Počítačová grafika RHINOCEROS
|
|
|
- Miluše Valentová
- před 9 lety
- Počet zobrazení:
Transkript
1 Počítačová grafika RHINOCEROS Ing. Zuzana Benáková Základní otázkou grafických programů je způsob zobrazení určitého tvaru. Existují dva základní způsoby prezentace 3D modelů v počítači. První využívá polygonové sítě, které většinou nachází uplatnění při rendrování a animaci. I když se zdá, že programy pro polygonové modelování poskytují zcela přesné nástroje pro modelování objektů jako jsou koule, válec atd., nakonec jsou stejně všechny plochy převedeny na polygonové sítě. Ty jsou už od počátku nepřesné, protože polygonová síť je vlastně souborem plochých trojúhelníků, které se snaží ideální plochu aproximovat - i když je ale plocha zakřivená, reprezentuje ji polygonový modelář stále jako síť plošek - nejčastěji trojúhelníků a čtyřúhelníků. To je sice zcela dostačující pro rendrování, animaci a tvorbu herních postav, ne však pro strojírenskou výrobu. Druhou možností reprezentace 3D dat je NURBS geometrie. Většina modelářů pro CAD, CAM, CAE a CAID (včetně Rhina) reprezentuje plochy a tělesa volného tvaru jako NURBS objekty. Pokud modelovací programy implementují NURBS geometrii pečlivě, mohou popisovat obecné tvary s přesností, která je dostatečná pro většinu náročných aplikací. Pokud je však prvotním zaměřením této aplikace strojírenství a ne tvorba obecných ploch, je jasné, že implementace NURBS geometrie bude z hlediska možnosti tvorby složitých ploch volného tvaru slabší. To je typické pro parametrické modeláře střední třídy, které jsou dnes tak populární. Rhinoceros je 3D NURBS modelář pro Windows, který využívá NURBS geometrie. NURBS modely však na polygonové sítě může převést a exportovat je do jiných programů. Umožňuje tvořit křivky, plochy a tělesa volného tvaru. Poskytuje pružné, přesné a rychlé pracovní prostředí. Další výhodou je snadné a rychlé ovládání. A v neposlední řadě je to také dostupná cena při dosažení obdobných vlastností mnohem dražších modelářů. Je stejně přesný či dokonce ještě přesnější, než většina CADů, které jsou v současné době na trhu. Navíc poskytuje možnost uživatelského nastavení přesnosti a jednotek, k dispozici jsou také nástroje pro vyhodnocení a dosažení spojitosti ploch, což jsou nástroje, které ve většině jiných CADů obsaženy nejsou. NURBS (Non-Uniformn Rational B-Splines) neuniformní racionální B-spline křivky jsou dvojím zobecnění B-spline křivek. Termín neuniformní je odvozen od vzdálenosti uzlů (ve smyslu parametru), která nemusí být u těchto křivek konstantní. Racionalita znamená, že body jsou reprezentovány svými homogenními souřadnicemi. Křivka Nurbs je určena :
2 Body řídícího polygonu Pi Váha bodu wi Normalizované B-spline bázové funkcenurbs umožňují generovat klasické geometrické prvky (počínaje jednoduchou čarou, kružnicí, obloukem nebo kvádrem.) za pomoci stejných metod, které umožňují vytvořit křivky a plochy složitých organických tvarů. Díky své pružnosti a přesnosti můžeme použít NURBS modely v jakémkoliv procesu od ilustrace a animace přes design až po sériovou výrobu. Typy geometrie v Rhinu Rhino rozeznává čtyři základní typy geometrie: body (1), křivky (2), NURBS plochy (3) (a tělesa, což je soustava ploch spojených tak, že beze zbytku uzavírají objem) a polygonové sítě (4): Polygonové objekty se používají většinou v programech pro výpočet obrázků a animací, stereolitografii, VRML a metodu konečných prvků. Polygonová síť je aproximací ideální matematické plochy. Rhino umí z NURBS ploch vytvořit polygonové sítě libovolné složitosti a exportovat je do těchto programů.
3 Tvorba ploch v Rhinu Vytvoření plochy z hraničních křivek Vytvoří plochu ze tří nebo čtyř křivek, které definují její hrany. Rotace křivky kolem osy Rotací profilové křivky kolem osy vytvoříme rotační plochu. Výsledkem může být buď otevřená plocha nebo uzavřené těleso, podle toho, zda byla nebo nebyla vstupní křivka uzavřená a o kolik stupňů ji necháme rotovali. Rotace křivky po trase vytvoří plochu, určenou rotací profilu kolem osy, přičemž tento profil navíc sleduje tvar trasy. V podstatě se jedná o obdobu tažení křivky po dvou trasách s tím, že jedna trasa byla zdegenerována do bodu.
4 Přímé vytažení křivky, tažení křívky po křivce Vytažením vytvoříme z křivky plochu. Pokud byla vstupní křivka rovinná, proběhne vytažení kolmo k rovině, v níž křivka leží. Pokud křivka není rovinná, závisí směr vytažení na aktivní konstrukční rovině. Šablonovaní (dvourozměrné) křivky po jedné (trojrozměrné) trase řezy vytvořené plochy zachovávají původní orientaci profilové křivky (či křivek) vůči trase. Na rozdíl od plochy vytvořené přímým tažením, které zachovává původní orientaci profilu vůči konstrukční rovině. Můžeme zadat libovolný počet řezů (může se jednat i o bod), které má plocha obsahovat. Šablonování křivky po dvou trasách vytvoří hladkou plochu, které prochází jedním nebo více řezy a
5 přitom sleduje dvě trasy. Tyto trasy rovněž ovlivňují celkový tvar plochy, což je vhodné v případě, kdy. chceme přesně určit tvar hran výsledné plochy. Plynulý přechod mezi plochami vytvoří novou plochu mezi plochami - plynulý přechod, který obě tyto plochy hladce spojuje. Potažení křivek plochou vytvoří plochu, která hladce prochází vybranými obrysovými křivkami. Hrany výsledné plochy vznikly proložením koncových bodů profilů hladkou křivkou. Další způsoby tvorby ploch Mezi plochami můžeme vytvářet nejen plynulé přechody, ale i zaoblení nebo zkosení, Booleovské operace (sjednocení, rozdíl, průnik), ofset v zadané vzdálenosti. Je možná i tvorba sítě polygonů: rovina, válec, kužel, koule, konverze z NURBS do polygonů. Editační nástroje: kopírování, přesunování, rotace, zmenšování/zvětšování, zrcadlení, protažení, přizpůsobení, stříhání, rozdělení, rozpojení, spojování, prodloužení, zkosení, zaoblení, ekvidistanta, kroucení, ohyb, zúžení, střih, pole Analýza: plocha, objem, střed, těžiště, momenty, spojitost, křivost (vč. grafu), směry tečen
6 Vytvoření složitějších těles: Nůž použito: přímé tažení křivky, zaoblení hran, odečtení objemu plochy, tažení křivky po dvou trasách, sjednocení ploch Ruka použito: potažení křivek, vytvoření křivky průmětem na plochu, oříznutí plochy křivkou, plynulý přechod ploch
7 Příklady vizualizací profesionálů Kuchyně autor: Greg Truen, modelovano v Rhinu, rendrováno ve Flamingu Sklípek autor: Greg Truen, modelovano v Rhinu, rendrováno ve Flamingu
8 Ložnice autor: Jang Moo Hyun, modelovano v Rhinu, rendrováno ve Flamingu Foyer autor: J. Kroeker, modelovano v Rhinu, rendrováno ve Flamingu
9 Použité zdroje informací Moderní počítačová grafika - J. Žára, B. Beneš, J. Sochor, P. Felker ISBN
Typy geometrie v. Rhinu. Body
 Typy geometrie v 16 Rhinu Rhino rozeznává pět základních typů geometrie: body (points), křivky (curves), plochy (surfaces) a spojené plochy (polysurfaces). Navíc jsou plochy nebo spojené plochy, které
Typy geometrie v 16 Rhinu Rhino rozeznává pět základních typů geometrie: body (points), křivky (curves), plochy (surfaces) a spojené plochy (polysurfaces). Navíc jsou plochy nebo spojené plochy, které
Zobrazování těles. problematika geometrického modelování. základní typy modelů. datové reprezentace modelů základní metody geometrického modelování
 problematika geometrického modelování manifold, Eulerova rovnost základní typy modelů hranový model stěnový model objemový model datové reprezentace modelů základní metody geometrického modelování těleso
problematika geometrického modelování manifold, Eulerova rovnost základní typy modelů hranový model stěnový model objemový model datové reprezentace modelů základní metody geometrického modelování těleso
1.8. Úprava uživatelského prostředí AutoCADu 25 Přednostní klávesy 25 Pracovní prostory 25
 Obsah 1 Novinky v AutoCADu 2006 11 1.1. Kreslení 11 Dynamické zadávání 11 Zvýraznění objektu po najetí kurzorem 12 Zvýraznění výběrové oblasti 13 Nový příkaz Spoj 14 Zkosení a zaoblení 15 Vytvoření kopie
Obsah 1 Novinky v AutoCADu 2006 11 1.1. Kreslení 11 Dynamické zadávání 11 Zvýraznění objektu po najetí kurzorem 12 Zvýraznění výběrové oblasti 13 Nový příkaz Spoj 14 Zkosení a zaoblení 15 Vytvoření kopie
9 Prostorová grafika a modelování těles
 9 Prostorová grafika a modelování těles Studijní cíl Tento blok je věnován základům 3D grafiky. Jedná se především o vysvětlení principů vytváření modelů 3D objektů, jejich reprezentace v paměti počítače.
9 Prostorová grafika a modelování těles Studijní cíl Tento blok je věnován základům 3D grafiky. Jedná se především o vysvětlení principů vytváření modelů 3D objektů, jejich reprezentace v paměti počítače.
Jana Dannhoferová Ústav informatiky, PEF MZLU
 Počítačová grafika Křivky Jana Dannhoferová (jana.dannhoferova@mendelu.cz) Ústav informatiky, PEF MZLU Základní vlastnosti křivek křivka soustava parametrů nějaké rovnice, která je posléze generativně
Počítačová grafika Křivky Jana Dannhoferová (jana.dannhoferova@mendelu.cz) Ústav informatiky, PEF MZLU Základní vlastnosti křivek křivka soustava parametrů nějaké rovnice, která je posléze generativně
Obsah. Úvod do prostorového modelování 9. Prostředí AutoCADu při práci ve 3D 15 KAPITOLA 1 KAPITOLA 2
 KAPITOLA 1 Úvod do prostorového modelování 9 Produkty společnosti Autodesk 9 3D řešení 10 Vertikální řešení založené na platformě AutoCAD 10 Obecný AutoCAD 11 Obecné 2D kreslení 11 Prohlížeče a pomocné
KAPITOLA 1 Úvod do prostorového modelování 9 Produkty společnosti Autodesk 9 3D řešení 10 Vertikální řešení založené na platformě AutoCAD 10 Obecný AutoCAD 11 Obecné 2D kreslení 11 Prohlížeče a pomocné
Singularity rotačních obalových ploch
 Singularity rotačních obalových ploch Ivana Linkeová ČVUT v Praze, Fakulta strojní, Ústav technické matematiky Karlovo nám. 13, 121 35 Praha 2 Nové Město Ivana.Linkeova@fs.cvut.cz Abstrakt. V příspěvku
Singularity rotačních obalových ploch Ivana Linkeová ČVUT v Praze, Fakulta strojní, Ústav technické matematiky Karlovo nám. 13, 121 35 Praha 2 Nové Město Ivana.Linkeova@fs.cvut.cz Abstrakt. V příspěvku
Aproximační křivky. Trocha historie. geometrické modelování veliký pokrok v oblasti letectví 1944 Roy Liming
 Trocha historie geometrické modelování veliký pokrok v oblasti letectví 944 Roy Liming analytik, North American Aviation (výrobce letadel) společně s konstruktérem a designérem Edgardem Schmuedem matematizace
Trocha historie geometrické modelování veliký pokrok v oblasti letectví 944 Roy Liming analytik, North American Aviation (výrobce letadel) společně s konstruktérem a designérem Edgardem Schmuedem matematizace
Prostředí Inventoru. Název školy. Střední škola informatiky, elektrotechniky a řemesel Rožnov pod Radhoštěm
 Prostředí u Prostředí u Číslo DUM v digitálním archivu školy VY_32_INOVACE_04_02_01 Vytvořeno Září 2013 Materiál slouží k podpoře výuky programu ve čtvrtém ročníku oboru. Učební materiál má žákům ukázat
Prostředí u Prostředí u Číslo DUM v digitálním archivu školy VY_32_INOVACE_04_02_01 Vytvořeno Září 2013 Materiál slouží k podpoře výuky programu ve čtvrtém ročníku oboru. Učební materiál má žákům ukázat
Křivky a plochy technické praxe
 Kapitola 7 Křivky a plochy technické praxe V technické praxi se setkáváme s tím, že potřebujeme křivky a plochy, které se dají libovolně upravovat a zároveň je jejich matematické vyjádření jednoduché.
Kapitola 7 Křivky a plochy technické praxe V technické praxi se setkáváme s tím, že potřebujeme křivky a plochy, které se dají libovolně upravovat a zároveň je jejich matematické vyjádření jednoduché.
Matematický ústav UK Matematicko-fyzikální fakulta
 Geometrické modelování Zbyněk Šír Matematický ústav UK Matematicko-fyzikální fakulta 5. října 2016 Zbyněk Šír (MÚ UK) - Geometrické modelování 5. října 2016 1 / 14 Obsah dnešní přednášky Co je to geometrické
Geometrické modelování Zbyněk Šír Matematický ústav UK Matematicko-fyzikální fakulta 5. října 2016 Zbyněk Šír (MÚ UK) - Geometrické modelování 5. října 2016 1 / 14 Obsah dnešní přednášky Co je to geometrické
Interaktivní modely pro Konstruktivní geometrii
 Interaktivní modely pro Konstruktivní geometrii Jakub Makarovský Abstrakt V příspěvku jsou prezentovány interaktivní modely základních úloh z Konstruktivní geometrie (1. ročník, zimní semestr) zaměřující
Interaktivní modely pro Konstruktivní geometrii Jakub Makarovský Abstrakt V příspěvku jsou prezentovány interaktivní modely základních úloh z Konstruktivní geometrie (1. ročník, zimní semestr) zaměřující
Gymnázium Jiřího Ortena, Kutná Hora
 Předmět: Náplň: Cvičení z matematiky geometrie (CZMg) Systematizace a prohloubení učiva matematiky Planimetrie, Stereometrie, Analytická geometrie, Kombinatorika, Pravděpodobnost a statistika Třída: 4.
Předmět: Náplň: Cvičení z matematiky geometrie (CZMg) Systematizace a prohloubení učiva matematiky Planimetrie, Stereometrie, Analytická geometrie, Kombinatorika, Pravděpodobnost a statistika Třída: 4.
Grafické programy pro tvorbu 3D modelů
 přednáška 1 Grafické programy pro tvorbu 3D modelů Úvodní přednáška bude věnována vysvětlení obecných základních pojmů, které se v souvislosti s počítačovým modelováním používají a principu, na kterém
přednáška 1 Grafické programy pro tvorbu 3D modelů Úvodní přednáška bude věnována vysvětlení obecných základních pojmů, které se v souvislosti s počítačovým modelováním používají a principu, na kterém
Jana Dannhoferová Ústav informatiky, PEF MZLU
 Počítačová grafika 1. Definice oblasti souvisí: a) s definováním množiny všech bodů, které náleží do hranice a zároveň do jejího vnitřku b) s popisem její hranice c) s definováním množiny všech bodů, které
Počítačová grafika 1. Definice oblasti souvisí: a) s definováním množiny všech bodů, které náleží do hranice a zároveň do jejího vnitřku b) s popisem její hranice c) s definováním množiny všech bodů, které
Geometrické transformace pomocí matic
 Geometrické transformace pomocí matic Pavel Strachota FJFI ČVUT v Praze 2. dubna 2010 Obsah 1 Úvod 2 Geometrické transformace ve 2D 3 Geometrické transformace ve 3D Obsah 1 Úvod 2 Geometrické transformace
Geometrické transformace pomocí matic Pavel Strachota FJFI ČVUT v Praze 2. dubna 2010 Obsah 1 Úvod 2 Geometrické transformace ve 2D 3 Geometrické transformace ve 3D Obsah 1 Úvod 2 Geometrické transformace
Rekonstrukce ploch: Polygonální a analytická reprezentace Vybrané metody aproximace ploch
 Rekonstrukce ploch: Polygonální a analytická reprezentace Vybrané metody aproximace ploch Petra Surynková Matematicko-fyzikální fakulta Univerzita Karlova v Praze petra.surynkova@mff.cuni.cz Přehled (1)
Rekonstrukce ploch: Polygonální a analytická reprezentace Vybrané metody aproximace ploch Petra Surynková Matematicko-fyzikální fakulta Univerzita Karlova v Praze petra.surynkova@mff.cuni.cz Přehled (1)
Základní topologické pojmy:
 Křivky Marie Ennemond Camille Jordan (88 9): Křivka je množina bodů, která je surjektivním obrazem nějakého intervalu Giuseppe Peano (858 9): Zobrazení intervalu na čtverec Wacław Franciszek Sierpiński
Křivky Marie Ennemond Camille Jordan (88 9): Křivka je množina bodů, která je surjektivním obrazem nějakého intervalu Giuseppe Peano (858 9): Zobrazení intervalu na čtverec Wacław Franciszek Sierpiński
3D kontaktní skener MicroScribe-3D výukový modul. 3D kontaktní skener MicroScribe-3D Výukový modul
 3D kontaktní skener MicroScribe-3D Výukový modul Kontaktní skener Microscribe-3D MicroScribe je 3D kontaktní flexibilní a cenově dostupný digitizér pro oblast reverzního inženýrství, pro vytváření modelů
3D kontaktní skener MicroScribe-3D Výukový modul Kontaktní skener Microscribe-3D MicroScribe je 3D kontaktní flexibilní a cenově dostupný digitizér pro oblast reverzního inženýrství, pro vytváření modelů
Generování sítě konečných prvků
 Generování sítě konečných prvků Jaroslav Beran Modelování a simulace Tvorba výpočtového modelu s využitím MKP zahrnuje: Tvorbu (import) geometrického modelu Generování sítě konečných prvků Definování vlastností
Generování sítě konečných prvků Jaroslav Beran Modelování a simulace Tvorba výpočtového modelu s využitím MKP zahrnuje: Tvorbu (import) geometrického modelu Generování sítě konečných prvků Definování vlastností
Příklad 1: Nakreslete libovolnou uzavřenou rovinnou křivku a sestrojte rovinnou plochu, Návod:
 Křivky a plochy Plocha z rovinné křivky, vytažená z křivky, vytvořená rotací a rotací po křivce. Plocha přechodová, potažená, tažená po 1 a 2 trasách, odsazená. Příklad 1: Nakreslete libovolnou uzavřenou
Křivky a plochy Plocha z rovinné křivky, vytažená z křivky, vytvořená rotací a rotací po křivce. Plocha přechodová, potažená, tažená po 1 a 2 trasách, odsazená. Příklad 1: Nakreslete libovolnou uzavřenou
Mgr. Ladislav Zemánek Maturitní okruhy Matematika 2013-2014. 1. Obor reálných čísel
 Mgr. Ladislav Zemánek Maturitní okruhy Matematika 2013-2014 1. Obor reálných čísel - obor přirozených, celých, racionálních a reálných čísel - vlastnosti operací (sčítání, odčítání, násobení, dělení) -
Mgr. Ladislav Zemánek Maturitní okruhy Matematika 2013-2014 1. Obor reálných čísel - obor přirozených, celých, racionálních a reálných čísel - vlastnosti operací (sčítání, odčítání, násobení, dělení) -
Animované modely šroubových ploch
 Animované modely šroubových ploch Jaroslav Bušek Abstrakt V příspěvku jsou prezentovány animované prostorové modely přímkových a cyklických šroubových ploch, které byly vytvořeny jako didaktické pomůcky
Animované modely šroubových ploch Jaroslav Bušek Abstrakt V příspěvku jsou prezentovány animované prostorové modely přímkových a cyklických šroubových ploch, které byly vytvořeny jako didaktické pomůcky
Obsah. Předmluva 1. Úvod do studia 3 Komu je tato kniha určena 4 Co byste měli předem znát 4 Co se naučíte v učebnici AutoCADu? 5
 Obsah Předmluva 1 KAPITOLA 1 Úvod do studia 3 Komu je tato kniha určena 4 Co byste měli předem znát 4 Co se naučíte v učebnici AutoCADu? 5 CA technologie 6 Product Lifecycle Management 7 Aplikační programy
Obsah Předmluva 1 KAPITOLA 1 Úvod do studia 3 Komu je tato kniha určena 4 Co byste měli předem znát 4 Co se naučíte v učebnici AutoCADu? 5 CA technologie 6 Product Lifecycle Management 7 Aplikační programy
Využití programu AutoCAD při vytváření geometrie konstrukce v prostředí programu ANSYS
 Využití programu AutoCAD při vytváření geometrie konstrukce v prostředí programu ANSYS Abstrakt Jan Pěnčík 1 Článek popisuje a porovnává způsoby možného vytváření geometrie konstrukce v prostředí programu
Využití programu AutoCAD při vytváření geometrie konstrukce v prostředí programu ANSYS Abstrakt Jan Pěnčík 1 Článek popisuje a porovnává způsoby možného vytváření geometrie konstrukce v prostředí programu
Plochy počítačové grafiky II. Interpolační plochy Bezierovy pláty nad obdélníkovou a trojúhelníkovou sítí Recionální Bezierovy pláty B-spline NURBS
 II Interpolační plochy Bezierovy pláty nad obdélníkovou a trojúhelníkovou sítí Recionální Bezierovy pláty B-spline NURBS Konstrukce a zadání plochy hraniční křivky sítí bodů Kinematicky vytvořené křivky
II Interpolační plochy Bezierovy pláty nad obdélníkovou a trojúhelníkovou sítí Recionální Bezierovy pláty B-spline NURBS Konstrukce a zadání plochy hraniční křivky sítí bodů Kinematicky vytvořené křivky
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Základy parametrického modelování Skicovací nástroje
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Základy parametrického modelování Skicovací nástroje
NURBS REPREZENTACE KŘIVEK V MAPLE
 25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE Karolína Kundrátová NURBS REPREZENTACE KŘIVEK V MAPLE Abstrakt Parametrizace křivek jako NURBS (tj. neuniformní racionální B-spliny) patří k moderním postupům
25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE Karolína Kundrátová NURBS REPREZENTACE KŘIVEK V MAPLE Abstrakt Parametrizace křivek jako NURBS (tj. neuniformní racionální B-spliny) patří k moderním postupům
Aproximační křivky. Trocha historie. geometrické modelování veliký pokrok v oblasti letectví 1944 Roy Liming
 Trocha historie geometrické modelování veliký pokrok v oblasti letectví 944 Roy Liming analytik, North American Aviation (výrobce letadel) společně s konstruktérem a designérem Edgardem Schmuedem matematizace
Trocha historie geometrické modelování veliký pokrok v oblasti letectví 944 Roy Liming analytik, North American Aviation (výrobce letadel) společně s konstruktérem a designérem Edgardem Schmuedem matematizace
HVrchlík DVrchlík. Anuloid Hrana 3D síť
 TVORBA PLOCH Plochy mají oproti 3D drátovým modelům velkou výhodu, pro snadnější vizualizaci modelů můžeme skrýt zadní plochy a vytvořit stínované obrázky. Plochy dále umožňují vytvoření neobvyklých tvarů.
TVORBA PLOCH Plochy mají oproti 3D drátovým modelům velkou výhodu, pro snadnější vizualizaci modelů můžeme skrýt zadní plochy a vytvořit stínované obrázky. Plochy dále umožňují vytvoření neobvyklých tvarů.
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Základy parametrického modelování Základní prvky modelování
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Základy parametrického modelování Základní prvky modelování
Novinky v Solid Edge ST7
 Novinky v Solid Edge ST7 Primitiva Nově lze vytvořit základní geometrii pomocí jednoho příkazu Funkce primitiv je dostupná pouze v synchronním prostředí Těleso vytvoříme ve dvou navazujících krocích, kde
Novinky v Solid Edge ST7 Primitiva Nově lze vytvořit základní geometrii pomocí jednoho příkazu Funkce primitiv je dostupná pouze v synchronním prostředí Těleso vytvoříme ve dvou navazujících krocích, kde
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Pokročilé metody parametrického modelování Modelování
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Pokročilé metody parametrického modelování Modelování
Základní vlastnosti ploch
 plocha zpravidla se definuje jako výsledek spojitého pohybu jisté tvořící křivky podél zadané trajektorie lze obohatit o možnost spojitých změn tvaru tvořící křivky x v průběhu pohybu podél trajektorie
plocha zpravidla se definuje jako výsledek spojitého pohybu jisté tvořící křivky podél zadané trajektorie lze obohatit o možnost spojitých změn tvaru tvořící křivky x v průběhu pohybu podél trajektorie
SEZNÁMENÍ S PROGRAMEM AUTODESK INVENTOR
 1 SEZNÁMENÍ S PROGRAMEM AUTODESK INVENTOR PRACOVNÍ PROSTŘEDÍ 2 Panel nástrojů Prohlížeč součástí Modelovací prostor Nástroj ViewCube pro ovládání pohledu na model 3 Panel nástrojů Obsahuje základní ovládací
1 SEZNÁMENÍ S PROGRAMEM AUTODESK INVENTOR PRACOVNÍ PROSTŘEDÍ 2 Panel nástrojů Prohlížeč součástí Modelovací prostor Nástroj ViewCube pro ovládání pohledu na model 3 Panel nástrojů Obsahuje základní ovládací
Matematický ústav UK Matematicko-fyzikální fakulta
 Geometrické modelování Zbyněk Šír Matematický ústav UK Matematicko-fyzikální fakulta 2. října 2018 Zbyněk Šír (MÚ UK) - Geometrické modelování 2. října 2018 1 / 15 Obsah dnešní přednášky Co je to geometrické
Geometrické modelování Zbyněk Šír Matematický ústav UK Matematicko-fyzikální fakulta 2. října 2018 Zbyněk Šír (MÚ UK) - Geometrické modelování 2. října 2018 1 / 15 Obsah dnešní přednášky Co je to geometrické
Obecný princip 3D numerického modelování výrubu
 Obecný princip 3D numerického modelování výrubu Modelovaná situace Svislé zatížení nadloží se přenáší horninovým masivem na bok tunelu Soustava lineárních rovnic Soustavou lineárních rovnic popíšeme určované
Obecný princip 3D numerického modelování výrubu Modelovaná situace Svislé zatížení nadloží se přenáší horninovým masivem na bok tunelu Soustava lineárních rovnic Soustavou lineárních rovnic popíšeme určované
Základy 3D modelování a animace v CGI systémech Cinema 4D C4D
 EVROPSKÝ SOCIÁLNÍ FOND Základy 3D modelování a animace v CGI systémech Cinema 4D C4D PRAHA & EU INVESTUJEME DO VAŠÍ BUDOUCNOSTI Mgr. David Frýbert 2013 CGI systémy Computer - generated imagery - aplikace
EVROPSKÝ SOCIÁLNÍ FOND Základy 3D modelování a animace v CGI systémech Cinema 4D C4D PRAHA & EU INVESTUJEME DO VAŠÍ BUDOUCNOSTI Mgr. David Frýbert 2013 CGI systémy Computer - generated imagery - aplikace
Obsah. Předmluva 15 KAPITOLA 1 17 KAPITOLA 2 39
 Předmluva 15 KAPITOLA 1 17 AutoCAD Tour 17 Úvod 17 Spuštění programu AutoCAD 18 Okno aplikace AutoCAD 20 Ovládací prvky 22 Příkazový řádek 25 Dynamická výzva 28 Vizuální nastavení 29 Práce s výkresovými
Předmluva 15 KAPITOLA 1 17 AutoCAD Tour 17 Úvod 17 Spuštění programu AutoCAD 18 Okno aplikace AutoCAD 20 Ovládací prvky 22 Příkazový řádek 25 Dynamická výzva 28 Vizuální nastavení 29 Práce s výkresovými
Obsah. Úvod 9. Orientace v prostředí programu SolidWorks 11. Skica 29. Kapitola 1 11. Kapitola 2 29
 Úvod 9 Kapitola 1 11 Orientace v prostředí programu SolidWorks 11 Pruh nabídky 12 Nabídka Možnosti 14 Nápověda 14 Podokno úloh 15 Zdroje SolidWorks 15 Knihovna návrhů 15 Průzkumník souborů 16 Paleta pohledů
Úvod 9 Kapitola 1 11 Orientace v prostředí programu SolidWorks 11 Pruh nabídky 12 Nabídka Možnosti 14 Nápověda 14 Podokno úloh 15 Zdroje SolidWorks 15 Knihovna návrhů 15 Průzkumník souborů 16 Paleta pohledů
Obsah. Předmluva 13 KAPITOLA 1 KAPITOLA 2
 Předmluva 13 KAPITOLA 1 AutoCAD Tour 15 Úvod 15 Spuštění programu AutoCAD 15 Okno aplikace AutoCAD 17 Ovládací prvky 19 Příkazový řádek 22 Dynamická výzva 25 Vizuální nastavení 26 Práce s výkresovými soubory
Předmluva 13 KAPITOLA 1 AutoCAD Tour 15 Úvod 15 Spuštění programu AutoCAD 15 Okno aplikace AutoCAD 17 Ovládací prvky 19 Příkazový řádek 22 Dynamická výzva 25 Vizuální nastavení 26 Práce s výkresovými soubory
Obsah KAPITOLA 1 13 KAPITOLA 2 33
 Obsah KAPITOLA 1 13 Seznámení s programem AutoCAD 13 Úvod 13 Spuštění programu AutoCAD 13 Okno aplikace AutoCAD 16 Ovládací prvky 17 Příkazový řádek 20 Dynamická výzva 24 Vizuální nastavení 24 Práce s
Obsah KAPITOLA 1 13 Seznámení s programem AutoCAD 13 Úvod 13 Spuštění programu AutoCAD 13 Okno aplikace AutoCAD 16 Ovládací prvky 17 Příkazový řádek 20 Dynamická výzva 24 Vizuální nastavení 24 Práce s
GIS Geografické informační systémy
 GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
MATEMATIKA 5. TŘÍDA. C) Tabulky, grafy, diagramy 1 - Tabulky, doplnění řady čísel podle závislosti 2 - Grafy, jízní řády 3 - Magické čtverce
 MATEMATIKA 5. TŘÍDA 1 - Přirozená čísla a číslo nula a číselná osa, porovnávání b zaokrouhlování c zápis čísla v desítkové soustavě d součet, rozdíl e násobek, činitel, součin f dělení, dělení se zbytkem
MATEMATIKA 5. TŘÍDA 1 - Přirozená čísla a číslo nula a číselná osa, porovnávání b zaokrouhlování c zápis čísla v desítkové soustavě d součet, rozdíl e násobek, činitel, součin f dělení, dělení se zbytkem
CAD_Inventor -cvičení k modelování a tvorbě technické obrazové dokumentace Spirála
 Předmět: Ročník: Vytvořil: Datum: CAD druhý, třetí Petr Machanec 25.5.2013 Název zpracovaného celku: CAD_Inventor -cvičení k modelování a tvorbě technické obrazové dokumentace Spirála Spirála vrták s válcovou
Předmět: Ročník: Vytvořil: Datum: CAD druhý, třetí Petr Machanec 25.5.2013 Název zpracovaného celku: CAD_Inventor -cvičení k modelování a tvorbě technické obrazové dokumentace Spirála Spirála vrták s válcovou
Základní vlastnosti křivek
 křivka množina bodů v rovině nebo v prostoru lze chápat jako trajektorii pohybu v rovině či v prostoru nalezneme je také jako množiny bodů na ploše křivky jako řezy plochy rovinou, křivky jako průniky
křivka množina bodů v rovině nebo v prostoru lze chápat jako trajektorii pohybu v rovině či v prostoru nalezneme je také jako množiny bodů na ploše křivky jako řezy plochy rovinou, křivky jako průniky
PARAMETRICKÉ MODELOVÁNÍ A KONSTRUOVÁNÍ ÚVOD DO PARAMETRICKÉHO MODELOVÁNÍ A KONSTRUOVÁNÍ
 PARAMETRICKÉ MODELOVÁNÍ A KONSTRUOVÁNÍ ÚVOD DO PARAMETRICKÉHO MODELOVÁNÍ A KONSTRUOVÁNÍ Ing. Zdeněk Hodis, Ph.D. Úvod S rozvojem nových poznatků v oblasti technické grafiky je kladen důraz na jejich začlenění
PARAMETRICKÉ MODELOVÁNÍ A KONSTRUOVÁNÍ ÚVOD DO PARAMETRICKÉHO MODELOVÁNÍ A KONSTRUOVÁNÍ Ing. Zdeněk Hodis, Ph.D. Úvod S rozvojem nových poznatků v oblasti technické grafiky je kladen důraz na jejich začlenění
Maturitní témata z matematiky
 Maturitní témata z matematiky G y m n á z i u m J i h l a v a Výroky, množiny jednoduché výroky, pravdivostní hodnoty výroků, negace operace s výroky, složené výroky, tabulky pravdivostních hodnot důkazy
Maturitní témata z matematiky G y m n á z i u m J i h l a v a Výroky, množiny jednoduché výroky, pravdivostní hodnoty výroků, negace operace s výroky, složené výroky, tabulky pravdivostních hodnot důkazy
Využití 3D tisku při výrobě fyzikálních pomůcek
 LŠUMF Šluknov 2018 Projektové dopoledne čtvrtek 9.8.2018 Ing. Stanislav Jakoubek Využití 3D tisku při výrobě fyzikálních pomůcek Úvodní chytrosti Dostupnost 3D tiskáren ve školách i v domácnostech Financování
LŠUMF Šluknov 2018 Projektové dopoledne čtvrtek 9.8.2018 Ing. Stanislav Jakoubek Využití 3D tisku při výrobě fyzikálních pomůcek Úvodní chytrosti Dostupnost 3D tiskáren ve školách i v domácnostech Financování
Gymnázium Česká a Olympijských nadějí, České Budějovice, Česká 64, 37021
 Maturitní témata MATEMATIKA 1. Funkce a jejich základní vlastnosti. Definice funkce, def. obor a obor hodnot funkce, funkce sudá, lichá, monotónnost funkce, funkce omezená, lokální a globální extrémy funkce,
Maturitní témata MATEMATIKA 1. Funkce a jejich základní vlastnosti. Definice funkce, def. obor a obor hodnot funkce, funkce sudá, lichá, monotónnost funkce, funkce omezená, lokální a globální extrémy funkce,
Gymnázium Jiřího Ortena, Kutná Hora. Průřezová témata Poznámky. Téma Školní výstupy Učivo (pojmy) volné rovnoběžné promítání průmětna
 Předmět: Matematika Náplň: Stereometrie, Analytická geometrie Třída: 3. ročník a septima Počet hodin: 4 hodiny týdně Pomůcky: PC a dataprojektor, učebnice Stereometrie Volné rovnoběžné promítání Zobrazí
Předmět: Matematika Náplň: Stereometrie, Analytická geometrie Třída: 3. ročník a septima Počet hodin: 4 hodiny týdně Pomůcky: PC a dataprojektor, učebnice Stereometrie Volné rovnoběžné promítání Zobrazí
Maturitní otázky z předmětu MATEMATIKA
 Wichterlovo gymnázium, Ostrava-Poruba, příspěvková organizace Maturitní otázky z předmětu MATEMATIKA 1. Výrazy a jejich úpravy vzorce (a+b)2,(a+b)3,a2-b2,a3+b3, dělení mnohočlenů, mocniny, odmocniny, vlastnosti
Wichterlovo gymnázium, Ostrava-Poruba, příspěvková organizace Maturitní otázky z předmětu MATEMATIKA 1. Výrazy a jejich úpravy vzorce (a+b)2,(a+b)3,a2-b2,a3+b3, dělení mnohočlenů, mocniny, odmocniny, vlastnosti
TECHNICKÁ DOKUMENTACE
 TECHNICKÁ DOKUMENTACE Jan Petřík 2013 Projekt ESF CZ.1.07/2.2.00/28.0050 Modernizace didaktických metod a inovace výuky technických předmětů. Obsah přednášek 1. Úvod do problematiky tvorby technické dokumentace
TECHNICKÁ DOKUMENTACE Jan Petřík 2013 Projekt ESF CZ.1.07/2.2.00/28.0050 Modernizace didaktických metod a inovace výuky technických předmětů. Obsah přednášek 1. Úvod do problematiky tvorby technické dokumentace
SurfCAM. Modelování ploch
 SurfCAM Modelování ploch Modelování Ploch 1. Úvod Pro dokonalé obrobení načteného modelu obrobku z různých CAD systémů je mnohdy nutné vytvořit pomocné a doplňující plochy na tomto modelu. V SURFCAMu je
SurfCAM Modelování ploch Modelování Ploch 1. Úvod Pro dokonalé obrobení načteného modelu obrobku z různých CAD systémů je mnohdy nutné vytvořit pomocné a doplňující plochy na tomto modelu. V SURFCAMu je
Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Jiří Haňáček [ÚLOHA 20 KŘIVKY]
![Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Jiří Haňáček [ÚLOHA 20 KŘIVKY] Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Jiří Haňáček [ÚLOHA 20 KŘIVKY]](/thumbs/24/2637057.jpg) Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Jiří Haňáček [ÚLOHA 20 KŘIVKY] 1 CÍL KAPITOLY Cílem tohoto dokumentu je přiblížit uživateli přehledovým způsobem oblast použití křivek v rámci dnes
Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Jiří Haňáček [ÚLOHA 20 KŘIVKY] 1 CÍL KAPITOLY Cílem tohoto dokumentu je přiblížit uživateli přehledovým způsobem oblast použití křivek v rámci dnes
Cvičení 5 z předmětu CAD I PARAMETRICKÉ 3D MODELOVÁNÍ ODLITKU - OBROBKU
 Cvičení 5 z předmětu CAD I PARAMETRICKÉ 3D MODELOVÁNÍ ODLITKU - OBROBKU Cílem cvičení je vytvořit jednoduchý model obrobku z odlitku. Obrobek je odvozen z předem vytvořeného odlitku z předcházejícího cvičení.
Cvičení 5 z předmětu CAD I PARAMETRICKÉ 3D MODELOVÁNÍ ODLITKU - OBROBKU Cílem cvičení je vytvořit jednoduchý model obrobku z odlitku. Obrobek je odvozen z předem vytvořeného odlitku z předcházejícího cvičení.
Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Jan Boháček [ÚLOHA 27 NÁSTROJE KRESLENÍ]
![Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Jan Boháček [ÚLOHA 27 NÁSTROJE KRESLENÍ] Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Jan Boháček [ÚLOHA 27 NÁSTROJE KRESLENÍ]](/thumbs/24/3705963.jpg) Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Jan Boháček [ÚLOHA 27 NÁSTROJE KRESLENÍ] 1 CÍL KAPITOLY V této kapitole si představíme Nástroje kreslení pro tvorbu 2D skic v modulu Objemová součást
Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Jan Boháček [ÚLOHA 27 NÁSTROJE KRESLENÍ] 1 CÍL KAPITOLY V této kapitole si představíme Nástroje kreslení pro tvorbu 2D skic v modulu Objemová součást
Zavedeme-li souřadnicový systém {0, x, y, z}, pak můžeme křivku definovat pomocí vektorové funkce.
 KŘIVKY Křivka = dráha pohybujícího se bodu = = množina nekonečného počtu bodů, které závisí na parametru (čase). Proto můžeme křivku také nazvat jednoparametrickou množinou bodů. Zavedeme-li souřadnicový
KŘIVKY Křivka = dráha pohybujícího se bodu = = množina nekonečného počtu bodů, které závisí na parametru (čase). Proto můžeme křivku také nazvat jednoparametrickou množinou bodů. Zavedeme-li souřadnicový
Elementární plochy-základní pojmy
 -základní pojmy Kulová plocha je množina bodů v prostoru, které mají od pevného bodu S stejnou vzdálenost r. Hranolová plocha je určena lomenou čarou k (k σ) a směrem s, který nenáleží dané rovině (s σ),
-základní pojmy Kulová plocha je množina bodů v prostoru, které mají od pevného bodu S stejnou vzdálenost r. Hranolová plocha je určena lomenou čarou k (k σ) a směrem s, který nenáleží dané rovině (s σ),
8 Plochy - vytvoření, rozdělení, tečná rovina a normála. Šroubové plochy - přímkové, cyklické. Literatura:
 8 Plochy - vytvoření, rozdělení, tečná rovina a normála. Šroubové plochy - přímkové, cyklické. Literatura: (1)Poláček, J., Doležal, M.: Základy deskriptivní a konstruktivní geometrie, díl 5, Křivky a plochy
8 Plochy - vytvoření, rozdělení, tečná rovina a normála. Šroubové plochy - přímkové, cyklické. Literatura: (1)Poláček, J., Doležal, M.: Základy deskriptivní a konstruktivní geometrie, díl 5, Křivky a plochy
KŘIVKY A PLOCHY. Obrázky (popř. slajdy) převzaty od
 KŘIVKY A PLOCHY JANA ŠTANCLOVÁ jana.stanclova@ruk.cuni.cz Obrázky (popř. slajdy) převzaty od RNDr. Josef Pelikán, CSc., KSVI MFF UK Obsah matematický popis křivek a ploch křivky v rovině implicitní tvar
KŘIVKY A PLOCHY JANA ŠTANCLOVÁ jana.stanclova@ruk.cuni.cz Obrázky (popř. slajdy) převzaty od RNDr. Josef Pelikán, CSc., KSVI MFF UK Obsah matematický popis křivek a ploch křivky v rovině implicitní tvar
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Pokročilé metody parametrického modelování Speciální
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Pokročilé metody parametrického modelování Speciální
Maturitní témata profilová část
 Seznam témat Výroková logika, úsudky a operace s množinami Základní pojmy výrokové logiky, logické spojky a kvantifikátory, složené výroky (konjunkce, disjunkce, implikace, ekvivalence), pravdivostní tabulky,
Seznam témat Výroková logika, úsudky a operace s množinami Základní pojmy výrokové logiky, logické spojky a kvantifikátory, složené výroky (konjunkce, disjunkce, implikace, ekvivalence), pravdivostní tabulky,
Předpokládané znalosti žáka 1. stupeň:
 Předpokládané znalosti žáka 1. stupeň: ČÍSLO A POČETNÍ OPERACE používá přirozená čísla k modelování reálných situací, počítá předměty v daném souboru, vytváří soubory s daným počtem prvků čte, zapisuje
Předpokládané znalosti žáka 1. stupeň: ČÍSLO A POČETNÍ OPERACE používá přirozená čísla k modelování reálných situací, počítá předměty v daném souboru, vytváří soubory s daným počtem prvků čte, zapisuje
Modelování součásti pomocí ploch
 Modelování součásti pomocí ploch Číslo publikace spse01560 Poznámky a omezení vlastnických práv Tento software a související dokumentace je majetkem společnosti Siemens Product Lifecycle Management Software
Modelování součásti pomocí ploch Číslo publikace spse01560 Poznámky a omezení vlastnických práv Tento software a související dokumentace je majetkem společnosti Siemens Product Lifecycle Management Software
Geometrické vidění světa KMA/GVS ak. rok 2013/2014 letní semestr
 Polyedry, polyedrické (diskrétní) plochy Geometrické vidění světa KMA/GVS ak. rok 2013/2014 letní semestr Základní tělesa 1 Co jsou základní tělesa? Základní tělesa pro tvorbu modelů standardní výbava
Polyedry, polyedrické (diskrétní) plochy Geometrické vidění světa KMA/GVS ak. rok 2013/2014 letní semestr Základní tělesa 1 Co jsou základní tělesa? Základní tělesa pro tvorbu modelů standardní výbava
Gymnázium Jiřího Ortena, Kutná Hora
 Předmět: Cvičení z matematiky Náplň: Systematizace a prohloubení učiva matematiky Třída: 4. ročník Počet hodin: 2 Pomůcky: Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné obory
Předmět: Cvičení z matematiky Náplň: Systematizace a prohloubení učiva matematiky Třída: 4. ročník Počet hodin: 2 Pomůcky: Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné obory
Polygonální objekty v Rhinoceros Volné modelování
 přednáška 10 Polygonální objekty v Rhinoceros Volné modelování 10.1 Polygonální objekty v Rhinoceros Jak již bylo zmíněno v první přednášce, program Rhinoceros je plošný modelář a při popisu svých objektů
přednáška 10 Polygonální objekty v Rhinoceros Volné modelování 10.1 Polygonální objekty v Rhinoceros Jak již bylo zmíněno v první přednášce, program Rhinoceros je plošný modelář a při popisu svých objektů
Systematizace a prohloubení učiva matematiky. Učebna s dataprojektorem, PC, grafický program, tabulkový procesor. Gymnázium Jiřího Ortena, Kutná Hora
 Předmět: Náplň: Třída: Počet hodin: Pomůcky: Cvičení z matematiky Systematizace a prohloubení učiva matematiky 4. ročník 2 hodiny Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné
Předmět: Náplň: Třída: Počet hodin: Pomůcky: Cvičení z matematiky Systematizace a prohloubení učiva matematiky 4. ročník 2 hodiny Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Základy parametrického modelování Základní prvky modelování
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Základy parametrického modelování Základní prvky modelování
Plochy zadané okrajovými křivkami
 Plochy zadané okrajovými křivkami Lineární plát plocha je určena dvěma okrajovými křivkami, pokud by pro tyto křivky byly intervaly, v nichž leží hodnoty parametru, různé, provedeme lineární transformaci
Plochy zadané okrajovými křivkami Lineární plát plocha je určena dvěma okrajovými křivkami, pokud by pro tyto křivky byly intervaly, v nichž leží hodnoty parametru, různé, provedeme lineární transformaci
MOCNINY A ODMOCNINY. Standardy: M-9-1-01 M-9-1-02 PYTHAGOROVA VĚTA. Standardy: M-9-3-04 M-9-3-01
 matematických pojmů a vztahů, k poznávání základě těchto vlastností k určování a zařazování pojmů matematického aparátu Zapisuje a počítá mocniny a odmocniny racionálních čísel Používá pro počítání s mocninami
matematických pojmů a vztahů, k poznávání základě těchto vlastností k určování a zařazování pojmů matematického aparátu Zapisuje a počítá mocniny a odmocniny racionálních čísel Používá pro počítání s mocninami
Obsah. Co je nového v Advance CAD 2015 NOVINKY... 5 VYLEPŠENÍ... 8
 Obsah NOVINKY... 5 1: Nová ukotvitelná paleta nástrojů...5 2: Oříznutí výřezu...5 3: Různé typy licencí...5 4: Uživatelské nastavení stránky...6 5: Nastavení barev pro šrafy...7 6: Asociativita úhlových
Obsah NOVINKY... 5 1: Nová ukotvitelná paleta nástrojů...5 2: Oříznutí výřezu...5 3: Různé typy licencí...5 4: Uživatelské nastavení stránky...6 5: Nastavení barev pro šrafy...7 6: Asociativita úhlových
Potenciální proudění
 Hydromechanické procesy Potenciální proudění + plíživé obtékání koule M. Jahoda Proudění tekutiny Pohyby elementu tekutiny 2 čas t čas t + dt obecný pohyb posunutí lineární deformace rotace úhlová deformace
Hydromechanické procesy Potenciální proudění + plíživé obtékání koule M. Jahoda Proudění tekutiny Pohyby elementu tekutiny 2 čas t čas t + dt obecný pohyb posunutí lineární deformace rotace úhlová deformace
Laserové skenování (1)
 (1) Prohloubení nabídky dalšího vzdělávání v oblasti zeměměřictví a katastru nemovitostí ve Středočeském kraji CZ.1.07/3.2.11/03.0115 Projekt je finančně podpořen Evropským sociálním fondem astátním rozpočtem
(1) Prohloubení nabídky dalšího vzdělávání v oblasti zeměměřictví a katastru nemovitostí ve Středočeském kraji CZ.1.07/3.2.11/03.0115 Projekt je finančně podpořen Evropským sociálním fondem astátním rozpočtem
MATURITNÍ TÉMATA Z MATEMATIKY
 MATURITNÍ TÉMATA Z MATEMATIKY 1. Základní poznatky z logiky a teorie množin Pojem konstanty a proměnné. Obor proměnné. Pojem výroku a jeho pravdivostní hodnota. Operace s výroky, složené výroky, logické
MATURITNÍ TÉMATA Z MATEMATIKY 1. Základní poznatky z logiky a teorie množin Pojem konstanty a proměnné. Obor proměnné. Pojem výroku a jeho pravdivostní hodnota. Operace s výroky, složené výroky, logické
Vytvořte si svůj svět
 Vytvořte si svůj svět Vytváření návrhů a prostorové zobrazení v programu AutoCAD Rychlý průvodce Použití systému nápovědy vyhledání položek v rejstříku zadání dotazu nebo výrazu pro verzi v přirozeném
Vytvořte si svůj svět Vytváření návrhů a prostorové zobrazení v programu AutoCAD Rychlý průvodce Použití systému nápovědy vyhledání položek v rejstříku zadání dotazu nebo výrazu pro verzi v přirozeném
Žák plní standard v průběhu primy a sekundy, učivo absolutní hodnota v kvartě.
 STANDARDY MATEMATIKA 2. stupeň ČÍSLO A PROMĚNNÁ 1. M-9-1-01 Žák provádí početní operace v oboru celých a racionálních čísel; užívá ve výpočtech druhou mocninu a odmocninu 1. žák provádí základní početní
STANDARDY MATEMATIKA 2. stupeň ČÍSLO A PROMĚNNÁ 1. M-9-1-01 Žák provádí početní operace v oboru celých a racionálních čísel; užívá ve výpočtech druhou mocninu a odmocninu 1. žák provádí základní početní
5. Statika poloha střediska sil
 5. Statika poloha střediska sil 5.1 Rovnoběžné sily a jejich střed Uvažujeme soustavu vzájemně rovnoběžných sil v prostoru s pevnými působišti. Každá síla má působiště dané polohovým vektorem. Všechny
5. Statika poloha střediska sil 5.1 Rovnoběžné sily a jejich střed Uvažujeme soustavu vzájemně rovnoběžných sil v prostoru s pevnými působišti. Každá síla má působiště dané polohovým vektorem. Všechny
Tématická oblast Počítačová grafika Modelování objektů
 Číslo projektu CZ.1.07/1.5.00/34.0556 Číslo materiálu VY_32_INOVACE_VC_IKT_18 Název školy Střední průmyslová škola a Vyšší odborná škola Příbram, Hrabákova 271, Příbram II Autor Martin Vacek Tématická
Číslo projektu CZ.1.07/1.5.00/34.0556 Číslo materiálu VY_32_INOVACE_VC_IKT_18 Název školy Střední průmyslová škola a Vyšší odborná škola Příbram, Hrabákova 271, Příbram II Autor Martin Vacek Tématická
Bézierovy křivky Bohumír Bastl KMA/GPM Geometrické a počítačové modelování Bézierovy křivky GPM 1 / 26
 Bézierovy křivky Bohumír Bastl (bastl@kma.zcu.cz) KMA/GPM Geometrické a počítačové modelování Bézierovy křivky GPM 1 / 26 Opakování Spline křivky opakování Bézierovy křivky GPM 2 / 26 Opakování Interpolace
Bézierovy křivky Bohumír Bastl (bastl@kma.zcu.cz) KMA/GPM Geometrické a počítačové modelování Bézierovy křivky GPM 1 / 26 Opakování Spline křivky opakování Bézierovy křivky GPM 2 / 26 Opakování Interpolace
Vzdělávací obsah vyučovacího předmětu
 Vzdělávací obsah vyučovacího předmětu Matematika 7. ročník Zpracovala: Mgr. Michaela Krůtová Číslo a početní operace provádí početní operace v oboru celých a racionálních čísel zaokrouhluje, provádí odhady
Vzdělávací obsah vyučovacího předmětu Matematika 7. ročník Zpracovala: Mgr. Michaela Krůtová Číslo a početní operace provádí početní operace v oboru celých a racionálních čísel zaokrouhluje, provádí odhady
Kooperace v automobilovém průmyslu - podpora konstrukčních prací 3D modelování
 Vyšší odborná škola, Střední odborná škola a Střední odborné učiliště, Kopřivnice, příspěvková organizace Kooperace v automobilovém průmyslu - podpora konstrukčních prací 3D modelování učební text Ing.
Vyšší odborná škola, Střední odborná škola a Střední odborné učiliště, Kopřivnice, příspěvková organizace Kooperace v automobilovém průmyslu - podpora konstrukčních prací 3D modelování učební text Ing.
Příloha č. 6 MATEMATIKA A JEJÍ APLIKACE
 Žák cvičí prostorovou představivost Žák využívá při paměťovém i písemném počítání komutativnost i asociativní sčítání a násobení Žák provádí písemné početní operace v oboru Opakování učiva 3. ročníku Písemné
Žák cvičí prostorovou představivost Žák využívá při paměťovém i písemném počítání komutativnost i asociativní sčítání a násobení Žák provádí písemné početní operace v oboru Opakování učiva 3. ročníku Písemné
Referenční plochy a souřadnice na těchto plochách Zeměpisné, pravoúhlé, polární a kartografické souřadnice
 Referenční plochy a souřadnice na těchto plochách Zeměpisné, pravoúhlé, polární a kartografické souřadnice Kartografie přednáška 5 Referenční plochy souřadnicových soustav slouží k lokalizaci bodů, objektů
Referenční plochy a souřadnice na těchto plochách Zeměpisné, pravoúhlé, polární a kartografické souřadnice Kartografie přednáška 5 Referenční plochy souřadnicových soustav slouží k lokalizaci bodů, objektů
7 Editace bodů. Editace bodů. NURBS křivky
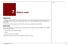 7 Editace bodů Editace bodů U objektů si můžete zobrazit řídicí nebo editační body a pomocí jejich přemisťování můžete lokálně upravovat tvar objektů namísto manipulace s objektem jako celkem. To se nazývá
7 Editace bodů Editace bodů U objektů si můžete zobrazit řídicí nebo editační body a pomocí jejich přemisťování můžete lokálně upravovat tvar objektů namísto manipulace s objektem jako celkem. To se nazývá
Výpočet průsečíků paprsku se scénou
 Výpočet průsečíků paprsku se scénou 1996-2018 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ Intersection 2018 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 26 Průsečík
Výpočet průsečíků paprsku se scénou 1996-2018 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ Intersection 2018 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 26 Průsečík
Vzdělávací obor matematika
 "Cesta k osobnosti" 6.ročník Hlavní okruhy Očekávané výstupy dle RVP ZV Metody práce (praktická cvičení) obor navázání na již zvládnuté ročník 1. ČÍSLO A Žák používá početní operace v oboru de- Dělitelnost
"Cesta k osobnosti" 6.ročník Hlavní okruhy Očekávané výstupy dle RVP ZV Metody práce (praktická cvičení) obor navázání na již zvládnuté ročník 1. ČÍSLO A Žák používá početní operace v oboru de- Dělitelnost
GIS Geografické informační systémy
 GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
Kreslení obrazů součástí Zobrazování geometrických těles. Zobrazení kvádru
 Kreslení obrazů součástí Zobrazování geometrických těles Zobrazení kvádru Kreslení obrazů součástí Zobrazování geometrických těles Zobrazení jehlanu s čtvercovou podstavou Kreslení obrazů součástí Zobrazování
Kreslení obrazů součástí Zobrazování geometrických těles Zobrazení kvádru Kreslení obrazů součástí Zobrazování geometrických těles Zobrazení jehlanu s čtvercovou podstavou Kreslení obrazů součástí Zobrazování
Rhino transformace, pole (kruhové, rovinné), tělesa editace těles (sjednocení, rozdíl, ), tvorba složených objektů (šroubovák)
 Rhino transformace, pole (kruhové, rovinné), tělesa editace těles (sjednocení, rozdíl, ), tvorba složených objektů (šroubovák) Výpočty dělící poměr, dělící dvojpoměr, transformace Příklad 1: Pracujte v
Rhino transformace, pole (kruhové, rovinné), tělesa editace těles (sjednocení, rozdíl, ), tvorba složených objektů (šroubovák) Výpočty dělící poměr, dělící dvojpoměr, transformace Příklad 1: Pracujte v
37. PARABOLA V ANALYTICKÉ GEOMETRII
 37.. Napiš rovnici paraboly, která má osu rovnoběžnou s osou y a prochází body A 0; 60, B 4; 8, C 8;36. 0m p60n 4m p8n 8m p36n m p pn 0 6 8 6 mm p pn 64 6 7 3 mm p pn 6 8m64 p 3 64 6m9 p Je-li osa rovnoběžná
37.. Napiš rovnici paraboly, která má osu rovnoběžnou s osou y a prochází body A 0; 60, B 4; 8, C 8;36. 0m p60n 4m p8n 8m p36n m p pn 0 6 8 6 mm p pn 64 6 7 3 mm p pn 6 8m64 p 3 64 6m9 p Je-li osa rovnoběžná
Terestrické 3D skenování
 Jan Říha, SPŠ zeměměřická www.leica-geosystems.us Laserové skenování Technologie, která zprostředkovává nové možnosti v pořizování geodetických dat a výrazně rozšiřuje jejich využitelnost. Metoda bezkontaktního
Jan Říha, SPŠ zeměměřická www.leica-geosystems.us Laserové skenování Technologie, která zprostředkovává nové možnosti v pořizování geodetických dat a výrazně rozšiřuje jejich využitelnost. Metoda bezkontaktního
Témata ke státní závěrečné zkoušce z matematiky ARITMETIKA
 Státní zkouška aritmetika Témata ke státní závěrečné zkoušce z matematiky ARITMETIKA Teoretická aritmetika 1. Prvky výrokové logiky - výrok, skládání výroků, abeceda výrokové logiky, výrokové formule,
Státní zkouška aritmetika Témata ke státní závěrečné zkoušce z matematiky ARITMETIKA Teoretická aritmetika 1. Prvky výrokové logiky - výrok, skládání výroků, abeceda výrokové logiky, výrokové formule,
ŠVP Školní očekávané výstupy. - vytváří konkrétní soubory (peníze, milimetrový papír, apod.) s daným počtem prvků do 100
 5.2 MATEMATIKA A JEJÍ APLIKACE 5.2.1 MATEMATIKA A JEJÍ APLIKACE Matematika 1. období 3. ročník RVP ZV Obsah RVP ZV Kód RVP ZV Očekávané výstupy ŠVP Školní očekávané výstupy ŠVP Učivo M3101 používá přirozená
5.2 MATEMATIKA A JEJÍ APLIKACE 5.2.1 MATEMATIKA A JEJÍ APLIKACE Matematika 1. období 3. ročník RVP ZV Obsah RVP ZV Kód RVP ZV Očekávané výstupy ŠVP Školní očekávané výstupy ŠVP Učivo M3101 používá přirozená
Výpočet průsečíků paprsku se scénou
 Výpočet průsečíků paprsku se scénou 1996-2008 Josef Pelikán, MFF UK Praha http://cgg.ms.mff.cuni.cz/~pepca/ Josef.Pelikan@mff.cuni.cz NPGR004, intersection.pdf 2008 Josef Pelikán, http://cgg.ms.mff.cuni.cz/~pepca
Výpočet průsečíků paprsku se scénou 1996-2008 Josef Pelikán, MFF UK Praha http://cgg.ms.mff.cuni.cz/~pepca/ Josef.Pelikan@mff.cuni.cz NPGR004, intersection.pdf 2008 Josef Pelikán, http://cgg.ms.mff.cuni.cz/~pepca
Copyright 2013 Martin Kaňka;
 Copyright 2013 Martin Kaňka; http://dalest.kenynet.cz Popis aplikace Aplikace Bottle design, jak je již z názvu patrné, je aplikace, která umožňuje vytvářet tělesa tvaru lahve. To znamená, že můžeme vytvořit
Copyright 2013 Martin Kaňka; http://dalest.kenynet.cz Popis aplikace Aplikace Bottle design, jak je již z názvu patrné, je aplikace, která umožňuje vytvářet tělesa tvaru lahve. To znamená, že můžeme vytvořit
Tento materiál byl vytvořen vrámci projektu. Inovace ve vzdělávání na naší škole V rámci OP Vzdělávání pro konkurenceschopnost
 Střední odborná škola stavební a Střední odborné učiliště stavební Rybitví Vzdělávací oblast: Odborné vzdělávání profilující okruhy Název: Technické kreslení a CAD I. Autor: ing. Milan Hanus Datum, třída:
Střední odborná škola stavební a Střední odborné učiliště stavební Rybitví Vzdělávací oblast: Odborné vzdělávání profilující okruhy Název: Technické kreslení a CAD I. Autor: ing. Milan Hanus Datum, třída:
Multimediální systémy. 11 3d grafika
 Multimediální systémy 11 3d grafika Michal Kačmařík Institut geoinformatiky, VŠB-TUO Osnova přednášky Princip 3d objekty a jejich reprezentace Scéna a její osvětlení Promítání Renderování Oblasti využití
Multimediální systémy 11 3d grafika Michal Kačmařík Institut geoinformatiky, VŠB-TUO Osnova přednášky Princip 3d objekty a jejich reprezentace Scéna a její osvětlení Promítání Renderování Oblasti využití
Voronoiův diagram. RNDr. Petra Surynková, Ph.D. Univerzita Karlova v Praze Matematicko-fyzikální fakulta
 12 RNDr., Ph.D. Katedra didaktiky matematiky Univerzita Karlova v Praze Matematicko-fyzikální fakulta petra.surynkova@mff.cuni.cz http://surynkova.info Definice V( P) nad množinou bodů P { p v rovině 1,
12 RNDr., Ph.D. Katedra didaktiky matematiky Univerzita Karlova v Praze Matematicko-fyzikální fakulta petra.surynkova@mff.cuni.cz http://surynkova.info Definice V( P) nad množinou bodů P { p v rovině 1,
