Vysoká škola ekonomická v Praze Fakulta managementu. Jindřichův Hradec. Bakalářská práce. Lenka Hadáčková
|
|
|
- Vladimír Neduchal
- před 6 lety
- Počet zobrazení:
Transkript
1 Vysoká škola ekonomická v Praze Fakulta managementu Jindřichův Hradec Bakalářská práce Lenka Hadáčková 2007
2 Vysoká škola ekonomická v Praze Fakulta managementu Jindřichův Hradec Bakalářská práce Lenka Hadáčková
3 Vysoká škola ekonomická v Praze Fakulta managementu v Jindřichově Hradci Katedra managementu informací Modelování dynamických procesů v ekonomii s využitím programu Derive5 ( Economic Process Modelling in Derive5 ) Vypracovala: Lenka Hadáčková Vedoucí bakalářské práce: RNDr. Jitka Bartošová Milevsko, červen
4 Prohlášení Prohlašuji, že bakalářskou práci na téma Modelování dynamických procesů v ekonomii s využitím programu Derive5 jsem vypracovala samostatně. Použitou literaturu a podkladové materiály uvádím v přiloženém seznamu literatury. Milevsko, červen 2007 Podpis studenta 3
5 Anotace Modelování dynamických procesů v ekonomii s využitím programu Derive5 Cílem práce je popis metod používaných k modelování dynamických problémů v mikroekonomii a makroekonomii a ukázky jejich řešení s využitím programu Derive5. Červen
6 Poděkování Za pomoc, ochotu, vstřícný postoj a cenné rady při tvorbě mé bakalářské práce bych chtěla poděkovat vedoucímu práce, RNDr. Jitce Bartošové 5
7 Obsah: 1. Úvod Teoretická část Hospodářský růst Bariéry ekonomického růstu Teorie ekonomického růstu Neoklasická teorie růstu Nové teorie růstu Ekonomická problematika Dynamická analýza ekonomických procesů Regresní a korelační analýza Vícenásobná regrese a korelace Praktická část Česká republika Vývoj hrubého domácího produktu Vývoj počtu pracujících Vývoj kapitálu Vývoj úrovně technologií Dánsko Vývoj hrubého domácího produktu Vývoj počtu pracujících Vývoj kapitálu Vývoj úrovně technologií Slovensko Vývoj hrubého domácího produktu Vývoj počtu pracujících Vývoj kapitálu Porovnání stavu v ČR, v Dánsku a na Slovensku Srovnání vývoje HDP v České republice, Dánsku a na Slovensku Srovnání vývoje počtu pracovníků v ČR, Dánsku a na Slovensku Srovnání vývoje kapitálu v ČR, Dánsku a na Slovensku Srovnání vývoje úrovně technologií v ČR, Dánsku a na Slovensku Regresní a korelační analýza Zjištění závislosti hrubého domácího produktu a kapitálu Zjištění závislosti HDP a úrovní technického pokroku Zjištění závislosti HDP a počtu pracovníků Vícenásobná regrese Závěr Literatura Knihy Internetové odkazy Přílohy
8 1. Úvod Za cíl své bakalářské práce jsem si zvolila teoreticky popsat a prakticky využít modely dynamických procesů v ekonomii. Vybrala jsem si především Solowův neoklasický model, jehož využití v praxi je velmi jednoduché. Má práce je rozdělena do několika částí. V první části se mimo jiné teoreticky věnuji problematice hospodářského růstu, který s dynamickými procesy úzce souvisí. Dále se zaměřuji na jednotlivé teorie, které vysvětlují hospodářský růst, a které obsahují jednotlivé modely. V dalších dvou částech se zabývám rozdělením ekonomické problematiky a popisem základů regresní a korelační analýzy. Potom se zaměřím hlavně na využití Solowova modelu, jeho porovnání se skutečností a posouzení, zda se skutečnost může shodovat s modelem. Toto provedu nejen s daty České republiky, ale i s dalšími členy Evropské unie, a to s Dánskem a Slovenskem. Pro lepší orientaci v problematice provedu srovnání ekonomik všech těchto zmíněných států. Na závěr porovnám a graficky znázorním závislosti mezi jednotlivými proměnnými, které jsou potřebné k jeho konstrukci. Pro zjednodušení bude v mé práci použito několika počítačových programů, a to program Derive5, MS Excel 2000 a statistický program Statgraphics. Pro lepší přehlednost jsou všechny rovnice vyskytující se v této bakalářské práci vytvořeny v editoru rovnic. 7
9 2. Teoretická část 2. 1 Hospodářský růst Pod pojmem hospodářský růst si můžeme představit vzestup hospodářského potenciálu země, ke kterému dochází v souvislosti s růstem hrubého domácího produktu (HDP). [26] uvádí, že ekonomický růst je pokládán za jeden z dominantních cílů hospodářské politiky. V obdobích, kdy země dosahují relativně vysoká tempa ekonomického růstu a jejich ekonomika se rozvíjí na vzestupné úrovni, je zpravidla hospodářský a politický život země stabilizovaný. Naopak, v dobách recese se zvětšují hospodářské potíže. Při sledování růstu produktu je podle [11] potřeba odlišovat dvojí situaci: 1. zvýšení krátkodobé, které je po určité době vystřídané poklesem produktu 2. dlouhodobý trend, který se obvykle spojený s víceméně plynulým zvyšováním produkčních možností ekonomiky V prvním případě jde o růst skutečného produktu ve smyslu jeho cyklického kolísání, ve druhém případě jde o dlouhodobý růst potenciálního produktu, neboli o hospodářský růst. Růst potenciálního produktu umožňují zdroje tvořené dle [11] několika složkami: 1. Lidské zdroje o množství práce o lidský kapitál, tj. vzdělání, zručnost a zkušenosti pracovníků, náklady na jejich získání, zvýšení a udržení, a dále i motivace a schopnost podnikání 2. Přírodní zdroje o množství půdy a nerostného bohatství o kvalita těchto zdrojů (úrodnost půdy, kvalita nerostů, klimatické podmínky) 3. Kapitálové zdroje v podobě kapitálových statků o stroje a zařízení, budovy, stavby apod. o technická úroveň těchto statků - jejich výkonnost, přesnost, pracovní a energetická náročnost 8
10 Dle [11] se pojem ekonomický růst často používá jako synonymum vývoje skutečného reálného produktu. Tento vývoj se dá vyjádřit buď absolutně jako přírůstek produktu v mld. Kč v daném období t, anebo tempem růstu reálného produktu. Ekonomický růst je určován dle [26] do značné míry formálními pravidly, neformálními normami a způsoby jejich vynucování. Formální pravidla se mohou měnit rychle, neformální se ale mění velmi pomalu. Proto i rozvojové ekonomiky, které přijmou formální ekonomická pravidla úspěšných ekonomik, často velký úspěch nezažívají Bariéry ekonomického růstu Vývoj ekonomické úrovně vykazuje v různých zemích a regionech výrazně rozdílnou podobu. Tempo růstu produktu je dle [11] závislé: na tempu prohlubování kapitálu, tj. na vývoji obyvatelstva a na vývoji zásoby kapitálu na vývoji technologických změn Zatímco v rozvinutých ekonomikách roční tempo růstu obyvatelstva málokdy překračuje 1 %, v rozvojových zemích činí většinou několikanásobek, což ale snižuje růst produktu. Za základní bariéru ekonomického růstu bývá často považována nedostatečná zásoba kapitálu. Na problém nedostatku kapitálových statků navazuje nedostatečný technologický pokrok. Nedostatečnou úroveň vykazuje i pracovní síla. Další brzdou hospodářského růstu mohou být i faktory jako náboženství, různé kulturní tradice a nebo příbuzenské vztahy. Brzdit hospodářský růst může i vysoké zdanění úspor, které jsou podmínkou pro tvorbu kapitálu. Toto vysoké zdanění může vést k poklesu množství práce, která tvoří hrubý domácí produkt (HDP), dochází k omezení úspor a tvorby kapitálu a tedy k nízkému produktu. Naopak nízké zdanění ukazuje vysokou zaměstnanost, tvorbu kapitálu a tím i vysokou úroveň produktu. Nezanedbatelným problémem ekonomického vývoje v čase je to, že po určité době ekonomického růstu se začnou vytvářet silné zájmové skupiny, které omezují trhy, zvyšují transakční náklady a snižují růst produktivity. Dochází k vytváření podnětů pro ekonomicky škodlivé aktivity typu hospodářské kriminality, tunelování a korupce. 9
11 Právě fenomén korupce je faktor, který je v poslední době považován za jednu ze základních překážek dynamizace hospodářského růstu. Hospodářský růst bývá vysvětlován pomocí několika teorií. Tyto teorie mohou být rozděleny na keynesiánskou teorii růstu, neoklasickou teorii růstu a novou teorii růstu Teorie ekonomického růstu U zrodu této teorie byl A.Smith a jeho dílo Inquiry into the Nature and Causes of the Wealth of Nations z roku Smith totiž došel k závěru, že je důležitá dělba práce, akumulace kapitálu a technický pokrok. Mimo jiné také přišel na to, že svobodný mezinárodní obchod umožňuje chudším zemím přibližovat se zemím bohatším. Ve své době tyto teorie vzbuzovaly velkou pozornost, ale dnes se jeví jako nevýznamné. Základy moderní teorie růstu pak byly dle [26] položeny v 50. letech R. Solowem (1956) a T. Swanem (1956). Výsledkem jejich práce byl model, který je dnes označován za neoklasický model neboli také Solowův model a který se stal základním rámcem pro analýzu ekonomického růstu na dlouhou dobu. O tomto modelu se zmíním podrobněji v dalším textu. Tehdejší ekonomové se zabývali otázkami, kterými se zabývají i dnešní ekonomové, mezi ně patří: Co ovlivňuje bohatství národů? Proč některé země rostou rychleji než druhé? Co by měly a neměly vlády dělat, aby jejich země dosahovaly rychlého růstu životní úrovně? Dle [26] bylo definováno několik pravd o ekonomickém růstu: 1. Důchod na osobu v čase roste a tempo růstu nevykazuje tendenci k poklesu. 2. Fyzický kapitál na osobu v čase roste. 3. Míra výnosu z kapitálu je téměř konstantní. 4. Poměr fyzického kapitálu k výstupu je téměř konstantní. 5. Podíly práce a fyzického kapitálu na důchodu jsou téměř konstantní. 6. Tempo růstu důchodu na osobu mezi zeměmi se významně odlišuje. Ekonomická teorie obsahuje řadu konkrétnějších přístupu v podobě různých růstových modelů, které rozdílně zohledňují význam jednotlivých zdrojů růstu a zkoumají pohled na hospodářský růst včetně jeho omezení. 10
12 Mezi nejjednodušší modely patří klasický model, který byl vytvořen T. R. Malthusem. Tento model pracuje s konstantním množstvím a kvalitou půdy a neuvažuje ani významnější růst množství kapitálu, ani jeho technický rozvoj. Jediným zdrojem ekonomického růstu je v tomto modelu růst obyvatelstva, jinak také množství pracovních vstupů, což je ale spojeno s klesajícím mezním produktem práce. Tempo růstu produktu se postupně snižuje, až se dostane pod tempo růstu obyvatelstva. Klesá proto produkt na 1 obyvatele a klesají reálné mzdy až na úroveň životního minima, kde se růst obyvatelstva zastaví. Dle [10] je zvýšení produktu na 1 obyvatele a reálné mzdy možné za podmínek, kdy nastává zvýšená úmrtnost, např. kvůli válkám nebo epidemii a nebo také snížením porodnosti. Růst reálných mezd však povede k růstu porodnosti a opět k ustálení produktu na úrovni, která odpovídá životnímu minimu Neoklasická teorie růstu Neoklasická teorie růstu vychází z neoklasické produkční funkce (1), která má tvar: Y = f ( K, AL), (1) kde Y je reálný důchod K je kapitál L je lidský kapitál A je měřítko úrovně technologií Součin A a L vyjadřuje pracovní sílu vyjádřenou v efektivnostních jednotkách a zahrnuje množství práce i její produktivitu. 11
13 Solowův model Solowův Swanův model je dle [26] nejznámějším neoklasickým modelem. Tento model je dílem nositele Nobelovy ceny za ekonomii, amerického ekonoma Roberta Solowa a australského ekonoma Trevora Swana. Stal se základem pro analýzu ekonomického růstu. Výše zmíněná produkční funkce je jeho základem. Zaměřuje se na růst úspor, kapitálové akumulace a populační expanze na jedné straně a na úlohu technického pokroku na straně druhé. Díky tomuto modelu se dá odpovědět na spoustu otázek jako např.: Jak se růst důchodu na osobu v dané zemi vyvíjí v čase? Existují nějaké ekonomické síly, které ve velmi dlouhém období umožní chudým zemím přibližovat se životní úrovni zemí vyspělých? Solowův model předpokládá, že ekonomika má v každém časovém okamžiku k dispozici určitý počet pracujícího obyvatelstva L, které roste stabilním tempem. Ekonomika má dále v daném časovém okamžiku k dispozici určitou kapitálovou zásobu K. S těmito zdroji ekonomika vyrábí ročně reálný důchod Y. Dále se předpokládá, že ekonomika je uzavřená, což znamená, že nemá žádný export ani import. A také, že neexistují státní výdaje a daně. Solowův model studuje jak se hrubý domácí produkt, kapitál a pracující obyvatelstvo vyvíjejí v čase. Pro konstrukci Solowova modelu musí být splněny určité předpoklady: produkce roste, ale tempo růstu se zpomaluje, takže dle [8] platí vztah (2) f > K 2 f f > 0 2 L K 2 f < 0 L 0 2 limitní chování produkce je dáno těmito vztahy (3) f f lim = 0 lim = K K K 0 K f f lim = 0 lim = K L K 0 L produkční funkce (4) je homogenní 1. stupně < 0 (2) (3) f ( ak, aal) = af ( K, AL) (4) 12
14 výnosy z rozsahu (5) jsou konstantní Y = f ( K, AL) = AL f ( k), (5) kde K k = je kapitál na jednotku efektivní práce AL Y y= je produkce na jednotku efektivní práce. AL Dalšími předpoklady dle [27] jsou předpoklady o tvaru produkční funkce (6): f (0) = 0 f ( k) > 0 f ( k) < 0 (6) kde f ( k) > 0 je mezní produkt kapitálu Tvar produkční funkce, která je použitá v Solowově a Swanově obrázek č. 1 modelu znázorňuje Obrázek č. 1 Tvar produkční funkce v Solowově modelu Zdroj: Semestrální práce (vondrasek_sem2.pdf), [9] Dalšími podmínkami, které ovšem nejsou tak striktně vyžadovány jsou tzv. Inadovy podmínky (7). lim f ( k) = k 0 lim f ( k) = 0, (7) k které v podstatě říkají, že čím více se množství kapitálu blíží nule, tím větší je jeho mezní produkt a to až do nekonečna a naopak, čím větší je množství kapitálu, tím menší je jeho mezní produkt a tato hodnota konverguje k nule. 13
15 Posledním předpokladem je konstantní tempo růstu pracovní síly n a míra technického pokroku g, pokud platí dle [8] vztahy (8). L= nl. A= na. L = n= konst. L. A = g = konst. A (8) pak pro časový vývoj pracovních sil platí vztah (9) nt L( t) = L0e (9) pro časový vývoj míry technického pokroku (10) platí gt A( t ) = A 0 e (10) pro růst produktu v čase platí vztah (11): Y ( t ) ( n+ g ) t = Y 0 e (11) a pro růst kapitálu v čase (12) platí K ( t ) ( n+ g ) t = K 0e (12) kde L 0 = L(0), A 0 = A(0), Y 0 = Y (0) a K 0 = K(0) jsou počáteční hodnoty velikosti populace, úrovně technologií, produktu a kapitálu (v čase t = 0 ). Tyto vztahy tvoří v podstatě jádro Solowova modelu. Při použití tohoto modelu se objevují tři základní problémy: mezinárodní rozdíly v životní úrovni výnosy kapitálu v jednotlivých ekonomikách konvergence ekonomik Hypotéza konvergence znamená, že země s nižším počátečním důchodem na osobu rostou rychleji než země s vyšším počátečním důchodem na osobu. 14
16 Celkově lze dle [26] shrnout předpovědi Solowova modelu ohledně dlouhodobého růstu do několika bodů: celkový reálný důchod (Y) roste tempem, které odpovídá míře růstu rozšířené práce, tj. míře růstu populace plus míře technického pokroku (n + g) reálný důchod na osobu (Y/L) roste tempem, které odpovídá míře technického pokroku (g) v úspěšně se rozvíjejících ekonomikách, kde je míra růstu kapitálu [(n + x)k] vyšší než míra růstu rozšířené práce (n + g), bude míra růstu reálného důchodu na osobu vyšší než míra odpovídající dlouhodobému stálému růstu u vyspělých stagnujících ekonomik bude tempo růstu reálného důchodu na osobu stejné nebo nižší než tempo odpovídající dlouhodobému stálému růstu, ale díky technickému pokroku bude stále pozitivní. Jediným závěrem neoklasického modelu je to, že růst existuje. Pokud si např. položíme otázku, proč v určité ekonomice roste životní úroveň, dá nám neoklasický model celkem jednoznačnou odpověď, a to, kvůli tomu, že se zvyšuje zásoba kapitálu a produktivita faktorů. Pokud si ale položíme otázku např. proč některé země rostou rychleji a některé pomaleji, pak jednoznačnou odpověď z tohoto modelu nezískáme Nové teorie růstu Ve druhé polovině 80. let dochází ke vzniku nových modelů růstu, které opouští některé základní předpoklady neoklasického modelu, jako byly exogennost technického pokroku a dostupnost stejné technologie pro všechny země. Nové teorie by měly lépe vysvětlit trvalý ekonomický růst světové ekonomiky a rozdíly mezi jednotlivými zeměmi. Cílem nových růstových teoretiků je vysvětlit, proč země, které více spoří a investují, rostou dlouhodobě rychleji. Dlouhodobý růst v takovém modelovém světě závisí na vládní politice, a to na zdanění, zajišťování zákona a pravidel, údržbě ekonomické infrastruktury, podpoře vzdělávání, regulaci mezinárodního obchodu atd. Počátky tzv. nové teorie růstu jsou spojeny s pracemi P. Romera a R. Lucase. 15
17 Endogenní růstové modely Endogenní růstové modely patří mezi lineární dynamické modely deterministického typu, o kterých bude řeč později. V těchto modelech se ekonomové zaměřují na endogenizaci technického pokroku. Dle [8] je tento technický pokrok podmíněn: 1. určitou výchozí kvantitativní i kvalitativní úrovní fyzického kapitálu 2. novými objevy a různými zlepšeními 3. určitými institucionálními podmínkami, jako je např. vládní podporou výzkumu Endogenního ekonomického růstu nelze tedy dosáhnout pouhým jednorázovým poskytnutím moderního kapitálového vybavení, ale je výsledkem dlouhodobého ekonomického vývoje. Endogenní růstové modely se mohou rozdělit na modely, které mají velmi blízko k modelu Solowa a Swana, tzv. AK modely. A na modely výzkumu a vývoje, tzv. R&D modely. Blížeji se zmíním o AK modelech. Mezi AK modely patří Romerův a Lucasův model a samostatný AK model. V AK modelech má významný vliv na růst ekonomiky především daňová politika, která ovlivňuje akumulaci fyzického nebo lidského kapitálu. Romerův model Tento model je považován za rovnovážný model endogenního technického pokroku, ve kterém je dlouhodobý růst poháněn zvyšováním znalostí. Produkční funkce (13) podle Romera má tento tvar Y = A( K, L) KL (13) Podle Romera může celková produkce mít konstantní nebo dokonce rostoucí výnosy z rozsahu. Pokud bude přijat předpoklad konstantních nebo rostoucích výnosů z rozsahu, může růst i ve stabilním stavu pokračovat nekonečně i bez technického pokroku. 16
18 Lucasův model Druhý z modelů nové teorie růstu nabídl R.Lucas. Podle něj je technický pokrok spojen s investicemi do lidského kapitálu. Lucas vidí lidský kapitál jako obecnou úroveň dovedností dělníků. Je velice zajímavé, že investice do lidského kapitálu způsobují kromě růstu vlastní produktivity dělníka i růst produktivity ostatních dělníků. Z toho vyplývá dle [8] několik poznatků: Lidský kapitál zvyšuje produktivitu fyzického kapitálu i práce Mezní produkt fyzického kapitálu má tendenci zůstávat konstantní Produkční funkce (14) typu Romer-Lucas může být zaznamenána ve tvaru Y = A( K, HC) f ( K, HC, L), (14) kde K je kapitál L je lidský kapitál HC jsou znalosti Tyto tři faktory jsou hlavními faktory, které vyvolávají rostoucí výnosy z rozsahu. K i HC přitom závisí na růstu a tím je endogenizována úroveň technologií. AK model AK model je posledním ze tří AK modelů. Základem teorie endogenního růstu je produkční funkce (15) ve tvaru Y = AK, (15) která z definice udržuje předpoklad konstantních výnosů z rozsahu a nepředpokládá klesající výnosy z akumulovaného faktoru Základní skupina modelů endogenního růstu je tedy často označována za AK modely, protože faktorem, který zahrnuje všechny produkční vstupy, je kapitál. Produkční funkce dle [8] vychází z rovnice akumulace (16). K K = sy δk (16) 17
19 Tato rovnice (16) spolu s produkční funkcí Y = AK zajišťuje, že platí vztah (17). Y Y. K = = sa δ K (17) Pokud je sa > δ pak důchod roste trvale i bez předpokladu exogenního technického pokroku. Tzn., že ke zvýšení dlouhodobého růstu stačí zvýšit míru úspor. V endogenním růstovém modelu vede růst míry úspor k trvalému zvýšení ekonomického růstu. Z tohoto modelu mohou být dle [8] vyvozeny čtyři důležité závěry: Rozdíly v míře úspor mezi zeměmi vedou ke zvyšujícím se rozdílům důchodu v čase. Bohaté země tak mohou růst stále Velké rozdíly důchodu nejsou spojeny s rozdíly ve výnosu kapitálu. Svět tak může vykazovat velké rozdíly v důchodu, aniž dochází k pohybu kapitálu z bohatých do chudých zemí Chudší země, u kterých je stejná úroveň technologií jako u jiných zemí, porostou stejným tempem jako země bohatší, bez ohledu na počáteční úroveň důchodu Cokoli, co ovlivňuje podněty lidí spořit a investovat, může ovlivnit dlouhodobý růst. Mezi klíčové faktory může patřit např. daňová politika Podle ekonomů endogenního růstu totiž stačí lépe měřit základní veličiny v neoklasickém modelu. Tím se získají v podstatě stejné výsledky jako u nových růstových modelů. Podle názorů ekonomů je třeba přidat k práci nebo kapitálu lidský kapitál a přizpůsobit oba faktory růstu jejich kvality znalostí. Ekonomové tvrdí, že jak neoklasická teorie tak teorie endogenního růstu trpí jedním zásadním nedostatkem. Neoklasická teorie předpokládá, že nejrychleji by měla růst skupina nejchudších zemí, zatímco podle Romerova a Lucasova modelu by to měla být spíše skupina nejbohatších zemí. 18
20 2. 3 Ekonomická problematika Ekonomickou problematiku můžeme rozdělit do dvou základních skupin, a to: Statická analýza ekonomických procesů Dynamická analýza ekonomických procesů Dynamická analýza ekonomických procesů se může dále dělit na: Dynamické modely nespojitých ekonomických procesů Dynamické modely spojitých ekonomických procesů Dynamická analýza ekonomických procesů Stav a vývoj ekonomických systémů dle [3] může být obecně zachycen pomocí diferenciálních nebo diferenčních rovnic. Rozlišují se dvě metody analýzy časového vývoje ekonomických systémů, které určují dva základní typy modelů. První typ modelu je založen na diskrétním chápání času a pracuje s diferenčními rovnicemi. Dynamika je zde zachycena pomocí zpožděných endogenních a exogenních proměnných. Druhý typ modelu je založen na chápání času jako spojité veličiny a k popisu dynamiky procesu tento model využívá diferenciální rovnice. Na oba typy modelů je možné pohlížet buď jako na modely deterministické, tzn. bez náhodných vlivů, nebo jako na modely stochastické, do kterých jsou zahrnuty i náhodné vlivy. Dynamické modely deterministického typu Deterministické dynamické systémy jsou založeny na předpokladu, že následné hodnoty stavových proměnných jsou určeny předcházejícími hodnotami. Hlavní výhodou těchto modelů je, že při popisu dynamiky systémů může být využito diferenciálních rovnic. Deterministický model dynamického ekonomického systému může být dle [3] soustava obyčejných diferenciálních rovnic ve tvaru (18) r r r x T = F (18) ( t, x) 19
21 r T kde x = ( x x,... x ) T je vektor transponovaný k x = ( x x,... ) 1, 2 n t je čas, r F t x r, je vektorová funkce času a stavových proměnných. ( ) r 1, 2 x n, Deterministické dynamické modely se dále mohou dělit na lineární a nelineární. Lineární dynamické modely deterministického typu Lineární dynamické systémy jsou relativně jednoduché a dobře prozkoumané. Za lineární r r dynamický model se považuje takový model, ve kterém je funkce F( t, x) lineární. Jestliže r funkce F(x r ) neobsahuje čas, jedná se o tzv. autonomní systém. Každý neautonomní systém lze převést na autonomní, když nahradíme čas další stavovou proměnnou x n+ 1 a přidáme diferenciální rovnice x = +1 1 do soustavy. n Nelineární dynamické modely deterministického typu Nelineární dynamické systémy se mohou chovat velmi složitě, takže dokonce i deterministicky definované nelineární modely mohou mít vývoj, který nelze předpovědět. Analýza nelineárních systémů je zaměřena především na hledání bodů stability a na počítačové simulace chování těchto systémů. Vyšetřování nelineárních dynamických systémů je omezeno na hledání okolí kritických bodů, ve kterých je lokální fázový profil stejný s některým lineárním systémem. Na okolí těchto kritických bodů je provedena linearizace systému pomocí Taylorova rozvoje. Nelineární dynamické modely nám dávají možnost modelovat takové stavy, kdy v systému existují body nestability. Dynamické modely stochastického typu Stochastické dynamické modely obsahují narozdíl od deterministických dynamických modelů navíc náhodnou složku a neumožňují proto přímé vytvoření vhodného tvaru funkce, který by odpovídal charakteru zkoumaných veličin. Je nutné zvolit metodu odhadu parametrů modelu podle předem zvolené struktury. Odhad je proveden na základě průběhu posloupnosti naměřených hodnot stavových veličin v různých časových okamžicích. 20
22 2. 4 Regresní a korelační analýza Regresní analýza se zabývá hledáním, zkoumáním a hodnocením souvislostí mezi dvěma i více statistickými znaky. Z hlediska metody zkoumání je možné rozlišit závislosti na pevné a volné. Pevnou závislost představuje případ, kdy výskytu jednoho jevu nutně odpovídá výskyt druhého jevu. Tento vztah musí mít stoprocentní jistotu. O závislosti volné je možné potom hovořit v případech, kdy výskyt jednoho jevu ovlivňuje výskyt druhého jevu v tom smyslu, že se zvýšila pravděpodobnost nastoupení druhého jevu při nastoupení prvního jevu. Se závislostmi pevnými se většinou můžeme setkat v teoretické oblasti, kdy se vztahy mezi proměnnými formulují na základě deduktivních úvah a v souladu se zkušenostmi. Takovým způsobem dle [12] vznikl např. Newtonův gravitační zákon nebo Ohmův fyzikální zákon. V reálných situacích se setkáváme prakticky výhradně s volnými závislostmi. V ekonomické oblasti se regresní analýza rozšířila asi nejvíc při analýze a prognózování spotřeby a poptávky, kdy se kostruovaly různé regresní modely sloužící k odhadu střední spotřeby nebo poptávky domácností s různým příjmem, s různým počtem členů, s různým počtem dětí apod. Podkladem pro regresní analýzu jsou vždy nějaká data získaná pozorováním. Někdy se pracuje s hodnotami číselných proměnných zjištěných v určitém období nebo okamžiku u nějakých jednotek, kterými mohou být osoby, domácnosti, prodeje atd. Jsou-li k dispozici hodnoty číselných proměnných získaných v n po sobě jdoucích obdobích, týká se regresní analýza časových řad. Regresní modely K regresní analýze se využívají regresní modely, které tvoří určité funkce známé z matematiky. Poměrně často se používají funkce, které jsou lineární z hlediska proměnných. K nim patří přímka, dále rovina a regresní nadrovina. Kromě nich se užívá i řada dalších regresních funkcí, které nejsou lineární z hlediska proměnných a jsou lineární jen z hlediska parametrů. K nim patří parabola, dále hyperbola, logaritmická funkce a řada dalších. 21
23 Dle [2] se regresní funkce, které jsou lineární z hlediska parametrů, nazývají lineární regresní funkce a regresní modely s takovými funkcemi se nazývají lineární regresní modely. V praxi se však využívají takové regresní funkce, které nejsou lineární z hlediska parametrů. Jsou to například exponenciální funkce, mocninná funkce a mnohé jiné. Nazývají se nelineární regresní funkce a regresní modely s takovými funkcemi se nazývají nelineární regresní modely. Někdy lze při volbě regresní funkce využít i zkušenost. Regresní funkce je zvolena dříve, než se začne zkoumat, jak se závislost projevuje ve zjištěných údajích. Obvykle se vymezí určitá skupina možných regresních funkcí a pak se zkoumá, které z těchto funkcí dobře přiléhají zjištěným údajům. Regresní funkce je dle [2] vyjádřena pomocí regresních parametrů, ty se označují řeckým písmenem β. V případě regresní přímky je parametr β 1 její směrnicí, což znamená, že udává, jaký přírůstek střední hodnoty proměnné y odpovídá jednotkovému přírůstku hodnoty proměnné x. Lineární regrese, která je dle [1] dána následujícími vztahy: Regresní přímka, jejíž vztah (1) je = β 0 + β x+ ε (1) y 1 Regresní parabola daná vztahem (2) 2 y = β + β x+ β + ε (2) x Regresní hyperbola daná funkcí (3) β1 y= β + + ε x 0 (3) Regresní logaritmická funkce ve vztahu (4) y= β 0 + β1 log x+ ε (4) 22
24 Nelineární regrese, která je dle [1] dána následujícími vztahy: Regresní exponenciála ve vztahu (5) x y 1 = β0 β ε (5) Regresní mocninná funkce daná vztahem (6) β β 1 y = ε (6) 0 x kde β 0, β1, β2 jsou regresní koeficienty Regresní testování Ve vybrané regresní funkci lze zjistit a otestovat, zda jsou regresní parametry významné a zda je významný celý regresní model. K otestování toho, zda je některý z regresních koeficientů významný, slouží jednotlivé t-testy (7). Tyto testy o nulových hodnotách jednotlivých regresních parametrů vycházejí z rozdělení náhodných veličin. bi T i = (7) s b ) Hypotézou je nulová hodnota regresního parametru, který je tím nevýznamný ( i Oborem přijetí H 0 (8) je pak H 0 : b i = 0 T i < t ( n p) 1 α (8) 2 Pokud je tento test prováděn v Excelu, pak se může vycházet z tzv. p-hodnoty. Je-li p-hodnota menší než hladina významnosti, která je obecně určena hodnotou 0,05, pak zamítáme hypotézu o nulovosti koeficientu a testovaný parametr je významný. 23
25 Jak již bylo výše řečeno, může být testována i významnost celého regresního modelu a to celkovým F-testem (9). Při tomto testování se vychází z Fischerova rozdělení F(p-1;n-p) F = S T p 1 S R n p (9) Hypotézou je stejně jako u předchozích t-testů nulová hodnota regresních parametrů Oborem přijetí hypotézy H 0 je vztah (10) F < F α ( p 1; n ) (10) 1 p V regresním modelu může být také zjištěna síla závislosti mezi proměnnými. K tomu se využívá korelační analýza. K určení síly závislosti se používají různé korelační indexy. Mezi ně patří: index determinace, který je dán vztahem (11) R 2 S S 2 T = I = = 1 y S S R y, (11) kde S T je teoretický součet čtverců, ten se považuje za tu část součtu čtverců S y, která je vysvětlena zvolenou výběrovou regresní funkcí. Zatímco reziduální součet čtverců S R se považuje za tu část, která zvolenou výběrovou regresní funkcí vysvětlena není. Další index, který vystihuje sílu závislosti je: index korelace, jehož vztah (12) je I = 2 2 = I R (12) 2. 5 Vícenásobná regrese a korelace Hodnoty závislé proměnné y lze sledovat v důsledku působení více různých vlivů, tj. nezávisle proměnných x j, kde j = 1,2,... m. Při vícenásobné regresi může nastat situace, kdy se v modelu objeví nežádoucí závislost mezi vysvětlujícími proměnnými. Tento jev se dle [1] nazývá multikolinearita. Dle [1] je multikolinearita velmi běžným jevem. Informace o ní se dají získat z korelačních koeficientů mezi jednotlivými vysvětlujícími proměnnými. 24
26 Význam multikolinearity Podle [1] znamená, že snaha přidávat další vysvětlující proměnné do modelu není účelná. Jde-li o silnou multikolinearitu, pak je některá proměnná v modelu zbytečná a může být z modelu vyloučena bez jeho ovlivnění. 25
27 3. Praktická část Při řešení konkrétních případů bude použit program Derive5 a tabulkový kalkulátor MS Excel K výpočtům budou použity vzorce z teoretické části. Kromě vybraného Solowova modelu ve své práci využiji jednoduchou a vícenásobnou regresi. Budu se zabývat výší hrubého domácího produktu, kapitálu, počtem pracovníků a úrovní míry technického pokroku v zemi. Všechny tyto faktory budu zkoumat jednotlivě i ve spojení s ostatními. V případě regrese budu využívat statistický program Statgraphics. Pro svou praktickou část jsem si tedy vybrala využití Solowova modelu. Ve své práci jsem se rozhodla porovnat pomocí tohoto modelu Českou republiku s dalšími státy Evropské unie. Vybrala jsem si Dánsko a Slovensko. Data, která jsou potřebná pro tento model, jsem získala z webových stránek jednotlivých zemí a ze stránek Ministerstva práce a sociálních věcí. Tato data zachycují období od roku 1995 do roku U každého z vybraných států provedu srovnání skutečných hodnot s hodnotami získanými pomocí Solowova modelu. Jednotlivé ukazatele budu dále porovnávat mezi sebou. Každou situaci názorně předvedu na grafech, vytvořených v programu Derive5 nebo pro lepší přesnost programem MS Excel Pro lepší přehlednost jsou použité vzorce vkládány pomocí editoru rovnic. Data potřebná ke grafům jsou k nalezení v příslušných přílohách. Jednou z nejdůležitějších potřeb Solowova modelu je určení konstant, pro tento model nepostradatelných. Jde o konstanty n, g, n+g. Konstanta n Tato konstanta udává tempo růstu pracovní síly. Vypočítá se tak, že z poměru růstu pracovní síly utvoříme geometrický průměr a ten se pak následně zlogaritmuje. ČR : n= 0,0018 DK : n= 0,00639 SK : n= 0,
28 Konstanta n+g Konstanta udává tempo růstu hrubého domácího produktu v jednotlivých letech. Vypočítá se zase zlogaritmováním geometrického průměru jednotlivých přírůstků HDP. ČR : n+ g = 0,0715 DK : n+ g = 0,00279 SK : n+ g = 0, Konstanta g Tato konstanta vyjadřuje úroveň technologií neboli míru technického pokroku. Vypočítá se dopočtem, pokud již známe konstanty n+g a n. ČR : g = 0,0733 DK : g = 0,00918 SK : g = 0, Pro potřeby modelu se musí nejprve vypočítat jednotlivé přírůstky HDP, kapitálu a počtu pracovníků. Dále je potřeba zjistit ze zjištěných dat úroveň technologií, a to podle vzorce (1), který vyjadřuje, že úroveň technologie se dá vyjádřit jako podíl produktu na kapitálu Y A= (1) K Hodnoty v políčkách s názvem poměr růstu se získají pomocí vzorce (2) hodnota roku ( n+1) hodnota roku n (2) 27
29 Z těchto hodnot se pak vypočítá geometrický průměr pomocí příkazu v programu MS Excel 2000, a ten se potom zlogaritmuje, tím vyjdou hledané konstanty. Tyto konstanty se mohou vypočítat také pomocí regrese. V tomto případě se bude postupovat tak, že se hodnoty zlogaritmují a dále se postupuje pomocí příkazu v programu MS Excel 2000 Analýza dat Regrese. Podle mého názoru je lepší první způsob a proto jsem ho také využila ve své práci. Takto vypočítané konstanty jednotlivých zemí jsou výše uvedené Česká republika Jako státní útvar přestalo Československo existovat 1. ledna 1993, kdy se mírovou cestou rozdělilo na Česko a Slovensko. Česká republika spolu se Slovenskem schválily v referendu v roce 2003 svůj přístup k Evropské unii, který nabyl účinnosti 1. května Získaná data, potřebná k sestrojení modelu, byla nejprve upravena do přehledných tabulek: Tabulka č. 1 Údaje o České republice potřebné k použití Solowova modelu ČESKÁ REPUBLIKA HDP v mld. (Y) 1466, , , , , ,17 - poměr růstu x 1,1478 1,0759 1, , , Pracovníci v tis. (L) 5054, , , , , ,40 - poměr růstu x 1,0118 0,982 0, , ,01927 Hrubý fixní kapitál v mld. (K) 477,68 567,02 551,86 566,90 563,77 645,12 - poměr růstu x 1,187 0,9733 1, , , Míra techn. pokroku (A) 3,0701 2,9687 3,2818 3, , , HDP v mld. (Y) 2352, , , , , ,26 - poměr růstu 1,0745 1,0477 1,0457 1, , , Pracovníci v tis. (L) 4956, , , , , ,00 - poměr růstu 1,0033 1,0017 0,9988 0, , , Hrubý fixní kapitál v mld. (K) 694,06 703,96 700,26 774,37 772,77 873,77 - poměr růstu 1,0759 1,0143 0,9948 1, , , Míra techn. pokroku (A) 3,389 3,5008 3,6802 3, , ,
30 Vývoj hrubého domácího produktu Základní vztah (1) pro růst produktu v čase je: Y ( n+ g ) t ( t) = Y0 e (1) Funkce, z které budu nadále vycházet, je dána vztahem (2): Y 0,0715 t ( t) = Y0 e (2) kde Y 0 je výchozí hodnota neboli hodnota v čase 0 Z grafu č. 1 je patrné, že vývoj celkového důchodu (HDP) je téměř totožný s vývojem v modelové situaci. Odchylka se pohybuje kolem 10%, což je podle mě při takto vysokých hodnotách zanedbatelné. To znamená, že výkyvy ve vývoji jsou minimální. V této situaci by se dala udělat předpověď na další roky. To by se zjistilo tím, že se do vzorce dosadí další následující hodnoty času t. A pak by byl vývoj v dalších letech popsán v následujícím grafu č. 2. V roce 2007 sice produkt poroste, ale už ne takovým tempem jako v posledních třech letech. Graf č. 1 Vývoj HDP v ČR v letech Data viz. Příloha č. 1 29
31 Hrubý domácí produkt České republiky dosahuje v posledních třech letech hodnot vyspělých států světa. Vzrostl ve stálých cenách přibližně o 6 %, což je téměř dvojnásobná rychlost celé Evropské unie. V letech se zaostávání České republiky za ekonomickou úrovní vyspělé Evropy mírně snížilo. Koncem roku 1996 vstupuje Česká republika do obtížného období, které je charakterizované značným poklesem ekonomického růstu. Roku 1999 domácí poptávka stagnovala a vliv zahraničního sektoru, který působil pozitivně na růst HDP v roce 1997 a 1998 se změnil na brzdící faktor v důsledku silného kurzu koruny. Hlavním zdrojem hospodářského růstu v roce 2005 se stala domácí poptávka, tedy tvorba hrubého kapitálu a konečná spotřeba. Graf č. 2 Předpověď vývoje HDP v ČR v letech Předpověď vývoje HDP ,00 HDP v mld.kč 6000, , ,00 Predikce HDP 0, Rok Data viz. Příloha č. 18 Dle předpovědi je možné, že v roce 2018 bude výše hrubého domácího produktu dosahovat hodnoty zhruba 7500 mld. Kč. Podle mého názoru tomu tak ale nebude, jelikož zde nejsou brány v potaz další faktory jako je např. přijetí Eura v roce Podle výzkumů tato situace velmi zasáhne českou ekonomiku. Pro zajímavost jsem zde na následujícím obrázku č. 1 a tabulce (viz. Příloha č. 19) uvedla podíl jednotlivých regionů na tvorbě HDP v České republice. Přirozeně má největší podíl naše hlavní město, hned za ním následují Středočeský kraj a Jihomoravský kraj. 30
32 Obrázek č. 1 Zdroj: ČSÚ Vývoj počtu pracujících Ekonomický růst také velmi ovlivňuje míra nezaměstnanosti. Vztahem (1) pro zjištění růstu pracujících v čase pomocí Solowova modelu je: L n t ( t) = L 0 e (1) funkce, z které budu nadále vycházet, je dána vztahem (2): L 0,0018 t ( t) = L0 e (2) Dá se říci, že Solowův model vidí situaci znázorněnou na grafu č. 3 o mnohem lépe než je tomu ve skutečnosti. Je to patrné především v letech 1998, 1999, 2000 a Snad nejvíce se model rozchází se skutečností v roce 1999, kde je model velmi optimistický. Z grafu také vidíme, že modelová situace má klesající tendenci, ve skutečnosti tomu tak není. Situaci na trhu práce komplikuje i odliv některých mladých kvalifikovaných pracovníků do zahraničí. Proto je v České republice třeba vytvářet takové atraktivní prostředí, aby mladí lidé do zahraničí neodcházeli. 31
33 Pružnost pracovního trhu a dostupnost pracovní síly je proto vhodné zvýšit zlepšením právních podmínek a snížením zdanění skupin s nízkým příjmem Pro zajímavost průměrná hrubá mzda v České republice byla v loňském roce Kč, přičemž vyšší plat pobírají zaměstnanci v podnikatelské sféře. Počet pracovníků vzrostl zejména v sekundárním a terciárním sektoru na úkor primárního. Graf č. 3 Vývoj počtu pracujících v ČR v letech Pracovníci 5150, , , , , , , , , ,00 Vývoj počtu pracujících v čase Počet pracovníků L (t) Rok Data viz. Příloha č. 2 V České republice byla v roce 2006 podle Ministerstva financí míra nezaměstnanosti nejnižší za posledních 9 let, přesto jsou hodnoty zaměstnaných poměrně nízké. Nejnižší míra nezaměstnanosti byla zjištěna v Praze, Mladé Boleslavi a Pelhřimově. Nejvíce lidí bez práce naopak evidovaly úřady práce v Mostě, Karviné a Teplicích. Pokles nezaměstnanosti je podle statistického úřadu způsoben tím, že byla vytvořena nová pracovní místa v ekonomice. V tomto roce existovalo o 80 tis. míst více než v roce Míra nezaměstnanosti bude ještě více klesat, jestliže se současné vládě podaří uskutečnit již plánované reformy, které ukončí plýtvání financemi a lidskou energií a dojde ke snížení daní. Pokud se toto ale nepodaří, pak bude naše míra nezaměstnanosti vyšší než na Slovensku. Kde nezaměstnanost vykazuje velmi vysoké hodnoty. 32
34 Podle informací ministerstva financí dnešní nástroje hospodářské politiky rozhodně nevystačí do budoucna. Pro další soutěž v rámci světového trhu se musí zvýšit vzdělanost obyvatelstva, jazykové dovednosti a pružnost přizpůsobení se novým podmínkám Vývoj kapitálu Vztah (1) pro růst kapitálu v čase je: K ( n+ g ) t ( t) = K0 e (1) Funkce, z které budu nadále vycházet, je dána vztahem (2) K 0,0715 t ( t) = K0 e (2) Z grafu č. 4 můžeme zjistit, že vývoj velikosti kapitálu má stejný trend jako modelová situace a to od roku zhruba 1997 do roku Dá se říci, že podle Solowova modelu je vývoj optimističtější než je tomu ve skutečnosti. A to především od roku Graf č. 4 Vývoj kapitálu v ČR v letech Data viz. Příloha č. 3 K dobrému vývoji české ekonomiky přispěly hlavně výdaje domácností. Negativním překvapením roku 2006 byly naopak investice, neboli hrubá tvorba fixního kapitálu. Což do budoucna podle ministerstva financí nevěstí nic dobrého. 33
35 Vývoj úrovně technologií Vztah (1) pro úroveň technologií v čase je: A g t ( t) = A 0 e (1) Funkce, z které budu nadále vycházet, je dána vztahem (2) A 0,0733 t ( t) = A0 e (2) Jak lze poznat z grafu č. 5, je vývoj technologií zhruba stejný jako modelová situace od roku 1995 do roku Od roku 2001 je vývoj technologií podle modelové situace mnohem optimističtější než je tomu ve skutečnosti. V těchto letech je odchylka opravdu značná; její hodnota se pohybuje do 50 %. Graf č. 5 Vývoj technologií v ČR v letech Vývoj technologií Úroveň technologie Rok Technologie A (t) Data viz. Příloha č. 4 Česká republika se zařadila k nejrychleji rostoucím ekonomikám Evropské unie. V rámci středoevropského regionu stojí za zmínku růst ještě Slovenska, Polska a Maďarska. 34
36 3. 2 Dánsko Dánsko patří mezi státy s moderním tržním hospodářstvím, technicky vyspělým zemědělstvím a rozsáhlou vládní sociální politikou. Vyspělost dánské ekonomiky se projevuje vysokou životní úrovní a pevnou měnou. Ačkoli Dánsko splňovalo ekonomická kritéria Evropské měnové unie (EMU), rozhodli Dánové v referendu roku 2000 o nepřipojení se. Dánsko má tedy stále svou měnu a to dánskou korunu. V padesátých a šedesátých letech začalo Dánsko úspěšně budovat systém univerzální sociální péče pro všechny občany. V sedmdesátých letech byly zrušeny příspěvky na zdravotní pojištění a byl zaveden všeobecný systém národní zdravotní péče financovaný z daní. Dánsko se tak stalo sociálním státem, který poskytuje služby nejen chudým a potřebným, ale bez rozdílu všem občanům. Tento přístup sice přinesl značné zvýšení životní úrovně, ale vedl i k nevídanému nárůstu veřejných výdajů a tím vyšší míru zdanění. Tabulka č. 2 Údaje o Dánsku potřebné k použití Solowova modelu DÁNSKO HDP v mld. (Y) 4726, , , , , ,60 - poměr růstu x 1, , , , , Pracovníci v tis. (L) 2554, , , , , ,08 - poměr růstu x 1, , , , , Hrubý fixní kapitál v mld. (K) 596,10 644,80 677,00 734,00 769,80 845,40 - poměr růstu x 1, , , , , Míra techn. pokroku (A) 7, , , , , , HDP v mld. (Y) 5194, , , , , ,30 - poměr růstu 0, , , , , , Pracovníci v tis. (L) 2764, , , , , ,00 - poměr růstu 1, , , , , , Hrubý fixní kapitál v mld. (K) 855,80 863,40 815,30 860,30 897,90 899,00 - poměr růstu 1, , , , , , Míra techn. pokroku (A) 6, , , , , ,
37 Dánsko překonalo útlum z roku 2002, což se ukázalo především hospodářským růstem v roce 2004, který s ještě větší intenzitou pokračoval i v roce 2005 a V roce 2005 byla významným přispěvatelem k výši HDP průmyslová výroba Vývoj hrubého domácího produktu Funkce, z které budu vycházet, je dána vztahem (1): Y 0,00279 t ( t) = Y0 e (1) O grafu č. 6 by se dalo říci, že vývoj HDP je v modelové situaci Solowova modelu mírně kritičtější než jsou skutečné hodnoty. Odchylka se pohybuje kolem 20%, což není zas tak vysoké číslo. Graf č. 6 Vývoj HDP v Dánsku v letech Data viz. Příloha č Vývoj počtu pracujících Funkce, z které budu vycházet, je dána vztahem (2): L 0, t ( t) = L0 e (2) Dle vypočtených hodnot a dále i podle grafického znázornění (graf č. 7), se dá říci, že počet pracovníků by měl podle modelu stále přibývat. Můžeme si povšimnout, že skutečné hodnoty tento názor nezastávají, ve skutečnosti počet pracovníků neustále kolísá. 36
38 Graf č. 7 Vývoj počtu pracujících v Dánsku v letech Vývoj počtu pracovníků v čase Pracovníci v tis Počet pracovníků L (t) Rok Data viz. Příloha č. 6 Z ekonomického hlediska je významná míra nezaměstnanosti, která dosáhla svého třicetiletého minima. V roce 2006 byla míra nezaměstnanosti dokonce pouhých 3,9 % Vývoj kapitálu Funkce, z které budu vycházet v případě růstu kapitálu, je dána vztahem (3): K 0,00279 t ( t) = K0 e (3) Z grafu č. 8 můžeme zjistit, že vývoj velikosti kapitálu má velmi rozdílný trend jako modelová situace a to převážně od roku zhruba 1999 do roku Dá se říci, že podle Solowova modelu je vývoj mnohem pesimističtější než je tomu ve skutečnosti. Graf č. 8 Vývoj kapitálu v Dánsku v letech Vývoj kapitálu v čase Kapitál v mld. 1000,00 900,00 800,00 700,00 600,00 500,00 400,00 300,00 200,00 100,00 0,00 Kapitál K (t) Rok Data viz. Příloha č. 7 37
39 Vývoj úrovně technologií Základním vztahem (4) pro úroveň technologií je: A 0,00918 t ( t) = A0 e (4) Jak lze poznat z grafu č. 9, je vývoj technologií na velmi vysoké úrovni, technický pokrok je dán hrubým domácím produktem a kapitálem. Od roku 2000 je vývoj technologií podle modelové situace mnohem optimističtější než ve skutečnosti. Dalo by se říci, že je stále na stejné úrovni. Graf č. 9 Vývoj technologií v Dánsku v letech Vývoj technologií Úroveň technologie 9,00 8,00 7,00 6,00 5,00 4,00 3,00 2,00 1,00 0, Rok Technologie A (t) Data viz. Příloha č Slovensko Slovenská ekonomika patří mezi úspěšné ekonomiky zemí, které roku 2004 vstoupily do Evropské unie a v 90. letech 20. století zažily transformaci ekonomiky socialistického centrálního plánování na hospodářství volného trhu. Po vzniku samostatného státu byla země, stejně jako Česká republika, postižená neudržitelnou strukturou průmyslu, orientovanou především na těžký průmysl. 38
40 V prvních letech nezávislosti však došlo ke zpomalení reforem a to především díky politice tehdejší vlády. Objevila se zde hlavně korupce a tím vzrostl také státní dluh, a to převážně kvůli vysokým státním výdajům. Údaje potřebné k Solowovu modelu jsou zaznamenány v následující tabulce č. 3 Tabulka č. 3 Údaje o Slovensku potřebné k použití Solowova modelu SLOVENSKÁ REPUBLIKA HDP v mld. (Y) 585,78 655,24 724,90 790,05 852,17 941,31 - poměr růstu x 1, , , , ,10461 Pracovníci v tis. (L) 480,76 528,58 527,39 549,77 579,86 719,09 - poměr růstu x 1, , , , , Hrubý fixní kapitál v mld. (K) 144,25 205,85 243,54 281,77 249,79 242,28 - poměr růstu x 1, , , , , Míra techn. pokroku (A) 4, , , , , , HDP v mld. (Y) 1020, , , , , ,26 - poměr růstu 1, , , , , , Pracovníci v tis. (L) 663,83 634,52 539,19 545,68 599,55 649,06 - poměr růstu 0, , , , , ,08258 Hrubý fixní kapitál v mld. (K) 291,03 303,48 302,78 327,09 394,62 432,08 - poměr růstu 1, , , , , , Míra techn. pokroku (A) 3, , , , , , Vývoj hrubého domácího produktu Funkce, z které budu vycházet, je dána vztahem (1): Y 0, t ( t) = Y0 e (1) Z grafu č. 10 je patrné, že celkový důchod (HDP) je téměř totožný, ne-li shodný s vývojem v modelové situaci. V této situaci by se dala udělat předpověď na další roky. To by se zjistilo tím, že se do vzorce dosadí další následující hodnoty času t. A pak by byl vývoj v dalších letech popsán v následujícím grafu č
41 Graf č. 10 Vývoj HDP na Slovensku v letech Data viz. Příloha č. 9 Roku 1995 rostl slovenský hrubý domácí produkt o 6,5 % ročně, ale na konci 90. let došlo k propadu, stejně jako v jiných zemích Střední Evropy. V roce 1998 se ekonomika mírně stabilizovala pod vedením nové vlády široké koalice stran. Zvýšila se ale inflace i nezaměstnanost. Graf č. 11 Predikce vývoje HDP v letech Předpověď vývoje HDP na Slovensku , ,00 HDP v mld. Sk 4000, , , ,00 Predikce HDP 0, Rok Data viz. Příloha č. 17 Protože se v poslední době na Slovensku objevila celá řada příznivých hospodářských faktorů, jako jsou nízké přímé daně, nízké úrokové sazby, příliv zahraničních investic, hospodářské reformy, lze očekávat, že v příštích letech překročí tempo hospodářského růstu hranici 6%. 40
42 Vývoj počtu pracujících Vztah (2) pro vývoj pracujících je: L 0, t ( t) = L0 e (2) Dá se říci, že Solowův model znázorňuje situaci na grafu č. 12, která je až na malé výjimky shodná se skutečností. Odchylky od skutečného stavu jsou patrné hlavně v letech 2000, 2001 a V letech se opět zvýšil ekonomický růst, také země v té době vstoupila do Evropské unie i do NATO. Nezaměstnanost, která dosahovala dvouciferných čísel začala rychle klesat. Graf č. 12 Vývoj počtu pracujících na Slovensku v letech Vývoj počtu pracujících v čase Pracovníci v tis Rok Počet pracovníků L (t) Data viz. Příloha č. 10 V roce 2003 klesl počet nezaměstnaných na 12,6%. Míra evidované nezaměstnanosti se tak na Slovensku dostala na nejnižší hodnotu za posledních 7 let. Lze předpokládat, že nezaměstnanost bude stále klesat a za pár let překročí magickou hranici 10 %. 41
Makroekonomie I. Podstata a východiska. Definice: Přednáška 2. Ekonomický růst. Osnova přednášky: Ekonomický růst. Definování ekonomického růstu
 Přednáška 2. Ekonomický růst Makroekonomie I Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Osnova přednášky: Podstatné ukazatele výkonnosti ekonomiky souhrnné opakování předchozí přednášky Potenciální produkt
Přednáška 2. Ekonomický růst Makroekonomie I Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Osnova přednášky: Podstatné ukazatele výkonnosti ekonomiky souhrnné opakování předchozí přednášky Potenciální produkt
Cvičení č. 4, 5 MAE 1. Pokud vycházíme ze speciální formy produkční funkce, můžeme rovnici pro tempo růstu potenciální produktu vyjádřit následovně
 Ekonomický růst Pokud vycházíme ze speciální formy produkční funkce, můžeme rovnici pro tempo růstu potenciální produktu vyjádřit následovně ΔY/Y = (1 α) x ΔL/L + α x ΔK/K + ΔA/A, kde ΔY/Y.. tempo růstu
Ekonomický růst Pokud vycházíme ze speciální formy produkční funkce, můžeme rovnici pro tempo růstu potenciální produktu vyjádřit následovně ΔY/Y = (1 α) x ΔL/L + α x ΔK/K + ΔA/A, kde ΔY/Y.. tempo růstu
Makroekonomická rovnováha, ekonomický růst a hospodářské cykly
 Ústav stavební ekonomiky a řízení Fakulta stavební VUT Makroekonomická rovnováha, ekonomický růst a hospodářské cykly Ing. Dagmar Palatová dagmar@mail.muni.cz Agregátní nabídka a agregátní poptávka cena
Ústav stavební ekonomiky a řízení Fakulta stavební VUT Makroekonomická rovnováha, ekonomický růst a hospodářské cykly Ing. Dagmar Palatová dagmar@mail.muni.cz Agregátní nabídka a agregátní poptávka cena
EKONOMETRIE 7. přednáška Fáze ekonometrické analýzy
 EKONOMETRIE 7. přednáška Fáze ekonometrické analýzy Ekonometrická analýza proces, skládající se z následujících fází: a) specifikace b) kvantifikace c) verifikace d) aplikace Postupné zpřesňování jednotlivých
EKONOMETRIE 7. přednáška Fáze ekonometrické analýzy Ekonometrická analýza proces, skládající se z následujících fází: a) specifikace b) kvantifikace c) verifikace d) aplikace Postupné zpřesňování jednotlivých
Obsah. Nedostatky v měření HDP. Ekonomický růst. Hrubý domácí produkt
 Obsah Nedostatky v měření HDP Ekonomický růst Hrubý domácí produkt HDP ČR HDP nominální a reálný HDP nominální- celková peněžní hodnota HDP, vyjádřená v.. HDP reálný- celková peněžní hodnota HDP, vyjádřená
Obsah Nedostatky v měření HDP Ekonomický růst Hrubý domácí produkt HDP ČR HDP nominální a reálný HDP nominální- celková peněžní hodnota HDP, vyjádřená v.. HDP reálný- celková peněžní hodnota HDP, vyjádřená
Měření závislosti statistických dat
 5.1 Měření závislosti statistických dat Každý pořádný astronom je schopen vám předpovědět, kde se bude nacházet daná hvězda půl hodiny před půlnocí. Ne každý je však téhož schopen předpovědět v případě
5.1 Měření závislosti statistických dat Každý pořádný astronom je schopen vám předpovědět, kde se bude nacházet daná hvězda půl hodiny před půlnocí. Ne každý je však téhož schopen předpovědět v případě
ÚVOD. Nyní opuštění předpokladů Zkoumání vývoje potenciálního produktu. Cíl: Ujasnit si pojmy před představením různých teorií k ekonomickému růstu
 HOSPODÁŘSKÝ RŮST ÚVOD V předchozích částech: Kolísání skutečného produktu kolem potenciálního produktu Neexistence technologického pokroku Stály počet obyvatel Fixní zásoba kapitálu Nyní opuštění předpokladů
HOSPODÁŘSKÝ RŮST ÚVOD V předchozích částech: Kolísání skutečného produktu kolem potenciálního produktu Neexistence technologického pokroku Stály počet obyvatel Fixní zásoba kapitálu Nyní opuštění předpokladů
Makroekonomie I. Co je podstatné z Mikroekonomie - co již známe obecně. Nabídka a poptávka mikroekonomické kategorie
 Model AS - AD Makroekonomie I Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Osnova: Agregátní poptávka a agregátní nabídka : Agregátní poptávka a její změny Agregátní nabídka krátkodobá a dlouhodobá Rovnováha
Model AS - AD Makroekonomie I Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Osnova: Agregátní poptávka a agregátní nabídka : Agregátní poptávka a její změny Agregátní nabídka krátkodobá a dlouhodobá Rovnováha
1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004.
 Prostá regresní a korelační analýza 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Problematika závislosti V podstatě lze rozlišovat mezi závislostí nepodstatnou, čili náhodnou
Prostá regresní a korelační analýza 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Problematika závislosti V podstatě lze rozlišovat mezi závislostí nepodstatnou, čili náhodnou
7. Veřejné výdaje. Prof. Ing. Václav Vybíhal, CSc.
 7. Veřejné výdaje Prof. Ing. Václav Vybíhal, CSc. Obsah : 7.1 Charakteristika veřejných 7.2 Ukazatele dynamiky, objemu a struktury veřejných 7.3 Klasifikace veřejných 7.4 Teorie růstu veřejných 7.5 Faktory
7. Veřejné výdaje Prof. Ing. Václav Vybíhal, CSc. Obsah : 7.1 Charakteristika veřejných 7.2 Ukazatele dynamiky, objemu a struktury veřejných 7.3 Klasifikace veřejných 7.4 Teorie růstu veřejných 7.5 Faktory
Makroekonomie I. Dvousektorová ekonomika. Téma. Opakování. Praktický příklad. Řešení. Řešení Dvousektorová ekonomika opakování Inflace
 Téma Makroekonomie I Dvousektorová ekonomika opakování Inflace Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Opakování Dvousektorová ekonomika Praktický příklad Dvousektorová ekonomika je charakterizována
Téma Makroekonomie I Dvousektorová ekonomika opakování Inflace Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Opakování Dvousektorová ekonomika Praktický příklad Dvousektorová ekonomika je charakterizována
VZOROVÝ STIPENDIJNÍ TEST Z EKONOMIE
 VZOROVÝ STIPENDIJNÍ TEST Z EKONOMIE Jméno a příjmení: Datum narození: Datum testu: 1. Akcie jsou ve své podstatě: a) cenné papíry nesoucí fixní výnos b) cenné papíry jejichž hodnota v čase vždy roste c)
VZOROVÝ STIPENDIJNÍ TEST Z EKONOMIE Jméno a příjmení: Datum narození: Datum testu: 1. Akcie jsou ve své podstatě: a) cenné papíry nesoucí fixní výnos b) cenné papíry jejichž hodnota v čase vždy roste c)
Makroekonomie I cvičení
 Téma Makroekonomie I cvičení 25. 3. 015 Dvousektorový model ekonomiky Spotřební funkce Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Model 45 - jak je dosaženo rovnovážného HDP Východiska - graf: Osa x.
Téma Makroekonomie I cvičení 25. 3. 015 Dvousektorový model ekonomiky Spotřební funkce Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Model 45 - jak je dosaženo rovnovážného HDP Východiska - graf: Osa x.
4. Aplikace matematiky v ekonomii
 4. Aplikace matematiky v ekonomii 1 Lineární algebra Soustavy 1) Na základě statistických údajů se zjistilo, že závislost množství statku z poptávaného v průběhu jednoho týdne lze popsat vztahem q d =
4. Aplikace matematiky v ekonomii 1 Lineární algebra Soustavy 1) Na základě statistických údajů se zjistilo, že závislost množství statku z poptávaného v průběhu jednoho týdne lze popsat vztahem q d =
1) Úvod do makroekonomie, makroekonomické identity, hrubý domácí produkt. 2) Celkové výdaje, rovnovážný produkt (model 45 ), rovnováha v modelu AD AS
 Makroekonomie (Bc) LS 2005/06 Podkladové materiály na cvičení 1) Úvod do makroekonomie, makroekonomické identity, hrubý domácí produkt 2) Celkové výdaje, rovnovážný produkt (model 45 ), rovnováha v modelu
Makroekonomie (Bc) LS 2005/06 Podkladové materiály na cvičení 1) Úvod do makroekonomie, makroekonomické identity, hrubý domácí produkt 2) Celkové výdaje, rovnovážný produkt (model 45 ), rovnováha v modelu
Regresní analýza 1. Regresní analýza
 Regresní analýza 1 1 Regresní funkce Regresní analýza Důležitou statistickou úlohou je hledání a zkoumání závislostí proměnných, jejichž hodnoty získáme při realizaci experimentů Vzhledem k jejich náhodnému
Regresní analýza 1 1 Regresní funkce Regresní analýza Důležitou statistickou úlohou je hledání a zkoumání závislostí proměnných, jejichž hodnoty získáme při realizaci experimentů Vzhledem k jejich náhodnému
Téma č. 2: Rovnovážný výstup hospodářství
 Základy ekonomie II Téma č. 2: Rovnovážný výstup hospodářství Petr Musil Struktura Pojetí ekonomické rovnováhy Agregátní poptávka, agregátní nabídka Rovnovážný výstup v dlouhém období Rovnovážný výstup
Základy ekonomie II Téma č. 2: Rovnovážný výstup hospodářství Petr Musil Struktura Pojetí ekonomické rovnováhy Agregátní poptávka, agregátní nabídka Rovnovážný výstup v dlouhém období Rovnovážný výstup
VZOROVÝ STIPENDIJNÍ TEST Z EKONOMIE
 VZOROVÝ STIPENDIJNÍ TEST Z EKONOMIE 1. Povinná míra rezerv je: a) procento z depozit, které komerční banka musí držet u centrální banky b) rezerva, kterou si komerční banka nechává pro případ okamžitých
VZOROVÝ STIPENDIJNÍ TEST Z EKONOMIE 1. Povinná míra rezerv je: a) procento z depozit, které komerční banka musí držet u centrální banky b) rezerva, kterou si komerční banka nechává pro případ okamžitých
Inovace bakalářského studijního oboru Aplikovaná chemie
 http://aplchem.upol.cz CZ.1.07/2.2.00/15.0247 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. 10. Lekce Ekonomický růst a cyklický vývoj tržního hospodářství
http://aplchem.upol.cz CZ.1.07/2.2.00/15.0247 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. 10. Lekce Ekonomický růst a cyklický vývoj tržního hospodářství
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
8 NEZAMĚSTNANOST. 8.1 Klíčové pojmy
 8 NEZAMĚSTNANOST 8.1 Klíčové pojmy Ekonomicky aktivní obyvatelstvo je definováno jako suma zaměstnaných a nezaměstnaných a míra nezaměstnanosti je definovaná jako procento ekonomicky aktivního obyvatelstva,
8 NEZAMĚSTNANOST 8.1 Klíčové pojmy Ekonomicky aktivní obyvatelstvo je definováno jako suma zaměstnaných a nezaměstnaných a míra nezaměstnanosti je definovaná jako procento ekonomicky aktivního obyvatelstva,
Obsah. Hospodářský cyklus. Hospodářský cyklus Fáze HC, příčiny HC Druhy HC, dopady a indikátor HC Sektory národního hospodářství
 Obsah Hospodářský cyklus Fáze HC, příčiny HC Druhy HC, dopady a indikátor HC Sektory národního hospodářství Vývoj ekonomiky Klasického pohledu - samoregulující se systém Sayův zákon - co se vyrobí bude
Obsah Hospodářský cyklus Fáze HC, příčiny HC Druhy HC, dopady a indikátor HC Sektory národního hospodářství Vývoj ekonomiky Klasického pohledu - samoregulující se systém Sayův zákon - co se vyrobí bude
cíl teorie růstu zjistit příčiny bohatství národů
 Ekonomický růst Problematika růstu hospodářský růst = zvyšování potenciálního produktu v dané ekonomice cíl teorie růstu zjistit příčiny hospodářského růstu první náznaky teorie růstu Adam Smith: Pojednání
Ekonomický růst Problematika růstu hospodářský růst = zvyšování potenciálního produktu v dané ekonomice cíl teorie růstu zjistit příčiny hospodářského růstu první náznaky teorie růstu Adam Smith: Pojednání
Česká ekonomika v roce 2014. Ing. Jaroslav Vomastek, MBA Ředitel odboru
 Česká ekonomika v roce 2014 Přehled ekonomiky České republiky HDP Zaměstnanost Inflace Cenový vývoj Zahraniční investice Platební bilance Průmysl Zahraniční obchod Hlavní charakteristiky české ekonomiky
Česká ekonomika v roce 2014 Přehled ekonomiky České republiky HDP Zaměstnanost Inflace Cenový vývoj Zahraniční investice Platební bilance Průmysl Zahraniční obchod Hlavní charakteristiky české ekonomiky
ČESKÁ EKONOMIKA 2015. Ing. Martin Hronza ČESKÁ EKONOMIKA 2015. ředitel odboru ekonomických analýz
 1 Přehled ekonomiky České republiky HDP Trh práce Inflace Platební bilance Zahraniční investice Průmysl Zahraniční obchod 2 Hlavní charakteristiky české ekonomiky Malá, otevřená ekonomika, výrazně závislá
1 Přehled ekonomiky České republiky HDP Trh práce Inflace Platební bilance Zahraniční investice Průmysl Zahraniční obchod 2 Hlavní charakteristiky české ekonomiky Malá, otevřená ekonomika, výrazně závislá
Plán přednášek makroekonomie
 Plán přednášek makroekonomie Úvod do makroekonomie, makroekonomické agregáty Agregátní poptávka a agregátní nabídka Ekonomické modely rovnováhy Hospodářský růst a cyklus, výpočet HDP Hlavní ekonomické
Plán přednášek makroekonomie Úvod do makroekonomie, makroekonomické agregáty Agregátní poptávka a agregátní nabídka Ekonomické modely rovnováhy Hospodářský růst a cyklus, výpočet HDP Hlavní ekonomické
Cíl: analýza modelu makroekonomické rovnováhy s pohyblivou cenovou hladinou
 Vysoká škola finanční a správní, o. p. s. Akademický rok 2005/06, letní semestr Kombinované studium Předmět: Makroekonomie (Bc.) Metodický list č. 2 5) Makroekonomická rovnováha (model AD AS) 6) Ekonomický
Vysoká škola finanční a správní, o. p. s. Akademický rok 2005/06, letní semestr Kombinované studium Předmět: Makroekonomie (Bc.) Metodický list č. 2 5) Makroekonomická rovnováha (model AD AS) 6) Ekonomický
Všeobecná rovnováha 1 Statistický pohled
 Makroekonomická analýza přednáška 4 1 Všeobecná rovnováha 1 Statistický pohled Předpoklady Úspory (resp.spotřeba) a investice (resp.kapitál), kterými jsme se zabývali v minulých lekcích, jsou spolu s technologickým
Makroekonomická analýza přednáška 4 1 Všeobecná rovnováha 1 Statistický pohled Předpoklady Úspory (resp.spotřeba) a investice (resp.kapitál), kterými jsme se zabývali v minulých lekcích, jsou spolu s technologickým
Základy makroekonomie
 Základy makroekonomie Ing. Martin Petříček Struktura přednášky Úvod do makroekonomie Sektory NH HDP Úspory, spotřeba, investice Inflace, peníze Nezaměstnanost Fiskální a monetární politika Hospodářský
Základy makroekonomie Ing. Martin Petříček Struktura přednášky Úvod do makroekonomie Sektory NH HDP Úspory, spotřeba, investice Inflace, peníze Nezaměstnanost Fiskální a monetární politika Hospodářský
Opakování. Makroekonomie I cvičení 8. března HDP, HNP. Ing. Jaroslav ŠETEK, Ph.D. 1. Co z následujícího není součástí HDP měřeného důchodovou metodou:
 Makroekonomie I cvičení 8. března Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Opakování HDP, HNP 1. Co z následujícího není součástí HDP měřeného důchodovou metodou: a) nájemné za pronájem půdy b) nákup
Makroekonomie I cvičení 8. března Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Opakování HDP, HNP 1. Co z následujícího není součástí HDP měřeného důchodovou metodou: a) nájemné za pronájem půdy b) nákup
Inflace. Makroekonomie I. Osnova k teorii inflace. Co již známe? Vymezení podstata inflace. Definice inflace
 Makroekonomie I Teorie inflace Praktické příklady Příklady k opakování Inflace Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Co již známe? Osnova k teorii inflace Deflátor HDP způsob měření inflace Agregátní
Makroekonomie I Teorie inflace Praktické příklady Příklady k opakování Inflace Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Co již známe? Osnova k teorii inflace Deflátor HDP způsob měření inflace Agregátní
10. téma: Krátkodobá a dlouhodobá fiskální nerovnováha*) **) Krátkodobá fiskální nerovnováha Dlouhodobá fiskální nerovnováha
 10. téma: Krátkodobá a dlouhodobá fiskální nerovnováha*) **) 10.1. Krátkodobá fiskální nerovnováha 10.2. Dlouhodobá fiskální nerovnováha *) Viz 10. kap. učebnice; Dodatek J P (povinně); X. případová studie
10. téma: Krátkodobá a dlouhodobá fiskální nerovnováha*) **) 10.1. Krátkodobá fiskální nerovnováha 10.2. Dlouhodobá fiskální nerovnováha *) Viz 10. kap. učebnice; Dodatek J P (povinně); X. případová studie
Makroekonomie I. Opakování. Řešení. Příklad. Řešení. Příklad Příklady k zápočtu. Ing. Jaroslav ŠETEK, Ph.D.
 Opakování Makroekonomie I y k zápočtu Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Co je znázorněno? 1). 2).. 1) Růst AD 2) Inflace tažená AD Náklady cyklické nezaměstnanosti v podobě odchylky skutečně
Opakování Makroekonomie I y k zápočtu Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Co je znázorněno? 1). 2).. 1) Růst AD 2) Inflace tažená AD Náklady cyklické nezaměstnanosti v podobě odchylky skutečně
Životní úroveň, rodinné finance a sociální podmínky z pohledu veřejného mínění
 TISKOVÁ ZPRÁVA Centrum pro výzkum veřejného mínění Sociologický ústav AV ČR V Holešovičkách 41, Praha 8 Tel./fax: 286 840 129, 130 E-mail: cervenka@soc.cas.cz Životní úroveň, rodinné finance a sociální
TISKOVÁ ZPRÁVA Centrum pro výzkum veřejného mínění Sociologický ústav AV ČR V Holešovičkách 41, Praha 8 Tel./fax: 286 840 129, 130 E-mail: cervenka@soc.cas.cz Životní úroveň, rodinné finance a sociální
Určeno studentům středního vzdělávání s maturitní zkouškou, předmět Ekonomika, okruh Národní a mezinárodní ekonomika
 Určeno studentům středního vzdělávání s maturitní zkouškou, předmět Ekonomika, okruh Národní a mezinárodní ekonomika Materiál vytvořil: Ing. Karel Průcha Období vytvoření VM: říjen 2013 Klíčová slova:
Určeno studentům středního vzdělávání s maturitní zkouškou, předmět Ekonomika, okruh Národní a mezinárodní ekonomika Materiál vytvořil: Ing. Karel Průcha Období vytvoření VM: říjen 2013 Klíčová slova:
Kapitola 5 AGREGÁTNÍ POPTÁVKA A AGREGÁTNÍ NABÍDKA
 Kapitola 5 AGREGÁTNÍ POPTÁVKA A AGREGÁTNÍ NABÍDKA Agregátní poptávka (AD): agregátní poptávka vyjadřuje různá množství statků a služeb (reálného produktu), která chtějí spotřebitelé, firmy, vláda a zahraniční
Kapitola 5 AGREGÁTNÍ POPTÁVKA A AGREGÁTNÍ NABÍDKA Agregátní poptávka (AD): agregátní poptávka vyjadřuje různá množství statků a služeb (reálného produktu), která chtějí spotřebitelé, firmy, vláda a zahraniční
Cíl: seznámení s pojetím peněz v ekonomické teorii a s fungováním trhu peněz. Peníze jako prostředek směny, zúčtovací jednotka a uchovatel hodnoty.
 Vysoká škola finanční a správní, o. p. s. Akademický rok 2006/07, letní semestr Kombinované studium Předmět: Makroekonomie (Bc.) Metodický list č. 3 7) Peníze a trh peněz. 8) Otevřená ekonomika 7) Peníze
Vysoká škola finanční a správní, o. p. s. Akademický rok 2006/07, letní semestr Kombinované studium Předmět: Makroekonomie (Bc.) Metodický list č. 3 7) Peníze a trh peněz. 8) Otevřená ekonomika 7) Peníze
Solowův model dlouhodobého ekonomického růstu
 Solowův model dlouhodobého ekonomického růstu Neoklasický model hospodářského růstu. Model byl publikován v 50. a 60. letech, stal se učebnicovým standardem. Solow za model dostal Nobelovu cenu v roce
Solowův model dlouhodobého ekonomického růstu Neoklasický model hospodářského růstu. Model byl publikován v 50. a 60. letech, stal se učebnicovým standardem. Solow za model dostal Nobelovu cenu v roce
Seminární práce. Vybrané makroekonomické nástroje státu
 Seminární práce Vybrané makroekonomické nástroje státu 1 Obsah Úvod... 3 1 Fiskální politika... 3 1.1 Rozdíly mezi fiskální a rozpočtovou politikou... 3 1.2 Státní rozpočet... 4 2 Monetární politika...
Seminární práce Vybrané makroekonomické nástroje státu 1 Obsah Úvod... 3 1 Fiskální politika... 3 1.1 Rozdíly mezi fiskální a rozpočtovou politikou... 3 1.2 Státní rozpočet... 4 2 Monetární politika...
ALTERNATIVNÍ UKAZATELÉ EKONOMICKÉ VÝKONNOSTI A BLAHOBYTU. Vojtěch Spěváček Centrum ekonomických studií VŠEM. www.cesvsem.cz. Bratislava, 9.
 ALTERNATIVNÍ UKAZATELÉ EKONOMICKÉ VÝKONNOSTI A BLAHOBYTU Vojtěch Spěváček Centrum ekonomických studií VŠEM www.cesvsem.cz Bratislava, 9. února 2007 Obsah: 1. Hrubý domácí produkt (HDP) a růstová výkonnost
ALTERNATIVNÍ UKAZATELÉ EKONOMICKÉ VÝKONNOSTI A BLAHOBYTU Vojtěch Spěváček Centrum ekonomických studií VŠEM www.cesvsem.cz Bratislava, 9. února 2007 Obsah: 1. Hrubý domácí produkt (HDP) a růstová výkonnost
4EK211 Základy ekonometrie
 4EK211 Základy ekonometrie Úvod do předmětu obecné informace Základní pojmy ze statistiky / ekonometrie Úvod do programu EViews, Gretl Některé užitečné funkce v MS Excel Cvičení 1 Zuzana Dlouhá Úvod do
4EK211 Základy ekonometrie Úvod do předmětu obecné informace Základní pojmy ze statistiky / ekonometrie Úvod do programu EViews, Gretl Některé užitečné funkce v MS Excel Cvičení 1 Zuzana Dlouhá Úvod do
Matematicky lze ekonomický růst vyjádřit jako změna (růst, pokles) reálného produktu ekonomiky za určité období (1 rok):
 Ekonomie 1 RNDr. Ondřej Pavlačka, Ph.D. pracovna 5.052 tel. 585 63 4027 e-mail: ondrej.pavlacka@upol.cz 5. Ekonomický růst 5.1 Základní terminologie Každá ekonomika má za cíl svůj růst, tj. produkovat
Ekonomie 1 RNDr. Ondřej Pavlačka, Ph.D. pracovna 5.052 tel. 585 63 4027 e-mail: ondrej.pavlacka@upol.cz 5. Ekonomický růst 5.1 Základní terminologie Každá ekonomika má za cíl svůj růst, tj. produkovat
ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR LISTOPAD. Samostatný odbor finanční stability
 ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR LISTOPAD Samostatný odbor finanční stability 0 ZÁTĚŽOVÉ TESTY LISTOPAD 0 ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR (LISTOPAD 0) SHRNUTÍ Výsledky zátěžových testů bankovního
ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR LISTOPAD Samostatný odbor finanční stability 0 ZÁTĚŽOVÉ TESTY LISTOPAD 0 ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR (LISTOPAD 0) SHRNUTÍ Výsledky zátěžových testů bankovního
ROVNOVÁHA. 5. Jak by se změnila účinnost fiskální politiky, pokud by spotřeba kromě důchodu závisela i na úrokové sazbě?
 ROVNOVÁHA Zadání 1. Použijte neoklasickou teorii rozdělování k předpovědi efektu následujících událostí na reálnou mzdu a reálnou cenu kapitálu: a) Vlna imigrace zvýší množství pracovníků v zemi. b) Zemětřesení
ROVNOVÁHA Zadání 1. Použijte neoklasickou teorii rozdělování k předpovědi efektu následujících událostí na reálnou mzdu a reálnou cenu kapitálu: a) Vlna imigrace zvýší množství pracovníků v zemi. b) Zemětřesení
i R = i N π Makroekonomie I i R. reálná úroková míra i N. nominální úroková míra π. míra inflace Téma cvičení
 Téma cvičení Makroekonomie I Nominální a reálná úroková míra Otevřená ekonomika Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Nominální a reálná úroková míra Zahrnutí míry inflace v rámci peněžního trhu
Téma cvičení Makroekonomie I Nominální a reálná úroková míra Otevřená ekonomika Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Nominální a reálná úroková míra Zahrnutí míry inflace v rámci peněžního trhu
MĚŘENÍ VÝKONU NÁRODNÍHO HOSPODÁŘSTVÍ
 MĚŘENÍ VÝKONU NÁRODNÍHO HOSPODÁŘSTVÍ ALENA KERLINOVÁ ALENA.KERLINOVA@LAW.MUNI.CZ VÝKON NÁRODNÍHO HOSPODÁŘSTVÍ Založen na využívání výrobních faktorů: půda vnitřně nehomogenní faktor (liší se kvalitou),
MĚŘENÍ VÝKONU NÁRODNÍHO HOSPODÁŘSTVÍ ALENA KERLINOVÁ ALENA.KERLINOVA@LAW.MUNI.CZ VÝKON NÁRODNÍHO HOSPODÁŘSTVÍ Založen na využívání výrobních faktorů: půda vnitřně nehomogenní faktor (liší se kvalitou),
4EK211 Základy ekonometrie
 4EK211 Základy ekonometrie Predikce Multikolinearita Cvičení 4 Zuzana Dlouhá Aplikace EM predikce obecně ekonomické prognózování, předpověď, předvídání hlavním cílem je odhad hodnot vysvětlované proměnné
4EK211 Základy ekonometrie Predikce Multikolinearita Cvičení 4 Zuzana Dlouhá Aplikace EM predikce obecně ekonomické prognózování, předpověď, předvídání hlavním cílem je odhad hodnot vysvětlované proměnné
Analýza vývoje zahraničního obchodu v zemích Visegrádské čtyřky
 Analýza vývoje zahraničního obchodu v zemích Visegrádské čtyřky Ing. Jaroslav Kovárník, Ph.D. Ing. Eva Hamplová, Ph.D. Univerzita Hradec Králové Fakulta informatiky a managementu Katedra ekonomie makroekonomická
Analýza vývoje zahraničního obchodu v zemích Visegrádské čtyřky Ing. Jaroslav Kovárník, Ph.D. Ing. Eva Hamplová, Ph.D. Univerzita Hradec Králové Fakulta informatiky a managementu Katedra ekonomie makroekonomická
Kvízové otázky Obecná ekonomie I. Teorie firmy
 1. Firmy působí: a) na trhu výrobních faktorů b) na trhu statků a služeb c) na žádném z těchto trhů d) na obou těchto trzích Kvízové otázky Obecná ekonomie I. Teorie firmy 2. Firma na trhu statků a služeb
1. Firmy působí: a) na trhu výrobních faktorů b) na trhu statků a služeb c) na žádném z těchto trhů d) na obou těchto trzích Kvízové otázky Obecná ekonomie I. Teorie firmy 2. Firma na trhu statků a služeb
4EK211 Základy ekonometrie
 4EK211 Základy ekonometrie Predikce Multikolinearita Cvičení 4 Zuzana Dlouhá Aplikace EM predikce obecně ekonomické prognózování, předpověď, předvídání hlavním cílem je odhad hodnot vysvětlované proměnné
4EK211 Základy ekonometrie Predikce Multikolinearita Cvičení 4 Zuzana Dlouhá Aplikace EM predikce obecně ekonomické prognózování, předpověď, předvídání hlavním cílem je odhad hodnot vysvětlované proměnné
Determinanty regionáln. lní konkurenceschopnosti a regionáln
 Determinanty regionáln lní konkurenceschopnosti a regionáln lních disparit v ČR Přednáška Studentského ekonomického klubu Marta Šlehoferová 20.5.2010 Struktura přednášky pojem konkurenceschopnost regionů
Determinanty regionáln lní konkurenceschopnosti a regionáln lních disparit v ČR Přednáška Studentského ekonomického klubu Marta Šlehoferová 20.5.2010 Struktura přednášky pojem konkurenceschopnost regionů
STAV VEŘEJNÝCH FINANCÍ V ROCE 2007 A V DALŠÍCH LETECH
 STAV VEŘEJNÝCH FINANCÍ V ROCE 27 A V DALŠÍCH LETECH Mirek Topolánek předseda vlády ČR Stav veřejných financí vládní deficit Trvale deficitní hospodaření -1-2 -3 % HDP -4-5 -6-7 -8 Saldo vládního sektoru
STAV VEŘEJNÝCH FINANCÍ V ROCE 27 A V DALŠÍCH LETECH Mirek Topolánek předseda vlády ČR Stav veřejných financí vládní deficit Trvale deficitní hospodaření -1-2 -3 % HDP -4-5 -6-7 -8 Saldo vládního sektoru
časovém horizontu na rozdíl od experimentu lépe odhalit chybné poznání reality.
 Modelování dynamických systémů Matematické modelování dynamických systémů se využívá v různých oborech přírodních, technických, ekonomických a sociálních věd. Použití matematického modelu umožňuje popsat
Modelování dynamických systémů Matematické modelování dynamických systémů se využívá v různých oborech přírodních, technických, ekonomických a sociálních věd. Použití matematického modelu umožňuje popsat
4. 3. Váha nefinančních firem pod zahraniční kontrolou na investicích sektoru nefinančních podniků a v české ekonomice
 4. 3. Váha nefinančních firem kontrolou na investicích sektoru nefinančních podniků a v české ekonomice 4.3.1. Spojitost s přílivem přímých investic Odlišnost pojmů Je třeba rozlišovat termín příliv přímých
4. 3. Váha nefinančních firem kontrolou na investicích sektoru nefinančních podniků a v české ekonomice 4.3.1. Spojitost s přílivem přímých investic Odlišnost pojmů Je třeba rozlišovat termín příliv přímých
Nezaměstnanost. Makroekonomie I. Opakování. Příklad. Řešení. Nezaměstnanost. Téma cvičení. Nezaměstnanost, Okunův zákon
 Opakování Makroekonomie I Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Uvažujte následující úsporovou funkci: S = -300 + 0,15 YD. Určete výši důchodu, při kterém bude platit YD = C. S = -300 + 0,15 YD
Opakování Makroekonomie I Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Uvažujte následující úsporovou funkci: S = -300 + 0,15 YD. Určete výši důchodu, při kterém bude platit YD = C. S = -300 + 0,15 YD
Šetření prognóz. makroekonomického vývoje ČR. Ministerstvo financí odbor Hospodářská politika
 šetření prognóz makroekonomického vývoje v ČR, HDP zemí EA9, cena ropy Brent, M PRIBOR, výnos do splatnosti R státních dluhopisů, měnový kurz CZK/EUR, měnový kurz USD/EUR, hrubý domácí produkt, příspěvek
šetření prognóz makroekonomického vývoje v ČR, HDP zemí EA9, cena ropy Brent, M PRIBOR, výnos do splatnosti R státních dluhopisů, měnový kurz CZK/EUR, měnový kurz USD/EUR, hrubý domácí produkt, příspěvek
MODELY HOSPODÁŘSKÉHO RŮSTU
 MODELY HOSPODÁŘSKÉHO RŮSTU ÚVOD Několik teorií Exogenní vs. Endogenní technologický pokrok Lidský kapitál SOLOWŮV MODEL Předpoklad: Existují pouze 2 sektor (domácnosti + firm) Y=C+I Technologický pokrok
MODELY HOSPODÁŘSKÉHO RŮSTU ÚVOD Několik teorií Exogenní vs. Endogenní technologický pokrok Lidský kapitál SOLOWŮV MODEL Předpoklad: Existují pouze 2 sektor (domácnosti + firm) Y=C+I Technologický pokrok
Otázky k přijímacímu řízení magisterského civilního studia
 Univerzita obrany Fakulta ekonomiky a managementu ----------------------------------------------------------------------------------------------------- Otázky k přijímacímu řízení magisterského civilního
Univerzita obrany Fakulta ekonomiky a managementu ----------------------------------------------------------------------------------------------------- Otázky k přijímacímu řízení magisterského civilního
Analýzy stupně ekonomické sladěnosti ČR s eurozónou 2008
 Analýzy stupně ekonomické sladěnosti ČR s eurozónou 2008 Mojmír r Hampl viceguvernér Praha, 16. ledna 2009 Je ČR R připravena p na přijetp ijetí eura? Schopnost ekonomiky dobře fungovat bez vlastní měnové
Analýzy stupně ekonomické sladěnosti ČR s eurozónou 2008 Mojmír r Hampl viceguvernér Praha, 16. ledna 2009 Je ČR R připravena p na přijetp ijetí eura? Schopnost ekonomiky dobře fungovat bez vlastní měnové
ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR LISTOPAD Samostatný odbor finanční stability
 ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR LISTOPAD Samostatný odbor finanční stability ZÁTĚŽOVÉ TESTY LISTOPAD SHRNUTÍ Výsledky zátěžových testů bankovního sektoru v ČR, které byly provedeny na datech ke konci
ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR LISTOPAD Samostatný odbor finanční stability ZÁTĚŽOVÉ TESTY LISTOPAD SHRNUTÍ Výsledky zátěžových testů bankovního sektoru v ČR, které byly provedeny na datech ke konci
Využití pracovní síly
 Využití pracovní síly HDP na konci sledovaného období klesal výrazněji než v celé Rozhodující význam má v kraji zpracovatelský průmysl Hrubý domácí produkt na Vysočině obdobně jako v celé České republice
Využití pracovní síly HDP na konci sledovaného období klesal výrazněji než v celé Rozhodující význam má v kraji zpracovatelský průmysl Hrubý domácí produkt na Vysočině obdobně jako v celé České republice
Vývoj české ekonomiky
 Přehled ekonomiky České republiky HDP Trh práce Inflace Platební bilance Zahraniční investice Průmysl Zahraniční obchod Hlavní charakteristiky české ekonomiky Malá, otevřená ekonomika, výrazně závislá
Přehled ekonomiky České republiky HDP Trh práce Inflace Platební bilance Zahraniční investice Průmysl Zahraniční obchod Hlavní charakteristiky české ekonomiky Malá, otevřená ekonomika, výrazně závislá
1. Vývoj počtu ekonomických subjektů v ČR od roku 2000
 1. Vývoj počtu ekonomických subjektů v ČR od u 2000 1.1. Celkový vývoj Charakteristika celkového vývoje ekonomických subjektů v ČR vychází z údajů registru ekonomických subjektů (RES), kde se evidují všechny
1. Vývoj počtu ekonomických subjektů v ČR od u 2000 1.1. Celkový vývoj Charakteristika celkového vývoje ekonomických subjektů v ČR vychází z údajů registru ekonomických subjektů (RES), kde se evidují všechny
Statistika. Regresní a korelační analýza Úvod do problému. Roman Biskup
 Statistika Regresní a korelační analýza Úvod do problému Roman Biskup Jihočeská univerzita v Českých Budějovicích Ekonomická fakulta (Zemědělská fakulta) Katedra aplikované matematiky a informatiky 2008/2009
Statistika Regresní a korelační analýza Úvod do problému Roman Biskup Jihočeská univerzita v Českých Budějovicích Ekonomická fakulta (Zemědělská fakulta) Katedra aplikované matematiky a informatiky 2008/2009
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
4. Křivka nabídky monopolní firmy je totožná s částí křivky mezních nákladů.
 Firma v nedokonalé konkurenci 1. Zdroji nedokonalé konkurence jsou: - jednak nákladové podmínky podnikání, - jednak. 2. Zapište vzorec Lernerova indexu. K čemu slouží? 3. Zakreslete celkový příjem monopolní
Firma v nedokonalé konkurenci 1. Zdroji nedokonalé konkurence jsou: - jednak nákladové podmínky podnikání, - jednak. 2. Zapište vzorec Lernerova indexu. K čemu slouží? 3. Zakreslete celkový příjem monopolní
Průzkum prognóz makroekonomického vývoje ČR
 Průzkum prognóz makroekonomického vývoje ČR Cílem průzkumu makroekonomických prognóz (tzv. Kolokvia), který provádí MF ČR, je zjistit názor relevantních institucí na budoucí vývoj české ekonomiky a vyhodnotit
Průzkum prognóz makroekonomického vývoje ČR Cílem průzkumu makroekonomických prognóz (tzv. Kolokvia), který provádí MF ČR, je zjistit názor relevantních institucí na budoucí vývoj české ekonomiky a vyhodnotit
nejen Ing. Jaroslav Zlámal, Ph.D. Ing. Zdeněk Mendl Vzdìlávání, které baví www.computermedia.cz Nakladatelství a vydavatelství
 nejen 1. díl Obecná ekonomie Ing. Jaroslav Zlámal, Ph.D. Ing. Zdeněk Mendl Nakladatelství a vydavatelství R Vzdìlávání, které baví www.computermedia.cz TEMATICKÉ ROZDĚLENÍ DÍLŮ KNIHY EKONOMIE NEJEN K MATURITĚ
nejen 1. díl Obecná ekonomie Ing. Jaroslav Zlámal, Ph.D. Ing. Zdeněk Mendl Nakladatelství a vydavatelství R Vzdìlávání, které baví www.computermedia.cz TEMATICKÉ ROZDĚLENÍ DÍLŮ KNIHY EKONOMIE NEJEN K MATURITĚ
OTEVŘENÁ EKONOMIKA. b) Předpokládejte, že se vládní výdaje zvýší na Spočítejte národní úspory, investice,
 OTEVŘENÁ EKONOMIKA Zadání 1. Pomocí modelu malé otevřené ekonomiky předpovězte, jak následující události ovlivní čisté vývozy, reálný směnný kurz a nominální směnný kurz: a) Klesne spotřebitelská důvěra
OTEVŘENÁ EKONOMIKA Zadání 1. Pomocí modelu malé otevřené ekonomiky předpovězte, jak následující události ovlivní čisté vývozy, reálný směnný kurz a nominální směnný kurz: a) Klesne spotřebitelská důvěra
Mezi makroekonomické subjekty náleží: a) domácnosti b) podniky c) vláda d) zahraničí e) vše výše uvedené
 Makroekonomická rovnováha může být představována: a) tempem růstu skutečného produktu, odpovídající vývoji tzv. potenciálního produktu b) vyrovnanou platební bilancí c) mírou nezaměstnanosti na úrovni
Makroekonomická rovnováha může být představována: a) tempem růstu skutečného produktu, odpovídající vývoji tzv. potenciálního produktu b) vyrovnanou platební bilancí c) mírou nezaměstnanosti na úrovni
4EK211 Základy ekonometrie
 4EK Základy ekonometrie Odhad klasického lineárního regresního modelu II Cvičení 3 Zuzana Dlouhá Klasický lineární regresní model - zadání příkladu Soubor: CV3_PR.xls Data: y = maloobchodní obrat potřeb
4EK Základy ekonometrie Odhad klasického lineárního regresního modelu II Cvičení 3 Zuzana Dlouhá Klasický lineární regresní model - zadání příkladu Soubor: CV3_PR.xls Data: y = maloobchodní obrat potřeb
MÍRY ZÁVISLOSTI (KORELACE A REGRESE)
 zhanel@fsps.muni.cz MÍRY ZÁVISLOSTI (KORELACE A REGRESE) 2.5 MÍRY ZÁVISLOSTI 2.5.1 ZÁVISLOST PEVNÁ, VOLNÁ, STATISTICKÁ A KORELAČNÍ Jednorozměrné soubory - charakterizovány jednotlivými statistickými znaky
zhanel@fsps.muni.cz MÍRY ZÁVISLOSTI (KORELACE A REGRESE) 2.5 MÍRY ZÁVISLOSTI 2.5.1 ZÁVISLOST PEVNÁ, VOLNÁ, STATISTICKÁ A KORELAČNÍ Jednorozměrné soubory - charakterizovány jednotlivými statistickými znaky
Model ekonomiky. Model ekonomiky. Typy ekonomik. Model makroekonomiky. PŘEDNÁŠKA č. 2 Hospodářské cykly Ekonomický růst
 PŘEDNÁŠKA č. 2 Hospodářské cykly Ekonomický růst Pro všechny přístupy, směry a školy makroekonomie je charakteristické, že: zkoumají souhrnnou úroveň národohospodářského produktu, zaměstnanosti, cen a
PŘEDNÁŠKA č. 2 Hospodářské cykly Ekonomický růst Pro všechny přístupy, směry a školy makroekonomie je charakteristické, že: zkoumají souhrnnou úroveň národohospodářského produktu, zaměstnanosti, cen a
ALTERNATIVNÍ UKAZATELÉ EKONOMICKÉ VÝKONNOSTI A BLAHOBYTU. Vojtěch Spěváček Centrum ekonomických studií VŠEM. www.cesvsem.cz. Praha 25. 11.
 ALTERNATIVNÍ UKAZATELÉ EKONOMICKÉ VÝKONNOSTI A BLAHOBYTU Vojtěch Spěváček Centrum ekonomických studií VŠEM www.cesvsem.cz Praha 25. 11. 2006 Obsah: 1. Jak rychle rostla česká ekonomika a jaká je její ekonomická
ALTERNATIVNÍ UKAZATELÉ EKONOMICKÉ VÝKONNOSTI A BLAHOBYTU Vojtěch Spěváček Centrum ekonomických studií VŠEM www.cesvsem.cz Praha 25. 11. 2006 Obsah: 1. Jak rychle rostla česká ekonomika a jaká je její ekonomická
Makroekonomická predikce (listopad 2018)
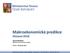 Ministerstvo financí České republiky, Letenská 15, 118 10 Praha 1, +420 257 041 111 Ministerstvo financí Makroekonomická predikce (listopad 2018) David PRUŠVIC Ministerstvo financí České republiky Praha,
Ministerstvo financí České republiky, Letenská 15, 118 10 Praha 1, +420 257 041 111 Ministerstvo financí Makroekonomická predikce (listopad 2018) David PRUŠVIC Ministerstvo financí České republiky Praha,
VÝVOJ EKONOMIKY ČR WWW.SPCR.CZ
 VÝVOJ EKONOMIKY ČR WWW.SPCR.CZ VÝVOJ EKONOMIKY ČR: PŘEHLED A KOMENTÁŘE SP ČR ZPRACOVAL: BOHUSLAV ČÍŽEK (BCIZEK@SPCR.CZ) ZPRACOVÁNO K 30.10.2015 VÝZNAM PRŮMYSLU Průmysl (2014) 32,4% podíl na přidané hodnotě
VÝVOJ EKONOMIKY ČR WWW.SPCR.CZ VÝVOJ EKONOMIKY ČR: PŘEHLED A KOMENTÁŘE SP ČR ZPRACOVAL: BOHUSLAV ČÍŽEK (BCIZEK@SPCR.CZ) ZPRACOVÁNO K 30.10.2015 VÝZNAM PRŮMYSLU Průmysl (2014) 32,4% podíl na přidané hodnotě
Politika zaměstnanosti České republiky v letech 2004 až 2011
 Politika zaměstnanosti České republiky v letech 2004 až 2011 Teoretický úvod Politika zaměstnanosti je jedním z nejdůležitějších segmentů každého vyspělého státu. V České republice je upravena především
Politika zaměstnanosti České republiky v letech 2004 až 2011 Teoretický úvod Politika zaměstnanosti je jedním z nejdůležitějších segmentů každého vyspělého státu. V České republice je upravena především
Makroekonomie I. Model Agregátní nabídky Agregátní poptávky
 Přednáška 4. Model AS -AD Makroekonomie I Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Osnova přednášky: Souhrnné opakování předchozí přednášky : Hospodářské cykly a sektory ekonomiky Agregátní poptávka
Přednáška 4. Model AS -AD Makroekonomie I Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky Osnova přednášky: Souhrnné opakování předchozí přednášky : Hospodářské cykly a sektory ekonomiky Agregátní poptávka
Mikroekonomie. Minulá přednáška - podstatné. Náklady firmy v krátkém a dlouhém období. Důležité vzorce. Náklady v krátkém období - graficky
 Minulá přednáška - podstatné Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Typologie nákladů firmy Náklady v krátkém období Náklady v dlouhém období Důležité vzorce TC = FC + VC AC =
Minulá přednáška - podstatné Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Typologie nákladů firmy Náklady v krátkém období Náklady v dlouhém období Důležité vzorce TC = FC + VC AC =
Téma 4 - metodika. Ekonomický vývoj ČR od roku 1995
 Hospodářská politika - VŠFS Jiří Mihola, jiri.mihola@quick.cz, 2010 www.median-os.cz, www.ak-ol.cz Téma 4 - metodika Ekonomický vývoj ČR od roku 1995 Charakteristika metody Výchozí studijní materiál: Analýza
Hospodářská politika - VŠFS Jiří Mihola, jiri.mihola@quick.cz, 2010 www.median-os.cz, www.ak-ol.cz Téma 4 - metodika Ekonomický vývoj ČR od roku 1995 Charakteristika metody Výchozí studijní materiál: Analýza
RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr.
 Analýza dat pro Neurovědy RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr. Jaro 2014 Institut biostatistiky Janoušová, a analýz Dušek: Analýza dat pro neurovědy Blok 7 Jak hodnotit vztah spojitých proměnných
Analýza dat pro Neurovědy RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr. Jaro 2014 Institut biostatistiky Janoušová, a analýz Dušek: Analýza dat pro neurovědy Blok 7 Jak hodnotit vztah spojitých proměnných
INDUKTIVNÍ STATISTIKA
 10. SEMINÁŘ INDUKTIVNÍ STATISTIKA 3. HODNOCENÍ ZÁVISLOSTÍ HODNOCENÍ ZÁVISLOSTÍ KVALITATIVNÍ VELIČINY - Vychází se z kombinační (kontingenční) tabulky, která je výsledkem třídění druhého stupně KVANTITATIVNÍ
10. SEMINÁŘ INDUKTIVNÍ STATISTIKA 3. HODNOCENÍ ZÁVISLOSTÍ HODNOCENÍ ZÁVISLOSTÍ KVALITATIVNÍ VELIČINY - Vychází se z kombinační (kontingenční) tabulky, která je výsledkem třídění druhého stupně KVANTITATIVNÍ
Některé pozoruhodné tendence ve vývoji kultury
 Některé pozoruhodné tendence ve vývoji kultury PhDr. Ing. Jaroslav Novák, CSc. Centrum informací a statistik kultury A) OBECNÝ POHLED Časové řady statistických dat odhalují nově vznikající změny a tendence
Některé pozoruhodné tendence ve vývoji kultury PhDr. Ing. Jaroslav Novák, CSc. Centrum informací a statistik kultury A) OBECNÝ POHLED Časové řady statistických dat odhalují nově vznikající změny a tendence
INFLACE A NEZAMĚSTNANOST
 INFLACE A NEZAMĚSTNANOST Úvod Hypotéza zda-li existuje vztah mezi mírou inflace a nezaměstnaností (trade off) Negativní korelace veličin? Růst inflace pokles nezaměstnanosti a naopak Phillipsova křivka
INFLACE A NEZAMĚSTNANOST Úvod Hypotéza zda-li existuje vztah mezi mírou inflace a nezaměstnaností (trade off) Negativní korelace veličin? Růst inflace pokles nezaměstnanosti a naopak Phillipsova křivka
Mikroekonomie Nabídka, poptávka
 Téma cvičení č. 2: Mikroekonomie Nabídka, poptávka Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Podstatné z minulého cvičení Matematický pojmový aparát v Mikroekonomii Důležité minulé cvičení kontrolní
Téma cvičení č. 2: Mikroekonomie Nabídka, poptávka Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Podstatné z minulého cvičení Matematický pojmový aparát v Mikroekonomii Důležité minulé cvičení kontrolní
Komentář k makroekonomickému vývoji ovlivňujícímu vývoj registrací nových vozidel v České republice
 Komentář k makroekonomickému vývoji ovlivňujícímu vývoj registrací nových vozidel v České republice Expertní pohled PricewaterhouseCoopers Česká republika ; 1 Přestože ekonomika České republiky nadále
Komentář k makroekonomickému vývoji ovlivňujícímu vývoj registrací nových vozidel v České republice Expertní pohled PricewaterhouseCoopers Česká republika ; 1 Přestože ekonomika České republiky nadále
Metodický list č. 2. Metodický list pro 2. soustředění kombinovaného Mgr. studia předmětu. Makroekonomie II (Mgr.) LS
 Metodický list č. 2 Metodický list pro 2. soustředění kombinovaného Mgr. studia předmětu Makroekonomie II (Mgr.) LS 2008-09 Název tématického celku: Makroekonomie II 2. blok. Tento tématický blok je rozdělen
Metodický list č. 2 Metodický list pro 2. soustředění kombinovaného Mgr. studia předmětu Makroekonomie II (Mgr.) LS 2008-09 Název tématického celku: Makroekonomie II 2. blok. Tento tématický blok je rozdělen
předmětu MAKROEKONOMIE
 Metodický list pro první soustředění kombinovaného studia předmětu Přednášející: doc. Ing. Božena Kadeřábková, CSc. Úvod do makroekonomie a hrubý domácí produkt, model 45 1. Úvod do makroekonomie, pojem
Metodický list pro první soustředění kombinovaného studia předmětu Přednášející: doc. Ing. Božena Kadeřábková, CSc. Úvod do makroekonomie a hrubý domácí produkt, model 45 1. Úvod do makroekonomie, pojem
Spotřeba domácností má významný sociální rozměr
 Spotřeba domácností má významný sociální rozměr Výdaje domácností výrazně přispívají k celkové výkonnosti ekonomiky. Podobně jako jiné sektory v ekonomice jsou i ony ovlivněny hospodářským cyklem. Jejich
Spotřeba domácností má významný sociální rozměr Výdaje domácností výrazně přispívají k celkové výkonnosti ekonomiky. Podobně jako jiné sektory v ekonomice jsou i ony ovlivněny hospodářským cyklem. Jejich
ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR LISTOPAD. Samostatný odbor finanční stability
 ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR LISTOPAD Samostatný odbor finanční stability ZÁTĚŽOVÉ TESTY LISTOPAD ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR (LISTOPAD ) SHRNUTÍ Výsledky zátěžových testů bankovního sektoru
ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR LISTOPAD Samostatný odbor finanční stability ZÁTĚŽOVÉ TESTY LISTOPAD ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR (LISTOPAD ) SHRNUTÍ Výsledky zátěžových testů bankovního sektoru
I. Dopady změn ve výplatě nemocenských dávek
 Tisková zpráva ze dne 17. dubna 2009 I. Dopady změn ve výplatě nemocenských dávek V roce 2008 meziročně pokleslo průměrné procento pracovní neschopnosti z 5,62 % na 5,18 %, což je nejnižší výsledek v historii
Tisková zpráva ze dne 17. dubna 2009 I. Dopady změn ve výplatě nemocenských dávek V roce 2008 meziročně pokleslo průměrné procento pracovní neschopnosti z 5,62 % na 5,18 %, což je nejnižší výsledek v historii
I. Vývoj čistých mezd zaměstnanců
 Tisková zpráva ze dne 11. září 2008 I. Vývoj čistých mezd zaměstnanců Ministerstvo práce a sociálních věcí zpracovalo očekávaný vývoj čistých mezd zaměstnanců v podnikatelském a nepodnikatelském sektoru
Tisková zpráva ze dne 11. září 2008 I. Vývoj čistých mezd zaměstnanců Ministerstvo práce a sociálních věcí zpracovalo očekávaný vývoj čistých mezd zaměstnanců v podnikatelském a nepodnikatelském sektoru
Základy ekonomie II. Téma č. 3: Modely ekonomické rovnováhy Petr Musil
 Základy ekonomie II Téma č. 3: Modely ekonomické rovnováhy Petr Musil Struktura Opakování: ekonomická rovnováha Klasický model ekonomické rovnováhy: trh kapitálu trh práce důsledky v modelu AS-AD Keynesiánský
Základy ekonomie II Téma č. 3: Modely ekonomické rovnováhy Petr Musil Struktura Opakování: ekonomická rovnováha Klasický model ekonomické rovnováhy: trh kapitálu trh práce důsledky v modelu AS-AD Keynesiánský
Úvod do ekonomie Týden 3. Tomáš Cahlík
 Úvod do ekonomie Týden 3 Tomáš Cahlík Obsah Ekonomika v dlouhém časovém horizontu Výrobní faktory, Hrubý domácí produkt a Produkční funkce Inflace, nominální a reálný HDP, nezaměstnanost Instituce a hospodářský
Úvod do ekonomie Týden 3 Tomáš Cahlík Obsah Ekonomika v dlouhém časovém horizontu Výrobní faktory, Hrubý domácí produkt a Produkční funkce Inflace, nominální a reálný HDP, nezaměstnanost Instituce a hospodářský
0 z 25 b. Ekonomia: 0 z 25 b.
 Ekonomia: 1. Roste-li mzdová sazba,: nabízené množství práce se nemění nabízené množství práce může růst i klesat nabízené množství práce roste nabízené množství práce klesá Zvýšení peněžní zásoby vede
Ekonomia: 1. Roste-li mzdová sazba,: nabízené množství práce se nemění nabízené množství práce může růst i klesat nabízené množství práce roste nabízené množství práce klesá Zvýšení peněžní zásoby vede
MAKROEKONOMIE. Blok č. 5: ROVNOVÁHA V UZAVŘENÉ EKONOMICE
 MAKROEKONOMIE Blok č. 5: ROVNOVÁHA V UZAVŘENÉ EKONOMICE CÍL A STRUKTURA TÉMATU.odpovědět na následující typy otázek: Kolik se toho v ekonomice vyprodukuje? Kdo obdrží důchody z produkce? Kdo nakoupí celkový
MAKROEKONOMIE Blok č. 5: ROVNOVÁHA V UZAVŘENÉ EKONOMICE CÍL A STRUKTURA TÉMATU.odpovědět na následující typy otázek: Kolik se toho v ekonomice vyprodukuje? Kdo obdrží důchody z produkce? Kdo nakoupí celkový
Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115
 Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115 Číslo projektu: CZ.1.07/1.5.00/34.0410 Číslo šablony: Název materiálu: Národní hospodářství 3 Ročník: Identifikace materiálu: Jméno autora:
Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115 Číslo projektu: CZ.1.07/1.5.00/34.0410 Číslo šablony: Název materiálu: Národní hospodářství 3 Ročník: Identifikace materiálu: Jméno autora:
Korelační a regresní analýza
 Korelační a regresní analýza Analýza závislosti v normálním rozdělení Pearsonův (výběrový) korelační koeficient: r = s XY s X s Y, kde s XY = 1 n (x n 1 i=0 i x )(y i y ), s X (s Y ) je výběrová směrodatná
Korelační a regresní analýza Analýza závislosti v normálním rozdělení Pearsonův (výběrový) korelační koeficient: r = s XY s X s Y, kde s XY = 1 n (x n 1 i=0 i x )(y i y ), s X (s Y ) je výběrová směrodatná
4EK201 Matematické modelování. 11. Ekonometrie
 4EK201 Matematické modelování 11. Ekonometrie 11. Ekonometrie Ekonometrie Interdisciplinární vědní disciplína Zkoumá vztahy mezi ekonomickými veličinami Mikroekonomickými i makroekonomickými Ekonomie ekonomické
4EK201 Matematické modelování 11. Ekonometrie 11. Ekonometrie Ekonometrie Interdisciplinární vědní disciplína Zkoumá vztahy mezi ekonomickými veličinami Mikroekonomickými i makroekonomickými Ekonomie ekonomické
