MODELOVÁNÍ ARTEFAKTŮ PROCESU CT RTG ZOBRAZENÍ
|
|
|
- Miloslav Čermák
- před 6 lety
- Počet zobrazení:
Transkript
1 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV BIOMEDICÍNSKÉHO INŽENÝRSTVÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF BIOMEDICAL ENGINEERING MODELOVÁNÍ ARTEFAKTŮ PROCESU CT RTG ZOBRAZENÍ BAKALÁŘSKÁ PRÁCE BACHELOR S THESIS AUTOR PRÁCE AUTHOR MARKÉTA KOŤOVÁ BRNO 2011
2 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV BIOMEDICÍNSKÉHO INŽENÝRSTVÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF BIOMEDICAL ENGINEERING MODELOVÁNÍ ARTEFAKTŮ PROCESU CT RTG ZOBRAZENÍ X-RAY COMPUTED TOMOGRAPHY ARTIFACTS SIMULATION BAKALÁŘSKÁ PRÁCE BACHELOR S THESIS AUTOR PRÁCE AUTHOR VEDOUCÍ PRÁCE SUPERVISOR MARKÉTA KOŤOVÁ doc. Ing. ALEŠ DRASTICH, CSc. BRNO 2011
3 ZDE VLOŽIT LIST ZADÁNÍ Z důvodu správného číslování stránek
4 ABSTRAKT Bakalářská Práce se zabývá modelováním artefaktů vznikajících během vyšetřovaní počítačovou tomografií. Teoretická část shrnuje poznatky o principech výpočetní tomografie a vzniku jednotlivých artefaktů. V praktické části byl vytvořen simulátor artefaktů, který obsahuje následující artefakty: kruhový, pohybový, aliasing, kovový, artefakt vlivem kvantového šumu. V další části je navržena laboratorní úloha. KLÍČOVÁ SLOVA CT RTG, Radonova transformace, pohybový artefakt, kruhový artefakt, aliasing artefakt, kovový artefakt, artefakt vlivem kvantového šumu, simulátor, laboratorní úloha ABSTRACT The bachelor s thesis deals with CT artifacts modeling generated during the acquisition process. The theoretical part summarizes principles of CT and origin of artifacts. The practical part consists of a newly developed simulator, which includes ring, motion, metal, streak and aliasing artifacts. Finally, the new laboratory exercise was designed. KEYWORDS CT RTG, Radon transform, motion artifact, ring artifact, metal artifact, streak artifact, aliasing artifact, simulator, laboratory exercise KOŤOVÁ, Markéta Modelování artefaktů procesu CT RTG zobrazení: bakalářská práce. Brno: Vysoké učení technické v Brně, Fakulta elektrotechniky a komunikačních technologií, Ústav biomedicínského inženýrství, s. Vedoucí práce byl doc. Ing. Aleš Drastich, CSc.
5 PROHLÁŠENÍ Prohlašuji, že svou bakalářskou práci na téma Modelování artefaktů procesu CT RTG zobrazení jsem vypracoval samostatně pod vedením vedoucího bakalářské práce a s použitím odborné literatury a dalších informačních zdrojů, které jsou všechny citovány v práci a uvedeny v seznamu literatury na konci práce. Jako autor uvedené bakalářské práce dále prohlašuji, že v souvislosti s vytvořením této bakalářské práce jsem neporušil autorská práva třetích osob, zejména jsem nezasáhl nedovoleným způsobem do cizích autorských práv osobnostních a jsem si plně vědom následků porušení ustanovení 11 a následujících autorského zákona č. 121/2000 Sb., včetně možných trestněprávních důsledků vyplývajících z ustanovení 152 trestního zákona č. 140/1961 Sb. V Brně (podpis autora)
6 PODĚKOVÁNÍ Děkuji vedoucímu semestrálního projektu doc. Ing. Aleši Drastichovi CSc. za účinnou metodickou, pedagogickou a odbornou pomoc a další cenné rady při zpracování mého semestrálního projektu. Děkuji také své rodině a svému příteli Ondrovi za veškerou podporu. V Brně (Podpis autora)
7 OBSAH 1 Úvod 1 2 Výpočetní tomografie Rentgenové záření Vznik obrazu Radonova transformace Inverzní Radonova transformace Artefakty CT Kruhový artefakt Pohybový artefakt Kovový artefakt Aliasing artefakt Pruhový artefakt Partial volume artefakt Artefakty vlivem helikální akvizice Artefakty vlivem cone-beam akvizice Artefakty vlivem jevu utvrzování svazku rtg záření Artefakty vlivem překročení omezení spojeného s FOM Simulátor CT artefaktů Matlab Uživatelské rozhraní Vývojový diagram Akviziční parametry Kruhový artefakt Pohybový artefakt Aliasing artefakt Kovový artefakt Artefakt vlivem kvantového šumu Návrh laboratorní úlohy 29 6 Závěr 37 Literatura 38 Seznam příloh 40
8 A Obsah přiloženého DVD 41
9 SEZNAM OBRÁZKŮ 2.1 CT Toshiba Aquilion Biologické účinky IZ Princip sběru dat CT RTG Diskretizace scény a definice voxelu Princip snímaní Vztah mezi prostorovou doménou a Radonovou transformací Princip tvorby kruhového artefaktu Princip tvorby kovového artefaktu Aliasing Princip tvorby Partial Volume artefaktu Princip tvorby helikálního artefaktu a cone-beam jevu Hlavní zobrazovací okno programu Vývojový diagram programu Projevení počtu detektorů Projevení počtu projekcí Shepp - Logan Cosine Hamming Hann Projevení typu filtru Kruhový artefakt Pohybový artefakt Aliasing artefakt Aliasing artefakt Kovový artefakt Ovlivňování detektorů při otáčení Pohybový artefakt Pohybový artefakt Kruhový artefakt Kruhový artefakt Aliasing artefakt Aliasing artefakt Kovový artefakt Artefakt vlivem kvantového šumu
10 SEZNAM TABULEK 2.1 Hounsfieldova stupnice
11 1 ÚVOD V současné době vzrůstá v lékařství význam zobrazovacích metod. Pod pojmem zobrazovací metody se shrnují všechny metody, používané v medicíně pro zobrazení určité části těla. Mezi tyto zobrazovací metody patří například ultrazvuk, magnetická rezonance, výpočetní tomografie, ale také třeba systémy, které jsou využitelné v nukleární medicíně jako jsou např. PET a SPECT. Výpočetní tomografie je velmi důležitou součástí vyšetření, kde napomáhá k diagnostice širokého spektra poranění a chorob. Během vyšetření dochází při zobrazení k nenáhodnému šumu v obraze nebo-li k artefaktům. Artefakty mohou vznikat z různých důvodů a příčin. Tyto nesrovnalosti v obraze komplikují lékařům interpretování snímků a proto se snažíme artefakty potlačit (nikdy je neodstraníme úplně). Úkolem této bakalářské práce je modelování artefaktů procesu CT RTG zobrazení. Význam této práce spočívá v tom, že na těchto modelech se dají potlačovat artefakty. Uživatel si vyzkouší jakými parametry artefakt vzniká a jak se mění, když se změní některý z parametrů, jak tyto artefakty ovlivňují akviziční parametry (počet detektorů, počet projekcí a filtry pro zpětnou Radonovu transformaci). To mu umožní lepší pochopení principu vzniku a projevu artefaktů. 1
12 2 VÝPOČETNÍ TOMOGRAFIE Výpočetní tomografie je velmi rozšířená vyšetřovací metoda v medicíně. Přestože je stále dosti drahá, stala se standardem, využívaným v diagnóze velkého množství různých nemocí. CT se začalo využívat i jako prevence nejrůznějších onemocnění. Velmi často jde například o pacienty s vysokým rizikem rakoviny tlustého střeva. CT se využívá také pro odhalování jak akutních, tak chronických změn v plicním parenchymu, břišních onemocnění... Pokud se jedná o určení stadia rakoviny, tak lékaři velmi často využívají právě CT. Dále se CT využívá při méně závažných onemocnění, jako jsou ledvinové kameny, zánět slepého střeva, zánět slinivky břišní, zánět divertikulu, břišní aortální výduť a ucpání střeva. Složité fraktury končetin, především kloubů se zobrazují také pomocí CT, nikoliv RTG, a to z toho důvodu, že zlomeniny, zranění vazů a dislokace se dají snadno rozpoznat s rozlišením 0,2 mm [4]. Obr. 2.1: CT Toshiba Aquilion 64, převzato z [11] CT je založeno na rentgenovém záření, které objevil německý fyzik Wilhelm Conrad Röntgen, který za tento objev získal Nobelovu cenu za fyziku v roce Samotná teorie rekonstrukce tomografického řezu z mnoha sumačních snímků byla vypracována Allanem MacCormackem a Godfreyem Newboldem Hounsfieldem. Vzhledem k náročnosti rekonstrukce však uplynulo takřka deset let, než byl v praxi zkonstruován první použitelný tomograf. Oba dostali Nobelovu cenu za medicínu [12]. Pořízení prvního CT obrázku trvalo několik hodin a jeho rekonstrukce dalších 24 hodin (dáno možnostmi výpočetní techniky). V dnešní době je rekonstrukce dat hotova ve zlomcích sekundy. V roce 1986 byl sestrojen první CT skener s kontinuální rotací (3-4 snímky za vteřinu) firmou Bio-Imaging Research. Metoda kontinuální 2
13 rotace umožnila vývoj revolučního spirálního CT. V roce 1999 byl přiveden na trh první tzv. Multi-Slice CT firmou Toshiba.[10], [13] 2.1 Rentgenové záření Rentgenové záření je elektromagnetické vlnění o vlnové délce 10nm až 100pm. Rentgenové záření má kratší vlnovou délku a větší energii než světlo. Zdrojem X-záření pro rtg zobrazení je rentgenka. Svazek záření vycházející z rentgenky je vycloněn do tvaru vějíře. Záření, které prochází pacientem, potom dopadá na detektory uložené na části kruhové výseče naproti rentgence. Zde je dopadající záření převedeno na elektrický signál, který je odeslán ke zpracování do počítače. Během expozice jedné vrstvy se systém (rentgenka - detektory), otočí kolem pacienta o 360. Doba rotace se pohybuje v rozmezí 0,5-7 sekund - záleží na typu CT přístroje. U nových přístrojů se pracuje s expozičními časy 1-2 sekundy. Ionizující záření je pro člověka nebezpečné. Pracovníci, kteří pracují na pracovišti, kde se vyskytuje rentgenové záření, musí dodržovat určité předpisy. Nejdůležitější ochranou před zářením je snižovat expozici, které jsou pracovníci a zejména pacienti vystavěni. Pracovníci jsou pod dozimetrickou kontrolou a nesmí překročit maximální dávku záření, pacienti nejsou kontrolováni nijak. Proto se může stát, že je pacient vyšetřován na dvou různých pracovištích během krátké doby. Maximální dávka pro pracovníky je 50 msv/rok, pro pacienty je tato hodnota nižší a to 1 msv/rok [8]. Ochrana před zářením je tedy: Čas maximální zkrácení doby vystavení se záření Vzdálenost dávka se snižuje s druhou mocninou vzdálenosti Stínění používání ochranných pomůcek Dávka záření závisí na velikosti místa, které je snímáno. CT patří mezi aktivní systém - potenciální nebezpečí překročení prahové dávky ionizujícího záření (somatické a genetické účinky) aplikace principu ALARA (As Low As Reasonable Achievable). Na obrázku 2.2 vidíme biologické účinky ionizujícího záření na organismus. 3
14 Obr. 2.2: Biologické účinky IZ, převzato z [1] 2.2 Vznik obrazu Základní princip je založen na zeslabování svazku rentgenového záření při průchodu vyšetřovaným objektem. CT RTG se liší od RTG tím, že vytváří sérii tomografických řezů. Každý řez je vytvořen matematickou rekonstrukcí. Principem CT zobrazení je detekční systém, který změří úbytek záření mezi rentgenkou a detektorem. Tento úbytek nastane, protože dojde k pohlcení záření prostředím (tkání). Scéna je snímána do souboru projekcí získaných pod různým úhlem. Jednotlivé projekce jsou tvořeny souborem paprskových integrálů. Na obrázku 2.3 je zobrazen princip sběru dat CT RTG. Můžeme vidět 2 typy pohybů: translace a rotace. Během translace se sejme jedna projekce scény. Poté se natočí rentgenka a detektor a nastane rotace. Následuje další sejmutí projekce téže scény, ale pod jiným úhlem [3]. Získávané obrazy vrstev jsou obrazy digitální - jsou tvořeny maticí bodů, nejčastěji v počtu 512 x 512. Denzita v prostoru je definována pomocí Hounsfieldovi stupnice (používá se zkratka H nebo HU). Hodnota denzity vyjadřuje stupeň absorpce záření voxelem vzhledem k absorpci zářeni vodou [3]. CT cislo = K µ tkane µ vody µ vody [HU], (2.1) kde µ vody = 0, 19cm 1 při 73 kev, K je konstanta. Hounsfieldova stupnice je v odstínech šedi. V stupnici jsou důležité dva body: HU, což odpovídá denzitě vzduchu a 0 HU, což odpovídá denzitě vody. Denzity ostatních tkání jsou různé, viz tabulka
15 Obr. 2.3: Princip sběru dat CT RTG, převzato z [2] Výsledný CT obraz se skládá z dvourozměrné sítě čtverců - z matice. Tato matice se skládá z voxelů a pixelů. Voxely jsou objemové elementy matice a pixely jsou plošné elementy výsledné matice jak je znázorněno na obrázku 2.4. Objekt Denzita [HU] Vzduch Tuk -40 až -120 Voda 0 Starý hematon +18 až +40 Metastázy +25 až +50 Nádory +30 až +50 Čerstvý hematon +65 až +85 Kompaktní kost 1000 a více Tab. 2.1: Hounsfieldovi stupnice, převzato z [12] Nejdůležitější mechanizmy interakce rtg záření se scénou jsou vnitřní fotoelektrický jev a Comptonův rozptyl. Schopnost tkáně absorbovat záření je zahrnuta v lineárním koeficientu zeslabení µ(ρ, Z, E). 5
16 Obr. 2.4: Diskretizace scény a definice voxelu, převzato z [2] Fotoelektrický jev - (fotoefekt) je fyzikální jev, při němž jsou elektrony emitovány z látky v důsledku absorpce elektromagnetického záření (např. rentgenové záření) látkou. Část energie se spotřebuje na uvolnění elektronu a zbytek tvoří kinetickou energii vzniklého fotoelektronu. Původní foton zaniká a jeho energii získává fotoelektron, který je směrově odchýlen od dráhy původního fotonu a který dále ionizuje své okolí. Atom, ze kterého byl vyražen elektron přechází do základního stavu a vyzáří tak energii odpovídající rozdílu vzbuzeného a základního stavu. Comptonův rozptyl - (Comptonův jev)je fyzikální děj, při kterém se po srážce elektromagnetického záření s atomy pevné látky mění vlnová délka záření v důsledku předání části své energie atomům nebo jejich elektronům. Oba tyto jevy přispívají ke zkreslení obrazu a objasňují účelnost sekundárních clon (např. Buckyho clona), které pohlcují fotony RTG záření odchýlené od primárního svazku. 6
17 2.3 Radonova transformace V praxi se k řešení obrazové rekonstrukce používá Radonova transformace a zpětná Radonova transformace. Radonova transformace je matematická transformace, která je pojmenována po českém matematikovi německé národnosti Johannovi Radonovi. Jedná se o integrální transformaci, která spočívá v integrálu funkce přes přímky. Matematicky lze Radonovu transformaci zapsat: p Φ (x ) p(x, Φ) R[o(x, y)], (2.2) kde R[o(x, y)] je Radonův operátor R[o(x, y)] = = kde + + [ x y o(x, y) (xcosφ + ysinφ x )dxdy = (2.3) o(x cosφ y sinφ, x sinφ + y cosφ)dy, ] [ ] [ ] cosφ sinφ x =. (2.4) sinφ cosφ y Je možné zavést funkci R(Φ, x ) = p Φ, ( x ), pro Φ R. Tato funkce je periodická vzhledem k Φ s periodou 2π. Dále platí R(Φ + π, x ) = R(Φ, x ). Z této rovnosti vyplývá, že akviziční projekce pro rekonstrukci obrazu je možno provádět pouze pro Φ 0, π) [3]. Soubor všech sejmutých projekcí v jasové modulaci se nazývá sinogram. Obrázek 2.6 ukazuje jak se projevuje Radonova transformace při prostorovém posunutí a při rotaci. 2.4 Inverzní Radonova transformace Filtrovaná zpětná projekce je založena na původní prosté zpětné projekci. Tato metoda odstraňuje nevýhody prosté zpětné projekce. Odlišnost od prosté zpětné projekce spočívá v tom, že se použije inverzní přenosová funkce H-filtru. Tímto filtrem se koriguje zkreslení původní prosté zpětné projekce. Používají se Ramp-filtry, které mají nekonečnou přenosovou charakteristiku a také se zvyšuje prostorová frekvence. Tyto filtry potlačují stejnosměrnou složku jednotlivých projekcí, umožňují přímý 7
18 Obr. 2.5: Princip snímaní - Radonova transformace je dána datovým souborem všech možných paprskových integrálů snímaného objektu, převzato z [17] Obr. 2.6: Vztah mezi prostorovou doménou a Radonovou transformací, převzato z [17] součet projekcí při zpětném promítání. Ramp-filtry jsou ale fyzikálně nerealizovatelné, proto se používají filtry, které kombinují Ramp-filtry s filtry pro filtraci šumu. Mohou to být Ramp-Lak či Sheep-Logan[3], [5]. Podrobněji jsou tyto filtry rozebrány v kapitole
19 3 ARTEFAKTY CT Obrazové artefakty, nebo-li nenáhodný šum v obraze jsou systematické neshody v CT číslech v rekonstruovaném obraze oproti skutečné hodnotě útlumu rtg záření. Artefakty můžeme rozlišit podle druhu či původu [6]. Druhy artefaktů máme například: Proužky Stíny Kruhy Spirály (zkroucení) Častější rozdělení je podle zdroje artefaktů. Ty nejdůležitější zdroje jsou: Fyzikální podvzorkování, atd. Pacient kovy v těle, pohyb pacienta, atd. Přistroj (skener) citlivost detektorů, atd. V této části bakalářské práce budou popsány příklady artefaktů, které mohou vznikat při CT snímání. 3.1 Kruhový artefakt Jedná se o změnu detekční účinnosti nebo citlivosti detekčních kanálů. Jak se artefakt projevuje záleží na počtu detektorů, u kterých je snížena citlivost a také jak moc je tato citlivost snížena. Tento artefakt je typický pro 3. generaci CT (systém rotace rotace). Využívá rotační pohyb systému rentgenka detektory. Detektory jsou umístěny na kruhové výseči rotující spolu s rentgenkou [3]. Tento artefakt se projevuje ve tvaru kruhu kruhový artefakt. K potlačení tohoto typu artefaktu je důležité najít chybný detektor či detektory a provést jejich následnou rekalibraci. 9
20 Obr. 3.1: Princip tvorby kruhového artefaktu, převzato z [2] 3.2 Pohybový artefakt Artefakt vzniký v důsledku pohybu pacienta, který může být: Úmyslný pohyb pacienta při průběhu vyšetřování (pohyb hlavou,... ) atd. Neúmyslný pulzace srdce, dýchání, atd. Pohybový artefakt se projevuje světelnými pruhy v tangenciálním směru, vysokokontrastních hran pohybujících se částí [3]. Většina artefaktů je způsobena nespoluprací pacienta pacient nevydrží zadržet dech po dobu skenu. Proto se zdravotníci snaží alespoň zminimalizovat tento problém fixací hlavy či končetin a samozřejmě urychlit dobu skenu. 3.3 Kovový artefakt Kovový artefakt je způsoben nežádoucími výpady obrazu (data se dostanou do saturace), které mohou být vyvolané přítomností objektu s největší absorpcí v místě skenu [3]. Objekt absorbuje záření a způsobuje artefakt. Princip tvorby artefaktu je zobrazen na obrázku 3.2. Tento předmět je kovového charakteru jako mohou být dentální materiály, spony, šrouby či elektrody. Kovový artefakt se projevuje výraznými, jasnými pruhy, často až do hvězdicového útvaru. Potlačení tohoto artefaktu můžeme dojít interpolací [7]. 10
21 Obr. 3.2: Princip tvorby kovového artefaktu, převzato z [2] 3.4 Aliasing artefakt Artefakty jsou způsobeny chybně navzorkovanou scénou. K aliasingu nedochází, pokud je splněn Shannonův vzorkovací teorém, to znamená, že f f vz /2. Aliasing se projevuje překrýváním spekter a dochází k neobnovitelné ztrátě informace. K tomuto artefaktu dochází pokud je počet projekcí nebo počet detektorů příliš malý. Aliasingu je nutné předcházet, protože pokud k němu dojde, jeho následky nelze odstranit. K předcházení vzniku aliasingu se používají antialiasingové filtry, které odfiltrovávají frekvence vyšší než odpovídají Shannonovu teorému. Vznik aliasingu vidíme na obrázku 3.3. Aliasing, nebo-li překrytí spekter je vyznačeno červenou barvou. Obr. 3.3: Aliasing, převzato z [9] 11
22 3.5 Pruhový artefakt Pruhové artefakty, které vznikají vlivem kvantového šumu, pokud rtg záření prochází velkou vrstvou tkáně - například v oblasti pánve, ramen. Tento artefakt se také vyskytuje u obézních lidí. K potlačení pruhového typu artefaktu se využívá adaptivní filtrace nebo adaptivní modulace anodového proudu [3]. U pruhového artefaktu je důležité zmínit Lambert-Beerův zákon exponenciálního útlumu: I = I 0 e µ d. (3.1) fotonový tok intenzity I 0 rtg svazku záření s energií E bude mít po průchodu vrstvou tloušťky d velikost I, absorpční koeficient µ se nazývá lineární součinitel zeslabení. Jeho hodnota závisí na hustotě a protonovém čísle absorpčního materiálu a výrazně též na energii záření. 3.6 Partial volume artefakt Tento artefakt je způsobem výskytem více struktur v objemu voxelu - výsledek je dán zprůměrováním jednotlivých lineárních součinitelů zeslabení [3]. Partial volume artefakt je také znám pod názvem Hounsfieldovy pruhy. K potlačení artefaktu dochází pomocí snímání po tenkých vrstvách s následných sečtením nebo zprůměrováním obrazů. Obr. 3.4: Princip tvorby Partial Volume artefaktu, převzato z [2] 12
23 3.7 Artefakty vlivem helikální akvizice Rekonstrukce obrazu při helikální akvizici je stejná jako při sekvenční akvizici. V průběhu rekonstrukce je přidán jeden krok jedná se o tzv. z-interpolaci, která potlačí pohybový artefakt. U helikální akvizice vzniká artefakt vlivem nehomogenity distribuce šumu v jednotlivých pixelech obrazu, která se mění v závislosti na z-pozici. Tento artefakt se nazývá zebra artefakt, protože se projevuje střídáním podélných světlých a tmavých pruhů. Potlačení artefaktu se provádí volbou interpolační metody a nebo upraveným interpolačním algoritmem[3]. 3.8 Artefakty vlivem cone-beam akvizice Jestliže jsou objekty, které jsou lokalizované mimo centrální řadu detekční mozaiky viděny různými řadami detektorů v závislosti na úhlu snímání projekce, je to způsobeno cone - beam efektem. Princip cone-beam jevu způsobeného velkou axiální rozbíhavostí rtg záření je znázorněn na obrázku 3.5b. Artefakt se projevuje na okrajích obrazů ze surových dat získaných krajními řadami detektorů detekční mozaiky. K potlačení artefaktu se používají rekonstrukční algoritmy[3]. Obr. 3.5: Princip tvorby helikálního artefaktu a cone-beam jevu, a) Princip tvorby helikálního artefaktu, b) Princip tvorby cone-beam jevu, převzato z [2] 3.9 Artefakty vlivem jevu utvrzování svazku rtg záření Vlivem utvrzování svazku rtg záření dochází ke vzniku cupping artefaktu. Jde o to, že pokud snímáme např. válcovitý předmět, uplatňují se více detektory ve středu, 13
24 než detektory krajní. Tento artefakt způsobuje nehomogenitu procesu zobrazení. Cupping artefakt se projevuje mezi kostními strukturami. Artefakt se dá potlačit pomocí klínových filtrů (bowtie filter), kalibrace nebo BHC (Beam Hardenning Correction)[2] Artefakty vlivem překročení omezení spojeného s FOM Tento artefakt se projevuje tehdy, když pacient je umístěn v gantry, ale jejich polohování je mimo skenovací zorné pole (FOM - Field Of Measurement). Artefakt můžeme potlačit pomocí speciálních korekčních měření [3]. 14
25 4 SIMULÁTOR CT ARTEFAKTŮ V této kapitole je popsána praktická realizace bakalářské práce od zvoleného programovacího prostředí (4.1), přes vývojový diagram navrženého simulátoru (4.3), až po popis realizace konkrétních artefaktů. Po domluvě s vedoucím práce byly vybrány artefakty: kruhový, pohybový, aliasing, kovový a artefakt vlivem kvantového šumu. 4.1 Matlab Simulátor CT artefaktů byl vytvořen v programu Matlab(verze 2009b). Matlab je programovací prostředí a skriptovací programovací jazyk - pomocí jehož lze provádět matematické výpočty, modelování, analýzu a zpracování dat, vývoj algoritmů atd. Matlab je maticově orientován. Součástí Matlabu je i nástroj Guide pro interaktivní tvorbu grafického prostředí (GUI graphical user interface) [16]. 4.2 Uživatelské rozhraní Na obrázku 4.1 je hlavní zobrazovací okno. V horní části se nachází nabídka, která slouží k obsluze programu. V první nabídce je Soubor, kde nalezneme tyto možnosti: Otevření obrázku volba modelu scény Uložení obrázku na výběr je uložení artefaktu či porovnání rekonstrukce bez artefaktu a s artefaktem Konec slouží k ukončení programu V nabídce Artefakty si uživatel volí akviziční parametry a následně konkrétní artefakt: Akviziční parametry Konkrétní artefakty Poslední nabídka je zobrazení, které je vhodné pro lepší pochopení vzniku artefaktu: Sinogram Prostorové zobrazení Projekce 15
26 Obr. 4.1: Hlavní zobrazovací okno programu Nejprve si uživatel zvolí model scény, který se zobrazí v levém horním okně. Následně jsou zvoleny akviziční parametry - tato rekonstrukce bez artefaktu (I 0 ) je zobrazena v pravé horní části. Rekonstrukce s artefaktem (I 1 ) po zvolení parametrů vybraného artefaktu se poté nachází v levé dolní části. Porovnání těchto dvou rekonstrukcí je zobrazeno v pravé dolní části. I porovnani (x, y) = I 1 (x, y) I 0 (x, y). (4.1) 4.3 Vývojový diagram Při inicializaci programu se program zavede do paměti počítače, nastaví se cesty k artefaktům a počáteční hodnoty globálních proměnných. Načtou se jednotlivé artefakty jako zásuvné moduly (plug-in). Následně si uživatel otevře obrázek, buď z knihovny obrázků, která obsahuje fantomy, nebo svůj libovolný obrázek. Podporované jsou standardní formáty jako png, jpg, bmp, gif. Na hlavní liště si uživatel zvolí akviziční parametry (počet detektorů, počet projekcí, typ filtru pro zpětnou RT), vybere typ artefaktu a zvolí jeho parametry. Následně proběhne výpočet artefaktu, který se nám zobrazí. 16
27 Obr. 4.2: Vývojový diagram programu 17
28 4.4 Akviziční parametry Volba počtu detektorů - udává počet detektorů v řadě na jednu snímanou projekci a odpovídá počtu paprskových integrálů. Jejich počet ovlivňuje prostorovou rozlišovací schopnost v rekonstruovaném obraze a vzorkovací kmitočet projekce. Obr. 4.3: Projevení počtu detektorů, počet projekcí: 180, typ filtru: Ram-Lak, a) 100 detektorů, b) 200 detektorů, c) 300 detektorů, d) 400 detektorů Počet projekcí - udává počet snímaných projekcí, které jsou jednotlivě pořízeny s úhlovým inkrementem v definovaném úhlovém rozsahu. Úhlový krok pro snímaní dané projekce je u většiny CT systémů menší než 1 stupeň. Celkový počet sejmutých projekcí je poté 500 až 1500 na jeden obraz [3]. Filtry pro zpětnou Radonovu transformaci uživatel si zvolí typ filtru, kterým chce aby se prováděla zpětná filtrovaná RT. Ram-Lak je základní filtr, který zesiluje vyšší prostorové frekvence Frekvenční odezva tohoto filtru je absolutní f. Tento filtr je citlivý na šum v projekci. Filtry, 18
29 Obr. 4.4: Projevení počtu projekcí, počet detektorů: 360, typ filtru: Ram-Lak, a) 50 projekcí, b) 90 projekcí, c) 120 projekcí, d) 150 projekcí které jsou uvedeny níže vynásobí Ram-Lak filtr oknem a tím potlačí vysoké frekvence. Sheep-Logan filtr, který představuje ideální pásmovou propust, protože ve frekvenčním spektru mu odpovídá obdélník. Vynásobí Ram-Lak filtr pomocí sinc funkce: kde sinc je: 2n ω(n) = sinc 1, (4.2) N 1 sinc(x) = sin(x), (4.3) x Cosine vynásobí Ram-Lak filtr pomocí cosinova okna: ω(n) = cos πn N 1 π 2, (4.4) 19
30 1 Sheep logan okno 0 Frekvenèní charakteristika Sheep logan okna amplituda db N 1 vzorky koeficienty Obr. 4.5: Shepp - Logan: a) Shepp - Logan okno, b) Frekvenční charakteristika, převzato z [14] 1 Cosine okno 0 Frekvenèní charakteristika Cosine okna amplituda db N 1 vzorky koeficienty Obr. 4.6: Cosine: a) Cosine okno, b) Frekvenční charakteristika, převzato z [14] Hamming Toto okno je navrženo tak, aby nejbližší postranní lalok (ve spektru) byl utlumen. Vynásobí Ram-Lak filtr pomocí Hammingova okna: ω(n) = 0, 54 0, 46cos 2πn N 1, (4.5) Hann hlavní lalok je širší oproti Hammingovu oknu, ale na druhou stranu dochází k lepšímu potlačení na vyšších frekvencích. Vynásobí Ram-Lak filtr pomocí Hannova okna: None nefiltruje ( ( )) 2πn ω(n) = 0, 5 1 cos, (4.6) N 1 20
31 1 Hammingovo okno 0 Frekvenèní charakteristika Hammingova okna amplituda db N 1 vzorky koeficienty Obr. 4.7: Hamming: a) Hammingovo okno, b) Frekvenční charakteristika, převzato z [14] 1 Hannovo okno 0 Frekvenèní charakteristika Hannova okna amplituda db N 1 vzorky koeficienty Obr. 4.8: Hann: a) Hannovo okno, b) Frekvenční charakteristika, převzato z [14] 21
32 Obr. 4.9: Projevení typu filtru, počet detektorů: 360, počet projekcí: 180, a) Ram- Lak, b) Sheep-Logan, c) Cosine, d) Hamming 22
33 4.5 Kruhový artefakt Tak jak bylo zmíněno v kapitole 3.1, jedná se o změnu detekční účinnosti nebo citlivosti detekčních kanálů. Uživatel má možnost si artefakt vygenerovat automaticky a nebo manuálně. Při automatickém generování si uživatel volí pouze počet měněných detektorů a parametr SNR (odstup signál šum). Následně se náhodně vyberou detektory, které budou chybné - jejich detekční účinnost se bude měnit - pomocí funkce randi. Funkce randi vygeneruje náhodná čísla, tudíž detektory. Všechny detekční účinnosti jsou nastaveny na 100 procent, pomocí funkce awgn se přidá k náhodně vybraným detektorům bílý šum, který je určen pomocí parametrů, které udávají odstup signálu od šumu v db. Při manuálním generování si uživatel volí daný detektor a jeho detekční účinnost. Poté co, jsou určeny detekční účinnosti jednotlivých detektorů, tak se provede samotný výpočet kruhového artefaktu, který probíhá následovně: nejdříve se vypočte Radonova transformace vstupního obrazu, tím získáme jeho sinogram. Poté každý sloupec sinogramu násobíme prvek po prvku s vektorem detekční účinnosti detektoru. I kruh (Θ, x ) = I sinogram (Θ, x ). w (4.7) w = (w 1, w 2,..., w n ) T vektor detekční účinnosti, kde. znamená násobení prvku po prvku. I sinogram je sinogram vstupního obrázku. Nakonec se provede zpětná Radonova transformace, čím se získá obraz s kruhovým artefaktem. Na obrázku 5.5 jsou znázorněny 3 artefakty, které mají následující parametry: První artefakt: Akviziční parametry: Počet detektorů: 400; Počet projekcí: 220; Filtr: Shepp- Logan Nastavení parametrů artefaktu: Změna SNR u počtu detektorů: 50; Volba SNR: 35 Druhý artefakt: Akviziční parametry: Počet detektorů: 380; Počet projekcí: 180; Filtr: Ram- Lak 23
34 Nastavení parametrů artefaktu: Změna SNR u počtu detektorů: 80; Volba SNR: 35 Třetí artefakt: Akviziční parametry: Počet detektorů: 380; Počet projekcí: 180; Filtr: Ram- Lak Nastavení parametrů artefaktu: Změna SNR u počtu detektorů: 20; Volba SNR: 20 Obr. 4.10: Kruhový artefakt : a) první artefakt, b) druhý artefakt, c) třetí artefakt 4.6 Pohybový artefakt Pohybový artefakt vzniká pohybem pacienta během vyšetřování. Pro naši simulaci je použita změna velikosti vstupního obrazu, která zhruba simuluje dýchání pacienta. Jako základní funkce, z které se generuje posloupnost obrazů je použita harmonická funkce sinus: krivka(t) = 1 + Asin(2πf) (4.8) kde A je hloubka nádechu, f frekvence dýchání, což jsou parametry pomocích kterých se určuje měřítko pro tvorbu artefaktu. Pomocí těchto parametrů se vygeneruje křivka, simulující dýchání a uživatel zvolí začátek a konec scénu. Vyznačená část křivky popisuje pacienta během snímání. Následně se spustí cyklus, který probíhá: vyznačená část křivky je navzorkována a poté se v každém kroku snímání vytvoří obrázek, jehož velikost je volena podle hodnoty funkce v daném vzorku. Tento obrázek je zarovnán na střed, je spočítána Radonova transformace 24
35 pod daným úhlem a výsledek této transformace což je jeden sloupec sinogramu je uložen do zásobníku (bufferu) na příslušnou pozici. Po skončení cyklu se vypočítá zpětná Radonova transformace a je vygenerován obrázek s artefaktem. Příklad simulace pohybového artefaktu je zobrazen na obrázku 4.11 Obr. 4.11: Simulace pohybového artefaktu - počet projekcí: 180, počet detektorů: 360, filtr: Ram-Lak, hloubka nádechu: 0,05, frekvence dýchání: 4 a) křivka dýchání, b) artefakt 4.7 Aliasing artefakt Artefakty vznikají chybně navzorkovanou scénou. K aliasingu nedochází, když f f vz /2. Aliasingový artefakt vzniká dvojím způsobem. Buď špatnou volbou počtu projekcí a nebo volbou počtu detektorů (případně jejich kombinací). Uživatel mění vždy pouze jeden z těchto parametrů, nikdy ne oba zároveň, aby bylo názorné, jak se změna projeví. Artefakt je naprogramován takto, aby si uživatel vyzkoušel vliv jednoho parametru na jeho vznik. Chování tohoto artefaktu je jiné než ostatních a to tak, že zvolený parametr (počet detektorů nebo počet projekcí) změní původní nastavení akvizičního parametru. Z výsledků viz obrázek 5.7 a 5.5 je patrné, že při zvyšování počtu detektorů a počtu projekcí se artefakt projevuje méně. Při zvolení počtu detektoru se vypočítá Radonova transformace pomocí Matlabu, ve které se použije zvolený počet detektorů a projekcí, které byly zvoleny v akvizičních parametrech. Pomocí zvoleného filtru se poté provede zpětná RT a zobrazí se výsledný artefakt. Při zvolení počtu projekcí se opět vypočítá RT, ve které se použije počet projekcí, které si uživatel zvolil a počet detektorů, který byl zvolen v akvizičních parametrech. 25
36 Provede se zpětná RT a zobrazí se výsledný artefakt. Obr. 4.12: Simulace aliasing artefaktu - projekce, počet projekcí: a) 70, b) 120, c) 180 Obr. 4.13: Simulace aliasing artefaktu - detektory, počet detektorů: a) 70, b) 120, c) Kovový artefakt Kovový artefakt je způsoben nežádoucími výpady obrazu (data se dostanou do saturace). Tato saturace je způsobena kovem v místě skenu. Aby měl uživatel dobrou volbu - u tohoto artefaktu se nevolí žádné parametry jako je tvar kovu, velikost kovu atd. Místo toho si uživatel nakreslí binární obrázek podle toho jaký objekt chce mít zobrazen. Model scény a nakreslený kov musí mít stejné velikosti. Pokud se velikosti neshodují, zobrazí se upozornění: Rozměry obrázků se neshodují. V nákresu se používají dvě barvy a to bílá a černá, kde bílá barva znázorňuje kov. 26
37 Vypočítaná Radonova transformace obou obrázků se uchová v paměti. Výsledný sinogram se skládá tak, že se postupně prochází bod po bodu sinogramu kovu a pokud je hodnota větší než nula, což znamená, že v tomto bodě se kov projevuje, tak dojde k saturaci odpovídajícího bodu ve výsledném sinogramu. Pokud se kov neprojevuje, zkopíruje se bod ze sinogramu modelu scény. Provede se zpětná RT a zobrazí se kovový artefakt. Obr. 4.14: Kovový artefakt: a) počet detektorů: 400, počet projekcí: 220, filtr: Hamming, b) počet detektorů: 360, počet projekcí: 180, filtr: Hamming, c) počet detektorů: 360, počet projekcí: 180, filtr: Ram-Lak 4.9 Artefakt vlivem kvantového šumu Jak již bylo řečeno artefakt vzniká, když záření prochází velkou vrstvou tkáně, například v oblasti pánve, ramen. Na obrázku je vidět, že při různých úhlech je ovlivněn různý počet detektorů a dokonce mohou být ovlivněny i jiné detektory. Při nulovém natočení je ovlivněn pouze středový detektor. U 10 stupňů jsou zasaženy detektory napravo od středu ale při 20 stupňovém natočení už je zasaženo více detektorů. Z výše uvedeného rozboru je zřejmé, že vytvoření artefaktu je nejdůležitější určit, při které projekci jsou zasaženy které detektory. Model scény se otočí o požadovaný úhel, spočítá se jedna projekce RT. Kromě RT je potřeba také mít informace o útlumu pro danou projekci a proto je vypočítána suma v jednotlivých sloupcích otočeného obrazu. Následně je určen počátek a konec v RT a v sesumovaném obraze a přizpůsobíme jeho velikost RT. Vypočítá se rovnice 3.1. Výsledek je uložen do bufferu. Po vypočtení všech dílčích projekcí je do obrazu přidán náhodný šum. 27
38 Obr. 4.15: Ovlivňování detektorů při otáčení, převzato z [15] Při přidávání šumu je nejdříve omezena oblast, kde se artefakt projeví podle zvoleného prahu. Pokud je velikost daného bodu v bufferu větší než zvolený práh, vygeneruje se šum, jehož útlum je určen právě podle velikosti daného bodu. Tento šum se přičte k sinogramu a provede se zpětná RT. 28
39 5 NÁVRH LABORATORNÍ ÚLOHY Cílem této laboratorní úlohy je seznámení uživatele (studenta) s artefakty, které vznikají při CT RTG zobrazení (3 generace CT). Uživatel si vyzkouší simulovat artefakt, jak se mění, pokud se změní jeden z parametrů, či jak se liší, pokud se změní akviziční parametry (volba počtu detektorů, volba počtu projekcí, volba filtru pro zpětnou RT). Obsah laboratorní úlohy Simulace pohybového artefaktu Simulace kruhového artefaktu Simulace aliasing artefaktu Simulace kovového artefaktu Simulace artefaktu vlivem kvantového šumu Simulace pohybového artefaktu V této části se bude simulovat pohybový artefakt. Artefakt simuluje dýchání - určujeme parametry jako jsou hloubka nádechu, frekvence nádechu a křivka simulující pohyb (změna objemu) pacienta. Uživatel si vyzkouší dva artefakty, při kterých změní jak akviziční parametry, tak parametry artefaktu. První artefakt: Načtení modelu scény: Soubor/ Otevřít / Obrázky / Čtverec Zvolení akvizičních parametrů: Artefakt / Akviziční parametry / Počet detektorů: 360; Počet projekcí: 180; Filtr: Ram-Lak / Ok Nastavení parametrů artefaktu: Artefakt / Pohybový / Hloubka nádechu: 0,05; Frekvence dýchání: 2,0; Pohyb pacienta: viz obr. (5.1)a / Ok Druhý artefakt: Zvolení akvizičních parametrů: Artefakt / Akviziční parametry / Počet detektorů: 280; Počet projekcí: 100; Filtr: Shepp-Logan / Ok Nastavení parametrů artefaktu: Artefakt / Pohybový / Hloubka nádechu: 0,1; Frekvence dýchání: 3,0; Pohyb pacienta: viz obr. (5.2)a / Ok 29
40 Obr. 5.1: Simulace pohybového artefaktu- první, a) Pohyb pacienta, b) Artefakt, c) Porovnání Obr. 5.2: Simulace pohybového artefaktu- druhý, a) Pohyb pacienta, b) Artefakt, c) Porovnání Pozorujte změnu vzniku artefaktu, pro lepší pochopení se podívejte na sinogram či na prostorové zobrazení, které naleznete v menu: Zobrazení. Dále si vyzkoušejte takové parametry, při kterých artefakt nevzniká: začátek a konec dýchání v pohybové křivce je na stejné pozici. Simulace kruhového artefaktu Kruhový artefakt se simuluje dvojím způsobem: automaticky (pouze počet poškozených detektorů a jejich SNR) a manuálně (konkrétní detektory a jejich detekční účinnost). Nejprve si vytvořte automaticky zvolený kruhový artefakt: nechejte stejné akviziční parametry a změňte parametry artefaktu - pozorujte změnu. Při manuálně zvoleném artefaktu si nechte stejné detektory ale změňte jejich detekční účinnost - opět pozorujte změnu. Nakonec si vyzkoušejte parametry, u kterých artefakt nevzniká: u automatického volení: změna SNR u počtu detektorů: 0; volba SNR: 0; při manuálním volení: detekční účinnost u detektorů nastavte na 100 procent. Opět 30
41 pro lepší pochopení si zvolte sinogram či prostorové zobrazení a porovnejte, jak se změnil, když se artefakt projevuje a kdy nikoliv. Automaticky zvolení artefaktu První artefakt: Načtení modelu scény: Soubor/ Otevřít / Obrázky / Phantom Zvolení akvizičních parametrů: Artefakt / Akviziční parametry / Počet detektorů: 400; Počet projekcí: 220; Filtr: Ram-Lak / Ok Nastavení parametrů artefaktu: Artefakt / Kruhový / Automaticky / Změna SNR u počtu detektorů: 50; Volba SNR: 40/ Ok Druhý artefakt: Nastavení parametrů artefaktu: Artefakt / Kruhový / Automaticky / Změna SNR u počtu detektorů: 80; Volba SNR: 30/ Ok Obr. 5.3: Simulace Kruhového artefaktu - automaticky, a) První artefakt, b) Druhý artefakt Manuálně zvolení artefaktu První artefakt: Zvolení akvizičních parametrů: Artefakt / Akviziční parametry / Počet detektorů: 250; Počet projekcí: 125; Filtr: Hamming / Ok Nastavení parametrů artefaktu: Artefakt / Kruhový / Manuálně / Počet měněných detektorů: 10; Číslo detektoru: 90, 94, 96, 100, 105, 125, 134, 141, 156, 164; Citlivost: 95, 94, 96,95, 97, 99, 95, 96, 98, 94 / Ok Druhý artefakt: 31
42 Nastavení parametrů artefaktu: Artefakt / Kruhový / Manuálně / Počet měněných detektorů: 10; Číslo detektoru: 90, 94, 96, 100, 105, 125, 134, 141, 156, 164; Citlivost: 75, 82, 76, 86, 84, 79, 81, 81, 89, 80/ Ok Obr. 5.4: Simulace Kruhového artefaktu - manuálně, a) První artefakt, b) Druhý artefakt Simulace aliasing artefaktu Aliasing artefakt si můžeme vyzkoušet opět dvojím způsobem a to volbou počtu detektorů nebo volbou počtu projekcí. Nejprve si vyzkoušejte volbu počtu detektorů. A následně volbu počtem projekcí. Zvyšujícím počtem detektorů a projekcí se aliasing artefakt projevuje méně. Podívejte se na sinogramy různých artefaktů. Volba počtu detektorů První artefakt: Načtení modelu scény: Soubor/ Otevřít / Obrázky / Phantom3 Zvolení akvizičních parametrů: Artefakt / Akviziční parametry / Počet detektorů: 360; Počet projekcí: 180; Filtr: Ram-Lak / Ok Nastavení parametrů artefaktu: Artefakt / Aliasing / Detektory / Volba počtu detektorů: 70/ Ok Druhý artefakt: Nastavení parametrů artefaktu: Artefakt / Aliasing / Detektory / Volba počtu detektorů: 120/ Ok Třetí artefakt: Nastavení parametrů artefaktu: Artefakt / Aliasing / Detektory / Volba počtu detektorů: 360/ Ok 32
43 Obr. 5.5: Simulace aliasing artefaktu-detektory,počet detektorů: a) 70, b) 120, c) 360 Volba počtu projekcí První artefakt: Nastavení parametrů artefaktu: Artefakt / Aliasing / Projekce / Volba počtu detektorů: 70/ Ok Druhý artefakt: Nastavení parametrů artefaktu: Artefakt / Aliasing / Projekce / Volba počtu detektorů: 120/ Ok Třetí artefakt: Nastavení parametrů artefaktu: Artefakt / Aliasing / Projekce / Volba počtu detektorů: 180/ Ok Obr. 5.6: Simulace aliasing artefaktu- projekce,počet projekcí: a) 70, b) 120, c)
44 Simulace kovového artefaktu U kovového artefaktu simulujte, jak se změní artefakt pokud změníte jeden z akvizičních parametrů (filtr pro zpětnou RT) a zanecháme stejný kov a stejný model scény. Zde si určitě zobrazte sinogram artefaktu a sinogram bez artefaktu. Dále si namodelujte artefakt s úplně jinými akvizičními parametry- změňte jak počet detektorů tak i počet projekcí. První artefakt: Načtení modelu scény: Soubor/ Otevřít / Obrázky / Phantom3 Zvolení akvizičních parametrů: Artefakt / Akviziční parametry / Počet detektorů: 360; Počet projekcí: 180; Filtr: Ram-Lak / Ok Nastavení parametrů artefaktu: Artefakt / Kovový / Obrázky / Kov3/ Ok Druhý artefakt: Zvolení akvizičních parametrů: Artefakt / Akviziční parametry / Počet detektorů: 360; Počet projekcí: 180; Filtr: Hann / Ok Nastavení parametrů artefaktu: Artefakt / Kovový / Obrázky / Kov3/ Ok Třetí artefakt: Zvolení akvizičních parametrů: Artefakt / Akviziční parametry / Počet detektorů: 360; Počet projekcí: 180; Filtr: Shepp-Logan / Ok Nastavení parametrů artefaktu: Artefakt / Kovový / Obrázky / Kov3/ Ok Obr. 5.7: Simulace kovového artefaktu, Filtr: a) Ram-Lak, b) Hann, c) Shepp-Logan Simulace artefaktu vlivem kvantového šumu 34
45 U tohoto artefaktu si vyzkoušejte vliv počtu projekcí a počtu detektorů na jeho vznik. Při stejných akvizičních parametrech zvyšte úroveň artefaktu a pozorujte změnu. Poté změňte akviziční parametry a zadejte stejné úrovně artefaktu jako v předchozích případech. Při zvyšování úrovně artefaktu se nám artefakt projevuje méně. První artefakt: Načtení modelu scény: Soubor/ Otevřít / Obrázky / Phantom8 Zvolení akvizičních parametrů: Artefakt / Akviziční parametry / Počet detektorů: 360; Počet projekcí: 180; Filtr: Ram-Lak / Ok Nastavení parametrů artefaktu: Artefakt / Kvantový šum / Volba úrovně artefaktu: 1,8 / Ok Obr. 5.8: Simulace artefaktu vlivem kvantového šumu- artefakt: a) první, b) druhý, c) třetí, d) čtvrtý Druhý artefakt: Nastavení parametrů artefaktu: Artefakt / Kvantový šum / Volba úrovně artefaktu: 1,85 / Ok Třetí artefakt: Zvolení akvizičních parametrů: Artefakt / Akviziční parametry / Počet detektorů: 250; Počet projekcí: 125; Filtr: Ram-Lak / Ok Nastavení parametrů artefaktu: Artefakt / Kvantový šum / Volba úrovně artefaktu: 1,8 / Ok Čtvrtý artefakt: 35
46 Nastavení parametrů artefaktu: Artefakt / Kvantový šum / Volba úrovně artefaktu: 1,85 / Ok 36
47 6 ZÁVĚR Cílem této bakalářské práce je modelování artefaktů procesu CT RTG zobrazení. Práce byla vytvořena v prostředí Matlab (verze 2009b). V první čísti práce je popsán princip výpočetní tomografie, jsou popsány artefakty, které mohou vznikat při procesu zobrazení. Ve druhé části je popsán program a vybrané artefakty pro modelování. Po domluvě s vedoucím práce byly vybrány následující artefakty: kruhový, pohybový, aliasing, kovový a artefakty vlivem kvantového šumu. Uživatel má možnost volby jejich parametrů. Parametry se u každého artefaktu liší - záleží na konkrétním artefaktu. Vyzkouší si, jakými parametry artefakt vzniká a jak se mění, když se změní některý z parametrů. Dále si vyzkouší jak tyto artefakty ovlivňují akviziční parametry. Součástí zadání bakalářské práce bylo vytvoření laboratorní úlohy pro předmět zabývající se procesem zobrazení, včetně postupu práce s programem a následující výsledky. Toto všechno umožní uživateli lepší pochopení principu vzniku a projevu artefaktu. Program navržený v této bakalářské práci je možné poměrně snadno rozšířit. Tím je myšleno nasimulování dalších artefaktů nebo jejich potlačení. 37
48 LITERATURA [1] Bradáčová, K.: Ochrana před zářením. Výukový materiál předmětu Radiologie a nukleární medicína (ARAD). [2] Drastich, A.: Zobrazovací systémy v lékařství-ct RTG. Výukový materiál předmětu Zobrazovací systémy v lékařství (AZSL). [3] Drastich, A.: Tomografické zobrazovací systémy. První vydání, Vysoké učení technické v Brně, 2004, ISBN , 208 s. [4] Ferda, J.: Výpočetní tomografie. První vydání, Galén, 2002, 663 s. [5] Jan, J.: Číslicová filtrace, analýza a restaurace signálů. druhé vydání, VUTIUM, 2002, 427 s. [6] Kubínek, R.: CT-artefakty. [online], Navštíveno URL [7] Sorapong Aootaphao, C. P.; Sotthivirat, S.: Penalized-Likelihood Reconstruction for Metal Artifact Reduction in Cone-Beam CT. In International IEEE EMBS Conference, [8] SÚJB. [online], Navštíveno URL [9] The Sampling Theorem. [online], Navštíveno URL [10] Toshiba. [online], Navštíveno URL [11] Toshiba Medical. [online], Navštíveno URL index.php [12] Válek, V.; Eliáš, P.; Petr Máca, J. N.: Moderní diagnostické metody-ii. díl- Výpočetní tomografie. Institut pro další vzdělávání pracovníků ve zdravotníků v Brně. [13] Varian medical systems. [online], Navštíveno URL [14] Wikipedia. [online], Navštíveno URL 38
49 [15] Youngshin Kim, S. Y.; Yi, J.: EFFECTIVE SINOGRAM-INPAINTING FOR METAL ARTIFACTS REDUCTION IN X-RAY CT IMAGES. In International Conference on Image Processing, [16] Zaplatílek, K.; Doňar, B.: Matlab - tvorba uživatelských aplikací. První vydání, BEN - technická literatura, 2008, ISBN , 216 s. [17] Zerfowski, D.: Motion artifact compensation in CT. In Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Presented at the Society of Photo-Optical Instrumentation Engineers (SPIE) Conference, ročník 3338, editace K. M. Hanson, Červen 1998, s
50 SEZNAM PŘÍLOH A Obsah přiloženého DVD 41 40
51 A OBSAH PŘILOŽENÉHO DVD Přiložené DVD obsahuje: Bakalářská práce v PDF Laboratorní úloha Simulátor CT artefaktů Knihovna modelů scén 41
CT - artefakty. Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová fyzika
 CT - artefakty Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová fyzika Artefakty v CT Systematické neshody v CT číslech v rekonstruovaném obraze oproti skutečné hodnotě koeficientu zeslabení
CT - artefakty Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová fyzika Artefakty v CT Systematické neshody v CT číslech v rekonstruovaném obraze oproti skutečné hodnotě koeficientu zeslabení
Základy výpočetní tomografie
 Základy výpočetní tomografie Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová technika Základní principy výpočetní tomografie Výpočetní tomografie - CT (Computed Tomography) CT je obecné označení
Základy výpočetní tomografie Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová technika Základní principy výpočetní tomografie Výpočetní tomografie - CT (Computed Tomography) CT je obecné označení
Šum v obraze CT. Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová fyzika
 Šum v obraze CT Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová fyzika Šum v CT obraze co to je? proč je důležitý jak ho měřit? šum a skenovací parametry - osové skenovací parametry - spirálové
Šum v obraze CT Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová fyzika Šum v CT obraze co to je? proč je důležitý jak ho měřit? šum a skenovací parametry - osové skenovací parametry - spirálové
Princip CT. MUDr. Lukáš Mikšík, KZM FN Motol
 Princip CT MUDr. Lukáš Mikšík, KZM FN Motol Tomografie tomos = řez; graphein = psát definice - zobrazení objektu pomocí řezů Damien Hirst Autopsy with Sliced Human Brain 2004 Historie 1924 - matematická
Princip CT MUDr. Lukáš Mikšík, KZM FN Motol Tomografie tomos = řez; graphein = psát definice - zobrazení objektu pomocí řezů Damien Hirst Autopsy with Sliced Human Brain 2004 Historie 1924 - matematická
CT-prostorové rozlišení a citlivost z
 CT-prostorové rozlišení a citlivost z Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová fyzika Prostorové rozlišení a citlivost z Prostorové rozlišení význam vyjádření rozlišení měření rozlišení
CT-prostorové rozlišení a citlivost z Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová fyzika Prostorové rozlišení a citlivost z Prostorové rozlišení význam vyjádření rozlišení měření rozlišení
Konstrukce výpočetního tomografu. Jiří Ferda, Hynek Mírka Klinika zobrazovacích metod LFUK a FN v Plzni
 Konstrukce výpočetního tomografu Jiří Ferda, Hynek Mírka Klinika zobrazovacích metod LFUK a FN v Plzni Výpočetní tomografie Hlavní indikace Urgentní diagnostika Plicní parenchym Skelet Srdce a cévy CT
Konstrukce výpočetního tomografu Jiří Ferda, Hynek Mírka Klinika zobrazovacích metod LFUK a FN v Plzni Výpočetní tomografie Hlavní indikace Urgentní diagnostika Plicní parenchym Skelet Srdce a cévy CT
Měření absorbce záření gama
 Měření absorbce záření gama Úkol : 1. Změřte záření gama přirozeného pozadí. 2. Změřte záření gama vyzářené gamazářičem. 3. Změřte záření gama vyzářené gamazářičem přes absorbátor. 4. Naměřené závislosti
Měření absorbce záření gama Úkol : 1. Změřte záření gama přirozeného pozadí. 2. Změřte záření gama vyzářené gamazářičem. 3. Změřte záření gama vyzářené gamazářičem přes absorbátor. 4. Naměřené závislosti
Rekonstrukce obrazu. Jiří Ferda, Hynek Mírka. Klinika zobrazovacích metod LFUK a FN v Plzni
 Rekonstrukce obrazu Jiří Ferda, Hynek Mírka Klinika zobrazovacích metod LFUK a FN v Plzni Hrubá data Raw data Data získaná detektorovou soustavou Výchozí soubor pro výpočet atenuace a rekonstrukci obrazů
Rekonstrukce obrazu Jiří Ferda, Hynek Mírka Klinika zobrazovacích metod LFUK a FN v Plzni Hrubá data Raw data Data získaná detektorovou soustavou Výchozí soubor pro výpočet atenuace a rekonstrukci obrazů
Skenovací parametry. H.Mírka, J. Ferda, KZM LFUK a FN Plzeň
 Skenovací parametry H.Mírka, J. Ferda, KZM LFUK a FN Plzeň Skenovací parametry Expozice Kolimace Faktor stoupání Perioda rotace Akvizice. ovlivňují způsob akvizice. závisí na nich kvalita hrubých dat.
Skenovací parametry H.Mírka, J. Ferda, KZM LFUK a FN Plzeň Skenovací parametry Expozice Kolimace Faktor stoupání Perioda rotace Akvizice. ovlivňují způsob akvizice. závisí na nich kvalita hrubých dat.
VYUŽITÍ MATLABU PRO PODPORU VÝUKY A PŘI ŘEŠENÍ VÝZKUMNÝCH ÚKOLŮ NA KATEDŘE KOMUNIKAČNÍCH A INFORMAČNÍCH SYSTÉMŮ
 VYUŽITÍ MATLABU PRO PODPORU VÝUKY A PŘI ŘEŠENÍ VÝZKUMNÝCH ÚKOLŮ NA KATEDŘE KOMUNIKAČNÍCH A INFORMAČNÍCH SYSTÉMŮ Markéta Mazálková Katedra komunikačních a informačních systémů Fakulta vojenských technologií,
VYUŽITÍ MATLABU PRO PODPORU VÝUKY A PŘI ŘEŠENÍ VÝZKUMNÝCH ÚKOLŮ NA KATEDŘE KOMUNIKAČNÍCH A INFORMAČNÍCH SYSTÉMŮ Markéta Mazálková Katedra komunikačních a informačních systémů Fakulta vojenských technologií,
Obrazové parametry. H.Mírka, J. Ferda, KZM LFUK a FN Plzeň. Z jedné sady hrubých dat je možno vytvořit mnoho obrazů různé kvality
 Obrazové parametry H.Mírka, J. Ferda, KZM LFUK a FN Plzeň Z jedné sady hrubých dat je možno vytvořit mnoho obrazů různé kvality Obrazové parametry. výpočet obrazu z hrubých dat. je možno je opakovaně měnit
Obrazové parametry H.Mírka, J. Ferda, KZM LFUK a FN Plzeň Z jedné sady hrubých dat je možno vytvořit mnoho obrazů různé kvality Obrazové parametry. výpočet obrazu z hrubých dat. je možno je opakovaně měnit
Pohled do historie. -Wilhelm Conrad Röntgen - objev X-paprsků ,
 RTG a CT biofyzika Pohled do historie -Wilhelm Conrad Röntgen - objev X-paprsků 11.8.1895, Nobelova cena za fyziku - 1901-1897 - první vyráběné rentgeny (plynem plněná rentgenka) - 1902 - změření vlnové
RTG a CT biofyzika Pohled do historie -Wilhelm Conrad Röntgen - objev X-paprsků 11.8.1895, Nobelova cena za fyziku - 1901-1897 - první vyráběné rentgeny (plynem plněná rentgenka) - 1902 - změření vlnové
Ultrazvukové diagnostické přístroje. X31ZLE Základy lékařské elektroniky Jan Havlík Katedra teorie obvodů xhavlikj@fel.cvut.cz
 Ultrazvukové diagnostické přístroje X31ZLE Základy lékařské elektroniky Jan Havlík Katedra teorie obvodů xhavlikj@fel.cvut.cz Ultrazvuková diagnostika v medicíně Ultrazvuková diagnostika diagnostická zobrazovací
Ultrazvukové diagnostické přístroje X31ZLE Základy lékařské elektroniky Jan Havlík Katedra teorie obvodů xhavlikj@fel.cvut.cz Ultrazvuková diagnostika v medicíně Ultrazvuková diagnostika diagnostická zobrazovací
Zobrazování. Zdeněk Tošner
 Zobrazování Zdeněk Tošner Ultrazvuk Zobrazování pomocí magnetické rezonance Rentgen a počítačová tomografie (CT) Ultrazvuk Akustické vlnění 20 khz 1 GHz materiálová defektoskopie sonar sonografie (v lékařství
Zobrazování Zdeněk Tošner Ultrazvuk Zobrazování pomocí magnetické rezonance Rentgen a počítačová tomografie (CT) Ultrazvuk Akustické vlnění 20 khz 1 GHz materiálová defektoskopie sonar sonografie (v lékařství
Zobrazovací systémy v transmisní radiografii a kvalita obrazu. Kateřina Boušková Nemocnice Na Františku
 Zobrazovací systémy v transmisní radiografii a kvalita obrazu Kateřina Boušková Nemocnice Na Františku Rentgenové záření Elektromagnetické záření o λ= 10-8 10-13 m V lékařství obvykle zdrojem rentgenová
Zobrazovací systémy v transmisní radiografii a kvalita obrazu Kateřina Boušková Nemocnice Na Františku Rentgenové záření Elektromagnetické záření o λ= 10-8 10-13 m V lékařství obvykle zdrojem rentgenová
VÝUKOVÝ MATERIÁL. 0301 Ing. Yvona Bečičková Tematická oblast. Vlnění, optika Číslo a název materiálu VY_32_INOVACE_0301_0310 Anotace
 VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
Signál v čase a jeho spektrum
 Signál v čase a jeho spektrum Signály v časovém průběhu (tak jak je vidíme na osciloskopu) můžeme dělit na periodické a neperiodické. V obou případech je lze popsat spektrálně určit jaké kmitočty v sobě
Signál v čase a jeho spektrum Signály v časovém průběhu (tak jak je vidíme na osciloskopu) můžeme dělit na periodické a neperiodické. V obou případech je lze popsat spektrálně určit jaké kmitočty v sobě
SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY
 SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY TEMATICKÉ OKRUHY Signály se spojitým časem Základní signály se spojitým časem (základní spojité signály) Jednotkový skok σ (t), jednotkový impuls (Diracův impuls)
SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY TEMATICKÉ OKRUHY Signály se spojitým časem Základní signály se spojitým časem (základní spojité signály) Jednotkový skok σ (t), jednotkový impuls (Diracův impuls)
Ultrazvukové diagnostické přístroje. X31LET Lékařskátechnika Jan Havlík Katedra teorie obvodů xhavlikj@fel.cvut.cz
 Ultrazvukové diagnostické přístroje X31LET Lékařskátechnika Jan Havlík Katedra teorie obvodů xhavlikj@fel.cvut.cz Ultrazvukové diagnostické přístroje 1. Ultrazvuková diagnostika v medicíně 2. Fyzikální
Ultrazvukové diagnostické přístroje X31LET Lékařskátechnika Jan Havlík Katedra teorie obvodů xhavlikj@fel.cvut.cz Ultrazvukové diagnostické přístroje 1. Ultrazvuková diagnostika v medicíně 2. Fyzikální
Fotonásobič. fotokatoda. typicky: - koeficient sekundární emise = počet dynod N = zisk: G = fokusační elektrononová optika
 Fotonásobič vstupní okno fotokatoda E h fokusační elektrononová optika systém dynod anoda e zesílení G N typicky: - koeficient sekundární emise = 3 4 - počet dynod N = 10 12 - zisk: G = 10 5-10 7 Fotonásobič
Fotonásobič vstupní okno fotokatoda E h fokusační elektrononová optika systém dynod anoda e zesílení G N typicky: - koeficient sekundární emise = 3 4 - počet dynod N = 10 12 - zisk: G = 10 5-10 7 Fotonásobič
Fourierovské metody v teorii difrakce a ve strukturní analýze
 Osnova přednášky na 31 kolokviu Krystalografické společnosti Výpočetní metody v rtg a neutronové strukturní analýze Nové Hrady, 16 20 6 2003 Fourierovské metody v teorii difrakce a ve strukturní analýze
Osnova přednášky na 31 kolokviu Krystalografické společnosti Výpočetní metody v rtg a neutronové strukturní analýze Nové Hrady, 16 20 6 2003 Fourierovské metody v teorii difrakce a ve strukturní analýze
Spektrální charakteristiky
 Spektrální charakteristiky Cíl cvičení: Měření spektrálních charakteristik filtrů a zdrojů osvětlení 1 Teoretický úvod Interakcí elektromagnetického vlnění s libovolnou látkou vzniká optický jev, který
Spektrální charakteristiky Cíl cvičení: Měření spektrálních charakteristik filtrů a zdrojů osvětlení 1 Teoretický úvod Interakcí elektromagnetického vlnění s libovolnou látkou vzniká optický jev, který
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV BIOMEDICÍNSKÉHO INŽENÝRSTVÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV BIOMEDICÍNSKÉHO INŽENÝRSTVÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT
MODELOVÁNÍ REKONSTRUKCE OBRAZU PŘI CT RTG FLUOROSKOPII
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV BIOMEDICÍNSKÉHO INŽENÝRSTVÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV BIOMEDICÍNSKÉHO INŽENÝRSTVÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT
Konference radiologické fyziky 2010 a členská schůze ČSFM
 Konference radiologické fyziky 2010 a členská schůze ČSFM Kouty nad Desnou, 2.-4.6.2010 Vladimír Dufek Diplomová práce Stanovení dávek pacientů z lokalizačních a verifikačních metod používaných v obrazem
Konference radiologické fyziky 2010 a členská schůze ČSFM Kouty nad Desnou, 2.-4.6.2010 Vladimír Dufek Diplomová práce Stanovení dávek pacientů z lokalizačních a verifikačních metod používaných v obrazem
Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného)
 Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného) 1 Obecný popis metody Particle Image Velocimetry, nebo-li zkráceně PIV, je měřící
Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného) 1 Obecný popis metody Particle Image Velocimetry, nebo-li zkráceně PIV, je měřící
VYUŽITÍ PRAVDĚPODOBNOSTNÍ METODY MONTE CARLO V SOUDNÍM INŽENÝRSTVÍ
 VYUŽITÍ PRAVDĚPODOBNOSTNÍ METODY MONTE CARLO V SOUDNÍM INŽENÝRSTVÍ Michal Kořenář 1 Abstrakt Rozvoj výpočetní techniky v poslední době umožnil také rozvoj výpočetních metod, které nejsou založeny na bázi
VYUŽITÍ PRAVDĚPODOBNOSTNÍ METODY MONTE CARLO V SOUDNÍM INŽENÝRSTVÍ Michal Kořenář 1 Abstrakt Rozvoj výpočetní techniky v poslední době umožnil také rozvoj výpočetních metod, které nejsou založeny na bázi
DETEKCE HRAN V BIOMEDICÍNSKÝCH OBRAZECH
 DETEKCE HRAN V BIOMEDICÍNSKÝCH OBRAZECH Viktor Haškovec, Martina Mudrová Vysoká škola chemicko-technologická v Praze, Ústav počítačové a řídicí techniky Abstrakt Příspěvek je věnován zpracování biomedicínských
DETEKCE HRAN V BIOMEDICÍNSKÝCH OBRAZECH Viktor Haškovec, Martina Mudrová Vysoká škola chemicko-technologická v Praze, Ústav počítačové a řídicí techniky Abstrakt Příspěvek je věnován zpracování biomedicínských
MĚŘENÍ A ANALÝZA ELEKTROAKUSTICKÝCH SOUSTAV NA MODELECH. Petr Kopecký ČVUT, Fakulta elektrotechnická, Katedra Radioelektroniky
 MĚŘENÍ A ANALÝZA ELEKTROAKUSTICKÝCH SOUSTAV NA MODELECH Petr Kopecký ČVUT, Fakulta elektrotechnická, Katedra Radioelektroniky Při návrhu elektroakustických soustav, ale i jiných systémů, je vhodné nejprve
MĚŘENÍ A ANALÝZA ELEKTROAKUSTICKÝCH SOUSTAV NA MODELECH Petr Kopecký ČVUT, Fakulta elektrotechnická, Katedra Radioelektroniky Při návrhu elektroakustických soustav, ale i jiných systémů, je vhodné nejprve
BBZS - Zobrazovací systémy
 2016-06-05 06:59 1/11 BBZS - Zobrazovací systémy BBZS - Zobrazovací systémy Převodní charakteristiky Otázky ke zkoušce Energie elektromagnetického zárení se dá vyjádrit jako E = h.v a jednotkou bude J.
2016-06-05 06:59 1/11 BBZS - Zobrazovací systémy BBZS - Zobrazovací systémy Převodní charakteristiky Otázky ke zkoušce Energie elektromagnetického zárení se dá vyjádrit jako E = h.v a jednotkou bude J.
Měření vlastností datového kanálu
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta elektrotechnická ÚLOHA E Měření vlastností datového kanálu Vypracoval: V rámci předmětu: Jan HLÍDEK Základy datové komunikace (X32ZDK) Měřeno: 14. 4. 2008 Cvičení:
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta elektrotechnická ÚLOHA E Měření vlastností datového kanálu Vypracoval: V rámci předmětu: Jan HLÍDEK Základy datové komunikace (X32ZDK) Měřeno: 14. 4. 2008 Cvičení:
Úvod do zpracování signálů
 1 / 25 Úvod do zpracování signálů Karel Horák Rozvrh přednášky: 1. Spojitý a diskrétní signál. 2. Spektrum signálu. 3. Vzorkovací věta. 4. Konvoluce signálů. 5. Korelace signálů. 2 / 25 Úvod do zpracování
1 / 25 Úvod do zpracování signálů Karel Horák Rozvrh přednášky: 1. Spojitý a diskrétní signál. 2. Spektrum signálu. 3. Vzorkovací věta. 4. Konvoluce signálů. 5. Korelace signálů. 2 / 25 Úvod do zpracování
Ultrasonografická diagnostika v medicíně. Daniel Smutek 3. interní klinika 1.LF UK a VFN
 Ultrasonografická diagnostika v medicíně Daniel Smutek 3. interní klinika 1.LF UK a VFN frekvence 2-15 MHz rychlost šíření vzduch: 330 m.s -1 kost: 1080 m.s -1 měkké tkáně: průměrně 1540 m.s -1 tuk: 1450
Ultrasonografická diagnostika v medicíně Daniel Smutek 3. interní klinika 1.LF UK a VFN frekvence 2-15 MHz rychlost šíření vzduch: 330 m.s -1 kost: 1080 m.s -1 měkké tkáně: průměrně 1540 m.s -1 tuk: 1450
Voda a život Wasser und Leben
 Počítání fólií měřením úbytku světla Cíl: Cílem této úlohy je připravit u žáků půdu pro pochopení důležité fyzikálně-chemické metody: stanovení koncentrace měřením absorbance s využitím Lambertova-Beerova
Počítání fólií měřením úbytku světla Cíl: Cílem této úlohy je připravit u žáků půdu pro pochopení důležité fyzikálně-chemické metody: stanovení koncentrace měřením absorbance s využitím Lambertova-Beerova
ZÁKLADNÍ METODY REFLEKTOMETRIE
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV RADIOELEKTRONIKY FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV RADIOELEKTRONIKY FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF
MATLAB PRO PODPORU VÝUKY KOMUNIKAČNÍCH SYSTÉMŮ
 MATLAB PRO PODPORU VÝUKY KOMUNIKAČNÍCH SYSTÉMŮ Aneta Coufalíková, Markéta Smejkalová Mazálková Univerzita obrany Katedra Komunikačních a informačních systémů Matlab ve výuce V rámci modernizace výuky byl
MATLAB PRO PODPORU VÝUKY KOMUNIKAČNÍCH SYSTÉMŮ Aneta Coufalíková, Markéta Smejkalová Mazálková Univerzita obrany Katedra Komunikačních a informačních systémů Matlab ve výuce V rámci modernizace výuky byl
31SCS Speciální číslicové systémy Antialiasing
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE 2006/2007 31SCS Speciální číslicové systémy Antialiasing Vypracoval: Ivo Vágner Email: Vagnei1@seznam.cz 1/7 Převod analogového signálu na digitální Složité operace,
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE 2006/2007 31SCS Speciální číslicové systémy Antialiasing Vypracoval: Ivo Vágner Email: Vagnei1@seznam.cz 1/7 Převod analogového signálu na digitální Složité operace,
VÝUKOVÝ SOFTWARE PRO ANALÝZU A VIZUALIZACI INTERFERENČNÍCH JEVŮ
 VÝUKOVÝ SOFTWARE PRO ANALÝZU A VIZUALIZACI INTERFERENČNÍCH JEVŮ P. Novák, J. Novák Katedra fyziky, Fakulta stavební, České vysoké učení technické v Praze Abstrakt V práci je popsán výukový software pro
VÝUKOVÝ SOFTWARE PRO ANALÝZU A VIZUALIZACI INTERFERENČNÍCH JEVŮ P. Novák, J. Novák Katedra fyziky, Fakulta stavební, České vysoké učení technické v Praze Abstrakt V práci je popsán výukový software pro
Operace s obrazem I. Biofyzikální ústav Lékařské fakulty Masarykovy univerzity Brno. prezentace je součástí projektu FRVŠ č.
 Operace s obrazem I Biofyzikální ústav Lékařské fakulty Masarykovy univerzity Brno prezentace je součástí projektu FRVŠ č.2487/2011 Osnova 1 Filtrování obrazu 2 Lineární a nelineární filtry 3 Fourierova
Operace s obrazem I Biofyzikální ústav Lékařské fakulty Masarykovy univerzity Brno prezentace je součástí projektu FRVŠ č.2487/2011 Osnova 1 Filtrování obrazu 2 Lineární a nelineární filtry 3 Fourierova
KTE/TEVS - Rychlá Fourierova transformace. Pavel Karban. Katedra teoretické elektrotechniky Fakulta elektrotechnická Západočeská univerzita v Plzni
 KTE/TEVS - Rychlá Fourierova transformace Pavel Karban Katedra teoretické elektrotechniky Fakulta elektrotechnická Západočeská univerzita v Plzni 10.11.011 Outline 1 Motivace FT Fourierova transformace
KTE/TEVS - Rychlá Fourierova transformace Pavel Karban Katedra teoretické elektrotechniky Fakulta elektrotechnická Západočeská univerzita v Plzni 10.11.011 Outline 1 Motivace FT Fourierova transformace
13 Barvy a úpravy rastrového
 13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
pracovní list studenta
 Výstup RVP: Klíčová slova: pracovní list studenta Goniometrické funkce Mirek Kubera žák načrtne grafy elementárních funkcí a určí jejich vlastnosti, při konstrukci grafů aplikuje znalosti o zobrazeních,
Výstup RVP: Klíčová slova: pracovní list studenta Goniometrické funkce Mirek Kubera žák načrtne grafy elementárních funkcí a určí jejich vlastnosti, při konstrukci grafů aplikuje znalosti o zobrazeních,
Quantization of acoustic low level signals. David Bursík, Miroslav Lukeš
 KVANTOVÁNÍ ZVUKOVÝCH SIGNÁLŮ NÍZKÉ ÚROVNĚ Abstrakt Quantization of acoustic low level signals David Bursík, Miroslav Lukeš Při testování kvality A/D převodníků se používají nejrůznější testovací signály.
KVANTOVÁNÍ ZVUKOVÝCH SIGNÁLŮ NÍZKÉ ÚROVNĚ Abstrakt Quantization of acoustic low level signals David Bursík, Miroslav Lukeš Při testování kvality A/D převodníků se používají nejrůznější testovací signály.
POČÍTAČOVÁ TOMOGRAFIE V ZOBRAZOVÁNÍ MALÝCH ZVÍŘAT ÚVOD. René Kizek. Název: Školitel: Datum: 20.09.2013
 Název: Školitel: POČÍTAČOVÁ TOMOGRAFIE V ZOBRAZOVÁNÍ MALÝCH ZVÍŘAT ÚVOD René Kizek Datum: 20.09.2013 Základy počítačové tomografie položil W. C. Röntgen, který roku 1895 objevil paprsky X. Tyto paprsky,
Název: Školitel: POČÍTAČOVÁ TOMOGRAFIE V ZOBRAZOVÁNÍ MALÝCH ZVÍŘAT ÚVOD René Kizek Datum: 20.09.2013 Základy počítačové tomografie položil W. C. Röntgen, který roku 1895 objevil paprsky X. Tyto paprsky,
Rovinné přetvoření. Posunutí (translace) TEORIE K M2A+ULA
 Rovinné přetvoření Rovinné přetvoření, neboli, jak se také často nazývá, geometrická transformace je vlastně lineární zobrazení v prostoru s nějakou soustavou souřadnic. Jde v něm o přepočet souřadnic
Rovinné přetvoření Rovinné přetvoření, neboli, jak se také často nazývá, geometrická transformace je vlastně lineární zobrazení v prostoru s nějakou soustavou souřadnic. Jde v něm o přepočet souřadnic
Úloha 4: Totální účinný průřez interakce γ záření absorpční koeficient záření gama pro některé elementy
 Petra Suková, 3.ročník 1 Úloha 4: Totální účinný průřez interakce γ záření absorpční koeficient záření gama pro některé elementy 1 Zadání 1. UrčeteabsorpčníkoeficientzářenígamaproelementyFe,CdaPbvzávislostinaenergii
Petra Suková, 3.ročník 1 Úloha 4: Totální účinný průřez interakce γ záření absorpční koeficient záření gama pro některé elementy 1 Zadání 1. UrčeteabsorpčníkoeficientzářenígamaproelementyFe,CdaPbvzávislostinaenergii
Modulace a šum signálu
 Modulace a šum signálu PATRIK KANIA a ŠTĚPÁN URBAN Nejlepší laboratoř molekulové spektroskopie vysokého rozlišení Ústav analytické chemie, VŠCHT Praha kaniap@vscht.cz a urbans@vscht.cz http://www.vscht.cz/anl/lmsvr
Modulace a šum signálu PATRIK KANIA a ŠTĚPÁN URBAN Nejlepší laboratoř molekulové spektroskopie vysokého rozlišení Ústav analytické chemie, VŠCHT Praha kaniap@vscht.cz a urbans@vscht.cz http://www.vscht.cz/anl/lmsvr
FRVŠ 2829/2011/G1. Tvorba modelu materiálu pro živé tkáně
 FOND ROZVOJE VYSOKÝCH ŠKOL 2011 FRVŠ 2829/2011/G1 Tvorba modelu materiálu pro živé tkáně Řešitel: Ing. Jiří Valášek Vysoké učení technické v Brně Fakulta strojního inženýrství Spoluřešitel 1: Ing. David
FOND ROZVOJE VYSOKÝCH ŠKOL 2011 FRVŠ 2829/2011/G1 Tvorba modelu materiálu pro živé tkáně Řešitel: Ing. Jiří Valášek Vysoké učení technické v Brně Fakulta strojního inženýrství Spoluřešitel 1: Ing. David
25 A Vypracoval : Zdeněk Žák Pyrometrie υ = -40 C.. +10000 C. Výhody termovize Senzory infračerveného záření Rozdělení tepelné senzory
 25 A Vypracoval : Zdeněk Žák Pyrometrie Bezdotykové měření Pyrometrie (obrázky viz. sešit) Bezdotykové měření teplot je měření povrchové teploty těles na základě elektromagnetického záření mezi tělesem
25 A Vypracoval : Zdeněk Žák Pyrometrie Bezdotykové měření Pyrometrie (obrázky viz. sešit) Bezdotykové měření teplot je měření povrchové teploty těles na základě elektromagnetického záření mezi tělesem
Interpolace trojrozměrných dat magnetické rezonance
 Rok / Year: Svazek / Volume: Číslo / Number: 2010 12 2 Interpolace trojrozměrných dat magnetické rezonance Interpolation of magnetic resonance threedimensional data Jan Mikulka mikulka@feec.vutbr.cz Ústav
Rok / Year: Svazek / Volume: Číslo / Number: 2010 12 2 Interpolace trojrozměrných dat magnetické rezonance Interpolation of magnetic resonance threedimensional data Jan Mikulka mikulka@feec.vutbr.cz Ústav
Ing. Jan Buriánek. Katedra softwarového inženýrství Fakulta informačních technologií České vysoké učení technické v Praze Jan Buriánek, 2010
 Ing. Jan Buriánek (ČVUT FIT) Reprezentace bodu a zobrazení BI-MGA, 2010, Přednáška 2 1/33 Ing. Jan Buriánek Katedra softwarového inženýrství Fakulta informačních technologií České vysoké učení technické
Ing. Jan Buriánek (ČVUT FIT) Reprezentace bodu a zobrazení BI-MGA, 2010, Přednáška 2 1/33 Ing. Jan Buriánek Katedra softwarového inženýrství Fakulta informačních technologií České vysoké učení technické
FYZIKA Elektromagnetické vlnění
 Výukový materiál zpracován v rámci operačního projektu EU peníze školám Registrační číslo projektu: CZ.1.07/1.5.00/34.0512 Střední škola ekonomiky, obchodu a služeb SČMSD Benešov, s.r.o. FYZIKA Elektromagnetické
Výukový materiál zpracován v rámci operačního projektu EU peníze školám Registrační číslo projektu: CZ.1.07/1.5.00/34.0512 Střední škola ekonomiky, obchodu a služeb SČMSD Benešov, s.r.o. FYZIKA Elektromagnetické
Radioterapie. X31LET Lékařská technika Jan Havlík Katedra teorie obvodů xhavlikj@fel.cvut.cz
 Radioterapie X31LET Lékařská technika Jan Havlík Katedra teorie obvodů xhavlikj@fel.cvut.cz Radioterapie je klinický obor využívající účinků ionizujícího záření v léčbě jak zhoubných, tak nezhoubných nádorů
Radioterapie X31LET Lékařská technika Jan Havlík Katedra teorie obvodů xhavlikj@fel.cvut.cz Radioterapie je klinický obor využívající účinků ionizujícího záření v léčbě jak zhoubných, tak nezhoubných nádorů
Fyzikální sekce přírodovědecké fakulty Masarykovy univerzity v Brně FYZIKÁLNÍ PRAKTIKUM. Praktikum z pevných látek (F6390)
 Fyzikální sekce přírodovědecké fakulty Masarykovy univerzity v Brně FYZIKÁLNÍ PRAKTIKUM Praktikum z pevných látek (F6390) Zpracoval: Michal Truhlář Naměřeno: 6. března 2007 Obor: Fyzika Ročník: III Semestr:
Fyzikální sekce přírodovědecké fakulty Masarykovy univerzity v Brně FYZIKÁLNÍ PRAKTIKUM Praktikum z pevných látek (F6390) Zpracoval: Michal Truhlář Naměřeno: 6. března 2007 Obor: Fyzika Ročník: III Semestr:
Dosah γ záření ve vzduchu
 Dosah γ záření ve vzduchu Intenzita bodového zdroje γ záření se mění podobně jako intenzita bodového zdroje světla. Ve dvojnásobné vzdálenosti, paprsek pokrývá dvakrát větší oblast povrchu, což znamená,
Dosah γ záření ve vzduchu Intenzita bodového zdroje γ záření se mění podobně jako intenzita bodového zdroje světla. Ve dvojnásobné vzdálenosti, paprsek pokrývá dvakrát větší oblast povrchu, což znamená,
Fázorové diagramy pro ideální rezistor, skutečná cívka, ideální cívka, skutečný kondenzátor, ideální kondenzátor.
 FREKVENČNĚ ZÁVISLÉ OBVODY Základní pojmy: IMPEDANCE Z (Ω)- charakterizuje vlastnosti prvku pro střídavý proud. Impedance je základní vlastností, kterou potřebujeme znát pro analýzu střídavých elektrických
FREKVENČNĚ ZÁVISLÉ OBVODY Základní pojmy: IMPEDANCE Z (Ω)- charakterizuje vlastnosti prvku pro střídavý proud. Impedance je základní vlastností, kterou potřebujeme znát pro analýzu střídavých elektrických
Laboratoř RTG tomografice CET
 Výzkumná zpráva Pro projekt NAKI DF12P01OVV020 Komplexní metodika pro výběr a řemeslné opracování náhradního kamene pro opravy kvádrového zdiva historických objektů Laboratoř RTG tomografice CET Vypracovala:
Výzkumná zpráva Pro projekt NAKI DF12P01OVV020 Komplexní metodika pro výběr a řemeslné opracování náhradního kamene pro opravy kvádrového zdiva historických objektů Laboratoř RTG tomografice CET Vypracovala:
Primární zpracování radarového signálu dopplerovská filtrace
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE K13137 - Katedra radioelektroniky A2M37RSY Jméno Stud. rok Stud. skupina Ročník Lab. skupina Václav Dajčar 2011/2012 2. 101 - Datum zadání Datum odevzdání Klasifikace
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE K13137 - Katedra radioelektroniky A2M37RSY Jméno Stud. rok Stud. skupina Ročník Lab. skupina Václav Dajčar 2011/2012 2. 101 - Datum zadání Datum odevzdání Klasifikace
DECT S VYUŽITÍM ITERATIVNÍ REKONSTRUKCE DAT ALGORITMEM SAFIRE
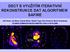 DECT S VYUŽITÍM ITERATIVNÍ REKONSTRUKCE DAT ALGORITMEM SAFIRE Jiří Ferda, Jan Baxa, Hynek Mírka, Radek Tupý, Eva Ferdová, Boris Kreuzberg KLINIKA ZOBRAZOVACÍCH METOD LFUK A FN PLZEŇ CÍL Porovnat MDCT
DECT S VYUŽITÍM ITERATIVNÍ REKONSTRUKCE DAT ALGORITMEM SAFIRE Jiří Ferda, Jan Baxa, Hynek Mírka, Radek Tupý, Eva Ferdová, Boris Kreuzberg KLINIKA ZOBRAZOVACÍCH METOD LFUK A FN PLZEŇ CÍL Porovnat MDCT
TSO NEBO A INVARIANTNÍ ROZPOZNÁVACÍ SYSTÉMY
 TSO NEBO A INVARIANTNÍ ROZPOZNÁVACÍ SYSTÉMY V PROSTŘEDÍ MATLAB K. Nováková, J. Kukal FJFI, ČVUT v Praze ÚPŘT, VŠCHT Praha Abstrakt Při rozpoznávání D binárních objektů z jejich diskrétní realizace se využívají
TSO NEBO A INVARIANTNÍ ROZPOZNÁVACÍ SYSTÉMY V PROSTŘEDÍ MATLAB K. Nováková, J. Kukal FJFI, ČVUT v Praze ÚPŘT, VŠCHT Praha Abstrakt Při rozpoznávání D binárních objektů z jejich diskrétní realizace se využívají
Zjistil, že při dopadu elektronů s velkou kinetickou energií na kovovou anodu vzniká záření, které proniká i neprůhlednými předměty.
 2.snímek Historie rentgenového záření Na počátku vzniku stál německý fyzik W.C. Röntgen (1845-1923). V roce 1895 objevil při studiu výbojů v plynech neznámý druh záření. Röntgen zkoumal katodové záření,
2.snímek Historie rentgenového záření Na počátku vzniku stál německý fyzik W.C. Röntgen (1845-1923). V roce 1895 objevil při studiu výbojů v plynech neznámý druh záření. Röntgen zkoumal katodové záření,
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Příklady použití tenkých vrstev Jaromír Křepelka
 Příklady použití tenkých vrstev Jaromír Křepelka Příklad 01 Spočtěte odrazivost prostého rozhraní dvou izotropních homogenních materiálů s indexy lomu n 0 = 1 a n 1 = 1,52 v závislosti na úhlu dopadu pro
Příklady použití tenkých vrstev Jaromír Křepelka Příklad 01 Spočtěte odrazivost prostého rozhraní dvou izotropních homogenních materiálů s indexy lomu n 0 = 1 a n 1 = 1,52 v závislosti na úhlu dopadu pro
Algoritmizace prostorových úloh
 INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Úlohy nad rastrovými daty Daniela
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Úlohy nad rastrovými daty Daniela
Reprezentace bodu, zobrazení
 Reprezentace bodu, zobrazení Ing. Jan Buriánek VOŠ a SŠSE P9 Jan.Burianek@gmail.com Obsah Témata Základní dělení grafických elementů Rastrový vs. vektorový obraz Rozlišení Interpolace Aliasing, moiré Zdroje
Reprezentace bodu, zobrazení Ing. Jan Buriánek VOŠ a SŠSE P9 Jan.Burianek@gmail.com Obsah Témata Základní dělení grafických elementů Rastrový vs. vektorový obraz Rozlišení Interpolace Aliasing, moiré Zdroje
M ASARYKŮ V ONKOLOGICKÝ ÚSTAV Žlutý kopec 7, Brno
 PET. PET / CT, PET Centrum, Cyklotron Pozitronová emisní tomografie ( PET ) je neinvazivní vyšetřovací metoda nukleární medicíny založená na detekci záření z radiofarmaka podaného pacientovi.nejčastěji
PET. PET / CT, PET Centrum, Cyklotron Pozitronová emisní tomografie ( PET ) je neinvazivní vyšetřovací metoda nukleární medicíny založená na detekci záření z radiofarmaka podaného pacientovi.nejčastěji
MODELOVÁNÍ REKONSTRUKCE OBRAZU PŘI CT RTG FLUOROSKOPII
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV BIOMEDICÍNSKÉHO INŽENÝRSTVÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV BIOMEDICÍNSKÉHO INŽENÝRSTVÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT
ELT1 - Přednáška č. 6
 ELT1 - Přednáška č. 6 Elektrotechnická terminologie a odborné výrazy, měřicí jednotky a činitelé, které je ovlivňují. Rozdíl potenciálů, elektromotorická síla, napětí, el. napětí, proud, odpor, vodivost,
ELT1 - Přednáška č. 6 Elektrotechnická terminologie a odborné výrazy, měřicí jednotky a činitelé, které je ovlivňují. Rozdíl potenciálů, elektromotorická síla, napětí, el. napětí, proud, odpor, vodivost,
CT - dozimetrie. Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová fyzika
 CT - dozimetrie Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová fyzika CT dozimetrie Rozdělení dávky Definice dávky Instrumentace Definice CTDI Rizika, efektivní dávka Diagnostické referenční
CT - dozimetrie Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová fyzika CT dozimetrie Rozdělení dávky Definice dávky Instrumentace Definice CTDI Rizika, efektivní dávka Diagnostické referenční
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ KVANTITATIVNÍ HODNOCENÍ KVALITY CT RTG ZOBRAZENÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV BIOMEDICÍNSKÉHO INŽENÝRSTVÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV BIOMEDICÍNSKÉHO INŽENÝRSTVÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT
Identifikace typu záření
 Identifikace typu záření U radioaktivního záření rozeznáváme několik druhů, jejichž vlastnosti se diametrálně liší. Jednotlivé druhy rozeznáváme podle druhu emitovaného záření. Tyto druhy radioaktivity
Identifikace typu záření U radioaktivního záření rozeznáváme několik druhů, jejichž vlastnosti se diametrálně liší. Jednotlivé druhy rozeznáváme podle druhu emitovaného záření. Tyto druhy radioaktivity
DECT S VYUŽITÍM ITERATIVNÍ REKONSTRUKCE DAT ALGORITMEM SAFIRE
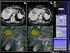 DECT S VYUŽITÍM ITERATIVNÍ REKONSTRUKCE DAT ALGORITMEM SAFIRE Jiří Ferda, Jan Baxa, Hynek Mírka, Radek Tupý, Eva Ferdová, Boris Kreuzberg KLINIKA ZOBRAZOVACÍCH METOD LFUK A FN PLZEŇ CÍL Porovnat MDCT
DECT S VYUŽITÍM ITERATIVNÍ REKONSTRUKCE DAT ALGORITMEM SAFIRE Jiří Ferda, Jan Baxa, Hynek Mírka, Radek Tupý, Eva Ferdová, Boris Kreuzberg KLINIKA ZOBRAZOVACÍCH METOD LFUK A FN PLZEŇ CÍL Porovnat MDCT
1 Základní funkce pro zpracování obrazových dat
 1 Základní funkce pro zpracování obrazových dat 1.1 Teoretický rozbor 1.1.1 Úvod do zpracování obrazu v MATLABu MATLAB je primárně určen pro zpracování a analýzu numerických dat. Pro analýzu obrazových
1 Základní funkce pro zpracování obrazových dat 1.1 Teoretický rozbor 1.1.1 Úvod do zpracování obrazu v MATLABu MATLAB je primárně určen pro zpracování a analýzu numerických dat. Pro analýzu obrazových
Pozorování Slunce s vysokým rozlišením. Michal Sobotka Astronomický ústav AV ČR, Ondřejov
 Pozorování Slunce s vysokým rozlišením Michal Sobotka Astronomický ústav AV ČR, Ondřejov Úvod Na Slunci se důležité děje odehrávají na malých prostorových škálách (desítky až stovky km). Granule mají typickou
Pozorování Slunce s vysokým rozlišením Michal Sobotka Astronomický ústav AV ČR, Ondřejov Úvod Na Slunci se důležité děje odehrávají na malých prostorových škálách (desítky až stovky km). Granule mají typickou
HISTORIE ZOBRAZOVACÍCH METOD V MEDICÍNĚ
 HISTORIE ZOBRAZOVACÍCH METOD V MEDICÍNĚ Doc.RNDr. Roman Kubínek, CSc. předmět: lékařská přístrojová technika Rozvoj radiologie, jako medicínského oboru začíná v prvním desetiletí 20. století objevem rtg.
HISTORIE ZOBRAZOVACÍCH METOD V MEDICÍNĚ Doc.RNDr. Roman Kubínek, CSc. předmět: lékařská přístrojová technika Rozvoj radiologie, jako medicínského oboru začíná v prvním desetiletí 20. století objevem rtg.
Absorpční polovrstva pro záření γ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojního inženýrství VUT FSI ÚFI 1ZM-10-ZS Ústav fyzikálního inženýrství Technická 2, Brno 616 69 Laboratoř A2-128 Absorpční polovrstva pro záření γ 12.10.2010 Měření
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojního inženýrství VUT FSI ÚFI 1ZM-10-ZS Ústav fyzikálního inženýrství Technická 2, Brno 616 69 Laboratoř A2-128 Absorpční polovrstva pro záření γ 12.10.2010 Měření
Speciální spektrometrické metody. Zpracování signálu ve spektroskopii
 Speciální spektrometrické metody Zpracování signálu ve spektroskopii detekce slabých signálů synchronní detekce (Lock-in) čítaní fotonů měření časového průběhu signálů metoda fázového posuvu časově korelované
Speciální spektrometrické metody Zpracování signálu ve spektroskopii detekce slabých signálů synchronní detekce (Lock-in) čítaní fotonů měření časového průběhu signálů metoda fázového posuvu časově korelované
Planmeca ProMax. zobrazovací možnosti panoramatického rentgenu
 Planmeca ProMax zobrazovací možnosti panoramatického rentgenu U panoramatického rentgenu nové generace Planmeca ProMax neexistuje žádné mechanické omezení geometrie zobrazení. Nastavit lze libovolné požadované
Planmeca ProMax zobrazovací možnosti panoramatického rentgenu U panoramatického rentgenu nové generace Planmeca ProMax neexistuje žádné mechanické omezení geometrie zobrazení. Nastavit lze libovolné požadované
Měření průtoku kapaliny s využitím digitální kamery
 Měření průtoku kapaliny s využitím digitální kamery Mareš, J., Vacek, M. Koudela, D. Vysoká škola chemicko-technologická Praha, Ústav počítačové a řídicí techniky, Technická 5, 166 28, Praha 6 e-mail:
Měření průtoku kapaliny s využitím digitální kamery Mareš, J., Vacek, M. Koudela, D. Vysoká škola chemicko-technologická Praha, Ústav počítačové a řídicí techniky, Technická 5, 166 28, Praha 6 e-mail:
Grafika na počítači. Bc. Veronika Tomsová
 Grafika na počítači Bc. Veronika Tomsová Proces zpracování obrazu Proces zpracování obrazu 1. Snímání obrazu 2. Digitalizace obrazu převod spojitého signálu na matici čísel reprezentující obraz 3. Předzpracování
Grafika na počítači Bc. Veronika Tomsová Proces zpracování obrazu Proces zpracování obrazu 1. Snímání obrazu 2. Digitalizace obrazu převod spojitého signálu na matici čísel reprezentující obraz 3. Předzpracování
Ultrazvuková defektoskopie. Vypracoval Jan Janský
 Ultrazvuková defektoskopie Vypracoval Jan Janský Základní principy použití vysokých akustických frekvencí pro zjištění vlastností máteriálu a vad typické zařízení: generátor/přijímač pulsů snímač zobrazovací
Ultrazvuková defektoskopie Vypracoval Jan Janský Základní principy použití vysokých akustických frekvencí pro zjištění vlastností máteriálu a vad typické zařízení: generátor/přijímač pulsů snímač zobrazovací
Elektrický signál - základní elektrické veličiny
 EVROPSKÝ SOCIÁLNÍ FOND Elektrický signál - základní elektrické veličiny PRAHA & EU INVESTUJEME DO VAŠÍ BUDOUCNOSTI Podpora kvality výuky informačních a telekomunikačních technologií ITTEL CZ.2.17/3.1.00/36206
EVROPSKÝ SOCIÁLNÍ FOND Elektrický signál - základní elektrické veličiny PRAHA & EU INVESTUJEME DO VAŠÍ BUDOUCNOSTI Podpora kvality výuky informačních a telekomunikačních technologií ITTEL CZ.2.17/3.1.00/36206
Balmerova série. F. Grepl 1, M. Benc 2, J. Stuchlý 3 Gymnázium Havlíčkův Brod 1, Gymnázium Mnichovo Hradiště 2, Gymnázium Šumperk 3
 Balmerova série F. Grepl 1, M. Benc 2, J. Stuchlý 3 Gymnázium Havlíčkův Brod 1, Gymnázium Mnichovo Hradiště 2, Gymnázium Šumperk 3 Grepl.F@seznam.cz Abstrakt: Metodou dělených svazků jsme určili lámavý
Balmerova série F. Grepl 1, M. Benc 2, J. Stuchlý 3 Gymnázium Havlíčkův Brod 1, Gymnázium Mnichovo Hradiště 2, Gymnázium Šumperk 3 Grepl.F@seznam.cz Abstrakt: Metodou dělených svazků jsme určili lámavý
Praktikum III - Optika
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum III - Optika Úloha č. 13 Název: Vlastnosti rentgenového záření Pracoval: Matyáš Řehák stud.sk.: 13 dne: 3. 4. 2008 Odevzdal
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum III - Optika Úloha č. 13 Název: Vlastnosti rentgenového záření Pracoval: Matyáš Řehák stud.sk.: 13 dne: 3. 4. 2008 Odevzdal
Fyzikální korespondenční seminář MFF UK
 Úloha V.E... nezbedné fotony 1 bodů; (chybí statistiky) Spolu se zadáním úlohy vám přišly polarizační brýle. Máte tedy polarizační filtry. Když je dáte za sebe tak, aby směry jejich polarizace byly na
Úloha V.E... nezbedné fotony 1 bodů; (chybí statistiky) Spolu se zadáním úlohy vám přišly polarizační brýle. Máte tedy polarizační filtry. Když je dáte za sebe tak, aby směry jejich polarizace byly na
Co se skrývá v ultrazvukové vyšetřovací sondě?
 Co se skrývá v ultrazvukové vyšetřovací sondě? Ultrazvukové vlnění o frekvencích, které jsou používány v medicíně, je generováno pomocí piezoelektrických měničů. Piezoelektrický jev objevili v roce 1880
Co se skrývá v ultrazvukové vyšetřovací sondě? Ultrazvukové vlnění o frekvencích, které jsou používány v medicíně, je generováno pomocí piezoelektrických měničů. Piezoelektrický jev objevili v roce 1880
Světlo jako elektromagnetické záření
 Světlo jako elektromagnetické záření Základní pojmy: Homogenní prostředí prostředí, jehož dané vlastnosti jsou ve všech místech v prostředí stejné. Izotropní prostředí prostředí, jehož dané vlastnosti
Světlo jako elektromagnetické záření Základní pojmy: Homogenní prostředí prostředí, jehož dané vlastnosti jsou ve všech místech v prostředí stejné. Izotropní prostředí prostředí, jehož dané vlastnosti
VÍŘIVÉ PROUDY DZM 2013 1
 VÍŘIVÉ PROUDY DZM 2013 1 2 VÍŘIVÉ PROUDY ÚVOD Vířivé proudy tvoří druhou skupinu v metodách, které využívají ke zjišťování vad materiálu a výrobků působení elektromagnetického pole. Na rozdíl od metody
VÍŘIVÉ PROUDY DZM 2013 1 2 VÍŘIVÉ PROUDY ÚVOD Vířivé proudy tvoří druhou skupinu v metodách, které využívají ke zjišťování vad materiálu a výrobků působení elektromagnetického pole. Na rozdíl od metody
Předmluva 9 Obsah knihy 9 Typografické konvence 10 Informace o autorovi 10 Poděkování 10
 Obsah Předmluva 9 Obsah knihy 9 Typografické konvence 10 Informace o autorovi 10 Poděkování 10 KAPITOLA 1 Úvod 11 Dostupná rozšíření Matlabu 13 Alternativa zdarma GNU Octave 13 KAPITOLA 2 Popis prostředí
Obsah Předmluva 9 Obsah knihy 9 Typografické konvence 10 Informace o autorovi 10 Poděkování 10 KAPITOLA 1 Úvod 11 Dostupná rozšíření Matlabu 13 Alternativa zdarma GNU Octave 13 KAPITOLA 2 Popis prostředí
Jaký význam má kritický kmitočet vedení? - nejnižší kmitočet vlny, při kterém se vlna začíná šířit vedením.
 Jaký význam má kritický kmitočet vedení? - nejnižší kmitočet vlny, při kterém se vlna začíná šířit vedením. Na čem závisí účinnost vedení? účinnost vedení závisí na činiteli útlumu β a na činiteli odrazu
Jaký význam má kritický kmitočet vedení? - nejnižší kmitočet vlny, při kterém se vlna začíná šířit vedením. Na čem závisí účinnost vedení? účinnost vedení závisí na činiteli útlumu β a na činiteli odrazu
1. Zadání Pracovní úkol Pomůcky
 1. 1. Pracovní úkol 1. Zadání 1. Ověřte měřením, že směry výletu anihilačních fotonů vznikajících po β + rozpadu jader 22 Na svírají úhel 180. 2. Určete pološířku úhlového rozdělení. 3. Vysvětlete tvar
1. 1. Pracovní úkol 1. Zadání 1. Ověřte měřením, že směry výletu anihilačních fotonů vznikajících po β + rozpadu jader 22 Na svírají úhel 180. 2. Určete pološířku úhlového rozdělení. 3. Vysvětlete tvar
doc. Dr. Ing. Elias TOMEH Elias Tomeh / Snímek 1
 doc. Dr. Ing. Elias TOMEH e-mail: elias.tomeh@tul.cz Elias Tomeh / Snímek 1 Frekvenční spektrum Dělení frekvenčního pásma (počet čar) Průměrování Časovou váhovou funkci Elias Tomeh / Snímek 2 Vzorkovací
doc. Dr. Ing. Elias TOMEH e-mail: elias.tomeh@tul.cz Elias Tomeh / Snímek 1 Frekvenční spektrum Dělení frekvenčního pásma (počet čar) Průměrování Časovou váhovou funkci Elias Tomeh / Snímek 2 Vzorkovací
Komplexní obálka pásmového signálu
 České vysoké učení technické v Praze, Fakulta elektrotechnická X37SGS Signály a systémy Komplexní obálka pásmového signálu Daniel Tureček 8.11.8 1 Úkol měření Nalezněte vzorky komplexní obálky pásmového
České vysoké učení technické v Praze, Fakulta elektrotechnická X37SGS Signály a systémy Komplexní obálka pásmového signálu Daniel Tureček 8.11.8 1 Úkol měření Nalezněte vzorky komplexní obálky pásmového
Semestrální práce Mozaika aneb Co všechno umí pan Voronoi
 Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra informatiky a výpočetní techniky Semestrální práce Mozaika aneb Co všechno umí pan Voronoi Plzeň, 2008 Aubrecht Vladimír Obsah 1 Zadání...
Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra informatiky a výpočetní techniky Semestrální práce Mozaika aneb Co všechno umí pan Voronoi Plzeň, 2008 Aubrecht Vladimír Obsah 1 Zadání...
filtry FIR zpracování signálů FIR & IIR Tomáš Novák
 filtry FIR 1) Maximální překývnutí amplitudové frekvenční charakteristiky dolní propusti FIR řádu 100 je podle obr. 1 na frekvenci f=50hz o velikosti 0,15 tedy 1,1dB; přechodové pásmo je v rozsahu frekvencí
filtry FIR 1) Maximální překývnutí amplitudové frekvenční charakteristiky dolní propusti FIR řádu 100 je podle obr. 1 na frekvenci f=50hz o velikosti 0,15 tedy 1,1dB; přechodové pásmo je v rozsahu frekvencí
Modelování blízkého pole soustavy dipólů
 1 Úvod Modelování blízkého pole soustavy dipólů J. Puskely, Z. Nováček Ústav radioelektroniky, Fakulta elektrotechniky a komunikačních technologií, VUT v Brně Purkyňova 118, 612 00 Brno Abstrakt Tento
1 Úvod Modelování blízkého pole soustavy dipólů J. Puskely, Z. Nováček Ústav radioelektroniky, Fakulta elektrotechniky a komunikačních technologií, VUT v Brně Purkyňova 118, 612 00 Brno Abstrakt Tento
Vybrané spektroskopické metody
 Vybrané spektroskopické metody a jejich porovnání s Ramanovou spektroskopií Předmět: Kapitoly o nanostrukturách (2012/2013) Autor: Bc. Michal Martinek Školitel: Ing. Ivan Gregora, CSc. Obsah přednášky
Vybrané spektroskopické metody a jejich porovnání s Ramanovou spektroskopií Předmět: Kapitoly o nanostrukturách (2012/2013) Autor: Bc. Michal Martinek Školitel: Ing. Ivan Gregora, CSc. Obsah přednášky
elektrické filtry Jiří Petržela filtry založené na jiných fyzikálních principech
 Jiří Petržela filtry založené na jiných fyzikálních principech piezoelektrický jev při mechanickém namáhání krystalu ve správném směru na něm vzniká elektrické napětí po přiložení elektrického napětí se
Jiří Petržela filtry založené na jiných fyzikálních principech piezoelektrický jev při mechanickém namáhání krystalu ve správném směru na něm vzniká elektrické napětí po přiložení elektrického napětí se
Lineární a adaptivní zpracování dat. 1. ÚVOD: SIGNÁLY a SYSTÉMY
 Lineární a adaptivní zpracování dat 1. ÚVOD: SIGNÁLY a SYSTÉMY Daniel Schwarz Investice do rozvoje vzdělávání Osnova Úvodní informace o předmětu Signály, časové řady klasifikace, příklady, vlastnosti Vzorkovací
Lineární a adaptivní zpracování dat 1. ÚVOD: SIGNÁLY a SYSTÉMY Daniel Schwarz Investice do rozvoje vzdělávání Osnova Úvodní informace o předmětu Signály, časové řady klasifikace, příklady, vlastnosti Vzorkovací
Jméno a příjmení. Ročník. Měřeno dne. 21.3.2012 Příprava Opravy Učitel Hodnocení
 FYZIKÁLNÍ PRAKTIKUM Ústav fyziky FEKT VUT BRNO Jméno a příjmení Vojtěch Přikryl Ročník 1 Předmět IFY Kroužek 35 ID 143762 Spolupracoval Měřeno dne Odevzdáno dne Daniel Radoš 7.3.2012 21.3.2012 Příprava
FYZIKÁLNÍ PRAKTIKUM Ústav fyziky FEKT VUT BRNO Jméno a příjmení Vojtěch Přikryl Ročník 1 Předmět IFY Kroužek 35 ID 143762 Spolupracoval Měřeno dne Odevzdáno dne Daniel Radoš 7.3.2012 21.3.2012 Příprava
