ZÁPADOČESKÁ UNIVERZITA V PLZNI FAKULTA ELEKTROTECHNICKÁ KATEDRA TECHNOLOGIÍ A MĚŘENÍ BAKALÁŘSKÁ PRÁCE
|
|
|
- Magdalena Šimková
- před 9 lety
- Počet zobrazení:
Transkript
1 ZÁPADOČESKÁ UNIVERZITA V PLZNI FAKULTA ELEKTROTECHNICKÁ KATEDRA TECHNOLOGIÍ A MĚŘENÍ BAKALÁŘSKÁ PRÁCE Magnetické pole transformátoru Jan Maňhal 2013
2 2
3 3
4 Abstrakt Hlavním tématem bakalářské práce je zaměření na magnetické pole transformátoru. Výsledkem práce je 2D model reálného univerzitního transformátoru, na kterém jsou modelovány stavy podle předešlého měření. Klíčová slova Transformátor, náhradní schéma transformátoru, magnetické pole transformátoru, 2D model transformátoru, rovnice transformátoru, magnetické pole, magnetický tok, matematické modelování. 4
5 Abstract The main topic of this thesis is to focus on the magnetic field of the transformer. The result is a 2D model of a real university transformer, where the states are modeled by previous measurements. Key words Transformer, the transformer equivalent circuit, the magnetic field of the transformer, the transformer 2D model, equation transformers, magnetic field, magnetic flux, mathematical modeling. 5
6 Prohlášení Prohlašuji, ţe jsem tuto bakalářskou práci vypracoval samostatně, s pouţitím odborné literatury a pramenů uvedených v seznamu, který je součástí této bakalářské práce. Dále prohlašuji, ţe veškerý software, pouţitý při řešení této bakalářské práce, je legální.... podpis V Plzni dne Jan Maňhal 6
7 Poděkování Tímto bych rád poděkoval vedoucímu bakalářské práce Ing. Lukáši Bouzkoviza cenné profesionální rady, připomínky a metodické vedení práce. Poděkování si zaslouţí i Ing. Vladimír Kindl Ph.D. za pomoc a rady s počítačovým modelováním. Dále bych rád poděkoval rodičům za umoţněné studium a jejich mimořádnou trpělivost během mého studia. 7
8 Obsah OBSAH... 8 SEZNAM SYMBOLŮ A ZKRATEK... 9 ÚVOD TRANSFORMÁTOR PRINCIP TRANSFORMÁTORU NÁHRADNÍ SCHÉMA IDEÁLNÍHO TRANSFORMÁTORU NÁHRADNÍ SCHÉMA REÁLNÉHO TRANSFORMÁTORU TRANSFORMÁTOR NAPRÁZDNO TRANSFORMÁTOR NAKRÁTKO TROJFÁZOVÉ TRANSFORMÁTORY MAGNETICKÝ OBVOD TRANSFORMÁTORU DĚLENÍ KONSTRUKCE MAGNETICKÉHO OBVODU KONSTRUKCE MAGNETICKÉHO OBVODU TRANSFORMÁTORU TRANSFORMÁTOROVÉ PLECHY TVARY TRANSFORMÁTOROVÝCH PLECHŮ A JEJICH SKLÁDÁNÍ MODELOVÁNÍ MAGNETICKÉHO POLE METODA KONEČNÝCH PRVKŮ MODELOVÝ TRANSFORMÁTOR TNC F POSTUP MODELOVÁNÍ Pre-procesing Solution Post-procesing VÝSLEDKY MODELOVÁNÍ STAV - NAPRÁZDNO STAV ŢÁROVKA NESVÍTÍ STAV ŢÁROVKA SVÍTÍ ZÁVĚR SEZNAM LITERATURY A INFORMAČNÍCH ZDROJŮ PŘÍLOHY
9 Seznam symbolů a zkratek NN... nízké napětí VN... vysoké napětí VVN... velmi vysoké napětí V, mv, µv... napětí [V] X 1σ, X 2σ... reaktance W... Watt Φ 1, Φ 2... magnetický tok N 1, N 2... počet závitů p 1... ztrátové číslo elektrotech. plechu L... indukčnost[h] Z... impedance[ohm] k... převod transformátoru I... proud[a] R... odpor[ohm] Y(y)... zapojení transformátoru od hvězdy D(d)... zapojení transformátoru do trojúhelníka Z(z)... zapojení transformátoru do lomené hvězdy T... Tesla B... indukce J... proudová hustota 9
10 Úvod Transformátor je netočivý elektrický stroj, jehoţ princip a funkce je od svého vzniku prakticky nezměněna. Transformátor můţe přeměňovat přivedené hodnoty napětí a proudu o vstupním výkonu na jiné poţadované parametry. Díky transformátoru můţeme transformovat střídavé jednofázové i vícefázové elektrické výkony. Dále lze transformátory vyuţívat kromě transformace napětí a proudu i k transformování počtu fází. Tato vlastnost se nejčastěji vyuţívá u transformátorů, které napájejí usměrňovače. Během transformace zůstává výkon transformátoru prakticky nezměněný, pokud ne přihlíţíme k malé spotřebě činného a jalového výkonu v samotném transformátoru. U transformátorů středních výkonů se lze s účinností dostat aţ k 98%. Dalším velkým plusem jsou nízké náklady na chod a údrţbu transformátoru, které jsou takřka zanedbatelné i díky tomu, ţe neobsahují ţádný točivý předmět a poměrně jednoduché konstrukci. Rukou v ruce jde s tímto faktem i jejich větší spolehlivost. Výše zmíněné vlastnosti napomáhají přenosu vysokých a velmi vysokých napětí při malém proudu, neboť pro ekonomický přenos je nutné elektrickou energii během její cesty od výrobce ke spotřebiteli několikrát transformovat, jak je znázorněno na Obr Tím se transformátory stávají nepostradatelnou sloţkou v celém energetickém systému.[1] Obr. 1.1 Schéma rozvodné sítě [2] 10
11 1 Transformátor Konstrukčně se transformátor skládá ze čtyř základních pilířů, tak jak je tomu zobrazeno na Obr První nepostradatelnou součástí transformátoru je magnetický obvod, sloţený z plechů, které jsou z transformátorové elektrotechnické oceli. [3] Druhou důleţitou součástí jsou elektrické obvody, které mohou být z dvou nebo několika vinutí nasazených na magnetickém obvodu. Vinutí je od magnetického obvodu navzájem izolováno. [3] Dalším prvkem transformátoru je zařízení na jeho chlazení. Můţe být chlazen vzduchem, nebo kapalinou, kterou nejčastěji zastupuje transformátorový olej. Je moţné pouţívat i jejich kombinace, avšak jejich funkce je stále stejná a to odvádět teplo, které vzniká přeměnou ztrát v magnetickém obvodu a ve vinutí.[3] Posledním důleţitým prvkem transformátoru jsou jeho mechanické části konstrukce. Tyto části zajišťují mechanickou pevnost všech komponentů konstrukce, které slouţí k manipulaci, transportu, přívodu a odvodu elektrické energie. [3] 1 magnetický obvod transformátoru 2, 3 sekundární a primární vinutí 4, 5 průchodky vyššího a nižšího napět 6 olejová nádoba 7 radiátory na chlazení oleje 8 dilatační nádoba 9 olej Obr. 1.2 Konstrukční schéma jednofázového olejového transformátoru, převzato z [3] 11
12 1.1 Princip transformátoru Jednofázový transformátor má dvě vinutí s různým počtem závitů N 1 a N 2, kde index 1 označuje primární vinutí a index 2 vinutí sekundární. Vinutí jsou navinuta na feromagnetickém jádře a snahou je, aby vinutí měla společnou osu. Dojde-li k připojení primárního vinutí ke zdroji, protéká jím proud i(t), následkem čehoţ je buzen magnetický tok Φ 1. [1] Transformátor se můţe nacházet ve dvou stavech ve stavu naprázdno, kdy obvod sekundárního vinutí je rozpojen, nebo ve stavu nakrátko, kdy výstupní svorky jsou spojeny. Pokud jsou svorky sekundárního vinutí rozpojeny, magnetický tok Φ 1 se dělí na dvě sloţky. První sloţkou je hlavní magnetický tok Φ 1h, který se uzavírá přes jádro transformátoru a zabírá s druhým vinutím. Druhou sloţkou magnetického toku je rozptylový tok Φ 1σ, který se uzavírá pouze kolem primárního vinutí a přenosu energie se neúčastní. Matematicky lze popsat magnetický tok Φ 1 rovnicí: Φ 1 t = Φ 1h t + Φ 1σ t, (1.1) kde jednotlivým sloţkám toku odpovídají reaktance a tedy i jejich indukčnosti Φ 1h X 1h L 1h, (1.2) Φ 1σ X 1σ L 1σ. (1.3) Připojíme-li zátěţ na svorky sekundárního vinutí, začne vinutím protékat proud i 2, který vyvolává tok Φ 2 t = Φ 2h t + Φ 2σ t. (1.4) Sloţky Φ 1h (t)a Φ 2h (t)jsou fiktivními toky, které byly se zavedeny pro jejich pouţití v matematickém popisu. Ve skutečnosti však v jádře existuje jen výsledný magnetický tok. Tyto dvě sloţkyφ 1h (t)a Φ 2h (t)působí na stejné trajektorii jádra transformátoru a jejich vzájemným působením vzniká výsledný hlavní magnetický tok Φ h t = Φ 1h t + Φ 2h t. (1.5) Díky výslednému magnetickému toku se na jednotlivých vinutích indukuje vnitřní napětí 12
13 u i 1 = N 1 d Φ d t a u i 2 = N 2 d Φ d t. (1.6) Jestliţe předpokládáme harmonický průběh magnetického toku Φ platí, ţe u i = d d t ( N Φ m si n(ωt ))= N Φ m ω co s(ωt ) (1.7) a pro efektivní hodnotu indukovaného napětí 2πf U i = NΦ = 4,44 fnφ. (1.8) 2 Jedním ze základních parametrů transformátoru je převod, který je označován písmenem k. Převod transformátoru lze získat poměrem vnitřních indukovaných napětí, nebo poměrem počtu závitů. Pro převod k platí, u u i1 i2 4,44N1Φ = 4,44N Φ 2 m m f f = N N 1 2 = k U 1N. (1.9) U 2N Za pouţití zákona o celkovém proudu můţeme vyjádřit vztah pro převod proudu U m = Hdl = I = N1I1 + N2I 2 (1.10) Pro siločáry hlavního magnetického toku, které vedou ţelezným jádrem transformátoru platí, ţe: μ Fe 1 2 H Fe = 0 N1 I1 = N 2I 2 a k = =. (1.11) N 2 I1 N I Takto lze popsat princip transformátoru matematicky. Pokud chceme popsat princip transformátoru prakticky platí,ţe po připojení transformátoru na střídavé sinusového napětí u 1, které je přivedeno na primární svorky na primární vinutí, dochází k průchodu proudu i 1 vinutím. Tento proud i 1 vytváří magnetický tok, který na základě indukčního zákona vytváří v sekundárním vinutí napětí u 2. Pokud sekundární cívku transformátoru zatíţíme zátěţí, začne sekundární stranou transformátoru procházet proud o okamţité hodnotě i 2. [1][6] 13
14 1.2 Náhradní schéma ideálního transformátoru Ideální transformátor je definován jako transformátor, jehoţ odpor vinut je nulový a jehoţ magnetická vodivost vazebního obvodu je nekonečně velká. Stejně tak i rozptylové toky ideálního transformátoru jsou nulové. Pokud budeme uvaţovat převod transformátoru roven jedné, lze schéma ideálního transformátoru nakreslit jako je tomu na obrázku 1.3. Vzhledem k tomu, ţe je převod transformátoru roven jedné, je moţné vinutí galvanicky spojit. Pokud však bude převod transformátoru jiný neţ jedna, je nutné všechny hodnoty na sekundární straně přepočítat podle strany primární. Reaktance X µ, která je zobrazena ve schématu představuje vazební, neboli magnetizační reaktanci, která je nazývána hlavní reaktancí. [6] Obr. 1.3Náhradní schéma ideálního transformátoru, převzato z [6] 1.3 Náhradní schéma reálného transformátoru Náhradním schématem u transformátoru se rozumí kombinace pasivních prvků obvodu, kam patří odpory společně s indukčnostmi, jejichţ vlastnosti za pouţití zjednodušujících předpokladů odpovídají vlastnostem transformátoru. Náhradní schéma reálného transformátoru platí pro harmonické průběhy veličin a zároveň pro ustálený stav transformátoru. Transformátor lze díky náhradnímu obvodu popsat pomocí algebraických rovnic, musí se však dodrţovat pravidla Kirchhoffových zákonů. Řešením těchto rovnic lze získat průběhy proudů ve schématu a při znalostech vztahů mezi náhradním schématem a reálným transformátorem i velikosti proudů skutečného transformátoru. Známe-li charakteristiky transformátoru naprázdno a nakrátko, můţeme vypočítat parametry hodnot transformátoru, jimiţ jsou odpory primárního a sekundárního vinutí a jednotlivé reaktance. Na obrázku 1.4 je znázorněno náhradní schéma reálného transformátoru, které je ve tvaru T článku.[1] 14
15 Obr. 1.4Náhradní schéma reálného transformátoru, převzato z [1] Na schématu je patrné, ţe veličiny vyskytující se na sekundární straně, jsou převedeny na stranu primární. Takové to veličiny jsou označeny čárkou v horním indexu a platí pro transformátor s převodem jedna. Schéma je platné pro všechny transformátory, které mají libovolný počet závitů N 1 a N 2. Skutečné hodnoty prvků na sekundární straně lze získat vyřešením rovnic, pro které platí vztahy: U 2, = ku 2, (1.12) I 2, = 1 k I 2 a (1.13) Z 2, = k 2 Z 2. (1.14) Pro napěťové rovnice náhradního schématu platí: U 1 = R 1 I 1 + jx 1σ I 1 + U i = R 1 I 1 + jx 1σ I 1 + jx μ I 1 + I 2, a (1.15) U 2, = R 2, I 2,,, + jx 2σ I 2 + U i = R 2, I 2,,, + jx 2σ I 2 + jx μ I 1 + I 2,. (1.16) Po úpravě těchto rovnic dostaneme rovnice ve tvaru U 1 = R 1 + jx 1 I 1 + jx μ I 2, a (1.17) U 2, = jx μ I 1 + R 2, + jx 2, I 2,. (1.18) 15
16 Celkové reaktance primárního a sekundárního vinut lze vyjádřit jako X 1 = X 1σ + X μ a (1.19) X 2,, = X 2σ + X μ. (1.20) Tyto rovnice byly pouţity z literatury [1] a [6]. 1.4 Transformátor naprázdno Obr. 1.5 Náhradní schéma transformátoru naprázdno, převzato z [6] Na obrázku 1.5 je moţné vidět náhradní schéma transformátoru naprázdno, coţ představuje nezatíţený transformátor, kdy na sekundárních svorkách není nic připojeno. Proud I 2 se tedy rovná nule a transformátor je pouze pod napětím. Při tomto ději odebírá transformátor ze sítě pouze proud I 0, který je nazýván proudem magnetizačním a jeho velikost je relativně malá. Většinou se jeho hodnota pohybuje od 1 % do 10 % proudu jmenovitého. V transformátoru dochází pouze ke vzniku ztrát naprázdno a pokud se zaměříme na náhradní schéma, můţeme z něho vypozorovat, co určuje ztráty naprázdno. Ztráty v transformátoru budou představovat Joulovy ztráty, které budou vznikat na odporech R 1 a R Fe. Ztráty R 1 reprezentují činné ztráty, R Fe ztráty v ţeleze.[6] 16
17 Při měření transformátoru naprázdno se určuje proud I 0, napětí naprázdno U 0 a příkon naprázdno P 0. Příkon takového transformátoru bude spotřebován na krytí ztrát a platí pro něj: P o = P 1j0 + P Fe, (1.21) kde P Fe je součtem hysterezních ztrát a ztrát vířivými proudy v ţeleze. U trojfázového transformátoru platí, ţe hodnota Joulových ztrát ve vinutí se dá určit z rovnice 1.22, pro kterou musíme znát hodnotu odporu R s a magnetizačního proudu I 0.[7] P 1j0 = 3 2 R SI 0 2 (1.22) 1.5 Transformátor nakrátko Obr. 1.7 Náhradní schéma transformátoru nakrátko, převzato z [6] V tomto stavu se můţe transformátor nacházet buď poruchou, nebo vyzkratováním sekundárních svorek, jak je patrné na obrázku 1.7. V prvním případě poruše, je transformátor napájen jmenovitým napětím. Vznikne-li zkrat, proběhne přechodový děj a vinutím protéká přibliţně 25 násobek jmenovitého proudu. Tím se mnohonásobně zvýší Joulovy ztráty - pokud proud je 25 násobkem, pak Joulovy ztráty jsou 625krát větší neţ 17
18 jmenovité ztráty. Takto vznikne teplo, které pokud nezapůsobí nějaké ochrany, zničí transformátor. [6] Při zapojení transformátoru nakrátko je napětí U 21 rovno nule, také jinak je sekundární vinutí vyzkratováno vodičem. Při průchodu jmenovitého proudu transformátorem je hodnota napětí na primárním vinutí U kn napětí nakrátko. Toto napětí se většinou uvádí v poměrných hodnotách a pro lineární magnetický obvod v chodu nakrátko platí vztah u k = U kn U n = I n U k = Z k = z U n I k Z k. (1.23) n Velikost napětí nakrátko se pohybuje v poměrných hodnotách v rozmezí přibliţně 4 % aţ 12 % pro transformátory o velkých výkonech. U transformátorů pro výkonovou elektroniku se horní mez můţe pohybovat aţ k 30 procentům. Hodnota napětí nakrátko je měřítkem pro tvrdost zdroje, kdy malá hodnota u k znamená menší úbytek napětí na impedanci transformátoru a transformátor je tedy tvrdší. Niţší hodnota také znamená menší zkratuvzdornost v porovnání s transformátorem, který má hodnotu u k větší. Jediné, co omezuje zkratový proud je velikost impedance z k. Měření transformátoru nakrátko se provádí podobně jako při chodu naprázdno, také jinak příkon transformátoru je spotřebovává na krytí Joulových ztrát v primárním a sekundárním vinutí a ztrát přídavných, jak je moţné vidět v rovnici P k = P jk + P d (1.24) Ve stavu nakrátko se nachází magnetický obvod v nenasyceném stavu, neboť proudy procházející primárním a sekundárním vinutím jsou v protifázi. To platí, pokud je zanedbán proud procházející příčnou větví. [1][7] 1.6 Trojfázové transformátory Během transformace trojfázového proudu se můţou pouţít dva druhy transformátorů. Jedním druhem jsou transformátory jednofázové, které jsou samostatně zapojené do kaţdé ze tří fází. Druhou moţností je pouţít transformátor trojfázový, neboli transformátor, který díky svojí konstrukci obsahuje tři vinutí, které protíná jedno společné magnetické jádro. Více se 18
19 však pouţívají transformátory trojfázové, protoţe nevyţadují tolik materiálu tak, jako spotřebují tři jednofázové transformátory. Naopak v případě pouţití tří jednofázových transformátorů není potřeba mít v záloze velké mnoţství instalovaného výkonu v záloţních řešeních. Neboť v případě výpadku nedojde ke kompletní odstávce, jak by tomu bylo u transformátoru trojfázového, ale je moţné dělat potřebná opatření na jednotlivých transformátorech bez omezení funkce ostatních. [3] Při spojení transformátorů tak, ţe se jejich vertikální spojky vzájemně dotýkají, vytvářejí magnetické toky, které procházejí jednotlivými jádry souměrné soustavy. Ve středním jádře je součet okamţitých magnetických toků, které jsou od sebe navzájem natočeny o 120 stupňů roven nule a je moţné prostřední sloupek vynechat, protoţe platí rovnice 1.25: u + v + w = 0 (1.25) Tímto krokem sice vznikne jistá nesymetrie, kdy krajní fáze mají větší magnetický odpor a tedy i jejich magnetizační proud musí být větší pro poţadované napětí. Tato nesymetrie však není překáţkou, neboť proud I μ I 1n. [1] Trojfázové transformátory je moţno zapojit třemi různými způsoby. Prvním způsobem je zapojení do hvězdy, které je označováno jako Y(y). Druhým způsobem je zapojení do trojúhelníku, označované jako D(d) a posledním způsobem je zapojení do lomené hvězdy Z(z). Velká písmena značí primární stranu vinutí, písmena malá označují stranu sekundárního vinutí. Dalším parametrem, který informuje o vlastnostech transformátoru je hodinové číslo. Hodinové číslo je vzájemné fázové natočení fázorů primárního a sekundárního napětí stejnojmenných fází. Je měřené od strany vyššího ke straně niţšího napětí ve smyslu sledu fází. Tato hodnota není neměnná, záměnou svorek začátků a konců vinutí se hodnota hodinového čísla změní o 6, cyklickou záměnou svorek se změní o 4 a necyklickou záměnou o 10. Takovéto hodinové číslo je udáváno za označením zapojení transformátoru, například Yy0. [3] 19
20 2 Magnetický obvod transformátoru Jádra magnetických obvodů jsou velmi důleţitou součástkou pro výrobu transformátorů a na jejich vlastnostech jsou závislé finální parametry magnetického obvodu, popřípadě celého transformátoru. Jádro transformátoru vytváří magnetický obvod, přes který protéká indukční tok, který je vyvolán průchodem proudu přes primární vynutí. Díky tomu se indukuje elektrické napětí v sekundárním vinutí. Obr. 2.1 Schématické znázornění transformátoru, převzato z [1]; (a) jádrový transformátor, (b) plášťový transformátor 2.1 Dělení konstrukce magnetického obvodu Jádrové transformátory Jádrový transformátor na obr. 2.1 (a) má primární i sekundární vinutí rozdělené na dvou jádrech a umístěné na sobě tak, ţe vinutí na niţší napětí je blíţe k jádru. Jádra jsou spojený tzv. spojkami a u tohoto typu transformátoru mají jádra i spojky přibliţně stejný průřez, protoţe vedou celý magnetický tok.[1] Plášťovétransformátory U plášťového transformátoru na obr 2.1 (b) jsou vinutí umístěna na středním sloupku, přes který teče celý hlavní magnetický tok. Následně se magnetický tok rozděluje a uzavírá se spojkami a krajními jádry, na kterých uţ není umístěno ţádné vinutí. Spojky mají zpravidla poloviční průřez v porovnání s transformátorem jádrovým, coţ je významné zejména u výkonových trojfázových transformátorů. Plášťový transformátor má také menší rozptylové magnetické toky a tedy X 1σ i 1 ax 2σ i 2, jeho sekundární napětí kolísá méně s měnící se zátěţí a je povaţován za tvrdší neţ transformátor jádrový.[1] 20
21 Toroidní transformátory Transformátory s toroidními jádry se vyznačují nízkým rozptylem elektromagnetického pole a nízkým proudem naprázdno. Dalším kladem toroidního transformátoru je jeho vysoká účinnost a snadná montáţ, kde se vývody standardně vyvádějí na jedné straně toroidu. Toroidy jsou vyráběny z orientovaného transformátorového plechu, kde je obsah křemíku kolem 3%.Na obrázku 2.2 je znázorněné uspořádání toroidu. [4] Obr. 2.2 Schématické znázornění toroidního transformátoru, převzato z [11]; 2.2 Konstrukce magnetického obvodu transformátoru Kostra transformátoru, jinak řečeno magnetický obvod (feromagnetické jádro) je sloţen z jednotlivých od sebe navzájem izolovaných transformátorových plechů. Díky tomu, ţe jsou plechy od sebe navzájem odizolovány, dochází ke sníţení ztrát v ţeleze. Tomu napomáhá i to, ţe pouţité transformátorové plechy jsou orientované a za tepla válcované. Tyto typy plechů umoţňují navýšit hodnoty indukce v jádře aţ na 1,8T ve směru orientace. Ve směru orientace je také veden magnetický tok v jádře. Vyšší hodnoty indukce dovolují zmenšit průřez jádra a tím lze sníţit i celkovou hmotnost transformátoru.[1] Feromagnetické jádro je zpravidla odstupňováno tak, aby co nejlépe vyplňovalo kruhovou plochu mezi jádrem a vinutím. Úsporou místa se zkrátí délka závitů, čímţ se sníţí ztráty ve mědi. Transformátorové plechy jsou voleny s ohledem na frekvenci, při které bude transformátor pouţíván. Do stovek Hz se pouţívají křemíkové oceli o tloušťce 0,35 mm, pro vysoké frekvence se pouţívají lisované práškové slitiny. Pro vysokofrekvenční transformátory je nutné pouţít materiály s vysokou počáteční magnetickou vodivostí, neboť vstupní napětí jsou řádově v mv a proudy v µv.[1] 21
22 2.3 Transformátorové plechy Elektrotechnické plechy Et Plechy Et byly vyráběny v několika magnetických vlastnostech, které byly charakterizovány ztrátovým číslem p 1. U nás se vyráběly plechy Et 1,3 a Et 1,3s. Plech Et 1,3 se vyráběl o tloušťce 0,35 mm, který byl za studena doválcovaný pro zvýšení činitele plnění. Činitel plnění díky tomuto postupu vzrostl z 92 % na 96 %. Plech Et 1,3s se vyráběl v tloušťce 0,5 mm. Plechy Et se ztrátovým číslem p 1 do 1,8 W/kg se označovaly jako transformátorové plechy. Pokud ztrátový činitel byl vyšší jak 1,8 W/kg, plechy byly označovány jako dynamové plechy, které slouţily převáţně k výrobě motorů. V dnešní době jsou Et plechy zastaralé a nahrazují je plechy typu Eo a dynamové plechy Ei.Magnetizační charakteristiky plechů Eo v porovnání s plechem Et jsou zobrazeny v tabulce Tab. 2.1.[5] Tab 2.1 Porovnání vlastností plechů Eo s plechy Et 1,3 [5] H B (T) (A/cm) Eo 10 Eo 11 Eo 12 Eo 13 Eo 15 Eo 17 Et 1,3 (amplituda) 0,30 mm 0,30 mm 0,35 mm 0,35 mm 0,35 mm 0,35 mm 0,35 mm 0,3 1,2 1,12 1,1 0,97 0,84 0,74 0,05 1 1,6 1,56 1,52 1,48 1,41 1,35 0,6 5 1,74 1,7 1,64 1,7 1,65 1,6 0,8 10 1,8 1,76 1,76 1,74 1,72 1,67 1,2 25 1,88 1,84 1,8 1,85 1,82 1,77 1, ,98 1,96 1,94 1,98 1,96 1,94 1,82 p 0,5 0,14 0,15 0,16 0,17 0,18 0,2 0,38 p 1,0 0,49 0,52 0,56 0,59 0,64 0,7 1,3 p 1,5 1,02 1,12 1,23 1,35 1,48 1,62 3,2 p 1,7 1,65 1,75 1,9 1,93 2,16 2,36 4,2 (při cca 0,5 A/cm) µ max Elektrotechnické plechy Eo V dnešní době jsou tabulové plechy pro stavbu transformátorů nahrazovány kontinuálně vyráběnými svitky pásu Eo (elektrotechnický plech orientovaný) válcovanými za studena. Technologickým zpracováním se orientuje uspořádání krystalů a tím vzniká magnetická textura. Ţelezo, které krystaluje v kubické soustavě má hranu krychle ve směru snadné 22
23 magnetizace, kdeţto ve směru plošné úhlopříčky je magnetizace nesnadná. Po válcování za studena následuje tepelné zpracování pásů v průběţných pecích v ochranné atmosféře. Při tomto procesu dochází k oduhličení a rekrystalizaci. Současně probíhá opatření pásů tenkou vrstvou izolace Kerizol o tloušťce 2 aţ 5µm, která jednak zabraňuje vzájemnému svaření jednotlivých svitků při tepelném zpracování a v druhé řadě izoluje plechy v magnetickém obvodu, co má za následek zmenšení ztrát vířivými proudy. Takto připravené pásy mají hladký povrch a rovnoměrné magnetické i mechanické vlastnosti.[5] Plechy Eo se vyrábějí v druzích kvality od Eo 9, Eo 10, Eo 11, Eo12, Eo 13, Eo 14, Eo 15 po Eo 17 a v tloušťkách 0,28 aţ 0,35 mm. Nejpouţívanějším plechem je plech Eo 10 a Eo 11. Číslo, které je vyznačeno za Eo určuje ztrátové číslo, které je vyjádřeno v desetinách W/kg. Takto nízké ztráty dosahují plechy jen v případě, ţe indukční tok, který jimi teče je orientován ve směru snadné magnetizace a dosahují rovněţ indukci blízkou nasycení při niţších polích neţ plechy Et. Díky těmto vlastnostem, které jsou uvedeny v tabulce Tab 2.2, jsou Eo plechy hojně vyuţívány i kdyţ je jejich cena oproti plechům Et několikanásobně vyšší. [5] Tab 2.2 Magnetické vlastnosti plechů a pásů pro elektroniku válcovaných za studena s magnetickou texturou [5] Jakost VP Tl. (mm) p 1,5 p 1,7 Minimální indukce (T) při amplitudě int. magnetického pole (A/m) Značka výrobce AISI DIN 46400/3 EN B 100 B 1000 B 2500 B Eo N 0,27 0,89 1,30 1,82 Eo 9 M-4 VM 89-27N M N Eo N 0,85 1,34 1,84 Eo 9 Eo N 0,92 1,30 1,6 1,8 1,90 1,98 Eo 10 M-4 0,3 Eo N 0,97 1,45 1,6 1,77 1,85 1,98 Eo 10 M-5 VM 97-30N M N Eo N 1,07 1,50 1,56 1,77 1,80 1,96 Eo 11 Eo N 1,01 1,60 1,52 1,8 1,88 1,98 Eo 11 M-5 VM 111- Eo N 1,11 1,58 1,52 1,7 1,84 1,96 Eo 11 M-6 M N 35N 0,35 Eo N 1,20 1,65 1,52 1,7 1,80 1,94 Eo 12 Eo N 1,30 1,75 1,48 1,67 1,80 1,92 Eo 13 Eo N 1,50 1,90 1,41 1,62 1,76 1,90 Eo 15 23
24 Elektrotechnické plechy Ei Ei plechy se pouţívají převáţně při výrobě asynchronních motorů a pro výseky plechů pro jádra malých transformátorů. Tyto plechy jsou magneticky izotropní, coţ znamená, ţe mají ve všech směrech přibliţně stejné vlastnosti. Oproti plechům Et mají plechy Ei podstatně niţší ztráty, především však ztráty hysterezní. Májí také lepší mechanické vlastnosti, jsou hladší a dosahují dobrého činitele plnění. Tabulka Tab 2.3 ukazuje vlastnosti plechů a pásů pro elektrotechniku, které jsou válcované za studena a jsou magneticky izotropní. Tyto plechy jsou vyráběny v kvalitách od Ei 33, Ei 35, Ei 40, Ei 45, Ei 50, Ei 55, Ei 60, Ei 70 aţ do Ei 80 o tloušťkách 0,5 mm a 0, 65 mm, kdy číslo opět ukazuje ztráty ve W/kg při 1,5 T a 50 Hz. [5] Tab 2.3 Zaručované vlastnosti plechů a pásů pro elektrotechniku válcovaných za studena magneticky izotropní[5] Jakost Tloušťka (mm) p1,0 (W/kg) p1,5 (W/kg) Min hodnota magn. indukce (T) při amplitudě mag. pole (A/m) Max. anizotropie (%) Ei 33 0,50 1,40 3,30 1,50 1,60 1,70 18 Ei 35 0,50 1,50 3,50 1,50 1,60 1,71 14 Ei 40 0,50 1,70 4,00 1,53 1,62 1,73 14 Ei 45 0,50 1,80 4,30 1,54 1,64 1,74 14 Ei 50 0,50 2,00 4,70 1,55 1,64 1,75 14 Ei 55 0,50 2,30 5,30 1,56 1,65 1,76 14 Ei 60 0,50 3,60 6,00 1,58 1,67 1,78 14 Ei 70 0,50 3,00 6,80 1,58 1,67 1,78 14 Ei 80 0,50 3,50 8,00 1,58 1,68 1,78 14 Ei 55 0,65 2,30 5,30 1,55 1,64 1,75 14 Ei 60 0,65 2,60 6,00 1,58 1,67 1,78 12 Ei 70 0,65 3,00 6,80 1,58 1,67 1,78 12 Ei 80 0,65 3,59 8,00 1,58 1,68 1,
25 2.4 Tvary transformátorových plechů a jejich skládání Dle způsobu spojení jader se spojkami se rozlišují magnetické obvody s tupým stykem a magnetické obvody, kde v místě jejich styku jsou plechy přeplátovány. V magnetických obvodech s tupým stykem se jádra a spojky skládají z plechů samostatně, poté jsou pomocí vertikálních stahovacích nosníků spojovány. U těchto obvodů se jádra i spojky skládají současně, aby tvořily uzavřený obvod. Po jejich sloţení dochází k vyjmutí spojky, na jádra jsou umístěna vinutí a následně je spojka vrácena zpět. Výhodou tupých styků je poměrně snadná montáţ a demontáţ magnetického obvodu společně s vinutím. To je jedna z mála výhod, neboť u jader skládaných natupo jsou značnou nevýhodou vířivé proudy. Ty vznikají v místech styku, které vznikají překrytím spojky a jádra. Vířivými proudy vzniknou dodatečné ztráty, způsobující ohřátí ţeleza v místech styku. Proto je konstrukce těchto typů jader omezena a pouţívá se jen málokdy například pro výrobu tlumivky. [3] U spojení přeplátováním vzniká v místech spojení jader a spojek také ke vzniku ztrát, úbytku magnetického napětí a ztrátám v ţeleze. Tyto ztráty jsou však podstatně menší, neţ u jader skládaných natupo. Proto jsou v dnešní době pouţívány magnetické obvody z orientovaných válcovaných plechů, u kterých magnetické vlastnosti jsou lepšími ve směru válcování, neţ ve směru na něj kolmém. Úbytky magnetického napětí a ztráty v ţeleze jsou v místech ohybu indukčních siločár při jejich přechodu z jádra do spojky větší, neţ ve vlastním jádře a spojce. Tento jev se dá částečně odstranit pouţitím listů plechů takových, které mají zkosené hrany a jejich způsob přeplátování se liší od klasického přeplátování.výhodou jsou niţší ztráty, oproti tomu je konstrukce o něco sloţitější. [3] Obr. 2.3Transformátorové plechy EI, převzato z [9] 25
26 EI jádra Jádra tvaru EI dostaly název podle svého tvaru. Jsou tvořeny prvky, které mají tvar písmene E a písmene I, jak je patrné na obrázku 2.3. Vyrábí se vysekáváním z ocelokřemíkových plechů a pro výrobu jsou nejvýhodnější, neboť mají malý výrobní odpad. Proto se jim také někdy říká plechy bezodpadové.nevýhodou těchto typů jader je však přechod magnetického toku, který musí překonat úhel o velikosti 90 stupňů. Plechy jsou na sebe kladeny střídavě, coţ se pouţívá pro síťové transformátory, nebo jsou na sebe pokládány shodně, kde se tohoto vyuţívá u transformátorů se stejnosměrným sycením.[8] M jádra M jádra jsou také vysekávány z transformátorových plechů, jejich nevýhodou je však značný odpad oproti plechům EI. Mají o něco menší magnetický rozptyl neţ ostatní skládaná jádra. Pouţití našly M jádra v telekomunikační technice. Avšak díky svojí vyšší ceně, která je způsobena odpadem při výrobě těchto plechů se M jádra na trhu moc neobjevují. [10] I a L jádra Obr. 2.4 Postup při skládání I a L plechů, [10]; a) I plech 1. vrstva, b) I plech 2. vrstva c) L plech 1. vrstva, d) L plech 2. vrstva V praxi se pouţívají transformátorové plechy vyseknuté ve tvaru písmene I. Takto vyseknuté plechy jsou následně přes sebe překládány tak, ţe na místě, kde ve vrstvě pod byl plech vedle sebe je následující plech v nové řadě v celku. Výrobně jsou tyto plechy nejjednodušší, avšak jejich nevýhodou je větší rozptyl magnetického toku. Pouţití nacházejí například u transformátorů slouţících ke svařování. Plechy ve tvaru písmene L jsou skládány podobně jako plechy I, tedy také přes sebe a jsou překládány jejich spoje. Na výrobu jsou tyto 26
27 plechy o něco nákladnější neţ plechy I, jelikoţ se nedají stříhat strojními nůţkami a musejí být vysekávány. Na obrázku 2.4 je znázorněno, jakým způsobem jsou přes sebe plechy překládány. [10] 3 Modelování magnetického pole V této kapitole se bakalářská práce bude věnovat jiţ samotnému modelování. Bude zde popsána metoda konečných prvků, bude zde popsán program Ansys a následně i průběh modelování samotného transformátoru. 3.1 Metoda konečných prvků Metoda konečných prvků vznikla kvůli potřebě řešit sloţité úlohy z inţenýrské praxe. Především byla vyvinuta na řešení úloh z pruţnosti a strukturní analýzy. Počátky metody konečných prvků lze nalézt jiţ v roce 1941 v práci Alexandera Hrennikoffa a Richarda Couranta v roce Metody, které pouţili byly na první pohled odlišné, přesto se však shodovali v jednom bodě. Tím bodem bylo rozdělení spojité oblasti do oblasti mnoţin samostatných podoblastí. Jedna z prací rozdělovala oblast pomocí mříţky, druhá práce rozdělovala oblast do konečného mnoţství trojúhelníkových elementů. Vývoj metody konečných prvků začal v padesátých letech 20. století na univerzitě ve Stuttgartu prací Johna Argyrise a po něm pokračoval v 60. letech na univerzitě v Berkeley Ray W. Clough. Koncem šedesátých let se do této metody zapojila NASA, která vyvinula software NASTRAN, který pracuje na principu metody konečných prvků. [12] Metoda konečných prvků je numerickou metodou slouţící k simulaci průběhu napětí, deformací, vlastních frekvencí, proudění tepla, proudění tekutin a pro tuto práci důleţitou simulací jevů elektromagnetismu na vytvořeném fyzikálním modelu. Principem metody konečných prvků je diskretizace spojitého kontinua do určitého počtu prvků, kde zjišťované parametry jsou určovány v jednotlivých uzlových bodech. Metoda konečných prvků je pouţívána především pro kontrolu jiţ navrţených zařízení, nebo pro stanovení kritického místa konstrukce. Principy metody jsou známy jiţ delší dobu, její masové pouţití se rozmohlo aţ s nástupem výpočetní techniky. [12] 27
28 Princip metody je zaloţen na řešení soustavy diferenciálních rovnic, které popisují vlastnosti určitého fyzikálního problému. Analytické řešení diferenciálních rovnic nepředstavuje problém dokud se jedná o základní fyzikální úlohy a jednoduché tvary geometrických těles. U sloţitějších analýz, jsou naopak charakteristické fyzikálně komplexní, matematicky diskontinuální soustavy u těles s mnohdy velmi sloţitou geometrií. Právě pro řešení těchto problémů se ukázala jako nejvhodnější numerická aproximační metoda, která je právě onou metodou konečných prvků. Nejprve je nutné rozdělit geometricky definovaný objekt na konečný počet elementů, které vyplňují s dostatečnou přesností jeho tvar. Obr. 3.1Rozdělení oblasti na elementy Jednotlivé elementy jsou vzájemně spojeny v místech zvaných uzel. Tyto uzly jsou matematické body, které mají známé souřadnice v prostoru a zjednodušeně lze říci, ţe jsou počítány hodnoty pro tyto body právě v těchto uzlech. Vlastnosti kaţdého z elementů jsou popsány matematicky a popis celého objektu dostáváme soustavu rovnic. Řešení diferenciálních rovnic je poté převedeno na řešení algebraických rovnic, jejichţ neznámé představují parametry poţadovaného fyzikálního problému, který jsme se rozhodli řešit. Pro vyřešení vlastností celého objektu dostáváme soustavu s tisíci aţ miliony rovnic. [13] 28
29 3.2 Modelový transformátor TNC F Pro modelování byl vybrán univerzitní transformátor o zdánlivém výkonu 900 VA. Jedná se o třífázový jádrový transformátor, který byl rozměrově změřen a následně pouţit pro modelování příkladu z magnetického pole. Transformátor je zobrazen na obrázku 3.2 a štítkové hodnoty transformátoru v tabulce 3.1. Obr. 3.2TransformátorTNC F Tab 3.1Štítkové hodnoty transformátoru TNC F Typ TNC F výkon 900 [VA] zapojení Yy0 primární strana 400 [V] 230 [V] 2,26 [A] sekundární strana 230 [V] 132 [V] 2,26 [A] výrobce Elektrokov Znojmo 29
30 3.3 Postup modelování Samotné modelování lze rozdělit do několika kroků. Prvním krokem je definice problému, coţ zahrnuje celkem široký pojem. Pro tuto bakalářskou práci bylo úkolem namodelovat magnetické pole transformátoru ve stavu naprázdno, tedy problém z oblasti elektromagnetismu. Po namodelování tohoto stavu a proniknutí do problematiky modelování jsem přišel ještě s doplněním simulací o stav, který jsem našel na internetu [14]. Úloha byla zajímavá a hezky se na ní ukázalo chování transformátoru. Jak jiţ bylo zmíněno, pro tuto úlohu poslouţil univerzitní třífázový transformátor, který jsem pouţil jako jednofázový transformátor se dvěma postranními vinutími, kdy jedním sekundárním vinutím se ovládala ţárovka připojená na druhém sekundárním vinutí, viz obrázek 3.3. Obr. 3.3TransformátorTNC F zapojení měření Po připojení transformátoru ke zdroji napětí bylo prováděno měření proudů, které protékají napájecími kabely, pravou stranou sekundárního vinutí - ţárovkou a levou stranou sekundárního vinutí zkratovacím kabelem. Pokud se sekundární vinutí na levé straně transformátoru nechalo vyzkratované, došlo k rozsvícení ţárovky. Druhý případ, kdy levé svorky sekundárního vinutí byly rozpojeny, došlo ke zhasnutí ţárovky. Naměřené hodnoty, které byly pouţity pro modelování jsou zobrazeny v tabulce
31 Tab 3.2Naměřené hodnoty transformátoru TNC F žárovka svítí I [ma] J[A/m 2 ] I [ma] J[A/m 2 ] vstup vstup žárovka žárovka nesvítí žárovka svorky svorky 0 - rozpojeno 0 Problém je tedy definován, nyní nastává samotný postup modelování. První nepostradatelnou součástí modelování je tzv. Pre-procesing Pre-procesing V této fázi dochází k vytvoření fyzikálního modelu, kde se zvolí materiálové vlastnosti a generuje se výpočet sítě. Často se zde přidávají i okrajové podmínky, které jsou podstatné pro správné vypočítání výsledků. Následuje zatěţování buď proudovou hustotou, nebo napětím. Tvorba modelu Po změření geometrie transformátoru bylo moţné zanést hodnoty do počítače a vytvořit počítačový 2D model v programu Ansys, který je k vidění na obrázku3.3. Obr. 3.3Počítačový 2D model transformátoru Pro představu velikosti transformátoru je jeho velikost 160 mm na šířku, 160 mm na výšku, šířa sloupků je 26 mm. 31
32 Volba atributů a zadávání materiálových vlastností Zde jsou zadávány informace o materiálu, volí se typy elementů a tzv. real konstantym, které představují matematické vyjádření některých geometrických funkcí při volbě určitého elementu. Na obrázku 3.4 je printscreen z programu Ansys, kde jsou voleny typy elementů. Obr. 3.4Volba elementů Na obrázku 3.4 je vidět, ţe je model rozdělen na 4 druhy elementů, přičemţ všechny jsou jednoho druhu Plane 53. Model je tedy rozdělen na 4 části vzduchové okolí, primární vinutí (blíţe k jádru), sekundární vinutí a jádro transformátoru. 32
33 Dalším krokem při modelování je zadání hodnot, které charakterizují určité vlastnosti materiálů. První je vzduch, který je definován permeabilitou o hodnotě 1 Hm -1. Primární a sekundární vinutí modelu je charakterizované také permeabilitou o hodnotě 1 Hm -1 aby se předešlo zkreslení výsledků měření vířivými proudy. Poslední součástí modelu je jádro transformátoru, které je popsáno BH charakteristikou, vyobrazenou na obrázku 3.5. Obr. 3.5BH charakteristika a okénko s možností navolení vlastností materiálů Zasíťování objektu meshování, okrajové podmínky Jsou-li nadefinované materiály, je moţné přistoupit k dalšímu kroku, který na modelu vytvoří síť mesh. Zasíťováním objektu dojde k rozdělení na mnoho malých trojúhelníčků, které mají danou velikost své hrany. Význam zasíťování je důleţitý pro následné počítání výsledků a je na nich zaloţena metoda konečných prvků. Následuje jiţ jen nastavení okrajové podmínky pro vzduchové okolí, která zjednodušuje a urychluje výpočet. Nastavení a výpočet proudových hustot Nejprve se proudová hustota musí vypočítat z naměřených hodnot. Plocha jednoho vinutí v řezu je 6,02e10-4 m 2. Proud, který protéká vinutím je známý, proto je moţné vypočítat proudovou hustotu tak, ţe proud vydělíme plochou vinutí. Tuto vypočítanou hodnotu je moţné pouţít pro modelování a je vypočítána v tabulce 3.3Podle typu vybrané úlohy existují 33
34 různé způsoby zadávání proudových hustot. Při simulaci stavu naprázdno jsou napájena jen prostřední vinutí. Jedno vinutí je napájeno s kladnou polaritou, druhé se zápornou. Ostatní vinutí (boční sloupky) jsou rozepnuta hodnota proudové hustoty je nula. Simulujeme-li případ, kdy ţárovka svítí, na prostředním vinutí a obou postranních vinutích nastavíme proudovou hustotu podle tabulky 3.3. Stejně postupujeme i při simulaci stavu, kdy ţárovka nesvítí, rozdíl je pouze v nastavení vinutí na straně kde je ţárovka. Tam je hodnota proudové hustoty 0. Tab 3.3Proudové hustoty transformátoru žárovka svítí J[A/m2] J[A/m2] J[A/m2] vstup 2093 vstup 558 vstup 2000 žárovka žárovka 631 žárovka 358 Naprázdno žárovka 0 nesvítí svorky 2059 svorky 0 svorky Solution Po části zvané pre-procesing následuje část zvaná solution. Zde probíhá volba typu analýzy (zda je statická, harmonická, transientní), výběr řešiče, který je vhodný pro daný typ úlohy a je optimalizován pro dané fyzikální pole a nastavuje se poţadovaná přesnost výsledků. V našem případě se jedná o harmonickou analýzu o frekvenci 50 Hz a ostatní hodnoty a nastavení jsou volena automaticky. [13] Post-procesing V této závěrečné fázi modelování se provádí samotné vyhodnocení modelované úlohy. Je velké mnoţství moţností, jakým lze interpretovat dosaţené výsledky, z nichţ nejpouţívanějšími je zobrazení mapy elektromagnetického pole, nebo vynesení závislosti elektromagnetických veličin na čase, frekvenci, teplotě a podobně. Interpretace výsledků ze simulovaných úloh v této práci budou zobrazeny v nové kapitole. [13] 34
35 4 Výsledky modelování Jak jiţ bylo napsáno v předchozí kapitole, je modelování magnetického pole transformátoru rozděleno na tři různé stavy transformátoru. Proto i vyhodnocení bude rozděleno podle jednotlivých stavů. 4.1 Stav - naprázdno Tento stav představuje transformátor, který je pouze připojen k síti a není zatíţen. Při modelování to znamenalo, ţe bylo napájeno pouze prostřední vinutí a obě postranní byla odpojena. Obr. 4.1Magnetické siločáry - naprázdno 35
36 Obr. 4.2Magnetická indukce naprázdno Obr. 4.3Magnetická indukce - naprázdno 36
37 4.2 Stav žárovka nesvítí Stav, kdy připojená ţárovka nesvítí představuje transformátor, který je připojen k síti a jeho levé sekundární vinutí je vyzkratováno. Na pravém vinutí je připojena ţárovka, která díky vyzkratovanému levému vinutí nemá dostatek energie na to, aby se rozsvítila. Obr. 4.4Magnetické siločáry žárovka nesvítí Obr. 4.5Magnetická indukce žárovka nesvítí 37
38 Obr. 4.6Magnetická indukce žárovka nesvítí 4.3 Stav žárovka svítí Obr. 4.7Magnetické siločáry žárovka svítí 38
39 Posledním modelovaným stavem byl stav, kdy připojená ţárovka svítila. Při modelování to představovalo transformátor připojený k síti a obě sekundární vinutí byla napájena proudovou hustotou, která byla naměřena při simulaci pokusu a následně vypočítána. Obr. 4.8Magnetická indukce žárovka svítí Obr. 4.9Magnetická indukce žárovka svítí 39
40 Závěr Kdyţ jsem si vybíral z velkého mnoţství zadání bakalářských prací, vybral jsem si právě toto téma, neboť to nebylo téma jenom teoretické, ale i praktické. S prací jsem začal na podzim roku 2012, kdy bylo součástí předmětu MPS namodelovat a prezentovat elektrický stroj. Tento předmět mi hodně pomohl k napsání bakalářské práce, moţná i proto, ţe jsem si z velké části modelování připravil uţ tam. Po novém roce jsem pomalu začal psát teorii a postupně od úvodu byly plněny ostatní stránky, aţ jsem se dostal aţ sem. První část bakalářské práce zahrnuje především teoretické poznatky o transformátoru a jsou zde shrnuta fakta o principu a funkci transformátoru, dále jsou zde popsána náhradní schémata a rovnice popisující chování transformátoru. To vše je součástí kapitoly první. Ve druhé kapitole jsem se věnoval magnetickému obvodu. Ten je zde popsán od rozdělení podle tvarů, podle pouţitých materiálů a částečně je zde popsán i pracovní postup při výrobě magnetických jader transformátoru. Můj největší přínos k této bakalářské práci přichází společně s kapitolou třetí. Po namodelování základního stavu transformátoru stavu naprázdno jsem ještě modelování doplnil o pokus, který jsem nalezl na internetu. Tento pokus mi přišel jako zajímavý a bylo proveditelné i samotné namodelování na počítači v programu Ansys. Následovalo provedení pokusu v laboratoři, naměření potřebných hodnot a následně bylo zkoušeno ideální provedení pokusu, které by přehledně zobrazilo poţadované stavy transformátoru. Pomocí naměřených hodnot byl vytvořen 2D model transformátoru v počítačovém programu Ansys, který se stal terčem útoku všech moţných zatěţování a simulací. Nakonec jsem vybral tři stavy, které dle mého názoru hezky popisují chování transformátoru. Výsledkyzobrazují transformátor naprázdno, druhý a třetí stav si pohrává se sycením transformátoru. 40
41 Seznam literatury a informačních zdrojů [1] BARTOŠ, Václav et al. Elektrické stroje. 1. vyd. V Plzni: Západočeská univerzita, s. ISBN [2] Miniencyklopedie : Elektřina. [online]. [cit ].Dostupné z: [3] PETROV, Georgij N. Elektrické stroje 1: úvod-transformátory. Vyd. 1. Praha: Academia, s. [4] Toroidní transformátory. [online]. [cit ]. Dostupné z: [5] FAKTOR, Zdeňek. Transformátory a cívky. Vyd. 1. Praha: BEN, s. ISBN X [6] Elektrické stroje. [online]. s. 23 [cit ]. Dostupné z: [7] BARTOŠ, Václav. Teorie a měření elektrických strojů: laboratorní cvičení - měření. 4. vyd. Plzeň: VŠSE, s. [8] Prezentace VTP. [online]. s. 71 [cit ]. Dostupné z: [9] Trafoplech. In: Wikipedia: the free encyclopedia [online]. San Francisco (CA): Wikimedia Foundation, [cit ]. Dostupné z: [10] Transformátor. [online]. s. 30 [cit ]. Dostupné z: [11] ECOM.CZ. [online]. [cit ]. Dostupné z: [12] Metoda konečných prvků. In: Wikipedia: the free encyclopedia [online]. San Francisco (CA): Wikimedia Foundation, 2013 [cit ]. Dostupné z: [13] KINDL, Vladimír. Modelování polí v elektrických strojích. [online]. [cit ]. Dostupné z: [14] Sbírka fyzikálních pokusů Transformátor se dvěma sekundáry. [online]. s. 1 [cit ]. Dostupné z: 41
42 Přílohy Příloha A - zdrojový kód z program Ansys pro model transformátoru naprázdno. Ostatní případy se liší pouze zadávanou proudovou hustotou označeno červeně /PREP7 *SET,a,160e-3 RECTING, 0,a,0,a, RECTING, 26e-3,67e-3,32e-3,128e-3, RECTING, 93e-3,134e-3,32e-3,128e-3, RECTING, -9e-3,-2e-3,37e-3,123e-3, RECTING, -17e-3,-10e-3,37e-3,123e-3, RECTING, 28e-3,35e-3,37e-3,123e-3, RECTING, 36e-3,43e-3,37e-3,123e-3, RECTING, 50e-3,57e-3,37e-3,123e-3, RECTING, 58e-3,65e-3,37e-3,123e-3, RECTING, 95e-3,102e-3,37e-3,123e-3, RECTING, 103e-3,110e-3,37e-3,123e-3, RECTING, 117e-3,124e-3,37e-3,123e-3, RECTING, 125e-3,132e-3,37e-3,123e-3, RECTING, 162e-3,169e-3,37e-3,123e-3, RECTING, 170e-3,177e-3,37e-3,123e-3,, RECTING, -80e-3,240e-3,-80e-3,240e-3, APTN,all ET,1,plane 53 ET,2,plane 53 ET,3,plane 53 ET,4,plane 53 KEYOPT,1,1,0 KEYOPT,1,2,0 KEYOPT,1,3,0 KEYOPT,1,4,0 KEYOPT,1,5,0 KEYOPT,1,7,0 KEYOPT,2,1,0 KEYOPT,2,2,0 KEYOPT,2,3,0 KEYOPT,2,4,0 KEYOPT,2,5,0 KEYOPT,2,7,0 KEYOPT,3,1,0 KEYOPT,3,2,0 KEYOPT,3,3,0 KEYOPT,3,4,0 KEYOPT,3,5,0 KEYOPT,3,7,0 KEYOPT,4,1,0 KEYOPT,4,2,0 KEYOPT,4,3,0 KEYOPT,4,4,0 KEYOPT,4,5,0 42
43 KEYOPT,4,7,0 MPTEMP,,,,,,,, MPTEMP,1,0 MPDATA,MURX,1,,1 MPTEMP,,,,,,,, MPTEMP,1,0 MPDATA,MURX,2,,1 MPTEMP,,,,,,,, MPTEMP,1,0 MPDATA,MURX,3,,1 MPTEMP,,,,,,,, MPTEMP,1,0 MPTEMP,,,,,,,, MPTEMP,1,0 TB,BH,4,1,15, TBTEMP,0 TBPT,,10000,0.5 TBPT,,20000,1 TBPT,,30000,1.5 TBPT,,40000,2 TBPT,,50000,2.02 TBPT,,70000,2.04 TBPT,,100000,2.08 TBPT,,250000,2.13 TBPT,,500000,2.18 TBPT,,750000,2.23 TBPT,, ,2.25 TBPT,, ,2.27 TBPT,, ,2.29 TBPT,, ,2.31 TBPT,, ,2.33 aplot FLST,5,3,5,ORDE,2 FITEM,5,18 FITEM,5,-20 CM,_Y,AREA ASEL,,,,P51X CM,_Y1,AREA CMSEL,S,_Y CMSEL,S,_Y1 AATT, 1,, 1, 0, CMSEL,S,_Y CMDELE,_Y CMDELE,_Y1 CM,_Y,AREA ASEL,,,, 17 CM,_Y1,AREA CMSEL,S,_Y CMSEL,S,_Y1 AATT, 4,, 4, 0, CMSEL,S,_Y CMDELE,_Y CMDELE,_Y1 FLST,5,6,5,ORDE,6 43
44 FITEM,5,4 FITEM,5,6 FITEM,5,9 FITEM,5,-10 FITEM,5,13 FITEM,5,-14 CM,_Y,AREA ASEL,,,,P51X CM,_Y1,AREA CMSEL,S,_Y CMSEL,S,_Y1 AATT, 2,, 2, 0, CMSEL,S,_Y CMDELE,_Y CMDELE,_Y1 FLST,5,6,5,ORDE,6 FITEM,5,5 FITEM,5,7 FITEM,5,-8 FITEM,5,11 FITEM,5,-12 FITEM,5,15 CM,_Y,AREA ASEL,,,,P51X CM,_Y1,AREA CMSEL,S,_Y CMSEL,S,_Y1 AATT, 3,, 3, 0, CMSEL,S,_Y CMDELE,_Y CMDELE,_Y1 ESIZE,0.0025,0, MSHAPE,1,2D MSHKEY,0 FLST,5,16,5,ORDE,4 FITEM,5,4 FITEM,5,-15 FITEM,5,17 FITEM,5,-20 CM,_Y,AREA ASEL,,,,P51X CM,_Y1,AREA CHKMSH,'AREA' CMSEL,S,_Y AMESH,_Y1 CMDELE,_Y CMDELE,_Y1 CMDELE,_Y2 ANTYPE,3 HARFRQ,0,50, NSUBST,, KBC,0 44
45 FLST,2,4,4,ORDE,2 FITEM,2,61 FITEM,2,-64 DL,P51X,,AZ,0,0, aplot FLST,2,1,5,ORDE,1 FITEM,2,5 BFA,P51X,JS,,,0,0 FLST,2,1,5,ORDE,1 FITEM,2,7 BFA,P51X,JS,,,-0,0 FLST,2,1,5,ORDE,1 FITEM,2,8 BFA,P51X,JS,,,2000,0 FLST,2,1,5,ORDE,1 FITEM,2,11 BFA,P51X,JS,,,-2000,0 FLST,2,1,5,ORDE,1 FITEM,2,12 BFA,P51X,JS,,,0,0 FLST,2,1,5,ORDE,1 FITEM,2,15 BFA,P51X,JS,,,-0,0 FINISH /SOL ANTYPE,3 HARFRQ,0,50, NSUBST,, KBC,0 solve FINISH 45
ZÁPADOČESKÁ UNIVERZITA V PLZNI FAKULTA ELEKTROTECHNICKÁ
 ZÁPADOČESKÁ UNIVERZITA V PLZNI FAKULTA ELEKTROTECHNICKÁ Katedra elektromechaniky a výkonové elektroniky BAKALÁŘSKÁ PRÁCE Měření na vzduchovém trojfázovém transformátoru Vojtěch Behrík 2012 Abstrakt Cílem
ZÁPADOČESKÁ UNIVERZITA V PLZNI FAKULTA ELEKTROTECHNICKÁ Katedra elektromechaniky a výkonové elektroniky BAKALÁŘSKÁ PRÁCE Měření na vzduchovém trojfázovém transformátoru Vojtěch Behrík 2012 Abstrakt Cílem
Praktikum II Elektřina a magnetismus
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum II Elektřina a magnetismus Úloha č. VII Název: Měření indukčnosti a kapacity metodou přímou Pracoval: Matyáš Řehák stud.sk.:
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum II Elektřina a magnetismus Úloha č. VII Název: Měření indukčnosti a kapacity metodou přímou Pracoval: Matyáš Řehák stud.sk.:
4.6.6 Složený sériový RLC obvod střídavého proudu
 4.6.6 Složený sériový LC obvod střídavého proudu Předpoklady: 41, 4605 Minulá hodina: odpor i induktance omezují proud ve střídavém obvodu, nemůžeme je však sčítat normálně, ale musíme použít Pythagorovu
4.6.6 Složený sériový LC obvod střídavého proudu Předpoklady: 41, 4605 Minulá hodina: odpor i induktance omezují proud ve střídavém obvodu, nemůžeme je však sčítat normálně, ale musíme použít Pythagorovu
4.2.7 Voltampérová charakteristika rezistoru a žárovky
 4.2.7 Voltampérová charakteristika rezistoru a žárovky Předpoklady: 4205 Pedagogická poznámka: Tuto hodinu učím jako běžnou jednohodinovku s celou třídou. Některé dvojice stihnou naměřit více odporů. Voltampérová
4.2.7 Voltampérová charakteristika rezistoru a žárovky Předpoklady: 4205 Pedagogická poznámka: Tuto hodinu učím jako běžnou jednohodinovku s celou třídou. Některé dvojice stihnou naměřit více odporů. Voltampérová
Napájecí soustava automobilu. 2) Odsimulujte a diskutujte stavy které mohou v napájecí soustavě vzniknout.
 VŠB-TU Ostrava Datum měření: 3. KATEDRA ELEKTRONIKY Napájecí soustava automobilu Fakulta elektrotechniky a informatiky Jména, studijní skupiny: Zadání: 1) Zapojte úlohu podle návodu. 2) Odsimulujte a diskutujte
VŠB-TU Ostrava Datum měření: 3. KATEDRA ELEKTRONIKY Napájecí soustava automobilu Fakulta elektrotechniky a informatiky Jména, studijní skupiny: Zadání: 1) Zapojte úlohu podle návodu. 2) Odsimulujte a diskutujte
ISŠT Mělník. Integrovaná střední škola technická Mělník, K učilišti 2566, 276 01 Mělník Ing.František Moravec
 ISŠT Mělník Číslo projektu Označení materiálu Název školy Autor Tematická oblast CZ.1.07/1.5.00/34.0061 VY_32_INOVACE_H.2.19 Integrovaná střední škola technická Mělník, K učilišti 2566, 276 01 Mělník Ing.František
ISŠT Mělník Číslo projektu Označení materiálu Název školy Autor Tematická oblast CZ.1.07/1.5.00/34.0061 VY_32_INOVACE_H.2.19 Integrovaná střední škola technická Mělník, K učilišti 2566, 276 01 Mělník Ing.František
LABORATORNÍ CVIČENÍ Elektrotechnika a elektronika
 VUT FSI BRNO ÚVSSaR, ODBOR ELEKTROTECHNIKY JMÉNO: ŠKOLNÍ ROK: 2010/2011 PŘEDNÁŠKOVÁ SKUPINA: 1E/95 LABORATORNÍ CVIČENÍ Elektrotechnika a elektronika ROČNÍK: 1. KROUŽEK: 2EL SEMESTR: LETNÍ UČITEL: Ing.
VUT FSI BRNO ÚVSSaR, ODBOR ELEKTROTECHNIKY JMÉNO: ŠKOLNÍ ROK: 2010/2011 PŘEDNÁŠKOVÁ SKUPINA: 1E/95 LABORATORNÍ CVIČENÍ Elektrotechnika a elektronika ROČNÍK: 1. KROUŽEK: 2EL SEMESTR: LETNÍ UČITEL: Ing.
2.4.11 Nerovnice s absolutní hodnotou
 .. Nerovnice s absolutní hodnotou Předpoklady: 06, 09, 0 Pedagogická poznámka: Hlavním záměrem hodiny je, aby si studenti uvědomili, že se neučí nic nového. Pouze používají věci, které dávno znají, na
.. Nerovnice s absolutní hodnotou Předpoklady: 06, 09, 0 Pedagogická poznámka: Hlavním záměrem hodiny je, aby si studenti uvědomili, že se neučí nic nového. Pouze používají věci, které dávno znají, na
Semestrální práce NÁVRH ÚZKOPÁSMOVÉHO ZESILOVAČE. Daniel Tureček zadání číslo 18 cvičení: sudý týden 14:30
 Semestrální práce NÁVRH ÚZKOPÁSMOVÉHO ZESILOVAČE Daniel Tureček zadání číslo 18 cvičení: sudý týden 14:30 1. Ověření stability tranzistoru Při návrhu úzkopásmového zesilovače s tranzistorem je potřeba
Semestrální práce NÁVRH ÚZKOPÁSMOVÉHO ZESILOVAČE Daniel Tureček zadání číslo 18 cvičení: sudý týden 14:30 1. Ověření stability tranzistoru Při návrhu úzkopásmového zesilovače s tranzistorem je potřeba
ELEKTROTECHNICKÁ MĚŘENÍ PRACOVNÍ SEŠIT 2-3
 ELEKTROTECHNICKÁ MĚŘENÍ PRACOVNÍ SEŠIT - Název úlohy: Měření vlastností regulačních prvků Listů: List: Zadání: Pro daný regulační prvek zapojený jako dělič napětí změřte a stanovte: a, Minimálně regulační
ELEKTROTECHNICKÁ MĚŘENÍ PRACOVNÍ SEŠIT - Název úlohy: Měření vlastností regulačních prvků Listů: List: Zadání: Pro daný regulační prvek zapojený jako dělič napětí změřte a stanovte: a, Minimálně regulační
Indukční děliče napětí
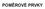 POMĚROVÉ PRVKY Indukční děliče napětí 2 Jednoduchý indukční dělič napětí k v D D i1 U Ui D 1α jβ U D k / m Jádro toroidního tvaru z materiálu s vysokou permeabilitou. Všechny sekce navinuty současně kabelem
POMĚROVÉ PRVKY Indukční děliče napětí 2 Jednoduchý indukční dělič napětí k v D D i1 U Ui D 1α jβ U D k / m Jádro toroidního tvaru z materiálu s vysokou permeabilitou. Všechny sekce navinuty současně kabelem
Kvadratické rovnice pro učební obory
 Variace 1 Kvadratické rovnice pro učební obory Autor: Mgr. Jaromír JUŘEK Kopírování a jkaékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
Variace 1 Kvadratické rovnice pro učební obory Autor: Mgr. Jaromír JUŘEK Kopírování a jkaékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
3.2.4 Podobnost trojúhelníků II
 3..4 odobnost trojúhelníků II ředpoklady: 33 ř. 1: Na obrázku jsou nakresleny podobné trojúhelníky. Zapiš jejich podobnost (aby bylo zřejmé, který vrchol prvního trojúhelníku odpovídá vrcholu druhého trojúhelníku).
3..4 odobnost trojúhelníků II ředpoklady: 33 ř. 1: Na obrázku jsou nakresleny podobné trojúhelníky. Zapiš jejich podobnost (aby bylo zřejmé, který vrchol prvního trojúhelníku odpovídá vrcholu druhého trojúhelníku).
Pracovní list vzdáleně ovládaný experiment. Obr. 1: Schéma sériového RLC obvodu, převzato z [3].
![Pracovní list vzdáleně ovládaný experiment. Obr. 1: Schéma sériového RLC obvodu, převzato z [3]. Pracovní list vzdáleně ovládaný experiment. Obr. 1: Schéma sériového RLC obvodu, převzato z [3].](/thumbs/40/21550192.jpg) Pracovní list vzdáleně ovládaný experiment Střídavý proud (SŠ) Sériový obvod RLC Fyzikální princip Obvod střídavého proudu může mít současně odpor, indukčnost i kapacitu. Pokud jsou tyto prvky v sérii,
Pracovní list vzdáleně ovládaný experiment Střídavý proud (SŠ) Sériový obvod RLC Fyzikální princip Obvod střídavého proudu může mít současně odpor, indukčnost i kapacitu. Pokud jsou tyto prvky v sérii,
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita V. 2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V. 2.15 Konstrukční materiály Kapitola 1 Vlastnosti
Zvyšování kvality výuky technických oborů Klíčová aktivita V. 2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V. 2.15 Konstrukční materiály Kapitola 1 Vlastnosti
A1B14SP1 ELEKTRICKÉ STROJE A PŘÍSTROJE 1
 A1B14SP1 ELEKTRICKÉ STROJE A PŘÍSTROJE 1 3+2 z,zk Doc. Ing. Petr Voženílek, CSc. 2 2435 2135 T2:B3-257 Doc. Ing. Vladimír Novotný, CSc. 2 2435 2150 T2:B3-247 Doc. Ing. Pavel Mindl, CSc. 2 2435 2150 T2:B3-247
A1B14SP1 ELEKTRICKÉ STROJE A PŘÍSTROJE 1 3+2 z,zk Doc. Ing. Petr Voženílek, CSc. 2 2435 2135 T2:B3-257 Doc. Ing. Vladimír Novotný, CSc. 2 2435 2150 T2:B3-247 Doc. Ing. Pavel Mindl, CSc. 2 2435 2150 T2:B3-247
PRAKTIKUM II Elektřina a magnetismus
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM II Elektřina a magnetismus Úloha č.: XIV Název: Relaxační kmity Pracoval: Pavel Brožek stud. skup. 12 dne 5.12.2008 Odevzdal
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM II Elektřina a magnetismus Úloha č.: XIV Název: Relaxační kmity Pracoval: Pavel Brožek stud. skup. 12 dne 5.12.2008 Odevzdal
Tvorba trendové funkce a extrapolace pro roční časové řady
 Tvorba trendové funkce a extrapolace pro roční časové řady Příklad: Základem pro analýzu je časová řada živě narozených mezi lety 1970 a 2005. Prvním úkolem je vybrat vhodnou trendovou funkci pro vystižení
Tvorba trendové funkce a extrapolace pro roční časové řady Příklad: Základem pro analýzu je časová řada živě narozených mezi lety 1970 a 2005. Prvním úkolem je vybrat vhodnou trendovou funkci pro vystižení
Jednofázový alternátor
 Jednofázový alternátor - 1 - Jednofázový alternátor Ing. Ladislav Kopecký, 2007 Ke generování elektrického napětí pro energetické účely se nejčastěji využívá dvou principů. Prvním z nich je indukce elektrického
Jednofázový alternátor - 1 - Jednofázový alternátor Ing. Ladislav Kopecký, 2007 Ke generování elektrického napětí pro energetické účely se nejčastěji využívá dvou principů. Prvním z nich je indukce elektrického
Rozložení magnetického pole v elektrických strojích část 1
 Rozložení magnetického pole v elektrických strojích část 1 Ing. Miroslav Skalka, Ing. Roman Bok, Doc. Ing. Čestmír Ondrůšek, CSc. Vysoké učení technické v Brně, Fakulta elektrotechniky a komunikačních
Rozložení magnetického pole v elektrických strojích část 1 Ing. Miroslav Skalka, Ing. Roman Bok, Doc. Ing. Čestmír Ondrůšek, CSc. Vysoké učení technické v Brně, Fakulta elektrotechniky a komunikačních
ZADÁNÍ: ÚVOD: SCHÉMA:
 ZADÁNÍ: ) U daného síťového transformátoru vyhodnoťte osciloskopickou metodou ze zobrazení hysterezní smyčky hlavní magnetické vlastnosti jádra - H MAX,H 0,B r při B MAX T. 2) Ze zjištěného průběhu hysterezní
ZADÁNÍ: ) U daného síťového transformátoru vyhodnoťte osciloskopickou metodou ze zobrazení hysterezní smyčky hlavní magnetické vlastnosti jádra - H MAX,H 0,B r při B MAX T. 2) Ze zjištěného průběhu hysterezní
Kvadratické rovnice pro studijní obory
 Variace 1 Kvadratické rovnice pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
Variace 1 Kvadratické rovnice pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
http://www.zlinskedumy.cz
 Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor Ročník 2, 3 Obor Anotace CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Elektronické obvody, vy_32_inovace_ma_42_06
Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor Ročník 2, 3 Obor Anotace CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Elektronické obvody, vy_32_inovace_ma_42_06
Sériově a paralelně řazené rezistory. Tematický celek: Elektrický proud. Úkol:
 Název: Sériově a paralelně řazené rezistory. Tematický celek: Elektrický proud. Úkol: Zopakujte si, co platí pro sériově a paralelně řazené rezistory. Sestrojte elektrické obvody dle schématu. Pomocí senzorů
Název: Sériově a paralelně řazené rezistory. Tematický celek: Elektrický proud. Úkol: Zopakujte si, co platí pro sériově a paralelně řazené rezistory. Sestrojte elektrické obvody dle schématu. Pomocí senzorů
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV VÝKONOVÉ ELEKTROTECHNIKY A ELEKTRONIKY FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV VÝKONOVÉ ELEKTROTECHNIKY A ELEKTRONIKY FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION
Učební osnova vyučovacího předmětu Silnoproudá zařízení. 3. ročník (2 hodiny týdně, celkem 52 hodin)
 Učební osnova vyučovacího předmětu Silnoproudá zařízení 3. ročník (2 hodiny týdně, celkem 52 hodin) Obor vzdělání: Forma vzdělávání: 26-41-M/01 Elektrotechnika denní studium Celkový počet týdenních vyuč.
Učební osnova vyučovacího předmětu Silnoproudá zařízení 3. ročník (2 hodiny týdně, celkem 52 hodin) Obor vzdělání: Forma vzdělávání: 26-41-M/01 Elektrotechnika denní studium Celkový počet týdenních vyuč.
STEREOMETRIE. Vzdálenost bodu od přímky. Mgr. Jakub Němec. VY_32_INOVACE_M3r0113
 STEREOMETRIE Vzdálenost bodu od přímky Mgr. Jakub Němec VY_32_INOVACE_M3r0113 VZDÁLENOST BODU OD PŘÍMKY V PROSTORU Při hledání vzdálenosti bodu od geometrického útvaru v prostoru je nutné si vždy úlohu
STEREOMETRIE Vzdálenost bodu od přímky Mgr. Jakub Němec VY_32_INOVACE_M3r0113 VZDÁLENOST BODU OD PŘÍMKY V PROSTORU Při hledání vzdálenosti bodu od geometrického útvaru v prostoru je nutné si vždy úlohu
M - Rovnice - lineární a s absolutní hodnotou
 Rovnice a jejich ekvivalentní úpravy Co je rovnice Rovnice je matematický zápis rovnosti dvou výrazů. př.: x + 5 = 7x - M - Rovnice - lineární a s absolutní hodnotou Písmeno zapsané v rovnici nazýváme
Rovnice a jejich ekvivalentní úpravy Co je rovnice Rovnice je matematický zápis rovnosti dvou výrazů. př.: x + 5 = 7x - M - Rovnice - lineární a s absolutní hodnotou Písmeno zapsané v rovnici nazýváme
Napájení elektrifikovaných tratí
 Napájení elektrifikovaných tratí Elektrická trakce je pohon hnacího vozidla pomocí metrického točivého stroje elektromotoru kterému říkáme trakční motor. Přívod proudu do elektrických vozidel je realizovaný
Napájení elektrifikovaných tratí Elektrická trakce je pohon hnacího vozidla pomocí metrického točivého stroje elektromotoru kterému říkáme trakční motor. Přívod proudu do elektrických vozidel je realizovaný
Bipolární tranzistor. Bipolární tranzistor. Otevřený tranzistor
 Bipolární tranzistor Bipolární tranzistor polovodičová součástka se dvěma PN přechody a 3 elektrodami: C - kolektorem E - emitorem B - bází vrstvy mohou být v pořadí NPN nebo PNP, častější je varianta
Bipolární tranzistor Bipolární tranzistor polovodičová součástka se dvěma PN přechody a 3 elektrodami: C - kolektorem E - emitorem B - bází vrstvy mohou být v pořadí NPN nebo PNP, častější je varianta
(a) = (a) = 0. x (a) > 0 a 2 ( pak funkce má v bodě a ostré lokální maximum, resp. ostré lokální minimum. Pokud je. x 2 (a) 2 y (a) f.
 I. Funkce dvou a více reálných proměnných 5. Lokální extrémy. Budeme uvažovat funkci f = f(x 1, x 2,..., x n ), která je definovaná v otevřené množině G R n. Řekneme, že funkce f = f(x 1, x 2,..., x n
I. Funkce dvou a více reálných proměnných 5. Lokální extrémy. Budeme uvažovat funkci f = f(x 1, x 2,..., x n ), která je definovaná v otevřené množině G R n. Řekneme, že funkce f = f(x 1, x 2,..., x n
VY_52_INOVACE_2NOV37. Autor: Mgr. Jakub Novák. Datum: 5. 9. 2012 Ročník: 8. a 9.
 VY_52_INOVACE_2NOV37 Autor: Mgr. Jakub Novák Datum: 5. 9. 2012 Ročník: 8. a 9. Vzdělávací oblast: Člověk a příroda Vzdělávací obor: Fyzika Tematický okruh: Elektromagnetické a světelné děje Téma: Měření
VY_52_INOVACE_2NOV37 Autor: Mgr. Jakub Novák Datum: 5. 9. 2012 Ročník: 8. a 9. Vzdělávací oblast: Člověk a příroda Vzdělávací obor: Fyzika Tematický okruh: Elektromagnetické a světelné děje Téma: Měření
4.5.2 Magnetické pole vodiče s proudem
 4.5.2 Magnetické pole vodiče s proudem Předpoklady: 4501 1820 H. Ch. Oersted objevil, že vodič s proudem působí na magnetku elektrický proud vytváří ve svém okolí magnetické pole (dříve nebyly k dispozici
4.5.2 Magnetické pole vodiče s proudem Předpoklady: 4501 1820 H. Ch. Oersted objevil, že vodič s proudem působí na magnetku elektrický proud vytváří ve svém okolí magnetické pole (dříve nebyly k dispozici
Číselné soustavy Ing. M. Kotlíková, Ing. A. Netrvalová Strana 1 (celkem 7) Číselné soustavy
 Číselné soustavy Ing. M. Kotlíková, Ing. A. Netrvalová Strana (celkem 7) Polyadické - zobrazené mnohočlenem desítková soustava 3 2 532 = 5 + 3 + 2 + Číselné soustavy Číslice tvořící zápis čísla jsou vlastně
Číselné soustavy Ing. M. Kotlíková, Ing. A. Netrvalová Strana (celkem 7) Polyadické - zobrazené mnohočlenem desítková soustava 3 2 532 = 5 + 3 + 2 + Číselné soustavy Číslice tvořící zápis čísla jsou vlastně
VÝUKOVÝ MATERIÁL. Pro vzdělanější Šluknovsko. 32 Inovace a zkvalitnění výuky prostřednictvím ICT. 0210 Bc. David Pietschmann.
 VÝUKOVÝ MATERIÁL Identifikační údaje školy Číslo projektu Název projektu Číslo a název šablony Autor Tematická oblast Číslo a název materiálu Anotace Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková
VÝUKOVÝ MATERIÁL Identifikační údaje školy Číslo projektu Název projektu Číslo a název šablony Autor Tematická oblast Číslo a název materiálu Anotace Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková
2.8.9 Parametrické rovnice a nerovnice s absolutní hodnotou
 .8.9 Parametrické rovnice a nerovnice s absolutní hodnotou Předpoklady: 0,, 806 Pedagogická poznámka: Opět si napíšeme na začátku hodiny na tabuli jednotlivé kroky postupu při řešení rovnic (nerovnic)
.8.9 Parametrické rovnice a nerovnice s absolutní hodnotou Předpoklady: 0,, 806 Pedagogická poznámka: Opět si napíšeme na začátku hodiny na tabuli jednotlivé kroky postupu při řešení rovnic (nerovnic)
M7061 ROTAČNÍ POHONY VENTILŮ
 M7061 ROTAČNÍ POHONY VENTILŮ TECHNICKÉ INFORMACE VLASTNOSTI Chráněno proti přetížení a zablokování Bezúdržbový elektrický pohon pro rotační ventily Zřetelný indikátor polohy Přímá montáž na rotační ventily
M7061 ROTAČNÍ POHONY VENTILŮ TECHNICKÉ INFORMACE VLASTNOSTI Chráněno proti přetížení a zablokování Bezúdržbový elektrický pohon pro rotační ventily Zřetelný indikátor polohy Přímá montáž na rotační ventily
Fyzika - Kvarta Fyzika kvarta Výchovné a vzdělávací strategie Učivo ŠVP výstupy
 - Kvarta Fyzika Výchovné a vzdělávací strategie Kompetence k řešení problémů Kompetence komunikativní Kompetence sociální a personální Kompetence občanská Kompetence k učení Kompetence pracovní Učivo magnetické
- Kvarta Fyzika Výchovné a vzdělávací strategie Kompetence k řešení problémů Kompetence komunikativní Kompetence sociální a personální Kompetence občanská Kompetence k učení Kompetence pracovní Učivo magnetické
2.3. POLARIZACE VLN, POLARIZAČNÍ KOEFICIENTY A POMĚR E/B
 .3. POLARIZACE VLN, POLARIZAČNÍ KOEFICIENTY A POMĚR E/B V řadě případů je užitečné znát polarizaci vlny a poměry mezi jednotlivými složkami vektoru elektrické intenzity E takzvané polarizační koeficienty,
.3. POLARIZACE VLN, POLARIZAČNÍ KOEFICIENTY A POMĚR E/B V řadě případů je užitečné znát polarizaci vlny a poměry mezi jednotlivými složkami vektoru elektrické intenzity E takzvané polarizační koeficienty,
EATON TOUR 2014. Pojistkové systémy Eaton. Eaton Elektrotechnika. 2010 Eaton Corporation. All rights reserved.
 EATON TOUR 2014 Pojistkové systémy Eaton Eaton Elektrotechnika Historie pojistek Patent z roku 1881 (T.A. Edison) k ochraně žárovek Patent z roku 1883 (C.V. Boys a H.H. Cunningham) Patent z roku 1890 (W.M.
EATON TOUR 2014 Pojistkové systémy Eaton Eaton Elektrotechnika Historie pojistek Patent z roku 1881 (T.A. Edison) k ochraně žárovek Patent z roku 1883 (C.V. Boys a H.H. Cunningham) Patent z roku 1890 (W.M.
PROGRAMOVÁNÍ SVĚTELNÝCH OZDOB
 Středoškolská technika 2016 Setkání a prezentace prací středoškolských studentů na ČVUT PROGRAMOVÁNÍ SVĚTELNÝCH OZDOB Jiří Bendík, Martin Bárta Střední odborná škola strojní a elektrotechnická U Hřiště
Středoškolská technika 2016 Setkání a prezentace prací středoškolských studentů na ČVUT PROGRAMOVÁNÍ SVĚTELNÝCH OZDOB Jiří Bendík, Martin Bárta Střední odborná škola strojní a elektrotechnická U Hřiště
ISŠT Mělník. Integrovaná střední škola technická Mělník, K učilišti 2566, 276 01 Mělník Ing.František Moravec
 ISŠT Mělník Číslo projektu Označení materiálu Název školy Autor Tematická oblast Ročník Anotace Metodický pokyn CZ.1.07/1.5.00/34.0061 VY_32_ INOVACE_C.3.17 Integrovaná střední škola technická Mělník,
ISŠT Mělník Číslo projektu Označení materiálu Název školy Autor Tematická oblast Ročník Anotace Metodický pokyn CZ.1.07/1.5.00/34.0061 VY_32_ INOVACE_C.3.17 Integrovaná střední škola technická Mělník,
Oddělení teplárenství sekce regulace VYHODNOCENÍ CEN TEPELNÉ ENERGIE
 Oddělení teplárenství sekce regulace VYHODNOCENÍ CEN TEPELNÉ ENERGIE Obsah: 1. Úvod 2. Přehled průměrných cen 3. Porovnání cen s úrovněmi cen 4. Vývoj průměrné ceny v období 21 26 5. Rozbor cen za rok
Oddělení teplárenství sekce regulace VYHODNOCENÍ CEN TEPELNÉ ENERGIE Obsah: 1. Úvod 2. Přehled průměrných cen 3. Porovnání cen s úrovněmi cen 4. Vývoj průměrné ceny v období 21 26 5. Rozbor cen za rok
2.7.2 Mocninné funkce se záporným celým mocnitelem
 .7. Mocninné funkce se záporným celým mocnitelem Předpoklady: 70 Mocninné funkce se záporným celým mocnitelem: znamená? 3 y = = = = 3 y y y 3 = ; = ; = ;.... Co to Pedagogická poznámka: Nechávám studenty,
.7. Mocninné funkce se záporným celým mocnitelem Předpoklady: 70 Mocninné funkce se záporným celým mocnitelem: znamená? 3 y = = = = 3 y y y 3 = ; = ; = ;.... Co to Pedagogická poznámka: Nechávám studenty,
Laboratorní práce č. 3: Měření indukčnosti cívky pomocí střídavého proudu
 Přírodní vědy moderně a interaktivně FYZIKA 5. ročník šestiletého a 3. ročník čtyřletého studia aboratorní práce č. 3: Měření indukčnosti cívky pomocí střídavého proudu ymnázium Přírodní vědy moderně
Přírodní vědy moderně a interaktivně FYZIKA 5. ročník šestiletého a 3. ročník čtyřletého studia aboratorní práce č. 3: Měření indukčnosti cívky pomocí střídavého proudu ymnázium Přírodní vědy moderně
1. Stejnosměrný proud základní pojmy
 1. Stejnosměrný proud základní pojmy Stejnosměrný elektrický proud je takový proud, který v čase nemění svoji velikost a smysl. 1.1. Mezinárodní soustava jednotek Fyzikální veličina je stanovena s fyzikálního
1. Stejnosměrný proud základní pojmy Stejnosměrný elektrický proud je takový proud, který v čase nemění svoji velikost a smysl. 1.1. Mezinárodní soustava jednotek Fyzikální veličina je stanovena s fyzikálního
Zvlhčovače vzduchu řady UX
 Návod k používání a obsluze Zvlhčovače vzduchu řady UX Výrobek název: Zvlhčovač vzduchu FRANCO typ: UX56-M, UX56-T, UX71-TT, UX71-TS Dodavatel název: AGRICO s.r.o. adresa: Rybářská 671, 379 01 Třeboň IČO:
Návod k používání a obsluze Zvlhčovače vzduchu řady UX Výrobek název: Zvlhčovač vzduchu FRANCO typ: UX56-M, UX56-T, UX71-TT, UX71-TS Dodavatel název: AGRICO s.r.o. adresa: Rybářská 671, 379 01 Třeboň IČO:
MĚŘENÍ Laboratorní cvičení z měření Měření parametrů operačních zesilovačů část 3-7-2 Test
 MĚŘENÍ Laboratorní cvičení z měření část 3-7- Test Výukový materiál Číslo projektu: CZ..07/.5.00/34.0093 Šablona: III/ Inovace a zkvalitnění výuky prostřednictvím ICT Sada: Číslo materiálu: VY_3_INOVACE_
MĚŘENÍ Laboratorní cvičení z měření část 3-7- Test Výukový materiál Číslo projektu: CZ..07/.5.00/34.0093 Šablona: III/ Inovace a zkvalitnění výuky prostřednictvím ICT Sada: Číslo materiálu: VY_3_INOVACE_
TPU 4x.xx. Přístrojový transformátor proudu
 Přístrojový transformátor proudu TPU 4x.xx Nejvyšší napětí soustavy [kv] 12-17,5 Zkušební napětí střídavé, 1 min. [kv] 28-42 Zkušební napětí impulsní [kv] 75-95 Jmenovitý primární proud [A] 10-3200 Jmenovitý
Přístrojový transformátor proudu TPU 4x.xx Nejvyšší napětí soustavy [kv] 12-17,5 Zkušební napětí střídavé, 1 min. [kv] 28-42 Zkušební napětí impulsní [kv] 75-95 Jmenovitý primární proud [A] 10-3200 Jmenovitý
( ) ( ) ( ) 2 ( ) 2.7.16 Rovnice s neznámou pod odmocninou II. Předpoklady: 2715
 .7.6 Rovnice s neznámou pod odmocninou II Předpoklady: 75 Př. : Vyřeš rovnici y + + y = 4 y + + y = 4 / ( y + + y ) = ( 4) y + + 4 y + y + 4 y = 6 5y + 4 y + y = 8 5y + 4 y + y = 8 - v tomto stavu nemůžeme
.7.6 Rovnice s neznámou pod odmocninou II Předpoklady: 75 Př. : Vyřeš rovnici y + + y = 4 y + + y = 4 / ( y + + y ) = ( 4) y + + 4 y + y + 4 y = 6 5y + 4 y + y = 8 5y + 4 y + y = 8 - v tomto stavu nemůžeme
Popis připojení elektroměru k modulům SDS Micro, Macro a TTC.
 Popis připojení elektroměru k modulům SDS Micro, Macro a TTC. V tomhle případě předpokládáme, že modul SDS je již zapojen do sítě a zprovozněn. První zapojení a nastavení modulů SDS najdete v návodech
Popis připojení elektroměru k modulům SDS Micro, Macro a TTC. V tomhle případě předpokládáme, že modul SDS je již zapojen do sítě a zprovozněn. První zapojení a nastavení modulů SDS najdete v návodech
Systém zvukové signalizace a spouštění motoru na základě stavu světla
 Systém zvukové signalizace a spouštění motoru na základě stavu světla vzorová úloha (SŠ) Jméno Třída.. Datum.. 1. Teoretický úvod Cílem této úlohy je sestavit systém sledující stav světla, které bude vyhodnocováno
Systém zvukové signalizace a spouštění motoru na základě stavu světla vzorová úloha (SŠ) Jméno Třída.. Datum.. 1. Teoretický úvod Cílem této úlohy je sestavit systém sledující stav světla, které bude vyhodnocováno
Dopravní úloha. Jiří Neubauer. Katedra ekonometrie FEM UO Brno
 Přednáška č. 9 Katedra ekonometrie FEM UO Brno Distribuční úlohy Budeme se zabývat 2 typy distribučních úloh dopravní úloha přiřazovací problém Dopravní úloha V dopravním problému se v typickém případě
Přednáška č. 9 Katedra ekonometrie FEM UO Brno Distribuční úlohy Budeme se zabývat 2 typy distribučních úloh dopravní úloha přiřazovací problém Dopravní úloha V dopravním problému se v typickém případě
1. Cizinci v České republice
 1. Cizinci v České republice Počet cizinců v ČR se již delší dobu udržuje na přibližně stejné úrovni, přičemž na území České republiky bylo k 31. 12. 2011 evidováno 434 153 osob III. Pokud vezmeme v úvahu
1. Cizinci v České republice Počet cizinců v ČR se již delší dobu udržuje na přibližně stejné úrovni, přičemž na území České republiky bylo k 31. 12. 2011 evidováno 434 153 osob III. Pokud vezmeme v úvahu
Energetický regulační
 Energetický regulační ENERGETICKÝ REGULAČNÍ ÚŘAD ROČNÍK 16 V JIHLAVĚ 25. 5. 2016 ČÁSTKA 4/2016 OBSAH: str. 1. Zpráva o dosažené úrovni nepřetržitosti přenosu nebo distribuce elektřiny za rok 2015 2 Zpráva
Energetický regulační ENERGETICKÝ REGULAČNÍ ÚŘAD ROČNÍK 16 V JIHLAVĚ 25. 5. 2016 ČÁSTKA 4/2016 OBSAH: str. 1. Zpráva o dosažené úrovni nepřetržitosti přenosu nebo distribuce elektřiny za rok 2015 2 Zpráva
( ) 2.4.4 Kreslení grafů funkcí metodou dělení definičního oboru I. Předpoklady: 2401, 2208
 .. Kreslení grafů funkcí metodou dělení definičního oboru I Předpoklady: 01, 08 Opakování: Pokud jsme při řešení nerovnic potřebovali vynásobit nerovnici výrazem, nemohli jsme postupovat pro všechna čísla
.. Kreslení grafů funkcí metodou dělení definičního oboru I Předpoklady: 01, 08 Opakování: Pokud jsme při řešení nerovnic potřebovali vynásobit nerovnici výrazem, nemohli jsme postupovat pro všechna čísla
Měření statických parametrů tranzistorů
 Měření statických parametrů tranzistorů 1. Úkol měření Změřte: a.) závislost prahového napětí UT unipolárních tranzistorů typu MIS KF522 a KF521 na napětí UBS mezi substrátem a sourcem UT = f(ubs) b.)
Měření statických parametrů tranzistorů 1. Úkol měření Změřte: a.) závislost prahového napětí UT unipolárních tranzistorů typu MIS KF522 a KF521 na napětí UBS mezi substrátem a sourcem UT = f(ubs) b.)
ESII-2.1 Elektroměry
 Projekt: ODBORNÝ VÝCVIK VE 3. TISÍCILETÍ Téma: ESII-2.1 Elektroměry Obor: Elektrikář - silnoproud Ročník: 2. Zpracoval(a): Bc. Josef Dulínek Střední průmyslová škola Uherský Brod, 2010 OBSAH 1. Měření
Projekt: ODBORNÝ VÝCVIK VE 3. TISÍCILETÍ Téma: ESII-2.1 Elektroměry Obor: Elektrikář - silnoproud Ročník: 2. Zpracoval(a): Bc. Josef Dulínek Střední průmyslová škola Uherský Brod, 2010 OBSAH 1. Měření
Poznámky k verzi. Scania Diagnos & Programmer 3, verze 2.27
 cs-cz Poznámky k verzi Scania Diagnos & Programmer 3, verze 2.27 Verze 2.27 nahrazuje verzi 2.26 programu Scania Diagnos & Programmer 3 a podporuje systémy ve vozidlech řady P, G, R a T a řady F, K a N
cs-cz Poznámky k verzi Scania Diagnos & Programmer 3, verze 2.27 Verze 2.27 nahrazuje verzi 2.26 programu Scania Diagnos & Programmer 3 a podporuje systémy ve vozidlech řady P, G, R a T a řady F, K a N
Pojem stability v elektrizační soustavě
 Pojem stability v elektrizační soustavě Pro KEE/PJS Karel Noháč 2015 1 Úhlová stabilita: Rozdělení stabilit v ES Interakce přenášeného činného výkonu a rozdílu úhlu napětí uzlu připojení zdroje (elektrárny)
Pojem stability v elektrizační soustavě Pro KEE/PJS Karel Noháč 2015 1 Úhlová stabilita: Rozdělení stabilit v ES Interakce přenášeného činného výkonu a rozdílu úhlu napětí uzlu připojení zdroje (elektrárny)
Indukce, Kapacita, Odpor, Diody LCR MULTIMETR. Model : LCR-9083
 Indukce, Kapacita, Odpor, Diody LCR MULTIMETR Model : LCR-9083 OBSAH 1. Vlastnosti... 1 2. Specifikace....1 2-1 Základní specifikace....1 2-2 Elektrické specifikace....2 A. Indukce...2 B. Kapacita....2
Indukce, Kapacita, Odpor, Diody LCR MULTIMETR Model : LCR-9083 OBSAH 1. Vlastnosti... 1 2. Specifikace....1 2-1 Základní specifikace....1 2-2 Elektrické specifikace....2 A. Indukce...2 B. Kapacita....2
Úloha č. 6 Stanovení průběhu koncentrace příměsí polovodičů
 Úloha č. 6 Stanovení průběhu koncentrace příměsí polovodičů Úkol měření: 1. Změřte průběh resistivity podél monokrystalu polovodiče. 2. Vypočtěte koncentraci příměsí N A, D z naměřených hodnot resistivity.
Úloha č. 6 Stanovení průběhu koncentrace příměsí polovodičů Úkol měření: 1. Změřte průběh resistivity podél monokrystalu polovodiče. 2. Vypočtěte koncentraci příměsí N A, D z naměřených hodnot resistivity.
Pro vš echny body platí U CC = ± 15 V (pokud není uvedeno jinak). Ke kaž dému bodu nakreslete jednoduché schéma zapojení.
 OPEAČNÍ ZESILOVAČ 304 4 Pro vš echny body platí U CC = ± 15 V (pokud není uvedeno jinak). Ke kaž dému bodu nakreslete jednoduché schéma zapojení. 1. Ověřte měření m některé katalogové údaje OZ MAC 157
OPEAČNÍ ZESILOVAČ 304 4 Pro vš echny body platí U CC = ± 15 V (pokud není uvedeno jinak). Ke kaž dému bodu nakreslete jednoduché schéma zapojení. 1. Ověřte měření m některé katalogové údaje OZ MAC 157
STŘEDNÍ ODBORNÁ ŠKOLA a STŘEDNÍ ODBORNÉ UČILIŠTĚ, Česká Lípa, 28. října 2707, příspěvková organizace
 Název školy: STŘEDNÍ ODBORNÁ ŠKOLA a STŘEDNÍ ODBORNÉ UČILIŠTĚ, Česká Lípa, 28. října 2707, příspěvková organizace Číslo a název projektu: Číslo a název šablony klíčové aktivity: CZ.1.07/1.5.00/34.0880
Název školy: STŘEDNÍ ODBORNÁ ŠKOLA a STŘEDNÍ ODBORNÉ UČILIŠTĚ, Česká Lípa, 28. října 2707, příspěvková organizace Číslo a název projektu: Číslo a název šablony klíčové aktivity: CZ.1.07/1.5.00/34.0880
DUM téma: KALK Výrobek sestavy
 DUM téma: KALK Výrobek sestavy ze sady: 2 tematický okruh sady: Příprava výroby a ruční programování CNC ze šablony: 6 Příprava a zadání projektu Určeno pro : 3 a 4 ročník vzdělávací obor: 23-41-M/01 Strojírenství
DUM téma: KALK Výrobek sestavy ze sady: 2 tematický okruh sady: Příprava výroby a ruční programování CNC ze šablony: 6 Příprava a zadání projektu Určeno pro : 3 a 4 ročník vzdělávací obor: 23-41-M/01 Strojírenství
Využití ICT pro rozvoj klíčových kompetencí CZ.1.07/1.5.00/34.0448
 Střední odborná škola elektrotechnická, Centrum odborné přípravy Zvolenovská 537, Hluboká nad Vltavou Využití ICT pro rozvoj klíčových kompetencí CZ.1.07/1.5.00/34.0448 CZ.1.07/1.5.00/34.0448 1 Číslo projektu
Střední odborná škola elektrotechnická, Centrum odborné přípravy Zvolenovská 537, Hluboká nad Vltavou Využití ICT pro rozvoj klíčových kompetencí CZ.1.07/1.5.00/34.0448 CZ.1.07/1.5.00/34.0448 1 Číslo projektu
{ } 9.1.9 Kombinace II. Předpoklady: 9108. =. Vypiš všechny dvoučlenné kombinace sestavené z těchto pěti prvků. Urči počet kombinací pomocí vzorce.
 9.1.9 Kombinace II Předpoklady: 9108 Př. 1: Je dána pěti prvková množina: M { a; b; c; d; e} =. Vypiš všechny dvoučlenné kombinace sestavené z těchto pěti prvků. Urči počet kombinací pomocí vzorce. Vypisujeme
9.1.9 Kombinace II Předpoklady: 9108 Př. 1: Je dána pěti prvková množina: M { a; b; c; d; e} =. Vypiš všechny dvoučlenné kombinace sestavené z těchto pěti prvků. Urči počet kombinací pomocí vzorce. Vypisujeme
Osnova kurzu. Základy teorie elektrických obvodů 1
 Osnova kurzu 1) Úvodní informace; zopakování nejdůležitějších vztahů 2) Základy teorie elektrických obvodů 1 3) Základy teorie elektrických obvodů 2 4) Základy teorie elektrických obvodů 3 5) Základy teorie
Osnova kurzu 1) Úvodní informace; zopakování nejdůležitějších vztahů 2) Základy teorie elektrických obvodů 1 3) Základy teorie elektrických obvodů 2 4) Základy teorie elektrických obvodů 3 5) Základy teorie
MĚŘENÍ Laboratorní cvičení z měření Měření nízkofrekvenčního koncového zesilovače, část 3-13-4
 MĚŘENÍ Laboratorní cvičení z měření Měření nízkofrekvenčního koncového zesilovače, část 3-13-4 Výukový materiál Číslo projektu: CZ.1.07/1.5.00/34.0093 Šablona: III/2 Inovace a zkvalitnění výuky prostřednictvím
MĚŘENÍ Laboratorní cvičení z měření Měření nízkofrekvenčního koncového zesilovače, část 3-13-4 Výukový materiál Číslo projektu: CZ.1.07/1.5.00/34.0093 Šablona: III/2 Inovace a zkvalitnění výuky prostřednictvím
rozvaděče BTS - skříně
 rozvaděče BTS - skříně Společné znaky: skříně jsou vyrobeny z moderního materiálu ALUZINKU, což je speciální legovaný, proti korozi velmi odolný plech. Skříně jsou opatřeny nátěrem fasádní strukturní barvou
rozvaděče BTS - skříně Společné znaky: skříně jsou vyrobeny z moderního materiálu ALUZINKU, což je speciální legovaný, proti korozi velmi odolný plech. Skříně jsou opatřeny nátěrem fasádní strukturní barvou
Podpěrné transformátory proudu pro vnitřní prostředí
 Podpěrné transformátory proudu pro vnitřní prostředí TPU 6x.xx Nejvyšší napětí soustavy [kv] 24 až do 25 Zkušební napětí střídavé, 1 min. [kv] 50 až do 55 Zkušební napětí impulsní [kv] až do 125 Jmenovitý
Podpěrné transformátory proudu pro vnitřní prostředí TPU 6x.xx Nejvyšší napětí soustavy [kv] 24 až do 25 Zkušební napětí střídavé, 1 min. [kv] 50 až do 55 Zkušební napětí impulsní [kv] až do 125 Jmenovitý
Plechy válcované za tepla
 Plechy válcované za tepla Plechy válcované za tepla jsou vyráběny na širokopásové válcovací trati P 500 Steckel do svitků, které jsou dále příčně děleny za studena na dělících linkách výrobního závodu.
Plechy válcované za tepla Plechy válcované za tepla jsou vyráběny na širokopásové válcovací trati P 500 Steckel do svitků, které jsou dále příčně děleny za studena na dělících linkách výrobního závodu.
Pingpongový míček. Petr Školník, Michal Menkina. TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií
 Petr Školník, Michal Menkina TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Tento materiál vznikl v rámci projektu ESF CZ.1.7/../7.47, který je spolufinancován
Petr Školník, Michal Menkina TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Tento materiál vznikl v rámci projektu ESF CZ.1.7/../7.47, který je spolufinancován
TECHNICKÁ UNIVERZITA V LIBERCI
 TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Otáčky DC motoru DC motor se zátěží Osvald Modrlák Lukáš Hubka Liberec 2010 Materiál vznikl v rámci projektu ESF
TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Otáčky DC motoru DC motor se zátěží Osvald Modrlák Lukáš Hubka Liberec 2010 Materiál vznikl v rámci projektu ESF
Ročník: 1. Mgr. Jan Zmátlík Zpracováno dne: 25.9.2012
 Označení materiálu: VY_32_INOVACE_ZMAJA_VODARENSTVI_15 Název materiálu: Přehled vlastností a struktura materiálu Tematická oblast: Vodárenství 1. ročník instalatér Anotace: Prezentace uvádí základní vlastnosti
Označení materiálu: VY_32_INOVACE_ZMAJA_VODARENSTVI_15 Název materiálu: Přehled vlastností a struktura materiálu Tematická oblast: Vodárenství 1. ročník instalatér Anotace: Prezentace uvádí základní vlastnosti
Střední škola obchodu, řemesel a služeb Žamberk. Výukový materiál zpracovaný v rámci projektu EU Peníze SŠ
 Střední škola obchodu, řemesel a služeb Žamberk Výukový materiál zpracovaný v rámci projektu EU Peníze SŠ Registrační číslo projektu: CZ.1.07/1.5.00/34.0130 Šablona: III/2 Ověřeno ve výuce dne: 7.10.2013
Střední škola obchodu, řemesel a služeb Žamberk Výukový materiál zpracovaný v rámci projektu EU Peníze SŠ Registrační číslo projektu: CZ.1.07/1.5.00/34.0130 Šablona: III/2 Ověřeno ve výuce dne: 7.10.2013
FEROMAGNETICKÉ ANALOGOVÉ MĚŘICÍ PŘÍSTROJE TYP EA16, EB16, EA17, EA19, EA12
 FEROMAGNETICKÉ ANALOGOVÉ MĚŘICÍ PŘÍSTROJE TYP EA16, EB16, EA17, EA19, EA12 AMPÉRMETRY a VOLTMETRY EA12 144x144 EA19 96x96 EA17 72x72 EA16 48x48 EB16 DIN 35 EA16, EB16, EA17, EA19 a EA12 feromagnetické
FEROMAGNETICKÉ ANALOGOVÉ MĚŘICÍ PŘÍSTROJE TYP EA16, EB16, EA17, EA19, EA12 AMPÉRMETRY a VOLTMETRY EA12 144x144 EA19 96x96 EA17 72x72 EA16 48x48 EB16 DIN 35 EA16, EB16, EA17, EA19 a EA12 feromagnetické
Mřížky a vyústky NOVA-C-2-R2. Vyústka do kruhového potrubí. Obr. 1: Rozměry vyústky
 -1-1-H Vyústka do kruhového potrubí - Jednořadá 1 Dvouřadá 2 L x H Typ regulačního ústrojí 1) R1, RS1, RN1 R2, RS2, RN2 R, RS, RN Lamely horizontální 2) H vertikální V Provedení nerez A- A-16 Povrchová
-1-1-H Vyústka do kruhového potrubí - Jednořadá 1 Dvouřadá 2 L x H Typ regulačního ústrojí 1) R1, RS1, RN1 R2, RS2, RN2 R, RS, RN Lamely horizontální 2) H vertikální V Provedení nerez A- A-16 Povrchová
Dualita v úlohách LP Ekonomická interpretace duální úlohy. Jiří Neubauer. Katedra ekonometrie FEM UO Brno
 Přednáška č. 6 Katedra ekonometrie FEM UO Brno Uvažujme obecnou úlohu lineárního programování, tj. úlohu nalezení takového řešení vlastních omezujících podmínek a 11 x 1 + a 1 x +... + a 1n x n = b 1 a
Přednáška č. 6 Katedra ekonometrie FEM UO Brno Uvažujme obecnou úlohu lineárního programování, tj. úlohu nalezení takového řešení vlastních omezujících podmínek a 11 x 1 + a 1 x +... + a 1n x n = b 1 a
Tepelná výměna. výměna tepla může probíhat vedením (kondukce), sáláním (radiace) nebo prouděním (konvekce).
 Tepelná výměna tepelná výměna je termodynamický děj, při kterém dochází k samovolné výměně tepla mezi dvěma tělesy s různou teplotou. Tepelná výměna vždy probíhá tak, že teplejší těleso předává svou vnitřní
Tepelná výměna tepelná výměna je termodynamický děj, při kterém dochází k samovolné výměně tepla mezi dvěma tělesy s různou teplotou. Tepelná výměna vždy probíhá tak, že teplejší těleso předává svou vnitřní
Dutý plastický trojúhelník by Gianelle
 Dutý plastický trojúhelník by Gianelle Připravíme si rokajl dle našeho výběru pro začátek nejlépe dvě barvy jedné velikosti Já používám korálky Miyuki Delica v tmavě červené barvě, matné s AB úpravou na
Dutý plastický trojúhelník by Gianelle Připravíme si rokajl dle našeho výběru pro začátek nejlépe dvě barvy jedné velikosti Já používám korálky Miyuki Delica v tmavě červené barvě, matné s AB úpravou na
E-ZAK. metody hodnocení nabídek. verze dokumentu: 1.1. 2011 QCM, s.r.o.
 E-ZAK metody hodnocení nabídek verze dokumentu: 1.1 2011 QCM, s.r.o. Obsah Úvod... 3 Základní hodnotící kritérium... 3 Dílčí hodnotící kritéria... 3 Metody porovnání nabídek... 3 Indexace na nejlepší hodnotu...4
E-ZAK metody hodnocení nabídek verze dokumentu: 1.1 2011 QCM, s.r.o. Obsah Úvod... 3 Základní hodnotící kritérium... 3 Dílčí hodnotící kritéria... 3 Metody porovnání nabídek... 3 Indexace na nejlepší hodnotu...4
Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Aleš Najman [ÚLOHA 18 TVORBA PLOCH]
![Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Aleš Najman [ÚLOHA 18 TVORBA PLOCH] Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Aleš Najman [ÚLOHA 18 TVORBA PLOCH]](/thumbs/41/22292385.jpg) Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Aleš Najman [ÚLOHA 18 TVORBA PLOCH] 1 ÚVOD V této kapitole je probírána tématika tvorby ploch pomocí funkcí vysunutí, rotace a tažení. V moderním světě,
Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Aleš Najman [ÚLOHA 18 TVORBA PLOCH] 1 ÚVOD V této kapitole je probírána tématika tvorby ploch pomocí funkcí vysunutí, rotace a tažení. V moderním světě,
NAMÁHÁNÍ NA TAH NAMÁHÁNÍ NA TAH
 Předmět: Ročník: Vytvořil: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 10. BŘEZNA 2013 Název zpracovaného celku: NAMÁHÁNÍ NA TAH NAMÁHÁNÍ NA TAH Přímá tyč je namáhána na tah, je-li zatíţena dvěma silami
Předmět: Ročník: Vytvořil: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 10. BŘEZNA 2013 Název zpracovaného celku: NAMÁHÁNÍ NA TAH NAMÁHÁNÍ NA TAH Přímá tyč je namáhána na tah, je-li zatíţena dvěma silami
STROPNÍ DÍLCE PŘEDPJATÉ STROPNÍ PANELY SPIROLL
 4.1.1 PŘEDPJATÉ STROPNÍ PANELY SPIROLL POUŽITÍ Předpjaté stropní panely SPIROLL slouží k vytvoření stropních a střešních konstrukcí pozemních staveb. Pro svou vysokou únosnost, odlehčení dutinami a dokonalému
4.1.1 PŘEDPJATÉ STROPNÍ PANELY SPIROLL POUŽITÍ Předpjaté stropní panely SPIROLL slouží k vytvoření stropních a střešních konstrukcí pozemních staveb. Pro svou vysokou únosnost, odlehčení dutinami a dokonalému
Převodníky analogových a číslicových signálů
 Převodníky analogových a číslicových signálů Převodníky umožňující transformaci číslicově vyjádřené informace na analogové napětí a naopak zaujímají v řídícím systému klíčové postavení. Značná část měřených
Převodníky analogových a číslicových signálů Převodníky umožňující transformaci číslicově vyjádřené informace na analogové napětí a naopak zaujímají v řídícím systému klíčové postavení. Značná část měřených
C v celé výkonnostní třídě.
 Dobrý den. Aktuální informace k 01.09.2013 Emisní třída 4 a automatický kotel na uhlí = Benekov C S potěšením Vám mohu oznámit, že jako první v ČR má firma Benekov certifikovaný automatický kotel na uhlí
Dobrý den. Aktuální informace k 01.09.2013 Emisní třída 4 a automatický kotel na uhlí = Benekov C S potěšením Vám mohu oznámit, že jako první v ČR má firma Benekov certifikovaný automatický kotel na uhlí
Zkratové proudy I. Listopad 2010. Ing. René Vápeník
 Zkratové proudy I. Listopad 2010 Ing. René Vápeník Zkrat - příčiny Zkrat je spojení mezi fázemi nebo mezi fázemi a zemí, které se za normálního provozu nepředpokládá a které je důsledkem porušení izolace
Zkratové proudy I. Listopad 2010 Ing. René Vápeník Zkrat - příčiny Zkrat je spojení mezi fázemi nebo mezi fázemi a zemí, které se za normálního provozu nepředpokládá a které je důsledkem porušení izolace
1 Statické zkoušky. 1.1 Zkouška tahem L L. R = e [MPa] S S
![1 Statické zkoušky. 1.1 Zkouška tahem L L. R = e [MPa] S S 1 Statické zkoušky. 1.1 Zkouška tahem L L. R = e [MPa] S S](/thumbs/40/21731773.jpg) 1 Statické zkoušky 1.1 Zkouška tahem Zkouška tahem je základní a nejrozšířenější mechanická zkouška. Princip: Přetržení zkušební tyče a následné stanovení tzv. napěťových a deformačních charakteristik
1 Statické zkoušky 1.1 Zkouška tahem Zkouška tahem je základní a nejrozšířenější mechanická zkouška. Princip: Přetržení zkušební tyče a následné stanovení tzv. napěťových a deformačních charakteristik
1 Měření kapacity kondenzátorů
 . Zadání úlohy a) Změřte kapacitu kondenzátorů, 2 a 3 LR můstkem. b) Vypočítejte výslednou kapacitu jejich sériového a paralelního zapojení. Hodnoty kapacit těchto zapojení změř LR můstkem. c) Změřte kapacitu
. Zadání úlohy a) Změřte kapacitu kondenzátorů, 2 a 3 LR můstkem. b) Vypočítejte výslednou kapacitu jejich sériového a paralelního zapojení. Hodnoty kapacit těchto zapojení změř LR můstkem. c) Změřte kapacitu
Univerzita Tomáše Bati ve Zlíně
 Univerzita Tomáše Bati ve líně LABORATORNÍ CVIČENÍ ELEKTROTECHNIKY A PRŮMYSLOVÉ ELEKTRONIKY Název úlohy: pracovali: Měření činného výkonu střídavého proudu v jednofázové síti wattmetrem Petr Luzar, Josef
Univerzita Tomáše Bati ve líně LABORATORNÍ CVIČENÍ ELEKTROTECHNIKY A PRŮMYSLOVÉ ELEKTRONIKY Název úlohy: pracovali: Měření činného výkonu střídavého proudu v jednofázové síti wattmetrem Petr Luzar, Josef
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita IV. Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma IV.. Kvadratické funkce, rovnice a nerovnice
Zvyšování kvality výuky technických oborů Klíčová aktivita IV. Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma IV.. Kvadratické funkce, rovnice a nerovnice
IMPORT A EXPORT MODULŮ V PROSTŘEDÍ MOODLE
 Nové formy výuky s podporou ICT ve školách Libereckého kraje IMPORT A EXPORT MODULŮ V PROSTŘEDÍ MOODLE Podrobný návod Autor: Mgr. Michal Stehlík IMPORT A EXPORT MODULŮ V PROSTŘEDÍ MOODLE 1 Úvodem Tento
Nové formy výuky s podporou ICT ve školách Libereckého kraje IMPORT A EXPORT MODULŮ V PROSTŘEDÍ MOODLE Podrobný návod Autor: Mgr. Michal Stehlík IMPORT A EXPORT MODULŮ V PROSTŘEDÍ MOODLE 1 Úvodem Tento
1. Kruh, kružnice. Mezi poloměrem a průměrem kružnice platí vztah : d = 2. r. Zapíšeme k ( S ; r ) Čteme kružnice k je určena středem S a poloměrem r.
 Kruh, kružnice, válec 1. Kruh, kružnice 1.1. Základní pojmy Kružnice je množina bodů mající od daného bodu stejnou vzdálenost. Daný bod označujeme jako střed kružnice. Stejnou vzdálenost nazýváme poloměr
Kruh, kružnice, válec 1. Kruh, kružnice 1.1. Základní pojmy Kružnice je množina bodů mající od daného bodu stejnou vzdálenost. Daný bod označujeme jako střed kružnice. Stejnou vzdálenost nazýváme poloměr
Google Apps. pošta 2. verze 2012
 Google Apps pošta verze 0 Obsah Obsah... Úvod... Přečtení emailu... Napsání emailu... Odpověď na email... 6 Úvod V dnešní době chce mít každý své informace po ruce. Díky Internetu a online aplikacím je
Google Apps pošta verze 0 Obsah Obsah... Úvod... Přečtení emailu... Napsání emailu... Odpověď na email... 6 Úvod V dnešní době chce mít každý své informace po ruce. Díky Internetu a online aplikacím je
10 Měření parametrů vzduchové cívky
 10 10.1 adání úlohy a) měřte indukčnost a ohmický (činný) odpor vzduchové cívky ohmovou metodou. b) měřte indukčnost a ohmický odpor cívky rezonanční metodou. c) měřte indukčnost a ohmický odpor cívky
10 10.1 adání úlohy a) měřte indukčnost a ohmický (činný) odpor vzduchové cívky ohmovou metodou. b) měřte indukčnost a ohmický odpor cívky rezonanční metodou. c) měřte indukčnost a ohmický odpor cívky
Výsledky testování školy. Druhá celoplošná generální zkouška ověřování výsledků žáků na úrovni 5. a 9. ročníků základní školy. Školní rok 2012/2013
 Výsledky testování školy Druhá celoplošná generální zkouška ověřování výsledků žáků na úrovni 5. a 9. ročníků základní školy Školní rok 2012/2013 Gymnázium, Šternberk, Horní náměstí 5 Termín zkoušky: 13.
Výsledky testování školy Druhá celoplošná generální zkouška ověřování výsledků žáků na úrovni 5. a 9. ročníků základní školy Školní rok 2012/2013 Gymnázium, Šternberk, Horní náměstí 5 Termín zkoušky: 13.
Historie výpočetní techniky Vývoj počítačů 4. generace. 4. generace mikroprocesor
 4. generace mikroprocesor V roce 1971 se podařilo dosáhnout takové hustoty integrace (množství součástek v jednom obvodu), která umožňovala postavení celého mozku počítače z jednoho obvodu tento obvod
4. generace mikroprocesor V roce 1971 se podařilo dosáhnout takové hustoty integrace (množství součástek v jednom obvodu), která umožňovala postavení celého mozku počítače z jednoho obvodu tento obvod
Inovace výuky prostřednictvím ICT v SPŠ Zlín, CZ.1.07/1.5.00/34.0333 Vzdělávání v informačních a komunikačních technologií
 VY_32_INOVACE_33_12 Škola Střední průmyslová škola Zlín Název projektu, reg. č. Inovace výuky prostřednictvím ICT v SPŠ Zlín, CZ.1.07/1.5.00/34.0333 Vzdělávací oblast Vzdělávání v informačních a komunikačních
VY_32_INOVACE_33_12 Škola Střední průmyslová škola Zlín Název projektu, reg. č. Inovace výuky prostřednictvím ICT v SPŠ Zlín, CZ.1.07/1.5.00/34.0333 Vzdělávací oblast Vzdělávání v informačních a komunikačních
Kapitola I - Množiny bodů daných vlastností I.a Co je množinou všech bodů v rovině, které mají od daných dvou různých bodů stejnou vzdálenost? I.
 Kapitola I - Množiny bodů daných vlastností I.a Co je množinou všech bodů v rovině, které mají od daných dvou různých bodů stejnou vzdálenost? I.b Co je množinou středů všech kružnic v rovině, které prochází
Kapitola I - Množiny bodů daných vlastností I.a Co je množinou všech bodů v rovině, které mají od daných dvou různých bodů stejnou vzdálenost? I.b Co je množinou středů všech kružnic v rovině, které prochází
