Řešení příkladu - klasifikace testovacího subjektu podle minimální vzdálenosti:
|
|
|
- Libuše Štěpánková
- před 7 lety
- Počet zobrazení:
Transkript
1 Řešení příkladu - klasifikace testovacího subjektu podle minimální vzdálenosti: Postup: I) zvolení metriky pro výpočet vzdáleností dvou bodů II) zvolení metriky pro určení vzdálenosti mezi dvěma množinami bodů Předpoklad: budeme shlukovací algoritmy využívat jako neučící se algoritmy (klasifikátor natrénujeme na celé trénovací množině a pak už pouze klasifikujeme nové subjekty (např. už nepřepočítáváme centroid po zařazení každého nového subjektu či objektu apod.)) 1.1 Metoda k nejbližších sousedů + Euklidova metrika: Znázornění výpočtu vzdálenosti dvou bodů pomocí Euklidovy metriky je uvedeno na Obr Obr.1: Ilustrace výpočtu vzdálenosti dvou bodů pomocí Euklidovy metriky (vlevo) a znázornění klasifikace podle nejbližšího souseda (vpravo). Modře je vyznačena množina bodů, které mají od testovacího subjektu stejnou vzdálenost. d E (x 1, x 0 ) = (x x 01 ) 2 + (x x 02 ) 2 = (2,) 2 + ( ) 2 = 2,2 + =, d E (x 2, x 0 ) = (x 21 x 01 ) 2 + (x 22 x 02 ) 2 = (,) 2 + ( ) 2 = 0,2 + 1 = 1, d E (x, x 0 ) = (x 1 x 01 ) 2 + (x 2 x 02 ) 2 = (,) 2 + ( ) 2 = 0,2 + 1 = 1, d E (x, x 0 ) = (x 1 x 01 ) 2 + (x 2 x 02 ) 2 = (,) 2 + ( ) 2 = 2,2 + = 2, d E (x, x 0 ) = (x 1 x 01 ) 2 + (x 2 x 02 ) 2 = (,) 2 + ( ) 2 = 0,2 d E (x, x 0 ) = (x 1 x 01 ) 2 + (x 2 x 02 ) 2 = (,) 2 + ( ) 2 = 0,2 + 1 =,0 d E (x, x 0 ) < d E (x 2, x 0 ) d E (x, x 0 ) < d E (x, x 0 ) < d E (x 1, x 0 ) < d E (x, x 0 ) 1
2 pro k = 1: nejbližší soused bodu x 0 je bod x, protože d E (x, x 0 ) je nejmenší ; lze rovněž zapsat jako: d NN (D, x 0 ) = min d E (x i, x 0 ) = 1,, kde i = 1,2,, a d NN (H, x 0 ) = min d E (x i, x 0 ), kde i =,,; protože d NN (H, x 0 ) < d NN (D, x 0 ), pro k = : subjekt zařazen do třídy pacientů, protože mezi nejbližšími sousedy jsou 2 a 1 pro k = : nelze rozhodnout pro k = : subjekt zařazen do třídy pacientů, protože mezi nejbližšími sousedy jsou a 2 y pro k = : nelze rozhodnout Poznámka: je nutné volit liché k Poznámka 2: závisí na volbě k, kam subjekt zařadíme (tzn., pro různá k se zařazení může lišit např. v tomto případě pro k = 1 subjekt zařazen do třídy kontrolních subjektů a pro k = a k = subjekt zařazen do třídy pacientů) 1.2 Metoda průměrné vazby + Euklidova metrika: d GG (D, x 0 ) = d E(x 1,x 0 )+d E (x 2,x 0 )+d E (x,x 0 ) d GG (H, x 0 ) = d E(x,x 0 )+d E (x,x 0 )+d E (x,x 0 ) =,+1,+1, = 2,+0,+,0 = 1, = 2, Protože d GG (D, x 0 ) < d GG (H, x 0 ), bude zařazen do třídy pacientů. 1. Centroidová metoda + Euklidova metrika: x D = 1 n D 1 n x n i1 D D i=1 x n i2 D i=1 = 1 (2 + + ) 1 ( + + ) = [ ] centroid pacientů x H = 1 n H 1 n x n i1 H i=1 H x n i2 H i=1 = 1 ( + + ) 1 ( + + ) = [ ] centroid kontrol d CC (D, x 0 ) = d E (x D, x 0 ) = (,) 2 + ( ) 2 = 0,2 + 1 = 1, d CC (H, x 0 ) = d E (x H, x 0 ) = (,) 2 + ( ) 2 = 0,2 + = 2,0 Protože d CC (D, x 0 ) < d CC (H, x 0 ), bude zařazen do třídy pacientů. Znázornění klasifikace testovacího subjektu pomocí centroidové metody, přičemž vzdálenosti testovacího subjektu od centroidů skupin jsou počítány pomocí Euklidovy metriky, je na Obr. 2. Medoid (odvozen vizuálně spočítal by se tak, že by se našel nejbližší bod k centroidu u dané skupiny nebo jako bod s nejmenší sumou vzdáleností od ostatních bodů) medoid pro pacienty: x D = x 2 = [ ] medoid pro : x H = x = [ ] d CCC (D, x 0 ) = d E (x D, x 0 ) = d E (x 2, x 0 ) = (,) 2 + ( ) 2 = 0,2 + 1 = 1, d CCC (H, x 0 ) = d E (x H, x 0 ) = d E (x, x 0 ) = (,) 2 + ( ) 2 = 2,2 + = 2, Protože d CCC (D, x 0 ) < d CCC (H, x 0 ), bude zařazen do třídy pacientů. 2
3 1 centroid pacientů centroid kontrol 1 2 Obr. 2: Ilustrace klasifikace testovacího subjektu pomocí centroidové metody, přičemž vzdálenosti testovacího subjektu od centroidů skupin jsou počítány pomocí Euklidovy metriky. Je patrné, že subjekt bude zařazen do třídy pacientů, protože jeho Euklidova vzdálenost od centroidu pacientů je menší než od centroidu kontrol. 2.1 Metoda k nejbližších sousedů + Hammingova (manhattanská) metrika: Znázornění výpočtu vzdálenosti dvou bodů pomocí Hammingovy (manhattanské) metriky je uvedeno na Obr.. d H (x 1, x 0 ) = x x 01 + x x 02 = 2, + = 1, + =, d H (x 2, x 0 ) = x 21 x 01 + x 22 x 02 =, = 1, d H (x, x 0 ) = x 1 x 01 + x 2 x 02 =, = 1, d H (x, x 0 ) = x 1 x 01 + x 2 x 02 =, + = 1, + 2 =, d H (x, x 0 ) = x 1 x 01 + x 2 x 02 =, d H (x, x 0 ) = x 1 x 01 + x 2 x 02 =, + + =, d H (x, x 0 ) < d H (x 2, x 0 ) d H (x, x 0 ) < d H (x, x 0 ) < d H (x 1, x 0 ) d E (x, x 0 ) pro k = 1: nejbližší soused bodu x 0 je bod x, protože d H (x, x 0 ) je nejmenší pro k = : subjekt zařazen do třídy pacientů, protože mezi nejbližšími sousedy jsou 2 a 1 pro k = : nelze rozhodnout pro k = : nelze rozhodnout pro k = : nelze rozhodnout
4 Obr. : Ilustrace výpočtu vzdálenosti dvou bodů pomocí Hammingovy (manhattanské) metriky (vlevo) a znázornění klasifikace podle nejbližšího souseda (vpravo). Modře je vyznačena množina bodů, které mají od testovacího subjektu stejnou vzdálenost. 2.2 Metoda průměrné vazby + Hammingova (manhattanská) metrika: d GG (D, x 0 ) = d H(x 1,x 0 )+d H (x 2,x 0 )+d H (x,x 0 ) d GG (H, x 0 ) = d H(x,x 0 )+d H (x,x 0 )+d H (x,x 0 ) =,+1,+1, =,+0,+, = 2, = 2, Protože d GG (D, x 0 ) < d GG (H, x 0 ), bude zařazen do třídy pacientů. 2. Centroidová metoda + Hammingova (manhattanská) metrika: d CC (D, x 0 ) = d H (x D, x 0 ) =, = 1, d CC (H, x 0 ) = d H (x H, x 0 ) =, = 2, Protože d CC (D, x 0 ) < d CC (H, x 0 ), bude zařazen do třídy pacientů. Znázornění klasifikace testovacího subjektu pomocí centroidové metody, přičemž vzdálenosti testovacího subjektu od centroidů skupin jsou počítány pomocí Hammingovy (manhattanské) metriky, je na Obr.. d CCC (D, x 0 ) = d H (x D, x 0 ) = d H (x 2, x 0 ) =, = 1, d CCC (H, x 0 ) = d H (x H, x 0 ) = d H (x, x 0 ) =, + = 1, + 2 =, Protože d CCC (D, x 0 ) < d CCC (H, x 0 ), bude zařazen do třídy pacientů.
5 1 centroid pacientů centroid kontrol 1 2 Obr. : Ilustrace klasifikace testovacího subjektu pomocí centroidové metody, přičemž vzdálenosti testovacího subjektu od centroidů skupin jsou počítány pomocí Hammingovy (manhattanské) metriky. Je patrné, že subjekt bude zařazen do třídy pacientů, protože jeho Hammingova (manhattanská) vzdálenost od centroidu pacientů je menší než od centroidu kontrol..1 Metoda k nejbližších sousedů + Čebyševova metrika: d C (x 1, x 0 ) = max( x x 01 ; x x 02 ) = max( 2, ; ) = max(1,; ) = d C (x 2, x 0 ) = max( x 21 x 01 ; x 22 x 02 ) = max(, ; ) = max(0,; 1) = 1 d C (x, x 0 ) = max( x 1 x 01 ; x 2 x 02 ) = max(, ; ) = max(0,; 1) = 1 d C (x, x 0 ) = max( x 1 x 01 ; x 2 x 02 ) = max(, ; ) = max(1,; 2) = 2 d C (x, x 0 ) = max( x 1 x 01 ; x 2 x 02 ) = max(, ; ) = max(0,; 0) d C (x, x 0 ) = max( x 1 x 01 ; x 2 x 02 ) = max(, ; ) = max(0,; ) = d C (x, x 0 ) < d C (x 2, x 0 ) d C (x, x 0 ) < d C (x, x 0 ) < d C (x 1, x 0 ) < d C (x, x 0 ) pro k = 1: nejbližší soused bodu x 0 je bod x, protože d C (x, x 0 ) je nejmenší pro k = : subjekt zařazen do třídy pacientů, protože mezi nejbližšími sousedy jsou 2 a 1 pro k = : nelze rozhodnout pro k = : subjekt zařazen do třídy pacientů, protože mezi nejbližšími sousedy jsou a 2 y pro k = : nelze rozhodnout.2 Metoda průměrné vazby + Čebyševova metrika: d GG (D, x 0 ) = d C(x 1,x 0 )+d C (x 2,x 0 )+d C (x,x 0 ) = +1+1 = 1,
6 d GG (H, x 0 ) = d C(x,x 0 )+d C (x,x 0 )+d C (x,x 0 ) = 2+0,+ = 2,1 Protože d GG (D, x 0 ) < d GG (H, x 0 ), bude zařazen do třídy pacientů.. Centroidová metoda + Čebyševova metrika: d CC (D, x 0 ) = d C (x D, x 0 ) = max(, ; ) = max(0,; 1) = 1 d CC (H, x 0 ) = d C (x H, x 0 ) = max (, ; ) = max(0,; 2) = 2 Protože d CC (D, x 0 ) < d CC (H, x 0 ), bude zařazen do třídy pacientů. d CCC (D, x 0 ) = d C (x D, x 0 ) = d C (x 2, x 0 ) = max(, ; ) = max(0,; 1) = 1 d CCC (H, x 0 ) = d C (x H, x 0 ) = d C (x, x 0 ) = max(, ; ) = max(1,; 2) = 2 Protože d CCC (D, x 0 ) < d CCC (H, x 0 ), bude zařazen do třídy pacientů..1 Metoda k nejbližších sousedů + Canberrská metrika: d CC (x 1, x 0 ) = x x 01 + x x 02 = 2, + = 1, + = 0,2 x + x 01 x + x , +, 21 d CC (x 2, x 0 ) = x 21 x 01 + x 22 x 02 =, = 0, x 21 + x 01 x 22 + x 02 +, +, 1 d CC (x, x 0 ) = x 1 x 01 + x 2 x 02 =, = 0,1 x 1 + x 01 x 2 + x 02 +, +, 1 d CC (x, x 0 ) = x 1 x 01 + x 2 x 02 =, + = 1, + 2 = 0,0 x 1 + x 01 x 2 + x 02 +, +, 1 d CC (x, x 0 ) = x 1 x 01 + x 2 x 02 =, = 0,0 x 1 + x 01 x 2 + x 02 +, +, 1 d CC (x, x 0 ) = x 1 x 01 + x 2 x 02 =, + + x 1 + x 01 x 2 + x 02 +, +, 1 d CC (x, x 0 ) < d CC (x 2, x 0 ) < d CC (x, x 0 ) < d CC (x, x 0 ) < d CC (x, x 0 ) < d CC (x 1, x 0 ) pro k = 1: nejbližší soused bodu x 0 je bod x, protože d CC (x, x 0 ) je nejmenší pro k = : subjekt zařazen do třídy pacientů, protože mezi nejbližšími sousedy jsou 2 a 1 pro k = : nelze rozhodnout pro k = : subjekt zařazen do třídy kontrolních subjektů, protože mezi nejbližšími sousedy jsou 2 a y pro k = : nelze rozhodnout.2 Metoda průměrné vazby + Canberrská metrika: d GG (D, x 0 ) = d CC(x 1,x 0 )+d CC (x 2,x 0 )+d CC (x,x 0 ) d GG (H, x 0 ) = d CC(x,x 0 )+d CC (x,x 0 )+d CC (x,x 0 ) = 0,2+0,+0,1 = 0,0+0,0+0, = 0,2 = 0,2 Protože d GG (D, x 0 ) < d GG (H, x 0 ), bude zařazen do třídy pacientů.
7 . Centroidová metoda + Canberrská metrika: d CC (D, x 0 ) = d CC (x D, x 0 ) =, = 0,1 +, +, 1 d CC (H, x 0 ) = d CC (x H, x 0 ) =, = 0,1 +, +, 1 Protože d CC (D, x 0 ) < d CC (H, x 0 ), bude zařazen do třídy pacientů. d CCC (D, x 0 ) = d CC (x D, x 0 ) = d CC (x 2, x 0 ) =, = 0, +, +, 1 d CCC (H, x 0 ) = d CC (x H, x 0 ) = d CC (x, x 0 ) =, + = 1, + 2 = 0,0 +, +, 1 Protože d CCC (D, x 0 ) < d CCC (H, x 0 ), bude zařazen do třídy pacientů..1 Metoda k nejbližších sousedů + Mahalanobisova metrika: Nejprve je potřeba vypočítat výběrové kovarianční matice pro třídu pacientů a kontrol, tzn. S D = a S H = 1 1 (výpočet výběrových kovariančních matic lze nalézt ve Cvičení 1) 1 a jejich inverzi její inverzi S 1 D = a S H 1 = d MM (x 1, x 0 ) = (x 1 x 0 ) T S 1 D (x 1 x 0 ) = [2, ] 1, 2 = 1, 1 1 d MM (x 2, x 0 ) = (x 2 x 0 ) T S 1 D (x 2 x 0 ) = [, ] 1, 1 1 = 1 d MM (x, x 0 ) = (x x 0 ) T S 1 D (x x 0 ) = [, ] 1, 1 1 = 1 d MM (x, x 0 ) = (x x 0 ) T S 1 H (x x 0 ) = [, ] 1, = 1, 1 1 d MM (x, x 0 ) = (x x 0 ) T S 1 H (x x 0 ) = [, ] 1, 1 1 d MM (x, x 0 ) = (x x 0 ) T S 1 H (x x 0 ) = [, ] 1, = 2,0 1 1 d MM (x, x 0 ) < d MM (x 2, x 0 ) d MM (x, x 0 ) < d MM (x, x 0 ) < d MM (x 1, x 0 ) < d MM (x, x 0 ) pro k = 1: nejbližší soused bodu x 0 je bod x, protože d CC (x, x 0 ) je nejmenší pro k = : subjekt zařazen do třídy pacientů, protože mezi nejbližšími sousedy jsou 2 a 1
8 pro k = : nelze rozhodnout pro k = : subjekt zařazen do třídy pacientů, protože mezi nejbližšími sousedy jsou a 2 y pro k = : nelze rozhodnout.2 Metoda průměrné vazby + Mahalanobisova metrika: d GG (D, x 0 ) = d MM(x 1,x 0 )+d MM (x 2,x 0 )+d MM (x,x 0 ) d GG (H, x 0 ) = d MM(x,x 0 )+d MM (x,x 0 )+d MM (x,x 0 ) = 1,+1+1 = 1,2 = 1,0 Protože d GG (D, x 0 ) < d GG (H, x 0 ), bude zařazen do třídy pacientů.. Centroidová metoda + Mahalanobisova metrika: = 1,+0,+2,0 d CC (D, x 0 ) = d MM (x D, x 0 ) = [, ] 1, 1 1 d CC (H, x 0 ) = d CC (x H, x 0 ) = [, ] 1, 1 1 = 1 Protože d CC (D, x 0 ) < d CC (H, x 0 ), bude zařazen do třídy pacientů. d CCC (D, x 0 ) = d MM (x D, x 0 ) = d MM (x 2, x 0 ) = 1 d CCC (H, x 0 ) = d MM (x H, x 0 ) = d MM (x, x 0 ) = 1, Protože d CCC (D, x 0 ) < d CCC (H, x 0 ), bude zařazen do třídy pacientů. Výsledky uspořádáme do tabulky: metrika Euklidova Hammingova Čebyševova Canberrská Mahalanobisova NN H H H H H -NN D D D D D -NN D - D H D GA D D D D D CE-centroid D D D D D CE-medoid D D D D D Je patrné, že výsledek klasifikace se může lišit při použití různých metrik vzdálenosti.
Obr. 1: Vizualizace dat pacientů, kontrolních subjektů a testovacího subjektu.
Řešení příkladu - klasifikace testovacího subjektu pomocí Bayesova klasifikátoru: ata si vizualizujeme (Obr. ). Objem mozkových komor 9 8 7 6 5 pacienti kontroly testovací subjekt 5 6 Objem hipokampu Obr.
uvedení do problematiky i Bezpečnostní kódy: detekční kódy = kódy zjišťující chyby samoopravné kódy = kódy opravující chyby příklady kódů:
I. Bezpečnostníkódy úvod základní pojmy počet zjistitelných a opravitelných chyb 2prvkové těleso a lineární prostor jednoduché bezpečnostní kódy lineární kódy Hammingův kód smysluplnost bezpečnostních
Vícerozměrné statistické metody
Vícerozměrné statistické metody Vícerozměrné statistické rozdělení a testy, operace s vektory a maticemi Jiří Jarkovský, Simona Littnerová FSTA: Pokročilé statistické metody Vícerozměrné statistické rozdělení
Shluková analýza. Jiří Militky. Analýza experimentálních dat V. Červeně označené slide jsou jen pro doplnění informací a nezkouší se.
Červeně označené slide jsou jen pro doplnění informací a nezkouší se. Shluková analýza Jiří Militky Analýza experimentálních dat V Klasifikace objektů Rozdělení objektů do shluků dle jejich podobnosti
Úloha - rozpoznávání číslic
Úloha - rozpoznávání číslic Vojtěch Franc, Tomáš Pajdla a Tomáš Svoboda http://cmp.felk.cvut.cz 27. listopadu 26 Abstrakt Podpůrný text pro cvičení předmětu X33KUI. Vysvětluje tři způsoby rozpoznávání
Shluková analýza dat a stanovení počtu shluků
Shluková analýza dat a stanovení počtu shluků Autor: Tomáš Löster Vysoká škola ekonomická v Praze Ostrava, červen 2017 Osnova prezentace Úvod a teorie shlukové analýzy Podrobný popis shlukování na příkladu
Cvičná bakalářská zkouška, 1. varianta
jméno: studijní obor: PřF BIMAT počet listů(včetně tohoto): 1 2 3 4 5 celkem Cvičná bakalářská zkouška, 1. varianta 1. Matematická analýza Najdětelokálníextrémyfunkce f(x,y)=e 4(x y) x2 y 2. 2. Lineární
Vícerozměrné statistické metody
Vícerozměrné statistické metody Shluková analýza Jiří Jarkovský, Simona Littnerová FSTA: Pokročilé statistické metody Typy shlukových analýz Shluková analýza: cíle a postupy Shluková analýza se snaží o
ANALÝZA A KLASIFIKACE DAT. Institut biostatistiky a analýz
ANALÝZA A KLASIFIKACE DAT prof. Ing. Jiří Holčík,, CSc. VII. VOLBA A VÝBĚR PŘÍZNAKŮ ZAČÍNÁME kolik a jaké příznaky? málo příznaků možná chyba klasifikace; moc příznaků možná nepřiměřená pracnost, vysoké
Metody založené na analogii
Metody založené na analogii V neznámé situaci lze použít to řešení, které se osvědčilo v situaci podobné případové usuzování (Case-Based Reasoning CBR) pravidlo nejbližšího souseda (nearest neighbour rule)
Fakulta chemicko-technologická Katedra analytické chemie. 3.2 Metody s latentními proměnnými a klasifikační metody
Fakulta chemicko-technologická Katedra analytické chemie 3.2 Metody s latentními proměnnými a klasifikační metody Vypracoval: Ing. Tomáš Nekola Studium: licenční Datum: 21. 1. 2008 Otázka 1. Vypočtěte
ANALÝZA A KLASIFIKACE DAT
ANALÝZA A KLASIFIKACE DAT RNDr. Eva Janoušová INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ HODNOCENÍ ÚSPĚŠNOSTI KLASIFIKACE A SROVNÁNÍ KLASIFIKÁTORŮ ÚVOD Vstupní data Subjekt Objem hipokampu Objem komor Skutečnost
Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na. x 2 x 1
Kapitola 4 Rasterizace objektů Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na rastrově definované obrazy. Při zobrazení reálného modelu ve světových souřadnicích na výstupní
Státnice odborné č. 20
Státnice odborné č. 20 Shlukování dat Shlukování dat. Metoda k-středů, hierarchické (aglomerativní) shlukování, Kohonenova mapa SOM Shlukování dat Shluková analýza je snaha o seskupení objektů do skupin
Klasifikace podle nejbližších sousedů Nearest Neighbour Classification [k-nn]
![Klasifikace podle nejbližších sousedů Nearest Neighbour Classification [k-nn]](/thumbs/93/111339850.jpg "Klasifikace podle nejbližších sousedů Nearest Neighbour Classification [k-nn]")
Klasifikace podle nejbližších sousedů Nearest Neighbour Classification [k-nn] Michal Houdek, Tomáš Svoboda, Tomáš Procházka 6. června 2001 1 Obsah 1 Úvod 3 2 Definice a postup klasifikace 3 3 Příklady
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV AUTOMATIZACE A MĚŘÍCÍ TECHNIKY FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION
ÚLOHY S POLYGONEM. Polygon řetězec úseček, poslední bod je totožný s prvním. 6 bodů: X1, Y1 až X6,Y6 Y1=X6, Y1=Y6 STANOVENÍ PLOCHY JEDNOHO POLYGONU
ÚLOHY S POLYGONEM Polygon řetězec úseček, poslední bod je totožný s prvním 6 bodů: X1, Y1 až X6,Y6 Y1=X6, Y1=Y6 STANOVENÍ PLOCHY JEDNOHO POLYGONU 3 úsečky (segmenty) v horní části 2 úsečky ve spodní části
Rosenblattův perceptron
Perceptron Přenosové funkce Rosenblattův perceptron Rosenblatt r. 1958. Inspirace lidským okem Podle fyziologického vzoru je třívrstvá: Vstupní vrstva rozvětvovací jejím úkolem je mapování dvourozměrného
Cyklickékódy. MI-AAK(Aritmetika a kódy)
MI-AAK(Aritmetika a kódy) Cyklickékódy c doc. Ing. Alois Pluháček, CSc., 2011 Katedra číslicového návrhu Fakulta informačních technologií České vysoké učení technické v Praze Evropský sociální fond Praha&
SHLUKOVÁ ANALÝZA KRAJŮ ČESKÉ REPUBLIKY DLE VYBRANÝCH CHARAKTERISTIK ZEMĚDĚLSTVÍ V PROGRAMU STATISTICA
SHLUKOVÁ ANALÝZA KRAJŮ ČESKÉ REPUBLIKY DLE VYBRANÝCH CHARAKTERISTIK ZEMĚDĚLSTVÍ V PROGRAMU STATISTICA CLUSTER ANALYSIS OF REGIONS OF CZECH REPUBLIC BY SELECTED CHARACTERISTICS OF AGRICULTURE IN PROGRAM
Pseudospektrální metody
Pseudospektrální metody Obecně: založeny na rozvoji do bázových funkcí s globálním nosičem řešení diferenciální rovnice aproximuje sumou kde jsou např. Čebyševovy polynomy nebo trigonometrické funkce tyto
Kybernetika a umělá inteligence, cvičení 10/11
Kybernetika a umělá inteligence, cvičení 10/11 Program 1. seminární cvičení: základní typy klasifikátorů a jejich princip 2. počítačové cvičení: procvičení na problému rozpoznávání číslic... body za aktivitu
Algoritmy a struktury neuropočítačů ASN P3
Algoritmy a struktury neuropočítačů ASN P3 SOM algoritmus s učitelem i bez učitele U-matice Vektorová kvantizace Samoorganizující se mapy ( Self-Organizing Maps ) PROČ? Základní myšlenka: analogie s činností
Instance based learning
Učení založené na instancích Instance based learning Charakteristika IBL (nejbližších sousedů) Tyto metody nepředpokládají určitý model nejsou strukturované a typicky nejsou příliš užitečné pro porozumění
Vytyčení polohy bodu polární metodou
Obsah Vytyčení polohy bodu polární metodou... 2 1 Vliv měření na přesnost souřadnic... 3 2 Vliv měření na polohovou a souřadnicovou směrodatnou odchylku... 4 3 Vliv podkladu na přesnost souřadnic... 5
Informační systémy pro podporu rozhodování
Informační systémy pro podporu rozhodování 3 Jan Žižka, Naděžda Chalupová Ústav informatiky PEF Mendelova universita v Brně Nejbližší sousedi k NN Algoritmus k-nejbližších sousedů (k-nearest neighbors)
DĚLENÍ SE ZBYTKEM (DĚLITEL 6, 7, 8, 9)
VY_32_INOVACE_M_191 DĚLENÍ SE ZBYTKEM (DĚLITEL 6, 7, 8, 9) Autor: Mgr. Irena Štěpánová Použití: 3. třída Datum vypracování: 21. 10. 2012 Datum pilotáže: 26. 4. 2013 Anotace: Procvičení dělení se zbytkem
Interpolace Uvažujme třídu funkcí jedné proměnné ψ(x; a 0,..., a n ), kde a 0,..., a n jsou parametry, které popisují jednotlivé funkce této třídy. Mějme dány body x 0, x 1,..., x n, x i x k, i, k = 0,
Aproximace funkcí. x je systém m 1 jednoduchých, LN a dostatečně hladkých funkcí. x c m. g 1. g m. a 1. x a 2. x 2 a k. x k b 1. x b 2.
Aproximace funkcí Aproximace je výpočet funkčních hodnot funkce z nějaké třídy funkcí, která je v určitém smyslu nejbližší funkci nebo datům, která chceme aproximovat. Třída funkcí, ze které volíme aproximace
Detekce neznámých typů mutantů na základě odlišnosti kinetiky fluorescence
Detekce neznámých typů mutantů na základě odlišnosti kinetiky fluorescence Jan Vaněk 1, Radek Tesař 1, Jan Urban 1, Karel Matouš 2 1 Katedra kybernetiky, Fakulta aplikovaných věd, Západočeská univerzita
Klasifikace a rozpoznávání. Lineární klasifikátory
Klasifikace a rozpoznávání Lineární klasifikátory Opakování - Skalární součin x = x1 x 2 w = w T x = w 1 w 2 x 1 x 2 w1 w 2 = w 1 x 1 + w 2 x 2 x. w w T x w Lineární klasifikátor y(x) = w T x + w 0 Vyber
1 Mnohočleny a algebraické rovnice
1 Mnohočleny a algebraické rovnice 1.1 Pojem mnohočlenu (polynomu) Připomeňme, že výrazům typu a 2 x 2 + a 1 x + a 0 říkáme kvadratický trojčlen, když a 2 0. Číslům a 0, a 1, a 2 říkáme koeficienty a písmenem
AVDAT Mnohorozměrné metody, metody klasifikace Shluková analýza
AVDAT Mnohorozměrné metody, metody klasifikace Shluková analýza Josef Tvrdík Katedra informatiky Přírodovědecká fakulta Ostravská univerzita Shluková analýza Cílem shlukové analýzy je nalézt v datech podmnožiny
[1] Determinant. det A = 0 pro singulární matici, det A 0 pro regulární matici
![[1] Determinant. det A = 0 pro singulární matici, det A 0 pro regulární matici](/thumbs/94/118721039.jpg "[1] Determinant. det A = 0 pro singulární matici, det A 0 pro regulární matici")
[1] Determinant je číslo jistým způsobem charakterizující čtvercovou matici det A = 0 pro singulární matici, det A 0 pro regulární matici používá se při řešení lineárních soustav... a v mnoha dalších aplikacích
UČENÍ BEZ UČITELE. Václav Hlaváč
UČENÍ BEZ UČITELE Václav Hlaváč Fakulta elektrotechnická ČVUT v Praze katedra kybernetiky, Centrum strojového vnímání hlavac@fel.cvut.cz, http://cmp.felk.cvut.cz/~hlavac 1/22 OBSAH PŘEDNÁŠKY ÚVOD Učení
Algoritmizace prostorových úloh
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Grafové úlohy Daniela Szturcová Tento
4 STATISTICKÁ ANALÝZA VÍCEROZMĚRNÝCH DAT
4 SAISICKÁ ANALÝZA VÍCEROZMĚRNÝCH DA V technické biologické ale také lékařské praxi se často vedle informací obsažených v náhodném skaláru ξ vyskytují i informace obsažené v náhodném vektoru ξ s m složkami
Univerzita Pardubice 8. licenční studium chemometrie
Univerzita Pardubice 8. licenční studium chemometrie Statistické zpracování dat při managementu jakosti Semestrální práce Metody s latentními proměnnými a klasifikační metody Ing. Jan Balcárek, Ph.D. vedoucí
Lineární klasifikátory
Lineární klasifikátory Lineární klasifikátory obsah: perceptronový algoritmus základní verze varianta perceptronového algoritmu přihrádkový algoritmus podpůrné vektorové stroje Lineární klasifikátor navrhnout
ANALÝZA A KLASIFIKACE BIOMEDICÍNSKÝCH DAT. Institut biostatistiky a analýz
ANALÝZA A KLASIFIKACE BIOMEDICÍNSKÝCH DAT prof. Ing. Jiří Holčík, CSc. VII. VOLBA A VÝBĚR PŘÍZNAKŮ ZAČÍNÁME kolik a jaké příznaky? málo příznaků možná chyba klasifikace; moc příznaků možná nepřiměřená
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Příklady použití tenkých vrstev Jaromír Křepelka
Příklady použití tenkých vrstev Jaromír Křepelka Příklad 01 Spočtěte odrazivost prostého rozhraní dvou izotropních homogenních materiálů s indexy lomu n 0 = 1 a n 1 = 1,52 v závislosti na úhlu dopadu pro
1 Vektorové prostory.
1 Vektorové prostory DefiniceMnožinu V, jejíž prvky budeme označovat a, b, c, z, budeme nazývat vektorovým prostorem právě tehdy, když budou splněny následující podmínky: 1 Je dáno zobrazení V V V, které
kamerou. Dle optických parametrů objektivu mohou v získaném obraze nastat geometrická
Odstranění geometrických zkreslení obrazu Vstupní obraz pro naše úlohy získáváme pomocí optické soustavy tvořené objektivem a kamerou. Dle optických parametrů objektivu mohou v získaném obraze nastat geometrická
Metody zpracování a analýzy medicínských obrazových dat: možnosti využití v neurovědním výzkumu
Metody zpracování a analýzy medicínských obrazových dat: možnosti využití v neurovědním výzkumu Ing. Daniel Schwarz, Ph.D. Bc. Eva Janoušov ová INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ O čem budu mluvit? Neurovědy
Rozdělování dat do trénovacích a testovacích množin
Rozdělování dat do trénovacích a testovacích množin Marcel Jiřina Rozpoznávání je důležitou metodou při zpracování reálných úloh. Rozpoznávání je definováno dvěma kroky a to pořízením dat o reálném rozpoznávaném
RNDr. Tomáš Pavlík, PhD. RNDr. Jiří Jarkovský, PhD. Doc. RNDr. Ladislav Dušek, PhD. Ústav zdravotnických informací a statistiky České republiky
Metodika vı cerozme rne analy zy Na rodnı ho registru hospitalizovany ch za u c elem vy be ru reprezentativnı sı te poskytovatelu zdravotnı ch sluz eb CČR RNDr. Tomáš Pavlík, PhD. RNDr. Jiří Jarkovský,
Tento výukový materiál byl vytvořen v rámci projektu MatemaTech Matematickou cestou k technice. Cyklistický převod výpočet rychlosti pohybu cyklisty
Tento výukový materiál byl vytvořen v rámci projektu MatemaTech Matematickou cestou k technice. Předmět: Matematika, fyzika Téma: Cyklistický převod výpočet rychlosti pohybu cyklisty Věk žáků: 16-19 Časová
NADSTAVBOVÝ MODUL MOHSA V1
NADSTAVBOVÝ MODUL MOHSA V1 Nadstavbový modul pro hierarchické shlukování se jmenuje Mod_Sh_Hier (MOHSA V1) je součástí souboru Shluk_Hier.xls. Tento soubor je přístupný na http://jonasova.upce.cz, a je
Profilování vzorků heroinu s využitím vícerozměrné statistické analýzy
Profilování vzorků heroinu s využitím vícerozměrné statistické analýzy Autor práce : RNDr. Ivo Beroun,CSc. Vedoucí práce: prof. RNDr. Milan Meloun, DrSc. PROFILOVÁNÍ Profilování = klasifikace a rozlišování
Příklad 2: Obsah PCB v játrech zemřelých lidí. Zadání: Data: Program:
Příklad 2: Obsah PCB v játrech zemřelých lidí Zadání: V rámci Monitoringu zdraví byly měřeny koncentrace polychlorovaných bifenylů vjátrech lidí zemřelých náhodnou smrtí ve věku 40 let a více. Sedm vybraných
Algoritmy pro shlukování prostorových dat
Algoritmy pro shlukování prostorových dat Marta Žambochová Katedra matematiky a informatiky Fakulta sociálně ekonomická Univerzita J. E. Purkyně v Ústí nad Labem ROBUST 21. 26. leden 2018 Rybník - Hostouň
Hammingovy kódy. dekódování H.kódů. konstrukce. šifrování. Fanova rovina charakteristický vektor. princip generující a prověrková matice
Hammingovy kódy konstrukce Fanova rovina charakteristický vektor šifrování princip generující a prověrková matice dekódování H.kódů třída lineárních binárních kódů s A n, 3 n = délka kódu, d = distance
Algoritmy a struktury neuropočítačů ASN P9 SVM Support vector machines Support vector networks (Algoritmus podpůrných vektorů)
Algoritmy a struktury neuropočítačů ASN P9 SVM Support vector machines Support vector networks (Algoritmus podpůrných vektorů) Autor: Vladimir Vapnik Vapnik, V. The Nature of Statistical Learning Theory.
2D transformací. červen Odvození transformačního klíče vybraných 2D transformací Metody vyrovnání... 2
Výpočet transformačních koeficinetů vybraných 2D transformací Jan Ježek červen 2008 Obsah Odvození transformačního klíče vybraných 2D transformací 2 Meto vyrovnání 2 2 Obecné vyjádření lineárních 2D transformací
X = x, y = h(x) Y = y. hodnotám x a jedné hodnotě y. Dostaneme tabulku hodnot pravděpodobnostní
..08 8cv7.tex 7. cvičení - transformace náhodné veličiny Definice pojmů a základní vzorce Je-li X náhodná veličina a h : R R je měřitelná funkce, pak náhodnou veličinu Y, která je definovaná vztahem X
Nehierarchické shlukování
Základní informace Následující text je součástí učebních textů předmětu Vícerozměrné statistické metody a je určen zejména pro studenty Matematické biologie. Může být ovšem přínosný i pro další studenty
Dobývání znalostí. Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické informatiky Matematicko-fyzikální fakulta Univerzity Karlovy v Praze
Dobývání znalostí Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické informatiky Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Dobývání znalostí Pravděpodobnost a učení Doc. RNDr. Iveta Mrázová,
Trénování sítě pomocí učení s učitelem
Trénování sítě pomocí učení s učitelem! předpokládá se, že máme k dispozici trénovací množinu, tj. množinu P dvojic [vstup x p, požadovaný výstup u p ]! chceme nastavit váhy a prahy sítě tak, aby výstup
øada LS Koncové spínaèe Popis Konstrukce Technické údaje Dostupnost vybraných typù
Popis Koncové spínaèe øady LS se už dlouhá léta úspìšnì dodávají pro široké spektrum prùmyslových aplikací. Peèlivý návrh konstrukce u- možòující pøesné spínání po miliony pracovních cyklù se osvìdèil
ZÍSKÁVÁNÍ ZNALOSTÍ Z DATABÁZÍ
Metodický list č. 1 Dobývání znalostí z databází Cílem tohoto tematického celku je vysvětlení základních pojmů z oblasti dobývání znalostí z databází i východisek dobývání znalostí z databází inspirovaných
Strojové učení Marta Vomlelová
Strojové učení Marta Vomlelová marta@ktiml.mff.cuni.cz KTIML, S303 Literatura 1.T. Hastie, R. Tishirani, and J. Friedman. The Elements of Statistical Learning, Data Mining, Inference and Prediction. Springer
Informace v počítači. Výpočetní technika I. Ing. Pavel Haluza ústav informatiky PEF MENDELU v Brně haluza@mendelu.cz
.. Informace v počítači Ing. Pavel Haluza ústav informatiky PEF MENDELU v Brně haluza@mendelu.cz Osnova přednášky Úvod do teorie informace základní pojmy měření množství informace ve zprávě přenos a kódování
Čebyševovy aproximace
Čebyševovy aproximace Čebyševova aproximace je tzv hledání nejlepší stejnoměrné aproximace funkce v daném intervalu Hledáme funkci h x, která v intervalu a,b minimalizuje maximální absolutní hodnotu rozdílu
Cvičení 11. Klasifikace. Jan Přikryl. 14. března 2018 ČVUT FD
Cvičení 11 Klasifikace Jan Přikryl ČVUT FD 14. března 2018 Příklad 1 Data z akciového trhu Nejprve prozkoumáme data z akciových trhů, konkrétně denní vývoj indexu S&P v letech 2001 2005. Načteme a zobrazíme
Kombinatorická minimalizace
Kombinatorická minimalizace Cílem je nalézt globální minimum ve velké diskrétní množině, kde může být mnoho lokálních minim. Úloha obchodního cestujícího Cílem je najít nejkratší cestu, která spojuje všechny
Ing. Petr Hájek, Ph.D. Podpora přednášky kurzu Aplikace umělé inteligence
APLIKACE UMĚLÉ INTELIGENCE Ing. Petr Hájek, Ph.D. Podpora přednášky kurzu Aplikace umělé inteligence Aplikace umělé inteligence - seminář ING. PETR HÁJEK, PH.D. ÚSTAV SYSTÉMOVÉHO INŽENÝRSTVÍ A INFORMATIKY
Zada ní 1. Semina rní pra ce z pr edme tu Matematický software (KI/MSW)
Zada ní. Semina rní pra ce z pr edme tu Matematický software (KI/MSW) Datum zadání: 5.. 06 Podmínky vypracování: - Seminární práce se skládá z programové části (kódy v Matlabu) a textové části (protokol
Dálkový průzkum Země. Klasifikace obrazu
Dálkový průzkum Země Klasifikace obrazu Neřízená klasifikace v IDRISI Modul CLUSTER (Image Processing / Hard Classifiers) využívá techniku histogramových vrcholů pásma pro klasifikaci výsledný obraz volba
Naučte se víc... Microsoft Office Excel 2007 PŘÍKLADY
Naučte se víc... Microsoft Office Excel 2007 PŘÍKLADY Autor: Lukáš Polák Příklady MS Excel 2007 Tato publikace vznikla za přispění společnosti Microsoft ČR v rámci iniciativy Microsoft Partneři ve vzdělávání.
Varianta Pravděpodobnost Výnos A 1 Výnos A 2 1 0,1 1% 0,1 3% 0,3 2 0,2 12% 2,4 28% 5,6 3 0,3 6% 1,8 14% 4,2
Dobrý den. Kladno, 22. 3. 2007 21:35 Chtěl bych se všem omluvit za ten závěr přednášky. Bohužel mě chyba v jednom z příkladů vykolejila natolik, že jsem se již velice těžko soustředil na svůj výkon. Chtěl
Determinant. Definice determinantu. Permutace. Permutace, vlastnosti. Definice: Necht A = (a i,j ) R n,n je čtvercová matice.
[] Definice determinantu BI-LIN, determinant, 9, P Olšák [2] Determinant je číslo jistým způsobem charakterizující čtvercovou matici det A 0 pro singulární matici, det A 0 pro regulární matici používá
Přednáška 13 Redukce dimenzionality
Vytěžování Dat Přednáška 13 Redukce dimenzionality Miroslav Čepek Fakulta Elektrotechnická, ČVUT Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti ČVUT (FEL) Redukce dimenzionality 1 /
Klasifikace předmětů a jevů
Klasifikace předmětů a jevů 1. Úvod Rozpoznávání neboli klasifikace je základní znak lidské činnosti. Rozpoznávání (klasifikace) předmětů a jevů spočívá v jejich zařazování do jednotlivých tříd. Třídou
Matice. Modifikace matic eliminační metodou. α A = α a 2,1, α a 2,2,..., α a 2,n α a m,1, α a m,2,..., α a m,n
[1] Základní pojmy [2] Matice mezi sebou sčítáme a násobíme konstantou (lineární prostor) měníme je na jiné matice eliminační metodou násobíme je mezi sebou... Matice je tabulka čísel s konečným počtem
Náhodný vektor a jeho charakteristiky
Náhodný vektor a jeho číselné charakteristiky 1 Náhodný vektor a jeho charakteristiky V následující kapitole budeme věnovat pozornost pouze dvourozměřnému náhodnému vektoru, i když uvedené pojmy a jejich
PROSTOROVÉ HIERARCHICKÉ SHLUKOVÁNÍ
PROSTOROVÉ HIERARCHICKÉ SHLUKOVÁNÍ Jiří HORÁK 1, Igor IVAN 1, Tomáš INSPEKTOR 1 1 Institut geoinformatiky, Hornicko-geologická fakulta, VŠB-TUO, 17. listopadu 15/2172, 708 33, Ostrava- Poruba, ČR Abstrakt
Odhad stavu matematického modelu křižovatek
Odhad stavu matematického modelu křižovatek Miroslav Šimandl, Miroslav Flídr a Jindřich Duník Katedra kybernetiky & Výzkumné centrum Data-Algoritmy-Rozhodování Fakulta aplikovaných věd Západočeská univerzita
Interpolace obrazu pro experimentální měřiče plošného teplotního rozložení
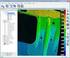Interpolace obrazu pro experimentální měřiče plošného teplotního rozložení Bc. Zdeněk Martinásek Vysoké učení technické v Brně, Fakulta elektrotechniky a komunikačních technologií, Ústav telekomunikací,
13 Barvy a úpravy rastrového
13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
i=1 Přímka a úsečka. Body, které leží na přímce procházející body a a b můžeme zapsat pomocí parametrické rovnice
I. Funkce dvou a více reálných proměnných 1. Úvod Značení: V textu budeme používat označení: N pro množinu všech přirozených čísel; R pro množinu všech reálných čísel; R n pro množinu všech uspořádaných
= cos sin = sin + cos = 1, = 6 = 9. 6 sin 9. = 1 cos 9. = 1 sin 9. + 6 cos 9 = 1 0,939692621 6 ( 0,342020143) = 1 ( 0,342020143) + 6 0,939692621
ŘEŠENÉ PŘÍKLADY Z MA+ULA ČÁST Příklad Bod má vůči souřadné soustavě souřadnice uvedené níže. Vypočtěte jeho souřadnice vzhledem k soustavě, která je vůči otočená dle zadání uvedeného níže. Výsledky zaokrouhlete
Věra Keselicová. březen 2013
VY_52_INOVACE_VK46 Jméno autora výukového materiálu Datum (období), ve kterém byl VM vytvořen Ročník, pro který je VM určen Vzdělávací oblast, obor, okruh, téma Anotace Věra Keselicová březen 2013 6. ročník
ZÍSKÁVÁNÍ ZNALOSTÍ Z DATABÁZÍ
metodický list č. 1 Dobývání znalostí z databází Cílem tohoto tematického celku je vysvětlení základních pojmů z oblasti dobývání znalostí z databází i východisek dobývání znalostí z databází inspirovaných
Odpřednesenou látku naleznete v kapitole 3.3 skript Diskrétní matematika.
Lineární kódy, část 2 Odpřednesenou látku naleznete v kapitole 3.3 skript Diskrétní matematika. Jiří Velebil: A7B01LAG 22.12.2014: Lineární kódy, část 2 1/12 Dnešní přednáška 1 Analýza Hammingova (7, 4)-kódu.
SYLABUS PŘEDNÁŠKY 10 Z GEODÉZIE 1
SYLABUS PŘEDNÁŠKY 10 Z GEODÉZIE 1 (Souřadnicové výpočty 4, Orientace osnovy vodorovných směrů) 1. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec
Program Denoiser v1.4 (10.11.2012)
Program Denoiser v1.4 (10.11.2012) doc. Ing. Martin Štroner, Ph.D., ČVUT Fakulta stavební, Praha Anotace Program pro potlačení šumu v datech 3D skenování na základě využití okolních dat prokládáním bivariantními
SF2 Podklady pro cvičení
SF Podklady pro cvičení Úloha 7 D přenos tepla riziko růstu plísní a kondenzace na vnitřním povrchu konstrukce Ing. Kamil Staněk 11/010 kamil.stanek@fsv.cvut.cz 1 D přenos tepla 1.1 Úvodem Dosud jsme se
Návod na cvičení VoIP Hodnocení kvality řeči neintrusivní metodou
Fakulta elektrotechniky a informatiky, VSB-TU Ostrava Návod na cvičení VoIP Hodnocení kvality řeči neintrusivní metodou Datum: 15.2.2013 Autor: Ing. Karel Tomala Kontakt: karel.tomala@vsb.cz Předmět: Telekomunikační
11 Analýza hlavních komponet
11 Analýza hlavních komponet Tato úloha provádí transformaci měřených dat na menší počet tzv. fiktivních dat tak, aby většina informace obsažená v původních datech zůstala zachována. Jedná se tedy o úlohu
cv3.tex. Vzorec pro úplnou pravděpodobnost
3 cvičení - pravděpodobnost 2102018 18cv3tex n i=1 Vzorec pro úplnou pravděpodobnost Systém náhodných jevů nazýváme úplným, jestliže pro něj platí: B i = 1 a pro i k je B i B k = 0 Jestliže je (Ω, A, P
ROZPOZNÁNÍ TITULU GRAMOFONOVÉ DESKY PODLE KRÁTKÉ UKÁZKY
ROZPOZNÁNÍ TITULU GRAMOFONOVÉ DESKY PODLE KRÁTKÉ UKÁZKY V. Moldan, F. Rund Katedra radioelektroniky, fakulta elektrotechnická České vysoké učení technické v Praze, Česká republika Abstrakt Tento článek
20. května Abstrakt V následujícím dokumentu je popsán způsob jakým analyzovat problém. výstřelu zasáhnout bod na zemi v definované vzdálenosti.
Ukázková semestrální práce z předmětu VSME Tomáš Kroupa 20. května 2014 Abstrakt V následujícím dokumentu je popsán způsob jakým analyzovat problém lučištníka, který má při pevně daném natažení luku jen
Autor: Ing. Martin Varga
TZB - modul TZ: VÝPOČET TEPLOTY VNITŘNÍHO VZDUCHU 2. 11. 2018 Autor: Ing. Martin Varga 2.11.2018 byla vystavena nová verze programu TZB 3.1.0. S touto verzí programu byla do modulu tepelné ztráty (TZ)
100 1500 1200 1000 875 750 675 600 550 500 - - 775 650 550 500 450 400 350 325 - -
Prostý kružnicový oblouk Prostý kružnicový oblouk se používá buď jako samostatné řešení změny směru osy nebo nám slouží jako součást směrové změny v kombinaci s přechodnicemi nebo složenými oblouky. Nejmenší
rovnic), Definice y + p(x)y = q(x), Je-li q(x) = 0 na M, nazývá se y + p(x)y =
Cíle Přehled základních typů diferenciálních rovnic prvního řádu zakončíme pojednáním o lineárních rovnicích, které patří v praktických úlohách k nejfrekventovanějším. Ukážeme například, že jejich řešení
Popis metod CLIDATA-GIS. Martin Stříž
Popis metod CLIDATA-GIS Martin Stříž Říjen 2008 Obsah 1CLIDATA-SIMPLE...3 2CLIDATA-DEM...3 2.1Metodika výpočtu...3 2.1.1Výpočet regresních koeficientů...3 2.1.2 nalezených koeficientu...5 2.1.3Výpočet
Iterační výpočty. Dokumentace k projektu č. 2 do IZP. 24. listopadu 2004
Dokumentace k projektu č. 2 do IZP Iterační výpočty 24. listopadu 2004 Autor: Kamil Dudka, xdudka00@stud.fit.vutbr.cz Fakulta Informačních Technologií Vysoké Učení Technické v Brně Obsah 1. Úvod...3 2.
3. Reálná čísla. většinou racionálních čísel. V analytických úvahách, které praktickým výpočtům
RACIONÁLNÍ A IRACIONÁLNÍ ČÍSLA Význačnými množinami jsou číselné množiny K nejvýznamnějším patří množina reálných čísel, obsahující jako podmnožiny množiny přirozených, celých, racionálních a iracionálních