Povídání o hrách(ke druhé sérii)
|
|
|
- Jitka Hájková
- před 8 lety
- Počet zobrazení:
Transkript
1 Povídání o hrách(ke druhé sérii) Milá řešitelko, milý řešiteli, prosím, nelekni se, že tato série nezačíná hned zadáním úloh, ale je tu napřed tento podivný text. Občas totiž píšeme úvod k sérii, ve kterém Ti vysvětlíme některé pojmy,kterésetřebaobjevujívzadáních,atrochuporadíme,jakúlohyřešit.atotojeprvní letošní povídání. Cojetohra,asikaždýví.Vtétosériisepotkámejenomshrami,kteréhrajídvahráči. Hráčisestřídajívtazích,vzadáníkaždéúlohyjenapsáno,comůžehráčpřisvémtahuudělat. (Pokudtonenívzadáníuvedeno,hráčmusívždytáhnout,nesmívynechattah.)Ajetamtaké napsané, kdy který z hráčů vyhraje. Každý samozřejmě chce vyhrát nebo přinejhorším aspoň neprohrát,takžehozajímá,jakhrátconejlépe.aprávětobudetvýmúkolemvevětšiněpřípadů zjistit, který z hráčů má takzvanou vyhrávající strategii neboli postup, podle nějž může hrát a mítjistotu,žestejněvždyckyvyhraje,aťbudesoupeřhrátjakkoli.občassetakémůžestát,že si ani jeden z hráčů nemůže zajistit vítězství, pak je dobré najít aspoň neprohrávající strategii takový postup, s jehož pomocí jistě neprohraje. Vždy by ses samozřejmě měl pokusit dokázat, že tomu je skutečně tak, jak tvrdíš například, že tebou navržená strategie funguje. Předchozí odstavec byl asi celkem hutný, vše si tedy osvětlíme na příkladě, který navíc ještě ukazuje celkem užitečný způsob, jak hledat strategie. Na stole jsou dvě hromádky sirek, na každé znichjepřesně18sirek.ten,kdojenatahu,sivyberejednuzhromádekaseberezníjednu sirku. Prohraje ten hráč, který sebere poslední sirku z některé hromádky. Ukážeme, že druhý hráč(tedy ten, který nezačíná, říkejme mu třeba šnek) má vyhrávající strategii: Vždyvezmisirkuzopačnéhromádkynežsoupeř. Nenítěžkésirozmyslet,žekdyž podleníbudehrát,budevždypošnekovětahunaobouhromádkáchstejnýpočetsirek.toale takéznamená,žepředjehotahembudenahromádce H,zekterémábrát,ojednusirkuvícnež na té druhé. Pokud tedy soupeř svým předchozím tahem nevyprázdnil hromádku, ze které bral sirku, určitě ani šnek nevyprázdní hromádku H. Pokud tedy soupeř neprohrál, může šnek vždy hrát tak, aby také neprohrál. Sirek je jenom konečně mnoho, takže hra časem skončí. A protože šnek používající naši strategii nemůže prohrát, musí vyhrát. Snad jsme Tě tímto povídáním příliš neunavili nebo neznechutili; pokud by Ti cokoli nebylo jasné, neboj se zeptat třeba v chatu na našich stránkách Přejeme Ti pěknou zábavu při řešení úloh(: 2. série Téma: Datumodeslání: Hry ½¾º Ð ØÓÔ Ù ¾¼¼ ¼º ÐÓ ½ Ó µ Vymysli co nejvypečenější podfuk do libovolné(klidně i vlastní) hry. ½º ÐÓ Ó Ýµ Vbodě AstojílupičPavel,vbodě BjedetektivRasťo,kterýjejhoní.Střídajísevtazích,hráč na tahu se vždy přesune do nějakého sousedního bodu. Začíná Pavel, Rasťo vyhraje, pokud jej někdychytí.márasťovyhrávajícístrategii 1? 1 Neboli:můžeRasťohráttak,abyPavlachytil,aťužPavelhrajesebelépe?
2 E A D F B C ¾º ÐÓ Ó Ýµ Čert rozložil před ubohého Víťu lícem dospod všech osm žaludových karet a řekl: Jednu si vyber.bude-litoeso,ušetřímtě,jinakpropadnetvádušepeklu. Víťasáhlpojednézkaret. Užužsechtělnanipodívat,čerthovšakzarazil.Sebralzestolušestzesedmiostatníchkareta řekl: Esojejednazedvoukaret,kterénastolezbyly. Víťasepoškrábalnahlavě: Tohleděláš pokaždé?aťužjsemsiprvněvybraleso,nebone? Čertsezasmál: Samozřejmě,chytráku. Ateďužvybírej! Vyplatí se Víťovi změnit původní tip, nebo má raději zůstat u karty, kterou si zvolil na začátku, aby ušel pekelným mukám? º ÐÓ Ó Ýµ Stojedenáctlidístojívkruhu,mezinimiiFrantaaMartin,kteříalenestojívedlesebe.Franta smartinemsestřídajívtazích,začínáfranta.každýsevesvémtahudotknejednohozesvých sousedů,řekne Uglabuglagoblong! adotčenýmusíopustitkruh 2.Vyhrávátenhráč,kterýse takto první dotkne svého protihráče. Který z nich má vyhrávající strategii? º ÐÓ Ó µ OndraaSašahrajínásledujícíhru:NazačátkusiOndravyberenějaké(reálné)čísloanapíšeho najednuzvolnýchpozicvtétorovnici: x x x x+...=0 PakzaseSašaněkamnapíšečíslo,pakzaseOndraanakonecještěSaša,ažjsouvšechnamísta zaplněná. Pokud má výsledná rovnice(aspoň jedno) reálné řešení, vyhraje Saša, jinak vyhraje Ondra. Kdo má vyhrávající strategii? º ÐÓ Ó µ Proradní loupežníci Kenny a Jarda ukořistili obrovskou truhlu plnou zlatých mincí. Jak už to tak bývá, loupežníci se neradi dělí, tak se rozhodli si o poklad zahrát hru. Odněkud vytáhli čtvercový stůlapostupněnanějpokládajímince.ten,kdojezrovnanatahu,nastůlpoložíjednuminci tak,aby(anizčásti)neleželanajinémincianepřesahovalaokrajstolu 3.ZačínáKenny;prohraje ten, kdo už na stůl nemůže položit další minci. Kdo má vyhrávající strategii? º ÐÓ Ó µ Dva lovci pokladů, doktor Zelený a profesorka Červená, stojí uprostřed Duhové bažiny, která sestává z mnoha ostrůvků spojených barevnými lávkami. Mají dokonalou mapu bažiny, bohužel 2 Prošťouralypoznamenejme,želidéstojínaobvodukruhuaipoté,coněkdoodejde,má každý dva sousedy. 3 Všechnymincejsoustejněvelkéastůljetakobrovský,žesenanějvejdeaspoňjednamince.
3 ale jenom jednu, takže musí chodit spolu. Dohodli se, že se budou střídat ve vybírání cesty (ZelenýjegalantníanecháČervenouzačínat).Ten,nakomjeřada,můžebuďzůstatstát,nebo vést dvojici po lávce své oblíbené barvy(zelený zelené, Červená červené) na sousední ostrůvek. Podle mapy leží na některých ostrůvcích diamanty. Dr. Zelený hledá zelený diamant, prof. Červená prahne po diamantu červeném. Ve chvíli, kdy dvojice najde zelený nebo červený diamant, honzapoklademkončívítězstvímodpovídajícíhodobrodruha 4. Duhová bažina má ještě jednu zajímavou vlastnost: Když uděláme středovou symetrii se středem v počátečním ostrůvku, dostaneme stejnou bažinu, jen barvy(lávek i diamantů) se prohodí (cobylozelené,ječervenéanaopak).dokaž,žeaťužbažinavypadájakkoli 5,můžeprof.Červená zabránit tomu, aby se zelený drahokam našel jako první(má neprohrávající strategii). Podotýkáme, že neprohrávající strategii nemusíš do detailu popsat, stačí ukázat, že nějaká existuje. º ÐÓ Ó µ Zlomyslnému upírovi se do spárů dostaly Háňa a Zuzka. Aby je trochu potrápil, rozhodl se zahrát si s nimi jednu velice zákeřnou hru. Každá z nebohých dívek si musí vymyslet nějaké přirozené čísloapošeptatjeupírovi.tenjimpakřeknedvěčísla.jednoznichjesoučetčíseloboudívek(a druhé si prostě vymyslel, hráčky ale neví, které je které). Ta, která jako první zjistí číslo, které si myslela druhá nebožačka, vyhraje a za odměnu se stane upírovou manželkou, zatímco poraženou upír nemilosrdně rozsápe na kusy. Háňa po pravdě řekne, že neumí určit Zuzčino číslo. Zuzka zas pravdivěodpoví,žeanionaháninočísloještěnezná.pakzasháňadí,žezuzčinočíslonezná, ataksepořádstřídají.předpokládejme,žeupírřeklčísla900a777 6.Dokaž,žečasemjedna znichzjistíčíslotédruhéavyhraje. º ÐÓ Ó µ Dva hráči hrají piškvorky, pro osvěžení na nekonečně velkém trojúhelníkovém papíře. Hráči se střídají v tazích, ten, kdo je na tahu, vždy nakreslí svou značku do některého volného políčka. Vyhrajehráč,kterýmájakoprvnínepřerušenourovnouřadu 7 aspoň nsvýchznaků,kde nje nějaké přirozené číslo. V závislosti na n urči, kdo má vyhrávající nebo neprohrávající strategii. Pro upřesnění ještě dodejme, že na obrázku posloupnost křížků není řadou a posloupnost koleček je řadou. 4 Kdyžnajdounajednomostrůvkuobadrahokamynajednou,jetoremíza. 5 Tedyaťjetojedinýostrůvek,nebosložitéuskupenímilionůostrůvků krompodmínky symetrie vzhled bažiny nic neomezuje. 6 PokudbyTěvzadáníobtěžovalakonkrétnostčísel900a777,klidněúlohuřešsobecnými čísly man.nařešenísetéměřnicnezmění. 7 Směřujícíjednímzetřímožnýchsměrůpodélčartrojúhelníkovésítě.
4 Řešení 2. série 0. úloha Vymysli co nejvypečenější podfuk do libovolné(klidně i vlastní) hry. Pro ukázku zveřejňujeme některé z nejzajímavějších podfuků: Karolína Rezková VneděliosméhosesešlinejznámějšíekonomovéEvropy. 8 Začalisitakpovídatonovinkách, až se dostali k vážnějším otázkám, začali totiž řešit otázku svých platů. Ovšem nikdo nechtěl nahlasříct,jakýmásvůjhrubýpříjem,... jenžeekonomyčíslazajímají,aprotosedohodli po dlouhé, předlouhé diskuzi(konečně), že si alespoň zahrají a dozví se průměrný hrubý příjem všech přítomných. A to následujícím postupem. Všichni ekonomové si sedli do řady. Každý z nich dostal papírek. Na tento papírek musel první napsat svůj hrubý příjem a k němu přičíst libovolné náhodné číslo. Tento papírek podal svému sousedovi, ten k číslu na papírku přičetl zase svůj plat a libovolné náhodné číslo. Celý tento součet napsalnasvůjpapírekaposlaldále,ataktošloažnakonec.poté,coposledníprovedltentoúkon, předal zase papírek prvnímu hráči. Nyní si zase všichni rozdali papírek. Každý z ekonomů nyní (když na něj přijde řada) odečte sebou vymyšlené číslo a výsledek pošle dalšímu. Až poslední dostane papírek, odečte svůj hrubý příjem a výsledek vydělí počtem ekonomů. Tak dostanou všichni informaci o jejich průměrném platu, ale přitom nikdo nezjistil ničí hrubý příjem. Ovšem, co se nestalo. Dva britští ekonomové se dohodli na francouzského a sedli si oba vedle něj... Nyní se tito dva Britové mohou(spoluprací) jednoduše dobrat k hrubému platu Francouze. Stačí, aby si zapamatovali, jaké číslo první Brit podává Francouzovi. Pokud tuto hodnotu odečtou od hodnoty, kterou podá Francouz druhému Britovi, dostanou součet Francouzovy mzdy a jím vymyšleného náhodného čísla. V druhém kole si zase první Brit zapamatuje číslo, které podává Francouzovi a druhý Brit číslo, které od Francouze dostane. Rozdíl těchto dvou čísel se rovná Francouzově hrubé mzdě. Michal Hagara Dúfám,žepoznátepravidláhry Mamute,nehnevajsa! lebosamivámichsemnechcevysvetľovať.anibysasemvšetkynezmestili.šakúplnenajväčšípodfukje,keďchetitzelenýakolembas sa postaví na políčko D9, pričom hneď vedľa na I13 stojí chetit červený ako lembas prefarbený chameleónom na červeno. Vidíte ten podfuk? Že nie? Nojasné,niekdotunepoznápravidlátejtohry... Alejatoniesom... Josef Tkadlec Hrajejednoduchá.Dvahráčiházíkostkou 9,vyhráváten,kdohodívyššíčíslo.Abytonebyla takovánuda,jsoukmáníčtyřirůznékostky(vizpláště).obahráčisipředhodemvyberoukostku ahodí.dokaždéhohodusimůžouvybratkostkujinou. 8 Bylojichvícejak2. 9 Jetokostkakompletněbezděr!
5 Můjpodfukneníanitakpodfuk,jakospíšfinta(alezatojakořemen).Nechámsoupeře,abysi vybralkostku,kterájepodlenějnejlepší,ažpaksivyberujá.fórjevtom,žeaťsisoupeřvybere jakoukoliv, já si můžu vybrat takovou, že budu vyhrávat dvakrát častěji:-)(laskavá čtenářka si jistěsamadokáže... ).Stakovýmišancemiužsehrátvyplatí Poznámka: Tohlevšeplatí,jenpokudnehrajetesněkýmjakojeChuck 10,protožeten,jak známo, vyhrává za všech podmínek. 1. úloha Vbodě AstojílupičPavel,vbodě BjedetektivRasťo,kterýjejhoní.Střídajísevtazích,hráč na tahu se vždy přesune do nějakého sousedního bodu. Začíná Pavel, Rasťo vyhraje, pokud jej někdychytí.márasťovyhrávajícístrategii 11? E A D F B C Veliceelegantníjerešenípomocíobarvení.Nechťpolíčka A, Ca Fjsoučernáapolíčka B, D a Ebílá.(Můžešsipředstavit,žejdeodvěskupinysrůznýmivlastnostmi,alesbarvičkamije to pěkně názorné.) Nyní se lupič i detektiv z jakéhokoli políčka, při libovolném povoleném tahu, přesunounapolíčkobarvydruhé.tomimojinéznamená,žepojednomkole(lupičidetektiv odehrajekaždýjedentah)stojíopětjedenznichnapoličernémadruhýnabílém.potkatse protomohoujenvpřípadě,ževaktuálnímkoletáhlpouzejedenzhráčů,cožjelupič(vždy začíná) a ten sotva půjde dobrovolně do náruče detektiva, když z každého místa existují alespoň dvě různé cesty. Pavel má neprohrávající strategii, a proto Rasťo nemá vyhrávající strategii. Jiné řešení Pokaždé,kdyžjedenzhráčůtáhne,změnísevzdálenosthráčůo1.Toznamená,žepokudbyla předtímsudá,nyníbudelicháanaopak.počátečnívzdálenostjelichá.potahulupičebudetedy vždy vzdálenost mezi hráči sudá a naopak po tahu detektiva bude lichá. Koncová vzdálenost by 10 Norris,pozn.red. 11 Neboli:můžeRasťohráttak,abyPavlachytil,aťužPavelhrajesebelépe?
6 byla nula(když Rasťo Pavla dostihne), tedy sudá. Setkat se tedy mohou pouze po sudém tahu, to jest tahu lupiče, který ale nikdy není nucen padnout detektivovi do náruče. 2. úloha Čert rozložil před ubohého Víťu lícem dospod všech osm žaludových karet a řekl: Jednu si vyber.bude-litoeso,ušetřímtě,jinakpropadnetvádušepeklu. Víťasáhlpojednézkaret. Užužsechtělnanipodívat,čerthovšakzarazil.Sebralzestolušestzesedmiostatníchkareta řekl: Esojejednazedvoukaret,kterénastolezbyly. Víťasepoškrábalnahlavě: Tohleděláš pokaždé?aťužjsemsiprvněvybraleso,nebone? Čertsezasmál: Samozřejmě,chytráku. Ateďužvybírej! Vyplatí se Víťovi změnit původní tip, nebo má raději zůstat u karty, kterou si zvolil na začátku, aby ušel pekelným mukám? Pravděpodobnost,žesiVíťavytáhneesonaprvnípokus,je 1 8.Naopak,jinoukartunežeso vytáhnespravděpodobností 7 8. Pokudčertmluvípravdu 12,jednazedvoukaret,kterézůstalynastole,jeeso.Pravděpodobnost,žeprvníkartajeeso,jerovna 1 8.Druhákartajeeso,právěkdyžprvníkartanebyla eso,tedyspravděpodobností 7 8.Odtudjevidět,žeseVíťovivyplatízměnitpůvodnítipavolit druhou kartu. 3. úloha Stojedenáctlidístojívkruhu,mezinimiiFrantaaMartin,kteříalenestojívedlesebe.Franta smartinemsestřídajívtazích,začínáfranta.každýsevesvémtahudotknejednohozesvých sousedů,řekne Uglabuglagoblong! adotčenýmusíopustitkruh 13.Vyhrávátenhráč,kterýse takto první dotkne svého protihráče. Který z nich má vyhrávající strategii? VyhrávajícístrategiimáFranta.PojednérucehoodMartinadělísudýapodruhélichýpočet lidí.frantabudevždyodebíratztéstrany,kdejedělísudýpočetlidí,tímnechámartinovidvě liché skupinky. Zároveň se po každém kole (po tazích obou dvou) snižuje celkový počet lidí o dva, tedy před každým Martinovým tahem zbývá sudý počet lidí. Hra tedy nutně, pokud někdoneuděláchybu,dojdedosituace,kdyjenatahumartinazbývajítamještědvanehrající lidé,každýzjednéstrany.avdalšímtahuhofrantaužjistěvyřadí. 4. úloha OndraaSašahrajínásledujícíhru:NazačátkusiOndravyberenějaké(reálné)čísloanapíšeho najednuzvolnýchpozicvtétorovnici: x x x x+...=0 PakzaseSašaněkamnapíšečíslo,pakzaseOndraanakonecještěSaša,ažjsouvšechnamísta zaplněná. Pokud má výsledná rovnice(aspoň jedno) reálné řešení, vyhraje Saša, jinak vyhraje Ondra. Kdo má vyhrávající strategii? 12 Pokudčertvněkterémzesvýchvýrokůlhal,jepravděpodobné,želhalivtom,žeVíťu ušetří, jak správně poznamenal řešitel Karel Kolář. 13 Prošťouralypoznamenejme,želidéstojínaobvodukruhuaipoté,coněkdoodejde,má každý dva sousedy.
7 Ukážeme, že vyhrávající strategii má Saša. Všimneme si, že když součet koeficientů libovolnéhopolynomuje0,potommárovnicekořen1.stačítedy,abysašavhodnězvolilsvůjposlední tah. Označíme-li poslední Sašou doplňovaný koeficient a a ostatní již doplněné koeficienty postupnězlevadopravapísmeny b, c, d,potomsašovistačízvolit a= 1 b c davýsledná rovnice bude mít kořen 1. Samozřejmě Saša by uspěl i s obecnější strategií, ve které by si dopředu vymyslel nenulový kořen x 0 (vpředchozímjsmevolili x 0 =1)avposlednímtahuzahráltak,abyvzniklárovnice měla kořen x 0. Pokud například posledním tahem doplňuje koeficient a před x 3, zvolí a = = x4 0 bx2 0 cx 0 d x 3 0 (x 0 0)avýslednárovnice x 4 + x4 0 bx2 0 cx 0 d x 3 x 3 + bx 2 + cx+d=0 0 budemítvskutkukořen x 0.AnalogickybySašapostupoval,kdybyposledníkoeficientdoplňoval jinam. Ještě si dokážeš rozmyslet, že Sašovi dokonce stačí zvolit poslední koeficient tak, aby hodnotapolynomuvbodě x 0 bylazáporná. 5. úloha Proradní loupežníci Kenny a Jarda ukořistili obrovskou truhlu plnou zlatých mincí. Jak už to tak bývá, loupežníci se neradi dělí, tak se rozhodli si o poklad zahrát hru. Odněkud vytáhli čtvercový stůlapostupněnanějpokládajímince.ten,kdojezrovnanatahu,nastůlpoložíjednuminci tak,aby(anizčásti)neleželanajinémincianepřesahovalaokrajstolu 14.ZačínáKenny;prohraje ten, kdo už na stůl nemůže položit další minci. Kdo má vyhrávající strategii? Hledejme výherní strategii pro Kennyho. Mějme stůl, na který se vejde aspoň jedna mince. Začínající hráč, Kenny, ji položí doprostřed stolu.pokudsenastůlnevejdeužžádnádalšímince,kennyrovnouvyhrává.pokudsenastůl vejdeještěaspoňjednamince,jenatahujarda.aťtenpoložísvoumincikamkoli,zestředové souměrnosti stolu a prostřední mince(všechny mince jsou kulaté) vyplývá, že existuje aspoň jedno volné místo na stole obraz Jardovy mince ve středové souměrnosti podle středu stolu. Přesně na toto místo Kenny položí svou minci. Dále opět pokládá Jarda a Kenny reaguje položením mince na místo obrazu Jardovy mince podle středu stolu, a tak dále. Jelikož je stůl konečný, musí nastat situace, kdy už nepůjde nikam mince pokládat. Nemůže-li nakonec položit Jarda, vyhrál Kenny. Nemůže-li Kenny, znamená to, že Jarda nemohl položit svou předcházející minci, neboť Kenny vždy reaguje na Jardův tah, tedy Kenny ve skutečnosti vyhrál. Máme tedy krásnou výherní strategii pro Kennyho(zjevně nemůže nastat remíza). 6. úloha Dva lovci pokladů, doktor Zelený a profesorka Červená, stojí uprostřed Duhové bažiny, která sestává z mnoha ostrůvků spojených barevnými lávkami. Mají dokonalou mapu bažiny, bohužel ale jenom jednu, takže musí chodit spolu. Dohodli se, že se budou střídat ve vybírání cesty (ZelenýjegalantníanecháČervenouzačínat).Ten,nakomjeřada,můžebuďzůstatstát,nebo vést dvojici po lávce své oblíbené barvy(zelený zelené, Červená červené) na sousední ostrůvek. Podle mapy leží na některých ostrůvcích diamanty. Dr. Zelený hledá zelený diamant, prof. Červená prahne po diamantu červeném. Ve chvíli, kdy dvojice najde zelený nebo červený diamant, honzapoklademkončívítězstvímodpovídajícíhodobrodruha Všechnymincejsoustejněvelkéastůljetakobrovský,žesenanějvejdeaspoňjednamince. 15 Kdyžnajdounajednomostrůvkuobadrahokamynajednou,jetoremíza.
8 Duhová bažina má ještě jednu zajímavou vlastnost: Když uděláme středovou symetrii se středem v počátečním ostrůvku, dostaneme stejnou bažinu, jen barvy(lávek i diamantů) se prohodí (cobylozelené,ječervenéanaopak).dokaž,žeaťužbažinavypadájakkoli 16,můžeprof.Červená zabránit tomu, aby se zelený drahokam našel jako první(má neprohrávající strategii). Podotýkáme, že neprohrávající strategii nemusíš do detailu popsat, stačí ukázat, že nějaká existuje. SohledemnadokonaloumapuDuhovébažinyjižnazačátkudobrodruzivědí,kdoznichmá vítěznou strategii(má-li ji někdo). Z inverzní středové souměrnosti pak oba mají stejné možnosti dostat se ke svému drahokamu. Ve hře mohou nastat dvě varianty: (i) První hráč(v našem případě profesorka Červená) má neprohrávající strategii. V tomto případěsejítedystačídržetacíljesplněn. (ii) První hráč, který se pohne, nemá neprohrávající strategii. To znamená, že druhý(nezačínající) hráč má vítěznou strategii. Ať se první hráč pohne kamkoli, druhý hráč ho dotlačí ke svému vítězství. Profesorka Červená se ale v této situaci může vzdát tahu, přenechat první tah doktoru Zelenému a stát se tak vlastně nezačínajícím hráčem. Ani doktor ale nechce prohrát, a proto budou stále stát na místě, což je také neprohrávající strategie paní Červené. 7. úloha Zlomyslnému upírovi se do spárů dostaly Háňa a Zuzka. Aby je trochu potrápil, rozhodl se zahrát si s nimi jednu velice zákeřnou hru. Každá z nebohých dívek si musí vymyslet nějaké přirozené čísloapošeptatjeupírovi.tenjimpakřeknedvěčísla.jednoznichjesoučetčíseloboudívek(a druhé si prostě vymyslel, hráčky ale neví, které je které). Ta, která jako první zjistí číslo, které si myslela druhá nebožačka, vyhraje a za odměnu se stane upírovou manželkou, zatímco poraženou upír nemilosrdně rozsápe na kusy. Háňa po pravdě řekne, že neumí určit Zuzčino číslo. Zuzka zas pravdivěodpoví,žeanionaháninočísloještěnezná.pakzasháňadí,žezuzčinočíslonezná, ataksepořádstřídají.předpokládejme,žeupírřeklčísla900a Dokaž,žečasemjedna znichzjistíčíslotédruhéavyhraje. Úlohasedalařešitiobecně,alenejpřístupnějšíjeasinásledující polopatické řešení.označmesi hčíslo,kterésinazačátkumyslelaháňa,azčíslo,kterésinapočátkuzvolilazuzka.obě tato čísla jsou přirozená. Zlomyslnýupírdívkámřeklčísla777a900,jednoznichjevymyšlenéadruhéjesoučtemobou dívčinýchčísel,dívkyalenevědí,kteréjekteré.platítedybuďto h+z=777,nebo h+z=900. KdyžHáňanejdříveřekne,ženeumíurčitZuzčinočíslo,dávátímZuzceinformaci,žeje h <777. Kdyby totiž h bylo alespoň rovno 777, potom by pravým součtem dívčiných čísel nemohlo být číslo 777, neboť by pak Zuzčino číslo z nebylo přirozené. Háňa by pak dopočítala číslo své sokyně jako900 h.kdyžpotomzuzkazasetvrdí,ženeznáčísloháni,zestejnéhodůvodumusíbýt z <777,pakjíaletakédávánavědomost,že z > =123.Kdybytotižbylo znejvýše 123,ajakužvíme,je h <777,bylobyih+z <900,tímpádembytedysoučetčíseldívek bylnutně777azuzkabydokázalaurčitháninočíslojako777 z.pakzaseháňaoznamuje,že 16 Tedyaťjetojedinýostrůvek,nebosložitéuskupenímilionůostrůvků krompodmínky symetrie vzhled bažiny nic neomezuje. 17 PokudbyTěvzadáníobtěžovalakonkrétnostčísel900a777,klidněúlohuřešsobecnými čísly man.nařešenísetéměřnicnezmění.
9 pořádnedokážeurčitčíslozuzky.tímzuzcedávánajevonejento,žeje h >123(důkazbybyl podobnýjakouzuzkyvýše),aleito,že h < =654.Kdybytotižbylo halespoň654, pakby(protožeje z >123)bylo h+z >777,pravýmsoučtemčíseldívekbymuselobýtčíslo 900aHáňabymohlaZuzčinočíslodopočítatjako900 h,tímpádembyneřekla,ženeznáčíslo soupeřky.pokudzuzkaopětnedokážeurčitčíslohániasdělíjíto,prozuzčinočíslo zpakplatí z <654(zjižznáméhodůvodu)adále z > =246.Proč?Kdybybylo znejvýše246, pakby(kvůlitomu,žeje h <654)bylo h+z <900,čímžpádembybylsoučetčíseldívekjistě 777aZuzkabymohladopočítatHáninočíslojako777 h. Vtomtostyluseodvíjíhradál.Pokudbymohlaněkterádívkavzávislostinasvémčísle odvoditčíslosvéprotihráčky,učinítakavyhraje.pokudne,budousedívkyopětstřídatvopakovánípravdivéfráze Neumímurčitčíslosvésoupeřky. avduchusistálevíceomezovatmožné hodnoty čísla své sokyně. Důkazy následujících tvrzení ponechám na laskavé čtenářce, jsou hodně podobné těm již uvedeným. ZnásledujícívýpovědiHáni,ženeumíurčitZuzčinočíslo,vyplývá =246 < h < < =531,tedy246 < h <531.ZuzkapakzaseHáňusvýmvýrokem zpraví otom,že =369 < z < =531,neboli369 < z <531.NatoHáňadalšínegativnívětou nasvéčísloprozradí =369 < h < =408,takže369 < h <408.Jevidět, žeháninočísloteďmůženabývatnejvýše38hodnot.teďužzuzkamusíháninočíslo hnutně poznat,podíváseještějednoupořádněnasvéčíslo zapřičtehobleskurychlepostupněkevšem (maximálně)38možnýmhodnotám h.vtomtosoučtubudeurčitějenjednozčísel777a900 (rozdíl těchto čísel je mnohem větší než 38), naopak právě jedno tam bude, pokud dívky celou dobu mluvily pravdu(a to mluvily). Tím Zuzka zjistí Hánino číslo. Vyhrát mohla i Háňa, pokud v některé fázi nereagovala notorickyznámoufrází NeznámčísloZuzky.,alečíslomohladopočítat(jakbylovýšenaznačeno). Každopádně jedna z dívek nakonec zjistí číslo té druhé a vyhraje. 8. úloha Dva hráči hrají piškvorky, pro osvěžení na nekonečně velkém trojúhelníkovém papíře. Hráči se střídají v tazích, ten, kdo je na tahu, vždy nakreslí svou značku do některého volného políčka. Vyhrajehráč,kterýmájakoprvnínepřerušenourovnouřadu 18 aspoň nsvýchznaků,kde nje nějaké přirozené číslo. V závislosti na n urči, kdo má vyhrávající nebo neprohrávající strategii. Pro upřesnění ještě dodejme, že na obrázku posloupnost křížků není řadou a posloupnost koleček je řadou. Zkušenost z klasických piškvorek nám říká, že pro malé délky vyhrávající sekvence bude vyhrávat první hráč, a když už bude vyhrávající sekvence dost dlouhá, zvládnou se oba hráči 18 Směřujícíjednímzetřímožnýchsměrůpodélčartrojúhelníkovésítě.
10 navzájemubránit.aopravdujetomutak.pro n 3triviálněvítězízačínajícíhráčaužpro n=4 existuje pro oba neprohrávající strategie. K jejímu pochopení potřebujeme nejprve porozumět následujícímu obrázku(za jehož poskytnutí mnohokrát děkuji Mirkovi Olšákovi). Až nám z tohoto obrázku přestanou přecházet oči, všimneme si, že znázorňuje rozdělení trojúhelníkovésítěna kosočtverečky nebolinadvojicetrojúhelníků.dobrouvlastnostítakového rozdělení je, že jakákoliv vyhrávající řada délky alespoň 4 prochází jedním celým kosočtverečkem.abychomtedysoupeřizabránilivevýhře,stačímuzabránitvovládnutí kosočtverečku, no a to je snadné. Kdykoliv náš soupeř zahraje do jednoho z dvojice trojúhelníků tvořícího kosočtverec, my zahrajeme do toho druhého. No a protože v ovládnutí celého kosočtverce si umí oba hráčinavzájemzabránit(rozmyslisi!),nikdoznichnemůževyhrát.pro n=4anásledněipro n >4nemánikdozhráčůvítěznoustrategii.
Teorie her(povídání ke čtvrté sérii)
 Teorie her(povídání ke čtvrté sérii) Je velice obtížné definovat obecně, co je to hra. Navíc tento pojem intuitivně chápeme. Budeme se zabývat takovými hrami jako jsou šachy nebo pišqorky hrami dvou hráčů,
Teorie her(povídání ke čtvrté sérii) Je velice obtížné definovat obecně, co je to hra. Navíc tento pojem intuitivně chápeme. Budeme se zabývat takovými hrami jako jsou šachy nebo pišqorky hrami dvou hráčů,
Abstrakt. V příspěvku se budeme zabývat kombinatorickými hrami s úplnou informací
 Teorie her Viki Němeček Abstrakt. V příspěvku se budeme zabývat kombinatorickými hrami s úplnou informací pro dva hráče. Vysvětlíme si základní pojmy, zahrajeme si několik jednodušších her a naučíme se
Teorie her Viki Němeček Abstrakt. V příspěvku se budeme zabývat kombinatorickými hrami s úplnou informací pro dva hráče. Vysvětlíme si základní pojmy, zahrajeme si několik jednodušších her a naučíme se
Přijímací zkouška na MFF UK v Praze
 Přijímací zkouška na MFF UK v Praze Studijní program Matematika, bakalářské studium Studijní program Informatika, bakalářské studium 2014, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a,
Přijímací zkouška na MFF UK v Praze Studijní program Matematika, bakalářské studium Studijní program Informatika, bakalářské studium 2014, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a,
Teorie her. (ii) pouze triomina typu L:? 1 Ořechynelzejístpočástech.Např.zbývá-li11ořechů,sníhráč1,2nebo3kusy.
 ½º Ö ÐÓ ½º ÐÓÚ Ö Teorie her ÐÓ ¾º ÐÓ º Ì ÖÑ ÒÓ Ð Ò ºÔÖÓ Ò ¾¼½¾ ( Ó ) ( Ó ) Vkošíkuje17ořechů.MíšasFilipemsepravidelněstřídajívtazích,začínáMíša.Vkaždém tahusníhráčminimálnějedenořechamaximálnětřetinu 1
½º Ö ÐÓ ½º ÐÓÚ Ö Teorie her ÐÓ ¾º ÐÓ º Ì ÖÑ ÒÓ Ð Ò ºÔÖÓ Ò ¾¼½¾ ( Ó ) ( Ó ) Vkošíkuje17ořechů.MíšasFilipemsepravidelněstřídajívtazích,začínáMíša.Vkaždém tahusníhráčminimálnějedenořechamaximálnětřetinu 1
Návody k domácí části I. kola kategorie C
 61. ročník Matematické olympiády Návody k domácí části I. kola kategorie C 1. Najděte všechny trojčleny p(x) = ax 2 + bx + c, které dávají při dělení dvojčlenem x + 1 zbytek 2 a při dělení dvojčlenem x
61. ročník Matematické olympiády Návody k domácí části I. kola kategorie C 1. Najděte všechny trojčleny p(x) = ax 2 + bx + c, které dávají při dělení dvojčlenem x + 1 zbytek 2 a při dělení dvojčlenem x
Dobble HRA PLNÁ DIVOKÉ ATMOSFÉRY A RYCHLÝCH REFLEXŮ 2 AŽ 8 HRÁČŮ DOPORUČENÝ VĚK 6 A VÍCE LET. Pravidla
 Dobble HRA PLNÁ DIVOKÉ ATMOSFÉRY A RYCHLÝCH REFLEXŮ 2 AŽ 8 HRÁČŮ DOPORUČENÝ VĚK 6 A VÍCE LET Pravidla Co je to Dobble? Dobble, to je více než 50 symbolů na 55 kartách. Na jedné je vždy 8 různých symbolů
Dobble HRA PLNÁ DIVOKÉ ATMOSFÉRY A RYCHLÝCH REFLEXŮ 2 AŽ 8 HRÁČŮ DOPORUČENÝ VĚK 6 A VÍCE LET Pravidla Co je to Dobble? Dobble, to je více než 50 symbolů na 55 kartách. Na jedné je vždy 8 různých symbolů
Habermaaß-hra 4646. Chutná nebo nechutná?
 CZ Habermaaß-hra 4646 Chutná nebo nechutná? Chutná nebo nechutná? Hra podporující exekutivní funkce pro 2 4 hráče ve věku od 4 do 99 let. Využívá Fex-efekt na zvýšení stupně obtížnosti hry. Autoři: Markus
CZ Habermaaß-hra 4646 Chutná nebo nechutná? Chutná nebo nechutná? Hra podporující exekutivní funkce pro 2 4 hráče ve věku od 4 do 99 let. Využívá Fex-efekt na zvýšení stupně obtížnosti hry. Autoři: Markus
Čtvercové, krychlové a teseraktové minipiškvorky
 Čtvercové, krychlové a teseraktové minipiškvorky strategie hry Mgr. Michal Musílek červen 2006 1 Pravidla hry minipiškvorky Minipiškvorky jsou zjednodušená verze piškvorek, která se hraje v omezeném prostoru
Čtvercové, krychlové a teseraktové minipiškvorky strategie hry Mgr. Michal Musílek červen 2006 1 Pravidla hry minipiškvorky Minipiškvorky jsou zjednodušená verze piškvorek, která se hraje v omezeném prostoru
Habermaaß-hra 3389A /4521N. Počítání s piráty (mini verze)
 CZ Habermaaß-hra 3389A /4521N Počítání s piráty (mini verze) Počítání s piráty mini verze Vzdělávací hra pro 2 až 4 piráty ve věku od 6 do 99 let. Obsahuje variantu pro jednoho hráče. Autor: Wolfgang Dirscherl
CZ Habermaaß-hra 3389A /4521N Počítání s piráty (mini verze) Počítání s piráty mini verze Vzdělávací hra pro 2 až 4 piráty ve věku od 6 do 99 let. Obsahuje variantu pro jednoho hráče. Autor: Wolfgang Dirscherl
B) EX = 0,5, C) EX = 1, F) nemáme dostatek informací.
 Hlasovací otázka 9 Náhodná veličina X nabývá jen dvou různých hodnot, 0 a 1. Předpokládejme P(X = 0) = 0,5. Co můžeme říci o EX? Hlasovací otázka 9 Náhodná veličina X nabývá jen dvou různých hodnot, 0
Hlasovací otázka 9 Náhodná veličina X nabývá jen dvou různých hodnot, 0 a 1. Předpokládejme P(X = 0) = 0,5. Co můžeme říci o EX? Hlasovací otázka 9 Náhodná veličina X nabývá jen dvou různých hodnot, 0
TEORIE HER
 TEORIE HER 15. 10. 2014 HRA HRA Definice Hra je činnost jednoho či více lidí, která nemusí mít konkrétní smysl, ale přitom má za cíl radost či relaxaci. HRA Definice Hra je činnost jednoho či více lidí,
TEORIE HER 15. 10. 2014 HRA HRA Definice Hra je činnost jednoho či více lidí, která nemusí mít konkrétní smysl, ale přitom má za cíl radost či relaxaci. HRA Definice Hra je činnost jednoho či více lidí,
Habermaaß-hra 3615A /4714N. Kartová hra Najdi správný pár
 CZ Habermaaß-hra 3615A /4714N Kartová hra Najdi správný pár Kartová hra Najdi správný pár Monstrózně rychlá vyhledávací hra pro 2 až 6 hráčů ve věku od 4 do 99 let. Zahrnuje variantu pro experty na sbírání
CZ Habermaaß-hra 3615A /4714N Kartová hra Najdi správný pár Kartová hra Najdi správný pár Monstrózně rychlá vyhledávací hra pro 2 až 6 hráčů ve věku od 4 do 99 let. Zahrnuje variantu pro experty na sbírání
1. podzimní série. KdyžseLenkatuhleozkouškovémnudila,přišlanato,žepokudproreálnáčísla a, b, cplatí nerovnosti
 1. podzimní série Téma: Triky Datumodeslání: ½½º Ò ¾¼½¼ ½º ÐÓ Ó Ýµ Miško vymyslel trik! Nejdříve požádá Tomáška, ať si vybere osmičku nebo devítku. Potom mu řekne, aby zvolené číslo vynásobil jakýmkoliv
1. podzimní série Téma: Triky Datumodeslání: ½½º Ò ¾¼½¼ ½º ÐÓ Ó Ýµ Miško vymyslel trik! Nejdříve požádá Tomáška, ať si vybere osmičku nebo devítku. Potom mu řekne, aby zvolené číslo vynásobil jakýmkoliv
NÁVOD LOGIX mini Hra pro 2-4 hráče
 NÁVOD LOGIX mini Hra pro 2-4 hráče Cíl hry: Každý hráč si na začátku vylosuje kartu s tajným kódem (vzorem rozložení kuliček). V průběhu partie hráči pokládají na desku nové kuličky nebo přemisťují stávající
NÁVOD LOGIX mini Hra pro 2-4 hráče Cíl hry: Každý hráč si na začátku vylosuje kartu s tajným kódem (vzorem rozložení kuliček). V průběhu partie hráči pokládají na desku nové kuličky nebo přemisťují stávající
Úlohy krajského kola kategorie C
 6. ročník matematické olympiády Úlohy krajského kola kategorie C. Pro libovolná reálná čísla x, y, z taková, že x < y < z, dokažte nerovnost x 2 y 2 + z 2 > (x y + z) 2. 2. Honza má tři kartičky, na každé
6. ročník matematické olympiády Úlohy krajského kola kategorie C. Pro libovolná reálná čísla x, y, z taková, že x < y < z, dokažte nerovnost x 2 y 2 + z 2 > (x y + z) 2. 2. Honza má tři kartičky, na každé
Čtvercové puzzle úloha za 2 body
 Čtvercové puzzle úloha za 2 body Poskládejte uvedené dílky do čtverce 5 5 polí tak, aby v každém řádku a každém sloupci byla obarvena právě tři pole: jedno červené, jedno žluté a jedno modré. Úloha č.
Čtvercové puzzle úloha za 2 body Poskládejte uvedené dílky do čtverce 5 5 polí tak, aby v každém řádku a každém sloupci byla obarvena právě tři pole: jedno červené, jedno žluté a jedno modré. Úloha č.
Teorie her a ekonomické rozhodování. 7. Hry s neúplnou informací
 Teorie her a ekonomické rozhodování 7. Hry s neúplnou informací 7.1 Informace Dosud hráči měli úplnou informaci o hře, např. znali svou výplatní funkci, ale i výplatní funkce ostatních hráčů často to tak
Teorie her a ekonomické rozhodování 7. Hry s neúplnou informací 7.1 Informace Dosud hráči měli úplnou informaci o hře, např. znali svou výplatní funkci, ale i výplatní funkce ostatních hráčů často to tak
V zemi skřítků se hráči snaží navštívit co nejvíce měst. Musíte kombinovat jakou krajinou a jakým dopravním prostředkem budete cestovat.
 Elfenland Počet hráčů: 2-6 Doporučený věk: nejméně 10 let Délka hry: 60 až 80 minut Vydavatel: Amigo Rok vydání: 1998 Autor: Alan R. Moon V zemi skřítků se hráči snaží navštívit co nejvíce měst. Musíte
Elfenland Počet hráčů: 2-6 Doporučený věk: nejméně 10 let Délka hry: 60 až 80 minut Vydavatel: Amigo Rok vydání: 1998 Autor: Alan R. Moon V zemi skřítků se hráči snaží navštívit co nejvíce měst. Musíte
Chytrý medvěd učí počítat
 CZ Habermaaß-hra 3151A /4547N Chytrý medvěd učí počítat Medvědí kolekce vzdělávacích her pro 2 až 5 hráčů ve věku od 4 do 8 let. S navlékacím počítadlem Chytrého medvěda a třemi extra velkými kostkami.
CZ Habermaaß-hra 3151A /4547N Chytrý medvěd učí počítat Medvědí kolekce vzdělávacích her pro 2 až 5 hráčů ve věku od 4 do 8 let. S navlékacím počítadlem Chytrého medvěda a třemi extra velkými kostkami.
Habermaaß-hra 3616A /4717N. Zvířecí pyramida karetní hra
 CZ Habermaaß-hra 3616A /4717N Zvířecí pyramida karetní hra Zvířecí pyramida karetní hra Rozechvělá hra pro 2-4 hráče ve věku od 5 do 99 let. Obsahuje dvě herní varianty. Autor: Ilustrace: Poskytovatel
CZ Habermaaß-hra 3616A /4717N Zvířecí pyramida karetní hra Zvířecí pyramida karetní hra Rozechvělá hra pro 2-4 hráče ve věku od 5 do 99 let. Obsahuje dvě herní varianty. Autor: Ilustrace: Poskytovatel
101 Střední škola, město Zadání - Náboj 2008 Úloha 1. Kolik různých trojúhelníků s celočíselnými délkami stran má obvod 7? Které to jsou?
 Úloha 1. Kolik různých trojúhelníků s celočíselnými délkami stran má obvod 7? Které to jsou? Úloha 2. V růžovém království se platí mincemi v hodnotě 3 a 7. Určete největší částku, která se nedá pomocí
Úloha 1. Kolik různých trojúhelníků s celočíselnými délkami stran má obvod 7? Které to jsou? Úloha 2. V růžovém království se platí mincemi v hodnotě 3 a 7. Určete největší částku, která se nedá pomocí
Povídání k sedmé sérii
 Povídání k sedmé sérii Tato série se zabývá hrami. Pojem hra není pro řešení zadaných úloh potřeba nějak přesně vymezovat, čtenář si vystačí s intuitivní představou. Naše hry mají charakter her pro dva
Povídání k sedmé sérii Tato série se zabývá hrami. Pojem hra není pro řešení zadaných úloh potřeba nějak přesně vymezovat, čtenář si vystačí s intuitivní představou. Naše hry mají charakter her pro dva
Medvídek Teddy barvy a tvary
 CZ Habermaaß-hra 5878 Moje první hra Medvídek Teddy barvy a tvary Moje první hra Medvídek Teddy barvy a tvary První umísťovací hra pro 1 až 4 malé medvídky od 2 let. Autor: Christiane Hüpper Ilustrace:
CZ Habermaaß-hra 5878 Moje první hra Medvídek Teddy barvy a tvary Moje první hra Medvídek Teddy barvy a tvary První umísťovací hra pro 1 až 4 malé medvídky od 2 let. Autor: Christiane Hüpper Ilustrace:
Habermaaß-hra 8679A /4716N. Hrad Strašidlákov karetní hra
 CZ Habermaaß-hra 8679A /4716N Hrad Strašidlákov karetní hra Hrad Strašidlákov karetní hra Roztřesená hra pro 2-4 malé duchy ve věku 4 do 99 let. Autoři: Kai Haferkamp & Markus Nikisch Ilustrace: Sabine
CZ Habermaaß-hra 8679A /4716N Hrad Strašidlákov karetní hra Hrad Strašidlákov karetní hra Roztřesená hra pro 2-4 malé duchy ve věku 4 do 99 let. Autoři: Kai Haferkamp & Markus Nikisch Ilustrace: Sabine
ZAZVOŇ A VYHRAJ! Počet hráčů: 2 6 osob Věk: od 6 let Délka hry: cca 20 minut
 ZAZVOŇ A VYHRAJ! Počet hráčů: 2 6 osob Věk: od 6 let Délka hry: cca 20 minut Obsah: 72 hracích karet - 64 karet s ovocem, 3 karty se slonem, 3 karty s opicí, 2 karty s prasátkem 1 zvonek 1 pravidla hry
ZAZVOŇ A VYHRAJ! Počet hráčů: 2 6 osob Věk: od 6 let Délka hry: cca 20 minut Obsah: 72 hracích karet - 64 karet s ovocem, 3 karty se slonem, 3 karty s opicí, 2 karty s prasátkem 1 zvonek 1 pravidla hry
Habermaaß-hra 4280. Nešikovná čarodějnice
 CZ Habermaaß-hra 4280 Nešikovná čarodějnice Nešikovná čarodějnice Okouzlující sledovací hra podporující rychlé rozhodování, pro 2 až 4 hráče ve věku od 5 do 99 let. Hra má FEX efekt pro zvýšení stupně
CZ Habermaaß-hra 4280 Nešikovná čarodějnice Nešikovná čarodějnice Okouzlující sledovací hra podporující rychlé rozhodování, pro 2 až 4 hráče ve věku od 5 do 99 let. Hra má FEX efekt pro zvýšení stupně
N Q Z N N N, kde A Bjesymbolprokartézskýsoučinmnožin A, B(tj.množinuvšechuspořádanýchdvojic [a, b],kde a A, b B).Opětprosímpřijmětejakofakt, 1 že
![N Q Z N N N, kde A Bjesymbolprokartézskýsoučinmnožin A, B(tj.množinuvšechuspořádanýchdvojic [a, b],kde a A, b B).Opětprosímpřijmětejakofakt, 1 že N Q Z N N N, kde A Bjesymbolprokartézskýsoučinmnožin A, B(tj.množinuvšechuspořádanýchdvojic [a, b],kde a A, b B).Opětprosímpřijmětejakofakt, 1 že](/thumbs/88/115751012.jpg) Jak rozeznáváme nekonečné množiny. Nejprve něco o zobrazeních: Nášvýkladbudezaložennaintuitivnípředstavězobrazení f: A Bjakoněčeho,cokaždému prvku a Apřiřazujenějakýprvek f(a) B. Mějmezobrazení f: A B.Řekneme,že
Jak rozeznáváme nekonečné množiny. Nejprve něco o zobrazeních: Nášvýkladbudezaložennaintuitivnípředstavězobrazení f: A Bjakoněčeho,cokaždému prvku a Apřiřazujenějakýprvek f(a) B. Mějmezobrazení f: A B.Řekneme,že
Usekne-li Honza 1 hlavu, narostou dva ocasy. Tento tah můžeme zakreslit následujícím způsobem: Usekne-li 2 hlavy, nic nenaroste.
 Řešení 2. série Řešení J-I-2-1 1. krok: Číslici 2 ve třetím řádku můžeme dostat jedině násobením 5 4 = 20, 5 5 = 25. Tedy na posledním místě v prvním řádku může být číslice 4 nebo 5. Odtud máme i dvě možnosti
Řešení 2. série Řešení J-I-2-1 1. krok: Číslici 2 ve třetím řádku můžeme dostat jedině násobením 5 4 = 20, 5 5 = 25. Tedy na posledním místě v prvním řádku může být číslice 4 nebo 5. Odtud máme i dvě možnosti
Hra pro 2 10 hráčů od deseti let. OBSAH HRY CÍL HRY
 Hra pro 2 10 hráčů od deseti let. OBSAH HRY 104 hracích karet s čísly 1 104, pravidla hry CÍL HRY Na všech kartách jsou symboly krav. Každá kráva, kterou během hry vezmete, znamená jeden minusový bod.
Hra pro 2 10 hráčů od deseti let. OBSAH HRY 104 hracích karet s čísly 1 104, pravidla hry CÍL HRY Na všech kartách jsou symboly krav. Každá kráva, kterou během hry vezmete, znamená jeden minusový bod.
Habermaaß-hra 2404. Domino Had z číslic a obrázků
 CZ Habermaaß-hra 2404 Domino Had z číslic a obrázků Domino Had z číslic a obrázků Barevná a veselá paměťová hra s čísly pro 2-4 děti ve věku od 4 let. Obsahuje i variantu pro jednoho hráče. Design: Jutta
CZ Habermaaß-hra 2404 Domino Had z číslic a obrázků Domino Had z číslic a obrázků Barevná a veselá paměťová hra s čísly pro 2-4 děti ve věku od 4 let. Obsahuje i variantu pro jednoho hráče. Design: Jutta
Úlohy krajského kola kategorie B
 65. ročník matematické olympiády Úlohy krajského kola kategorie B 1. Určete všechny trojice celých kladných čísel k, l a m, pro které platí 3l + 1 3kl + k + 3 = lm + 1 5lm + m + 5. 2. Je dána úsečka AB,
65. ročník matematické olympiády Úlohy krajského kola kategorie B 1. Určete všechny trojice celých kladných čísel k, l a m, pro které platí 3l + 1 3kl + k + 3 = lm + 1 5lm + m + 5. 2. Je dána úsečka AB,
ODDVILLE hra pro 2 4 hráče od 10 let
 ODDVILLE hra pro 2 4 hráče od 10 let Obsah hry: 64 karet budov/mincí 1 karta startovního náměstí 16 karet dělníků (4 od barvy) 36 figurek (9 od barvy) 1 deska zdrojů 12 karet postav (3 od jené gildy) Hráči
ODDVILLE hra pro 2 4 hráče od 10 let Obsah hry: 64 karet budov/mincí 1 karta startovního náměstí 16 karet dělníků (4 od barvy) 36 figurek (9 od barvy) 1 deska zdrojů 12 karet postav (3 od jené gildy) Hráči
PRAVIDLA: ÚROVEŇ 4 BALÍČEK VS BALÍČEK
 PRAVIDLA: ÚROVEŇ 4 BALÍČEK VS BALÍČEK PŘÍPRAVA NA HRU Každý hráč si připraví balíček s 20 kartami hrdinů a s 20 kartami zbraní. Do balíčku může dát maximálně 4 karty stejného typu (např. 4 Naftové rytíře
PRAVIDLA: ÚROVEŇ 4 BALÍČEK VS BALÍČEK PŘÍPRAVA NA HRU Každý hráč si připraví balíček s 20 kartami hrdinů a s 20 kartami zbraní. Do balíčku může dát maximálně 4 karty stejného typu (např. 4 Naftové rytíře
Habermaaß-hra 4530. Terra Kids Země světa
 CZ Habermaaß-hra 4530 Terra Kids Země světa Terra kids Země světa Vzrušující poznávací hra pro 2-4 cestovatele ve věku od 8 do 99 let. Herní nápad: zaměstnanci Haba Ilustrace: Albert Kokai Délka hry: cca.
CZ Habermaaß-hra 4530 Terra Kids Země světa Terra kids Země světa Vzrušující poznávací hra pro 2-4 cestovatele ve věku od 8 do 99 let. Herní nápad: zaměstnanci Haba Ilustrace: Albert Kokai Délka hry: cca.
Teorie her a ekonomické rozhodování. 4. Hry v rozvinutém tvaru
 Teorie her a ekonomické rozhodování 4. Hry v rozvinutém tvaru 4.1 Hry v rozvinutém tvaru Hra v normálním tvaru hráči provedou jediné rozhodnutí a to všichni najednou v rozvinutém tvaru řada po sobě následujících
Teorie her a ekonomické rozhodování 4. Hry v rozvinutém tvaru 4.1 Hry v rozvinutém tvaru Hra v normálním tvaru hráči provedou jediné rozhodnutí a to všichni najednou v rozvinutém tvaru řada po sobě následujících
Od Uwe Rosenberga Pro 2 až 5 hráčů od 10 let, 40 minut
 Od Uwe Rosenberga Pro 2 až 5 hráčů od 10 let, 40 minut Herní materiál 65 karet přísad na pizzu (13 od každého druhu: olivy, papričky, žampiony, salám a ananas) 40 karet s objednávkami (8 od každé v 5 barvách
Od Uwe Rosenberga Pro 2 až 5 hráčů od 10 let, 40 minut Herní materiál 65 karet přísad na pizzu (13 od každého druhu: olivy, papričky, žampiony, salám a ananas) 40 karet s objednávkami (8 od každé v 5 barvách
40 označovacích kamenů vždy 10 v červené, oranžové, černé, modré barvě. 7 slonů 3 lvi 6 normálních 1 super
 Lev, zebra, slon - divoká, daleká, krásná země! Počet hráčů: 2-4 Věk: od 8 let Herní doba: okolo 20 min. Andreas Spies Karty Celkem 42 kopytníků (pakůň, zebra, antilopa) se chce dostat z jedné strany africké
Lev, zebra, slon - divoká, daleká, krásná země! Počet hráčů: 2-4 Věk: od 8 let Herní doba: okolo 20 min. Andreas Spies Karty Celkem 42 kopytníků (pakůň, zebra, antilopa) se chce dostat z jedné strany africké
Návody k úlohám domácí části I. kola 59. ročníku MO kategorie B
 Návody k úlohám domácí části I kola 59 ročníku MO kategorie B Soutěžní úloha 1 Na stole leží tři hromádky zápalek: v jedné 009, ve druhé 010 a v poslední 011 Hráč, který je na tahu, zvolí dvě hromádky
Návody k úlohám domácí části I kola 59 ročníku MO kategorie B Soutěžní úloha 1 Na stole leží tři hromádky zápalek: v jedné 009, ve druhé 010 a v poslední 011 Hráč, který je na tahu, zvolí dvě hromádky
Pravděpodobnost kolem nás
 Brno, 17. 6. 2011 Pravděpodobnost kolem nás - jak spravedlivě losovat? - je možnost volby vždy výhodou? - který šifrovací zámek chrání nejlépe? - je známka z testu věrohodná? - proč prosperuje casino?
Brno, 17. 6. 2011 Pravděpodobnost kolem nás - jak spravedlivě losovat? - je možnost volby vždy výhodou? - který šifrovací zámek chrání nejlépe? - je známka z testu věrohodná? - proč prosperuje casino?
Habermaaß-hra 4094. Princezna Kouzelná víla
 CZ Habermaaß-hra 4094 Princezna Kouzelná víla Princezna Kouzelná víla Paměťová a kreslící hra pro družstva pro 2-4 víly od 4 do 10 let. Autor: Ilustrace: Délka hry: Thilo Hutzler Anja Rieger přibližně
CZ Habermaaß-hra 4094 Princezna Kouzelná víla Princezna Kouzelná víla Paměťová a kreslící hra pro družstva pro 2-4 víly od 4 do 10 let. Autor: Ilustrace: Délka hry: Thilo Hutzler Anja Rieger přibližně
pro bakalářské studijní programy fyzika, informatika a matematika 2018, varianta A
 Přijímací zkouška na MFF UK pro bakalářské studijní programy fyzika, informatika a matematika 2018, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a, b, c, d, e. Vaším úkolem je u každé úlohy
Přijímací zkouška na MFF UK pro bakalářské studijní programy fyzika, informatika a matematika 2018, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a, b, c, d, e. Vaším úkolem je u každé úlohy
KACÍŘI a bitva o Evropu
 KACÍŘI a bitva o Evropu Historická karetní hra Kacíři jsou karetní hra na motivy náboženských bojů v 15.-17. století, v níž se hrající snaží získat evropská města pro náboženskou frakci, kterou si vybrali.
KACÍŘI a bitva o Evropu Historická karetní hra Kacíři jsou karetní hra na motivy náboženských bojů v 15.-17. století, v níž se hrající snaží získat evropská města pro náboženskou frakci, kterou si vybrali.
2. série. Prvočísla. Téma: Datumodeslání: Dokažte,žekaždéprvočíslovětšínež5jdepsátvetvaru6k+1nebo6k 1,kde kjenějaké přirozené číslo.
 2. série Téma: Datumodeslání: Prvočísla º Ð ØÓÔ Ù ¾¼¼ ½º ÐÓ Ó Ýµ Dokažte,žekaždéprvočíslovětšínež5jdepsátvetvaru6k+1nebo6k 1,kde kjenějaké přirozené číslo. ¾º ÐÓ Ó Ýµ Mějme libovolné přirozené číslo n,
2. série Téma: Datumodeslání: Prvočísla º Ð ØÓÔ Ù ¾¼¼ ½º ÐÓ Ó Ýµ Dokažte,žekaždéprvočíslovětšínež5jdepsátvetvaru6k+1nebo6k 1,kde kjenějaké přirozené číslo. ¾º ÐÓ Ó Ýµ Mějme libovolné přirozené číslo n,
9 karet alibi. Každá z nich představuje postavu ze světa Mr. Jacka. Každá z těchto karet také zobrazuje počet přesýpacích hodin (0,1 nebo 2).
 Materiál 9 destiček ulic, dále jen hrací pole. - jsou oboustranné a slouží jako hrací plocha (městská čtvrť) Na jedné straně není vyobrazena žádná postava to je prázdná strana. Na druhé straně postava
Materiál 9 destiček ulic, dále jen hrací pole. - jsou oboustranné a slouží jako hrací plocha (městská čtvrť) Na jedné straně není vyobrazena žádná postava to je prázdná strana. Na druhé straně postava
NA ZÁPAD! (Go West!)
 NA ZÁPAD! (Go West!) Leo Colovini 1.0 ÚVOD Na konci 18. století se zájmy USA upíraly díky osidlování vnitrozemí a přistěhovalectví ze západní, střední a severní Evropy stále více k dobytí Západu rozšiřování
NA ZÁPAD! (Go West!) Leo Colovini 1.0 ÚVOD Na konci 18. století se zájmy USA upíraly díky osidlování vnitrozemí a přistěhovalectví ze západní, střední a severní Evropy stále více k dobytí Západu rozšiřování
Každý hráč dostane 1 list s herním plánem. Připraví se 6 kostek. Navíc potřebuje každý hráč tužku. Určí se, kdo začíná.
 Herní materiál 6 kostek se surovinami blok s 60 herními plány Příprava Každý hráč dostane list s herním plánem. Připraví se 6 kostek. Navíc potřebuje každý hráč tužku. Určí se, kdo začíná. Princip hry
Herní materiál 6 kostek se surovinami blok s 60 herními plány Příprava Každý hráč dostane list s herním plánem. Připraví se 6 kostek. Navíc potřebuje každý hráč tužku. Určí se, kdo začíná. Princip hry
Zadání soutěžních úloh
 20. až 22. dubna 2017 Krajské kolo 2016/2017 Úlohy můžete řešit v libovolném pořadí a samozřejmě je nemusíte vyřešit všechny. Počet bodů za každou úlohu je uveden přímo v jejím zadání. Hodnotí se shoda
20. až 22. dubna 2017 Krajské kolo 2016/2017 Úlohy můžete řešit v libovolném pořadí a samozřejmě je nemusíte vyřešit všechny. Počet bodů za každou úlohu je uveden přímo v jejím zadání. Hodnotí se shoda
Úloha2.Naleznětevšechnydvojicereálnýchčísel(a,b)takové,žečísla10, a, b, abtvořívtomtopořadí aritmetickou posloupnost.
 Úloha. V Americe se pro měření teploty používají místo Celsiových stupňů stupně Fahrenheitovy. PřepočetzCelsiovýchstupňůnaFahrenheitovylzeprovéstpodlevzorce f = 9 5 c+32(cjsoustupně Celsiovy, f Farenheitovy).
Úloha. V Americe se pro měření teploty používají místo Celsiových stupňů stupně Fahrenheitovy. PřepočetzCelsiovýchstupňůnaFahrenheitovylzeprovéstpodlevzorce f = 9 5 c+32(cjsoustupně Celsiovy, f Farenheitovy).
Habermaaß-hra 4748A /4287N a jeden poklad
 CZ Habermaaß-hra 4748A /4287N 1000 a jeden poklad 1000 a jeden poklad Dobrodružná hra na motivy pohádek 1000 a jedné noci pro 2-4 hráče od 5 do 99 let. Obsahuje základní variantu pro mladší hráče. Autor:
CZ Habermaaß-hra 4748A /4287N 1000 a jeden poklad 1000 a jeden poklad Dobrodružná hra na motivy pohádek 1000 a jedné noci pro 2-4 hráče od 5 do 99 let. Obsahuje základní variantu pro mladší hráče. Autor:
návod ke hře GWINT Gwint je karetní hra pro 2 hráče, ve které se spolu na bojišti utkají dvě armády.
 návod ke hře GWINT Gwint je karetní hra pro 2 hráče, ve které se spolu na bojišti utkají dvě armády. Hráči se střídají a každý ve svém tahu na bojiště vynese jednu kartu. Na konci každého kola si hráči
návod ke hře GWINT Gwint je karetní hra pro 2 hráče, ve které se spolu na bojišti utkají dvě armády. Hráči se střídají a každý ve svém tahu na bojiště vynese jednu kartu. Na konci každého kola si hráči
27-SEP-10. Black Cyan Magenta Yellow. CÍL HRY Jako první vytlačit šest. v tazích - své kuličky lze posunout. pole.
 Návod ke hře Hra 2 hráčů CÍL HRY Jako první vytlačit šest soupeřových kuliček z hracího pole. PŘÍPRAVA HRY: - hráči si připraví kuličky do startovních pozic, jak je uvedeno na obr. 1 - hráči se domluví,
Návod ke hře Hra 2 hráčů CÍL HRY Jako první vytlačit šest soupeřových kuliček z hracího pole. PŘÍPRAVA HRY: - hráči si připraví kuličky do startovních pozic, jak je uvedeno na obr. 1 - hráči se domluví,
NÁVOD. SPOJUJ SLŮVKA téma: DŮM. vzdělávací hra ve 2 variantách od 7 let
 NÁVOD SPOJUJ SLŮVKA téma: DŮM vzdělávací hra ve 2 variantách od 7 let Dílky s obrázky a anglickými slovíčky, které popisující obsah těchto obrázků jsou jednoduchou a atraktivní formou výuky pro nejmladší.
NÁVOD SPOJUJ SLŮVKA téma: DŮM vzdělávací hra ve 2 variantách od 7 let Dílky s obrázky a anglickými slovíčky, které popisující obsah těchto obrázků jsou jednoduchou a atraktivní formou výuky pro nejmladší.
Zadání soutěžních úloh
 Zadání soutěžních úloh Kategorie žáci Soutěž v programování 24. ročník Krajské kolo 2009/2010 15. až 17. dubna 2010 Úlohy můžete řešit v libovolném pořadí a samozřejmě je nemusíte vyřešit všechny. Za každou
Zadání soutěžních úloh Kategorie žáci Soutěž v programování 24. ročník Krajské kolo 2009/2010 15. až 17. dubna 2010 Úlohy můžete řešit v libovolném pořadí a samozřejmě je nemusíte vyřešit všechny. Za každou
RA PLNÁ DIVOKÉ ATMOSFÉRY A RYCHLÝCH REAKCÍ 2 AŽ 8 HRÁČŮ DOPORUČENÝ VĚK 6 A VÍCE L
 HRA PLNÁ DIVOKÉ ATMOSFÉRY A RYCHLÝCH REAKCÍ 2 AŽ 8 HRÁČŮ DOPORUČENÝ VĚK 6 A VÍCE LET Pravidla Co je to Dobble? Dobble, to je více než 50 symbolů na 55 kartách. Na jedné je vždy 8 různých symbolů a každé
HRA PLNÁ DIVOKÉ ATMOSFÉRY A RYCHLÝCH REAKCÍ 2 AŽ 8 HRÁČŮ DOPORUČENÝ VĚK 6 A VÍCE LET Pravidla Co je to Dobble? Dobble, to je více než 50 symbolů na 55 kartách. Na jedné je vždy 8 různých symbolů a každé
Materiál. 4 hodnotící karty 1 karta hracích kol 4 tužky. 100 křížů pokladů Počet hráčů: 2-4 Věk: od 8 let Herní doba: okolo 20 min.
 Phil Walker-Harding 100 křížů - 1000 pokladů Počet hráčů: 2-4 Věk: od 8 let Herní doba: okolo 20 min. Materiál 47 map pokladů Od každé barvy (fialová, oranžová, zelená, šedá) je k dispozici vždy 12 karet
Phil Walker-Harding 100 křížů - 1000 pokladů Počet hráčů: 2-4 Věk: od 8 let Herní doba: okolo 20 min. Materiál 47 map pokladů Od každé barvy (fialová, oranžová, zelená, šedá) je k dispozici vždy 12 karet
Habermaaß-hra 5663A /4794N. Mili nosí poštu
 CZ Habermaaß-hra 5663A /4794N Mili nosí poštu Mili nosí poštu Bláznivá paměťová hra pro 2-4 hráče ve věku od 4 let. Na motivy knižního bestselleru "Lieselotte lauert", kterou vydalo vydavatelství Sauerländer.
CZ Habermaaß-hra 5663A /4794N Mili nosí poštu Mili nosí poštu Bláznivá paměťová hra pro 2-4 hráče ve věku od 4 let. Na motivy knižního bestselleru "Lieselotte lauert", kterou vydalo vydavatelství Sauerländer.
Úlohy domácí části I. kola kategorie C
 6. ročník Matematické olympiády Úlohy domácí části I. kola kategorie C 1. Určete všechny dvojice (x, y) reálných čísel, která vyhovují soustavě rovnic (x + )2 = y, (y )2 = x + 8. Řešení. Vzhledem k tomu,
6. ročník Matematické olympiády Úlohy domácí části I. kola kategorie C 1. Určete všechny dvojice (x, y) reálných čísel, která vyhovují soustavě rovnic (x + )2 = y, (y )2 = x + 8. Řešení. Vzhledem k tomu,
3. podzimní série. ... {z }
 3. podzimní série Téma: Kombinatorika Datumodeslání: º ÔÖÓ Ò ¾¼¼ ½º ÐÓ Ó Ýµ Monča potřebuje zatelefonovat Pepovi, avšak nemá u sebe svůj telefonní seznam PraSátek. Zná však předvolbu 723 a vzpomněla si,
3. podzimní série Téma: Kombinatorika Datumodeslání: º ÔÖÓ Ò ¾¼¼ ½º ÐÓ Ó Ýµ Monča potřebuje zatelefonovat Pepovi, avšak nemá u sebe svůj telefonní seznam PraSátek. Zná však předvolbu 723 a vzpomněla si,
Napínavé letecké závody pro dva chytré havrany od 10 let
 Napínavé letecké závody pro dva chytré havrany od 10 let CELKOVÝ POHLED Odin, otec bohů, posílá své dva havrany: Hugina a Mugina do světa, aby dohlíželi na Zemi. Hráči vykládají karty, aby pohybovali opeřenými
Napínavé letecké závody pro dva chytré havrany od 10 let CELKOVÝ POHLED Odin, otec bohů, posílá své dva havrany: Hugina a Mugina do světa, aby dohlíželi na Zemi. Hráči vykládají karty, aby pohybovali opeřenými
Dokažte Větu 2(Minimax) ze třetího dílu seriálu pro libovolnou hru s nulovým součtem, ve kterémákaždýhráčnavýběrprávězedvoustrategií.
 Teorie her º Ö ÐÓÚ Ö Ì ÖÑ Ò Ó Ð Ò º Ù Ò ¾¼½ ÐÓ ½º HráčIsitajněnapíšenapapírnějaképřirozenéčíslozrozmezíaž noznačmeho ivestejnou chvílisirovněžhráčiinapíšenapapírnějaképřirozenéčíslozrozmezíaž noznačmeho
Teorie her º Ö ÐÓÚ Ö Ì ÖÑ Ò Ó Ð Ò º Ù Ò ¾¼½ ÐÓ ½º HráčIsitajněnapíšenapapírnějaképřirozenéčíslozrozmezíaž noznačmeho ivestejnou chvílisirovněžhráčiinapíšenapapírnějaképřirozenéčíslozrozmezíaž noznačmeho
Úlohy domácí části I. kola kategorie B
 6. ročník Matematické olympiády Úlohy domácí části I. kola kategorie B. Mezi všemi desetimístnými čísly dělitelnými jedenácti, v nichž se žádná číslice neopakuje, najděte nejmenší a největší. Řešení. Uvažovaná
6. ročník Matematické olympiády Úlohy domácí části I. kola kategorie B. Mezi všemi desetimístnými čísly dělitelnými jedenácti, v nichž se žádná číslice neopakuje, najděte nejmenší a největší. Řešení. Uvažovaná
Základy umělé inteligence
 Základy umělé inteligence Hraní her (pro 2 hráče) Základy umělé inteligence - hraní her. Vlasta Radová, ZČU, katedra kybernetiky 1 Hraní her (pro dva hráče) Hraní her je přirozeně spjato s metodami prohledávání
Základy umělé inteligence Hraní her (pro 2 hráče) Základy umělé inteligence - hraní her. Vlasta Radová, ZČU, katedra kybernetiky 1 Hraní her (pro dva hráče) Hraní her je přirozeně spjato s metodami prohledávání
Složka případu. Neobvyklí podezřelí
 Policie se již několik měsíců neúspěšně snaží dopadnout ne známého zloděje. A teď byl konečně přistižen při činu. Svědek má ale dost zvláštní paměť. Na tvář zloděje si vzpo menout nedokáže, zato o jeho
Policie se již několik měsíců neúspěšně snaží dopadnout ne známého zloděje. A teď byl konečně přistižen při činu. Svědek má ale dost zvláštní paměť. Na tvář zloděje si vzpo menout nedokáže, zato o jeho
Razzia!. Od Reinera Knizia
 Razzia!. Od Reinera Knizia Počet hráčů: 2 5 Věk: od 12 let Hrací doba: přibližně 45 minut Herní materiál. 99 karet kořistí (obsahují 6 typů karet s barevně odlišným rámečkem) 20 červených 20 cetek (4 od
Razzia!. Od Reinera Knizia Počet hráčů: 2 5 Věk: od 12 let Hrací doba: přibližně 45 minut Herní materiál. 99 karet kořistí (obsahují 6 typů karet s barevně odlišným rámečkem) 20 červených 20 cetek (4 od
2. ročník, 2012/ 2013 Medzinárodný korešpondenčný seminár iks. i d 1azároveň p α i+1. i d. Konečně definujme k. L = p d/p i α i
 Řešení 2. série ÚlohaN2. Jedánopřirozenéčíslo d.dokažte,žejemožnénajíttakovékladnéreálnéčíslo c, žeprovšechnapřirozenáčísla n > dplatínerovnost [n 1,n 2,...,n d] > cn d. Hranatými závorkami značíme nejmenší
Řešení 2. série ÚlohaN2. Jedánopřirozenéčíslo d.dokažte,žejemožnénajíttakovékladnéreálnéčíslo c, žeprovšechnapřirozenáčísla n > dplatínerovnost [n 1,n 2,...,n d] > cn d. Hranatými závorkami značíme nejmenší
2.1.4 Funkce, definiční obor funkce. π 4. Předpoklady: 2103. Pedagogická poznámka: Následující ukázky si studenti do sešitů nepřepisují.
 .. Funkce, definiční obor funkce Předpoklady: 03 Pedagogická poznámka: Následující ukázky si studenti do sešitů nepřepisují. Uděláme si na tabuli jenom krátký seznam: S = a, y = x, s = vt, výška lidí v
.. Funkce, definiční obor funkce Předpoklady: 03 Pedagogická poznámka: Následující ukázky si studenti do sešitů nepřepisují. Uděláme si na tabuli jenom krátký seznam: S = a, y = x, s = vt, výška lidí v
Úlohy klauzurní části školního kola kategorie B
 65. ročník matematické olympiády Úlohy klauzurní části školního kola kategorie B 1. Kolika způsoby je možno vyplnit čtvercovou tabulku 3 3 čísly,, 3, 3, 3, 4, 4, 4, 4 tak, aby součet čísel v každém čtverci
65. ročník matematické olympiády Úlohy klauzurní části školního kola kategorie B 1. Kolika způsoby je možno vyplnit čtvercovou tabulku 3 3 čísly,, 3, 3, 3, 4, 4, 4, 4 tak, aby součet čísel v každém čtverci
Povídání o paměti a paměťových hrách. Hana Kotinová, KND Praha
 Povídání o paměti a paměťových hrách Hana Kotinová, KND Praha Motto * Všichni po mně ve škole chtějí, abych si něco zapamatovala, ale nedali mi na to návod... *... naštěstí mi to šlo vždy samo od sebe
Povídání o paměti a paměťových hrách Hana Kotinová, KND Praha Motto * Všichni po mně ve škole chtějí, abych si něco zapamatovala, ale nedali mi na to návod... *... naštěstí mi to šlo vždy samo od sebe
Micro:bit lekce 3. - Konstrukci If Then a If Then Else najdete v kategorii Logic - Podmínky od If (např. porovnání < >= atd.) najdete taktéž v Logic
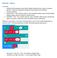 Micro:bit lekce 3. Podmínky - Rozvětvení běhu programu podle splnění nějakých podmínek typu pravda / nepravda - splněno / nesplněno (výsledkem podmínky musí být vždy jen dvě možnosti) - Dva typy podmínek:
Micro:bit lekce 3. Podmínky - Rozvětvení běhu programu podle splnění nějakých podmínek typu pravda / nepravda - splněno / nesplněno (výsledkem podmínky musí být vždy jen dvě možnosti) - Dva typy podmínek:
The Mind. Wolfgang Warsch Pro profesionální telepaty! hvězdice vrhací hvězdice. Bílé (1-50) Červené (1-50)
 The Mind Wolfgang Warsch Pro profesionální telepaty! Počet hráčů: 2-4 Věk: od 8 let Herní doba: okolo 20 min. Co je na Extreme nového? Na základních pravidlech originální hry The Mind se nic nemění. V
The Mind Wolfgang Warsch Pro profesionální telepaty! Počet hráčů: 2-4 Věk: od 8 let Herní doba: okolo 20 min. Co je na Extreme nového? Na základních pravidlech originální hry The Mind se nic nemění. V
Nejmladší kategorie tenisu....a jejich rozdíly
 jmladší kategorie tenisu...a jejich rozdíly Cíl prezentace Rámcově představit 3 nejmladší kategorie tenisu Upozornit na rozdíly mezi nejmladšími kategoriemi A jak na kurtu se správně chovat Popis role
jmladší kategorie tenisu...a jejich rozdíly Cíl prezentace Rámcově představit 3 nejmladší kategorie tenisu Upozornit na rozdíly mezi nejmladšími kategoriemi A jak na kurtu se správně chovat Popis role
S hrací deskou pro ještě více možností!
 S hrací deskou pro ještě více možností! Steffen Benndorf Reinhard Staupe Počet hráčů: 2-4 Věk: od 8 let Herní doba: okolo 20 min. Pozor: Pokud už znáte vyznamenaný originál Qwixx, stačí si jen přečíst
S hrací deskou pro ještě více možností! Steffen Benndorf Reinhard Staupe Počet hráčů: 2-4 Věk: od 8 let Herní doba: okolo 20 min. Pozor: Pokud už znáte vyznamenaný originál Qwixx, stačí si jen přečíst
III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Označení šablony/označení sady VY_32_INOVACE_04_M3 M 3
 Záznamový arch Název školy: Základní škola a Mateřská škola Brno, Bosonožské nám. 44, příspěvková organizace Číslo projektu: CZ.1.07/1.4.00/21.2499 Číslo a název šablony klíčové aktivity: III/2 Inovace
Záznamový arch Název školy: Základní škola a Mateřská škola Brno, Bosonožské nám. 44, příspěvková organizace Číslo projektu: CZ.1.07/1.4.00/21.2499 Číslo a název šablony klíčové aktivity: III/2 Inovace
1. série. Iracionální čísla. Téma: Datumodeslání: Dokažte, že 0, (píšeme za sebou všechna přirozená čísla) je iracionální.
 Téma: Datumodeslání: 1. série Iracionální čísla ¾½º Ò ½ ½º ÐÓ Ó µ Dokažte, že 0,12345678910111213... (píšeme za sebou všechna přirozená čísla) je iracionální. ¾º ÐÓ Ó µ Dokažte,že 2+ 3+ 4+ 5jeiracionálníčíslo.
Téma: Datumodeslání: 1. série Iracionální čísla ¾½º Ò ½ ½º ÐÓ Ó µ Dokažte, že 0,12345678910111213... (píšeme za sebou všechna přirozená čísla) je iracionální. ¾º ÐÓ Ó µ Dokažte,že 2+ 3+ 4+ 5jeiracionálníčíslo.
Habermaaß-hra 4446. Nadýchaný koláč
 CZ Habermaaß-hra 4446 Nadýchaný koláč Nadýchaný koláč Foukací hra pro 1-4 hráče ve věku od 4 do 12 let s herní variantou pro foukače profesionály. Tato hra procvičuje motoriku rtů a úst čímž se hravou
CZ Habermaaß-hra 4446 Nadýchaný koláč Nadýchaný koláč Foukací hra pro 1-4 hráče ve věku od 4 do 12 let s herní variantou pro foukače profesionály. Tato hra procvičuje motoriku rtů a úst čímž se hravou
Míčové hry - pravidla. Stolní tenis Badminton
 Míčové hry - pravidla Stolní tenis Badminton Pravidla stolního tenisu http://www.pingpongweb.cz/pingpong-na-olympijskych-hrach-12 Odehrání míčku Míček je odehráván výhradně pálkou, a to kteroukoliv její
Míčové hry - pravidla Stolní tenis Badminton Pravidla stolního tenisu http://www.pingpongweb.cz/pingpong-na-olympijskych-hrach-12 Odehrání míčku Míček je odehráván výhradně pálkou, a to kteroukoliv její
ZOOLORETTO. Herní materiál 16 kulatých destiček mláďat (Nachwuchsplättchen) 2 od každého z 8 druhů
 ZOOLORETTO Michael Schacht Herní idea Každý hráč vlastní jednu zoo. Hráči se pokoušejí přilákat do svých zoo co nejvíce návštěvníků, aby získali vítězné body. Za tímto účelem musí shromažďovat vhodná zvířata.
ZOOLORETTO Michael Schacht Herní idea Každý hráč vlastní jednu zoo. Hráči se pokoušejí přilákat do svých zoo co nejvíce návštěvníků, aby získali vítězné body. Za tímto účelem musí shromažďovat vhodná zvířata.
1 Linearní prostory nad komplexními čísly
 1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
Datum odevzdání 12. prosince Vypočtěte velikost strany čtverce ABCD s vrcholem A = [0, 0], jestliže
![Datum odevzdání 12. prosince Vypočtěte velikost strany čtverce ABCD s vrcholem A = [0, 0], jestliže Datum odevzdání 12. prosince Vypočtěte velikost strany čtverce ABCD s vrcholem A = [0, 0], jestliže](/thumbs/57/40473291.jpg) Příklady k řešení (. kolo) Datum odevzdání. prosince 00 PŘÍKLAD. Vypočtěte velikost strany čtverce ABCD s vrcholem A = [0, 0], jestliže úhlopříčka BD leží na přímce p :x +y = 0. PŘÍKLAD. Jsou dány body
Příklady k řešení (. kolo) Datum odevzdání. prosince 00 PŘÍKLAD. Vypočtěte velikost strany čtverce ABCD s vrcholem A = [0, 0], jestliže úhlopříčka BD leží na přímce p :x +y = 0. PŘÍKLAD. Jsou dány body
Před první hrou setřiďte karty podle přiloženého pořadníku do drážek v krabici. 500 karet 130 karet peněz Název
 Něco visí ve vzduchu. Správce vypadá, jako by skrýval tajemství. Tvůj věrný sluha tě však varuje. Chystá se spiknutí. Tohle si přece nenecháš líbit. Vymysli vlastní plán, využij svého vlivu a známostí.
Něco visí ve vzduchu. Správce vypadá, jako by skrýval tajemství. Tvůj věrný sluha tě však varuje. Chystá se spiknutí. Tohle si přece nenecháš líbit. Vymysli vlastní plán, využij svého vlivu a známostí.
====== ZAČÁTEK UKÁZKY ======
 ====== ZAČÁTEK UKÁZKY ====== Na závěr kapitoly poslední poznámka, která se týká obou variant. Praxí poznáte, že ačkoliv je startovních prémiových kombinací v Omaha pokeru víc než v Texas Hold'em, nedostanete
====== ZAČÁTEK UKÁZKY ====== Na závěr kapitoly poslední poznámka, která se týká obou variant. Praxí poznáte, že ačkoliv je startovních prémiových kombinací v Omaha pokeru víc než v Texas Hold'em, nedostanete
Habermaaß-hra 4232. Černý pirát
 CZ Habermaaß-hra 4232 Černý pirát Černý pirát Hra pro 2-4 hráče, ve věku od 5-99 let. Dobří a poctiví mořeplavci plují od jednoho ostrova pokladů k dalšímu. V patách je jim ale Černý pirát Černovous Mořský
CZ Habermaaß-hra 4232 Černý pirát Černý pirát Hra pro 2-4 hráče, ve věku od 5-99 let. Dobří a poctiví mořeplavci plují od jednoho ostrova pokladů k dalšímu. V patách je jim ale Černý pirát Černovous Mořský
CVIČNÝ TEST 48. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17
 CVIČNÝ TEST 48 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Je dán konvexní čtyřúhelník, jehož vnitřní
CVIČNÝ TEST 48 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Je dán konvexní čtyřúhelník, jehož vnitřní
Dokumentace programu piskvorek
 Dokumentace programu piskvorek Zápočtového programu z Programování II PRM045 Ondřej Vostal 20. září 2011, Letní semestr, 2010/2011 1 Stručné zadání Napsat textovou hru piškvorky se soupeřem s umělou inteligencí.
Dokumentace programu piskvorek Zápočtového programu z Programování II PRM045 Ondřej Vostal 20. září 2011, Letní semestr, 2010/2011 1 Stručné zadání Napsat textovou hru piškvorky se soupeřem s umělou inteligencí.
A. Cíl hry. Vítězem je hráč s nejvíce vítěznými body po 5 kole. Vítězné body můžete získat dvěma způsoby. a) každé kolo -za darování zboží do senátu
 A. Cíl hry Vítězem je hráč s nejvíce vítěznými body po 5 kole. Vítězné body můžete získat dvěma způsoby. a) každé kolo -za darování zboží do senátu b) na konci hry -za nejvíce peněz - za největší rozmanitost
A. Cíl hry Vítězem je hráč s nejvíce vítěznými body po 5 kole. Vítězné body můžete získat dvěma způsoby. a) každé kolo -za darování zboží do senátu b) na konci hry -za nejvíce peněz - za největší rozmanitost
CVIČNÝ TEST 25. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 13 IV. Záznamový list 15
 CVIČNÝ TEST 25 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 13 IV. Záznamový list 15 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 V lidové výkupně barevných kovů vykoupili
CVIČNÝ TEST 25 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 13 IV. Záznamový list 15 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 V lidové výkupně barevných kovů vykoupili
1. Cíl hry. 2. Komponenty
 1. Cíl hry Hráči se stávají dračími Akolyty, kteří hledají magické krystaly, aby se stali dračími králi či královnami. Krystalem zobrazeným na kartě bojiště je odměněn hráč, který vyhraje boj na bojišti,
1. Cíl hry Hráči se stávají dračími Akolyty, kteří hledají magické krystaly, aby se stali dračími králi či královnami. Krystalem zobrazeným na kartě bojiště je odměněn hráč, který vyhraje boj na bojišti,
Pravidla fotbalpoolu. Rozdělení stolu
 Pravidla fotbalpoolu Vychází se z pravidel kulečníkové hry Poolu a všech jejích disciplín. Kulečníkové tágo je nahrazeno samotným hráčem a hraje se na zvětšeném stole o rozměrech 7m x 3,5m s dírami pro
Pravidla fotbalpoolu Vychází se z pravidel kulečníkové hry Poolu a všech jejích disciplín. Kulečníkové tágo je nahrazeno samotným hráčem a hraje se na zvětšeném stole o rozměrech 7m x 3,5m s dírami pro
Habermaaß-hra 2523 CZ
 CZ Habermaaß-hra 2523 Hra Habermaaß č. 2523 Pirát Joe Jednooký pirát Rychlá hra pro 2 až 4 nelítostné piráty ve věku 4-99 let. Autoři: Ilustrace: Délka hry: Markus Nikisch Susanne Krinke asi 10 minut Na
CZ Habermaaß-hra 2523 Hra Habermaaß č. 2523 Pirát Joe Jednooký pirát Rychlá hra pro 2 až 4 nelítostné piráty ve věku 4-99 let. Autoři: Ilustrace: Délka hry: Markus Nikisch Susanne Krinke asi 10 minut Na
Autor hry: Hervé Marly Ilustrátor: Thomas Vuarchex Počet hráčů: 3 6 Věk hráčů: 10+ Doba hraní: min OBSAH KRABIČKY:
 Autor hry: Hervé Marly Ilustrátor: Thomas Vuarchex Počet hráčů: 3 6 Věk hráčů: 10+ Doba hraní: 15 30 min OBSAH KRABIČKY: 24 žetonů rozdělených do 6 sad (každá po 4 žetonech). Každá sada obsahuje 3 žetony
Autor hry: Hervé Marly Ilustrátor: Thomas Vuarchex Počet hráčů: 3 6 Věk hráčů: 10+ Doba hraní: 15 30 min OBSAH KRABIČKY: 24 žetonů rozdělených do 6 sad (každá po 4 žetonech). Každá sada obsahuje 3 žetony
JAK HRÁT Petr Vojtěch Jindřich Pavlásek
 JAK HRÁT Petr Vojtěch Jindřich Pavlásek Cíl Představte si, že jste velryba. Jste velryba. Nyní jste připraveni hrát hru. Herní materiál Hráči se jako velrybí generálové pokouší sestavit nejsilnější možnou
JAK HRÁT Petr Vojtěch Jindřich Pavlásek Cíl Představte si, že jste velryba. Jste velryba. Nyní jste připraveni hrát hru. Herní materiál Hráči se jako velrybí generálové pokouší sestavit nejsilnější možnou
NĚKOLIK NEDOKONČENÝCH. Karel Řezba
 NĚKOLIK NEDOKONČENÝCH Karel Řezba ba Stoh slámy Bokorys, půdorys nárys 4 patra, v prvním 7 1*7 + 2*8 + 3*9 + 4*10 různé rozměry kolik balíků v pyramidě obrácená úloha mám počet balíků a chci postavit pyramidu,
NĚKOLIK NEDOKONČENÝCH Karel Řezba ba Stoh slámy Bokorys, půdorys nárys 4 patra, v prvním 7 1*7 + 2*8 + 3*9 + 4*10 různé rozměry kolik balíků v pyramidě obrácená úloha mám počet balíků a chci postavit pyramidu,
Habermaaß-hra 4931. Koza s motýlkem
 CZ Habermaaß-hra 4931 Koza s motýlkem Koza s motýlkem Kombinační hra pro 2-6 hráčů ve věku od 5 do 99let. S "Fex efektem" pro větší zábavu a větší namáhání mozkových závitů! Autoři: Christiane Hüpper,
CZ Habermaaß-hra 4931 Koza s motýlkem Koza s motýlkem Kombinační hra pro 2-6 hráčů ve věku od 5 do 99let. S "Fex efektem" pro větší zábavu a větší namáhání mozkových závitů! Autoři: Christiane Hüpper,
Pravděpodobnost a statistika (BI-PST) Cvičení č. 1
 Pravděpodobnost a statistika (BI-PST) Cvičení č. 1 Katedra aplikované matematiky Fakulta informačních technologií České vysoké učení technické v Praze ZS 2014/2015 (FIT ČVUT) BI-PST, Cvičení č. 1 ZS 2014/2015
Pravděpodobnost a statistika (BI-PST) Cvičení č. 1 Katedra aplikované matematiky Fakulta informačních technologií České vysoké učení technické v Praze ZS 2014/2015 (FIT ČVUT) BI-PST, Cvičení č. 1 ZS 2014/2015
Cíl hry: Cílem hry je získat počet bodů, který si hráči stanoví na začátku. Body lze získat za slova složená z písmen na vylosovaných kostkách.
 Návod PÍSMENKOBRANÍ naučná hra ve 2 variantách - doporučený věk od 7 let - počet hráčů: 2-3 Obsah balení: 1) kostky s písmeny 25 ks 2) sáček 1 ks 3) provázky 3 ks 4) kostka s čísly 1 ks 5) poznámkový blok
Návod PÍSMENKOBRANÍ naučná hra ve 2 variantách - doporučený věk od 7 let - počet hráčů: 2-3 Obsah balení: 1) kostky s písmeny 25 ks 2) sáček 1 ks 3) provázky 3 ks 4) kostka s čísly 1 ks 5) poznámkový blok
SEMINÁRNÍ PRÁCE Z MATEMATIKY
 SEMINÁRNÍ PRÁCE Z MATEMATIKY PETROHRADSKÝ PARADOX TEREZA KIŠOVÁ 4.B 28.10.2016 MOTIVACE: K napsání této práce mě inspiroval název tématu. Když jsem si o petrohradském paradoxu zjistila nějaké informace
SEMINÁRNÍ PRÁCE Z MATEMATIKY PETROHRADSKÝ PARADOX TEREZA KIŠOVÁ 4.B 28.10.2016 MOTIVACE: K napsání této práce mě inspiroval název tématu. Když jsem si o petrohradském paradoxu zjistila nějaké informace
Habermaaß-hra 4511. Divocí Vikingové
 CZ Habermaaß-hra 4511 Divocí Vikingové Hra Habermaaß č. 4511 Divocí Vikingové Riskantní sázková hra pro 2 5 odvážných Vikingů ve věku 6 99 let. Autor: Ilustrace: Délka hry: Wolfgang Dirscherl Michael Menzel
CZ Habermaaß-hra 4511 Divocí Vikingové Hra Habermaaß č. 4511 Divocí Vikingové Riskantní sázková hra pro 2 5 odvážných Vikingů ve věku 6 99 let. Autor: Ilustrace: Délka hry: Wolfgang Dirscherl Michael Menzel
FAZOLE KOSTKOVÁ HRA POPIS
 od Uweho Rosenberga Hráči: 2-5 hráčů Věk: 10+ Herní doba: 45 min FAZOLE KOSTKOVÁ HRA POPIS I pěstitelé fazolí si po těžké celodenní dřině na poli chtějí užít trochu zábavy s kostkami. Zde se jim naskýtá
od Uweho Rosenberga Hráči: 2-5 hráčů Věk: 10+ Herní doba: 45 min FAZOLE KOSTKOVÁ HRA POPIS I pěstitelé fazolí si po těžké celodenní dřině na poli chtějí užít trochu zábavy s kostkami. Zde se jim naskýtá
