Transparentní intenzionální logika (TIL)
|
|
|
- Kristina Müllerová
- před 7 lety
- Počet zobrazení:
Transkript
1 Marek Rychlý Ústav informačních systémů, Fakulta informačních technologií, Vysoké učení technické v Brně, Božetěchova 2, Brno , Czech Republic rychly@fit.vutbr.cz Abstrakt Transparentní intenzionální logika představuje ve filozofické logice moderní a jednoduché pojetí intenzionální logiky. Tato seminární práce pojednává o extenzionální a intenzionální logice, neformální konstrukci transparentní intenzionální logiky a o jejím uplatnění v softwarovém inženýrství. Klíčová slova: filozofická logika, modální logika, teorie možných světů, extenzionální model, lambda-kategoriální gramatika, transparentní intenzionální logika Obsah 1. Úvod Modální logika Kripkeho teorie možných světů Základní extenzionální model a predikátová logika Lambda-kategoriální gramatika Transparentní intenzionální logika (TIL) Příklad Využití transparentní intenzionální logiky v SW inženýrství Závěr... 7 Bibliografie Úvod Ve vědě je pod obecným pojmem logika zařazeno několik navzájem odlišných a přesto úzce spjatých a prolínajících se vědních disciplín, mezi které patří např. původní sylogistická logika (tj. původní Aristotelovská logika), predikátová logika (dnes známá jako logika 1. a 2. řádu), modální logika (v současné době velmi populární v teoretické informatice) nebo obecná matematická logika (formální aplikace logiky na matematické problémy). Specifickou větev logiky pak tvoří filozofická logika, která navazuje na původní nematematické pojetí logiky ve filozofii, jako prostředku pro porozumění systému reálného světa. 1
2 Filozofická logika je zaměřena na formální aplikaci logiky na filozofické problémy, zejména s využitím prostředků formální logické analýzy přirozeného jazyka. Cílem filozofické logiky je porozumění hlubší sémantice tvrzení formulovaných pomocí přirozeného jazyka. Formální vyjádření sémantiky tvrzení pak umožní překlad přirozeného jazyka do formální logiky, kde mohou být uplatněny klasické logické operace (významnou roli hraje zejména důsledek ). Tato práce se bude zabývat transparentní intenzionální logikou, stěžejním dílem významného českého filozofa a logika prof. Pavla Tichého. Transparentní intenzionální logika patří mezi filozofické logiky a zasahuje také významně do modálních logik. V posledních letech má transparentní intenzionální logika velký význam v informatice, konkrétně v oblasti konceptuálního modelování v softwarovém inženýrství, kde je využívána pro formálně korektní transformaci uživatelských požadavků na datový model informačního systému. V následujících kapitolách budou nejprve zavedeny základní pojmy a teorie filozofické a modální logiky, nezbytné pro konstrukci transparentní intenzionální logiky, která bude poté stručně představena s důrazem na její využití v softwarovém inženýrství. 2. Modální logika Modální logika zavádí do formální logiky prostředky pro vyjádření pravděpodobnostních atributů logických tvrzení (tzv. modalit). Patří sem vyjádření (ne)možnosti a nutnosti platnosti tvrzení. Tyto pravděpodobnostní atributy tedy vyjadřují diskrétní pravděpodobnost s jakou nastane platnost tvrzení. Základní modální logika zavádí společně s klasickými logickými symboly také dva modální operátory 1 (tzv. denotáty): F φ = někdy platí tvrzení φ (denotát možná ) G φ = vždy platí tvrzení φ (denotát nutně ) Existuje mnoho modifikací či rozšíření modální logiky, např. tempolární logiky (zkoumající časové závislosti modalit), deontologické logiky (zkoumající druhy modalit) s v neposlední řadě intenzionální logiky, zmiňované v této práci Kripkeho teorie možných světů [1] Definujme možný svět jako maximální konsistentní (bezrozporný) soubor faktů, které mohou platit. Pak aktuální svět je jeden z možných světů (množina všech platících faktů). Jako logický prostor se zde označuje soubor všech možných světů. Kripke přistupuje k sémantice modální logiky pomocí teorie modelů, kde model představuje trojice (G, K, R), kde: K je množina možných světů, G je prvek z K představující aktuální (reálný) svět, R je relace na množině K, tzv. relace dostupnosti jednoho světa z druhého. 1 Přitom z definice platí rovnost G φ = (F φ). 2
3 Pro Kripkeho je možný svět něco, co umožňuje odlišovat pravdivé věty od nepravdivých. Ve filozofické logice je tedy význam věty charakteristická funkce z K do množiny pravdivostních hodnot (sémantika je závislá na aktuálním světě). Kripkeho sémantika založená na teorii možných světů rozšiřuje význam modální logiky (upřesňuje sémantiku denotátů) i intenztionální logiky, kde z ní vychází prof. Tichý při specifikaci epistémické báze (viz dále). 3. Základní extenzionální model a predikátová logika [2] Zavedeme syntax a sémantiku prvků základního extensionálního modelu. V rámci modelu definujeme následující kategorie (množiny): jména (J) neomezený počet jednoduchých jmen, predikáty (P) neomezený počet jednoduchých predikátů, unární výrokové operátory (O1) jediný jednoduchý výraz, a sice, binární výrokové operátory (O2) tři jednoduché výrazy (výrokové spojky), a sice, a, kvantifikátory (Q) dva jednoduché výrazy, a sice Σ a Π, výroky (V) pouze složené výrazy (žádné jednoduché výrazy): je-li P predikát a J jméno, je P(J) výrok, je-li Q kvantifikátor a P predikát, je Q(P) výrok, je-li O unární výrokový operátor a V výrok, je O V výrok, je-li O binární výrokový operátor a V, W výroky, je V O W výrok, pomocné symboly a závorky. Pokud U je množina individuí (tzv. universum diskursu) a B je množina pravdivostních hodnot, pak významy jednotlivých výrazů definujeme následovně: významem jména je prvek daného univerza U, významem predikátu je funkce z U do B (tj. prvek množiny [U B], tzv. klasifikátorů individuí), významem unárního výrokového operátoru je funkce z B do B (tj. prvek množiny [B B]), konkrétně významem operátoru je ta funkce, která je dána pravdivostní tabulkou negace, významem binárního výrokového operátoru je funkce z B B do B (tj. prvek množiny [B B B]), konkrétně významem operátorů,, jsou funkce dány příslušnými pravdivostními tabulkami, významem kvantifikátoru je funkce z [U B] do B (tj. prvek množiny [[U B] B], tzv. klasifikátorů klasifikátorů individuí), konkrétně: významem kvantifikátoru Π je funkce, která přiřazuje pravdivou hodnotu z B pouze plnému klasifikátoru (tj. klasifikátoru, který pro všechny prvky univerza vrací pravdivou hodnotu), významem Σ je ta funkce, která přiřazuje pravdivou hodnotu pouze neprázdnému klasifikátoru (tj. klasifikátoru, který pro nějaký prvek univerza vrací pravdivou hodnotu), 3
4 významem výroku je pravdivostní hodnota, tedy prvek B, konkrétně pokud P značí význam výroku P, pak: je-li P predikát a J jméno, pak P(J) = P ( J ), je-li Q kvantifikátor a P predikát, pak Q(P) = Q ( P ), je-li O unární výrokový operátor a V výrok, pak O V = O ( V ), je-li O binární výrokový operátor a V, W výroky, pak V O W = O ( V, W ). Pro vyjádření základního extensionálního modelu v predikátové logice prvního řádu zavedeme dále proměnné následující modifikací definice kategorie jmen a sémantiky kvantifikátoru: jména (J) neomezený počet jednoduchých jmen a neomezený počet proměnných, je-li Q kvantifikátor, x proměnná a V výrok, je Qx.V výrok s významem Qx.V = Q ( V x ), kde V x značí klasifikátor individuí splňujících výrok V po dosazení za x. Pak klasifikátory Π a Σ mají význam klasifikátorů a predikátové logiky. Například pokud predikát prezident(x) je pravdivý pokud x je prezidentem a dramatik(x) pokud x je dramatikem, pak (z [2], str. 16): 1. Πx.prezident(x) je v univerzu osob v současném reálném světě nepravdivé, 2. Σx.prezident(x) dramatik(x) je v univerzu osob v reálném světě k 1. lednu 2000 pravdivé. 4. Lambda-kategoriální gramatika [2] Zavedeme syntax a sémantiku lambda-abstrakce, která nám umožní vytvářet z výrazů funkce: jestliže p P a x Q, pak (λx.p) je prvek množiny P/Q, jestliže navíc q Q, pak (λx.p)(q) = p[x q], kde p[x q] značí substituci q za x v p. Gramatickou kategorii definujeme indukcí z kategorie (K) představené v předchozí kapitole následujícím způsobem: 1. je-li k K, pak k je gramatickou kategorií, 2. jsou A, B gramatickými kategoriemi, je gramatickou kategorií i B/A. Definujeme gramatická pravidla, která umožní sestavovat z kategorií složené výrazy: je-li b výraz gram. kat. B/A, a výraz gram. kat. A, pak b(a) je výraz gram. kat. B, je-li b výraz gram. kat. B, a výraz gram. kat. A, x prom. gram. kat. A, pak λx.b[a x], kde b[a x] značí substituci x za a v b, je výraz gram. kat. B/A. Zavedeme doménu D K kategorie K, jako množinu významů prvků z K tak, že pokud k K, pak k D K. Doména kategorie B/A je [D A D B ]. Význam složených výrazů je definován následujícím způsobem: B(A) = B ( A ), λx.b[a x] je funkce f z D A do D B, která pro d D A je f(d)= b a =d. Příklad: (λx.spisovatel(x))(eco) = spisovatel(eco) 4
5 5. Transparentní intenzionální logika (TIL) Intenzionální logika je kombinace lambda-kategoriální gramatiky s kripkovskou možnosvětovou sémantikou [2]. Obecná intenzionální logika zavádí dva základní pojmy: extenze (intenze 0. řádu) funkce z možných světů do kategorie (pravdivostních hodnot, individuí, klasifikátorů individuí atd.), intenze k. řádu (pro k>0 prostě intenze ) je-li T intezne k. řádu, pak funkce z možných světů do T je intezne (k+1). řádu. Extensionální logika pracuje pouze s inteznemi 0. řádu (dále jen extenzemi ). Zavedení intenzí nenulových řádů (dále jen intenzí ) umožňuje pracovat s možnými světy. Např. tvrzení teplota je 30 stupňů Celsia a stoupá nelze v extenzionální logice analyzovat jako (teplota=30) stoupá(teplota), protože z toho lze dokázat stoupá(30), což není význam tvrzení zde tedy potřebujeme vyjádřit vztah aktuálního světa (teplota=30) se světem v relaci dostupnosti (viz 2.1). Montague zavádí rozšířenou gramatiku (tzv. Montaguova intenzionální logika) s motivem minimálního rozšíření extensionální sémantiky o intenze (kde to nejde, vzít do hry intenze). Definuje unární operátor ^ pro zvýšení řádu intenze a k němu inverzní operátor ~ pro snížení řádu intenze: extenze ^E = intenze E, intenze ~E = extenze E, ^~E = ~^E = E. Tím je umožněno posunutí inteze do role extenze a následné uplatnění postupů klasické extenzionální sémantiky. Operátory je definovány pomocí lambda-abstrakce operátor ^ konstruuje funkci možných světů a extenze vzniklá pomocí operátoru ~ je pak považovaná za danou tím, že původní intenze platí pro všechny možné světy: ^A (w)= A, ~A (w) je ta funkce f, že pro každé v W platí f(v)= A (w)(v). Transparentní intenzionální logika (TIL), jejímž autorem je prof. Tichý, rozšiřuje Montaguovu intenzionální logiku, přestože oba přístupy vznikly nezávisle Montague publikoval svou práci v roce 1970 a Tichý v roce Přestože originalita byla díky dřívější publikaci přiznána spíše Montaguově práci, pojetí intenzionální logiky podle prof. Tichého se ukázalo vhodnější [3]. Zatímco Montague upravoval extenzionální model tak, aby do syntaxe a sémantiky zanesl možné světy (úprava pravidel), Tichý prohlásil množinu možný světů za gramatickou kategorii. Tím bylo rozšíření extenzionální logiky na intenzionální tzv. transparentní. Tato logika bývá označována také jako globálně intenzionální logika Příklad Mějme extenzi predikátu spát, extenzi predikátu hlavakatcirkve, jméno papež a jeho extenzi. Aplikaci extenze P na aktuálním světě w budeme označovat jako P w. 1. Větu papež spí analyzujeme v TIL jako λw.spát w (papež w ). 5
6 2. Větu Papež je hlavou katolické církve analyzujeme v TIL jako λw.hlavakatcirkve w (papež). V prvním případě věta vypovídala o úřadu a jeho obsazení závisí na možném světě (proto je zde papež extenze jména), v druhém případě je reč o tom, kdo úřad zastává (proto je zde Papež pouze jméno, tj. individuum). Další příklady viz [2] strana Využití transparentní intenzionální logiky v SW inženýrství Tichý uvádí, že aktuální svět nelze nikdy poznat, protože je to nespočetná množina platných faktů. Argumentuje tvrzením, že pokud by se jednalo o spočetnou množinu, byla by dána výčtem svých prvků, což by vyžadovalo vědět všechna platná fakta a to není možné. Toto je zásadní problém SW inženýrství, které se snaží zachytit v informačním systému model určité oblasti aktuálního světa. Aktuální svět sice nelze logicky vypočítat, ale lze ho empiricky zjišťovat pomocí platných poznatků. Poznatky sdělujeme oznamovacími větami, tzv. propozicemi, kde každá propozice vyčleňuje v množině možných světů podmnožinu, ve kterých je ona pravdivá. Propozice pravdivé v daném časovém okamžiku vyčleňují tedy podmnožinu možných světů, která zaručeně obsahuje aktuální svět. Mějme čtveřici (B, T, U, W), tzv. epistémickou bázi, kde B je množina pravdivostních hodnot, T množina časových okamžiků (používají se také jako reálná čísla), U množina individuí a W množina možných světů (tzv. logický prostor, který je dán a priori). Typ nad epistémickou bází je objekt určený prvky epistémické báze. Pak objekt P je: extenze (intenze 0. řádu) pokud neexistuje Q nad epistémickou bází tak, že P=(W T) Q, intezne k. řádu (pro k>0) je-li Q intezne (k-1). řádu a P=(W T) Q. Pro objekty nad epistémickou bází platí: 1. třídy individuí = (U B)-objekty = extenze, 2. vlastnosti individuí = ((W T U) B)-objekty = intenze, 3. propozice = ((W T) B)-objekty = intenze, 4. individuové úřady = ((W T) U)-objekty = intenze, 5. veličiny = ((W T) T)-objekty = intenze, 6. třídy vlastností = (((W T U) B) B)-objekty = extenze. Příklady z praxe: 1. třídy individuí: lidé, zaměstnanci, produkty, faktury atd. 2, 2. vlastnosti individuí: být zaměstnancem, být oprávněným uživatelem, být proplacenou fakturou, 3. propozice: uživatel (Jan Novák) vystavil k datu ( ) fakturu (1274/2006), 4. individuové úřady = jednatel dané společnosti, 5. veličiny = mzda daného zaměstnance za daný měsíc, 2 Jen pokud individua nemění svoje zařazení, tj. nejsou zařazeny vlastnostmi individuí. 6
7 6. třídy vlastností = položky tvořící adresu zaměstnance. Při vyjádření specifikace informačního systému (konceptuální modelování) pomocí analýzy v TIL lze převést sémantiku na formule intenzionální logiky. S těmi pak lze provádět různé operace při zachování sémantické korektnosti. Podrobněji viz [4]. 7. Závěr Transparentní intenzionální logika patří mezi nejvýznamnější teorie moderní filozofické logiky. Své uplatnění nalezne především v místech, kde je třeba analyzovat sémantiku tvrzení přirozeného jazyka se závislostí na možných světech (extenzionální logika je zde slabá). Jednou z takový oblastí je konceptuální modelování (datové modelování, část SW inženýrství) v podobě datového modelu HIT [4]. Tato seminární práce stručně představila filozofickou logiku teorii možných světů, extenzionální a původní intenzionální logiku a Tichého transparentní intenzionální logiku. Transparentní intenzionální logika byla z didaktických důvodů představena jako rozšíření Montaguovy intenzionální logiky (autor se snažil nezacházet do problematiky objektuální sémantiky, kterou představil Gottlob Frege a ze které původně vychází prof. Tichý [3]). Je třeba upozornit, že tato práce prezentuje neformálně pouze vybranou část filozofické logiky (z prostorových důvodů nebyly mimo jiné formálně zavedeny definice některých pojmů, které se v této práci vyskytují) a zásadně nepokrývá celou problematiku transparentní intenzionální logiky, ale pouze nastiňuje její myšlenku. Podrobnější úvod do transparentní intenzionální logiky lze nalézt například v [3]. Bibliografie 1. Jiří Raclavský. Předmět Filosofická logika. Studijní materiály. Masarykova univerzita v Brně, Filozofická fakulta. Brno. URL [ Jaroslav Peregrin. Úvod do teoretické sémantiky. Komplet studijních materiálů (rozšířený sylabus). Univerzita Karlova v Praze, Filozofická fakulta. Praha. URL [ Andrew Holster. An Introduction to Pavel Tichy and Transparent Intensional Logic. URL [ to Pavel Tichy and Transparent Intensional Logic.doc] Marie Duží. Konceptuální modelování - datový model HIT. Filozoficko-přírodovědecká fakulta, Slezská universita Opava. Opava
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
4.2 Syntaxe predikátové logiky
 36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
Unární je také spojka negace. pro je operace binární - příkladem může být funkce se signaturou. Binární je velká většina logických spojek
 Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Inteligentní systémy (TIL) Marie Duží
 Inteligentní systémy (TIL) Marie Duží http://www.cs.vsb.cz/duzi/ /d Přednáška 3 Sémantické schéma Výraz vyjadřuje označuje Význam (konstrukce konstrukce) k ) konstruuje denotát Ontologie TIL: rozvětvená
Inteligentní systémy (TIL) Marie Duží http://www.cs.vsb.cz/duzi/ /d Přednáška 3 Sémantické schéma Výraz vyjadřuje označuje Význam (konstrukce konstrukce) k ) konstruuje denotát Ontologie TIL: rozvětvená
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz
 Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Okruh č.3: Sémantický výklad predikátové logiky
 Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
ZÁKLADY LOGIKY A METODOLOGIE
 ZÁKLADY LOGIKY A METODOLOGIE Metodický list č. 1 Téma: Předmět logiky a metodologie, základy logiky a formalizace. Toto téma lze rozdělit do tří základních tématických oblastí: 1) Předmět logiky a metodologie
ZÁKLADY LOGIKY A METODOLOGIE Metodický list č. 1 Téma: Předmět logiky a metodologie, základy logiky a formalizace. Toto téma lze rozdělit do tří základních tématických oblastí: 1) Předmět logiky a metodologie
Úvod do predikátové logiky. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
 Úvod do predikátové logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 1 Relace Neuspořádaná vs. uspořádaná dvojice {m, n} je neuspořádaná dvojice. m, n je uspořádaná dvojice. (FLÚ AV ČR) Logika:
Úvod do predikátové logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 1 Relace Neuspořádaná vs. uspořádaná dvojice {m, n} je neuspořádaná dvojice. m, n je uspořádaná dvojice. (FLÚ AV ČR) Logika:
Logika a jazyk. filosofický slovník, Praha:Svoboda 1966)
 Logika a jazyk V úvodu bylo řečeno, že logika je věda o správnosti (lidského) usuzování. A protože veškeré usuzování, odvozování a myšlení vůbec se odehrává v jazyce, je problematika jazyka a jeho analýza
Logika a jazyk V úvodu bylo řečeno, že logika je věda o správnosti (lidského) usuzování. A protože veškeré usuzování, odvozování a myšlení vůbec se odehrává v jazyce, je problematika jazyka a jeho analýza
Logický důsledek. Petr Kuchyňka (7765@mail.muni.cz)
 Logický důsledek Petr Kuchyňka (7765@mail.muni.cz) Úvod P 1 Logický důsledek je hlavním předmětem zájmu logiky. Je to relace mezi premisami a závěry logicky platných úsudků: v logicky platném úsudku závěr
Logický důsledek Petr Kuchyňka (7765@mail.muni.cz) Úvod P 1 Logický důsledek je hlavním předmětem zájmu logiky. Je to relace mezi premisami a závěry logicky platných úsudků: v logicky platném úsudku závěr
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
2.2 Sémantika predikátové logiky
 14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
Matematická logika. Lekce 1: Motivace a seznámení s klasickou výrokovou logikou. Petr Cintula. Ústav informatiky Akademie věd České republiky
 Matematická logika Lekce 1: Motivace a seznámení s klasickou výrokovou logikou Petr Cintula Ústav informatiky Akademie věd České republiky www.cs.cas.cz/cintula/mal Petr Cintula (ÚI AV ČR) Matematická
Matematická logika Lekce 1: Motivace a seznámení s klasickou výrokovou logikou Petr Cintula Ústav informatiky Akademie věd České republiky www.cs.cas.cz/cintula/mal Petr Cintula (ÚI AV ČR) Matematická
Predikátová logika. prvního řádu
 Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
Sémantika predikátové logiky
 Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Výroková logika. Sémantika výrokové logiky
 Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
Obsah Předmluva Rekapitulace základních pojmů logiky a výrokové logiky Uvedení do predikátové logiky...17
 Obsah Předmluva...3 0. Rekapitulace základních pojmů logiky a výrokové logiky...11 0.1 Logika jako věda o vyplývání... 11 1. Uvedení do predikátové logiky...17 1.1 Základní terminologie... 17 1.2 Základní
Obsah Předmluva...3 0. Rekapitulace základních pojmů logiky a výrokové logiky...11 0.1 Logika jako věda o vyplývání... 11 1. Uvedení do predikátové logiky...17 1.1 Základní terminologie... 17 1.2 Základní
KMA/MDS Matematické důkazy a jejich struktura
 Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 KMA/MDS Matematické důkazy a jejich struktura Seminář 3 Predikátový počet Uvažujme následující úsudek.
Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 KMA/MDS Matematické důkazy a jejich struktura Seminář 3 Predikátový počet Uvažujme následující úsudek.
Logika pro sémantický web
 ZVYŠOVÁNÍ ODBORNÝCH KOMPETENCÍ AKADEMICKÝCH PRACOVNÍKŮ OSTRAVSKÉ UNIVERZITY V OSTRAVĚ A SLEZSKÉ UNIVERZITY V OPAVĚ Logika pro sémantický web Martin Žáček PROČ BALÍČEK? 1. balíček Formální logické systémy
ZVYŠOVÁNÍ ODBORNÝCH KOMPETENCÍ AKADEMICKÝCH PRACOVNÍKŮ OSTRAVSKÉ UNIVERZITY V OSTRAVĚ A SLEZSKÉ UNIVERZITY V OPAVĚ Logika pro sémantický web Martin Žáček PROČ BALÍČEK? 1. balíček Formální logické systémy
platné nejsou Sokrates je smrtelný. (r) 1/??
 Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2018/2019 1 / 13 Dokončené tablo Chceme, aby dokončená bezesporná
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2018/2019 1 / 13 Dokončené tablo Chceme, aby dokončená bezesporná
Výroková a predikátová logika - IV
 Výroková a predikátová logika - IV Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IV ZS 2018/2019 1 / 17 Tablo metoda Tablo Tablo - příklady F (((p q)
Výroková a predikátová logika - IV Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IV ZS 2018/2019 1 / 17 Tablo metoda Tablo Tablo - příklady F (((p q)
Logické programy Deklarativní interpretace
 Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
Přednáška 2: Formalizace v jazyce logiky.
 Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
Formálnílogickésystémy pro aplikaci v informatice Martin Žáček
 ZVYŠOVÁNÍODBORNÝCH KOMPETENCÍAKADEMICKÝCH PRACOVNÍKŮ OSTRAVSKÉUNIVERZITY V OSTRAVĚ A SLEZSKÉ UNIVERZITY V OPAVĚ Formálnílogickésystémy pro aplikaci v informatice Martin Žáček PŘEDMĚTY NA OU Logické základy
ZVYŠOVÁNÍODBORNÝCH KOMPETENCÍAKADEMICKÝCH PRACOVNÍKŮ OSTRAVSKÉUNIVERZITY V OSTRAVĚ A SLEZSKÉ UNIVERZITY V OPAVĚ Formálnílogickésystémy pro aplikaci v informatice Martin Žáček PŘEDMĚTY NA OU Logické základy
Predikátová logika dokončení
 Predikátová logika dokončení Jiří Velebil: X01DML 1. října 2010: Predikátová logika dokončení 1/18 Syntaktická analýza Jako ve výrokové logice (syntaktické stromy). Každý list úspěšného stromu je obsazen
Predikátová logika dokončení Jiří Velebil: X01DML 1. října 2010: Predikátová logika dokončení 1/18 Syntaktická analýza Jako ve výrokové logice (syntaktické stromy). Každý list úspěšného stromu je obsazen
Metody tvorby ontologií a sémantický web. Martin Malčík, Rostislav Miarka
 Metody tvorby ontologií a sémantický web Martin Malčík, Rostislav Miarka Obsah Reprezentace znalostí Ontologie a sémantický web Tvorba ontologií Hierarchie znalostí (D.R.Tobin) Data jakékoliv znakové řetězce
Metody tvorby ontologií a sémantický web Martin Malčík, Rostislav Miarka Obsah Reprezentace znalostí Ontologie a sémantický web Tvorba ontologií Hierarchie znalostí (D.R.Tobin) Data jakékoliv znakové řetězce
Další (neklasické) logiky. Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20
 Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Pravděpodobnost a statistika
 Pravděpodobnost a statistika 1 Náhodné pokusy a náhodné jevy Činnostem, jejichž výsledek není jednoznačně určen podmínkami, za kterých probíhají, a které jsou (alespoň teoreticky) neomezeně opakovatelné,
Pravděpodobnost a statistika 1 Náhodné pokusy a náhodné jevy Činnostem, jejichž výsledek není jednoznačně určen podmínkami, za kterých probíhají, a které jsou (alespoň teoreticky) neomezeně opakovatelné,
Každé formuli výrokového počtu přiřadíme hodnotu 0, půjde-li o formuli nepravdivou, a hodnotu 1, půjde-li. α neplatí. β je nutná podmínka pro α
 1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
Matematika B101MA1, B101MA2
 Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Výroková a predikátová logika - VI
 Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
Úvod do informatiky. Miroslav Kolařík
 Úvod do informatiky přednáška první Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Co a k čemu je logika? 2 Výroky a logické spojky
Úvod do informatiky přednáška první Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Co a k čemu je logika? 2 Výroky a logické spojky
7 Jemný úvod do Logiky
 7 Jemný úvod do Logiky Základem přesného matematického vyjadřování je správné používání (matematické) logiky a logických úsudků. Logika jako filozofická discipĺına se intenzivně vyvíjí už od dob antiky,
7 Jemný úvod do Logiky Základem přesného matematického vyjadřování je správné používání (matematické) logiky a logických úsudků. Logika jako filozofická discipĺına se intenzivně vyvíjí už od dob antiky,
Základní pojmy matematické logiky
 KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
Místo pojmu výroková formule budeme používat zkráceně jen formule. Při jejich zápisu
 VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
SINGULÁRNÍ VÝROKY: Jednoduchý singulární výrok vznikne spojením singulárního termínu s termínem obecným pomocí spony=slova je.
 Studijní text Co je singulární výrok SINGULÁRNÍ VÝROKY: PETR Petr je veselý. Jednoduchý singulární výrok vznikne spojením singulárního termínu s termínem obecným pomocí spony=slova je. Příklad: Pavel je
Studijní text Co je singulární výrok SINGULÁRNÍ VÝROKY: PETR Petr je veselý. Jednoduchý singulární výrok vznikne spojením singulárního termínu s termínem obecným pomocí spony=slova je. Příklad: Pavel je
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce
 Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Formální systém výrokové logiky
 Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
Základy logiky a teorie množin
 Pracovní text k přednášce Logika a teorie množin (I/2007) 1 1 Struktura přednášky Matematická logika 2 Výroková logika Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz Predikátová logika 1. řádu
Pracovní text k přednášce Logika a teorie množin (I/2007) 1 1 Struktura přednášky Matematická logika 2 Výroková logika Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz Predikátová logika 1. řádu
1. Matematická logika
 Moderní technologie ve studiu aplikované fyziky CZ.1.07/2.2.00/07.0018 1. Matematická logika Základem každé vědy (tedy i matematiky i fyziky) je soubor jistých znalostí. To, co z těchto izolovaných poznatků
Moderní technologie ve studiu aplikované fyziky CZ.1.07/2.2.00/07.0018 1. Matematická logika Základem každé vědy (tedy i matematiky i fyziky) je soubor jistých znalostí. To, co z těchto izolovaných poznatků
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška pátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška pátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
přednáška 2 Marie Duží
 Logika v praxi přednáška 2 Marie Duží marie.duzi@vsb.cz 1 1 Výroková logika Analyzuje způsoby skládání jednoduchých výroků do výroků složených pomocí logických spojek. Co je to výrok? Výrok je tvrzení,
Logika v praxi přednáška 2 Marie Duží marie.duzi@vsb.cz 1 1 Výroková logika Analyzuje způsoby skládání jednoduchých výroků do výroků složených pomocí logických spojek. Co je to výrok? Výrok je tvrzení,
Úvod do logiky a logického programování.
 Úvod do logiky a logického programování Luboš Popelínský popel@fi.muni.cz www.fi.muni.cz/~popel Přehled učiva Opakování základů výrokové a predikátové logiky Normální formy ve výrokové a predikátové logice
Úvod do logiky a logického programování Luboš Popelínský popel@fi.muni.cz www.fi.muni.cz/~popel Přehled učiva Opakování základů výrokové a predikátové logiky Normální formy ve výrokové a predikátové logice
Systém přirozené dedukce výrokové logiky
 Systém přirozené dedukce výrokové logiky Korektnost, úplnost a bezespornost Šárka Vavrečková Ústav informatiky, FPF SU Opava Poslední aktualizace: 6. října 2008 Věta o korektnosti Věta (O korektnosti Systému
Systém přirozené dedukce výrokové logiky Korektnost, úplnost a bezespornost Šárka Vavrečková Ústav informatiky, FPF SU Opava Poslední aktualizace: 6. října 2008 Věta o korektnosti Věta (O korektnosti Systému
Výroková logika - opakování
 - opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
- opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
Výroková a predikátová logika - VIII
 Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2017/2018 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2017/2018 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Modely Herbrandovské interpretace
 Modely Herbrandovské interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 8 1 Uvedli jsme termové interpretace a termové modely pro logické programy a také nejmenší
Modely Herbrandovské interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 8 1 Uvedli jsme termové interpretace a termové modely pro logické programy a také nejmenší
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška desátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. Obsah 1 Úvod do modální logiky 2 Logické programování a Prolog 3
Matematická logika přednáška desátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. Obsah 1 Úvod do modální logiky 2 Logické programování a Prolog 3
Převyprávění Gödelova důkazu nutné existence Boha
 Převyprávění Gödelova důkazu nutné existence Boha Technické podrobnosti Důkaz: Konečná posloupnost výrokůkorektně utvořených formulí nějakého logického kalkulu), z nichž každý jelogickým) axiomem, postulátemteorie),
Převyprávění Gödelova důkazu nutné existence Boha Technické podrobnosti Důkaz: Konečná posloupnost výrokůkorektně utvořených formulí nějakého logického kalkulu), z nichž každý jelogickým) axiomem, postulátemteorie),
Výroková logika. Teoretická informatika Tomáš Foltýnek
 Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Pro každé formule α, β, γ, δ platí: Pro každé formule α, β, γ platí: Poznámka: Platí právě tehdy, když je tautologie.
 Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
Predikátová logika. Teoretická informatika Tomáš Foltýnek
 Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
1 Báze a dimenze vektorového prostoru 1
 1 Báze a dimenze vektorového prostoru 1 Báze a dimenze vektorového prostoru 1 2 Aritmetické vektorové prostory 7 3 Eukleidovské vektorové prostory 9 Levá vnější operace Definice 5.1 Necht A B. Levou vnější
1 Báze a dimenze vektorového prostoru 1 Báze a dimenze vektorového prostoru 1 2 Aritmetické vektorové prostory 7 3 Eukleidovské vektorové prostory 9 Levá vnější operace Definice 5.1 Necht A B. Levou vnější
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2013/2014 1 / 20 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2013/2014 1 / 20 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2018/2019 1 / 15 Platnost (pravdivost) Platnost ve struktuře
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2018/2019 1 / 15 Platnost (pravdivost) Platnost ve struktuře
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2015/2016 1 / 18 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2015/2016 1 / 18 Základní syntax Jazyk Výroková logika je logikou
Fuzzy logika a reálný svět, aneb jsou všechny hromady skutečně malé?
 Fuzzy logika a reálný svět, aneb jsou všechny hromady skutečně malé? Jiří Močkoř University of Ostrava Department of Mathematics Institute for Research and Applications of Fuzzy Modeling 30. dubna 22,
Fuzzy logika a reálný svět, aneb jsou všechny hromady skutečně malé? Jiří Močkoř University of Ostrava Department of Mathematics Institute for Research and Applications of Fuzzy Modeling 30. dubna 22,
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
Rovnost lze vyjádřit jako predikát, např. můžeme zvolit, že P(x, y) reprezentujetvrzení xjerovnoy.
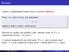 Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Matematická analýza 1
 Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Výroková a predikátová logika - VIII
 Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2016/2017 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2016/2017 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2016/2017 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2016/2017 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Sémantická věta o dedukci Věta Pro
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Sémantická věta o dedukci Věta Pro
Klauzulární logika. Znalostní báze. Šárka Vavrečková
 Klauzulární logika Znalostní báze Šárka Vavrečková Ústav informatiky, Filozoficko-přírodovědecká fakulta Slezské univerzity v Opavě sarka.vavreckova@fpf.slu.cz 26. listopadu 2007 (Znalostní báze) Klauzulární
Klauzulární logika Znalostní báze Šárka Vavrečková Ústav informatiky, Filozoficko-přírodovědecká fakulta Slezské univerzity v Opavě sarka.vavreckova@fpf.slu.cz 26. listopadu 2007 (Znalostní báze) Klauzulární
Booleovská algebra. Booleovské binární a unární funkce. Základní zákony.
 Booleovská algebra. Booleovské binární a unární funkce. Základní zákony. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Booleovská algebra. Booleovské binární a unární funkce. Základní zákony. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Matematika I. Přednášky: Mgr. Radek Výrut, Zkouška:
 Přednášky: Mgr. Radek Výrut, Matematika I katedra matematiky, UL-605, rvyrut@kma.zcu.cz tel.: 377 63 2658 Zkouška: Písemná část zkoušky - příklady v rozsahu zápočtových prací Ústní část zkoušky - základní
Přednášky: Mgr. Radek Výrut, Matematika I katedra matematiky, UL-605, rvyrut@kma.zcu.cz tel.: 377 63 2658 Zkouška: Písemná část zkoušky - příklady v rozsahu zápočtových prací Ústní část zkoušky - základní
teorie logických spojek chápaných jako pravdivostní funkce
 Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Sémantika výrokové logiky. Alena Gollová Výroková logika 1/23
 Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
Výroková a predikátová logika - III
 Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2017/2018 1 / 16 2-SAT 2-SAT Výrok je v k-cnf, je-li v CNF a
Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2017/2018 1 / 16 2-SAT 2-SAT Výrok je v k-cnf, je-li v CNF a
Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka
 Celkové hodnocení BI-MLO (nevyplňujte!) Semestr Zkouška Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka BI-MLO Písemná zkouška 9. února 2016 Matematická logika FIT ČVUT v Praze Varianta B
Celkové hodnocení BI-MLO (nevyplňujte!) Semestr Zkouška Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka BI-MLO Písemná zkouška 9. února 2016 Matematická logika FIT ČVUT v Praze Varianta B
Sylogistika. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 16
 (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 16 Výstavba logické teorie Sylogistika 1) Syntax základní symboly (logické, mimologické) gramatická pravidla (pojem formule) 2) Sémantika pojem interpretace
(FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 16 Výstavba logické teorie Sylogistika 1) Syntax základní symboly (logické, mimologické) gramatická pravidla (pojem formule) 2) Sémantika pojem interpretace
Cvičení ke kursu Logika II, část III
 Cvičení ke kursu Logika II, část III (30. listopadu 2008) Osnova přednášky přednáška je určena studentům, kteří absolvovali úvodní kursy logiky a teorie rekurzívních funkcí. Předpokládané znalosti: syntax
Cvičení ke kursu Logika II, část III (30. listopadu 2008) Osnova přednášky přednáška je určena studentům, kteří absolvovali úvodní kursy logiky a teorie rekurzívních funkcí. Předpokládané znalosti: syntax
prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. BI-ZMA ZS 2009/2010
 Základní pojmy prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy
Základní pojmy prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy
10. Techniky formální verifikace a validace
 Fakulta informačních technologií MI-NFA, zimní semestr 2011/2012 Jan Schmidt EVROPSKÝ SOCIÁLNÍ FOND PRAHA & EU: INVESTUJENE DO VAŠÍ BUDOUCNOSTI 10. Techniky formální verifikace a validace 1 Simulace není
Fakulta informačních technologií MI-NFA, zimní semestr 2011/2012 Jan Schmidt EVROPSKÝ SOCIÁLNÍ FOND PRAHA & EU: INVESTUJENE DO VAŠÍ BUDOUCNOSTI 10. Techniky formální verifikace a validace 1 Simulace není
Predik atov a logika - pˇredn aˇska () Predik atov a logika - pˇredn aˇska / 16
 Predikátová logika - přednáška 3 6. 1. 2015 () Predikátová logika - přednáška 3 6. 1. 2015 1 / 16 Věta (o dedukci) Bud L jazyk, T teorie pro L, ϕ L-sentence a ψ L-formule. Pak Věta (o kompaktnosti) T ϕ
Predikátová logika - přednáška 3 6. 1. 2015 () Predikátová logika - přednáška 3 6. 1. 2015 1 / 16 Věta (o dedukci) Bud L jazyk, T teorie pro L, ϕ L-sentence a ψ L-formule. Pak Věta (o kompaktnosti) T ϕ
Matematika pro informatiky KMA/MATA
 Matematika pro informatiky KMA/MATA Informace k předmětu Mgr. Přemysl Rosa rosapr00@pf.jcu.cz, J349 Konzultační hodiny v ZS: úterý 10-11, čtvrtek 15-16 nebo individuálně po předchozí domluvě aktivní účast
Matematika pro informatiky KMA/MATA Informace k předmětu Mgr. Přemysl Rosa rosapr00@pf.jcu.cz, J349 Konzultační hodiny v ZS: úterý 10-11, čtvrtek 15-16 nebo individuálně po předchozí domluvě aktivní účast
Logika 5. Základní zadání k sérii otázek: V uvedených tezích doplňte z nabízených adekvátní pojem, termín, slovo. Otázka číslo: 1. Logika je věda o...
 Logika 5 Základní zadání k sérii otázek: V uvedených tezích doplňte z nabízených adekvátní pojem, termín, slovo. Otázka číslo: 1 Logika je věda o.... slovech správném myšlení myšlení Otázka číslo: 2 Základy
Logika 5 Základní zadání k sérii otázek: V uvedených tezích doplňte z nabízených adekvátní pojem, termín, slovo. Otázka číslo: 1 Logika je věda o.... slovech správném myšlení myšlení Otázka číslo: 2 Základy
Predikátová logika Individua a termy Predikáty
 Predikátová logika Predikátová logika je rozšířením logiky výrokové o kvantifikační výrazy jako každý, všichni, někteří či žádný. Nejmenší jazykovou jednotkou, kterou byla výroková logika schopna identifikovat,
Predikátová logika Predikátová logika je rozšířením logiky výrokové o kvantifikační výrazy jako každý, všichni, někteří či žádný. Nejmenší jazykovou jednotkou, kterou byla výroková logika schopna identifikovat,
1 Pravdivost formulí v interpretaci a daném ohodnocení
 1 Pravdivost formulí v interpretaci a daném ohodnocení Než uvedeme konkrétní příklady, zopakujme si definici interpretace, ohodnocení a pravdivosti. Necht L je nějaký jazyk. Interpretaci U, jazyka L tvoří
1 Pravdivost formulí v interpretaci a daném ohodnocení Než uvedeme konkrétní příklady, zopakujme si definici interpretace, ohodnocení a pravdivosti. Necht L je nějaký jazyk. Interpretaci U, jazyka L tvoří
Logika. Akademie managementu a komunikace, Praha PhDr. Peter Jan Kosmály, PhD.
 Akademie managementu a komunikace, Praha PhDr. Peter Jan Kosmály, PhD. Tematické okruhy: 1. Stručné dějiny logiky a její postavění ve vědě 2. Analýza složených výroků pomocí pravdivostní tabulky 3. Subjekt-predikátová
Akademie managementu a komunikace, Praha PhDr. Peter Jan Kosmály, PhD. Tematické okruhy: 1. Stručné dějiny logiky a její postavění ve vědě 2. Analýza složených výroků pomocí pravdivostní tabulky 3. Subjekt-predikátová
Primární a sekundární výskyt označující fráze. Martina Juříková Katedra filozofie, FF UP v Olomouci Bertrand Russell, 17. - 18. 5.
 Primární a sekundární výskyt označující fráze Martina Juříková Katedra filozofie, FF UP v Olomouci Bertrand Russell, 17. - 18. 5. 2012 Russellovo rozlišení jména a popisu Označující fráze Primární a sekundární
Primární a sekundární výskyt označující fráze Martina Juříková Katedra filozofie, FF UP v Olomouci Bertrand Russell, 17. - 18. 5. 2012 Russellovo rozlišení jména a popisu Označující fráze Primární a sekundární
Obsah ZÁKLADNÍ POJMY LOGIKA DESKRIPTIVNÍHO JAZYKA 2 VÝROKOVÁ LOGIKA 49 3 VNITŘNÍ STAVBA VÝROKŮ 78
 259 Obsah PŘEDMLUVA 5 ZÁKLADNÍ POJMY 1 ÚVODNÍ ÚVAHY 1.1 o povaze a úkolech logiky 1.2 Logika a právo. Pojem právní logiky 1.3 Vyjadřovací soustava a sdělovací proces. 1.4 Několik základních pojmů potřebných
259 Obsah PŘEDMLUVA 5 ZÁKLADNÍ POJMY 1 ÚVODNÍ ÚVAHY 1.1 o povaze a úkolech logiky 1.2 Logika a právo. Pojem právní logiky 1.3 Vyjadřovací soustava a sdělovací proces. 1.4 Několik základních pojmů potřebných
Negativní informace. Petr Štěpánek. S použitím materiálu M.Gelfonda a V. Lifschitze. Logické programování 15 1
 Negativní informace Petr Štěpánek S použitím materiálu M.Gelfonda a V. Lifschitze 2009 Logické programování 15 1 Negace jako neúspěch Motivace: Tvrzení p (atomická formule) neplatí, jestliže nelze odvodit
Negativní informace Petr Štěpánek S použitím materiálu M.Gelfonda a V. Lifschitze 2009 Logické programování 15 1 Negace jako neúspěch Motivace: Tvrzení p (atomická formule) neplatí, jestliže nelze odvodit
Aplikace: Znalostní báze
 Aplikace: Znalostní báze 1 Znalostní báze je systém, který dostává fakta o prostředí a dotazy o něm. Znalostní báze je agentem ve větším systému, který obsahuje prostředí (také agent), správce (agent),
Aplikace: Znalostní báze 1 Znalostní báze je systém, který dostává fakta o prostředí a dotazy o něm. Znalostní báze je agentem ve větším systému, který obsahuje prostředí (také agent), správce (agent),
Logika, výroky, množiny
 Logika, výroky, množiny Martina Šimůnková 23. srpna 2017 Učební text k předmětu Matematická analýza pro studenty FP TUL Jazyk matematiky Budeme používat dva jazyky: jazyk matematiky a běžně používaný jazyk.
Logika, výroky, množiny Martina Šimůnková 23. srpna 2017 Učební text k předmětu Matematická analýza pro studenty FP TUL Jazyk matematiky Budeme používat dva jazyky: jazyk matematiky a běžně používaný jazyk.
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 2014
 Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 204 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 204 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
NAIVNÍ TEORIE MNOŽIN, okruh č. 5
 NAIVNÍ TEORIE MNOŽIN, okruh č. 5 Definování množiny a jejích prvků Množina je souhrn nějakých věcí. Patří-li věc do množiny X, říkáme, že v ní leží, že je jejím prvkem nebo že množina X tuto věc obsahuje.
NAIVNÍ TEORIE MNOŽIN, okruh č. 5 Definování množiny a jejích prvků Množina je souhrn nějakých věcí. Patří-li věc do množiny X, říkáme, že v ní leží, že je jejím prvkem nebo že množina X tuto věc obsahuje.
Modely datové. Další úrovní je logická úroveň Databázové modely Relační, Síťový, Hierarchický. Na fyzické úrovni se jedná o množinu souborů.
 Modely datové Existují různé úrovně pohledu na data. Nejvyšší úroveň je úroveň, která zachycuje pouze vztahy a struktury dat samotných. Konceptuální model - E-R model. Další úrovní je logická úroveň Databázové
Modely datové Existují různé úrovně pohledu na data. Nejvyšší úroveň je úroveň, která zachycuje pouze vztahy a struktury dat samotných. Konceptuální model - E-R model. Další úrovní je logická úroveň Databázové
Logický čtverec. Tradiční logický čtverec
 Logický čtverec Tradiční logický čtverec Logický čtverec je schéma, do kterého lze poměrně přehledně znázornit následující vztahy mezi tvrzeními: Kontradikce je vztah mezi dvěma tvrzeními s přesně opačnými
Logický čtverec Tradiční logický čtverec Logický čtverec je schéma, do kterého lze poměrně přehledně znázornit následující vztahy mezi tvrzeními: Kontradikce je vztah mezi dvěma tvrzeními s přesně opačnými
Výroková a predikátová logika - XIII
 Výroková a predikátová logika - XIII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XIII ZS 2013/2014 1 / 13 Úvod Algoritmická (ne)rozhodnutelnost Které
Výroková a predikátová logika - XIII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XIII ZS 2013/2014 1 / 13 Úvod Algoritmická (ne)rozhodnutelnost Které
Logika. 1. Úvod, Výroková logika
 Logika 1. Úvod, Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216,
Logika 1. Úvod, Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216,
Úvod do logiky (PL): sémantika predikátové logiky
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): sémantika predikátové logiky doc. PhDr. Jiří
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): sémantika predikátové logiky doc. PhDr. Jiří
Výroková a predikátová logika - III
 Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2014/2015 1 / 21 Výroková logika Horn-SAT Horn-SAT Jednotková
Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2014/2015 1 / 21 Výroková logika Horn-SAT Horn-SAT Jednotková
Zobecněné kvantifikátory, empirické argumenty pro unifikovanou sémantiku NP, negativně 1 / 20 p
 Zobecněné kvantifikátory, empirické argumenty pro unifikovanou sémantiku NP, negativně polaritní výrazy FF MU Mojmír Dočekal ÚJABL Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik
Zobecněné kvantifikátory, empirické argumenty pro unifikovanou sémantiku NP, negativně polaritní výrazy FF MU Mojmír Dočekal ÚJABL Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik
Inteligentní systémy (TIL)
 Inteligentní systémy (TIL) Marie Duží http://www.cs.vsb.cz/duzi/ Přednáška 9 hyperintensionální kontext Celá konstrukce C je objektem predikace (argumentem), tedy její výstup funkce, kterou konstruuje,
Inteligentní systémy (TIL) Marie Duží http://www.cs.vsb.cz/duzi/ Přednáška 9 hyperintensionální kontext Celá konstrukce C je objektem predikace (argumentem), tedy její výstup funkce, kterou konstruuje,
Kapitola Základní množinové pojmy Princip rovnosti. Dvě množiny S a T jsou si rovny (píšeme S = T ) prvek T je také prvkem S.
 1 Kapitola 1 Množiny 11 Základní množinové pojmy Pojem množiny nedefinujeme, pouze připomínáme, že množina je souhrn, nebo soubor navzájem rozlišitelných objektů, kterým říkáme prvky 111 Princip rovnosti
1 Kapitola 1 Množiny 11 Základní množinové pojmy Pojem množiny nedefinujeme, pouze připomínáme, že množina je souhrn, nebo soubor navzájem rozlišitelných objektů, kterým říkáme prvky 111 Princip rovnosti
