Algoritmy. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
|
|
|
- Miloš Sedlák
- před 6 lety
- Počet zobrazení:
Transkript
1 Algoritmy Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
2 Algoritmy Příklad: Popis algoritmu pomocí pseudokódu: Algoritmus 1: Algoritmus pro nalezení největšího prvku v poli 1 Find-Max(A,n): 2 begin 3 k :=0 4 fori:=1ton 1do 5 ifa[i] >A[k]then 6 k :=i 7 end 8 end 9 return A[k] 10 end Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
3 Algoritmy Algoritmus zpracovává vstup generuje výstup Z hlediska analýzy toho, jak daný algoritmus funguje, většinou není příliš podstatný rozdíl v tom, jestli algoritmus: nebo čte vstupní data z nějakého vstupního zařízení(např. ze souboru na disku, z klávesnice, apod.) zapisuje data na nějaké výstupní zařízení(např. do souboru, na obrazovku, apod.) čte vstupní data z paměti(např. jsou mu předány jako parametry) zapisuje data na do paměti(např. je vrátí jako návratovou hodnotu) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
4 Řídící tok Instrukce lze zhruba rozdělit na dvě skupiny: instrukce přímo pracující s daty: přiřazení vyhodnocení hodnot výrazů v podmínkách čtení vstupu, zápis na výstup... instrukce ovlivňující řídící tok určují, které instrukce se budou provádět, v jakém pořadí, apod.: větvení(if,switch,...) cykly(while,do..while,for,...) uspořádání instrukcí do bloků návratyzpodpogramů(return,...)... Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
5 Graf řídícího toku 0 Sfrag replacements 1 k :=0 i :=1 [i n] 2 6 [i <n] result := A[k] 3 [A[i] >A[k]] i :=i +1 7 [A[i] A[k]] 4 k :=i 5 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
6 Některé základní konstrukce strukturovaného programování S 1 [B] [ B] [B] [ B] PSfrag replacements S 1 S 2 PSfragreplacements S ements S 2 S 1 ;S 2 ifbthens 1 elses 2 ifbthens Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
7 Některé základní konstrukce strukturovaného programování [ B] ag replacements [B] S PSfrag replacements [ B] S [B] whilebdos doswhileb Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
8 Některé základní konstrukce strukturovaného programování acements [i >b] i :=a [i b] S i :=i +1 i :=a whilei bdo S i :=i +1 end fori:=atobdos Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
9 Některé základní konstrukce strukturovaného programování Zkrácené vyhodnocování složených podmínek, např.: whilei <nanda[i] >xdo... [B 1] g replacements[b 2] [ B 2] [ B 1] PSfrag replacements [B 1] [B 2] [ B 1] [ B 2] S 1 S 2 S 1 S 2 ifb 1 andb 2 thens 1 elses 2 ifb 1 orb 2 thens 1 elses 2 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
10 Řídící tok realizovaný pomocí goto goto l nepodmíněný skok ifbthengoto l podmíněnýskok Příklad: 0: k :=0 1: i :=1 2: goto6 3: ifa[i] A[k]thengoto5 4: k :=i 5: i :=i +1 6: ifi <nthengoto3 7: return A[k] Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
11 Řídící tok realizovaný pomocí goto goto l nepodmíněný skok ifbthengoto l podmíněnýskok Příklad: start: k :=0 i :=1 goto L3 L1: ifa[i] A[k]thengotoL2 k :=i L2: i :=i +1 L3: ifi <nthengotol1 return A[k] Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
12 Vyhodnocení složitých výrazů Vyhodnocení složitého výrazu, jako třeba A[i +s] := (B[3 j +1]+x) y +8 může být na nižší úrovni nahrazeno posloupností jednodušších příkazů, jako třeba t 1 :=i +s t 2 :=3 j t 2 :=t 2 +1 t 3 :=B[t 2 ] t 3 :=t 3 +x t 3 :=t 3 y t 3 :=t 3 +8 A[t 1 ] :=t 3 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
13 Výpočet algoritmu Algoritmus je vykonáván strojem může to být například: skutečný počítač vykonává instrukce strojového kódu virtuální stroj vykonává instrukce bytekódu nějaký idealizovaný matematický model počítače... Stroj může být: jednoúčelový vykonává jen jeden algoritmus obecnější algoritmus dostává ve formě programu Stroj pracuje po krocích. Algoritmus během výpočtu zpracovává konkrétní vstup. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
14 Výpočet algoritmu Během výpočtu si stroj musí pamatovat: která instrukce se právě provádí obsah pracovní paměti Podle typu stroje je určeno: s jakým typem dat stroj pracuje jak jsou tato data v paměti organizována Podle typu algoritmu a typu analýzy, kterou chceme provádět, se můžeme rozhodnout, zda má smysl mezi obsah paměti zahranout i místa odkud se čtou vstupní data kam se zapisují výstupní data Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
15 Výpočet algoritmu Konfigurace popis celkového stavu stroje v nějakém okamžiku během výpočtu Příklad: Konfigurace tvaru kde (q, mem) q aktuálnířídícístav mem představuje aktuální obsah paměti stroje jaké hodnoty jsou momentálně přiřazeny jednotlivým proměnným. Příklad obsahu paměti mem: A: [3,8,1,3,6], n:5, i:1, k:0, result:? Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
16 Výpočet algoritmu Příklad konfigurace: (2, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) Výpočet stroje M provádějícího algoritmus Alg, kde zpracovává vstup w, je posloupnost konfigurací. Začíná se v počáteční konfiguraci. Každým krokem se přejde z jedné konfigurace do druhé. Výpočet končí v koncové konfiguraci. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
17 Výpočet algoritmu 0 Sfrag replacements 1 k :=0 i :=1 [i n] 2 6 [i <n] result := A[k] 3 [A[i] >A[k]] i :=i +1 7 [A[i] A[k]] 4 k :=i 5 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
18 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
19 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) α 1 : (1, A: [3,8,1,3,6], n:5, i:?, k:0, result:? ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
20 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) α 1 : (1, A: [3,8,1,3,6], n:5, i:?, k:0, result:? ) α 2 : (2, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
21 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) α 1 : (1, A: [3,8,1,3,6], n:5, i:?, k:0, result:? ) α 2 : (2, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 3 : (3, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
22 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) α 1 : (1, A: [3,8,1,3,6], n:5, i:?, k:0, result:? ) α 2 : (2, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 3 : (3, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 4 : (4, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
23 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) α 1 : (1, A: [3,8,1,3,6], n:5, i:?, k:0, result:? ) α 2 : (2, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 3 : (3, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 4 : (4, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 5 : (5, A: [3,8,1,3,6], n:5, i:1, k:1, result:? ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
24 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) α 1 : (1, A: [3,8,1,3,6], n:5, i:?, k:0, result:? ) α 2 : (2, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 3 : (3, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 4 : (4, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 5 : (5, A: [3,8,1,3,6], n:5, i:1, k:1, result:? ) α 6 : (2, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
25 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) α 1 : (1, A: [3,8,1,3,6], n:5, i:?, k:0, result:? ) α 2 : (2, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 3 : (3, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 4 : (4, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 5 : (5, A: [3,8,1,3,6], n:5, i:1, k:1, result:? ) α 6 : (2, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 7 : (3, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
26 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) α 1 : (1, A: [3,8,1,3,6], n:5, i:?, k:0, result:? ) α 2 : (2, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 3 : (3, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 4 : (4, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 5 : (5, A: [3,8,1,3,6], n:5, i:1, k:1, result:? ) α 6 : (2, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 7 : (3, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 8 : (5, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
27 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) α 1 : (1, A: [3,8,1,3,6], n:5, i:?, k:0, result:? ) α 2 : (2, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 3 : (3, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 4 : (4, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 5 : (5, A: [3,8,1,3,6], n:5, i:1, k:1, result:? ) α 6 : (2, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 7 : (3, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 8 : (5, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 9 : (2, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
28 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) α 1 : (1, A: [3,8,1,3,6], n:5, i:?, k:0, result:? ) α 2 : (2, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 3 : (3, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 4 : (4, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 5 : (5, A: [3,8,1,3,6], n:5, i:1, k:1, result:? ) α 6 : (2, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 7 : (3, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 8 : (5, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 9 : (2, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 10 : (3, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
29 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) α 1 : (1, A: [3,8,1,3,6], n:5, i:?, k:0, result:? ) α 2 : (2, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 3 : (3, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 4 : (4, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 5 : (5, A: [3,8,1,3,6], n:5, i:1, k:1, result:? ) α 6 : (2, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 7 : (3, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 8 : (5, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 9 : (2, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 10 : (3, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 11 : (5, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
30 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) α 1 : (1, A: [3,8,1,3,6], n:5, i:?, k:0, result:? ) α 2 : (2, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 3 : (3, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 4 : (4, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 5 : (5, A: [3,8,1,3,6], n:5, i:1, k:1, result:? ) α 6 : (2, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 7 : (3, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 8 : (5, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 9 : (2, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 10 : (3, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 11 : (5, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 12 : (2, A: [3,8,1,3,6], n:5, i:4, k:1, result:? ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
31 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) α 1 : (1, A: [3,8,1,3,6], n:5, i:?, k:0, result:? ) α 2 : (2, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 3 : (3, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 4 : (4, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 5 : (5, A: [3,8,1,3,6], n:5, i:1, k:1, result:? ) α 6 : (2, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 7 : (3, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 8 : (5, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 9 : (2, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 10 : (3, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 11 : (5, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 12 : (2, A: [3,8,1,3,6], n:5, i:4, k:1, result:? ) α 13 : (3, A: [3,8,1,3,6], n:5, i:4, k:1, result:? ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
32 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) α 1 : (1, A: [3,8,1,3,6], n:5, i:?, k:0, result:? ) α 2 : (2, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 3 : (3, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 4 : (4, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 5 : (5, A: [3,8,1,3,6], n:5, i:1, k:1, result:? ) α 6 : (2, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 7 : (3, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 8 : (5, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 9 : (2, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 10 : (3, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 11 : (5, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 12 : (2, A: [3,8,1,3,6], n:5, i:4, k:1, result:? ) α 13 : (3, A: [3,8,1,3,6], n:5, i:4, k:1, result:? ) α 14 : (5, A: [3,8,1,3,6], n:5, i:4, k:1, result:? ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
33 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) α 1 : (1, A: [3,8,1,3,6], n:5, i:?, k:0, result:? ) α 2 : (2, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 3 : (3, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 4 : (4, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 5 : (5, A: [3,8,1,3,6], n:5, i:1, k:1, result:? ) α 6 : (2, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 7 : (3, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 8 : (5, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 9 : (2, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 10 : (3, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 11 : (5, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 12 : (2, A: [3,8,1,3,6], n:5, i:4, k:1, result:? ) α 13 : (3, A: [3,8,1,3,6], n:5, i:4, k:1, result:? ) α 14 : (5, A: [3,8,1,3,6], n:5, i:4, k:1, result:? ) α 15 : (2, A: [3,8,1,3,6], n:5, i:5, k:1, result:? ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
34 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) α 1 : (1, A: [3,8,1,3,6], n:5, i:?, k:0, result:? ) α 2 : (2, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 3 : (3, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 4 : (4, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 5 : (5, A: [3,8,1,3,6], n:5, i:1, k:1, result:? ) α 6 : (2, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 7 : (3, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 8 : (5, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 9 : (2, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 10 : (3, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 11 : (5, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 12 : (2, A: [3,8,1,3,6], n:5, i:4, k:1, result:? ) α 13 : (3, A: [3,8,1,3,6], n:5, i:4, k:1, result:? ) α 14 : (5, A: [3,8,1,3,6], n:5, i:4, k:1, result:? ) α 15 : (2, A: [3,8,1,3,6], n:5, i:5, k:1, result:? ) α 16 : (6, A: [3,8,1,3,6], n:5, i:5, k:1, result:? ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
35 Výpočet algoritmu Příklad: Výpočet, kde algoritmus Find-Max zpracovává vstup, kde A = [3,8,1,3,6]an =5. α 0 : (0, A: [3,8,1,3,6], n:5, i:?, k:?, result:? ) α 1 : (1, A: [3,8,1,3,6], n:5, i:?, k:0, result:? ) α 2 : (2, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 3 : (3, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 4 : (4, A: [3,8,1,3,6], n:5, i:1, k:0, result:? ) α 5 : (5, A: [3,8,1,3,6], n:5, i:1, k:1, result:? ) α 6 : (2, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 7 : (3, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 8 : (5, A: [3,8,1,3,6], n:5, i:2, k:1, result:? ) α 9 : (2, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 10 : (3, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 11 : (5, A: [3,8,1,3,6], n:5, i:3, k:1, result:? ) α 12 : (2, A: [3,8,1,3,6], n:5, i:4, k:1, result:? ) α 13 : (3, A: [3,8,1,3,6], n:5, i:4, k:1, result:? ) α 14 : (5, A: [3,8,1,3,6], n:5, i:4, k:1, result:? ) α 15 : (2, A: [3,8,1,3,6], n:5, i:5, k:1, result:? ) α 16 : (6, A: [3,8,1,3,6], n:5, i:5, k:1, result:? ) α 17 : (7, A: [3,8,1,3,6], n:5, i:5, k:1, result:8 ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
36 Výpočet algoritmu ProvedeníminstrukceIsepřejdezkonfigurace αdokonfigurace α : α I α Výpočet může být: Konečný: I α 0 I 0 1 I α1 2 I α2 3 I α3 4 I t 2 I t 1 α4 αt 1 αt kde α t jekoncovákonfigurace Nekonečný: I α 0 I 0 1 I α1 2 I α2 3 I α3 4 α4 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
37 Výpočet algoritmu Výpočet je možné popsat dvěma různými způsoby: jakoposloupnostkonfigurací α 0,α 1,α 2,... jakoposloupnostprovedenýchinstrukcíi 0,I 1,I 2,... Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
38 Korektnost algoritmu Algoritmy slouží k řešení problémů. Problém specifikace toho, co má algoritmus dělat: Popis vstupu Popis výstupu Vztah mezi vstupy a výstupy Algoritmus konkrétní postup, jak při výpočtu postupovat Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
39 Korektnost algoritmu Příklad: Problém nalezení maximálního prvku v poli: Vstup:PoleAindexovanéodnulyačíslonudávajícípočetprvků vtomtopoli,přičemžsepředpokládá,žen 1. Výstup: Hodnota result, která je hodnotou maximálního prvku vpolia,tj.hodnota result,prokterouplatí: A[j] resultprovšechnaj N,kde0 j <n,a existujej Ntakové,že0 j <naa[j] = result. Instance problému konkrétní vstup, např. A = [3,8,1,3,6],n =5. Pro tuto instanci je výstupem hodnota 8. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
40 Korektnost algoritmu Definice Algoritmus Alg řeší problém P, jestliže pro každou instanci w problému P jsou splněny následující dvě podmínky: (a) Výpočetalgoritmu Algnadvstupemwsepokonečnémpočtukroků (korektně) zastaví. (b) Algoritmus Alg vygeneruje pro vstup w výstup, který odpovídá podmínkám kladeným na výstup ve specifikaci problému P. Algoritmus, který řeší problém P, je korektním řešením tohoto problému. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
41 Korektnost algoritmu Algoritmus Alg není korektním řešení problému P, jestliže existuje vstup w takový, že při výpočtu nad tímto vstupem nastane některá z následujících chyb: provedení nějaké chybné nepovolené operace(přístup k prvku pole mimopovolenýrozsahindexů,dělenínulou,...), vygenerovaný výstup neodpovídá podmínkám specifikovaným v zadání problému P, výpočet se nikdy nezastaví. Testování spustění algoritmu nad různými vstupy a zkontrolování, zda sealgoritmusprotytovstupychová správně. Testování může prokázat přítomnost chyb, ale ne to, že se algoritmus chová korektně pro všechny vstupy. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
42 Korektnost algoritmu Důkaz korektnosti algoritmu je obecně vhodné rozdělit na dvě části: Zdůvodnění toho, že algoritmus pro žádný vstup nikdy neudělá nic špatně : během výpočtu nedojde k žádné chybné operaci pokudprogramskončí,výstupbude správně Zdůvodnění toho, že se algoritmus pro každý vstup po konečném počtu kroků zastaví. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
43 Korektnost algoritmu Invariant podmínka, která musí být v určitém místě kódu algoritmu vždy(tj. ve všech možných výpočtech pro všechny možné vstupy) splněna v okamžiku, kdy algoritmus tímto místem prochází. Řekneme, že konfigurace α je dosažitelná, jestliže existuje vstup w takový, že je α jednou z konfigurací, kterými algoritmus Alg projde při výpočtunadvstupemw. Pokud je algoritmus reprezentován ve formě grafu řídícího toku, můžeme pro řídící stav q(tj. vrchol grafu) specifikovat invarianty, které platí v každé dosažitelné konfiguraci, kde je řídícím stavem q. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
44 Invarianty Invarianty můžeme zapisovat formulemi predikátové logiky: volné proměnné odpovídají proměnným programu valuace je dána hodnotami proměnných programu v dané konfiguraci Příklad: Formule (1 i) (i n) budeplatitnapříkladvkonfiguraci,kdeproměnnáimáhodnotu5a proměnná n má hodnotu 14. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
45 Invarianty 0 Sfrag replacements 1 k :=0 i :=1 [i n] 2 6 [i <n] result := A[k] 3 [A[i] >A[k]] i :=i +1 7 [A[i] A[k]] 4 k :=i 5 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
46 Invarianty Příklady invariantů: invariantvřídícímstavuqzapíšemeformulí ϕ q Invarianty v jednotlivých řídících stavech(zatím jen hypotézy): ϕ 0 : (n 1) ϕ 1 : (n 1) (k =0) ϕ 2 : (n 1) (1 i n) (0 k <i) ϕ 3 : (n 1) (1 i <n) (0 k <i) ϕ 4 : (n 1) (1 i <n) (0 k <i) ϕ 5 : (n 1) (1 i <n) (0 k i) ϕ 6 : (n 1) (i =n) (0 k <n) ϕ 7 : (n 1) (i =n) (0 k <n) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
47 Invarianty Příklady invariantů: invariantvřídícímstavuqzapíšemeformulí ϕ q Invarianty v jednotlivých řídících stavech(zatím jen hypotézy): ϕ 0 :n 1 ϕ 1 :n 1, k =0 ϕ 2 :n 1, 1 i n, 0 k <i ϕ 3 :n 1, 1 i <n, 0 k <i ϕ 4 :n 1, 1 i <n, 0 k <i ϕ 5 :n 1, 1 i <n, 0 k i ϕ 6 :n 1, i =n, 0 k <n ϕ 7 :n 1, i =n, 0 k <n Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
48 Invarianty Zkontrolování toho, že invarianty opravdu platí: Pro každou instrukci algoritmu je třeba zkontrolovat, zda za předpokladu, že bude platit příslušný invariant před provedením této instrukce, bude platit i příslušný invariant po provedení této instrukce. Předpokládejme algoritmus ve formě grafu řídícího toku: hrany odpovídají instrukcím vezměmesihranuzestavuqdostavuq označenouinstrukcíi řekněme,že(zatímneověřené)invariantyprostavyqaq jsou vyjádřenyformulemi ϕaϕ pro tuto hranu musíme zkontrolovat, že pro všechny konfigurace α = (q,mem)aα = (q,mem )takové,že α I α,platí,že pokud vkonfiguraci αplatí ϕ, pak vkonfiguraci α platí ϕ Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
49 Invarianty Zkontrolování instrukcí, které jsou testy podmínek: hrana označená testem podmínky [B] Obsah paměti se nemění. Stačí ověřit, že platí implikace (ϕ B) ϕ Poznámka: Příslušná implikace musí platit pro všechny možné hodnoty proměnných. Příklad: Předpokládáme, že se formulích objevují jen proměnné n, i, k, a že hodnotami těchto proměnných mohou být jen celá čísla: ( n Z)( i Z)( k Z)(ϕ B ϕ ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
50 Invarianty Zkontrolování instrukcí, které přiřazují hodnoty proměnným(mění obsah paměti): hrana označená přiřazením x := E ϕ formule,kteroudostanemezformule ϕ přejmenovánímvšech volnýchvýskytůproměnnéxnaproměnnoux Je třeba ověřit platnost implikace Příklad:Přiřazeník:=3 k +i +1: (ϕ (x =E)) ϕ ( n Z)( i Z)( k Z)( k Z)(ϕ (k =3 k +i +1) ϕ ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
51 Invarianty Dokončení ověření toho, že algoritmus pro nalezení maximálního prvku v poli vrací správný výsledek(za předpokladu, že skončí): ψ 0 : ϕ 0 ψ 1 : ϕ 1 ( j N)(0 j <1 A[j] A[k]) ψ 2 : ϕ 2 ( j N)(0 j <i A[j] A[k]) ψ 3 : ϕ 3 ( j N)(0 j <i A[j] A[k]) ψ 4 : ϕ 4 ( j N)(0 j <i A[j] A[k]) (A[i] >A[k]) ψ 5 : ϕ 5 ( j N)(0 j i A[j] A[k]) ψ 6 : ϕ 6 ( j N)(0 j <n A[j] A[k]) ψ 7 : ϕ 7 (result =A[k]) ( j N)(0 j <n A[j] result) ( j N)(0 j <n A[j] = result) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
52 Invarianty Často není třeba specifikovat invarianty ve všech řídících stavech, ale je vněkterých důležitých zejménastavy,kdesevstupujedonebo vystupuje z cyklů: Je pak třeba ověřit: Že invariant platí před vstupem do cyklu. Že pokud invariant platí před provedením cyklu, tak bude platit i po jeho provedení. Že invariant platí při opuštění cyklu. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
53 Invarianty Příklad:ValgoritmuFind-Maxjetakovým důležitým stavemstav2. Vestavu2platí: n 1 1 i n 0 k <i Provšechnajtaková,že0 j <i,platía[j] A[k]. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
54 Konečnost výpočtu Dva možné případy, jak může vypadat nekonečný výpočet: nějaká konfigurace se zopakuje následující konfigurace se opakují stále dokola objevují se stále nové a nové konfigurace Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
55 Konečnost výpočtu Jeden z běžných způsobů dokazování toho, že se algoritmus zaručeně pro každý vstup po konečném počtu kroků zastaví: každé(dosažitelné) konfiguraci přiřadit hodnotu z nějaké vhodně zvolené množiny W na množině W definovat uspořádání takové, že ve W neexistují nekonečné(ostře) klesající posloupnosti ukázat, že s provedením každé instrukce se hodnota přiřazená konfiguracizmenšuje,tj.pro α I α je f(α) >f(α ) (f(α),f(α )jsouhodnotyzmnožinywpřiřazenékonfiguracím α a α ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
56 Konečnost výpočtu Jako množinu W je možno použít například: Množinupřirozenýchčísel N = {0,1,2,3,...}suspořádáním. Množinu vektorů přirozených číslel s lexikografickým uspořádáním, tj.suspořádáním,kdevektor (a 1,a 2,...,a m )jemenšínežvektor (b 1,b 2,...,b n ),jestliže existujeitakové,že1 i mai n,kdea i <b i aprovšechnaj taková,že1 j <i,platía j =b j,nebo m <naprovšechnajtaková,že1 j m,jea j =b j. Například (5,1,3,6,4) < (5,1,4,1)a(4,1,1) < (4,1,1,3). Poznámka: Počet prvků vektorů musí být omezen nějakou konstantou. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
57 Konečnost výpočtu 0 Sfrag replacements 1 k :=0 i :=1 [i n] 2 6 [i <n] result := A[k] 3 [A[i] >A[k]] i :=i +1 7 [A[i] A[k]] 4 k :=i 5 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
58 Konečnost výpočtu Příklad: Vektory přiřazené jednotlivým konfiguracím: Stav0:f(α) = (4) Stav1:f(α) = (3) Stav2:f(α) = (2,n i,3) Stav3:f(α) = (2,n i,2) Stav4:f(α) = (2,n i,1) Stav5:f(α) = (2,n i,0) Stav6:f(α) = (1) Stav7:f(α) = (0) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
Úvod do teoretické informatiky(2017/2018) cvičení 11 1
Úvod do teoretické informatiky(2017/2018) cvičení 11 1 Cvičení 11 Příklad 1: Vezměme si následující Algoritmus 1. Vstupem tohoto algoritmu může být libovolné přirozené číslo n. Algoritmus 1: 1 PrintSeq(n):
Algoritmus. Přesné znění definice algoritmu zní: Algoritmus je procedura proveditelná Turingovým strojem.
Algoritmus Algoritmus je schematický postup pro řešení určitého druhu problémů, který je prováděn pomocí konečného množství přesně definovaných kroků. nebo Algoritmus lze definovat jako jednoznačně určenou
Úvod do teoretické informatiky
Úvod do teoretické informatiky Zdeněk Sawa Katedra informatiky, FEI, Vysoká škola báňská Technická universita Ostrava 17. listopadu 15, Ostrava-Poruba 708 33 Česká republika 11. února 2018 Z. Sawa (VŠB-TUO)
ŘÍKÁME, ŽE FUNKCE JE ČÁSTEČNĚ SPRÁVNÁ (PARTIALLY CORRECT), POKUD KDYŽ JE SPLNĚNA PRECONDITION
ŘÍKÁME, ŽE FUNKCE JE ČÁSTEČNĚ SPRÁVNÁ (PARTIALLY CORRECT), POKUD KDYŽ JE SPLNĚNA PRECONDITION FUNKCE PŘI JEJÍM ZAVOLÁNÍ, JEJÍ POSTCONDITION JE SPLNĚNA PŘI NÁVRATU Z FUNKCE (POKUD NASTANE) OBECNĚ FUNKCE
doplněk, zřetězení, Kleeneho operaci a reverzi. Ukážeme ještě další operace s jazyky, na které je
28 [181105-1236 ] 2.7 Další uzávěrové vlastnosti třídy regulárních jazyků Z předchozích přednášek víme, že třída regulárních jazyků je uzavřena na sjednocení, průnik, doplněk, zřetězení, Kleeneho operaci
NP-úplnost problému SAT
Problém SAT je definován následovně: SAT(splnitelnost booleovských formulí) Vstup: Booleovská formule ϕ. Otázka: Je ϕ splnitelná? Příklad: Formule ϕ 1 =x 1 ( x 2 x 3 )jesplnitelná: např.přiohodnocení ν,kde[x
Zpracoval: hypspave@fel.cvut.cz 7. Matematická indukce a rekurse. Řešení rekurentních (diferenčních) rovnic s konstantními koeficienty.
Zpracoval: hypspave@fel.cvut.cz 7. Matematická indukce a rekurse. Řešení rekurentních (diferenčních) rovnic s konstantními koeficienty. (A7B01MCS) I. Matematická indukce a rekurse. Indukční principy patří
Lekce 01 Úvod do algoritmizace
Počítačové laboratoře bez tajemství aneb naučme se učit algoritmizaci a programování s využitím robotů Lekce 01 Úvod do algoritmizace Tento projekt CZ.1.07/1.3.12/04.0006 je spolufinancován Evropským sociálním
Algoritmizace. 1. Úvod. Algoritmus
1. Úvod Algoritmizace V dnešní době již počítače pronikly snad do všech oblastí lidské činnosti, využívají se k řešení nejrůznějších úkolů. Postup, který je v počítači prováděn nějakým programem se nazývá
Paralelní programování
Paralelní programování přednášky Jan Outrata únor duben 2011 Jan Outrata (KI UP) Paralelní programování únor duben 2011 1 / 14 Atomické akce dále nedělitelná = neproložitelná jiným procesem izolovaná =
NPRG030 Programování I RNDr.Tomáš Holan, Ph.D. 4.patro, č
NPRG030 Programování I RNDr.Tomáš Holan, Ph.D. 4.patro, č.404 http://ksvi.mff.cuni.cz/~holan/ Tomas.Holan@mff.cuni.cz NPRG030 Programování I, 2014/15 1 / 37 6. 10. 2014 11:42:59 NPRG030 Programování I,
Rovnost lze vyjádřit jako predikát, např. můžeme zvolit, že P(x, y) reprezentujetvrzení xjerovnoy.
Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Základy algoritmizace
Algoritmus Toto je sice na první pohled pravdivá, ale při bližším prozkoumání nepřesná definice. Například některé matematické postupy by této definici vyhovovaly, ale nejsou algoritmy. Přesné znění definice
Principy indukce a rekursivní algoritmy
Principy indukce a rekursivní algoritmy Jiří Velebil: A7B01MCS 19. září 2011: Indukce 1/20 Příklad Místností rozměru n budeme rozumět šachovnici rozměru 2 n 2 n, ze které je jedno (libovolné) pole vyjmuto.
Vlastnosti algoritmu. elementárnost. determinovanost. rezultativnost. konečnost. hromadnost. efektivnost
Programování Algoritmus návod na vykonání činnosti, který nás od (měnitelných) vstupních dat přivede v konečném čase k výsledku přesně definovaná konečná posloupnost činností vedoucích k výsledku (postup,
Výroková a predikátová logika - IV
Výroková a predikátová logika - IV Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IV ZS 2018/2019 1 / 17 Tablo metoda Tablo Tablo - příklady F (((p q)
Vyhledávání. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 21.
Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 21. září 2018 Jiří Dvorský (VŠB TUO) Vyhledávání 242 / 433 Osnova přednášky
2. lekce Algoritmus, cyklus Miroslav Jílek
2. lekce Algoritmus, cyklus Miroslav Jílek 1/36 Algoritmus 2/36 Algoritmus je konečná posloupnost operací, která dává řešení skupiny problémů 3/36 Algoritmus je konečná posloupnost operací, která dává
Z. Sawa (VŠB-TUO) Teoretická informatika 11. prosince / 63
Výpočetní modely Z. Sawa (VŠB-TUO) Teoretická informatika 11. prosince 2018 1/ 63 Nutnost upřesnění pojmu algoritmus Dosavadní definice pojmu algoritmus byla poněkud vágní. Pokud bychom pro nějaký problém
Vyučovací hodina. 1vyučovací hodina: 2vyučovací hodiny: Opakování z minulé hodiny. Procvičení nové látky
Vyučovací hodina 1vyučovací hodina: Opakování z minulé hodiny Nová látka Procvičení nové látky Shrnutí 5 min 20 min 15 min 5 min 2vyučovací hodiny: Opakování z minulé hodiny Nová látka Procvičení nové
PODOBÁ SE JAZYKU C S NĚKTERÝMI OMEZENÍMI GLOBÁLNÍ PROMĚNNÉ. NSWI162: Sémantika programů 2
PI JE JEDNODUCHÝ IMPERATIVNÍ PROGRAMOVACÍ JAZYK OBSAHUJE PODPORU ANOTACÍ NEOBSAHUJE NĚKTERÉ TYPICKÉ KONSTRUKTY PROGRAMOVACÍCH JAZYKŮ JAKO JSOU REFERENCE, UKAZATELE, GLOBÁLNÍ PROMĚNNÉ PODOBÁ SE JAZYKU C
IV113 Validace a verifikace. Formální verifikace algoritmů. Jiří Barnat
IV113 Validace a verifikace Formální verifikace algoritmů Jiří Barnat Verifikace algoritmů IV113 Úvod do validace a verifikace: Formální verifikace str. 2/29 Validace a Verifikace Jeden z obecných cílů
Úvod do programovacích jazyků (Java)
Úvod do programovacích jazyků (Java) Michal Krátký Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programovacích jazyků (Java), 2007/2008 c 2006 2008 Michal Krátký Úvod do programovacích
Výroková a predikátová logika - II
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2015/2016 1 / 18 Základní syntax Jazyk Výroková logika je logikou
Čtvrtek 8. prosince. Pascal - opakování základů. Struktura programu:
Čtvrtek 8 prosince Pascal - opakování základů Struktura programu: 1 hlavička obsahuje název programu, použité programové jednotky (knihovny), definice konstant, deklarace proměnných, všechny použité procedury
Výroková a predikátová logika - III
Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2017/2018 1 / 16 2-SAT 2-SAT Výrok je v k-cnf, je-li v CNF a
Princip funkce počítače
Princip funkce počítače Princip funkce počítače prvotní úlohou počítačů bylo zrychlit provádění matematických výpočtů první počítače kopírovaly obvyklý postup manuálního provádění výpočtů pokyny pro zpracování
Algoritmus pro hledání nejkratší cesty orientovaným grafem
1.1 Úvod Algoritmus pro hledání nejkratší cesty orientovaným grafem Naprogramoval jsem v Matlabu funkci, která dokáže určit nejkratší cestu v orientovaném grafu mezi libovolnými dvěma vrcholy. Nastudoval
for (i = 0, j = 5; i < 10; i++) { // tělo cyklu }
5. Operátor čárka, - slouží k jistému určení pořadí vykonání dvou příkazů - oddělím-li čárkou dva příkazy, je jisté, že ten první bude vykonán dříve než příkaz druhý. Např.: i = 5; j = 8; - po překladu
Úvod do informatiky. Miroslav Kolařík
Úvod do informatiky přednáška první Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Co a k čemu je logika? 2 Výroky a logické spojky
Složitost algoritmů. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava
Složitost algoritmů doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 27. prosince 2015 Jiří Dvorský (VŠB TUO) Složitost algoritmů
Třídy složitosti P a NP, NP-úplnost
Třídy složitosti P a NP, NP-úplnost Cíle přednášky: 1. Definovat, za jakých okolností můžeme problém považovat za efektivně algoritmicky řešitelný. 2. Charakterizovat určitou skupinu úloh, pro které není
Stefan Ratschan. Fakulta informačních technologíı. Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
Logika pro každodenní přežití Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
Logika a logické programování
Logika a logické programování témata ke zkoušce Poslední aktualizace: 16. prosince 2009 Zkouška je písemná, skládá se obvykle ze sedmi otázek (může být více nebo méně, podle náročnosti otázek), z toho
Obsah přednášky. programovacího jazyka. Motivace. Princip denotační sémantiky Sémantické funkce Výrazy Příkazy Vstup a výstup Kontinuace Program
Denotační sémantika programovacího jazyka doc. Dr. Ing. Miroslav Beneš katedra informatiky, A-1007 59 732 4213 Obsah přednášky Princip denotační sémantiky Sémantické funkce Výrazy Příkazy Vstup a výstup
Algoritmizace. Obrázek 1: Přeložení programu překladačem
Algoritmizace V každém okamžiku ví procesor počítače přesně, co má vykonat. Pojmem procesor se v souvislosti s algoritmy označuje objekt (např. stroj i člověk), který vykonává činnost popisovanou algoritmem.
Sada 1 - Základy programování
S třední škola stavební Jihlava Sada 1 - Základy programování 07. Základní příkazy vstup a výstup hodnot Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284
10. Techniky formální verifikace a validace
Fakulta informačních technologií MI-NFA, zimní semestr 2011/2012 Jan Schmidt EVROPSKÝ SOCIÁLNÍ FOND PRAHA & EU: INVESTUJENE DO VAŠÍ BUDOUCNOSTI 10. Techniky formální verifikace a validace 1 Simulace není
6 Příkazy řízení toku
6 Příkazy řízení toku Studijní cíl Tento studijní blok má za cíl pokračovat v základních prvcích jazyka Java. Konkrétně bude věnována pozornost příkazům pro řízení toku programu. Pro všechny tyto základní
Definice 7.2. Nejmenší přirozené číslo k, pro které je graf G k-obarvitelný, se nazývá chromatické číslo (barevnost) grafu G a značí se χ(g).
7 Barevnost grafu Definice 71 Graf G se nazývá k-obarvitelný, jestliže každému jeho uzlu lze přiřadit jednu z barev 1 k tak, že žádné dva sousední uzly nemají stejnou barvu Definice 72 Nejmenší přirozené
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 2014
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 204 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
2.1 Podmínka typu case Cykly Cyklus s podmínkou na začátku Cyklus s podmínkou na konci... 5
Obsah Obsah 1 Řídicí struktury 1 2 Podmínka 1 2.1 Podmínka typu case......................... 2 3 Příkaz skoku 3 4 Cykly 4 4.1 Cyklus s podmínkou na začátku................... 4 4.2 Cyklus s podmínkou
Negativní informace. Petr Štěpánek. S použitím materiálu M.Gelfonda a V. Lifschitze. Logické programování 15 1
Negativní informace Petr Štěpánek S použitím materiálu M.Gelfonda a V. Lifschitze 2009 Logické programování 15 1 Negace jako neúspěch Motivace: Tvrzení p (atomická formule) neplatí, jestliže nelze odvodit
Matematická indukce a správnost programů. Základy diskrétní matematiky, BI-ZDM ZS 2011/12, Lekce 13
Matematická indukce a správnost programů doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky FIT České vysoké učení technické v Praze c Josef Kolar, 2011 Základy diskrétní matematiky, BI-ZDM ZS
Unbounded Model Checking
Unbounded Model Checking Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze 25. října 2011 Evropský sociální fond Praha & EU: Investujeme do
Seminář z IVT Algoritmizace. Slovanské gymnázium Olomouc Tomáš Kühr
Seminář z IVT Algoritmizace Slovanské gymnázium Olomouc Tomáš Kühr Algoritmizace - o čem to je? Zatím jsme se zabývali především tím, jak určitý postup zapsat v konkrétním programovacím jazyce (např. C#)
Systém přirozené dedukce výrokové logiky
Systém přirozené dedukce výrokové logiky Korektnost, úplnost a bezespornost Šárka Vavrečková Ústav informatiky, FPF SU Opava Poslední aktualizace: 6. října 2008 Věta o korektnosti Věta (O korektnosti Systému
Úvod do programování - Java. Cvičení č.4
Úvod do programování - Java Cvičení č.4 1 Sekvence (posloupnost) Sekvence je tvořena posloupností jednoho nebo více příkazů, které se provádějí v pevně daném pořadí. Příkaz se začne provádět až po ukončení
Algoritmizace a programování
Algoritmizace a programování Řídicí struktury jazyka Java Struktura programu Příkazy jazyka Blok příkazů Logické příkazy Ternární logický operátor Verze pro akademický rok 2012/2013 1 Struktura programu
Digitální učební materiál
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_145_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
V každém kroku se a + b zmenší o min(a, b), tedy vždy alespoň o 1. Jestliže jsme na začátku dostali 2
Euklidův algoritmus Doprovodný materiál pro cvičení Programování I. NPRM044 Autor: Markéta Popelová Datum: 31.10.2010 Euklidův algoritmus verze 1.0 Zadání: Určete největšího společného dělitele dvou zadaných
Práce se soubory. Základy programování 2 Tomáš Kühr
Práce se soubory Základy programování 2 Tomáš Kühr Soubory z pohledu C Soubor zjednodušeně chápeme jako posloupnost bytů uložených někde na disku Datový proud (anglicky stream) Ještě obecnější přístup
Konstrukce relace. Postupně konstruujeme na množině všech stavů Q relace i,
[161014-1204 ] 11 2.1.35 Konstrukce relace. Postupně konstruujeme na množině všech stavů Q relace i, kde i = 0, 1,..., takto: p 0 q právě tehdy, když bud p, q F nebo p, q F. Dokud i+1 i konstruujeme p
Modely Herbrandovské interpretace
Modely Herbrandovské interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 8 1 Uvedli jsme termové interpretace a termové modely pro logické programy a také nejmenší
setup() { I = 0; } loop() { I = I + 1; }
PŘERUŠENÍ Procesor pracuje tak, že načítá z paměti jednotlivé instrukce a ty následně zpracovává. Instrukce se zpracovávají v pořadí v jakém jsou uloženy v paměti. Vezměme jednoduchý program, který v nekonečném
Výroková a predikátová logika - VIII
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2017/2018 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Vyhledávání. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 12.
Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 12. září 2016 Jiří Dvorský (VŠB TUO) Vyhledávání 201 / 344 Osnova přednášky
Pascal. Katedra aplikované kybernetiky. Ing. Miroslav Vavroušek. Verze 7
Pascal Katedra aplikované kybernetiky Ing. Miroslav Vavroušek Verze 7 Proměnné Proměnná uchovává nějakou informaci potřebnou pro práci programu. Má ve svém oboru platnosti unikátní jméno. (Připadne, musí
Analýza toku dat. Petr Krajča. Katedra informatiky Univerzita Palackého v Olomouci. 15. listopad, 2012
Překladače 2 Analýza toku dat Petr Krajča Katedra informatiky Univerzita Palackého v Olomouci 15. listopad, 2012 Petr Krajča (UP) KMI/PRKL2: Přednáška I. 15. listopad, 2012 1 / 33 Lokální analýza: živost
10. Složitost a výkon
Jiří Vokřínek, 2016 B6B36ZAL - Přednáška 10 1 Základy algoritmizace 10. Složitost a výkon doc. Ing. Jiří Vokřínek, Ph.D. Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Jiří
Základy programovaní 3 - Java. Unit testy. Petr Krajča. Katedra informatiky Univerzita Palackého v Olomouci. 26.,27.
Základy programovaní 3 - Java Unit testy Petr Krajča Katedra informatiky Univerzita Palackého v Olomouci 26.,27. listopad, 2014 Petr Krajča (UP) Unit testy 26.,27. listopad, 2014 1 / 14 Testování zásadní
Základy algoritmizace, návrh algoritmu
Základy algoritmizace, návrh algoritmu Algoritmus Předpoklady automatického výpočtu: předem stanovit (rozmyslet) přesný postup během opakovaného provádění postupu již nepřemýšlet a postupovat mechanicky
Dijkstrův algoritmus
Dijkstrův algoritmus Hledání nejkratší cesty v nezáporně hranově ohodnoceném grafu Necht je dán orientovaný graf G = (V, H) a funkce, která každé hraně h = (u, v) H přiřadí nezáporné reálné číslo označované
8. lekce Úvod do jazyka C 3. část Základní příkazy jazyka C Miroslav Jílek
8. lekce Úvod do jazyka C 3. část Základní příkazy jazyka C Miroslav Jílek 1/41 Základní příkazy Všechny příkazy se píšou malými písmeny! Za většinou příkazů musí být středník (;)! 2/41 Základní příkazy
Výroková a predikátová logika - II
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2013/2014 1 / 20 Základní syntax Jazyk Výroková logika je logikou
Algoritmizace a programování. Ak. rok 2012/2013 vbp 1. ze 44
Algoritmizace a programování Ak. rok 2012/2013 vbp 1. ze 44 Vladimír Beneš Petrovický K101 katedra matematiky, statistiky a informačních technologií vedoucí katedry E-mail: vbenes@bivs.cz Telefon: 251
Výrazy a operátory. Operátory Unární - unární a unární + Např.: a +b
Výrazy a operátory i = 2 i = 2; to je výraz to je příkaz 4. Operátory Unární - unární a unární + Např.: +5-5 -8.345 -a +b - unární ++ - inkrement - zvýší hodnotu proměnné o 1 - unární -- - dekrement -
Funkce, podmíněný příkaz if-else, příkaz cyklu for
Funkce, podmíněný příkaz if-else, příkaz cyklu for Definice funkce Funkce je pojmenovaná část programu, kterou lze dále zavolat v jiné části programu. V Pythonu je definována klíčovým slovem def. Za tímto
Složitost problémů. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 25. dubna / 23
Složitost problémů Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 25. dubna 2012 1/ 23 Složitost problémů Ukazuje se, že různé(algoritmické) problémy jsou různě těžké. Obtížnější jsou ty problémy, k
Výpočet globálního stavu
PDV 09 2017/2018 Výpočet globálního stavu Michal Jakob michal.jakob@fel.cvut.cz Centrum umělé inteligence, katedra počítačů, FEL ČVUT Globální Stav Globální stav: množina lokální stavů procesů v DS a stavů
PŘEDNÁŠKA 2 POSLOUPNOSTI
PŘEDNÁŠKA 2 POSLOUPNOSTI 2.1 Zobrazení 2 Definice 1. Uvažujme libovolné neprázdné množiny A, B. Zobrazení množiny A do množiny B je definováno jako množina F uspořádaných dvojic (x, y A B, kde ke každému
Programovací jazyk Pascal
Programovací jazyk Pascal Syntaktická pravidla (syntaxe jazyka) přesná pravidla pro zápis příkazů Sémantická pravidla (sémantika jazyka) pravidla, která každému příkazu přiřadí přesný význam Všechny konstrukce
Výroková a predikátová logika - VIII
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2016/2017 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2016/2017 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
PODPROGRAMY PROCEDURY A FUNKCE
PODPROGRAMY PROCEDURY A FUNKCE Programy bez podprogramů Příklady: a) Napište program, který na obrazovku nakreslí čáru složenou ze znaků pomlčka. program Cara; b) Napište program, který na obrazovku nakreslí
Algoritmizace prostorových úloh
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Algoritmus Daniela Szturcová Tento
ROZHODOVACÍ PROCEDURY A VERIFIKACE PAVEL SURYNEK, KTIML HTTP://KTIML.MFF.CUNI.CZ/~SURYNEK/NAIL094
10 ROZHODOVACÍ PROCEDURY A VERIFIKACE PAVEL SURYNEK, KTIML HTTP://KTIML.MFF.CUNI.CZ/~SURYNEK/NAIL094 Matematicko-fyzikální fakulta Univerzita Karlova v Praze 1 ROZHODOVÁNÍ TEORIÍ POMOCÍ SAT ŘEŠIČE (SMT)
Predik atov a logika - pˇredn aˇska () Predik atov a logika - pˇredn aˇska / 16
Predikátová logika - přednáška 3 6. 1. 2015 () Predikátová logika - přednáška 3 6. 1. 2015 1 / 16 Věta (o dedukci) Bud L jazyk, T teorie pro L, ϕ L-sentence a ψ L-formule. Pak Věta (o kompaktnosti) T ϕ
Algoritmy I. Cvičení č. 2, 3 ALGI 2018/19
Algoritmy I Cvičení č. 2, 3 1 ALG I, informace Cvičící RNDr. Eliška Ochodková, Ph.D., kancelář EA439 eliska.ochodkova@vsb.cz www.cs.vsb.cz/ochodkova Přednášející doc. Mgr. Jiří Dvorský, Ph.D., kancelář
Algoritmizace, základy programování, VY_32_INOVACE_PRG_ALGO_01
Anotace sady: Algoritmizace, základy programování, VY_32_INOVACE_PRG_ALGO_01 Autor: Blanka Sadovská Klíčová slova: Algoritmus, proměnná, diagram Stupeň a typ vzdělávání: gymnaziální vzdělávání, 3. ročník
VISUAL BASIC. Práce se soubory
VISUAL BASIC Práce se soubory Práce se soubory 1/2 2 Vstupní data pro programy bývají uloženy do souborů Vstupy pro výpočet, nastavení vzhledu aplikace Výsledky práce programu je potřeba uchovat uložit
Složitost 1.1 Opera ní a pam ová složitost 1.2 Opera ní složitost v pr rném, nejhorším a nejlepším p ípad 1.3 Asymptotická složitost
1 Složitost 1.1 Operační a paměťová složitost Nezávislé určení na konkrétní implementaci Několik typů operací = sčítání T+, logické T L, přiřazení T A(assign), porovnání T C(compare), výpočet adresy pole
zapište obslužnou metodu události Click tlačítka a vyzkoušejte chování polevýsledek.text = polečíslo1.text + polečíslo2.text;
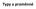Typy a proměnné zapište obslužnou metodu události Click tlačítka a vyzkoušejte chování polevýsledek.text = polečíslo1.text + polečíslo2.text; Typy Hodnoty, kterých mohou nabývat vlastnosti prvků nejsou
Činnost počítače po zapnutí
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Činnost počítače po zapnutí Paměť RWM(Read Write Memory - paměť pro čtení a zápis, označovaná také jako RAM)
Výroková a predikátová logika - V
Výroková a predikátová logika - V Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - V ZS 2015/2016 1 / 21 Dokazovací systémy VL Hilbertovský kalkul Hilbertovský
Katedra informatiky a výpočetní techniky. 10. prosince Ing. Tomáš Zahradnický doc. Ing. Róbert Lórencz, CSc.
Katedra informatiky a výpočetní techniky České vysoké učení technické, fakulta elektrotechnická Ing. Tomáš Zahradnický doc. Ing. Róbert Lórencz, CSc. 10. prosince 2007 Pamět ové banky S výhodou používáme
Algoritmy a datové struktury
Algoritmy a datové struktury 1 / 34 Obsah přednášky Základní řídící struktury posloupnost příkazů podmínka cyklus s podmínkou na začátku cyklus s podmínkou na konci cyklus s pevným počtem opakování Jednoduchá
2) Napište algoritmus pro vložení položky na konec dvousměrného seznamu. 3) Napište algoritmus pro vyhledání položky v binárním stromu.
Informatika 10. 9. 2013 Jméno a příjmení Rodné číslo 1) Napište algoritmus pro rychlé třídění (quicksort). 2) Napište algoritmus pro vložení položky na konec dvousměrného seznamu. 3) Napište algoritmus
NP-ÚPLNÉ PROBLÉMY. Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze
NP-ÚPLNÉ PROBLÉMY Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze BI-GRA, LS 2010/2011, Lekce 13 Evropský sociální fond Praha & EU: Investujeme do
Dobývání znalostí. Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické informatiky Matematicko-fyzikální fakulta Univerzity Karlovy v Praze
Dobývání znalostí Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické informatiky Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Dobývání znalostí Pravděpodobnost a učení Doc. RNDr. Iveta Mrázová,
ÚVODNÍ ZNALOSTI. datové struktury. správnost programů. analýza algoritmů
ÚVODNÍ ZNALOSTI datové struktury správnost programů analýza algoritmů Datové struktury základní, primitivní, jednoduché datové typy: int, char,... hodnoty: celá čísla, znaky, jednoduché proměnné: int i;
Řídicí struktury. alg3 1
Řídicí struktury Řídicí struktura je programová konstrukce, která se skládá z dílčích příkazů a předepisuje pro ně způsob provedení Tři druhy řídicích struktur: posloupnost, předepisující postupné provedení
Práce se soubory. Úvod do programování 2 Tomáš Kühr
Práce se soubory Úvod do programování 2 Tomáš Kühr Soubory z pohledu C u Soubor chápeme jako posloupnost bytů uložených na disku u Datový proud (anglicky stream) u Ještě obecnější přístup u Sjednocuje
Lekce 04 Řídící struktury
Počítačové laboratoře bez tajemství aneb naučme se učit algoritmizaci a programování s využitím robotů Lekce 04 Řídící struktury Tento projekt CZ.1.07/1.3.12/04.0006 je spolufinancován Evropským sociálním
Rozhodnutelné a nerozhodnutelné problémy. M. Kot, Z. Sawa (VŠB-TU Ostrava) Úvod do teoretické informatiky 24. dubna / 49
Rozhodnutelné a nerozhodnutelné problémy M. Kot, Z. Sawa (VŠB-TU Ostrava) Úvod do teoretické informatiky 24. dubna 2007 1/ 49 Co je to algoritmus? Algoritmus Algoritmus je mechanický postup skládající
Predikátová logika. Teoretická informatika Tomáš Foltýnek
Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Maturitní otázky z předmětu PROGRAMOVÁNÍ
Wichterlovo gymnázium, Ostrava-Poruba, příspěvková organizace Maturitní otázky z předmětu PROGRAMOVÁNÍ 1. Algoritmus a jeho vlastnosti algoritmus a jeho vlastnosti, formy zápisu algoritmu ověřování správnosti
Matematická logika. Rostislav Horčík. horcik
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Splnitelnost množin Definice Množina
Michal Krátký. Úvod do programovacích jazyků (Java), 2006/2007
Úvod do programovacích jazyků (Java) Michal Krátký 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programovacích jazyků (Java), 2006/2007 c 2006 Michal Krátký Úvod do programovacích jazyků
IB108 Sada 1, Příklad 1 Vypracovali: Tomáš Krajča (255676), Martin Milata (256615)
IB108 Sada 1, Příklad 1 ( ) Složitost třídícího algoritmu 1/-Sort je v O n log O (n.71 ). Necht n = j i (velikost pole, které je vstupním parametrem funkce 1/-Sort). Lehce spočítáme, že velikost pole předávaná
1. lekce. do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme:
1. lekce 1. Minimální program do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme: #include #include int main() { printf("hello world!\n"); return 0; 2.