2. Bodové pole a souřadnicové výpočty
|
|
|
- Emil Vaněk
- před 9 lety
- Počet zobrazení:
Transkript
1 2. Bodové pole a souřadnicové výpočty 2.1 Body 2.2 Bodová pole 2.3 Polohové bodové pole Rozdělení polohového bodového pole Dokumentace geodetického bodu Stabilizace a signalizace bodů. 2.4 Souřadnicové výpočty Délka Směrník Polární metoda Protínání vpřed z úhlů Protínání vpřed z délek Polygonové pořady Protínání zpět, volné stanovisko. 1
2 2.1 Body. Měřické body : - Geodetické : jsou stabilizovány, popř. signalizovány a je k nim vyhotovena dokumentace geodetických údajů. - Ostatní : předpokládá se pouze dočasná stabilizace a speciální použití. Geodetický bod: - trvale označený bod, stanovenými měřickými značkami a signalizačními nebo ochrannými zařízeními. GB vytváří bodová pole (BP) a geodetické sítě (GS). Každý GB je vždy označen číslem a může mít i název. Zároveň je možné aby jeden GB patřil do více BP. Ke GB se vyplňuje předepsaný formulář. 2
3 2.2 Bodová pole - Polohové bodové pole. - Základní polohové bodové pole (σ xy = 15 mm). - Zhušťovací body (σ xy = 20 mm). - Podrobné polohové bodové pole (σ xy = 60 mm) - Výškové bodové pole. - Základní. - Podrobné. - Stabilizované body technických nivelací. - Tíhové bodové pole. (potřebné pro určování výšek a věd. účely) - Základní. - Podrobné. 3
4 2.2 Bodová pole Bodová pole a jejich správa a údržba jsou v ČR dána zákony a vyhláškami, konkrétní formulace lze nalézt v: [1] Vyhláška č. 31/1995 Sb., o zeměměřictví [2] Vyhláška č. 26/2007 Sb., o zápisech vlastnických a jiných věcných práv k nemovitostem 4
5 2.3 Polohové bodové pole Bodová pole byla po roce 1918 budována jednotně v rámci celé tehdejší ČSR. Výpočet v S-JTSK. - Základní polohové bodové pole. - Body referenční sítě NULRAD (nultý řád) - Body Astronomicko-Geodetické sítě (AGS) - Body České státní trigonometrické sítě (ČSTS) - Body geodynamické sítě. - Zhušťovací body. - Podrobné polohové bodové pole (ČSTS byla dokončena v 50. letech našeho století na území celé ČSR. Síť se člení na pět řádů, body nižšího řádu plošně zhušťují síť bodů řádu vyššího. Hustota bodů V. řádu je 1 3 km. Relativní polohová přesnost vztažená k sousedním bodům sítě je udávána hodnotou cca 15 mm. Na území ČR se nachází cca 30 tisíc trigonometrických bodů.) 5
6 2.3.1 Rozdělení polohového bodového pole. ČSTS I. řád 6
7 2.3.1 Rozdělení polohového bodového pole. ČS AGS (strana cca 36 km) 7
8 2.3.1 Rozdělení polohového bodového pole. NULRAD GPS zpřesňování BP (od 1991) 8
9 2.3.1 Rozdělení polohového bodového pole. NULRAD GPS zpřesňování BP 9
10 2.3.1 Rozdělení polohového bodového pole. Základní geodynamická síť 10
11 2.3.2 Dokumentace geodetického bodu. Geodetické údaje : Ke každému GB se vyplňuje předepsaný formulář. U každého GB si uživatelé sami musí ověřit, zda se geodetické údaje nezměnily. GB se podle potřeby chrání ochrannými zařízeními (ochranné tyče, výstražné tabulky). 11
12 2.3.2 Dokumentace geodetického bodu. 12
13 2.3.2 Dokumentace geodetického bodu. 13
14 2.3.3 Stabilizace a signalizace bodů. Trigonometrické body se stabilizují v terénu kamenem délky asi 0,8 m, jehož hlava tvaru krychle o straně 0,2 m má na horní ploše vytesaný křížek. Tato povrchová značka je jištěna dvěma podzemními značkami. Obvykle jde o kamennou a skleněnou desku s křížkem na horní ploše, uložené asi 0,2 m pod předcházející značkou. Stabilizační značky musí být umístěny na svislici s přesností 3 mm. Jáma se poté zasype odlišným materiálem, který slouží k usnadnění vyhledání značky. 14
15 2.3.3 Stabilizace a signalizace bodů. Pokud nelze použít podzemní značky (věž kostela), stabilizují se zajišťovací body, které musí být mezi sebou vzájemně viditelné a vzdálené max. 500 m od trigonometrického bodu. Z každého bodu musí být vidět alespoň jedna orientace (TB nebo bod 1.tř. PBPP), pokud není, zřizuje se nejméně jeden orientační bod. Zajišťovací body se stabilizují v terénu kamenem s hlavou o straně 0,15 m, která má na horní ploše vytesaný křížek a jednou podzemní značkou. Orientační body se stabilizují stejně jako zajišťovací. 15
16 2.3.3 Stabilizace a signalizace bodů. Body PBPP 1. tř. př. se stabilizují stejně jako zajišťovací body, pokud jsou tyto body trvale signalizovány, opět jsou nutné zajišťovacími body. Body PBPP tř. př. se volí na objektech s osazenou stabilizační značkou kteréhokoli bodového pole, na hraničních kamenech, jako znak na šachtách, poklopech a dalších objektech apod. Lze je také stabilizovat kamennými hranoly s křížkem nebo důlkem na horní ploše, ocelovými trubkami nebo roxory v betonu nebo plnostěnnými trubkami, atd. K dočasné stabilizaci se užívá dřevěných kolíků (s křížkem nebo nastřeleným hřebíčkem) nebo křížků vyznačených křídou na objektu. 16
17 2.3.3 Stabilizace a signalizace bodů. Signalizace bodů Na bodech ČSTS byly vystavěny měřické pyramidy, v jejichž vrcholu je umístěna černobílá výtyčka. Pro signalizaci bodů tř. př. se používá především výtyček umístěných ve stojánku, hrotu svisle drženého měřického hřebu nebo tužky. 17
18 2.4 Souřadnicové výpočty. Podkladem pro polohové měření jsou body polohového bodového pole. Poloha těchto bodů je dána pravoúhlými rovinnými souřadnicemi Y,X v daném souřadnicovém systému. V tomtéž systému se udává poloha nově určovaných bodů. Výpočty se odehrávají v rovině, přímo měřené hodnoty je nutno redukovat z nadmořské výšky a kartografického zobrazení! Souřadnicové rozdíly : x 12 = x 2 - x 1, y 12 = y 2 - y 1, x 21 = x 1 - x 2, y 21 = y 1 - y 2. 18
19 2.4.1 Délka. Vzdálenost dvou bodů, platí s 12 = s 21. Znaménko je vždy kladné. s = x12 + y12 Z pravoúhlého trojúhelníku lze odvodit další možnosti výpočtu s. 19
20 2.4.2 Směrník. Směrník je orientovaný úhel, který svírá spojnice dvou bodů s rovnoběžkou s kladnou osou X souřadnicové soustavy. Z obrázku vyplývá : σ 12 = 200 g + σ 21 tg ϕ 12 = y x Tabulkový úhel ϕ je třeba přepočítat do správného kvadrantu. 20
21 2.4.2 Směrník. Kvadranty I. II. III. IV. y x σ 12 = ϕ g - ϕ g + ϕ g - ϕ 12 21
22 2.4.2 Směrník. Tento postup výpočtu byl vytvořen pro výpočty z tabulek goniom. funkcí, kde byly hodnoty tabelovány pouze pro kladné argumenty. Při použití kalkulačky je možný jednodušší výpočet, neboť funkce arctan(x) je jednoznačná v rozsahu (-100 gon, 100 gon). Pomocný úhel ϕ: =arctan Δ 1,2 Δ 1,2 Směrník se pak v případě, že X 1,2 < 0 vypočítá takto: 1,2 =+200, V opačném případě, kdy X 1,2 > 0, platí: 1,2 =, Výsledek výpočtu je stejný jako u předchozího postupu. Pro oba postupy platí, že je-li jeden souřadnicový rozdíl roven nule, lze hodnotu směrníku odvodit pouze na základě znalosti znaménka druhého souřadnicového rozdílu. Pokud X = 0, pak má směrník hodnotu 100 gon pro Y > 0 a 300 gon pro Y < 0. Pokud Y = 0, pak má směrník hodnotu 0 gon pro X > 0 a 200 gon pro X < 0. Jsou-li oba souřadnicové rozdíly rovny nule, směrník nelze vypočítat 22 poloha obou bodů je v rovině XY totožná.
23 2.4.3 Polární metoda. Slouží k výpočtu souřadnic bodu P 3, je-li měřeno : měřená délka strany d 13, vodorovný úhel ω. Známo : Y,X bodů P 1 a P 2. Postup výpočtu: α 13 = σ 12 + ω, y 13 = d 13. sin α 13, x 13 = d 13. cos α 13, y 3 = y 1 + y 13, x 3 = x 1 + x
24 2.4.4 Protínání vpřed z úhlů. Slouží k výpočtu souřadnic bodu P 3, je-li měřeno : vodorovné úhly ω 1, ω 2. Známo : Y,X bodů P 1 a P 2. s s = s = s sin sin ( ω ) 2 ( ω + ω ) sin 1 2 ( ω ) 1 ( ω + ω ) sin 1 2 Dále polární metoda, pro kontrolu se bod P 3 počítá z obou stanovisek. (P 1 : s 13,ω 1 ; P 2 : s 23,ω 2 ). 24
25 2.4.5 Protínání vpřed z délek. Slouží k výpočtu souřadnic bodu (P 3 ), je-li měřeno : vodorovné délky s 13, s 23. Známo : Y,X bodů P 1 a P 2. cos ( ω ) 1 = s + s s s s Dále polární metoda, pro kontrolu lze počítat z obou stanovisek. (P 1 : s 13,ω 1 ; P 2 : s 23,ω 2 ). 25
26 2.4.6 Polygonové pořady. Slouží k současnému určení souřadnic více bodů. Měří se délky všech stran a levostranné vrcholové úhly na všech polygonových bodech. Rozdělení : Jednostranně /oboustranně připojený /nepřipojený, Orientovaný /neorientovaný. Vetknutý (oboustranně připojený, neorientovaný). Uzavřený (začíná a končí na stejném bodě). Volný (jednostranně připojený a orientovaný). 26
27 2.4.6 Polygonové pořady. Oboustranně připojený a orientovaný. Známo : Y,X bodů A, B, 1, n. Měřeno : ω 1, ω 2 ω n ; d 12, d 23 d n-1,n. Určuje se : Y,X bodů 2, 3 n-1. 27
28 2.4.6 Polygonové pořady. Přibližný výpočet souřadnic s odděleným vyrovnáním uhlů a souřadnicových rozdílů. Postup výpočtu : 1. Výpočet směrníků na orientační body. 2. Úhlové vyrovnání. 3. Výpočet směrníků v polygonu. 4. Výpočet souřadnicových rozdílů. 5. Souřadnicové uzávěry. 6. Výpočet opravených souřadnicových rozdílů. 7. Výpočet souřadnic polygonových bodů. 28
29 2.4.6 Polygonové pořady. 1. Výpočet směrníků na orientační body σ 1A, σ nb. 2. Úhlové vyrovnání Úhlový uzávěr : ( ) g Oω = σ nb σ A + 1 ω i n i Nesmí překročit mezní hodnotu Oω um ω g u = 0 ω, 01 n + 3 M Rozdělení úhlové odchylky se provádí vždy úměrně počtu vrcholů: = O ω δω i i ω n, n počet bodů pořadu. ω = ω + δ 29
30 2.4.6 Polygonové pořady. 3. Výpočet směrníků v polygonu : α 12 = σ 1A + ω 1, α 23 = α 12 + ω 2 ± 200 g, α n-1,n = α n-2,n-1 + ω n-1 ± 200 g, α nb = α n-1,n + ω n ± 200 g = σ nb. Kontrola! 4. Výpočet souřadnicových rozdílů y 12 = d 12.sin α 12, x 12 =d 12.cos α 12, y n-1,n = d n-1,n.sin α n-1,n, x n-1,n = d n-1,n.cos α n-1,n. 30
31 2.4.6 Polygonové pořady. 5. Souřadnicové uzávěry : Souřadnicové uzávěry : O = y y, y 1n i i O = x x. x 1n i i Polohový uzávěr : O = O + O. 2 2 p x y u = 0, 01 d + 0, 10; M p p O u. M p i i 31
32 2.4.6 Polygonové pořady. 6. Výpočet opravených souřadnicových rozdílů : (úměrně souřadnicovým rozdílům) δ y i Oy = y y, i δ x i Ox = x x. i. Opravené souřadnicové rozdíly : y = y + δ, i i y i x = x + δ. i i x i Kontrola! y i = y 1n x i = x1n i i 32
33 2.4.6 Polygonové pořady. 7. Výpočet souřadnic y 1 = dáno, x 1 = dáno, y 2 = y 1 + y 12, x 2 = x 1 + x 12, y n = y n-1 + y n-1,n, x n = x n-1 + x n-1,n.. Kontrola! 33
34 2.4.6 Polygonové pořady. O. O ω ω Uzavřený polygonový pořad : Známo : Y,X bodů A (orientace), P 1. Měřeno : ω 1, ω 2 ω n ; d 12, d 23 d n-1,n. Určuje se : Y,X bodů 2, 3 n-1. Úhlový uzávěr : pro vnitřní úhly ( n 2) 200 i = ω pro vnější úhly ( n 2) 200 i = + ω Musí platit : Σ x = Σ y =0. Výpočet podle dříve popsaného postupu. 34
35 2.4.6 Polygonové pořady. O. O ω ω Uzavřený polygonový pořad (lokální soustava): Voleno : Y,X např. bodu P 1, souřadnicový systém. Měřeno : ω 1, ω 2 ω n ; d 12, d 23 d n-1,n. Určuje se : Y,X bodů 2, 3 n-1. Úhlový uzávěr : pro vnitřní úhly ( n 2) 200 i = ω pro vnější úhly ( n 2) 200 i = + ω Musí platit : Σ x = Σ y =0. Výpočet podle dříve popsaného postupu. 35
36 2.4.7 Protínání zpět. Z úhlů : Slouží k výpočtu souřadnic bodu (P 4 ), je-li na určovaném bodě měřeno : vodorovné úhly ω 12, ω 23. Je známo : Y,X bodů P 1, P 2, P 3. Volné stanovisko : Slouží k výpočtu souřadnic bodu (S), jsou-li na určovaném bodě měřeny vodorovné úhly a délky na body P i. Minimum jsou 2 délky a 1 úhel. Je známo : Y,X bodů P i. Složitý výpočet, řeší se nejlépe vyrovnáním MNČ, v současné době v geodetické praxi často využíváno. 36
3. Souřadnicové výpočty
 3. Souřadncové výpočty 3.1 Délka. 3.2 Směrník. 3.3 Polární metoda. 3.4 Protínání vpřed z úhlů. 3.5 Protínání vpřed z délek. 3.6 Polygonové pořady. 3.7 Protínání zpět. 3.8 Transformace souřadnc. 3.9 Volné
3. Souřadncové výpočty 3.1 Délka. 3.2 Směrník. 3.3 Polární metoda. 3.4 Protínání vpřed z úhlů. 3.5 Protínání vpřed z délek. 3.6 Polygonové pořady. 3.7 Protínání zpět. 3.8 Transformace souřadnc. 3.9 Volné
2. Bodové pole a souřadnicové výpočty
 2. Bodové pole a souřadnicové výpočty 2.1 Body 2.2 Bodová pole 2.3 Polohové bodové pole. 2.3.1 Rozdělení polohového bodového pole. 2.3.2 Dokumentace geodetického bodu. 2.3.3 Stabilizace a signalizace bodů.
2. Bodové pole a souřadnicové výpočty 2.1 Body 2.2 Bodová pole 2.3 Polohové bodové pole. 2.3.1 Rozdělení polohového bodového pole. 2.3.2 Dokumentace geodetického bodu. 2.3.3 Stabilizace a signalizace bodů.
2.2 Bodová pole. - Výškové bodové pole. - Základní. - Podrobné. - Stabilizované body technických nivelací.
 2. Bodová pole 2.1 Body 2.2 Bodová pole 2.3 Polohové bodové pole. 2.3.1 Rozdělení polohového bodového pole. 2.3.2 Dokumentace geodetického bodu. 2.3.3 Stabilizace a signalizace bodů. 2.4 Výškové bodové
2. Bodová pole 2.1 Body 2.2 Bodová pole 2.3 Polohové bodové pole. 2.3.1 Rozdělení polohového bodového pole. 2.3.2 Dokumentace geodetického bodu. 2.3.3 Stabilizace a signalizace bodů. 2.4 Výškové bodové
Předloha č. 1 výpočty v bodovém poli
 Předloha č. 1 výpočty v bodovém poli 1. Zadání 2. Zápisníky 3. Stručný návod Groma 4. Protokol Groma 5. Stručný návod Geus 6. Protokol Geus 7. Stručný návod Kokeš 8. Protokol Kokeš 1 Zadání 1) Vložte dané
Předloha č. 1 výpočty v bodovém poli 1. Zadání 2. Zápisníky 3. Stručný návod Groma 4. Protokol Groma 5. Stručný návod Geus 6. Protokol Geus 7. Stručný návod Kokeš 8. Protokol Kokeš 1 Zadání 1) Vložte dané
3. Souřadnicové výpočty
 3. Souřadnicové výpočty 3.1 Délka. 3.2 Směrník. 3.3 Polární metoda. 3.4 Protínání vpřed z úhlů. 3.5 Protínání vpřed z délek. 3.6 Polygonové pořady. 3.7 Protínání zpět. 3.8 Transformace souřadnic. 3.9 Volné
3. Souřadnicové výpočty 3.1 Délka. 3.2 Směrník. 3.3 Polární metoda. 3.4 Protínání vpřed z úhlů. 3.5 Protínání vpřed z délek. 3.6 Polygonové pořady. 3.7 Protínání zpět. 3.8 Transformace souřadnic. 3.9 Volné
2. Bodová pole. 154GUI1 Geodézie 1
 2. Bodová pole 2.1 Body 2.2 Bodová pole 2.3 Polohové bodové pole. 2.3.1 Rozdělení polohového bodového pole. 2.3.2 Dokumentace geodetického bodu. 2.3.3 Stabilizace a signalizace bodů. 2.4 Výškové bodové
2. Bodová pole 2.1 Body 2.2 Bodová pole 2.3 Polohové bodové pole. 2.3.1 Rozdělení polohového bodového pole. 2.3.2 Dokumentace geodetického bodu. 2.3.3 Stabilizace a signalizace bodů. 2.4 Výškové bodové
STEREOMETRIE. Vzdálenost bodu od přímky. Mgr. Jakub Němec. VY_32_INOVACE_M3r0113
 STEREOMETRIE Vzdálenost bodu od přímky Mgr. Jakub Němec VY_32_INOVACE_M3r0113 VZDÁLENOST BODU OD PŘÍMKY V PROSTORU Při hledání vzdálenosti bodu od geometrického útvaru v prostoru je nutné si vždy úlohu
STEREOMETRIE Vzdálenost bodu od přímky Mgr. Jakub Němec VY_32_INOVACE_M3r0113 VZDÁLENOST BODU OD PŘÍMKY V PROSTORU Při hledání vzdálenosti bodu od geometrického útvaru v prostoru je nutné si vždy úlohu
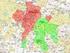
Ukázka hustoty bodového pole
 Ing. Pavel Hánek, Ph.D. hanek00@zf.jcu.cz síť bodů pokrývající území ČR u bodů jsou známé souřadnice Y, X v S-JTSK, případně souřadnice B, L v ERTS pro každý bod jsou vyhotoveny geodetické údaje (GÚ) ukázka
Ing. Pavel Hánek, Ph.D. hanek00@zf.jcu.cz síť bodů pokrývající území ČR u bodů jsou známé souřadnice Y, X v S-JTSK, případně souřadnice B, L v ERTS pro každý bod jsou vyhotoveny geodetické údaje (GÚ) ukázka
Energetický regulační
 Energetický regulační ENERGETICKÝ REGULAČNÍ ÚŘAD ROČNÍK 16 V JIHLAVĚ 25. 5. 2016 ČÁSTKA 4/2016 OBSAH: str. 1. Zpráva o dosažené úrovni nepřetržitosti přenosu nebo distribuce elektřiny za rok 2015 2 Zpráva
Energetický regulační ENERGETICKÝ REGULAČNÍ ÚŘAD ROČNÍK 16 V JIHLAVĚ 25. 5. 2016 ČÁSTKA 4/2016 OBSAH: str. 1. Zpráva o dosažené úrovni nepřetržitosti přenosu nebo distribuce elektřiny za rok 2015 2 Zpráva
PŘEHLED ZÁKLADNÍCH ZKUŠEBNÍCH OTÁZEK ke zkoušce odborné způsobilosti k udělení úředního oprávnění pro ověřování výsledků zeměměřických činností
 PŘEHLED ZÁKLADNÍCH ZKUŠEBNÍCH OTÁZEK ke zkoušce odborné způsobilosti k udělení úředního oprávnění pro ověřování výsledků zeměměřických činností Obecná část 1. Základní ustanovení katastrálního zákona,
PŘEHLED ZÁKLADNÍCH ZKUŠEBNÍCH OTÁZEK ke zkoušce odborné způsobilosti k udělení úředního oprávnění pro ověřování výsledků zeměměřických činností Obecná část 1. Základní ustanovení katastrálního zákona,
4.6.6 Složený sériový RLC obvod střídavého proudu
 4.6.6 Složený sériový LC obvod střídavého proudu Předpoklady: 41, 4605 Minulá hodina: odpor i induktance omezují proud ve střídavém obvodu, nemůžeme je však sčítat normálně, ale musíme použít Pythagorovu
4.6.6 Složený sériový LC obvod střídavého proudu Předpoklady: 41, 4605 Minulá hodina: odpor i induktance omezují proud ve střídavém obvodu, nemůžeme je však sčítat normálně, ale musíme použít Pythagorovu
3.2.4 Podobnost trojúhelníků II
 3..4 odobnost trojúhelníků II ředpoklady: 33 ř. 1: Na obrázku jsou nakresleny podobné trojúhelníky. Zapiš jejich podobnost (aby bylo zřejmé, který vrchol prvního trojúhelníku odpovídá vrcholu druhého trojúhelníku).
3..4 odobnost trojúhelníků II ředpoklady: 33 ř. 1: Na obrázku jsou nakresleny podobné trojúhelníky. Zapiš jejich podobnost (aby bylo zřejmé, který vrchol prvního trojúhelníku odpovídá vrcholu druhého trojúhelníku).
Vývoj polohových základz. kladů na. Ing. Eva Sálová
 MAPOVÁNÍ Vývoj polohových základz kladů na území České republiky Ing. Eva Sálová Klasické geodetické polohové systémy 1. Katastráln lní triangulace na území bývalé rakouské monarchie 2. Vojenská triangulace
MAPOVÁNÍ Vývoj polohových základz kladů na území České republiky Ing. Eva Sálová Klasické geodetické polohové systémy 1. Katastráln lní triangulace na území bývalé rakouské monarchie 2. Vojenská triangulace
(a) = (a) = 0. x (a) > 0 a 2 ( pak funkce má v bodě a ostré lokální maximum, resp. ostré lokální minimum. Pokud je. x 2 (a) 2 y (a) f.
 I. Funkce dvou a více reálných proměnných 5. Lokální extrémy. Budeme uvažovat funkci f = f(x 1, x 2,..., x n ), která je definovaná v otevřené množině G R n. Řekneme, že funkce f = f(x 1, x 2,..., x n
I. Funkce dvou a více reálných proměnných 5. Lokální extrémy. Budeme uvažovat funkci f = f(x 1, x 2,..., x n ), která je definovaná v otevřené množině G R n. Řekneme, že funkce f = f(x 1, x 2,..., x n
Vrtání závitů bez vyrovnávací hlavičky (G331, G332)
 Předpoklady Funkce Technickým předpokladem pro vrtání závitů bez vyrovnávací hlavičky je vřeteno s regulací polohy a systémem pro měření dráhy. Vrtání závitů bez vyrovnávací hlavičky se programuje pomocí
Předpoklady Funkce Technickým předpokladem pro vrtání závitů bez vyrovnávací hlavičky je vřeteno s regulací polohy a systémem pro měření dráhy. Vrtání závitů bez vyrovnávací hlavičky se programuje pomocí
Sada 2 Geodezie II. 11. Určování ploch z map a plánů
 S třední škola stavební Jihlava Sada 2 Geodezie II 11. Určování ploch z map a plánů Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2
S třední škola stavební Jihlava Sada 2 Geodezie II 11. Určování ploch z map a plánů Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2
Post-Processingové zpracování V módu post-processingu je možné s tímto přístrojem docílit až centimetrovou přesnost z běžné 0,5m.
 Výjimečná EVEREST technologie Aplikovaná EVEREST technologie pro dobrou ochranu vícecestného šíření GNSS signálu a pro spolehlivé a přesné řešení. To je důležité pro kvalitní měření s minimální chybou.
Výjimečná EVEREST technologie Aplikovaná EVEREST technologie pro dobrou ochranu vícecestného šíření GNSS signálu a pro spolehlivé a přesné řešení. To je důležité pro kvalitní měření s minimální chybou.
1.3.1 Kruhový pohyb. Předpoklady: 1105
 .. Kruhový pohyb Předpoklady: 05 Předměty kolem nás se pohybují různými způsoby. Nejde pouze o přímočaré nebo křivočaré posuvné pohyby. Velmi často se předměty otáčí (a některé se přitom pohybují zároveň
.. Kruhový pohyb Předpoklady: 05 Předměty kolem nás se pohybují různými způsoby. Nejde pouze o přímočaré nebo křivočaré posuvné pohyby. Velmi často se předměty otáčí (a některé se přitom pohybují zároveň
SYLABUS PŘEDNÁŠKY 6a Z INŽENÝRSKÉ GEODÉZIE (Polohové vytyčovací sítě) 4. ročník bakalářského studia studijní program G studijní obor G
 SYLABUS PŘEDNÁŠKY 6a Z INŽENÝRSKÉ GEODÉZIE (Polohové vytyčovací sítě) 4. ročník bakalářského studia studijní program G studijní obor G říjen 2014 1 7. POLOHOVÉ VYTYČOVACÍ SÍTĚ Vytyčení je součástí realizace
SYLABUS PŘEDNÁŠKY 6a Z INŽENÝRSKÉ GEODÉZIE (Polohové vytyčovací sítě) 4. ročník bakalářského studia studijní program G studijní obor G říjen 2014 1 7. POLOHOVÉ VYTYČOVACÍ SÍTĚ Vytyčení je součástí realizace
Testování výškové přesnosti navigační GPS pro účely (cyklo)turistiky
 Fakulta aplikovaných věd Katedra matematiky Testování výškové přesnosti navigační GPS pro účely (cyklo)turistiky Kompletní grafické přílohy bakalářské práce Plzeň 2006 David Velhartický Seznam příloh Praktický
Fakulta aplikovaných věd Katedra matematiky Testování výškové přesnosti navigační GPS pro účely (cyklo)turistiky Kompletní grafické přílohy bakalářské práce Plzeň 2006 David Velhartický Seznam příloh Praktický
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE. 1 Zaměření a vyrovnání rovinné sítě
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ - OBOR GEODÉZIE, KARTOGRAFIE A GEOINFORMATIKA KATEDRA SPECIÁLNÍ GEODÉZIE název předmětu GEODÉZIE 1 číslo úlohy název úlohy 1 Zaměření a vyrovnání rovnné
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ - OBOR GEODÉZIE, KARTOGRAFIE A GEOINFORMATIKA KATEDRA SPECIÁLNÍ GEODÉZIE název předmětu GEODÉZIE 1 číslo úlohy název úlohy 1 Zaměření a vyrovnání rovnné
Staveniště a zařízení staveniště
 Staveniště a zařízení staveniště Staveniště - místo určené k realizaci stavby nebo udržovacích prací - zahrnuje zejména pozemek ve vlastnictví investora, ale i další pozemky, které jsou nutné k provedení
Staveniště a zařízení staveniště Staveniště - místo určené k realizaci stavby nebo udržovacích prací - zahrnuje zejména pozemek ve vlastnictví investora, ale i další pozemky, které jsou nutné k provedení
2.8.9 Parametrické rovnice a nerovnice s absolutní hodnotou
 .8.9 Parametrické rovnice a nerovnice s absolutní hodnotou Předpoklady: 0,, 806 Pedagogická poznámka: Opět si napíšeme na začátku hodiny na tabuli jednotlivé kroky postupu při řešení rovnic (nerovnic)
.8.9 Parametrické rovnice a nerovnice s absolutní hodnotou Předpoklady: 0,, 806 Pedagogická poznámka: Opět si napíšeme na začátku hodiny na tabuli jednotlivé kroky postupu při řešení rovnic (nerovnic)
Funkce více proměnných
 Funkce více proměnných Funkce více proměnných Euklidův prostor Body, souřadnice, vzdálenost bodů Množina bodů, které mají od bodu A stejnou vzdálenost Uzavřený interval, otevřený interval Okolí bodu
Funkce více proměnných Funkce více proměnných Euklidův prostor Body, souřadnice, vzdálenost bodů Množina bodů, které mají od bodu A stejnou vzdálenost Uzavřený interval, otevřený interval Okolí bodu
Zásady označování budov
 MĚSTSKÝ ÚŘAD HORNÍ SLAVKOV Zásady označování budov Článek 1 Úvodní ustanovení Městský úřad Horní Slavkov určuje podle 32 odst. 1 zákona č. 128/2000 Sb., o obcích v pl. znění barvu a provedení čísel popisných,
MĚSTSKÝ ÚŘAD HORNÍ SLAVKOV Zásady označování budov Článek 1 Úvodní ustanovení Městský úřad Horní Slavkov určuje podle 32 odst. 1 zákona č. 128/2000 Sb., o obcích v pl. znění barvu a provedení čísel popisných,
Zřizování věcných břemen na pozemcích ve vlastnictví města Zábřeh
 1. Identifikační číslo 2. Kód 3. Pojmenování (název) životní situace Zřizování věcných břemen na pozemcích ve vlastnictví města Zábřeh 4. Základní informace Jedná se o uložení inženýrských sítí v souvislosti
1. Identifikační číslo 2. Kód 3. Pojmenování (název) životní situace Zřizování věcných břemen na pozemcích ve vlastnictví města Zábřeh 4. Základní informace Jedná se o uložení inženýrských sítí v souvislosti
PŘEJÍMACÍ A PERIODICKÉ ZKOUŠKY SOUŘADNICOVÝCH MĚŘICÍCH STROJŮ
 ČVUT - Fakulta strojní Ústav technologie obrábění, projektování a metrologie Měrové a školicí středisko Carl Zeiss PŘEJÍMACÍ A PERIODICKÉ ZKOUŠKY SOUŘADNICOVÝCH MĚŘICÍCH STROJŮ Ing. Libor Beránek Aktivity
ČVUT - Fakulta strojní Ústav technologie obrábění, projektování a metrologie Měrové a školicí středisko Carl Zeiss PŘEJÍMACÍ A PERIODICKÉ ZKOUŠKY SOUŘADNICOVÝCH MĚŘICÍCH STROJŮ Ing. Libor Beránek Aktivity
Dopravní úloha. Jiří Neubauer. Katedra ekonometrie FEM UO Brno
 Přednáška č. 9 Katedra ekonometrie FEM UO Brno Distribuční úlohy Budeme se zabývat 2 typy distribučních úloh dopravní úloha přiřazovací problém Dopravní úloha V dopravním problému se v typickém případě
Přednáška č. 9 Katedra ekonometrie FEM UO Brno Distribuční úlohy Budeme se zabývat 2 typy distribučních úloh dopravní úloha přiřazovací problém Dopravní úloha V dopravním problému se v typickém případě
E-ZAK. metody hodnocení nabídek. verze dokumentu: 1.1. 2011 QCM, s.r.o.
 E-ZAK metody hodnocení nabídek verze dokumentu: 1.1 2011 QCM, s.r.o. Obsah Úvod... 3 Základní hodnotící kritérium... 3 Dílčí hodnotící kritéria... 3 Metody porovnání nabídek... 3 Indexace na nejlepší hodnotu...4
E-ZAK metody hodnocení nabídek verze dokumentu: 1.1 2011 QCM, s.r.o. Obsah Úvod... 3 Základní hodnotící kritérium... 3 Dílčí hodnotící kritéria... 3 Metody porovnání nabídek... 3 Indexace na nejlepší hodnotu...4
PŘEJÍMACÍ A PERIODICKÉ ZKOUŠKY SOUŘADNICOVÝCH MĚŘICÍCH STROJŮ
 ČVUT - Fakulta strojní Ústav technologie obrábění, projektování a metrologie Ing. Libor Beránek Průmyslová metrologie PŘEJÍMACÍ A PERIODICKÉ ZKOUŠKY SOUŘADNICOVÝCH MĚŘICÍCH STROJŮ Aktivity mezinárodní
ČVUT - Fakulta strojní Ústav technologie obrábění, projektování a metrologie Ing. Libor Beránek Průmyslová metrologie PŘEJÍMACÍ A PERIODICKÉ ZKOUŠKY SOUŘADNICOVÝCH MĚŘICÍCH STROJŮ Aktivity mezinárodní
SYLABUS 7. a 8. PŘEDNÁŠKY Z GEODÉZIE 2 (Podrobné polohopisné měření)
 SYLABUS 7. a 8. PŘEDNÁŠKY Z GEODÉZIE 2 (Podrobné polohopisné měření) 1. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. duben 2016 1 Geodézie 2 přednáška
SYLABUS 7. a 8. PŘEDNÁŠKY Z GEODÉZIE 2 (Podrobné polohopisné měření) 1. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. duben 2016 1 Geodézie 2 přednáška
2.4.11 Nerovnice s absolutní hodnotou
 .. Nerovnice s absolutní hodnotou Předpoklady: 06, 09, 0 Pedagogická poznámka: Hlavním záměrem hodiny je, aby si studenti uvědomili, že se neučí nic nového. Pouze používají věci, které dávno znají, na
.. Nerovnice s absolutní hodnotou Předpoklady: 06, 09, 0 Pedagogická poznámka: Hlavním záměrem hodiny je, aby si studenti uvědomili, že se neučí nic nového. Pouze používají věci, které dávno znají, na
15 s. Analytická geometrie lineárních útvarů
 5 s Analytická geometrie lineárních útvarů ) Na přímce: a) Souřadnice bodu na přímce: Bod P nazýváme počátek - jeho souřadnice je P [0] Nalevo od počátku leží čísla záporná, napravo čísla kladná. Každý
5 s Analytická geometrie lineárních útvarů ) Na přímce: a) Souřadnice bodu na přímce: Bod P nazýváme počátek - jeho souřadnice je P [0] Nalevo od počátku leží čísla záporná, napravo čísla kladná. Každý
Kapitola I - Množiny bodů daných vlastností I.a Co je množinou všech bodů v rovině, které mají od daných dvou různých bodů stejnou vzdálenost? I.
 Kapitola I - Množiny bodů daných vlastností I.a Co je množinou všech bodů v rovině, které mají od daných dvou různých bodů stejnou vzdálenost? I.b Co je množinou středů všech kružnic v rovině, které prochází
Kapitola I - Množiny bodů daných vlastností I.a Co je množinou všech bodů v rovině, které mají od daných dvou různých bodů stejnou vzdálenost? I.b Co je množinou středů všech kružnic v rovině, které prochází
ISÚI Informační systém územní identifikace Proč? Co? Kde? Kdo? Jak? Kdy?
 ISÚI Informační systém územní identifikace Proč? Co? Kde? Kdo? Jak? Kdy? Jiří Formánek Český úřad zeměměřický a katastrální (ČÚZK) Projekt RÚIAN Projekt Vybudování Registru územní identifikace, adres a
ISÚI Informační systém územní identifikace Proč? Co? Kde? Kdo? Jak? Kdy? Jiří Formánek Český úřad zeměměřický a katastrální (ČÚZK) Projekt RÚIAN Projekt Vybudování Registru územní identifikace, adres a
Úlohy 22. ročníku Mezinárodní fyzikální olympiády - Havana, Cuba
 Úlohy 22. ročníku Mezinárodní fyzikální olympiády - Havana, Cuba Petr Pošta Text pro soutěžící FO a ostatní zájemce o fyziku 2 1. úloha Obrázek 1.1 ukazuje pevný, homogenní míč poloměru R. Před pádem na
Úlohy 22. ročníku Mezinárodní fyzikální olympiády - Havana, Cuba Petr Pošta Text pro soutěžící FO a ostatní zájemce o fyziku 2 1. úloha Obrázek 1.1 ukazuje pevný, homogenní míč poloměru R. Před pádem na
Cvičení č. 4 : Tachymetrie s TS postup, výpočet, zpracování, podklad
 Cvičení č. 4 : Tachymetrie s TS postup, výpočet, zpracování, podklad Obsah: 1 STRUČNÉ SEZNÁMENÍ S METODOU TACHYMETRIE...2 2 POLOHOVÉ A VÝŠKOVÉ PŘIPOJENÍ S TS PŘI TACHYMETRII...2 2.1 URČENÍ NOVÉHO BODU
Cvičení č. 4 : Tachymetrie s TS postup, výpočet, zpracování, podklad Obsah: 1 STRUČNÉ SEZNÁMENÍ S METODOU TACHYMETRIE...2 2 POLOHOVÉ A VÝŠKOVÉ PŘIPOJENÍ S TS PŘI TACHYMETRII...2 2.1 URČENÍ NOVÉHO BODU
Metodický materiál odboru dozoru a kontroly veřejné správy Ministerstva vnitra
 Metodický materiál odboru dozoru a kontroly veřejné správy Ministerstva vnitra Právní předpisy a jejich ustanovení související se zákonným zmocněním k vydání obecně závazné vyhlášky obce o vedení technické
Metodický materiál odboru dozoru a kontroly veřejné správy Ministerstva vnitra Právní předpisy a jejich ustanovení související se zákonným zmocněním k vydání obecně závazné vyhlášky obce o vedení technické
Otázky z kapitoly Stereometrie
 Otázky z kapitoly Stereometrie 10. února 015 Obsah 1 Krokované příklady (0 otázek) 1 Metrické vlastnosti (30 otázek) 1.1 Obtížnost 1 (16 otázek)....................................... 1. Obtížnost (14
Otázky z kapitoly Stereometrie 10. února 015 Obsah 1 Krokované příklady (0 otázek) 1 Metrické vlastnosti (30 otázek) 1.1 Obtížnost 1 (16 otázek)....................................... 1. Obtížnost (14
Číselné soustavy Ing. M. Kotlíková, Ing. A. Netrvalová Strana 1 (celkem 7) Číselné soustavy
 Číselné soustavy Ing. M. Kotlíková, Ing. A. Netrvalová Strana (celkem 7) Polyadické - zobrazené mnohočlenem desítková soustava 3 2 532 = 5 + 3 + 2 + Číselné soustavy Číslice tvořící zápis čísla jsou vlastně
Číselné soustavy Ing. M. Kotlíková, Ing. A. Netrvalová Strana (celkem 7) Polyadické - zobrazené mnohočlenem desítková soustava 3 2 532 = 5 + 3 + 2 + Číselné soustavy Číslice tvořící zápis čísla jsou vlastně
Kvadratické rovnice pro učební obory
 Variace 1 Kvadratické rovnice pro učební obory Autor: Mgr. Jaromír JUŘEK Kopírování a jkaékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
Variace 1 Kvadratické rovnice pro učební obory Autor: Mgr. Jaromír JUŘEK Kopírování a jkaékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
http://www.zlinskedumy.cz
 Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor Ročník 2, 3 Obor Anotace CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Elektronické obvody, vy_32_inovace_ma_42_06
Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor Ročník 2, 3 Obor Anotace CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Elektronické obvody, vy_32_inovace_ma_42_06
SYLABUS 6. PŘEDNÁŠKY Z INŽENÝRSKÉ GEODÉZIE
 SYLABUS 6. PŘEDNÁŠKY Z INŽENÝRSKÉ GEODÉZIE (Polohové vytyčovací sítě, Polohové vytyčování) 3. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. listopad 2015
SYLABUS 6. PŘEDNÁŠKY Z INŽENÝRSKÉ GEODÉZIE (Polohové vytyčovací sítě, Polohové vytyčování) 3. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. listopad 2015
Bezpečnostní úschovné objekty
 Příloha č. 1: Mechanické zábranné prostředky - písm. a) 30 zákona Příloha č.. 1.1: Bezpečnostní úschovné objekty a jejich zámky Bezpečnostní úschovné objekty Výstup Certifikát shody podle certifikačního
Příloha č. 1: Mechanické zábranné prostředky - písm. a) 30 zákona Příloha č.. 1.1: Bezpečnostní úschovné objekty a jejich zámky Bezpečnostní úschovné objekty Výstup Certifikát shody podle certifikačního
3. Rozměry a hmotnosti... 3. 4. Přiřazení typů a velikostí čelních desek... 7. 5. Odchylka od TPM... 8
 Tyto technické podmínky stanovují řadu vyráběných velikostí připojovacích skříní v ekonomickém provedení, které lze použít k čelním deskám VVM, VVPM, ALCM a ALKM. Platí pro výrobu, navrhování, objednávání,
Tyto technické podmínky stanovují řadu vyráběných velikostí připojovacích skříní v ekonomickém provedení, které lze použít k čelním deskám VVM, VVPM, ALCM a ALKM. Platí pro výrobu, navrhování, objednávání,
Geodetické polohové a výškové vytyčovací práce
 Geodézie přednáška 3 Geodetické polohové a výškové vytyčovací práce Ústav geoinformačních technologií Lesnická a dřevařská fakulta ugt.mendelu.cz tel.: 545134015 Geodetické vytyčovací práce řeší úlohu
Geodézie přednáška 3 Geodetické polohové a výškové vytyčovací práce Ústav geoinformačních technologií Lesnická a dřevařská fakulta ugt.mendelu.cz tel.: 545134015 Geodetické vytyčovací práce řeší úlohu
Úloha č. 6 Stanovení průběhu koncentrace příměsí polovodičů
 Úloha č. 6 Stanovení průběhu koncentrace příměsí polovodičů Úkol měření: 1. Změřte průběh resistivity podél monokrystalu polovodiče. 2. Vypočtěte koncentraci příměsí N A, D z naměřených hodnot resistivity.
Úloha č. 6 Stanovení průběhu koncentrace příměsí polovodičů Úkol měření: 1. Změřte průběh resistivity podél monokrystalu polovodiče. 2. Vypočtěte koncentraci příměsí N A, D z naměřených hodnot resistivity.
Metodické principy NIL
 Ústav pro hospodářskou úpravu lesů Brandýs nad Labem Metodické principy NIL Radim Adolt Analyticko metodické centrum NIL ÚHÚL, pobočka Kroměříž Adolt.Radim@uhul.cz 7. října 2015 Ústav pro hospodářskou
Ústav pro hospodářskou úpravu lesů Brandýs nad Labem Metodické principy NIL Radim Adolt Analyticko metodické centrum NIL ÚHÚL, pobočka Kroměříž Adolt.Radim@uhul.cz 7. října 2015 Ústav pro hospodářskou
Diferenciální počet funkcí jedné proměnné
 Diferenciální počet funkcí jedné proměnné 1 Diferenciální počet funkcí jedné proměnné - Úvod Diferenciální počet funkcí jedné proměnné - úvod V přírodě se neustále dějí změny. Naší snahou je nalézt příčiny
Diferenciální počet funkcí jedné proměnné 1 Diferenciální počet funkcí jedné proměnné - Úvod Diferenciální počet funkcí jedné proměnné - úvod V přírodě se neustále dějí změny. Naší snahou je nalézt příčiny
1. Kruh, kružnice. Mezi poloměrem a průměrem kružnice platí vztah : d = 2. r. Zapíšeme k ( S ; r ) Čteme kružnice k je určena středem S a poloměrem r.
 Kruh, kružnice, válec 1. Kruh, kružnice 1.1. Základní pojmy Kružnice je množina bodů mající od daného bodu stejnou vzdálenost. Daný bod označujeme jako střed kružnice. Stejnou vzdálenost nazýváme poloměr
Kruh, kružnice, válec 1. Kruh, kružnice 1.1. Základní pojmy Kružnice je množina bodů mající od daného bodu stejnou vzdálenost. Daný bod označujeme jako střed kružnice. Stejnou vzdálenost nazýváme poloměr
NAŘÍZENÍ JIHOČESKÉHO KRAJE
 NAŘÍZENÍ JIHOČESKÉHO KRAJE č. 1/2011, kterým se zřizuje přírodní památka Granátová skála Rada Jihočeského kraje vydává dne 8. 3. 2011 podle 77a odst. 2 v souladu s ustanovením 36 zákona č. 114/1992 Sb.,
NAŘÍZENÍ JIHOČESKÉHO KRAJE č. 1/2011, kterým se zřizuje přírodní památka Granátová skála Rada Jihočeského kraje vydává dne 8. 3. 2011 podle 77a odst. 2 v souladu s ustanovením 36 zákona č. 114/1992 Sb.,
KONSTRUKČNÍ ÚLOHY ŘEŠENÉ UŽITÍM MNOŽIN BODŮ
 Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol KONSTRUKČNÍ
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol KONSTRUKČNÍ
Sada 2 Microsoft Word 2007
 S třední škola stavební Jihlava Sada 2 Microsoft Word 2007 04. Text v záhlaví, zápatí, číslování stránek Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284
S třední škola stavební Jihlava Sada 2 Microsoft Word 2007 04. Text v záhlaví, zápatí, číslování stránek Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284
Adresa příslušného úřadu
 Příloha č. 9 k vyhlášce č. 503/2006 Sb. Adresa příslušného úřadu Úřad: Obecní úřad Výprachtice Stavební úřad PSČ, obec: Výprachtice č.p.3, 561 34 Výprachtice Věc: ŽÁDOST O STAVEBNÍ POVOLENÍ podle ustvení
Příloha č. 9 k vyhlášce č. 503/2006 Sb. Adresa příslušného úřadu Úřad: Obecní úřad Výprachtice Stavební úřad PSČ, obec: Výprachtice č.p.3, 561 34 Výprachtice Věc: ŽÁDOST O STAVEBNÍ POVOLENÍ podle ustvení
Zobrazování zemského povrchu
 Zobrazování zemského povrchu Země je kulatá Mapy jsou placaté Zemský povrch je zvlněný a země není kulatá Fyzický povrch potřebuji promítnout na nějaký matematicky popsatelný povrch http://photojournal.jpl.nasa.gov/jpeg/pia03399.jpg
Zobrazování zemského povrchu Země je kulatá Mapy jsou placaté Zemský povrch je zvlněný a země není kulatá Fyzický povrch potřebuji promítnout na nějaký matematicky popsatelný povrch http://photojournal.jpl.nasa.gov/jpeg/pia03399.jpg
Sada 2 Geodezie II. 19. Katastr
 S třední škola stavební Jihlava Sada 2 Geodezie II 19. Katastr Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2 - inovace a zkvalitnění
S třední škola stavební Jihlava Sada 2 Geodezie II 19. Katastr Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2 - inovace a zkvalitnění
APSLAN. Komunikační převodník APS mini Plus <-> Ethernet nebo WIEGAND -> Ethernet. Uživatelský manuál
 APSLAN Komunikační převodník APS mini Plus Ethernet nebo WIEGAND -> Ethernet Uživatelský manuál 2004 2014, TECHFASS s.r.o., Věštínská 1611/19, 153 00 Praha 5, www.techfass.cz, techfass@techfass.cz
APSLAN Komunikační převodník APS mini Plus Ethernet nebo WIEGAND -> Ethernet Uživatelský manuál 2004 2014, TECHFASS s.r.o., Věštínská 1611/19, 153 00 Praha 5, www.techfass.cz, techfass@techfass.cz
Sada 1 Geodezie I. 08. Nivelační přístroje a pomůcky
 S třední škola stavební Jihlava Sada 1 Geodezie I 08. Nivelační přístroje a pomůcky Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2
S třední škola stavební Jihlava Sada 1 Geodezie I 08. Nivelační přístroje a pomůcky Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2
Plánované investice v distribučních sítích E.ON Distribuce, a.s. Lukáš Svoboda, Miroslav Točín E.ON Česká republika, s.r.o.
 Plánované investice v distribučních sítích E.ON Distribuce, a.s. Lukáš Svoboda, Miroslav Točín E.ON Česká republika, s.r.o. Legislativa upravující provozování distribuční sítě Distribuční síť dále jen
Plánované investice v distribučních sítích E.ON Distribuce, a.s. Lukáš Svoboda, Miroslav Točín E.ON Česká republika, s.r.o. Legislativa upravující provozování distribuční sítě Distribuční síť dále jen
Kanalizačního řádu stokové sítě Vysoký Újezd
 Dodatek č.1 Kanalizačního řádu stokové sítě Vysoký Újezd Doplnění: Kuchař Provozovatel kanalizace pro veřejnou potřebu: Vodovody a kanalizace Beroun, a.s. Mostníkovská 255 266 41 Beroun www.vakberoun.cz
Dodatek č.1 Kanalizačního řádu stokové sítě Vysoký Újezd Doplnění: Kuchař Provozovatel kanalizace pro veřejnou potřebu: Vodovody a kanalizace Beroun, a.s. Mostníkovská 255 266 41 Beroun www.vakberoun.cz
Kontrola stavebních objektů bez vazby na MOMC v ISÚI
 Kontrola stavebních objektů bez vazby na MOMC v ISÚI Seznam zkratek a pojmů použitých v tomto dokumentu: Pojem/zkratka Číslo domovní ČÚZK Definiční bod Vysvětlení číslo popisné nebo evidenční Český úřad
Kontrola stavebních objektů bez vazby na MOMC v ISÚI Seznam zkratek a pojmů použitých v tomto dokumentu: Pojem/zkratka Číslo domovní ČÚZK Definiční bod Vysvětlení číslo popisné nebo evidenční Český úřad
ČÁST I. IDENTIFIKACE ŽADATELE: Vyplňte, popř. proškrtněte
 Žádost o dofinancování sociální služby pro r. 2016 v rámci Podmínek dotačního Programu na podporu poskytování sociálních služeb a způsobu rozdělení a čerpání dotace z kapitoly 313 MPSV státního rozpočtu
Žádost o dofinancování sociální služby pro r. 2016 v rámci Podmínek dotačního Programu na podporu poskytování sociálních služeb a způsobu rozdělení a čerpání dotace z kapitoly 313 MPSV státního rozpočtu
SYLABUS 2. a 3. PŘEDNÁŠKY Z INŽENÝRSKÉ GEODÉZIE
 SYLABUS 2. a 3. PŘEDNÁŠKY Z INŽENÝRSKÉ GEODÉZIE (Plánování přesnosti měření v IG) 3. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. říjen 2015 1 3. PLÁNOVÁNÍ
SYLABUS 2. a 3. PŘEDNÁŠKY Z INŽENÝRSKÉ GEODÉZIE (Plánování přesnosti měření v IG) 3. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. říjen 2015 1 3. PLÁNOVÁNÍ
9.2.5 Sčítání pravděpodobností I
 9.2.5 Sčítání pravděpodobností I Předpoklady: 9203 Pedagogická poznámka: Následující problém sice zadávám jako příklad, ale minimálně na začátku s žáky počítám na tabuli. I kvůli tomu, aby jejich úprava
9.2.5 Sčítání pravděpodobností I Předpoklady: 9203 Pedagogická poznámka: Následující problém sice zadávám jako příklad, ale minimálně na začátku s žáky počítám na tabuli. I kvůli tomu, aby jejich úprava
Bodová pole (1) Bodová pole. Úvod. Úvod. Přednáší: Ing. Michal Volkmann
 Bodová pole (1) Bodová pole Přednáší: Ing. Michal Volkmann Prohloubení nabídky dalšího vzdělávání v oblasti zeměměřictví a katastru nemovitostí ve Středočeském kraji CZ.1.07/3.2.11/03.0115 Projekt je finančně
Bodová pole (1) Bodová pole Přednáší: Ing. Michal Volkmann Prohloubení nabídky dalšího vzdělávání v oblasti zeměměřictví a katastru nemovitostí ve Středočeském kraji CZ.1.07/3.2.11/03.0115 Projekt je finančně
IMPORT A EXPORT MODULŮ V PROSTŘEDÍ MOODLE
 Nové formy výuky s podporou ICT ve školách Libereckého kraje IMPORT A EXPORT MODULŮ V PROSTŘEDÍ MOODLE Podrobný návod Autor: Mgr. Michal Stehlík IMPORT A EXPORT MODULŮ V PROSTŘEDÍ MOODLE 1 Úvodem Tento
Nové formy výuky s podporou ICT ve školách Libereckého kraje IMPORT A EXPORT MODULŮ V PROSTŘEDÍ MOODLE Podrobný návod Autor: Mgr. Michal Stehlík IMPORT A EXPORT MODULŮ V PROSTŘEDÍ MOODLE 1 Úvodem Tento
VOLBA TYPU REGULÁTORU PRO BĚŽNÉ REGULAČNÍ SMYČKY
 VOLBA TYPU REGULÁTORU PRO BĚŽNÉ REGULAČNÍ SMYČKY Jaroslav Hlava TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Tento materiál vznikl v rámci projektu ESF CZ.1.07/2.2.00/07.0247,
VOLBA TYPU REGULÁTORU PRO BĚŽNÉ REGULAČNÍ SMYČKY Jaroslav Hlava TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Tento materiál vznikl v rámci projektu ESF CZ.1.07/2.2.00/07.0247,
Zateplovací systémy Baumit. Požární bezpečnost staveb PKO - 14-001 PKO - 14-002 PKO - 13-011
 Zateplovací systémy Baumit Požární bezpečnost staveb PKO - 14-001 PKO - 14-002 PKO - 13-011 www.baumit.cz duben 2014 Při provádění zateplovacích systémů je nutno dodržovat požadavky požárních norem, mimo
Zateplovací systémy Baumit Požární bezpečnost staveb PKO - 14-001 PKO - 14-002 PKO - 13-011 www.baumit.cz duben 2014 Při provádění zateplovacích systémů je nutno dodržovat požadavky požárních norem, mimo
Digitální učební materiál
 Digitální učební materiál Projekt Šablona CZ.1.07/1.5.00/34.0415 Inovujeme, inovujeme III/2 Inovace a zkvalitnění výuky prostřednictvím ICT (DUM) DUM č. VY_32_INOVACE_CH29_2_03 ŠVP Podnikání RVP 64-41-L/51
Digitální učební materiál Projekt Šablona CZ.1.07/1.5.00/34.0415 Inovujeme, inovujeme III/2 Inovace a zkvalitnění výuky prostřednictvím ICT (DUM) DUM č. VY_32_INOVACE_CH29_2_03 ŠVP Podnikání RVP 64-41-L/51
Kvadratické rovnice pro studijní obory
 Variace 1 Kvadratické rovnice pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
Variace 1 Kvadratické rovnice pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
Pohyb v listu. Řady a posloupnosti
 Pohyb v listu. Řady a posloupnosti EU peníze středním školám Didaktický učební materiál Anotace Označení DUMU: VY_32_INOVACE_IT4.05 Předmět: IVT Tematická oblast: Microsoft Office 2007 Autor: Ing. Vladimír
Pohyb v listu. Řady a posloupnosti EU peníze středním školám Didaktický učební materiál Anotace Označení DUMU: VY_32_INOVACE_IT4.05 Předmět: IVT Tematická oblast: Microsoft Office 2007 Autor: Ing. Vladimír
Obecně závazná vyhláška č. 1/2013
 OBEC SULKOVEC Obecně závazná vyhláška č. 1/2013 o místním poplatku za provoz systému shromažďování, sběru, přepravy, třídění, využívání a odstraňování komunálních odpadů Zastupitelstvo obce Sulkovec se
OBEC SULKOVEC Obecně závazná vyhláška č. 1/2013 o místním poplatku za provoz systému shromažďování, sběru, přepravy, třídění, využívání a odstraňování komunálních odpadů Zastupitelstvo obce Sulkovec se
UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE
 MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin
Mřížky a vyústky NOVA-C-2-R2. Vyústka do kruhového potrubí. Obr. 1: Rozměry vyústky
 -1-1-H Vyústka do kruhového potrubí - Jednořadá 1 Dvouřadá 2 L x H Typ regulačního ústrojí 1) R1, RS1, RN1 R2, RS2, RN2 R, RS, RN Lamely horizontální 2) H vertikální V Provedení nerez A- A-16 Povrchová
-1-1-H Vyústka do kruhového potrubí - Jednořadá 1 Dvouřadá 2 L x H Typ regulačního ústrojí 1) R1, RS1, RN1 R2, RS2, RN2 R, RS, RN Lamely horizontální 2) H vertikální V Provedení nerez A- A-16 Povrchová
imedicus - internetové objednávání
 imedicus - internetové objednávání verze: 27. červenec 2009 2 1. Medicus Komfort imedicus - internetové objednávání imedicus slouží k internetovému objednávání pacientů. Přispívá ke zvýšení pohodlí pacientů
imedicus - internetové objednávání verze: 27. červenec 2009 2 1. Medicus Komfort imedicus - internetové objednávání imedicus slouží k internetovému objednávání pacientů. Přispívá ke zvýšení pohodlí pacientů
Informace o prohlížecích službách pro Katastrální mapu (KM)
 Český úřad zeměměřický a katastrální Sekce centrální databáze Informace o prohlížecích službách pro Katastrální mapu (KM) Zpracoval: Ing. Michal Med Datum: 22. dubna 2014 Verze: 1.2 Popis: Dokument obsahuje
Český úřad zeměměřický a katastrální Sekce centrální databáze Informace o prohlížecích službách pro Katastrální mapu (KM) Zpracoval: Ing. Michal Med Datum: 22. dubna 2014 Verze: 1.2 Popis: Dokument obsahuje
Google AdWords - návod
 Google AdWords - návod Systém Google AdWords je reklamním systémem typu PPC, který provozuje společnost Google, Inc. Zobrazuje reklamy ve výsledcích vyhledávání či v obsahových sítích. Platí se za proklik,
Google AdWords - návod Systém Google AdWords je reklamním systémem typu PPC, který provozuje společnost Google, Inc. Zobrazuje reklamy ve výsledcích vyhledávání či v obsahových sítích. Platí se za proklik,
7 Vstup na nemovitosti
 7 Zeměměřictví bodu podle 83 stavebního zákona nebo při místním šetření údajů o geografických objektech základních státních mapových děl. 43. Pokud fyzické nebo právnické osobě oprávněné vykonávat zeměměřické
7 Zeměměřictví bodu podle 83 stavebního zákona nebo při místním šetření údajů o geografických objektech základních státních mapových děl. 43. Pokud fyzické nebo právnické osobě oprávněné vykonávat zeměměřické
= musíme dát pozor na: jmenovatel 2a, zda je a = 0 výraz pod odmocninou, zda je > 0, < 0, = 0 (pak je jediný kořen)
 .8.7 Kvadratické rovnice s parametrem Předpoklady: 507, 803 Pedagogická poznámka: Na první pohled asi každého zarazí, že takřka celá hodina je psána jako příklady a studenti by ji měli vypracovat samostatně.
.8.7 Kvadratické rovnice s parametrem Předpoklady: 507, 803 Pedagogická poznámka: Na první pohled asi každého zarazí, že takřka celá hodina je psána jako příklady a studenti by ji měli vypracovat samostatně.
REVITALIZACE BYTOVÉHO DOMU ZMĚNA 2 (BŘEZEN 2012) Mezilesí 2056-2057 Praha 20 Horní Počernice
 AKCE: REVITALIZACE BYTOVÉHO DOMU ZMĚNA 2 (BŘEZEN 2012) Mezilesí 2056-2057 Praha 20 Horní Počernice STUPEŇ DOKUMENTACE: ČÁST DOKUMENTACE: DSP A. Průvodní zpráva Č.ZAKÁZKY: ZAK-2011-041-Tp VYPRACOVAL: Ing.
AKCE: REVITALIZACE BYTOVÉHO DOMU ZMĚNA 2 (BŘEZEN 2012) Mezilesí 2056-2057 Praha 20 Horní Počernice STUPEŇ DOKUMENTACE: ČÁST DOKUMENTACE: DSP A. Průvodní zpráva Č.ZAKÁZKY: ZAK-2011-041-Tp VYPRACOVAL: Ing.
Střední škola obchodu, řemesel a služeb Žamberk. Výukový materiál zpracovaný v rámci projektu EU Peníze SŠ
 Střední škola obchodu, řemesel a služeb Žamberk Výukový materiál zpracovaný v rámci projektu EU Peníze SŠ Registrační číslo projektu: CZ.1.07/1.5.00/34.0130 Šablona: III/2 Ověřeno ve výuce dne: 7.10.2013
Střední škola obchodu, řemesel a služeb Žamberk Výukový materiál zpracovaný v rámci projektu EU Peníze SŠ Registrační číslo projektu: CZ.1.07/1.5.00/34.0130 Šablona: III/2 Ověřeno ve výuce dne: 7.10.2013
Android OpenGL. Animace a ovládání pomocí dotykové obrazovky
 Android OpenGL Animace a ovládání pomocí dotykové obrazovky Principy animace Animace udává pohyb objektů v čase Může být reprezentována mnoha způsoby Procedurální Pozice objektů se počítá přímo v programu
Android OpenGL Animace a ovládání pomocí dotykové obrazovky Principy animace Animace udává pohyb objektů v čase Může být reprezentována mnoha způsoby Procedurální Pozice objektů se počítá přímo v programu
Bipolární tranzistor. Bipolární tranzistor. Otevřený tranzistor
 Bipolární tranzistor Bipolární tranzistor polovodičová součástka se dvěma PN přechody a 3 elektrodami: C - kolektorem E - emitorem B - bází vrstvy mohou být v pořadí NPN nebo PNP, častější je varianta
Bipolární tranzistor Bipolární tranzistor polovodičová součástka se dvěma PN přechody a 3 elektrodami: C - kolektorem E - emitorem B - bází vrstvy mohou být v pořadí NPN nebo PNP, častější je varianta
Digitální učební materiál
 Digitální učební materiál Projekt Šablona CZ.1.07/1.5.00/34.0415 Inovujeme, inovujeme III/2 Inovace a zkvalitnění výuky prostřednictvím ICT (DUM) DUM č. VY_32_INOVACE_CH29_1_16 ŠVP Podnikání RVP 64-41-L/51
Digitální učební materiál Projekt Šablona CZ.1.07/1.5.00/34.0415 Inovujeme, inovujeme III/2 Inovace a zkvalitnění výuky prostřednictvím ICT (DUM) DUM č. VY_32_INOVACE_CH29_1_16 ŠVP Podnikání RVP 64-41-L/51
PŘIJÍMACÍ ZKOUŠKY 2010 - I.termín
 MATEMATIKA Obor: 79-41-K/81 Součet bodů: Opravil: Kontroloval: Vítáme vás na gymnáziu Omská a přejeme úspěšné vyřešení všech úloh. Úlohy můžete řešit v libovolném pořadí. V matematice pracujeme s čísly
MATEMATIKA Obor: 79-41-K/81 Součet bodů: Opravil: Kontroloval: Vítáme vás na gymnáziu Omská a přejeme úspěšné vyřešení všech úloh. Úlohy můžete řešit v libovolném pořadí. V matematice pracujeme s čísly
Označování dle 11/2002 označování dle ADR, označování dle CLP
 Označování dle 11/2002 označování dle ADR, označování dle CLP Nařízení 11/2002 Sb., Bezpečnostní značky a signály 4 odst. 1 nařízení 11/2002 Sb. Nádoby pro skladování nebezpečných chemických látek, přípravků
Označování dle 11/2002 označování dle ADR, označování dle CLP Nařízení 11/2002 Sb., Bezpečnostní značky a signály 4 odst. 1 nařízení 11/2002 Sb. Nádoby pro skladování nebezpečných chemických látek, přípravků
1 Typografie. 1.1 Rozpal verzálek. Typografie je organizace písma v ploše.
 1 Typografie Typografie je organizace písma v ploše. 1.1 Rozpal verzálek vzájemné vyrovnání mezer mezi písmeny tak, aby vzdálenosti mezi písmeny byly opticky stejné, aby bylo slovo, řádek a celý text opticky
1 Typografie Typografie je organizace písma v ploše. 1.1 Rozpal verzálek vzájemné vyrovnání mezer mezi písmeny tak, aby vzdálenosti mezi písmeny byly opticky stejné, aby bylo slovo, řádek a celý text opticky
INŽENÝRSKÁ MATEMATIKA LOKÁLNÍ EXTRÉMY
 INŽENÝRSKÁ MATEMATIKA LOKÁLNÍ EXTRÉMY FUNKCÍ DVOU PROMĚNNÝCH Robert Mařík 2. října 2009 Obsah z = x 4 +y 4 4xy + 30..................... 3 z = x 2 y 2 x 2 y 2........................ 18 z = y ln(x 2 +y)..........................
INŽENÝRSKÁ MATEMATIKA LOKÁLNÍ EXTRÉMY FUNKCÍ DVOU PROMĚNNÝCH Robert Mařík 2. října 2009 Obsah z = x 4 +y 4 4xy + 30..................... 3 z = x 2 y 2 x 2 y 2........................ 18 z = y ln(x 2 +y)..........................
Sada 2 - MS Office, Excel
 S třední škola stavební Jihlava Sada 2 - MS Office, Excel 03. Úvod do Excelu 2007. Vkládání dat, vzorce Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284
S třední škola stavební Jihlava Sada 2 - MS Office, Excel 03. Úvod do Excelu 2007. Vkládání dat, vzorce Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284
Praktikum II Elektřina a magnetismus
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum II Elektřina a magnetismus Úloha č. VII Název: Měření indukčnosti a kapacity metodou přímou Pracoval: Matyáš Řehák stud.sk.:
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum II Elektřina a magnetismus Úloha č. VII Název: Měření indukčnosti a kapacity metodou přímou Pracoval: Matyáš Řehák stud.sk.:
NAMÁHÁNÍ NA TAH NAMÁHÁNÍ NA TAH
 Předmět: Ročník: Vytvořil: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 10. BŘEZNA 2013 Název zpracovaného celku: NAMÁHÁNÍ NA TAH NAMÁHÁNÍ NA TAH Přímá tyč je namáhána na tah, je-li zatíţena dvěma silami
Předmět: Ročník: Vytvořil: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 10. BŘEZNA 2013 Název zpracovaného celku: NAMÁHÁNÍ NA TAH NAMÁHÁNÍ NA TAH Přímá tyč je namáhána na tah, je-li zatíţena dvěma silami
M - Rovnice - lineární a s absolutní hodnotou
 Rovnice a jejich ekvivalentní úpravy Co je rovnice Rovnice je matematický zápis rovnosti dvou výrazů. př.: x + 5 = 7x - M - Rovnice - lineární a s absolutní hodnotou Písmeno zapsané v rovnici nazýváme
Rovnice a jejich ekvivalentní úpravy Co je rovnice Rovnice je matematický zápis rovnosti dvou výrazů. př.: x + 5 = 7x - M - Rovnice - lineární a s absolutní hodnotou Písmeno zapsané v rovnici nazýváme
souřadné systémy geometrické určení polohy pevně spojené se vztažným tělesem
 souřadné systémy geometrické určení polohy pevně spojené se vztažným tělesem kartézský souřadný systém Z Y X kartézský souřadný systém Z Y X kartézský souřadný systém Z x y Y X kartézský souřadný systém
souřadné systémy geometrické určení polohy pevně spojené se vztažným tělesem kartézský souřadný systém Z Y X kartézský souřadný systém Z Y X kartézský souřadný systém Z x y Y X kartézský souřadný systém
28.9.2014. Prezentace, promítané na přednášce, jsou dostupné na http://www2.zf.jcu.cz/~hanek00/geoda/
 Ing. Pavel Hánek, Ph.D. Prezentace, promítané na přednášce, jsou dostupné na http://www2.zf.jcu.cz/~hanek00/geoda/ HÁNEK, P. (ST.) - KOZA, P. - HÁNEK, P.: Geodezie pro SPŠ stavební. 4. upravené a rozšířené
Ing. Pavel Hánek, Ph.D. Prezentace, promítané na přednášce, jsou dostupné na http://www2.zf.jcu.cz/~hanek00/geoda/ HÁNEK, P. (ST.) - KOZA, P. - HÁNEK, P.: Geodezie pro SPŠ stavební. 4. upravené a rozšířené
Liga mladších žáků 2000 (6001 6180). Utkání zahajuje ročník 2000 Liga starších žáků 1998 (8001 8180)
 Liga mladších žáků 2000 (6001 6180). Utkání zahajuje ročník 2000 Liga starších žáků 1998 (8001 8180) Žákovská liga 2000 a 1998 (6. a 8. třídy) technické normy Startují : ŽL 2000 - startují hráči ročníku
Liga mladších žáků 2000 (6001 6180). Utkání zahajuje ročník 2000 Liga starších žáků 1998 (8001 8180) Žákovská liga 2000 a 1998 (6. a 8. třídy) technické normy Startují : ŽL 2000 - startují hráči ročníku
Využití EduBase ve výuce 2
 B.I.B.S., a. s. Využití EduBase ve výuce 2 Projekt Vzdělávání pedagogů v prostředí cloudu reg. č. CZ.1.07/1.3.00/51.0011 Mgr. Jitka Kominácká, Ph.D. a kol. 2015 1 Obsah 1 Obsah... 2 2 Úvod... 3 3 Aktivita:
B.I.B.S., a. s. Využití EduBase ve výuce 2 Projekt Vzdělávání pedagogů v prostředí cloudu reg. č. CZ.1.07/1.3.00/51.0011 Mgr. Jitka Kominácká, Ph.D. a kol. 2015 1 Obsah 1 Obsah... 2 2 Úvod... 3 3 Aktivita:
Optický komplex brýlí a očí I. LF MU Brno Brýlová technika
 Optický komplex brýlí a očí I LF MU Brno Brýlová technika Struktura prezentace Definice základních pojmů centrace, vycházející z Gullstrandova systému oka Schéma polohy vztažných bodů do dálky 2 Základní
Optický komplex brýlí a očí I LF MU Brno Brýlová technika Struktura prezentace Definice základních pojmů centrace, vycházející z Gullstrandova systému oka Schéma polohy vztažných bodů do dálky 2 Základní
Příloha č. 1 Vzor smlouvy o založení svěřenského fondu a statutu svěřenského fondu
 Příloha č. 1 Vzor smlouvy o založení svěřenského fondu a statutu svěřenského fondu Strana první. NZ [ ]/[ ] N [ ]/[ ] Notářský zápis sepsaný dne [ ] (slovy: [ ])[jméno a příjmení], notářem v [ ], na adrese
Příloha č. 1 Vzor smlouvy o založení svěřenského fondu a statutu svěřenského fondu Strana první. NZ [ ]/[ ] N [ ]/[ ] Notářský zápis sepsaný dne [ ] (slovy: [ ])[jméno a příjmení], notářem v [ ], na adrese
SPOLEHLIVOST KONSTRUKCÍ & TEORIE SPOLEHLIVOSTI část 2: Statistika a pravděpodobnost
 SPOLEHLIVOST KONSTRUKCÍ & TEORIE SPOLEHLIVOSTI část 2: Statistika a pravděpodobnost Drahomír Novák Jan Eliáš 2012 Spolehlivost konstrukcí, Drahomír Novák & Jan Eliáš 1 část 2 Statistika a pravděpodobnost
SPOLEHLIVOST KONSTRUKCÍ & TEORIE SPOLEHLIVOSTI část 2: Statistika a pravděpodobnost Drahomír Novák Jan Eliáš 2012 Spolehlivost konstrukcí, Drahomír Novák & Jan Eliáš 1 část 2 Statistika a pravděpodobnost
