Dlaždicemi rotujeme tak, aby nám nezbyly žádné volné konce :
|
|
|
- Vendula Jandová
- před 8 lety
- Počet zobrazení:
Transkript
1 11. Dlaždice Dlaždicemi rotujeme tak, aby nám nezbyly žádné volné konce : Heslo je STRAKAPOUD. 12. Dva texty Každý řádek textu je asociace na šestipísmenné slovo, přičemž slova na stejném řádku jsou vzájmenými přesmyčkami. Způsob jak převést první slovo na druhé využijeme jako klíč k transpozici písmen v mřížce uprostřed. simona - osmina kostel - stolek svatba - stavba kobyla - oblaky slanit - stalin brusle - brusel kostra - troska chleba - blecha VIAOAO ESVMNR MKAIAP OVISAE CRJTVC ANMRYI SYEATV NPNJVO Po sloupcích čteme: vem ocasni skvrny pava i jmeno mistra jana a vytvor pecivo. Použijeme tedy ještě jednou stejný princip šestipísmenných přesmyček: oka hus - houska. Heslo je HOUSKA.
2 13. Obrázky Obrázky jsou dvou typů: asociace na světové strany a na města (jsou mimochodem rozlišena tím, že u měst je číslo psáno italikou). Čísla u měst udávají, kolikáté písmeno z názvu města máme brát. Čísla u světových stran udávají, o kolik kilometrů se posunujeme při přesunu do dalšího města. Některé asociace na města jsou záměrně mlhavé (např. černá nebo pivo), aby bylo nutné použít i směry (případně i vzdálenosti). zlín - Z - S - velké losiny - Z - J - česká Třebová - V - J -Ostrava - Z - S - Mladá boleslav - J - Z - písek - V - S - pardubice - S - Z - jičín - J - humpolec - V - S - litovel Heslo je LITOMERICE. 14. Čtverce 1. pozorování: malé bílé čtverečky dělí mřížku na sektory velikosti pozorování: v mřížce 5 3 je celkem 26 čtverců. Heslo je SPILBERK.
3 21. Trojúhelníky a čísla 1. pozorování: Do zadání lze vepsat dvakrát abecedu. 2. pozorování: Do zadání lze doplnit čísla 1-5 tak, že po doplnění bude v každém řádku v každém ze 3 směrů každé číslo od 1 do 5 právě jedenkrát ( Sudoku princip ). Pak již jen podle čísel přečteme příslušná písmena. Heslo je PRASE. 22. V obchoďáku Klasická staganografická slohovka vybíráme k-té písmeno ze slov. Tato šifra je speciální v tom, že vybíráme písmena ze slov, která v zadání vůbec nejsou. Číslovky určují jak tato skrytá slova, tak pořadí písmene, které máme vybrat. Byl to takový pohodový den v obchoďáku. Nejdřív jsem zašel do drogerie a vzal si tam kartáček a pastu, po které se moje přerostlé horní jedničky budou jen blyštět (Zuby). Měli tam moc šikovnou pokladní takhle hezké čtyřky (prsa) jsem už dlouho neviděl. Pak jsem se zastavil v obuvi vybrat něco pro ženu k narozeninám. Koupil jsem jí trojky (boty), i když má dvojky (nohy) však si do nich může vzít silné ponožky. Ještě kalkulačku pro syna, ať z matematiky nemá samé pětky (známky). A sobě nové karty na poker. Včera jsem shrábl pěkný balík jenom na červené dvojky (karty). Heslo je ZATOKA. 23. Čáry v obdélníku Podle tlustých čar vystřihneme 10 obdélníků (proužků). Podle tenkých čar proužky přehneme. Dostaneme písmenka. Heslo je POUSTEVNIK.
4 31. Spermie Pozorování: Na základě vnitřku hlaviček a polohy zobáčku, můžeme spermie jednoznačně spárovat. Nápad: Hlavičky překryjeme a dvojice tak vytvoří písmena v semaforu. Pak už odhalit jen správné natočení zobáčku (nahoru) a písmenka seřadit (primárně podle počtu vyplněných částí, sekundárně podle jejich polohy). 32. Scrabble pro pokročilé Šifra je založena na principu a pravidlech klasické verze hry Scrabble upravené do rozměrů 3D. Cílem je odkrýt třípísmenná slova skrytá v sloupečcích. Dolní (první) písmeno těchto slov musí zároveň umožnit utvoření smysluplného slova s křížícím se výrazem (resp. výrazy). Heslo pak tvoří prostřední písmenka trojic. vztah/výtah (zlý), přisaj/přisaď (jeď), rudl-štípl/rudá-štípá (lká), prs/prý (stý), drsná/dusná (rvu), oslaben/oslaven (bav), návodné/náhodné (vrh). Některé části křížovky nabízejí na první pohled i jiné možné varianty spodních slov (např. prs, prd, pro). Tyto alternativy ale neumožňují složit žádné smysluplné trojpísmenné slovo a nelze je tedy využít. Řešením šifry je heslo LEKTVAR.
5 41. Různý zápis V každé z šesti kružnic jsou písmena zakódována v určitém systému: klávesy zmáčknuté při psaní SMSky, semafor, vlajková abeceda, pořadí písmene v abecedě, Braillova abeceda, morseovka. Při řešení je dobré se zeptat: Proč jsou použita různá kódování? Jen proto, aby nás organizátoři zdrželi tím, že je budeme muset vyhledávat v tabulkách? Nikoliv, různá kódování tvoří princip šifry. Kódy převedeme na písmena, která napíšeme v kódování, jež následuje (podle šipek). Pak dostaneme skupiny kódů se společným znakem. V každé skupině však jedno písmeno chybí: Semaforová písmena, u kterých ruce svírají pravý úhel chybí P. Vlajky obsahující žlutou barvu chybí O. Prvočísla chybí K. Braillova písmena s třemi plnými a třemi prázdnými tečkami chybí O. Písmena morseovkovy délky tři chybí R. Písmena, která lze na mobilu napsat jediným stlačením klávesy chybí A. Heslo je POKORA.
6 51. Barvy a kolečka Užitečná pozorování: Barvy tvoří 4 hady, kteří se v některých políčkách překrývají. Velká kolečka tvoří zjevně písmena v Braillově abecedě, jsou však různě natočena. Malá kolečka tvoří čísla 1-6 tak, jak jsou na kostce. Princip šifry: Válíme barevné kostky, které na sobě mají Brailova písmena - na některých polích jsou tato písmena otisknuta, jinde ne. Pokud se dvě barvy na některém poli potkávají, musí se otisknout stejným písmenem. Musíme doplnit chybějící otisky - viz obrázek. Poté přečteme písmena na polích označených čísly 1-6. Dostáváme heslo STROMY. Poznámky k šifře: K vyluštění není samozřejmě třeba hledat všechny otisky, obrázek ukazující všechny dohledatelné otisky je zde jen pro kontrolu. Šifra obsahuje několik prvků, které na správný postup navádí, případně jej potvrzují (např. opakované výskyty písmen T a E blízko sebe, písmeno U, které je na průniku žluté a šedé i na obou dvou barvách). Přebytečná písmena v zadání a použití množného čísla v heslu jsou primárně opatření proti uhádnutí hesla scrabblením z písmen vyskytujících se v zadání.
10. ročník. Řešení 1. a 2. sada
 101. Vaši organizátoři 10. ročník Řešení 1. a 2. sada Název šifry a umístění úlohy jako 1. úloha jubilejního 10. ročníku navádí k tomu, že šifra je o organizátorech Sendviče. Pokud náhodou neumíte odříkat
101. Vaši organizátoři 10. ročník Řešení 1. a 2. sada Název šifry a umístění úlohy jako 1. úloha jubilejního 10. ročníku navádí k tomu, že šifra je o organizátorech Sendviče. Pokud náhodou neumíte odříkat
Úlohy klauzurní části školního kola kategorie B
 65. ročník matematické olympiády Úlohy klauzurní části školního kola kategorie B 1. Kolika způsoby je možno vyplnit čtvercovou tabulku 3 3 čísly,, 3, 3, 3, 4, 4, 4, 4 tak, aby součet čísel v každém čtverci
65. ročník matematické olympiády Úlohy klauzurní části školního kola kategorie B 1. Kolika způsoby je možno vyplnit čtvercovou tabulku 3 3 čísly,, 3, 3, 3, 4, 4, 4, 4 tak, aby součet čísel v každém čtverci
Nápovědy k numerickému myšlení TSP MU
 Nápovědy k numerickému myšlení TSP MU Numerické myšlení 2011/var. 01 26. Ciferné součty čísel v každém z kruhů mají tutéž hodnotu. Pozor, hledáme číslo, které se nehodí na místo otazníku. Jedná se o dvě
Nápovědy k numerickému myšlení TSP MU Numerické myšlení 2011/var. 01 26. Ciferné součty čísel v každém z kruhů mají tutéž hodnotu. Pozor, hledáme číslo, které se nehodí na místo otazníku. Jedná se o dvě
12. ročník Řešení: 3. a 4. sada
 12. ročník Řešení: 3. a 4. sada 301. Padesáté zvíře V každém sloupci má 6 zvířat jednu společnou vlastnost, ale jedno zvíře ji nemá: 1. sloupec zvířata ze zvěrokruhu + krysa 2. sloupec jednoslabičná zvířata
12. ročník Řešení: 3. a 4. sada 301. Padesáté zvíře V každém sloupci má 6 zvířat jednu společnou vlastnost, ale jedno zvíře ji nemá: 1. sloupec zvířata ze zvěrokruhu + krysa 2. sloupec jednoslabičná zvířata
ŠIFRY. 1) Morseova abeceda
 ŠIFRY V následujícím textu je shrnuto několik základních typů šifer, které by měla vlčata znát před tím, než se stanou skauty. U skautů se pak naučí mnohým dalším šifrám. 1) Morseova abeceda Nejdůležitější
ŠIFRY V následujícím textu je shrnuto několik základních typů šifer, které by měla vlčata znát před tím, než se stanou skauty. U skautů se pak naučí mnohým dalším šifrám. 1) Morseova abeceda Nejdůležitější
11. ročník. Řešení: 3. a 4. sada
 11. ročník Řešení: 3. a 4. sada 301. Mřížka s tvary Pro informatiky: Hledáme Hamiltonovskou cestu v grafu, jehož vrcholy jsou písmena, která jsou spojena orientovanou hranou právě tehdy, když jejich manhatanovská
11. ročník Řešení: 3. a 4. sada 301. Mřížka s tvary Pro informatiky: Hledáme Hamiltonovskou cestu v grafu, jehož vrcholy jsou písmena, která jsou spojena orientovanou hranou právě tehdy, když jejich manhatanovská
Gabriela Janská. Středočeský vzdělávací institut akademie J. A. Komenského www.sviajak.cz
 PŘÍRUČKA KE KURZU: ZÁKLADY PRÁCE NA PC MS WORD 2003 Gabriela Janská Středočeský vzdělávací institut akademie J. A. Komenského www.sviajak.cz Obsah: 1. Písmo, velikost písma, tučně, kurzíva, podtrhnout
PŘÍRUČKA KE KURZU: ZÁKLADY PRÁCE NA PC MS WORD 2003 Gabriela Janská Středočeský vzdělávací institut akademie J. A. Komenského www.sviajak.cz Obsah: 1. Písmo, velikost písma, tučně, kurzíva, podtrhnout
Polodokreslovka křížovka (časový limit 15 minut)
 Polodokreslovka křížovka (časový limit 15 minut) V obrazci nejsou vyznačené dělící linky mezi slovy. Je třeba je doplnit, přičemž rozmístění těchto linek v obrazci je symetrické. A B C D E F G H I 1 2
Polodokreslovka křížovka (časový limit 15 minut) V obrazci nejsou vyznačené dělící linky mezi slovy. Je třeba je doplnit, přičemž rozmístění těchto linek v obrazci je symetrické. A B C D E F G H I 1 2
Logika je logika Úlohy na dvoudenní turnaj v Brně 2012
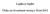 Logika je logika Úlohy na dvoudenní turnaj v Brně 2012 MOSTY Spojte všechny ostrovy (tj. kroužky s čísly) pomocí mostů tak, aby bylo možno dojít z každého ostrova na kterýkoliv jiný. Mosty je přitom dovoleno
Logika je logika Úlohy na dvoudenní turnaj v Brně 2012 MOSTY Spojte všechny ostrovy (tj. kroužky s čísly) pomocí mostů tak, aby bylo možno dojít z každého ostrova na kterýkoliv jiný. Mosty je přitom dovoleno
jsme se spustili do nádherného dómu (obr. A2, E5, H2), s mnohou excentrickou výzdobou na stěnách = ŽALUDEK
 301. Z deníku prof. Absolona Text je sice zdánlivě stylizován jako speleologické zápisky (všechny jmenované postavy skutečně existovaly), jedná se však o metaforický popis trávicí soustavy - od dutiny
301. Z deníku prof. Absolona Text je sice zdánlivě stylizován jako speleologické zápisky (všechny jmenované postavy skutečně existovaly), jedná se však o metaforický popis trávicí soustavy - od dutiny
Obsah Navigace... 2 Primární ovládací prvky... 3 Sekundární ovládací prvky... 4 Slovní zásoba... 12 Ukončení programu... 14
 V tomto dokumentu se nachází cenné rady pro používání našeho výukového programu anglického jazyka. Program byl koncipován, aby každému uživateli přinesl jednoduché a intuitivní prostředí. Jak funguje navigace
V tomto dokumentu se nachází cenné rady pro používání našeho výukového programu anglického jazyka. Program byl koncipován, aby každému uživateli přinesl jednoduché a intuitivní prostředí. Jak funguje navigace
Výukový materiál zpracován v rámci projektu EU peníze školám
 Výukový materiál zpracován v rámci projektu EU peníze školám Registrační číslo projektu: CZ.1.07/1.4.00/21.3665 Šablona: I/2 č. materiálu: VY_32_INOVACE_363 Jméno autora: Třída/ročník: Mgr. Tomáš Vaculík
Výukový materiál zpracován v rámci projektu EU peníze školám Registrační číslo projektu: CZ.1.07/1.4.00/21.3665 Šablona: I/2 č. materiálu: VY_32_INOVACE_363 Jméno autora: Třída/ročník: Mgr. Tomáš Vaculík
Digitální učební materiál
 Digitální učební materiál Číslo projektu Označení materiálu Název školy Autor Tematická oblast Ročník Anotace Metodický pokyn Zhotoveno CZ.1.07/1.5.00/34.0061 VY_42_INOVACE_M.2.01 Integrovaná střední škola
Digitální učební materiál Číslo projektu Označení materiálu Název školy Autor Tematická oblast Ročník Anotace Metodický pokyn Zhotoveno CZ.1.07/1.5.00/34.0061 VY_42_INOVACE_M.2.01 Integrovaná střední škola
Matematický KLOKAN : ( ) = (A) 1 (B) 9 (C) 214 (D) 223 (E) 2 007
 Matematický KLOKN 007 kategorie enjamín Úlohy za 3 body. Které číslo patří do prázdného rámečku? 007 : ( + 0 + 0 + 7) 0 0 7 = () () 9 (C) 4 (D) 3 (E) 007. Který z dílů stavebnice musíš přiložit k dílu
Matematický KLOKN 007 kategorie enjamín Úlohy za 3 body. Které číslo patří do prázdného rámečku? 007 : ( + 0 + 0 + 7) 0 0 7 = () () 9 (C) 4 (D) 3 (E) 007. Který z dílů stavebnice musíš přiložit k dílu
3. podzimní série. ... {z }
 3. podzimní série Téma: Kombinatorika Datumodeslání: º ÔÖÓ Ò ¾¼¼ ½º ÐÓ Ó Ýµ Monča potřebuje zatelefonovat Pepovi, avšak nemá u sebe svůj telefonní seznam PraSátek. Zná však předvolbu 723 a vzpomněla si,
3. podzimní série Téma: Kombinatorika Datumodeslání: º ÔÖÓ Ò ¾¼¼ ½º ÐÓ Ó Ýµ Monča potřebuje zatelefonovat Pepovi, avšak nemá u sebe svůj telefonní seznam PraSátek. Zná však předvolbu 723 a vzpomněla si,
1. otázka. 2. otázka = Ve které z následujících možností je výsledek uvedeného výpočtu? 3. otázka
 1. otázka Paní Irena měla černé, bílé a černobílé kočky. elkově jich měla dvanáct. Z toho bylo šest černých a čtyři bílé. Jakou část z celkového počtu představují černobílé kočky? 2. otázka 24 + 12 3 5
1. otázka Paní Irena měla černé, bílé a černobílé kočky. elkově jich měla dvanáct. Z toho bylo šest černých a čtyři bílé. Jakou část z celkového počtu představují černobílé kočky? 2. otázka 24 + 12 3 5
20 b. 45 b. 25 b. 20 b. Kolo J Klasické S. 9. Klasické R. 8. Klasické Č. 7. Klasické M. 5 b. 10 b. 5 b. 5 b. 3. Klasické
 body: Soutěž jednotlivců b. Nepravidelné b b 0 b 0 b b 0 b b. Klasické Č. Klasické R 0. Klasické S. Klasické. Klasické 0. Klasické. Klasické Brno,. a. září 0 www.sudokualogika.cz logických her a sudoku
body: Soutěž jednotlivců b. Nepravidelné b b 0 b 0 b b 0 b b. Klasické Č. Klasické R 0. Klasické S. Klasické. Klasické 0. Klasické. Klasické Brno,. a. září 0 www.sudokualogika.cz logických her a sudoku
(13)(5)(B)(14)(F)(12)(15)
 LIST ŠIFER 1.1 červeně je napsáno řešení, nebo alespoň návod, jak řešit Šifra 02 - šestnáctková soustava, Šifra 05 - Braillovo písmo, Ř: Číslo z hodin, ke kterému je otvor nejblíž Šifra 10 Ř: Zvíře v sektoru
LIST ŠIFER 1.1 červeně je napsáno řešení, nebo alespoň návod, jak řešit Šifra 02 - šestnáctková soustava, Šifra 05 - Braillovo písmo, Ř: Číslo z hodin, ke kterému je otvor nejblíž Šifra 10 Ř: Zvíře v sektoru
8. MČR v řešení sudoku, Brno, Přehled úloh
 . MČR v řešení sudoku, Brno,.-..0 Přehled úloh Na mistrovství se budou řešit zde uvedené typy úloh. V úlohách ve tvaru čtverce n n rozděleného na n oblastí platí standardní pravidla sudoku, tj. je potřeba
. MČR v řešení sudoku, Brno,.-..0 Přehled úloh Na mistrovství se budou řešit zde uvedené typy úloh. V úlohách ve tvaru čtverce n n rozděleného na n oblastí platí standardní pravidla sudoku, tj. je potřeba
1. sada. 9. ročník. 101. Šifrovací tutoriál
 9. ročník 1. sada 101. Šifrovací tutoriál Protože se luštitelské zkušenosti týmů velmi liší, rozhodli jsme se na začátek letošního ročníku zařadit úlohu, při které si všichni zopakují základní šifrovací
9. ročník 1. sada 101. Šifrovací tutoriál Protože se luštitelské zkušenosti týmů velmi liší, rozhodli jsme se na začátek letošního ročníku zařadit úlohu, při které si všichni zopakují základní šifrovací
HROMADNÉ ÚPRAVY NAJÍT A NAHRADIT
 HROMADNÉ ÚPRAVY NAJÍT A NAHRADIT Funkce Najít a nahradit slouží k rychlému vyhledávání určitých slov a jejich nahrazování jinými slovy. Lze hledat i určité varianty slov a nahrazovat je buď hromadně (všechny
HROMADNÉ ÚPRAVY NAJÍT A NAHRADIT Funkce Najít a nahradit slouží k rychlému vyhledávání určitých slov a jejich nahrazování jinými slovy. Lze hledat i určité varianty slov a nahrazovat je buď hromadně (všechny
Školní kolo soutěže Mladý programátor 2013, kategorie C, D
 Doporučené hodnocení školního kola: Hodnotit mohou buď učitelé školy, tým rodičů nebo si žáci, kteří se zúčastní soutěže, mohou ohodnotit úlohy navzájem sami (v tomto případě doporučujeme, aby si žáci
Doporučené hodnocení školního kola: Hodnotit mohou buď učitelé školy, tým rodičů nebo si žáci, kteří se zúčastní soutěže, mohou ohodnotit úlohy navzájem sami (v tomto případě doporučujeme, aby si žáci
Vánoční turnaj GP Praha 2012
 Vánoční turnaj GP Praha 0 konaný péčí HALAS o.s. dne. prosince 0 Jméno hráče: Pravidla obecná: Do každého políčka vepište jednu číslici -N podle velikosti tabulky není-li v zadání jinak zmíněno. Zadání
Vánoční turnaj GP Praha 0 konaný péčí HALAS o.s. dne. prosince 0 Jméno hráče: Pravidla obecná: Do každého políčka vepište jednu číslici -N podle velikosti tabulky není-li v zadání jinak zmíněno. Zadání
SOUBOR OTÁZEK. 5. ročník
 SOUBOR OTÁZEK 5. ročník 2016 Mezinárodní matematická soutěž Pangea v Evropě Název země Počet registrovaných účastníků Název země Počet registrovaných účastníků 1 Německo 147 000 10 Dánsko 5 068 2 Polsko
SOUBOR OTÁZEK 5. ročník 2016 Mezinárodní matematická soutěž Pangea v Evropě Název země Počet registrovaných účastníků Název země Počet registrovaných účastníků 1 Německo 147 000 10 Dánsko 5 068 2 Polsko
Přijímací zkouška na MFF UK v Praze
 Přijímací zkouška na MFF UK v Praze pro bakalářské studijní programy fyzika, informatika a matematika 2016, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a, b, c, d, e. Vaším úkolem je u každé
Přijímací zkouška na MFF UK v Praze pro bakalářské studijní programy fyzika, informatika a matematika 2016, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a, b, c, d, e. Vaším úkolem je u každé
Jméno a příjmení. 2.1 Pokyny k otevřeným úlohám. 2.2 Pokyny k uzavřeným úlohám TESTOVÝ SEŠIT NEOTVÍREJTE, POČKEJTE NA POKYN!
 MATEMATIKA 9 M9PAD9C0T0 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 6 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby Základní informace k zadání zkoušky Časový limit
MATEMATIKA 9 M9PAD9C0T0 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 6 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby Základní informace k zadání zkoušky Časový limit
PSANÍ VZORCŮ A ROVNIC
 PSANÍ VZORCŮ A ROVNIC aneb matematikem bez nesnází Jednoduché matematické, fyzikální či chemické vzorce a rovnice můžeme zapsat poměrně snadno za pomoci znaků na klávesnici a použitím horního nebo dolního
PSANÍ VZORCŮ A ROVNIC aneb matematikem bez nesnází Jednoduché matematické, fyzikální či chemické vzorce a rovnice můžeme zapsat poměrně snadno za pomoci znaků na klávesnici a použitím horního nebo dolního
INFORMATIKA 5. ROČNÍK TABULKY PROCVIČOVÁNÍ
 INFORMATIKA 5. ROČNÍK TABULKY PROCVIČOVÁNÍ 1. PRACOVNÍ ÚKOL Rozvrh hodin Vytvoř si svůj vlastní rozvrh hodin pomocí zadaných úkolů. Rozvrh hodin 5. třída 1. 2. 3. 4. 5. Pondělí M ČJ AnJ ČaS HV Úterý ČJ
INFORMATIKA 5. ROČNÍK TABULKY PROCVIČOVÁNÍ 1. PRACOVNÍ ÚKOL Rozvrh hodin Vytvoř si svůj vlastní rozvrh hodin pomocí zadaných úkolů. Rozvrh hodin 5. třída 1. 2. 3. 4. 5. Pondělí M ČJ AnJ ČaS HV Úterý ČJ
Téma: Práce se základními objekty, výplní a obrysem
 Téma: Práce se základními objekty, výplní a obrysem Vypracovala: Ing. Jana Wasserbauerová TE NTO PR OJ E KT J E S POLUFINANC OVÁN EVR OPS KÝ M S OC IÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY. Cíl:
Téma: Práce se základními objekty, výplní a obrysem Vypracovala: Ing. Jana Wasserbauerová TE NTO PR OJ E KT J E S POLUFINANC OVÁN EVR OPS KÝ M S OC IÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY. Cíl:
Booklet soutěže družstev
 tým: body: 11. mistrovství ČR v řešení sudoku Booklet soutěže družstev HALAS Hráčská asociace logických her a sudoku www.sudokualogika.cz Soutěž družstev Brno, 17. a 18. září 2016 Antidiagonální Každá
tým: body: 11. mistrovství ČR v řešení sudoku Booklet soutěže družstev HALAS Hráčská asociace logických her a sudoku www.sudokualogika.cz Soutěž družstev Brno, 17. a 18. září 2016 Antidiagonální Každá
KAPITOLA 4 ZPRACOVÁNÍ TEXTU
 KAPITOLA 4 ZPRACOVÁNÍ TEXTU TABULÁTORY Jsou to značky (zarážky), ke kterým se zarovná text. Můžeme je nastavit kliknutím na pravítku nebo v dialogovém okně, které vyvoláme kliknutím na tlačítko Tabulátory
KAPITOLA 4 ZPRACOVÁNÍ TEXTU TABULÁTORY Jsou to značky (zarážky), ke kterým se zarovná text. Můžeme je nastavit kliknutím na pravítku nebo v dialogovém okně, které vyvoláme kliknutím na tlačítko Tabulátory
ČT 2 15% ČT 1? nesleduje 42% Nova 13% Prima 10% a. 210 b. 100 c. 75 d. 50
 1. Rada pro televizní vysílání prováděla průzkum sledovanosti českých televizních stanic. Průzkumu se zúčastnilo 500 tzv. respondentů. Sledovanost stanic ČT1, ČT2, Nova a Prima je uvedena v diagramu. Kolik
1. Rada pro televizní vysílání prováděla průzkum sledovanosti českých televizních stanic. Průzkumu se zúčastnilo 500 tzv. respondentů. Sledovanost stanic ČT1, ČT2, Nova a Prima je uvedena v diagramu. Kolik
MATÝSKOVA MATEMATIKA
 MTÝSKOV MTEMTIK PRO ROČNÍK ZÁKLDNÍ ŠKOLY DÍL učebnice podporující čtenářské dovednosti vytvořená v souladu s RVP ZV Vážení vyučující, nová učebnice matematiky mimo jiné aplikuje čtení jako prostředek k
MTÝSKOV MTEMTIK PRO ROČNÍK ZÁKLDNÍ ŠKOLY DÍL učebnice podporující čtenářské dovednosti vytvořená v souladu s RVP ZV Vážení vyučující, nová učebnice matematiky mimo jiné aplikuje čtení jako prostředek k
Test žáka. Zdroj testu: Celoplošná zkouška 2. Školní rok 2012/2013 MATEMATIKA. Jméno: Třída: Škola: Termín provedení testu:
 Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Kolik os souměrnosti má kruh?
Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Kolik os souměrnosti má kruh?
Jednoduché cykly 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45.
 Jednoduché cykly Tento oddíl obsahuje úlohy na první procvičení práce s cykly. Při řešení každé ze zde uvedených úloh stačí použít vedle podmíněných příkazů jen jediný cyklus. Nepotřebujeme používat ani
Jednoduché cykly Tento oddíl obsahuje úlohy na první procvičení práce s cykly. Při řešení každé ze zde uvedených úloh stačí použít vedle podmíněných příkazů jen jediný cyklus. Nepotřebujeme používat ani
Brlohovská úloha za 2 body
 Brlohovská úloha za 2 body Určete, kolika nejméně barvami můžeme obarvit naše logo tak, aby žádné dvě sousední oblasti neměly stejnou barvu. Za sousední se považují oblasti, které mají společný více než
Brlohovská úloha za 2 body Určete, kolika nejméně barvami můžeme obarvit naše logo tak, aby žádné dvě sousední oblasti neměly stejnou barvu. Za sousední se považují oblasti, které mají společný více než
Výroková logika II. Negace. Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0).
 Výroková logika II Negace Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0). Na konkrétních příkladech si ukážeme, jak se dají výroky negovat. Obecně se výrok dá negovat tak, že před
Výroková logika II Negace Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0). Na konkrétních příkladech si ukážeme, jak se dají výroky negovat. Obecně se výrok dá negovat tak, že před
Kolo 1. Mistrovství akademiků v řešení sudoku HALAS. Hráčská asociace logických her a sudoku
 jméno: body: Mistrovství akademiků v řešení sudoku Kolo. Klasické b. Klasické b. Klasické b. Klasické b. Klasické b. Klasické b 7. Klasické 9 9 b. Klasické 9 9 b 9. Sudé b 0. Liché b. Malá-střední-velká
jméno: body: Mistrovství akademiků v řešení sudoku Kolo. Klasické b. Klasické b. Klasické b. Klasické b. Klasické b. Klasické b 7. Klasické 9 9 b. Klasické 9 9 b 9. Sudé b 0. Liché b. Malá-střední-velká
101. Ať žije císař. 102. Lidový soud
 101. Ať žije císař Spojnice mezi body obsahují 26 písmen abecedy. Šipky tvoří dráhu, která podle určitých tajných pravidel prochází od počátečního bodu ke koncovému. Černé šipky znamenají pouze průchod,
101. Ať žije císař Spojnice mezi body obsahují 26 písmen abecedy. Šipky tvoří dráhu, která podle určitých tajných pravidel prochází od počátečního bodu ke koncovému. Černé šipky znamenají pouze průchod,
HOT POTATOES PRO PEDAGOGY - orientace v programu
 HOT POTATOES PRO PEDAGOGY - orientace v programu Mgr. Magda Sováková ESF PROJEKT OP VK ČÍSLO PROJEKTU CZ.1.07/1.1.07/11.0047 EFEKTIVNÍ VYUŽÍVÁNÍ ICT VE VÝUCE VŠEOBECNĚ VZDĚLÁVACÍCH A ODBORNÝCH PŘEDMĚTŮ
HOT POTATOES PRO PEDAGOGY - orientace v programu Mgr. Magda Sováková ESF PROJEKT OP VK ČÍSLO PROJEKTU CZ.1.07/1.1.07/11.0047 EFEKTIVNÍ VYUŽÍVÁNÍ ICT VE VÝUCE VŠEOBECNĚ VZDĚLÁVACÍCH A ODBORNÝCH PŘEDMĚTŮ
BARVY. Příkaz barva. Barvy TrueColor. Se objeví dialogové okno
 BARVY Příkaz barva Se objeví dialogové okno Lze vybrat barvu přímo Nebo vložíme do programu a za tento prvek číslo Baltíkovy barvy nebo konstantyu Za prvek lze vložit náhodnou barvu přímo nebo pomocí proměnné
BARVY Příkaz barva Se objeví dialogové okno Lze vybrat barvu přímo Nebo vložíme do programu a za tento prvek číslo Baltíkovy barvy nebo konstantyu Za prvek lze vložit náhodnou barvu přímo nebo pomocí proměnné
Čtvrtek 3. listopadu. Makra v Excelu. Obecná definice makra: Spouštění makra: Druhy maker, způsoby tvorby a jejich ukládání
 Čtvrtek 3. listopadu Makra v Excelu Obecná definice makra: Podle definice je makro strukturovanou definicí jedné nebo několika akcí, které chceme, aby MS Excel vykonal jako odezvu na nějakou námi definovanou
Čtvrtek 3. listopadu Makra v Excelu Obecná definice makra: Podle definice je makro strukturovanou definicí jedné nebo několika akcí, které chceme, aby MS Excel vykonal jako odezvu na nějakou námi definovanou
Formulář pro křížový filtr
 Formulář pro křížový filtr Formulář pro křížový filtr je určen zejména autorům křížovek a má sloužit jako pomůcka při jejich tvorbě. Levé části formuláře dominuje tzv. šablona, což je síť 20 krát 20 políček
Formulář pro křížový filtr Formulář pro křížový filtr je určen zejména autorům křížovek a má sloužit jako pomůcka při jejich tvorbě. Levé části formuláře dominuje tzv. šablona, což je síť 20 krát 20 políček
Flash - animace. 17. Změna tvaru - Flash. Vytvořila: Radka Veverková Vytvořeno dne: 10. 1. 2013. www.isspolygr.cz. Flash. DUM číslo: 16 Název: Flash
 - animace 17. Změna tvaru - www.isspolygr.cz Vytvořila: Radka Veverková Vytvořeno dne: 10. 1. 2013 DUM číslo: 16 Strana: 1/11 Škola Ročník 4. ročník (SOŠ, SOU) Název projektu Interaktivní metody zdokonalující
- animace 17. Změna tvaru - www.isspolygr.cz Vytvořila: Radka Veverková Vytvořeno dne: 10. 1. 2013 DUM číslo: 16 Strana: 1/11 Škola Ročník 4. ročník (SOŠ, SOU) Název projektu Interaktivní metody zdokonalující
1. KOMBINATORIKA - PŘÍKLADY
 1. KOMBINATORIKA - PŘÍKLADY Úlohy k samostatnému řešení 1.1. Zjednodušte a vypočtěte: 1.2. Kolik třítónových akordů je možné zahrát z 8 tónů? 1.3. Kolik různých optických signálů je možno dát vytahováním
1. KOMBINATORIKA - PŘÍKLADY Úlohy k samostatnému řešení 1.1. Zjednodušte a vypočtěte: 1.2. Kolik třítónových akordů je možné zahrát z 8 tónů? 1.3. Kolik různých optických signálů je možno dát vytahováním
Školní kolo soutěže Baltík 2007, kategorie A a B
 Úloha č. 1: Baltík - obkladač a. Baltík si koupil nový dvoupokojový byt. Po spuštění programu se na pracovní ploše objeví tyto dva pokoje. Zdi pokojů jsou tvořené předměty č. 1150 z banky 1. Baltík stojí
Úloha č. 1: Baltík - obkladač a. Baltík si koupil nový dvoupokojový byt. Po spuštění programu se na pracovní ploše objeví tyto dva pokoje. Zdi pokojů jsou tvořené předměty č. 1150 z banky 1. Baltík stojí
Výhody a nevýhody jednotlivých reprezentací jsou shrnuty na konci kapitoly.
 Kapitola Reprezentace grafu V kapitole?? jsme se dozvěděli, co to jsou grafy a k čemu jsou dobré. rzo budeme chtít napsat nějaký program, který s grafy pracuje. le jak si takový graf uložit do počítače?
Kapitola Reprezentace grafu V kapitole?? jsme se dozvěděli, co to jsou grafy a k čemu jsou dobré. rzo budeme chtít napsat nějaký program, který s grafy pracuje. le jak si takový graf uložit do počítače?
( n) ( ) ( ) 9.1.11 Kombinatorické úlohy bez opakování. Předpoklady: 9109
 9.1.11 Kombinatorické úlohy bez opakování Předpoklady: 9109 Pedagogická poznámka: Tato hodina slouží jednak ke zopakování probraného, ale zejména k praktickému nácviku kombinatoriky v situaci, ve které
9.1.11 Kombinatorické úlohy bez opakování Předpoklady: 9109 Pedagogická poznámka: Tato hodina slouží jednak ke zopakování probraného, ale zejména k praktickému nácviku kombinatoriky v situaci, ve které
KOMBINATORIKA. 1. cvičení
 KOMBINATORIKA 1. cvičení Co to je kombinatorika Kombinatorika je vstupní branou do teorie pravděpodobnosti. Zabývá se různými způsoby výběru prvků z daného souboru. 2011 Ing. Janurová Kateřina, FEI VŠB-TU
KOMBINATORIKA 1. cvičení Co to je kombinatorika Kombinatorika je vstupní branou do teorie pravděpodobnosti. Zabývá se různými způsoby výběru prvků z daného souboru. 2011 Ing. Janurová Kateřina, FEI VŠB-TU
Mistrovství České republiky v logických úlohách
 Mistrovství České republiky v logických úlohách Blok 1 - Logický mixer 10:00-11:40 Řešitel 1 Praha 013 Mrakodrapy 3 Heywake 4 Rybáři 5 Dvojblok Pentomina 7 Nádraží 8 Slalom 9 Plot 10 Kriskros 11 Cesta
Mistrovství České republiky v logických úlohách Blok 1 - Logický mixer 10:00-11:40 Řešitel 1 Praha 013 Mrakodrapy 3 Heywake 4 Rybáři 5 Dvojblok Pentomina 7 Nádraží 8 Slalom 9 Plot 10 Kriskros 11 Cesta
Pokyny pro žáky k testování písemné zkoušky na počítači
 Pokyny pro žáky k testování písemné zkoušky na počítači Posadíte se na určené místo v počítačové učebně, kde již předtím správce zkoušky spustil určený internetový prohlížeč s IP adresou zkouškového serveru.
Pokyny pro žáky k testování písemné zkoušky na počítači Posadíte se na určené místo v počítačové učebně, kde již předtím správce zkoušky spustil určený internetový prohlížeč s IP adresou zkouškového serveru.
4a) Racionální čísla a početní operace s nimi
 Racionální čísla a početní operace s nimi Množinu racionálních čísel získáme z množiny čísel celých, jejím rozšířením o čísla desetinná s ukončeným des. rozvojem nebo periodická a zlomky, které lze na
Racionální čísla a početní operace s nimi Množinu racionálních čísel získáme z množiny čísel celých, jejím rozšířením o čísla desetinná s ukončeným des. rozvojem nebo periodická a zlomky, které lze na
Řešte s námi! Dlouhodobá soutěž v řešení sudoku a logických úloh TOP 10
 Řešte s námi! Dlouhodobá soutěž v řešení sudoku a logických úloh TOP 7 Nurikabe loop Zakreslete do obrazce několik ostrovů (stranově souvislých oblastí) tak, aby každý z nich obsahoval přesně jedno zadané
Řešte s námi! Dlouhodobá soutěž v řešení sudoku a logických úloh TOP 7 Nurikabe loop Zakreslete do obrazce několik ostrovů (stranově souvislých oblastí) tak, aby každý z nich obsahoval přesně jedno zadané
Programy na PODMÍNĚNÝ příkaz IF a CASE
 Vstupy a výstupy budou vždy upraveny tak, aby bylo zřejmé, co zadáváme a co se zobrazuje. Není-li určeno, zadáváme přirozená čísla. Je-li to možné, používej generátor náhodných čísel vysvětli, co a jak
Vstupy a výstupy budou vždy upraveny tak, aby bylo zřejmé, co zadáváme a co se zobrazuje. Není-li určeno, zadáváme přirozená čísla. Je-li to možné, používej generátor náhodných čísel vysvětli, co a jak
Povrchy, objemy. Krychle = = = + =2 = 2 = 2 = 2 = 2 =( 2) + = ( 2) + = 2+ =3 = 3 = 3 = 3 = 3
 y, objemy nám vlastně říká, kolik tapety potřebujeme k polepení daného tělesa. Základní jednotkou jsou metry čtverečné (m 2 ). nám pak říká, kolik vody se do daného tělesa vejde. Základní jednotkou jsou
y, objemy nám vlastně říká, kolik tapety potřebujeme k polepení daného tělesa. Základní jednotkou jsou metry čtverečné (m 2 ). nám pak říká, kolik vody se do daného tělesa vejde. Základní jednotkou jsou
Řešení čtvrté série (14. dubna 2009)
 13. Tento seminář pro Vás připravuje vzdělávací agentura Kurzy-Fido.cz...s námi TSP zvládnete! Řešení čtvrté série (14. dubna 2009) Řešení společně připravili lektoři Aleph.cz a Kurzy-Fido.cz Úlohy z varianty
13. Tento seminář pro Vás připravuje vzdělávací agentura Kurzy-Fido.cz...s námi TSP zvládnete! Řešení čtvrté série (14. dubna 2009) Řešení společně připravili lektoři Aleph.cz a Kurzy-Fido.cz Úlohy z varianty
Sada 2 Microsoft Word 2007
 S třední škola stavební Jihlava Sada 2 Microsoft Word 2007 18. Editor rovnic Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2 - inovace
S třední škola stavební Jihlava Sada 2 Microsoft Word 2007 18. Editor rovnic Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2 - inovace
Matematický KLOKAN 2005 kategorie Junior
 Matematický KLOKAN 2005 kategorie Junior Vážení přátelé, v následujících 75 minutách vás čeká stejný úkol jako mnoho vašich vrstevníků v řadě dalších evropských zemí. V níže uvedeném testu je zadáno čtyřiadvacet
Matematický KLOKAN 2005 kategorie Junior Vážení přátelé, v následujících 75 minutách vás čeká stejný úkol jako mnoho vašich vrstevníků v řadě dalších evropských zemí. V níže uvedeném testu je zadáno čtyřiadvacet
Řešení: 1. a 2. sada
 14. ročník Řešení: 1. a 2. sada 101. Domino Kartičky rozstříháme a poskládáme za sebe tak, aby dvojice slov vedle sebe tvořily asociace na ptáky. Barva odpovídá rodu (mužský, ženský), pravé číslo udává
14. ročník Řešení: 1. a 2. sada 101. Domino Kartičky rozstříháme a poskládáme za sebe tak, aby dvojice slov vedle sebe tvořily asociace na ptáky. Barva odpovídá rodu (mužský, ženský), pravé číslo udává
Šablona pro zadávání otázek pro přijímací řízení pro akademický rok 2009/2010
 Šablona pro zadávání otázek pro přijímací řízení pro akademický rok 00/010 Zadavatel: Ekonomický přehled: kód 1 Matematické myšlení: kód Společensko historický přehled: kód Zadejte kód místo x do níže
Šablona pro zadávání otázek pro přijímací řízení pro akademický rok 00/010 Zadavatel: Ekonomický přehled: kód 1 Matematické myšlení: kód Společensko historický přehled: kód Zadejte kód místo x do níže
Výukový materiál zpracovaný v rámci projektu EU peníze do škol. Zašifrované verše
 Výukový materiál zpracovaný v rámci projektu EU peníze do škol ZŠ Litoměřice, Ladova Ladova 5 412 01 Litoměřice www.zsladovaltm.cz vedeni@zsladovaltm.cz Pořadové číslo projektu: CZ.1.07/1.4.00/21.0948
Výukový materiál zpracovaný v rámci projektu EU peníze do škol ZŠ Litoměřice, Ladova Ladova 5 412 01 Litoměřice www.zsladovaltm.cz vedeni@zsladovaltm.cz Pořadové číslo projektu: CZ.1.07/1.4.00/21.0948
9. ročník. Řešení 1. a 2. sada
 101. Šifrovací tutoriál 9. ročník Řešení 1. a 2. sada Substituční šifra ROT13, snadno viz např. rot13.com heslo obsahuje logicky soucin logický součin je and. Transpoziční šifra čteme vždy trojice písmen
101. Šifrovací tutoriál 9. ročník Řešení 1. a 2. sada Substituční šifra ROT13, snadno viz např. rot13.com heslo obsahuje logicky soucin logický součin je and. Transpoziční šifra čteme vždy trojice písmen
CO UMÍ EXCEL? CVIČEBNICE PŘÍKLADŮ PRO UČITELE. Modulární systém dalšího vzdělávání pedagogických pracovníků JmK. v přírodních vědách a informatice
 Modulární systém dalšího vzdělávání pedagogických pracovníků JmK v přírodních vědách a informatice CZ.1.07/1.3.10/02.0024 CO UMÍ EXCEL? CVIČEBNICE PŘÍKLADŮ PRO UČITELE 1 Tabulkový kalkulátor představuje
Modulární systém dalšího vzdělávání pedagogických pracovníků JmK v přírodních vědách a informatice CZ.1.07/1.3.10/02.0024 CO UMÍ EXCEL? CVIČEBNICE PŘÍKLADŮ PRO UČITELE 1 Tabulkový kalkulátor představuje
Základní vzorce a funkce v tabulkovém procesoru
 Základní vzorce a funkce v tabulkovém procesoru Na tabulkovém programu je asi nejzajímavější práce se vzorci a funkcemi. Když jednou nastavíte, jak se mají dané údaje zpracovávat (některé buňky sečíst,
Základní vzorce a funkce v tabulkovém procesoru Na tabulkovém programu je asi nejzajímavější práce se vzorci a funkcemi. Když jednou nastavíte, jak se mají dané údaje zpracovávat (některé buňky sečíst,
Slovní úlohy řešené lineární rovnicí. pracovní list. Základní škola Zaječí, okres Břeclav Školní 402, 691 05, příspěvková organizace
 Slovní úlohy řešené lineární rovnicí pracovní list Název školy: Číslo projektu: Autor: Základní škola Zaječí, okres Břeclav Školní 402, 691 05, příspěvková organizace CZ.1.07/1.4.00/21.1131 Mgr. Lenka
Slovní úlohy řešené lineární rovnicí pracovní list Název školy: Číslo projektu: Autor: Základní škola Zaječí, okres Břeclav Školní 402, 691 05, příspěvková organizace CZ.1.07/1.4.00/21.1131 Mgr. Lenka
Datum odevzdání 12. prosince Vypočtěte velikost strany čtverce ABCD s vrcholem A = [0, 0], jestliže
![Datum odevzdání 12. prosince Vypočtěte velikost strany čtverce ABCD s vrcholem A = [0, 0], jestliže Datum odevzdání 12. prosince Vypočtěte velikost strany čtverce ABCD s vrcholem A = [0, 0], jestliže](/thumbs/57/40473291.jpg) Příklady k řešení (. kolo) Datum odevzdání. prosince 00 PŘÍKLAD. Vypočtěte velikost strany čtverce ABCD s vrcholem A = [0, 0], jestliže úhlopříčka BD leží na přímce p :x +y = 0. PŘÍKLAD. Jsou dány body
Příklady k řešení (. kolo) Datum odevzdání. prosince 00 PŘÍKLAD. Vypočtěte velikost strany čtverce ABCD s vrcholem A = [0, 0], jestliže úhlopříčka BD leží na přímce p :x +y = 0. PŘÍKLAD. Jsou dány body
MS Excel Filtr automatický, rozšířený
 MS Excel Filtr automatický, rozšířený Obsah kapitoly V této lekci se seznámíme s nástrojem, který se používá pro výběry dat z rozsáhlých tabulek s filtrem automatickým a rozšířeným. Studijní cíle Studenti
MS Excel Filtr automatický, rozšířený Obsah kapitoly V této lekci se seznámíme s nástrojem, který se používá pro výběry dat z rozsáhlých tabulek s filtrem automatickým a rozšířeným. Studijní cíle Studenti
Zdokonalování gramotnosti v oblasti ICT. Kurz MS Excel kurz 3. Inovace a modernizace studijních oborů FSpS (IMPACT) CZ.1.07/2.2.00/28.
 Zdokonalování gramotnosti v oblasti ICT Kurz MS Excel kurz 3 1 Obsah Řazení dat... 3 Seřazení textu a čísel... 3 Další možné seřazení je možné podle barev, písma a ikon... 4 Filtry, rozšířené filtry...
Zdokonalování gramotnosti v oblasti ICT Kurz MS Excel kurz 3 1 Obsah Řazení dat... 3 Seřazení textu a čísel... 3 Další možné seřazení je možné podle barev, písma a ikon... 4 Filtry, rozšířené filtry...
SYLABUS RODINNÉHO KURZU ČEŠTINY Centrum pro integraci cizinců, o.p.s. www.cicpraha.org
 SYLABUS RODINNÉHO KURZU ČEŠTINY Centrum pro integraci cizinců, o.p.s. www.cicpraha.org 1 - SEZNÁMENÍ, PŘEDSTAVOVÁNÍ - rodič se umí představit - rodič umí představit své dítě - rodič umí hláskovat své jméno
SYLABUS RODINNÉHO KURZU ČEŠTINY Centrum pro integraci cizinců, o.p.s. www.cicpraha.org 1 - SEZNÁMENÍ, PŘEDSTAVOVÁNÍ - rodič se umí představit - rodič umí představit své dítě - rodič umí hláskovat své jméno
aplikační software pro práci s informacemi
 INFORMATIKA aplikační software pro práci s informacemi CITÁTY Pracovní list pro žáky Autor: RNDr. Ivanka Dvořáčková 2013 Citáty pracovní list Podle pokynů vyučujícího vyhledejte soubor IT 35Citáty pracovní
INFORMATIKA aplikační software pro práci s informacemi CITÁTY Pracovní list pro žáky Autor: RNDr. Ivanka Dvořáčková 2013 Citáty pracovní list Podle pokynů vyučujícího vyhledejte soubor IT 35Citáty pracovní
CVIČNÝ TEST 15. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17
 CVIČNÝ TEST 15 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Je dána čtvercová mřížka, v níž každý čtverec má délku
CVIČNÝ TEST 15 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Je dána čtvercová mřížka, v níž každý čtverec má délku
1. Základní pojmy, používané v tomto manuálu. 2. Stránky
 Redakční systém manuál 1. Základní pojmy, používané v tomto manuálu Hlavní menu Menu v horní světlemodré liště obsahující 7 základních položek: Publikovat, Správa, Vzhled, Komentáře, Nastavení, Pluginy,
Redakční systém manuál 1. Základní pojmy, používané v tomto manuálu Hlavní menu Menu v horní světlemodré liště obsahující 7 základních položek: Publikovat, Správa, Vzhled, Komentáře, Nastavení, Pluginy,
Obsah. Vymezení použitých pojmů
 Obsah Vymezení použitých pojmů Základní pravidla pro svazování kvadrantů v Karnaughových mapách Základní pravidla pro tvorbu rovnic Postup při zápisu rovnice z Karnaughovy mapy Příklady řešení Vymezení
Obsah Vymezení použitých pojmů Základní pravidla pro svazování kvadrantů v Karnaughových mapách Základní pravidla pro tvorbu rovnic Postup při zápisu rovnice z Karnaughovy mapy Příklady řešení Vymezení
Zadání soutěžních úloh
 20. až 22. dubna 2017 Krajské kolo 2016/2017 Úlohy můžete řešit v libovolném pořadí a samozřejmě je nemusíte vyřešit všechny. Za každou úlohu můžete dostat maximálně 10 bodů, z nichž je většinou 9 bodů
20. až 22. dubna 2017 Krajské kolo 2016/2017 Úlohy můžete řešit v libovolném pořadí a samozřejmě je nemusíte vyřešit všechny. Za každou úlohu můžete dostat maximálně 10 bodů, z nichž je většinou 9 bodů
Základy práce s programem pro interaktivní tabuli SMART notebook
 ZŠ praktická a ZŠ speciální Chodov, okres Sokolov, příspěvková organizace Základy práce s programem pro interaktivní tabuli SMART notebook Metodický materiál k základnímu školení Materiál vznikl v rámci
ZŠ praktická a ZŠ speciální Chodov, okres Sokolov, příspěvková organizace Základy práce s programem pro interaktivní tabuli SMART notebook Metodický materiál k základnímu školení Materiál vznikl v rámci
Mlýnek (typový výrobek)
 Mlýnek (typový výrobek) Popis: Středověká a dodnes oblíbená desková hra, známá po celé Evropě (například u Velkomoravanů). Hra je určena pro dva hráče. Počet žetonů celkem: 9 vs. 9 Parametry: Čtvercová
Mlýnek (typový výrobek) Popis: Středověká a dodnes oblíbená desková hra, známá po celé Evropě (například u Velkomoravanů). Hra je určena pro dva hráče. Počet žetonů celkem: 9 vs. 9 Parametry: Čtvercová
Jevy A a B jsou nezávislé, jestliže uskutečnění jednoho jevu nemá vliv na uskutečnění nebo neuskutečnění jevu druhého
 8. Základy teorie pravděpodobnosti 8. ročník 8. Základy teorie pravděpodobnosti Pravděpodobnost se zabývá matematickými zákonitostmi, které se projevují v náhodných pokusech. Tyto zákonitosti mají opodstatnění
8. Základy teorie pravděpodobnosti 8. ročník 8. Základy teorie pravděpodobnosti Pravděpodobnost se zabývá matematickými zákonitostmi, které se projevují v náhodných pokusech. Tyto zákonitosti mají opodstatnění
RNDr. Zdeněk Horák 23. 11. 2013 VII.
 Jméno RNDr. Zdeněk Horák Datum 23. 11. 2013 Ročník VII. Vzdělávací oblast MATEMATIKA A JEJÍ APLIKACE Vzdělávací obor MATEMATIKA Tematický okruh ZLOMKY Téma klíčová slova Slovní úlohy se zlomky, početní
Jméno RNDr. Zdeněk Horák Datum 23. 11. 2013 Ročník VII. Vzdělávací oblast MATEMATIKA A JEJÍ APLIKACE Vzdělávací obor MATEMATIKA Tematický okruh ZLOMKY Téma klíčová slova Slovní úlohy se zlomky, početní
Výběr báze. u n. a 1 u 1
 Výběr báze Mějme vektorový prostor zadán množinou generátorů. To jest V = M, kde M = {u,..., u n }. Pokud je naším úkolem najít nějakou bázi V, nejpřímočařejším postupem je napsat si vektory jako řádky
Výběr báze Mějme vektorový prostor zadán množinou generátorů. To jest V = M, kde M = {u,..., u n }. Pokud je naším úkolem najít nějakou bázi V, nejpřímočařejším postupem je napsat si vektory jako řádky
Pracovní list korekce hlásky B
 Pracovní list korekce hlásky B Pojmenuj všechny předměty na obrázcích a ty, které začínají písmenkem B, spoj červenou pastelkou s písmenkem uprostřed kroužku. Spočítej, kolik je na obrázku zvířátek, každé
Pracovní list korekce hlásky B Pojmenuj všechny předměty na obrázcích a ty, které začínají písmenkem B, spoj červenou pastelkou s písmenkem uprostřed kroužku. Spočítej, kolik je na obrázku zvířátek, každé
Celostátní kolo soutěže Mladý programátor 2013, kategorie C, D
 Pokyny: 1. Kategorie C i D řeší úlohy 1, 2, 3. 2. Řešení úloh ukládejte do složky, která se nachází na pracovní ploše počítače. Její název je stejný, jako je kód, který váš tým dostal přidělený (C05, D10
Pokyny: 1. Kategorie C i D řeší úlohy 1, 2, 3. 2. Řešení úloh ukládejte do složky, která se nachází na pracovní ploše počítače. Její název je stejný, jako je kód, který váš tým dostal přidělený (C05, D10
Změna velikosti písmen
 Změna velikosti písmen U aplikace Word můžeme změnit velikost písmen v textu bez toho, aniž bychom museli daný text přepisovat ručně. Postup je následující: 1) Vyberte text, u kterého chcete změnit psaní
Změna velikosti písmen U aplikace Word můžeme změnit velikost písmen v textu bez toho, aniž bychom museli daný text přepisovat ručně. Postup je následující: 1) Vyberte text, u kterého chcete změnit psaní
II. Elektronická pošta
 II. Chceme-li si přečíst poštu, klikneme v levém sloupci na nápis Doručená pošta. Máme před sebou seznam e-mailů seřazených podle data a času přijetí. Pokud máme zapnuto zobrazení náhledu, ve spodní nebo
II. Chceme-li si přečíst poštu, klikneme v levém sloupci na nápis Doručená pošta. Máme před sebou seznam e-mailů seřazených podle data a času přijetí. Pokud máme zapnuto zobrazení náhledu, ve spodní nebo
KAPITOLA 3 - ZPRACOVÁNÍ TEXTU
 KAPITOLA 3 - ZPRACOVÁNÍ TEXTU KLÍČOVÉ POJMY textové editory formát textu tabulka grafické objekty odrážky a číslování odstavec CÍLE KAPITOLY Pracovat s textovými dokumenty a ukládat je v souborech různého
KAPITOLA 3 - ZPRACOVÁNÍ TEXTU KLÍČOVÉ POJMY textové editory formát textu tabulka grafické objekty odrážky a číslování odstavec CÍLE KAPITOLY Pracovat s textovými dokumenty a ukládat je v souborech různého
Vkládání dalších objektů
 Vkládání dalších objektů Do textu v aplikaci Word, můžeme vkládat další objekty. Jedním z takových objektů je tabulka, o které jsme si už něco ukázali. Dalšími jsou obrázky, kliparty, grafy a kreslené
Vkládání dalších objektů Do textu v aplikaci Word, můžeme vkládat další objekty. Jedním z takových objektů je tabulka, o které jsme si už něco ukázali. Dalšími jsou obrázky, kliparty, grafy a kreslené
Matematika se Čtyřlístkem 1
 Matematika se Čtyřlístkem SPOČÍTEJ, KOLIK VĚCÍ JE V KAŽDÉ SKUPINĚ. DO RÁMEČKU NAKRESLI STEJNÝ POČET PUNTÍKŮ. ŘEKNI, CO VIDÍŠ, NAPŘ. TŘI TYČINKY. DO OKÉNEK NAKRESLI STEJNÝ POČET TVARŮ. POTOM NA OKÉNKA PŘILOŽ
Matematika se Čtyřlístkem SPOČÍTEJ, KOLIK VĚCÍ JE V KAŽDÉ SKUPINĚ. DO RÁMEČKU NAKRESLI STEJNÝ POČET PUNTÍKŮ. ŘEKNI, CO VIDÍŠ, NAPŘ. TŘI TYČINKY. DO OKÉNEK NAKRESLI STEJNÝ POČET TVARŮ. POTOM NA OKÉNKA PŘILOŽ
Čtvercové puzzle úloha za 2 body
 Čtvercové puzzle úloha za 2 body Poskládejte uvedené dílky do čtverce 5 5 polí tak, aby v každém řádku a každém sloupci byla obarvena právě tři pole: jedno červené, jedno žluté a jedno modré. Úloha č.
Čtvercové puzzle úloha za 2 body Poskládejte uvedené dílky do čtverce 5 5 polí tak, aby v každém řádku a každém sloupci byla obarvena právě tři pole: jedno červené, jedno žluté a jedno modré. Úloha č.
vzdělávací oblast vyučovací předmět ročník zodpovídá MATEMATIKA A JEJÍ APLIKACE MATEMATIKA 4. BÁRTOVÁ, VOJTÍŠKOVÁ
 Výstupy žáka ZŠ Chrudim, U Stadionu Učivo obsah Mezipředmětové vztahy Metody + formy práce, projekty, pomůcky a učební materiály ad. Poznámky 4. ročník OPAKOVÁNÍ UČIVA 3. ROČNÍKU Rozvíjí dovednosti s danými
Výstupy žáka ZŠ Chrudim, U Stadionu Učivo obsah Mezipředmětové vztahy Metody + formy práce, projekty, pomůcky a učební materiály ad. Poznámky 4. ročník OPAKOVÁNÍ UČIVA 3. ROČNÍKU Rozvíjí dovednosti s danými
1.4.6 Stavba matematiky, důkazy
 1.4.6 tavba matematiky, důkazy Předpoklady: 1401, 1404 Pedagogická poznámka: Tato hodina se velmi liší od většiny ostatních neboť jde v podstatě o přednášku. Také ji neprobíráme v prvním ročníku, ale přednáším
1.4.6 tavba matematiky, důkazy Předpoklady: 1401, 1404 Pedagogická poznámka: Tato hodina se velmi liší od většiny ostatních neboť jde v podstatě o přednášku. Také ji neprobíráme v prvním ročníku, ale přednáším
CVIČNÝ TEST 37. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15
 CVIČNÝ TEST 37 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Na staré hliněné desce je namalován čtverec
CVIČNÝ TEST 37 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Na staré hliněné desce je namalován čtverec
Digitalizace dat metodika
 Digitalizace dat metodika Digitalizace Jak počítač získá jedničky a nuly, se kterými potom počítá a které je schopen si pamatovat? Pomocí různých přístrojů a zařízení (mikrofon, fotoaparát, skener, kamera,
Digitalizace dat metodika Digitalizace Jak počítač získá jedničky a nuly, se kterými potom počítá a které je schopen si pamatovat? Pomocí různých přístrojů a zařízení (mikrofon, fotoaparát, skener, kamera,
Magické čtverce. Tomáš Roskovec. Úvod
 Magické čtverce Tomáš Roskovec Úvod Magické čtverce patří k dávným matematickým hrátkám, které i přes dvoutisíciletou historii dodnes nejsou zcela prozkoumány. Během přednášky se budeme zabývat nejprve
Magické čtverce Tomáš Roskovec Úvod Magické čtverce patří k dávným matematickým hrátkám, které i přes dvoutisíciletou historii dodnes nejsou zcela prozkoumány. Během přednášky se budeme zabývat nejprve
Jméno a příjmení. Pokud budete chtít svou odpověď opravit, zabarvěte původně zakřížkovaný čtvereček a zakřížkujte nový čtvereček.
 MATEMATIKA 5 M5PCD19C0T03 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 14 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby Časový limit pro řešení didaktického testu
MATEMATIKA 5 M5PCD19C0T03 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 14 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby Časový limit pro řešení didaktického testu
Test žáka. Zdroj testu: Celoplošná zkouška 2. Školní rok 2012/2013 MATEMATIKA. Jméno: Třída: Škola: Termín provedení testu:
 Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Trojúhelník má jeden úhel tupý,
Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Trojúhelník má jeden úhel tupý,
Mezinárodní kolo soutěže Baltík 2009, kategorie A a B
 Pokyny: 1. Kategorie A řeší pouze úlohy 1, 2, 3 a kategorie B pouze úlohy 2, 3, 4! 2. Řešení úloh ukládejte do složky, která se nachází na pracovní ploše počítače. Její název je stejný, jako je kód, který
Pokyny: 1. Kategorie A řeší pouze úlohy 1, 2, 3 a kategorie B pouze úlohy 2, 3, 4! 2. Řešení úloh ukládejte do složky, která se nachází na pracovní ploše počítače. Její název je stejný, jako je kód, který
kombinatorika září, 2015 Kombinatorika Opakovací kurz 2015 Radka Hájková
 Kombinatorika Opakovací kurz 2015 Radka Hájková 1) Děti z hudební školy Písnička, mezi nimiž byla i dvojčata Dita a Zita, psaly v rámci hudební nauky písemnou práci z not. Kolik možností oznámkování mohla
Kombinatorika Opakovací kurz 2015 Radka Hájková 1) Děti z hudební školy Písnička, mezi nimiž byla i dvojčata Dita a Zita, psaly v rámci hudební nauky písemnou práci z not. Kolik možností oznámkování mohla
Formuláře. Téma 3.2. Řešený příklad č Zadání: V databázi formulare_a_sestavy.accdb vytvořte formulář pro tabulku student.
 Téma 3.2 Formuláře Formuláře usnadňují zadávání, zobrazování, upravování nebo odstraňování dat z tabulky nebo z výsledku dotazu. Do formuláře lze vybrat jen určitá pole z tabulky, která obsahuje mnoho
Téma 3.2 Formuláře Formuláře usnadňují zadávání, zobrazování, upravování nebo odstraňování dat z tabulky nebo z výsledku dotazu. Do formuláře lze vybrat jen určitá pole z tabulky, která obsahuje mnoho
Algebra - druhý díl. Lenka Zalabová. zima Ústav matematiky a biomatematiky, Přírodovědecká fakulta, Jihočeská univerzita
 Algebra - druhý díl Lenka Zalabová Ústav matematiky a biomatematiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích zima 2012 Obsah 1 Permutace 2 Grupa permutací 3 Více o permutacích
Algebra - druhý díl Lenka Zalabová Ústav matematiky a biomatematiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích zima 2012 Obsah 1 Permutace 2 Grupa permutací 3 Více o permutacích
Zlatý řez nejen v matematice
 Zlatý řez nejen v matematice Příloha A In: Vlasta Chmelíková (author): Zlatý řez nejen v matematice. (Czech). Praha: Katedra didaktiky matematiky MFF UK, 2009. pp. 157 166. Persistent URL: http://dml.cz/dmlcz/400805
Zlatý řez nejen v matematice Příloha A In: Vlasta Chmelíková (author): Zlatý řez nejen v matematice. (Czech). Praha: Katedra didaktiky matematiky MFF UK, 2009. pp. 157 166. Persistent URL: http://dml.cz/dmlcz/400805
