Základy algoritmizace a programování
|
|
|
- Štěpánka Slavíková
- před 9 lety
- Počet zobrazení:
Transkript
1 Základy algoritmizace a programování Přednáška 1 Olga Majlingová Katedra matematiky, ČVUT v Praze 21. září 2009
2 Obsah Úvodní informace 1 Úvodní informace 2 3 4
3 Organizace předmětu Přednášky Základní konstrukce C Numerické algoritmy Některé konstrukce MATLABu Cvičení Navazují na přednášky.
4 Klasifikovaný zápočet Podmínky udělení zápočtu: hodnocení E : První test hodnocení D,C : + Druhý test hodnocení B,A : + Semestrální práce
5 Klasifikovaný zápočet Podmínky udělení zápočtu: hodnocení E : První test hodnocení D,C : + Druhý test hodnocení B,A : + Semestrální práce
6 Klasifikovaný zápočet Podmínky udělení zápočtu: hodnocení E : První test hodnocení D,C : + Druhý test hodnocení B,A : + Semestrální práce
7 Doporučená literatura web: zapg Resumé přednášek, informace k předmětu, aktuální informace... Herout, P.:Učebnice jazyka C Kernighan, B.W., Ritchie, D.M. Programovací jazyk C
8 Cíle předmětu být schopen číst a psát jednoduché programy v C rozumět základním konstrukcím jayzka C a umět je použít být schopen použít MATLAB pro řešení jednoduchých úloh
9 Algoritmus Úvodní informace Tvoříme-li program, musíme nejprve sami znát podrobný postup neboli algoritmus řešení úlohy. Algoritmus chápeme jako přesný popis výpočtového procesu, který vede od měnitelných výchozích údajů k požadovanému výsledku. Algoritmus má formu posloupnosti jednoduchých pravidel - elementárních kroků (operací). Kroky algoritmu musí být tak podrobné, aby byly srozumitelné tomu, kdo má podle algoritmu postupovat.
10 Algoritmizace a programování Program pro počítač musí splňovat všechny znaky algoritmu. K zápisu programu se používá programovací jazyk. Přípravu programu obvykle dělíme na dvě etapy: Algoritmizace V průběhu analýzy úlohy nebo po jejím ukončení sestavíme algoritmus řešení, který můžeme znázornit např. graficky, např. ve formě vývojového diagramu. Programování Podle zápisu algoritmu sestavíme program v programovacím jazyku.
11 Algoritmizace Při algoritmizaci pro počítač členíme postup řešení úlohy na tak podrobné kroky (operace), aby šly jednoduše vyjádřit programovacím jazykem. Při řešení numerických úloh jde o operace: výpočet hodnoty aritmetického výrazu, kde se smí vyskytovat operace sčítání, odčítání, násobení, dělení a výpočty hodnot elementárních funkcí (sin x, log x, x n, a x ) srovnání dvou hodnot podle velikosti, tj. rozhodnutí o pravdivosti relací rovno, nerovno, větší, menší určení pravdivostní hodnoty logického výrazu, k jehož sestavení bylo užito logických spojek konjunkce, disjunkce, negace přiřazení hodnoty proměnné
12 Proměnné a konstanty Konstanty: hodnoty, které se v průběhu výpočtu nemění. Např. čísla... 1, 1.2, nebo pojmenované konstanty (π) Proměnné:pamět ová místa, označená jménem proměnné (identifikátorem) jednoduché: kam se vejde jedna hodnota. v: složené: kam se vejde několik hodnot. p:
13 Příklad algoritmizace Úloha: Určit, zda přirozené číslo N je prvočíslo. Vstupní data: číslo N. Výstupní data (výsledek): ANO nebo NE. Musíme vědět, že přirozené číslo je prvočíslo když má právě 2 dělitele: jedničku a samo sebe. Také víme, že číslo a je dělitelné číslem b, když zbytek po dělení je nula.
14 Analyzujeme úlohu 1. přečteme N 2. zjistíme zbytek po po dělení čísla N číslem 2 3. když je zbytek 0, máme výsledek: NE, končíme v opačném případě pokračujeme 4. zjistíme zbytek po po dělení čísla N číslem 3 5. když je zbytek 0, máme výsledek: NE, končíme v opačném případě pokračujeme... zjistíme zbytek po dělení čísla N číslem K když je zbytek 0, máme výsledek: NE, končíme v opačném případě pokračujeme... jak dlouho?
15 Algoritmus (není dokonalý! PROČ?) 1. Přečteme N. Přejdeme ke kroku Když N je rovno 2 přejdeme ke kroku 8, v opačném případě přejdeme ke kroku Když zbytek po dělení čísla N číslem 2 je 0 v opačném případě přejdeme ke kroku Proměnné K přiřadíme 3. Přejdeme ke kroku Když zbytek po dělení čísla N číslem K je 0 v opačném případě přejdeme ke kroku Hodnotu K zvětšíme o 2. Přejdeme ke kroku Když je pravdivé : K K < N přejdeme ke kroku 5, v opačném případě přejdeme ke kroku Tiskneme ANO. Přejdeme ke kroku Tiskneme NE. Přejdeme ke kroku KONEC
16 Algoritmus (není dokonalý! PROČ?) 1. Přečteme N. Přejdeme ke kroku Když N je rovno 2 přejdeme ke kroku 8, v opačném případě přejdeme ke kroku Když zbytek po dělení čísla N číslem 2 je 0 v opačném případě přejdeme ke kroku Proměnné K přiřadíme 3. Přejdeme ke kroku Když zbytek po dělení čísla N číslem K je 0 v opačném případě přejdeme ke kroku Hodnotu K zvětšíme o 2. Přejdeme ke kroku Když je pravdivé : K K < N přejdeme ke kroku 5, v opačném případě přejdeme ke kroku Tiskneme ANO. Přejdeme ke kroku Tiskneme NE. Přejdeme ke kroku KONEC
17 Algoritmus (není dokonalý! PROČ?) 1. Přečteme N. Přejdeme ke kroku Když N je rovno 2 přejdeme ke kroku 8, v opačném případě přejdeme ke kroku Když zbytek po dělení čísla N číslem 2 je 0 v opačném případě přejdeme ke kroku Proměnné K přiřadíme 3. Přejdeme ke kroku Když zbytek po dělení čísla N číslem K je 0 v opačném případě přejdeme ke kroku Hodnotu K zvětšíme o 2. Přejdeme ke kroku Když je pravdivé : K K < N přejdeme ke kroku 5, v opačném případě přejdeme ke kroku Tiskneme ANO. Přejdeme ke kroku Tiskneme NE. Přejdeme ke kroku KONEC
18 Algoritmus (není dokonalý! PROČ?) 1. Přečteme N. Přejdeme ke kroku Když N je rovno 2 přejdeme ke kroku 8, v opačném případě přejdeme ke kroku Když zbytek po dělení čísla N číslem 2 je 0 v opačném případě přejdeme ke kroku Proměnné K přiřadíme 3. Přejdeme ke kroku Když zbytek po dělení čísla N číslem K je 0 v opačném případě přejdeme ke kroku Hodnotu K zvětšíme o 2. Přejdeme ke kroku Když je pravdivé : K K < N přejdeme ke kroku 5, v opačném případě přejdeme ke kroku Tiskneme ANO. Přejdeme ke kroku Tiskneme NE. Přejdeme ke kroku KONEC
19 Algoritmus (není dokonalý! PROČ?) 1. Přečteme N. Přejdeme ke kroku Když N je rovno 2 přejdeme ke kroku 8, v opačném případě přejdeme ke kroku Když zbytek po dělení čísla N číslem 2 je 0 v opačném případě přejdeme ke kroku Proměnné K přiřadíme 3. Přejdeme ke kroku Když zbytek po dělení čísla N číslem K je 0 v opačném případě přejdeme ke kroku Hodnotu K zvětšíme o 2. Přejdeme ke kroku Když je pravdivé : K K < N přejdeme ke kroku 5, v opačném případě přejdeme ke kroku Tiskneme ANO. Přejdeme ke kroku Tiskneme NE. Přejdeme ke kroku KONEC
20 Algoritmus (není dokonalý! PROČ?) 1. Přečteme N. Přejdeme ke kroku Když N je rovno 2 přejdeme ke kroku 8, v opačném případě přejdeme ke kroku Když zbytek po dělení čísla N číslem 2 je 0 v opačném případě přejdeme ke kroku Proměnné K přiřadíme 3. Přejdeme ke kroku Když zbytek po dělení čísla N číslem K je 0 v opačném případě přejdeme ke kroku Hodnotu K zvětšíme o 2. Přejdeme ke kroku Když je pravdivé : K K < N přejdeme ke kroku 5, v opačném případě přejdeme ke kroku Tiskneme ANO. Přejdeme ke kroku Tiskneme NE. Přejdeme ke kroku KONEC
21 Algoritmus (není dokonalý! PROČ?) 1. Přečteme N. Přejdeme ke kroku Když N je rovno 2 přejdeme ke kroku 8, v opačném případě přejdeme ke kroku Když zbytek po dělení čísla N číslem 2 je 0 v opačném případě přejdeme ke kroku Proměnné K přiřadíme 3. Přejdeme ke kroku Když zbytek po dělení čísla N číslem K je 0 v opačném případě přejdeme ke kroku Hodnotu K zvětšíme o 2. Přejdeme ke kroku Když je pravdivé : K K < N přejdeme ke kroku 5, v opačném případě přejdeme ke kroku Tiskneme ANO. Přejdeme ke kroku Tiskneme NE. Přejdeme ke kroku KONEC
22 Algoritmus (není dokonalý! PROČ?) 1. Přečteme N. Přejdeme ke kroku Když N je rovno 2 přejdeme ke kroku 8, v opačném případě přejdeme ke kroku Když zbytek po dělení čísla N číslem 2 je 0 v opačném případě přejdeme ke kroku Proměnné K přiřadíme 3. Přejdeme ke kroku Když zbytek po dělení čísla N číslem K je 0 v opačném případě přejdeme ke kroku Hodnotu K zvětšíme o 2. Přejdeme ke kroku Když je pravdivé : K K < N přejdeme ke kroku 5, v opačném případě přejdeme ke kroku Tiskneme ANO. Přejdeme ke kroku Tiskneme NE. Přejdeme ke kroku KONEC
23 Algoritmus (není dokonalý! PROČ?) 1. Přečteme N. Přejdeme ke kroku Když N je rovno 2 přejdeme ke kroku 8, v opačném případě přejdeme ke kroku Když zbytek po dělení čísla N číslem 2 je 0 v opačném případě přejdeme ke kroku Proměnné K přiřadíme 3. Přejdeme ke kroku Když zbytek po dělení čísla N číslem K je 0 v opačném případě přejdeme ke kroku Hodnotu K zvětšíme o 2. Přejdeme ke kroku Když je pravdivé : K K < N přejdeme ke kroku 5, v opačném případě přejdeme ke kroku Tiskneme ANO. Přejdeme ke kroku Tiskneme NE. Přejdeme ke kroku KONEC
24 Algoritmus (není dokonalý! PROČ?) 1. Přečteme N. Přejdeme ke kroku Když N je rovno 2 přejdeme ke kroku 8, v opačném případě přejdeme ke kroku Když zbytek po dělení čísla N číslem 2 je 0 v opačném případě přejdeme ke kroku Proměnné K přiřadíme 3. Přejdeme ke kroku Když zbytek po dělení čísla N číslem K je 0 v opačném případě přejdeme ke kroku Hodnotu K zvětšíme o 2. Přejdeme ke kroku Když je pravdivé : K K < N přejdeme ke kroku 5, v opačném případě přejdeme ke kroku Tiskneme ANO. Přejdeme ke kroku Tiskneme NE. Přejdeme ke kroku KONEC
25 Algoritmus (není dokonalý! PROČ?) 1. Přečteme N. Přejdeme ke kroku Když N je rovno 2 přejdeme ke kroku 8, v opačném případě přejdeme ke kroku Když zbytek po dělení čísla N číslem 2 je 0 v opačném případě přejdeme ke kroku Proměnné K přiřadíme 3. Přejdeme ke kroku Když zbytek po dělení čísla N číslem K je 0 v opačném případě přejdeme ke kroku Hodnotu K zvětšíme o 2. Přejdeme ke kroku Když je pravdivé : K K < N přejdeme ke kroku 5, v opačném případě přejdeme ke kroku Tiskneme ANO. Přejdeme ke kroku Tiskneme NE. Přejdeme ke kroku KONEC
26 Algoritmus (není dokonalý! PROČ?) 1. Přečteme N. Přejdeme ke kroku Když N je rovno 2 přejdeme ke kroku 8, v opačném případě přejdeme ke kroku Když zbytek po dělení čísla N číslem 2 je 0 v opačném případě přejdeme ke kroku Proměnné K přiřadíme 3. Přejdeme ke kroku Když zbytek po dělení čísla N číslem K je 0 v opačném případě přejdeme ke kroku Hodnotu K zvětšíme o 2. Přejdeme ke kroku Když je pravdivé : K K < N přejdeme ke kroku 5, v opačném případě přejdeme ke kroku Tiskneme ANO. Přejdeme ke kroku Tiskneme NE. Přejdeme ke kroku KONEC
27 Algoritmus (není dokonalý! PROČ?) 1. Přečteme N. Přejdeme ke kroku Když N je rovno 2 přejdeme ke kroku 8, v opačném případě přejdeme ke kroku Když zbytek po dělení čísla N číslem 2 je 0 v opačném případě přejdeme ke kroku Proměnné K přiřadíme 3. Přejdeme ke kroku Když zbytek po dělení čísla N číslem K je 0 v opačném případě přejdeme ke kroku Hodnotu K zvětšíme o 2. Přejdeme ke kroku Když je pravdivé : K K < N přejdeme ke kroku 5, v opačném případě přejdeme ke kroku Tiskneme ANO. Přejdeme ke kroku Tiskneme NE. Přejdeme ke kroku KONEC
28 Testování algoritmu Zvolíme si číslo N =... a budeme postupovat podle uvedeného algoritmu. Jaká N jsou vhodná? Najdeme nedokonalosti?
29 algoritmus myšlenka editor překladač linker OS gramatika funkce
30 algoritmus myšlenka editor překladač linker OS gramatika funkce
31 algoritmus myšlenka editor překladač linker OS gramatika funkce
32 algoritmus myšlenka editor překladač linker OS gramatika funkce
33 algoritmus myšlenka editor překladač linker OS gramatika funkce
34 algoritmus myšlenka editor překladač linker OS gramatika funkce
35 algoritmus myšlenka editor překladač linker OS gramatika funkce
36 algoritmus myšlenka editor překladač linker OS gramatika funkce
37 Úvodní informace Zápis programu: prostý textový soubor (ASCII) mezery, tabulátory,... překladač ignoruje mezery a tabulátory slouží ke zvýšení čitelnosti nešetřit mezerami! příkazy se ukončují středníkem IDENTIFIKÁTORY (jména) : pouze aa..zz, _, číslice 0..9 nesmí začínat číslicí rozlišují se velká a malá písmena!!! (id, Id, ID jsou 3 různé identifikátory) všechna klíčová slova a názvy funkcí ze standardní knihovny jsou malými písmeny
38 Nejjednodušší program main() {} o trochu větší: int main() { return 0 ;}
39 Program, který umí psát #include<stdio.h> main() { printf("hello world!"); }
40 Proměnné a zápis výrazů Proměnné musíme deklarovat: int a, b; float c; Aritmetické výrazy: sčítání + odčítání - násobení dělení / zbytek po dělení % umocňování... NENÍ! ZLKY! POZOR: celočíselné nebo reálné POZOR: pouze pro celočíselné a/b*c nebo a/(b*c)! a=5*3-12%4; b = 1/3*3; c=1/3*3;
41 Přiřazení Úvodní informace PRĚNNÁ = VÝRAZ ; int a, b, c; a = 5; b = 2; c = 3; a = a + b ; b = a - b ; a = a - b ; c = c + 1; a = c ; a = b ; c = a ; b = c ; c = a ;
42 Program, který umí také číst # include<stdio.h> main() { int a; float x; printf("zadejte celé číslo!"); scanf("%d",&a); printf("zadejte reálné číslo!"); scanf("%f",&x); printf("zadali jste %d a %f", a, f); printf("zadejte 1 celé a 1 reálné číslo!"); scanf("%d%f",&a,&x); printf("zadali jste %d a %5.3f", a, f); }
43 Použtí matematických funkcí ve výrazech MATEMATICKÁ KNIHOVNA: #include<math.h> mocnina: odmocnina: goniometrické: inverzní: logaritmy: pow(co, na_ kolikátou); sqrt(x); sin(x); cos(x); tan(x); asin(x); acos(x); atan(x); log(x); log10(x);
44 Prográmek pro výpočet obsahů a obvodů # include<stdio.h> # include<math.h> main() { float a,b,o_c,s, o; printf("zadejte stranu ctverce"); scanf("%f",&a); o_c = 4 a; S=pow(a,2); printf("ctverec:o=%5.3f, S=%6.4f",o_c,S); printf("zadejte strany obdelnika"); scanf("%f%f",&a,&b); o = (a+b) 2 ; printf("obdelnik o=%6.4f,s=%5.3f" o,a b); }
45 Dále... Úvodní informace Na příští přednášce: Logické výrazy Větvení (příkazy if - else, switch) Cykly
Základy algoritmizace a programování
 Základy algoritmizace a programování Přednáška 1 Olga Majlingová Katedra matematiky, ČVUT v Praze 19. září 2011 Obsah Úvodní informace 1 Úvodní informace 2 3 4 Doporučená literatura web: http://marian.fsik.cvut.cz/zapg
Základy algoritmizace a programování Přednáška 1 Olga Majlingová Katedra matematiky, ČVUT v Praze 19. září 2011 Obsah Úvodní informace 1 Úvodní informace 2 3 4 Doporučená literatura web: http://marian.fsik.cvut.cz/zapg
1. lekce. do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme:
 1. lekce 1. Minimální program do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme: #include #include int main() { printf("hello world!\n"); return 0; 2.
1. lekce 1. Minimální program do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme: #include #include int main() { printf("hello world!\n"); return 0; 2.
1. lekce. do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme:
 1. lekce 1. Minimální program do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme: #include #include int main() { printf("hello world!\n"); return 0; 2.
1. lekce 1. Minimální program do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme: #include #include int main() { printf("hello world!\n"); return 0; 2.
Úvod do programování. Lekce 1
 Úvod do programování Lekce 1 Základní pojmy vytvoření spustitelného kódu editor - psaní zdrojových souborů preprocesor - zpracování zdrojových souborů (vypuštění komentářů atd.) kompilátor (compiler) -
Úvod do programování Lekce 1 Základní pojmy vytvoření spustitelného kódu editor - psaní zdrojových souborů preprocesor - zpracování zdrojových souborů (vypuštění komentářů atd.) kompilátor (compiler) -
Algoritmizace a programování
 Algoritmizace a programování Výrazy Operátory Výrazy Verze pro akademický rok 2012/2013 1 Operace, operátory Unární jeden operand, operátor se zapisuje ve většině případů před operand, v některých případech
Algoritmizace a programování Výrazy Operátory Výrazy Verze pro akademický rok 2012/2013 1 Operace, operátory Unární jeden operand, operátor se zapisuje ve většině případů před operand, v některých případech
Lekce 01 Úvod do algoritmizace
 Počítačové laboratoře bez tajemství aneb naučme se učit algoritmizaci a programování s využitím robotů Lekce 01 Úvod do algoritmizace Tento projekt CZ.1.07/1.3.12/04.0006 je spolufinancován Evropským sociálním
Počítačové laboratoře bez tajemství aneb naučme se učit algoritmizaci a programování s využitím robotů Lekce 01 Úvod do algoritmizace Tento projekt CZ.1.07/1.3.12/04.0006 je spolufinancován Evropským sociálním
Operátory pro maticové operace (operace s celými maticemi) * násobení maticové Pro čísla platí: 2*2
 * násobení maticové Pro čísla platí: Pro matice - násobení inverzní maticí inv inverzní matice A -1 k dané matici A je taková matice, která po vynásobení s původní maticí dá jednotkovou matici. Inverzní
* násobení maticové Pro čísla platí: Pro matice - násobení inverzní maticí inv inverzní matice A -1 k dané matici A je taková matice, která po vynásobení s původní maticí dá jednotkovou matici. Inverzní
Základy jazyka C. Základy programování 1 Martin Kauer (Tomáš Kühr)
 Základy jazyka C Základy programování 1 Martin Kauer (Tomáš Kühr) Organizační záležitosti Konzultace Pracovna 5.076 Úterý 15:00 16:30 Emailem martin.kauer@upol.cz Web předmětu http://tux.inf.upol.cz/~kauer/index.php?content=var&class=zp1
Základy jazyka C Základy programování 1 Martin Kauer (Tomáš Kühr) Organizační záležitosti Konzultace Pracovna 5.076 Úterý 15:00 16:30 Emailem martin.kauer@upol.cz Web předmětu http://tux.inf.upol.cz/~kauer/index.php?content=var&class=zp1
Operátory. Základy programování 1 Tomáš Kühr
 Operátory Základy programování 1 Tomáš Kühr Operátory a jejich vlastnosti Základní konstrukce (skoro) každého jazyka Z daných operandů vytvoří výsledek, který je možné dále využívat Arita udává počet operandů
Operátory Základy programování 1 Tomáš Kühr Operátory a jejich vlastnosti Základní konstrukce (skoro) každého jazyka Z daných operandů vytvoří výsledek, který je možné dále využívat Arita udává počet operandů
- speciální symboly + - * / =., < > <> <= >= a další. Klíčová slova jsou chráněnými útvary, které nelze použít ve významu identifikátorů.
 Základní symboly - písmena A B C Y Z a b c y z - číslice 0 1 2 9 - speciální symboly + - * / =., < > = a další - klíčová slova and array begin case const a další Klíčová slova jsou chráněnými útvary,
Základní symboly - písmena A B C Y Z a b c y z - číslice 0 1 2 9 - speciální symboly + - * / =., < > = a další - klíčová slova and array begin case const a další Klíčová slova jsou chráněnými útvary,
Vlastnosti algoritmu. elementárnost. determinovanost. rezultativnost. konečnost. hromadnost. efektivnost
 Programování Algoritmus návod na vykonání činnosti, který nás od (měnitelných) vstupních dat přivede v konečném čase k výsledku přesně definovaná konečná posloupnost činností vedoucích k výsledku (postup,
Programování Algoritmus návod na vykonání činnosti, který nás od (měnitelných) vstupních dat přivede v konečném čase k výsledku přesně definovaná konečná posloupnost činností vedoucích k výsledku (postup,
Úvod do jazyka C. Ing. Jan Fikejz (KST, FEI) Fakulta elektrotechniky a informatiky Katedra softwarových technologií
 1 Fakulta elektrotechniky a informatiky Katedra softwarových technologií 12. října 2009 Organizace výuky Přednášky Teoretické základy dle normy jazyka C Cvičení Praktické úlohy odpřednášené látky Prostřední
1 Fakulta elektrotechniky a informatiky Katedra softwarových technologií 12. října 2009 Organizace výuky Přednášky Teoretické základy dle normy jazyka C Cvičení Praktické úlohy odpřednášené látky Prostřední
Racionální čísla, operátory, výrazy, knihovní funkce
 Příprava studijního programu Informatika je podporována projektem financovaným z Evropského sociálního fondu a rozpočtu hlavního města Prahy. Praha & EU: Investujeme do vaší budoucnosti Racionální čísla,
Příprava studijního programu Informatika je podporována projektem financovaným z Evropského sociálního fondu a rozpočtu hlavního města Prahy. Praha & EU: Investujeme do vaší budoucnosti Racionální čísla,
Výrazy a operátory. Operátory Unární - unární a unární + Např.: a +b
 Výrazy a operátory i = 2 i = 2; to je výraz to je příkaz 4. Operátory Unární - unární a unární + Např.: +5-5 -8.345 -a +b - unární ++ - inkrement - zvýší hodnotu proměnné o 1 - unární -- - dekrement -
Výrazy a operátory i = 2 i = 2; to je výraz to je příkaz 4. Operátory Unární - unární a unární + Např.: +5-5 -8.345 -a +b - unární ++ - inkrement - zvýší hodnotu proměnné o 1 - unární -- - dekrement -
Algoritmy a algoritmizace
 Otázka 21 Algoritmy a algoritmizace Počítačové programy (neboli software) umožňují počítačům, aby přestaly být pouhou stavebnicí elektronických a jiných součástek a staly se pomocníkem v mnoha lidských
Otázka 21 Algoritmy a algoritmizace Počítačové programy (neboli software) umožňují počítačům, aby přestaly být pouhou stavebnicí elektronických a jiných součástek a staly se pomocníkem v mnoha lidských
Základní pojmy. Úvod do programování. Základní pojmy. Zápis algoritmu. Výraz. Základní pojmy
 Úvod do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programování, 2004/2005 Procesor Procesorem je objekt, který vykonává algoritmem popisovanou
Úvod do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programování, 2004/2005 Procesor Procesorem je objekt, který vykonává algoritmem popisovanou
Logické operace. Datový typ bool. Relační operátory. Logické operátory. IAJCE Přednáška č. 3. může nabýt hodnot: o true o false
 Logické operace Datový typ bool může nabýt hodnot: o true o false Relační operátory pravda, 1, nepravda, 0, hodnoty všech primitivních datových typů (int, double ) jsou uspořádané lze je porovnávat binární
Logické operace Datový typ bool může nabýt hodnot: o true o false Relační operátory pravda, 1, nepravda, 0, hodnoty všech primitivních datových typů (int, double ) jsou uspořádané lze je porovnávat binární
Algoritmizace a programování. Ak. rok 2012/2013 vbp 1. ze 44
 Algoritmizace a programování Ak. rok 2012/2013 vbp 1. ze 44 Vladimír Beneš Petrovický K101 katedra matematiky, statistiky a informačních technologií vedoucí katedry E-mail: vbenes@bivs.cz Telefon: 251
Algoritmizace a programování Ak. rok 2012/2013 vbp 1. ze 44 Vladimír Beneš Petrovický K101 katedra matematiky, statistiky a informačních technologií vedoucí katedry E-mail: vbenes@bivs.cz Telefon: 251
Racionální čísla, operátory, výrazy, knihovní funkce
 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Racionální čísla, operátory, výrazy, knihovní funkce BI-PA1 Programování a algoritmizace 1 Katedra teoretické informatiky Miroslav Balík
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Racionální čísla, operátory, výrazy, knihovní funkce BI-PA1 Programování a algoritmizace 1 Katedra teoretické informatiky Miroslav Balík
Algoritmus. Přesné znění definice algoritmu zní: Algoritmus je procedura proveditelná Turingovým strojem.
 Algoritmus Algoritmus je schematický postup pro řešení určitého druhu problémů, který je prováděn pomocí konečného množství přesně definovaných kroků. nebo Algoritmus lze definovat jako jednoznačně určenou
Algoritmus Algoritmus je schematický postup pro řešení určitého druhu problémů, který je prováděn pomocí konečného množství přesně definovaných kroků. nebo Algoritmus lze definovat jako jednoznačně určenou
Výukový materiál zpracován v rámci projektu EU peníze školám
 Výukový materiál zpracován v rámci projektu EU peníze školám Registrační číslo projektu: CZ. 1.07/1.5.00/34.0637 Šablona III/2 Název VY_32_INOVACE_39_Algoritmizace_teorie Název školy Základní škola a Střední
Výukový materiál zpracován v rámci projektu EU peníze školám Registrační číslo projektu: CZ. 1.07/1.5.00/34.0637 Šablona III/2 Název VY_32_INOVACE_39_Algoritmizace_teorie Název školy Základní škola a Střední
Operátory. Základy programování 1 Martin Kauer (Tomáš Kühr)
 Operátory Základy programování 1 Martin Kauer (Tomáš Kühr) Organizační poznámky Formátujte kód přehledně! Pomůžete sobě i mně. Spusťte si vaše programy a zkuste různé vstupy! Pokud program nedává správné
Operátory Základy programování 1 Martin Kauer (Tomáš Kühr) Organizační poznámky Formátujte kód přehledně! Pomůžete sobě i mně. Spusťte si vaše programy a zkuste různé vstupy! Pokud program nedává správné
Učební plán 4. letého studia předmětu matematiky. Učební plán 6. letého studia předmětu matematiky
 Učební plán 4. letého studia předmětu matematiky Ročník I II III IV Dotace 3 3+1 2+1 2+2 Povinnost povinný povinný povinný povinný Učební plán 6. letého studia předmětu matematiky Ročník 1 2 3 4 5 6 Dotace
Učební plán 4. letého studia předmětu matematiky Ročník I II III IV Dotace 3 3+1 2+1 2+2 Povinnost povinný povinný povinný povinný Učební plán 6. letého studia předmětu matematiky Ročník 1 2 3 4 5 6 Dotace
Matematická indukce, sumy a produkty, matematická logika
 Matematická indukce, sumy a produkty, matematická logika 8.9. -.0.009 Matematická indukce Jde o následující vlastnost přirozených čísel: Předpokládejme:. Nějaké tvrzení platí pro.. Platí-li tvrzení pro
Matematická indukce, sumy a produkty, matematická logika 8.9. -.0.009 Matematická indukce Jde o následující vlastnost přirozených čísel: Předpokládejme:. Nějaké tvrzení platí pro.. Platí-li tvrzení pro
Booleovská algebra. Booleovské binární a unární funkce. Základní zákony.
 Booleovská algebra. Booleovské binární a unární funkce. Základní zákony. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Booleovská algebra. Booleovské binární a unární funkce. Základní zákony. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Algoritmizace prostorových úloh
 INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Algoritmus Daniela Szturcová Tento
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Algoritmus Daniela Szturcová Tento
Algoritmizace a programování
 Algoritmizace a programování Řídicí struktury, standardní metody Problematika načítání pomocí Scanner Některé poznámky k příkazům Psaní kódu programu Metody třídy Math Obalové třídy primitivních datových
Algoritmizace a programování Řídicí struktury, standardní metody Problematika načítání pomocí Scanner Některé poznámky k příkazům Psaní kódu programu Metody třídy Math Obalové třídy primitivních datových
PROGRAMOVACÍ JAZYKY A PŘEKLADAČE REALIZACE PŘEKLADAČE I
 PROGRAMOVACÍ JAZYKY A PŘEKLADAČE REALIZACE PŘEKLADAČE I 2011 Jan Janoušek BI-PJP Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Programová realizace DKA typedef enum {q0, q1,... qn,
PROGRAMOVACÍ JAZYKY A PŘEKLADAČE REALIZACE PŘEKLADAČE I 2011 Jan Janoušek BI-PJP Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Programová realizace DKA typedef enum {q0, q1,... qn,
Programování v jazyce C pro chemiky (C2160) 3. Příkaz switch, příkaz cyklu for, operátory ++ a --, pole
 Programování v jazyce C pro chemiky (C2160) 3. Příkaz switch, příkaz cyklu for, operátory ++ a --, pole Příkaz switch Příkaz switch provede příslušnou skupinu příkazů na základě hodnoty proměnné (celočíselné
Programování v jazyce C pro chemiky (C2160) 3. Příkaz switch, příkaz cyklu for, operátory ++ a --, pole Příkaz switch Příkaz switch provede příslušnou skupinu příkazů na základě hodnoty proměnné (celočíselné
Algoritmizace. 1. Úvod. Algoritmus
 1. Úvod Algoritmizace V dnešní době již počítače pronikly snad do všech oblastí lidské činnosti, využívají se k řešení nejrůznějších úkolů. Postup, který je v počítači prováděn nějakým programem se nazývá
1. Úvod Algoritmizace V dnešní době již počítače pronikly snad do všech oblastí lidské činnosti, využívají se k řešení nejrůznějších úkolů. Postup, který je v počítači prováděn nějakým programem se nazývá
Inovace bakalářského studijního oboru Aplikovaná chemie http://aplchem.upol.cz
 Inovace bakalářského studijního oboru Aplikovaná chemie http://aplchem.upol.cz CZ.1.07/2.2.00/15.0247 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. Tvorba
Inovace bakalářského studijního oboru Aplikovaná chemie http://aplchem.upol.cz CZ.1.07/2.2.00/15.0247 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. Tvorba
Sada 1 - Základy programování
 S třední škola stavební Jihlava Sada 1 - Základy programování 04. Datové typy, operace, logické operátory Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284
S třední škola stavební Jihlava Sada 1 - Základy programování 04. Datové typy, operace, logické operátory Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284
Algoritmizace prostorových úloh
 INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Algoritmus Daniela Szturcová Tento
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Algoritmus Daniela Szturcová Tento
Mgr. Ladislav Zemánek Maturitní okruhy Matematika 2013-2014. 1. Obor reálných čísel
 Mgr. Ladislav Zemánek Maturitní okruhy Matematika 2013-2014 1. Obor reálných čísel - obor přirozených, celých, racionálních a reálných čísel - vlastnosti operací (sčítání, odčítání, násobení, dělení) -
Mgr. Ladislav Zemánek Maturitní okruhy Matematika 2013-2014 1. Obor reálných čísel - obor přirozených, celých, racionálních a reálných čísel - vlastnosti operací (sčítání, odčítání, násobení, dělení) -
8. lekce Úvod do jazyka C 3. část Základní příkazy jazyka C Miroslav Jílek
 8. lekce Úvod do jazyka C 3. část Základní příkazy jazyka C Miroslav Jílek 1/41 Základní příkazy Všechny příkazy se píšou malými písmeny! Za většinou příkazů musí být středník (;)! 2/41 Základní příkazy
8. lekce Úvod do jazyka C 3. část Základní příkazy jazyka C Miroslav Jílek 1/41 Základní příkazy Všechny příkazy se píšou malými písmeny! Za většinou příkazů musí být středník (;)! 2/41 Základní příkazy
Funkce, intuitivní chápání složitosti
 Příprava studijního programu Informatika je podporována projektem financovaným z Evropského sociálního fondu a rozpočtu hlavního města Prahy. Praha & EU: Investujeme do vaší budoucnosti Funkce, intuitivní
Příprava studijního programu Informatika je podporována projektem financovaným z Evropského sociálního fondu a rozpočtu hlavního města Prahy. Praha & EU: Investujeme do vaší budoucnosti Funkce, intuitivní
KTE / PPEL Počítačová podpora v elektrotechnice
 KTE / PPEL Počítačová podpora v elektrotechnice Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz http://home.zcu.cz/~lsroubov 3. 10. 2012 Základy práce s výpočetními systémy opakování a pokračování
KTE / PPEL Počítačová podpora v elektrotechnice Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz http://home.zcu.cz/~lsroubov 3. 10. 2012 Základy práce s výpočetními systémy opakování a pokračování
Vyhledávání. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 21.
 Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 21. září 2018 Jiří Dvorský (VŠB TUO) Vyhledávání 242 / 433 Osnova přednášky
Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 21. září 2018 Jiří Dvorský (VŠB TUO) Vyhledávání 242 / 433 Osnova přednášky
MATURITNÍ TÉMATA Z MATEMATIKY
 MATURITNÍ TÉMATA Z MATEMATIKY 1. Základní poznatky z logiky a teorie množin Pojem konstanty a proměnné. Obor proměnné. Pojem výroku a jeho pravdivostní hodnota. Operace s výroky, složené výroky, logické
MATURITNÍ TÉMATA Z MATEMATIKY 1. Základní poznatky z logiky a teorie množin Pojem konstanty a proměnné. Obor proměnné. Pojem výroku a jeho pravdivostní hodnota. Operace s výroky, složené výroky, logické
KTE / PPEL Počítačová podpora v elektrotechnice
 24. 9. 2014 KTE / PPEL Počítačová podpora v elektrotechnice Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz ICQ: 361057825 http://home.zcu.cz/~lsroubov tel.: +420 377 634 623 Místnost: EK602 Katedra
24. 9. 2014 KTE / PPEL Počítačová podpora v elektrotechnice Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz ICQ: 361057825 http://home.zcu.cz/~lsroubov tel.: +420 377 634 623 Místnost: EK602 Katedra
Paměť počítače. alg2 1
 Paměť počítače Výpočetní proces je posloupnost akcí nad daty uloženými v paměti počítače Data jsou v paměti reprezentována posloupnostmi bitů (bit = 0 nebo 1) Připomeňme: paměť je tvořena řadou 8-mi bitových
Paměť počítače Výpočetní proces je posloupnost akcí nad daty uloženými v paměti počítače Data jsou v paměti reprezentována posloupnostmi bitů (bit = 0 nebo 1) Připomeňme: paměť je tvořena řadou 8-mi bitových
ZŠ ÚnO, Bratří Čapků 1332
 Úvodní obrazovka Menu Návrat na hlavní stránku Obsah Výsledky Poznámky Záložky edunet Konec Matematika 1 (pro 9-12 let) LangMaster Obsah (střední část) výběr tématu - dvojklikem v seznamu témat (horní
Úvodní obrazovka Menu Návrat na hlavní stránku Obsah Výsledky Poznámky Záložky edunet Konec Matematika 1 (pro 9-12 let) LangMaster Obsah (střední část) výběr tématu - dvojklikem v seznamu témat (horní
VÝUKOVÝ MATERIÁL. Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632 Číslo projektu
 VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
Čtvrtek 8. prosince. Pascal - opakování základů. Struktura programu:
 Čtvrtek 8 prosince Pascal - opakování základů Struktura programu: 1 hlavička obsahuje název programu, použité programové jednotky (knihovny), definice konstant, deklarace proměnných, všechny použité procedury
Čtvrtek 8 prosince Pascal - opakování základů Struktura programu: 1 hlavička obsahuje název programu, použité programové jednotky (knihovny), definice konstant, deklarace proměnných, všechny použité procedury
9.3.2010 Program převod z desítkové na dvojkovou soustavu: /* Prevod desitkove na binarni */ #include <stdio.h>
 9.3.2010 Program převod z desítkové na dvojkovou soustavu: /* Prevod desitkove na binarni */ #include int main(void) { int dcislo, kolikbcislic = 0, mezivysledek = 0, i; int vysledek[1000]; printf("zadejte
9.3.2010 Program převod z desítkové na dvojkovou soustavu: /* Prevod desitkove na binarni */ #include int main(void) { int dcislo, kolikbcislic = 0, mezivysledek = 0, i; int vysledek[1000]; printf("zadejte
Základy algoritmizace
 Algoritmus Toto je sice na první pohled pravdivá, ale při bližším prozkoumání nepřesná definice. Například některé matematické postupy by této definici vyhovovaly, ale nejsou algoritmy. Přesné znění definice
Algoritmus Toto je sice na první pohled pravdivá, ale při bližším prozkoumání nepřesná definice. Například některé matematické postupy by této definici vyhovovaly, ale nejsou algoritmy. Přesné znění definice
Úvod do Matlabu. Praha & EU: Investujeme do vaší budoucnosti. 1 / 24 Úvod do Matlabu
 Vytěžování dat, cvičení 1: Úvod do Matlabu Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Fakulta elektrotechnická, ČVUT 1 / 24 Úvod do Matlabu Proč proboha Matlab? Matlab je SW pro
Vytěžování dat, cvičení 1: Úvod do Matlabu Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Fakulta elektrotechnická, ČVUT 1 / 24 Úvod do Matlabu Proč proboha Matlab? Matlab je SW pro
Algoritmizace a programování
 Algoritmizace a programování Řídicí struktury jazyka Java Struktura programu Příkazy jazyka Blok příkazů Logické příkazy Ternární logický operátor Verze pro akademický rok 2012/2013 1 Struktura programu
Algoritmizace a programování Řídicí struktury jazyka Java Struktura programu Příkazy jazyka Blok příkazů Logické příkazy Ternární logický operátor Verze pro akademický rok 2012/2013 1 Struktura programu
Základy algoritmizace a programování
 Základy algoritmizace a programování Příklady v MATLABu Přednáška 10 30. listopadu 2009 Řídící instrukce if else C Matlab if ( podmínka ) { } else { } Podmíněný příkaz if podmínka elseif podmínka2... else
Základy algoritmizace a programování Příklady v MATLABu Přednáška 10 30. listopadu 2009 Řídící instrukce if else C Matlab if ( podmínka ) { } else { } Podmíněný příkaz if podmínka elseif podmínka2... else
Příklady: (y + (sin(2*x) + 1)*2)/ /2 * 5 = 8.5 (1+3)/2 * 5 = /(2 * 5) = 1.3. Pavel Töpfer, 2017 Programování 1-3 1
 Výraz - syntaxe i sémantika podobné jako v matematice - obsahuje proměnné, konstanty, operátory, závorky, volání funkcí - všechny operátory nutno zapisovat (nelze např. vynechat znak násobení) - argumenty
Výraz - syntaxe i sémantika podobné jako v matematice - obsahuje proměnné, konstanty, operátory, závorky, volání funkcí - všechny operátory nutno zapisovat (nelze např. vynechat znak násobení) - argumenty
Doňar B., Zaplatílek K.: MATLAB - tvorba uživatelských aplikací, BEN - technická literatura, Praha, (ISBN:
 http://portal.zcu.cz > Portál ZČU > Courseware (sem lze i přímo: http://courseware.zcu.cz) > Předměty po fakultách > Fakulta elektrotechnická > Katedra teoretické elektrotechniky > PPEL Doňar B., Zaplatílek
http://portal.zcu.cz > Portál ZČU > Courseware (sem lze i přímo: http://courseware.zcu.cz) > Předměty po fakultách > Fakulta elektrotechnická > Katedra teoretické elektrotechniky > PPEL Doňar B., Zaplatílek
ALGORITMIZACE A PROGRAMOVÁNÍ
 Metodický list č. 1 Algoritmus a jeho implementace počítačovým programem Základním cílem tohoto tematického celku je vysvětlení pojmů algoritmus a programová implementace algoritmu. Dále je cílem seznámení
Metodický list č. 1 Algoritmus a jeho implementace počítačovým programem Základním cílem tohoto tematického celku je vysvětlení pojmů algoritmus a programová implementace algoritmu. Dále je cílem seznámení
1 Výroková logika 1. 2 Predikátová logika 3. 3 Důkazy matematických vět 4. 4 Doporučená literatura 7
 1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
I. ZÁVĚREČNÁ ZPRÁVA PROJEKTU
 I. ZÁVĚREČNÁ ZPRÁVA PROJEKTU IGA číslo projektu C_VŠCHT_2015_ ifis číslo projektu 445-17-5642 Název projektu Řešitel Inovace a modernizace předmětu Úvod do programování a algoritmů Ing. Jana Finkeová,
I. ZÁVĚREČNÁ ZPRÁVA PROJEKTU IGA číslo projektu C_VŠCHT_2015_ ifis číslo projektu 445-17-5642 Název projektu Řešitel Inovace a modernizace předmětu Úvod do programování a algoritmů Ing. Jana Finkeová,
Jazyk C Program v jazyku C má následující strukturu: konstanty nebo proměnné musí Jednoduché datové typy: Strukturované datové typy Výrazy operátory
 Jazyk C Program v jazyku C má následující strukturu: Direktivy procesoru Globální definice (platné a známé v celém programu) Funkce Hlavička funkce Tělo funkce je uzavřeno mezi složené závorky { Lokální
Jazyk C Program v jazyku C má následující strukturu: Direktivy procesoru Globální definice (platné a známé v celém programu) Funkce Hlavička funkce Tělo funkce je uzavřeno mezi složené závorky { Lokální
Úvod do programování. Lekce 3
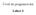 Úvod do programování Lekce 3 Řízení běhu programu - pokračování /2 příklad: program vypisuje hodnotu sin x dx pro různé délky integračního kroku 0 #include #include // budeme pouzivat funkci
Úvod do programování Lekce 3 Řízení běhu programu - pokračování /2 příklad: program vypisuje hodnotu sin x dx pro různé délky integračního kroku 0 #include #include // budeme pouzivat funkci
1.1 Struktura programu v Pascalu Vstup a výstup Operátory a některé matematické funkce 5
 Obsah Obsah 1 Programovací jazyk Pascal 1 1.1 Struktura programu v Pascalu.................... 1 2 Proměnné 2 2.1 Vstup a výstup............................ 3 3 Operátory a některé matematické funkce 5
Obsah Obsah 1 Programovací jazyk Pascal 1 1.1 Struktura programu v Pascalu.................... 1 2 Proměnné 2 2.1 Vstup a výstup............................ 3 3 Operátory a některé matematické funkce 5
Zápis programu v jazyce C#
 Zápis programu v jazyce C# Základní syntaktická pravidla C# = case sensitive jazyk rozlišuje velikost písmen Tzv. bílé znaky (Enter, mezera, tab ) ve ZK překladač ignoruje každý příkaz končí ; oddělovač
Zápis programu v jazyce C# Základní syntaktická pravidla C# = case sensitive jazyk rozlišuje velikost písmen Tzv. bílé znaky (Enter, mezera, tab ) ve ZK překladač ignoruje každý příkaz končí ; oddělovač
Poslední nenulová číslice faktoriálu
 Poslední nenulová číslice faktoriálu Kateřina Bambušková BAM015, I206 Abstrakt V tomto článku je popsán a vyřešen problém s určením poslední nenulové číslice faktoriálu přirozeného čísla N. Celý princip
Poslední nenulová číslice faktoriálu Kateřina Bambušková BAM015, I206 Abstrakt V tomto článku je popsán a vyřešen problém s určením poslední nenulové číslice faktoriálu přirozeného čísla N. Celý princip
Základy algoritmizace a programování. 1. a 8.října 2018
 Základy algoritmizace a programování Přednáška 1 a 2 1. a 8.října 2018 Obsah 1 Úvodní informace 2 Metoda půlení intervalu Vykoušíme algoritmus 3 Algoritmus a algoritmizace 4 Exkurze do MATLABu Podmíněný
Základy algoritmizace a programování Přednáška 1 a 2 1. a 8.října 2018 Obsah 1 Úvodní informace 2 Metoda půlení intervalu Vykoušíme algoritmus 3 Algoritmus a algoritmizace 4 Exkurze do MATLABu Podmíněný
GEODETICKÉ VÝPOČTY I.
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. ÚVOD ZÁKLADNÍ POČETNÍ ÚKONY A ZKOUŠKY ZÁKLADNÍ POČETNÍ ÚKONY A ZKOUŠKY ZÁPIS, DIKTOVÁNÍ A KONTROLA ZAOKROUHLOVÁNÍ ČÍSEL
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. ÚVOD ZÁKLADNÍ POČETNÍ ÚKONY A ZKOUŠKY ZÁKLADNÍ POČETNÍ ÚKONY A ZKOUŠKY ZÁPIS, DIKTOVÁNÍ A KONTROLA ZAOKROUHLOVÁNÍ ČÍSEL
Matematika I (KMI/PMATE)
 Přednáška první aneb Úvod do matematické analýzy Funkce a její vlastnosti Úvod do matematické analýzy Osnova přednášky pojem funkce definice funkce graf funkce definiční obor funkce obor hodnot funkce
Přednáška první aneb Úvod do matematické analýzy Funkce a její vlastnosti Úvod do matematické analýzy Osnova přednášky pojem funkce definice funkce graf funkce definiční obor funkce obor hodnot funkce
Algoritmizace. Cíle předmětu
 Cíle předmětu Algoritmizace naučit se sestavovat algoritmy řešení jednoduchých problémů a zapisovat je v jazyku Java Organizace předmětu přednášky (učast nepovinná, ale doporučená) cvičení střídavě u tabule
Cíle předmětu Algoritmizace naučit se sestavovat algoritmy řešení jednoduchých problémů a zapisovat je v jazyku Java Organizace předmětu přednášky (učast nepovinná, ale doporučená) cvičení střídavě u tabule
Anotace: Digitální učební materiály slouží k zopakování a k testování získaných znalostí a dovedností.
 Tematická oblast: (VY_32_INOVACE_04 1 M1) Autor: RNDr. Yvetta Bartáková, Mgr. Petra Drápelová, Mgr. Jaroslava Vrbková, Mgr. Jarmila Zelená Vytvořeno: 2013-2014 Anotace: Digitální učební materiály slouží
Tematická oblast: (VY_32_INOVACE_04 1 M1) Autor: RNDr. Yvetta Bartáková, Mgr. Petra Drápelová, Mgr. Jaroslava Vrbková, Mgr. Jarmila Zelená Vytvořeno: 2013-2014 Anotace: Digitální učební materiály slouží
Programování: základní konstrukce, příklady, aplikace. IB111 Programování a algoritmizace
 Programování: základní konstrukce, příklady, aplikace IB111 Programování a algoritmizace 2011 Připomenutí z minule, ze cvičení proměnné, výrazy, operace řízení výpočtu: if, for, while funkce příklady:
Programování: základní konstrukce, příklady, aplikace IB111 Programování a algoritmizace 2011 Připomenutí z minule, ze cvičení proměnné, výrazy, operace řízení výpočtu: if, for, while funkce příklady:
M - Výroková logika VARIACE
 M - Výroková logika Autor: Mgr. Jaromír Juřek Kopírování a další šíření povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu
M - Výroková logika Autor: Mgr. Jaromír Juřek Kopírování a další šíření povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu
Disjunktivní a konjunktivní lní tvar formule. 2.přednáška
 Disjunktivní a konjunktivní normáln lní tvar formule 2.přednáška Disjunktivní normáln lní forma Definice Řekneme, že formule ( A ) je v disjunktivním normálním tvaru (formě), zkráceně v DNF, jestliže je
Disjunktivní a konjunktivní normáln lní tvar formule 2.přednáška Disjunktivní normáln lní forma Definice Řekneme, že formule ( A ) je v disjunktivním normálním tvaru (formě), zkráceně v DNF, jestliže je
Rozklad na součin vytýkáním
 Rozklad na součin vytýkáním 1. Rozložte na součin prvočísel číslo: 165 = 210 = 546 = 2. Rozložte na součin mocnin prvočísel číslo: 96 = 432 = B. Rozklad na součin vytýkáním 1. Rozložte na součin vytýkáním:
Rozklad na součin vytýkáním 1. Rozložte na součin prvočísel číslo: 165 = 210 = 546 = 2. Rozložte na součin mocnin prvočísel číslo: 96 = 432 = B. Rozklad na součin vytýkáním 1. Rozložte na součin vytýkáním:
Autoevaluační karta. Škola: Obchodní akademie Pelhřimov, Jirsíkova 875. obchodní akademie. ekonomika, účetnictví, daně. Školní rok: Jméno:
 Autoevaluační karta Škola: Obchodní akademie Pelhřimov, Jirsíkova 875 Obor: obchodní akademie Zaměření: ekonomika, účetnictví, daně Školní rok: Předmět: matematika Třída: 1. A Jméno: TEMATICKÝ CELEK: Znalosti
Autoevaluační karta Škola: Obchodní akademie Pelhřimov, Jirsíkova 875 Obor: obchodní akademie Zaměření: ekonomika, účetnictví, daně Školní rok: Předmět: matematika Třída: 1. A Jméno: TEMATICKÝ CELEK: Znalosti
Objektově orientované programování
 10. října 2011 Pragmatické informace Volitelný předmět, zápočet: zápočtový program(s dokumentací), aktivní účast na cvičení(body v CodExu), praktický test, zkouška: zkoušková písemka na objektový návrh
10. října 2011 Pragmatické informace Volitelný předmět, zápočet: zápočtový program(s dokumentací), aktivní účast na cvičení(body v CodExu), praktický test, zkouška: zkoušková písemka na objektový návrh
TEMATICKÝ PLÁN. září říjen
 TEMATICKÝ PLÁN Předmět: MATEMATIKA Literatura: Matematika doc. RNDr. Oldřich Odvárko, DrSc., doc. RNDr. Jiří Kadleček, CSc Matematicko fyzikální tabulky pro základní školy UČIVO - ARITMETIKA: 1. Rozšířené
TEMATICKÝ PLÁN Předmět: MATEMATIKA Literatura: Matematika doc. RNDr. Oldřich Odvárko, DrSc., doc. RNDr. Jiří Kadleček, CSc Matematicko fyzikální tabulky pro základní školy UČIVO - ARITMETIKA: 1. Rozšířené
Základy jazyka C. Základy programování 1 Tomáš Kühr
 Základy jazyka C Základy programování 1 Tomáš Kühr Organizační záležitosti Konzultace Osobně v pracovně 5.043 Pondělí 15.00 16.00 Úterý 14.00 16.00 Čtvrtek 13.00 15.00 Pátek 9.30 11.30 Něco jde vyřešit
Základy jazyka C Základy programování 1 Tomáš Kühr Organizační záležitosti Konzultace Osobně v pracovně 5.043 Pondělí 15.00 16.00 Úterý 14.00 16.00 Čtvrtek 13.00 15.00 Pátek 9.30 11.30 Něco jde vyřešit
Algoritmizace prostorových úloh
 INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Datové struktury Daniela Szturcová
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Datové struktury Daniela Szturcová
Algoritmy I. Cvičení č. 2, 3 ALGI 2018/19
 Algoritmy I Cvičení č. 2, 3 1 ALG I, informace Cvičící RNDr. Eliška Ochodková, Ph.D., kancelář EA439 eliska.ochodkova@vsb.cz www.cs.vsb.cz/ochodkova Přednášející doc. Mgr. Jiří Dvorský, Ph.D., kancelář
Algoritmy I Cvičení č. 2, 3 1 ALG I, informace Cvičící RNDr. Eliška Ochodková, Ph.D., kancelář EA439 eliska.ochodkova@vsb.cz www.cs.vsb.cz/ochodkova Přednášející doc. Mgr. Jiří Dvorský, Ph.D., kancelář
Programovací jazyk Pascal
 Programovací jazyk Pascal Syntaktická pravidla (syntaxe jazyka) přesná pravidla pro zápis příkazů Sémantická pravidla (sémantika jazyka) pravidla, která každému příkazu přiřadí přesný význam Všechny konstrukce
Programovací jazyk Pascal Syntaktická pravidla (syntaxe jazyka) přesná pravidla pro zápis příkazů Sémantická pravidla (sémantika jazyka) pravidla, která každému příkazu přiřadí přesný význam Všechny konstrukce
Algoritmy a datové struktury
 Algoritmy a datové struktury 1 / 34 Obsah přednášky Základní řídící struktury posloupnost příkazů podmínka cyklus s podmínkou na začátku cyklus s podmínkou na konci cyklus s pevným počtem opakování Jednoduchá
Algoritmy a datové struktury 1 / 34 Obsah přednášky Základní řídící struktury posloupnost příkazů podmínka cyklus s podmínkou na začátku cyklus s podmínkou na konci cyklus s pevným počtem opakování Jednoduchá
for (i = 0, j = 5; i < 10; i++) { // tělo cyklu }
 5. Operátor čárka, - slouží k jistému určení pořadí vykonání dvou příkazů - oddělím-li čárkou dva příkazy, je jisté, že ten první bude vykonán dříve než příkaz druhý. Např.: i = 5; j = 8; - po překladu
5. Operátor čárka, - slouží k jistému určení pořadí vykonání dvou příkazů - oddělím-li čárkou dva příkazy, je jisté, že ten první bude vykonán dříve než příkaz druhý. Např.: i = 5; j = 8; - po překladu
CHARAKTERISTIKA. VZDĚLÁVACÍ OBLAST VYUČOVACÍ PŘEDMĚT ZODPOVÍDÁ VOLITELNÉ PŘEDMĚTY Seminář z matematiky Mgr. Dana Rauchová
 CHARAKTERISTIKA VZDĚLÁVACÍ OBLAST VYUČOVACÍ PŘEDMĚT ZODPOVÍDÁ VOLITELNÉ PŘEDMĚTY Seminář z matematiky Mgr. Dana Rauchová Vyučovací volitelný předmět Cvičení z matematiky je zařazen samostatně na druhém
CHARAKTERISTIKA VZDĚLÁVACÍ OBLAST VYUČOVACÍ PŘEDMĚT ZODPOVÍDÁ VOLITELNÉ PŘEDMĚTY Seminář z matematiky Mgr. Dana Rauchová Vyučovací volitelný předmět Cvičení z matematiky je zařazen samostatně na druhém
Martin Hejtmánek hejtmmar@fjfi.cvut.cz http://kmlinux.fjfi.cvut.cz/ hejtmmar
 Základy programování Martin Hejtmánek hejtmmar@fjfi.cvut.cz http://kmlinux.fjfi.cvut.cz/ hejtmmar Počítačový kurs Univerzity třetího věku na FJFI ČVUT Pokročilý 21. května 2009 Dnešní přednáška 1 Počátky
Základy programování Martin Hejtmánek hejtmmar@fjfi.cvut.cz http://kmlinux.fjfi.cvut.cz/ hejtmmar Počítačový kurs Univerzity třetího věku na FJFI ČVUT Pokročilý 21. května 2009 Dnešní přednáška 1 Počátky
Maturitní témata profilová část
 Seznam témat Výroková logika, úsudky a operace s množinami Základní pojmy výrokové logiky, logické spojky a kvantifikátory, složené výroky (konjunkce, disjunkce, implikace, ekvivalence), pravdivostní tabulky,
Seznam témat Výroková logika, úsudky a operace s množinami Základní pojmy výrokové logiky, logické spojky a kvantifikátory, složené výroky (konjunkce, disjunkce, implikace, ekvivalence), pravdivostní tabulky,
Systém je citlivý na velikost písmen CASE SENSITIVE rozeznává malá velká písmena, např. PROM=1; PROm=1; PRom=1; Prom=1; prom=1; - 5 různých proměnných
 Systém je citlivý na velikost písmen CASE SENSITIVE rozeznává malá velká písmena, např. PROM=1; PROm=1; PRom=1; Prom=1; prom=1; - 5 různých proměnných jakési nádoby na hodnoty jsou různých typů při běžné
Systém je citlivý na velikost písmen CASE SENSITIVE rozeznává malá velká písmena, např. PROM=1; PROm=1; PRom=1; Prom=1; prom=1; - 5 různých proměnných jakési nádoby na hodnoty jsou různých typů při běžné
MATEMATIKA 5. TŘÍDA. C) Tabulky, grafy, diagramy 1 - Tabulky, doplnění řady čísel podle závislosti 2 - Grafy, jízní řády 3 - Magické čtverce
 MATEMATIKA 5. TŘÍDA 1 - Přirozená čísla a číslo nula a číselná osa, porovnávání b zaokrouhlování c zápis čísla v desítkové soustavě d součet, rozdíl e násobek, činitel, součin f dělení, dělení se zbytkem
MATEMATIKA 5. TŘÍDA 1 - Přirozená čísla a číslo nula a číselná osa, porovnávání b zaokrouhlování c zápis čísla v desítkové soustavě d součet, rozdíl e násobek, činitel, součin f dělení, dělení se zbytkem
Základy jazyka C. Úvod do programování 1 Tomáš Kühr
 Základy jazyka C Úvod do programování 1 Tomáš Kühr Organizační záležitosti Konzultace Pracovna 5.043 Pondělí 9.30 11.30, středa 10.00 11.30 a 13.00 14.30 (oficiální) Pátek 8.00 9.30 (někdy), 12.30-13.00
Základy jazyka C Úvod do programování 1 Tomáš Kühr Organizační záležitosti Konzultace Pracovna 5.043 Pondělí 9.30 11.30, středa 10.00 11.30 a 13.00 14.30 (oficiální) Pátek 8.00 9.30 (někdy), 12.30-13.00
Matematika - 6. ročník Vzdělávací obsah
 Matematika - 6. ročník Září Opakování učiva Obor přirozených čísel do 1000, početní operace v daném oboru Čte, píše, porovnává čísla v oboru do 1000, orientuje se na číselné ose Rozlišuje sudá a lichá
Matematika - 6. ročník Září Opakování učiva Obor přirozených čísel do 1000, početní operace v daném oboru Čte, píše, porovnává čísla v oboru do 1000, orientuje se na číselné ose Rozlišuje sudá a lichá
Operační systémy. Cvičení 4: Programování v C pod Unixem
 Operační systémy Cvičení 4: Programování v C pod Unixem 1 Obsah cvičení Řídící struktury Funkce Dynamická alokace paměti Ladění programu Kde najít další informace Poznámka: uvedené příklady jsou dostupné
Operační systémy Cvičení 4: Programování v C pod Unixem 1 Obsah cvičení Řídící struktury Funkce Dynamická alokace paměti Ladění programu Kde najít další informace Poznámka: uvedené příklady jsou dostupné
2 Datové typy v jazyce C
 1 Procedurální programování a strukturované programování Charakteristické pro procedurální programování je organizace programu, který řeší daný problém, do bloků (procedur, funkcí, subrutin). Původně jednolitý,
1 Procedurální programování a strukturované programování Charakteristické pro procedurální programování je organizace programu, který řeší daný problém, do bloků (procedur, funkcí, subrutin). Původně jednolitý,
12. Booleova algebra, logická funkce určitá a neurčitá, realizace logických funkcí, binární kódy pro algebraické operace.
 12. Booleova algebra, logická funkce určitá a neurčitá, realizace logických funkcí, binární kódy pro algebraické operace. Logická proměnná - proměnná nesoucí logickou hodnotu Logická funkce - funkce přiřazující
12. Booleova algebra, logická funkce určitá a neurčitá, realizace logických funkcí, binární kódy pro algebraické operace. Logická proměnná - proměnná nesoucí logickou hodnotu Logická funkce - funkce přiřazující
Algoritmizace a programování. Ak. rok 2012/2013 vbp 1. ze 44
 Algoritmizace a programování Ak. rok 2012/2013 vbp 1. ze 44 Vladimír Beneš Petrovický K101 katedra matematiky, statistiky a informačních technologií vedoucí katedry E-mail: vbenes@bivs.cz Telefon: 251
Algoritmizace a programování Ak. rok 2012/2013 vbp 1. ze 44 Vladimír Beneš Petrovický K101 katedra matematiky, statistiky a informačních technologií vedoucí katedry E-mail: vbenes@bivs.cz Telefon: 251
EVROPSKÝ SOCIÁLNÍ FOND. Úvod do PHP PRAHA & EU INVESTUJEME DO VAŠÍ BUDOUCNOSTI
 EVROPSKÝ SOCIÁLNÍ FOND Úvod do PHP PRAHA & EU INVESTUJEME DO VAŠÍ BUDOUCNOSTI Úvod do PHP PHP Personal Home Page Hypertext Preprocessor jazyk na tvorbu dokumentů přípona: *.php skript je součást HTML stránky!
EVROPSKÝ SOCIÁLNÍ FOND Úvod do PHP PRAHA & EU INVESTUJEME DO VAŠÍ BUDOUCNOSTI Úvod do PHP PHP Personal Home Page Hypertext Preprocessor jazyk na tvorbu dokumentů přípona: *.php skript je součást HTML stránky!
Univerzitní licence MATLABu. Pište mail na: se žádostí o nejnovější licenci MATLABu.
 Univerzitní licence MATLABu Pište mail na: operator@service.zcu.cz se žádostí o nejnovější licenci MATLABu. * násobení maticové K = L = 1 2 5 6 3 4 7 8 Příklad: M = K * L N = L * K (2,2) = (2,2) * (2,2)
Univerzitní licence MATLABu Pište mail na: operator@service.zcu.cz se žádostí o nejnovější licenci MATLABu. * násobení maticové K = L = 1 2 5 6 3 4 7 8 Příklad: M = K * L N = L * K (2,2) = (2,2) * (2,2)
0. ÚVOD - matematické symboly, značení,
 0. ÚVOD - matematické symboly, značení, číselné množiny Výroky Výrok je každé sdělení, u kterého lze jednoznačně rozhodnout, zda je či není pravdivé. Každému výroku lze proto přiřadit jedinou pravdivostní
0. ÚVOD - matematické symboly, značení, číselné množiny Výroky Výrok je každé sdělení, u kterého lze jednoznačně rozhodnout, zda je či není pravdivé. Každému výroku lze proto přiřadit jedinou pravdivostní
Matematika pro informatiky KMA/MATA
 Matematika pro informatiky KMA/MATA Informace k předmětu Mgr. Přemysl Rosa rosapr00@pf.jcu.cz, J349 Konzultační hodiny v ZS: úterý 10-11, čtvrtek 15-16 nebo individuálně po předchozí domluvě aktivní účast
Matematika pro informatiky KMA/MATA Informace k předmětu Mgr. Přemysl Rosa rosapr00@pf.jcu.cz, J349 Konzultační hodiny v ZS: úterý 10-11, čtvrtek 15-16 nebo individuálně po předchozí domluvě aktivní účast
NPRG030 Programování I, 2018/19 1 / :25:37
 NPRG030 Programování I, 2018/19 1 / 26 24. 9. 2018 10:25:37 Čísla v algoritmech a programech 10 26 Poloměr vesmíru 2651 studujících studentů MFF UK 3.142857... Ludolfovo číslo 10 16 stáří vesmíru v sekundách!!!
NPRG030 Programování I, 2018/19 1 / 26 24. 9. 2018 10:25:37 Čísla v algoritmech a programech 10 26 Poloměr vesmíru 2651 studujících studentů MFF UK 3.142857... Ludolfovo číslo 10 16 stáří vesmíru v sekundách!!!
Booleovská algebra. Pravdivostní tabulka. Karnaughova mapa. Booleovské n-krychle. Základní zákony. Unární a binární funkce. Podmínky.
 Booleovská algebra. Pravdivostní tabulka. Karnaughova mapa. Booleovské n-krychle. Základní zákony. Unární a binární funkce. Podmínky. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky
Booleovská algebra. Pravdivostní tabulka. Karnaughova mapa. Booleovské n-krychle. Základní zákony. Unární a binární funkce. Podmínky. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky
Výroková logika II. Negace. Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0).
 Výroková logika II Negace Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0). Na konkrétních příkladech si ukážeme, jak se dají výroky negovat. Obecně se výrok dá negovat tak, že před
Výroková logika II Negace Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0). Na konkrétních příkladech si ukážeme, jak se dají výroky negovat. Obecně se výrok dá negovat tak, že před
Matematika. Vlastnosti početních operací s přirozenými čísly. Sčítání a odčítání dvojciferných čísel do 1 000, zpaměti i písemně.
 1 Matematika Matematika Učivo Vlastnosti početních operací s přirozenými čísly Sčítání a odčítání dvojciferných čísel do 1 000, 1 000 000 zpaměti i písemně Násobení dvojciferných čísel jednociferným činitelem
1 Matematika Matematika Učivo Vlastnosti početních operací s přirozenými čísly Sčítání a odčítání dvojciferných čísel do 1 000, 1 000 000 zpaměti i písemně Násobení dvojciferných čísel jednociferným činitelem
Testování prvočíselnosti
 Dokumentace zápočtového programu z Programování II (NPRG031) Testování prvočíselnosti David Pěgřímek http://davpe.net Úvodem V různých oborech (například v kryptografii) je potřeba zjistit, zda je číslo
Dokumentace zápočtového programu z Programování II (NPRG031) Testování prvočíselnosti David Pěgřímek http://davpe.net Úvodem V různých oborech (například v kryptografii) je potřeba zjistit, zda je číslo
CVIČNÝ TEST 5. OBSAH I. Cvičný test 2. Mgr. Václav Zemek. II. Autorské řešení 6 III. Klíč 17 IV. Záznamový list 19
 CVIČNÝ TEST 5 Mgr. Václav Zemek OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 17 IV. Záznamový list 19 I. CVIČNÝ TEST 1 Zjednodušte výraz (2x 5) 2 (2x 5) (2x + 5) + 20x. 2 Určete nejmenší trojciferné
CVIČNÝ TEST 5 Mgr. Václav Zemek OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 17 IV. Záznamový list 19 I. CVIČNÝ TEST 1 Zjednodušte výraz (2x 5) 2 (2x 5) (2x + 5) + 20x. 2 Určete nejmenší trojciferné
Bakalářská matematika I
 1. Funkce Diferenciální počet Mgr. Jaroslav Drobek, Ph. D. Katedra matematiky a deskriptivní geometrie Bakalářská matematika I Některé užitečné pojmy Kartézský součin podrobnosti Definice 1.1 Nechť A,
1. Funkce Diferenciální počet Mgr. Jaroslav Drobek, Ph. D. Katedra matematiky a deskriptivní geometrie Bakalářská matematika I Některé užitečné pojmy Kartézský součin podrobnosti Definice 1.1 Nechť A,
Matematika (KMI/PMATE)
 Úvod do matematické analýzy Funkce a její vlastnosti Funkce a její vlastnosti Veličina Veličina - pojem, který popisuje kvantitativní (číselné) vlastnosti reálných i abstraktních objektů. Funkce a její
Úvod do matematické analýzy Funkce a její vlastnosti Funkce a její vlastnosti Veličina Veličina - pojem, který popisuje kvantitativní (číselné) vlastnosti reálných i abstraktních objektů. Funkce a její
