Geodézie pro stavitelství KMA/GES
|
|
|
- Radka Marešová
- před 9 lety
- Počet zobrazení:
Transkript
1 Geodézie pro stavitelství KMA/GES ZÁPADOČESKÁ UNIVERZITA V PLZNI Fakulta aplikovaných věd - KMA oddělení geomatiky Ing. Martina Vichrová, Ph.D. vichrova@kma.zcu.cz Vytvoření materiálů bylo podpořeno prostředky z projektu FRVŠ č. 584/2011. Přístroje a metody měření úhlů TISK 1
2 Přístroje pro měření úhlů - teodolit videa: teodolit 1. část teodolit 2. část (You Tube: (You Tube: Základní součásti geodetických přístrojů 1. Mechanické součásti 2. Optické součásti 3. Jednoduché optické přístroje 4. Odečítací pomůcky 5. Příslušenství 2
3 1. Mechanické součásti přístrojů Šrouby, ustanovky, nosná zařízení a čepy. Šrouby Umožňují trvalé nebo dočasné spojení mechanických dílů, jemný pohyb součástí, zajišťují spojení přístroje s podstavcem, správnou polohu os přístroje během měření,.. Šroub se skládá z hlavy (opatřené drážkou, šestihranem nebo otvorem pro trn) a vřetena se závitem, na které se může našroubovat matice (matka). Šroub stavěcí slouží k urovnání třínožky a tím i přístroje do správné polohy Šroub rektifikační - slouží k uvedení některých částí přístroje do vzájemně správné polohy Šrouby drobnoměrné - slouží jako zařízení k jemnému posunu nebo jako šrouby měřící. U geodetických přístrojů se mikrometrické šrouby používají jako jemné ustanovky. 1. Mechanické součásti přístrojů Ustanovky Mechanické pomůcky pro hrubé přibližné nastavení a jemné nastavení (navedení alhidády i dalekohledu na zaměřovaný bod). Tato zařízení jsou v geodézii označována jako hrubá a jemná ustanovka. Pro dělení těchto mechanických pomůcek jsou různá kritéria: smysl pohybu (lineární/nelineární ustanovky), tvar (páčkové ustanovky), poloha (vodorovné/svislé ustanovky), konstrukce, citlivost (hrubé /jemné ustanovky), Nosná zařízení Geodetické přístroje se staví při měření na přiměřeně vysoké podstavce stativy, observační pilíře, konzoly nebo rozpěry. Kpřipevnění teodolitu na nosné zařízení se používá spojovací článek podložka. Čepy a pouzdra umožňují vzájemný pohyb pevné a otočné části přístroje. Vyrábějí se z oceli, bronzu nebo pro méně přesné přístroje z mosazi. K lehkému chodu točné osy přístroje je třeba, aby tření čepu v pouzdře bylo co nejmenší. 3
4 2. Optické součásti Zrcadla, hranoly, planparalelní deska a čočky Zrcadla U geodetických přístrojů se používají většinou zrcadla rovinná. Jsou to broušené skleněné desky z jedné strany opatřené odrazivou vrstvou (stříbro, chrom, hliník ). Používají se k odklonu světelných paprsků od původního směru. Dráha dopadajícího světelného paprsku se řídí zákonem odrazu. Zákon dopadu a odrazu. Hranoly Hranoly jsou skleněná tělesa omezená dokonale vybroušenými rovinami. Jsou vyráběny z kvalitního optického skla. Užívají se k odklonu paprsků nebo k převracení či posunutí obrazů optických soustav. Dráha dopadajícího světelného paprsku se řídí zákonem lomu. 2. Optické součásti odrazné hranoly: trojboký hranol k odchýlení paprsku o 90 a k otočení obrazu o 180 v původním směru, pětiboký hranol pentagon - působí jako dvojice zrcadel svírajících úhel 45 rombický hranol k paralelnímu posunutí paprsků, střechový hranol ke stranovému obrácení a posunu paprsku, složené hranoly k otočení obrazu o 90 a posunutí obrazu. Nejdůležitějším lámavým hranolem je optický klín. 4
5 2. Optické součásti Planparalelní deska Planparalelní deska je tvořena dvěma paralelními optickými rozhraními. Je zhotovena z optického skla o indexu lomu n. Dopadne-li paprsek kolmo, prochází deskou beze změny směru. Dopadne-li pod úhlem α, který je menší než úhel mezní ( ~42 ), dochází k lomu paprsku na obou plochách desky. Na prvním rozhraní dochází k lomu ke kolmici, na druhém od kolmice. Vycházející paprsek je rovnoběžný s paprskem dopadajícím, leží v rovině dopadu a je posunutý o hodnotu p. Čočky se dělí na tenké a tlusté. Podle toho, zda čočky poskytují skutečné obrazy či neskutečné, je dělíme na spojky a rozptylky. Spojky mají okraje tenčí než středy, u rozptylek je tomu opačně. Čočka je těleso ohraničené dvěma většinou kulovými plochami. 3. Jednoduché optické přístroje Úkolem jednoduchých optických přístrojů je zobrazit předmět tak, aby bylo výhodnější pozorovat okem jeho obraz než pozorovat okem vlastní předmět. Oko, lupa, mikroskop a dalekohled. Lupa Lupa je nejjednodušším optickým přístrojem. Slouží k pozorování detailů drobných blízkých předmětů, které jsou menší než asi 0,075 mm. Jako lupa slouží spojná čočka Obraz předmětu je neskutečný, zvětšený a vzpřímený. Základní charakteristikou lupy je její zvětšení. V geodézii se lupy používají jako čtecí pomůcky při čtení na vernierech, bubíncích mikrometrů a jiných malých stupnic. 5
6 3. Jednoduché optické přístroje Mikroskop Mikroskop slouží k rozlišení podrobností blízkých předmětů. Mikroskop se skládá ze dvou optických soustav z objektivu a z okuláru. Obě součásti jsou umístěny ve společném tubusu. Za objektivem se vytvoří skutečný, zvětšený a převrácený obraz, který se pozoruje okulárem jako lupou. Okulár vytváří neskutečný, zvětšený obraz. 3. Jednoduché optické přístroje Dalekohled Dalekohled slouží k pozorování vzdálených předmětů a k rozlišení detailů na těchto předmětech. Je tvořen dvěma optickými soustavami objektivem a okulárem. Objektiv vytváří skutečný, zmenšený a převrácený obraz, který se pozoruje okulárem jako lupou. V geodetických přístrojích se využívá dalekohledu k zaměření na pozorovaný vzdálený předmět (cílovou značku terč, či měřickou stupnici lať). Kvalita dalekohledu závisí na jeho zvětšení, na zorném poli, světelnosti a rozlišovací schopnosti dalekohledu. 6
7 3. Jednoduché optické přístroje Zvětšení dalekohledu z je poměr úhlu u, pod kterým je vidět obraz předmětu dalekohledem, k úhlu u, pod kterým je vidět předmět pouhým okem. Zorné pole dalekohledu je skutečné a zdánlivé. Skutečné vstupní zorné pole je prostor, který se v dalekohledu rázem přehlédne. Světelnost dalekohledu je poměr světelného toku, který dopadne do oka z obrazu předmětu po průchodu dalekohledem, k světelnému toku, který dopadá do oka přímo z předmětu Rozlišovací schopnost je nejmenší úhel, pod kterým lze při zobrazení optickým přístrojem navzájem rozlišit obrazy dvou bodů. Před vlastním cílením (nastavením nitkového kříže na obraz signálu zaměřovaného bodu) je třeba, aby se prvky nitkového kříže jevily ostré a zřetelné (= byly zaostřeny). Zaostření dosáhneme tak, že zamíříme dalekohledem na světlé pozadí a otáčíme objímkou okuláru dokud neuvidí oko obrazec ostře. 4. Odečítací pomůcky Index, vernier, mřížka, optický mikrometr, elektronické odečítací systémy. Odečítací pomůcky můžeme rozdělit do 3 skupin: mechanické (index, vernier, mřížka), optické (mikroskopy, mikrometry), elektronické. Odečítání mechanických a optických odečítacích pomůcek vykonáváme vizuálně, u elektronických pomůcek se odečítání vykonává plně automaticky a digitálně. Vizuální odečítání neprovádíme pouhým okem. Oko totiž dokáže rozdělit na desetiny ještě dílek velikosti 1 mm, je-li však interval dělení stupnice odečítací pomůcky menší, musíme jej opticky zvětšit. K tomu využíváme lupy a mikroskopy. Index Index je nejjednodušší odečítací pomůckou. Pomocí indexu odečítáme na hlavní stupnici nejbližší nižší vyznačený údaj a toto čtení doplníme odhadem zbytku dílku mezi dílkem stupnice, který jsme přečetli, a ryskou. 7
8 4. Odečítací pomůcky Vernier Vernier je odečítací pomůcka, která nám umožňuje přesnější odečítání zbytku z dílku hlavní stupnice. Vernier je pomocná stupnice, která se pohybuje podél hlavní stupnice. Nebo-li n dílkům vernieru odpovídá (n 1) dílků hlavní stupnice (vernier stejnosměrný) nebo (n + 1) dílků hlavní stupnice (vernier protisměrný). Čtení pomocí vernieru se skládá ze čtení hlavní stupnice a ze čtení vernieru. Na hlavním měřítku přečteme podle nulové rysky vernieru počet celých dílků (hrubé čtení) a na vernieru zjistíme, kolikátý dílek vernieru splývá s některým dílkem hlavní stupnice. Výsledné čtení je rovno součtu hrubého a jemného čtení. 4. Odečítací pomůcky Mřížka je jemně dělená stupnice v rozsahu jednoho dílku obrazu hlavní stupnice je číslována opačným směrem než hlavní stupnice Čtení spočívá v odečtení hodnoty hlavní stupnice, kterou mřížka protíná (hrubé čtení) a počtu celých dílků mřížky (jemné čtení) odečítací ryskou je ryska hlavní stupnice. Optický mikrometr Základem optického mikrometru je pohyblivý optický prvek. Tímto prvkem mohou být planparalelní desky nebo posuvné klíny. Podle způsobu odečítání se optické mikrometry dělí na mikrometry jednoduché (s jednou planparalelní deskou) a mikrometry koincidenční (se dvěma planparalelními deskami popř. klíny). Jednoduchý optický mikrometr Koincidenční mikrometr u koincidenčního mikrometru snímáme směry na dvou protilehlých místech kruhu, která se do zorného pole mikroskopu převádí optickou cestou 8
9 4. Odečítací pomůcky Elektronické odečítací systémy Odečítací systém tvoří úhloměrné převodníky, které optoelektronicky či elektronicky mění údaje o poloze kruhu na digitální údaje v jednotkách rovinného úhlu. Impulsový systém Při otáčení kruhu a jeho prosvětlování vzniká určitý počet světelných signálů, které jsou snímané a přeměňované na elektrické impulsy fotodiodami. Celý proces měření řídí vhodný mikroprocesorový systém. Kódový systém Skládá se z kódových kruhů, na kterých se nachází několik koncentrických kruhových stop. Stopy jsou vytvořené ze světlých a tmavých plošek různých tvarů, velikostí a uspořádání. Slouží jako analogové signály (kódy) a odpovídají konkrétním úhlovým hodnotám. 5. Příslušenství Pomůcky pro stanovení vodorovného a svislého směru. K určení vodorovného a svislého směru se používají olovnice, libely a kompenzátory. Olovnice Olovnice slouží k realizaci svislého směru. Používají se závěsné olovnice, tyčové olovnice a optické olovnice (klasické a laserové). Závěsnou olovnici tvoří závaží (100 až 250 gramů těžké) tvaru rotačního tělesa a závěs o vhodné délce. Nevýhodou závěsných olovnic je velká citlivost vůči větru. Tyčová olovnice se skládá ze dvou kovových tyčí, které lze do sebe zasouvat a tím měnit jejich délku. Výhodou tyčové olovnice je možnost použití i za větru. Optická olovnice je jednoduchý dalekohled, jehož optická osa je hranolem zalomena v pravém úhlu. Umožňuje přesnou centraci přístroje či samostatné třínožky nad daným bodem. Výhodou optických olovnic je vysoká přesnost centrace. U laserové olovnice je v dalekohledu umístěný laserový zdroj, který vytváří kruhovou laserovou stopu. To umožňuje rychlejší centrování. 9
10 5. Příslušenství Libely Libely jsou vzduchotěsně uzavřené skleněné nádobky z větší části naplněné vhodnou kapalinou s nízkým bodem varu (lihem, sirouhlíkem, éterem) tak, aby se vytvořila dostatečně velká bublina. Používají se k určení jak vodorovného tak i svislého směru. Podle tvaru rozeznáváme libely: krabicové a trubicové Libely jsou chráněné kovovým pouzdrem s výřezem na čtení polohy bubliny. V pouzdru je libela utěsněná korkem a zalitá sádrou. Oba materiály slouží také jako tepelná izolace. Základní charakteristikou libely je její citlivost. Citlivost libely je úhel, o který se osa libely odchýlí od horizontální roviny, jestliže se bublina posune o jeden dílek. Čím je tento úhel menší, tím je libela citlivější. Kompenzátory U elektronických Kompenzátory teodolitů mohou se být můžeme mechanické, setkat optické, s elektronickými opticko-mechanické, libelami. Ty libelové, využívají kapalinové činnost a tzv. další. automatického křížového kompenzátoru (jeho úlohou je určování Používají odklonu se osy zejména od svislice u nivelačních a korekce přístrojů příslušného a teodolitů vlivu na měřené úhly). Teodolit Teodolit je geodetický přístroj na přesné měření a vytyčování vodorovných a svislých úhlů libovolné velikosti. Teodolity prošly dlouhým vývojem: teodolity s kovovými kruhy přes optické teodolity elektronické teodolity, které umožňují automatické odečítání a registraci úhlů. videa: základní součásti teodolitu Theo10 základní součásti GTS Topcon 225 Teodolit Theo 10 10
11 Totální stanice Topcon GTS 700 na pilíři nucené centrace Topcon GTS 720 Topcon GPT 7000 automatická registrace dat Řez teodolitem 1. alhidáda 2. limbus 3. třínožka doplňkové části, které zvyšují jejich využitelnost trojnožky teodolitů s nucenou centrací, filtry, zalomené okuláry, sázecí libela, výměnné okuláry, gyroskopické doplňky, dálkoměrné doplňky 11
12 Řez teodolitem Matěj Pokora a kol. Geodézie pro stavební fakulty. Praha Dělení teodolitů teodolity je možné dělit: podle konstrukce podle přesnosti materiálu, ze kterého jsou vyrobené kruhy podle materiálu, z něhož jsou vyrobené kruhy: teodolity s kovovými kruhy teodolity se skleněnými kruhy podle způsobu čtení naměřených hodnot na kruzích: teodolity vernierové teodolity mikroskopové teodolity digitální (výstup měřených hodnot na displej v podobě číslic) teodolity registrační (registrace naměřených hodnot na paměťové médium) teodolity kódové (fotografická registrace zakódovaného záznamu měřených dat) 12
13 Dělení teodolitů podle konstrukce jednoduché - limbus L je pevně spojen s podstavnou částí pouzdrem repetiční - je možné otáčet buď jen alhidádou nebo alhidádou společně s limbem s limbem na postrk - limbus je možné otáčet pomocí pastorku P zcela nezávisle na alhidádě U repetičních teodolitů a teodolitů s limbem na postrk lze nastavit určité čtení do žádaného směru. Dělení teodolitů podle přesnosti podle přesnosti se teodolity dělí na teodolity: technické (minutové) běžné práce. Přesnost čtení je 0,01 gon přesné (vteřinové) budování bodových polí, podrobné měření. Přesnost čtení je 0,2 mgon. velmi přesné (triangulační) inženýrská geodézie, budování přesných úhlových sítí. Přesnost čtení je 0,05 mgon. další dělení teodolitů podle přesnosti - kritériem dělení je střední chyba směru měřeném jedenkrát v obou polohách dalekohledu - mα teodolity nejvyšší přesnosti triangulační (třída přesnosti 1) mα < 2 mgon (0,67"), teodolity vyšší přesnosti vteřinové (třída přesnosti 2) mα < 6 mgon (2"), teodolity střední přesnosti minutové (třída přesnosti 3) mα < 20 mgon (6,7"), teodolity nejnižší přesnosti stavební (třída přesnosti 4) mα > 20 mgon (6,7"). 13
14 Zkoušky a rektifikace teodolitů Rektifikovaný teodolit musí splňovat geometrické podmínky vzájemné polohy hlavních os. Základními osami teodolitu jsou: vertikální osa (alhidádová osa) V točná osa dalekohledu (horizontální osa) H osa alhidádové libely L osa záměrné přímky Z Podmínky (označované jako osové) pak jsou: V kolmá k L, při nesplnění vzniká chyba alhidádové libely, H kolmá k V, při nesplnění vzniká chyba úklonná, Z kolmá k H, při nesplnění vzniká chyba kolimační. Osové podmínky lze však splnit pouze s určitou přesností, kterou charakterizujeme tzv. osovými chybami. Jedná se o chyby systematické, které je tudíž třeba z měření vyloučit nebo alespoň jejich vliv snížit. Úklonnou a kolimační chybu lze kromě rektifikace vyloučit metodou měření měřením ve dvou polohách dalekohledu. Chyba alhidádové libely se musí odstranit rektifikací. Zkoušky a rektifikace teodolitů Rektifikovaný teodolit musí splňovat geometrické podmínky vzájemné polohy hlavních os. Základními osami teodolitu jsou: vertikální osa (alhidádová osa) V točná osa dalekohledu (horizontální osa) H osa alhidádové libely L osa záměrné přímky Z Podmínky (označované jako osové) pak jsou: V kolmá k L, při nesplnění vzniká chyba alhidádové libely, H kolmá k V, při nesplnění vzniká chyba úklonná, Z kolmá k H, při nesplnění vzniká chyba kolimační. Všechny tři chyby je možno rektifikovat pomocí rektifikačního zařízení. Chyby Osové podmínky lze však splnit pouze s určitou přesností, kterou charakterizujeme tzv. osovými chybami. Jedná se o chyby systematické, které úklonnou a kolimační lze odstranit měřením je tudíž třeba z měření vyloučit nebo alespoň jejich vliv snížit. Úklonnou a kolimační v obou chybu polohách lze kromě rektifikace dalekohledu. vyloučit metodou měření měřením ve dvou polohách dalekohledu. Chyba alhidádové libely se musí odstranit rektifikací. 14
15 Vodorovný směr nebo úhel??? Vrcholový úhel, který leží ve všeobecné rovině (jeho ramena mají různý sklon), určujeme jako průmět do vodorovné a svislé roviny. Tím vzniká vodorovný a svislý úhel. Vodorovný úhel ω mezi body L a P získáme tak, že směry CL, CP promítneme kolmo do vodorovné roviny π. Úhel mezi průměty (CL 1, CP 1 ) je vodorovný úhel ω. vodorovné úhly - odměřovány na vodorovném kruhu teodolitu Pokud by levý směr byl: rovnob. s kladným směrem osy x úhel ω - směrník vložen do směru sev. větve zeměp. pol. úhel ω - astronomický azimut vložen do směru sev. magnetického pol. úhel ω - magnetický azimut Vodorovný směr nebo úhel??? Svislý úhel ε - měřen ve svislé rovině z 1 (z 2 ), odměřován na svislém kruhu teodolitu Svislý úhel výškový úhel ε 1 hloubkový úhel ε 2 zenitový úhel z ε > 0: ε < 0: z = R ε z = R + ε Opačným úkonem k měření úhlů je jejich vytýčení (do terénu vynášíme úhel známé velikosti). 15
16 Jednotky a převodní vztahy velikost úhlu - oblouková nebo stupňová míra oblouková míra - radián (rad) - nevhodný pro geodetické měření a výpočty stupňová míra šedesátinné dělení - 1 (úhlový stupeň), 1' (úhlová minuta), 1'' (úhlová sekunda), plný kruh setinné dělení - 1 gon, 1 mgon (miligon), plný kruh 400 gon Pozn. Dříve se používalo dělení gradu (g) na centigrady (1c = 1/100g) a centicentigrady (1cc = 1/100c). Nelze měřit přímo vodorovný úhel měříme směry a vodorovný úhel je rozdílem dvou směrů. Svislé úhly měříme přímo. Určování úhlů konst. velikosti pásmo trojboký hranol pentagonální hranol pentagonální hranol dvojitý pentagonální hranol 16
17 Určování úhlů libovolné velikosti Příprava stroje na stanovisku Před začátkem měření je třeba zajistit, aby vertikální osa teodolitu byla ve svislé poloze horizontace teodolitu, a byla ztotožněná se svislicí jdoucí vrcholem měřeného úhlu centrace teodolitu. Příprava teodolitu na stanovisku zahrnuje následující úkony: hrubá centrace hrubá horizontace přesná centrace přesná horizontace video: příprava stroje na stanovisku Příprava stroje na stanovisku Hrubá centrace Stativ teodolitu se postaví nad stabilizovaným geodetickým bodem tak, aby střed hlavy stativu byl přibližně nad tímto bodem a hlava stativu byla přibližně vodorovná. Centrace se provádí pomocí olovnice (závěsné, tyčové nebo optické, popř. laserové). Centrace pomocí závěsné olovnice: Fixovaná je jedna noha stativu (ve svahu nejvýše postavená), zbylé dvě volné nohy se posouvají do polohy, v níž hrot olovnice směřuje nad stabilizační znaku bodu. Centrace optickou (laserovou) olovnicí: Fixovány jsou všechny tři nohy stativu, bod se nachází přibližně v těžišti trojúhelníka vymezeného nohama stativu. Stavěcími šrouby se provede nastavení středu optické olovnice (laserové stopy) na značku bodu. Změnou délky nohou stativu dosáhneme urovnání krabicové libely 17
18 Příprava stroje na stanovisku Hrubá horizontace Horizontaci provádíme podle kruhové libely nebo alhidádové libely teodolitu třemi stavěcími šrouby teodolitu. Přístroj se nejprve urovná ve směru dvou stavěcích šroubů (současným protisměrným otáčením těchto šroubů), otočí se o 90 a urovná se pomocí třetího šroubu. Přesná centrace Přístroj se posouvá po desce stativu dokud hrot olovnice (záměrný obrazec) není přesně nad značkou stabilizovaného bodu. Pak se přístroj upevní k desce stativu středovým šroubem. Přesná horizontace Přístroj se horizontuje alhidádovou libelou ve dvou na sebe kolmých směrech stavěcími šrouby. Poté přístrojem otočíme o 360 a pokud se bublina alhidádové libely nevychýlí, je přístroj horizontován. Pokud tomu tak není, je třeba provést rektifikaci alhidádové libely. Před měřením je ještě potřeba upravit dalekohled zaostřit nitkový kříž a obraz zacíleného předmětu!!! Metody měření vodorovných směrů v jedné poloze dalekohledu rozdíl dvou směrů, přístrojové chyby násobením v laboratorních jednotkách J. Křovák, (LPPL) a (PLLP) ve všech kombinacích (Schreiberova metoda) vodorovných směrů ve skupinách 18
19 Měření vodorovných směrů v 1 poloze Používá se při podrobném polohovém měření (polární metodě, tachymetrii). Úhly jsou zatíženy všemi přístrojovými chybami!!! Dalekohledem se zacílí v první poloze na signál, který je ve směru levého ramene úhlu. Na vodorovném kruhu se přečte čtení o 1. Stejným způsobem se provede zacílení ve směru pravého ramene úhlu. Na vodorovném kruhu se přečte čtení o 2. Výsledný úhel se určí ω = o 2 -o 1. Pokud o 2 < o 1, potom ω = ( ) - o 1. Měření vodorovných směrů násobením repeticí / násobením pro měření malých úhlů střídavé zaměřování levého a pravého směru při posouvání vodorovného kruhu o daný měřený úhel (hodnota pravého ramene se posune do levého ramene) dochází k mechanickému sčítání úhlů umožňuje měřit úhel s větší přesností než je přesnost odečítací pomůcky teodolitu, lze ji použít pouze u přístrojů repetičních v současnosti se používá již jen ojediněle Schreiberova metoda Při této metodě se měří všechny úhly na stanovisku. Měření v laboratorních jednotkách Měření v laboratorních jednotkách Metoda zavedená roku 1936 Ing. Josefem Křovákem se používá ke snížení vlivu všech chyb soustavy teodolit observační pilíř na minimum. Měření trvá krátkou dobu, takže lze předpokládat stejnou refrakci. Označení laboratorní má vyjádřit, že po krátkou dobu měření mají spojnice teodolit cíl laboratorní vlastnosti. Laboratorní jednotka sestává ze zaměření na levý a pravý signál (L P) a opakovaného měření téhož úhlu v obráceném pořadí (P L) při dvojnásobném cílení i odečítání, tedy (LPPL). Po proložení dalekohledu do druhé polohy se postup opakuje, ovšem opačně (PLLP). Další laboratorní jednotky se měří na jiných místech děleného kruhu. 19
20 Měření vodorovných směrů ve skupinách Jedná se o základní metodu při určování bodů polohového pole a většiny měření. Výchozí směr má být dobře viditelný po celou dobu měření. Měří se v obou polohách dalekohledu. Při každé další skupině se nastavuje na počáteční směr čtení změněné o hodnotu 200 gon/s, kde s je počet skupin. Výsledky se ukládají do paměti teodolitu nebo se zapisují do zápisníku. Zápisník měřených vodorovných směrů 20
21 Zápisník měřených vodorovných směrů Zápisník měřených vodorovných směrů (charakteristiky přesnosti) Zápisník měřených vodorovných směrů 21
22 Chyby při měření vodorovných úhlů přístrojové chyby chyba alhidádové libely úklonná chyba kolimační chyba,. měřické chyby chyba z nesprávné horizontace chyba z nesprávné centrace stroje chyba z nesprávné centrace signálu chyba z nepevného postavení stroje chyba z cílení chyba ze čtení stupnice vnější chyby (z prostředí) refrakce vibrace Magnetické azimuty K orientaci vodorovných směrů, resp. k měření úhlů tam, kde není možné připojení na body bodového pole, lze využít magnetického pole Země. V důsledku působení magnetického pole Země ukazuje jeden konec volně zavěšené magnetky vždy k severnímu magnetickému pólu. Směr severního magnetického poledníku je základním směrem pro měření magnetických azimutů. Magnetický meridián pozorovacího místa je průsečnice svislé roviny, proložené osou ustálené deklinační magnetky se zemským povrchem (Osou magnetky je spojnice obou koncových hrotů, která prochází středem magnetky) Magnetický azimut je úhel měřený v místě pozorování od severní větve magnetického meridiánu na určovaný bod ve směru číslování na hodinách. Je vždy kladný a počítá se od 0 do 360 (příp. od 0 gon do 400 gon). 22
23 Magnetické azimuty Magnetická deklinace δ je úhel, který v místě pozorování svírá směr magnetického meridiánu SM s astronomickým meridiánem SA. Jestliže se severní hrot magnetky odklání k západu od astronomického meridiánu, je deklinace západní záporná, odklání-li se k východu, je deklinace východní kladná. Astronomický azimut A tedy získáme přičtením magnetické deklinace k naměřenému magnetickému azimutu. Změna deklinace s místem je patrná z magnetických map, na kterých čáry spojující místa se stejnou hodnotou magnetické deklinace se nazývají izogony. Izogony probíhají přibližně ve směru zemských poledníků. Největší změna deklinace se změnou pozorovacího místa nastává ve tedy směru východ západ. Magnetické azimuty Pokud změny velikosti magnetické deklinace s časem probíhají v pravidelných časových obdobích, nazývají se variace. Podle délky periody rozlišujeme variace denní, roční a sekulární. Pro přesné práce je tedy třeba znát místo a dobu (epochu), kde a kdy se měření konalo. Kromě poměrně pravidelných změn magnetické deklinace mohou nastat také nepravidelné změny, neboli poruchy. Příčinou magnetických poruch mohou být např. magnetické bouře provázející polární záři nebo související s obdobím výskytu zvýšeného počtu slunečních skvrn, příčinou může také být vliv feromagnetických kovů, vliv elektrického proudu, vliv nepravidelně rozložených železných a ocelových součástí vlastního přístroje atd. Magnetické přístroje: Součástí každého magnetického přístroje je deklinační magnetka, která je umístěna v pouzdru z nemagnetického materiálu, opatřeném děleným kruhem, nazývaným též hodinovým. Deklinační magnetka je tenká, lehká, ocelová, silně zmagnetizovaná tyčinka různého tvaru. Mezi magnetické přístroje patří kompasy, busoly, busolní teodolity 23
24 Magnetické azimuty Pokud změny velikosti magnetické deklinace s časem probíhají v pravidelných časových obdobích, nazývají se variace. Podle délky periody rozlišujeme variace denní, roční a sekulární. Pro přesné práce je tedy třeba znát místo a dobu (epochu), kde a kdy se měření konalo. Kromě poměrně pravidelných změn magnetické deklinace mohou nastat také nepravidelné změny, neboli poruchy. Příčinou magnetických poruch mohou být např. magnetické bouře provázející polární záři nebo související s obdobím výskytu zvýšeného počtu slunečních skvrn, příčinou může také být vliv feromagnetických kovů, vliv elektrického proudu, vliv nepravidelně rozložených železných a ocelových součástí vlastního přístroje atd. Magnetické přístroje: Součástí každého magnetického přístroje je deklinační magnetka, která je umístěna v pouzdru z nemagnetického materiálu, opatřeném děleným kruhem, nazývaným též hodinovým. Deklinační magnetka je tenká, lehká, ocelová, silně zmagnetizovaná tyčinka různého tvaru. Mezi magnetické přístroje patří kompasy, busoly, busolní teodolity Astronomické azimuty Astronomický azimut úhel, který svírá svislá záměrná rovina s rovinou astronomického meridiánu v místě pozorování měří se od severní větve poledníku ve směru číslování na hodinách od 0 do 360 pro určení astronomického azimutu je tedy třeba předem znát směr místního poledníku jako základního směru Magnetická deklinace δ je úhel, který v místě pozorování svírá směr magnetického meridiánu SM s astronomickým meridiánem SA (obr.). 24
25 Měření svislých úhlů Svislý úhel se na rozdíl od vodorovného úhlu získá zaměřením pouze jednoho směru (na cílovou značku příslušného signálu). Druhým směrem je směr základní vodorovný pro výškový úhel, svislý pro zenitový úhel. Velikost svislého úhlu se odečítá na vertikálním kruhu, který se na rozdíl od vodorovného kruhu při sklápění dalekohledu otáčí současně s vodorovnou točnou osou dalekohledu, se kterou je pevně spojen. Odečítací indexy jsou spojené s dalekohledovou vidlicí, zůstávají pevné. Zařízením, které realizuje základní směr, je indexová libela nebo kompenzátor. Indexovou libelu je nutné urovnat před každým měřením!!! Svislý úhel svírá záměrná přímka s vodorovnou rovinou. Značí se ± ε (výškový/hloubkový). Nabývá hodnot od 0 až do ±100 gon. Zenitový úhel svírá záměrná přímka se svislou rovinou. Značí se z a nabývá hodnot od 0 až 200gon. Vodorovná záměra má hodnotu z = 100gon. Měření svislých úhlů metody měření svislých úhlů v jedné poloze dalekohledu měříme v první poloze dalekohledu nutno znát hodnotu indexové chyby před začátkem měření v obou polohách dalekohledu výsledek je průměr z měření v obou polohách dalekohledu měření v obou polohách realizovat bez prodlev indexová ch.!!! přístrojové chyby úklonná chyba, kolimační chyba, chyba alhidádové libely, indexová, měřické chyby chyba z nesprávné horizontace, chyba z nesprávného dostředění přístroje, chyba v cílení a odečtení, chyba z urovnání indexové libely vnější chyby (z prostředí) chyba z refrakce a z vibrace 25
26 Měření svislých úhlů Zápisník zenitových úhlů 26
27 Prameny a literatura : Matěj Pokora a kol. Geodézie pro stavební fakulty. Praha Děkuji za pozornost Dotazy ZÁPADOČESKÁ UNIVERZITA V PLZNI Fakulta aplikovaných věd - KMA oddělení geomatiky Ing. Martina Vichrová, Ph.D. vichrova@kma.zcu.cz 27
6.1 Základní pojmy - zákonné měřící jednotky
 6. Měření úhlů 6.1 Základní pojmy 6.2 Teodolity 6.3 Totální stanice 6.4 Osové podmínky, konstrukční chyby a chyby při měření 6.5 Měření úhlů 6.6 Postup při měření vodorovného úhlu 6.7 Postup při měření
6. Měření úhlů 6.1 Základní pojmy 6.2 Teodolity 6.3 Totální stanice 6.4 Osové podmínky, konstrukční chyby a chyby při měření 6.5 Měření úhlů 6.6 Postup při měření vodorovného úhlu 6.7 Postup při měření
4.1 Základní pojmy Zákonné měřicí jednotky.
 4. Měření úhlů. 4.1 Základní pojmy 4.1.1 Zákonné měřicí jednotky. 4.1.2 Vodorovný úhel, směr. 4.1.3 Svislý úhel, zenitový úhel. 4.2 Teodolity 4.2.1 Součásti. 4.2.2 Čtecí pomůcky optickomechanických teodolitů.
4. Měření úhlů. 4.1 Základní pojmy 4.1.1 Zákonné měřicí jednotky. 4.1.2 Vodorovný úhel, směr. 4.1.3 Svislý úhel, zenitový úhel. 4.2 Teodolity 4.2.1 Součásti. 4.2.2 Čtecí pomůcky optickomechanických teodolitů.
SPŠ STAVEBNÍ České Budějovice GEODÉZIE. Teodolit a měření úhlů
 SPŠ STAVEBNÍ České Budějovice GEODÉZIE Teodolit a měření úhlů ještě doplnění k výškovému systému jadranský systém udává pro stejný bod hodnotu výšky o cca 0,40 m větší než systém Bpv Potřebujeme vědět
SPŠ STAVEBNÍ České Budějovice GEODÉZIE Teodolit a měření úhlů ještě doplnění k výškovému systému jadranský systém udává pro stejný bod hodnotu výšky o cca 0,40 m větší než systém Bpv Potřebujeme vědět
Popis teodolitu Podmínky správnosti teodolitu Metody měření úhlů
 5. PŘEDNÁŠKA LETNÍ 00 Ing. Hana Staňková, Ph.D. Měření úhlů Popis teodolitu Podmínky správnosti teodolitu Metody měření úhlů GEODÉZIE 5. PŘEDNÁŠKA LETNÍ 00 POPIS TEODOLITU THEO 00 THEO 00 kolimátor dalekohled
5. PŘEDNÁŠKA LETNÍ 00 Ing. Hana Staňková, Ph.D. Měření úhlů Popis teodolitu Podmínky správnosti teodolitu Metody měření úhlů GEODÉZIE 5. PŘEDNÁŠKA LETNÍ 00 POPIS TEODOLITU THEO 00 THEO 00 kolimátor dalekohled
SPŠ STAVEBNÍ České Budějovice GEODÉZIE. Teodolit a měření úhlů
 SPŠ STAVEBNÍ České Budějovice GEODÉZIE Teodolit a měření úhlů ještě doplnění k výškovému systému jadranský systém udává pro stejný bod hodnotu výšky o cca 0,40 m větší než systém Bpv Potřebujeme vědět
SPŠ STAVEBNÍ České Budějovice GEODÉZIE Teodolit a měření úhlů ještě doplnění k výškovému systému jadranský systém udává pro stejný bod hodnotu výšky o cca 0,40 m větší než systém Bpv Potřebujeme vědět
Přednášející: Ing. M. Čábelka Katedra aplikované geoinformatiky a kartografie PřF UK v Praze
 Seminář z geoinformatiky Měření vodorovných úhlů Seminář z geo oinform matiky Přednášející: Ing. M. Čábelka cabelka@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie PřF UK v Praze Základním
Seminář z geoinformatiky Měření vodorovných úhlů Seminář z geo oinform matiky Přednášející: Ing. M. Čábelka cabelka@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie PřF UK v Praze Základním
Měření horizontálních a vertikálních úhlů Úhloměrné přístroje a jejich konstrukce Horizontace a centrace Přesnost a chyby v měření úhlů.
 Měření horizontálních a vertikálních úhlů Úhloměrné přístroje a jejich konstrukce Horizontace a centrace Přesnost a chyby v měření úhlů Kartografie přednáška 10 Měření úhlů prostorovou polohu směru, vycházejícího
Měření horizontálních a vertikálních úhlů Úhloměrné přístroje a jejich konstrukce Horizontace a centrace Přesnost a chyby v měření úhlů Kartografie přednáška 10 Měření úhlů prostorovou polohu směru, vycházejícího
SYLABUS PŘEDNÁŠKY 4 Z GEODÉZIE 1
 SYLABUS PŘEDNÁŠKY 4 Z GEODÉZIE 1 (Měření svislých úhlů Chyby ovlivňující úhlová měření a jejich eliminace) 1 ročník bakalářského studia studijní program G studijní obor G doc Ing Jaromír Procházka CSc
SYLABUS PŘEDNÁŠKY 4 Z GEODÉZIE 1 (Měření svislých úhlů Chyby ovlivňující úhlová měření a jejich eliminace) 1 ročník bakalářského studia studijní program G studijní obor G doc Ing Jaromír Procházka CSc
ÚHLŮ METODY MĚŘENÍ ÚHLŮ A SMĚRŮ CHYBY PŘI MĚŘENÍ ÚHLŮ A SMĚRŮ
 5. PŘEDNÁŠKA LETNÍ 00 ING. HANA STAŇKOVÁ, Ph.D. MĚŘENÍ ÚHLŮ METODY MĚŘENÍ ÚHLŮ A SMĚRŮ CHYBY PŘI MĚŘENÍ ÚHLŮ A SMĚRŮ GEODÉZIE 5. PŘEDNÁŠKA LETNÍ 00 METODY MĚŘENÍ ÚHLŮ. měření úhlů v jedné poloze dalekohledu.
5. PŘEDNÁŠKA LETNÍ 00 ING. HANA STAŇKOVÁ, Ph.D. MĚŘENÍ ÚHLŮ METODY MĚŘENÍ ÚHLŮ A SMĚRŮ CHYBY PŘI MĚŘENÍ ÚHLŮ A SMĚRŮ GEODÉZIE 5. PŘEDNÁŠKA LETNÍ 00 METODY MĚŘENÍ ÚHLŮ. měření úhlů v jedné poloze dalekohledu.
Sada 1 Geodezie I. 03. Drobné geodetické pomůcky
 S třední škola stavební Jihlava Sada 1 Geodezie I 03. Drobné geodetické pomůcky Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2
S třední škola stavební Jihlava Sada 1 Geodezie I 03. Drobné geodetické pomůcky Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2
Geodézie Přednáška. Měření úhlů Přístroje pro měření úhlů Přesnost a chyby při měření úhlů
 Geodézie Přednáška Měření úhlů Přístroje pro měření úhlů Přesnost a chyby při měření úhlů Měření úhlů strana 2 úhly jsou pro geodézii jednou ze základních veličin a jejich měření představuje základ pro
Geodézie Přednáška Měření úhlů Přístroje pro měření úhlů Přesnost a chyby při měření úhlů Měření úhlů strana 2 úhly jsou pro geodézii jednou ze základních veličin a jejich měření představuje základ pro
Přípravný kurz k vykonání maturitní zkoušky v oboru Dopravní stavitelství. Výšky relativní a absolutní
 Přípravný kurz k vykonání maturitní zkoušky v oboru Dopravní stavitelství MĚŘENÍ VÝŠEK Ing. Bc. Pavel Voříšek (úředně oprávněný zeměměřický inženýr). Vysoké Mýto leden 2017 Výšky relativní a absolutní
Přípravný kurz k vykonání maturitní zkoušky v oboru Dopravní stavitelství MĚŘENÍ VÝŠEK Ing. Bc. Pavel Voříšek (úředně oprávněný zeměměřický inženýr). Vysoké Mýto leden 2017 Výšky relativní a absolutní
SPŠ STAVEBNÍ České Budějovice GEODÉZIE STA NIVELACE VÝŠKOVÉ MĚŘENÍ A VÝŠKOVÉ BODOVÉ POLE JS
 SPŠ STAVEBNÍ České Budějovice GEODÉZIE STA NIVELACE VÝŠKOVÉ MĚŘENÍ A VÝŠKOVÉ BODOVÉ POLE JS NIVELACE - úvod NIVELACE je měření výškového rozdílu od realizované (vytyčené) vodorovné roviny Provádí se pomocí
SPŠ STAVEBNÍ České Budějovice GEODÉZIE STA NIVELACE VÝŠKOVÉ MĚŘENÍ A VÝŠKOVÉ BODOVÉ POLE JS NIVELACE - úvod NIVELACE je měření výškového rozdílu od realizované (vytyčené) vodorovné roviny Provádí se pomocí
Sada 1 Geodezie I. 13. Měření vodorovných směrů
 S třední škola stavební Jihlava Sada 1 Geodezie I 13. Měření vodorovných směrů Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2 -
S třední škola stavební Jihlava Sada 1 Geodezie I 13. Měření vodorovných směrů Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2 -
6.1 Základní pojmy. 6.1.1 Zákonné měřicí jednotky.
 6. Měření úhlů. 6.1 Základní pojmy 6.1.1 Zákonné měřicí jednotky. 6.1.2 Vodorovný úhel, směr. 6.1.3 Svislý úhel, zenitový úhel. 6.2 Teodolity 6.2.1 Součásti. 6.2.2 Čtecí pomůcky optickomechanických teodolitů.
6. Měření úhlů. 6.1 Základní pojmy 6.1.1 Zákonné měřicí jednotky. 6.1.2 Vodorovný úhel, směr. 6.1.3 Svislý úhel, zenitový úhel. 6.2 Teodolity 6.2.1 Součásti. 6.2.2 Čtecí pomůcky optickomechanických teodolitů.
ZÁKLADNÍ GEODETICKÉ POMŮCKY
 Přípravný kurz k vykonání maturitní zkoušky v oboru Dopravní stavitelství Ing. Pavel Voříšek ZÁKLADNÍ GEODETICKÉ POMŮCKY VOŠ a SŠS Vysoké Mýto prosinec 2007 ZÁKLADNÍ GEODETICKÉ POMŮCKY POMŮCKY K URČOVÁNÍ
Přípravný kurz k vykonání maturitní zkoušky v oboru Dopravní stavitelství Ing. Pavel Voříšek ZÁKLADNÍ GEODETICKÉ POMŮCKY VOŠ a SŠS Vysoké Mýto prosinec 2007 ZÁKLADNÍ GEODETICKÉ POMŮCKY POMŮCKY K URČOVÁNÍ
Automatický nivelační přístroj RUNNER 20/24
 Automatický nivelační přístroj RUNNER 20/24 RUNNER 20/24 patří k nové generaci stavebních nivelačních přístrojů. Je vhodný pro všechny aplikace spojené s přenášením výšek, pro měření vzdáleností a pro
Automatický nivelační přístroj RUNNER 20/24 RUNNER 20/24 patří k nové generaci stavebních nivelačních přístrojů. Je vhodný pro všechny aplikace spojené s přenášením výšek, pro měření vzdáleností a pro
GEOMETRICKÁ OPTIKA. Znáš pojmy A. 1. Znázorni chod význačných paprsků pro spojku. Čočku popiš a uveď pro ni znaménkovou konvenci.
 Znáš pojmy A. Znázorni chod význačných paprsků pro spojku. Čočku popiš a uveď pro ni znaménkovou konvenci. Tenká spojka při zobrazování stačí k popisu zavést pouze ohniskovou vzdálenost a její střed. Znaménková
Znáš pojmy A. Znázorni chod význačných paprsků pro spojku. Čočku popiš a uveď pro ni znaménkovou konvenci. Tenká spojka při zobrazování stačí k popisu zavést pouze ohniskovou vzdálenost a její střed. Znaménková
Určení svislosti. Ing. Zuzana Matochová
 Určení svislosti Ing. Zuzana Matochová Svislost stěn Jedná se o jeden z geometrických parametrů, který udává orientaci části konstrukce vzhledem ke stanovenému směru. Geometrické parametry jsou kontrolovány
Určení svislosti Ing. Zuzana Matochová Svislost stěn Jedná se o jeden z geometrických parametrů, který udává orientaci části konstrukce vzhledem ke stanovenému směru. Geometrické parametry jsou kontrolovány
Základní pojmy Zobrazení zrcadlem, Zobrazení čočkou Lidské oko, Optické přístroje
 Optické zobrazování Základní pojmy Zobrazení zrcadlem, Zobrazení čočkou Lidské oko, Optické přístroje Základní pojmy Optické zobrazování - pomocí paprskové (geometrické) optiky - využívá model světelného
Optické zobrazování Základní pojmy Zobrazení zrcadlem, Zobrazení čočkou Lidské oko, Optické přístroje Základní pojmy Optické zobrazování - pomocí paprskové (geometrické) optiky - využívá model světelného
7. Určování výšek II.
 7. Určování výšek II. 7.1 Geometrická nivelace ze středu. 7.1.1 Princip geometrické nivelace. 7.1.2 Výhody geometrické nivelace ze středu. 7.1.3 Dělení nivelace dle přesnosti. 7.1.4 Nivelační přístroje.
7. Určování výšek II. 7.1 Geometrická nivelace ze středu. 7.1.1 Princip geometrické nivelace. 7.1.2 Výhody geometrické nivelace ze středu. 7.1.3 Dělení nivelace dle přesnosti. 7.1.4 Nivelační přístroje.
Klasická měření v geodetických sítích. Poznámka. Klasická měření v polohových sítích
 Klasická měření v geodetických sítích Poznámka Detailněji budou popsány metody, které se používaly v minulosti pro budování polohových, výškových a tíhových základů. Pokud se některé z nich používají i
Klasická měření v geodetických sítích Poznámka Detailněji budou popsány metody, které se používaly v minulosti pro budování polohových, výškových a tíhových základů. Pokud se některé z nich používají i
Geodézie pro stavitelství KMA/GES
 Geodézie pro stavitelství KMA/GES ZÁPADOČESKÁ UNIVERZITA V PLZNI Fakulta aplikovaných věd - KMA oddělení geomatiky Ing. Martina Vichrová, Ph.D. vichrova@kma.zcu.cz Vytvoření materiálů bylo podpořeno prostředky
Geodézie pro stavitelství KMA/GES ZÁPADOČESKÁ UNIVERZITA V PLZNI Fakulta aplikovaných věd - KMA oddělení geomatiky Ing. Martina Vichrová, Ph.D. vichrova@kma.zcu.cz Vytvoření materiálů bylo podpořeno prostředky
Průmyslová střední škola Letohrad
 Průmyslová střední škola Letohrad Manuál pro obsluhu geodetických přístrojů 2014 Zpracoval: Ing. Jiří Štěpánek Tento projekt je realizovaný v rámci OP VK a je financovaný ze Strukturálních fondů EU (ESF)
Průmyslová střední škola Letohrad Manuál pro obsluhu geodetických přístrojů 2014 Zpracoval: Ing. Jiří Štěpánek Tento projekt je realizovaný v rámci OP VK a je financovaný ze Strukturálních fondů EU (ESF)
GEODÉZIE II. Metody určov. Geometrická nivelace ze středu. vzdálenost
 Vysoká škola báňská technická univerzita Ostrava Hornicko-geologická fakulta Institut geodézie a důlního měřictví GEODÉZIE II 1. URČOV OVÁNÍ VÝŠEK Metody určov ování převýšení Geometrická nivelace Ing.
Vysoká škola báňská technická univerzita Ostrava Hornicko-geologická fakulta Institut geodézie a důlního měřictví GEODÉZIE II 1. URČOV OVÁNÍ VÝŠEK Metody určov ování převýšení Geometrická nivelace Ing.
7. Určování výšek II.
 7. Určování výšek II. 7.1 Geometrická nivelace ze středu. 7.1.1 Princip geometrické nivelace. 7.1.2 Výhody geometrické nivelace ze středu. 7.1.3 Dělení nivelace dle přesnosti. 7.1.4 Nivelační přístroje.
7. Určování výšek II. 7.1 Geometrická nivelace ze středu. 7.1.1 Princip geometrické nivelace. 7.1.2 Výhody geometrické nivelace ze středu. 7.1.3 Dělení nivelace dle přesnosti. 7.1.4 Nivelační přístroje.
Optika. Zápisy do sešitu
 Optika Zápisy do sešitu Světelné zdroje. Šíření světla. 1/3 Světelné zdroje - bodové - plošné Optická prostředí - průhledné (sklo, vzduch) - průsvitné (matné sklo) - neprůsvitné (nešíří se světlo) - čirá
Optika Zápisy do sešitu Světelné zdroje. Šíření světla. 1/3 Světelné zdroje - bodové - plošné Optická prostředí - průhledné (sklo, vzduch) - průsvitné (matné sklo) - neprůsvitné (nešíří se světlo) - čirá
Geodézie pro stavitelství KMA/GES
 Geodézie pro stavitelství KMA/GES ZÁPADOČESKÁ UNIVERZITA V PLZNI Fakulta aplikovaných věd - KMA oddělení geomatiky Ing. Martina Vichrová, Ph.D. vichrova@kma.zcu.cz Vytvoření materiálů bylo podpořeno prostředky
Geodézie pro stavitelství KMA/GES ZÁPADOČESKÁ UNIVERZITA V PLZNI Fakulta aplikovaných věd - KMA oddělení geomatiky Ing. Martina Vichrová, Ph.D. vichrova@kma.zcu.cz Vytvoření materiálů bylo podpořeno prostředky
Výuka v terénu I. Obory: Inženýrská geodézie a Důlní měřictví. Skupiny: GB1IGE01, GB1IGE02, GB1DME
 Výuka v terénu I Obory: Inženýrská geodézie a Důlní měřictví Skupiny: GB1IGE01, GB1IGE02, GB1DME01 27. 4-30. 4. 2015 1. Trojúhelníkový řetězec Zásady pro zpracování úlohy: Zaměřte ve skupinách úhly potřebné
Výuka v terénu I Obory: Inženýrská geodézie a Důlní měřictví Skupiny: GB1IGE01, GB1IGE02, GB1DME01 27. 4-30. 4. 2015 1. Trojúhelníkový řetězec Zásady pro zpracování úlohy: Zaměřte ve skupinách úhly potřebné
4. přednáška ze stavební geodézie SG01. Ing. Tomáš Křemen, Ph.D.
 4. přednáška ze stavební geodézie SG01 Ing. Tomáš Křemen, Ph.D. Měření úhlů Základní pojmy Optickomechanické teodolity Elektronické teodolity, totální stanice Osové podmínky, chyby při měření úhlů Měření
4. přednáška ze stavební geodézie SG01 Ing. Tomáš Křemen, Ph.D. Měření úhlů Základní pojmy Optickomechanické teodolity Elektronické teodolity, totální stanice Osové podmínky, chyby při měření úhlů Měření
SYLABUS PŘEDNÁŠKY 2 Z GEODÉZIE 1
 SYLABUS PŘEDNÁŠKY 2 Z GEODÉZIE 1 (Tvar a rozměry Země, základní součásti geodetických přístrojů) 1. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. říjen
SYLABUS PŘEDNÁŠKY 2 Z GEODÉZIE 1 (Tvar a rozměry Země, základní součásti geodetických přístrojů) 1. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. říjen
Přípravný kurz k vykonání maturitní zkoušky v oboru Dopravní stavitelství. Ing. Pavel Voříšek MĚŘENÍ VZDÁLENOSTÍ. VOŠ a SŠS Vysoké Mýto leden 2008
 Přípravný kurz k vykonání maturitní zkoušky v oboru Dopravní stavitelství Ing. Pavel Voříšek MĚŘENÍ VZDÁLENOSTÍ VOŠ a SŠS Vysoké Mýto leden 2008 METODY MĚŘENÍ DÉLEK PŘÍMÉ (měřidlo klademe přímo do měřené
Přípravný kurz k vykonání maturitní zkoušky v oboru Dopravní stavitelství Ing. Pavel Voříšek MĚŘENÍ VZDÁLENOSTÍ VOŠ a SŠS Vysoké Mýto leden 2008 METODY MĚŘENÍ DÉLEK PŘÍMÉ (měřidlo klademe přímo do měřené
Vytyčování pozemních stavebních objektů s prostorovou skladbou
 Vytyčování pozemních stavebních objektů s prostorovou skladbou ZÁPADOČESKÁ UNIVERZITA V PLZNI Ing. Martina Vichrová, Ph.D. Fakulta aplikovaných věd - KMA oddělení geomatiky vichrova@kma.zcu.cz Vytvoření
Vytyčování pozemních stavebních objektů s prostorovou skladbou ZÁPADOČESKÁ UNIVERZITA V PLZNI Ing. Martina Vichrová, Ph.D. Fakulta aplikovaných věd - KMA oddělení geomatiky vichrova@kma.zcu.cz Vytvoření
Odraz světla na rozhraní dvou optických prostředí
 Odraz světla na rozhraní dvou optických prostředí Může kulová nádoba naplněná vodou sloužit jako optická čočka? Exponát demonstruje zaostření světla procházejícího skrz vodní kulovou čočku. Pohyblivý světelný
Odraz světla na rozhraní dvou optických prostředí Může kulová nádoba naplněná vodou sloužit jako optická čočka? Exponát demonstruje zaostření světla procházejícího skrz vodní kulovou čočku. Pohyblivý světelný
VY_32_INOVACE_FY.12 OPTIKA II
 VY_32_INOVACE_FY.12 OPTIKA II Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 Optická čočka je optická soustava dvou centrovaných
VY_32_INOVACE_FY.12 OPTIKA II Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 Optická čočka je optická soustava dvou centrovaných
SBÍRKA ŘEŠENÝCH FYZIKÁLNÍCH ÚLOH
 SBÍRKA ŘEŠENÝCH FYZIKÁLNÍCH ÚLOH MECHANIKA MOLEKULOVÁ FYZIKA A TERMIKA ELEKTŘINA A MAGNETISMUS KMITÁNÍ A VLNĚNÍ OPTIKA FYZIKA MIKROSVĚTA ODRAZ A LOM SVĚTLA 1) Index lomu vody je 1,33. Jakou rychlost má
SBÍRKA ŘEŠENÝCH FYZIKÁLNÍCH ÚLOH MECHANIKA MOLEKULOVÁ FYZIKA A TERMIKA ELEKTŘINA A MAGNETISMUS KMITÁNÍ A VLNĚNÍ OPTIKA FYZIKA MIKROSVĚTA ODRAZ A LOM SVĚTLA 1) Index lomu vody je 1,33. Jakou rychlost má
11. Měření závitů. Profil metrického závitu je určen jmenovitými rozměry:
 11. Měření závitů Závit je geometricky určen závitovou plochou. Rozeznáváme závit matice (vnitřní) a závit šroubu (vnější). Závitová plocha vznikne pohybem profilu závitu tak, že každý jeho bod opisuje
11. Měření závitů Závit je geometricky určen závitovou plochou. Rozeznáváme závit matice (vnitřní) a závit šroubu (vnější). Závitová plocha vznikne pohybem profilu závitu tak, že každý jeho bod opisuje
Kontrola svislosti montované budovy
 1. Zadání Kontrola svislosti montované budovy Určete skutečné odchylky svislosti panelů na budově ČVUT. Objednatel požaduje kontrolu svislosti štítové stěny objektu. Při konstrukční výšce jednoho podlaží
1. Zadání Kontrola svislosti montované budovy Určete skutečné odchylky svislosti panelů na budově ČVUT. Objednatel požaduje kontrolu svislosti štítové stěny objektu. Při konstrukční výšce jednoho podlaží
Geometrická optika. předmětu. Obrazový prostor prostor za optickou soustavou (většinou vpravo), v němž může ležet obraz - - - 1 -
 Geometrická optika Optika je část fyziky, která zkoumá podstatu světla a zákonitosti světelných jevů, které vznikají při šíření světla a při vzájemném působení světla a látky. Světlo je elektromagnetické
Geometrická optika Optika je část fyziky, která zkoumá podstatu světla a zákonitosti světelných jevů, které vznikají při šíření světla a při vzájemném působení světla a látky. Světlo je elektromagnetické
Trigonometrické určení výšek nepřístupných bodů na stavebním objektu
 Trigonometrické určení výšek nepřístupných bodů na stavebním objektu Prof. Ing. Jiří Pospíšil, CSc., 2010 V urbanismu a pozemním stavitelství lze trigonometrického určování výšek užít při zjišťování relativních
Trigonometrické určení výšek nepřístupných bodů na stavebním objektu Prof. Ing. Jiří Pospíšil, CSc., 2010 V urbanismu a pozemním stavitelství lze trigonometrického určování výšek užít při zjišťování relativních
Přednášející: Ing. M. Čábelka Katedra aplikované geoinformatiky a kartografie PřF UK v Praze
 Seminář z geoinformatiky Metody měření výškopisu, Tachymetrie Seminář z geo oinform matiky Přednášející: Ing. M. Čábelka cabelka@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie PřF UK v Praze
Seminář z geoinformatiky Metody měření výškopisu, Tachymetrie Seminář z geo oinform matiky Přednášející: Ing. M. Čábelka cabelka@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie PřF UK v Praze
ČOS 124002 1. vydání ČESKÝ OBRANNÝ STANDARD ÚSŤOVÉ REKTIFIKAČNÍ DALEKOHLEDY ZBRANÍ TYPY, ZÁKLADNÍ PARAMETRY
 ČESKÝ OBRANNÝ STANDARD ÚSŤOVÉ REKTIFIKAČNÍ DALEKOHLEDY ZBRANÍ TYPY, ZÁKLADNÍ PARAMETRY (VOLNÁ STRANA) 2 ČESKÝ OBRANNÝ STANDARD ÚSŤOVÉ REKTIFIKAČNÍ DALEKOHLEDY ZBRANÍ TYPY, ZÁKLADNÍ PARAMETRY Základem pro
ČESKÝ OBRANNÝ STANDARD ÚSŤOVÉ REKTIFIKAČNÍ DALEKOHLEDY ZBRANÍ TYPY, ZÁKLADNÍ PARAMETRY (VOLNÁ STRANA) 2 ČESKÝ OBRANNÝ STANDARD ÚSŤOVÉ REKTIFIKAČNÍ DALEKOHLEDY ZBRANÍ TYPY, ZÁKLADNÍ PARAMETRY Základem pro
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Zrcadla Zobrazení zrcadlem Zrcadla jistě všichni znáte z každodenního života ráno se do něj v koupelně díváte,
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Zrcadla Zobrazení zrcadlem Zrcadla jistě všichni znáte z každodenního života ráno se do něj v koupelně díváte,
Bodový zdroj světla A vytvoří svazek rozbíhajících se paprsků, které necháme projít optickou soustavou.
 Optické zobrazení Optické zobrazení je proces, kterým optické soustavy vytvářejí obrazy reálných předmětů. Tyto soustavy mění chod světelných paprsků. Obsahují zrcadla, čočky, odrazné hranoly aj. Princip
Optické zobrazení Optické zobrazení je proces, kterým optické soustavy vytvářejí obrazy reálných předmětů. Tyto soustavy mění chod světelných paprsků. Obsahují zrcadla, čočky, odrazné hranoly aj. Princip
Optika pro mikroskopii materiálů I
 Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
7.ročník Optika Lom světla
 LOM SVĚTLA. ZOBRAZENÍ ČOČKAMI 1. LOM SVĚTLA NA ROVINNÉM ROZHRANÍ DVOU OPTICKÝCH PROSTŘEDÍ Sluneční světlo se od vodní hladiny částečně odráží a částečně proniká do vody. V čisté vodě jezera vidíme rostliny,
LOM SVĚTLA. ZOBRAZENÍ ČOČKAMI 1. LOM SVĚTLA NA ROVINNÉM ROZHRANÍ DVOU OPTICKÝCH PROSTŘEDÍ Sluneční světlo se od vodní hladiny částečně odráží a částečně proniká do vody. V čisté vodě jezera vidíme rostliny,
Oblast podpory: 1.5 - Zlepšení podmínek pro vzdělávání na středních školách. Karlovy Vary nám. Karla Sabiny 16 Karlovy Vary
 Prioritní osa: 1 Počáteční vzdělávání Oblast podpory: 1.5 - Zlepšení podmínek pro vzdělávání na středních školách Registrační číslo projektu: CZ.1.07/1.5.00/34. 1077 Název projektu: Zkvalitnění výuky SOŠ
Prioritní osa: 1 Počáteční vzdělávání Oblast podpory: 1.5 - Zlepšení podmínek pro vzdělávání na středních školách Registrační číslo projektu: CZ.1.07/1.5.00/34. 1077 Název projektu: Zkvalitnění výuky SOŠ
SYLABUS PŘEDNÁŠKY 5 Z GEODÉZIE 1
 SYLABUS PŘEDNÁŠKY 5 Z GEODÉZIE 1 (Měření délek) 1. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. říjen 2015 1 Geodézie 1 přednáška č.5 MĚŘENÍ DÉLEK Podle
SYLABUS PŘEDNÁŠKY 5 Z GEODÉZIE 1 (Měření délek) 1. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. říjen 2015 1 Geodézie 1 přednáška č.5 MĚŘENÍ DÉLEK Podle
Polohopisná měření Metody měření Jednoduché pomůcky pro měření
 Geodézie přednáška 1 Polohopisná měření Metody měření Jednoduché pomůcky pro měření Ústav geoinformačních technologií Lesnická a dřevařská fakulta ugt.mendelu.cz tel.: 545134015 Polohopisné měření úkolem
Geodézie přednáška 1 Polohopisná měření Metody měření Jednoduché pomůcky pro měření Ústav geoinformačních technologií Lesnická a dřevařská fakulta ugt.mendelu.cz tel.: 545134015 Polohopisné měření úkolem
Geodézie Přednáška. Polohopisná měření Metody měření Jednoduché pomůcky pro měření
 Geodézie Přednáška Polohopisná měření Metody měření Jednoduché pomůcky pro měření strana 2 téměř všechna geodetická měření jsou vztažena ke dvěma základním směrům směru vodorovnému a směru svislému úkolem
Geodézie Přednáška Polohopisná měření Metody měření Jednoduché pomůcky pro měření strana 2 téměř všechna geodetická měření jsou vztažena ke dvěma základním směrům směru vodorovnému a směru svislému úkolem
Polohopisná měření Jednoduché pomůcky k zaměřování Metody zaměřování pozemků
 Polohopisná měření Jednoduché pomůcky k zaměřování Metody zaměřování pozemků Kartografie přednáška 8 Polohopisná měření úkolem polohopisného měření je určení vzájemné polohy bodů na povrchu Země ve směru
Polohopisná měření Jednoduché pomůcky k zaměřování Metody zaměřování pozemků Kartografie přednáška 8 Polohopisná měření úkolem polohopisného měření je určení vzájemné polohy bodů na povrchu Země ve směru
Seznámení s moderní přístrojovou technikou Totální stanice a digitální nivelační přístroje
 Prohloubení nabídky dalšího vzdělávání v oblasti zeměměřictví a katastru nemovitostí ve Středočeském kraji CZ.1.07/3.2.11/03.0115 Projekt je finančně podpořen Evropským sociálním fondem a státním rozpočtem
Prohloubení nabídky dalšího vzdělávání v oblasti zeměměřictví a katastru nemovitostí ve Středočeském kraji CZ.1.07/3.2.11/03.0115 Projekt je finančně podpořen Evropským sociálním fondem a státním rozpočtem
Úloha č. 1 : TROJÚHELNÍK. Určení prostorových posunů stavebního objektu
 Václav Čech, ČVUT v Praze, Fakulta stavební, 008 Úloha č. 1 : TROJÚHELNÍK Určení prostorových posunů stavebního objektu Zadání : Zjistěte posun bodu P do P, umístěného na horní terase Stavební fakulty.
Václav Čech, ČVUT v Praze, Fakulta stavební, 008 Úloha č. 1 : TROJÚHELNÍK Určení prostorových posunů stavebního objektu Zadání : Zjistěte posun bodu P do P, umístěného na horní terase Stavební fakulty.
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA SPECIÁLNÍ GEODÉZIE název předmětu Geodézie v podzemních prostorách 10 úloha/zadání U1-U2/190-4 název úlohy Připojovací
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA SPECIÁLNÍ GEODÉZIE název předmětu Geodézie v podzemních prostorách 10 úloha/zadání U1-U2/190-4 název úlohy Připojovací
Seznam součástek. A. Seznam prvků soupravy GON. Rozměry (cm) nebo Poloměry* (cm) Značka Název prvku
 Seznam součástek Sklo, ze kterého jsou zhotoveny optické prvky, má index lomu 1, 5 a tloušťku 15 mm. V následujících tabulkách uvádíme seznam prvků v soupravách GON a GON+ a absolutní hodnoty velikostí
Seznam součástek Sklo, ze kterého jsou zhotoveny optické prvky, má index lomu 1, 5 a tloušťku 15 mm. V následujících tabulkách uvádíme seznam prvků v soupravách GON a GON+ a absolutní hodnoty velikostí
M I K R O S K O P I E
 Inovace předmětu KBB/MIK SVĚTELNÁ A ELEKTRONOVÁ M I K R O S K O P I E Rozvoj a internacionalizace chemických a biologických studijních programů na Univerzitě Palackého v Olomouci CZ.1.07/2.2.00/28.0066
Inovace předmětu KBB/MIK SVĚTELNÁ A ELEKTRONOVÁ M I K R O S K O P I E Rozvoj a internacionalizace chemických a biologických studijních programů na Univerzitě Palackého v Olomouci CZ.1.07/2.2.00/28.0066
Otázky z optiky. Fyzika 4. ročník. Základní vlastnosti, lom, odraz, index lomu
 Otázky z optiky Základní vlastnosti, lom, odraz, index lomu ) o je světlo z fyzikálního hlediska? Jaké vlnové délky přísluší viditelnému záření? - elektromagnetické záření (viditelné záření) o vlnové délce
Otázky z optiky Základní vlastnosti, lom, odraz, index lomu ) o je světlo z fyzikálního hlediska? Jaké vlnové délky přísluší viditelnému záření? - elektromagnetické záření (viditelné záření) o vlnové délce
3. Optika III. 3.1. Přímočaré šíření světla
 3. Optika III Popis soupravy: Souprava Haftoptik s níž je prováděn soubor experimentů Optika III je určena k demonstraci optických jevů pomocí segmentů se silnými magnety. Ty umožňují jejich fixaci na
3. Optika III Popis soupravy: Souprava Haftoptik s níž je prováděn soubor experimentů Optika III je určena k demonstraci optických jevů pomocí segmentů se silnými magnety. Ty umožňují jejich fixaci na
Obr. 4 Změna deklinace a vzdálenosti Země od Slunce v průběhu roku
 4 ZÁKLADY SFÉRICKÉ ASTRONOMIE K posouzení proslunění budovy nebo oslunění pozemku je vždy nutné stanovit polohu slunce na obloze. K tomu slouží vztahy sférické astronomie slunce. Pro sledování změn slunečního
4 ZÁKLADY SFÉRICKÉ ASTRONOMIE K posouzení proslunění budovy nebo oslunění pozemku je vždy nutné stanovit polohu slunce na obloze. K tomu slouží vztahy sférické astronomie slunce. Pro sledování změn slunečního
Ing. Jakub Ulmann. Zavádění inovativních metod a výukových materiálů do přírodovědných předmětů na Gymnáziu v Krnově
 Zavádění inovativních metod a výukových materiálů do přírodovědných předmětů na Gymnáziu v Krnově 07_10_Zobrazování optickými soustavami II Ing. Jakub Ulmann Zobrazování optickými soustavami 1. Optické
Zavádění inovativních metod a výukových materiálů do přírodovědných předmětů na Gymnáziu v Krnově 07_10_Zobrazování optickými soustavami II Ing. Jakub Ulmann Zobrazování optickými soustavami 1. Optické
Světlo je elektromagnetické vlnění, které má ve vakuu vlnové délky od 390 nm do 770 nm.
 1. Podstata světla Světlo je elektromagnetické vlnění, které má ve vakuu vlnové délky od 390 nm do 770 nm. Vznik elektromagnetických vln (záření): 1. při pohybu elektricky nabitých částic s nenulovým zrychlením
1. Podstata světla Světlo je elektromagnetické vlnění, které má ve vakuu vlnové délky od 390 nm do 770 nm. Vznik elektromagnetických vln (záření): 1. při pohybu elektricky nabitých částic s nenulovým zrychlením
GEODETICKÝ MONITORING PŘIROZENÝCH PODZEMNÍCH PROSTOR
 XV. konference SDMG Kutná Hora 2008 GEODETICKÝ MONITORING PŘIROZENÝCH PODZEMNÍCH PROSTOR Pavel Hánek Ilona Janžurová Alena Roušarová (SMALL spol. s r. o.) Podzemní dutiny - Umělé (historické, současné),
XV. konference SDMG Kutná Hora 2008 GEODETICKÝ MONITORING PŘIROZENÝCH PODZEMNÍCH PROSTOR Pavel Hánek Ilona Janžurová Alena Roušarová (SMALL spol. s r. o.) Podzemní dutiny - Umělé (historické, současné),
Automatický nivelační přístroj. Příručka uživatele
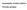 Automatický nivelační přístroj Příručka uživatele Obsah 1. Technické údaje 2. Vnější vzhled 3. Použití 4. Zamíření a zaostření 5. Měření 5.1. Měření výšky 5.2. Měření vzdálenosti 5. 3. Měření úhlu 6. Kontrola
Automatický nivelační přístroj Příručka uživatele Obsah 1. Technické údaje 2. Vnější vzhled 3. Použití 4. Zamíření a zaostření 5. Měření 5.1. Měření výšky 5.2. Měření vzdálenosti 5. 3. Měření úhlu 6. Kontrola
Chyby měřidel a metody měření vybraných fyzikálních veličin
 Chyby měřidel a metody měření vybraných fyzikálních veličin Jaké měřidlo je vhodné zvolit? Pravidla: Přesnost měřidla má být pětkrát až desetkrát vyšší, než je požadovaná přesnost měření. Např. chceme-li
Chyby měřidel a metody měření vybraných fyzikálních veličin Jaké měřidlo je vhodné zvolit? Pravidla: Přesnost měřidla má být pětkrát až desetkrát vyšší, než je požadovaná přesnost měření. Např. chceme-li
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ JOSEF VITÁSEK - ZDENĚK NEVOSÁD GEODÉZIE I. Prùvodce 01 PRŮVODCE PŘEDMĚTEM GEODÉZIE I
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ JOSEF VITÁSEK - ZDENĚK NEVOSÁD GEODÉZIE I Prùvodce 01 PRŮVODCE PŘEDMĚTEM GEODÉZIE I STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Průvodce
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ JOSEF VITÁSEK - ZDENĚK NEVOSÁD GEODÉZIE I Prùvodce 01 PRŮVODCE PŘEDMĚTEM GEODÉZIE I STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Průvodce
Geodézie a pozemková evidence
 2012, Brno Ing.Tomáš Mikita, Ph.D. Geodézie a pozemková evidence Přednáška č.5 Metody výškového měření, měření vzdáleností, měřické přístroje Podpořeno projektem Průřezová inovace studijních programů Lesnické
2012, Brno Ing.Tomáš Mikita, Ph.D. Geodézie a pozemková evidence Přednáška č.5 Metody výškového měření, měření vzdáleností, měřické přístroje Podpořeno projektem Průřezová inovace studijních programů Lesnické
Zavádění inovativních metod a výukových materiálů do přírodovědných předmětů na Gymnáziu v Krnově 07_10_Zobrazování optickými soustavami 1
 Zavádění inovativních metod a výukových materiálů do přírodovědných předmětů na Gymnáziu v Krnově 07_10_Zobrazování optickými soustavami 1 Ing. Jakub Ulmann Zobrazování optickými soustavami 1. Optické
Zavádění inovativních metod a výukových materiálů do přírodovědných předmětů na Gymnáziu v Krnově 07_10_Zobrazování optickými soustavami 1 Ing. Jakub Ulmann Zobrazování optickými soustavami 1. Optické
OPTIKA. Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda
 OPTIKA Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda Základní poznatky Zdroje světla světlo vzniká různými procesy (Slunce, žárovka, svíčka, Měsíc) Bodový zdroj Plošný zdroj Základní poznatky Optická prostředí
OPTIKA Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda Základní poznatky Zdroje světla světlo vzniká různými procesy (Slunce, žárovka, svíčka, Měsíc) Bodový zdroj Plošný zdroj Základní poznatky Optická prostředí
MĚŘENÍ VLNOVÝCH DÉLEK SVĚTLA MŘÍŽKOVÝM SPEKTROMETREM
 MĚŘENÍ VLNOVÝCH DÉLEK SVĚTLA MŘÍŽKOVÝM SPEKTROMETREM Difrakce (ohyb) světla je jedním z několika projevů vlnových vlastností světla. Z těchto důvodů světlo při setkání s překážkou nepostupuje dále vždy
MĚŘENÍ VLNOVÝCH DÉLEK SVĚTLA MŘÍŽKOVÝM SPEKTROMETREM Difrakce (ohyb) světla je jedním z několika projevů vlnových vlastností světla. Z těchto důvodů světlo při setkání s překážkou nepostupuje dále vždy
S v ě telné jevy. Optika - nauka - o světle, jeho vlastnostech a účincích - o přístrojích, které jsou založeny na zákonech šíření světla
 S v ě telné jevy Optika - nauka - o světle, jeho vlastnostech a účincích - o přístrojích, které jsou založeny na zákonech šíření světla Světelný zdroj - těleso v kterém světlo vzniká a vysílá je do okolí
S v ě telné jevy Optika - nauka - o světle, jeho vlastnostech a účincích - o přístrojích, které jsou založeny na zákonech šíření světla Světelný zdroj - těleso v kterém světlo vzniká a vysílá je do okolí
17. března 2000. Optická lavice s jezdci a držáky čoček, světelný zdroj pro optickou lavici, mikroskopický
 Úloha č. 6 Ohniskové vzdálenosti a vady čoček, zvětšení optických přístrojů Václav Štěpán, sk. 5 17. března 2000 Pomůcky: Optická lavice s jezdci a držáky čoček, světelný zdroj pro optickou lavici, mikroskopický
Úloha č. 6 Ohniskové vzdálenosti a vady čoček, zvětšení optických přístrojů Václav Štěpán, sk. 5 17. března 2000 Pomůcky: Optická lavice s jezdci a držáky čoček, světelný zdroj pro optickou lavici, mikroskopický
 Terénní kurz kartografie a topografie Den 1. OPAKOVÁNÍ: 1. Co je to mapa? - zmenšený, zgeneralizovaný povrch Země zobrazený v rovině 2. Jaká máme kartografická zobrazení? Dle kartografického zkreslení:
Terénní kurz kartografie a topografie Den 1. OPAKOVÁNÍ: 1. Co je to mapa? - zmenšený, zgeneralizovaný povrch Země zobrazený v rovině 2. Jaká máme kartografická zobrazení? Dle kartografického zkreslení:
Geometrická optika. Optické přístroje a soustavy. převážně jsou založeny na vzájemné interakci světelného pole s látkou nebo s jiným fyzikálním polem
 Optické přístroje a soustav Geometrická optika převážně jsou založen na vzájemné interakci světelného pole s látkou nebo s jiným fzikálním polem Důsledkem této t to interakce je: změna fzikáln lních vlastností
Optické přístroje a soustav Geometrická optika převážně jsou založen na vzájemné interakci světelného pole s látkou nebo s jiným fzikálním polem Důsledkem této t to interakce je: změna fzikáln lních vlastností
SPŠ STAVEBNÍ České Budějovice GEODÉZIE STA NIVELACE VÝŠKOVÉ MĚŘENÍ A VÝŠKOVÉ BODOVÉ POLE JS
 SPŠ STAVEBNÍ České Budějovice GEODÉZIE STA NIVELACE VÝŠKOVÉ MĚŘENÍ A VÝŠKOVÉ BODOVÉ POLE JS NIVELACE - úvod NIVELACE je měření výškového rozdílu od realizované (vytyčené) vodorovné roviny Provádí se pomocí
SPŠ STAVEBNÍ České Budějovice GEODÉZIE STA NIVELACE VÝŠKOVÉ MĚŘENÍ A VÝŠKOVÉ BODOVÉ POLE JS NIVELACE - úvod NIVELACE je měření výškového rozdílu od realizované (vytyčené) vodorovné roviny Provádí se pomocí
9.1 Geometrická nivelace ze středu, princip
 9 Určování výšek II 9.1 Princip geometrické nivelace, její výhody 9.2 Dělení nivelace dle přesnosti 9.3 Nivelační přístroje 9.4 Osové podmínky nivelačních přístrojů 9.5 Zkouška nivelačního přístroje (nevodorovnost
9 Určování výšek II 9.1 Princip geometrické nivelace, její výhody 9.2 Dělení nivelace dle přesnosti 9.3 Nivelační přístroje 9.4 Osové podmínky nivelačních přístrojů 9.5 Zkouška nivelačního přístroje (nevodorovnost
Přesný goniometr-spektrometr S Go 1.1
 1 Popis přístroje 1.1 Uspořádání Přesný goniometr-spektrometr S Go 1.1 Na podstavci (1) je připevněna svislá osa přístroje, kolem které se otáčí rameno () s dalekohledem (3) a mikroskopem (). Nastavení
1 Popis přístroje 1.1 Uspořádání Přesný goniometr-spektrometr S Go 1.1 Na podstavci (1) je připevněna svislá osa přístroje, kolem které se otáčí rameno () s dalekohledem (3) a mikroskopem (). Nastavení
Fyzikální praktikum FJFI ČVUT v Praze
 Fyzikální praktikum FJFI ČVUT v Praze Úloha 6: Geometrická optika Datum měření: 8. 4. 2016 Doba vypracovávání: 10 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V přípravě
Fyzikální praktikum FJFI ČVUT v Praze Úloha 6: Geometrická optika Datum měření: 8. 4. 2016 Doba vypracovávání: 10 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V přípravě
Cvičení č. 1 : Seznámení s TS TOPCON GPT-2006
 Cvičení č. 1 : Seznámení s TS TOPCON GPT-2006 Obsah 1. Typ a charakteristiky přístroje...2 2. Popis částí a ovládacích prvků...4 3. Ovládací klávesy...6 4. Displej, princip ovládání...7 5. Centrace a horizontace
Cvičení č. 1 : Seznámení s TS TOPCON GPT-2006 Obsah 1. Typ a charakteristiky přístroje...2 2. Popis částí a ovládacích prvků...4 3. Ovládací klávesy...6 4. Displej, princip ovládání...7 5. Centrace a horizontace
Laboratorní práce č. 1: Měření délky
 Přírodní vědy moderně a interaktivně FYZIKA 3. ročník šestiletého a 1. ročník čtyřletého studia Laboratorní práce č. 1: Měření délky G Gymnázium Hranice Přírodní vědy moderně a interaktivně FYZIKA 3.
Přírodní vědy moderně a interaktivně FYZIKA 3. ročník šestiletého a 1. ročník čtyřletého studia Laboratorní práce č. 1: Měření délky G Gymnázium Hranice Přírodní vědy moderně a interaktivně FYZIKA 3.
Optika OPTIKA. June 04, 2012. VY_32_INOVACE_113.notebook
 Optika Základní škola Nový Bor, náměstí Míru 128, okres Česká Lípa, příspěvková organizace e mail: info@zsnamesti.cz; www.zsnamesti.cz; telefon: 487 722 010; fax: 487 722 378 Registrační číslo: CZ.1.07/1.4.00/21.3267
Optika Základní škola Nový Bor, náměstí Míru 128, okres Česká Lípa, příspěvková organizace e mail: info@zsnamesti.cz; www.zsnamesti.cz; telefon: 487 722 010; fax: 487 722 378 Registrační číslo: CZ.1.07/1.4.00/21.3267
25. Zobrazování optickými soustavami
 25. Zobrazování optickými soustavami Zobrazování zrcadli a čočkami. Lidské oko. Optické přístroje. Při optickém zobrazování nemusíme uvažovat vlnové vlastnosti světla a stačí považovat světlo za svazek
25. Zobrazování optickými soustavami Zobrazování zrcadli a čočkami. Lidské oko. Optické přístroje. Při optickém zobrazování nemusíme uvažovat vlnové vlastnosti světla a stačí považovat světlo za svazek
Kvantový topografický dálkoměr KTD-1. Stručný technický popis a návod k obsluze
 Kvantový topografický dálkoměr KTD-1 Stručný technický popis a návod k obsluze Made in U.S.S.R 1987 1. Určení přístroje Kvantový topografický dálkoměr KTD-1 slouží k topografickému průzkumu terénu, hledání
Kvantový topografický dálkoměr KTD-1 Stručný technický popis a návod k obsluze Made in U.S.S.R 1987 1. Určení přístroje Kvantový topografický dálkoměr KTD-1 slouží k topografickému průzkumu terénu, hledání
Rozdělení přístroje zobrazovací
 Optické přístroje úvod Rozdělení přístroje zobrazovací obraz zdánlivý subjektivní přístroje lupa mikroskop dalekohled obraz skutečný objektivní přístroje fotoaparát projekční přístroje přístroje laboratorní
Optické přístroje úvod Rozdělení přístroje zobrazovací obraz zdánlivý subjektivní přístroje lupa mikroskop dalekohled obraz skutečný objektivní přístroje fotoaparát projekční přístroje přístroje laboratorní
Optika nauka o světle
 Optika nauka o světle 50_Světelný zdroj, šíření světla... 2 51_Stín, fáze Měsíce... 3 52_Zatmění Měsíce, zatmění Slunce... 3 53_Odraz světla... 4 54_Zobrazení předmětu rovinným zrcadlem... 4 55_Zobrazení
Optika nauka o světle 50_Světelný zdroj, šíření světla... 2 51_Stín, fáze Měsíce... 3 52_Zatmění Měsíce, zatmění Slunce... 3 53_Odraz světla... 4 54_Zobrazení předmětu rovinným zrcadlem... 4 55_Zobrazení
Chyby měřidel a metody měření vybraných fyzikálních veličin
 Chyby měřidel a metody měření vybraných fyzikálních veličin Jaké měřidlo je vhodné zvolit? Pravidla: Přesnost měřidla má být pětkrát až desetkrát vyšší, než je požadovaná přesnost měření. Např. chceme-li
Chyby měřidel a metody měření vybraných fyzikálních veličin Jaké měřidlo je vhodné zvolit? Pravidla: Přesnost měřidla má být pětkrát až desetkrát vyšší, než je požadovaná přesnost měření. Např. chceme-li
Měření vzdáleností, určování azimutu, práce s buzolou.
 Měření vzdáleností, určování azimutu, práce s buzolou. Měření vzdáleností Odhadem Vzdálenost lze odhadnout pomocí rozlišení detailů na pozorovaných objektech. Přesnost odhadu závisí na viditelnosti předmětu
Měření vzdáleností, určování azimutu, práce s buzolou. Měření vzdáleností Odhadem Vzdálenost lze odhadnout pomocí rozlišení detailů na pozorovaných objektech. Přesnost odhadu závisí na viditelnosti předmětu
10.1 Šíření světla, Fermatův princip, refrakce
 10 Refrakce 10.1 Šíření světla, Fermatův princip, refrakce 10.2 Refrakce - dělení 10.3 Způsoby posuzování a určování vlivu refrakce 10.4 Refrakční koeficient 10.5 Zjednodušený model profesora Böhma 10.6
10 Refrakce 10.1 Šíření světla, Fermatův princip, refrakce 10.2 Refrakce - dělení 10.3 Způsoby posuzování a určování vlivu refrakce 10.4 Refrakční koeficient 10.5 Zjednodušený model profesora Böhma 10.6
Základní pojmy a vztahy: Vlnová délka (λ): vzdálenost dvou nejbližších bodů vlnění kmitajících ve stejné fázi
 LRR/BUBCV CVIČENÍ Z BUNĚČNÉ BIOLOGIE 1. SVĚTELNÁ MIKROSKOPIE A PREPARÁTY V MIKROSKOPII TEORETICKÝ ÚVOD: Mikroskopie je základní metoda, která nám umožňuje pozorovat velmi malé biologické objekty. Díky
LRR/BUBCV CVIČENÍ Z BUNĚČNÉ BIOLOGIE 1. SVĚTELNÁ MIKROSKOPIE A PREPARÁTY V MIKROSKOPII TEORETICKÝ ÚVOD: Mikroskopie je základní metoda, která nám umožňuje pozorovat velmi malé biologické objekty. Díky
16.2.2015. Ing. Pavel Hánek, Ph.D. hanek00@zf.jcu.cz
 Ing. Pavel Hánek, Ph.D. hanek00@zf.jcu.cz Výškový referenční systém je definován v nařízení vlády 430/2006 Sb. Výškový systém baltský - po vyrovnání je určen a) výchozím výškovým bodem, kterým je nula
Ing. Pavel Hánek, Ph.D. hanek00@zf.jcu.cz Výškový referenční systém je definován v nařízení vlády 430/2006 Sb. Výškový systém baltský - po vyrovnání je určen a) výchozím výškovým bodem, kterým je nula
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/ Protokol měření. Kontrola a měření závitů
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Protokol měření Tolerování závitů Kontrola a měření závitů Řetězec norem, které se zabývají závity, zahrnuje
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Protokol měření Tolerování závitů Kontrola a měření závitů Řetězec norem, které se zabývají závity, zahrnuje
GEODÉZIE II. metody Trigonometrická metoda Hydrostatická nivelace Barometrická nivelace GNSS metoda. Trigonometricky určen. ení. Princip určen.
 Vysoká škola báňská technická univerzita Ostrava Hornicko-geologická fakulta Institut geodézie a důlního měřictví GEODÉZIE II Ing. Hana Staňková, Ph.D. 3. URČOV OVÁNÍ VÝŠEK metody Trigonometrická metoda
Vysoká škola báňská technická univerzita Ostrava Hornicko-geologická fakulta Institut geodézie a důlního měřictví GEODÉZIE II Ing. Hana Staňková, Ph.D. 3. URČOV OVÁNÍ VÝŠEK metody Trigonometrická metoda
Návody na cvičení Geodézie I
 Návody na cvičení Geodézie I Institut geodézie a důlního měřictví Ročník 1 Semestr: letní Cvičící: Ing. Jiří Pospíšil Forma studia a rozsah Prezenční: Zápočet a zkouška 3+3 Kombinovaná: Zápočet a zkouška
Návody na cvičení Geodézie I Institut geodézie a důlního měřictví Ročník 1 Semestr: letní Cvičící: Ing. Jiří Pospíšil Forma studia a rozsah Prezenční: Zápočet a zkouška 3+3 Kombinovaná: Zápočet a zkouška
Aplikovaná optika I: příklady k procvičení celku Geometrická optika. Jana Jurmanová
 Aplikovaná optika I: příklady k procvičení celku Geometrická optika Jana Jurmanová Geometrická optika Následující úlohy řešte graficky či výpočtem. 1. Předmět vysoký 1cm je umístěn 30cm od spojky, která
Aplikovaná optika I: příklady k procvičení celku Geometrická optika Jana Jurmanová Geometrická optika Následující úlohy řešte graficky či výpočtem. 1. Předmět vysoký 1cm je umístěn 30cm od spojky, která
OLS 26. Návod k použití
 OLS 26 cs Návod k použití 2018 1 2 3 6 4 3 2 1 12 8 11 7 9 2 5 1 10 cs Návod k použití Nivelační přístroj STIL OLS 26 lze využít při rozmanitých zaměřovacích pracích na stavbě. Může být používán pro optický
OLS 26 cs Návod k použití 2018 1 2 3 6 4 3 2 1 12 8 11 7 9 2 5 1 10 cs Návod k použití Nivelační přístroj STIL OLS 26 lze využít při rozmanitých zaměřovacích pracích na stavbě. Může být používán pro optický
ZOBRAZOVÁNÍ ROVINNÝM ZRCADLEM
 ZOBRAZOVÁNÍ ROVINNÝM ZRCADLEM Pozorně se podívejte na obrázky. Kterou rukou si nevěsta maluje rty? Na které straně cesty je automobil ve zpětném zrcátku? Zrcadla jsou vyleštěné, zpravidla kovové plochy
ZOBRAZOVÁNÍ ROVINNÝM ZRCADLEM Pozorně se podívejte na obrázky. Kterou rukou si nevěsta maluje rty? Na které straně cesty je automobil ve zpětném zrcátku? Zrcadla jsou vyleštěné, zpravidla kovové plochy
2012, Brno Ing.Tomáš Mikita, Ph.D. Geodézie a pozemková evidence
 2012, Brno Ing.Tomáš Mikita, Ph.D. Geodézie a pozemková evidence Přednáška č.7 Vytyčování, souřadnicové výpočty, podélné a příčné profily Vytyčování Geodetická činnost uskutečněná odborně a nestranně na
2012, Brno Ing.Tomáš Mikita, Ph.D. Geodézie a pozemková evidence Přednáška č.7 Vytyčování, souřadnicové výpočty, podélné a příčné profily Vytyčování Geodetická činnost uskutečněná odborně a nestranně na
CZ.1.07/2.2.00/28.0021)
 Metody geoinženýrstv enýrství Ing. Miloš Cibulka, Ph.D. Brno, 2015 Cvičen ení č.. 1 Vytvořeno s podporou projektu Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
Metody geoinženýrstv enýrství Ing. Miloš Cibulka, Ph.D. Brno, 2015 Cvičen ení č.. 1 Vytvořeno s podporou projektu Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
Sada 1 Geodezie I. 09. Nivelace pořadová, ze středu, plošná
 S třední škola stavební Jihlava Sada 1 Geodezie I 09. Nivelace pořadová, ze středu, plošná Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona:
S třední škola stavební Jihlava Sada 1 Geodezie I 09. Nivelace pořadová, ze středu, plošná Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona:
8 SOUČÁSTI MĚŘICKÝCH PŘÍSTROJŮ
 8 SOUČÁSTI MĚŘICKÝCH PŘÍSTROJŮ Měřické přístroje jsou složeny z různých skupin součástí. Dále se při používání přístrojů setkáváme s doplňky a příslušenstvím. Pro využívání všech možností, jež nám konstruktéři
8 SOUČÁSTI MĚŘICKÝCH PŘÍSTROJŮ Měřické přístroje jsou složeny z různých skupin součástí. Dále se při používání přístrojů setkáváme s doplňky a příslušenstvím. Pro využívání všech možností, jež nám konstruktéři
Nivelační přístroje GeoFennel
 Internetový obchod Měřící přístroje stavební Nivelační přístroje GeoFennel FAL 24 optický nivelační přístroj Cena: 5 600 Kč bez DPH přesnost 2,5mm/km, zvětšení 24x Technická specifikace: průměr objektivu
Internetový obchod Měřící přístroje stavební Nivelační přístroje GeoFennel FAL 24 optický nivelační přístroj Cena: 5 600 Kč bez DPH přesnost 2,5mm/km, zvětšení 24x Technická specifikace: průměr objektivu
