Využití Pythagorovy věty III
|
|
|
- Stanislav Janda
- před 9 lety
- Počet zobrazení:
Transkript
1 .8.3 Využití Pythagorovy věty III Předpoklady: 008 Př. 1: Urči obsah rovnoramenného trojúhelníku se základnou 8 cm a rameny 5,8 cm. Pro výpočet obsahu potřebujeme znát jednu ze stran a odpovídající výšku. v V rovnoramenném trojúhelníku je výška k základně zároveň těžnicí a vychází ze středu základny rozděluje trojúhelník na dva stejné pravoúhlé trojúhelníky. v 5,8 cm cm Výška je odvěsnou v tomto trojúhelníku. a + b = c / b a = c b a c b = = = / 5,8 cm, cm a v, Obsah trojúhelníku: a S = = cm = 8,cm. Rovnoramenný trojúhelník se základnou dlouhou 8 cm a rameny dlouhými 5,8 cm má obsah 8, cm. 1
2 Př. : Stožár má být ukotven pomocí čtyř bočních lan připevněných ke stožáru ve výšce,5 m a ukotvených do země ve vzdálenosti 3 m od paty stožáru. Kolik metrů lana bude k ukotvení třeba? K vypočtené přímé délce přidej ještě 7% na upevnění.,5 m 3 m Délka každého bočního lana představuje přeponu v pravoúhlém trojúhelníku s odvěsnami 3 m a,5 m. = + = + lana: 3,9 m = 15,6m,5 3 m 3,9m Výpočet rezervy na upevnění 100 % 15,6 m 107 % x x 15,6 = x = 15,6 107 m 16,7 m Na ukotvení stožáru bude potřeba celkem 16,7 m lana. Pedagogická poznámka: Nakreslení obrázku je velký problém. Žáci často kreslí obrázek prostorový se všemi čtyřmi lany a pak do něj nejsou schopni dokreslit zadané vzdálenosti (nejčastěji kreslí 3 m od jednoho lana k druhému). Chci co nejjednodušší obrázek (jak tam musíme lana přidělat, aby stožár držela), pak se bavíme o tom, co znamená pata u člověka a co asi bude znamenat pata stožáru. Př. 3: Bouřka zlomila smrk ve výšce 1,5 m. Jeho špička se dotýká země 6 m od pařezu. Jak byl strom původně vysoký? 1,5 m 6 m Délku ulomené část stromu můžeme vypočítat jako přeponu v pravoúhlém trojúhelníku. = + = + 1,5 6 m 6, m
3 Celková výška stromu: 1,5 + 6, m = 7, 7 m. Před zlomením měl smrk výšku 7,7 m. Př. : Jana přechovává přes zimu dřevěné tyčky k rajčatům v prázdném zahradním sudu o průměru 70 cm a výšce 10 cm. Jakou největší délku mohou tyčky mít, aby se celé schovaly do sudu a Jana mohla sud přiklopit víkem? 10 cm 70 cm Nejdelší tyčky se do sudu vejdou, kdy je položíme napříč (podobně jako tyčku do kufru auta v předchozí hodině). V takovém případě tvoří tyčka přeponu v pravoúhlém trojúhelníku. = + = cm 139 cm Nejdelší tyčky, které se vejdou do sudu, mají délku 139 cm. Př. 5: Vypočti obvod kosočtverce, jehož úhlopříčky mají délky 9,6 cm a 11 cm. Obvod kosočtverce je čtyřnásobek délky strany. 9,6 cm 11 cm Speciální vlastnost kosočtverce: Úhlopříčky jsou navzájem kolmé a navzájem se půlí rozdělí kosočtverec na čtyři shodné pravoúhlé trojúhelníky, jejichž přeponami jsou strany kosočtverce. 5,5 cm,8 cm a c = a + b / 3
4 = + = + = 5,5,8 cm 7,3cm o = a = 7,3cm = 9, cm Kosočtverec má obvod 9, cm. Pedagogická poznámka: Většině žáků je třeba poradit, jakou speciální vlastnost mají úhlopříčky kosočtverce. Př. 6: Čtyřúhelníková parcela má v katastru uvedeny tyto rozměry. Urči její výměru. 0 m 36 m 1 m Parcela se skládá ze dvou pravoúhlých trojúhelníků. Přepona levého trojúhelníku je odvěsnou pravého. = + = + = 0 1 cm 9 cm a b 0 1 Obsah levého trojúhelníku: S1 = = m = 10m. a b 9 36 Obsah pravého trojúhelníku: S = = m = 5m. Celková výměra: S = S1 + S = m = 73 m Parcela má výměru 73 m. Pedagogická poznámka: Největším problémem je slovo výměra. Ptám se, co je u pozemků nejdůležitější. Př. 7: Urči délky úhlopříček kosočtverce cm Zdá se, že máme málo údajů. Hledáme cestu, jak využít zadanou hodnotu úhlu.
5 7 cm 7 cm 60 7 cm Kosočtverec je kratší úhlopříčkou rozdělen na dva shodné trojúhelníky. Modrý trojúhelník má úhel 60 a dvě shodné strany 7 cm je rovnostranný a jeho třetí strana (kratší úhlopříčka) má také velikost 7 cm. Stále platí, že úhlopříčky kosočtverce jsou na sebe kolmé a půlí se. 7 cm 7 cm 60 3,5 cm 7 cm Delší odvěsna v zeleném trojúhelníku představuje polovinu úhlopříčky. a + b = c / b a = c b a c b = = = / 7 3,5 cm 6,1cm Celá úhlopříčka: 6,1 cm = 1, cm. Pedagogická poznámka: Rozhodujícím okamžikem je nalezení rovnostranného trojúhelníka. Snažím se to neprozradit, a proto nejdříve doporučuji zjistit, k čemu by mohla být dobrá hodnota úhlu. Př. 8: V kartézských souřadnicích jsou dány body A[ 1;3], B [ 3;0], [ 1; 1] zda je trojúhelník ABC pravoúhlý. C. Rozhodni, A[-1; 3] 5 3 y 1 3 B [3; 0] x 1-1 C [1; -1] - 5
6 Př. 9: Valbová střecha má zakrýt půdorys 8 m x 16 m. Hřeben střechy má být dlouhý 9 m a má být 3 m nad základnou střechy. Nakresli obrázek situace a spočti plochu střechy. Shrnutí: 6
Výroba Hofmanových bočních louček pomocí hoblovky. Napsal uživatel Milan Čáp Čtvrtek, 30 Duben 2009 17:47
 Zveřejňujeme příspěvek, který byl před časem publikován ve Včelařských novinách. Tento elektronický včelařský web je již delší dobu mimo provoz, proto návod na výrobu bočních louček Hoffmanova typu dnes
Zveřejňujeme příspěvek, který byl před časem publikován ve Včelařských novinách. Tento elektronický včelařský web je již delší dobu mimo provoz, proto návod na výrobu bočních louček Hoffmanova typu dnes
( x ) 2 ( ) 2.5.4 Další úlohy s kvadratickými funkcemi. Předpoklady: 2501, 2502
 .5. Další úlohy s kvadratickými funkcemi Předpoklady: 50, 50 Pedagogická poznámka: Tato hodina patří mezi ty méně organizované. Společně řešíme příklad, při dalším počítání se třída rozpadá. Já řeším příklady
.5. Další úlohy s kvadratickými funkcemi Předpoklady: 50, 50 Pedagogická poznámka: Tato hodina patří mezi ty méně organizované. Společně řešíme příklad, při dalším počítání se třída rozpadá. Já řeším příklady
Strojní součásti, konstrukční prvky a spoje
 Strojní součásti, konstrukční prvky a spoje Šroubové spoje Šrouby jsou nejčastěji používané strojní součástí a neexistuje snad stroj, kde by se nevyskytovaly. Mimo šroubů jsou u některých šroubových spojů
Strojní součásti, konstrukční prvky a spoje Šroubové spoje Šrouby jsou nejčastěji používané strojní součástí a neexistuje snad stroj, kde by se nevyskytovaly. Mimo šroubů jsou u některých šroubových spojů
Digitální učební materiál
 Digitální učební materiál Číslo projektu Číslo materiálu Název školy Autor Tematický celek Ročník CZ.1.07/1.5.00/34.0029 VY_32_INOVACE_29-19 Střední průmyslová škola stavební, Resslova 2, České Budějovice
Digitální učební materiál Číslo projektu Číslo materiálu Název školy Autor Tematický celek Ročník CZ.1.07/1.5.00/34.0029 VY_32_INOVACE_29-19 Střední průmyslová škola stavební, Resslova 2, České Budějovice
Gymnázium Christiana Dopplera, Zborovská 45, Praha 5. ROČNÍKOVÁ PRÁCE Teoretické řešení střech
 Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 ROČNÍKOVÁ PRÁCE Teoretické řešení střech Vypracoval: Michal Drašnar Třída: 8.M Školní rok: 2015/2016 Seminář: Deskriptivní geometrie Prohlašuji, že
Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 ROČNÍKOVÁ PRÁCE Teoretické řešení střech Vypracoval: Michal Drašnar Třída: 8.M Školní rok: 2015/2016 Seminář: Deskriptivní geometrie Prohlašuji, že
ZAHRADNÍ DŘEVĚNÉ DOMKY
 ZAHRADNÍ DŘEVĚNÉ DOMKY Jak správně vybrat dřevěný domek? "Klasický dřevěný zahradní domek zajistí souznění Vaší zahrady s přírodou." www.lanitplast.cz 1.3.2016 1 Jak správně vybrat dřevěný domek Zahradní
ZAHRADNÍ DŘEVĚNÉ DOMKY Jak správně vybrat dřevěný domek? "Klasický dřevěný zahradní domek zajistí souznění Vaší zahrady s přírodou." www.lanitplast.cz 1.3.2016 1 Jak správně vybrat dřevěný domek Zahradní
Využití Pythagorovy věty III
 .8. Využití Pythagorovy věty III Předpoklady: 008 Př. 1: Urči obsah rovnoramenného trojúhelníku se základnou 8 cm a rameny 5,8 cm. Pro výpočet obsahu potřebujeme znát jednu ze stran a odpovídající výšku.
.8. Využití Pythagorovy věty III Předpoklady: 008 Př. 1: Urči obsah rovnoramenného trojúhelníku se základnou 8 cm a rameny 5,8 cm. Pro výpočet obsahu potřebujeme znát jednu ze stran a odpovídající výšku.
Mezní kalibry. Druhy kalibrů podle přesnosti: - dílenské kalibry - používají ve výrobě, - porovnávací kalibry - pro kontrolu dílenských kalibrů.
 Mezní kalibry Mezními kalibry zjistíme, zda je rozměr součástky v povolených mezích, tj. v toleranci. Mají dobrou a zmetkovou stranu. Zmetková strana je označená červenou barvou. Délka zmetkové části je
Mezní kalibry Mezními kalibry zjistíme, zda je rozměr součástky v povolených mezích, tj. v toleranci. Mají dobrou a zmetkovou stranu. Zmetková strana je označená červenou barvou. Délka zmetkové části je
Válec - slovní úlohy
 Válec - slovní úlohy VY_32_INOVACE_M-Ge. 7., 8. 20 Anotace: Žák řeší slovní úlohy z praxe. Využívá k řešení matematický aparát. Vzdělávací oblast: Matematika Autor: Mgr. Robert Kecskés Jazyk: Český Očekávaný
Válec - slovní úlohy VY_32_INOVACE_M-Ge. 7., 8. 20 Anotace: Žák řeší slovní úlohy z praxe. Využívá k řešení matematický aparát. Vzdělávací oblast: Matematika Autor: Mgr. Robert Kecskés Jazyk: Český Očekávaný
2.2.2 Zlomky I. Předpoklady: 020201
 .. Zlomky I Předpoklady: 0001 Pedagogická poznámka: V hodině je třeba postupovat tak, aby se ještě před jejím koncem začala vyplňovat tabulka u posledního příkladu 9. V loňském roce jsme si zopakovali
.. Zlomky I Předpoklady: 0001 Pedagogická poznámka: V hodině je třeba postupovat tak, aby se ještě před jejím koncem začala vyplňovat tabulka u posledního příkladu 9. V loňském roce jsme si zopakovali
1.9.5 Středově souměrné útvary
 1.9.5 Středově souměrné útvary Předpoklady: 010904 Př. 1: V obdélníkových rámech jsou nakresleny tři obrázky. Každý je sestaven z jedné přímky a jednoho obdélníku. Jeden z obrázků je středově souměrný.
1.9.5 Středově souměrné útvary Předpoklady: 010904 Př. 1: V obdélníkových rámech jsou nakresleny tři obrázky. Každý je sestaven z jedné přímky a jednoho obdélníku. Jeden z obrázků je středově souměrný.
Bod, přímka a rovina. bezrozměrnost, jeden rozměr a dva rozměry
 Úvod Posvátná geometrie mapuje rozkrývání významu čísel v prostoru. Základní trasa vede z izolovaného bodu do přímky, následuje rozprostření do roviny, poté do třetího rozměru, ba až za jeho hranice, a
Úvod Posvátná geometrie mapuje rozkrývání významu čísel v prostoru. Základní trasa vede z izolovaného bodu do přímky, následuje rozprostření do roviny, poté do třetího rozměru, ba až za jeho hranice, a
na tyč působit moment síly M, určený ze vztahu (9). Periodu kmitu T tohoto kyvadla lze určit ze vztahu:
 Úloha Autoři Zaměření FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE 2. Měření modulu pružnosti v tahu a modulu pružnosti ve smyku Martin Dlask Měřeno 11. 10., 18. 10., 25. 10. 2012 Jakub Šnor SOFE Klasifikace
Úloha Autoři Zaměření FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE 2. Měření modulu pružnosti v tahu a modulu pružnosti ve smyku Martin Dlask Měřeno 11. 10., 18. 10., 25. 10. 2012 Jakub Šnor SOFE Klasifikace
1.2.5 Reálná čísla I. Předpoklady: 010204
 .2.5 Reálná čísla I Předpoklady: 00204 Značíme R. Reálná čísla jsou čísla, kterými se vyjadřují délky úseček, čísla jim opačná a 0. Každé reálné číslo je na číselné ose znázorněno právě jedním bodem. Každý
.2.5 Reálná čísla I Předpoklady: 00204 Značíme R. Reálná čísla jsou čísla, kterými se vyjadřují délky úseček, čísla jim opačná a 0. Každé reálné číslo je na číselné ose znázorněno právě jedním bodem. Každý
1.1.11 Poměry a úměrnosti I
 1.1.11 Poměry a úměrnosti I Předpoklady: základní početní operace, 010110 Poznámka: Následující látka bohužel patří mezi ty, kde je nejvíce rozšířené používání samospasitelných postupů, které umožňují
1.1.11 Poměry a úměrnosti I Předpoklady: základní početní operace, 010110 Poznámka: Následující látka bohužel patří mezi ty, kde je nejvíce rozšířené používání samospasitelných postupů, které umožňují
Výroba ozubených kol. Použití ozubených kol. Převody ozubenými koly a tvary ozubených kol
 Výroba ozubených kol Použití ozubených kol Ozubenými koly se přenášejí otáčivé pohyby a kroutící momenty. Přenos je zde nucený, protože zuby a zubní mezery do sebe zabírají. Kola mohou mít vnější nebo
Výroba ozubených kol Použití ozubených kol Ozubenými koly se přenášejí otáčivé pohyby a kroutící momenty. Přenos je zde nucený, protože zuby a zubní mezery do sebe zabírají. Kola mohou mít vnější nebo
SBÍRKA PŘÍKLADŮ PRO OPAKOVÁNÍ NA PŘIJÍMACÍ ZKOUŠKY 2
 STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJNÍ A STAVEBNÍ TÁBOR, KOMENSKÉHO 1670 SBÍRKA PŘÍKLADŮ PRO OPAKOVÁNÍ NA PŘIJÍMACÍ ZKOUŠKY 2 ŠKOLNÍ ROK 2014/2015 Obsah 1 Dělitelnost přirozených čísel... 3 2 Obvody a obsahy
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJNÍ A STAVEBNÍ TÁBOR, KOMENSKÉHO 1670 SBÍRKA PŘÍKLADŮ PRO OPAKOVÁNÍ NA PŘIJÍMACÍ ZKOUŠKY 2 ŠKOLNÍ ROK 2014/2015 Obsah 1 Dělitelnost přirozených čísel... 3 2 Obvody a obsahy
Žáci mají k dispozici pracovní list. Formou kolektivní diskuze a výkladu si osvojí grafickou minimalizaci zápisu logické funkce
 Číslo projektu Číslo materiálu Název školy Autor Název Téma hodiny Předmět Ročník /y/ CZ.1.07/1.5.00/34.0394 VY_32_INOVACE_9_ČT_1.09_ grafická minimalizace Střední odborná škola a Střední odborné učiliště,
Číslo projektu Číslo materiálu Název školy Autor Název Téma hodiny Předmět Ročník /y/ CZ.1.07/1.5.00/34.0394 VY_32_INOVACE_9_ČT_1.09_ grafická minimalizace Střední odborná škola a Střední odborné učiliště,
Matematický KLOKAN 2009 www.matematickyklokan.net. kategorie Benjamín
 Matematický KLOKAN 2009 www.matematickyklokan.net kategorie Benjamín Úlohy za 3 body 1. Hodnota kterého výrazu je sudé číslo? (A) 200 + 9 (B) 200 9 (C) 200 9 (D) 2 + 0 + 0 + 9 (E) 2 0 + 0 + 9 2. Kolik
Matematický KLOKAN 2009 www.matematickyklokan.net kategorie Benjamín Úlohy za 3 body 1. Hodnota kterého výrazu je sudé číslo? (A) 200 + 9 (B) 200 9 (C) 200 9 (D) 2 + 0 + 0 + 9 (E) 2 0 + 0 + 9 2. Kolik
2.1 Pokyny k otevřeným úlohám. 2.2 Pokyny k uzavřeným úlohám TESTOVÝ SEŠIT NEOTVÍREJTE, POČKEJTE NA POKYN!
 MATEMATIKA DIDAKTICKÝ TEST Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % Základní informace k zadání zkoušky Didaktický test obsahuje 26 úloh. Časový limit pro řešení didaktického testu
MATEMATIKA DIDAKTICKÝ TEST Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % Základní informace k zadání zkoušky Didaktický test obsahuje 26 úloh. Časový limit pro řešení didaktického testu
Po etní geometrie. Výpo et délky p epony: c 2 = a 2 + b 2 Výpo et délky odv sny: a 2 = c 2 b 2, b 2 = c 2 a 2
 Po etní geometrie Pythagorova v ta Obsah tverce nad p eponou je roven sou tu obsah tverc nad ob ma odv snami. Výpo et délky p epony: c = a + b Výpo et délky odv sny: a = c b, b = c a P íklad 1: Vypo t
Po etní geometrie Pythagorova v ta Obsah tverce nad p eponou je roven sou tu obsah tverc nad ob ma odv snami. Výpo et délky p epony: c = a + b Výpo et délky odv sny: a = c b, b = c a P íklad 1: Vypo t
2.3.6 Vektory - shrnutí
 .3.6 Vektory - shrnutí Předpoklady: 0070 Pomůcky: lano, tři knížky, závaží 5 kg Pedagogická poznámka: V úvodu řešíme poslední příklad z minulé hodiny. Př. : Jirka s Honzou nesou společně tašku. Jirkovo
.3.6 Vektory - shrnutí Předpoklady: 0070 Pomůcky: lano, tři knížky, závaží 5 kg Pedagogická poznámka: V úvodu řešíme poslední příklad z minulé hodiny. Př. : Jirka s Honzou nesou společně tašku. Jirkovo
Č část četnost. 部 分 频 率 relativní četnost 率, 相 对 频 数
 A absolutní člen 常 量 成 员 absolutní hodnota čísla 绝 对 值 algebraický výraz 代 数 表 达 式 ar 公 亩 aritmetický průměr 算 术 均 数 aritmetika 算 术, 算 法 B boční hrana 侧 棱 boční hrany jehlanu 角 锥 的 侧 棱 boční stěny jehlanu
A absolutní člen 常 量 成 员 absolutní hodnota čísla 绝 对 值 algebraický výraz 代 数 表 达 式 ar 公 亩 aritmetický průměr 算 术 均 数 aritmetika 算 术, 算 法 B boční hrana 侧 棱 boční hrany jehlanu 角 锥 的 侧 棱 boční stěny jehlanu
1.2.7 Druhá odmocnina
 ..7 Druhá odmocnina Předpoklady: umocňování čísel na druhou Pedagogická poznámka: Probrat obsah této hodiny není možné ve 4 minutách. Já osobně druhou část (usměrňování) probírám v další hodině, jejíž
..7 Druhá odmocnina Předpoklady: umocňování čísel na druhou Pedagogická poznámka: Probrat obsah této hodiny není možné ve 4 minutách. Já osobně druhou část (usměrňování) probírám v další hodině, jejíž
4. cvičení: Pole kruhové, rovinné, Tělesa editace těles (sjednocení, rozdíl, ), tvorba složených objektů
 4. cvičení: Pole kruhové, rovinné, Tělesa editace těles (sjednocení, rozdíl, ), tvorba složených objektů Příklad 1: Pracujte v pohledu Shora. Sestrojte kružnici se středem [0,0,0], poloměrem 10 a kružnici
4. cvičení: Pole kruhové, rovinné, Tělesa editace těles (sjednocení, rozdíl, ), tvorba složených objektů Příklad 1: Pracujte v pohledu Shora. Sestrojte kružnici se středem [0,0,0], poloměrem 10 a kružnici
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita V.2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V.2.5 Karosářské Know how (Vědět jak) Kapitola
Zvyšování kvality výuky technických oborů Klíčová aktivita V.2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V.2.5 Karosářské Know how (Vědět jak) Kapitola
Název školy. Moravské gymnázium Brno s.r.o. Mgr. Marie Chadimová Mgr. Věra Jeřábková. Autor. Matematika. Planimetrie. Trojúhelníky. Teorie a příklady.
 Číslo projektu Z.1.07/1.5.00/34.0743 Název školy Moravské gymnázium rno s.r.o. utor Tematická oblast Mgr. Marie hadimová Mgr. Věra Jeřábková Matematika. Planimetrie. Trojúhelníky. Teorie a příklady. Ročník
Číslo projektu Z.1.07/1.5.00/34.0743 Název školy Moravské gymnázium rno s.r.o. utor Tematická oblast Mgr. Marie hadimová Mgr. Věra Jeřábková Matematika. Planimetrie. Trojúhelníky. Teorie a příklady. Ročník
Obsah: Archivní rešerše. Popis stávajícího stavu mostků č.1 5. Stavební vývoj. Vyjádření k hodnotě mostků. Vyjádření ke stavu mostků.
 OPERATIVNÍ DOKUMENTACE PĚTI MOSTKŮ V PODZÁMECKÉ ZAHRADĚ V KROMĚŘÍŽI NPÚ ÚOP V KROMĚŘÍÍŽII RADIIM VRLA ZÁŘÍÍ- PROSIINEC 2011 1 2 Obsah: Úvod Archivní rešerše Popis stávajícího stavu mostků č.1 5 Stavební
OPERATIVNÍ DOKUMENTACE PĚTI MOSTKŮ V PODZÁMECKÉ ZAHRADĚ V KROMĚŘÍŽI NPÚ ÚOP V KROMĚŘÍÍŽII RADIIM VRLA ZÁŘÍÍ- PROSIINEC 2011 1 2 Obsah: Úvod Archivní rešerše Popis stávajícího stavu mostků č.1 5 Stavební
Sada 1 Geodezie I. 06. Přímé měření délek pásmem
 S třední škola stavební Jihlava Sada 1 Geodezie I 06. Přímé měření délek pásmem Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2
S třední škola stavební Jihlava Sada 1 Geodezie I 06. Přímé měření délek pásmem Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2
Omezovač otvírání dveří. s hydraulickým koncovým tlumením ve směru otvírání. Technické údaje Průměr válce TB: 23 / 28 mm ; TBR: 28
 Omezovače DICTATOR se starají o to, aby se otočné dveře neotvíraly netlumeně. Tlumí pohyb dveří při otvírání a omezuje úhel jejich otevření. Tím se šetří dveře i jejich kování. Dveřmi můžete snadno pohybovat
Omezovače DICTATOR se starají o to, aby se otočné dveře neotvíraly netlumeně. Tlumí pohyb dveří při otvírání a omezuje úhel jejich otevření. Tím se šetří dveře i jejich kování. Dveřmi můžete snadno pohybovat
Výstupy Učivo Téma. Čas. Základní škola a mateřská škola Hať. Školní vzdělávací program. Průřezová témata, kontexty a přesahy,další poznámky
 provádí pamětné a písemné početní Čísla přirozená Opakování září, říjen operace v oboru přirozených čísel porovnává a uspořádává čísla celá a Čísla celá, racionální racionální, provádí početní operace
provádí pamětné a písemné početní Čísla přirozená Opakování září, říjen operace v oboru přirozených čísel porovnává a uspořádává čísla celá a Čísla celá, racionální racionální, provádí početní operace
2.2.10 Slovní úlohy vedoucí na lineární rovnice I
 Slovní úlohy vedoucí na lineární rovnice I Předpoklady: 0, 06 Pedagogická poznámka: Řešení slovních úloh představuje pro značnou část studentů nejobtížnější část matematiky Důvod je jednoduchý Po celou
Slovní úlohy vedoucí na lineární rovnice I Předpoklady: 0, 06 Pedagogická poznámka: Řešení slovních úloh představuje pro značnou část studentů nejobtížnější část matematiky Důvod je jednoduchý Po celou
1 Zadání konstrukce. Výška stěny nad terénem (horní líc) h= 3,5 m Sedlová střecha, sklon 45, hřeben ve směru delší stěny
 1 1 Zadání konstrukce Základní půdorysné uspořádání i výškové uspořádání je patrné z obrázků. Dřevostavba má obytné zateplené podkroví. Detailní uspořádání a skladby konstrukcí stěny, stropu i střechy
1 1 Zadání konstrukce Základní půdorysné uspořádání i výškové uspořádání je patrné z obrázků. Dřevostavba má obytné zateplené podkroví. Detailní uspořádání a skladby konstrukcí stěny, stropu i střechy
1. POLOVODIČOVÁ DIODA 1N4148 JAKO USMĚRŇOVAČ
 1. POLOVODIČOVÁ DIODA JAKO SMĚRŇOVAČ Zadání laboratorní úlohy a) Zaznamenejte datum a čas měření, atmosférické podmínky, při nichž dané měření probíhá (teplota, tlak, vlhkost). b) Proednictvím digitálního
1. POLOVODIČOVÁ DIODA JAKO SMĚRŇOVAČ Zadání laboratorní úlohy a) Zaznamenejte datum a čas měření, atmosférické podmínky, při nichž dané měření probíhá (teplota, tlak, vlhkost). b) Proednictvím digitálního
3.5.8 Otočení. Předpoklady: 3506
 3.5.8 Otočení Předpoklady: 3506 efinice úhlu ze základní školy: Úhel je část roviny ohraničená dvojicí polopřímek se společným počátečním bodem (konvexní a nekonvexní úhel). Nevýhody této definice: Nevíme,
3.5.8 Otočení Předpoklady: 3506 efinice úhlu ze základní školy: Úhel je část roviny ohraničená dvojicí polopřímek se společným počátečním bodem (konvexní a nekonvexní úhel). Nevýhody této definice: Nevíme,
Obsah: 1. Bezpečnost práce 2. Měření a orýsování 3. Řezání, stříhání, sekání 4. Pilování 5. Ohýbání, rovnání 6. Vrtání 7.
 Obsah: 1. Bezpečnost práce 2. Měření a orýsování 3. Řezání, stříhání, sekání 4. Pilování 5. Ohýbání, rovnání 6. Vrtání 7. Řezání závitů 1. Bezpečnost práce 1. Počínej si při práci tak, abys neohrožoval
Obsah: 1. Bezpečnost práce 2. Měření a orýsování 3. Řezání, stříhání, sekání 4. Pilování 5. Ohýbání, rovnání 6. Vrtání 7. Řezání závitů 1. Bezpečnost práce 1. Počínej si při práci tak, abys neohrožoval
ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ
 ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ Pozemkem se podle 2 písm. a) katastrálního zákona rozumí část zemského povrchu, a to část taková, která je od sousedních částí zemského povrchu (sousedních pozemků)
ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ Pozemkem se podle 2 písm. a) katastrálního zákona rozumí část zemského povrchu, a to část taková, která je od sousedních částí zemského povrchu (sousedních pozemků)
Znalectví středověké hmotné kultury referát Koňský postroj ve středověku. Alžběta Čerevková učo: 330952
 Znalectví středověké hmotné kultury referát Koňský postroj ve středověku Alžběta Čerevková učo: 330952 Úvod Středověk je považován za zlatý věk koně, neboť využití tohoto všestranného zvířete můžeme pozorovat
Znalectví středověké hmotné kultury referát Koňský postroj ve středověku Alžběta Čerevková učo: 330952 Úvod Středověk je považován za zlatý věk koně, neboť využití tohoto všestranného zvířete můžeme pozorovat
Šipka sa skladá z hrotu, těla, násadky a letky.
 Šipkový sport - s čím a jak na něj Výstroj Na to, abyste si zahráli šipky nepotřebujete žádnou 'extra' výstroj. Oblečení by mělo být pohodlné. V žádném případě by vám nemělo bránit v pohybu odhodové ruky.
Šipkový sport - s čím a jak na něj Výstroj Na to, abyste si zahráli šipky nepotřebujete žádnou 'extra' výstroj. Oblečení by mělo být pohodlné. V žádném případě by vám nemělo bránit v pohybu odhodové ruky.
MATEMATIKA. 1 Základní informace k zadání zkoušky
 MATEMATIKA PŘIJÍMAČKY LIK 2012 DIDAKTICKÝ TEST Maximální bodové hodnocení: 50 bodů 1 Základní informace k zadání zkoušky Didaktický test obsahuje 15 úloh. Časový limit pro řešení didaktického testu je
MATEMATIKA PŘIJÍMAČKY LIK 2012 DIDAKTICKÝ TEST Maximální bodové hodnocení: 50 bodů 1 Základní informace k zadání zkoušky Didaktický test obsahuje 15 úloh. Časový limit pro řešení didaktického testu je
3.2.13 Slovní úlohy II
 3..13 Slovní úlohy II Předpoklady: 0301 Pedagogická poznámka: První příklad je opakování z minulé hodiny. Při prvním průchodu se ukázalo, že žáci mají problém s tím, co zvolit za neznámou a jak vyjadřovat.
3..13 Slovní úlohy II Předpoklady: 0301 Pedagogická poznámka: První příklad je opakování z minulé hodiny. Při prvním průchodu se ukázalo, že žáci mají problém s tím, co zvolit za neznámou a jak vyjadřovat.
Integrace kolektorů TS
 Integrace kolektorů TS do šikmé střechy Návod na montáž /3 OBSAH. Použití...3... 2. Popis...3 3. Montáž.....7 A. Postup montáže dvouřadé integrace...7. Odkrytí potřebné plochy střešní krytiny...7 2. Určení
Integrace kolektorů TS do šikmé střechy Návod na montáž /3 OBSAH. Použití...3... 2. Popis...3 3. Montáž.....7 A. Postup montáže dvouřadé integrace...7. Odkrytí potřebné plochy střešní krytiny...7 2. Určení
Úlohy domácího kola kategorie C
 50. ročník Matematické olympiády Úlohy domácího kola kategorie 1. Najděte všechna trojmístná čísla n taková, že poslední trojčíslí čísla n 2 je shodné s číslem n. Student může při řešení úlohy postupovat
50. ročník Matematické olympiády Úlohy domácího kola kategorie 1. Najděte všechna trojmístná čísla n taková, že poslední trojčíslí čísla n 2 je shodné s číslem n. Student může při řešení úlohy postupovat
ÚPRAVA PÁNSKÉHO SAKA - ROZŠÍŘENÍ ŠÍŘKY NÁRAMENICE
 ÚPRAVA PÁNSKÉHO SAKA - ROZŠÍŘENÍ ŠÍŘKY NÁRAMENICE Název úpravy v systému PGS: PS PD ZD BD 1 A-SIRKY NÁRAMENICE (obr. č.1) Název souboru: PSASN Přípona: TXT Hodnota učení: 100% 1. 1. 4. 3. 3. 4. 2. 1. 3.
ÚPRAVA PÁNSKÉHO SAKA - ROZŠÍŘENÍ ŠÍŘKY NÁRAMENICE Název úpravy v systému PGS: PS PD ZD BD 1 A-SIRKY NÁRAMENICE (obr. č.1) Název souboru: PSASN Přípona: TXT Hodnota učení: 100% 1. 1. 4. 3. 3. 4. 2. 1. 3.
3. NEZAMĚSTNANOST A VOLNÁ PRACOVNÍ MÍSTA
 3. NEZAMĚSTNANOST A VOLNÁ PRACOVNÍ MÍSTA V České republice je nezaměstnanost definována dvojím způsobem: Národní metodika, používaná Ministerstvem práce a sociálních věcí (MPSV), vychází z administrativních
3. NEZAMĚSTNANOST A VOLNÁ PRACOVNÍ MÍSTA V České republice je nezaměstnanost definována dvojím způsobem: Národní metodika, používaná Ministerstvem práce a sociálních věcí (MPSV), vychází z administrativních
ROZCVIČKY. (v nižší verzi může být posunuta grafika a špatně funkční některé odkazy).
 ROZCVIČKY Z MATEMATIKY 8. ROČ Prezentace jsou vytvořeny v MS PowerPoint 2010 (v nižší verzi může být posunuta grafika a špatně funkční některé odkazy). Anotace: Materiál slouží k procvičení základních
ROZCVIČKY Z MATEMATIKY 8. ROČ Prezentace jsou vytvořeny v MS PowerPoint 2010 (v nižší verzi může být posunuta grafika a špatně funkční některé odkazy). Anotace: Materiál slouží k procvičení základních
Název: O co nejvyšší věž
 Název: O co nejvyšší věž Výukové materiály Téma: Pevnost, stabilita, síly Úroveň: 1. stupeň ZŠ Tematický celek: Jak se co dělá Věci a jejich původ (Suroviny a jejich zdroje) Předmět (obor): prvouka a přírodopis
Název: O co nejvyšší věž Výukové materiály Téma: Pevnost, stabilita, síly Úroveň: 1. stupeň ZŠ Tematický celek: Jak se co dělá Věci a jejich původ (Suroviny a jejich zdroje) Předmět (obor): prvouka a přírodopis
1 NÁPRAVA De-Dion Představuje přechod mezi tuhou nápravou a nápravou výkyvnou. Používá se (výhradně) jako náprava hnací.
 1 NÁPRAVA De-Dion Představuje přechod mezi tuhou nápravou a nápravou výkyvnou. Používá se (výhradně) jako náprava hnací. Skříň rozvodovky spojena s rámem zmenšení neodpružené hmoty. Přenos točivého momentu
1 NÁPRAVA De-Dion Představuje přechod mezi tuhou nápravou a nápravou výkyvnou. Používá se (výhradně) jako náprava hnací. Skříň rozvodovky spojena s rámem zmenšení neodpružené hmoty. Přenos točivého momentu
1. a) Přirozená čísla
 jednotky desítky stovky tisíce desetitisíce statisíce miliony 1. a) Přirozená čísla Přirozená čísla jsou nejčastějšími čísly, se kterými se setkáváme v běžném životě. Jejich pomocí zapisujeme počet věcí
jednotky desítky stovky tisíce desetitisíce statisíce miliony 1. a) Přirozená čísla Přirozená čísla jsou nejčastějšími čísly, se kterými se setkáváme v běžném životě. Jejich pomocí zapisujeme počet věcí
Přednáška č.4 Tolerování
 Fakulta strojní VŠB-TUO Přednáška č.4 Tolerování Tolerování Pro sériovou a hromadnou výrobu je nutná zaměnitelnost a vyměnitelnost součástí strojů. Aby se mohla dodržet tato podmínka je nutné vyrobit součást
Fakulta strojní VŠB-TUO Přednáška č.4 Tolerování Tolerování Pro sériovou a hromadnou výrobu je nutná zaměnitelnost a vyměnitelnost součástí strojů. Aby se mohla dodržet tato podmínka je nutné vyrobit součást
Přírodovědný KLOKAN 2007
 Přírodovědný KLOKAN 2007 Junior Úlohy za 3 body 1. Na proužek papíru délky 1m zakreslíme nejprve značky, které jej rozdělí na stejně dlouhé části a potom další značky, které jej rozdělí na 3 stejně dlouhé
Přírodovědný KLOKAN 2007 Junior Úlohy za 3 body 1. Na proužek papíru délky 1m zakreslíme nejprve značky, které jej rozdělí na stejně dlouhé části a potom další značky, které jej rozdělí na 3 stejně dlouhé
Jakýkoliv jiný způsob záznamu odpovědí (např. dva křížky u jedné úlohy) bude považován za nesprávnou odpověď.
 MATEMATIKA 5 M5PZD16C0T01 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 16 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: psací a rýsovací potřeby Časový limit pro řešení didaktického testu je 60
MATEMATIKA 5 M5PZD16C0T01 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 16 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: psací a rýsovací potřeby Časový limit pro řešení didaktického testu je 60
Měření změny objemu vody při tuhnutí
 Měření změny objemu vody při tuhnutí VÁCLAVA KOPECKÁ Katedra didaktiky fyziky, Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Anotace Od prosince 2012 jsou na webovém portálu Alik.cz publikovány
Měření změny objemu vody při tuhnutí VÁCLAVA KOPECKÁ Katedra didaktiky fyziky, Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Anotace Od prosince 2012 jsou na webovém portálu Alik.cz publikovány
MOBILNÍ KOMUNIKACE STRUKTURA GSM SÍTĚ
 MOBILNÍ KOMUNIKACE STRUKTURA GSM SÍTĚ Jiří Čermák Letní semestr 2005/2006 Struktura sítě GSM Mobilní sítě GSM byly původně vyvíjeny za účelem přenosu hlasu. Protože ale fungují na digitálním principu i
MOBILNÍ KOMUNIKACE STRUKTURA GSM SÍTĚ Jiří Čermák Letní semestr 2005/2006 Struktura sítě GSM Mobilní sítě GSM byly původně vyvíjeny za účelem přenosu hlasu. Protože ale fungují na digitálním principu i
Jak vybrat outdoorový nůž
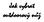 Jak vybrat outdoorový nůž Hledáme nůž, který nám umožní výrobu různých předmětů. Pro činnosti, jako je vyřezávání, zahrocování kůlů či třeba dlabání zářezů, nesmí být nůž příliš těžký. Takový nůž vede
Jak vybrat outdoorový nůž Hledáme nůž, který nám umožní výrobu různých předmětů. Pro činnosti, jako je vyřezávání, zahrocování kůlů či třeba dlabání zářezů, nesmí být nůž příliš těžký. Takový nůž vede
145 905 R01 Hzs-revize provoz.souboru a st.obj. - Revize otopného systému viz.tz kč 1,00
 ÚŘAD MĚSTSKÉ ČÁSTI, ORGANIZAČNÍ ODBOR, JÍROVA 2, 628 00 BRNO VÁŠ DOPIS ČJ.: ZE DNE: NAŠE ČJ.: SPIS. ZN.: VYŘIZUJE: TEL.: FAX: E-MAIL: DATUM: XX/000/0000 20/2013 Alexandra Černá 544 42 48 40, 724 925 260
ÚŘAD MĚSTSKÉ ČÁSTI, ORGANIZAČNÍ ODBOR, JÍROVA 2, 628 00 BRNO VÁŠ DOPIS ČJ.: ZE DNE: NAŠE ČJ.: SPIS. ZN.: VYŘIZUJE: TEL.: FAX: E-MAIL: DATUM: XX/000/0000 20/2013 Alexandra Černá 544 42 48 40, 724 925 260
PATENTOVÝ SPIS N O. CO 00 co OO CM CZ0129446. Obálka pro kontejnery na přepravu a skladování radioaktivních a zvláště nebezpečných materiálů
 PATENTOVÝ SPIS (19) ČESKÁ REPUBLIKA (2 l)čislo přihlášky: 1999-2458 (22) Přihlášeno. 12.07.1999 (40) Zveřejněno: 17.01.2001 (Věstník č. 1/2001) (47) Uděleno: 07.11.2000 (24) Oznámeno udělení ve Včstníku:
PATENTOVÝ SPIS (19) ČESKÁ REPUBLIKA (2 l)čislo přihlášky: 1999-2458 (22) Přihlášeno. 12.07.1999 (40) Zveřejněno: 17.01.2001 (Věstník č. 1/2001) (47) Uděleno: 07.11.2000 (24) Oznámeno udělení ve Včstníku:
Koučování PER Personální management
 Koučování PER Personální management Möbius Jan 25.3.2013 Fakulta textilní Technické univerzity v Liberci 1 OBSAH ÚVOD... 3 1. Co je koučování?... 3 2. Kdo může koučovat?... 3 3. Koho lze koučovat?... 3
Koučování PER Personální management Möbius Jan 25.3.2013 Fakulta textilní Technické univerzity v Liberci 1 OBSAH ÚVOD... 3 1. Co je koučování?... 3 2. Kdo může koučovat?... 3 3. Koho lze koučovat?... 3
Věty o pravoúhlém trojúhelníku. Vztahy pro výpočet obvodu a obsahu. Eukleidova věta o výšce. Druhá mocnina výšky k přeponě je rovna součinu
 Věty o pravoúhlém trojúhelníku Eukleidova věta o výšce. Druhá mocnina výšky k přeponě je rovna součinu b v a obou úseků přepony: v 2 = c a c b c b c a Eukleidova věta o odvěsně A c B Druhá mocnina délky
Věty o pravoúhlém trojúhelníku Eukleidova věta o výšce. Druhá mocnina výšky k přeponě je rovna součinu b v a obou úseků přepony: v 2 = c a c b c b c a Eukleidova věta o odvěsně A c B Druhá mocnina délky
MATEMATIKA A BYZNYS. Finanční řízení firmy. Příjmení: Rajská Jméno: Ivana
 MATEMATIKA A BYZNYS Finanční řízení firmy Příjmení: Rajská Jméno: Ivana Os. číslo: A06483 Datum: 5.2.2009 FINANČNÍ ŘÍZENÍ FIRMY Finanční analýza, plánování a controlling Důležité pro rozhodování o řízení
MATEMATIKA A BYZNYS Finanční řízení firmy Příjmení: Rajská Jméno: Ivana Os. číslo: A06483 Datum: 5.2.2009 FINANČNÍ ŘÍZENÍ FIRMY Finanční analýza, plánování a controlling Důležité pro rozhodování o řízení
NÁVOD NA POKLÁDKU kamenný koberec - INTERIÉR
 NÁVOD NA POKLÁDKU kamenný koberec - INTERIÉR KAMENNÝ KOBEREC je certifikovaný systém pryskyřice a přírodních oblázků. TYPY KAMENNÉHO KOBERCE S UZAVŘENOU STRUKTUROU DO INTERIÉRU 1. uzavřená struktura -
NÁVOD NA POKLÁDKU kamenný koberec - INTERIÉR KAMENNÝ KOBEREC je certifikovaný systém pryskyřice a přírodních oblázků. TYPY KAMENNÉHO KOBERCE S UZAVŘENOU STRUKTUROU DO INTERIÉRU 1. uzavřená struktura -
novostavba polyfunkčního domu
 ARCHITEKTONICKÁ STUDIE 7/2014 údaje o stavbě Petra Bezruče 40 747 62 Mokré Lazce údaje o objednateli obec Mokré Lazce Pavla Křížkovského 158 747 62 Mokré Lazce údaje o zhotoviteli datum Ing.arch. Jiří
ARCHITEKTONICKÁ STUDIE 7/2014 údaje o stavbě Petra Bezruče 40 747 62 Mokré Lazce údaje o objednateli obec Mokré Lazce Pavla Křížkovského 158 747 62 Mokré Lazce údaje o zhotoviteli datum Ing.arch. Jiří
Kapitola 8 Kůň našíř. Článek 30 Popis sestavy na koni našíř. Článek 31 Informace o provedení sestavy
 Kapitola 8 Kůň našíř Výška: 105 cm od horní plochy žíněnky Článek 30 Popis sestavy na koni našíř Současná sestava na koni našíř je charakteristická různými typy kol v provedení s roznožením a snožmo, prováděných
Kapitola 8 Kůň našíř Výška: 105 cm od horní plochy žíněnky Článek 30 Popis sestavy na koni našíř Současná sestava na koni našíř je charakteristická různými typy kol v provedení s roznožením a snožmo, prováděných
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita V. 2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V. 2. 10 Základní části strojů Kapitola 6 Matice
Zvyšování kvality výuky technických oborů Klíčová aktivita V. 2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V. 2. 10 Základní části strojů Kapitola 6 Matice
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita V.2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V.2.8 Realizace klempířských prací a dovedností
Zvyšování kvality výuky technických oborů Klíčová aktivita V.2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V.2.8 Realizace klempířských prací a dovedností
5.1.6 Vzájemná poloha dvou přímek
 5.1.6 Vzájemná oloha dvou římek Předoklady: 5105 Planimetrie: dvě možností ro vzájemnou olohu římek různoběžky rávě jeden solečný bod (různý směr) rovnoběžky žádný solečný bod (stejný směr) Př. 1: Najdi
5.1.6 Vzájemná oloha dvou římek Předoklady: 5105 Planimetrie: dvě možností ro vzájemnou olohu římek různoběžky rávě jeden solečný bod (různý směr) rovnoběžky žádný solečný bod (stejný směr) Př. 1: Najdi
Měřidla. Existují dva druhy měření:
 V této kapitole se seznámíte s většinou klasických druhů měřidel a se způsobem jejich použití. A co že má dělat měření na prvním místě mezi kapitolami o ručním obrábění kovu? Je to jednoduché - proto,
V této kapitole se seznámíte s většinou klasických druhů měřidel a se způsobem jejich použití. A co že má dělat měření na prvním místě mezi kapitolami o ručním obrábění kovu? Je to jednoduché - proto,
Technická zpráva. 1. Všeobecné údaje. 2. Základní údaje charakterizující stavbu. 3. Stavebně technické řešení. 3.1 Zemní práce. 3.2 Svislé konstrukce
 Příloha č. 2 Technická zpráva 1. Všeobecné údaje Název stavby: Dřevostavba pro rekreační účely Místo stavby: Teplá, Máchova, č. parcely 2 358/1 a 2 358/3 Vypracoval: Tadeáš Domin Kontroloval: Ing. Martin
Příloha č. 2 Technická zpráva 1. Všeobecné údaje Název stavby: Dřevostavba pro rekreační účely Místo stavby: Teplá, Máchova, č. parcely 2 358/1 a 2 358/3 Vypracoval: Tadeáš Domin Kontroloval: Ing. Martin
7. Stropní chlazení, Sálavé panely a pasy - 1. část
 Základy sálavého vytápění (2162063) 7. Stropní chlazení, Sálavé panely a pasy - 1. část 30. 3. 2016 Ing. Jindřich Boháč Obsah přednášek ZSV 1. Obecný úvod o sdílení tepla 2. Tepelná pohoda 3. Velkoplošné
Základy sálavého vytápění (2162063) 7. Stropní chlazení, Sálavé panely a pasy - 1. část 30. 3. 2016 Ing. Jindřich Boháč Obsah přednášek ZSV 1. Obecný úvod o sdílení tepla 2. Tepelná pohoda 3. Velkoplošné
Tématická oblast Programování CNC strojů a CAM systémy Příprava součásti pro obrábění
 Číslo projektu CZ.1.07/1.5.00/34.0556 Číslo materiálu VY_32_INOVACE_VC_CAM_11 Název školy Střední průmyslová škola a Vyšší odborná škola Příbram, Hrabákova 271, Příbram II Autor Martin Vacek Tématická
Číslo projektu CZ.1.07/1.5.00/34.0556 Číslo materiálu VY_32_INOVACE_VC_CAM_11 Název školy Střední průmyslová škola a Vyšší odborná škola Příbram, Hrabákova 271, Příbram II Autor Martin Vacek Tématická
Inovace a zkvalitnění výuky prostřednictvím ICT. Obrábění. Název: Ing. Kubíček Miroslav. Autor: Číslo: VY_32_INOVACE_19 09 Anotace:
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Obrábění Frézování Ing. Kubíček Miroslav Číslo: VY_32_INOVACE_19
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Obrábění Frézování Ing. Kubíček Miroslav Číslo: VY_32_INOVACE_19
10 Ostatní aplikace desek CETRIS. 10.5 Záhonový obrubník CETRIS. www.cetris.cz/produkty/deska-cetris-hobby-zahonovy-obrubnik/
 www.cetris.cz/produkty/deska-cetris-hobby-zahonovy-obrubnik/ 10.5 Záhonový obrubník CETRIS Záhonový obrubník CETRIS HOBBY je deska pravo úhlého formátu o rozměru 1 28 mm vzniká dělením desky CETRIS. Horní
www.cetris.cz/produkty/deska-cetris-hobby-zahonovy-obrubnik/ 10.5 Záhonový obrubník CETRIS Záhonový obrubník CETRIS HOBBY je deska pravo úhlého formátu o rozměru 1 28 mm vzniká dělením desky CETRIS. Horní
1.3 Druhy a metody měření
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 1.3 Druhy a metody měření Měření je soubor činností, jejichž cílem je stanovit hodnotu měřené fyzikální veličiny.
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 1.3 Druhy a metody měření Měření je soubor činností, jejichž cílem je stanovit hodnotu měřené fyzikální veličiny.
Rozdělení metod tlakového odporového svařování
 Rozdělení metod tlakového odporového svařování Podle konstrukčního uspořádání elektrod a pracovního postupu tohoto elektromechanického procesu rozdělujeme odporové svařování na čtyři hlavní druhy: a) bodové
Rozdělení metod tlakového odporového svařování Podle konstrukčního uspořádání elektrod a pracovního postupu tohoto elektromechanického procesu rozdělujeme odporové svařování na čtyři hlavní druhy: a) bodové
Algoritmizace a programování
 Algoritmizace a programování V algoritmizaci a programování je důležitá schopnost analyzovat a myslet. Všeobecně jsou odrazovým můstkem pro řešení neobvyklých, ale i každodenních problémů. Naučí nás rozdělit
Algoritmizace a programování V algoritmizaci a programování je důležitá schopnost analyzovat a myslet. Všeobecně jsou odrazovým můstkem pro řešení neobvyklých, ale i každodenních problémů. Naučí nás rozdělit
Rolovací sítě okenní Vyobrazenívýrobku ROLOVACÍ SÍTĚ OKENNÍ
 Rolovací sítě okenní Vyobrazenívýrobku Rolovací síť okenní Technickýpopis Celý výrobek se skládá z extrudovaného hliníkového boxu (1). Uvnitř boxu se nachází kulatá hliníková hřídel (2) o průměru 25mm.
Rolovací sítě okenní Vyobrazenívýrobku Rolovací síť okenní Technickýpopis Celý výrobek se skládá z extrudovaného hliníkového boxu (1). Uvnitř boxu se nachází kulatá hliníková hřídel (2) o průměru 25mm.
Škola VOŠ a SPŠE Plzeň, IČO 49774301, REDIZO 600009491
 Škola VOŠ a SPŠE Plzeň, IČO 49774301, REDIZO 600009491 Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Kód DUMu Název DUMu Autor DUMu Studijní obor Ročník Předmět Anotace CZ.1.07/1.5.00/34.0560
Škola VOŠ a SPŠE Plzeň, IČO 49774301, REDIZO 600009491 Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Kód DUMu Název DUMu Autor DUMu Studijní obor Ročník Předmět Anotace CZ.1.07/1.5.00/34.0560
371/2002 Sb. VYHLÁŠKA
 371/2002 Sb. VYHLÁŠKA Ministerstva průmyslu a obchodu ze dne 26. července 2002, kterou se stanoví postup při znehodnocování a ničení zbraně, střeliva a výrobě jejich řezů ve znění vyhlášky č. 632/2004
371/2002 Sb. VYHLÁŠKA Ministerstva průmyslu a obchodu ze dne 26. července 2002, kterou se stanoví postup při znehodnocování a ničení zbraně, střeliva a výrobě jejich řezů ve znění vyhlášky č. 632/2004
Technická zpráva ke konstrukční části:
 Technická zpráva ke konstrukční části: ČOV Skalka: Popis navrženého konstrukčního systému: Objekt ČOV je dvoupodlažní. Nadzemní část je provedena jako tradiční zděná stavba, kterou lze charakterizovat
Technická zpráva ke konstrukční části: ČOV Skalka: Popis navrženého konstrukčního systému: Objekt ČOV je dvoupodlažní. Nadzemní část je provedena jako tradiční zděná stavba, kterou lze charakterizovat
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita V.2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V.2.14 Konstrukce stolového a lůžkového nábytku
Zvyšování kvality výuky technických oborů Klíčová aktivita V.2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V.2.14 Konstrukce stolového a lůžkového nábytku
Veterinární stůl VT 804ON
 Veterinární stůl VT 804ON Výrobce: CIRA cz. spol. s r. o., Hradišťská 149, 538 25 Nasavrky, Česká republika, IČ. 288 14 193 Prohlášení o shodě: podle směrnice Evropského parlamentu a Rady 2006/42/ES (nařízení
Veterinární stůl VT 804ON Výrobce: CIRA cz. spol. s r. o., Hradišťská 149, 538 25 Nasavrky, Česká republika, IČ. 288 14 193 Prohlášení o shodě: podle směrnice Evropského parlamentu a Rady 2006/42/ES (nařízení
Příloha Průběžné zprávy. Shrnutí návrhu algoritmu
 Příloha Průběžné zprávy Shrnutí návrhu algoritmu Obsah 1. Zadání a definice 2. Předpoklady použitíalgoritmu 3. Ocenění lesní půdy Ocenění zemědělské půdy Oceněníbudov a zastavěných ploch Ocenění vodních
Příloha Průběžné zprávy Shrnutí návrhu algoritmu Obsah 1. Zadání a definice 2. Předpoklady použitíalgoritmu 3. Ocenění lesní půdy Ocenění zemědělské půdy Oceněníbudov a zastavěných ploch Ocenění vodních
Seznámení s možnostmi Autodesk Inventoru 2012
 Název a adresa školy: Střední škola průmyslová a umělecká, Opava, příspěvková organizace, Praskova 399/8, Opava, 746 01 Název operačního programu: OP Vzdělávání pro konkurenceschopnost, oblast podpory
Název a adresa školy: Střední škola průmyslová a umělecká, Opava, příspěvková organizace, Praskova 399/8, Opava, 746 01 Název operačního programu: OP Vzdělávání pro konkurenceschopnost, oblast podpory
Kam s ním. Při navrhování úložných. Bydlení pod střechou ZKOSENÉ STĚNY A NEPŘÍSTUPNÁ ZÁKOUTÍ DODÁVAJÍ SICE PODKROVNÍM MÍSTNOSTEM ROMANTICKÝ VZHLED,
 138 Bydlení pod střechou ZKOSENÉ STĚNY A NEPŘÍSTUPNÁ ZÁKOUTÍ DODÁVAJÍ SICE PODKROVNÍM MÍSTNOSTEM ROMANTICKÝ VZHLED, PŘINÁŠEJÍ ALE TAKÉ ŘADU STAROSTÍ PŘI JEJICH ZAŘIZOVÁNÍ NÁBYTKEM. SE ŠIKMINAMI SE MUSÍME
138 Bydlení pod střechou ZKOSENÉ STĚNY A NEPŘÍSTUPNÁ ZÁKOUTÍ DODÁVAJÍ SICE PODKROVNÍM MÍSTNOSTEM ROMANTICKÝ VZHLED, PŘINÁŠEJÍ ALE TAKÉ ŘADU STAROSTÍ PŘI JEJICH ZAŘIZOVÁNÍ NÁBYTKEM. SE ŠIKMINAMI SE MUSÍME
TECHNICKÉ KRESLENÍ A CAD
 Přednáška č. 7 V ELEKTROTECHNICE Kótování Zjednodušené kótování základních geometrických prvků Někdy stačí k zobrazení pouze jeden pohled Tenké součásti kvádr Kótování Kvádr (základna čtverec) jehlan Kvalitativní
Přednáška č. 7 V ELEKTROTECHNICE Kótování Zjednodušené kótování základních geometrických prvků Někdy stačí k zobrazení pouze jeden pohled Tenké součásti kvádr Kótování Kvádr (základna čtverec) jehlan Kvalitativní
STŘEŠNÍ SYSTÉM BRAMAC 7
 STŘEŠNÍ SYSTÉM BRAMAC 7 Řešení pro šikmé střechy od sklonu 7 Člen MONIER GROUP ZÁSADY PRO NAVRHOVÁNÍ STŘEŠNÍHO SYSTÉMU BRAMAC 7 Střešní systém Bramac 7 je založen na upravené betonové střešní tašce Bramac
STŘEŠNÍ SYSTÉM BRAMAC 7 Řešení pro šikmé střechy od sklonu 7 Člen MONIER GROUP ZÁSADY PRO NAVRHOVÁNÍ STŘEŠNÍHO SYSTÉMU BRAMAC 7 Střešní systém Bramac 7 je založen na upravené betonové střešní tašce Bramac
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita V.2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V.2.11 Diagnostika automobilů Kapitola 1 Snímač
Zvyšování kvality výuky technických oborů Klíčová aktivita V.2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V.2.11 Diagnostika automobilů Kapitola 1 Snímač
Obr. 1 Jednokvadrantový proudový regulátor otáček (dioda plní funkci ochrany tranzistoru proti zápornému napětí generovaného vinutím motoru)
 http://www.coptkm.cz/ Regulace otáček stejnosměrných motorů pomocí PWM Otáčky stejnosměrných motorů lze řídit pomocí stejnosměrného napájení. Tato plynulá regulace otáček motoru však není vhodná s energetického
http://www.coptkm.cz/ Regulace otáček stejnosměrných motorů pomocí PWM Otáčky stejnosměrných motorů lze řídit pomocí stejnosměrného napájení. Tato plynulá regulace otáček motoru však není vhodná s energetického
MSSF Benefit praktický průvodce pro žadatele v rámci Operačního programu Rozvoj lidských zdrojů
 MSSF Benefit praktický průvodce pro žadatele v rámci Operačního programu Rozvoj lidských zdrojů MSSF Benefit dostupnost a instalace MSSF Benefit bude dostupný ke stažení na stránkách www.kr-olomoucky.cz
MSSF Benefit praktický průvodce pro žadatele v rámci Operačního programu Rozvoj lidských zdrojů MSSF Benefit dostupnost a instalace MSSF Benefit bude dostupný ke stažení na stránkách www.kr-olomoucky.cz
Ovocné pálenky. Velmi dobré je i vložení dřevěného roštu do kádě, kterým se pevné součástky kvasu vtlačí pod povrch tekutiny.
 1. Kvasné nádoby a kvašení. 1.1 Kvasné nádoby. Ovocné pálenky. V minulosti se používaly dřevěné kádě nebo sudy a v současnosti se nejčastěji používají plastové sudy. Tyto nesmí být od nevhodných popř.
1. Kvasné nádoby a kvašení. 1.1 Kvasné nádoby. Ovocné pálenky. V minulosti se používaly dřevěné kádě nebo sudy a v současnosti se nejčastěji používají plastové sudy. Tyto nesmí být od nevhodných popř.
NÁVOD K OBSLUZE DRAK ROGALO. Obj. č.: 22 44 46
 NÁVOD K OBSLUZE DRAK ROGALO Obj. č.: 22 44 46 Ideální pro uživatele, kteří začínají s létáním se sportovními rogaly-draky. Neboť díky nepatrné hmotnosti je již možné při slabém větru snadno a lehce provádět
NÁVOD K OBSLUZE DRAK ROGALO Obj. č.: 22 44 46 Ideální pro uživatele, kteří začínají s létáním se sportovními rogaly-draky. Neboť díky nepatrné hmotnosti je již možné při slabém větru snadno a lehce provádět
Osvětlovací modely v počítačové grafice
 Západočeská univerzita v Plzni Fakulta aplikovaných věd Semestrální práce z předmětu Matematické modelování Osvětlovací modely v počítačové grafice 27. ledna 2008 Martin Dohnal A07060 mdohnal@students.zcu.cz
Západočeská univerzita v Plzni Fakulta aplikovaných věd Semestrální práce z předmětu Matematické modelování Osvětlovací modely v počítačové grafice 27. ledna 2008 Martin Dohnal A07060 mdohnal@students.zcu.cz
Zásady pro prodej bytových domů Městské části Praha 5
 Zásady pro prodej bytových domů Městské části Praha 5 Základní pojmy Pro účely těchto Zásad pro prodej nemovitostí (pozemků, jejichž součástí jsou bytové domy) Městské části Praha 5 (dále jen Zásady )
Zásady pro prodej bytových domů Městské části Praha 5 Základní pojmy Pro účely těchto Zásad pro prodej nemovitostí (pozemků, jejichž součástí jsou bytové domy) Městské části Praha 5 (dále jen Zásady )
Václav Meškan - PF JČU v Českých Budějovicích, ZŠ L. Kuby, České Budějovice
 Tvůrčí řešení problémových úloh Divergentní fyzikální úlohy Václav Meškan - PF JČU v Českých Budějovicích, ZŠ L. Kuby, České Budějovice Problémové fyzikální úlohy Úlohy, k jejichž vyřešení nestačí pouhá
Tvůrčí řešení problémových úloh Divergentní fyzikální úlohy Václav Meškan - PF JČU v Českých Budějovicích, ZŠ L. Kuby, České Budějovice Problémové fyzikální úlohy Úlohy, k jejichž vyřešení nestačí pouhá
Studijní materiál KA 1
 Z.1.07/1.1.14/01.0032 2012 2014 Studijní materiál KA 1 Předmět: Fyzika Ročník: 3. ročník Téma vyučovací hodiny: Řešení obvodů s kondenzátory Vypracoval: Mgr. Luboš Vejvoda Téma čivo je zaměřeno na vysvětlení
Z.1.07/1.1.14/01.0032 2012 2014 Studijní materiál KA 1 Předmět: Fyzika Ročník: 3. ročník Téma vyučovací hodiny: Řešení obvodů s kondenzátory Vypracoval: Mgr. Luboš Vejvoda Téma čivo je zaměřeno na vysvětlení
MASARYKOVA UNIVERZITA UNIVERZITNÍ CENTRUM TELČ
 Výpočet doby Návrh akustické úpravy prostoru MASARYKOVA UNIVERZITA UNIVERZITNÍ CENTRUM TELČ UČEBNY 110, 111, 112, 218, 219 Objednatel: Masarykova univerzita Univerzitní centrum Telč Náměstí Zachariáše
Výpočet doby Návrh akustické úpravy prostoru MASARYKOVA UNIVERZITA UNIVERZITNÍ CENTRUM TELČ UČEBNY 110, 111, 112, 218, 219 Objednatel: Masarykova univerzita Univerzitní centrum Telč Náměstí Zachariáše
MANUÁL PRO HODNOCENÍ OTEVŘENÝCH TESTOVÝCH ÚLOH MATEMATIKA SADA B (TEST PRO PŘIJÍMACÍ ZKOUŠKY DO 8LETÉHO GYMNÁZIA)
 PH-M5MBCINT MANUÁL PRO HODNOCENÍ OTEVŘENÝCH TESTOVÝCH ÚLOH MATEMATIKA SADA B (TEST PRO PŘIJÍMACÍ ZKOUŠKY DO 8LETÉHO GYMNÁZIA) 1. TYPY TESTOVÝCH ÚLOH V TESTU První dvě úlohy (1 2) jsou tzv. úzce otevřené
PH-M5MBCINT MANUÁL PRO HODNOCENÍ OTEVŘENÝCH TESTOVÝCH ÚLOH MATEMATIKA SADA B (TEST PRO PŘIJÍMACÍ ZKOUŠKY DO 8LETÉHO GYMNÁZIA) 1. TYPY TESTOVÝCH ÚLOH V TESTU První dvě úlohy (1 2) jsou tzv. úzce otevřené
Montážní návod LC 45... S-15-02
 Montážní návod LC 45... S-15-02 2 Při čtení přihlížejte k vyobrazení na posledních stranách. Důležitá upozornění Starý odsavač není bezcenným odpadem. Jeho likvidací, příznivou k životnímu prostředí, můžete
Montážní návod LC 45... S-15-02 2 Při čtení přihlížejte k vyobrazení na posledních stranách. Důležitá upozornění Starý odsavač není bezcenným odpadem. Jeho likvidací, příznivou k životnímu prostředí, můžete
Pracovní list. Workshop: Hospodaření domácnosti
 Pracovní list Workshop: Hospodaření domácnosti Úkol č. 1 Příjmy a výdaje Úkolem je roztřídit níže uvedené pojmy na příjmy a výdaje. Současně také na příjmy aktivní, pasivní, nahodilé a výdaje na zbytné,
Pracovní list Workshop: Hospodaření domácnosti Úkol č. 1 Příjmy a výdaje Úkolem je roztřídit níže uvedené pojmy na příjmy a výdaje. Současně také na příjmy aktivní, pasivní, nahodilé a výdaje na zbytné,
MECHANICKÁ PRÁCE A ENERGIE
 MECHANICKÁ RÁCE A ENERGIE MECHANICKÁ RÁCE Konání práce je podmíněno silovým působením a pohybem Na čem závisí velikost vykonané práce Snadno určíme práci pro případ F s ráci nekonáme, pokud se těleso nepřemísťuje
MECHANICKÁ RÁCE A ENERGIE MECHANICKÁ RÁCE Konání práce je podmíněno silovým působením a pohybem Na čem závisí velikost vykonané práce Snadno určíme práci pro případ F s ráci nekonáme, pokud se těleso nepřemísťuje
