VYUŽITÍ STROMOVÝCH AUTOMATŮ PŘI VERIFIKACI BEZPEČNOSTNÍCH KOMUNIKAČNÍCH PROTOKOLŮ
|
|
|
- Kristýna Krausová
- před 10 lety
- Počet zobrazení:
Transkript
1 VYUŽITÍ STROMOVÝCH AUTOMATŮ PŘI VERIFIKACI BEZPEČNOSTNÍCH KOMUNIKAČNÍCH PROTOKOLŮ STUDIE DO PŘEDMĚTU TID prosinec 2004 Ing. Pavel OČENÁŠEK Ústav informačních systémů, FIT, VUT Brno ABSTRACT Security protocols use cryptography to set up private communication channels on an insecure network. Many protocols contain flaws, and because security goals are seldom specified in detail, we cannot be certain what constitutes a flaw. The paper attempts to draw an approach based on the use of tree automata. 1 ÚVOD Běžná elektronická komunikace mezi uživateli / stanicemi bývá lehce napadnutelná. Příkladem může být komunikace po nezabezpečené síti Internet. Než se zpráva dostane k adresátovi, musí projít přes mnoho dalších počítačů. Na této cestě ji mohou další subjekty analyzovat nebo pozměnit. Případně mohou odeslat adresátovi falešnou zprávu (podvrh) a vydávat se tak za původního odesílatele. 2 BEZPEČNOSTNÍ PROTOKOLY Pro zabezpečení běžné elektronické komunikace se používají bezpečnostní protokoly. Pojmem protokol je myšlen sled interakcí mezi entitami. Příkladem bezpečnostního protokolu může být protokol SSL, který se používá pro zajištění šifrované komunikace mezi klientem a web-serverem.
2 Obr. 1: Příklad bezpečnostního protokolu Aby bylo možné takový protokol pro zabezpečení použít, musí obstát při pokusu o jeho prolomení vnějšími útočníky, kteří se snaží komunikaci odposlechnout nebo jinak napadnout. Obecná zabezpečená komunikace probíhá tak, že se zasílají zprávy šifrované dočasnými klíči, které nejsou známé vnějším pozorovatelům spojení (útočníkům). Zdálo by se, že takto je vše v pořádku a komunikace probíhá v šifrované formě. Mnoho protokolů však zahrnuje chyby a jsou popsány metody prolomení protokolů útočníky. Samotné tvrzení že protokol je bezpečný není dostačující. Jednou z možností, jak toto tvrzení dokázat, případně nalézt chyby, je použití některých formálních postupů, jak bude popsáno dále. 2.1 ZPRÁVA Základním prvkem komunikace mezi účastníky A, B je zpráva. Při formálním zápisu zpráv bereme v úvahu její následující charakteristiky: označení účastníků A, B, ; nonces Na, Nb, ; klíče Ka, Kb, Kab, ; složená zpráva { X, X, hašovaná zpráva Hash X, šifrovaná zpráva klíčem K Crypt K X.
3 Při použití šifrování metodou veřejného klíče předpokládáme, že K -1 je inverzní ke klíči K. V případě rovnosti K -1 = K se jedná o symetrické klíče. Dále předpokládáme (K -1 ) -1 = K pro všechny klíče K. Předpokládáme, že šifrovaná zpráva nemůže být nikdy přečtena bez znalosti příslušných klíčů. Nonces, někdy překládané jako keksíky, jsou náhodně vygenerovaná čísla. Někdy bývají rozlišována jako odhadnutelná (sekvenčně generovaná čísla, časové razítko) nebo neodhadnutelná (např. náhodné 40-bitové číslo). 2.2 ÚTOK NA ZPRÁVU Bezpečnostní protokol musí odolat všem formám pokusů o jeho prolomení. Aktivní útočník, tedy ten který může zasílat zprávy, je mnohem nebezpečnější než pasivní sledovatel komunikace. Vzhledem k tomu, že typů útoků je velké množství, pak tvrzení, že protokol je bezpečný by mělo být doplněno o poznámku, proti kterým typům útoku je tato ochrana zaručena. Základní metody útoku Možnosti útoku na komunikaci subjektů A, B: odposlouchávání přerušení komunikace podvržení identity modifikace zprávy Útok přehráváním Tento typ útoku je založen na principu, že komunikace mezi zúčastněnými subjekty je odposlouchávána a útočník si tuto komunikaci ukládá za účelem její další analýzy. Poté co jsou zachycená data analyzována, mohou být použita pro podvrhnutí identity útočníka vůči některému ze subjektů. Vzdálený subjekt totiž nemá žádnou možnost ověřit čerstvost zprávy (freshness).
4 Jako obrana proti tomuto typu útoku se používá časové razítkování zprávy, čímž se zabrání možnosti pozdějšího použití odposlechnuté informace. Útok ze středu Další z možností jak protokol napadnout je použití útoku ze středu (man-in-themiddle attack, middle-person attack). V tomto případě existuje kromě dvou komunikujících stran A a B ještě aktivní útočník C. Tento naváže komunikaci jak s A, tak s B, přičemž se vždy vydává za regulérního partnera. S využitím informací odposlechnutých od druhé strany se jeví pro A jako B a naopak. Útočník C má tedy možnost monitorovat veškerý přenos. 2.3 ROZDĚLENÍ PROTOKOLŮ Symetrické protokoly V tradiční kryptografii je základem aplikace symetrických šifrovacích algoritmů (DES), kdy se pro zašifrování a dešifrování zpráv používá stejného sdíleného klíče. Před odesláním je zpráva zašifrována pomocí klíče, který zná jak odesílatel, tak příjemce zprávy. Tato zpráva je pak příjemcem standardně dešifrována. Při uvedené komunikaci často vyskytuje třetí subjekt (Key Distribution Center), který zajišťuje výměnu klíče mezi dvěma hlavními subjekty bezpečnou formou, obvykle po zvláštním zabezpečeném komunikačním kanále. Příkladem symetrického protokolu je Otway-Rees protokol. Asymetrické protokoly Alternativou je použití asymetrických protokolů, které používají šifrovací algoritmy založené na dvojici veřejný a privátní klíč. Privátní klíč reprezentuje identitu jeho vlastníka, veřejný klíč je volně k dispozici všem ostatním subjektům, kteří se na komunikaci podílejí. Do této skupiny patří mnoho protokolů, například IKE (Internet Key Exchange protocol), SET (Secure Electronic Transaction protocol), TMN protokol a dále také známý Needham-Schroederův autentizační protokol. 2.4 PŘÍKLADY PROTOKOLŮ Otway-Rees protokol Tento protokol je určen k tomu, aby mohl jakýkoliv uživatel vytvořit bezpečné spojení s kýmkoliv jiným. Předpokládejme opět pokus o navázání komunikace mezi subjekty A a B, přičemž S je důvěryhodný server (trusted key server). Formální zápis: 1. A B : Na, A, B, { Na, A, B Ka 2. B S : Na, A, B, { Na, A, B Ka, Nb, { Na, A, B Kb 3. S B : Na, {Na, Kab Ka, { Nb, Kab Kb 4. B A : Na, { Na, Kab Ka
5 Zde Ka znamená klíč uživatele A a Kb klíč uživatele B. { X K značí zprávu X šifrovanou klíčem K. Přičemž předpokládáme, že nikdo nemůže získat originál zprávy X nebo vytvořit novou šifrovanou zprávu { X K bez znalosti klíče K. Obr. 2: Neformální popis Otway-Rees protokolu (s chybou) 1. A kontaktuje B, vytvoří nonce Na pro identifikaci spojení 2. B kontaktuje S, vytvoří nonce Nb. Nemůže ale přečíst zprávu { Na, A, B Ka protože je zašifrována klíčem uživatele A, takže ji pouze přepošle S. Navíc zašifruje přijatou zprávu svým klíčem a přepošle ji S. 3. S zná klíče všech zúčastněných stran, takže obě zprávy může dešifrovat. Vytvoří nový relační klíč Kab. Pro subjekt A zašifruje zprávu obsahující Kab a Na klíčem Ka. Taková šifrovaná zpráva bývá často označována jako certifikát. 4. B převezme svůj certifikát. Zkontroluje zda přijatá nonce Nb je stejná jako jím odeslaná v kroku 2. Pokud souhlasí, pak přepošle druhý certifikát subjektu A, který podobně ověří přijatý certifikát. Nyní následuje šifrovaná komunikace s použitím klíče Kab jako relačního klíče. Uvedený protokol lze však napadnou útočníkem C, a to z těchto důvodů: oba certifikáty zaslané v kroku 3 mají stejný formát v kroku 2 se nonce Nb posílá v nezabezpečené formě Útok pak bude mít následující formu (C A značí, že se subjekt C vydává za A apod.): 1. A C B : Na, A, B, { Na, A, B Ka 1. C A : Nc, C, A, { Nc, C, A Kc Subjekt A se snaží kontaktovat B, ale C zachytí uvedenou zprávu a kontaktuje A 2. A C S : Nc, C, A, { Nc, C, A Kc, Na, { Nc, C, A Ka 2. C A S : Nc, C, A, { Nc, C, A Kc, Na, { Nc, C, A Ka
6 Subjekt A odpovídá na zprávu od C podle pravidel protokolu, snaží se kontaktovat S. Ale C modifikuje tuto zprávu a nahradí původní nonce Na novým nonce Na. 3. S C A : Nc, { Nc, Kca Kc, { Na, Kca Ka Jako odpověď posílá S subjektu A relační klíč, který se pak bude sdílet mezi A a C. 4. C B A : Na, { Na, Kca Ka Útočník C získává oba certifikáty a posílá subjektu A ten špatný. Tento obsahuje Na, tedy A akceptuje Kca jako relační klíč zaslaný od B. Ale tento klíč je již sdílený s C. Yahalom protokol Protokol má následující specifikaci: 1. A B : A, Na 2. B S : B, Nb, { A, Na Kb 3. S A : { B, Kab, Na, Nb Ka, { A, Kab Kb 4. A B : { A, Kab Kb, { Nb Kab Trojúhelníková konfigurace předurčuje subjektům A i B možnost získat informaci o tom, zda další strana je aktivní: Obr. 3: Yahalom protokol (s chybou) Protokol obsahuje následující chybu - certifikát subjektu B { A, Kab Kb neobsahuje žádné nonces, proto nepodává žádnou časovou informaci. Pokud bude K starým relačním klíčem který již jednou byl sdílen subjekty A a B, pak pokud C nějakým způsobem získá K a uloží si starý certifikát { A, K Kb obsahující tento klíč, pak může provést následující konverzaci s B: 1. C A B : A, Nc 2. B C S : B, Nb, { A, Nc Kb
7 4. C A B : { A, K Kb, { Nb K Nyní B přijme starý kompromitovaný relační klíč. Podobně jako u Otway-Rees protokolu, správná verze protokolu zašifruje nonce Nb v kroku 2. Poznámky k bezpečnosti obou protokolů: Otway-Rees protokol vyžaduje ochranu Nb před modifikací. Útok je proveden zevnitř systému. Oběť útoku získá klíč, který je bohužel sdílen s nesprávnou osobou. Yahalom vyžaduje zašifrování Nb. Útok je jednoduchý a může být proveden zvenčí. Oběť útoku získá klíč který je později zkompromitován. Needham-Schroeder protokol Tento protokol patří mezi asymetrické bezpečnostní protokoly. Je znám svoji jednoduchostí a bývá uváděn jako příklad pro analýzu v mnoha verifikačních technikách. Specifikace protokolu: 1. A S: A, B S A: { K B Ks 3. A B: { Na, A Kb 4. B S: B, A 5. S B: { Ka, A Ks B A: { Na, Nb Ka 7. A B: { Nb Kb Obr. 4: Needham-Schroederův autentizační protokol
8 Symboly Ka, Kb, Ks jsou veřejné klíče subjektů A, B, S. Inverzní klíče jsou privátní klíče, které jsou známé pouze svým vlastníkům. Přepokládá se, že každý subjekt zná veřejný klíč Ks, tedy každý si může přečíst zprávu odeslanou serverem S a zašifrovanou jeho privátním klíčem Ks -1. V případě, že některý subjekt potřebuje veřejný klíč jiného subjektu, pošle svůj požadavek serveru S. Kroky 1,2,4,5 se týkají zjištění veřejných klíčů, přičemž v 3,6,7 pak provádí autentizace A a B. V kroku 3 posílá subjekt A svůj nonce a svoji identitu zašifrovanou klíčem Kb. Protože pouze B vlastní privátní klíč Kb -1, může A předpokládat, že takto zašifrovanou zprávu nepřečte nikdo jiný než B. Subjekt B pak vrací tento nonce spolu se svým Nb, zašifrované veřejným klíčem Ka. 3 FORMÁLNÍ VERIFIKAČNÍ TECHNIKY Proces formální kontroly modelu systému, zda splňuje specifikované požadavky, se nazývá formální verifikace. Tato technika hraje v oblasti bezpečnosti významnou roli. V zásadě můžeme říci, že vývoj formální technik se ubírá třemi hlavními směry. Jeden z nich využívá modální logiky (modal logic), další provádí verifikaci metodou procházení stavového prostoru (state enumeration/exploration), poslední se pak označuje jako theorem proving. Přehled jednotlivých přístupů je k dispozici například v [2], [5] a [6]. Mezi prostřední uvedenou kategorii (stavový prostor) patří použití stromových automatů [1] (angl. tree automata). Detailněji je tento přístup popsán v následující kapitole. 4 STROMOVÉ AUTOMATY 4.1 NEFORMÁLNÍ SÉMANTIKA Nejběžnějším postupem v analýze kryptografických protokolů je abstrakce elementárních funkcí (např. šifrování veřejným/privátním klíčem, hash funkce, ). Uvažujme např. symetrickou funkci Encrypt(X, K), která převezme data X a zašifruje je klíčem K. Pojem symetričnost funkce znamená takovou vlastnost, kdy stejný klíč K je použit jak pro šifrování tak pro dešifrování dat. Protokol používající symetrické kryptografické funkce je pak modelován zprávami založenými na následující algebře: encrypt(-, -) (šifrování) a pair(-, -) (párování). Takové modely kryptografických protokolů již byly představeny autory Dolev a Yao [2] [5]. Specifikace protokolů obsahuje: pojmenování a aritu základních elementů vlastnosti těchto elementů jednotlivé kroky protokolu Techniky využívající stromových automatů omezují třídu vlastností jež lze vyjádřit. Stejně tak jsou omezena přechodová pravidla reprezentující jednotlivé kroky protokolu. Přes tato omezení lze vhodně specifikovat protokol, jehož bezpečnost chceme prověřit. Pro specifikaci protokolu používáme programovou syntaxi.
9 Základní elementy (klauzule CONSTRUCTORS) Příklad specifikace základních elementů protokolu: CONSTRUCTORS { pair(p,p); proj1(n); proj2(n); encrypt(p,n); decrypt(p,n); private Na; Základní elementy protokolu mohou být specifikovány jako veřejné (public, implicitní, bez klíčového slova) nebo privátní (klíčové slovo private). Veřejné elementy jsou volně k dispozici útočníkovi. Privátní elementy reprezentují prvky nebo operace, které úročník nezná: například některé utajené konstanty (jsou specifikovány jako elementy s 0-ní (nulární) aritou). Písmena P a N jsou užity pro zavedení určité logičnosti v používání vybraných akcí jednotlivými komunikujícími subjekty. Subjekt může použít funkci ověřování (patternmatching) pro získání informací z položek označených jako P (pattern), ne však z položek označených N. Tedy pokud subjekt zná klíč K, může odvodit příchozí zprávu x zašifrovanou v encrypt(x, K). Na druhou stranu by bylo nesmyslné pokoušet se analyzovat encrypt(x, k) a získat položku k zašifrovanou klíčem X. Toto označení nemá vliv na analýzu, ale je použito pouze pro předejití některým možným chybám ve specifikaci. Přepisovací pravidla V našem případě jsou pravidla následující: proj1(pair(x,y)) => x; proj2(pair(x,y)) => y; decrypt(encrypt(x, k), k) => x; Tato pravidla znamenají: útočník může získat levý prvek z páru, který vlastní útočník může získat pravý prvek z páru, který vlastní útočník může dešifrovat zašifrovanou zprávu, v případě, že zná odpovídající klíč k Asymetrické šifrování je pak možné modelovat následovně: publicdecrypt(publicencrypt(x, k), privatekey(k)) => x
10 kde privatekey je privátní unární konstruktor (deklarován jako PRIVATE). Pokud je x veřejný klíč, pak privatekey(x) je odpovídající soukromý klíč. Útočník Předpokládáme, že všechna komunikace jde přes útočníka. Tedy pokud subjekt odešle zprávu, je tato zpráva zaslána útočníkovi. Pokud subjekt přijme zprávu, obdrží ji od útočníka. Tímto modelujeme skutečnost, že útočník má přístup ke komunikaci mezi zúčastněnými subjekty, dokonce může také zprávy pozměňovat. Na počátku komunikace je útočník inicializován množinou známých informací (dat) a tuto množinu rozšiřuje podle zpráv, které obdržel od zúčastněných subjektů. Množinu tak může rozšířit o všeobecně (public) známé elementy nebo pomocí přepisovacích pravidel. Počáteční množina znalostí útočníka je specifikována klauzulí INTRUDER_KNOWLEDGE. Subjekty (klauzule PRINCIPALS) Každý zúčastněný subjekt si řídí svou část komunikace. Podle běžné notace označujeme subjekty písmeny A, B, nebo S pro servery. Registry (klauzule REGISTERS) Každý subjekt vlastní konečný počet registrů, pro každý platí že buď nemá přiřazenou žádnou hodnotu nebo obsahuje terminál. Označení registrů koresponduje s významem dat, který obsahuje. Například registr kab obsahuje klíč Kab používaný pro šifrování komunikace mezi subjekty A a B. Specifikace akcí (klauzule PROGRAM) Subjekty mohou, podle kroku ve kterém se zrovna nachází, provést následující akce: Načtení zprávy do registru (?r). Zpráva přichází od útočníka a může jí být jakákoliv informace, kterou může útočník odvodit z jemu přístupných (znalých) informací. Příklad: pokud útočník již zná zprávu X a obdržel od subjektu Y, cílovému subjektu může poslat např. zprávu pair(x, Y). Tento subjekt provede operaci?r a načte přijatou zprávu do registru. Odeslání zprávy (!message). V naší notaci je zprávou výraz obsahující konstruktory, konstanty nebo jména registrů. Subjekt vytvoří aktuální zprávu tak, že nahradí jména registrů příslušnými hodnotami. Tuto zprávu pak zašle útočníkovi, který z ní odvodí potřebné informace a může si tak rozšířit množinu znalostí. Ověření registru, zda obsahuje specifikovaný výraz (register =~ pattern). Výrazem (pattern) zde může být konstanta, aktuální hodnota registru (register) nebo cílový registr ($register). Pokud výraz selže, subjekt prohlásí že protokol selhal a provádění protokolu se zastaví. Příklad: předpokládejme, že registr r obsahuje encrypt($data, kab), registr kab pak obsahuje klíč Kab. Poté co se provede akce r =~ encrypt($data, kab), registr data bude obsahovat X. Pokud r obsahoval encrypt(x, Kas), pak ověření selhalo a subjekt provádění protokolu zastaví.
11 Příklad: Otway-Rees protokol Specifikace protokolu Otway-Rees (viz. kapitola 2) je následující: (1) A B: M; A; B; {Na;M;A;B Kas (2) B S: M; A; B; {Na;M;A;B Kas ; {Nb;M;A;B Kbs (3) S B: M; {Na;Kab Kas ; {Nb;Kab Kbs (4) B A: M; {Na;Kab Kas V tomto protokolu komunikují 3 subjekty, dva klienti označení A, B a server S. Takový protokol můžeme modelovat následujícím kódem: CONSTRUCTORS { pair(p,p); proj1(n); proj2(n); encrypt(p,n); decrypt(p,n); private Kas; private Kbs; private Kab; private M; private Na; private Nb; private X; private A; private B; S; RULES { proj1(pair(x,y)) => x; proj2(pair(x,y)) => y; decrypt(encrypt(x, k), k) => x;
12 INTRUDER_KNOWLEDGE { SECRETS { X PRINCIPAL A { REGISTERS { r, kab PROGRAM {! pair(a, pair(b, pair(m, encrypt(pair(pair(na, M), pair(a, B)), Kas))));? r; r =~ pair(b, pair(a, encrypt(pair(na, $kab), Kas)));! encrypt(x, kab); PRINCIPAL B { REGISTERS { r, m, a, z, kab PROGRAM {? r; r =~ pair($a, pair(b, pair($m, $z)));!pair(b, pair(s, pair(a, pair(z, encrypt(pair(pair(nb, m), pair(a, B)), Kbs)))));? r; r =~ pair(s, pair(b, pair($z, encrypt(pair(nb, $kab), Kbs))));! pair(b, pair(a, z)); PRINCIPAL S { REGISTERS { m, r, a, b, na, nb PROGRAM {? r; r =~ pair($b, pair(s, pair($m, pair($a, pair($b, pair( encrypt(pair(pair($na, $m), pair($a, $b)), Kas), encrypt(pair(pair($nb, $m), pair($a, $b)), Kbs)))))));! pair(s, pair(b, pair(m, pair( encrypt(pair(na, Kab), Kas),
13 encrypt(pair(nb, Kab), Kbs))))); 4.2 FORMÁLNÍ SÉMANTIKA V této kapitole nadefinujeme formální popis komunikačního protokolu. Označme F dvojici (, a) kde je množina názvů funkcí a a je funkce nazývaná arita, která přiřazuje prvku z množiny nezáporné číslo: a x N. Příkladem názvů funkcí může být pair, encrypt, obě s aritou 2, taktéž pak konstanty, např. Na s aritou 0. Uvažujme volnou algebru T(F) nad F jako množinu syntaktických výrazů vytvořenou jednoduše z uvedených názvů funkcí (např. encrypt(na, Kas)). Zprávy zaslané mezi subjekty jsou pak prvky této algebry. Uvažujme dále algebru T(F, X) výrazů s proměnnými z X. Pokud t T(F, X), (X i ) i I je rodina proměnných, (t i ) i I je rodina výrazů, zapisujeme t[t i /X i ] výraz získaný paralelní substitucí t i za X i v t. Přitom bereme v úvahu FV(t) množinu volných proměnných v t. Dále uvažujme pojem možné odvození. Tento pojem je definován funkcí K: p(t(f)) p(t(f)) jenž spočítá uzávěr podmnožiny T(F) pomocí následujících operací: podmnožina O funkčních symbolů nalezených v F; pokud symbol f spadá do podmnožiny O n mocniny elementů O arity n, pak pro všechny n-tice (x i ) 1 i n elementů z K(X) platí, že f(x 1,,x n ) patří do K(X); množina R pravidel tvaru t=>x, kde t je výraz s proměnnými a x je proměnná, která se v t vyskytuje právě jednou (collapsing rules) Pak se můžeme uvažovat, že prvek x T(F) je odvoditelný z X T(F) pokud x K(X). Zapisujeme p(t(f)) K. 4.3 KONKRÉTNÍ SÉMANTIKA Uvažujme konečnou množinu subjektů P. Každý subjekt p P má konečnou množinu registrů R p, každý obsahující prvek z T(F) {Ω prvek Ω znamená neinicializováno a program x p k provedení. Zpočátku budeme ignorovat neinicializované prvky, protože protokol používající neinicializované prvky nedává smysl. Program je pak konečná posloupnost (i prázdná) příkazů, které mohou být jedním ze tří typů: Vyslání zprávy:!t kde t T(F, R p ); Ověření: r 0 =~t, kde r 0 {1,, r p a t T(F, R p $R p ); $R p ={$r r R p je kopie R p získaná přidáním znaku $ před název každého registru. Přijetí zprávy:?r, kde r R p. Nechť h :: t je posloupnost, jejíž záhlaví je h a zápatí t, ε pak označíme prázdnou posloupnost. Lokální stav každého subjektu pak tvoří obsah jeho registrů a zbytek programu, který je třeba
14 vykonat. Globální stav je pak n-tice tvořená lokálními stavy spolu se stavem útočníka, který je prvkem p(t(f)) K. Množina globálních stavů je označena. Sémantiku systému definujeme nedeterministickými přechody. Mějme S a S dva globální stavy. Označme S.p lokální stav subjektu p v S a S.I znalosti útočníka v S. V lokálním stavu pak označme L.r obsah registru r a L.P program. Definice přechodu je pak následující: S S pokud existuje p 0 P takové, že: pro všechna p P takové, že p p 0, S.p = S.p; S.p 0.P = h::t a buďto o (přijetí zprávy) h =?r 0 a zároveň pro všechna r R p0, S.p 0.r=S.p 0.r, S.p 0.r 0 S.I S.p 0.P = t o (zaslání zprávy) h =!t a zároveň pro všechna r R p0, S.p 0.r = S.p 0.r (nemění stav žádného registru) S.I = K(S.I {t[s.p 0.r/r r R p0 ]) (útočník nyní zná I a použije jej k rozšíření své množiny znalostí) S.p 0.P = t (subjekt p 0 má za úkol spustit zbytek svého programu) o (ověření) h = r 0 =~t a buďto existuje substituce σ 1 : $R p T(F) tak, že r 0 =t[σ 1 ; σ 2 ] kde σ 2 je substituce r a S.p 0.r a t[σ 1 ; σ 2 ] je výsledek aplikace obou substitucí σ 1, σ 2 na výraz t; pak pro každé r R p0 takové že $r není volná v t, S.p 0.r = S.p 0.r pro každé r R p0 takové že $r není volná v t, S.p 0.r = σ 1 (r) S I = S I (žádná komunikace) S.p 0.P = t (subjekt p 0 nedokončil provádění svého programu) pokud taková substituce neexistuje, pak pro každé r R p0, S.p 0.r = S.p 0.r ; S I = S I (žádná komunikace) S.p 0.P = ε (subjekt zjistil že protokol selhal a ukončil činnost) 4.4 STROMOVÉ AUTOMATY A OPERACE NAD NIMI Pro reprezentaci podmnožin T(F) jsou použity nedeterministické top-down stromové automaty. Automat je konečnou reprezentací podmnožin výrazů, které rozezná. Top-down automat nad F je trojice A=<Q, q 0, > kde Q je konečná množina stavů, q 0 je počáteční stav a
15 je množina pravidel nad F Q kde stavy jsou unárními symboly. Pravidla z jsou následujícího typu: q(f(x 1,, x n )) A f(q 1 (x 1 ),, q n (x n )) kde n 0, f F n, q, q 1,. q n Q, x 1,, x n jsou proměnné. Pokud n=0, pak je pravidlo ve tvaru q(a) a. Pak získáváme L q (a)={t T(F) q(t) * A t, je L(a) = L q0 (a) jazyk rozpoznatelný automatem A. q0(encrypt(x; y)) A encrypt(q1(x); q2(y)) q0(k1) A K1 q0(k2) A K2 q1(x) A X q3(k1) A K1 q4(k2) A K2 (a) Strom Zakroužkované uzly reprezentují stavy, ostatní uzly symboly. (b) Odpovídající množina pravidel Obr. : Automat ({q 0,, q 4, q 0, ) s množinou konstant {X, K 1, K 2 který rozpoznává {encrypt(x, encrypt(k 1, K 2 )), K 1, K 2.
16 Takto zkonstruovaný automat má dva typy uzlů: stavy, které mají o (neuspořádaný a také možný prázdný) seznam poduzlů, které všechny jsou symboly o značku (hodnotu) typu boolean. Pokud true (reprezentováno ) znamená množinu pravidel { f q (s(x 1 ; ; x n )) A s(q(x 1 ); ; q(x n )) s O n, n N. symboly, které mají uspořádaný seznam poduzlů; těchto poduzlů je právě takový počet jaká je arita uvedeného symbolu Nad zkonstruovaným automatem lze definovat mnohé další operace, které však již převyšují rámec této práce. Více informací lze nalézt v literatuře [1]. 5 PRŮBĚH VERIFIKACE Verifikační program zkonstruovaný autory této teorie [1] čte vstupní soubor obsahující následující informace: algebra rozdělená na public a private konstruktory; přičemž privátní konstruktory nejsou přístupné útočníkovi přepisovací systém počáteční množina znalostí útočníka množina L definující jakých znalostí chce útočník dosáhnout programy spustitelné jednotlivými subjekty Verifikační program pak prochází (spouští) instrukce jednotlivých subjektů s ohledem na abstraktnost operací, a zobrazuje mezistavy, ve byly překročeny bezpečnostní požadavky. To se stane v momentě, kdy se v množině znalostí útočníka vyskytne prvek z množiny L. 6 ZÁVĚR Tato práce měla za úkol nastínit princip abstrakce bezpečnostních protokolů za použití stromových automatů. Hlavní nevýhodou tohoto přístupu je velké množství mezistavů, které je třeba zkontrolovat. Toto znemožňuje současnou analýzu rozsáhlejších protokolů. Náročnost analýzy je také dána složitostí algoritmů, které pracují s abstraktními množinami stromů. Nicméně je tato metoda vhodná pro analýzu menších protokolů (ideálně max. 4 zúčastněné subjekty). Výhodou je přehledná specifikace pravidel a programových kroků jednotlivých subjektů. Další nespornou výhodou je možnost okamžitého vypsání stavu, ve kterém je porušena bezpečnost.
17 LITERATURA [1] Monniaux, D.: Abstracting Cryptographic Protocols with Tree automata. In Proc. 6th International Static Analysis Symposium (SAS'99), vol of Lecture Notes in Computer Science, Springer- Verlag, [2] Očenášek, P.: Verification of Security Protocols, In: Proceedings of the 9th Conference and Competition STUDENT EEICT 2003, Brno, CZ, FEKT VUT, 2003, p , ISBN [3] Očenášek, P.: On Inductive Approach in Security Protocol Verification, In: Proceedings of the 10th Conference and Competition STUDENT EEICT 2004, Brno, CZ, FEKT VUT, 2004, p , ISBN [4] Paulson, C. L.: Proving Security Protocols Correct, Computer Laboratory at University of Cambridge, 1998 [5] Pitt, Martin: Modeling and verification of security protocols, Dresden University of Technology, November 2002 [6] Ma L., Tsai Jeffrey: Formal verification techniques for computer communication security protocols, University of Illinois, Chicago, 2000 [7] Huima A., Efficient Infnite-State Analysis of Security Protocols, [8] Leathrum J.F., Morsi R., Leathrum T.E.: Formal Verification of Communication Protocols,
Andrew Kozlík KA MFF UK
 Autentizační kód zprávy Andrew Kozlík KA MFF UK Autentizační kód zprávy Anglicky: message authentication code (MAC). MAC algoritmus je v podstatě hashovací funkce s klíčem: MAC : {0, 1} k {0, 1} {0, 1}
Autentizační kód zprávy Andrew Kozlík KA MFF UK Autentizační kód zprávy Anglicky: message authentication code (MAC). MAC algoritmus je v podstatě hashovací funkce s klíčem: MAC : {0, 1} k {0, 1} {0, 1}
PSK2-16. Šifrování a elektronický podpis I
 PSK2-16 Název školy: Autor: Anotace: Vzdělávací oblast: Předmět: Vyšší odborná škola a Střední průmyslová škola, Božetěchova 3 Ing. Marek Nožka Jak funguje asymetrická šifra a elektronický podpis Informační
PSK2-16 Název školy: Autor: Anotace: Vzdělávací oblast: Předmět: Vyšší odborná škola a Střední průmyslová škola, Božetěchova 3 Ing. Marek Nožka Jak funguje asymetrická šifra a elektronický podpis Informační
Protokol pro zabezpečení elektronických transakcí - SET
 Protokol pro zabezpečení elektronických transakcí - SET Ing. Petr Číka Vysoké učení technické v Brně, Fakulta elektrotechniky a komunikačních technologií, Ústav telekomunikací, Purkyňova 118, 612 00 Brno,
Protokol pro zabezpečení elektronických transakcí - SET Ing. Petr Číka Vysoké učení technické v Brně, Fakulta elektrotechniky a komunikačních technologií, Ústav telekomunikací, Purkyňova 118, 612 00 Brno,
ElGamal, Diffie-Hellman
 Asymetrické šifrování 22. dubna 2010 Prezentace do předmětu UKRY Osnova 1 Diskrétní logaritmus 2 ElGamal 3 Diffie-Hellman Osnova 1 Diskrétní logaritmus 2 ElGamal 3 Diffie-Hellman Osnova 1 Diskrétní logaritmus
Asymetrické šifrování 22. dubna 2010 Prezentace do předmětu UKRY Osnova 1 Diskrétní logaritmus 2 ElGamal 3 Diffie-Hellman Osnova 1 Diskrétní logaritmus 2 ElGamal 3 Diffie-Hellman Osnova 1 Diskrétní logaritmus
Bezpečnost internetového bankovnictví, bankomaty
 , bankomaty Filip Marada, filipmarada@gmail.com KM FJFI 15. května 2014 15. května 2014 1 / 18 Obsah prezentace 1 Bezpečnost internetového bankovnictví Možná rizika 2 Bankomaty Výběr z bankomatu Možná
, bankomaty Filip Marada, filipmarada@gmail.com KM FJFI 15. května 2014 15. května 2014 1 / 18 Obsah prezentace 1 Bezpečnost internetového bankovnictví Možná rizika 2 Bankomaty Výběr z bankomatu Možná
Kryptografie založená na problému diskrétního logaritmu
 Kryptografie založená na problému diskrétního logaritmu Andrew Kozlík KA MFF UK Diffieho-Hellmanův protokol ustanovení klíče (1976) Před zahájením protokolu se ustanoví veřejně známé parametry: Konečná
Kryptografie založená na problému diskrétního logaritmu Andrew Kozlík KA MFF UK Diffieho-Hellmanův protokol ustanovení klíče (1976) Před zahájením protokolu se ustanoví veřejně známé parametry: Konečná
Identifikátor materiálu: ICT-2-04
 Identifikátor materiálu: ICT-2-04 Předmět Téma sady Informační a komunikační technologie Téma materiálu Zabezpečení informací Autor Ing. Bohuslav Nepovím Anotace Student si procvičí / osvojí kryptografii.
Identifikátor materiálu: ICT-2-04 Předmět Téma sady Informační a komunikační technologie Téma materiálu Zabezpečení informací Autor Ing. Bohuslav Nepovím Anotace Student si procvičí / osvojí kryptografii.
Šifrování Autentizace Bezpečnostní slabiny. Bezpečnost. Lenka Kosková Třísková, NTI TUL. 22. března 2013
 Šifrování Autentizace ní slabiny 22. března 2013 Šifrování Autentizace ní slabiny Technologie Symetrické vs. asymetrické šifry (dnes kombinace) HTTPS Funguje nad HTTP Šifrování s pomocí SSL nebo TLS Šifrování
Šifrování Autentizace ní slabiny 22. března 2013 Šifrování Autentizace ní slabiny Technologie Symetrické vs. asymetrické šifry (dnes kombinace) HTTPS Funguje nad HTTP Šifrování s pomocí SSL nebo TLS Šifrování
Směry rozvoje v oblasti ochrany informací PS 7
 1 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Směry rozvoje v oblasti ochrany informací PS 7 2 Osnova vývoj symetrických a asymetrických metod; bezpečnostní protokoly; PKI; šifrováochranavinternetu;
1 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Směry rozvoje v oblasti ochrany informací PS 7 2 Osnova vývoj symetrických a asymetrických metod; bezpečnostní protokoly; PKI; šifrováochranavinternetu;
SSL Secure Sockets Layer
 SSL Secure Sockets Layer internetové aplikační protokoly jsou nezabezpečené SSL vkládá do architektury šifrující vrstvu aplikační (HTTP, IMAP,...) SSL transportní (TCP, UDP) síťová (IP) SSL poskytuje zabezpečenou
SSL Secure Sockets Layer internetové aplikační protokoly jsou nezabezpečené SSL vkládá do architektury šifrující vrstvu aplikační (HTTP, IMAP,...) SSL transportní (TCP, UDP) síťová (IP) SSL poskytuje zabezpečenou
Základy kryptografie. Beret CryptoParty 11.02.2013. 11.02.2013 Základy kryptografie 1/17
 Základy kryptografie Beret CryptoParty 11.02.2013 11.02.2013 Základy kryptografie 1/17 Obsah prezentace 1. Co je to kryptografie 2. Symetrická kryptografie 3. Asymetrická kryptografie Asymetrické šifrování
Základy kryptografie Beret CryptoParty 11.02.2013 11.02.2013 Základy kryptografie 1/17 Obsah prezentace 1. Co je to kryptografie 2. Symetrická kryptografie 3. Asymetrická kryptografie Asymetrické šifrování
Y36PSI Bezpečnost v počítačových sítích. Jan Kubr - 10_11_bezpecnost Jan Kubr 1/41
 Y36PSI Bezpečnost v počítačových sítích Jan Kubr - 10_11_bezpecnost Jan Kubr 1/41 Osnova základní pojmy typy šifer autentizace integrita distribuce klíčů firewally typy útoků zabezpečení aplikací Jan Kubr
Y36PSI Bezpečnost v počítačových sítích Jan Kubr - 10_11_bezpecnost Jan Kubr 1/41 Osnova základní pojmy typy šifer autentizace integrita distribuce klíčů firewally typy útoků zabezpečení aplikací Jan Kubr
Projekt: 1.5, Registrační číslo: CZ.1.07/1.5.00/ Digitální podpisy
 VY_32_INOVACE_BEZP_08 Projekt: 1.5, Registrační číslo: CZ.1.07/1.5.00/34.0304 Digitální podpisy Základní myšlenkou elektronického podpisu je obdoba klasického podpisu, jež má zaručit jednoznačnou identifikaci
VY_32_INOVACE_BEZP_08 Projekt: 1.5, Registrační číslo: CZ.1.07/1.5.00/34.0304 Digitální podpisy Základní myšlenkou elektronického podpisu je obdoba klasického podpisu, jež má zaručit jednoznačnou identifikaci
9. DSA, PKI a infrastruktura. doc. Ing. Róbert Lórencz, CSc.
 Bezpečnost 9. DSA, PKI a infrastruktura doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních programů Informatika
Bezpečnost 9. DSA, PKI a infrastruktura doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních programů Informatika
Správa přístupu PS3-2
 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Správa přístupu PS3-2 1 Osnova II základní metody pro zajištění oprávněného přístupu; autentizace; autorizace; správa uživatelských účtů; srovnání současných
Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Správa přístupu PS3-2 1 Osnova II základní metody pro zajištění oprávněného přístupu; autentizace; autorizace; správa uživatelských účtů; srovnání současných
PV157 Autentizace a řízení přístupu
 PV157 Autentizace a řízení přístupu Zdeněk Říha Vašek Matyáš Konzultační hodiny FI MU: B415 St 17:00 18:00 část semestru mimo CZ Microsoft Research Cambridge Email: zriha / matyas @fi.muni.cz Průběh kurzu
PV157 Autentizace a řízení přístupu Zdeněk Říha Vašek Matyáš Konzultační hodiny FI MU: B415 St 17:00 18:00 část semestru mimo CZ Microsoft Research Cambridge Email: zriha / matyas @fi.muni.cz Průběh kurzu
Diffieho-Hellmanův protokol ustanovení klíče
 Diffieho-Hellmanův protokol ustanovení klíče Andrew Kozlík KA MFF UK Diffieho-Hellmanův protokol ustanovení klíče (1976) Před zahájením protokolu se ustanoví veřejně známé parametry: Konečná grupa (G,
Diffieho-Hellmanův protokol ustanovení klíče Andrew Kozlík KA MFF UK Diffieho-Hellmanův protokol ustanovení klíče (1976) Před zahájením protokolu se ustanoví veřejně známé parametry: Konečná grupa (G,
Kryptografie, elektronický podpis. Ing. Miloslav Hub, Ph.D. 27. listopadu 2007
 Kryptografie, elektronický podpis Ing. Miloslav Hub, Ph.D. 27. listopadu 2007 Kryptologie Kryptologie věda o šifrování, dělí se: Kryptografie nauka o metodách utajování smyslu zpráv převodem do podoby,
Kryptografie, elektronický podpis Ing. Miloslav Hub, Ph.D. 27. listopadu 2007 Kryptologie Kryptologie věda o šifrování, dělí se: Kryptografie nauka o metodách utajování smyslu zpráv převodem do podoby,
Hesla a bezpečnost na internetu MjUNI 2019 Dětská univerzita,
 Hesla a bezpečnost na internetu MjUNI 2019 Dětská univerzita, 13. 4. 2019 Vladimír Sedláček, vlada.sedlacek@mail.muni.cz Marek Sýs, syso@mail.muni.cz Osnova Hesla: Jaké jsou typické problémy? Jak si zvolit
Hesla a bezpečnost na internetu MjUNI 2019 Dětská univerzita, 13. 4. 2019 Vladimír Sedláček, vlada.sedlacek@mail.muni.cz Marek Sýs, syso@mail.muni.cz Osnova Hesla: Jaké jsou typické problémy? Jak si zvolit
8. RSA, kryptografie s veřejným klíčem. doc. Ing. Róbert Lórencz, CSc.
 Bezpečnost 8. RSA, kryptografie s veřejným klíčem doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních programů
Bezpečnost 8. RSA, kryptografie s veřejným klíčem doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních programů
Seminární práce do předmětu: Bezpečnost informačních systémů. téma: IPsec. Vypracoval: Libor Stránský
 Seminární práce do předmětu: Bezpečnost informačních systémů téma: IPsec Vypracoval: Libor Stránský Co je to IPsec? Jedná se o skupinu protokolů zabezpečujících komunikaci na úrovni protokolu IP (jak už
Seminární práce do předmětu: Bezpečnost informačních systémů téma: IPsec Vypracoval: Libor Stránský Co je to IPsec? Jedná se o skupinu protokolů zabezpečujících komunikaci na úrovni protokolu IP (jak už
Elektronický podpis. Základní princip. Digitální podpis. Podpis vs. šifrování. Hashování. Jednosměrné funkce. Odesílatel. Příjemce
 Základní princip Elektronický podpis Odesílatel podepíše otevřený text vznikne digitálně podepsaný text Příjemce ověří zda podpis patří odesílateli uvěří v pravost podpisu ověří zda podpis a text k sobě
Základní princip Elektronický podpis Odesílatel podepíše otevřený text vznikne digitálně podepsaný text Příjemce ověří zda podpis patří odesílateli uvěří v pravost podpisu ověří zda podpis a text k sobě
ERP-001, verze 2_10, platnost od
 ERP-001, verze 2_10, platnost od 2010.08.01. ELEKTRONICKÉ PŘEDEPISOVÁNÍ HUMÁNNÍCH LÉČIVÝCH PŘÍPRAVKŮ ERP-001.pdf (208,89 KB) Tímto technickým dokumentem jsou, v souladu s 80 zákona č. 378/2007 Sb., o léčivech
ERP-001, verze 2_10, platnost od 2010.08.01. ELEKTRONICKÉ PŘEDEPISOVÁNÍ HUMÁNNÍCH LÉČIVÝCH PŘÍPRAVKŮ ERP-001.pdf (208,89 KB) Tímto technickým dokumentem jsou, v souladu s 80 zákona č. 378/2007 Sb., o léčivech
Asymetrická kryptografie a elektronický podpis. Ing. Mgr. Martin Henzl Mgr. Radim Janča ijanca@fit.vutbr.cz
 Asymetrická kryptografie a elektronický podpis Ing. Mgr. Martin Henzl Mgr. Radim Janča ijanca@fit.vutbr.cz Obsah cvičení Asymetrická, symetrická a hybridní kryptografie Matematické problémy, na kterých
Asymetrická kryptografie a elektronický podpis Ing. Mgr. Martin Henzl Mgr. Radim Janča ijanca@fit.vutbr.cz Obsah cvičení Asymetrická, symetrická a hybridní kryptografie Matematické problémy, na kterých
Desktop systémy Microsoft Windows
 Desktop systémy Microsoft Windows IW1/XMW1 2013/2014 Jan Fiedor, přednášející Peter Solár ifiedor@fit.vutbr.cz, solar@pocitacoveskoleni.cz Fakulta Informačních Technologií Vysoké Učení Technické v Brně
Desktop systémy Microsoft Windows IW1/XMW1 2013/2014 Jan Fiedor, přednášející Peter Solár ifiedor@fit.vutbr.cz, solar@pocitacoveskoleni.cz Fakulta Informačních Technologií Vysoké Učení Technické v Brně
DNSSEC. Proč je důležité chránit internetové domény? CZ.NIC z.s.p.o. Pavel Tůma pavel.tuma@nic.cz 11. 2. 2009
 DNSSEC Proč je důležité chránit internetové domény? CZ.NIC z.s.p.o. Pavel Tůma pavel.tuma@nic.cz 11. 2. 2009 1 Systém doménových jmen Proč vlastně doménová jména? IP adresa 124.45.10.231 2001:1488:800:200:217:a4ff:fea7:49fe
DNSSEC Proč je důležité chránit internetové domény? CZ.NIC z.s.p.o. Pavel Tůma pavel.tuma@nic.cz 11. 2. 2009 1 Systém doménových jmen Proč vlastně doménová jména? IP adresa 124.45.10.231 2001:1488:800:200:217:a4ff:fea7:49fe
PA159 - Bezpečnostní aspekty
 PA159 - Bezpečnostní aspekty 19. 10. 2007 Formulace oblasti Kryptografie (v moderním slova smyslu) se snaží minimalizovat škodu, kterou může způsobit nečestný účastník Oblast bezpečnosti počítačových sítí
PA159 - Bezpečnostní aspekty 19. 10. 2007 Formulace oblasti Kryptografie (v moderním slova smyslu) se snaží minimalizovat škodu, kterou může způsobit nečestný účastník Oblast bezpečnosti počítačových sítí
KRYPTOGRAFIE VER EJNE HO KLI Č E
 KRYPTOGRAFIE VER EJNE HO KLI Č E ÚVOD Patricie Vyzinová Jako téma jsem si vybrala asymetrickou kryptografii (kryptografie s veřejným klíčem), což je skupina kryptografických metod, ve kterých se pro šifrování
KRYPTOGRAFIE VER EJNE HO KLI Č E ÚVOD Patricie Vyzinová Jako téma jsem si vybrala asymetrickou kryptografii (kryptografie s veřejným klíčem), což je skupina kryptografických metod, ve kterých se pro šifrování
asymetrická kryptografie
 asymetrická kryptografie princip šifrování Zavazadlový algoritmus RSA EL GAMAL další asymetrické blokové algoritmy Skipjack a Kea, DSA, ECDSA D H, ECDH asymetrická kryptografie jeden klíč pro šifrování
asymetrická kryptografie princip šifrování Zavazadlový algoritmus RSA EL GAMAL další asymetrické blokové algoritmy Skipjack a Kea, DSA, ECDSA D H, ECDH asymetrická kryptografie jeden klíč pro šifrování
Množinu všech slov nad abecedou Σ značíme Σ * Množinu všech neprázdných slov Σ + Jazyk nad abecedou Σ je libovolná množina slov nad Σ
 Abecedou se rozumí libovolná konečná množina Σ. Prvky abecedy nazýváme znaky (symboly) Slovo (řetězec) v nad abecedou Σ je libovolná konečná posloupnost znaků této abecedy. Prázdné posloupnosti znaků odpovídá
Abecedou se rozumí libovolná konečná množina Σ. Prvky abecedy nazýváme znaky (symboly) Slovo (řetězec) v nad abecedou Σ je libovolná konečná posloupnost znaků této abecedy. Prázdné posloupnosti znaků odpovídá
bit/p6d-h.d 22. března
 bit/pd-h.d 22. března 2003 Needham-Schroederův protokol... * základní varianta Needham a Schroeder 978 * zajímavý zejména z historických důvodů, protože je základem mnoha autentizačních protokolů a protokolů
bit/pd-h.d 22. března 2003 Needham-Schroederův protokol... * základní varianta Needham a Schroeder 978 * zajímavý zejména z historických důvodů, protože je základem mnoha autentizačních protokolů a protokolů
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Protokol TELNET. Schéma funkčních modulů komunikace protokolem TELNET. Telnet klient. login shell. Telnet server TCP/IP.
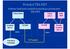 Protokol TELNET Schéma funkčních modulů komunikace protokolem TELNET Telnet klient Telnet server login shell terminal driver Jádro TCP/IP TCP/IP Jádro Pseudo terminal driver Uživatel u terminálu TCP spojení
Protokol TELNET Schéma funkčních modulů komunikace protokolem TELNET Telnet klient Telnet server login shell terminal driver Jádro TCP/IP TCP/IP Jádro Pseudo terminal driver Uživatel u terminálu TCP spojení
KLASICKÝ MAN-IN-THE-MIDDLE
 SNIFFING SNIFFING je technika, při které dochází k ukládání a následnému čtení TCP paketů. Používá se zejména při diagnostice sítě, zjištění používaných služeb a protokolů a odposlechu datové komunikace.
SNIFFING SNIFFING je technika, při které dochází k ukládání a následnému čtení TCP paketů. Používá se zejména při diagnostice sítě, zjištění používaných služeb a protokolů a odposlechu datové komunikace.
Úlohy k procvičování textu o univerzální algebře
 Úlohy k procvičování textu o univerzální algebře Číslo za pomlčkou v označení úlohy je číslo kapitoly textu, která je úlohou procvičovaná. Každá úloha je vyřešena o několik stránek později. Kontrolní otázky
Úlohy k procvičování textu o univerzální algebře Číslo za pomlčkou v označení úlohy je číslo kapitoly textu, která je úlohou procvičovaná. Každá úloha je vyřešena o několik stránek později. Kontrolní otázky
Asymetrické šifry. Pavla Henzlová 28.3.2011. FJFI ČVUT v Praze. Pavla Henzlová (FJFI ČVUT v Praze) Asymetrické šifry 28.3.
 Asymetrické šifry Pavla Henzlová FJFI ČVUT v Praze 28.3.2011 Pavla Henzlová (FJFI ČVUT v Praze) Asymetrické šifry 28.3.2011 1 / 16 Obsah 1 Asymetrická kryptografie 2 Diskrétní logaritmus 3 Baby step -
Asymetrické šifry Pavla Henzlová FJFI ČVUT v Praze 28.3.2011 Pavla Henzlová (FJFI ČVUT v Praze) Asymetrické šifry 28.3.2011 1 / 16 Obsah 1 Asymetrická kryptografie 2 Diskrétní logaritmus 3 Baby step -
Asymetrická kryptografie
 PEF MZLU v Brně 12. listopadu 2007 Problém výměny klíčů Problém výměny klíčů mezi odesílatelem a příjemcem zprávy trápil kryptografy po několik století. Problém spočívá ve výměně tajné informace tak, aby
PEF MZLU v Brně 12. listopadu 2007 Problém výměny klíčů Problém výměny klíčů mezi odesílatelem a příjemcem zprávy trápil kryptografy po několik století. Problém spočívá ve výměně tajné informace tak, aby
ELEKTRONICKÝ PODPIS V PODNIKOVÝCH APLIKACÍCH. Tomáš Vaněk ICT Security Consultant
 ELEKTRONICKÝ PODPIS V PODNIKOVÝCH APLIKACÍCH Tomáš Vaněk ICT Security Consultant ELEKTRONICKÝ PODPIS A JEHO VLASTNOSTI Uplatnění elektronického podpisu a časového razítka Integrita Identifikace Nepopiratelnost
ELEKTRONICKÝ PODPIS V PODNIKOVÝCH APLIKACÍCH Tomáš Vaněk ICT Security Consultant ELEKTRONICKÝ PODPIS A JEHO VLASTNOSTI Uplatnění elektronického podpisu a časového razítka Integrita Identifikace Nepopiratelnost
Informatika / bezpečnost
 Informatika / bezpečnost Bezpečnost, šifry, elektronický podpis ZS 2015 KIT.PEF.CZU Bezpečnost IS pojmy aktiva IS hardware software data citlivá data hlavně ta chceme chránit autorizace subjekt má právo
Informatika / bezpečnost Bezpečnost, šifry, elektronický podpis ZS 2015 KIT.PEF.CZU Bezpečnost IS pojmy aktiva IS hardware software data citlivá data hlavně ta chceme chránit autorizace subjekt má právo
Matematické základy šifrování a kódování
 Matematické základy šifrování a kódování Permutace Pojem permutace patří mezi základní pojmy a nachází uplatnění v mnoha oblastech, např. kombinatorice, algebře apod. Definice Nechť je n-prvková množina.
Matematické základy šifrování a kódování Permutace Pojem permutace patří mezi základní pojmy a nachází uplatnění v mnoha oblastech, např. kombinatorice, algebře apod. Definice Nechť je n-prvková množina.
Autentizace uživatelů
 Autentizace uživatelů základní prvek ochrany sítí a systémů kromě povolování přístupu lze uživatele členit do skupin, nastavovat různá oprávnění apod. nejčastěji dvojicí jméno a heslo další varianty: jednorázová
Autentizace uživatelů základní prvek ochrany sítí a systémů kromě povolování přístupu lze uživatele členit do skupin, nastavovat různá oprávnění apod. nejčastěji dvojicí jméno a heslo další varianty: jednorázová
Strukturování Petriho Nadpis 2 Nadpis 3
 Strukturování Petriho Nadpissítí 1 Nadpis 2 Nadpis 3 Vladimír JménoJanoušek Příjmení VysokéVysoké učení technické učení technické v Brně,vFakulta Brně, Fakulta informačních informačních technologií technologií
Strukturování Petriho Nadpissítí 1 Nadpis 2 Nadpis 3 Vladimír JménoJanoušek Příjmení VysokéVysoké učení technické učení technické v Brně,vFakulta Brně, Fakulta informačních informačních technologií technologií
Přednáška 10. X Window. Secure shell. Úvod do Operačních Systémů Přednáška 10
 Přednáška 10 X Window. Secure shell. 1 X Window systém I Systém pro správu oken. Poskytuje nástroje pro tvorbu GUI (Graphical User Interface) a grafických aplikací. Nezávislý na hardwaru. Transparentní
Přednáška 10 X Window. Secure shell. 1 X Window systém I Systém pro správu oken. Poskytuje nástroje pro tvorbu GUI (Graphical User Interface) a grafických aplikací. Nezávislý na hardwaru. Transparentní
Digitální podepisování pomocí asymetrické kryptografie
 Digitální podepisování pomocí asymetrické kryptografie 11. dubna 2011 Trocha historie Asymetrické metody Historie Historie Vlastnosti Asymetrické šifrování 1976 Whitfield Diffie a Martin Hellman první
Digitální podepisování pomocí asymetrické kryptografie 11. dubna 2011 Trocha historie Asymetrické metody Historie Historie Vlastnosti Asymetrické šifrování 1976 Whitfield Diffie a Martin Hellman první
platné nejsou Sokrates je smrtelný. (r) 1/??
 Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Protokol TELNET. Schéma funkčních modulů komunikace protokolem TELNET. Telnet klient. login shell. Telnet server TCP/IP TCP/IP.
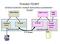 Protokol TELNET Schéma funkčních modulů komunikace protokolem TELNET Telnet klient Telnet server login shell terminal driver Operační systém TCP/IP TCP spojení TCP/IP Pseudo terminal driver Operační systém
Protokol TELNET Schéma funkčních modulů komunikace protokolem TELNET Telnet klient Telnet server login shell terminal driver Operační systém TCP/IP TCP spojení TCP/IP Pseudo terminal driver Operační systém
SIM karty a bezpečnost v mobilních sítích
 Spojujeme software, technologie a služby SIM karty a bezpečnost v mobilních sítích Václav Lín programátor 19.5.2009 1 Osnova SIM karty Role SIM karet v telekomunikacích Hardwarové charakteristiky Bezpečnost
Spojujeme software, technologie a služby SIM karty a bezpečnost v mobilních sítích Václav Lín programátor 19.5.2009 1 Osnova SIM karty Role SIM karet v telekomunikacích Hardwarové charakteristiky Bezpečnost
Digitální měna Bitcoin. Dalibor Hula Slezská univerzita v Opavě OPF v Karviné
 Digitální měna Bitcoin Dalibor Hula Slezská univerzita v Opavě OPF v Karviné Výpomoc bankám Blokáda Wikileaks Peníze kryty zlatem Platby do zahraničí Peníze Odkud se berou? Co jim dává hodnotu? Kolik jich
Digitální měna Bitcoin Dalibor Hula Slezská univerzita v Opavě OPF v Karviné Výpomoc bankám Blokáda Wikileaks Peníze kryty zlatem Platby do zahraničí Peníze Odkud se berou? Co jim dává hodnotu? Kolik jich
Co je Czech Point? Podací Ověřovací Informační Národní Terminál, zredukovat přílišnou byrokracii ve vztahu
 Czech Point Co je Czech Point? Podací Ověřovací Informační Národní Terminál, tedy Czech POINT je projektem, který by měl zredukovat přílišnou byrokracii ve vztahu občan veřejná správa. Czech POINT bude
Czech Point Co je Czech Point? Podací Ověřovací Informační Národní Terminál, tedy Czech POINT je projektem, který by měl zredukovat přílišnou byrokracii ve vztahu občan veřejná správa. Czech POINT bude
Naproti tomu gramatika je vlastně soupis pravidel, jak
 1 Kapitola 1 Úvod V přednášce se zaměříme hlavně na konečný popis obecně nekonečných množin řetězců symbolů dané množiny A. Prvkům množiny A budeme říkat písmena, řetězcům (konečným posloupnostem) písmen
1 Kapitola 1 Úvod V přednášce se zaměříme hlavně na konečný popis obecně nekonečných množin řetězců symbolů dané množiny A. Prvkům množiny A budeme říkat písmena, řetězcům (konečným posloupnostem) písmen
4.2 Syntaxe predikátové logiky
 36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
Projekt 2 - Nejčastější chyby. Ing. Dominik Breitenbacher
 Projekt 2 - Nejčastější chyby Ing. Dominik Breitenbacher ibreiten@fit.vutbr.cz Projekt 2 - Nejčastější chyby Překlepy a interpunkce Estetika Kvalita obrázků Zdrojové kódy v textu Text nebyl rozdělen na
Projekt 2 - Nejčastější chyby Ing. Dominik Breitenbacher ibreiten@fit.vutbr.cz Projekt 2 - Nejčastější chyby Překlepy a interpunkce Estetika Kvalita obrázků Zdrojové kódy v textu Text nebyl rozdělen na
Šifrování ve Windows. EFS IPSec SSL. - Encrypting File System - Internet Protocol Security - Secure Socket Layer - Private Point to Point Protocol
 Šifrování ve Windows EFS IPSec SSL PPTP - Encrypting File System - Internet Protocol Security - Secure Socket Layer - Private Point to Point Protocol 18.11.2003 vjj 1 Bezpečnost? co chci chránit? systém
Šifrování ve Windows EFS IPSec SSL PPTP - Encrypting File System - Internet Protocol Security - Secure Socket Layer - Private Point to Point Protocol 18.11.2003 vjj 1 Bezpečnost? co chci chránit? systém
Šifrování (2), FTP. Petr Koloros p.koloros [at] sh.cvut.cz. http://sut.sh.cvut.cz
![Šifrování (2), FTP. Petr Koloros p.koloros [at] sh.cvut.cz. http://sut.sh.cvut.cz Šifrování (2), FTP. Petr Koloros p.koloros [at] sh.cvut.cz. http://sut.sh.cvut.cz](/thumbs/25/5884225.jpg) Šifrování (2), FTP Petr Koloros p.koloros [at] sh.cvut.cz http://sut.sh.cvut.cz Obsah Úvod do šifrování FTP FTP server ProFTPd Šifrovaný přístup Virtuální servery Síť FTPek na klíč FTP File Transfer Protokol
Šifrování (2), FTP Petr Koloros p.koloros [at] sh.cvut.cz http://sut.sh.cvut.cz Obsah Úvod do šifrování FTP FTP server ProFTPd Šifrovaný přístup Virtuální servery Síť FTPek na klíč FTP File Transfer Protokol
7. Aplikační vrstva. Aplikační vrstva. Počítačové sítě I. 1 (5) KST/IPS1. Studijní cíl. Představíme si funkci aplikační vrstvy a jednotlivé protokoly.
 7. Aplikační vrstva Studijní cíl Představíme si funkci aplikační vrstvy a jednotlivé protokoly. Doba nutná k nastudování 2 hodiny Aplikační vrstva Účelem aplikační vrstvy je poskytnout aplikačním procesům
7. Aplikační vrstva Studijní cíl Představíme si funkci aplikační vrstvy a jednotlivé protokoly. Doba nutná k nastudování 2 hodiny Aplikační vrstva Účelem aplikační vrstvy je poskytnout aplikačním procesům
Výroková a predikátová logika - III
 Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2014/2015 1 / 21 Výroková logika Horn-SAT Horn-SAT Jednotková
Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2014/2015 1 / 21 Výroková logika Horn-SAT Horn-SAT Jednotková
doplněk, zřetězení, Kleeneho operaci a reverzi. Ukážeme ještě další operace s jazyky, na které je
 28 [181105-1236 ] 2.7 Další uzávěrové vlastnosti třídy regulárních jazyků Z předchozích přednášek víme, že třída regulárních jazyků je uzavřena na sjednocení, průnik, doplněk, zřetězení, Kleeneho operaci
28 [181105-1236 ] 2.7 Další uzávěrové vlastnosti třídy regulárních jazyků Z předchozích přednášek víme, že třída regulárních jazyků je uzavřena na sjednocení, průnik, doplněk, zřetězení, Kleeneho operaci
Šifrová ochrana informací věk počítačů PS5-2
 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 1 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací věk počítačů PS5-2 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 2 Osnova
VŠFS; Aplikovaná informatika; SW systémy 2005/2006 1 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací věk počítačů PS5-2 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 2 Osnova
496/2004 Sb. VYHLÁŠKA Ministerstva informatiky ze dne 29. července 2004 o elektronických podatelnách
 496/2004 Sb. VYHLÁŠKA Ministerstva informatiky ze dne 29. července 2004 o elektronických podatelnách Ministerstvo informatiky stanoví podle 20 odst. 4 zákona č. 227/2000 Sb., o elektronickém podpisu a
496/2004 Sb. VYHLÁŠKA Ministerstva informatiky ze dne 29. července 2004 o elektronických podatelnách Ministerstvo informatiky stanoví podle 20 odst. 4 zákona č. 227/2000 Sb., o elektronickém podpisu a
Šifrová ochrana informací věk počítačů PS5-2
 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací věk počítačů PS5-2 1 Osnova šifrová ochrana využívající výpočetní techniku např. Feistelova šifra; symetrické a asymetrické šifry;
Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací věk počítačů PS5-2 1 Osnova šifrová ochrana využívající výpočetní techniku např. Feistelova šifra; symetrické a asymetrické šifry;
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Výroková a predikátová logika - III
 Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2017/2018 1 / 16 2-SAT 2-SAT Výrok je v k-cnf, je-li v CNF a
Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2017/2018 1 / 16 2-SAT 2-SAT Výrok je v k-cnf, je-li v CNF a
Představíme základy bezdrátových sítí. Popíšeme jednotlivé typy sítí a zabezpečení.
 10. Bezdrátové sítě Studijní cíl Představíme základy bezdrátových sítí. Popíšeme jednotlivé typy sítí a zabezpečení. Doba nutná k nastudování 1,5 hodiny Bezdrátové komunikační technologie Uvedená kapitola
10. Bezdrátové sítě Studijní cíl Představíme základy bezdrátových sítí. Popíšeme jednotlivé typy sítí a zabezpečení. Doba nutná k nastudování 1,5 hodiny Bezdrátové komunikační technologie Uvedená kapitola
Množiny, relace, zobrazení
 Množiny, relace, zobrazení Množiny Množinou rozumíme každý soubor určitých objektů shrnutých v jeden celek. Zmíněné objekty pak nazýváme prvky dané množiny. Pojem množina je tedy synonymem pojmů typu soubor,
Množiny, relace, zobrazení Množiny Množinou rozumíme každý soubor určitých objektů shrnutých v jeden celek. Zmíněné objekty pak nazýváme prvky dané množiny. Pojem množina je tedy synonymem pojmů typu soubor,
Programování II. Návrh programu I 2018/19
 Programování II Návrh programu I 2018/19 Osnova přednášky Co víme? Objektový návrh programu. Příklad. Co víme? Třída Třída je popisem objektů se společnými vlastnostmi. class private:
Programování II Návrh programu I 2018/19 Osnova přednášky Co víme? Objektový návrh programu. Příklad. Co víme? Třída Třída je popisem objektů se společnými vlastnostmi. class private:
Unární je také spojka negace. pro je operace binární - příkladem může být funkce se signaturou. Binární je velká většina logických spojek
 Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Integrovaný informační systém Státní pokladny (IISSP) Dokumentace API - integrační dokumentace
 Česká republika Vlastník: Logica Czech Republic s.r.o. Page 1 of 10 Česká republika Obsah 1. Úvod...3 2. Východiska a postupy...4 2.1 Způsob dešifrování a ověření sady přístupových údajů...4 2.2 Způsob
Česká republika Vlastník: Logica Czech Republic s.r.o. Page 1 of 10 Česká republika Obsah 1. Úvod...3 2. Východiska a postupy...4 2.1 Způsob dešifrování a ověření sady přístupových údajů...4 2.2 Způsob
Systém Přenos verze 3.0
 Systém Přenos verze 3.0 (bezpečná komunikace a automatizované zpracování dat) CTlabs spol. s r.o. Pernštejnské Janovice 28, 593 01 Bystřice nad Pernštejnem, tel/fax.: 0505-551 011 www.ctlabs.cz info@ctlabs.cz
Systém Přenos verze 3.0 (bezpečná komunikace a automatizované zpracování dat) CTlabs spol. s r.o. Pernštejnské Janovice 28, 593 01 Bystřice nad Pernštejnem, tel/fax.: 0505-551 011 www.ctlabs.cz info@ctlabs.cz
Inovace bakalářského studijního oboru Aplikovaná chemie http://aplchem.upol.cz
 http://aplchem.upol.cz CZ.1.07/2.2.00/15.0247 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. Internet a zdroje Elektronická pošta a její správa, bezpečnost
http://aplchem.upol.cz CZ.1.07/2.2.00/15.0247 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. Internet a zdroje Elektronická pošta a její správa, bezpečnost
Příručka pro dodavatele. Systém EZVR 1.1 Verze dokumentu 1.3 Datum vydání:
 Příručka pro dodavatele Systém EZVR 1.1 Verze dokumentu 1.3 Datum vydání: 1.10.2017 1 2 1. Úvod do systému...3 2. Technické požadavky a zabezpečení systému...3 3. Registrace nového dodavatele...4 4. Přihlášení
Příručka pro dodavatele Systém EZVR 1.1 Verze dokumentu 1.3 Datum vydání: 1.10.2017 1 2 1. Úvod do systému...3 2. Technické požadavky a zabezpečení systému...3 3. Registrace nového dodavatele...4 4. Přihlášení
Internet, www, el. pošta, prohlížeče, služby, bezpečnost
 Internet, www, el. pošta, prohlížeče, služby, bezpečnost Internet jedná se o fyzické propojení komponent nacházejících se v počítačových sítí všech rozsahů LAN, MAN, WAN. Patří sem koncové uživatelské
Internet, www, el. pošta, prohlížeče, služby, bezpečnost Internet jedná se o fyzické propojení komponent nacházejících se v počítačových sítí všech rozsahů LAN, MAN, WAN. Patří sem koncové uživatelské
Hashovací funkce. Andrew Kozlík KA MFF UK
 Hashovací funkce Andrew Kozlík KA MFF UK Hashovací funkce Hashovací funkce je zobrazení h : {0, 1} {0, 1} n. Typicky n {128, 160, 192, 224, 256, 384, 512}. Obraz h(x) nazýváme otisk, hash nebo digest prvku
Hashovací funkce Andrew Kozlík KA MFF UK Hashovací funkce Hashovací funkce je zobrazení h : {0, 1} {0, 1} n. Typicky n {128, 160, 192, 224, 256, 384, 512}. Obraz h(x) nazýváme otisk, hash nebo digest prvku
EXTRAKT z mezinárodní normy
 EXTRAKT z mezinárodní normy Extrakt nenahrazuje samotnou technickou normu, je pouze informativním materiálem o normě ICS: 03.220.01; 35.240.60 CALM Základní přístupy k ochraně osobních dat z informačních
EXTRAKT z mezinárodní normy Extrakt nenahrazuje samotnou technickou normu, je pouze informativním materiálem o normě ICS: 03.220.01; 35.240.60 CALM Základní přístupy k ochraně osobních dat z informačních
Predikátová logika. prvního řádu
 Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
10. Techniky formální verifikace a validace
 Fakulta informačních technologií MI-NFA, zimní semestr 2011/2012 Jan Schmidt EVROPSKÝ SOCIÁLNÍ FOND PRAHA & EU: INVESTUJENE DO VAŠÍ BUDOUCNOSTI 10. Techniky formální verifikace a validace 1 Simulace není
Fakulta informačních technologií MI-NFA, zimní semestr 2011/2012 Jan Schmidt EVROPSKÝ SOCIÁLNÍ FOND PRAHA & EU: INVESTUJENE DO VAŠÍ BUDOUCNOSTI 10. Techniky formální verifikace a validace 1 Simulace není
Secure Shell. X Window.
 Přednáška 10 Secure Shell. X Window. Katedra číslicových systémů FIT, České vysoké učení technické v Praze Jan Trdlička, 2011 Příprava studijního programu Informatika je podporována projektem financovaným
Přednáška 10 Secure Shell. X Window. Katedra číslicových systémů FIT, České vysoké učení technické v Praze Jan Trdlička, 2011 Příprava studijního programu Informatika je podporována projektem financovaným
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Odesílání citlivých dat prostřednictvím šifrovaného emailu s elektronickým podpisem standardem S/MIME
 Odesílání citlivých dat prostřednictvím šifrovaného emailu s elektronickým podpisem standardem S/MIME Je dostupnou možností, jak lze zaslat lékařskou dokumentaci elektronicky. Co je třeba k odeslání šifrovaného
Odesílání citlivých dat prostřednictvím šifrovaného emailu s elektronickým podpisem standardem S/MIME Je dostupnou možností, jak lze zaslat lékařskou dokumentaci elektronicky. Co je třeba k odeslání šifrovaného
Bezpečnost vzdáleného přístupu. Jan Kubr
 Bezpečnost vzdáleného přístupu Jan Kubr Vzdálené připojení - protokoly IPsec PPTP, P2TP SSL, TSL IPsec I RFC 4301-4309 IPv6, IPv4 autentizace Authentication Header (AH) šifrování Encapsulating Security
Bezpečnost vzdáleného přístupu Jan Kubr Vzdálené připojení - protokoly IPsec PPTP, P2TP SSL, TSL IPsec I RFC 4301-4309 IPv6, IPv4 autentizace Authentication Header (AH) šifrování Encapsulating Security
INFORMATIKA (ŠIFROVÁNÍ A PODPIS) 2010/11
 INFORMATIKA (ŠIFROVÁNÍ A PODPIS) 2010/11 1.1 Šifrovaná a nešifrovaná komunikace Při přenosu dat (v technice i v živých organismech) se užívá: Kódování realizace nebo usnadnění přenosu informace. Morse
INFORMATIKA (ŠIFROVÁNÍ A PODPIS) 2010/11 1.1 Šifrovaná a nešifrovaná komunikace Při přenosu dat (v technice i v živých organismech) se užívá: Kódování realizace nebo usnadnění přenosu informace. Morse
Substituce. Petr Štěpánek. S využitím materialu Krysztofa R. Apta. Logické programování 2 1
 Substituce Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 2 1 Algebra termů Předpokládáme, že je dán jazyk termů. L, definovali jsme množinu jeho Zavedeme některé užitečné
Substituce Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 2 1 Algebra termů Předpokládáme, že je dán jazyk termů. L, definovali jsme množinu jeho Zavedeme některé užitečné
Turingovy stroje. Teoretická informatika Tomáš Foltýnek
 Turingovy stroje Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Jaké znáte algebraické struktury s jednou operací? Co je to okruh,
Turingovy stroje Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Jaké znáte algebraické struktury s jednou operací? Co je to okruh,
Náhled testu. Přijímací zkouška magisterského studia. konečný automat bez zbytečných stavů, který přijímá jazyk popsaný tímto výrazem, má:
 1 z 6 14.11.2017 0:03 Přijímací zkouška magisterského studia Moodle Test MSP Testy VzorTest-2 Pokus 1 Jste přihlášeni jako Josef Kolář (Odhlásit se) Náhled testu 1 Je dán regulární výraz. Minimální deterministický
1 z 6 14.11.2017 0:03 Přijímací zkouška magisterského studia Moodle Test MSP Testy VzorTest-2 Pokus 1 Jste přihlášeni jako Josef Kolář (Odhlásit se) Náhled testu 1 Je dán regulární výraz. Minimální deterministický
Kapitola 9. Kryptografie v běžném životě. Úvod. Výběr hotovosti z bankomatu
 Kapitola 9 Úvod V této knize jsme už opakovaně zdůrazňovali vliv kryptografie na podobu moderního světa a některé z důležitých prvků jsme ilustrovali na situacích z běžného života. V následující kapitole
Kapitola 9 Úvod V této knize jsme už opakovaně zdůrazňovali vliv kryptografie na podobu moderního světa a některé z důležitých prvků jsme ilustrovali na situacích z běžného života. V následující kapitole
teorie logických spojek chápaných jako pravdivostní funkce
 Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
TÉMATICKÝ OKRUH Softwarové inženýrství
 TÉMATICKÝ OKRUH Softwarové inženýrství Číslo otázky : 24. Otázka : Implementační fáze. Postupy při specifikaci organizace softwarových komponent pomocí UML. Mapování modelů na struktury programovacího
TÉMATICKÝ OKRUH Softwarové inženýrství Číslo otázky : 24. Otázka : Implementační fáze. Postupy při specifikaci organizace softwarových komponent pomocí UML. Mapování modelů na struktury programovacího
AUTOMATY A GRAMATIKY. Pavel Surynek. Kontextové uzávěrové vlastnosti Turingův stroj Rekurzivně spočetné jazyky Kódování, enumerace
 AUTOMATY A 11 GRAMATIKY Pavel Surynek Univerzita Karlova v Praze Matematicko-fyzikální fakulta Katedra teoretické informatiky a matematické logiky Kontextové uzávěrové vlastnosti Turingův stroj Rekurzivně
AUTOMATY A 11 GRAMATIKY Pavel Surynek Univerzita Karlova v Praze Matematicko-fyzikální fakulta Katedra teoretické informatiky a matematické logiky Kontextové uzávěrové vlastnosti Turingův stroj Rekurzivně
Jan Hrdinka. Bakalářská práce
 Vysoká škola ekonomická v Praze Fakulta informatiky a statistiky Vyšší odborná škola informačních služeb v Praze Jan Hrdinka Realizace zabezpečeného FTP serveru (SFTP a FTPS) a zabezpečeného HTTP (HTTPS)
Vysoká škola ekonomická v Praze Fakulta informatiky a statistiky Vyšší odborná škola informačních služeb v Praze Jan Hrdinka Realizace zabezpečeného FTP serveru (SFTP a FTPS) a zabezpečeného HTTP (HTTPS)
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti MI-SOC: 11 METODY VERIFIKACE SYSTÉMŮ NA ČIPU Hana Kubátov vá doc. Ing. Hana Kubátová, CSc. Katedra číslicového návrhu Fakulta 1 informačních
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti MI-SOC: 11 METODY VERIFIKACE SYSTÉMŮ NA ČIPU Hana Kubátov vá doc. Ing. Hana Kubátová, CSc. Katedra číslicového návrhu Fakulta 1 informačních
Sémantika predikátové logiky
 Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Náhled testu. Přijímací zkouška magisterského studia. konečný automat bez zbytečných stavů, který přijímá jazyk popsaný tímto výrazem, má:
 Přijímací zkouška magisterského studia Moodle Test MSP Testy VzorTest-2 Pokus 1 Jste přihlášeni jako Josef Kolář (Odhlásit se) Info Výsledky Náhled Upravit Náhled testu 1 Je dán regulární výraz. Minimální
Přijímací zkouška magisterského studia Moodle Test MSP Testy VzorTest-2 Pokus 1 Jste přihlášeni jako Josef Kolář (Odhlásit se) Info Výsledky Náhled Upravit Náhled testu 1 Je dán regulární výraz. Minimální
ŠIFROVACÍ METODA ZALOŽENÁ NA FRAKTÁLNÍ KOMPRESI. 1. Úvod. V posledních letech se ukázalo, že teorii fraktálů lze využít v mnoha teoretických
 Kvaternion 2 (2012, 83 89 83 ŠIFROVACÍ METODA ZALOŽENÁ NA FRAKTÁLNÍ KOMPRESI TOMÁŠ GRÍSA Abstrakt Tento článek se zabývá teoretickými principy fraktální komprese a využitím modifikovaného algoritmu fraktální
Kvaternion 2 (2012, 83 89 83 ŠIFROVACÍ METODA ZALOŽENÁ NA FRAKTÁLNÍ KOMPRESI TOMÁŠ GRÍSA Abstrakt Tento článek se zabývá teoretickými principy fraktální komprese a využitím modifikovaného algoritmu fraktální
Kryptografie - Síla šifer
 Kryptografie - Síla šifer Rozdělení šifrovacích systémů Krátká charakteristika Historie a současnost kryptografie Metody, odolnost Praktické příklady Slabá místa systémů Lidský faktor Rozdělení šifer Obousměrné
Kryptografie - Síla šifer Rozdělení šifrovacích systémů Krátká charakteristika Historie a současnost kryptografie Metody, odolnost Praktické příklady Slabá místa systémů Lidský faktor Rozdělení šifer Obousměrné
Počítačové sítě II. 20. Útoky na síť a její ochrana Miroslav Spousta, 2006 <qiq@ucw.cz>, http://www.ucw.cz/~qiq/vsfs/
 Počítačové sítě II 20. Útoky na síť a její ochrana Miroslav Spousta, 2006 , http://www.ucw.cz/~qiq/vsfs/ 1 Bezpečnost sítí cílem je ochránit počítačovou síť a především data/zařízení v nich
Počítačové sítě II 20. Útoky na síť a její ochrana Miroslav Spousta, 2006 , http://www.ucw.cz/~qiq/vsfs/ 1 Bezpečnost sítí cílem je ochránit počítačovou síť a především data/zařízení v nich
BEZPEČNOST INFORMACÍ
 Předmět Bezpečnost informací je zaměřen na bezpečnostní aspekty informačních systémů a na zkoumání základních prvků vytvářeného bezpečnostního programu v organizacích. Tyto prvky technologie, procesy a
Předmět Bezpečnost informací je zaměřen na bezpečnostní aspekty informačních systémů a na zkoumání základních prvků vytvářeného bezpečnostního programu v organizacích. Tyto prvky technologie, procesy a
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz
 Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti
 Kapitola 5 Vektorové prostory V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti operací sčítání a násobení
Kapitola 5 Vektorové prostory V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti operací sčítání a násobení
MATLABLINK - VZDÁLENÉ OVLÁDÁNÍ A MONITOROVÁNÍ TECHNOLOGICKÝCH PROCESŮ
 MATLABLINK - VZDÁLENÉ OVLÁDÁNÍ A MONITOROVÁNÍ TECHNOLOGICKÝCH PROCESŮ M. Sysel, I. Pomykacz Univerzita Tomáše Bati ve Zlíně, Fakulta aplikované informatiky Nad Stráněmi 4511, 760 05 Zlín, Česká republika
MATLABLINK - VZDÁLENÉ OVLÁDÁNÍ A MONITOROVÁNÍ TECHNOLOGICKÝCH PROCESŮ M. Sysel, I. Pomykacz Univerzita Tomáše Bati ve Zlíně, Fakulta aplikované informatiky Nad Stráněmi 4511, 760 05 Zlín, Česká republika
Miroslav Kureš. Aplikovaná matematika Ostravice 2012 2. workshop A-Math-Net Sít pro transfer znalostí v aplikované matematice
 O Weilově párování na eliptických křivkách Miroslav Kureš Aplikovaná matematika Ostravice 2012 2. workshop A-Math-Net Sít pro transfer znalostí v aplikované matematice Abstrakt. Pracovní seminární text,
O Weilově párování na eliptických křivkách Miroslav Kureš Aplikovaná matematika Ostravice 2012 2. workshop A-Math-Net Sít pro transfer znalostí v aplikované matematice Abstrakt. Pracovní seminární text,
