Rozptylování, stromy - zákl. vlastnosti
|
|
|
- Marta Mašková
- před 6 lety
- Počet zobrazení:
Transkript
1 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 1/55 Rozptylování, stromy - zákl. vlastnosti Ing. Josef Vogel, CSc Katedra softwarového inženýrství Katedra teoretické informatiky, Fakulta informačních technologii, ČVUT v Praze Karel Müller, Josef Vogel, 2011 Programování a algoritmizace 2, BI-PA2, 2011, Přednáška 12 BI-PA2 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
2 Témata Rozptylování princip otevřené rozptylování (open hashing) řetězení (chaining) = interpolační rozptylování uzavřené rozptylování (closed hashing) = otevřené adresování (open addressing) Stromy základní vlastnosti Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 2/55
3 Rozptylování Připomeňme si nejefektivnější metodu implementace množiny a tabulky: jsou-li hodnotami klíčů celá čísla z intervalu 0 až max, lze pro implementaci použít pole, jehož indexy jsou klíče a hodnotou prvku je v případě množiny true nebo false, v případě tabulky to jsou hodnoty odpovídající klíčům vyhledávání se v tomto případě nazývá adresním vyhledáváním (z klíče lze určit adresu umístění prvku v datové struktuře) a jeho složitost je O(1) Jestliže nelze stanovit vzájemně jednoznačné zobrazení mezi klíči a adresami umístění v datové struktuře, lze použít techniku rozptylování (hashing) Princip rozptylování (patří mezi adresní vyhledávání): pro klíč se vypočte adresa, zobrazení mezi klíči a adresami však není vzájemně jednoznačné (několika různým klíčům odpovídá stejná adresa) klíče, kterým odpovídá stejná adresa, se nazývají synonyma, a je pro ně třeba stanovit náhradní způsob umístění Funkce pro výpočet (základní) adresy umístění klíče se nazývá rozptylovací funkce (hash function) Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 3/55
4 Rozptylovací funkce Předpokládejme, že klíče chceme transformovat na indexy pole z intervalu 0 až m-1 (pole obsahuje m prvků) Příklad 1: klíče jsou kladná celá čísla int hash(int k, int m) {return k % m; Příklad 2: klíče jsou C-čkovské řetězce int hash(const char* s, int m) { int h = 0, len = strlen(s); for (int i=0; i<len; i++) h += s[i]; return h % m; Příklad 3: klíče jsou řetězce typu string int hash(string s, int m) { int h = 0, len = s.length(); for (int i=0; i<len; i++) h += s[i]; return h % m; Pozor: funkci hash nelze zavést pomocí šablony Podrobněji se bude rozptylovací funkcí zabývat předmět BI-EFA Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 4/55
5 Otevřené rozptylování Pole tvořené m prvky obsahuje m dílčích tabulek, v tabulce s indexem i jsou synonyma, pro které rozptylovací funkce dá výsledek i 0 1 tabulka pro hash(k,m)=0 tabulka pro hash(k,m)=1 Key hash(k, m) m-1 tabulka pro hash(k,m)=m-1 Dílčí tabulku lze realizovat různým způsobem, např. spojovým seznamem rozšiřitelným polem atd. Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 5/55
6 p12\hashset1\lnklst.h Otevřené rozptylování - řetězení Realizace dílčích tabulek pomocí spojového seznamu Šablona pro spojový seznam: // lnklst.h #include <iostream> using namespace std; template <class T> class LinkList { struct Elem { T key; Elem *next; Elem(T v, Elem *n) { key = v; next = n; ; Elem *head; Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 6/55
7 p12\hashset1\lnklst.h Otevřené rozptylování - řetězení Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 7/55 Pokračování šablony pro spojový seznam: public: LinkList() {head = NULL; bool isempty() const { return head == NULL; void add(t x) { if (!incl(x)) head = new Elem(x, head); void del(t x) { Elem *p=head, *pp=null; while (p && p->key!=x) { pp = p; p = p->next; if (p==null) return; if (pp==null) head = p->next; else pp->next = p->next; delete p;
8 p12\hashset1\lnklst.h Otevřené rozptylování - řetězení Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 8/55 Pokračování šablony pro spojový seznam: bool incl(t x) { Elem *p = head; while (p) if (p->key==x) return true; else p = p->next; return false; friend ostream& operator<<(ostream& s, const LinkList& l) { Elem *p = l.head; while (p) { s << p->key << ' '; p = p->next; return s; ;
9 p12\hashset1\hashset.h Otevřené rozptylování - řetězení Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 9/55 Deklarace třídy HashSet: // hashset.h #include "hash.h" #include "lnklst.h" #include <iostream> using namespace std; template <class Key> class HashSet { int m; LinkList<Key> *keys; public: HashSet(int m); ~HashSet(); void ins(key); bool incl(key) const; void del(key); void print() const; ;
10 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 10/55 Metody třídy HashSet: p12\hashset1\hashset.h Otevřené rozptylování - řetězení template <class Key> HashSet::HashSet(int m) { this->m = m; keys = new LinkList<Key>[m]; template <class Key> HashSet::~HashSet() { delete [] keys; template <class Key> void HashSet::ins(Key k) { int i = hash(k, m); keys[i].add(k); template <class Key> bool HashSet::incl(Key k) const { int i = hash(k, m); return keys[i].incl(k);
11 p12\hashset1\hashset.h Otevřené rozptylování - řetězení Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 11/55 Metody třídy HashSet (pokračování): template <class Key> void HashSet::del(Key k) { int i = hash(k, m); keys[i].del(k); template <class Key> void HashSet::print() const { for (int i=0; i<m; i++) if (!keys[i].isempty()) { cout << setw(3) << i << ": "; cout << keys[i] << endl; cout << endl;
12 p12\hashset2\hashset.h Uzavřené rozptylování Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 12/55 Klíče (včetně případné hodnoty) se ukládají do pole, jehož velikost omezuje počet prvků množiny (tabulky) Synonyma se ukládají do dalších prvků pole, např.s krokem 1 Podobně se postupuje při hledání Příklad: template <class Key> class HashSet { int m; int n; Key *keys; Key none; int search(key) const; public: HashSet(int m); ~HashSet(); bool incl(key) const; void ins(key); void del(key); void print() const; ;
13 p12\hashset2\hashset.h Uzavřené rozptylování Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 13/55 Příklad: template <class Key> HashSet::HashSet(int m) { this->m = m; n = 0; none = Key(); // co bude hodnotou pro int a string? keys = new Key[m]; for (int i=0; i<m; i++) keys[i] = none; template <class Key> HashSet::~HashSet() { delete [] keys;
14 p12\hashset2\hashset.h Uzavřené rozptylování Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 14/55 Příklad: template <class Key> int HashSet<Key>::search(Key k) const { int i = hash(k, m); while (keys[i]!=none) { if (keys[i]==k) return i; i = (i+1) % m; return i; template <class Key> bool HashSet<Key>::incl(Key k) const { int i = search(k); if (keys[i]==k) return true; return false;
15 p12\hashset2\hashset.h Uzavřené rozptylování Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 15/55 Příklad: template <class Key> void HashSet<Key>::ins(Key k) { cout << "vklada se klic " << k; int i = search(k); if (keys[i]==none) { int j = hash(k,m); cout << " s hash-kodem " << j; if (j!=i) cout << " - synonymum " << i; cout << endl; else { cout << " - klic uz v tabulce existuje" << endl; return; n++; if (n==m) { n--; throw "Ins: Hash table full!"; keys[i]=k;
16 p12\hashset2\hashset.h Uzavřené rozptylování Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 16/55 Příklad: template <class Key> void HashSet<Key>::del(Key k) { int i = hash(k, m); cout << "odebira se klic " << k << " s hash-kodem " << i << endl; i = search(k); if (keys[i]==none) return; n--; keys[i]=none; i = (i+1) % m; while (keys[i]!=none) { k = keys[i]; n--; keys[i] = none; ins(k); i = (i+1) % m;
17 p12\hashset2\hashset.h Uzavřené rozptylování Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 17/55 Příklad: template <class Key> void HashSet::print() const { cout << "n= << n << " faktor zaplneni << setprecision(2) << (float)n/m << endl; for (int i=0; i<m; i++) if (keys[i]!=none) cout << keys[i] << ' '; cout << endl;
18 Stromy Podle teorie grafů: Strom je souvislý neorientovaný graf bez kružnic Kořenový strom je orientovaný strom, ve kterém jeden uzel kořen je spojen s každým jiným uzlem jedinou orientovanou cestou V informatice se obvykle rozumí: Příklad grafického vyjádření: strom = kořenový strom Orientaci hran obvykle nekreslíme ale předpokládáme shora dolů Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 18/55
19 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 19/55 Stromy Strom bývá obvykle uzlově ohodnocený každý uzel obsahuje hodnotu určitého typu hodnota uzlu (případně její část, jde-li o strukturovanou hodnotu) je klíčem uzlu Příklad:
20 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 20/55 Stromy Některé pojmy: předchůdce (rodič) následník (potomek) kořen (nemá předchůdce) vnitřní uzel (má následníky) list (nemá následníky)
21 Stromy Stromy chápeme jako uspořádané, tzn. následníci každého vnitřního uzlu jsou pevným způsobem uspořádáni (první, druhý,..., v grafickém vyjádření zleva doprava) Příklad: následující dva stromy jsou různé Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 21/55
22 Stromy Hloubka uzlu délka (počet hran) cesty z kořene do uzlu Uzly, které mají stejnou hloubku, jsou na stejné úrovni (někdy se úrovně uzlů číslují od 1, tj. úroveň uzlu = hloubka uzlu + 1) Hloubka stromu (= výška stromu) délka nejdelší cesty hloubka uzlu 0 hloubka stromu Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 22/55
23 Stromy výška stromu hloubka uzlu úroveň uzlu H 0 1 C M K P 2 3 J 3 4 kořen stromu: H C M K J P výška stromu: Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 23/55
24 Stromy Pravidelný strom stupně r (r>0): každý uzel má 0 nebo r následníků Úplný pravidelný strom stupně r (r>0): všechny listy mají hloubku stromu pravidelný strom stupně 3 úplný pravidelný strom stupně 3 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 24/55
25 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 25/55 Binární stromy Binární strom: každý uzel má nanejvýš dva následníky levý následník pravý následník levý podstrom pravý podstrom
26 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 26/55 Binární stromy Pravidelný binární strom: každý uzel má 0 nebo 2 následníků Vyvážený binární strom: hloubky všech listů se liší nanejvýš o 1
27 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 27/55 Hloubka a počet uzlů vyváženého binárního stromu Úplný pravidelný binární strom (je vyvážený) hloubka uzlů počet uzlů N = 2 H+1-1 hloubka H = log 2 (N + 1) - 1 k 2 k 2 k+1-1
28 Hloubka a počet uzlů extrémně nevyváženého binárního stromu Extrémně nevyvážený pravidelný binární strom hloubka uzlů k-1 2 k 2 2k+1 počet uzlů N = 2H + 1 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 28/55
29 Haldově uspořádaný strom Haldově uspořádaný strom je binární strom, ve kterém klíč každého uzlu je větší nebo roven klíčům následníků (max-heap) Alternativní definice: Haldově uspořádaný strom je binární strom, ve kterém klíč každého uzlu je menší nebo roven klíčům následníků (min-heap) Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 29/55
30 Vyhledávací strom Vyhledávací strom je binární strom, ve kterém klíč každého vnitřního uzlu je větší než klíče uzlů v levém podstromu a menší než klíče uzlů v pravém podstromu Alternativní definice: Vyhledávací strom je binární strom, ve kterém klíč každého vnitřního uzlu je menší než klíče uzlů v levém podstromu a větší než klíče uzlů v pravém podstromu Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 30/55
31 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 31/55 Programová realizace stromu Kořenový strom, jehož uzly mohou mít libovolný počet následníků, lze realizovat pomocí spojového seznamu, jehož prvky jsou zase spojové seznamy Nelineární spojová struktura
32 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 32/55 Programová realizace stromu Pro uzly zavedeme třídu potomek bratr class Node { public: Node *child; T info; Node *brother; Node(Node *c, T x, Node *b) { child =c; info = x; brother = b; ;
33 Programová realizace stromu Jestliže strom je pravidelný stupně r nebo každý uzel má nanejvýš r následníků, můžeme spojový seznam nahradit objektem, který obsahuje pole ukazatelů na následníky Například: class Node { enum {R = 6;; T info; Node* childs[r]; Node(T x) { info = x; for (int i=0; i<r; i++) childs[i] = NULL; ; Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 33/55
34 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 34/55 Programová realizace binárního stromu Binární strom lze realizovat pomocí nelineární spojové struktury, jejíž uzly budou obsahovat ukazatele na levého a pravého následníka
35 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 35/55 Programová realizace binárního stromu Pro uzly zavedeme třídu levý následník pravý následník class Node { public: T info; Node *left; Node *right; Node(T i, Node l=null; Node r=null) { info = i; left = l; right = r; ;
36 p12\btree\binstrom1.cpp Programová realizace binárního stromu Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 36/55 Příklad: funkce pro vytvoření náhodného binárního stromu dané maximální hloubky inline int random(int m) { // vysledkem je pseudonahodne cislo z intervalu 0 az m-1 return rand()%m; Node *randtree(int depth) { if (depth<=0 random(10)>7) return NULL; return new Node(random(100), randtree(depth-1), randtree(depth-1)); pokud tento test vypustíme, bude vytvořený strom vždy pravidelný a úplný
37 p12\btree\binstrom2.cpp Výpis binárního stromu Předchozí program vytvořil náhodný binární strom (pomocí rekurzívní funkce), ale jak ho vypsat? Pomocí rekurzívní funkce, která: vypíše hodnotu v uzlu, na který ukazuje parametr funkce, rekurzívním voláním vypíše uzly v levém podstromu rekurzívním voláním vypíše uzly v pravém podstromu Parametrem funkce bude kromě ukazatele na uzel také číslo udávající, kolik mezer má být vypsáno před hodnotou uzlu (odsazení podle hloubky uzlu) void print(node *p, int s) { if (p) { cout << setw(s) << ' ' << p->info << endl; print(p->left, s+1); print(p->right, s+1); else cout << setw(s) << ' ' << "null" << endl; Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 37/55
38 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 38/55 Výpis binárního stromu Program binstrom2.cpp např. vypíše: 67 0 null 78 null 64 null null null null 42 null null 36 4 null null 53 null null grafické vyjádření vytvořeného stromu
39 Průchody binárním stromem Funkce print v programu binstrom2.cpp je příkladem průchodu binárním stromem shora dolů v pořadí Preorder Další způsoby průchodu binárním stromem jsou Inorder a Postorder Preorder: pro každý uzel se provede: operace s hodnotou uzlu vyvolání průchodu pro levého následníka vyvolání průchodu pro pravého následníka Inorder: pro každý uzel se provede: vyvolání průchodu pro levého následníka operace s hodnotou uzlu vyvolání průchodu pro pravého následníka Postorder: pro každý uzel se provede: vyvolání průchodu pro levého následníka vyvolání průchodu pro pravého následníka operace s hodnotou uzlu Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 39/55
40 p12\btree\binstrom3.cpp Výpis binárního stromu Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 40/55 Průchodem Inorder: void printinorder(node *p, int s) { if (p) { printinorder(p->left, s+1); cout << setw(s) << ' ' << p->info << endl; printinorder(p->right, s+1); else cout << setw(s) << ' ' << "null" << endl; Průchodem Postorder: void printpostorder(node *p, int s) { if (p) { printpostorder(p->left, s+1); printpostorder(p->right, s+1); cout << setw(s) << ' ' << p->info << endl; else cout << setw(s) << ' ' << "null" << endl;
41 p12\btree\pocetuzlu.cpp Počet uzlů binárního stromu Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 41/55 Funkce pro výpočet počtu uzlů binárního stromu int count(node *p) { if (p) return count(p->left)+count(p->right)+1; else return 0;
42 p12\btree\hloubkastromu.cpp Hloubka binárního stromu Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 42/55 inline int max(int x, int y) { return x>y? x : y; int depth(node *p) { if (p) return max(depth(p->left), depth(p->right)) + 1; else return -1;
43 p12\btree\pocetuzlu2.cpp Implementace rekurze pomocí zásobníku Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 43/55 Funkci pro výpočet počtu uzlů binárního stromu napíšeme nerekurzívně Postup: požijeme zásobník ukazatelů na uzly stromu opakovaně, dokud se zásobník nevyprázdní, odebereme z vrcholu ukazatel a pokud není NULL, zvětšíme počítadlo uzlů a a do zásobníku vložíme ukazatele na levého a pravého potomka na začátku do zásobníku vložíme ukazatel na kořen stromu int count2(node *p) { Stack<Node*> stc; int cnt = 0; stc.push(p); while (!stc.empty()) { Node *q = stc.pop(); if (q) { cnt++; stc.push(q->right); stc.push(q->left); return cnt;
44 Implementace rekurze pomocí zásobníku Proceduru pro výpis stromu metodou preorder napíšeme nerekurzívně Postup: do zásobníku budeme ukládat dvojice <ukazatel na uzel, počet mezer> opakovaně, dokud se zásobník nevyprázdní, odebereme z vrcholu dvojici, vypíšeme počet mezer, a pokud ukazatel není NULL, vložíme do zásobníku ukazatel na pravého následníka a pak ukazatel na levého následníka (pořadí je důležité); pokud je ukazatel null, vypíšeme null na začátku vložíme do zásobníku dvojici obsahující ukazatel na kořen a 1 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 44/55
45 p12\btree\binstrom4.cpp Implementace rekurze pomocí zásobníku struct Pair { Node *ptr; int spc; Pair(Node *p, int s) { ptr = p; spc = s; ; void print2(node *p, int s) { Stack<Pair> stc; stc.push(pair(p,s)); while (!stc.empty()) { Pair pair = stc.pop(); cout << setw(pair.spc) << ' '; if (pair.ptr) { cout << pair.ptr->info << endl; stc.push(pair(pair.ptr->right, pair.spc+1)); stc.push(pair(pair.ptr->left, pair.spc+1)); else cout << "null" << endl; Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 45/55
46 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 46/55 Binární vyhledávací strom Připomenuti: Binární vyhledávací strom je binární strom, ve kterém klíč každého vnitřního uzlu je větší než klíče uzlů v levém podstromu a menší než klíče uzlů v pravém podstromu (ostrá nerovnost může být nahrazena neostrou) Alternativní definice: Vyhledávací strom je binární strom, ve kterém klíč každého vnitřního uzlu je menší než klíče uzlů v levém podstromu a větší než klíče uzlů v pravém podstromu (ostrá nerovnost může být nahrazena neostrou)
47 p12\bstree\node.h, bstree.h Programová realizace BVS Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 47/55 BVS je tvořen uzly, každý uzel obsahuje: klíč (případně další data) ukazatele na levého a pravého potomka class Node { key Key key; Node *left; left right Node *right; public: Node(... ); key key Key getkey() const; Node *getleft() const; left right left right Node *getright() const; ; Objekt typu BVS obsahuje ukazatel na kořen stromu class BSTree { Node *root; public: BSTree() {root = NULL;... ;
48 Programová realizace BVS Pro některé operace s BVS je třeba k uzlu najít rodiče Pro určení rodiče uzlu lze zavést metodu stromu (časově náročné), nebo doplnit ukazatel na rodiče do každého uzlu class Node { Node *parent; Key key; Node *left; Node *right; public: Node(... ); Node *getparent() const; Key getkey() const; Node *getleft() const; Node *getright() const; ; parent key left right parent parent key key left right left right Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 48/55
49 Počet uzlů ~ hloubka stromu Pro hloubku h BVS s n uzly platí: v nejhorším případě je h = n 1 v nejlepším případě je h = Příklad pro n = 5 nejlepší případ (h=2) nejhorší případ (h=4) vyvážený strom nevyvážený strom Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 49/55
50 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 50/55 Výpis BVS průchodem Inorder Vypíšeme-li uzly BVS průchodem Inorder, dostaneme vzestupnou posloupnost klíčů všech uzlů void printio(node *p) { if (p) { printio(p->getleft()); cout << ' ' << p->getkey(); printio(p->getright());
51 Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 51/55 Výpis BVS průchodem Inorder Pro strom H D N B F J S A C E G I M P bude výstupem A B C D E F G H I J M N P S
52 p12\bstree\node.cpp Vyhledávání v BVS Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 52/55 Rekurzivní: Node *searchr(node *x, Key k) { if (x==null x->key==k) return x; if (k<x->key) return searchr(x->left, k); else return searchr(x->right, k); Iterační: Node *search(node *x, Key k) { while (x && x->key!= k) if (k < x->key) x = x->left; else x = x->right; return x; Realizace pomocí šablon je v adresáři bstree-s
53 p12\bstree1\bstree.cpp Vložení uzlu do BVS Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 53/55 Najde se rodič pp pro nový uzel n Nový uzel n (je to list) se stane potomkem uzlu pp H ins( F ) H D pp N D N B F n B F void BSTree::ins(Key k) { Node *p = root, *pp = NULL; if (p==null) {root = new Node(k); return; do { pp = p; if (k < p->key) p = p->left; else if (k > p->key) p = p->right; else return; while (p); Node *n = new Node(k); if (k < pp->key) pp->left = n; else pp->right = n;
54 p12\bstree1\main.cpp Vložení uzlu do BVS Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 54/55 Jaký strom vznikne, vkládáme-li uzly v pořadí daném následujícím polem: char a[] = {'H','D','N','B','F','J','S','A','C','E','G','I','M','P'; int na = sizeof(a)/sizeof(char); BSTree t; for (int i=0; i<na; i++) t.ins(a[i]); H D N B F J S A C E G I M P
55 p12\bstree1\main.cpp Vložení uzlu do BVS Karel Müller, Josef Vogel (ČVUT FIT) Rozptylování, stromy - zákl. vlastnosti BI-PA2, 2011, Přednáška 12 55/55 Jaký strom vznikne, vkládáme-li uzly v pořadí daném následujícím polem: char b[] = {'A','B','C','D','E','F','G','H','I','J','M','N','P','S'; int nb = sizeof(b)/sizeof(char); BSTree tb; for (int i=0; i<nb; i++) tb.ins(a[i]); A B C D P S
Stromy. Karel Richta a kol. Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Karel Richta a kol.
 Stromy Karel Richta a kol. Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Karel Richta a kol., 2018, B6B36DSA 01/2018, Lekce 9 https://cw.fel.cvut.cz/wiki/courses/b6b36dsa/start
Stromy Karel Richta a kol. Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Karel Richta a kol., 2018, B6B36DSA 01/2018, Lekce 9 https://cw.fel.cvut.cz/wiki/courses/b6b36dsa/start
ALGORITMIZACE 2010/03 STROMY, BINÁRNÍ STROMY VZTAH STROMŮ A REKURZE ZÁSOBNÍK IMPLEMENTUJE REKURZI PROHLEDÁVÁNÍ S NÁVRATEM (BACKTRACK)
 ALGORITMIZACE 2010/03 STROMY, BINÁRNÍ STROMY VZTAH STROMŮ A REKURZE ZÁSOBNÍK IMPLEMENTUJE REKURZI PROHLEDÁVÁNÍ S NÁVRATEM (BACKTRACK) Strom / tree uzel, vrchol / node, vertex hrana / edge vnitřní uzel
ALGORITMIZACE 2010/03 STROMY, BINÁRNÍ STROMY VZTAH STROMŮ A REKURZE ZÁSOBNÍK IMPLEMENTUJE REKURZI PROHLEDÁVÁNÍ S NÁVRATEM (BACKTRACK) Strom / tree uzel, vrchol / node, vertex hrana / edge vnitřní uzel
Základní datové struktury III: Stromy, haldy
 Základní datové struktury III: Stromy, haldy prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní
Základní datové struktury III: Stromy, haldy prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní
Stromy. Strom: souvislý graf bez kružnic využití: počítačová grafika seznam objektů efektivní vyhledávání výpočetní stromy rozhodovací stromy
 Stromy úvod Stromy Strom: souvislý graf bez kružnic využití: počítačová grafika seznam objektů efektivní vyhledávání výpočetní stromy rozhodovací stromy Neorientovaný strom Orientovaný strom Kořenový orientovaný
Stromy úvod Stromy Strom: souvislý graf bez kružnic využití: počítačová grafika seznam objektů efektivní vyhledávání výpočetní stromy rozhodovací stromy Neorientovaný strom Orientovaný strom Kořenový orientovaný
Abstraktní datové typy
 Karel Müller, Josef Vogel (ČVUT FIT) Abstraktní datové typy BI-PA2, 2011, Přednáška 10 1/27 Abstraktní datové typy Ing. Josef Vogel, CSc Katedra softwarového inženýrství Katedra teoretické informatiky,
Karel Müller, Josef Vogel (ČVUT FIT) Abstraktní datové typy BI-PA2, 2011, Přednáška 10 1/27 Abstraktní datové typy Ing. Josef Vogel, CSc Katedra softwarového inženýrství Katedra teoretické informatiky,
Stromy. Příklady. Rekurzivní datové struktury. Základní pojmy
 Základní pojmy Stromy doc. Ing. Miroslav Beneš, Ph.D. katedra informatiky FEI VŠB-TUO A-1007 / 597 324 213 http://www.cs.vsb.cz/benes Miroslav.Benes@vsb.cz Graf uzly hrany orientované / neorientované Souvislý
Základní pojmy Stromy doc. Ing. Miroslav Beneš, Ph.D. katedra informatiky FEI VŠB-TUO A-1007 / 597 324 213 http://www.cs.vsb.cz/benes Miroslav.Benes@vsb.cz Graf uzly hrany orientované / neorientované Souvislý
Rekurzivní algoritmy
 Rekurzivní algoritmy prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA) ZS
Rekurzivní algoritmy prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA) ZS
ALGORITMIZACE 2010/03 STROMY, BINÁRNÍ STROMY VZTAH STROMŮ A REKURZE ZÁSOBNÍK IMPLEMENTUJE REKURZI PROHLEDÁVÁNÍ S NÁVRATEM (BACKTRACK)
 ALGORITMIZACE 2010/03 STROMY, BINÁRNÍ STROMY VZTAH STROMŮ A REKURZE ZÁSOBNÍK IMPLEMENTUJE REKURZI PROHLEDÁVÁNÍ S NÁVRATEM (BACKTRACK) Strom / tree uzel, vrchol / node, vertex hrana / edge vnitřní uzel
ALGORITMIZACE 2010/03 STROMY, BINÁRNÍ STROMY VZTAH STROMŮ A REKURZE ZÁSOBNÍK IMPLEMENTUJE REKURZI PROHLEDÁVÁNÍ S NÁVRATEM (BACKTRACK) Strom / tree uzel, vrchol / node, vertex hrana / edge vnitřní uzel
Abstraktní třídy, polymorfní struktury
 Karel Müller, Josef Vogel (ČVUT FIT) Abstraktní třídy, polymorfní struktury BI-PA2, 2011, Přednáška 9 1/32 Abstraktní třídy, polymorfní struktury Ing. Josef Vogel, CSc Katedra softwarového inženýrství
Karel Müller, Josef Vogel (ČVUT FIT) Abstraktní třídy, polymorfní struktury BI-PA2, 2011, Přednáška 9 1/32 Abstraktní třídy, polymorfní struktury Ing. Josef Vogel, CSc Katedra softwarového inženýrství
Datové struktury 2: Rozptylovací tabulky
 Datové struktury 2: Rozptylovací tabulky prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy
Datové struktury 2: Rozptylovací tabulky prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy
Stromy, haldy, prioritní fronty
 Stromy, haldy, prioritní fronty prof. Ing. Pavel Tvrdík CSc. Katedra počítačů FEL České vysoké učení technické DSA, ZS 2008/9, Přednáška 6 http://service.felk.cvut.cz/courses/x36dsa/ prof. Pavel Tvrdík
Stromy, haldy, prioritní fronty prof. Ing. Pavel Tvrdík CSc. Katedra počítačů FEL České vysoké učení technické DSA, ZS 2008/9, Přednáška 6 http://service.felk.cvut.cz/courses/x36dsa/ prof. Pavel Tvrdík
Mělká a hluboká kopie
 Karel Müller, Josef Vogel (ČVUT FIT) Mělká a hluboká kopie BI-PA2, 2011, Přednáška 5 1/28 Mělká a hluboká kopie Ing. Josef Vogel, CSc Katedra softwarového inženýrství Katedra teoretické informatiky, Fakulta
Karel Müller, Josef Vogel (ČVUT FIT) Mělká a hluboká kopie BI-PA2, 2011, Přednáška 5 1/28 Mělká a hluboká kopie Ing. Josef Vogel, CSc Katedra softwarového inženýrství Katedra teoretické informatiky, Fakulta
Programování v C++ 1, 16. cvičení
 Programování v C++ 1, 16. cvičení binární vyhledávací strom 1 1 Fakulta jaderná a fyzikálně inženýrská České vysoké učení technické v Praze Zimní semestr 2018/2019 Přehled 1 2 Shrnutí minule procvičené
Programování v C++ 1, 16. cvičení binární vyhledávací strom 1 1 Fakulta jaderná a fyzikálně inženýrská České vysoké učení technické v Praze Zimní semestr 2018/2019 Přehled 1 2 Shrnutí minule procvičené
Jazyk C++, některá rozšíření oproti C
 Karel Müller, Josef Vogel (ČVUT FIT) Jazyk C++, některá rozšíření oproti C BI-PA2, 2011, Přednáška 1 1/22 Jazyk C++, některá rozšíření oproti C Ing. Josef Vogel, CSc Katedra softwarového inženýrství Katedra
Karel Müller, Josef Vogel (ČVUT FIT) Jazyk C++, některá rozšíření oproti C BI-PA2, 2011, Přednáška 1 1/22 Jazyk C++, některá rozšíření oproti C Ing. Josef Vogel, CSc Katedra softwarového inženýrství Katedra
Základy algoritmizace c2005, 2007 Michal Krátký, Jiří Dvorský1/39
 Základy algoritmizace Michal Krátký 1, Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Základy algoritmizace, 2006/2007 Základy algoritmizace c2005, 2007 Michal Krátký, Jiří Dvorský1/39
Základy algoritmizace Michal Krátký 1, Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Základy algoritmizace, 2006/2007 Základy algoritmizace c2005, 2007 Michal Krátký, Jiří Dvorský1/39
Dynamicky vázané metody. Pozdní vazba, virtuální metody
 Dynamicky vázané metody Pozdní vazba, virtuální metody Motivace... class TBod protected: float x,y; public: int vrat_pocet_bodu() return 1; ; od třídy TBod odvodíme: class TUsecka: public TBod protected:
Dynamicky vázané metody Pozdní vazba, virtuální metody Motivace... class TBod protected: float x,y; public: int vrat_pocet_bodu() return 1; ; od třídy TBod odvodíme: class TUsecka: public TBod protected:
Algoritmy a datové struktury
 Algoritmy a datové struktury Stromy 1 / 32 Obsah přednášky Pole a seznamy Stromy Procházení stromů Binární stromy Procházení BS Binární vyhledávací stromy 2 / 32 Pole Hledání v poli metodou půlení intervalu
Algoritmy a datové struktury Stromy 1 / 32 Obsah přednášky Pole a seznamy Stromy Procházení stromů Binární stromy Procházení BS Binární vyhledávací stromy 2 / 32 Pole Hledání v poli metodou půlení intervalu
Pole, množina, tabulka
 Karel Müller, Josef Vogel (ČVUT FIT) Pole, množina, tabulka BI-PA2, 2011, Přednáška 11 1/53 Pole, množina, tabulka Ing. Josef Vogel, CSc Katedra softwarového inženýrství Katedra teoretické informatiky,
Karel Müller, Josef Vogel (ČVUT FIT) Pole, množina, tabulka BI-PA2, 2011, Přednáška 11 1/53 Pole, množina, tabulka Ing. Josef Vogel, CSc Katedra softwarového inženýrství Katedra teoretické informatiky,
5 Rekurze a zásobník. Rekurzivní volání metody
 5 Rekurze a zásobník Při volání metody z metody main() se do zásobníku uloží aktivační záznam obsahující - parametry - návratovou adresu, tedy adresu, kde bude program pokračovat v metodě main () po skončení
5 Rekurze a zásobník Při volání metody z metody main() se do zásobníku uloží aktivační záznam obsahující - parametry - návratovou adresu, tedy adresu, kde bude program pokračovat v metodě main () po skončení
Volné stromy. Úvod do programování. Kořenové stromy a seřazené stromy. Volné stromy
 Volné stromy Úvod do programování Souvislý, acyklický, neorientovaný graf nazýváme volným stromem (free tree). Často vynecháváme adjektivum volný, a říkáme jen, že daný graf je strom. Michal Krátký 1,Jiří
Volné stromy Úvod do programování Souvislý, acyklický, neorientovaný graf nazýváme volným stromem (free tree). Často vynecháváme adjektivum volný, a říkáme jen, že daný graf je strom. Michal Krátký 1,Jiří
Adresní vyhledávání (přímý přístup, zřetězené a otevřené rozptylování, rozptylovací funkce)
 13. Metody vyhledávání. Adresní vyhledávání (přímý přístup, zřetězené a otevřené rozptylování, rozptylovací funkce). Asociativní vyhledávání (sekvenční, binárním půlením, interpolační, binární vyhledávací
13. Metody vyhledávání. Adresní vyhledávání (přímý přístup, zřetězené a otevřené rozptylování, rozptylovací funkce). Asociativní vyhledávání (sekvenční, binárním půlením, interpolační, binární vyhledávací
Programování 3. hodina. RNDr. Jan Lánský, Ph.D. Katedra informatiky a matematiky Fakulta ekonomických studií Vysoká škola finanční a správní 2015
 Programování 3. hodina RNDr. Jan Lánský, Ph.D. Katedra informatiky a matematiky Fakulta ekonomických studií Vysoká škola finanční a správní 2015 Umíme z minulé hodiny Implementace zásobníku a fronty pomocí
Programování 3. hodina RNDr. Jan Lánský, Ph.D. Katedra informatiky a matematiky Fakulta ekonomických studií Vysoká škola finanční a správní 2015 Umíme z minulé hodiny Implementace zásobníku a fronty pomocí
Reprezentace aritmetického výrazu - binární strom reprezentující aritmetický výraz
 Reprezentace aritmetického výrazu - binární strom reprezentující aritmetický výraz (2 + 5) * (13-4) * + - 2 5 13 4 - listy stromu obsahují operandy (čísla) - vnitřní uzly obsahují operátory (znaménka)
Reprezentace aritmetického výrazu - binární strom reprezentující aritmetický výraz (2 + 5) * (13-4) * + - 2 5 13 4 - listy stromu obsahují operandy (čísla) - vnitřní uzly obsahují operátory (znaménka)
2) Napište algoritmus pro vložení položky na konec dvousměrného seznamu. 3) Napište algoritmus pro vyhledání položky v binárním stromu.
 Informatika 10. 9. 2013 Jméno a příjmení Rodné číslo 1) Napište algoritmus pro rychlé třídění (quicksort). 2) Napište algoritmus pro vložení položky na konec dvousměrného seznamu. 3) Napište algoritmus
Informatika 10. 9. 2013 Jméno a příjmení Rodné číslo 1) Napište algoritmus pro rychlé třídění (quicksort). 2) Napište algoritmus pro vložení položky na konec dvousměrného seznamu. 3) Napište algoritmus
NEJKRATŠÍ CESTY I. Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze
 NEJKRATŠÍ CESTY I Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze BI-GRA, LS 2010/2011, Lekce 7 Evropský sociální fond Praha & EU: Investujeme do vaší
NEJKRATŠÍ CESTY I Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze BI-GRA, LS 2010/2011, Lekce 7 Evropský sociální fond Praha & EU: Investujeme do vaší
Stromy. Jan Hnilica Počítačové modelování 14
 Stromy Jan Hnilica Počítačové modelování 14 1 Základní pojmy strom = dynamická datová struktura, složená z vrcholů (uzlů, prvků) propojených hranami hrany chápeme jako orientované, tzn. vedou z uzlu A
Stromy Jan Hnilica Počítačové modelování 14 1 Základní pojmy strom = dynamická datová struktura, složená z vrcholů (uzlů, prvků) propojených hranami hrany chápeme jako orientované, tzn. vedou z uzlu A
bin arn ı vyhled av an ı a bst Karel Hor ak, Petr Ryˇsav y 23. bˇrezna 2016 Katedra poˇ c ıtaˇ c u, FEL, ˇ CVUT
 binární vyhledávání a bst Karel Horák, Petr Ryšavý 23. března 2016 Katedra počítačů, FEL, ČVUT Příklad 1 Naimplementujte binární vyhledávání. Upravte metodu BinarySearch::binarySearch. 1 Příklad 2 Mysĺım
binární vyhledávání a bst Karel Horák, Petr Ryšavý 23. března 2016 Katedra počítačů, FEL, ČVUT Příklad 1 Naimplementujte binární vyhledávání. Upravte metodu BinarySearch::binarySearch. 1 Příklad 2 Mysĺım
Standardní algoritmy vyhledávací.
 Standardní algoritmy vyhledávací. Vyhledávací algoritmy v C++ nám umožňují vyhledávat prvky v datových kontejnerech podle různých kritérií. Také se podíváme na vyhledávání metodou půlením intervalu (binární
Standardní algoritmy vyhledávací. Vyhledávací algoritmy v C++ nám umožňují vyhledávat prvky v datových kontejnerech podle různých kritérií. Také se podíváme na vyhledávání metodou půlením intervalu (binární
Přetěžování operátorů
 Karel Müller, Josef Vogel (ČVUT FIT) Přetěžování operátorů BI-PA2, 2011, Přednáška 4 1/31 Přetěžování operátorů Ing. Josef Vogel, CSc Katedra softwarového inženýrství Katedra teoretické informatiky, Fakulta
Karel Müller, Josef Vogel (ČVUT FIT) Přetěžování operátorů BI-PA2, 2011, Přednáška 4 1/31 Přetěžování operátorů Ing. Josef Vogel, CSc Katedra softwarového inženýrství Katedra teoretické informatiky, Fakulta
Rekurze a zásobník. Jak se vypočítá rekurzivní program? volání metody. vyšší adresy. main(){... fa(); //push ret1... } ret1
 Rekurze a zásobník Jak se vypočítá rekurzivní program? volání metody vyšší adresy ret1 main(){... fa(); //push ret1... PC ret2 void fa(){... fb(); //push ret2... return //pop void fb(){... return //pop
Rekurze a zásobník Jak se vypočítá rekurzivní program? volání metody vyšší adresy ret1 main(){... fa(); //push ret1... PC ret2 void fa(){... fb(); //push ret2... return //pop void fb(){... return //pop
Pokročilé haldy. prof. Ing. Pavel Tvrdík CSc. Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010
 Pokročilé haldy prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (I-EFA) ZS 2010/11,
Pokročilé haldy prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (I-EFA) ZS 2010/11,
Programování v C++ 1, 17. cvičení
 Programování v C++ 1, 17. cvičení výjimky 1 1 Fakulta jaderná a fyzikálně inženýrská České vysoké učení technické v Praze Zimní semestr 2018/2019 Přehled 1 2 Shrnutí minule procvičené látky Binární vyhledávací
Programování v C++ 1, 17. cvičení výjimky 1 1 Fakulta jaderná a fyzikálně inženýrská České vysoké učení technické v Praze Zimní semestr 2018/2019 Přehled 1 2 Shrnutí minule procvičené látky Binární vyhledávací
Red Black strom (Red Black Tree) Úvod do programování. Rotace. Red Black strom. Rotace. Rotace
 Úvod do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programování, 2004/2005 Red Black strom je binární strom s jedním dvouhodnotovým příznakem
Úvod do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programování, 2004/2005 Red Black strom je binární strom s jedním dvouhodnotovým příznakem
Dynamické datové struktury II.
 Dynamické datové struktury II. Stromy. Binární vyhledávací strom. DFS. BFS. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Dynamické datové struktury II. Stromy. Binární vyhledávací strom. DFS. BFS. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
BINARY SEARCH TREE
 ---------------------------------------- BINARY SEARCH TREE --------------------------------------------------- Je dán BVS s n uzly. Máme za úkol spočítat hodnotu součtu všech klíčů v tomto stromě. Když
---------------------------------------- BINARY SEARCH TREE --------------------------------------------------- Je dán BVS s n uzly. Máme za úkol spočítat hodnotu součtu všech klíčů v tomto stromě. Když
Algoritmy výpočetní geometrie
 Algoritmy výpočetní geometrie prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
Algoritmy výpočetní geometrie prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
Úvod do teorie grafů
 Úvod do teorie grafů Neorientovaný graf G = (V,E,I) V množina uzlů (vrcholů) - vertices E množina hran - edges I incidence incidence je zobrazení, buď: funkce: I: E V x V relace: I E V V incidence přiřadí
Úvod do teorie grafů Neorientovaný graf G = (V,E,I) V množina uzlů (vrcholů) - vertices E množina hran - edges I incidence incidence je zobrazení, buď: funkce: I: E V x V relace: I E V V incidence přiřadí
Stromy. Jan Kybic.
 Stromy Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 1 / 44 Stromy Binární vyhledávací stromy Množiny a mapy 2 / 44 Strom (Tree) Strom skládá se s uzlů (nodes) spojených hranami (edges).
Stromy Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 1 / 44 Stromy Binární vyhledávací stromy Množiny a mapy 2 / 44 Strom (Tree) Strom skládá se s uzlů (nodes) spojených hranami (edges).
Dynamické datové struktury IV.
 Dynamické datové struktury IV. Prioritní fronta. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz (Katedra
Dynamické datové struktury IV. Prioritní fronta. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz (Katedra
2 Datové struktury. Pole Seznam Zásobník Fronty FIFO Haldy a prioritní fronty Stromy Hash tabulky Slovníky
 Pole Seznam Zásobník Fronty FIFO Haldy a prioritní fronty Stromy Hash tabulky Slovníky 25 Pole Datová struktura kolekce elementů (hodnot či proměnných), identifikovaných jedním nebo více indexy, ze kterých
Pole Seznam Zásobník Fronty FIFO Haldy a prioritní fronty Stromy Hash tabulky Slovníky 25 Pole Datová struktura kolekce elementů (hodnot či proměnných), identifikovaných jedním nebo více indexy, ze kterých
Spojové struktury. Spojová struktura (linked structure):
 Spojová struktura (linked structure): Spojové struktury množina objektů propojených pomocí spojů (odkazů, referencí, ukazatelů) Spoj často vyjadřuje vztah předchůdce následník Lineární spojové struktury
Spojová struktura (linked structure): Spojové struktury množina objektů propojených pomocí spojů (odkazů, referencí, ukazatelů) Spoj často vyjadřuje vztah předchůdce následník Lineární spojové struktury
PROHLEDÁVÁNÍ GRAFŮ. Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze
 PROHLEDÁVÁNÍ GRAFŮ Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze BI-GRA, LS 2010/2011, Lekce 4 Evropský sociální fond Praha & EU: Investujeme do
PROHLEDÁVÁNÍ GRAFŮ Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze BI-GRA, LS 2010/2011, Lekce 4 Evropský sociální fond Praha & EU: Investujeme do
Další příklady. Katedra softwarového inženýrství. Katedra teoretické informatiky, Fakulta informačních technologii, ČVUT v Praze. Karel Müller, 2011
 Karel Müller (ČVUT FIT) BI-PA2, 2011, Cvičení 11-13 1/5 Katedra softwarového inženýrství Katedra teoretické informatiky, Fakulta informačních technologii, ČVUT v Praze Karel Müller, 2011 Programování a
Karel Müller (ČVUT FIT) BI-PA2, 2011, Cvičení 11-13 1/5 Katedra softwarového inženýrství Katedra teoretické informatiky, Fakulta informačních technologii, ČVUT v Praze Karel Müller, 2011 Programování a
a) b) c) Radek Mařík
 2012-03-20 Radek Mařík 1. Čísla ze zadané posloupnosti postupně vkládejte do prázdného binárního vyhledávacího stromu (BVS), který nevyvažujte. Jak bude vypadat takto vytvořený BVS? Poté postupně odstraňte
2012-03-20 Radek Mařík 1. Čísla ze zadané posloupnosti postupně vkládejte do prázdného binárního vyhledávacího stromu (BVS), který nevyvažujte. Jak bude vypadat takto vytvořený BVS? Poté postupně odstraňte
BINARY SEARCH TREE
 Níže uvedené úlohy představují přehled otázek, které se vyskytly v tomto nebo v minulých semestrech ve cvičení nebo v minulých semestrech u zkoušky. Mezi otázkami semestrovými a zkouškovými není žádný
Níže uvedené úlohy představují přehled otázek, které se vyskytly v tomto nebo v minulých semestrech ve cvičení nebo v minulých semestrech u zkoušky. Mezi otázkami semestrovými a zkouškovými není žádný
Dynamické datové struktury III.
 Dynamické datové struktury III. Halda. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz (Katedra aplikované
Dynamické datové struktury III. Halda. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz (Katedra aplikované
Dynamické programování
 Dynamické programování prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
Dynamické programování prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
Dynamické programování. Optimální binární vyhledávací strom
 The complexity of different algorithms varies: O(n), Ω(n ), Θ(n log (n)), Dynamické programování Optimální binární vyhledávací strom Různé algoritmy mají různou složitost: O(n), Ω(n ), Θ(n log (n)), The
The complexity of different algorithms varies: O(n), Ω(n ), Θ(n log (n)), Dynamické programování Optimální binární vyhledávací strom Různé algoritmy mají různou složitost: O(n), Ω(n ), Θ(n log (n)), The
ALG 04. Zásobník Fronta Operace Enqueue, Dequeue, Front, Empty... Cyklická implementace fronty. Průchod stromem do šířky
 LG 04 Zásobník Fronta Operace nqueue, equeue, Front, mpty... yklická implementace fronty Průchod stromem do šířky Grafy průchod grafem do šířky průchod grafem do hloubky Ořezávání a heuristiky 1 Zásobník
LG 04 Zásobník Fronta Operace nqueue, equeue, Front, mpty... yklická implementace fronty Průchod stromem do šířky Grafy průchod grafem do šířky průchod grafem do hloubky Ořezávání a heuristiky 1 Zásobník
Vyhledávání. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 21.
 Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 21. září 2018 Jiří Dvorský (VŠB TUO) Vyhledávání 242 / 433 Osnova přednášky
Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 21. září 2018 Jiří Dvorský (VŠB TUO) Vyhledávání 242 / 433 Osnova přednášky
R zné algoritmy mají r znou složitost
 / / zné algoritmy mají r znou složitost Dynamické programování / / Definice funkce Otázka Program f(x,y) = (x = ) (y = ) f(x, y-) + f(x-,y) (x > ) && (y > ) f(,) =? int f(int x, int y) { if ( (x == ) (y
/ / zné algoritmy mají r znou složitost Dynamické programování / / Definice funkce Otázka Program f(x,y) = (x = ) (y = ) f(x, y-) + f(x-,y) (x > ) && (y > ) f(,) =? int f(int x, int y) { if ( (x == ) (y
Šablony, kontejnery a iterátory
 7. října 2010, Brno Připravil: David Procházka Šablony, kontejnery a iterátory Programovací jazyk C++ Šablony Strana 2 / 21 Šablona funkce/metody Šablona je obecný popis (třídy, funkce) bez toho, že by
7. října 2010, Brno Připravil: David Procházka Šablony, kontejnery a iterátory Programovací jazyk C++ Šablony Strana 2 / 21 Šablona funkce/metody Šablona je obecný popis (třídy, funkce) bez toho, že by
TGH07 - Chytré stromové datové struktury
 TGH07 - Chytré stromové datové struktury Jan Březina Technical University of Liberec 1. dubna 2014 Prioritní fronta Datová struktura s operacemi: Odeber Minum (AccessMin, DeleteMin) - vrat prvek s minimálním
TGH07 - Chytré stromové datové struktury Jan Březina Technical University of Liberec 1. dubna 2014 Prioritní fronta Datová struktura s operacemi: Odeber Minum (AccessMin, DeleteMin) - vrat prvek s minimálním
bfs, dfs, fronta, zásobník, prioritní fronta, halda
 bfs, dfs, fronta, zásobník, prioritní fronta, halda Petr Ryšavý 20. září 2016 Katedra počítačů, FEL, ČVUT prohledávání grafů Proč prohledávání grafů Zkontrolovat, zda je sít spojitá. Hledání nejkratší
bfs, dfs, fronta, zásobník, prioritní fronta, halda Petr Ryšavý 20. září 2016 Katedra počítačů, FEL, ČVUT prohledávání grafů Proč prohledávání grafů Zkontrolovat, zda je sít spojitá. Hledání nejkratší
Programování v C++ 2, 8. cvičení
 Programování v C++ 2, 8. cvičení návrhový vzor iterátor 1 1 Fakulta jaderná a fyzikálně inženýrská České vysoké učení technické v Praze Zimní semestr 2018/2019 Přehled 1 2 Shrnutí minule procvičené látky
Programování v C++ 2, 8. cvičení návrhový vzor iterátor 1 1 Fakulta jaderná a fyzikálně inženýrská České vysoké učení technické v Praze Zimní semestr 2018/2019 Přehled 1 2 Shrnutí minule procvičené látky
1 Nejkratší cesta grafem
 Bakalářské zkoušky (příklady otázek) podzim 2014 1 Nejkratší cesta grafem 1. Uvažujte graf s kladným ohodnocením hran (délka). Definujte formálně problém hledání nejkratší cesty mezi dvěma uzly tohoto
Bakalářské zkoušky (příklady otázek) podzim 2014 1 Nejkratší cesta grafem 1. Uvažujte graf s kladným ohodnocením hran (délka). Definujte formálně problém hledání nejkratší cesty mezi dvěma uzly tohoto
DobSort. Úvod do programování. DobSort Implementace 1/3. DobSort Implementace 2/3. DobSort - Příklad. DobSort Implementace 3/3
 DobSort Úvod do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programování, 2004/2005 V roce 1980 navrhl Dobosiewicz variantu (tzv. DobSort),
DobSort Úvod do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programování, 2004/2005 V roce 1980 navrhl Dobosiewicz variantu (tzv. DobSort),
B3B33ALP - Algoritmy a programování - Zkouška z předmětu B3B33ALP. Marek Boháč bohacm11
 333LP - lgoritmy a programování - Zkouška z předmětu 333LP Jméno Příjmení Už. jméno Marek oháč bohacm11 Zkouškový test Otázka 1 Jaká je hodnota proměnné count po vykonání následujícího kódu: data=[4,4,5,5,6,6,6,7,7,7,7,8,8]
333LP - lgoritmy a programování - Zkouška z předmětu 333LP Jméno Příjmení Už. jméno Marek oháč bohacm11 Zkouškový test Otázka 1 Jaká je hodnota proměnné count po vykonání následujícího kódu: data=[4,4,5,5,6,6,6,7,7,7,7,8,8]
TGH07 - Chytré stromové datové struktury
 TGH07 - Chytré stromové datové struktury Jan Březina Technical University of Liberec 5. dubna 2017 Prioritní fronta Datová struktura s operacemi: Odeber Minum (AccessMin, DeleteMin) - vrat prvek s minimálním
TGH07 - Chytré stromové datové struktury Jan Březina Technical University of Liberec 5. dubna 2017 Prioritní fronta Datová struktura s operacemi: Odeber Minum (AccessMin, DeleteMin) - vrat prvek s minimálním
bfs, dfs, fronta, zásobník, prioritní fronta, halda
 bfs, dfs, fronta, zásobník, prioritní fronta, halda Petr Ryšavý 19. září 2017 Katedra počítačů, FEL, ČVUT prohledávání grafů Proč prohledávání grafů Zkontrolovat, zda je sít spojitá. Hledání nejkratší
bfs, dfs, fronta, zásobník, prioritní fronta, halda Petr Ryšavý 19. září 2017 Katedra počítačů, FEL, ČVUT prohledávání grafů Proč prohledávání grafů Zkontrolovat, zda je sít spojitá. Hledání nejkratší
Martin Flusser. Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague. October 17, 2016
 ZPRO cvičení 2 Martin Flusser Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague October 17, 2016 Outline I 1 Outline 2 Proměnné 3 Proměnné - cvičení 4 Funkce 5 Funkce
ZPRO cvičení 2 Martin Flusser Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague October 17, 2016 Outline I 1 Outline 2 Proměnné 3 Proměnné - cvičení 4 Funkce 5 Funkce
Algoritmizace Dynamické programování. Jiří Vyskočil, Marko Genyg-Berezovskyj 2010
 Dynamické programování Jiří Vyskočil, Marko Genyg-Berezovskyj 2010 Rozděl a panuj (divide-and-conquer) Rozděl (Divide): Rozděl problém na několik podproblémů tak, aby tyto podproblémy odpovídaly původnímu
Dynamické programování Jiří Vyskočil, Marko Genyg-Berezovskyj 2010 Rozděl a panuj (divide-and-conquer) Rozděl (Divide): Rozděl problém na několik podproblémů tak, aby tyto podproblémy odpovídaly původnímu
STACK
 Níže uvedené úlohy představují přehled otázek, které se vyskytly v tomto nebo v minulých semestrech ve cvičení nebo v minulých semestrech u zkoušky. Mezi otázkami semestrovými a zkouškovými není žádný
Níže uvedené úlohy představují přehled otázek, které se vyskytly v tomto nebo v minulých semestrech ve cvičení nebo v minulých semestrech u zkoušky. Mezi otázkami semestrovými a zkouškovými není žádný
Michal Krátký. Úvod do programovacích jazyků (Java), 2006/2007
 Úvod do programovacích jazyků (Java) Michal Krátký Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programovacích jazyků (Java), 2006/2007 c 2006 Michal Krátký Úvod do programovacích jazyků
Úvod do programovacích jazyků (Java) Michal Krátký Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programovacích jazyků (Java), 2006/2007 c 2006 Michal Krátký Úvod do programovacích jazyků
4. Rekurze. BI-EP1 Efektivní programování Martin Kačer
 4. Rekurze BI-EP1 Efektivní programování 1 ZS 2011/2012 Ing. Martin Kačer, Ph.D. 2010-11 Martin Kačer Katedra teoretické informatiky Fakulta informačních technologií České vysoké učení technické v Praze
4. Rekurze BI-EP1 Efektivní programování 1 ZS 2011/2012 Ing. Martin Kačer, Ph.D. 2010-11 Martin Kačer Katedra teoretické informatiky Fakulta informačních technologií České vysoké učení technické v Praze
Vyhledávání. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 12.
 Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 12. září 2016 Jiří Dvorský (VŠB TUO) Vyhledávání 201 / 344 Osnova přednášky
Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 12. září 2016 Jiří Dvorský (VŠB TUO) Vyhledávání 201 / 344 Osnova přednášky
Základní pojmy. Úvod do programování. Základní pojmy. Zápis algoritmu. Výraz. Základní pojmy
 Úvod do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programování, 2004/2005 Procesor Procesorem je objekt, který vykonává algoritmem popisovanou
Úvod do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programování, 2004/2005 Procesor Procesorem je objekt, který vykonává algoritmem popisovanou
Základy algoritmizace. Hašování
 Základy algoritmizace Hašování Problematika hašování Hašování - nástroj na jednoduchý způsob "zakódování vstupních dat. Vstupní data jsou zpracována hašovací funkcí jsou jistým způsobem komprimována. Relativně
Základy algoritmizace Hašování Problematika hašování Hašování - nástroj na jednoduchý způsob "zakódování vstupních dat. Vstupní data jsou zpracována hašovací funkcí jsou jistým způsobem komprimována. Relativně
1 2 3 4 5 6 součet cvičení celkem. známka. Úloha č.: max. bodů: skut. bodů:
 Úloha č.: max. bodů: skut. bodů: 1 2 3 4 5 6 součet cvičení celkem 20 12 20 20 14 14 100 známka UPOZORNĚNÍ : a) Písemná zkouška obsahuje 6 úloh, jejichž řešení musí být vepsáno do připraveného formuláře.
Úloha č.: max. bodů: skut. bodů: 1 2 3 4 5 6 součet cvičení celkem 20 12 20 20 14 14 100 známka UPOZORNĚNÍ : a) Písemná zkouška obsahuje 6 úloh, jejichž řešení musí být vepsáno do připraveného formuláře.
B3B33ALP - Algoritmy a programování - Zkouška z předmětu B3B33ALP. Marek Boháč bohacm11
 Jméno Příjmení Už. jméno Marek oháč bohacm11 Zkouškový test Otázka 1 Jaká je hodnota proměnné count po vykonání následujícího kódu: data=[4,4,5,5,6,6,6,7,7,7,7,8,8] count=0 for i in range(1,len(data)):
Jméno Příjmení Už. jméno Marek oháč bohacm11 Zkouškový test Otázka 1 Jaká je hodnota proměnné count po vykonání následujícího kódu: data=[4,4,5,5,6,6,6,7,7,7,7,8,8] count=0 for i in range(1,len(data)):
Grafové algoritmy. Programovací techniky
 Grafové algoritmy Programovací techniky Grafy Úvod - Terminologie Graf je datová struktura, skládá se z množiny vrcholů V a množiny hran mezi vrcholy E Počet vrcholů a hran musí být konečný a nesmí být
Grafové algoritmy Programovací techniky Grafy Úvod - Terminologie Graf je datová struktura, skládá se z množiny vrcholů V a množiny hran mezi vrcholy E Počet vrcholů a hran musí být konečný a nesmí být
DSA, První krok: máme dokázat, že pro left = right vrátí volání f(array, elem, left, right)
 Indukcí dokažte následující výrok: pokud lef t a right jsou parametry funkce f a platí left right, pak volání f(array, left, right) vrátí minimální hodnotu z hodnot všech prvků v poli array na indexech
Indukcí dokažte následující výrok: pokud lef t a right jsou parametry funkce f a platí left right, pak volání f(array, left, right) vrátí minimální hodnotu z hodnot všech prvků v poli array na indexech
Datové struktury. alg12 1
 Datové struktury Jedna z klasických knih o programování (autor prof. Wirth) má název Algorithms + Data structures = Programs Datová struktura je množina dat (prvků, složek, datových objektů), pro kterou
Datové struktury Jedna z klasických knih o programování (autor prof. Wirth) má název Algorithms + Data structures = Programs Datová struktura je množina dat (prvků, složek, datových objektů), pro kterou
Dědičnost. Časová náročnost lekce: 3 hodiny Datum ukončení a splnění lekce: 23.března
 Dědičnost Cíle lekce Cílem lekce je naučit se pracovat a využívat dědičnosti při návrhu a tvorbě programů. Lekce je zaměřena hlavně na jednoduchou dědičnost. Bude rovněž vysvětlen rozdíl mezi dědičností
Dědičnost Cíle lekce Cílem lekce je naučit se pracovat a využívat dědičnosti při návrhu a tvorbě programů. Lekce je zaměřena hlavně na jednoduchou dědičnost. Bude rovněž vysvětlen rozdíl mezi dědičností
1. Převeďte dané číslo do dvojkové, osmičkové a šestnáctkové soustavy: a) 759 10 b) 2578 10
 Úlohy- 2.cvičení 1. Převeďte dané číslo do dvojkové, osmičkové a šestnáctkové soustavy: a) 759 10 b) 2578 10 2. Převeďte dané desetinné číslo do dvojkové soustavy (DEC -> BIN): a) 0,8125 10 b) 0,35 10
Úlohy- 2.cvičení 1. Převeďte dané číslo do dvojkové, osmičkové a šestnáctkové soustavy: a) 759 10 b) 2578 10 2. Převeďte dané desetinné číslo do dvojkové soustavy (DEC -> BIN): a) 0,8125 10 b) 0,35 10
Spojové struktury. x, y, a, b. X1 y1 X2 y2 X3 y3. Grafické objekty bod. kružnice. obdélník. lomenáčára
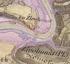 Spojové struktury Grafické objekty bod x y kružnice x y r obdélník x, y, a, b lomenáčára X1 y1 X2 y2 X3 y3 Algoritmizace (Y36ALG), Šumperk - 13. přednáška 1 Spojové seznamy I Prvek seznamu: class Prvek
Spojové struktury Grafické objekty bod x y kružnice x y r obdélník x, y, a, b lomenáčára X1 y1 X2 y2 X3 y3 Algoritmizace (Y36ALG), Šumperk - 13. přednáška 1 Spojové seznamy I Prvek seznamu: class Prvek
6. Tahy / Kostry / Nejkratší cesty
 6. Tahy / Kostry / Nejkratší cesty BI-EP2 Efektivní programování 2 LS 2017/2018 Ing. Martin Kačer, Ph.D. 2011-18 Martin Kačer Katedra teoretické informatiky Fakulta informačních technologií České vysoké
6. Tahy / Kostry / Nejkratší cesty BI-EP2 Efektivní programování 2 LS 2017/2018 Ing. Martin Kačer, Ph.D. 2011-18 Martin Kačer Katedra teoretické informatiky Fakulta informačních technologií České vysoké
Vyhledávací stromy. Slouží jako pomůcka pro organizaci dat umožňující efektivní vyhledávání.
 Vyhledávací stromy Slouží jako pomůcka pro organizaci dat umožňující efektivní vyhledávání. Vytvářejí se vždy nad již existující datovou strukturou (zpravidla tabulkou). Vyhledávací stromy můžeme rozdělit
Vyhledávací stromy Slouží jako pomůcka pro organizaci dat umožňující efektivní vyhledávání. Vytvářejí se vždy nad již existující datovou strukturou (zpravidla tabulkou). Vyhledávací stromy můžeme rozdělit
STROMY A KOSTRY. Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze. BI-GRA, LS 2010/2011, Lekce 6
 STROMY A KOSTRY Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze BI-GRA, LS 010/011, Lekce 6 Evropský sociální fond Praha & EU: Investujeme do vaší
STROMY A KOSTRY Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze BI-GRA, LS 010/011, Lekce 6 Evropský sociální fond Praha & EU: Investujeme do vaší
Select sort: krok 1: krok 2: krok 3: atd. celkem porovnání. výběr nejmenšího klíče z n prvků vyžaduje 1 porovnání
 Select sort: krok 1: výběr klíče z n prvků vyžaduje 1 porovnání krok 2: výběr klíče z 1 prvků vyžaduje 2 porovnání krok 3: výběr klíče z 2 prvků vyžaduje 3 porovnání atd. celkem porovnání Zlepšení = použít
Select sort: krok 1: výběr klíče z n prvků vyžaduje 1 porovnání krok 2: výběr klíče z 1 prvků vyžaduje 2 porovnání krok 3: výběr klíče z 2 prvků vyžaduje 3 porovnání atd. celkem porovnání Zlepšení = použít
V případě jazyka Java bychom abstraktní datový typ Time reprezentující čas mohli definovat pomocí třídy takto:
 20. Programovací techniky: Abstraktní datový typ, jeho specifikace a implementace. Datový typ zásobník, fronta, tabulka, strom, seznam. Základní algoritmy řazení a vyhledávání. Složitost algoritmů. Abstraktní
20. Programovací techniky: Abstraktní datový typ, jeho specifikace a implementace. Datový typ zásobník, fronta, tabulka, strom, seznam. Základní algoritmy řazení a vyhledávání. Složitost algoritmů. Abstraktní
Dynamické datové struktury I.
 Dynamické datové struktury I. Seznam. Fronta. Zásobník. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Dynamické datové struktury I. Seznam. Fronta. Zásobník. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Algoritmy na ohodnoceném grafu
 Algoritmy na ohodnoceném grafu Dvě základní optimalizační úlohy: Jak najít nejkratší cestu mezi dvěma vrcholy? Dijkstrův algoritmus s t Jak najít minimální kostru grafu? Jarníkův a Kruskalův algoritmus
Algoritmy na ohodnoceném grafu Dvě základní optimalizační úlohy: Jak najít nejkratší cestu mezi dvěma vrcholy? Dijkstrův algoritmus s t Jak najít minimální kostru grafu? Jarníkův a Kruskalův algoritmus
C++ Akademie SH. 2. Prom nné, podmínky, cykly, funkce, rekurze, operátory. Michal Kvasni ka. 20. b ezna Za áte níci C++
 C++ Akademie SH 2. Prom nné, podmínky, cykly, funkce, rekurze, operátory Za áte níci C++ 20. b ezna 2011 Obsah 1 Prom nné - primitivní typy Celá ísla ƒísla s pohyblivou desetinnou árkou, typ bool 2 Podmínka
C++ Akademie SH 2. Prom nné, podmínky, cykly, funkce, rekurze, operátory Za áte níci C++ 20. b ezna 2011 Obsah 1 Prom nné - primitivní typy Celá ísla ƒísla s pohyblivou desetinnou árkou, typ bool 2 Podmínka
ORIENTOVANÉ GRAFY, REPREZENTACE GRAFŮ
 ORIENTOVANÉ GRAFY, REPREZENTACE GRAFŮ Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze BI-GRA, LS 2/2, Lekce Evropský sociální fond Praha & EU: Investujeme
ORIENTOVANÉ GRAFY, REPREZENTACE GRAFŮ Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze BI-GRA, LS 2/2, Lekce Evropský sociální fond Praha & EU: Investujeme
Grafové algoritmy. Programovací techniky
 Grafové algoritmy Programovací techniky Grafy Úvod - Terminologie Graf je datová struktura, skládá se z množiny vrcholů V a množiny hran mezi vrcholy E Počet vrcholů a hran musí být konečný a nesmí být
Grafové algoritmy Programovací techniky Grafy Úvod - Terminologie Graf je datová struktura, skládá se z množiny vrcholů V a množiny hran mezi vrcholy E Počet vrcholů a hran musí být konečný a nesmí být
Dynamické struktury a Abstraktní Datový Typy (ADT)
 Dynamické struktury a Abstraktní Datový Typy (ADT) Jan Faigl Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Přednáška 11 A0B36PR1 Programování 1 Jan Faigl, 2015 A0B36PR1
Dynamické struktury a Abstraktní Datový Typy (ADT) Jan Faigl Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Přednáška 11 A0B36PR1 Programování 1 Jan Faigl, 2015 A0B36PR1
Rekurze. Pavel Töpfer, 2017 Programování 1-8 1
 Rekurze V programování ve dvou hladinách: - rekurzivní algoritmus (řešení úlohy je definováno pomocí řešení podúloh stejného charakteru) - rekurzivní volání procedury nebo funkce (volá sama sebe přímo
Rekurze V programování ve dvou hladinách: - rekurzivní algoritmus (řešení úlohy je definováno pomocí řešení podúloh stejného charakteru) - rekurzivní volání procedury nebo funkce (volá sama sebe přímo
Lineární datové struktury
 Lineární datové struktury doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 13. března 2017 Jiří Dvorský (VŠB TUO) Lineární datové
Lineární datové struktury doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 13. března 2017 Jiří Dvorský (VŠB TUO) Lineární datové
Šablony, kontejnery a iterátory
 11. března 2015, Brno Připravil: David Procházka Šablony, kontejnery a iterátory Programovací jazyk C++ Šablony Strana 2 / 31 Obsah přednášky 1 Šablony 2 Abstraktní datové struktury 3 Iterátory 4 Array
11. března 2015, Brno Připravil: David Procházka Šablony, kontejnery a iterátory Programovací jazyk C++ Šablony Strana 2 / 31 Obsah přednášky 1 Šablony 2 Abstraktní datové struktury 3 Iterátory 4 Array
Část 1 Spojové struktury (stromy) Dynamické struktury a Abstraktní Datový Typy (ADT) Část 2 Abstraktní datový typ. Část 3 Příklad ADT Prioritní fronta
 Část 1 Spojové struktury (stromy) Dynamické struktury a Abstraktní Datový Typy (ADT) Stromy Jan Faigl Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Přednáška 11 A0B36PR1
Část 1 Spojové struktury (stromy) Dynamické struktury a Abstraktní Datový Typy (ADT) Stromy Jan Faigl Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Přednáška 11 A0B36PR1
Dynamické programování
 ALG 0 Dynamické programování zkratka: DP Zdroje, přehledy, ukázky viz https://cw.fel.cvut.cz/wiki/courses/a4balg/literatura_odkazy 0 Dynamické programování Charakteristika Neřeší jeden konkrétní typ úlohy,
ALG 0 Dynamické programování zkratka: DP Zdroje, přehledy, ukázky viz https://cw.fel.cvut.cz/wiki/courses/a4balg/literatura_odkazy 0 Dynamické programování Charakteristika Neřeší jeden konkrétní typ úlohy,
Algoritmy II. Otázky k průběžnému testu znalostí
 Algoritmy II Otázky k průběžnému testu znalostí Revize ze dne 19. února 2018 2 Lineární datové struktury 1 1. Vysvětlete co znamená, že zásobník představuje paměť typu LIFO. 2. Co je to vrchol zásobníku?
Algoritmy II Otázky k průběžnému testu znalostí Revize ze dne 19. února 2018 2 Lineární datové struktury 1 1. Vysvětlete co znamená, že zásobník představuje paměť typu LIFO. 2. Co je to vrchol zásobníku?
Zápis programu v jazyce C#
 Zápis programu v jazyce C# Základní syntaktická pravidla C# = case sensitive jazyk rozlišuje velikost písmen Tzv. bílé znaky (Enter, mezera, tab ) ve ZK překladač ignoruje každý příkaz končí ; oddělovač
Zápis programu v jazyce C# Základní syntaktická pravidla C# = case sensitive jazyk rozlišuje velikost písmen Tzv. bílé znaky (Enter, mezera, tab ) ve ZK překladač ignoruje každý příkaz končí ; oddělovač
Vyvažování a rotace v BVS, všude se předpokládá AVL strom
 Vyvažování a rotace v BVS, všude se předpokládá AVL strom 1. Jednoduchá levá rotace v uzlu u má operační složitost a) závislou na výšce levého podstromu uzlu u b) mezi O(1) a Θ(n) c) závislou na hloubce
Vyvažování a rotace v BVS, všude se předpokládá AVL strom 1. Jednoduchá levá rotace v uzlu u má operační složitost a) závislou na výšce levého podstromu uzlu u b) mezi O(1) a Θ(n) c) závislou na hloubce
Binární vyhledávací stromy II
 Binární vyhledávací stromy II doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 19. března 2019 Jiří Dvorský (VŠB TUO) Binární vyhledávací
Binární vyhledávací stromy II doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 19. března 2019 Jiří Dvorský (VŠB TUO) Binární vyhledávací
Základy C++ I. Jan Hnilica Počítačové modelování 18
 Základy C++ I 1 Přechod z C na C++ jazyk C++ je nadmnožinou jazyka C z hlediska syntaxe se jedná o velmi podobné jazyky, spolu s dalšími jazyky "céčkovské" rodiny, jako je např. C# každý platný program
Základy C++ I 1 Přechod z C na C++ jazyk C++ je nadmnožinou jazyka C z hlediska syntaxe se jedná o velmi podobné jazyky, spolu s dalšími jazyky "céčkovské" rodiny, jako je např. C# každý platný program
AVL stromy. pro každý uzel u stromu platí, že rozdíl mezi výškou jeho levého a pravého podstromu je nejvýše 1 stromy jsou samovyvažující
 Stromy 2 AVL AVL stromy jména tvůrců stromů: dva Rusové Adelson-Velskii, Landis vyvážené binární stromy pro každý uzel u stromu platí, že rozdíl mezi výškou jeho levého a pravého podstromu je nejvýše 1
Stromy 2 AVL AVL stromy jména tvůrců stromů: dva Rusové Adelson-Velskii, Landis vyvážené binární stromy pro každý uzel u stromu platí, že rozdíl mezi výškou jeho levého a pravého podstromu je nejvýše 1
Datové struktury. Obsah přednášky: Definice pojmů. Abstraktní datové typy a jejich implementace. Algoritmizace (Y36ALG), Šumperk - 12.
 Obsah přednášky: Definice pojmů o datový typ, o abstraktní datový typ Datové struktury Abstraktní datové typy a jejich implementace o Fronta (Queue) o Zásobník (Stack) o Množina (Set) Algoritmizace (Y36ALG),
Obsah přednášky: Definice pojmů o datový typ, o abstraktní datový typ Datové struktury Abstraktní datové typy a jejich implementace o Fronta (Queue) o Zásobník (Stack) o Množina (Set) Algoritmizace (Y36ALG),
Jazyk C++ II. Šablony a implementace
 Jazyk C++ II Šablony a implementace AR 2013/2014 Jazyk C++ II Úvod Dědičnost a kompozice nejsou vždy tou správnou odpovědí na požadavky znovupoužitelnosti kódu. Proto máme možnost definování určité třídy
Jazyk C++ II Šablony a implementace AR 2013/2014 Jazyk C++ II Úvod Dědičnost a kompozice nejsou vždy tou správnou odpovědí na požadavky znovupoužitelnosti kódu. Proto máme možnost definování určité třídy
