Algoritmy prostorových analýz KMA/APA
|
|
|
- Tadeáš Beran
- před 6 lety
- Počet zobrazení:
Transkript
1 Algoritmy prostorových analýz KMA/APA Testování vhodnosti použití vybrané interpolace na soubor dat Michal Kepka
2 Obsah 1. Úvod Metodika testování Hodnotící kritéria Příprava dat Sběr dat Prostorová lokalizace dat Konvexní obálka Přidání zkratek Programová část Skript SelectStations Skripty pro testování Zjednodušený model testovacích skriptů Výstupní soubor Skript pro porovnání výsledků Vyhodnocení testování Pomocí interpolovaných rastrů Interpolace Natural Neighbor Interpolace IDW Interpolace Kriging Hodnocení Pomocí kritéria kvadrátů odchylek Pomocí kritéria kvadrátů odchylek u více souborů dat Závěr Literatura a zdroje
3 1. Úvod Úkolem práce je vytvořit programový nástroj pro testování vhodnosti použití vybrané interpolace na předložený soubor dat. Neméně důležitým úkolem je také prověření samotné použité metodiky testování jako objektivního hodnotícího nástroje. Výsledkem je nástroj, který na předložených datech prověří několik interpolací a z nich vybere jednu, která interpoluje zadaná data s nejmenší chybou. Pro testování byly zvoleny soubory teplotních dat, která naměřily vybrané měřické stanice Českého hydrometeorologického úřadu (dále ČHMÚ). 2. Metodika testování Metodika testování spočívá v myšlence postupného vynechávání jednotlivých naměřených hodnot ze souboru dat, následné interpolaci zbylých dat, odečtení vyinterpolované hodnoty ve vynechaném bodě a výsledném porovnání s původní měřenou hodnotou. Do souboru vynechávaných bodů nebyly ovšem zařazeny okrajové body, ve kterých je předem jasné, že by následná interpolace nebyla bezchybná Hodnotící kritéria Hlavním hodnotícím kritériem je zde součet druhých mocnin odchylek na jednotlivých vynechaných bodech (v dalším textu jako kritérium kvadrátů odchylek). Kde pojmem odchylka o je myšlena celá část desetinásobku absolutní hodnoty rozdílu původní h p a nově interpolované h i hodnoty (viz vzorec 2.1). o 10 h p h i (2.1) Např. pro rozdíl -1,234 [ C] činí odchylka 12 [10-1 C]. Celá část desetinásobku je zvolena z důvodu zachování stejné přesnosti jako u vstupních dat (přesnost 0,1 C), kvadrát je zvolen proto, aby se větší odchylka projevila v hodnocení více než menší. Jako vedlejší kritéria a spíše pro porovnání, je také vyhodnocována suma odchylek (dále jako kritérium odchylek) a celková suma rozdílů na jednotlivých bodech (dále jako kritérium rozdílů). Rozdílem je myšlen rozdíl mezi původní hodnotou a interpolovanou. Myšlenkou kritéria rozdílů je případné ověření, zda se suma rozdílů může blížit nule, tj. kladné a záporné chyby se vzájemně odečtou. Jako nejvhodnější metoda interpolace je vyhodnocena taková metoda, která má nejmenší hodnotu kritéria kvadrátů odchylek. 3
4 3. Příprava dat Příprava dat spočívala jednak v samotném získání těchto dat, jednak v jejich prostorovém umístění a ve vytvoření vektorové bodové vrstvy Sběr dat Po neúspěšném jednání s ČHMÚ o poskytnutí většího souboru dat z celého území České republiky, byl zvolen postup sběru uveřejňovaných hodnot [CHMU1] z vybraných měřických stanic na území republiky. Tímto způsobem byla získána data z 38 stanic. Teploty byly zaznamenávány v přibližně denních intervalech mezi až Výsledkem je 7 souborů hodnot, z čehož pouze 2 jsou úplné (soubory č. 6. a 8.), u zbylých 5 chybí údaj ze stanice Kopisty (soubory č. 1., 2., 3., 5., 7.), která v té době neposkytovala data. Soubor č. 4. byl vyřazen, protože neobsahoval měření z více stanic Prostorová lokalizace dat Prostorová lokalizace spočívala ve zjištění souřadnic měřických stanic. ČHMÚ zveřejňuje pouze geografické souřadnice s přesností jedné úhlové minuty, což přibližně odpovídá polohové přesnosti 1,2 km v zeměpisné šířce a 1,8 km v zeměpisné délce. Tato přesnost nebyla nepovažována za dostatečnou. Proto byla pomocí uveřejněných souřadnic, adres stanic, katastrální mapy a ortofota [MAP1] jejich poloha zpřesněna. Zpřesnění spočívalo v nalezení stanice pomocí výše uvedených podkladů na ortofoto snímku a následném odečtu souřadnic ze snímku v systému WGS84 s přesností na 1 úhlovou vteřinu, tj. s přesností 20 m v zeměpisné šířce, resp. 30 m v zeměpisné délce. U některých stanic na letištích byl problém lokalizovat přesnou polohu měřící stanice na snímku, proto byla odečtena souřadnice řídící věže s předpokladem, že meteorologická zahrádka se bude nacházet v jejím blízkém okolí. Tabulka souřadnic byla pomocí funkce Add XY Data v ArcGIS převedena na vektorovou bodovou vrstvu a transformována do systému UTM 33N. Následně byla k vektorové vrstvě připojena tabulka měřených teplotních dat. Tímto vznikla surová vstupní datová vrstva, kterou byla dále zpracovávána. Výsledné rozložení stanic na území ČR ukazuje následující obrázek
5 Obr. 3.1.: Rozložení stanic 3.3. Konvexní obálka Z důvodu snadné identifikace, které stanice lze při testování vypouštět, bylo nutné vytvořit k použité bodové vrstvě konvexní obálku. Obálka bude zároveň použita k ořezání interpolovaných rastrů. Po vytvoření obálky bylo možné přiřadit k bodům stanic nový atribut, vyjadřující, zda daný bod leží na hranici oblasti či nikoliv. Tento atribut byl nazván Hranicni a nabývá hodnoty 1 pro stanici tvořící obálku (11 stanic) a 0 pro vnitřní a tudíž vypustitelnou stanici (27 stanic). Stanice tvořící obálku budu dále v textu nazývat hraniční, stanice ležící uvnitř obálky budu označovat jako vypustitelné. Vytvořenou konvexní obálku lze vidět na obrázku Přidání zkratek Během odečtu interpolované hodnoty v bodě rastru, vyvstala nutnost přidat jako další atribut zkratku stanice. Volba použití zkratek přišla z důvodu snadného pojmenování vytvářených souborů, jelikož některé názvy stanic jsou víceslovné a většina obsahuje diakritiku. Zkratka byla použita pro vytvoření shapefile pro každou vypustitelnou stanici. Zkratka je dvou až tří písmenná, neobsahuje diakritiku a skládá se většinou z prvních písmen názvu stanice, při shodě byla zvolena jiná podobná kombinace písmen, případně zažité pojmenování (např. pro Karlovy Vary je použita zkratka KV). 5
6 4. Programová část Hlavní součástí práce jsou vytvořené skripty v programovacím jazyce Python, které využívají některé funkce z programu ArcGIS. Testovací program je rozdělen na jednotlivé skripty, kdy každý skript testuje jednu interpolaci nad jedním souborem dat. Popis jednotlivých skriptů je uveden dále. Důvodem vytvoření více skriptů bylo jednak hledisko paměťové ale i časové náročnosti testování (viz kap. 4.2). K testování byly použity vybrané interpolační metody z nabídky Toolbox ArcGIS, konkrétně Inverse Distance Weighing (dále IDW), Kriging a Natural Neighbor. Bližší popis a vlastnosti jednotlivých interpolací jsou dostupné v literatuře Skript SelectStations Tento skript patří ještě k přípravné části před samostatným testováním. Slouží k vytvoření jednobodových shapefile obsahující vždy jednu vypustitelnou stanici. Tento krok je důležitý proto, že při testování byla k získání hodnoty rastru v bodě využita funkce Extract Values to Points, která potřebuje jako jeden ze vstupů bodovou vektorovou vrstvu, podle které odečítá hodnoty rastru v daných bodech a vkládá je do atributové tabulky jako atribut RASTERVALU. Skript se v podstatě spouští pouze před úplně prvním testováním. Testovací skripty následně předpokládají přítomnost shapefile vypustitelných stanic v nastaveném adresáři Skripty pro testování Testovací skripty jsou pro každou interpolaci napsané zvlášť, ovšem liší se pouze použitou interpolací. Jedná se o skripty Kriging_komplet.py, IDW_komplet.py a NaturalNeighbor_komplet.py. Základem skriptů je kursor, který prochází vstupní shapefile s daty a u stanic, kde je atribut Hranicni roven nule, zavolá příslušnou funkci. Jedná se o prototypové skripty, které by byly v další verzi sloučeny do jednoho skriptu a uživatel by prováděl zadání vstupního souboru dat a volbu testované interpolace. Funkce ve skriptech vyjme vybranou stanici ze vstupního souboru, provede příslušnou interpolaci zbylých dat, pak ořízne rastr dříve vytvořenou konvexní obálkou (viz kap. 3.3), následně je využita funkce pro odečet hodnoty rastru (viz kap. 4.1), která vytvoří shapefile stejný jako vstupní jednobodový, ale navíc s hodnotou rastru v daném bodě jako novým atributem. Pak je odečtena interpolovaná hodnota od původní měřené a rozdíl se vrací jako výsledek celé funkce. 6
7 Získaný rozdíl z funkce je zapsán do výstupního textového souboru. Výstupem všech testovacích skriptů je textový soubor se získanými rozdíly hodnot. Skripty také produkují velké množství vedlejších souborů každé volání funkce vytvoří 3 shapefile a 2 rastry o celkové velikosti 80 MB, což po otestování celého souboru dat (27 vypuštěných stanic) jednou interpolací dosahuje objemu kolem 3 GB dat, oproti vstupnímu shapefile o velikosti 30 kb. Tento obrovský nárůst dat byl také jeden z důvodů pro rozdělení skriptů podle jednotlivých interpolačních metod a jejich odděleného spouštění. Druhým důvodem byla také časová náročnost testu jedné interpolace, která dosahovala od 40 do 220 minut při vypouštění 27 stanic Zjednodušený model testovacích skriptů Strukturu výše popsaných testovacích skriptů představuje ve zjednodušené formě následující modelový diagram na obrázku 4.1. Tento diagram byl základem pro funkci skriptu používající interpolační metodu Kriging, zbylé skripty se liší jen použitou interpolační metodou. Obr. 4.1.:Diagram testovací funkce Diagram představuje základ testovací funkce pro metodu Kriging. Názvy meziproduktových vrstev jsou i v dalších případech zachovány ve stejné konvenci interpolacnimetoda_zkratkastanice_produkt. Kde produkt IR značí interpolated raster, MR označuje masked raster a P je označení pro point, 7
8 nebo-li bodovou vrstvu s vypustitelnou stanicí a hodnotou rastru jako novým atributem Výstupní soubor Výstupem každého testovacího skriptu je textový soubor s hodnotami rozdílů v jednotlivých vynechaných stanicích. Testovací soubor se nachází ve vytvořeném podadresáři pojmenovaném jako sloupec s testovacími daty a je vždy pojmenován interpolacnimetoda_nazevsloupce.txt Skript pro porovnání výsledků Pro vyhodnocení získaných rozdílů byl vytvořen skript Compare.py, který přečte všechny tři získané výstupní soubory a spočítá pro každou metodu výslednou sumu kvadrátů odchylek, sumu rozdílů a sumu odchylek. Získané hodnoty kritérií vypíše uživateli na obrazovku i do textového souboru s názvem Hodnoceni_nazevSloupce.txt. Uživatel již jen pouhým porovnáním vypsaných hodnot lehce usoudí na vhodnost použití té které interpolační metody, protože nejvhodnější metoda má nejmenší hodnotu součtu kvadrátů odchylek. Výstup hodnotícího skriptu: Testovany soubor dat: TEST3 Kriterium: >---< suma((diff*10)^2) >---< suma(diff) >---< suma(diff*10) > < Kriging: >---< >---< >---< 387 IDW: >---< 8995 >---< >---< 335 Nat. Neighbor: >---< >---< >---< 409 Z výpisu lze snadno nahlédnout, která z interpolačních metod byla výše uvedeným kritériem kvadrátů odchylek vyhodnocena jako nejvhodnější. 8
9 5. Vyhodnocení testování V této části jsou představeny možné způsoby hodnocení testování s využitím části meziproduktů testovacích skriptů, dále jsou zde předloženy důvody pro vytvoření hodnotícího kritéria kvadrátů odchylek (viz kap. 2.1) a následně shrnuty výsledky testování pomocí kritéria kvadrátů odchylek pro několik souborů dat Pomocí interpolovaných rastrů Jak je popsáno výše (viz kap. 4.2) základem testovacího skriptu je funkce, která provádí selekci stanice, interpolaci rastru a extrakci hodnot z rastru. Následují ukázky interpolovaných rastrů pro vybrané interpolační metody při vypuštění konkrétní stanice (Čáslav) během testování jednoho souboru dat, konkrétně souboru č. 8. (TEST8). Jako možné hodnotící kritérium je použita maximální hodnota rozdílového rastru, který vznikne odečtením rastru bez vypuštěné stanice od rastru se všemi stanicemi. Veškeré hodnoty rastrů jsou ve stupních Celsia Interpolace Natural Neighbor Obr. 5.1.: Interpolace Natural Neighbor kompletní rastr 9
10 Obr. 5.2.: Interpolace Natural Neighbor testovací rastr Obr. 5.3.: Interpolace Natural Neighbor- rozdílový rastr 10
11 Z interpolovaných rastrů (Obr. 5.1., Obr. 5.2.) je patrná změna hodnot po vypuštění stanice Čáslav. Rozsah změny rastru je nejlépe viditelný z rozdílového rastru (Obr. 5.3.), kde zabarvená oblast vymezuje prostor, kde není rozdíl mezi rastry nulový. Je patrné, že při metodě Natural Neighbor ovlivní vypuštění jedné stanice hodnoty rastru jen v blízkém okolí této stanice. Ovšem maximální rozdíl mezi rastry činí 1,8 C Interpolace IDW Obr. 5.4.: Interpolace IDW kompletní rastr 11
12 Obr. 5.5.: Interpolace IDW testovací rastr Obr. 5.6.: Interpolace IDW rozdílový rastr 12
13 Z interpolovaných rastrů (Obr. 5.4., Obr. 5.5.) je opět viditelná změna hodnot po vypuštění stanice Čáslav. Rozsah změny ukazuje rozdílový rastr (Obr. 5.6.), kde opět zabarvená oblast vymezuje prostor, kde není rozdíl mezi rastry nulový. Je patrné, že při metodě IDW již dochází k mnohem většímu ovlivnění hodnot rastru. Maximální rozdíl činí 2,2 C Interpolace Kriging Obr. 5.7.: Interpolace Kriging kompletní rastr 13
14 Obr. 5.8.: Interpolace Kriging testovací rastr Obr. 5.9.: Interpolace Kriging rozdílový rastr 14
15 Opět je z rastrů (Obr. 5.7., Obr. 5.8.) patrná změna hodnot po vypuštění stanice Čáslav. Rozdílový rastr (Obr. 5.9.) je v tomto případě kompletní, tzn. že vypuštění jedné stanice ovlivní hodnoty v celém novém rastru. Ovšem rozdíl mezi rastry činí maximálně 0,5 C Hodnocení Při vypuštění pouze jedné stanice lze dojít k závěru, že pro daný soubor dat je pořadí vhodnosti použití metod následující: 1. Kriging, 2. Natural Neighbor, 3. IDW. Tento způsob testování nevyžaduje vytvořené skripty a je také mnohem méně časově náročný. Ovšem jak je později ukázáno, nemusí vést ke správnému výsledku Pomocí kritéria kvadrátů odchylek Nyní je vyhodnocení stejného souboru dat provedeno pomocí vytvořených skriptů a vypočítána vhodnost daných interpolací pomocí hodnotícího kritéria kvadrátů odchylek. Po provedení testů byla získána následující tabulka (Tabulka 5.1) rozdílů a odchylek (viz kap. 2.1). 15
16 Tab. 5.1.: Rozdíly a odchylky pro soubor č. 8. TEST 8 Natural Neighbor Kriging IDW čas testu [min] Stanice Rozdíl Odchylka Rozdíl Odchylka Rozdíl Odchylka [ C] [10-1 C] [ C] [10-1 C] [ C] [10-1 C] Karlovy Vary -0, , , Tušimice 0, , , Plzeň-Mikulka 1, , , Milešovka -3, , , Kocelovice -1, , , Doksany 2, , , Praha-Ruzyně -0, , , Praha-Karlov 0, , , Praha-Libuš -0, , , Temelín -0, , , Praha-Kbely -0, , , Čáslav 1, , , Košetice 1, , , Kostelní Myslová -2, , , Pardubice -1, , , Přibyslav -0, , , Polom 2, , , Ústí n. Orlicí -0, , , Svratouch 0, , , Náměšť n. Oslavou 0, , , Dukovany -0, , , Luká -1, , , Brno-Tuřany 0, , , Přerov -0, , , Červená 0, , , Holešov -1, , , Ostrava-Mošnov 3, , , Hodnotící skript spočítal následující součty kvadrátů odchylek, rozdílů a odchylek: Testovany soubor dat: TEST8 Kriterium: >---< suma((diff*10)^2) >---< suma(diff) >---< suma(diff*10) > < Kriging: >---< 4771 >---< >---< 275 IDW: >---< 4428 >---< >---< 254 Nat. Neighbor: >---< 5065 >---< >---< 281 Z výstupu hodnotícího skriptu lze po porovnání hodnot kritéria kvadrátů odchylek snadno nahlédnout, že nyní je pořadí vhodnosti použití metod následující: 1. IDW, 2. Kriging, 3. Natural Neighbor. Je zajímavé všimnout si i časové náročnosti jednotlivých testů, zatímco otestovat metody Natural Neighbor a IDW zabralo cca 40 minut, testování metody Kriging potřebovalo třikrát více času. Čímž se potvrzuje správnost počátečního rozdělení skriptů 16
17 Součet kvadrátů podle metod, při jednom společném skriptu by testování zabralo přes 3,5 hodiny. Dále je možné si všimnout, že při použití kritéria součtu rozdílů, je pořadí opět trochu jiné: 1. Natural Neighbor, 2. Kriging, 3. IDW. Takže ačkoliv byly rozdíly u metody Natural Neighbor větší než u ostatních (viz hodnoty odchylek), v součtu se blíží nule. Hodnoty kritéria odchylek udávají stejné pořadí jako hodnoty kritéria kvadrátů odchylek, ovšem s nižší odlišitelností jednotlivých metod, zvláště metody IDW a Kriging Pomocí kritéria kvadrátů odchylek u více souborů dat Po testování pěti souborů dat, konkrétně souborů číslo 1, 2, 3, 6 a 8, bylo již možno sestavit přehlednou tabulku (Tabulka 5.2.) vývoje součtů kvadrátů odchylek pro jednotlivé metody a vykreslit je do grafu (Graf 5.1). Soubory č. 5. a 7. nebyly testovány, protože jednotlivá měření neměla 24 hodinový odstup od ostatních měření. Tabulka 5.2.: Součty kvadrátů odchylek pro soubory dat TEST1 TEST2 TEST3 TEST6 TEST8 IDW Kriging Nat. Neighbor Graf 5.1 Součty kvadrátů odchylek pro soubory dat IDW Kriging Nat. Neighbor TEST1 TEST2 TEST3 TEST6 TEST8 Soubor dat 17
18 Součet rozdílů Z grafu 5.1. je patrné, že pořadí vhodnosti interpolačních metod se s různými soubory podobných dat nemění. Mění se pouze hodnoty odchylek, což je dáno změnou hodnot dat v jednotlivých souborech. Pokud ovšem je stejná tabulka (Tabulka 5.3.) i graf (Graf 5.2) sestavena pro součty rozdílů v rámci jednotlivých testovaných souborů nejsou výsledky tak jednoznačné. Tabulka 5.3.: Součty rozdílů pro soubory dat TEST1 TEST2 TEST3 TEST6 TEST8 IDW 6, ,1414 6, , , Kriging 15, , , , , Nat. Neighbor 18, , , , , Graf 5.2 Součet rozdílů podle souborů dat IDW Kriging Nat. Neighbor TEST1 TEST2 TEST3 TEST6 TEST8 Soubor dat Z grafu 5.3 je patrné, že pořadí vhodnosti není již tak jednoznačné, z pěti souborů jsou tři soubory s pořadím ve shodě, zbylé dva naznačují každý jiné pořadí, tzn. pro pět souborů existují tři možná pořadí. Což není možné nepovažovat za uspokojivý výsledek, který ovšem potvrzuje správnost použití kritéria kvadrátů odchylek. Další možností je sestavit tabulku i pro součty odchylek (Tabulka 5.4) a vykreslit obdobný graf (Graf 5.3). 18
19 Součet odchylek Tabulka 5.4.: Součty odchylek pro soubory dat TEST1 TEST2 TEST3 TEST6 TEST8 IDW Kriging Nat. Neighbor Graf 5.3 Součty odchylek pro soubory dat 600 IDW Kriging Nat. Neighbor TEST1 TEST2 TEST3 TEST6 TEST8 Soubor dat Z grafu 5.3 pro součty odchylek je vidět stejné pořadí vhodnosti interpolací jako pro graf 5.1, tedy pro kritérium kvadrátů odchylek. Pouze není tolik zvýrazněn rozdíl mezi interpolační metodou IDW a Kriging. 19
20 6. Závěr Po počátečním získání teplotních dat a jejich prostorové lokalizaci, bylo provedeno předzpracování, které usnadnilo další kroky během testování. V programové části byly vytvořeny skripty, které jednak dokončí předzpracování, další otestují data a poskytnou surové výpisy a nakonec byl vytvořen hodnotící skript, který uživateli určitým postupem spočítá číselnou hodnotu ze získaných rozdílů a jejíž nejnižší hodnota označuje nejvhodnější interpolační metodu z testované množiny metod. Vytvořené skripty lze po menších úpravách využít i pro další soubory dat jiného charakteru než zde uvedená teplotní data. Skripty jsou dostatečné komentovány ve zdrojových kódech a nutné úpravy lze snadno identifikovat. V poslední části bylo provedeno vyhodnocení metod pomocí rozdílných kritérií a postupů, čímž měla být potvrzena správnost volby použitého hodnotícího kritéria kvadrátů odchylek. K čemuž také došlo, jelikož použité kritérium kvadrátů odchylek poskytovalo jednoznačné výsledky. Stejné výsledky poskytuje i kritérium odchylek, ovšem s menší rozlišovací schopností výsledků hodnocení jednotlivých interpolačních metod. Závěrem lze tedy konstatovat, že pro zvolená meteorologická data s danou nepravidelnou hustotou rozložení po území republiky a daným ročním obdobím, ve kterém byla měřena, se ukázala jako nejvhodnější interpolační metoda IDW. Je samozřejmě možné diskutovat o charakteru samotných dat, jak by se změnily výsledky při jiném ročním období měření, při kombinaci období, při změně hustoty měřících stanic. Práce bude mít pokračování v rámci předmětu Aplikace GIS, kde bude testovací program vytvořen pomocí jazyku VisualBasic for Aplications a bude součástí programu ArcGIS. Zároveň bude příležitost otestovat i data jiného charakteru, např. gravimetrická. 7. Literatura a zdroje [CHMU1] Aktuální informace o počasí na území ČR. [online]. URL adresa: pozadi=mapareg&graf=ne [CHMU2] Poloha meteorologických stanic. [online]. URL adresa: [MAP1] Ortofotomapa. [online]. URL adresa: 20
Popis metod CLIDATA-GIS. Martin Stříž
 Popis metod CLIDATA-GIS Martin Stříž Říjen 2008 Obsah 1CLIDATA-SIMPLE...3 2CLIDATA-DEM...3 2.1Metodika výpočtu...3 2.1.1Výpočet regresních koeficientů...3 2.1.2 nalezených koeficientu...5 2.1.3Výpočet
Popis metod CLIDATA-GIS Martin Stříž Říjen 2008 Obsah 1CLIDATA-SIMPLE...3 2CLIDATA-DEM...3 2.1Metodika výpočtu...3 2.1.1Výpočet regresních koeficientů...3 2.1.2 nalezených koeficientu...5 2.1.3Výpočet
Testování neuronových sítí pro prostorovou interpolaci v softwaru GRASS GIS
 Testování neuronových sítí pro prostorovou interpolaci v softwaru GRASS GIS Veronika NEVTÍPILOVÁ Gisáček 2013 Katedra Geoinformatiky Univerzita Palackého v Olomouci Cíle otestovat kvalitu interpolace pomocí
Testování neuronových sítí pro prostorovou interpolaci v softwaru GRASS GIS Veronika NEVTÍPILOVÁ Gisáček 2013 Katedra Geoinformatiky Univerzita Palackého v Olomouci Cíle otestovat kvalitu interpolace pomocí
Horské meteorologické stanice v Česku a výškové členění staniční sítě ČHMÚ
 ČESKÁ METEOROLOGICKÁ SPOLEČNOST Horské meteorologické stanice v Česku a výškové členění staniční sítě ČHMÚ Pavel Lipina Lysá hora 120 let meteorologických měření a pozorování Bezručova chata, Lysá hora
ČESKÁ METEOROLOGICKÁ SPOLEČNOST Horské meteorologické stanice v Česku a výškové členění staniční sítě ČHMÚ Pavel Lipina Lysá hora 120 let meteorologických měření a pozorování Bezručova chata, Lysá hora
Rastrové digitální modely terénu
 Rastrové digitální modely terénu Rastr je tvořen maticí buněk (pixelů), které obsahují určitou informaci. Stejně, jako mohou touto informací být typ vegetace, poloha sídel nebo kvalita ovzduší, může každá
Rastrové digitální modely terénu Rastr je tvořen maticí buněk (pixelů), které obsahují určitou informaci. Stejně, jako mohou touto informací být typ vegetace, poloha sídel nebo kvalita ovzduší, může každá
Digitální model reliéfu (terénu) a analýzy modelů terénu
 Digitální model reliéfu (terénu) a analýzy modelů terénu Digitální modely terénu jsou dnes v geoinformačních systémech hojně využívány pro různé účely. Naměřená terénní data jsou často zpracována do podoby
Digitální model reliéfu (terénu) a analýzy modelů terénu Digitální modely terénu jsou dnes v geoinformačních systémech hojně využívány pro různé účely. Naměřená terénní data jsou často zpracována do podoby
ÚLOHY S POLYGONEM. Polygon řetězec úseček, poslední bod je totožný s prvním. 6 bodů: X1, Y1 až X6,Y6 Y1=X6, Y1=Y6 STANOVENÍ PLOCHY JEDNOHO POLYGONU
 ÚLOHY S POLYGONEM Polygon řetězec úseček, poslední bod je totožný s prvním 6 bodů: X1, Y1 až X6,Y6 Y1=X6, Y1=Y6 STANOVENÍ PLOCHY JEDNOHO POLYGONU 3 úsečky (segmenty) v horní části 2 úsečky ve spodní části
ÚLOHY S POLYGONEM Polygon řetězec úseček, poslední bod je totožný s prvním 6 bodů: X1, Y1 až X6,Y6 Y1=X6, Y1=Y6 STANOVENÍ PLOCHY JEDNOHO POLYGONU 3 úsečky (segmenty) v horní části 2 úsečky ve spodní části
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ, OBOR GEODÉZIE A KARTOGRAFIE KATEDRA MAPOVÁNÍ A KARTOGRAFIE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ, OBOR GEODÉZIE A KARTOGRAFIE KATEDRA MAPOVÁNÍ A KARTOGRAFIE název předmětu TOPOGRAFICKÁ A TEMATICKÁ KARTOGRAFIE číslo úlohy název úlohy 2 Tvorba tematických
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ, OBOR GEODÉZIE A KARTOGRAFIE KATEDRA MAPOVÁNÍ A KARTOGRAFIE název předmětu TOPOGRAFICKÁ A TEMATICKÁ KARTOGRAFIE číslo úlohy název úlohy 2 Tvorba tematických
9. přednáška z předmětu GIS1 Digitální model reliéfu a odvozené povrchy. Vyučující: Ing. Jan Pacina, Ph.D.
 9. přednáška z předmětu GIS1 Digitální model reliéfu a odvozené povrchy Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Lehký úvod Digitální modely terénu jsou dnes v geoinformačních systémech
9. přednáška z předmětu GIS1 Digitální model reliéfu a odvozené povrchy Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Lehký úvod Digitální modely terénu jsou dnes v geoinformačních systémech
2. úkol MI-PAA. Jan Jůna (junajan) 3.11.2013
 2. úkol MI-PAA Jan Jůna (junajan) 3.11.2013 Specifikaci úlohy Problém batohu je jedním z nejjednodušších NP-těžkých problémů. V literatuře najdeme množství jeho variant, které mají obecně různé nároky
2. úkol MI-PAA Jan Jůna (junajan) 3.11.2013 Specifikaci úlohy Problém batohu je jedním z nejjednodušších NP-těžkých problémů. V literatuře najdeme množství jeho variant, které mají obecně různé nároky
Digitální kartografie 7
 Digitální kartografie 7 digitální modely terénu základní analýzy a vizualizace strana 2 ArcGIS 3D Analyst je zaměřen na tvorbu, analýzu a zobrazení dat ve 3D. Poskytuje jak nástroje pro interpolaci rastrových
Digitální kartografie 7 digitální modely terénu základní analýzy a vizualizace strana 2 ArcGIS 3D Analyst je zaměřen na tvorbu, analýzu a zobrazení dat ve 3D. Poskytuje jak nástroje pro interpolaci rastrových
Digitální modely terénu a vizualizace strana 2. ArcGIS 3D Analyst
 Brno, 2014 Ing. Miloš Cibulka, Ph.D. Cvičení č. 7 Digitální kartografie Vytvořeno s podporou projektu Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na
Brno, 2014 Ing. Miloš Cibulka, Ph.D. Cvičení č. 7 Digitální kartografie Vytvořeno s podporou projektu Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Fyzikální geodézie 2/7 Gravitační potenciál a jeho derivace
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Fyzikální geodézie 2/7 Gravitační potenciál a jeho derivace
Příloha P.1 Mapa větrných oblastí
 Příloha P.1 Mapa větrných oblastí P.1.1 Úvod Podle metodiky Eurokódů se velikost zatížení větrem odvozuje z výchozí hodnoty základní rychlosti větru, definované jako střední rychlost větru v intervalu
Příloha P.1 Mapa větrných oblastí P.1.1 Úvod Podle metodiky Eurokódů se velikost zatížení větrem odvozuje z výchozí hodnoty základní rychlosti větru, definované jako střední rychlost větru v intervalu
TECHNICKÉ POŽADAVKY NA FORMU SDĚLENÍ OBCE SPRÁVCI REGISTRU
 TECHNICKÉ POŽADAVKY NA FORMU SDĚLENÍ OBCE SPRÁVCI REGISTRU Leden 2017 Strana 1/5 1. Sdělení údajů o definiční čáře ulice Sdělení údajů o definiční čáře ulice vychází z 9 vyhlášky č. 359/2011 Sb., o základním
TECHNICKÉ POŽADAVKY NA FORMU SDĚLENÍ OBCE SPRÁVCI REGISTRU Leden 2017 Strana 1/5 1. Sdělení údajů o definiční čáře ulice Sdělení údajů o definiční čáře ulice vychází z 9 vyhlášky č. 359/2011 Sb., o základním
Triangulace. Význam triangulace. trojúhelník je základní grafický element aproximace ploch předzpracování pro jiné algoritmy. příklad triangulace
 Význam triangulace trojúhelník je základní grafický element aproximace ploch předzpracování pro jiné algoritmy příklad triangulace Definice Triangulace nad množinou bodů v rovině představuje takové planární
Význam triangulace trojúhelník je základní grafický element aproximace ploch předzpracování pro jiné algoritmy příklad triangulace Definice Triangulace nad množinou bodů v rovině představuje takové planární
N-LETOST SRÁŽEK A PRŮTOKŮ PŘI POVODNI 2002
 N-LETOST SRÁŽEK A PRŮTOKŮ PŘI POVODNI 2002 MARTIN STEHLÍK* * Oddělení povrchových vod, ČHMÚ; e-mail: stehlikm@chmi.cz 1. ÚVOD Povodeň v srpnu 2002 v České republice byla způsobena přechodem dvou frontálních
N-LETOST SRÁŽEK A PRŮTOKŮ PŘI POVODNI 2002 MARTIN STEHLÍK* * Oddělení povrchových vod, ČHMÚ; e-mail: stehlikm@chmi.cz 1. ÚVOD Povodeň v srpnu 2002 v České republice byla způsobena přechodem dvou frontálních
Tvorba povrchů pomocí interpolací
 Tvorba povrchů pomocí interpolací Rastrová data, která souvisle zobrazují průběh hodnot nějakého měřitelného fenoménu, jsou zpravidla vypočítávána pomocí interpolací naměřených hodnot vztažených k bodům
Tvorba povrchů pomocí interpolací Rastrová data, která souvisle zobrazují průběh hodnot nějakého měřitelného fenoménu, jsou zpravidla vypočítávána pomocí interpolací naměřených hodnot vztažených k bodům
DETEKCE FUGITIVNÍCH EMISÍ Z POVRCHOVÝCH UHELNÝCH LOMŮ. Josef Keder Lubomír Paroha
 DETEKCE FUGITIVNÍCH EMISÍ Z POVRCHOVÝCH UHELNÝCH LOMŮ Josef Keder keder@chmi.cz Lubomír Paroha paroha@acnend.cz Motivace V současné době začala být akcentována otázka příspěvku fugitivních emisí z povrchových
DETEKCE FUGITIVNÍCH EMISÍ Z POVRCHOVÝCH UHELNÝCH LOMŮ Josef Keder keder@chmi.cz Lubomír Paroha paroha@acnend.cz Motivace V současné době začala být akcentována otázka příspěvku fugitivních emisí z povrchových
Pravidla pro tvorbu ÚKM Jihočeského kraje
 Pravidla pro tvorbu ÚKM Jihočeského kraje Pravidla pro tvorbu ÚKM Jihočeského kraje stanovují způsob tvorby ÚKM Jihočeského kraje a její aktualizace do doby než dojde ke zprovoznění RUIAN, poté přechází
Pravidla pro tvorbu ÚKM Jihočeského kraje Pravidla pro tvorbu ÚKM Jihočeského kraje stanovují způsob tvorby ÚKM Jihočeského kraje a její aktualizace do doby než dojde ke zprovoznění RUIAN, poté přechází
Tabulka 1. Výběr z datové tabulky
 1. Zadání domácího úkolu Vyberte si datový soubor obsahující alespoň jednu kvalitativní a jednu kvantitativní proměnnou s alespoň 30 statistickými jednotkami (alespoň 30 jednotlivých údajů). Zdroje dat
1. Zadání domácího úkolu Vyberte si datový soubor obsahující alespoň jednu kvalitativní a jednu kvantitativní proměnnou s alespoň 30 statistickými jednotkami (alespoň 30 jednotlivých údajů). Zdroje dat
Statistická analýza dat podzemních vod. Statistical analysis of ground water data. Vladimír Sosna 1
 Statistická analýza dat podzemních vod. Statistical analysis of ground water data. Vladimír Sosna 1 1 ČHMÚ, OPZV, Na Šabatce 17, 143 06 Praha 4 - Komořany sosna@chmi.cz, tel. 377 256 617 Abstrakt: Referát
Statistická analýza dat podzemních vod. Statistical analysis of ground water data. Vladimír Sosna 1 1 ČHMÚ, OPZV, Na Šabatce 17, 143 06 Praha 4 - Komořany sosna@chmi.cz, tel. 377 256 617 Abstrakt: Referát
Vyvinuté programové vybavení (projekt čís. TA02030806)
 Vyvinuté programové vybavení (projekt čís. TA02030806) 1.část programů Předzpracování dat Program sloužící k vytvoření Digitálního modelu reliéfu, povrchu a bezpečnostní hladiny, do formátu grid, s konstantním
Vyvinuté programové vybavení (projekt čís. TA02030806) 1.část programů Předzpracování dat Program sloužící k vytvoření Digitálního modelu reliéfu, povrchu a bezpečnostní hladiny, do formátu grid, s konstantním
Použití splinů pro popis tvarové křivky kmene
 NAZV QI102A079: Výzkum biomasy listnatých dřevin Česká zemědělská univerzita v Praze Fakulta lesnická a dřevařská 9. února 2011 Cíl práce Cíl projektu: Vytvořit a ověřit metodiku pro sestavení lokálního
NAZV QI102A079: Výzkum biomasy listnatých dřevin Česká zemědělská univerzita v Praze Fakulta lesnická a dřevařská 9. února 2011 Cíl práce Cíl projektu: Vytvořit a ověřit metodiku pro sestavení lokálního
II. Úlohy na vložené cykly a podprogramy
 II. Úlohy na vložené cykly a podprogramy Společné zadání pro příklady 1. - 10. začíná jednou ze dvou možností popisu vstupních dat. Je dána posloupnost (neboli řada) N reálných (resp. celočíselných) hodnot.
II. Úlohy na vložené cykly a podprogramy Společné zadání pro příklady 1. - 10. začíná jednou ze dvou možností popisu vstupních dat. Je dána posloupnost (neboli řada) N reálných (resp. celočíselných) hodnot.
Semestrální práce. 2. semestr
 Licenční studium č. 89002 Semestrální práce 2. semestr PŘEDMĚT 2.2 KALIBRACE A LIMITY JEJÍ PŘESNOSTI Příklad 1 Lineární kalibrace Příklad 2 Nelineární kalibrace Příklad 3 Rozlišení mezi lineární a nelineární
Licenční studium č. 89002 Semestrální práce 2. semestr PŘEDMĚT 2.2 KALIBRACE A LIMITY JEJÍ PŘESNOSTI Příklad 1 Lineární kalibrace Příklad 2 Nelineární kalibrace Příklad 3 Rozlišení mezi lineární a nelineární
1 Obsah přípravné fáze projektu Poohří
 1 Obsah přípravné fáze projektu Poohří V rámci projektu Poohří budou pro účely zatápění povrchových hnědouhelných dolů modelovány a predikovány pohyby nadzemních i podzemních vod a jejich předpokládané
1 Obsah přípravné fáze projektu Poohří V rámci projektu Poohří budou pro účely zatápění povrchových hnědouhelných dolů modelovány a predikovány pohyby nadzemních i podzemních vod a jejich předpokládané
Strategie ochrany před negativními dopady povodní a erozními jevy přírodě blízkými opatřeními v České republice
 Strategie ochrany před negativními dopady povodní a erozními jevy přírodě blízkými opatřeními v České republice Návod k prezentačnímu mapovému portálu Obsah: 1. Úvod... 3 2. Obecná část mapového portálu...
Strategie ochrany před negativními dopady povodní a erozními jevy přírodě blízkými opatřeními v České republice Návod k prezentačnímu mapovému portálu Obsah: 1. Úvod... 3 2. Obecná část mapového portálu...
2. Charakteristika navržených variant vymezení venkova
 2. Charakteristika navržených variant vymezení venkova Pro účely této publikace bylo zvoleno osm způsobů vymezení venkovského u, přičemž je na čtenáři, aby posoudil, která z těchto variant mu nejvíce vyhovuje.
2. Charakteristika navržených variant vymezení venkova Pro účely této publikace bylo zvoleno osm způsobů vymezení venkovského u, přičemž je na čtenáři, aby posoudil, která z těchto variant mu nejvíce vyhovuje.
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
GEODETICKÉ VÝPOČTY I.
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. TABELACE FUNKCE LINEÁRNÍ INTERPOLACE TABELACE FUNKCE Tabelace funkce se v minulosti často využívala z důvodu usnadnění
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. TABELACE FUNKCE LINEÁRNÍ INTERPOLACE TABELACE FUNKCE Tabelace funkce se v minulosti často využívala z důvodu usnadnění
Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného)
 Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného) 1 Obecný popis metody Particle Image Velocimetry, nebo-li zkráceně PIV, je měřící
Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného) 1 Obecný popis metody Particle Image Velocimetry, nebo-li zkráceně PIV, je měřící
VIZUALIZACE TRANSPORTU ZNEČIŠTĚNÍ V OSTRAVSKO KATOVICKÉ PRŮMYSLOVÉ OBLASTI (manažerské shrnutí)
 VIZUALIZACE TRANSPORTU ZNEČIŠTĚNÍ V OSTRAVSKO KATOVICKÉ PRŮMYSLOVÉ OBLASTI (manažerské shrnutí) MANAŽERSKÉ SHRNUTÍ 1. Identifikační údaje projektu 1.1 Název projektu Vizualizace transportu znečištění v
VIZUALIZACE TRANSPORTU ZNEČIŠTĚNÍ V OSTRAVSKO KATOVICKÉ PRŮMYSLOVÉ OBLASTI (manažerské shrnutí) MANAŽERSKÉ SHRNUTÍ 1. Identifikační údaje projektu 1.1 Název projektu Vizualizace transportu znečištění v
Porovnání rychlosti mapového serveru GeoServer při přístupu k různým datovým skladům
 Porovnání rychlosti mapového serveru GeoServer při přístupu k různým datovým skladům Bakalářská práce 2014 Autor: Adam Schreier Garant práce: Jan Růžička Obsah prezentace 1.Seznámení s řešeným problémem
Porovnání rychlosti mapového serveru GeoServer při přístupu k různým datovým skladům Bakalářská práce 2014 Autor: Adam Schreier Garant práce: Jan Růžička Obsah prezentace 1.Seznámení s řešeným problémem
Základní jednotky používané ve výpočetní technice
 Základní jednotky používané ve výpočetní technice Nejmenší jednotkou informace je bit [b], který může nabývat pouze dvou hodnot 1/0 (ano/ne, true/false). Tato jednotka není dostatečná pro praktické použití,
Základní jednotky používané ve výpočetní technice Nejmenší jednotkou informace je bit [b], který může nabývat pouze dvou hodnot 1/0 (ano/ne, true/false). Tato jednotka není dostatečná pro praktické použití,
INFORMACE o stavu bodového systému v České republice BODOVANÍ ŘIDIČI
 INFORMACE o stavu bodového systému v České republice BODOVANÍ ŘIDIČI Rok 216 Obsah Počet bodovaných řidičů, počet dvanáctibodových řidičů 3 Přírůstky bodů za poslední rok, složení udělených bodů. 4 Srovnání
INFORMACE o stavu bodového systému v České republice BODOVANÍ ŘIDIČI Rok 216 Obsah Počet bodovaných řidičů, počet dvanáctibodových řidičů 3 Přírůstky bodů za poslední rok, složení udělených bodů. 4 Srovnání
INFORMACE o stavu bodového systému v České republice BODOVANÍ ŘIDIČI
 INFORMACE o stavu bodového systému v České republice BODOVANÍ ŘIDIČI Rok 217 Obsah Počet bodovaných řidičů, počet dvanáctibodových řidičů 3 Přírůstky bodů za poslední rok, složení udělených bodů. 4 Srovnání
INFORMACE o stavu bodového systému v České republice BODOVANÍ ŘIDIČI Rok 217 Obsah Počet bodovaných řidičů, počet dvanáctibodových řidičů 3 Přírůstky bodů za poslední rok, složení udělených bodů. 4 Srovnání
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Iterační výpočty. Dokumentace k projektu č. 2 do IZP. 24. listopadu 2004
 Dokumentace k projektu č. 2 do IZP Iterační výpočty 24. listopadu 2004 Autor: Kamil Dudka, xdudka00@stud.fit.vutbr.cz Fakulta Informačních Technologií Vysoké Učení Technické v Brně Obsah 1. Úvod...3 2.
Dokumentace k projektu č. 2 do IZP Iterační výpočty 24. listopadu 2004 Autor: Kamil Dudka, xdudka00@stud.fit.vutbr.cz Fakulta Informačních Technologií Vysoké Učení Technické v Brně Obsah 1. Úvod...3 2.
ANOVA. Semestrální práce UNIVERZITA PARDUBICE. Fakulta chemicko-technologická Katedra analytické chemie
 UNIVERZITA PARDUBICE Fakulta chemicko-technologická Katedra analytické chemie ANOVA Semestrální práce Licenční studium Galileo Interaktivní statistická analýza dat Brno 2015 Ing. Petra Hlaváčková, Ph.D.
UNIVERZITA PARDUBICE Fakulta chemicko-technologická Katedra analytické chemie ANOVA Semestrální práce Licenční studium Galileo Interaktivní statistická analýza dat Brno 2015 Ing. Petra Hlaváčková, Ph.D.
Návod pro obnovu katastrálního operátu a převod
 Český úřad zeměměřický a katastrální Návod pro obnovu katastrálního operátu a převod Dodatek č. 3 Praha 2013 Zpracoval: Český úřad zeměměřický a katastrální Schválil: Ing. Karel Štencel, místopředseda
Český úřad zeměměřický a katastrální Návod pro obnovu katastrálního operátu a převod Dodatek č. 3 Praha 2013 Zpracoval: Český úřad zeměměřický a katastrální Schválil: Ing. Karel Štencel, místopředseda
Semestrální projekt. Vyhodnocení přesnosti sebelokalizace VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ. Fakulta elektrotechniky a komunikačních technologií
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta elektrotechniky a komunikačních technologií Semestrální projekt Vyhodnocení přesnosti sebelokalizace Vedoucí práce: Ing. Tomáš Jílek Vypracovali: Michaela Homzová,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta elektrotechniky a komunikačních technologií Semestrální projekt Vyhodnocení přesnosti sebelokalizace Vedoucí práce: Ing. Tomáš Jílek Vypracovali: Michaela Homzová,
Téma: Geografické a kartografické základy map
 Topografická příprava Téma: Geografické a kartografické základy map Osnova : 1. Topografické mapy, měřítko mapy 2. Mapové značky 3. Souřadnicové systémy 2 3 1. Topografické mapy, měřítko mapy Topografická
Topografická příprava Téma: Geografické a kartografické základy map Osnova : 1. Topografické mapy, měřítko mapy 2. Mapové značky 3. Souřadnicové systémy 2 3 1. Topografické mapy, měřítko mapy Topografická
Pomůcka k aplikaci ustanovení katastrální vyhlášky vztahujících se k souřadnicím podrobných bodů
 Příloha k č.j. ČÚZK 6495/2009-22 Pomůcka k aplikaci ustanovení katastrální vyhlášky vztahujících se k souřadnicím podrobných bodů 1. Geometrické a polohové určení 1.1. Katastrální území a nemovitosti evidované
Příloha k č.j. ČÚZK 6495/2009-22 Pomůcka k aplikaci ustanovení katastrální vyhlášky vztahujících se k souřadnicím podrobných bodů 1. Geometrické a polohové určení 1.1. Katastrální území a nemovitosti evidované
Základní popis Toolboxu MPSV nástroje
 Základní popis Toolboxu MPSV nástroje Nástroj XLS2DBF ze sady MPSV nástroje slouží pro zkonvertování souboru ve formátu XLS do formátu DBF. Nástroj umožňuje konvertovat buď vybraný list nebo listy ze sešitu
Základní popis Toolboxu MPSV nástroje Nástroj XLS2DBF ze sady MPSV nástroje slouží pro zkonvertování souboru ve formátu XLS do formátu DBF. Nástroj umožňuje konvertovat buď vybraný list nebo listy ze sešitu
Vypracoval: Datum: Název projektu (oblast, číslo mapy) Závěrečná zpráva
 Vypracoval: Datum: Název projektu (oblast, číslo mapy) Závěrečná zpráva Zadání a nastínění postupu práce: Proveďte pohledové analýzy pro existující větrnou elektrárnu v ČR (dle vlastního výběru). Použijte
Vypracoval: Datum: Název projektu (oblast, číslo mapy) Závěrečná zpráva Zadání a nastínění postupu práce: Proveďte pohledové analýzy pro existující větrnou elektrárnu v ČR (dle vlastního výběru). Použijte
8. přednáška z předmětu GIS1 Rastrový datový model a mapová algebra
 8. přednáška z předmětu GIS1 Rastrový datový model a mapová algebra Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Pro přednášku byly použity texty a obrázky z www.gis.zcu.cz Předmět KMA/UGI,
8. přednáška z předmětu GIS1 Rastrový datový model a mapová algebra Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Pro přednášku byly použity texty a obrázky z www.gis.zcu.cz Předmět KMA/UGI,
Základní popis Toolboxu MPSV nástroje
 Základní popis Toolboxu MPSV nástroje Nástroj XLS2DBF ze sady MPSV nástroje slouží pro zkonvertování souboru ve formátu XLS do formátu DBF. Nástroj umožňuje konvertovat buď vybraný list nebo listy ze sešitu
Základní popis Toolboxu MPSV nástroje Nástroj XLS2DBF ze sady MPSV nástroje slouží pro zkonvertování souboru ve formátu XLS do formátu DBF. Nástroj umožňuje konvertovat buď vybraný list nebo listy ze sešitu
TECHNICKÁ UNIVERZITA V LIBERCI
 TECHNICKÁ UNIVERZITA V LIBERCI Ekonomická fakulta Semestrální práce Statistický rozbor dat z dotazníkového šetření Počet stran: 10 Datum odevzdání: 13. 5. 2016 Pavel Kubát Obsah Úvod... 3 1 Charakterizujte
TECHNICKÁ UNIVERZITA V LIBERCI Ekonomická fakulta Semestrální práce Statistický rozbor dat z dotazníkového šetření Počet stran: 10 Datum odevzdání: 13. 5. 2016 Pavel Kubát Obsah Úvod... 3 1 Charakterizujte
MRBT M8. VIDITELNOST OBJEKTŮ VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ. Bc. MARTIN MAŠTERA
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV AUTOMATIZACE A MĚŘICÍ TECHNIKY MRBT M8. VIDITELNOST OBJEKTŮ AUTOŘI PRÁCE Bc. JAKUB BERÁNEK Bc. MARTIN MAŠTERA VEDOUCÍ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV AUTOMATIZACE A MĚŘICÍ TECHNIKY MRBT M8. VIDITELNOST OBJEKTŮ AUTOŘI PRÁCE Bc. JAKUB BERÁNEK Bc. MARTIN MAŠTERA VEDOUCÍ
Nástroj pro výpočet času vítěze tratě v orientačním běhu.
 Uživatelský manuál pro práci s nástrojem pro výpočet času vítěze tratě v orientačním běhu v prostředí ArcGIS Desktop 10.1 Nástroj pro výpočet času vítěze tratě v orientačním běhu. Martin KLÍCHA Olomouc,
Uživatelský manuál pro práci s nástrojem pro výpočet času vítěze tratě v orientačním běhu v prostředí ArcGIS Desktop 10.1 Nástroj pro výpočet času vítěze tratě v orientačním běhu. Martin KLÍCHA Olomouc,
2 Zpracování naměřených dat. 2.1 Gaussův zákon chyb. 2.2 Náhodná veličina a její rozdělení
 2 Zpracování naměřených dat Důležitou součástí každé experimentální práce je statistické zpracování naměřených dat. V této krátké kapitole se budeme věnovat určení intervalů spolehlivosti získaných výsledků
2 Zpracování naměřených dat Důležitou součástí každé experimentální práce je statistické zpracování naměřených dat. V této krátké kapitole se budeme věnovat určení intervalů spolehlivosti získaných výsledků
Metodika Standardizovaný postup identifikace segmentů předindustriální krajiny platný pro regiony Moravy
 Metodika Standardizovaný postup identifikace segmentů předindustriální krajiny platný pro regiony Moravy Vyhledávání segmentů předindustriální krajiny vychází z komparace kartografických podkladů různého
Metodika Standardizovaný postup identifikace segmentů předindustriální krajiny platný pro regiony Moravy Vyhledávání segmentů předindustriální krajiny vychází z komparace kartografických podkladů různého
INFORMACE o stavu bodového systému v České republice BODOVANÍ ŘIDIČI
 INFORMACE o stavu bodového systému v České republice BODOVANÍ ŘIDIČI Rok 218 Obsah Počet bodovaných řidičů, počet dvanáctibodových řidičů 3 Přírůstky bodů za poslední rok, složení udělených bodů. 4 Srovnání
INFORMACE o stavu bodového systému v České republice BODOVANÍ ŘIDIČI Rok 218 Obsah Počet bodovaných řidičů, počet dvanáctibodových řidičů 3 Přírůstky bodů za poslední rok, složení udělených bodů. 4 Srovnání
INFLUENCE OF SPEED RADAR SIGN ON VELOCITY CHANGE IN THE SELECTED LOCATION
 VLIV INFORMATIVNÍ TABULE NA ZMĚNU RYCHLOSTI VE VYBRANÉ LOKALITĚ INFLUENCE OF SPEED RADAR SIGN ON VELOCITY CHANGE IN THE SELECTED LOCATION Martin Lindovský 1 Anotace: Článek popisuje měření prováděné na
VLIV INFORMATIVNÍ TABULE NA ZMĚNU RYCHLOSTI VE VYBRANÉ LOKALITĚ INFLUENCE OF SPEED RADAR SIGN ON VELOCITY CHANGE IN THE SELECTED LOCATION Martin Lindovský 1 Anotace: Článek popisuje měření prováděné na
Matematické modelování dopravního proudu
 Matematické modelování dopravního proudu Ondřej Lanč, Alena Girglová, Kateřina Papežová, Lucie Obšilová Gymnázium Otokara Březiny a SOŠ Telč lancondrej@centrum.cz Abstrakt: Cílem projektu bylo seznámení
Matematické modelování dopravního proudu Ondřej Lanč, Alena Girglová, Kateřina Papežová, Lucie Obšilová Gymnázium Otokara Březiny a SOŠ Telč lancondrej@centrum.cz Abstrakt: Cílem projektu bylo seznámení
DTM DMVS Plzeňského kraje
 Směrnice DTM DMVS Plzeňského kraje Verze 2.1 DTM DMVS Plzeňského kraje Zpracoval Datum 18. 7. 2013 Popis Vydavatel URL GEOREAL spol. s r.o., Hálkova 12, 301 00 Plzeň Směrnice obsahuje základní údaje o
Směrnice DTM DMVS Plzeňského kraje Verze 2.1 DTM DMVS Plzeňského kraje Zpracoval Datum 18. 7. 2013 Popis Vydavatel URL GEOREAL spol. s r.o., Hálkova 12, 301 00 Plzeň Směrnice obsahuje základní údaje o
Vliv Mosteckého jezera na teplotu a vlhkost vzduchu a rychlost větru. Lukáš Pop Ústav fyziky atmosféry v. v. i. AV ČR
 Vliv Mosteckého jezera na teplotu a vlhkost vzduchu a rychlost větru Lukáš Pop Ústav fyziky atmosféry v. v. i. AV ČR Motivace a cíle výzkumu Vznik nové vodní plochy mění charakter povrchu (teplotní charakteristiky,
Vliv Mosteckého jezera na teplotu a vlhkost vzduchu a rychlost větru Lukáš Pop Ústav fyziky atmosféry v. v. i. AV ČR Motivace a cíle výzkumu Vznik nové vodní plochy mění charakter povrchu (teplotní charakteristiky,
Diskusní příspěvek. Seminář Revize katastru nemovitostí a nové trendy v zeměměřictví. Praha, Doc. Ing. Jiří Šíma, CSc.
 Diskusní příspěvek Seminář Revize katastru nemovitostí a nové trendy v zeměměřictví Praha, 16. 1. 2019 Doc. Ing. Jiří Šíma, CSc. Bloky LMS pro tvorbu Ortofota ČR ve dvouletém intervalu Západ:2013 2015-2017
Diskusní příspěvek Seminář Revize katastru nemovitostí a nové trendy v zeměměřictví Praha, 16. 1. 2019 Doc. Ing. Jiří Šíma, CSc. Bloky LMS pro tvorbu Ortofota ČR ve dvouletém intervalu Západ:2013 2015-2017
Předpoklad o normalitě rozdělení je zamítnut, protože hodnota testovacího kritéria χ exp je vyšší než tabulkový 2
 Na úloze ukážeme postup analýzy velkého výběru s odlehlými prvky pro určení typu rozdělení koncentrace kyseliny močové u 50 dárců krve. Jaká je míra polohy a rozptýlení uvedeného výběru? Z grafických diagnostik
Na úloze ukážeme postup analýzy velkého výběru s odlehlými prvky pro určení typu rozdělení koncentrace kyseliny močové u 50 dárců krve. Jaká je míra polohy a rozptýlení uvedeného výběru? Z grafických diagnostik
Android Elizabeth. Verze: 1.1
 Android Elizabeth Program pro měření mezičasů na zařízeních s OS Android Verze: 1.1 Naposledy upraveno: 15. února 2013 Aleš Razým Historie verzí Verze Datum Popis 1.0 7.1.2013 Původní verze pro OS Android
Android Elizabeth Program pro měření mezičasů na zařízeních s OS Android Verze: 1.1 Naposledy upraveno: 15. února 2013 Aleš Razým Historie verzí Verze Datum Popis 1.0 7.1.2013 Původní verze pro OS Android
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Vliv přístroje SOMAVEDIC Medic na poruchy magnetických polí
 IIREC Dr. Medinger e.u. Mezinárodní institut pro výzkum elektromagnetické kompatibility elektromagnetická kompatibilita na biofyzikálním základě projektová kancelář v oboru ekologické techniky Ringstr.
IIREC Dr. Medinger e.u. Mezinárodní institut pro výzkum elektromagnetické kompatibility elektromagnetická kompatibilita na biofyzikálním základě projektová kancelář v oboru ekologické techniky Ringstr.
Digitální modely terénu (9-10) DMT v ArcGIS Desktop
 Digitální modely terénu (9-10) DMT v Desktop Ing. Martin KLIMÁNEK, Ph.D. 411 Ústav geoinformačních technologií Lesnická a dřevařská fakulta, Mendelova zemědělská a lesnická univerzita v Brně 1 Digitální
Digitální modely terénu (9-10) DMT v Desktop Ing. Martin KLIMÁNEK, Ph.D. 411 Ústav geoinformačních technologií Lesnická a dřevařská fakulta, Mendelova zemědělská a lesnická univerzita v Brně 1 Digitální
Využití geografických informačních systémů v analýzách místních trhů práce
 Využití geografických informačních systémů v analýzách místních trhů práce Šimek Milan - Horák Jiří VŠB Technická univerzita Ostrava tř. 17. listopadu, 708 33 Ostrava Poruba e-mail: milan.simek@vsb.cz,
Využití geografických informačních systémů v analýzách místních trhů práce Šimek Milan - Horák Jiří VŠB Technická univerzita Ostrava tř. 17. listopadu, 708 33 Ostrava Poruba e-mail: milan.simek@vsb.cz,
ROZVOJ SLUŽEB GEOPORTÁLU ČÚZK
 Zeměměřický úřad ROZVOJ SLUŽEB GEOPORTÁLU ČÚZK Ing. Petr Dvořáček Zeměměřický úřad 9. dubna 2013, Hradec Králové http://geoportal.cuzk.cz ČÚZK - jaké geografické informace poskytuje Informace z katastru
Zeměměřický úřad ROZVOJ SLUŽEB GEOPORTÁLU ČÚZK Ing. Petr Dvořáček Zeměměřický úřad 9. dubna 2013, Hradec Králové http://geoportal.cuzk.cz ČÚZK - jaké geografické informace poskytuje Informace z katastru
GIS ANALÝZA VLIVU DÁLNIČNÍ SÍTĚ NA OKOLNÍ KRAJINU. Veronika Berková 1
 GIS ANALÝZA VLIVU DÁLNIČNÍ SÍTĚ NA OKOLNÍ KRAJINU Veronika Berková 1 1 Katedra mapování a kartografie, Fakulta stavební, ČVUT, Thákurova 7, 166 29, Praha, ČR veronika.berkova@fsv.cvut.cz Abstrakt. Metody
GIS ANALÝZA VLIVU DÁLNIČNÍ SÍTĚ NA OKOLNÍ KRAJINU Veronika Berková 1 1 Katedra mapování a kartografie, Fakulta stavební, ČVUT, Thákurova 7, 166 29, Praha, ČR veronika.berkova@fsv.cvut.cz Abstrakt. Metody
Popisná statistika. Komentované řešení pomocí MS Excel
 Popisná statistika Komentované řešení pomocí MS Excel Vstupní data Máme k dispozici data o počtech bodů z 1. a 2. zápočtového testu z Matematiky I v zimním semestru 2015/2016 a to za všech 762 studentů,
Popisná statistika Komentované řešení pomocí MS Excel Vstupní data Máme k dispozici data o počtech bodů z 1. a 2. zápočtového testu z Matematiky I v zimním semestru 2015/2016 a to za všech 762 studentů,
KAPITOLA 9 - POKROČILÁ PRÁCE S TABULKOVÝM PROCESOREM
 KAPITOLA 9 - POKROČILÁ PRÁCE S TABULKOVÝM PROCESOREM CÍLE KAPITOLY Využívat pokročilé možnosti formátování, jako je podmíněné formátování, používat vlastní formát čísel a umět pracovat s listy. Používat
KAPITOLA 9 - POKROČILÁ PRÁCE S TABULKOVÝM PROCESOREM CÍLE KAPITOLY Využívat pokročilé možnosti formátování, jako je podmíněné formátování, používat vlastní formát čísel a umět pracovat s listy. Používat
ROZPTYLOVÉ PODMÍNKY A JEJICH VLIV NA KONCENTRACI AEROSOLOVÝCH ČÁSTIC PM 10 V LOKALITĚ MOSTECKÉHO JEZERA
 ROZPTYLOVÉ PODMÍNKY A JEJICH VLIV NA KONCENTRACI AEROSOLOVÝCH ČÁSTIC PM 10 V LOKALITĚ MOSTECKÉHO JEZERA Ing. Jan Brejcha, Výzkumný ústav pro hnědé uhlí a.s., brejcha@vuhu.cz Vodárenská a biologie 2015
ROZPTYLOVÉ PODMÍNKY A JEJICH VLIV NA KONCENTRACI AEROSOLOVÝCH ČÁSTIC PM 10 V LOKALITĚ MOSTECKÉHO JEZERA Ing. Jan Brejcha, Výzkumný ústav pro hnědé uhlí a.s., brejcha@vuhu.cz Vodárenská a biologie 2015
1. Vymezení předmětu veřejné zakázky a podmínek plnění
 1. Vymezení předmětu veřejné zakázky a podmínek plnění a) Vytvoření vektorové sítě místních komunikací silnic, parkovišť, parkovacích stání, chodníků a stezek. b) Kategorizace místních komunikací podle
1. Vymezení předmětu veřejné zakázky a podmínek plnění a) Vytvoření vektorové sítě místních komunikací silnic, parkovišť, parkovacích stání, chodníků a stezek. b) Kategorizace místních komunikací podle
e-mail: RadkaZahradnikova@seznam.cz 1. července 2010
 Optimální výrobní program Radka Zahradníková e-mail: RadkaZahradnikova@seznam.cz 1. července 2010 Obsah 1 Lineární programování 2 Simplexová metoda 3 Grafická metoda 4 Optimální výrobní program Řešení
Optimální výrobní program Radka Zahradníková e-mail: RadkaZahradnikova@seznam.cz 1. července 2010 Obsah 1 Lineární programování 2 Simplexová metoda 3 Grafická metoda 4 Optimální výrobní program Řešení
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
ZEMĚMĚŘICKÝ ÚŘAD. Poskytování dat a služeb Geoportál ČÚZK. Petr Dvořáček
 ZEMĚMĚŘICKÝ ÚŘAD Poskytování dat a služeb Geoportál ČÚZK Petr Dvořáček Ústí nad Labem 25. 10. 2016 Formy poskytování geografických podkladů Tištěné mapy Data Mapové listy Souborová data Mapové služby WMS,
ZEMĚMĚŘICKÝ ÚŘAD Poskytování dat a služeb Geoportál ČÚZK Petr Dvořáček Ústí nad Labem 25. 10. 2016 Formy poskytování geografických podkladů Tištěné mapy Data Mapové listy Souborová data Mapové služby WMS,
VYHODNOCENÍ METEOROLOGICKÝCH PRVKŮ ZA ROK 2014
 VYHODNOCENÍ METEOROLOGICKÝCH PRVKŮ ZA ROK 2014 Měření denní teploty a množství srážek na stanici Ústředního kontrolního a zkušebního ústavu zemědělského (ÚKZÚZ) se datuje už od roku 1945. Postupně přibývají
VYHODNOCENÍ METEOROLOGICKÝCH PRVKŮ ZA ROK 2014 Měření denní teploty a množství srážek na stanici Ústředního kontrolního a zkušebního ústavu zemědělského (ÚKZÚZ) se datuje už od roku 1945. Postupně přibývají
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Algoritmy pro shlukování prostorových dat
 Algoritmy pro shlukování prostorových dat Marta Žambochová Katedra matematiky a informatiky Fakulta sociálně ekonomická Univerzita J. E. Purkyně v Ústí nad Labem ROBUST 21. 26. leden 2018 Rybník - Hostouň
Algoritmy pro shlukování prostorových dat Marta Žambochová Katedra matematiky a informatiky Fakulta sociálně ekonomická Univerzita J. E. Purkyně v Ústí nad Labem ROBUST 21. 26. leden 2018 Rybník - Hostouň
Geomorfologie vybraných skalních útvarů v okolí Bělé pod Bezdězem, Mimoně a České Lípy
 Geomorfologie vybraných skalních útvarů v okolí Bělé pod Bezdězem, Mimoně a České Lípy Vedoucí práce: RNDr. Marek Matura, Ph.D. Jakub Koutník, Františka Ektrtová, Andrea Suchánková, Ester Burgerová, Tomáš
Geomorfologie vybraných skalních útvarů v okolí Bělé pod Bezdězem, Mimoně a České Lípy Vedoucí práce: RNDr. Marek Matura, Ph.D. Jakub Koutník, Františka Ektrtová, Andrea Suchánková, Ester Burgerová, Tomáš
DTM DMVS Plzeňského kraje
 Směrnice DTM DMVS Plzeňského kraje Verze 3.1 DTM DMVS Plzeňského kraje Zpracoval Datum 1. 3. 2015 Popis Vydavatel URL Platnost Práva Zpracováno ve spolupráci partnerů DTM DMVS Plzeňského kraje: - Plzeňský
Směrnice DTM DMVS Plzeňského kraje Verze 3.1 DTM DMVS Plzeňského kraje Zpracoval Datum 1. 3. 2015 Popis Vydavatel URL Platnost Práva Zpracováno ve spolupráci partnerů DTM DMVS Plzeňského kraje: - Plzeňský
ZABAGED Mgr. Petr Neckář
 ZEMĚMĚŘICKÝ ÚŘAD ZABAGED Mgr. Petr Neckář Zeměměřický úřad 27. 4. 2017, Pardubice ZABAGED ZÁKLADNÍ BÁZE GEOGRAFICKÝCH DAT digitální geografický model území České republiky, který je spravován Zeměměřickým
ZEMĚMĚŘICKÝ ÚŘAD ZABAGED Mgr. Petr Neckář Zeměměřický úřad 27. 4. 2017, Pardubice ZABAGED ZÁKLADNÍ BÁZE GEOGRAFICKÝCH DAT digitální geografický model území České republiky, který je spravován Zeměměřickým
Zadání soutěžních úloh
 16. až 18. dubna 2015 Krajské kolo 2014/2015 Úlohy můžete řešit v libovolném pořadí a samozřejmě je nemusíte vyřešit všechny. Za každou úlohu můžete dostat maximálně 10 bodů, z nichž je většinou 9 bodů
16. až 18. dubna 2015 Krajské kolo 2014/2015 Úlohy můžete řešit v libovolném pořadí a samozřejmě je nemusíte vyřešit všechny. Za každou úlohu můžete dostat maximálně 10 bodů, z nichž je většinou 9 bodů
Dostupné zdroje geodat v ČR
 Dostupné zdroje geodat v ČR Geografická data nekomerční nebo volně dostupná komerční státní správa privátní sféra všeobecná specializovaná pokrývají celé území pokrývají zájmovou oblast Volně dostupná
Dostupné zdroje geodat v ČR Geografická data nekomerční nebo volně dostupná komerční státní správa privátní sféra všeobecná specializovaná pokrývají celé území pokrývají zájmovou oblast Volně dostupná
Kartodiagramy. Přednáška z předmětu Tematická kartografie (KMA/TKA) Otakar Čerba Západočeská univerzita
 Kartodiagramy Přednáška z předmětu Tematická kartografie (KMA/TKA) Otakar Čerba Západočeská univerzita Datum vztvoření dokumentu: 29. 10. 2007 Poslední aktualizace: 24. 10. 2011 Obsah přednášky Úvodní
Kartodiagramy Přednáška z předmětu Tematická kartografie (KMA/TKA) Otakar Čerba Západočeská univerzita Datum vztvoření dokumentu: 29. 10. 2007 Poslední aktualizace: 24. 10. 2011 Obsah přednášky Úvodní
Tomáš Hudeček Zuzana Žáková
 Tomáš Hudeček Zuzana Žáková disertační, diplomové a bakalářské práce v tématech analýzy dostupnosti různých částíúzemí s využitím různých dopravních módů změny dostupnosti v čase vztahy dostupnosti a dalších
Tomáš Hudeček Zuzana Žáková disertační, diplomové a bakalářské práce v tématech analýzy dostupnosti různých částíúzemí s využitím různých dopravních módů změny dostupnosti v čase vztahy dostupnosti a dalších
Interpolace obrazu pro experimentální měřiče plošného teplotního rozložení
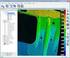 Interpolace obrazu pro experimentální měřiče plošného teplotního rozložení Bc. Zdeněk Martinásek Vysoké učení technické v Brně, Fakulta elektrotechniky a komunikačních technologií, Ústav telekomunikací,
Interpolace obrazu pro experimentální měřiče plošného teplotního rozložení Bc. Zdeněk Martinásek Vysoké učení technické v Brně, Fakulta elektrotechniky a komunikačních technologií, Ústav telekomunikací,
NADSTAVBOVÝ MODUL MOHSA V1
 NADSTAVBOVÝ MODUL MOHSA V1 Nadstavbový modul pro hierarchické shlukování se jmenuje Mod_Sh_Hier (MOHSA V1) je součástí souboru Shluk_Hier.xls. Tento soubor je přístupný na http://jonasova.upce.cz, a je
NADSTAVBOVÝ MODUL MOHSA V1 Nadstavbový modul pro hierarchické shlukování se jmenuje Mod_Sh_Hier (MOHSA V1) je součástí souboru Shluk_Hier.xls. Tento soubor je přístupný na http://jonasova.upce.cz, a je
Obsah přednášky Jaká asi bude chyba modelu na nových datech?
 Obsah přednášky Jaká asi bude chyba modelu na nových datech? Chyba modelu Bootstrap Cross Validation Vapnik-Chervonenkisova dimenze 2 Chyba skutečná a trénovací Máme 30 záznamů, rozhodli jsme se na jejich
Obsah přednášky Jaká asi bude chyba modelu na nových datech? Chyba modelu Bootstrap Cross Validation Vapnik-Chervonenkisova dimenze 2 Chyba skutečná a trénovací Máme 30 záznamů, rozhodli jsme se na jejich
INFORMACE o stavu bodového systému v České republice BODOVANÍ ŘIDIČI. Rok 2017 (1. pololetí)
 INFORMACE o stavu bodového systému v České republice BODOVANÍ ŘIDIČI Rok 217 (1. pololetí) Obsah Počet bodovaných řidičů, počet dvanáctibodových řidičů 3 Přírůstky bodů za poslední rok, složení udělených
INFORMACE o stavu bodového systému v České republice BODOVANÍ ŘIDIČI Rok 217 (1. pololetí) Obsah Počet bodovaných řidičů, počet dvanáctibodových řidičů 3 Přírůstky bodů za poslední rok, složení udělených
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Základy fyzikální geodézie 3/19 Legendreovy přidružené funkce
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Základy fyzikální geodézie 3/19 Legendreovy přidružené funkce
STRUKTURA RASTROVÝCH DAT
 STRUKTURA RASTROVÝCH DAT dva typy rastrové vrstvy v GIS 1) Digitální obraz TV, počítač, mobil - obrazovka obraz z bodů mapa - mřížka s barevnými plochami 2) Rastrová data data pro analýzu a) binární -
STRUKTURA RASTROVÝCH DAT dva typy rastrové vrstvy v GIS 1) Digitální obraz TV, počítač, mobil - obrazovka obraz z bodů mapa - mřížka s barevnými plochami 2) Rastrová data data pro analýzu a) binární -
Digitální model reliéfu (terénu) a analýzy modelů terénu
 Digitální model reliéfu (terénu) a analýzy modelů terénu Digitální modely terénu jsou dnes v geoinformačních systémech hojně využívány pro různé účely. Naměřená terénní data jsou často zpracována do podoby
Digitální model reliéfu (terénu) a analýzy modelů terénu Digitální modely terénu jsou dnes v geoinformačních systémech hojně využívány pro různé účely. Naměřená terénní data jsou často zpracována do podoby
Rudné. Kategorie. Kritéria. Přehledná mapa přispívající plochy. KONEČNÁ VERZE - výstupy kompletního projektu
 KONEČNÁ VERZE výstupy kompletního projektu ID plochy: 72641_4 : Obec: Vysoká Pec ORP: Karlovy Vary Souřadnice GPS (ve stupních): N 5.353133 E 12.685271 Kategorie Kategorie plochy dle nebezpečí: Kategorie
KONEČNÁ VERZE výstupy kompletního projektu ID plochy: 72641_4 : Obec: Vysoká Pec ORP: Karlovy Vary Souřadnice GPS (ve stupních): N 5.353133 E 12.685271 Kategorie Kategorie plochy dle nebezpečí: Kategorie
GEOGRAFICKÁ SLUŽBA ARMÁDY ČESKÉ REPUBLIKY
 GEOGRAFICKÁ SLUŽBA ARMÁDY ČESKÉ REPUBLIKY VOJENSKÝ GEOGRAFICKÝ A HYDROMETEOROLOGICKÝ ÚŘAD Popis a zásady používání světového geodetického referenčního systému 1984 v AČR POPIS A ZÁSADY POUŽÍVÁNÍ V AČR
GEOGRAFICKÁ SLUŽBA ARMÁDY ČESKÉ REPUBLIKY VOJENSKÝ GEOGRAFICKÝ A HYDROMETEOROLOGICKÝ ÚŘAD Popis a zásady používání světového geodetického referenčního systému 1984 v AČR POPIS A ZÁSADY POUŽÍVÁNÍ V AČR
Výběr hodnot z modisovského rastru v místech, kde se nacházela jedna ze zeber
 Výběr hodnot z modisovského rastru v místech, kde se nacházela jedna ze zeber - pro ukázku je zde vybrán rastr s hodnotami indexu EVI v jednom únorovém dni - a místa výskytu dané zebry celkem za celý rok
Výběr hodnot z modisovského rastru v místech, kde se nacházela jedna ze zeber - pro ukázku je zde vybrán rastr s hodnotami indexu EVI v jednom únorovém dni - a místa výskytu dané zebry celkem za celý rok
Autorizovaný software DRUM LK 3D SOFTWARE PRO VYHODNOCENÍ MĚŘENÍ ODCHYLEK HÁZIVOSTI BUBNOVÝCH ROTAČNÍCH SOUČÁSTÍ
 Autorizovaný software DRUM LK 3D SOFTWARE PRO VYHODNOCENÍ MĚŘENÍ ODCHYLEK HÁZIVOSTI BUBNOVÝCH ROTAČNÍCH SOUČÁSTÍ Ing. Michal Švantner, Ph.D. Doc. Ing. Milan Honner, Ph.D. 1/10 Anotace Popisuje se software,
Autorizovaný software DRUM LK 3D SOFTWARE PRO VYHODNOCENÍ MĚŘENÍ ODCHYLEK HÁZIVOSTI BUBNOVÝCH ROTAČNÍCH SOUČÁSTÍ Ing. Michal Švantner, Ph.D. Doc. Ing. Milan Honner, Ph.D. 1/10 Anotace Popisuje se software,
Ing. Libor Ansorge. Vodní stopa představení ISO 14046
 Ing. Libor Ansorge Vodní stopa představení ISO 14046 Obsah přednášky 1. Koncept vodní stopy jeden pojem, dva významy 2. ISO 14046 3. Představení projektu QJ1520322 4. Ukázka výsledků pilotní studie Vznik
Ing. Libor Ansorge Vodní stopa představení ISO 14046 Obsah přednášky 1. Koncept vodní stopy jeden pojem, dva významy 2. ISO 14046 3. Představení projektu QJ1520322 4. Ukázka výsledků pilotní studie Vznik
Metodický pokyn. k zadávání fotogrammetrických činností pro potřeby vymezování záplavových území
 Ministerstvo zemědělství ČR Č.j.: 28181/2005-16000 Metodický pokyn k zadávání fotogrammetrických činností pro potřeby vymezování záplavových území Určeno: K využití: státním podnikům Povodí Zemědělské
Ministerstvo zemědělství ČR Č.j.: 28181/2005-16000 Metodický pokyn k zadávání fotogrammetrických činností pro potřeby vymezování záplavových území Určeno: K využití: státním podnikům Povodí Zemědělské
PowerPoint 2010 Kurz 4
 PowerPoint 2010 Kurz 4 Animace... 1 Texty vkládání, formátování... 3 Grafy vkládání, formátování... 5 Grafické objekty... 6 Přechody mezi snímky... 7 CZ.1.07/2.2.00/28.0221 Animace Animace jsou umístěny
PowerPoint 2010 Kurz 4 Animace... 1 Texty vkládání, formátování... 3 Grafy vkládání, formátování... 5 Grafické objekty... 6 Přechody mezi snímky... 7 CZ.1.07/2.2.00/28.0221 Animace Animace jsou umístěny
Jak vytvořit pocitovou mapu v QGIS s využitím WMS služeb
 geografie a Škola Jak vytvořit pocitovou mapu v QIS s využitím WMS služeb 1 IS Software Pro vytvoření pocitové mapy je možné využít některý z IS softwarů, které mají různé licencování. Vhodným IS softwarem
geografie a Škola Jak vytvořit pocitovou mapu v QIS s využitím WMS služeb 1 IS Software Pro vytvoření pocitové mapy je možné využít některý z IS softwarů, které mají různé licencování. Vhodným IS softwarem
