Úvod Základy Fyzika MRI. Magnetická rezonance. J. Kybic, J. Hornak 1, M. Bock, J. Hozman, P.Doubek. 1

Transkript

1 Úvod Základy Fyzika MRI Magnetická rezonance J. Kybic, J. Hornak 1, M. Bock, J. Hozman, P.Doubek

2 Úvod Základy Fyzika MRI Magnetická rezonance Úvod a motivace Fyzikální základy NMR spektroskopie Prostorové zobrazování Lékařské MR systémy Speciální techniky: rychlé techniky, funkční MRI,...

3 Úvod Základy Fyzika MRI Úvod Základy Historie Všeobecně... Fyzika MRI Jaderný spin Interakce Boltzmannova statistika Makroskopický pohled Relaxace a precese Excitace Blochova rovnice

4 Úvod Základy Fyzika MRI Názvy a zkratky pro MRI MR MRI MRT MRS NMR JMR KST pmri fmri Magnetic Resonance Magnetic Resonance Imaging (zobrazování magnetickou rezonancí) Magnetic Resonance Tomography Magnetic Resonance Technology Magnetic Resonance Spectroscopy Nuclear Magnetic Resonance Jaderná Magnetická Rezonance Kernspintomografie positional MRI functional MRI MR scanner

5 Úvod Základy Fyzika MRI Princip MRI ve zkratce NMR Nuclei Magnetic field Resonance absorbce fotonu excitace relaxace MRI Magnetic field RF pulse Induction

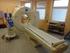
6 Úvod Základy Fyzika MRI Permanentní magnety - architektura OPEN

7 Úvod Základy Fyzika MRI Elektromagnety - architektura OPEN Philips-Marconi Panorama 0.23T a 0.6T FONAR Stand-Up MRI

8 Úvod Základy Fyzika MRI Supravodivé magnety - architektura OPEN

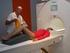
9 Úvod Základy Fyzika MRI ÚVOD -pr$bh MRI 1. Umístní objektu do silného magnetického pole 2. Do objektu vyšleme rádiové vlny (2 až 10 ms) 3. Vypneme rádiový vysílaþ 4. Detekce rádiových vln vysílaných objektem 5. Uložení namených dat (rádiové vlny v þase) 6. Opakování bodu 2. Pro získání více dat 7. Zpracování surových dat za úþelem rekonstrukce 8. Objekt opouští silné magnetické pole

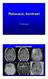
10 Úvod Základy Fyzika MRI MRI Example Brain slice:

11 Úvod Základy Fyzika MRI Historie Všeobecně... Úvod Základy Historie Všeobecně... Fyzika MRI Jaderný spin Interakce Boltzmannova statistika Makroskopický pohled Relaxace a precese Excitace Blochova rovnice

12 Úvod Základy Fyzika MRI Historie Všeobecně... Stručná historie MRI 1946 Felix Bloch, Edward Purcell, nezávislý objev jevu NMR, spektroskopická analýza 1971 Raymond Damadian, relaxační časy tkání jsou různé 1973 Hounsfield, CT ukázalo ochotu nemocnic investovat do zobrazování 1973 Paul Lauterbur, tomografické MRI (zpětná projekce) 1975 Richard Ernst, Fourier MRI 1977 Peter Mansfield, echo-planar imaging (EPI), později umožní 30 ms/řez

13 Úvod Základy Fyzika MRI Historie Všeobecně... Stručná historie MRI (2) 1980 Edelstein, MRI těla (3D), 5 min/řez 1986 MRI těla (3D), 5 s 1986 MRI+NMR mikroskop, rozlišení 10 µm v 1 cm vzorku 1987 zobrazení srdečního cyklu v reálném čase 1987 MRA (angiografie), tok krve (bez kontrast. látek) 1992 funkční MRI, mapování funkcí mozku

14 Úvod Základy Fyzika MRI Historie Všeobecně... Nobelovy ceny 1952 Felix Bloch, Edward Purcell, fyzika, objev jevu 1991 Richard Ernst, chemie, Fourier MRI 2003 Paul Lauterbur, Peter Mansfield, lékařství, MRI v medicíně

15 Úvod Základy Fyzika MRI Historie Všeobecně... Rozšíření MRI V r bylo ve světě asi MRI skenerů 75 miliónů vyšetření za den (20/den na každém skeneru) V ČR desítky (17 v roce 2000, 80 v roce 2013) Zařízení stojí mil. Kč Jedno vyšetření 10 tis. Kč

16 Úvod Základy Fyzika MRI Historie Všeobecně... Potřebné profese, možnosti uplatnění Při vyšetření Lékař radiolog ( čte MR obrazy) Operátor skeneru Operátor dodatečného zpracování Zdravotní sestra Údržba Technik Vývoj Fyzika magnetické rezonance Fyzika supravodivých magnetů Mechanika konstrukce Zpracování signálů a obrazů Elektronika, výpočetní technika Architektura

17 Úvod Základy Fyzika MRI Historie Všeobecně... Výrobci Fonar, General Electric, Hitachi, Philips, Siemens, Toshiba

18 Úvod Základy Fyzika MRI Historie Všeobecně... Tomografické zobrazování

21 Úvod Základy Fyzika MRI Historie Všeobecně... Rozlišení Abbe, Rayleigh nelze zobrazovat objekty o mnoho menší než λ U MRI λ 5 10 m, rozlišení 1 mm. Jak to?

22 Úvod Základy Fyzika MRI Historie Všeobecně... Rozlišení Abbe, Rayleigh nelze zobrazovat objekty o mnoho menší než λ U MRI λ 5 10 m, rozlišení 1 mm. Jak to? Standardní zobrazování používá prostorovou závislost amplitudy absorbovaného či emitovaného záření. MRI používá prostorovou závislost frekvence a fáze absorbovaného a emitovaného záření.

23 Úvod Základy Fyzika MRI Historie Všeobecně... Principy MRI Lidské tělo: tuk a voda. 63 % vodíku. Jádro vodíku = proton. Proton má vlastnost zvanou jaderný spin (podobně jako hmotnost a elektrický náboj). Něco jako rotace kolem své osy. Částice s nenulovým spinem se přibližně chová jako magnet MRI signál

24 Úvod Základy Historie Všeobecně... Fyzika MRI Jaderný spin Interakce Boltzmannova statistika Makroskopický pohled Relaxace a precese Excitace Blochova rovnice

25 Jaderný spin Jaderný spin I je násobkem 1/2 Volné protony, neutrony, elektrony mají spin 1/2 Atom deuteria 2 H (elektron, proton, neutron): celkový elektronový spin 1/2, celkový jaderný spin 1. U párů částic se spin může vyrušit. Helium (He, 2 elektrony, 2 protony, 2 neutrony): celkový spin 0 Jen nespárované spiny (I 0) jsou užitečné pro MRI sudé hmotové číslo & sudé atomové číslo I = 0 ( 12 C, 16 O) sudé hmotové číslo & liché atomové číslo I {1, 2...} ( 14 N, 2 H, 10 B) liché hmotové číslo I { 1 2, 3 2,...} (1 H, 13 C, 15 N)

26 Magnetické kvantové číslo, magnetický moment magnetické kvantové číslo m {I, I 1,..., I } udává spinový stav jádra, pro 1 H, 13 C, 15 N, 19 N, 31 P (nejběžnější jádra) I = 1/2 m = ±1/2 jádro má tedy dva možné spinové stavy magnetický moment µ je vektorová veličina µ = γ I h kde h = Js je Planckova konstanta

27 Spin v magnetickém poli f = γb f resonanční frekvence, také Larmorova frekvence B [Tesla] intenzita magnetického pole γ gyromagnetická konstanta daného jádra Pro 1 H, γ = MHz/T (někdy udávaná v [rad/t], pak se píše γ 2π místo γ) Spin (částice) může absorbovat foton o frekvenci právě f

28 Vlastnosti relevantních prvků Izotop Nukleární spin I γ [MHz/T] citlivost [%] 1 H 1/ % 2 H C 1/ % 19 F 1/ % 23 Na 3/ % 31 P 1/ %

29 Spin v magnetickém poli (2) Konfigurace: nízká energie vysoká energie

30 Přechod mezi energetickými stavy Absorbováním fotonu s energíı E = hf = hν = hγb může spin přejít do vysokoenergetického stavu (excitace) Při zpětném přechodu (relaxace) se foton vyzáří

31 Energetický diagram E = hf = hγb Pro H, typicky f = MHz.

33 Continous wave NMR (1) Konstantní frekvence Proměnné magnetické pole Měříme absorbovanou energii

36 Continous wave NMR (2) Konstantní magnetické pole Proměnná frekvence Měříme absorbovanou energii

40 Spin v magnetickém poli (2) Konfigurace: nízká energie vysoká energie

41 Boltzmannova statistika Spiny v magnetickém poli Počet spinů s nízkou energíı N Počet spinů s vysokou energíı N + N N + = e E kt kde k = je Boltzmannova konstanta T [Kelvin] je teplota

42 Boltzmannova statistika a NMR N N + = e E kt NMR detekuje (velmi malý) rozdíl N N + rezonance citlivost NMR nízká T větší rozdíl vysoká T N N + 0

43 Odvození Boltzmannovy statistiky Systém S + rezervoár R (s teplotou T ) Mějme stavy s i s energíı ε i s N i částicemi. Jaké jsou pravděpodobnosti stavů s i?

44 Odvození Boltzmannovy statistiky (2) Fundamentální předpoklad termodynamiky (2.zákon): Izolovaný systém v rovnováze má maximální entropii Izolovaný systém má všechny stavy stejně pravděpodobné S + R je izolovaný Zachování energie: U R + U S = U 0 = const

45 Odvození Boltzmannovy statistiky (2) Fundamentální předpoklad termodynamiky (2.zákon): Izolovaný systém v rovnováze má maximální entropii Izolovaný systém má všechny stavy stejně pravděpodobné S + R je izolovaný Zachování energie: U R + U S = U 0 = const Necht počet stavů R s energíı U je Ω(U) Pravděpodobnost P(U) Ω(U) Pravděpodobnost P(s i ) Ω R (U 0 ε i )Ω S (ε i ) = Ω R (U 0 )

46 Odvození Boltzmannovy statistiky (2) Fundamentální předpoklad termodynamiky (2.zákon): Izolovaný systém v rovnováze má maximální entropii Izolovaný systém má všechny stavy stejně pravděpodobné S + R je izolovaný Zachování energie: U R + U S = U 0 = const Necht počet stavů R s energíı U je Ω(U) Pravděpodobnost P(U) Ω(U) Pravděpodobnost P(s i ) Ω R (U 0 ε i )Ω S (ε i ) = Ω R (U 0 ) P(s 1 ) P(s 2 ) = Ω R(U 0 ε 1 ) Ω R (U 0 ε 2 )

47 Entropie Entropie = míra neuspořádanosti Statistická definice Termodynamická definice S = k log Ω ds = du T kde Ω je počet stavů a U je rozptýlená nevyužitelná energie.

48 Odvození Boltzmannovy statistiky (3) Odvozené pravděpodobnosti: P(s 1 ) P(s 2 ) = Ω R(U 0 ε 1 ) Ω R (U 0 ε 2 ) z definice entropie: S = k log Ω Ω = e S/k P(s 1 ) P(s 2 ) = esr(u0 ε1)/k e S R(U 0 ε 2 )/k = es R(U 0 ε 1 )/k S R (U 0 ε 2 )/k = e S R k

49 Odvození Boltzmannovy statistiky (3) P(s 1 ) P(s 2 ) = es R(U 0 ε 1 )/k S R (U 0 ε 2 )/k = e SR k jelikož ε i U 0 S R (U 0 ε i ) S R (U 0 ) ε i ds r du U=U 0 S R = (ε 1 ε 2 ) ds r du U=U 0 z termodynamické definice ds = du/t : S R = (ε 1 ε 2 ) T

50 Odvození Boltzmannovy statistiky (3) P(s 1 ) P(s 2 ) = es R(U 0 ε 1 )/k S R (U 0 ε 2 )/k = e SR k S R = (ε 1 ε 2 ) T P(s 1 ) P(s 2 ) = e ε1/(kt ) e ε 2/(kT ) P(s i ) e ε i /(kt ) kde e ε i /(kt ) je Boltzmannův faktor.

51 Boltzmannova statistika Spiny v magnetickém poli Počet spinů s nízkou energíı N Počet spinů s vysokou energíı N + N N + = e E kt kde k = je Boltzmannova konstanta T [Kelvin] je teplota

52 Vliv magnetického pole (I = 1/2) V základním stavu (a) jsou jaderné spiny orientovány náhodně a neexistuje mezi nimi energetický rozdíl (jsou tzv. degenerované). Vlivem silného externího magnetického pole (b) dojde k orientaci spinů bud v souhlasném nebo opačném směru. Vždy existuje malý přebytek spinů v souhlasném směru (nižší energetický stav).

53 Vliv magnetického pole (I = 1/2) příklad 1 H: f = 400 MHz B = 9.5 T E = Kcal mol N N + =

55 Vlastnosti relevantních prvků Izotop Nukleární spin I γ [MHz/T] citlivost [%] 1 H 1/ % 2 H C 1/ % 19 F 1/ % 23 Na 3/ % 31 P 1/ %

56 Výskyt izotopů v přírodě Prvek Četnost [%] 1 H H C N N Na P K Ca 0.145

57 Biologická četnost prvků Prvek Četnost [%] H 63 O 26 hlavní izotop 16 O s nulovým spinem C 9.4 hlavní izotop 12 C s nulovým spinem N 1.5 P 0.24 Ca 0.22 Na 0.041

58 Macroscopic Magnetisation M 0 P B = 0 S N B = B 0 6 = M 0

59 Spinový paket Spinový paket = prostorově ohraničený soubor spinů, na které působí stejné magnetické pole. Vektor magnetizace M magnetické pole spinového paketu M = µ M N + N Celková/čistá Magnetizace (net magnetization) = součet magnetizací od všech paketů Soubor spinů = v NMR všechny spinové pakety v měřeném vzorku

61 T 1 relaxace V rovnováze, M = M 0 e z, M z = M 0 klidová magnetizace.

62 T 1 relaxace V rovnováze, M = M 0 e z, M z = M 0 klidová magnetizace. Vyšleme elmag. (RF) impuls. Vhodnou energíı M z = 0

65 T 1 relaxace (2) Po odeznění impulsu se M z vrací do rovnovážného stavu. M z = M 0 ( 1 e t T 1 ) T 1 mřížková relaxační časová konstanta (spin-lattice relaxation time) energie se přenáší na mřížku (lattice) jako teplo

66 T 1 relaxace (3) Silnější impuls může překlopit M z = M 0. M z = M 0 ( 1 2e t T 1 )

74 Precese Pokud je M překlopena do xy...

77 Precese Pokud je M překlopena do xy M začne rotovat s Larmorovou frekvencí f = γb

87 Precese Pokud je M překlopena do xy M začne rotovat s Larmorovou frekvencí f = γb Frekvence je stejná jako rezonanční frekvence pro změnu orientace.

88 Precese použití pro měření Jak uvidíme později, měřitelný signál vyvolává pouze rotující komponenta magnetizace v rovině xy, nebot pro indukci napětí v RF cívce (které je měřeno) je nutný magnetický tok měnící se v čase. Komponenta M z takové napětí neindukuje.

89 Precese (2) klasický popis Magnetické pole se snaží natočit spin µ do směru B 0. To vytváří moment síly C = µ B 0

98 Precese (3) Pro magnetizaci ne zcela v rovině xy

103 T 2 relaxace Precese každého spinu s trochu jinou f ztráta synchronizace

108 T 2 relaxace (2) Transversální magnetizace M xy postupně klesá M xy = M xy0 e t T 2 T 2 spinová relaxační časová konstanta (spin-spin relaxation time), T 2 < T 1

109 T 1 a T 2 relaxace Transversální magnetizace M xy postupně klesá Zároveň (ale pomaleji) dochází k návratu M z M 0.

113 Důvody T 2 relaxace Molekulární interakce (T 2 ) Nehomogenita magnetického pole (T inhom 2 ) Kombinovaná časová konstanta T 2 : 1 T 2 = 1 T T inhom 2

114 Další faktory ovlivňující relaxaci Pohyb molekul (vlivem nehomogenity mag. pole) Teplota Viskozita Fluktuace Časy relaxace (1.5 T) tkáň T 1 [ms] T 2 [ms] tuk sval mozek (šedá hmota) mozek (bílá hmota) játra mozkomíšní tekutina

115 Rotující soustava souřadnic... rotuje kolem osy z s Larmorovou frekvencí f

119 Rotující soustava souřadnic (2) µ rotující s frekvencí f se zdá stacionární

120 Rotující soustava souřadnic (3) µ rotující rychleji se otáčí souhlasně

124 Rotující soustava souřadnic (4) µ rotující pomaleji se otáčí nesouhlasně

128 Rotující soustava souřadnic (5)... a desynchronizace vypadá takto:

133 Elektromagnetická excitace Cívka s osou x vytvoří magnetické pole ve směru x

134 Elektromagnetická excitace Cívka s osou x vytvoří magnetické pole ve směru x Střídavý proud s frekvencí f vytvoří pole B 1 s frekvencí f

135 Elektromagnetická excitace Cívka s osou x vytvoří magnetické pole ve směru x Střídavý proud s frekvencí f vytvoří pole B 1 s frekvencí f B 1 se dá rozložit na B B 1, rotující okolo z s frekvencí ±f

136 Elektromagnetická excitace Cívka s osou x vytvoří magnetické pole ve směru x Střídavý proud s frekvencí f vytvoří pole B 1 s frekvencí f B 1 se dá rozložit na B B 1, rotující okolo z s frekvencí ±f B + 1 bude v rotující soustavě souřadnic stacionární.

137 Elektromagnetická excitace Cívka s osou x vytvoří magnetické pole ve směru x Střídavý proud s frekvencí f vytvoří pole B 1 s frekvencí f B 1 se dá rozložit na B B 1, rotující okolo z s frekvencí ±f B + 1 bude v rotující soustavě souřadnic stacionární. B 1 bude mít frekvencí 2f, daleko od rezonance, zanedbáme.

138 Elektromagnetická excitace Cívka s osou x vytvoří magnetické pole ve směru x Střídavý proud s frekvencí f vytvoří pole B 1 s frekvencí f B 1 se dá rozložit na B B 1, rotující okolo z s frekvencí ±f B + 1 bude v rotující soustavě souřadnic stacionární. B 1 bude mít frekvencí 2f, daleko od rezonance, zanedbáme. pole B 1 se bude v rotující soustave jevit stacionární, ve směru x.

139 Natočení vektoru magnetizace Impuls o Larmorově frekvenci f (tzv. rezonanční podmínka), amplitudě B 1 a délce trvání τ magnetizace M se natočí podle osy B 1 (x ) o úhel α = 2πγτB 1 flip angle

140 Natočení vektoru magnetizace Impuls o Larmorově frekvenci f (tzv. rezonanční podmínka), amplitudě B 1 a délce trvání τ magnetizace M se natočí podle osy B 1 (x ) o úhel α = 2πγτB 1 90 impuls natočí M do směru y flip angle

144 Natočení vektoru magnetizace Impuls o Larmorově frekvenci f (tzv. rezonanční podmínka), amplitudě B 1 a délce trvání τ magnetizace M se natočí podle osy B 1 (x ) o úhel α = 2πγτB 1 flip angle 90 impuls natočí M do směru y 180 impuls natočí M do směru z

145 Natočení vektoru magnetizace Impuls o Larmorově frekvenci f (tzv. rezonanční podmínka), amplitudě B 1 a délce trvání τ magnetizace M se natočí podle osy B 1 (x ) o úhel α = 2πγτB 1 flip angle 90 impuls natočí M do směru y 180 impuls natočí M do směru z v nerotující soustavě souřadnic...

154 Natočení vektoru magnetizace (2) Magnetizace je otočena o úhel α z libovolné počáteční pozice 180 impuls pro M y

159 Blochova rovnice dm = γm B dt kde B je celkové magnetické pole (B 0 + B 1 ).

160 Blochovy rovnice (2) dm = γm B dt dosadíme za B, přidáme ztráty a přejdeme do rotujícího systému dm x dt dm y dt dm z dt = (ω 0 ω)m y M x T 2 = (ω 0 ω)m x + 2πγB 1 M z M y T 2 = 2πγB 1 M y M z M z0 T 1 kde ω 0 = 2πf 0 = 2πγB 0, ω je frekvence rotace spinu.