Úvod do logiky: PL analýza vět mimo logický čtverec (cvičení)
|
|
|
- Pavlína Bednářová
- před 8 lety
- Počet zobrazení:
Transkript
1 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/ , OPVK) Úvod do logiky: PL analýza vět mimo logický čtverec (cvičení) doc. PhDr. Jiří Raclavský, Ph.D. (raclavsky@phil.muni.cz) 1
2 4. Cvičení - analýza vět, které nespadají pod logický čtverec 4.1 Cvičení věty zahrnující monadické i binární predikáty Následující věty přirozeného jazyka vyjádřete formulemi predikátové logiky: 1) Misantrop každého nenávidí. 2) Včely sbírají med. 3) Někteří studenti nemají hudební nadání. 4) Pes je věrný přítel člověka. 5) Adam má rád pouze analytické filosofy. 6) Adam nemá rád nikoho, kdo není analytickým filosofem. 7) Neexistuje nikdo takový, že ho má Adam rád a nebyl to analytický filosof. 8) Někdo má rád každého, ale ne sám sebe. 9) Každé číslo dělitelné 8 je dělitelné 4. 10) Vše, co se děje, má svou příčinu. 11) Žádný učený z nebe nespadl. 12) Kdo nic nedělá, nic nezkazí. 13) Kdo jinému jámu kopá, sám do ní padá. 14) Všichni přítomní jsou starší než někteří členové klubu. 15) Žádný dobrý učitel nikoho zbytečně nepotrestal. 16) Jablka i hrušky rostou na stromech. 17) Bohdan půjde do kina pouze tehdy, pokud jeho žena nebude doma. 18) Všichni savci rodí živá mláďata. 19) Posláním mudrce je vytvářet řád. 20) Myslí dobře ten, kdo se k věcem dobře postaví. 4.2 Cvičení věty s jedním ternárním predikátem Nechť výraz P(a,b,g) znamená Adam půjčuje Báře Goffyho. Přepište do symbolismu predikátové logiky následující výroky: 2
3 1) Někdo půjčuje Báře Goffyho. 2) Bára půjčuje někomu Goffyho. 3) Bára někomu něco půjčuje. 4) Někdo někomu něco půjčuje. 5) Adam každému něco půjčuje. 6) Někdo někomu všechno půjčuje. 7) Každý někomu něco půjčuje. 8) Někdo každému všechno půjčuje. 9) Někdo nikomu nic nepůjčuje. 4.3 Cvičení věty s jedním binárním predikátem Nechť binární predikátový symbol R znamená binární predikát x rozumí y. Zapište symbolismem predikátové logiky věty: 1) Každý něčemu rozumí. 2) Všemu někdo nerozumí. 3) Každý něčemu nerozumí. 4) Všemu někdo rozumí. 5) Každý rozumí všemu. 6) Něčemu někdo nerozumí. 7) Každý nerozumí všemu. 8) Něčemu někdo rozumí. 9) Někdo rozumí něčemu. 10) Všemu každý nerozumí. 11) Někdo něčemu nerozumí. 12) Všemu každý rozumí. 13) Někdo rozumí všemu. 14) Něčemu nikdo nerozumí. 3
4 15) Někdo nerozumí ničemu. 16) Něčemu rozumí každý. 4.1 Řešení věty s monadickými i binárními predikáty 1) x (M(x) y N(x,y)) 2) x (V(x) y (M(y) S(x,y)) Pro všechna x platí, že je-li x včelou, tak existuje nějaké y, které je medem (nesbírá totiž každý med) a x sbírá to y. 3) x (S(x) y( (H(y) N(y)) M(x,y)) Existuje nějaké x, které je studentem a existuje nějaké y, které je hudební a je nadáním a x nemá to y. 4) x (P(x) y (Č(y) (V(x) P (x,y)) ) Pro všechna x platí, že je-li x psem, tak pokud to y je člověkem, tak to x je věrné a přítelem toho y. 5) x (R(a,x) AF(x)) Pro všechna x platí, že jestliže Adam má rád x, pak je x analytickým filosofem (nedělíme na být analytickým a být filozofem ). 6) x ( AF(x) R(a,x)) Pro všechna x platí, že není-li x zároveň analytickým filosofem, pak Adam ho nemá rád. 7) x (R(a,x) AF(x)) Není pravda, že existuje někdo takový, že Adam ho má rád a současně není analytickým filosofem. Této větě je ekvivalentní věta: Každý, koho má Adam rád, je analytickým filosofem. x (R(p,x) (AF(x)) 8) x y (R(x,y) R(x,x)) Čili: Někdo má rád všechny ostatní. 9) x (D8(x) D4(x)) 4
5 Lepší analýza odliší predikáty být dělitelný 8 a být dělitelný 4 : x (Č(x) (D8(x) D4(x))) Ještě lepší analýza odliší predikáty být dělitelný čím od čísel, jimiž je nějaké x dělitelné. Ten je totiž vyjádřen tranzitivním slovesem: x (Č(x) (D(x,8) D(x,4))) Pro všechna x platí, že je-li x číslem, tak pokud to x je dělitelné osmi, tak je to x dělitelné čtyřmi. 10) x (D(x) y P(y,x)) Pro všechna x platí, že pokud se děje, tak existuje nějaké y, které je příčinou y. (Nikoli: Pro všechna x platí, že pokud se děje, tak existuje nějaké y, které je příčinou a které x má. Mít totiž nechápeme jako svébytný predikát.) 11) x (U(x) y (N(y) S(x,y)) ) Pro všechna x platí, že pokud je x učené, tak existuje nějaké y, které je nebem a x spadl z toho y. 12) x ( D(x) Z(x)) Lepší analýza: x y ( D(x,y) Z(x,y)) ) Pro všechna x a y platí, že pokud x nedělá to y, tak x nezkazí to y. 13) x ( y ( J(y) (K(x,y) P(x,y)) ) ) ) Pro všechna x a y platí, že pokud je y jáma, tak jestliže x kope to y, tak x padá do y. 14) x(p(x) yz (K(y) Č(z,y) S(x,y))) Pro všechna x platí, že pokud x je přítomný, tak existují y a z taková, že y je klub a z je člen y a x jsou starší než ti (někteří) z. 15) x (D(x) y P(x,y)) Lepší analýza: x ( (D(x) U(x)) y z (Z(z) P(x,y,z)) ) 5
6 Pro všechna x platí, že existuje takové y a z, že z je zbytečné a ten x toho y potrestal (způsobem) z (P je ternární predikát). To je ekvivalentní větě formalizovatelné (ekvivalentní) formulí: x ( (D(x) U(x)) yz (Z(z) P(x,y,z)) ). 16) xy ( (J(x) H(y)) z (S(z) (R(x,z) R(y,z)) ) Pro všechna x a y platí, že je-li x jablkem a y hruškou, tak existuje něco, co je strom a x roste na z a y roste na z. 17) xy ((K(x) P(b,x)) ( D(y) Ž(y,b)) Existují x a y taková, že x je kino a Bohdan půjde do x právě tehdy, když y nebude doma a y je ženou Bohdana. 18) x ( S(x) y((ž(y) M(y)) R(x,y)) ) Pro všechna x platí, že jestliže je savcem, tak některá y, která jsou živým mládětem, jsou taková, že x rodí to y. Analýza x (S(x) y((ž(y) M(y)) R(x,y))) by byla chybná proto, že jsou i taková živá mláďata, která nejsou rozena savci, ale např. ptactvem či plazy. 19) x (M(x) y ((Ř(y) V(x,y)) P(x,y))) Pro všechna x platí, že je-li mudrcem, tak existuje nějaké y, které je řádem a je vytvářeno díky x, a x má poslání k tomu y. 20) x ( [ y V(y) z (D(z) P(x,y,z)) ] [ z (D(z) M(x,z)) ] ) Pro všechna x, platí, že pokud existuje y, které je věc, a zároveň existuje z takové, které je dobré, a x se postaví k tomu y způsobem z, tak tedy způsobem z, který je dobrý, ten x myslí Řešení věty s jedním ternárním predikátem 1) x P(x,b,g) 2) x P(b,x,g) 3) x y P(b,x,y) 4) x y z P(x,y,z) 5) x y P(a,x,y) 6
7 6) x y z P(x,y,z) 7) x y z P(x,y,z) 8) x y z P(x,y,z) 9) x y z P(x,y,z) 4.3 Řešení věty s jedním binárním predikátem 1) x y R(x,y) 2) y x R(x,y) 3) x y R(x,y) 4) y x R(x,y) 5) x y R(x,y) 6) y x R(x,y) 7) x y R(x,y) 8) y x R(x,y) 9) x y R(x,y) 10) y x R(x,y) 11) x y R(x,y) 12) y x R(x,y) 13) x y R(x,y) 14) y x R(x,y) 15) x y R(x,y) 16) y x R(x,y) 7
Úvod do logiky (PL): negace a ekvivalence vět mimo logický
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): negace a ekvivalence vět mimo logický čtverec
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): negace a ekvivalence vět mimo logický čtverec
Úvod do logiky (PL): analýza vět mimo logický čtverec
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): analýza vět mimo logický čtverec doc. PhDr.
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): analýza vět mimo logický čtverec doc. PhDr.
Úvod do logiky (PL): ekvivalence a negace výroků logického
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): ekvivalence a negace výroků logického čtverce
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): ekvivalence a negace výroků logického čtverce
Úvod do logiky (PL): logický čtverec (cvičení)
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): logický čtverec (cvičení) doc. PhDr. Jiří
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): logický čtverec (cvičení) doc. PhDr. Jiří
Úvod do logiky (PL): analýza vět přirozeného jazyka
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): analýza vět přirozeného jazyka doc. PhDr.
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): analýza vět přirozeného jazyka doc. PhDr.
Úvod do logiky (PL): sémantika predikátové logiky
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): sémantika predikátové logiky doc. PhDr. Jiří
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): sémantika predikátové logiky doc. PhDr. Jiří
I) Příklady (převeďte následující věty do formulí PL1 a ověřte jejich ekvivalenci pomocí de Morganových zákonů):
 I) Příklady (převeďte následující věty do formulí PL1 a ověřte jejich ekvivalenci pomocí de Morganových zákonů): 1. Všechna prvočísla větší než 2 jsou lichá. Je-li prvočíslo větší než 2, pak je liché.
I) Příklady (převeďte následující věty do formulí PL1 a ověřte jejich ekvivalenci pomocí de Morganových zákonů): 1. Všechna prvočísla větší než 2 jsou lichá. Je-li prvočíslo větší než 2, pak je liché.
Obsah Předmluva Rekapitulace základních pojmů logiky a výrokové logiky Uvedení do predikátové logiky...17
 Obsah Předmluva...3 0. Rekapitulace základních pojmů logiky a výrokové logiky...11 0.1 Logika jako věda o vyplývání... 11 1. Uvedení do predikátové logiky...17 1.1 Základní terminologie... 17 1.2 Základní
Obsah Předmluva...3 0. Rekapitulace základních pojmů logiky a výrokové logiky...11 0.1 Logika jako věda o vyplývání... 11 1. Uvedení do predikátové logiky...17 1.1 Základní terminologie... 17 1.2 Základní
Úvod do logiky (VL): 5. Odvození výrokových spojek z jiných
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (VL): 5. Odvození z jiných doc. PhDr. Jiří Raclavský,
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (VL): 5. Odvození z jiných doc. PhDr. Jiří Raclavský,
UDL 2004/2005 Cvičení č.6 řešení Strana 1/5
 UDL 2004/2005 Cvičení č.6 řešení Strana 1/5 Opakování pojmů relace a funkce Relace R nad množinami A, B je podmnožina kartézského součinu: R A B Kartézský součin množin A = {a 1, a 2,, a 4 }, B = {b 1,
UDL 2004/2005 Cvičení č.6 řešení Strana 1/5 Opakování pojmů relace a funkce Relace R nad množinami A, B je podmnožina kartézského součinu: R A B Kartézský součin množin A = {a 1, a 2,, a 4 }, B = {b 1,
2016 Česká republika ŽENY (aktuální k )
 2016 Česká republika ŽENY (aktuální k 27. 11. 2017) věk qx px lx dx Lx Tx ex Dx Cx Nx Mx Sx Rx 0 0.002462 0.997538 100 000.00 246.23 99787 8205207 82.05 100 000.00 243.07 5 066 877.57 34 975.90 176 922
2016 Česká republika ŽENY (aktuální k 27. 11. 2017) věk qx px lx dx Lx Tx ex Dx Cx Nx Mx Sx Rx 0 0.002462 0.997538 100 000.00 246.23 99787 8205207 82.05 100 000.00 243.07 5 066 877.57 34 975.90 176 922
Česká republika - ŽENY
 2012 Česká republika - ŽENY věk qx px lx dx Lx Tx ex Dx Cx Nx Mx Sx Rx 0 0.002338 0.997662 100000 234 99804 8088058 80.88 100 000.00 229.43 4 164 194.04 22 355.11 130 483 842.84 1 731 180.86 1 0.000144
2012 Česká republika - ŽENY věk qx px lx dx Lx Tx ex Dx Cx Nx Mx Sx Rx 0 0.002338 0.997662 100000 234 99804 8088058 80.88 100 000.00 229.43 4 164 194.04 22 355.11 130 483 842.84 1 731 180.86 1 0.000144
Logika XI. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı BI-MLO, ZS 2011/12
 Logika XI. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Logika XI. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
2.1 Formule predikátové logiky. větám. Použijte k tomu predikátových symbolu uvedených v textu.
 6 Kapitola 2 Příklady z predikátové logiky 2.1 Formule predikátové logiky 2.1.1 Příklad. Napište formule predikátové logiky odpovídající následujícím větám. Použijte k tomu predikátových symbolu uvedených
6 Kapitola 2 Příklady z predikátové logiky 2.1 Formule predikátové logiky 2.1.1 Příklad. Napište formule predikátové logiky odpovídající následujícím větám. Použijte k tomu predikátových symbolu uvedených
Úvod do logiky (VL): 7. Ekvivalentní transformace
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (VL): 7. Ekvivalentní transformace doc. PhDr. Jiří
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (VL): 7. Ekvivalentní transformace doc. PhDr. Jiří
Úvod do teoretické informatiky(2017/2018) cvičení 6 1
 Úvod do teoretické informatiky(2017/2018) cvičení 6 1 Cvičení 6 Příklad 1: Pro každou z následujících sekvencí symbolů rozhodněte, zda se jedná o a) term, b) formuli predikátové logiky(používejte běžné
Úvod do teoretické informatiky(2017/2018) cvičení 6 1 Cvičení 6 Příklad 1: Pro každou z následujících sekvencí symbolů rozhodněte, zda se jedná o a) term, b) formuli predikátové logiky(používejte běžné
Úvod do logiky (PL): logický čtverec
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): logický čtverec doc. PhDr. Jiří Raclavský,
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): logický čtverec doc. PhDr. Jiří Raclavský,
Úvod do predikátové logiky. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
 Úvod do predikátové logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 1 Relace Neuspořádaná vs. uspořádaná dvojice {m, n} je neuspořádaná dvojice. m, n je uspořádaná dvojice. (FLÚ AV ČR) Logika:
Úvod do predikátové logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 1 Relace Neuspořádaná vs. uspořádaná dvojice {m, n} je neuspořádaná dvojice. m, n je uspořádaná dvojice. (FLÚ AV ČR) Logika:
 Á É Č ď ý ý Č Ť ž ý ý ť žž Ž ý ú ž š ý ž ž ž š š š ý Š ť ý ý š ž ž ý ž ž Ň ý ž ť ť ú ž ý š ž š ž ž š ž š ž ý ý šť ý Ý Ú ň ý ý Ý ž ý ý ť ý ž ý ý ž ý ď ý ý š ý ž ú ú ď ý ž š ž ý ž ť ý ý ý ý ý Á ý ď ž š ž
Á É Č ď ý ý Č Ť ž ý ý ť žž Ž ý ú ž š ý ž ž ž š š š ý Š ť ý ý š ž ž ý ž ž Ň ý ž ť ť ú ž ý š ž š ž ž š ž š ž ý ý šť ý Ý Ú ň ý ý Ý ž ý ý ť ý ž ý ý ž ý ď ý ý š ý ž ú ú ď ý ž š ž ý ž ť ý ý ý ý ý Á ý ď ž š ž
Úvod do logiky (VL): 12. Ověřování platnosti úsudků metodou protipříkladu
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (VL): 12. Ověřování platnosti úsudků metodou protipříkladu
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (VL): 12. Ověřování platnosti úsudků metodou protipříkladu
Úvod do logiky (VL): 4. Zjištění průběhu pravdivostních hodnot formule tabulkovou metodou
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (VL): 4. Zjištění průběhu pravdivostních hodnot
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (VL): 4. Zjištění průběhu pravdivostních hodnot
Úvod do logiky (VL): 8. Negace výroků
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (VL): 8. Negace výroků doc. PhDr. Jiří Raclavský,
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (VL): 8. Negace výroků doc. PhDr. Jiří Raclavský,
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Úvod do logiky (PL): sylogismy (cvičení)
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): sylogismy (cvičení) doc. PhDr. Jiří Raclavský,
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): sylogismy (cvičení) doc. PhDr. Jiří Raclavský,
Predikátová logika Individua a termy Predikáty
 Predikátová logika Predikátová logika je rozšířením logiky výrokové o kvantifikační výrazy jako každý, všichni, někteří či žádný. Nejmenší jazykovou jednotkou, kterou byla výroková logika schopna identifikovat,
Predikátová logika Predikátová logika je rozšířením logiky výrokové o kvantifikační výrazy jako každý, všichni, někteří či žádný. Nejmenší jazykovou jednotkou, kterou byla výroková logika schopna identifikovat,
Predikátová logika. 3.1 Formule predikátové logiky
 12 Kapitola 3 Predikátová logika 3.1 Formule predikátové logiky 3.1.1 Příklad. Napište formule predikátové logiky odpovídající následujícím větám. Použijte k tomu predikátových symbolů uvedených v textu.
12 Kapitola 3 Predikátová logika 3.1 Formule predikátové logiky 3.1.1 Příklad. Napište formule predikátové logiky odpovídající následujícím větám. Použijte k tomu predikátových symbolů uvedených v textu.
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz
 Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Úvod do logiky (VL): 11. Ověřování, zda je formule tautologií metodou protipříkladu
 Jiří Raclavský (214): Úvod do logiky: klasická výroková logika Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.7/2.2./28.216, OPVK) Úvod
Jiří Raclavský (214): Úvod do logiky: klasická výroková logika Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.7/2.2./28.216, OPVK) Úvod
Transformujte diferenciální výraz x f x + y f do polárních souřadnic r a ϕ, které jsou definovány vztahy x = r cos ϕ a y = r sin ϕ.
 Ukázka 1 Necht má funkce z = f(x, y) spojité parciální derivace. Napište rovnici tečné roviny ke grafu této funkce v bodě A = [ x 0, y 0, z 0 ]. Transformujte diferenciální výraz x f x + y f y do polárních
Ukázka 1 Necht má funkce z = f(x, y) spojité parciální derivace. Napište rovnici tečné roviny ke grafu této funkce v bodě A = [ x 0, y 0, z 0 ]. Transformujte diferenciální výraz x f x + y f y do polárních
Sylogistika. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 16
 (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 16 Výstavba logické teorie Sylogistika 1) Syntax základní symboly (logické, mimologické) gramatická pravidla (pojem formule) 2) Sémantika pojem interpretace
(FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 16 Výstavba logické teorie Sylogistika 1) Syntax základní symboly (logické, mimologické) gramatická pravidla (pojem formule) 2) Sémantika pojem interpretace
1 Pravdivost formulí v interpretaci a daném ohodnocení
 1 Pravdivost formulí v interpretaci a daném ohodnocení Než uvedeme konkrétní příklady, zopakujme si definici interpretace, ohodnocení a pravdivosti. Necht L je nějaký jazyk. Interpretaci U, jazyka L tvoří
1 Pravdivost formulí v interpretaci a daném ohodnocení Než uvedeme konkrétní příklady, zopakujme si definici interpretace, ohodnocení a pravdivosti. Necht L je nějaký jazyk. Interpretaci U, jazyka L tvoří
Okruh č.9: sémantické metody dokazování v PL1 model formule Tradiční Aristotelova logika kategorický sylogismus subjekt predikátové výroky
 Okruh č.9: sémantické metody dokazování v PL1 Pomocí metody Vennových diagramů a relačních struktur vytváříme grafický model situace, která je úsudkem vyjádřena. Ověřujeme, zda náš graficky znázorněný
Okruh č.9: sémantické metody dokazování v PL1 Pomocí metody Vennových diagramů a relačních struktur vytváříme grafický model situace, která je úsudkem vyjádřena. Ověřujeme, zda náš graficky znázorněný
Úvod do logiky: PL Kategorický sylogismus
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky: PL Kategorický sylogismus doc. PhDr. Jiří Raclavský,
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky: PL Kategorický sylogismus doc. PhDr. Jiří Raclavský,
λογος - LOGOS slovo, smysluplná řeč )
 MATA P1: Výroky, množiny a operace s nimi Matematická logika (z řeckého slova λογος - LOGOS slovo, smysluplná řeč ) Výrok primitivní pojem matematické logiky. Tvrzení, pro které má smysl otázka o jeho
MATA P1: Výroky, množiny a operace s nimi Matematická logika (z řeckého slova λογος - LOGOS slovo, smysluplná řeč ) Výrok primitivní pojem matematické logiky. Tvrzení, pro které má smysl otázka o jeho
Typy predikátů: slovesa, predikativní jména, adjektiva, tranzitivní slovesa, relativní 1 věty / 10
 : slovesa, predikativní jména, adjektiva, tranzitivní slovesa, relativní věty FF MU Mojmír Dočekal ÚJABL Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia
: slovesa, predikativní jména, adjektiva, tranzitivní slovesa, relativní věty FF MU Mojmír Dočekal ÚJABL Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia
Predikátová logika. Kapitola 2. 2.1 Formule predikátové logiky
 5 Kapitola 2 Predikátová logika 2.1 Formule predikátové logiky 2.1.1 Příklad. Napište formule predikátové logiky odpovídající následujícím větám. Použijte k tomu predikátových symbolů uvedených v textu.
5 Kapitola 2 Predikátová logika 2.1 Formule predikátové logiky 2.1.1 Příklad. Napište formule predikátové logiky odpovídající následujícím větám. Použijte k tomu predikátových symbolů uvedených v textu.
Polynomy nad Z p Konstrukce faktorových okruhů modulo polynom. Alena Gollová, TIK Počítání modulo polynom 1/30
 Počítání modulo polynom 3. přednáška z algebraického kódování Alena Gollová, TIK Počítání modulo polynom 1/30 Obsah 1 Polynomy nad Zp Okruh Zp[x] a věta o dělení se zbytkem 2 Kongruence modulo polynom,
Počítání modulo polynom 3. přednáška z algebraického kódování Alena Gollová, TIK Počítání modulo polynom 1/30 Obsah 1 Polynomy nad Zp Okruh Zp[x] a věta o dělení se zbytkem 2 Kongruence modulo polynom,
Zobecněné kvantifikátory, empirické argumenty pro unifikovanou sémantiku NP, negativně 1 / 20 p
 Zobecněné kvantifikátory, empirické argumenty pro unifikovanou sémantiku NP, negativně polaritní výrazy FF MU Mojmír Dočekal ÚJABL Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik
Zobecněné kvantifikátory, empirické argumenty pro unifikovanou sémantiku NP, negativně polaritní výrazy FF MU Mojmír Dočekal ÚJABL Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik
Predikátová logika. Teoretická informatika Tomáš Foltýnek
 Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce
 Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
1 Predikátová logika. 1.1 Syntax. jaký mohou mít formule význam (sémantiku). 1. Logických symbolů: 2. Speciálních (mimologických) symbolů:
 1 Predikátová logika 1.1 Syntax Podobně jako ve výrokové logice začneme nejprve se syntaxí predikátové logiky, která nám říká, co jsou správně utvořené formule predikátové logiky. V další části tohoto
1 Predikátová logika 1.1 Syntax Podobně jako ve výrokové logice začneme nejprve se syntaxí predikátové logiky, která nám říká, co jsou správně utvořené formule predikátové logiky. V další části tohoto
Rovnost lze vyjádřit jako predikát, např. můžeme zvolit, že P(x, y) reprezentujetvrzení xjerovnoy.
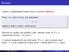 Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Přednáška 2: Formalizace v jazyce logiky.
 Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
Cvičení z logiky II.
 Cvičení z logiky II. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 https://edux.fit.cvut.cz/courses/bi-mlo/lectures/
Cvičení z logiky II. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 https://edux.fit.cvut.cz/courses/bi-mlo/lectures/
Predikátová logika. prvního řádu
 Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
diferenciální rovnice verze 1.1
 Diferenciální rovnice vyšších řádů, snižování řádu diferenciální rovnice verze 1.1 1 Úvod Následující text popisuje řešení diferenciálních rovnic, konkrétně diferenciálních rovnic vyšších řádů a snižování
Diferenciální rovnice vyšších řádů, snižování řádu diferenciální rovnice verze 1.1 1 Úvod Následující text popisuje řešení diferenciálních rovnic, konkrétně diferenciálních rovnic vyšších řádů a snižování
Úvod do TI - logika Aristotelova logika. Marie Duží
 Úvod do TI - logika Aristotelova logika Marie Duží marie.duzi@vsb.cz Platón, Aristoteles (vpravo) 384 322 Mine is the first step and therefore a small one, though worked out with much thought and hard
Úvod do TI - logika Aristotelova logika Marie Duží marie.duzi@vsb.cz Platón, Aristoteles (vpravo) 384 322 Mine is the first step and therefore a small one, though worked out with much thought and hard
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška pátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška pátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Sublexikální sémantika: události, sémantické role; formalizace: množiny a funkce, lambda 1 / 12 a
 Sublexikální sémantika: události, sémantické role; formalizace: množiny a funkce, lambda abstrakce FF MU Mojmír Dočekal ÚJABL Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik
Sublexikální sémantika: události, sémantické role; formalizace: množiny a funkce, lambda abstrakce FF MU Mojmír Dočekal ÚJABL Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik
Marie Duží
 Marie Duží marie.duzi@vsb.cz Platón, Aristoteles (vpravo) 384 322 Mine is the first step and therefore a small one, though worked out with much thought and hard labour. You, my readers or hearers of my
Marie Duží marie.duzi@vsb.cz Platón, Aristoteles (vpravo) 384 322 Mine is the first step and therefore a small one, though worked out with much thought and hard labour. You, my readers or hearers of my
Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka
 Celkové hodnocení BI-MLO (nevyplňujte!) Semestr Zkouška Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka BI-MLO Písemná zkouška 9. února 2016 Matematická logika FIT ČVUT v Praze Varianta B
Celkové hodnocení BI-MLO (nevyplňujte!) Semestr Zkouška Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka BI-MLO Písemná zkouška 9. února 2016 Matematická logika FIT ČVUT v Praze Varianta B
Negace bázového atomu Negace atomu s existenčním termem Negace klauzule Negace množiny klauzulí Predikát rovnosti. Klauzulární logika
 Vlastnosti klauzulí, negace Šárka Vavrečková Ústav informatiky, Filozoficko-přírodovědecká fakulta Slezské univerzity v Opavě sarka.vavreckova@fpf.slu.cz 27. října 2008 Věta o transferu bázového atomu
Vlastnosti klauzulí, negace Šárka Vavrečková Ústav informatiky, Filozoficko-přírodovědecká fakulta Slezské univerzity v Opavě sarka.vavreckova@fpf.slu.cz 27. října 2008 Věta o transferu bázového atomu
Logika. Akademie managementu a komunikace, Praha PhDr. Peter Jan Kosmály, PhD.
 Akademie managementu a komunikace, Praha PhDr. Peter Jan Kosmály, PhD. Tematické okruhy: 1. Stručné dějiny logiky a její postavění ve vědě 2. Analýza složených výroků pomocí pravdivostní tabulky 3. Subjekt-predikátová
Akademie managementu a komunikace, Praha PhDr. Peter Jan Kosmály, PhD. Tematické okruhy: 1. Stručné dějiny logiky a její postavění ve vědě 2. Analýza složených výroků pomocí pravdivostní tabulky 3. Subjekt-predikátová
$ x. $ z. divg # G. z divg + 0. rotg # G. Dt DT. x y. z y x z y
 t x, y, z t x F x, y, z, t # #,,, #,,, y F x y z t z F3 x y z t x y z u #, v #, w # t t t u x v y w z # t t t 3 #, # t t #, # # t u f x, y, z, t v f x, y, z, t w f3 x, y, z, t # # # u v w #, #, 3 # t t
t x, y, z t x F x, y, z, t # #,,, #,,, y F x y z t z F3 x y z t x y z u #, v #, w # t t t u x v y w z # t t t 3 #, # t t #, # # t u f x, y, z, t v f x, y, z, t w f3 x, y, z, t # # # u v w #, #, 3 # t t
2.2 Sémantika predikátové logiky
 14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
Protože se neobejdeme bez základních poznatků vektorové algebry, připomeneme si nejdůležitější pojmy., pak - skalární součin vektorů u,
 4 VEKTOROVÁ ANALÝZA 41 Vektorová funkce Protože se neobejdeme bez základních poznatků vektorové algebry, připomeneme si nejdůležitější pojmy Jsou-li dány tři nenulové vektory, uu ( 1, u, u), vv ( 1, v,
4 VEKTOROVÁ ANALÝZA 41 Vektorová funkce Protože se neobejdeme bez základních poznatků vektorové algebry, připomeneme si nejdůležitější pojmy Jsou-li dány tři nenulové vektory, uu ( 1, u, u), vv ( 1, v,
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
Soužití občanů. Metodický materiál pro učitele
 Soužití občanů. Metodický materiál pro učitele Spolufinancováno ESF a státním rozpočtem ČR, reg. č. projektu CZ.1.07/1.1.00/14.0143 OPVK 1 Soužití občanů právní předpisy Práva občanů jsou upravena v právních
Soužití občanů. Metodický materiál pro učitele Spolufinancováno ESF a státním rozpočtem ČR, reg. č. projektu CZ.1.07/1.1.00/14.0143 OPVK 1 Soužití občanů právní předpisy Práva občanů jsou upravena v právních
Kvantita (u subjektu) všechny prvky množiny (všichni, každý, nikdo, žádní ) některé prvky množiny (některý, existuje,.) predikát.
 Studijní text Hledisko kvality a kvantity, vztahy pravdivostních hodnot Nyní se zaměříme na obecné a částečné výroky se stejným em a em. Kvantita (u u) všechny prvky množiny (všichni, každý, nikdo, žádní
Studijní text Hledisko kvality a kvantity, vztahy pravdivostních hodnot Nyní se zaměříme na obecné a částečné výroky se stejným em a em. Kvantita (u u) všechny prvky množiny (všichni, každý, nikdo, žádní
výrok-každésdělení,uněhožmásmyslseptát,zdaječinenípravdivé, aproněžprávějednaztěchtodvoumožnostínastává.
 1 Základní pojmy matematické logiky Výrokový počet... syntaktické hledisko Predikátový počet... sémantické hledisko 1.1 VÝROKOVÝ POČET výrok-každésdělení,uněhožmásmyslseptát,zdaječinenípravdivé, aproněžprávějednaztěchtodvoumožnostínastává.
1 Základní pojmy matematické logiky Výrokový počet... syntaktické hledisko Predikátový počet... sémantické hledisko 1.1 VÝROKOVÝ POČET výrok-každésdělení,uněhožmásmyslseptát,zdaječinenípravdivé, aproněžprávějednaztěchtodvoumožnostínastává.
Databázové systémy. * relační kalkuly. Tomáš Skopal. - relační model
 Databázové systémy Tomáš Skopal - relační model * relační kalkuly Osnova přednášky relační kalkuly doménový n-ticový Relační kalkuly využití aparátu predikátové logiky 1. řádu pro dotazování rozšíření
Databázové systémy Tomáš Skopal - relační model * relační kalkuly Osnova přednášky relační kalkuly doménový n-ticový Relační kalkuly využití aparátu predikátové logiky 1. řádu pro dotazování rozšíření
platné nejsou Sokrates je smrtelný. (r) 1/??
 Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
3. Celistvé výrazy a jejich úprava 3.1. Číselné výrazy
 . Celistvé výrazy a jejich úprava.1. Číselné výrazy 8. ročník. Celistvé výrazy a jejich úprava Proměnná je znak, zpravidla ve tvaru písmene, který zastupuje čísla z dané množiny čísel. Většinou se setkáváme
. Celistvé výrazy a jejich úprava.1. Číselné výrazy 8. ročník. Celistvé výrazy a jejich úprava Proměnná je znak, zpravidla ve tvaru písmene, který zastupuje čísla z dané množiny čísel. Většinou se setkáváme
RUČNÍ PROGRAMOVÁNÍ FRÉZOVÁNÍ UOV Petr Svoboda
 RUČNÍ PROGRAMOVÁNÍ FRÉZOVÁNÍ UOV Petr Svoboda Přípravné funkce G VY_32_INOVACE_OVS_2_16 OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/34.0116 Modernizace výuky na učilišti 6.3.2014 1 Název školy Název
RUČNÍ PROGRAMOVÁNÍ FRÉZOVÁNÍ UOV Petr Svoboda Přípravné funkce G VY_32_INOVACE_OVS_2_16 OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/34.0116 Modernizace výuky na učilišti 6.3.2014 1 Název školy Název
Úvod do teorie deskripcí (pokračování)
 Úvod do teorie deskripcí (pokračování) Označující fráze je esenciálně součástí věty a nemá význam sama o sobě. Scott byl člověk x byl člověk : Scott je subjektem výroku. Autor Wawerly byl člověk x byl
Úvod do teorie deskripcí (pokračování) Označující fráze je esenciálně součástí věty a nemá význam sama o sobě. Scott byl člověk x byl člověk : Scott je subjektem výroku. Autor Wawerly byl člověk x byl
1 Výroková logika 1. 2 Predikátová logika 3. 3 Důkazy matematických vět 4. 4 Doporučená literatura 7
 1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
Okruh č.3: Sémantický výklad predikátové logiky
 Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
MATEMATIKA. Diofantovské rovnice 2. stupně
 MATEMATIKA Diofantovské rovnice 2. stupně LADISLAVA FRANCOVÁ JITKA KÜHNOVÁ Přírodovědecká fakulta, Univerzita Hradec Králové V tomto článku se budeme zabývat některými případy diofantovských rovnic 2.
MATEMATIKA Diofantovské rovnice 2. stupně LADISLAVA FRANCOVÁ JITKA KÜHNOVÁ Přírodovědecká fakulta, Univerzita Hradec Králové V tomto článku se budeme zabývat některými případy diofantovských rovnic 2.
Úvod do logiky (PL): základní úvaha
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): základní úvaha doc. PhDr. Jiří Raclavský,
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): základní úvaha doc. PhDr. Jiří Raclavský,
Výroková logika. Sémantika výrokové logiky
 Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
13. Kvadratické rovnice 2 body
 13. Kvadratické rovnice 2 body 13.1. Rovnice x 2 + 2x + 2 m = 0 (s neznámou x) má dva různé reálné kořeny, které jsou oba menší než tři, právě a) m (1, 17), b) m = 2, c) m = 2 m = 5, d) m 2, 5, e) m >
13. Kvadratické rovnice 2 body 13.1. Rovnice x 2 + 2x + 2 m = 0 (s neznámou x) má dva různé reálné kořeny, které jsou oba menší než tři, právě a) m (1, 17), b) m = 2, c) m = 2 m = 5, d) m 2, 5, e) m >
)(x 2 + 3x + 4),
 3 IREDUCIBILNÍ ROZKLADY POLYNOMŮ V T [X] 3 Ireducibilní rozklady polynomů v T [x] - rozklady polynomů na ireducibilní (dále nerozložitelné) prvky v oboru integrity polynomů jedné neurčité x nad tělesem
3 IREDUCIBILNÍ ROZKLADY POLYNOMŮ V T [X] 3 Ireducibilní rozklady polynomů v T [x] - rozklady polynomů na ireducibilní (dále nerozložitelné) prvky v oboru integrity polynomů jedné neurčité x nad tělesem
Funkce více proměnných. April 29, 2016
 Funkce více proměnných April 29, 2016 Příklad (Derivace vyšších řádů) Daná je funkce f (x, y) = x 2 y + y 3 x 4, určte její parc. derivace podle x a podle y prvního i druhého řádu, i smíšené. f x = 2xy
Funkce více proměnných April 29, 2016 Příklad (Derivace vyšších řádů) Daná je funkce f (x, y) = x 2 y + y 3 x 4, určte její parc. derivace podle x a podle y prvního i druhého řádu, i smíšené. f x = 2xy
Logika II. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı BI-MLO, ZS 2011/12
 Logika II. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Logika II. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Základní pojmy matematické logiky
 KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
Místo pojmu výroková formule budeme používat zkráceně jen formule. Při jejich zápisu
 VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
Výroková a predikátová logika - X
 Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
Matematika vzorce. Ing. Petr Šídlo. verze
 Matematika vzorce Ing. Petr Šídlo verze 0050409 Obsah Jazyk matematiky 3. Výrokový počet.......................... 3.. Logické spojky...................... 3.. Tautologie výrokového počtu...............
Matematika vzorce Ing. Petr Šídlo verze 0050409 Obsah Jazyk matematiky 3. Výrokový počet.......................... 3.. Logické spojky...................... 3.. Tautologie výrokového počtu...............
IA008 Computational logic Version: 6. května Formule je v konjunktivní normální formě (CNF), pokud má tvar α 1... α n,
 1 Převody do normálních forem Příklad 1.1: Vyjádřete následující formule v DNF pomocí pravdivostní tabulky a pomocí převodu logických spojek. a) (A B) C b) (A B) C c) (A B) (C D) Formule je v disjunktivní
1 Převody do normálních forem Příklad 1.1: Vyjádřete následující formule v DNF pomocí pravdivostní tabulky a pomocí převodu logických spojek. a) (A B) C b) (A B) C c) (A B) (C D) Formule je v disjunktivní
Náhled testu. Přijímací zkouška magisterského studia. konečný automat bez zbytečných stavů, který přijímá jazyk popsaný tímto výrazem, má:
 1 z 6 14.11.2017 0:03 Přijímací zkouška magisterského studia Moodle Test MSP Testy VzorTest-2 Pokus 1 Jste přihlášeni jako Josef Kolář (Odhlásit se) Náhled testu 1 Je dán regulární výraz. Minimální deterministický
1 z 6 14.11.2017 0:03 Přijímací zkouška magisterského studia Moodle Test MSP Testy VzorTest-2 Pokus 1 Jste přihlášeni jako Josef Kolář (Odhlásit se) Náhled testu 1 Je dán regulární výraz. Minimální deterministický
Úvod do matematiky. Mgr. Radek Horenský, Ph.D. Důkazy
 Úvod do matematiky Mgr. Radek Horenský, Ph.D. Důkazy Matematika a matematické chápání jako takové je založeno na logické výstavbě. Základními stavebními prvky jsou definice, věty a důkazy. Definice zavádějí
Úvod do matematiky Mgr. Radek Horenský, Ph.D. Důkazy Matematika a matematické chápání jako takové je založeno na logické výstavbě. Základními stavebními prvky jsou definice, věty a důkazy. Definice zavádějí
Náhled testu. Přijímací zkouška magisterského studia. konečný automat bez zbytečných stavů, který přijímá jazyk popsaný tímto výrazem, má:
 Přijímací zkouška magisterského studia Moodle Test MSP Testy VzorTest-2 Pokus 1 Jste přihlášeni jako Josef Kolář (Odhlásit se) Info Výsledky Náhled Upravit Náhled testu 1 Je dán regulární výraz. Minimální
Přijímací zkouška magisterského studia Moodle Test MSP Testy VzorTest-2 Pokus 1 Jste přihlášeni jako Josef Kolář (Odhlásit se) Info Výsledky Náhled Upravit Náhled testu 1 Je dán regulární výraz. Minimální
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Každé formuli výrokového počtu přiřadíme hodnotu 0, půjde-li o formuli nepravdivou, a hodnotu 1, půjde-li. α neplatí. β je nutná podmínka pro α
 1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
Úvod do TI - logika 1. přednáška. Marie Duží
 Úvod do TI - logika 1. přednáška Marie Duží marie.duzi@vsb.cz Úvod do TI - logika Učební texty: http://www.cs.vsb.cz/duzi Courses Introduction to Logic: Informace pro studenty Učební texty: Kapitoly: Úvod
Úvod do TI - logika 1. přednáška Marie Duží marie.duzi@vsb.cz Úvod do TI - logika Učební texty: http://www.cs.vsb.cz/duzi Courses Introduction to Logic: Informace pro studenty Učební texty: Kapitoly: Úvod
Kapitola 11: Lineární diferenciální rovnice 1/15
 Kapitola 11: Lineární diferenciální rovnice 1/15 Lineární diferenciální rovnice 2. řádu Definice: Lineární diferenciální rovnice 2-tého řádu je rovnice tvaru kde: y C 2 (I) je hledaná funkce a 0 (x)y +
Kapitola 11: Lineární diferenciální rovnice 1/15 Lineární diferenciální rovnice 2. řádu Definice: Lineární diferenciální rovnice 2-tého řádu je rovnice tvaru kde: y C 2 (I) je hledaná funkce a 0 (x)y +
pouze u některých typů rovnic a v tomto textu se jím nebudeme až na
 Matematika II 7.1. Zavedení diferenciálních rovnic Definice 7.1.1. Rovnice tvaru F(y (n), y (n 1),, y, y, x) = 0 se nazývá diferenciální rovnice n-tého řádu pro funkci y = y(x). Speciálně je F(y, y, x)
Matematika II 7.1. Zavedení diferenciálních rovnic Definice 7.1.1. Rovnice tvaru F(y (n), y (n 1),, y, y, x) = 0 se nazývá diferenciální rovnice n-tého řádu pro funkci y = y(x). Speciálně je F(y, y, x)
Úvod do logiky: klasická predikátová logika. Jiří Raclavský. Masarykova univerzita
 Úvod do logiky: klasická predikátová logika Jiří Raclavský Masarykova univerzita Úvod do logiky: klasická predikátová logika Jiří Raclavský Masarykova univerzita Brno 2015 Práce na publikaci a její tisk
Úvod do logiky: klasická predikátová logika Jiří Raclavský Masarykova univerzita Úvod do logiky: klasická predikátová logika Jiří Raclavský Masarykova univerzita Brno 2015 Práce na publikaci a její tisk
VÝROKOVÁ LOGIKA. Výrok srozumitelná oznamovací věta (výraz, sdělení), která může být buď jen pravdivá nebo jen nepravdivá..
 VÝROKOVÁ LOGIKA Teorie: Logika je vědní obor zabývající se studiem různých forem vyjadřování a pravidel správného posuzování. (Matematická logika je součástí tohoto vědního oboru a ve velké míře užívá
VÝROKOVÁ LOGIKA Teorie: Logika je vědní obor zabývající se studiem různých forem vyjadřování a pravidel správného posuzování. (Matematická logika je součástí tohoto vědního oboru a ve velké míře užívá
OBYČEJNÉ DIFERENCIÁLNÍ ROVNICE DIFERENCIÁLNÍ ROVNICE 1.ŘÁDU
 OBYČEJNÉ DIFERENCIÁLNÍ ROVNICE Diferenciální rovnice patří mezi nejužívanější nástroje matematiky v aplikacích. Jsou to rovnice, kde neznámou je funkce a rovnice obsahuje i derivace této funkce. Lze očekávat,
OBYČEJNÉ DIFERENCIÁLNÍ ROVNICE Diferenciální rovnice patří mezi nejužívanější nástroje matematiky v aplikacích. Jsou to rovnice, kde neznámou je funkce a rovnice obsahuje i derivace této funkce. Lze očekávat,
LOGIKA VÝROKOVÁ LOGIKA
 LOGIKA Popisuje pravidla odvozování jedněch tvrzení z druhých. Je to myšlenková cesta ke správným závěrům. Vznikla jako součást filosofie. Zakladatelem byl Aristoteles. VÝROKOVÁ LOGIKA Obsahuje syntaktická,
LOGIKA Popisuje pravidla odvozování jedněch tvrzení z druhých. Je to myšlenková cesta ke správným závěrům. Vznikla jako součást filosofie. Zakladatelem byl Aristoteles. VÝROKOVÁ LOGIKA Obsahuje syntaktická,
rovnic), Definice y + p(x)y = q(x), Je-li q(x) = 0 na M, nazývá se y + p(x)y =
 Cíle Přehled základních typů diferenciálních rovnic prvního řádu zakončíme pojednáním o lineárních rovnicích, které patří v praktických úlohách k nejfrekventovanějším. Ukážeme například, že jejich řešení
Cíle Přehled základních typů diferenciálních rovnic prvního řádu zakončíme pojednáním o lineárních rovnicích, které patří v praktických úlohách k nejfrekventovanějším. Ukážeme například, že jejich řešení
8.2. Exaktní rovnice. F(x, y) x. dy. df = dx + y. Nyní budeme hledat odpověd na otázku, zda a jak lze od této diferenciální formule
 Cíle Ve výkladu o funkcích dvou proměnných jsme se seznámili také s jejich diferenciálem prvního řádu, který je pro funkci F(x, y) vyjádřen výrazem df dx + dy. Nyní budeme hledat odpověd na otázku, zda
Cíle Ve výkladu o funkcích dvou proměnných jsme se seznámili také s jejich diferenciálem prvního řádu, který je pro funkci F(x, y) vyjádřen výrazem df dx + dy. Nyní budeme hledat odpověd na otázku, zda
Unární je také spojka negace. pro je operace binární - příkladem může být funkce se signaturou. Binární je velká většina logických spojek
 Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Automaty a gramatiky(bi-aag) Formální překlady. 5. Překladové konečné automaty. h(ε) = ε, h(xa) = h(x)h(a), x, x T, a T.
 BI-AAG (2011/2012) J. Holub: 5. Překladové konečné automaty p. 2/41 Formální překlady BI-AAG (2011/2012) J. Holub: 5. Překladové konečné automaty p. 4/41 Automaty a gramatiky(bi-aag) 5. Překladové konečné
BI-AAG (2011/2012) J. Holub: 5. Překladové konečné automaty p. 2/41 Formální překlady BI-AAG (2011/2012) J. Holub: 5. Překladové konečné automaty p. 4/41 Automaty a gramatiky(bi-aag) 5. Překladové konečné
2.5 Rezoluční metoda v predikátové logice
 2.5. Rezoluční metoda v predikátové logice [101104-1520] 19 2.5 Rezoluční metoda v predikátové logice Rezoluční metoda v predikátové logice je obdobná stejnojmenné metodě ve výrokové logice. Ovšem vzhledem
2.5. Rezoluční metoda v predikátové logice [101104-1520] 19 2.5 Rezoluční metoda v predikátové logice Rezoluční metoda v predikátové logice je obdobná stejnojmenné metodě ve výrokové logice. Ovšem vzhledem
Funkce zadané implicitně
 Kapitola 8 Funkce zadané implicitně Začneme několika příklady. Prvním je známá rovnice pro jednotkovou kružnici x 2 + y 2 1 = 0. Tato rovnice popisuje křivku, kterou si však nelze představit jako graf
Kapitola 8 Funkce zadané implicitně Začneme několika příklady. Prvním je známá rovnice pro jednotkovou kružnici x 2 + y 2 1 = 0. Tato rovnice popisuje křivku, kterou si však nelze představit jako graf
Výroková a predikátová logika - VI
 Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
4. OBYČEJNÉ DIFERENCIÁLNÍ ROVNICE
 FBI VŠB-TUO 28. března 2014 4.1. Základní pojmy Definice 4.1. Rovnice tvaru F (x, y, y, y,..., y (n) ) = 0 se nazývá obyčejná diferenciální rovnice n-tého řádu a vyjadřuje vztah mezi neznámou funkcí y
FBI VŠB-TUO 28. března 2014 4.1. Základní pojmy Definice 4.1. Rovnice tvaru F (x, y, y, y,..., y (n) ) = 0 se nazývá obyčejná diferenciální rovnice n-tého řádu a vyjadřuje vztah mezi neznámou funkcí y
