(c) 2015 Pro potřeby žáků ZŠ Čerčany ŠIFROVACÍ KROUŢEK - 1. hodina
|
|
|
- Naděžda Kolářová
- před 9 lety
- Počet zobrazení:
Transkript
1 ŠIFROVACÍ KROUŢEK - 1. hodina Pokud Vás zajímá I.Quest šifrovací soutěž, kterou pořádáme, více informací i šifry najdete zde. Odkazy: Na konci roku si uděláme malou jednoduchou šifrovací soutěž také. Šifrování se řekně cizím slovem kryptografie. Pochází z řečtiny kryptós znamená skrytý a graphein znamená psát. Kryptografie je nauka o metodách utajování smyslu zpráv a to převedením do formy, která je čitelná jenom s určitou speciální znalostí. Informace můžeme schovat nebo utajit velkým množstvím různých způsobů, mezi které patří i třeba hádanky, rébusy a další. Kroužek se bude zabývat nejrůznějšími z nich. Cvičení během kroužku: Autobus, Puzzle, Test selektivní pozornosti Naše první šifra: Při šifrování obvykle nepouţíváme diakritiku, protoţe komplikuje šifrování i de-šifrování. TRANSPOZIČNÍ transpozice znamená přenos, nebo změna vzájemné polohy. Jedná se o šifru, ve které jsou správná písmenka na jiných než původních místech textu. Příklad textu, který budeme šifrovat: SIFROVACIKROUZEK nebo na dvou řádcích: SIFROVAC IKROUZEK Při šifrování se velmi často pro pořádek i pro zmatení dešifrujícího výsledný text zapisuje ve skupinách, nejčastěji po pěti písmenech. Náš text má celkem 16 znaků, což je ideální k zápisu ve skupinách po čtyřech.
2 1. Psaní textu odzadu: Na této šifře není co vysvětlovat, píšeme text odzadu dopředu. KEZUORKICAVORFIS Výsledek: KEZU ORKI CAVO RFIS 2. První poslední: V této šifře je vždy první písmeno na začátku textu, poslední druhé na konci. Třetí je druhé, čtvrté předposlední, atd. SFOAIRUEKZOKCVRI Výsledek: SFOA IRUE KZOK CVRI 3. Ob písmeno: K výrobě této šifry nám pomůže původní text napsaný ve dvou řádkách. Lichá písmena textu jsou první řádek, sudá pak druhý. SIIKFRROOUVZAECK Výsledek: SIIK FRRO OUVZ AECK 4. Hradby: V této šifře zapisujeme text do dvou řádek, ve tvaru hradeb, snadno rozlušíte: SROCIOUK IFVAKRZE Výsledek: SROC IOUK IFVA KRZE 5. Uhlopříčka: V této šifře zapisujeme text do čtverce v úhlopříčkách, čteme zleva: ARZK RCOE IOIU SFVK Výsledek: ARZK RCOE IOIU SFVK
3 6. Kaţdé x-té písmeno ve sloupci: V této šifře používáme každé x-té písmenko. Můžeme sifrování zjednodušit zápisem do sloupečků: Pokud nám při potřebě seřadit šifrovaný text do nějakého vzorce nevychází potřebný počet písmenek, doplníme na konec nějaké málo používané písměno, většinou X SIFR OVAC IKRO UZEK Výsledek (každé čtvrté): SOIU IVKZ FARE RCOK SIFROV ACIKRO UZEKXX Výsledek (každé třetí): SAU ICZ FIE RKK ORX VOX 7. Šnek: V této šifře se piše odstředu dokola (doprava nebo doleva). ACIK VSIR ORFO KEZU Seskupování písmen: Zašifrovaný text se většinou seskupuje po určitém počtu písmenek (často je to 5), aby se znesnadnilo dešifrování. My jsme si dosud seskupili písmenka po takových skupinách, aby se nám naopak snadno šifrovalo i dešifrovalo. Seskupování může být i zajímavá varianta, rozlušíte tento text? ANY NIV IDI TEJ EDE NZE ZPU SOB UJA KZA SIF ROV ATN EJA KYT EXT
4 Cvičení č. 1 Kterým směrem jede autobus? Nebo na které straně má předek? Cvičení č. 2 Cvičení č. 3: Selektivní pozornost
5 Úkoly na příště: 1. Zkuste vymyslet nějakou vlastní transpoziční šifru. Zašifrujte do ní text: JSEMTENNEJLEPSISIFRANTVCERCANECH Na příští hodině ukážete šifru ostatním. 2. Pohledejte pomocí internetového vyhledávače transpoziční šifry. Zkuste najít nějaký další druh transpoziční šifry, zkuste pochopit jak funguje, zašifrujte do ní stejný text jako ve cvičení 1. Když nebudete vědět, napište mi mail, rád poradím. 3. Zkuste najít nebo vymyslet nějakou zajímavou hádanku, rébus, chyták, cokoli připravte si na příští hodinu. 4. Zkuste si dešifrovat následující jednoduchou šifru: AZB UDU VEL KYS TAN USE SIF RAN TEM 5. Pokud se to povedlo, pak následující zvládnete také OST RAD MIT DOU EBU ZEM ICE ROD
A B C D E 2 F G H I J 3 K L M N O 4 P Q R S T 5 U/V W X Y Z
 ŠIFROVACÍ KROUŽEK - 4. hodina 1. Polybiův čtverec Polybios (cca 230 př.n.l. cca 120 př.n.l.) byl starověký řecký politik, historik, matematik a spisovatel. Polibiův čtverec je matice 5x5, do které vepíšeme
ŠIFROVACÍ KROUŽEK - 4. hodina 1. Polybiův čtverec Polybios (cca 230 př.n.l. cca 120 př.n.l.) byl starověký řecký politik, historik, matematik a spisovatel. Polibiův čtverec je matice 5x5, do které vepíšeme
Šifrovací kroužek, 2015 Pro potřeby žáků ZŠ Čerčany ŠIFROVACÍ KROUŽEK - 3. hodina
 ŠIFROVACÍ KROUŽEK - 3. hodina Substituční šifry: V šifrovaném textu jsou nahrazeny jednotlivé znaky jinými znaky, nebo symboly. Nejjednodušší (co se týče dešifrování) substituční šifry jsou monoalfabetické,
ŠIFROVACÍ KROUŽEK - 3. hodina Substituční šifry: V šifrovaném textu jsou nahrazeny jednotlivé znaky jinými znaky, nebo symboly. Nejjednodušší (co se týče dešifrování) substituční šifry jsou monoalfabetické,
Kryptografie, elektronický podpis. Ing. Miloslav Hub, Ph.D. 27. listopadu 2007
 Kryptografie, elektronický podpis Ing. Miloslav Hub, Ph.D. 27. listopadu 2007 Kryptologie Kryptologie věda o šifrování, dělí se: Kryptografie nauka o metodách utajování smyslu zpráv převodem do podoby,
Kryptografie, elektronický podpis Ing. Miloslav Hub, Ph.D. 27. listopadu 2007 Kryptologie Kryptologie věda o šifrování, dělí se: Kryptografie nauka o metodách utajování smyslu zpráv převodem do podoby,
Matematické základy šifrování a kódování
 Matematické základy šifrování a kódování Permutace Pojem permutace patří mezi základní pojmy a nachází uplatnění v mnoha oblastech, např. kombinatorice, algebře apod. Definice Nechť je n-prvková množina.
Matematické základy šifrování a kódování Permutace Pojem permutace patří mezi základní pojmy a nachází uplatnění v mnoha oblastech, např. kombinatorice, algebře apod. Definice Nechť je n-prvková množina.
ŠIFROVÁNÍ, EL. PODPIS. Kryptografie Elektronický podpis Datové schránky
 ŠIFROVÁNÍ, EL. PODPIS Kryptografie Elektronický podpis Datové schránky Kryptografie Kryptografie neboli šifrování je nauka o metodách utajování smyslu zpráv převodem do podoby, která je čitelná jen se
ŠIFROVÁNÍ, EL. PODPIS Kryptografie Elektronický podpis Datové schránky Kryptografie Kryptografie neboli šifrování je nauka o metodách utajování smyslu zpráv převodem do podoby, která je čitelná jen se
ŠIFRY. 1) Morseova abeceda
 ŠIFRY V následujícím textu je shrnuto několik základních typů šifer, které by měla vlčata znát před tím, než se stanou skauty. U skautů se pak naučí mnohým dalším šifrám. 1) Morseova abeceda Nejdůležitější
ŠIFRY V následujícím textu je shrnuto několik základních typů šifer, které by měla vlčata znát před tím, než se stanou skauty. U skautů se pak naučí mnohým dalším šifrám. 1) Morseova abeceda Nejdůležitější
Celostátní kolo soutěže Baltík 2008, kategorie C
 Pokyny: 1. Pracujte pouze v ikonkových reţimech! 2. Řešení úloh ukládejte do sloţky, která se nachází na pracovní ploše počítače. Její název je stejný, jako je kód, který dostal váš tým přidělený (např.
Pokyny: 1. Pracujte pouze v ikonkových reţimech! 2. Řešení úloh ukládejte do sloţky, která se nachází na pracovní ploše počítače. Její název je stejný, jako je kód, který dostal váš tým přidělený (např.
Permutační grupy Cykly a transpozice Aplikace. Permutace. Rostislav Horčík: Y01DMA 11. května 2010: Permutace 1/17
 Permutace Rostislav Horčík: Y01DMA 11. května 2010: Permutace 1/17 Motivace Permutace jsou důležitou částí matematiky viz použití v pravděpodobnosti, algebře (např. determinanty) a mnoho dalších. Jsou
Permutace Rostislav Horčík: Y01DMA 11. května 2010: Permutace 1/17 Motivace Permutace jsou důležitou částí matematiky viz použití v pravděpodobnosti, algebře (např. determinanty) a mnoho dalších. Jsou
MANUÁL K LUŠTĚNÍ ŠIFER
 FHJŮMPŮDFJKEPDFMDMVCŮPJMFNONSLNCSLOCNSPCNPSDESLNVCSLPJMCVSDOP VNHOPWNFOWPFNCŮSPŮ MXP MXPS MXPCSKBCSOKBCSNCSCKCSDKJVNODVNOVM MANUÁL K FHJŮMPŮDFJKEPDFMDMVCŮPJMFNONDESVMDSVPDSMVSPCSPCMKSPYCMSPCYSP LUŠTĚNÍ
FHJŮMPŮDFJKEPDFMDMVCŮPJMFNONSLNCSLOCNSPCNPSDESLNVCSLPJMCVSDOP VNHOPWNFOWPFNCŮSPŮ MXP MXPS MXPCSKBCSOKBCSNCSCKCSDKJVNODVNOVM MANUÁL K FHJŮMPŮDFJKEPDFMDMVCŮPJMFNONDESVMDSVPDSMVSPCSPCMKSPYCMSPCYSP LUŠTĚNÍ
Šifry. Rozdělení šifer:
 Šifry Od té doby, kdy si lidé začali posílat důležité zprávy, snažili se jiní lidé tyto zprávy zachytit. Jednou z možností, jak ochránit své vzkazy před zvědavci bylo zajistit jim silný (pokud možno ozbrojený
Šifry Od té doby, kdy si lidé začali posílat důležité zprávy, snažili se jiní lidé tyto zprávy zachytit. Jednou z možností, jak ochránit své vzkazy před zvědavci bylo zajistit jim silný (pokud možno ozbrojený
Střední odborné učiliště a Střední odborná škola Hustopeče, Masarykovo nám. 1 Ing. Miriam Sedláčková Číslo
 Číslo projektu CZ.1.07/1.5.00/34.0394 Škola Střední odborné učiliště a Střední odborná škola Hustopeče, Masarykovo nám. 1 Autor Ing. Miriam Sedláčková Číslo VY_32_INOVACE_ICT.3.15 Název Hodnota a ochrana
Číslo projektu CZ.1.07/1.5.00/34.0394 Škola Střední odborné učiliště a Střední odborná škola Hustopeče, Masarykovo nám. 1 Autor Ing. Miriam Sedláčková Číslo VY_32_INOVACE_ICT.3.15 Název Hodnota a ochrana
Šifrová ochrana informací historie KS4
 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 1 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací historie KS4 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 2 Osnova
VŠFS; Aplikovaná informatika; SW systémy 2005/2006 1 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací historie KS4 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 2 Osnova
Základy šifrování a kódování
 Materiál byl vytvořen v rámci projektu Nové výzvy, nové příležitosti, nová škola Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky Základy šifrování a kódování
Materiál byl vytvořen v rámci projektu Nové výzvy, nové příležitosti, nová škola Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky Základy šifrování a kódování
klasická kryptologie základní pojmy požadavky na kryptosystém typologie šifer transpoziční šifry substituční šifry
 klasická kryptologie transpoziční šifry substituční šifry základní pojmy požadavky na kryptosystém pravidla bezpečnosti silný kryptosystém typologie šifer bloková x proudová s tajným klíčem x s veřejným
klasická kryptologie transpoziční šifry substituční šifry základní pojmy požadavky na kryptosystém pravidla bezpečnosti silný kryptosystém typologie šifer bloková x proudová s tajným klíčem x s veřejným
Základy kryptografie. Beret CryptoParty 11.02.2013. 11.02.2013 Základy kryptografie 1/17
 Základy kryptografie Beret CryptoParty 11.02.2013 11.02.2013 Základy kryptografie 1/17 Obsah prezentace 1. Co je to kryptografie 2. Symetrická kryptografie 3. Asymetrická kryptografie Asymetrické šifrování
Základy kryptografie Beret CryptoParty 11.02.2013 11.02.2013 Základy kryptografie 1/17 Obsah prezentace 1. Co je to kryptografie 2. Symetrická kryptografie 3. Asymetrická kryptografie Asymetrické šifrování
KRYPTOGRAFIE VER EJNE HO KLI Č E
 KRYPTOGRAFIE VER EJNE HO KLI Č E ÚVOD Patricie Vyzinová Jako téma jsem si vybrala asymetrickou kryptografii (kryptografie s veřejným klíčem), což je skupina kryptografických metod, ve kterých se pro šifrování
KRYPTOGRAFIE VER EJNE HO KLI Č E ÚVOD Patricie Vyzinová Jako téma jsem si vybrala asymetrickou kryptografii (kryptografie s veřejným klíčem), což je skupina kryptografických metod, ve kterých se pro šifrování
Různé psaní zpráv. Hadovka. Sloupce. Šnek
 Psaní podle slovního klíče ejme tomu, že chceme zašifrovat "sraz všech v neděli ráno" za použití klíče "PH". Napíšeme zprávu takto : P H klíč 4 5 1 3 2 pořadí písmen v klíči podle abecedy S V zpráva S
Psaní podle slovního klíče ejme tomu, že chceme zašifrovat "sraz všech v neděli ráno" za použití klíče "PH". Napíšeme zprávu takto : P H klíč 4 5 1 3 2 pořadí písmen v klíči podle abecedy S V zpráva S
klasická kryptologie základní pojmy požadavky na kryptosystém typologie šifer transpoziční šifry substituční šifry
 Květuše Sýkorová Květuše Sýkorová klasická kryptologie transpoziční šifry substituční šifry základní pojmy požadavky na kryptosystém pravidla bezpečnosti silný kryptosystém typologie šifer bloková x proudová
Květuše Sýkorová Květuše Sýkorová klasická kryptologie transpoziční šifry substituční šifry základní pojmy požadavky na kryptosystém pravidla bezpečnosti silný kryptosystém typologie šifer bloková x proudová
Magické čtverce. Tomáš Roskovec. Úvod
 Magické čtverce Tomáš Roskovec Úvod Magické čtverce patří k dávným matematickým hrátkám, které i přes dvoutisíciletou historii dodnes nejsou zcela prozkoumány. Během přednášky se budeme zabývat nejprve
Magické čtverce Tomáš Roskovec Úvod Magické čtverce patří k dávným matematickým hrátkám, které i přes dvoutisíciletou historii dodnes nejsou zcela prozkoumány. Během přednášky se budeme zabývat nejprve
Šifrová ochrana informací historie PS4
 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací historie PS4 1 Osnova úvod, definice pojmů; substituční šifry; transpoziční šifry; první prakticky používané šifrové systémy;
Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací historie PS4 1 Osnova úvod, definice pojmů; substituční šifry; transpoziční šifry; první prakticky používané šifrové systémy;
 Šifrování Kafková Petra Kryptografie Věda o tvorbě šifer (z řečtiny: kryptós = skrytý, gráphein = psát) Kryptoanalýza Věda o prolamování/luštění šifer Kryptologie Věda o šifrování obecné označení pro kryptografii
Šifrování Kafková Petra Kryptografie Věda o tvorbě šifer (z řečtiny: kryptós = skrytý, gráphein = psát) Kryptoanalýza Věda o prolamování/luštění šifer Kryptologie Věda o šifrování obecné označení pro kryptografii
Šifrová ochrana informací historie PS4
 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 1 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací historie PS4 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 2 Osnova
VŠFS; Aplikovaná informatika; SW systémy 2005/2006 1 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací historie PS4 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 2 Osnova
Micro:bit lekce 3. - Konstrukci If Then a If Then Else najdete v kategorii Logic - Podmínky od If (např. porovnání < >= atd.) najdete taktéž v Logic
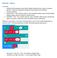 Micro:bit lekce 3. Podmínky - Rozvětvení běhu programu podle splnění nějakých podmínek typu pravda / nepravda - splněno / nesplněno (výsledkem podmínky musí být vždy jen dvě možnosti) - Dva typy podmínek:
Micro:bit lekce 3. Podmínky - Rozvětvení běhu programu podle splnění nějakých podmínek typu pravda / nepravda - splněno / nesplněno (výsledkem podmínky musí být vždy jen dvě možnosti) - Dva typy podmínek:
Výroková logika II. Negace. Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0).
 Výroková logika II Negace Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0). Na konkrétních příkladech si ukážeme, jak se dají výroky negovat. Obecně se výrok dá negovat tak, že před
Výroková logika II Negace Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0). Na konkrétních příkladech si ukážeme, jak se dají výroky negovat. Obecně se výrok dá negovat tak, že před
Aplikovaná informatika
 1 Aplikovaná informatika Cvičení - Opakování tématu 3 Řešení bezpečnostních incidentů PLUSKAL, D. SMETANA, B. Operační program Vzdělávání pro konkurenceschopnost Projekt: Vzdělávání pro bezpečnostní systém
1 Aplikovaná informatika Cvičení - Opakování tématu 3 Řešení bezpečnostních incidentů PLUSKAL, D. SMETANA, B. Operační program Vzdělávání pro konkurenceschopnost Projekt: Vzdělávání pro bezpečnostní systém
vysvětlení pravidel + rozdělení žáků do skupinek (cca 5 minut)
 Didaktika matematiky s praxí II. PhDr. Eva Bomerová Cíl hodiny: Procvičení násobení a dělení z paměti hravou formou - Lovení matematických bobříků Před začátkem vyučovací hodiny si upravíme třídu tak,
Didaktika matematiky s praxí II. PhDr. Eva Bomerová Cíl hodiny: Procvičení násobení a dělení z paměti hravou formou - Lovení matematických bobříků Před začátkem vyučovací hodiny si upravíme třídu tak,
Středoškolská technika 2015. Encryption Protection System
 Středoškolská technika 2015 Setkání a prezentace prací středoškolských studentů na ČVUT Encryption Protection System Jaroslav Vondrák Vyšší odborná a Střední škola Varnsdorf Mariánská 1100, Varnsdorf 1
Středoškolská technika 2015 Setkání a prezentace prací středoškolských studentů na ČVUT Encryption Protection System Jaroslav Vondrák Vyšší odborná a Střední škola Varnsdorf Mariánská 1100, Varnsdorf 1
1.1.8 Sčítání přirozených čísel
 .. Sčítání přirozených čísel Předpoklady: 000 Pedagogická poznámka: Pokud při formulaci pravidel necháváte žáky zapisovat samostatně, nedostanete se dále než k příkladu. Což využívám schválně, další hodinu
.. Sčítání přirozených čísel Předpoklady: 000 Pedagogická poznámka: Pokud při formulaci pravidel necháváte žáky zapisovat samostatně, nedostanete se dále než k příkladu. Což využívám schválně, další hodinu
6. Cvičení [MI-KRY Pokročilá kryptologie]
![6. Cvičení [MI-KRY Pokročilá kryptologie] 6. Cvičení [MI-KRY Pokročilá kryptologie]](/thumbs/89/98710672.jpg) 6. Cvičení Náplň cv. 6 Náplní šestého cvičení jsou módy blokových šifer. Výběr módu by neměl nikdy oslabit bezpečnost samotné šifry, ale vhodně podpořit vlastnosti, které od bezpečnostního řešení očekáváme.
6. Cvičení Náplň cv. 6 Náplní šestého cvičení jsou módy blokových šifer. Výběr módu by neměl nikdy oslabit bezpečnost samotné šifry, ale vhodně podpořit vlastnosti, které od bezpečnostního řešení očekáváme.
P4 Ukecaný program InterLoS 2014
 P4 Ukecaný program Stáhněte si zdrojový kód P4-ukecany.c, zkopilujte jej pomocí kompilátoru jazyka C a spusťte. Program je psaný podle standartu C89, takže by měl jít zkompilovat libovolným C kompilátorem,
P4 Ukecaný program Stáhněte si zdrojový kód P4-ukecany.c, zkopilujte jej pomocí kompilátoru jazyka C a spusťte. Program je psaný podle standartu C89, takže by měl jít zkompilovat libovolným C kompilátorem,
Šifry s morseovkou. Opačná morseovka. Čísla. Písmena. Grafická morseovka
 Šifry s morseovkou Opačná morseovka v opačné morseovce píšeme místo teček čárky a naopak -. / - - - - /... / -... // = AHOJ Čísla místo teček píšeme čísla od 0 do 4 a místo čárek čísla 5 až 9. 16;0403;676;2579
Šifry s morseovkou Opačná morseovka v opačné morseovce píšeme místo teček čárky a naopak -. / - - - - /... / -... // = AHOJ Čísla místo teček píšeme čísla od 0 do 4 a místo čárek čísla 5 až 9. 16;0403;676;2579
INFORMAČNÍ TECHNOLOGIE A SPOLEČNOST
 INFORMAČNÍ TECHNOLOGIE A SPOLEČNOST Témata Termíny Utajená komunikace Elektronický podpis Datové schránky Sociální sítě Všimnete si! Kontrolní otázky TERMÍNY E-komerce (Electronic Commerce (elektronický
INFORMAČNÍ TECHNOLOGIE A SPOLEČNOST Témata Termíny Utajená komunikace Elektronický podpis Datové schránky Sociální sítě Všimnete si! Kontrolní otázky TERMÍNY E-komerce (Electronic Commerce (elektronický
Složitost a moderní kryptografie
 Složitost a moderní kryptografie Radek Pelánek Modulární systém dalšího vzdělávání pedagogických pracovníků JmK v přírodních vědách a informatice CZ.1.07/1.3.10/02.0024 Složitost a moderní kryptografie
Složitost a moderní kryptografie Radek Pelánek Modulární systém dalšího vzdělávání pedagogických pracovníků JmK v přírodních vědách a informatice CZ.1.07/1.3.10/02.0024 Složitost a moderní kryptografie
Identifikátor materiálu: ICT-2-04
 Identifikátor materiálu: ICT-2-04 Předmět Téma sady Informační a komunikační technologie Téma materiálu Zabezpečení informací Autor Ing. Bohuslav Nepovím Anotace Student si procvičí / osvojí kryptografii.
Identifikátor materiálu: ICT-2-04 Předmět Téma sady Informační a komunikační technologie Téma materiálu Zabezpečení informací Autor Ing. Bohuslav Nepovím Anotace Student si procvičí / osvojí kryptografii.
Substituční šifry a frekvenční analýza. Mgr. Radim Janča ijanca@fit.vutbr.cz
 Substituční šifry a frekvenční analýza Mgr. Radim Janča ijanca@fit.vutbr.cz Harmonogram Celkově 4 cvičení v P256 Prezentace z cvičení budou zveřejňovány na http://buslab.fit.vutbr.cz/kib/ 3 samostatné
Substituční šifry a frekvenční analýza Mgr. Radim Janča ijanca@fit.vutbr.cz Harmonogram Celkově 4 cvičení v P256 Prezentace z cvičení budou zveřejňovány na http://buslab.fit.vutbr.cz/kib/ 3 samostatné
8. MČR v řešení sudoku, Brno, Přehled úloh
 . MČR v řešení sudoku, Brno,.-..0 Přehled úloh Na mistrovství se budou řešit zde uvedené typy úloh. V úlohách ve tvaru čtverce n n rozděleného na n oblastí platí standardní pravidla sudoku, tj. je potřeba
. MČR v řešení sudoku, Brno,.-..0 Přehled úloh Na mistrovství se budou řešit zde uvedené typy úloh. V úlohách ve tvaru čtverce n n rozděleného na n oblastí platí standardní pravidla sudoku, tj. je potřeba
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Informační
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Informační
INDIÁNI NEJPRVE SI VEZMĚTE PRACOVNÍ SEŠIT K ŽIVÉ ABECEDĚ. NA INDIÁNSKÉ STRÁNCE 13 VYPRACUJTE KAŽDÝ SÁM CVIČENÍ 4.
 CENTRUM ČTENÍ, TI SE MAJÍ, CELÝ DEN SI JENOM HRAJÍ. POJĎME SI HRÁT NEJEN S PÍSMENKEM I NEJPRVE SI VEZMĚTE PRACOVNÍ SEŠIT K ŽIVÉ ABECEDĚ. NA INDIÁNSKÉ STRÁNCE 13 VYPRACUJTE KAŽDÝ SÁM CVIČENÍ 4. UDĚLEJTE
CENTRUM ČTENÍ, TI SE MAJÍ, CELÝ DEN SI JENOM HRAJÍ. POJĎME SI HRÁT NEJEN S PÍSMENKEM I NEJPRVE SI VEZMĚTE PRACOVNÍ SEŠIT K ŽIVÉ ABECEDĚ. NA INDIÁNSKÉ STRÁNCE 13 VYPRACUJTE KAŽDÝ SÁM CVIČENÍ 4. UDĚLEJTE
Asymetrické šifry. Pavla Henzlová 28.3.2011. FJFI ČVUT v Praze. Pavla Henzlová (FJFI ČVUT v Praze) Asymetrické šifry 28.3.
 Asymetrické šifry Pavla Henzlová FJFI ČVUT v Praze 28.3.2011 Pavla Henzlová (FJFI ČVUT v Praze) Asymetrické šifry 28.3.2011 1 / 16 Obsah 1 Asymetrická kryptografie 2 Diskrétní logaritmus 3 Baby step -
Asymetrické šifry Pavla Henzlová FJFI ČVUT v Praze 28.3.2011 Pavla Henzlová (FJFI ČVUT v Praze) Asymetrické šifry 28.3.2011 1 / 16 Obsah 1 Asymetrická kryptografie 2 Diskrétní logaritmus 3 Baby step -
Algebra - druhý díl. Lenka Zalabová. zima Ústav matematiky a biomatematiky, Přírodovědecká fakulta, Jihočeská univerzita
 Algebra - druhý díl Lenka Zalabová Ústav matematiky a biomatematiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích zima 2012 Obsah 1 Permutace 2 Grupa permutací 3 Více o permutacích
Algebra - druhý díl Lenka Zalabová Ústav matematiky a biomatematiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích zima 2012 Obsah 1 Permutace 2 Grupa permutací 3 Více o permutacích
1. sada. 9. ročník. 101. Šifrovací tutoriál
 9. ročník 1. sada 101. Šifrovací tutoriál Protože se luštitelské zkušenosti týmů velmi liší, rozhodli jsme se na začátek letošního ročníku zařadit úlohu, při které si všichni zopakují základní šifrovací
9. ročník 1. sada 101. Šifrovací tutoriál Protože se luštitelské zkušenosti týmů velmi liší, rozhodli jsme se na začátek letošního ročníku zařadit úlohu, při které si všichni zopakují základní šifrovací
Výukový materiál zpracovaný v rámci projektu EU peníze do škol. Zašifrované verše
 Výukový materiál zpracovaný v rámci projektu EU peníze do škol ZŠ Litoměřice, Ladova Ladova 5 412 01 Litoměřice www.zsladovaltm.cz vedeni@zsladovaltm.cz Pořadové číslo projektu: CZ.1.07/1.4.00/21.0948
Výukový materiál zpracovaný v rámci projektu EU peníze do škol ZŠ Litoměřice, Ladova Ladova 5 412 01 Litoměřice www.zsladovaltm.cz vedeni@zsladovaltm.cz Pořadové číslo projektu: CZ.1.07/1.4.00/21.0948
koordinátor (řídí práci ve skupině, prezentuje práci skupiny) člen týmu (spolupracuje s koordinátorem a pomáhá jeho činnosti)
 Užitečné weby Co se naučíte Získáte přehled o užitečných webových stránkách různého druhu a o tom, jak je můžete v životě využít. Vytvoříte si myšlenkovou mapu o různých druzích užitečných webů na internetu.
Užitečné weby Co se naučíte Získáte přehled o užitečných webových stránkách různého druhu a o tom, jak je můžete v životě využít. Vytvoříte si myšlenkovou mapu o různých druzích užitečných webů na internetu.
Jak funguje asymetrické šifrování?
 Jak funguje asymetrické šifrování? Petr Vodstrčil petr.vodstrcil@vsb.cz Katedra aplikované matematiky, Fakulta elektrotechniky a informatiky, Vysoká škola báňská Technická univerzita Ostrava Petr Vodstrčil
Jak funguje asymetrické šifrování? Petr Vodstrčil petr.vodstrcil@vsb.cz Katedra aplikované matematiky, Fakulta elektrotechniky a informatiky, Vysoká škola báňská Technická univerzita Ostrava Petr Vodstrčil
Číslo projektu CZ.1.07/1.5.00/34.0394 Škola SOŠ a SOU Hustopeče, Masarykovo nám. 1 Ing. Miriam Sedláčková Číslo
 Číslo projektu CZ.1.07/1.5.00/34.0394 Škola SOŠ a SOU Hustopeče, Masarykovo nám. 1 Autor Ing. Miriam Sedláčková Číslo VY_32_INOVACE_ICT.3.05 Název Teorie internetu- e-mail Téma hodiny Teorie internetu
Číslo projektu CZ.1.07/1.5.00/34.0394 Škola SOŠ a SOU Hustopeče, Masarykovo nám. 1 Autor Ing. Miriam Sedláčková Číslo VY_32_INOVACE_ICT.3.05 Název Teorie internetu- e-mail Téma hodiny Teorie internetu
KAPITOLA 5 - POKROČILÉ ZPRACOVÁNÍ TEXTU
 KAPITOLA 5 - POKROČILÉ ZPRACOVÁNÍ TEXTU KLÍČOVÉ POJMY Oddíly, styly, poznámka pod čarou, revize, obsah, rejstřík, záložka, citace a seznamy literatury, vzorce, vložené a propojené objekty, oddíly, zabezpečení.
KAPITOLA 5 - POKROČILÉ ZPRACOVÁNÍ TEXTU KLÍČOVÉ POJMY Oddíly, styly, poznámka pod čarou, revize, obsah, rejstřík, záložka, citace a seznamy literatury, vzorce, vložené a propojené objekty, oddíly, zabezpečení.
Klasická kryptologie: Historické šifry
 Klasická kryptologie: Historické šifry L ubomíra Balková Úvod do kryptologie 18. únor 2010 L. Balková (ČVUT FJFI) Kryptologie 18. únor 2010 1 / 32 Obsah 1 Základní pojmy 2 Formální definice kryptosystému
Klasická kryptologie: Historické šifry L ubomíra Balková Úvod do kryptologie 18. únor 2010 L. Balková (ČVUT FJFI) Kryptologie 18. únor 2010 1 / 32 Obsah 1 Základní pojmy 2 Formální definice kryptosystému
PSK2-16. Šifrování a elektronický podpis I
 PSK2-16 Název školy: Autor: Anotace: Vzdělávací oblast: Předmět: Vyšší odborná škola a Střední průmyslová škola, Božetěchova 3 Ing. Marek Nožka Jak funguje asymetrická šifra a elektronický podpis Informační
PSK2-16 Název školy: Autor: Anotace: Vzdělávací oblast: Předmět: Vyšší odborná škola a Střední průmyslová škola, Božetěchova 3 Ing. Marek Nožka Jak funguje asymetrická šifra a elektronický podpis Informační
DSY-6. Přenosový kanál kódy pro zabezpečení dat Základy šifrování, autentizace Digitální podpis Základy měření kvality přenosu signálu
 DSY-6 Přenosový kanál kódy pro zabezpečení dat Základy šifrování, autentizace Digitální podpis Základy měření kvality přenosu signálu Kódové zabezpečení přenosu dat Popis přiřazení kódových slov jednotlivým
DSY-6 Přenosový kanál kódy pro zabezpečení dat Základy šifrování, autentizace Digitální podpis Základy měření kvality přenosu signálu Kódové zabezpečení přenosu dat Popis přiřazení kódových slov jednotlivým
6. Formátování: Formátování odstavce
 6. Formátování: Formátování odstavce Obrázek 1: Formát / Odstavec Odstavec je text mezi dvěma znaky konce odstavce. Konec odstavce je skrytý znak a vkládáme jej během psaní při každém stisknutí klávesy
6. Formátování: Formátování odstavce Obrázek 1: Formát / Odstavec Odstavec je text mezi dvěma znaky konce odstavce. Konec odstavce je skrytý znak a vkládáme jej během psaní při každém stisknutí klávesy
Kódy a kódování dat. Binární (dvojkové) kódy. Kód Aikenův
 Kódy a kódování dat Kódování je proces, při kterém se každému znaku nebo postupnosti znaků daného souboru znaků jednoznačně přiřadí znak nebo postupnost znaků z jiného souboru znaků. Kódování je tedy transformace
Kódy a kódování dat Kódování je proces, při kterém se každému znaku nebo postupnosti znaků daného souboru znaků jednoznačně přiřadí znak nebo postupnost znaků z jiného souboru znaků. Kódování je tedy transformace
MANUÁL. k šifrovací hře - 1 -
 MANUÁL k šifrovací hře - 1 - ÚVOD Tuto brožurku berte jako malý exkurz po šifrách. Jejich výčet zde není vyčerpávající a ani být nemůže šifry vznikají stále nové, stále nápaditější a složitější. Zde uvádíme
MANUÁL k šifrovací hře - 1 - ÚVOD Tuto brožurku berte jako malý exkurz po šifrách. Jejich výčet zde není vyčerpávající a ani být nemůže šifry vznikají stále nové, stále nápaditější a složitější. Zde uvádíme
Regionální kolo soutěže Mladý programátor 2016, kategorie A, B
 Pokyny: 1. Kategorie A řeší jen úlohy 1, 2, 3 a kategorie B jen úlohy 2, 3, 4! 2. Řešení úloh ukládejte do složky, která se nachází na pracovní ploše počítače. Její název je stejný, jako je kód, který
Pokyny: 1. Kategorie A řeší jen úlohy 1, 2, 3 a kategorie B jen úlohy 2, 3, 4! 2. Řešení úloh ukládejte do složky, která se nachází na pracovní ploše počítače. Její název je stejný, jako je kód, který
Praktické šifrování dat pomocí programu PGP
 Instalace prostředí Praktické šifrování dat pomocí programu PGP Jako první je nutné stáhnout program GPG a extrahovat jeho obsah do vybraného adresáře. Program získáme např. na adrese http://www.gnupg.org/.
Instalace prostředí Praktické šifrování dat pomocí programu PGP Jako první je nutné stáhnout program GPG a extrahovat jeho obsah do vybraného adresáře. Program získáme např. na adrese http://www.gnupg.org/.
8. RSA, kryptografie s veřejným klíčem. doc. Ing. Róbert Lórencz, CSc.
 Bezpečnost 8. RSA, kryptografie s veřejným klíčem doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních programů
Bezpečnost 8. RSA, kryptografie s veřejným klíčem doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních programů
P = 1;3;3; 4; Množiny. Předpoklady:
 3218 Množiny Předpoklady: 030201 Př 1: Kolik lidí může v souladu s předpisy cestovat v běžném osobním autě (například Škoda Octavia)? Hledej různé způsoby, jak odpověď vyjádřit 1 způsob: Autem může cestovat
3218 Množiny Předpoklady: 030201 Př 1: Kolik lidí může v souladu s předpisy cestovat v běžném osobním autě (například Škoda Octavia)? Hledej různé způsoby, jak odpověď vyjádřit 1 způsob: Autem může cestovat
Definice. Fingerprint = soubor znaků sloužících k identifikaci vydání starého tisku nebo jeho variantního vydání.
 FINGERPRINT Definice Fingerprint = soubor znaků sloužících k identifikaci vydání starého tisku nebo jeho variantního vydání. Skládá se z 16 znaků rozdělených do 4 skupin a doplňkových znaků. Výběr znaků
FINGERPRINT Definice Fingerprint = soubor znaků sloužících k identifikaci vydání starého tisku nebo jeho variantního vydání. Skládá se z 16 znaků rozdělených do 4 skupin a doplňkových znaků. Výběr znaků
Nerovnice a nerovnice v součinovém nebo v podílovém tvaru
 Variace 1 Nerovnice a nerovnice v součinovém nebo v podílovém tvaru Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz
Variace 1 Nerovnice a nerovnice v součinovém nebo v podílovém tvaru Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz
CO JE KRYPTOGRAFIE Šifrovací algoritmy Kódovací algoritmus Prolomení algoritmu
 KRYPTOGRAFIE CO JE KRYPTOGRAFIE Kryptografie je matematický vědní obor, který se zabývá šifrovacími a kódovacími algoritmy. Dělí se na dvě skupiny návrh kryptografických algoritmů a kryptoanalýzu, která
KRYPTOGRAFIE CO JE KRYPTOGRAFIE Kryptografie je matematický vědní obor, který se zabývá šifrovacími a kódovacími algoritmy. Dělí se na dvě skupiny návrh kryptografických algoritmů a kryptoanalýzu, která
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Informační
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Informační
Úvod do teorie informace
 PEF MZLU v Brně 24. září 2007 Úvod Výměna informací s okolím nám umožňuje udržovat vlastní existenci. Proces zpracování informací je trvalý, nepřetržitý, ale ovlivnitelný. Zabezpečení informací je spojeno
PEF MZLU v Brně 24. září 2007 Úvod Výměna informací s okolím nám umožňuje udržovat vlastní existenci. Proces zpracování informací je trvalý, nepřetržitý, ale ovlivnitelný. Zabezpečení informací je spojeno
Kód trezoru 1 je liché číslo.
 1 Kód trezoru 1 je liché číslo. Kód trezoru 1 není prvočíslo. Každá číslice kódu trezoru 1 je prvočíslo. Ciferný součet kódu trezoru 1 je 12. Druhá cifra kódu trezoru 1 je sudá, ostatní jsou liché. Jeden
1 Kód trezoru 1 je liché číslo. Kód trezoru 1 není prvočíslo. Každá číslice kódu trezoru 1 je prvočíslo. Ciferný součet kódu trezoru 1 je 12. Druhá cifra kódu trezoru 1 je sudá, ostatní jsou liché. Jeden
Šifrování v oddíle. František Fladung (Frfla) TK Draci Roztoky
 Šifrování v oddíle 2017 František Fladung (Frfla) TK Draci Roztoky Úvod V této práci se chci zabývat tím, jak vytvářet šifry pro děti a jak je učit je luštit. Toto téma jsem si zvolil, protože šifrování
Šifrování v oddíle 2017 František Fladung (Frfla) TK Draci Roztoky Úvod V této práci se chci zabývat tím, jak vytvářet šifry pro děti a jak je učit je luštit. Toto téma jsem si zvolil, protože šifrování
FUNKCE SVYHLEDAT() ZLÍNSKÝ KRAJ. Obchodní akademie, Vyšší odborná škola a Jazyková škola s právem státní jazykové zkoušky Uherské Hradiště
 FUNKCE SVYHLEDAT() Název školy Obchodní akademie, Vyšší odborná škola a Jazyková škola s právem státní jazykové zkoušky Uherské Hradiště Název DUMu Funkce SVYHLEDAT() Autor Ing. Bc. Martin Šimůnek Datum
FUNKCE SVYHLEDAT() Název školy Obchodní akademie, Vyšší odborná škola a Jazyková škola s právem státní jazykové zkoušky Uherské Hradiště Název DUMu Funkce SVYHLEDAT() Autor Ing. Bc. Martin Šimůnek Datum
kryptosystémy obecně další zajímavé substituční šifry klíčové hospodářství kryptografická pravidla Hillova šifra Vernamova šifra Knižní šifra
 kryptosystémy obecně klíčové hospodářství klíč K, prostor klíčů T K kryptografická pravidla další zajímavé substituční šifry Hillova šifra Vernamova šifra Knižní šifra klíč K různě dlouhá posloupnost znaků
kryptosystémy obecně klíčové hospodářství klíč K, prostor klíčů T K kryptografická pravidla další zajímavé substituční šifry Hillova šifra Vernamova šifra Knižní šifra klíč K různě dlouhá posloupnost znaků
Magické čtverce. Bára Kociánová
 Magické čtverce Bára Kociánová Abstrakt. Příspěvek se zabývá magickými čtverci, které patří spíše do rekreační matematiky. Popisuje jejich základní vlastnosti, uvádí zajímavosti z historie a na závěr podává
Magické čtverce Bára Kociánová Abstrakt. Příspěvek se zabývá magickými čtverci, které patří spíše do rekreační matematiky. Popisuje jejich základní vlastnosti, uvádí zajímavosti z historie a na závěr podává
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Informační
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Informační
Pokročilá kryptologie
 Pokročilá kryptologie RSA doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních programů Informatika pro
Pokročilá kryptologie RSA doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních programů Informatika pro
( ) Jako základ mocnin nemusíme používat jen 10. Pokud není jasné, že číslo je uvedeno v desítkové soustavě, píšeme jej takto: ( 12054 ) 10
 .. Číselné soustavy I Předpoklady: základní početní operace Pedagogická poznámka: Tato a následující hodina není součástí klasické gymnaziální sady. Upřímně řečeno nevím proč. Jednak se všichni studenti
.. Číselné soustavy I Předpoklady: základní početní operace Pedagogická poznámka: Tato a následující hodina není součástí klasické gymnaziální sady. Upřímně řečeno nevím proč. Jednak se všichni studenti
INFORMATIKA. V minulých článcích našeho seriálu jsme se seznámili s pojmy otevřený
 INFORMATIKA Počítačová bezpečnost ve výuce informatiky (7. část: snadné transpoziční šifry a výuka programování) MICHAL MUSÍLEK ŠTĚPÁN HUBÁLOVSKÝ Přírodovědecká fakulta Univerzity Hradec Králové V minulých
INFORMATIKA Počítačová bezpečnost ve výuce informatiky (7. část: snadné transpoziční šifry a výuka programování) MICHAL MUSÍLEK ŠTĚPÁN HUBÁLOVSKÝ Přírodovědecká fakulta Univerzity Hradec Králové V minulých
Školní kolo soutěže Mladý programátor 2013, kategorie A, B. Úloha č. 1 - Baltík v zoo
 Úloha č. 1 - Baltík v zoo 30 bodů a) Baltík má rád zvířátka. Šel se na ně podívat do zoologické zahrady. Tvým úkolem je vyčarovat tři stejné prázdné klece (předměty jsou z bank 0 a 2). 10 bodů b) Baltík
Úloha č. 1 - Baltík v zoo 30 bodů a) Baltík má rád zvířátka. Šel se na ně podívat do zoologické zahrady. Tvým úkolem je vyčarovat tři stejné prázdné klece (předměty jsou z bank 0 a 2). 10 bodů b) Baltík
Podzim 2008. Boot možnosti
 Sedí dva velmi smutní informatici v serverové místnosti. Přijde k nim třetí a ptá se: "A cože jste tak smutní?" "No, včera jsme se trošku ožrali a měnili jsme hesla... Podzim 2008 PV175 SPRÁVA MS WINDOWS
Sedí dva velmi smutní informatici v serverové místnosti. Přijde k nim třetí a ptá se: "A cože jste tak smutní?" "No, včera jsme se trošku ožrali a měnili jsme hesla... Podzim 2008 PV175 SPRÁVA MS WINDOWS
Mgr. et Mgr. Jan Petrov, LL.M. Ph.D. BYZNYS A PRÁVO
 BYZNYS A PRÁVO Byznys a právo OBSAH ZÁKLADNÍ FUNKCE EXCELU... 2 FUNKCE ODMOCNINA A ZAOKROULIT... 4 FORMÁT A OBSAH BUNĚK... 5 RELATIVNÍ ODKAZY... 9 ABSOLUTNÍ ODKAZY... 11 Byznys a právo ZÁKLADNÍ FUNKCE
BYZNYS A PRÁVO Byznys a právo OBSAH ZÁKLADNÍ FUNKCE EXCELU... 2 FUNKCE ODMOCNINA A ZAOKROULIT... 4 FORMÁT A OBSAH BUNĚK... 5 RELATIVNÍ ODKAZY... 9 ABSOLUTNÍ ODKAZY... 11 Byznys a právo ZÁKLADNÍ FUNKCE
základní informace o kurzu základní pojmy literatura ukončení, požadavky, podmiňující předměty,
 základní informace o kurzu ukončení, požadavky, podmiňující předměty, základní pojmy kód x šifra kryptologie x steganografie kryptografie x kryptoanalyza literatura klasická x moderní kryptologie základní,
základní informace o kurzu ukončení, požadavky, podmiňující předměty, základní pojmy kód x šifra kryptologie x steganografie kryptografie x kryptoanalyza literatura klasická x moderní kryptologie základní,
téma: psaní v pojetí montessori
 téma: psaní v pojetí montessori Důvody, proč psát psacím písmem dříve než tiskacím 1. Psací písmo je přirozenějším a pohodlnějším způsobem psaní. Jelikož psaní předchází čtení, měla by pro jeho výuku být
téma: psaní v pojetí montessori Důvody, proč psát psacím písmem dříve než tiskacím 1. Psací písmo je přirozenějším a pohodlnějším způsobem psaní. Jelikož psaní předchází čtení, měla by pro jeho výuku být
Ukázkyaplikacímatematiky
 Ukázkyaplikacímatematiky Jiří Tůma 2015 http://www.karlin.mff.cuni.cz/ tuma/aplikace15.htm tuma@karlin.mff.cuni.cz 0-1 Kapitola1 Úvod do šifrování 1-1 Základní pojmy- obsah Základnípojmy Ceasarova šifra
Ukázkyaplikacímatematiky Jiří Tůma 2015 http://www.karlin.mff.cuni.cz/ tuma/aplikace15.htm tuma@karlin.mff.cuni.cz 0-1 Kapitola1 Úvod do šifrování 1-1 Základní pojmy- obsah Základnípojmy Ceasarova šifra
Konstrukce šifer. Andrew Kozlík KA MFF UK
 Konstrukce šifer Andrew Kozlík KA MFF UK Kerckhoffsův princip V roce 1883 stanovil Auguste Kerckhoffs 6 principů, kterými by se měl řídit návrh šifrovacích zařízení. Například, že zařízení by mělo být
Konstrukce šifer Andrew Kozlík KA MFF UK Kerckhoffsův princip V roce 1883 stanovil Auguste Kerckhoffs 6 principů, kterými by se měl řídit návrh šifrovacích zařízení. Například, že zařízení by mělo být
Ukázky aplikací matematiky. Kapitola 1. Jiří Tůma. Úvod do šifrování. Základní pojmy- obsah. Historie šifrování
 Ukázky aplikací matematiky Jiří Tůma 2015 http://www.karlin.mff.cuni.cz/ tuma/aplikace15.htm tuma@karlin.mff.cuni.cz Kapitola 1 0-1 1-1 Základní pojmy- obsah Historie šifrování Základnípojmy Ceasarova
Ukázky aplikací matematiky Jiří Tůma 2015 http://www.karlin.mff.cuni.cz/ tuma/aplikace15.htm tuma@karlin.mff.cuni.cz Kapitola 1 0-1 1-1 Základní pojmy- obsah Historie šifrování Základnípojmy Ceasarova
JčU - Cvičení z matematiky pro zemědělské obory (doc. RNDr. Nýdl, CSc & spol.) Minitest MT4
 ŘEŠENÍ MINITESTŮ JčU - Cvičení z matematiky pro zemědělské obory (doc. RNDr. Nýdl, CSc & spol.) Minitest MT4. Z daných tří soustav rovnic o neznámých x, x vyberte právě všechny ty, které jsou regulární.
ŘEŠENÍ MINITESTŮ JčU - Cvičení z matematiky pro zemědělské obory (doc. RNDr. Nýdl, CSc & spol.) Minitest MT4. Z daných tří soustav rovnic o neznámých x, x vyberte právě všechny ty, které jsou regulární.
Jazyková výchova. Materiál slouží k procvičení abecedy. Předpokládá se, že žáci již umí abecedu zpaměti.
 Šablona č. Ii, sada č. 2 Vzdělávací oblast Vzdělávací obor Tematický okruh Téma Český jazyk a literatura Jazyková výchova Abeceda Řazení slov podle abecedy Ročník 2. Anotace Materiál slouží k procvičení
Šablona č. Ii, sada č. 2 Vzdělávací oblast Vzdělávací obor Tematický okruh Téma Český jazyk a literatura Jazyková výchova Abeceda Řazení slov podle abecedy Ročník 2. Anotace Materiál slouží k procvičení
Monoalfabetické substituční šifry
 PEF MZLU v Brně 21. října 2010 Úvod Jeden z prvních popisů substituční šifry se objevuje v Kámasútře z 4. stol, vychází však z rukopisů o 800 let starších. Princip substitučních šifer spočívá v nahrazení
PEF MZLU v Brně 21. října 2010 Úvod Jeden z prvních popisů substituční šifry se objevuje v Kámasútře z 4. stol, vychází však z rukopisů o 800 let starších. Princip substitučních šifer spočívá v nahrazení
Šiška. Cíle lekce tematické, obsahové. Motivace 5 MINUT. Získávání informací, rozdělení do skupin 10 MINUT
 Šiška Autor Mgr. Markéta Vokurková, ZŠ Kunratice Cílová skupina 1. stupeň ZŠ Potřebný čas 90 minut Kde lekce proběhne? V lese, za nepříznivého počasí ve třídě 5 Cíl aktivity: Motivace Cíle lekce tematické,
Šiška Autor Mgr. Markéta Vokurková, ZŠ Kunratice Cílová skupina 1. stupeň ZŠ Potřebný čas 90 minut Kde lekce proběhne? V lese, za nepříznivého počasí ve třídě 5 Cíl aktivity: Motivace Cíle lekce tematické,
Zpracování seminární práce. AD7B32KBE semestrální práce
 Zpracování seminární práce AD7B32KBE semestrální práce ČVUT FEL obor STM-Softwarové inženýrství, kombinované studium 4. semestr Radek Horáček Úloha 1: Metoda: prostý posun Zadání: WUEHWUQHHYLYDWCQTUJXUIULUDJXQDTCQDOEVJXUSXQCFYEDIXQTMYJXJXUCJXUVQYHBQTYUIJX
Zpracování seminární práce AD7B32KBE semestrální práce ČVUT FEL obor STM-Softwarové inženýrství, kombinované studium 4. semestr Radek Horáček Úloha 1: Metoda: prostý posun Zadání: WUEHWUQHHYLYDWCQTUJXUIULUDJXQDTCQDOEVJXUSXQCFYEDIXQTMYJXJXUCJXUVQYHBQTYUIJX
Asymetrická kryptografie a elektronický podpis. Ing. Dominik Breitenbacher Mgr. Radim Janča
 Asymetrická kryptografie a elektronický podpis Ing. Dominik Breitenbacher ibreiten@fit.vutbr.cz Mgr. Radim Janča ijanca@fit.vutbr.cz Obsah cvičení Asymetrická, symetrická a hybridní kryptografie Kryptoanalýza
Asymetrická kryptografie a elektronický podpis Ing. Dominik Breitenbacher ibreiten@fit.vutbr.cz Mgr. Radim Janča ijanca@fit.vutbr.cz Obsah cvičení Asymetrická, symetrická a hybridní kryptografie Kryptoanalýza
1.4.3 Složené výroky konjunkce a disjunkce
 1.4.3 Složené výroky konjunkce a disjunkce Předpoklady: 010402 Složené výroky = souvětí, výroky složené z více jednoduchých výroků. Výrok: Číslo 5 je sudé a je prvočíslo. Sestavený ze dvou výroků: 1. výrok:
1.4.3 Složené výroky konjunkce a disjunkce Předpoklady: 010402 Složené výroky = souvětí, výroky složené z více jednoduchých výroků. Výrok: Číslo 5 je sudé a je prvočíslo. Sestavený ze dvou výroků: 1. výrok:
2. ZÁKLADY MATICOVÉ ALGEGRY 2.1. ZÁKLADNÍ POJMY
 2. ZÁKLADY MAICOVÉ ALGEGRY 2.1. ZÁKLADNÍ POJMY V této kapitole se dozvíte: jak je definována reálná nebo komplexní matice a co rozumíme jejím typem; co jsou to prvky matice, co vyjadřují jejich indexy
2. ZÁKLADY MAICOVÉ ALGEGRY 2.1. ZÁKLADNÍ POJMY V této kapitole se dozvíte: jak je definována reálná nebo komplexní matice a co rozumíme jejím typem; co jsou to prvky matice, co vyjadřují jejich indexy
4.2.3 Oblouková míra. π r2. π π. Předpoklady: Obloukovou míru známe z geometrie nebo z fyziky (kruhový pohyb) rychlé zopakování.
 .. Oblouková míra Předpoklady: 8 Obloukovou míru známe z geometrie nebo z fyziky (kruhový pohyb) rychlé zopakování. Př. : Jsou dány dvě kružnice o poloměrech r a r. Do tabulky doplň délky oblouků těchto
.. Oblouková míra Předpoklady: 8 Obloukovou míru známe z geometrie nebo z fyziky (kruhový pohyb) rychlé zopakování. Př. : Jsou dány dvě kružnice o poloměrech r a r. Do tabulky doplň délky oblouků těchto
Jak vyhledávat. Vyhledávače KAPITOLA 3
 KAPITOLA 3 Jak vyhledávat Už víme, jak zacházet s programem Microsoft Internet Explorer, a můžeme se pustit do surfování. Ostatně, stejně jsme to při seznamování s funkcemi programu chtíce nechtíce dělali.
KAPITOLA 3 Jak vyhledávat Už víme, jak zacházet s programem Microsoft Internet Explorer, a můžeme se pustit do surfování. Ostatně, stejně jsme to při seznamování s funkcemi programu chtíce nechtíce dělali.
Gabriela Janská. Středočeský vzdělávací institut akademie J. A. Komenského www.sviajak.cz
 PŘÍRUČKA KE KURZU: ZÁKLADY PRÁCE NA PC MS WORD 2003 Gabriela Janská Středočeský vzdělávací institut akademie J. A. Komenského www.sviajak.cz Obsah: 1. Písmo, velikost písma, tučně, kurzíva, podtrhnout
PŘÍRUČKA KE KURZU: ZÁKLADY PRÁCE NA PC MS WORD 2003 Gabriela Janská Středočeský vzdělávací institut akademie J. A. Komenského www.sviajak.cz Obsah: 1. Písmo, velikost písma, tučně, kurzíva, podtrhnout
Autentizace uživatelů
 Autentizace uživatelů základní prvek ochrany sítí a systémů kromě povolování přístupu lze uživatele členit do skupin, nastavovat různá oprávnění apod. nejčastěji dvojicí jméno a heslo další varianty: jednorázová
Autentizace uživatelů základní prvek ochrany sítí a systémů kromě povolování přístupu lze uživatele členit do skupin, nastavovat různá oprávnění apod. nejčastěji dvojicí jméno a heslo další varianty: jednorázová
Informatika / bezpečnost
 Informatika / bezpečnost Bezpečnost, šifry, elektronický podpis ZS 2015 KIT.PEF.CZU Bezpečnost IS pojmy aktiva IS hardware software data citlivá data hlavně ta chceme chránit autorizace subjekt má právo
Informatika / bezpečnost Bezpečnost, šifry, elektronický podpis ZS 2015 KIT.PEF.CZU Bezpečnost IS pojmy aktiva IS hardware software data citlivá data hlavně ta chceme chránit autorizace subjekt má právo
Aplikovaná informatika Bezpečné přenášení, ukládání a archivace dat. ZEMÁNEK, Z. - PLUSKAL,D. - SMETANA, B.
 Aplikovaná informatika Bezpečné přenášení, ukládání a archivace dat. ZEMÁNEK, Z. - PLUSKAL,D. - SMETANA, B. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního
Aplikovaná informatika Bezpečné přenášení, ukládání a archivace dat. ZEMÁNEK, Z. - PLUSKAL,D. - SMETANA, B. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního
Šifrování flash a jiných datových úložišť
 24. dubna 2014 Obsah přednášky Úvod Pár slov úvodem Proč šifrovat? ochrana citlivých dat nebo záloh sdílení dat jen s vybranými osobami Pár slov úvodem Proč šifrovat? ochrana citlivých dat nebo záloh sdílení
24. dubna 2014 Obsah přednášky Úvod Pár slov úvodem Proč šifrovat? ochrana citlivých dat nebo záloh sdílení dat jen s vybranými osobami Pár slov úvodem Proč šifrovat? ochrana citlivých dat nebo záloh sdílení
Tvorba fotogalerie v HTML str.1
 Tvorba fotogalerie v HTML str.1 obr. A obr. B 1) Spustíme PsPad, vytvoříme nový dokument a otevře se nám okno nový soubor, kde si můžeme zvolit jaký chceme typ. My označíme HTML a potvrdíme. 2) Pro správné
Tvorba fotogalerie v HTML str.1 obr. A obr. B 1) Spustíme PsPad, vytvoříme nový dokument a otevře se nám okno nový soubor, kde si můžeme zvolit jaký chceme typ. My označíme HTML a potvrdíme. 2) Pro správné
Hromadná korespondence
 Kapitola dvanáctá Hromadná korespondence Učební text Mgr. Radek Hoszowski Hromadná korespondence Hromadná korespondence Představíme si jednoduchý nástroj, který nám může ušetřit velké množství práce. Je
Kapitola dvanáctá Hromadná korespondence Učební text Mgr. Radek Hoszowski Hromadná korespondence Hromadná korespondence Představíme si jednoduchý nástroj, který nám může ušetřit velké množství práce. Je
(a kryptografické odbočky) IB111 Úvod do programování skrze Python
 Řetězce a seznamy (a kryptografické odbočky) IB111 Úvod do programování skrze Python 2013 1 / 50 Rozcvička: šifry 1 C S A R B V E K T E O A 2 C S B U J T M B W B 3 A J L B N O C E 2 / 50 Transpoziční šifry
Řetězce a seznamy (a kryptografické odbočky) IB111 Úvod do programování skrze Python 2013 1 / 50 Rozcvička: šifry 1 C S A R B V E K T E O A 2 C S B U J T M B W B 3 A J L B N O C E 2 / 50 Transpoziční šifry
HROMADNÉ ÚPRAVY NAJÍT A NAHRADIT
 HROMADNÉ ÚPRAVY NAJÍT A NAHRADIT Funkce Najít a nahradit slouží k rychlému vyhledávání určitých slov a jejich nahrazování jinými slovy. Lze hledat i určité varianty slov a nahrazovat je buď hromadně (všechny
HROMADNÉ ÚPRAVY NAJÍT A NAHRADIT Funkce Najít a nahradit slouží k rychlému vyhledávání určitých slov a jejich nahrazování jinými slovy. Lze hledat i určité varianty slov a nahrazovat je buď hromadně (všechny
Kombinované úlohy - cvičení
 DUM Vyšší odborná škola, Obchodní akademie a Střední odborná škola EKONOM, o. p. s. Algoritmy DUM III/2-T1-1-16 PRG-01A-var1 Téma: Kombinované úlohy cvičení Střední škola Rok: 2012 2013 Varianta: A Zpracoval:
DUM Vyšší odborná škola, Obchodní akademie a Střední odborná škola EKONOM, o. p. s. Algoritmy DUM III/2-T1-1-16 PRG-01A-var1 Téma: Kombinované úlohy cvičení Střední škola Rok: 2012 2013 Varianta: A Zpracoval:
Moderní metody substitučního šifrování
 PEF MZLU v Brně 11. listopadu 2010 Úvod V současné době se pro bezpečnou komunikaci používají elektronická média. Zprávy se před šifrováním převádí do tvaru zpracovatelného technickým vybavením, do binární
PEF MZLU v Brně 11. listopadu 2010 Úvod V současné době se pro bezpečnou komunikaci používají elektronická média. Zprávy se před šifrováním převádí do tvaru zpracovatelného technickým vybavením, do binární
Druhá část odpovědi na mail ohledně zpracování případů užití
 Druhá část odpovědi na mail ohledně zpracování případů užití Autor RNDr. Ilja Kraval leden 2008 www.objects.cz Úvod Tento článek navazuje jako pokračování na článek předešlý. Minule jsme si vysvětlili,
Druhá část odpovědi na mail ohledně zpracování případů užití Autor RNDr. Ilja Kraval leden 2008 www.objects.cz Úvod Tento článek navazuje jako pokračování na článek předešlý. Minule jsme si vysvětlili,
