kamerou. Dle optických parametrů objektivu mohou v získaném obraze nastat geometrická
|
|
|
- Sára Moravcová
- před 9 lety
- Počet zobrazení:
Transkript
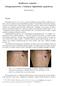
1 Odstranění geometrických zkreslení obrazu Vstupní obraz pro naše úlohy získáváme pomocí optické soustavy tvořené objektivem a kamerou. Dle optických parametrů objektivu mohou v získaném obraze nastat geometrická zkreslení způsobená jeho optikou. Jedním z nejznámějších zkreslení je zkreslení typu fisheye, které vzniká u širokoúhlých objektivů s extrémně malou ohniskovou vzdáleností. Dalšími typy zkreslení jsou barel a polštář. Tato zkreslení jsou, spolu s nezkresleným obrazem, znázorněna na obrázku 1 Obrázek 1: Nezkreslený obraz, zkreslení typu barel barrel) a polštář pincushion) Zkreslení typu barel je způsobeno vlastností širokoúhlých objektivů, která zapříčiňuje větší zvětšení středu obrazu než jeho okrajových částí. Podle výsledného efektu je také odvozen název deformace. Polštářový efekt je deformací inverzní. Pokud bychom obraz, ve kterém je nějaký typ zkreslení, podrobili například detekci pohybu v obraze, výsledná detekce by trpěla chybou, kdy různé části takovéhoto obrazu by pro objekt pohybující se konstantní rychlostí vykazovaly rychlost objektu proměnlivou a to v závislosti na míře zkreslení. Z takovýchto důvodů je žádoucí, aby bylo na zkresleném obrazu před aplikováním nějaké operace nejprve provedeno odstranění tohoto geometrického zkreslení. V následující části popíšeme princip odstranění geometrického zkreslení, možnost jeho ručního nastavení a nakonec metodu, která automaticky najde nezkreslený obraz z původního deformovaného obrazu. 1
2 0.1 Popis metody odstranění zkreslení Zkreslení typu barel nebo polštář jsou tzv. radiální zkreslení. Nejjednodušším způsobem jak namodelovat takovéto zkreslení je pomocí posunu souřadnic obrazu. Necht q = x n,y n ) T reprezentuje nezkreslené souřadnice, zatímco q = x d, ) T reprezentuje souřadnice pozorované tedy souřadnice v deformovaném obraze). Každé radiálně symetrické zkreslení může být aproximováno pomocí Taylorova polynomu ve tvaru: φr 2 ) = 1+K1r 2 +K2r , 1) kde r 2 = x 2 +ȳ 2 a K1, K2,...jsou koeficienty radiálního zkreslení. Aby byly koeficienty nezávislé na velikosti vstupního obrazu, jsou souřadnice x, ȳ bezrozměrné. Navíc pro zachování radiální symetrie musíme přesunout počátek souřadnicového systému do středu obrazu. Souřadnice požadovaných vlastností obdržíme snadno s pomocí následujícího předpisu: x = xn cu R ȳ = yn cv R, 2) kde R = c 2 u +c 2 v a souřadnice středu obrazu c u = w/2, c v = h/2 w je šířka a h výška obrazu). Výslednou transformaci přechodu ze souřadnic x n, y n rekonstruovaného obrazu do souřadnic x d, původního deformovaného obrazu lze zapsat následující rovnicí: ) xn c = u y n c v ) φ 1 r 2 )+ cu c v ). 3) Postupněprocházímevýstupníobrazpojednotlivýchpixelechx n,y n ) T avypočítáváme souřadnicekorespondujícíhopixeluvnámznámémvstupnímdeformovanémobrazex d, ) T. Získané souřadnice jsou obecně reálná čísla, takže musíme zvolit vhodnou interpolaci. Jednoduchou interpolaci nejbližším sousedem docílíme přijatelného výsledku. Pro kvalitnější výstup je nutné využít interpolaci bilineární. Výsledek dosažený pomocí popsané metody je zobrazen na obr Popis metody aplikace zkreslení V praxi exitují úholy, kde chceme do obrazu, který obsahuje nějaké geometrické zkreslení, vložit nové objekty. Takovýto postup je běžně využíván v počítačové grafice, kdy jsou do nasnímaného filmu vkládány nové objekty, např. vizuálních efektů, virtuálních postav, apod. Ve své podstatě jde tedy o postup opačný k dříve popsané metodě. Důvodem takovéhoto postupu je to, že jednou nasnímaný kino)film má jednou provždané rozlišení. Počítačem generovaný obsah však můžeme renderovat i ve velmi vysokém rozlišení a takovýto obraz pak vkládat do původníhogeometricky zkresleného) obrazu. Tímto způsobem je kvalita vstupního kino)filmu zachována. 2
3 Obrázek 2: Původní zkreslený obraz vlevo), obraz po odstranění radiálního zkreslení vpravo) K aplikaci zkreslení je nutné najít inverzní mapování funkce g 1 z rovnice 3. Řešení takovéto transformace však není možné najít analyticky a proto je nutné využít numerického řešení. V zásadě je cílem najít zkreslené souřadnice x d, ) T k nezkresleným souřadnicím x n,y n ) T. Dále víme, že ) ) xn = g, 4) y n kde g = φr 2 ). Rovnice iteračního algoritmu podle metody Newton-Raphson bude vypadat následovně: ) j+1) = ) j) g x d, ) j)) x d, ) j)) 1 g ) j) xn y n ) ). 5) Kvalita výsledku je závislá na dvou faktorech: počtu iterací a počáteční inicializaci. K dosažení dobrého výsledku zpravidla postačí 5 iterací, zatímco k dosažení přesného výsledku může být potřeba i 30 iterací. Jako počáteční podmínku x d, ) T je s úspěchem možno použít hodnotu 0,0) T. Tento iterační algoritmus je však nutno provádět pro každý pixel a proto je tento postup časově náročný. 0.3 Automatická kalibrace Kdybychom chtěli nastavovat koeficienty radiálního zkreslení ručně, jistě bychom záhy přišli na to, že je tato operace poměrně náročná na přesnost a čas uživatele, který ji provádí. Existuje několik metod, které si kladou za cíl automatickou kalibraci zmíněných parametrů. Většina takových metod vyžaduje bud obrazy kalibrační mřížky nebo referenčního objektu, 3
4 u nějž jsou známe rozměry. V praxi jsou však takovéto obrazy nedostupné a je třeba postupovat jiným způsobem. V následujících odstavcích si popíšeme metodu, která vychází z jednoduchého předpokladu a poskytuje kvalitní výsledky. Základním principem je tvrzení, že přímé linie ve snímané scéně by měly být přímé i ve výslednémnezkresleném) obraze. Algoritmus, který využívá tohoto tvrzení, se též anglicky nazývá plumb line. Jednotlivé kroky algoritmu narovnávání je možno popsat následovně: 1. Uživatel ve zkresleném obraze vyznačí několik bodů tvořící čáru, která ve scéně tvoří přímku, 2. algoritmus hledá takové koeficienty radiálního zkreslení, při kterých jsou body co možná nejvíce v přímce, 3. pro nalezené koeficienty se aplikuje postup, kdy se každý bod zkresleného obrazu promítá do obrazu bez zkreslení Hledání koeficientů radiálního zkreslení Hledání koeficientů radiálního zkreslení je opět prováděno iteračním algoritmem. Pseudokód algoritmu je popsán níže: step = 0.1 threshold = 1.0e-4 while!good: error minus = test param - step ) error here = test param ) error plus = test param + step ) if error here is smallest: step /= 2 if error minus is smallest: param -= step if error plus is smallest: param += step if step < threshold: good = True Funkce test transformuje uživatelem definované body podle aktuální hodnoty koeficientu. Podle velikosti chyby, která je vrácena funkcí test, pak algoritmus upravuje parametr tak, aby ve výsledku postupně narovnával uživatelem definovanou lomenou čáru do přímky. Funkce test po transformaci bodů jimi proloží přímku pomocí metody nejmenších čtverců, 4
5 která je popsána dále. Následně funkce vrací sumu vzdáleností vnitřních bodů definované lomené čáry od proložené přímky. Tato chyba je definována následujícím vzorcem: Err = d 2 i, 6) i kde d i je vzdálenost bodu od přímky. Proložení přímky množinou bodů pomocí metody nejmenších čtverců Mějme množinu n bodu x i,y i ), i = 1,2,...,n). Chceme najít takovou přímku y = ax+b, která nejlépe prokládá zadanou množinu bodů. Musíme proto najít parametry a, b, které nejlépe řeší předeterminovanou soustavu rovnic. b 1 x 1 a 1 b 2 x 2 a 2.. b n x n a n = y 1 y 2. y n. 7) Pro jednoduchost si popišme, jak můžeme koeficienty odpovídající zadání nalézt pomocí následujících dvou rovnic: a = n xy) y) x) n x 2 ) x) 2, 8) 1 ) 1 ) b = y a x = y) x 2 ) x) xy) n n n x 2 ) x) 2. 9) Pomocí takto získaných koeficientů a, b si vytvoříme přímku, se kterou budeme dále pracovat Odstranění zkreslení pomocí koeficientů získaných autokalibrací V této chvíli již známe koeficienty radiálního zkreslení. Je nutné si uvědomit, že takto získané koeficienty nelze použít pro transformaci uvedenou v odstavci 0.1. Můžeme však provést transformaci opačnou, tedy ze souřadnic x d, ) T zkresleného obrazu do souřadnic y n,y n ) T obrazu nedeformovaného. K takové transformaci použijeme následující vztah: ) ) ) xn cu c = + u φr 2 ). 10) y n c v c v Opětpostupněprocházímevstupníobrazpojednotlivýchpixelechx d, ) T avypočítáváme souřadnice korespondujícího pixelu v nám neznámém výstupním nedeformovaném obraze x n,y n ) T. Takto získaný výstup však trpí tím, že některým pixelům ve výstupním obraze nebude přiřazena funkční hodnota ze vstupního obrazu. Tento jev můžeme odstranit tak, 5
6 Obrázek 3: Původní zkreslený obraz s uživatelem definovanou lomenou čárou vlevo), obraz po odstranění zkreslení pomocí automatické kalibrace vpravo) že bud použijeme metodu popsanou v odstavci 0.2 nebo můžeme využít jednoduchého triku v podobě supersamplingu. V takovém případě budeme vstupní deformovaný obraz procházet ne po celých pixelech, ale po jejich částech subpixelech). V takovém případě je však nutné vstupní barevnou hodnotu opět interpolovat pomocí bilineární interpolace. Výsledek popsané metody s nakreslenou kalibrační lomenou čárou je zobrazen na obr Zadání úlohy 1. Implementujte problém korekce radiálního zkreslení metodou popsanou v odstavci 0.1. Koeficienty upravujte ručně dokud nedocílíte výsledku zobrazeného v příkladu. 2. Nadefinujte několik bodů v původním zkresleném obraze. Naimplementujte autokalibrační metodu popsanou v odstavci 0.3. Výstupní obraz s odstraněným zkreslením vytvořte pomocí supersamplingu ze vstupního obrazu. 3. Autokalibrační metodu doplňte tak, aby využívala iterační metodu aplikace zkreslení z odstavce
úloh pro ODR jednokrokové metody
 Numerické metody pro řešení počátečních úloh pro ODR jednokrokové metody Formulace: Hledáme řešení y = y() rovnice () s počáteční podmínkou () y () = f(, y()) () y( ) = y. () Smysl: Analyticky lze spočítat
Numerické metody pro řešení počátečních úloh pro ODR jednokrokové metody Formulace: Hledáme řešení y = y() rovnice () s počáteční podmínkou () y () = f(, y()) () y( ) = y. () Smysl: Analyticky lze spočítat
2D transformací. červen Odvození transformačního klíče vybraných 2D transformací Metody vyrovnání... 2
 Výpočet transformačních koeficinetů vybraných 2D transformací Jan Ježek červen 2008 Obsah Odvození transformačního klíče vybraných 2D transformací 2 Meto vyrovnání 2 2 Obecné vyjádření lineárních 2D transformací
Výpočet transformačních koeficinetů vybraných 2D transformací Jan Ježek červen 2008 Obsah Odvození transformačního klíče vybraných 2D transformací 2 Meto vyrovnání 2 2 Obecné vyjádření lineárních 2D transformací
Geometrické transformace obrazu
 Geometrické transformace obrazu a související témata 9. přednáška předmětu Zpracování obrazů Martina Mudrová 2004 Téma přednášk O čem bude tato přednáška? Geometrické transformace obrazu Interpolace v
Geometrické transformace obrazu a související témata 9. přednáška předmětu Zpracování obrazů Martina Mudrová 2004 Téma přednášk O čem bude tato přednáška? Geometrické transformace obrazu Interpolace v
Geometrické transformace obrazu a související témata. 9. přednáška předmětu Zpracování obrazů
 Geometrické transformace obrazu a související témata 9. přednáška předmětu Zpracování obrazů Martina Mudrová 2004 Téma přednášk O čem bude tato přednáška? Geometrické transformace obrazu Interpolace v
Geometrické transformace obrazu a související témata 9. přednáška předmětu Zpracování obrazů Martina Mudrová 2004 Téma přednášk O čem bude tato přednáška? Geometrické transformace obrazu Interpolace v
Geometrické transformace
 1/15 Předzpracování v prostoru obrazů Geometrické transformace Václav Hlaváč, Jan Kybic Fakulta elektrotechnická ČVUT v Praze katedra kybernetiky, Centrum strojového vnímání hlavac@fel.cvut.cz http://cmp.felk.cvut.cz/
1/15 Předzpracování v prostoru obrazů Geometrické transformace Václav Hlaváč, Jan Kybic Fakulta elektrotechnická ČVUT v Praze katedra kybernetiky, Centrum strojového vnímání hlavac@fel.cvut.cz http://cmp.felk.cvut.cz/
1 Linearní prostory nad komplexními čísly
 1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice
 Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice Vektorové podprostory K množina reálných nebo komplexních čísel, U vektorový prostor nad K. Lineární kombinace vektorů u 1, u 2,...,u
Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice Vektorové podprostory K množina reálných nebo komplexních čísel, U vektorový prostor nad K. Lineární kombinace vektorů u 1, u 2,...,u
Metoda nejmenších čtverců Michal Čihák 26. listopadu 2012
 Metoda nejmenších čtverců Michal Čihák 26. listopadu 2012 Metoda nejmenších čtverců Matematicko-statistická metoda používaná zejména při zpracování nepřesných dat (typicky experimentálních empirických
Metoda nejmenších čtverců Michal Čihák 26. listopadu 2012 Metoda nejmenších čtverců Matematicko-statistická metoda používaná zejména při zpracování nepřesných dat (typicky experimentálních empirických
Algoritmizace prostorových úloh
 INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Úlohy nad rastrovými daty Daniela
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Úlohy nad rastrovými daty Daniela
13 Barvy a úpravy rastrového
 13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
Kalibrace snímků. Jakub Šolc
 Kalibrace snímků fotogrammetrie s běžným digitálním aparátem Jakub Šolc Úvod Fotogrammetrie je obor, který se zabývá analýzou geometrických vztahů mezi objekty, jež jsou zachyceny na fotografickém snímku.
Kalibrace snímků fotogrammetrie s běžným digitálním aparátem Jakub Šolc Úvod Fotogrammetrie je obor, který se zabývá analýzou geometrických vztahů mezi objekty, jež jsou zachyceny na fotografickém snímku.
1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004.
 Prostá regresní a korelační analýza 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Problematika závislosti V podstatě lze rozlišovat mezi závislostí nepodstatnou, čili náhodnou
Prostá regresní a korelační analýza 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Problematika závislosti V podstatě lze rozlišovat mezi závislostí nepodstatnou, čili náhodnou
Kalibrační proces ve 3D
 Kalibrační proces ve 3D FCC průmyslové systémy společnost byla založena v roce 1995 jako součást holdingu FCC dodávky komponent pro průmyslovou automatizaci integrace systémů kontroly výroby, strojového
Kalibrační proces ve 3D FCC průmyslové systémy společnost byla založena v roce 1995 jako součást holdingu FCC dodávky komponent pro průmyslovou automatizaci integrace systémů kontroly výroby, strojového
= je prostý orientovaný graf., formálně c ( u, v) 0. dva speciální uzly: zdrojový uzel s a cílový uzel t. Dále budeme bez
 Síť Síť je čtveřice N = ( G, s, t, c) kde G ( V, A) = je prostý orientovaný graf a každé orientované hraně ( u, v) je přiřazeno nezáporné číslo, které se nazývá kapacita hrany ( u, v), formálně c ( u,
Síť Síť je čtveřice N = ( G, s, t, c) kde G ( V, A) = je prostý orientovaný graf a každé orientované hraně ( u, v) je přiřazeno nezáporné číslo, které se nazývá kapacita hrany ( u, v), formálně c ( u,
ZPRACOVÁNÍ DAT DÁLKOVÉHO PRŮZKUMU
 A - zdroj záření B - záření v atmosféře C - interakce s objektem D - změření záření přístrojem E - přenos, příjem dat F - zpracování dat G - využití informace v aplikaci Typ informace získávaný DPZ - vnitřní
A - zdroj záření B - záření v atmosféře C - interakce s objektem D - změření záření přístrojem E - přenos, příjem dat F - zpracování dat G - využití informace v aplikaci Typ informace získávaný DPZ - vnitřní
Grafika na počítači. Bc. Veronika Tomsová
 Grafika na počítači Bc. Veronika Tomsová Proces zpracování obrazu Proces zpracování obrazu 1. Snímání obrazu 2. Digitalizace obrazu převod spojitého signálu na matici čísel reprezentující obraz 3. Předzpracování
Grafika na počítači Bc. Veronika Tomsová Proces zpracování obrazu Proces zpracování obrazu 1. Snímání obrazu 2. Digitalizace obrazu převod spojitého signálu na matici čísel reprezentující obraz 3. Předzpracování
Aplikovaná matematika I
 Metoda nejmenších čtverců Aplikovaná matematika I Dana Říhová Mendelu Brno c Dana Říhová (Mendelu Brno) Metoda nejmenších čtverců 1 / 8 Obsah 1 Formulace problému 2 Princip metody nejmenších čtverců 3
Metoda nejmenších čtverců Aplikovaná matematika I Dana Říhová Mendelu Brno c Dana Říhová (Mendelu Brno) Metoda nejmenších čtverců 1 / 8 Obsah 1 Formulace problému 2 Princip metody nejmenších čtverců 3
Úvod do mobilní robotiky AIL028
 md at robotika.cz http://robotika.cz/guide/umor07/cs 20. prosince 2007 1 2 3D model světa ProMIS Cvičení hledání domečku Model štěrbinové kamery Idealizovaný jednoduchý model kamery Paprsek světla vychází
md at robotika.cz http://robotika.cz/guide/umor07/cs 20. prosince 2007 1 2 3D model světa ProMIS Cvičení hledání domečku Model štěrbinové kamery Idealizovaný jednoduchý model kamery Paprsek světla vychází
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.
 INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 Báze vektorových prostorů, transformace souřadnic Michal Botur Přednáška
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 Báze vektorových prostorů, transformace souřadnic Michal Botur Přednáška
Integrace. Numerické metody 7. května FJFI ČVUT v Praze
 Integrace Numerické metody 7. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod 1D Kvadraturní vzorce Gaussovy kvadratury Více dimenzí Programy 1 Úvod Úvod - Úloha Máme funkci f( x) a snažíme se najít určitý integrál
Integrace Numerické metody 7. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod 1D Kvadraturní vzorce Gaussovy kvadratury Více dimenzí Programy 1 Úvod Úvod - Úloha Máme funkci f( x) a snažíme se najít určitý integrál
ROZ1 CVIČENÍ VI. Geometrická registrace (matching) obrazů
 ROZ1 CVIČENÍ VI. Geometrická registrace (matching) obrazů REGISTRACI OBRAZU (IMAGE REGISTRATION) Více snímků téže scény Odpovídající pixely v těchto snímcích musí mít stejné souřadnice Pokud je nemají
ROZ1 CVIČENÍ VI. Geometrická registrace (matching) obrazů REGISTRACI OBRAZU (IMAGE REGISTRATION) Více snímků téže scény Odpovídající pixely v těchto snímcích musí mít stejné souřadnice Pokud je nemají
 Interpolace Uvažujme třídu funkcí jedné proměnné ψ(x; a 0,..., a n ), kde a 0,..., a n jsou parametry, které popisují jednotlivé funkce této třídy. Mějme dány body x 0, x 1,..., x n, x i x k, i, k = 0,
Interpolace Uvažujme třídu funkcí jedné proměnné ψ(x; a 0,..., a n ), kde a 0,..., a n jsou parametry, které popisují jednotlivé funkce této třídy. Mějme dány body x 0, x 1,..., x n, x i x k, i, k = 0,
VYBRANÉ PARTIE Z NUMERICKÉ MATEMATIKY
 VYBRANÉ PARTIE Z NUMERICKÉ MATEMATIKY Jan Krejčí 31. srpna 2006 jkrejci@physics.ujep.cz http://physics.ujep.cz/~jkrejci Obsah 1 Přímé metody řešení soustav lineárních rovnic 3 1.1 Gaussova eliminace...............................
VYBRANÉ PARTIE Z NUMERICKÉ MATEMATIKY Jan Krejčí 31. srpna 2006 jkrejci@physics.ujep.cz http://physics.ujep.cz/~jkrejci Obsah 1 Přímé metody řešení soustav lineárních rovnic 3 1.1 Gaussova eliminace...............................
9 Kolmost vektorových podprostorů
 9 Kolmost vektorových podprostorů Od kolmosti dvou vektorů nyní přejdeme ke kolmosti dvou vektorových podprostorů. Budeme se zabývat otázkou, kdy jsou dva vektorové podprostory na sebe kolmé a jak to poznáme.
9 Kolmost vektorových podprostorů Od kolmosti dvou vektorů nyní přejdeme ke kolmosti dvou vektorových podprostorů. Budeme se zabývat otázkou, kdy jsou dva vektorové podprostory na sebe kolmé a jak to poznáme.
Aplikovaná numerická matematika - ANM
 Aplikovaná numerická matematika - ANM 3 Řešení soustav lineárních rovnic iterační metody doc Ing Róbert Lórencz, CSc České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových
Aplikovaná numerická matematika - ANM 3 Řešení soustav lineárních rovnic iterační metody doc Ing Róbert Lórencz, CSc České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových
11MAMY LS 2017/2018. Úvod do Matlabu. 21. února Skupina 01. reseni2.m a tak dále + M souborem zadané funkce z příkladu 3 + souborem skupina.
 11MAMY LS 2017/2018 Cvičení č. 2: 21. 2. 2018 Úvod do Matlabu. Jan Přikryl 21. února 2018 Po skupinách, na které jste se doufám rozdělili samostatně včera, vyřešte tak, jak nejlépe svedete, níže uvedená
11MAMY LS 2017/2018 Cvičení č. 2: 21. 2. 2018 Úvod do Matlabu. Jan Přikryl 21. února 2018 Po skupinách, na které jste se doufám rozdělili samostatně včera, vyřešte tak, jak nejlépe svedete, níže uvedená
Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného)
 Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného) 1 Obecný popis metody Particle Image Velocimetry, nebo-li zkráceně PIV, je měřící
Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného) 1 Obecný popis metody Particle Image Velocimetry, nebo-li zkráceně PIV, je měřící
Úlohy k přednášce NMAG 101 a 120: Lineární algebra a geometrie 1 a 2,
 Úlohy k přednášce NMAG a : Lineární algebra a geometrie a Verze ze dne. května Toto je seznam přímočarých příkladů k přednášce. Úlohy z tohoto seznamu je nezbytně nutné umět řešit. Podobné typy úloh se
Úlohy k přednášce NMAG a : Lineární algebra a geometrie a Verze ze dne. května Toto je seznam přímočarých příkladů k přednášce. Úlohy z tohoto seznamu je nezbytně nutné umět řešit. Podobné typy úloh se
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník MĚŘICKÝ SNÍMEK PRVKY VNITŘNÍ A VNĚJŠÍ ORIENTACE CHYBY SNÍMKU
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník MĚŘICKÝ SNÍMEK PRVKY VNITŘNÍ A VNĚJŠÍ ORIENTACE CHYBY SNÍMKU MĚŘICKÝ SNÍMEK Základem měření je fotografický snímek, který je v ideálním případě
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník MĚŘICKÝ SNÍMEK PRVKY VNITŘNÍ A VNĚJŠÍ ORIENTACE CHYBY SNÍMKU MĚŘICKÝ SNÍMEK Základem měření je fotografický snímek, který je v ideálním případě
1 0 0 u 22 u 23 l 31. l u11
 LU dekompozice Jedná se o rozklad matice A na dvě trojúhelníkové matice L a U, A=LU. Matice L je dolní trojúhelníková s jedničkami na diagonále a matice U je horní trojúhelníková. a a2 a3 a 2 a 22 a 23
LU dekompozice Jedná se o rozklad matice A na dvě trojúhelníkové matice L a U, A=LU. Matice L je dolní trojúhelníková s jedničkami na diagonále a matice U je horní trojúhelníková. a a2 a3 a 2 a 22 a 23
Aplikovaná numerická matematika
 Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Lingebraické kapitolky - Analytická geometrie
 Lingebraické kapitolky - Analytická geometrie Jaroslav Horáček KAM MFF UK 2013 Co je to vektor? Šipička na tabuli? Ehm? Množina orientovaných úseček majících stejný směr. Prvek vektorového prostoru. V
Lingebraické kapitolky - Analytická geometrie Jaroslav Horáček KAM MFF UK 2013 Co je to vektor? Šipička na tabuli? Ehm? Množina orientovaných úseček majících stejný směr. Prvek vektorového prostoru. V
Algoritmus pro hledání nejkratší cesty orientovaným grafem
 1.1 Úvod Algoritmus pro hledání nejkratší cesty orientovaným grafem Naprogramoval jsem v Matlabu funkci, která dokáže určit nejkratší cestu v orientovaném grafu mezi libovolnými dvěma vrcholy. Nastudoval
1.1 Úvod Algoritmus pro hledání nejkratší cesty orientovaným grafem Naprogramoval jsem v Matlabu funkci, která dokáže určit nejkratší cestu v orientovaném grafu mezi libovolnými dvěma vrcholy. Nastudoval
Interpolace, aproximace
 11 Interpolace, aproximace Metoda nejmenších čtverců 11.1 Interpolace Mějme body [x i,y i ], i =0, 1,...,n 1. Cílem interpolace je najít funkci f(x), jejíž graf prochází všemi těmito body, tj. f(x i )=y
11 Interpolace, aproximace Metoda nejmenších čtverců 11.1 Interpolace Mějme body [x i,y i ], i =0, 1,...,n 1. Cílem interpolace je najít funkci f(x), jejíž graf prochází všemi těmito body, tj. f(x i )=y
transformace je posunutí plus lineární transformace má svou matici vzhledem k homogenním souřadnicím [1]
![transformace je posunutí plus lineární transformace má svou matici vzhledem k homogenním souřadnicím [1] transformace je posunutí plus lineární transformace má svou matici vzhledem k homogenním souřadnicím [1]](/thumbs/88/115112143.jpg) [1] Afinní transformace je posunutí plus lineární transformace má svou matici vzhledem k homogenním souřadnicím využití například v počítačové grafice Evropský sociální fond Praha & EU. Investujeme do
[1] Afinní transformace je posunutí plus lineární transformace má svou matici vzhledem k homogenním souřadnicím využití například v počítačové grafice Evropský sociální fond Praha & EU. Investujeme do
DIGITÁLNÍ ORTOFOTO. SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník
 DIGITÁLNÍ ORTOFOTO SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník DIGITÁLNÍ SNÍMEK Ortofotomapa se skládá ze všech prvků, které byly v době expozice přítomné na povrchu snímkované oblasti.
DIGITÁLNÍ ORTOFOTO SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník DIGITÁLNÍ SNÍMEK Ortofotomapa se skládá ze všech prvků, které byly v době expozice přítomné na povrchu snímkované oblasti.
Úloha - rozpoznávání číslic
 Úloha - rozpoznávání číslic Vojtěch Franc, Tomáš Pajdla a Tomáš Svoboda http://cmp.felk.cvut.cz 27. listopadu 26 Abstrakt Podpůrný text pro cvičení předmětu X33KUI. Vysvětluje tři způsoby rozpoznávání
Úloha - rozpoznávání číslic Vojtěch Franc, Tomáš Pajdla a Tomáš Svoboda http://cmp.felk.cvut.cz 27. listopadu 26 Abstrakt Podpůrný text pro cvičení předmětu X33KUI. Vysvětluje tři způsoby rozpoznávání
11 Zobrazování objektů 3D grafiky
 11 Zobrazování objektů 3D grafiky Studijní cíl Tento blok je věnován základním algoritmům zobrazení 3D grafiky. Postupně budou probrány základní metody projekce kolmé promítání, rovnoběžné promítání a
11 Zobrazování objektů 3D grafiky Studijní cíl Tento blok je věnován základním algoritmům zobrazení 3D grafiky. Postupně budou probrány základní metody projekce kolmé promítání, rovnoběžné promítání a
VYUŽITÍ PRAVDĚPODOBNOSTNÍ METODY MONTE CARLO V SOUDNÍM INŽENÝRSTVÍ
 VYUŽITÍ PRAVDĚPODOBNOSTNÍ METODY MONTE CARLO V SOUDNÍM INŽENÝRSTVÍ Michal Kořenář 1 Abstrakt Rozvoj výpočetní techniky v poslední době umožnil také rozvoj výpočetních metod, které nejsou založeny na bázi
VYUŽITÍ PRAVDĚPODOBNOSTNÍ METODY MONTE CARLO V SOUDNÍM INŽENÝRSTVÍ Michal Kořenář 1 Abstrakt Rozvoj výpočetní techniky v poslední době umožnil také rozvoj výpočetních metod, které nejsou založeny na bázi
Téma: Vektorová grafika. Určete pravdivost následujícího tvrzení: "Grafická data jsou u 2D vektorové grafiky uložena ve voxelech."
 Téma: Vektorová grafika. Určete pravdivost následujícího tvrzení: "Grafická data jsou u 2D vektorové grafiky uložena ve voxelech." Téma: Vektorová grafika. Určete pravdivost následujícího tvrzení: "Na
Téma: Vektorová grafika. Určete pravdivost následujícího tvrzení: "Grafická data jsou u 2D vektorové grafiky uložena ve voxelech." Téma: Vektorová grafika. Určete pravdivost následujícího tvrzení: "Na
Teorie informace a kódování (KMI/TIK) Reed-Mullerovy kódy
 Teorie informace a kódování (KMI/TIK) Reed-Mullerovy kódy Lukáš Havrlant Univerzita Palackého 10. ledna 2014 Primární zdroj Jiří Adámek: Foundations of Coding. Strany 137 160. Na webu ke stažení, heslo:
Teorie informace a kódování (KMI/TIK) Reed-Mullerovy kódy Lukáš Havrlant Univerzita Palackého 10. ledna 2014 Primární zdroj Jiří Adámek: Foundations of Coding. Strany 137 160. Na webu ke stažení, heslo:
Polynomy a interpolace text neobsahuje přesné matematické definice, pouze jejich vysvětlení
 Polynomy a interpolace text neobsahuje přesné matematické definice, pouze jejich vysvětlení Polynom nad R = zobrazení f : R R f(x) = a n x n + a n 1 x n 1 +... + a 1 x + a 0, kde a i R jsou pevně daná
Polynomy a interpolace text neobsahuje přesné matematické definice, pouze jejich vysvětlení Polynom nad R = zobrazení f : R R f(x) = a n x n + a n 1 x n 1 +... + a 1 x + a 0, kde a i R jsou pevně daná
1 Polynomiální interpolace
 Polynomiální interpolace. Metoda neurčitých koeficientů Příklad.. Nalezněte polynom p co nejmenšího stupně, pro který platí p() = 0, p(2) =, p( ) = 6. Řešení. Polynom hledáme metodou neurčitých koeficientů,
Polynomiální interpolace. Metoda neurčitých koeficientů Příklad.. Nalezněte polynom p co nejmenšího stupně, pro který platí p() = 0, p(2) =, p( ) = 6. Řešení. Polynom hledáme metodou neurčitých koeficientů,
Kinematika příklad. Robotika. Vladimír Smutný. Centrum strojového vnímání. České vysoké učení technické v Praze
 Kinematika příklad Robotika Kinematika příklad Vladimír Smutný Centrum strojového vnímání České vysoké učení technické v Praze ROBOTICS: Vladimír Smutný Slide, Page Příklad praktické úlohy D měřicí stroj
Kinematika příklad Robotika Kinematika příklad Vladimír Smutný Centrum strojového vnímání České vysoké učení technické v Praze ROBOTICS: Vladimír Smutný Slide, Page Příklad praktické úlohy D měřicí stroj
Aproximace a interpolace
 Aproximace a interpolace Aproximace dat = náhrada nearitmetické veličiny (resp. složité funkce) pomocí aritmetických veličin. Nejčastěji jde o náhradu hodnot složité funkce g(x) nebo funkce zadané pouze
Aproximace a interpolace Aproximace dat = náhrada nearitmetické veličiny (resp. složité funkce) pomocí aritmetických veličin. Nejčastěji jde o náhradu hodnot složité funkce g(x) nebo funkce zadané pouze
8.3). S ohledem na jednoduchost a názornost je výhodné seznámit se s touto Základní pojmy a vztahy. Definice
 9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
Figurální čísla, Pascalův trojúhelník, aritmetické posloupnost vyšších řádů
 Figurální čísla, Pascalův trojúhelník, aritmetické posloupnost vyšších řádů Jaroslav Zhouf, PedF UK, Praha Úvod Pascalův trojúhelník je schéma přirozených čísel, která má své využití např. v binomické
Figurální čísla, Pascalův trojúhelník, aritmetické posloupnost vyšších řádů Jaroslav Zhouf, PedF UK, Praha Úvod Pascalův trojúhelník je schéma přirozených čísel, která má své využití např. v binomické
Nelineární rovnice. Numerické metody 6. května FJFI ČVUT v Praze
 Nelineární rovnice Numerické metody 6. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod Ohraničení kořene Hledání kořene Soustava Programy 1 Úvod Úvod - Úloha Hledáme bod x, ve kterém je splněno pro zadanou funkci
Nelineární rovnice Numerické metody 6. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod Ohraničení kořene Hledání kořene Soustava Programy 1 Úvod Úvod - Úloha Hledáme bod x, ve kterém je splněno pro zadanou funkci
Pořízení rastrového obrazu
 Pořízení rastrového obrazu Poznámky k předmětu POČÍTAČOVÁ GRAFIKA Martina Mudrová duben 2006 Úvod Nejčastější metody pořízení rastrového obrazu: digitální fotografie skenování rasterizace vektorových obrázků
Pořízení rastrového obrazu Poznámky k předmětu POČÍTAČOVÁ GRAFIKA Martina Mudrová duben 2006 Úvod Nejčastější metody pořízení rastrového obrazu: digitální fotografie skenování rasterizace vektorových obrázků
Vektory a matice. Obsah. Aplikovaná matematika I. Carl Friedrich Gauss. Základní pojmy a operace
 Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Numerické řešení diferenciálních rovnic
 Numerické řešení diferenciálních rovnic Omezení: obyčejné (nikoli parciální) diferenciální rovnice, Cauchyho počáteční úloha, pouze jedna diferenciální rovnice 1. řádu 1/1 Numerické řešení diferenciálních
Numerické řešení diferenciálních rovnic Omezení: obyčejné (nikoli parciální) diferenciální rovnice, Cauchyho počáteční úloha, pouze jedna diferenciální rovnice 1. řádu 1/1 Numerické řešení diferenciálních
Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika)
 Inovace studijního oboru Geotechnika Reg. č. CZ.1.07/2.2.00/28.0009 Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika) Doc. RNDr.
Inovace studijního oboru Geotechnika Reg. č. CZ.1.07/2.2.00/28.0009 Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika) Doc. RNDr.
UNIVERZITA PARDUBICE. 4.4 Aproximace křivek a vyhlazování křivek
 UNIVERZITA PARDUBICE Licenční Studium Archimedes Statistické zpracování dat a informatika 4.4 Aproximace křivek a vyhlazování křivek Mgr. Jana Kubátová Endokrinologický ústav V Praze, leden 2012 Obsah
UNIVERZITA PARDUBICE Licenční Studium Archimedes Statistické zpracování dat a informatika 4.4 Aproximace křivek a vyhlazování křivek Mgr. Jana Kubátová Endokrinologický ústav V Praze, leden 2012 Obsah
Kombinatorická minimalizace
 Kombinatorická minimalizace Cílem je nalézt globální minimum ve velké diskrétní množině, kde může být mnoho lokálních minim. Úloha obchodního cestujícího Cílem je najít nejkratší cestu, která spojuje všechny
Kombinatorická minimalizace Cílem je nalézt globální minimum ve velké diskrétní množině, kde může být mnoho lokálních minim. Úloha obchodního cestujícího Cílem je najít nejkratší cestu, která spojuje všechny
Vzdálenost uzlů v neorientovaném grafu
 Vzdálenosti a grafy Vzdálenost uzlů v neorientovaném grafu Je dán neorientovaný neohodnocený graf G = (V,E,I) vzdálenost uzlů u a v v neorientovaném souvislém grafu G je délka nejkratší cesty spojující
Vzdálenosti a grafy Vzdálenost uzlů v neorientovaném grafu Je dán neorientovaný neohodnocený graf G = (V,E,I) vzdálenost uzlů u a v v neorientovaném souvislém grafu G je délka nejkratší cesty spojující
CVIČNÝ TEST 15. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17
 CVIČNÝ TEST 15 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Je dána čtvercová mřížka, v níž každý čtverec má délku
CVIČNÝ TEST 15 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Je dána čtvercová mřížka, v níž každý čtverec má délku
7. Funkce jedné reálné proměnné, základní pojmy
 , základní pojmy POJEM FUNKCE JEDNÉ PROMĚNNÉ Reálná funkce f jedné reálné proměnné je funkce (zobrazení) f: X Y, kde X, Y R. Jde o zvláštní případ obecného pojmu funkce definovaného v přednášce. Poznámka:
, základní pojmy POJEM FUNKCE JEDNÉ PROMĚNNÉ Reálná funkce f jedné reálné proměnné je funkce (zobrazení) f: X Y, kde X, Y R. Jde o zvláštní případ obecného pojmu funkce definovaného v přednášce. Poznámka:
Omezení barevného prostoru
 Úpravy obrazu Omezení barevného prostoru Omezení počtu barev v obraze při zachování obrazového vjemu z obrazu Vytváření barevné palety v některých souborových formátech Různé filtry v grafických programech
Úpravy obrazu Omezení barevného prostoru Omezení počtu barev v obraze při zachování obrazového vjemu z obrazu Vytváření barevné palety v některých souborových formátech Různé filtry v grafických programech
Aproximace funkcí. Numerické metody 6. května FJFI ČVUT v Praze
 Aproximace funkcí Numerické metody 6. května 2018 FJFI ČVUT v Praze 1 Úvod Dělení Interpolace 1D Více dimenzí Minimalizace Důvody 1 Dělení Dělení - Získané data zadané data 2 Dělení - Získané data Obecně
Aproximace funkcí Numerické metody 6. května 2018 FJFI ČVUT v Praze 1 Úvod Dělení Interpolace 1D Více dimenzí Minimalizace Důvody 1 Dělení Dělení - Získané data zadané data 2 Dělení - Získané data Obecně
Iterační metody řešení soustav lineárních rovnic. 27. prosince 2011
 Iterační metody řešení soustav lineárních rovnic Michal Čihák 27. prosince 2011 Přímé metody řešení soustav lineárních rovnic V přednáškách z lineární algebry jste se seznámili s několika metodami řešení
Iterační metody řešení soustav lineárních rovnic Michal Čihák 27. prosince 2011 Přímé metody řešení soustav lineárních rovnic V přednáškách z lineární algebry jste se seznámili s několika metodami řešení
Numerická matematika 1
 Numerická matematika 1 Obsah 1 Řešení nelineárních rovnic 3 1.1 Metoda půlení intervalu....................... 3 1.2 Metoda jednoduché iterace..................... 4 1.3 Newtonova metoda..........................
Numerická matematika 1 Obsah 1 Řešení nelineárních rovnic 3 1.1 Metoda půlení intervalu....................... 3 1.2 Metoda jednoduché iterace..................... 4 1.3 Newtonova metoda..........................
REÁLNÁ FUNKCE JEDNÉ PROMĚNNÉ
 REÁLNÁ FUNKCE JEDNÉ PROMĚNNÉ 5 přednáška S funkcemi se setkáváme na každém kroku ve všech přírodních vědách ale i v každodenním životě Každá situace kdy jsou nějaký jev nebo veličina jednoznačně určeny
REÁLNÁ FUNKCE JEDNÉ PROMĚNNÉ 5 přednáška S funkcemi se setkáváme na každém kroku ve všech přírodních vědách ale i v každodenním životě Každá situace kdy jsou nějaký jev nebo veličina jednoznačně určeny
Vektorový prostor. Př.1. R 2 ; R 3 ; R n Dvě operace v R n : u + v = (u 1 + v 1,...u n + v n ), V (E 3 )...množina vektorů v E 3,
 Vektorový prostor Příklady: Př.1. R 2 ; R 3 ; R n...aritmetický n-rozměrný prostor Dvě operace v R n : součet vektorů u = (u 1,...u n ) a v = (v 1,...v n ) je vektor u + v = (u 1 + v 1,...u n + v n ),
Vektorový prostor Příklady: Př.1. R 2 ; R 3 ; R n...aritmetický n-rozměrný prostor Dvě operace v R n : součet vektorů u = (u 1,...u n ) a v = (v 1,...v n ) je vektor u + v = (u 1 + v 1,...u n + v n ),
Jaroslav Tuma. 8. února 2010
 Semestrální práce z předmětu KMA/MM Odstraňování šumu z obrazu Jaroslav Tuma 8. února 2010 1 1 Zpracování obrazu Zpracování obrazu je disciplína zabývající se zpracováním obrazových dat různého původu.
Semestrální práce z předmětu KMA/MM Odstraňování šumu z obrazu Jaroslav Tuma 8. února 2010 1 1 Zpracování obrazu Zpracování obrazu je disciplína zabývající se zpracováním obrazových dat různého původu.
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na. x 2 x 1
 Kapitola 4 Rasterizace objektů Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na rastrově definované obrazy. Při zobrazení reálného modelu ve světových souřadnicích na výstupní
Kapitola 4 Rasterizace objektů Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na rastrově definované obrazy. Při zobrazení reálného modelu ve světových souřadnicích na výstupní
Digitalizace dat metodika
 Digitalizace dat metodika Digitalizace Jak počítač získá jedničky a nuly, se kterými potom počítá a které je schopen si pamatovat? Pomocí různých přístrojů a zařízení (mikrofon, fotoaparát, skener, kamera,
Digitalizace dat metodika Digitalizace Jak počítač získá jedničky a nuly, se kterými potom počítá a které je schopen si pamatovat? Pomocí různých přístrojů a zařízení (mikrofon, fotoaparát, skener, kamera,
Matematika (a fyzika) schovaná za GPS. Global Positioning system. Michal Bulant. Brno, 2011
 Matematika (a fyzika) schovaná za GPS Michal Bulant Masarykova univerzita Přírodovědecká fakulta Ústav matematiky a statistiky Brno, 2011 Michal Bulant (PřF MU) Matematika (a fyzika) schovaná za GPS Brno,
Matematika (a fyzika) schovaná za GPS Michal Bulant Masarykova univerzita Přírodovědecká fakulta Ústav matematiky a statistiky Brno, 2011 Michal Bulant (PřF MU) Matematika (a fyzika) schovaná za GPS Brno,
Algoritmy a struktury neuropočítačů ASN - P11
 Aplikace UNS při rozpoznání obrazů Základní úloha segmentace obrazu rozdělení obrazu do několika významných oblastí klasifikační úloha, clusterová analýza target Metody Kohonenova metoda KSOM Kohonenova
Aplikace UNS při rozpoznání obrazů Základní úloha segmentace obrazu rozdělení obrazu do několika významných oblastí klasifikační úloha, clusterová analýza target Metody Kohonenova metoda KSOM Kohonenova
GIS Geografické informační systémy
 GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
6. ANALYTICKÁ GEOMETRIE
 Vektorová algebra 6. ANALYTICKÁ GEOMETRIE Pravoúhlé souřadnice bodu v prostoru Poloha bodu v prostoru je vzhledem ke třem osám k sobě kolmým určena třemi souřadnicemi, které tvoří uspořádanou trojici reálných
Vektorová algebra 6. ANALYTICKÁ GEOMETRIE Pravoúhlé souřadnice bodu v prostoru Poloha bodu v prostoru je vzhledem ke třem osám k sobě kolmým určena třemi souřadnicemi, které tvoří uspořádanou trojici reálných
9.5. Soustavy diferenciálních rovnic
 Cíle Budeme se nyní zabývat úlohami, v nichž je cílem najít dvojici funkcí y(x), z(x), pro které jsou zadány dvě lineární rovnice prvního řádu, obsahující tyto funkce a jejich derivace. Výklad Omezíme-li
Cíle Budeme se nyní zabývat úlohami, v nichž je cílem najít dvojici funkcí y(x), z(x), pro které jsou zadány dvě lineární rovnice prvního řádu, obsahující tyto funkce a jejich derivace. Výklad Omezíme-li
Odhad stavu matematického modelu křižovatek
 Odhad stavu matematického modelu křižovatek Miroslav Šimandl, Miroslav Flídr a Jindřich Duník Katedra kybernetiky & Výzkumné centrum Data-Algoritmy-Rozhodování Fakulta aplikovaných věd Západočeská univerzita
Odhad stavu matematického modelu křižovatek Miroslav Šimandl, Miroslav Flídr a Jindřich Duník Katedra kybernetiky & Výzkumné centrum Data-Algoritmy-Rozhodování Fakulta aplikovaných věd Západočeská univerzita
Rozvoj tepla v betonových konstrukcích
 Úvod do problematiky K novinkám v požární odolnosti nosných konstrukcí Praha, 11. září 2012 Ing. Radek Štefan prof. Ing. Jaroslav Procházka, CSc. Znalost rozložení teploty v betonové konstrukci nebo její
Úvod do problematiky K novinkám v požární odolnosti nosných konstrukcí Praha, 11. září 2012 Ing. Radek Štefan prof. Ing. Jaroslav Procházka, CSc. Znalost rozložení teploty v betonové konstrukci nebo její
Úvod do zpracování signálů
 1 / 25 Úvod do zpracování signálů Karel Horák Rozvrh přednášky: 1. Spojitý a diskrétní signál. 2. Spektrum signálu. 3. Vzorkovací věta. 4. Konvoluce signálů. 5. Korelace signálů. 2 / 25 Úvod do zpracování
1 / 25 Úvod do zpracování signálů Karel Horák Rozvrh přednášky: 1. Spojitý a diskrétní signál. 2. Spektrum signálu. 3. Vzorkovací věta. 4. Konvoluce signálů. 5. Korelace signálů. 2 / 25 Úvod do zpracování
1 Projekce a projektory
 Cvičení 3 - zadání a řešení úloh Základy numerické matematiky - NMNM20 Verze z 5. října 208 Projekce a projektory Opakování ortogonální projekce Definice (Ortogonální projekce). Uvažujme V vektorový prostor
Cvičení 3 - zadání a řešení úloh Základy numerické matematiky - NMNM20 Verze z 5. října 208 Projekce a projektory Opakování ortogonální projekce Definice (Ortogonální projekce). Uvažujme V vektorový prostor
SEMESTRÁLNÍ PRÁCE X. Aproximace křivek Numerické vyhlazování
 KATEDRA ANALYTICKÉ CHEMIE FAKULTY CHEMICKO TECHNOLOGICKÉ UNIVERSITA PARDUBICE - Licenční studium chemometrie LS96/1 SEMESTRÁLNÍ PRÁCE X. Aproximace křivek Numerické vyhlazování Praha, leden 1999 0 Úloha
KATEDRA ANALYTICKÉ CHEMIE FAKULTY CHEMICKO TECHNOLOGICKÉ UNIVERSITA PARDUBICE - Licenční studium chemometrie LS96/1 SEMESTRÁLNÍ PRÁCE X. Aproximace křivek Numerické vyhlazování Praha, leden 1999 0 Úloha
Lineární zobrazení. 1. A(x y) = A(x) A(y) (vlastnost aditivity) 2. A(α x) = α A(x) (vlastnost homogenity)
 4 Lineární zobrazení Definice: Nechť V a W jsou vektorové prostory Zobrazení A : V W (zobrazení z V do W nazýváme lineárním zobrazením, pokud pro všechna x V, y V a α R platí 1 A(x y = A(x A(y (vlastnost
4 Lineární zobrazení Definice: Nechť V a W jsou vektorové prostory Zobrazení A : V W (zobrazení z V do W nazýváme lineárním zobrazením, pokud pro všechna x V, y V a α R platí 1 A(x y = A(x A(y (vlastnost
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník RELATIVNÍ A ABSOLUTNÍ ORIENTACE AAT ANALYTICKÁ AEROTRIANGULACE
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník RELATIVNÍ A ABSOLUTNÍ ORIENTACE AAT ANALYTICKÁ AEROTRIANGULACE PŘÍPRAVA STEREODVOJICE PRO VYHODNOCENÍ Příprava stereodvojice pro vyhodnocení
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník RELATIVNÍ A ABSOLUTNÍ ORIENTACE AAT ANALYTICKÁ AEROTRIANGULACE PŘÍPRAVA STEREODVOJICE PRO VYHODNOCENÍ Příprava stereodvojice pro vyhodnocení
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
pracovní list studenta
 Výstup RVP: Klíčová slova: pracovní list studenta Funkce kvadratická funkce Mirek Kubera žák načrtne grafy požadovaných funkcí, formuluje a zdůvodňuje vlastnosti studovaných funkcí, modeluje závislosti
Výstup RVP: Klíčová slova: pracovní list studenta Funkce kvadratická funkce Mirek Kubera žák načrtne grafy požadovaných funkcí, formuluje a zdůvodňuje vlastnosti studovaných funkcí, modeluje závislosti
VY_32_INOVACE_INF.10. Grafika v IT
 VY_32_INOVACE_INF.10 Grafika v IT Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 GRAFIKA Grafika ve smyslu umělecké grafiky
VY_32_INOVACE_INF.10 Grafika v IT Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 GRAFIKA Grafika ve smyslu umělecké grafiky
bin arn ı vyhled av an ı a bst Karel Hor ak, Petr Ryˇsav y 23. bˇrezna 2016 Katedra poˇ c ıtaˇ c u, FEL, ˇ CVUT
 binární vyhledávání a bst Karel Horák, Petr Ryšavý 23. března 2016 Katedra počítačů, FEL, ČVUT Příklad 1 Naimplementujte binární vyhledávání. Upravte metodu BinarySearch::binarySearch. 1 Příklad 2 Mysĺım
binární vyhledávání a bst Karel Horák, Petr Ryšavý 23. března 2016 Katedra počítačů, FEL, ČVUT Příklad 1 Naimplementujte binární vyhledávání. Upravte metodu BinarySearch::binarySearch. 1 Příklad 2 Mysĺım
Lineární algebra : Metrická geometrie
 Lineární algebra : Metrická geometrie (16. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 6. května 2014, 10:42 1 2 Úvod Zatím jsme se lineární geometrii věnovali v kapitole o lineárních
Lineární algebra : Metrická geometrie (16. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 6. května 2014, 10:42 1 2 Úvod Zatím jsme se lineární geometrii věnovali v kapitole o lineárních
Geometrická optika. předmětu. Obrazový prostor prostor za optickou soustavou (většinou vpravo), v němž může ležet obraz - - - 1 -
 Geometrická optika Optika je část fyziky, která zkoumá podstatu světla a zákonitosti světelných jevů, které vznikají při šíření světla a při vzájemném působení světla a látky. Světlo je elektromagnetické
Geometrická optika Optika je část fyziky, která zkoumá podstatu světla a zákonitosti světelných jevů, které vznikají při šíření světla a při vzájemném působení světla a látky. Světlo je elektromagnetické
Kreslení elipsy Andrej Podzimek 22. prosince 2005
 Kreslení elipsy Andrej Podzimek 22. prosince 2005 Kreslení elipsy v obecné poloze O co půjde Ukázat přesný matematický model elipsy Odvodit vzorce pro výpočet souřadnic důležitých bodů Nalézt algoritmus
Kreslení elipsy Andrej Podzimek 22. prosince 2005 Kreslení elipsy v obecné poloze O co půjde Ukázat přesný matematický model elipsy Odvodit vzorce pro výpočet souřadnic důležitých bodů Nalézt algoritmus
Rosenblattův perceptron
 Perceptron Přenosové funkce Rosenblattův perceptron Rosenblatt r. 1958. Inspirace lidským okem Podle fyziologického vzoru je třívrstvá: Vstupní vrstva rozvětvovací jejím úkolem je mapování dvourozměrného
Perceptron Přenosové funkce Rosenblattův perceptron Rosenblatt r. 1958. Inspirace lidským okem Podle fyziologického vzoru je třívrstvá: Vstupní vrstva rozvětvovací jejím úkolem je mapování dvourozměrného
i=1 Přímka a úsečka. Body, které leží na přímce procházející body a a b můžeme zapsat pomocí parametrické rovnice
 I. Funkce dvou a více reálných proměnných 1. Úvod Značení: V textu budeme používat označení: N pro množinu všech přirozených čísel; R pro množinu všech reálných čísel; R n pro množinu všech uspořádaných
I. Funkce dvou a více reálných proměnných 1. Úvod Značení: V textu budeme používat označení: N pro množinu všech přirozených čísel; R pro množinu všech reálných čísel; R n pro množinu všech uspořádaných
DZDDPZ3 Digitální zpracování obrazových dat DPZ. Doc. Dr. Ing. Jiří Horák Institut geoinformatiky VŠB-TU Ostrava
 DZDDPZ3 Digitální zpracování obrazových dat DPZ Doc. Dr. Ing. Jiří Horák Institut geoinformatiky VŠB-TU Ostrava Digitální zpracování obrazových dat DPZ Předzpracování (rektifikace a restaurace) Geometrické
DZDDPZ3 Digitální zpracování obrazových dat DPZ Doc. Dr. Ing. Jiří Horák Institut geoinformatiky VŠB-TU Ostrava Digitální zpracování obrazových dat DPZ Předzpracování (rektifikace a restaurace) Geometrické
maticeteorie 1. Matice A je typu 2 4, matice B je typu 4 3. Jakých rozměrů musí být matice X, aby se dala provést
 Úlohy k zamyšlení 1. Zdůvodněte, proč třetí řádek Hornerova schématu pro vyhodnocení polynomu p v bodě c obsahuje koeficienty polynomu r, pro který platí p(x) = (x c) r(x) + p(c). 2. Dokažte, že pokud
Úlohy k zamyšlení 1. Zdůvodněte, proč třetí řádek Hornerova schématu pro vyhodnocení polynomu p v bodě c obsahuje koeficienty polynomu r, pro který platí p(x) = (x c) r(x) + p(c). 2. Dokažte, že pokud
5. Plochy v počítačové grafice. (Bézier, Coons)
 5. PLOCHY V POČÍAČOVÉ GRAFICE Cíl Po prostudování této kapitoly budete umět popsat plochy používané v počítačové grafice řešit příklady z praxe, kdy jsou použity plochy Výklad Interpolační plochy - plochy,
5. PLOCHY V POČÍAČOVÉ GRAFICE Cíl Po prostudování této kapitoly budete umět popsat plochy používané v počítačové grafice řešit příklady z praxe, kdy jsou použity plochy Výklad Interpolační plochy - plochy,
2D grafika. Jak pracuje grafik s 2D daty Fotografie Statické záběry Záběry s pohybem kamery PC animace. Počítačová grafika, 2D grafika 2
 2D grafika Jak pracuje grafik s 2D daty Fotografie Statické záběry Záběry s pohybem kamery PC animace Počítačová grafika, 2D grafika 2 2D grafika PC pracuje s daným počtem pixelů s 3 (4) kanály barev (RGB
2D grafika Jak pracuje grafik s 2D daty Fotografie Statické záběry Záběry s pohybem kamery PC animace Počítačová grafika, 2D grafika 2 2D grafika PC pracuje s daným počtem pixelů s 3 (4) kanály barev (RGB
Zpracování digitalizovaného obrazu (ZDO) - Analýza pohybu
 Zpracování digitalizovaného obrazu (ZDO) - Analýza pohybu Úvod Ing. Zdeněk Krňoul, Ph.D. Katedra Kybernetiky Fakulta aplikovaných věd Západočeská univerzita v Plzni Zpracování digitalizovaného obrazu (ZDO)
Zpracování digitalizovaného obrazu (ZDO) - Analýza pohybu Úvod Ing. Zdeněk Krňoul, Ph.D. Katedra Kybernetiky Fakulta aplikovaných věd Západočeská univerzita v Plzni Zpracování digitalizovaného obrazu (ZDO)
REALIZACE BAREVNÉHO KONTRASTU DEFEKTŮ V OPTICKÉ PROSTOVĚ-FREKVENČNÍ OBLASTI SPEKTRA
 REALIZACE AREVNÉHO KONTRASTU DEFEKTŮ V OPTICKÉ PROSTOVĚFREKVENČNÍ OLASTI SPEKTRA. Úvod Antonín Mikš Jiří Novák Fakulta stavební ČVUT katedra fyziky Thákurova 7 66 9 Praha 6 V technické praxi se často vyskytuje
REALIZACE AREVNÉHO KONTRASTU DEFEKTŮ V OPTICKÉ PROSTOVĚFREKVENČNÍ OLASTI SPEKTRA. Úvod Antonín Mikš Jiří Novák Fakulta stavební ČVUT katedra fyziky Thákurova 7 66 9 Praha 6 V technické praxi se často vyskytuje
Úloha 1. Napište matici pro případ lineárního regresního spline vyjádřeného přes useknuté
 Úloha 1. Napište matici pro případ lineárního regresního spline vyjádřeného přes useknuté polynomy pro případ dvou uzlových bodů ξ 1 = 1 a ξ 2 = 4. Experimentální body jsou x = [0.2 0.4 0.6 1.5 2.0 3.0
Úloha 1. Napište matici pro případ lineárního regresního spline vyjádřeného přes useknuté polynomy pro případ dvou uzlových bodů ξ 1 = 1 a ξ 2 = 4. Experimentální body jsou x = [0.2 0.4 0.6 1.5 2.0 3.0
PŘÍMKA A JEJÍ VYJÁDŘENÍ V ANALYTICKÉ GEOMETRII
 PŘÍMKA A JEJÍ VYJÁDŘENÍ V ANALYTICKÉ GEOMETRII V úvodu analytické geometrie jsme vysvětlili, že její hlavní snahou je popsat geometrické útvary (body, vektory, přímky, kružnice,...) pomocí čísel nebo proměnných.
PŘÍMKA A JEJÍ VYJÁDŘENÍ V ANALYTICKÉ GEOMETRII V úvodu analytické geometrie jsme vysvětlili, že její hlavní snahou je popsat geometrické útvary (body, vektory, přímky, kružnice,...) pomocí čísel nebo proměnných.
Úloha 1: Lineární kalibrace
 Úloha 1: Lineární kalibrace U pacientů s podezřením na rakovinu prostaty byl metodou GC/MS měřen obsah sarkosinu v moči. Pro kvantitativní stanovení bylo nutné změřit řadu kalibračních roztoků o různé
Úloha 1: Lineární kalibrace U pacientů s podezřením na rakovinu prostaty byl metodou GC/MS měřen obsah sarkosinu v moči. Pro kvantitativní stanovení bylo nutné změřit řadu kalibračních roztoků o různé
GEODETICKÉ VÝPOČTY I.
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. TABELACE FUNKCE LINEÁRNÍ INTERPOLACE TABELACE FUNKCE Tabelace funkce se v minulosti často využívala z důvodu usnadnění
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. TABELACE FUNKCE LINEÁRNÍ INTERPOLACE TABELACE FUNKCE Tabelace funkce se v minulosti často využívala z důvodu usnadnění
Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6)
![Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6) Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6)](/thumbs/96/128965676.jpg) 1. Lineární diferenciální rovnice řádu n [MA1-18:P1.7] rovnice typu y n) + p n 1 )y n 1) +... + p 1 )y + p 0 )y = q) 6) počáteční podmínky: y 0 ) = y 0 y 0 ) = y 1 y n 1) 0 ) = y n 1. 7) Věta 1.3 : Necht
1. Lineární diferenciální rovnice řádu n [MA1-18:P1.7] rovnice typu y n) + p n 1 )y n 1) +... + p 1 )y + p 0 )y = q) 6) počáteční podmínky: y 0 ) = y 0 y 0 ) = y 1 y n 1) 0 ) = y n 1. 7) Věta 1.3 : Necht
3 Lineární kombinace vektorů. Lineární závislost a nezávislost
 3 Lineární kombinace vektorů. Lineární závislost a nezávislost vektorů. Obrázek 5: Vektor w je lineární kombinací vektorů u a v. Vektory u, v a w jsou lineárně závislé. Obrázek 6: Vektor q je lineární
3 Lineární kombinace vektorů. Lineární závislost a nezávislost vektorů. Obrázek 5: Vektor w je lineární kombinací vektorů u a v. Vektory u, v a w jsou lineárně závislé. Obrázek 6: Vektor q je lineární
