Svobodná chebská škola, základní škola a gymnázium s.r.o. Dělitelnost slovní úlohy. Dušan Astaloš. samostatná práce, případně skupinová práce
|
|
|
- Romana Němcová
- před 8 lety
- Počet zobrazení:
Transkript
1 METODICKÝ LIST DA12 Název tématu: Autor: Předmět: Dělitelnost slovní úlohy Dušan Astaloš Matematika Ročník: 6. Učebnice: Kapitola, oddíl: Metody výuky: Formy výuky: frontální, fixační samostatná práce, případně skupinová práce Cíl výuky: Získané dovednosti: Stručný obsah: Pomůcky: Slovní úlohy pracovní list Vytvořeno: 02/2010 tabulky nebo list s prvočísly
2 Slovní úlohy 1) Tři ocelové tyče o délkách 24 dm, 3 m a 160 cm mají být rozřezány na stejně dlouhé části. Urči jejich největší možnou délku a počet. 2) Na vánoční besídce dostaly děti ve škole stejné balíčky. Kolik balíčků se celkem rozdalo, když bylo do balíčků rozděleno 96 jablek, 320 bonbónů, 80 žvýkaček a 112 ořechů? Co bylo v každém balíčku? 3) Hřiště má běžeckou dráhu délky 250 metrů. Ze startovní čáry vybíhají současně dva běžci. První uběhne jedno kolo za 56 sekund, druhý za 1 minutu a 4 sekundy. Kolik kol by museli uběhnout, aby se opět ve stejnou dobu setkali na startovní čáře? Za jakou dobu se tak stane? Kolik kilometrů uběhne do té doby každý z nich? 4) Na míse leží švestky. Kolik by jich tam muselo nejméně ležet, abychom je mohli podělit rovným dílem mezi osm, deset i dvanáct dětí? 5) Z kolika dlaždic o rozměrech 15 cm a 20 cm se dá sestavit čtverec, je-li k dispozici 120 dlaždic? 6) Prodavačce květin přivezli ze zahradnictví 208 tulipánů a 156 narcisů. Kolik nejvíce kytic mohla prodavačka svázat, chtěla-li mít všechny kytice stejné? Klik tulipánů a narcisů bude v každé kytici? 7) Urči nejmenší možný počet sešitů, které by se daly rozdělit na hromádky po 6, 8, 9 nebo 10 kusech? 8) Učitelka první třídy měla na začátku roku spravedlivě rozdělit mezi své žáky 87 tužek, 145 malých sešitů a 116 velkých sešitů. Kolik dětí má paní učitelka v první třídě? Co dostal každý žák? 9) V dílně rovnají zboží zabalené v krabičkách tvaru krychle do velikých beden s rozměry 52 cm, 78 cm a 65 cm. Urči rozměr krychlové krabičky a jejich počet v plné bedně, když v bedně nesmí zůstat žádný nevyplněný prostor. 10) Ze startovní čáry vystartovali současně dva rychlobruslaři. První, jedoucí po vnitřním okruhu absolvuje celý ovál vždy za 75 sekund. Druhý, jedoucí po vnějším okruhu, za 90 sekund. Urči nejkratší možnou dobu, za kterou projedou současně prostorem startu. 11) Na veřejném vystoupení se cvičenci seřadili postupně do dvojstupů, třístupů, čtyřstupů, pětistupů a šestistupů. Urči nejmenší možný počet cvičenců, byl-li přítomen ještě jeden náhradník.
3 12) V 9:00 se na konečné zastávce místní hromadné dopravy setkaly tři autobusy. První autobus má intervaly po 20 minutách, druhý po 25 minutách a třetí po 30 minutách. V kolik hodin se opět na konečné zastávce potkají? 13) Hotelová hala obdélníkového tvaru má rozměry 12 metrů a 5,6 metru. Urči počet mramorových čtvercových dlaždic a jejich největší možný rozměr tak, aby se s nimi podlaha přesně pokryla a nemusela se žádná z dlaždic řezat. 14) Jana a Hana začali číst stejnou knihu. Jana přečetla denně 16 stránek, Hana o dvě více a tak měla knihu přečtenou o dva dny dříve než Jana. Kolik stran měla kniha, kterou děvčata četla? 15) Farmář potřebuje oplotit nově koupený pozemek pro své stádo dobytka. Pozemek má tvar obdélníka s rozměry 126 metrů a 96 metrů. Kolik kůlů na oplocení pozemku si musí farmář připravit, když chce, aby mezery mezi kůly byly stejné a větší než 5 metrů? Má více možností?
4 Výsledky: 1) Převedení na stejné jednotky: 24 dm, 30 dm, 16 dm D(24; 30; 16) = 2 24 = 2 x 2 x 2 x 3 24 : 2 = = = 2 x 3 X 5 30 : 2 = = 2 x 2 x 2 x 2 16 : 2 = 8 Tyče budou dlouhé 20 cm a bude jich celkem 35 kusů. 2) D (96; 320; 80; 112) = = 2 x 2 x 2 x 2 x 2 x 3 96 : 16 = = 2 x 2 x 2 x 2 x 2 x 2 x : 16 = = 2 x 2 x 2 x 2 x 5 80 : 16 = = 2 x 2 x 2 x 2 x : 16 = 7 Na vánoční besídce se rozdalo 16 balíčků. V jednom balíčku je 6 jablek, 20 bonbonů, 5 žvýkaček a 7 ořechů. 3) Převedeme na stejné jednotky 1 min 4 s = 64 s. n (56; 64) = 2 6 x 7 = 448 (448 s = 7 min a 28 s) 56 = 2 x 2 x 2 x 7 64 = 2 x 2 x 2 x 2 x 2 x 2 1. běžec 448 : 56 = 8 kol (8 x 250 = 2000 metrů) 2. běžec 448 : 64 = 7 kol (7 x 250 = 1750 metrů) První běžec uběhl za 8 kol 2000 metrů. Druhý běžec uběhl za 7 kol 1750 metrů. Uvedenou vzdálenost uběhli za 7 minut 28 sekund. 4) n (8; 10; 12) = 2 3 x 3 x 5 = = 2 x 2 x 2 10 = 2 x 5 12 = 2 x 2 x 3 Na míse by muselo být 120 švestek.
5 5) n (15; 20) = 2 2 x 3 x 5 = = 3 x 5 20 = 2 x 2 x 5 60 : 15 = 4 (4 x 3 = 12 dl) 120 : 15 = 8 (8 x 6 = 48 dl) 180 : 15 = 12 (12 x 9 = 108 dl) 60 : 20 = : 20 = : 20 = 9 Čtverec můžeme složit z 12, 48 nebo 108 dlaždic. 6) D (208, 156) = 2 2 x 13 = = 2 x 2 x 2 x 2 x = 2 x 2 x 3 x 13 Prodavačka svázala 52 kytic. Kytice obsahovala 4 tulipány a 3 narcisy. 7) n (6; 8; 9; 10) = 2 3 x 3 2 x 5 = = 2 x 3 8 = 2 x 2 x 2 9 = 3 x 3 10 = 2 x 5 Sešitů musí být nejméně 360 kusů. 8) D (87; 145; 116) = = 3 x = 5 x = 2 x 2 x 29 Do první třídy chodí 29 žáků. Každý žák dostal 3 tužky, 5 malých a 4 velké sešity. 9) D (52; 78; 65) = = 2 x 2 x 13 4 x 6 x 5 = = 2 x 3 x = 5 x 13 Hrana krabičky je dlouhá 13 cm. Do bedny se jich vejde ) n (75; 90) = 3 x 3 x 2 x 5 x 5 = 450 (7 min 30 s)
6 75 = 3 x 5 x 5 90 = 2 x 3 x 3 x 5 Oba rychlobruslaři projedou současně startem za 7,5 minuty. 11) n (2; 3; 4; 5; 6) = 2 2 x 3 x 5 = 60 4 = 2 x = 61 6 = 2 x 3 12) n (20; 25; 30) = 2 2 x 3 x 5 2 = 300 (5 hodin) 20 = 2 x 2 x = = 5 x 5 30 = 2 x 3 x 5 Autobusy se na konečné setkají opět ve 14 hodin. 13) Převedeme na stejné jednotky 120 dm a 56 dm. D (120; 56) = 8 dm 120 = 2 x 2 x 2 x 3 x 5 15 x 7 = = 2 x 2 x 2 x 7 Bude třeba 105 dlaždic o straně 8 dm. 14) n (16; 18) = 2 4 x 3 2 = = 2 x 2 x 2 x : 16 = : 16 = = 2 x 3 x : 18 = : 18 = 16 Kniha měla 288 stran. 15) D126 = {1; 2; 3; 6; 7; 9; 14; 18; 21; 42; 63; 126} D96 = {1; 2; 3; 4; 6; 8; 12; 16; 24; 32; 48; 96} D126 D 96 = {1; 2; 3; 6} 6 > : 6 = 21 o = 2 x x 96 = 444 m 444 : 6 = 74 k. 96 : 6 = 16 Farmář si musí připravit 74 kůlů. Je jen jediná možná délka mezery a to 6 metrů.
1,2,3,6,9,18, 1,2,3,5,6,10,15,30.
 ARNP 1 2015 Př. 9 Společný dělitel a společný násobek Společný dělitel Příklad 1: Najděte množinu všech dělitelů čísla 18 a množinu všech dělitelů čísla 30. Řešení: Množina všech dělitelů čísla 18 je množina
ARNP 1 2015 Př. 9 Společný dělitel a společný násobek Společný dělitel Příklad 1: Najděte množinu všech dělitelů čísla 18 a množinu všech dělitelů čísla 30. Řešení: Množina všech dělitelů čísla 18 je množina
Příklady pro přijímací zkoušku z matematiky školní rok 2012/2013
 Příklady pro přijímací zkoušku z matematiky školní rok 2012/2013 Test přijímací zkoušky bude obsahovat úlohy uzavřené, kdy žák vybírá správnou odpověď ze čtyř nabízených variant (správná je vždy právě
Příklady pro přijímací zkoušku z matematiky školní rok 2012/2013 Test přijímací zkoušky bude obsahovat úlohy uzavřené, kdy žák vybírá správnou odpověď ze čtyř nabízených variant (správná je vždy právě
Opakování na 2. trimestrální test z MATEMATIKY PRIMA. Dělitelnost. 3. Rozložte daná čísla na součin prvočísel: 128; 96; 78; 105; 150.
 Opakování na 2. trimestrální test z MATEMATIKY PRIMA Dělitelnost 1. Z čísel 1800; 356; 168; 855; 380; 768; 2880; 435; 2000 vyberte čísla: a) dělitelná dvěma: b) dělitelná třemi: c) dělitelná čtyřmi: d)
Opakování na 2. trimestrální test z MATEMATIKY PRIMA Dělitelnost 1. Z čísel 1800; 356; 168; 855; 380; 768; 2880; 435; 2000 vyberte čísla: a) dělitelná dvěma: b) dělitelná třemi: c) dělitelná čtyřmi: d)
8. ročník - školní kolo
 PVTHAGORIÁDA 2012/2013 8. ročník - školní kolo ZADÁNí 1) Které číslo nepatří mezi ostatní? 225; 168; 144; 289; 324; 196; 121; 361 2) Tyč byla rozříznuta na poloviny, poté jednu část dále rozřízli na dva
PVTHAGORIÁDA 2012/2013 8. ročník - školní kolo ZADÁNí 1) Které číslo nepatří mezi ostatní? 225; 168; 144; 289; 324; 196; 121; 361 2) Tyč byla rozříznuta na poloviny, poté jednu část dále rozřízli na dva
M08-01 Přijímačky nanečisto osmileté studium matematika
 M08-01 Přijímačky nanečisto osmileté studium matematika Řešení 1) Bratři Martin a Tomáš dostali stolní hru, ve které se hrálo o papírové peníze - dolary. Martin rozdělil peníze před začátkem hry tak, že
M08-01 Přijímačky nanečisto osmileté studium matematika Řešení 1) Bratři Martin a Tomáš dostali stolní hru, ve které se hrálo o papírové peníze - dolary. Martin rozdělil peníze před začátkem hry tak, že
Kód uchazeče ID:... Varianta: 14
 Fakulta informačních technologií ČVUT v Praze Přijímací zkouška z matematiky 2013 Kód uchazeče ID:.................. Varianta: 14 1. V lednu byla zaměstnancům zvýšena mzda o 16 % prosincové mzdy. Následně
Fakulta informačních technologií ČVUT v Praze Přijímací zkouška z matematiky 2013 Kód uchazeče ID:.................. Varianta: 14 1. V lednu byla zaměstnancům zvýšena mzda o 16 % prosincové mzdy. Následně
Svobodná chebská škola, základní škola a gymnázium s.r.o. procvičování obsahu a objemu prostorových těles
 METODICKÝ LIST DA55 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný obsah: Prostorová tělesa VII. slovní úlohy Astaloš Dušan Matematika šestý/sedmý
METODICKÝ LIST DA55 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný obsah: Prostorová tělesa VII. slovní úlohy Astaloš Dušan Matematika šestý/sedmý
Matematický KLOKAN 2005 (A) 2 005 002 005 (B) 20 052 005 (C) 2 007 005 (D) 202 555 (E) 202 505 (A) 8 (B) 6 (C) 4 (D) 2 (E) 1
 Matematický KLOKAN 2005 kategorie Benjamín Úlohy za 3 body 1. Vypočítej 2 005. 100 + 2 005. (A) 2 005 002 005 (B) 20 052 005 (C) 2 007 005 (D) 202 555 (E) 202 505 2. Anička a Bětka mají dohromady 10 bonbonů.
Matematický KLOKAN 2005 kategorie Benjamín Úlohy za 3 body 1. Vypočítej 2 005. 100 + 2 005. (A) 2 005 002 005 (B) 20 052 005 (C) 2 007 005 (D) 202 555 (E) 202 505 2. Anička a Bětka mají dohromady 10 bonbonů.
ILUSTRAÈNÍ TEST LIBERECKÝ KRAJ
 ILUSTRAÈNÍ TEST LIBERECKÝ KRAJ 5 NEOTVÍREJ, DOKUD NEDOSTANEŠ POKYN! Test obsahuje 30 úloh na 60 minut. Každá úloha má právì jedno správné øešení. Za správné øešení získáš 2 body. Za chybnou odpovìï ztratíš
ILUSTRAÈNÍ TEST LIBERECKÝ KRAJ 5 NEOTVÍREJ, DOKUD NEDOSTANEŠ POKYN! Test obsahuje 30 úloh na 60 minut. Každá úloha má právì jedno správné øešení. Za správné øešení získáš 2 body. Za chybnou odpovìï ztratíš
Test žáka. Zdroj testu: Celoplošná zkouška 2. Školní rok 2012/2013 MATEMATIKA. Jméno: Třída: Škola: Termín provedení testu:
 Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Ke každé z jednoduchých úloh přiřaď,
Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Ke každé z jednoduchých úloh přiřaď,
Příprava na závěrečnou písemnou práci
 Příprava na závěrečnou písemnou práci Dělitelnost přirozených čísel Osová a středová souměrnost Povrch a objem krychle a kvádru Zlomky 1) Určete, zdali jsou pravdivé následující věty. 2) a) Číslo 544 721
Příprava na závěrečnou písemnou práci Dělitelnost přirozených čísel Osová a středová souměrnost Povrch a objem krychle a kvádru Zlomky 1) Určete, zdali jsou pravdivé následující věty. 2) a) Číslo 544 721
Test žáka. Zdroj testu: Celoplošná zkouška 2. Školní rok 2012/2013 MATEMATIKA. Jméno: Třída: Škola: Termín provedení testu:
 Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Železná trubka o délce 3 metry
Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Železná trubka o délce 3 metry
Otázky z kapitoly Základní poznatky
 Otázky z kapitoly Základní poznatky 4. ledna 2016 Obsah 1 Krokované příklady (0 otázek) 1 2 Mnohočleny a lomené výrazy (88 otázek) 1 2.1 Obtížnost 2 (78 otázek)....................................... 1
Otázky z kapitoly Základní poznatky 4. ledna 2016 Obsah 1 Krokované příklady (0 otázek) 1 2 Mnohočleny a lomené výrazy (88 otázek) 1 2.1 Obtížnost 2 (78 otázek)....................................... 1
Úloha č. 1 Rozměry fotografie jsou a = 12 cm a b = 9 cm. Fotografii zvětšíme v poměru 5 : 3. Určete rozměry zvětšené fotografie.
 Slovní úlohy - řešené úlohy Úměra, poměr Úloha č. 1 Rozměry fotografie jsou a = 12 cm a b = 9 cm. Fotografii zvětšíme v poměru 5 : 3. Určete rozměry zvětšené fotografie. Každý rozměr zvětšíme tak, že jeho
Slovní úlohy - řešené úlohy Úměra, poměr Úloha č. 1 Rozměry fotografie jsou a = 12 cm a b = 9 cm. Fotografii zvětšíme v poměru 5 : 3. Určete rozměry zvětšené fotografie. Každý rozměr zvětšíme tak, že jeho
1. V závodě jsou dvě jídelny a v obou jsou stejně velké stoly. Při úplném obsazení jídelen může v jedné obědvat 72 osob a v druhé 42.
 1. V závodě jsou dvě jídelny a v obou jsou stejně velké stoly. Při úplném obsazení jídelen může v jedné obědvat 72 osob a v druhé 42. Kolik osob může nejvíce současně obědvat u jednoho stolu? Kolik je
1. V závodě jsou dvě jídelny a v obou jsou stejně velké stoly. Při úplném obsazení jídelen může v jedné obědvat 72 osob a v druhé 42. Kolik osob může nejvíce současně obědvat u jednoho stolu? Kolik je
ZLOMKY A DESETINNÁ ČÍSLA. Růžena Blažková
 ZLOMKY A DESETINNÁ ČÍSLA Růžena Blažková Úvod Se zlomky a s desetinnými čísly se setkává každý člověk, jak v běžném životě, tak v pracovních či zájmových činnostech. Z matematického hlediska není rozdíl
ZLOMKY A DESETINNÁ ČÍSLA Růžena Blažková Úvod Se zlomky a s desetinnými čísly se setkává každý člověk, jak v běžném životě, tak v pracovních či zájmových činnostech. Z matematického hlediska není rozdíl
Mária Sadloňová. Fajn MATIKA. 150 řešených příkladů (vzorek)
 Mária adloňová Fajn MATIKA (nejen) na přijímačky 50 řešených příkladů (vorek) 0 Mgr. Mária adloňová FajnMATIKA (nejen) na přijímačky 50 řešených příkladů (reklamní vorek) Mgr. Mária adloňová, 0 Vydavatel
Mária adloňová Fajn MATIKA (nejen) na přijímačky 50 řešených příkladů (vorek) 0 Mgr. Mária adloňová FajnMATIKA (nejen) na přijímačky 50 řešených příkladů (reklamní vorek) Mgr. Mária adloňová, 0 Vydavatel
Svobodná chebská škola, základní škola a gymnázium s.r.o. procvičení a zapamatování počítání a měření úhlů
 METODICKÝ LIST DA50 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný obsah: Úhly II. - Počítání a měření úhlů Astaloš Dušan Matematika šestý frontální,
METODICKÝ LIST DA50 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný obsah: Úhly II. - Počítání a měření úhlů Astaloš Dušan Matematika šestý frontální,
S = 2. π. r ( r + v )
 horní podstava plášť výška válce průměr podstavy poloměr podstavy dolní podstava Válec se skládá ze dvou shodných podstav (horní a dolní) a pláště. Podstavou je kruh. Plášť má tvar obdélníka, který má
horní podstava plášť výška válce průměr podstavy poloměr podstavy dolní podstava Válec se skládá ze dvou shodných podstav (horní a dolní) a pláště. Podstavou je kruh. Plášť má tvar obdélníka, který má
Test žáka. Zdroj testu: Celoplošná zkouška 2. Školní rok 2012/2013 MATEMATIKA. Jméno: Třída: Škola: Termín provedení testu:
 Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Trojúhelník má jeden úhel tupý,
Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Trojúhelník má jeden úhel tupý,
Matematika 9. ročník
 Matematika 9. ročník Náhradník NáhradníkJ evátá třída (Testovací klíč: SVFMFRIH) Počet správně zodpovězených otázek Počet nesprávně zodpovězených otázek 0 26 Počítání s čísly / Geometrie / Slovní úlohy
Matematika 9. ročník Náhradník NáhradníkJ evátá třída (Testovací klíč: SVFMFRIH) Počet správně zodpovězených otázek Počet nesprávně zodpovězených otázek 0 26 Počítání s čísly / Geometrie / Slovní úlohy
1 z 7 18.6.2012 8:14. 1. otázka. Které číslo musíme odečíst od čísla 250, aby výsledné číslo bylo osminásobkem čísla 25? 2. otázka
 Stonožka 9 - M 2011 - náhled testu http://ib.scio.cz/test?t=ceow8rrhgtr79v2xq7/zcppky1fbxbzulq... 1 z 7 18.6.2012 8:14 1. otázka Které číslo musíme odečíst od čísla 250, aby výsledné číslo bylo osminásobkem
Stonožka 9 - M 2011 - náhled testu http://ib.scio.cz/test?t=ceow8rrhgtr79v2xq7/zcppky1fbxbzulq... 1 z 7 18.6.2012 8:14 1. otázka Které číslo musíme odečíst od čísla 250, aby výsledné číslo bylo osminásobkem
1. Na stole jsou tři hromádky jablek. Na první je o třináct jablek méně než na druhé, na třetí hromádce je o osm
 1. Na stole jsou tři hromádky jablek. Na první je o třináct jablek méně než na druhé, na třetí hromádce je o osm jablek více než na první. Kolik jablek je dohromady na stole, víš-li, že na druhé hromádce
1. Na stole jsou tři hromádky jablek. Na první je o třináct jablek méně než na druhé, na třetí hromádce je o osm jablek více než na první. Kolik jablek je dohromady na stole, víš-li, že na druhé hromádce
ILUSTRAÈNÍ TEST LIBERECKÝ KRAJ
 ILUSTRAÈNÍ TEST LIBERECKÝ KRAJ NEOTVÍREJ, DOKUD NEDOSTANEŠ POKYN! Test obsahuje 30 úloh na 60 minut. Každá úloha má právì jedno správné øešení. Za správné øešení získáš 2 body. Za chybnou odpovìï ztratíš
ILUSTRAÈNÍ TEST LIBERECKÝ KRAJ NEOTVÍREJ, DOKUD NEDOSTANEŠ POKYN! Test obsahuje 30 úloh na 60 minut. Každá úloha má právì jedno správné øešení. Za správné øešení získáš 2 body. Za chybnou odpovìï ztratíš
Test z celoplošné zkoušky I. MATEMATIKA. 9. ročník ZŠ (kvarta G8, sekunda G6)
 Test žáka Zdroj testu: Domácí testování Školní rok 2014/2015 Test z celoplošné zkoušky I. MATEMATIKA 9. ročník ZŠ (kvarta G8, sekunda G6) Jméno: Třída: Škola: Termín testování: Datum tisku: 01. 02. 2015
Test žáka Zdroj testu: Domácí testování Školní rok 2014/2015 Test z celoplošné zkoušky I. MATEMATIKA 9. ročník ZŠ (kvarta G8, sekunda G6) Jméno: Třída: Škola: Termín testování: Datum tisku: 01. 02. 2015
Výpočet rychlosti. Autor: Pavel Broža Datum: 14. 3. 2014 Cílový ročník: 7. Život jako leporelo, registrační číslo CZ.1.07/1.4.00/21.
 Výpočet rychlosti Autor: Pavel Broža Datum: 14. 3. 2014 Cílový ročník: 7. Život jako leporelo, registrační číslo CZ.1.07/1.4.00/21.3763 Výpočet rychlosti vzor 1 Auto ujelo celkovou dráhu 14 km za celkový
Výpočet rychlosti Autor: Pavel Broža Datum: 14. 3. 2014 Cílový ročník: 7. Život jako leporelo, registrační číslo CZ.1.07/1.4.00/21.3763 Výpočet rychlosti vzor 1 Auto ujelo celkovou dráhu 14 km za celkový
Slovní úlohy řešené soustavou rovnic
 Slovní úlohy řešené soustavou rovnic Jirka s maminkou byl na nákupu. Maminka koupila 2 kg broskví a 5 kg brambor a platila 173 Kč. Sousedka koupila 3 kg broskví a 4 kg brambor a platila 186 Kč. Kolik stál
Slovní úlohy řešené soustavou rovnic Jirka s maminkou byl na nákupu. Maminka koupila 2 kg broskví a 5 kg brambor a platila 173 Kč. Sousedka koupila 3 kg broskví a 4 kg brambor a platila 186 Kč. Kolik stál
Kategorie mladší. Řešení 1. kola VI. ročník
 Kategorie mladší Úloha 1A Korálky Řešení 1. kola Způsobů, jak korálky při splnění všech Heleniných podmínek navléci, je celá řada a dá se říci, že správné jsou všechny postupy, které nakonec vedou ke správnému
Kategorie mladší Úloha 1A Korálky Řešení 1. kola Způsobů, jak korálky při splnění všech Heleniných podmínek navléci, je celá řada a dá se říci, že správné jsou všechny postupy, které nakonec vedou ke správnému
Autor: Jana Krchová Obor: Matematika. Hranoly
 Převeď na jednotky v závorce: Hranoly a) 0,5 cm 2 (mm 2 ) = 8,4 dm 2 (cm 2 ) = b) 2,3 m 2 (dm 2 ) = 0,078 m 2 (cm 2 ) = c) 0,09 ha (a) = 0,006 km 2 (a) = d) 4 a (m 2 ) = 540 cm 2 (m 2 ) = e) 23 cm 3 (mm
Převeď na jednotky v závorce: Hranoly a) 0,5 cm 2 (mm 2 ) = 8,4 dm 2 (cm 2 ) = b) 2,3 m 2 (dm 2 ) = 0,078 m 2 (cm 2 ) = c) 0,09 ha (a) = 0,006 km 2 (a) = d) 4 a (m 2 ) = 540 cm 2 (m 2 ) = e) 23 cm 3 (mm
PASPORT MÍSTNÍCH KOMUNIKACÍ - Obec Deštné - ZIMNÍ ÚDRŽBA
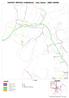 ÚK51 ÚK50 ÚK53 ÚK45 19c ÚK46 ÚK49 ÚK52 II/309 ÚK58 ÚK48 II/309 ÚK47 ÚK41 21c ÚK40 ÚK42 20c III/3093 ÚK43 ÚK44 ÚK38 13d II/310 13d ÚK30 ÚK39 ÚK37 ÚK36 ÚK35 ÚK34 ÚK21 10d 9c ÚK15 7c ÚK19 ÚK17 26c 27c 26c-M1
ÚK51 ÚK50 ÚK53 ÚK45 19c ÚK46 ÚK49 ÚK52 II/309 ÚK58 ÚK48 II/309 ÚK47 ÚK41 21c ÚK40 ÚK42 20c III/3093 ÚK43 ÚK44 ÚK38 13d II/310 13d ÚK30 ÚK39 ÚK37 ÚK36 ÚK35 ÚK34 ÚK21 10d 9c ÚK15 7c ÚK19 ÚK17 26c 27c 26c-M1
MATEMATIKA vyšší úroveň obtížnosti
 MATEMATIKA vyšší úroveň obtížnosti DIDAKTICKÝ TEST MAIVD11C0T01 ILUSTRAČNÍ TEST Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % 1 Základní informace k zadání zkoušky Didaktický test obsahuje
MATEMATIKA vyšší úroveň obtížnosti DIDAKTICKÝ TEST MAIVD11C0T01 ILUSTRAČNÍ TEST Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % 1 Základní informace k zadání zkoušky Didaktický test obsahuje
MATEMATIKA / 1. ROČNÍK. Strategie (metody a formy práce)
 MATEMATIKA / 1. ROČNÍK Učivo Čas Strategie (metody a formy práce) Pomůcky Numerace v oboru do 7 30 pokládání koleček rozlišování čísel znázorňování kreslení a představivost třídění - číselné obrázky -
MATEMATIKA / 1. ROČNÍK Učivo Čas Strategie (metody a formy práce) Pomůcky Numerace v oboru do 7 30 pokládání koleček rozlišování čísel znázorňování kreslení a představivost třídění - číselné obrázky -
(ukázky tématického celku učiva zpracovaného formou žákovských projektů)
 Krabicování (ukázky tématického celku učiva zpracovaného formou žákovských projektů) Úvod hledání vhodného přístupu Moje zkušenosti z dlouhodobého vyučování na základní škole opřené o studium literatury
Krabicování (ukázky tématického celku učiva zpracovaného formou žákovských projektů) Úvod hledání vhodného přístupu Moje zkušenosti z dlouhodobého vyučování na základní škole opřené o studium literatury
Matematika I: Aplikované úlohy
 Matematika I: Aplikované úlohy Zuzana Morávková Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava 260. Řy 283 - Pálkař Zadání Pálkař odpálí míč pod úhlem α = 30 a rychlostí
Matematika I: Aplikované úlohy Zuzana Morávková Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava 260. Řy 283 - Pálkař Zadání Pálkař odpálí míč pod úhlem α = 30 a rychlostí
Přiřaď k páčkám 1, 2, 3, 4, 5, 6, 7 písmena a, b, c, d a urči,
 21. Na obrázku je robot, který na sobě má 7 páček, osmá schází. Přiřaď k páčkám 1, 2, 3, 4, 5, 6, 7 písmena a, b, c, d a urči, jak má vypadat osmá, chybějící páčka. 32 6. Na obrázku je podivný letící hmyz
21. Na obrázku je robot, který na sobě má 7 páček, osmá schází. Přiřaď k páčkám 1, 2, 3, 4, 5, 6, 7 písmena a, b, c, d a urči, jak má vypadat osmá, chybějící páčka. 32 6. Na obrázku je podivný letící hmyz
MATEMATIKA základní úroveň obtížnosti
 MATEMATIKA základní úroveň obtížnosti DIDAKTICKÝ TEST Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % Základní informace k zadání zkoušky Didaktický test obsahuje 26 úloh. Časový limit pro
MATEMATIKA základní úroveň obtížnosti DIDAKTICKÝ TEST Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % Základní informace k zadání zkoušky Didaktický test obsahuje 26 úloh. Časový limit pro
MATEMATIKA+ MAMPD14C0T01 DIDAKTICKÝ TEST. 2.1 Pokyny k otevřeným úlohám. 1 Základní informace k zadání zkoušky. 2.2 Pokyny k uzavřeným úlohám
 MATEMATIKA+ DIDAKTICKÝ TEST MAMPD14C0T01 Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % 1 Základní informace k zadání zkoušky Didaktický test obsahuje 3 úloh. Časový limit pro řešení didaktického
MATEMATIKA+ DIDAKTICKÝ TEST MAMPD14C0T01 Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % 1 Základní informace k zadání zkoušky Didaktický test obsahuje 3 úloh. Časový limit pro řešení didaktického
MATEMATIKA Charakteristika vyučovacího předmětu 1. stupeň
 MATEMATIKA Charakteristika vyučovacího předmětu 1. stupeň Obsahové, časové a organizační vymezení Předmět se vyučuje jako samostatný předmět v 1. - 5. ročníku 5 hodin týdně. Vzdělávání v matematice zaměřeno
MATEMATIKA Charakteristika vyučovacího předmětu 1. stupeň Obsahové, časové a organizační vymezení Předmět se vyučuje jako samostatný předmět v 1. - 5. ročníku 5 hodin týdně. Vzdělávání v matematice zaměřeno
Mateřská škola a Základní škola při dětské léčebně, Křetín 12
 VY_32_INOVACE_DUM.M.14 Mateřská škola a Základní škola při dětské léčebně, Křetín 12 Autor: Mgr. Miroslav Páteček Vytvořeno: duben 2012 Klíčová slova: Matematika a její aplikace Početní operace s přirozenými
VY_32_INOVACE_DUM.M.14 Mateřská škola a Základní škola při dětské léčebně, Křetín 12 Autor: Mgr. Miroslav Páteček Vytvořeno: duben 2012 Klíčová slova: Matematika a její aplikace Početní operace s přirozenými
MATEMATIKA. 1 Základní informace k zadání zkoušky. 2 Pravidla správného zápisu řešení. 3.2 Pokyny k uzavřeným úlohám 7-15 DIDAKTICKÝ TEST
 MATEMATIKA PŘIJÍMACÍ ZKOUŠKY DIDAKTICKÝ TEST B TS-M5MBCINT Maximální bodové hodnocení: 50 bodů 1 Základní informace k zadání zkoušky Didaktický test obsahuje 15 úloh. Časový limit pro řešení didaktického
MATEMATIKA PŘIJÍMACÍ ZKOUŠKY DIDAKTICKÝ TEST B TS-M5MBCINT Maximální bodové hodnocení: 50 bodů 1 Základní informace k zadání zkoušky Didaktický test obsahuje 15 úloh. Časový limit pro řešení didaktického
Základní škola Moravský Beroun, okres Olomouc
 Charakteristika vyučovacího předmětu matematika Vyučovací předmět má časovou dotaci čtyři hodiny týdně v prvním ročníku, pět hodin týdně ve druhém až pátém ročníku, pět hodin týdně v šestém ročníku a čtyři
Charakteristika vyučovacího předmětu matematika Vyučovací předmět má časovou dotaci čtyři hodiny týdně v prvním ročníku, pět hodin týdně ve druhém až pátém ročníku, pět hodin týdně v šestém ročníku a čtyři
Autor: Jana Krchová Obor: Matematika. Procenta
 Procenta Vypočítej zpaměti: a) 123 : 78 : 4356 : 10 82 : 28 190 : 6 : b) 9 : 0,5 : 0,34 : 6,4 : 0,072 : 0,73 : Vypočítej: 3 a) : 4 2 5 : 6 7 : 5 12 : 7 15 : 1 2 3 4 8 b) 1 : 2 : 3 : 2 : 5 : 2 5 4 7 9 1
Procenta Vypočítej zpaměti: a) 123 : 78 : 4356 : 10 82 : 28 190 : 6 : b) 9 : 0,5 : 0,34 : 6,4 : 0,072 : 0,73 : Vypočítej: 3 a) : 4 2 5 : 6 7 : 5 12 : 7 15 : 1 2 3 4 8 b) 1 : 2 : 3 : 2 : 5 : 2 5 4 7 9 1
RNDr. Zdeněk Horák 23. 11. 2013 VII.
 Jméno RNDr. Zdeněk Horák Datum 23. 11. 2013 Ročník VII. Vzdělávací oblast MATEMATIKA A JEJÍ APLIKACE Vzdělávací obor MATEMATIKA Tematický okruh ZLOMKY Téma klíčová slova Slovní úlohy se zlomky, početní
Jméno RNDr. Zdeněk Horák Datum 23. 11. 2013 Ročník VII. Vzdělávací oblast MATEMATIKA A JEJÍ APLIKACE Vzdělávací obor MATEMATIKA Tematický okruh ZLOMKY Téma klíčová slova Slovní úlohy se zlomky, početní
1. Určete proud procházející vodičem, jestliže za jednu minutu prošel jeho průřezem náboj a) 150 C, b) 30 C.
 ELEKTRICKÝ PROUD 1. Určete proud procházející vodičem, jestliže za jednu minutu prošel jeho průřezem náboj a) 150 C, b) 30 C. 2. Vodičem prochází stejnosměrný proud. Za 30 minut jím prošel náboj 1 800
ELEKTRICKÝ PROUD 1. Určete proud procházející vodičem, jestliže za jednu minutu prošel jeho průřezem náboj a) 150 C, b) 30 C. 2. Vodičem prochází stejnosměrný proud. Za 30 minut jím prošel náboj 1 800
Komunikativní Sociální a personální
 Název programu Název cyklu Vypracoval Anotace Cílová skupina Časová dotace Potřebné čtenářské dovednosti (porozumění textu, rychlost) Osnova programu Vzdělávací oblasti Klíčové kompetence Jak to chodí
Název programu Název cyklu Vypracoval Anotace Cílová skupina Časová dotace Potřebné čtenářské dovednosti (porozumění textu, rychlost) Osnova programu Vzdělávací oblasti Klíčové kompetence Jak to chodí
I. kolo kategorie Z5
 62. ročník Matematické olympiády I. kolo kategorie Z5 Z5 I 1 Maminka zaplatila v knihkupectví 2 700 Kč. Platila dvěma druhy bankovek, dvousetkorunovými a pětisetkorunovými, a přesně. Kolik kterých bankovek
62. ročník Matematické olympiády I. kolo kategorie Z5 Z5 I 1 Maminka zaplatila v knihkupectví 2 700 Kč. Platila dvěma druhy bankovek, dvousetkorunovými a pětisetkorunovými, a přesně. Kolik kterých bankovek
MIŠ MAŠ. 17 OBVODY, obsahy 7.4.2014.notebook. May 18, 2015. Základní škola Nýrsko, Školní ulice, příspěvková organizace.
 Základní škola Nýrsko, Školní ulice, příspěvková organizace (www.sumavanet.cz/zsskolni/projekt2 zakladni.asp) Název projektu: MIŠ MAŠ Moderní Interaktivní Škola Možností a Šancí (pro každého žáka) Číslo
Základní škola Nýrsko, Školní ulice, příspěvková organizace (www.sumavanet.cz/zsskolni/projekt2 zakladni.asp) Název projektu: MIŠ MAŠ Moderní Interaktivní Škola Možností a Šancí (pro každého žáka) Číslo
Páťáci a matematika I. Přirozená čísla větší než milión. 1. Zapište čísla do tabulky. 2. Přečtěte čísla zapsaná v tabulce. Rozepište do tabulky čísla:
 Páťáci a matematika I Přirozená čísla větší než milión 1. Zapište čísla do tabulky 2. Přečtěte čísla zapsaná v tabulce. Rozepište do tabulky čísla: 1 3. Napočítejte deset čísel od nuly při počítání 4.
Páťáci a matematika I Přirozená čísla větší než milión 1. Zapište čísla do tabulky 2. Přečtěte čísla zapsaná v tabulce. Rozepište do tabulky čísla: 1 3. Napočítejte deset čísel od nuly při počítání 4.
Přijímačky nanečisto - 2011
 Přijímačky nanečisto - 2011 1. Vypočtěte: 0,5 2 + (-0,5) 2 (- 0,1) 3 = a) 0,001 b) 0,51 c) 0,499 d) 0,501 2. Vypočtěte: a) 0,4 b) - 0,08 c) 2 3 d) 2 3. Určete číslo s tímto rozvinutým zápisem v desítkové
Přijímačky nanečisto - 2011 1. Vypočtěte: 0,5 2 + (-0,5) 2 (- 0,1) 3 = a) 0,001 b) 0,51 c) 0,499 d) 0,501 2. Vypočtěte: a) 0,4 b) - 0,08 c) 2 3 d) 2 3. Určete číslo s tímto rozvinutým zápisem v desítkové
Jméno a příjmení. Pokud budete chtít svou odpověď opravit, zabarvěte původně zakřížkovaný čtvereček a zakřížkujte nový čtvereček.
 MATEMATIKA 5 M5PDD19C0T04 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 14 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby Časový limit pro řešení didaktického testu
MATEMATIKA 5 M5PDD19C0T04 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 14 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby Časový limit pro řešení didaktického testu
HMOTNÝ BOD, POHYB, POLOHA, TRAJEKTORIE, DRÁHA, RYCHLOST
 Škola: Autor: Šablona: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Vladislav Válek VY_32_INOVACE_MGV_F_SS_1S1_D02_Z_MECH_Hmotny_bod_r ychlost_pl Člověk a příroda Fyzika Mechanika
Škola: Autor: Šablona: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Vladislav Válek VY_32_INOVACE_MGV_F_SS_1S1_D02_Z_MECH_Hmotny_bod_r ychlost_pl Člověk a příroda Fyzika Mechanika
Vypočítejte délku tělesové úhlopříčky krychle o hraně délky a cm.
 Vypočítejte délku tělesové úhlopříčky krychle o hraně délky a cm. 8 cm u s = 11,3137085 cm pomocí Pythagorovy věty z pravoúhlého ABC u t = 13,85640646 cm opět pomocí Pythagorovy věty z pravoúhlého ACA'
Vypočítejte délku tělesové úhlopříčky krychle o hraně délky a cm. 8 cm u s = 11,3137085 cm pomocí Pythagorovy věty z pravoúhlého ABC u t = 13,85640646 cm opět pomocí Pythagorovy věty z pravoúhlého ACA'
Matematika číslo a početní operace PDF MZ 4 / VY_MA2_42_01-36
 VY_42_INOVACE_MA2_01-36 Název školy Základní škola Benešov, Jiráskova 888 Číslo projektu CZ.1.07/1.4.00/21.1278 Název projektu Pojďte s námi Číslo a název šablony klíčové aktivity IV/2 Inovace a zkvalitnění
VY_42_INOVACE_MA2_01-36 Název školy Základní škola Benešov, Jiráskova 888 Číslo projektu CZ.1.07/1.4.00/21.1278 Název projektu Pojďte s námi Číslo a název šablony klíčové aktivity IV/2 Inovace a zkvalitnění
PŘIJÍMACÍ ZKOUŠKY II.termín
 MATEMATIKA Obor: 79-41-K/81 Součet bodů: Opravil: Kontroloval: Vítejte na Gymnáziu v Omské u přijímacích zkoušek z matematiky. Dnes budete řešit úlohy čtverečkové a kostičkové. Úlohy můžete řešit v libovolném
MATEMATIKA Obor: 79-41-K/81 Součet bodů: Opravil: Kontroloval: Vítejte na Gymnáziu v Omské u přijímacích zkoušek z matematiky. Dnes budete řešit úlohy čtverečkové a kostičkové. Úlohy můžete řešit v libovolném
3. Mocnina a odmocnina. Pythagorova věta
 . Mocnina a odmocnina. Pythagorova věta 7. ročník -. Mocnina, odmocnina, Pythagorovavěta.. Mocnina... Vymezení pojmu Součin stejných činitelů můţeme napsat v podobě mocniny. Například : součin...... můţeme
. Mocnina a odmocnina. Pythagorova věta 7. ročník -. Mocnina, odmocnina, Pythagorovavěta.. Mocnina... Vymezení pojmu Součin stejných činitelů můţeme napsat v podobě mocniny. Například : součin...... můţeme
1.2.1 Desetinná čísla I
 1.2.1 Desetinná čísla I Předpoklady: S přirozenými čísly dokážeme hodně, ale vždy s nimi nevystačíme. Takto by například vypadalo olympijské finále v běhu na 1 m mužů, kdybychom uměli měřit pouze na celé
1.2.1 Desetinná čísla I Předpoklady: S přirozenými čísly dokážeme hodně, ale vždy s nimi nevystačíme. Takto by například vypadalo olympijské finále v běhu na 1 m mužů, kdybychom uměli měřit pouze na celé
3. Středoškolská stereometrie v anaglyfech
 3. Středoškolská stereometrie v anaglyfech V předchozích dvou kapitolách jsme zjistili, jak se zobrazují tělesa ve středovém promítání a hlavně v lineární perspektivě, a jak pomocí těchto promítání vytvořit
3. Středoškolská stereometrie v anaglyfech V předchozích dvou kapitolách jsme zjistili, jak se zobrazují tělesa ve středovém promítání a hlavně v lineární perspektivě, a jak pomocí těchto promítání vytvořit
Fyzikální veličiny. Převádění jednotek
 Fyzikální veličiny Vlastnosti těles, které můžeme měřit nebo porovnávat nazýváme fyzikální veličiny. Značka fyzikální veličiny je písmeno, kterým se název fyzikální veličiny nahradí pro zjednodušení zápisu.
Fyzikální veličiny Vlastnosti těles, které můžeme měřit nebo porovnávat nazýváme fyzikální veličiny. Značka fyzikální veličiny je písmeno, kterým se název fyzikální veličiny nahradí pro zjednodušení zápisu.
Název: VY_32_INOVACE_01_C_12_Slovní úlohy obvod a obsah kruhu
 SLOVNÍ ÚLOHY OBVOD A OBSAH KRUHU Název školy: Základní škola Karla Klíče Hostinné Autor: Mgr. Hana Kuříková Název: VY_32_INOVACE_01_C_12_Slovní úlohy obvod a obsah kruhu Téma: Matematika 8.ročník Číslo
SLOVNÍ ÚLOHY OBVOD A OBSAH KRUHU Název školy: Základní škola Karla Klíče Hostinné Autor: Mgr. Hana Kuříková Název: VY_32_INOVACE_01_C_12_Slovní úlohy obvod a obsah kruhu Téma: Matematika 8.ročník Číslo
Digitální učební materiál
 Digitální učební materiál Projekt Šablona CZ.1.07/1.5.00/34.0415 Inovujeme, inovujeme III/2 Inovace a zkvalitnění výuky prostřednictvím ICT (DUM) DUM č. VY_32_INOVACE_CH29_1_15 ŠVP Podnikání RVP 64-41-L/51
Digitální učební materiál Projekt Šablona CZ.1.07/1.5.00/34.0415 Inovujeme, inovujeme III/2 Inovace a zkvalitnění výuky prostřednictvím ICT (DUM) DUM č. VY_32_INOVACE_CH29_1_15 ŠVP Podnikání RVP 64-41-L/51
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost.
 Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
1. Vypočítejte: 775522 : 11. 2. Základní čtvercová síť má délky strany čtverců 1 cm. Určete obsah vyznačeného obrazce, odpověď zdůvodněte.
 Z A D Á N Í Gymnázium Ohradní Praha 4 / 5. třída / 03-04 / 1. kolo 1. Vypočítejte: 775522 : 11 2. Základní čtvercová síť má délky strany čtverců 1 cm. Určete obsah vyznačeného obrazce, odpověď zdůvodněte.
Z A D Á N Í Gymnázium Ohradní Praha 4 / 5. třída / 03-04 / 1. kolo 1. Vypočítejte: 775522 : 11 2. Základní čtvercová síť má délky strany čtverců 1 cm. Určete obsah vyznačeného obrazce, odpověď zdůvodněte.
V jídelně jsou tři stoly se stejným počtem židlí. Celkem si k nim posedalo 18 dětí, žádná židle nezbyla prázdná. Kolik dětí sedělo u každého stolu?
 Úloha 1 Ke každé z jednoduchých úloh přiřaď, jaký výpočet určuje správný výsledek úlohy. 18 : 3 = 18 + 3 = 18. 3 = 18-3 = V jídelně jsou tři stoly se stejným počtem židlí. Celkem si k nim posedalo 18 dětí,
Úloha 1 Ke každé z jednoduchých úloh přiřaď, jaký výpočet určuje správný výsledek úlohy. 18 : 3 = 18 + 3 = 18. 3 = 18-3 = V jídelně jsou tři stoly se stejným počtem židlí. Celkem si k nim posedalo 18 dětí,
Test žáka. Zdroj testu: Celoplošná zkouška 2. Školní rok 2012/2013 MATEMATIKA. Jméno: Třída: Škola: Termín provedení testu:
 Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Trojúhelník má jeden úhel tupý,
Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Trojúhelník má jeden úhel tupý,
Název projektu: Poznáváme sebe a svět, chceme poznat více
 Název projektu: Poznáváme sebe a svět, chceme poznat více Registrační číslo projektu: CZ.1.07/1.4.00/21.2970 Identifikátor materiálu Název klíčové aktivity Vzdělávací oblast Vzdělávací předmět / obor Tematický
Název projektu: Poznáváme sebe a svět, chceme poznat více Registrační číslo projektu: CZ.1.07/1.4.00/21.2970 Identifikátor materiálu Název klíčové aktivity Vzdělávací oblast Vzdělávací předmět / obor Tematický
Očekávané výstupy podle RVP ZV Učivo Přesahy a vazby
 Předmět: MATEMATIKA Ročník: 3. Časová dotace: 5 hodin týdně Očekávané výstupy podle RVP ZV Učivo Přesahy a vazby Používá přirozená čísla k modelování reálných situací, počítá předměty v daném souboru,
Předmět: MATEMATIKA Ročník: 3. Časová dotace: 5 hodin týdně Očekávané výstupy podle RVP ZV Učivo Přesahy a vazby Používá přirozená čísla k modelování reálných situací, počítá předměty v daném souboru,
Určete všechna čísla z množiny {0,2,3,4,5,6,7,8,9,10}, která jsou děliteli čísel: a) 24 b) 210 c) 240 d) 216 e)7560
 Dělitelnost čísel Prvočíslo je přirozené číslo, které je beze zbtku dělitelné právě dvěma různými čísl, a to číslem jedna a sebou samým (ted není prvočíslo). Přirozená čísla různá od jedné, která nejsou
Dělitelnost čísel Prvočíslo je přirozené číslo, které je beze zbtku dělitelné právě dvěma různými čísl, a to číslem jedna a sebou samým (ted není prvočíslo). Přirozená čísla různá od jedné, která nejsou
Matematická statistika
 Matematická statistika Daniel Husek Gymnázium Rožnov pod Radhoštěm, 8. A8 Dne 12. 12. 2010 v Rožnově pod Radhoštěm Osnova Strana 1) Úvod 3 2) Historie matematické statistiky 4 3) Základní pojmy matematické
Matematická statistika Daniel Husek Gymnázium Rožnov pod Radhoštěm, 8. A8 Dne 12. 12. 2010 v Rožnově pod Radhoštěm Osnova Strana 1) Úvod 3 2) Historie matematické statistiky 4 3) Základní pojmy matematické
Slovní úlohy v učivu matematiky 1. stupně základní školy
 Slovní úlohy v učivu matematiky 1. stupně základní školy V každé matematické úloze jde o to, abychom dokázali platnost (pravdivost) nějakého výroku. Podle toho, o jaký výrok jde, máme různé druhy úloh.
Slovní úlohy v učivu matematiky 1. stupně základní školy V každé matematické úloze jde o to, abychom dokázali platnost (pravdivost) nějakého výroku. Podle toho, o jaký výrok jde, máme různé druhy úloh.
Svobodná chebská škola, základní škola a gymnázium s.r.o.
 METODICKÝ LIST DA42 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Poměry IV. měřítko mapy Astaloš Dušan Matematika sedmý frontální, fixační samostatná práce upevnění znalostí
METODICKÝ LIST DA42 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Poměry IV. měřítko mapy Astaloš Dušan Matematika sedmý frontální, fixační samostatná práce upevnění znalostí
Svobodná chebská škola, základní škola a gymnázium s.r.o. Dušan Astaloš. samostatná práce, případně skupinová práce. pochopení znaků vztahů mezi čísly
 METODICKÝ LIST DA6 Název tématu: Autor: Předmět: Dělitelnost dělitel a násobek, sudá a lichá čísla, prvočísla a čísla složená Dušan Astaloš Matematika Ročník: 6. Učebnice: Kapitola, oddíl: Metody výuky:
METODICKÝ LIST DA6 Název tématu: Autor: Předmět: Dělitelnost dělitel a násobek, sudá a lichá čísla, prvočísla a čísla složená Dušan Astaloš Matematika Ročník: 6. Učebnice: Kapitola, oddíl: Metody výuky:
1. otázka. 2. otázka = Ve které z následujících možností je výsledek uvedeného výpočtu? 3. otázka
 1. otázka Paní Irena měla černé, bílé a černobílé kočky. elkově jich měla dvanáct. Z toho bylo šest černých a čtyři bílé. Jakou část z celkového počtu představují černobílé kočky? 2. otázka 24 + 12 3 5
1. otázka Paní Irena měla černé, bílé a černobílé kočky. elkově jich měla dvanáct. Z toho bylo šest černých a čtyři bílé. Jakou část z celkového počtu představují černobílé kočky? 2. otázka 24 + 12 3 5
Jméno a příjmení. Pokud budete chtít svou odpověď opravit, zabarvěte původně zakřížkovaný čtvereček a zakřížkujte nový čtvereček.
 MATEMATIKA 5 M5PCD19C0T03 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 14 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby Časový limit pro řešení didaktického testu
MATEMATIKA 5 M5PCD19C0T03 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 14 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby Časový limit pro řešení didaktického testu
1.2.2 Měříme délku II
 1.2.2 Měříme délku II Předpoklady: 010201 Pomůcky: metr, zavinovací metr, krejčovský metr, šuplera, metrický šroub, pásmo, provázek s vyznačeným metrem, provázek s vyznačenými decimetry, pravítko 30 cm
1.2.2 Měříme délku II Předpoklady: 010201 Pomůcky: metr, zavinovací metr, krejčovský metr, šuplera, metrický šroub, pásmo, provázek s vyznačeným metrem, provázek s vyznačenými decimetry, pravítko 30 cm
Vzorové příklady k přijímacím zkouškám. 1) Doplňte číselné řady o další dvě čísla. a) 3, 6, 12, 24, 48, 96,... b) 875, 764, 653, 542, 431,...
 Vzorové příklady k přijímacím zkouškám ) Doplňte číselné řady o další dvě čísla. a), 6,, 4, 48, 96,... b) 87, 764, 6, 4, 4,... c), 6, 8,,, 0, 6,... d),,, 7,,, 7, 9,,... e) ; ; ; ; ; 8 ) Doplňte číslo místo.
Vzorové příklady k přijímacím zkouškám ) Doplňte číselné řady o další dvě čísla. a), 6,, 4, 48, 96,... b) 87, 764, 6, 4, 4,... c), 6, 8,,, 0, 6,... d),,, 7,,, 7, 9,,... e) ; ; ; ; ; 8 ) Doplňte číslo místo.
1.2.5 Měříme objem III
 1.2.5 Měříme objem III Předpoklady: 0204 Pomůcky: odměrné válce, 8 kostek Př. 1: Nakresli z pamětí schéma pro převádění jednotek objemu. Schéma pro převádění jednotek objemu: dvě řádky: o krychlové jednotky
1.2.5 Měříme objem III Předpoklady: 0204 Pomůcky: odměrné válce, 8 kostek Př. 1: Nakresli z pamětí schéma pro převádění jednotek objemu. Schéma pro převádění jednotek objemu: dvě řádky: o krychlové jednotky
VM 2. Dělitelnost přir. čísel násobek, dělitel, znaky dělitelnosti.notebook. September 21, 2015. 1. Vzdělávací oblast: Matematika a její aplikace
 Registrační číslo projektu: Název projektu: Název a číslo globálního grantu: CZ.1.07/1.1.12/02.0010 Šumavská škola = evropská škola Zvyšování kvality ve vzdělání v Plzeňském kraji CZ.1.07/1.1.12 Název
Registrační číslo projektu: Název projektu: Název a číslo globálního grantu: CZ.1.07/1.1.12/02.0010 Šumavská škola = evropská škola Zvyšování kvality ve vzdělání v Plzeňském kraji CZ.1.07/1.1.12 Název
Číslo projektu CZ.1.07/1.4.00/21.1405 Název sady materiálů Technické práce 6. ročník Název materiálu VY_32_INOVACE_15_Měření a orýsování kovů Autor
 Číslo projektu CZ.1.07/1.4.00/21.1405 Název sady materiálů Technické práce 6. ročník Název materiálu VY_32_INOVACE_15_Měření a orýsování kovů Autor Frait Josef Měření a orýsování kovů Abychom mohli začít
Číslo projektu CZ.1.07/1.4.00/21.1405 Název sady materiálů Technické práce 6. ročník Název materiálu VY_32_INOVACE_15_Měření a orýsování kovů Autor Frait Josef Měření a orýsování kovů Abychom mohli začít
Kinematika pohyb rovnoměrný
 DUM Základy přírodních věd DUM III/2-T3-03 Téma: Kinematika rovnoměrný Střední škola Rok: 2012 2013 Varianta: A Zpracoval: Mgr. Pavel Hrubý VÝKLAD Kinematika rovnoměrný Kinematika je jedna ze základních
DUM Základy přírodních věd DUM III/2-T3-03 Téma: Kinematika rovnoměrný Střední škola Rok: 2012 2013 Varianta: A Zpracoval: Mgr. Pavel Hrubý VÝKLAD Kinematika rovnoměrný Kinematika je jedna ze základních
Test žáka. Zdroj testu: Celoplošná zkouška 2. Školní rok 2012/2013 MATEMATIKA. Jméno: Třída: Škola: Termín provedení testu:
 Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Prohlédni si obrázek a vyber správnou
Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Prohlédni si obrázek a vyber správnou
Jakýkoliv jiný způsob záznamu odpovědí (např. dva křížky u jedné úlohy) bude považován za nesprávnou odpověď.
 MATEMATIKA 5 M5PZD16C0T02 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 16 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: psací a rýsovací potřeby Časový limit pro řešení didaktického testu je 60
MATEMATIKA 5 M5PZD16C0T02 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 16 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: psací a rýsovací potřeby Časový limit pro řešení didaktického testu je 60
MATEMATIKA. 5. třída. Čemu se rovná uvedený součet v metrech? (A) 1,65015 m (B) 16,515 m (C) 16,0515 m (D) 16,5 m
 MATEMATIKA 5. třída 1. Jaké číslo je o 12 stovek, 4 desítky a 9 jednotek menší než 2000? (A) 751 (B) 861 (C) 1249 (D) 1831 2. Které z následujících tvrzení o pravoúhlém trojúhelníku je správné? (A) Dvě
MATEMATIKA 5. třída 1. Jaké číslo je o 12 stovek, 4 desítky a 9 jednotek menší než 2000? (A) 751 (B) 861 (C) 1249 (D) 1831 2. Které z následujících tvrzení o pravoúhlém trojúhelníku je správné? (A) Dvě
Stereometrie pro učební obory
 Variace 1 Stereometrie pro učební obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz 1. Vzájemná poloha prostorových
Variace 1 Stereometrie pro učební obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz 1. Vzájemná poloha prostorových
Převody jednotek Vedlejší jednotky objemu
 Převody jednotek Vedlejší jednotky objemu Pár užitečných rad, jak postupovat při převádění jednotek objemu. Zopakujme si již známé jednotky objemu: Základní jednotka: metr krychlový ( kubík značka m Odvozené
Převody jednotek Vedlejší jednotky objemu Pár užitečných rad, jak postupovat při převádění jednotek objemu. Zopakujme si již známé jednotky objemu: Základní jednotka: metr krychlový ( kubík značka m Odvozené
Základní škola Karviná Nové Město tř. Družby 1383
 Základní škola Karviná Nové Město tř. Družby 1383 Projekt OP VK oblast podpory 1.4 Zlepšení podmínek pro vzdělávání na základních školách Registrační číslo projektu: CZ.1.07/1.4.00/21.3526 Název projektu:
Základní škola Karviná Nové Město tř. Družby 1383 Projekt OP VK oblast podpory 1.4 Zlepšení podmínek pro vzdělávání na základních školách Registrační číslo projektu: CZ.1.07/1.4.00/21.3526 Název projektu:
Modely diskrétní náhodné veličiny. Jiří Neubauer. Katedra ekonometrie, FVL, UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.
 Katedra ekonometrie, FVL, UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Po(λ) je možné použít jako model náhodné veličiny, která nabývá hodnot 0, 1, 2,... a udává buď počet událostí,
Katedra ekonometrie, FVL, UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Po(λ) je možné použít jako model náhodné veličiny, která nabývá hodnot 0, 1, 2,... a udává buď počet událostí,
Přehled učiva matematiky 7. ročník ZŠ
 Přehled učiva matematiky 7. ročník ZŠ I. ARITMETIKA 1. Zlomky a racionální čísla Jestliže rozdělíme něco (= celek) na několik stejných dílů, nazývá se každá část celku zlomkem. Zlomek tři čtvrtiny = tři
Přehled učiva matematiky 7. ročník ZŠ I. ARITMETIKA 1. Zlomky a racionální čísla Jestliže rozdělíme něco (= celek) na několik stejných dílů, nazývá se každá část celku zlomkem. Zlomek tři čtvrtiny = tři
MATEMATIKA 6. ROČNÍK. Sada pracovních listů CZ.1.07/1.1.16/
 MATEMATIKA 6. ROČNÍK CZ.1.07/1.1.16/02.0079 Sada pracovních listů Resumé Sada pracovních listů zaměřená na opakování, procvičení a upevnění učiva 6. ročníku přirozená čísla a desetinná čísla. Může být
MATEMATIKA 6. ROČNÍK CZ.1.07/1.1.16/02.0079 Sada pracovních listů Resumé Sada pracovních listů zaměřená na opakování, procvičení a upevnění učiva 6. ročníku přirozená čísla a desetinná čísla. Může být
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost.
 Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu ázev projektu školy Klíčová aktivita III/2 EU PEÍZE ŠKOLÁM CZ.1.7/1.4./21.2146
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu ázev projektu školy Klíčová aktivita III/2 EU PEÍZE ŠKOLÁM CZ.1.7/1.4./21.2146
MATEMATIKA NEOTVÍREJ, DOKUD NEDOSTANEŠ POKYN OD ZADÁVAJÍCÍHO! 5. třída
 MATEMATIKA 5. třída NEOTVÍREJ, DOKUD NEDOSTANEŠ POKYN OD ZADÁVAJÍCÍHO! JMÉNO TŘÍDA ČÍSLO ŽÁKA AŽ ZAHÁJÍŠ PRÁCI, NEZAPOMEŇ: www.scio.cz, s.r.o. Pobřežní 34, 186 00 Praha 8 tel.: 234 705 555 fax: 234 705
MATEMATIKA 5. třída NEOTVÍREJ, DOKUD NEDOSTANEŠ POKYN OD ZADÁVAJÍCÍHO! JMÉNO TŘÍDA ČÍSLO ŽÁKA AŽ ZAHÁJÍŠ PRÁCI, NEZAPOMEŇ: www.scio.cz, s.r.o. Pobřežní 34, 186 00 Praha 8 tel.: 234 705 555 fax: 234 705
- zvládá orientaci na číselné ose
 Příklady možné konkretizace minimální doporučené úrovně pro úpravy očekávaných výstupů v rámci podpůrných opatření pro využití v IVP předmětu Matematika Ukázka zpracována s využitím školního vzdělávacího
Příklady možné konkretizace minimální doporučené úrovně pro úpravy očekávaných výstupů v rámci podpůrných opatření pro využití v IVP předmětu Matematika Ukázka zpracována s využitím školního vzdělávacího
Cvičení podporující prostorovou představivost. Josef Molnár molnar@inf.upol.cz. Podpořit prostorovou představivost pomocí cvičení různé úrovně.
 ROMOTE MSc OIS TÉMATU MATEMATIKA 3 ázev Tematický celek Jméno a e-mailová adresa autora Cíle Obsah omůcky Cvičení podporující prostorovou představivost Geometrie Josef Molnár molnar@inf.upol.cz odpořit
ROMOTE MSc OIS TÉMATU MATEMATIKA 3 ázev Tematický celek Jméno a e-mailová adresa autora Cíle Obsah omůcky Cvičení podporující prostorovou představivost Geometrie Josef Molnár molnar@inf.upol.cz odpořit
Dělitelnost přirozených čísel - opakování
 Dělitelnost přirozených čísel - opakování Do kolika různých obdélníků můžeme sestavit 60 čtvercových dlaždic tak, abychom vždycky spotřebovali všechny dlaždice a nerozbíjeli je? Závěr: Všichni tito dělitelé
Dělitelnost přirozených čísel - opakování Do kolika různých obdélníků můžeme sestavit 60 čtvercových dlaždic tak, abychom vždycky spotřebovali všechny dlaždice a nerozbíjeli je? Závěr: Všichni tito dělitelé
Projekt: Zlepšení výuky na ZŠ Schulzovy sady registrační číslo: CZ.1.07./1.4.00/21.2581. Datum: 7. 02. - 10. 2. 2012. Ročník: 7.
 Projekt: Zlepšení výuky na ZŠ Schulzovy sady registrační číslo: CZ.1.07./1.4.00/21.2581 Autor: Marie Smolíková Datum: 7. 02. - 10. 2. 2012 Ročník: 7. Vzdělávací oblast: Vzdělávací obor: Tematický okruh:
Projekt: Zlepšení výuky na ZŠ Schulzovy sady registrační číslo: CZ.1.07./1.4.00/21.2581 Autor: Marie Smolíková Datum: 7. 02. - 10. 2. 2012 Ročník: 7. Vzdělávací oblast: Vzdělávací obor: Tematický okruh:
Přijímací test z českého jazyka - osmileté studium
 Přijímací test z českého jazyka - osmileté studium (1) Edudant a Francimor, s nimi školní mládež, osaměli v domě, kterýžto se nazývá Loupežnická beseda. (2) Pan loupežník Kokrhelini mínil, že by se měl
Přijímací test z českého jazyka - osmileté studium (1) Edudant a Francimor, s nimi školní mládež, osaměli v domě, kterýžto se nazývá Loupežnická beseda. (2) Pan loupežník Kokrhelini mínil, že by se měl
Test žáka. Zdroj testu: Celoplošná zkouška 2. Školní rok 2012/2013 MATEMATIKA. Jméno: Třída: Škola: Termín provedení testu:
 Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Na obrázku jsou čtyři červené
Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Na obrázku jsou čtyři červené
Racionální čísla. Množinu racionálních čísel značíme Q. Zlomky můžeme při počítání s nimi:
 Racionální čísla Racionální číslo je číslo vyjádřené ve tvaru zlomku p kde p je celé číslo a q je q číslo přirozené. Tento zápis je jednoznačný pokud čísla p, q jsou nesoudělná, zlomek je v základním tvaru.
Racionální čísla Racionální číslo je číslo vyjádřené ve tvaru zlomku p kde p je celé číslo a q je q číslo přirozené. Tento zápis je jednoznačný pokud čísla p, q jsou nesoudělná, zlomek je v základním tvaru.
Seminární práce k předmětu Didaktika matematiky. Téma práce: Aplikační matematické úlohy
 Seminární práce k předmětu Didaktika matematiky Téma práce: Aplikační matematické úlohy Vypracovala: Kateřina Fišerová 25. dubna 2009 Příklad 1 (Derivace funkce jedné proměnné) Do stejnosměrného elektrického
Seminární práce k předmětu Didaktika matematiky Téma práce: Aplikační matematické úlohy Vypracovala: Kateřina Fišerová 25. dubna 2009 Příklad 1 (Derivace funkce jedné proměnné) Do stejnosměrného elektrického
1. VYMEZENÍ ODBORNÉ STÁŽE
 1. VYMEZENÍ ODBORNÉ STÁŽE Šablona stáže představuje rámec odborné stáže pro typovou pozici a obsahuje požadavky na obsah a průběh stáže, na stážistu i na poskytovatele stáže. Bílá pole označují text, který
1. VYMEZENÍ ODBORNÉ STÁŽE Šablona stáže představuje rámec odborné stáže pro typovou pozici a obsahuje požadavky na obsah a průběh stáže, na stážistu i na poskytovatele stáže. Bílá pole označují text, který

