54. ročník Matematické olympiády 2004/2005
|
|
|
- Božena Sedláková
- před 4 lety
- Počet zobrazení:
Transkript
1 54. ročník Matematické olympiády 004/005 Úlohy ústředního kola kategorie P 1. soutěžní den Na řešení úloh máte 4,5 hodiny čistého času. Řešení každého příkladu musí obsahovat: Popis řešení, to znamená slovní popis použitého algoritmu, argumenty zdůvodňující jeho správnost (případně důkaz správnosti algoritmu), diskusi o efektivitě vašeho řešení (časová a paměťová složitost). Slovní popis řešení musí být jasný a srozumitelný i bez nahlédnutí do samotného zápisu algoritmu (do programu). Program. V úlohách P-III-1 a P-III- je třeba uvést dostatečně podrobný zápis algoritmu, nejlépe ve tvaru zdrojového textu nejdůležitějších částí programu v jazyce Pascal nebo C. Ze zápisu můžete vynechat jednoduché operace jako vstupy, výstupy, implementaci jednoduchých matematických vztahů apod. V úloze P-III-3 zapište navržený algoritmus ve formě programu v jazyce Alik. Hodnotí se nejen správnost programu, ale také kvalita popisu řešení a efektivita zvoleného algoritmu. P-III-1 Náhrdelníky K. O. Lektor je sběratel náhrdelníků. Náhrdelníky se liší počtem, pořadím a druhy použitých drahokamů. Jeho finanční zdroje nejsou neomezené, proto by se chtěl vyhnout tomu, aby kupoval více kusů stejného typu náhrdelníku. Vymyslel tedy kódování, které funguje takto: každému druhu drahokamů přiřadil písmeno abecedy a tyto kódy zapsal v pořadí, v jakém se nacházejí na náhrdelníku, počínaje libovolným z nich. Dále si pořídil stroj, který pro zadaný kód zjistí, zda již má příslušný náhrdelník ve sbírce. Obchodníci s náhrdelníky si samozřejmě rychle povšimli slabiny tohoto systému pokud náhrdelník pootočili, případně obrátili, kód se změnil a K. O. Lektor si tak nakoupil několik duplikátů například náhrdelník ABCA si koupil i jako AABC a ACBA. Chtěl by tedy svůj stroj vylepšit tak, aby tuto situaci rozeznal. Napište program implementující toto vylepšení. Program dostane na vstupu několik kódů náhrdelníků x 1,..., x N (1 N ) a měl by pro každý z nich vypsat, zda si ho má K. O. Lektor koupit nebo ne tak, aby získal každý typ náhrdelníků právě jednou. Pokud je náhrdelník x i různý od všech náhrdelníků x 1,..., x i 1 (včetně rotací a zrcadlení), program odpoví Kup to, v opačném případě odpoví Podvod. Program může využívat starý stroj jako černou skříňku, která si pamatuje množinu kódů náhrdelníků (na počátku práce množinu prázdnou) a je schopna do této množiny kódy přidávat (zavoláním procedury Pridej) a zjišťovat, jestli stroj již nějaký kód zná (zavoláním funkce UzMam, která vrací true (1 v C), pokud někdy předtím byla zavolána procedure Pridej pro stejný kód): int UzMam (const char *kod); /* v C */ void Pridej (const char *kod); function UzMam (var kod:string):boolean; { v Pascalu } procedure Pridej (var kod:string); K. O. Lektor má na váš program následující požadavky: Paměťová složitost nesmí záviset na počtu testovaných náhrdelníků. Časová složitost by měla být co nejnižší, přičemž volání funkce starého stroje počítáme jako operace běžící v lineárním čase. Ze dvou programů o stejné časové složitosti pak považuje za lepší ten, který funkce starého stroje volá méněkrát. Příklad: V levém sloupci je vstup, v pravém jediný správný výstup: ABCA ACBA AABC P-III- Mosty Kup to Podvod Podvod Magické observatoře (MO) nedávno otevřely nový areál v Horních Mokřadech. Podnebí v Horních Mokřadech je bohužel poměrně deštivé, a tak se vedení MO rozhodlo, že propojí všechny budovy v areálu nadzemními krytými mosty. Vedení MO samozřejmě chce, aby si dodatečné stavební úpravy vyžádaly co nejmenší náklady. Proto požaduje, aby celková délka mostů, které propojí budovy v areálu, byla co nejmenší. Navíc, kvůli vlivu energetických zón v okolí Horních Mokřad, musí všechny mosty vést severojižně. Vaším úkolem je vytvořit algoritmus, který pro zadanou mapu areálu MO navrhne nejlepší možné propojení budov severojižními mosty. Pokud všechny budovy nelze navzájem propojit, pak algoritmus vypíše vhodnou zprávu. Na vstupu algoritmus obdrží mapu areálu MO jako čtvercovou síť o N řádcích a M sloupcích. Budovy v areálu jsou reprezentovány znaky x, volná prostranství tečkami. Budova je maximální oblast tvořená políčky x, která se mezi sebou dotýkají hranami. Vaším úkolem je navrhnout propojení budov severojižními (na mapě svislými) mosty tak, aby mezi každými dvěma budovami existovala cesta používající pouze políček x a mostů: Mezi dvěma políčky x lze přejít, pokud sousedí hranou, mosty lze používat pouze v severojižním směru, tj. seshora dolů nebo zdola nahoru v jejich směru na mapě. Při (popisu) řešení této úlohy se soustřeďte na efektivní nalezení optimálního propojení mezi budovami a zdůvodnění správnosti navrženého algoritmu. 1
2 Příklad 1: Pro M = 8 a N = 5 uvažme následující mapu areálu:..xxxxx....x...x...x.x.x....xxx..xx Areál je tvořen čtyřmi budovami (na následujícím obrázku jsou jejich políčka označena čísly 1 až 4; všimněte si, že políčka s čísly 1 a tvoří dvě různé budovy): Optimální řešení úlohy pro zadanou mapu je propojit dvojici budov 1 a 3 mostem délky jedna, dvojici budov a 4 rovněž mostem délky jedna a budovy 1 a 4 mostem délky tři: Protože mosty lze používat pouze severojižně, nemůžeme z mostu spojujícího budovy 1 a 4 přejít do budovy a je třeba vybudovat i most mezi budovami a 4. Příklad : Pro M = 6 a N = 5 uvažme následující mapu areálu: x...x x.xx.x x...x Areál je tvořen dvěma budovami a k jejich propojení stačí vybudovat jeden most délky 1: Příklad 3: x...x x.xx.x x...x Pro M = 5 a N = 4 uvažme následující mapu areálu: xxx..... xxx.....xx Areál je tvořen třemi budovami. Protože budovu v pravém dolním rohu nelze spojit s žádnou jinou budovou mostem, všechny budovy nelze vzájemně propojit. P-III-3 ALÍK Sestrojte program pro stroj Alik, který spočte dvojkový logaritmus zadaného nenulového čísla x, tedy pozici nejlevější jedničky v x. Pozice bitů rostou zprava doleva, nejnižší řád je na pozici 0. Příklad: Dvojkový logaritmus dvojkového čísla je 5, logaritmus z je 0. Studijní text: (stejný jako v krajském kole) Aritmeticko-logický integerový kalkulátor (zkráceně Alik) je počítací stroj pracující s W -bitovými celými čísly v rozsahu 0 až W 1 včetně; kdykoliv budeme hovořit o číslech, půjde o tato čísla. Budeme je obvykle zapisovat ve dvojkové soustavě polotučnými číslicemi a vždy si na začátek dvojkového zápisu doplníme příslušný počet nul, aby číslic (bitů) bylo právě W. Většinou také nebudeme rozlišovat mezi číslem a jeho dvojkovým zápisem, takže i-tým bitem čísla budeme rozumět i-tý bit jeho dvojkového zápisu (bity číslujeme zprava doleva od 0 do W 1). Paměť stroje je tvořena 6 registry pojmenovanými a až z. Každý registr vždy obsahuje jedno číslo. Alik se řídí programem, což je posloupnost přiřazovacích příkazů typu registr := výraz, přičemž výraz může obsahovat konstanty (čísla zapsaná ve dvojkové soustavě), registry, závorky a následující operátory (řecká písmena značí podvýrazy, v pravém sloupci jsou priority operátorů): α + β sečte čísla α a β. Pokud je výsledek větší než W 1, číslice vyšších řádů odřízne. Jinými 4 slovy, počítá součet modulo W. α β odečte od čísla α číslo β. Pokud je α < β, spočte W + α β, čili rozdíl modulo W. 4 α β vynásobí dvě čísla, výsledek opět modulo W. 6 α / β vydělí číslo α číslem β; dělení nulou dá vždy výsledek 0. 6 α % β vrátí zbytek po dělení čísla α číslem β, čili α β (α / β); pokud je β = 0, je výsledek roven α. 6 α spočte bitovou negaci čísla α, což je číslo, jehož i-tý bit je 0 právě tehdy, je-li i-tý bit čísla α roven 1, a naopak. α β bitové operace: and, or a xor. Vyhodnocují se tak, že se i-tý bit výsledku spočte z i-tého bitu α β čísla α a i-tého bitu čísla β podle následujících tabulek: α β 0 0 = = = = = = = = = = = =
3 α << β α >> β posune číslo α o β bitů doleva, čili doplní doprava β nul a odřízne prvních β bitů zleva, aby byl výsledek opět W -bitový. posune číslo α o β bitů doprava, čili doplní doleva β nul a odřízne posledních β bitů vpravo, aby byl výsledek opět W -bitový. Pokud závorky neurčí jinak, vyhodnocují se operátory s vyšší prioritou před operátory s nižší prioritou. V rámci stejné priority se pak vyhodnocuje zleva doprava (s výjimkou operátoru, který je unární, a tudíž se musí vyhodnocovat zprava doleva). Příklad 0: (jak fungují operátory; zde máme W = 4) a + b c + d = (a + (b c)) + d zde zafungují priority operátorů = 0011 nejvyšší bit výsledku se již oříznul = 0010 odčítáme modulo 16 = = 0001 takto funguje and = 0111 takto or = 0110 a takto xor (1 << 11) 1 = = 0111 jak vyrobit pomocí << posloupnost jedniček a a = 1111 jak získat z čehokoliv samé jedničky Výpočet probíhá takto: Nejprve se do registru x nastaví vstup (to je vždy jedno číslo) a do ostatních registrů nuly. Poté se provedou všechny příkazy v pořadí, v jakém jsou v programu uvedeny, přičemž vždy se nejprve vyhodnotí výraz na pravé straně a teprve poté se jeho výsledek uloží do registru, takže uvnitř výrazu je ještě možné pracovat s původní hodnotou registru. Po dokončení posledního příkazu se hodnota v registru y interpretuje jako výsledek výpočtu. Hodnoty v ostatních registrech mohou být libovolné. Často budeme potřebovat, aby program mohl pracovat s většími čísly, než je číslo na vstupu, takže budeme rozlišovat velikost vstupu N (tj. počet bitů potřebných k zapisu vstupní hodnoty) a velikost W registrů a mezivýsledků, kterou si při psaní programu sami určíme. Pokud bychom ovšem povolili exponenciálně velká čísla (tedy W = N ), mohli bychom cokoliv spočíst v konstantním čase stačilo by do jedné dlouhatánské konstanty uvedené v programu zakódovat všechny možné výsledky programu pro všechny hodnoty vstupu. Tak dlouhé registry lze však stěží považovat za realistické, proto přijměme omezení, že W musí být polynomiální ve velikosti vstupu, čili že existuje konstanta k taková, že pro každé N je W N k. Ne vždy si ovšem vystačíme s jedním programem, který funguje pro všechny velikosti vstupu mnohdy potřebujeme podle N měnit hodnoty pomocných konstant v programu, někdy také nějakou operaci opakovat vícekrát v závislosti na velikosti vstupu. Povolíme si tedy programy zapisovat obecněji, a to tak, že uvedeme seznam pravidel, jež nám pro každé N vytvoří program, který počítá správně pro všechny vstupy velikosti N. [Formálně bychom tato pravidla mohli zavést třeba jako programy v nějakém klasickém programovacím jazyce. My si ale formalismus odpustíme a budeme je popisovat slovně.] Při řešení úloh budeme chtít, aby časová složitost vygenerovaných programů, tedy jejich délka v závislosti na N, byla co nejmenší. Mezi stejně rychlými programy je pak lepší ten, který si vystačí s kratšími čísly, čili s menším W (to je analogie prostorové složitosti). Podobně jako u klasických programů ovšem budeme v obou případech přehlížet multiplikativní konstanty. Příklad 1: Sestrojte program pro Alik, který dostane na vstupu nenulové číslo a vrátí výsledek 1 právě tehdy, je-li toto číslo mocninou dvojky, jinak vrátí nulu. Řešení: Nejdříve si všimněme, že mocniny dvojky jsou právě čísla, která obsahují právě jeden jedničkový bit. Sledujme chování následujícího jednoduchého programu. Zmiňme ale ještě konvence, které budeme používat při psaní všech ukázkových programů: V levém sloupci naleznete jednotlivé příkazy, v pravém sloupci obecný tvar spočítané hodnoty pro libovolné N. Pokud se nějaká číslice nebo skupina číslic opakuje vícekrát, značíme opakování exponentem, tedy 0 8 je osm nul, (01) 3 je zkratka za Řeckými písmeny značíme blíže neurčené skupiny bitů. a := x 1 b := x a x = α10 i a = α01 i b = α00 i Číslo v registru a se od x vždy liší tím, že nejpravější 1 se změní na 0 a všechny 0 vpravo od ní se změní na 1. Proto b = x a se musí od x lišit právě přepsáním nejpravější 1 na 0. (To proto, že bity vlevo od této 1 jsou stále stejné a α α = α, zatímco ve zbytku čísla se vždy anduje 0 s 1, což dá nulu.) A jelikož mocniny dvojky jsou právě čísla, v jejichž dvojkovém zápisu je právě jedna 1, spočte náš program v b nulu právě tehdy, je-li x mocninou dvojky (nebo nulou, což jsme si ale zakázali). Zbývá tedy vyřešit, jak z nuly udělat požadovanou jedničku a z nenuly nulu. K tomu si zavedeme operaci r := if (s, t, u), která bude realizovat podmínku: pokud s 0, přiřadí r := t, jinak r := u. Provedeme to jednoduchým trikem: rozšíříme si registry o jeden pomocný bit vlevo, nastavíme v r tento bit na jedničku a sledujeme, zda se zmenšením vzniklého čísla o jedničku tento bit změní na nulu nebo ne: v := s 10 N v = 1s v := v 1 v = 1s (je-li s 0), jinak 01 N v := v 10 N v = 10 N nebo 00 N v := v >> N v = 0 N 1 nebo 0 N 0 v := v 1 v = 0 N+1 nebo 1 N+1 3
4 r := (u v) (t v) r = t nebo u Stačí tedy na konec našeho programu přidat y := if (b, 0, 1) y = 0 nebo 1 a máme program, který rozpoznává mocniny dvojky v konstantním čase a používá k tomu čísla o N + 1 = O(N) bitech. Ještě si ukažme, jak bude probíhat výpočet pro dva konkrétní 8-bitové vstupy (tehdy je N = 8 a W = 9): x = x = a := x 1 a = a = b := x a b = b = v := b v = v = v := v 1 v = v = v := v v = v = v := v >> 8 v = v = v := v 1 v = v = y := ( v) ( v) y = y = Příklad : Sestrojte program pro Alik, který spočte binární paritu vstupního čísla, čili vrátí 0 nebo 1 podle toho, zda je v tomto čísle sudý nebo lichý počet jedničkových bitů. Řešení: Binární parita P (x) čísla x = x N 1... x 1 x 0 je podle definice rovna x 0 x 1... x N 1. Jelikož operace je asociativní (α (β γ) = (α β) γ) a komutativní (α β = β α), můžeme tento vztah pro N = k (to opět můžeme bez újmy na obecnosti předpokládat) přeuspořádat na P (x) = (x 0 x N/ ) (x 1 x N/+1 )... (x N/ 1 x N 1 ), což je ovšem parita čísla vzniklého vyxorováním horní a dolní poloviny čísla x. Takže výpočet parity N-bitového čísla můžeme na konstantní počet příkazů převést na výpočet parity N/-bitového čísla, ten zase na výpočet parity N/4-bitového čísla atd., až po log N krocích na paritu 1-bitového čísla, která je ovšem rovna číslu samému. Paritu tedy vypočteme na logaritmický počet příkazů pracujících s N-bitovými čísly takto: p := x >> N/ p = horních N/ bitů x q := x 1 N/ q = dolních N/ bitů x x := p q x = N/-bitové číslo s paritou jako původní x x := (x >> N/4) (x 1 N/4 ) x = N/4-bitové... (můžeme psát zkráceně)... x := (x >> 1) (x 1) x = 1-bitové... y := x y = x (už jen zkopírovat výsledek) Náš programovací jazyk samozřejmě 1 N/ a podobné operace nemá, ale to vůbec nevadí, protože je vždy používáme jen na podvýrazy závisící pouze na N, takže je v programu můžeme pro každé N uvést jako konstanty. Například pro N = 8 bude výpočet probíhat takto: x = p := x >> 4 p = 0011 q := x 1111 q = 0110 x := p q x = 0101 x := (x >> ) (x 11) x = 00 x := (x >> 1) (x 1) x = 0 y := x y = Příklad 3: Ve vzorovém řešení úlohy P-I-4 b) jsme potřebovali přesunout posloupnost jedniček na konec čísla, tedy číslo tvaru 0 i 1 j 0 k převést na 0 i 0 k 1 j. To je pomocí dělení možné provést v konstantním čase třeba takto: x = 0 i 1 j 0 k a := x (x 1) a = 0 i 1 j 1 00 k (viz Příklad 1) b := x a b = 0 i 0 j 1 10 k y := x / b b = 0 i 0 k 1 j Zde jsme využili toho, že dělení mocninou dvojky je možné použít jako bitový posun doprava, ovšem zadaný místo počtu bitů, o které se má posouvat, číslem majícím 1 na pozici, která se má po posunu objevit úplně vpravo. 4
5 54. ročník Matematické olympiády 004/005 Úlohy ústředního kola kategorie P. soutěžní den P-III-4 Zaklínadla Program: Vstup: Výstup: magie.pas / magie.c / magie.cpp magie.in magie.out Při výzkumu vlivu přesmyček na magická zaklínadla se podařilo dokázat, že výměna takových dvou sousedních písmen v zaklínadle, která se nevyskytují v (anglické) abecedě těsně vedle sebe, nemá vliv na magický účinek zaklínadla. Například místo oblíbeného abraka lze stejně dobře použít arbaka, ale nikoliv již baraka. Samozřejmě lze sousední písmena v zaklínadle prohazovat vícekrát, takže z abraka lze postupně odvodit následující (stejně účinná) zaklínadla: abraka arbaka rabaka rabkaa rakbaa rkabaa krabaa. Povšimněte si, že pořadí výměn sousedních písmen v zaklínadle můžeme otočit, a tedy ze zaklínadla krabaa lze též získat původní abraka. Dvě zaklínadla nazveme ekvivalentní, jestliže je lze mezi sebou převést posloupností výměn dvou sousedních písmen, která se nevyskytují v abecedě těsně vedle sebe. Například zaklínadla abraka a krabaa jsou ekvivalentní, ale zaklínadla dabra a badar ne. Soutěžní úloha: Napište program, který pro zadané dvojice zaklínadel určí, zda jsou či nejsou ekvivalentní. Vstup: Vstupní soubor magie.in obsahuje několik bloků, z nichž každý odpovídá jedné dvojici zaklínadel. Obě zaklínadla v jednom bloku mají vždy stejný počet písmen N, 1 N , který je uveden na prvním řádku každého bloku. Následuje N řádků, z nichž každý obsahuje dvě malá písmena anglické abecedy (tzn. znaky z rozmezí a... z), která jsou oddělená jednou mezerou. První znak na i-tém z těchto řádků je i-tý znak prvního zaklínadla, druhý znak je i-tý znak druhého zaklínadla. Vstupní soubor je ukončen řádkem, který obsahuje jediné číslo 0. Výstup: Výstupní soubor magie.out obsahuje pro každý blok vstupního souboru jeden řádek. Tento řádek obsahuje slovo ekvivalentni, pokud jsou zadaná zaklínadla ekvivalentní, a slovo neekvivalentni, pokud nejsou. Řádky musí být vypsány v pořadí, v jakém se jim odpovídající bloky vyskytují v souboru magie.in. Příklad: Soubor magie.in 6 a k b r r a a b k a a a 5 d b a a b d r a a r 0 Soubor magie.out ekvivalentni neekvivalentni 1
6 P-III-5 Asfaltéři Program: Vstup: Výstup: asfalt.pas / asfalt.c / asfalt.cpp asfalt.in asfalt.out Ve Viácii si občané již dlouho stěžovali na nekvalitní silnice. Když si jednou i vrchní cestář při cestě do práce v kočáře vyrazil zub, rozhodl se k radikální akci. Doslechl se, že v sousední zemi začali na cesty používat novinku zvanou asfalt, a myšlenka na vyasfaltování všech silnic ve Viácii byla na světě. A jak si vrchní cestář usmyslel, tak se i stalo. Při realizaci nápadu se ale nižší cestáři museli potýkat s nemilým problémem: asfalt se do Viácie dovážel v ohromných barelech, ve kterých bylo asfaltu tak akorát na dvě cesty (byly to opravdu ohromné barely). Potíž byla v tom, že jakmile se barel narazil a asfalt z něj začal vytékat, nedal se už proud asfaltu ničím zastavit a bylo tedy nutné vyasfaltovat najednou dvě na sebe navazující cesty. Jenže jak rozvrhnout asfaltování, aby cestáři neskončili ve městě s poloplným barelem a se všemi cestami vedoucími do města už vyasfaltovanými? Důsledky zalití náměstí a několika přilehlých čtvrtí do asfaltu by byly pro cestáře jistě nemilé... Rozhodli se proto přizvat k problému vás, jakožto na asfalt vzaté odborníky. Soutěžní úloha: Napište program, který pro zadané propojení měst cestami rozhodne, zda je možno cesty podle popsaných pravidel vyasfaltovat, a pokud ano, vypíše jednu z možností, jak rozvrhnout, která dvojice cest bude asfaltována ze kterého barelu. Vstup: Na prvním řádku vstupního souboru asfalt.in se nacházejí dvě celá čísla N a M oddělená mezerou, 1 N , 1 M počet měst a počet cest ve Viácii. Dále ve vstupním souboru následuje M řádků popisujících jednotlivé cesty. Každý řádek obsahuje dvě celá čísla A a B oddělená mezerou čísla měst (města číslujeme od jedné do N), mezi kterými cesta vede. Předpokládejte, že mezi každými dvěma městy se lze po cestách dostat (pokud ne přímo, tak přes jiná města). Výstup: Výstupní soubor asfalt.out bude buď obsahovat jediný řádek s textem Cesty nelze vyasfaltovat., pokud neexistuje způsob, jak vyasfaltovat všechny cesty a neskončit s poloplným barelem v nějakém městě, nebo bude obsahovat M/ řádků s popisem postupu asfaltování. Každý řádek postupu bude popisovat využití jednoho barelu s asfaltem. Bude obsahovat tři celá čísla oddělená mezerou číslo města, ve kterém má asfaltování začít, číslo města, do kterého se má pokračovat a číslo města, ve kterém má asfaltování skončit. Každá cesta musí být vyasfaltována právě jednou. Příklad 1: Soubor asfalt.in Příklad : Soubor asfalt.in Soubor asfalt.out Cesty nelze vyasfaltovat. Soubor asfalt.out
Algoritmizace a programování
 Algoritmizace a programování Výrazy Operátory Výrazy Verze pro akademický rok 2012/2013 1 Operace, operátory Unární jeden operand, operátor se zapisuje ve většině případů před operand, v některých případech
Algoritmizace a programování Výrazy Operátory Výrazy Verze pro akademický rok 2012/2013 1 Operace, operátory Unární jeden operand, operátor se zapisuje ve většině případů před operand, v některých případech
MATEMATICKÁ OLYMPIÁDA
 MATEMATICKÁ OLYMPIÁDA NA STŘEDNÍCH ŠKOLÁCH kategorie A, B, C a P 54. ROČNÍK, 2004/2005 http://home.pf.jcu.cz/mo Studenti středních škol, zveme vás k účasti v matematické olympiádě, jejíž soutěžní kategorie
MATEMATICKÁ OLYMPIÁDA NA STŘEDNÍCH ŠKOLÁCH kategorie A, B, C a P 54. ROČNÍK, 2004/2005 http://home.pf.jcu.cz/mo Studenti středních škol, zveme vás k účasti v matematické olympiádě, jejíž soutěžní kategorie
Čtvrtek 8. prosince. Pascal - opakování základů. Struktura programu:
 Čtvrtek 8 prosince Pascal - opakování základů Struktura programu: 1 hlavička obsahuje název programu, použité programové jednotky (knihovny), definice konstant, deklarace proměnných, všechny použité procedury
Čtvrtek 8 prosince Pascal - opakování základů Struktura programu: 1 hlavička obsahuje název programu, použité programové jednotky (knihovny), definice konstant, deklarace proměnných, všechny použité procedury
59. ročník Matematické olympiády 2009/2010
 59. ročník Matematické olympiády 2009/2010 Úlohy ústředního kola kategorie P 1. soutěžní den Na řešení úloh máte 4,5 hodiny čistého času. Řešení každé úlohy pište na samostatný list papíru. Při soutěži
59. ročník Matematické olympiády 2009/2010 Úlohy ústředního kola kategorie P 1. soutěžní den Na řešení úloh máte 4,5 hodiny čistého času. Řešení každé úlohy pište na samostatný list papíru. Při soutěži
1. lekce. do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme:
 1. lekce 1. Minimální program do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme: #include #include int main() { printf("hello world!\n"); return 0; 2.
1. lekce 1. Minimální program do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme: #include #include int main() { printf("hello world!\n"); return 0; 2.
1.1 Struktura programu v Pascalu Vstup a výstup Operátory a některé matematické funkce 5
 Obsah Obsah 1 Programovací jazyk Pascal 1 1.1 Struktura programu v Pascalu.................... 1 2 Proměnné 2 2.1 Vstup a výstup............................ 3 3 Operátory a některé matematické funkce 5
Obsah Obsah 1 Programovací jazyk Pascal 1 1.1 Struktura programu v Pascalu.................... 1 2 Proměnné 2 2.1 Vstup a výstup............................ 3 3 Operátory a některé matematické funkce 5
Paměť počítače. alg2 1
 Paměť počítače Výpočetní proces je posloupnost akcí nad daty uloženými v paměti počítače Data jsou v paměti reprezentována posloupnostmi bitů (bit = 0 nebo 1) Připomeňme: paměť je tvořena řadou 8-mi bitových
Paměť počítače Výpočetní proces je posloupnost akcí nad daty uloženými v paměti počítače Data jsou v paměti reprezentována posloupnostmi bitů (bit = 0 nebo 1) Připomeňme: paměť je tvořena řadou 8-mi bitových
Programovací jazyk Pascal
 Programovací jazyk Pascal Syntaktická pravidla (syntaxe jazyka) přesná pravidla pro zápis příkazů Sémantická pravidla (sémantika jazyka) pravidla, která každému příkazu přiřadí přesný význam Všechny konstrukce
Programovací jazyk Pascal Syntaktická pravidla (syntaxe jazyka) přesná pravidla pro zápis příkazů Sémantická pravidla (sémantika jazyka) pravidla, která každému příkazu přiřadí přesný význam Všechny konstrukce
1. lekce. do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme:
 1. lekce 1. Minimální program do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme: #include #include int main() { printf("hello world!\n"); return 0; 2.
1. lekce 1. Minimální program do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme: #include #include int main() { printf("hello world!\n"); return 0; 2.
5 Přehled operátorů, příkazy, přetypování
 5 Přehled operátorů, příkazy, přetypování Studijní cíl Tento studijní blok má za cíl pokračovat v základních prvcích jazyka Java. Konkrétně budou uvedeny detaily týkající se operátorů. Doba nutná k nastudování
5 Přehled operátorů, příkazy, přetypování Studijní cíl Tento studijní blok má za cíl pokračovat v základních prvcích jazyka Java. Konkrétně budou uvedeny detaily týkající se operátorů. Doba nutná k nastudování
53. ročník Matematické olympiády 2003/2004
 5. ročník Matematické olympiády 00/004 Úlohy celostátního kola kategorie P. soutěžní den Na řešení úloh máte 4,5 hodiny čistého času. Řešení každého příkladu musí obsahovat: Popis řešení, to znamená slovní
5. ročník Matematické olympiády 00/004 Úlohy celostátního kola kategorie P. soutěžní den Na řešení úloh máte 4,5 hodiny čistého času. Řešení každého příkladu musí obsahovat: Popis řešení, to znamená slovní
LEKCE 6. Operátory. V této lekci najdete:
 LEKCE 6 Operátory V této lekci najdete: Aritmetické operátory...94 Porovnávací operátory...96 Operátor řetězení...97 Bitové logické operátory...97 Další operátory...101 92 ČÁST I: Programování v jazyce
LEKCE 6 Operátory V této lekci najdete: Aritmetické operátory...94 Porovnávací operátory...96 Operátor řetězení...97 Bitové logické operátory...97 Další operátory...101 92 ČÁST I: Programování v jazyce
Programy na PODMÍNĚNÝ příkaz IF a CASE
 Vstupy a výstupy budou vždy upraveny tak, aby bylo zřejmé, co zadáváme a co se zobrazuje. Není-li určeno, zadáváme přirozená čísla. Je-li to možné, používej generátor náhodných čísel vysvětli, co a jak
Vstupy a výstupy budou vždy upraveny tak, aby bylo zřejmé, co zadáváme a co se zobrazuje. Není-li určeno, zadáváme přirozená čísla. Je-li to možné, používej generátor náhodných čísel vysvětli, co a jak
Jak v Javě primitivní datové typy a jejich reprezentace. BD6B36PJV 002 Fakulta elektrotechnická České vysoké učení technické
 Jak v Javě primitivní datové typy a jejich reprezentace BD6B36PJV 002 Fakulta elektrotechnická České vysoké učení technické Obsah Celočíselný datový typ Reálný datový typ Logický datový typ, typ Boolean
Jak v Javě primitivní datové typy a jejich reprezentace BD6B36PJV 002 Fakulta elektrotechnická České vysoké učení technické Obsah Celočíselný datový typ Reálný datový typ Logický datový typ, typ Boolean
ALGORITMIZACE A PROGRAMOVÁNÍ
 Metodický list č. 1 Algoritmus a jeho implementace počítačovým programem Základním cílem tohoto tematického celku je vysvětlení pojmů algoritmus a programová implementace algoritmu. Dále je cílem seznámení
Metodický list č. 1 Algoritmus a jeho implementace počítačovým programem Základním cílem tohoto tematického celku je vysvětlení pojmů algoritmus a programová implementace algoritmu. Dále je cílem seznámení
Jednoduché cykly 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45.
 Jednoduché cykly Tento oddíl obsahuje úlohy na první procvičení práce s cykly. Při řešení každé ze zde uvedených úloh stačí použít vedle podmíněných příkazů jen jediný cyklus. Nepotřebujeme používat ani
Jednoduché cykly Tento oddíl obsahuje úlohy na první procvičení práce s cykly. Při řešení každé ze zde uvedených úloh stačí použít vedle podmíněných příkazů jen jediný cyklus. Nepotřebujeme používat ani
63. ročník Matematické olympiády 2013/2014
 63. ročník Matematické olympiády 2013/2014 Úlohy ústředního kola kategorie P 2. soutěžní den Na řešení úloh máte 4,5 hodiny čistého času. Při soutěži je zakázáno používat jakékoliv pomůcky kromě psacích
63. ročník Matematické olympiády 2013/2014 Úlohy ústředního kola kategorie P 2. soutěžní den Na řešení úloh máte 4,5 hodiny čistého času. Při soutěži je zakázáno používat jakékoliv pomůcky kromě psacích
Vyhledávání. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 21.
 Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 21. září 2018 Jiří Dvorský (VŠB TUO) Vyhledávání 242 / 433 Osnova přednášky
Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 21. září 2018 Jiří Dvorský (VŠB TUO) Vyhledávání 242 / 433 Osnova přednášky
NPRG030 Programování I, 2016/17 1 / :58:13
 NPRG030 Programování I, 2016/17 1 / 31 10. 10. 2016 10:58:13 Podmínka = něco, co JE, nebo NENÍ splněno typ Boolean hodnoty: TRUE pravda FALSE lež domluva (optimistická): FALSE < TRUE NPRG030 Programování
NPRG030 Programování I, 2016/17 1 / 31 10. 10. 2016 10:58:13 Podmínka = něco, co JE, nebo NENÍ splněno typ Boolean hodnoty: TRUE pravda FALSE lež domluva (optimistická): FALSE < TRUE NPRG030 Programování
II. Úlohy na vložené cykly a podprogramy
 II. Úlohy na vložené cykly a podprogramy Společné zadání pro příklady 1. - 10. začíná jednou ze dvou možností popisu vstupních dat. Je dána posloupnost (neboli řada) N reálných (resp. celočíselných) hodnot.
II. Úlohy na vložené cykly a podprogramy Společné zadání pro příklady 1. - 10. začíná jednou ze dvou možností popisu vstupních dat. Je dána posloupnost (neboli řada) N reálných (resp. celočíselných) hodnot.
Intervalové stromy. Představme si, že máme posloupnost celých čísel p 0, p 1,... p N 1, se kterou budeme. 1. Změna jednoho čísla v posloupnosti.
 Intervalové stromy Představme si, že máme posloupnost celých čísel p 0, p 1,... p N 1, se kterou budeme průběžně provádět tyto dvě operace: 1. Změna jednoho čísla v posloupnosti. 2. Zjištění součtu čísel
Intervalové stromy Představme si, že máme posloupnost celých čísel p 0, p 1,... p N 1, se kterou budeme průběžně provádět tyto dvě operace: 1. Změna jednoho čísla v posloupnosti. 2. Zjištění součtu čísel
Přednáška 7. Celočíselná aritmetika. Návratový kód. Příkazy pro větvení výpočtu. Cykly. Předčasné ukončení cyklu.
 Přednáška 7 Celočíselná aritmetika. Návratový kód. Příkazy pro větvení výpočtu. Cykly. Předčasné ukončení cyklu. 1 Příkaz expr výraz Celočíselná aritmetika I Zašle na standardní výstup vyhodnocení výrazu
Přednáška 7 Celočíselná aritmetika. Návratový kód. Příkazy pro větvení výpočtu. Cykly. Předčasné ukončení cyklu. 1 Příkaz expr výraz Celočíselná aritmetika I Zašle na standardní výstup vyhodnocení výrazu
Teorie informace a kódování (KMI/TIK) Reed-Mullerovy kódy
 Teorie informace a kódování (KMI/TIK) Reed-Mullerovy kódy Lukáš Havrlant Univerzita Palackého 10. ledna 2014 Primární zdroj Jiří Adámek: Foundations of Coding. Strany 137 160. Na webu ke stažení, heslo:
Teorie informace a kódování (KMI/TIK) Reed-Mullerovy kódy Lukáš Havrlant Univerzita Palackého 10. ledna 2014 Primární zdroj Jiří Adámek: Foundations of Coding. Strany 137 160. Na webu ke stažení, heslo:
Úvod do programování. Lekce 1
 Úvod do programování Lekce 1 Základní pojmy vytvoření spustitelného kódu editor - psaní zdrojových souborů preprocesor - zpracování zdrojových souborů (vypuštění komentářů atd.) kompilátor (compiler) -
Úvod do programování Lekce 1 Základní pojmy vytvoření spustitelného kódu editor - psaní zdrojových souborů preprocesor - zpracování zdrojových souborů (vypuštění komentářů atd.) kompilátor (compiler) -
NPRG030 Programování I, 2010/11
 Podmínka = něco, co JE, nebo NENÍ splněno typ Boolean hodnoty: TRUE pravda FALSE lež domluva (optimistická): FALSE < TRUE když X, Y jsou (číselné) výrazy, potom X = Y X Y X < Y X > Y X = Y jsou
Podmínka = něco, co JE, nebo NENÍ splněno typ Boolean hodnoty: TRUE pravda FALSE lež domluva (optimistická): FALSE < TRUE když X, Y jsou (číselné) výrazy, potom X = Y X Y X < Y X > Y X = Y jsou
Zadání druhého zápočtového projektu Základy algoritmizace, 2005
 Zadání druhého zápočtového projektu Základy algoritmizace, 2005 Jiří Dvorský 2 května 2006 Obecné pokyny Celkem je k dispozici 8 zadání příkladů Každý student obdrží jedno zadání Vzhledem k tomu, že odpadly
Zadání druhého zápočtového projektu Základy algoritmizace, 2005 Jiří Dvorský 2 května 2006 Obecné pokyny Celkem je k dispozici 8 zadání příkladů Každý student obdrží jedno zadání Vzhledem k tomu, že odpadly
Logické operace. Datový typ bool. Relační operátory. Logické operátory. IAJCE Přednáška č. 3. může nabýt hodnot: o true o false
 Logické operace Datový typ bool může nabýt hodnot: o true o false Relační operátory pravda, 1, nepravda, 0, hodnoty všech primitivních datových typů (int, double ) jsou uspořádané lze je porovnávat binární
Logické operace Datový typ bool může nabýt hodnot: o true o false Relační operátory pravda, 1, nepravda, 0, hodnoty všech primitivních datových typů (int, double ) jsou uspořádané lze je porovnávat binární
- speciální symboly + - * / =., < > <> <= >= a další. Klíčová slova jsou chráněnými útvary, které nelze použít ve významu identifikátorů.
 Základní symboly - písmena A B C Y Z a b c y z - číslice 0 1 2 9 - speciální symboly + - * / =., < > = a další - klíčová slova and array begin case const a další Klíčová slova jsou chráněnými útvary,
Základní symboly - písmena A B C Y Z a b c y z - číslice 0 1 2 9 - speciální symboly + - * / =., < > = a další - klíčová slova and array begin case const a další Klíčová slova jsou chráněnými útvary,
Algoritmizace a programování
 Algoritmizace a programování Řídicí struktury jazyka Java Struktura programu Příkazy jazyka Blok příkazů Logické příkazy Ternární logický operátor Verze pro akademický rok 2012/2013 1 Struktura programu
Algoritmizace a programování Řídicí struktury jazyka Java Struktura programu Příkazy jazyka Blok příkazů Logické příkazy Ternární logický operátor Verze pro akademický rok 2012/2013 1 Struktura programu
Příklad 1/23. Pro rostoucí spojité fukce f(x), g(x) platí f(x) Ω(g(x)). Z toho plyne, že: a) f(x) Ο(g(x)) b) f(x) Θ(g(x)) d) g(x) Ω(f(x))
 Příklad 1/23 Pro rostoucí spojité fukce f(x), g(x) platí f(x) Ω(g(x)). Z toho plyne, že: a) f(x) Ο(g(x)) b) f(x) Θ(g(x)) c) g(x) Θ(f(x)) d) g(x) Ω(f(x)) e) g(x) Ο(f(x)) 1 Příklad 2/23 Pro rostoucí spojité
Příklad 1/23 Pro rostoucí spojité fukce f(x), g(x) platí f(x) Ω(g(x)). Z toho plyne, že: a) f(x) Ο(g(x)) b) f(x) Θ(g(x)) c) g(x) Θ(f(x)) d) g(x) Ω(f(x)) e) g(x) Ο(f(x)) 1 Příklad 2/23 Pro rostoucí spojité
67. ročník Matematické olympiády 2017/2018
 67. ročník Matematické olympiády 2017/2018 Úlohy ústředního kola kategorie P 2. soutěžní den Na řešení úloh máte 4,5 hodiny čistého času. Při soutěži je zakázáno používat jakékoliv pomůcky kromě psacích
67. ročník Matematické olympiády 2017/2018 Úlohy ústředního kola kategorie P 2. soutěžní den Na řešení úloh máte 4,5 hodiny čistého času. Při soutěži je zakázáno používat jakékoliv pomůcky kromě psacích
68. ročník Matematické olympiády 2018/2019
 68. ročník Matematické olympiády 2018/2019 Řešení úloh krajského kola kategorie P P-II-1 Tulipány Budeme řešit o něco obecnější úlohu: dovolíme si předepsat, zda má na n-té pozici být tulipán, a pokud
68. ročník Matematické olympiády 2018/2019 Řešení úloh krajského kola kategorie P P-II-1 Tulipány Budeme řešit o něco obecnější úlohu: dovolíme si předepsat, zda má na n-té pozici být tulipán, a pokud
[1] samoopravné kódy: terminologie, princip
![[1] samoopravné kódy: terminologie, princip [1] samoopravné kódy: terminologie, princip](/thumbs/51/27813178.jpg) [1] Úvod do kódování samoopravné kódy: terminologie, princip blokové lineární kódy Hammingův kód Samoopravné kódy, k čemu to je [2] Data jsou uložena (nebo posílána do linky) kodérem podle určitého pravidla
[1] Úvod do kódování samoopravné kódy: terminologie, princip blokové lineární kódy Hammingův kód Samoopravné kódy, k čemu to je [2] Data jsou uložena (nebo posílána do linky) kodérem podle určitého pravidla
Racionální čísla, operátory, výrazy, knihovní funkce
 Příprava studijního programu Informatika je podporována projektem financovaným z Evropského sociálního fondu a rozpočtu hlavního města Prahy. Praha & EU: Investujeme do vaší budoucnosti Racionální čísla,
Příprava studijního programu Informatika je podporována projektem financovaným z Evropského sociálního fondu a rozpočtu hlavního města Prahy. Praha & EU: Investujeme do vaší budoucnosti Racionální čísla,
[1] Determinant. det A = 0 pro singulární matici, det A 0 pro regulární matici
![[1] Determinant. det A = 0 pro singulární matici, det A 0 pro regulární matici [1] Determinant. det A = 0 pro singulární matici, det A 0 pro regulární matici](/thumbs/94/118721039.jpg) [1] Determinant je číslo jistým způsobem charakterizující čtvercovou matici det A = 0 pro singulární matici, det A 0 pro regulární matici používá se při řešení lineárních soustav... a v mnoha dalších aplikacích
[1] Determinant je číslo jistým způsobem charakterizující čtvercovou matici det A = 0 pro singulární matici, det A 0 pro regulární matici používá se při řešení lineárních soustav... a v mnoha dalších aplikacích
Algoritmizace prostorových úloh
 INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Algoritmus Daniela Szturcová Tento
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Algoritmus Daniela Szturcová Tento
Algoritmy I. Číselné soustavy přečíst!!! ALGI 2018/19
 Algoritmy I Číselné soustavy přečíst!!! Číselné soustavy Každé číslo lze zapsat v poziční číselné soustavě ve tvaru: a n *z n +a n-1 *z n-1 +. +a 1 *z 1 +a 0 *z 0 +a -1 *z n-1 +a -2 *z -2 +.. V dekadické
Algoritmy I Číselné soustavy přečíst!!! Číselné soustavy Každé číslo lze zapsat v poziční číselné soustavě ve tvaru: a n *z n +a n-1 *z n-1 +. +a 1 *z 1 +a 0 *z 0 +a -1 *z n-1 +a -2 *z -2 +.. V dekadické
Složitost Filip Hlásek
 Složitost Filip Hlásek Abstrakt. Příspěvek popisuje dva základní koncepty teoretické informatiky, Turingovy stroje a složitost. Kromě definic důležitých pojmů uvádí také několik souvisejících tvrzení,
Složitost Filip Hlásek Abstrakt. Příspěvek popisuje dva základní koncepty teoretické informatiky, Turingovy stroje a složitost. Kromě definic důležitých pojmů uvádí také několik souvisejících tvrzení,
Prohledávání do šířky = algoritmus vlny
 Prohledávání do šířky = algoritmus vlny - souběžně zkoušet všechny možné varianty pokračování výpočtu, dokud nenajdeme řešení úlohy průchod stromem všech možných cest výpočtu do šířky, po vrstvách (v každé
Prohledávání do šířky = algoritmus vlny - souběžně zkoušet všechny možné varianty pokračování výpočtu, dokud nenajdeme řešení úlohy průchod stromem všech možných cest výpočtu do šířky, po vrstvách (v každé
Výrazy a operátory. Operátory Unární - unární a unární + Např.: a +b
 Výrazy a operátory i = 2 i = 2; to je výraz to je příkaz 4. Operátory Unární - unární a unární + Např.: +5-5 -8.345 -a +b - unární ++ - inkrement - zvýší hodnotu proměnné o 1 - unární -- - dekrement -
Výrazy a operátory i = 2 i = 2; to je výraz to je příkaz 4. Operátory Unární - unární a unární + Např.: +5-5 -8.345 -a +b - unární ++ - inkrement - zvýší hodnotu proměnné o 1 - unární -- - dekrement -
MQL4 COURSE. By Coders guru www.forex-tsd.com. -4 Operace & Výrazy
 MQL4 COURSE By Coders guru www.forex-tsd.com -4 Operace & Výrazy Vítejte ve čtvrté lekci mého kurzu MQL4. Předchozí lekce Datové Typy prezentovaly mnoho nových konceptů ; Doufám, že jste všemu porozuměli,
MQL4 COURSE By Coders guru www.forex-tsd.com -4 Operace & Výrazy Vítejte ve čtvrté lekci mého kurzu MQL4. Předchozí lekce Datové Typy prezentovaly mnoho nových konceptů ; Doufám, že jste všemu porozuměli,
Data v počítači. Informační data. Logické hodnoty. Znakové hodnoty
 Data v počítači Informační data (elementární datové typy) Logické hodnoty Znaky Čísla v pevné řádové čárce (celá čísla) v pohyblivé (plovoucí) řád. čárce (reálná čísla) Povelová data (instrukce programu)
Data v počítači Informační data (elementární datové typy) Logické hodnoty Znaky Čísla v pevné řádové čárce (celá čísla) v pohyblivé (plovoucí) řád. čárce (reálná čísla) Povelová data (instrukce programu)
61. ročník Matematické olympiády 2011/2012
 61. ročník Matematické olympiády 2011/2012 Úlohy ústředního kola kategorie P 1. soutěžní den Na řešení úloh máte 4,5 hodiny čistého času. Řešení každé úlohy pište na samostatný list papíru. Při soutěži
61. ročník Matematické olympiády 2011/2012 Úlohy ústředního kola kategorie P 1. soutěžní den Na řešení úloh máte 4,5 hodiny čistého času. Řešení každé úlohy pište na samostatný list papíru. Při soutěži
Vyhledávání. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 12.
 Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 12. září 2016 Jiří Dvorský (VŠB TUO) Vyhledávání 201 / 344 Osnova přednášky
Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 12. září 2016 Jiří Dvorský (VŠB TUO) Vyhledávání 201 / 344 Osnova přednášky
Příklady: (y + (sin(2*x) + 1)*2)/ /2 * 5 = 8.5 (1+3)/2 * 5 = /(2 * 5) = 1.3. Pavel Töpfer, 2017 Programování 1-3 1
 Výraz - syntaxe i sémantika podobné jako v matematice - obsahuje proměnné, konstanty, operátory, závorky, volání funkcí - všechny operátory nutno zapisovat (nelze např. vynechat znak násobení) - argumenty
Výraz - syntaxe i sémantika podobné jako v matematice - obsahuje proměnné, konstanty, operátory, závorky, volání funkcí - všechny operátory nutno zapisovat (nelze např. vynechat znak násobení) - argumenty
Booleovská algebra. Booleovské binární a unární funkce. Základní zákony.
 Booleovská algebra. Booleovské binární a unární funkce. Základní zákony. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Booleovská algebra. Booleovské binární a unární funkce. Základní zákony. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Operace s maticemi
 Operace s maticemi Seminář druhý 17.10. 2018 Obsah 1 Operace s maticemi 2 Hodnost matice 3 Regulární matice 4 Inverzní matice Matice Definice (Matice). Reálná matice typu m n je obdélníkové schema A =
Operace s maticemi Seminář druhý 17.10. 2018 Obsah 1 Operace s maticemi 2 Hodnost matice 3 Regulární matice 4 Inverzní matice Matice Definice (Matice). Reálná matice typu m n je obdélníkové schema A =
Úvod do programování 7. hodina
 Úvod do programování 7. hodina RNDr. Jan Lánský, Ph.D. Katedra informatiky a matematiky Fakulta ekonomických studií Vysoká škola finanční a správní 2015 Umíme z minulé hodiny Syntax Znaky Vlastní implementace
Úvod do programování 7. hodina RNDr. Jan Lánský, Ph.D. Katedra informatiky a matematiky Fakulta ekonomických studií Vysoká škola finanční a správní 2015 Umíme z minulé hodiny Syntax Znaky Vlastní implementace
Výhody a nevýhody jednotlivých reprezentací jsou shrnuty na konci kapitoly.
 Kapitola Reprezentace grafu V kapitole?? jsme se dozvěděli, co to jsou grafy a k čemu jsou dobré. rzo budeme chtít napsat nějaký program, který s grafy pracuje. le jak si takový graf uložit do počítače?
Kapitola Reprezentace grafu V kapitole?? jsme se dozvěděli, co to jsou grafy a k čemu jsou dobré. rzo budeme chtít napsat nějaký program, který s grafy pracuje. le jak si takový graf uložit do počítače?
PQ-stromy a rozpoznávání intervalových grafů v lineárním čase
 -stromy a rozpoznávání intervalových grafů v lineárním čase ermutace s předepsanými intervaly Označme [n] množinu {1, 2,..., n}. Mějme permutaci π = π 1, π 2,..., π n množiny [n]. Řekneme, že množina S
-stromy a rozpoznávání intervalových grafů v lineárním čase ermutace s předepsanými intervaly Označme [n] množinu {1, 2,..., n}. Mějme permutaci π = π 1, π 2,..., π n množiny [n]. Řekneme, že množina S
for (i = 0, j = 5; i < 10; i++) { // tělo cyklu }
 5. Operátor čárka, - slouží k jistému určení pořadí vykonání dvou příkazů - oddělím-li čárkou dva příkazy, je jisté, že ten první bude vykonán dříve než příkaz druhý. Např.: i = 5; j = 8; - po překladu
5. Operátor čárka, - slouží k jistému určení pořadí vykonání dvou příkazů - oddělím-li čárkou dva příkazy, je jisté, že ten první bude vykonán dříve než příkaz druhý. Např.: i = 5; j = 8; - po překladu
PHP - úvod. Kapitola seznamuje se základy jazyka PHP a jeho začleněním do HTML stránky.
 PHP - úvod Kapitola seznamuje se základy jazyka PHP a jeho začleněním do HTML stránky. Klíčové pojmy: PHP, webový prohlížeč, HTTP, FTP Základní pojmy služba WWW = 1990 první prototyp serveru, od roku 1994
PHP - úvod Kapitola seznamuje se základy jazyka PHP a jeho začleněním do HTML stránky. Klíčové pojmy: PHP, webový prohlížeč, HTTP, FTP Základní pojmy služba WWW = 1990 první prototyp serveru, od roku 1994
α β ) právě tehdy, když pro jednotlivé hodnoty platí β1 αn βn. Danou relaci nazýváme relace
 Monotónní a Lineární Funkce 1. Relace předcházení a to Uvažujme dva vektory hodnot proměnných α = α,, 1 αn ( ) a β = ( β β ) 1,, n x,, 1 xn. Říkáme, že vekto r hodnot α předchází vektor hodnot β (značíme
Monotónní a Lineární Funkce 1. Relace předcházení a to Uvažujme dva vektory hodnot proměnných α = α,, 1 αn ( ) a β = ( β β ) 1,, n x,, 1 xn. Říkáme, že vekto r hodnot α předchází vektor hodnot β (značíme
Cykly a pole 103. 104. 105. 106. 107. 108. 109. 110. 111. 112. 113. 114. 115. 116.
 Cykly a pole Tato část sbírky je tvořena dalšími úlohami na práci s cykly. Na rozdíl od předchozího oddílu se zde již v řešeních úloh objevuje více cyklů, ať už prováděných po sobě nebo vnořených do sebe.
Cykly a pole Tato část sbírky je tvořena dalšími úlohami na práci s cykly. Na rozdíl od předchozího oddílu se zde již v řešeních úloh objevuje více cyklů, ať už prováděných po sobě nebo vnořených do sebe.
63. ročník Matematické olympiády 2013/2014
 6. ročník Matematické olympiády 0/0 Úlohy ústředního kola kategorie P. soutěžní den Na řešení úloh máte, hodiny čistého času. Řešení každé úlohy pište na samostatný list papíru. Při soutěži je zakázáno
6. ročník Matematické olympiády 0/0 Úlohy ústředního kola kategorie P. soutěžní den Na řešení úloh máte, hodiny čistého času. Řešení každé úlohy pište na samostatný list papíru. Při soutěži je zakázáno
Dělení. INP 2008 FIT VUT v Brně
 ělení INP 28 FIT VUT v Brně ělení čísel s pevnou řádovou čárkou Nejdříve se budeme zabývat dělením čísel s pevnou řádovou čárkou bez znaménka. Pro jednotlivé činitele operace dělení zavedeme symboly d
ělení INP 28 FIT VUT v Brně ělení čísel s pevnou řádovou čárkou Nejdříve se budeme zabývat dělením čísel s pevnou řádovou čárkou bez znaménka. Pro jednotlivé činitele operace dělení zavedeme symboly d
20 b. 45 b. 25 b. 20 b. Kolo J Klasické S. 9. Klasické R. 8. Klasické Č. 7. Klasické M. 5 b. 10 b. 5 b. 5 b. 3. Klasické
 body: Soutěž jednotlivců b. Nepravidelné b b 0 b 0 b b 0 b b. Klasické Č. Klasické R 0. Klasické S. Klasické. Klasické 0. Klasické. Klasické Brno,. a. září 0 www.sudokualogika.cz logických her a sudoku
body: Soutěž jednotlivců b. Nepravidelné b b 0 b 0 b b 0 b b. Klasické Č. Klasické R 0. Klasické S. Klasické. Klasické 0. Klasické. Klasické Brno,. a. září 0 www.sudokualogika.cz logických her a sudoku
Algoritmizace prostorových úloh
 INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Algoritmus Daniela Szturcová Tento
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Algoritmus Daniela Szturcová Tento
Struktura a architektura počítačů (BI-SAP) 5
 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Struktura a architektura počítačů (BI-SAP) 5 doc. Ing. Hana Kubátová, CSc. Katedra číslicového návrhu Fakulta informačních technologii
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Struktura a architektura počítačů (BI-SAP) 5 doc. Ing. Hana Kubátová, CSc. Katedra číslicového návrhu Fakulta informačních technologii
Obsah. Euler-Fermatova věta. Reziduální aritmetika. 3. a 4. přednáška z kryptografie
 Obsah Počítání modulo n a jeho časová složitost 3. a 4. přednáška z kryptografie 1 Počítání modulo n - dokončení Umocňování v Zn 2 Časová složitost výpočtů modulo n Asymptotická notace Základní aritmetické
Obsah Počítání modulo n a jeho časová složitost 3. a 4. přednáška z kryptografie 1 Počítání modulo n - dokončení Umocňování v Zn 2 Časová složitost výpočtů modulo n Asymptotická notace Základní aritmetické
Třídy složitosti P a NP, NP-úplnost
 Třídy složitosti P a NP, NP-úplnost Cíle přednášky: 1. Definovat, za jakých okolností můžeme problém považovat za efektivně algoritmicky řešitelný. 2. Charakterizovat určitou skupinu úloh, pro které není
Třídy složitosti P a NP, NP-úplnost Cíle přednášky: 1. Definovat, za jakých okolností můžeme problém považovat za efektivně algoritmicky řešitelný. 2. Charakterizovat určitou skupinu úloh, pro které není
Číselné vyjádření hodnoty. Kolik váží hrouda zlata?
 Čísla a logika Číselné vyjádření hodnoty Au Kolik váží hrouda zlata? Dekadické vážení Když přidám osmé závaží g, váha se převáží => závaží zase odeberu a začnu přidávat závaží x menší 7 závaží g 2 závaží
Čísla a logika Číselné vyjádření hodnoty Au Kolik váží hrouda zlata? Dekadické vážení Když přidám osmé závaží g, váha se převáží => závaží zase odeberu a začnu přidávat závaží x menší 7 závaží g 2 závaží
Jednoduchá exponenciální rovnice
 Jednoduchá exponenciální rovnice Z běžné rovnice se exponenciální stává, pokud obsahuje proměnnou v exponentu. Obecně bychom mohli exponenciální rovnici zapsat takto: a f(x) = b g(x), kde a, b > 0. Typickým
Jednoduchá exponenciální rovnice Z běžné rovnice se exponenciální stává, pokud obsahuje proměnnou v exponentu. Obecně bychom mohli exponenciální rovnici zapsat takto: a f(x) = b g(x), kde a, b > 0. Typickým
Y36SAP - aritmetika. Osnova
 Y36SAP - aritmetika Čísla se znaménkem a aritmetické operace pevná a pohyblivá řádová čárka Kubátová 2007 Y36SAP-aritmetika 1 Osnova Zobrazení záporných čísel Přímý, aditivní a doplňkový kód a operace
Y36SAP - aritmetika Čísla se znaménkem a aritmetické operace pevná a pohyblivá řádová čárka Kubátová 2007 Y36SAP-aritmetika 1 Osnova Zobrazení záporných čísel Přímý, aditivní a doplňkový kód a operace
Inovace a zkvalitnění výuky prostřednictvím ICT Základy programování a algoritmizace úloh. Ing. Hodál Jaroslav, Ph.D. VY_32_INOVACE_25 09
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Inovace a zkvalitnění výuky prostřednictvím ICT Základy programování a algoritmizace úloh Operátory Autor:
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Inovace a zkvalitnění výuky prostřednictvím ICT Základy programování a algoritmizace úloh Operátory Autor:
Lineární algebra : Polynomy
 Lineární algebra : Polynomy (2. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 15. dubna 2014, 11:21 1 2 2.1 Značení a těleso komplexních čísel Značení N := {1, 2, 3... }... množina
Lineární algebra : Polynomy (2. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 15. dubna 2014, 11:21 1 2 2.1 Značení a těleso komplexních čísel Značení N := {1, 2, 3... }... množina
Architektury počítačů a procesorů
 Kapitola 3 Architektury počítačů a procesorů 3.1 Von Neumannova (a harvardská) architektura Von Neumann 1. počítač se skládá z funkčních jednotek - paměť, řadič, aritmetická jednotka, vstupní a výstupní
Kapitola 3 Architektury počítačů a procesorů 3.1 Von Neumannova (a harvardská) architektura Von Neumann 1. počítač se skládá z funkčních jednotek - paměť, řadič, aritmetická jednotka, vstupní a výstupní
. je zlomkem. Ten je smysluplný pro jakýkoli jmenovatel různý od nuly. Musí tedy platit = 0
 Příklad 1 Určete definiční obor funkce: a) = b) = c) = d) = e) = 9 f) = Řešení 1a Máme určit definiční obor funkce =. Výraz je zlomkem. Ten je smysluplný pro jakýkoli jmenovatel různý od nuly. Musí tedy
Příklad 1 Určete definiční obor funkce: a) = b) = c) = d) = e) = 9 f) = Řešení 1a Máme určit definiční obor funkce =. Výraz je zlomkem. Ten je smysluplný pro jakýkoli jmenovatel různý od nuly. Musí tedy
Maticí typu (m, n), kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru:
 3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
Úvod do programovacích jazyků (Java)
 Úvod do programovacích jazyků (Java) Michal Krátký Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programovacích jazyků (Java), 2007/2008 c 2006 2008 Michal Krátký Úvod do programovacích
Úvod do programovacích jazyků (Java) Michal Krátký Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programovacích jazyků (Java), 2007/2008 c 2006 2008 Michal Krátký Úvod do programovacích
1 Mnohočleny a algebraické rovnice
 1 Mnohočleny a algebraické rovnice 1.1 Pojem mnohočlenu (polynomu) Připomeňme, že výrazům typu a 2 x 2 + a 1 x + a 0 říkáme kvadratický trojčlen, když a 2 0. Číslům a 0, a 1, a 2 říkáme koeficienty a písmenem
1 Mnohočleny a algebraické rovnice 1.1 Pojem mnohočlenu (polynomu) Připomeňme, že výrazům typu a 2 x 2 + a 1 x + a 0 říkáme kvadratický trojčlen, když a 2 0. Číslům a 0, a 1, a 2 říkáme koeficienty a písmenem
Binární soubory (datové, typované)
 Binární soubory (datové, typované) - na rozdíl od textových souborů data uložena binárně (ve vnitřním tvaru jako v proměnných programu) není čitelné pro člověka - všechny záznamy téhož typu (může být i
Binární soubory (datové, typované) - na rozdíl od textových souborů data uložena binárně (ve vnitřním tvaru jako v proměnných programu) není čitelné pro člověka - všechny záznamy téhož typu (může být i
Úlohy krajského kola kategorie C
 67. ročník matematické olympiády Úlohy krajského kola kategorie C 1. Najděte nejmenší přirozené číslo končící čtyřčíslím 2018, které je násobkem čísla 2017. 2. Pro celá čísla x, y, z platí x 2 + y z =
67. ročník matematické olympiády Úlohy krajského kola kategorie C 1. Najděte nejmenší přirozené číslo končící čtyřčíslím 2018, které je násobkem čísla 2017. 2. Pro celá čísla x, y, z platí x 2 + y z =
Struktura a architektura počítačů (BI-SAP) 6
 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Struktura a architektura počítačů (BI-SAP) 6 doc. Ing. Hana Kubátová, CSc. Katedra číslicového návrhu Fakulta informačních technologii
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Struktura a architektura počítačů (BI-SAP) 6 doc. Ing. Hana Kubátová, CSc. Katedra číslicového návrhu Fakulta informačních technologii
Informatika 8. třída/6
 Rekurze Jedním z důležitých principů pro návrh procedur je tzv. rekurze. Nejlépe uvidíme tento princip na příkladech dvou velmi jednoduchých procedur (hvězdička označuje násobení). Rekurze vlastně označuje
Rekurze Jedním z důležitých principů pro návrh procedur je tzv. rekurze. Nejlépe uvidíme tento princip na příkladech dvou velmi jednoduchých procedur (hvězdička označuje násobení). Rekurze vlastně označuje
ARITMETICKÉ OPERACE V BINÁRNÍ SOUSTAVĚ
 Sčítání binárních čísel Binární čísla je možné sčítat stejným způsobem, jakým sčítáme čísla desítková. Příklad je uveden v tabulce níže. K přenosu jedničky do vyššího řádu dojde tehdy, jeli výsledkem součtu
Sčítání binárních čísel Binární čísla je možné sčítat stejným způsobem, jakým sčítáme čísla desítková. Příklad je uveden v tabulce níže. K přenosu jedničky do vyššího řádu dojde tehdy, jeli výsledkem součtu
doplněk, zřetězení, Kleeneho operaci a reverzi. Ukážeme ještě další operace s jazyky, na které je
 28 [181105-1236 ] 2.7 Další uzávěrové vlastnosti třídy regulárních jazyků Z předchozích přednášek víme, že třída regulárních jazyků je uzavřena na sjednocení, průnik, doplněk, zřetězení, Kleeneho operaci
28 [181105-1236 ] 2.7 Další uzávěrové vlastnosti třídy regulárních jazyků Z předchozích přednášek víme, že třída regulárních jazyků je uzavřena na sjednocení, průnik, doplněk, zřetězení, Kleeneho operaci
Algoritmus. Přesné znění definice algoritmu zní: Algoritmus je procedura proveditelná Turingovým strojem.
 Algoritmus Algoritmus je schematický postup pro řešení určitého druhu problémů, který je prováděn pomocí konečného množství přesně definovaných kroků. nebo Algoritmus lze definovat jako jednoznačně určenou
Algoritmus Algoritmus je schematický postup pro řešení určitého druhu problémů, který je prováděn pomocí konečného množství přesně definovaných kroků. nebo Algoritmus lze definovat jako jednoznačně určenou
Fz =a z + a z +...+a z +a z =
 Polyadické číselné soustavy - převody M-místná skupina prvků se z-stavovou abecedou umožňuje zobrazit z m čísel. Zjistíme, že stačí vhodně zvolit číslo m, abychom mohli zobrazit libovolné číslo menší než
Polyadické číselné soustavy - převody M-místná skupina prvků se z-stavovou abecedou umožňuje zobrazit z m čísel. Zjistíme, že stačí vhodně zvolit číslo m, abychom mohli zobrazit libovolné číslo menší než
5. Sekvenční logické obvody
 5. Sekvenční logické obvody 3. Sekvenční logické obvody - úvod Sledujme chování jednoduchého logického obvodu se zpětnou vazbou 3. Sekvenční logické obvody - příklad asynchronního sekvenčního obvodu 3.
5. Sekvenční logické obvody 3. Sekvenční logické obvody - úvod Sledujme chování jednoduchého logického obvodu se zpětnou vazbou 3. Sekvenční logické obvody - příklad asynchronního sekvenčního obvodu 3.
Funkce a lineární funkce pro studijní obory
 Variace 1 Funkce a lineární funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce
Variace 1 Funkce a lineární funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce
Pointery II. Jan Hnilica Počítačové modelování 17
 Pointery II 1 Pointery a pole Dosavadní způsob práce s poli zahrnoval: definici pole jakožto kolekce proměnných (prvků) jednoho typu, umístěných v paměti za sebou int pole[10]; práci s jednotlivými prvky
Pointery II 1 Pointery a pole Dosavadní způsob práce s poli zahrnoval: definici pole jakožto kolekce proměnných (prvků) jednoho typu, umístěných v paměti za sebou int pole[10]; práci s jednotlivými prvky
4EK213 Lineární modely. 12. Dopravní problém výchozí řešení
 4EK213 Lineární modely 12. Dopravní problém výchozí řešení 12. Distribuční úlohy LP Úlohy výrobního plánování (alokace zdrojů) Úlohy finančního plánování (optimalizace portfolia) Úlohy reklamního plánování
4EK213 Lineární modely 12. Dopravní problém výchozí řešení 12. Distribuční úlohy LP Úlohy výrobního plánování (alokace zdrojů) Úlohy finančního plánování (optimalizace portfolia) Úlohy reklamního plánování
Operace s maticemi. 19. února 2018
 Operace s maticemi Přednáška druhá 19. února 2018 Obsah 1 Operace s maticemi 2 Hodnost matice (opakování) 3 Regulární matice 4 Inverzní matice 5 Determinant matice Matice Definice (Matice). Reálná matice
Operace s maticemi Přednáška druhá 19. února 2018 Obsah 1 Operace s maticemi 2 Hodnost matice (opakování) 3 Regulární matice 4 Inverzní matice 5 Determinant matice Matice Definice (Matice). Reálná matice
1.3. Číselné množiny. Cíle. Průvodce studiem. Výklad
 1.3. Cíle Cílem kapitoly je seznámení čtenáře s axiomy číselných oborů a jejich podmnožin (intervalů) a zavedení nových pojmů, které nejsou náplní středoškolských osnov. Průvodce studiem Vývoj matematiky
1.3. Cíle Cílem kapitoly je seznámení čtenáře s axiomy číselných oborů a jejich podmnožin (intervalů) a zavedení nových pojmů, které nejsou náplní středoškolských osnov. Průvodce studiem Vývoj matematiky
Micro:bit lekce 3. - Konstrukci If Then a If Then Else najdete v kategorii Logic - Podmínky od If (např. porovnání < >= atd.) najdete taktéž v Logic
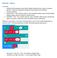 Micro:bit lekce 3. Podmínky - Rozvětvení běhu programu podle splnění nějakých podmínek typu pravda / nepravda - splněno / nesplněno (výsledkem podmínky musí být vždy jen dvě možnosti) - Dva typy podmínek:
Micro:bit lekce 3. Podmínky - Rozvětvení běhu programu podle splnění nějakých podmínek typu pravda / nepravda - splněno / nesplněno (výsledkem podmínky musí být vždy jen dvě možnosti) - Dva typy podmínek:
Operátory. Základy programování 1 Tomáš Kühr
 Operátory Základy programování 1 Tomáš Kühr Operátory a jejich vlastnosti Základní konstrukce (skoro) každého jazyka Z daných operandů vytvoří výsledek, který je možné dále využívat Arita udává počet operandů
Operátory Základy programování 1 Tomáš Kühr Operátory a jejich vlastnosti Základní konstrukce (skoro) každého jazyka Z daných operandů vytvoří výsledek, který je možné dále využívat Arita udává počet operandů
Hledání v textu algoritmem Boyer Moore
 Zápočtová práce z Algoritmů a Datových Struktur II (NTIN061) Hledání v textu algoritmem Boyer Moore David Pěgřímek http://davpe.net Algoritmus Boyer Moore[1] slouží k vyhledání vzoru V v zadaném textu
Zápočtová práce z Algoritmů a Datových Struktur II (NTIN061) Hledání v textu algoritmem Boyer Moore David Pěgřímek http://davpe.net Algoritmus Boyer Moore[1] slouží k vyhledání vzoru V v zadaném textu
IB112 Základy matematiky
 IB112 Základy matematiky Řešení soustavy lineárních rovnic, matice, vektory Jan Strejček IB112 Základy matematiky: Řešení soustavy lineárních rovnic, matice, vektory 2/53 Obsah Soustava lineárních rovnic
IB112 Základy matematiky Řešení soustavy lineárních rovnic, matice, vektory Jan Strejček IB112 Základy matematiky: Řešení soustavy lineárních rovnic, matice, vektory 2/53 Obsah Soustava lineárních rovnic
Algoritmus pro generování normálních magických čtverců
 1.1 Úvod Algoritmus pro generování normálních magických čtverců Naprogramoval jsem v Matlabu funkci, která dokáže vypočítat magický čtverec libovolného přípustného rozměru. Za pomocí tří algoritmů, které
1.1 Úvod Algoritmus pro generování normálních magických čtverců Naprogramoval jsem v Matlabu funkci, která dokáže vypočítat magický čtverec libovolného přípustného rozměru. Za pomocí tří algoritmů, které
Hledání správné cesty
 Semestrální práce z předmětu A6M33AST Závěrečná zpráva Hledání správné cesty Nela Grimová, Lenka Houdková 2015/2016 1. Zadání Naším úkolem bylo vytvoření úlohy Hledání cesty, kterou by bylo možné použít
Semestrální práce z předmětu A6M33AST Závěrečná zpráva Hledání správné cesty Nela Grimová, Lenka Houdková 2015/2016 1. Zadání Naším úkolem bylo vytvoření úlohy Hledání cesty, kterou by bylo možné použít
Informatika navazující magisterské studium Přijímací zkouška z informatiky 2018 varianta A
 Informatika navazující magisterské studium Přijímací zkouška z informatiky 2018 varianta A Každá úloha je hodnocena maximálně 25 body. Všechny své odpovědi zdůvodněte! 1. Postavte na stůl do řady vedle
Informatika navazující magisterské studium Přijímací zkouška z informatiky 2018 varianta A Každá úloha je hodnocena maximálně 25 body. Všechny své odpovědi zdůvodněte! 1. Postavte na stůl do řady vedle
Nápovědy k numerickému myšlení TSP MU
 Nápovědy k numerickému myšlení TSP MU Numerické myšlení 2011/var. 01 26. Ciferné součty čísel v každém z kruhů mají tutéž hodnotu. Pozor, hledáme číslo, které se nehodí na místo otazníku. Jedná se o dvě
Nápovědy k numerickému myšlení TSP MU Numerické myšlení 2011/var. 01 26. Ciferné součty čísel v každém z kruhů mají tutéž hodnotu. Pozor, hledáme číslo, které se nehodí na místo otazníku. Jedná se o dvě
Programování v jazyce JavaScript
 Programování v jazyce JavaScript Katedra softwarového inženýrství Fakulta informačních technologií České vysoké učení technické v Praze Pavel Štěpán, 2011 Operátory a příkazy BI-JSC Evropský sociální fond
Programování v jazyce JavaScript Katedra softwarového inženýrství Fakulta informačních technologií České vysoké učení technické v Praze Pavel Štěpán, 2011 Operátory a příkazy BI-JSC Evropský sociální fond
Poslední nenulová číslice faktoriálu
 Poslední nenulová číslice faktoriálu Kateřina Bambušková BAM015, I206 Abstrakt V tomto článku je popsán a vyřešen problém s určením poslední nenulové číslice faktoriálu přirozeného čísla N. Celý princip
Poslední nenulová číslice faktoriálu Kateřina Bambušková BAM015, I206 Abstrakt V tomto článku je popsán a vyřešen problém s určením poslední nenulové číslice faktoriálu přirozeného čísla N. Celý princip
Úvod do programování 6. hodina
 Úvod do programování 6. hodina RNDr. Jan Lánský, Ph.D. Katedra informatiky a matematiky Fakulta ekonomických studií Vysoká škola finanční a správní 2015 Umíme z minulé hodiny Algoritmy Třídění pole: Selection
Úvod do programování 6. hodina RNDr. Jan Lánský, Ph.D. Katedra informatiky a matematiky Fakulta ekonomických studií Vysoká škola finanční a správní 2015 Umíme z minulé hodiny Algoritmy Třídění pole: Selection
Lineární algebra : Polynomy
 Lineární algebra : Polynomy (2. přednáška) František Štampach, Karel Klouda frantisek.stampach@fit.cvut.cz, karel.klouda@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních technologií České
Lineární algebra : Polynomy (2. přednáška) František Štampach, Karel Klouda frantisek.stampach@fit.cvut.cz, karel.klouda@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních technologií České
9.3.2010 Program převod z desítkové na dvojkovou soustavu: /* Prevod desitkove na binarni */ #include <stdio.h>
 9.3.2010 Program převod z desítkové na dvojkovou soustavu: /* Prevod desitkove na binarni */ #include int main(void) { int dcislo, kolikbcislic = 0, mezivysledek = 0, i; int vysledek[1000]; printf("zadejte
9.3.2010 Program převod z desítkové na dvojkovou soustavu: /* Prevod desitkove na binarni */ #include int main(void) { int dcislo, kolikbcislic = 0, mezivysledek = 0, i; int vysledek[1000]; printf("zadejte
Test prvočíselnosti. Úkol: otestovat dané číslo N, zda je prvočíslem
 Test prvočíselnosti Úkol: otestovat dané číslo N, zda je prvočíslem 1. zkusit všechny dělitele od 2 do N-1 časová složitost O(N) cca N testů 2. stačí zkoušet všechny dělitele od 2 do N/2 (větší dělitel
Test prvočíselnosti Úkol: otestovat dané číslo N, zda je prvočíslem 1. zkusit všechny dělitele od 2 do N-1 časová složitost O(N) cca N testů 2. stačí zkoušet všechny dělitele od 2 do N/2 (větší dělitel
Kódováni dat. Kódy používané pro strojové operace
 Kódováni dat Před zpracováním dat například v počítači je třeba znaky převést do tvaru, kterému počítač rozumí, tj. přiřadit jim určité kombinace bitů. Tomuto převodu se říká kódování. Kód je předpis pro
Kódováni dat Před zpracováním dat například v počítači je třeba znaky převést do tvaru, kterému počítač rozumí, tj. přiřadit jim určité kombinace bitů. Tomuto převodu se říká kódování. Kód je předpis pro
