Metody analýzy dat I (Data Analysis I) Modely - pokračování
|
|
|
- Aneta Slavíková
- před 7 lety
- Počet zobrazení:
Transkript
1 Metody analýzy dat I (Data Analysis I) Modely - pokračování
2 Literatura Zaki, M. J., Meira Jr, W. (2014). Data Mining and Analysis: Fundamental Concepts and Algorithms. Cambridge University Press. [ ]
3 Model malého světa Víme že, řídké náhodné grafy: průměrný stupeň <d> = np nejsou místně strukturovány všechny hrany jsou stejně pravděpodobné a k sousedům vrcholů se nepřistupuje nijak speciálně, malý shlukovací koeficient (při průměrném stupni vrcholů <d> a rostoucím n se p hrany snižuje, hodnota shlukovacího koeficientu C klesá, C=p) vzdálenosti v nich jsou malé, průměrně log n/log <d> Mřížka pravidelný stupeň vrcholu velké vzdálenosti velký shlukovací koeficient (např. mřížka) (ale C=0 pro čtvercovou mřížku)
4 Model malého světa Existuje řídký graf s velkým s.k. C a malou průměrnou vzdáleností L? Důležité v lidských sítích, lidé se shlukují; je přirozené, že lidské sítě mají velký s.k. Sítě malého světa vs. náhodné sítě srovnatelné velikosti C sw >> C rand, L sw L rand (sw = small world) Vlastnost malého světa L log n Vlastnost ultra-small-world L log n
5 Model malého světa Stanley Milgram, 1967 experiment s dopisy odeslanými z Nebrasky příteli v Bostonu pojem šest stupňů odloučení. 160 dopisů (odesílatelů) z Kansasu a Nebrasky mělo doručit dopis adresátovi z Massachusetts: neznáte-li adresáta, předejte dopis osobě, se kterou si tykáte, a o které předpokl., že by adresáta znát mohla, každá osoba měla odeslat potvrzující dopis zpět na Harvard (to umožnilo sledovat cesty dopisů). 42 dopisů dorazilo do cíle, průměr byl D = 12, průměrná vzdálenost L = 5.5 U G n,p víme, že je-li <d>=1, graf obsahuje obrovskou souvislou komponentu, kde je průměrná vzdálenost malá malý svět
6 Baconovo, Erdősovo číslo Erdősovo číslo síť spolupráce spoluautoři, viz P. Erdős má číslo 0, Ti, kdo s ním měli společný článek, mají číslo 1,... Př. Einstein má EČ dva, N.Chomsky má EČ čtyři, B.Gates také čtyři, S.Hawking 4, A.Turing 5 Baconovo číslo ( Ch. Chaplin má BČ 3, E. Presley 2, R. Steiger 2 Průměrné Baconovo číslo (08/2016) - 1. Eric Roberts (L= ), nejvyšší průměrné BČ je Viz
7 K. Bacon, E. Roberts Průměrné Baconovo číslo k 8/
8 y Tým z Kolumbijské university v New Yorku Dodds, Muhamad, Watts, (Science 301, 2003) 18 cílových adres ve 13 zemích (z registrovaných účastníků) úkolem bylo doručit zprávu jim přidělenému cíli předáním zprávy osobě, o které si mysleli, že má k cíli blíže než oni sami cest pro jednotlivé zprávy, 384 dosáhlo cíle, +60,000 osob celkem, 166 zemí L = columbia.pdf
9 y profesor na univerzitě Ivy League inspektor v Estonsku, technologický konzultant v Indii, policista v Austrálii, veterinář v norské armádě. Cíl v Chorvatsku nabyl dosažen
10 Model malého světa N m <d> L D log n / log <d>
11 Model malého světa Topologie malého světa malé vzdálenosti s velkým shlukovacím koeficientem - nezávisle na velikosti sítě. Model Watts-Strogatz 1998, kruhová mřížka o n vrcholech, m hranách, kde každý vrchol sousedí s prvními k sousedy a hrana je přepojena náhodně s pravděpodobností p (smyčky a multihrany nejsou povoleny). Pst p je tedy pst přepojení hrany
12 Watts - Strogatz WS model sítě spoluprací (herci), biologická síť (PPI síť, červ C.elegans) p=0 p=1
13 Watts - Strogatz n = 20, m = 40, <d> = 4 0, 5, 200 přepojení (mřížka, sw, rand) L =2.89, 2.35, 2.21, C = 0.5, 0.40, 0.23, D = 5,4,5
14 Watts - Strogatz Je-li p=0, máme pravidelnou mřížku s vysokým shlukovacím koeficientem C(p) asi C(0)=(3* <d>-6)/(4*<d>-4), a průměrnou nejkratší cestou L(p) asi L(0)=n/2* <d>, která se mění lineárně s rostoucím n. Je-li p=1, model konverguje k náhodnému grafu s nízkým shlukovacím koeficientem C(p) asi C(1)=<d>/n a průměrnou nejkratší cestou L(p) asi L(1)=log n/log<d>, která se mění logaritmicky s rostoucím n.
15 Watts - Strogatz Z p=0 a p=1 se může zdát, že vysoký C je asociován s velkou L a naopak malý C s malou L. Ale Watts-Strogatz dokázali (experimentálně), že existuje velký interval p, pro který se L(p) blíží L(1) zatímco C(p)>> C(1), (malé L a velké C jsou vlastnosti reálných sítí). 15
16 C(p)/Cmax L(p)/Lmax Watts numericky simuloval, že s p rostoucí od 0 k 1 Se rychle snižuje L Pomalu snižuje C A že existuje interval pro <p1,p2>, který generuje síť s malou L a velkým C.
17 Watts - Newman Watts-Newman 1999: kruhová mřížka o n vrcholech, m hranách, kde každý vrchol sousedí s prvními k sousedy a náhodně je přidána hrana (ale žádná původní hrana mřížky není přemístěna) s pstí p. Lépe se analyzuje, nevznikají izolované komponenty jako u WS modelu (potravní sítě popisující vztahy v ekosystému, elektrorozvodná síť v USA, schéma zapojení mikroprocesoru).
18 Model malého světa WN: shlukovací koeficient C(p) = 2*(2* < 3*( < d > -1) d > -1) + 4* < d > *p*(p + 2) WS: shlukovací koeficient 3*( < d > -1) 3 C(p) = *(1 p) 2*(2* < d > -1) Určení průměrné nejkratší cesty obtížné, Watts: L se nezačne snižovat dokud p<2/n*<d> n L(n, p) = *f (n < d > < d > p) kde
19 Model malého světa Distribuce stupňů u obou modelů malého světa neodpovídá distribuci u reálných sítí (což také nebylo cílem modelů). Přesná charakterizace je složitá, dostáváme však podobnou distribuci jako pro náh. grafy. WS model, mřížka s <d>=3, n=1000, hodnoty pro různá p (přítomny jen pro d> <d>/2),
20 Existují v rand a SW grafech centra? Malé vzdálenosti jsou charakteristické pro rand a SW grafy Distribuce stupňů má pro velká d exponenciální charakter, nedovolují existenci velkých center (vrcholů s vysokým stupněm) na obr. k je stupeň N = 10^6,<d>=4, Random Graph
21 Nový model Potřebujeme model, kde distribuce stupňů bude mít dlouhý konec (bude heavy tailed, right skewed), odrážející existenci center v reálných sítích Kandidát mocninné rozdělení (power law distribution) p(d) d -α na obr. k je stupeň N = 10^6,<d>=4, Random Graph & Scale/free
22 MADI Bezškálové grafy (Scale-free graphs)
23 Předchozí modely Mřížka pravidelný stupeň, velký shlukovací koeficient C, velká průměrná délka L Náhodné grafy všechny hrany stejně pravděpodobné (s pstí p), malý C, malá L Zobecněné náhodné grafy, vlastnosti jako náhodný graf ale respektuje distribuci stupňů dle mocninného zákona Wats Strogatzův model (Wats Newmanův model ) velký C, malá L
24 Centra (hubs) 2000 Malcom Gladwell - The Tipping Point existence prostředníků v sociální síti 248 příjmení z tel. seznamu pro Manhattan, bod za každého známého s příjmením ze seznamu Různé skupiny lidí (cca 400 osob), různé výsledky (nejméně 2 body, nejvíce 118) 1999 ( zároveň s WS modelem (1998)) Barabási, Jeong, Albertová zkoumali WWW existence center v síti Webu (doména nd.edu) z stránek v doméně univerzity Notre Dame mělo (82%) vstupní stupeň 3, 24 stránek vstupní stupeň cca 1000
25 Centra (hubs) Web později Z 203 mil. stránek mělo in stupeň 10 90% stránek, 3 měly in stupeň cca milion Herecká síť (08/2016) 1. Eric Roberts (d = 9403, L= ), 2. Michael Madsen (d = 6417, L= ), 3. Danny Trejo (d = 7432, L= ), 4. Samuel L. Jackson (d = 6649, L = ), 435. Kevin Bacon (d=3303, L= ) Objev shluků v sítích odporoval modelu n.g. WS model přizpůsobil model n.g. faktu existence shluků objev center definitivně vedl k opuštění náhodného pohledu na reálné sítě.
26 Centra (hubs) Kdyby zmíněné sítě byly n.g.: Gladwell - <d> = 39, nejspolečenštější osoba by musela mít méně než 118 známých Web pravděpodobnost stránky s in stupněm 500 by byla tj. centra nemohou existovat Hollywood E. Roberts by neexistoval, pst existence takového vrcholu Centra i v jiných sítích Buňka centra v síti molekul spojených chem. vazbami (voda, ATP) Studie AT&T vysoký podíl hovorů připadá na malý počet tel. čísel (call centra apod.)
27 Nový model Potřebujeme model, kde distribuce stupňů bude mít dlouhý konec (bude heavy tailed, right skewed), odrážející existenci center v reálných sítích Kandidát mocninné rozdělení (power law distribution) p(x) x -α
28 Co znamená heavy tailed? Heavy tailed, také right skew Distribuce stupňů Normální rozdělení: Např. výška mužské populace je vycentrována okolo 180cm Mocninné rozdělení: např. městská populace: NYC 8.3 mil. obyv., ale mnoho malých měst Vysoký poměr max k min Výška: Nejvyšší muž 272cm, nejnižší: 74cm, poměr cca 3.7 Populace: NYC 8.3 mil. obyv., Duffield, Virginia 52 obyv., poměr cca
29 Mocninné rozdělení Sklon α lineární měřítko log-log měřítko Velmi šikmé (asymetrie) Přímka v logaritmickém měřítku (rovnice přímky y=c+mx) f(x)=bx α, log(f(x))= log(b) + αlog(x) 29
30 Invariant Invariance - neměnnost, stálost jevů nebo veličin vůči změnám, Invariant - vztah nebo útvar neměnící se při určité transformaci nebo neměnný v různých variacích Invariant vzhledem ke změně měřítka (scale invariant) př. fraktály, Kochova vločka
31 Mocninný zákon Mocninný zákon je polynomiální závislost f(x) (ve které závislá proměnná x obsahuje exponent α) vyjadřující vlastnost invariance vzhledem k měřítku. Nejobvyklejší mocninný zákon má tvar f(x)=bx α +o(x α ), kde b, α jsou konstanty a o(x α ) je vzhledem k bx α asymptoticky menší funkce. Exponent α se nazývá měřítkový exponent. Měřítkový znamená, že mocninná funkce vyhovuje f(cx) f(x), kde c je konstanta (vyjadřuje, že zvětšením argumentu konstantním poměrem se změní pouze měřítko funkce, ne však její tvar). Pro znázornění funkce v grafické podobě se často používá tzv. loglog tvar zápisu log(f(x))= log b + α *log x Tento zápis představuje lineární závislost, kde α je parametr funkce určující její sklon (je vidět nezávislost tvaru na násobící konstantě argumentu b, tato konstanta nijak neovlivňuje parametr α).
32 log(d) Mocninný zákon Pro potřeby v bezškálových sítích se tedy používá vztah m.z. p(d) d -α, d je stupeň vrcholu U reálných bezškálových sítí je exponent α typicky v rozmezí 2 α 3 (ale není to pravidlem). Mocninný zákon vypadá stejně, nezávisle na měřítku, ve kterém se na něj díváme Tedy bezškálová distribuce vyhovuje: p(cd) = g(c)p(d), Tedy p(cd) p(d) tvar rozdělení je stále stejný až na multiplikativní konstantu, p(cd)=(cd) -α = c -α d -α d c*d log(p(d))
33 Co znamená bezškálovost? Barabási a Albertová - vysvětlili bezškálovost webu pomocí násl. principů: neustálý růst sítě - síť je dynamická a neustále se proměňuje, v každém kroku časového vývoje se k síti přidá jeden uzel, preferenční připojování nového uzlu k starším -nezáleží tedy na obsahu stránky, ale na počtu stránek, které na ni odkazují. Pojem bezškálový původně jen pro generativní model bohatí bohatnou a chudí chudnou (a za určitých podmínek vítěz bere vše)
34 BA model BA model obecně pro neorientované grafy Mechanismy Růst sítě nejsou statické (na rozdíl od modelu NG), ale rostou (pro každé časové období přidáme k síti jeden vrchol) Preferenční připojování nové vazby (hrany) nejsou náhodné, ale preferují zdatnější vrcholy, pst, že se nový vrchol připojí k vrcholu i závisí proporcionálně na stupni d i přes sumu všech stupňů
35 BA model BA model (neorientovaný graf) vstup: počáteční (pod)graf G 0 s m 0 vrcholy a m (m m 0 ) počet hran pro nový vrchol proces: Vrcholy přidávány jeden po druhém Každý vrchol se připojí k m jiným vrcholům, vybere je s pstí úměrnou jejich stupni jestliže [d 1,,d t ] je posloupnost stupňů v čase t, vrchol t+1 se připojí k vrcholu i s pstí d j i = d j di 2mt
36 BA model Po t krocích máme graf s N=t+m 0 vrcholy a mt hranami Experimentálně Výsledkem je mocninné rozdělení distribuce stupňů s α = 3 (α = 2+1/m, bere m=1) Exponent je nezávislý na m, tedy na jediném parametru modelu Růst lineární (linear preferential attachment), což vede ke konstantnímu průměrnému stupni (a k tomu, že distribuce stupňů je mocninná pro všechny stupně, což ale není v reálu příliš časté (zpravidla mocninné na konci, obecně od nějakého minimálního stupně > 1))
37 Simulace preferenčního připojování Naivní přístup vyžaduje určení stupňů vrcholů a celý proces konstrukce grafu s n vrcholy bude vyžadovat O(n 2 ) kroků Lepší přístup O(n) vrcholy uložíme do pole a prvek pole vybíráme náhodně Pst výběru vrcholu je úměrná počtu výskytů prvku v poli (což koresponduje se stupněm vrcholu)
38 Simulace preferenčního připojování 3 Start každý vrchol má stejný stupeň (2), pst výběru vrcholu je 1/3 Přidáme nový vrchol s m hranami, např. m = Vybereme náhodně dva prvky z pole např. 2 a Po přidání vrcholu 4 jsou psti výběru vrcholu 1, 2, 3 nebo 4 1/5, 3/10, 3/10, 1/5 Přidej nový vrchol náhodně vyber vrchol z pole atd
39 Vlastnosti BA modelu Graf je souvislý Každý nový vrchol vzniká s vazbou nebo více vazbami (podle toho zda m = 1 nebo m > 1) Připojí se ke staršímu vrcholu, který je sám s pojen s jiným vrcholem A začali jsme od souvislého grafu (podgrafu, jádra) Starší vrcholy jsou bohatší Vrcholy postupem času shromažďují vazby, což přináší starším vrcholům výhodu nové vrcholy se připojují preferenčně a starší vrcholy mají vyšší stupně
40 Vlastnosti BA modelu Struktura core-pheriphery, vrcholy s vysokým stupněm mají často vysokou closeness a betweenness
41 Jak je to se scale-free sítěmi? Síť je často nazývána bezškálovou, pokud distribuce stupňů odpovídá mocninnému zákonu. Pojem bezškálový je však někdy používán chybně, pozor na to tento pojem původně jen pro generativní model Barabási- Albertová, Li: Towards a Theory of Scale-Free Graphs, Sec 3., ( Hlavní vlastnosti grafů SF (podle literatury) SF sítě mají mocninné rozdělení distribuce stupňů SF sítě mohou být generovány náhodnými procesy, jako je např. preferenční připojování SF sítě mají vysoce propojená centra, která drží sítě pohromadě a činí SF sítě odolnými vůči chybám ale zranitelnými vzhledem k cíleným útokům SF sítě jsou obecné v tom smyslu že distribuce stupňů zůstává zachována i při náhodném přepojování hran SF sítě jsou univerzální v tom smyslu, že nezávisí na specifických detailech domény
42 Příklady bezškálových sítí Moby Dick scientific papers AOL users visiting sites 97 bestsellers AT&T customers on 1 day California
43 Příklady Web různé experimenty různé hodnoty α α in = 2.1, α out = 2.45 α in = 2.1, α out = 2.72 α in = 2.1, α out = 2.38 Herci α = 2.3±0.1 Síť telef. hovorů α in = α out = 2.1
44 Další příklady exponent α (in/out degree) film actors 2.3 telephone call graph 2.1 networks 1.5/2.0 sexual contacts 3.2 WWW 2.3/2.7 internet 2.5 peer-to-peer 2.1 metabolic network 2.2 protein interactions 2.4
Metody analýzy dat I (Data Analysis I) Modely pokračování Model malého světa
 Metody analýzy dat I (Data Analysis I) Modely pokračování Model malého světa Literatura Zaki, M. J., Meira Jr, W. (2014). Data Mining and Analysis: Fundamental Concepts and Algorithms. Cambridge University
Metody analýzy dat I (Data Analysis I) Modely pokračování Model malého světa Literatura Zaki, M. J., Meira Jr, W. (2014). Data Mining and Analysis: Fundamental Concepts and Algorithms. Cambridge University
MADI. Model bezškálového grafu (Scale-free graphs) - pokračování
 MADI Model bezškálového grafu (Scale-free graphs) - pokračování Předchozí modely Mřížka pravidelný stupeň, velký shlukovací koeficient C, velká průměrná vzdálenost L Náhodné grafy všechny hrany stejně
MADI Model bezškálového grafu (Scale-free graphs) - pokračování Předchozí modely Mřížka pravidelný stupeň, velký shlukovací koeficient C, velká průměrná vzdálenost L Náhodné grafy všechny hrany stejně
Metody analýzy dat I (Data Analysis I) Rozsáhlé struktury a vlastnosti sítí (Large-scale Structures and Properties of Networks) - pokračování
 Metody analýzy dat I (Data Analysis I) Rozsáhlé struktury a vlastnosti sítí (Large-scale Structures and Properties of Networks) - pokračování Základní (strukturální) vlastnosti sítí Stupně vrcholů a jejich
Metody analýzy dat I (Data Analysis I) Rozsáhlé struktury a vlastnosti sítí (Large-scale Structures and Properties of Networks) - pokračování Základní (strukturální) vlastnosti sítí Stupně vrcholů a jejich
Metody analýzy dat I. Míry a metriky - pokračování
 Metody analýzy dat I Míry a metriky - pokračování Literatura Newman, M. (2010). Networks: an introduction. Oxford University Press. [168-193] Zaki, M. J., Meira Jr, W. (2014). Data Mining and Analysis:
Metody analýzy dat I Míry a metriky - pokračování Literatura Newman, M. (2010). Networks: an introduction. Oxford University Press. [168-193] Zaki, M. J., Meira Jr, W. (2014). Data Mining and Analysis:
Metody analýzy dat I (Data Analysis I) Strukturální vlastnosti sítí 1. krok analýzy
 Metody analýzy dat I (Data Analysis I) Strukturální vlastnosti sítí 1. krok analýzy Literatura Newman, M. (2010). Networks: an introduction. Oxford University Press. [235-270] Zaki, M. J., Meira Jr, W.
Metody analýzy dat I (Data Analysis I) Strukturální vlastnosti sítí 1. krok analýzy Literatura Newman, M. (2010). Networks: an introduction. Oxford University Press. [235-270] Zaki, M. J., Meira Jr, W.
Metody analýzy dat I (Data Analysis I) Míry a metriky (Measures and Metrics) - - pokračování
 Metody analýzy dat I (Data Analysis I) Míry a metriky (Measures and Metrics) - - pokračování Literatura Newman, M. (2010). Networks: an introduction. Oxford University Press. [168-193] Zaki, M. J., Meira
Metody analýzy dat I (Data Analysis I) Míry a metriky (Measures and Metrics) - - pokračování Literatura Newman, M. (2010). Networks: an introduction. Oxford University Press. [168-193] Zaki, M. J., Meira
Moderní aplikace statistické fyziky II - TMF050
 Moderní aplikace statistické fyziky II - TMF050 Body 2, E-Kredity 3, 2/0 Zk - LS Miroslav Kotrla a František Slanina kotrla@fzu.cz slanina@fzu fzu.cz kmenově: externě: ÚTF UK FZÚ AV ČR, v.v.i. oddělení
Moderní aplikace statistické fyziky II - TMF050 Body 2, E-Kredity 3, 2/0 Zk - LS Miroslav Kotrla a František Slanina kotrla@fzu.cz slanina@fzu fzu.cz kmenově: externě: ÚTF UK FZÚ AV ČR, v.v.i. oddělení
Metody analýzy dat I (Data Analysis I) Úvod do sítí (Networks Basics)
 Metody analýzy dat I (Data Analysis I) Úvod do sítí (Networks Basics) Literatura Albert-László Barabási. Network Science http://barabasi.com/networksciencebook/ kapitoly 1 a 2 http://tuvalu.santafe.edu/~aaronc/courses/5352/csci5352_
Metody analýzy dat I (Data Analysis I) Úvod do sítí (Networks Basics) Literatura Albert-László Barabási. Network Science http://barabasi.com/networksciencebook/ kapitoly 1 a 2 http://tuvalu.santafe.edu/~aaronc/courses/5352/csci5352_
Metody analýzy dat I (Data Analysis I) Úvod do sítí (Networks Basics)
 Metody analýzy dat I (Data Analysis I) Úvod do sítí (Networks Basics) Literatura Newman, M. (2010). Networks: An Introduction. Oxford University Press. [15-77] Leskovec, J., Rajaraman, A., Ullman, J. D.
Metody analýzy dat I (Data Analysis I) Úvod do sítí (Networks Basics) Literatura Newman, M. (2010). Networks: An Introduction. Oxford University Press. [15-77] Leskovec, J., Rajaraman, A., Ullman, J. D.
Metody analýzy dat I (Data Analysis I) Úvod do sítí (Networks Basics)
 Metody analýzy dat I (Data Analysis I) Úvod do sítí (Networks Basics) Literatura Newman, M. (2010). Networks: An Introduction. Oxford University Press. [15-77] Leskovec, J., Rajaraman, A., Ullman, J. D.
Metody analýzy dat I (Data Analysis I) Úvod do sítí (Networks Basics) Literatura Newman, M. (2010). Networks: An Introduction. Oxford University Press. [15-77] Leskovec, J., Rajaraman, A., Ullman, J. D.
Úvod do mobilní robotiky AIL028
 Pravděpodobnostní plánování zbynek.winkler at mff.cuni.cz, md at robotika.cz http://robotika.cz/guide/umor05/cs 12. prosince 2005 1 Co už umíme a co ne? Jak řešit složitější případy? Definice konfiguračního
Pravděpodobnostní plánování zbynek.winkler at mff.cuni.cz, md at robotika.cz http://robotika.cz/guide/umor05/cs 12. prosince 2005 1 Co už umíme a co ne? Jak řešit složitější případy? Definice konfiguračního
Redukce bezškálových grafů pomocí genetických algoritmů Scale-free Network Reduction by Genetic Algorithms
 VŠB Technická univerzita Ostrava Fakulta elektrotechniky a informatiky Katedra informatiky Redukce bezškálových grafů pomocí genetických algoritmů Scale-free Network Reduction by Genetic Algorithms 2014
VŠB Technická univerzita Ostrava Fakulta elektrotechniky a informatiky Katedra informatiky Redukce bezškálových grafů pomocí genetických algoritmů Scale-free Network Reduction by Genetic Algorithms 2014
PROSTOROVÉ ANALÝZY DAT
 PROSTOROVÉ ANALÝZY DAT doc. Dr. Ing. Jiří Horák VŠB-TU Ostrava, HGF, Institut geoinformatiky, 2018 7.vydání část C linie, grafy a sítě 1 Obsah: 1 Linie... 4 1.1 Analýza interakčních dat... 4 1.1.1 Prostorové
PROSTOROVÉ ANALÝZY DAT doc. Dr. Ing. Jiří Horák VŠB-TU Ostrava, HGF, Institut geoinformatiky, 2018 7.vydání část C linie, grafy a sítě 1 Obsah: 1 Linie... 4 1.1 Analýza interakčních dat... 4 1.1.1 Prostorové
Logaritmické a exponenciální funkce
 Kapitola 4 Logaritmické a exponenciální funkce V této kapitole se budeme zabývat exponenciálními a logaritmickými funkcemi. Uvedeme si definice vlastnosti a vztah mezi nimi. 4.1 Exponenciální funkce Exponenciální
Kapitola 4 Logaritmické a exponenciální funkce V této kapitole se budeme zabývat exponenciálními a logaritmickými funkcemi. Uvedeme si definice vlastnosti a vztah mezi nimi. 4.1 Exponenciální funkce Exponenciální
Zdůvodněte, proč funkce n lg(n) roste alespoň stejně rychle nebo rychleji než než funkce lg(n!). Symbolem lg značíme logaritmus o základu 2.
 1 3 4 5 6 7 8 9 10 11 1 13 14 15 16 17 18 19 0 1 3 4 5 6 7 8 9 30 31 3 Zdůvodněte, proč funkce f(n) = n log(n) 1 n 1/ roste rychleji než funkce g(n) = n. Zdůvodněte, proč funkce f(n) = n 3/ log(n) roste
1 3 4 5 6 7 8 9 10 11 1 13 14 15 16 17 18 19 0 1 3 4 5 6 7 8 9 30 31 3 Zdůvodněte, proč funkce f(n) = n log(n) 1 n 1/ roste rychleji než funkce g(n) = n. Zdůvodněte, proč funkce f(n) = n 3/ log(n) roste
PB050: Modelování a predikce v systémové biologii
 PB050: Modelování a predikce v systémové biologii David Šafránek 21.10.2009 Obsah Pojem modelu a simulace in silico opakování Obsah Pojem modelu a simulace in silico opakování Workflow systémové biologie
PB050: Modelování a predikce v systémové biologii David Šafránek 21.10.2009 Obsah Pojem modelu a simulace in silico opakování Obsah Pojem modelu a simulace in silico opakování Workflow systémové biologie
Časová složitost / Time complexity
 Časová složitost / Time complexity Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 2018 1 / 24 Složitost algoritmů Algorithm complexity Časová a paměťová složitost Trvání výpočtu v závislosti
Časová složitost / Time complexity Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 2018 1 / 24 Složitost algoritmů Algorithm complexity Časová a paměťová složitost Trvání výpočtu v závislosti
Ukážeme si lineární algoritmus, který pro pevné k rozhodne, zda vstupní. stromový rozklad. Poznamenejme, že je-li k součástí vstupu, pak rozhodnout
 Ukážeme si lineární algoritmus, který pro pevné k rozhodne, zda vstupní graf má stromovou šířku nejvýše k, a je-li tomu tak, také vrátí příslušný stromový rozklad. Poznamenejme, že je-li k součástí vstupu,
Ukážeme si lineární algoritmus, který pro pevné k rozhodne, zda vstupní graf má stromovou šířku nejvýše k, a je-li tomu tak, také vrátí příslušný stromový rozklad. Poznamenejme, že je-li k součástí vstupu,
ALGORITMY A DATOVÉ STRUKTURY
 Název tématického celku: Cíl: ALGORITMY A DATOVÉ STRUKTURY Metodický list č. 1 Časová složitost algoritmů Základním cílem tohoto tematického celku je vysvětlení potřebných pojmů a definic nutných k popisu
Název tématického celku: Cíl: ALGORITMY A DATOVÉ STRUKTURY Metodický list č. 1 Časová složitost algoritmů Základním cílem tohoto tematického celku je vysvětlení potřebných pojmů a definic nutných k popisu
MATURITNÍ TÉMATA Z MATEMATIKY
 MATURITNÍ TÉMATA Z MATEMATIKY 1. Základní poznatky z logiky a teorie množin Pojem konstanty a proměnné. Obor proměnné. Pojem výroku a jeho pravdivostní hodnota. Operace s výroky, složené výroky, logické
MATURITNÍ TÉMATA Z MATEMATIKY 1. Základní poznatky z logiky a teorie množin Pojem konstanty a proměnné. Obor proměnné. Pojem výroku a jeho pravdivostní hodnota. Operace s výroky, složené výroky, logické
Počítačové zobrazování fraktálních množin. J. Bednář*, J. Fábera**, B. Fürstová*** *Gymnázium Děčín **SPŠ Hronov ***Gymnázium Plasy
 Počítačové zobrazování fraktálních množin J. Bednář*, J. Fábera**, B. Fürstová*** *Gymnázium Děčín **SPŠ Hronov ***Gymnázium Plasy *jurij.jurjevic@centrum.cz **icarosai@seznam.cz ***barborafurstova7@seznam.cz
Počítačové zobrazování fraktálních množin J. Bednář*, J. Fábera**, B. Fürstová*** *Gymnázium Děčín **SPŠ Hronov ***Gymnázium Plasy *jurij.jurjevic@centrum.cz **icarosai@seznam.cz ***barborafurstova7@seznam.cz
Fraktály. krásné obrázky v matematice
 Fraktály aneb krásné obrázky v matematice Mgr. Jan Šustek 22. 10. 2009 Grafy funkcí Grafy funkcí Mějme funkce f, g : [ 6, 6] R definované vztahy f(x) = 2 3 Jak vypadají jejich grafy? x 2 + x 6 x 2 + x
Fraktály aneb krásné obrázky v matematice Mgr. Jan Šustek 22. 10. 2009 Grafy funkcí Grafy funkcí Mějme funkce f, g : [ 6, 6] R definované vztahy f(x) = 2 3 Jak vypadají jejich grafy? x 2 + x 6 x 2 + x
Časové řady, typy trendových funkcí a odhady trendů
 Statistika II Katedra ekonometrie FVL UO Brno kancelář 69a, tel 973 442029 email:jirineubauer@unobcz Stochastický proces Posloupnost náhodných veličin {Y t, t = 0, ±1, ±2 } se nazývá stochastický proces
Statistika II Katedra ekonometrie FVL UO Brno kancelář 69a, tel 973 442029 email:jirineubauer@unobcz Stochastický proces Posloupnost náhodných veličin {Y t, t = 0, ±1, ±2 } se nazývá stochastický proces
Časové řady, typy trendových funkcí a odhady trendů
 Časové řady, typy trendových funkcí a odhady trendů Jiří Neubauer Katedra ekonometrie FVL UO Brno kancelář 69a, tel 973 442029 email:jirineubauer@unobcz Jiří Neubauer (Katedra ekonometrie UO Brno) Časové
Časové řady, typy trendových funkcí a odhady trendů Jiří Neubauer Katedra ekonometrie FVL UO Brno kancelář 69a, tel 973 442029 email:jirineubauer@unobcz Jiří Neubauer (Katedra ekonometrie UO Brno) Časové
U Úvod do modelování a simulace systémů
 U Úvod do modelování a simulace systémů Vyšetřování rozsáhlých soustav mnohdy nelze provádět analytickým výpočtem.často je nutné zkoumat chování zařízení v mezních situacích, do kterých se skutečné zařízení
U Úvod do modelování a simulace systémů Vyšetřování rozsáhlých soustav mnohdy nelze provádět analytickým výpočtem.často je nutné zkoumat chování zařízení v mezních situacích, do kterých se skutečné zařízení
7. Rozdělení pravděpodobnosti ve statistice
 7. Rozdělení pravděpodobnosti ve statistice Statistika nuda je, má však cenné údaje, neklesejte na mysli, ona nám to vyčíslí Jednou z úloh statistiky je odhad (výpočet) hodnot statistického znaku x i,
7. Rozdělení pravděpodobnosti ve statistice Statistika nuda je, má však cenné údaje, neklesejte na mysli, ona nám to vyčíslí Jednou z úloh statistiky je odhad (výpočet) hodnot statistického znaku x i,
Metody analýzy dat II
 Metody analýzy dat II Vzorkování (Sampling) MAD2 2018/19 1 Literatura http://tuvalu.santafe.edu/~aaronc/courses/53 52/csci5352 2017 L9.pdf https://cs.stanford.edu/~jure/pubs/samplingkdd06.pdf https://www.cs.purdue.edu/homes/neville/co
Metody analýzy dat II Vzorkování (Sampling) MAD2 2018/19 1 Literatura http://tuvalu.santafe.edu/~aaronc/courses/53 52/csci5352 2017 L9.pdf https://cs.stanford.edu/~jure/pubs/samplingkdd06.pdf https://www.cs.purdue.edu/homes/neville/co
Pravděpodobnost, náhoda, kostky
 Pravděpodobnost, náhoda, kostky Radek Pelánek IV122, jaro 2015 Výhled pravděpodobnost náhodná čísla lineární regrese detekce shluků Dnes lehce nesourodá směs úloh souvisejících s pravděpodobností krátké
Pravděpodobnost, náhoda, kostky Radek Pelánek IV122, jaro 2015 Výhled pravděpodobnost náhodná čísla lineární regrese detekce shluků Dnes lehce nesourodá směs úloh souvisejících s pravděpodobností krátké
Monte Carlo. Simulační metoda založená na užití stochastických procesů a generace náhodných čísel.
 Monte Carlo Simulační metoda založená na užití stochastických procesů a generace náhodných čísel. Typy MC simulací a) MC integrace b) Geometrické MC c) Termodynamické MC d) Modelování vývoje na strukturální
Monte Carlo Simulační metoda založená na užití stochastických procesů a generace náhodných čísel. Typy MC simulací a) MC integrace b) Geometrické MC c) Termodynamické MC d) Modelování vývoje na strukturální
Algoritmy I, složitost
 A0B36PRI - PROGRAMOVÁNÍ Algoritmy I, složitost České vysoké učení technické Fakulta elektrotechnická v 1.01 Rychlost... Jeden algoritmus (program, postup, metoda ) je rychlejší než druhý. Co ta věta znamená??
A0B36PRI - PROGRAMOVÁNÍ Algoritmy I, složitost České vysoké učení technické Fakulta elektrotechnická v 1.01 Rychlost... Jeden algoritmus (program, postup, metoda ) je rychlejší než druhý. Co ta věta znamená??
AVDAT Nelineární regresní model
 AVDAT Nelineární regresní model Josef Tvrdík Katedra informatiky Přírodovědecká fakulta Ostravská univerzita Nelineární regresní model Ey i = f (x i, β) kde x i je k-členný vektor vysvětlujících proměnných
AVDAT Nelineární regresní model Josef Tvrdík Katedra informatiky Přírodovědecká fakulta Ostravská univerzita Nelineární regresní model Ey i = f (x i, β) kde x i je k-členný vektor vysvětlujících proměnných
You created this PDF from an application that is not licensed to print to novapdf printer (http://www.novapdf.com)
 Závislost náhodných veličin Úvod Předchozí přednášky: - statistické charakteristiky jednoho výběrového nebo základního souboru - vztahy mezi výběrovým a základním souborem - vztahy statistických charakteristik
Závislost náhodných veličin Úvod Předchozí přednášky: - statistické charakteristiky jednoho výběrového nebo základního souboru - vztahy mezi výběrovým a základním souborem - vztahy statistických charakteristik
oddělení Inteligentní Datové Analýzy (IDA)
 Vytěžování dat Filip Železný Katedra počítačů oddělení Inteligentní Datové Analýzy (IDA) 22. září 2014 Filip Železný (ČVUT) Vytěžování dat 22. září 2014 1 / 25 Odhad rozdělení Úloha: Vstup: data D = {
Vytěžování dat Filip Železný Katedra počítačů oddělení Inteligentní Datové Analýzy (IDA) 22. září 2014 Filip Železný (ČVUT) Vytěžování dat 22. září 2014 1 / 25 Odhad rozdělení Úloha: Vstup: data D = {
Projekční algoritmus. Urychlení evolučních algoritmů pomocí regresních stromů a jejich zobecnění. Jan Klíma
 Urychlení evolučních algoritmů pomocí regresních stromů a jejich zobecnění Jan Klíma Obsah Motivace & cíle práce Evoluční algoritmy Náhradní modelování Stromové regresní metody Implementace a výsledky
Urychlení evolučních algoritmů pomocí regresních stromů a jejich zobecnění Jan Klíma Obsah Motivace & cíle práce Evoluční algoritmy Náhradní modelování Stromové regresní metody Implementace a výsledky
Odhad parametrů N(µ, σ 2 )
 Odhad parametrů N(µ, σ 2 ) Mějme statistický soubor x 1, x 2,, x n modelovaný jako realizaci náhodného výběru z normálního rozdělení N(µ, σ 2 ) s neznámými parametry µ a σ. Jaký je maximální věrohodný
Odhad parametrů N(µ, σ 2 ) Mějme statistický soubor x 1, x 2,, x n modelovaný jako realizaci náhodného výběru z normálního rozdělení N(µ, σ 2 ) s neznámými parametry µ a σ. Jaký je maximální věrohodný
Usuzování za neurčitosti
 Usuzování za neurčitosti 25.11.2014 8-1 Usuzování za neurčitosti Hypotetické usuzování a zpětná indukce Míry postačitelnosti a nezbytnosti Kombinace důkazů Šíření pravděpodobnosti v inferenčních sítích
Usuzování za neurčitosti 25.11.2014 8-1 Usuzování za neurčitosti Hypotetické usuzování a zpětná indukce Míry postačitelnosti a nezbytnosti Kombinace důkazů Šíření pravděpodobnosti v inferenčních sítích
Téma 22. Ondřej Nývlt
 Téma 22 Ondřej Nývlt nyvlto1@fel.cvut.cz Náhodná veličina a náhodný vektor. Distribuční funkce, hustota a pravděpodobnostní funkce náhodné veličiny. Střední hodnota a rozptyl náhodné veličiny. Sdružené
Téma 22 Ondřej Nývlt nyvlto1@fel.cvut.cz Náhodná veličina a náhodný vektor. Distribuční funkce, hustota a pravděpodobnostní funkce náhodné veličiny. Střední hodnota a rozptyl náhodné veličiny. Sdružené
10. Předpovídání - aplikace regresní úlohy
 10. Předpovídání - aplikace regresní úlohy Regresní úloha (analýza) je označení pro statistickou metodu, pomocí nichž odhadujeme hodnotu náhodné veličiny (tzv. závislé proměnné, cílové proměnné, regresandu
10. Předpovídání - aplikace regresní úlohy Regresní úloha (analýza) je označení pro statistickou metodu, pomocí nichž odhadujeme hodnotu náhodné veličiny (tzv. závislé proměnné, cílové proměnné, regresandu
Regrese. používáme tehdy, jestliže je vysvětlující proměnná kontinuální pokud je kategoriální, jde o ANOVA
 Regrese používáme tehd, jestliže je vsvětlující proměnná kontinuální pokud je kategoriální, jde o ANOVA Specifikace modelu = a + bx a závisle proměnná b x vsvětlující proměnná Cíl analýz Odhadnout hodnot
Regrese používáme tehd, jestliže je vsvětlující proměnná kontinuální pokud je kategoriální, jde o ANOVA Specifikace modelu = a + bx a závisle proměnná b x vsvětlující proměnná Cíl analýz Odhadnout hodnot
Regresní analýza 1. Regresní analýza
 Regresní analýza 1 1 Regresní funkce Regresní analýza Důležitou statistickou úlohou je hledání a zkoumání závislostí proměnných, jejichž hodnoty získáme při realizaci experimentů Vzhledem k jejich náhodnému
Regresní analýza 1 1 Regresní funkce Regresní analýza Důležitou statistickou úlohou je hledání a zkoumání závislostí proměnných, jejichž hodnoty získáme při realizaci experimentů Vzhledem k jejich náhodnému
4EK311 Operační výzkum. 5. Teorie grafů
 4EK311 Operační výzkum 5. Teorie grafů 5. Teorie grafů definice grafu Graf G = uspořádaná dvojice (V, E), kde V označuje množinu n uzlů u 1, u 2,, u n (u i, i = 1, 2,, n) a E označuje množinu hran h ij,
4EK311 Operační výzkum 5. Teorie grafů 5. Teorie grafů definice grafu Graf G = uspořádaná dvojice (V, E), kde V označuje množinu n uzlů u 1, u 2,, u n (u i, i = 1, 2,, n) a E označuje množinu hran h ij,
Pravděpodobnost, náhoda, kostky
 Pravděpodobnost, náhoda, kostky Radek Pelánek IV122 Výhled pravděpodobnost náhodná čísla lineární regrese detekce shluků Dnes lehce nesourodá směs úloh souvisejících s pravděpodobností připomenutí, souvislosti
Pravděpodobnost, náhoda, kostky Radek Pelánek IV122 Výhled pravděpodobnost náhodná čísla lineární regrese detekce shluků Dnes lehce nesourodá směs úloh souvisejících s pravděpodobností připomenutí, souvislosti
Modelování a simulace Lukáš Otte
 Modelování a simulace 2013 Lukáš Otte Význam, účel a výhody MaS Simulační modely jsou nezbytné pro: oblast vědy a výzkumu (základní i aplikovaný výzkum) analýzy složitých dyn. systémů a tech. procesů oblast
Modelování a simulace 2013 Lukáš Otte Význam, účel a výhody MaS Simulační modely jsou nezbytné pro: oblast vědy a výzkumu (základní i aplikovaný výzkum) analýzy složitých dyn. systémů a tech. procesů oblast
Generování pseudonáhodných. Ing. Michal Dorda, Ph.D.
 Generování pseudonáhodných čísel při simulaci Ing. Michal Dorda, Ph.D. 1 Úvodní poznámky V simulačních modelech se velice často vyskytují náhodné proměnné. Proto se budeme zabývat otázkou, jak při simulaci
Generování pseudonáhodných čísel při simulaci Ing. Michal Dorda, Ph.D. 1 Úvodní poznámky V simulačních modelech se velice často vyskytují náhodné proměnné. Proto se budeme zabývat otázkou, jak při simulaci
1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004.
 Prostá regresní a korelační analýza 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Problematika závislosti V podstatě lze rozlišovat mezi závislostí nepodstatnou, čili náhodnou
Prostá regresní a korelační analýza 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Problematika závislosti V podstatě lze rozlišovat mezi závislostí nepodstatnou, čili náhodnou
časovém horizontu na rozdíl od experimentu lépe odhalit chybné poznání reality.
 Modelování dynamických systémů Matematické modelování dynamických systémů se využívá v různých oborech přírodních, technických, ekonomických a sociálních věd. Použití matematického modelu umožňuje popsat
Modelování dynamických systémů Matematické modelování dynamických systémů se využívá v různých oborech přírodních, technických, ekonomických a sociálních věd. Použití matematického modelu umožňuje popsat
Funkce jedné reálné proměnné. lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou
 Funkce jedné reálné proměnné lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou lineární y = ax + b Průsečíky s osami: Px [-b/a; 0] Py [0; b] grafem je přímka (získá se pomocí
Funkce jedné reálné proměnné lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou lineární y = ax + b Průsečíky s osami: Px [-b/a; 0] Py [0; b] grafem je přímka (získá se pomocí
4. OBYČEJNÉ DIFERENCIÁLNÍ ROVNICE
 FBI VŠB-TUO 28. března 2014 4.1. Základní pojmy Definice 4.1. Rovnice tvaru F (x, y, y, y,..., y (n) ) = 0 se nazývá obyčejná diferenciální rovnice n-tého řádu a vyjadřuje vztah mezi neznámou funkcí y
FBI VŠB-TUO 28. března 2014 4.1. Základní pojmy Definice 4.1. Rovnice tvaru F (x, y, y, y,..., y (n) ) = 0 se nazývá obyčejná diferenciální rovnice n-tého řádu a vyjadřuje vztah mezi neznámou funkcí y
E(X) = np D(X) = np(1 p) 1 2p np(1 p) (n + 1)p 1 ˆx (n + 1)p. A 3 (X) =
 Základní rozdělení pravděpodobnosti Diskrétní rozdělení pravděpodobnosti. Pojem Náhodná veličina s Binomickým rozdělením Bi(n, p), kde n je přirozené číslo, p je reálné číslo, < p < má pravděpodobnostní
Základní rozdělení pravděpodobnosti Diskrétní rozdělení pravděpodobnosti. Pojem Náhodná veličina s Binomickým rozdělením Bi(n, p), kde n je přirozené číslo, p je reálné číslo, < p < má pravděpodobnostní
Obsah prezentace. Základní pojmy v teorii o grafech Úlohy a prohledávání grafů Hledání nejkratších cest
 Obsah prezentace Základní pojmy v teorii o grafech Úlohy a prohledávání grafů Hledání nejkratších cest 1 Základní pojmy Vrchol grafu: {množina V} Je to styčná vazba v grafu, nazývá se též uzlem, prvkem
Obsah prezentace Základní pojmy v teorii o grafech Úlohy a prohledávání grafů Hledání nejkratších cest 1 Základní pojmy Vrchol grafu: {množina V} Je to styčná vazba v grafu, nazývá se též uzlem, prvkem
Různé algoritmy mají různou složitost
 / 1 Různé algoritmy mají různou složitost 1/ 1 Rychlost... Jeden algoritmus (program, postup, metoda ) je rychlejší než druhý. Co ta věta znamená?? 2/ 1 Asymptotická složitost y y x x Každému algoritmu
/ 1 Různé algoritmy mají různou složitost 1/ 1 Rychlost... Jeden algoritmus (program, postup, metoda ) je rychlejší než druhý. Co ta věta znamená?? 2/ 1 Asymptotická složitost y y x x Každému algoritmu
Vybrané technologie povrchových úprav. Základy vakuové techniky Doc. Ing. Karel Daďourek 2006
 Vybrané technologie povrchových úprav Základy vakuové techniky Doc. Ing. Karel Daďourek 2006 Střední rychlost plynů Rychlost molekuly v p = (2 k N A ) * (T/M 0 ), N A = 6. 10 23 molekul na mol (Avogadrova
Vybrané technologie povrchových úprav Základy vakuové techniky Doc. Ing. Karel Daďourek 2006 Střední rychlost plynů Rychlost molekuly v p = (2 k N A ) * (T/M 0 ), N A = 6. 10 23 molekul na mol (Avogadrova
Regresní analýza. Eva Jarošová
 Regresní analýza Eva Jarošová 1 Obsah 1. Regresní přímka 2. Možnosti zlepšení modelu 3. Testy v regresním modelu 4. Regresní diagnostika 5. Speciální využití Lineární model 2 1. Regresní přímka 3 nosnost
Regresní analýza Eva Jarošová 1 Obsah 1. Regresní přímka 2. Možnosti zlepšení modelu 3. Testy v regresním modelu 4. Regresní diagnostika 5. Speciální využití Lineární model 2 1. Regresní přímka 3 nosnost
2. Složitost, grafové algoritmy (zapsal Martin Koutecký)
 2. Složitost, grafové algoritmy (zapsal Martin Koutecký) Model Ram Při analýze algoritmu bychom chtěli nějak popsat jeho složitost. Abychom mohli udělat toto, potřebujeme nejprve definovat výpočetní model.
2. Složitost, grafové algoritmy (zapsal Martin Koutecký) Model Ram Při analýze algoritmu bychom chtěli nějak popsat jeho složitost. Abychom mohli udělat toto, potřebujeme nejprve definovat výpočetní model.
Základy teorie pravděpodobnosti
 Základy teorie pravděpodobnosti Náhodná veličina Roman Biskup (zapálený) statistik ve výslužbě, aktuálně analytik v praxi ;-) roman.biskup(at)email.cz 12. února 2012 Statistika by Birom Základy teorie
Základy teorie pravděpodobnosti Náhodná veličina Roman Biskup (zapálený) statistik ve výslužbě, aktuálně analytik v praxi ;-) roman.biskup(at)email.cz 12. února 2012 Statistika by Birom Základy teorie
Cvičné texty ke státní maturitě z matematiky
 Cvičné texty ke státní maturitě z matematiky Pracovní listy s postupy řešení Brno 2010 RNDr. Rudolf Schwarz, CSc. Státní maturita z matematiky Obsah Obsah NIŽŠÍ úroveň obtížnosti 4 MAGZD10C0K01 říjen 2010..........................
Cvičné texty ke státní maturitě z matematiky Pracovní listy s postupy řešení Brno 2010 RNDr. Rudolf Schwarz, CSc. Státní maturita z matematiky Obsah Obsah NIŽŠÍ úroveň obtížnosti 4 MAGZD10C0K01 říjen 2010..........................
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
IV117: Úvod do systémové biologie
 IV117: Úvod do systémové biologie David Šafránek 1.10.2008 Obsah Pojem modelu a simulace in silico Statická analýza modelu Dynamická analýza modelu Obsah Pojem modelu a simulace in silico Statická analýza
IV117: Úvod do systémové biologie David Šafránek 1.10.2008 Obsah Pojem modelu a simulace in silico Statická analýza modelu Dynamická analýza modelu Obsah Pojem modelu a simulace in silico Statická analýza
Kolik existuje různých stromů na pevně dané n-prvkové množině vrcholů?
 Kapitola 9 Matice a počet koster Graf (orientovaný i neorientovaný) lze popsat maticí, a to hned několika různými způsoby. Tématem této kapitoly jsou incidenční matice orientovaných grafů a souvislosti
Kapitola 9 Matice a počet koster Graf (orientovaný i neorientovaný) lze popsat maticí, a to hned několika různými způsoby. Tématem této kapitoly jsou incidenční matice orientovaných grafů a souvislosti
Základy vakuové techniky
 Základy vakuové techniky Střední rychlost plynů Rychlost molekuly v p = (2 k N A ) * (T/M 0 ), N A = 6. 10 23 molekul na mol (Avogadrova konstanta), k = 1,38. 10-23 J/K.. Boltzmannova konstanta, T.. absolutní
Základy vakuové techniky Střední rychlost plynů Rychlost molekuly v p = (2 k N A ) * (T/M 0 ), N A = 6. 10 23 molekul na mol (Avogadrova konstanta), k = 1,38. 10-23 J/K.. Boltzmannova konstanta, T.. absolutní
Základní pojmy teorie grafů [Graph theory]
![Základní pojmy teorie grafů [Graph theory] Základní pojmy teorie grafů [Graph theory]](/thumbs/25/4817299.jpg) Část I Základní pojmy teorie grafů [Graph theory] V matematice grafem obvykle rozumíme grafické znázornění funkční závislosti. Pro tento předmět je však podstatnější pohled jiný. V teorii grafů rozumíme
Část I Základní pojmy teorie grafů [Graph theory] V matematice grafem obvykle rozumíme grafické znázornění funkční závislosti. Pro tento předmět je však podstatnější pohled jiný. V teorii grafů rozumíme
Binární vyhledávací stromy pokročilé partie
 Binární vyhledávací stromy pokročilé partie KMI/ALS lekce Jan Konečný 30.9.204 Literatura Cormen Thomas H., Introduction to Algorithms, 2nd edition MIT Press, 200. ISBN 0-262-5396-8 6, 3, A Knuth Donald
Binární vyhledávací stromy pokročilé partie KMI/ALS lekce Jan Konečný 30.9.204 Literatura Cormen Thomas H., Introduction to Algorithms, 2nd edition MIT Press, 200. ISBN 0-262-5396-8 6, 3, A Knuth Donald
Regresní analýza. Ekonometrie. Jiří Neubauer. Katedra ekonometrie FVL UO Brno kancelář 69a, tel
 Regresní analýza Ekonometrie Jiří Neubauer Katedra ekonometrie FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Jiří Neubauer (Katedra ekonometrie UO Brno) Regresní analýza 1 / 23
Regresní analýza Ekonometrie Jiří Neubauer Katedra ekonometrie FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Jiří Neubauer (Katedra ekonometrie UO Brno) Regresní analýza 1 / 23
Diskrétní náhodná veličina. November 12, 2008
 Diskrétní náhodná veličina November 12, 2008 (Náhodná veličina (náhodná proměnná)) Náhodná veličina (nebo též náhodná proměnná) je veličina X, jejíž hodnota je jednoznačně určena výsledkem náhodného pokusu.
Diskrétní náhodná veličina November 12, 2008 (Náhodná veličina (náhodná proměnná)) Náhodná veličina (nebo též náhodná proměnná) je veličina X, jejíž hodnota je jednoznačně určena výsledkem náhodného pokusu.
Měření závislosti statistických dat
 5.1 Měření závislosti statistických dat Každý pořádný astronom je schopen vám předpovědět, kde se bude nacházet daná hvězda půl hodiny před půlnocí. Ne každý je však téhož schopen předpovědět v případě
5.1 Měření závislosti statistických dat Každý pořádný astronom je schopen vám předpovědět, kde se bude nacházet daná hvězda půl hodiny před půlnocí. Ne každý je však téhož schopen předpovědět v případě
Charakterizace rozdělení
 Charakterizace rozdělení Momenty f(x) f(x) f(x) μ >μ 1 σ 1 σ >σ 1 g 1 g σ μ 1 μ x μ x x N K MK = x f( x) dx 1 M K = x N CK = ( x M ) f( x) dx ( xi M 1 C = 1 K 1) N i= 1 K i K N i= 1 K μ = E ( X ) = xf
Charakterizace rozdělení Momenty f(x) f(x) f(x) μ >μ 1 σ 1 σ >σ 1 g 1 g σ μ 1 μ x μ x x N K MK = x f( x) dx 1 M K = x N CK = ( x M ) f( x) dx ( xi M 1 C = 1 K 1) N i= 1 K i K N i= 1 K μ = E ( X ) = xf
Metody síťové analýzy
 Metody síťové analýzy Řeší problematiku složitých systémů, zejména pak vazby mezi jejich jednotlivými prvky. Vychází z teorie grafů. Základní metody síťové analýzy: CPM (Critical Path Method) deterministický
Metody síťové analýzy Řeší problematiku složitých systémů, zejména pak vazby mezi jejich jednotlivými prvky. Vychází z teorie grafů. Základní metody síťové analýzy: CPM (Critical Path Method) deterministický
Funkce. Úkol: Uveďte příklady závislosti dvou veličin.
 Funkce Pojem funkce Dostupné z Metodického portálu www.rvp.cz, ISSN: 1802-4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze. Funkce vyjadřuje závislost
Funkce Pojem funkce Dostupné z Metodického portálu www.rvp.cz, ISSN: 1802-4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze. Funkce vyjadřuje závislost
www.pedagogika.skolni.eu
 2. Důležitost grafů v ekonomických modelech. Náležitosti grafů. Typy grafů. Formy závislosti zkoumaných ekonomických jevů a jejich grafické znázornění. Grafy prezentují údaje a zachytávají vztahy mezi
2. Důležitost grafů v ekonomických modelech. Náležitosti grafů. Typy grafů. Formy závislosti zkoumaných ekonomických jevů a jejich grafické znázornění. Grafy prezentují údaje a zachytávají vztahy mezi
MĚŘENÍ STATISTICKÝCH ZÁVISLOSTÍ
 MĚŘENÍ STATISTICKÝCH ZÁVISLOSTÍ v praxi u jednoho prvku souboru se často zkoumá více veličin, které mohou na sobě různě záviset jednorozměrný výběrový soubor VSS X vícerozměrným výběrovým souborem VSS
MĚŘENÍ STATISTICKÝCH ZÁVISLOSTÍ v praxi u jednoho prvku souboru se často zkoumá více veličin, které mohou na sobě různě záviset jednorozměrný výběrový soubor VSS X vícerozměrným výběrovým souborem VSS
1. Statistická analýza dat Jak vznikají informace Rozložení dat
 1. Statistická analýza dat Jak vznikají informace Rozložení dat J. Jarkovský, L. Dušek, S. Littnerová, J. Kalina Význam statistické analýzy dat Sběr a vyhodnocování dat je způsobem k uchopení a pochopení
1. Statistická analýza dat Jak vznikají informace Rozložení dat J. Jarkovský, L. Dušek, S. Littnerová, J. Kalina Význam statistické analýzy dat Sběr a vyhodnocování dat je způsobem k uchopení a pochopení
COMPLEXITY
 Níže uvedené úlohy představují přehled otázek, které se vyskytly v tomto nebo v minulých semestrech ve cvičení nebo v minulých semestrech u zkoušky. Mezi otázkami semestrovými a zkouškovými není žádný
Níže uvedené úlohy představují přehled otázek, které se vyskytly v tomto nebo v minulých semestrech ve cvičení nebo v minulých semestrech u zkoušky. Mezi otázkami semestrovými a zkouškovými není žádný
HAZARDY V LOGICKÝCH SYSTÉMECH
 HAZARDY V LOGICKÝCH SYSTÉMECH 1. FUNKČNÍ HAZARD : Při změně vstupního stavu vstupních proměnných, kdy se bude měnit více jak jedna proměnná - v reálné praxi však současná změna nenastává a ke změnám hodnot
HAZARDY V LOGICKÝCH SYSTÉMECH 1. FUNKČNÍ HAZARD : Při změně vstupního stavu vstupních proměnných, kdy se bude měnit více jak jedna proměnná - v reálné praxi však současná změna nenastává a ke změnám hodnot
Metody analýzy dat II
 Metody analýzy dat II Detekce komunit MADII 2018/19 1 Zachary s club, Collaboration network in Santa Fe Institute, Lusseau s network of Bottlenose Dolphins 2 Web Pages, Overlaping communities of word associations
Metody analýzy dat II Detekce komunit MADII 2018/19 1 Zachary s club, Collaboration network in Santa Fe Institute, Lusseau s network of Bottlenose Dolphins 2 Web Pages, Overlaping communities of word associations
Úvod do analýzy časových řad
 Přednáška STATISTIKA II - EKONOMETRIE Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Posloupnost náhodných veličin {Y t, t = 0, ±1, ±2... } se nazývá stochastický
Přednáška STATISTIKA II - EKONOMETRIE Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Posloupnost náhodných veličin {Y t, t = 0, ±1, ±2... } se nazývá stochastický
1 Test 1 naivní vs standardní
 . DÚ Nafukovací pole Datové Struktury I Studentus Maximus Takto jsou zobrazeny poznámky cvičících k tomu, co a jak je tu napsáno, skutečný text je mimo oranžové rámečky. Počítač, na kterém byly provedeny
. DÚ Nafukovací pole Datové Struktury I Studentus Maximus Takto jsou zobrazeny poznámky cvičících k tomu, co a jak je tu napsáno, skutečný text je mimo oranžové rámečky. Počítač, na kterém byly provedeny
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Kostry. 9. týden. Grafy. Marie Demlová (úpravy Matěj Dostál) 16. dubna 2019
 Grafy 16. dubna 2019 Tvrzení. Je dán graf G, pak následující je ekvivalentní. 1 G je strom. 2 Graf G nemá kružnice a přidáme-li ke grafu libovolnou hranu, uzavřeme přesně jednu kružnici. 3 Graf G je souvislý
Grafy 16. dubna 2019 Tvrzení. Je dán graf G, pak následující je ekvivalentní. 1 G je strom. 2 Graf G nemá kružnice a přidáme-li ke grafu libovolnou hranu, uzavřeme přesně jednu kružnici. 3 Graf G je souvislý
CVIČNÝ TEST 48. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17
 CVIČNÝ TEST 48 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Je dán konvexní čtyřúhelník, jehož vnitřní
CVIČNÝ TEST 48 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Je dán konvexní čtyřúhelník, jehož vnitřní
Teoretická informatika Tomáš Foltýnek Barvení grafů Platónská tělesa
 Tomáš Foltýnek foltynek@pef.mendelu.cz Barvení grafů Platónská tělesa strana 2 Opakování z minulé přednášky Co je to prohledávání grafu? Jaké způsoby prohledávání grafu známe? Jak nalézt východ z bludiště?
Tomáš Foltýnek foltynek@pef.mendelu.cz Barvení grafů Platónská tělesa strana 2 Opakování z minulé přednášky Co je to prohledávání grafu? Jaké způsoby prohledávání grafu známe? Jak nalézt východ z bludiště?
Grafy. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 13.
 Grafy doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 13. března 2017 Jiří Dvorský (VŠB TUO) Grafy 104 / 309 Osnova přednášky Grafy
Grafy doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 13. března 2017 Jiří Dvorský (VŠB TUO) Grafy 104 / 309 Osnova přednášky Grafy
ÚLOHA 1. EXPONENCIÁLNÍ MODEL...2 ÚLOHA 2. MOCNINNÝ MODEL...7
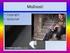 OBSAH ÚLOHA 1. EXPONENCIÁLNÍ MODEL...2 ÚLOHA 2. MOCNINNÝ MODEL...7 Úloha 1. Exponenciální model Zadání: Použijte exponenciální model pro stanovení počáteční hodnoty aktivity radionuklidu Ag 110m. Aktivita
OBSAH ÚLOHA 1. EXPONENCIÁLNÍ MODEL...2 ÚLOHA 2. MOCNINNÝ MODEL...7 Úloha 1. Exponenciální model Zadání: Použijte exponenciální model pro stanovení počáteční hodnoty aktivity radionuklidu Ag 110m. Aktivita
Statistika. Regresní a korelační analýza Úvod do problému. Roman Biskup
 Statistika Regresní a korelační analýza Úvod do problému Roman Biskup Jihočeská univerzita v Českých Budějovicích Ekonomická fakulta (Zemědělská fakulta) Katedra aplikované matematiky a informatiky 2008/2009
Statistika Regresní a korelační analýza Úvod do problému Roman Biskup Jihočeská univerzita v Českých Budějovicích Ekonomická fakulta (Zemědělská fakulta) Katedra aplikované matematiky a informatiky 2008/2009
2.7.6 Rovnice vyšších řádů (separace kořenů)
 76 Rovnice vyšších řádů (separace kořenů) Předpoklady: 00507, 00705 Přehled rovnic: Řád rovnice Tvar Název způsob řešení (vzorec) ax + b = 0 lineární b a 0, x = a ax + bx + c = 0 kvadratická ± a 0, x,
76 Rovnice vyšších řádů (separace kořenů) Předpoklady: 00507, 00705 Přehled rovnic: Řád rovnice Tvar Název způsob řešení (vzorec) ax + b = 0 lineární b a 0, x = a ax + bx + c = 0 kvadratická ± a 0, x,
Odhad parametrů N(µ, σ 2 )
 Odhad parametrů N(µ, σ 2 ) Mějme statistický soubor x 1, x 2,, x n modelovaný jako realizaci náhodného výběru z normálního rozdělení N(µ, σ 2 ) s neznámými parametry µ a σ. Jaký je maximální věrohodný
Odhad parametrů N(µ, σ 2 ) Mějme statistický soubor x 1, x 2,, x n modelovaný jako realizaci náhodného výběru z normálního rozdělení N(µ, σ 2 ) s neznámými parametry µ a σ. Jaký je maximální věrohodný
Elegantní algoritmus pro konstrukci sufixových polí
 Elegantní algoritmus pro konstrukci sufixových polí 22.10.2014 Zadání Obsah Zadání... 3 Definice... 3 Analýza problému... 4 Jednotlivé algoritmy... 4 Algoritmus SA1... 4 Algoritmus SA2... 5 Algoritmus
Elegantní algoritmus pro konstrukci sufixových polí 22.10.2014 Zadání Obsah Zadání... 3 Definice... 3 Analýza problému... 4 Jednotlivé algoritmy... 4 Algoritmus SA1... 4 Algoritmus SA2... 5 Algoritmus
Odhady Parametrů Lineární Regrese
 Odhady Parametrů Lineární Regrese Mgr. Rudolf B. Blažek, Ph.D. prof. RNDr. Roman Kotecký, DrSc. Katedra počítačových systémů Katedra teoretické informatiky Fakulta informačních technologií České vysoké
Odhady Parametrů Lineární Regrese Mgr. Rudolf B. Blažek, Ph.D. prof. RNDr. Roman Kotecký, DrSc. Katedra počítačových systémů Katedra teoretické informatiky Fakulta informačních technologií České vysoké
jednoduchá heuristika asymetrické okolí stavový prostor, kde nelze zabloudit připustit zhoršují cí tahy Pokročilé heuristiky
 Pokročilé heuristiky jednoduchá heuristika asymetrické stavový prostor, kde nelze zabloudit připustit zhoršují cí tahy pokročilá heuristika symetrické stavový prostor, který vyžaduje řízení 1 2 Paměť pouze
Pokročilé heuristiky jednoduchá heuristika asymetrické stavový prostor, kde nelze zabloudit připustit zhoršují cí tahy pokročilá heuristika symetrické stavový prostor, který vyžaduje řízení 1 2 Paměť pouze
Úvod do teorie grafů
 Úvod do teorie grafů Neorientovaný graf G = (V,E,I) V množina uzlů (vrcholů) - vertices E množina hran - edges I incidence incidence je zobrazení, buď: funkce: I: E V x V relace: I E V V incidence přiřadí
Úvod do teorie grafů Neorientovaný graf G = (V,E,I) V množina uzlů (vrcholů) - vertices E množina hran - edges I incidence incidence je zobrazení, buď: funkce: I: E V x V relace: I E V V incidence přiřadí
Přijímací zkouška - matematika
 Přijímací zkouška - matematika Jméno a příjmení pište do okénka Číslo přihlášky Číslo zadání 1 Grafy 1 Pro který z následujících problémů není znám žádný algoritmus s polynomiální časovou složitostí? Problém,
Přijímací zkouška - matematika Jméno a příjmení pište do okénka Číslo přihlášky Číslo zadání 1 Grafy 1 Pro který z následujících problémů není znám žádný algoritmus s polynomiální časovou složitostí? Problém,
Statistická teorie učení
 Statistická teorie učení Petr Havel Marek Myslivec přednáška z 9. týdne 1 Úvod Představme si situaci výrobce a zákazníka, který si u výrobce objednal algoritmus rozpoznávání. Zákazník dodal experimentální
Statistická teorie učení Petr Havel Marek Myslivec přednáška z 9. týdne 1 Úvod Představme si situaci výrobce a zákazníka, který si u výrobce objednal algoritmus rozpoznávání. Zákazník dodal experimentální
1. Náhodný vektor (X, Y ) má diskrétní rozdělení s pravděpodobnostní funkcí p, kde. p(x, y) = a(x + y + 1), x, y {0, 1, 2}.
 VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
Fraktály. Ondřej Bouchala, George Dzhanezashvili, Viktor Skoupý
 Fraktály Ondřej Bouchala, George Dzhanezashvili, Viktor Skoupý 19.6.2012 Abstrakt Tato práce se zabývá vlastnostmi a vykreslováním fraktálů. Popisuje fraktální dimenzi (soběpodobnostní a mřížkovou), dále
Fraktály Ondřej Bouchala, George Dzhanezashvili, Viktor Skoupý 19.6.2012 Abstrakt Tato práce se zabývá vlastnostmi a vykreslováním fraktálů. Popisuje fraktální dimenzi (soběpodobnostní a mřížkovou), dále
VYBRANÁ ROZDĚLENÍ. SPOJITÉ NÁH. VELIČINY Martina Litschmannová
 VYBRANÁ ROZDĚLENÍ SPOJITÉ NÁH. VELIČINY Martina Litschmannová Opakování hustota pravděpodobnosti f(x) Funkce f(x) je hustotou pravděpodobností (na intervalu a x b), jestliže splňuje následující podmínky:
VYBRANÁ ROZDĚLENÍ SPOJITÉ NÁH. VELIČINY Martina Litschmannová Opakování hustota pravděpodobnosti f(x) Funkce f(x) je hustotou pravděpodobností (na intervalu a x b), jestliže splňuje následující podmínky:
Přehled funkcí. Funkce na množině D R je předpis, který každému číslu z množiny D přiřazuje právě jedno reálné číslo. přehled fcí.
 Přehled funkcí Martina Hetmerová Gymnázium Přípotoční 1337 Praha 10 Vlastnosti funkcí Funkce na množině D R je předpis, který každému číslu z množiny D přiřazuje právě jedno reálné číslo Zapisujeme: f:y=f(x)
Přehled funkcí Martina Hetmerová Gymnázium Přípotoční 1337 Praha 10 Vlastnosti funkcí Funkce na množině D R je předpis, který každému číslu z množiny D přiřazuje právě jedno reálné číslo Zapisujeme: f:y=f(x)
Funkce - pro třídu 1EB
 Variace 1 Funkce - pro třídu 1EB Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv využití výukového materiálu je povoleno pouze s odkazem na www.jarjurek.cz. 1. Funkce Funkce je přiřazení, které každému
Variace 1 Funkce - pro třídu 1EB Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv využití výukového materiálu je povoleno pouze s odkazem na www.jarjurek.cz. 1. Funkce Funkce je přiřazení, které každému
PRŮZKUMOVÁ ANALÝZA JEDNOROZMĚRNÝCH DAT Exploratory Data Analysis (EDA)
 PRŮZKUMOVÁ ANALÝZA JEDNOROZMĚRNÝCH DAT Exploratory Data Analysis (EDA) Reprezentativní náhodný výběr: 1. Prvky výběru x i jsou vzájemně nezávislé. 2. Výběr je homogenní, tj. všechna x i jsou ze stejného
PRŮZKUMOVÁ ANALÝZA JEDNOROZMĚRNÝCH DAT Exploratory Data Analysis (EDA) Reprezentativní náhodný výběr: 1. Prvky výběru x i jsou vzájemně nezávislé. 2. Výběr je homogenní, tj. všechna x i jsou ze stejného
Cvičné texty ke státní maturitě z matematiky
 Cvičné texty ke státní maturitě z matematiky Pracovní listy s postupy řešení Brno 2010 RNDr. Rudolf Schwarz, CSc. Státní maturita z matematiky Úloha 1 1. a = s : 45 = 9.10180 45 = 9.101+179 45 = 9.10.10179
Cvičné texty ke státní maturitě z matematiky Pracovní listy s postupy řešení Brno 2010 RNDr. Rudolf Schwarz, CSc. Státní maturita z matematiky Úloha 1 1. a = s : 45 = 9.10180 45 = 9.101+179 45 = 9.10.10179
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
