Co bych býval byl rád věděl v prváku
|
|
|
- Vít Kučera
- před 6 lety
- Počet zobrazení:
Transkript
1 aneb prvák jako nutné "zlo" 10. října 2018
2 Outline Motivace přednášky 1 Motivace přednášky Každý prvák se jednou zeptá 2
3 Každý prvák se jednou zeptá Každý prvák se jednou zeptá Proč?
4 Každý prvák se jednou zeptá Každý prvák se jednou zeptá Proč? je to tak těžké to není ztracený rok života
5 Každý prvák se jednou zeptá Každý prvák se jednou zeptá Proč? je to tak těžké to není ztracený rok života Co?
6 Každý prvák se jednou zeptá Každý prvák se jednou zeptá Proč? je to tak těžké to není ztracený rok života Co? je potřeba si odnést získám jako člověk
7 Každý prvák se jednou zeptá Každý prvák se jednou zeptá Proč? je to tak těžké to není ztracený rok života Co? je potřeba si odnést získám jako člověk Jak?
8 Každý prvák se jednou zeptá Každý prvák se jednou zeptá Proč? je to tak těžké to není ztracený rok života Co? je potřeba si odnést získám jako člověk Jak? to přežít v psychickém a fyzickém zdraví
9 "Příliš zkušení"lektoři Motivace přednášky "To je zřejmé." "To určitě znáte ze střední školy." většina lektorů nemá pedagogické vzdělání ptejte se vydolujte to z nich naučte ho učit
10 Stavba základů bolí nejvíce velmi abstraktní základy není vidět, kam to vede první setkání s typy vět (BC) a důkazů (ɛ δ) chybí užitečné věty, poznatky složitější, delší důkazy chybí terminologie potřeba se naučit analyticky myslet, ne důkazy nazpaměť
11 Matematický aparát ve fyzice Fyzici zachází s matematikou jako zločinci se zákony.
12 Matematický aparát ve fyzice Fyzici zachází s matematikou jako zločinci se zákony. matematika popis fyziky pokročilejší aparát ve fyzice
13 Vstřebávat stovky let poznání je náročné přehledovky vidíme jen část teorie (fyzika) zdá se nekonzistentní šprtání není vidět, k čemu to je triky v důkazech (matematika) nenašly se během hodiny
14 Opakování matka studenta MA1,2 + stejnoměrná konvergence + topologie = MAA3,4 MECH, ELMA + Hamiltonův/Lagrangeův formal. = TEF1,2 TER + víc statistiky = TSFA ZFM + víc kv + železné nervy = PRA1,2 MECH + samosdružené operátory = KVAN Důsledky neslyšíte to naposled hlubší pochopení pojmů
15 LHO kmity na všechny způsoby MECH LHO ELMA EM pole TEF záření dipólu VOAF kmitání soustav MAA3, MMF Fourierova analýza KVAN KLHO DIFR lin. diferenciální rovnice NUM simulace PRA experimenty Důsledky hluboké chápání pojmu schopnost přenést chápání na jiné sféry ẍ + ω 2 x = 0 (1)
16 LA je prostě všude Motivace přednášky linearizovaný pohled na problémy (DIM, DIFR, VOAF) linearizace ve fyzice metrika (MAA3) SLAR a matice (NUM) vlastní čísla (KVAN) skalární součin (KVAN, MAA3,... )
17 Počítač prodloužená ruka mysli nepostradatelné seznámení s prostředím (L A TEX, GNU/Linux, C/C++, Python,... ) záleží na oboru
18 Hodiny cizích jazyků kultivace vědce kultivace jazyka akademický styl psaní prezentování své práce také na FYS
19 Na těchto základech můžete stavět terminologie + intuitivní chápání termínů schopnost si najít a dostudovat detaily práce s PC vědecká komunikace
20 Pracovitý student spí dobře body za práci DIM, LA, MA, písemky odpuštění/zmírnění příkladů u zkoušky počítání příkladů ze sbírek získání intuice asymptotické cítění zlaté slovo Dr. Škody
21 Pracovitý student spí dobře body za práci DIM, LA, MA, písemky odpuštění/zmírnění příkladů u zkoušky počítání příkladů ze sbírek získání intuice asymptotické cítění zlaté slovo Dr. Škody průběžně
22 Volba vhodné úrovně matematiky A "teoretická" B "praktická" alternativní pohled lepší/horší, těžší/lehčí individuálně vhodná (každý myslí jinak)
23 Připravený student přednášejícímu rozumí číst si skripta před přednáškou intuitivní pochopení struktura problematiky neztratím se nové pojmy nepřekvapí mě, můžu si udělat představu doprovodné materiály (na internetu)
24 Sokratova metoda Motivace přednášky přednášející se dotazy nesnaží nachytat není se čeho bát, ale lámat ledy musíte vy nejde přednesení informací, ale o jejich předání (komunikaci)
25 Zkouškové metla studenta předtermíny (fyzika) ušetří stres (TER) málo termínů pro velký ročník 2 týdny učení na MA/LA není moc hodin v semestru hodin ve zkouškovém vstupy pro plánování (lektor, vyšší ročníky): kolik termínů a kdy vypsané? jak probíhá zkouška? jak fungují opravné termíny (a jak rychle se plní) komplexní (i varianty) plánování celého zkouškového: Gantt grafy zkouška jdu zkusit své schopnosti
26 Jak se učit Motivace přednášky každý ma jiný typ paměti, chápání třeba najít adekvátní metodu ( zeptejte se CIPS) neučit se (důkazy) úplně nazpamět (až na triky), důležité nasát analytické myšlení a přístup důležité hledat strukturu, souvislosti, vzory myšlenkové mapy barvičky, zvýrazňovače
27 Závěrečné, ročníkové, seminární práce nenechat na poslední chvíli průběžné reporty nakonec zkompilovat do celku reprodukovatelnost - snadné se vrátit a poupravit dřívější analýzu grafy, výpočty
28 IT tipy pro začátečníky L A TEX LyX (WSIWYG), TeXMaker, Overleaf (cloud, kolaborace) Linux/GNU lepší začít ve VirtualBox, LinuxMint Secure Shell (SSH) OpenSSH (Linux, OSX), Windows Subsystem for Linux C/C++ Code::Blocks IDE + MinGW zpracování dat Python (Gnuplot omezený, Matlab omezený nedostatkem licencí) revizní systém Mercurial (TortoiseHg GUI), Git (GitKraken GUI) texťáky dobrý textový editor (Kate, Gedit, Notepad++,..., (spac)emacs, Vim) myšlenkové mapy Freeplane, Docear (+citační systém)
29 Python Motivace přednášky intepretovaný jazyk (nekompilovaný), ale lze optimalizovat multiplatformní (včetně většiny knihoven) rozvinutý ekosystém vědeckých (a všech jiných) knihoven snadná instalace (včetně knihoven) skrze Anaconda distribuci interaktivní výukové materiály/reporty: Jupyter notebook předmět 12PYTH, interaktivná materiály na pythonic.eu/fjfi
30 Zvídavý student si místo najde cvičící a přednášející loví talenty stačí projevit zájem o věc a pracovitost práce ve škole/ústavu navíc motivuje ke studiu (vím, že to k něčemu je) odměny (výjezdy na konference, pomvěd) bonus při žádání o stipendia
31 Závěr Shrnutí Shrnutí pro nikoho to nebylo lehké bez prváku se dál nepohnete aktivní student přežije bez problémů
Co bych býval byl rád věděl v prváku
 aneb prvák jako nutné "zlo" 14. října 2015 Osnova 1 2 Osnova 1 2 Proč? Proč? je to tak těžké to není ztracený rok života Proč? je to tak těžké to není ztracený rok života Co? Proč? je to tak těžké to není
aneb prvák jako nutné "zlo" 14. října 2015 Osnova 1 2 Osnova 1 2 Proč? Proč? je to tak těžké to není ztracený rok života Proč? je to tak těžké to není ztracený rok života Co? Proč? je to tak těžké to není
Základy matematické analýzy
 Základy matematické analýzy Informace o předmětu Ing. Tomáš Kalvoda, Ph.D. 1, Ing. Daniel Vašata 2 1 tomas.kalvoda@fit.cvut.cz 2 daniel.vasata@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
Základy matematické analýzy Informace o předmětu Ing. Tomáš Kalvoda, Ph.D. 1, Ing. Daniel Vašata 2 1 tomas.kalvoda@fit.cvut.cz 2 daniel.vasata@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
Netradiční výklad tradičních témat
 Netradiční výklad tradičních témat J. Musilová, P. Musilová: Matematika pro porozumění i praxi I. VUTIUM, Brno 2006 (291 s.), 2009 (349 s.). J. Musilová, P. Musilová: Matematika pro porozumění i praxi
Netradiční výklad tradičních témat J. Musilová, P. Musilová: Matematika pro porozumění i praxi I. VUTIUM, Brno 2006 (291 s.), 2009 (349 s.). J. Musilová, P. Musilová: Matematika pro porozumění i praxi
aneb jiný úhel pohledu na prvák
 Účelná matematika aneb jiný úhel pohledu na prvák Jan Hejtmánek FEL, ČVUT v Praze 24. června 2015 Jan Hejtmánek (FEL, ČVUT v Praze) Technokrati 2015 24. června 2015 1 / 18 Outline 1 Motivace 2 Proč tolik
Účelná matematika aneb jiný úhel pohledu na prvák Jan Hejtmánek FEL, ČVUT v Praze 24. června 2015 Jan Hejtmánek (FEL, ČVUT v Praze) Technokrati 2015 24. června 2015 1 / 18 Outline 1 Motivace 2 Proč tolik
Diskrétní matematika. DiM /01, zimní semestr 2016/2017
 Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2016/2017 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2016/2017 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
Diskrétní matematika. DiM /01, zimní semestr 2017/2018
 Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2017/2018 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2017/2018 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
Rovnice matematické fyziky cvičení pro akademický školní rok 2013-2014
 Harmonogram výuky předmětu Rovnice matematické fyziky cvičení pro akademický školní rok 2013-2014 Vedoucí cvičení: ing. Václav Klika, Ph.D. & MSc. Karolína Korvasová & & ing. Matěj Tušek, Ph.D. Katedra
Harmonogram výuky předmětu Rovnice matematické fyziky cvičení pro akademický školní rok 2013-2014 Vedoucí cvičení: ing. Václav Klika, Ph.D. & MSc. Karolína Korvasová & & ing. Matěj Tušek, Ph.D. Katedra
Co je to matematika?
 Co je to matematika? Hello FIT 2018 Daniel Dombek, Tomáš Kalvoda, Karel Klouda KAM FIT ČVUT 27. září 2018 Přednášející Daniel Dombek Tomáš Kalvoda Úvod Úvod Úvod Blíží se akademický Nový rok! Již příští
Co je to matematika? Hello FIT 2018 Daniel Dombek, Tomáš Kalvoda, Karel Klouda KAM FIT ČVUT 27. září 2018 Přednášející Daniel Dombek Tomáš Kalvoda Úvod Úvod Úvod Blíží se akademický Nový rok! Již příští
Modelování a simulace: o předmětu. Radek Pelánek
 Modelování a simulace: o předmětu Radek Pelánek Vymezení zájmu Modelování a simulace komplexních systémů modely formulovatelné matematicky (včetně programovacích jazyků), simulace prováděné počítačem aplikace
Modelování a simulace: o předmětu Radek Pelánek Vymezení zájmu Modelování a simulace komplexních systémů modely formulovatelné matematicky (včetně programovacích jazyků), simulace prováděné počítačem aplikace
Bonn, Rheinischen Friedrich-Wilhelms-Universität
 Bonn, Rheinischen Friedrich-Wilhelms-Universität Seznam přednášek Bc s anotacemi http://www.mathematics.uni-bonn.de/files/bachelor/ba_modulhandbuch.pdf Studijní plán-požadavky http://www.mathematics.uni-bonn.de/studium/bachelor/studienprogramm
Bonn, Rheinischen Friedrich-Wilhelms-Universität Seznam přednášek Bc s anotacemi http://www.mathematics.uni-bonn.de/files/bachelor/ba_modulhandbuch.pdf Studijní plán-požadavky http://www.mathematics.uni-bonn.de/studium/bachelor/studienprogramm
Modelování a simulace: o předmětu. Radek Pelánek
 Modelování a simulace: o předmětu Radek Pelánek Vymezení zájmu Modelování a simulace komplexních systémů modely formulovatelné matematicky (včetně programovacích jazyků), simulace prováděné počítačem aplikace
Modelování a simulace: o předmětu Radek Pelánek Vymezení zájmu Modelování a simulace komplexních systémů modely formulovatelné matematicky (včetně programovacích jazyků), simulace prováděné počítačem aplikace
Matematika pro inženýry 21. století
 Matematika pro inženýry 21. století Schůzka realizačního týmu 2. 12. 2010 Tato prezentace je spolufinancována Evropským sociálním fondem a státním rozpočtem České republiky Program schůzky: Informace o
Matematika pro inženýry 21. století Schůzka realizačního týmu 2. 12. 2010 Tato prezentace je spolufinancována Evropským sociálním fondem a státním rozpočtem České republiky Program schůzky: Informace o
Principy počítačů a operačních systémů
 Principy počítačů a operačních systémů Agenda Zimní semestr 2011/2012 Kdo jsem? Lubomír Bulej Katedra distribuovaných a spolehlivých systémů 2. patro, místnost č. 205 lubomir.bulej@d3s.mff.cuni.cz Přednášky
Principy počítačů a operačních systémů Agenda Zimní semestr 2011/2012 Kdo jsem? Lubomír Bulej Katedra distribuovaných a spolehlivých systémů 2. patro, místnost č. 205 lubomir.bulej@d3s.mff.cuni.cz Přednášky
Studijní program Aplikované matematicko-stochastické metody. Předmět kód učitel zim. sem. let. sem. kr kr
 1. ročník Matematická analýza 1 01MA1 Pošta, 4+4 z, zk - 8 - Pelantová Lineární algebra 1 01LA1 Dvořáková, 2+2 z, zk - 4 - Ambrož Matematická analýza 2 01MA2 Pelantová, - 4+4 z, zk - 8 Pošta Lineární algebra
1. ročník Matematická analýza 1 01MA1 Pošta, 4+4 z, zk - 8 - Pelantová Lineární algebra 1 01LA1 Dvořáková, 2+2 z, zk - 4 - Ambrož Matematická analýza 2 01MA2 Pelantová, - 4+4 z, zk - 8 Pošta Lineární algebra
Diskrétní matematika. DiM /01, zimní semestr 2016/2017
 Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2016/2017 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2016/2017 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
MATLAB Úvod. Úvod do Matlabu. Miloslav Čapek
 MATLAB Úvod Úvod do Matlabu Miloslav Čapek Proč se na FELu učit Matlab? Matlab je světový standard pro výuku v technických oborech využívá ho více než 3500 univerzit licence vlastní tisíce velkých firem
MATLAB Úvod Úvod do Matlabu Miloslav Čapek Proč se na FELu učit Matlab? Matlab je světový standard pro výuku v technických oborech využívá ho více než 3500 univerzit licence vlastní tisíce velkých firem
Diskrétní matematika. DiM /01, zimní semestr 2018/2019
 Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2018/2019 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2018/2019 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
ZS: 2017/2018 NMAF061 F/2 J. MÁLEK. Matematika pro fyziky I. Posluchárna: T2 T1 Konzultační hodiny: pátek 9:40-10:30, posluchárna T5
 ZS: 2017/2018 NMAF061 F/2 J. MÁLEK Matematika pro fyziky I OBECNÉ INFORMACE A SYLABUS Přednášející: Cvičící: Josef Málek Michal Báthory, Tomáš Los, Michal Pavelka, Vít Průša Termíny přednášek: Čtvrtek
ZS: 2017/2018 NMAF061 F/2 J. MÁLEK Matematika pro fyziky I OBECNÉ INFORMACE A SYLABUS Přednášející: Cvičící: Josef Málek Michal Báthory, Tomáš Los, Michal Pavelka, Vít Průša Termíny přednášek: Čtvrtek
DIDAKTIKA FYZIKY DIDAKTICKÉ PRINCIPY (ZÁSADY) Prof. RNDr. Emanuel Svoboda, CSc.
 DIDAKTIKA FYZIKY DIDAKTICKÉ PRINCIPY (ZÁSADY) Prof. RNDr. Emanuel Svoboda, CSc. CITÁTY KOMENSKÉHO Poněvadž při všem je nesnadněji odučovati se než učiti se, musí být opatrně přihlíženo k tomu, aby se ničemu
DIDAKTIKA FYZIKY DIDAKTICKÉ PRINCIPY (ZÁSADY) Prof. RNDr. Emanuel Svoboda, CSc. CITÁTY KOMENSKÉHO Poněvadž při všem je nesnadněji odučovati se než učiti se, musí být opatrně přihlíženo k tomu, aby se ničemu
PB029 Elektronická příprava dokumentů
 PB029 Elektronická příprava dokumentů 1. demopřednáška, seznámení se software Vít Novotný witiko@mail.muni.cz 20. září 2018 Obsah prezentace Informace pro podzim 2018 Seznámení s použitým software TEX
PB029 Elektronická příprava dokumentů 1. demopřednáška, seznámení se software Vít Novotný witiko@mail.muni.cz 20. září 2018 Obsah prezentace Informace pro podzim 2018 Seznámení s použitým software TEX
Bakalářské a diplomové práce. katedra matematiky
 Bakalářské a diplomové práce katedra matematiky 31.10.2011 Závěrečné práce obecné informace databáze VŠKP výběr a zadání témat -kdy -jak zpracování práce odevzdání a obhajoba práce -kdy -jak okruhy témat
Bakalářské a diplomové práce katedra matematiky 31.10.2011 Závěrečné práce obecné informace databáze VŠKP výběr a zadání témat -kdy -jak zpracování práce odevzdání a obhajoba práce -kdy -jak okruhy témat
DEFINICE,VĚTYADŮKAZYKÚSTNÍZKOUŠCEZMAT.ANALÝZY Ib
 INFORMACE O PRŮBĚHU A POŽADAVKY KE ZKOUŠCE Z MAT. ANALÝZYIbVLS2010/11 Ke zkoušce mohou přistoupit studenti, kteří získali zápočet. Do indexu jej zapíši na zkoušce, pokud cvičící potvrdí, že na něj student
INFORMACE O PRŮBĚHU A POŽADAVKY KE ZKOUŠCE Z MAT. ANALÝZYIbVLS2010/11 Ke zkoušce mohou přistoupit studenti, kteří získali zápočet. Do indexu jej zapíši na zkoušce, pokud cvičící potvrdí, že na něj student
Výuka základů mikroekonomie na ESF MU
 Výuka základů mikroekonomie na ESF MU y Michal Kvasnička ESF MU michal.kvasnicka@econ.muni.cz y y x E C x E U 1 U 2 x Struktura prezentace představení předmětu Mikroekonomie I výzvy masové výuky naše řešení
Výuka základů mikroekonomie na ESF MU y Michal Kvasnička ESF MU michal.kvasnicka@econ.muni.cz y y x E C x E U 1 U 2 x Struktura prezentace představení předmětu Mikroekonomie I výzvy masové výuky naše řešení
Gymnázium Uherské Hradiště Charakteristika volitelných předmětů 3. ročník (dvouhodinové předměty, žák si vybírá dva)
 Gymnázium Uherské Hradiště Charakteristika volitelných předmětů 3. ročník (dvouhodinové předměty, žák si vybírá dva) Seminář z českého jazyka Rozšiřuje, prohlubuje a procvičuje učivo gramatiky, slohu a
Gymnázium Uherské Hradiště Charakteristika volitelných předmětů 3. ročník (dvouhodinové předměty, žák si vybírá dva) Seminář z českého jazyka Rozšiřuje, prohlubuje a procvičuje učivo gramatiky, slohu a
Základy matematiky pro FEK
 Základy matematiky pro FEK 1. přednáška 22.9.2016 Blanka Šedivá KMA zimní semestr 2016/2017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 2016/2017 1 / 19 Organizační pokyny přednášející:
Základy matematiky pro FEK 1. přednáška 22.9.2016 Blanka Šedivá KMA zimní semestr 2016/2017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 2016/2017 1 / 19 Organizační pokyny přednášející:
Zpracování elektronických studijních opor pro nově otevíranou kombinovanou formu učitelského studia matematiky
 Zpracování elektronických studijních opor pro nově otevíranou kombinovanou formu učitelského studia matematiky IP 12251 Alena Kopáčková (KMD) 24. 1. 2017 Projekt č. 12251 Návaznost na DZ TUL 2016-2020
Zpracování elektronických studijních opor pro nově otevíranou kombinovanou formu učitelského studia matematiky IP 12251 Alena Kopáčková (KMD) 24. 1. 2017 Projekt č. 12251 Návaznost na DZ TUL 2016-2020
Požadavky na zápočet a zkoušku
 1/6 Požadavky na zápočet a zkoušku Zápočet vstupní test aktivní účast na cvičeních dva zápočtové testy Maximální počet bodů, který můžete získat je 200 bodů. 80 bodů zápočet 50-79 bodů souhrnný test (1
1/6 Požadavky na zápočet a zkoušku Zápočet vstupní test aktivní účast na cvičeních dva zápočtové testy Maximální počet bodů, který můžete získat je 200 bodů. 80 bodů zápočet 50-79 bodů souhrnný test (1
Nikolić Aleksandra Matěj Martin
 POSTAVENÍ Í PEDAGOGIKY MEZI VĚDAMI Nikolić Aleksandra Matěj Martin PŮVOD NÁZVU Paidagogos = pais + agein Pais = dítě Agein = vést průvodce dětí, často vzdělaný otrok pečoval o výchovu dětí ze zámožných
POSTAVENÍ Í PEDAGOGIKY MEZI VĚDAMI Nikolić Aleksandra Matěj Martin PŮVOD NÁZVU Paidagogos = pais + agein Pais = dítě Agein = vést průvodce dětí, často vzdělaný otrok pečoval o výchovu dětí ze zámožných
Komplexní analýza. Fourierovy řady. Martin Bohata. Katedra matematiky FEL ČVUT v Praze
 Komplexní analýza Fourierovy řady Martin Bohata Katedra matematiky FEL ČVU v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Fourierovy řady 1 / 20 Úvod Často se setkáváme s periodickými
Komplexní analýza Fourierovy řady Martin Bohata Katedra matematiky FEL ČVU v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Fourierovy řady 1 / 20 Úvod Často se setkáváme s periodickými
MATEMATIKA PRO INŽENÝRY 21. STOLETÍ
 MATEMATIKA PRO INŽENÝRY 21. STOLETÍ Schůzka realizačního týmu 8. 9. 2011 Tato prezentace je spolufinancována Evropským sociálním fondem a státním rozpočtem České republiky PROGRAM SCHŮZKY: Pilotní kurzy
MATEMATIKA PRO INŽENÝRY 21. STOLETÍ Schůzka realizačního týmu 8. 9. 2011 Tato prezentace je spolufinancována Evropským sociálním fondem a státním rozpočtem České republiky PROGRAM SCHŮZKY: Pilotní kurzy
Renáta Bednárová, Petr Sládek. Pedagogická fakulta MU Brno, Univerzita obrany Brno
 Renáta Bednárová, Petr Sládek Pedagogická fakulta MU Brno, Univerzita obrany Brno Cíle Úvod Cíle projektu Charakteristika e-kurzu Několik poznámek k pedagogickému šetření Využití e-kurzu v praxi Možnosti
Renáta Bednárová, Petr Sládek Pedagogická fakulta MU Brno, Univerzita obrany Brno Cíle Úvod Cíle projektu Charakteristika e-kurzu Několik poznámek k pedagogickému šetření Využití e-kurzu v praxi Možnosti
Anketa pro učitele fyziky všech typů škol k případným změnám RVP VÝSLEDKY
 Anketa pro učitele fyziky všech typů škol k případným změnám RVP VÝSLEDKY Leoš Dvořák, Irena Dvořáková Základní informace Cíl: Sesbírat názory co největšího počtu učitelů před tímto setkáním (jako podklad
Anketa pro učitele fyziky všech typů škol k případným změnám RVP VÝSLEDKY Leoš Dvořák, Irena Dvořáková Základní informace Cíl: Sesbírat názory co největšího počtu učitelů před tímto setkáním (jako podklad
Příprava lekce v knihovně o informační bezpečnosti pro děti a seniory
 Příprava lekce v knihovně o informační bezpečnosti pro děti a seniory Pavla Kovářová Kabinet informačních studií a knihovnictví Filozofická fakulta Masarykovy univerzity Kdo z vás by teď přijal žádost
Příprava lekce v knihovně o informační bezpečnosti pro děti a seniory Pavla Kovářová Kabinet informačních studií a knihovnictví Filozofická fakulta Masarykovy univerzity Kdo z vás by teď přijal žádost
A1 Marketingové minimum pro posílení výchovy k podnikavosti (8h)
 A1 Marketingové minimum pro posílení výchovy k podnikavosti (8h) 2.1 Základy marketingové strategie (2,5h) Učitelé se seznámí se základní marketingovou terminologií a s možnými cestami rozvoje firmy. V
A1 Marketingové minimum pro posílení výchovy k podnikavosti (8h) 2.1 Základy marketingové strategie (2,5h) Učitelé se seznámí se základní marketingovou terminologií a s možnými cestami rozvoje firmy. V
Matematický software pro Linux
 Matematický software pro Linux Michal Černý LinuxAlt 2010 Abstrakt Příspěvek stručně představí základní matematické aplikace, které jsou k dispozici jako open source pro Linux, se zvláštním zřetelem na
Matematický software pro Linux Michal Černý LinuxAlt 2010 Abstrakt Příspěvek stručně představí základní matematické aplikace, které jsou k dispozici jako open source pro Linux, se zvláštním zřetelem na
Úvodní slovo studentům informatických oborů
 Úvodní slovo studentům informatických oborů prof. RNDr. Radim Bělohlávek, DSc. KATEDRA INFORMATIKY UNIVERZITA PALACKÉHO V OLOMOUCI Obsah 1 Univerzita Palackého v Olomouci 2 Katedra informatiky 3 Informatika
Úvodní slovo studentům informatických oborů prof. RNDr. Radim Bělohlávek, DSc. KATEDRA INFORMATIKY UNIVERZITA PALACKÉHO V OLOMOUCI Obsah 1 Univerzita Palackého v Olomouci 2 Katedra informatiky 3 Informatika
Přednášky z předmětu Aplikovaná matematika, rok 2012
 Přednášky z předmětu Aplikovaná matematika, rok 2012 Robert Mařík 23. ledna 2015 2 Obsah 1 Přednášky 2012 5 2 Písemky 2012 9 3 4 OBSAH Kapitola 1 Přednášky 2012 1. prednaska, 16.2.2012 -----------------------
Přednášky z předmětu Aplikovaná matematika, rok 2012 Robert Mařík 23. ledna 2015 2 Obsah 1 Přednášky 2012 5 2 Písemky 2012 9 3 4 OBSAH Kapitola 1 Přednášky 2012 1. prednaska, 16.2.2012 -----------------------
B) výchovné a vzdělávací strategie jsou totožné se strategiemi vyučovacího předmětu Matematika.
 4.8.3. Cvičení z matematiky Předmět Cvičení z matematiky je vyučován v sextě a v septimě jako volitelný předmět. Vzdělávací obsah vyučovacího předmětu Cvičení z matematiky vychází ze vzdělávací oblasti
4.8.3. Cvičení z matematiky Předmět Cvičení z matematiky je vyučován v sextě a v septimě jako volitelný předmět. Vzdělávací obsah vyučovacího předmětu Cvičení z matematiky vychází ze vzdělávací oblasti
Biostatistika a e-learning na Lékařské fakultě UK v Hradci Králové
 Univerzita Karlova v Praze Lékařská fakulta v Hradci Králové Ústav lékařské biofyziky Biostatistika a e-learning na Lékařské fakultě UK v Hradci Králové Josef Hanuš, Josef Bukač, Iva Selke-Krulichová,
Univerzita Karlova v Praze Lékařská fakulta v Hradci Králové Ústav lékařské biofyziky Biostatistika a e-learning na Lékařské fakultě UK v Hradci Králové Josef Hanuš, Josef Bukač, Iva Selke-Krulichová,
Středoškolská technika SCI-Lab
 Středoškolská technika 2016 Setkání a prezentace prací středoškolských studentů na ČVUT SCI-Lab Kamil Mudruňka Gymnázium Dašická 1083 Dašická 1083, Pardubice O projektu SCI-Lab je program napsaný v jazyce
Středoškolská technika 2016 Setkání a prezentace prací středoškolských studentů na ČVUT SCI-Lab Kamil Mudruňka Gymnázium Dašická 1083 Dašická 1083, Pardubice O projektu SCI-Lab je program napsaný v jazyce
Transformace souřadnic
 Transformace souřadnic Odpřednesenou látku naleznete v kapitolách 8.2 a 8.3 skript Abstraktní a konkrétní lineární algebra. Jiří Velebil: A7B01AG 5.11.2015: Transformace souřadnic 1/17 Minulá přednáška
Transformace souřadnic Odpřednesenou látku naleznete v kapitolách 8.2 a 8.3 skript Abstraktní a konkrétní lineární algebra. Jiří Velebil: A7B01AG 5.11.2015: Transformace souřadnic 1/17 Minulá přednáška
PRAVDĚPODOBNOST A STATISTIKA 1 Metodický list č 1.
 Metodický list č 1. Název tématického celku: Elementární statistické zpracování 1 - Kolekce a interpretace statistických dat, základní pojmy deskriptivní statistiky. Cíl: Základním cílem tohoto tematického
Metodický list č 1. Název tématického celku: Elementární statistické zpracování 1 - Kolekce a interpretace statistických dat, základní pojmy deskriptivní statistiky. Cíl: Základním cílem tohoto tematického
Organizace výuky, podmínky zápočtu a zkoušky. Vyučovací metody formy a metody vyučování. Vyučovací jednotka, praktické dokumenty ve výuce
 1 4.10. 2 11.10.* 3 18.10. 4 25.10. * datum téma Organizace výuky, podmínky zápočtu a zkoušky. Pravidla prezentace Vyučovací metody formy a metody vyučování Vyučovací jednotka, praktické dokumenty ve výuce
1 4.10. 2 11.10.* 3 18.10. 4 25.10. * datum téma Organizace výuky, podmínky zápočtu a zkoušky. Pravidla prezentace Vyučovací metody formy a metody vyučování Vyučovací jednotka, praktické dokumenty ve výuce
Základy počítačových sítí. Motivace
 Základy počítačových sítí Motivace V čem je předmět KIV/ZPS přínosný např. pro studenta humanitní fakulty? o Určitě ne jen v tom, že dostane kredity, tj. zápočet a zkoušku alespoň za tři, jen proto, že
Základy počítačových sítí Motivace V čem je předmět KIV/ZPS přínosný např. pro studenta humanitní fakulty? o Určitě ne jen v tom, že dostane kredity, tj. zápočet a zkoušku alespoň za tři, jen proto, že
REFIMAT INOVACE VÝUKY MATEMATIKY V TECHNICKÉM A. NEÚSPĚŠNOSTI, reg. číslo CZ.1.07/2.2.00/ listopad, 2010 FIM UHK
 REFIMAT INOVACE VÝUKY MATEMATIKY V TECHNICKÉM A EKONOMICKÉM VZDĚLÁVÁNÍ S CÍLEM SNÍŽENÍ STUDIJNÍ NEÚSPĚŠNOSTI, reg. číslo CZ.1.07/2.2.00/15.0016 Pavel Pražák, Táňa Gavalcová FIM UHK 16. listopad, 2010 Pavel
REFIMAT INOVACE VÝUKY MATEMATIKY V TECHNICKÉM A EKONOMICKÉM VZDĚLÁVÁNÍ S CÍLEM SNÍŽENÍ STUDIJNÍ NEÚSPĚŠNOSTI, reg. číslo CZ.1.07/2.2.00/15.0016 Pavel Pražák, Táňa Gavalcová FIM UHK 16. listopad, 2010 Pavel
Měření efektivity informačního vzdělávání. Mgr. Gabriela Šimková gsimkova@phil.muni.cz KISK, Filozofická fakulta MU
 Měření efektivity informačního vzdělávání Mgr. Gabriela Šimková gsimkova@phil.muni.cz KISK, Filozofická fakulta MU Evaluace jako výzkumný proces Formy informačního vzdělávání CEINVE Kontaktní (face to
Měření efektivity informačního vzdělávání Mgr. Gabriela Šimková gsimkova@phil.muni.cz KISK, Filozofická fakulta MU Evaluace jako výzkumný proces Formy informačního vzdělávání CEINVE Kontaktní (face to
VYUŽITÍ MATLABU PRO PODPORU VÝUKY A PŘI ŘEŠENÍ VÝZKUMNÝCH ÚKOLŮ NA KATEDŘE KOMUNIKAČNÍCH A INFORMAČNÍCH SYSTÉMŮ
 VYUŽITÍ MATLABU PRO PODPORU VÝUKY A PŘI ŘEŠENÍ VÝZKUMNÝCH ÚKOLŮ NA KATEDŘE KOMUNIKAČNÍCH A INFORMAČNÍCH SYSTÉMŮ Markéta Mazálková Katedra komunikačních a informačních systémů Fakulta vojenských technologií,
VYUŽITÍ MATLABU PRO PODPORU VÝUKY A PŘI ŘEŠENÍ VÝZKUMNÝCH ÚKOLŮ NA KATEDŘE KOMUNIKAČNÍCH A INFORMAČNÍCH SYSTÉMŮ Markéta Mazálková Katedra komunikačních a informačních systémů Fakulta vojenských technologií,
Matematická analýza pro informatiky I. Limita posloupnosti (I)
 Matematická analýza pro informatiky I. 3. přednáška Limita posloupnosti (I) Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 25. února 2011 tomecek@inf.upol.cz
Matematická analýza pro informatiky I. 3. přednáška Limita posloupnosti (I) Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 25. února 2011 tomecek@inf.upol.cz
ZS: 2018/2019 NMAF063 F/3 Josef MÁLEK. Matematika pro fyziky III
 ZS: 2018/2019 NMAF063 F/3 Josef MÁLEK Matematika pro fyziky III OBECNÉ INFORMACE A SYLABUS Přednášející: Cvičící: Josef Málek Tomáš Los, Michal Pavelka, Michal Pavelka, Vít Průša Termíny přednášek: čtvrtek
ZS: 2018/2019 NMAF063 F/3 Josef MÁLEK Matematika pro fyziky III OBECNÉ INFORMACE A SYLABUS Přednášející: Cvičící: Josef Málek Tomáš Los, Michal Pavelka, Michal Pavelka, Vít Průša Termíny přednášek: čtvrtek
Koncept odborného vzdělávání
 Koncept odborného vzdělávání Škola SPŠCH Pardubice (CZ) Oblast vzdělávání Odborné vzdělávání Zaměření (ŠVP) 1. Analytická chemie 2. Farmaceutické substance 3. Chemicko-farmaceutická výroba 4. Analýza chemických
Koncept odborného vzdělávání Škola SPŠCH Pardubice (CZ) Oblast vzdělávání Odborné vzdělávání Zaměření (ŠVP) 1. Analytická chemie 2. Farmaceutické substance 3. Chemicko-farmaceutická výroba 4. Analýza chemických
IB013 Logické programování I Hana Rudová. jaro 2011
 IB013 Logické programování I Hana Rudová jaro 2011 Hodnocení předmětu Zápočtový projekt: celkem až 40 bodů Průběžná písemná práce: až 30 bodů (základy programování v Prologu) pro každého jediný termín:
IB013 Logické programování I Hana Rudová jaro 2011 Hodnocení předmětu Zápočtový projekt: celkem až 40 bodů Průběžná písemná práce: až 30 bodů (základy programování v Prologu) pro každého jediný termín:
Nástroje pro vývoj software
 Nástroje pro vývoj software http://d3s.mff.cuni.cz Pavel Parízek parizek@d3s.mff.cuni.cz CHARLES UNIVERSITY IN PRAGUE faculty of mathematics and physics Cíl předmětu Základní přehled o dostupných nástrojích
Nástroje pro vývoj software http://d3s.mff.cuni.cz Pavel Parízek parizek@d3s.mff.cuni.cz CHARLES UNIVERSITY IN PRAGUE faculty of mathematics and physics Cíl předmětu Základní přehled o dostupných nástrojích
Vzdělávací oblast: Matematika a její aplikace Vzdělávací obor: Matematický kroužek pro nadané žáky ročník 9.
 Vzdělávací oblast: Matematika a její aplikace Vzdělávací obor: Matematický kroužek pro nadané žáky ročník 9. Školní rok 2013/2014 Mgr. Lenka Mateová Kapitola Téma (Učivo) Znalosti a dovednosti (výstup)
Vzdělávací oblast: Matematika a její aplikace Vzdělávací obor: Matematický kroužek pro nadané žáky ročník 9. Školní rok 2013/2014 Mgr. Lenka Mateová Kapitola Téma (Učivo) Znalosti a dovednosti (výstup)
Fyzikální laboratoř. Kamil Mudruňka. Gymnázium, Pardubice, Dašická /8
 Středoškolská technika 2015 Setkání a prezentace prací středoškolských studentů na ČVUT Fyzikální laboratoř Kamil Mudruňka Gymnázium, Pardubice, Dašická 1083 1/8 O projektu Cílem projektu bylo vytvořit
Středoškolská technika 2015 Setkání a prezentace prací středoškolských studentů na ČVUT Fyzikální laboratoř Kamil Mudruňka Gymnázium, Pardubice, Dašická 1083 1/8 O projektu Cílem projektu bylo vytvořit
Interaktivní výukový program pro demonstraci principů tvorby tomografických obrazů
 Interaktivní výukový program pro demonstraci principů tvorby tomografických obrazů Projekt: FRVŠ 583/2013 Tématický okruh / specifikace: B3 / d Řešitel: Ing. Jaroslav Ptáček1,2 Spoluřešitelé: Mgr. Pavel
Interaktivní výukový program pro demonstraci principů tvorby tomografických obrazů Projekt: FRVŠ 583/2013 Tématický okruh / specifikace: B3 / d Řešitel: Ing. Jaroslav Ptáček1,2 Spoluřešitelé: Mgr. Pavel
Užití software Wolfram Alpha při výuce matematiky
 Jednalo se tedy o ukázku propojení klasického středoškolského učiva s problematikou běžného života v oblasti financí za pomoci využití informačních technologií dnešní doby. Hlavním přínosem příspěvku je
Jednalo se tedy o ukázku propojení klasického středoškolského učiva s problematikou běžného života v oblasti financí za pomoci využití informačních technologií dnešní doby. Hlavním přínosem příspěvku je
Závěrečná zpráva o seminářích Rozvíjíme matematickou gramotnost na základní a střední škole v roce 2015
 Závěrečná zpráva o seminářích Rozvíjíme matematickou gramotnost na základní a střední škole v roce 20. Úvod Vzhledem k závažnosti matematického vzdělávání, které provází děti a žáky od předškolního věku
Závěrečná zpráva o seminářích Rozvíjíme matematickou gramotnost na základní a střední škole v roce 20. Úvod Vzhledem k závažnosti matematického vzdělávání, které provází děti a žáky od předškolního věku
Zásady zpracování vědecké práce
 Zásady zpracování vědecké práce Kontakt: Doc. Hana Čížková Katedra biologických disciplín ZF JU Na Zlaté stoce 10, 1. patro č. 203 hcizkova@zf.jcu.cz Pro 2. ročník BOZO, PÚPN, LS 2011 1. Úvod 1.1 Co je
Zásady zpracování vědecké práce Kontakt: Doc. Hana Čížková Katedra biologických disciplín ZF JU Na Zlaté stoce 10, 1. patro č. 203 hcizkova@zf.jcu.cz Pro 2. ročník BOZO, PÚPN, LS 2011 1. Úvod 1.1 Co je
VZDĚLÁVÁNÍ PRO 21. STOLETÍ. Lukáš Herout Institut vzdělávání a poradenství ČZU, Praha
 VZDĚLÁVÁNÍ PRO 21. STOLETÍ Lukáš Herout Institut vzdělávání a poradenství ČZU, Praha ZMĚNY VE VZDĚLÁVÁNÍ Změny ve vzdělávacích systémech Transmisivní x konstruktivistický přístup Digitální technologie
VZDĚLÁVÁNÍ PRO 21. STOLETÍ Lukáš Herout Institut vzdělávání a poradenství ČZU, Praha ZMĚNY VE VZDĚLÁVÁNÍ Změny ve vzdělávacích systémech Transmisivní x konstruktivistický přístup Digitální technologie
Úvod do Informatiky. 0 Organizační pokyny k výuce IB000. Organizátor předmětu: Ondrej Moriš Cvičící (online přes IS MU):
 0 Organizační pokyny k výuce IB000 Úvod do Informatiky 2010 Přednášející: Petr Hliněný hlineny@fi.muni.cz Organizátor předmětu: Ondrej Moriš xmoris@mail.muni.cz Cvičící (online přes IS MU): Martin Derka,
0 Organizační pokyny k výuce IB000 Úvod do Informatiky 2010 Přednášející: Petr Hliněný hlineny@fi.muni.cz Organizátor předmětu: Ondrej Moriš xmoris@mail.muni.cz Cvičící (online přes IS MU): Martin Derka,
Matematická analýza pro informatiky I. Spojitost funkce
 Matematická analýza pro informatiky I. 6. přednáška Spojitost funkce Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 18. března 2011 Jan Tomeček, tomecek@inf.upol.cz
Matematická analýza pro informatiky I. 6. přednáška Spojitost funkce Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 18. března 2011 Jan Tomeček, tomecek@inf.upol.cz
Studijní program Matematika Obor Pravděpodobnost, matematická statistika a ekonometrie
 Studijní program Matematika Obor Pravděpodobnost, matematická statistika a ekonometrie Doporučené průběhy studia pro rok 2014/15 24. září 2014 Vysvětlivky: Tento dokument obsahuje několik alternativních
Studijní program Matematika Obor Pravděpodobnost, matematická statistika a ekonometrie Doporučené průběhy studia pro rok 2014/15 24. září 2014 Vysvětlivky: Tento dokument obsahuje několik alternativních
Co jsme udělali: Au = f, u D(A)
 Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Místní akční plán rozvoje vzdělávání II ORP Strakonice CZ /0.0/0.0/17_047/
 Místní akční plán rozvoje vzdělávání II ORP Strakonice CZ.02.3.68/0.0/0.0/17_047/0009074 Členové pracovní skupiny ve spolupráci s realizačním týmem identifikovali a popsali příčiny problémů ke každé prioritní
Místní akční plán rozvoje vzdělávání II ORP Strakonice CZ.02.3.68/0.0/0.0/17_047/0009074 Členové pracovní skupiny ve spolupráci s realizačním týmem identifikovali a popsali příčiny problémů ke každé prioritní
DOTAZNÍK PRO URČENÍ UČEBNÍHO STYLU
 DOTAZNÍK PRO URČENÍ UČEBNÍHO STYLU Projekt MOTIVALUE Jméno: Třida: Pokyny Prosím vyplňte vaše celé jméno. Vaše jméno bude vytištěno na informačním listu s výsledky. U každé ze 44 otázek vyberte a nebo
DOTAZNÍK PRO URČENÍ UČEBNÍHO STYLU Projekt MOTIVALUE Jméno: Třida: Pokyny Prosím vyplňte vaše celé jméno. Vaše jméno bude vytištěno na informačním listu s výsledky. U každé ze 44 otázek vyberte a nebo
Angličtina program k procvičování slovní zásoby
 Středoškolská technika 2011 Setkání a prezentace prací středoškolských studentů na ČVUT Angličtina program k procvičování slovní zásoby Kamil Hanus Střední průmyslová škola elektrotechniky a informačních
Středoškolská technika 2011 Setkání a prezentace prací středoškolských studentů na ČVUT Angličtina program k procvičování slovní zásoby Kamil Hanus Střední průmyslová škola elektrotechniky a informačních
Karta předmětu prezenční studium
 Karta předmětu prezenční studium Název předmětu: Číslo předmětu: 714-0513 Garantující institut: Garant předmětu: Vybrané kapitoly z matematiky (VKM) Katedra matematiky a deskriptivní geometrie doc. RNDr.
Karta předmětu prezenční studium Název předmětu: Číslo předmětu: 714-0513 Garantující institut: Garant předmětu: Vybrané kapitoly z matematiky (VKM) Katedra matematiky a deskriptivní geometrie doc. RNDr.
Směrnice rektora č. 3/2014 Hodnocení kvality studia z pohledu studentů
 Vysoká škola sociálně správní, Institut celoživotního vzdělávání Havířov o.p.s. Vysoká škola sociálně správní, Havířov Směrnice rektora č. 3/2014 Hodnocení kvality studia z pohledu studentů Článek 1 Úvodní
Vysoká škola sociálně správní, Institut celoživotního vzdělávání Havířov o.p.s. Vysoká škola sociálně správní, Havířov Směrnice rektora č. 3/2014 Hodnocení kvality studia z pohledu studentů Článek 1 Úvodní
Gymnázium, Český Krumlov
 Gymnázium, Český Krumlov Vyučovací předmět Fyzika Třída: 6.A - Prima (ročník 1.O) Úvod do předmětu FYZIKA Jan Kučera, 2011 1 Organizační záležitosti výuky Pomůcky související s výukou: Pracovní sešit (formát
Gymnázium, Český Krumlov Vyučovací předmět Fyzika Třída: 6.A - Prima (ročník 1.O) Úvod do předmětu FYZIKA Jan Kučera, 2011 1 Organizační záležitosti výuky Pomůcky související s výukou: Pracovní sešit (formát
Bankovní institut vysoká škola, a.s. Praha Karlovy Vary Písek Teplice Břeclav
 Bankovní institut vysoká škola, a.s. Kdo jsme? První soukromá vysoká škola Atraktivní studijní obory Univerzitní informační systém Skvělé zázemí a nejnovější technika Moderní bezbariérová budova Jsme součástí
Bankovní institut vysoká škola, a.s. Kdo jsme? První soukromá vysoká škola Atraktivní studijní obory Univerzitní informační systém Skvělé zázemí a nejnovější technika Moderní bezbariérová budova Jsme součástí
Příklad dobré praxe XXI
 Projekt Další vzdělávání pedagogických pracovníků středních škol v oblasti kariérového poradenství CZ 1.07/1.3.00/08.0181 Příklad dobré praxe XXI pro průřezové téma Člověk a svět práce Ing. Iva Černá 2010
Projekt Další vzdělávání pedagogických pracovníků středních škol v oblasti kariérového poradenství CZ 1.07/1.3.00/08.0181 Příklad dobré praxe XXI pro průřezové téma Člověk a svět práce Ing. Iva Černá 2010
Struktura článku. Chemická literatura. Struktura článku. Struktura článku 10/25/ Struktura článku, cílová skupina
 Chemická literatura 17.10. 2017, cílová skupina Shrnuje celý článek TOC Volně k dispozici (Supporting Information) Připravuje + motivuje čtenáře k dalšímu čtení Shrnuje současný stav poznání!! Zohledňuje
Chemická literatura 17.10. 2017, cílová skupina Shrnuje celý článek TOC Volně k dispozici (Supporting Information) Připravuje + motivuje čtenáře k dalšímu čtení Shrnuje současný stav poznání!! Zohledňuje
Metody analýzy modelů. Radek Pelánek
 Metody analýzy modelů Radek Pelánek Fáze modelování 1 Formulace problému 2 Základní návrh modelu 3 Budování modelu 4 Verifikace a validace 5 Simulace a analýza 6 Sumarizace výsledků Simulace a analýza
Metody analýzy modelů Radek Pelánek Fáze modelování 1 Formulace problému 2 Základní návrh modelu 3 Budování modelu 4 Verifikace a validace 5 Simulace a analýza 6 Sumarizace výsledků Simulace a analýza
Co je L Y X? Vlastnosti a nástroje Instalace Zdroje. Adam Farnik. V B - TU Ostrava. Elektronické publikování, 2008
 LYX Adam Farnik V B - TU Ostrava Elektronické publikování, 2008 Osnova 1 Co je LYX? 2 Vlastnosti a nástroje Formatování textu Matematický reºim Dal²í moºnosti 3 Instalace 4 Zdroje WYSIWYM WYSIWYG prost
LYX Adam Farnik V B - TU Ostrava Elektronické publikování, 2008 Osnova 1 Co je LYX? 2 Vlastnosti a nástroje Formatování textu Matematický reºim Dal²í moºnosti 3 Instalace 4 Zdroje WYSIWYM WYSIWYG prost
Matematika I. dvouletý volitelný předmět
 Název předmětu: Zařazení v učebním plánu: Matematika I O7A, C3A, O8A, C4A dvouletý volitelný předmět Cíle předmětu Tento předmět je koncipován s cílem usnadnit absolventům gymnázia přechod na vysoké školy
Název předmětu: Zařazení v učebním plánu: Matematika I O7A, C3A, O8A, C4A dvouletý volitelný předmět Cíle předmětu Tento předmět je koncipován s cílem usnadnit absolventům gymnázia přechod na vysoké školy
Zřízení studijního oboru HPC (High performance computing)
 Zřízení studijního oboru HPC (High performance computing) Návrh oboru je koncipován tak, aby byl zajímavý pro široký okruh zájemců, kteří pak mohou později pracovat při využití HPC v projekčních a výzkumných
Zřízení studijního oboru HPC (High performance computing) Návrh oboru je koncipován tak, aby byl zajímavý pro široký okruh zájemců, kteří pak mohou později pracovat při využití HPC v projekčních a výzkumných
Osm let po přijímačkách: jak se dnes daří zájemcům o vysoké školy?
 Osm let po přijímačkách: jak se dnes daří zájemcům o vysoké školy? Longitudinální studie 2010-2018 2010: respondenti skládali test Obecných studijních předpokladů (OSP) 2018: respondenti vyplnili dotazník
Osm let po přijímačkách: jak se dnes daří zájemcům o vysoké školy? Longitudinální studie 2010-2018 2010: respondenti skládali test Obecných studijních předpokladů (OSP) 2018: respondenti vyplnili dotazník
Odpřednesenou látku naleznete v kapitolách skript Abstraktní a konkrétní lineární algebra.
 nad obecným tělesem a lineární kombinace Odpřednesenou látku naleznete v kapitolách 1.1 1.4 skript Abstraktní a konkrétní lineární algebra. Jiří Velebil: A7B01LAG 1.10.2015: 1/20 nad obecným tělesem Co
nad obecným tělesem a lineární kombinace Odpřednesenou látku naleznete v kapitolách 1.1 1.4 skript Abstraktní a konkrétní lineární algebra. Jiří Velebil: A7B01LAG 1.10.2015: 1/20 nad obecným tělesem Co
1 Test 1 naivní vs standardní
 . DÚ Nafukovací pole Datové Struktury I Studentus Maximus Takto jsou zobrazeny poznámky cvičících k tomu, co a jak je tu napsáno, skutečný text je mimo oranžové rámečky. Počítač, na kterém byly provedeny
. DÚ Nafukovací pole Datové Struktury I Studentus Maximus Takto jsou zobrazeny poznámky cvičících k tomu, co a jak je tu napsáno, skutečný text je mimo oranžové rámečky. Počítač, na kterém byly provedeny
VYUČOVACÍ PROCE S A JEHO FÁZE
 VYUČOVACÍ PROCE S A JEHO FÁZE I. Klasické pojetí II. Konstruktivistické pojetí Motivace Expozice Fixace Evokace Uvědomění si významu Reflexe Diagnóza Aplikace MOTIVACE - prostředek zvyšování efektivity
VYUČOVACÍ PROCE S A JEHO FÁZE I. Klasické pojetí II. Konstruktivistické pojetí Motivace Expozice Fixace Evokace Uvědomění si významu Reflexe Diagnóza Aplikace MOTIVACE - prostředek zvyšování efektivity
MATEMATIKA A 3 Metodický list č. 1
 Metodický list č. 1 Název tématického celku: Úvod do problematiky diskrétní matematiky Cíl: Cílem tohoto tématického celku je vymezení oblasti diskrétní matematiky a příprava na další výklad kurzu. Jedná
Metodický list č. 1 Název tématického celku: Úvod do problematiky diskrétní matematiky Cíl: Cílem tohoto tématického celku je vymezení oblasti diskrétní matematiky a příprava na další výklad kurzu. Jedná
SVD rozklad a pseudoinverse
 SVD rozklad a pseudoinverse Odpřednesenou látku naleznete v kapitole 12 skript Abstraktní a konkrétní lineární algebra. Jiří Velebil: Lineární algebra 19.12.2016: SVD rozklad a pseudoinverse 1/21 Cíle
SVD rozklad a pseudoinverse Odpřednesenou látku naleznete v kapitole 12 skript Abstraktní a konkrétní lineární algebra. Jiří Velebil: Lineární algebra 19.12.2016: SVD rozklad a pseudoinverse 1/21 Cíle
Studijní program Elektrotechnika a komunikační technologie. prof. Ing. Aleš Prokeš, Ph.D Ústav radioelektroniky FEKT VUT v Brně
 Studijní program Elektrotechnika a komunikační technologie prof. Ing. Aleš Prokeš, Ph.D Ústav radioelektroniky FEKT VUT v Brně Studijní obory Studijní obory doktorského studijního programu Elektrotechnika
Studijní program Elektrotechnika a komunikační technologie prof. Ing. Aleš Prokeš, Ph.D Ústav radioelektroniky FEKT VUT v Brně Studijní obory Studijní obory doktorského studijního programu Elektrotechnika
Výstupy z pracovní skupiny ČTENÁŘSKÁ A MATEMATICKÁ GRAMOSTNOST
 Výstupy z pracovní skupiny ČTENÁŘSKÁ A MATEMATICKÁ GRAMOSTNOST Vymezení problémových oblastí a klíčových problémů Problémové okruhy ČTENÁŘSKÁ GRAMOTNOST Vysoký počet žáků v hodině hlavně ve velkých školách
Výstupy z pracovní skupiny ČTENÁŘSKÁ A MATEMATICKÁ GRAMOSTNOST Vymezení problémových oblastí a klíčových problémů Problémové okruhy ČTENÁŘSKÁ GRAMOTNOST Vysoký počet žáků v hodině hlavně ve velkých školách
1.5.1 Číselné soustavy
 .. Číselné soustavy Předpoklady: základní početní operace Pedagogická poznámka: Tato hodina není součástí klasické gymnaziální sady. Upřímně řečeno nevím proč. Jednak se všichni studenti určitě setkávají
.. Číselné soustavy Předpoklady: základní početní operace Pedagogická poznámka: Tato hodina není součástí klasické gymnaziální sady. Upřímně řečeno nevím proč. Jednak se všichni studenti určitě setkávají
CELOŽIVOTNÍ VZDĚLÁVÁNÍ NA FAKULTĚ DOPRAVNÍ
 CELOŽIVOTNÍ VZDĚLÁVÁNÍ NA FAKULTĚ DOPRAVNÍ Celoživotní vzdělávaní (CŽV) bylo přijato na ČVUT jako logický a nezbytný doplněk základní pedagogické činnosti. Legislativní rámec CŽV na ČVUT je vymezen platným
CELOŽIVOTNÍ VZDĚLÁVÁNÍ NA FAKULTĚ DOPRAVNÍ Celoživotní vzdělávaní (CŽV) bylo přijato na ČVUT jako logický a nezbytný doplněk základní pedagogické činnosti. Legislativní rámec CŽV na ČVUT je vymezen platným
Využití volně dostupných simulátorů pole v elektromagnetické kompatibilitě
 Využití volně dostupných simulátorů pole v elektromagnetické kompatibilitě UEM FAI Zlín STOČ 2009, Ostrava Bc. Jan Strnad Anotace Studentský projekt se zabývá numerickou simulaci vybraných problémů z elektromagnetické
Využití volně dostupných simulátorů pole v elektromagnetické kompatibilitě UEM FAI Zlín STOČ 2009, Ostrava Bc. Jan Strnad Anotace Studentský projekt se zabývá numerickou simulaci vybraných problémů z elektromagnetické
Odborný článek. Petr Klán, VŠE v Praze, IMRAD Introduction, Material and Method, Results, Discussion
 Odborný článek Petr Klán, VŠE v Praze, petr.klan@vse.cz Části odborného článku IMRAD Introduction, Material and Method, Results, Discussion NADPIS Do 10 slov Autor (autoři) Jméno, adresa, e-mail Abstrakt
Odborný článek Petr Klán, VŠE v Praze, petr.klan@vse.cz Části odborného článku IMRAD Introduction, Material and Method, Results, Discussion NADPIS Do 10 slov Autor (autoři) Jméno, adresa, e-mail Abstrakt
Informační a databázové systémy v rostlinolékařství. Zdeněk Landa & Helena Landová
 Informační a databázové systémy v rostlinolékařství Zdeněk Landa & Helena Landová Úvodem charakteristika kurzu - cíle, obsah informační gramotnost - definice, význam význam informací a práce s nimi škola,
Informační a databázové systémy v rostlinolékařství Zdeněk Landa & Helena Landová Úvodem charakteristika kurzu - cíle, obsah informační gramotnost - definice, význam význam informací a práce s nimi škola,
SEZNAM ANOTACÍ. CZ.1.07/1.5.00/ III/2 Inovace a zkvalitnění výuky prostřednictvím ICT VY_32_INOVACE_MA4 Analytická geometrie
 SEZNAM ANOTACÍ Číslo projektu Číslo a název šablony klíčové aktivity Označení sady DUM Tematická oblast CZ.1.07/1.5.00/34.0527 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT VY_32_INOVACE_MA4 Analytická
SEZNAM ANOTACÍ Číslo projektu Číslo a název šablony klíčové aktivity Označení sady DUM Tematická oblast CZ.1.07/1.5.00/34.0527 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT VY_32_INOVACE_MA4 Analytická
Cloudy a gridy v národní einfrastruktuře
 Cloudy a gridy v národní einfrastruktuře Tomáš Rebok MetaCentrum, CESNET z.s.p.o. CERIT-SC, Masarykova Univerzita (rebok@ics.muni.cz) Ostrava, 5. 4. 2012 PRACE a IT4Innovations Workshop Cestovní mapa národních
Cloudy a gridy v národní einfrastruktuře Tomáš Rebok MetaCentrum, CESNET z.s.p.o. CERIT-SC, Masarykova Univerzita (rebok@ics.muni.cz) Ostrava, 5. 4. 2012 PRACE a IT4Innovations Workshop Cestovní mapa národních
POŽADAVKY K SOUBORNÉ ZKOUŠCE Z MATEMATIKY
 POŽADAVKY K SOUBORNÉ ZKOUŠCE Z MATEMATIKY Bakalářský studijní program B1101 (studijní obory - Aplikovaná matematika, Matematické metody v ekonomice, Aplikovaná matematika pro řešení krizových situací)
POŽADAVKY K SOUBORNÉ ZKOUŠCE Z MATEMATIKY Bakalářský studijní program B1101 (studijní obory - Aplikovaná matematika, Matematické metody v ekonomice, Aplikovaná matematika pro řešení krizových situací)
Doktorský studijní program Elektrotechnika a komunikační technologie. prof. Ing. Aleš Prokeš, Ph.D Ústav radioelektroniky FEKT VUT v Brně
 Doktorský studijní program Elektrotechnika a komunikační technologie prof. Ing. Aleš Prokeš, Ph.D Ústav radioelektroniky FEKT VUT v Brně Doktorský studijní program Garant: Prof. RNDr. Vladimír Aubrecht,
Doktorský studijní program Elektrotechnika a komunikační technologie prof. Ing. Aleš Prokeš, Ph.D Ústav radioelektroniky FEKT VUT v Brně Doktorský studijní program Garant: Prof. RNDr. Vladimír Aubrecht,
Dnešní látka: Literatura: Kapitoly 3 a 4 ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Úvod do Informatiky 2006
 0 Organizační pokyny k výuce IB000 Úvod do Informatiky 2006 Přednášející: Petr Hliněný hlineny@fi.muni.cz Konzultant: Jan Holeček holecek@fi.muni.cz Cvičící: Václav Brožek, Jitka Kudrnáčová, Zdeněk Řehák,
0 Organizační pokyny k výuce IB000 Úvod do Informatiky 2006 Přednášející: Petr Hliněný hlineny@fi.muni.cz Konzultant: Jan Holeček holecek@fi.muni.cz Cvičící: Václav Brožek, Jitka Kudrnáčová, Zdeněk Řehák,
Reálné gymnázium a základní škola města Prostějova Školní vzdělávací program pro ZV Ruku v ruce
 2 MATEMATIKA A JEJÍ APLIKACE UČEBNÍ OSNOVY 2. 2 Cvičení z matematiky Časová dotace 7. ročník 1 hodina 8. ročník 1 hodina 9. ročník 1 hodina Charakteristika: Předmět cvičení z matematiky doplňuje vzdělávací
2 MATEMATIKA A JEJÍ APLIKACE UČEBNÍ OSNOVY 2. 2 Cvičení z matematiky Časová dotace 7. ročník 1 hodina 8. ročník 1 hodina 9. ročník 1 hodina Charakteristika: Předmět cvičení z matematiky doplňuje vzdělávací
2 MATEMATIKA A JEJÍ APLIKACE UČEBNÍ OSNOVY
 2 MATEMATIKA A JEJÍ APLIKACE UČEBNÍ OSNOVY 2. 2 Cvičení z matematiky Časová dotace 7. ročník 1 hodina 8. ročník 1 hodina 9. ročník 1 hodina Charakteristika: Předmět cvičení z matematiky doplňuje vzdělávací
2 MATEMATIKA A JEJÍ APLIKACE UČEBNÍ OSNOVY 2. 2 Cvičení z matematiky Časová dotace 7. ročník 1 hodina 8. ročník 1 hodina 9. ročník 1 hodina Charakteristika: Předmět cvičení z matematiky doplňuje vzdělávací
2.6. VLASTNÍ ČÍSLA A VEKTORY MATIC
 .6. VLASTNÍ ČÍSLA A VEKTORY MATIC V této kapitole se dozvíte: jak jsou definována vlastní (charakteristická) čísla a vektory čtvercové matice; co je to charakteristická matice a charakteristický polynom
.6. VLASTNÍ ČÍSLA A VEKTORY MATIC V této kapitole se dozvíte: jak jsou definována vlastní (charakteristická) čísla a vektory čtvercové matice; co je to charakteristická matice a charakteristický polynom
Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVUT v Praze. Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A
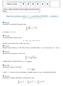 Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
Měření hodnoty g z periody kmitů kyvadla
 Měření hodnoty g z periody kmitů kyvadla Online: http://www.sclpx.eu/lab2r.php?exp=8 Úvod Při určení hodnoty tíhové zrychlení z periody kmitů kyvadla o délce l vycházíme ze známého vztahu (2.4.1) pro periodu
Měření hodnoty g z periody kmitů kyvadla Online: http://www.sclpx.eu/lab2r.php?exp=8 Úvod Při určení hodnoty tíhové zrychlení z periody kmitů kyvadla o délce l vycházíme ze známého vztahu (2.4.1) pro periodu
