JAK NA ZEBRY? Marta Volfová, garant oboru matematika
|
|
|
- Otto Musil
- před 10 lety
- Počet zobrazení:
Transkript
1 JAK NA ZEBRY? Marta Volfová, garant oboru matematika Učitel autoškoly říká adeptovi šoférského umění: Právě jste přejel zebru! Ten sebou trhne a ptá se: Propána, co se jí stalo? Žije? Tak o těchto zebrách řeč nebude. Nebudeme hovořit ani o tom, jak osedlat zebru ze ZOO. Zebrami nazýváme zajímavé logické kombinatorické úlohy, které vyžadují správně k sobě přiřadit prvky několika různých množin na základě několika (zdánlivě nepostačujících) informací. Název zebra dostaly podle úlohy, která asi před 50 lety okouzlila celý svět a která končila otázkou: Kdo chová zebru? (U nás se tato úloha prvně objevila v r v časopise, který může mladým matematickým talentům hodně dát, neboť stále vychází a mívá zajímavé články a úlohy, totiž v Rozhledech matematickofyzikálních.) Několik posledních let však tato úloha putuje v různě obměněných verzích po internetu pod názvem Einsteinova úloha (i s informací, že 98 % lidí ji vyřešit neumí). Úloha 1 V ulici cizinecké čtvrti stojí vedle sebe pět domků různých barev. V každém bydlí muž jiné národnosti, v každém se pije jiný oblíbený nápoj, v každém domku je oblíben jiný sport, resp. se nesportuje vůbec a konečně v každém se pěstuje jiný druh zvířat. O domcích a jejich obyvatelích známe tyto informace: A) Angličan bydlí v červeném domku. B) Španěl chová psa. C) Káva se pije v zeleném domku. D) Polák pije vodku. E) Zelený domek stojí vedle domku bílého (z hlediska pozorovatele domků). F) Fotbalista pěstuje hlemýždě. G) Ve žlutém domku bydlí cyklista. H) Mléko se pije v prostředním domku. I) V prvním domku bydlí Nor. J) Nesportovec bydlí vedle domku, v němž je chována liška. K) Domek cyklisty sousedí s domkem, v němž je chován kůň. L) Zápasník pije pomerančovou šťávu. M) Japonec je hokejista. 1
2 N) Nor bydlí vedle modrého domku. O) V jednom domku se pije voda. P) V jednom domku je chována zebra. Kdo chová zebru a kdo pije vodu? Jestli jste už takové úlohy řešili, můžete ji zkusit bez dalšího čtení řešit. Jestliže ne, začneme úlohou lehčí a ukážeme, jak se takové úlohy řešit dají. Stará a oblíbená je tato úloha 2 (vyskytuje se v přemnoha variantách) Tři známí sedí spolu v kavárně, povídají si a najednou jeden povídá: to je legrace, my máme stejná zaměstnání jako jsou naše jména, ale nikomu se jméno a zaměstnání nekryje! Na to odpoví pekař: To máte pravdu, pane Zahradníku! Jaké zaměstnání měl pan Tesař? Lze řešit usuzováním, kombinováním, někdo řeší tzv. vhledem. Dobré je u podobných úloh užívat tabulku. pekař zahradník tesař pan Pekař pan Zahradník pan Tesař Proškrtneme dvojice, které se vylučují (Pekař pekař atd.), pak i dvojici těch, co spolu hovořili (a nemohou tedy tvořit jednu osobu): pekař Zahradník. Zbyde-li v nějaké řádce či sloupci jen jedna možnost, vyznačíme ji jako správnou a v příslušném sloupci či řádce vyškrtáme zbylé možnosti. Zde ve 2. řádce zbývá jediná možnost pan Zahradník je tesařem tedy tesařem není pan Pekař, proto ve 3. sloupci vyloučíme možnost Pekař tesař a tabulku dokončíme. pekař zahradník tesař pan Pekař pan Zahradník pan Tesař Pan Pekař je tedy zahradníkem a pan Tesař pekařem. Tuto tabulkovou metodu můžeme využít i u složitějších úloh, jak ukážeme dále. Nejdřív ale připomeneme ještě dvě jiné metody řešení Zeber. 2
3 Úloha 3 Na studiích se sešly tři studentky Kája, Jana a Lenka. Každá dělá jiný sport a pochází z jiného města. Víme o nich, že 1. Jana nedělá balet, 2. Lenka nedělá gymnastiku, 3. gymnastka je z města krajky, 4. ta, co baletí, není z Hradce, 5. Lenka není z Plzně, 6. jedna pěstuje aikido. Můžeme řešit tzv. stromem logických možností např. ke každé dívce připíšeme všechny možnosti prováděného sportu (to je 3. 3 = 9 případů) a ke každému z nich všechna tři města (celkem 27 možností) a pak budeme vyškrtávat podle sdělených informací neslučitelné. Z 1. a 2. však plyne, že u Jany a Lenky přicházejí v úvahu jen dva sporty, z 3., že ke gymnastce přiřadíme jen Vamberk, k baletu by podle 4. patřil Vamberk nebo Plzeň, protože ale Vamberk je přiřazen gymnastce, může být balet spojen jen s Plzní. Pro Lenku přichází v úvahu jen Hradec nebo Vamberk. Tedy Vamberk bude jen u gymnastiky a Plzeň u baletu. Jana gymnastika - Vamberk aikido - Hradec Lenka balet Plzeň (ale podle 5. Lenka z Plzně není) aikido - Hradec Kája balet Plzeň gymnastika - Vamberk aikido Hradec Vidíme, že pro Lenku vychází jen možnost aikido Hradec (škrtneme aikido u druhých děvčat) pak Janě vychází Vamberk a gymnastika a Káje balet a Plzeň. Další metodou, vhodnou pro jednodušší úlohy, je užívat grafického znázornění. Načrtneme trojúhelník (případně i čtyř- nebo pětiúhelník) a na každou jeho stranu vyznačíme prvky jedné z množin (např. lidi, města, pohoří, ). Pak spojíme plnou čarou prvky, které k sobě patří a čárkovaně, které nepatří. 3
4 Užití ukážeme na úloze 4 Každý ze tří kamarádů (Petr, Karel, Jan) o prázdninách podnikal turistické túry právě v jednom z pohoří Alpy, Tatry, Krkonoše a navštívil právě jedno ze zajímavých měst Hradec Králové, Salzburg, Kežmarok. Určete, kdo byl kde, víte-li, že: - Karel si opět zopakoval svou oblíbenou tatranskou túru na Kriváň. - Ten, kdo jel do Krkonoš, si cestou prohlédl Gočárovo řešení Hradce. - Petr říkal, že v Krkonoších byl už aspoň desetkrát, a jel jinam. - Ten, kdo byl v Tatrách, uvěřil reklamě, že při špatném počasí je nejlepší řešení navštívit půvabné městečko Kežmarok a své návštěvy nelitoval. Načrtneme trojúhelník, na každou stranu napíšeme prvky jedné z množin a vyznačíme plnou čarou podle textu pravdivá spojení, čárkovanou neuskutečněná. Dále: - Karel byl v Tatrách, tedy ne v Krkonoších spojíme Karel Krkonoše přerušovanou čarou. - Krkonoše nejsou spojeny plnou čarou ani s Petrem ani s Karlem musí být s Janem. A protože jsou plnou čarou spojeny s Hradcem, dostáváme 1. řešení trojúhelník Jan Krkonoše Hradec Králové. - Petr nejel do Krkonoš ani do Tater (tam byl Karel), jel tedy do Alp. (Vyznačíme plnou čarou.) - Plzně je spojeno Karel Tatry, Tatry Kežmarok, bude i spojení Karel Kežmarok (2. řešení). - Petr je spojen s Alpami, z měst zbývá jediné, tedy propojíme a máme 3. řešení: trojúhelník Petr Alpy Salzburg. 4
5 Vždy platí: každý prvek je spojen právě s jedním prvkem z každé další množiny (spojení vyznačíme plnou čarou); s ostatními prvky té množiny již být spojen nemůže (čárkovaná čára). Má-li prvek vyloučeny z nějaké další množiny již všechny prvky až na jeden, musí být spojen s ním. Tato metoda je výhodná jen pro jednodušší úlohy. Pro trochu složitější úlohy si získala oblibu metoda tabulková. Její užití ukážeme na úloze 5 Určete, kdo má jakého psa, víte-li, že Královi nemají boxera, ale mají psa jménem Nero nebo Dick, Staňkovi mají psa, co se jmenuje Nero nebo Filip a není to určitě vlčák, knírač Alan se se Šmídovým Filipem nemá moc rád. Vlčák není Filip ani Argo, boxer má jméno Nero nebo Dick, u Valentů mají vždy krásně ostříhaného pudla, Majerovi nedali psovi jméno Argo. Jeden pes je jezevčík. Připravíme tabulku a podle textu budeme vyznačovat (to, co platí, tečkou, co neplatí, vodorovnou čarou). boxer vlčák jezevčík knírač pudl Alan Nero Dick Argo Filip Královi Staňkovi Šmídovi Majerovi Valentovi Alan Nero Dick Argo Filip - Královi nemají boxera, jejich pes se nejmenuje ani Alan ani Argo ani Filip (protože je Nero nebo Dick), - Staňkovi nemají vlčáka; jejich pes není Alan ani Dick ani Argo, - knírač je Alan; ke dvojici Alan knírač vyškrtáme zbývající část řádku i (dolního) sloupce, protože knírač Alan nemá rád Filipa od Šmídových, tedy Šmídovi nemají knírače, nemají Alana; mají Filipa; ke dvojici Šmídovi Filip vyškrtáme opět zbylé v řádku i sloupci, - Valentovi mají pudla; k dvojici Valentovi pudl vyškrtáme v příslušném řádku i sloupci zbylá okénka, - Majerovi nemají Arga, 5
6 - uplatníme, že vlčák není Argo a boxer že není Alan ani Argo ani Filip (protože je Nero nebo Dick). (Výsledná podoba tabulky po tomto doplňování informací je na obrázku.) - Nyní ve sloupci Argo zbývá jediné volné políčko Valentovi; k dvojici Valentovi Argo proškrtáme zbylé v řádku i sloupci; Valentovi mají pudla Argo doplníme v dolní tabulce Argo pudl a proškrtáme zbytek sloupce i řádku. - V posledním řádku Filip je teď jediné volné okénko jezevčík ; Filipa mají Šmídovi, tedy mají jezevčíka (vyškrtáme vše k dvojici Filip jezevčík a Šmídovi jezevčík). - V pravé horní tabulce vyznačíme Staňkovi Nero (jediné volné políčko) a proškrtáme sloupec; dále Královi Dick (totéž) a Majerovi Alan (opět táž situace). - Víme tedy, že Majerovi mají Alana a že Alan je knírač; vyznačíme dvojici Majerovi knírač a proškrtáme zbylé v příslušném sloupci i řádku. - Zbývá doplnit, že Královi mají vlčáka; jejich pes se jmenuje Dick; Dick je tedy vlčák. - Uzavřeme posledními dosud volnými políčky: Staňkovi boxer, Nero boxer. Výsledná tabulka sděluje, že Královi mají vlčáka Dicka, Staňkovi boxera Nera, Šmídovi jezevčíka Filipa, Majerovi knírače Alana a Valentovi pudla Arga. Nejsložitější úlohy řešíme úvahou. Pomáháme si tak, že prvky, o nichž již víme, že k sobě patří, skládáme do jakýchsi bloků. Úloha 6 Čtyři manželské páry vyrazily na jarní výlet na české hrady a zámky. Každý pár zvolil jiný dopravní prostředek a jiný cíl. - Užíkovi se jeli podívat na hrad do Litic nad Orlicí. - Jedni manželé jeli vlakem. - Petra byla na zámku Opočno. - Olda se ženou navštívil zámek Doudleby nad Orlicí. - Radka Vlčková na Bezdězu nebyla. - Pan Bárta se nejmenuje Jarda. - Manžel Věry se jmenuje Vili. - Olda nemá příjmení Staněk. - Busem jel Láďa s manželkou. - Jana a její muž vyrazili na kolech. 6
7 - Bártovi si udělali výlet autem. Budeme řešit úvahou a využijeme schémat (bloků). Vypišme cíle cest a co kolem nich víme a jména, která k sobě patří spolu s dopravními prostředky. Opočno Doudleby Vlčkovi Užíkovi Petra (ne Bezděz) Litice Olda Radka Bártovi Staňkovi Užíkovi ne Jarda Věra Láďa Jana Vili ne Olda bus kolo auto Víme, že Radka Vlčková nebyla na Bezdězi, nebyla ani na zámku Opočno (tam byla Petra) ani v Liticích (tam byli Užíkovi), byla tedy v Doudlebech a to s manželem Oldou. Nejeli autem (tím se dopravovali Bártovi) ani na kolech (tak jela Jana s manželem), ani busem (tím jel Láďa se ženou) tedy využili vlak. Věra a Vili nejeli busem (tím jel Láďa) ani na kole (na tom jela Jana) ani vlakem, jak jsme výše usoudili tedy autem byli to tedy Bártovi; nebyli proto ani v Liticích (tam byli Užíkovi) ani v Doudlebách (Vlčkovi) ani v Opočně (tam byla Petra, ne Věra) byli tedy na Bezdězi. Jana jela na kole, jejím manželem tedy nemůže být Láďa (jel busem) Láďa tedy patří k Petře. Láďa s Petrou byli busem v Opočně, jmenují se Staňkovi a k Janě přiřadíme Jardu a příjmení Užíkovi, byli v Liticích. Závěr: Radka a Olda Vlčkovi byli vlakem v Doudlebách, Věra a Vili Bártovi autem na Bezdězi, Petra a Láďa Staňkovi busem v Opočně a Jana a Jarda Užíkovi zajeli na kolech do Litic. Poslední úloha 7 V ulici stojí vedle sebe pět domků (každý jiné barvy). Zjistěte, v jakém pořadí domky stojí, který muž a žena v nich bydlí, jaké zvíře chovají a jaké vlastní auto, víte-li, že: - Adam bydlí v červeném domku, - Leoš má psa, - Milan bydlí v 1. domku zleva, - Jiřina bydlí ve žlutém domku, - Iveta má sousedy, co chovají rybičky, - Milan bydlí vedle modrého domku, 7
8 - Berta má kočku, - Eva jezdí v autě Fiat, - Tomáš vlastní auto Seat, - Karel se oženil s Lucií, - sousedi Jiřiny chovají koně, - S Mazdou jsou spokojeni v zeleném domku, - zelený domek je hned nalevo od bílého, - Škodu vlastní v prostředním domku, - někdo vlastní auto Renault, - v jednom domku chovají želvu. Řešení: Nejprve si informace z textu úlohy zaznamenáme do bloků, řešíme postupně úvahou. Dobré je vytvořit si schéma (zde pět domků vedle sebe) a již zjištěná umístění prvků zapisovat na správné místo červený žlutý modrý zelen ý Adam Le oš pes Mila n Jiřina Iveta Ber ta kůň ryby koč ka Ev a Fia t Tomá š Seat Kare l Luci e bílý Mazd a Škod a Uvažujeme a doplňujeme do schématu: 1) Kolikátý je zelený domek? ne 1. to by vedle něj byl modrý ale má být bílý. ne 2. ten je modrý, ne zelený. ne 3. tam mají Škodovku, ne Mazdu. ne 5. má být nalevo od bílého, nemůže být poslední. Je tedy čtvrtý a bílý domek je pátý. 2) Jakou barvu má první domek? ne zelenou tu má 4. ne bílou tu má 5. 8
9 chovají koně). ne modrou tu má 2. ne červenou tam bydlí Adam, ne Milan Je tedy žlutý, proto tam bydlí i Jiřina (a vedle ve 2. domě 3. domek (s Adamem a škodovkou) musí být červený. 3) Ze schématu vidíme, že Eva (s Fiatem) může bydlet jen ve 2. nebo 5. domku a také Tomáš (se Seatem) může bydlet jen ve 2. nebo 5. domku, ale buď bydlí Eva ve 2. a Tomáš v 5., nebo Tomáš ve 2. a Eva v 5. (mají různá auta nepatří do téže rodiny každá má právě jedno auto). 4) Dvojici Karla s Lucií můžeme umístit už jen do 4. domku (v 1. už jsou Milan s Jiřinou, ve 2. je Eva nebo Tomáš, stejně tak v 5., a ve 3. je Adam). 5) Leoš se psem se nyní vejde už jen do 5. domku; bude tam s Evou (a s Fiatem) a tedy Tomáš se svým Seatem bude v domku č. 2. 6) Berta s kočkou se vejde už jen do 3. domku. 7) Iveta bude ve 2. domku a sousedi, co pěstují rybičky, budou v 1. 8) Doplníme: auto Renault vlastní v 1. domě, želvu chovají ve 4., úloha je vyřešena. Zkuste nyní vyřešit úvodní Einsteinovu úlohu. (Další úlohy lze nalézt v [1] či [2].) Literatura: [1] Volfová, M.: Metody řešení matematických úloh, Gaudeamus, Hradec Králové, [2] Pěnčík, J. Pěnčíková, J.: Lámejte si hlavu. Prometheus Praha,
Soutěž Vodní světy (CZ) 2.kolo listopad (kategorie 2)
 Projekt Pestrý BUNT, Přátelé biodiverzity v Krušných horácch Soutěž Vodní světy 2011 2012 (CZ) 2.kolo listopad (kategorie 2) Základní škola: Třída: 1. Voda v Krušných horách Krušné hory, jejich dlouhý
Projekt Pestrý BUNT, Přátelé biodiverzity v Krušných horácch Soutěž Vodní světy 2011 2012 (CZ) 2.kolo listopad (kategorie 2) Základní škola: Třída: 1. Voda v Krušných horách Krušné hory, jejich dlouhý
1.1.6 Porovnávání přirozených čísel
 1.1.6 Porovnávání přirozených čísel Předpoklady: 010105 Př. 1: Porovnej následující dvojice čísel: a) 11 11 b) 5486 5468 c) 98765 13456 a) 11 > 11 b) 5486 > 5468 c) 98765 < 13456 Př. : Česká republika
1.1.6 Porovnávání přirozených čísel Předpoklady: 010105 Př. 1: Porovnej následující dvojice čísel: a) 11 11 b) 5486 5468 c) 98765 13456 a) 11 > 11 b) 5486 > 5468 c) 98765 < 13456 Př. : Česká republika
Logické úlohy, vč. řešení. Marta Volfová
 Logické úlohy, vč. řešení Marta Volfová Centrum talentů M&F&I, Univerzita Hradec Králové, 2010 Logické úlohy 1. Muž cestuje s (částečně ochočeným) vlkem, kozou a pytlem zelí. Dojde k dosti široké a hluboké
Logické úlohy, vč. řešení Marta Volfová Centrum talentů M&F&I, Univerzita Hradec Králové, 2010 Logické úlohy 1. Muž cestuje s (částečně ochočeným) vlkem, kozou a pytlem zelí. Dojde k dosti široké a hluboké
1.1.5 Porovnávání přirozených čísel
 1.1.5 Porovnávání přirozených čísel Předpoklady: 010104 Př. 1: Porovnej následující dvojice čísel: a) 11 11 b) 5486 5468 c) 98765 13456 a) 11 > 11 b) 5486 > 5468 c) 98765 < 13456 Př. : Česká republika
1.1.5 Porovnávání přirozených čísel Předpoklady: 010104 Př. 1: Porovnej následující dvojice čísel: a) 11 11 b) 5486 5468 c) 98765 13456 a) 11 > 11 b) 5486 > 5468 c) 98765 < 13456 Př. : Česká republika
Zebra(5x5) - Farmáři. Metoda 3: Hledání cesty - Podrobné řešení
 Zebra(5x5) - Farmáři Metoda 3: Hledání cesty - Podrobné řešení Zadání: Na venkově vedle sebe leží pět farem. Každou farmu vlastní jiný z pěti mužů, každý z nich jiného psa, pěstuje právě jinou plodinu
Zebra(5x5) - Farmáři Metoda 3: Hledání cesty - Podrobné řešení Zadání: Na venkově vedle sebe leží pět farem. Každou farmu vlastní jiný z pěti mužů, každý z nich jiného psa, pěstuje právě jinou plodinu
Výroková logika II. Negace. Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0).
 Výroková logika II Negace Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0). Na konkrétních příkladech si ukážeme, jak se dají výroky negovat. Obecně se výrok dá negovat tak, že před
Výroková logika II Negace Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0). Na konkrétních příkladech si ukážeme, jak se dají výroky negovat. Obecně se výrok dá negovat tak, že před
Úvod do logiky (VL): 4. Zjištění průběhu pravdivostních hodnot formule tabulkovou metodou
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (VL): 4. Zjištění průběhu pravdivostních hodnot
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (VL): 4. Zjištění průběhu pravdivostních hodnot
3.10 Rezoluční metoda ve výrokové logice
 3.10. Rezoluční metoda ve výrokové logice [070405-1102 ] 27 3.10 Rezoluční metoda ve výrokové logice Rezoluční metoda rozhoduje, zda daná množina klausulí je splnitelná nebo je nesplnitelná. Tím je také
3.10. Rezoluční metoda ve výrokové logice [070405-1102 ] 27 3.10 Rezoluční metoda ve výrokové logice Rezoluční metoda rozhoduje, zda daná množina klausulí je splnitelná nebo je nesplnitelná. Tím je také
MATEMATIKA NEOTVÍREJ, DOKUD NEDOSTANEŠ POKYN OD ZADÁVAJÍCÍHO! 5. třída
 MATEMATIKA 5. třída NEOTVÍREJ, DOKUD NEDOSTANEŠ POKYN OD ZADÁVAJÍCÍHO! JMÉNO TŘÍDA ČÍSLO ŽÁKA AŽ ZAHÁJÍŠ PRÁCI, NEZAPOMEŇ: www.scio.cz, s.r.o. Pobřežní 34, 186 00 Praha 8 tel.: 234 705 555 fax: 234 705
MATEMATIKA 5. třída NEOTVÍREJ, DOKUD NEDOSTANEŠ POKYN OD ZADÁVAJÍCÍHO! JMÉNO TŘÍDA ČÍSLO ŽÁKA AŽ ZAHÁJÍŠ PRÁCI, NEZAPOMEŇ: www.scio.cz, s.r.o. Pobřežní 34, 186 00 Praha 8 tel.: 234 705 555 fax: 234 705
Digitální učební materiál
 Digitální učební materiál Číslo projektu Označení materiálu Název školy Autor Tematická oblast Ročník Anotace Metodický pokyn Zhotoveno CZ.1.07/1.5.00/34.0061 VY_42_INOVACE_M.2.01 Integrovaná střední škola
Digitální učební materiál Číslo projektu Označení materiálu Název školy Autor Tematická oblast Ročník Anotace Metodický pokyn Zhotoveno CZ.1.07/1.5.00/34.0061 VY_42_INOVACE_M.2.01 Integrovaná střední škola
V roce 1998 se v Liberci oženili muži a vdaly ženy v jednotlivých věkových skupinách v následujících počtech:
 Příklad 1 V roce 1998 se v Liberci oženili muži a vdaly ženy v jednotlivých věkových skupinách v následujících počtech: Skupina Počet ženichů Počet nevěst 15-19 let 11 30 20-24 let 166 272 25-29 let 191
Příklad 1 V roce 1998 se v Liberci oženili muži a vdaly ženy v jednotlivých věkových skupinách v následujících počtech: Skupina Počet ženichů Počet nevěst 15-19 let 11 30 20-24 let 166 272 25-29 let 191
Úlohy klauzurní části školního kola kategorie B
 65. ročník matematické olympiády Úlohy klauzurní části školního kola kategorie B 1. Kolika způsoby je možno vyplnit čtvercovou tabulku 3 3 čísly,, 3, 3, 3, 4, 4, 4, 4 tak, aby součet čísel v každém čtverci
65. ročník matematické olympiády Úlohy klauzurní části školního kola kategorie B 1. Kolika způsoby je možno vyplnit čtvercovou tabulku 3 3 čísly,, 3, 3, 3, 4, 4, 4, 4 tak, aby součet čísel v každém čtverci
Úlohy krajského kola kategorie C
 67. ročník matematické olympiády Úlohy krajského kola kategorie C 1. Najděte nejmenší přirozené číslo končící čtyřčíslím 2018, které je násobkem čísla 2017. 2. Pro celá čísla x, y, z platí x 2 + y z =
67. ročník matematické olympiády Úlohy krajského kola kategorie C 1. Najděte nejmenší přirozené číslo končící čtyřčíslím 2018, které je násobkem čísla 2017. 2. Pro celá čísla x, y, z platí x 2 + y z =
Nerovnice a nerovnice v součinovém nebo v podílovém tvaru
 Variace 1 Nerovnice a nerovnice v součinovém nebo v podílovém tvaru Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz
Variace 1 Nerovnice a nerovnice v součinovém nebo v podílovém tvaru Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz
JčU - Cvičení z matematiky pro zemědělské obory (doc. RNDr. Nýdl, CSc & spol.) Minitest MT4
 ŘEŠENÍ MINITESTŮ JčU - Cvičení z matematiky pro zemědělské obory (doc. RNDr. Nýdl, CSc & spol.) Minitest MT4. Z daných tří soustav rovnic o neznámých x, x vyberte právě všechny ty, které jsou regulární.
ŘEŠENÍ MINITESTŮ JčU - Cvičení z matematiky pro zemědělské obory (doc. RNDr. Nýdl, CSc & spol.) Minitest MT4. Z daných tří soustav rovnic o neznámých x, x vyberte právě všechny ty, které jsou regulární.
Střeštěnov a jeho obyvatelé
 Střeštěnov a jeho obyvatelé Město Střěštěnov Střeštěnov je malé městečko ležící na severu Čech. Město je to plnohodnotné. Vše co potřebujete k žití a bytí tu naleznete. Uprostřed města je náměstí s historickou
Střeštěnov a jeho obyvatelé Město Střěštěnov Střeštěnov je malé městečko ležící na severu Čech. Město je to plnohodnotné. Vše co potřebujete k žití a bytí tu naleznete. Uprostřed města je náměstí s historickou
Podkrušnohorské gymnázium, Most
 Aktivita je spolufinancována Evropským sociálním fondem a státním rozpočtem České republiky V rámci projektu Nebojte se matematiky č. CZ.1.07/1.1.34/01.0022 Podkrušnohorské gymnázium, Most 10.-11 11.4.201.2013
Aktivita je spolufinancována Evropským sociálním fondem a státním rozpočtem České republiky V rámci projektu Nebojte se matematiky č. CZ.1.07/1.1.34/01.0022 Podkrušnohorské gymnázium, Most 10.-11 11.4.201.2013
22. Základní škola Plzeň. Až já budu velká. Třída: 7. B. Datum: 8. 12. 2008. Jméno: Kamila Šilhánková
 22. Základní škola Plzeň Až já budu velká Třída: 7. B Datum: 8. 12. 2008 Jméno: Kamila Šilhánková V pěti letech jsem onemocněla zánětem ledvin a ležela jsem v nemocnici u svatého Jiří. Byla tam veliká
22. Základní škola Plzeň Až já budu velká Třída: 7. B Datum: 8. 12. 2008 Jméno: Kamila Šilhánková V pěti letech jsem onemocněla zánětem ledvin a ležela jsem v nemocnici u svatého Jiří. Byla tam veliká
P R A C O V N Í L I S T Domácí mazlíčci. Domácí mazlíčci stupeň ZŠ
 10 1. stupeň ZŠ PL-1 1. stupeň ZŠ 11 PL-2 Pes Kočka Morče Křeček Rybičky Želva Chameleon Králík Papoušek 12 1. stupeň ZŠ PL-3a Druh zvířete: Popis (věk, velikost, barva, tvar těla, dovednosti ) Potrava:
10 1. stupeň ZŠ PL-1 1. stupeň ZŠ 11 PL-2 Pes Kočka Morče Křeček Rybičky Želva Chameleon Králík Papoušek 12 1. stupeň ZŠ PL-3a Druh zvířete: Popis (věk, velikost, barva, tvar těla, dovednosti ) Potrava:
Algebrogramy. PaedDr. Libuše Sekaninová Martin Blahák (grafická úprava)
 Algebrogramy PaedDr. Libuše Sekaninová Martin Blahák (grafická úprava) Materiál byl zpracován v rámci projektu "Systémová podpora trvalého profesního rozvoje (CPD) pedagogických pracovníků propojením pedagogické
Algebrogramy PaedDr. Libuše Sekaninová Martin Blahák (grafická úprava) Materiál byl zpracován v rámci projektu "Systémová podpora trvalého profesního rozvoje (CPD) pedagogických pracovníků propojením pedagogické
Matematický KLOKAN 2007 kategorie Junior (A) 8 (B) 9 (C) 11 (D) 13 (E) 15 AEF? (A) 16 (B) 24 (C) 32 (D) 36 (E) 48
 Matematický KLOKAN 007 kategorie Junior Úlohy za 3 body 1. Lucka, Radek a David mají dohromady 30 míčů. Jestliže Radek dá 5 míčů Davidovi, David dá 4 míče Lucce a Lucka dá míče Radkovi, budou mít oba chlapci
Matematický KLOKAN 007 kategorie Junior Úlohy za 3 body 1. Lucka, Radek a David mají dohromady 30 míčů. Jestliže Radek dá 5 míčů Davidovi, David dá 4 míče Lucce a Lucka dá míče Radkovi, budou mít oba chlapci
Jméno a příjmení. 2.1 Pokyny k otevřeným úlohám. 2.2 Pokyny k uzavřeným úlohám TESTOVÝ SEŠIT NEOTVÍREJTE, POČKEJTE NA POKYN!
 MATEMATIKA 7 M7PBD19C0T02 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 16 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby 1 Základní informace k zadání zkoušky Časový
MATEMATIKA 7 M7PBD19C0T02 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 16 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby 1 Základní informace k zadání zkoušky Časový
Determinant matice řádu 5 budeme počítat opakovaným použitím rozvoje determinantu podle vybraného řádku nebo sloupce. Aby byl náš výpočet
 Řešené příklady z lineární algebry - část 2 Příklad 2.: Určete determinant matice A: A = 4 4. Řešení: Determinant matice řádu budeme počítat opakovaným použitím rozvoje determinantu podle vybraného řádku
Řešené příklady z lineární algebry - část 2 Příklad 2.: Určete determinant matice A: A = 4 4. Řešení: Determinant matice řádu budeme počítat opakovaným použitím rozvoje determinantu podle vybraného řádku
Čteme se skřítkem Alfrédem
 Jiřina Bednářová Čteme se skřítkem Alfrédem Čtení s porozuměním a hry s jazykem Edika Brno 2012 Čteme se skřítkem Alfrédem Čtení s porozuměním a hry s jazykem Jiřina Bednářová Odborná korektura: Alena
Jiřina Bednářová Čteme se skřítkem Alfrédem Čtení s porozuměním a hry s jazykem Edika Brno 2012 Čteme se skřítkem Alfrédem Čtení s porozuměním a hry s jazykem Jiřina Bednářová Odborná korektura: Alena
ZŠ a MŠ Panenské Břežany
 Hlavní 63, 250 70 Panenské Břežany www.zsmsbrezany.cz, zsbrezany@seznam.cz Výukový materiál zpracovaný v rámci projektu EU peníze do škol Číslo projektu: Šablona: Cz.1.07/1.4.00/21.1997 VY_32_INOVACE_41-60
Hlavní 63, 250 70 Panenské Břežany www.zsmsbrezany.cz, zsbrezany@seznam.cz Výukový materiál zpracovaný v rámci projektu EU peníze do škol Číslo projektu: Šablona: Cz.1.07/1.4.00/21.1997 VY_32_INOVACE_41-60
Einsteinova hádanka. Pokud si nevíte rady, podívejte se na další stránku. Patříte mezi 2 % nejinteligentnějších lidí na světě?
 Einsteinova hádanka. Patříte mezi 2 % nejinteligentnějších lidí na světě? Einstein vytvořil tuto hádanku v minulém století. Tvrdil, že 98% lidí na světě není schopno ji vyřešit. Budete-li mít tabulku celou
Einsteinova hádanka. Patříte mezi 2 % nejinteligentnějších lidí na světě? Einstein vytvořil tuto hádanku v minulém století. Tvrdil, že 98% lidí na světě není schopno ji vyřešit. Budete-li mít tabulku celou
I. kolo kategorie Z6
 68. ročník atematické olympiády I. kolo kategorie Z6 Z6 I Ivan a irka se dělili o hrušky na míse. Ivan si vždy bere dvě hrušky a irka polovinu toho, co na míse zbývá. Takto postupně odebírali Ivan, irka,
68. ročník atematické olympiády I. kolo kategorie Z6 Z6 I Ivan a irka se dělili o hrušky na míse. Ivan si vždy bere dvě hrušky a irka polovinu toho, co na míse zbývá. Takto postupně odebírali Ivan, irka,
Matematický KLOKAN kategorie Benjamín
 Matematický KLOKAN 2011 www.matematickyklokan.net kategorie Benjamín Úlohy za 3 body 1. Motocyklista ujel vzdálenost 28 km za 30 minut. Jakou průměrnou rychlostí jel? (A) 28 km/h (B) 36 km/h (C) 56 km/h
Matematický KLOKAN 2011 www.matematickyklokan.net kategorie Benjamín Úlohy za 3 body 1. Motocyklista ujel vzdálenost 28 km za 30 minut. Jakou průměrnou rychlostí jel? (A) 28 km/h (B) 36 km/h (C) 56 km/h
Matice přechodu. Pozorování 2. Základní úkol: Určete matici přechodu od báze M k bázi N. Každou bázi napíšeme do sloupců matice, např.
 Matice přechodu Základní úkol: Určete matici přechodu od báze M k bázi N. Každou bázi napíšeme do sloupců matice, např. u příkladu 7 (v ) dostaneme: Nyní bychom mohli postupovat jako u matice homomorfismu
Matice přechodu Základní úkol: Určete matici přechodu od báze M k bázi N. Každou bázi napíšeme do sloupců matice, např. u příkladu 7 (v ) dostaneme: Nyní bychom mohli postupovat jako u matice homomorfismu
VÝUKOVÝ MATERIÁL zpracovaný v rámci projektu
 VÝUKOVÝ MATERIÁL zpracovaný v rámci projektu Číslo projektu Škola Šablona klíčové aktivity V/2 Sada Fyzika 6+7 CZ.1.07/1.4.00/21.1825 Základní škola s rozšířenou výukou výtvarné výchovy, Teplice, Koperníkova
VÝUKOVÝ MATERIÁL zpracovaný v rámci projektu Číslo projektu Škola Šablona klíčové aktivity V/2 Sada Fyzika 6+7 CZ.1.07/1.4.00/21.1825 Základní škola s rozšířenou výukou výtvarné výchovy, Teplice, Koperníkova
Největší společný dělitel
 1..1 Největší společný dělitel Předpoklady: 01016 Číslo Číslo nsn Platí pravidlo "nsn získáme jako součin obou čísel"? = 1 = Násobící pravidlo platí. 1 = Násobící pravidlo platí. 1 = Násobící pravidlo
1..1 Největší společný dělitel Předpoklady: 01016 Číslo Číslo nsn Platí pravidlo "nsn získáme jako součin obou čísel"? = 1 = Násobící pravidlo platí. 1 = Násobící pravidlo platí. 1 = Násobící pravidlo
{ 3;4;5;6 } pravděpodobnost je zřejmě 4 = 2.
 9..3 Pravděpodobnosti jevů I Předpoklady: 90 Opět se vrátíme k hodu kostkou. Pokus má šest stejně pravděpodobných náhodných výsledků pravděpodobnost každého z nich je 6. Do domečku nám chybí tři políčka.
9..3 Pravděpodobnosti jevů I Předpoklady: 90 Opět se vrátíme k hodu kostkou. Pokus má šest stejně pravděpodobných náhodných výsledků pravděpodobnost každého z nich je 6. Do domečku nám chybí tři políčka.
Přípravný kurz - Matematika
 Přípravný kurz - Matematika Téma: Základy statistiky, kombinační úsudek v úlohách Klíčová slova: tabulky, grafy, diagramy Autor: Mlynářová 12 19 9:02 Základy statistiky Statistika je vědní obor, který
Přípravný kurz - Matematika Téma: Základy statistiky, kombinační úsudek v úlohách Klíčová slova: tabulky, grafy, diagramy Autor: Mlynářová 12 19 9:02 Základy statistiky Statistika je vědní obor, který
StatSoft Jak vyzrát na datum
 StatSoft Jak vyzrát na datum Tento článek se věnuje podrobně možnostem práce s proměnnými, které jsou ve formě datumu. A že jich není málo. Pokud potřebujete pracovat s datumem, pak se Vám bude tento článek
StatSoft Jak vyzrát na datum Tento článek se věnuje podrobně možnostem práce s proměnnými, které jsou ve formě datumu. A že jich není málo. Pokud potřebujete pracovat s datumem, pak se Vám bude tento článek
I. kolo kategorie Z7
 60. ročník Matematické olympiády I. kolo kategorie Z7 Z7 I 1 Součin číslic libovolného vícemístného čísla je vždy menší než toto číslo. Pokud počítáme součin číslic daného vícemístného čísla, potom součin
60. ročník Matematické olympiády I. kolo kategorie Z7 Z7 I 1 Součin číslic libovolného vícemístného čísla je vždy menší než toto číslo. Pokud počítáme součin číslic daného vícemístného čísla, potom součin
Parametrické programování
 Parametrické programování Příklad 1 Parametrické pravé strany Firma vyrábí tři výrobky. K jejich výrobě potřebuje jednak surovinu a jednak stroje, na kterých dochází ke zpracování. Na první výrobek jsou
Parametrické programování Příklad 1 Parametrické pravé strany Firma vyrábí tři výrobky. K jejich výrobě potřebuje jednak surovinu a jednak stroje, na kterých dochází ke zpracování. Na první výrobek jsou
Název DUM: Úlohy o pohybu
 ZŠ a MŠ Štramberk Projekt EU peníze školám Šablona III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Název sady: Poznáváme svět algebry Název DUM: Úlohy o pohybu Vzdělávací oblast: Vzdělávací obor:
ZŠ a MŠ Štramberk Projekt EU peníze školám Šablona III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Název sady: Poznáváme svět algebry Název DUM: Úlohy o pohybu Vzdělávací oblast: Vzdělávací obor:
63. ročník matematické olympiády Řešení úloh krajského kola kategorie B. 1. Odečtením druhé rovnice od první a třetí od druhé dostaneme dvě rovnice
 63. ročník matematické olympiády Řešení úloh krajského kola kategorie B 1. Odečtením druhé rovnice od první a třetí od druhé dostaneme dvě rovnice (x y)(x + y 6) = 0, (y z)(y + z 6) = 0, které spolu s
63. ročník matematické olympiády Řešení úloh krajského kola kategorie B 1. Odečtením druhé rovnice od první a třetí od druhé dostaneme dvě rovnice (x y)(x + y 6) = 0, (y z)(y + z 6) = 0, které spolu s
analytické geometrie v prostoru s počátkem 18. stol.
 4.. Funkce více proměnných, definice, vlastnosti Funkce více proměnných Funkce více proměnných se v matematice začal používat v rámci rozvoje analtické geometrie v prostoru s počátkem 8. stol. I v sami
4.. Funkce více proměnných, definice, vlastnosti Funkce více proměnných Funkce více proměnných se v matematice začal používat v rámci rozvoje analtické geometrie v prostoru s počátkem 8. stol. I v sami
(Cramerovo pravidlo, determinanty, inverzní matice)
 KMA/MAT1 Přednáška a cvičení, Lineární algebra 2 Řešení soustav lineárních rovnic se čtvercovou maticí soustavy (Cramerovo pravidlo, determinanty, inverzní matice) 16 a 21 října 2014 V dnešní přednášce
KMA/MAT1 Přednáška a cvičení, Lineární algebra 2 Řešení soustav lineárních rovnic se čtvercovou maticí soustavy (Cramerovo pravidlo, determinanty, inverzní matice) 16 a 21 října 2014 V dnešní přednášce
6. blok část C Množinové operátory
 6. blok část C Množinové operátory Studijní cíl Tento blok je věnován problematice množinových operátorů a práce s množinovými operátory v jazyce SQL. Čtenáři se seznámí s operátory, UNION, a INTERSECT.
6. blok část C Množinové operátory Studijní cíl Tento blok je věnován problematice množinových operátorů a práce s množinovými operátory v jazyce SQL. Čtenáři se seznámí s operátory, UNION, a INTERSECT.
Školní kolo soutěže Mladý programátor 2014, kategorie A, B
 Doporučené hodnocení školního kola: Hodnotit mohou buď učitelé školy, tým rodičů nebo si žáci, kteří se zúčastní soutěže, mohou ohodnotit úlohy navzájem sami (v tomto případě doporučujeme, aby si žáci
Doporučené hodnocení školního kola: Hodnotit mohou buď učitelé školy, tým rodičů nebo si žáci, kteří se zúčastní soutěže, mohou ohodnotit úlohy navzájem sami (v tomto případě doporučujeme, aby si žáci
2.1.4 Funkce, definiční obor funkce. π 4. Předpoklady: 2103. Pedagogická poznámka: Následující ukázky si studenti do sešitů nepřepisují.
 .. Funkce, definiční obor funkce Předpoklady: 03 Pedagogická poznámka: Následující ukázky si studenti do sešitů nepřepisují. Uděláme si na tabuli jenom krátký seznam: S = a, y = x, s = vt, výška lidí v
.. Funkce, definiční obor funkce Předpoklady: 03 Pedagogická poznámka: Následující ukázky si studenti do sešitů nepřepisují. Uděláme si na tabuli jenom krátký seznam: S = a, y = x, s = vt, výška lidí v
v z t sin ψ = Po úpravě dostaneme: sin ψ = v z v p v p v p 0 sin ϕ 1, 0 < v z sin ϕ < 1.
 Řešení S-I-4-1 Hledáme vlastně místo, kde se setkají. A to tak, aby nemusel pes na zajíce čekat nebo ho dohánět. X...místo setkání P...místo, kde vybíhá pes Z...místo, kde vybíhá zajíc ZX = v z t P X =
Řešení S-I-4-1 Hledáme vlastně místo, kde se setkají. A to tak, aby nemusel pes na zajíce čekat nebo ho dohánět. X...místo setkání P...místo, kde vybíhá pes Z...místo, kde vybíhá zajíc ZX = v z t P X =
PREZENTACE DAT: SLOŽITĚJŠÍ GRAFY
 PREZENTACE DAT: SLOŽITĚJŠÍ GRAFY V kombinační tabulce 8.7 jsme roztřídili soubor pracovníků dle znaku pracovní kategorie na 4 třídy dělníci, techničtí pracovníci, hospodářští pracovníci, provozní a obsluhující
PREZENTACE DAT: SLOŽITĚJŠÍ GRAFY V kombinační tabulce 8.7 jsme roztřídili soubor pracovníků dle znaku pracovní kategorie na 4 třídy dělníci, techničtí pracovníci, hospodářští pracovníci, provozní a obsluhující
Statistika babyboxů ke dni 12. listopadu 2015
 Statistika babyboxů ke dni. listopadu 2015 pořadí den datum čas jméno místo 2006 1. sobota 17. 2. 2006 20:10 Sonička Praha Hloubětín 2. sobota 25. 2. 2006 21:30 Lenka Praha Hloubětín 3. neděle 26. 2. 2006
Statistika babyboxů ke dni. listopadu 2015 pořadí den datum čas jméno místo 2006 1. sobota 17. 2. 2006 20:10 Sonička Praha Hloubětín 2. sobota 25. 2. 2006 21:30 Lenka Praha Hloubětín 3. neděle 26. 2. 2006
Statistika babyboxů ke dni 5. září 2016
 Statistika babyboxů ke dni 5. září 2016 pořadí den datum čas jméno místo 2006 1. sobota 17. 2. 2006 20:10 Sonička Praha Hloubětín 2. sobota 25. 2. 2006 21:30 Lenka Praha Hloubětín 3. neděle 26. 2. 2006
Statistika babyboxů ke dni 5. září 2016 pořadí den datum čas jméno místo 2006 1. sobota 17. 2. 2006 20:10 Sonička Praha Hloubětín 2. sobota 25. 2. 2006 21:30 Lenka Praha Hloubětín 3. neděle 26. 2. 2006
Obecné studijní předpoklady TEST 1
 Obecné studijní předpoklady TEST 1 A.) Text k první sérii otázek ( porozumění textu ) Před 2,5 až 2 miliardami let se začala tvářnost Země výrazně měnit. Mnoho radioaktivních prvků přítomných při vzniku
Obecné studijní předpoklady TEST 1 A.) Text k první sérii otázek ( porozumění textu ) Před 2,5 až 2 miliardami let se začala tvářnost Země výrazně měnit. Mnoho radioaktivních prvků přítomných při vzniku
Přehled vzdělávacích materiálů
 Přehled vzdělávacích materiálů Název školy Název a číslo OP Název šablony klíčové aktivity Název sady vzdělávacích materiálů Jméno tvůrce vzdělávací sady Číslo sady Anotace Základní škola Ţeliv Novými
Přehled vzdělávacích materiálů Název školy Název a číslo OP Název šablony klíčové aktivity Název sady vzdělávacích materiálů Jméno tvůrce vzdělávací sady Číslo sady Anotace Základní škola Ţeliv Novými
Pana školníka se ptali Martin Kubík a Jakub Gregor.
 Pana školníka se ptali Martin Kubík a Jakub Gregor. 1. Máte rád svoje povolání? Proč? - pro svoji pestrost a i určitou volnost volby pořadí této práce - možnosti tvůrčí práce - a pod. 2. Jak dlouho děláte
Pana školníka se ptali Martin Kubík a Jakub Gregor. 1. Máte rád svoje povolání? Proč? - pro svoji pestrost a i určitou volnost volby pořadí této práce - možnosti tvůrčí práce - a pod. 2. Jak dlouho děláte
Matematický KLOKAN : ( ) = (A) 1 (B) 9 (C) 214 (D) 223 (E) 2 007
 Matematický KLOKN 007 kategorie enjamín Úlohy za 3 body. Které číslo patří do prázdného rámečku? 007 : ( + 0 + 0 + 7) 0 0 7 = () () 9 (C) 4 (D) 3 (E) 007. Který z dílů stavebnice musíš přiložit k dílu
Matematický KLOKN 007 kategorie enjamín Úlohy za 3 body. Které číslo patří do prázdného rámečku? 007 : ( + 0 + 0 + 7) 0 0 7 = () () 9 (C) 4 (D) 3 (E) 007. Který z dílů stavebnice musíš přiložit k dílu
Jméno a příjmení. Pokud budete chtít svou odpověď opravit, zabarvěte původně zakřížkovaný čtvereček a zakřížkujte nový čtvereček.
 MATEMATIKA 5 M5PBD19C0T02 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 14 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby Časový limit pro řešení didaktického testu
MATEMATIKA 5 M5PBD19C0T02 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 14 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby Časový limit pro řešení didaktického testu
( n) ( ) ( ) 9.1.11 Kombinatorické úlohy bez opakování. Předpoklady: 9109
 9.1.11 Kombinatorické úlohy bez opakování Předpoklady: 9109 Pedagogická poznámka: Tato hodina slouží jednak ke zopakování probraného, ale zejména k praktickému nácviku kombinatoriky v situaci, ve které
9.1.11 Kombinatorické úlohy bez opakování Předpoklady: 9109 Pedagogická poznámka: Tato hodina slouží jednak ke zopakování probraného, ale zejména k praktickému nácviku kombinatoriky v situaci, ve které
( ) ( ) 9.2.7 Nezávislé jevy I. Předpoklady: 9204
 9.2.7 Nezávislé jevy I Předpoklady: 9204 Př. : Předpokládej, že pravděpodobnost narození chlapce je stejná jako pravděpodobnost narození dívky (a tedy v obou případech rovna 0,5) a není ovlivněna genetickými
9.2.7 Nezávislé jevy I Předpoklady: 9204 Př. : Předpokládej, že pravděpodobnost narození chlapce je stejná jako pravděpodobnost narození dívky (a tedy v obou případech rovna 0,5) a není ovlivněna genetickými
1. Jméno. jméno. příjmení. mapa. Jaroslav. stůl. Antonín. moře. Vladimír. Jan. vana. sprcha. Blanka. Trénink funkcionální komunikace I.
 1. Jméno 1 Václav Procházka jméno příjmení 1. VYBERTE JENOM JMÉNA. mapa Antonín moře Jan sprcha Jaroslav stůl Vladimír vana Blanka 1 2. JAK SE JMENUJE AUTOR TOHOTO TEXTU. Dobrý den, jmenuji se Robert Kouba,
1. Jméno 1 Václav Procházka jméno příjmení 1. VYBERTE JENOM JMÉNA. mapa Antonín moře Jan sprcha Jaroslav stůl Vladimír vana Blanka 1 2. JAK SE JMENUJE AUTOR TOHOTO TEXTU. Dobrý den, jmenuji se Robert Kouba,
Základy Hejného metody zpracovala Ivana Čiháková Matematika dle metody VOBS.
 Základy Hejného metody zpracovala Ivana Čiháková ivana.cihakova@centrum.cz Matematika dle metody VOBS. Úlohy jsou z učebnic matematiky pro 1. 5. ročník vydané nakladatelstvím Fraus v letech 2007-2011 Autoři
Základy Hejného metody zpracovala Ivana Čiháková ivana.cihakova@centrum.cz Matematika dle metody VOBS. Úlohy jsou z učebnic matematiky pro 1. 5. ročník vydané nakladatelstvím Fraus v letech 2007-2011 Autoři
Mistrovství České republiky v logických úlohách
 Mistrovství České republiky v logických úlohách Blok 1 - Logický mixer 10:00-11:40 Řešitel 1 Praha 013 Mrakodrapy 3 Heywake 4 Rybáři 5 Dvojblok Pentomina 7 Nádraží 8 Slalom 9 Plot 10 Kriskros 11 Cesta
Mistrovství České republiky v logických úlohách Blok 1 - Logický mixer 10:00-11:40 Řešitel 1 Praha 013 Mrakodrapy 3 Heywake 4 Rybáři 5 Dvojblok Pentomina 7 Nádraží 8 Slalom 9 Plot 10 Kriskros 11 Cesta
Řešení úloh z TSP MU SADY S 1
 Řešení úloh z TSP MU SADY S 1 projekt RESENI-TSP.CZ úlohy jsou vybírány z dříve použitých TSP MU autoři řešení jsou zkušení lektoři vzdělávací agentury Kurzy-Fido.cz Masarykova univerzita nabízí uchazečům
Řešení úloh z TSP MU SADY S 1 projekt RESENI-TSP.CZ úlohy jsou vybírány z dříve použitých TSP MU autoři řešení jsou zkušení lektoři vzdělávací agentury Kurzy-Fido.cz Masarykova univerzita nabízí uchazečům
61.ročník Matematické olympiády. I.kolo kategorie Z5
 61.ročník Matematické olympiády I.kolo kategorie Z5 Z5 I 1 Tři kamarádi Pankrác, Servác a Bonifác šli o prázdninách na noční procházku přírodním labyrintem. U vstupu dostal každý svíčku a vydali se různými
61.ročník Matematické olympiády I.kolo kategorie Z5 Z5 I 1 Tři kamarádi Pankrác, Servác a Bonifác šli o prázdninách na noční procházku přírodním labyrintem. U vstupu dostal každý svíčku a vydali se různými
SINOVÁ A KOSINOVÁ VĚTA VZORCE PRO OBSAH TROJÚHELNÍKU
 Projekt ŠLONY N GVM Gymnázium Velké Meziříčí registrační číslo projektu: Z.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol SINOVÁ KOSINOVÁ
Projekt ŠLONY N GVM Gymnázium Velké Meziříčí registrační číslo projektu: Z.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol SINOVÁ KOSINOVÁ
III/2 Inovace a zkvalitnění výuky prostřednictvím ICT
 Název školy Gymnázium, Šternberk, Horní nám. 5 Číslo projektu CZ.1.07/1.5.00/34.0218 Šablona III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Označení materiálu VY_32_INOVACE_Hor014 Vypracoval(a),
Název školy Gymnázium, Šternberk, Horní nám. 5 Číslo projektu CZ.1.07/1.5.00/34.0218 Šablona III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Označení materiálu VY_32_INOVACE_Hor014 Vypracoval(a),
Datum odevzdání 12. prosince Vypočtěte velikost strany čtverce ABCD s vrcholem A = [0, 0], jestliže
![Datum odevzdání 12. prosince Vypočtěte velikost strany čtverce ABCD s vrcholem A = [0, 0], jestliže Datum odevzdání 12. prosince Vypočtěte velikost strany čtverce ABCD s vrcholem A = [0, 0], jestliže](/thumbs/57/40473291.jpg) Příklady k řešení (. kolo) Datum odevzdání. prosince 00 PŘÍKLAD. Vypočtěte velikost strany čtverce ABCD s vrcholem A = [0, 0], jestliže úhlopříčka BD leží na přímce p :x +y = 0. PŘÍKLAD. Jsou dány body
Příklady k řešení (. kolo) Datum odevzdání. prosince 00 PŘÍKLAD. Vypočtěte velikost strany čtverce ABCD s vrcholem A = [0, 0], jestliže úhlopříčka BD leží na přímce p :x +y = 0. PŘÍKLAD. Jsou dány body
2581/21/7.1.4/2010 PROJEKTU: Pracovní list pro žáky 5. ročníku. Žáci doplňují neúplné věty, pracují s příruční mapou a vyřeší si křížovku.
 NÁZEV ŠKOLY: Základní škola a Mateřská škola Jakubčovice nad Odrou okres Nový Jičín, příspěvková organizace AUTOR: Mgr. Martina Pajurková NÁZEV: VY_12_INOVACE_1.2.19.5._VL TÉMA: Vlastivěda- Královehradecký
NÁZEV ŠKOLY: Základní škola a Mateřská škola Jakubčovice nad Odrou okres Nový Jičín, příspěvková organizace AUTOR: Mgr. Martina Pajurková NÁZEV: VY_12_INOVACE_1.2.19.5._VL TÉMA: Vlastivěda- Královehradecký
Úvod do matematiky. Mgr. Radek Horenský, Ph.D. Důkazy
 Úvod do matematiky Mgr. Radek Horenský, Ph.D. Důkazy Matematika a matematické chápání jako takové je založeno na logické výstavbě. Základními stavebními prvky jsou definice, věty a důkazy. Definice zavádějí
Úvod do matematiky Mgr. Radek Horenský, Ph.D. Důkazy Matematika a matematické chápání jako takové je založeno na logické výstavbě. Základními stavebními prvky jsou definice, věty a důkazy. Definice zavádějí
M - Kvadratické rovnice a kvadratické nerovnice
 M - Kvadratické rovnice a kvadratické nerovnice Určeno jako učební tet pro studenty dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase.
M - Kvadratické rovnice a kvadratické nerovnice Určeno jako učební tet pro studenty dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase.
Přípravný kurz - Matematika
 Přípravný kurz - Matematika Téma: Základy statistiky, kombinační úsudek v úlohách Klíčová slova: tabulky, grafy, diagramy Autor: Mlynářová 1 Základy statistiky Statistika je vědní obor, který se zabývá
Přípravný kurz - Matematika Téma: Základy statistiky, kombinační úsudek v úlohách Klíčová slova: tabulky, grafy, diagramy Autor: Mlynářová 1 Základy statistiky Statistika je vědní obor, který se zabývá
Logika je logika Úlohy na dvoudenní turnaj v Brně 2012
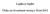 Logika je logika Úlohy na dvoudenní turnaj v Brně 2012 MOSTY Spojte všechny ostrovy (tj. kroužky s čísly) pomocí mostů tak, aby bylo možno dojít z každého ostrova na kterýkoliv jiný. Mosty je přitom dovoleno
Logika je logika Úlohy na dvoudenní turnaj v Brně 2012 MOSTY Spojte všechny ostrovy (tj. kroužky s čísly) pomocí mostů tak, aby bylo možno dojít z každého ostrova na kterýkoliv jiný. Mosty je přitom dovoleno
Matematický KLOKAN 2005 kategorie Junior
 Matematický KLOKAN 2005 kategorie Junior Vážení přátelé, v následujících 75 minutách vás čeká stejný úkol jako mnoho vašich vrstevníků v řadě dalších evropských zemí. V níže uvedeném testu je zadáno čtyřiadvacet
Matematický KLOKAN 2005 kategorie Junior Vážení přátelé, v následujících 75 minutách vás čeká stejný úkol jako mnoho vašich vrstevníků v řadě dalších evropských zemí. V níže uvedeném testu je zadáno čtyřiadvacet
Úvod do řešení lineárních rovnic a jejich soustav
 Úvod do řešení lineárních rovnic a jejich soustav Rovnice je zápis rovnosti dvou výrazů, ve kterém máme najít neznámé číslo (neznámou). Po jeho dosazení do rovnice musí platit rovnost. Existuje-li takové
Úvod do řešení lineárních rovnic a jejich soustav Rovnice je zápis rovnosti dvou výrazů, ve kterém máme najít neznámé číslo (neznámou). Po jeho dosazení do rovnice musí platit rovnost. Existuje-li takové
1 Řešení soustav lineárních rovnic
 1 Řešení soustav lineárních rovnic 1.1 Lineární rovnice Lineární rovnicí o n neznámých x 1,x 2,..., x n s reálnými koeficienty rozumíme rovnici ve tvaru a 1 x 1 + a 2 x 2 +... + a n x n = b, (1) kde koeficienty
1 Řešení soustav lineárních rovnic 1.1 Lineární rovnice Lineární rovnicí o n neznámých x 1,x 2,..., x n s reálnými koeficienty rozumíme rovnici ve tvaru a 1 x 1 + a 2 x 2 +... + a n x n = b, (1) kde koeficienty
II. kolo kategorie Z5
 II. kolo ktegorie Z5 Z5 II 1 Z prvé kpsy klhot jsem přendl 4 pětikoruny do levé kpsy z levé kpsy jsem přendl 16 dvoukorun do prvé kpsy. Teď mám v levé kpse o 13 korun méně než v prvé. Ve které kpse jsem
II. kolo ktegorie Z5 Z5 II 1 Z prvé kpsy klhot jsem přendl 4 pětikoruny do levé kpsy z levé kpsy jsem přendl 16 dvoukorun do prvé kpsy. Teď mám v levé kpse o 13 korun méně než v prvé. Ve které kpse jsem
Kombinatorika. November 12, 2008
 Kombinatorika November 12, 2008 Příklad Do školní jídelny přišla skupina 35 žáků. Určete kolika způsoby se mohli seřadit do fronty u výdeje obědů. Řešení: Počet možností je 1 2... 35 = 35! (Permutace bez
Kombinatorika November 12, 2008 Příklad Do školní jídelny přišla skupina 35 žáků. Určete kolika způsoby se mohli seřadit do fronty u výdeje obědů. Řešení: Počet možností je 1 2... 35 = 35! (Permutace bez
1.4.6 Stavba matematiky, důkazy
 1.4.6 tavba matematiky, důkazy Předpoklady: 1401, 1404 Pedagogická poznámka: Tato hodina se velmi liší od většiny ostatních neboť jde v podstatě o přednášku. Také ji neprobíráme v prvním ročníku, ale přednáším
1.4.6 tavba matematiky, důkazy Předpoklady: 1401, 1404 Pedagogická poznámka: Tato hodina se velmi liší od většiny ostatních neboť jde v podstatě o přednášku. Také ji neprobíráme v prvním ročníku, ale přednáším
Voltampérová charakteristika diody
 Voltampérová charakteristika diody Pozn.: Voltampérovou charakteristiku diod, resp. i rezistorů, žárovek aj. lze proměřovat se soupravou ISES-PCI a též i s ISES-USB. Souprava ISES-PCI, resp. ISES-PCI Professional
Voltampérová charakteristika diody Pozn.: Voltampérovou charakteristiku diod, resp. i rezistorů, žárovek aj. lze proměřovat se soupravou ISES-PCI a též i s ISES-USB. Souprava ISES-PCI, resp. ISES-PCI Professional
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/
 Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol BINOMICKÉ
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol BINOMICKÉ
Magické čtverce. Tomáš Roskovec. Úvod
 Magické čtverce Tomáš Roskovec Úvod Magické čtverce patří k dávným matematickým hrátkám, které i přes dvoutisíciletou historii dodnes nejsou zcela prozkoumány. Během přednášky se budeme zabývat nejprve
Magické čtverce Tomáš Roskovec Úvod Magické čtverce patří k dávným matematickým hrátkám, které i přes dvoutisíciletou historii dodnes nejsou zcela prozkoumány. Během přednášky se budeme zabývat nejprve
Maticí typu (m, n), kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru:
 3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
M08-01 Přijímačky nanečisto osmileté studium matematika
 M08-01 Přijímačky nanečisto osmileté studium matematika Řešení 1) Bratři Martin a Tomáš dostali stolní hru, ve které se hrálo o papírové peníze - dolary. Martin rozdělil peníze před začátkem hry tak, že
M08-01 Přijímačky nanečisto osmileté studium matematika Řešení 1) Bratři Martin a Tomáš dostali stolní hru, ve které se hrálo o papírové peníze - dolary. Martin rozdělil peníze před začátkem hry tak, že
Faktoriály a kombinační čísla
 Faktoriály a kombinační čísla 7. kapitola. Různé In: Jiří Sedláček (author): Faktoriály a kombinační čísla. (Czech). Praha: Mladá fronta, 1964. pp. 72 81. Persistent URL: http://dml.cz/dmlcz/403522 Terms
Faktoriály a kombinační čísla 7. kapitola. Různé In: Jiří Sedláček (author): Faktoriály a kombinační čísla. (Czech). Praha: Mladá fronta, 1964. pp. 72 81. Persistent URL: http://dml.cz/dmlcz/403522 Terms
MATEMATIKA. Doc. RNDr. Eduard Fuchs, CSc., Přírodovědecká fakulta MU Brno. Ing. Milan Hausner, ZŠ Lupáčova, Praha 3
 MATEMATIKA Vypracovala skupina pro přípravu standardů z matematiky ve složení: Vedoucí: Koordinátor za VÚP: Členové: Doc. RNDr. Eduard Fuchs, CSc., Přírodovědecká fakulta MU Brno RNDr. Eva Zelendová, VÚP
MATEMATIKA Vypracovala skupina pro přípravu standardů z matematiky ve složení: Vedoucí: Koordinátor za VÚP: Členové: Doc. RNDr. Eduard Fuchs, CSc., Přírodovědecká fakulta MU Brno RNDr. Eva Zelendová, VÚP
Řešení geometrické úlohy spočívá v nalezení geometrického útvaru (útvarů) daných vlastností.
 Řešení geometrické úlohy spočívá v nalezení geometrického útvaru (útvarů) daných vlastností. Metody řešení konstrukčních úloh: množinou bodů zobrazením výpočtem kombinací předchozích způsobů Konstrukční
Řešení geometrické úlohy spočívá v nalezení geometrického útvaru (útvarů) daných vlastností. Metody řešení konstrukčních úloh: množinou bodů zobrazením výpočtem kombinací předchozích způsobů Konstrukční
Poměry a úměrnosti II
 1.1.12 Poměry a úměrnosti II Předpoklady: 010111 U následujících úloh je nutné poznat, zda jde o přímou nebo nepřímou úměrnost případně příklad, který není možné řešit ani jedním z obou postupů. Pedagogická
1.1.12 Poměry a úměrnosti II Předpoklady: 010111 U následujících úloh je nutné poznat, zda jde o přímou nebo nepřímou úměrnost případně příklad, který není možné řešit ani jedním z obou postupů. Pedagogická
KALENDÁŘOVÉ ÚLOHY PRO TALENTY, vč. metodického listu. doc. PhDr. Marta Volfová, CSc.
 KALENDÁŘOVÉ ÚLOHY PRO TALENTY, vč. metodického listu doc. PhDr. Marta Volfová, CSc. Centrum talentů M&F&I, Univerzita Hradec Králové, 2010 Kalendářové úlohy jsou zahaleny určitou tajemností a přitahují
KALENDÁŘOVÉ ÚLOHY PRO TALENTY, vč. metodického listu doc. PhDr. Marta Volfová, CSc. Centrum talentů M&F&I, Univerzita Hradec Králové, 2010 Kalendářové úlohy jsou zahaleny určitou tajemností a přitahují
V tomto prostředí jsou postupně zaváděny různé typy úloh.
 Matematické prostředí Děda Lesoň umožňuje dětem pracovat s veličinou zapsanou ikonicky (nikoliv číslem). Uvedeno je příběhem o dědovi Lesoňovi, ochránci zvířátek. Nejprve jsou u Lesoně pouze tři druhy
Matematické prostředí Děda Lesoň umožňuje dětem pracovat s veličinou zapsanou ikonicky (nikoliv číslem). Uvedeno je příběhem o dědovi Lesoňovi, ochránci zvířátek. Nejprve jsou u Lesoně pouze tři druhy
N á z e v š k o l y : Z Š A M Š Ú D O L Í D E S N É, D R U Ž S T E V N Í 1 2 5, R A P O T Í N N á z e v p r o j e k t u : V e s v a z k o v é š k o l
 N á z e v š k o l y : Z Š A M Š Ú D O L Í D E S N É, D R U Ž S T E V N Í 1 2 5, R A P O T Í N N á z e v p r o j e k t u : V e s v a z k o v é š k o l e a k t i v n ě - i n t e r a k t i v n ě Č í s l o
N á z e v š k o l y : Z Š A M Š Ú D O L Í D E S N É, D R U Ž S T E V N Í 1 2 5, R A P O T Í N N á z e v p r o j e k t u : V e s v a z k o v é š k o l e a k t i v n ě - i n t e r a k t i v n ě Č í s l o
2. ZÁKLADY MATICOVÉ ALGEGRY 2.1. ZÁKLADNÍ POJMY
 2. ZÁKLADY MAICOVÉ ALGEGRY 2.1. ZÁKLADNÍ POJMY V této kapitole se dozvíte: jak je definována reálná nebo komplexní matice a co rozumíme jejím typem; co jsou to prvky matice, co vyjadřují jejich indexy
2. ZÁKLADY MAICOVÉ ALGEGRY 2.1. ZÁKLADNÍ POJMY V této kapitole se dozvíte: jak je definována reálná nebo komplexní matice a co rozumíme jejím typem; co jsou to prvky matice, co vyjadřují jejich indexy
III/2 Inovace a zkvalitnění výuky prostřednictvím ICT
 Název školy Gymnázium, Šternberk, Horní nám. 5 Číslo projektu CZ.1.0/1.5.00/4.018 Šablona III/ Inovace a zkvalitnění výuky prostřednictvím ICT Označení materiálu VY INOVACE_Hor015 Vypracoval(a), dne Mgr.
Název školy Gymnázium, Šternberk, Horní nám. 5 Číslo projektu CZ.1.0/1.5.00/4.018 Šablona III/ Inovace a zkvalitnění výuky prostřednictvím ICT Označení materiálu VY INOVACE_Hor015 Vypracoval(a), dne Mgr.
Matematika se Čtyřlístkem 1
 Matematika se Čtyřlístkem SPOČÍTEJ, KOLIK VĚCÍ JE V KAŽDÉ SKUPINĚ. DO RÁMEČKU NAKRESLI STEJNÝ POČET PUNTÍKŮ. ŘEKNI, CO VIDÍŠ, NAPŘ. TŘI TYČINKY. DO OKÉNEK NAKRESLI STEJNÝ POČET TVARŮ. POTOM NA OKÉNKA PŘILOŽ
Matematika se Čtyřlístkem SPOČÍTEJ, KOLIK VĚCÍ JE V KAŽDÉ SKUPINĚ. DO RÁMEČKU NAKRESLI STEJNÝ POČET PUNTÍKŮ. ŘEKNI, CO VIDÍŠ, NAPŘ. TŘI TYČINKY. DO OKÉNEK NAKRESLI STEJNÝ POČET TVARŮ. POTOM NA OKÉNKA PŘILOŽ
1.4.3 Složené výroky implikace a ekvivalence
 1.4.3 Složené výroky implikace a ekvivalence Předpoklady: 1401, 1402 Pedagogická poznámka: Látka zabere spíše jeden a půl vyučovací hodiny. Buď můžete využít písemku nebo se podělit o čas s následující
1.4.3 Složené výroky implikace a ekvivalence Předpoklady: 1401, 1402 Pedagogická poznámka: Látka zabere spíše jeden a půl vyučovací hodiny. Buď můžete využít písemku nebo se podělit o čas s následující
Řešíme slovní úlohy Růžena Blažková Pedagogická fakulta MU
 Řešíme slovní úlohy Růžena Blažková Pedagogická fakulta MU blazkova@ped.muni.cz V úvodu si položme několik otázek: - Proč řešíme slovní úlohy? - Je řešení slovních úloh žáky oblíbené? - Jaká tématika slovních
Řešíme slovní úlohy Růžena Blažková Pedagogická fakulta MU blazkova@ped.muni.cz V úvodu si položme několik otázek: - Proč řešíme slovní úlohy? - Je řešení slovních úloh žáky oblíbené? - Jaká tématika slovních
KOMBINATORIKA. 1. cvičení
 KOMBINATORIKA 1. cvičení Co to je kombinatorika Kombinatorika je vstupní branou do teorie pravděpodobnosti. Zabývá se různými způsoby výběru prvků z daného souboru. 2011 Ing. Janurová Kateřina, FEI VŠB-TU
KOMBINATORIKA 1. cvičení Co to je kombinatorika Kombinatorika je vstupní branou do teorie pravděpodobnosti. Zabývá se různými způsoby výběru prvků z daného souboru. 2011 Ing. Janurová Kateřina, FEI VŠB-TU
Úvod do informatiky. Miroslav Kolařík
 Úvod do informatiky přednáška osmá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Kombinatorika: pravidla součtu a součinu 2 Kombinatorika:
Úvod do informatiky přednáška osmá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Kombinatorika: pravidla součtu a součinu 2 Kombinatorika:
PSANÍ VZORCŮ A ROVNIC
 PSANÍ VZORCŮ A ROVNIC aneb matematikem bez nesnází Jednoduché matematické, fyzikální či chemické vzorce a rovnice můžeme zapsat poměrně snadno za pomoci znaků na klávesnici a použitím horního nebo dolního
PSANÍ VZORCŮ A ROVNIC aneb matematikem bez nesnází Jednoduché matematické, fyzikální či chemické vzorce a rovnice můžeme zapsat poměrně snadno za pomoci znaků na klávesnici a použitím horního nebo dolního
Magické čtverce. Bára Kociánová
 Magické čtverce Bára Kociánová Abstrakt. Příspěvek se zabývá magickými čtverci, které patří spíše do rekreační matematiky. Popisuje jejich základní vlastnosti, uvádí zajímavosti z historie a na závěr podává
Magické čtverce Bára Kociánová Abstrakt. Příspěvek se zabývá magickými čtverci, které patří spíše do rekreační matematiky. Popisuje jejich základní vlastnosti, uvádí zajímavosti z historie a na závěr podává
4.3. GONIOMETRICKÉ ROVNICE A NEROVNICE
 4.3. GONIOMETRICKÉ ROVNICE A NEROVNICE V této kapitole se dozvíte: jak jsou definovány goniometrické rovnice a nerovnice; jak se řeší základní typy goniometrických rovnic a nerovnic. Klíčová slova této
4.3. GONIOMETRICKÉ ROVNICE A NEROVNICE V této kapitole se dozvíte: jak jsou definovány goniometrické rovnice a nerovnice; jak se řeší základní typy goniometrických rovnic a nerovnic. Klíčová slova této
příkladů do cvičení. V textu se objeví i pár detailů, které jsem nestihl (na které jsem zapomněl) a(b u) = (ab) u, u + ( u) = 0 = ( u) + u.
 Několik řešených příkladů do Matematiky Vektory V tomto textu je spočteno několik ukázkových příkladů které vám snad pomohou při řešení příkladů do cvičení. V textu se objeví i pár detailů které jsem nestihl
Několik řešených příkladů do Matematiky Vektory V tomto textu je spočteno několik ukázkových příkladů které vám snad pomohou při řešení příkladů do cvičení. V textu se objeví i pár detailů které jsem nestihl
ÚLOHY SE SPORTOVNÍ TÉMATIKOU PRO MATEMATICKÉ TALENTY, vč. metodického listu. doc. PhDr. Marta Volfová, CSc.
 ÚLOHY SE SPORTOVNÍ TÉMATIKOU PRO MATEMATICKÉ TALENTY, vč. metodického listu doc. PhDr. Marta Volfová, CSc. Centrum talentů M&F&I, Univerzita Hradec Králové, 2010 Úlohy se sportovní tematikou pro matematické
ÚLOHY SE SPORTOVNÍ TÉMATIKOU PRO MATEMATICKÉ TALENTY, vč. metodického listu doc. PhDr. Marta Volfová, CSc. Centrum talentů M&F&I, Univerzita Hradec Králové, 2010 Úlohy se sportovní tematikou pro matematické
Poznávání struktury a PROSTŘEDÍ RODINA. Darina Jirotková
 Poznávání struktury a PROSTŘEDÍ RODINA Darina Jirotková poznávání struktury Co se vám vybaví v mysli, když se řekne struktura? Jaké struktury v matematice znáte? Jaké struktury se tvoří ve vědomí dítěte?
Poznávání struktury a PROSTŘEDÍ RODINA Darina Jirotková poznávání struktury Co se vám vybaví v mysli, když se řekne struktura? Jaké struktury v matematice znáte? Jaké struktury se tvoří ve vědomí dítěte?
Řešení 1H, 2D, 3B, 4C, 5F, 6E, 7J, 8G, 9I, 10A
 Materiál pro domácí VY_07_Vla5E_26 přípravu žáků: Název programu: Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovativní metody v prvouce, vlastivědě a zeměpisu Registrační číslo
Materiál pro domácí VY_07_Vla5E_26 přípravu žáků: Název programu: Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovativní metody v prvouce, vlastivědě a zeměpisu Registrační číslo
Statistika babyboxů ke dni 3. prosince 2018
 Statistika babyboxů ke dni 3. prosince 2018 pořadí den datum čas jméno místo 2006 1. sobota 17. 2. 2006 20:10 Sonička Praha Hloubětín 2. sobota 25. 2. 2006 21:30 Lenka Praha Hloubětín 3. neděle 26. 2.
Statistika babyboxů ke dni 3. prosince 2018 pořadí den datum čas jméno místo 2006 1. sobota 17. 2. 2006 20:10 Sonička Praha Hloubětín 2. sobota 25. 2. 2006 21:30 Lenka Praha Hloubětín 3. neděle 26. 2.
