Katedra fyziky. Zaměření: Fyzika a technika termojaderné fúze DIPLOMOVÁ PRÁCE
|
|
|
- Libuše Růžena Pešková
- před 6 lety
- Počet zobrazení:
Transkript
1 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta jaderná a fyzikálně inženýrská Katedra fyziky Obor: Fyzikální inženýrství Zaměření: Fyzika a technika termojaderné fúze DIPLOMOVÁ PRÁCE Studium okrajového plazmatu tokamaku COMPASS pomocí dvojice reciprokých sond Study of edge plasma physics of tokamak COMPASS by means of two reciprocating probes Vypracoval: Bc. Petr Vondráček Vedoucí práce: Mgr. Jan Horáček, docteur ès sciences Rok: 2011/2012
2 Prohlášení Prohlašuji, že jsem svou diplomovou práci vypracoval samostatně a použil jsem pouze podklady (literaturu, projekty, SW atd.) uvedené v přiloženém seznamu. Nemám závažný důvod proti užití tohoto školního díla ve smyslu 60 Zákona č. 121/2000 Sb., o právu autorském, o právech souvisejících s právem autorským a o změně některých zákonů (autorský zákon). V Praze dne 7. května podpis
3 Poděkování Děkuji dr. Janu Horáčkovi za odborné vedení mé práce posledních několik let na Ústavu fyziky plazmatu AV ČR v oddělení tokamak za ochotu, shovívavost i podnětné rady, stejně tak jako všem ostatním zaměstnancům oddělení, kteří svou radou či pomocí přispěli ke zdárnému dokončení této diplomové práce.
4 Název práce: Studium okrajového plazmatu tokamaku COMPASS pomocí dvojice reciprokých sond Autor: Bc. Petr Vondráček Obor: Fyzikální inženýrství Zaměření: Fyzika a technika termojaderné fúze Druh práce: Diplomová práce Vedoucí práce: Mgr. Jan Horáček, dr. ès sc., Ústav fyziky plazmatu, AV ČR, v.v.i. Abstrakt: Diplomová práce shrnuje činnosti související s optimalizací ovládacího systému 2 reciprokých sond tokamaku Compass, experimentální měření charakteristické šířky pro pokles paralelního toku energie v SOL tohoto tokamaku a podrobné porovnání experimentálních dat naměřených na tokamaku ASDEX Upgrade s výstupy numerického modelu ESEL. Navíc obsahuje přehled základní teorie sondových měření plazmatu a způsobu zpracování naměřených dat. Klíčová slova: tokamak, sondová měření, diagnostika plazmatu, šířka SOL, ESEL Title: Study of edge plasma physics of tokamak COMPASS by means of two reciprocating probes Author: Bc. Petr Vondráček Abstract: This master s thesis summarizes activities connected with control system optimization of 2 reciprocating probes at the Compass tokamak, experimental measurements of characteristic power decay length for parallel heat flux in the SOL of the tokamak and a detailed comparison of experimental data from the ASDEX Upgrade tokamak with numerical model ESEL. Basic overview of probe measurement theory and data processing is included. Key words: tokamak, probe measurements, plasma diagnostics, SOL length, ESEL
5 Obsah Předmluva 9 I Úvod 10 1 Okraj plazmatu tokamaku Základy magnetického držení plazmatu Drifty B B drift Drift zakřivení Magnetizační drift E B drift Stěnová vrstva Bohmovo kritérium Maxwellovský tok částic Pokles potenciálu na stěnové vrstvě Nabitá stěna Tepelný tok Transport částic Difúze Turbulentní transport Šířka SOL Sondová měření Langmuirova sonda Teorie Langmuirovy sondy Zpracování voltampérové charakteristiky Ball-pen sonda Rychlá reciproká sonda II Práce na tokamaku COMPASS 30 3 Upgrade reciprokých sond tokamaku COMPASS Reciproké sondy na tokamaku COMPASS
6 OBSAH Horizontální sonda Vertikální sonda Ovládací systém Elektronika Ovládací software Optimalizace reciprokého pohybu Pneumatický systém Zrychlení obrátky reciprokého pohybu Šířka SOL limiterového plazmatu Motivace Měření na tokamaku Compass Uspořádání experimentu Určení pozice LCFS Naměřená data III ESEL ASDEX analýza 44 5 Vstupní data Experimentální měření na tokamaku ASDEX Numerický model ESEL Parametry vyhodnocované simulace Porovnání výsledků Ustálené radiální profily Střední hodnota Fluktuace Časové a prostorové charakteristiky Časová korelace Prostorová korelace Rychlost transportu Podmíněný průměr (CAV) Hustota Potenciál Teplota Shrnutí Závěr 61 IV Dodatky 62 A Základy pravděpodobnosti a statistiky 63 A.1 Distribuční funkce, hustota pravděpodobnosti A.2 Momenty náhodných veličin
7 OBSAH 8 A.3 Výběrové statistiky A.4 Vzájemná korelace A.5 Nelineární regresní analýza B GUI ovládání reciprokých sond 67 C Komunikační protokol ovládacího systému sond 71 Seznam obrázků 74 Seznam použitých zdrojů 75 Rejstřík 81
8 Předmluva V rámci své diplomové práce jsem se zaměřil na 3 vzájemně provázané nicméně poměrně různorodé oblasti. Prvně to bylo pokračování v úpravách horizontálního a vertikálního manipulátoru reciprokých sond tokamaku Compass, na kterých jsem se podílel již během své bakalářské práce [54] a výzkumného úkolu [55]. Především šlo o vyladění ovládacího systému obou manipulátorů (doplnění ovládacího softwaru, úpravy elektroniky) a optimalizaci jejich pohybu. Tuto část popisuji v kapitole 3. Druhou oblastí bylo využití sond v praxi experimentální měření charakteristické šířky pro pokles paralelního toku energie ve SOL tokamaku Compass. To je velice aktuální téma důležité pro design první stěny mezinárodního tokamaku ITER. Popis experimentu s výsledky je v kapitole 4. Třetí část diplomové práce (kapitoly 5 a 6) tvoří analýza experimentálních dat naměřených reciprokou sondou na tokamaku ASDEX Upgrade a výsledků simulací numerického modelu ESEL a jejich vzájemné porovnání. Navíc lze v úvodní části práce nalézt seznámení s některými později použitými pojmy, odvození základní fyzikální teorie potřebné pro sondová měření a pro studium turbulentního transportu i uvedení do problematiky zpracování dat sondových měření (kapitoly 1 a 2). V dodatcích je pak přehled potřebných vztahů z pravděpodobnosti a statistiky (dodatek A), návod k obsluze mnou sestaveného grafického rozhraní ovládacího systému reciprokých sond tokamaku Compass (dodatek B) a popis komunikačního protokolu, který je v ovládacím systému použit (dodatek C). Na přiloženém CD je k nahlédnutí elektronická verze diplomové práce ve formátu PDF, aktuální verze ovládacího softwaru reciprokých sond tokamaku Compass, zpomalený videozáznam rychlého reciprokého pohybu vertikální sondy při použití různých hnacích plynů (hélium a dusík) a videosekvence 2D snímků hustoty, teploty, potenciálu a vorticity simulace numerického modelu ESEL. 9
9 Část I Úvod 10
10 Kapitola 1 Okraj plazmatu tokamaku 1.1 Základy magnetického držení plazmatu Experimentální fúzní zařízení založená na principu magnetického držení plazmatu (MCF magnetic confinement fusion) využívají omezení pohybu částic plazmatu tj. nabitých částic (elektronů a iontů) ve směru kolmém na magnetické pole díky působení Lorentzovy síly. Nabité částice se mohou pohybovat volně ve směru magnetického pole, ve směru kolmém je jejich pohyb zakřiven a celkově tedy obecně vykonávají šroubovicovitý pohyb podél magnetických siločar s Larmorovým poloměrem ρ L = mv QB (1.1) (m je hmotnost částice, v velikost složky rychlosti kolmé na magnetické pole, Q náboj částice a B velikost magnetické indukce dále označováno pouze jako magnetické pole) a cyklotronní frekvencí ω c = QB m. (1.2) Jedním z nejjednodušších způsobů jak zabránit úniku částic ve směru magnetického pole je silokřivky uzavřít např. do tvaru toroidu. Tento princip využívá zařízení tokamak. Při pouhém stočení magnetických siločar do toroidu by se však nutně objevil vliv nehomogenity magnetického pole (pole je silnější na vnitřní straně toroidu tzv. high field side, HFS oproti vnější low field side, LFS) v podobě B B driftu zapříčiňujícího polarizaci plazmatu, ke které by přispěl také vliv zakřivení magnetického pole. Následkem by byl E B drift a únik plazmatu mimo požadovanou oblast. Z tohoto důvodu mají magnetické silokřivky v tokamaku helicitní šroubovicovitý tvar. Díky tomu se plazma pohybuje nejen v toroidálním, ale i v poloidálním směru, a efekt B B driftu se vyruší. Vzhledem k helicitnímu tvaru magnetických siločar lze tomuto uspořádání přiřadit systém myšlených magnetických povrchů, na nichž silokřivky leží. Strmost stoupání šroubovice lze pro každý magnetický povrch popsat tzv. bezpečnostním faktorem q, který udává, kolik oběhů v toroidálním směru 11
11 KAPITOLA 1. OKRAJ PLAZMATU TOKAMAKU 12 Obrázek 1.1: Magnetická pole tokamaku toroidální je generováno externími cívkami, poloidální proudem v plazmatu. Převzato z [43]. magnetická silokřivka vykoná, než jednou oběhne v poloidálním směru. q = ϕ 2π = 1 1 B T ds rb T, (1.3) 2π R B pol R 0 B pol ϕ zde značí toroidální úhel, R velký poloměr (od hlavní osy prstence), r malý poloměr (od vedlejší osy prstence), B T toroidální magnetické pole, B pol poloidální magnetické pole. Integrál probíhá přes celý obvod poloidálního řezu daného magnetického povrchu. Uvedená aproximace platí pro tokamaky s velkým aspektem (poměrem mezi hlavním a vedlejším poloměrem) [56]. Helicitního uspořádání magnetického pole je dosaženo přidáním malého poloidálního pole (typicky B pol 1/10B T ), které je generováno elektrickým proudem procházejícím prstencem plazmatu viz obrázek 1.1. Tvarováním magnetických povrchů lze docílit různých tvarů průřezu prstence plazmatu od kruhového přes eliptický až po často používáný průřez ve tvaru písmene D. Velice důležitou roli hraje magnetický povrch označovaný jako LCFS (z ang. Last Close Flux Surface) příp. separatrix jde o poslední uzavřený magnetický povrch uvnitř komory tokamaku v tom smyslu, že magnetické silokřivky na něm ležící se volně uzavírají sami do sebe, aniž by procházely nějakou překážkou (stěnou vakuové komory, limiterem či divertorem viz dále). Pozice LCFS je v tokamacích určena buďto limiterem pevným objektem schopným odolávat vysokým tepelným tokům, který je v přímém kontaktu s plazmatem, nebo za pomoci tvarování magnetického pole externími cívkami (poloidálního pole) vytvořením tzv. X-bodu. V druhém případě je
12 KAPITOLA 1. OKRAJ PLAZMATU TOKAMAKU 13 Obrázek 1.2: Znázornění řezu komorou tokamaku s vyobrazenými magnetickými povrchy v limiterové a divertorové konfiguraci. Převzato z [43]. komora tokamaku doplněna tzv. divertorem, na který je koncentrována většina tepelného toku. Oba případy jsou znázorněny na obrázku 1.2. Výhodou divertoru je větší vzdálenost od LCFS, díky níž se atomy uvolněné tokem dopadajících částic nedostávají přímo do vnitřního objemu plazmatu jako v případě limiteru. Vzhledem k malému poloidálnímu poli v oblasti X-bodu musí navíc částice urazit velice dlouhou dráhu než dopadne na desky divertoru. U tokamaků s divertorovým uspořádáním je též možný přechod do H-módu (módu s vyšším udržením poprvé pozorovaným v osmdesátých letech minulého století na tokamaku ASDEX). LCFS dělí plazma držené v tokamaku na 2 po fyzikální stránce odlišné oblasti. Uvnitř LCFS se částice volně pohybují podél uzavřených magnetických siločar a unikat mohou jen díky různým driftům a difúzi napříč magnetickým polem. Je to tedy oblast klasického magnetického držení plazmatu. Oproti tomu v oblasti vně LCFS, označované jako scrape-off layer (SOL), platí značně odlišná fyzika, jelikož zde rychlý transport částic podél magnetických siločar na divertor či limiter vytvoří prudký gradient tlaku, jehož důsledkem je tzv. výměnná nestabilita, jež je motorem turbulence. Do hry navíc vstupují atomové procesy atd. V dalším textu je oblast cektrálního plazmatu přiléhající k LCFS označována jako okrajové plazma, oblast vně LCFS pak jako SOL příp. wall-shadow či limiterový stín což je ta část vakuové komory tokamaku s divertorovou konfigurací, kterou procházejí magnetické povrchy protínající stěnu (ne pouze divertor). V počátcích výzkumu řízené termojaderné fúze byl okraj plazmatu poněkud opomíjen díky přesvědčení, že není nezbytně nutné zcela rozumět tamějším procesům a není nutné do nich nikterak zasahovat. Již v 80. letech minulého století ovšem začalo být jasné, že tomu tak není a bez řešení problémů souvisejících s okrajovým magneticky drženým plazmatem nebude možné dosáhnout kýžených výsledků v ří-
13 KAPITOLA 1. OKRAJ PLAZMATU TOKAMAKU 14 zené termojaderné fúzi [50]. Jde především o transport částic a energie napříč i podél magnetického pole, ústící jednak ve ztráty energie z centrální části plazmatu a jednak způsobující extrémní tepelnou zátěž stěn vakuové komory fúzního zařízení, zejména limiteru příp. divertoru. S tepelným tokem na stěny fúzního zařízení velice úzce souvisí i uvolňování nečistot díky interakci plazmatu se stěnou (recyklace částic). Nečistoty dostávající se skrze SOL do centrálního plazmatu způsobují radiační tepelné ztráty a ředění vodíkového paliva, což jsou opět velice závažné problémy. 1.2 Drifty Témata řešená v této práci se týkají především oblasti SOL. Vzhledem k tomu, že částice pohybující se ve SOL dopadnou na pevný povrch dříve než dokončí celý poloidální oběh, nevyruší se působení nehomogenity a zakřivení magnetického pole a drifty zmiňované v sekci 1.1 hrají v této oblasti důležitou roli. Jak uvidíme dál, jsou původcem nestabilit a transportu makroskopických plazmatických struktur tzv. blobů. Je tedy na místě se jim věnovat trochu podrobněji. Důkladnou analýzu driftů lze nalézt v každé základní učebnici fyziky plazmatu např. v [39, 13, 8, 49, 12]. Jde především o následující drifty: B B drift Tento drift se také někdy označuje pouze jako grad-b příp. B drift. Je způsoben změnou velikosti magnetického pole podél trajektorie gyrující částice v oblasti vyššího magnetického pole je poloměr křivosti trajektorie nižší než v oblasti s nižším magnetickým polem a částice driftuje ve směru kolmém na směr magnetického pole i jeho gradient. Driftová rychlost má podobu v B = mv2 2Q B B B 3. (1.4) v značí složku rychlosti částice kolmou na magnetické pole. Směr B B driftu je závislý na náboji částice. Je tedy opačný pro elektrony a ionty a způsobuje vznik elektrického proudu a separaci náboje v plazmatu Drift zakřivení Pokud jsou silokřivky magnetického pole zakřivené, dochází k driftu zakřivení, jehož rychlost je v R = mv2 R k B QB 2 2, (1.5) R k kde R k je poloměr křivosti magnetické silokřivky a v značí složku rychlosti částice ve směru magnetického pole. Drift zakřivení obdobně jako drift B B závisí na náboji a způsobuje vznik elektrického proudu a separaci náboje v plazmatu. Oba drifty se sčítají, separací náboje vzniká elektrické pole, což následně způsobuje E B drift.
14 KAPITOLA 1. OKRAJ PLAZMATU TOKAMAKU Magnetizační drift Magnetizační drift není driftem v pravém slova smyslu nedochází při něm k posunu gyračního středu napříč magnetickým polem ani k makroskopickému toku částic či energie. Jde o tekutinový efekt v prostředí s gradientem hustoty částic způsobující lokální nenulový tok částic tok způsobený gyračním pohybem částic stejného náboje v kladném směru osy kolmé na magnetické pole i gradient hustoty se nevyruší s tokem částic v záporném směru (daným prostorovým bodem prochází více trajektorií částic stejného náboje s gyračním středem umístěným ve směru vyšší koncentrace než trajektorií částic s gyračním středem umístěným ve směru k oblastem s nižší koncentrací) E B drift Tento drift vzniká za přítomnosti vzájemně různoběžného elektrického a magnetického pole. Jeho rychlost je v E = E B B 2. (1.6) Drift není závislý na náboji. Nevede tedy ke vzniku elektrického proudu v plazmatu. 1.3 Stěnová vrstva Bohmovo kritérium Díky vyšší pohyblivosti (nižší hmotnosti, vyšší rychlosti při stejné teplotě) oproti iontům unikají elektrony na stěny komory (desky divertoru, limiter, příp. na jiné předměty, které jsou ve styku s plazmatem) bezprostředně po vzniku plazmatu rychleji než ionty. Stěny tak získávají ve srovnání s plazmatem záporný potenciál a v jejich okolí vzniká tzv. stěnová vrstva (ang. plasma sheath). V ní dochází směrem z plazmatu ke stěně k pozvolnému poklesu hustoty, tlaku i elektrického potenciálu a vzniku elektrického pole takové hodnoty, aby se vyrovnal tok elektronů a iontů. Stěna je nabita na plovoucí potenciál φ fl, který je záporný ve srovnání s potenciálem vzdáleného (neporušeného) plazmatu. Elektrické pole je na vzdálenosti tloušťky stěnové vrstvy téměř odstíněno, nicméně slabé elektrické pole zasahuje ještě do vzdálených oblastí. Přítomnost tohoto slabého elektrického pole, předstěnové vrstvy (angl. pre-sheath), je naprosto klíčová pro ustanovení stabilní stěnové vrstvy, neboť zajišťuje dostatečný přítok iontů. Okraj stěnové vrstvy (tj. přechod mezi stěnovou a předstěnovou vrstvou) je dále značen indexem se. Pokles elektronové hustoty ve stěnové vrstvě je dán Boltzmannovým faktorem ( ) e (φ(x) φse ) n e (x) = n se exp. (1.7) k B T e Lze ukázat, že k udržení stabilní stěnové vrstvy musí ionty splňovat tzv. Bohmovo kritérium, které říká, že rychlost v se iontů vstupujících do stěnové vrstvy musí být
15 KAPITOLA 1. OKRAJ PLAZMATU TOKAMAKU 16 rovna alespoň akustické rychlosti c s. Pro akustickou rychlost platí k B (T i + ZT e ) c s =. (1.8) m i k B je Boltzmanova konstanta, T i iontová teplota, T e elektronová teplota, m i hmotnost iontů a Z stupeň ionizace iontů. Zároveň však částice unikající z neporušeného plazmatu nemohou (alespoň v izotermickém přiblížení předpokládajícím konstantní teplotu podél magnetické siločáry) dosáhnout vyšší rychlosti než je c s. U běžného deuteriového plazmatu je stěnová vrstva tlustá přibližně 10λ D (Debyeových délek). λ D je vzdálenost, na které plazma odstíní elektrický potenciál vloženého statického náboje na 1/e jeho velikosti bez přítomnosti plazmatu. Pro Debyeovu délku platí ɛ0 k B T e λ D =. (1.9) ne Maxwellovský tok částic Stěnová vrstva je velice tenká a můžeme ji považovat za bezesrážkovou [50, str. 64]. Elektrony na okraji stěnové vrstvy mají přibližně Maxwellovské rozdělení rychlostí chybí pouze malá část z jednoho konce rozdělení tj. vysokoenergetické elektrony, které překonaly záporný potenciál stěnové vrstvy a dopadly na stěnu. Střední rychlost elektronů na okraji stěnové vrstvy (daná absencí zpětně se pohybujících energetických elektronů) je stejná jako střední rychlost iontů (1.8). Tato rychlost je velice malá ve srovnání se střední hodnotou velikosti rychlosti elektronů (1.12). Mnohé vlastnosti stěnové vrstvy jsou tedy odvozeny od Maxwellovské povahy neporušeného plazmatu [50]. Pro hustotu pravděpodobnosti Maxwellova rozdělení (oproti dodatku A zde není normováno na 1 ale na hustotu n) ( ) m f Max (v) = n exp 2πk B T je hustota toku částic ve směru osy x rovna Γ Max x = + v z= + v y= + v x=0 ( m ( vx 2 + vy 2 + vz 2 2k B T kde c je střední hodnota velikosti rychlosti (tepelná rychlost) c = 1 n + 0 vf Max (v)dv = )) (1.10) v x f Max (v)dv x dv y dv z = 1 n c, (1.11) 4 ( 8kB T πm ) 1 2. (1.12) Hustotu toku elektronů na stěnu získáme spojením (1.7) a (1.11) ve tvaru Γ e w = 1 4 ne w c e = 1 ( ) ( ) 1 e 4 n (φw φ se ) 8kB T 2 e se exp. (1.13) k B T e πm e
16 KAPITOLA 1. OKRAJ PLAZMATU TOKAMAKU 17 Hustota toku iontů na stěnu musí být rovna hustotě toku iontů okrajem stěnové vrstvy Γ i w = Γ i se = 1 Z n sec s. (1.14) Pokles potenciálu na stěnové vrstvě Po vytvoření stěnové vrstvy musí být tok iontů a elektronů na stěnu vyrovnaný, tj. Γ e w (φ w = φ fl ) = ZΓ i w. (1.15) Dosazením (1.13) a (1.14) do (1.15) získáme [50, str. 647] [( φ fl φ se = 0.5 ln 2π m ) ( e Z + T ) ] i (1 δ e ) 2 kb m i T e e T e. (1.16) Do vztahu (1.16) byl přidán člen s δ e, který popisuje sekundární elektronovou emisi z povrchu stěny, způsobenou dopadem částic plazmatu. Sekundární emise elektronů působí jako zdroj elektronů v oblasti stěnové vrstvy a může významně ovlivnit hodnotu plovoucího potenciálu. Uvažujeme-li δ e = 0, T e = T i a deuteriové plazma, je φ fl φ se 2.8 k B e T e. Uvažujeme-li, že teplota v předstěnové vrstvě zůstává podél magnetické silokřivky konstantní (izotermický model), lze pro pokles potenciálu na této oblasti ukázat [50, str. 48] φ se φ p 0.7 k B e T e, (1.17) čemuž odpovídá pokles hustoty n se 1 2 n p, (1.18) kde φ p a n p jsou potenciál plazmatu resp. elektronová hustota plazmatu (tj. ve vzdálené oblasti mimo předstěnovou vrstvu). Izotermický předpoklad lze dobře použít v případě limiterového plazmatu. Poněkud odlišná situace ovšem nastává v divertorové konfiguraci s tzv. detachmentem. Tento režim využívá přítomnosti oblaku neutrálního plynu v oblasti divertoru, který brzdí přilétávající částice a vede tudíž ke vzniku gradientu teploty podél magnetického pole viz [50, kap. 5] Nabitá stěna Nabijeme-li vodivý předmět, který je ve styku s plazmatem, na potenciál odlišný od plovoucího potenciálu (1.16) a nižší, než je potenciál plazmatu (např. přiložením elektrického napětí mezi tento předmět a podobný předmět jinde v plazmatu), znemožníme vytvoření standardní stěnové vrstvy. Na předmět budou dopadat odlišné toky iontů a elektronů. Hustota toku elektronů závisí na daném potenciálu předmětu (stěny) podle vztahu (1.13). Při velikosti potenciálu rovné potenciálu plazmatu nabývá proud elektronů hodnoty označované jako elektronový nasycený proud. Hustota
17 KAPITOLA 1. OKRAJ PLAZMATU TOKAMAKU 18 toku iontů (1.14) se s potenciálem nemění odpovídající proud můžeme označit jako iontový nasycený proud, jehož hustotu lze pomocí (1.13), (1.14) a (1.15) zapsat jako jsat i = en se c s = 1 ( ) ( ) 1 e 4 en (φfl φ se ) 8kB T 2 e se exp. (1.19) k B T e πm e Výsledná závislost elektrického proudu na potenciálu předmětu daná rozdílem toku iontů a elektronů bude mít podobu j = e ( ( ( )) ) ZΓ i w Γ e w = j i e (φ φfl ) sat 1 exp. (1.20) k B T e Pro δ e = 0 lze s využitím definice iontového a elektronového nasyceného proudu rovnici (1.16) přepsat jako φ fl = φ p ln Isat e k B T e e. (1.21) Tepelný tok Podobně jako hustotu toku částic můžeme pro Maxwellovský soubor částic definovat hustotu toku energie ve směru osy x q Max x = + v z= + v y= + v x=0 I i sat 1 2 m ( ) vx 2 + vy 2 + vz 2 vx f Max (v)dv x dv y dv z = 2k B T Γ Max x. (1.22) Vzhledem k tomu, že se v brzdném elektrostatickém poli stěnové vrstvy zachovává Maxwellovské rozdělení rychlostí elektronů s parametrem T e, můžeme pro elektrony dopadající na stěnu psát q e w = 2k B T e Γ e w. (1.23) Částice dopadající na stěnu měly původně energii vyšší o energii ekvivalentní potenciálovému skoku na stěnové a předstěnové vrstvě (1.16) resp. (1.17), (1.23) tedy odpovídá tepelnému toku z neporušeného plazmatu kde q e = γ e k B T e Γ e w, (1.24) γ e = 2 + e (φ w φ se ) /k B T e + e (φ se φ p ) /k B T e (1.25) V případě iontů je situace o něco složitější, jelikož je obtížné stanovit přesné rozdělení jejich rychlostí to je ovlivněno srážkami a dalšími procesy během pohybu skrz předstěnovou vrstvu. Pro tok iontů rozhraním stěnové a předstěnové vrstvy alespoň přibližně platí [50, str. 634] q i se 2.5k B T i Γ i se. (1.26) Odpovídající tepelný tok z neporušeného plazmatu je nižší o energii, kterou ionty získají průchodem předstěnové vrstvy, tedy q i = γ i k B T e Γ e w, (1.27)
18 KAPITOLA 1. OKRAJ PLAZMATU TOKAMAKU 19 kde γ i 2.5 T i ZT e e (φ se φ p ) /k B T e. (1.28) Při započtení vlivu sekundární elektronové emise má celkový koeficient přenosu tepla podobu [50, str. 649] γ 2.5 T i + 2 [( 0.5 ln 2π m ) ( e Z + T ) ] i (1 δ e ) 2. (1.29) ZT e 1 δ e m i T e Uvažujeme-li δ e = 0, T e = T i a deuteriové plazma, získáme γ 7 8. (1.30) Při reálném měření tepelného toku se projevují některé další efekty, které zde nejsou podrobněji rozebírány. Experimenty na tokamaku TCV poskytly výsledek γ = 6 ± 2 [41]. Při těchto experimentech byl tepelný tok měřen za pomoci divertorových Langmuirových sond a infračervené kamery. Ukázalo se, že na velikost koeficientu γ má poměrně velký vliv velikost úhlu mezi magnetickými silokřivkami a divertorovými deskami (resp. povrchem Langmuirovy sondy) naměřený rozsah cca 4 8 v hodnotě koeficientu γ odpovídá rozsahu úhlu 1 3. Celková hustota tepelného toku na plovoucí stěnu je q = γk B T e Γ e w. (1.31) V literatuře se předchozí vztahy běžně odvozují pro Z = 1, vzhledem k výhradnímu používání vodíku příp. deuteria v tokamacích. Nicméně jak je dobře známo, zvláště na okraji plazmatu je vždy řada nečistot, které způsobují, že měřené plazma je směsí iontů různých prvků s různým stupněm ionizace. Toto složení popisuje na tokamacích často měřený parametr Z eff definovaný jako Z eff = i n izi 2 i n, (1.32) iz i kde n i je hustota iontů i-tého druhu a Z i jejich stupeň ionizace. Já jsem při odvozování výše uvedených vztahů zachovával obecné Z jak je vidět např. v rovnici (1.29) pro velikost koeficientu γ, složení plazmatu resp. stupeň ionizace iontů hraje poměrně důležitou roli. Viz též [37] 1.4 Transport částic Tepelný tok na stěny tokamaku je přímo spjatý s transportem částic ve SOL, který určuje radiální profil hustoty SOL. Zásadní roli hraje transport kolmý na magnetické pole, který zabezpečuje přítok čístic z okrajového plazmatu do SOL, kde je kombinován s rychlým podélným transportem na desky divertoru či limiter.
19 KAPITOLA 1. OKRAJ PLAZMATU TOKAMAKU Difúze Kolmý transport je kombinací difúzních procesů (založených na srážkách) popsaných Fickovým zákonem a konvektivního transportu. Kolmý tok částic tak lze zapsat jako [31] Γ r = D r n + v eff n e. (1.33) První člen představuje Fickův zákon difúze, druhý člen popisuje konvektivní transport. Pro koeficient difúze D platí [39] D k [ ] BT 1 k BT mν = ρ 2 mν 1 + (ω c /ν) Q 2 B Lν, (1.34) 0 2 kde ν je srážková frekvence. Aproximace je platná pro silná magnetická pole, tedy pro ω c ν. Z experimentů vyplývá, že radiální profil hustoty má exponenciální tvar ( n(r) = n(0)exp r λ n SOL ) λ n SOL = n r n. (1.35) Experimentálně naměřené hodnoty charakteristické šířky SOL λ n SOL, což je vzdálenost, na které hustota poklesne na 1/e své hodnoty, jsou však několikanásobně vyšší oproti těm, které by mohl způsobit pouhý difúzní transport s koeficientem difúze (1.34). Ukazuje se, že kolmý transport je ve SOL velice významný [23] podélný transport nezabezpečuje dostatečně rychlý odtok částic na divertor. λ n SOL se navíc zvyšuje s rostoucí hustotou centrálního plazmatu [23] a plošší profil hustoty ve SOL má za následek nežádoucí tok částic na stěny tokamaku s negativním dopadem na životnost komponent první stěny, příp. vedoucí ke zvýšené depozici tritia v těchto komponentách. Nadměrný tok plazmatu na stěnu též v této oblasti způsobuje recyklaci částic, ke které by mělo ideálně docházet pouze na divertoru. Zvyšování centrální hustoty může tímto mechanismem vést k disrupci (náhlému zániku plazmatu). S tím spojený náhlý zánik proudu plazmatem je velice problematický zvláště u větších tokamaků s vysokou energií magnetického pole, která je náhle uvolněna Turbulentní transport Dnes se má za to, že hlavním zdrojem kolmého toku částic je turbulentní konvektivní transport. Rozvoj nestabilit vedoucích k turbulentnímu transportu je připisován okrajovému plazmatu (okolí LCFS) v oblasti okolo midplane na LFS, kde fluktuace hustoty a elektrického potenciálu vedou díky vlivu B B driftu a driftu zakřivení ke vzniku lokálního elektrického pole, které nestabilitu dále zvětšuje a vytváří makroskopické koherentní plazmatické útvary nazývané bloby. Ty se pak poměrně rychle šíří napříč magnetickým polem skrz SOL. Vlivů podílejících se na vzniku turbulencí je více, jedním z hlavních je výměnná nestabilita. Na principu výměnné nestability je založen numerický model ESEL, který s úspěchem popisuje mnohé aspekty SOL a je mu věnována pozornost v části III.
20 KAPITOLA 1. OKRAJ PLAZMATU TOKAMAKU 21 (a) const (b) A B v ExB drift elektronů drift iontů x Obrázek 1.3: Znázornění výměnné nestability. Upraveno z [42]. Výměnná nestabilita Výměnná nestabilita někdy též označovaná jako Rayleighova-Taylorova či žlábková nestabilita se rozvíjí na rozhraní 2 tekutin různé hustoty, příp. v prostředích s gradientem hustoty, kde působí zrychlení ve směru od hustší k řidší tekutině [39]. V takové situaci se snaží hustší tekutina zaujmout polohu pod řidší tekutinou (v daném poli) a počáteční poruchy na rozhraní se rozvinou do charakteristických útvarů podobných prstům a později kloboučkům hub. Typickým příkladem jsou dvě nemísící se kapaliny nalité do sklenice tak, aby hustší kapalina byla nad řidší. RT nestabilita ale vzniká i při inverzi na rozhraní dvou vzdušných mas nebo při interakci expandujícího hvězdného větru s Krabí mlhovinou, jež je pozůstatkem po explozi supernovy pozorované v roce RT nestabilita je zodpovědná i za hřibovitý útvar vznikající při atomovém výbuchu. V místě exploze vznikne lehký a horký plyn, který za pomoci RT nestability proniká vzhůru [39]. Roli zrychlení nutného pro rozvoj nestability přebírá v případě LFS tokamaku E B drift Mechanismus jeho vzniku je ilustrován na obrázku 1.3a. Předpokládámeli radiální gradient tlaku a hustoty vě směru k ose tokamaku a zavedeme-li malou sinusovou poruchu hustoty, povede tato konfigurace díky B B driftu, driftu zakřivení a magnetizačnímu driftu k lokální separaci náboje a vzniku vertikálního (poloidálního) elektrického pole, které bude mechanismem E B driftu dále zvětšovat poruchu. Radiálně směrem ven z tokamaku se bude pohybovat objekt s vyšší hustotou (blob), směrem do centra naopak 2 objekty s nižší hustotou oproti okolnímu plazmatu (díry) [17, 42, 31, 48, 14]. Při radiálním pohybu blobu skrz SOL se na jeho spodním a horním okraji začne rozvíjet Kelvinova-Helmholtzova nestabilita (rozvíjí se na rozhraní 2 různě hustých vzájemně se tečně pohybujících prostředí). KH nestabilita se projeví roztočením okrajů blobu každého v opačném směru. Blob tak získá vorticitu horní polovina kladnou, dolní polovina zápornou viz obrázek 1.3b. Vorticita je pojem používaný v teorii proudění. V našem případě je definována jako rotace vektoru rychlosti E B driftu [31] Ω v E 2 φ. (1.36) Odvození rovnosti vorticity s laplacem potenciálu lze nalézt např. v [31]. Z poissonovy
21 KAPITOLA 1. OKRAJ PLAZMATU TOKAMAKU 22 (a) (b) Obrázek 1.4: (a) Schematické znázornění filamentární struktury blobu [14]. (b) Fotografie záření na frekvenci čáry D α znázorňující toroidální protažení blobů na tokamaku Alcator C-Mod. Přerušovaná čára naznačuje směr magnetického pole. Expoziční čas 6 µs [25]. rovnice 2 φ = ρ ɛ 0 (1.37) vyplývá, že vorticitu lze až na multiplikativní konstantu ztotožnit s nábojovou hustotou. Bloby Bloby, vznikající v důsledku výměnné nestability, jsou makroskopické plazmové struktury generované v okrajovém plazmatu a šířící se napříč SOL. Vzhledem k tomu, že je jejich vznik spjatý s B B driftem a driftem zakřivení, je jejich výskyt omezen přibližně na výseč π/6 nahoru a dolu od ekvatoriální roviny (midplane) na LFS, kde se působení těchto driftů sčítá [53]. Naopak na HFS se B B drift s driftem zakřivení vzájemně vyruší a bloby v této oblasti pozorovány nejsou[14]. V poloidálním řezu mají bloby velikost typicky několik cm v radiálním směru jsou typicky sploštělé zhruba na polovina oproti poloidálnímu směru. V toroidálním směru tvoří několik metrů dlouhlé filamenty podél magnetických silokřivek, jak je znázorněno na obrázku 1.4. Ač jsou bloby 3D prostorovými objekty, lze jejich vznik a šíření s úspěchem popisovat pouze ve 2 dimenzích poloidálního řezu to umožňuje 2D numerické modelování výměnné nestability (viz popis numerického modelu ESEL v kapitole 5.2). Radiálně směrem ke stěně se bloby typicky šíří rychlostí o velikosti několika jednotek až desítek procent rychlosti zvuku c s (tj. jednotky km/s). Doba života blobu je několik desítek µs. Díky klesajícímu radiálnímu profilu elektrického potenciálu směrem ke stěně uvnitř SOL a s tím spojenému elektrickému poli, získávají bloby díky E B
22 KAPITOLA 1. OKRAJ PLAZMATU TOKAMAKU 23 Obrázek 1.5: Vznik a šíření blobu zachycené metodou gas puff imaging na tokamaku NSTX. Velikost snímané oblasti je 25x25 cm a snímky jsou časově posunuty o 7 µs. Blob vzniká v oblasti LCFS (plná čára) a šíří se radiálně skrz SOL do limiterového stínu (přerušovaná čára) rychlostí 1km/s. Převzato z [40]. driftu poloidální rychlost (1.6) [33] v pol = 1 B Důležitou roli hraje střih poloidální rychlosti ω E B dv pol dr dφ dr. (1.38) = 1 B d 2 φ dr 2, (1.39) který je zodpovědný za rozbíjení struktury blobu a ovlivňuje tak jeho velikost [31]. Střih poloidální rychlosti zhruba odpovídá převrácené hodnotě autokorelačního času τ c hustoty měřené statickou Langmuirovou sondou [31] ω E B τ 1 c. (1.40) Autokorelační čas τ c odpovídá času τ v autokorelační funkci (A.17), pro který hodnota autokorelační funkce exponenciálně poklesne na 1/e (viz dodatek A.4 a kapitola 6.2). Ukazuje se, že rozměr blobů je srovnatelný s charakteristickou délkou λ n SOL popisovanou níže L blob v pol τ c λ n SOL. (1.41) Tento vztah je upřesněn a blíže rozebírán v kapitole 6.2. Výskyt blobů ve SOL způsobuje značné fluktuace hustoty, potenciálu i teploty. Relativní fluktuace hustoty stoupají se vzdáleností od LCFS a řádově se pohybují až okolo 1, teplota a potenciál fluktuují o něco méně [24, 11, 14]. Experimenty ukazují, že přibližně platí [11] σ Te ( ) σ n. (1.42) µ Te µ n Ač např. při sondovém měření bloby zaujímají méně než 20% signálu, zapříčiňují okolo 50% veškerého radiálního transportu v blízkosti LCFS, ve vzdálenějších oblastech SOL ještě více [7].
23 KAPITOLA 1. OKRAJ PLAZMATU TOKAMAKU Šířka SOL Podobně jako pro hustotu (1.35) můžeme definovat charakteristickou šířku SOL pro další veličiny s exponenciálně klesajícím radiálním profilem - např. pro elektronovou teplotu T e, paralelní tok energie q či elektrický potenciál φ. ( a(r) = a(0)exp r ), a = [n, T e, q, φ]. (1.43) Charakteristická šířka SOL λ a SOL λ a SOL = a r a (1.44) udává vzdálenost, na které radiální profil dané veličiny klesne na 1/e. Dobrá znalost šířky SOL je nutná pro konstrukci nových tokamaků. SOL musí být dostatečně široká na to, aby podélný transport odvedl částice na divertor, nebyla namáhána stěna vakuové komory a nedocházelo k významné recyklaci částic na stěně. Měření λ q SOL na tokamaku Compass je podrobněji popsáno v kapitole 4. V kapitole 6 lze mj. nalézt porovnání experimentálně naměřených hodnot charakteristické šířky SOL ostatních výše jmenovaných veličin tokamaku ASDEX Upgrade s výsledky numerického modelu ESEL.
24 Kapitola 2 Sondová měření Na experimentálních fúzních zařízeních (zejména tokamacích) se používá velká škála diagnostických metod a systémů pro zjišťování (fyzikálních) parametrů produkovaného plazmatu. Jednou z nejzákladnějších, velice rozšířených a v principu i nejjednodušších diagnostik je Langmuirova sonda a sondy z ní odvozené, využívající podobný princip, příp. se snažící odstranit některé nevýhody Langmuirovy sondy. Mezi ně patří např. Katsumata sonda [36], ball-pen sonda [2, 3, 4], tunelová sonda [27, 29] a další. Langmuirova sonda je v podstatě malý vodivý drátek (hrot) zasunutý do plazmatu. Ostatní jmenované sondy využívají rozličné způsoby stínění některých částic plazmatu, což má různé výhody. Měřením napětí a proudů mohou tyto sondy poskytnout informace o základních parametrech plazmatu především o plovoucím potenciálu, potenciálu plazmatu, jeho hustotě, teplotě a o fluktuacích těchto veličin. 2.1 Langmuirova sonda Langmuirova sonda je malý kus vodiče typicky váleček o průměru několika desetin až jednotek milimetrů vyrobený z wolframu, molybdenu, grafitu či jiného materiálu schopného odolávat vysokým teplotám. V nejjednodušším případě je tento pin pouze vnořen do plazmatu a sbírá elektrony a ionty na něj dopadající, příp. je na sondu aplikováno konstantní či proměnné (rozmítané) napětí a je měřen procházející proud. Obecně je velkou předností Langmuirovy sondy jedinečné prostorové ( 3 mm) i časové ( 1 µs) rozlišení, což z ní (v kombinaci s reciprokým manipulátorem) dělá diagnostiku číslo 1 na poli studia turbulentního transportu. Langmuirovy sondy se běžně používají i na řadě dalších zařízení než jen na tokamacích Teorie Langmuirovy sondy V plovoucím režimu (bez přiloženého externího napětí) se v okolí Langmuirovy sondy vytvoří standardní stěnová vrstva a sonda se nabije na plovoucí potenciál daný rovnicí (1.16). Připomeňme, že tato hodnota se dá v běžných případech pro vodíkové plazma považovat za přibližně rovnou potenciálu plazmatu sníženého o zhruba 3 elektronové 25
25 KAPITOLA 2. SONDOVÁ MĚŘENÍ 26 teploty (v ev). Známe-li elektronovou teplotu, můžeme pomocí plovoucího potenciálu určit potenciál plazmatu. V magnetizovaném plazmatu je chování Langmuirovy sondy ovlivněno poměrem mezi Larmorovým poloměrem a velikostí sondy [34]. Díky většímu Larmorovu poloměru má Langmuirova sonda větší efektivní plochu pro sběr iontů než pro sběr elektronů. Ionty tedy vyrovnají tok elektronů již při menším poklesu potenciálu, než jaký by vyplýval z (1.16). Přesná hodnota závisí na tvaru a rozměrech Langmuirovy sondy a na velikosti magnetického pole. Pomocí efektivních ploch pro sběr elektronů a iontů lze vztah (1.21) pro plovoucí potenciál přepsat jako φ fl = φ p α k BT e, kde α = ln jsata e e e. (2.1) j i sata i A e a A i značí právě efektivní plochu sondy pro sběr elektronů resp. iontů. Efektivní plocha pro sběr iontů je obecně funkcí iontové teploty a mnohdy tedy není možné ji přesně určit. Pro Langmuirovu sondu v deuteriovém plazmatu za předpokladu T e = T i a A e /A i = 1 platí α lp = 3.5. Za přítomnosti magnetického pole je poměr A e /A i < 1 a velikost koeficientu α se tudíž sníží. Nabijeme-li Langmuirovu sondu na dostatečně nízký potenciál ve srovnání s potenciálem plazmatu tj. přiložíme-li patřičné napětí mezi sondu a komoru tokamaku (resp. místo, kterým prochází druhý konec magnetických silokřivek procházejících sondou), nebudou mít přicházející elektrony dostatečnou energii na překonání potenciálové bariéry a sondou poteče iontový nasycený proud I i sat = fn p ea i c s. (2.2) Efektivní plocha sondy A i se v prvním přiblížení často pokládá rovna ploše projekce sondy ve směru magnetického pole. f je faktor popisující změnu hustoty na předstěnové vrstvě. Jeho velikost je závislá na použitém modelu v již zmiňovaném izotermickém přiblížení je f 0.5 (viz vztah (1.18)). Přesnost sondových měření není většinou taková, aby velikost tohoto koeficientu hrála nějakou zásadní roli bližší informace o přesnějších modelech a hodnotách f lze nalézt např. v [26] či [34]. Celková hustota tepelného toku (1.31) měřená Langmuirovou sondou je [41] Voltampérová charakteristika q lp = γk B T e j i sat e. (2.3) Aplikací rozmítaného napětí na sondu získáme voltampérovou charakteristiku, pro niž teoreticky až po potenciál plazmatu platí ( ( )) e (U I = Isat i Ufl ) 1 exp. (2.4) k B T e Typicky má voltampérová charakteristika takovou podobu, že pro dostatečně nízké napětí se proud saturuje na iontovém nasyceném proudu, s rostoucím napětím má
26 KAPITOLA 2. SONDOVÁ MĚŘENÍ 27 proud exponenciální průběh a nabývá nulové hodnoty pro napětí rovné plovoucímu potenciálu. Po průchodu nulou proud nadále klesá až po potenciál plazmatu, ve kterém se křivka saturuje na hodnotě elektronového nasyceného proudu. V praxi je již po průchodu nulou často exponenciální závislost deformována a elektronový proud různě osciluje. V magnetizovaném plazmatu se navíc rozdělení rychlostí elektronů často odlišuje od Maxwellovského malá část elektronů má vyšší teplotu (tzv. supratermální elektrony) a rozdělení rychlostí lze považovat za bi-maxwellovské [45]. I malé zastoupení elektronů s vysokou teplotou ale může značně ovlivnit tvar elektronové části voltampérové charakteristiky (oblast nad plovoucím potenciálem) a způsobit nadhodnocení určené elektronové teploty [51]. SOL tokamaku je velice turbulentní zvláště v oblasti LFS, kde se šíří bloby charakteristické časy těchto turbulencí teploty a potenciálu jsou typicky několikanásobně kratší než jaká je perioda rozmítání sondy a projevují se tak fluktuacemi signálu voltampérovy charakteristiky. To představuje jeden z hlavních rozdílů oproti sondovým měřením např. v nízkoteplotním laboratorním plazmatu a způsobuje mnohdy značné komplikace při zpracování a vyhodnocování voltamperových charakteristik sondových měření v tokamacích Zpracování voltampérové charakteristiky Nafitováním voltampérové charakteristiky Langmuirovy sondy je možné určit elektronovou teplotu, plovoucí potenciál i iontový nasycený proud viz vztah (2.4). Fitování charakteristiky bývá ale často značně obtížné především díky fluktuacím signálu (viz výše) a efektům projevujícím se v elektronové části charakteristiky (supratermální elektrony, saturace pro napětí nad potenciálem plazmatu). V praxi se používají různé metody fitování, zde uvádím jen některé z nich. Metoda U < U fl Vzheldem k tomu, že největší potíže většinou způsobuje elektronová část voltampérové charakteristiky, která se v magnetizovaném plazmatu často odchyluje od exponenciálního průběhu, je první variantou fitovat exponenciálou pouze iontovou část křivky tedy od nejzápornějších hodnot napětí až po plovoucí potenciál (průchod křivky napěťovou osou nulový proud). Metoda minimální T e Další možností je vybrat namísto plovoucího potenciálu za koncový bod fitovaných dat takový bod z oblasti U > U fl, pro který bude výsledná teplota T e minimální [32]. Tento způsob vychází čistě z experimentální praxe, která ukazuje, že teplota měřená Langmuirovou sondou je vyšší ve srovnání s ostatními diagnostikami. Metoda minimální chyby fitu Další možností je za koncový bod fitovaných dat vzít takový bod z oblasti U > U fl, pro který má fit nejmenší chybu ve smyslu co nejvyšší hodnoty (adjustovaného)
27 KAPITOLA 2. SONDOVÁ MĚŘENÍ 28 koeficientu determinace (A.24) resp. (A.24) příp. co nejmenšího relativního rozptylu teploty σ Te /T e (A.21) viz též [5][28]. V kapitole 4 je k optimalizaci fitu použita minimalizace hodnoty výrazu spojujícího jak relativní rozptyl teploty, tak adjustovaný koeficient determinace ( ) 1 R 2 σ Te adj. (2.5) T e 2.2 Ball-pen sonda Jednou z nevýhod Langmuirovy sondy je nutnost znalosti elektronové a iontové teploty k určení potenciálu plazmatu viz (1.16) resp. (2.1). Jak již bylo řečeno v části 2.1.1, přítomnost magnetického pole ovlivňuje efektivní plochu Langmuirovy sondy pro sběr elektronů a iontů a tím pádem i velikost koeficientu u T e v rovnici (2.1). Stejného principu využívá ball-pen sonda, jejímž cílem je přiblížit poměr elektronového a iontového nasyceného proudu co nejvíce jedničce, aby koeficient α u elektronové teploty v (2.1) byl co nejmenší. Podobně jako u Katsumata sondy je změny poměru iontového a elektronového proudu docíleno umístěním Langmuirovy sondy do magnetického stínu (např. zasunutím do kovové trubičky v případě Katsumata sondy či do trubičky z dielektrika, např. keramiky, v případě ball-pen sondy), což redukuje především efektivní plochu sondy pro sběr elektronů A e a tedy i I e sat. Ve SOL L-módu tokamaku ASDEX Upgrade s deuteriem a magnetickým polem velikosti 2.5T bylo pro ball-pen sondu experimentálně nalezeno [4] α bpp 0.6 ± 0.3. (2.6) Vzhledem k rozdílným hodnotám koeficientu α v (2.1) lze porovnáním hodnoty plovoucího potenciálu Langmuirovy a ball-pen sondy získat hodnotu elektronové teploty k B T ( ) e = φ bpp fl φ lp fl δα, kde δα = α lp α bpp. (2.7) e Takovéto přímé měření potenciálu plazmatu je daleko vhodnější pro studium rychlých turbulentních procesů ve SOL, než měření za použití rozmítaného napětí a fitování voltampérové charakteristiky, kde je časové rozlišení značně limitováno rychlostí rozmítání [1]. 2.3 Rychlá reciproká sonda Vysokou tepelnou zátěž sondových diagnostik při kontaktu s plazmatem se snaží omezit koncept rychlé reciproké sondy. Základním principem je co možná nejvíce zkrátit dobu kontaktu aktivní části sondy (např. Langmuirovy či ball-pen sondy) s horkým plazmatem. Reciproká sonda tedy spojuje rychlý reciproký manipulátor s některou ze sondových diagnostik. Manipulátor velice rychle zasune měřící hlavici osazenou sondou, příp. několika sondami, do plazmatu (typicky do SOL nedaleko LCFS) a okamžitě, dříve než se tepelným tokem poničí, ji zase vytáhne. Kontakt s nejteplejším plazmatem se tak zkrátí typicky na několik jednotek až desítek ms.
28 KAPITOLA 2. SONDOVÁ MĚŘENÍ 29 Jak již bylo řečeno, hlavice reciproké sondy se často osazuje hned několika Langmuirovými či jinými sondami. Klíčovými parametry při výběru materiálu pro samotnou hlavici jsou bod tání, tepelná vodivost a energetický práh pro odprašování daného materiálu v plazmatu, příp. atomové číslo. Jednotlivé sondy musí být samozřejmě od hlavice elektricky izolované. Běžně se tedy využívá elektrický izolant nitrid boritý, často v kombinaci s grafitem, příp. molybden či wolfram. Slibné parametry pro možné budoucí využití mají i diamant a grafen. Konstrukce reciproké sondy může být rozličná, reciproký pohyb typicky zajišťuje píst poháněný stlačeným plynem nejčastěji vzduchem či héliem. Navíc je možné před výbojem sondu pomalým posuvem nastavit na potřebnou pozici vůči komoře tokamaku. Podrobnosti lze nalézt např. v [9, 10, 31]. Vysoké nároky jsou kladeny na mechanickou konstrukci sondy, která při reciprokém pohybu odolává přetížení několika g, i na přesný řídící systém sondy, který musí být schopen časově i prostorově sesynchronizovat pohyb sondy s plazmatem.
29 Část II Práce na tokamaku COMPASS 30
30 Kapitola 3 Upgrade reciprokých sond tokamaku COMPASS 3.1 Reciproké sondy na tokamaku COMPASS Na tokamaku Compass jsou v současnosti k dispozici 2 rychlé reciproké sondy jedna vertikální a druhá horizontální. Bližší informace o sondách a jejich instalaci na tokamaku Compass lze nalézt v mé bakalářské práci [54] a výzkumném úkolu [55] Horizontální sonda Současná horizontální reciproká sonda byla na tokamaku Compass používána již ve Velké Británii před přesunem tokamaku do Prahy. Tam byla ovšem instalována ve vertikální poloze, v Praze tedy musela projít úpravami, zcela nově byl vyvinut ovládací systém sondy [54][55]. Oproti vertikální sondě je poněkud robustnější, je osazena větším počtem signálních koaxiálních vodičů a umožňuje tedy připojení větší hlavice s více sondami. Daní za tyto výhody je ovšem menší rychlost, zrychlení i celková délka reciprokého pohybu. Sonda měří parametry plazmatu přibližně na midplane LFS. Tělo reciprokého manipulátoru ukrývá celkem 18 koaxiálních signálních vodičů, které je možno připojit k jednotlivým Langmuirovým sondám hlavice (příp. ball-pen sondám apod.). V minulém roce byla provedena první měření, při kterých byl manipulátor osazen hlavicí se čtyřmi ball-pen sondami a čtyřmi Langmuirovými sondami viz obrázek 5.1b a [4]. Celý mechanismus je umístěn na masivním kovovém stole, zajišťujícím dostatečnou stabilitu a znemožňujícím jakékoli nežádoucí pohyby či vibrace sondy při rychlém pohybu během měření. Hlavní pohonnou silou 190 cm dlouhé sondy je stlačený vzduch, kterým je pro účely pomalého posuvu poháněn pneumatický motor, jehož otáčivý pohyb se pomocí mechanických převodů mění na lineární. Posuv na požadovanou pozici před měřením (výbojem) lze též provádět ručně. Rychlý pohyb směrem do komory tokamaku a následně ven zajišťuje dvoucestný pneumatický píst. Rozsah pomalého posuvu je zhruba 610 mm, rychlého pak maximálně 60 mm hloubku rychlého zásunu lze měnit nastavením ovládacího systému. Tlak vzduchu přiváděného k sondě z centrálního 31
31 KAPITOLA 3. UPGRADE RECIPROKÝCH SOND TOKAMAKU COMPASS 32 (a) (b) (c) Obrázek 3.1: Fotografie (a) horizontálního a (b) vertikálního reciprokého manipulátoru tokamaku Compass. (c) Nákres vertikálního reciprokého manipulátoru. rozvodu tokamaku je řízen redukčním ventilem. Vzhledem k technické konstrukci zařízení a bezpečnosti je používán tlak 5 bar, při kterém rychlý pohyb sondy dosahuje maximální rychlosti v 1.3 m s 1 a maximálního zrychlení a 5 g. Celý pohyb při nejhlubším možném zásunu 60 mm trvá přibližně 170 ms. Průběh reciprokého pohybu je podrobněji popsán v sekci 3.3. Vzhledem k současnému umístění v horizontální poloze, bylo třeba tělo reciprokého manipulátoru doplnit o distanční kroužek a posuvnou podpěru vnějšího konce sondy zajišťující centraci rychle se pohybující části vzhledem k podélné ose (směru pohybu). Bez této úpravy se při reciprokém pohybu sonda rozkmitávala, což bylo s nějvětší pravděpodobností příčinou poničení instalované hlavice během poslední experimentální kampaně Vertikální sonda Vertikální sonda tokamaku Compass byla původně navržena pro horizontální umístění. Vyvinuta a zkonstruována byla výzkumnou skupinou na University of California v San Diegu v USA, řadu let ji úspěšně používali na tokamacích TEXTOR a DIII-D, s některými úpravami pak na TCV ve švýcarském Lausanne, odkud byla v roce 2009 převezena do ČR. Pro výměnu umístění původně vertikální britské sondy do horizontální polohy a původně horizontální americké sondy do vertikální pozice bylo rozhodnuto z důvodu možnosti osadit britský reciproký manipulátor hlavicí s větším množstvím sond, což je vhodné ke studiu turbulentních struktur generovaných v oblasti okolo midplane na LFS. Vertikální reciproká sonda je připojena na horní oválný port v jihozápadní části komory tokamaku a měří tedy v nejvrchnějších částech plazmatu. Tělem manipulátoru
32 KAPITOLA 3. UPGRADE RECIPROKÝCH SOND TOKAMAKU COMPASS 33 je vedeno 5 koaxiálních signálních vodičů, maximální počet sond na hlavici je tedy 5. Oproti horizontálnímu manipulátoru, kde pomalý posuv zajišťuje pneumatický motor, jsou zde oba pohyby, tedy rychlý i pomalý, zajištěny dvoucestnými pneumatickými písty. Nastavení koncové polohy pomalého posuvu se provádí pomocí dorazu v podobě elektrickými motorky polohovatelného vozíku. Délka rychlého pohybu je dána pevně na 150 mm. Podobně jako u horizontální sondy je i u této pomalý pohyb poháněn stlačeným vzduchem z centrálního rozvodu tokamaku, jehož tlak je redukován na 5 bar. Pohonnou sílu rychlého pohybu zajišťuje hélium pod tlakem 6 bar, při jehož použití reciproký pohyb dosahuje maximální rychlosti v 2.5 m s 1 a maximálního zrychlení a 10 g (resp. a 15 g v místě obrátky reciprokého pohybu). Celý pohyb trvá zhruba 200 ms. Průběh reciprokého pohybu je znázorněn na obrázku Ovládací systém Ovládací systém obou reciprokých sond tokamaku Compass byl postupně vyvíjen v posledních třech letech. Nyní je již plně funkční a otestovaný během experimentálních kampaní. Vzhledem k tomu, že byl systém vytvářen zcela nově, bylo možné jej uzpůsobit na míru místním standardům a potřebám Elektronika Srdcem ovládacího systému každé ze sond je mikrokontrolér dspic30f4013 osazený do na Compassu již standardizované elektronické desky zajišťující rozhraní pro sériovou komunikaci RS232 a napájení mikrokontroléru. Deska mikrokontroléru je pomocí 96-pinového DIN konektoru napojena na rozšiřující elektronickou desku poskytující úpravu vstupů a výstupů mikrokontroléru dle potřeb každé ze sond. V případě horizontální sondy jde především o galvanické optické oddělení, změnu napětí z 5V (pracovní napětí dspic) na 24V potřebných pro ovládání pneumatických ventilů apod. Vertikální sonda není ovládána přímo mikrokontrolérem dspic o bezprostřední ovládání systémů sondy (tj. pneumatických ventilů a motoru pro posun dorazu pomalého posuvu) a snímání stavu sondy (koncové polohy pomalého posuvu a koncové polohy dorazu) se stará původní elektronika sondy, které dspic zasílá 4bitové binární příkazy v podobě různých kombinací 0 a 1 (v TTL logice) na 4 vstupech. Rozšiřující desky jsou osazeny konektory pro snadné připojování a odpojování signálních kabelů vedoucích k sondám (RJ-45, BNC, příp. svorkovnice) Ovládací software Provoz každého z reciprokých manipulátorů je bezprostředně řízen programem v mikrokontroléru dspic. Ten obstarává ovládání sondy v reálném čase tj. zachytává externí trigger, v potřebném okamžiku spíná pneumatické ventily, sbírá polohu reciprokého pohybu v čase atd. Uživateli je komunikace s mikrokontrolérem a jeho nastavení před samotným měřením umožněno skrze ovládací software s grafickým
33 KAPITOLA 3. UPGRADE RECIPROKÝCH SOND TOKAMAKU COMPASS 34 uživatelským rozhraním (GUI) běžící na linuxovém serveru propojeném s mikrokontrolérem pomocí sériového rozhraní. dspic Současná podoba kódu řídícího dspic obou sond vychází z programu popsaného v mé bakalářské práci [54]. Program je psán v jazyce C. Postupně došlo k jeho doplnění a úpravám, což se týká především způsobu uživatelského řízení a nastavování potřebných parametrů. Původní jednoznakové příkazy zasílané prostřednictvím sériového rozhraní nahradil ucelený komunikační protokol založený na podobné filozofii jako protokoly používáne u dalších systémů tokamaku Compass (řízení vakuového systému, doutnavého výboje apod.) [52]. Nový komunikační protokol navíc obsahuje zabezpečení v podobě kontrolního součtu na konci každého příkazu pro případ porušení datového paketu během přenosu. Jednotlivé příkazy je možné buďto přímo zasílat po sériovém portu nebo využít grafické uživatelské rozhraní, k jehož obsluze vůbec není nutné komunikační protokol znát a ovládání sondy za pomoci klikacího prostředí je tak velice snadné. Komunikační protokol je podrobně popsán v dodatku C. GUI Grafické uživatelské rozhraní ovládacího softwaru reciprokých sond umožňuje intuitivní řízení chodu sond bez potřeby bližší znalosti samotného systému. Rozhraní je vytvořeno v jazyce Python za využití multiplatformní grafické knihovny Qt. Uživatel obsluhující sondu jej spustí po přihlášení se na server thermoc a je tudíž možné sondu ovládat z libovolné počítačové stanice v ovládací místnosti tokamaku či z libovolného jiného PC s připojením na intranet. GUI převádí uživatelské vstupy (stisk tlačítka, zaškrtnutí některé volby, zadání číselné hodnoty apod.) na patřičné datové pakety komunikačního protokolu, které odesílá přes sériový port mikrokontroléru dspic. Ten vždy ověří, zda je příslušná akce proveditelná (např. že je sonda zasunutá do tokamaku, v případě požadavku na rychlý reciproký pohyb), pokud je to přípustné, provede ji a odpoví datovým paketem opět v patřičném formátu s uvedením výsledku. Podrobný návod k obsluze GUI lze nalézt v dodatku B. Aktuální verze GUI i kódu programu pro mikrokontroléry dspic je přiložena na CD. 3.3 Optimalizace reciprokého pohybu Pneumatický systém Ze zkušeností provozu reciprokých sond na různých tokamacích i z teoretických předpokladů vyplývá, že klíčovým parametrem rychlosti reciprokého pohybu sondy je rychlost šíření zvuku c s v používaném hnacím plynu [10][9]. To prokázaly i provedené testy s vertikální reciprokou sondou na tokamaku Compass: při použití dusíku (c s = 334 m s 1 [38]), jakožto hnacího média, trval reciproký pohyb 480 ms, při
34 KAPITOLA 3. UPGRADE RECIPROKÝCH SOND TOKAMAKU COMPASS 35 0 Shot #2162 Z [mm] t [ms] 2 v [m/s] t [ms] 5 a [g] t [ms] Obrázek 3.2: Průběh polohy, rychlosti a zrychlení hlavice horizontální rychlé reciproké sondy v čase (výstřel #2162). použití hélia (c s = 971 m s 1 [38]) se doba pohybu snížila na 200 ms (viz obrázek 3.3). Zpomalené videozáznamy rychlého reciprokého pohybu s héliem i dusíkem lze nalézt na přiloženém CD. Zásadní roli v optimalizaci rychlého reciprokého pohybu také hraje zařazení plynového reservoáru před píst. Reservoár eliminuje pokles tlaku v pneumatickém systému během rychlého pohybu a významně vylepšuje jeho rychlost [10][9]. Nastavováním časů přepínání pneumatických ventilů, lze docílit různých průběhů reciprokého pohybu. Nejlepší výsledky průběhu rychlého reciprokého pohybu horizontální a vertikální sondy v současné konfiguraci (horizontální sonda poháněná vzduchem, vertikální sonda poháněná heliem, bez přídavných pružin) jsou znázorněny na obrázcích 3.2 a 3.3.
35 KAPITOLA 3. UPGRADE RECIPROKÝCH SOND TOKAMAKU COMPASS 36 0 Shot #2721 Z [mm] t [ms] 4 2 v [m/s] t [ms] a [g] t [ms] Obrázek 3.3: Průběh polohy, rychlosti a zrychlení hlavice vertikální rychlé reciproké sondy v čase (výstřel #2721).
36 KAPITOLA 3. UPGRADE RECIPROKÝCH SOND TOKAMAKU COMPASS Zrychlení obrátky reciprokého pohybu Smyslem reciprokého manipulátoru je zajistit co nejkratší dobu kontaktu měřící sondy s horkým plazmatem zásadních je především několik posledních cm zanoření sondy. Jedním z možných způsobů zrychlení reciprokého pohybu je zvětšení brzdné síly a zrychlení během obrátky např. přidáním pružiny v koncovém bodu reciprokého pohybu. V takovém případě by bylo možné urychlovat sondu na delší vzdálenosti zkrátil by se tak i celkový čas pohybu. V běžné konfiguraci je totiž k brždění dopředného pohybu horizontální sondy používána stejná síla jako k jeho urychlování tj. síla pohonného plynu a nechceme-li, aby sonda narazila do koncového bodu, může být urychlována pouze na polovině dráhy a v druhé polovině musí být opět bržděna. Přesněji vzato má samozřejmě ještě vliv tření při pohybu manipulátoru a rozdíl atmosférického tlaku a tlaku uvnitř komory tokamaku. Navíc je doba urychlování a brždění ještě kratší díky prodlevě mezi těmito fázemi dané dobou přepnutí pneumatického ventilu a dobou potřebnou k natlakování hadičky propojující ventil a zpětnou větev pístu. Píst rychlého pohybu vertikálního manipulátoru umožňuje omezit výtok pracovního plynu při pohybu pístu v několika posledních centimetrech u koncových poloh vzniká tak jakýsi plynový polštář, který též přispívá k brždění pohybu a k jeho plynulosti. Různá nastavení tohoto systému byla otestována během odstávky reciproké sondy, nyní je třeba nastavení vyladit po opětovném připojení k tokamaku (kdy bude mít vliv snížený tlaku v komoře a vertikální umístění sondy), příp. nakombinovat s přidáním pružiny podobně jako bylo zmiňováno výše pro horizontální sondu. Z provedených simulací vyplývá, že by takto mohl být poměrně jednoduše zkrácen čas, který hlavice sondy stráví v oblasti několika cm nejhlubšího zanoření, např. na polovinu (záleží na tuhosti a délce použité pružiny a požadovaném omezení maximálního zrychlení/přetížení hlavice daném její konstrukcí).
37 Kapitola 4 Šířka SOL limiterového plazmatu 4.1 Motivace V současnoti je již v plném proudu výstavba technického zázemí mezinárodníko tokamaku ITER 1 a finišují přípravy samotného zařízení. Stále však panují nejasnosti okolo designu některých komponent. Podstatným parametrem pro návrh a výrobu komponent první stěny vakuové komory tokamaku je tepelný tok, který bude skrze SOL na stěnu deponován. Klíčovou roli v této otázce hraje charakteristická šířka SOL λ q SOL pro radiální pokles paralelního toku energie. Současné znalosti fyziky tokamaků neumožňují prediktivní výpočet λ q SOL a je tudíž nutno provést odhad na základě experimentů na tokamacích různých parametrů. Teoretické pochopení nám umožní určit, které parametry by měly být podstatné. Ty zase bohužel často nejsou známy pro ITER. Design první stěny ITERu vychází z požadavku umožnit limiterový start-up výboje na aktivně chlazených beriliových panelech jak na LFS tak na HFS. Možné tepelné toky na tyto panely jsou velmi vysoké, avšak musí splnit limity pro povrchovou teplotu beriliových komponent. Tento tepelný tok se odvíjí od tvaru panelů a paralelního tepelného toku na ně dopadajícího, který je spjat s charakteristickou délkou exponenciálního poklesu tepelného toku ve SOL λ q SOL. V ITER Thermal Load Specifications jsou hodnoty λ q SOL pro limiterovou fázi odvozeny od škálování pro L- mód divertorového plazmatu. Vzhledem k tomu, že design tvaru první stěny ITERu je již v závěrečném stádiu, je vysokou prioritou ověření platnosti tohoto škálování λ q SOL. (Volně přeloženo z [47].) Používané škálování λ q SOL pro L-mód ITERu [35] má podobu λ q SOL R2 0P 0.8 SOL n0.9 e q Zeff 0.6, (4.1) kde R 0 je hlavní poloměr, P SOL tepelný tok do SOL, n e line averaged hustota, Z eff efektivní náboj plazmatu a q 95 je bezpečnostní faktor 95% magnetického povrchu. 1 ITER je zkratkou anglického International Thermonuclear Experimental Reactor, příp. latinsky cesta. Tento velkolepý projekt by měl demonstrovat možnost komerčního využití termojaderné fúze jakožto zdroje energie. Na realizaci ITERu spolupracují Čína, Evropská unie, Indie, Japonsko, Jižní Korea, Rusko a USA. Výstavba probíhá ve francouzském Cadarache a tokamak by měl vytvořit první plazma v roce Projektovou hodnotou fúzního zisku ITERu je Q
38 KAPITOLA 4. ŠÍŘKA SOL LIMITEROVÉHO PLAZMATU 39 Dříve provedené experimenty naznačují [29], že toto škálování není vhodné pro limiterovou start-up fázi. Významným úkolem tedy je takové škálování provést to však zahrnuje vytvoření databáze λ q SOL z mnoha výbojů řady tokamaků a na základě těchto dat statistickými metodami stanovit funkční závislost λ q SOL na základních parametrech výboje jako jsou R 0, P, Z eff, q, n e. Experimenty na stávajících tokamacích ukázaly, že šířka SOL je větší (radiální profil tepelného toku klesá pomaleji) pro plazma limitované na HFS než-li při využití limiteru na LFS. Tento předpoklad je třeba též ověřit, tzn. provést škálování pro obě variatny ořez plazmatu na HFS i na LFS. Měření λ q SOL již dříve proběhlo na tokamacích DIII-D a Tore Supra, v září 2011 pak na tokamaku JET a v následujících měsících také na tokamaku COMPASS. V následující části jsou shrnuty výsledky posledně jmenovaného měření. 4.2 Měření na tokamaku Compass Uspořádání experimentu Pro stanovení λ q SOL na tokamaku Compass bylo nutné naměřit radiální profil paralelního toku energie (2.3) ve SOL. To lze poměrně snadno provést pomocí reciproké sondy. Za předpokladu T e = T i postačí znalost iontového nasyceného proudu, elektronové teploty, aktivní plochy sondy a její polohy v čase vůči separatrix. Pro měření byla využita vertikální reciproká sonda. Základní popis sondy lze nalézt v kapitole Reciproký manipulátor byl za tímto účelem osazen hlavicí s jedinou Langmuirovou sondou. Hlavice je vyobrazena na obrázku 4.1a, vyrobena byla ve spolupráci se St Kliment Ohridski University of Sofia. V následujících měřeních byla uvažována aktivní plocha Langmuirovy sondy A 16 mm 2, což představuje celý povrch sondy nikoli pouze průmět ve směru magnetického pole vzhledem k tomu, že sonda je poměrně veliká a sbírá částice i v kolmém směru. Stanovení korektní plochy není triviální, nicméně pro určení hledané λ q SOL není absolutní kalibrace příliš důležitá. Tato měření byla vůbec prvními měřeními vertikální reciproké sondy tokamaku Compass s využitím reciprokého pohybu po její reinstalaci v Praze. Jako zdroj rozmítaného napětí sondy byla využita elektronika na Compassu běžně užívaná pro měření s divertorovými Langmuirovými sondami. Rozmítáno bylo od -100 V do 100 V s frekvencí 1 khz. Data byla sbírána s frekvencí 2 MHz Určení pozice LCFS Pro určení λ q SOL není znalost přesné polohy LCFS nutná, nicméně užitečné by mohly být hodnoty elektronové hustoty n LCFS e a teploty Te LCFS na separatrix pro účely škálování. Vzhledem k tomu, že v době experimentu nebyla ještě na tokamaku Compass k dispozici rekonstrukce magnetických povrchů (což by v blízké budoucnosti měl zajišťovat kód EFIT), bylo nutné vystačit si s informacemi o proudech magnetickými cívkami a s údaji magnetických detektorů. Z těchto podkladů lze za předpokladu kru-
39 KAPITOLA 4. ŠÍŘKA SOL LIMITEROVÉHO PLAZMATU 40 (a) (b) Obrázek 4.1: (a) Hlavice vertikální reciproké sondy použitá při měření λ q SOL. Hlavice je osazena jedinou Langmuirovou sondou. (b) Určování polohy plazmatu a LCFS z údajů o proudech magnetickými cívkami. Výboj #2614, t = 1078 ms. [J. Horáček ] hového průřezu plazmatu a parabolického profilu proudu plazmatem přibližně určit časový vývoj polohy středu plazmatu a pozice separatrix graficky je výpočet polohy plazmatu znázorněn na obrázku 4.1b. Systematická chyba takovéhoto určení pozice LCFS byla ovšem až 3 cm, což významně ovlivnilo nepřesnost stanovení hodnoty elektronové hustoty n LCFS e a teploty Te LCFS na separatrix, stejně tak jako paralelní vzdálenosti na limiter L (vzdálenosti podél magnetické silokřivky od sondy na limiter ang. connection length) Naměřená data Experimentální měření charakteristické šířky SOL pro radiální pokles paralelního toku energie λ q SOL proběhlo na tokamaku Compass v prosinci Celkem bylo provedeno 19 výbojů použitých následně při zpracování dat. Plazma bylo ořezáváno limiterem na HFS (malý poloměr plazmového prstence a 0.2 m, velký poloměr R 0.55 m, magnetické pole B = 1.1 T). Hodnota λ q SOL se v jednotlivých provedených výbojích liší v závislosti na parametrech výboje v následující části pro ukázku popisuji výsledky výboje #2568. Nalézt funkční závislost λ q SOL na parametrech výboje bude důležitým úkolem po vytvoření dostatečně obsáhlé databáze měření z různých tokamaků.
40 KAPITOLA 4. ŠÍŘKA SOL LIMITEROVÉHO PLAZMATU 41 Ke stanovení λ q SOL bylo třeba určit radiální profil paralelního tepelného toku q daného rovnicí (1.31) resp. (2.3). Elektronová teplota T e a iontový nasycený proud Isat i byly získány z voltampérových charakteristik rozmítané sondy fitováním metodou výběru koncového bodu fitovaných dat tak, aby byl minimální vztah (2.5) (tj. požadavek na minimální relativní rozptyl σ Te /T e naměřené teploty a maximální hodnotu adjustovaného koeficientu determinace Radj 2 ) viz sekce Podrobnější popis použitého postupu fitování (resp. nelineární regresní analýzy) včetně stanovení směrodatných odchylek získaných parametrů (T e, Isat, i U fl ) a adjustovaného koeficientu determinace (Radj 2 ) lze nalézt v dodatku A.5. Naměřené voltampérové charakteristiky se mnohdy značně odchylovaly od ideální exponenciály zvláště elektronová část často oscilovala což snižovalo spolehlivost fitu. Několik příkladů voltampérových charakteristik a jejich fitů je znázorněno na obrázku 4.2. Jednotlivým nafitovaným hodnotám iontového nasyceného proudu Isat i a elektronové teploty T e byly přiřazeny váhy dle spolehlivosti daného fitu dané převrácenou hodnotou výrazu (2.5). Z takto vážených dat byla následně určena charakteristická šířka SOL vzhledem k iontovému nasycenému proudu, teplotě i paralelnímu tepelnému toku, jak znázorňují obrázky 4.3a, 4.3b a 4.3d. Na obrázku 4.3c jsou ještě pro úplnost vyneseny naměřené hodnoty plovoucího potenciálu. Velikost jednotlivých bodů na obrázcích odpovídá spolehlivosti fitů, ze kterých byly body vypočteny (tj. jejich vahám při dalším zpracování). Jak je zřejmé z obrázku 4.3b, naměřené hodnoty teploty v blízkosti separatrix značně fluktuují, což je s největší pravděpodobností následek především nepřesného fitování voltampérových charakteristik díky rychlým fluktuacím signálu (rychlejším než rozmítací frekvence). Tento fakt vnáší významný rozptyl i do výsledné charakteristické šířky λ q SOL = 16 ± 12 mm.
41 KAPITOLA 4. ŠÍŘKA SOL LIMITEROVÉHO PLAZMATU Up, 255mm, t=1011ms. T e =9±9eV, R adj = Down, 292mm, t=995ms. T e =5±2eV, R adj = I [A] Original data Taken for fit BCKG fit φ interval I s interval I [A] Original data Taken for fit BCKG fit φ interval I s interval 1 U [V] 0.2 U [V] (a) (b) Up, 234mm, t=1021ms. T e =16±13eV, R adj = Down, 268mm, t=1005ms. T e =9±5eV, R adj = I [A] Original data Taken for fit BCKG fit φ interval I s interval I [A] Original data Taken for fit BCKG fit φ interval I s interval 1 U [V] 0.3 U [V] (c) (d) Obrázek 4.2: Fitování voltampérové charakteristiky. Použitá metoda plovoucího koncového bodu dat použitých pro fit poměrně úspěšně eliminuje vliv fluktuací (saturace) na konci voltampérové charakteristiky. I tak je však často spolehlivost fitu poměrně malá díky fluktuacím v průběhu celého rozmítání. Modré body představují surová data, červené byly získány odečtením pozadí (proudu měřeného i mimo plazma díky kapacitě kabelů) a mírným vyhlazením dat. [J. Horáček , úprava P. Vondráček ]
42 i KAPITOLA 4. ŠÍŘKA SOL LIMITEROVÉHO PLAZMATU 43 2 λ i Isat =24±7mm, R adj =76% λ Te =39±32mm, R adj =28% [A] I sat 10 1 T [ev] r r [mm] LCFS (a) Nafitované hodnoty iontového nasyceného proudu I i sat. λ Ii sat SOL = 24 ± 7 mm, R2 adj = r r LCFS [mm] (b) Nafitované hodnoty elektronové teploty T e. λ Te SOL = 39 ± 32 mm, R2 adj = λ =16±12mm, R =43% q adj 10 5 U fl [V] 0 5 q [W/m 2 ] r r [mm] LCFS r r [mm] LCFS (c) Nafitované hodnoty plovoucího potenciálu U fl. (d) Výsledné hodnoty paralelního toku energie q. λ q SOL = 16 ± 12 mm, R2 adj = Obrázek 4.3: Nafitované hodnoty I i sat, T e, U fl, příslušné charakteristické šířky SOL λ SOL a výsledný paralelní tok energie q. [J. Horáček , úprava P. Vondráček ]
43 Část III Srovnání měření reciproké sondy s numerickým modelem ESEL 44
44 Kapitola 5 Vstupní data V této části srovnávám experimentální data získaná měřením reciproké sondy ve SOL tokamaku ASDEX Upgrade s výstupy numerického modelu ESEL. Podobná srovnání v minulosti proběhla již pro řadu tokamaků např. pro TCV [19, 20, 23, 18, 31], MAST [15], Textor [53], JET [44]. Doposud byla demonstrována poměrně dobrá shoda experimentálních pozorování s modelem v oblasti fluktuací hustoty. Srovnání popisované v následující části diplomové práce je jedinečné především díky unikátnímu časovému (1 µs) a prostorovému (2-4 mm) rozlišení experimentálních dat díky použití ball-pen sond, které v kombinaci s Langmuirovými sondami umožnily velice rychlé měření teploty a potenciálu plazmatu (omezené pouze rychlostí sběru dat) [33]. To umožnilo srovnání turbulentních struktur (fluktuací) modelu a experimentu i po stránce teploty a potenciálu! Dosavadní experimentální data toto neumožňovala vzhledem k nedostatečnému prostorovému rozlišení (např. při použití tunelové sondy) nebo časovému rozlišení (díky omezené rychlosti rozmítání při použití Langmuirových sond). 5.1 Experimentální měření na tokamaku ASDEX Experimentální data byla získána během měření pomocí horizontální reciproké sondy na tokamaku ASDEX Upgrade v roce Jejich analýza je podrobně popsána v [33], odkud je též převzata většina zde prezentovaných zpracovaných dat (radiální profily, korelační charakteristiky, podmíněné průměry). Analyzovaná data pocházejí z výboje #24349 (L-mód, vstřik svazku neutrálních částic [NBI] o výkonu 1 MW, toroidální magnetické pole B = 2.5 T resp. B = 1.9 T ve SOL, proud plazmatem I p = 0.8 MA a line averaged hustota n e = m 3 ). Data byla sbírána se vzorkovací frekvencí 2 MHz. Reciproký manipulátor byl umístěn cca 30 cm nad midplane LFS tokamaku, jak znázorňuje obrázek 5.1a. Hlavice manipulátoru byla osazena čtyřmi ball-pen sondami (BPP0-3) a čtyřmi Langmuirovými sondami (LP1-4) tak, aby žádné ze sond nebyly vzájemně v zákrytu z pohledu magnetického pole viz obrázek 5.1b. Sonda LP1 byla nabita na -150 V a poskytovala měření iontového nasyceného proudu (2.2). LP3 byla rozmítána s frekvencí 100 khz za účelem měření voltampérové charakteristiky 45
45 KAPITOLA 5. VSTUPNÍ DATA (a) 46 (b) Obrázek 5.1: (a) Umístění reciprokého manipulátoru nad midplane LFS tokamaku ASDEX Upgrade (Z = m). (b) Hlavice horizontálního reciprokého manipulátoru tokamaku ASDEX Upgrade osazená čtyřmi Langmuirovými a čtyřmi ball-pen sondami. Horizontální směr fotografie odpovídá poloidálnímu (vertikálnímu) směru v tokamaku. Převzato z [33]. (2.4). Ostatní sondy byly ponechány v plovoucím režimu (2.1). Velikost koeficientu α v rovnici (2.1) byla pro Langmuirovu sondu v této konfiguraci experimentálně stanovena jako αlp =2.3 3 [46], pro ball-pen sondu pak αbpp = 0.6 ± 0.3 [4]. V souladu s [33] používám αlp = 2.8. Rozdílnost koeficientu αlp a αbpp Langmuirovy a ball-pen sondy umožnila určení elektronové teploty (viz vztah (2.7)) a potenciálu plazmatu (za předpokladu, že potenciálové prostorové škály turbulentních struktur jsou větší než vzdálenost sond a Te Ti ). 5.2 Numerický model ESEL Jak se ukazuje v experimentech, pohybuje se hladina relativních fluktuací hustoty, teploty a elektrického potenciálu ve SOL v řádech (fluktuace hustoty jsou největší viz vztah (1.42)), zatímco fluktuace magnetického pole jsou zde typicky o několik řádů nižší [11]. Toho využívá numerický tekutinový model ESEL (z ang. Edge SOL Electrostatic) [19, 48] specializovaný na simulaci turbulentních procesů ve SOL v okolí midplane LFS tokamaků. Jde o elektrostatický model vyvíjený fyziky v dánském Risø, který uvažuje pouze fluktuace elektrického potenciálu φ s časově konstantním magnetickým polem s radiálním gradientem a popisuje fluktuace 3 skalárních polí: hustoty částic n, elektronové teploty Te a vorticity Ω[15]. Model je dvoudimenzionální rovnice modelu popisují skalární veličiny v rovině kolmé k magnetickému poli. Třetí dimenze je simulována zavedením paralelních ztrát,
46 KAPITOLA 5. VSTUPNÍ DATA 47 které jsou silnější pro teplotu než pro hustotu a vorticitu vzhledem k dominantním ztrátám vysokoteplotních elektronů [53]. Rovnice modelu jsou bezrozměrné díky Bohmově normalizaci: n = n n 0, T e = T e T e,0, φ = eφ k B T e,0, B = B B 0, t = tω ci,0, x = x ρ s,0, (5.1a) (5.1b) kde ρ s,0 c s,0 /ω ci,0 je hybridní Larmorův poloměr (Larmorův poloměr iontů s tepelnou rychlostí 1 Maxwellova rozdělení s elektronovou teplotou), c s k B T e,0 /m i je rychlost zvuku v přiblížení chladných iontů a iontová cyklotronní frekvence ω ci je dána rovnicí (1.2). Nulový index označuje hodnotu dané veličiny na separatrix. Model je založen na sadě redukovaných tekutinových rovnic [16] dt e dt dn dt + n C(φ ) C(n T ) = Λ n, 2 (5.2a) + 2T e 3 C(φ ) 7T e 3 C(T e) 2T e C(n ) = Λ 3n Te, (5.2b) dω C(n T dt e) = Λ Ω (5.2c) Vorticita Ω je spojena s potenciálem φ podle vztahu (1.36). Časová derivace d/dt, operátor zakřivení C a magnetické pole B jsou definovány jako d = dt t + B φ C = ρ s,0 R 0 y, B 2, (5.3a) (5.3b) 1 B = 1 + r 0 + ρ s,0 x R o. (5.3c) Operátor Λ a (a = [n, T e, Ω]) popisuje kolmou difúzi a paralelní ztráty Λ a = D a 2 a, (5.4) τ a kde D a je koeficient difúze a τ a paralelní ztrátový čas. Podrobnější informace o numerickém modelu ESEL lze nalézt např. v [21, 16] Parametry vyhodnocované simulace Pro účely tohoto porovnání bylo vytvořeno několik simulací, které se lišily např. rozlišením, ale také zahrnutím různých fyzikálních předpokladů příp. okrajových podmínek tak, aby model co nejlépe popisoval skutečnost. Níže je sepsán popis některých důležitých parametrů simulace s pracovním označením 002, která byla použita pro srovnání s experimentálními daty popsané v následující kapitole. 1 Zde se na rozdíl od kapitoly tepelnou rychlostí míní 1D střední kvadratická rychlost daná odmocninou ze střední hodnoty kvadrátu některé složky vektoru rychlosti.
47 KAPITOLA 5. VSTUPNÍ DATA 48 y [mm] r r LCFS [mm] (a) Hustota. 2 1 n [m 3 ] x y [mm] r r LCFS [mm] (b) Teplota T [ev] e y [mm] r r LCFS [mm] (c) Potenciál. φ [V] y [mm] r r LCFS [mm] (d) Vorticita Ω Obrázek 5.2: Hustota, teplota, potenciál a vorticita v ESELu. Horizontální osa odpovídá radiálnímu směru v tokamaku, vertikální osa poloidálnímu směru. Přerušované čáry značí LCFS (r r LCFS = 0) a okraj limiteru (r r LCFS 45mm pozice limiteru v ESELu nekoresponduje zcela přesně s reálnou polohou r r LCFS 50mm). Dobře patrný je radiálně se šířící blob (z okrajového plazmatu na levé straně do limiterového stínu na pravé straně). Rozměry simulace Modelovaná oblast zahrnuje okrajové plazma, SOL a limiterový stín viz obrázek 5.2. Rozměry modelované oblasti i ostatní parametry jsou nastaveny tak, aby byly v co nejlepším souladu s experimentálně pozorovanou oblastí tokamaku ASDEX Upgrade. Model neuvažuje zakřivení magnetických povrchů v poloidálním směru, tzn. separatrix i stěna jsou v něm rovné. Pro popis polohy v simulované oblasti používám souřadnicový systém x, y x lze přibližně ztotožnit s radiálním směrem v tokamaku, y s poloidálním směrem. Simulace 002 měla ve směru osy x (radiálním směru) rozměr L x = 220ρ s (90ρ s okrajové plazma, 90ρ s SOL, 40ρ s limiterový stín) s rozlišením 1252 bodů, ve směru osy y (poloidálním směru) L y = 90ρ s a 512 bodů. Na 21 radiálně rovnoměrně rozmístěných pozicích vzájemně vzdálených 10ρ s byly umístěny sady sond odpovídající sondám hlavice reciprokého manipulátoru (celkem 8 sond s patřičným poloidálním rozmístěním). Pozice sond jsou též znázorněny na obrázku 5.2. V místech těchto sond byly každých 10 kroků vnitřního cyklu simulace (10 jednotek normalizovaného času) ukládány hodnoty základních veličin (T e, n, φ, Ω). Každý krok pak byla ukládána data v plném rozlišení ( 2D snímky ) a časově ustředněné radiální profily (poloidálně zprůměrované hodnoty veličin). Videosekvenci sestavenou z 2D snímků hustoty, teploty, potenciálu a vorticity simulace 002 lze nalézt na přiloženém CD.
48 KAPITOLA 5. VSTUPNÍ DATA 49 Parametry na separatrix Parametry základních veličin na separatrix byly nastaveny tak, aby pokud možno odpovídaly hodnotám tokamaku ASDEX Upgrade, tj. B 0 = 2.34 T, n 0 = m 3, T e,0 = 40 ev, T i,0 = 40 ev. Okrajové podmínky Velice důležitá je volba okrajových podmínek, které řídí tok částic a energie okraji modelované oblasti. V poloidálním směru je aplikována periodická okrajová podmínka a(x, 0, t) = a(x, L y, t), pro a = [n, T e, Ω, φ]. (5.5) V radiálním směru pro x = 0 má podmínka tvar a pro x = L x (na stěně) platí T e 2 = n 2 = Ω = φ x = 0 (5.6) T e x = n x = Ω x = φ 0.07 = 0. (5.7) V běhu simulace 002 byl zahrnut vliv stěnové vrstvy v paralelním směru (sheath condition) uvnitř SOL a limiterového stínu v podobě předpisu pro paralelní ztrátový čas vorticity 1 = c ( s 2.8 φ ), (5.8) τ Ω L T e což mělo za následek snížení v předchozích simulacích nadměrné rychlosti poloidálního toku plazmatu. Rychlost zvuku Na obrázku 6.1a jsou časově ustředněné radiální profily simulace s pracovním označením 137 radiální profil hustoty je zde ve SOL příliš plochý, což je dáno neefektivitou paralelních ztrát ve vzdálenějších oblastech SOL, kde je nízká elektronová teplota a tedy i rychlost c s, která řídí rychlost paralelních ztrát. V simulaci 002 byla ve vztahu pro rychlost zvuku uvažována i nenulová (konstantní) teplota iontů, která byla dříve zanedbávána: c s = k B (T e + T i,0 ) /m i.
49 Kapitola 6 Porovnání výsledků Po odstranění šumu na pozadí (pravidelných píků) byla experimentální data zpracovávána po intervalech dlouhých 2.7 ms (tj. při vzorkovací frekvenci 2 MHz celkem 60 intervalů po 5400 vzorcích). Interval 2.7 ms je v porovnání s autokorelačním časem dostatečně dlouhý (zahrnuje průměrně 3-15 blobů) na to, aby bylo možné v něm provést základní statistickou analýzu. Zároveň je dostatečně krátký na to, aby se během něho dala sonda považovat za statickou (pohne se maximálně o 2.7 mm, což je výrazně méně, než jaká je charakteristická šířka SOL λ SOL ) [33]. Každému intervalu byla přiřazena střední radiální poloha a takto vytvořený radiální profil experimentálních měření je v následujícím textu porovnáván s radiálními profily modelu ESEL příp. s daty z modelových radiálně rozmístěných sond. 6.1 Ustálené radiální profily První důležitou informací v analýze shody experimentálních pozorování s modelem je porovnání radiálních profilů základních veličin a jejich (relativních) fluktuací. Pro všechny 2.7 ms intervaly dat reciproké sondy byly spočítány první 4 statistické momenty (střední hodnota, směrodatná odchylka, koeficient šikmosti a špičatosti viz dodatek A.2), čímž bylo získáno 60 bodů radiálního profilu každého momentu zhruba polovina pro pohyb sondy směrem do středu komory tokamaku, druhá polovina pro zpětný pohyb. Jak je vidět na obrázku 6.2, hodnoty se mírně liší v závislosti na směru pohybu sondy, což může být dáno zahřátím hlavice sondy, příp. dalšími efekty, které doposud nejsou zcela zřejmé. Časově a poloidálně ustředněné radiální profily základních veličin jsou přímým výstupem kódu ESEL, pro stanovení vyšších statistických momentů jsem použil data ze sond, která jsou generována dostatečně často a v dostatečném množství pro statistickou analýzu Střední hodnota Jak je zřejmé z obrázku 6.2a, experimentální a modelované radiální profily střední hodnoty hustoty, teploty i potenciálu si poměrně dobře odpovídají. Profily všech 3 50
50 KAPITOLA 6. POROVNÁNÍ VÝSLEDKŮ μ a n e [10 19 m 3 ] ESEL n e [10 19 m 3 ] T e [ev] ESEL T e [ev] T e [ev] Thomson φ [V] ESEL φ= φ bpp +0.6 T e [V] λ pol /τ c [km.s 1 ] 10 1 n ESEL T e ESEL φ ESEL V p ESEL T e φ bpp r r LCFS [mm] (a) r r LCFS [mm] (b) Obrázek 6.1: Porovnání experimentálních a modelových (a) časově ustředněných radiálních profilů hustoty, teploty, potenciálu a (b) radiálních profilů poloidální rychlosti pro simulaci s pracovním označením 137. Nesoulad je částečně odstraněn v simulaci 002 viz obrázky 6.2a a 6.6. Červenými křížky jsou vyznačeny hodnoty teploty naměřené thomsonovým rozptylem (převzato z [4]) μ a n e [10 19 m 3 ] ESEL n e [10 19 m 3 ] T e [ev] ESEL T e [ev] T e [ev] Thomson φ [V] ESEL φ= φ bpp +0.6 T e [V] r r LCFS [mm] (a) σ a /μ a 10 1 n ESEL n e T e ESEL T e φ ESEL φ bpp r r LCFS [mm] (b) Obrázek 6.2: Porovnání experimentálních a modelových (a) časově ustředněných radiálních profilů hustoty, teploty, potenciálu a (b) relativních fluktuací těchto veličin (směrodatných odchylek normovaných na střední hodnotu). Experimentální data jsou pospojována tak, jak šla v čase za sebou - naměřené střední hodnoty jsou o něco vyšší pro pohyb sondy směrem do tokamaku. Simulace s pracovním označením 002. Červenými křížky jsou vyznačeny hodnoty teploty naměřené thomsonovým rozptylem (převzato z [4]).
51 KAPITOLA 6. POROVNÁNÍ VÝSLEDKŮ 52 veličin mají přibližně exponenciální průběh (1.43). Profily experimentálních dat mají v oblasti SOL a v limiterovém stínu výrazně rozdílnou strmost, která je popisována charakteristickou šířkou λ: λ ne,te,φ SOL 30mm, λ ne,te,φ shadow 5mm (to koresponduje s rozdílnou srážkovostí v těchto oblastech viz [22, 33]). V případě modelu je rozdíl o něco menší a charakteristická šířka v limiterovém stínu je zhruba dvojnásobná ve srovnání s experimentem, tj. λ ne,te,φ shadow 10mm Fluktuace Při porovnání fluktuací jsou rozdíly významnější obrázek 6.2b zachycuje směrodatné odchylky normované na střední hodnotu. Model vykazuje vyšší míru fluktuací především teploty a potenciálu, jehož fluktuace jsou dokonce v rozporu s experimentálními pozorováními (1.42) několikanásobně vyšší oproti fluktuacím hustoty. Jak ukazuji později, projevuje se nepoměr mezi fluktuacemi modelu a experimentálních dat také rozdílností charakteristik podmíněného průměru (CAV), které jsou u ESELu daleko výraznější. Možných příčin nesouladu je několik buďto ESEL z nějakého důvodu nepopisuje situaci realisticky, nebo hodnoty experimentálních fluktuací ovlivňuje kombinace signálů ze 2 různých prostorových bodů (Langmuirova a ball-pen sonda), příp. sondy nedokážou fluktuace v dostatečné míře zachytit. 6.2 Časové a prostorové charakteristiky Další důležitou oblastí porovnání modelu s experimentem jsou časové a prostorové škály výměnnou nestabilitou generovaných turbulentních struktur blobů. K určení charakteristických rozměrů a rychlostí blobů posloužila korelační analýza. Pro hustotu, teplotu i potenciál je vzájemná korelace 2 vůči sobě časově či prostorově posunutých signálů v okolí nuly klesající funkcí tohoto posunutí. Pokles je možné aproximovat exponenciálou a pro korelační funkci (A.17) lze tedy psát [33] ( ) ρ a,a (δt, δz) exp δz δt. (6.1) λ a pol τc a Časová korelace Charakteristický autokorelační čas τc a v rovnici (6.1) představuje čas δt, za který autokorelační funkce v konkrétním pevně daném místě poklesne zhruba na 1/e jde tedy o parametr exponenciálního fitu autokorelační funkce časové řady hodnot veličiny a = [T e, n, φ]. Autokorelační čas poskytuje informaci o tom, jak dlouho blobu typicky trvá, než přeletí přes daný prostorový bod (resp. statickou sondu). 1 Zde je na místě podotknout, že měření teploty rozmítanou Langmuirovou sondou nezaznamenalo pokles charakteristické šířky v limiterovém stínu a její hodnota měřená touto cestou je tedy naopak vyšší než v ESELu. Nicméně hodnoty poskytované ball-pen sondou jsou v lepší shodě s teoretickými očekáváními založenými na srážkovosti.
52 KAPITOLA 6. POROVNÁNÍ VÝSLEDKŮ 53 Pro experimentální data byla autokorelační funkce spočtena v každém ze 60 výše zmiňovaných 2.7 ms dlouhých intervalů (pohyb sondy v rámci intervalu byl zanedbán). Pro model jsem autokorelační funkce a jejich fity spočetl pro radiálně rozmístěné sondy odpovídající LP1 a LP2 (v poloidálním směru ve středu simulované oblasti v ESELu jsou tyto sondy ztotožněny vzhledem k tomu, že jsou vzájemně poloidálně posunuty pouze nepatrně). Ukázka autokorelačních funkcí a jejich exponenciálních fitů přibližně ze středu SOL je na obrázku 6.3a. Je vidět, že exponenciála neaproximuje korelační funkce příliš dobře, nicméně jak ukazuji později, poskytnuté výsledky rychlosti kolmého transportu blobů jsou v dobré shodě s očekávanými parametry a exponenciální aproximace se tak zdá být uspokojivá. Výsledné radiální profily autokorelačních časů jsou vyneseny v obrázku 6.3b Prostorová korelace Podobně jako autokorelační čas τ c v časové doméně, představuje charakteristická autokorelační délka λ a pol resp. λ a rad prostorovou vzdálenost δz, na které (prostorová) autokorelační funkce v pevně daném okamžiku poklesne zhruba na 1/e jde tedy o parametr exponenciálního fitu autokorelační funkce prostorové řady hodnot veličiny a = [T e, n, φ] v poloidálním resp. radiálním směru. Korelační délka udává typické rozměry blobu z pohledu veličiny a poměr mezi λ a pol a λ a rad vypovídá o prostorové deformaci blobu. Ze znalosti autokorelačního času a délky lze usuzovat typickou rychlost šíření blobů. Pro model jsem prostorové korelační funkce spočetl pro všechny 2D snímky na radiálních pozicích zabudovaných sond. V poloidálním směru jsem vždy prováděl korelaci sloupce dat s radiální souřadnicí dané sondy; v radiálním směru jsem zpracovával řádky dat dlouhé 60ρ s : 30ρ s doleva a 30ρ s doprava od dané sondy (všechny pouze poloidálně ve středu modelované oblasti, jelikož na poloidální poloze časový průměr radiální korelační délky nezávisí). Korelační funkce jsem následně časově ustřednil (zprůměroval údaje z jednotlivých 2D snímků) a nafitoval exponenciálou. Ukázka prostorových korelačních funkcí v poloidálním směru a jejich exponenciálních fitů je na obrázku 6.4a. Zvláště v oblasti limiterového stínu se na mnoha snímcích nevyskytovala žádná turbulentní struktura prostorová korelační funkce v takovém případě klesá téměř okamžitě (již pro malé vzájemné posunutí dat) k nule. Jelikož je cílem této korelační analýzy popis vlastností blobů, bylo třeba tyto korelační funkce z časového průměru vyřadit. Vhodnost zařazení do časového průměru jsem tedy podmiňoval minimální hodnotou dané korelační funkce pro prostorové posunutí 1 mm jako ρ(δz = 1 mm) = 1/e. Tato podmínka nemá ve SOL takřka žádný efekt, nicméně v limiterovém stínu zajistila plynulé pokračování radiálního profilu korelační délky (viz obrázek 6.4b) bez ní padá hodnota vypočtené prostorové korelace v limiterovém stínu k nule. Z experimentálních dat není možné určit radiální korelační délku (v každém časovém okamžiku jsou všechny sondy na stejné radiální pozici). Poloidální korelační délka byla určena vypočítáním vzájemné korelace signálů 2 sond s nulovým časovým posunem a známým prostorovým posunem (např. pro BPP1 a BPP2 = 10 mm)
53 KAPITOLA 6. POROVNÁNÍ VÝSLEDKŮ n ESEL T e ESEL 10 2 φ ESEL n e 10 0 n, τ =4.4 μs c T, τ =5.8 μs e c φ, τ =3.5 μs c τ c [μs] 10 1 T e φ bpp ρ a,a δ t [μs] (a) r r LCFS [mm] (b) Obrázek 6.3: (a) Časová autokorelační funkce hustoty, teploty a potenciálu ESELu pro r r LCFS 40 mm. Přerušované čáry znázorňují exponenciální fit. Hodnota 1/e je naznačena čerchovanou čarou. (b) Radiální profily autokorelačních časů tj. času, za který časová autokorelační funkce v daném místě poklesne na 1/e. n ESEL T e ESEL φ ESEL T e φ bpp 10 0 λ pol [mm] 10 1 ρ a,a n, λ pol =3.3 mm T e, λ pol =4.3 mm φ, λ pol =8.5 mm δ z [mm] (a) r r [mm] LCFS (b) Obrázek 6.4: (a) Poloidální prostorová korelační funkce hustoty, teploty a potenciálu ESELu pro r r LCFS 40 mm. Přerušované čáry znázorňují exponenciální fit. Hodnota 1/e je naznačena čerchovanou čarou. (b) Radiální profily poloidálních korelačních délek tj. poloidální vzdálenosti, na které prostorová korelační funkce v dané radiální pozici poklesne na 1/e.
54 KAPITOLA 6. POROVNÁNÍ VÝSLEDKŮ 55 jako λ a δz pol = ln [ρ a,a (δt = 0, δz = )]. (6.2) Nebylo tudíž možné určit prostorovou korelační délku hustoty, která byla měřena jedinou I sat sondou. Porovnání modelových a experimentálních radiálních profilů poloidálních prostorových korelačních délek je vyneseno v obrázku 6.4b. Jak pro model tak pro experimentální data je dobře patrná výrazně vyšší hodnota korelační délky potenciálu λ φ pol ve srovnání s korelační délkou teploty λ Te pol a v případě modelu i hustoty λ n pol, jak je také vidět na obrázku 5.2. V grafu 6.5a jsou pak radiální profily radiálních prostorových korelačních délek modelu Rychlost transportu Rychlost pohybu blobu napříč magnetickým polem můžeme vyjádřit jako v = vpol 2 + v2 rad ɛλ pol, (6.3) τ c kde v pol je určeno E rad B driftem viz Velikost koeficientu ɛ nelze bez znalosti směru pohybu blobu přesně stanovit, nicméně bude ležet mezi jedničkou a hodnotou danou poměrem mezi radiální a poloidální korelační délkou λ rad /λ pol. Radiální profil tohoto poměru pro modelová data je vynesen v grafu 6.5b, z něhož je zřejmé, že ve SOL se ɛ příliš neliší od 1. Odhad velikosti rychlosti transportu blobů napříč magnetickým polem daný poměrem λ pol /τ c je vyobrazen na obrázku 6.6. Rychlost spočtená z experimentálních dat dobře odpovídá modelu v první polovině SOL s narůstající vzdáleností od LCFS experimentálně pozorovaná rychlost dále klesá na rozdíl od modelové, která opět stoupá. Modelová rychlost určená korelační analýzou je v dobré shodě s poloidální rychlostí vypočtenou z radiálního profilu potenciálu pomocí vztahu (1.38). 6.3 Podmíněný průměr (CAV) Podstatnou informaci o podobě blobu podává časový průběh signálů měřených veličin při přechodu blobu přes statickou sondu. Průměru mnoha takovýchto krátkých úseků signálu se říká podmíněný průměr (ang. conditional average CAV) a lze ho zapsat jako CAV a (dt) a I sat > I sat + βσ Isat 1 N b N b i=1 a (t i + dt), (6.4) kde a = [T e, n e, φ, V fl ], N b je počet blobů splňujících podmínku, že na signálu iontového nasyceného proudu I sat vytvářejí pík alespoň o β směrodatných odchylek vyšší oproti střední hodnotě signálu navíc signál nad touto úrovní musí být dlouhý alespoň
55 KAPITOLA 6. POROVNÁNÍ VÝSLEDKŮ n ESEL T e ESEL φ ESEL λ rad [mm] 4 λ rad /λ pol r r LCFS [mm] (a) r r LCFS [mm] (b) Obrázek 6.5: (a) Radiální profily radiálních korelačních délek ESELu tj. radiální vzdálenosti, na které prostorová korelační funkce poklesne na 1/e. (b) Poměr mezi poloidální a radiální korelační délkou. Červenou přerušovanou čarou je zobrazena průměrná hodnota poměrů z celé oblasti simulace λ pol /τ c [km.s 1 ] 10 1 n ESEL T e ESEL φ ESEL V p ESEL T e φ bpp r r LCFS [mm] Obrázek 6.6: Radiální profil rychlosti kolmého transportu plazmatu. V p značí poloidální rychlost vypočtenou z radiálního profilu potenciálu pomocí vztahu (1.38) tedy zcela nezávislou metodou.
56 KAPITOLA 6. POROVNÁNÍ VÝSLEDKŮ n [10 19 m 3 ] t [ms] Obrázek 6.7: Detekce blobů v signálu hustoty 17-té sondy (r r LCFS 40 mm) modelu ESEL. Vodorovné linky označují střední hodnotu a úroveň 2.5-násobku směrodatné odchylky nad střední hodnotou. 4 µs a od minulého rozpoznaného blobu být vzdálen minimálně 25 µs. U modelových dat jsem namísto I sat pro detekci blobů používal signál hustoty n e a podmínku minimální délky a separace blobů modifikoval tak, že signál splňující podmínku 6.4 musí být dlouhý alespoň τ c /4 a od minulého rozpoznaného blobu být vzdálen minimálně o τ c (τ c je autokorelační čas hustoty v místě sondy, pro jejíž data je podmíněný průměr počítán). Ukázka signálu hustoty modelu s označenými detekovanými píky je na obrázku 6.7. Porovnání podmíněných průměrů experimentálních dat s modelovými ve 3 různých vzdálenostech od LCFS je na obrázku 6.8. Je vidět, že rozdíly mezi měřením a modelem jsou poměrně značné jak v absolutní výšce píků jednotlivých veličin, tak ve tvaru jejich časového průběhu. Poměrně dobrá shoda je pouze v hustotě. Rozdílnost výšky píků vyplývá z vyšší míry fluktuací v ESELu, jak bylo diskutováno v sekci viz obrázek 6.2b Hustota Modelová data se nejlépe shodují s experimentem v podmíněných průměrech hustoty. Signály jsou vůči sobě lehce posunuté, což je dáno nedokonalou shodou časově ustředněných radiálních profilů hustoty především v druhé polovině SOL viz 6.2a. Průběh signálu je podobný, pík ESELu je však zhruba pětinásobný, což odpovídá vyšším fluktuacím ESELu viz obrázek 6.2b. V obou případech jsou píky poměrně strmé a úzké, což je dáno především tím, že hustota (resp. I sat ) byla použita pro detekci blobů Potenciál Průběh podmíněného průměru potenciálu modelu vykazuje zcela odlišné chování oproti experimentálním datům. Zatímco signál potenciálu ball-pen sondy je téměř
57 KAPITOLA 6. POROVNÁNÍ VÝSLEDKŮ 58 konstantní a plovoucí potenciál Langmuirovy sondy obsahuje malý pík v kladném směru (o velikosti řádově maximálně několik směrodatných odchylek), signál potenciálu plazmatu modelu značně osciluje a plovoucí potenciál spočtený jako φ 2.8T e vykazuje výrazný pík v záporném směru (dominuje vliv velkého píku teploty, který se ještě násobí faktorem 2.8) Teplota Z neshody modelu s experimentem v průběhu podmíněného průměru potenciálu přímo vyplývá i rozdílnost v teplotě. V experimentu je teplota měřena porovnáním plovoucího potenciálu Langmuirovy a ball-pen sondy (2.7) a jelikož signál ball-pen sondy je oproti plovoucímu potenciálu téměř konstantní, udává tvar podmíněného průměru teploty plovoucí potenciál. Ten má ve vztahu (2.7) záporné znaménko a na signálu teploty se tedy objevuje pík v záporném směru. U modelových dat je tomu přesně naopak podmíněný průměr teploty má průběh takřka identický s hustotou, tedy úzký strmý pík v kladném směru. Názornější porovnání tvarů jednotlivých podmíněných průměrů lze nalézt na obrázku 6.9, kde je eliminován vliv různé úrovně fluktuací i středních hodnot experimentálních a modelových dat díky odečtení střední hodnoty a normalizaci podmíněného průměru na směrodatnou odchylku na svislé ose grafů jsou tedy vynášeny hodnoty (CAV a µ a ) /σ a. 6.4 Shrnutí Zahrnutím některých potřebných fyzikálních předpokladů a rozšířením modelované oblasti okrajového plazmatu se podařilo docílit poměrně dobré shody časově ustředněných radiálních profilů pozorovaných veličin numerického modelu ESEL s experimentálním pozorováním na tokamaku ASDEX Upgrade. Uspokojivá shoda byla též pomocí prostorové a časové korelační analýzy pozorována ve velikosti turbulentních struktur hustoty a teploty a v profilech rychlosti jejich kolmého transportu v 1. polovině SOL. Stále však model vykazuje neúměrně velké fluktuace (především potenciálu a teploty), což se následně projevuje značnými rozdíly ve velikostech podmíněných průměrů signálů generovaných blobem přecházejícím přes statickou Langmuirovu sondu. Zde je třeba provést další analýzu, příp. srovnání s dlašími experimentálními daty, aby bylo zřejmé, zda je původcem chybný model nebo nesprávně interpretovaná experimentální data.
58 KAPITOLA 6. POROVNÁNÍ VÝSLEDKŮ ESEL probe #13 r r LCFS =20mm, ASDEX r r LCFS =22mm 100 ESEL probe #15 r r LCFS =31mm, ASDEX r r LCFS =30mm 100 ESEL probe #17 r r LCFS =41mm, ASDEX r r LCFS =39mm CAV φ [V] ESEL φ 2 bpp [V] V fl [V] ESEL V fl2 [V] δ t [μs] (a) CAV φ [V] ESEL φ 2 bpp [V] V fl [V] ESEL V fl2 [V] δ t [μs] (b) CAV 0 50 φ [V] ESEL φ 2 bpp [V] V fl [V] ESEL V fl2 [V] δ t [μs] (c) n [10 18 m 3 ] ESEL n e [10 18 m 3 ] n [10 18 m 3 ] ESEL n e [10 18 m 3 ] n [10 18 m 3 ] ESEL n e [10 18 m 3 ] CAV 15 CAV 15 CAV δ t [μs] (d) δ t [μs] (e) δ t [μs] (f) T e [ev] ESEL T e [ev] T e [ev] ESEL T e [ev] T e [ev] ESEL T e [ev] CAV 40 CAV CAV δ t [μs] (g) δ t [μs] (h) δ t [μs] (i) Obrázek 6.8: Podmíněné průměry (a c) potenciálu, plovoucího potenciálu, (d f) hustoty a (g i) teploty ve 3 radiálních pozicích pro experimentální i modelová data.
59 KAPITOLA 6. POROVNÁNÍ VÝSLEDKŮ ESEL probe #13 r r LCFS =20mm, ASDEX r r LCFS =22mm 1.5 ESEL probe #15 r r LCFS =31mm, ASDEX r r LCFS =30mm 1 ESEL probe #17 r r LCFS =41mm, ASDEX r r LCFS =39mm (CAV μ a )/σ a φ ESEL φ 2 bpp V fl ESEL V fl2 (CAV μ a )/σ a φ ESEL φ 2 bpp V fl ESEL V fl2 (CAV μ a )/σ a φ ESEL φ 2 bpp V fl ESEL V fl δ t [μs] (a) δ t [μs] (b) δ t [μs] (c) 5 4 n ESEL n e n ESEL n e n ESEL n e (CAV μ n )/σ n 2 1 (CAV μ n )/σ n (CAV μ n )/σ n δ t [μs] (d) δ t [μs] (e) δ t [μs] (f) T e ESEL T e T e ESEL T e 4 3 T e ESEL T e (CAV μ Te )/σ Te (CAV μ Te )/σ Te (CAV μ Te )/σ Te δ t [μs] δ t [μs] δ t [μs] (g) (h) (i) Obrázek 6.9: Podmíněné průměry (a c) potenciálu, plovoucího potenciálu, (d f) hustoty a (g i) teploty normalizované na směrodatnou odchylku spočtené ve 3 radiálních pozicích pro experimentální i modelová data.
60 Závěr Diplomová práce mi přinesla řadu nových zkušeností, poznatků i dovedností. Vyzkoušel jsem si vědeckou práci od ryze technické optimalizace diagnostiky, přes experimentální měření a rozsáhlé zpracování dat, až po jejich porovnání s numerickým modelem. Prvním hmatatelným výsledkem mé práce je přispění k tomu, že obě reciproké sondy tokamaku Compass již mohly být otestovány během experimentálních kampaní, poskytly měření parametrů plazmatu ve SOL a je možné je využívat v rutinním provozu. To umožnilo změření charakteristické šířky SOL pro pokles paralelního toku energie λ q SOL kruhového plazmatu a poskytlo výsledky do mezinárodní databáze podobných měření s účelem predikce této veličiny pro tokamak ITER. V dnešní fyzice plazmatu hrají klíčovou roli numerické simulace. Proto věřím, že přínosem bude i třetí část mé práce porovnání experimentálních dat s numerickým modelem ESEL, které by mělo přispět k rozvoji modelu, tak aby lépe popisoval skutečnost. Všechny zmiňované oblasti nicméně nejsou uzavřené a je třeba v práci dále pokračovat pohyb reciprokých sond dále optimalizovat a současně vyvinout odolnější hlavice, aby bylo možné dosáhnout hlubších částí plazmatu; z databáze měření charakteristické šířky SOL λ q SOL v mezinárodní spolupráci sestavit škálování hodnot pro ITER; porovnat výstupy numerického modelu ESEL s dalšími experimentálními pozorováními a příp. navrhnout vhodné úpravy modelu tak, aby lépe popisoval realitu. 61
61 Část IV Dodatky 62
62 Dodatek A Základy pravděpodobnosti a statistiky Data poskytovaná sondovými měřeními mají charakter náhodných veličin. Užitečnou informaci mohou poskytnout většinou až po zpracování statistickými metodami. Vzhledem k tomu, že to je velice rozsáhlý obor, přináším zde pouze stručný výčet v této práci potřebných pojmů a vztahů mnohdy bez exaktních definic (se všemi potřebnými předpoklady atd.). Zcela základní výrazy přebírám tak, jak se běžně užívají viz např. [30]. A.1 Distribuční funkce, hustota pravděpodobnosti Distribuční funkce F vyjadřuje pravděpodobnost, že náhodná funkce nabude hodnoty menší než nebo rovné x, tedy F (x) = P(X x). (A.1) Absolutně spojitá náhodná veličina je taková náhodná veličina, pro kterou existuje nezáporná reálná funkce f(x) taková, že pro každé x R platí F (x) = x f(t)dt. (A.2) Funkce f(x) se nazývá hustota pravděpodobnosti. 63
63 DODATEK A. ZÁKLADY PRAVDĚPODOBNOSTI A STATISTIKY 64 A.2 Momenty náhodných veličin X a Y v následujícím textu značí náhodné veličiny. normování hustoty pr.: 1 = střední hodnota: EX = µ = rozptyl: VarX = σ 2 = směrodatná odchylka: σ = koeficient šikmosti: S = koeficient špičatosti: K = k-tý obecný moment: µ k = k-tý centrální moment: µ k = ( f(x)dx xf(x)dx (A.3) (A.4) (x µ) 2 f(x)dx (A.5) (x µ) 2 f(x)dx ) 1 2 (A.6) (x µ) 3 f(x)dx/σ 3 (A.7) (x µ) 4 f(x)dx/σ 4 3 (A.8) x k f(x)dx/σ k (A.9) (x µ) k f(x)dx/σ k (A.10) kovariance náh. veličin: Cov(X, Y ) = E[(X EX)(Y EY )] (A.11) koeficient korelace: ρ(x, Y ) = Cov(X, Y ) Var(X)Var(Y ) (A.12) Střední hodnota se někdy též značí jako x příp. x. A.3 Výběrové statistiky N-tici nezávislých náhodných veličin X 1,..., X n, stejně rozdělených s distribuční funkcí F, nazýváme náhodný výběr z rozdělení F. Podobnými charakteristikami jaké se používají pro rozdělení pravděpodobnosti lze popsat i náhodný výběr. Mluvíme pak o výběrových statistikách. Výběrové statistiky se používají k odhadu charakteristik rozdělení pravděpodobnosti náhodných veličin výběru. Výběrový průměr X n = 1 n n X i, i=1 (A.13) protějšek střední hodnoty. Pokud EX i = µ a VarX i = σ 2, potom EX n = µ a VarX n = σ 2 /n.
64 DODATEK A. ZÁKLADY PRAVDĚPODOBNOSTI A STATISTIKY 65 Výběrový rozptyl protějšek rozptylu, Es 2 n = σ 2. Výběrová směrodatná odchylka Výběrový k-tý moment s 2 n = 1 n 1 [ 1 s n = n 1 n ( ) 2 Xi X n, (A.14) i=1 n i=1 ( Xi X n ) 2 ] 1 2. (A.15) m k = 1 n n Xi k, k = 1, 2,... i=1 (A.16) A.4 Vzájemná korelace Významnou pomůckou pro vyhodnocení náhodných procesů (např. v čase se vyvíjejícího signálu Langmuirovy sondy) je vzájemná korelační funkce a autokorelační funkce. Vzájemnou korelační funkci slabě stacionárních náhodných procesů X t a Y t definujeme jako ρ X,Y (τ) ρ(x t, Y t+τ ) = E [(X t µ X )(Y t+τ µ Y )] σ X σ Y. (A.17) t čísluje např. jednotlivá měření v čase (vzorky signálu), příp. prostorovou pozici apod. Vzájemná korelační funkce nabývá hodnoty -1 až 1 a popisuje míru závislosti náhodných procesů. Např. pro 2 shodné signály s časovým posunem bude vzájemná korelační funkce nabývat 1 pro τ rovné posunutí signálů. Jako o autokorelační funkci náhodného procesu X t mluvíme o funkci ρ X,X (τ). V experimentální praxi odhadujeme střední hodnotu µ X a rozptyl σ X výběrovým průměrem a výběrovým rozptylem souboru naměřených dat X. A.5 Nelineární regresní analýza Jako regresní analýza se obecně označuje řešení úlohy z n bodů dat určit m neznámých parametrů β 1,..., β m závislosti Y k = f(x k ; β 1,..., β m ) + e k, k = 1,..., n (A.18) kde x označuje nezávisle proměnnou (vysvětlující proměnnou), Y značí vysvětlovanou proměnnou a e k jsou náhodné veličiny s nulovými středními hodnotami a neznámými rozptyly σ 2 [6].
65 DODATEK A. ZÁKLADY PRAVDĚPODOBNOSTI A STATISTIKY 66 Hledaná závislost se nazývá model. Regresní modely lze rozdělit na lineární a nelineární vzhledem ke koeficientům β j. Typickým příkladem linearizovatelného nelineárního modelu je exponenciální voltampérová charakteristika (2.4) při sondových měřeních Y k = I ( ( ( )) ) e U k ; Isat, i U fl, T e + ek = Isat i (Uk U fl ) 1 exp + e k. (A.19) k B T e Neznámé parametry jsou zde β = [ I i sat, U fl, T e ]. Odhadem neznámého vektoru β bude vektor b, který minimalizuje výraz S(β) = n [Y k I k ] 2. (A.20) k=1 Směrodatné odchylky hledaných parametrů pak lze odhadnout jako [σ I isat, σ Ufl, σ Te ] = u α S(β) n m [F (b) IF (b)] 1, m = 3, (A.21) kde u α je koeficient spolehlivosti pro zvolenou úroveň spolehlivosti α a matice F je definovaná jako ( ) [ f (xk, β) I F kj = F =, e ( Isat i I ), e ( I i sat I ) ] (U U fl ). (A.22) β j Isat i k B T e k B Te 2 Jako indikátor síly závislosti mezi závisle proměnnou veličinou a nezávislou veličinou tj. jakési kvality fitu lze využít koeficient determinace definovaný jako R 2 = n i=1 ( Yk Y ) 2 n i=1 ( Ik I ) 2, (A.23) příp. adjustovaný koeficient determinace Radj 2 = 1 (1 R 2 ) n 1, m = 3. (A.24) n m
66 Dodatek B GUI ovládání reciprokých sond Zde naleznete stručný návod k ovládání reciprokých sond tokamaku Compass za pomoci GUI popisovaného v sekci Grafické uživatelské rozhraní softwaru horizontální sondy je znázorněno na obrázku B.1, vertikální sondy pak na obrázku B.2. Menu umožňuje uložení aktuálního nastavení sondy do zvoleného souboru, příp. načtení dříve uloženého nastavení a ukončení programu (klávesová zkratka Ctrl + Q). Mimo to programy zaznamenávají do textového souboru jakýsi logbook práce sond (změny nastavení, poloha sondy, detekce externího triggeru, provedení reciprokého pohybu atd.). Podle data a času tak není problém dohledat např. nastavení sondy při některém z měření. Do samostatných souborů se též zaznamenává časový průběh každého reciprokého pohybu (poloha hlavice sondy v čase). Program pomocí vytváření zámkového souboru povoluje spuštění pouze 1 instance programu. Po vykonání reciprokého pohybu se automaticky dotáže na místo a název pro uložení souboru s daty časového průběhu polohy hlavice sondy. Vysvětlivky k obrázkům B.1 a B.2: 1. Kontrolka navázání komunikace se sondou (mikrokontrolérem dspic). 2. Zapnutí/vypnutí automatické detekce externího triggeru. 3. Aktuální poloha vozíku pomalého posuvu sondy a tlačítko pro vyvolání dialogového okna pro pomalý posuv na požadovanou pozici. 4. Výběr počtu reciprokých pohybů po obdržení triggeru. 5. Nastavená prodleva mezi triggerem a prvním reciprokým pohybem a tlačítko pro její změnu. 6. Nastavená prodleva mezi triggerem a druhým reciprokým pohybem a tlačítko pro její změnu. 7. Nastavení časů přepnutí pneumatického ventilu pro pohon rychlého reciprokého pohybu (nastavení hloubky pohybu, dobrždění apod.). 8. Logbook. 67
67 DODATEK B. GUI OVLÁDÁNÍ RECIPROKÝCH SOND Pole pro zadání vlastních poznámek do logbooku (např. číslo výstřelu apod.). 10. Ruční spuštění externího triggeru. 11. Zastavení akce (pomalého posuvu). 12. Zapnutí/vypnutí automatického připojení napájení hrotů sondy při reciprokém pohybu (měření Isat). 13. Znázornění aktuální polohy sondy vůči komoře tokamaku. 14. Časový průběh polohy hlavice sondy při posledním reciprokém pohybu. 15. Pomalé zasunutí vertikální sondy. 16. Pomalé vysunutí vertikální sondy. 17. Indikátor aktuálního napětí kondenzátoru pro napájení sond hlavice a tlačítko pro jeho změnu.
68 DODATEK B. GUI OVLÁDÁNÍ RECIPROKÝCH SOND 69 Obrázek B.1: Grafické uživatelské rozhraní ovládacího systému horizontální reciproké sondy.
69 DODATEK B. GUI OVLÁDÁNÍ RECIPROKÝCH SOND 70 Obrázek B.2: Grafické uživatelské rozhraní ovládacího systému vertikální reciproké sondy.
DOUTNAVÝ VÝBOJ. Další technologie využívající doutnavý výboj
 DOUTNAVÝ VÝBOJ Další technologie využívající doutnavý výboj Plazma doutnavého výboje je využíváno v technologiích depozice povlaků nebo modifikace povrchů. Jedná se zejména o : - depozici povlaků magnetronovým
DOUTNAVÝ VÝBOJ Další technologie využívající doutnavý výboj Plazma doutnavého výboje je využíváno v technologiích depozice povlaků nebo modifikace povrchů. Jedná se zejména o : - depozici povlaků magnetronovým
Petr Zikán. Studentský seminář, Březen 2011
 Sondová měření v plazmatu Petr Zikán Studentský seminář, Březen 2011 Přehled prezentace 1 Child-Langmuirův zákon Přehled prezentace 1 Child-Langmuirův zákon 2 Sheath a pre-sheath Přehled prezentace 1 Child-Langmuirův
Sondová měření v plazmatu Petr Zikán Studentský seminář, Březen 2011 Přehled prezentace 1 Child-Langmuirův zákon Přehled prezentace 1 Child-Langmuirův zákon 2 Sheath a pre-sheath Přehled prezentace 1 Child-Langmuirův
Vojtěch Hrubý: Esej pro předmět Seminář EVF
 Vojtěch Hrubý: Esej pro předmět Seminář EVF Plazma Pod pojmem plazma většinou myslíme plynné prostředí, které se skládá z neutrálních částic, iontů a elektronů. Poměr množství neutrálních a nabitých částic
Vojtěch Hrubý: Esej pro předmět Seminář EVF Plazma Pod pojmem plazma většinou myslíme plynné prostředí, které se skládá z neutrálních částic, iontů a elektronů. Poměr množství neutrálních a nabitých částic
Základní experiment fyziky plazmatu
 Základní experiment fyziky plazmatu D. Vašíček 1, R. Skoupý 2, J. Šupík 3, M. Kubič 4 1 Gymnázium Velké Meziříčí, david.vasicek@centrum.cz 2 Gymnázium Ostrava-Hrabůvka příspěvková organizace, jansupik@gmail.com
Základní experiment fyziky plazmatu D. Vašíček 1, R. Skoupý 2, J. Šupík 3, M. Kubič 4 1 Gymnázium Velké Meziříčí, david.vasicek@centrum.cz 2 Gymnázium Ostrava-Hrabůvka příspěvková organizace, jansupik@gmail.com
Plazma. magnetosféra komety. zbytky po výbuchu supernovy. formování hvězdy. slunce
 magnetosféra komety zbytky po výbuchu supernovy formování hvězdy slunce blesk polární záře sluneční vítr - plazma je označována jako čtvrté skupenství hmoty - plazma je plyn s významným množstvím iontů
magnetosféra komety zbytky po výbuchu supernovy formování hvězdy slunce blesk polární záře sluneční vítr - plazma je označována jako čtvrté skupenství hmoty - plazma je plyn s významným množstvím iontů
Skalární a vektorový popis silového pole
 Skalární a vektorový popis silového pole Elektrické pole Elektrický náboj Q [Q] = C Vlastnost materiálových objektů Interakce (vzájemné silové působení) Interakci (vzájemné silové působení) mezi dvěma
Skalární a vektorový popis silového pole Elektrické pole Elektrický náboj Q [Q] = C Vlastnost materiálových objektů Interakce (vzájemné silové působení) Interakci (vzájemné silové působení) mezi dvěma
Theory Česky (Czech Republic)
 Q3-1 Velký hadronový urychlovač (10 bodů) Než se do toho pustíte, přečtěte si prosím obecné pokyny v oddělené obálce. V této úloze se budeme bavit o fyzice částicového urychlovače LHC (Large Hadron Collider
Q3-1 Velký hadronový urychlovač (10 bodů) Než se do toho pustíte, přečtěte si prosím obecné pokyny v oddělené obálce. V této úloze se budeme bavit o fyzice částicového urychlovače LHC (Large Hadron Collider
ELEKTRICKÝ PROUD ELEKTRICKÝ ODPOR (REZISTANCE) REZISTIVITA
 ELEKTRICKÝ PROD ELEKTRICKÝ ODPOR (REZISTANCE) REZISTIVITA 1 ELEKTRICKÝ PROD Jevem Elektrický proud nazveme usměrněný pohyb elektrických nábojů. Např.:- proud vodivostních elektronů v kovech - pohyb nabitých
ELEKTRICKÝ PROD ELEKTRICKÝ ODPOR (REZISTANCE) REZISTIVITA 1 ELEKTRICKÝ PROD Jevem Elektrický proud nazveme usměrněný pohyb elektrických nábojů. Např.:- proud vodivostních elektronů v kovech - pohyb nabitých
Úvod do vln v plazmatu
 Úvod do vln v plazmatu Co je to vlna? (fázová a grupová rychlost) Přehled vln v plazmatu Plazmové oscilace Iontové akustické vlny Horní hybridní frekvence Elektrostatické iontové cyklotronové vlny Dolní
Úvod do vln v plazmatu Co je to vlna? (fázová a grupová rychlost) Přehled vln v plazmatu Plazmové oscilace Iontové akustické vlny Horní hybridní frekvence Elektrostatické iontové cyklotronové vlny Dolní
Základy vakuové techniky
 Základy vakuové techniky Střední rychlost plynů Rychlost molekuly v p = (2 k N A ) * (T/M 0 ), N A = 6. 10 23 molekul na mol (Avogadrova konstanta), k = 1,38. 10-23 J/K.. Boltzmannova konstanta, T.. absolutní
Základy vakuové techniky Střední rychlost plynů Rychlost molekuly v p = (2 k N A ) * (T/M 0 ), N A = 6. 10 23 molekul na mol (Avogadrova konstanta), k = 1,38. 10-23 J/K.. Boltzmannova konstanta, T.. absolutní
ATOMOVÁ SPEKTROMETRIE
 ATOMOVÁ SPEKTROMETRIE Atomová spektrometrie valenčních e - 1. OES (AES). AAS 3. AFS 1 Atomová spektra čárová spektra Tok záření P - množství zářivé energie (Q E ) přenesené od zdroje za jednotku času.
ATOMOVÁ SPEKTROMETRIE Atomová spektrometrie valenčních e - 1. OES (AES). AAS 3. AFS 1 Atomová spektra čárová spektra Tok záření P - množství zářivé energie (Q E ) přenesené od zdroje za jednotku času.
Počítačový model plazmatu. Vojtěch Hrubý listopad 2007
 Počítačový model plazmatu Vojtěch Hrubý listopad 2007 Situace Zajímá nás, co se děje v okolí kovové sondy ponořené do plazmatu. Na válcovou sondu přivedeme napětí U Očekáváme, že se okolo sondy vytvoří
Počítačový model plazmatu Vojtěch Hrubý listopad 2007 Situace Zajímá nás, co se děje v okolí kovové sondy ponořené do plazmatu. Na válcovou sondu přivedeme napětí U Očekáváme, že se okolo sondy vytvoří
ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Posuvný proud a Poyntingův vektor
 ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Posuvný proud a Poyntingův vektor Peter Dourmashkin MIT 006, překlad: Jan Pacák (007) Obsah 10. POSUVNÝ PROUD A POYNTINGŮV VEKTOR 3 10.1 ÚKOLY 3 10. POSUVNÝ
ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Posuvný proud a Poyntingův vektor Peter Dourmashkin MIT 006, překlad: Jan Pacák (007) Obsah 10. POSUVNÝ PROUD A POYNTINGŮV VEKTOR 3 10.1 ÚKOLY 3 10. POSUVNÝ
Úvod do fyziky plazmatu
 Úvod do fyziky plazmatu Plazma Velmi často se o plazmatu mluví jako o čtvrtém skupenství hmoty Název plazma pro ionizovaný plyn poprvé použil Irwing Langmuir (1881 1957) v roce 1928, protože mu chováním
Úvod do fyziky plazmatu Plazma Velmi často se o plazmatu mluví jako o čtvrtém skupenství hmoty Název plazma pro ionizovaný plyn poprvé použil Irwing Langmuir (1881 1957) v roce 1928, protože mu chováním
Plazmové metody. Základní vlastnosti a parametry plazmatu
 Plazmové metody Základní vlastnosti a parametry plazmatu Atom je základní částice běžné hmoty. Částice, kterou již chemickými prostředky dále nelze dělit a která definuje vlastnosti daného chemického prvku.
Plazmové metody Základní vlastnosti a parametry plazmatu Atom je základní částice běžné hmoty. Částice, kterou již chemickými prostředky dále nelze dělit a která definuje vlastnosti daného chemického prvku.
Záření KZ. Význam. Typy netermálního záření. studium zdrojů a vlastností KZ. energetické ztráty KZ. synchrotronní. brzdné.
 Zářivé procesy Podmínky vyzařování, Larmorův vzorec, Thomsonův rozptyl, synchrotronní záření, brzdné záření, Comptonův rozptyl, čerenkovské záření, spektum zdroje KZ Záření KZ Význam studium zdrojů a vlastností
Zářivé procesy Podmínky vyzařování, Larmorův vzorec, Thomsonův rozptyl, synchrotronní záření, brzdné záření, Comptonův rozptyl, čerenkovské záření, spektum zdroje KZ Záření KZ Význam studium zdrojů a vlastností
Vybrané technologie povrchových úprav. Základy vakuové techniky Doc. Ing. Karel Daďourek 2006
 Vybrané technologie povrchových úprav Základy vakuové techniky Doc. Ing. Karel Daďourek 2006 Střední rychlost plynů Rychlost molekuly v p = (2 k N A ) * (T/M 0 ), N A = 6. 10 23 molekul na mol (Avogadrova
Vybrané technologie povrchových úprav Základy vakuové techniky Doc. Ing. Karel Daďourek 2006 Střední rychlost plynů Rychlost molekuly v p = (2 k N A ) * (T/M 0 ), N A = 6. 10 23 molekul na mol (Avogadrova
ELT1 - Přednáška č. 6
 ELT1 - Přednáška č. 6 Elektrotechnická terminologie a odborné výrazy, měřicí jednotky a činitelé, které je ovlivňují. Rozdíl potenciálů, elektromotorická síla, napětí, el. napětí, proud, odpor, vodivost,
ELT1 - Přednáška č. 6 Elektrotechnická terminologie a odborné výrazy, měřicí jednotky a činitelé, které je ovlivňují. Rozdíl potenciálů, elektromotorická síla, napětí, el. napětí, proud, odpor, vodivost,
Gyrační poloměr jako invariant relativistického pohybu. 2 Nerovnoměrný pohyb po kružnici v R 2
 Gyrační poloměr jako invariant relativistického pohybu nabité částice v konfiguraci rovnoběžného konstantního vnějšího elektromagnetického pole 1 Popis problému Uvažujme pohyb nabité částice v E 3 v takové
Gyrační poloměr jako invariant relativistického pohybu nabité částice v konfiguraci rovnoběžného konstantního vnějšího elektromagnetického pole 1 Popis problému Uvažujme pohyb nabité částice v E 3 v takové
Opakování: shrnutí základních poznatků o struktuře atomu
 11. Polovodiče Polovodiče jsou krystalické nebo amorfní látky, jejichž elektrická vodivost leží mezi elektrickou vodivostí kovů a izolantů a závisí na teplotě nebo dopadajícím optickém záření. Elektrické
11. Polovodiče Polovodiče jsou krystalické nebo amorfní látky, jejichž elektrická vodivost leží mezi elektrickou vodivostí kovů a izolantů a závisí na teplotě nebo dopadajícím optickém záření. Elektrické
ČÁST V F Y Z I K Á L N Í P O L E. 18. Gravitační pole 19. Elektrostatické pole 20. Elektrický proud 21. Magnetické pole 22. Elektromagnetické pole
 Kde se nacházíme? ČÁST V F Y Z I K Á L N Í P O L E 18. Gravitační pole 19. Elektrostatické pole 20. Elektrický proud 21. Magnetické pole 22. Elektromagnetické pole Mapování elektrického pole -jak? Detektorem.Intenzita
Kde se nacházíme? ČÁST V F Y Z I K Á L N Í P O L E 18. Gravitační pole 19. Elektrostatické pole 20. Elektrický proud 21. Magnetické pole 22. Elektromagnetické pole Mapování elektrického pole -jak? Detektorem.Intenzita
O symetrii tokamaku. Vtomto článku opustíme tematiku konkrétních. Jan Mlynář. 50 let UFP AV ČR
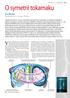 č. 4 Čs. čas. fyz. 59 (2009) 207 O symetrii tokamaku Jan Mlynář Ústav fyziky plazmatu AV ČR, v. v. i., Za Slovankou 3, 182 00 Praha 8 Loňské čtvrté číslo Čs. čas. fyz. se podrobně věnovalo historii tokamaků
č. 4 Čs. čas. fyz. 59 (2009) 207 O symetrii tokamaku Jan Mlynář Ústav fyziky plazmatu AV ČR, v. v. i., Za Slovankou 3, 182 00 Praha 8 Loňské čtvrté číslo Čs. čas. fyz. se podrobně věnovalo historii tokamaků
Pokroky matematiky, fyziky a astronomie
 Pokroky matematiky, fyziky a astronomie Jan Mlynář Rovnováha plazmatu a magnetického pole v termojaderných reaktorech typu tokamak Pokroky matematiky, fyziky a astronomie, Vol. 57 (2012), No. 2, 122--139
Pokroky matematiky, fyziky a astronomie Jan Mlynář Rovnováha plazmatu a magnetického pole v termojaderných reaktorech typu tokamak Pokroky matematiky, fyziky a astronomie, Vol. 57 (2012), No. 2, 122--139
Základní zákony a terminologie v elektrotechnice
 Základní zákony a terminologie v elektrotechnice (opakování učiva SŠ, Fyziky) Určeno pro studenty komb. formy FMMI předmětu 452702 / 04 Elektrotechnika Zpracoval: Jan Dudek Prosinec 2006 Elektrický náboj
Základní zákony a terminologie v elektrotechnice (opakování učiva SŠ, Fyziky) Určeno pro studenty komb. formy FMMI předmětu 452702 / 04 Elektrotechnika Zpracoval: Jan Dudek Prosinec 2006 Elektrický náboj
vysokoteplotního plazmatu na tokamaku GOLEM
 Měření základních parametů vysokoteplotního plazmatu na tokamaku GOLEM J. Krbec 1 1 České vysoké učení technické v Praze Fakulta jaderná a fyzikálně inženýrská U3V Fyzika přátelsky / Aplikované přírodní
Měření základních parametů vysokoteplotního plazmatu na tokamaku GOLEM J. Krbec 1 1 České vysoké učení technické v Praze Fakulta jaderná a fyzikálně inženýrská U3V Fyzika přátelsky / Aplikované přírodní
VÝKONOVÉ TRANZISTORY MOS
 VÝKONOVÉ TANZSTOY MOS Pro výkonové aplikace mají tranzistory MOS přednosti: - vysoká vstupní impedance, - vysoké výkonové zesílení, - napěťové řízení, - teplotní stabilita PNP FNKE TANZSTO MOS Prahové
VÝKONOVÉ TANZSTOY MOS Pro výkonové aplikace mají tranzistory MOS přednosti: - vysoká vstupní impedance, - vysoké výkonové zesílení, - napěťové řízení, - teplotní stabilita PNP FNKE TANZSTO MOS Prahové
Šíření tepla. Obecnéprincipy
 Šíření tepla Obecnéprincipy Šíření tepla Obecně: Šíření tepla je výměna tepelné energie v tělese nebo mezi tělesy, která nastává při rozdílu teplot. Těleso s vyšší teplotou má větší tepelnou energii. Šíření
Šíření tepla Obecnéprincipy Šíření tepla Obecně: Šíření tepla je výměna tepelné energie v tělese nebo mezi tělesy, která nastává při rozdílu teplot. Těleso s vyšší teplotou má větší tepelnou energii. Šíření
FYZIKA II. Petr Praus 10. Přednáška Magnetické pole v látce
 FYZIKA II Petr Praus 10. Přednáška Magnetické pole v látce Osnova přednášky Magnetické pole v látkovém prostředí, Ampérovy proudové smyčky, veličiny B, M, H materiálové vztahy, susceptibilita a permeabilita
FYZIKA II Petr Praus 10. Přednáška Magnetické pole v látce Osnova přednášky Magnetické pole v látkovém prostředí, Ampérovy proudové smyčky, veličiny B, M, H materiálové vztahy, susceptibilita a permeabilita
Interakce laserového impulsu s plazmatem v souvislosti s inerciální fúzí zapálenou rázovou vlnou
 Interakce laserového impulsu s plazmatem v souvislosti s inerciální fúzí zapálenou rázovou vlnou Autor práce: Petr Valenta Vedoucí práce: Ing. Ondřej Klimo, Ph.D. Konzultanti: prof. Ing. Jiří Limpouch,
Interakce laserového impulsu s plazmatem v souvislosti s inerciální fúzí zapálenou rázovou vlnou Autor práce: Petr Valenta Vedoucí práce: Ing. Ondřej Klimo, Ph.D. Konzultanti: prof. Ing. Jiří Limpouch,
Užití mikrovlnné techniky v termojaderné fúzi. A. Křivská 1,2. Ústav fyziky plazmatu AV ČR, v.v.i., Česká republika
 Užití mikrovlnné techniky v termojaderné fúzi A. Křivská 1,2 1 Ústav fyziky plazmatu AV ČR, v.v.i., Česká republika 2 České vysoké učení technické v Praze, Fakulta elektrotechnická, katedra telekomunikační
Užití mikrovlnné techniky v termojaderné fúzi A. Křivská 1,2 1 Ústav fyziky plazmatu AV ČR, v.v.i., Česká republika 2 České vysoké učení technické v Praze, Fakulta elektrotechnická, katedra telekomunikační
Hydromechanické procesy Obtékání těles
 Hydromechanické procesy Obtékání těles M. Jahoda Klasifikace těles 2 Typy externích toků dvourozměrné osově symetrické třírozměrné (s/bez osy symetrie) nebo: aerodynamické vs. neaerodynamické Odpor a vztlak
Hydromechanické procesy Obtékání těles M. Jahoda Klasifikace těles 2 Typy externích toků dvourozměrné osově symetrické třírozměrné (s/bez osy symetrie) nebo: aerodynamické vs. neaerodynamické Odpor a vztlak
7 Hallůvjevvkovuapolovodiči
 Zadání 7 Hallůvjevvkovuapolovodiči 1. Změřte Hallův koeficient pro kov a polovodič při laboratorní teplotě. 2. Změřte měrnou vodivost obou vzorků. 3. Pro několik hodnot proudu a magnetické indukce ověřte,
Zadání 7 Hallůvjevvkovuapolovodiči 1. Změřte Hallův koeficient pro kov a polovodič při laboratorní teplotě. 2. Změřte měrnou vodivost obou vzorků. 3. Pro několik hodnot proudu a magnetické indukce ověřte,
Ionizační manometry. Při ionizaci plynu o koncentraci n nejsou ionizovány všechny molekuly, ale jenom část z nich n i = γn ; γ < 1.
 Ionizační manometry Princip: ionizace molekul a měření počtu nabitých částic Rozdělení podle způsobu ionizace: Manometry se žhavenou katodou Manometry se studenou katodou Manometry s radioaktivním zářičem
Ionizační manometry Princip: ionizace molekul a měření počtu nabitých částic Rozdělení podle způsobu ionizace: Manometry se žhavenou katodou Manometry se studenou katodou Manometry s radioaktivním zářičem
Úvod do fyziky plazmatu
 Úvod do fyziky plazmatu Lenka Zajíčková, Ústav fyz. elektroniky Doporučená literatura: J. A. Bittencourt, Fundamentals of Plasma Physics, 2003 (3. vydání) ISBN 85-900100-3-1 Navazující a související přednášky:
Úvod do fyziky plazmatu Lenka Zajíčková, Ústav fyz. elektroniky Doporučená literatura: J. A. Bittencourt, Fundamentals of Plasma Physics, 2003 (3. vydání) ISBN 85-900100-3-1 Navazující a související přednášky:
Přehled veličin elektrických obvodů
 Přehled veličin elektrických obvodů Ing. Martin Černík, Ph.D Projekt ESF CZ.1.7/2.2./28.5 Modernizace didaktických metod a inovace. Elektrický náboj - základní vlastnost některých elementárních částic
Přehled veličin elektrických obvodů Ing. Martin Černík, Ph.D Projekt ESF CZ.1.7/2.2./28.5 Modernizace didaktických metod a inovace. Elektrický náboj - základní vlastnost některých elementárních částic
Metodický návod: 5. Zvyšování vnějšího napětí na 3 V. Dochází k dalšímu zakřivování hladin a rozšiřování hradlové vrstvy.
 Metodický návod: 1. Spuštění souborem a.4.3_p-n.exe. Zobrazeny jsou oddělené polovodiče P a N, majoritní nositelé náboje (elektrony červené, díry modré), ionty příměsí (čtverečky) a Fermiho energetické
Metodický návod: 1. Spuštění souborem a.4.3_p-n.exe. Zobrazeny jsou oddělené polovodiče P a N, majoritní nositelé náboje (elektrony červené, díry modré), ionty příměsí (čtverečky) a Fermiho energetické
Základní otázky pro teoretickou část zkoušky.
 Základní otázky pro teoretickou část zkoušky. Platí shodně pro prezenční i kombinovanou formu studia. 1. Síla současně působící na elektrický náboj v elektrickém a magnetickém poli (Lorentzova síla) 2.
Základní otázky pro teoretickou část zkoušky. Platí shodně pro prezenční i kombinovanou formu studia. 1. Síla současně působící na elektrický náboj v elektrickém a magnetickém poli (Lorentzova síla) 2.
Technika vysokých napětí. Elektrické výboje v elektroenergetice
 Elektrické výboje v elektroenergetice Korónový výboj V homogenním elektrickém poli dochází k celkovému přeskoku mezi elektrodami najednou U nehomogenních uspořádání dochází k optickým a akustickým projevům
Elektrické výboje v elektroenergetice Korónový výboj V homogenním elektrickém poli dochází k celkovému přeskoku mezi elektrodami najednou U nehomogenních uspořádání dochází k optickým a akustickým projevům
TECHNIKA VYSOKÝCH NAPĚŤÍ. #4 Elektrické výboje v elektroenergetice
 TECHNIKA VYSOKÝCH NAPĚŤÍ #4 Elektrické výboje v elektroenergetice Korónový výboj V homogenním elektrickém poli dochází k celkovému přeskoku mezi elektrodami najednou U nehomogenních uspořádání dochází
TECHNIKA VYSOKÝCH NAPĚŤÍ #4 Elektrické výboje v elektroenergetice Korónový výboj V homogenním elektrickém poli dochází k celkovému přeskoku mezi elektrodami najednou U nehomogenních uspořádání dochází
Základy magnetohydrodynamiky. aneb MHD v jedné přednášce?! To si snad děláte legraci!
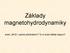 Základy magnetohydrodynamiky aneb MHD v jedné přednášce?! To si snad děláte legraci! Osnova Magnetohydrodynamika Maxwellovy rovnice Aplikace pinče, MHD generátory, geofyzika, astrofyzika... Magnetohydrodynamika
Základy magnetohydrodynamiky aneb MHD v jedné přednášce?! To si snad děláte legraci! Osnova Magnetohydrodynamika Maxwellovy rovnice Aplikace pinče, MHD generátory, geofyzika, astrofyzika... Magnetohydrodynamika
VEDENÍ ELEKTRICKÉHO PROUDU V LÁTKÁCH
 VEDENÍ ELEKTRICKÉHO PROUDU V LÁTKÁCH Jan Hruška TV-FYZ Ahoj, tak jsme tady znovu a pokusíme se Vám vysvětlit problematiku vedení elektrického proudu v látkách. Co je to vlastně elektrický proud? Na to
VEDENÍ ELEKTRICKÉHO PROUDU V LÁTKÁCH Jan Hruška TV-FYZ Ahoj, tak jsme tady znovu a pokusíme se Vám vysvětlit problematiku vedení elektrického proudu v látkách. Co je to vlastně elektrický proud? Na to
Detekce nabitých částic Jak se ztrácí energie průchodem částice hmotou?
 Detekce nabitých částic Jak se ztrácí energie průchodem částice hmotou? 10/20/2004 1 Bethe Blochova formule (1) je maximální možná předaná energie elektronu N r e - vogadrovo čislo - klasický poloměr elektronu
Detekce nabitých částic Jak se ztrácí energie průchodem částice hmotou? 10/20/2004 1 Bethe Blochova formule (1) je maximální možná předaná energie elektronu N r e - vogadrovo čislo - klasický poloměr elektronu
Atom vodíku. Nejjednodušší soustava: p + e Řešitelná exaktně. Kulová symetrie. Potenciální energie mezi p + e. e =
 Atom vodíku Nejjednodušší soustava: p + e Řešitelná exaktně Kulová symetrie Potenciální energie mezi p + e V 2 e = 4πε r 0 1 Polární souřadnice využití kulové symetrie atomu Ψ(x,y,z) Ψ(r,θ, φ) x =? y=?
Atom vodíku Nejjednodušší soustava: p + e Řešitelná exaktně Kulová symetrie Potenciální energie mezi p + e V 2 e = 4πε r 0 1 Polární souřadnice využití kulové symetrie atomu Ψ(x,y,z) Ψ(r,θ, φ) x =? y=?
ZÁŘENÍ V ASTROFYZICE
 ZÁŘENÍ V ASTROFYZICE Plazmový vesmír Uvádí se, že 99 % veškeré hmoty ve vesmíru je v plazmovém skupenství (hvězdy, mlhoviny, ) I na Zemi se vyskytuje plazma, např. v podobě blesků, polárních září Ve sluneční
ZÁŘENÍ V ASTROFYZICE Plazmový vesmír Uvádí se, že 99 % veškeré hmoty ve vesmíru je v plazmovém skupenství (hvězdy, mlhoviny, ) I na Zemi se vyskytuje plazma, např. v podobě blesků, polárních září Ve sluneční
TERMOMECHANIKA 15. Základy přenosu tepla
 FSI VUT v Brně, Energetický ústav Odbor termomechaniky a techniky prostředí Prof. Ing. Milan Pavelek, CSc. TERMOMECHANIKA 15. Základy přenosu tepla OSNOVA 15. KAPITOLY Tři mechanizmy přenosu tepla Tepelný
FSI VUT v Brně, Energetický ústav Odbor termomechaniky a techniky prostředí Prof. Ing. Milan Pavelek, CSc. TERMOMECHANIKA 15. Základy přenosu tepla OSNOVA 15. KAPITOLY Tři mechanizmy přenosu tepla Tepelný
4. Stanovení teplotního součinitele odporu kovů
 4. Stanovení teplotního součinitele odporu kovů 4.. Zadání úlohy. Změřte teplotní součinitel odporu mědi v rozmezí 20 80 C. 2. Změřte teplotní součinitel odporu platiny v rozmezí 20 80 C. 3. Vyneste graf
4. Stanovení teplotního součinitele odporu kovů 4.. Zadání úlohy. Změřte teplotní součinitel odporu mědi v rozmezí 20 80 C. 2. Změřte teplotní součinitel odporu platiny v rozmezí 20 80 C. 3. Vyneste graf
Vibrace atomů v mřížce, tepelná kapacita pevných látek
 Vibrace atomů v mřížce, tepelná kapacita pevných látek Atomy vázané v mřížce nejsou v klidu. Míru jejich pohybu vyjadřuje podobně jako u plynů a kapalin teplota. - Elastické vlny v kontinuu neatomární
Vibrace atomů v mřížce, tepelná kapacita pevných látek Atomy vázané v mřížce nejsou v klidu. Míru jejich pohybu vyjadřuje podobně jako u plynů a kapalin teplota. - Elastické vlny v kontinuu neatomární
Charakterizace fluktuací okrajového plazmatu tokamaku COMPASS. Characterization of edge plasma fluctuations in tokamak COMPASS
 České vysoké učení technické v Praze Fakulta jaderná a fyzikálně inženýrská Charakterizace fluktuací okrajového plazmatu tokamaku COMPASS Characterization of edge plasma fluctuations in tokamak COMPASS
České vysoké učení technické v Praze Fakulta jaderná a fyzikálně inženýrská Charakterizace fluktuací okrajového plazmatu tokamaku COMPASS Characterization of edge plasma fluctuations in tokamak COMPASS
Obr. 141: První tři Bernsteinovy iontové módy. Na vodorovné ose je bezrozměrný vlnový vektor a na svislé ose reálná část bezrozměrné frekvence.
 Mikronestability 33 m Re( ) ( m1) m1,,3, (5.18) ci Imaginární část frekvence, která je zodpovědná za útlum, razantně roste, pokud se vlny nešíří kolmo na magnetické pole. Útlum také roste s číslem módu
Mikronestability 33 m Re( ) ( m1) m1,,3, (5.18) ci Imaginární část frekvence, která je zodpovědná za útlum, razantně roste, pokud se vlny nešíří kolmo na magnetické pole. Útlum také roste s číslem módu
STACIONÁRNÍ MAGNETICKÉ POLE. Mgr. Jan Ptáčník - GJVJ - Fyzika - Elektřina a magnetismus - 3. ročník
 STACIONÁRNÍ MAGNETICKÉ POLE Mgr. Jan Ptáčník - GJVJ - Fyzika - Elektřina a magnetismus - 3. ročník Magnetické pole Vytváří se okolo trvalého magnetu. Magnetické pole vodiče Na základě experimentů bylo
STACIONÁRNÍ MAGNETICKÉ POLE Mgr. Jan Ptáčník - GJVJ - Fyzika - Elektřina a magnetismus - 3. ročník Magnetické pole Vytváří se okolo trvalého magnetu. Magnetické pole vodiče Na základě experimentů bylo
VY_32_INOVACE_6/15_ČLOVĚK A PŘÍRODA. Předmět: Fyzika Ročník: 6. Poznámka: Vodiče a izolanty Vypracoval: Pták
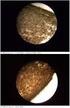 VY_32_INOVACE_6/15_ČLOVĚK A PŘÍRODA Předmět: Fyzika Ročník: 6. Poznámka: Vodiče a izolanty Vypracoval: Pták Izolant je látka, která nevede elektrický proud izolant neobsahuje volné částice s elektrický
VY_32_INOVACE_6/15_ČLOVĚK A PŘÍRODA Předmět: Fyzika Ročník: 6. Poznámka: Vodiče a izolanty Vypracoval: Pták Izolant je látka, která nevede elektrický proud izolant neobsahuje volné částice s elektrický
ρ = 0 (nepřítomnost volných nábojů)
 Učební text k přednášce UFY Světlo v izotropním látkovém prostředí Maxwellovy rovnice v izotropním látkovém prostředí: B rot + D rot H ( r, t) div D ρ rt, ( ) div B a materiálové vztahy D ε pro dielektrika
Učební text k přednášce UFY Světlo v izotropním látkovém prostředí Maxwellovy rovnice v izotropním látkovém prostředí: B rot + D rot H ( r, t) div D ρ rt, ( ) div B a materiálové vztahy D ε pro dielektrika
Elektromagnetické pole je generováno elektrickými náboji a jejich pohybem. Je-li zdroj charakterizován nábojovou hustotou ( r r
 Záření Hertzova dipólu, kulové vlny, Rovnice elektromagnetického pole jsou vektorové diferenciální rovnice a podle symetrie bývá vhodné je řešit v křivočarých souřadnicích. Základní diferenciální operátory
Záření Hertzova dipólu, kulové vlny, Rovnice elektromagnetického pole jsou vektorové diferenciální rovnice a podle symetrie bývá vhodné je řešit v křivočarých souřadnicích. Základní diferenciální operátory
Mechanika kontinua. Mechanika elastických těles Mechanika kapalin
 Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
Od kvantové mechaniky k chemii
 Od kvantové mechaniky k chemii Jan Řezáč UOCHB AV ČR 19. září 2017 Jan Řezáč (UOCHB AV ČR) Od kvantové mechaniky k chemii 19. září 2017 1 / 33 Úvod Vztah mezi molekulovou strukturou a makroskopickými vlastnostmi
Od kvantové mechaniky k chemii Jan Řezáč UOCHB AV ČR 19. září 2017 Jan Řezáč (UOCHB AV ČR) Od kvantové mechaniky k chemii 19. září 2017 1 / 33 Úvod Vztah mezi molekulovou strukturou a makroskopickými vlastnostmi
Charakteristika a mrtvá doba Geiger-Müllerova počítače
 Charakteristika a mrtvá doba Geiger-Müllerova počítače Úkol : 1. Proměřte charakteristiku Geiger-Müllerova počítače. K jednotlivým naměřeným hodnotám určete střední kvadratickou chybu a vyznačte ji do
Charakteristika a mrtvá doba Geiger-Müllerova počítače Úkol : 1. Proměřte charakteristiku Geiger-Müllerova počítače. K jednotlivým naměřeným hodnotám určete střední kvadratickou chybu a vyznačte ji do
Urychlovače částic principy standardních urychlovačů částic
 Urychlovače částic principy standardních urychlovačů částic Základní info technické zařízení, které dodává kinetickou energii částicím, které je potřeba urychlit nabité částice jsou v urychlovači urychleny
Urychlovače částic principy standardních urychlovačů částic Základní info technické zařízení, které dodává kinetickou energii částicím, které je potřeba urychlit nabité částice jsou v urychlovači urychleny
Kovy - model volných elektronů
 Kovy - model volných elektronů Kovová vazba 1. Preferuje ji většina prvků vyskytujících se v přírodě. Kov je tvořen kladně nabitými ionty (s konfigurací vzácného plynu) a relativně velmi volnými elektrony.
Kovy - model volných elektronů Kovová vazba 1. Preferuje ji většina prvků vyskytujících se v přírodě. Kov je tvořen kladně nabitými ionty (s konfigurací vzácného plynu) a relativně velmi volnými elektrony.
Vysoké frekvence a mikrovlny
 Vysoké frekvence a mikrovlny Osnova Úvod Maxwellovy rovnice Typy mikrovlnného vedení Použití ve fyzice plazmatu Úvod Mikrovlny jsou elektromagnetické vlny o vlnové délce větší než 1mm a menší než 1m, což
Vysoké frekvence a mikrovlny Osnova Úvod Maxwellovy rovnice Typy mikrovlnného vedení Použití ve fyzice plazmatu Úvod Mikrovlny jsou elektromagnetické vlny o vlnové délce větší než 1mm a menší než 1m, což
Plazma v kosmickém prostoru
 Plazma v kosmickém prostoru Literatura F. F. Chen, Úvod do fyziky plazmatu Academia, Praha, 1984 D. A. Gurnett, A. Bhattacharjee, Introduction to Plasma Physics: With Space and Laboratory Applications
Plazma v kosmickém prostoru Literatura F. F. Chen, Úvod do fyziky plazmatu Academia, Praha, 1984 D. A. Gurnett, A. Bhattacharjee, Introduction to Plasma Physics: With Space and Laboratory Applications
GAUSSŮV ZÁKON ELEKTROSTATIKY
 GAUSSŮV ZÁKON ELEKTROSTATIKY PLOCHA JAKO VEKTOR Matematický doplněk n n Elementární plocha ΔS ds Ploše přiřadíme vektor, který 1) je k této ploše kolmý 2) má velikost rovnou velikosti (obsahu) plochy Δ
GAUSSŮV ZÁKON ELEKTROSTATIKY PLOCHA JAKO VEKTOR Matematický doplněk n n Elementární plocha ΔS ds Ploše přiřadíme vektor, který 1) je k této ploše kolmý 2) má velikost rovnou velikosti (obsahu) plochy Δ
OPVK CZ.1.07/2.2.00/
 18.2.2013 OPVK CZ.1.07/2.2.00/28.0184 Cvičení z NMR OCH/NMR Mgr. Tomáš Pospíšil, Ph.D. LS 2012/2013 18.2.2013 NMR základní principy NMR Nukleární Magnetická Resonance N - nukleární (studujeme vlastnosti
18.2.2013 OPVK CZ.1.07/2.2.00/28.0184 Cvičení z NMR OCH/NMR Mgr. Tomáš Pospíšil, Ph.D. LS 2012/2013 18.2.2013 NMR základní principy NMR Nukleární Magnetická Resonance N - nukleární (studujeme vlastnosti
4.1.7 Rozložení náboje na vodiči
 4.1.7 Rozložení náboje na vodiči Předpoklady: 4101, 4102, 4104, 4105, 4106 Opakování: vodič látka, ve které se mohou volně pohybovat nosiče náboje (většinou elektrony), nemohou ji však opustit (bez doteku
4.1.7 Rozložení náboje na vodiči Předpoklady: 4101, 4102, 4104, 4105, 4106 Opakování: vodič látka, ve které se mohou volně pohybovat nosiče náboje (většinou elektrony), nemohou ji však opustit (bez doteku
BIOMECHANIKA KINEMATIKA
 BIOMECHANIKA KINEMATIKA MECHANIKA Mechanika je nejstarším oborem fyziky (z řeckého méchané stroj). Byla původně vědou, která se zabývala konstrukcí strojů a jejich činností. Mechanika studuje zákonitosti
BIOMECHANIKA KINEMATIKA MECHANIKA Mechanika je nejstarším oborem fyziky (z řeckého méchané stroj). Byla původně vědou, která se zabývala konstrukcí strojů a jejich činností. Mechanika studuje zákonitosti
Obvodové prvky a jejich
 Obvodové prvky a jejich parametry Ing. Martin Černík, Ph.D. Projekt ESF CZ.1.07/2.2.00/28.0050 Modernizace didaktických metod a inovace. Elektrický obvod Uspořádaný systém elektrických prvků a vodičů sloužící
Obvodové prvky a jejich parametry Ing. Martin Černík, Ph.D. Projekt ESF CZ.1.07/2.2.00/28.0050 Modernizace didaktických metod a inovace. Elektrický obvod Uspořádaný systém elektrických prvků a vodičů sloužící
Poloautomatizovaná VA charakteristika doutnavého výboje na tokamaku GOLEM
 Poloautomatizovaná VA charakteristika doutnavého výboje na tokamaku GOLEM O. Tinka, Š. Malec, M. Bárta Fakulta jaderná a fyzikálně inženýrská, Břehová 7, 115 19 Praha 1 malecste@fjfi.cvut.cz Abstrakt Uvažovali
Poloautomatizovaná VA charakteristika doutnavého výboje na tokamaku GOLEM O. Tinka, Š. Malec, M. Bárta Fakulta jaderná a fyzikálně inženýrská, Břehová 7, 115 19 Praha 1 malecste@fjfi.cvut.cz Abstrakt Uvažovali
Řešení: Nejdříve musíme určit sílu, kterou působí kladka proti směru pohybu padajícího vědra a napíná tak lano. Moment síly otáčení kladky je:
 Přijímací zkouška na navazující magisterské studium - 16 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Jak dlouho bude padat
Přijímací zkouška na navazující magisterské studium - 16 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Jak dlouho bude padat
Nauka o materiálu. Přednáška č.2 Poruchy krystalické mřížky
 Nauka o materiálu Přednáška č.2 Poruchy krystalické mřížky Opakování z minula Materiál Degradační procesy Vnitřní stavba atomy, vazby Krystalické, amorfní, semikrystalické Vlastnosti materiálů chemické,
Nauka o materiálu Přednáška č.2 Poruchy krystalické mřížky Opakování z minula Materiál Degradační procesy Vnitřní stavba atomy, vazby Krystalické, amorfní, semikrystalické Vlastnosti materiálů chemické,
Mlžnákomora. PavelMotal,SOŠaSOUKuřim Martin Veselý, FJFI ČVUT Praha
 Mlžnákomora PavelMotal,SOŠaSOUKuřim Martin Veselý, FJFI ČVUT Praha Historie vývoje mlžné komory Jelikož není možné částice hmoty pozorovat pouhým okem, bylo vyvinutozařízení,ježzviditelňujedráhytěchtočásticvytvářenímmlžné
Mlžnákomora PavelMotal,SOŠaSOUKuřim Martin Veselý, FJFI ČVUT Praha Historie vývoje mlžné komory Jelikož není možné částice hmoty pozorovat pouhým okem, bylo vyvinutozařízení,ježzviditelňujedráhytěchtočásticvytvářenímmlžné
Základní otázky ke zkoušce A2B17EPV. České vysoké učení technické v Praze ID Fakulta elektrotechnická
 Základní otázky ke zkoušce A2B17EPV Materiál z přednášky dne 10/5/2010 1. Síla současně působící na elektrický náboj v elektrickém a magnetickém poli (Lorentzova síla) 2. Coulombův zákon, orientace vektorů
Základní otázky ke zkoušce A2B17EPV Materiál z přednášky dne 10/5/2010 1. Síla současně působící na elektrický náboj v elektrickém a magnetickém poli (Lorentzova síla) 2. Coulombův zákon, orientace vektorů
102FYZB-Termomechanika
 České vysoké učení technické v Praze Fakulta stavební katedra fyziky 102FYZB-Termomechanika Sbírka úloh (koncept) Autor: Doc. RNDr. Vítězslav Vydra, CSc Poslední aktualizace dne 20. prosince 2018 OBSAH
České vysoké učení technické v Praze Fakulta stavební katedra fyziky 102FYZB-Termomechanika Sbírka úloh (koncept) Autor: Doc. RNDr. Vítězslav Vydra, CSc Poslední aktualizace dne 20. prosince 2018 OBSAH
ATOMOVÁ SPEKTROMETRIE
 ATOMOVÁ SPEKTROMETRIE doc. Ing. David MILDE, Ph.D. tel.: 585634443 E-mail: david.milde@upol.cz (c) -017 Doporučená literatura Černohorský T., Jandera P.: Atomová spektrometrie. Univerzita Pardubice 1997.
ATOMOVÁ SPEKTROMETRIE doc. Ing. David MILDE, Ph.D. tel.: 585634443 E-mail: david.milde@upol.cz (c) -017 Doporučená literatura Černohorský T., Jandera P.: Atomová spektrometrie. Univerzita Pardubice 1997.
Fakulta elektrotechniky a komunikačních technologíı Ústav automatizace a měřicí techniky v Brně
 Vysoké učení technické v Brně Fakulta elektrotechniky a komunikačních technologíı Ústav automatizace a měřicí techniky Algoritmy řízení topného článku tepelného hmotnostního průtokoměru Autor práce: Vedoucí
Vysoké učení technické v Brně Fakulta elektrotechniky a komunikačních technologíı Ústav automatizace a měřicí techniky Algoritmy řízení topného článku tepelného hmotnostního průtokoměru Autor práce: Vedoucí
Laserová technika prosince Katedra fyzikální elektroniky.
 Laserová technika 1 Aktivní prostředí Šíření rezonančního záření dvouhladinovým prostředím Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program
Laserová technika 1 Aktivní prostředí Šíření rezonančního záření dvouhladinovým prostředím Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program
Potenciální proudění
 Hydromechanické procesy Potenciální proudění + plíživé obtékání koule M. Jahoda Proudění tekutiny Pohyby elementu tekutiny 2 čas t čas t + dt obecný pohyb posunutí lineární deformace rotace úhlová deformace
Hydromechanické procesy Potenciální proudění + plíživé obtékání koule M. Jahoda Proudění tekutiny Pohyby elementu tekutiny 2 čas t čas t + dt obecný pohyb posunutí lineární deformace rotace úhlová deformace
c) vysvětlení jednotlivých veličin ve vztahu pro okamžitou výchylku, jejich jednotky
 Harmonický kmitavý pohyb a) vysvětlení harmonického kmitavého pohybu b) zápis vztahu pro okamžitou výchylku c) vysvětlení jednotlivých veličin ve vztahu pro okamžitou výchylku, jejich jednotky d) perioda
Harmonický kmitavý pohyb a) vysvětlení harmonického kmitavého pohybu b) zápis vztahu pro okamžitou výchylku c) vysvětlení jednotlivých veličin ve vztahu pro okamžitou výchylku, jejich jednotky d) perioda
Úvod do moderní fyziky. lekce 3 stavba a struktura atomu
 Úvod do moderní fyziky lekce 3 stavba a struktura atomu Vývoj představ o stavbě atomu 1904 J. J. Thomson pudinkový model atomu 1909 H. Geiger, E. Marsden experiment s ozařováním zlaté fólie alfa částicemi
Úvod do moderní fyziky lekce 3 stavba a struktura atomu Vývoj představ o stavbě atomu 1904 J. J. Thomson pudinkový model atomu 1909 H. Geiger, E. Marsden experiment s ozařováním zlaté fólie alfa částicemi
Měření absorbce záření gama
 Měření absorbce záření gama Úkol : 1. Změřte záření gama přirozeného pozadí. 2. Změřte záření gama vyzářené gamazářičem. 3. Změřte záření gama vyzářené gamazářičem přes absorbátor. 4. Naměřené závislosti
Měření absorbce záření gama Úkol : 1. Změřte záření gama přirozeného pozadí. 2. Změřte záření gama vyzářené gamazářičem. 3. Změřte záření gama vyzářené gamazářičem přes absorbátor. 4. Naměřené závislosti
5.2.4 Rayleighova Taylorova nestabilita
 74 Nestability v plazmatu 5..4 Rayleighova Taylorova nestabilita Rayleighova Taylorova nestabilita (RT nestabilita) vzniká na rozhraní dvou tekutin různých hustot (například je-li v gravitačním poli hustší
74 Nestability v plazmatu 5..4 Rayleighova Taylorova nestabilita Rayleighova Taylorova nestabilita (RT nestabilita) vzniká na rozhraní dvou tekutin různých hustot (například je-li v gravitačním poli hustší
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE. Úloha 11: Termická emise elektronů
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 15.4.2011 Jméno: Jakub Kákona Pracovní skupina: 4 Ročník a kroužek: Pa 9:30 Spolupracovníci: Jana Navrátilová Hodnocení: Úloha 11: Termická emise elektronů
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 15.4.2011 Jméno: Jakub Kákona Pracovní skupina: 4 Ročník a kroužek: Pa 9:30 Spolupracovníci: Jana Navrátilová Hodnocení: Úloha 11: Termická emise elektronů
Úvod do analýzy časových řad
 Přednáška STATISTIKA II - EKONOMETRIE Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Posloupnost náhodných veličin {Y t, t = 0, ±1, ±2... } se nazývá stochastický
Přednáška STATISTIKA II - EKONOMETRIE Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Posloupnost náhodných veličin {Y t, t = 0, ±1, ±2... } se nazývá stochastický
Pokud proudění splňuje všechny výše vypsané atributy, lze o něm prohlásit, že je turbulentní (atributy je třeba znát).
 Laminární proudění je jeden z typů proudění reálné, tedy vazké, tekutiny. Laminární proudění vzniká obecně při nižších rychlostech (přesněji Re). Proudnice laminárního proudu jsou rovnoběžné a vytvářejí
Laminární proudění je jeden z typů proudění reálné, tedy vazké, tekutiny. Laminární proudění vzniká obecně při nižších rychlostech (přesněji Re). Proudnice laminárního proudu jsou rovnoběžné a vytvářejí
Elektromagnetismus 163
 Elektromagnetismus 163 I I H= 2πr Magnetické pole v blízkosti vodi e s proudem x r H Relativní permeabilita Materiály paramagnetické feromagnetické (nap. elezo, nikl, kobalt) diamagnetické Ve vzduchu je
Elektromagnetismus 163 I I H= 2πr Magnetické pole v blízkosti vodi e s proudem x r H Relativní permeabilita Materiály paramagnetické feromagnetické (nap. elezo, nikl, kobalt) diamagnetické Ve vzduchu je
Zajímavé vlastnosti sluneční atmosféry: magnetická a rychlostní pole
 Zajímavé vlastnosti sluneční atmosféry: magnetická a rychlostní pole Spektroskopie (nejen) ve sluneční fyzice LS 2011/2012 Michal Švanda Astronomický ústav MFF UK Astronomický ústav AV ČR Vliv na tvar
Zajímavé vlastnosti sluneční atmosféry: magnetická a rychlostní pole Spektroskopie (nejen) ve sluneční fyzice LS 2011/2012 Michal Švanda Astronomický ústav MFF UK Astronomický ústav AV ČR Vliv na tvar
FYZIKA II. Petr Praus 6. Přednáška elektrický proud
 FYZIKA II Petr Praus 6. Přednáška elektrický proud Osnova přednášky Elektrický proud proudová hustota Elektrický odpor a Ohmův zákon měrná vodivost driftová rychlost Pohyblivost nosičů náboje teplotní
FYZIKA II Petr Praus 6. Přednáška elektrický proud Osnova přednášky Elektrický proud proudová hustota Elektrický odpor a Ohmův zákon měrná vodivost driftová rychlost Pohyblivost nosičů náboje teplotní
1. Dva dlouhé přímé rovnoběžné vodiče vzdálené od sebe 0,75 cm leží kolmo k rovine obrázku 1. Vodičem 1 protéká proud o velikosti 6,5A směrem od nás.
 Příklady: 30. Magnetické pole elektrického proudu 1. Dva dlouhé přímé rovnoběžné vodiče vzdálené od sebe 0,75 cm leží kolmo k rovine obrázku 1. Vodičem 1 protéká proud o velikosti 6,5A směrem od nás. a)
Příklady: 30. Magnetické pole elektrického proudu 1. Dva dlouhé přímé rovnoběžné vodiče vzdálené od sebe 0,75 cm leží kolmo k rovine obrázku 1. Vodičem 1 protéká proud o velikosti 6,5A směrem od nás. a)
7. Elektrický proud v polovodičích
 7. Elektrický proud v polovodičích 7.1 Elektrické vlastnosti polovodičů Kromě vodičů a izolantů existují polovodiče. Definice polovodiče: Je to řada minerálů, rud, krystalů i amorfních látek, řada oxidů
7. Elektrický proud v polovodičích 7.1 Elektrické vlastnosti polovodičů Kromě vodičů a izolantů existují polovodiče. Definice polovodiče: Je to řada minerálů, rud, krystalů i amorfních látek, řada oxidů
Urychlení KZ. Obecné principy, Fermiho urychlení, druhý řád, první řád, spektrum
 Urychlení KZ Obecné principy, Fermiho urychlení, druhý řád, první řád, spektrum Obecné principy Netermální vznik nekompatibilní se spektrem KZ nerealistické teploty E k =3/2 k B T, Univerzalita tvaru spektra
Urychlení KZ Obecné principy, Fermiho urychlení, druhý řád, první řád, spektrum Obecné principy Netermální vznik nekompatibilní se spektrem KZ nerealistické teploty E k =3/2 k B T, Univerzalita tvaru spektra
PRAKTIKUM I. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Pracoval: Pavel Ševeček stud. skup.: F/F1X/11 dne:
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I. Úloha č. VII Název: Studium kmitů vázaných oscilátorů Pracoval: Pavel Ševeček stud. skup.: F/F1X/11 dne: 27. 2. 2012 Odevzdal
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I. Úloha č. VII Název: Studium kmitů vázaných oscilátorů Pracoval: Pavel Ševeček stud. skup.: F/F1X/11 dne: 27. 2. 2012 Odevzdal
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Praktikum IV
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum IV Úloha č. A13 Určení měrného náboje elektronu z charakteristik magnetronu Název: Pracoval: Martin Dlask. stud. sk.: 11 dne:
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum IV Úloha č. A13 Určení měrného náboje elektronu z charakteristik magnetronu Název: Pracoval: Martin Dlask. stud. sk.: 11 dne:
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY STUDIE TURBÍNY S VÍŘIVÝM OBĚŽNÝM KOLEM STUDY OF TURBINE WITH SIDE CHANNEL RUNNER
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ENERGETICKÝ ÚSTAV FACULTY OF MECHANICAL ENGINEERING ENERGY INSTITUTE STUDIE TURBÍNY S VÍŘIVÝM OBĚŽNÝM KOLEM STUDY
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ENERGETICKÝ ÚSTAV FACULTY OF MECHANICAL ENGINEERING ENERGY INSTITUTE STUDIE TURBÍNY S VÍŘIVÝM OBĚŽNÝM KOLEM STUDY
Fakulta biomedic ınsk eho inˇzen yrstv ı Teoretick a elektrotechnika Prof. Ing. Jan Uhl ıˇr, CSc. L eto 2017
 Fakulta biomedicínského inženýrství Teoretická elektrotechnika Prof. Ing. Jan Uhlíř, CSc. Léto 2017 8. Nelineární obvody nesetrvačné dvojpóly 1 Obvodové veličiny nelineárního dvojpólu 3. 0 i 1 i 1 1.5
Fakulta biomedicínského inženýrství Teoretická elektrotechnika Prof. Ing. Jan Uhlíř, CSc. Léto 2017 8. Nelineární obvody nesetrvačné dvojpóly 1 Obvodové veličiny nelineárního dvojpólu 3. 0 i 1 i 1 1.5
Integrovaná střední škola, Sokolnice 496
 Název projektu: Moderní škola Integrovaná střední škola, Sokolnice 496 Registrační číslo: CZ.1.07/1.5.00/34.0467 Název klíčové aktivity: V/2 - Inovace a zkvalitnění výuky směřující k rozvoji odborných
Název projektu: Moderní škola Integrovaná střední škola, Sokolnice 496 Registrační číslo: CZ.1.07/1.5.00/34.0467 Název klíčové aktivity: V/2 - Inovace a zkvalitnění výuky směřující k rozvoji odborných
SNÍMAČE PRO MĚŘENÍ TEPLOTY
 SNÍMAČE PRO MĚŘENÍ TEPLOTY 10.1. Kontaktní snímače teploty 10.2. Bezkontaktní snímače teploty 10.1. KONTAKTNÍ SNÍMAČE TEPLOTY Experimentální metody přednáška 10 snímač je připevněn na měřený objekt 10.1.1.
SNÍMAČE PRO MĚŘENÍ TEPLOTY 10.1. Kontaktní snímače teploty 10.2. Bezkontaktní snímače teploty 10.1. KONTAKTNÍ SNÍMAČE TEPLOTY Experimentální metody přednáška 10 snímač je připevněn na měřený objekt 10.1.1.
TERMIKA II. Stacionární vedení s dokonalou i nedokonalou izolací; Obecná rovnice vedení tepla; Přestup a prostup tepla;
 TERMIKA II Šíření tepla vedením, prouděním a zářením; Stacionární vedení s dokonalou i nedokonalou izolací; Nestacionární vedení tepla; Obecná rovnice vedení tepla; Přestup a prostup tepla; 1 Šíření tepla
TERMIKA II Šíření tepla vedením, prouděním a zářením; Stacionární vedení s dokonalou i nedokonalou izolací; Nestacionární vedení tepla; Obecná rovnice vedení tepla; Přestup a prostup tepla; 1 Šíření tepla
V nejnižším energetickém stavu valenční elektrony úplně obsazují všechny hladiny ve valenčním pásu, nemohou zprostředkovat vedení proudu.
 POLOVODIČE Vlastní polovodiče Podle typu nosiče náboje dělíme polovodiče na vlastní (intrinsické) a příměsové. Příměsové polovodiče mohou být dopované typu N (majoritními nosiči volného náboje jsou elektrony)
POLOVODIČE Vlastní polovodiče Podle typu nosiče náboje dělíme polovodiče na vlastní (intrinsické) a příměsové. Příměsové polovodiče mohou být dopované typu N (majoritními nosiči volného náboje jsou elektrony)
FYZIKA II. Petr Praus 9. Přednáška Elektromagnetická indukce (pokračování) Elektromagnetické kmity a střídavé proudy
 FYZIKA II Petr Praus 9. Přednáška Elektromagnetická indukce (pokračování) Elektromagnetické kmity a střídavé proudy Osnova přednášky Energie magnetického pole v cívce Vzájemná indukčnost Kvazistacionární
FYZIKA II Petr Praus 9. Přednáška Elektromagnetická indukce (pokračování) Elektromagnetické kmity a střídavé proudy Osnova přednášky Energie magnetického pole v cívce Vzájemná indukčnost Kvazistacionární
B. Hvězdy s větší hmotností spalují termojaderné palivo pomaleji,
 HVĚZDY 1. Většina hvězd se při pozorování v průběhu noci pohybuje od A. Západu k východu, B. Východu k západu, C. Severu k jihu, D. Jihu k severu. 2. Ve většině hvězd se energie uvolňuje A. Prudkou rotací
HVĚZDY 1. Většina hvězd se při pozorování v průběhu noci pohybuje od A. Západu k východu, B. Východu k západu, C. Severu k jihu, D. Jihu k severu. 2. Ve většině hvězd se energie uvolňuje A. Prudkou rotací
Software pro analýzu transportu nosičů náboje u autoemisních katod
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV FYZIKY Software pro analýzu transportu nosičů náboje u autoemisních katod Číslo projektu: GAP102/11/0995 Číslo výsledku:
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV FYZIKY Software pro analýzu transportu nosičů náboje u autoemisních katod Číslo projektu: GAP102/11/0995 Číslo výsledku:
