epojení) magnetického pole
|
|
|
- Adam Rohla
- před 9 lety
- Počet zobrazení:
Transkript
1 Rekonexe magnetického pole, current-sheet, X-bodX
2 Rekonexe (rekonekce, přepojenp epojení) magnetického pole Ve fyzice plazmatu je jev rekonexe magnetického pole velmi důležitým jevem Jde o jev, s jehož pomocí se daří vysvětlovat řadu dosud ne plně pochopených dějů v plazmatu. Mezi ně patří například sluneční erupce, jevy na hranici magnetosféry Země a meziplanetárního prostoru, jevy v atmosférách magnetarů, stejně tak jako jevy v laboratorním plazmatu. K přepojení magnetických silokřivek dochází na všech nám dostupných škálách
3 Rekonexe (rekonekce, přepojenp epojení) magnetického pole Přepojení magnetických silokřivek, rekonekce, rekonexe (původní anglický termín je reconnection) nebo mluvíme o tzv. o magnetickém zkratu Dochází k tomu, že magnetické silokřivky prudce změní svou dosavadní topologii do jiné, energeticky výhodnější podoby Při tom dojde k uvolnění energie, která zahřeje okolní plazma. Někdy natolik, že plazma zazáří i v RTG oboru. V každém případě však změna topologie magnetických silokřivek znamená zásadní změnu v chování plazmatu.
4 Rekonexe magnetického pole Rezistivní a Alfvénův čas Doba rekonexe Občas se ještě v plazmatu zavádí tzv. Lundquistovo číslo Pro posouzení rychlosti rekonexe se ještě používá tzv. index rekonexe (následující vztah platí pro samovolnou rekonexi):
5 Rekonexe magnetického pole
6 Rovnice rezistivní MHD Pro popis přepojení magnetických indukčních čar je třeba použít tzv. rezistivní MHD, ve které má plazma nenulový odpor
7 Difúze a zamrzání plazmatu Vyjdeme z rovnice popisující magnetické pole v plazmatu: Člen zamrzání Člen difúze Magnetické pole v plazmatu se tedy může měnit dvěma způsoby Difúze pomalé pronikání magnetického pole do okolního plazmatu Zamrznutí magnetické indukční čáry sledují pohyb plazmatu a zdá se nám jako by byly zamrzlé v plazmatu
8 Magnetické Reynoldsovočíslo slo Pokud odhadneme příspěvky obou zmíněných členů, tj. členu difúze a zamrzání, dostaneme tzv. magnetické Reynoldsovo číslo: Pokud je plazma ideálně vodivé, pak magnetické Reynoldsovočíslo Rm >> 1 a převládá člen zamrzání magnetického pole v plazmatu Naopak pro pomalé pohyby plazmatu dominuje difúze, tj. R m << 1 Na Slunci je toto číslo obvykle dost vysoké, např. ve slunečních skvrnách η 10 3 m 2 s -1, L 10 4 km, v 1 km s -1 vychází R m 10 7 Obecně můžeme říct, že ve slunečním plazmatu dominuje člen zamrzání, existují ovšem výjimky okolí X-bodů, rekonexe při erupcích
9 Člen zamrzání plazmatu
10 Člen difúze plazmatu Teoretický rozbor difúzního členu je příliš složitý a proto se jím nebudeme zabývat Rezistivní čas:
11 Rekonexe magnetického pole Jde o proces přepojení magnetických silokřivek do jiné, energeticky výhodnější konfigurace uvolní se magnetická energie ve formě tepla, které zahřeje okolní plazma K přepojování dochází v oblastech, kde magnetické siločáry míří opačným směrem, to je v astrofyzice velice časté smyčky magnetického pole v koróně, magnetosféra Země, atd.
12 Rekonexe magnetického pole
13 Rekonexe magnetického pole
14 Rekonexe magnetického pole Pokud má plazma konečnou vodivost, může dojít k transformaci mezi magnetickou, tepelnou a kinetickou složkou energie. Přispívají k tomu proudy tekoucí v plazmatu a následný ohmický ohřev Představme si, že v plazmatu se k sobě přiblíží dvě oblasti magnetického pole s opačně orientovanými silokřivkami. V této oblasti vzniká tzv. difúzní region. Ten je charakteristický velmi nízkou hodnotou magnetického pole. Právě zde dojde ke změně topologie magnetických silokřivek, jejich přepojení do nové konfigurace s nižší energií
15 Rekonexe magnetického pole Při přepojení tečou v difúzním regionu velké elektrické proudy, které zahřívají plazma. Energie magnetického pole je transformována do tepelné energie plazmatu. Horké plazma nadbytečnou energii intenzivně vyzařuje do okolí V některých situacích způsobí nestability opakované přepojení magnetických silokřivek s periodicky se opakujícími body nulového pole tvaru X a O.
16 Řízená 2D rekonexe (Sweetův-Parkerův model) V malé oblasti v okolí proudové vrstvy dochází k podstatnému zvýšení odporu taková oblast se nazývá difúzní region Na konci 60. let minulého století navrhli Sweet a Parker model řízené rekonexe, kde předpokládají, že platí
17 Sweet-Parker Parkerův model Sweetův-Parkerův model, je založen na třech předpokladech Rychlost vtékajícího plazmatu Rychlost vytékajícího plazmatu Vztah mezi oběma rychlostmi Index (rychlost řízené rekonexe)
18 Rychlá 2D rekonexe (Petschekův model) Idex řízené rekonexe je vyšší, nž samovolné, tj. probíhá rychleji, avšak některé děje jsou ještě rychlejší, než odpovídá tomuto modelu Proto H. Petschek navrhl v roce 1964 jiný model, kde k rekonexi dochází ve velmi malé oblasti, kde se ještě vytvoří rázová vlna, která celý proces urychlí Tento model je tedy schopen popsat některé procesy vedoucí k rychlé rekonexi, jeho význačným omezením je ale to, že se předpokládá malý difúzní region
19 Turbulentní rekonexe Rychlost rekonexe magnetického pole může urychlit ještě existence přítomnost vln a turbulence v plazmatu V modelu turbulentní rekonexe (GS95) lze nalézt index rekonexe jako Charakter difúzního regionu je fraktální, tj. struktury se na menších rozměrech opakují (až do Larmorova poloměru pro ionty)
20 Simulace turbulentní rekonexe Shibata a Tanuma (Earth, Planets, Space 53, 2001) navrhli schematický koncept tzv. fraktální rekonexe Bárta et al. použili AMR pro řešení tohoto problému
21 Simulace turbulentní rekonexe Bárta, M. - Büchner, J. - Karlický, M. - Skála, J.: Spontaneous Current-Layer Fragmentation and Cascading Reconnection in Solar Flares I: Model and Analysis., The Astrophysical Journal 737 (2011)
22 Rekonexe ve 3D Pokud má magnetické pole i výraznou složku kolmou na proudovou vrstvu, hovoříme o 3D rekonexi Situace může být podobná jako na následujícím obrázku Zatím jsou mechanizmy 3D rekonexe prozkoumány jen velmi málo Parnell, C.E., Smith, J.M. Neukirch, T. and Priest, E.R. ''The structure of threedimensional magnetic neutral points'' Physics of Plasmas, 3, No. 3: (1996)
23 Magnetary Neutronová hvězda s mimořádně silným magnetickým polem až T Povrch magnetaru tvoří kůra z neutronů a magnetického pole, ve které dochází k rekonexi, přičemž se uvolní značné množství energie, které zahřeje magnetickou korónu magnetaru Vznikne horký oblak elektron pozitronových párů (jsou zachyceny a drženy silným magnetickým polem ) a fotonů (fotony unikají v podobě vzplanutí RTG nebo gama záření) Někdy dojde ke katastrofické rekonexi magnetických silokřivek a k gigantickému záblesku, který je tisíckrát energetičtější než běžně se opakující vzplanutí. Zatím byly pozorovány tři takové případy (1979, 1998, 2004), v posledním byla uvolněná energie doposud nejvyšší, a to J.
24 Vyvržen ení koronáln lní hmoty Je to oblak plazmatu vyvržený z koróny Slunce do meziplanetárního prostoru V případě srážky s magnetickým polem Země dochází nejen k polárním zářím, ale také geomagnetické bouře, které mohou vést k poruchám na telekomunkačních družicích, problémům v letecké dopravě nebo k poruchám rozvodných sítí elektrické energie
25 Magnetary
26 Harris CS bez a s gravitací
27 Harris CS MHD model
28 Příklady Najděte vztahy pro výpočet rozložení hustoty a tlaku pro strukturu tzv. X-bodu, popsaného vektorovým potenciálem ve tvaru Vyjádřete podmínku rovnováhy current-sheetu v charakteristických rychlostech zvukové a Alfvénovy Určete tlak v centru a na okraji current-sheetu v erupci, víte-li, že n cs = m -3, T = K a plasma β = 0,1. Jaká je Alfvénova a zvuková rychlost v centru a na okraji takové struktury? Jaký je vztah mezi Alfvénovou a zvukovou rychlostí? Odhadněte za jak dlouho by vymizelo magnetické pole difúzí ze sluneční skvrny o poloměru 10 Mm a koeficient difúze je η = 10 3 m 2 s -1.
29 V textu byly použity některé obrázky a text z knihy: P. Kulhánek, Úvod do teorie plazmatu, AGA 2011, Praha.
epojení) magnetického pole
 Rekonexe magnetického pole, current-sheet, X-bodX Rekonexe (rekonekce, přepojenp epojení) magnetického pole Ve fyzice plazmatu je jev rekonexe magnetického pole velmi důležitým jevem Jde o jev, s jehož
Rekonexe magnetického pole, current-sheet, X-bodX Rekonexe (rekonekce, přepojenp epojení) magnetického pole Ve fyzice plazmatu je jev rekonexe magnetického pole velmi důležitým jevem Jde o jev, s jehož
Základy magnetohydrodynamiky. aneb MHD v jedné přednášce?! To si snad děláte legraci!
 Základy magnetohydrodynamiky aneb MHD v jedné přednášce?! To si snad děláte legraci! Osnova Magnetohydrodynamika Maxwellovy rovnice Aplikace pinče, MHD generátory, geofyzika, astrofyzika... Magnetohydrodynamika
Základy magnetohydrodynamiky aneb MHD v jedné přednášce?! To si snad děláte legraci! Osnova Magnetohydrodynamika Maxwellovy rovnice Aplikace pinče, MHD generátory, geofyzika, astrofyzika... Magnetohydrodynamika
Slunce, erupce, ohřev sluneční koróny
 Slunce, erupce, ohřev sluneční koróny Slunce jako božstvo Mnoho kultur uctívalo Slunce jako božstvo modlitbami i přinášením (lidských) obětí Egypt Re Indie Surya Řecko a Řím Apollón a Helios Mezopotámie
Slunce, erupce, ohřev sluneční koróny Slunce jako božstvo Mnoho kultur uctívalo Slunce jako božstvo modlitbami i přinášením (lidských) obětí Egypt Re Indie Surya Řecko a Řím Apollón a Helios Mezopotámie
2.4.11 Nerovnice s absolutní hodnotou
 .. Nerovnice s absolutní hodnotou Předpoklady: 06, 09, 0 Pedagogická poznámka: Hlavním záměrem hodiny je, aby si studenti uvědomili, že se neučí nic nového. Pouze používají věci, které dávno znají, na
.. Nerovnice s absolutní hodnotou Předpoklady: 06, 09, 0 Pedagogická poznámka: Hlavním záměrem hodiny je, aby si studenti uvědomili, že se neučí nic nového. Pouze používají věci, které dávno znají, na
3.2.4 Podobnost trojúhelníků II
 3..4 odobnost trojúhelníků II ředpoklady: 33 ř. 1: Na obrázku jsou nakresleny podobné trojúhelníky. Zapiš jejich podobnost (aby bylo zřejmé, který vrchol prvního trojúhelníku odpovídá vrcholu druhého trojúhelníku).
3..4 odobnost trojúhelníků II ředpoklady: 33 ř. 1: Na obrázku jsou nakresleny podobné trojúhelníky. Zapiš jejich podobnost (aby bylo zřejmé, který vrchol prvního trojúhelníku odpovídá vrcholu druhého trojúhelníku).
(a) = (a) = 0. x (a) > 0 a 2 ( pak funkce má v bodě a ostré lokální maximum, resp. ostré lokální minimum. Pokud je. x 2 (a) 2 y (a) f.
 I. Funkce dvou a více reálných proměnných 5. Lokální extrémy. Budeme uvažovat funkci f = f(x 1, x 2,..., x n ), která je definovaná v otevřené množině G R n. Řekneme, že funkce f = f(x 1, x 2,..., x n
I. Funkce dvou a více reálných proměnných 5. Lokální extrémy. Budeme uvažovat funkci f = f(x 1, x 2,..., x n ), která je definovaná v otevřené množině G R n. Řekneme, že funkce f = f(x 1, x 2,..., x n
Petr Kulhánek České vysoké učení technické v Praze, Fakulta elektrotechnická, katedra fyziky
 PLAZMA ČTVRTÉ SKUPENSTVÍ HMOTY Petr Kulhánek České vysoké učení technické v Praze, Fakulta elektrotechnická, katedra fyziky Abstrakt: Příspěvek pojednává o vlastnostech laboratorního i vesmírného plazmatu,
PLAZMA ČTVRTÉ SKUPENSTVÍ HMOTY Petr Kulhánek České vysoké učení technické v Praze, Fakulta elektrotechnická, katedra fyziky Abstrakt: Příspěvek pojednává o vlastnostech laboratorního i vesmírného plazmatu,
Úvod do teorie plazmatu
 Úvod do teorie plazmatu Petr Kulhánek AGA 2011 Text Petr Kulhánek ISBN: 978-80-904582-2-2 Obsah PŘEDMLUVA...9 ÚVOD...11 1. POHYBY NABITÝCH ČÁSTIC...15 1.1 NERELATIVISTICKÉ POHYBY... 16 1.1.1 Lagrangeova
Úvod do teorie plazmatu Petr Kulhánek AGA 2011 Text Petr Kulhánek ISBN: 978-80-904582-2-2 Obsah PŘEDMLUVA...9 ÚVOD...11 1. POHYBY NABITÝCH ČÁSTIC...15 1.1 NERELATIVISTICKÉ POHYBY... 16 1.1.1 Lagrangeova
Složení hvězdy. Hvězda - gravitačně vázaný objekt, složený z vysokoteplotního plazmatu; hmotnost 0,08 M ʘ cca 150 M ʘ, ale R136a1 (LMC) má 265 M ʘ
 Hvězdy zblízka Složení hvězdy Hvězda - gravitačně vázaný objekt, složený z vysokoteplotního plazmatu; hmotnost 0,08 M ʘ cca 150 M ʘ, ale R136a1 (LMC) má 265 M ʘ Plazma zcela nebo částečně ionizovaný plyn,
Hvězdy zblízka Složení hvězdy Hvězda - gravitačně vázaný objekt, složený z vysokoteplotního plazmatu; hmotnost 0,08 M ʘ cca 150 M ʘ, ale R136a1 (LMC) má 265 M ʘ Plazma zcela nebo částečně ionizovaný plyn,
Numerické simulace v astrofyzice
 Numerické simulace v astrofyzice Petr Jelínek Jihočeská univerzita, Přírodovědecká fakulta, České Budějovice, Česká republika Astronomický ústav, Akademie věd České republiky v.v.i., Ondřejov, Česká republika
Numerické simulace v astrofyzice Petr Jelínek Jihočeská univerzita, Přírodovědecká fakulta, České Budějovice, Česká republika Astronomický ústav, Akademie věd České republiky v.v.i., Ondřejov, Česká republika
2.8.9 Parametrické rovnice a nerovnice s absolutní hodnotou
 .8.9 Parametrické rovnice a nerovnice s absolutní hodnotou Předpoklady: 0,, 806 Pedagogická poznámka: Opět si napíšeme na začátku hodiny na tabuli jednotlivé kroky postupu při řešení rovnic (nerovnic)
.8.9 Parametrické rovnice a nerovnice s absolutní hodnotou Předpoklady: 0,, 806 Pedagogická poznámka: Opět si napíšeme na začátku hodiny na tabuli jednotlivé kroky postupu při řešení rovnic (nerovnic)
Tepelná výměna. výměna tepla může probíhat vedením (kondukce), sáláním (radiace) nebo prouděním (konvekce).
 Tepelná výměna tepelná výměna je termodynamický děj, při kterém dochází k samovolné výměně tepla mezi dvěma tělesy s různou teplotou. Tepelná výměna vždy probíhá tak, že teplejší těleso předává svou vnitřní
Tepelná výměna tepelná výměna je termodynamický děj, při kterém dochází k samovolné výměně tepla mezi dvěma tělesy s různou teplotou. Tepelná výměna vždy probíhá tak, že teplejší těleso předává svou vnitřní
Fyzika - Kvarta Fyzika kvarta Výchovné a vzdělávací strategie Učivo ŠVP výstupy
 - Kvarta Fyzika Výchovné a vzdělávací strategie Kompetence k řešení problémů Kompetence komunikativní Kompetence sociální a personální Kompetence občanská Kompetence k učení Kompetence pracovní Učivo magnetické
- Kvarta Fyzika Výchovné a vzdělávací strategie Kompetence k řešení problémů Kompetence komunikativní Kompetence sociální a personální Kompetence občanská Kompetence k učení Kompetence pracovní Učivo magnetické
Střední škola obchodu, řemesel a služeb Žamberk. Výukový materiál zpracovaný v rámci projektu EU Peníze SŠ
 Střední škola obchodu, řemesel a služeb Žamberk Výukový materiál zpracovaný v rámci projektu EU Peníze SŠ Registrační číslo projektu: CZ.1.07/1.5.00/34.0130 Šablona: III/2 Ověřeno ve výuce dne: 7.10.2013
Střední škola obchodu, řemesel a služeb Žamberk Výukový materiál zpracovaný v rámci projektu EU Peníze SŠ Registrační číslo projektu: CZ.1.07/1.5.00/34.0130 Šablona: III/2 Ověřeno ve výuce dne: 7.10.2013
Vlny ve sluneční atmosféře. Petr Jelínek
 Vlny ve sluneční atmosféře Petr Jelínek Obsah přednášek Slunce a sluneční koróna, ohřev sluneční koróny, sluneční erupce Plazma, vlny v plazmatu, vlny ve sluneční koróně Popis plazmatu, magnetohydrodynamika
Vlny ve sluneční atmosféře Petr Jelínek Obsah přednášek Slunce a sluneční koróna, ohřev sluneční koróny, sluneční erupce Plazma, vlny v plazmatu, vlny ve sluneční koróně Popis plazmatu, magnetohydrodynamika
Věra Keselicová. červen 2013
 VY_52_INOVACE_VK67 Jméno autora výukového materiálu Datum (období), ve kterém byl VM vytvořen Ročník, pro který je VM určen Vzdělávací oblast, obor, okruh, téma Anotace Věra Keselicová červen 2013 9. ročník
VY_52_INOVACE_VK67 Jméno autora výukového materiálu Datum (období), ve kterém byl VM vytvořen Ročník, pro který je VM určen Vzdělávací oblast, obor, okruh, téma Anotace Věra Keselicová červen 2013 9. ročník
Eruptivní procesy na Slunci a jejich optická, radiová a EUV diagnostika
 Eruptivní procesy na Slunci a jejich optická, radiová a EUV diagnostika Miroslav Bárta Astronomický ústav AV ČR, Ondřejov barta@asu.cas.cz 26. prosince 2013 1. ČS setkání pozorovatelů Slunce, Valašské
Eruptivní procesy na Slunci a jejich optická, radiová a EUV diagnostika Miroslav Bárta Astronomický ústav AV ČR, Ondřejov barta@asu.cas.cz 26. prosince 2013 1. ČS setkání pozorovatelů Slunce, Valašské
Úvod do fyziky plazmatu
 Úvod do fyziky plazmatu Lenka Zajíčková, Ústav fyz. elektroniky Doporučená literatura: J. A. Bittencourt, Fundamentals of Plasma Physics, 2003 (3. vydání) ISBN 85-900100-3-1 Navazující a související přednášky:
Úvod do fyziky plazmatu Lenka Zajíčková, Ústav fyz. elektroniky Doporučená literatura: J. A. Bittencourt, Fundamentals of Plasma Physics, 2003 (3. vydání) ISBN 85-900100-3-1 Navazující a související přednášky:
M - Rovnice - lineární a s absolutní hodnotou
 Rovnice a jejich ekvivalentní úpravy Co je rovnice Rovnice je matematický zápis rovnosti dvou výrazů. př.: x + 5 = 7x - M - Rovnice - lineární a s absolutní hodnotou Písmeno zapsané v rovnici nazýváme
Rovnice a jejich ekvivalentní úpravy Co je rovnice Rovnice je matematický zápis rovnosti dvou výrazů. př.: x + 5 = 7x - M - Rovnice - lineární a s absolutní hodnotou Písmeno zapsané v rovnici nazýváme
2.7.2 Mocninné funkce se záporným celým mocnitelem
 .7. Mocninné funkce se záporným celým mocnitelem Předpoklady: 70 Mocninné funkce se záporným celým mocnitelem: znamená? 3 y = = = = 3 y y y 3 = ; = ; = ;.... Co to Pedagogická poznámka: Nechávám studenty,
.7. Mocninné funkce se záporným celým mocnitelem Předpoklady: 70 Mocninné funkce se záporným celým mocnitelem: znamená? 3 y = = = = 3 y y y 3 = ; = ; = ;.... Co to Pedagogická poznámka: Nechávám studenty,
Optika. VIII - Seminář
 Optika VIII - Seminář Op-1: Šíření světla Optika - pojem Historie - dva pohledy na světlo ČÁSTICOVÁ TEORIE (I. Newton): světlo je proud částic VLNOVÁ TEORIE (Ch.Huygens): světlo je vlnění prostředí Dělení
Optika VIII - Seminář Op-1: Šíření světla Optika - pojem Historie - dva pohledy na světlo ČÁSTICOVÁ TEORIE (I. Newton): světlo je proud částic VLNOVÁ TEORIE (Ch.Huygens): světlo je vlnění prostředí Dělení
4.6.6 Složený sériový RLC obvod střídavého proudu
 4.6.6 Složený sériový LC obvod střídavého proudu Předpoklady: 41, 4605 Minulá hodina: odpor i induktance omezují proud ve střídavém obvodu, nemůžeme je však sčítat normálně, ale musíme použít Pythagorovu
4.6.6 Složený sériový LC obvod střídavého proudu Předpoklady: 41, 4605 Minulá hodina: odpor i induktance omezují proud ve střídavém obvodu, nemůžeme je však sčítat normálně, ale musíme použít Pythagorovu
Pingpongový míček. Petr Školník, Michal Menkina. TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií
 Petr Školník, Michal Menkina TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Tento materiál vznikl v rámci projektu ESF CZ.1.7/../7.47, který je spolufinancován
Petr Školník, Michal Menkina TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Tento materiál vznikl v rámci projektu ESF CZ.1.7/../7.47, který je spolufinancován
Kvadratické rovnice pro učební obory
 Variace 1 Kvadratické rovnice pro učební obory Autor: Mgr. Jaromír JUŘEK Kopírování a jkaékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
Variace 1 Kvadratické rovnice pro učební obory Autor: Mgr. Jaromír JUŘEK Kopírování a jkaékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
2.3. POLARIZACE VLN, POLARIZAČNÍ KOEFICIENTY A POMĚR E/B
 .3. POLARIZACE VLN, POLARIZAČNÍ KOEFICIENTY A POMĚR E/B V řadě případů je užitečné znát polarizaci vlny a poměry mezi jednotlivými složkami vektoru elektrické intenzity E takzvané polarizační koeficienty,
.3. POLARIZACE VLN, POLARIZAČNÍ KOEFICIENTY A POMĚR E/B V řadě případů je užitečné znát polarizaci vlny a poměry mezi jednotlivými složkami vektoru elektrické intenzity E takzvané polarizační koeficienty,
SMĚŠOVACÍ KALORIMETR -tepelně izolovaná nádoba s míchačkou a teploměrem, která je naplněná kapalinou
 KALORIMETRIE Kalorimetr slouží k měření tepla, tepelné kapacity, případně měrné tepelné kapacity Kalorimetrická rovnice vyjadřuje energetickou bilanci při tepelné výměně mezi kalorimetrem a tělesy v kalorimetru.
KALORIMETRIE Kalorimetr slouží k měření tepla, tepelné kapacity, případně měrné tepelné kapacity Kalorimetrická rovnice vyjadřuje energetickou bilanci při tepelné výměně mezi kalorimetrem a tělesy v kalorimetru.
Srovnání posledních dvou verzí studijních plánů pro studijní obor. Informační systémy. (studijní program Aplikovaná informatika)
 Srovnání posledních dvou verzí studijních plánů pro studijní obor Informační systémy (studijní program Aplikovaná informatika) Úvod Ve STAGu jsou poslední verze studijních plánů pro studijní obor Informační
Srovnání posledních dvou verzí studijních plánů pro studijní obor Informační systémy (studijní program Aplikovaná informatika) Úvod Ve STAGu jsou poslední verze studijních plánů pro studijní obor Informační
( ) 2.4.4 Kreslení grafů funkcí metodou dělení definičního oboru I. Předpoklady: 2401, 2208
 .. Kreslení grafů funkcí metodou dělení definičního oboru I Předpoklady: 01, 08 Opakování: Pokud jsme při řešení nerovnic potřebovali vynásobit nerovnici výrazem, nemohli jsme postupovat pro všechna čísla
.. Kreslení grafů funkcí metodou dělení definičního oboru I Předpoklady: 01, 08 Opakování: Pokud jsme při řešení nerovnic potřebovali vynásobit nerovnici výrazem, nemohli jsme postupovat pro všechna čísla
Koróna, sluneční vítr
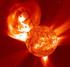 Koróna, sluneční vítr Sluneční fyzika ZS 2011/2012 Michal Švanda Astronomický ústav MFF UK Astronomický ústav AV ČR Přechodová oblast Změna teplotní režimu mezi chromosférou (104 K) a korónou (106 K) Nehomogenní,
Koróna, sluneční vítr Sluneční fyzika ZS 2011/2012 Michal Švanda Astronomický ústav MFF UK Astronomický ústav AV ČR Přechodová oblast Změna teplotní režimu mezi chromosférou (104 K) a korónou (106 K) Nehomogenní,
3. Ve zbylé množině hledat prvky, které ve srovnání nikdy nejsou napravo (nevedou do nich šipky). Dát do třetí
 DMA Přednáška Speciální relace Nechť R je relace na nějaké množině A. Řekneme, že R je částečné uspořádání, jestliže je reflexivní, antisymetrická a tranzitivní. V tom případě značíme relaci a řekneme,
DMA Přednáška Speciální relace Nechť R je relace na nějaké množině A. Řekneme, že R je částečné uspořádání, jestliže je reflexivní, antisymetrická a tranzitivní. V tom případě značíme relaci a řekneme,
O symetrii tokamaku. Vtomto článku opustíme tematiku konkrétních. Jan Mlynář. 50 let UFP AV ČR
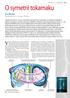 č. 4 Čs. čas. fyz. 59 (2009) 207 O symetrii tokamaku Jan Mlynář Ústav fyziky plazmatu AV ČR, v. v. i., Za Slovankou 3, 182 00 Praha 8 Loňské čtvrté číslo Čs. čas. fyz. se podrobně věnovalo historii tokamaků
č. 4 Čs. čas. fyz. 59 (2009) 207 O symetrii tokamaku Jan Mlynář Ústav fyziky plazmatu AV ČR, v. v. i., Za Slovankou 3, 182 00 Praha 8 Loňské čtvrté číslo Čs. čas. fyz. se podrobně věnovalo historii tokamaků
1.3.1 Kruhový pohyb. Předpoklady: 1105
 .. Kruhový pohyb Předpoklady: 05 Předměty kolem nás se pohybují různými způsoby. Nejde pouze o přímočaré nebo křivočaré posuvné pohyby. Velmi často se předměty otáčí (a některé se přitom pohybují zároveň
.. Kruhový pohyb Předpoklady: 05 Předměty kolem nás se pohybují různými způsoby. Nejde pouze o přímočaré nebo křivočaré posuvné pohyby. Velmi často se předměty otáčí (a některé se přitom pohybují zároveň
Vztah mezi dvěma čísly, které se rovnají, se nazývá rovnost, jako například : ( 2) 3 = 8 4 = 2 ; 16 = 4 ; 1 = 1 a podobně. 2
 Lineární rovnice o jedné neznámé O rovnicích obecně Vztah mezi dvěma čísly, které se rovnají, se nazývá rovnost, jako například : ( ) 8 ; 6 ; a podobně. ; Na rozdíl od rovností obsahuje rovnice kromě čísel
Lineární rovnice o jedné neznámé O rovnicích obecně Vztah mezi dvěma čísly, které se rovnají, se nazývá rovnost, jako například : ( ) 8 ; 6 ; a podobně. ; Na rozdíl od rovností obsahuje rovnice kromě čísel
4.2.7 Voltampérová charakteristika rezistoru a žárovky
 4.2.7 Voltampérová charakteristika rezistoru a žárovky Předpoklady: 4205 Pedagogická poznámka: Tuto hodinu učím jako běžnou jednohodinovku s celou třídou. Některé dvojice stihnou naměřit více odporů. Voltampérová
4.2.7 Voltampérová charakteristika rezistoru a žárovky Předpoklady: 4205 Pedagogická poznámka: Tuto hodinu učím jako běžnou jednohodinovku s celou třídou. Některé dvojice stihnou naměřit více odporů. Voltampérová
Sada: VY_32_INOVACE_4IS
 Registrační číslo projektu: CZ.1.07/1.4.00/21.3075 Šablona: III/2 Sada: VY_32_INOVACE_4IS Pořadové číslo: 12 Ověření ve výuce Třída: 8.A Datum: 20. 3. 2013 1 Elektrické pole Předmět: Ročník: Fyzika 8.
Registrační číslo projektu: CZ.1.07/1.4.00/21.3075 Šablona: III/2 Sada: VY_32_INOVACE_4IS Pořadové číslo: 12 Ověření ve výuce Třída: 8.A Datum: 20. 3. 2013 1 Elektrické pole Předmět: Ročník: Fyzika 8.
Kvadratické rovnice pro studijní obory
 Variace 1 Kvadratické rovnice pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
Variace 1 Kvadratické rovnice pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
4.5.2 Magnetické pole vodiče s proudem
 4.5.2 Magnetické pole vodiče s proudem Předpoklady: 4501 1820 H. Ch. Oersted objevil, že vodič s proudem působí na magnetku elektrický proud vytváří ve svém okolí magnetické pole (dříve nebyly k dispozici
4.5.2 Magnetické pole vodiče s proudem Předpoklady: 4501 1820 H. Ch. Oersted objevil, že vodič s proudem působí na magnetku elektrický proud vytváří ve svém okolí magnetické pole (dříve nebyly k dispozici
11. Koróna, sluneční vítr
 11. Koróna, sluneční vítr Sluneční fyzika LS 2007/2008 Michal Švanda Astronomický ústav MFF UK Astronomický ústav AV ČR Přechodová oblast Změna teplotní režimu mezi chromosférou (104 K) a korónou (106
11. Koróna, sluneční vítr Sluneční fyzika LS 2007/2008 Michal Švanda Astronomický ústav MFF UK Astronomický ústav AV ČR Přechodová oblast Změna teplotní režimu mezi chromosférou (104 K) a korónou (106
3M OH&ES/EMEA. Úvod do legislativy / Co je to hluk?
 Úvod do legislativy / Co je to hluk? Agenda: Něco málo z legislativy Co je vlastně hluk? Něco málo ze statistických údajů 2 3M 2008. All Rights Reserved. Co je vlastně hluk? 3 3M 2008. All Rights Reserved.
Úvod do legislativy / Co je to hluk? Agenda: Něco málo z legislativy Co je vlastně hluk? Něco málo ze statistických údajů 2 3M 2008. All Rights Reserved. Co je vlastně hluk? 3 3M 2008. All Rights Reserved.
Plazma v mikrovlnné troubě
 Plazma v mikrovlnné troubě JIŘÍ KOHOUT Katedra obecné fyziky, Fakulta pedagogická, Západočeská univerzita v Plzni V tomto příspěvku prezentuji sérii netradičních experimentů souvisejících se vznikem plazmatu
Plazma v mikrovlnné troubě JIŘÍ KOHOUT Katedra obecné fyziky, Fakulta pedagogická, Západočeská univerzita v Plzni V tomto příspěvku prezentuji sérii netradičních experimentů souvisejících se vznikem plazmatu
Relativistická dynamika
 Relativistická dynamika 1. Jaké napětí urychlí elektron na rychlost světla podle klasické fyziky? Jakou rychlost získá při tomto napětí elektron ve skutečnosti? [256 kv, 2,236.10 8 m.s -1 ] 2. Vypočtěte
Relativistická dynamika 1. Jaké napětí urychlí elektron na rychlost světla podle klasické fyziky? Jakou rychlost získá při tomto napětí elektron ve skutečnosti? [256 kv, 2,236.10 8 m.s -1 ] 2. Vypočtěte
1. Cizinci v České republice
 1. Cizinci v České republice Počet cizinců v ČR se již delší dobu udržuje na přibližně stejné úrovni, přičemž na území České republiky bylo k 31. 12. 2011 evidováno 434 153 osob III. Pokud vezmeme v úvahu
1. Cizinci v České republice Počet cizinců v ČR se již delší dobu udržuje na přibližně stejné úrovni, přičemž na území České republiky bylo k 31. 12. 2011 evidováno 434 153 osob III. Pokud vezmeme v úvahu
Dualita v úlohách LP Ekonomická interpretace duální úlohy. Jiří Neubauer. Katedra ekonometrie FEM UO Brno
 Přednáška č. 6 Katedra ekonometrie FEM UO Brno Uvažujme obecnou úlohu lineárního programování, tj. úlohu nalezení takového řešení vlastních omezujících podmínek a 11 x 1 + a 1 x +... + a 1n x n = b 1 a
Přednáška č. 6 Katedra ekonometrie FEM UO Brno Uvažujme obecnou úlohu lineárního programování, tj. úlohu nalezení takového řešení vlastních omezujících podmínek a 11 x 1 + a 1 x +... + a 1n x n = b 1 a
Astronomie 1 ... 3. Dopiš do správných míst schématu vývoje hvězdy následující pojmy: bílý trpaslík, černá díra, globule, neutronová hvězda, obr
 Astronomie Autor: Miroslav Randa. Poloměr Slunce je přibližně stokrát větší než poloměr Země. Kolikrát je větší objem Slunce než objem Země? Poloměr Země je 6 78 km.. Doplňovačka se skrytou tajenkou nejvzdálenější
Astronomie Autor: Miroslav Randa. Poloměr Slunce je přibližně stokrát větší než poloměr Země. Kolikrát je větší objem Slunce než objem Země? Poloměr Země je 6 78 km.. Doplňovačka se skrytou tajenkou nejvzdálenější
Zadání bakalářské/diplomové práce
 Analýza systémového chování experimentální smyčky S-ALLEGRO V rámci projektu SUSEN Udržitelná energetika bude vyprojektována a postavena experimentální heliová smyčka S-Allegro. Tato smyčka má modelově
Analýza systémového chování experimentální smyčky S-ALLEGRO V rámci projektu SUSEN Udržitelná energetika bude vyprojektována a postavena experimentální heliová smyčka S-Allegro. Tato smyčka má modelově
Rostislav Horčík. 13. října 2006
 3. přednáška Rostislav Horčík 13. října 2006 1 Lineární prostory Definice 1 Lineárním prostorem nazýváme každou neprázdnou množinu L, na které je definováno sčítání + : L L L a násobení reálným číslem
3. přednáška Rostislav Horčík 13. října 2006 1 Lineární prostory Definice 1 Lineárním prostorem nazýváme každou neprázdnou množinu L, na které je definováno sčítání + : L L L a násobení reálným číslem
( ) 2.5.7 Neúplné kvadratické rovnice. Předpoklady: 020501
 ..7 Neúplné kvadratické rovnice Předpoklady: Pedagogická poznámka: Tato hodina patří mezi vzácné výjimky, kdy naprostá většina studentů skončí více než pět minut před zvoněním. Nechávám je dělat něco jiného
..7 Neúplné kvadratické rovnice Předpoklady: Pedagogická poznámka: Tato hodina patří mezi vzácné výjimky, kdy naprostá většina studentů skončí více než pět minut před zvoněním. Nechávám je dělat něco jiného
OPTIKA Vlastnosti světla TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY.
 OPTIKA Vlastnosti světla TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY. Vlastnosti světla Světlo je příčina našich zrakových vjemů. Vidíme jen ty předměty,
OPTIKA Vlastnosti světla TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY. Vlastnosti světla Světlo je příčina našich zrakových vjemů. Vidíme jen ty předměty,
Praktikum II Elektřina a magnetismus
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum II Elektřina a magnetismus Úloha č. VII Název: Měření indukčnosti a kapacity metodou přímou Pracoval: Matyáš Řehák stud.sk.:
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum II Elektřina a magnetismus Úloha č. VII Název: Měření indukčnosti a kapacity metodou přímou Pracoval: Matyáš Řehák stud.sk.:
Pokroky matematiky, fyziky a astronomie
 Pokroky matematiky, fyziky a astronomie Jan Mlynář Rovnováha plazmatu a magnetického pole v termojaderných reaktorech typu tokamak Pokroky matematiky, fyziky a astronomie, Vol. 57 (2012), No. 2, 122--139
Pokroky matematiky, fyziky a astronomie Jan Mlynář Rovnováha plazmatu a magnetického pole v termojaderných reaktorech typu tokamak Pokroky matematiky, fyziky a astronomie, Vol. 57 (2012), No. 2, 122--139
Tvorba trendové funkce a extrapolace pro roční časové řady
 Tvorba trendové funkce a extrapolace pro roční časové řady Příklad: Základem pro analýzu je časová řada živě narozených mezi lety 1970 a 2005. Prvním úkolem je vybrat vhodnou trendovou funkci pro vystižení
Tvorba trendové funkce a extrapolace pro roční časové řady Příklad: Základem pro analýzu je časová řada živě narozených mezi lety 1970 a 2005. Prvním úkolem je vybrat vhodnou trendovou funkci pro vystižení
SLUNCE A JEHO POZOROVÁNÍ I FYZIKA PLAZMATU
 POZVÁNKA NA WORKSHOP PROJEKTU SE SLUNCEM SPOLEČNĚ SLUNCE A JEHO POZOROVÁNÍ I FYZIKA PLAZMATU 28. 30. června 2013, Hvězdárna Valašské Meziříčí Milí přátelé, Hvězdárna Valašské Meziříčí, p. o. ve spolupráci
POZVÁNKA NA WORKSHOP PROJEKTU SE SLUNCEM SPOLEČNĚ SLUNCE A JEHO POZOROVÁNÍ I FYZIKA PLAZMATU 28. 30. června 2013, Hvězdárna Valašské Meziříčí Milí přátelé, Hvězdárna Valašské Meziříčí, p. o. ve spolupráci
KVADRATICKÉ ROVNICE A NEROVNICE (včetně řešení v C)
 Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol KVADRATICKÉ
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol KVADRATICKÉ
Soustavy lineárních rovnic
 Soustavy lineárních rovnic Buď (T, +, ) těleso. Pak soustava rovnic a 11 x 1 + a 12 x 2 + + a 1n x n = b 1, a 21 x 1 + a 22 x 2 + + a 2n x n = b 2,................................... a m1 x 1 + a m2 x
Soustavy lineárních rovnic Buď (T, +, ) těleso. Pak soustava rovnic a 11 x 1 + a 12 x 2 + + a 1n x n = b 1, a 21 x 1 + a 22 x 2 + + a 2n x n = b 2,................................... a m1 x 1 + a m2 x
KINETICKÁ TEORIE STAVBY LÁTEK
 KINETICKÁ TEORIE STAVBY LÁTEK Látky kteréhokoliv skupenství se skládají z částic. Prostor, který těleso zaujímá, není částicemi beze zbytku vyplněn (diskrétní struktura látek). Rozměry částic jsou řádově
KINETICKÁ TEORIE STAVBY LÁTEK Látky kteréhokoliv skupenství se skládají z částic. Prostor, který těleso zaujímá, není částicemi beze zbytku vyplněn (diskrétní struktura látek). Rozměry částic jsou řádově
{ } 9.1.9 Kombinace II. Předpoklady: 9108. =. Vypiš všechny dvoučlenné kombinace sestavené z těchto pěti prvků. Urči počet kombinací pomocí vzorce.
 9.1.9 Kombinace II Předpoklady: 9108 Př. 1: Je dána pěti prvková množina: M { a; b; c; d; e} =. Vypiš všechny dvoučlenné kombinace sestavené z těchto pěti prvků. Urči počet kombinací pomocí vzorce. Vypisujeme
9.1.9 Kombinace II Předpoklady: 9108 Př. 1: Je dána pěti prvková množina: M { a; b; c; d; e} =. Vypiš všechny dvoučlenné kombinace sestavené z těchto pěti prvků. Urči počet kombinací pomocí vzorce. Vypisujeme
12/40 Zdroj kmitů budí počátek bodové řady podle vztahu u(o, t) = 2.10 3 m. 14/40 Harmonické vlnění o frekvenci 500 Hz a amplitudě výchylky 0,25 mm
 Vlnění a akustika 1/40 Zdroj kmitů budí počátek bodové řady podle vztahu u(o, t) =.10 3 m, 5π s 1 t. Napište rovnici vlnění, které se šíří bodovou řadou v kladném smyslu osy x rychlostí 300 m.s 1. c =
Vlnění a akustika 1/40 Zdroj kmitů budí počátek bodové řady podle vztahu u(o, t) =.10 3 m, 5π s 1 t. Napište rovnici vlnění, které se šíří bodovou řadou v kladném smyslu osy x rychlostí 300 m.s 1. c =
PROGRAMOVÁNÍ SVĚTELNÝCH OZDOB
 Středoškolská technika 2016 Setkání a prezentace prací středoškolských studentů na ČVUT PROGRAMOVÁNÍ SVĚTELNÝCH OZDOB Jiří Bendík, Martin Bárta Střední odborná škola strojní a elektrotechnická U Hřiště
Středoškolská technika 2016 Setkání a prezentace prací středoškolských studentů na ČVUT PROGRAMOVÁNÍ SVĚTELNÝCH OZDOB Jiří Bendík, Martin Bárta Střední odborná škola strojní a elektrotechnická U Hřiště
Číslo projektu: CZ.1.07/1.5.00/34.0290. Ročník: 1.
 Zlepšení podmínek pro vzdělávání na středních školách Operačního programu Vzdělávání pro konkurenceschopnost Název a adresa školy: Integrovaná střední škola Cheb, Obrněné brigády 6, 350 11 Cheb Číslo projektu:
Zlepšení podmínek pro vzdělávání na středních školách Operačního programu Vzdělávání pro konkurenceschopnost Název a adresa školy: Integrovaná střední škola Cheb, Obrněné brigády 6, 350 11 Cheb Číslo projektu:
1. Kruh, kružnice. Mezi poloměrem a průměrem kružnice platí vztah : d = 2. r. Zapíšeme k ( S ; r ) Čteme kružnice k je určena středem S a poloměrem r.
 Kruh, kružnice, válec 1. Kruh, kružnice 1.1. Základní pojmy Kružnice je množina bodů mající od daného bodu stejnou vzdálenost. Daný bod označujeme jako střed kružnice. Stejnou vzdálenost nazýváme poloměr
Kruh, kružnice, válec 1. Kruh, kružnice 1.1. Základní pojmy Kružnice je množina bodů mající od daného bodu stejnou vzdálenost. Daný bod označujeme jako střed kružnice. Stejnou vzdálenost nazýváme poloměr
Ohrozí nás Slunce v roce 2013, tedy rok po konci světa? Krátká odpověď: Ne více než kdy jindy.
 Ohrozí nás Slunce v roce 2013, tedy rok po konci světa? Krátká odpověď: Ne více než kdy jindy. Vztah Slunce Země Slunce je nejvýznamnějším tělesem Sluneční soustavy. Ovlivňuje ji nejen gravitačním působením,
Ohrozí nás Slunce v roce 2013, tedy rok po konci světa? Krátká odpověď: Ne více než kdy jindy. Vztah Slunce Země Slunce je nejvýznamnějším tělesem Sluneční soustavy. Ovlivňuje ji nejen gravitačním působením,
Kapitola 7: Integrál. 1/14
 Kapitola 7: Integrál. 1/14 Neurčitý integrál. Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f (x) x I nazýváme primitivní funkcí k
Kapitola 7: Integrál. 1/14 Neurčitý integrál. Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f (x) x I nazýváme primitivní funkcí k
DUM 11 téma: Nástroje pro transformaci obrázku
 DUM 11 téma: Nástroje pro transformaci obrázku ze sady: 2 tematický okruh sady: Bitmapová grafika ze šablony: 09 Počítačová grafika určeno pro: 2. ročník vzdělávací obor: vzdělávací oblast: číslo projektu:
DUM 11 téma: Nástroje pro transformaci obrázku ze sady: 2 tematický okruh sady: Bitmapová grafika ze šablony: 09 Počítačová grafika určeno pro: 2. ročník vzdělávací obor: vzdělávací oblast: číslo projektu:
= musíme dát pozor na: jmenovatel 2a, zda je a = 0 výraz pod odmocninou, zda je > 0, < 0, = 0 (pak je jediný kořen)
 .8.7 Kvadratické rovnice s parametrem Předpoklady: 507, 803 Pedagogická poznámka: Na první pohled asi každého zarazí, že takřka celá hodina je psána jako příklady a studenti by ji měli vypracovat samostatně.
.8.7 Kvadratické rovnice s parametrem Předpoklady: 507, 803 Pedagogická poznámka: Na první pohled asi každého zarazí, že takřka celá hodina je psána jako příklady a studenti by ji měli vypracovat samostatně.
Průřezové téma - Enviromentální výchova Lidské aktivity a životní prostředí Zdroje energie I.
 Průřezové téma - Enviromentální výchova Lidské aktivity a životní prostředí Zdroje energie I. Anotace: Prezentace slouží jako výukový materiál k průřezovému tématu EV Lidské aktivity a životní prostředí
Průřezové téma - Enviromentální výchova Lidské aktivity a životní prostředí Zdroje energie I. Anotace: Prezentace slouží jako výukový materiál k průřezovému tématu EV Lidské aktivity a životní prostředí
Pedagogická fakulta Katedra fyziky. Rekonexe magnetického pole a její důsledky v plazmové astrofyzice
 Jihočeská univerzita v Českých Budějovicích Pedagogická fakulta Katedra fyziky Rekonexe magnetického pole a její důsledky v plazmové astrofyzice Bakalářská práce Vedoucí práce: RNDr. Petr Jelínek, Ph.D.
Jihočeská univerzita v Českých Budějovicích Pedagogická fakulta Katedra fyziky Rekonexe magnetického pole a její důsledky v plazmové astrofyzice Bakalářská práce Vedoucí práce: RNDr. Petr Jelínek, Ph.D.
M-10. AU = astronomická jednotka = vzdálenost Země-Slunce = přibližně 150 mil. km. V následující tabulce je závislost doby
 M-10 Jméno a příjmení holka nebo kluk * Třída Datum Škola AU = astronomická jednotka = vzdálenost Země-Slunce = přibližně 150 mil. km V následující tabulce je závislost doby a/au T/rok oběhu planety (okolo
M-10 Jméno a příjmení holka nebo kluk * Třída Datum Škola AU = astronomická jednotka = vzdálenost Země-Slunce = přibližně 150 mil. km V následující tabulce je závislost doby a/au T/rok oběhu planety (okolo
Funkce více proměnných
 Funkce více proměnných Funkce více proměnných Euklidův prostor Body, souřadnice, vzdálenost bodů Množina bodů, které mají od bodu A stejnou vzdálenost Uzavřený interval, otevřený interval Okolí bodu
Funkce více proměnných Funkce více proměnných Euklidův prostor Body, souřadnice, vzdálenost bodů Množina bodů, které mají od bodu A stejnou vzdálenost Uzavřený interval, otevřený interval Okolí bodu
Proudění viskózní tekutiny. Renata Holubova renata.holubova@upol.cz
 Název Tematický celek Jméno a e-mailová adresa autora Cíle Obsah Pomůcky Poznámky Proudění viskózní tekutiny Mechanika kapalin Renata Holubova renata.holubova@upol.cz Popis základních zákonitostí v mechanice
Název Tematický celek Jméno a e-mailová adresa autora Cíle Obsah Pomůcky Poznámky Proudění viskózní tekutiny Mechanika kapalin Renata Holubova renata.holubova@upol.cz Popis základních zákonitostí v mechanice
http://www.zlinskedumy.cz
 Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor Ročník 2, 3 Obor Anotace CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Elektronické obvody, vy_32_inovace_ma_42_06
Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor Ročník 2, 3 Obor Anotace CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Elektronické obvody, vy_32_inovace_ma_42_06
Urychlené částice z pohledu sluneční rentgenové emise
 Urychlené částice z pohledu sluneční rentgenové emise Jana Kašparová Astronomický ústav AV ČR, Ondřejov kasparov@asu.cas.cz Vybrané kapitoly z astrofyziky, MFF UK, 25. října 2006 sluneční erupce stručný
Urychlené částice z pohledu sluneční rentgenové emise Jana Kašparová Astronomický ústav AV ČR, Ondřejov kasparov@asu.cas.cz Vybrané kapitoly z astrofyziky, MFF UK, 25. října 2006 sluneční erupce stručný
Další aplikace magnetohydrodynamiky v astrofyzice, nestability v plazmatu
 Další aplikace magnetohydrodynamiky v astrofyzice, nestability v plazmatu MHD dynamo, sluneční a hvězdný vítr, MHD vlny při srážkách HVC s galaktickým diskem Tekutinové dynamo Velmi důležitou částí magnetohydrodynamiky
Další aplikace magnetohydrodynamiky v astrofyzice, nestability v plazmatu MHD dynamo, sluneční a hvězdný vítr, MHD vlny při srážkách HVC s galaktickým diskem Tekutinové dynamo Velmi důležitou částí magnetohydrodynamiky
ATMOSFÉRA. Obecná část
 ATMOSFÉRA Obecná část Co je to ATMOSFÉRA? Nejjednodušší definice říká: Atmosféra = plynný obal Země Tato definice však pravdě úplně neodpovídá. Proč? Složky atmosféry: plynné (kyslík, dusík, vodní pára,...)
ATMOSFÉRA Obecná část Co je to ATMOSFÉRA? Nejjednodušší definice říká: Atmosféra = plynný obal Země Tato definice však pravdě úplně neodpovídá. Proč? Složky atmosféry: plynné (kyslík, dusík, vodní pára,...)
HOVORKOVÁ M., LINC O.: OPTICKÉ ÚKAZY V ATMOSFÉŘE
 OPTICKÉ ÚKAZY V ATMOSFÉŘE M. Hovorková, O. Linc 4. D, Gymnázium Na Vítězné pláni 1126, Praha 4, šk. rok 2005/2006 Abstrakt: Článek se zabývá vysvětlením několika světelných jevů, viditelných na obloze.
OPTICKÉ ÚKAZY V ATMOSFÉŘE M. Hovorková, O. Linc 4. D, Gymnázium Na Vítězné pláni 1126, Praha 4, šk. rok 2005/2006 Abstrakt: Článek se zabývá vysvětlením několika světelných jevů, viditelných na obloze.
Motivace, zvyšování energie lidstva a smysl života
 Motivace, zvyšování energie lidstva a smysl života 3. přednáška z cyklu Jak se dělá sociální síť Implementace, Startup, Motivace David Čápka, 2015 Co je to motivace? Motivace Definice: Motivace je vnitřní
Motivace, zvyšování energie lidstva a smysl života 3. přednáška z cyklu Jak se dělá sociální síť Implementace, Startup, Motivace David Čápka, 2015 Co je to motivace? Motivace Definice: Motivace je vnitřní
Bipolární tranzistor. Bipolární tranzistor. Otevřený tranzistor
 Bipolární tranzistor Bipolární tranzistor polovodičová součástka se dvěma PN přechody a 3 elektrodami: C - kolektorem E - emitorem B - bází vrstvy mohou být v pořadí NPN nebo PNP, častější je varianta
Bipolární tranzistor Bipolární tranzistor polovodičová součástka se dvěma PN přechody a 3 elektrodami: C - kolektorem E - emitorem B - bází vrstvy mohou být v pořadí NPN nebo PNP, častější je varianta
PRŮBĚH CHEMICKÉ REAKCE
 PRŮBĚH CHEMICKÉ REAKCE Autor: Mgr. Stanislava Bubíková Datum (období) tvorby: 12. 12. 2012 Ročník: osmý Vzdělávací oblast: Člověk a příroda / Chemie / Chemické reakce 1 Anotace: Žáci se seznámí s chemickou
PRŮBĚH CHEMICKÉ REAKCE Autor: Mgr. Stanislava Bubíková Datum (období) tvorby: 12. 12. 2012 Ročník: osmý Vzdělávací oblast: Člověk a příroda / Chemie / Chemické reakce 1 Anotace: Žáci se seznámí s chemickou
Proudìní fotosférického plazmatu po sluneèním povrchu
 Proudìní fotosférického plazmatu po sluneèním povrchu M. Klvaòa, Astronomický ústav Akademie vìd Èeské republiky, observatoø Ondøejov, Èeská republika, mklvana@asu.cas.cz M. Švanda, Matematicko-fyzikální
Proudìní fotosférického plazmatu po sluneèním povrchu M. Klvaòa, Astronomický ústav Akademie vìd Èeské republiky, observatoø Ondøejov, Èeská republika, mklvana@asu.cas.cz M. Švanda, Matematicko-fyzikální
IMPORT A EXPORT MODULŮ V PROSTŘEDÍ MOODLE
 Nové formy výuky s podporou ICT ve školách Libereckého kraje IMPORT A EXPORT MODULŮ V PROSTŘEDÍ MOODLE Podrobný návod Autor: Mgr. Michal Stehlík IMPORT A EXPORT MODULŮ V PROSTŘEDÍ MOODLE 1 Úvodem Tento
Nové formy výuky s podporou ICT ve školách Libereckého kraje IMPORT A EXPORT MODULŮ V PROSTŘEDÍ MOODLE Podrobný návod Autor: Mgr. Michal Stehlík IMPORT A EXPORT MODULŮ V PROSTŘEDÍ MOODLE 1 Úvodem Tento
Př. 3: Dláždíme čtverec 12 x 12. a) dlaždice 2 x 3 12 je dělitelné 2 i 3 čtverec 12 x 12 můžeme vydláždit dlaždicemi 2 x 3.
 1..20 Dláždění III Předpoklady: 01019 Př. 1: Najdi n ( 84,96), ( 84,96) D. 84 = 4 21 = 2 2 7 96 = 2 = 4 8 = 2 2 2 2 2 D 84,96 = 2 2 = 12 (společné části rozkladů) ( ) n ( 84,96) = 2 2 2 2 2 7 = 672 (nejmenší
1..20 Dláždění III Předpoklady: 01019 Př. 1: Najdi n ( 84,96), ( 84,96) D. 84 = 4 21 = 2 2 7 96 = 2 = 4 8 = 2 2 2 2 2 D 84,96 = 2 2 = 12 (společné části rozkladů) ( ) n ( 84,96) = 2 2 2 2 2 7 = 672 (nejmenší
λ, (20.1) 3.10-6 infračervené záření ultrafialové γ a kosmické mikrovlny
 Elektromagnetické vlny Optika, část fyziky zabývající se světlem, patří spolu s mechanikou k nejstarším fyzikálním oborům. Podle jedné ze starověkých teorií je světlo vyzařováno z oka a oko si jím ohmatává
Elektromagnetické vlny Optika, část fyziky zabývající se světlem, patří spolu s mechanikou k nejstarším fyzikálním oborům. Podle jedné ze starověkých teorií je světlo vyzařováno z oka a oko si jím ohmatává
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto
 Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Polarita σ vazeb v organických sloučeninách V uhlovodíkových řetězcích může být atom uhlíku vázán s jiným atomem prvku s výrazně nižší nebo
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Polarita σ vazeb v organických sloučeninách V uhlovodíkových řetězcích může být atom uhlíku vázán s jiným atomem prvku s výrazně nižší nebo
Koróna, sluneční vítr. Michal Švanda Sluneční fyzika LS 2014/2015
 Koróna, sluneční vítr Michal Švanda Sluneční fyzika LS 2014/2015 Přechodová oblast Změna teplotní režimu mezi chromosférou (10 4 K) a korónou (10 6 K) Nehomogenní, pohyby (doppler-shift), vývoj S výškou
Koróna, sluneční vítr Michal Švanda Sluneční fyzika LS 2014/2015 Přechodová oblast Změna teplotní režimu mezi chromosférou (10 4 K) a korónou (10 6 K) Nehomogenní, pohyby (doppler-shift), vývoj S výškou
2.1. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné x je taková
 .. Funkce a jejich graf.. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné je taková binární relace z množin R do množin R, že pro každé R eistuje nejvýše jedno R, pro které [, ] f.
.. Funkce a jejich graf.. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné je taková binární relace z množin R do množin R, že pro každé R eistuje nejvýše jedno R, pro které [, ] f.
Laboratorní práce č. 3: Měření indukčnosti cívky pomocí střídavého proudu
 Přírodní vědy moderně a interaktivně FYZIKA 5. ročník šestiletého a 3. ročník čtyřletého studia aboratorní práce č. 3: Měření indukčnosti cívky pomocí střídavého proudu ymnázium Přírodní vědy moderně
Přírodní vědy moderně a interaktivně FYZIKA 5. ročník šestiletého a 3. ročník čtyřletého studia aboratorní práce č. 3: Měření indukčnosti cívky pomocí střídavého proudu ymnázium Přírodní vědy moderně
Dopravní úloha. Jiří Neubauer. Katedra ekonometrie FEM UO Brno
 Přednáška č. 9 Katedra ekonometrie FEM UO Brno Distribuční úlohy Budeme se zabývat 2 typy distribučních úloh dopravní úloha přiřazovací problém Dopravní úloha V dopravním problému se v typickém případě
Přednáška č. 9 Katedra ekonometrie FEM UO Brno Distribuční úlohy Budeme se zabývat 2 typy distribučních úloh dopravní úloha přiřazovací problém Dopravní úloha V dopravním problému se v typickém případě
10. Polynomy a racionálně lomenné funkce
 10 Polynomy a racionálně lomenné funkce A Polynomy Definice 101 Reálný polynom stupně n (neboli mnohočlen) je funkce tvaru p(x) = a n x n + a n 1 x n 1 + + a 0, kde a 1,, a n R, a n 0, která každému komplexnímu
10 Polynomy a racionálně lomenné funkce A Polynomy Definice 101 Reálný polynom stupně n (neboli mnohočlen) je funkce tvaru p(x) = a n x n + a n 1 x n 1 + + a 0, kde a 1,, a n R, a n 0, která každému komplexnímu
ZÁŘENÍ V ASTROFYZICE
 ZÁŘENÍ V ASTROFYZICE Plazmový vesmír Uvádí se, že 99 % veškeré hmoty ve vesmíru je v plazmovém skupenství (hvězdy, mlhoviny, ) I na Zemi se vyskytuje plazma, např. v podobě blesků, polárních září Ve sluneční
ZÁŘENÍ V ASTROFYZICE Plazmový vesmír Uvádí se, že 99 % veškeré hmoty ve vesmíru je v plazmovém skupenství (hvězdy, mlhoviny, ) I na Zemi se vyskytuje plazma, např. v podobě blesků, polárních září Ve sluneční
VESMÍR. za počátek vesmíru považujeme velký třesk před 13,7 miliardami let. dochází k obrovskému uvolnění energie, která se rozpíná
 VESMÍR za počátek vesmíru považujeme velký třesk před 13,7 miliardami let dochází k obrovskému uvolnění energie, která se rozpíná vznikají první atomy, jako první se tvoří atomy vodíku HVĚZDY vznikají
VESMÍR za počátek vesmíru považujeme velký třesk před 13,7 miliardami let dochází k obrovskému uvolnění energie, která se rozpíná vznikají první atomy, jako první se tvoří atomy vodíku HVĚZDY vznikají
Sluneční fyzika. Vojtěch Sidorin. Praha,
 Sluneční fyzika OHŘEV KORÓNY Vojtěch Sidorin Astronomický ústav Univerzity Karlovy v Praze Praha, 29.4.2008 Struktura prezentace 1 V čem je problém 2 Navrhnutá řešení 3 Které řešení je správné 4 Není to
Sluneční fyzika OHŘEV KORÓNY Vojtěch Sidorin Astronomický ústav Univerzity Karlovy v Praze Praha, 29.4.2008 Struktura prezentace 1 V čem je problém 2 Navrhnutá řešení 3 Které řešení je správné 4 Není to
1 Rozbor vývoje smrtelných následků dopravních nehod v ČR
 1 Rozbor vývoje smrtelných následků dopravních nehod v ČR 1.1 Úvod Následující analýza je zaměřena na problematiku vývoje smrtelných následků nehodovosti v ČR především v období 2006-2012 (období, kdy
1 Rozbor vývoje smrtelných následků dopravních nehod v ČR 1.1 Úvod Následující analýza je zaměřena na problematiku vývoje smrtelných následků nehodovosti v ČR především v období 2006-2012 (období, kdy
Informace o stavu bodového systému v České republice PŘESTUPKY A TRESTNÉ ČINY I. Q 2014. O 070 Odbor kabinet ministra O 072 Oddělení tiskové
 Informace o stavu bodového systému v České republice PŘESTUPKY A TRESTNÉ ČINY I. 2014 O 070 Odbor kabinet ministra O 072 Oddělení tiskové OBSAH Návod Ministerstva dopravy Jak nedostat body... 3 Souhrn
Informace o stavu bodového systému v České republice PŘESTUPKY A TRESTNÉ ČINY I. 2014 O 070 Odbor kabinet ministra O 072 Oddělení tiskové OBSAH Návod Ministerstva dopravy Jak nedostat body... 3 Souhrn
Bohrova disertační práce o elektronové teorii kovů
 Niels Bohr jako vědec, filosof a občan 1 I. Úvod Bohrova disertační práce o elektronové teorii kovů do angličtiny. Výsledek byl ale ne moc zdařilý. Bohrova disertační práce byla obhájena na jaře roku 1911
Niels Bohr jako vědec, filosof a občan 1 I. Úvod Bohrova disertační práce o elektronové teorii kovů do angličtiny. Výsledek byl ale ne moc zdařilý. Bohrova disertační práce byla obhájena na jaře roku 1911
R10 F Y Z I K A M I K R O S V Ě T A. R10.1 Fotovoltaika
 Fyzika pro střední školy II 84 R10 F Y Z I K A M I K R O S V Ě T A R10.1 Fotovoltaika Sluneční záření je spojeno s přenosem značné energie na povrch Země. Její velikost je dána sluneční neboli solární
Fyzika pro střední školy II 84 R10 F Y Z I K A M I K R O S V Ě T A R10.1 Fotovoltaika Sluneční záření je spojeno s přenosem značné energie na povrch Země. Její velikost je dána sluneční neboli solární
Experimentální metody EVF II.: Mikrovlnná
 Experimentální metody EVF II.: Mikrovlnná měření parametrů plazmatu Vypracovali: Štěpán Roučka, Jan Klusoň Zadání: Měření admitance kolíku impedančního transformátoru v závislosti na hloubce zapuštění.
Experimentální metody EVF II.: Mikrovlnná měření parametrů plazmatu Vypracovali: Štěpán Roučka, Jan Klusoň Zadání: Měření admitance kolíku impedančního transformátoru v závislosti na hloubce zapuštění.
ISŠT Mělník. Integrovaná střední škola technická Mělník, K učilišti 2566, 276 01 Mělník Ing.František Moravec
 ISŠT Mělník Číslo projektu Označení materiálu Název školy Autor Tematická oblast Ročník Anotace Metodický pokyn CZ.1.07/1.5.00/34.0061 VY_32_ INOVACE_C.3.17 Integrovaná střední škola technická Mělník,
ISŠT Mělník Číslo projektu Označení materiálu Název školy Autor Tematická oblast Ročník Anotace Metodický pokyn CZ.1.07/1.5.00/34.0061 VY_32_ INOVACE_C.3.17 Integrovaná střední škola technická Mělník,
2.8.10 Rovnice s neznámou pod odmocninou a parametrem
 .8.10 Rovnie s neznámou pod odmoninou a parametrem Předpoklady: 806, 808 Budeme postupovat stejně jako v předhozíh hodináh. Nejdříve si zopakujeme obený postup při řešení rovni s neznámou pod odmoninou
.8.10 Rovnie s neznámou pod odmoninou a parametrem Předpoklady: 806, 808 Budeme postupovat stejně jako v předhozíh hodináh. Nejdříve si zopakujeme obený postup při řešení rovni s neznámou pod odmoninou
Diferenciální počet funkcí jedné proměnné
 Diferenciální počet funkcí jedné proměnné 1 Diferenciální počet funkcí jedné proměnné - Úvod Diferenciální počet funkcí jedné proměnné - úvod V přírodě se neustále dějí změny. Naší snahou je nalézt příčiny
Diferenciální počet funkcí jedné proměnné 1 Diferenciální počet funkcí jedné proměnné - Úvod Diferenciální počet funkcí jedné proměnné - úvod V přírodě se neustále dějí změny. Naší snahou je nalézt příčiny
1.1.1 Kvadratické rovnice (dosazení do vzorce) I
 .. Kvadratické rovnice (dosazení do vzorce) I Předpoklady: základní početní operace Rovnicí se nazývá vztah rovnosti mezi dvěma výrazy obsahujícími jednu nebo více neznámých. V této kapitole se budeme
.. Kvadratické rovnice (dosazení do vzorce) I Předpoklady: základní početní operace Rovnicí se nazývá vztah rovnosti mezi dvěma výrazy obsahujícími jednu nebo více neznámých. V této kapitole se budeme
Vzdělávání výzkumných pracovníků v Regionálním centru pokročilých technologií a materiálů reg. č.: CZ.1.07/2.3.00/09.0042
 Vzdělávání výzkumných pracovníků v Regionálním centru pokročilých technologií a materiálů reg. č.: CZ.1.07/2.3.00/09.0042 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem
Vzdělávání výzkumných pracovníků v Regionálním centru pokročilých technologií a materiálů reg. č.: CZ.1.07/2.3.00/09.0042 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem
