TEORIE HER, FORMOVÁNÍ KOALIC A KONCENTRACE POLITICKÉ MOCI V ZASTUPITELSTVU HLAVNÍHO MĚSTA PRAHY
|
|
|
- Štěpán Rohla
- před 8 lety
- Počet zobrazení:
Transkript
1 TEORIE HER, FORMOVÁNÍ KOALIC A KONCENTRACE POLITICKÉ MOCI V ZASTUPITELSTVU HLAVNÍHO MĚSTA PRAHY DOI: /j.polek.1107 Martin 1 Dlouhý* Abstract Game Theory, Coalition Formation and Political Power Concentration in the Prague City Assembly The objective of the paper is to study the political development in the Prague City Assembly after three elections in 2006, 2010, and The theory of voting games, the Shapley-Shubik and Banzhaf power indexes, and theories of coalition formation are used for an analysis of possible majority coalitions. We developed the mayor s power index that measures the probability that the party will be the strongest party in the majority coalition with the right having a mayor. Measures of concentration of political power are used for evaluating the processes of political fragmentation. The increased number of political parties represented in the Prague City Assembly highly increased the number of possible coalitions and the number of political parties needed to form majority coalitions. The process of political fragmentation is probably not limited only to the Prague City Assembly. Keywords: game theory, coalition formation, Shapley-Shubik power index, mayor s power index, Prague City Assembly JEL Classification: H70, C71 Úvod Teorie her se zabývá studiem konfliktních či kooperativních rozhodovacích situací s více účastníky. Hra má této v teorii velmi obecný význam, který nezahrnuje pouze salónní hry typu šachy či poker, ale v podstatě jakoukoli konfliktní či kooperativní situaci mezi jedinci, firmami, vojenskými jednotkami, politickými stranami, biologickými druhy. Tato různorodost možných aplikačních oblastí ukazuje na univerzalitu modelů vyvinutých v rámci teorie her (např. Binmore, 2014, Dlouhý, Fiala, 2015, Houdek, 2008, Shermer, 2008). Účastníci rozhodovací situace jsou hráči. Každý hráč volí strategii ze svého prostoru strategií podle hodnot výplatní funkce. Výplatní funkce určitého hráče závisí nejen na rozhodnutí hráče samotného, ale také na rozhodnutí všech ostatních hráčů. Strategie, která hráči v dané hře zajišťuje nejvyšší dosažitelnou hodnotu výplatní funkce, je optimální (rovnovážnou) strategií. O hráčích předpokládáme, že mají veškeré informace o hře a maximalizují své výplaty. Mezi aplikační oblastí teorie her mimo oblast ekonomie patří zejména politologie. Je možné například zmínit povolební komentáře politologů o tom, jaké koalice jsou možné sestavit, a to jak početně z hlediska získaných mandátů, tak z hlediska ideologických *1 Martin Dlouhý (martin.dlouhy@vse.cz), Vysoká škola ekonomická v Praze, Fakulta informatiky a statistiky. Výzkum byl podpořen Grantovou agenturou ČR, projekt č S. 747
2 pozic politických stran. Hráči v takové hře jsou tedy politické strany a výplatní funkce je dána účastí či neúčastí politické strany ve vládní koalici. Pomocí různých ukazatelů síly lze také hodnotit vyjednávací sílu politických stran, která se může významně lišit od volebního výsledku v podobě počtu mandátů. Jiné politologické aplikace se zaměřují na rozbor volebních systémů a na možnosti jejich zlepšení tak, aby volební systém co nejlépe vystihoval skutečné preference voličů, nebo aby zajistil vznik silné, stabilní vlády. Obecněji lze závěry teorie her ze zastupitelských sborů aplikovat i na volby a hlasování v mezinárodních institucích, v různých komisích, v orgánech akciových společností atd. V mezinárodních vztazích je možné teorii her využívat při vyjednávání, při použití hrozeb a zastrašování. Dá se proto říci, že poznatky teorie her patří do vzdělání každého politologa. Například v učebnici Přehled moderních politologických teorií (Říchová, 2000) najdeme hned dvě kapitoly, které jsou věnovány využití teorie her v politologii. Cílem příspěvku je aplikace přístupů z oblasti teorie her na analýzu vývoje politické situace v Zastupitelstvu hl. města Prahy (ZHMP) za poslední tři volební období (volby 2006, 2010, 2014). Zaměříme se na problém formování většinové koalice, jehož obtížnost závisí na počtu stran v ZHMP a jejich početní síle. Pro hodnocení síly stran využijeme jednak tradičních ukazatelů síly a jednak definujeme nový ukazatel (primátorský ukazatel síly). Dále se budeme zabývat mírou politické koncentrace v ZHMP a jejím vývojem. 1. Metody teorie her a zdroj dat Teorie her provádí analýzu rozhodovacích situací pomocí specifických matematických modelů, které na přiměřené míře abstrakce popisují podstatné charakteristiky dané situace. Výchozím matematickým modelem je hra v normálním tvaru, která je určena množinou hráčů N = {1, 2,, N}, množinou prostorů strategií X = {X 1, X 2,, X N } a množinou výplatních funkcí F = {f 1 (x 1, x 2,, x N ), f 2 (x 1, x 2,, x N ),, f N (x 1, x 2,, x N )}. Výplatní funkce hráčů jsou definovány na kartézském součinu prostoru strategií, neboť musí stanovit výhru hráče pro všechny možné kombinace strategií. Souhrnný přehled o tomto a dalších modelech teorie her lze najít v českých i zahraničních učebních textech, jako např. (Maňas, 1991, Myerson, 1991, Osborne, 2004, Dlouhý, Fiala, 2009, 2015, Chvoj, 2013). Pokud platí, že co jeden hráč získá, jiný hráč musí ztratit, tak se jedná o hru s konstantním součtem. Hra s konstantním součtem je sice zjednodušeným, ale přesto dostatečným modelem pro mnoho reálných situací. Například v politickém boji platí, že celkový počet poslanců, zastupitelů, ministrů či radních je konstantní. Když vládne jeden, nemůže vládnout druhý. 1.1 Koaliční hry Jestliže hráči mají možnost uzavírat závazné dohody o volbě strategií, provádíme analýzu pomocí kooperativní hry (např. Dlouhý, Fiala, 2015). Ve hře s dvěma hráči existují pouze dvě možnosti řešení: buď se hráči dohodnou na vzájemné spolupráci, nebo budou vystupovat jako konkurenti. Kooperace vznikne jen tehdy, pokud bude pro oba hráče výhodná. V kooperativní teorii při větším počtu hráčů (N > 2) vzniká hráčům nový problém, totiž s kým spolupracovat a proti komu. Skupinu hráčů, kteří spolupracují při volbě strategií, nazveme koalicí. Proto také kooperativní hry s N hráči nazýváme též jako koaliční 748
3 hry. Nechť N je množina hráčů, potom koalicí hráčů rozumíme každou podmnožinu S množiny hráčů N. V případě, že S se shoduje s množinou N, jsou v koalici všichni hráči a hovoříme o velké koalici. Zde nutno upozornit, že politologové si pod pojmem velká koalice představují něco jiného, než teorii her. I když nějaký hráč nevstoupí do žádné koalice s dalšími hráči, budeme ho přesto nazývat koalicí (jednoprvkovou). To je další odlišnost teorie her od politologie. Množinu utvořených koalic v rámci určité hry budeme nazývat koaliční strukturou. Optimální (rovnovážná) koaliční struktura je řešením koaliční hry tehdy, když žádný z hráčů nemá důvod přestoupit do jiné koalice. Ve hře o pěti hráčích můžeme popsat koaliční strukturu například následovně: ({1, 4},{2, 3},{5}). Spolupracují hráči 1 a 4, hráči 2 a 3, hráč 5 hraje samostatně. V typických hrách budeme předpokládat volnou disjunktní koaliční strukturu, ve které jsou přípustné jakékoli koalice a ve které je každý hráč členem pouze jedné koalice. Uvažujme koalici S. Každý hráč má možnost být nebo nebýt členem koalice S. Počet možností být, či nebýt členem koalice S pro všechny hráče je dán podle počtu hráčů, čili 2 N. Obvykle vynecháme možnost, že všichni hráči se rozhodli nebýt členy koalice (vzniká tzv. prázdná koalice {0}), a tím se dostáváme k výsledku, že ve hře s N hráči je možné vytvořit 2 N 1 koalic. Počet možných koalic tudíž poměrně rychle roste s počtem hráčů. Pro hru se třemi hráči dostaneme 7 koalic, čtyři hráči mohou vytvořit 15 koalic, pět hráčů 31 koalic a tak dále. Při modelování kooperativních her je výhodné přejít od hry v normálním tvaru ke hře ve tvaru charakteristické funkce. Charakteristickou funkcí hry s množinou hráčů N nazveme takovou funkci v, která je definována pro všechny podmnožiny S, to jest pro všechny koalice, kterých je 2 N 1. Každé koalici charakteristická funkce přiřazuje hodnotu v(s), což je výplata koalice S. Charakteristická funkce je obdobou výplatní funkce, s tím rozdílem, že charakteristická funkce přiřazuje výplaty koalicím, nikoliv hráčům. Jestliže pro každou možnou koaliční strukturu je součet výplat všech utvořených koalic roven určité konstantě, jde o hru s konstantním součtem. Příkladem hry s konstantním součtem je hlasovací hra (viz oddíl 1.2), ve které většinová koalice získává výplatu označenou symbolicky 1 (vládnutí) a menšinová koalice získává výhru 0 (opozice). Shapley (1953) navrhl metodu odhadu síly hráče z hlediska jeho mezního přínosu ke všem koalicím, v nichž může být členem. Toto řešení se označuje jako Shapleyův vektor a jeho složky bývají označovány jako Shapleyovy hodnoty. Pro kooperativní hru o N hráčích je N-rozměrný Shapleyův vektor definován jako h = (h 1, h 2,..., h N ), přičemž jednotlivé složky označují střední hodnotu mezního přínosu i-tého hráče ke všem koalicím, ve kterých může být daný hráč členem. 1.2 Hlasovací hry Specifickým typem koaličních her jsou hry hlasovací. Nechť N = {1, 2,..., N} je množina poslaneckých klubů v parlamentu. Počet poslanců i-tého klubu bude označován jako a i a celkový počet poslanců v parlamentu a 0 lze vyjádřit jako součet poslanců všech klubů. Důležitým faktorem, který určuje reálný vliv a hlasovací sílu určitého politického seskupení je tzv. hlasovací pravidlo vyjádřené prostřednictvím hodnoty α. Hlasovací pravidlo určuje minimální počet hlasujících, který je potřeba k vítězství v daném hlasování: 749
4 int a 0 1, (1) kde symbol int označuje celou část součinu αa 0. Pokud je respektováno hlasovací pravidlo, pak pro vítěznou (většinovou) m-člennou koalici (1 m N) platí: m ai int a0 0. (2) i 1 V opačném případě se jedná o koalici menšinovou. Obvykle má hlasovací pravidlo α hodnotu 0,5, což vyjadřuje nutnost získat nadpoloviční většinu, ale není neobvyklé, že je stanovena vyšší hodnota. Například požadavek 2/3 hlasů pro ústavní změny. Pro měření síly hráčů je možno použít koncepci kooperativní hry N hráčů ve tvaru charakteristické funkce. Pokud pro všechny koalice S hry ve tvaru charakteristické funkce platí v(s) = 0 nebo v(s) = 1, používá se pro tuto hru (N, v) označení prostá hra. Charakteristická funkce v(s) = 1, je-li S vítěznou (většinovou) koalicí, v(s) = 0, je-li S poraženou (menšinovou) koalicí. Prostá hra (N, v, α) s takto definovanou charakteristickou funkcí je pak označována jako hlasovací hra. V české literatuře jsou tyto hry též známy jako hry volební (např. Fiala, 2003). My se přikláníme k názvu hra hlasovací, neboť nejde o volby, ale o formování koalice pro hlasování již zvolených zástupců. Pro analýzu hlasovacích her pomocí ukazatelů síly hráčů je nutné přijmout následující předpoklady: Všichni zástupci jedné strany hlasují vždy jednotně. Vytvoří-li se v určité fázi hlasovacího procesu nějaká koalice, pak také všichni členové této koalice hlasují jednotně. Je možno vytvořit libovolnou koalici stran a všechny koalice jsou stejně pravděpodobné. Všechny tyto předpoklady však v politické praxi bývají splněny zřídka a po celé volební období, což dokladují případy odpadlíků a přeběhlíků, kteří rozhodovali o bytí či nebytí vlád. Linek a Rakušanová (2005) ukazují, že čeští poslanci se poměrně často odchylují od jednotného hlasování klubů. V obecních zastupitelstvech má ovšem požadavek disciplinovaného hlasování vyšší váhu, neboť v poslanecké sněmovně stačí pro přijetí návrhu většina z přítomných, zatímco v obecním zastupitelstvu většina ze všech zastupitelů. Přes tyto nedostatky jsou ukazatelé síly hráčů zajímavým a dobře použitelným indikátorem situace v parlamentu či zastupitelstvu. Ukazatelé síly vycházejí ze skutečnosti, že pouze samotné rozdělení zástupců mezi jednotlivé strany v hlasovací hře není postačujícím ukazatelem síly a vlivu politických subjektů. Záleží také na síle strany pro vytvoření většinové koalice. Mezi v literatuře nejčastěji zmiňované a v praxi nejpoužívanější ukazatele síly hráčů patří ukazatele Shapleyův-Shubikův a Banzhafův (např. Straffin, 1994, Loužek, 2004, Dlouhý, Fiala, 2009). Jelikož naším cílem není úplný výčet ukazatelů síly, ani není jejich použití z hlediska cílů příspěvku nutné, nebudeme zde další ukazatele z jinak bohaté literatury uvádět (např. Deegan, Packel, 1978; Straffin, 1994; Felsenthal, Machover, 2005; Turnovec, 2007). Shapleyův-Shubikův ukazatel síly vychází ze Shapleyovy hodnoty pro kooperativní hry (Shapley, Shubik, 1954). V případě koaličních her s charakteristickou funkcí 750
5 s hodnotou 1 (vláda) nebo 0 (opozice) se Shapleyova hodnota zjednoduší tak, že složky vektoru h = (h 1, h 2,..., h N ) vyjadřujeme pomocí vztahu: N 1!! hi S S, (3) i S N! kde symbolem S je označen počet členů koalice S a sumace probíhá přes všechny většinové koalice S takové, že i S a S {i} je menšinová koalice. Pro hodnoty vypočtené dle (3) platí: N hi 1, hi 0. (4) i 1 Hodnota h i je označována jako Shapleyův-Shubikův ukazatel síly pro i-tého hráče. Lze ji interpretovat jako pravděpodobnost, že i-tá strana bude nezbytná při sestavování většinových koalicí. Dalším ukazatelem síly koalice je Banzhafův ukazatel síly. Nechť (N, v, α) definuje hlasovací hru. Nechť pro charakteristickou funkci platí v(s) = 1, v(s {i}) = 0, potom hráče i lze označovat jako nepostradatelného pro vítězství koalice S. Symbolem e i budeme značit počet všech většinových koalic S takových, pro které je hráč i S nepostradatelný. Tato míra se obvykle značí jako vektor b. Její jednotlivé složky jsou definovány jako: ei i. N (5) e k k 1 Koeficient β i vyjadřuje pravděpodobnost situace, při které strana svým odstoupením může anulovat vítězné postavení většinové koalice. Důležitým hlediskem při formování koalice je rovněž obsazení funkce primátora (starosty, předsedy vlády apod.), která symbolizuje moc dané strany a její možnost být lídrem ve vyjednávání. Obvykle tuto funkci získává nejsilnější strana, která je součástí většinové koalice. Shapley-Shubikův a Banzhafův ukazatel síly však s tímto faktem nepracují. Z tohoto důvodu navrhujeme nový ukazatel m i, který bude definován jako pravděpodobnost, že daná strana bude v utvořené většinové koalici nejsilnějším hráčem (podle počtu zastupitelů). V případě, že ve většinové koalici je více nejsilnějších stran se stejným počtem zastupitelů, předpokládáme, že všechny strany mají stejnou pravděpodobnost získat primátora. Jelikož jde o pravděpodobnost, bude součet těchto ukazatelů pro všechny strany roven jedné. Tento ukazatel nazveme podle naší aplikace na ZHMP jako primátorský ukazatel síly. Obecně je však lhostejno, zda jde o starostu, předsedu vlády, předsedu sněmovny atd. Symbolem f i budeme značit počet všech většinových koalic S takových, ve kterých je hráč i S hráčem s maximálním počtem zastupitelů. Primátorský ukazatel síly je pak možné vyjádřit ve tvaru: m i N f k 1 i f k. (6) 751
6 1.3 Formování koalic a politická koncentrace Teorie formování koalic se používají k předpovídání struktury většinových koalic. Pochopení, jak dané volební výsledky vedou k vytvoření vlády, je jednou z důležitých prognóz v politologii. Teorie nabízejí množinu koalic podstatně menší, než je množina všech přípustných koalic, kterých je 2 N 1, kde N je počet účastníků. Různé teorie poskytují různé předpovědi pro vytvoření většinové koalice a jejich vypovídací schopnost může být srovnávána se skutečnou vládní koalicí, což zpětně umožňuje ohodnocení teorií. Jsou dva základní druhy teorií, nepolitické (mocenské) teorie formování koalic a politické teorie formování koalic (např. Dlouhý, Fiala, 2009). Tyto teorie se liší v tom, zda účastníci koaličního vyjednávání při formování koalice přihlížejí či nepřihlížejí k politickým pozicím účastníků. Mezi nepolitické (mocenské) teorie formování koalic patří teorie von Neumanna a Morgensterna (1944), podle které se utvoří minimální většinová koalice. Minimální většinová koalice je taková koalice, která se stane menšinovou v případě, že ji opustí libovolný člen. Tím sice autoři redukovali celkový počet možných většinových koalic, avšak nevýhodou této teorie zůstává, že obvykle existuje více minimálních většinových koalic, takže příliš nepomůže při predikci možného výsledku. Riker (1962) navrhl koncepci nejmenší minimální většinové koalice, která redukuje počet predikovaných koalic. Z množiny minimálních většinových koalic jsou vybrány koalice s nejmenším počtem poslanců. Myšlenka Rikerovy teorie spočívá v předpokladu, že každá politická strana maximalizuje svůj vliv v utvořené koalici. Podíl politické strany s daným počtem poslanců bude tím větší, čím menší bude celkový počet poslanců koalice. Praktickým problémem této teorie ovšem je předpoklad, že poslanci se chovají jako hlasovací stroje. Tak tomu obvykle nebývá a koalice s malou většinou může být vydírána skupinou poslanců či může velmi snadno ztratit většinu při odchodu několika poslanců. Proto lze v realitě očekávat, že nejmenší minimální většinová koalice nebude v politické praxi až tak oblíbena. Jiný způsob pro redukci počtu predikovaných koalic je koncepce vyjednávacího návrhu. Z množiny minimálních většinových koalic jsou vybrány koalice s nejmenším počtem členů. Tato koncepce je založena na předpokladu, že čím menší bude počet politických stran, tím snadněji dosáhnou dohody. Politické teorie formování koalic přihlížejí k politickým pozicím účastníků koalice. Například teorie minimální souvislé většinové koalice vychází z předpokladu, že je možné politické strany uspořádat podle ideologické dimenze od levicových po pravicové a vytvořená koalice bude ideologicky souvislá v tom smyslu, že všichni členové koalice budou navzájem sousední podle této dimenze. Souvislá většinová koalice bude minimální v tom smyslu, že jestliže ji opustí libovolný člen, koalice už nebude většinová nebo souvislá. Predikovaná koalice s nejmenším vnitřním konfliktem se bude snadněji formovat, snáze zůstane stabilní, a proto bude preferována před jinými. Jinou teorií je koncepce uzavřené koalice s minimálním rozpětím. Je to taková minimální souvislá koalice, která má nejmenší ideologické rozpětí. Jednodimenzionální teorie vyjednávání při formaci koalice předvídá diktátorskou roli pro stranu, která kontroluje mediánového poslance. Tím má totiž strana zaručenu účast ve většinové koalici. Při určitých hlasováních však může hrát kromě ideologické dimenze důležitou roli i faktor lokálního patriotismu. Kupříkladu poslanci Evropského parlamentu jsou 752
7 sice členy celoevropského politického klubu, zároveň však vytvářejí hlasovací koalici s poslanci ze stejné země (Turnovec, Mercik, Mazurkiewicz, 2008). V případě ZHMP lze tento jev pozorovat na zájmu zastupitele za určitý klub zastupovat i městskou část, ze které pochází. To se může projevit například při určování pravidel pro rozdělování dotacím městským částem (např. Dlouhý, 2013, 2014). Důležitým aspektem složitosti koaličního vyjednávání je celkový počet hráčů a struktura rozdělení hlasů, což můžeme zachytit a měřit pomocí ukazatelů politické koncentrace. Nejjednodušší mírou koncentrace je počet klubů (N), případně od toho odvozený celkový počet koalic (2 N 1). Další ukazatelem je z ekonomie známá míra koncentrace, jež vyjadřuje podíl stanoveného počtu největších firem v odvětví. Nic nebrání použít tuto míru i pro naše účely a jako míry koncentrace použít podíl dvou a podíl tří nejsilnějších zastupitelských klubů na celkovém počtu zastupitelů. Jiným ukazatelem je pravděpodobnost, že dva náhodně vybraní zastupitelé budou ze stejného klubu (volební strany). Pro zastupitelský sbor s nekonečným počtem členů je výpočet je matematicky shodný s výpočtem v případě Herfindahlova indexu koncentrace: N H a, (7) i 1 kde a i jsou podíly jednotlivých klubů zastupitelů z celkového počtu zastupitelů v rozmezí nula až jedna. 2 i 1.4 Zdroj dat Veškeré údaje o volbách v České republice od roku 1990 jsou volně dostupné na webové prezentaci Českého statistického úřadu na adrese Odtud také pocházejí všechny údaje o výsledcích voleb do ZHMP, které jsme při výpočtech využili. 2. Analýza koaličních her v Zastupitelstvu hlavního města Prahy 2.1 Volební období Ve volbách do Zastupitelstva hlavního města Prahy (ZHMP), které se konaly ve dnech , si občané vybírali mezi 24 kandidátními listinami. Ve volbách uspělo 5 volebních stran: ODS, ČSSD, Strana zelených, KSČM a SNK Evropští demokraté (tabulka 1). Vítězná ODS získala 54,4 % hlasů, což znamenalo nadpoloviční většinu zastupitelů, celkem 42 ze 70 zastupitelů. Analýza síly volebních stran je tudíž zbytečná, neboť sto procent moci držela ODS, síla ostatních stran byla nulová. Analýza většinových koalic je rovněž zbytečná, neboť žádná většinová koalice bez ODS nešla sestavit. Samotná ODS mohla vytvořit minimální většinovou koalici, Rikerovu nejmenší minimální většinovou koalici, minimální souvislou většinovou koalici, vyjednávací návrh, uzavřenou koalici s minimálním rozpětím. Ve skutečnosti vznikla v Praze koalice tří volebních stran: ODS, Strany zelených, SNK ED. Zástupci dvou menších stran však Radu HMP během volebního období opustili. ODS měla v ZHMP postavení hráče diktátora. Hráč diktátor je hráč, jehož hlasovací síla je rovna nebo větší než hlasovací pravidlo. Hráč diktátor tudíž absolutně rozhoduje o tom, který návrh je či není přijat v hlasovací hře. 753
8 Tabulka 1 Výsledky voleb do ZHMP v roce 2006 Volební strana Počet hlasů v % Počet zastupitelů (%) Shapleyův- Shubikův ukazatel síly Banzhafův ukazatel síly Primátorský ukazatel síly ODS 54,43 42 (60,00) ČSSD 15,88 12 (17,14) KSČM 7,93 6 (8,57) Strana zelených 7,80 6 (8,57) SNK ED 5,39 4 (5,71) Celkem Volební období Ve volbách roku 2010 do ZHMP kandidovalo 23 volebních stran. Praha byla rozdělena do sedmi obvodů pro devíti mandátech, což zřejmě zvýhodnilo velké volební strany. Volební strany Věci veřejné a Koalice SZ, SNK sice překročily nutnou pětiprocentní hranici, přesto ovšem v malých volebních odvodech po přepočtech na mandáty nezískaly žádného zastupitele. Do ZHMP se nakonec dostaly čtyři volební strany: TOP 09, ODS, ČSSD a KSČM. Počty získaných zastupitelů pro tyto strany jsou uvedeny v tabulce 2. Počet členů pražského zastupitelstva byl v daných volbách stanoven na 63, takže většinová koalice potřebovala minimálně 32 zastupitelů. V tabulce 2 jsme vypočetli Shapleyův-Shubikův, Banzhafův a primátorský ukazatel síly. Tři nejsilnější strany mají podle Shapleyova-Shubikova a Banzhofova ukazatele shodnou vyjednávací sílu, přestože má TOP 09 téměř dvojnásobný počet zastupitelů než ČSSD. Síla KSČM je v dané situaci nulová podle obou ukazatelů síly. Naopak primátorský ukazatel vypovídá o dominantní pozici TOP 09 při získání primátorské pozice. Tabulka 2 Výsledky voleb do ZHMP v roce 2010 Volební strana Počet hlasů v % Počet zastupitelů (%) Shapleyův- Shubikův ukazatel síly Banzhafův ukazatel síly Primátorský ukazatel síly TOP 09 30,26 26 (41,27) 33,3 33,3 75,0 ODS 23,10 20 (31,75) 33,3 33,3 25,0 ČSSD 17,85 14 (22,22) 33,3 33,3 0,0 KSČM 6,82 4 (4,76) 0,0 0,0 0,0 Koalice SZ, SNK 5,90 0 (0,00) Věci veřejné 5,66 0 (0,00) Celkem % 100 % 100 % 754
9 Počet možných koalic ve hře se čtyřmi hráči je celkem 15. Z toho většinových koalic, které mají 32 a více zastupitelů, je možných 8. Z toho je jedna koalice čtyřčlenná (velká koalice), čtyři koalice jsou trojčlenné a tři koalice dvoučlenné (tabulka 3). Z hlediska primátorského ukazatele síly by TOP 09 uspěla šestkrát a ODS by uspěla dvakrát. Tabulka 3 Většinové koalice v ZHMP 2010 Většinové koalice Počet koaličních zastupitelů TOP 09 + ODS + ČSSD + KSČM 63 TOP 09 + ODS + ČSSD 60 TOP 09 + ODS + KSČM 49 TOP 09 + ČSSD + KSČM 43 ODS + ČSSD + KSČM 37 TOP 09 + ODS 46 TOP 09 + ČSSD 40 ODS + ČSSD 34 Nyní z většinových koalic vybereme pouze minimální většinové koalice. Například velká koalice všech čtyř politických stran není minimální většinovou koalicí, protože jakákoliv ze stran může koalici opustit, aniž by svým rozhodnutím ohrozila většinový status koalice. V ZHMP šlo sestavit pouze tři minimální většinové koalice, které shodou okolností během volebního období všechny střídavě vládly (koalice ODS a ČSSD, potom koalice ODS a TOP 09, nakonec koalice TOP 09 a ČSSD). Rikerova nejmenší minimální většinová koalice by v ZHMP byla ve složení ODS a ČSSD a měla by 34 zastupitelů. To se také stalo a jako první vznikla v ZHMP v roce 2010 právě tato nejmenší minimální většinová koalice. Z hlediska možného maximálního počtu získaných členů rady, kterých je 11, byla z mocenského (nikoliv ideologického) hlediska koalice ODS a ČSSD pro obě strany racionální volbou. Během volebního období došlo k odchodu několika zastupitelů z klubu ODS, kteří postupně vytvořili vlastní zastupitelských klub Nezávislých. Tím se zvýšil počet zastupitelských klubů v ZHMP na pět. Ovšem v posledním roce volebního období již nebyl takový zájem na další změnu koalice a do konce období dovládla jednobarevná rada TOP 09 s koaliční podporou ČSSD. 2.3 ZHMP po volbách 2014 V obecních volbách se do ZHMP volilo v jednom celopražském volebním obvodu. Počet členů zastupitelstva byl ve volbách roku 2014 stanoven na 65, takže většinová koalice potřebovala minimálně 33 zastupitelů. Zvýšený počet zastupitelů a jediný pražský obvod zvýšil šance úspěchu pro menší volební strany. Dalo se 755
10 tedy očekávat, že ZHMP by mohlo být politicky více rozmanité, což se také potvrdilo. Do ZHMP se v roce 2014 dostalo celkem sedm volebních stran. Počty získaných zastupitelů jsou uvedeny v tabulce 4. V tabulce 4 jsme také vypočetli hodnoty Shapleyova-Shubikova, Banzhafova a primátorského ukazatele síly. Za povšimnutí stojí zejména rozdíl v síle ANO 2011 a TOP 09, který vzniká v důsledku toho, že TOP 09 má pouze o jednoho zastupitele méně. Z hlediska ukazatelů síly získává největší výhodu volební strana ANO 2011, která má v ZHMP 26,2 % zastupitelů, ale její vyjednávací síla je odhadována Shapleyovým-Shubikových ukazatelem síly na 34,3 % a Banzhafovým ukazatelem síly na 32,2 %. Ještě větší rozdíl ukazuje primátorský ukazatel síly, podle kterého díky jednomu hlasu navíc má ANO 2011 téměř 80% šanci na primátora. Tabulka 4 Výsledky voleb do ZHMP v roce 2014 Volební strana Počet hlasů v % Počet zastupitelů (%) Shapleyův- Shubikův ukazatel síly Banzhafův ukazatel síly Primátorský ukazatel síly ANO ,08 17 (26,2) 34,3 32,2 79,7 TOP 09 20,07 16 (24,6) 24,3 22,0 20,3 Trojkoalice 11,22 8 (12,3) 11,0 11,9 0 ODS 10,97 8 (12,3) 11,0 11,9 0 ČSSD 10,43 8 (12,3) 11,0 11,9 0 KSČM 5,91 4 (6,2) 4,3 5,1 0 Piráti 5,31 4 (6,2) 4,3 5,1 0 Celkem 65 (100 %) 100 % 100 % 100 % Počet možných koalic ve hře se sedmi hráči je 127, což je zhruba osmkrát více než v předešlém volebním období Již tento údaj svědčí o tom, jak roztříštěnost politického spektra ve volebním období násobně komplikuje analýzu situace a formování koalic v ZHMP. Počet možných většinových koalic je celkem 64. Obecně je počet většinových koalic v zastupitelstvu s lichým počtem zastupitelů 2 N /2 (tedy 2 N-1 ), protože ke každé většinové koalici nutně existuje kolice menšinová. Výjimkou je velká koalice, která je spárována s prázdnou koalicí {0}. Pro sudý počet zastupitelů toto neplatí, protože v případě remízového stavu hlasů budou obě koalice menšinové. Počet kombinací koalic s rovným počtem hlasů závisí na konkrétní struktuře velikosti klubů v zastupitelstvu, takže hodnota 2 N-1 má pro sudý počet zastupitelů význam teoreticky maximálního počtu většinových koalic v dané hlasovací hře. Pokud by pro ostatní volební strany v ZHMP bylo nepřípustné uzavřít koalici s KSČM, tak by počet většinových koalic poklesl na 29. Ve skutečnosti byla v listopadu 2014 uzavřena koalice ANO 2011, Trojkoalice a ČSSD. Tato koalice je jednou z minimálních většinových koalic. Během dvakrát přerušeného zasedání ZHMP v říjnu 2015 byla tato koalice vypovězena ze strany ČSSD. 756
11 V roce 2014 mohla v ZHMP teoreticky vzniknout jediná dvoučlenná většinová koalice, a to koalice ANO 2011 a TOP 09, která by měla 33 zastupitelů. Vzhledem k vyhraněné volební kampani však tato koalice byla v té době politicky nemožná a navíc krátce po volbách došlo k odchodu čtyř zastupitelů z klubu TOP 09. Tím již možnost dvoučlenné většinové koalice v ZHMP neexistuje. V červnu 2015 bylo v ZHMP devět možných hráčů, neboť kolem bývalého primátora Tomáše Hudečka vznikl klub Nezávislí a dále je v ZHMP jeden nezařazený zastupitel (tabulka 5). Počet všech možných koalic stoupl na 511. Odchod čtyř zastupitelů z TOP 09 samozřejmě oslabil sílu klubu TOP 09, ovšem zároveň trochu paradoxně snížil mírně i sílu zastupitelského klubu ANO Naopak podle ukazatelů síly vznikem dvou nových klubů mírné posílily malé zastupitelské kluby KSČM a Piráti, což je v literatuře známo jako tzv. paradox nového člena (např. Straffin, 1994, Loužek, 2004a). Tabulka 5 Zastupitelské kluby v ZHMP, červen 2015 Kluby zastupitelů Počet koaličních zastupitelů Shapleyův- Shubikův ukazatel Banzhafův ukazatel síly Primátorský ukazatel síly ANO ,8 31,2 80,9 TOP 09 a nezávislí 12 17,5 17,0 18,0 Trojkoalice 8 11,6 11,5 0,4 ODS 8 11,6 11,5 0,4 ČSSD 8 11,6 11,5 0,4 KSČM 4 5,6 5,9 0 Piráti 4 5,6 5,9 0 Nezávislí 3 2,3 2,8 0 Nezařazený zastupitel 1 2,3 2,8 0 Celkem % 100 % 100 % Pokud bychom v situaci devíti možných hráčů (tabulka 5) vyřadili klub KSČM a nezařazeného zastupitele, neboť jejich účast na koalici není příliš pravděpodobná, mohlo by vzniknout 53 většinových koalic. Jestliže by klub TOP 09 chtěl zformovat bez podpory klubu KSČM a nezařazeného zastupitele většinovou koalici, kterou by poslal vítěze voleb ANO 2011 do opozice, měl by klub TOP 09 k dispozici 7 možností v rozmezí čtyřkoalice až šestikoalice. Z toho čtyři koalice jsou minimálními většinovými koalicemi. Určitou zajímavostí je, že koalice ANO 2011, Trojkoalice a ČSSD byla během tří posledních volebních období početně nejslabší většinovou koalicí. Koalice disponovala 33 hlasy z celkových 65, takže vždy museli hlasovat pro všichni koaliční zastupitelé a nikdo z nich se nemohl omluvit ze zasedání ZHMP ani z důvodu nemoci. Kromě obvyklého požadavku na jednotné hlasování zastupitelů koaliční smlouva tak nadstandardně obsahuje v bodě č. 5 ustanovení: Smluvní strany zajistí, aby se všichni jejich zastupitelé 757
12 učastnili každého zasedání ZHMP (hl. m. Praha, 2014). Poprvé problém nastal při hlasování na zasedání ZHMP dne , kdy pro tisk Z-3154 (Zajištění komplexního systému nakládání s komunálním odpadem) nehlasoval koaliční zastupitel Matěj Stropnický. Tisk byl však schválen díky jednomu hlasu nezávislého zastupitele, takže koaliční konflikt kvůli nejednotnému hlasování byl tehdy oddálen. Na zasedání v červnu 2015 došlo k druhému narušení jednoty koaličních zastupitelů při hlasování o hazardu, které skončilo vyvoláním dohadovacího řízení. Třetí narušení jednoty koaličního hlasování nastalo při hlasování o odvolání radních na zasedání v říjnu 2015, které vedlo k rozpadu koalice. 2.4 Míra politické koncentrace Míru politické koncentrace v ZHMP měříme pomocí pěti ukazatelů, které jsme popsali v oddíle 1.3, a to počtem klubů, celkovým počtem možných koalic, podílem dvou nejsilnějších zastupitelských klubů na celkovém počtu zastupitelů, podílem tří nejsilnějších zastupitelských klubů a Herfindahlovým indexem koncentrace (tabulka 6). Výpočty míry politické koncentrace provádíme pro tři obecní volby (2006, 2010, 2014) a navíc pro situaci v ZHMP v červnu 2015, kdy byl počet hráčů (klubů) zvýšen na devět. Podle všech ukazatelů politické koncentrace se ukazuje situace v ZHMP v roce 2014 jako politicky komplikovanější oproti dřívějším volebním obdobím, což je dáno větším počtem zastupitelských klubů. Po roce od voleb roku 2014 je situace v ZHMP dokonce ještě více politicky fragmentovaná. Proces rostoucí politické roztříštěnosti sice ještě nebyl vidět při srovnání voleb v říjnu 2006 a v říjnu 2010, bylo to však zřejmě díky tomu, že Praha byla rozdělena na sedm obvodů a dvě volební strany (Věci veřejné a Koalice SZ, SNK) tak byly díky upravenému volebnímu systému připraveny o vstup do ZHMP. Tabulka 6 Míra politické koncentrace v ZHMP, období let Ukazatel koncentrace 10/ / / /2015 Počet klubů v ZHMP Počet možných koalic Podíl 2 největších klubů 77,1 % 71,9 % 50,8 % 44,6 % Podíl 3 největších klubů 85,7 % 93,8 % 63,1 % 56,9 % Herfindahlův index 0,4073 0,3145 0,1820 0, Diskuse Věnovali jsme se analýze výsledku obecních voleb a formování koalic v ZHMP po třech obecních volbách v letech 2006, 2010 a Volby roku 2006 skončily absolutním vítězství ODS, takže analýza voleb a analýza formování koalic byly v podstatě zbytečné. V roce 2010 dominovaly zastupitelstvu tři strany (TOP 09, ODS, ČSSD), které se sice lišily v počtu mandátů, ale jejich vyjednávací síla, jak ukázaly i ukazatele síly, byla shodná. Ve volbách 2014 získalo hnutí ANO 2011 o jeden mandát více než druhá TOP 09, což však stačilo k výraznému posílení vyjednávací pozice (tabulka 4). Z hlediska primátorského ukazatele je ANO 2011 zcela dominantním hráčem v ZHMP. 758
13 Je možné pozorovat určitý dlouhodobý trend ve fragmentaci politického spektra, který ovšem jistě není omezen pouze na případ ZHMP. Sledujeme určitou krizi tradičních stran (minulostí je bývalé dělení ČSSD versus ODS), která se projevila vznikem nových politických stran a hnutí, jako například Věci veřejné, TOP 09, ANO 2011, Úsvit, Piráti, Svobodní apod. Vznik nových stran a hnutí asi není ničím výjimečným, spíše jde o to, jak rychle se podařilo těmto novým stranám a hnutím získat dostatečný počet hlasů pro úspěch v parlamentních či obecních volbách. Tím narostl počet stran v mnoha zastupitelských sborech. Jak je známo z teoretických výsledků, větší počet volebních stran ovšem vyvolává narůst počtu možných většinových koalic a zvyšuje počet stran, které se ve většinové koalici musí dohodnout. Snížená míra politické koncentrace, kterou měřit lze, spolu s určitou politickou nezkušeností mnoha nových zastupitelů (což se měří obtížněji) vede k nižší stabilitě většinových koalic všech úrovních. Z dnešního pohledu je už stěží neuvěřitelné, že v roce 2006 mohla v Praze vzniknout jednobarevná Rada HMP. Závěr Politický systém na národní i lokální úrovni lze studovat pomocí teorie her jako tzv. hlasovací hru. Pro tento účel teorie her nabízí rovněž možnost odhadovat sílu jednotlivých hráčů (volebních stran) při vyjednávání pomocí různých ukazatelů síly, z nichž jsme v tomto příspěvku použili Shapleyův-Shubikův a Banzhafův ukazatel síly. Pro tento účel jsme v příspěvku navrhli primátorský ukazatel síly, který měří pravděpodobnost, že daná volební strana získá ve většinové koalici primátorskou pozici. Primátorský ukazatel se svou definicí liší od ostatních ukazatelů síly, protože svou pozornost soustřeďuje pouze na klíčové hráče (největší strany). Jde tedy spíše o hodnocení, které ukazuje, zda daná strana může zaujímat rozhodující pozici při tvorbě koalice. Na druhé straně pro malé volební strany je pak logicky primátorský ukazatel nulový a nemůže pro jejich vzájemné hodnocení nic nabídnout. Dále teorie her nabízí možnost predikovat formování většinové koalice na základě politických i nepolitických (mocenských) teorií formování koalic. Teorie minimální většinové koalice v ZHMP v posledních dvou obdobích funguje. Naopak je nutné odmítnout teorii souvislé koalice, protože ta je v rozporu se třemi různými koalicemi ve volebním období Pro měření politické koncentrace si lze vypůjčit v ekonomii známé ukazatele koncentrace oligopolních odvětví, jako např. míru koncentrace či Herfindahlův index. Z hlediska politologického lze pozorovat a změřit určitou politickou dekoncentraci moci, která zřejmě není omezena pouze na studovaný případ ZHMP. Můžeme spekulovat o tom, že v období politické dekoncentrace dojde k volání po většinovém systému (ČT24, 2013), a to i v obecních volbách, dojde k volání po elektronických referendech a přímé demokracii apod. Nebo také po nových volbách, které však na rozdíl od voleb do Poslanecké sněmovny Parlamentu ČR nejsou na obecní úrovni prakticky uskutečnitelné. Prvním empirickým testem této naší spekulace mohou být výsledky krajských voleb na podzim roku Literatura Binmore, K. (2014). Teorie her a jak může změnit váš život. Praha: Nakladatelství Dokořán a Argo. ISBN: ČT24 (2013). Zeman oprášil svůj návrh: Změnu volebního systému ve prospěch velkých stran. Praha: ČT24. Dostupné z: -zeman-oprasil-svuj-navrh-zmenu-volebniho-systemu-ve-prospech-velkych-stran 759
14 Deegan, J.; Packel, E. W. (1978). A New Index of Power for Simple n-person Games. International Journal of Game Theory, 7(2), , Dlouhý, M. (2013). Subsidy Allocation as a Coalition Game, in Mathematical Methods in Economics. Jihlava: College of Polytechnics Jihlava, ISBN Dlouhý, M. (2014). Models of Subsidy Allocation among City Districts. Prague Economic Papers, 23(1), , Dlouhý, M.; Fiala, P. (2009). Úvod do teorie her. Praha: Nakladatelství Oeconomica. ISBN Dlouhý, M.; Fiala, P. (2015). Teorie ekonomických a politických her. Praha: Nakladatelství Oeconomica. ISBN Felsenthal, D. S.; Machover, M. (2005). Voting Power Measurement: a Story of Misreinvention. London: LSE Research Online. Fiala, P. (2003). Modely a metody rozhodování. Praha: Vysoká škola ekonomická v Praze. ISBN X. Hlavní město Praha (2014). Koaliční smlouva o spolupráci v ZHMP ve volebním období mezi Hnutím ANO, Trojkoalicí SZ, KDU-ČSL a STAN a Českou stranou sociálně demokratickou. Hlavní město Praha. Dostupné z: koalicni_smlouva_ano_2011_trojkoalice_cssd.pdf Houdek, P. (2008). Proč brankáři skáčou a ženy mají knoflíky vlevo. Vesmír, 87, Dostupné z: proc-brankari-skacou-a-zeny-maji-knofliky-vlevo Chvoj, M. (2013). Pokročilá teorie her ve světě kolem nás. Praha: Grada Publishing. ISBN: Linek, L.; Rakušanová, P. (2005). Why Czech Parliamentary Party Groups Vote Less Unitedly. The Role of Frequent Voting and Big Majorities in Passing Bills. Sociologický časopis/ Czech Sociological Review, 43(3), Dostupné z: default/files/linek-rakunasova%20-%20why%20czech%20parliamentary%20party%20 Groups%20Vote%20Less%20Unitedly%20-%202005%20-%20EN%20-%20PI.pdf Loužek, M. (2004). Indikátory hlasovací síly v Evropské unii. Politická ekonomie, 52(3), , Loužek, M. (2004a). Voting Power Indicators in the European Union. Prague Economic Papers, 13(3), , Maňas, M. (1991). Teorie her a její aplikace. Praha: SNTL. Myerson, R. B. (1991). Game Theory: Analysis of Conflict. Cambridge: Harvard University Press. ISBN Osborne, M. J. (2004). An Introduction to Game Theory. New York: Oxford University Press. Riker, W. H. (1962). A Theory of Political Coalitions. New Haven: Yale University Press. Říchová, B. (2000). Přehled moderních politologických teorií. Praha: Portál. ISBN: Shapley, L. S. (1953). A value of n-person game, in Kuhn, H.; Tucker, A. W. ed., Contributions to the Theory of Games. Princeton: Princeton University Press, pp Shapley, L. S.; Shubik, M. (1954). A Method of Evaluating the Distribution of Power in a Committee System. American Polical Science Review, 48(3), , org/ /
15 Shermer, M. (2008). Dilema dopingu. Scientific American české vydání, 4 5, Straffin, P. D. (1994). Power and Stability in Politics, in Aumann, R.; Hart, S., ed., Handbook of Game Theory with Economic Applications Volume 2. Amsterdam: North-Holland, Chapter 32. ISBN Turnovec, F. (2007). New Measure of Voting Power. Czech Economic Review, 1(1), Turnovec, F.; Mercik, J. W.; Mazurkiewicz, M. (2008). National and ideological influence in the European Parliament. Control and Cybernetics, 37(3), von Neumann, J.; Morgenstern, O. (1944). Theory of Games and Economic Behavior. Princeton: Princeton University Press. 761
Teorie her a ekonomické rozhodování 6. Kooperativní hry více hráčů
 Teorie her a ekonomické rozhodování 6. Kooperativní hry více hráčů (chyby ve skriptech) 6.1 Koaliční hra Kooperativní hra hráči mají možnost před samotnou hrou uzavírat závazné dohody dva hráči (hra má
Teorie her a ekonomické rozhodování 6. Kooperativní hry více hráčů (chyby ve skriptech) 6.1 Koaliční hra Kooperativní hra hráči mají možnost před samotnou hrou uzavírat závazné dohody dva hráči (hra má
Kooperativní hra N hráčů
 Hry bez opakování - kooperativní hra N hráčů Obsah kapitoly Studijní cíle Doba potřebná ke studiu 1) Hry bez opakování - kooperativní hra N hráčů a) Úvod b) Volební hry c) Teorie formování koalic I. Nepolitické
Hry bez opakování - kooperativní hra N hráčů Obsah kapitoly Studijní cíle Doba potřebná ke studiu 1) Hry bez opakování - kooperativní hra N hráčů a) Úvod b) Volební hry c) Teorie formování koalic I. Nepolitické
KOOPERATIVNÍ HRY FORMULACE, KONCEPCE ŘEŠENÍ, JÁDRO HRY, HRA VE TVARU CHARAKTERISTICKÉ FUNKCE, SHAPLEYOVA HODNOTA CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ?
 KOOPERATIVNÍ HRY FORMULACE, KONCEPCE ŘEŠENÍ, JÁDRO HRY, HRA VE TVARU CHARAKTERISTICKÉ FUNKCE, SHAPLEYOVA HODNOTA CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekonomická vědní disciplína, která se
KOOPERATIVNÍ HRY FORMULACE, KONCEPCE ŘEŠENÍ, JÁDRO HRY, HRA VE TVARU CHARAKTERISTICKÉ FUNKCE, SHAPLEYOVA HODNOTA CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekonomická vědní disciplína, která se
Politická síla. Semestrální práce MAB. Jakub Štaif A08B0116P
 Semestrální práce MAB A08B0116P Obsah 1 Úvod... 3 2 Shapley-Shubikův index síly (Shapley-Shubik index of power)... 3 3 Teorie hlasovacích bloků... 4 4 Banzhafův index síly (The Banzhaf index of power)...
Semestrální práce MAB A08B0116P Obsah 1 Úvod... 3 2 Shapley-Shubikův index síly (Shapley-Shubik index of power)... 3 3 Teorie hlasovacích bloků... 4 4 Banzhafův index síly (The Banzhaf index of power)...
Koaliční hry. Kooperativní hra dvou hráčů
 Koaliční hry Obsah kapitoly. Koalice dvou hráčů 2. Koalice N hráčů Studijní cíle Cílem tohoto tematického bloku je získání základního přehledu o kooperativních hrách a jejich aplikovatelnosti. Student
Koaliční hry Obsah kapitoly. Koalice dvou hráčů 2. Koalice N hráčů Studijní cíle Cílem tohoto tematického bloku je získání základního přehledu o kooperativních hrách a jejich aplikovatelnosti. Student
Favoritem komunálních voleb je ČSSD, většinově však vítězí pravice
 Favoritem komunálních voleb je ČSSD, většinově však vítězí pravice Z modelového exkluzivního průzkumu společnosti SANEP, který se zaměřil na politické nálady občanů ČR, Pražanů a obyvatel Brna a Ostravy
Favoritem komunálních voleb je ČSSD, většinově však vítězí pravice Z modelového exkluzivního průzkumu společnosti SANEP, který se zaměřil na politické nálady občanů ČR, Pražanů a obyvatel Brna a Ostravy
Úvod do teorie her. 6. Koaliční hry
 Úvod do teorie her 6. Koaliční hry Tomáš Kroupa http://staff.utia.cas.cz/kroupa/ 2018 ÚTIA AV ČR Různé formy her Známé formy her jsou: rozvinutá, strategická, koaliční. Pro danou množinu hráčů N = {1,...,
Úvod do teorie her 6. Koaliční hry Tomáš Kroupa http://staff.utia.cas.cz/kroupa/ 2018 ÚTIA AV ČR Různé formy her Známé formy her jsou: rozvinutá, strategická, koaliční. Pro danou množinu hráčů N = {1,...,
Úvod do teorie her ZVYŠOVÁNÍ ODBORNÝCH KOMPETENCÍ AKADEMICKÝCH PRACOVNÍKŮ OSTRAVSKÉ UNIVERZITY V OSTRAVĚ A SLEZSKÉ UNIVERZITY V OPAVĚ
 ZVYŠOVÁNÍ ODBORNÝCH KOMPETENCÍ AKADEMICKÝCH PRACOVNÍKŮ OSTRAVSKÉ UNIVERZITY V OSTRAVĚ A SLEZSKÉ UNIVERZITY V OPAVĚ Úvod do teorie her David Bartl, Lenka Ploháková OSNOVA Úvod (hra n hráčů ve strategickém
ZVYŠOVÁNÍ ODBORNÝCH KOMPETENCÍ AKADEMICKÝCH PRACOVNÍKŮ OSTRAVSKÉ UNIVERZITY V OSTRAVĚ A SLEZSKÉ UNIVERZITY V OPAVĚ Úvod do teorie her David Bartl, Lenka Ploháková OSNOVA Úvod (hra n hráčů ve strategickém
Operační výzkum. Teorie her. Hra v normálním tvaru. Optimální strategie. Maticové hry.
 Operační výzkum Hra v normálním tvaru. Optimální strategie. Maticové hry. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky
Operační výzkum Hra v normálním tvaru. Optimální strategie. Maticové hry. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky
TGH13 - Teorie her I.
 TGH13 - Teorie her I. Jan Březina Technical University of Liberec 19. května 2015 Hra s bankéřem Máte právo sehrát s bankéřem hru: 1. hází se korunou dokud nepadne hlava 2. pokud hlava padne v hodu N,
TGH13 - Teorie her I. Jan Březina Technical University of Liberec 19. května 2015 Hra s bankéřem Máte právo sehrát s bankéřem hru: 1. hází se korunou dokud nepadne hlava 2. pokud hlava padne v hodu N,
STEM VOLEBNÍ PREFERENCE ČERVEN 2014
 STEM VOLEBNÍ PREFERENCE ČERVEN 201 V červnovém volebním modelu STEM by se do Poslanecké sněmovny nedostalo hnutí Úsvit, sněmovna by tak byla složena ze šesti stran. Poslední tři měsíce před prázdninami
STEM VOLEBNÍ PREFERENCE ČERVEN 201 V červnovém volebním modelu STEM by se do Poslanecké sněmovny nedostalo hnutí Úsvit, sněmovna by tak byla složena ze šesti stran. Poslední tři měsíce před prázdninami
11,0% 10,5% 7,9% 6,3% 5,8% 5,5% 3,4% 2,5% 2,0% 1,7% 1,3% ANO ČSSD nevím KSČM ODS KDU-ČSL TOP09 jiné strany Piráti STAN Strana zelených
 Preference listopad 214 sběr 22.11. - 11.12.214 S 1 1/ Přehled politických subjektů 2 1 79% 63% 8% % 34% 2% 2% 13% ANO ČSSD nevím KSČM ODS KDU-ČSL TOP9 jiné strany Piráti STAN Strana zelených Úsvit Svobodní
Preference listopad 214 sběr 22.11. - 11.12.214 S 1 1/ Přehled politických subjektů 2 1 79% 63% 8% % 34% 2% 2% 13% ANO ČSSD nevím KSČM ODS KDU-ČSL TOP9 jiné strany Piráti STAN Strana zelených Úsvit Svobodní
Bleskový výzkum SC&C a STEM pro Českou televizi
 Marketingový a sociologický výzkum Držitel certifikátu ISO 9001:2001 - člen ESOMAR www.scac.cz Závěrečná zpráva VOLBY DO PS 2010 - Jihomoravský kraj Bleskový výzkum SC&C a STEM pro Českou televizi Praha,
Marketingový a sociologický výzkum Držitel certifikátu ISO 9001:2001 - člen ESOMAR www.scac.cz Závěrečná zpráva VOLBY DO PS 2010 - Jihomoravský kraj Bleskový výzkum SC&C a STEM pro Českou televizi Praha,
1/5. volební výzkum PRAHA 1.9.2014-18.9.2014. Praha S 1 5. preference a potenciál
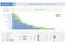 S 1 1/ preference a potenciál preference potenciál Domov 6 TOP Demokratů 09 ### 89 ## Jana Kasla ANO 2011 ### 68 Restart ## 2014 ČSSD### Úsvit přímé 26 ## demokracie SZ + KDU-ČSL 91 32 + ## PRO PRAHU STAN
S 1 1/ preference a potenciál preference potenciál Domov 6 TOP Demokratů 09 ### 89 ## Jana Kasla ANO 2011 ### 68 Restart ## 2014 ČSSD### Úsvit přímé 26 ## demokracie SZ + KDU-ČSL 91 32 + ## PRO PRAHU STAN
Preference politických subjektů - prosinec celkový přehled 10,4% 10,3% 9,1% 6,5% 5,0% 5,0% 4,6% 1,5% 1,3% 1,2% 1,2% 1,1%
 14% SOŠ 1 1/8 Preference politických subjektů - prosinec 2015 celkový přehled 30% 243% 20% 185% 10% 0% 104% 103% 9 65% 50% 50% 46% 13% 12% 12% 1 35+ 45+ 55+ 35% ZŠ 19% OU SŠ 33% 14% VŠ 35% 33% 19% 2 2/8
14% SOŠ 1 1/8 Preference politických subjektů - prosinec 2015 celkový přehled 30% 243% 20% 185% 10% 0% 104% 103% 9 65% 50% 50% 46% 13% 12% 12% 1 35+ 45+ 55+ 35% ZŠ 19% OU SŠ 33% 14% VŠ 35% 33% 19% 2 2/8
ANO ČSSD KSČM nevím jiné strany ODS TOP09 KDU-ČSL Piráti STAN Svobodní Strana zelených
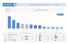 S 1 1/ Přehled politických subjektů 30 2 243 20 169 1 10 110 88 83 77 64 9 32 21 21 17 16 0 ANO ČSSD KSČM nevím jiné strany ODS TOP09 KDU-ČSL Piráti STAN Svobodní Strana zelených Úsvit 18+ 1 112 2+ 3+
S 1 1/ Přehled politických subjektů 30 2 243 20 169 1 10 110 88 83 77 64 9 32 21 21 17 16 0 ANO ČSSD KSČM nevím jiné strany ODS TOP09 KDU-ČSL Piráti STAN Svobodní Strana zelených Úsvit 18+ 1 112 2+ 3+
15,4 2,4 0,0 5,0 10,0 15,0 20,0 25,0 30,0. cílová skupina pohlaví respondentů věk respondentů vzdělání respondentů % 19% % 19%
 5 5 volební výzkum PRAHA 1.9.2014-30.9.2014 S 1 1/ preference a potenciál Demokraté Jana Kasla Domov SVOBODNÍ Úsvit přímé demokracie Restart 2014 ostatní Česká pirátská strana prefepotenciál TOP ### 59
5 5 volební výzkum PRAHA 1.9.2014-30.9.2014 S 1 1/ preference a potenciál Demokraté Jana Kasla Domov SVOBODNÍ Úsvit přímé demokracie Restart 2014 ostatní Česká pirátská strana prefepotenciál TOP ### 59
6,8% 6,6% 6,5% 5,6% 0% ANO ČSSD KSČM nevím KDU-ČSL ODS TOP09 Ostatní STAN Piráti Svobodní Úsvit SZ
 Preference leden 201 sběr 12.12.2014-12.1.201 S 1 1/ Přehled politických subjektů 236% 20% 168% 120% 119% 10% % 68% 66% 6% 6% 2% 2% 18% 0% ANO ČSSD KSČM nevím KDU-ČSL ODS TOP09 Ostatní STAN Piráti Svobodní
Preference leden 201 sběr 12.12.2014-12.1.201 S 1 1/ Přehled politických subjektů 236% 20% 168% 120% 119% 10% % 68% 66% 6% 6% 2% 2% 18% 0% ANO ČSSD KSČM nevím KDU-ČSL ODS TOP09 Ostatní STAN Piráti Svobodní
Preference politických subjektů - leden celkový přehled. cílová skupina pohlaví respondentů věk respondentů vzdělání respondentů % 35+
 5 5 SOŠ 1 1/9 Preference politických subjektů - leden 2016 celkový přehled 30% 244% 20% 18 10% 105% 102% 89% 62% 52% 50% 50% 0% 16% 12% 12% 10% 18+ 35+ 45+ 55+ 35% 35% 16% ZŠ 16% OU VŠ 2 2/9 Preference
5 5 SOŠ 1 1/9 Preference politických subjektů - leden 2016 celkový přehled 30% 244% 20% 18 10% 105% 102% 89% 62% 52% 50% 50% 0% 16% 12% 12% 10% 18+ 35+ 45+ 55+ 35% 35% 16% ZŠ 16% OU VŠ 2 2/9 Preference
STEM VOLEBNÍ PREFERENCE KVĚTEN 2015
 STEM VOLEBNÍ PREFERENCE KVĚTEN 2015 Na konci května by se do Poslanecké sněmovny dostalo 6 stran. Hnutí ANO vede žebříček preferencí, ale ztrácí. Snižuje se tak jeho odstup od druhé ČSSD. Nadále je patrna
STEM VOLEBNÍ PREFERENCE KVĚTEN 2015 Na konci května by se do Poslanecké sněmovny dostalo 6 stran. Hnutí ANO vede žebříček preferencí, ale ztrácí. Snižuje se tak jeho odstup od druhé ČSSD. Nadále je patrna
STEM VOLEBNÍ PREFERENCE LEDEN 2016
 STEM VOLEBNÍ PREFERENCE LEDEN 2016 Na startovní čáře roku 2016 potvrzuje hnutí ANO svoji vedoucí pozici v žebříčku volebních preferencí před druhou ČSSD. Obě strany oproti konci roku mírně získaly. Příznivci
STEM VOLEBNÍ PREFERENCE LEDEN 2016 Na startovní čáře roku 2016 potvrzuje hnutí ANO svoji vedoucí pozici v žebříčku volebních preferencí před druhou ČSSD. Obě strany oproti konci roku mírně získaly. Příznivci
STEM VOLEBNÍ PREFERENCE PROSINEC 2015
 STEM VOLEBNÍ PREFERENCE PROSINEC 2015 Prosincový výzkum přináší jen dílčí posuny volebních preferencí. Nadále vede hnutí ANO, druhá ČSSD však stáhla svůj odstup na 3,5 procentního bodu. Za poslední rok
STEM VOLEBNÍ PREFERENCE PROSINEC 2015 Prosincový výzkum přináší jen dílčí posuny volebních preferencí. Nadále vede hnutí ANO, druhá ČSSD však stáhla svůj odstup na 3,5 procentního bodu. Za poslední rok
METODOLOGIE. SANEP s.r.o. kvótní výběr. multiplechoice
 METODOLOGIE TÉMA PRŮZKUMU: Volební preference (duben 2017) REALIZÁTOR: VÝBĚR RESPONDENTŮ: TYP OTÁZEK: SANEP s.r.o. kvótní výběr multiplechoice REPREZENTATIVITA: ve věku 18+let Reprezentativní vzorek odpovídá
METODOLOGIE TÉMA PRŮZKUMU: Volební preference (duben 2017) REALIZÁTOR: VÝBĚR RESPONDENTŮ: TYP OTÁZEK: SANEP s.r.o. kvótní výběr multiplechoice REPREZENTATIVITA: ve věku 18+let Reprezentativní vzorek odpovídá
5.7 Kooperativní hry 5.7.1 Kooperativní hra 2 hráčů 5.7.2 Kooperativní hra N hráčů 5.8 Modely oligopolu 5.9 Teorie redistribučních systémů 5.
 Mikroekonomie bakalářský kurz - VŠFS Jiří Mihola, jiri.mihola@quick.cz, www.median-os.cz, 2010 Téma 6 Teorie her, volby teorie redistribučních systémů a teorie veřejné Obsah 5.7 Kooperativní hry 5.7.1
Mikroekonomie bakalářský kurz - VŠFS Jiří Mihola, jiri.mihola@quick.cz, www.median-os.cz, 2010 Téma 6 Teorie her, volby teorie redistribučních systémů a teorie veřejné Obsah 5.7 Kooperativní hry 5.7.1
Teorie her a ekonomické rozhodování. 8. Vyjednávací hry
 Teorie her a ekonomické rozhodování 8. Vyjednávací hry 8. Vyjednávání Teorie her Věda o řešení konfliktů Ale také věda o hledání vzájemně výhodné spolupráce Teorie vyjednávání Odvětví teorie her dohoda
Teorie her a ekonomické rozhodování 8. Vyjednávací hry 8. Vyjednávání Teorie her Věda o řešení konfliktů Ale také věda o hledání vzájemně výhodné spolupráce Teorie vyjednávání Odvětví teorie her dohoda
Souboj ANO a ČSSD se vyrovnal
 TISKOVÁ ZPRÁVA 1. dubna 2016 Souboj ANO a ČSSD se vyrovnal Pokud by se předčasné volby do PSP ČR konaly nyní, do poslanecké sněmovny by se dostalo šest stran. Současná vládní koalice by získala ústavní
TISKOVÁ ZPRÁVA 1. dubna 2016 Souboj ANO a ČSSD se vyrovnal Pokud by se předčasné volby do PSP ČR konaly nyní, do poslanecké sněmovny by se dostalo šest stran. Současná vládní koalice by získala ústavní
PODOBY DEMOKRACIE Přímá a nepřímá demokracie.
 PODOBY DEMOKRACIE Přímá a nepřímá demokracie. Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Mgr. Michaela Holubová. PODOBY DEMOKRACIE PŘÍMÁ DEMOKRACIE = možnost občanů bezprostředně rozhodovat
PODOBY DEMOKRACIE Přímá a nepřímá demokracie. Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Mgr. Michaela Holubová. PODOBY DEMOKRACIE PŘÍMÁ DEMOKRACIE = možnost občanů bezprostředně rozhodovat
STEM VOLEBNÍ PREFERENCE PROSINEC 2016
 STEM VOLEBNÍ PREFERENCE PROSINEC 2016 V říjnu preference odrážely emotivně vzepjatou situaci těsně po volbách. Obraz počátku prosince ukazuje určité zklidnění. Sociální demokracie si dílčím způsobem polepšila,
STEM VOLEBNÍ PREFERENCE PROSINEC 2016 V říjnu preference odrážely emotivně vzepjatou situaci těsně po volbách. Obraz počátku prosince ukazuje určité zklidnění. Sociální demokracie si dílčím způsobem polepšila,
Úvod do teorie her. David Bartl, Lenka Ploháková
 Úvod do teorie her David Bartl, Lenka Ploháková Abstrakt Předložený text Úvod do teorie her pokrývá čtyři nejdůležitější, vybrané kapitoly z této oblasti. Nejprve je čtenář seznámen s předmětem studia
Úvod do teorie her David Bartl, Lenka Ploháková Abstrakt Předložený text Úvod do teorie her pokrývá čtyři nejdůležitější, vybrané kapitoly z této oblasti. Nejprve je čtenář seznámen s předmětem studia
PREFERENCE KVĚTEN 2017 sběr: ,7% 10,3% 7,7% 7,4% 5,9% 4,9% 3,8% 3,4% 2,8% 1,6% 1,3% 1,1%
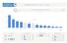 1 1/8 71 216 1162 638 Preference politických subjektů - KVĚTEN 2017 celkový přehled 22,9% 20% 15,2% 10% 11,7% 10,3% 7,7% 7,4% 5,9% 4,9% 3,8% 3,4% 2,8% 1,6% 1,3% 1,1% 0% ANO ČSSD KSČM KDU-ČSL a STAN nevím
1 1/8 71 216 1162 638 Preference politických subjektů - KVĚTEN 2017 celkový přehled 22,9% 20% 15,2% 10% 11,7% 10,3% 7,7% 7,4% 5,9% 4,9% 3,8% 3,4% 2,8% 1,6% 1,3% 1,1% 0% ANO ČSSD KSČM KDU-ČSL a STAN nevím
VOLEBNÍ PREFERENCE ČR + PRAHA ZÁŘÍ 2018
 VOLEBNÍ PREFERENCE ČR + PRAHA ZÁŘÍ 2018 Komentář Hnutí ANO nedává svým soupeřům šanci, TOP 09 je s největším nárůstem zpět nad pěti procenty Hnutí ANO nadále nechává své politické soupeře daleko za sebou
VOLEBNÍ PREFERENCE ČR + PRAHA ZÁŘÍ 2018 Komentář Hnutí ANO nedává svým soupeřům šanci, TOP 09 je s největším nárůstem zpět nad pěti procenty Hnutí ANO nadále nechává své politické soupeře daleko za sebou
Kdo skutečně vyhrál komunální volby 2018
 Kdo skutečně vyhrál komunální volby 2018 POLICY PAPER / ŘÍJEN 2018 JAKUB KONRÁD Kdo skutečně vyhrál komunální volby 2018 Policy Paper Jakub Konrád, říjen 2018 Hodnotit komunální volby je nesmírně obtížné.
Kdo skutečně vyhrál komunální volby 2018 POLICY PAPER / ŘÍJEN 2018 JAKUB KONRÁD Kdo skutečně vyhrál komunální volby 2018 Policy Paper Jakub Konrád, říjen 2018 Hodnotit komunální volby je nesmírně obtížné.
Výzkum před komunálními volbami 2018 Volební potenciál. Závěrečná zpráva, Zpracováno exkluzivně pro
 Výzkum před komunálními volbami 2018 Volební potenciál Závěrečná zpráva, 7. 9. 2018 Zpracováno exkluzivně pro Metodika výzkumu Velikost vzorku N = 1 210 respondentů ve věku 18 a více let Termín dotazování
Výzkum před komunálními volbami 2018 Volební potenciál Závěrečná zpráva, 7. 9. 2018 Zpracováno exkluzivně pro Metodika výzkumu Velikost vzorku N = 1 210 respondentů ve věku 18 a více let Termín dotazování
ČSSD by si mohla vybírat
 4. dubna 2013 ČSSD by si mohla vybírat Vládu by ČSSD mohla vytvořit s účastí, podporou nebo tolerancí TOP 09 a Starostů (104 mandátů), KSČM (102 mandátů) nebo ODS (101 mandátů). Volební model, který ppm
4. dubna 2013 ČSSD by si mohla vybírat Vládu by ČSSD mohla vytvořit s účastí, podporou nebo tolerancí TOP 09 a Starostů (104 mandátů), KSČM (102 mandátů) nebo ODS (101 mandátů). Volební model, který ppm
ČÁST IV VOLBY DO ZASTUPITELSTEV OBCÍ
 ČÁST IV VOLBY DO ZASTUPITELSTEV OBCÍ 4.1. Volební účast Nejvyšší volební účast ve volbách do obecních zastupitelstev byla na začátku analyzovaného období v roce 1994, kdy se voleb zúčastnilo více než 62
ČÁST IV VOLBY DO ZASTUPITELSTEV OBCÍ 4.1. Volební účast Nejvyšší volební účast ve volbách do obecních zastupitelstev byla na začátku analyzovaného období v roce 1994, kdy se voleb zúčastnilo více než 62
VÝSLEDKŮ VOLEB DO ZASTUPITELSTEV KRAJŮ V ROCE [Zadejte podtitul dokumentu.]
![VÝSLEDKŮ VOLEB DO ZASTUPITELSTEV KRAJŮ V ROCE [Zadejte podtitul dokumentu.] VÝSLEDKŮ VOLEB DO ZASTUPITELSTEV KRAJŮ V ROCE [Zadejte podtitul dokumentu.]](/thumbs/59/42912767.jpg) GENDEROVÁ [Zadejte podtitul dokumentu.] ANALÝZA VÝSLEDKŮ VOLEB [Vyberte datum.] [Zadejte název společnosti.] jana Kavková DO ZASTUPITELSTEV KRAJŮ V ROCE 2012 Analýza vznikla v rámci projektu Dámy mají
GENDEROVÁ [Zadejte podtitul dokumentu.] ANALÝZA VÝSLEDKŮ VOLEB [Vyberte datum.] [Zadejte název společnosti.] jana Kavková DO ZASTUPITELSTEV KRAJŮ V ROCE 2012 Analýza vznikla v rámci projektu Dámy mají
Volební model MEDIAN (duben-květen 2012)
 VÝZKUM TRHU, MÉDIÍ a VEŘEJNÉHO MÍNĚNÍ, VÝVOJ SOFTWARE MEDIAN, Národních hrdinů 73, 190 12 Praha 9, tel.: 225 301 111, fax: 225 301 101, http: //www.median.cz, e-mail: median@median.cz oficiální partner
VÝZKUM TRHU, MÉDIÍ a VEŘEJNÉHO MÍNĚNÍ, VÝVOJ SOFTWARE MEDIAN, Národních hrdinů 73, 190 12 Praha 9, tel.: 225 301 111, fax: 225 301 101, http: //www.median.cz, e-mail: median@median.cz oficiální partner
VÝSLEDKŮ VOLEB DO ZASTUPITELSTEV KRAJŮ A DO SENÁTU [Zadejte podtitul dokumentu.]
![VÝSLEDKŮ VOLEB DO ZASTUPITELSTEV KRAJŮ A DO SENÁTU [Zadejte podtitul dokumentu.] VÝSLEDKŮ VOLEB DO ZASTUPITELSTEV KRAJŮ A DO SENÁTU [Zadejte podtitul dokumentu.]](/thumbs/56/39065989.jpg) GENDEROVÁ [Zadejte podtitul dokumentu.] ANALÝZA VÝSLEDKŮ VOLEB [Vyberte datum.] [Zadejte název společnosti.] jana Kavková DO ZASTUPITELSTEV KRAJŮ A DO SENÁTU 2012 Analýza vznikla v rámci projektu Dámy
GENDEROVÁ [Zadejte podtitul dokumentu.] ANALÝZA VÝSLEDKŮ VOLEB [Vyberte datum.] [Zadejte název společnosti.] jana Kavková DO ZASTUPITELSTEV KRAJŮ A DO SENÁTU 2012 Analýza vznikla v rámci projektu Dámy
1/5. Celá ČR. PREFERENCE PROSINEC 2018 sběr: Celá ČR Preference politických subjektů - PROSINEC % 20% 10%
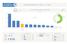 1 1/5 Preference politických subjektů - PROSINEC 2018 celkový přehled 30% 29,7% volební účast 20% 53,9% 14,2% 14,1% 10% 6,3% 6,1% 5,5% 5,1% 4,9% 0% ANO ODS Piráti Nevím, neumím odpovědět 3,5% 3,0% 0,4%
1 1/5 Preference politických subjektů - PROSINEC 2018 celkový přehled 30% 29,7% volební účast 20% 53,9% 14,2% 14,1% 10% 6,3% 6,1% 5,5% 5,1% 4,9% 0% ANO ODS Piráti Nevím, neumím odpovědět 3,5% 3,0% 0,4%
10. Volební podpora ostatních politických subjektů v Zastupitelstvu Pardubického kraje
 10. Volební podpora ostatních politických subjektů v Zastupitelstvu Pardubického kraje V předchozích kapitolách byla věnována pozornost těm politickým subjektům, které patřily k nejúspěšnějším ve všech
10. Volební podpora ostatních politických subjektů v Zastupitelstvu Pardubického kraje V předchozích kapitolách byla věnována pozornost těm politickým subjektům, které patřily k nejúspěšnějším ve všech
Volby do PS 2013. Volební účast. Výsledky jednotlivých stran podle regionů, zde v členění podle okresů.
 Volby do PS 213 Výsledky jednotlivých stran podle regionů, zde v členění podle okresů. Analýza vychází z OpenData ze serveru www.volby.cz Českého statistického úřadu. Soubor s podklady ve formátu ODS (OpenOffice),
Volby do PS 213 Výsledky jednotlivých stran podle regionů, zde v členění podle okresů. Analýza vychází z OpenData ze serveru www.volby.cz Českého statistického úřadu. Soubor s podklady ve formátu ODS (OpenOffice),
nezávislá analýza nad daty pro
 VOLBY DO EVROPSKÉHO PARLAMENTU volební účast a pravděpodobná volba podle věku a vzdělání a minulé preference nezávislá analýza nad daty pro 19. 5..5. 019 metodika výzkumu Velikost vzorku Termín dotazování
VOLBY DO EVROPSKÉHO PARLAMENTU volební účast a pravděpodobná volba podle věku a vzdělání a minulé preference nezávislá analýza nad daty pro 19. 5..5. 019 metodika výzkumu Velikost vzorku Termín dotazování
Výsledky voleb do EP jsou velmi nejisté, ANO 2011 by ovšem jasně vyhrálo
 V Praze 16.5.2014 Výsledky voleb do EP jsou velmi nejisté, ANO 2011 by ovšem jasně vyhrálo Tisková zpráva Předpokládaná účast ve volbách do EP činí 29,6 %. Pětiprocentní hranici nutnou pro přidělení mandátů
V Praze 16.5.2014 Výsledky voleb do EP jsou velmi nejisté, ANO 2011 by ovšem jasně vyhrálo Tisková zpráva Předpokládaná účast ve volbách do EP činí 29,6 %. Pětiprocentní hranici nutnou pro přidělení mandátů
Pravděpodobnost a její vlastnosti
 Pravděpodobnost a její vlastnosti 1 Pravděpodobnost a její vlastnosti Náhodné jevy Náhodný jev je výsledek pokusu (tj. realizace určitého systému podmínek) a jeho charakteristickým rysem je, že může, ale
Pravděpodobnost a její vlastnosti 1 Pravděpodobnost a její vlastnosti Náhodné jevy Náhodný jev je výsledek pokusu (tj. realizace určitého systému podmínek) a jeho charakteristickým rysem je, že může, ale
STŘEDNÍ ODBORNÁ ŠKOLA a STŘEDNÍ ODBORNÉ UČILIŠTĚ, Česká Lípa, 28. října 2707, příspěvková organizace
 FORMY DEMOKRACIE Název školy: Číslo a název projektu: Číslo a název šablony klíčové aktivity: Označení materiálu: Typ materiálu: Předmět, ročník, obor: STŘEDNÍ ODBORNÁ ŠKOLA a STŘEDNÍ ODBORNÉ UČILIŠTĚ,
FORMY DEMOKRACIE Název školy: Číslo a název projektu: Číslo a název šablony klíčové aktivity: Označení materiálu: Typ materiálu: Předmět, ročník, obor: STŘEDNÍ ODBORNÁ ŠKOLA a STŘEDNÍ ODBORNÉ UČILIŠTĚ,
VOLEBNÍ PREFERENCE LISTOPAD 2018
 VOLEBNÍ PREFERENCE LISTOPAD 2018 METODOLOGIE TÉMA PRŮZKUMU: Volební preference (listopad 2018) REALIZÁTOR: VÝBĚR RESPONDENTŮ: TYP OTÁZEK: SANEP s.r.o. kvótní výběr multiplechoice REPREZENTATIVITA: ve věku
VOLEBNÍ PREFERENCE LISTOPAD 2018 METODOLOGIE TÉMA PRŮZKUMU: Volební preference (listopad 2018) REALIZÁTOR: VÝBĚR RESPONDENTŮ: TYP OTÁZEK: SANEP s.r.o. kvótní výběr multiplechoice REPREZENTATIVITA: ve věku
Teorie her a ekonomické rozhodování 5. Opakované hry
 Teorie her a ekonomické rozhodování 5. Opakované hry (chybějící či chybná indexace ve skriptech) 5.1 Opakovaná hra Hra až dosud hráči hráli hru jen jednou v reálu se konflikty neustále opakují (firmy nabízí
Teorie her a ekonomické rozhodování 5. Opakované hry (chybějící či chybná indexace ve skriptech) 5.1 Opakovaná hra Hra až dosud hráči hráli hru jen jednou v reálu se konflikty neustále opakují (firmy nabízí
Teorie her a ekonomické rozhodování. 2. Maticové hry
 Teorie her a ekonomické rozhodování 2. Maticové hry 2.1 Maticová hra Teorie her = ekonomická vědní disciplína, která se zabývá studiem konfliktních situací pomocí matematických modelů Hra v normálním tvaru
Teorie her a ekonomické rozhodování 2. Maticové hry 2.1 Maticová hra Teorie her = ekonomická vědní disciplína, která se zabývá studiem konfliktních situací pomocí matematických modelů Hra v normálním tvaru
METODOLOGIE. SANEP s.r.o. kvótní výběr. multiplechoice
 METODOLOGIE TÉMA PRŮZKUMU: Volební preference (srpen 2016) REALIZÁTOR: VÝBĚR RESPONDENTŮ: TYP OTÁZEK: SANEP s.r.o. kvótní výběr multiplechoice REPREZENTATIVITA: ve věku 18+let Reprezentativní vzorek odpovídá
METODOLOGIE TÉMA PRŮZKUMU: Volební preference (srpen 2016) REALIZÁTOR: VÝBĚR RESPONDENTŮ: TYP OTÁZEK: SANEP s.r.o. kvótní výběr multiplechoice REPREZENTATIVITA: ve věku 18+let Reprezentativní vzorek odpovídá
SSOS_ON_2.13 Člověk jako občan
 Číslo a název projektu Číslo a název šablony DUM číslo a název CZ.1.07/1.5.00/34.0378 Zefektivnění výuky prostřednictvím ICT technologií III/2 - Inovace a zkvalitnění výuky prostřednictvím ICT SSOS_ON_2.13
Číslo a název projektu Číslo a název šablony DUM číslo a název CZ.1.07/1.5.00/34.0378 Zefektivnění výuky prostřednictvím ICT technologií III/2 - Inovace a zkvalitnění výuky prostřednictvím ICT SSOS_ON_2.13
Znalost log politických stran
 Sociologie politiky Sociologický ústav AV ČR, v.v.i. Jilská 1, Praha 1 Aleš Kudrnáč E-mail: ales.kudrnac@soc.cas.cz Znalost log politických stran Technické parametry Výzkum: Naše společnost, v14-11 Realizátor:
Sociologie politiky Sociologický ústav AV ČR, v.v.i. Jilská 1, Praha 1 Aleš Kudrnáč E-mail: ales.kudrnac@soc.cas.cz Znalost log politických stran Technické parametry Výzkum: Naše společnost, v14-11 Realizátor:
Sněmovní volební model MEDIAN (říjen-listopad 2012)
 VÝZKUM TRHU, MÉDIÍ a VEŘEJNÉHO MÍNĚNÍ, VÝVOJ SOFTWARE MEDIAN, Národních hrdinů 73, 190 12 Praha 9, tel.: 225 301 111, fax: 225 301 101, http: //www.median.cz, e-mail: median@median.cz oficiální partner
VÝZKUM TRHU, MÉDIÍ a VEŘEJNÉHO MÍNĚNÍ, VÝVOJ SOFTWARE MEDIAN, Národních hrdinů 73, 190 12 Praha 9, tel.: 225 301 111, fax: 225 301 101, http: //www.median.cz, e-mail: median@median.cz oficiální partner
POLITICKÉ STRANY. Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Mgr. Michaela Holubová.
 POLITICKÉ STRANY Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Mgr. Michaela Holubová. POLITICKÝ PLURALISMUS = existence mnoha politických stran a zájmových skupin působí ve společnosti
POLITICKÉ STRANY Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Mgr. Michaela Holubová. POLITICKÝ PLURALISMUS = existence mnoha politických stran a zájmových skupin působí ve společnosti
Volební preference v pěti největších krajích ČR
 Volební preference v pěti největších krajích ČR V Praze vítězí TOP 09, v Ústeckém kraji KSČM a v Moravskoslezském, Jihomoravském a Středočeském kraji ČSSD Před nadcházejícími volbami, kdy ještě nejsou
Volební preference v pěti největších krajích ČR V Praze vítězí TOP 09, v Ústeckém kraji KSČM a v Moravskoslezském, Jihomoravském a Středočeském kraji ČSSD Před nadcházejícími volbami, kdy ještě nejsou
Černá skříňka demokracie? Volební systémy
 Černá skříňka demokracie? Volební systémy Funkce voleb (D. Nohlen) 1. Legitimace politické moci 2. Výběr, kontrola a výměna politické elity 3. Pokojné řešení politických konfliktů 4. Aktivizace voličů
Černá skříňka demokracie? Volební systémy Funkce voleb (D. Nohlen) 1. Legitimace politické moci 2. Výběr, kontrola a výměna politické elity 3. Pokojné řešení politických konfliktů 4. Aktivizace voličů
VOLEBNÍ POTENCIÁL ZÁŘÍ 2017 sběr: ? Piráti 5,9% KDU-ČSL 5,7% Realisté 5,5%
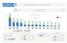 1 100,0% 71 216 1227 638 1/4 volební potenciál září2017 výstup: graf 100% skládaný sloupcový 5,2% 35,0% 30,0% 23,0% Preference Potenciál 25,0% 20,0% 3,4% 10,5% 2,3% 10,6% 2,6% 8,3% 1,8% 1,8% 1,6% 0,7%
1 100,0% 71 216 1227 638 1/4 volební potenciál září2017 výstup: graf 100% skládaný sloupcový 5,2% 35,0% 30,0% 23,0% Preference Potenciál 25,0% 20,0% 3,4% 10,5% 2,3% 10,6% 2,6% 8,3% 1,8% 1,8% 1,6% 0,7%
1. Hlasy a mandáty parlamentních stran v PS PČR
 1. Hlasy a mandáty parlamentních stran v PS PČR 1.1 Kandidující strany a jejich úspěšnost Ve volbách do PS kandidovaly převážně samostatné politické strany a hnutí. Pouze v roce 2006 kandidovala 1 koalice
1. Hlasy a mandáty parlamentních stran v PS PČR 1.1 Kandidující strany a jejich úspěšnost Ve volbách do PS kandidovaly převážně samostatné politické strany a hnutí. Pouze v roce 2006 kandidovala 1 koalice
Vektory a matice. Obsah. Aplikovaná matematika I. Carl Friedrich Gauss. Základní pojmy a operace
 Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Zpráva z bleskového výzkumu
 STEM - Středisko empirických výzkumů, Sabinova 3, 0 02 Praha 3 Zpráva z bleskového výzkumu STEM pro Friedrich Naumann Stiftung V Praze dne 15. dubna 0 I. Údaje o výzkumu Typ výzkumu: bleskový reprezentativní
STEM - Středisko empirických výzkumů, Sabinova 3, 0 02 Praha 3 Zpráva z bleskového výzkumu STEM pro Friedrich Naumann Stiftung V Praze dne 15. dubna 0 I. Údaje o výzkumu Typ výzkumu: bleskový reprezentativní
VOLBY DO EVROPSKÉHO PARLAMENTU volební model (duben 2019), vliv účasti, potenciál stran
 VOLBY DO EVROPSKÉHO PARLAMENTU volební model (duben 2019), vliv účasti, potenciál stran shrnutí Volební model není volební predikcí, ale ukazuje, jak by se v době dotazování (16. 3. 3. 5. 2019) měnil pravděpodobný
VOLBY DO EVROPSKÉHO PARLAMENTU volební model (duben 2019), vliv účasti, potenciál stran shrnutí Volební model není volební predikcí, ale ukazuje, jak by se v době dotazování (16. 3. 3. 5. 2019) měnil pravděpodobný
Preference politických subjektů - březen celkový přehled 5,5% 5,5% 5,4% 4,5% 2,0% 1,6% 1,5% 1,5% 1,4%
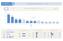 1 1/9 Preference politických subjektů - březen 2016 celkový přehled 30% 250% 20% 180% 10% 0% 102% 102% 77% ANO ČSSD KSČM ODS nevím KDU-ČSL Úsvit s Blokem proti Islámu 55% 55% 54% 45% 20% TOP 09 ostatní
1 1/9 Preference politických subjektů - březen 2016 celkový přehled 30% 250% 20% 180% 10% 0% 102% 102% 77% ANO ČSSD KSČM ODS nevím KDU-ČSL Úsvit s Blokem proti Islámu 55% 55% 54% 45% 20% TOP 09 ostatní
ANTAGONISTICKE HRY 172
 5 ANTAGONISTICKÉ HRY 172 Antagonistický konflikt je rozhodovací situace, v níž vystupují dva inteligentní rozhodovatelé, kteří se po volbě svých rozhodnutí rozdělí o pevnou částku, jejíž výše nezávisí
5 ANTAGONISTICKÉ HRY 172 Antagonistický konflikt je rozhodovací situace, v níž vystupují dva inteligentní rozhodovatelé, kteří se po volbě svých rozhodnutí rozdělí o pevnou částku, jejíž výše nezávisí
Úvod do teorie her
 Úvod do teorie her 2. Garanční řešení, hry s nulovým součtem a smíšené strategie Tomáš Kroupa http://staff.utia.cas.cz/kroupa/ 2017 ÚTIA AV ČR Program 1. Zavedeme řešení, které zabezpečuje minimální výplatu
Úvod do teorie her 2. Garanční řešení, hry s nulovým součtem a smíšené strategie Tomáš Kroupa http://staff.utia.cas.cz/kroupa/ 2017 ÚTIA AV ČR Program 1. Zavedeme řešení, které zabezpečuje minimální výplatu
U S N E S E N Í. t a k t o : I. Návrh na neplatnost volby kandidátů ve volebním kraji Hlavní město Praha s e z a m í t á.
 č. j. Vol 59/2006-31 U S N E S E N Í Nejvyšší správní soud rozhodl v senátě složeném z předsedy JUDr. Vojtěcha Šimíčka a soudců JUDr. Miluše Doškové, JUDr. Josefa Baxy, JUDr. Brigity Chrastilové, JUDr.
č. j. Vol 59/2006-31 U S N E S E N Í Nejvyšší správní soud rozhodl v senátě složeném z předsedy JUDr. Vojtěcha Šimíčka a soudců JUDr. Miluše Doškové, JUDr. Josefa Baxy, JUDr. Brigity Chrastilové, JUDr.
VOLEBNÍ PREFERENCE ČERVEN 2018
 VOLEBNÍ PREFERENCE ČERVEN 2018 METODOLOGIE TÉMA PRŮZKUMU: Volební preference (červen 2018) REALIZÁTOR: VÝBĚR RESPONDENTŮ: TYP OTÁZEK: SANEP s.r.o. kvótní výběr multiplechoice REPREZENTATIVITA: ve věku
VOLEBNÍ PREFERENCE ČERVEN 2018 METODOLOGIE TÉMA PRŮZKUMU: Volební preference (červen 2018) REALIZÁTOR: VÝBĚR RESPONDENTŮ: TYP OTÁZEK: SANEP s.r.o. kvótní výběr multiplechoice REPREZENTATIVITA: ve věku
ŘECKÁ FINANČNÍ KRIZE Z POHLEDU TEORIE HER
 ŘECKÁ FINANČNÍ KRIZE Z POHLEDU TEORIE HER TOMÁŠ KOSIČKA Abstrakt Obsahem příspěvku je hodnocení řecké finanční krize z pohledu teorie her. V první části je popis historických událostí vedoucích k přijetí
ŘECKÁ FINANČNÍ KRIZE Z POHLEDU TEORIE HER TOMÁŠ KOSIČKA Abstrakt Obsahem příspěvku je hodnocení řecké finanční krize z pohledu teorie her. V první části je popis historických událostí vedoucích k přijetí
VOLEBNÍ PREFERENCE BŘEZEN 2018
 VOLEBNÍ PREFERENCE BŘEZEN 2018 METODOLOGIE TÉMA PRŮZKUMU: Volební preference (březen 2018) REALIZÁTOR: VÝBĚR RESPONDENTŮ: TYP OTÁZEK: SANEP s.r.o. kvótní výběr multiplechoice REPREZENTATIVITA: ve věku
VOLEBNÍ PREFERENCE BŘEZEN 2018 METODOLOGIE TÉMA PRŮZKUMU: Volební preference (březen 2018) REALIZÁTOR: VÝBĚR RESPONDENTŮ: TYP OTÁZEK: SANEP s.r.o. kvótní výběr multiplechoice REPREZENTATIVITA: ve věku
1. dílčí téma: Úvod do teorie her a historie
 Cíl tematického celku: Cílem tohoto tematického celku je seznámit se se základy teorie her, její historií proniknout do matematických základů. Tento tematický celek je rozdělen do následujících dílčích
Cíl tematického celku: Cílem tohoto tematického celku je seznámit se se základy teorie her, její historií proniknout do matematických základů. Tento tematický celek je rozdělen do následujících dílčích
Bleskový výzkum SC&C pro Českou televizi
 Bleskový výzkum SC&C pro Českou televizi Volby do zastupitelstva Ostravy Praha 20. září 2010 Marketingový a sociologický výzkum Držitel certifikátu ISO 9001:2001 - člen ESOMAR www.scac.cz Metodologie Cíle
Bleskový výzkum SC&C pro Českou televizi Volby do zastupitelstva Ostravy Praha 20. září 2010 Marketingový a sociologický výzkum Držitel certifikátu ISO 9001:2001 - člen ESOMAR www.scac.cz Metodologie Cíle
Výsledky volebních stran se ziskem mandátů krajského zastupitelstva v roce v tom okres Moravskoslezský Frýdek-
 Historie voleb do zastupitelstva Moravskoslezského kraje V průběhu 1. pololetí 2000 přijal Parlament ČR nový zákon o volbách do zastupitelstev krajů a dne 12. listopadu 2000 se tak v ČR uskutečnily první
Historie voleb do zastupitelstva Moravskoslezského kraje V průběhu 1. pololetí 2000 přijal Parlament ČR nový zákon o volbách do zastupitelstev krajů a dne 12. listopadu 2000 se tak v ČR uskutečnily první
ANALÝZA ZASTOUPENÍ ŽEN NA KANDIDÁTNÍCH LISTINÁCH DO PŘEDČASNÝCH VOLEB DO PS PČR 2013
 [Zadejte podtitul dokumentu.] [Vyberte datum.] [Zadejte název společnosti.] jana Kavková ANALÝZA ZASTOUPENÍ ŽEN NA KANDIDÁTNÍCH LISTINÁCH DO PŘEDČASNÝCH VOLEB DO PS PČR 2013 Analýza vznikla v rámci projektu
[Zadejte podtitul dokumentu.] [Vyberte datum.] [Zadejte název společnosti.] jana Kavková ANALÝZA ZASTOUPENÍ ŽEN NA KANDIDÁTNÍCH LISTINÁCH DO PŘEDČASNÝCH VOLEB DO PS PČR 2013 Analýza vznikla v rámci projektu
TEORIE HER - ÚVOD PŘEDNÁŠKA. OPTIMALIZACE A ROZHODOVÁNÍ V DOPRAVĚ část druhá Přednáška 2. Zuzana Bělinová
 PŘEDNÁŠKA 2 TEORIE HER - ÚVOD Teorie her matematická teorie rozhodování dvou racionálních hráčů, kteří jsou na sobě závislí Naznačuje, jak by se v takové situaci chovali racionální a informovaní hráči.
PŘEDNÁŠKA 2 TEORIE HER - ÚVOD Teorie her matematická teorie rozhodování dvou racionálních hráčů, kteří jsou na sobě závislí Naznačuje, jak by se v takové situaci chovali racionální a informovaní hráči.
Teorie her a ekonomické rozhodování. 4. Hry v rozvinutém tvaru
 Teorie her a ekonomické rozhodování 4. Hry v rozvinutém tvaru 4.1 Hry v rozvinutém tvaru Hra v normálním tvaru hráči provedou jediné rozhodnutí a to všichni najednou v rozvinutém tvaru řada po sobě následujících
Teorie her a ekonomické rozhodování 4. Hry v rozvinutém tvaru 4.1 Hry v rozvinutém tvaru Hra v normálním tvaru hráči provedou jediné rozhodnutí a to všichni najednou v rozvinutém tvaru řada po sobě následujících
sněmovní volební model srpen 2018 (sběr 25. července 28. srpna 2018)
 sněmovní volební model srpen 2018 (sběr 25. července 28. srpna 2018) 2 metodika volebního modelu Společnost MEDIAN kontinuálně vydává nezávislý volební model pro volby do Poslanecké sněmovny parlamentu
sněmovní volební model srpen 2018 (sběr 25. července 28. srpna 2018) 2 metodika volebního modelu Společnost MEDIAN kontinuálně vydává nezávislý volební model pro volby do Poslanecké sněmovny parlamentu
ANALÝZA NOMINACÍ ŽEN A MUŽŮ DO SENÁTNÍCH VOLEB V ROCE 2014
 ANALÝZA NOMINACÍ ŽEN A MUŽŮ DO SENÁTNÍCH VOLEB V ROCE 2014 Podpořeno grantem z Islandu, Lichtenštejnska a Norska v rámci EHP fondů. Mgr. Veronika Šprincová Fórum 50 %, o.p.s www.padesatprocent.cz Úvod
ANALÝZA NOMINACÍ ŽEN A MUŽŮ DO SENÁTNÍCH VOLEB V ROCE 2014 Podpořeno grantem z Islandu, Lichtenštejnska a Norska v rámci EHP fondů. Mgr. Veronika Šprincová Fórum 50 %, o.p.s www.padesatprocent.cz Úvod
Teorie her a ekonomické rozhodování. Úvodní informace Obsah kursu 1. Úvod do teorie her
 Teorie her a ekonomické Úvodní informace Obsah kursu 1. Úvod do teorie her Úvodní informace Mgr. Jana SEKNIČKOVÁ, Ph.D. Místnost: 433 NB Konzultace: Středa 6:30 7:30, 19:30 20:30 Čtvrtek E-mail: jana.seknickova@vse.cz
Teorie her a ekonomické Úvodní informace Obsah kursu 1. Úvod do teorie her Úvodní informace Mgr. Jana SEKNIČKOVÁ, Ph.D. Místnost: 433 NB Konzultace: Středa 6:30 7:30, 19:30 20:30 Čtvrtek E-mail: jana.seknickova@vse.cz
ŘÍJEN 2017 VOLEBNÍ POTENCIÁL
 ŘÍJEN 2017 VOLEBNÍ POTENCIÁL METODOLOGIE TÉMA PRŮZKUMU: REALIZÁTOR: VÝBĚR RESPONDENTŮ: TYP OTÁZEK: Volební potenciál (říjen2017) SANEP s.r.o. kvótní výběr multiplechoice REPREZENTATIVITA: ve věku 18+let
ŘÍJEN 2017 VOLEBNÍ POTENCIÁL METODOLOGIE TÉMA PRŮZKUMU: REALIZÁTOR: VÝBĚR RESPONDENTŮ: TYP OTÁZEK: Volební potenciál (říjen2017) SANEP s.r.o. kvótní výběr multiplechoice REPREZENTATIVITA: ve věku 18+let
Bleskový výzkum SC&C a STEM pro Českou televizi
 Marketingový a sociologický výzkum Držitel certifikátu ISO 9001:2001 - člen ESOMAR www.scac.cz Závěrečná zpráva VOLBY DO PS 2010 - Středočeský kraj Bleskový výzkum SC&C a STEM pro Českou televizi Praha,
Marketingový a sociologický výzkum Držitel certifikátu ISO 9001:2001 - člen ESOMAR www.scac.cz Závěrečná zpráva VOLBY DO PS 2010 - Středočeský kraj Bleskový výzkum SC&C a STEM pro Českou televizi Praha,
METODOLOGIE. SANEP s.r.o. kvótní výběr. multiplechoice
 METODOLOGIE TÉMA PRŮZKUMU: Volební preference (listopad 2016) REALIZÁTOR: VÝBĚR RESPONDENTŮ: TYP OTÁZEK: SANEP s.r.o. kvótní výběr multiplechoice REPREZENTATIVITA: ve věku 18+let Reprezenta)vní vzorek
METODOLOGIE TÉMA PRŮZKUMU: Volební preference (listopad 2016) REALIZÁTOR: VÝBĚR RESPONDENTŮ: TYP OTÁZEK: SANEP s.r.o. kvótní výběr multiplechoice REPREZENTATIVITA: ve věku 18+let Reprezenta)vní vzorek
ANALÝZA ZASTOUPENÍ ŽEN NA KANDIDÁTNÍCH LISTINÁCH DO VOLEB DO EVROPSKÉHO PARLAMENTU 2014
 ANALÝZA ZASTOUPENÍ ŽEN NA KANDIDÁTNÍCH LISTINÁCH DO VOLEB DO EVROPSKÉHO PARLAMENTU 2014 Finančně podpořeno z programu Evropské unie Základní práva a občanství Mgr. Veronika Šprincová Fórum 50 %, o.p.s
ANALÝZA ZASTOUPENÍ ŽEN NA KANDIDÁTNÍCH LISTINÁCH DO VOLEB DO EVROPSKÉHO PARLAMENTU 2014 Finančně podpořeno z programu Evropské unie Základní práva a občanství Mgr. Veronika Šprincová Fórum 50 %, o.p.s
Modely oligopolu. I. Dokonalý trh II. Nedokonalý trh 1. Modely oligopolu. Dokonalý trh. Nedokonalý trh
 Modely oligopolu Obsah kapitoly Studijní cíle I. Dokonalý trh II. Nedokonalý trh 1. Modely oligopolu Student získá komplexní přehled teorií oligopolu, které lze úspěšně aplikovat v realitě. Doba potřebná
Modely oligopolu Obsah kapitoly Studijní cíle I. Dokonalý trh II. Nedokonalý trh 1. Modely oligopolu Student získá komplexní přehled teorií oligopolu, které lze úspěšně aplikovat v realitě. Doba potřebná
10,2% 9,8% 8,4% 7,9% 6,1% 4,0% 3,4% 2,2% 2,2% 1,5% 1,2% 1,0% 0% ANO ČSSD KSČM nevím ODS TOP 09 KDU-ČSL ostatní Úsvit STAN Piráti Svobodní SZ SPD
 14% OŠ PREFERENCE RPEN 2015 sběr: 30.7. - 10.8.2015 1 1/8 Preference politických subjektů - srpen 2015 234% 20% 187% 10% 5% 102% 98% 84% 79% 6 40% 34% 22% 22% 12% 10% 0% ANO ČD KČM nevím OD TOP 09 KDU-ČL
14% OŠ PREFERENCE RPEN 2015 sběr: 30.7. - 10.8.2015 1 1/8 Preference politických subjektů - srpen 2015 234% 20% 187% 10% 5% 102% 98% 84% 79% 6 40% 34% 22% 22% 12% 10% 0% ANO ČD KČM nevím OD TOP 09 KDU-ČL
Systémy politických stran základní klasifikace a typologie
 Systémy politických stran základní klasifikace a typologie Obsah bloku Co to je systém politických stran vymezení a kritéria pro třídění Faktory ovlivňující podobu stranického systému Technické ústavní
Systémy politických stran základní klasifikace a typologie Obsah bloku Co to je systém politických stran vymezení a kritéria pro třídění Faktory ovlivňující podobu stranického systému Technické ústavní
Znalost a hodnocení zastupitelů MHMP sběr: nejvíce známých politiků 6% 8% 9% 12% 13% 18% 23% 29% 38% 57% 57%
 00,0% Znalost a hodnocení zastupitelů MHMP sběr:.6. - 9.6.06 /7 0 nejvíce známých politiků 00% 90% 80% 70% 60% 50% 0% 0% 0% 0% 0% 6% 8% 9% % % 8% % 9% 8% 57% 57% 9% 9% 9% 88% 87% 8% 77% 7% 6% % % Adriana
00,0% Znalost a hodnocení zastupitelů MHMP sběr:.6. - 9.6.06 /7 0 nejvíce známých politiků 00% 90% 80% 70% 60% 50% 0% 0% 0% 0% 0% 6% 8% 9% % % 8% % 9% 8% 57% 57% 9% 9% 9% 88% 87% 8% 77% 7% 6% % % Adriana
Kdo je podle Pražanů nejlepším kandidátem na primátora?
 Kdo je podle Pražanů nejlepším kandidátem na primátora? Závěrečná zpráva z výzkumu Analytické centrum s.r.o. Bulharská 20, 101 00 Praha 6. 10. 2014 Praha OBSAH: 1. Důvodová zpráva 3 2. O nás 3 3. Shrnutí
Kdo je podle Pražanů nejlepším kandidátem na primátora? Závěrečná zpráva z výzkumu Analytické centrum s.r.o. Bulharská 20, 101 00 Praha 6. 10. 2014 Praha OBSAH: 1. Důvodová zpráva 3 2. O nás 3 3. Shrnutí
Postoje populace ČR k ekonomické krizi a k předvolebním tématům
 Postoje populace ČR k ekonomické krizi a k předvolebním tématům Vybrané výsledky aktuálního výzkumu Ipsos Tambor pro Zlatou korunu u příležitosti konání VII. Finančního fóra Zlaté koruny Květen 2010 Nobody
Postoje populace ČR k ekonomické krizi a k předvolebním tématům Vybrané výsledky aktuálního výzkumu Ipsos Tambor pro Zlatou korunu u příležitosti konání VII. Finančního fóra Zlaté koruny Květen 2010 Nobody
Sněmovní volební model MEDIAN KVĚTEN 2014
 Sněmovní volební model MEDIAN VÝZKUM TRHU, MÉDIÍ A VEŘEJNÉHO MÍNĚNÍ, VÝVOJ SOFTWARE Národních hrdinů 73, 190 12 Praha 9, tel.: 225 301 111, fax: 225 301 101 e-mail: median@median.cz www.median.cz OFICIÁLNÍ
Sněmovní volební model MEDIAN VÝZKUM TRHU, MÉDIÍ A VEŘEJNÉHO MÍNĚNÍ, VÝVOJ SOFTWARE Národních hrdinů 73, 190 12 Praha 9, tel.: 225 301 111, fax: 225 301 101 e-mail: median@median.cz www.median.cz OFICIÁLNÍ
VÝVOJ DŮVĚRYHODNOSTI VÁCLAVA KLAUSE CELKOVÝ PŘEHLED
 Informace STEM ze dne 5. 3. 13 CESTA VÁCLAVA KLAUSE ČESKOU POLITIKOU I. VÝVOJ DŮVĚRYHODNOSTI VÁCLAVA KLAUSE CELKOVÝ PŘEHLED První část seriálu věnovaného osobnosti Václava Klause sleduje důvěru veřejnosti
Informace STEM ze dne 5. 3. 13 CESTA VÁCLAVA KLAUSE ČESKOU POLITIKOU I. VÝVOJ DŮVĚRYHODNOSTI VÁCLAVA KLAUSE CELKOVÝ PŘEHLED První část seriálu věnovaného osobnosti Václava Klause sleduje důvěru veřejnosti
Teorie her a ekonomické rozhodování. 3. Dvoumaticové hry (Bimaticové hry)
 Teorie her a ekonomické rozhodování 3. Dvoumaticové hry (Bimaticové hry) 3.1 Neantagonistický konflikt Hra v normálním tvaru hráči provedou jediné rozhodnutí a to všichni najednou v rozvinutém tvaru řada
Teorie her a ekonomické rozhodování 3. Dvoumaticové hry (Bimaticové hry) 3.1 Neantagonistický konflikt Hra v normálním tvaru hráči provedou jediné rozhodnutí a to všichni najednou v rozvinutém tvaru řada
Veřejné finance - základní otázky
 Veřejné finance - základní otázky - jak rozsáhlá má být redistribuce důchodů? - jak ovlivňovat hospodářský cyklus (dynamiku HDP)? - co a kolik se má vyrábět ve veřejném sektoru? - jak se uskutečňují kolektivní
Veřejné finance - základní otázky - jak rozsáhlá má být redistribuce důchodů? - jak ovlivňovat hospodářský cyklus (dynamiku HDP)? - co a kolik se má vyrábět ve veřejném sektoru? - jak se uskutečňují kolektivní
3. ANTAGONISTICKÉ HRY
 3. ANTAGONISTICKÉ HRY ANTAGONISTICKÝ KONFLIKT Antagonistický konflikt je rozhodovací situace, v níž vystupují dva inteligentní rozhodovatelé, kteří se po volbě svých rozhodnutí rozdělí o pevnou částku,
3. ANTAGONISTICKÉ HRY ANTAGONISTICKÝ KONFLIKT Antagonistický konflikt je rozhodovací situace, v níž vystupují dva inteligentní rozhodovatelé, kteří se po volbě svých rozhodnutí rozdělí o pevnou částku,
PARLAMENT ČESKÉ REPUBLIKY POSLANECKÁ SNĚMOVNA. VI. volební období 599/0
 PARLAMENT ČESKÉ REPUBLIKY POSLANECKÁ SNĚMOVNA VI. volební období 599/0 Návrh poslanců Stanislava Polčáka, Petra Gazdíka, Heleny Langšádlové, Jana Chvojky, Jiřího Petrů, Stanislava Křečka, Milady Halíkové,
PARLAMENT ČESKÉ REPUBLIKY POSLANECKÁ SNĚMOVNA VI. volební období 599/0 Návrh poslanců Stanislava Polčáka, Petra Gazdíka, Heleny Langšádlové, Jana Chvojky, Jiřího Petrů, Stanislava Křečka, Milady Halíkové,
2,9% 2,6% 2,5% 1,9% 1,7% 1,5% ANO ČSSD nevím KSČM ODS TOP 09 KDU-ČSL STAN Úsvit ostatní Piráti Svobodní SZ
 Preference květen 201 sběr 20.4-8..201 S 1 1/ Přehled politických subjektů 30% 244% 20% 180% 10% 13% 10% 79% 73% 70% % 0% 29% 26% 2% ANO ČSSD nevím KSČM ODS TOP 09 KDU-ČSL STAN Úsvit ostatní Piráti Svobodní
Preference květen 201 sběr 20.4-8..201 S 1 1/ Přehled politických subjektů 30% 244% 20% 180% 10% 13% 10% 79% 73% 70% % 0% 29% 26% 2% ANO ČSSD nevím KSČM ODS TOP 09 KDU-ČSL STAN Úsvit ostatní Piráti Svobodní
Výzkum před komunálními volbami 2018 Volební potenciál
 Výzkum před komunálními volbami 2018 Volební potenciál Závěrečná zpráva, 7. 9. 2018 Zpracováno exkluzivně pro Metodika výzkumu Velikost vzorku N = 1 229 respondentů ve věku 18 a více let Termín dotazování
Výzkum před komunálními volbami 2018 Volební potenciál Závěrečná zpráva, 7. 9. 2018 Zpracováno exkluzivně pro Metodika výzkumu Velikost vzorku N = 1 229 respondentů ve věku 18 a více let Termín dotazování
Volby do EP by nyní vyhrálo ANO 2011
 V Praze 22.4.2014 Volby do EP by nyní vyhrálo ANO 2011 Tisková zpráva Předpokládaná účast ve volbách do EP činí 32,4 %, zvyšují ji příznivci ANO 2011 a Úsvitu. Pětiprocentní hranici nutnou pro přidělení
V Praze 22.4.2014 Volby do EP by nyní vyhrálo ANO 2011 Tisková zpráva Předpokládaná účast ve volbách do EP činí 32,4 %, zvyšují ji příznivci ANO 2011 a Úsvitu. Pětiprocentní hranici nutnou pro přidělení
7. Rozdělení pravděpodobnosti ve statistice
 7. Rozdělení pravděpodobnosti ve statistice Statistika nuda je, má však cenné údaje, neklesejte na mysli, ona nám to vyčíslí Jednou z úloh statistiky je odhad (výpočet) hodnot statistického znaku x i,
7. Rozdělení pravděpodobnosti ve statistice Statistika nuda je, má však cenné údaje, neklesejte na mysli, ona nám to vyčíslí Jednou z úloh statistiky je odhad (výpočet) hodnot statistického znaku x i,
Lineární algebra : Báze a dimenze
 Lineární algebra : Báze a dimenze (5. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 9. dubna 2014, 13:33 1 2 5.1 Báze lineárního prostoru Definice 1. O množině vektorů M z LP V řekneme,
Lineární algebra : Báze a dimenze (5. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 9. dubna 2014, 13:33 1 2 5.1 Báze lineárního prostoru Definice 1. O množině vektorů M z LP V řekneme,
Patové situace a volební systém pro volbu Poslanecké sněmovny Parlamentu České republiky * Jakub Šedo
 Patové situace a volební systém pro volbu Poslanecké sněmovny Parlamentu České republiky * Jakub Šedo Od voleb do Poslanecké sněmovny Parlamentu České republiky (PS PČR) v roce 1996 se opakuje v každých
Patové situace a volební systém pro volbu Poslanecké sněmovny Parlamentu České republiky * Jakub Šedo Od voleb do Poslanecké sněmovny Parlamentu České republiky (PS PČR) v roce 1996 se opakuje v každých
volební zisky kandidujících stran pravice
 Zadání Ve volbách do dolní komory parlamentu kandidovalo 8 politických stran. Ve čtyřech volebních obvodech bylo zvoleno dohromady 29 poslanců. Výsledky voleb ve všech volebních obvodech uvádí tabulka
Zadání Ve volbách do dolní komory parlamentu kandidovalo 8 politických stran. Ve čtyřech volebních obvodech bylo zvoleno dohromady 29 poslanců. Výsledky voleb ve všech volebních obvodech uvádí tabulka
Teorie pravěpodobnosti 1
 Teorie pravěpodobnosti 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Náhodný jev a pravděpodobnost Každou zákonitost sledovanou v přírodě lze zjednodušeně charakterizovat jako
Teorie pravěpodobnosti 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Náhodný jev a pravděpodobnost Každou zákonitost sledovanou v přírodě lze zjednodušeně charakterizovat jako
