Teorie her a ekonomické rozhodování 5. Opakované hry
|
|
|
- Břetislav Müller
- před 9 lety
- Počet zobrazení:
Transkript
1 Teorie her a ekonomické rozhodování 5. Opakované hry (chybějící či chybná indexace ve skriptech)
2 5.1 Opakovaná hra Hra až dosud hráči hráli hru jen jednou v reálu se konflikty neustále opakují (firmy nabízí množství výrobků trh stanovuje cenu výrobci reagují dodávají výrobky atd.) a tak analyzujeme opakovanou hru Mgr. Jana Sekničková, Ph.D. 2
3 5.1 Opakovaná hra Informace o opakování hry ovlivňuje chování hráčů Odlišně hrajeme, pokud hráče již nikdy neuvidíme, a jinak, pokud očekáváme další hru Nedodržení dohody v kooperativní hře (např. kartelové dohody) může mít následky v budoucnosti Mgr. Jana Sekničková, Ph.D. 3
4 5.1 Opakovaná hra Jednokolová hra G v normálním tvaru s N hráči strategie hráče v jednokolové hře = akce ai neprázdný prostor strategií hráče i v jednokolové hře = prostor akcí Ai Mgr. Jana Sekničková, Ph.D. 4
5 5.1 Opakovaná hra Příklad 1 Kámen nůžky papír Akce hráče i: a i, i = 1, 2 a i = kámen nebo a i = nůžky nebo a i = papír Prostor akcí hráče i: A i, i = 1, 2 A i = kámen, nůžky, papír Mgr. Jana Sekničková, Ph.D. 5
6 5.1 Opakovaná hra Příklad 2 Vězňovo dilema Akce hráče i: a i, i = 1, 2 a i a i = spolupráce (nepřiznat) nebo = podvod (přiznat) Prostor akcí hráče i: A i, i = 1, 2 A i = spolupráce nepřiznat, podvod (přiznat) Mgr. Jana Sekničková, Ph.D. 6
7 5.1 Opakovaná hra Opakovaná hra G* (superhra) je-li hra G hrána opakovaně, je řada her G sama o sobě také hrou (opakovanou) strategie hráče i = posloupnost zvolených akcí v rámci celé opakované hry hraje se v diskrétních okamžicích t = 0, 1,, T celkový počet kol = T+1 (t počet opakování) T < konečně opakovaná hra T = nekonečně opakovaná hra Mgr. Jana Sekničková, Ph.D. 7
8 5.1 Opakovaná hra Příklad 1 Kámen nůžky papír Jak může vypadat strategie prvního hráče ve dvoukolové hře? Kámen, kámen Nůžky, papír Papír, zopakuji tah druhého hráče z prvního kola Mgr. Jana Sekničková, Ph.D. 8
9 5.1 Opakovaná hra Příklad 2 Vězňovo dilema Jak může vypadat strategie prvního hráče ve dvoukolové hře? Spolupráce, spolupráce Spolupráce, podvod Spolupráce, zopakuji tah druhého hráče z prvního kola Mgr. Jana Sekničková, Ph.D. 9
10 5.1 Opakovaná hra Nutno rozlišovat index hráče i budeme používat dolní index index času t budeme používat horní index Akce, kterou hraje hráč i v okamžiku t: a i t Prostor akcí hráče i v čase t: A i t (a i t A i t ) Profil akcí v čase t: a t = (a 1 t, a 2 t,, a n t ) Mgr. Jana Sekničková, Ph.D. 10
11 5.1 Opakovaná hra Příklad 1 Kámen nůžky papír Prostor akcí hráče i v čase t: A i t = kámen, nůžky, papír, i = 1, 2, t = 0, 1, Profil akcí v čase 0: a 0 = (kámen, nůžky) Profil akcí v čase 1: a 1 = (papír, kámen) Profil akcí v čase 2: a 2 = (papír, papír) Mgr. Jana Sekničková, Ph.D. 11
12 5.1 Opakovaná hra Předpoklady: Prostor akcí Ai každého hráče i se mezi jednotlivými Hráč volí v každém koly nemění kole akci (A t i =A v závislosti t+1 i ) na minulých rozhodnutích ostatních hráčů Výplaty pro hráče se v jednotlivých kolech nemění, mohou však být diskontovány Výplaty pro hráče závisí pouze na profilu akcí daného kola (nezávisí na pořadí kola) Prostředí Hráči volí pro a realizují opakovanou akce hru v kole je stacionární současně výplatní Hráči znají matice akce má ostatních v každém hráčů kole stejný v předchozích rozměr a kolech stejné hodnoty Mgr. Jana Sekničková, Ph.D. 12
13 5.1 Opakovaná hra Za těchto předpokladů: Akce, kterou hraje hráč i v čase t: a i t Prostor akcí hráče i v čase t nezávisí na kole: A i (a i t A i ) Profil akcí v čase t: a t = (a 1 t, a 2 t,, a n t ) Prostor profilů akcí: A = A 1 A 2 A n Mgr. Jana Sekničková, Ph.D. 13
14 5.1 Opakovaná hra Historie hry představuje všechny předchozí realizované profily akcí: při 0. opakování: a 0 = (a 1 0, a 2 0,, a n 0 ) při 1. opakování: a 1 = (a 1 1, a 2 1,, a n 1 ) při T. opakování: a T = (a 1 T, a 2 T,, a n T ) Historie v čase t: h t = (a 0, a 1,, a t 1 ) Mgr. Jana Sekničková, Ph.D. 14
15 5.1 Opakovaná hra Příklad 1 Kámen nůžky papír Prostor akcí hráče i v čase t: A i = kámen, nůžky, papír, i = 1,2 Historie v čase 0: h 0 = Profil akcí v čase 0: a 0 = (kámen, nůžky) Historie v čase 1: h 1 = (kámen, nůžky) Profil akcí v čase 1: a 1 = (papír, kámen) Historie v čase 2: h 2 = kámen, nůžky, (papír, kámen) Mgr. Jana Sekničková, Ph.D. 15
16 5.1 Opakovaná hra Pro historii platí: historie h 0 je prázdná historie h t v sobě obsahuje také informaci o předchozích historiích h t 1, h t 2,, h 0 historie h T se nazývá konečná historie (konečná historie v nekonečné hře má nekonečnou délku, T = ) historie h t označuje historii po t+1. kole (po t- tém opakování hry, neboť hra začíná v čase 0) Mgr. Jana Sekničková, Ph.D. 16
17 5.1 Opakovaná hra Prostor historií hry: H t množina všech možných historií v čase t H t = (A) t = A 0 A 1 A t kartézský součin prostorů profilů akcí jednotlivých kol opakované hry Mgr. Jana Sekničková, Ph.D. 17
18 5.1 Opakovaná hra Příklad 1 Kámen nůžky papír Prostor historií po 1. kole (pro 2. kolo, t = 1): H 1 = {(kámen, kámen), (kámen, nůžky), (kámen, papír), (nůžky, kámen), (nůžky, nůžky), (nůžky, papír), (papír, kámen), (papír, nůžky), (papír, papír)} Prostor historií po 2. kole (t = 2) má již 9 x 9 možných historií h 2 Mgr. Jana Sekničková, Ph.D. 18
19 5.1 Opakovaná hra Ryzí strategie hráče i: s i h t : H t A i Ryzí strategie tedy přiřazuje hráči i akci a i t A i po odehrané historii h t H t Hráč tedy vyhodnotí výsledek odehrané hry až do času t 1 a na jeho základě zvolí akci pro čas t Na začátku hry hráč nemá žádné informace Mgr. Jana Sekničková, Ph.D. 19
20 5.1 Opakovaná hra Profil strategií odehraných hráči v čase t: s t = s 1 h t, s 2 h t,, s n h t Strategie hráče i v opakované hře: s i = s i h 0, s i h 1,, s i h T tento vektor má T+1 složek vektor ryzích strategií z každého kola hry Mgr. Jana Sekničková, Ph.D. 20
21 5.1 Opakovaná hra Prostor strategií hráče i: S i množina všech strategií s i, které může hráč i uskutečnit Prostor profilů strategií: S množina všech prostorů strategií, které mohou ve hře nastat Mgr. Jana Sekničková, Ph.D. 21
22 5.1 Opakovaná hra Příklad 2 Vězňovo dilema Prostor akcí hráče i v čase t: A i = spolupráce nepřiznat, podvod (přiznat) Ryzí strategie hráče i může být např.: s i h t = spolupráce, t = 0 spolupráce, když a τ j = spolupráce j i, τ = 1 t 1 podvod, jinak spolupracuj, dokud všichni hráči spolupracují Mgr. Jana Sekničková, Ph.D. 22
23 5.1 Opakovaná hra Jak probíhá hra? na počátku je historie prázdná h 0 = každý hráč volí akci pro nulté kolo a i 0 po ukončení kola se vytvoří historie h 1 = a 0 všichni hráči jsou s touto historií seznámeni volí strategii pro první kolo s i h 1 aktualizuje se historie, hráči jsou s ní seznámeni a volí strategii pro další kolo, Mgr. Jana Sekničková, Ph.D. 23
24 5.1 Opakovaná hra Pro výplatní funkci u i použijeme přístup založený na diskontování s diskontním faktorem δ i (0,1) Diskontní faktor je společný pro výplaty ze všech kol g i a t výplata pro hráče i při profilu akcí a t Tento faktor se teoreticky může lišit pro jednotlivé hráče a jednotlivá kola Mgr. Jana Sekničková, Ph.D. 24
25 5.1 Opakovaná hra Diskontní faktor přidává do výplatní funkce hodnotu času popisuje míru netrpělivosti hráčů δ i 0 hráč je netrpělivý, má sklon podvádět, hrozba budoucího trestu má malý význam δ i 1 hráč je trpělivý, má sklon spolupracovat, hrozba budoucího trestu má velký význam Mgr. Jana Sekničková, Ph.D. 25
26 5.1 Opakovaná hra Výplatní funkci hráče i lze definovat jako diskontovaný součet výplat z každého kola: u i = g i a 0 + δ i g i a 1 + δ i 2 g i a 2 + neboli u i = T t=0 δ i t g i a t Mgr. Jana Sekničková, Ph.D. 26
27 5.1 Opakovaná hra Přenásobení užitkové funkce kladnou konstantou nemění preference, takže místo T diskontovaného součtu výplat u i = t=0 δ t i g i a t lze použít diskontovanou průměrnou výplatu u i = (1 δ i ) T t=0 δ i t g i a t Mgr. Jana Sekničková, Ph.D. 27
28 5.1 Opakovaná hra Tato úprava umožňuje srovnání s jednorázovou hrou u i = (1 δ i ) Opakovaná hra s výplatami (v, v, v,, v) T má užitek u i = 1 δ i t=0 δ t i v = T = 1 δ i v t=0 δ t i = = 1 δ i v 1 = v 1 δ i T t=0 δ i t g i a t Mgr. Jana Sekničková, Ph.D. 28
29 5.1 Opakovaná hra Nashova rovnováha Strategie hráče i s i = s i h 0, s i h 1,, s i h T je Nashovou rovnováhou v opakované hře, jestliže s i je nejlepší odezvou hráče i vůči chování ostatních hráčů, kteří se drží svých rovnovážných strategií Mgr. Jana Sekničková, Ph.D. 29
30 5.2 Konečně opakovaná hra Je dán všem hráčům známý počet opakování T < V důsledku této informace může v posledních kolech hry dojít ke změně chování hráčů Často spolupracují téměř až do konce, na úplném konci (kdy už nehrozí postih za podvod) spolupracovat přestanou Mgr. Jana Sekničková, Ph.D. 30
31 5.2 Konečně opakovaná hra Příklad: Vězňovo dilema P N P 6, 6 0, 10 N 10,0 2, 2 Jednorázová hra má Nashovo rovnovážné řešení (podvod, podvod) dominování Mgr. Jana Sekničková, Ph.D. 31
32 5.2 Konečně opakovaná hra P N P 6, 6 0, 10 N 10,0 2, 2 Předpokládejme nyní opakovanou hru Je dán počet opakování hry T a diskontní faktor δ Dokonalá rovnováha podhry V posledním kole je výhodné podvádět (protihráč již nemůže podvod trestat) a tak bude výsledkem řešení (podvod, podvod) Mgr. Jana Sekničková, Ph.D. 32
33 5.2 Konečně opakovaná hra V posledním kole tedy hrají (podvod, podvod) stejně jako v jednorázové hře V předposledním kole je opět výhodnější podvod než spolupráce za podvod může protihráč trestat tak, že bude podvádět ale podvádět bude stejně, takže to žádný trest není Mgr. Jana Sekničková, Ph.D. 33
34 5.2 Konečně opakovaná hra Postupně dojdeme stejnou úvahou až na začátek hry Nashovou rovnováhou je tedy strategie: s i h t = podvod t = 0, 1,, T Platí: V konečně opakované hře vězňovo dilema existuje jediná Nashova rovnováha (a jediná dokonalá rovnováha podhry), ve které všichni hráči volí podvod Mgr. Jana Sekničková, Ph.D. 34
35 5.3 Nekonečně opakovaná hra Je dán nekonečný časový horizont T = Hráči nevědí, ve kterém kole hra skončí a zda vůbec skončí Není tedy stanoveno poslední kolo, ve kterém by hráči mohli beztrestně podvádět Hráči se tedy drží dohodnuté spolupráce pod hrozbou trestu z nedodržení dohody Mgr. Jana Sekničková, Ph.D. 35
36 5.3 Nekonečně opakovaná hra Místo jedné rovnovážné strategie (jako v jednorázové hře nebo v konečně opakované hře) existuje řada potenciálně rovnovážných strategií Ukážeme si ty nejznámější pro vězňovo dilema Jaké strategie napadají Vás? Mgr. Jana Sekničková, Ph.D. 36
37 5.3 Nekonečně opakovaná hra 1. Vždy podvádějte (Always Defect) Jestřábí strategie Hráč podvádí bez ohledu na historii s i h t = podvod t = 0, 1, 2, Mgr. Jana Sekničková, Ph.D. 37
38 5.3 Nekonečně opakovaná hra 2. Vždy spolupracujte (Always Cooperate) Holubí strategie Hráč spolupracuje bez ohledu na historii s i h t = spolupráce t = 0, 1, 2, Mgr. Jana Sekničková, Ph.D. 38
39 5.3 Nekonečně opakovaná hra 3. Naivní GrimTrigger Hráč spolupracuje až do chvíle, než někdo spolupráci poruší, pak již podvádí Podvod protihráče je navždy trestán s i h t = spolupráce, t = 0 spolupráce, když a τ j = spolupráce j i, τ = 0,1,, t 1 podvod, jinak Mgr. Jana Sekničková, Ph.D. 39
40 5.3 Nekonečně opakovaná hra 4. GrimTrigger Hráč spolupracuje až do chvíle, než někdo spolupráci poruší, pak již podvádí Postihuje zradu protihráčů i hráče samého s i h t = spolupráce, t = 0 spolupráce, když a τ j = spolupráce j, τ = 0,1,, t 1 podvod, jinak Mgr. Jana Sekničková, Ph.D. 40
41 5.3 Nekonečně opakovaná hra 5. Oko za oko (Tit-for-Tat) Strategie Půjčka za oplátku Začít spoluprací a dále kopírovat strategie protihráčů z předchozího kola spolupráce, t = 0 s i h t = spolupráce, když a t 1 j = spolupráce j i podvod, jinak Mgr. Jana Sekničková, Ph.D. 41
42 5.3 Nekonečně opakovaná hra 6. Omezená odplata (Limited Retaliation) Strategie Odpouštějící trigger Začít spoluprací Pokud kdokoliv zradí, k kol podvádět jako trest za zradu Pak opět spolupracovat bez ohledu na historii během odvety Mgr. Jana Sekničková, Ph.D. 42
43 5.3 Nekonečně opakovaná hra 7. Win-Stay, Lose-Shift Začít spoluprací a dále spolupracovat, pokud hráči hráli stejně, a podvádět, pokud hráli různě s i h t = spolupráce, t = 0 spolupráce, když a t 1 j = spolupráce j nebo a t 1 j = podvod j podvod, jinak Mgr. Jana Sekničková, Ph.D. 43
44 5.3 Nekonečně opakovaná hra 8. Jednou podvádějte (Deviate Once) Použít Oko za oko až do kola L V kole L podvod, v L+1 spolupráce a dále Oko za oko s i h t = spolupráce, t = 0, L + 1 spolupráce, když a t 1 j = spolupráce j i, t L podvod, jinak t = L Mgr. Jana Sekničková, Ph.D. 44
45 5.3 Nekonečně opakovaná hra 9. Grim Deviate Once Použít Grim Trigger až do kola L V kole L a následujících podvádět s i h t = spolupráce, t = 0 spolupráce, když a τ j = spolupráce τ = 0, 1,, t 1, t < L podvod, jinak t L Mgr. Jana Sekničková, Ph.D. 45
46 5.3 Nekonečně opakovaná hra Pro řešení opakované hry potřebujeme určit Nashovy rovnovážné strategie obou hráčů Jednou možností jsou strategie Grim Trigger Jsou rovnovážnými strategiemi? Bude výsledkem hry trvalá spolupráce? Na čem závisí rozhodnutí hráčů? Mgr. Jana Sekničková, Ph.D. 46
47 5.3 Nekonečně opakovaná hra Příklad: GrimTrigger Hráč spolupracuje až do chvíle, než někdo (i on) spolupráci poruší, pak již podvádí Oba začínají spoluprací, v dalším kole opět spolupracují (nikdo dohodu neporušil) atd. Výplaty v jednotlivých kolech tedy budou: 2, 2, 2 P N P 6, 6 N 0, 10 10,0 2, 2 Mgr. Jana Sekničková, Ph.D. 47
48 5.3 Nekonečně opakovaná hra Příklad: GrimTrigger Pokud by někdo podváděl, bude protihráč dále volit podvod Podvodník tedy získá 0, 6, 6, 6, V prvním kole získá o 2 jednotky více, v každém dalším však o 4 jednotky P více Nztratí Pokud je velmi netrpělivý, P 6, může 6pro 0, něj 10 být tato strategie výhodnější N 10,0 2, 2 Mgr. Jana Sekničková, Ph.D. 48
49 5.3 Nekonečně opakovaná hra Příklad: GrimTrigger Pro opakovanou spolupráci s výplatami ( 2, 2, 2 ) je diskontovaná průměrná výplata u i = 1 δ i = 1 δ i 2 t=0 δ i t 2 = 1 1 δ i = 2 Mgr. Jana Sekničková, Ph.D. 49
50 5.3 Nekonečně opakovaná hra Příklad: GrimTrigger Pro podvod v kroku τ s výplatami ( 2, 2, 2, 2, 0, 6, 6, 6, ) je diskontovaná průměrná výplata = 1 δ i u i = 1 δ i τ 1 t=0 t=0 δ i t δ i t g i a t = t=τ+1 δ i t 6 Mgr. Jana Sekničková, Ph.D. 50
51 5.3 Nekonečně opakovaná hra Příklad: GrimTrigger u i = 1 δ i τ 1 t=0 τ 1 δ i t = 1 1 δ i τ t=0 u i = 1 δ i δ i t δ i t=τ+1 t=τ+1 δ i t 6 δ i t = δ i τ+1 1 δ i 2 1 δ i τ + 6 δ τ+1 i 1 δ i 1 δ i Mgr. Jana Sekničková, Ph.D. 51
52 5.3 Nekonečně opakovaná hra Příklad: GrimTrigger u i = 2 1 δ i τ 6δ i τ+1 = 2 + 2δ i τ 6δ i τ+1 Hráč bude spolupracovat, pokud u i (spolupráce) u i (podvod) δ i τ 6δ i τ+1 6δ i τ+1 2δ i τ δ i τ+1 δ i τ 2 6 δ i 1 3 Mgr. Jana Sekničková, Ph.D. 52
53 5.3 Nekonečně opakovaná hra Příklad: GrimTrigger Hráč tedy bude spolupracovat, pokud pro jeho diskontní faktor platí δ i 1 3 Pro trpělivé hráče s δ i 1 3 se podvádění nevyplatí Naopak netrpěliví hráči (s nízkým diskontním faktorem) preferují krátkodobý zisk Mgr. Jana Sekničková, Ph.D. 53
54 5.3 Nekonečně opakovaná hra Příklad: GrimTrigger Strategie GrimTrigger je Nashovou rovnováhou v uvedeném příkladě pro trpělivé hráče s δ i 1 3 Mgr. Jana Sekničková, Ph.D. 54
55 5.3 Nekonečně opakovaná hra Závěr: Odchýlením od rovnovážné strategie si trpělivý hráč nemůže polepšit Pro opakované hry s vysokým diskontním faktorem (blízkým 1) existuje mnoho rovnovážných strategií Pro trpělivého hráče libovolná strategie zajišťující výhry alespoň rovné zaručené maximinové výhře může představovat Nashovu rovnovážnou strategii Mgr. Jana Sekničková, Ph.D. 55
56 KONEC Mgr. Jana Sekničková, Ph.D. 56
Hry v rozvinutém tvaru a opakované hry. Hry v rozvinutém tvaru
 Hry v rozvinutém tvaru a opakované hry Obsah kapitoly Studijní cíle Doba potřebná ke studiu Pojmy k zapamatování Úvod Výkladová část 1) Hry v rozvinutém tvaru 2) Opakované hry I. Konečně opakované hry
Hry v rozvinutém tvaru a opakované hry Obsah kapitoly Studijní cíle Doba potřebná ke studiu Pojmy k zapamatování Úvod Výkladová část 1) Hry v rozvinutém tvaru 2) Opakované hry I. Konečně opakované hry
Teorie her a ekonomické rozhodování. 3. Dvoumaticové hry (Bimaticové hry)
 Teorie her a ekonomické rozhodování 3. Dvoumaticové hry (Bimaticové hry) 3.1 Neantagonistický konflikt Hra v normálním tvaru hráči provedou jediné rozhodnutí a to všichni najednou v rozvinutém tvaru řada
Teorie her a ekonomické rozhodování 3. Dvoumaticové hry (Bimaticové hry) 3.1 Neantagonistický konflikt Hra v normálním tvaru hráči provedou jediné rozhodnutí a to všichni najednou v rozvinutém tvaru řada
Teorie her a ekonomické rozhodování. 7. Hry s neúplnou informací
 Teorie her a ekonomické rozhodování 7. Hry s neúplnou informací 7.1 Informace Dosud hráči měli úplnou informaci o hře, např. znali svou výplatní funkci, ale i výplatní funkce ostatních hráčů často to tak
Teorie her a ekonomické rozhodování 7. Hry s neúplnou informací 7.1 Informace Dosud hráči měli úplnou informaci o hře, např. znali svou výplatní funkci, ale i výplatní funkce ostatních hráčů často to tak
TGH13 - Teorie her I.
 TGH13 - Teorie her I. Jan Březina Technical University of Liberec 19. května 2015 Hra s bankéřem Máte právo sehrát s bankéřem hru: 1. hází se korunou dokud nepadne hlava 2. pokud hlava padne v hodu N,
TGH13 - Teorie her I. Jan Březina Technical University of Liberec 19. května 2015 Hra s bankéřem Máte právo sehrát s bankéřem hru: 1. hází se korunou dokud nepadne hlava 2. pokud hlava padne v hodu N,
Teorie her a ekonomické rozhodování. 2. Maticové hry
 Teorie her a ekonomické rozhodování 2. Maticové hry 2.1 Maticová hra Teorie her = ekonomická vědní disciplína, která se zabývá studiem konfliktních situací pomocí matematických modelů Hra v normálním tvaru
Teorie her a ekonomické rozhodování 2. Maticové hry 2.1 Maticová hra Teorie her = ekonomická vědní disciplína, která se zabývá studiem konfliktních situací pomocí matematických modelů Hra v normálním tvaru
3. ANTAGONISTICKÉ HRY
 3. ANTAGONISTICKÉ HRY ANTAGONISTICKÝ KONFLIKT Antagonistický konflikt je rozhodovací situace, v níž vystupují dva inteligentní rozhodovatelé, kteří se po volbě svých rozhodnutí rozdělí o pevnou částku,
3. ANTAGONISTICKÉ HRY ANTAGONISTICKÝ KONFLIKT Antagonistický konflikt je rozhodovací situace, v níž vystupují dva inteligentní rozhodovatelé, kteří se po volbě svých rozhodnutí rozdělí o pevnou částku,
Teorie her a ekonomické rozhodování. 4. Hry v rozvinutém tvaru
 Teorie her a ekonomické rozhodování 4. Hry v rozvinutém tvaru 4.1 Hry v rozvinutém tvaru Hra v normálním tvaru hráči provedou jediné rozhodnutí a to všichni najednou v rozvinutém tvaru řada po sobě následujících
Teorie her a ekonomické rozhodování 4. Hry v rozvinutém tvaru 4.1 Hry v rozvinutém tvaru Hra v normálním tvaru hráči provedou jediné rozhodnutí a to všichni najednou v rozvinutém tvaru řada po sobě následujících
ANTAGONISTICKE HRY 172
 5 ANTAGONISTICKÉ HRY 172 Antagonistický konflikt je rozhodovací situace, v níž vystupují dva inteligentní rozhodovatelé, kteří se po volbě svých rozhodnutí rozdělí o pevnou částku, jejíž výše nezávisí
5 ANTAGONISTICKÉ HRY 172 Antagonistický konflikt je rozhodovací situace, v níž vystupují dva inteligentní rozhodovatelé, kteří se po volbě svých rozhodnutí rozdělí o pevnou částku, jejíž výše nezávisí
Teorie her a ekonomické rozhodování 6. Kooperativní hry více hráčů
 Teorie her a ekonomické rozhodování 6. Kooperativní hry více hráčů (chyby ve skriptech) 6.1 Koaliční hra Kooperativní hra hráči mají možnost před samotnou hrou uzavírat závazné dohody dva hráči (hra má
Teorie her a ekonomické rozhodování 6. Kooperativní hry více hráčů (chyby ve skriptech) 6.1 Koaliční hra Kooperativní hra hráči mají možnost před samotnou hrou uzavírat závazné dohody dva hráči (hra má
Dvou-maticové hry a jejich aplikace
 Dvou-maticové hry a jejich aplikace Obsah kapitoly. Hry s konstantním součtem Hra v normálním tvaru (ryzí strategie) Smíšené strategie. Hry s nekonstantním součtem Nekooperativní hra Dvou-maticová hra
Dvou-maticové hry a jejich aplikace Obsah kapitoly. Hry s konstantním součtem Hra v normálním tvaru (ryzí strategie) Smíšené strategie. Hry s nekonstantním součtem Nekooperativní hra Dvou-maticová hra
Operační výzkum. Teorie her. Hra v normálním tvaru. Optimální strategie. Maticové hry.
 Operační výzkum Hra v normálním tvaru. Optimální strategie. Maticové hry. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky
Operační výzkum Hra v normálním tvaru. Optimální strategie. Maticové hry. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky
TEORIE HER Meta hry PŘEDNÁŠKA. OPTIMALIZACE A ROZHODOVÁNÍ V DOPRAVĚ část druhá Přednáška 4. Zuzana Bělinová
 PŘEDNÁŠKA 4a TEORIE HER Meta hry OPTIMALIZACE A ROZHODOVÁNÍ V DOPRAVĚ část druhá Přednáška 4 Strategické hry se nenulovým součtem počet hráčů není dán, ale dále uvažujeme 2 hráče hrající racionálně Meta
PŘEDNÁŠKA 4a TEORIE HER Meta hry OPTIMALIZACE A ROZHODOVÁNÍ V DOPRAVĚ část druhá Přednáška 4 Strategické hry se nenulovým součtem počet hráčů není dán, ale dále uvažujeme 2 hráče hrající racionálně Meta
Dva podniky vedou mezi sebou spor, k jehož vyřešení může každý z nich podniknout jednu
 Zadání příkladu: Dva podniky vedou mezi sebou spor, k jehož vyřešení může každý z nich podniknout jednu ze tří akcí: a/ žalovat druhý podnik u soudu strategie Z b/ nabídnout druhému podniku spojení strategie
Zadání příkladu: Dva podniky vedou mezi sebou spor, k jehož vyřešení může každý z nich podniknout jednu ze tří akcí: a/ žalovat druhý podnik u soudu strategie Z b/ nabídnout druhému podniku spojení strategie
5.7 Kooperativní hry 5.7.1 Kooperativní hra 2 hráčů 5.7.2 Kooperativní hra N hráčů 5.8 Modely oligopolu 5.9 Teorie redistribučních systémů 5.
 Mikroekonomie bakalářský kurz - VŠFS Jiří Mihola, jiri.mihola@quick.cz, www.median-os.cz, 2010 Téma 6 Teorie her, volby teorie redistribučních systémů a teorie veřejné Obsah 5.7 Kooperativní hry 5.7.1
Mikroekonomie bakalářský kurz - VŠFS Jiří Mihola, jiri.mihola@quick.cz, www.median-os.cz, 2010 Téma 6 Teorie her, volby teorie redistribučních systémů a teorie veřejné Obsah 5.7 Kooperativní hry 5.7.1
Úvod do teorie her
 Úvod do teorie her 2. Garanční řešení, hry s nulovým součtem a smíšené strategie Tomáš Kroupa http://staff.utia.cas.cz/kroupa/ 2017 ÚTIA AV ČR Program 1. Zavedeme řešení, které zabezpečuje minimální výplatu
Úvod do teorie her 2. Garanční řešení, hry s nulovým součtem a smíšené strategie Tomáš Kroupa http://staff.utia.cas.cz/kroupa/ 2017 ÚTIA AV ČR Program 1. Zavedeme řešení, které zabezpečuje minimální výplatu
Úvod do teorie her
 Úvod do teorie her. Formy her a rovnovážné řešení Tomáš Kroupa http://staff.utia.cas.cz/kroupa/ 208 ÚTIA AV ČR Program. Definujeme 2 základní formy pro studium různých her: rozvinutou, strategickou. 2.
Úvod do teorie her. Formy her a rovnovážné řešení Tomáš Kroupa http://staff.utia.cas.cz/kroupa/ 208 ÚTIA AV ČR Program. Definujeme 2 základní formy pro studium různých her: rozvinutou, strategickou. 2.
KOOPERATIVNÍ HRY FORMULACE, KONCEPCE ŘEŠENÍ, JÁDRO HRY, HRA VE TVARU CHARAKTERISTICKÉ FUNKCE, SHAPLEYOVA HODNOTA CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ?
 KOOPERATIVNÍ HRY FORMULACE, KONCEPCE ŘEŠENÍ, JÁDRO HRY, HRA VE TVARU CHARAKTERISTICKÉ FUNKCE, SHAPLEYOVA HODNOTA CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekonomická vědní disciplína, která se
KOOPERATIVNÍ HRY FORMULACE, KONCEPCE ŘEŠENÍ, JÁDRO HRY, HRA VE TVARU CHARAKTERISTICKÉ FUNKCE, SHAPLEYOVA HODNOTA CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekonomická vědní disciplína, která se
4EK201 Matematické modelování. 10. Teorie rozhodování
 4EK201 Matematické modelování 10. Teorie rozhodování 10. Rozhodování Rozhodování = proces výběru nějaké možnosti (varianty) podle stanoveného kritéria za účelem dosažení stanovených cílů Rozhodovatel =
4EK201 Matematické modelování 10. Teorie rozhodování 10. Rozhodování Rozhodování = proces výběru nějaké možnosti (varianty) podle stanoveného kritéria za účelem dosažení stanovených cílů Rozhodovatel =
Úvod do teorie her ZVYŠOVÁNÍ ODBORNÝCH KOMPETENCÍ AKADEMICKÝCH PRACOVNÍKŮ OSTRAVSKÉ UNIVERZITY V OSTRAVĚ A SLEZSKÉ UNIVERZITY V OPAVĚ
 ZVYŠOVÁNÍ ODBORNÝCH KOMPETENCÍ AKADEMICKÝCH PRACOVNÍKŮ OSTRAVSKÉ UNIVERZITY V OSTRAVĚ A SLEZSKÉ UNIVERZITY V OPAVĚ Úvod do teorie her David Bartl, Lenka Ploháková OSNOVA Úvod (hra n hráčů ve strategickém
ZVYŠOVÁNÍ ODBORNÝCH KOMPETENCÍ AKADEMICKÝCH PRACOVNÍKŮ OSTRAVSKÉ UNIVERZITY V OSTRAVĚ A SLEZSKÉ UNIVERZITY V OPAVĚ Úvod do teorie her David Bartl, Lenka Ploháková OSNOVA Úvod (hra n hráčů ve strategickém
Aplikace teorie her. V ekonomice a politice Ing. Václav Janoušek
 Aplikace teorie her V ekonomice a politice Ing. Václav Janoušek Co je teorie her a její využití Teorie her obor aplikované matematiky a operační analýzy, sloužící k analýze konfliktních a strategických
Aplikace teorie her V ekonomice a politice Ing. Václav Janoušek Co je teorie her a její využití Teorie her obor aplikované matematiky a operační analýzy, sloužící k analýze konfliktních a strategických
Rozhodovací procesy v ŽP HRY A SIMULAČNÍ MODELY
 Rozhodovací procesy v ŽP HRY A SIMULAČNÍ MODELY Teorie her proč využívat hry? Hry a rozhodování varianty her cíle a vítězné strategie (simulační) Modely Operační hra WRENCH Cv. Katedra hydromeliorací a
Rozhodovací procesy v ŽP HRY A SIMULAČNÍ MODELY Teorie her proč využívat hry? Hry a rozhodování varianty her cíle a vítězné strategie (simulační) Modely Operační hra WRENCH Cv. Katedra hydromeliorací a
Teorie her a ekonomické rozhodování. 9. Modely nedokonalých trhů
 Teorie her a ekonomické rozhodování 9. Modely nedokonalých trhů 9.1 Dokonalý trh Dokonalý trh Dokonalá informovanost kupujících Dokonalá informovanost prodávajících Nulové náklady na změnu dodavatele Homogenní
Teorie her a ekonomické rozhodování 9. Modely nedokonalých trhů 9.1 Dokonalý trh Dokonalý trh Dokonalá informovanost kupujících Dokonalá informovanost prodávajících Nulové náklady na změnu dodavatele Homogenní
Teorie her a ekonomické rozhodování. 8. Vyjednávací hry
 Teorie her a ekonomické rozhodování 8. Vyjednávací hry 8. Vyjednávání Teorie her Věda o řešení konfliktů Ale také věda o hledání vzájemně výhodné spolupráce Teorie vyjednávání Odvětví teorie her dohoda
Teorie her a ekonomické rozhodování 8. Vyjednávací hry 8. Vyjednávání Teorie her Věda o řešení konfliktů Ale také věda o hledání vzájemně výhodné spolupráce Teorie vyjednávání Odvětví teorie her dohoda
(Ne)kooperativní hry
 (Ne)kooperativní hry Tomáš Svoboda, svobodat@fel.cvut.cz katedra kybernetiky, centrum strojového vnímání 5. října 2015 Tomáš Svoboda, svobodat@fel.cvut.cz / katedra kybernetiky, CMP / (Ne)kooperativní
(Ne)kooperativní hry Tomáš Svoboda, svobodat@fel.cvut.cz katedra kybernetiky, centrum strojového vnímání 5. října 2015 Tomáš Svoboda, svobodat@fel.cvut.cz / katedra kybernetiky, CMP / (Ne)kooperativní
charakteristika oligopolu kartel Cournotův model duopolu oligopol s dominantní firmou Sweezyho model (se zalomenou křivkou poptávky) Nashova
 charakteristika oligopolu kartel Cournotův model duopolu oligopol s dominantní firmou Sweezyho model (se zalomenou křivkou poptávky) Nashova rovnováha Soukupová et al.: Mikroekonomie. Kapitola 11, str.
charakteristika oligopolu kartel Cournotův model duopolu oligopol s dominantní firmou Sweezyho model (se zalomenou křivkou poptávky) Nashova rovnováha Soukupová et al.: Mikroekonomie. Kapitola 11, str.
KOOPERATIVNI HRY DVOU HRA CˇU
 8 KOOPERATIVNÍ HRY DVOU HRÁČŮ 291 V této kapitole se budeme zabývat situacemi, kdy hráči mohou před začátkem hry uzavřít závaznou dohodu o tom, jaké použijí strategie, vygenerovaný zisk si však nemohou
8 KOOPERATIVNÍ HRY DVOU HRÁČŮ 291 V této kapitole se budeme zabývat situacemi, kdy hráči mohou před začátkem hry uzavřít závaznou dohodu o tom, jaké použijí strategie, vygenerovaný zisk si však nemohou
Teorie her a ekonomické rozhodování. 11. Aukce
 Teorie her a ekonomické rozhodování 11. Aukce 11. Aukce Příklady tržních mechanismů prodej s pevnou cenou cenové vyjednávání aukce Využití aukcí prodej uměleckých předmětů, nemovitostí, prodej květin,
Teorie her a ekonomické rozhodování 11. Aukce 11. Aukce Příklady tržních mechanismů prodej s pevnou cenou cenové vyjednávání aukce Využití aukcí prodej uměleckých předmětů, nemovitostí, prodej květin,
Stručný úvod do teorie her. Michal Bulant
 Stručný úvod do teorie her Michal Bulant Čím se budeme zabývat Alespoň 2 hráči (osoby, firmy, státy, biologické druhy apod.) Každý hráč má určitou množinu strategií, konkrétní situace (outcome) ve hře
Stručný úvod do teorie her Michal Bulant Čím se budeme zabývat Alespoň 2 hráči (osoby, firmy, státy, biologické druhy apod.) Každý hráč má určitou množinu strategií, konkrétní situace (outcome) ve hře
Přednáška #8. Základy mikroekonomie TEORIE HER
 Přednáška #8 Základy mikroekonomie TEORIE HER 14.11.2012 V minulé přednášce jsme si vysvětlili, co je to oligopolistické tržní uspořádání Oligopol jako tržní uspořádání stojí mezi monopolem a režimem dokonalé
Přednáška #8 Základy mikroekonomie TEORIE HER 14.11.2012 V minulé přednášce jsme si vysvětlili, co je to oligopolistické tržní uspořádání Oligopol jako tržní uspořádání stojí mezi monopolem a režimem dokonalé
{Q={1,2};S,T;u(s,t)} (3.3) Prorovnovážnéstrategie s,t vehřesnulovýmsoučtemmusíplatit:
 3 ANTAGONISTICKÉ HRY 3. ANTAGONISTICKÝ KONFLIKT Antagonistický konflikt je rozhodovací situace, v níž vystupují dva inteligentní rozhodovatelé, kteří se po volbě svých rozhodnutí rozdělí o pevnou částku,
3 ANTAGONISTICKÉ HRY 3. ANTAGONISTICKÝ KONFLIKT Antagonistický konflikt je rozhodovací situace, v níž vystupují dva inteligentní rozhodovatelé, kteří se po volbě svých rozhodnutí rozdělí o pevnou částku,
Koaliční hry. Kooperativní hra dvou hráčů
 Koaliční hry Obsah kapitoly. Koalice dvou hráčů 2. Koalice N hráčů Studijní cíle Cílem tohoto tematického bloku je získání základního přehledu o kooperativních hrách a jejich aplikovatelnosti. Student
Koaliční hry Obsah kapitoly. Koalice dvou hráčů 2. Koalice N hráčů Studijní cíle Cílem tohoto tematického bloku je získání základního přehledu o kooperativních hrách a jejich aplikovatelnosti. Student
VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE. Model tahové hry s finančními odměnami
 VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY Obor: Statistika a ekonometrie Název bakalářské práce Model tahové hry s finančními odměnami Autor: Vedoucí bakalářské práce: Rok: 009 Markéta
VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY Obor: Statistika a ekonometrie Název bakalářské práce Model tahové hry s finančními odměnami Autor: Vedoucí bakalářské práce: Rok: 009 Markéta
Teorie her. RNDr. Magdalena Hykšová, Ph.D. online prostředí, Operační program Praha Adaptabilita, registrační číslo CZ.2.17/3.1.00/31165.
 Teorie her RNDr. Magdalena Hykšová, Ph.D. Kurz vznikl v rámci projektu Rozvoj systému vzdělávacích příležitostí pro nadané žáky a studenty v přírodních vědách a matematice s využitím online prostředí,
Teorie her RNDr. Magdalena Hykšová, Ph.D. Kurz vznikl v rámci projektu Rozvoj systému vzdělávacích příležitostí pro nadané žáky a studenty v přírodních vědách a matematice s využitím online prostředí,
12 HRY S NEÚPLNOU INFORMACÍ
 12 HRY S NEÚPLNOU INFORMACÍ 543 Ne v každé hře mají všichni hráči úplné informace o výplatních funkcích ostatních. Ve skutečnosti je většina situací s informací neúplnou. Například: V aukcích zpravidla
12 HRY S NEÚPLNOU INFORMACÍ 543 Ne v každé hře mají všichni hráči úplné informace o výplatních funkcích ostatních. Ve skutečnosti je většina situací s informací neúplnou. Například: V aukcích zpravidla
 Mikroekonomie magisterský kurz - VŠFS Jiří Mihola, jiri.mihola@quick.cz, www.median-os.cz, 2010 Téma 1 Teorie her pro manažery Obsah 5.1 Teorie her jako součást mikroekonomie 5.2 Základní pojmy teorie
Mikroekonomie magisterský kurz - VŠFS Jiří Mihola, jiri.mihola@quick.cz, www.median-os.cz, 2010 Téma 1 Teorie her pro manažery Obsah 5.1 Teorie her jako součást mikroekonomie 5.2 Základní pojmy teorie
TEORIE HER
 TEORIE HER 15. 10. 2014 HRA HRA Definice Hra je činnost jednoho či více lidí, která nemusí mít konkrétní smysl, ale přitom má za cíl radost či relaxaci. HRA Definice Hra je činnost jednoho či více lidí,
TEORIE HER 15. 10. 2014 HRA HRA Definice Hra je činnost jednoho či více lidí, která nemusí mít konkrétní smysl, ale přitom má za cíl radost či relaxaci. HRA Definice Hra je činnost jednoho či více lidí,
Mezi firmami v oligopolu dochází ke strategickým interakcím. Při zkoumání strategických interakcí používáme teorii her.
 Teorie her a oligopol Varian: Mikroekonomie: moderní přístup, oddíly 26.1-9, 27.1-3 a 27.7-8 Varian: Intermediate Microeconomics, Sections 27.1-9, 28.1-3, 28.7-8 () 1 / 36 Obsah přednášky V této přednášce
Teorie her a oligopol Varian: Mikroekonomie: moderní přístup, oddíly 26.1-9, 27.1-3 a 27.7-8 Varian: Intermediate Microeconomics, Sections 27.1-9, 28.1-3, 28.7-8 () 1 / 36 Obsah přednášky V této přednášce
Dva kompletně řešené příklady
 Markl: Příloha 1: Dva kompletně řešené příklady /TEH_app1_2006/ Strana 1 Dva kompletně řešené příklady Úvod V této příloze uvedeme úplné a podrobné řešení dvou her počínaje jejich slovním neformálním popisem
Markl: Příloha 1: Dva kompletně řešené příklady /TEH_app1_2006/ Strana 1 Dva kompletně řešené příklady Úvod V této příloze uvedeme úplné a podrobné řešení dvou her počínaje jejich slovním neformálním popisem
Teorie her a ekonomické rozhodování. Úvodní informace Obsah kursu 1. Úvod do teorie her
 Teorie her a ekonomické Úvodní informace Obsah kursu 1. Úvod do teorie her Úvodní informace Mgr. Jana SEKNIČKOVÁ, Ph.D. Místnost: 433 NB Konzultace: Středa 6:30 7:30, 19:30 20:30 Čtvrtek E-mail: jana.seknickova@vse.cz
Teorie her a ekonomické Úvodní informace Obsah kursu 1. Úvod do teorie her Úvodní informace Mgr. Jana SEKNIČKOVÁ, Ph.D. Místnost: 433 NB Konzultace: Středa 6:30 7:30, 19:30 20:30 Čtvrtek E-mail: jana.seknickova@vse.cz
 Mikroekonomie magisterský kurz - VŠFS Jiří Mihola, jiri.mihola@quick.cz, www.median-os.cz, 2013 Téma 4 Teorie her pro manažery Obsah 5.7 Kooperativní hry 5.7.1 Kooperativní hra 2 hráčů 5.7.2 Kooperativní
Mikroekonomie magisterský kurz - VŠFS Jiří Mihola, jiri.mihola@quick.cz, www.median-os.cz, 2013 Téma 4 Teorie her pro manažery Obsah 5.7 Kooperativní hry 5.7.1 Kooperativní hra 2 hráčů 5.7.2 Kooperativní
Operační výzkum. Teorie her cv. Hra v normálním tvaru. Optimální strategie. Maticové hry.
 Operační výzkum Teorie her cv. Hra v normálním tvaru. Optimální strategie. Maticové hry. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty
Operační výzkum Teorie her cv. Hra v normálním tvaru. Optimální strategie. Maticové hry. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty
Teorie her. Kapitola 1. 1.1 Základní pojmy. 1.1.1 Základní pojmy
 Kapitola 1 Teorie her Dosud jsme se věnovali jednokriteriální či vícekriteriální optimalizaci, kde ve všech úlohách byly předem pevně dané podmínky a ty se nijak neměnily v závislosti na našem rozhodnutí.
Kapitola 1 Teorie her Dosud jsme se věnovali jednokriteriální či vícekriteriální optimalizaci, kde ve všech úlohách byly předem pevně dané podmínky a ty se nijak neměnily v závislosti na našem rozhodnutí.
TEORIE HER. Základní pojmy teorie her. buď racionální (usiluje o optimální výsledek hry) nebo indiferentní (výsledek hry je mu lhostejný)
 TEORIE HER V dosavadních přednáškách jsme probírali jedno či vícekriteriální optimalizaci, ale v těchto úlohách byly předem pevně dané podmínky a ty se nijak neměnily v závislosti na našem rozhodnutí Také
TEORIE HER V dosavadních přednáškách jsme probírali jedno či vícekriteriální optimalizaci, ale v těchto úlohách byly předem pevně dané podmínky a ty se nijak neměnily v závislosti na našem rozhodnutí Také
MATEMATICKÁ TEORIE ROZHODOVÁNÍ
 MATEMATICKÁ TEORIE ROZHODOVÁNÍ Podklady k soustředění č. 1 Řešení úloh 1. dílčí téma: Řešení úloh ve stavovém prostoru Počáteční období výzkumu v oblasti umělé inteligence (50. a 60. léta) bylo charakterizováno
MATEMATICKÁ TEORIE ROZHODOVÁNÍ Podklady k soustředění č. 1 Řešení úloh 1. dílčí téma: Řešení úloh ve stavovém prostoru Počáteční období výzkumu v oblasti umělé inteligence (50. a 60. léta) bylo charakterizováno
MODELY OLIGOPOLU COURNOTŮV MODEL, STACKELBERGŮV MODEL
 MODELY OLIGOPOLU COURNOTŮV MODEL, STACKELBERGŮV MODEL DOKONALÁ KONKURENCE Trh dokonalé konkurence je charakterizován velkým počtem prodávajících, kteří vyrábějí homogenní produkt a nemohou ovlivnit tržní
MODELY OLIGOPOLU COURNOTŮV MODEL, STACKELBERGŮV MODEL DOKONALÁ KONKURENCE Trh dokonalé konkurence je charakterizován velkým počtem prodávajících, kteří vyrábějí homogenní produkt a nemohou ovlivnit tržní
2 HRA V EXPLICITNÍM TVARU
 2 HRA V EXPLICITNÍM TVARU 59 Příklad 1 Hra Nim. Uvažujme jednoduchou hru, kdy dva hráči označme je čísly 1, 2 mají před sebou dvě hromádky, z nichž každá je tvořena dvěma fazolemi. Hráč 1 musí vzít z jedné
2 HRA V EXPLICITNÍM TVARU 59 Příklad 1 Hra Nim. Uvažujme jednoduchou hru, kdy dva hráči označme je čísly 1, 2 mají před sebou dvě hromádky, z nichž každá je tvořena dvěma fazolemi. Hráč 1 musí vzít z jedné
Dokažte Větu 2(Minimax) ze třetího dílu seriálu pro libovolnou hru s nulovým součtem, ve kterémákaždýhráčnavýběrprávězedvoustrategií.
 Teorie her º Ö ÐÓÚ Ö Ì ÖÑ Ò Ó Ð Ò º Ù Ò ¾¼½ ÐÓ ½º HráčIsitajněnapíšenapapírnějaképřirozenéčíslozrozmezíaž noznačmeho ivestejnou chvílisirovněžhráčiinapíšenapapírnějaképřirozenéčíslozrozmezíaž noznačmeho
Teorie her º Ö ÐÓÚ Ö Ì ÖÑ Ò Ó Ð Ò º Ù Ò ¾¼½ ÐÓ ½º HráčIsitajněnapíšenapapírnějaképřirozenéčíslozrozmezíaž noznačmeho ivestejnou chvílisirovněžhráčiinapíšenapapírnějaképřirozenéčíslozrozmezíaž noznačmeho
TEORIE HER - ÚVOD PŘEDNÁŠKA. OPTIMALIZACE A ROZHODOVÁNÍ V DOPRAVĚ část druhá Přednáška 2. Zuzana Bělinová
 PŘEDNÁŠKA 2 TEORIE HER - ÚVOD Teorie her matematická teorie rozhodování dvou racionálních hráčů, kteří jsou na sobě závislí Naznačuje, jak by se v takové situaci chovali racionální a informovaní hráči.
PŘEDNÁŠKA 2 TEORIE HER - ÚVOD Teorie her matematická teorie rozhodování dvou racionálních hráčů, kteří jsou na sobě závislí Naznačuje, jak by se v takové situaci chovali racionální a informovaní hráči.
Charakteristika oligopolu
 Oligopol Charakteristika oligopolu Oligopol v ekonomice převažuje - základní rysy: malý počet firem - činnost několika firem v odvětví vyráběný produkt může být homogenní (čistý oligopol) nebo heterogenní
Oligopol Charakteristika oligopolu Oligopol v ekonomice převažuje - základní rysy: malý počet firem - činnost několika firem v odvětví vyráběný produkt může být homogenní (čistý oligopol) nebo heterogenní
nutně znamenat ztrátu), ve které mají oba hráči dvě možnosti kooperovat nebo zradit.
 Vě zň ovo dilěma Vojtěch Ptáčník K tomuto tématu jsem se dostal úplnou náhodou. Měli jsme udělat projekt dle své vlastní volby. V té době jsem vůbec nevěděl, jaké téma si mám zvolit. Jednoho dne nám do
Vě zň ovo dilěma Vojtěch Ptáčník K tomuto tématu jsem se dostal úplnou náhodou. Měli jsme udělat projekt dle své vlastní volby. V té době jsem vůbec nevěděl, jaké téma si mám zvolit. Jednoho dne nám do
Úvod do teorie her. David Bartl, Lenka Ploháková
 Úvod do teorie her David Bartl, Lenka Ploháková Abstrakt Předložený text Úvod do teorie her pokrývá čtyři nejdůležitější, vybrané kapitoly z této oblasti. Nejprve je čtenář seznámen s předmětem studia
Úvod do teorie her David Bartl, Lenka Ploháková Abstrakt Předložený text Úvod do teorie her pokrývá čtyři nejdůležitější, vybrané kapitoly z této oblasti. Nejprve je čtenář seznámen s předmětem studia
Úvod do teorie her. druhé upravené vydání. Martin Dlouhý Petr Fiala
 Úvod do teorie her druhé upravené vydání Martin Dlouhý Petr Fiala 2009 2 Teorie her: analýza konfliktů a spolupráce Teorie her: analýza konfliktů a spolupráce 3 Obsah Předmluva... 5 1. Úvod do teorie her
Úvod do teorie her druhé upravené vydání Martin Dlouhý Petr Fiala 2009 2 Teorie her: analýza konfliktů a spolupráce Teorie her: analýza konfliktů a spolupráce 3 Obsah Předmluva... 5 1. Úvod do teorie her
MASARYKOVA UNIVERZITA ÚSTAV MATEMATIKY A STATISTIKY
 MSRYKOV UIVERZIT PŘÍRODOVĚDECKÁ FKULT ÚSTV MTEMTIKY STTISTIKY Bakalářská práce BRO 04 MREK VLŠÍ MSRYKOV UIVERZIT PŘÍRODOVĚDECKÁ FKULT ÚSTV MTEMTIKY STTISTIKY Hry s diskrétní pravděpodobností Bakalářská
MSRYKOV UIVERZIT PŘÍRODOVĚDECKÁ FKULT ÚSTV MTEMTIKY STTISTIKY Bakalářská práce BRO 04 MREK VLŠÍ MSRYKOV UIVERZIT PŘÍRODOVĚDECKÁ FKULT ÚSTV MTEMTIKY STTISTIKY Hry s diskrétní pravděpodobností Bakalářská
co je vězňovo dilema, jak funguje kartel a kdy je kartel stabilní.
 Kartel a asymetrické informace Varian: Mikroekonomie: moderní přístup, kapitoly 26.10-11, 27.4-6, 34 Varian: Intermediate Microeconomics, Chapters 27.10-11, 28.4-6, 37 () 1 / 42 Na této přednášce se dozvíte
Kartel a asymetrické informace Varian: Mikroekonomie: moderní přístup, kapitoly 26.10-11, 27.4-6, 34 Varian: Intermediate Microeconomics, Chapters 27.10-11, 28.4-6, 37 () 1 / 42 Na této přednášce se dozvíte
PŘÍKLADY DVOJMATICOVÉ HRY
 PŘÍKLADY DVOJMATICOVÉ HRY Příklad 1 SOUTĚŽ O ZAKÁZKY Investor chce vybudovat dva hotely Jeden nazveme Velký (zkratka V); ze získání zakázky na něj se očekává zisk ve výši 30 milionů Druhý nazveme Malý
PŘÍKLADY DVOJMATICOVÉ HRY Příklad 1 SOUTĚŽ O ZAKÁZKY Investor chce vybudovat dva hotely Jeden nazveme Velký (zkratka V); ze získání zakázky na něj se očekává zisk ve výši 30 milionů Druhý nazveme Malý
Usekne-li Honza 1 hlavu, narostou dva ocasy. Tento tah můžeme zakreslit následujícím způsobem: Usekne-li 2 hlavy, nic nenaroste.
 Řešení 2. série Řešení J-I-2-1 1. krok: Číslici 2 ve třetím řádku můžeme dostat jedině násobením 5 4 = 20, 5 5 = 25. Tedy na posledním místě v prvním řádku může být číslice 4 nebo 5. Odtud máme i dvě možnosti
Řešení 2. série Řešení J-I-2-1 1. krok: Číslici 2 ve třetím řádku můžeme dostat jedině násobením 5 4 = 20, 5 5 = 25. Tedy na posledním místě v prvním řádku může být číslice 4 nebo 5. Odtud máme i dvě možnosti
VĚZŇOVO DILEMA. Markéta Reichenbachová II.B. Gymnázium a Střední odborná škola Cihelní 410
 VĚZŇOVO DILEMA Markéta Reichenbachová II.B Gymnázium a Střední odborná škola Cihelní 410 Vězňovo dilema je typ hry s nenulovým součtem, ve které mají oba hráči dvě možnosti spolupracovat (cooperate) nebo
VĚZŇOVO DILEMA Markéta Reichenbachová II.B Gymnázium a Střední odborná škola Cihelní 410 Vězňovo dilema je typ hry s nenulovým součtem, ve které mají oba hráči dvě možnosti spolupracovat (cooperate) nebo
HRA V NORMA LNI M TVARU
 3 HRA V NORMÁLNÍM TVARU 91 Hra v normálním tvaru Definice 1. Necht je dána konečná neprázdná n-prvková množina Q = {1, 2,..., n}, n množin S 1, S 2,..., S n a n reálných funkcí u 1, u 2,..., u n definovaných
3 HRA V NORMÁLNÍM TVARU 91 Hra v normálním tvaru Definice 1. Necht je dána konečná neprázdná n-prvková množina Q = {1, 2,..., n}, n množin S 1, S 2,..., S n a n reálných funkcí u 1, u 2,..., u n definovaných
V této části se budeme věnovat nejjednoduššímu typu her, ve kterých rozhodováníprobíhávjednomkrokuakaždýhráčmáúplnouinformacijako
 Kapitola 1 Aplikace teorie her Teorie her není úplně nejvýstižnější pojmenování. Předmětem teorie her nejsou hry v obvyklém smyslu slova, hrané pro zábavu. Výstižnější název by asi byl teorie interaktivního
Kapitola 1 Aplikace teorie her Teorie her není úplně nejvýstižnější pojmenování. Předmětem teorie her nejsou hry v obvyklém smyslu slova, hrané pro zábavu. Výstižnější název by asi byl teorie interaktivního
Dalibor Pražák, KMA MFF UK
 Zajímavé příklady z teorie her Dalibor Pražák, KMA MFF UK 1. Úvod Z matematického hlediska je,,hra strategická či potenciálně konfliktní situace, kde zisk či ztráta každého jednotlivého aktéra (,,hráče
Zajímavé příklady z teorie her Dalibor Pražák, KMA MFF UK 1. Úvod Z matematického hlediska je,,hra strategická či potenciálně konfliktní situace, kde zisk či ztráta každého jednotlivého aktéra (,,hráče
Algoritmizace diskrétních. Ing. Michal Dorda, Ph.D.
 Algoritmizace diskrétních simulačních modelů Ing. Michal Dorda, Ph.D. 1 Úvodní poznámky Při programování simulačních modelů lze hlavní dílčí problémy shrnout do následujících bodů: 1) Zachycení statických
Algoritmizace diskrétních simulačních modelů Ing. Michal Dorda, Ph.D. 1 Úvodní poznámky Při programování simulačních modelů lze hlavní dílčí problémy shrnout do následujících bodů: 1) Zachycení statických
1. MATEMATICKÉ MODELY ROZHODOVACÍCH SITUACÍ
 Markl: Matematické modely rozhodovacích situací /nhry.doc/ Strana. MATEMATICKÉ MODELY ROZHODOVACÍCH SITUACÍ Popis obecné rozhodovací situace (rozhodovacího procesu) vyžaduje zadání následujících údajů:.
Markl: Matematické modely rozhodovacích situací /nhry.doc/ Strana. MATEMATICKÉ MODELY ROZHODOVACÍCH SITUACÍ Popis obecné rozhodovací situace (rozhodovacího procesu) vyžaduje zadání následujících údajů:.
Úvod Game designer Struktura hry Formální a dramatické elementy Dynamika her Konec. Úvod do game designu 1 / 37
 Počítačové hry Úvod do game designu 1 / 37 Obsah přednášky Role game designera Struktura hry Formální a dramatické elementy Dynamika herních systémů 2 / 37 Literatura a odkazy Chris Crawford. The Art of
Počítačové hry Úvod do game designu 1 / 37 Obsah přednášky Role game designera Struktura hry Formální a dramatické elementy Dynamika herních systémů 2 / 37 Literatura a odkazy Chris Crawford. The Art of
MATICOVÉ HRY MATICOVÝCH HER
 MATICOVÉ HRY FORMULACE, KONCEPCE ŘEŠENÍ, SMÍŠENÉ ROZŠÍŘENÍ MATICOVÝCH HER, ZÁKLADNÍ VĚTA MATICOVÝCH HER CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekoomická vědí disciplía, která se zabývá studiem
MATICOVÉ HRY FORMULACE, KONCEPCE ŘEŠENÍ, SMÍŠENÉ ROZŠÍŘENÍ MATICOVÝCH HER, ZÁKLADNÍ VĚTA MATICOVÝCH HER CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekoomická vědí disciplía, která se zabývá studiem
Contents. 1 Repeated games Úvod Definice opakované hry Folk theorems Jak lidé hrají v opakovaných hrách...
 Contents 1 Repeated games 2 1.1 Úvod.......................................... 2 1.2 Opakované vězňovo dilema............................... 4 1.3 Preference a očekávaný užitek v opakované hře....................
Contents 1 Repeated games 2 1.1 Úvod.......................................... 2 1.2 Opakované vězňovo dilema............................... 4 1.3 Preference a očekávaný užitek v opakované hře....................
13. cvičení z PSI ledna 2017
 cvičení z PSI - 7 ledna 07 Asymptotické pravděpodobnosti stavů Najděte asymptotické pravděpodobnosti stavů Markovova řetězce s maticí přechodu / / / 0 P / / 0 / 0 0 0 0 0 0 jestliže počáteční stav je Řešení:
cvičení z PSI - 7 ledna 07 Asymptotické pravděpodobnosti stavů Najděte asymptotické pravděpodobnosti stavů Markovova řetězce s maticí přechodu / / / 0 P / / 0 / 0 0 0 0 0 0 jestliže počáteční stav je Řešení:
Kajot Casino Ltd. Popis hry Joker 27
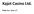 Joker 27 Joker 27 Popis a pravidla Joker 27 je hra se třemi kotouči. Zobrazený výsledek se skládá ze tří řad po třech symbolech (každý kotouč zobrazuje tři symboly). Náhledy Uvedený obrázek představuje
Joker 27 Joker 27 Popis a pravidla Joker 27 je hra se třemi kotouči. Zobrazený výsledek se skládá ze tří řad po třech symbolech (každý kotouč zobrazuje tři symboly). Náhledy Uvedený obrázek představuje
1 Odvození poptávkové křivky
 Odvození poptávkové křivky Optimalizační chování domácností (maximalizace užitku) vzhledem k rozpočtovému omezení. Nejprve odvodíme deterministický model, který potom rozšíříme o stochastické prvky. Odvozené
Odvození poptávkové křivky Optimalizační chování domácností (maximalizace užitku) vzhledem k rozpočtovému omezení. Nejprve odvodíme deterministický model, který potom rozšíříme o stochastické prvky. Odvozené
ŘECKÁ FINANČNÍ KRIZE Z POHLEDU TEORIE HER
 ŘECKÁ FINANČNÍ KRIZE Z POHLEDU TEORIE HER TOMÁŠ KOSIČKA Abstrakt Obsahem příspěvku je hodnocení řecké finanční krize z pohledu teorie her. V první části je popis historických událostí vedoucích k přijetí
ŘECKÁ FINANČNÍ KRIZE Z POHLEDU TEORIE HER TOMÁŠ KOSIČKA Abstrakt Obsahem příspěvku je hodnocení řecké finanční krize z pohledu teorie her. V první části je popis historických událostí vedoucích k přijetí
HERNÍ PLÁN GANGSTER WORLD APOLLO GAMES APOLLO SOFT k. s.
 HERNÍ PLÁN GANGSTER WORLD APOLLO GAMES HISTORIE REVIZÍ Datum Verze Popis změn Autor změn 12. 10. 2015 1.0 První naplnění dokumentu Milena Charvátová 27. 10. 2015 1.1 Oprava, doplněni Radoslav Hrčka 08.
HERNÍ PLÁN GANGSTER WORLD APOLLO GAMES HISTORIE REVIZÍ Datum Verze Popis změn Autor změn 12. 10. 2015 1.0 První naplnění dokumentu Milena Charvátová 27. 10. 2015 1.1 Oprava, doplněni Radoslav Hrčka 08.
Míčové hry - pravidla. Stolní tenis Badminton
 Míčové hry - pravidla Stolní tenis Badminton Pravidla stolního tenisu http://www.pingpongweb.cz/pingpong-na-olympijskych-hrach-12 Odehrání míčku Míček je odehráván výhradně pálkou, a to kteroukoliv její
Míčové hry - pravidla Stolní tenis Badminton Pravidla stolního tenisu http://www.pingpongweb.cz/pingpong-na-olympijskych-hrach-12 Odehrání míčku Míček je odehráván výhradně pálkou, a to kteroukoliv její
Dokumentace programu piskvorek
 Dokumentace programu piskvorek Zápočtového programu z Programování II PRM045 Ondřej Vostal 20. září 2011, Letní semestr, 2010/2011 1 Stručné zadání Napsat textovou hru piškvorky se soupeřem s umělou inteligencí.
Dokumentace programu piskvorek Zápočtového programu z Programování II PRM045 Ondřej Vostal 20. září 2011, Letní semestr, 2010/2011 1 Stručné zadání Napsat textovou hru piškvorky se soupeřem s umělou inteligencí.
Věk: 6+ Jak hrát. Goro-Goro Zvířátkové Shogi. Japonská Shogi Asociace / Shogi.cz
 Věk: 6+ Jak hrát Goro-Goro Zvířátkové Shogi Japonská Shogi Asociace / Shogi.cz Jak začít hrát Území Oblohy Postavte kameny tak, jak je vyznačeno na obrázku. Rozhodněte, kdo bude hrát první "Furigomou"
Věk: 6+ Jak hrát Goro-Goro Zvířátkové Shogi Japonská Shogi Asociace / Shogi.cz Jak začít hrát Území Oblohy Postavte kameny tak, jak je vyznačeno na obrázku. Rozhodněte, kdo bude hrát první "Furigomou"
Úvod do teorie her. podzim 2010 v.1.0
 Úvod do teorie her podzim 2010 v.1.0 1 Obsah 1 Matematická teorie her 3 1.1 Matematický model.................................. 3 1.2 Maticové hry...................................... 6 1.3 Bi maticové
Úvod do teorie her podzim 2010 v.1.0 1 Obsah 1 Matematická teorie her 3 1.1 Matematický model.................................. 3 1.2 Maticové hry...................................... 6 1.3 Bi maticové
SEMINÁRNÍ PRÁCE Z MATEMATIKY
 SEMINÁRNÍ PRÁCE Z MATEMATIKY PETROHRADSKÝ PARADOX TEREZA KIŠOVÁ 4.B 28.10.2016 MOTIVACE: K napsání této práce mě inspiroval název tématu. Když jsem si o petrohradském paradoxu zjistila nějaké informace
SEMINÁRNÍ PRÁCE Z MATEMATIKY PETROHRADSKÝ PARADOX TEREZA KIŠOVÁ 4.B 28.10.2016 MOTIVACE: K napsání této práce mě inspiroval název tématu. Když jsem si o petrohradském paradoxu zjistila nějaké informace
27-SEP-10. Black Cyan Magenta Yellow. CÍL HRY Jako první vytlačit šest. v tazích - své kuličky lze posunout. pole.
 Návod ke hře Hra 2 hráčů CÍL HRY Jako první vytlačit šest soupeřových kuliček z hracího pole. PŘÍPRAVA HRY: - hráči si připraví kuličky do startovních pozic, jak je uvedeno na obr. 1 - hráči se domluví,
Návod ke hře Hra 2 hráčů CÍL HRY Jako první vytlačit šest soupeřových kuliček z hracího pole. PŘÍPRAVA HRY: - hráči si připraví kuličky do startovních pozic, jak je uvedeno na obr. 1 - hráči se domluví,
Dijkstrův algoritmus
 Dijkstrův algoritmus Hledání nejkratší cesty v nezáporně hranově ohodnoceném grafu Necht je dán orientovaný graf G = (V, H) a funkce, která každé hraně h = (u, v) H přiřadí nezáporné reálné číslo označované
Dijkstrův algoritmus Hledání nejkratší cesty v nezáporně hranově ohodnoceném grafu Necht je dán orientovaný graf G = (V, H) a funkce, která každé hraně h = (u, v) H přiřadí nezáporné reálné číslo označované
Lineární algebra Operace s vektory a maticemi
 Lineární algebra Operace s vektory a maticemi Robert Mařík 26. září 2008 Obsah Operace s řádkovými vektory..................... 3 Operace se sloupcovými vektory................... 12 Matice..................................
Lineární algebra Operace s vektory a maticemi Robert Mařík 26. září 2008 Obsah Operace s řádkovými vektory..................... 3 Operace se sloupcovými vektory................... 12 Matice..................................
Představení počítačové hry Titan. Alena Králová
 Představení počítačové hry Titan Alena Králová Ekonomické hry aktivizující metody vyučování Různé druhy her Motivační x expoziční x fixační Postihují všeobecnou problematiku x dílčí Ručně hrané (deskové)
Představení počítačové hry Titan Alena Králová Ekonomické hry aktivizující metody vyučování Různé druhy her Motivační x expoziční x fixační Postihují všeobecnou problematiku x dílčí Ručně hrané (deskové)
Strategické hry v bezpečnostním inženýrství
 Strategické hry v bezpečnostním inženýrství Strategic games in security engineering Bc. Jan Cibulka Diplomová práce 2010 ABSTRAKT Diplomová práce je zaměřena na vyuţití teorie her a optimálního rozhodování
Strategické hry v bezpečnostním inženýrství Strategic games in security engineering Bc. Jan Cibulka Diplomová práce 2010 ABSTRAKT Diplomová práce je zaměřena na vyuţití teorie her a optimálního rozhodování
Teorie her. Nepřiznat se 1 rok; 1 rok 20 let; 0 let Lupič Dale Přiznat se 0 let; 20 let 10 let; 10 let
 Teorie her Teorie her je definována jako analýza matematických modelů konfliktu a spolupráce mezi inteligentními a racionálními subjekty. Teorie her tedy nabízí obecné matematické techniky využitelné pro
Teorie her Teorie her je definována jako analýza matematických modelů konfliktu a spolupráce mezi inteligentními a racionálními subjekty. Teorie her tedy nabízí obecné matematické techniky využitelné pro
Micro:bit lekce 3. - Konstrukci If Then a If Then Else najdete v kategorii Logic - Podmínky od If (např. porovnání < >= atd.) najdete taktéž v Logic
 Micro:bit lekce 3. Podmínky - Rozvětvení běhu programu podle splnění nějakých podmínek typu pravda / nepravda - splněno / nesplněno (výsledkem podmínky musí být vždy jen dvě možnosti) - Dva typy podmínek:
Micro:bit lekce 3. Podmínky - Rozvětvení běhu programu podle splnění nějakých podmínek typu pravda / nepravda - splněno / nesplněno (výsledkem podmínky musí být vždy jen dvě možnosti) - Dva typy podmínek:
1. dílčí téma: Úvod do teorie her a historie
 Cíl tematického celku: Cílem tohoto tematického celku je seznámit se se základy teorie her, její historií proniknout do matematických základů. Tento tematický celek je rozdělen do následujících dílčích
Cíl tematického celku: Cílem tohoto tematického celku je seznámit se se základy teorie her, její historií proniknout do matematických základů. Tento tematický celek je rozdělen do následujících dílčích
HERNÍ PLÁN A POPIS HRY
 Přijímané mince: 10, 20, 50 Kč Přijímané bankovky: 100, 200, 500, 1000, 2000, 5000 Kč Maximální sázka do hry: 50 Kč Maximální výhra z jedné hry: 50 000 Kč Výherní podíl: 93-97 % Výplata kreditu je možná
Přijímané mince: 10, 20, 50 Kč Přijímané bankovky: 100, 200, 500, 1000, 2000, 5000 Kč Maximální sázka do hry: 50 Kč Maximální výhra z jedné hry: 50 000 Kč Výherní podíl: 93-97 % Výplata kreditu je možná
Obsah herní sady: 40x dřevěný kámen hrací deska návod
 Obsah herní sady: 40x dřevěný kámen hrací deska návod www.shogi.cz info@shogi.cz /Shogicz Online návod: http://www.shogi.cz/zviratkanavod.pdf CZ Rychlá pravidla 1 Rozestavění kamenů 3 Hrací kameny a pohyb
Obsah herní sady: 40x dřevěný kámen hrací deska návod www.shogi.cz info@shogi.cz /Shogicz Online návod: http://www.shogi.cz/zviratkanavod.pdf CZ Rychlá pravidla 1 Rozestavění kamenů 3 Hrací kameny a pohyb
Oligopoly a teorie her
 Oligopoly a teorie her Co se dnes naučíte co je to oligopol jaké výsledky jsou v oligopolu možné proč je pro oligopolní firmy obtížné spolupracovat jak antimonopolní zákonodárství může prospět konkurenci
Oligopoly a teorie her Co se dnes naučíte co je to oligopol jaké výsledky jsou v oligopolu možné proč je pro oligopolní firmy obtížné spolupracovat jak antimonopolní zákonodárství může prospět konkurenci
OPAKOVANE HRY. JJ x II 197
 6 OPAKOVANE HRY JJ x II 197 VĚZŇOVO DILEMA Píší se třicátá léta dvacátého století. V tehdejším Sovětském svazu cestuje jistý dirigent vlakem do Moskvy, kde jej večer čeká koncert se symfonickým orchestrem.
6 OPAKOVANE HRY JJ x II 197 VĚZŇOVO DILEMA Píší se třicátá léta dvacátého století. V tehdejším Sovětském svazu cestuje jistý dirigent vlakem do Moskvy, kde jej večer čeká koncert se symfonickým orchestrem.
Universita Karlova v Praze Matematicko-fyzikální fakulta RIGORÓZNÍ PRÁCE. Mgr. Martin Chvoj. Pokročilé partie teorie her a jejich aplikace
 Universita Karlova v Praze Matematicko-fyzikální fakulta RIGORÓZNÍ PRÁCE Mgr. Martin Chvoj Pokročilé partie teorie her a jejich aplikace Katedra pravděpodobnosti a matematické statistiky Vedoucí rigorózní
Universita Karlova v Praze Matematicko-fyzikální fakulta RIGORÓZNÍ PRÁCE Mgr. Martin Chvoj Pokročilé partie teorie her a jejich aplikace Katedra pravděpodobnosti a matematické statistiky Vedoucí rigorózní
AUKCE S PLATBOU ZA PŘÍHOZ - MODEL A DATA. Vojtěch Kuna ESF MUNI
 AUKCE S PLATBOU ZA PŘÍHOZ - MODEL A DATA Vojtěch Kuna ESF MUNI 31.10. 2013 aukce server Bonus.cz datový soubor a jeho vlastnosti teoretický model ekonometrický model odhad teoretického modelu AUKCE S PLATBOU
AUKCE S PLATBOU ZA PŘÍHOZ - MODEL A DATA Vojtěch Kuna ESF MUNI 31.10. 2013 aukce server Bonus.cz datový soubor a jeho vlastnosti teoretický model ekonometrický model odhad teoretického modelu AUKCE S PLATBOU
CATE VLT VŠEOBECNÝ HERNÍ PLÁN - CZ VERZE. CAMPANULA spol.s r.o. 28. října 892/11 790 01 Jeseník Česká republika IČ: 561207 DIČ: CZ00561207
 CATE VLT CAMPANULA spol.s r.o. 28. října 892/11 790 01 Jeseník Česká republika IČ: 561207 DIČ: CZ00561207 Verze: 1.00.CZ 1 / 8 CAMPANULA spol.s r.o. Obsah Historie verzí... 3 Základní údaje... 4 Název
CATE VLT CAMPANULA spol.s r.o. 28. října 892/11 790 01 Jeseník Česká republika IČ: 561207 DIČ: CZ00561207 Verze: 1.00.CZ 1 / 8 CAMPANULA spol.s r.o. Obsah Historie verzí... 3 Základní údaje... 4 Název
strategická desková hra pro dva hráče
 strategická desková hra pro dva hráče Hrací potřeby: Sada 10 hracích kamenů pro každého hráče: 2 Pěšáci, 2 Rytíři, 1 Věž, 1 Zvěd, 1 Generál, 1 Katapult, 1 Lučištník, 1 Král 1 kámen se symbolem vlajky 4
strategická desková hra pro dva hráče Hrací potřeby: Sada 10 hracích kamenů pro každého hráče: 2 Pěšáci, 2 Rytíři, 1 Věž, 1 Zvěd, 1 Generál, 1 Katapult, 1 Lučištník, 1 Král 1 kámen se symbolem vlajky 4
4EK311 Operační výzkum. 5. Teorie grafů
 4EK311 Operační výzkum 5. Teorie grafů 5. Teorie grafů definice grafu Graf G = uspořádaná dvojice (V, E), kde V označuje množinu n uzlů u 1, u 2,, u n (u i, i = 1, 2,, n) a E označuje množinu hran h ij,
4EK311 Operační výzkum 5. Teorie grafů 5. Teorie grafů definice grafu Graf G = uspořádaná dvojice (V, E), kde V označuje množinu n uzlů u 1, u 2,, u n (u i, i = 1, 2,, n) a E označuje množinu hran h ij,
K vymezení hry Titanic. Jan Mertl
 K vymezení hry Titanic Jan Mertl Otázka Podstatou hry Titanic je (v případě, kdy vznikne situace, za které nemohou přežít všichni) dilema těch, kteří mají informace a kompetence: Maximalizovat počet zachráněných
K vymezení hry Titanic Jan Mertl Otázka Podstatou hry Titanic je (v případě, kdy vznikne situace, za které nemohou přežít všichni) dilema těch, kteří mají informace a kompetence: Maximalizovat počet zachráněných
NÁVOD. SPOJUJ SLŮVKA téma: DŮM. vzdělávací hra ve 2 variantách od 7 let
 NÁVOD SPOJUJ SLŮVKA téma: DŮM vzdělávací hra ve 2 variantách od 7 let Dílky s obrázky a anglickými slovíčky, které popisující obsah těchto obrázků jsou jednoduchou a atraktivní formou výuky pro nejmladší.
NÁVOD SPOJUJ SLŮVKA téma: DŮM vzdělávací hra ve 2 variantách od 7 let Dílky s obrázky a anglickými slovíčky, které popisující obsah těchto obrázků jsou jednoduchou a atraktivní formou výuky pro nejmladší.
Otázky ke státní závěrečné zkoušce
 Otázky ke státní závěrečné zkoušce obor Ekonometrie a operační výzkum a) Diskrétní modely, Simulace, Nelineární programování. b) Teorie rozhodování, Teorie her. c) Ekonometrie. Otázka č. 1 a) Úlohy konvexního
Otázky ke státní závěrečné zkoušce obor Ekonometrie a operační výzkum a) Diskrétní modely, Simulace, Nelineární programování. b) Teorie rozhodování, Teorie her. c) Ekonometrie. Otázka č. 1 a) Úlohy konvexního
PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO KATEDRA INFORMATIKY ROČNÍKOVÝ PROJEKT KLOKAN. Informatika, II. ročník
 PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO KATEDRA INFORMATIKY ROČNÍKOVÝ PROJEKT KLOKAN Květen 2010 Libor Valouch Informatika, II. ročník 1 Abstrakt Dokumentace ročníkového projektu Klokan. Jedná se o
PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO KATEDRA INFORMATIKY ROČNÍKOVÝ PROJEKT KLOKAN Květen 2010 Libor Valouch Informatika, II. ročník 1 Abstrakt Dokumentace ročníkového projektu Klokan. Jedná se o
Hodnocení ekonomické efektivnosti projektů Průměrný výnos z investice, doba návratnosti, ČSH, VVP
 Hodnocení ekonomické efektivnosti projektů Průměrný výnos z investice, doba návratnosti, ČSH, VVP Investice je charakterizována jako odložená spotřeba. Podnikové investice jsou ty statky, které nejsou
Hodnocení ekonomické efektivnosti projektů Průměrný výnos z investice, doba návratnosti, ČSH, VVP Investice je charakterizována jako odložená spotřeba. Podnikové investice jsou ty statky, které nejsou
UPPAAL příklady. Jiří Vyskočil 2010
 UPPAAL příklady Jiří Vyskočil 2010 Hra NIM Někdy se také označuje jako odebírání zápalek (existuje velké množství variant této hry). Hra dvou hráčů Na začátku si oba hráči stanoví počet zápalek, se kterými
UPPAAL příklady Jiří Vyskočil 2010 Hra NIM Někdy se také označuje jako odebírání zápalek (existuje velké množství variant této hry). Hra dvou hráčů Na začátku si oba hráči stanoví počet zápalek, se kterými
Dobble HRA PLNÁ DIVOKÉ ATMOSFÉRY A RYCHLÝCH REFLEXŮ 2 AŽ 8 HRÁČŮ DOPORUČENÝ VĚK 6 A VÍCE LET. Pravidla
 Dobble HRA PLNÁ DIVOKÉ ATMOSFÉRY A RYCHLÝCH REFLEXŮ 2 AŽ 8 HRÁČŮ DOPORUČENÝ VĚK 6 A VÍCE LET Pravidla Co je to Dobble? Dobble, to je více než 50 symbolů na 55 kartách. Na jedné je vždy 8 různých symbolů
Dobble HRA PLNÁ DIVOKÉ ATMOSFÉRY A RYCHLÝCH REFLEXŮ 2 AŽ 8 HRÁČŮ DOPORUČENÝ VĚK 6 A VÍCE LET Pravidla Co je to Dobble? Dobble, to je více než 50 symbolů na 55 kartách. Na jedné je vždy 8 různých symbolů
Czech SILESIA BC 2011-1.ROČNÍK. Propozice Turnaje
 Czech SILESIA BC 2011-1.ROČNÍK Propozice Turnaje 1.verze 02/2011 Pořadatel turnaje: Občanské sdružení BOWLING CZECH SILESIA Partner turnaje: Amatérská Bowlingová Liga ABL ( www.ablweb.cz ) Kontaktní osoby:
Czech SILESIA BC 2011-1.ROČNÍK Propozice Turnaje 1.verze 02/2011 Pořadatel turnaje: Občanské sdružení BOWLING CZECH SILESIA Partner turnaje: Amatérská Bowlingová Liga ABL ( www.ablweb.cz ) Kontaktní osoby:
