}w!"#$%&'()+,-./012345<ya
|
|
|
- Vít Bláha
- před 8 lety
- Počet zobrazení:
Transkript
1 MASARYKOVA UNIVERZITA FAKULTA INFORMATIKY }w!"#$%&'()+,-./012345<ya Knihovna pro genetické algoritmy v C#.NET DIPLOMOVÁ PRÁCE Martin Huněk Brno, jaro 2016
2 Prohlášení Prohlašuji, že tato diplomová práce je mým původním autorským dílem, které jsem vypracoval samostatně. Všechny zdroje, prameny a literaturu, které jsem při vypracování používal nebo z nich čerpal, v práci řádně cituji s uvedením úplného odkazu na příslušný zdroj. Vedoucí práce: RNDr. Martin Stehlík ii
3 Poděkování Rád bych poděkoval vedoucímu své práce RNDr. Martinu Stehlíkovi, za jeho pomoc při řešení této práce, společnosti SeaComp za podporu a Mgr. Tamaře Spoustové za korekturu práce. iii
4 Shrnutí Cílem této práce je vytvořit přehled a srovnání existujících knihoven pro genetické algoritmy v C#.NET a dle zjištěných nedostatků exisujících knihoven vytvořit knihovnu novou. iv
5 Klíčová slova genetické algoritmy, evoluční algoritmy, metaheuristiky, návrh knihovny v
6 Obsah 1 Úvod Cíle práce Struktura Evoluční algoritmy Principy evolučních algoritmů Evoluční strategie Evoluční programování Genetické programování Shrnutí Genetické algoritmy Populace Chromozom Schopnost učení Tvorba populace Vyhodnocovací funkce Selekce Křížení Mutace Nahrazení staré populace Ukončovací podmínka Typy genetických algoritmů Využití genetických algoritmů Příklady použití Klasifikační systémy Požadavky a existující řešení Vlastní rozšíření knihovny
7 5.1 Programování na grafických kartách Využití grafických karet pro genetické algoritmy Speciální operace Využití speciálních operací v kódu Null gene Návrh tříd Chromosomes Population Configuration GALConfig GALConfigClass GALVariableClass Fitness GenerationEndAction GenerationHandlers IGenerationHandler IParentSelector ICrossBreed IMutator Special operations Utils Výkon knihovny Porovnání s existujícími řešeními Test rychlosti Test problému obchodního cestujícího Práce s více vlákny Další možnosti optimalizace Závěr
8 1 Úvod Jako student na Fakultě informatiky jsem velmi často diskutoval se svými spolužáky o tématech, na kterých pracují během svých závěrečných prací, nebo na co se zaměřuje firma, kde pracují. Poslední dobou pozoruji, že se některá témata začínají objevovat velmi často. Dobrý příkladem je umělá inteligence a samoučící se algoritmy. I já jsem si nakonec toto zaměření vybral, nebot mě samotného tento přístup zajímal. Mým konkrétním oborem jsou genetické algoritmy. Jednouchý koncept převzatý z přírody, který dovoluje vytvářet velmi zajímavé věci. Mou oblíbenou ukázkou, díky které jsem nakonec zůstal u genetických algoritmů, je experiment z roku 1994, kdy se za pomocí genetických algoritmů sledovalo, jak se organismy učí pohybovat 1. Takové využití ovšem není úplně běžné a vzhledem k situaci, kdy jsem chtěl na diplomové práci spolupracovat s průmyslovým partnerem (společnost SeaComp 2 ), bylo třeba najít, zda by genetické algoritmy mohly mít uplatnění i pro něj. Hledání bylo krátké, nebot problém obchodního cestujícího a jemu podobné problémy jsou jedním z obvyklých problémů, řešených genetickými algoritmy. A průmyslový partner zabývající se programováním logistických systémů souhlasil. 1.1 Cíle práce Cílem této práce bylo navrhnout a následně implementovat knihovnu pro genetické algoritmy v jazyku C# a použit bude.net framework 4.0. Jazyk C# byl zvolen na základě kritérií a po konzultaci s průmyslovým partnerem. Knihovna má být ve formě souboru dll (dynamicky linkovaná knihovna) a s přiloženými zdrojovými kódy. Kód musí být komentovaný a jeho funkcionalita se bude testovat na schopnosti řešit problém obchodního cestujícího. Knihovna bude možné bez obtíží rozšířit o novou funkcionalitu a upravit pro téměř
9 1. ÚVOD libovolný problém. Součástí práce bude také jednouchý manuál s ukázkou na konkrétním příkladu. Prozkoumám také možnosti, jak, a pokud vůbec, lze efektivně využit výpočtu na grafické kartě pro genetické algoritmy. V textové části práce bylo mým úkolem popsat genetické algoritmy, jejich možnosti a využití a následně porovnat vytvořené řešení s již existujícími řešeními. 1.2 Struktura Práci začínám úvodem do evolučních algoritmů, do kterých genetické algoritmy patří. Popisuji základní společné principy a porovnávám jednotlivé používané principy. Druhá kapitola Genetické programování se zaměřuje výhradně na genetické algoritmy, kde podrobněji popisuji jednotlivé části algoritmu včetně typických přístupů a zmiňuji, které z nich jsem se rozhodl implementovat. Těmito kapitolami pokrývám převážnou část teorie o genetických algoritmech. V následující kapitole, nazývané Požadavky a existující řešení, podrobně rozebírám, jaké požadavky byly kladeny na knihovnu a proč jsem nezvolil existující řešení a rozhodl jsem se implementovat nové. Další dvě kapitoly pojednávají o projektové části práce, konkrétně o mých vlastních rozšířeních, které nebývají součástí standardních genetických algoritmů, a o mnou vytvořené knihovně. Součástí je samozřejmě i UML návrh a detailnější popis jednotlivých částí knihovny. Předposlední kapitola, věnující se výkonu aplikace, je stěžejní pro rozhodnutí, zda jsem naplnil cíle dané práce, nebot v ní porovnávám existující řešení se mnou vytvořenou knihovnou. Také obsahuje několik dílčích testů výkonů některých částí knihovny. Tyto testu ukazují, které přístupy je třeba zvolit na daný problém, jestli chceme být maximálně efektivní při hledání řešení pomocí této knihovny. V závěru pak hodnotím výsledky a popisuji možnosti rozšíření této knihovny. 4
10 2 Evoluční algoritmy Při řešení problémů se lidé velmi často inspirovali v přírodě, odkud přejímali dobře fungující a osvědčené systémy. V oblasti umělé inteligence (kam bych genetické algoritmy zařadil), jsou podle mého názoru nejznámějšími inspiračními zdroji lidský mozek (neuronové sítě) a evoluce (evoluční algoritmy). Evoluční algoritmy jsou algoritmy metaheuristicky pracující s populacemi (Populationbased metaheuristics). Metaheuristika je termín nejčastěji užívaný jako hlavní podobor stochastické optimalizace. Stochastická optimalizace je obecná třída algoritmů, které využívají určitou formu náhody k nalezení optimálního (či téměř optimálního) řešení pro těžké problémy. Metaheuristiky jsou nejobecnější z těchto algoritmů a jsou použitelné k řešení velkého množství problémů [18]. Mezi metaheuristiky také patří například simulované žíhání, inteligence hejna a mnohé další. Tato práce se ale věnuje genetickým algoritmům jakožto podkategorie evolučních algoritmů. 2.1 Principy evolučních algoritmů Evoluční algoritmus je postup řešení problémů, který se inspiroval evolučními mechanismy fungujícími v přírodě. Pro daný problém se vytvoří několik potenciálních řešení (například náhodným vygenerováním), kterým se říká populace. Potenciální řešení (jedinec v populaci) je reprezentováno sadou dat (genů), která se používá pro tvorbu potomků. V populaci existují lepší a horší řešení, což je důsledek toho, jak se tato řešení vytvořila. Z populace se vyberou (selekce) ta lepší řešení (většinou na principu čím lepší řešení, tím větší šance se stát rodičem nové generace), která se zkombinují (křížení) mezi sebou a vzniknou tak řešení nová. Během křížení se může přidat trochu náhody (mutace), která dává řešením větší 5
11 2. EVOLUČNÍ ALGORITMY rozmanitost a umožňuje překonávat lokální optima. Selekci, křížení a mutaci poté opakujeme tak dlouho, jak uznáme za vhodné pro konkrétní problém. Tento systém je velmi podobný tomu, jak funguje přirozený výběr. Také máme populaci, která obsahuje jedince (jedno možné řešení) s různými geny. Geny jedinců se při rozmnožování kříží a vzniká tak jedinec nový (s malou šancí mutace). Přirozený výběr zařizuje, že úspěšnější jedinec má větší šanci mít potomky, než méně úspěšný (selekce). V části nazývané Genetické algoritmy (str. 8) rozebírám tyto mechanismy podrobněji. Mezi evoluční algoritmy patří: genetické algoritmy, evoluční programování, genetické programování, evoluční strategie a některé zdroje [14] sem řadí i klasifikační systémy. Klasifikační systémy jsem osobně raději zařadil mezi možnosti využití genetických algoritmů než jako samostatný přístup k evolučním algoritmům. Existují detaily, ve kterých se jednotlivé přístupy liší a které zmíním v následujících podkapitolách Evoluční strategie Původní verzi algoritmu navrhli v roce 1964 Schwefel a Rechenberg. Stalo se tak na Technické univerzitě v Berlíně [9]. Základní princip je podobný náhodnému prohledávání, ale hlavní rozdíl je ten, že každý krok v hledání je mutací předchozího kroku. Pokud například hledáme maximální hodnotu funkce, tak každý krok kontrolujeme, zda bod X je maximem, kde bod X je mutací bodu Y, který jsme kontrolovali v předchozím kroku. Vznik bodu X mutací funguje dle následující rovnice X = Y + U, kde U N(0, σ 2 ) pokud X je vektor, tak U = (U 1, U 2..., U n ), kde každé U X = N(0, σ 2 ), tedy mutace za využití Gaussova normálního rozložení. Evoluční strategie také umožňuje postupné vyvíjení parametrů stejně jako dané populace. Umožňuje například používání větší směrodatně odchylky σ při úvodních mutacích a postupem času její následné zmenšování, jak se algoritmus dostává blíže ke 6
12 2. EVOLUČNÍ ALGORITMY svému cíli. Původní návrh algoritmu počítal pouze s jedním iniciálním bodem (vektorem) a jedním potomkem. Tato idea byla následně opuštěna a byly vytvořeny dvě verze evoluční strategie s větší populací. 1. ES(M+L) generace potomků M je tvořena těmi nejlepšími z M+L jedinců (tj. jak z potomků, tak z rodičů). Používá se tedy elitismus (nejlepší jedinec přežije do další generace) 2. ES(M,L) generace potomků M je vytvořena z generace rodičů L a potomci kompletně nahradí rodiče. Koncept popsaný v bodu A se nazývá elitismus a můžeme jej najít v ostatních evolučních algoritmech. Oproti genetickým algoritmům se evoluční strategie liší hlavně absencí křížení a také tím, že mutace se odvíjí od Gaussova normálního rozdělení. Absenci křížení vidím jako velkou nevýhodu v případě toho, že existuje v daném problému lokální optimum, které dokáže (pokud nebude nastavená dostatečně velká směrodatná odchylka) řešení zastavit právě v lokálním optimu. Na druhou stranu je tento způsob bez použití křížení rychlejší, resp. jedna generace při stejně velké populaci se spočítá rychleji díky absenci křížení. Existují i rozšíření evolučních strategií, které využívají křížení, ale na úkor pamět ové a procesorové náročnosti výpočtu Evoluční programování Evoluční programování bylo vytvořeno v roce 1960 Lawrencem J. Fogelem a je velmi podobné evolučním strategiím. Také obsahuje mutaci podle Gaussova normálního rozdělení, dovoluje změny ve směrodatné odchylce a také nepoužívá křížení (zde striktně nepoužívá na rozdíl od evolučních strategií). 7
13 2. EVOLUČNÍ ALGORITMY Oproti evolučním strategiím se také liší v tom, že pro výběr rodičů (selekci) používá typicky stochastický výběr, zatímco evoluční strategie standardně využívá deterministické řešení a vybírá vždy ty lepší na úkor horších. Čím se liší oproti genetickým algoritmům, je mnohem volnější možnost reprezentace, zatímco genetické algoritmy využívají určitou formu genomu (sady genů, například čísel, nesoucí informace), evoluční programování, které nepracuje s křížením, může pracovat například s neuronovou sítí jako takovou. Další rozdíly oproti genetickým algoritmům jsou stejné, jako měly evoluční strategie (použití Gaussova normálního rozdělení při mutaci) [11] Genetické programování Genetické programování je nejmladší ze čtveřice evoluční algoritmů. Bylo publikováno v roce 1992 panem Johnem R. Kozou. Typickým znakem genetického programování je využití stromů a grafů jako reprezentace chromozomů [12]. Pomocí stromy chromosomy často reprezentují matematické výrazy či například zdrojové kódy programu. Genetické programování se dá využít například k nalezení nejkratšího programu, který plní určitou funkcionalitu. Díky této reprezentaci se také používá jiný systém křížení a mutace (vždy se vybere jedna z možností). Při obou těchto postupech se nahrazuje určitá část podstromu (či podgrafu) bud úplně nově vytvořenou, nebo převzatou z druhého rodiče (viz obrázek 2.1). 8
14 2. EVOLUČNÍ ALGORITMY Obrázek 2.1: Genetické programování - křížení Na obrázku je vidět, jak funguje křížení, pokud stromy reprezentují matematické vzorce. Ze vzorců cos(x) + (1.5/10) a X (8.3 * ( )) vznikne potomek cos(x) + (8.3 * ( )). Křížení a mutace je díky tomu jednoduchá a rychlá, ovšem za cenu neustále rostoucího stromu, který se stává nejkritičtějším místem. Je třeba hloubku stromu hlídat a v případě potřeby strom vyrovnávat (balanced tree). Také se uvádí, že genetické programování potřebuje populaci o velikosti tisíců jedinců, což je třeba oproti genetickým algoritmům s několika desítkami jedinců značný rozdíl [3, str. 204] Shrnutí Z předchozího textu je jasné, že evoluční algoritmy jsou si navzájem velice podobné, a zdálo by se, že navzájem plně nahraditelné. Opak je pravdou, právě ty malé detaily mohou být rozhodující v určování, který z přístupů bude použit. Jinou možností by bylo vzít jeden přístup a ten rozšířit o techniky z jiného přístupu. Například pro genetické algoritmy není problém doimplementovat mutaci pomocí Gaussova normálního rozdělení, nebo například úplně vypustit křížení. Lze zajít 9
15 2. EVOLUČNÍ ALGORITMY až tak daleko, že je možno stromovou/grafovou reprezentaci genů (binární strom se dá reprezentovat jako pole, se kterým genetické algoritmy fungují standardně), a ty následně křížit a mutovat za použití vhodně upravených operací. Závěrem bych chtěl ukázat dobře zpracovanou tabulku rozdílů (základních/původních verzí) mezi jednotlivými přístupy [3, str ]. Obrázek 2.2: Přehled jednotlivých přístupů 10
16 3 Genetické algoritmy Genetické algoritmy byly vymyšleny v roce 1960 Johnem Hollandem na na Michiganské univerzitě. Několik dalších let byly Hollandem a jeho studenty a kolegy dále rozvíjeny [13]. Genetické algoritmy se objevují ve stejné době jako evoluční strategie a evoluční programování. Na rozdíl od nich jsou genetické algoritmy studovány za účelem pochopeni principu evoluce v přírodě a za účelem přenesení těchto konceptů do informačních technologií, a to ne pouze za účelem řešení jednoho konkrétního problému, či sady podobných problémů. Využití genetických algoritmů se může v některých částech značně lišit od původního konceptu J. Hollanda, ale základní kostra zůstává vždy stejná, jak byla v roce 1975 prezentována v knize Adaptation in Natural and Artificial Systems [5] a rozvíjeno v An introduction to Genetic Algorithm [13]. Základní prvky (někdy nazývané také operátory) jsou: 1. Populace chromozomů 2. Selekce (výběr rodičů) na základně vyhodnocovací (fitness) funkce 3. Křížení (crossover) 4. Mutace Prvky jsou již několikrát zmíněny na začátku kapitoly, kde jsem se věnoval ostatním evolučním algoritmům. Tam se také nachází základní popis běhu evolučních algoritmů, který v podání genetických algoritmů vypadá následovně: 11
17 3. GENETICKÉ ALGORITMY Obrázek 3.1: Životní cyklus genetických algoritmů Jak si můžete všimnout, až na populaci chromozomů, jsou prvky (operátory) obsaženy jako oddělené kroky běhu algoritmu. Populace chromozomů je obsažena ve všech bodech, nebot to jsou data, se kterými algoritmus pracuje. Nyní rozeberu jednotlivé části genetických algoritmů do větších detailů, včetně používaných principů v jednotlivých částech. 3.1 Populace Použijeme-li genetický algoritmus na řešení problému (více v podkapitole Využití genetických algoritmů), tak populace chromozomů je vlastně sada možných řešení. Jeden chromozom je jedno potenciální řešení. Pokud bychom řešili například maximální hodnotu funkce o n proměnných, tak jeden chromozom by bylo pole (n-tice) čísel sloužících jako vstup funkce. 12
18 3. GENETICKÉ ALGORITMY Chromozom Chromozom je ekvivalent jednoho jedince v populaci, který zpravidla obsahuje n-tici genů. Gen je datová položka/nosič části informace-řešení. V původním návrhu genetických algoritmů byl chromozom n-tice bitů (a tedy gen byl datová položka bit nabývající hodnoty 0,1). Důvodem byla efektivnost, kdy se díky n-tici bitů neplýtvalo délkou a bylo možno vyjádřit libovolná data. Z toho se odvíjel i původní návrh mutace, který byl jen změna hodnoty bitu (bit flipping). Dnes lze mít v n-tici jakoukoliv datovou strukturu a je možné si tedy vybrat, jaká reprezentace dat (genů) se nejlépe hodí k danému problému, a tedy jakým způsobem chceme, aby se chovalo křížení a mutace. Čím komplikovanější datová struktura, tím komplikovanější musí být mutace, ale na druhou stranu zase umožňuje lepší křížení. Kdybychom se například rozhodli, že chceme použít genetické algoritmy pro sledování evoluce zvířat (jedno zvíře jeden chromozom), kdy každé zvíře budeme reprezentovat sekvencí DNA (tedy hodnotami A, T, G, C ). Každá vlastnost zvířete je reprezentována různě velkou sekvencí. Taková reprezentace je blízká realitě, ale pro mutaci a křížení to znamená potenciální komplikace. Mutace tady znamená, že jeden gen v chromozomu změní svou hodnotu. Implementace je jednoduchá, problém nastává s následním vyhodnocením, jaké následky má jedna změna hodnoty genu na výsledný stav. Situace, kdy bychom měli místo několika proměnných pouze jednu, by znamenala, že mutace může nastavit hodnoty z široké škály možností (je rozdíl, když musíme deseti proměnným nastavit hodnotu 1 nebo 0, nebo jedné hodnotě nastavit hodnotu 0 až 20). Pro křížení může nastat větší problém, a tím je rozbití sekvencí. Pokud by náš chromozom obsahoval například tři sekvence (inteligence, síla, rychlost), každá vyjádřená několika geny, a my se snažili najít maximálně efektivní kombinaci těchto tří vlastností, může se stát, že v křížení se vezme polovina genů z první vlastnosti a druhá polovina genu z první vlastnosti přijde od druhého rodiče, zatímco v přírodě se standardně dědí celé sekvence a takovéto změny patří pod mutaci, nikoliv křížení. Řešením by bylo znát 13
19 3. GENETICKÉ ALGORITMY délky sekvencí a podle toho řídit křížení, ale to vyžaduje logiku navíc oproti stavu, kdy jedna proměnná znamená jednu vlastnost. Proto je třeba vždy vhodně zvolit reprezentaci chromozomů vzhledem k použitým operátorům mutace a křížení(případně naopak) Schopnost učení Schopnost učení je důležitá vlastnost živých organismů, která jim pomáhá přežít. Naučit se učit je mnohem rychlejší proces, jak dosáhnout nějaké dovednosti, než čekat na evoluci, až danou vlastnost přinese do genetické výbavy. Implementace dovednosti učení v genetických algoritmech není obtížná. Pokud bychom například měli geny s hodnotami 0 (nemá danou vlastnost) a 1 (má danou vlastnost), stačí gen rozšířit o hodnotu 2 (vlastnost nemá, ale je schopen se naučit). V takovém případě ovšem na reprezentaci jednoho genu nebude stačit bit, ale bity alespoň dva. Obecně stačí přidat do genu další možnost navíc, která značí, že daná hodnota se dokáže přizpůsobit situaci (fitness funkci). Takové přizpůsobení nemusí být dokonalé, ale třeba i částečné, nebo dokonce úplně náhodné. Náhodná změna může být použita například v situaci, kdy gen modeluje chování v nějaké situaci, a pokud gen značí, že situace je neznámá, tak jedinec zkusí úplně náhodné chování. Je nutné si také uvědomit důsledek implementace takové změny a přizpůsobit tomu fitness funkce. Fitness funkce si vyžádá změnu v tom, že již nehodnotí jen dva stavy, ale i stav naučil se danou dovednost. Je také vhodné ohodnotit naučenou dovednost jako slabší než dovednost obsaženou v genech, nebot potom by to vedlo k populaci, kde by mohli převládat tyto geny (bez konkrétní hodnoty) Tvorba populace Genetické algoritmy jsou založené na práci s potenciálními řešeními a hledáním lepších řešeních na základě předchozích pokusů. Vytvoření počáteční populace je tedy důleži- 14
20 3. GENETICKÉ ALGORITMY tým krokem ke splnění tohoto cíle. Základním požadavkem je různorodost počáteční populace, protože ze stejnorodé populace se pomocí křížení nedá dosáhnout žádných nových výsledků a muselo by se spoléhat pouze na mutaci. Existuje několik způsobů, jak vytvořit úvodní populac [3, str.193]: Základní prvky (někdy nazývané také operátory) jsou: 1. Náhodné generování (pseudo, kvazi) je nejjednodušší možností, kdy pomocí opakovaného volání náhodného generování vytvoříme postupně celou populaci. Vysvětlení rozdílu mezi kvazi- a pseudo- náhodného generování je dobře vysvětleno zde 3 a stejné pravidla jako pro generování čísel platí také pro generování populace. 2. Sekvenční diverzifikace generuje populaci postupně a snaží se o maximální rozdílnost od všech předchozích vygenerovaných hodnot, např. Simple sequential inhibition process 3. Paralelní diverzifikace je generování hodnot nezávisle paralelně s cílem o maximální rozdílnost hodnot, např. Uniform sampling using Latin hypercube sampling, Diversified initial population of permutations 4. Heuristika generování pomocí heuristických přístupů (například lokálního prohledávání), velmi závislé na konkrétním problému a potencionálně nízká diverzifikace 194].. V níže uvedené tabulce lze vidět základní srovnání jednotlivých přístupů [3, str
21 3. GENETICKÉ ALGORITMY Obrázek 3.2: Tvorba populace Vyhodnocovací funkce Pokud se potřebujeme rozhodovat, musíme být schopni rozlišit správné řešení od špatného a k tomu slouží vyhodnocovací funkce (dále v textu zmiňovaná jako fitness funkce nebo pouze fitness kvůli konzistenci se zdroji). Výstup z fitness funkce je nadále používán pro selekci a výběr rodičů, kde se standardně vybírají ti lepší jedinci na úkor slabších. Pro některé případy pak není potřeba, aby fitness funkce byla schopna rozlišit ideální řešení, a stačí pouze rozlišit, zda jedno řešení je lepší nebo horší (a už ne třeba o kolik). To platí například o selekcích Tournament selection, Rank Based Selection, které jsem probral v další podkapitole Selekce. Pro jiné to ovšem neplatí a je třeba konkrétních hodnot (v původním návrhu hodnoty , kde 1.0 znamenalo ideální řešení). Problémem ovšem je, že ne vždy je možné pracovat s dobrou fitness funkcí, at už z důvodu vysoké výpočetní náročnosti, nebo neexistence přesného matematického modelu, který daný problém popisuje. V takových situacích je možné zkusit hodnotu fitness funkcí různě aproximovat (použít fitness funkci nepřesnou, ale dostatečně přesnou/rychlou pro dané potřeby) či jen přibližně určit například s pomocí fitness funkce rodičů (za předpokladu, že takové informace jsou uloženy). Je dobré si také uvědomit, že fitness funkce nemusí být nutně číselná. Například pro výše uvedený příklad s geny je například třeba převést pole znaků na hodnotu fitness 16
22 3. GENETICKÉ ALGORITMY funkce Selekce Výběr chromozomů (jedinců) z populace s nejlepšími vlastnosti proto, aby předal své geny další generaci, se nazývá selekce. V genetických algoritmech najdeme nejčastěji dva základní směry: 1. Fitness proportionate selection fungující na principu čím větší hodnota fitness pro daného jedince v populaci, tím větší šance, že bude vybrán. Například pokud má celá populace součet fitness funkcí 100 a pokud má jedinec má hodnotu fitness funkce 23, tak má šanci 23/100. Potenciálním problémem tohoto přístupu je situace, kdy jeden jedinec má oproti zbylé populaci vysokou fitness a jeho šance, že bude vybrán, je oproti zbytku velmi vysoká. Tento přístup také neřeší pořadí, nebot i druhý v pořadí může mít velmi mizivou šanci být vybrán, protože fitness všech ostatních kromě jednoho chromozomu je velmi nízká. Tyto problémy mohou dlouhodobě vést k málo různorodé populaci. Nejznámější implementace Fitness proportionate selection jsou Roullete-wheel selection a Stochastic universal sampling (částečně řeší problém s jedním chromozomem s příliš velkou fitness) 2. Ordinal selection tento princip funguje na seřazení celé populace podle hodnoty její fitness funkce a následnému vybírání podle pořadí, nikoliv absolutní hodnoty fitness. Zde tedy nerozlišujeme, zda rozdíl mezi prvním a druhým místem byl velmi malý, a jsou to tedy řešení skoro stejně dobrá, nebo naopak propastná, a je tedy k tomu potřeba přihlédnout více. Nejznámější implementací jsou Tournament selection a Rank-Based selection. Ve své práci jsem se rozhodl implementovat Roullete-wheel selection, Stochastic universal sampling, Trounament selection a Rank-Based Selection. V části pro průmyslo- 17
23 3. GENETICKÉ ALGORITMY vého partnera jsem některé z těchto přístupů rozšířil o jejich výpočetně efektivnější varianty Křížení Je operace, která vezme dva či více chromozomů (rodičů) na vstupu, zkombinuje jejich geny a vytvoří potomstvo (1 n potomků). Křížení je hlavní způsob genetických algoritmů, jak najít řešení (mutace slouží hlavně k řešení lokálních optim). Při volbě vhodného křížení je třeba si uvědomit, zda není řešením hledání vhodné permutace genů, a tedy záleží na pořadí a sada genu je pevně daná, například problém obchodního cestujícího. V takovém případě je potom nutné zvolit odpovídající křížení. Představované přístupy jsou popsány pro situace, kdy pracujeme se dvěma rodiči, i když u většiny z nich není problém rozšířit i pro situaci, kdy rodičů může být více. Standardní implementace také počítá, že všechny chromozomy mají stejnou délku genů (více v části Vlastní rozšíření knihovny str. 36). Mezi typické představitele patří: 1. K-point crossover v chromozomu najdeme k pozic (navzájem různých), kde budeme měnit chromozom, ze kterého čerpáme geny. Nejjednodušší případ je pro One-point crossover, kdy zvolíme v chromozomu pozici, do které potomek dědí geny z prvního rodiče a od které už dostane geny z druhého rodiče (druhý potomek funguje na stejném principu, jen začíná brát geny z druhého rodiče). 2. Uniform crossover pro každý gen potomka se vypočítá pravděpodobnost (nejčastěji 1 ), s jakou bude brát gen od prvního z rodičů Order-based crossover křížení, které pracuje s permutacemi (řešení obchodního cestujícího), funguje na principu, že se označí část genu (jeden nebo více bloků) z prvního rodiče a ty se umístí do prvního potomka, zbylá prázdná pole se postupně doplňují z druhého rodiče, jak jdou postupně v pořadí. Ve své práci jsem se rozhodl implementovat hlavně mutace pracující s permutací 18
24 3. GENETICKÉ ALGORITMY prvků, které jsou více univerzální, než mutace používané pro změnění hodnoty genu, které jsou více závislé na konkrétním typu problému. V práci jsou implementované tyto přístupy: K-point crossover, Uniform crossover, Order-based crossover (dvě varianty) Mutace Při křížení se může stát, že oba rodiče mají v konkrétní pozici gen se stejnou hodnotou, v takovém případě se pomocí křížení nedostaneme k nové hodnotě. Nebo naopak problém lokálního optima, se kterým se musí genetické algoritmy potýkat. To jsou případy, kdy je mutace důležitou součástí genetických algoritmů. Mutace přichází na řadu pro každého nově vytvořeného potomka a s určitou šancí provede malou změnu v hodnotách genů. Je nutné si uvědomit, že mutace silně závisí na reprezentaci dat a zároveň musí splňovat některá základní pravidla: 1. Mutace nesmí vytvářet nevalidní zadání. Například pro geny obsahující znaky abecedy platí, že nesmí mutací vzniknout číslo. od které už dostane geny z druhého rodiče (druhý potomek funguje na stejném principu, jen začíná brát geny z druhého rodiče). 2. Mutace musí mít šanci dosáhnout každé hodnoty v dané množině. Pokud umím mutovat jen na číslo 1 až 10 a geny jsou v rozmezí 1 až 100, tak mutace neplní svůj účel. 3. Mutace slouží pouze k malým změnám hodnoty jednoho genu, a tedy by teoreticky neměla sloužit k vytváření sad nových řešení (k tomu slouží primárně křížení). rodiče, jak jdou postupně v pořadí. V původním návrhu byla mutace jednoduchou záležitostí. S určitou pravděpodobností daný gen změnil hodnotu z 0 na 1 či naopak. Pro geny, které jsou reprezentovány složitějšími hodnotami, nejde použít jednoduchá inverze. 19
25 3. GENETICKÉ ALGORITMY Pokud se pracuje s geny, které mohou nabývat diskrétních hodnot (číslo, znak, slovo) je možné udělat změnu na novou hodnotu za předpokladu, že známe daný rozsah. Tuto změnu je možné provést úplně náhodně nebo například pomocí normálního rozdělení, kdy budeme mít větší šanci, že hodnota bude blízko hodnotě původní. Pokud se pracuje se složitějšími strukturami, jako je například strom, je možné nejen měnit hodnoty v kořenech, ale i strom rozšiřovat či zmenšovat. Další možností jsou mutace, které se mohou přizpůsobovat, například si pamatovat úspěšnost takové mutace (hodnota fitness před a po mutaci), brát informace ohledně konkrétní mutace z externího zdroje (databáze, pozorování, internet). Implementované přístupy jsou: Insert mutation, Inversion mutation, Scramble mutation, Swap mutation, doplněné o jednoduchou mutaci nad celými čísly (změna hodnoty v intervalu, s maximálním možným posunem hodnoty) Nahrazení staré populace Pomocí křížení a mutace vzniká nová generace chromozomů, které mají nahradit ty staré. Nahrazení nových chromozomů je logickým krokem, nebot z aktuální populace jsme vybírali ty lepší (pomocí fitness) a pomocí jejich kombinací jsme se snažili dostat ještě lepší potomky. Může se stát, že část nové generace nepřináší nic nového, nebo dokonce naopak je v něčem horší. Různé přístupy se takovým situacím snaží předejít. Nejčastěji tak, že část staré generace, nejčastěji nejúspěšnější, nebude nahrazena novou (elitismus). 1. Smazat všechny nová generace kompletně nahradí tu starou, jednoduché a velmi často dostačující. 2. Ustálený stav (Steady-state) nová generace bude nahrazovat jen část staré, pouze X chromozomů ze staré generace bude nahrazeno stejným počtem nových chromozomů. Podle implementace se pak rozhodne, které chromozomy nahradíme (nejhorší, náhodně, rodiče potomků..) 20
26 3. GENETICKÉ ALGORITMY 3. Ustálený stav bez duplikací (Steady-state-no-duplication) stejné jako v předchozím bodu, ale dělá se navíc kontrola, aby se našly a odstranily dva stejné chromozomy v jedné populaci. Implementované přístupy: kompletní nahrazení nové generace, nahrazení poloviny (s horší fitness), elitismus Ukončovací podmínka Genetický algoritmus může běžet neomezeně dlouho. Může běžet i poté co najde řešení, a dokonce může v dalších generacích řešení ztratit. Právě proto je nutné mít ukončovací podmínku, která algoritmus zastaví ve vhodné chvíli. Existují dva základní přístupy: 1. Zastavení za pevně stanovenou hodnotu za konkrétní počet generací, po konkrétním spotřebování času (procesorového). S tímto přístupem lze předem docela přesně odhadnout, kdy algoritmus skončí. 2. Zastavení po nastalé událost po dosažení maximální hodnoty fitness, když několik generací se maximální hodnota fitness nezmění. Implementovány jsou podmínky: dosaženo maximální fitness nebo počtu generací a několik generací bez změny hodnoty fitness. 3.2 Typy genetických algoritmů Díky změnám těchto částí a jejich parametrů lze vytvořit velké množství rozdílných genetických algoritmů(ga), které jsou vhodné pro různé situace. Objevil jsem zdroj [15] popisující šest druhů genetických algoritmů. Zdroj ukazuje různorodost genetických algoritmů v závislosti na zvolených operátorech (částech GA). 21
27 3. GENETICKÉ ALGORITMY Po detailnější popis jsem si zvolil GA se stochastickým kódováním, který ukazuje, jak je možné řešit situace, kdy stavový prostor (možné řešení) je příliš velký, ale stejně je potřeba, alespoň částečně, stavový prostor prohledat. Jednotlivé typy GA [15]: 1. Jednoduchý GA (Simple GA - SGA) Prakticky identické s původním návrhem GA. Populace se převážně generuje celá. 2. GA se stálým stavem (Steady-State GA) Podobná předcházejícímu popisu, zde ale většinou populace částečně přetrvává. 3. Inkrementální GA Typickým znakem je velmi malý přírůstek nových jedinců (jednotky), kteři postupně nahrazují aktuální populaci. 4. Mikro GA (μga) Pracuje s velmi malými populacemi okolo pěti jedinců. Je závislé na častém vytváření nových řešení, a to kvůli problému s malou diverzitou. 5. GA se stochastickým kódováním (Stochastic GA) Tento algoritmus se uplatňuje hlavně při optimalizačních úlohách s velkým počtem parametrů. Tyto úlohy mívají obvykle velice obsáhlý stavový prostor, jehož prohledání by trvalo neúnosně dlouho. Je proto třeba soustředit se do slibných oblastí stavového prostoru, zatímco v méně slibných ho omezit, nikoli však úplně zrušit. To je zajištěno dynamickým kódováním řetězců, které nepředstavují konkrétní řešení daného problému, ale prohledávané regiony stavového prostoru. Každý region je charakterizován normálním Gaussovým rozložením s vektorem středních hodnot a s variační maticí. Vektor středních hodnot udává očekávané hodnoty parametrů v prohledávaném regionu, zatímco variační matice udává pravděpodobnost nalezení optimálního řešení v určité oblasti prohledávaného 22
28 3. GENETICKÉ ALGORITMY regionu. V průběhu evoluce se pak mění právě popis rozdělení, tj. střední hodnoty a variační matice, čímž se celá rozdělení (prohledávané regiony) posouvají do slibnějších oblastí stavového prostoru. 6. Nalezení většího počtu extrémů Niching Používá se v situacích, kdy je třeba stabilní různorodá populace, která není okolo jednoho globálního extrému. Používá se technika, která extrémy (pomocí fitness funkce), povětšinou lehce negativně, upravuje vzhledem k tomu, jak moc je daný extrém dobrý (čím lepší, tím větší zpětná vazba). Výsledkem jsou skupiny populací okolo lokálních (a globálního) extrémů. 3.3 Využití genetických algoritmů Genetické algoritmy jsou populární a především účinnou metodou pro hledání dostatečně vyhovujícího řešení ve velkých stavových prostorech, které nelze definovat snadno řešitelnou funkcí a v nichž z výpočetních a časových důvodů selhává klasické prohledávání obyčejnou hrubou silou [8]. Pro možnost použití genetických algoritmů pro konkrétní problém je nutné, aby platily jenom dvě podmínky: 1. Poznáme dobré a špatné řešení, když ho uvidíme. Jsme tedy schopni vytvořit na daný problém fitness funkci. 2. Řešení jsme schopni reprezentovat pomocí chromozomu (sady genu viz Chromozom). Hlavní otázkou tedy zůstává, kdy je vhodné genetické algoritmy použít. Podmínky nejsou závazné a existuje jistě spousta hraničních případů, které nemusí zapadat. Navíc opomíjím faktor vývoje/použití takového řešení z hlediska přípravy, která se odvíjí i od toho, zda jsou již nějaké zkušenosti z použití genetických algoritmů, či naopak z použití jiného řešení. 23
29 3. GENETICKÉ ALGORITMY 1. Prohledávaný prostor je velký typickým příkladem je problém obchodního cestujícího, kdy neznáme žádný jiný algoritmus, který najde zaručeně správně řešení, než vyzkoušení všech možností. Je nutné upozornit, že ani genetické algoritmy nenajdou s jistotou nejlepší řešení. 2. Prostor není vyhlazený ani unimodální pokud by byl, tak by stačilo hledat globální extrémy tradičnímu přístupy. 3. Struktura prostoru je komplikovaná tím pádem nejsme schopni navrhnout vhodné heuristiky. 4. Není třeba najít optimum globální, ale stačí přijatelné řešení v přijatelném čase pokud dopředu neznáme vlastnosti hledaného řešení (například délka hledané cesty), tak pomocí genetického algoritmu nejsme schopni určit, zda jsme už globální extrém našli, pokud jsme ho ovšem vůbec našli, a nejednalo se pouze o lokální extrém. Posledním bodem jsme se dostaly k hlavní nevýhodě genetických algoritmů, a tím jsou lokální extrémy. Na obrázku je ukázán příklad lokálního extrému (pro hodnotu 1111), ale globální extrém se nachází pro hodnotu Obrázek 3.3: Lokální maximum 24
30 3. GENETICKÉ ALGORITMY Z obrázku 5 je velmi pravděpodobné, že pouze pomocí selekce se dostaneme k řešení 1111, což je pouze lokální maximum. V takových případech je nutné použít vhodnou mutaci, ale ani ta nezaručuje (pracuje s náhodou), že se k danému řešení algoritmus dostane. Čím více lokálních extrémů existuje, tím menší je šance, že algoritmus najde správné (maximální) řešení. Problém lokálních optim však není pouze problémem genetických algoritmů a evoluce obecně. Naopak lze evoluci velmi úspěšně použít, a je to jedna z lepších možností jak lokální optima řešit (oproti například Gradientnímu algoritmu Hill-climbing), když není možnost prohledávat celý stavový prostor. Problém také může vzniknout, pokud nepřizpůsobíme genetický algoritmus konkrétnímu problému, například že zvolíme špatnou reprezentaci chromozomů, či použijeme špatné křížení. 3.4 Příklady použití Oblíbeným příkladem použití genetických algoritmů je problém obchodního cestujícího (Traveling salesman problem), což je jeden ze známých NP-úplných problémů. Tento příklad zmiňuji proto, že výsledná knihovna bude použita pro průmyslového partnera pro podobný typ problému. Další známé využití genetických algoritmů je využití v chemii pro hledání a předpovídání vlastností proteinů. Názorné využití genetických algoritmů lze například najít i zde 6, kde se algoritmus využívá v aplikaci, která hledá ideální auto na danou cestu (aplikace a cesta jsou ve 2D). Poslední použití, které bych chtěl zmínit, je sledování vývoje populace. Na rozdíl od klasického problému, kdy hledáme jedno ideální řešení, zde sledujeme vývoj populace a její změnu v závislosti na okolních podmínkách (fitness funkce) a možnostech populace (křížení). Během práce jsem již několikrát takové využití zmiňoval a například speciální verze genetického algoritmu nalezení většího počtu extrémů Niching, kterou jsem 5. slide
31 3. GENETICKÉ ALGORITMY zmínil v kapitole Typy genetických algoritmů, se používá přesně pro tyto případy. Algoritmus ale musí s tímto využitím počítat a obsahovat alespoň základní prostředky, jak hlásit aktuální stav populace v každé generaci (v pravidelném časovém úseku). V mé knihovně pro tyto situace lze využít třídy GenerationEndAction, která v základu počítá s pravidelnými reporty každou generaci, a na neočekávané či nepravidelné zprávy lze vždy implementovat Special operation (více detailů najdete v kapitole Návrh tříd). 3.5 Klasifikační systémy Jak jsem zmiňoval na začátku kapitoly o evolučních algoritmech (Evoluční algoritmy str. 5), klasifikační systémy jsou někdy považovány za samostatnou kategorii. Já se ovšem přikláním k názoru, že se jedná spíše o využití genetických algoritmů, a proto je uvádím zde. Klasifikační systémy byly původně zamýšleny jako framework, který využívá genetické algoritmy pro studium systému na bázi pravidel (podmínka akce) [6]. Poprvé je zmínil John J. Holland v knize Adaptation in Natural and Artificial Systems. Klasifikační systémy využívají tři základní techniky v přístupu ke strojovému učení: 1. Paralelismus při vyhodnocování podmínek. Místo jedné velké podmínky se použije více podmínek menších, které se budou hodnotit nezávisle. Například vytvořit a následně vyhodnotit podmínku: modré Volvo mimo silnici v příkopu, kterému neběží motor, je složité, vyhodnotit tři podmínky modré Volvo (auto), mimo v silnici v příkopu a neběží motor, to jsou tři jednodušší pravidla, která když se vyhodnotí paralelně, dají stejný výsledek jako původní složitější pravidlo. 2. Kreditový systém, který se využívá pro naučení, za jakých podmínek uděláme jakou akci. Nevýhodou tohoto systému mohou být počáteční špatné reakce, kdy 26
32 3. GENETICKÉ ALGORITMY se systém ještě učí. 3. Objevování nových pravidel je ve strojovém učení jeden z těžších problémů, který se standardně řeší pomocí kreditového systému tak, že nejhůře hodnocené funkce nahradí novými, náhodně vygenerovanými (se zapojeným různých pomocných podmínek) pravidly. 27
33 4 Požadavky a existující řešení Před každým psaním programu je dobré si zjistit, zda již neexistuje řešení, které vytvořil někdo jiný, a zda by takové řešení nebylo vhodné pro aktuálně řešený problém. Existující řešení je možno jen upravit na náš konkrétní problém a tím ušetřit spoustu času a zbytečné práce. Proto jsem si sepsal požadavky na svůj program a následně jsem se podíval, zda již takové řešení neexistuje. Požadavky jsou rozdělené do dvou kategorií, kdy jsem napřed uvedl ty důležité, které po již hotovém řešení požaduji. Druhou kategorií je funkcionalita, kterou lze doimplementovat, pokud to bude možné, popřípadě požadavky obsahují více možností, jak danou situaci řešit, a bylo by vhodné obsáhnout alespoň část z nich, ideálně všechny. Základní požadavky: 1. Platforma.NET rozšířená a stabilní platforma podporovaná firmou Microsoft. Navíc existuje projekt Mono 7, s cílem udělat.net do budoucna plně použitelným na platformách založených na jádře Unix 2. Minimální závislost na knihovnách třetích stran aby se zamezilo potenciálním problémům v budoucnu, kdy se může lehce stát, že autor knihovny přestane vydávat aktualizace 3. Dokončený vývoj požadavek na stabilní verzi bez známých problémů zabraňujících použitelnosti a vedoucích k pádům programu. 4. Dokumentace kvalitní dokumentace jak na úrovni kódu (komentáře), tak na úrovni celé knihovny, díky které jde rychle zjistit, jaká funkcionalita je v kódu obsažena a jak ji použít. Bez takové dokumentace je velmi časově náročné používat cizí kód. 5. Rychlý a efektivní SW řešení by mělo podporovat použití více vláken (nutná
34 4. POŽADAVKY A EXISTUJÍCÍ ŘEŠENÍ podmínka), nesmí plýtvat pamětí, neprovádět zbytečné výpočty, a žádné úniky paměti. 6. Snadná rozšiřitelnost knihovnu je nutno navrhnout tak, aby bylo možné jednotlivé části programu upravit nebo nahradit vlastním kódem. 7. Přístup ke zdrojovým kódům pro potenciální nasazení v komerční sféře je třeba mít nějaké záruky na funkčnost, nebo přístup ke zdrojovým kódům. Další požadavky: 8 Možnost provádět alespoň část výpočtů na grafické kartě u tohoto bodu neočekávám, že knihovna již bude implementovat výpočty na grafické kartě, ale že bude možné jej jednoduše o tuto funkcionalitu rozšířit) platformách založených na jádře Unix. 9 Načítání konfigurace ze souboru aby se zamezilo potenciálním problémům v budoucnu, kdy se může lehce stát, že autor knihovny přestane vydávat aktualizace. 10 Změna vyhodnocovací funkce za běhu vyhodnocovací funkce (fitness funkce) je základem evoluce, nebot určuje, kteří jedinci jsou úspěšní a kteří ne. Během algoritmu vlastně říkáme, že jedinec, který vyhovuje dané funkci, je naše hledané řešení. Můžeme ovšem místo řešení problému využit genetické algoritmy pro pozorování evoluce samotné a pro takové situace je vhodné měnit fitness funkci (čímž říkáme, že se pro danou populaci změnilo prostředí, a tudíž jsou třeba jiné vlastnosti k tomu být nejlepší), další možností je zlepšení výkonu, kdy oproti jedné vyhodnocovací funkci, která hodnotí více parametrů, budeme mít více vyhodnocovacích funkcí, které řeší pouze jeden parametr. Tyto funkce postupně střídáme. V takovém případě bude populace oscilovat kolem ideálního řešení a jsem přesvědčen, že by k němu měla dlouhodobě konvergovat (toto tvrzení bude nutné ovšem otestovat, stejně jako 29
35 4. POŽADAVKY A EXISTUJÍCÍ ŘEŠENÍ jeho případnou rychlost) (viz Speciální operace 37 v kapitole Vlastní rozšíření knihovny). 11 Přidávání a odebírání existujících jedinců za běhu díky této funkcionalitě jsme schopni včas odstranit řešení, o kterých víme, že jsou lokálně nejvýhodnější, ale globálně nevedou k cíli,jsme také schopni řešit situace, kdy je populace příliš homogenní (což se řeší i mutací) a přináší to další možnosti při křížení. Standardně se pro řešení těchto problémů používá mutace, ale díky této funkcionalitě se značně rozšíří možnosti, jak pracovat s populací z konkrétních situací (př. zajímá mě, jestli jsem schopen najít při druhém pokusu, jiné řešení, a tedy budu cíleně odstraňovat jedince, které vedou k již objevenému řešení) (viz Speciální operace 37 v kapitole Vlastní rozšíření knihovny). 12 Selekce a křížení novou generaci vždy tvoří dva rodiče, kdy z těchto rodičů mohou vzniknout bud dva potomci, kteří dohromady nesou celou genetickou výbavu rodičů, nebo jen jeden potomek, který nese část genetické výbavy od obou rodičů. Stará generace může zmizet nebo může zůstat. Tyto všechny možnosti by měla standardní knihovna nabízet. 13 Maximální počet populace maximální počet populace by měl být nastavitelný bud na pevnou hranici, kdy veškerá populace nad tímto limitem bude odstraněna, nebo zde naopak bude určitá (volná) hranice, která se bude řídit například náhodou. 14 Chromozomy budou podporovat více datových typů pro různé situace se hodí různá reprezentace, nehledě na možnost, že chromozomy mohou být objekty, které se budou používat jinde, a není proto důvod nutit nikoho používat int[], když je mnohem vhodnější jiná reprezentace Body 1 8 vyplývaly ze zadání průmyslovým partnerem při řešení tématu. Bod 9 beru jako standardní požadavek, nebot takto se dosahuje změny konfigurace bez nut- 30
36 4. POŽADAVKY A EXISTUJÍCÍ ŘEŠENÍ nosti měnit kód. Body 10 a 11 jsou má vlastní rozšíření, o kterých si myslím, že dovolí větší rozmanitost při použití vytvářené knihovny. Zbylé body jsou požadavky na genetické algoritmy obecně. Při hledání jsem našel tato tři existující.net řešení. Obrázek 4.1: Existující řešení AForge.NET framework [1] Framework obsahující více částí, zpracování obrazu, umělá inteligence, genetické algoritmy. 1. C#.NET (verze 2.0/3.0) 2. Všechny knihovny a závislosti součástí projektu při stáhnutí a otevření projektu se nepovedlo nalinkovat všechny třídy, což přidává potenciálně další práci (problém pravděpodobně stejný jako v bodu 3 staré assembly a starý projekt) 3. Stabilní a ukončený vývoj, ale využívá starý.net a při otevírání ve Visual Studiu 2012 se objevila chybová hláška: Genetic (mono).csproj: Your project is targeting.net Framework 2.0 or 3.0. If your project uses assemblies requiring a newer.net Framework, your project will fail to build. You can change the.net Framework version by clicking Properties on the project menu and then selecting a new version in the.net 31
37 4. POŽADAVKY A EXISTUJÍCÍ ŘEŠENÍ Framework dropdown box. (In Visual Basic, this is located on the Compile tab by clicking the Advanced Compiler Options... button.) Při druhém spuštění projektu se již tato hláška neobjevila, a ani celý projekt nehlásí další chyby, ale framework díky tomu nevypadá důvěryhodně 4. Dokumentace obsáhlá a dostačující. Navíc existuje fórum. 5. Více vláken existuje jen na úrovni, kdy se více populací může počítat naráz, ale jedna populace využívající více vláken v knihovně není. 6. Ano 7. Ano 8. Ne Tato vylepšení framework nepodporuje, ale je možné jednotlivé třídy vytvořit/rozšířit existující 12. Částečně pouze jedna možnost křížení a selekce 13. Pevně nastavená velikost populace 14. Z části, podporuje více datových typů Závěr: Framework se snaží obsáhnout více témat (například zpracování obrazu), a kvůli tomu se podle mého názoru genetickým algoritmům příliš nevěnuje, nebo spíše se dokončil vývoj a nyní se zaměřuje na jiné části frameworku. Poslední update genetického algoritmu je z Pokud bych potřeboval více částí frameworku, tak bych byl s daným stavem spokojený. Vzhledem k tomu, že potřebujeme jen jednu velmi malou část, která není navíc podle všeho dále vyvíjená, neobsahuje většinu rozšiřujících požadavků a nepodporuje více vláken, bylo by podle mého odhadu skoro stejně časově náročné doimplementovat zbývající požadavky jako vytvořit framework vlastní. Navíc chyba při otevírání projektu nebudí příliš velkou důvěru pro nasazování ve firemním 32
38 4. POŽADAVKY A EXISTUJÍCÍ ŘEŠENÍ sektoru. Genetic Algorithm Framework for.net [7] 1. C#.NET, k dostání skrze Visual Studio prostřednictvím NuGet packages 2. Jedna knihovna dostupná NuGet packages 3. Knihovna je aktuální, neustále se přidávají nové funkce, vývoj je dle stránek autora dokončen 4. Na stránkách autora je dokumentace tvořená soustavou článků s ukázkami a odkazy na jednochodé příklady použití na Bitbucketu. Metody a třídy v kódu komentovány nejsou. 5. V knihovně existuje Namespace Threading obsahující jedinou třídu, bez dalšího komentáře, a ani na stránkách se neobjevuje komentář, že knihovna podporuje více vláken, také jsem našel v knihovně použití reflexe, což je technika, která není příliš efektivní. 6. Kód je rozšiřitelný a autor poskytuje i ukázky na Bitbucketu. 7. Ne 8. Ne 9. Ano 12. Ano Tato vylepšení framework nepodporuje, ale je možné jednotlivé třídy vytvořit/rozšířit existující 13. Pevně nastavená velikost populace 14. Z části, podporuje více datových typů 33
39 4. POŽADAVKY A EXISTUJÍCÍ ŘEŠENÍ Závěr: nejlépe zpracovaná knihovna. Chybí komentáře v kódu, což ale není tak velký problém, ukázky a články na stránce projektu jsou dostačující. Co se výkonu týče, chybějící podpora více vláken a použití reflexe mohou zpomalit program. Pro firemní sektor je podle mého názoru nevhodná, protože autor neposkytuje zdrojové kódy, ale jen knihovnu, a rychlost je taky možné vylepšit. BraneCloud.Evolution [2] 1. Opensource projekt postavený na C# - tento projekt je port z knihovny napsané v Javě 2. Dostupný pouze v alfa verzi z roku Vývoj nedokončený, na stránkách jsou hlášeny neopravené chyby 4. V projektu dobře komentovaný kód. Součástí zdrojového kódu je i dokumentace, místy ale nekompletní, jinak podrobná. Poznámky v kódu taktéž svědčí o nedokončené práci. This project is a placeholder for planned refactoring.do not delete! 5. Knihovna práci s více vlákny umí. 6. Knihovna je rozšiřitelná, bohužel bez přehledného návrhu a částí je rozšíření obtížné. 7. Ano 8. Ne 9. Ano Tato vylepšení framework nepodporuje, ale je možné jednotlivé třídy vytvořit/rozšířit existující Ano 34
40 4. POŽADAVKY A EXISTUJÍCÍ ŘEŠENÍ Závěr: Pokud by byl projekt dokončený, jednalo by se o nejkomplexnější použitelný projekt, který se mi podařilo najít. Bohužel nedokončený vývoj a chybějící dokumentace použití zabraňují. V případě tvorby knihovny pro jazyk Java doporučují prostudovat projekt, ze kterého tento port vychází 8 Výsledek je takový, že se mi nepovedlo najít dostatečně vhodný již existující projekt, který splňoval dostatek požadavků, aby si jeho úprava a rozšíření nevyžádalo tolik práce, že by bylo výhodnější vytvořit řešení vlastní. Je však možné se z těchto řešení poučit a vzít si příklady z jejich slabých a silných stránek
41 5 Vlastní rozšíření knihovny Při získávání požadavků na program a jeho následném návrhu se velmi často stává, že autora napadne nějaké vylepšení či nestandardní řešení části kódu. Tyto návrhy mohou vzniknout díky zkušenosti z jiných oblastí, nebo například díky specifickým požadavkům. V mé práci se vyskytují takové situace čtyři: 1. Řešení konfigurace projektu, o kterém se rozepisuje v následující kapitole 2. Návrh na využití grafických karet při výpočtu genetických algoritmů 3. Speciální operace, které také zmiňuji v následující kapitole, ale zde vysvětlím důvod, proč jsem zvolil takové řešení. 4. Null gene jako vlastnost chromozomu a využití. 5.1 Programování na grafických kartách 1. Využití pro matematické výpočty (speciálně pro výpočty s plovoucí desetinnou čárkou) 2. Paralelizace (až tisíce jader /matematických procesorů/koprocesorů) 3. Úzká specializace - nehodí se na: (a) (b) (c) nepředvídatelnou práci s pamětí (sort, graph search) jednoduché úkoly (vše stále řídí cpu, a existuje určitá režie) úkoly, které nejde paralelizovat (hlavní výhoda GPU) Pro programování na GPU se dnes používají dvě hlavní možnosti: OpenCL a CUDA. Pro C# existuje několik knihoven, které dovolují pracovat s GPU, například CUDAfy.NET
42 5. VLASTNÍ ROZŠÍŘENÍ KNIHOVNY Využití grafických karet pro genetické algoritmy V genetických algoritmech je teoreticky možné využít výpočty na GPU v těchto částech (místa, kde se vyplatí vysoká paralelizace): 1. Fitness funkce při složitější fitness funkci je zde jednoznačné využití GPU výhodou, za předpokladu, že fitness funkce je něco, co je třeba spočítat (například matematický model) 2. Křížení zde se neprovádí výpočty, maximálně se kombinují datové struktury, žádné využití pro GPU 3. Výběr rodičů zde se standardně neprovádí žádné velké operace, často je silně závislý na generování náhodného čísla (při velké paralelizaci je problém generovat náhodná na sobě pro každé vlákno nezávislá čísla) 4. Mutace zde je znovu teoreticky možné nasadit GPU výpočty, sice zde záleží také na generování náhodných čísel, ale za předpokladu, že další výpočet mutace (př. komplikovanější způsob mutace než nahradit jednu hodnotu jinou), je teoreticky možné GPU využít Z uvedeného přehledu vyplývá, že využití grafických karet má smysl jen ve specifických případech. Implementace výpočtu na grafické kartě pro vytvářenou knihovnu využívá možnosti, že každou třídu lze nahradit vlastní implementací. Zde konkrétně se může jedna o nahrazení třídy FitnessHandler vlastní implementací. Vlastní implementace může místo volání fitness funkce pro všechny jedince v populaci pro tyto výpočty využít grafickou kartu. Konkrétní ukázkový příklad najdete v elektronické příloze pod názvem F itnesshandlergp U.cs. 5.2 Speciální operace Mezi požadavky na vytvořenou knihovnu (str. 28) se objevily dva, které jsem označil jako požadavky, které jsem si přidal sám. 37
43 5. VLASTNÍ ROZŠÍŘENÍ KNIHOVNY Prvním požadavkem byla možnost změnit fitness funkci za běhu a druhým požadavkem byla možnost přidávat a odebírat jedince z populace za běhu. Ani na jednu možnost jsem nepřišel sám, a obě existují v různých variantách. Práce s fitness funkcí z důvodu optimalizace [16] a problém s malou diverzitou populace [4] existují a je snaha je řešit, i když ani jedno není standardní součástí genetických algoritmů. V předchozím odstavci jsem uvedl několik odkazů, které ukazovaly využití speciálních operací pro genetické algoritmy. Zatímco přidávání a odebírání jedinců na základě například duplicitních výskytů nebo předem známých lokálních optim může byt jasné, změna fitness funkce si podle mě zaslouží i jiný příklad. Tím je už dříve zmíněné [odkaz] využití genetických algoritmů na sledování vývoje populace. Zde si lze jen obtížně představit, jak by se vytvářela fitness funkce (jež nesmí být příliš pomalá), která reflektuje měnící se prostředí. Ovšem vyměnit jednou za čas fitness funkci za jinou, to dokáže vytvořit stejný efekt a zachovává fitness funkci jednodušší Využití speciálních operací v kódu Všechny předchozí situace se dají řešit mnoha různými způsoby a existující implementace genetických algoritmů, pokud tuto funkcionalitu podporovaly, je také úspěšně vyřešily. Mým cílem bylo poskytnout co nejobecnější nástroj, který dovoluje rozšířit knihovnu o co největší množství neobvyklých případů. Zároveň jsem chtěl zabránit situaci, aby taková implementace zasahovala co nejméně invazivně do ostatních částí knihovny. Další detaily ohledně implementace najdete v následující kapitole v části Special Operation (str. 37). V knihovně jsem pro účely předvedení funkcionality implementoval vkládání jedinců. 38
44 5. VLASTNÍ ROZŠÍŘENÍ KNIHOVNY 5.3 Null gene Genetické algoritmy se dají použít na hledání ideální cesty v neznámém prostředí, problém obchodního cestujícího je nejznámějším příkladem. Jiný typ hledání cesty může být například navigace v neznámém prostředí a vyhýbání se překážkám v situaci, kdy máme jen omezené informace, příkladem je umělá inteligence hledající nejlepší cestu k cíli. Tento přístup lze samozřejmě řešit jinými algoritmy, ale pokud například dokážeme získat informace jen o místě, kde aktuálně stojíme, je nutné vyzkoušet náhodně několik cest a postupně se zlepšovat [17]. Reprezentace chromozomu bývá bud pole pozic, nebo pole směrů (dalších kroků) vedoucích k cíli. Jak ovšem rozlišit výhodnost řešení, pokud se k cíli dá dojít různě dlouhými cestami? Fitness funkce může penalizovat kroky navíc, jen pokud ví, jak dlouhá má být ideální cesta. Je tedy nutné penalizovat jakýkoliv krok. To vyžaduje, aby jednou z možných hodnot genu bylo čekání či nicnedělání. To se využije například v situaci, kdy očekáváme, že počet kroků bude maximálně dvacet, a algoritmus najde cestu o devatenácti krocích a jednoho kroku (genu) čekání. Alternativním řešením by bylo mít různě dlouhou délku genů [10], to ovšem přináší další nároky například na křížení. Já se rozhodl implementovat krok (gen) čekání obecněji, a proto každý chromozom musí znát hodnotu svého genu čekání pojmenovaného jako null gene (nulový gen). Tedy pokud máme chromozom (jedince v populaci), jsme schopni se od něj dozvědět tuto hodnotu a je poté na nás, jak s takovou informací naložíme. V popisovaném příkladu hledání cesty můžeme například tyto geny nepovažovat za kroky, a tudíž neuplatňovat penalizaci. Další možné využití této informace je při křížení. Obtíže při vhodné reprezentaci problému jsem probíral v podkapitole věnující se chromozomu. Pro připomenutí, jedním z problémů reprezentace je situace, kdy sekvence genů nese společně důležitou informaci. Tato informace se však může ztratit, pokud pomocí křížení vezmu část genů 39
45 5. VLASTNÍ ROZŠÍŘENÍ KNIHOVNY z prvního rodiče a část z druhého rodiče. Pokud dostatečně dobře znám daný problém, který chci pomocí genetického algoritmu řešit a zároveň si zvolím vhodnou reprezentaci dat, je možné využit tyto nulové geny, aby ukazovaly pozice, ve kterých může proběhnout křížení, a tím zabránit zmiňované situaci. Výhodou takového použití je jistota, že důležité sekvence genů se křížením neztratí, a nevýhodou je prodloužení chromozomu o nulové geny. Křížení jen na pozicích s nulovými geny jsem implementoval do své práce. 40
46 6 Návrh tříd Před začátkem programování je dobré si vždy ujasnit, co všechno má projekt obsahovat a jak se má chovat. Pro tento projekt jsem si napřed vytvořil UML diagram a také životní cyklus programu. Obrázek 6.1: UML návrhí Návrh reflektuje požadavky na snadnou použitelnost knihovny (snadná orientace, logicky členěné části, minimum nezbytných závislostí), jež by měla obsahovat všechnu nezbytnou funkcionalitu, která se od ní očekává pro efektivní řešení maximálního množství problémů, ale také by měla poskytnout dostatečné nástroje k jejímu jednoduchému rozšiřování a upravování pro konkrétní řešení specifických problémů. Knihovna se snaží v maximální míře využit obecné typy(generics) 10. Všechny třídy kromě těch sloužících ke konfiguraci rozšiřují rozhraní GALClass. Toto rozhraní slouží pouze k implementaci proměnné projectname, jež dovoluje rozeznat, která instance patří pod kterou konfiguraci (čímž dovoluje, aby více vláken mohlo ne
47 6. NÁVRH TŘÍD závisle využívat knihovnu i přes to, že obsahuje singleton). Knihovna obsahuje abstraktní třídy, které umožňují snadno implementovat vlastní rozšíření. V případě, že je třeba odlišné chování, lze využít rozhraní. UML Třídy u UML diagramu jsem si v kódu rozčlenil do jmenných prostorů (Namespaces) 11 na části: 1. Chromosomes 2. Population (nacházející se ve jmenném prostoru GAL) 3. Configuration 4. Fitness 5. GenerationEndAction 6. GenerationHandlers 7. Special operations 8. Utils Jmenný prostor Utils se nenachází v UML návrhu, nebot slouží pouze pro uchovávání pomocných objektů a metod, které se využívají při výpočtech v jiných částech programu. Životní cyklus mého programu: 1. Start systému 2. Načtení konfigurace a načtení tříd pro konkrétní kroky (tj. fitness funkce, tvorba populace atd.) 3. Načtení/vytvoření populace 4. Vyhodnocení populace (fitness funkce)
48 6. NÁVRH TŘÍD 5. Vyhodnocení podmínky na ukončení a report 6. Selekce (vybere chromozomy, které se mohou stát rodiči, výběr rodičů pro konkrétní křížení, případné přežití části původních chromozomů) 7. Křížení nová generace a mutace 8. Speciální akce (změna fitness funkce, přidání/odebírání populace atd.) (zmínit + odkázat se v kapitole o vlastních rozšířeních) 9. Zpět na krok Chromosomes Jmenný prostor obsahující pouze jednotlivé typy chromozomů (možné řešení problémů). Obsahuje generické rozhrani IChromosome<E>, které každý chromozom musí implementovat. Pokud je třeba nový typ chromozomu, který není implementován, lze využít abstraktní třídu Chromosome<E>, kde je třeba doimplementovat dvě metody CreateChild, která slouží k vytvoření instance dané třídy, a GetNullGene, který slouží jako pomocná informace fitness funkci, jež díky němu dokáže rozpoznat prázdný gen (gen, který může při vyhodnocování přeskočit). 6.2 Population Tato třída je vstupním bodem algoritmu, zde se vloží počáteční populace (metodou NewPopulation) a následně se spustí algoritmus pomocí metody Run. Tato třída následně postupně volá všechny ostatní potřebné třídy. Také umožňuje na začátku načíst speciální operace pomoci metody LoadSpecialOperations, jež si z konfigurace zjistí, které speciální operace je třeba načíst, a argumenty, které určují, kdy a s jakými parametry se speciální operace spustí. 43
49 6. NÁVRH TŘÍD 6.3 Configuration Zde se nacházejí všechny třídy, které slouží k nastavení běhu samotného algoritmu. Bylo nutné vyřešit situaci, kdy potřebuji změnit některé parametry algoritmu za běhu (viz požadavky str. 28). Napadly mě dva způsoby, jak tento problém vyřešit: 1. Každá třída si bude držet vlastní proměnné a třídy, které potřebuje. 2. Vytvoří se nějaké centrální místo, kde jsou tyto informace uložené První přístup je standardně používaný a pro většinu situací mnohem vhodnější (a blíž principům objektového programování). Je o trochu rychlejší, ale zase může být pamět ově náročnější. Hlavní rozdíl nastává v situaci, kdy chci měnit údaje za běhu. Zatímco u prvního přístupu je třeba pro každou hodnotu, kterou chci změnit, najít její výskyt (může se vyskytovat na více místech) a pak ji nahradit, v druhém případě se hodnota změní v centrálním úložišti a každá třída/objekt se potom dle vlastních pravidel rozhodne, kdy zkontroluje aktuálnost svých údajů. První přístup velmi spoléhá na to, že již dopředu vím, kde všude chceme údaje měnit, a to potom komplikuje rozšiřování, nebot je neustále třeba přidávat místa, kde se tato hodnota vyskytuje. Další problém se vyskytne v případě, že budeme používat více vláken, a my budeme zvenku a potenciálně z jiného vlákna nastavovat hodnoty, nebo naopak budeme muset vždycky počkat, dokud nedoběhnou všechny vlákna, aby se například půlka populace nepočítala s jinou fitness funkcí než druhá. Druhý problém lze vyřešit bud tím, že se dovolí změny konfigurace jen v určitých fázích, nebo tak, že na začátku každého výpočtu vezmu danou konfiguraci a ignoruji všechny její změny, než výpočet skončí. V knihovně jsem použil obě možností, kdy změna konfigurace se dovoluje vždy před výpočtem fitness funkce, a to pomocí implementace SpecialOperation. Zároveň třídy implementované v knihovně vždy na začátku nějaké dlouhotrvající operace najdou příslušnou proměnnou (hodnotu, třídu) a s ní pracují po celou dobu dané operace. 44
50 6. NÁVRH TŘÍD Rozhodl jsem se použít obě řešení, protože je to jistější z hlediska dalšího rozšiřování, kdy je možné tento problém přehlédnout, a tedy potenciálně nechat vzniknout problém. Z obou přístupů jsem si tedy nakonec vybral druhou možnost, a to inspirací návrhovým vzorem singleton, který jsem pro potřeby knihovny upravil GALConfig Tato třída u sebe ukládá veškerou konfiguraci celého projektu, a to ve dvou proměnných (GALConfigClass, textitgalconfigvariables). Tato třída je generická, tudíž nemůže být singleton (tj. nejůze zaručit, že bude existovat jen jedna instance dané třídy pro celý kód), což ale nevadí, nebot stačí zajistit, že třída bude vypadat jako singleton pro každý běžící algoritmus, tedy, že každá populace vždy najde jen jednu svoji a unikátní třídu, ve které bude mít uloženou konfiguraci. To je zajištěné proměnnou projectkey, která má za úkol jednoznačně identifikovat konkrétní řešení. V třídě GALConfig jsou potom ve slovníku pod daným projectkey uložené příslušné konfigurační soubory, ke kterým jsou díky využití principu singletonu přístupné z celého kódu GALConfigClass Zde se ukládají všechny instance tříd, které se používají (např. fitness funkce). Pro každou třídu je zde zvlášt proměnná. Pokud by bylo potřeba tuto třídu rozšířit, je zde připravená datová struktura (slovník), do které lze přistupovat. Problémem tohoto řešení je rychlost. Instance je uložena jako typ Object, a je tedy nutné si ji přetypovat, a tedy je to pomalejší než přístup k ostatním proměnným. Vzhledem k tomu, že se s využitím této datové struktury počítá jen pro neočekávané situace a rozšíření, ztráta části rychlosti by neměla být problémem. 45
51 6. NÁVRH TŘÍD GALVariableClass Tato třída je ekvivalentem třídy GALConfigClass, s tím rozdílem, že slouží pro ukládání a přistupování k hodnotám (př. procentuální šance na mutaci). Obsahuje stejnou datovou strukturu, tentokrát pro hodnoty (využití pro hodnoty není problémem díky boxing/unboxing 12 Při návrhu jsem zvažoval, zda slovník (viz předchozí podkapitola) neimplementovat pouze v jedné ze dvou konfiguračních tříd (GALConfigClass, GALVariableClass), protože díky používání třídy Object je možné uložit jak třídu, tak primitivní datový typ (proměnnou) do stejného slovníku. Pro větší přehlednost jsem ale zvolil rozdělení do těchto dvou tříd, kdy se třídy ukládají do konfigurace určené pro třídy a proměnné do své vlastní třídy 6.4 Fitness Zde se řeší výpočet hodnoty fitness pro aktuální generaci. Skládá se ze dvou tříd (IFitnessFunction, IFitnessHandler), kde první je samotná fitness funkce, která pro daný chromozom vrátí hodnotu fitness. Krom samotné hodnoty fitness jsou zde ještě metody, které zajišt ují další informace: 1. Compatibility kontroluje, zda daný chromozom lze použít pro tuto fitness funkci. V základu se řeší pouze typ (tato funkcionalita je implementována), a v případě potřeby lze rozšířit o specifičtější kontrolu. 2. FitnessMin a FitnessMax ukazují rozpětí, které muže fitness nabývat. Ftiness funkce je jedna z věcí specifických pro každý problém a je ji nutno doimplementovat pro každý konkrétní případ. Hodnoty proměnných FitnessMin a FitnessMax se nastavují v kódu dle typu fitness funkce, zodpovídá za ně autor třídy a během výpočtu se hodnoty neměnní, například
52 6. NÁVRH TŘÍD pokud máme fitness funkci, která kontroluje, na kolik procent se splnila zadaná kritéria, a rozmezí je nastaveno na 0% (FitnessMin) a 100% (FitnessMax). Pokud bychom naopak kontrolovali, kolik hodnot jsme správně přiřadili do pole délky 50, tak hodnoty budou nabývat od 0 do 50. Druhá třída (FitnessHandler) se stará o volání fitness funkce, a tedy převážně o to, jestli se bude volat z jednoho či více vláken. Je možno zde také umístit další logiku spjatou s počítáním fitness, nebot na rozdíl od fitness funkce má tato třída přístup k celé populaci. 6.5 GenerationEndAction Jak již název napovídá, zde se řeší akce, které se vykonávají po skončení práce s aktuální generací (čímž je myšleno po výpočtu fitness funkce). V základní implementaci se jedná především o vyhodnocení podmínky pro ukončení a následně o vytvoření vhodného výstupu. Třída také obsahuje metodu Report, která může sloužit k pravidelnému či jednorázovému ukládání stavu populace například do externího souboru. 6.6 GenerationHandlers Poslední velkou skupinou jsou třídy v GenerationsHandlers, které se starají o vytváření nové generace chromozomů. Stará se o následující kroky: 1. Vybrat z aktuální populace ty chromozomy, které mohou být rodiči 2. Vybrat rodiče pro konkrétní generování potomstva 3. Pomocí křížení a mutace vygenerovat potomstvo 47
53 6. NÁVRH TŘÍD IGenerationHandler Rozhraní poskytující dvě metody: NextGeneration, která se stará o veškeré volání dalších tříd a Selection, která se stará o selekci rodičů. Metoda NextGeneration napřed zavolá metodu Selection, tím se zařídí prvotní selekce, ve které je možno odstranit některé chromozomy, které by neměly být rodiči (například příliš nízká hodnota fitness oproti ostatním chromozomům). Pokud takové omezení nechceme, tak tato metoda vrátí veškeré chromozomy a my s nimi můžeme pracovat dále. To konkrétně znamená, že budeme v cyklu vybírat rodiče a následně pomocí křížení a mutace vytvářet potomky. Ve vlastní implementaci je třeba si hlídat, kolikrát se takové vytváření potomstva bude opakovat, ale k tomu slouží bud vlastní implementace, která si to bude hlídat, nebo připravená proměnná NewGenerationCall (obsažená v GALVariableClass) IParentSelector Třída starající se o výběr rodičů pro jedno vytváření potomstva. Třída vrací seznam chromozomů, které budou rodiči pro jedno křížení. Je to proto, že je na implementaci, kolik rodičů budu na jedno křížení chtít a je tedy teoreticky možné mít rodiče jen jednoho (a spoléhat se na mutaci), nebo naopak rodiče více než dva ICrossBreed Třída řešící samotné křížení, tedy na vstupu dostane rodiče a vygeneruje potomstvo. Standardně se generují dva potomci pro dva rodiče, ale není problém vygenerovat jiný počet potomků, protože metoda vrací seznam IMutator Jak lze již z názvu odvodit, tato třída se stará o mutaci, která se vykonává po křížení. Obsahuje dvě metody, kde první Mutate bere na vstupu chromozom, který je třeba zkusit, zda nebude mutovat. Pokud ano, zavolá se druhá metoda MutatePosition, kde se 48
54 6. NÁVRH TŘÍD společně s chromozomem pošle i konkrétní pozice genu, kde probíhá mutace. Toto rozdělení je z důvodu lepší rozšiřitelnosti mutací, kdy první metodu můžeme v potomku přepsat například na vícevláknový přístup. Také to podporuje lepší testovatelnost, kdy si můžeme kdykoliv vyzkoušet, jak se chová daná mutace pro konkrétní chromozom a pozici. Krom mutace jako takové také třída obsahuje metodu, která kontroluje kompatibilitu (v základu implementováno jen na porovnání typů), aby existoval mechanismus, který rozpozná špatné použití třídy pro mutaci. Mohlo by se totiž stát, že konkrétní implementace sice umí pracovat z chromozomy daného typu (například chromozomy s geny celých čísel), ale třída mutuje geny (čísla) jen v určitém rozmezí, pro dané použit v rozmezí nevhodném. 6.7 Special operations Nestandardní problémy vyžadují nestandardní řešení, a aby knihovna byla dostatečně flexibilní, bylo nutné vytvořit mechanismus, který dokáže co možná největší škálu takových speciální případů pokrýt. Bylo nutné vytvořit mechanismus, který tyto situace dokáže řešit systémově a nikoliv tak, aby každé rozšíření knihovny vedlo k nekompatibilní verzi. Speciální operace je jednorázová akce, která se provede ve specifikované generaci. Výsledkem je rozhraní ISpecialOperation, které obsahuje dvě metody: 1. LoadSpecialOperation,jež zajišt uje načítání dat, která jsou potřeba k provedení operace dané třídou. Jako argument pracuje s polem slov, které slouží jako argumenty pro načítání a je v nich možné specifikovat například cestu k souborům. Tyto parametry jsou měnitelné v konfiguraci před spuštěním algoritmu a uživatel tedy může tyto údaje používat a měnit bez nutnosti měnit kód. 2. Execute obsahuje vykonání dané operace, jako argument dostává aktuální populaci (nic specifičtějšího jsem nezvolil z důvodu, že není dopředu možné určit, 49
55 6. NÁVRH TŘÍD jaké údaje budou potřeba a jaké nikoliv, a tedy je třeba poslat objekt ideálně co nejuniverzálnější). Jako příklady takovýchto operací je možné uvést přidávání a ubírání konkrétních jedinců z populace, změnu fitness funkce, či třeba změnu některého z parametrů (Speciální operace str. 37). 6.8 Utils Během tvorby jednotlivých částí jsem zjistil, že některé části platformy.net jsou pro mě nedostačující a že je třeba, abych si je upravil. Tato rozšíření jsem se rozhodl dát na jedno místo pro větší přehlednost. V současné době jsou moje rozšíření následující. Vláknově bezpečný generátor náhodných čísel. V.NET není generátor vláknově bezpečný, a proto by se mohlo stát, že pokud budou dvě vlákna ve stejný okamžik chtít náhodné číslo, mohou dostatčíslo stejné. Problém byl vyřešen tak, že pro každé vlákno bude vytvořen vlastní generátor náhodných čísel. Pro lepší výběr jsem se také rozhodl, že krom základního jednoduchého (a rychlejšího) generátoru náhodných čísel do třídy umístím i generátor náhodných čísel, který se používá v kryptografii, který je sice pomalejší, ale generuje čísla více náhodně 13 Třída HelpFunctions obsahuje metody pro efektivní a vícevláknovou práci s poli, například vícevláknový Equals nad polem hodnot, či vlastní implementace for cyklu (důvodům se budu více věnovat v další kapitole Výkon knihovny). ValueWrapper slouží pouze jako obal pro struktury (například číslo), aby se s nimi dalo pracovat skrze reference, které se poté dají jednodušeji posílat mezi vlákny. Pokud při práci s více vlákny předáme objekt odkazem, může další vlákno hodnotu měnit dle potřeby a v kódu není třeba řešit, jak dostat výsledek operace z jiného vlákna (naopak je třeba řešit, aby objekt neměnilo více vláken najednou). Primitivní datové typy v C# se předávají hodnotou, a proto je pro ně nutné vytvořit tuto třídu yptoserviceprovider%28v=vs.110%29.aspx 50
56 6. NÁVRH TŘÍD GALDefaultRunConfigurations jsem vytvořil pro jednoduché běhy genetických algoritmů. Dovoluje velmi rychle vyzkoušet tuto knihovnu jen s minimem vlastní imlementace. 51
57 7 Výkon knihovny Jak rychle funguje již hotová aplikace, je důležitý údaj, na který je třeba klást důraz. Je vhodné výkon aplikace postupně kontrolovat během vývoje a v případě větších problémů (například v návrhu), je třeba řešit co nejdříve a nikoliv až na konci vývoje. Míra optimalizací ale velmi často naráží na problém čitelného kódu a na to, jestli kód je upravený na jeden konkrétní problém, nebo se snaží být obecnější, ale za cenu trochu nižšího výkonu. V testech se věnuji výkonu z pohledu procesoru. Prorycvhlost genetických algoritmů je podle mě výkon procesoru nejdůležitější parametr, a pokud se nejedná o speciální případy (chromozom si pamatuje všechny rodiče, problém s RAM, veškerá data jsou na disku nebo například na internetu), kdy bude právě procesor ten nejvíce vytížený. Veškeré testy, pokud nebude uvedeno jinak, jsem testoval na počítači s následující konfigurací: procesor i5 M GHz, 4.00 GB RAM, Windows 7 (64-bit),.NET Framework 4.5. Testy měřící rychlost využívaly třídu Stopwatch. 7.1 Porovnání s existujícími řešeními V kapitole Požadavky a existující řešení (str. 28) jsem popisoval další tři různá řešení genetických algoritmů v jazyce C#. Bylo proto třeba zjistit, zda je má knihovna z hlediska výkonu dostatečně rychlá. Knihovnu BraneCloud.Evolution jsem z testování vyřadil, nebot jak jsem již psal v porovnání (odkaz), tento projekt považuji na nedokončený, a tak se i prezentuje, tudíž není důvod se jím zabývat jakožto jednou z možností. Pro porovnání výkonu jsem použil problém obchodního cestujícího (Travelling Salesman Problem TSP). Ten byl vybrán, protože problém, který průmyslový partner potřebuje řešit, je na podobném principu a navíc obě zbývající řešení obsahují ukázku řešení problému obchodního cestujícího. 52
58 7. VÝKON KNIHOVNY Výkon jsem měřil dvěma různými testy. Prvním testem bylo měření, jak dlouho trvá, než v populaci o velikosti 100 jedinců proběhne 1000 generací. Tento test je podle mého názoru užitečný v tom, že ukazuje, kolik generací za daný časový úsek je možno stihnout. Druhým testem je řešení problému obchodního cestujícího mezi stejnými pozicemi. Zde jsem pozoroval hlavně to, jak rychle a jak dobře zvládnou dané knihovny problém vyřešit a na rozdíl od prvního testu jsem již neřešil, jak rychle dojde algoritmus k cíli. Knihovna AForge.Net obsahuje pouze implementaci TSP, která počítá s celými čísly, pro účely testu to ale nebylo důležité (za předpokladu, že to byla známá informace) a rozdíl ve výkonu by neměl být natolik znatelný. Všechny běhy TSP se odehrávali v prostory o velikosti 400x400, 50 pozic (měst) a cesta mezi vybranými body byla klasická eukleidovská vzdálenost Test rychlosti Parametry testu byly: 1. Populace o 100 jedincích 2. Každý jedinec 50 genů 3. Celkem 1000 generací 4. Všechny knihovny používají variantu křížení se závislosti na pořadí (Order-based crossover) 5. Počet opakování testu Swap mutation (dva geny si vymění pozici) Z vlastní knihovny jsem udělal testy se třemi různými třídami. První konfigurace využívala pomocnou tabulku a následně pracoval jen s čísly vyjadřující pozice dat v tabulce. Proto bylo možno na kontrolu již použitých genů použít pole pravdivostních hodnot 53
59 7. VÝKON KNIHOVNY (bool), které bylo mnohem rychlejší. Druhá konfigurace byla stejná jako předchozí, s tím rozdílem, že mutace probíhala ve více vláknech. Třetí test použil variantu Order-based crossover, která kontroluje, zda již není nějaký gen použitý pomocí kolekce HashSet. Pro knihovny jsem použil již hotové ukázky, které obě knihovny již obsahovaly, tedy problém obchodního cestujícího. Obrázek 7.1: porovnání rychlosti, udávané hodnoty jsou ve vteřinách. Jak je vidět z naměřených výsledků, využití kolekce a neustálé počítání hashovaní funkce dokázalo zpomalit běh až čtyř-násobně. Je také vidět, že využití více vláken pro mutaci přineslo zlepšení výkonu o přibližně 10%, ale naopak za cenu zvětšeného rozptylu. Pokud se jedná o porovnání s ostatními knihovnami, tak AForge.NET měl dobré výsledky a věřím, že s lehkou optimalizací, například v oblasti selekce a práce s chromozomy (knihovna pracuje s chromozomy jako s nositeli většího množství informací, což může během velmi častého vytváření a mazání způsobit zpomalení), by bylo dosáhnuto srovnatelného výkonu. Druhá knihovna ovšem výkonnostně propadla. Díky absenci otevřeného zdrojového kódu jsem nebyl schopen určit příčinu. Výsledky testů lze najít v elektronické příloze (ve složce Data k testům - TSP test 1000runs). 54
Genetické algoritmy. Informační a komunikační technologie ve zdravotnictví
 Genetické algoritmy Informační a komunikační technologie ve zdravotnictví Přehled přednášky Úvod Historie Základní pojmy Principy genetických algoritmů Možnosti použití Související metody AI Příklad problém
Genetické algoritmy Informační a komunikační technologie ve zdravotnictví Přehled přednášky Úvod Historie Základní pojmy Principy genetických algoritmů Možnosti použití Související metody AI Příklad problém
Jak se matematika poučila v biologii
 Jak se matematika poučila v biologii René Kalus IT4Innovations, VŠB TUO Role matematiky v (nejen) přírodních vědách Matematika inspirující a sloužící jazyk pro komunikaci s přírodou V 4 3 r 3 Matematika
Jak se matematika poučila v biologii René Kalus IT4Innovations, VŠB TUO Role matematiky v (nejen) přírodních vědách Matematika inspirující a sloužící jazyk pro komunikaci s přírodou V 4 3 r 3 Matematika
VYUŽITÍ PRAVDĚPODOBNOSTNÍ METODY MONTE CARLO V SOUDNÍM INŽENÝRSTVÍ
 VYUŽITÍ PRAVDĚPODOBNOSTNÍ METODY MONTE CARLO V SOUDNÍM INŽENÝRSTVÍ Michal Kořenář 1 Abstrakt Rozvoj výpočetní techniky v poslední době umožnil také rozvoj výpočetních metod, které nejsou založeny na bázi
VYUŽITÍ PRAVDĚPODOBNOSTNÍ METODY MONTE CARLO V SOUDNÍM INŽENÝRSTVÍ Michal Kořenář 1 Abstrakt Rozvoj výpočetní techniky v poslední době umožnil také rozvoj výpočetních metod, které nejsou založeny na bázi
Evoluční algoritmy. Podmínka zastavení počet iterací kvalita nejlepšího jedince v populaci změna kvality nejlepšího jedince mezi iteracemi
 Evoluční algoritmy Použítí evoluční principů, založených na metodách optimalizace funkcí a umělé inteligenci, pro hledání řešení nějaké úlohy. Populace množina jedinců, potenciálních řešení Fitness function
Evoluční algoritmy Použítí evoluční principů, založených na metodách optimalizace funkcí a umělé inteligenci, pro hledání řešení nějaké úlohy. Populace množina jedinců, potenciálních řešení Fitness function
Projekční algoritmus. Urychlení evolučních algoritmů pomocí regresních stromů a jejich zobecnění. Jan Klíma
 Urychlení evolučních algoritmů pomocí regresních stromů a jejich zobecnění Jan Klíma Obsah Motivace & cíle práce Evoluční algoritmy Náhradní modelování Stromové regresní metody Implementace a výsledky
Urychlení evolučních algoritmů pomocí regresních stromů a jejich zobecnění Jan Klíma Obsah Motivace & cíle práce Evoluční algoritmy Náhradní modelování Stromové regresní metody Implementace a výsledky
Genetické algoritmy. Vysoká škola ekonomická Praha. Tato prezentace je k dispozici na: http://www.utia.cas.cz/vomlel/
 Genetické algoritmy Jiří Vomlel Laboratoř inteligentních systémů Vysoká škola ekonomická Praha Tato prezentace je k dispozici na: http://www.utia.cas.cz/vomlel/ Motivace z Darwinovy teorie evoluce Přírodní
Genetické algoritmy Jiří Vomlel Laboratoř inteligentních systémů Vysoká škola ekonomická Praha Tato prezentace je k dispozici na: http://www.utia.cas.cz/vomlel/ Motivace z Darwinovy teorie evoluce Přírodní
Metaheuristiky s populacemi
 Metaheuristiky s populacemi 8. března 2018 1 Společné vlastnosti 2 Evoluční algoritmy 3 Optimalizace mravenčí kolonie Zdroj: El-Ghazali Talbi, Metaheuristics: From Design to Implementation. Wiley, 2009.
Metaheuristiky s populacemi 8. března 2018 1 Společné vlastnosti 2 Evoluční algoritmy 3 Optimalizace mravenčí kolonie Zdroj: El-Ghazali Talbi, Metaheuristics: From Design to Implementation. Wiley, 2009.
Genetické programování
 Genetické programování Vyvinuto v USA v 90. letech J. Kozou Typické problémy: Predikce, klasifikace, aproximace, tvorba programů Vlastnosti Soupeří s neuronovými sítěmi apod. Potřebuje značně velké populace
Genetické programování Vyvinuto v USA v 90. letech J. Kozou Typické problémy: Predikce, klasifikace, aproximace, tvorba programů Vlastnosti Soupeří s neuronovými sítěmi apod. Potřebuje značně velké populace
Masarykova univerzita. Fakulta informatiky. Evoluce pohybu
 Masarykova univerzita Fakulta informatiky Evoluce pohybu IV109 Tomáš Kotula, 265 287 Brno, 2009 Úvod Pohyb je jedním ze základních projevů života. Zdá se tedy logické, že stejně jako ostatní vlastnosti
Masarykova univerzita Fakulta informatiky Evoluce pohybu IV109 Tomáš Kotula, 265 287 Brno, 2009 Úvod Pohyb je jedním ze základních projevů života. Zdá se tedy logické, že stejně jako ostatní vlastnosti
Moderní systémy pro získávání znalostí z informací a dat
 Moderní systémy pro získávání znalostí z informací a dat Jan Žižka IBA Institut biostatistiky a analýz PřF & LF, Masarykova universita Kamenice 126/3, 625 00 Brno Email: zizka@iba.muni.cz Bioinformatika:
Moderní systémy pro získávání znalostí z informací a dat Jan Žižka IBA Institut biostatistiky a analýz PřF & LF, Masarykova universita Kamenice 126/3, 625 00 Brno Email: zizka@iba.muni.cz Bioinformatika:
Evoluční výpočetní techniky (EVT)
 Evoluční výpočetní techniky (EVT) - Nacházejí svoji inspiraci v přírodních vývojových procesech - Stejně jako přírodní jevy mají silnou náhodnou složku, která nezanedbatelným způsobem ovlivňuje jejich
Evoluční výpočetní techniky (EVT) - Nacházejí svoji inspiraci v přírodních vývojových procesech - Stejně jako přírodní jevy mají silnou náhodnou složku, která nezanedbatelným způsobem ovlivňuje jejich
Navrženy v 60. letech jako experimentální optimalizační metoda. Velice rychlá s dobrou podporou teorie
 Evoluční strategie Navrženy v 60. letech jako experimentální optimalizační metoda Založena na reálných číslech Velice rychlá s dobrou podporou teorie Jako první zavedla self-adaptation (úpravu sebe sama)
Evoluční strategie Navrženy v 60. letech jako experimentální optimalizační metoda Založena na reálných číslech Velice rychlá s dobrou podporou teorie Jako první zavedla self-adaptation (úpravu sebe sama)
Kontingenční tabulky v MS Excel 2010
 Kontingenční tabulky v MS Excel 2010 Autor: RNDr. Milan Myšák e-mail: milan.mysak@konero.cz Obsah 1 Vytvoření KT... 3 1.1 Data pro KT... 3 1.2 Tvorba KT... 3 2 Tvorba KT z dalších zdrojů dat... 5 2.1 Data
Kontingenční tabulky v MS Excel 2010 Autor: RNDr. Milan Myšák e-mail: milan.mysak@konero.cz Obsah 1 Vytvoření KT... 3 1.1 Data pro KT... 3 1.2 Tvorba KT... 3 2 Tvorba KT z dalších zdrojů dat... 5 2.1 Data
Algoritmizace Dynamické programování. Jiří Vyskočil, Marko Genyg-Berezovskyj 2010
 Dynamické programování Jiří Vyskočil, Marko Genyg-Berezovskyj 2010 Rozděl a panuj (divide-and-conquer) Rozděl (Divide): Rozděl problém na několik podproblémů tak, aby tyto podproblémy odpovídaly původnímu
Dynamické programování Jiří Vyskočil, Marko Genyg-Berezovskyj 2010 Rozděl a panuj (divide-and-conquer) Rozděl (Divide): Rozděl problém na několik podproblémů tak, aby tyto podproblémy odpovídaly původnímu
A0M33EOA: Evoluční optimalizační algoritmy
 A0M33EOA: Evoluční optimalizační algoritmy Zkouškový test Pátek 8. února 2011 Vaše jméno: Známka, kterou byste si z předmětu sami dali, a její zdůvodnění: Otázka: 1 2 3 4 5 6 7 8 Celkem Body: 1 3 2 1 4
A0M33EOA: Evoluční optimalizační algoritmy Zkouškový test Pátek 8. února 2011 Vaše jméno: Známka, kterou byste si z předmětu sami dali, a její zdůvodnění: Otázka: 1 2 3 4 5 6 7 8 Celkem Body: 1 3 2 1 4
Pokročilé operace s obrazem
 Získávání a analýza obrazové informace Pokročilé operace s obrazem Biofyzikální ústav Lékařské fakulty Masarykovy univerzity Brno prezentace je součástí projektu FRVŠ č.2487/2011 (BFÚ LF MU) Získávání
Získávání a analýza obrazové informace Pokročilé operace s obrazem Biofyzikální ústav Lékařské fakulty Masarykovy univerzity Brno prezentace je součástí projektu FRVŠ č.2487/2011 (BFÚ LF MU) Získávání
2. úkol MI-PAA. Jan Jůna (junajan) 3.11.2013
 2. úkol MI-PAA Jan Jůna (junajan) 3.11.2013 Specifikaci úlohy Problém batohu je jedním z nejjednodušších NP-těžkých problémů. V literatuře najdeme množství jeho variant, které mají obecně různé nároky
2. úkol MI-PAA Jan Jůna (junajan) 3.11.2013 Specifikaci úlohy Problém batohu je jedním z nejjednodušších NP-těžkých problémů. V literatuře najdeme množství jeho variant, které mají obecně různé nároky
Dobývání znalostí. Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické informatiky Matematicko-fyzikální fakulta Univerzity Karlovy v Praze
 Dobývání znalostí Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické informatiky Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Dobývání znalostí Pravděpodobnost a učení Doc. RNDr. Iveta Mrázová,
Dobývání znalostí Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické informatiky Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Dobývání znalostí Pravděpodobnost a učení Doc. RNDr. Iveta Mrázová,
Uživatelský manuál. Aplikace GraphViewer. Vytvořil: Viktor Dlouhý
 Uživatelský manuál Aplikace GraphViewer Vytvořil: Viktor Dlouhý Obsah 1. Obecně... 3 2. Co aplikace umí... 3 3. Struktura aplikace... 4 4. Mobilní verze aplikace... 5 5. Vytvoření projektu... 6 6. Části
Uživatelský manuál Aplikace GraphViewer Vytvořil: Viktor Dlouhý Obsah 1. Obecně... 3 2. Co aplikace umí... 3 3. Struktura aplikace... 4 4. Mobilní verze aplikace... 5 5. Vytvoření projektu... 6 6. Části
Gramatická evoluce a softwarový projekt AGE
 Gramatická evoluce a softwarový projekt AGE Adam Nohejl Matematicko-fyzikální fakulta Univerzita Karlova v Praze http://nohejl.name/ 4. 4. 2010 Poznámka: Prezentace založené na variantách těchto slajdů
Gramatická evoluce a softwarový projekt AGE Adam Nohejl Matematicko-fyzikální fakulta Univerzita Karlova v Praze http://nohejl.name/ 4. 4. 2010 Poznámka: Prezentace založené na variantách těchto slajdů
Statistická teorie učení
 Statistická teorie učení Petr Havel Marek Myslivec přednáška z 9. týdne 1 Úvod Představme si situaci výrobce a zákazníka, který si u výrobce objednal algoritmus rozpoznávání. Zákazník dodal experimentální
Statistická teorie učení Petr Havel Marek Myslivec přednáška z 9. týdne 1 Úvod Představme si situaci výrobce a zákazníka, který si u výrobce objednal algoritmus rozpoznávání. Zákazník dodal experimentální
Algoritmizace diskrétních. Ing. Michal Dorda, Ph.D.
 Algoritmizace diskrétních simulačních modelů Ing. Michal Dorda, Ph.D. 1 Úvodní poznámky Při programování simulačních modelů lze hlavní dílčí problémy shrnout do následujících bodů: 1) Zachycení statických
Algoritmizace diskrétních simulačních modelů Ing. Michal Dorda, Ph.D. 1 Úvodní poznámky Při programování simulačních modelů lze hlavní dílčí problémy shrnout do následujících bodů: 1) Zachycení statických
 2015 http://excel.fit.vutbr.cz Kartézské genetické programování s LUT Karolína Hajná* Abstract Tato práce se zabývá problematikou návrhu obvodů pomocí kartézského genetického programování na úrovni třívstupových
2015 http://excel.fit.vutbr.cz Kartézské genetické programování s LUT Karolína Hajná* Abstract Tato práce se zabývá problematikou návrhu obvodů pomocí kartézského genetického programování na úrovni třívstupových
Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague
 1 / 23 Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague 2 / 23 biologové často potřebují najít často se opakující sekvence DNA tyto sekvence bývají relativně krátké,
1 / 23 Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague 2 / 23 biologové často potřebují najít často se opakující sekvence DNA tyto sekvence bývají relativně krátké,
1.5.2 Číselné soustavy II
 .. Číselné soustavy II Předpoklady: Př. : Převeď do desítkové soustavy čísla. a) ( ) b) ( ) 4 c) ( ) 6 = + + + = 7 + 9 + = a) = 4 + 4 + 4 = 6 + 4 + = 9 b) 4 = 6 + 6 + 6 = 6 + 6 + = 6 + + = 69. c) 6 Pedagogická
.. Číselné soustavy II Předpoklady: Př. : Převeď do desítkové soustavy čísla. a) ( ) b) ( ) 4 c) ( ) 6 = + + + = 7 + 9 + = a) = 4 + 4 + 4 = 6 + 4 + = 9 b) 4 = 6 + 6 + 6 = 6 + 6 + = 6 + + = 69. c) 6 Pedagogická
Základy umělé inteligence
 Základy umělé inteligence Automatické řešení úloh Základy umělé inteligence - prohledávání. Vlasta Radová, ZČU, katedra kybernetiky 1 Formalizace úlohy UI chápe řešení úloh jako proces hledání řešení v
Základy umělé inteligence Automatické řešení úloh Základy umělé inteligence - prohledávání. Vlasta Radová, ZČU, katedra kybernetiky 1 Formalizace úlohy UI chápe řešení úloh jako proces hledání řešení v
StatSoft Jak vyzrát na datum
 StatSoft Jak vyzrát na datum Tento článek se věnuje podrobně možnostem práce s proměnnými, které jsou ve formě datumu. A že jich není málo. Pokud potřebujete pracovat s datumem, pak se Vám bude tento článek
StatSoft Jak vyzrát na datum Tento článek se věnuje podrobně možnostem práce s proměnnými, které jsou ve formě datumu. A že jich není málo. Pokud potřebujete pracovat s datumem, pak se Vám bude tento článek
Markov Chain Monte Carlo. Jan Kracík.
 Markov Chain Monte Carlo Jan Kracík jan.kracik@vsb.cz Princip Monte Carlo integrace Cílem je (přibližný) výpočet integrálu I(g) = E f [g(x)] = g(x)f (x)dx. (1) Umíme-li generovat nezávislé vzorky x (1),
Markov Chain Monte Carlo Jan Kracík jan.kracik@vsb.cz Princip Monte Carlo integrace Cílem je (přibližný) výpočet integrálu I(g) = E f [g(x)] = g(x)f (x)dx. (1) Umíme-li generovat nezávislé vzorky x (1),
Programujeme v softwaru Statistica
 Programujeme v softwaru Statistica díl třetí Newsletter Statistica ACADEMY Téma: Programování, makra, skripty Typ článku: Návody V předchozích článcích (díl první, díl druhý) jsme si osvětlili základní
Programujeme v softwaru Statistica díl třetí Newsletter Statistica ACADEMY Téma: Programování, makra, skripty Typ článku: Návody V předchozích článcích (díl první, díl druhý) jsme si osvětlili základní
Emergence chování robotických agentů: neuroevoluce
 Emergence chování robotických agentů: neuroevoluce Petra Vidnerová, Stanislav Slušný, Roman Neruda Ústav Informatiky, AV ČR Kognice a umělý život VIII Praha 28. 5. 2008 Evoluční robotika: EA & neuronové
Emergence chování robotických agentů: neuroevoluce Petra Vidnerová, Stanislav Slušný, Roman Neruda Ústav Informatiky, AV ČR Kognice a umělý život VIII Praha 28. 5. 2008 Evoluční robotika: EA & neuronové
1. Přednáška. Ing. Miroslav Šulai, MBA
 N_OFI_2 1. Přednáška Počet pravděpodobnosti Statistický aparát používaný ve financích Ing. Miroslav Šulai, MBA 1 Počet pravděpodobnosti -náhodné veličiny 2 Počet pravděpodobnosti -náhodné veličiny 3 Jevy
N_OFI_2 1. Přednáška Počet pravděpodobnosti Statistický aparát používaný ve financích Ing. Miroslav Šulai, MBA 1 Počet pravděpodobnosti -náhodné veličiny 2 Počet pravděpodobnosti -náhodné veličiny 3 Jevy
PŘEDNÁŠKA 03 OPTIMALIZAČNÍ METODY Optimization methods
 CW057 Logistika (R) PŘEDNÁŠKA 03 Optimization methods Ing. Václav Venkrbec skupina obecných modelů slouží k nalezení nejlepšího řešení problémů a modelovaných reálií přináší řešení: prvky konečné / nekonečné
CW057 Logistika (R) PŘEDNÁŠKA 03 Optimization methods Ing. Václav Venkrbec skupina obecných modelů slouží k nalezení nejlepšího řešení problémů a modelovaných reálií přináší řešení: prvky konečné / nekonečné
Agent pracující v částečně pozorovatelném prostředí udržuje na základě senzorického modelu odhaduje, jak se svět může vyvíjet.
 Umělá inteligence II Roman Barták, KTIML roman.bartak@mff.cuni.cz http://ktiml.mff.cuni.cz/~bartak Dnešní program Agent pracující v částečně pozorovatelném prostředí udržuje na základě senzorického modelu
Umělá inteligence II Roman Barták, KTIML roman.bartak@mff.cuni.cz http://ktiml.mff.cuni.cz/~bartak Dnešní program Agent pracující v částečně pozorovatelném prostředí udržuje na základě senzorického modelu
Úvod do optimalizace, metody hladké optimalizace
 Evropský sociální fond Investujeme do vaší budoucnosti Úvod do optimalizace, metody hladké optimalizace Matematika pro informatiky, FIT ČVUT Martin Holeňa, 13. týden LS 2010/2011 O čem to bude? Příklady
Evropský sociální fond Investujeme do vaší budoucnosti Úvod do optimalizace, metody hladké optimalizace Matematika pro informatiky, FIT ČVUT Martin Holeňa, 13. týden LS 2010/2011 O čem to bude? Příklady
Hledání extrémů funkcí
 Hledání extrémů funkcí Budeme se zabývat téměř výhradně hledáním minima. Přes nost nalezeného extrému Obecně není hledání extrému tak přesné jako řešení rovnic. Demonstrovat to můžeme na příkladu hledání
Hledání extrémů funkcí Budeme se zabývat téměř výhradně hledáním minima. Přes nost nalezeného extrému Obecně není hledání extrému tak přesné jako řešení rovnic. Demonstrovat to můžeme na příkladu hledání
ZÁKLADY STATISTICKÉHO ZPRACOVÁNÍ ÚDAJŮ 5. hodina , zapsala Veronika Vinklátová Revize zápisu Martin Holub,
 ZÁKLADY STATISTICKÉHO ZPRACOVÁNÍ ÚDAJŮ 5. hodina - 22. 3. 2018, zapsala Revize zápisu Martin Holub, 27. 3. 2018 I. Frekvenční tabulky opakování z minulé hodiny Frekvenční tabulka je nejzákladnější nástroj
ZÁKLADY STATISTICKÉHO ZPRACOVÁNÍ ÚDAJŮ 5. hodina - 22. 3. 2018, zapsala Revize zápisu Martin Holub, 27. 3. 2018 I. Frekvenční tabulky opakování z minulé hodiny Frekvenční tabulka je nejzákladnější nástroj
STATISTICKÉ ODHADY Odhady populačních charakteristik
 STATISTICKÉ ODHADY Odhady populačních charakteristik Jak stanovit charakteristiky rozložení sledované veličiny v základní populaci? Populaci většinou nemáme celou k dispozici, musíme se spokojit jen s
STATISTICKÉ ODHADY Odhady populačních charakteristik Jak stanovit charakteristiky rozložení sledované veličiny v základní populaci? Populaci většinou nemáme celou k dispozici, musíme se spokojit jen s
Výhody a nevýhody jednotlivých reprezentací jsou shrnuty na konci kapitoly.
 Kapitola Reprezentace grafu V kapitole?? jsme se dozvěděli, co to jsou grafy a k čemu jsou dobré. rzo budeme chtít napsat nějaký program, který s grafy pracuje. le jak si takový graf uložit do počítače?
Kapitola Reprezentace grafu V kapitole?? jsme se dozvěděli, co to jsou grafy a k čemu jsou dobré. rzo budeme chtít napsat nějaký program, který s grafy pracuje. le jak si takový graf uložit do počítače?
DOTAZNÍK PRO URČENÍ UČEBNÍHO STYLU
 DOTAZNÍK PRO URČENÍ UČEBNÍHO STYLU Projekt MOTIVALUE Jméno: Třida: Pokyny Prosím vyplňte vaše celé jméno. Vaše jméno bude vytištěno na informačním listu s výsledky. U každé ze 44 otázek vyberte a nebo
DOTAZNÍK PRO URČENÍ UČEBNÍHO STYLU Projekt MOTIVALUE Jméno: Třida: Pokyny Prosím vyplňte vaše celé jméno. Vaše jméno bude vytištěno na informačním listu s výsledky. U každé ze 44 otázek vyberte a nebo
Vyhledávání. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 21.
 Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 21. září 2018 Jiří Dvorský (VŠB TUO) Vyhledávání 242 / 433 Osnova přednášky
Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 21. září 2018 Jiří Dvorský (VŠB TUO) Vyhledávání 242 / 433 Osnova přednášky
Slučování tabulek. Sloučení dvou tabulek
 Slučování tabulek Newsletter Statistica ACADEMY Téma: Příprava dat Typ článku: Návody Máte informace ve více tabulkách a chcete je sloučit dohromady? Pak je tento článek právě pro Vás. Vysvětlíme, jaké
Slučování tabulek Newsletter Statistica ACADEMY Téma: Příprava dat Typ článku: Návody Máte informace ve více tabulkách a chcete je sloučit dohromady? Pak je tento článek právě pro Vás. Vysvětlíme, jaké
METODY DOLOVÁNÍ V DATECH DATOVÉ SKLADY TEREZA HYNČICOVÁ H2IGE1
 METODY DOLOVÁNÍ V DATECH DATOVÉ SKLADY TEREZA HYNČICOVÁ H2IGE1 DOLOVÁNÍ V DATECH (DATA MINING) OBJEVUJE SE JIŽ OD 60. LET 20. ST. S ROZVOJEM POČÍTAČOVÉ TECHNIKY DEFINICE PROCES VÝBĚRU, PROHLEDÁVÁNÍ A MODELOVÁNÍ
METODY DOLOVÁNÍ V DATECH DATOVÉ SKLADY TEREZA HYNČICOVÁ H2IGE1 DOLOVÁNÍ V DATECH (DATA MINING) OBJEVUJE SE JIŽ OD 60. LET 20. ST. S ROZVOJEM POČÍTAČOVÉ TECHNIKY DEFINICE PROCES VÝBĚRU, PROHLEDÁVÁNÍ A MODELOVÁNÍ
Seminář z umělé inteligence. Otakar Trunda
 Seminář z umělé inteligence Otakar Trunda Plánování Vstup: Satisficing task: počáteční stav, cílové stavy, přípustné akce Optimization task: počáteční stav, cílové stavy, přípustné akce, ceny akcí Výstup:
Seminář z umělé inteligence Otakar Trunda Plánování Vstup: Satisficing task: počáteční stav, cílové stavy, přípustné akce Optimization task: počáteční stav, cílové stavy, přípustné akce, ceny akcí Výstup:
12 Metody snižování barevného prostoru
 12 Metody snižování barevného prostoru Studijní cíl Tento blok je věnován základním metodám pro snižování barevného rozsahu pro rastrové obrázky. Postupně zde jsou vysvětleny důvody k použití těchto algoritmů
12 Metody snižování barevného prostoru Studijní cíl Tento blok je věnován základním metodám pro snižování barevného rozsahu pro rastrové obrázky. Postupně zde jsou vysvětleny důvody k použití těchto algoritmů
Inferenční statistika - úvod. z-skóry normální rozdělení pravděpodobnost rozdělení výběrových průměrů
 Inferenční statistika - úvod z-skóry normální rozdělení pravděpodobnost rozdělení výběrových průměrů Pravděpodobnost postupy induktivní statistiky vycházejí z teorie pravděpodobnosti pravděpodobnost, že
Inferenční statistika - úvod z-skóry normální rozdělení pravděpodobnost rozdělení výběrových průměrů Pravděpodobnost postupy induktivní statistiky vycházejí z teorie pravděpodobnosti pravděpodobnost, že
X36SIN: Softwarové inženýrství. Životní cyklus a plánování
 X36SIN: Softwarové inženýrství Životní cyklus a plánování 1 Kontext Minule jsme si řekli, co to je deklarace záměru, odborný článek, katalog požadavků, seznam aktérů a seznam událostí. Seznam aktérů a
X36SIN: Softwarové inženýrství Životní cyklus a plánování 1 Kontext Minule jsme si řekli, co to je deklarace záměru, odborný článek, katalog požadavků, seznam aktérů a seznam událostí. Seznam aktérů a
1. Statistická analýza dat Jak vznikají informace Rozložení dat
 1. Statistická analýza dat Jak vznikají informace Rozložení dat J. Jarkovský, L. Dušek, S. Littnerová, J. Kalina Význam statistické analýzy dat Sběr a vyhodnocování dat je způsobem k uchopení a pochopení
1. Statistická analýza dat Jak vznikají informace Rozložení dat J. Jarkovský, L. Dušek, S. Littnerová, J. Kalina Význam statistické analýzy dat Sběr a vyhodnocování dat je způsobem k uchopení a pochopení
Parametrické programování
 Parametrické programování Příklad 1 Parametrické pravé strany Firma vyrábí tři výrobky. K jejich výrobě potřebuje jednak surovinu a jednak stroje, na kterých dochází ke zpracování. Na první výrobek jsou
Parametrické programování Příklad 1 Parametrické pravé strany Firma vyrábí tři výrobky. K jejich výrobě potřebuje jednak surovinu a jednak stroje, na kterých dochází ke zpracování. Na první výrobek jsou
Algoritmy pro spojitou optimalizaci
 Algoritmy pro spojitou optimalizaci Vladimír Bičík Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze 10.6.2010 Vladimír Bičík (ČVUT Praha) Algoritmy pro spojitou optimalizaci
Algoritmy pro spojitou optimalizaci Vladimír Bičík Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze 10.6.2010 Vladimír Bičík (ČVUT Praha) Algoritmy pro spojitou optimalizaci
1.5.1 Číselné soustavy
 .. Číselné soustavy Předpoklady: základní početní operace Pedagogická poznámka: Tato hodina není součástí klasické gymnaziální sady. Upřímně řečeno nevím proč. Jednak se všichni studenti určitě setkávají
.. Číselné soustavy Předpoklady: základní početní operace Pedagogická poznámka: Tato hodina není součástí klasické gymnaziální sady. Upřímně řečeno nevím proč. Jednak se všichni studenti určitě setkávají
Vyhledávání. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 12.
 Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 12. září 2016 Jiří Dvorský (VŠB TUO) Vyhledávání 201 / 344 Osnova přednášky
Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 12. září 2016 Jiří Dvorský (VŠB TUO) Vyhledávání 201 / 344 Osnova přednášky
Numerické metody 6. května FJFI ČVUT v Praze
 Extrémy funkcí Numerické metody 6. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod 1D Více dimenzí Kombinatorika Lineární programování Programy 1 Úvod Úvod - Úloha Snažíme se najít extrém funkce, at už jedné
Extrémy funkcí Numerické metody 6. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod 1D Více dimenzí Kombinatorika Lineární programování Programy 1 Úvod Úvod - Úloha Snažíme se najít extrém funkce, at už jedné
2.3.5 Ekvivalentní úpravy
 .. Ekvivalentní úpravy Předpoklady: 000 Př. : Vyřeš rovnice. Jaký je společný rys řešení všech příkladů? a) + = 7 b) = 9 c) = d) = a) + = 7 = 7 = 9 b) = 9 = 9: = 7 c) = d) = 0 = = 7 = + = + = = 9 9 9 9
.. Ekvivalentní úpravy Předpoklady: 000 Př. : Vyřeš rovnice. Jaký je společný rys řešení všech příkladů? a) + = 7 b) = 9 c) = d) = a) + = 7 = 7 = 9 b) = 9 = 9: = 7 c) = d) = 0 = = 7 = + = + = = 9 9 9 9
Algoritmus pro hledání nejkratší cesty orientovaným grafem
 1.1 Úvod Algoritmus pro hledání nejkratší cesty orientovaným grafem Naprogramoval jsem v Matlabu funkci, která dokáže určit nejkratší cestu v orientovaném grafu mezi libovolnými dvěma vrcholy. Nastudoval
1.1 Úvod Algoritmus pro hledání nejkratší cesty orientovaným grafem Naprogramoval jsem v Matlabu funkci, která dokáže určit nejkratší cestu v orientovaném grafu mezi libovolnými dvěma vrcholy. Nastudoval
ČVUT FEL X36PAA - Problémy a algoritmy. 4. úloha - Experimentální hodnocení algoritmů pro řešení problému batohu
 ČVUT FEL X36PAA - Problémy a algoritmy 4. úloha - Experimentální hodnocení algoritmů pro řešení problému batohu Jméno: Marek Handl Datum: 3. 2. 29 Cvičení: Pondělí 9: Zadání Prozkoumejte citlivost metod
ČVUT FEL X36PAA - Problémy a algoritmy 4. úloha - Experimentální hodnocení algoritmů pro řešení problému batohu Jméno: Marek Handl Datum: 3. 2. 29 Cvičení: Pondělí 9: Zadání Prozkoumejte citlivost metod
TÉMATICKÝ OKRUH Softwarové inženýrství
 TÉMATICKÝ OKRUH Softwarové inženýrství Číslo otázky : 24. Otázka : Implementační fáze. Postupy při specifikaci organizace softwarových komponent pomocí UML. Mapování modelů na struktury programovacího
TÉMATICKÝ OKRUH Softwarové inženýrství Číslo otázky : 24. Otázka : Implementační fáze. Postupy při specifikaci organizace softwarových komponent pomocí UML. Mapování modelů na struktury programovacího
4. blok část A Logické operátory
 4. blok část A Logické operátory Studijní cíl Tento blok je věnován představení logických operátorů AND, OR, NOT v jazyce SQL a práce s nimi. Doba nutná k nastudování 1-2 hodiny Průvodce studiem Při studiu
4. blok část A Logické operátory Studijní cíl Tento blok je věnován představení logických operátorů AND, OR, NOT v jazyce SQL a práce s nimi. Doba nutná k nastudování 1-2 hodiny Průvodce studiem Při studiu
Časová a prostorová složitost algoritmů
 .. Časová a prostorová složitost algoritmů Programovací techniky doc. Ing. Jiří Rybička, Dr. ústav informatiky PEF MENDELU v Brně rybicka@mendelu.cz Hodnocení algoritmů Programovací techniky Časová a prostorová
.. Časová a prostorová složitost algoritmů Programovací techniky doc. Ing. Jiří Rybička, Dr. ústav informatiky PEF MENDELU v Brně rybicka@mendelu.cz Hodnocení algoritmů Programovací techniky Časová a prostorová
Složitost Filip Hlásek
 Složitost Filip Hlásek Abstrakt. Příspěvek popisuje dva základní koncepty teoretické informatiky, Turingovy stroje a složitost. Kromě definic důležitých pojmů uvádí také několik souvisejících tvrzení,
Složitost Filip Hlásek Abstrakt. Příspěvek popisuje dva základní koncepty teoretické informatiky, Turingovy stroje a složitost. Kromě definic důležitých pojmů uvádí také několik souvisejících tvrzení,
Odhady - Sdružené rozdělení pravděpodobnosti
 Odhady - Sdružené rozdělení pravděpodobnosti 4. listopadu 203 Kdybych chtěl znát maximum informací o náhodné veličině, musel bych znát všechny hodnoty, které mohou padnout, a jejich pravděpodobnosti. Tedy
Odhady - Sdružené rozdělení pravděpodobnosti 4. listopadu 203 Kdybych chtěl znát maximum informací o náhodné veličině, musel bych znát všechny hodnoty, které mohou padnout, a jejich pravděpodobnosti. Tedy
Kategorická data METODOLOGICKÝ PROSEMINÁŘ II TÝDEN 7 4. DUBNA dubna 2018 Lukáš Hájek, Karel Höfer Metodologický proseminář II 1
 Kategorická data METODOLOGICKÝ PROSEMINÁŘ II TÝDEN 7 4. DUBNA 2018 4. dubna 2018 Lukáš Hájek, Karel Höfer Metodologický proseminář II 1 Typy proměnných nominální (nominal) o dvou hodnotách lze říci pouze
Kategorická data METODOLOGICKÝ PROSEMINÁŘ II TÝDEN 7 4. DUBNA 2018 4. dubna 2018 Lukáš Hájek, Karel Höfer Metodologický proseminář II 1 Typy proměnných nominální (nominal) o dvou hodnotách lze říci pouze
1. Úvod do genetických algoritmů (GA)
 Obsah 1. Úvod do genetických algoritmů (GA)... 2 1.1 Základní informace... 2 1.2 Výstupy z učení... 2 1.3 Základní pomy genetických algoritmů... 2 1.3.1 Úvod... 2 1.3.2 Základní pomy... 2 1.3.3 Operátor
Obsah 1. Úvod do genetických algoritmů (GA)... 2 1.1 Základní informace... 2 1.2 Výstupy z učení... 2 1.3 Základní pomy genetických algoritmů... 2 1.3.1 Úvod... 2 1.3.2 Základní pomy... 2 1.3.3 Operátor
StatSoft Jak poznat vliv faktorů vizuálně
 StatSoft Jak poznat vliv faktorů vizuálně V tomto článku bychom se rádi věnovali otázce, jak poznat již z grafického náhledu vztahy a závislosti v analýze rozptylu. Pomocí následujících grafických zobrazení
StatSoft Jak poznat vliv faktorů vizuálně V tomto článku bychom se rádi věnovali otázce, jak poznat již z grafického náhledu vztahy a závislosti v analýze rozptylu. Pomocí následujících grafických zobrazení
Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6)
![Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6) Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6)](/thumbs/96/128965676.jpg) 1. Lineární diferenciální rovnice řádu n [MA1-18:P1.7] rovnice typu y n) + p n 1 )y n 1) +... + p 1 )y + p 0 )y = q) 6) počáteční podmínky: y 0 ) = y 0 y 0 ) = y 1 y n 1) 0 ) = y n 1. 7) Věta 1.3 : Necht
1. Lineární diferenciální rovnice řádu n [MA1-18:P1.7] rovnice typu y n) + p n 1 )y n 1) +... + p 1 )y + p 0 )y = q) 6) počáteční podmínky: y 0 ) = y 0 y 0 ) = y 1 y n 1) 0 ) = y n 1. 7) Věta 1.3 : Necht
Modely teorie grafů, min.kostra, max.tok, CPM, MPM, PERT
 PEF ČZU Modely teorie grafů, min.kostra, max.tok, CPM, MPM, PERT Okruhy SZB č. 5 Zdroje: Demel, J., Operační výzkum Jablonský J., Operační výzkum Šubrt, T., Langrová, P., Projektové řízení I. a různá internetová
PEF ČZU Modely teorie grafů, min.kostra, max.tok, CPM, MPM, PERT Okruhy SZB č. 5 Zdroje: Demel, J., Operační výzkum Jablonský J., Operační výzkum Šubrt, T., Langrová, P., Projektové řízení I. a různá internetová
Stavový model a Kalmanův filtr
 Stavový model a Kalmanův filtr 2 prosince 23 Stav je veličina, kterou neznáme, ale chtěli bychom znát Dozvídáme se o ní zprostředkovaně prostřednictvím výstupů Příkladem může býapř nějaký zašuměný signál,
Stavový model a Kalmanův filtr 2 prosince 23 Stav je veličina, kterou neznáme, ale chtěli bychom znát Dozvídáme se o ní zprostředkovaně prostřednictvím výstupů Příkladem může býapř nějaký zašuměný signál,
Náhodné (statistické) chyby přímých měření
 Náhodné (statistické) chyby přímých měření Hodnoty náhodných chyb se nedají stanovit předem, ale na základě počtu pravděpodobnosti lze zjistit, která z možných naměřených hodnot je více a která je méně
Náhodné (statistické) chyby přímých měření Hodnoty náhodných chyb se nedají stanovit předem, ale na základě počtu pravděpodobnosti lze zjistit, která z možných naměřených hodnot je více a která je méně
09. Memory management. ZOS 2006, L.Pešička
 09. Memory management ZOS 2006, L.Pešička Správa paměti paměťová pyramida absolutní adresa relativní adresa počet bytů od absolutní adresy fyzický prostor adres fyzicky k dispozici výpočetnímu systému
09. Memory management ZOS 2006, L.Pešička Správa paměti paměťová pyramida absolutní adresa relativní adresa počet bytů od absolutní adresy fyzický prostor adres fyzicky k dispozici výpočetnímu systému
Aplikace. vliv na to, jakou mají strukturu i na to, jak pracné je je vyvinout. Bylo vypozorováno, že aplikace je možné rozdělit do skupin
 Aplikace Aplikace se liší tím, k jakému účelu jsou tvořeny. To má vliv na to, jakou mají strukturu i na to, jak pracné je je vyvinout. Bylo vypozorováno, že aplikace je možné rozdělit do skupin s podobnou
Aplikace Aplikace se liší tím, k jakému účelu jsou tvořeny. To má vliv na to, jakou mají strukturu i na to, jak pracné je je vyvinout. Bylo vypozorováno, že aplikace je možné rozdělit do skupin s podobnou
3. Optimalizace pomocí nástroje Řešitel
 3. Optimalizace pomocí nástroje Řešitel Rovnováha mechanické soustavy Uvažujme dvě různé nehmotné lineární pružiny P 1 a P 2 připevněné na pevné horizontální tyči splývající s osou x podle obrázku: (0,0)
3. Optimalizace pomocí nástroje Řešitel Rovnováha mechanické soustavy Uvažujme dvě různé nehmotné lineární pružiny P 1 a P 2 připevněné na pevné horizontální tyči splývající s osou x podle obrázku: (0,0)
4EK213 LINEÁRNÍ MODELY
 4EK213 LINEÁRNÍ MODELY Úterý 11:00 12:30 hod. učebna SB 324 3. přednáška SIMPLEXOVÁ METODA I. OSNOVA PŘEDNÁŠKY Standardní tvar MM Základní věta LP Princip simplexové metody Výchozí řešení SM Zlepšení řešení
4EK213 LINEÁRNÍ MODELY Úterý 11:00 12:30 hod. učebna SB 324 3. přednáška SIMPLEXOVÁ METODA I. OSNOVA PŘEDNÁŠKY Standardní tvar MM Základní věta LP Princip simplexové metody Výchozí řešení SM Zlepšení řešení
SPECIFICKÝCH MIKROPROGRAMOVÝCH ARCHITEKTUR
 EVOLUČNÍ NÁVRH A OPTIMALIZACE APLIKAČNĚ SPECIFICKÝCH MIKROPROGRAMOVÝCH ARCHITEKTUR Miloš Minařík DVI4, 2. ročník, prezenční studium Školitel: Lukáš Sekanina Fakulta informačních technologií, Vysoké učení
EVOLUČNÍ NÁVRH A OPTIMALIZACE APLIKAČNĚ SPECIFICKÝCH MIKROPROGRAMOVÝCH ARCHITEKTUR Miloš Minařík DVI4, 2. ročník, prezenční studium Školitel: Lukáš Sekanina Fakulta informačních technologií, Vysoké učení
Čtvrtek 8. prosince. Pascal - opakování základů. Struktura programu:
 Čtvrtek 8 prosince Pascal - opakování základů Struktura programu: 1 hlavička obsahuje název programu, použité programové jednotky (knihovny), definice konstant, deklarace proměnných, všechny použité procedury
Čtvrtek 8 prosince Pascal - opakování základů Struktura programu: 1 hlavička obsahuje název programu, použité programové jednotky (knihovny), definice konstant, deklarace proměnných, všechny použité procedury
ALGORITMY A DATOVÉ STRUKTURY
 Název tématického celku: Cíl: ALGORITMY A DATOVÉ STRUKTURY Metodický list č. 1 Časová složitost algoritmů Základním cílem tohoto tematického celku je vysvětlení potřebných pojmů a definic nutných k popisu
Název tématického celku: Cíl: ALGORITMY A DATOVÉ STRUKTURY Metodický list č. 1 Časová složitost algoritmů Základním cílem tohoto tematického celku je vysvětlení potřebných pojmů a definic nutných k popisu
STATISTICKÝ SOUBOR. je množina sledovaných objektů - statistických jednotek, které mají z hlediska statistického zkoumání společné vlastnosti
 ZÁKLADNÍ STATISTICKÉ POJMY HROMADNÝ JEV Statistika pracuje s tzv. HROMADNÝMI JEVY cílem statistického zpracování dat je podání informace o vlastnostech a zákonitostech hromadných jevů: velkého počtu jedinců
ZÁKLADNÍ STATISTICKÉ POJMY HROMADNÝ JEV Statistika pracuje s tzv. HROMADNÝMI JEVY cílem statistického zpracování dat je podání informace o vlastnostech a zákonitostech hromadných jevů: velkého počtu jedinců
Dynamické programování
 Dynamické programování prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
Dynamické programování prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
Kombinatorická minimalizace
 Kombinatorická minimalizace Cílem je nalézt globální minimum ve velké diskrétní množině, kde může být mnoho lokálních minim. Úloha obchodního cestujícího Cílem je najít nejkratší cestu, která spojuje všechny
Kombinatorická minimalizace Cílem je nalézt globální minimum ve velké diskrétní množině, kde může být mnoho lokálních minim. Úloha obchodního cestujícího Cílem je najít nejkratší cestu, která spojuje všechny
Náhodné chyby přímých měření
 Náhodné chyby přímých měření Hodnoty náhodných chyb se nedají stanovit předem, ale na základě počtu pravděpodobnosti lze zjistit, která z možných naměřených hodnot je více a která je méně pravděpodobná.
Náhodné chyby přímých měření Hodnoty náhodných chyb se nedají stanovit předem, ale na základě počtu pravděpodobnosti lze zjistit, která z možných naměřených hodnot je více a která je méně pravděpodobná.
Náplň. v.0.03 16.02.2014. - Jednoduché příklady na práci s poli v C - Vlastnosti třídění - Způsoby (algoritmy) třídění
 Náplň v.0.03 16.02.2014 - Jednoduché příklady na práci s poli v C - Vlastnosti třídění - Způsoby (algoritmy) třídění Spojení dvou samostatně setříděných polí void Spoj(double apole1[], int adelka1, double
Náplň v.0.03 16.02.2014 - Jednoduché příklady na práci s poli v C - Vlastnosti třídění - Způsoby (algoritmy) třídění Spojení dvou samostatně setříděných polí void Spoj(double apole1[], int adelka1, double
Elegantní algoritmus pro konstrukci sufixových polí
 Elegantní algoritmus pro konstrukci sufixových polí 22.10.2014 Zadání Obsah Zadání... 3 Definice... 3 Analýza problému... 4 Jednotlivé algoritmy... 4 Algoritmus SA1... 4 Algoritmus SA2... 5 Algoritmus
Elegantní algoritmus pro konstrukci sufixových polí 22.10.2014 Zadání Obsah Zadání... 3 Definice... 3 Analýza problému... 4 Jednotlivé algoritmy... 4 Algoritmus SA1... 4 Algoritmus SA2... 5 Algoritmus
Laboratorní zdroj - 6. část
 Laboratorní zdroj - 6. část Publikované: 20.05.2016, Kategória: Silové časti www.svetelektro.com V tomto článku popíšu způsob, jak dojít k rovnicím (regresní funkce), které budou přepočítávat milivolty
Laboratorní zdroj - 6. část Publikované: 20.05.2016, Kategória: Silové časti www.svetelektro.com V tomto článku popíšu způsob, jak dojít k rovnicím (regresní funkce), které budou přepočítávat milivolty
Funkcionální programování. Kristýna Kaslová
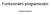 Funkcionální programování Kristýna Kaslová Historie Alonzo Church (30. léta) Netypovaný lambda kalkul Základ prvních funkcionálních jazyků Jeho konstrukce i v mnoha současných programovacích jazycích (Python)
Funkcionální programování Kristýna Kaslová Historie Alonzo Church (30. léta) Netypovaný lambda kalkul Základ prvních funkcionálních jazyků Jeho konstrukce i v mnoha současných programovacích jazycích (Python)
AVDAT Nelineární regresní model
 AVDAT Nelineární regresní model Josef Tvrdík Katedra informatiky Přírodovědecká fakulta Ostravská univerzita Nelineární regresní model Ey i = f (x i, β) kde x i je k-členný vektor vysvětlujících proměnných
AVDAT Nelineární regresní model Josef Tvrdík Katedra informatiky Přírodovědecká fakulta Ostravská univerzita Nelineární regresní model Ey i = f (x i, β) kde x i je k-členný vektor vysvětlujících proměnných
16. Goniometrické rovnice
 @198 16. Goniometrické rovnice Definice: Goniometrická rovnice je taková rovnice, ve které proměnná (neznámá) vystupuje pouze v goniometrických funkcích. Řešit goniometrické rovnice znamená nalézt všechny
@198 16. Goniometrické rovnice Definice: Goniometrická rovnice je taková rovnice, ve které proměnná (neznámá) vystupuje pouze v goniometrických funkcích. Řešit goniometrické rovnice znamená nalézt všechny
Státnice odborné č. 20
 Státnice odborné č. 20 Shlukování dat Shlukování dat. Metoda k-středů, hierarchické (aglomerativní) shlukování, Kohonenova mapa SOM Shlukování dat Shluková analýza je snaha o seskupení objektů do skupin
Státnice odborné č. 20 Shlukování dat Shlukování dat. Metoda k-středů, hierarchické (aglomerativní) shlukování, Kohonenova mapa SOM Shlukování dat Shluková analýza je snaha o seskupení objektů do skupin
Genetické algoritmy. a jejich praktické využití. Pavel Šturc. průmyslu, stejně tak je zde uvedeno i několik případů jejich úspěšné implementace.
 Genetické algoritmy a jejich praktické využití Pavel Šturc Úvod Cílem této práce je seznámit čtenáře se základním principem funkce genetických algoritmů a nastínit jejich možné aplikování do různých odvětví
Genetické algoritmy a jejich praktické využití Pavel Šturc Úvod Cílem této práce je seznámit čtenáře se základním principem funkce genetických algoritmů a nastínit jejich možné aplikování do různých odvětví
4a. Makra Visual Basic pro Microsoft Excel Cyklické odkazy a iterace Makra funkce a metody
 4a. Makra Visual Basic pro Microsoft Excel Cyklické odkazy a iterace Makra funkce a metody Vytvořil Institut biostatistiky a analýz, Masarykova univerzita J. Kalina Cyklické odkazy a iterativní výpočty
4a. Makra Visual Basic pro Microsoft Excel Cyklické odkazy a iterace Makra funkce a metody Vytvořil Institut biostatistiky a analýz, Masarykova univerzita J. Kalina Cyklické odkazy a iterativní výpočty
Tvar dat a nástroj přeskupování
 StatSoft Tvar dat a nástroj přeskupování Chtěli jste někdy použít data v jistém tvaru a STATISTICA Vám to nedovolila? Jistě se najde někdo, kdo se v této situaci již ocitl. Není ale potřeba propadat panice,
StatSoft Tvar dat a nástroj přeskupování Chtěli jste někdy použít data v jistém tvaru a STATISTICA Vám to nedovolila? Jistě se najde někdo, kdo se v této situaci již ocitl. Není ale potřeba propadat panice,
Unity a Objekty (NMIN102) RNDr. Michal Žemlička, Ph.D.
 Unity a Objekty Programování 2 (NMIN102) RNDr. Michal Žemlička, Ph.D. Větší programy Časté problémy: Ve více programech by se nám hodilo využít stejné řešení nějakého podproblému dalo by se vyřešit překopírováním
Unity a Objekty Programování 2 (NMIN102) RNDr. Michal Žemlička, Ph.D. Větší programy Časté problémy: Ve více programech by se nám hodilo využít stejné řešení nějakého podproblému dalo by se vyřešit překopírováním
Operační systémy. Jednoduché stránkování. Virtuální paměť. Příklad: jednoduché stránkování. Virtuální paměť se stránkování. Memory Management Unit
 Jednoduché stránkování Operační systémy Přednáška 8: Správa paměti II Hlavní paměť rozdělená na malé úseky stejné velikosti (např. 4kB) nazývané rámce (frames). Program rozdělen na malé úseky stejné velikosti
Jednoduché stránkování Operační systémy Přednáška 8: Správa paměti II Hlavní paměť rozdělená na malé úseky stejné velikosti (např. 4kB) nazývané rámce (frames). Program rozdělen na malé úseky stejné velikosti
- funkce, které integrujete aproximujte jejich Taylorovými řadami a ty následně zintegrujte. V obou případech vyzkoušejte Taylorovy řady
 Vzorové řešení domácího úkolu na 6. 1. 1. Integrály 1 1 x2 dx, ex2 dx spočítejte přibližně následují metodou - funkce, které integrujete aproximujte jejich Taylorovými řadami a ty následně zintegrujte.
Vzorové řešení domácího úkolu na 6. 1. 1. Integrály 1 1 x2 dx, ex2 dx spočítejte přibližně následují metodou - funkce, které integrujete aproximujte jejich Taylorovými řadami a ty následně zintegrujte.
Předpovídejte snadno a rychle
 Předpovídejte snadno a rychle Newsletter Statistica ACADEMY Téma: Časové řady, exponenciální vyrovnávání Typ článku: Příklad Dnes se budeme zabývat situací, kdy chceme předpovídat, jak se bude v čase vyvíjet
Předpovídejte snadno a rychle Newsletter Statistica ACADEMY Téma: Časové řady, exponenciální vyrovnávání Typ článku: Příklad Dnes se budeme zabývat situací, kdy chceme předpovídat, jak se bude v čase vyvíjet
13. Lineární procesy
 . Lineární procesy. Lineární procesy Našim cílem je studovat lineární (iterované) procesy. Každý takový proces je zadán čtvercovou maticí A Mat k k (R). Dále víme, že systém se v čase t n nachází ve stavu
. Lineární procesy. Lineární procesy Našim cílem je studovat lineární (iterované) procesy. Každý takový proces je zadán čtvercovou maticí A Mat k k (R). Dále víme, že systém se v čase t n nachází ve stavu
Multimediální prezentace MS PowerPoint I
 Multimediální prezentace MS PowerPoint I Informatika Multimediální prezentace zažívají v poslední době obrovský rozmach. Jsou používány například k reklamním účelům, k předvedení výrobků či služeb. Velmi
Multimediální prezentace MS PowerPoint I Informatika Multimediální prezentace zažívají v poslední době obrovský rozmach. Jsou používány například k reklamním účelům, k předvedení výrobků či služeb. Velmi
Programování 3. hodina. RNDr. Jan Lánský, Ph.D. Katedra informatiky a matematiky Fakulta ekonomických studií Vysoká škola finanční a správní 2015
 Programování 3. hodina RNDr. Jan Lánský, Ph.D. Katedra informatiky a matematiky Fakulta ekonomických studií Vysoká škola finanční a správní 2015 Umíme z minulé hodiny Implementace zásobníku a fronty pomocí
Programování 3. hodina RNDr. Jan Lánský, Ph.D. Katedra informatiky a matematiky Fakulta ekonomických studií Vysoká škola finanční a správní 2015 Umíme z minulé hodiny Implementace zásobníku a fronty pomocí
Relační DB struktury sloužící k optimalizaci dotazů - indexy, clustery, indexem organizované tabulky
 Otázka 20 A7B36DBS Zadání... 1 Slovníček pojmů... 1 Relační DB struktury sloužící k optimalizaci dotazů - indexy, clustery, indexem organizované tabulky... 1 Zadání Relační DB struktury sloužící k optimalizaci
Otázka 20 A7B36DBS Zadání... 1 Slovníček pojmů... 1 Relační DB struktury sloužící k optimalizaci dotazů - indexy, clustery, indexem organizované tabulky... 1 Zadání Relační DB struktury sloužící k optimalizaci
Reporting. Ukazatele je možno definovat nad libovolnou tabulkou Helios Orange, která je zapsána v nadstavbě firmy SAPERTA v souboru tabulek:
 Finanční analýza Pojem finanční analýza Finanční analýza umožňuje načítat data podle dimenzí a tyto součty dlouhodobě vyhodnocovat. Pojem finanční analýza není nejpřesnější, protože ukazatele mohou být
Finanční analýza Pojem finanční analýza Finanční analýza umožňuje načítat data podle dimenzí a tyto součty dlouhodobě vyhodnocovat. Pojem finanční analýza není nejpřesnější, protože ukazatele mohou být
Usuzování za neurčitosti
 Usuzování za neurčitosti 25.11.2014 8-1 Usuzování za neurčitosti Hypotetické usuzování a zpětná indukce Míry postačitelnosti a nezbytnosti Kombinace důkazů Šíření pravděpodobnosti v inferenčních sítích
Usuzování za neurčitosti 25.11.2014 8-1 Usuzování za neurčitosti Hypotetické usuzování a zpětná indukce Míry postačitelnosti a nezbytnosti Kombinace důkazů Šíření pravděpodobnosti v inferenčních sítích
3. úloha - problém batohu metodami branch & bound, dynamické programování, heuristika s testem
 ČVUT FEL X36PAA - Problémy a algoritmy 3. úloha - problém batohu metodami branch & bound, dynamické programování, heuristika s testem Jméno: Marek Handl Datum: 1. 1. 2009 Cvičení: Pondělí 9:00 Zadání Naprogramujte
ČVUT FEL X36PAA - Problémy a algoritmy 3. úloha - problém batohu metodami branch & bound, dynamické programování, heuristika s testem Jméno: Marek Handl Datum: 1. 1. 2009 Cvičení: Pondělí 9:00 Zadání Naprogramujte
5a. Makra Visual Basic pro Microsoft Escel. Vytvořil Institut biostatistiky a analýz, Masarykova univerzita J. Kalina
 5a. Makra Visual Basic pro Microsoft Escel Vytvořil Institut biostatistiky a analýz, Masarykova univerzita J. Kalina Cyklické odkazy a iterativní výpočty Zde bude stránka o cyklických odkazech a iteracích.
5a. Makra Visual Basic pro Microsoft Escel Vytvořil Institut biostatistiky a analýz, Masarykova univerzita J. Kalina Cyklické odkazy a iterativní výpočty Zde bude stránka o cyklických odkazech a iteracích.
