FRIKONOMIKON aneb frikulínské desatero o pětasedmdesáti bodech
|
|
|
- Michal Štěpánek
- před 9 lety
- Počet zobrazení:
Transkript
1 FRIKONOMIKON aneb frikulínské desatero o pětasedmdesáti bodech Co nevyluštíme, ukecáme a co neukecáme, uběháme. 1. První nápady a nejjednodušší postupy bývají často ty správné (viz. SUD [1], flašky [2]...). 2. Zkus odhadnout, ke kterému z následujících typů šifer by mohlo zadání patřit. Smysluplný text => steganografie, popis cesty nebo grafiky. Nesmyslný text => podle frekvenční analýzy buď substituce nebo transpozice. Heslo 3. Nemáš nějakého vhodného kandidáta na klíč? Zkus použít jako klíč/heslo názvev hry, název stanoviště, nápovědy z předchozího průběhu hry. 4. Proveď permutační vyčíslení klíče. Tj. přiřazení pořadí písmenům v klíči podle pořadí výskytu v abecedě. Může se to dále hodit při pokusech o transpozici. Základní počty 5. Není toho zhruba 26? => Abeceda. 6. Jsou tam 3 typy znaků? Mohla by to být nějaká forma morseovky, nebo římské číslice (I,V,X). 7. Jsou tam 2 typy znaků ve skupinách po nejvýše 5 znacích? Mohl by to být zápis v binární soustavě. 8. Jsou tam 2 typy znaků a 2x3 nějakých pozic/rastr? Mohlo by to být Braillovo písmo. 9. Není zadání rozděleno na 3(4) výrazné části? Nevyskytují se v něm 3(4) čísla? Není tam něco ve tvaru 3 prvky oddělovač 1 prvek? Pak by to mohla být kóta. 10. Není toho 12? Neobsahuje to nějakých prvků? => Kalendář měsíce, dny. 11. Nemá to velikost 8x8, nebo neobsahuje písmenka a-h a čísla 1-8? => Šachy. 12. Není tam něčeho 7/ 52? => Kalendář dny, týdny. 13. Není toho 12 nebo 24? Zkus hodiny/zobrazení na ciferníku hodin. 14. Nejsou tam 4(8) různé prvky? - navigace Nahoru, Dolů, Levo, Pravo, (S, SZ, SV, J, JZ, JV, V, Z) ve 2D a čtení/vykreslování v nějakém rastru. 15. Není tam něčeho 27? => kostka o rozměrech 3x3x3. 16 Není tam 6 různých prvků? - navigace Nahoru, Dolů, Levo, Pravo, Vpřed, Zpět ve 3D.
2 Substituce 17. Je tam zhruba 26 různých prvků? Zkus frekvenční analýzu a substituci. 18. Jsou tam běžné znaky abecedy, ale s divnými frekvencemi výskytu? Mohl by to být nějaký typ substituce: monoalfabetická šifra (Caesar) homofonní substituce nahrazení jednoho znaku více různými znaky polyalfabetická šifra (Vigenére) polygramová substituční šifra (Playfair) digrafická susbstituce (Polybiův čtverec) 19. Zkus posun hrubou silou všechny varianty. 20. Zkus posunout text podle nějakých zajímavých čísel vyskytujících se v zadání. 21. Čísla převeď na písmena/písmena převeď na čísla. Dál pracuj s výsledným textem. 22. Jsou tam nějaké dvojice znaků/čísel? Daly by se převést na desítková/šestnáctková čísla? Mohlo se jednat o ASCII kód intervaly s písmeny: velká /41 5A, malá /61 7A 23. Vyskytují se tam nepísmené znaky? Mohlo by jít o kód 1337 leetspeak využití nepísmenných znaků k vyjádření písmen. 24. Vyskytují se tam zlomky s malými čísly v čitateli i jmenovateli? Mohlo by jít o rozdělení abecedy na skupiny, ve zlomku by bylo zakódováno číslo skupiny a pořadí písmene v ní. 25. Zkus použít klávesnici mobilu/počítače/t9 využití znaků z klávesnice k jednoduché substituci (čísla->písmena, počet stisknutí->písmena...), nebo ke grafickému vykreslování znaků do rastru tvořeného klávesnicí. 26. Zkus vypsat vytipované heslo nad zašifrovaný text a provést následující algoritmus pro dešifrování polyalfabetických systémů: převeď písmena na čísla vyzkoušej pro každou dvojici heslo-šifrový text následující operace: systém šifrování dešifrování Vigenére O + K = Š Š K = O Varianta Beaufort O K = Š Š + K = O Beaufort K O = Š K Š = O if (a+b > 25) then return (a+b 25) else return (a+b) if (a-b < 0) then return (a-b + 25) else return (a-b) vrácené číslo převeď na písmeno 27. Vyskytují se v textu opakovaně dvojice pouze několika málo (5-6) písmen? Mohlo by se jednat o využití převodové tabulky s abecedou, kde by tato písmena tvořila souřadnice. (ADFGX, ADFGVX, MOTUX)
3 Transpozice 28. Zkus si zadání pořádně sepsat symetricky/pod sebe/vedle sebe a systematicky projdi jednotlivé sloupce, řádky a úhlopříčky, zda neobsahují další část šifry nebo řešení. 29. Zkus přečíst některé části zadání pozpátku, zepředu/zezadu. 30. Nebyl text rozdělen na poloviny/třetiny/čtvrtiny a potom nějakým způsobem prolnut/promíchán? 31. Není text zašifrován podle plotu lichá a sudá písmena na samostatných řádcích a řádky spojeny do jednoho? 32. Nedalo by se využít nějaké tabulky/obrazce/jiného rastru ve kterém by byl zapsán otevřený text? Šifrový text by byl vypsán po řádcích/sloupcích, případně složitějším způsobem spirálou, cikcak Nemohla by to být transpozice podle klíče? Můžeme zkusit provést následující algoritmus: - if máme kandidáta na klíč then provedem permutační vyčíslení a dešifrování textu else repeat určíme možné rozměry tabulky podle délky textu a možných dělitelů zkontrolujeme správnost tabulky if poměr samohlásky : souhlásky = 40 : 60 then rozstříháme sloupce a permutujeme s cílem nalézt vhodné bigramy a rozumné střídání souhlásek a samohlásek ve všech řádcích najednou 34. Nemohla by se využít Fleissnerova otočná mřížka? Nemáme k dispozici v zadání/jiných herních materiálech čtverec/mřížku, kde čtvrtinu políček tvoří otvory/označená místa? Pak můžeme zkusit otáčet mřížkou o 90 a číst ve vystřižených polích. 35. Nemohla by to být transpozice podle Roche? Máme k dispozici heslo. Určíme permutační vyčíslení. Vyznačíme posloupnost bloků příslušné délky. Do bloků vypíšeme zašifrovaný text. Z bloků postupně čteme otevřený text vždy první písmeno, po přečtení odmažeme. Steganografie 36. Zkus přečíst první/poslední/prostřední/sudá/lichá/x-tá... písmena/slova/věty z y-tých slov/vět/odstavců. 37. Zkus odpočítat písmena/slova v textu podle nějakých zajímavých čísel vyskytujících se v zadání. 38. Zkus v textu najít zajímavá písmena/znaky a číst písmena za nimi následující. Zajímavá jsou např. písmena kompletní abecedy, jinde získaného hesla, známé fráze (Máš IQ větší než 150?...), názvu hry, písmena nehodící se do okolního textu (méně frekventovaná fxwq, s diakritikou...). 39. Není součástí zadání nějaká mřížka s otvory? Nezískal jsi ji někde dříve? Případně nemáš k dispozici vhodný text (pravidla hry, text zadání, text hymny...), kam takovou mřížku přiložit? Mohla by to být Cardanova mřížka. 40. Děti, zazpíváme si! Kdo neumí, může recitovat... Nedá se v tom rozpoznat text známých písniček, básniček, hymny? A nějak se v textu dál navigovat, nebo vybírat písmena?
4 41. Když už nepomáhá nic, pomodli se ke správnýmu bohům (využití textu modliteb, náboženských textů Bible apod. k výběru písmen řešení) Grafika 42. Zkus metodu kouknu a vidím. 43. Nemohou být něco v zadání vyjádřené souřadnice nebo rastr? 44. Nedá se v zadání něco pospojovat? Posloupnost čísel, písmen, stejné prvky, doplnění nějakých logických řad Zkus si to prohlédnout proti světlu/prosvítit baterkou. 46. Zkus se na to podívat z jiného úhlu, případně zašilhat/zamhouřit oči. Mohl by to být stereogram, znetvořené písmo, řeky v textu, nějaké méně nápadné prvky vykreslující grafiku Zkus převést znaky na morseovku mohla by z toho vylézt grafika z teček, čárek a oddělovačů. 48. Nedá se to rozložit na víc vrstev nad sebou, tj. Do 3D? 49. Zkus to zobrazit na nějakém vhodném displeji/matrici/v digitálních číslech 50. Není to schéma/obrázek/fotka nějakého zajímavého místa/dalšího stanoviště? Není to plánek, nebo zjednodušená/zdeformovaná/zesložitěná mapa? 51. Není to graf? (Nedá se v něm nalézt nejkratší cesta, neljépe ohodnocená cesta, kořen, cesta mezi stejně/vzestupně/sestupně očíslovanými listy/uzly...? 52. Nedala by se část zadání překreslit na pauzák a vhodně přiložit/posunovat po originálním zadání? 53. Nejde to vhodně přeložit a následně prosvítít nebo probodnout špendlíkem? 54. Nejde z toho něco přímo vystříhat/poskládat/slepit? Nepomohlo by vystříhání při dalším kroku řešení? Další typy šifer 55. Není to popis cesty k další šifře? Není to popis cesty k nějakému místu v okolí/všeobecně známému místu, které by tě navedlo k dalšímu kroku řešení? 56. Zkus k zadání nalézt asociace/synonyma/antonyma. Dál pracuj s nimi. 57. Nelze v zadání vhodně doplnit nějaké řady? Číselné, písmenné, logické Pokud jsou v zadání prvky z kalendáře, nedaly by se využít jména svátků, státní svátky, znamení zvěrokruhu? 59. Nejsou v zadání nějaké noty, notová osnova (5 linek), stupnice, akordy? Nedala by se využít substituce za názvy not/akordů, případně nalézt odpovídající píseň a její text?
5 60. Zkus si v zadání zahrát karty neodpovídá něco počtu listů, očíslování/barvám/označení karet? 61. Zkus si v zadání zahrát šachy šachovnice (rozměry 8x8, označení 1-8, A-H), tahy figurek, označení figurek 62. Nepodobá se zadání nějaké jiné známé hře? Není to sudoku, patnáctka, sokoban, piškvorky...? Nedal by se pak průběh hry využít k vykreslení/přečtení/získání souřadnic řešení? 63. Nevyskytuje se tam několik opakujících se objektů a jejich vlastností? Není to Zebra (Einsteinova hádanka)? 64. Není v zadání něco napsaného neviditelným inkoustem? Zkus to zahřát nad plamenem/polít peroxidem nebo chemikálií získanou/doporučenou organizátory/prosvítít UV světlem/zářivkou. 65. Není v okolí nápověda v podobě nějakých zajímavých objektů (sud, cívka, vysílač...)/významných budov (radnice)/ulic/pamětihodností (pomíky, sochy (sv. Primitivus, ctnosti a neřesti...))? 66. Držíš se opravdu přesně instrukcí v zadání, případně v pravidlech hry? 67. Využil jsi už doporučenou mapu? Souřadnice GPS, zadní strana, legenda, mapové značky, označení čtverců Pro chvíle zoufalství Porozhlédni se kolem stanoviště nepřehlédl jsi nějakou důležitou indicii/organizátora/další části zadání/část šifry určenou pouze k obkreslení/prohlédnutí? 69. Opravdu využíváš všechny dostupné informace? Tedy vlastní zadání šifry/oficiální pravidla hry/poslední informace před hrou/informace a materály ze startovní obálky/ nezapomeňte z předchozích šifer/možnosti oficiální nápovědy? 70. Zkus zpětné inženýrství Aneb jak bys se ti mohlo podařit pravděpodobně jednoduchou zprávu, takhle blbě zašifrovat/zamaskovat/zdeformovat? 71. Prohlédni si na mapě dosavadní trasu, odhadni rozumnou vzdálenost, směr a oblasti a zkus vybrat sympatické místo, kam se dá rozumně dojít/dojet, které není nijak oplocené/chráněné/jinak nedostupné a nachází se u nějakého zajímavého/význačného bodu a zkus ho napasovat na zadání. 72. Když nevíš, najez se. 73. Když víš a máš hlad, předstírej, že nevíš, a nejdřív se najez ;). 74. Zkuste se projít kolem, zatancujte si, přesuňte se luštit někam jinam 75. Zkus využít pendrekovou kryptoanalýzu Jedná se o zisk klíče a dalších informací k používanému šifrovému systému, ale tentokrát se využívá vydírání, vyhrožování, mučení. [3] Ale pozor! Pravidla většiny her a zákony hostitelské země tuto sofistikovanou metodu luštění dost často neumožňují. Je potřeba se před startem hry řádně informovat, případně si zajistit dobrého právníka. A univerzální rada na závěr od Franty Vomáčky: Když nevíš, derivuj!
6 Zdroje [1] 10. šifra, Svíčky 2007 [2] 7. šifra, Osud 2008 [3] Pavel Vondruška Kryptologie, šifrování a tajná písma, Albatros, 2006
Kryptografie, elektronický podpis. Ing. Miloslav Hub, Ph.D. 27. listopadu 2007
 Kryptografie, elektronický podpis Ing. Miloslav Hub, Ph.D. 27. listopadu 2007 Kryptologie Kryptologie věda o šifrování, dělí se: Kryptografie nauka o metodách utajování smyslu zpráv převodem do podoby,
Kryptografie, elektronický podpis Ing. Miloslav Hub, Ph.D. 27. listopadu 2007 Kryptologie Kryptologie věda o šifrování, dělí se: Kryptografie nauka o metodách utajování smyslu zpráv převodem do podoby,
Šifrová ochrana informací historie KS4
 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 1 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací historie KS4 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 2 Osnova
VŠFS; Aplikovaná informatika; SW systémy 2005/2006 1 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací historie KS4 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 2 Osnova
P4 Ukecaný program InterLoS 2014
 P4 Ukecaný program Stáhněte si zdrojový kód P4-ukecany.c, zkopilujte jej pomocí kompilátoru jazyka C a spusťte. Program je psaný podle standartu C89, takže by měl jít zkompilovat libovolným C kompilátorem,
P4 Ukecaný program Stáhněte si zdrojový kód P4-ukecany.c, zkopilujte jej pomocí kompilátoru jazyka C a spusťte. Program je psaný podle standartu C89, takže by měl jít zkompilovat libovolným C kompilátorem,
Klasická kryptologie: Historické šifry
 Klasická kryptologie: Historické šifry L ubomíra Balková Úvod do kryptologie 18. únor 2010 L. Balková (ČVUT FJFI) Kryptologie 18. únor 2010 1 / 32 Obsah 1 Základní pojmy 2 Formální definice kryptosystému
Klasická kryptologie: Historické šifry L ubomíra Balková Úvod do kryptologie 18. únor 2010 L. Balková (ČVUT FJFI) Kryptologie 18. únor 2010 1 / 32 Obsah 1 Základní pojmy 2 Formální definice kryptosystému
Šifrová ochrana informací historie PS4
 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací historie PS4 1 Osnova úvod, definice pojmů; substituční šifry; transpoziční šifry; první prakticky používané šifrové systémy;
Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací historie PS4 1 Osnova úvod, definice pojmů; substituční šifry; transpoziční šifry; první prakticky používané šifrové systémy;
1. sada. 9. ročník. 101. Šifrovací tutoriál
 9. ročník 1. sada 101. Šifrovací tutoriál Protože se luštitelské zkušenosti týmů velmi liší, rozhodli jsme se na začátek letošního ročníku zařadit úlohu, při které si všichni zopakují základní šifrovací
9. ročník 1. sada 101. Šifrovací tutoriál Protože se luštitelské zkušenosti týmů velmi liší, rozhodli jsme se na začátek letošního ročníku zařadit úlohu, při které si všichni zopakují základní šifrovací
Matematické základy šifrování a kódování
 Matematické základy šifrování a kódování Permutace Pojem permutace patří mezi základní pojmy a nachází uplatnění v mnoha oblastech, např. kombinatorice, algebře apod. Definice Nechť je n-prvková množina.
Matematické základy šifrování a kódování Permutace Pojem permutace patří mezi základní pojmy a nachází uplatnění v mnoha oblastech, např. kombinatorice, algebře apod. Definice Nechť je n-prvková množina.
klasická kryptologie základní pojmy požadavky na kryptosystém typologie šifer transpoziční šifry substituční šifry
 klasická kryptologie transpoziční šifry substituční šifry základní pojmy požadavky na kryptosystém pravidla bezpečnosti silný kryptosystém typologie šifer bloková x proudová s tajným klíčem x s veřejným
klasická kryptologie transpoziční šifry substituční šifry základní pojmy požadavky na kryptosystém pravidla bezpečnosti silný kryptosystém typologie šifer bloková x proudová s tajným klíčem x s veřejným
MANUÁL. k šifrovací hře - 1 -
 MANUÁL k šifrovací hře - 1 - ÚVOD Tuto brožurku berte jako malý exkurz po šifrách. Jejich výčet zde není vyčerpávající a ani být nemůže šifry vznikají stále nové, stále nápaditější a složitější. Zde uvádíme
MANUÁL k šifrovací hře - 1 - ÚVOD Tuto brožurku berte jako malý exkurz po šifrách. Jejich výčet zde není vyčerpávající a ani být nemůže šifry vznikají stále nové, stále nápaditější a složitější. Zde uvádíme
12. ročník Řešení: 3. a 4. sada
 12. ročník Řešení: 3. a 4. sada 301. Padesáté zvíře V každém sloupci má 6 zvířat jednu společnou vlastnost, ale jedno zvíře ji nemá: 1. sloupec zvířata ze zvěrokruhu + krysa 2. sloupec jednoslabičná zvířata
12. ročník Řešení: 3. a 4. sada 301. Padesáté zvíře V každém sloupci má 6 zvířat jednu společnou vlastnost, ale jedno zvíře ji nemá: 1. sloupec zvířata ze zvěrokruhu + krysa 2. sloupec jednoslabičná zvířata
CO JE KRYPTOGRAFIE Šifrovací algoritmy Kódovací algoritmus Prolomení algoritmu
 KRYPTOGRAFIE CO JE KRYPTOGRAFIE Kryptografie je matematický vědní obor, který se zabývá šifrovacími a kódovacími algoritmy. Dělí se na dvě skupiny návrh kryptografických algoritmů a kryptoanalýzu, která
KRYPTOGRAFIE CO JE KRYPTOGRAFIE Kryptografie je matematický vědní obor, který se zabývá šifrovacími a kódovacími algoritmy. Dělí se na dvě skupiny návrh kryptografických algoritmů a kryptoanalýzu, která
Šifrová ochrana informací historie PS4
 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 1 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací historie PS4 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 2 Osnova
VŠFS; Aplikovaná informatika; SW systémy 2005/2006 1 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací historie PS4 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 2 Osnova
2000 zveřejnění dobové zprávy General Report on Tunny
 Luštění německého šifrovacího stroje Lorenz podle bakalářské práce Petra Veselého, MFF UK 25. února 2010 2000 zveřejnění dobové zprávy General Report on Tunny 2000 zveřejnění dobové zprávy General Report
Luštění německého šifrovacího stroje Lorenz podle bakalářské práce Petra Veselého, MFF UK 25. února 2010 2000 zveřejnění dobové zprávy General Report on Tunny 2000 zveřejnění dobové zprávy General Report
Klasická kryptologie: Historické šifry
 Klasická kryptologie: Historické šifry L ubomíra Balková Úvod do kryptologie 14. února 2011 L. Balková (ČVUT FJFI) Kryptologie 14. února 2011 1 / 32 Klasická kryptografie končí 2. světovou válkou a nástupem
Klasická kryptologie: Historické šifry L ubomíra Balková Úvod do kryptologie 14. února 2011 L. Balková (ČVUT FJFI) Kryptologie 14. února 2011 1 / 32 Klasická kryptografie končí 2. světovou válkou a nástupem
Celostátní kolo soutěže Baltík 2008, kategorie C
 Pokyny: 1. Pracujte pouze v ikonkových reţimech! 2. Řešení úloh ukládejte do sloţky, která se nachází na pracovní ploše počítače. Její název je stejný, jako je kód, který dostal váš tým přidělený (např.
Pokyny: 1. Pracujte pouze v ikonkových reţimech! 2. Řešení úloh ukládejte do sloţky, která se nachází na pracovní ploše počítače. Její název je stejný, jako je kód, který dostal váš tým přidělený (např.
Různé psaní zpráv. Hadovka. Sloupce. Šnek
 Psaní podle slovního klíče ejme tomu, že chceme zašifrovat "sraz všech v neděli ráno" za použití klíče "PH". Napíšeme zprávu takto : P H klíč 4 5 1 3 2 pořadí písmen v klíči podle abecedy S V zpráva S
Psaní podle slovního klíče ejme tomu, že chceme zašifrovat "sraz všech v neděli ráno" za použití klíče "PH". Napíšeme zprávu takto : P H klíč 4 5 1 3 2 pořadí písmen v klíči podle abecedy S V zpráva S
kryptosystémy obecně další zajímavé substituční šifry klíčové hospodářství kryptografická pravidla Hillova šifra Vernamova šifra Knižní šifra
 kryptosystémy obecně klíčové hospodářství klíč K, prostor klíčů T K kryptografická pravidla další zajímavé substituční šifry Hillova šifra Vernamova šifra Knižní šifra klíč K různě dlouhá posloupnost znaků
kryptosystémy obecně klíčové hospodářství klíč K, prostor klíčů T K kryptografická pravidla další zajímavé substituční šifry Hillova šifra Vernamova šifra Knižní šifra klíč K různě dlouhá posloupnost znaků
2000 zveřejnění dobové zprávy General Report on Tunny informací nedostatek k odvození konstrukce šifrátoru Lorenz cíl: odvození pravděpodobného
 Luštění německého šifrovacího stroje Lorenz podle bakalářské práce Petra Veselého, MFF UK 22. února 2012 2000 zveřejnění dobové zprávy General Report on Tunny informací nedostatek k odvození konstrukce
Luštění německého šifrovacího stroje Lorenz podle bakalářské práce Petra Veselého, MFF UK 22. února 2012 2000 zveřejnění dobové zprávy General Report on Tunny informací nedostatek k odvození konstrukce
Ukázkyaplikacímatematiky
 Ukázkyaplikacímatematiky Jiří Tůma 2015 http://www.karlin.mff.cuni.cz/ tuma/aplikace15.htm tuma@karlin.mff.cuni.cz 0-1 Kapitola1 Úvod do šifrování 1-1 Základní pojmy- obsah Základnípojmy Ceasarova šifra
Ukázkyaplikacímatematiky Jiří Tůma 2015 http://www.karlin.mff.cuni.cz/ tuma/aplikace15.htm tuma@karlin.mff.cuni.cz 0-1 Kapitola1 Úvod do šifrování 1-1 Základní pojmy- obsah Základnípojmy Ceasarova šifra
Ukázky aplikací matematiky. Kapitola 1. Jiří Tůma. Úvod do šifrování. Základní pojmy- obsah. Historie šifrování
 Ukázky aplikací matematiky Jiří Tůma 2015 http://www.karlin.mff.cuni.cz/ tuma/aplikace15.htm tuma@karlin.mff.cuni.cz Kapitola 1 0-1 1-1 Základní pojmy- obsah Historie šifrování Základnípojmy Ceasarova
Ukázky aplikací matematiky Jiří Tůma 2015 http://www.karlin.mff.cuni.cz/ tuma/aplikace15.htm tuma@karlin.mff.cuni.cz Kapitola 1 0-1 1-1 Základní pojmy- obsah Historie šifrování Základnípojmy Ceasarova
8. MČR v řešení sudoku, Brno, Přehled úloh
 . MČR v řešení sudoku, Brno,.-..0 Přehled úloh Na mistrovství se budou řešit zde uvedené typy úloh. V úlohách ve tvaru čtverce n n rozděleného na n oblastí platí standardní pravidla sudoku, tj. je potřeba
. MČR v řešení sudoku, Brno,.-..0 Přehled úloh Na mistrovství se budou řešit zde uvedené typy úloh. V úlohách ve tvaru čtverce n n rozděleného na n oblastí platí standardní pravidla sudoku, tj. je potřeba
20 b. 45 b. 25 b. 20 b. Kolo J Klasické S. 9. Klasické R. 8. Klasické Č. 7. Klasické M. 5 b. 10 b. 5 b. 5 b. 3. Klasické
 body: Soutěž jednotlivců b. Nepravidelné b b 0 b 0 b b 0 b b. Klasické Č. Klasické R 0. Klasické S. Klasické. Klasické 0. Klasické. Klasické Brno,. a. září 0 www.sudokualogika.cz logických her a sudoku
body: Soutěž jednotlivců b. Nepravidelné b b 0 b 0 b b 0 b b. Klasické Č. Klasické R 0. Klasické S. Klasické. Klasické 0. Klasické. Klasické Brno,. a. září 0 www.sudokualogika.cz logických her a sudoku
Aplikovaná informatika
 1 Aplikovaná informatika Cvičení - Opakování tématu 3 Řešení bezpečnostních incidentů PLUSKAL, D. SMETANA, B. Operační program Vzdělávání pro konkurenceschopnost Projekt: Vzdělávání pro bezpečnostní systém
1 Aplikovaná informatika Cvičení - Opakování tématu 3 Řešení bezpečnostních incidentů PLUSKAL, D. SMETANA, B. Operační program Vzdělávání pro konkurenceschopnost Projekt: Vzdělávání pro bezpečnostní systém
Monoalfabetické substituční šifry
 PEF MZLU v Brně 21. října 2010 Úvod Jeden z prvních popisů substituční šifry se objevuje v Kámasútře z 4. stol, vychází však z rukopisů o 800 let starších. Princip substitučních šifer spočívá v nahrazení
PEF MZLU v Brně 21. října 2010 Úvod Jeden z prvních popisů substituční šifry se objevuje v Kámasútře z 4. stol, vychází však z rukopisů o 800 let starších. Princip substitučních šifer spočívá v nahrazení
(a kryptografické odbočky) IB111 Úvod do programování skrze Python
 Řetězce a seznamy (a kryptografické odbočky) IB111 Úvod do programování skrze Python 2013 1 / 50 Rozcvička: šifry 1 C S A R B V E K T E O A 2 C S B U J T M B W B 3 A J L B N O C E 2 / 50 Transpoziční šifry
Řetězce a seznamy (a kryptografické odbočky) IB111 Úvod do programování skrze Python 2013 1 / 50 Rozcvička: šifry 1 C S A R B V E K T E O A 2 C S B U J T M B W B 3 A J L B N O C E 2 / 50 Transpoziční šifry
Booklet soutěže družstev
 tým: body: 11. mistrovství ČR v řešení sudoku Booklet soutěže družstev HALAS Hráčská asociace logických her a sudoku www.sudokualogika.cz Soutěž družstev Brno, 17. a 18. září 2016 Antidiagonální Každá
tým: body: 11. mistrovství ČR v řešení sudoku Booklet soutěže družstev HALAS Hráčská asociace logických her a sudoku www.sudokualogika.cz Soutěž družstev Brno, 17. a 18. září 2016 Antidiagonální Každá
klasická kryptologie základní pojmy požadavky na kryptosystém typologie šifer transpoziční šifry substituční šifry
 Květuše Sýkorová Květuše Sýkorová klasická kryptologie transpoziční šifry substituční šifry základní pojmy požadavky na kryptosystém pravidla bezpečnosti silný kryptosystém typologie šifer bloková x proudová
Květuše Sýkorová Květuše Sýkorová klasická kryptologie transpoziční šifry substituční šifry základní pojmy požadavky na kryptosystém pravidla bezpečnosti silný kryptosystém typologie šifer bloková x proudová
MANUÁL K LUŠTĚNÍ ŠIFER
 FHJŮMPŮDFJKEPDFMDMVCŮPJMFNONSLNCSLOCNSPCNPSDESLNVCSLPJMCVSDOP VNHOPWNFOWPFNCŮSPŮ MXP MXPS MXPCSKBCSOKBCSNCSCKCSDKJVNODVNOVM MANUÁL K FHJŮMPŮDFJKEPDFMDMVCŮPJMFNONDESVMDSVPDSMVSPCSPCMKSPYCMSPCYSP LUŠTĚNÍ
FHJŮMPŮDFJKEPDFMDMVCŮPJMFNONSLNCSLOCNSPCNPSDESLNVCSLPJMCVSDOP VNHOPWNFOWPFNCŮSPŮ MXP MXPS MXPCSKBCSOKBCSNCSCKCSDKJVNODVNOVM MANUÁL K FHJŮMPŮDFJKEPDFMDMVCŮPJMFNONDESVMDSVPDSMVSPCSPCMKSPYCMSPCYSP LUŠTĚNÍ
Zajímavosti z kryptologie
 chch Zajímavosti z kryptologie Vít Hrubý 22. 8. 2011 Kryptologie Hledání způsobu bezpečné komunikace, která by zajistila, že nikdo nepovolaný se ke zprávě nedostane Steganografie - ukrytí zprávy Kryptografie
chch Zajímavosti z kryptologie Vít Hrubý 22. 8. 2011 Kryptologie Hledání způsobu bezpečné komunikace, která by zajistila, že nikdo nepovolaný se ke zprávě nedostane Steganografie - ukrytí zprávy Kryptografie
Algebra - druhý díl. Lenka Zalabová. zima Ústav matematiky a biomatematiky, Přírodovědecká fakulta, Jihočeská univerzita
 Algebra - druhý díl Lenka Zalabová Ústav matematiky a biomatematiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích zima 2012 Obsah 1 Permutace 2 Grupa permutací 3 Více o permutacích
Algebra - druhý díl Lenka Zalabová Ústav matematiky a biomatematiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích zima 2012 Obsah 1 Permutace 2 Grupa permutací 3 Více o permutacích
Šifrovací kroužek, 2015 Pro potřeby žáků ZŠ Čerčany ŠIFROVACÍ KROUŽEK - 3. hodina
 ŠIFROVACÍ KROUŽEK - 3. hodina Substituční šifry: V šifrovaném textu jsou nahrazeny jednotlivé znaky jinými znaky, nebo symboly. Nejjednodušší (co se týče dešifrování) substituční šifry jsou monoalfabetické,
ŠIFROVACÍ KROUŽEK - 3. hodina Substituční šifry: V šifrovaném textu jsou nahrazeny jednotlivé znaky jinými znaky, nebo symboly. Nejjednodušší (co se týče dešifrování) substituční šifry jsou monoalfabetické,
Kódy a kódování dat. Binární (dvojkové) kódy. Kód Aikenův
 Kódy a kódování dat Kódování je proces, při kterém se každému znaku nebo postupnosti znaků daného souboru znaků jednoznačně přiřadí znak nebo postupnost znaků z jiného souboru znaků. Kódování je tedy transformace
Kódy a kódování dat Kódování je proces, při kterém se každému znaku nebo postupnosti znaků daného souboru znaků jednoznačně přiřadí znak nebo postupnost znaků z jiného souboru znaků. Kódování je tedy transformace
základní informace o kurzu základní pojmy literatura ukončení, požadavky, podmiňující předměty,
 základní informace o kurzu ukončení, požadavky, podmiňující předměty, základní pojmy kód x šifra kryptologie x steganografie kryptografie x kryptoanalyza literatura klasická x moderní kryptologie základní,
základní informace o kurzu ukončení, požadavky, podmiňující předměty, základní pojmy kód x šifra kryptologie x steganografie kryptografie x kryptoanalyza literatura klasická x moderní kryptologie základní,
11. ročník. Řešení: 3. a 4. sada
 11. ročník Řešení: 3. a 4. sada 301. Mřížka s tvary Pro informatiky: Hledáme Hamiltonovskou cestu v grafu, jehož vrcholy jsou písmena, která jsou spojena orientovanou hranou právě tehdy, když jejich manhatanovská
11. ročník Řešení: 3. a 4. sada 301. Mřížka s tvary Pro informatiky: Hledáme Hamiltonovskou cestu v grafu, jehož vrcholy jsou písmena, která jsou spojena orientovanou hranou právě tehdy, když jejich manhatanovská
Habermaaß-hra 4530. Terra Kids Země světa
 CZ Habermaaß-hra 4530 Terra Kids Země světa Terra kids Země světa Vzrušující poznávací hra pro 2-4 cestovatele ve věku od 8 do 99 let. Herní nápad: zaměstnanci Haba Ilustrace: Albert Kokai Délka hry: cca.
CZ Habermaaß-hra 4530 Terra Kids Země světa Terra kids Země světa Vzrušující poznávací hra pro 2-4 cestovatele ve věku od 8 do 99 let. Herní nápad: zaměstnanci Haba Ilustrace: Albert Kokai Délka hry: cca.
Šifry. Rozdělení šifer:
 Šifry Od té doby, kdy si lidé začali posílat důležité zprávy, snažili se jiní lidé tyto zprávy zachytit. Jednou z možností, jak ochránit své vzkazy před zvědavci bylo zajistit jim silný (pokud možno ozbrojený
Šifry Od té doby, kdy si lidé začali posílat důležité zprávy, snažili se jiní lidé tyto zprávy zachytit. Jednou z možností, jak ochránit své vzkazy před zvědavci bylo zajistit jim silný (pokud možno ozbrojený
Vánoční turnaj GP Praha 2012
 Vánoční turnaj GP Praha 0 konaný péčí HALAS o.s. dne. prosince 0 Jméno hráče: Pravidla obecná: Do každého políčka vepište jednu číslici -N podle velikosti tabulky není-li v zadání jinak zmíněno. Zadání
Vánoční turnaj GP Praha 0 konaný péčí HALAS o.s. dne. prosince 0 Jméno hráče: Pravidla obecná: Do každého políčka vepište jednu číslici -N podle velikosti tabulky není-li v zadání jinak zmíněno. Zadání
Téma 2 Principy kryptografie
 XXV/1/Téma 2 1 Téma 2 Principy kryptografie Substitučně-permutační sítě a AES V on-line světě každý den odešleme i přijmeme celou řadu šifrovaných zpráv. Obvykle se tak děje bez toho, abychom si to jakkoli
XXV/1/Téma 2 1 Téma 2 Principy kryptografie Substitučně-permutační sítě a AES V on-line světě každý den odešleme i přijmeme celou řadu šifrovaných zpráv. Obvykle se tak děje bez toho, abychom si to jakkoli
Zadání soutěžních úloh
 Zadání soutěžních úloh Kategorie žáci Soutěž v programování 24. ročník Krajské kolo 2009/2010 15. až 17. dubna 2010 Úlohy můžete řešit v libovolném pořadí a samozřejmě je nemusíte vyřešit všechny. Za každou
Zadání soutěžních úloh Kategorie žáci Soutěž v programování 24. ročník Krajské kolo 2009/2010 15. až 17. dubna 2010 Úlohy můžete řešit v libovolném pořadí a samozřejmě je nemusíte vyřešit všechny. Za každou
ŠIFRY. 1) Morseova abeceda
 ŠIFRY V následujícím textu je shrnuto několik základních typů šifer, které by měla vlčata znát před tím, než se stanou skauty. U skautů se pak naučí mnohým dalším šifrám. 1) Morseova abeceda Nejdůležitější
ŠIFRY V následujícím textu je shrnuto několik základních typů šifer, které by měla vlčata znát před tím, než se stanou skauty. U skautů se pak naučí mnohým dalším šifrám. 1) Morseova abeceda Nejdůležitější
CO UMÍ EXCEL? CVIČEBNICE PŘÍKLADŮ PRO UČITELE. Modulární systém dalšího vzdělávání pedagogických pracovníků JmK. v přírodních vědách a informatice
 Modulární systém dalšího vzdělávání pedagogických pracovníků JmK v přírodních vědách a informatice CZ.1.07/1.3.10/02.0024 CO UMÍ EXCEL? CVIČEBNICE PŘÍKLADŮ PRO UČITELE 1 Tabulkový kalkulátor představuje
Modulární systém dalšího vzdělávání pedagogických pracovníků JmK v přírodních vědách a informatice CZ.1.07/1.3.10/02.0024 CO UMÍ EXCEL? CVIČEBNICE PŘÍKLADŮ PRO UČITELE 1 Tabulkový kalkulátor představuje
Projdem Brodem A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
 Projdem Brodem Začátek: Havlíčkovo náměstí, Havlíčkův Brod Počet úkolů: 5 Délka: 1,5km Obtížnost: střední (s jasnou myslí by to neměl být problém) Nápovědy: Ano, dostupné na www.sifruj.cz. Heslo pro nápovědu
Projdem Brodem Začátek: Havlíčkovo náměstí, Havlíčkův Brod Počet úkolů: 5 Délka: 1,5km Obtížnost: střední (s jasnou myslí by to neměl být problém) Nápovědy: Ano, dostupné na www.sifruj.cz. Heslo pro nápovědu
Mistrovství České republiky v logických úlohách
 Mistrovství České republiky v logických úlohách Blok 1 - Logický mixer 10:00-11:40 Řešitel 1 Praha 013 Mrakodrapy 3 Heywake 4 Rybáři 5 Dvojblok Pentomina 7 Nádraží 8 Slalom 9 Plot 10 Kriskros 11 Cesta
Mistrovství České republiky v logických úlohách Blok 1 - Logický mixer 10:00-11:40 Řešitel 1 Praha 013 Mrakodrapy 3 Heywake 4 Rybáři 5 Dvojblok Pentomina 7 Nádraží 8 Slalom 9 Plot 10 Kriskros 11 Cesta
Školní kolo soutěže Baltík 2009, kategorie C
 Úloha 1 Sídliště Počet bodů: 40 b Pracujte v 3D režimu s Baltíkem. a) Bílý a šedivý Baltík si postaví šachovnici o rozměru 6x6 políček následujícím způsobem. Předměty SGP21.sgpm a SGP22.sgpm upravte na
Úloha 1 Sídliště Počet bodů: 40 b Pracujte v 3D režimu s Baltíkem. a) Bílý a šedivý Baltík si postaví šachovnici o rozměru 6x6 políček následujícím způsobem. Předměty SGP21.sgpm a SGP22.sgpm upravte na
CVIČNÝ TEST 15. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17
 CVIČNÝ TEST 15 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Je dána čtvercová mřížka, v níž každý čtverec má délku
CVIČNÝ TEST 15 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Je dána čtvercová mřížka, v níž každý čtverec má délku
Kolo 1. Mistrovství akademiků v řešení sudoku HALAS. Hráčská asociace logických her a sudoku
 jméno: body: Mistrovství akademiků v řešení sudoku Kolo. Klasické b. Klasické b. Klasické b. Klasické b. Klasické b. Klasické b 7. Klasické 9 9 b. Klasické 9 9 b 9. Sudé b 0. Liché b. Malá-střední-velká
jméno: body: Mistrovství akademiků v řešení sudoku Kolo. Klasické b. Klasické b. Klasické b. Klasické b. Klasické b. Klasické b 7. Klasické 9 9 b. Klasické 9 9 b 9. Sudé b 0. Liché b. Malá-střední-velká
Algoritmy I. Číselné soustavy přečíst!!! ALGI 2018/19
 Algoritmy I Číselné soustavy přečíst!!! Číselné soustavy Každé číslo lze zapsat v poziční číselné soustavě ve tvaru: a n *z n +a n-1 *z n-1 +. +a 1 *z 1 +a 0 *z 0 +a -1 *z n-1 +a -2 *z -2 +.. V dekadické
Algoritmy I Číselné soustavy přečíst!!! Číselné soustavy Každé číslo lze zapsat v poziční číselné soustavě ve tvaru: a n *z n +a n-1 *z n-1 +. +a 1 *z 1 +a 0 *z 0 +a -1 *z n-1 +a -2 *z -2 +.. V dekadické
Řešte s námi! Dlouhodobá soutěž v řešení sudoku a logických úloh TOP 10
 Řešte s námi! Dlouhodobá soutěž v řešení sudoku a logických úloh TOP 7 Nurikabe loop Zakreslete do obrazce několik ostrovů (stranově souvislých oblastí) tak, aby každý z nich obsahoval přesně jedno zadané
Řešte s námi! Dlouhodobá soutěž v řešení sudoku a logických úloh TOP 7 Nurikabe loop Zakreslete do obrazce několik ostrovů (stranově souvislých oblastí) tak, aby každý z nich obsahoval přesně jedno zadané
KL cm = mm U. ST cm = mm UV cm = mm XY cm = mm KL = mm mm PQ = mm mm ST = mm mm UV = mm mm XY = mm mm
 KARTA 19 ODHADY 1 1 a) Zkus uspořádat úsečky podle délky od nejkratší po nejdelší P T Y K L S X b) Odhadni délky čar v cm a převeď je na mm Q KL cm = mm U V PQ cm = mm c) Změř úsečky v mm O kolik mm se
KARTA 19 ODHADY 1 1 a) Zkus uspořádat úsečky podle délky od nejkratší po nejdelší P T Y K L S X b) Odhadni délky čar v cm a převeď je na mm Q KL cm = mm U V PQ cm = mm c) Změř úsečky v mm O kolik mm se
Kódováni dat. Kódy používané pro strojové operace
 Kódováni dat Před zpracováním dat například v počítači je třeba znaky převést do tvaru, kterému počítač rozumí, tj. přiřadit jim určité kombinace bitů. Tomuto převodu se říká kódování. Kód je předpis pro
Kódováni dat Před zpracováním dat například v počítači je třeba znaky převést do tvaru, kterému počítač rozumí, tj. přiřadit jim určité kombinace bitů. Tomuto převodu se říká kódování. Kód je předpis pro
Substituční šifry a frekvenční analýza. Mgr. Radim Janča ijanca@fit.vutbr.cz
 Substituční šifry a frekvenční analýza Mgr. Radim Janča ijanca@fit.vutbr.cz Harmonogram Celkově 4 cvičení v P256 Prezentace z cvičení budou zveřejňovány na http://buslab.fit.vutbr.cz/kib/ 3 samostatné
Substituční šifry a frekvenční analýza Mgr. Radim Janča ijanca@fit.vutbr.cz Harmonogram Celkově 4 cvičení v P256 Prezentace z cvičení budou zveřejňovány na http://buslab.fit.vutbr.cz/kib/ 3 samostatné
CODEWEEK 2014 Rozvoj algoritmického myšlení nejen pomocí programu MS Excel. Michaela Ševečková
 CODEWEEK 2014 Rozvoj algoritmického myšlení nejen pomocí programu MS Excel Michaela Ševečková Rozvoj technického myšlení nejmenších dětí práce s předměty charakteristika, diferenciace (hledání rozdílů),
CODEWEEK 2014 Rozvoj algoritmického myšlení nejen pomocí programu MS Excel Michaela Ševečková Rozvoj technického myšlení nejmenších dětí práce s předměty charakteristika, diferenciace (hledání rozdílů),
Polodokreslovka křížovka (časový limit 15 minut)
 Polodokreslovka křížovka (časový limit 15 minut) V obrazci nejsou vyznačené dělící linky mezi slovy. Je třeba je doplnit, přičemž rozmístění těchto linek v obrazci je symetrické. A B C D E F G H I 1 2
Polodokreslovka křížovka (časový limit 15 minut) V obrazci nejsou vyznačené dělící linky mezi slovy. Je třeba je doplnit, přičemž rozmístění těchto linek v obrazci je symetrické. A B C D E F G H I 1 2
ZŠ ÚnO, Bratří Čapků 1332
 Úvodní obrazovka Menu Návrat na hlavní stránku Obsah Výsledky Poznámky Záložky edunet Konec Matematika 1 (pro 9-12 let) LangMaster Obsah (střední část) výběr tématu - dvojklikem v seznamu témat (horní
Úvodní obrazovka Menu Návrat na hlavní stránku Obsah Výsledky Poznámky Záložky edunet Konec Matematika 1 (pro 9-12 let) LangMaster Obsah (střední část) výběr tématu - dvojklikem v seznamu témat (horní
A B C D E 2 F G H I J 3 K L M N O 4 P Q R S T 5 U/V W X Y Z
 ŠIFROVACÍ KROUŽEK - 4. hodina 1. Polybiův čtverec Polybios (cca 230 př.n.l. cca 120 př.n.l.) byl starověký řecký politik, historik, matematik a spisovatel. Polibiův čtverec je matice 5x5, do které vepíšeme
ŠIFROVACÍ KROUŽEK - 4. hodina 1. Polybiův čtverec Polybios (cca 230 př.n.l. cca 120 př.n.l.) byl starověký řecký politik, historik, matematik a spisovatel. Polibiův čtverec je matice 5x5, do které vepíšeme
MHD v mobilu. Instalace a spuštění. Co to umí
 MHD v mobilu Aplikace MHD v mobilu umí zobrazovat offline (bez nutnosti připojení) jízdní řády MHD na obrazovce mobilního telefonu. Aplikaci pro konkrétní město je možné stáhnout z našich stránek zdarma.
MHD v mobilu Aplikace MHD v mobilu umí zobrazovat offline (bez nutnosti připojení) jízdní řády MHD na obrazovce mobilního telefonu. Aplikaci pro konkrétní město je možné stáhnout z našich stránek zdarma.
. je zlomkem. Ten je smysluplný pro jakýkoli jmenovatel různý od nuly. Musí tedy platit = 0
 Příklad 1 Určete definiční obor funkce: a) = b) = c) = d) = e) = 9 f) = Řešení 1a Máme určit definiční obor funkce =. Výraz je zlomkem. Ten je smysluplný pro jakýkoli jmenovatel různý od nuly. Musí tedy
Příklad 1 Určete definiční obor funkce: a) = b) = c) = d) = e) = 9 f) = Řešení 1a Máme určit definiční obor funkce =. Výraz je zlomkem. Ten je smysluplný pro jakýkoli jmenovatel různý od nuly. Musí tedy
Úvod do kryptologie. Ing. Jan Přichystal, Ph.D. 12. listopadu 2008. PEF MZLU v Brně
 PEF MZLU v Brně 12. listopadu 2008 Úvod Od nepaměti lidé řeší problém: Jak předat zprávu tak, aby nikdo nežádoucí nezjistil její obsah? Dvě možnosti: ukrytí existence zprávy ukrytí smyslu zprávy S tím
PEF MZLU v Brně 12. listopadu 2008 Úvod Od nepaměti lidé řeší problém: Jak předat zprávu tak, aby nikdo nežádoucí nezjistil její obsah? Dvě možnosti: ukrytí existence zprávy ukrytí smyslu zprávy S tím
Fz =a z + a z +...+a z +a z =
 Polyadické číselné soustavy - převody M-místná skupina prvků se z-stavovou abecedou umožňuje zobrazit z m čísel. Zjistíme, že stačí vhodně zvolit číslo m, abychom mohli zobrazit libovolné číslo menší než
Polyadické číselné soustavy - převody M-místná skupina prvků se z-stavovou abecedou umožňuje zobrazit z m čísel. Zjistíme, že stačí vhodně zvolit číslo m, abychom mohli zobrazit libovolné číslo menší než
SOFTWAROVÁ PODPORA VÝUKY KLASICKÉ KRYPTOANALÝZY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV TELEKOMUNIKACÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF TELECOMMUNICATIONS
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV TELEKOMUNIKACÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF TELECOMMUNICATIONS
Modely teorie grafů, min.kostra, max.tok, CPM, MPM, PERT
 PEF ČZU Modely teorie grafů, min.kostra, max.tok, CPM, MPM, PERT Okruhy SZB č. 5 Zdroje: Demel, J., Operační výzkum Jablonský J., Operační výzkum Šubrt, T., Langrová, P., Projektové řízení I. a různá internetová
PEF ČZU Modely teorie grafů, min.kostra, max.tok, CPM, MPM, PERT Okruhy SZB č. 5 Zdroje: Demel, J., Operační výzkum Jablonský J., Operační výzkum Šubrt, T., Langrová, P., Projektové řízení I. a různá internetová
CVIČNÝ TEST 35. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17
 CVIČNÝ TEST 35 Mgr. Tomáš Kotler OBSAH I. Cvičný test II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST 1 Vypočtěte [( 3 3 ) ( 1 4 5 3 0,5 ) ] : 1 6 1. 1 bod VÝCHOZÍ TEXT K ÚLOZE
CVIČNÝ TEST 35 Mgr. Tomáš Kotler OBSAH I. Cvičný test II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST 1 Vypočtěte [( 3 3 ) ( 1 4 5 3 0,5 ) ] : 1 6 1. 1 bod VÝCHOZÍ TEXT K ÚLOZE
(a kryptografické odbočky) IB111 Úvod do programování skrze Python
 Řetězce a seznamy (a kryptografické odbočky) IB111 Úvod do programování skrze Python 2014 1 / 56 Rozcvička: šifry 1 C S A R B V E K T E O A 2 A J L B N O C E 3 C S B U J T M B W B 2 / 56 Transpoziční šifry
Řetězce a seznamy (a kryptografické odbočky) IB111 Úvod do programování skrze Python 2014 1 / 56 Rozcvička: šifry 1 C S A R B V E K T E O A 2 A J L B N O C E 3 C S B U J T M B W B 2 / 56 Transpoziční šifry
kryptoanalýza druhy útoků proti klasickým šifrám příklad útok hrubou silou frekvenční analýza Kasiskiho metoda index koincidence Jakobsenův algoritmus
 kryptoanalýza druhy útoků proti klasickým šifrám usnadnění útoku útok hrubou silou slovníkový, hybridní frekvenční analýza metoda ad hoc Kasiskiho metoda index koincidence přirozený jazyk struktura Jakobsenův
kryptoanalýza druhy útoků proti klasickým šifrám usnadnění útoku útok hrubou silou slovníkový, hybridní frekvenční analýza metoda ad hoc Kasiskiho metoda index koincidence přirozený jazyk struktura Jakobsenův
Zpracování seminární práce. AD7B32KBE semestrální práce
 Zpracování seminární práce AD7B32KBE semestrální práce ČVUT FEL obor STM-Softwarové inženýrství, kombinované studium 4. semestr Radek Horáček Úloha 1: Metoda: prostý posun Zadání: WUEHWUQHHYLYDWCQTUJXUIULUDJXQDTCQDOEVJXUSXQCFYEDIXQTMYJXJXUCJXUVQYHBQTYUIJX
Zpracování seminární práce AD7B32KBE semestrální práce ČVUT FEL obor STM-Softwarové inženýrství, kombinované studium 4. semestr Radek Horáček Úloha 1: Metoda: prostý posun Zadání: WUEHWUQHHYLYDWCQTUJXUIULUDJXQDTCQDOEVJXUSXQCFYEDIXQTMYJXJXUCJXUVQYHBQTYUIJX
Varianta: 1201 TEST STUDIJNÍCH PŘEDPOKLADŮ 4 strany 1. strana INSTRUKCE
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA PODNIKATELSKÁ Přijímací řízení 2016 Bakalářský studijní program: Systémové inženýrství a informatika VYPLNÍ UCHAZEČ: Kódové číslo Datum narození ZÁZNAM ZKUŠEBNÍ KOMISE
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA PODNIKATELSKÁ Přijímací řízení 2016 Bakalářský studijní program: Systémové inženýrství a informatika VYPLNÍ UCHAZEČ: Kódové číslo Datum narození ZÁZNAM ZKUŠEBNÍ KOMISE
Kódování a Šifrování. Iveta Nastoupilová
 Kódování a Šifrování Iveta Nastoupilová 12.11.2007 Kódování Přeměna, transformace, šifrování signálů Převádění informace z jednoho systému do jiného systému znaků Kódování Úzce souvisí s procesem komunikace
Kódování a Šifrování Iveta Nastoupilová 12.11.2007 Kódování Přeměna, transformace, šifrování signálů Převádění informace z jednoho systému do jiného systému znaků Kódování Úzce souvisí s procesem komunikace
Modulární systém dalšího vzdělávání pedagogických pracovníků JmK. v přírodních vědách a informatice CZ.1.07/1.3.10/
 Modulární systém dalšího vzdělávání pedagogických pracovníků JmK v přírodních vědách a informatice CZ.1.07/1.3.10/02.0024 Teorie grafů Sbírka cvičení Domečkologie Zkuste nakreslit domečky na obrázku. Které
Modulární systém dalšího vzdělávání pedagogických pracovníků JmK v přírodních vědách a informatice CZ.1.07/1.3.10/02.0024 Teorie grafů Sbírka cvičení Domečkologie Zkuste nakreslit domečky na obrázku. Které
10. ročník. Řešení 1. a 2. sada
 101. Vaši organizátoři 10. ročník Řešení 1. a 2. sada Název šifry a umístění úlohy jako 1. úloha jubilejního 10. ročníku navádí k tomu, že šifra je o organizátorech Sendviče. Pokud náhodou neumíte odříkat
101. Vaši organizátoři 10. ročník Řešení 1. a 2. sada Název šifry a umístění úlohy jako 1. úloha jubilejního 10. ročníku navádí k tomu, že šifra je o organizátorech Sendviče. Pokud náhodou neumíte odříkat
P1 Formule ve sněhu. P2 Double Cola
 P1 Formule ve sněhu Jak je obecně známo, losi mají spoustu různých zálib. Není tedy velkým překvapením, že existují losi, kteří se vyžívají v matematických prapodivnostech. Jeden takový los přišel s následující
P1 Formule ve sněhu Jak je obecně známo, losi mají spoustu různých zálib. Není tedy velkým překvapením, že existují losi, kteří se vyžívají v matematických prapodivnostech. Jeden takový los přišel s následující
jsme se spustili do nádherného dómu (obr. A2, E5, H2), s mnohou excentrickou výzdobou na stěnách = ŽALUDEK
 301. Z deníku prof. Absolona Text je sice zdánlivě stylizován jako speleologické zápisky (všechny jmenované postavy skutečně existovaly), jedná se však o metaforický popis trávicí soustavy - od dutiny
301. Z deníku prof. Absolona Text je sice zdánlivě stylizován jako speleologické zápisky (všechny jmenované postavy skutečně existovaly), jedná se však o metaforický popis trávicí soustavy - od dutiny
Zadání soutěžních úloh
 Zadání soutěžních úloh Kategorie žáci Soutěž v programování 25. ročník Krajské kolo 2010/2011 15. až 16. dubna 2011 Úlohy můžete řešit v libovolném pořadí a samozřejmě je nemusíte vyřešit všechny. Za každou
Zadání soutěžních úloh Kategorie žáci Soutěž v programování 25. ročník Krajské kolo 2010/2011 15. až 16. dubna 2011 Úlohy můžete řešit v libovolném pořadí a samozřejmě je nemusíte vyřešit všechny. Za každou
Magické čtverce. Bára Kociánová
 Magické čtverce Bára Kociánová Abstrakt. Příspěvek se zabývá magickými čtverci, které patří spíše do rekreační matematiky. Popisuje jejich základní vlastnosti, uvádí zajímavosti z historie a na závěr podává
Magické čtverce Bára Kociánová Abstrakt. Příspěvek se zabývá magickými čtverci, které patří spíše do rekreační matematiky. Popisuje jejich základní vlastnosti, uvádí zajímavosti z historie a na závěr podává
STRUKTURA RASTROVÝCH DAT
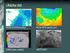 STRUKTURA RASTROVÝCH DAT dva typy rastrové vrstvy v GIS 1) Digitální obraz TV, počítač, mobil - obrazovka obraz z bodů mapa - mřížka s barevnými plochami 2) Rastrová data data pro analýzu a) binární -
STRUKTURA RASTROVÝCH DAT dva typy rastrové vrstvy v GIS 1) Digitální obraz TV, počítač, mobil - obrazovka obraz z bodů mapa - mřížka s barevnými plochami 2) Rastrová data data pro analýzu a) binární -
m.1.2. v prohlížeči vyhledat velikost katastrálního území a porovnat Jazyková komunikace ČESKÝ JAZYK 1. stupeň 1. období skládání slov, čtení textu
 Souhrnný 101 Ročník: 1 Matematika a její aplikace MATEMATIKA porovnávání čísel do 20, sčítání a odčítání do 20 M m.1.1. seřadit názvy vesnic podle velikosti území, odpovědět na otázky. Mapa se po kliknutí
Souhrnný 101 Ročník: 1 Matematika a její aplikace MATEMATIKA porovnávání čísel do 20, sčítání a odčítání do 20 M m.1.1. seřadit názvy vesnic podle velikosti území, odpovědět na otázky. Mapa se po kliknutí
Zadání soutěžních úloh
 19. až 21. dubna 2018 Krajské kolo 2017/2018 Úlohy můžete řešit v libovolném pořadí a samozřejmě je nemusíte vyřešit všechny. Za každou úlohu můžete dostat maximálně 10 bodů, z nichž je většinou 9 bodů
19. až 21. dubna 2018 Krajské kolo 2017/2018 Úlohy můžete řešit v libovolném pořadí a samozřejmě je nemusíte vyřešit všechny. Za každou úlohu můžete dostat maximálně 10 bodů, z nichž je většinou 9 bodů
Chytrý medvěd učí počítat
 CZ Habermaaß-hra 3151A /4547N Chytrý medvěd učí počítat Medvědí kolekce vzdělávacích her pro 2 až 5 hráčů ve věku od 4 do 8 let. S navlékacím počítadlem Chytrého medvěda a třemi extra velkými kostkami.
CZ Habermaaß-hra 3151A /4547N Chytrý medvěd učí počítat Medvědí kolekce vzdělávacích her pro 2 až 5 hráčů ve věku od 4 do 8 let. S navlékacím počítadlem Chytrého medvěda a třemi extra velkými kostkami.
Micro:bit lekce 3. - Konstrukci If Then a If Then Else najdete v kategorii Logic - Podmínky od If (např. porovnání < >= atd.) najdete taktéž v Logic
 Micro:bit lekce 3. Podmínky - Rozvětvení běhu programu podle splnění nějakých podmínek typu pravda / nepravda - splněno / nesplněno (výsledkem podmínky musí být vždy jen dvě možnosti) - Dva typy podmínek:
Micro:bit lekce 3. Podmínky - Rozvětvení běhu programu podle splnění nějakých podmínek typu pravda / nepravda - splněno / nesplněno (výsledkem podmínky musí být vždy jen dvě možnosti) - Dva typy podmínek:
2.4.9 Rovnice s absolutní hodnotou I
 ..9 Rovnice s absolutní hodnotou I Předpoklady: 0, 0, 05 Pedagogická poznámka: Obsah hodiny odpovídá přibližně 5 minutám. Je samozřejmě možné ji spojit s následující hodinou, pak ovšem část příkladů nestihnete
..9 Rovnice s absolutní hodnotou I Předpoklady: 0, 0, 05 Pedagogická poznámka: Obsah hodiny odpovídá přibližně 5 minutám. Je samozřejmě možné ji spojit s následující hodinou, pak ovšem část příkladů nestihnete
Základní škola Fr. Kupky, ul. Fr. Kupky 350, 518 01 Dobruška 5.2 MATEMATIKA A JEJÍ APLIKACE - 5.2.1 MATEMATIKA A JEJÍ APLIKACE Matematika 6.
 5.2 MATEMATIKA A JEJÍ APLIKACE 5.2.1 MATEMATIKA A JEJÍ APLIKACE Matematika 6. ročník RVP ZV Obsah RVP ZV Kód RVP ZV Očekávané výstupy ŠVP Školní očekávané výstupy ŠVP Učivo ČÍSLO A PROMĚNNÁ M9101 provádí
5.2 MATEMATIKA A JEJÍ APLIKACE 5.2.1 MATEMATIKA A JEJÍ APLIKACE Matematika 6. ročník RVP ZV Obsah RVP ZV Kód RVP ZV Očekávané výstupy ŠVP Školní očekávané výstupy ŠVP Učivo ČÍSLO A PROMĚNNÁ M9101 provádí
Práce s MS Excel v Portálu farmáře a využití pro stažení dat KN z LPIS a sestav z EPH
 Práce s MS Excel v Portálu farmáře a využití pro stažení dat KN z LPIS a sestav z EPH Leden 2012 1. Přehled sestav MS Excel v Portálu farmáře Registr půdy (LPIS) a Data ke stažení LPIS umožňuje na záložce
Práce s MS Excel v Portálu farmáře a využití pro stažení dat KN z LPIS a sestav z EPH Leden 2012 1. Přehled sestav MS Excel v Portálu farmáře Registr půdy (LPIS) a Data ke stažení LPIS umožňuje na záložce
2. Svoje řešení pojmenujte podle čísel zadání úloh: uloha1.sgpbprj uloha4.sgpbprj
 Pokyny: 1. Řešení úloh ukládejte do složky, která se nachází na pracovní ploše počítače. Její název je stejný, jako je kód, který váš tým dostal přidělený (C05, C10 apod.). Řešení, uložené v jiné složce,
Pokyny: 1. Řešení úloh ukládejte do složky, která se nachází na pracovní ploše počítače. Její název je stejný, jako je kód, který váš tým dostal přidělený (C05, C10 apod.). Řešení, uložené v jiné složce,
Třídy složitosti P a NP, NP-úplnost
 Třídy složitosti P a NP, NP-úplnost Cíle přednášky: 1. Definovat, za jakých okolností můžeme problém považovat za efektivně algoritmicky řešitelný. 2. Charakterizovat určitou skupinu úloh, pro které není
Třídy složitosti P a NP, NP-úplnost Cíle přednášky: 1. Definovat, za jakých okolností můžeme problém považovat za efektivně algoritmicky řešitelný. 2. Charakterizovat určitou skupinu úloh, pro které není
Základy šifrování a kódování
 Materiál byl vytvořen v rámci projektu Nové výzvy, nové příležitosti, nová škola Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky Základy šifrování a kódování
Materiál byl vytvořen v rámci projektu Nové výzvy, nové příležitosti, nová škola Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky Základy šifrování a kódování
Měsíc: učivo:. PROSINEC Numerace do 7, rozklad čísla 1 7. Sčítání a odčítání v oboru do 7, slovní úlohy.
 Předmět: MATEMATIKA Ročník: PRVNÍ Měsíc: učivo:. ZÁŘÍ Úvod k učivu o přirozeném čísle. Numerace do 5, čtení čísel 0-5. Vytváření souborů o daném počtu předmětů. Znaménka méně, více, rovná se, porovnávání
Předmět: MATEMATIKA Ročník: PRVNÍ Měsíc: učivo:. ZÁŘÍ Úvod k učivu o přirozeném čísle. Numerace do 5, čtení čísel 0-5. Vytváření souborů o daném počtu předmětů. Znaménka méně, více, rovná se, porovnávání
ZLOMKY A RACIONÁLNÍ ČÍSLA. Pojem zlomku. Zlomek zápis části celku. a b. a je část, b je celek, zlomková čára
 9... ZLOMKY A RACIONÁLNÍ ČÍSLA Pojem zlomku Zlomek zápis části celku a b a je část, b je celek, zlomková čára Každé číslo zapsané zlomkem lze vyjádřit jako číslo desetinné 7 Zlomková čára je dělící čára
9... ZLOMKY A RACIONÁLNÍ ČÍSLA Pojem zlomku Zlomek zápis části celku a b a je část, b je celek, zlomková čára Každé číslo zapsané zlomkem lze vyjádřit jako číslo desetinné 7 Zlomková čára je dělící čára
P7 Počítání vodíků CH3 C=CH-OH CH3. Příklad: CC(CC(C)O)=C je: CH3 CH3 C-CH-CH-OH CH3. jednoduše považujte c za zvláštní druh atomu.
 P7 Počítání vodíků V této úloze bude vaším úkolem spočítat počet vodíků v organické molekule. Molekuly dostanete zadané ve formátu SMILES, který vodíky neuvádí, nýbrž jsou doplněny podle jistých pravidel.
P7 Počítání vodíků V této úloze bude vaším úkolem spočítat počet vodíků v organické molekule. Molekuly dostanete zadané ve formátu SMILES, který vodíky neuvádí, nýbrž jsou doplněny podle jistých pravidel.
Informatika / bezpečnost
 Informatika / bezpečnost Bezpečnost, šifry, elektronický podpis ZS 2015 KIT.PEF.CZU Bezpečnost IS pojmy aktiva IS hardware software data citlivá data hlavně ta chceme chránit autorizace subjekt má právo
Informatika / bezpečnost Bezpečnost, šifry, elektronický podpis ZS 2015 KIT.PEF.CZU Bezpečnost IS pojmy aktiva IS hardware software data citlivá data hlavně ta chceme chránit autorizace subjekt má právo
1.5.1 Číselné soustavy
 .. Číselné soustavy Předpoklady: základní početní operace Pedagogická poznámka: Tato hodina není součástí klasické gymnaziální sady. Upřímně řečeno nevím proč. Jednak se všichni studenti určitě setkávají
.. Číselné soustavy Předpoklady: základní početní operace Pedagogická poznámka: Tato hodina není součástí klasické gymnaziální sady. Upřímně řečeno nevím proč. Jednak se všichni studenti určitě setkávají
Lekce 01 Úvod do algoritmizace
 Počítačové laboratoře bez tajemství aneb naučme se učit algoritmizaci a programování s využitím robotů Lekce 01 Úvod do algoritmizace Tento projekt CZ.1.07/1.3.12/04.0006 je spolufinancován Evropským sociálním
Počítačové laboratoře bez tajemství aneb naučme se učit algoritmizaci a programování s využitím robotů Lekce 01 Úvod do algoritmizace Tento projekt CZ.1.07/1.3.12/04.0006 je spolufinancován Evropským sociálním
Aplikovaná informatika Bezpečné přenášení, ukládání a archivace dat. ZEMÁNEK, Z. - PLUSKAL,D. - SMETANA, B.
 Aplikovaná informatika Bezpečné přenášení, ukládání a archivace dat. ZEMÁNEK, Z. - PLUSKAL,D. - SMETANA, B. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního
Aplikovaná informatika Bezpečné přenášení, ukládání a archivace dat. ZEMÁNEK, Z. - PLUSKAL,D. - SMETANA, B. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního
NPRG030 Programování I RNDr.Tomáš Holan, Ph.D. 4.patro, č
 NPRG030 Programování I RNDr.Tomáš Holan, Ph.D. 4.patro, č.404 http://ksvi.mff.cuni.cz/~holan/ Tomas.Holan@mff.cuni.cz NPRG030 Programování I, 2014/15 1 / 37 6. 10. 2014 11:42:59 NPRG030 Programování I,
NPRG030 Programování I RNDr.Tomáš Holan, Ph.D. 4.patro, č.404 http://ksvi.mff.cuni.cz/~holan/ Tomas.Holan@mff.cuni.cz NPRG030 Programování I, 2014/15 1 / 37 6. 10. 2014 11:42:59 NPRG030 Programování I,
Habermaaß-hra 4935. Magie stínů
 CZ Habermaaß-hra 4935 Magie stínů Magie stínů Magická stínová hra pro 2 až 4 hráče ve věku od 4 do 99 let. Autor: Kai Haferkamp Ilustrace: Marc Robitzky Délka hry: cca. 15 až 20 minut Obsah: 4 malé kouzelné
CZ Habermaaß-hra 4935 Magie stínů Magie stínů Magická stínová hra pro 2 až 4 hráče ve věku od 4 do 99 let. Autor: Kai Haferkamp Ilustrace: Marc Robitzky Délka hry: cca. 15 až 20 minut Obsah: 4 malé kouzelné
Zpracování chybějících dat a dat mimo rozsah
 StatSoft Zpracování chybějících dat a dat mimo rozsah V tomto článku si představíme jeden z možných postupů, jak se rychle a snadno vypořádat s detekcí chybějících dat a dat mimo stanovený rozsah. Načtení
StatSoft Zpracování chybějících dat a dat mimo rozsah V tomto článku si představíme jeden z možných postupů, jak se rychle a snadno vypořádat s detekcí chybějících dat a dat mimo stanovený rozsah. Načtení
CVIČNÝ TEST 37. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15
 CVIČNÝ TEST 37 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Na staré hliněné desce je namalován čtverec
CVIČNÝ TEST 37 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Na staré hliněné desce je namalován čtverec
2.4.9 Rovnice s absolutní hodnotou I
 ..9 Rovnice s absolutní hodnotou I Předpoklady: 0, 0, 05 Pedagogická poznámka: Obsah hodiny odpovídá přibližně 5 minutám. Je samozřejmě možné ji spojit s následující hodinou, pak ovšem část příkladů nestihnete
..9 Rovnice s absolutní hodnotou I Předpoklady: 0, 0, 05 Pedagogická poznámka: Obsah hodiny odpovídá přibližně 5 minutám. Je samozřejmě možné ji spojit s následující hodinou, pak ovšem část příkladů nestihnete
Úvod do Matlabu. Praha & EU: Investujeme do vaší budoucnosti. 1 / 24 Úvod do Matlabu
 Vytěžování dat, cvičení 1: Úvod do Matlabu Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Fakulta elektrotechnická, ČVUT 1 / 24 Úvod do Matlabu Proč proboha Matlab? Matlab je SW pro
Vytěžování dat, cvičení 1: Úvod do Matlabu Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Fakulta elektrotechnická, ČVUT 1 / 24 Úvod do Matlabu Proč proboha Matlab? Matlab je SW pro
CVIČNÝ TEST 48. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17
 CVIČNÝ TEST 48 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Je dán konvexní čtyřúhelník, jehož vnitřní
CVIČNÝ TEST 48 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Je dán konvexní čtyřúhelník, jehož vnitřní
Klasická kryptografie
 Klasická kryptografie Substituční kryptosystémy monoalfabetické homofonní polyalfabetické polygramové Transpoziční šifry jednoduchá transpozice transpozice s heslem dvojitá transpozice Součinové šifry
Klasická kryptografie Substituční kryptosystémy monoalfabetické homofonní polyalfabetické polygramové Transpoziční šifry jednoduchá transpozice transpozice s heslem dvojitá transpozice Součinové šifry
Šifry s morseovkou. Opačná morseovka. Čísla. Písmena. Grafická morseovka
 Šifry s morseovkou Opačná morseovka v opačné morseovce píšeme místo teček čárky a naopak -. / - - - - /... / -... // = AHOJ Čísla místo teček píšeme čísla od 0 do 4 a místo čárek čísla 5 až 9. 16;0403;676;2579
Šifry s morseovkou Opačná morseovka v opačné morseovce píšeme místo teček čárky a naopak -. / - - - - /... / -... // = AHOJ Čísla místo teček píšeme čísla od 0 do 4 a místo čárek čísla 5 až 9. 16;0403;676;2579
