Problém 1: Ceny nemovitostí Poznámkykřešení 1
|
|
|
- Jaromír Růžička
- před 8 lety
- Počet zobrazení:
Transkript
1 Problém 1: Ceny nemovitostí Poznámkykřešení 1 Zadání 1.Majínemovitostiurčenékbydlenívyššícenutam,kdeječistšíovzduší?Pokudano,okolik? 2. Lze vztah mezi znečištěním a cenou, pokud existuje, vysvětlit tím, že ve znečištěných oblastech bydlí chudší lidé, menšiny, jsou tam horší veřejné služby, atd.? 3. Myslíte, že cílený program na zlepšení čistoty ovzduší by vedl ke zvýšení cen rodinných domků v dané lokalitě? Postup Načtu data: data1 <- read.csv("cvic1.csv") Ověřím si velikost dat a jména veličin: names(data1); dim(data1) Vypíšu si základní popisné charakteristiky veličin: summary(data1) Vidím, že(i) v datech nejsou chybějící hodnoty;(ii) všechny veličiny jsou spojité kromě chas, která je nula-jedničková. Zajistím si přímý přístup k veličinám: attach(data1). Podívám se na nejdůležitější veličiny podrobněji. Např. histogramy(hist(medv), hist(nox)), tabulky četností: > table(cut(nox,c(-inf,seq(0.4,0.8,by=0.1),inf))) (-Inf,0.4] (0.4,0.5] (0.5,0.6] (0.6,0.7] (0.7,0.8] (0.8,Inf] > table(cut(medv,c(-inf,seq(5,30,by=5),inf))) (-Inf,5] (5,10] (10,15] (15,20] (20,25] (25,30](30,Inf] Prozkoumám popisně vztah mezi nox a medv. Např. obrázek(scatterplot) vyhlazený neparametrickou křivkou lowess:(plot(nox,medv); lines(lowess(nox,medv))) nebo tabulku průměrů medv podle intervalů nox: > tapply(medv,cut(nox,c(-inf,seq(0.4,0.8,by=0.1),inf)),mean) (-Inf,0.4] (0.4,0.5] (0.5,0.6] (0.6,0.7] (0.7,0.8] (0.8,Inf] Uvědomímsi,ženoxnabýváhodnotzhrubamezi0.4a0.9.Abychlépeviděl,coznamenajíparametryv mých modelech, udělám transformaci tnox <- (nox-0.4)/0.1. Absolutní člen v mých modelech bude nyníudávatprůměrnoucenunemovitostípřikoncentracino x = (nikoliv0)aparametrunox budeudávatzměnucenypřinárůstuno x o (nikolio1). První model, který vyzkouším, bude fit1 <- lm(medv~tnox). Dostanu 1 MichalKulich,KPMSMFFUK
2 Call: lm(formula = medv ~ tnox) Residuals: Min 1Q Median 3Q Max (Intercept) <2e-16*** tnox <2e-16*** Residual standard error: on 504 degrees of freedom Multiple R-Squared: , Adjusted R-squared: F-statistic: on 1 and 504 DF, p-value: < 2.2e-16 Vidím,žeprůměrnácenadomupřikoncentraciNO x =0.4jest$27780acenaklesáo$3392snárůstem koncentrace o 0.1. Nicméně z výběrových kvantilů pro residua ve výšeuvedeném výpisu si hned všimnu, že residua jsou silně asymetrická. Totéž potvrdí obrázek qqnorm(resid(fit1)). Zkusímztransformovatcenulogaritmem.Dostanumodellog(Y)=β 0 + β 1 X+ ε,čili Y =e β0 e β1x e ε. MámtedyE(Y X= x)=e β0 e β1x Ee ε.poděleníme(y X= x+1)ae(y X= x)dostanupřesně e β1,takže100(e β1 1)můžuinterpretovatjakopercentuálnípřírůstek/úbytekE Y přizměně Xojednu jednotku(tj.nárůstukoncentraceno x o0.1).obecněnemohutvrdit,žee β0 jestřednícenanemovitosti přikoncentracino x =0.4,alezapředpokladusymetrierozděleníchyb εlzeříci,žee β0 jemediánem cenynemovitostipřikoncentracino x =0.4. Tak tedy fit2 <- lm(log(medv)~tnox): Call: lm(formula = log(medv) ~ tnox) Residuals: Min 1Q Median 3Q Max (Intercept) <2e-16*** tnox <2e-16*** Residual standard error: on 504 degrees of freedom Multiple R-Squared: , Adjusted R-squared: F-statistic: on 1 and 504 DF, p-value: < 2.2e-16 Se symetrií residuí jsme si dost pomohli, což potvrdí i qqnorm(fit2). Ještě ztransformuji parametry: > exp(coef(fit2)) (Intercept) tnox
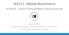
3 Obrázek 1: Porovnání lineárního a kubického modelu pro logaritmus ceny. medv tnox Odhadnutýmediáncenydomupřikoncentraci0.4jetedy$27471.Cenadomuvprůměruklesáo16.5% při nárůstu koncentrace o 0.1. JeštěsezabývejmenelineárnítransformacíNO x.zkusímetřebapolynomtřetíhořádu: > fit3 <- lm(log(medv)~poly(tnox,3)) > anova(fit2,fit3) Analysis of Variance Table Model 1: log(medv) ~ tnox Model 2: log(medv) ~ poly(tnox, 3) Res.Df RSS Df Sum of Sq F Pr(>F) e-06*** 3
4 Jelikož původní model je vnořený do tohoto modelu, můžeme otestovat rozdíl mezi nimi F-testem. Ten je vysoce významný. Teď je nejlepší udělat si obrázek, abychom viděli, v čem se oba modely liší. Nakreslíme si predikce odezvy z obou modelů do jednoho obrázku(všimněte si použití funkce predict()): noxpts <- seq(min(tnox),max(tnox),length=300) newdata <- data.frame(tnox=noxpts) fitted2 <- exp(predict(fit2,newdata)) fitted3 <- exp(predict(fit3,newdata)) plot(tnox,medv) lines(noxpts,fitted2,lty=1) lines(noxpts,fitted3,lty=2) Výsledekjenaobrázku1.Vidíme,že(i)vrozmezítnoxod0.5do3.5jevztahvpodstatělineárníaoba modely se liší jen málo;(ii) největší rozdíly mezi oběma jsou pro nejmenší a největší hodnoty znečištění; (iii) polynomiální model naznačuje, že pro znečištění menší než cca. 0.5 anebo větší než cca. 0.75(na původníškále)jevlivkoncentraceno x nacenuminimální. Cosepřesněnaoboukoncíchděje,tojetěžkosoudit.Zobrázku1jevidět,žedataoznečištěníjsou podezřele seskupená například hodnoty znečištění větší než 3 jsou prakticky diskrétní. To může být způsobeno metodikou měření(zaokrouhlování), nebo tím, že některé lokality jsou natolik blízko sebe, že jejich znečištění je prakticky stejné, nebo tím, že jeden měřicí přístroj udává hodnotu znečištění pro několik sousedních lokalit. V posledních dvou případech bychom měli problém s předpokladem nezávislosti data ve skutečnosti přicházejí ve shlucích, ale o struktuře těchto shluků nemáme žádnou informaci. Závislost mezi pozorováními pak může způsobit zakřivení regresního vztahu při vysokých hodnotách znečištění. Budeme dál pokračovat v aplikaci lineárního modelu, ale měli bychom si uvědomovat, že předpoklady modelu nejspíš neplatí a být opatrní při interpretaci výsledků, které dostaneme. Nyní máme dvě možnosti: buď můžeme zvolit lineární závislost(a nelpět příliš na výsledcích pro oba extrémyno x ),nebopřejítkekubickézávislosti(amítpotížesvysvětlovánímjehoparametrů).jemožné vymyslet i něco jiného(třeba spojitou po částech lineární křivku), ale vyberme si pro jednoduchost první variantu, lineární vztah. Vzhledem k tomu, že v modelu fit2 má znečištění vysoce významný vztah k ceně nemovitosti, můžeme si i při evidentním porušení předpokladu nezávislosti dovolit vyslovit dost jednoznačný závěr. Odpovězme na otázku 1 takto: Cena nemovitosti statisticky významně souvisí se znečištěním ovzduší. Střednícenanemovitostivrůznýchlokalitách,kteréselišívkoncentraciNO x,klesázhrubao16.5%na každých0.1nárůstukoncentraceno x.vlivkoncentraceno x navelmilevnéanebovelmidrahénemovitosti může však být nižší než oněch průměrných 16.5%. Otázkač.2:Podívejmesenejprve,jaksouvisíkoncentraceNO x sostatnímiveličinami:totojsoujejich korelace: crim zn indus chas nox rm age dis rad [1,] tax ptratio black lstat medv [1,] Vidíme, že vyšší znečištění může souviset s vyšší kriminalitou, nižším podílem velkých pozemků, vyšší industrialisací, vyšším stářím domů, větší blízkostí do centra, vyšší daňovou sazbou a vyšší mírou chudoby. Možná, že ve skutečnosti cenu pozemku ovlivňují jen tyto faktory, zatímco znečištění nehraje roli. Abychom zjistili, zdali tomu tak je, pokusíme se od vlivu znečištění odečíst vlivy těchto vedlejších matoucích(confounding) faktorů. V principu stačí sestavit model, který obsahuje kromě nox i ostatní potenciální vysvětlující veličiny, a podívat se, zdali i potom nox významně souvisí s cenou. 4
5 Zkusíme model fitm1 <- lm(log(medv)~tnox+crim+zn+indus+chas+rm+age+dis+ rad+tax+ptratio+black+lstat) summary(fitm1)... (Intercept) < 2e-16 *** tnox e-07***... Člověkihnedvidí,žetentomodelvysvětlujecenupozemkumnohemlépeažeřadaznověpřidaných veličinmávelmiúzkývztahkceněpozemků.těchpár,kterénemají,můžemealenemusímezmodelu odstranit. Nás totiž nejvíc zajímá, co se stalo s koeficientem veličiny tnox. Ten je stále signifikantně různý od nuly, ale jeho hodnota se změnila. Hleďme: getci <- function(fit,var) { # get estimateand se for variablevar a <- summary(fit)$coef[var,1:2] # get 95% confidence interv. ci <- rep(a[1],2)+c(-1,1)*a[2]*qt(0.975,fit$df.residual) names(ci) <- c("lower","upper") exp(c(a[1],ci)) } > getci(fit2,"tnox") Estimate Lower Upper > getci(fitm1,"tnox") Estimate Lower Upper Zavedli jsme novou funkci getci(fit,var), která vysaje z odhadnutého modelu fit výsledky pro veličinu var(zadatjakoznakovýřetězecvuvozovkách)aspočteeˆβa95%intervalspolehlivostiproe β. Tutofunkci 2 použijemenafit2afitm1aporovnámevýsledkyprotnox.jevidět,žepůvodní16.5%-ní sníženíprůměrnécenypřivzrůstukoncentraceno x o0.1(95%-níintervalspolehlivosti14% 19%;viz modelfit2)sezměnilona8.5%-nísníženívmodelufitm1(interval5% 10%).Jetedyvidět,žeostatní veličiny,kteréjsmevzalivúvahu,vysvětlujízhrubapolovinupůvodněodhadnutéhuvlivuno x,alenikoli vliv celý. Odpověďnaotázkuč.2:OstatníuvažovanéfaktoryvysvětlujízhrubapolovinuvlivukoncentraceNO x nacenunemovitosti. Ikdyžjevezmemevúvahu,koncentraceNO x mástálenegativnívztahkceně nemovitosti a nárůst koncentrace o 0.1 vede ke snížení průměrné ceny o zhruba 8.5%. Odpověďnaotázkuč.3:Nelzevyloučitaniprokázat,žezlepšeníčistotyovzdušíbyvedlokezvýšenícen nemovitostí. I kdyby se tak stalo, jednalo by se pravděpodobně o zvýšení relativně malé. Závěrečná poznámka: Kdybychom chtěli dělat věci pořádně, museli bychom řádně prozkoumat funkcionální vztah všech veličin v modelu fitm1 k odezvě log(medv)(tj., potenciální transformace regresorů) a museli bychom uvažovat možné interakce mezi nimi. 2 Jistěbyšlapoužítifunkceconfint vkombinacisexp.getcijevšaksnadnoupravitelnáipromodely,naněžconfint nefunguje. 5
Pokud data zadáme přes "Commands" okno: SDF1$X1<-c(1:15) //vytvoření řady čísel od 1 do 15 SDF1$Y1<-c(1.5,3,4.5,5,6,8,9,11,13,14,15,16,18.
 Regresní analýza; transformace dat Pro řešení vztahů mezi proměnnými kontinuálního typu používáme korelační a regresní analýzy. Korelace se používá pokud nelze určit "kauzalitu". Regresní analýza je určena
Regresní analýza; transformace dat Pro řešení vztahů mezi proměnnými kontinuálního typu používáme korelační a regresní analýzy. Korelace se používá pokud nelze určit "kauzalitu". Regresní analýza je určena
1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004.
 Vícenásobná regresní a korelační analýza 1 1 Tto materiál bl vtvořen za pomoci grantu FRVŠ číslo 1145/2004. O vícenásobné závislosti mluvíme tehd, jestliže je závisle proměnná závislá na více nezávislých
Vícenásobná regresní a korelační analýza 1 1 Tto materiál bl vtvořen za pomoci grantu FRVŠ číslo 1145/2004. O vícenásobné závislosti mluvíme tehd, jestliže je závisle proměnná závislá na více nezávislých
Statistické metody v marketingu. Ing. Michael Rost, Ph.D.
 Statistické metody v marketingu Ing. Michael Rost, Ph.D. Jihočeská univerzita v Českých Budějovicích Regresní analýza doplnění základů Vzhledem k požadavku Vašich kolegů zařazuji doplňující partii o regresní
Statistické metody v marketingu Ing. Michael Rost, Ph.D. Jihočeská univerzita v Českých Budějovicích Regresní analýza doplnění základů Vzhledem k požadavku Vašich kolegů zařazuji doplňující partii o regresní
Opravená data Úloha (A) + (E) Úloha (C) Úloha (B) Úloha (D) Lineární regrese
 - základní ukazatele Komentované řešení pomocí programu R Ústav matematiky Fakulta chemicko inženýrská Vysoká škola chemicko-technologická v Praze - základní ukazatele Načtení vstupních dat Vstupní data
- základní ukazatele Komentované řešení pomocí programu R Ústav matematiky Fakulta chemicko inženýrská Vysoká škola chemicko-technologická v Praze - základní ukazatele Načtení vstupních dat Vstupní data
05/29/08 cvic5.r. cv5.dat <- read.csv("cvic5.csv")
 Zobecněné lineární modely Úloha 5: Vzdělání a zájem o politiku cv5.dat
Zobecněné lineární modely Úloha 5: Vzdělání a zájem o politiku cv5.dat
Moderní regresní metody. Petr Šmilauer Biologická fakulta JU České Budějovice (c) 1998-2007
 Moderní regresní metody Petr Šmilauer Biologická fakulta JU České Budějovice (c) 1998-2007 Obsah Úvod... 5 1 Klasický lineární model a analýza variance... 7 Motivační příklad... 7 Fitování klasického lineárního
Moderní regresní metody Petr Šmilauer Biologická fakulta JU České Budějovice (c) 1998-2007 Obsah Úvod... 5 1 Klasický lineární model a analýza variance... 7 Motivační příklad... 7 Fitování klasického lineárního
Statistické metody v marketingu. Ing. Michael Rost, Ph.D.
 Statistické metody v marketingu Ing. Michael Rost, Ph.D. Jihočeská univerzita v Českých Budějovicích Úvodem Modelování vztahů mezi vysvětlující a vysvětlovanou (závisle) proměnnou patří mezi základní aktivity,
Statistické metody v marketingu Ing. Michael Rost, Ph.D. Jihočeská univerzita v Českých Budějovicích Úvodem Modelování vztahů mezi vysvětlující a vysvětlovanou (závisle) proměnnou patří mezi základní aktivity,
{ } ( 2) Příklad: Test nezávislosti kategoriálních znaků
 Příklad: Test nezávislosti kategoriálních znaků Určete na hladině významnosti 5 % na základě dat zjištěných v rámci dotazníkového šetření ve Šluknově, zda existuje závislost mezi pohlavím respondenta a
Příklad: Test nezávislosti kategoriálních znaků Určete na hladině významnosti 5 % na základě dat zjištěných v rámci dotazníkového šetření ve Šluknově, zda existuje závislost mezi pohlavím respondenta a
Statistické metody v marketingu. Ing. Michael Rost, Ph.D.
 Statistické metody v marketingu Ing. Michael Rost, Ph.D. Jihočeská univerzita v Českých Budějovicích Pojem závislosti Je nutné rozlišit mezi závislostí nepodstatnou a mezi příčinnou čili kauzální závislostí.ta
Statistické metody v marketingu Ing. Michael Rost, Ph.D. Jihočeská univerzita v Českých Budějovicích Pojem závislosti Je nutné rozlišit mezi závislostí nepodstatnou a mezi příčinnou čili kauzální závislostí.ta
(motto: An unsophisticated forecaster uses statistics as a drunken man uses lamp-posts - for support rather than for illumination.
 Neparametricke testy (motto: An unsophisticated forecaster uses statistics as a drunken man uses lamp-posts - for support rather than for illumination. Andrew Lang) 1. Příklad V následující tabulce jsou
Neparametricke testy (motto: An unsophisticated forecaster uses statistics as a drunken man uses lamp-posts - for support rather than for illumination. Andrew Lang) 1. Příklad V následující tabulce jsou
Zpracování studie týkající se průzkumu vlastností statistických proměnných a vztahů mezi nimi.
 SEMINÁRNÍ PRÁCE Zadání: Data: Statistické metody: Zpracování studie týkající se průzkumu vlastností statistických proměnných a vztahů mezi nimi. Minimálně 6 proměnných o 30 pozorováních (z toho 2 proměnné
SEMINÁRNÍ PRÁCE Zadání: Data: Statistické metody: Zpracování studie týkající se průzkumu vlastností statistických proměnných a vztahů mezi nimi. Minimálně 6 proměnných o 30 pozorováních (z toho 2 proměnné
Analýza rozptylu. Statistika II. Jiří Neubauer. Katedra ekonometrie FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.
 ANOVA Statistika II Katedra ekonometrie FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz ANOVA ANOVA je nástroj pro zkoumání vztahu mezi vysvětlovanými a vysvětlujícími proměnnými.
ANOVA Statistika II Katedra ekonometrie FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz ANOVA ANOVA je nástroj pro zkoumání vztahu mezi vysvětlovanými a vysvětlujícími proměnnými.
Analýza rozptylu. Přednáška STATISTIKA II - EKONOMETRIE. Jiří Neubauer
 ANOVA Přednáška STATISTIKA II - EKONOMETRIE Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz ANOVA ANOVA je nástroj pro zkoumání vztahu mezi vysvětlovanými a vysvětlujícími
ANOVA Přednáška STATISTIKA II - EKONOMETRIE Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz ANOVA ANOVA je nástroj pro zkoumání vztahu mezi vysvětlovanými a vysvětlujícími
Frekvenční analýza, čtyřpolní tabulky
 Frekvenční analýza, čtyřpolní tabulky V následujícím příkladě nás zajímá, zda sekání má pozitivní vliv na reprodukci studovaného druhu. V experimentu tedy máme dva druhy ošetření (sekané, nesekané) a pro
Frekvenční analýza, čtyřpolní tabulky V následujícím příkladě nás zajímá, zda sekání má pozitivní vliv na reprodukci studovaného druhu. V experimentu tedy máme dva druhy ošetření (sekané, nesekané) a pro
Analýza rozptylu. Ekonometrie. Jiří Neubauer. Katedra kvantitativních metod FVL UO Brno kancelář 69a, tel
 Analýza rozptylu Ekonometrie Jiří Neubauer Katedra kvantitativních metod FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Jiří Neubauer (Katedra UO Brno) Analýza rozptylu 1 / 30 Analýza
Analýza rozptylu Ekonometrie Jiří Neubauer Katedra kvantitativních metod FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Jiří Neubauer (Katedra UO Brno) Analýza rozptylu 1 / 30 Analýza
Analýza variance (ANOVA) - jednocestná; faktor s pevným efektem; mnohonásobná srovnání
 Analýza variance (ANOVA) - jednocestná; faktor s pevným efektem; mnohonásobná srovnání 1. Analýzu variance (ANOVu) používáme při studiu problémů, kdy máme závislou proměnou spojitého typu a nezávislé proměnné
Analýza variance (ANOVA) - jednocestná; faktor s pevným efektem; mnohonásobná srovnání 1. Analýzu variance (ANOVu) používáme při studiu problémů, kdy máme závislou proměnou spojitého typu a nezávislé proměnné
Univerzita Pardubice Chemicko-technologická fakulta Katedra analytické chemie
 Univerzita Pardubice Chemicko-technologická fakulta Katedra analytické chemie 12. licenční studium PYTHAGORAS Statistické zpracování dat 3.3 Tvorba nelineárních regresních modelů v analýze dat Semestrální
Univerzita Pardubice Chemicko-technologická fakulta Katedra analytické chemie 12. licenční studium PYTHAGORAS Statistické zpracování dat 3.3 Tvorba nelineárních regresních modelů v analýze dat Semestrální
4ST201 STATISTIKA CVIČENÍ Č. 10
 4ST201 STATISTIKA CVIČENÍ Č. 10 regresní analýza - vícenásobná lineární regrese korelační analýza Př. 10.1 Máte zadaný výstup regresní analýzy závislosti závisle proměnné Y na nezávisle proměnné X. Doplňte
4ST201 STATISTIKA CVIČENÍ Č. 10 regresní analýza - vícenásobná lineární regrese korelační analýza Př. 10.1 Máte zadaný výstup regresní analýzy závislosti závisle proměnné Y na nezávisle proměnné X. Doplňte
M cvičení : GLM03a (The Working Activities of Bees)
 RNDr. Marie Forbelská, Ph.D. 1 M7222 3. cvičení : GLM03a (The Working Activities of Bees) Popis dat je v souboru bees.txt, samotná data jsou uložena v souboru bees.dat. Nejprve načteme popisný soubor pomocí
RNDr. Marie Forbelská, Ph.D. 1 M7222 3. cvičení : GLM03a (The Working Activities of Bees) Popis dat je v souboru bees.txt, samotná data jsou uložena v souboru bees.dat. Nejprve načteme popisný soubor pomocí
STATISTIKA A INFORMATIKA - bc studium OZW, 1.roč. (zkušební otázky)
 STATISTIKA A INFORMATIKA - bc studium OZW, 1.roč. (zkušební otázky) 1) Význam a využití statistiky v biologických vědách a veterinárním lékařství ) Rozdělení znaků (veličin) ve statistice 3) Základní a
STATISTIKA A INFORMATIKA - bc studium OZW, 1.roč. (zkušební otázky) 1) Význam a využití statistiky v biologických vědách a veterinárním lékařství ) Rozdělení znaků (veličin) ve statistice 3) Základní a
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz
 Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická
Vliv odlehlých hodnot, korelační koeficient, mnohonásobná regrese
 Vliv odlehlých hodnot, korelační koeficient, mnohonásobná regrese 1. Vliv odlehlých hodnot Na následujících dvou příkladech ukážeme jak odlehlé hodnoty (outliers) ovlivňují výsledek analýzy a jak je identifikovat.
Vliv odlehlých hodnot, korelační koeficient, mnohonásobná regrese 1. Vliv odlehlých hodnot Na následujících dvou příkladech ukážeme jak odlehlé hodnoty (outliers) ovlivňují výsledek analýzy a jak je identifikovat.
4EK211 Základy ekonometrie
 4EK211 Základy ekonometrie ZS 2015/16 Cvičení 7: Časově řady, autokorelace LENKA FIŘTOVÁ KATEDRA EKONOMETRIE, FAKULTA INFORMATIKY A STATISTIKY VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE 1. Časové řady Data: HDP.wf1
4EK211 Základy ekonometrie ZS 2015/16 Cvičení 7: Časově řady, autokorelace LENKA FIŘTOVÁ KATEDRA EKONOMETRIE, FAKULTA INFORMATIKY A STATISTIKY VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE 1. Časové řady Data: HDP.wf1
Regresní analýza. Eva Jarošová
 Regresní analýza Eva Jarošová 1 Obsah 1. Regresní přímka 2. Možnosti zlepšení modelu 3. Testy v regresním modelu 4. Regresní diagnostika 5. Speciální využití Lineární model 2 1. Regresní přímka 3 nosnost
Regresní analýza Eva Jarošová 1 Obsah 1. Regresní přímka 2. Možnosti zlepšení modelu 3. Testy v regresním modelu 4. Regresní diagnostika 5. Speciální využití Lineární model 2 1. Regresní přímka 3 nosnost
M cvičení : GLM04b (Vztah mezi Poissonovým a
 RNDr. Marie Forbelská, Ph.D. 1 M7222 4. cvičení : GLM04b (Vztah mezi Poissonovým a binomických rozdělením) Připomeňme, že pomocí Poissonova rozdělení P o(λ) lze dobře aproximovat binomické rozdělení Bi(n,
RNDr. Marie Forbelská, Ph.D. 1 M7222 4. cvičení : GLM04b (Vztah mezi Poissonovým a binomických rozdělením) Připomeňme, že pomocí Poissonova rozdělení P o(λ) lze dobře aproximovat binomické rozdělení Bi(n,
Korelační a regresní analýza. 1. Pearsonův korelační koeficient 2. jednoduchá regresní analýza 3. vícenásobná regresní analýza
 Korelační a regresní analýza 1. Pearsonův korelační koeficient 2. jednoduchá regresní analýza 3. vícenásobná regresní analýza Pearsonův korelační koeficient u intervalových a poměrových dat můžeme jako
Korelační a regresní analýza 1. Pearsonův korelační koeficient 2. jednoduchá regresní analýza 3. vícenásobná regresní analýza Pearsonův korelační koeficient u intervalových a poměrových dat můžeme jako
POPISNÁ STATISTIKA Komentované řešení pomocí programu Statistica
 POPISNÁ STATISTIKA Komentované řešení pomocí programu Statistica Program Statistica I Statistica je velmi podobná Excelu. Na základní úrovni je to klikací program určený ke statistickému zpracování dat.
POPISNÁ STATISTIKA Komentované řešení pomocí programu Statistica Program Statistica I Statistica je velmi podobná Excelu. Na základní úrovni je to klikací program určený ke statistickému zpracování dat.
Statistika. Regresní a korelační analýza Úvod do problému. Roman Biskup
 Statistika Regresní a korelační analýza Úvod do problému Roman Biskup Jihočeská univerzita v Českých Budějovicích Ekonomická fakulta (Zemědělská fakulta) Katedra aplikované matematiky a informatiky 2008/2009
Statistika Regresní a korelační analýza Úvod do problému Roman Biskup Jihočeská univerzita v Českých Budějovicích Ekonomická fakulta (Zemědělská fakulta) Katedra aplikované matematiky a informatiky 2008/2009
Tabulární data, pozorované vs očekávané četnosti
 Tabulární data, pozorované vs očekávané četnosti Máme data o počtech např. samců a samic v populaci a zajímá nás, zda naše pozorované (observed) četnosti se liší od předpokládaného (expected). Příklad
Tabulární data, pozorované vs očekávané četnosti Máme data o počtech např. samců a samic v populaci a zajímá nás, zda naše pozorované (observed) četnosti se liší od předpokládaného (expected). Příklad
TECHNIKA UMĚLÝCH PROMĚNNÝCH V PRŮŘEZOVÉ ANALÝZE A V MODELECH ČASOVÝCH ŘAD
 TECHNIKA UMĚLÝCH PROMĚNNÝCH V PRŮŘEZOVÉ ANALÝZE A V MODELECH ČASOVÝCH ŘAD Umělé (dummy) proměnné se používají, pokud chceme do modelu zahrnout proměnné, které mají kvalitativní či diskrétní charakter,
TECHNIKA UMĚLÝCH PROMĚNNÝCH V PRŮŘEZOVÉ ANALÝZE A V MODELECH ČASOVÝCH ŘAD Umělé (dummy) proměnné se používají, pokud chceme do modelu zahrnout proměnné, které mají kvalitativní či diskrétní charakter,
RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr.
 Analýza dat pro Neurovědy RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr. Jaro 2014 Institut biostatistiky Janoušová, a analýz Dušek: Analýza dat pro neurovědy Blok 7 Jak hodnotit vztah spojitých proměnných
Analýza dat pro Neurovědy RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr. Jaro 2014 Institut biostatistiky Janoušová, a analýz Dušek: Analýza dat pro neurovědy Blok 7 Jak hodnotit vztah spojitých proměnných
M cvičení : GLM01a (Toxic Chemical Production Data)
 RNDr. Marie Forbelská, Ph.D. 1 M7222 1. cvičení : GLM01a (Toxic Chemical Production Data) Popis dat je v souboru toxic.txt, samotná data jsou uložena v souboru toxic.dat. Nejprve načteme popisný soubor
RNDr. Marie Forbelská, Ph.D. 1 M7222 1. cvičení : GLM01a (Toxic Chemical Production Data) Popis dat je v souboru toxic.txt, samotná data jsou uložena v souboru toxic.dat. Nejprve načteme popisný soubor
KORELACE. Komentované řešení pomocí programu Statistica
 KORELACE Komentované řešení pomocí programu Statistica Vstupní data I Data umístěná v excelovském souboru překopírujeme do tabulky ve Statistice a pojmenujeme proměnné, viz prezentace k tématu Popisná
KORELACE Komentované řešení pomocí programu Statistica Vstupní data I Data umístěná v excelovském souboru překopírujeme do tabulky ve Statistice a pojmenujeme proměnné, viz prezentace k tématu Popisná
Analýza dat na PC I.
 CENTRUM BIOSTATISTIKY A ANALÝZ Lékařská a Přírodovědecká fakulta, Masarykova univerzita Analýza dat na PC I. Popisná analýza v programu Statistica IBA výuka Základní popisná statistika Popisná statistika
CENTRUM BIOSTATISTIKY A ANALÝZ Lékařská a Přírodovědecká fakulta, Masarykova univerzita Analýza dat na PC I. Popisná analýza v programu Statistica IBA výuka Základní popisná statistika Popisná statistika
5EN306 Aplikované kvantitativní metody I
 5EN306 Aplikované kvantitativní metody I Přednáška 5 Zuzana Dlouhá Předmět a struktura kurzu 1. Úvod: struktura empirických výzkumů 2. Tvorba ekonomických modelů: teorie 3. Data: zdroje a typy dat, význam
5EN306 Aplikované kvantitativní metody I Přednáška 5 Zuzana Dlouhá Předmět a struktura kurzu 1. Úvod: struktura empirických výzkumů 2. Tvorba ekonomických modelů: teorie 3. Data: zdroje a typy dat, význam
Aplikovaná statistika v R - cvičení 3
 Aplikovaná statistika v R - cvičení 3 Filip Děchtěrenko Matematicko-fyzikální fakulta filip.dechterenko@gmail.com 5.8.2014 Filip Děchtěrenko (MFF UK) Aplikovaná statistika v R 5.8.2014 1 / 10 Lineární
Aplikovaná statistika v R - cvičení 3 Filip Děchtěrenko Matematicko-fyzikální fakulta filip.dechterenko@gmail.com 5.8.2014 Filip Děchtěrenko (MFF UK) Aplikovaná statistika v R 5.8.2014 1 / 10 Lineární
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc.
 Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika 010 1.týden (0.09.-4.09. ) Data, typy dat, variabilita, frekvenční analýza
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika 010 1.týden (0.09.-4.09. ) Data, typy dat, variabilita, frekvenční analýza
z dat nasbíraných v letech 1959 1994. Ke zpracování dat byl použit statistický software R. Základní model poptávkové funkce, ze kterého vycházíme,
 Úloha 1: V naší studii se zabýváme poptávkovou funkcí životního pojištění, vycházíme z dat nasbíraných v letech 1959 1994. Ke zpracování dat byl použit statistický software R. Základní model poptávkové
Úloha 1: V naší studii se zabýváme poptávkovou funkcí životního pojištění, vycházíme z dat nasbíraných v letech 1959 1994. Ke zpracování dat byl použit statistický software R. Základní model poptávkové
AVDAT Klasický lineární model, metoda nejmenších
 AVDAT Klasický lineární model, metoda nejmenších čtverců Josef Tvrdík Katedra informatiky Přírodovědecká fakulta Ostravská univerzita Lineární model y i = β 0 + β 1 x i1 + + β k x ik + ε i (1) kde y i
AVDAT Klasický lineární model, metoda nejmenších čtverců Josef Tvrdík Katedra informatiky Přírodovědecká fakulta Ostravská univerzita Lineární model y i = β 0 + β 1 x i1 + + β k x ik + ε i (1) kde y i
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Obecné momenty prosté tvary
 Obecné momenty prosté tvary První obecný moment: (Σy i )/n, i=1 n aritmetický průměr, těžiště dat y Druhý obecný moment: (Σy i2 )/n, i=1 n y 2 Obecné momenty prosté tvary Příklad 1 pokračování: y = (3+4+2+3+2+3+3+3)/8
Obecné momenty prosté tvary První obecný moment: (Σy i )/n, i=1 n aritmetický průměr, těžiště dat y Druhý obecný moment: (Σy i2 )/n, i=1 n y 2 Obecné momenty prosté tvary Příklad 1 pokračování: y = (3+4+2+3+2+3+3+3)/8
Lineární regrese. Komentované řešení pomocí MS Excel
 Lineární regrese Komentované řešení pomocí MS Excel Vstupní data Tabulka se vstupními daty je umístěna v oblasti A1:B11 (viz. obrázek) na listu cela data Postup Základní výpočty - regrese Výpočet základních
Lineární regrese Komentované řešení pomocí MS Excel Vstupní data Tabulka se vstupními daty je umístěna v oblasti A1:B11 (viz. obrázek) na listu cela data Postup Základní výpočty - regrese Výpočet základních
Základy biostatistiky II. Veřejné zdravotnictví 3.LF UK - II
 Základy biostatistiky II Veřejné zdravotnictví 3.LF UK - II Teoretické rozložení-matematické modely rozložení Naměřená data Výběrové rozložení Teoretické rozložení 1 e 2 x 2 Teoretické rozložení-matematické
Základy biostatistiky II Veřejné zdravotnictví 3.LF UK - II Teoretické rozložení-matematické modely rozložení Naměřená data Výběrové rozložení Teoretické rozložení 1 e 2 x 2 Teoretické rozložení-matematické
Intervalové odhady. Interval spolehlivosti pro střední hodnotu v N(µ, σ 2 ) Interpretace intervalu spolehlivosti. Interval spolehlivosti ilustrace
 Intervalové odhady Interval spolehlivosti pro střední hodnotu v Nµ, σ 2 ) Situace: X 1,..., X n náhodný výběr z Nµ, σ 2 ), kde σ 2 > 0 známe měli jsme: bodové odhady odhadem charakteristiky je číslo) nevyjadřuje
Intervalové odhady Interval spolehlivosti pro střední hodnotu v Nµ, σ 2 ) Situace: X 1,..., X n náhodný výběr z Nµ, σ 2 ), kde σ 2 > 0 známe měli jsme: bodové odhady odhadem charakteristiky je číslo) nevyjadřuje
PSY117/454 Statistická analýza dat v psychologii Přednáška 10
 PSY117/454 Statistická analýza dat v psychologii Přednáška 10 TESTY PRO NOMINÁLNÍ A ORDINÁLNÍ PROMĚNNÉ NEPARAMETRICKÉ METODY... a to mělo, jak sám vidíte, nedozírné následky. Smrť Analýza četností hodnot
PSY117/454 Statistická analýza dat v psychologii Přednáška 10 TESTY PRO NOMINÁLNÍ A ORDINÁLNÍ PROMĚNNÉ NEPARAMETRICKÉ METODY... a to mělo, jak sám vidíte, nedozírné následky. Smrť Analýza četností hodnot
odpovídá jedna a jen jedna hodnota jiných
 8. Regresní a korelační analýza Problém: hledání, zkoumání a hodnocení souvislostí, závislostí mezi dvěma a více statistickými znaky (veličinami). Typy závislostí: pevné a volné Pevná závislost každé hodnotě
8. Regresní a korelační analýza Problém: hledání, zkoumání a hodnocení souvislostí, závislostí mezi dvěma a více statistickými znaky (veličinami). Typy závislostí: pevné a volné Pevná závislost každé hodnotě
Matematika pro geometrickou morfometrii (5)
 Ján Dupej (jdupej@cgg.mff.cuni.cz) Laboratoř 3D zobrazovacích a analytických metod Katedra antropologie a genetiky člověka Přírodovědecká fakulta UK v Praze Cíle GM 1. Popsat tvar čísly 2. Čísla statisticky
Ján Dupej (jdupej@cgg.mff.cuni.cz) Laboratoř 3D zobrazovacích a analytických metod Katedra antropologie a genetiky člověka Přírodovědecká fakulta UK v Praze Cíle GM 1. Popsat tvar čísly 2. Čísla statisticky
letní semestr 2012 Katedra pravděpodobnosti a matematické statistiky Matematicko-fyzikální fakulta Univerzity Karlovy Matematická statistika
 Šárka Hudecová Katedra pravděpodobnosti a matematické statistiky Matematicko-fyzikální fakulta Univerzity Karlovy letní semestr 2012 Opakování t- vs. neparametrické Wilcoxonův jednovýběrový test Opakování
Šárka Hudecová Katedra pravděpodobnosti a matematické statistiky Matematicko-fyzikální fakulta Univerzity Karlovy letní semestr 2012 Opakování t- vs. neparametrické Wilcoxonův jednovýběrový test Opakování
ANALÝZA DAT V R 3. POPISNÉ STATISTIKY, NÁHODNÁ VELIČINA. Mgr. Markéta Pavlíková Katedra pravděpodobnosti a matematické statistiky MFF UK
 ANALÝZA DAT V R 3. POPISNÉ STATISTIKY, NÁHODNÁ VELIČINA Mgr. Markéta Pavlíková Katedra pravděpodobnosti a matematické statistiky MFF UK www.biostatisticka.cz POPISNÉ STATISTIKY - OPAKOVÁNÍ jedna kvalitativní
ANALÝZA DAT V R 3. POPISNÉ STATISTIKY, NÁHODNÁ VELIČINA Mgr. Markéta Pavlíková Katedra pravděpodobnosti a matematické statistiky MFF UK www.biostatisticka.cz POPISNÉ STATISTIKY - OPAKOVÁNÍ jedna kvalitativní
Intervalové odhady. Interval spolehlivosti pro střední hodnotu v N(µ, σ 2 ) Interpretace intervalu spolehlivosti. Interval spolehlivosti ilustrace
 Intervalové odhady Interval spolehlivosti pro střední hodnotu v Nµ, σ 2 ) Situace: X 1,..., X n náhodný výběr z Nµ, σ 2 ), kde σ 2 > 0 známe měli jsme: bodové odhady odhadem charakteristiky je číslo) nevyjadřuje
Intervalové odhady Interval spolehlivosti pro střední hodnotu v Nµ, σ 2 ) Situace: X 1,..., X n náhodný výběr z Nµ, σ 2 ), kde σ 2 > 0 známe měli jsme: bodové odhady odhadem charakteristiky je číslo) nevyjadřuje
Teorie časových řad Test 2 Varianta A HODNOCENÍ (max. 45 bodů z 50 možných)
 Teorie časových řad Test 2 Varianta A HODNOCENÍ (max. 45 bodů z 50 možných) 1. SPECIFIKACE (12 bodů): (1) Graf průběhu proměnných (1) Obě řady se chovají stejně, lze předpokládat jejich lineární vztah
Teorie časových řad Test 2 Varianta A HODNOCENÍ (max. 45 bodů z 50 možných) 1. SPECIFIKACE (12 bodů): (1) Graf průběhu proměnných (1) Obě řady se chovají stejně, lze předpokládat jejich lineární vztah
veličin, deskriptivní statistika Ing. Michael Rost, Ph.D.
 Vybraná rozdělení spojitých náhodných veličin, deskriptivní statistika Ing. Michael Rost, Ph.D. Třídění Základním zpracováním dat je jejich třídění. Jde o uspořádání získaných dat, kde volba třídícího
Vybraná rozdělení spojitých náhodných veličin, deskriptivní statistika Ing. Michael Rost, Ph.D. Třídění Základním zpracováním dat je jejich třídění. Jde o uspořádání získaných dat, kde volba třídícího
RNDr. Marie Forbelská, Ph.D. 1
 RNDr. Marie Forbelská, Ph.D. 1 M6120 7. cvičení : M6120cv07 (Klasický lineární regresní model) A. Klasický lineární regresní model, modely neúplné hodnosti, rozšířený lineární regresní model a vážená metoda
RNDr. Marie Forbelská, Ph.D. 1 M6120 7. cvičení : M6120cv07 (Klasický lineární regresní model) A. Klasický lineární regresní model, modely neúplné hodnosti, rozšířený lineární regresní model a vážená metoda
Jana Vránová, 3. lékařská fakulta, UK Praha
 Jana Vránová, 3. lékařská fakulta, UK Praha Byla navržena v 60tých letech jako alternativa k metodě nejmenších čtverců pro případ, že vysvětlovaná proměnná je binární Byla především používaná v medicíně
Jana Vránová, 3. lékařská fakulta, UK Praha Byla navržena v 60tých letech jako alternativa k metodě nejmenších čtverců pro případ, že vysvětlovaná proměnná je binární Byla především používaná v medicíně
Výběr hodnot z modisovského rastru v místech, kde se nacházela jedna ze zeber
 Výběr hodnot z modisovského rastru v místech, kde se nacházela jedna ze zeber - pro ukázku je zde vybrán rastr s hodnotami indexu EVI v jednom únorovém dni - a místa výskytu dané zebry celkem za celý rok
Výběr hodnot z modisovského rastru v místech, kde se nacházela jedna ze zeber - pro ukázku je zde vybrán rastr s hodnotami indexu EVI v jednom únorovém dni - a místa výskytu dané zebry celkem za celý rok
4EK211 Základy ekonometrie
 4EK211 Základy ekonometrie ZS 2014/15 Cvičení 6: Dummy proměnné, úvod do časových řad LENKA FIŘTOVÁ KATEDRA EKONOMETRIE, FAKULTA INFORMATIKY A STATISTIKY VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE 1. Multikolinearita
4EK211 Základy ekonometrie ZS 2014/15 Cvičení 6: Dummy proměnné, úvod do časových řad LENKA FIŘTOVÁ KATEDRA EKONOMETRIE, FAKULTA INFORMATIKY A STATISTIKY VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE 1. Multikolinearita
Pozn. přeskakuji zde popisnou statistiku, jinak by měla být součástí každé analýzy.
 Pozn. přeskakuji zde popisnou statistiku, jinak by měla být součástí každé analýzy. Z pastí na daném území byla odhadnuta abundance několika druhů: myšice lesní 250, myšice křovinná 200, hraboš polní 150,
Pozn. přeskakuji zde popisnou statistiku, jinak by měla být součástí každé analýzy. Z pastí na daném území byla odhadnuta abundance několika druhů: myšice lesní 250, myšice křovinná 200, hraboš polní 150,
Grafický a číselný popis rozložení dat 3.1 Způsoby zobrazení dat Metody zobrazení kvalitativních a ordinálních dat Metody zobrazení kvan
 1 Úvod 1.1 Empirický výzkum a jeho etapy 1.2 Význam teorie pro výzkum 1.2.1 Konstrukty a jejich operacionalizace 1.2.2 Role teorie ve výzkumu 1.2.3 Proces ověření hypotéz a teorií 1.3 Etika vědecké práce
1 Úvod 1.1 Empirický výzkum a jeho etapy 1.2 Význam teorie pro výzkum 1.2.1 Konstrukty a jejich operacionalizace 1.2.2 Role teorie ve výzkumu 1.2.3 Proces ověření hypotéz a teorií 1.3 Etika vědecké práce
Popisná statistika. Komentované řešení pomocí MS Excel
 Popisná statistika Komentované řešení pomocí MS Excel Vstupní data Máme k dispozici data o počtech bodů z 1. a 2. zápočtového testu z Matematiky I v zimním semestru 2015/2016 a to za všech 762 studentů,
Popisná statistika Komentované řešení pomocí MS Excel Vstupní data Máme k dispozici data o počtech bodů z 1. a 2. zápočtového testu z Matematiky I v zimním semestru 2015/2016 a to za všech 762 studentů,
4EK211 Základy ekonometrie
 4EK Základy ekonometrie Odhad klasického lineárního regresního modelu II Cvičení 3 Zuzana Dlouhá Klasický lineární regresní model - zadání příkladu Soubor: CV3_PR.xls Data: y = maloobchodní obrat potřeb
4EK Základy ekonometrie Odhad klasického lineárního regresního modelu II Cvičení 3 Zuzana Dlouhá Klasický lineární regresní model - zadání příkladu Soubor: CV3_PR.xls Data: y = maloobchodní obrat potřeb
STATISTIKA MIGRANTŮ PRO REGIONY V MORAVSKOSLEZSKÉM KRAJI A PRO KRAJ V OBDOBÍ 1992-2005
 VYSOKÁ ŠKOLA BÁŇSKÁ - TECHNICKÁ UNIVERZITA OSTRAVA Hornicko-geologická fakulta institut geoinformatiky STATISTIKA MIGRANTŮ PRO REGIONY V MORAVSKOSLEZSKÉM KRAJI A PRO KRAJ V OBDOBÍ 1992-2005 Speciální metody
VYSOKÁ ŠKOLA BÁŇSKÁ - TECHNICKÁ UNIVERZITA OSTRAVA Hornicko-geologická fakulta institut geoinformatiky STATISTIKA MIGRANTŮ PRO REGIONY V MORAVSKOSLEZSKÉM KRAJI A PRO KRAJ V OBDOBÍ 1992-2005 Speciální metody
7 Regresní modely v analýze přežití
 7 Regresní modely v analýze přežití Předpokládané výstupy z výuky: 1. Student rozumí významu regresního modelování dat o přežití 2. Student dokáže definovat pojmy poměr rizik a základní riziková funkce
7 Regresní modely v analýze přežití Předpokládané výstupy z výuky: 1. Student rozumí významu regresního modelování dat o přežití 2. Student dokáže definovat pojmy poměr rizik a základní riziková funkce
PSY117/454 Statistická analýza dat v psychologii přednáška 8. Statistické usuzování, odhady
 PSY117/454 Statistická analýza dat v psychologii přednáška 8 Statistické usuzování, odhady Výběr od deskripce k indukci Deskripce dat, odhad parametrů Usuzování = inference = indukce Počítá se s náhodným
PSY117/454 Statistická analýza dat v psychologii přednáška 8 Statistické usuzování, odhady Výběr od deskripce k indukci Deskripce dat, odhad parametrů Usuzování = inference = indukce Počítá se s náhodným
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc.
 Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika 2010 1.týden (20.09.-24.09. ) Data, typy dat, variabilita, frekvenční analýza
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika 2010 1.týden (20.09.-24.09. ) Data, typy dat, variabilita, frekvenční analýza
4EK211 Základy ekonometrie
 4EK211 Základy ekonometrie LS 2014/15 Cvičení 4: Statistické vlastnosti MNČ LENKA FIŘTOVÁ KATEDRA EKONOMETRIE, FAKULTA INFORMATIKY A STATISTIKY VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE Upřesnění k pojmům a značení
4EK211 Základy ekonometrie LS 2014/15 Cvičení 4: Statistické vlastnosti MNČ LENKA FIŘTOVÁ KATEDRA EKONOMETRIE, FAKULTA INFORMATIKY A STATISTIKY VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE Upřesnění k pojmům a značení
SEMESTRÁLNÍ PRÁCE X. Aproximace křivek Numerické vyhlazování
 KATEDRA ANALYTICKÉ CHEMIE FAKULTY CHEMICKO TECHNOLOGICKÉ UNIVERSITA PARDUBICE - Licenční studium chemometrie LS96/1 SEMESTRÁLNÍ PRÁCE X. Aproximace křivek Numerické vyhlazování Praha, leden 1999 0 Úloha
KATEDRA ANALYTICKÉ CHEMIE FAKULTY CHEMICKO TECHNOLOGICKÉ UNIVERSITA PARDUBICE - Licenční studium chemometrie LS96/1 SEMESTRÁLNÍ PRÁCE X. Aproximace křivek Numerické vyhlazování Praha, leden 1999 0 Úloha
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc.
 Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika 2010 1.týden (20.09.-24.09. ) Data, typy dat, variabilita, frekvenční analýza
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika 2010 1.týden (20.09.-24.09. ) Data, typy dat, variabilita, frekvenční analýza
INDUKTIVNÍ STATISTIKA
 10. SEMINÁŘ INDUKTIVNÍ STATISTIKA 3. HODNOCENÍ ZÁVISLOSTÍ HODNOCENÍ ZÁVISLOSTÍ KVALITATIVNÍ VELIČINY - Vychází se z kombinační (kontingenční) tabulky, která je výsledkem třídění druhého stupně KVANTITATIVNÍ
10. SEMINÁŘ INDUKTIVNÍ STATISTIKA 3. HODNOCENÍ ZÁVISLOSTÍ HODNOCENÍ ZÁVISLOSTÍ KVALITATIVNÍ VELIČINY - Vychází se z kombinační (kontingenční) tabulky, která je výsledkem třídění druhého stupně KVANTITATIVNÍ
VÝUKA: Biostatistika základní kurz CENTRUM BIOSTATISTIKY A ANALÝZ
 1 ANOVA analýza rozptylu Analýza rozptylu - ANOVA Základní technika sloužící k posouzení rozdílů mezi více úrovněmi pokusného zásahu Kontrola 1 Konce entrace Konce entrace 3 Konce entrace p Konce entrace
1 ANOVA analýza rozptylu Analýza rozptylu - ANOVA Základní technika sloužící k posouzení rozdílů mezi více úrovněmi pokusného zásahu Kontrola 1 Konce entrace Konce entrace 3 Konce entrace p Konce entrace
II. Statistické metody vyhodnocení kvantitativních dat Gejza Dohnal
 Základy navrhování průmyslových experimentů DOE II. Statistické metody vyhodnocení kvantitativních dat Gejza Dohnal! Testování statistických hypotéz kvalitativní odezva kvantitativní chí-kvadrát test homogenity,
Základy navrhování průmyslových experimentů DOE II. Statistické metody vyhodnocení kvantitativních dat Gejza Dohnal! Testování statistických hypotéz kvalitativní odezva kvantitativní chí-kvadrát test homogenity,
Cvičení ze statistiky - 9. Filip Děchtěrenko
 Cvičení ze statistiky - 9 Filip Děchtěrenko Minule bylo.. Dobrali jsme normální rozdělení Tyhle termíny by měly být známé: Inferenční statistika Konfidenční intervaly Z-test Postup při testování hypotéz
Cvičení ze statistiky - 9 Filip Děchtěrenko Minule bylo.. Dobrali jsme normální rozdělení Tyhle termíny by měly být známé: Inferenční statistika Konfidenční intervaly Z-test Postup při testování hypotéz
Bodové a intervalové odhady parametrů v regresním modelu
 Statistika II Katedra ekonometrie FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Lineární regresní model Mějme lineární regresní model (LRM) Y = Xβ + e, kde y 1 e 1 β y 2 Y =., e
Statistika II Katedra ekonometrie FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Lineární regresní model Mějme lineární regresní model (LRM) Y = Xβ + e, kde y 1 e 1 β y 2 Y =., e
Náhodný vektor. Náhodný vektor. Hustota náhodného vektoru. Hustota náhodného vektoru. Náhodný vektor je dvojice náhodných veličin (X, Y ) T = ( X
 Náhodný vektor Náhodný vektor zatím jsme sledovali jednu náhodnou veličinu, její rozdělení a charakteristiky často potřebujeme vyšetřovat vzájemný vztah několika náhodných veličin musíme sledovat jejich
Náhodný vektor Náhodný vektor zatím jsme sledovali jednu náhodnou veličinu, její rozdělení a charakteristiky často potřebujeme vyšetřovat vzájemný vztah několika náhodných veličin musíme sledovat jejich
Cvičení ze statistiky - 3. Filip Děchtěrenko
 Cvičení ze statistiky - 3 Filip Děchtěrenko Minule bylo.. Dokončili jsme základní statistiky, typy proměnných a začali analýzu kvalitativních dat Tyhle termíny by měly být známé: Histogram, krabicový graf
Cvičení ze statistiky - 3 Filip Děchtěrenko Minule bylo.. Dokončili jsme základní statistiky, typy proměnných a začali analýzu kvalitativních dat Tyhle termíny by měly být známé: Histogram, krabicový graf
KGG/STG Statistika pro geografy
 KGG/STG Statistika pro geografy 9. Korelační analýza Mgr. David Fiedor 20. dubna 2015 Analýza závislostí v řadě geografických disciplín studujeme jevy, u kterých vyšetřujeme nikoliv pouze jednu vlastnost
KGG/STG Statistika pro geografy 9. Korelační analýza Mgr. David Fiedor 20. dubna 2015 Analýza závislostí v řadě geografických disciplín studujeme jevy, u kterých vyšetřujeme nikoliv pouze jednu vlastnost
Aplikovaná statistika v R - cvičení 2
 Aplikovaná statistika v R - cvičení 2 Filip Děchtěrenko Matematicko-fyzikální fakulta filip.dechterenko@gmail.com 5.6.2014 Filip Děchtěrenko (MFF UK) Aplikovaná statistika v R 5.6.2014 1 / 18 Přehled Rkových
Aplikovaná statistika v R - cvičení 2 Filip Děchtěrenko Matematicko-fyzikální fakulta filip.dechterenko@gmail.com 5.6.2014 Filip Děchtěrenko (MFF UK) Aplikovaná statistika v R 5.6.2014 1 / 18 Přehled Rkových
Zadání Máme data hdp.wf1, která najdete zde: Bodová předpověď: Intervalová předpověď:
 Predikce Text o predikci pro upřesnění pro ty, které zajímá, kde se v EViews všechna ta čísla berou. Ruční výpočty u průběžného testu nebudou potřeba. Co bude v závěrečném testu, to nevím. Ale přečíst
Predikce Text o predikci pro upřesnění pro ty, které zajímá, kde se v EViews všechna ta čísla berou. Ruční výpočty u průběžného testu nebudou potřeba. Co bude v závěrečném testu, to nevím. Ale přečíst
Statistické metody vyhodnocení vlivu škodlivin na denní úmrtnost, hospitalizaci a příznaky kardiovaskulárních a respiračních onemocnění
 Statistické metody vyhodnocení vlivu škodlivin na denní úmrtnost, hospitalizaci a příznaky kardiovaskulárních a respiračních onemocnění Jiří Skorkovský Úvod a cíle studie vlivu PM10 na denní
Statistické metody vyhodnocení vlivu škodlivin na denní úmrtnost, hospitalizaci a příznaky kardiovaskulárních a respiračních onemocnění Jiří Skorkovský Úvod a cíle studie vlivu PM10 na denní
1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004.
 Prostá regresní a korelační analýza 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Problematika závislosti V podstatě lze rozlišovat mezi závislostí nepodstatnou, čili náhodnou
Prostá regresní a korelační analýza 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Problematika závislosti V podstatě lze rozlišovat mezi závislostí nepodstatnou, čili náhodnou
ZÁKLADNÍ STATISTICKÉ CHARAKTERISTIKY
 zhanel@fsps.muni.cz ZÁKLADNÍ STATISTICKÉ CHARAKTERISTIKY METODY DESKRIPTIVNÍ STATISTIKY 1. URČENÍ TYPU ŠKÁLY (nominální, ordinální, metrické) a) nominální + ordinální neparametrické stat. metody b) metrické
zhanel@fsps.muni.cz ZÁKLADNÍ STATISTICKÉ CHARAKTERISTIKY METODY DESKRIPTIVNÍ STATISTIKY 1. URČENÍ TYPU ŠKÁLY (nominální, ordinální, metrické) a) nominální + ordinální neparametrické stat. metody b) metrické
Seminář 6 statistické testy
 Seminář 6 statistické testy Část I. Volba správného testu Chceme zjistit, zda se Ježkovy a Širůčkovy seminární skupiny liší ve výsledcích v. průběžné písemce ze statistiky. Chceme zjistit, zda 1. průběžná
Seminář 6 statistické testy Část I. Volba správného testu Chceme zjistit, zda se Ježkovy a Širůčkovy seminární skupiny liší ve výsledcích v. průběžné písemce ze statistiky. Chceme zjistit, zda 1. průběžná
Jste aktivní sportovec?(pravidelně sportuji alespoň 2x týdně) Jakým sportovním činnostem se pravidelně věnujete? (alespoň 1 x za dva týdny v sezóně)
 Seznam příloh Příloha 1 Dotazník sportovních aktivit... 1 Příloha 2 Homogenita souboru věk... 3 Příloha 3 Homogenita souboru pohlaví... 4 Příloha 4 4Elements Inventory a sportovní aktivita... 5 Příloha
Seznam příloh Příloha 1 Dotazník sportovních aktivit... 1 Příloha 2 Homogenita souboru věk... 3 Příloha 3 Homogenita souboru pohlaví... 4 Příloha 4 4Elements Inventory a sportovní aktivita... 5 Příloha
Zkušenosti s použitím metod Counterfactual Impact Evaluation při evaluaci ESF v České republice. Jan Brůha IREAS
 Zkušenosti s použitím metod Counterfactual Impact Evaluation při evaluaci ESF v České republice Jan Brůha IREAS Pilotní projekt použití CIE pro hodnocení ESF OPLZZ V současné době byly použity tři metody
Zkušenosti s použitím metod Counterfactual Impact Evaluation při evaluaci ESF v České republice Jan Brůha IREAS Pilotní projekt použití CIE pro hodnocení ESF OPLZZ V současné době byly použity tři metody
Vytěžování znalostí z dat
 Pavel Kordík, Jan Motl (ČVUT FIT) Vytěžování znalostí z dat BI-VZD, 2012, Přednáška 1 1/32 Vytěžování znalostí z dat Pavel Kordík, Jan Motl Department of Computer Systems Faculty of Information Technology
Pavel Kordík, Jan Motl (ČVUT FIT) Vytěžování znalostí z dat BI-VZD, 2012, Přednáška 1 1/32 Vytěžování znalostí z dat Pavel Kordík, Jan Motl Department of Computer Systems Faculty of Information Technology
Design Experimentu a Statistika - AGA46E
 Design Experimentu a Statistika - AGA46E Czech University of Life Sciences in Prague Department of Genetics and Breeding Summer Term 2015 Matúš Maciak (@ A 211) Office Hours: T 9:00 10:30 or by appointment
Design Experimentu a Statistika - AGA46E Czech University of Life Sciences in Prague Department of Genetics and Breeding Summer Term 2015 Matúš Maciak (@ A 211) Office Hours: T 9:00 10:30 or by appointment
6. Lineární regresní modely
 6. Lineární regresní modely 6.1 Jednoduchá regrese a validace 6.2 Testy hypotéz v lineární regresi 6.3 Kritika dat v regresním tripletu 6.4 Multikolinearita a polynomy 6.5 Kritika modelu v regresním tripletu
6. Lineární regresní modely 6.1 Jednoduchá regrese a validace 6.2 Testy hypotéz v lineární regresi 6.3 Kritika dat v regresním tripletu 6.4 Multikolinearita a polynomy 6.5 Kritika modelu v regresním tripletu
LINEÁRNÍ REGRESE Komentované řešení pomocí programu Statistica
 LINEÁRNÍ REGRESE Komentované řešení pomocí programu Statistica Vstupní data Data umístěná v excelovském souboru překopírujeme do tabulky ve Statistice a pojmenujeme proměnné, viz prezentace k tématu Popisná
LINEÁRNÍ REGRESE Komentované řešení pomocí programu Statistica Vstupní data Data umístěná v excelovském souboru překopírujeme do tabulky ve Statistice a pojmenujeme proměnné, viz prezentace k tématu Popisná
vzorek1 0.0033390 0.0047277 0.0062653 0.0077811 0.0090141... vzorek 30 0.0056775 0.0058778 0.0066916 0.0076192 0.0087291
 Vzorová úloha 4.16 Postup vícerozměrné kalibrace Postup vícerozměrné kalibrace ukážeme na úloze C4.10 Vícerozměrný kalibrační model kvality bezolovnatého benzinu. Dle následujících kroků na základě naměřených
Vzorová úloha 4.16 Postup vícerozměrné kalibrace Postup vícerozměrné kalibrace ukážeme na úloze C4.10 Vícerozměrný kalibrační model kvality bezolovnatého benzinu. Dle následujících kroků na základě naměřených
Regrese. Karel Zvára. Poznámky k přednášce STP094, akademický rok 2001/2002
 1 Regrese Karel Zvára Poznámky k přednášce STP094, akademický rok 2001/2002 2 Uvítám všechny připomínky a zejména každé upozornění na chybu či nedopatření, ať už budou ústní, písemné nebo elektronickou
1 Regrese Karel Zvára Poznámky k přednášce STP094, akademický rok 2001/2002 2 Uvítám všechny připomínky a zejména každé upozornění na chybu či nedopatření, ať už budou ústní, písemné nebo elektronickou
Chyby měření 210DPSM
 Chyby měření 210DPSM Jan Zatloukal Stručný přehled Zdroje a druhy chyb Systematické chyby měření Náhodné chyby měření Spojité a diskrétní náhodné veličiny Normální rozdělení a jeho vlastnosti Odhad parametrů
Chyby měření 210DPSM Jan Zatloukal Stručný přehled Zdroje a druhy chyb Systematické chyby měření Náhodné chyby měření Spojité a diskrétní náhodné veličiny Normální rozdělení a jeho vlastnosti Odhad parametrů
Hloubka dat. kontury, klasifikace a konzistence. Daniel Hlubinka
 Hloubka dat kontury, klasifikace a konzistence Daniel Hlubinka Univerzita Karlova v Praze Matematicko-fyzikální fakulta Katedra pravděpodobnosti a matematické statistiky Robust Němčičky 2012 Hloubka Co
Hloubka dat kontury, klasifikace a konzistence Daniel Hlubinka Univerzita Karlova v Praze Matematicko-fyzikální fakulta Katedra pravděpodobnosti a matematické statistiky Robust Němčičky 2012 Hloubka Co
31. 3. 2014, Brno Hanuš Vavrčík Základy statistiky ve vědě
 31. 3. 2014, Brno Hanuš Vavrčík Základy statistiky ve vědě Motto Statistika nuda je, má však cenné údaje. strana 3 Statistické charakteristiky Charakteristiky polohy jsou kolem ní seskupeny ostatní hodnoty
31. 3. 2014, Brno Hanuš Vavrčík Základy statistiky ve vědě Motto Statistika nuda je, má však cenné údaje. strana 3 Statistické charakteristiky Charakteristiky polohy jsou kolem ní seskupeny ostatní hodnoty
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc.
 Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika 2010 1.týden (20.09.-24.09. ) Data, typy dat, variabilita, frekvenční analýza
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika 2010 1.týden (20.09.-24.09. ) Data, typy dat, variabilita, frekvenční analýza
Jana Vránová, 3. lékařská fakulta UK
 Jana Vránová, 3. lékařská fakulta UK Vznikají při zkoumání vztahů kvalitativních resp. diskrétních znaků Jedná se o analogii s korelační analýzou spojitých znaků Přitom předpokládáme, že každý prvek populace
Jana Vránová, 3. lékařská fakulta UK Vznikají při zkoumání vztahů kvalitativních resp. diskrétních znaků Jedná se o analogii s korelační analýzou spojitých znaků Přitom předpokládáme, že každý prvek populace
Testy nezávislosti kardinálních veličin
 Testy nezávislosti kardinálních veličin Komentované řešení pomocí programu R Ústav matematiky Fakulta chemicko inženýrská Vysoká škola chemicko-technologická v Praze Načtení vstupních dat Vstupní data
Testy nezávislosti kardinálních veličin Komentované řešení pomocí programu R Ústav matematiky Fakulta chemicko inženýrská Vysoká škola chemicko-technologická v Praze Načtení vstupních dat Vstupní data
Stav Svobodný Rozvedený Vdovec. Svobodná 37 10 6. Rozvedená 8 12 8. Vdova 5 8 6
 1. Příklad Byly sledovány rodinné stavy nevěst a ženichů při uzavírání sňatků a byla vytvořena následující tabulka četností. Stav Svobodný Rozvedený Vdovec Svobodná 37 10 6 Rozvedená 8 12 8 Vdova 5 8 6
1. Příklad Byly sledovány rodinné stavy nevěst a ženichů při uzavírání sňatků a byla vytvořena následující tabulka četností. Stav Svobodný Rozvedený Vdovec Svobodná 37 10 6 Rozvedená 8 12 8 Vdova 5 8 6
