7. Základy lineární teorie kmitání s jedním stupněm volnosti
|
|
|
- Michaela Říhová
- před 9 lety
- Počet zobrazení:
Transkript
1 7. Základy lineární teorie kmitání s jedním stupněm volnosti Úvod V této kapitole bude ukázán přístup k sestavení pohybové rovnice s využitím Lagrangeových rovnic druhého druhu a jejich analýza. Jeden stupeň volnosti se v současné době zejména s rozšířenou aplikací metody konečných prvků může zdát velmi jednoduchá, avšak z pohledu závěrů má podstatně obecnější platnost. Navíc pro určité soustavy s mnoha stupni volnosti lze použitím speciálních metod mechaniky soustavy zredukovat na jeden stupeň volnosti. Obr. 7.1 Na obr. 7.1 je nakresleno schéma soustavy, která kmitá s jedním stupněm volnosti. Zobecněná souřadnice může mít charakter posunutí a má v takovém případě rozměr m. V případě torzního kmitání má charakter natočení a má rozměr rad. Dále pak rychlosti mají rozměr, nebo a zrychlení mají rozměr, nebo. Tomu odpovídá i zobecněná vnější síla (buzení), která má pro první případ rozměr a ve druhém případě má charakter momentu s rozměrem. Těmto dvěma nejrozšířenějším případům odpovídá i charakter setrvačného, pružného a tlumícího členu. V prvním případě má setrvačný člen charakter hmotnosti s rozměrem kg a ve druhém případě moment setrvačnosti (v případě torzního kmitání) s rozměrem. V případě lineárního pružného členu má tuhost pružiny rozměr a ve druhém případě. Obdobná situace je také u tlumícího členu. V prvním případě má rozměr a ve druhém případě. Je tedy zřejmé, že obrázek 7.1 lze chápat jako ilustrativní obrázek, nikoliv jako výpočtový model. Poněkud jasnější situace je, v případě stanovení sil (momentů) v pružném a tlumícímčlenu. Síla v pružnémčlenu i s uvedením zmíněných dvou případů zobecněných souřadnic je dána vztahem (7.19) Síla v tlumícímčlenu i s uvedením zmíněných dvou případů zobecněných souřadnic je dána vztahem (7.20)
2 V případě torzního kmitání se jedná o torzní pružinu a torzní tlumič. Tlumícím členům se říká viskózní, protože silové (momentové) účinky jsou lineárně závislé na rychlostech ( úhlových rychlostech). V dalším bude věnována pozornost na stanovení kinetické a potenciální energie, zatlumené funkce a práce vnějších sil, které nemají potenciál. Tyto veličiny jsou nutné pro dosazení Lagrangeových rovnic druhého druhu. Pro kinetickou energii platí vztah Pro potenciální energii platí vztah (7.21) Pro zatlumenou funkci platí vztah (7.22) (7.23) Pro práci vnějších sil, které nemají potenciál platí vztah (7.24) a v případě výkonu (7.25) Po dosazení do Lagrangeových rovnic druhého druhu a provedení příslušných derivací se obdrží rovnice (7.26) kde je zobecněná souřadnice, je zobecněná hmotnost, je zobecněné tlumení, je zobecněná tuhost a je zobecněné buzení. Rovnice (7.26) je nehomogenní lineární diferenciální rovnice druhého řádu s konstantními koeficienty. Její řešení, jak je známo z matematiky, se skládá zřešení homogenníčásti a partikulárního integrálu. Nejdříve bude věnována pozornostřešení homogenníčásti. Volné tlumené kmitání Homogenní rovnice má tvar Obecnéřešení je dáno ve tvaru (7.27) (7.28) kde a jsou integrační konstanty, které se stanoví z počátečních podmínek a a jsou kořeny charakteristické rovnice. Tato má tvar
3 (7.29) Odtud jeřešení dáno vztahy (7.30) Podle znaménka pod odmocninou je určen celkový charakter čísel. Tato čísla se nazývají vlastní čísla soustavy. V případě jejich reálné hodnoty výsledný pohyb nebude kmitavý, ale bude probíhat po exponenciále. V případě záporné hodnoty bude děj utlumen (stabilní pohyb) a v případě kladné hodnoty bude výchylka neustále narůstat.výsledný pohyb bude nestabilní. pro praxi mnohem zajímavější případ nastane, když znaménko pod odmocninou bude záporné. V takovém případě je výhodnější rovnici (7.30) přepsat do tvaru (7.31) Odtud je zřejmé, že vlastní čísla jsou komplexně sdružená. Reálná část má charakter tlumení a je často označována koeficient doznívání V rovnici (7.31) dále je (7.32) (7.33) vlastní frekvence volného netlumeného kmitání. Pokud je požadován výsledek frekvence v, pro přepočet platí vztah. Vlastní frekvence volného netlumeného kmitání je jedna z nejdůležitějších charakteristik kmitavých dynamických systémů. V případě kmitání s jedním stupněm volnosti se obdrží hodnota jedna, v případě kmitání dynamických soustav s n stupni volnosti má soustava n vlastních frekvencí. V rovnici (7.31) dále je (7.34) vlastní frekvence tlumené soustavy. Z tohoto vztahu je dále zřejmé, že tlumení snižuje vlastní frekvenci. Kritické tlumení je charakterizováno tím, že vlastní frekvence tlumeného kmitání je nulová. Úpravou vztahu (7.34) pro tento případ se obdrží pro kritické tlumení vztah (7.35) Vlastní čísla jsou tedy komplexně sdružená, jak je i zřejmé z následujícího vztahu (7.36) V případě, že reálná část vlastního čísla je záporná, výsledný děj je kmitavý s frekvencí rovnou vlastní frekvenci tlumené soustavy s postupně se snižující amplitudou (stabilní kmitání). V případě, že reálná část vlastního čísla je kladná, výsledný děj je opět kmitavý s frekvencí rovnou vlastní frekvenci tlumené soustavy s postupně narůstající amplitudou (nestabilní kmitání). Z toho je zřejmé, že reálná část komplexního vlastního čísla je jedním z významných charakteristik, na základě kterého lze charakterizovat stabilitu kmitání.
4 Z pohledu kmitání soustavy, které je dáno rovnicí (7.28) pro stabilní dynamický systém přechodové a po určité době odezní. Tato analýza je důležitá zejména při přechodových stavech. V technické praxi se v souvislosti s vlastními čísly zavádí pojem poměrný útlum. Ten je dán vztahem (7.37) V této souvislosti je nutno se zmínit i o logaritmickém dekrementu tlumení. Ten je dán jako přirozený logaritmus dvou po sobě následujících amplitud, tedy vztahem Vynucené ustálené kmitání Nehomogenní rovnice má tvar (7.39) (7.38) Výsledná odezva, jak již bylo uvedeno je dána součtem homogenní části (přechodový děj) a ustálené složky kmitání, tedy z pohledu matematiky partikulárním integrálem. Tento integrál má tvar v závislosti na tom, jaké je buzení. V podstatě jeden způsob řešení je odhad odezvy v závislosti na tvaru pravé strany diferenciální rovnice. Harmonické buzení Jeden nejčastější případ technické praxe je harmonické buzení, tedy pohybová rovnice má tvar (7.40) V obecném případě může být amplituda budících sil komplexní. je budící frekvence. S ohledem na pravou stranu, lze i odhadnout, že i odezva (partikulární integrál) bude mít harmonický charakter s frekvencí rovnou budící, tedy ve tvaru. (7.41) Amplituda kmitání je zde komplexní. Po dosazení do (7.40) se pro komplexní amplitudu obdrží vztah (7.42) Na základě reálné a imaginárníčásti lze obdržet amplitudu kmitání a fázi. Pro obě veličiny platí vztahy (7.43) (7.44)
5 Fázový úhel je úhel mezi odezvou a budící silou. Oba děje jsou harmonické s různým fázovým posunutím. Nulový fázový úhel znamená, že v souladu se směrem budící síly se pohybuje i těleso. Obr. 7.2 Obr. 7.3 Vztahy (7.43) a (7.44) jsou důležité pro sestrojení amplitudové a fázové charakteristiky (amplitudo-frekvenční a fázově-frekvenční). Na vodorovných osách se vynáší budící frekvence a na svislých amplituda a fáze. Obě charakteristiky jsou na obr. 7.2 a 7.3. V podstatě mohou nastat tři případy. Buď je vlastní frekvence v pásmu provozního buzení a dochází k tzv. rezonanci. Nebo je vlastní frekvence nižší, než je pásmo provozního buzení, tomuto stavu seříká nadrezonanční, nebo je vlastní frekvence vyšší, než je pásmo provozního buzení, tomuto stavu říkáme podrezonanční. Je zřejmé, že z hlediska provozní bezpečnosti, kdy amplitudy dosahují nejnižších hodnot je v případě podrezonančního provozu. Tyto tři typické případy jsou nakresleny na obr. 7.4.
6 Obr. 7.4 Pro nulovou budící frekvenci je amplitudová odezva dána vztahem (7.45) což je v podstatě případ statiky, resp. pružnosti a pevnosti. podstatné ale je, že amplituda není nulová. Maximální amplitudy je dosaženo pro netlumené kmitání a pro stav, kdy je budící frekvence rovna vlastní netlumené frekvenci. tento stav se nazývá rezonanční a v provozních podmínkách bývá jako jeden z nejnebezpečnějších. Zpravidla je snaha se mu vyhnout. I v případě tlumených soustav je amplituda vyšší, než jsou statické amplitudy. Tomuto jevu seříká dynamické zesílení. Pro nekonečně velkou budící frekvenci se amplituda kmitání blíží k nule. Poznámka Ke stejným výsledkům lze rovněž dospět na základě řešení v reálném oboru. buzení má v tomto případě sinovou a cosinovou složku. Obdobně je to s předpokládanýmřešením ve tvaru součtu obou složek. V případě tuhostí, případně potenciálních energií je nutno vidět souvislosti s analýzou úloh pružnosti a pevnosti. Podélné kmitání má ekvivalent v tahu-tlaku, torzní kmitání v krutu. Poněkud komplikovanější situace je u ohybu, kde jak je známo, průřez se při současném posunutí i natočí. V této souvislosti nejjednodušší případ ohybového kmitání má dva stupně volnosti Buzení nevývahou
7 Obr. 7.5 Další velmičastý případ technické praxe je buzení od nevývahy, tedy v podstatě buzení odstředivou silou. Z pohledu aplikace v dynamice rotorových soustav střed hřídele kmitá v rovině kolmé na spojnici ložisek. Pro zjednodušení bude uvažováno kmitání pouze v jednom směru, jak je zřejmé z obr Pro jednoduchost nebudou uvažovány pasivní odpory ve stykové ploše mezi tělesem a základním tělesem. Pohybová rovnice má tvar (7.46) kde člen se nazývá nevývaha a je známá z vyvažování a je odstředivá síla. Řešení zde na rozdíl od předchozího případu bude provedeno v reálném oboru. S ohledem na pravou stranu, lze i odhadnout, že i odezva (partikulární integrál) bude mít harmonický charakter s frekvencí rovnou budící, tedy ve tvaru. Po dosazení do (7.46) se obdrží dvě rovnice pro dvě neznámé složky odezvy (7.47) a pro amplitudu kmitání (7.48) (7.49) Vztah (7.49) slouží pro sestrojení amplitudové charakteristiky (amplitudo-frekvenční), který je na obr. 7.6.
8 Obr. 7.6 Kinematické buzení Poslední analyzovaný případ technické praxe je kinematické buzení, tedy buzení od základu. Konkrétním případem to může být buzení při seismické události, tedy při zemětřesení. Schéma soustavy je na obr. 7.7.
9 Obr. 7.7 Opět pro zjednodušení bude uvažováno kmitání s jedním stupněm volnosti.časová závislost pohybujícího se základu je dána. Řešení lze provést dvěma způsoby. V prvním případě je výsledkem pohyb tělesa absolutně vzhledem k rámu, který se nepohybuje (absolutní souřadnice) a ve druhém případě je výsledkem relativní pohyb tělesa vzhledem k základu (relativní souřadnice). Mezi souřadnicemi platí vztah (7.50) Pro jednoduchost se bude předpokládat harmonický pohyb základu. Pohybová rovnice má tvar (7.51) přičemž není detailně analyzována potenciální energie v pružném členu a tlumící funkce, které jak je zřejmé jsou dány rozdílem absolutní souřadnice a základu. Analýza v absolutních souřadnicích Za předpokladu harmonického pohybu základu se úpravou rovnice (7.51) obdrží (7.52) což je rovnice po formální stránce shodná s rovnicí (7.40). Pro stanovení amplitudy kmitání a fáze lze použít všechny vztahy, které byly odvozeny pro harmonické buzení.
10 (7.53) Amplitudová charakteristika je na obr Odtud je zřejmé, že při budící frekvenci je odezva pro tlumený dynamický systém větší, než pro netlumený. Obr. 7.8 Analýza v relativních souřadnicích Za předpokladu harmonického pohybu základu se úpravou rovnice (7.51) obdrží (7.54) což je rovnice opět po formální stránce shodná s rovnicí (7.40). Pro stanovení amplitudy kmitání a fáze lze použít všechny vztahy, které byly odvozeny pro harmonické buzení. Amplitudová charakteristika je na obr (7.55)
11 Obr. 7.9 Závěr Možnosti jak potlačit (snížit dynamickou odezvu) jsou v podstatě zřejmé z charakteru rovnic pro odezvu a lze to provést třemi způsoby 1. Snížit amplitudu budících sil. V praxi to znamená např. stroj co možná nejlépe vyvážit, maximálně omezit aerodynamické buzení atd. 2. Pokud je snížena amplituda budících sil na minimum, druhá možnost je provést změnu vlastní frekvence. Zvýšení hmotnosti má za následek snížení vlastní frekvence a zvýšení tuhosti má za následek zvýšení vlastní frekvence. Cílem je stroj tzv. přeladit tak, aby se v pásmu provozního buzení nenacházela vlastní frekvence. 3. Třetí možný případ je takový, kdy jsou amplitudy budících sil sníženy na minimální hodnotu a konstrukčními změnami není možné soustavu přeladit. V tomto případě se do soustavy přidá tlumič, aby se snížila amplituda vibrací. Tlumič je vhodné umístit do míst s maximální rychlostí vibrací, aby bylo tlumení co nejvíce účinné. Příklad Je dána soustava těles podle obrázku 8. Kotouč o hmotnosti a poloměru je pevně spojen s tyčí o hmotnosti délky.,,,,,,,, kmity kolem této polohy.,. Soustava se nachází ve staticky rovnovážné poloze a předpokládejte malé Pro danou soustavuřešte: 1. Stanovte vlastní frekvenci netlumeného a tlumeného kmitání a znázorněte amplitudovou charakteristiku. 2. Rozhodněte, zda v pásmu provozního buzení nastane vymezení vůle v. Rozbor úlohy
12 Soustava těles představuje soustavu, která má jeden stupeň volnosti. K sestavení pohybové rovnice budou využity Lagrangeovy rovnice druhého druhu. K analýze kmitání lze přistovat dvěma způsoby. Schéma prvního způsobu je na obr. 9a. Jako zobecněná souřadnice je zvoleno natočení soustavy, tedy. Výsledkem bude kontrola vymezení vůle podle vztahu. Schéma druhého způsobu je na obr. 9b. Jako zobecněná souřadnice je zvoleno posunutí koncového bodu na tyčce, tedy. Výsledkem bude kontrola vymezení vůle podle vztahu. Mezi oběma přístupy, na základě kterých musí být dosaženy stejné výsledky a stejné závěry platí vztahy V obou případech je nutno stanovit úhel, pro která platí a také vzdálenost, pro kterou platí Poznámky 1. Přiřešení nebudou uvažovány tíhové síly, protože soustava je v rovnovážné poloze. 2. Pro odlišení zobecněných veličin (hmotnosti, tuhosti, tlumení a vnější síly), které jsou označeny v teoretické části od označení, které je použito v příkladu, budou zde tyto veličiny označeny nahoře hvězdičkou. Řešení dle 1. přístupu Pro aplikaci Lagrangeových rovnic druhého druhu je nutno stanovit kinetickou a potenciální energii, tlumící funkci a práci ( výkon) vnějších sil, které nemají potenciál. Kinetická energie Zobecněná hmotnost má charakter osového momentu setrvačnosti k ose kolmé na rovinu kmitání. Při jejím stanovení je nutno použít Steinerovu větu. Potenciální energie
13 odkud pro zobecněnou tuhost je Pro zatlumenou energii platí odkud pro zobecněné tlumení je Pro práci (výkon) vnějších sil, které nemají potenciál, přičemž bude uvažována pouze amplituda budících sil odkud pro amplitudu zobecněné budící síly je S ohledem na tvar kinetické energie, její parciální derivace podle zobecněné souřadnice je nulová. Výsledný tvar pohybové rovnice pak je Vlastní frekvence volného netlumeného kmitání Součinitel doznívání Vlastní frekvence tlumeného kmitání Na obr. 10 je nakreslena amplitudová charakteristika pro daný příklad. Poměrný útlum následně je
14 S ohledem na rozsah provozního buzení a vlastní frekvenci tlumeného kmitání, nastane v pásmu provozního buzení rezonanční stav, při kterém bude maximální odezva. Stačí tedy zkontrolovat amplitudu při rezonančním stavu. Obecný vztah pro odezvu je Rezonanční stav nastane, když je, což po dosazení Svislé posunutí koncového bodu na tyčce je dáno vztahem Vzhledem k tomu, že svislá amplituda kmitání koncového bodu je větší než vůle pásmu provozního buzení k vymezení vůle., nastane v daném Řešení dle 2. přístupu Pro aplikaci Lagrangeových rovnic druhého druhu je nutno stanovit kinetickou a potenciální energii, tlumící funkci a práci ( výkon) vnějších sil, které nemají potenciál. Kinetická energie Zobecněná hmotnost má rozměr jako klasická hmotnost. Při jejím stanovení je i v tomto případě nutno použít Steinerovu větu. Potenciální energie
15 odkud pro zobecněnou tuhost je Pro zatlumenou energii platí odkud pro zobecněné tlumení je Pro práci (výkon) vnějších sil, které nemají potenciál, přičemž bude uvažována pouze amplituda budících sil odkud pro amplitudu zobecněné budící síly je S ohledem na tvar kinetické energie, její parciální derivace podle zobecněné souřadnice je nulová. Výsledný tvar pohybové rovnice pak je Vlastní frekvence volného netlumeného kmitání Součinitel doznívání
16 Vlastní frekvence tlumeného kmitání Na obr. 10 je nakreslena amplitudová charakteristika pro daný příklad. Poměrný útlum následně je S ohledem na rozsah provozního buzení a vlastní frekvenci tlumeného kmitání, nastane v pásmu provozního buzení rezonanční stav, při kterém bude maximální odezva. Stačí tedy zkontrolovat amplitudu při rezonančním stavu. Obecný vztah pro odezvu je Rezonanční stav nastane, kdy je, což po dosazení což je přímo svislé posunutí konce tyče Vzhledem k tomu, že svislá amplituda kmitání koncového bodu je větší než vůle pásmu provozního buzení k vymezení vůle., nastane v daném Závěr Podle obou přístupů je nutno dojít ke stejným závěrům. Volba zobecněné souřadnice nemá vliv na výsledky řešení. V rámci pochopení dané problematiky se doporučuje provést analýzu za předpokladu volby zobecněné souřadnice jako posunutí těžiště tělesa 1. Na závěr pouze pro názornost bude provedena analýza pro případ podrezonančního a nadrezonančního provozu. V případě podrezonančního provozu by muselo být pásmo budící frekvence nižší, než je vlastní frekvence. Pouze pro ilustraci se předpokládá rozsah budící frekvence. Maximálních amplitud kmitání bude v tomto případě dosaženo při budící frekvenci amplitudy kmitání stanoveny pomocí vztahů. Pro oba případy volby zobecněné souřadnice budou
17 Svislé posunutí koncového bodu na tyčce je dáno vztahem Vzhledem k tomu, že svislá amplituda kmitání koncového bodu je menší než vůle daném pásmu provozního buzení k vymezení vůle., nenastane v což je přímo svislé posunutí konce tyče Vzhledem k tomu, že svislá amplituda kmitání koncového bodu je menší než vůle daném pásmu provozního buzení k vymezení vůle., nenastane v V případě nadrezonančního provozu by muselo být pásmo budící frekvence vyšší, než je vlastní frekvence. Pouze pro ilustraci se předpokládá rozsah budící frekvence. Maximálních amplitud kmitání bude v tomto případě dosaženo při budící frekvenci amplitudy kmitání stanoveny pomocí vztahů. Pro oba případy volby zobecněné souřadnice budou Svislé posunutí koncového bodu na tyčce je dáno vztahem Vzhledem k tomu, že svislá amplituda kmitání koncového bodu je menší než vůle daném pásmu provozního buzení k vymezení vůle., nenastane v což je přímo svislé posunutí konce tyče Vzhledem k tomu, že svislá amplituda kmitání koncového bodu je menší než vůle daném pásmu provozního buzení k vymezení vůle., nenastane v
18
ŘÍZENÍ ABSORBERU KMITŮ POMOCÍ MATLABU
 ŘÍZENÍ ABSORBERU KMITŮ POMOCÍ MATLABU Jiří Vondřich ; Evžen Thőndel Katedra mechaniky a materiálů, Fakulta elektrotechnická ČVUT Praha Abstrakt Periodické síly působící na strojní zařízení - například
ŘÍZENÍ ABSORBERU KMITŮ POMOCÍ MATLABU Jiří Vondřich ; Evžen Thőndel Katedra mechaniky a materiálů, Fakulta elektrotechnická ČVUT Praha Abstrakt Periodické síly působící na strojní zařízení - například
1.7. Mechanické kmitání
 1.7. Mechanické kmitání. 1. Umět vysvětlit princip netlumeného kmitavého pohybu.. Umět srovnat periodický kmitavý pohyb s periodickým pohybem po kružnici. 3. Znát charakteristické veličiny periodického
1.7. Mechanické kmitání. 1. Umět vysvětlit princip netlumeného kmitavého pohybu.. Umět srovnat periodický kmitavý pohyb s periodickým pohybem po kružnici. 3. Znát charakteristické veličiny periodického
Fyzikální praktikum 3 - úloha 7
 Fyzikální praktikum 3 - úloha 7 Operační zesilovač, jeho vlastnosti a využití Teorie: Operační zesilovač je elektronická součástka využívaná v měřící, regulační a výpočetní technice. Ideální model má nekonečně
Fyzikální praktikum 3 - úloha 7 Operační zesilovač, jeho vlastnosti a využití Teorie: Operační zesilovač je elektronická součástka využívaná v měřící, regulační a výpočetní technice. Ideální model má nekonečně
10.1.13 Asymptoty grafu funkce
 .. Asmptot grafu funkce Předpoklad:, Asmptot grafu už známe kreslili jsme si je jako přímk, ke kterým se graf funkce přibližuje. Nakreslení asmptot, pak umožňuje přesnější kreslení grafu. Například u hperbol
.. Asmptot grafu funkce Předpoklad:, Asmptot grafu už známe kreslili jsme si je jako přímk, ke kterým se graf funkce přibližuje. Nakreslení asmptot, pak umožňuje přesnější kreslení grafu. Například u hperbol
MS Word 2007 REVIZE DOKUMENTU A KOMENTÁŘE
 MS Word 2007 REVIZE DOKUMENTU A KOMENTÁŘE 1 ZAPNUTÍ SLEDOVÁNÍ ZMĚN Pokud zapnete funkci Sledování změn, aplikace Word vloží značky tam, kde provedete mazání, vkládání a změny formátu. Na kartě Revize klepněte
MS Word 2007 REVIZE DOKUMENTU A KOMENTÁŘE 1 ZAPNUTÍ SLEDOVÁNÍ ZMĚN Pokud zapnete funkci Sledování změn, aplikace Word vloží značky tam, kde provedete mazání, vkládání a změny formátu. Na kartě Revize klepněte
7. Silně zakřivený prut
 7. Silně zakřivený prut 2011/2012 Zadání Zjistěte rozložení napětí v průřezu silně zakřiveného prutu namáhaného ohybem analyticky a experimentálně. Výsledky ověřte numerickým výpočtem. Rozbor Pruty, které
7. Silně zakřivený prut 2011/2012 Zadání Zjistěte rozložení napětí v průřezu silně zakřiveného prutu namáhaného ohybem analyticky a experimentálně. Výsledky ověřte numerickým výpočtem. Rozbor Pruty, které
Lineární algebra. Vektorové prostory
 Lineární algebra Vektorové prostory Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo projektu:
Lineární algebra Vektorové prostory Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo projektu:
2.1. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné x je taková
 .. Funkce a jejich graf.. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné je taková binární relace z množin R do množin R, že pro každé R eistuje nejvýše jedno R, pro které [, ] f.
.. Funkce a jejich graf.. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné je taková binární relace z množin R do množin R, že pro každé R eistuje nejvýše jedno R, pro které [, ] f.
Definice 6.2.1. z = f(x,y) vázané podmínkou g(x,y) = 0 jsou z geometrického hlediska lokálními extrémy prostorové křivky k, Obr. 6.2.1. Obr. 6.2.
 Výklad Dalším typem extrémů, kterým se budeme zabývat jsou tzv. vázané extrémy. Hledáme extrémy nějaké funkce vzhledem k předem zadaným podmínkám. Definice 6.2.1. Řekneme, že funkce f : R n D f R má v
Výklad Dalším typem extrémů, kterým se budeme zabývat jsou tzv. vázané extrémy. Hledáme extrémy nějaké funkce vzhledem k předem zadaným podmínkám. Definice 6.2.1. Řekneme, že funkce f : R n D f R má v
Výrazy lze též zavést v nečíselných oborech, pak konstanty označuji jeden určitý prvek a obor proměnné není množina čísel.
 Výrazy. Rovnice a nerovnice. Výraz je matematický pojem používaný ve školské matematice. Prvním druhem matematických ů jsou konstanty. Konstanty označují právě jedno číslo z množiny reálných čísel. Například
Výrazy. Rovnice a nerovnice. Výraz je matematický pojem používaný ve školské matematice. Prvním druhem matematických ů jsou konstanty. Konstanty označují právě jedno číslo z množiny reálných čísel. Například
Gymnázium, Praha 10, Voděradská 2 Projekt OBZORY
 Gymnázium, Praha 10, Voděradská 2 Projekt OBZORY INDIVIDUÁLNÍ VÝUKA Matematika METODIKA Soustavy rovnic Mgr. Marie Souchová květen 2011 Tato část učiva následuje po kapitole Rovnice. Je rozdělena do částí
Gymnázium, Praha 10, Voděradská 2 Projekt OBZORY INDIVIDUÁLNÍ VÝUKA Matematika METODIKA Soustavy rovnic Mgr. Marie Souchová květen 2011 Tato část učiva následuje po kapitole Rovnice. Je rozdělena do částí
Rostislav Horčík. 13. října 2006
 3. přednáška Rostislav Horčík 13. října 2006 1 Lineární prostory Definice 1 Lineárním prostorem nazýváme každou neprázdnou množinu L, na které je definováno sčítání + : L L L a násobení reálným číslem
3. přednáška Rostislav Horčík 13. října 2006 1 Lineární prostory Definice 1 Lineárním prostorem nazýváme každou neprázdnou množinu L, na které je definováno sčítání + : L L L a násobení reálným číslem
Goniometrie trigonometrie
 Goniometrie trigonometrie Goniometrie se zabývá funkcemi sinus, kosinus, tangens, kotangens (goniometrické funkce). V tomto článku se budeme zabývat trigonometrií (součást goniometrie) používáním goniometrických
Goniometrie trigonometrie Goniometrie se zabývá funkcemi sinus, kosinus, tangens, kotangens (goniometrické funkce). V tomto článku se budeme zabývat trigonometrií (součást goniometrie) používáním goniometrických
SMĚŠOVACÍ KALORIMETR -tepelně izolovaná nádoba s míchačkou a teploměrem, která je naplněná kapalinou
 KALORIMETRIE Kalorimetr slouží k měření tepla, tepelné kapacity, případně měrné tepelné kapacity Kalorimetrická rovnice vyjadřuje energetickou bilanci při tepelné výměně mezi kalorimetrem a tělesy v kalorimetru.
KALORIMETRIE Kalorimetr slouží k měření tepla, tepelné kapacity, případně měrné tepelné kapacity Kalorimetrická rovnice vyjadřuje energetickou bilanci při tepelné výměně mezi kalorimetrem a tělesy v kalorimetru.
2.3.19 Grafické řešení soustav lineárních rovnic a nerovnic
 .3.19 Grafické řešení soustav lineárních rovnic a nerovnic Předpoklad: 307, 311 Př. 1: Vřeš soustavu rovnic + =. Pokud se také o grafické řešení. = 5 Tak jednoduchou soustavu už jsme dlouho neměli: + =
.3.19 Grafické řešení soustav lineárních rovnic a nerovnic Předpoklad: 307, 311 Př. 1: Vřeš soustavu rovnic + =. Pokud se také o grafické řešení. = 5 Tak jednoduchou soustavu už jsme dlouho neměli: + =
Numerická integrace. 6. listopadu 2012
 Numerická integrace Michal Čihák 6. listopadu 2012 Výpočty integrálů v praxi V přednáškách z matematické analýzy jste se seznámili s mnoha metodami výpočtu integrálů. V praxi se ale poměrně často můžeme
Numerická integrace Michal Čihák 6. listopadu 2012 Výpočty integrálů v praxi V přednáškách z matematické analýzy jste se seznámili s mnoha metodami výpočtu integrálů. V praxi se ale poměrně často můžeme
1 NÁPRAVA De-Dion Představuje přechod mezi tuhou nápravou a nápravou výkyvnou. Používá se (výhradně) jako náprava hnací.
 1 NÁPRAVA De-Dion Představuje přechod mezi tuhou nápravou a nápravou výkyvnou. Používá se (výhradně) jako náprava hnací. Skříň rozvodovky spojena s rámem zmenšení neodpružené hmoty. Přenos točivého momentu
1 NÁPRAVA De-Dion Představuje přechod mezi tuhou nápravou a nápravou výkyvnou. Používá se (výhradně) jako náprava hnací. Skříň rozvodovky spojena s rámem zmenšení neodpružené hmoty. Přenos točivého momentu
DYNAMICKÉ VÝPOČTY PROGRAMEM ESA PT
 DYNAMICKÉ VÝPOČTY PROGRAMEM ESA PT Doc. Ing. Daniel Makovička, DrSc.*, Ing. Daniel Makovička** *ČVUT v Praze, Kloknerův ústav, Praha 6, **Statika a dynamika konstrukcí, Kutná Hora 1 ÚVOD Obecně se dynamickým
DYNAMICKÉ VÝPOČTY PROGRAMEM ESA PT Doc. Ing. Daniel Makovička, DrSc.*, Ing. Daniel Makovička** *ČVUT v Praze, Kloknerův ústav, Praha 6, **Statika a dynamika konstrukcí, Kutná Hora 1 ÚVOD Obecně se dynamickým
UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE
 MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin
Posouzení únosnosti svaru se provádí podle zásad pružnosti a pevnosti v nebezpečném průřezu.
 Svarové spoje Posouzení únosnosti svaru se provádí podle zásad pružnosti a pevnosti v nebezpečném průřezu. Vybrané druhy svarů a jejich posouzení dle EN ČSN 1993-1-8. Koutový svar -T-spoj - přeplátovaný
Svarové spoje Posouzení únosnosti svaru se provádí podle zásad pružnosti a pevnosti v nebezpečném průřezu. Vybrané druhy svarů a jejich posouzení dle EN ČSN 1993-1-8. Koutový svar -T-spoj - přeplátovaný
2.6.4 Lineární lomené funkce s absolutní hodnotou
 .6. Lineární lomené funkce s absolutní hodnotou Předpoklady: 60, 603 Pedagogická poznámka: Hlavním cílem hodiny je nácvik volby odpovídajícího postupu. Proto je dobré nechat studentům chvíli, aby si metody
.6. Lineární lomené funkce s absolutní hodnotou Předpoklady: 60, 603 Pedagogická poznámka: Hlavním cílem hodiny je nácvik volby odpovídajícího postupu. Proto je dobré nechat studentům chvíli, aby si metody
(k 1)x k + 1. pro k 1 a x = 0 pro k = 1.
 . Funkce dvou a více proměnných. Úvod. Určete definiční obor funkce a proveďte klasifikaci bodů z R vzhledem k a rozhodněte zda je množina uzavřená či otevřená. Určete a načrtněte vrstevnice grafu funkce
. Funkce dvou a více proměnných. Úvod. Určete definiční obor funkce a proveďte klasifikaci bodů z R vzhledem k a rozhodněte zda je množina uzavřená či otevřená. Určete a načrtněte vrstevnice grafu funkce
Uložení potrubí. Postupy pro navrhování, provoz, kontrolu a údržbu. Volba a hodnocení rezervy posuvu podpěr potrubí
 Uložení potrubí Postupy pro navrhování, provoz, kontrolu a údržbu Volba a hodnocení rezervy posuvu podpěr potrubí Obsah: 1. Definice... 2 2. Rozměrový návrh komponent... 2 3. Podpěra nebo vedení na souosém
Uložení potrubí Postupy pro navrhování, provoz, kontrolu a údržbu Volba a hodnocení rezervy posuvu podpěr potrubí Obsah: 1. Definice... 2 2. Rozměrový návrh komponent... 2 3. Podpěra nebo vedení na souosém
doc. Dr. Ing. Elias TOMEH e-mail: elias.tomeh@tul.cz
 doc. Dr. Ing. Elias TOMEH e-mail: elias.tomeh@tul.cz Elias Tomeh / Snímek 1 Nevyváženost rotorů rotačních strojů je důsledkem změny polohy (posunutí, naklonění) hlavních os setrvačnosti rotorů vzhledem
doc. Dr. Ing. Elias TOMEH e-mail: elias.tomeh@tul.cz Elias Tomeh / Snímek 1 Nevyváženost rotorů rotačních strojů je důsledkem změny polohy (posunutí, naklonění) hlavních os setrvačnosti rotorů vzhledem
1 Měření kapacity kondenzátorů
 . Zadání úlohy a) Změřte kapacitu kondenzátorů, 2 a 3 LR můstkem. b) Vypočítejte výslednou kapacitu jejich sériového a paralelního zapojení. Hodnoty kapacit těchto zapojení změř LR můstkem. c) Změřte kapacitu
. Zadání úlohy a) Změřte kapacitu kondenzátorů, 2 a 3 LR můstkem. b) Vypočítejte výslednou kapacitu jejich sériového a paralelního zapojení. Hodnoty kapacit těchto zapojení změř LR můstkem. c) Změřte kapacitu
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1. Podpora digitalizace a využití ICT na SPŠ CZ.1.07/1.5.00/34.
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Uživatelská nastavení parametrických modelářů, využití
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Uživatelská nastavení parametrických modelářů, využití
ÚČEL zmírnit rázy a otřesy karosérie od nerovnosti vozovky, zmenšit namáhání rámu (zejména krutem), udržet všechna kola ve stálém styku s vozovkou.
 4 ODPRUŽENÍ Souhrn prvků automobilu, které vytvářejí pružné spojení mezi nápravami a nástavbou (karosérií). ÚČEL zmírnit rázy a otřesy karosérie od nerovnosti vozovky, zmenšit namáhání rámu (zejména krutem),
4 ODPRUŽENÍ Souhrn prvků automobilu, které vytvářejí pružné spojení mezi nápravami a nástavbou (karosérií). ÚČEL zmírnit rázy a otřesy karosérie od nerovnosti vozovky, zmenšit namáhání rámu (zejména krutem),
7. Stropní chlazení, Sálavé panely a pasy - 1. část
 Základy sálavého vytápění (2162063) 7. Stropní chlazení, Sálavé panely a pasy - 1. část 30. 3. 2016 Ing. Jindřich Boháč Obsah přednášek ZSV 1. Obecný úvod o sdílení tepla 2. Tepelná pohoda 3. Velkoplošné
Základy sálavého vytápění (2162063) 7. Stropní chlazení, Sálavé panely a pasy - 1. část 30. 3. 2016 Ing. Jindřich Boháč Obsah přednášek ZSV 1. Obecný úvod o sdílení tepla 2. Tepelná pohoda 3. Velkoplošné
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita V. 2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V. 2.4 Prvky elektronických obvodů Kapitola
Zvyšování kvality výuky technických oborů Klíčová aktivita V. 2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V. 2.4 Prvky elektronických obvodů Kapitola
Měření momentu setrvačnosti z doby kmitu
 Úloha č. 4 Měření momentu setrvačnosti z doby kmitu Úkoly měření:. Určete moment setrvačnosti vybraných těles, kruhové a obdélníkové desky.. Stanovení momentu setrvačnosti proveďte s využitím dvou rozdílných
Úloha č. 4 Měření momentu setrvačnosti z doby kmitu Úkoly měření:. Určete moment setrvačnosti vybraných těles, kruhové a obdélníkové desky.. Stanovení momentu setrvačnosti proveďte s využitím dvou rozdílných
Vítězslav Bártl. prosinec 2013
 VY_32_INOVACE_VB09_ČaP Jméno autora výukového materiálu Datum (období), ve kterém byl VM vytvořen Ročník, pro který je VM určen Vzdělávací oblast, vzdělávací obor, tematický okruh, téma Anotace Vítězslav
VY_32_INOVACE_VB09_ČaP Jméno autora výukového materiálu Datum (období), ve kterém byl VM vytvořen Ročník, pro který je VM určen Vzdělávací oblast, vzdělávací obor, tematický okruh, téma Anotace Vítězslav
Předmět: Ročník: Vytvořil: Datum: ŠČERBOVÁ M. PAVELKA V. NOSNÍKY NOSNÍKY
 Předmět: Ročník: Vytvořil: Datum: MECHANIKA PRVNÍ ŠČERBOVÁ M. PAVELKA V. 16. ČERVNA 2012 Název zpracovaného celku: NOSNÍKY NOSNÍKY Nosníky jsou zpravidla přímá tělesa (pruty) uloţená na podporách nebo
Předmět: Ročník: Vytvořil: Datum: MECHANIKA PRVNÍ ŠČERBOVÁ M. PAVELKA V. 16. ČERVNA 2012 Název zpracovaného celku: NOSNÍKY NOSNÍKY Nosníky jsou zpravidla přímá tělesa (pruty) uloţená na podporách nebo
Druhá mocnina. Druhá odmocnina. 2.8.5 Druhá odmocnina. Předpoklady: 020804. V této hodině jsou kalkulačky zakázány.
 .8.5 Druhá odmocnina Předpoklady: 0080 V této hodině jsou kalkulačky zakázány. Druhá mocnina nám umožňuje určit z délky strany plochu čtverce. Druhá mocnina 1 1 9 11 81 11 délky stran čtverců obsahy čtverců
.8.5 Druhá odmocnina Předpoklady: 0080 V této hodině jsou kalkulačky zakázány. Druhá mocnina nám umožňuje určit z délky strany plochu čtverce. Druhá mocnina 1 1 9 11 81 11 délky stran čtverců obsahy čtverců
Mechanismy. Vazby členů v mechanismech (v rovině):
 Mechanismy Mechanismus klikový, čtyřkloubový, kulisový, západkový a vačkový jsou nejčastějšími mechanismy ve strojích (kromě převodů). Mechanismy obsahují členy (kliky, ojnice, těhlice, křižáky a další).
Mechanismy Mechanismus klikový, čtyřkloubový, kulisový, západkový a vačkový jsou nejčastějšími mechanismy ve strojích (kromě převodů). Mechanismy obsahují členy (kliky, ojnice, těhlice, křižáky a další).
ESII-2.1 Elektroměry
 Projekt: ODBORNÝ VÝCVIK VE 3. TISÍCILETÍ Téma: ESII-2.1 Elektroměry Obor: Elektrikář - silnoproud Ročník: 2. Zpracoval(a): Bc. Josef Dulínek Střední průmyslová škola Uherský Brod, 2010 OBSAH 1. Měření
Projekt: ODBORNÝ VÝCVIK VE 3. TISÍCILETÍ Téma: ESII-2.1 Elektroměry Obor: Elektrikář - silnoproud Ročník: 2. Zpracoval(a): Bc. Josef Dulínek Střední průmyslová škola Uherský Brod, 2010 OBSAH 1. Měření
Analýza oběžného kola
 Vysoká škola báňská Technická univerzita 2011/2012 Analýza oběžného kola Radomír Bělík, Pavel Maršálek, Gȕnther Theisz Obsah 1. Zadání... 3 2. Experimentální měření... 4 2.1. Popis měřené struktury...
Vysoká škola báňská Technická univerzita 2011/2012 Analýza oběžného kola Radomír Bělík, Pavel Maršálek, Gȕnther Theisz Obsah 1. Zadání... 3 2. Experimentální měření... 4 2.1. Popis měřené struktury...
Hra a hry. Václav Vopravil. Teorie kombinatorických her se zabývá abstraktními hrami dvou hráčů. Hra je definována R },
 Hra a hry Václav Vopravil Úvod 1 Kombinatorické hry Teorie kombinatorických her se zabývá abstraktními hrami dvou hráčů. Hra je definována pomocí jednodušších her, tj. jako uspořádaná dvojice množin her.
Hra a hry Václav Vopravil Úvod 1 Kombinatorické hry Teorie kombinatorických her se zabývá abstraktními hrami dvou hráčů. Hra je definována pomocí jednodušších her, tj. jako uspořádaná dvojice množin her.
1 KOLA A PNEUMATIKY. Nejčastěji používaná kola automobilů se skládají z těchto částí : disky s ráfky, hlavy (paprskové hlavy), pneumatiky.
 1 KOLA A PNEUMATIKY Nejčastěji používaná kola automobilů se skládají z těchto částí : disky s ráfky, hlavy (paprskové hlavy), pneumatiky. DISKOVÉ KOLO Skládá se z : ráfku zabezpečuje spojení pneumatiky
1 KOLA A PNEUMATIKY Nejčastěji používaná kola automobilů se skládají z těchto částí : disky s ráfky, hlavy (paprskové hlavy), pneumatiky. DISKOVÉ KOLO Skládá se z : ráfku zabezpečuje spojení pneumatiky
COPY SPS. Návrh převodovky. Vypracoval Jaroslav Řezníček IV.B 2.KONSTRUKČNÍ CVIČENÍ ZA 4. ROČNÍK
 SPS 2.KONSTRUKČNÍ CVIČENÍ ZA 4. ROČNÍK Návrh převodovky Vypracoval Jaroslav Řezníček IV.B 26.listopadu 2001 Kinematika Výpočet převodového poměru (i), krouticích momentů počet zubů a modul P 8kW n n 1
SPS 2.KONSTRUKČNÍ CVIČENÍ ZA 4. ROČNÍK Návrh převodovky Vypracoval Jaroslav Řezníček IV.B 26.listopadu 2001 Kinematika Výpočet převodového poměru (i), krouticích momentů počet zubů a modul P 8kW n n 1
2.8.8 Kvadratické nerovnice s parametrem
 .8.8 Kvadratické nerovnice s arametrem Předoklady: 806 Pedagogická oznámka: Z hlediska orientace v tom, co studenti očítají, atří tato hodina určitě mezi nejtěžší během celého středoškolského studia. Proto
.8.8 Kvadratické nerovnice s arametrem Předoklady: 806 Pedagogická oznámka: Z hlediska orientace v tom, co studenti očítají, atří tato hodina určitě mezi nejtěžší během celého středoškolského studia. Proto
c sin Příklad 2 : v trojúhelníku ABC platí : a = 11,6 dm, c = 9 dm, α = 65 0 30. Vypočtěte stranu b a zbývající úhly.
 9. Úvod do středoškolského studia - rozšiřující učivo 9.. Další znalosti o trojúhelníku 9... Sinova věta a = sin b = sin c sin Příklad : V trojúhelníku BC platí : c = 0 cm, α = 45 0, β = 05 0. Vypočtěte
9. Úvod do středoškolského studia - rozšiřující učivo 9.. Další znalosti o trojúhelníku 9... Sinova věta a = sin b = sin c sin Příklad : V trojúhelníku BC platí : c = 0 cm, α = 45 0, β = 05 0. Vypočtěte
Matematika pro 9. ročník základní školy
 Matematika pro 9. ročník základní školy Řešení Ćíselné výrazy 1. Prvočíslo je přirozené číslo, které je beze zbytku dělitelné právě dvěma různými přirozenými čísly, a to číslem jedna a sebou samým (tedy
Matematika pro 9. ročník základní školy Řešení Ćíselné výrazy 1. Prvočíslo je přirozené číslo, které je beze zbytku dělitelné právě dvěma různými přirozenými čísly, a to číslem jedna a sebou samým (tedy
Jednofázový alternátor
 Jednofázový alternátor - 1 - Jednofázový alternátor Ing. Ladislav Kopecký, 2007 Ke generování elektrického napětí pro energetické účely se nejčastěji využívá dvou principů. Prvním z nich je indukce elektrického
Jednofázový alternátor - 1 - Jednofázový alternátor Ing. Ladislav Kopecký, 2007 Ke generování elektrického napětí pro energetické účely se nejčastěji využívá dvou principů. Prvním z nich je indukce elektrického
AMU1 Monitorování bezpečného života letounu (RYCHLÝ PŘEHLED)
 20. Července, 2009 AMU1 Monitorování bezpečného života letounu (RYCHLÝ PŘEHLED) ZLIN AIRCRAFT a.s. Oddělení Výpočtů letadel E-mail: safelife@zlinaircraft.eu AMU1 Monitorování bezpečného života letounu
20. Července, 2009 AMU1 Monitorování bezpečného života letounu (RYCHLÝ PŘEHLED) ZLIN AIRCRAFT a.s. Oddělení Výpočtů letadel E-mail: safelife@zlinaircraft.eu AMU1 Monitorování bezpečného života letounu
V. Zatížení stavebních konstrukcí stroji
 Jiří Máca - katedra mechaniky - B325 - tel. 2 2435 4500 maca@fsv.cvut.cz V. Zatížení stavebních konstrukcí stroji 1. Typy základových konstrukcí 2. Budicí síly 3. Výpočet odezvy 4. Zmenšování dynamických
Jiří Máca - katedra mechaniky - B325 - tel. 2 2435 4500 maca@fsv.cvut.cz V. Zatížení stavebních konstrukcí stroji 1. Typy základových konstrukcí 2. Budicí síly 3. Výpočet odezvy 4. Zmenšování dynamických
Pokusy s kolem na hřídeli (experimenty s výpočty)
 Zvyšování kvality výuky v přírodních a technických oblastech CZ.1.07/1.1.28/02.0055 Pokusy s kolem na hřídeli (experimenty s výpočty) Označení: EU-Inovace-F-7-08 Předmět: fyzika Cílová skupina: 7. třída
Zvyšování kvality výuky v přírodních a technických oblastech CZ.1.07/1.1.28/02.0055 Pokusy s kolem na hřídeli (experimenty s výpočty) Označení: EU-Inovace-F-7-08 Předmět: fyzika Cílová skupina: 7. třída
souřadné systémy geometrické určení polohy pevně spojené se vztažným tělesem
 souřadné systémy geometrické určení polohy pevně spojené se vztažným tělesem kartézský souřadný systém Z Y X kartézský souřadný systém Z Y X kartézský souřadný systém Z x y Y X kartézský souřadný systém
souřadné systémy geometrické určení polohy pevně spojené se vztažným tělesem kartézský souřadný systém Z Y X kartézský souřadný systém Z Y X kartézský souřadný systém Z x y Y X kartézský souřadný systém
Dynamika tuhých těles
 Dynamika tuhých těles V reálných technických aplikacích lze model bodového tělesa použít jen v omezené míře. Mnohem častější je použití modelu tuhého tělesa. Tuhé těleso je definováno jako těleso, u něhož
Dynamika tuhých těles V reálných technických aplikacích lze model bodového tělesa použít jen v omezené míře. Mnohem častější je použití modelu tuhého tělesa. Tuhé těleso je definováno jako těleso, u něhož
Antény. Zpracoval: Ing. Jiří. Sehnal. 1.Napájecí vedení 2.Charakteristické vlastnosti antén a základní druhy antén
 ANTÉNY Sehnal Zpracoval: Ing. Jiří Antény 1.Napájecí vedení 2.Charakteristické vlastnosti antén a základní druhy antén Pod pojmem anténa rozumíme obecně prvek, který zprostředkuje přechod elektromagnetické
ANTÉNY Sehnal Zpracoval: Ing. Jiří Antény 1.Napájecí vedení 2.Charakteristické vlastnosti antén a základní druhy antén Pod pojmem anténa rozumíme obecně prvek, který zprostředkuje přechod elektromagnetické
M-10. AU = astronomická jednotka = vzdálenost Země-Slunce = přibližně 150 mil. km. V následující tabulce je závislost doby
 M-10 Jméno a příjmení holka nebo kluk * Třída Datum Škola AU = astronomická jednotka = vzdálenost Země-Slunce = přibližně 150 mil. km V následující tabulce je závislost doby a/au T/rok oběhu planety (okolo
M-10 Jméno a příjmení holka nebo kluk * Třída Datum Škola AU = astronomická jednotka = vzdálenost Země-Slunce = přibližně 150 mil. km V následující tabulce je závislost doby a/au T/rok oběhu planety (okolo
Návod na sestavení naháněcí ohrady
 Návod na sestavení naháněcí ohrady Obj. č: 3552 ECONOMY 3509 STANDARD 3547 STANDARD+ 3510 STANDARD KOMPLET ECONOMY STANDARD STANDARD+ STANDARD KOMPLET Díly pro základní naháněcí ohradu 3521 1x Posuvné
Návod na sestavení naháněcí ohrady Obj. č: 3552 ECONOMY 3509 STANDARD 3547 STANDARD+ 3510 STANDARD KOMPLET ECONOMY STANDARD STANDARD+ STANDARD KOMPLET Díly pro základní naháněcí ohradu 3521 1x Posuvné
Stavební mechanika 3. 9. přednáška, 2. května 2016
 Stavební mechanika 3 9. přednáška,. května 06 Stavební mechanika 3 9. přednáška,. května 06 Silová metoda ) opakování použití principu virtuálních il ) vliv mykové deormace 3) motivační příklad 4) zobecnění
Stavební mechanika 3 9. přednáška,. května 06 Stavební mechanika 3 9. přednáška,. května 06 Silová metoda ) opakování použití principu virtuálních il ) vliv mykové deormace 3) motivační příklad 4) zobecnění
Střední škola pedagogická, hotelnictví a služeb, Litoměříce, příspěvková organizace
 Střední škola pedagogická, hotelnictví a služeb, Litoměříce, příspěvková organizace Předmět: Počítačové sítě Téma: Servery Vyučující: Ing. Milan Káža Třída: EK3 Hodina: 5 Číslo: III/2 S E R V E R Y 3.4.
Střední škola pedagogická, hotelnictví a služeb, Litoměříce, příspěvková organizace Předmět: Počítačové sítě Téma: Servery Vyučující: Ing. Milan Káža Třída: EK3 Hodina: 5 Číslo: III/2 S E R V E R Y 3.4.
MECHANIKA HORNIN A ZEMIN
 MECHANIKA HORNIN A ZEMIN podklady k přednáškám doc. Ing. Kořínek Robert, CSc. Místnost: C 314 Telefon: 597 321 942 E-mail: robert.korinek@vsb.cz Internetové stránky: fast10.vsb.cz/korinek Mechanické vlastnosti
MECHANIKA HORNIN A ZEMIN podklady k přednáškám doc. Ing. Kořínek Robert, CSc. Místnost: C 314 Telefon: 597 321 942 E-mail: robert.korinek@vsb.cz Internetové stránky: fast10.vsb.cz/korinek Mechanické vlastnosti
Vyvažování tuhého rotoru v jedné rovině přístrojem Adash 4900 - Vibrio
 Aplikační list Vyvažování tuhého rotoru v jedné rovině přístrojem Adash 4900 - Vibrio Ref: 15032007 KM Obsah Vyvažování v jedné rovině bez měření fáze signálu...3 Nevýhody vyvažování jednoduchými přístroji...3
Aplikační list Vyvažování tuhého rotoru v jedné rovině přístrojem Adash 4900 - Vibrio Ref: 15032007 KM Obsah Vyvažování v jedné rovině bez měření fáze signálu...3 Nevýhody vyvažování jednoduchými přístroji...3
1.3 Druhy a metody měření
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 1.3 Druhy a metody měření Měření je soubor činností, jejichž cílem je stanovit hodnotu měřené fyzikální veličiny.
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 1.3 Druhy a metody měření Měření je soubor činností, jejichž cílem je stanovit hodnotu měřené fyzikální veličiny.
IRACIONÁLNÍ ROVNICE. x /() 2 (umocnění obou stran rovnice na druhou) 2x 4 9 /(-4) (ekvivalentní úpravy) Motivace: Teorie: Řešené úlohy:
 IRACIONÁNÍ ROVNICE Motivace: V řadě matematických úloh je nutno ovládat práci s odmocninami a rovnicemi, které obsahují neznámou pod odmocninou, mj. při vyjádření neznámé z technických vzorců. Znalosti
IRACIONÁNÍ ROVNICE Motivace: V řadě matematických úloh je nutno ovládat práci s odmocninami a rovnicemi, které obsahují neznámou pod odmocninou, mj. při vyjádření neznámé z technických vzorců. Znalosti
MODEL MOSTU. Ing.Jiřina Strnadová. Evropský sociální fond Praha a EU Investujeme do vaší budoucnosti. Předmět:Fyzika
 MODEL MOSTU Ing.Jiřina Strnadová Předmět:Fyzika Praha a EU Investujeme do vaší budoucnosti Model mostu Teoretický úvod: Příhradové nosníky (prutové soustavy) jsou složené z prutů, které jsou vzájemně spojené
MODEL MOSTU Ing.Jiřina Strnadová Předmět:Fyzika Praha a EU Investujeme do vaší budoucnosti Model mostu Teoretický úvod: Příhradové nosníky (prutové soustavy) jsou složené z prutů, které jsou vzájemně spojené
Tematické okruhy otázek ke státním závěrečným zkouškám DIDC
 LINIOVÉ DOPRAVNÍ STAVBY (STAVBY KOLEJOVÉ DOPRAVY) 1. Navrhování železniční trasy (geometrické parametry koleje, vozidlo a kolej, průjezdný průřez, trasování) 2. Navrhování tělesa železničního spodku (navrhování
LINIOVÉ DOPRAVNÍ STAVBY (STAVBY KOLEJOVÉ DOPRAVY) 1. Navrhování železniční trasy (geometrické parametry koleje, vozidlo a kolej, průjezdný průřez, trasování) 2. Navrhování tělesa železničního spodku (navrhování
PROJEKT BAKALÁŘSKÉ PRÁCE
 PROJEKT BAKALÁŘSKÉ PRÁCE KOMUNIKACE A LIDSKÉ ZDROJE NÁZEV BAKALÁŘSKÉ PRÁCE PR jako cesta budování image firmy TERMÍN UKONČENÍ STUDIA A OBHAJOBA (MĚSÍC/ROK) Říjen 2012 JMÉNO A PŘÍJMENÍ / STUDIJNÍ SKUPINA
PROJEKT BAKALÁŘSKÉ PRÁCE KOMUNIKACE A LIDSKÉ ZDROJE NÁZEV BAKALÁŘSKÉ PRÁCE PR jako cesta budování image firmy TERMÍN UKONČENÍ STUDIA A OBHAJOBA (MĚSÍC/ROK) Říjen 2012 JMÉNO A PŘÍJMENÍ / STUDIJNÍ SKUPINA
DUM 06 téma: Náležitosti výkresu sestavení
 DUM 06 téma: Náležitosti výkresu sestavení ze sady: 01 tematický okruh sady: Kreslení výkres sestavení ze šablony: 04_Technická dokumentace Ur eno pro :1. ro ník vzd lávací obor: 26-41-M/01 Elektrotechnika
DUM 06 téma: Náležitosti výkresu sestavení ze sady: 01 tematický okruh sady: Kreslení výkres sestavení ze šablony: 04_Technická dokumentace Ur eno pro :1. ro ník vzd lávací obor: 26-41-M/01 Elektrotechnika
KATALOGOVÝ LIST. VENTILÁTORY RADIÁLNÍ STŘEDOTLAKÉ RSM 800 až 1250 jednostranně sací
 KATALOGOVÝ LIST VENTILÁTORY RADIÁLNÍ STŘEDOTLAKÉ RSM 800 až 1250 jednostranně sací KM 12 3219 Vydání: 12/10 Strana: 1 Stran: 6 Ventilátory radiální středotlaké RSM 800 až 1250 jednostranně sací (dále jen
KATALOGOVÝ LIST VENTILÁTORY RADIÁLNÍ STŘEDOTLAKÉ RSM 800 až 1250 jednostranně sací KM 12 3219 Vydání: 12/10 Strana: 1 Stran: 6 Ventilátory radiální středotlaké RSM 800 až 1250 jednostranně sací (dále jen
Jméno autora: Mgr. Zdeněk Chalupský Datum vytvoření: 14. 11. 2012 Číslo DUM: VY_32_INOVACE_12_FY_B
 Jméno autora: Mgr. Zdeněk Chalupský Datum vytvoření: 14. 11. 2012 Číslo DUM: VY_32_INOVACE_12_FY_B Ročník: I. Fyzika Vzdělávací oblast: Přírodovědné vzdělávání Vzdělávací obor: Fyzika Tematický okruh:
Jméno autora: Mgr. Zdeněk Chalupský Datum vytvoření: 14. 11. 2012 Číslo DUM: VY_32_INOVACE_12_FY_B Ročník: I. Fyzika Vzdělávací oblast: Přírodovědné vzdělávání Vzdělávací obor: Fyzika Tematický okruh:
Indukční děliče napětí
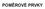 POMĚROVÉ PRVKY Indukční děliče napětí 2 Jednoduchý indukční dělič napětí k v D D i1 U Ui D 1α jβ U D k / m Jádro toroidního tvaru z materiálu s vysokou permeabilitou. Všechny sekce navinuty současně kabelem
POMĚROVÉ PRVKY Indukční děliče napětí 2 Jednoduchý indukční dělič napětí k v D D i1 U Ui D 1α jβ U D k / m Jádro toroidního tvaru z materiálu s vysokou permeabilitou. Všechny sekce navinuty současně kabelem
Tel/fax: +420 545 222 581 IČO:269 64 970
 PRÁŠKOVÁ NITRIDACE Pokud se chcete krátce a účinně poučit, přečtěte si stránku 6. 1. Teorie nitridace Nitridování je sycení povrchu součásti dusíkem v plynné, nebo kapalném prostředí. Výsledkem je tenká
PRÁŠKOVÁ NITRIDACE Pokud se chcete krátce a účinně poučit, přečtěte si stránku 6. 1. Teorie nitridace Nitridování je sycení povrchu součásti dusíkem v plynné, nebo kapalném prostředí. Výsledkem je tenká
Přednáška č.10 Ložiska
 Fakulta strojní VŠB-TUO Přednáška č.10 Ložiska LOŽISKA Ložiska jsou základním komponentem všech otáčivých strojů. Ložisko je strojní součást vymezující vzájemnou polohu dvou stýkajících se částí mechanismu
Fakulta strojní VŠB-TUO Přednáška č.10 Ložiska LOŽISKA Ložiska jsou základním komponentem všech otáčivých strojů. Ložisko je strojní součást vymezující vzájemnou polohu dvou stýkajících se částí mechanismu
III/2 Inovace a zkvalitnění výuky prostřednictvím ICT
 Název školy Gymnázium, Šternberk, Horní nám. 5 Číslo projektu CZ.1.07/1.5.00/34.0218 Šablona III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Označení materiálu VY_32_INOVACE_Hor013 Vypracoval(a),
Název školy Gymnázium, Šternberk, Horní nám. 5 Číslo projektu CZ.1.07/1.5.00/34.0218 Šablona III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Označení materiálu VY_32_INOVACE_Hor013 Vypracoval(a),
1 KLOUBOVÉ HŘÍDELE. Přenos točivého momentu u automobilu s klasickou koncepcí a výkyvnou zadní hnací nápravou
 1 KLOUBOVÉ HŘÍDELE ÚČEL přenášet točivý moment, umožnit vzájemnou výchylku os (klouby), vyrovnat axiální posuv (posuvný člen), tlumení vibrací (pružné klouby). Točivý moment je přenášen z převodovky do
1 KLOUBOVÉ HŘÍDELE ÚČEL přenášet točivý moment, umožnit vzájemnou výchylku os (klouby), vyrovnat axiální posuv (posuvný člen), tlumení vibrací (pružné klouby). Točivý moment je přenášen z převodovky do
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita V. 2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V. 2. 10 Základní části strojů Kapitola 26
Zvyšování kvality výuky technických oborů Klíčová aktivita V. 2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V. 2. 10 Základní části strojů Kapitola 26
na tyč působit moment síly M, určený ze vztahu (9). Periodu kmitu T tohoto kyvadla lze určit ze vztahu:
 Úloha Autoři Zaměření FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE 2. Měření modulu pružnosti v tahu a modulu pružnosti ve smyku Martin Dlask Měřeno 11. 10., 18. 10., 25. 10. 2012 Jakub Šnor SOFE Klasifikace
Úloha Autoři Zaměření FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE 2. Měření modulu pružnosti v tahu a modulu pružnosti ve smyku Martin Dlask Měřeno 11. 10., 18. 10., 25. 10. 2012 Jakub Šnor SOFE Klasifikace
Funkce Vypracovala: Mgr. Zuzana Kopečková
 Funkce Vypracovala: Mgr. Zuzana Kopečková Název školy Název a číslo projektu Název modulu Obchodní akademie a Střední odborné učiliště, Veselí nad Moravou Motivace žáků ke studiu technických předmětů OP
Funkce Vypracovala: Mgr. Zuzana Kopečková Název školy Název a číslo projektu Název modulu Obchodní akademie a Střední odborné učiliště, Veselí nad Moravou Motivace žáků ke studiu technických předmětů OP
Úloha 2 Tepelný odpor a vrstvená konstrukce
 SF Podklady pro cvičení Úloha Tepelný odpor a vrstvená konstrukce Ing. Kamil Staněk 10/010 kamil.stanek@fsv.cvut.cz 1 Tepelný odpor 1.1 Tepelný odpor materiálové vrstvy Tepelný odpor materiálové vrstvy
SF Podklady pro cvičení Úloha Tepelný odpor a vrstvená konstrukce Ing. Kamil Staněk 10/010 kamil.stanek@fsv.cvut.cz 1 Tepelný odpor 1.1 Tepelný odpor materiálové vrstvy Tepelný odpor materiálové vrstvy
Osvětlovací modely v počítačové grafice
 Západočeská univerzita v Plzni Fakulta aplikovaných věd Semestrální práce z předmětu Matematické modelování Osvětlovací modely v počítačové grafice 27. ledna 2008 Martin Dohnal A07060 mdohnal@students.zcu.cz
Západočeská univerzita v Plzni Fakulta aplikovaných věd Semestrální práce z předmětu Matematické modelování Osvětlovací modely v počítačové grafice 27. ledna 2008 Martin Dohnal A07060 mdohnal@students.zcu.cz
KVADRATICKÉ ROVNICE A NEROVNICE (početní a grafická řešení)
 KVADRATICKÉ ROVNICE A NEROVNICE (početní a grafická řešení) KVADRATICKÉ ROVNICE (početně) Teorie: Kvadratická rovnice o jedné neznámé se nazývá každá taková rovnice, kterou lze ekvivalentními úpravami
KVADRATICKÉ ROVNICE A NEROVNICE (početní a grafická řešení) KVADRATICKÉ ROVNICE (početně) Teorie: Kvadratická rovnice o jedné neznámé se nazývá každá taková rovnice, kterou lze ekvivalentními úpravami
ISŠT Mělník. Integrovaná střední škola technická Mělník, K učilišti 2566, 276 01 Mělník Ing.František Moravec
 ISŠT Mělník Číslo projektu Označení materiálu Název školy Autor Tematická oblast CZ.1.07/1.5.00/34.0061 VY_32_ INOVACE_C.2.07 Integrovaná střední škola technická Mělník, K učilišti 2566, 276 01 Mělník
ISŠT Mělník Číslo projektu Označení materiálu Název školy Autor Tematická oblast CZ.1.07/1.5.00/34.0061 VY_32_ INOVACE_C.2.07 Integrovaná střední škola technická Mělník, K učilišti 2566, 276 01 Mělník
Spoje se styčníkovými deskami s prolisovanými trny
 cvičení Dřevěné konstrukce Spoje se styčníkovými deskami s prolisovanými trny Úvodní poznámky Styčníkové desky s prolisovanými trny se používají pro spojování dřevěných prvků stejné tloušťky v jedné rovině,
cvičení Dřevěné konstrukce Spoje se styčníkovými deskami s prolisovanými trny Úvodní poznámky Styčníkové desky s prolisovanými trny se používají pro spojování dřevěných prvků stejné tloušťky v jedné rovině,
CZ.1.07/1.5.00/34.0581. Opravárenství a diagnostika. Pokud není uvedeno jinak, použitý materiál je z vlastních zdrojů autora
 Číslo projektu Číslo materiálu Název školy CZ.1.07/1.5.00/34.0581 VY_32_INOVACE_OAD_2.AE_05_ZAVADY PEROVANI MOTOROVYCH VOZIDEL Střední odborná škola a Střední odborné učiliště, Dubno Autor Ing. Pavel Štanc
Číslo projektu Číslo materiálu Název školy CZ.1.07/1.5.00/34.0581 VY_32_INOVACE_OAD_2.AE_05_ZAVADY PEROVANI MOTOROVYCH VOZIDEL Střední odborná škola a Střední odborné učiliště, Dubno Autor Ing. Pavel Štanc
TECHNICKÉ ODSTŘELY A JEJICH ÚČINKY
 TECHNICKÉ ODSTŘELY A JEJICH ÚČINKY Přednáška č.7 Demolici stavebních objektů lze provést: Inovace studijního oboru Geotechnika 7. Přednáška Trhací práce při destrukcích a) ručně (rozebírání objektu ruční
TECHNICKÉ ODSTŘELY A JEJICH ÚČINKY Přednáška č.7 Demolici stavebních objektů lze provést: Inovace studijního oboru Geotechnika 7. Přednáška Trhací práce při destrukcích a) ručně (rozebírání objektu ruční
Kótování na strojnických výkresech 1.část
 Kótování na strojnických výkresech 1.část Pro čtení výkresů, tj. určení rozměrů nebo polohy předmětu, jsou rozhodující kóty. Z tohoto důvodu je kótování jedna z nejzodpovědnějších prací na technických
Kótování na strojnických výkresech 1.část Pro čtení výkresů, tj. určení rozměrů nebo polohy předmětu, jsou rozhodující kóty. Z tohoto důvodu je kótování jedna z nejzodpovědnějších prací na technických
ZPRÁVA o stavebně technickém průzkumu železobetonové konstrukce v areálu Kolejí 17. listopadu UK, Pátkova ul., Praha 8 - Libeň
 Beranových 65 Letňany 199 21, Praha 9 tel. 283 920 588 ZPRÁVA o stavebně technickém průzkumu železobetonové konstrukce v areálu Kolejí 17. listopadu UK, Pátkova ul., Praha 8 - Libeň Číslo zakázky : Odpovědný
Beranových 65 Letňany 199 21, Praha 9 tel. 283 920 588 ZPRÁVA o stavebně technickém průzkumu železobetonové konstrukce v areálu Kolejí 17. listopadu UK, Pátkova ul., Praha 8 - Libeň Číslo zakázky : Odpovědný
Univerzita Tomáše Bati ve Zlíně
 Univerzita Tomáše Bati ve líně LABORATORNÍ CVIČENÍ ELEKTROTECHNIKY A PRŮMYSLOVÉ ELEKTRONIKY Název úlohy: pracovali: Měření činného výkonu střídavého proudu v jednofázové síti wattmetrem Petr Luzar, Josef
Univerzita Tomáše Bati ve líně LABORATORNÍ CVIČENÍ ELEKTROTECHNIKY A PRŮMYSLOVÉ ELEKTRONIKY Název úlohy: pracovali: Měření činného výkonu střídavého proudu v jednofázové síti wattmetrem Petr Luzar, Josef
Změnu DPH na kartách a v ceníku prací lze provést i v jednotlivých modulech.
 Způsob změny DPH pro rok 2013 Verze 2012.34 a vyšší Úvod Vzhledem k tomu, že dnes 23.11.2012 nikdo netuší, zda od 1.1.2013 bude DPH snížená i základní 17.5% nebo 15% a 21%, bylo nutné všechny programy
Způsob změny DPH pro rok 2013 Verze 2012.34 a vyšší Úvod Vzhledem k tomu, že dnes 23.11.2012 nikdo netuší, zda od 1.1.2013 bude DPH snížená i základní 17.5% nebo 15% a 21%, bylo nutné všechny programy
KALOVÉ KOŠE KOŠE DO ULIČNÍCH VPUSTÍ KOŠE DO DVORNÍCH VPUSTÍ LAPAČE NEČISTOT
 KALOVÉ KOŠE KOŠE DO ULIČNÍCH VPUSTÍ KOŠE DO DVORNÍCH VPUSTÍ LAPAČE NEČISTOT KALOVÉ KOŠE KOŠE DO ULIČNÍCH VPUSTÍ Koš do UV A4 vysoký pozinkovaný Ø 385 Koš podle DIN 4052-A4 pro uliční vpusti, vysoký hmotnost:
KALOVÉ KOŠE KOŠE DO ULIČNÍCH VPUSTÍ KOŠE DO DVORNÍCH VPUSTÍ LAPAČE NEČISTOT KALOVÉ KOŠE KOŠE DO ULIČNÍCH VPUSTÍ Koš do UV A4 vysoký pozinkovaný Ø 385 Koš podle DIN 4052-A4 pro uliční vpusti, vysoký hmotnost:
VY_52_INOVACE_2NOV70. Autor: Mgr. Jakub Novák. Datum: 19. 3. 2013 Ročník: 8. a 9.
 VY_52_INOVACE_2NOV70 Autor: Mgr. Jakub Novák Datum: 19. 3. 2013 Ročník: 8. a 9. Vzdělávací oblast: Člověk a příroda Vzdělávací obor: Fyzika Tematický okruh: Elektromagnetické a světelné děje Téma: Zapojení
VY_52_INOVACE_2NOV70 Autor: Mgr. Jakub Novák Datum: 19. 3. 2013 Ročník: 8. a 9. Vzdělávací oblast: Člověk a příroda Vzdělávací obor: Fyzika Tematický okruh: Elektromagnetické a světelné děje Téma: Zapojení
( ) ( ) 7.2.2 Sčítání vektorů. Předpoklady: 7201
 7.. Sčítání ektorů Předpoklady: 70 Pedagogická poznámka: Stdenti ětšino necítí potřeb postpoat při definici sčítání ektorů (obecně při zaádění jakékoli operace) tak striktně, jak yžadje matematika. Upozorňji
7.. Sčítání ektorů Předpoklady: 70 Pedagogická poznámka: Stdenti ětšino necítí potřeb postpoat při definici sčítání ektorů (obecně při zaádění jakékoli operace) tak striktně, jak yžadje matematika. Upozorňji
TECHNICKÉ KRESLENÍ A CAD
 Přednáška č. 7 V ELEKTROTECHNICE Kótování Zjednodušené kótování základních geometrických prvků Někdy stačí k zobrazení pouze jeden pohled Tenké součásti kvádr Kótování Kvádr (základna čtverec) jehlan Kvalitativní
Přednáška č. 7 V ELEKTROTECHNICE Kótování Zjednodušené kótování základních geometrických prvků Někdy stačí k zobrazení pouze jeden pohled Tenké součásti kvádr Kótování Kvádr (základna čtverec) jehlan Kvalitativní
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita V. 2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V. 2.3 Polovodiče a jejich využití Kapitola
Zvyšování kvality výuky technických oborů Klíčová aktivita V. 2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V. 2.3 Polovodiče a jejich využití Kapitola
2.7.15 Rovnice s neznámou pod odmocninou I
 .7.15 Rovnice s neznámou pod odmocninou I Předpoklady: 711, 71 Pedagogická poznámka: Látka této hodiny vyžaduje tak jeden a půl vyučovací hodiny, pokud nepospícháte můžete obětovat hodiny dvě a nechat
.7.15 Rovnice s neznámou pod odmocninou I Předpoklady: 711, 71 Pedagogická poznámka: Látka této hodiny vyžaduje tak jeden a půl vyučovací hodiny, pokud nepospícháte můžete obětovat hodiny dvě a nechat
Mechanika tuhého tělesa. Dynamika + statika
 Mechanika tuhého tělesa Dynamika + statika Moment hybnosti U tuhého tělesa není hybnost vhodnou veličinou pro posouzení dynamického stavu rotujícího tělesa Definujeme veličinu analogickou hybnosti, která
Mechanika tuhého tělesa Dynamika + statika Moment hybnosti U tuhého tělesa není hybnost vhodnou veličinou pro posouzení dynamického stavu rotujícího tělesa Definujeme veličinu analogickou hybnosti, která
4 Soustavy lineárních rovnic
 4 Soustavy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních rovnic, to znamená několika lineárními rovnicemi, které musí být současně splněny. 4.1 Základní pojmy Definice Soustavu
4 Soustavy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních rovnic, to znamená několika lineárními rovnicemi, které musí být současně splněny. 4.1 Základní pojmy Definice Soustavu
C. 2. Pořízení a implementace IS
 Název příjemce podpory: MĚSTO VESELÍ NAD MORAVOU tř. Masarykova 119 698 13 Veselí nad Moravou IMPLEMENTACE PROCESNÍHO ŘÍZENÍ V OBLASTI SAMOSTATNÉ PŮSOBNOSTI MĚSTA VESELÍ NAD MORAVOU C. 2. Pořízení a implementace
Název příjemce podpory: MĚSTO VESELÍ NAD MORAVOU tř. Masarykova 119 698 13 Veselí nad Moravou IMPLEMENTACE PROCESNÍHO ŘÍZENÍ V OBLASTI SAMOSTATNÉ PŮSOBNOSTI MĚSTA VESELÍ NAD MORAVOU C. 2. Pořízení a implementace
1) Vypočítej A) 32 B) 44 C) 48 D) 56. 2) Urči číslo, které se skrývá za A ve výpočtu: 8 5 A) 12 B) 13 C) 14 D) 15
 Varianta A 4 4 4 4 4 4 4 4 1) Vypočítej A) 32 B) 44 C) 48 D) 56 2) Urči číslo, které se skrývá za A ve výpočtu: 8 5 20 120 A. A) 12 B) 13 C) 14 D) 15 3) Najdi největší a nejmenší trojciferné číslo skládající
Varianta A 4 4 4 4 4 4 4 4 1) Vypočítej A) 32 B) 44 C) 48 D) 56 2) Urči číslo, které se skrývá za A ve výpočtu: 8 5 20 120 A. A) 12 B) 13 C) 14 D) 15 3) Najdi největší a nejmenší trojciferné číslo skládající
Měření hluku a vibrací zvukoměrem
 Úloha 1 Měření hluku a vibrací zvukoměrem 1.1 Zadání 1. Zkalibrujte, respektive ověřte kalibraci zvukoměru 2. Proveďte třetinooktávovou analýzu hluku zadaného zdroje v jednom místě 3. Zkalibrujte zvukoměr
Úloha 1 Měření hluku a vibrací zvukoměrem 1.1 Zadání 1. Zkalibrujte, respektive ověřte kalibraci zvukoměru 2. Proveďte třetinooktávovou analýzu hluku zadaného zdroje v jednom místě 3. Zkalibrujte zvukoměr
Ž Á D O S T O POSKYTNUTÍ NEINVESTIČNÍ DOTACE Z ROZPOČTU MORAVSKOSLEZSKÉHO KRAJE 2016/2017 OBECNÁ ČÁST
 Příloha č. 2 Dotačního programu Ž Á D O S T O POSKYTNUTÍ NEINVESTIČNÍ DOTACE Z ROZPOČTU MORAVSKOSLEZSKÉHO KRAJE Dotační program Podpora aktivit v oblasti prevence rizikových projevů chování u dětí a mládeže
Příloha č. 2 Dotačního programu Ž Á D O S T O POSKYTNUTÍ NEINVESTIČNÍ DOTACE Z ROZPOČTU MORAVSKOSLEZSKÉHO KRAJE Dotační program Podpora aktivit v oblasti prevence rizikových projevů chování u dětí a mládeže
LED svítidla - nové trendy ve světelných zdrojích
 LED svítidla - nové trendy ve světelných zdrojích Základní východiska Nejbouřlivější vývoj v posledním období probíhá v oblasti vývoje a zdokonalování světelných zdrojů nazývaných obecně LED - Light Emitting
LED svítidla - nové trendy ve světelných zdrojích Základní východiska Nejbouřlivější vývoj v posledním období probíhá v oblasti vývoje a zdokonalování světelných zdrojů nazývaných obecně LED - Light Emitting
Změna sazby DPH v HELIOS Red po 1. 1. 2013
 Změna sazby DPH v HELIOS Red po 1. 1. 2013 Uživatelé s platnou systémovou podporou budou mít HELIOS Red připravený k používání po stažení aktualizace. Uživatelé bez systémové podpory si mohou program nakonfigurovat
Změna sazby DPH v HELIOS Red po 1. 1. 2013 Uživatelé s platnou systémovou podporou budou mít HELIOS Red připravený k používání po stažení aktualizace. Uživatelé bez systémové podpory si mohou program nakonfigurovat
Grafický manuál jednotného vizuálního stylu. MACHINERY group
 Obsah 1. ZNAČKA VÍTKOVICE MACHINERY GROUP 1.1 Logotyp VÍTKOVICE MACHINERY GROUP 1.2 Konstrukce logotypu VÍTKOVICE MACHINERY GROUP 1.3 Základní barevné provedení logotypu 1.4 Černobílé a jednobarevné provedení
Obsah 1. ZNAČKA VÍTKOVICE MACHINERY GROUP 1.1 Logotyp VÍTKOVICE MACHINERY GROUP 1.2 Konstrukce logotypu VÍTKOVICE MACHINERY GROUP 1.3 Základní barevné provedení logotypu 1.4 Černobílé a jednobarevné provedení
Kritická síla imperfektovaných systémů
 Kritická síla imperfektovaných systémů Petr Frantík 1, Jiří Macur 2 Úvod V minulém století nově vzniklé obory, opírající se o studium silně nelineárních systémů, jako jsou teorie katastrof, teorie bifurkací
Kritická síla imperfektovaných systémů Petr Frantík 1, Jiří Macur 2 Úvod V minulém století nově vzniklé obory, opírající se o studium silně nelineárních systémů, jako jsou teorie katastrof, teorie bifurkací
Využití fixních a variabilních nákladů pro manažerské rozhodování a finanční řízení
 Využití fixních a variabilních nákladů pro manažerské rozhodování a finanční řízení Nákladové funkce Vývoj nákladů v závislosti na změně určité veličiny obvykle objemu výroby, výstupu lze vyjadřovat matematicky,
Využití fixních a variabilních nákladů pro manažerské rozhodování a finanční řízení Nákladové funkce Vývoj nákladů v závislosti na změně určité veličiny obvykle objemu výroby, výstupu lze vyjadřovat matematicky,
Přednáška č.4 Tolerování
 Fakulta strojní VŠB-TUO Přednáška č.4 Tolerování Tolerování Pro sériovou a hromadnou výrobu je nutná zaměnitelnost a vyměnitelnost součástí strojů. Aby se mohla dodržet tato podmínka je nutné vyrobit součást
Fakulta strojní VŠB-TUO Přednáška č.4 Tolerování Tolerování Pro sériovou a hromadnou výrobu je nutná zaměnitelnost a vyměnitelnost součástí strojů. Aby se mohla dodržet tato podmínka je nutné vyrobit součást
