FOTOM a System for Photogrammetrical Image Analysis FOTOM systém pro fotogrammetrickou analýzu obrazu

Transkript

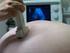
1 XXX. ASR '2005 Seminar, Instruments and Control, Ostrava, April 29, FOTOM a System for Photogrammetrical Image Analysis FOTOM systém pro fotogrammetrickou analýzu obrazu LIČEV, Lačezar 1 & PAJUREK, Ivo 2 1 doc. Ing., CSc., Katedra Informatiky-456, VŠB-TU Ostrava, 17. listopadu, Ostrava - Poruba, Lacezar.Licev@vsb.cz, 2 Ing., ivo.pajurek@vsb.cz Abstract: This contribution treats of the scientific field of photogrammetry and presents the results achieved at the Department of Computer Science of VŠB - Technical University of Ostrava during a long-termed research in this field. First we discuss photogrammetry and object recognition generally, then we describe FOTOM a system for photogrammetry image analysis. The system FOTOM was developed and used for geological metering of mining holes. Nowadays the research continues in cooperation with the teaching hospital of Ostrava and is focused on the medical applications (concretely ultrasound image analysis), which appear as highly perspective. This contribution also explains the basic concepts of image analysis and describes single parts of the modul and the way of usage of each part. FOTOM. Lastly advantages, disadvantages and chances of further development of the system are mentioned. Klíčová slova: Fotogrammetrie, lícovací bod, FOTOM 1 Úvod Fotogrammetrie je vědní obor, který se zabývá získáváním informací o objektech na základě jejich obrazového záznamu. V mnoha oblastech se jedná o jedinou možnou metodu analýzy objektů pomocí níž lze stanovit rozměry, tvar nebo polohu objektů. Snímek využitelný pro fotogrammetrii musí splňovat kritérium existence exaktní matematickogeometrické relace mezi měřeným objektem reálného světa a jeho dvourozměrným zobrazením na fotogrammetrickém snímku. Snímek tedy musí být pořízen speciálním zařízením, u něhož známe prvky jeho vnitřní orientace a přesný způsob zobrazování předmětu na záznamové médium. V souvislosti s fotogrammetrií je naprosto nezbytné zmínit tzv. lícovací body, což jsou právě body se známou polohou v reálném světě, které slouží k přizpůsobení geometrického modelu reálnému podkladu. 2 Technologie tvorby snímků Jelikož se v současné době na katedře informatiky orientujeme na výzkum využití fotogrammetrie v oblasti biomedicíny, a sice konkrétně na analýzu ultravukových snímků, ve zkratce popíšeme pouze nejpoužívanější metodu tvorby sonografických snímků. Metoda tvorby ultrazvukových snímků je založena na schopnosti ultrazvuku procházet různými materiály a odrážet se na jejich rozhraních. Nejlépe se ultrazvukové vlnění šíří v kapalinách. Výborně se tedy šíří v měkkých tkáních, které jsou ze značné části tvořeny vodou. Naopak pevné látky a plyny tvoří pro ultrazvuk téměř neproniknutelnou bariéru. Zdrojem i detektorem ultrazvukového vlnění bývá jeden piezzokrystal, který generuje mechanické vlnění a zároveň přijímá a převádí odraženou energii zpět na elektrický signál.

2 XXX. ASR '2005 Seminar, Instruments and Control, Ostrava, April 29, Nejčastějším typem 2D snímku v reálném čase je tzv. B-obraz (brightness modulated), což je de facto černobílý obraz, kde hodnota jasu v daném bodě je svázána s intenzitou echa ultrazvukového vlnění. Obrázek 1 - B-obraz ultrazvukové sonografie 3 Rozpoznávání objektů Segmentace obrazu: Aby bylo možné analyzovat reálné objekty na základě jejich obrazu, je nezbytné tyto zájmové objekty na jednotlivých snímcích definovat. Základním krokem analýzy zpracovávaných dat je segmentace obrazu neboli rozčlenění obrazu do částí, které mají souvislost s předměty a objekty reálného světa. V zásadě se využívají dva segmentační principy: princip detekce hran tento princip vychází z poznatku, že v místě hrany dvou objektů dochází k výrazné změně obrazové funkce vstupního obrazu. Nevýhodou této metody je, že ji nelze využít při analýze obrazu s vysokou úrovní šumu, neboť v takovém případě se hrany detekují i tam, kde se reálně žádné nevyskytují. princip detekce oblastí tento princip je v případě zašumněného obrazu spolehlivější než předchozí zmíněný. Základní myšlenkou tohoto principu je označení homogenních oblastí. Tato metoda se dále dělí na metodu spojování oblastí a metodu dělení oblastí. Prahování: Principem prahování je skutečnost, že objekty popředí mají odlišný jas než objekty pozadí. Stačí tedy nalézt vhodnou hodnotu prahu, který od sebe popředí a pozadí oddělí. Výsledkem prahování je pak binární obraz, v němž je bodům jednoho typu přiřazena hodnota 1, zatímco bodům druhého typu přísluší hodnota 0. Matematický zápis udává rovnice (3.1). 1, f ( x, y) t g( x, y) = (3.1) 0, jinak Stanovení vhodného prahu není jednoduchá záležitost. Je vypracována řada postupů, jak nalézt optimální práh, my se zmíníme pouze o metodě stanovení prahu pomocí histogramu jasu, která je v systému FOTOM implementována. Hlavní myšlenka spočívá v předpokladu, že v obraze existují pouze dva typy pixelů: pixely náležící hledaným objektům a pixely náležící pozadí, přičemž oba druhy jsou relativně četné a mají dost odlišný jas. Na následujícím obrázku je znázorněn typický příklad histogramu jasu, který se označuje jako bimodální (se dvěma vrcholy). Jako práh se určí hodnota jasu, v níž dosahuje histogram minima mezi oběma vrcholy.

3 XXX. ASR '2005 Seminar, Instruments and Control, Ostrava, April 29, Obrázek 2 Histogram jasu V reálných obrazech bývá situace složitější, obraz může mít v různých částech různou úroveň jasu a není tedy možno nalézt optimální práh, který by vyhovoval celému obrazu. V takovém případě se obraz rozdělí do menších částí a pro každou část se stanoví lokální hodnota prahu. V případě, že diference mezi maximální a minimální hodnotou jasu je příliš nízká, pak daná část obrazu pravděpodobně obsahuje pouze body jednoho typu (tj. buď popředí nebo pozadí) a práh se stanoví jako průměr prahů přilehlých oblastí. Stejným způsobem (stanovení prahu jako průměru prahů přilehlých oblastí) se postupuje i v případě, kdy v dané části převažují body pouze jednoho typu. Toto rozšíření metody stanovení prahu pomocí histogramu jasu metoda bývá označováno jako prahování s proměnným prahem. Eroze: Nechť B je vstupní a S pomocný binární obraz. Význam pomocného obrazu S je jako u konvoluce obdobný postupně jej budeme přikládat na různá místa obrazu B. Označení S xy budeme používat pro obraz, který vznikne translací pomocného obrazu tak, aby počátek obrazu S padl do bodu o souřadnicích (x,y). Erozí binárního obrazu B za použití masky S vznikne obraz E, který je opět binární. Předpokládejme, že jednotlivé body binárního obrazu nesou hodnotu 0 nebo 1. V bodě o souřadnicích (x,y) je v obraze E hodnota 1, jestliže je v obraze B hodnota 1 alespoň na těch místech, kde je hodnota 1 v masce S xy. Jinak je v obraze E o souřadnicích (x,y) hodnota 0. Matematická definice operace eroze je dána následující rovnicí (3.2): E B S = x, y S B (3.2) { } = x, y Ztenčování: Ztenčování slouží k eliminaci jevů, jako je např. rozmazání obrazu. Je realizováno opakovanou erozí, kdy postupně odstraňujeme krajní body objektu. Základním kritériem je neporušení souvislosti objektu. Určení hranice objektu: Výsledkem prahování je binární obraz, který určuje plochy náležící jednotlivým objektům. Ve většině praktických případů nás však zajímá explicitní hranice těchto objektů, kterou lze nalézt použitím následujícího algoritmu: Procházíme obraz z levého horního rohu po řádcích a sloupcích dokud nenarazíme na pixel spadající do zájmové oblasti. Tento bod je nepochybně bodem hranice. Z nalezeného počátečního pixelu sledujeme hranici objektu podle následujícího pravidla: je-li pixel uvnitř oblasti, otočíme se doleva a posuneme se o jeden pixel je-li pixel vně oblasti, otočíme se doprava a posuneme se o jeden pixel Algoritmus končí ve chvíli nalezení uzavřené hranice, tedy když se dostaneme zpět do výchozího bodu.

4 XXX. ASR '2005 Seminar, Instruments and Control, Ostrava, April 29, Přestože je tento algoritmus velmi jednoduchý, výsledky dosažené jeho aplikací jsou uspokojivé. V případě, že hranice obsahuje body sousedící jen rohem, může sice dojít ke ztrátě části hranice, ovšem tato ztráta je zanedbatelná. Určení hran gradientními metodami: Tyto metody vychází z poznatku, že v místě hrany dosahuje absolutní hodnota první derivace průběhu jasu v ortogonálním směru vzhledem ke směru hrany vysokých hodnot. Bod prohlásíme za součást hrany, pakliže je velikost hrany (tj. první derivace obrazové fukce) e(x,y) určená po značném zjednodušení rovnicí (3.3) vyšší nežli předem zvolená prahová hodnota. 2 2 e( x, y) = f x ( x, y) + f y ( x, y), (3.3) kde f x (x,y) a f y (x,y) jsou parciální derivace obrazové funkce podle x a y, které jsou určeny aplikací klasických numerických metod. Zjištění průběhu křivosti po délce křivky: Výstupem výše uvedených metod segmentace obrazu je vždy množina bodů určujících hranice objektů, my ovšem potřebujeme získat hranici ve formě křivky, která průběh hranice co nejlépe aproximuje. Pro získání průběhu křivosti je hranice aproximována kruhovými oblouky: ( x a) + ( y b) r = 0, (3.4) kde a, b jsou souřadnice středu kružnice a r její poloměr. Parametry rovnice kružnice určujeme metodou nejmenších čtverců s minimalizací rezidua kružnice. Výstupem této analýzy je zjištění průběhu křivosti po délce křivky, ze které se přímo (prahováním) popř. Fourierovou transformací generují zájmové body. Neuronové sítě metoda backpropagation: Nejdůležitější vlasností neuronových sítí pro naši aplikaci je učení se. V případě, že bychom měli k dispozici referenční vzory, které bychom použili v procesu učení sítě, mohli bychom proces rozpoznávání objektů automatizovat. Tuto myšlenku demonstruje Obrázek 3. Obrázek 3 schéma tréninkového a pracovního módu neuronové sítě

5 XXX. ASR '2005 Seminar, Instruments and Control, Ostrava, April 29, V systému FOTOM je implementována vrstvená neuronová síť s pevnou topologií, ve které jsou během procesu učení stanoveny váhy jednotlivých spojů metodou backpropagation. Proto se omezíme pouze na popis učení se pomocí této metody. Do vrstvy vstupních uzlů přivedeme první vzor trénovací množiny, provedeme dopředné šíření až k výstupní vrstvě neuronů, kde srovnáme výslednou odezvu s očekávanou. Jejich rozdíl představuje chybu neuronové sítě, kterou zpětně využíváme k úpravě vah mezi jednotlivými vrstvami směrem od vyšších vrstev k nižším tak, aby byla chyba při následující odezvě menší. Postup provádíme přes všechny vzory trénovací množiny. Po vyčerpání celé trénovací množiny se vyhodnotí celková chyba přes všechny vzory. Je-li tato chyba vyšší než předem stanovená hodnota, opakujeme celý proces znovu. Prvotní nastavení vazeb mezi vrstvami sítě se provádí náhodně. 4 Řešení na katedře informatiky FEI VŠB-TUO Systém FOTOM je na katedře informatiky FEI VŠB-TUO vyvíjen řadu let. Navazuje na systémy vytvářené původně ve Vědecko-výzkumném ústavu v Ostravě-Radvanicích a na Hornicko-geologické fakultě VŠB-TUO. Na katedře informatiky byl pak pod vedením doc. Ing. Ličeva dále rozšiřován. Přestože byl původní systém určen pro práci se snímky z důlního měřičství, kde sloužil především k sledování a zobrazování posunů profilů důlních jam, je díky jeho velmi obecné koncepci možno použít jej (nebo alespoň jeho části) i v jiných oblastech. V současné době se vývoj systému orientuje především na využití v biomedicíně. Hlavním prvkem pro práci se systémem je tzv. FTM snímek (interpretovaný jako soubor typu *.ftm), který v sobě spojuje tyto části: Bitmapový snímek odkaz na BMP soubor s přidruženým snímkem Parametry měření použité metody, jednotky, specifikace orientace snímku vzhledem k reálnému prostoru pomocí vlícovacích bodů Uživatelem definované body a objekty Zájmové objekty (objekty měření) jsou určeny skupinou zájmových bodů, což jsou obyčejné body v 2D prostoru roviny snímku. Orientace každého snímku vzhledem k reálnému prostoru je určena prostřednictvím lícovacích bodů, u kterých známe jak pozici na snímku, tak polohu v reálném světě. Systém FOTOM se skládá z několika modulů, jejichž funkci nyní krátce popíšeme. Nebudeme se jimi detailně zabývat, neboť většina již byla podrobně popsána dříve. Fotom1: Jedná se o hlavní aplikaci celého systému, která poskytuje nástroje pro vytváření a editaci FTM objektů. Slouží ke zpracování snímků ve formátu BMP a určení orientace snímku definováním vlícovacích bodů. Umožňuje definování parametrů, zadávání zájmových bodů a na jejich základě zadávání zájmových objektů a stanovení jejich parametrů (př. obsah, souřadnice těžiště ). Modul rovněž obsahuje funkci automatického vyhledávání zájmového bodu v uživatelem stanovené oblasti. Fotom2: Tento modul poskytuje grafové a tabulkové zobrazení a tisk vybraných charakteristik zadané množiny snímků. Dovoluje tak srovnat a sledovat vybrané parametry objektů v rámci definované série snímků a nalézt průměrné, maximální i minimální hodnoty těchto parametrů. Motivací implementace tohoto modulu byla potřeba sledovat vývoj vybraných parametrů. Jako klasický příklad v lékařské oblasti bychom uvedli sledování růstu aterického plátu na základě sady snímků pořízených v delším časovém intervalu, což popisuje vývoj zanášení tepny. Fotom3: Tato aplikace slouží k prostorovému zobrazení objektů vzniklých ze série FTM objektů jako řezů scénou. Máme-li k dispozici sérii snímků, které reprezentují řezy scénou v daných vzdálenostech, a na nich definované zájmové objekty, pak kanalizací skrze jednotlivé vstupní snímky dovoluje tento modul vytvořit trojrozměrný model jednotlivých

6 XXX. ASR '2005 Seminar, Instruments and Control, Ostrava, April 29, objektů. Např. je-li k dispozici sada ultrazvukových snímků reprezentujících cévu v po sobě jdoucích řezech, je možno vytvořit model pravděpodobného tvaru cévy. Fotom4: Modul Fotom4 umožňuje 2D animaci snímků a sledování pohybu geometrických objektů. Jedná se o prohlížeč množiny FTM snímků s možností animace pohybu vybraných zájmových objektů při průchodu touto množinou. Fotom5: modul pro měření odchylek. Velmi se podobá modulu Fotom2, ovšem na rozdíl od něj nezobrazuje hodnoty vybraných charakteristik, ale jejich odchylky od průměrných hodnot získaných průměrováním charakteristik napříč množinou vstupních snímků. Motivace vzniku tohoto modulu je zřejmá. Fotom6: tato aplikace vychází z modulů Fotom2 a Fotom5, přináší však jisté rozšíření. V praxi je často nezbytné srovnat podstatné charakteristiky objektů s hodnotami projektovanými, tj. hodnotami, které byly předem teoreticky určeny na základě výpočtů nebo na základě dlouhodobého sledování, Fotom6 toto srovnání umožňuje. Fotom7: Modul slouží k vyhledávání zájmových bodů na snímcích se snahou o plnou nebo alespoň částečnou automatizaci. Motivací vzniku tohoto modulu je vysoká časová náročnost manuálního zadávání zájmových objektů na jednotlivých snímcích uživatelem. 5 Využití fotomu pro analýzu důlních snímků Princip analýzy je v pořízení několika desítek až stovek snímků, na kterých je zachycen měřený úsek, přičemž vzdálenost mezi snímky se vždy liší o předem stanovený délkový interval (tzv. ekvidistantní dělení). Vzhledem k univerzálnosti většiny modulů systému FOTOM, které zpracovávají zájmové objekty, se těmito nebudeme zabývat a přistoupíme přímo k modulu, který byl vyvinut speciálně pro potřeby analýzy důlních snímků. Zcela zásadní nevýhodou původního systému FOTOM byla nutnost opakovaného zadávání zájmových bodů a objektů na každém snímku zvlášť. Při potřebě zpracovávat stovky snímků, tj. na každém zvlášť definovat zájmové body a oblasti (navíc s vysokou přesností, neboť každá odchylka způsobí nepřesnost měření), balancoval systém na hranici použitelnosti. Vzhledem ke skutečnosti, že dva po sobě snímky se liší jen v nepatrných detailech, byl nově implementován modul Fotom7, který slouží k automatickému zpracování důlních snímků na základě jednoho referenčního. Modul umožňuje nastavit, který snímek se bude považovat zareferenční pro analýzu následujících snímků. První možností je považovat za referenční vždy předchozí snímek. Tuto volbu využijeme v případě nekvalitních snímků, které obsahují zkreslení, které se s jednotlivými snímky zvětšuje. Daní za jistou eliminaci zkreslení je riziko kumulace chyb při chybném určení zájmového bodu. Naopak druhá metoda považuje za referenční parametry výchozího snímku. Tato metoda se nedokáže vyrovnat se zkreslením daným nekvalitním pořízením snímku, ovšem z principu vytváří při definování zájmových bodů pouze ojedinělé chyby. Další volbou, kterou modul umožňuje, je volba metody, která je použita při definování zájmových bodů. Nabízí se metoda zkoumání světelných stop a metoda s využitím neuronových sítí. Kombinací těchto nastavení lze dosáhnout až čtyř různých typů analýzy. Vzhledem k relativně obsáhlému popisu metod uvedenému v kapitole 3, popíšeme pouze posloupnost kroků, které systém provádí při automatickém generování zájmových bodů. V případě metody analýzy pomocí světelných stop se stanoví analyzovaná oblast velikosti 40x40 pixelů v jejímž středu je zájmový bod z předchozího měření (velikost oblasti byla určena experimentálně), je aplikována segmentace s proměnným prahem metodou histogramu jasu, následuje eroze sloužící k eliminaci šumu a nakonec je určen zájmový bod jako bod s nejmenší euklidovou vzdáleností od středu analyzované oblasti.

7 XXX. ASR '2005 Seminar, Instruments and Control, Ostrava, April 29, V případě analýzy pomocí neuronových sítí opět vycházíme z oblasti 40x40 pixelů, v jejímž středu se nachází zájmový bod z předchozího měření, po prahování a erozi zjistíme hranici objektu gradientní metodou první derivace, průběh křivosti hranice a pomocí Fourierovy transformace hraniční křivku, která je vstupem do neuronové sítě (metoda back propagation), jejímž výstupem je informace, zda se jedná o přímku či křivku. Tato výstupní informace se porovná s údajem uvedeným pro hledaný bod. Pakliže si údaje odpovídají, našli jsme správně odpovídající oblast a zájmový bod je určen jako její střed. V případě, že si údaje neodpovídají, je označen výchozí bod. Výhody: Automatické vyhledávání zájmových bodů na základě vzoru výrazně zjednodušuje práci se systémem. Nedostatky: V případě, že za referenční měření pro všechny snímky považujeme měření na prvním snímku a budu analyzovat snímek s nepříliš výraznou světelnou stopou, systém nenalezne žádný bod a chybně označí bod výchozí. Skutečný zájmový bod leží s velkou pravděpodobností jinde. Při analýze snímku, na němž je světelná stopa zamlžena (nevýrazná), ovšem jiná stopa je dostatečně výrazná, může dojít k chybnému označení zájmového bodu. V případě, že se v analyzované oblasti vyskytuje více zájmových bodů, může dojít k chybě, kdy jsou všechny tyto zájmové body totožné. a) původní bod b) zamlžená stopa c) napravený bod Obrázek 4 - Automatické rozpoznání metodou výchozího referenčního snímku 6 Využití Fotomu pro analýzu lékařských snímků Oproti důlním snímkům s ostrými plynulými objekty s relativně nízkou úrovní šumu jsou v důsledku nedokonalosti technické stránky ultrazvukové sonografie objekty na lékařských snímcích nespojitého zrnitého charakteru, výrazně zašuměné a mnohdy neúplné. Některé části orgánů jsou špatně viditelné nebo dokonce chybí úplně. Vzhledem k odlišné povaze lékařských snímků a skutečnosti, že při definici zájmových objektů je nutná asistence odborného lékaře, tedy nebylo možno využít modul FOTOM7 popsaný v předchozí kapitole. Zároveň byla nevyhovující koncepce zadávání zájmových bodů a objektů čistě manuálně v modulu Fotom1. Bylo žádoucí proces vyhledávání a zadávání objektů alespoň poloautomatizovat. Pro využití systému při analýze biomedicínských snímků byl modul Fotom7 nahrazen novým modulem (Fotom7-2004), který obsahuje nástroje pro grafickou práci se snímkem za účelem zjednodušení a urychlení práce při zadávání objektů. Modul Fotom7 je navržen na práci ve dvou režimech - v normálním režimu, kdy je na pozadí zobrazen originální snímek, a v režimu skica, který zobrazuje kopii originálního snímku s možností grafických úprav. Volba režimu nemá vliv na práci s objekty, ty jsou dostupné a viditelné v obou režimech. Mezi těmito módy je možno se kdykoli přepnout a porovnat tak modifikovanou skicu s originálem. Následuje stručný popis jednotlivých nástrojů určených ke grafické editaci skicy za účelem definování zájmových objektů.

8 XXX. ASR '2005 Seminar, Instruments and Control, Ostrava, April 29, Prahování: Práh je určen interaktivně uživatelem na základě jeho subjektivního vizuálního dojmu. Obešli jsme tak problém hledání optimálního prahu a spoléháme se na zkušenost uživatele. Vyplňování: Nástroj dovoluje vyplnit oblast bodů podobného jasu vybranou barvou. Slouží ke zpřehlednění obrazu. Hranice: Tento nástroj automaticky generuje hranici homogenní oblasti, která byla vytvořena kombinací nástrojů prahování a vyplňování (popř. i nástroje pero viz. dále). Pro vygenerování hranice stačí kliknout dovnitř zájmové oblasti. Modul postupuje v krocích: stanovení množiny bodů tvořících hranici; aproximace tvaru hranice a určení průběhu křivosti metodou uvedenou v kapitole 3; stanovení prahu křivosti, při jehož překročení se generuje zájmový bod; generování bodů. Rozmazávání: Tento nástroj slouží k vyhlazení objektu. Reálné objekty mívají tvar hladký, kdežto jejich obraz vlivem nedokonalosti snímací techniky může mít tvar značně roztříštěný. Algoritmus umožňující rozmazání je velmi jednoduchý. Hodnota jasu daného bodu je určena jako průměr jasu okolních bodů. Hloubka rozmazání je dána velikostí okolí, ze kterého se tento průměr stanovuje. Pero: Pero slouží k dokreslení chybějící části objektu. Již jsme zmínili, že na ultrazvukových snímcích mohou chybět části orgánů. Specialista může na základě zkušeností odhadnout a dokreslit chybějící část objektu. Speciální zadávání bodů: V případě, že úroveň šumu je tak vysoká, že nelze použít výše zmíněných nástrojů, nezbývá než zadat zájmové body manuálně. Pro usnadnění manuální definice zájmových bodů byl vytvořen režim speciálního zadávání bodů. Pro definici zájmového bodu stačí určit bod, v jehož okolí se zájmový bod nachází. Systém pak na okolí (101x101 bodů) tohoto bodu aplikuje prahování s prahem stanoveným metodou histogramu jasu, čímž dojde k oddělení popředí a pozadí. Za zájmový bod pak bude označen bod popředí s nejmenší euklidovou vzdáleností od výchozího bodu. Výhody: Svou velmi obecnou koncepcí částečně automatického definování zájmových bodů dovoluje systém nasazení i v jiných oblastech, než pro jaké byl původně vyvinut. Nevýhody: Zásadní nevýhodou zůstává i nadále nutnost zpracování každého snímku zvlášť a to za přispění uživatele odborníka s rozsáhlými odbornými znalostmi, zkušenostmi a praxí při analýze ultrazvukových snímků. Zároveň je bezpodmínečně nutné, aby uživatel dokonale ovládal jednotlivé nástroje pro rozpoznání objektů, což je opět podmíněno dlouhodobou praxí. 7 Závěr Příspěvek pojednával o fotogrammetrickém systému FOTOM vyvíjeném na katedře informatiky FEI VŠB-TUO. Cílem autorů nebyl kompletní popis tohoto složitého systému, nýbrž pouhé zdůraznění nejdůležitějších myšlenek, postupů a nástrojů implementovaných v tomto systému. I když byl původně tento systém zaměřen na práci se snímky důlního měřičství, dovoluje vzhledem k jeho obecné koncepci využití mnoha jeho částí i k práci se snímky z jiných odvětví (např. v lékařství). Základním předpokladem pro měření je správné definování zájmových objektů. Vzhledem ke značně různorodé povaze snímků charakteristických pro různé vědní obory není možno implementovat jednotný modul pro automatické definování zájmových bodů a oblastí. Pro každou specifickou oblast použití

9 XXX. ASR '2005 Seminar, Instruments and Control, Ostrava, April 29, je tedy vhodné vyvinout samostatný modul pro jednoduché a automatické (nebo alespoň částečně automatické) zadávání zájmových objektů. 8 Literatura DUDEK, R.: Rozpoznávání zájmových bodů na fotografii. Diplomová práce. VŠB TU Ostrava, FEI, SOJKA, E.: Sylaby k předmětu Aplikace obrazu a počítačového vidění. Ostrava, ŠEJDA, P.: Rozpoznávání objektů na snímku ultrazvuku. Diplomová práce. VŠB TU Ostrava, FEI, 2004.