Numerické řešení diferenciálních rovnic
|
|
|
- Julie Benešová
- před 5 lety
- Počet zobrazení:
Transkript
1 Numerické řešení diferenciálních rovnic Omezení: obyčejné (nikoli parciální) diferenciální rovnice, Cauchyho počáteční úloha, pouze jedna diferenciální rovnice 1. řádu 1/1
2 Numerické řešení diferenciálních rovnic Omezení: obyčejné (nikoli parciální) diferenciální rovnice, Cauchyho počáteční úloha, pouze jedna diferenciální rovnice 1. řádu 1/1 Úloha: Na intervalu x 0, x n máme řešit diferenciální rovnici y (x) = f(x, y(x)) s počáteční podmínkou y(x 0 ) = y 0, kde f je funkce dvou reálných proměnných a y 0 R.
3 Numerické řešení diferenciálních rovnic Omezení: obyčejné (nikoli parciální) diferenciální rovnice, Cauchyho počáteční úloha, pouze jedna diferenciální rovnice 1. řádu 1/1 Úloha: Na intervalu x 0, x n máme řešit diferenciální rovnici s počáteční podmínkou y (x) = f(x, y(x)) y(x 0 ) = y 0, kde f je funkce dvou reálných proměnných a y 0 R. Poznámka: Pokud f nezávisí na y, tj. f(x, y) = g(x), dostáváme numerickou integraci jako speciální případ řešení diferenciální rovnice y (x) = g(x)
4 Existence a jednoznačnost řešení Není obecně zaručena: 2/1 Příklad: Uvažujme diferenciální rovnici s počáteční podmínkou: y (x) = 3 y(x), y(0) = 0, kde třetí odmocninu považujeme za reálnou funkci definovanou i pro záporný argument. Má řešení např. y(x) = 0 a y(x) = ± ( 2 3 x) 3 2.
5 Existence a jednoznačnost řešení Není obecně zaručena: 2/1 Příklad: Uvažujme diferenciální rovnici s počáteční podmínkou: y (x) = 3 y(x), y(0) = 0, kde třetí odmocninu považujeme za reálnou funkci definovanou i pro záporný argument. Má řešení např. y(x) = 0 a y(x) = ± ( 2 3 x) 3 2. Věta: Nechť funkce f je definovaná a spojitá na x 0, x n R (tj. pro všechna x x 0, x n, y R). Nechť je splněna Lipschitzova podmínka L R x x 0, x n y 1, y 2 R : f(x, y 1 ) f(x, y 2 ) L y 1 y 2. Pak řešení naší úlohy na intervalu x 0, x n existuje a je jednoznačné.
6 Existence a jednoznačnost řešení Není obecně zaručena: 2/1 Příklad: Uvažujme diferenciální rovnici s počáteční podmínkou: y (x) = 3 y(x), y(0) = 0, kde třetí odmocninu považujeme za reálnou funkci definovanou i pro záporný argument. Má řešení např. y(x) = 0 a y(x) = ± ( 2 3 x) 3 2. Věta: Nechť funkce f je definovaná a spojitá na x 0, x n R (tj. pro všechna x x 0, x n, y R). Nechť je splněna Lipschitzova podmínka L R x x 0, x n y 1, y 2 R : f(x, y 1 ) f(x, y 2 ) L y 1 y 2. Pak řešení naší úlohy na intervalu x 0, x n existuje a je jednoznačné. Postačující podmínka: f y spojitá a omezená na x 0, x n R.
7 Interpretace úlohy a princip řešení Poznámka: Ekvivalentní formulace úlohy: řešení 3/1 y(x) = y 0 + x x 0 f(t, y(t)) dt lze chápat jako integrál (neznámé) funkce g(t) = f(t, y(t)) jedné proměnné nebo křivkový integrál známé funkce f přes (neznámou) křivku s parametrizací (t, y(t)), t x 0, x n.
8 Interpretace úlohy a princip řešení Poznámka: Ekvivalentní formulace úlohy: řešení 3/1 y(x) = y 0 + x x 0 f(t, y(t)) dt lze chápat jako integrál (neznámé) funkce g(t) = f(t, y(t)) jedné proměnné nebo křivkový integrál známé funkce f přes (neznámou) křivku s parametrizací (t, y(t)), t x 0, x n. Interval x 0, x n rozdělíme na n dílčích intervalů délky h = (x n x 0 )/n. Získáme uzlové body x i = x 0 + ih, i = 0,..., n. Správné hodnoty řešení v uzlových bodech, y(x i ), nahradíme odhady y i. Hodnoty derivace: f i = f(x i, y i ).
9 Obecný postup řešení Generujeme posloupnost y i, i = 0,..., n. V kroku i + 1 počítáme z odhadů y 0,..., y i odhad y i+1. Přesné řešení: 4/1 y(x i+1 ) y(x i ) = xi+1 x i f(t, y(t)) dt odhadujeme pomocí y i = y i+1 y i xi+1 x i f(t, y(t)) dt. y i+1 = y i + y i. Jednotlivé metody se liší pouze odhadem y i.
10 Rungovy-Kuttovy metody 1: Eulerova metoda Je zobecněním metody levého odhadu; funkci f(t, y(t)) nahrazujeme její hodnotou f(x i, y i ) v bodě x i 5/1 xi+1 y i = f(x i, y i ) dt = h f(x i, y i ), x i y i+1 = y i + h f(x i, y i ) = y i + h f i.
11 Rungovy-Kuttovy metody 1: Eulerova metoda Je zobecněním metody levého odhadu; funkci f(t, y(t)) nahrazujeme její hodnotou f(x i, y i ) v bodě x i 5/1 xi+1 y i = f(x i, y i ) dt = h f(x i, y i ), x i y i+1 = y i + h f(x i, y i ) = y i + h f i. Geometrický význam: f i = f(x i, y i ) je směrnice úsečky vedené body (x i, y i ), (x i+1, y i+1 ).
12 Odhad chyby Taylorův rozvoj funkce y se středem v x 0 vyhodnotíme v bodě x 1 : 6/1 y(x 1 ) = y(x 0 ) + h y (x 0 ) + h2 2 y (ξ), kde ξ x 0, x 1. y(x 1 ) = } y(x 0 ) + h {{ f(x 0, y 0 } ) + h2 2 y (ξ), y 1 y(x 1 ) y 1 = h2 2 y (ξ). Chyba na konci prvního kroku je úměrná h 2. V dalších krocích vycházíme z počáteční podmínky, která není přesná. Přesto lze za jistých podmínek odvodit, že chyba je zhruba úměrná h 2 a počtu kroků n = x n x 0 h. Chyba na konci daného intervalu je úměrná 1 h h2 = h metoda 1. řádu.
13 Rungovy-Kuttovy metody 2: První modifikace Eulerovy metody Je zobecněním obdélníkové metody; funkci f(t, y(t)) v ní nahradíme opět hodnotou v bodě x i+x i+1 2 = x i + h 2. Jako druhý argument funkce f použijeme výsledek pomocného kroku poloviční délky (Eulerovou metodou): 7/1 η i = y i + h 2 f i. f(t, y(t)) f(x i + h 2, η i) y i = xi+1 x i f(x i + h 2, η i) dt = h f(x i + h 2, η i). Metoda 2. řádu.
14 Rungovy-Kuttovy metody 3: Druhá modifikace Eulerovy metody (Heunova metoda) Je zobecněním lichoběžníkové metody integrace; funkci f(t, y(t)) nahradíme lineární funkcí, proloženou hodnotami v krajních bodech intervalu: v x i : f i = f(x i, y i ), v x i+1 : neznalost y-ové souřadnice řešíme pomocným krokem (délky h Eulerovou metodou): θ i = y i + h f i. Funkci f(t, y(t)) nahradíme lineární funkcí, jejíž graf prochází body ( xi, f(x i, y i ) ), ( x i+1, f(x i+1, θ i ) ). 8/1 y i = h 2 (f(x i, y i ) + f(x i+1, θ i )). Metoda 2. řádu.
15 Rungovy-Kuttovy metody 4: Rungova-Kuttova metoda 4. řádu Je zobecněním Simpsonovy metody; nejprve vypočteme pomocné body a hodnoty derivace v nich, 9/1 k i,1 = f(x i, y i ), k i,2 = f(x i + h 2, y i + h 2 k i,1), k i,3 = f(x i + h 2, y i + h 2 k i,2), k i,4 = f(x i + h, y i + h k i,3 ). Integrál nahradíme lineární kombinací těchto hodnot: y i = h 6 (k i,1 + 2k i,2 + 2k i,3 + k i,4 ).
16 Rungovy-Kuttovy metody 5: Obecné Rungovy-Kuttovy metody Odhadují integrál x i+1 f(t, y(t)) dt z několika hodnot funkce f v bodech, x i získaných z výchozích hodnot x i, y i a pomocných kroků. Tyto hodnoty jsou zkombinovány tak, aby se vykompenzovaly chyby nejnižších řádů. 10/1
17 Metody Vícekrokové metody 11/1 jednokrokové: využívají xi, yi a fi = f(xi, yi) (např. Rungeovy-Kuttovy),
18 Metody Vícekrokové metody 11/1 jednokrokové: využívají xi, yi a fi = f(xi, yi) (např. Rungeovy-Kuttovy), vícekrokové: využívají i výsledky předcházejících kroků, tj. xj, yj a f j = f(x j, y j ), j = i, i 1,..., i s + 1 (pro s-krokovou metodu). Vícekrokové metody dovolují zvýšit řád metody bez pomocných kroků. Nicméně k nastartování s-krokové metody potřebujeme s hodnot y 0, y 1,..., y s 1. Ty získáváme startovací metodou (některou z jednokrokových metod).
19 Adamsovy-Bashforthovy metody (explicitní) 12/1 s hodnotami derivace f i, f i 1,..., f i s+1 v uzlových bodech x i, x i 1,..., x i s+1 proložíme interpolační polynom ϕ i a ten integrujeme místo f(t, y(t)): y i = xi+1 x i ϕ i (t) dt. Není potřeba počítat ϕ i, neboť y i = h s 1 j=0 w j f i j, kde w j jsou předem známé koeficienty. Polynomem aproximujeme derivaci y (t) = f(t, y(t)), nikoli řešení, y(t)!
20 Pro s = 1: ϕ i = f i je konstantní Eulerova metoda. 13/1
21 Pro s = 1: ϕ i = f i je konstantní Eulerova metoda. 13/1 Pro s = 2: ϕ i je lineární polynom proložený body (x i, f i ), (x i 1, f i 1 ), y i = xi+1 ϕ i (t) = f i + f i f i 1 h (t x i ) x i ϕ i (t) dt = h f i + h 2 (f i f i 1 ) = h 2 (3f i f i 1 ).
22 Pro s = 1: ϕ i = f i je konstantní Eulerova metoda. 13/1 Pro s = 2: ϕ i je lineární polynom proložený body (x i, f i ), (x i 1, f i 1 ), Pro s = 3: y i = xi+1 ϕ i (t) = f i + f i f i 1 h (t x i ) x i ϕ i (t) dt = h f i + h 2 (f i f i 1 ) = h 2 (3f i f i 1 ). y i = h 12 (23f i 16f i 1 + 5f i 2 ),
23 Pro s = 1: ϕ i = f i je konstantní Eulerova metoda. 13/1 Pro s = 2: ϕ i je lineární polynom proložený body (x i, f i ), (x i 1, f i 1 ), Pro s = 3: Pro s = 4: y i = xi+1 ϕ i (t) = f i + f i f i 1 h (t x i ) x i ϕ i (t) dt = h f i + h 2 (f i f i 1 ) = h 2 (3f i f i 1 ). y i = h 12 (23f i 16f i 1 + 5f i 2 ), y i = h 24 (55f i 59f i f i 2 9f i 3 ).
24 Řád metody je s=počet bodů použitých v aproximaci. 14/1
25 Řád metody je s=počet bodů použitých v aproximaci. 14/1 Výhoda: jednoduchost
26 Řád metody je s=počet bodů použitých v aproximaci. 14/1 Výhoda: jednoduchost Nevýhody: různá znaménka koeficientů ( zaokrouhlovací chyby) chyba metody způsobená extrapolací polynomem snaha vyhnout se extrapolaci
27 Adamsovy-Moultonovy metody (implicitní) Pravou stranu f(t, y(t)) aproximujeme interpolačním polynomem ϕ i proloženým hodnotami f i, f i 1,..., f i s+1 a hodnotou v bodě x i+1, tj. f i+1 = f(x i+1, y i+1 ). 15/1
28 Adamsovy-Moultonovy metody (implicitní) Pravou stranu f(t, y(t)) aproximujeme interpolačním polynomem ϕ i proloženým hodnotami f i, f i 1,..., f i s+1 a hodnotou v bodě x i+1, tj. f i+1 = f(x i+1, y i+1 ). Opět se redukuje na tvar 15/1 y i+1 y i = y i = h s 1 j= 1 w j f i j, kde w j jsou předem vypočtené koeficienty (zde jiné).
29 Adamsovy-Moultonovy metody (implicitní) Pravou stranu f(t, y(t)) aproximujeme interpolačním polynomem ϕ i proloženým hodnotami f i, f i 1,..., f i s+1 a hodnotou v bodě x i+1, tj. f i+1 = f(x i+1, y i+1 ). Opět se redukuje na tvar 15/1 y i+1 y i = y i = h s 1 j= 1 w j f i j, kde w j jsou předem vypočtené koeficienty (zde jiné). Dostáváme rovnici y i+1 = y i + h w 1 f(x i+1, y i+1 ) + h s 1 j=0 w j f i j pro neznámou hodnotu y i+1, která je tímto určena implicitně.
30 Pro s = 1: ϕ i je lineární polynom proložený body (x i, f i ), (x i+1, f i+1 ), tj. 16/1 ϕ i (t) = f i + f i+1 f i h (t x i ). xi+1 y i = ϕ i (t) dt = h x i 2 (f i+1 + f i ), po dosazení f i+1 = f(x i+1, y i+1 ) y i+1 y i = h 2 ( f(xi+1, y i+1 ) + f i ).
31 Pro s = 1: ϕ i je lineární polynom proložený body (x i, f i ), (x i+1, f i+1 ), tj. 16/1 ϕ i (t) = f i + f i+1 f i h (t x i ). xi+1 y i = ϕ i (t) dt = h x i 2 (f i+1 + f i ), po dosazení f i+1 = f(x i+1, y i+1 ) y i+1 y i = h 2 ( f(xi+1, y i+1 ) + f i ). Pro s = 2: y i = h 12 ( 5f(xi+1, y i+1 ) + 8f i f i 1 ),
32 Pro s = 1: ϕ i je lineární polynom proložený body (x i, f i ), (x i+1, f i+1 ), tj. 16/1 ϕ i (t) = f i + f i+1 f i (t x i ). h xi+1 y i = ϕ i (t) dt = h x i 2 (f i+1 + f i ), po dosazení f i+1 = f(x i+1, y i+1 ) y i+1 y i = h 2 ( f(xi+1, y i+1 ) + f i ). Pro s = 2: y i = h 12 ( 5f(xi+1, y i+1 ) + 8f i f i 1 ), Pro s = 3: y i = h 24 ( 9f(xi+1, y i+1 ) + 19f i 5f i 1 + f i 2 ).
33 Řád metody je s + 1=počet bodů použitých v aproximaci. 17/1
34 Řád metody je s + 1=počet bodů použitých v aproximaci. 17/1 Výhoda: vyšší přesnost
35 Řád metody je s + 1=počet bodů použitých v aproximaci. 17/1 Výhoda: vyšší přesnost Nevýhody: obtížné řešení implicitní rovnice (zřídka možné exaktně, numerické řešení zvyšuje složitost) i chyba metody způsobená interpolací polynomem může být značná
36 Metody prediktor-korektor Základem je korektor, což je některá z implicitních metod, v níž se příslušná rovnice řeší numericky. V j-té iteraci z ní vypočítáme odhad y i+1,j hodnoty y i+1, přičemž na pravé straně použijeme odhad y i+1,j 1 získaný v předchozí iteraci: 18/1 y i+1,j = y i + h s 1 j=0 w j f i j + h w 1 f(x i+1, y i+1,j 1 ). Počáteční odhad y i+1,0 najdeme z výsledků předchozích kroků (event. z počátečních podmínek) jinou metodou, zvanou prediktor, např. některou z explicitních metod.
37 Řídicí mechanismus P = prediktor (Predictor) C = korektor (Corrector) E = vyhodnocení derivace (Evaluation) 19/1 Nejčastější možnosti: cyklus korektoru provádět tak dlouho, dokud není rozdíl yi+1,j yi+1,j 1 dostatečně malý, konstantní počet k opakování korektoru, P(EC)kE, jediný průchod korektorem, PECE.
38 Adamsovy metody Prediktor: Adamsova-Bashforthova metoda Korektor: Adamsova-Moultonova metoda 20/1 Příklad: Nejjednodušší varianta Adamsovy metody, s = 1: Prediktor: Eulerova metoda (1. řádu) y i+1,0 = y i + h f i. Korektor: Adamsova-Moultonova metoda 2. řádu y i+1,j+1 = y i + h 2 ( fi + f(x i+1, y i+1,j ) ).
39 Adamsovy metody Prediktor: Adamsova-Bashforthova metoda Korektor: Adamsova-Moultonova metoda 20/1 Příklad: Nejjednodušší varianta Adamsovy metody, s = 1: Prediktor: Eulerova metoda (1. řádu) y i+1,0 = y i + h f i. Korektor: Adamsova-Moultonova metoda 2. řádu y i+1,j+1 = y i + h 2 ( fi + f(x i+1, y i+1,j ) ). Volba startovací metody (jejího řádu)
40 Adamsovy metody Prediktor: Adamsova-Bashforthova metoda Korektor: Adamsova-Moultonova metoda 20/1 Příklad: Nejjednodušší varianta Adamsovy metody, s = 1: Prediktor: Eulerova metoda (1. řádu) y i+1,0 = y i + h f i. Korektor: Adamsova-Moultonova metoda 2. řádu y i+1,j+1 = y i + h 2 ( fi + f(x i+1, y i+1,j ) ). Volba startovací metody (jejího řádu) Volba kroku
41 Richardsonova extrapolace při řešení diferenciálních rovnic ỹ(x, h)... numerické řešení v bodě x, získané s krokem h ỹ(x, 2h)... numerické řešení v bodě x, získané s krokem 2h 21/1 (zde q = 2) Chyba odhadu ỹ(x, h) bude zhruba 2 p menší než chyba odhadu ỹ(x, 2h) odhad chyby výsledku ỹ(x, h) metodou polovičního kroku: ỹ(x, h) y(x) 1 2 p (ỹ(x, 2h) ỹ(x, h)). 1 Odhad výsledku zpřesněný Richardsonovou extrapolací: y(x) ỹ(x, h) p (ỹ(x, h) ỹ(x, 2h)). 1
42 Richardsonova extrapolace při řešení diferenciálních rovnic ỹ(x, h)... numerické řešení v bodě x, získané s krokem h ỹ(x, 2h)... numerické řešení v bodě x, získané s krokem 2h 21/1 (zde q = 2) Chyba odhadu ỹ(x, h) bude zhruba 2 p menší než chyba odhadu ỹ(x, 2h) odhad chyby výsledku ỹ(x, h) metodou polovičního kroku: ỹ(x, h) y(x) 1 2 p (ỹ(x, 2h) ỹ(x, h)). 1 Odhad výsledku zpřesněný Richardsonovou extrapolací: Richardsonova extrapolace pasivní aktivní y(x) ỹ(x, h) p (ỹ(x, h) ỹ(x, 2h)). 1
Numerické řešení diferenciálních rovnic
Numerické řešení diferenciálníc rovnic Mirko Navara ttp://cmp.felk.cvut.cz/ navara/ Centrum strojovéo vnímání, katedra kybernetiky FEL ČVUT Karlovo náměstí, budova G, místnost 104a ttp://mat.feld.cvut.cz/nemecek/nummet.tml
úloh pro ODR jednokrokové metody
Numerické metody pro řešení počátečních úloh pro ODR jednokrokové metody Formulace: Hledáme řešení y = y() rovnice () s počáteční podmínkou () y () = f(, y()) () y( ) = y. () Smysl: Analyticky lze spočítat
Numerické řešení obyčejných diferenciálních rovnic
Numerické řešení obyčejných diferenciálních rovnic Michal Menkina TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Tento materiál vznikl v rámci projektu ESF CZ.1.07/2.2.00/07.0247,
Numerická matematika. Zadání 25. Řešení diferenciální rovnice Rungovou Kuttovou metodou
Numerická matematika Zadání 25. Řešení diferenciální rovnice Rungovou Kuttovou metodou Václav Bubník, xbubni01, sk. 60 FIT VUT v Brně, 2004 Obsah Numerická matematika...1 1. Teorie... 3 1.1 Diferenciální
Obyčejné diferenciální rovnice počáteční úloha. KMA / NGM F. Ježek
Občejné diferenciální rovnice počáteční úloha KMA / NGM F. Ježek (JEZEK@KMA.ZCU.CZ) Základní pojm Tp rovnic a podmínek, řád rovnice Počáteční úloha pro občejné diferenciální rovnice Řád metod a počet kroků
Obyčejné diferenciální rovnice (ODE)
Obyčejné diferenciální rovnice (ODE) Obyčejné diferenciální rovnice N tého řádu převádíme na soustavy N diferenciálních rovnic prvního řádu. V rovnici f x, y, y ', y '',, y N =gx se substituují y '=z 1,
ODR metody Runge-Kutta
ODR metody Runge-Kutta Teorie (velmi stručný výběr z přednášek) Úloha s počátečními podmínkami (Cauchyova) 1 řádu Hledáme aprox řešení Y(x) soustavy obyčejných diferenciálních rovnic 1 řádu kde Y(x) =
Numerické řešení nelineárních rovnic
Numerické řešení nelineárních rovnic Mirko Navara http://cmp.felk.cvut.cz/ navara/ Centrum strojového vnímání, katedra kybernetiky FEL ČVUT Karlovo náměstí, budova G, místnost 104a http://math.feld.cvut.cz/nemecek/nummet.html
Kombinatorická minimalizace
Kombinatorická minimalizace Cílem je nalézt globální minimum ve velké diskrétní množině, kde může být mnoho lokálních minim. Úloha obchodního cestujícího Cílem je najít nejkratší cestu, která spojuje všechny
Kapitola 10: Diferenciální rovnice 1/14
Kapitola 10: Diferenciální rovnice 1/14 Co je to diferenciální rovnice? Definice: Diferenciální rovnice je vztah mezi hledanou funkcí y(x), jejími derivacemi y (x), y (x), y (x),... a nezávisle proměnnou
Fakt. Každou soustavu n lineárních ODR řádů n i lze eliminací převést ekvivalentně na jednu lineární ODR
DEN: ODR teoreticky: soustavy rovnic Soustava lineárních ODR 1 řádu s konstantními koeficienty je soustava ve tvaru y 1 = a 11 y 1 + a 12 y 2 + + a 1n y n + b 1 (x) y 2 = a 21 y 1 + a 22 y 2 + + a 2n y
Drsná matematika III 6. přednáška Obyčejné diferenciální rovnice vyšších řádů, Eulerovo přibližné řešení a poznámky o odhadech chyb
Drsná matematika III 6. přednáška Obyčejné diferenciální rovnice vyšších řádů, Eulerovo přibližné řešení a poznámky o odhadech chyb Jan Slovák Masarykova univerzita Fakulta informatiky 23. 10. 2006 Obsah
metody jsou proto často jedinou možností jak danou diferenciální rovnicivyřešit.
7. ODR počáteční úlohy Průvodce studiem Jen velmi málo diferenciálních rovnic, které se vyskytují při popisu praktických úloh, se dářešit exaktně, a i když dokážeme najít vzorce popisující analytickéřešení,
Numerické metody a statistika
Numerické metody a statistika Radek Kučera VŠB-TU Ostrava 016-017 ( ) Numerické metody a statistika 016-017 1 / Numerické integrování ( ) Numerické metody a statistika 016-017 / Geometrický význam integrálu
Studijní text pro obor G+K Katedra matematiky Fakulta stavební ROVNICE. Doc. RNDr. Milada Kočandrlová, CSc.
Studijní text pro obor G+K Katedra matematiky Fakulta stavební České vysoké učení technické OBYČEJNÉ DIFERENCIÁLNÍ ROVNICE Doc. RNDr. Milada Kočandrlová, CSc. Lektorovali: RNDr. Milan Kočandrle, CSc.,
Numerické řešení nelineárních rovnic
Numerické řešení nelineárních rovnic Mirko Navara http://cmp.felk.cvut.cz/ navara/ Centrum strojového vnímání, katedra kybernetiky FEL ČVUT Karlovo náměstí, budova G, místnost 104a http://math.feld.cvut.cz/nemecek/nummet.html
Integrace. Numerické metody 7. května FJFI ČVUT v Praze
Integrace Numerické metody 7. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod 1D Kvadraturní vzorce Gaussovy kvadratury Více dimenzí Programy 1 Úvod Úvod - Úloha Máme funkci f( x) a snažíme se najít určitý integrál
Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague
1 / 40 regula Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague regula 1 2 3 4 5 regula 6 7 8 2 / 40 2 / 40 regula Iterační pro nelineární e Bud f reálná funkce
4. OBYČEJNÉ DIFERENCIÁLNÍ ROVNICE
FBI VŠB-TUO 28. března 2014 4.1. Základní pojmy Definice 4.1. Rovnice tvaru F (x, y, y, y,..., y (n) ) = 0 se nazývá obyčejná diferenciální rovnice n-tého řádu a vyjadřuje vztah mezi neznámou funkcí y
METODA PŮLENÍ INTERVALU (METODA BISEKCE) METODA PROSTÉ ITERACE NEWTONOVA METODA
2-3. Metoda bisekce, met. prosté iterace, Newtonova metoda pro řešení f(x) = 0. Kateřina Konečná/ 1 ITERAČNÍ METODY ŘEŠENÍ NELINEÁRNÍCH ROVNIC - řešení nelineární rovnice f(x) = 0, - separace kořenů =
Typy příkladů na písemnou část zkoušky 2NU a vzorová řešení (doc. Martišek 2017)
Typy příkladů na písemnou část zkoušky NU a vzorová řešení (doc. Martišek 07). Vhodnou iterační metodou (tj. metodou se zaručenou konvergencí) řešte soustavu: x +x +4x 3 = 3.5 x 3x +x 3 =.5 x +x +x 3 =.5
MATEMATIKA III. Olga Majlingová. Učební text pro prezenční studium. Předběžná verze
Fakulta strojního inženýrství Univerzity J. E. Purkyně v Ústí nad Labem Pasteurova 7 Tel.: 475 285 511 400 96 Ústí nad Labem Fax: 475 285 566 Internet: www.ujep.cz E-mail: kontakt@ujep.cz MATEMATIKA III
Numerické řešení nelineárních rovnic
Numerické řešení nelineárních rovnic Mirko Navara http://cmp.felk.cvut.cz/~navara/ Centrum strojového vnímání, katedra kybernetiky FEL ČVUT Karlovo náměstí, budova G, místnost 104a http://math.feld.cvut.cz/nemecek/nummet.html
Obyčejnými diferenciálními rovnicemi (ODR) budeme nazývat rovnice, ve kterých
Obyčejné diferenciální rovnice Obyčejnými diferenciálními rovnicemi (ODR) budeme nazývat rovnice, ve kterých se vyskytují derivace neznámé funkce jedné reálné proměnné. Příklad. Bud dána funkce f : R R.
Úvod. Integrování je inverzní proces k derivování Máme zderivovanou funkci a integrací získáme původní funkci kterou jsme derivovali
NEURČITÝ INTEGRÁL Úvod Integrování je inverzní proces k derivování Máme zderivovanou funkci a integrací získáme původní funkci kterou jsme derivovali Umět pracovat s integrálním počtem Je důležité pro
Obsah Obyčejné diferenciální rovnice
Obsah 1 Obyčejné diferenciální rovnice 3 1.1 Základní pojmy............................................ 3 1.2 Obyčejné diferenciální rovnice 1. řádu................................ 5 1.3 Exaktní rovnice............................................
metody jsou proto často jedinou možností jak danou diferenciální rovnicivyřešit.
7. ODR POČÁTEČNÍ ÚLOHY Numerické metody 7. ODR počáteční úlohy Průvodce studiem Jen velmi málo diferenciálních rovnic, které se vyskytují při popisu praktických úloh, se dářešit exaktně, a i když dokážeme
Numerická matematika Písemky
Numerická matematika Písemky Bodování Každá písemka je bodována maximálně 20 body. Celkem student může získat za písemky až 40 bodů, pro udělení zápočtu musí získat minimálně 20 bodů. Písemka č. 1 Dva
4 Numerické derivování a integrace
Břetislav Fajmon, UMAT FEKT, VUT Brno Téma je podrobně zpracováno ve skriptech [1], kapitola 7, strany 85-94. Jedná se o úlohu výpočtu (první či druhé) derivace či o výpočet určitého integrálu jinými metodami,
Moderní numerické metody
Moderní numerické metody Sbírka příkladů doc. RNDr. Jaromír Baštinec, CSc. RNDr. Michal Novák, Ph.D. ÚSTAV MATEMATIKY Moderní numerické metody 1 Obsah 1 Soustavy lineárních rovnic 7 2 Řešení jedné nelineární
řešeny numericky 6 Obyčejné diferenciální rovnice řešeny numericky
řešeny numericky řešeny numericky Břetislav Fajmon, UMAT FEKT, VUT Brno Na minulé přednášce jsme viděli některé klasické metody a přístupy pro řešení diferenciálních rovnic: stručně řečeno, rovnice obsahující
NUMERICKÉ METODY. Problematika num. řešení úloh, chyby, podmíněnost, stabilita algoritmů. Aproximace funkcí.
NUMERICKÉ METODY. Problematika num. řešení úloh, chyby, podmíněnost, stabilita algoritmů. Aproximace funkcí. RNDr. Radovan Potůček, Ph.D., K-15, FVT UO, KŠ 5B/11, Radovan.Potucek@unob.cz, tel. 443056 -----
Interpolace, ortogonální polynomy, Gaussova kvadratura
Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
Obyčejné diferenciální rovnice numericky Je dána rovnice y (x) = F (x, y(x)) s počáteční podmínkou y(x 0 ) = y 0 (dohromady se tomu říká úloha,
Obyčejné diferenciální rovnice numericky Je dána rovnice y (x) = F (x, y(x)) s počáteční podmínkou y(x 0 ) = y 0 (dohromady se tomu říká úloha, přesněji počáteční úloha) pro interval I = x 0, x 0 + T Snažíme
Aproximace funkcí. Numerické metody 6. května FJFI ČVUT v Praze
Aproximace funkcí Numerické metody 6. května 2018 FJFI ČVUT v Praze 1 Úvod Dělení Interpolace 1D Více dimenzí Minimalizace Důvody 1 Dělení Dělení - Získané data zadané data 2 Dělení - Získané data Obecně
7. Derivace složené funkce. Budeme uvažovat složenou funkci F = f(g), kde některá z jejich součástí
202-m3b2/cvic/7slf.tex 7. Derivace složené funkce. Budeme uvažovat složenou funkci F = fg, kde některá z jejich součástí může být funkcí více proměnných. Předpokládáme, že uvažujeme funkce, které mají
y = 1 x (y2 y), dy dx = 1 x (y2 y) dy y 2 = dx dy y 2 y y(y 4) = A y + B 5 = A(y 1) + By, tj. A = 1, B = 1. dy y 1
ODR - řešené příkla 20 5 ANALYTICKÉ A NUMERICKÉ METODY ŘEŠENÍ ODR A. Analtické meto řešení Vzorové příkla: 5.. Příklad. Řešte diferenciální rovnici = 2. Řešení: Přepišme danou rovnici na tvar = (2 ), což
Aproximace a interpolace
Aproximace a interpolace Aproximace dat = náhrada nearitmetické veličiny (resp. složité funkce) pomocí aritmetických veličin. Nejčastěji jde o náhradu hodnot složité funkce g(x) nebo funkce zadané pouze
Transformujte diferenciální výraz x f x + y f do polárních souřadnic r a ϕ, které jsou definovány vztahy x = r cos ϕ a y = r sin ϕ.
Ukázka 1 Necht má funkce z = f(x, y) spojité parciální derivace. Napište rovnici tečné roviny ke grafu této funkce v bodě A = [ x 0, y 0, z 0 ]. Transformujte diferenciální výraz x f x + y f y do polárních
Matematická analýza III.
3. Implicitní funkce Miroslav Hušek, Lucie Loukotová UJEP 2010 V této kapitole se seznámíme s dalším možným zadáním funkce jejím implicitním vyjádřením. Doplní tak nám již známé explicitní a parametrické
Základní vlastnosti křivek
křivka množina bodů v rovině nebo v prostoru lze chápat jako trajektorii pohybu v rovině či v prostoru nalezneme je také jako množiny bodů na ploše křivky jako řezy plochy rovinou, křivky jako průniky
Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague
1 / 21 Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague 2 / 21 Řešíme následující úlohu: differencovatelnou funkci f : R R známe jen v konečném počtu bodů x 0,
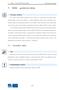
1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu
![1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu](/thumbs/102/155926571.jpg "1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu")
[M2-P1] KAPITOLA 1: Diferenciální rovnice 1. řádu diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu G(x, y, y, y,..., y (n) ) = 0 y (n) = F (x, y, y,..., y (n 1) ) Příklad 1.1:
Numerická matematika 1
Numerická matematika 1 Obsah 1 Řešení nelineárních rovnic 3 1.1 Metoda půlení intervalu....................... 3 1.2 Metoda jednoduché iterace..................... 4 1.3 Newtonova metoda..........................
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU 6.1 Křivkový integrál 1. druhu Definice 1. Množina R n se nazývá prostá regulární křivka v R n právě tehdy, když existuje vzájemně jednoznačné zobrazení
Soustavy lineárních rovnic
Soustavy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních diferenciálních rovnic y = a (x)y + a (x)y + + a n (x)y n + f (x) y = a (x)y + a (x)y + + a n (x)y n + f (x). y n = a
11. přednáška 10. prosince Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah
11. přednáška 10. prosince 2007 Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah F (x, y, y, y,..., y (n) ) = 0 mezi argumentem x funkce jedné
Diferenciální rovnice 1
Diferenciální rovnice 1 Základní pojmy Diferenciální rovnice n-tého řádu v implicitním tvaru je obecně rovnice ve tvaru,,,, = Řád diferenciální rovnice odpovídá nejvyššímu stupni derivace v rovnici použitému.
Q(y) dy = P(x) dx + C.
Cíle Naše nejbližší cíle spočívají v odpovědích na základní otázky, které si klademe v souvislosti s diferenciálními rovnicemi: 1. Má rovnice řešení? 2. Kolik je řešení a jakého jsou typu? 3. Jak se tato
Občas se používá značení f x (x 0, y 0 ), resp. f y (x 0, y 0 ). Parciální derivace f. rovnoběžného s osou y a z:
PARCIÁLNÍ DERIVACE Jak derivovat reálné funkce více proměnných aby bylo možné tyto derivace použít podobně jako derivace funkcí jedné proměnné? Jestliže se okopíruje definice z jedné proměnné dostane se
1. Obyčejné diferenciální rovnice
& 8..8 8: Josef Hekrdla obyčejné diferenciální rovnice-separace proměnných. Obyčejné diferenciální rovnice Rovnice, ve které je neznámá funkcí a v rovnici se vyskytuje spolu se svými derivacemi, se nazývá
Diferenciální rovnice a jejich aplikace. (Brkos 2011) Diferenciální rovnice a jejich aplikace 1 / 36
Diferenciální rovnice a jejich aplikace Zdeněk Kadeřábek (Brkos 2011) Diferenciální rovnice a jejich aplikace 1 / 36 Obsah 1 Co to je derivace? 2 Diferenciální rovnice 3 Systémy diferenciálních rovnic
Matematika I (KX001) Užití derivace v geometrii, ve fyzice 3. října f (x 0 ) (x x 0) Je-li f (x 0 ) = 0, tečna: x = 3, normála: y = 0
Rovnice tečny a normály Geometrický význam derivace funkce f(x) v bodě x 0 : f (x 0 ) = k t k t je směrnice tečny v bodě [x 0, y 0 = f(x 0 )] Tečna je přímka t : y = k t x + q, tj y = f (x 0 ) x + q; pokud
5.3. Implicitní funkce a její derivace
Výklad Podívejme se na následující problém. Uvažujme množinu M bodů [x,y] R 2, které splňují rovnici F(x, y) = 0, M = {[x,y] D F F(x,y) = 0}, kde z = F(x,y) je nějaká funkce dvou proměnných. Je-li F(x,y)
8. Okrajový problém pro LODR2
8. Okrajový problém pro LODR2 A. Základní poznatky o soustavách ODR1 V kapitole 6 jsme zavedli pojem lineární diferenciální rovnice n-tého řádu, která je pro n = 2 tvaru A 2 (x)y + A 1 (x)y + A 0 (x)y
Budeme hledat řešení y(x) okrajové úlohy pro diferenciální rovnici druhého řádu v samoadjungovaném tvaru na intervalu a, b : 2 ) y i p i+ 1
ODR - okrajová úloha Teorie (velmi stručný výběr z přednášek) Okrajová úloha 2. řádu Budeme hledat řešení y(x) okrajové úlohy pro diferenciální rovnici druhého řádu v samoadjungovaném tvaru na intervalu
VI. Derivace složené funkce.
VI. Derivace složené funkce. 17. Parciální derivace složené funkce Budeme uvažovat složenou funkci F = f(g, kde některá z jejich součástí může být funkcí více proměnných. Předpokládáme, že uvažujeme funkce,
ANALÝZA STIFF SOUSTAV DIFERENCIÁLNÍCH ROVNIC
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA INFORMAČNÍCH TECHNOLOGIÍ ÚSTAV INTELIGENTNÍCH SYSTÉMŮ FACULTY OF INFORMATION TECHNOLOGY DEPARTMENT OF INTELLIGENT SYSTEMS ANALÝZA STIFF
Integrace funkcí více proměnných, numerické metody
Matematika III 6. přednáška Integrace funkcí více proměnných, numerické metody Michal Bulant Masarykova univerzita Fakulta informatiky 27. 10. 2010 Obsah přednášky 1 Literatura 2 Integrální počet více
Aplikovaná numerická matematika
Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Řešení nelineárních rovnic
Řešení nelineárních rovnic Metody sečen (sekantová a regula falsi) Máme dva body x 1 a x mezi nimiž se nachází kořen Nový bod x 3 volíme v průsečíku spojnice bodů x 1, f x 1 a x, f x (sečny) s osou x ERRBISPAS
Tento dokument obsahuje zadání pro semestrální programy z PAA. Vypracování. vypracovanou úlohu podle níže uvedených zadání. To mimo jiné znamená, že
Kapitola Zadání Tento dokument obsahuje zadání pro semestrální programy z PAA. Vypracování alespoň jedné úlohy je nutnou podmínkou pro úspěšné složení zkoušky resp. získaní (klasifikovaného) zápočtu (viz.
Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
Jana Dannhoferová Ústav informatiky, PEF MZLU
Počítačová grafika Křivky Jana Dannhoferová (jana.dannhoferova@mendelu.cz) Ústav informatiky, PEF MZLU Základní vlastnosti křivek křivka soustava parametrů nějaké rovnice, která je posléze generativně
UNIVERZITA PARDUBICE. 4.4 Aproximace křivek a vyhlazování křivek
UNIVERZITA PARDUBICE Licenční Studium Archimedes Statistické zpracování dat a informatika 4.4 Aproximace křivek a vyhlazování křivek Mgr. Jana Kubátová Endokrinologický ústav V Praze, leden 2012 Obsah
8.4. Shrnutí ke kapitolám 7 a 8
8.4. Shrnutí ke kapitolám 7 a 8 Shrnutí lekce Úvodní 7. kapitola přinesla informace o druzích řešení diferenciálních rovnic prvního řádu a stručné teoretické poznatky o podmínkách existence a jednoznačnosti
teorie elektronických obvodů Jiří Petržela řešení nelineárních obvodů
Jiří Petržela vlastnosti lineárních obvodů přechodný děj obvodu je vždy tlumený, trvá omezenou dobu a je dán jeho vlastnostmi, počátečními podmínkami a buzením ustálený stav nezávisí na počátečních podmínkách
12. Křivkové integrály
12 Křivkové integrály Definice 121 Jednoduchou po částech hladkou křivkou v prostoru R n rozumíme množinu bodů [x 1,, x n ], které jsou dány parametrickými rovnicemi x 1 = ϕ 1 t), x 2 = ϕ 2 t), x n = ϕ
Interpolace Uvažujme třídu funkcí jedné proměnné ψ(x; a 0,..., a n ), kde a 0,..., a n jsou parametry, které popisují jednotlivé funkce této třídy. Mějme dány body x 0, x 1,..., x n, x i x k, i, k = 0,
Elementární křivky a plochy
Příloha A Elementární křivky a plochy A.1 Analytický popis geometrických objektů Geometrické vlastnosti, které jsme dosud studovali, se týkaly především základních geometrických objektů bodů, přímek, rovin
4.1 Řešení základních typů diferenciálních rovnic 1.řádu
4. Řešení základních tpů diferenciálních rovnic.řádu 4..4 Určete řešení z() Cauchov úloh pro rovnici + = 0 vhovující počáteční podmínce z =. Po separaci proměnných v rovnici dostaneme rovnici = d a po
s velmi malými čísly nevýhodou velký počet operací, proto je mnohdy postačující částečný výběr
1. Úvod 1.1. druhy chyb: ch. matematického modelu rozdíl mezi idealizovaným a reálným problémem ch. numerické metody výsledkem nepřesné řešení ch. zaokrouhlovací vystupují současaně 1.. chyba absolutní
Řešení 1D vedení tepla metodou sítí a metodou
ENumerická analýza transportních procesů - NTP2 Přednáška č. 9 Řešení 1D vedení tepla metodou sítí a metodou konečných objemů Metoda sítí (metoda konečných diferencí - MKD) Metoda sítí Základní myšlenka
Doc. RNDr. Libor Čermák, CSc. Numerické metody. Ústav matematiky FSI VUT v Brně
UČEBNÍ TEXTY VYSOKÝCH ŠKOL Vysoké učení technické v Brně Fakulta strojního inženýrství Doc. RNDr. Libor Čermák, CSc. Numerické metody pro řešení diferenciálních rovnic Ústav matematiky FSI VUT v Brně Obsah
Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
Derivace funkce Otázky
funkce je jedním z hlavních nástrojů matematické analýzy. V příští části ukážeme, jak mnoho různorodých aplikací derivace má. Geometricky lze derivaci funkce v nějakém bodě chápat jako směrnici tečny grafu
Diferenciální počet 1 1. f(x) = ln arcsin 1 + x 1 x. 1 x 1 a x 1 0. f(x) = (cos x) cosh x + 3x. x 0 je derivace funkce f(x) v bodě x0.
Nalezněte definiční obor funkce Diferenciální počet f = ln arcsin + Definiční obor funkce f je určen vztahy Z těchto nerovností plyne < + ln arcsin + je tedy D f =, Určete definiční obor funkce arcsin
I. Diferenciální rovnice. 3. Rovnici y = x+y+1. převeďte vhodnou transformací na rovnici homogenní (vzniklou
Typy příkladů pro I. část písemky ke zkoušce z MA II I. Diferenciální rovnice. 1. Určete obecné řešení rovnice y = y sin x.. Určete řešení rovnice y = y x splňující počáteční podmínku y(1) = 0. 3. Rovnici
Numerické metody a programování. Lekce 7
Numerické metody a programování Lekce 7 Řešení nelineárních rovnic hledáme řešení x problému f x = 0 strategie: odhad řešení iterační proces postupného zpřesňování řešení výpočet skončen pokud je splněno
Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
22. 2. 2016 Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
Učební texty k státní bakalářské zkoušce Matematika Diferenciální rovnice. študenti MFF 15. augusta 2008
Učební texty k státní bakalářské zkoušce Matematika Diferenciální rovnice študenti MFF 15. augusta 2008 1 7 Diferenciální rovnice Požadavky Soustavy lineárních diferenciálních rovnic prvního řádu lineární
Interpolace, aproximace
11 Interpolace, aproximace Metoda nejmenších čtverců 11.1 Interpolace Mějme body [x i,y i ], i =0, 1,...,n 1. Cílem interpolace je najít funkci f(x), jejíž graf prochází všemi těmito body, tj. f(x i )=y
Derivace funkce DERIVACE A SPOJITOST DERIVACE A KONSTRUKCE FUNKCÍ. Aritmetické operace
Derivace funkce Derivace je jedním z hlavních nástrojů matematické analýzy. V příští části ukážeme, jak mnoho různorodých aplikací derivace má. Geometricky lze derivaci funkce v nějakém bodě chápat jako
Diferenciální rovnice 3
Diferenciální rovnice 3 Lineární diferenciální rovnice n-tého řádu Lineární diferenciální rovnice (dále jen LDR) n-tého řádu je rovnice tvaru + + + + = kde = je hledaná funkce, pravá strana a koeficienty
7. Aplikace derivace
7. Aplikace derivace Verze 20. července 2017 Derivace funkce se využívá při řešení úloh technické praxe i teorie. Uvedeme několik z nich: vyčíslení hodnot funkce, výpočet limity, vyšetřování průběhu funkce
pouze u některých typů rovnic a v tomto textu se jím nebudeme až na
Matematika II 7.1. Zavedení diferenciálních rovnic Definice 7.1.1. Rovnice tvaru F(y (n), y (n 1),, y, y, x) = 0 se nazývá diferenciální rovnice n-tého řádu pro funkci y = y(x). Speciálně je F(y, y, x)
Interpolace Lagrangeovy polynomy. 29. října 2012
Interpolace Lagrangeovy polynomy Michal Čihák 29. října 2012 Problematika interpolace V praxi máme často k dispozici údaje z různých měření tzv. data. Data mohou mít například podobu n uspořádaných dvojic
Hledání kořenů rovnic jedné reálné proměnné metoda půlení intervalů Michal Čihák 23. října 2012
Hledání kořenů rovnic jedné reálné proměnné metoda půlení intervalů Michal Čihák 23. října 2012 Problém hledání kořenů rovnice f(x) = 0 jeden ze základních problémů numerické matematiky zároveň i jeden
Kapitola 12: Soustavy diferenciálních rovnic 1. řádu
Kapitola 12: Soustavy diferenciálních rovnic 1. řádu Základní pojmy Definice: Rovnice tvaru = f(t, x, y) = g(t, x, y), t I nazýváme soustavou dvou diferenciálních rovnic 1. řádu. Řešením soustavy rozumíme
INTERPOLAČNÍ POLYNOM. F (x)... hledaná funkce (polynom nebo funkce vytvořená z polynomů), pro kterou platí
8 Řešení Lagrangeovy a Hermiteovy úlohy interpolace Kateřina Konečná/1 INTERPOLAČNÍ POLYNOM aproximace zadaných hodnot nebo hledané funkce f funkcí F (x) (polynomem) F musí být k f co nejblíže značení:
Řešení "stiff soustav obyčejných diferenciálních rovnic
Řešení "stiff soustav obyčejných diferenciálních rovnic Jiří Škvára Katedra fyziky, Přírodovědecká fakulta Univerzity J.E. Purkyně v Ústí n.l.. ročník, počítačové metody ve vědě a technice Abstrakt Seminární
VYBRANÉ PARTIE Z NUMERICKÉ MATEMATIKY
VYBRANÉ PARTIE Z NUMERICKÉ MATEMATIKY Jan Krejčí 31. srpna 2006 jkrejci@physics.ujep.cz http://physics.ujep.cz/~jkrejci Obsah 1 Přímé metody řešení soustav lineárních rovnic 3 1.1 Gaussova eliminace...............................
LINEÁRNÍ ROVNICE S ABSOLUTNÍ HODNOTOU
LINEÁRNÍ ROVNICE S ABSOLUTNÍ HODNOTOU LINEÁRNÍ ROVNICE S ABSOLUTNÍ HODNOTOU je lineární rovnice, ve které se vyskytuje jeden nebo více výrazů v absolutní hodnotě. ABSOLUTNÍ HODNOTA x reálného čísla x je
Nyní využijeme slovník Laplaceovy transformace pro derivaci a přímé hodnoty a dostaneme běžnou algebraickou rovnici. ! 2 "
ŘEŠENÉ PŘÍKLADY Z MB ČÁST Příklad Nalezněte pomocí Laplaceovy transformace řešení dané Cauchyho úlohy lineární diferenciální rovnice prvního řádu s konstantními koeficienty v intervalu 0,, které vyhovuje
9. přednáška 26. listopadu f(a)h < 0 a pro h (0, δ) máme f(a 1 + h, a 2,..., a m ) f(a) > 1 2 x 1
9 přednáška 6 listopadu 007 Věta 11 Nechť f C U, kde U R m je otevřená množina, a a U je bod Pokud fa 0, nemá f v a ani neostrý lokální extrém Pokud fa = 0 a H f a je pozitivně negativně definitní, potom
Extrémy funkce dvou proměnných
Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
Matematika 5 FSV UK, ZS Miroslav Zelený
Matematika 5 FSV UK, ZS 2018-19 Miroslav Zelený 1. Stabilita řešení soustav diferenciálních rovnic 2. Úvod do variačního počtu 3. Globální extrémy 4. Teorie optimálního řízení 5. Různé 1. Stabilita řešení
Komplexní analýza. Laplaceova transformace. Martin Bohata. Katedra matematiky FEL ČVUT v Praze
Komplexní analýza Laplaceova transformace Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Laplaceova transformace 1 / 18 Definice Definice Laplaceovou
Nalezněte obecné řešení diferenciální rovnice (pomocí separace proměnných) a řešení Cauchyho úlohy: =, 0 = 1 = 1. ln = +,
Příklad Nalezněte obecné řešení diferenciální rovnice (pomocí separace proměnných) a řešení Cauchyho úlohy: a) =, 0= b) =, = c) =2, = d) =2, 0= e) =, 0= f) 2 =0, = g) + =0, h) =, = 2 = i) =, 0= j) sin+cos=0,
Diferenˇcní rovnice Diferenciální rovnice Matematika IV Matematika IV Program
Program Diferenční rovnice Program Diferenční rovnice Diferenciální rovnice Program Frisch a Samuelson: Systém je dynamický, jestliže jeho chování v čase je určeno funkcionální rovnicí, jejíž neznámé závisí