KONSTRUKČNÍ NÁVRH VÝUKOVÝCH MODELŮ HYDRAULICKÉHO OKRUHU LABORATOŘE CONSTRUCTION DESIGN OF INSTRUCTIONAL MODELS AT THE HYDRAULIC LABORATORY CIRCUIT
|
|
|
- Ondřej Macháček
- před 8 lety
- Počet zobrazení:
Transkript
1 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES KONSTRUKČNÍ NÁVRH VÝUKOVÝCH MODELŮ HYDRAULICKÉHO OKRUHU LABORATOŘE CONSTRUCTION DESIGN OF INSTRUCTIONAL MODELS AT THE HYDRAULIC LABORATORY CIRCUIT BAKALÁŘSKÁ PRÁCE BACHELOR'S THESIS AUTOR PRÁCE AUTHOR VEDOUCÍ PRÁCE SUPERVISOR MICHAL HAVLÁT Ing. MICHAL ŽOUŽELA, Ph.D. BRNO 2013
2 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ Studijní program Typ studijního programu Studijní obor Pracoviště B3607 Stavební inţenýrství Bakalářský studijní program s prezenční formou studia 3647R015 Vodní hospodářství a vodní stavby Ústav vodních staveb ZADÁNÍ BAKALÁŘSKÉ PRÁCE Student Michal Havlát Název Vedoucí bakalářské práce Konstrukční návrh výukových modelů hydraulického okruhu laboratoře Ing. Michal Ţouţela, Ph.D. Datum zadání bakalářské práce Datum odevzdání bakalářské práce V Brně dne prof. Ing. Jan Šulc, CSc. Vedoucí ústavu prof. Ing. Rostislav Drochytka, CSc. Děkan Fakulty stavební VUT 1
3 Podklady a literatura [1]Boor, B.,Kunštátský, J.,Patočka, C. Hydraulika pro vodohospodářské stavby, 1. vydání, SNTL Praha, 1968 [2] Ţouţela, M. Výstavba a provoz nové laboratoře Ústavu vodních staveb. Sborník příspěvků ze 3. Vodohospodářské konference 2003, Práce a studie Ústavu vodních staveb FAST VUT v Brně, 2003, str , ISBN [3] Ţouţela, M.: Návrh hydraulického okruhu laboratoře VOŠ stavební a SŠ stavební Vysoké Mýto. Výzkumná zpráva, LVV FAST VUT v Brně, 2011 Zásady pro vypracování Vyšší odborná škola stavební a Střední škola stavební ve Vysokém Mýtě bude v budoucnu budovat hydraulický laboratorní okruh, který bude slouţit především pro výuku studentů hydrauliky a hydrologie. Součástí laboratoře bude řada zmenšených hydraulických modelů. Ty budou simulovat především úlohy hydrauliky s prouděním o volné hladině či prouděním tlakovým. Konkrétně se bude jednat o simulaci přepadu, výtoku pod stavidlem, měření průtoku ţlabovými objekty, proudění propustkem, simulaci ztrát mechanické energie při protékání různými singularitami. V rámci zpracování bakalářské práce posluchač zhotoví projektovou dokumentaci pro všechny navrhované hydraulické modely. Předepsané přílohy... Ing. Michal Ţouţela, Ph.D. Vedoucí bakalářské práce 2
4 ABSTRAKT Vyšší odborná škola stavební a Střední škola stavební ve Vysokém Mýtě bude v budoucnu budovat hydraulický laboratorní okruh, který bude slouţit především pro výuku studentů hydrauliky a hydrologie. Součástí laboratoře bude řada zmenšených hydraulických modelů. Ty budou simulovat především úlohy hydrauliky s prouděním o volné hladině či prouděním tlakovým. Konkrétně se bude jednat o simulaci přepadu, měření průtoku ţlabovými objekty, proudění propustkem, simulaci ztrát mechanické energie třením po délce potrubí a při protékání různými singularitami. Předkládaná práce je zaměřena na hydrauliku simulovaných jevů, zhotovení projektové dokumentace a hydrotechnických výpočtů všech navrhovaných hydraulických modelů. Součástí dokumentace jsou pomocné prvky - měřicí vozík a obsluţné lávky. Práce obsahuje textovou teoretickou část, technickou zprávu navrţených objektů, hydrotechnické výpočty a výkresovou dokumentaci. KLÍČOVÁ SLOVA Ostrohranný přeliv, propustek, měrný ţlab, proudnicová přelivná plocha, ztráta třením po délce, místní ztráty ABSTRACT The Higher vocational school and The Secondary School of civil engineering in Vysoké Mýto is going to build a hydraulic laboratory circuit which will be used especially for teaching students of hydraulics and hydrology. Laboratory will include several scaled down models which simulate especially hydraulic tasks with open-channel flow or flow in pipes. It specifically means simulation of spillway, flow-measuring flumes, culvert flow and mechanic energy loss simulation per length of pipe and at singularity flow. This thesis is focused on hydraulics of the simulated tasks, project documentation and hydraulic calculations preparing for all designed models. The documentation also includes laboratory equipment - instrument 3
5 carrier and service stairs. This thesis includes theoretical text part, technical report, hydraulic calculations and drawing part. KEYWORDS Plate weirs, culver, flow-measuring flume, ogee-crested weir, energy loss per length of pipe, local energy loss 4
6 BIBLIOGRAFICKÁ CITACE VŠKP HAVLÁT, Michal. Konstrukční návrh výukových modelů hydraulického okruhu laboratoře. Brno, s., 51 s. příl. Bakalářská práce. Vysoké učení technické v Brně, Fakulta stavební, Ústav vodních staveb. Vedoucí práce Ing. Michal Ţouţela, Ph.D.. 5
7 Prohlášení: Prohlašuji, ţe jsem bakalářskou práci zpracoval(a) samostatně a ţe jsem uvedl(a) všechny pouţité informační zdroje. V Brně dne podpis autora Michal Havlát 6
8 PODĚKOVÁNÍ Tímto bych chtěl poděkovat svému vedoucímu bakalářské práce, Ing. Michalu Ţouţelovi, Ph.D. za zapůjčení vhodné literatury, trpělivost a pomoc při tvorbě a úpravě celé práce a čas strávený konzultacemi. Také bych chtěl poděkovat svému bratrovi Pavlovi Havlátovi za podporu, jeho připomínky a poznatky z oboru strojírenství. 7
9 SEZNAM PŘÍLOH 1. PRŮVODNÍ ZPRÁVA 2. HYDRAULIKA NAVRŢENÝCH MODELŮ A OBJEKTŮ 3. TECHNICKÁ ZPRÁVA NAVRŢENÉHO KONSTRUKČNÍHO ŘEŠENÍ 4. HYDROTECHNICKÉ VÝPOČTY 4.1. Výpočet Q/h charakteristiky měrného ostrohranného přelivu Ostrohranný přeliv s trojúhelníkovým výřezem Ostrohranný přeliv s trojúhelníkovým výřezem Ostrohranný přeliv s trojúhelníkovým výřezem Ostrohranný přeliv s obdélníkovým výřezem šířky 0,2 m Ostrohranný přeliv s lichoběţníkovým výřezem Q/h charakteristiky všech navrţených přelivů 4.2. Výpočet Q/h charakteristiky Scimemiho přelivné plochy 4.3. Výpočet Q/h charakteristiky Venturiho ţlabu 4.4. Výpočet proudění propustkem Proudění s volnou hladinou po celé délce bez ovlivnění dolní vodou Proudění s volnou hladinou a zahlceným vtokem bez ovlivnění dolní vodou Tlakové proudění propustkem 4.5. Hydrotechnické výpočty ztrát mechanické energie místních a třením po délce ve výukovém okruhu 5. VÝKRESOVÁ DOKUMENTACE 5.1. Ostrohranné měrné přelivy 5.2. Upevňovací rám měrných přelivů 8
10 5.3. Model propustku 5.4. Scimemiho přelivná plocha 5.5. Scimemiho přelivná plocha ţebro 5.6. Venturiho měrný ţlab 5.7. Měřicí vozík 5.8. Výukový okruh pro měření ztrát 5.9. Obsluţná lávka 6. SEZNAM POUŢITÉHO MATERIÁLU A PRVKŮ 9
11 SEZNAM POUŢITÝCH ZKRATEK A SYMBOLŮ Symbol Jednotka Význam symbolu Ce - součinitel přepadu určený z normy ČSN ISO 1438 h m výška, přepadová výška, hloubka vody g m/s 2 tíhové zrychlení, v našich podmínkách g = 9,81 m/s 2 m - součinitel přepadu p m převýšení přelivné hrany nad dnem měrného ţlabu S m 2 plocha, plocha průřezu C - součinitel přepadu (vzorec SIA) h n m návrhová přepadová výška σ z - součinitel zatopení σ s - součinitel šikmosti b 0 m účinná šířka přelivu h 0 m energetická přepadová výška; převýšení vtoku propustku nad dnem koryta (kap ) v m/s rychlost φ - rychlostní součinitel Venturiho ţlabu; rychlostní součinitel propustku R m hydraulický poloměr i 0 - sklon dna i k - kritický sklon h k m kritická hloubka D m průměr potrubí Q l/s; m 3 /s průtok 10
12 h c m sníţená hloubka vody za vtokem do propustku S c m 2 průtočná plocha v profilu se sníţenou hloubkou χ - součinitel výškového zúţení E m energetická výška Δ m tlaková výška na výtoku z propustku; absolutní drsnost ξ - součinitel místní ztráty λ - součinitel tření (odporový součinitel) h z m ztrátová výška Re - Reynoldsovo kritérium υ m 2 /s kinematická viskozita vody h m m místní ztrátová výška středový úhel kolen r s m poloměr zakřivení BSI SIA PMMA MVŢ DIN PA PP PVC British Standards Institution vzorec pro výpočet průtoku přes měrný ostrohranný přeliv s trojúhelníkovým výřezem 90, 53 8, 28 4 Societé suisse des ingénieurs et architectes vzorec pro výpočet průtoku přes měrný ostrohranný přeliv s obdélníkovým výřezem polymethylmethakrylát (akrylát) materiál propustku měrný Venturiho ţlab Deutsche Industrie Norm německá národní norma polyamid polypropylen polyvinilchlorid 11
13 SEZNAM POUŢITÝCH ZDROJŮ [1] BOOR, B., KUNŠTÁTSKÝ, J., PATOČKA, C. Hydraulika pro vodohospodářské stavby. 1. vydání, SNTL Praha, 1968 [2] ŢOUŢELA, M. Výstavba a provoz nové laboratoře Ústavu vodních staveb. Sborník příspěvků z 3. Vodohospodářské konference 2003, Práce a studie Ústavu vodních staveb FAST VUT v Brně, 2003, str , ISBN [3] ŢOUŢELA, M. Návrh hydraulického okruhu laboratoře VOŠ stavební a SŠ stavební Vysoké Mýto. Výzkumná zpráva, LVV FAST VUT v Brně, 2011 [4] ČSN ISO Hydrometrie Měření průtoku vody v otevřených korytech pomocí tenkostěnných přelivů. 2. vyd. Praha: Český normalizační institut 2008 [5] ČSN ISO 9826 Měření průtoku kapalin v otevřených korytech. Parshallovy žlaby a žlaby typu Saniiri. Praha: Český normalizační institut 1994 [6] ŠULC J. Doporučení k realizaci systémů pro stanovení průtoku využívajících vestavbových žlabů typu Venturi (hydraulická část). Vysoké učení technické v Brně, Fakulta stavební, Ústav vodních staveb, Laboratoř vodohospodářského výzkumu. Brno [7] KUNŠTÁTSKÝ J., PATOČKA C. Základy hydrauliky a hydrologie pro inženýrské konstrukce a dopravní stavby, 2. vydání, SNTL Praha, 1971 [8] SKALIČKA J., HOŘENÍ P. Ustálené tlakové proudění v potrubí s oblouky. 1. vydání, Výzkumný ústav vodohospodářský, Státní zemědělské nakladatelství, Praha 1985 [9] JANDORA, Jan; ŠULC Jan. Hydraulika: modul 01. Vyd. 1. Brno: Akademické nakladatelství CERM, 2006, 178 s. ISBN [10] HAMOUZ, Vladimír. Strojně technologický návrh hydraulického okruhu laboratoře Vyšší odborné školy stavební ve Vysokém Mýtě. Brno, s., 134 s. příl. Diplomová práce. Vysoké učení technické v Brně, Fakulta stavební, Ústav vodních staveb. Vedoucí práce Ing. Michal Ţouţela, Ph.D. [11] [12] firma OSMA 12
14 [13] [14] [15] [16] [17] [18] [19] 13
15 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES PŘÍLOHA Č. 1 PRŮVODNÍ ZPRÁVA BAKALÁŘSKÁ PRÁCE BACHELOR'S THESIS AUTOR PRÁCE AUTHOR VEDOUCÍ PRÁCE SUPERVISOR MICHAL HAVLÁT Ing. MICHAL ŽOUŽELA, Ph.D. BRNO 2013
16 1. PRŮVODNÍ ZPRÁVA OBSAH 1. Úvod Současný stav Popis navrhovaného hydraulického okruhu [10] Popis navrhovaných modelů a objektů Závěr
17 1. ÚVOD Vyšší odborná škola stavební a Střední škola stavební ve Vysokém Mýtě bude v budoucnu budovat hydraulický laboratorní okruh, který bude slouţit především pro výuku studentů hydrauliky a hydrologie. Součástí laboratoře bude řada zmenšených hydraulických modelů, které budou simulovat především úlohy hydrauliky s prouděním o volné hladině a proudění vody propustkem. Konkrétně se bude jednat o simulaci přepadu přes ostrohranný a proudnicový přeliv, zkoumání různých typů proudění kruhovým propustkem a měření průtoku ţlabovými objekty. Další úlohou práce je vytvoření výukového okruhu pro simulaci ztrát mechanické energie třením po délce potrubí a při protékání různými singularitami. Posledním cílem práce je návrh příslušenství k navrţenému měrnému ţlabu [10], konkrétně navrţení měřicího vozíku umoţňujícího pohyb měřicích přístrojů v podélném i příčném směru ţlabu a vytvoření obsluţných lávek pro lepší dostupnost a měření uvnitř měrného ţlabu. Součástí práce je výkresová dokumentace, hydrotechnické výpočty, jejich teoretický základ a technická zpráva ke všem navrţeným modelům a objektům. Bakalářská práce je zaměřena na vytvoření projektové dokumentace v dostatečném rozsahu pro výrobu a instalaci zmíněných prvků. V závěru práce je uveden seznam pouţitého materiálu a prvků. Základním podkladem pro návrh modelů a objektů je Strojně technologický návrh hydraulického okruhu laboratoře Vyšší odborné školy stavební ve Vysokém Mýtě [10] od Ing. Vladimíra Hamouze. 2
18 2. SOUČASNÝ STAV Současný stav místnosti budoucí laboratoře je detailně popsán v práci [10]. Prostor budoucí laboratoře s půdorysnými rozměry (9,43 x 2,45) m a přibliţnou plochou místnosti 23,1 m 2 se nachází v 1. NP budovy VOŠ stavební ve Vysokém Mýtě. Světlá výška místnosti je 3,19 m. Přístup z chodby je zajištěn vstupními dveřmi o šířce 900 mm. Na pravé straně (při pohledu ze vstupních dveří) je umístěna trojice oken (1500 x 1500) mm. Podlaha je tvořena čtvercovou dlaţbou. 3
19 3. POPIS NAVRHOVANÉHO HYDRAULICKÉHO OKRUHU [10] Z důvodu návaznosti této práce na projekt [10] si nyní uvedeme navrhovaný hydraulický okruh. V místech u vstupních dveří bude vybudována akumulační nádrţ s maximálním objemem 4,4 m 3, která bude zároveň slouţit jako čerpací jímka pro dvojici ponorných odstředivých čerpadel Flygt. V rohu místnosti u vstupních dveří bude umístěn elektro rozvaděč s dotykovým displejem pro snadné ovládání funkcí okruhu. Hydraulický okruh bude tvořen nerezovým potrubím DN50 a DN110, napájejícím tři měrné tratě s označením MŢ měrný ţlab, V výuka, R rezerva. Měrný ţlab a rezervní trať bude primárně napájen potrubím DN100, výuková část okruhu pomocí DN50. Součástí okruhu budou také nezbytné armatury, zpětné a uzavírací klapky ovládané servopohony a indukční průtokoměry. Největším navrţeným objektem je hydraulický měrný ţlab. Celková délka ţlabu bude 6,45 m, z toho 5,65 tvoří měřicí část. Konstrukce ţlabu bude vytvořena z ocelových nosných a opěrných částí, skleněných stěn tloušťky 12 mm a nerezového dna tl. 2 mm. Rozměry průtočného profilu mezi stěnami budou (š x v) (366 x 400) mm. Na vrchní části ocelové konstrukce bude po celé její délce upevněna plochá ocelová tyč (40 x 5) mm slouţící jako kolejnice pro měřicí vozík. Rozchod kolejnic bude 432 mm. Druhou měrnou trať tvoří rezerva R napájená nerezovým potrubím DN110, která můţe být pouţita pro připojení různých modelů (např. jezová konstrukce, přehrada, atd.) umístěných na podlaze laboratoře. Poslední měrná trať zajišťuje přísun vody do výukového okruhu simulující ztráty mechanické energie místní a třením po délce, navrhovaného v této práci. Výukový okruh je napájen nerezovým potrubím DN50, opatřeného na konci nerezové části kulovým uzávěrem a nipplem 2 s vnějším závitem. Základní prvek celého okruhu bude tvořit dvojice ponorných odstředivých čerpadel Flygt, umístěných v čerpací jímce. Obě čerpadla budou schopna dodat aţ 36 l/s v závislosti na napájené trati. Čerpadla jsou označena ČM1 a ČM2. Regulace čerpaného mnoţství bude probíhat pomocí změny frekvence otáček rotoru čerpadla. Podrobnější informace o konstrukci ţlabu, měrných tratí, strojním vybavením a řízení laboratoře je uvedeno v [10]. 4
20 4. POPIS NAVRHOVANÝCH MODELŮ A OBJEKTŮ S ohledem na rozměry měrného hydraulického ţlabu, způsobu jeho napájení vodou, připojení výukové trati (příloha 1, kap. 3; [10]) a rozměry prostoru laboratoře (příloha 1, kap. 2; [10]) jsou navrţeny následující modely a objekty: 1) měrné ostrohranné přelivy a jejich uchycení v měrném ţlabu (nerezové provedení), 2) model propustku (akrylát PMMA), 3) Scimemiho přelivná plocha (nerezové provedení), 4) Venturiho měrný ţlab (nerezové provedení), 5) měřicí vozík, 6) výukový okruh pro simulaci ztrát mechanické energie (PP a PVC potrubí), 7) obsluţné lávky. Hydraulika simulovaných jevů je podrobně popsána v příloze č. 2 Hydraulika navrţených modelů a objektů, konstrukční řešení v příloze č. 3 Technická zpráva navrţeného konstrukčního řešení. 5
21 5. ZÁVĚR Při navrhování výukových modelů simulujících různé úlohy hydrauliky s prouděním o volné hladině či tlakovým prouděním je důleţité zohlednit mnoho hydraulických, ekonomických, technologických a provozních nároků i poţadavků. Konstrukce objektů by měly být s ohledem na jejich výrobu snadno proveditelné, avšak jednoduchost řešení se nesmí projevit v neţádoucích hydraulických parametrech nebo naměřených výsledcích. Pro potřeby výuky v laboratoři je významným argumentem ovlivňujícím volbu finální řešení projektu názornost hydraulických jevů probíhajících na modelech, snadný přístup k jednotlivým objektům a jednoduchost měřicí a zobrazovací technologie, která se odráţí v moţném zapojení studentů do výuky a měření. Před samotnou tvorbou konstrukčního řešení a projektové dokumentace je nutné pečlivé seznámení se simulovanými hydraulickými jevy, nároky na měření sledovaných veličin a současným (resp. projektovaným) uspořádáním laboratoře a měrného hydraulického ţlabu. Při návrhu je vhodné vycházet z dokumentací jiţ dříve realizovaných projektů, provedených měření, studií a poznatků různých autorů, coţ zamezí vzniku konstrukčních chyb, které byly zjištěny při dlouhodobém provozu hydraulických laboratoří a jednotlivých modelů. Nezanedbatelný vliv na pouţití různých materiálů, provedení spojů a uchycení objektů má poţadovaná ţivotnost a provozní nároky s ohledem na údrţbu, potaţmo výměnu některých částí. Snahou při tvorbě této práce bylo vytvoření řešení zohledňující v maximální moţné míře všechny zmíněné poţadavky. Výstupem bakalářské práce je kompletní projektová dokumentace v prováděcím stupni pro měrné ostrohranné přelivy, jejich upevnění v měrném hydraulickém ţlabu, model propustku, nerezové provedení Scimemiho přelivné plochy, měrný Venturiho ţlab, měřicí vozík, výukovou trať simulující ztráty mechanické energie a trojici obsluţných lávek. Součástí práce je hydraulika jednotlivých simulovaných jevů, hydrotechnické výpočty pro navrţené řešení modelů, technická zpráva a výkresová dokumentace umoţňující snadnou výrobu objektů. 6
22 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES PŘÍLOHA Č. 2 HYDRAULIKA NAVRŽENÝCH MODELŮ A OBJEKTŮ BAKALÁŘSKÁ PRÁCE BACHELOR'S THESIS AUTOR PRÁCE AUTHOR VEDOUCÍ PRÁCE SUPERVISOR MICHAL HAVLÁT Ing. MICHAL ŽOUŽELA, Ph.D. BRNO 2013
23 2. HYDRAULIKA NAVRŽENÝCH MODELŮ A OBJEKTŮ OBSAH 1. Úvod Měrné ostrohranné přelivy Ostrohranný přeliv s trojúhelníkovým výřezem Ostrohranný přeliv s trojúhelníkovým výřezem Ostrohranný přeliv s trojúhelníkovým výřezem Ostrohranný přeliv s obdélníkovým výřezem Ostrohranný přeliv s lichoběžníkovým výřezem Scimemiho přelivná plocha Venturiho žlab Kruhový propustek Kruhové propustky s volnou hladinou po celé jejich délce bez ovlivnění dolní vodou Kruhové propustky se zatopeným vtokem bez ovlivnění dolní vodou Kruhové propustky s tlakovým prouděním po celé jejich délce Určování ztrát mechanické energie místních a třením po délce ve výukovém okruhu Ztráty třením po délce Ztráty místní Náhlé rozšíření průřezu Náhlé zúžení průřezu Kulový uzávěr Koleno Podmínky pro měření tlakových ztrát
24 1. ÚVOD V následujícím textu bude vysvětlena hydraulika všech navržených modelů a objektů, konkrétně přepad přes ostrohranné přelivy a Scimemiho přelivnou plochu, různé režimy proudění v propustku, měření průtoku pomocí Venturiho měrného žlabu a simulace ztrát mechanické energie místních a třením po délce ve výukovém okruhu. Uvedené vztahy a definice vycházejí z literatury [1], [4], [6], [7], [8] a [9]. 2
25 2. MĚRNÉ OSTROHRANNÉ PŘELIVY Přelivy můžeme obecně dělit dle tvaru a tloušťky přelivné hrany na čtyři základní typy: a) ostrohranné přelivy; b) jezové nebo přehradní přelivy; c) přelivy se širokou korunou; d) zvláštní typy přelivů. Ostrohranné přelivy se oproti ostatním vyznačují malou tloušťkou přelivné stěny. Přepad přes ostrou hranu nastává při splnění podmínky: t 0,66 h, kde t h tloušťka přelivné stěny, výška přepadového paprsku. Přepadová výška vyjadřuje vzdálenost hladiny od nejnižšího bodu přelivné hrany. Jednoduchost a geometrická jednoznačnost těchto přelivů se používá pro určení hodnoty průtoku pomocí měření úrovně hladiny u měrných ostrohranných přelivů. Pro tento způsob využití konstrukce je nutné splnit několik podmínek, které jsou uvedeny v normě [4]ČSN ISO Ostrohranné přelivy musí být umístěny v poloze svislé a kolmé ke stěnám přítokového koryta. Spojení přelivu s korytem musí být vodotěsné a natolik pevné, aby odolalo maximálnímu průtoku bez deformace, porušení či průsaku netěsnostmi. Pro měření průtoku je možné použít pouze dokonalý přepad, to znamená, že nesmí docházet k ovlivnění přepadového množství úrovní dolní vody. Při tloušťce přelivné hrany větší než 2 mm je nutné povodní hranu zkosit pro lepší odtržení přepadového paprsku. Proudění v přítokovém korytě musí být rovnoměrné a ustálené, čehož docílíme dostatečně dlouhým přímým úsekem před přelivem, dno koryta by mělo být pokud možno vodorovné. Minimální délka přímého přítokového koryta je dle [4] ČSN ISO 1438 desetinásobek výšky přepadového paprsku. Tvar a velikost koryta pod měrným profilem nemá, pokud nastává dokonalý přepad, vliv na naměřené hodnoty. Měření přepadové výšky probíhá v dostatečné vzdálenosti od přelivné hrany, aby nebylo ovlivněno poklesem hladiny způsobeného formováním přepadového paprsku. Doporučená vzdálenost měrného profilu se rovná 4 až 5 násobku maximální přepadové výšky. 3
26 Nejpoužívanější měrné ostrohranné přelivy mají trojúhelníkový, obdélníkový nebo lichoběžníkový výřez. Pokud jsou průtoky v korytě značně rozkolísané, je možné instalovat i jiné přelivy, například s výřezy tvaru složeného lichoběžníku, apod Ostrohranný přeliv s trojúhelníkovým výřezem 90 Přeliv s trojúhelníkovým výřezem o vrcholovém úhlu 90 neboli Thomsonův přeliv je konstrukčně i výpočtově nejjednodušší. Výpočet průtoku přes tento průřez lze řešit dle [4] pomocí tzv. BSI (British Standards Institution) vzorce, který platí pro trojici vzájemně svázaných vrcholových úhlů a to konkrétně: a) α = 90 = π/2 radiánů; tangens α/2 = 1; b) α = 53 8 = 0,9273 radiánů; tangens α/2 = 0,50; c) α = 28 4 = π/2 radiánů; tangens α/2 = 1. Vzorec BSI má pro tyto úhly tvar: Q = Ce 8 15 tan α 2 2g h 5 2. (2.1.1) Po dosazení α = 90 a následné úpravě dostáváme jednoduchý vztah: Q = 2,3625 Ce h 5 2, (2.1.2) kde Ce je součinitel určený experimentálně a jeho hodnoty lze získat z [4] ČSN ISO 1438 z tabulky Ostrohranný přeliv s trojúhelníkovým výřezem 53 8 Dalším často používaným typem měrného přelivu s trojúhelníkovým výřezem je profil s vrcholovým úhlem Výpočet průtoku lze provést dle BSI vzorce (2.1.1), který má po dosazení a následné úpravě tvar: Q = 1,18125 Ce h 5 2, (2.2.1) kde Ce je opět součinitel zapsaný v [4] ČSN ISO 1438, konkrétně z tabulky Ostrohranný přeliv s trojúhelníkovým výřezem 28 4 Poslední z pravidelně aplikovaných přelivů s trojúhelníkovým výřezem, u kterého je možné využít vzorce BSI (2.1.1) má vrcholový úhel Určení průtoku ze známé přepadové 4
27 výšky probíhá dosazením součinitele Ce z [4] ČSN ISO 1438, z tabulky 3 do vzorce vycházejícího ze vztahu (2.1.1): Q = 0,59059 Ce h 5 2 (2.3.1) 2.4. Ostrohranný přeliv s obdélníkovým výřezem Přelivy s obdélníkovým výřezem můžeme rozdělit podle poměru šířky přívodního koryta B a délky přelivné hrany b na dva typy. Při poměru b/b rovno 1 můžeme mluvit o přelivu bez bočního zúžení, tzv. Bazinův přeliv. Pokud zlomek b/b nabývá hodnot menších než 1, dochází ke kontrakcím proudu a mluvíme o přelivu s bočním zúžením neboli Ponceletově přelivu. Pro výpočet průtoku přes obdélníkové ostrohranné přelivy s dokonalým přepadem se používá následující vztah: Q = m b 2g h 3 2, (2.4.1) kde m b g h součinitel přepadu, šířka přelivné hrany, tíhové zrychlení, přepadová výška. Součinitel přepadu m pro Bazinův přeliv zahrnuje ztráty a kontrakci na přepadu a také vliv přítokové rychlosti. Při určování Q/h charakteristiky ostrohranného přelivu s obdélníkovým průřezem v této práci byl použit upravený vztah vycházející z (2.4.1), který je univerzální pro přelivy s i bez bočního zúžení, uvedený v [4] ČSN ISO 1438, tzv. vzorec SIA, který má tvar: Q = C 2 3 2g b h 3 2, (2.4.2) kde C označuje součinitel přepadu určený dle vztahu: C = 0, ,037 b B 2 0, ,003 b + B h+0, ,5 b B 4 h h+p 2. (2.4.3) 5
28 Praktické meze pro použití těchto vztahů jsou následující: a) h/p 1,0; b) b/b 0,3; c) h 0,025 B/b a h 0,8 m; d) p 0,3 m. Poslední podmínka nebyla z prostorového hlediska při návrhu měrného přelivu uvedeného v práci splněna Ostrohranný přeliv s lichoběžníkovým výřezem Poslední navržený ostrohranný přeliv má výřez ve tvaru jednoduchého lichoběžníku, se sklonem hran výřezu 1:4. Tento typ přelivu se nazývá Cipolettiho přeliv. Pro určení hodnoty průtoku příslušející naměřené přepadové výšce se používá jednoduchý vzorec: Q = 1,86 b h 3 2 (2.5.1) 6
29 3. SCIMEMIHO PŘELIVNÁ PLOCHA Scimemiho přelivná plocha patří mezi beztlakové proudnicové přelivné plochy. Její tvar vychází ze spodního obrysu volného přepadového paprsku přepadajícího přes ostrohranný přeliv. Při návrhové přepadové výšce obrys přelivu kopíruje tvar přepadového paprsku, který na něj teoreticky netlačí, ani se neodtrhává. Při přepadových výškách nižších než návrhová se stává přeliv tlakový, což se projeví ve snižování součinitele přepadu. Naopak při vyšších stavech hladiny dochází k odtrhávání přepadového paprsku od tělesa přelivu, vzniká podtlak, který může být provázen tlakovými pulsacemi. Tvar Scimemiho přelivné plochy je určen pro přepadovou výšku h = 1 m rovnicí [9]: y = a x n, (3.1) kde a parametr rovnice, a = 0,5; n parametr rovnice nabývající hodnoty n = 1,85. Počátek souřadnicového systému (x;y) je umístěn na přelivné hraně nejvyšším bodu přelivného tělesa (Obr. 1). Zakřivení přelivu před přelivnou hranou se navrhuje dle Bazinovy křivky. Křivka v praktickém použití přechází do různých sklonů, u námi navrženého modelu je to sklon 1:1. Pro navržený sklon a přepadovou výšku 1 m má bod dotyku T(x t ;y t ) souřadnice [1,096;0,593]. Obr. 1 Schéma Scimemiho přelivné plochy [9] Scimemiho plocha se vyznačuje poměrně velkým součinitelem přepadu, který má pro návrhovou přepadovou výšku hodnotu m = 0,51. Pro nižší přepadové výšky se návrhový součinitel přepadu přepočítá na hodnotu: 7
30 m = 0,51 0,63 + 0,37 h h n, (3.2) kde h h n je přepadová výška, pro kterou určujeme součinitel přepadu, je návrhová přepadová výška. Výpočet průtoku lze provést dle rovnice: kde σ z součinitel zatopení, pro dokonalý přepad σ z = 1, Q = σ z σ s m b 0 2g h 0 3 2, (3.3) σ s součinitel šikmosti vliv půdorysného uspořádání, pro přeliv kolmý na stěnu žlabu σ z = 1, b 0 účinná šířka přelivu, pro přeliv bez bočního zúžení b 0 = b, h 0 energetická přepadová výška zahrnuje rychlostní výšku v přítokovém korytě a vypočítá se jako: h 0 = h + αv 0 2. (3.4) 2g V případě navrženého modelu přelivu se Scimemiho beztlakovou přelivnou plochou se výpočet zjednoduší. Při hydrotechnickém výpočtu uvažujeme dokonalý přepad, přelivná hrana je umístněna kolmo ke stěnám měrného žlabu, u modelu nedochází k bočním kontrakcím. Vztah pro výpočet průtoku pak získává tvar: Q = m b 2g h (3.5) 8
31 4. VENTURIHO ŽLAB Další možností určení průtoku v otevřeném korytě pomocí měření hladiny je použití měrných žlabů. Mezi v praxi používané měrné žlaby můžeme zařadit Venturiho žlaby, Parshallovy žlaby a žlaby typu Saniiri. Volba konkrétního typu závisí na řadě faktorů, zejména rozsahu měřených průtoků, spádu a charakteristice koryta, možnosti prohloubení dna či vytvoření stupně ve dně, požadované přesnosti měření a také ekonomickém hledisku. Pro naše podmínky byl jako nejvhodnější zvolen Venturiho žlab (Obr. 2) a to zejména z důvodu konstrukční jednoduchosti, snadné instalace do měrného žlabu, výhodou je také vodorovné dno Venturiho žlabu, které těsně dosedne k nerezovému dnu měrného žlabu. Po celý měřený rozsah průtoků nesmí dojít k ovlivnění proudění v hrdle žlabu, kde musí nastat kritické proudění. Měření hladiny pro výpočet průtoku by mělo být realizováno dle [6] v protiproudní vzdálenosti maximálně A = 2 m od hrdla Venturiho žlabu. Velikost průtoku z naměřené úrovně hladiny se následně určí: Q = φ b g H3 2, (4.1) kde φ b H je součinitel zahrnující vliv ztrát mechanické energie, vliv nerovnoměrnosti rozložení rychlostí v profilu hrdla Venturiho žlabu a vliv rychlostní výšky v přítokovém korytě závislé na relativním zúžení b/b, šířka hrdla Venturiho žlabu, hloubka vody v přítokovém korytě měřená od výškové úrovně dna v profilu hrdla. Obr. 2 Schéma Venturiho žlabu 9
32 5. KRUHOVÝ PROPUSTEK S ohledem na rozměry a technologické řešení měrného hydraulického žlabu (příloha 1, kap. 3) byl navržen model propustku s kruhovým průřezem a sklonem svahů 1:1. Potrubí o vnitřním průměru 100 mm je uloženo na vtoku ve výšce 100 mm nad dnem žlabu ve sklonu 0,5 %. Kapitola vychází zejména z poznatků uvedených v literatuře [7] a [9]. Propustkem obvykle rozumíme menší objekt se stálým kruhovým nebo obdélníkovým průřezem a sklonem, kterým protéká voda pod komunikacemi, železnicemi, náhony apod. Přesné rozhraní mezi mostem a propustkem není definováno, propustek však na rozdíl od mostu obyčejně nepřeruší celou výšku násypu a většinou převažuje délka nad ostatními rozměry objektu. Hydraulicky je možné odlišit propustky od mostů pomocí uvažovaných ztrát mechanické energie. U mostních konstrukcí bývá ztráta třením po délce vzhledem ke ztrátám místím na vtoku zanedbatelná, u propustků nikoliv. Propustky mají na rozdíl od shybek po celé délce sklon ve směru proudění. Způsobů jakými může proudit voda v propustku je velké množství, a to v závislosti na sklonu potrubí propustku a jeho poměru ke kritickému sklonu, na délce propustku a na poměrech na vtoku a výtoku z propustku. V této práci se budeme zabývat pouze třemi základními typy proudění: a) proudění s volnou hladinou po celé délce propustku, na vtoku i výtoku, b) proudění se zatopeným vtokem a volnou hladinou ve zbytku propustku, c) proudění tlakové, při kterém je zaplněn celý průřez propustku vodou a to po celé délce. První a druhou variantu je dále možné rozdělit podle ovlivnění dolní vodou na proudění bez ovlivnění a proudění s ovlivněním dolní vodou, které v hydrotechnických výpočtech neuvažujeme. Ovlivnění dolní vodou může nastat při nízkém sklonu potrubí u dlouhého propustku, nebo pokud je hladina dolní vody tak vysoko, že ovlivňuje sníženou hloubku za vtokem do propustku. 10
33 5.1. Kruhové propustky s volnou hladinou po celé jejich délce bez ovlivnění dolní vodou Proudění s volnou hladinou po celé délce bez ovlivnění dolní vodou nastává při splnění následujících podmínek: a) Průtok Q je menší než kapacitní průtok potrubí propustku b) Hloubka vzduté hladiny před propustkem h je nižší než součin βd, kde β je součinitel zatopení vtoku závislý na konstrukčním řešení vtoku a D je průměr potrubí propustku c) Sklon dna propustku i 0 je větší nebo přibližně roven kritickému sklonu i k d) Hladina dolní vody není výše než snížená hladina za vtokem h c Výpočet kapacity potrubí můžeme určit ze vztahů Chezyho a Manninga: Q kap = 1 n R2 3 S i 0, (5.1.1) kde R je hydraulický poloměr, S plocha průřezu potrubí a i 0 sklon dna potrubí propustku. Kritický sklon i k je takový sklon, při kterém protéká voda v daném profilu právě kritickou hloubkou h k, kterou je možné určit například dle Abbotta [9] ze vztahu pro částečně plněné kruhové profily: h k = 0,32Q D 1 4. (5.1.2) Na kritické hloubce je přímo závislá snížená hloubka za vtokem do propustku h c : h c = χ h k, (5.1.3) kde χ je součinitel výškového zúžení závislý podobně jako β na konstrukčním uspořádání vtoku do propustku. Při hydrotechnických výpočtech proudění o volné hladině modelem navrženého propustku byl zvolen postup volby průtoku s konstantním krokem a současné ověřování podmínek tohoto typu proudění. Pro jednotlivé průtoky jsou vypočteny vzduté výšky hladiny před propustkem z Bernoulliho rovnice pro profily před propustkem a v místě snížené hloubky za vtokem (Obr. 3). Při výpočtu nebyl uvažován vliv rychlosti v přítokovém korytě, který je v celém rozsahu průtoků splňujících podmínky proudění v propustku o volné hladině zanedbatelný. Tvar Bernoulliho rovnice pro uvažované profily po matematických úpravách je: h = h c + h 0 + Q 2 2g φ 2 S c 2, (5.1.4) 11
34 kde h 0 φ S c převýšení dna vstupu do propustku nad dnem měrného žlabu, rychlostní součinitel závislý na konstrukčním řešení vstupu do propustku, průtočná plocha v profilu se sníženou hloubkou h c za vtokem. Obr. 3 Propustek s volnou hladinou po celé jeho délce 5.2. Kruhové propustky se zatopeným vtokem bez ovlivnění dolní vodou Při vzduté hladině h před propustkem vyšší než hodnota βd (viz. kap. 5.1) dochází k proudění v propustku o volné hladině se zatopeným vtokem (Obr. 4). V případě navrženého modelu uvažujeme při hydrotechnických výpočtech proudění bez ovlivnění dolní vodou. Výpočet průtoku propustkem se zahlceným vtokem a neovlivněným dolní vodou provedeme dle vztahu: Q = φ S c 2g E h c h 0, (5.2.1) kde φ rychlostní součinitel závislý na konstrukčním řešení vstupu do propustku, S c zúžená plocha v profilu za vtokem S c = 0,62 S, h c snížená hloubka v profilu za vtokem, pro kruhový propustek h c = 0,60 D, E h 0 energetická výška v profilu přítokového koryta před propustkem, převýšení vtoku propustku nad dnem přítokového koryta. 12
35 Obr. 4 Propustek s volnou hladinou a zatopeným vtokem 5.3. Kruhové propustky s tlakovým prouděním po celé jejich délce Tlakové proudění propustkem může nastat pouze při průtoku větším, než je kapacitní průtok potrubí propustku, které je možné určit dle vztahů Chezyho a Manninga (5.1.1). Při splnění této podmínky jsou možné dvě varianty proudění, s nezatopeným výtokem nebo se zatopeným výtokem z propustku. Při nezatopeném výtoku dochází k tlakovému proudění po celé délce propustku pouze v případě, kdy je kritická hloubka h k potrubí větší než jeho průměr D. Pokud tomu tak není, tlakový režim nastává pouze v části propustku. V hydrotechnických výpočtech modelu navrženého propustku uvažujeme jako jedinou variantu tlakového proudění propustek se zatopeným vtokem i výtokem (Obr. 5). Pro tento typ je nutné dodržet podmínku průtoku většího než kapacitního a také podmínku minimálního tlaku na konci výtokového průřezu, který musí být větší než tlak atmosférický: Δ > Δ min = v d v v d g, (5.3.1) kde v je rychlost v propustku, v d rychlost v odtokovém korytě. Při nedostatečném tlaku na výtoku může docházet k vzniku rušivých vlivů (tlakové pulsace), které nepříznivě působí na konstrukci propustku. Při splnění obou podmínek a při zanedbání přítokové rychlosti platí pro průtok: Q = S 2g h h d +i 0 L+Δ min 1+ξ v +λ L D, (5.3.2) kde S h plocha průřezu propustku, hloubka v přítokovém žlabu, 13
36 h d i 0 L hloubka v odtokovém žlabu, sklon dna propustku, délka potrubí propustku, Δ min minimální tlak na konci výtokového průřezu, ξ v λ D součinitel ztrát na výtoku, součinitel tření (odporový součinitel) určený z Colebrook-Whiteovy rovnice (6.1.4), průměr propustku. Obr. 5 Propustek s tlakovým prouděním a zatopeným výtokem Při řešení tlakového propustku v rámci hydrotechnických výpočtů navrženého modelu byl použit obrácený proces výpočtu. Pro zvolené průtoky Q a nastavené hloubky dolní vody h d byla stanovena hloubka vody v přítokovém žlabu h a došlo k ověření plnění podmínek pro minimální tlak Δ. 14
37 6. URČOVÁNÍ ZTRÁT MECHANICKÉ ENERGIE MÍSTNÍCH A TŘENÍM PO DÉLCE VE VÝUKOVÉM OKRUHU Při průtoku vody potrubím vznikají ztráty třením po délce, které můžeme pozorovat na úrovních hladin v piezometrických trubicích. Pokles úrovně hladin v piezometrických trubicích nastává také při průtoku vody různými singularitami (koleno, šoupě, náhlé rozšíření a zúžení), kde vznikají ztráty místní. Tohoto jevu je využito v navrženém výukovém okruhu pro simulaci ztrát pomocí 21 tlakových odběrů rozmístěných rovnoměrně po délce potrubí, zejména kolem zmiňovaných singularit Ztráty třením po délce Základním vzorcem pro výpočet ztrátových výšek při tření je Darcy-Weisbachova rovnice: h z = λ L D v 2 2g, (6.1.1) kde λ L D v součinitel tření (odporový součinitel) určený z Colebrook-Whiteovy rovnice (6.1.4), délka úseku potrubí, pro kterou určujeme ztrátu, průměr potrubí, rychlost vody v potrubí. Určení součinitele tření λ se mění v závislosti na režimu proudění v potrubí. Výpočet pro laminární a turbulentní proudění je odlišný. Laminární oblast je charakterizována hodnotou Reynoldsova kritéria Re < 2320, které je popsáno: Re = v D υ, (6.1.2) kde υ je kinematická viskozita vody. Pro laminární oblast můžeme určit součinitel tření λ dle: λ = 64 Re. (6.1.3) V praktických aplikacích se laminární proudění vyskytuje pouze ojediněle, proto je nutné použít závislost, která je vhodná pro popis celé oblasti turbulentního proudění. Vhodnou závislostí je Colebrook Whiteova vystižená vztahem: 15
38 1λ 2,51 = 2 log + Δ, (6.1.4) Re λ 3,7D kde Δ je absolutní drsnost neboli průměrná účinná výška nerovností stěn. Je zřejmé, že určení součinitele λ z rovnice nelze provést explicitně, pro jeho výpočet se používá postup několika (většinou postačí 3) iterací Ztráty místní Ztráty mechanické energie vznikají nejen třením po délce potrubí, ale také při změně směru proudnic a vířením u různých překážek v průtočném profilu, případně změn průřezu. Tato místa nazýváme singularity. Místní ztráty vyjadřujeme podobně jako ztráty třením ve tvaru násobku rychlostní výšky: h m = ξ v2 2g, (6.2.1) kde ξ je bezrozměrný součinitel místní ztráty, v rychlost, ke které se ztráta vztahuje (Obr. 6). Obr. 6 Vztažné rychlosti pro výpočet místních ztrát Velikost součinitele ξ se mění dle tvaru singularity, drsnosti stěn, hodnoty Reynoldsova kritéria Re, atd. Při výpočtech ztrát ve výukovém okruhu uvažujeme hodnotu ξ s měnícím se průtokem konstantní. Určení součinitele místní ztráty je pro jednotlivé singularity různý. V okruhu výukového modelu jsou navrženy následující singularity: koleno 90, koleno 45, kulový uzávěr, náhlé zúžení, náhlé rozšíření. Pro určení součinitele místní ztráty u ostatních objektů odkazujeme na literaturu [1], [7], [8], [9]. 16
39 Náhlé rozšíření průřezu Velikost místní ztráty při náhlém rozšíření průřezu, neboli Bordova ztráta, je závislé na rozdílu rychlostí v jednotlivých profilech: tedy h m = v 1 v 2 2 2g = S v2 2, ( ) S 1 2g ξ = S = D 2 2 S 1 D2 1 2 vztaženo k v 2 (Obr. 6). ( ) Náhlé zúžení průřezu Součinitel místní ztráty náhlého zúžení průřezu je stejně jako u náhlého rozšíření závislý pouze na poměru průměru, resp. ploše jednotlivých průřezů a určí se z: ξ = 1 0,57+ 0, ,1 S 2 S1 2 vztaženo k v 2. ( ) Kulový uzávěr Pro určení součinitele místní ztráty kulových uzávěrů, šoupat a dalších armatur neexistují žádné obecné výpočtové vztahy. Stanovení součinitele je možné pouze pomocí laboratorního měření. Velikost tlakové ztráty na uzávěru udávají jednotliví výrobci uzávěrů ve formě součinitele ξ, častěji však grafem tlakových ztrát vyjadřujícím závislost mezi průtokem a tlakovou ztrátou v metrech vodního sloupce (m v. sl.), případně barech. Příklad grafu tlakových ztrát je vidět na obrázku 6. Velikost součinitele místní ztráty závisí také na poloze otevření uzávěru. Obr. 7 Graf tlakových ztrát kulového uzávěru společnosti Ivar CS 17
40 Pro výpočet tlakové ztráty na navrženém kulovém uzávěru byl použit součinitel ξ = 0,08 při plném otevření uzávěru Koleno Při průtoku vody kolenem se uplatňují ztráty třením, ztráty odtržením proudu a vzniku úplavu při vnitřní stěně kolena a ztráta příčným pohybem. Převažující vliv na celkovou ztrátu má nesymetrické rozdělení rychlostí a tlaků v průtočném profilu. U obloukových kolen (resp. obloukového kolena dlouhého - oblouku), která jsou použita v navrženém výukovém okruhu, závisí součinitel místní ztráty na poloměru zakřivení r s, resp. na poměru poloměru zakřivení a průměru potrubí r s /D a středovém úhlu kolena. Hodnoty součinitelů ξ jsou určeny pro kolena se středovým úhlem = 90, pro menší úhly se součinitel přepočítá dle vztahu: ξ = ξ 90 δ 90. ( ) Tab. 1 Součinitel místní ztráty pravoúhlým kolenem pro hydraulicky hladká potrubí (Δ/D<0,001) r s /D 0,8 1,0 1,5 2,0 4,0 6, ξ 0,37 0,21 0,17 0,15 0,11 0,09 0,07 0,05 0,03 Pro hydraulicky drsná potrubí (Δ/D>0,001) jsou hodnoty ξ dvojnásobné. Pro ostrá kolena je charakteristické mohutnější odtržení proudu a to jak za vnitřní hranou, tak při vnější stěně kolena. Součinitel místní ztráty pak pochopitelně dosahuje vyšších hodnot. U segmentových kolen je součinitel ξ závislý na středovém úhlu a poměru a/d, kde a je délka jednoho segmentu. Hodnoty součinitele místní ztráty pro ostrá a segmentová kolena můžeme najít v literatuře [8] a [9]. Obr. 8 Koleno obloukové 90, ostré 45, segmentové jednoduché, segmentové dvojité [9] 18
41 Pro potřeby hydrotechnických výpočtů navržené měřicí tratě byly použity součinitele pro koleno 90 s poměrem r s /D = 1 a koleno dlouhé 90 neboli oblouk s poměrem r s /D = 1. Hodnoty součinitelů místních ztrát byly uvažovány pro hydraulicky drsná potrubí Podmínky pro měření tlakových ztrát Pro měření a simulaci tlakových ztrát s dostatečnou výpovědní hodnotou je nutné dodržet některá základní konstrukční pravidla, stanovená na základě výsledků provedených měření různých autorů. Následující poznatky vycházejí zejména z výzkumu Výzkumného ústavu vodohospodářského [8]. Při návrhu měřicího okruhu a umístění tlakových odběrů je velmi důležité vhodné rozmístění singularit pro zabránění jejich vzájemného ovlivňování. Jak uvádí Skalička a Hoření [8] hydraulická ztráta daná základní hodnotou součinitelů ztrát oblouků se plně realizuje uvnitř trubního systému jen tehdy, je li délka přímého potrubí za výstupem z oblouku větší než asi 40 až 50 D. Je však nutné přihlédnout i k dalším argumentům. U oblouků o velké křivosti (R/D 1,5), které jsou použity v navrženém okruhu, se ztráta realizuje převážně uvnitř oblouku a v přímém úseku za ním o délce rovné jednoho průměru potrubí. Další vliv na minimální délku přímého úseku za obloukem má středový úhel. U oblouků se středovým úhlem = 90 probíhá deformace rychlostního pole na vzdálenosti přibližně 9 D, ve větší vzdálenosti se již formuje téměř rovnoměrné pole rychlostí. Při středovém úhlu o velikosti 45 se tato vzdálenost zvětšuje až na 23 D. Významný rozdíl vzdáleností pro jednotlivé středové úhly je způsoben nepřímou úměrností mezi délkou ovlivnění a stupněm nerovnoměrnosti rozložení rychlostního pole. U oblouků s velkým středovým úhlem vychází z výtokového profilu proudění s velmi nerovnoměrným rozložením rychlostního pole, které se deformuje na kratší vzdálenosti, naopak u menších středových úhlů není rychlostní pole tolik nerovnoměrné a útlum příčných složek rychlostí probíhá na větších délkách potrubí. Pro vzdálenost tlakových odběrů od výtoku ze singularity je důležité dodržení minimálních délek, na kterých dochází k vyrovnání tlaků na protilehlých stěnách potrubí. Autoři Skalička a Hoření vycházejí z vlastních měření a uvádí [8]: Za oblouky o R / D = 1 dosahuje tlakový rozdíl u protilehlých stěn potrubí ve vzdálenosti 1,2 D za výstupním profilem 1 % až 6 % dynamického tlaku.(maximum je za obloukem o = 90, minimum za obloukem o = 180 ). Odchylku rozložení tlaku na stěně potrubí od hydrostatického zákona lze tedy bezpečně zanedbat až ve vzdálenosti 3 D až 8 D za výstupem z oblouků. 19
42 Při návrhu konstrukčního řešení výukového okruhu pro měření ztrát mechanické energie bylo nutné přihlédnout také k dispozičnímu řešení, proto byla navržena vzdálenost mezi singularitami min. 10 D, v jednom případě pouze 6 D na tomto úseku je možné zkoumat vzájemné ovlivnění singularit. Odstup tlakových piezometrických odběrů od objektů byl zvolen 1 D. 20
43 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES PŘÍLOHA Č. 3 TECHNICKÁ ZPRÁVA BAKALÁŘSKÁ PRÁCE BACHELOR'S THESIS AUTOR PRÁCE AUTHOR VEDOUCÍ PRÁCE SUPERVISOR MICHAL HAVLÁT Ing. MICHAL ŽOUŽELA, Ph.D. BRNO 2013
44 3. TECHNICKÁ ZPRÁVA NAVRŢENÉHO KONSTRUKČNÍHO ŘEŠENÍ OBSAH 1. Úvod Měrné ostrohranné přelivy Model propustku Scimemiho přelivná plocha Venturiho měrný ţlab Měřicí vozík Výukový okruh pro simulaci ztrát mechanické energie Trubní část výukového okruhu Soustava pro odběr a zobrazení tlakových piezometrických výšek Obsluţná lávka
45 1. ÚVOD Následující část práce se zabývá popisem konstrukčního řešení jednotlivých modelů výukového okruhu, měřicího vozíku a obsluţných lávek. Návrh jednotlivých modelů a objektů vychází z dispozičního řešení laboratoře (příloha č. 1, kap. 2; [10]), rozměrů měrného ţlabu (příloha č. 1, kap. 3; [10]) a hydraulických poţadavků na kapacitu a tvar konstrukcí (příloha č. 2 a z ní vycházející příloha č. 4). Nejdůleţitějšími podklady pro konstrukční návrh modelů a objektů byly rozměry ţlabu, pozice vyústění nerezového potrubí DN50 pro výukovou trať a umístění čerpací jímky v místnosti laboratoře pro usazení odpadního potrubí z výukového okruhu. Tato vstupní data byla získána z projektu [10]. 2. MĚRNÉ OSTROHRANNÉ PŘELIVY Základní charakteristiky: Počet měrných ostrohranných přelivů 5 Výřezy přelivů trojúhelníkový s výřezem 90, 53 8, 28 4, lichoběţníkový, obdélníkový Šířka přelivů Výška přelivů Výška přelivné hrany nad dnem ţlabu Materiál Uchycení přelivů k rámu 359 mm 380 mm (trojúhelníkový mm) 150 mm nerezová ocel 11 (resp. 9) ks šroubů M6x12 Všechny ostrohranné přelivy jsou navrţeny jako desky z nerezového plechu tloušťky 1,2 mm o šířce 359 mm. Tento rozměr vychází z rozměrů měrného ţlabu šířky 366 mm a rezervy 3,5 mm při stěnách pro snadnou výměnu jednotlivých přelivů. Malá tloušťka nerezového plechu zaručuje vhodné odtrţení přepadového paprsku, proto není nutné zkosení přelivné hrany uvedené v příloze č. 2, kap. 2. 2
46 Všechny ostrohranné přelivy mají přelivnou hranu, případně nejniţší bod výřezu ve výšce 150 mm. Uchycení přelivů v měrném ţlabu zajišťuje rám vyrobený z L profilů 20x20x3 mm z nerezové oceli, který je společný pro všechny typy přelivů, v daném okamţiku je moţné osazení pouze jednoho z nich. Celková pouţitá délka profilu je 1080 mm. L profily budou před jejich vzájemným svařením seříznuty pod úhlem 45 pro umoţnění jednoduššího a pevnějšího svaru. Po celém obvodu rámu i měrných přelivů bude vyvrtáno 11 otvorů průměru 6,5 mm pro šrouby. Na vnitřních stranách L profilu, tzn. z poproudní strany rámu budou v místech otvorů pro šrouby svarem připevněny matice 11xM6. Na návodní straně rámu bude nalepeno pryţové těsnění šířky 18 mm, tloušťka 2 mm zabraňující průsakům mezi rámem a stěnou přelivu. Celá konstrukce bude vodotěsně připevněna silikonovým tmelem ke stěnám a dnu měrného ţlabu. Při instalaci měrného přelivu budou pouţity nerezové šrouby M6x12 mm v počtu 11 ks. K uchycení ostrohranného přelivu s trojúhelníkovým výřezem 90 bude z důvodu menší výšky pouţito pouze 9 ks těchto šroubů. Rám ostrohranných přelivů bude trvale umístěn 900 mm od konce měrného ţlabu, coţ zajistí dostatečnou uklidňovací délku přítokového ţlabu. Rozměry rámu, měrných přelivů a umístění děr pro šrouby je zobrazeno v přílohách 5.1 Ostrohranné měrné přelivy a 5.2 Upevňovací rám měrných přelivů. 3. MODEL PROPUSTKU Základní parametry: Výška modelu Půdorysné rozměry (š x d) Vnitřní průměr potrubí D Materiál 300 mm (366 x 850) mm 100 mm akrylát PMMA čirý Sklon dna potrubí 0,5 % Sklon návodního a vzdušního svahu 1:1 Kapacitní průtok potrubím 4,75 l/s 3
47 Převýšení dna potrubí na vtoku nad dnem 100 mm Model propustku je navrţen z čirého akrylátu PMMA tloušťky 10 mm. Průhledná varianta umoţňuje názornou ukázku reţimů proudění propustkem. Model je navrţen jako miniatura silničního násypu s kruhovým propustkem se sklonem dna 0,5 %. Svahy násypu jsou ve sklonu 1:1. Objekt s celkovými rozměry (šířka x výška x délka) (362 x 300 x 850) mm bude upevněn v měrném ţlabu pomocí silikonového tmelu, který zaručí vodotěsnost spár. Potrubí propustku je tvořeno akrylátovou trubkou D 100 s tloušťkou stěny 5 mm. Dno potrubí je na návodní straně modelu ve výšce 100 mm nad dnem ţlabu, dno výtoku z propustku je nad dnem ţlabu převýšeno o 97 mm. Stropní deska propustku o rozměrech (250 x 362) mm má seříznuté delší hrany pro ideální dosednutí ke svahům modelu. Stěny tvořící svahy mají shodné půdorysné rozměry (424 x 366) mm, liší se pouze umístěním a rozměry otvoru pro potrubí propustku, coţ je způsobeno jeho sklonem. Výřezy mají půdorysný tvar elipsy, přesné rozměry jsou uvedeny v příloze 5.3. Celá konstrukce je vyztuţena dvojicí shodných ţeber tvaru rovnoramenného lichoběţníku s délkou základny 822 mm, výškou 290 mm a úhly u základny o velikosti 45. Rozestup ţeber je 152 mm. Jednotlivé díly modelu budou navzájem spojeny vhodným lepidlem. Celý objekt je vykreslen v příloze 5.3 Model propustku. Doporučené umístění modelu v měrném ţlabu je určeno vzdáleností 1670 mm od středu stropní desky ke konci ţlabu. Umístění modelu ve ţlabu bude pouze dočasné pro potřeby měření a výuky. Při měření na jiných modelech bude propustek z měrného ţlabu demontován. Doporučený postup výroby: 1) Vyříznutí jednotlivých dílů z akrylátové PMMA desky tloušťky 10 mm 2) Seříznutí hran dílů dle výkresu 3) Nalepení dvojice ţeber k stropní desce modelu 4) Nalepení desek tvořící svahy s nastrčeným potrubím 5) Utěsnění všech spojů vhodným lepidlem, případně silikonovým tmelem 6) Zabroušení případných výstupků a nepřesností 4
48 4. SCIMEMIHO PŘELIVNÁ PLOCHA Základní parametry: Maximální průtok Návrhová přepadová výška Výška přelivné hrany nad dnem ţlabu Půdorysné rozměry (š x d) shodný s max. průtokem dodaným na ţlab 115 mm 150 mm (362 x 242) mm Počet výztuţných ţeber 5 Konstrukce objektu je sloţena z čelní stěny, dna modelu, pěti kusů výztuţných ţeber z nerezového plechu tloušťky 1,2 mm, překryté přelivnou plochou vyrobenou taktéţ z nerezového plechu tloušťky 0,8 mm. Šířka modelu je 362 mm, délka 242 mm, převýšení přelivné hrany nad dnem ţlabu je 150 mm. Dno ţlabu tvoří nerezový plech o rozměrech (362 x 242) mm, na který je připevněno 5 kusů svislých výztuţných ţeber. Horní obrys ţeber je vytvořen podle křivky charakteristické pro Scimemiho přelivnou plochu (příloha č. 2, kap. 3) přecházející do sklonu 1:1. Přesný tvar ţebra je vykreslen pro účely výroby v příloze 5.5 Scimemiho přelivná plocha ţebro v měřítku 1:1. Umístění ţeber je naznačeno v příloze 5.4 Scimemiho přelivná plocha. Návodní stěna s rozměry (362 x 136) mm je spojena svarem ke dnu objektu a nerezovým ţebrům. Plášť modelu je tvořen přelivnou plochou z nerezového plechu tloušťky 0,8 mm. Zakřivení přelivné plochy je určeno tvarem výztuţných ţeber, na které bude materiál pláště postupně ohýbán a přichytáván bodovými svary. Jednotlivé části modelu budou spojeny svařením. Svary stýkající se s proudící vodou budou upraveny broušením. Rozměrové charakteristiky, umístění ţeber a jejich tvar jsou vykresleny v přílohách 5.4 a 5.5. Umístění návodní stěny modelu v měrném ţlabu je doporučeno ve vzdálenosti 1700 mm od konce ţlabu. 5
49 5. VENTURIHO MĚRNÝ ŢLAB Základní parametry: Rozměry (š x v x d) Materiál Šířka hrdla Maximální průtok Minimální měřitelný průtok Poloměr zakřivení vtoku Počet výztuţných ţeber (362 x 300 x 1050) mm nerezová ocel 122 mm 35 l/s 2,4 l/s 500 mm 2x7 Navrţené rozměry měrného Venturiho ţlabu (MVŢ) vychází z typizovaných řad Venturiho ţlabů uvedených ve zdroji [6], které však musely být adekvátně upraveny dle rozměrů ţlabu, do kterého bude MVŢ instalován. Navrţené konstrukční řešení zachovává relativní zúţení b/b = 0,333, které ovlivňuje hodnotu součinitele φ. Celá konstrukce MVŢ je navrţena z nerezové oceli. Zakřivené stěny tvoří nerezový plech tloušťky 0,8 mm, dno a výztuţná ţebra mají tloušťku 1,2 mm. Celková délka modelu je 1050 mm, šířka 362 mm a výška 300 mm. Dno MVŢ slouţí jako základna pro uchycení ţeber a obtékaného tvaru a jeho rozměry jsou shodné s půdorysnými rozměry modelu. Vtokovou část MVŢ tvoří oblouky o poloměru R = 500 mm, které přechází do stěn hrdla půdorysně rovnoběţných s osou ţlabu, vzájemně vzdálených 122 mm. Odtok z hrdla MVŢ je realizován postupným rozšířením v poměru 1:6 na délce 720 mm. Stabilita stěn ţlabu je zajištěna celkem 14 ţebry z nerezového plechu tloušťky 1,2 mm, připevněnými ke dnu objektu, dále dvojicí nerezových profilů L 20 x 20 x 3 mm délky 362 mm umístěných v horní části vtoku a výtoku z MVŢ a výztuţným pásem z nerezové oceli tloušťky 3 mm o rozměrech (40 x 130) mm umístěným v horní části stěn hrdla. Jednotlivé části modelu budou spojeny svařením. Svary stýkající se s proudící vodou budou upraveny broušením. Rozměrové charakteristiky, umístění ţeber a jejich rozměry jsou vykresleny v příloze
50 Doporučené umístění MVŢ je určeno usazením hrdla modelu ve vzdálenosti 1870 mm od konce měrného hydraulického ţlabu. 6. MĚŘICÍ VOZÍK Základní parametry: Rozměry základního rámu Rozchod kolejnic Rozsah měření hloubkoměru Typ hloubkoměru (300 x 406) mm 432 mm 500 mm digitální s výstupem dat Pro potřeby stanovení úrovně hladiny v měrném ţlabu je nutné umístění hloubkoměru na výškově stabilní, avšak půdorysně v obou směrech pohyblivé zařízení. Z tohoto důvodu je součástí této práce návrh měřicího vozíku pro měrný hydraulický ţlab. Základem vozíku je obdélníkový rám (300 x 406) mm vyrobený z nerezových uzavřených profilů obdélníkového průřezu (100 x 40) mm s tloušťkou stěny 2 mm, který je překrytý nerezovým plechem tloušťky 1,2 mm, který tvoří odkladní prostor pro měřicí pomůcky a další potřeby. Jednotlivé profily uzavřeného obdélníkového průřezu jsou seříznuty pod úhlem 45 a navzájem svařeny. Do bočních stěn (délky 300 mm) jsou vrtáním vytvořeny 4 otvory pro umístění hřídelí koleček. Hřídele o průměru 15 mm a délce 100 mm jsou opatřeny ve vzdálenosti 4 mm od kraje dráţkami pojistného krouţku šířky 1 mm s hloubkou dráţky 0,7 mm. Vysunutí hřídele z rámu na vnější stranu je 46 mm. Pohyb vozíku v podélném směru ţlabu zajišťují čtyři kola z plné oceli s nákolkem Blickle SPKVS 50K, průměr kola bez nákolku 50 mm, průměr nákolku 62 mm, šířka běhounu bez nákolku 30 mm. Kola jsou osazena kuličkovým loţiskem s průměrem otvoru pro hřídel 15 mm. Odsazení kol od rámu vozíku zajišťuje nerezová distanční podloţka průměru 15/21 mm, DIN 988. Posunu loţiska, resp. celého kolečka po hřídeli je zabráněno pouţitím pojistného krouţku z nerezové oceli A2, DIN 471 pro hřídele o průměru 15 mm. Na čelní stěně rámu vozíku je připevněna dvojice navzájem přiléhajících profilů L 30 x 30 x 3 mm délky 510 mm, které slouţí jako vodící kolejnice trojice plastových 7
51 koleček. Okraje kolejnice budou doplněny pojistnými šrouby M6, které zabrání vypadnutí koleček mimo prostor kolejnic. Uchycení šroubů musí zajistit případné demontování drţáku hloubkoměru. Plastová profilovaná kolečka Zabi s označením C30/4 jsou vyrobena z bílého polyamidu PA6, průměr kola 30 mm, průměr hřídele 5 mm, nejsou osazena loţiskem, otáčení probíhá kluzně. Pouţití třech koleček zajišťuje pohyb ve směru kolmém na směr proudění vody ve ţlabu, stabilitu hloubkoměru a zároveň zabraňuje zadrhávání koleček vlivem příčení. Hřídele těchto kol jsou opatřeny pojistnými krouţky z nerezové oceli A2, tloušťky 0,6 mm pro hřídele o průměru 4 aţ 5 mm, DIN Spojení hřídelí s pásovou nerezovým drţákem hloubkoměru bude provedeno nalisováním do předem připravených otvorů a následné spojení hřídele s drţákem svařením. Nerezová ocel tloušťky 3 mm s rozměry 130 x 115 mm zajišťuje pevné spojení třech hřídelí a připevnění hloubkoměru. Hloubkoměr bude spojen s drţákem z nerezového plechu pomocí dvou šroubů, jejichţ rozměr bude zvolen podle otvorů v měřicím můstku hloubkoměru. Na zadní stěně nerezového plechu budou připojeny svarem matky odpovídajícího rozměru. S ohledem na různé poţadavky na funkce hloubkoměru byl navrţen digitální hloubkoměr s výstupem dat IP 67 MAHR 30 EWR [15]. Parametry hloubkoměru: - Měřicí rozsah: 500 mm - Odečet: 0,01 mm - Mezní chyba 0,05 mm - Celková délka 584 mm - Délka měřícího můstku 150 mm - Výstup dat umoţňuje pouţít rozhraní USB, Digimatic nebo RS232C. Vodící tyč hloubkoměru bude dodatečně opatřena hrotem pro přesnější kontakt s hladinou, v případě potřeby jiným zařízením dle účelu měření. 8
52 7. VÝUKOVÝ OKRUH PRO SIMULACI ZTRÁT MECHANICKÉ ENERGIE Základní parametry: Potrubí Pouţité profily Materiál potrubí DYKA tlakové potrubí; HT systém Plus D50, D75, D110 PVC-U, PP Počet tlakových odběrů 21 Celková délka potrubí Maximální provozní průtok Zkoumané singularity mm 4,33 l/s koleno 90, koleno 90 dlouhé (oblouk), kulový uzávěr, náhlé rozšíření, náhlé zúţení, ztráta třením po délce Výukový okruh slouţí k názorné simulaci a měření ztrát mechanické energie třením po délce a ztrát místních při průtoku singularitami (koleno, kulový uzávěr, náhlé rozšíření a zúţení). Teoretická část problematiky je uvedena v příloze č. 2, kapitole 6. Návrh výukového okruhu můţeme rozdělit do dvou částí potrubí okruhu s jednotlivými tvarovkami, armaturami a kotevními prvky, druhou část tvoří systém odběrů piezometrických výšek, zobrazovací zařízení a napojení na odpadní potrubí pro případ překročení provozní hladiny v piezometrických trubicích nad zobrazovací oblast. 7.1 Trubní část výukového okruhu Potrubí pouţité v okruhu bude popisováno ve směru proudění vody. Umístění vtoku do výukového okruhu vychází z projektu hydraulického měrného ţlabu [10] a jeho zásobování vodou (příloha č. 1, kap. 3), v kterém byla budoucí výstavba výukového okruhu předpokládána a pro účel napojení byl navrţen zaslepený konec nerezového potrubí DN50 opatřený mosazným ventilem DN50, 2, PN 16 a nipplem DN50, 2 s vnějším závitem. Osa vyústění je umístněna 260 mm nad podlahou laboratoře, toto výškové umístění je 9
53 zachováno po celé délce úseku s tlakovými odběry. Okruh uzavírá čerpací jímka s dvojicí čerpadel. Pro tvorbu výukového okruhu bylo pouţito tlakové PVC potrubí DYKA s příslušnými tvarovkami a PP potrubí a tvarovky HT systém Plus od výrobce OSMA. PVC potrubí je spojováno pomocí lepených spojů nástrčných tvarovek. HT systém Plus pouţívá hrdlové spoje těsněné vícenásobným těsnícím elementem splňujícím nároky na těsnost a dlouhodobou pruţnost spoje. Kombinace dvou materiálů byla zvolena zejména z důvodů obtíţného lepení a těsnění spojů PP potrubí, které se tak stává nevhodné pro realizaci tlakových odběrů. Důvodem pro jeho pouţití je snadná montáţ i demontáţ pomocí hrdlových spojů, moţnost hrdlového spojení s PVC trubkami a sortiment tvarovek vhodných pro dispoziční řešení odpadní části okruhu. Výuková trať je sloţena ze dvou větví měřicí větev napojená na přívodní nerezové potrubí a odpadní větev odvádějící vodu přetékající z piezometrických trubic. Obě větve jsou spojeny pomocí odbočky 45 do společného odpadního potrubí DN110. Výpis potrubí, tvarovek a armatur v měřicí větvi po výtok do čerpací jímky (pořadí dle směru proudící vody): 1) Tl. potrubí PVC D 50, délka 635 mm 2) Tl. koleno 90, 2x lepený spoj, PVC D 50 3) Tl. potrubí PVC D 50, délka 785 mm 4) Tl. koleno 90 dlouhé, 2x lepený spoj, PVC D 50 5) Tl. potrubí PVC D 50, délka 610 mm 6) Tl. redukce 1x vnější závit PVC D 50/2 7) Uzávěr kulový závitový IVAR.BRA.A3.622, nerez 8) Tl. potrubí PVC D 50, délka 680 mm 9) Tl. koleno 90, 2x lepený spoj, PVC D 50 10) Tl. potrubí PVC D 50, délka 295 mm 11) Tl. koleno 90, 2x lepený spoj, PVC D 50 12) Tl. potrubí PVC D 50, délka 1065 mm 13) Tl. redukce krátká 75/50 PVC 14) Tl. potrubí PVC D 75, délka 3000 mm 15) Tl. redukce krátká 75/50 PVC 16) Tl. potrubí PVC D 50, délka 570 mm 10
54 17) Tl. koleno 90, 2x lepený spoj, PVC D 50 18) Tl. potrubí PVC D 50, délka 645 mm 19) Koleno 90 HTB D 50 20) Potrubí HT D 50 s hrdlem, délka 275 mm 21) Koleno 45 HTB D 50 22) Potrubí HT D 50 s hrdlem, délka 265 mm 23) Odbočka 45 HTEA 110/50 24) Potrubí HT D 110 s hrdlem, délka 840 mm 25) Koleno 90 HTB D ) Potrubí HT D 110 s hrdlem, délka 315 mm Délky potrubí měřicí větve v bodech 1) aţ 14) jsou voleny jako kompromisní poţadavky dispozičního řešení a podmínek uvedených v kap Výpis potrubí, tvarovek a armatur v odpadní větvi po napojení na měřicí větev (pořadí dle směru proudící vody): 1) Tl. zátka 1x lepený spoj, PVC D 50 2) Tl. potrubí PVC D 50, délka 670 mm 3) Potrubí HT DN50 s hrdlem, délka 2055 mm 4) Koleno 90 HTB DN50 5) Potrubí HT DN50 s hrdlem, délka 1590 mm 6) Redukce nesouosá dlouhá HTR 110/50 Všechny přímé části potrubí budou ukotveny do stěn, případně podlahy laboratoře pomocí trubkových objímek opatřených závitovými tyčemi. Objímky je moţné pouţít od různých výrobců. Pro kotvení obou větví výukového okruhu je zapotřebí 1 ks objímky pro D 110, 4 ks objímek pro D 75 a 19 ks objímek pro D 50. Délka závitové tyče bude upravena při instalaci okruhu, vychází však ze vzdálenosti osy potrubí od stěny laboratoře, která se pohybuje v rozmezí 63 aţ 100 mm. Uchycení závitových tyčí ve stěně bude provedeno chemickou kotvou. 7.2 Soustava pro odběr a zobrazení tlakových piezometrických výšek Prvním článkem soustavy je napojení piezometrických trubic na potrubí měřicí větve okruhu. Při instalaci tlakových odběru bude do PVC potrubí vyvrtán otvor průměru 12 mm 11
55 pro osazení GES spojky na hadici s vnějším závitem. Spojka je vyrobena z polyamidu PA6, odolá tlakům 8 10 bar. Obr. 9 Spojka GES pro hadice o vnitřním průměru 4 mm, GUMEX [11] Proti vytaţení spojky z PVC potrubí působí závit M12 x 1,5, který bude zbroušen na potřebnou délku odpovídající tloušťce PVC potrubí. Pevnost a těsnost spoje bude zaručena silikonovým tmelem. Spojka je určena pro hadici o vnitřním průměru 4 mm. Umístění tlakových odběrů pomocí GES spojek je navrţeno ve vzdálenosti 1 D (průměr potrubí) od hrdla kolen, profilů náhlého zúţení a rozšíření, resp. od vnějšího obrysu kulového uzávěru. Tato vzdálenost byla zvolena jako kompromis mezi poţadavky dispozičními a podmínkami uvedenými v příloze 2, kap Vzdálenost tlakových odběrů u přímých úseků větších délek je rozdělena dalším tlakovým odběrem do středu této vzdálenosti. Největší vzdálenost odběrů nastává na úseku s průměrem D 75, vzdálenost sousedních odběrů je 695 mm. Na měřicí větvi okruhu bude umístěno celkem 21 tlakových odběrů. Na tlakové odběry formou spojek GES budou napojeny průsvitné benzinové hadice z novoplastu s vnitřním průměrem 4 mm a tloušťkou stěny 1 mm. Nastrčení hadice na GES spojku bude provedeno po zahřátí konce hadice. Průsvitné hadice plní funkci transportní a zároveň zobrazovací. Hadičky budou vedeny při stěně laboratoře od místa odběru k měřícímu panelu, který bude umístěn na stěně mezi okny laboratoře 960 mm nad podlahou. Panel je tvořen čirým dvoustěnným polykarbonátem tloušťky 10 mm o rozměrech 1500 x 300 mm, jehoţ komůrkami budou protaţeny odběrné hadičky. Navrţené uspořádání zajišťuje dostatečnou viditelnost piezometrických hladin, stabilizaci hadiček v zobrazovací části ve vodorovném směru a moţnost výměny jednotlivých hadiček v případě ulpívání a sráţení nečistot vody na stěnách hadiček sniţující jejich průhlednost. Zobrazovací panel bude podloţen PVC deskou tl. 3 mm s nalepenou papírovou milimetrovou mříţkou chráněnou 12
KONSTRUKČNÍ NÁVRH VÝUKOVÝCH MODELŮ HYDRAULICKÉHO OKRUHU LABORATOŘE CONSTRUCTION DESIGN OF INSTRUCTIONAL MODELS AT THE HYDRAULIC LABORATORY CIRCUIT
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES KONSTRUKČNÍ NÁVRH VÝUKOVÝCH MODELŮ HYDRAULICKÉHO
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES KONSTRUKČNÍ NÁVRH VÝUKOVÝCH MODELŮ HYDRAULICKÉHO
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES KONSTRUKČNÍ NÁVRH VÝUKOVÉHO HYDRAULICKÉHO OKRUHU
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES KONSTRUKČNÍ NÁVRH VÝUKOVÉHO HYDRAULICKÉHO OKRUHU
(Aplikace pro mosty, propustky) K141 HYAR Hydraulika objektů na vodních tocích
 Hydraulika objektů na vodních tocích (Aplikace pro mosty, propustky) 0 Mostní pole provádějící vodní tok pod komunikací (při povodni v srpnu 2002) 14. století hydraulicky špatný návrh úzká pole, široké
Hydraulika objektů na vodních tocích (Aplikace pro mosty, propustky) 0 Mostní pole provádějící vodní tok pod komunikací (při povodni v srpnu 2002) 14. století hydraulicky špatný návrh úzká pole, široké
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTUTRES STANOVENÍ PRŮBĚHU SNÍŽENÍ HLADINY PROTIPROUDNĚ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTUTRES STANOVENÍ PRŮBĚHU SNÍŽENÍ HLADINY PROTIPROUDNĚ
Projekt 1 malé vodní nádrže 4. cvičení
 4. cvičení Václav David K143 e-mail: vaclav.david@fsv.cvut.cz Konzultační hodiny: viz web Obsah cvičení Účel spodní výpusti Součásti spodní výpusti Typy objektů spodní výpusti Umístění spodní výpusti Napojení
4. cvičení Václav David K143 e-mail: vaclav.david@fsv.cvut.cz Konzultační hodiny: viz web Obsah cvičení Účel spodní výpusti Součásti spodní výpusti Typy objektů spodní výpusti Umístění spodní výpusti Napojení
Hydraulika a hydrologie
 Hydraulika a hydrologie Cvičení č. 1 - HYDROSTATIKA Příklad č. 1.1 Jaký je tlak v hloubce (5+P) m pod hladinou moře (Obr. 1.1), je-li průměrná hustota mořské vody ρ mv = 1042 kg/m 3 (měrná tíha je tedy
Hydraulika a hydrologie Cvičení č. 1 - HYDROSTATIKA Příklad č. 1.1 Jaký je tlak v hloubce (5+P) m pod hladinou moře (Obr. 1.1), je-li průměrná hustota mořské vody ρ mv = 1042 kg/m 3 (měrná tíha je tedy
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES STANOVENÍ PRŮBĚHU SNÍŽENÍ HLADINY PROTIPROUDNĚ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES STANOVENÍ PRŮBĚHU SNÍŽENÍ HLADINY PROTIPROUDNĚ
HYDROTECHNICKÝ VÝPOČET
 Výstavba PZS Chrást u Plzně - Stupno v km 17,588, 17,904 a 18,397 SO 5.01.2 Rekonstrukce přejezdová konstrukce v km 17,904 Část objektu: Propustek v km 17,902 Hydrotechnický výpočet HYDROTECHNICKÝ VÝPOČET
Výstavba PZS Chrást u Plzně - Stupno v km 17,588, 17,904 a 18,397 SO 5.01.2 Rekonstrukce přejezdová konstrukce v km 17,904 Část objektu: Propustek v km 17,902 Hydrotechnický výpočet HYDROTECHNICKÝ VÝPOČET
PŘÍKLADY Z HYDRODYNAMIKY Poznámka: Za gravitační zrychlení je ve všech příkladech dosazována přibližná hodnota 10 m.s -2.
 PŘÍKLADY Z HYDRODYNAMIKY Poznámka: Za gravitační zrychlení je ve všech příkladech dosazována přibližná hodnota 10 m.s -. Řešené příklady z hydrodynamiky 1) Příklad užití rovnice kontinuity Zadání: Vodorovným
PŘÍKLADY Z HYDRODYNAMIKY Poznámka: Za gravitační zrychlení je ve všech příkladech dosazována přibližná hodnota 10 m.s -. Řešené příklady z hydrodynamiky 1) Příklad užití rovnice kontinuity Zadání: Vodorovným
2 Průběh výstavby a popis hydraulického okruhu laboratoře
 Výstavba Hydrotechnické laboratoře na Stavební škole ve Vysokém Mýtě Michal Žoužela, Vladimír Hamouz, Pavel Vacek, Lubomír Kříž 1 Úvod Jak jistě řada z nás ví, byla a je Stavební škola Vysoké Mýto již
Výstavba Hydrotechnické laboratoře na Stavební škole ve Vysokém Mýtě Michal Žoužela, Vladimír Hamouz, Pavel Vacek, Lubomír Kříž 1 Úvod Jak jistě řada z nás ví, byla a je Stavební škola Vysoké Mýto již
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES STUDIE MVE V LOKALITĚ PARDUBICE SVÍTKOV STUDY
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES STUDIE MVE V LOKALITĚ PARDUBICE SVÍTKOV STUDY
PŘÍRODĚ BLÍZKÁ POP A REVITALIZACE ÚDOLNÍ NIVY HLAVNÍCH BRNĚNSKÝCH TOKŮ 2.část
 PŘÍRODĚ BLÍZKÁ POP A REVITALIZACE ÚDOLNÍ NIVY HLAVNÍCH BRNĚNSKÝCH TOKŮ 2.část JEZ CACOVICE - NÁVRH RYBÍHO PŘECHODU A VODÁCKÉ PROPUSTI SO 18.3.2 - TECHNICKÁ ZPRÁVA 1.1. NÁVRH UMÍSTĚNÍ RYBÍHO PŘECHODU...
PŘÍRODĚ BLÍZKÁ POP A REVITALIZACE ÚDOLNÍ NIVY HLAVNÍCH BRNĚNSKÝCH TOKŮ 2.část JEZ CACOVICE - NÁVRH RYBÍHO PŘECHODU A VODÁCKÉ PROPUSTI SO 18.3.2 - TECHNICKÁ ZPRÁVA 1.1. NÁVRH UMÍSTĚNÍ RYBÍHO PŘECHODU...
IDENTIFIKAČNÍ ÚDAJE AKCE...
 Obsah 1. IDENTIFIKAČNÍ ÚDAJE AKCE... 2 2. ÚVOD... 2 3. POUŽITÉ PODKLADY... 2 3.1 Geodetické podklady... 2 3.2 Hydrologické podklady... 2 3.2.1 Odhad drsnosti... 3 3.3 Popis lokality... 3 3.4 Popis stavebních
Obsah 1. IDENTIFIKAČNÍ ÚDAJE AKCE... 2 2. ÚVOD... 2 3. POUŽITÉ PODKLADY... 2 3.1 Geodetické podklady... 2 3.2 Hydrologické podklady... 2 3.2.1 Odhad drsnosti... 3 3.3 Popis lokality... 3 3.4 Popis stavebních
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY VÍCEÚČELOVÁ SPORTOVNÍ HALA MULTI-FUNCTION SPORTS HALL
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES VÍCEÚČELOVÁ SPORTOVNÍ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES VÍCEÚČELOVÁ SPORTOVNÍ
1141 HYA (Hydraulika)
 ČVUT v Praze, fakulta stavební katedra hydrauliky a hydrologie (K4) Přednáškové slidy předmětu 4 HYA (Hydraulika) verze: 09/008 K4 Fv ČVUT Tato webová stránka nabízí k nahlédnutí/stažení řadu pdf souborů
ČVUT v Praze, fakulta stavební katedra hydrauliky a hydrologie (K4) Přednáškové slidy předmětu 4 HYA (Hydraulika) verze: 09/008 K4 Fv ČVUT Tato webová stránka nabízí k nahlédnutí/stažení řadu pdf souborů
ČVUT v Praze Fakulta stavební Katedra Technických zařízení budov. Modelování termohydraulických jevů 3.hodina. Hydraulika. Ing. Michal Kabrhel, Ph.D.
 ČVUT v Praze Fakulta stavební Katedra Technických zařízení budov Modelování termohydraulických jevů 3.hodina Hydraulika Ing. Michal Kabrhel, Ph.D. Letní semestr 008/009 Pracovní materiály pro výuku předmětu.
ČVUT v Praze Fakulta stavební Katedra Technických zařízení budov Modelování termohydraulických jevů 3.hodina Hydraulika Ing. Michal Kabrhel, Ph.D. Letní semestr 008/009 Pracovní materiály pro výuku předmětu.
Měřící žlaby FR Technické podmínky
 Měřící žlaby FR 200-250-300-400-500 Technické podmínky TP 9-2012 MI FLOW s.r.o. Zahradnická 12, PSČ 603 00 Brno Tel./fax:+420 515 540 166 Tel.:+420 603 810 247 Email: info@miflow.cz Základní technické
Měřící žlaby FR 200-250-300-400-500 Technické podmínky TP 9-2012 MI FLOW s.r.o. Zahradnická 12, PSČ 603 00 Brno Tel./fax:+420 515 540 166 Tel.:+420 603 810 247 Email: info@miflow.cz Základní technické
4. cvičení- vzorové příklady
 Příklad 4. cvičení- vzorové příklady ypočítejte kapacitu násosky a posuďte její funkci. Násoska převádí vodu z horní nádrže, která má hladinu na kótě H A = m, přes zvýšené místo a voda vytéká na konci
Příklad 4. cvičení- vzorové příklady ypočítejte kapacitu násosky a posuďte její funkci. Násoska převádí vodu z horní nádrže, která má hladinu na kótě H A = m, přes zvýšené místo a voda vytéká na konci
Základy hydrauliky vodních toků
 Základy hydrauliky vodních toků Jan Unucka, 014 Motivace pro začínajícího hydroinformatika Cesta do pravěku Síly ovlivňující proudění 1. Gravitace. Tření 3. Coriolisova síla 4. Vítr 5. Vztlak (rozdíly
Základy hydrauliky vodních toků Jan Unucka, 014 Motivace pro začínajícího hydroinformatika Cesta do pravěku Síly ovlivňující proudění 1. Gravitace. Tření 3. Coriolisova síla 4. Vítr 5. Vztlak (rozdíly
OCELOVÁ KONSTRUKCE ROZHLEDNY STEEL STRUCTURE OF VIEWING TOWER
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES OCELOVÁ KONSTRUKCE
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES OCELOVÁ KONSTRUKCE
(režimy proudění, průběh hladin) Proudění s volnou hladinou II
 Proudění s volnou hladinou (režimy proudění, průběh hladin) PROUDĚNÍ KRITICKÉ, ŘÍČNÍ A BYSTŘINNÉ Vztah mezi h (resp. y) a v: Ve žlabu za různých sklonů α a konst. Q: α 1 < α < α 3 => G s1 < G s < G s3
Proudění s volnou hladinou (režimy proudění, průběh hladin) PROUDĚNÍ KRITICKÉ, ŘÍČNÍ A BYSTŘINNÉ Vztah mezi h (resp. y) a v: Ve žlabu za různých sklonů α a konst. Q: α 1 < α < α 3 => G s1 < G s < G s3
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES INTERAKTIVNÍ VÝUKOVÉ MODELY VODOHOSPODÁŘSKÝCH
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES INTERAKTIVNÍ VÝUKOVÉ MODELY VODOHOSPODÁŘSKÝCH
P R OGR AM P R O NÁVRH VÝVAR U
 P R OGR AM P R O NÁVRH VÝVAR U Program Vývar je jednoduchá aplikace řešící problematiku vodního skoku. Zahrnuje interaktivní zadávání dat pro určení dimenze vývaru, tzn. jeho hloubku a délku. V aplikaci
P R OGR AM P R O NÁVRH VÝVAR U Program Vývar je jednoduchá aplikace řešící problematiku vodního skoku. Zahrnuje interaktivní zadávání dat pro určení dimenze vývaru, tzn. jeho hloubku a délku. V aplikaci
Zásady křížení vodních toků a komunikací Doc. Ing. Aleš Havlík, CSc.
 Zásady křížení vodních toků a Doc. Ing. Aleš Havlík, CSc. Respektování vodohospodářských zájmů Návrh křížení musí respektovat : Bezpečnost ochranných hrází. Splaveninový režim toku a stabilitu koryta toku.
Zásady křížení vodních toků a Doc. Ing. Aleš Havlík, CSc. Respektování vodohospodářských zájmů Návrh křížení musí respektovat : Bezpečnost ochranných hrází. Splaveninový režim toku a stabilitu koryta toku.
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY ZASTŘEŠENÍ SPORTOVNÍHO OBJEKTU THE ROOFING OF THE SPORT HALL ÚVODNÍ LISTY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES ZASTŘEŠENÍ SPORTOVNÍHO
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES ZASTŘEŠENÍ SPORTOVNÍHO
KRAJSKÁ KNIHOVNA V HAVLÍČKOVĚ BRODĚ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES KRAJSKÁ KNIHOVNA
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES KRAJSKÁ KNIHOVNA
Spodní výpusti 5. PŘEDNÁŠKA. BS053 Rybníky a účelové nádrže
 Spodní výpusti 5. PŘEDNÁŠKA BS053 Rybníky a účelové nádrže Spodní výpusti Obsah Rozdělení spodních výpustí Konstrukční zásady Dimenzování spodních výpustí Rekonstrukce a opravy Rozdělení spodních výpustí
Spodní výpusti 5. PŘEDNÁŠKA BS053 Rybníky a účelové nádrže Spodní výpusti Obsah Rozdělení spodních výpustí Konstrukční zásady Dimenzování spodních výpustí Rekonstrukce a opravy Rozdělení spodních výpustí
NOSNÁ KONSTRUKCE ZASTŘEŠENÍ FOTBALOVÉ TRIBUNY STEEL STRUCTURE OF FOOTBAL GRANDSTAND
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES NOSNÁ KONSTRUKCE
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES NOSNÁ KONSTRUKCE
Proudění s volnou hladinou (tj. v otevřených korytech)
 (tj. v otevřených korytech) TYPY OTEVŘENÝCH KORYT PŘÍRODNÍ přirozená a upravená KORYTA - přirozená: nepravidelného geometrického průřezu - upravená: zhruba pravidel. průřezu (upravené většinou jen břehy,
(tj. v otevřených korytech) TYPY OTEVŘENÝCH KORYT PŘÍRODNÍ přirozená a upravená KORYTA - přirozená: nepravidelného geometrického průřezu - upravená: zhruba pravidel. průřezu (upravené většinou jen břehy,
Sypaná hráz výpočet ustáleného proudění
 Inženýrský manuál č. 32 Aktualizace: 3/2016 Sypaná hráz výpočet ustáleného proudění Program: MKP Proudění Soubor: Demo_manual_32.gmk Úvod Tento příklad ilustruje použití modulu GEO5 MKP Proudění při analýze
Inženýrský manuál č. 32 Aktualizace: 3/2016 Sypaná hráz výpočet ustáleného proudění Program: MKP Proudění Soubor: Demo_manual_32.gmk Úvod Tento příklad ilustruje použití modulu GEO5 MKP Proudění při analýze
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV POZEMNÍCH KOMUNIKACÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF ROAD STRUCTURES VYHLEDÁVACÍ STUDIE OBCHVATU OBCE OSTROMĚŘ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV POZEMNÍCH KOMUNIKACÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF ROAD STRUCTURES VYHLEDÁVACÍ STUDIE OBCHVATU OBCE OSTROMĚŘ
Tlumení energie 7. PŘEDNÁŠKA. BS053 Rybníky a účelové nádrže
 Tlumení energie 7. PŘEDNÁŠKA BS053 Rybníky a účelové nádrže Tlumení energie Rozdělení podle způsobu vývarové (vodní skok, dimenzování) bezvývarové (umělá drsnost koryta) průběžná niveleta (max. 0,5 m převýšení)
Tlumení energie 7. PŘEDNÁŠKA BS053 Rybníky a účelové nádrže Tlumení energie Rozdělení podle způsobu vývarové (vodní skok, dimenzování) bezvývarové (umělá drsnost koryta) průběžná niveleta (max. 0,5 m převýšení)
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY STUDIE TURBÍNY S VÍŘIVÝM OBĚŽNÝM KOLEM STUDY OF TURBINE WITH SIDE CHANNEL RUNNER
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ENERGETICKÝ ÚSTAV FACULTY OF MECHANICAL ENGINEERING ENERGY INSTITUTE STUDIE TURBÍNY S VÍŘIVÝM OBĚŽNÝM KOLEM STUDY
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ENERGETICKÝ ÚSTAV FACULTY OF MECHANICAL ENGINEERING ENERGY INSTITUTE STUDIE TURBÍNY S VÍŘIVÝM OBĚŽNÝM KOLEM STUDY
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES STANOVENÍ MINIMÁLNÍ PROTIPROUDNÍ VZDÁLENOSTI
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES STANOVENÍ MINIMÁLNÍ PROTIPROUDNÍ VZDÁLENOSTI
Vodní skok, tlumení kinetické energie
 Fakulta stavební ČVUT v Praze Katedra a hdraulik a hdrologie og Předmět HYV K4 FSv ČVUT Vodní skok, tlumení kinetické energie Řešení průběhu hladin v otevřených kortech Doc. Ing. Aleš Havlík, CSc., Ing.
Fakulta stavební ČVUT v Praze Katedra a hdraulik a hdrologie og Předmět HYV K4 FSv ČVUT Vodní skok, tlumení kinetické energie Řešení průběhu hladin v otevřených kortech Doc. Ing. Aleš Havlík, CSc., Ing.
Mechanika tekutin. Tekutiny = plyny a kapaliny
 Mechanika tekutin Tekutiny = plyny a kapaliny Vlastnosti kapalin Kapaliny mění tvar, ale zachovávají objem jsou velmi málo stlačitelné Ideální kapalina: bez vnitřního tření je zcela nestlačitelná Viskozita
Mechanika tekutin Tekutiny = plyny a kapaliny Vlastnosti kapalin Kapaliny mění tvar, ale zachovávají objem jsou velmi málo stlačitelné Ideální kapalina: bez vnitřního tření je zcela nestlačitelná Viskozita
FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES BAKALÁŘSKÁ PRÁCE BACHELOR'S THESIS. prof. Ing. MARCELA KARMAZÍNOVÁ, CSc.
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES OCELOVÁ NOSNÁ KONSTRUKCE
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES OCELOVÁ NOSNÁ KONSTRUKCE
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES PŘEPOČET A VARIANTNÍ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES PŘEPOČET A VARIANTNÍ
FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB STUDIE PROTIPOVODŇOVÝCH OPATŘENÍ V LOKALITE DOLNÍ LOUČKY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERZITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES STUDIE PROTIPOVODŇOVÝCH OPATŘENÍ V LOKALITE
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERZITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES STUDIE PROTIPOVODŇOVÝCH OPATŘENÍ V LOKALITE
ŽELEZOBETONOVÁ SKELETOVÁ KONSTRUKCE
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES ŽELEZOBETONOVÁ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES ŽELEZOBETONOVÁ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ STATICKÉ ŘEŠENÍ SOUSTAVY ŽELEZOBETONOVÝCH NÁDRŽÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES STATICKÉ ŘEŠENÍ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES STATICKÉ ŘEŠENÍ
Otázky pro Státní závěrečné zkoušky
 Obor: Název SZZ: Strojírenství Mechanika Vypracoval: Doc. Ing. Petr Hrubý, CSc. Doc. Ing. Jiří Míka, CSc. Podpis: Schválil: Doc. Ing. Štefan Husár, PhD. Podpis: Datum vydání 8. září 2014 Platnost od: AR
Obor: Název SZZ: Strojírenství Mechanika Vypracoval: Doc. Ing. Petr Hrubý, CSc. Doc. Ing. Jiří Míka, CSc. Podpis: Schválil: Doc. Ing. Štefan Husár, PhD. Podpis: Datum vydání 8. září 2014 Platnost od: AR
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES PROJEKTOVÁNÍ LINIOVÝCH HYDROTECHNICKÝCH STAVEB
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES PROJEKTOVÁNÍ LINIOVÝCH HYDROTECHNICKÝCH STAVEB
Teoretické otázky z hydromechaniky
 Teoretické otázky z hydromechaniky 1. Napište vztah pro modul pružnosti kapaliny (+ popis jednotlivých členů a 2. Napište vztah pro Newtonův vztah pro tečné napětí (+ popis jednotlivých členů a 3. Jaká
Teoretické otázky z hydromechaniky 1. Napište vztah pro modul pružnosti kapaliny (+ popis jednotlivých členů a 2. Napište vztah pro Newtonův vztah pro tečné napětí (+ popis jednotlivých členů a 3. Jaká
Klíčová slova Autosalon Oblouk Vaznice Ocelová konstrukce Příhradový vazník
 Abstrakt Bakalářská práce se zabývá návrhem nosné příhradové ocelové konstrukce autosalonu v lokalitě města Blansko. Půdorysné rozměry objektu jsou 24 x 48 m. Hlavní nosnou částí je oblouková příčná vazba
Abstrakt Bakalářská práce se zabývá návrhem nosné příhradové ocelové konstrukce autosalonu v lokalitě města Blansko. Půdorysné rozměry objektu jsou 24 x 48 m. Hlavní nosnou částí je oblouková příčná vazba
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY VÍCEÚČELOVÁ SPORTOVNÍ HALA MULTIPURPOSE SPORT HALL
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES VÍCEÚČELOVÁ SPORTOVNÍ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES VÍCEÚČELOVÁ SPORTOVNÍ
HYDRAULICKÉ JEVY NA JEZECH
 HYDRAULICKÉ JEVY NA JEZECH Doc. Ing. Aleš Havlík, CSc. ČVUT v Praze, Fakulta stavební Katedra hydrauliky a hydrologie 1. REŽIMY PROUDĚNÍ S VOLNOU HLADINOU Proudění říční, kritické a bystřinné 2. PŘEPADY
HYDRAULICKÉ JEVY NA JEZECH Doc. Ing. Aleš Havlík, CSc. ČVUT v Praze, Fakulta stavební Katedra hydrauliky a hydrologie 1. REŽIMY PROUDĚNÍ S VOLNOU HLADINOU Proudění říční, kritické a bystřinné 2. PŘEPADY
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES NÁVRH NOSNÉ OCELOVÉ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES NÁVRH NOSNÉ OCELOVÉ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES ÚPRAVA HARTMANICKÉHO POTOKA REGULATION OF HARTMANICE
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES ÚPRAVA HARTMANICKÉHO POTOKA REGULATION OF HARTMANICE
Mechanika tekutin. Hydrostatika Hydrodynamika
 Mechanika tekutin Hydrostatika Hydrodynamika Hydrostatika Kapalinu považujeme za kontinuum, můžeme využít předchozí úvahy Studujeme kapalinu, která je v klidu hydrostatika Objem kapaliny bude v klidu,
Mechanika tekutin Hydrostatika Hydrodynamika Hydrostatika Kapalinu považujeme za kontinuum, můžeme využít předchozí úvahy Studujeme kapalinu, která je v klidu hydrostatika Objem kapaliny bude v klidu,
CVIČENÍ č. 11 ZTRÁTY PŘI PROUDĚNÍ POTRUBÍM
 CVIČENÍ č. 11 ZTRÁTY PŘI PROUDĚNÍ POTRUBÍM Místní ztráty, Tlakové ztráty Příklad č. 1: Jistá část potrubí rozvodného systému vody se skládá ze dvou paralelně uspořádaných větví. Obě potrubí mají průřez
CVIČENÍ č. 11 ZTRÁTY PŘI PROUDĚNÍ POTRUBÍM Místní ztráty, Tlakové ztráty Příklad č. 1: Jistá část potrubí rozvodného systému vody se skládá ze dvou paralelně uspořádaných větví. Obě potrubí mají průřez
PŘÍRODĚ BLÍZKÁ POP A REVITALIZACE ÚDOLNÍ NIVY HLAVNÍCH BRNĚNSKÝCH TOKŮ 2.část
 PŘÍRODĚ BLÍZKÁ POP A REVITALIZACE ÚDOLNÍ NIVY HLAVNÍCH BRNĚNSKÝCH TOKŮ 2.část KOMÍNSKÝ JEZ - NÁVRH RYBÍHO PŘECHODU A VODÁCKÉ PROPUSTI SO 03.3.2 - TECHNICKÁ ZPRÁVA 1.1. NÁVRH UMÍSTĚNÍ RYBÍHO PŘECHODU...
PŘÍRODĚ BLÍZKÁ POP A REVITALIZACE ÚDOLNÍ NIVY HLAVNÍCH BRNĚNSKÝCH TOKŮ 2.část KOMÍNSKÝ JEZ - NÁVRH RYBÍHO PŘECHODU A VODÁCKÉ PROPUSTI SO 03.3.2 - TECHNICKÁ ZPRÁVA 1.1. NÁVRH UMÍSTĚNÍ RYBÍHO PŘECHODU...
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV POZEMNÍHO STAVITELSTVÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF BUILDING STRUCTURES SLOŽKA A POLYFUNKČNÍ RODINNÝ DŮM
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV POZEMNÍHO STAVITELSTVÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF BUILDING STRUCTURES SLOŽKA A POLYFUNKČNÍ RODINNÝ DŮM
Průtoky. Q t Proteklé množství O (m 3 ) objem vody, který proteče průtočným profilem daným průtokem za delší čas (den, měsíc, rok)
 PRŮTOKY Průtoky Průtok Q (m 3 /s, l/s) objem vody, který proteče daným průtočným V profilem za jednotku doby (s) Q t Proteklé množství O (m 3 ) objem vody, který proteče průtočným profilem daným průtokem
PRŮTOKY Průtoky Průtok Q (m 3 /s, l/s) objem vody, který proteče daným průtočným V profilem za jednotku doby (s) Q t Proteklé množství O (m 3 ) objem vody, který proteče průtočným profilem daným průtokem
PROPUSTKY NA POZEMNÍCH KOMUNIKACÍCH. Michal Radimský
 PROPUSTKY NA POZEMNÍCH KOMUNIKACÍCH Michal Radimský PROPUSTKY NA PK propustky jsou mostní objekty s kolmou světlostí do 2 m (včetně) setkáme se s nimi jak v extravilánu, tak i v intravilánu trubní propustky
PROPUSTKY NA POZEMNÍCH KOMUNIKACÍCH Michal Radimský PROPUSTKY NA PK propustky jsou mostní objekty s kolmou světlostí do 2 m (včetně) setkáme se s nimi jak v extravilánu, tak i v intravilánu trubní propustky
Studentská tvůrčí činnost 2009
 Studentská tvůrčí činnost 2009 Numerické řešení proudového pole v kompresorové lopatkové mříži Balcarová Lucie Vedoucí práce: Prof. Ing. P. Šafařík, CSc. a Ing. T. Hyhlík, PhD. Numerické řešení proudového
Studentská tvůrčí činnost 2009 Numerické řešení proudového pole v kompresorové lopatkové mříži Balcarová Lucie Vedoucí práce: Prof. Ing. P. Šafařík, CSc. a Ing. T. Hyhlík, PhD. Numerické řešení proudového
1141 HYA (Hydraulika)
 ČVUT v Praze, fakulta stavení katedra ydrauliky a ydrologie (K141) Přednáškové slidy předmětu 1141 HYA (Hydraulika) verze: 1/011 K141 FSv ČVUT Tato weová stránka naízí k nalédnutí/stažení řadu pdf souorů
ČVUT v Praze, fakulta stavení katedra ydrauliky a ydrologie (K141) Přednáškové slidy předmětu 1141 HYA (Hydraulika) verze: 1/011 K141 FSv ČVUT Tato weová stránka naízí k nalédnutí/stažení řadu pdf souorů
Univerzita obrany. Měření součinitele tření potrubí K-216. Laboratorní cvičení z předmětu HYDROMECHANIKA. Protokol obsahuje 14 listů
 Univerzita obrany K-216 Laboratorní cvičení z předmětu HYDROMECHANIKA Měření součinitele tření potrubí Protokol obsahuje 14 listů Vypracoval: Vít Havránek Studijní skupina: 21-3LRT-C Datum zpracování:5.5.2011
Univerzita obrany K-216 Laboratorní cvičení z předmětu HYDROMECHANIKA Měření součinitele tření potrubí Protokol obsahuje 14 listů Vypracoval: Vít Havránek Studijní skupina: 21-3LRT-C Datum zpracování:5.5.2011
Rozumíme dobře Archimedovu zákonu?
 Rozumíme dobře Archimedovu zákonu? BOHUMIL VYBÍRAL Přírodovědecká fakulta Univerzity Hradec Králové K formulaci Archimedova zákona Archimedův zákon platí za podmínek, pro které byl odvozen, tj. že hydrostatické
Rozumíme dobře Archimedovu zákonu? BOHUMIL VYBÍRAL Přírodovědecká fakulta Univerzity Hradec Králové K formulaci Archimedova zákona Archimedův zákon platí za podmínek, pro které byl odvozen, tj. že hydrostatické
Bezpečnostní přelivy 6. PŘEDNÁŠKA. BS053 Rybníky a účelové nádrže
 Bezpečnostní přelivy 6. PŘEDNÁŠKA BS053 Rybníky a účelové nádrže Bezpečnostní přelivy Obsah Rozdělení přelivů a konstrukční zásady Dimenzování přelivů Bezpečnostní přelivy Bezpečnostní přelivy slouží k
Bezpečnostní přelivy 6. PŘEDNÁŠKA BS053 Rybníky a účelové nádrže Bezpečnostní přelivy Obsah Rozdělení přelivů a konstrukční zásady Dimenzování přelivů Bezpečnostní přelivy Bezpečnostní přelivy slouží k
p gh Hladinové (rovňové) plochy Tlak v kapalině, na niž působí pouze gravitační síla země
 Hladinové (rovňové) plochy Plochy, ve kterých je stálý statický tlak. Při posunu po takové ploše je přírůstek tlaku dp = 0. Hladinová plocha musí být všude kolmá ke směru výsledného zrychlení. Tlak v kapalině,
Hladinové (rovňové) plochy Plochy, ve kterých je stálý statický tlak. Při posunu po takové ploše je přírůstek tlaku dp = 0. Hladinová plocha musí být všude kolmá ke směru výsledného zrychlení. Tlak v kapalině,
Clony a dýzy Měření průtoku pomocí tlakové diference
 Clony a dýzy Měření průtoku pomocí tlakové diference - Ověřený normovaný způsob měření - Přesné měření i pro rychle proudící páru a plyn - Absence pohyblivých prvků - Robustní a variabilní provedení -
Clony a dýzy Měření průtoku pomocí tlakové diference - Ověřený normovaný způsob měření - Přesné měření i pro rychle proudící páru a plyn - Absence pohyblivých prvků - Robustní a variabilní provedení -
VLIV PŮDORYSNÉHO ZAKŘIVENÍ NA KAPACITU PŘELIVU INFLUENCE OF PLAN RADIUS ON DISCHARGING CAPACITY OF WEIR
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES VLIV PŮDORYSNÉHO ZAKŘIVENÍ NA KAPACITU PŘELIVU
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES VLIV PŮDORYSNÉHO ZAKŘIVENÍ NA KAPACITU PŘELIVU
Úvodní list. Zdravotní technika 4. ročník (TZB) Kanalizace Výpočet přečerpávané odpadní vody
 Úvodní list Název školy Integrovaná střední škola stavební, České Budějovice, Nerudova 59 Číslo šablony/ číslo sady 32/09 Poř. číslo v sadě 06 Jméno autora Období vytvoření materiálu Název souboru Zařazení
Úvodní list Název školy Integrovaná střední škola stavební, České Budějovice, Nerudova 59 Číslo šablony/ číslo sady 32/09 Poř. číslo v sadě 06 Jméno autora Období vytvoření materiálu Název souboru Zařazení
ČESKÁ TECHNICKÁ NORMA
 ČESKÁ TECHNICKÁ NORMA ICS 17.120.20 1998 Měření průtoku vody v otevřených korytech pomocí přelivů a Venturiho žlabů - Část 1: Tenkostěnné přelivy ČSN ISO 1438-1 25 9331 Červen Water flow measurement in
ČESKÁ TECHNICKÁ NORMA ICS 17.120.20 1998 Měření průtoku vody v otevřených korytech pomocí přelivů a Venturiho žlabů - Část 1: Tenkostěnné přelivy ČSN ISO 1438-1 25 9331 Červen Water flow measurement in
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY OCELOVÁ KONSTRUKCE HALY STEEL STRUCTURE OF A HALL
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES OCELOVÁ KONSTRUKCE
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES OCELOVÁ KONSTRUKCE
VLIV SKLONU NÁVODNÍHO LÍCE PŘELIVU SE ŠIROKOU KORUNOU NA SOUČINITEL PRŮTOKU
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES VLIV SKLONU NÁVODNÍHO LÍCE PŘELIVU SE ŠIROKOU
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV VODNÍCH STAVEB FACULTY OF CIVIL ENGINEERING INSTITUTE OF WATER STRUCTURES VLIV SKLONU NÁVODNÍHO LÍCE PŘELIVU SE ŠIROKOU
Proudění vody v potrubí. Martin Šimek
 Proudění vody v potrubí Martin Šimek Zadání problému Umělá vlna pro surfing Dosavadní řešení pomocí čerpadel Sestrojení modelu pro přívod vody z řeky Vyčíslení tohoto modelu Zhodnocení výsledků Návrh systému
Proudění vody v potrubí Martin Šimek Zadání problému Umělá vlna pro surfing Dosavadní řešení pomocí čerpadel Sestrojení modelu pro přívod vody z řeky Vyčíslení tohoto modelu Zhodnocení výsledků Návrh systému
Propustky a mosty malých rozpětí
 Distribuce: DIVYP Brno s.r.o., Hlavní 156/80, 64 00 Brno, ICO: 15530345, Tel.: 776614664, E-mail: info@divypbrno.cz TP 3 MINISTERSTVO DOPRAVY ODBOR POZEMNÍCH KOMUNIKACÍ TECHNICKÉ PODMÍNKY Schváleno MD
Distribuce: DIVYP Brno s.r.o., Hlavní 156/80, 64 00 Brno, ICO: 15530345, Tel.: 776614664, E-mail: info@divypbrno.cz TP 3 MINISTERSTVO DOPRAVY ODBOR POZEMNÍCH KOMUNIKACÍ TECHNICKÉ PODMÍNKY Schváleno MD
1 min. Zabarvení vody. 2 min. 5 min. 6 min. 7 min. 8 min.
 DIN 18800-7, PN-B-06200 DIN EN ISO 3834-2 Zabarvení vody 1 min. 2 min. 3 min. 4 min. 5 min. 6 min. 7 min. 8 min. AKVAHELP METAL spol. s r.o. VÝROBCE NEREZOVÝCH BAZÉNŮ Pobřežní 249/46, 186 00 Praha 8 -
DIN 18800-7, PN-B-06200 DIN EN ISO 3834-2 Zabarvení vody 1 min. 2 min. 3 min. 4 min. 5 min. 6 min. 7 min. 8 min. AKVAHELP METAL spol. s r.o. VÝROBCE NEREZOVÝCH BAZÉNŮ Pobřežní 249/46, 186 00 Praha 8 -
BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ENERGETICKÝ ÚSTAV FACULTY OF MECHANICAL ENGINEERING ENERGY INSTITUTE
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ENERGETICKÝ ÚSTAV FACULTY OF MECHANICAL ENGINEERING ENERGY INSTITUTE SAMONASÁVACÍ ČERPADLO SELF-PRIMING PUMP DIPLOMOVÁ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ENERGETICKÝ ÚSTAV FACULTY OF MECHANICAL ENGINEERING ENERGY INSTITUTE SAMONASÁVACÍ ČERPADLO SELF-PRIMING PUMP DIPLOMOVÁ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES PATROVÉ GARÁŽE PARK
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES PATROVÉ GARÁŽE PARK
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES ŽELEZOBETONOVÁ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES ŽELEZOBETONOVÁ
OCELOVÁ PRŮMYSLOVÁ HALA S JEŘÁBOVOU DRÁHOU STEEL INDUSTRIAL HALL WITH CRANE RAIL
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES OCELOVÁ PRŮMYSLOVÁ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES OCELOVÁ PRŮMYSLOVÁ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES MULTIFUNKČNÍ CENTRUM
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES MULTIFUNKČNÍ CENTRUM
Výpočet hltnosti odvodňovačů
 Výpočet hltnosti odvodňovačů Základní typy Rigolový V, L, M V České republice se zatím užíval postup, kdy za hltnost odvodňovačů bylo považováno množství vody, které přeteklo nad mříží. Nebyly řešeny malé
Výpočet hltnosti odvodňovačů Základní typy Rigolový V, L, M V České republice se zatím užíval postup, kdy za hltnost odvodňovačů bylo považováno množství vody, které přeteklo nad mříží. Nebyly řešeny malé
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES PŘEPOČET A ALTERNATIVNÍ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES PŘEPOČET A ALTERNATIVNÍ
Výpočet skořepiny tlakové nádoby.
 Václav Slaný BS design Bystřice nad Pernštejnem 1 Výpočet skořepiny tlakové nádoby. Úvod Indukční průtokoměry mají ve své podstatě svařovanou konstrukci základního tělesa. Její pevnost se musí posuzovat
Václav Slaný BS design Bystřice nad Pernštejnem 1 Výpočet skořepiny tlakové nádoby. Úvod Indukční průtokoměry mají ve své podstatě svařovanou konstrukci základního tělesa. Její pevnost se musí posuzovat
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY ODSTRANĚNÍ PILÍŘE V NOSNÉ STĚNĚ REMOVING OF MASONRY PILLAR FROM LOAD BEARING WALL
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES ODSTRANĚNÍ PILÍŘE
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES ODSTRANĚNÍ PILÍŘE
6. Mechanika kapalin a plynů
 6. Mechanika kapalin a plynů 1. Definice tekutin 2. Tlak 3. Pascalův zákon 4. Archimedův zákon 5. Rovnice spojitosti (kontinuity) 6. Bernoulliho rovnice 7. Fyzika letu Tekutiny: jejich rozdělení, jejich
6. Mechanika kapalin a plynů 1. Definice tekutin 2. Tlak 3. Pascalův zákon 4. Archimedův zákon 5. Rovnice spojitosti (kontinuity) 6. Bernoulliho rovnice 7. Fyzika letu Tekutiny: jejich rozdělení, jejich
Úvodní list. Prezentace pro interaktivní tabuli, pro projekci pomůcka pro výklad
 Úvodní list Název školy Integrovaná střední škola stavební, České Budějovice, Nerudova 59 Číslo šablony/ číslo sady 32/09 Poř. číslo v sadě 18 Jméno autora Období vytvoření materiálu Název souboru Zařazení
Úvodní list Název školy Integrovaná střední škola stavební, České Budějovice, Nerudova 59 Číslo šablony/ číslo sady 32/09 Poř. číslo v sadě 18 Jméno autora Období vytvoření materiálu Název souboru Zařazení
Proudění vzduchu v chladícím kanálu ventilátoru lokomotivy
 Proudění vzduchu v chladícím kanálu ventilátoru lokomotivy P. Šturm ŠKODA VÝZKUM s.r.o. Abstrakt: Příspěvek se věnuje optimalizaci průtoku vzduchu chladícím kanálem ventilátoru lokomotivy. Optimalizace
Proudění vzduchu v chladícím kanálu ventilátoru lokomotivy P. Šturm ŠKODA VÝZKUM s.r.o. Abstrakt: Příspěvek se věnuje optimalizaci průtoku vzduchu chladícím kanálem ventilátoru lokomotivy. Optimalizace
LABORATORNÍ ZKOUŠKY VZORKY LABORATORNÍ ZKOUŠKY. Postup laboratorních zkoušek
 LABORATORNÍ ZKOUŠKY Jednou z hlavních součástí grantového projektu jsou laboratorní zkoušky elastomerových ložisek. Cílem zkoušek je získání pracovního diagramu elastomerových ložisek v tlaku a porovnání
LABORATORNÍ ZKOUŠKY Jednou z hlavních součástí grantového projektu jsou laboratorní zkoušky elastomerových ložisek. Cílem zkoušek je získání pracovního diagramu elastomerových ložisek v tlaku a porovnání
Systém větrání využívající Coanda efekt
 Systém větrání využívající Coanda efekt Apollo ID: 24072 Datum: 23. 11. 2009 Typ projektu: G funkční vzorek Autoři: Jedelský Jan, Ing., Ph.D., Jícha Miroslav, prof. Ing., CSc., Vach Tomáš, Ing. Technický
Systém větrání využívající Coanda efekt Apollo ID: 24072 Datum: 23. 11. 2009 Typ projektu: G funkční vzorek Autoři: Jedelský Jan, Ing., Ph.D., Jícha Miroslav, prof. Ing., CSc., Vach Tomáš, Ing. Technický
VYSOKÉ U ENÍ TECHNICKÉ V BRN BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UENÍ TECHNICKÉ V BRN BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES ŽELEZOBETONOVÁ
VYSOKÉ UENÍ TECHNICKÉ V BRN BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES ŽELEZOBETONOVÁ
ZLATÝ POTOK (ř. km 0,000 12,267) stanovení záplavového území Technická zpráva
 ZLATÝ POTOK (ř. km 0,000 12,267) stanovení záplavového území Technická zpráva Povodí Labe, státní podnik Hradec Králové srpen 2016 výškový systém Bpv OBSAH 1. Úvod... 3 1.1. Podklady... 3 1.2. Popis zájmového
ZLATÝ POTOK (ř. km 0,000 12,267) stanovení záplavového území Technická zpráva Povodí Labe, státní podnik Hradec Králové srpen 2016 výškový systém Bpv OBSAH 1. Úvod... 3 1.1. Podklady... 3 1.2. Popis zájmového
FLOW PARAMETERS MEASUREMENT IN THE CURVED DIFFUSER OF THE RECTANGULAR CROSS-SECTION
 FLOW PARAMETERS MEASUREMENT IN THE CURVED DIFFUSER OF THE RECTANGULAR CROSS-SECTION Zubík. P., Šulc J. Summary: The article deals with measurement of flow parameters in the bend diffuser of the rectangular
FLOW PARAMETERS MEASUREMENT IN THE CURVED DIFFUSER OF THE RECTANGULAR CROSS-SECTION Zubík. P., Šulc J. Summary: The article deals with measurement of flow parameters in the bend diffuser of the rectangular
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ OCELOVÁ HALA PRO PRŮMYSLOVOU VÝROBU STEEL HALL STRUCTURE FOR INDUSTRIAL PRODUCTION
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES OCELOVÁ HALA PRO
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES OCELOVÁ HALA PRO
Příloha č. 1. Pevnostní výpočty
 Příloha č. 1 Pevnostní výpočty Pevnostní výpočty navrhovaného CKT byly provedeny podle normy ČSN 69 0010 Tlakové nádoby stabilní. Technická pravidla. Vzorce a texty v této příloze jsou převzaty z této
Příloha č. 1 Pevnostní výpočty Pevnostní výpočty navrhovaného CKT byly provedeny podle normy ČSN 69 0010 Tlakové nádoby stabilní. Technická pravidla. Vzorce a texty v této příloze jsou převzaty z této
Projekt 1 malé vodní nádrže 5. cvičení
 5. cvičení Václav David K143 e-mail: vaclav.david@fsv.cvut.cz Konzultační hodiny: viz web Obsah cvičení Typy objektů bezpečnostního přelivu Umístění bezpečnostního přelivu Konstrukce bezpečnostního přelivu
5. cvičení Václav David K143 e-mail: vaclav.david@fsv.cvut.cz Konzultační hodiny: viz web Obsah cvičení Typy objektů bezpečnostního přelivu Umístění bezpečnostního přelivu Konstrukce bezpečnostního přelivu
OFFSET VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 OFFSET VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES LÁVKA
OFFSET VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES LÁVKA
F.2.1 Technická zpráva ke stavebnímu objektu SO 01 část retenční přehrážka
 F.2.1 Technická zpráva ke stavebnímu objektu SO 01 část retenční přehrážka Ke zdůvodňování a vysvětlování návrhu změny stavby představované jediným stavebním objektem - vodohospodářské polyfunkční opatření
F.2.1 Technická zpráva ke stavebnímu objektu SO 01 část retenční přehrážka Ke zdůvodňování a vysvětlování návrhu změny stavby představované jediným stavebním objektem - vodohospodářské polyfunkční opatření
KOMENTÁŘ KE VZOROVÉMU LISTU SVĚTLÝ TUNELOVÝ PRŮŘEZ DVOUKOLEJNÉHO TUNELU
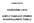 KOMENTÁŘ KE VZOROVÉMU LISTU SVĚTLÝ TUNELOVÝ PRŮŘEZ DVOUKOLEJNÉHO TUNELU OBSAH 1. ÚVOD... 3 1.1. Předmět a účel... 3 1.2. Platnost a závaznost použití... 3 2. SOUVISEJÍCÍ NORMY A PŘEDPISY... 3 3. ZÁKLADNÍ
KOMENTÁŘ KE VZOROVÉMU LISTU SVĚTLÝ TUNELOVÝ PRŮŘEZ DVOUKOLEJNÉHO TUNELU OBSAH 1. ÚVOD... 3 1.1. Předmět a účel... 3 1.2. Platnost a závaznost použití... 3 2. SOUVISEJÍCÍ NORMY A PŘEDPISY... 3 3. ZÁKLADNÍ
Vliv dolní vody na průtokové a zatěžovací charakteristiky jezové klapky
 Webová prezentace projektu 1939/2009/G1 Vliv dolní vody na průtokové a zatěžovací charakteristiky jezové klapky řešitel: spoluřešitel: Ing. Daniel Picka Prof. Ing. Jan Šulc, CSc. OBSAH Webová prezentace
Webová prezentace projektu 1939/2009/G1 Vliv dolní vody na průtokové a zatěžovací charakteristiky jezové klapky řešitel: spoluřešitel: Ing. Daniel Picka Prof. Ing. Jan Šulc, CSc. OBSAH Webová prezentace
A Průvodní dokument VŠKP
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES A Průvodní dokument
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES A Průvodní dokument
MECHANIKA KAPALIN A PLYNŮ. Mgr. Jan Ptáčník - GJVJ - Fyzika - Mechanika - 1. ročník
 MECHANIKA KAPALIN A PLYNŮ Mgr. Jan Ptáčník - GJVJ - Fyzika - Mechanika - 1. ročník Mechanika kapalin a plynů Hydrostatika - studuje podmínky rovnováhy kapalin. Aerostatika - studuje podmínky rovnováhy
MECHANIKA KAPALIN A PLYNŮ Mgr. Jan Ptáčník - GJVJ - Fyzika - Mechanika - 1. ročník Mechanika kapalin a plynů Hydrostatika - studuje podmínky rovnováhy kapalin. Aerostatika - studuje podmínky rovnováhy
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES ŽELEZOBETONOVÁ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES ŽELEZOBETONOVÁ
Proč funguje Clemův motor
 - 1 - Proč funguje Clemův motor Princip - výpočet - konstrukce (c) Ing. Ladislav Kopecký, 2004 Tento článek si klade za cíl odhalit podstatu funkce Clemova motoru, provést základní výpočty a navrhnout
- 1 - Proč funguje Clemův motor Princip - výpočet - konstrukce (c) Ing. Ladislav Kopecký, 2004 Tento článek si klade za cíl odhalit podstatu funkce Clemova motoru, provést základní výpočty a navrhnout
L.E.S. CR, spol. s r.o. Areál VÚLHM Jíloviště-Strnady, Praha 5 Zbraslav Tel.: ,
 VIAQUA FOREST 120 Popis výrobku Ocelová svodnice vody VIAQUA FOREST 120 je určena pro příčné odvodňování dopravních staveb. Je určena pro instalaci odvodňování dopravních staveb. Je určena pro instalaci
VIAQUA FOREST 120 Popis výrobku Ocelová svodnice vody VIAQUA FOREST 120 je určena pro příčné odvodňování dopravních staveb. Je určena pro instalaci odvodňování dopravních staveb. Je určena pro instalaci
Komponenta Vzorce a popis symbol propojení Hydraulický válec jednočinný. d: A: F s: p provoz.: v: Q přítok: s: t: zjednodušeně:
 Plánování a projektování hydraulických zařízení se provádí podle nejrůznějších hledisek, přičemž jsou hydraulické elementy voleny podle požadovaných funkčních procesů. Nejdůležitějším předpokladem k tomu
Plánování a projektování hydraulických zařízení se provádí podle nejrůznějších hledisek, přičemž jsou hydraulické elementy voleny podle požadovaných funkčních procesů. Nejdůležitějším předpokladem k tomu
