Technologie a maximalizace zisku Varian: Mikroekonomie: moderní přístup, kapitoly 17 a 18 Varian: Intermediate Microeconomics, 8e, Chapters 18 and 19
|
|
|
- Sabina Kopecká
- před 6 lety
- Počet zobrazení:
Transkript
1 Technologie a maximalizace zisku Varian: Mikroekonomie: moderní přístup, kapitoly 17 a 18 Varian: Intermediate Microeconomics, 8e, Chapters 18 and 19 () 1 / 40
2 Teorie firmy a tržní struktury Firmy maximalizují zisk. Výsledky interakce firem maximalizujících zisk závisí na struktuře trhu a vlastnostech produktu. Příštích pět témat: Technologie a maximalizace zisku Náklady Dokonalá konkurence Monopol a monopolní chování Oligopol () 2 / 40
3 Na této přednášce se dozvíte co jsou to technologická omezení firmy, co je to izokvanta a technická míra substituce, jaký je rozdíl mezi krátkým a dlouhým obdobím, co je to zisk, co víme o dokonale konkurenčních trzích, kde firmy maximalizují zisk, co je to projevená ziskovost. () 3 / 40
4 Produkce Produkce proces, který přeměňuje vstupy na výstupy. Příklady produkce: dělníci vyrobí auto právník sepíše smlouvu doktor vyšetří pacienta Woody Allen řekne vtip... () 4 / 40
5 Vstupy Výrobní faktory vstupy do výroby: práce půda (suroviny) kapitál Kapitálové statky vyrobené statky (kombinace práce a půdy) Vstupy a výstupy obvykle měříme v tokových veličinách: Určitý počet hodin práce + určitý počet strojových hodin za týden vyrobí určité množství výrobků za týden. () 5 / 40
6 Technologická omezení Produkční plán je určitá kombinace vstupů a výstupů. Technologická omezení jen některé ze všech možných produkčních plánů jsou technologicky přijatelné (feasible). Obvykle existuje několik přijatelných produkčních plánů. () 6 / 40
7 Popis technologických omezení Produkční množina (= technologie) množina všech přijatelných produkčních plánů. Produkční funkce maximální objem produkce pro dané vstupy. Graf technologická omezení pro jeden vstup: () 7 / 40
8 Popis technologických omezení - dva vstupy Produkční funkce y = f (x 1, x 2 ) měří maximální objem produkce, který vznikne kombinací x 1 jednotek vstupu 1 a x 2 jednotek vstupu 2. Izokvanta množina všech možných kombinací vstupů 1 a 2, které právě dostačují k vyrobení určitého množství výstupu. Izokvanty jsou podobné jako indiferenční křivky, ale číselná hodnota u izokvanty má konkrétní význam označuje množství výstupu. = Množství produkce nemůžeme transformovat jako užitky. () 8 / 40
9 Příklad rozdíl mezi užitkovou a produkční funkcí Užitková funkce dva spotřebitelé: spotřebitel 1 U 1 (x 1, x 2 ) = x 1 + x 2 spotřebitel 2 U 2 (x 1, x 2 ) = (x 1 + x 2 ) 2 Oba spotřebitelé mají stejný tvar IC a stejné preference = Při stejném rozpočtovém omezení si vyberou stejný spotřební koš. Produkční funkce dvě firmy: firma 1 f 1 (x 1, x 2 ) = x 1 + x 2 firma 2 f 2 (x 1, x 2 ) = (x 1 + x 2 ) 2 Firmy mají stejný tvar izokvant ale budou mít jinou technologii. Při stejných vstupech vyrobí jiné množství produktu (při x 1 + x 2 1). () 9 / 40
10 Příklady technologií dokonalé substituty Výkup lahví v maloobchodním řetězci člověk a stroj na výkup lahví. Produkční funkce f (x 1, x 2 ) = x 1 + x 2. () 10 / 40
11 Příklady technologií pevné proporce Prodej zmrzliny - každý zmrzlinář potřebuje jeden zmrzlinový stroj. Produkční funkce f (x 1, x 2 ) = min{x 1, x 2 }. () 11 / 40
12 Příklady technologií Cobb-Douglasova produkční funkce Cobb-Douglasova produkční funkce f (x 1, x 2 ) = Ax c 1 x d 2, kde parametr A určuje rozsah produkce, parametry c a d měří vliv změny vstupů na velikost výstupu. Cobb-Douglasovu užitkovou funkci je možné monotónně transformovat měli jsme A = 1 a obvykle c + d = 1. () 12 / 40
13 Vlastnosti technologií Monotónnost pokud zvýšíme alespoň jeden vstup, výstup by měl být alespoň tak velký jako doposud (izokvanta nesmí růst.) Volná dispozice firma se může zbavit přebytečných vstupů zdarma = zvýšení vstupů jí nemůže uškodit. Konvexnost pokud máme dvě kombinace vstupů (x 1, x 2 ) a (z 1, z 2 ), které vyrobí stejné množství výstupu y, pak pro všechna 0 t 1 i vstupy (tx 1 + (1 t)z 1, tx 2 + (1 t)z 2 ) vyrobí alespoň výstup y. Konvexnost je přirozený předpoklad příklad: Dvě technologie f (x 1, x 2 ) kombinující různá množství vstupů x 1 a x 2 : f A (sa 1, sa 2 ) = s, kde s > 0 např. f A (100a 1, 100a 2 ) = 100. f B (tb 1, tb 2 ) = t, kde t > 0 např. f B (100b 1, 100b 2 ) = 100. Možné kombinovat obě technologie: f AB (sa 1 + tb 1, sa 2 + tb 2 ) = s + t. () 13 / 40
14 Vlastnosti technologií (pokračování) 100 jednotek výstupu lze vyrobit např. s těmito množstvími vstupů: (100a 1, 100a 2 ), (100b 1, 100b 2 ) nebo (25a b 1, 25a b 2 ). () 14 / 40
15 Mezní produkt Mezní produkt faktoru 1 (MP 1 ) o kolik se zvýší celkový produkt, když zvýšíme x 1 o jednotku a x 2 zůstane stejný: MP 1 (x 1, x 2 ) = f (x 1 + x 1, x 2 ) f (x 1, x 2 ) x 1 Nebo pomocí parciálních derivací MP 1 (x 1, x 2 ) = f (x 1, x 2 ) x 1 MP je podobný jako MU, ale hodnota MP má konkrétní význam. () 15 / 40
16 Technická míra substituce Technická míra substituce (TRS) o kolik můžeme snížit x 2, pokud x 1 vzrostlo o jednotku a chceme zachovat stejný výstup? Někdy také mezní míra technické substituce (MRTS). Pro změny faktorů x 1 a x 2 musí platit, že y = MP 1 (x 1, x 2 ) x 1 + MP 2 (x 1, x 2 ) x 2 = 0. Úpravou této rovnice získáme TRS(x 1, x 2 ) = x 2 x 1 = MP 1(x 1, x 2 ) MP 2 (x 1, x 2 ). TRS = sklon izokvanty (podobně jako MRS = sklon IC). () 16 / 40
17 Snižující se mezní produkt Zákon klesajících výnosů (snižující se MP): Když roste množství jednoho vstupu (nad určitou hodnotou) a ostatní vstupy se nemění, mezní produkt tohoto vstupu klesá. Příklad: Jeden zahrádkář na malé zahrádce vypěstuje 100 mrkví. Druhý zahrádkář by zvýšil celkový produkt na 150 mrkví. Mezní produkt pracovníka by klesl ze 100 na 50 mrkví. Při velkém množství zahrádkářů by mohl dodatečný zahrádkář způsobit i pokles produkce. K poklesu nemůže dojít, pokud předpokládáme monotónnost (volnou dispozici). () 17 / 40
18 Snižující se technická míra substituce Snižující se TRS při posunu podél izokvanty doprava dolů absolutní hodnota TRS klesá (konvexní izokvanty). Jak souvisí snižující se MP a snižující se TRS? Není to to stejné, ale podobná logika: snižující se MP s růstem x 1 klesá MP 1, když x 2 je konstantní snižující se TRS s růstem x 1 podél izokvanty roste dodatečné množství vstupu 1 potřebné k nahrazení jedné jednotky vstupu 2. () 18 / 40
19 Krátké a dlouhé období Krátké období (SR) nemůžeme měnit množství alespoň u jednoho výrobního faktoru = alespoň jeden výrobní faktor je fixní. Fixní množství půdy, výrobní plochy továrny, fixní počet strojů,... Dlouhé období (LR) můžeme měnit množství všech výrobních faktorů = všechny výrobní faktory jsou variabilní. Jak dlouhé je krátké období? Nevíme, záleží na konkrétní situaci. () 19 / 40
20 Produkční funkce v SR Produkční funkce v krátkém období je f (x 1, x 2 ), kde vstup 1 je variabilní a vstup 2 je fixní. Funkce na obrázku má snižující se mezní produkt. Pro nízké x 1 by mohl MP 1 růst (funkce by měla tvar S). () 20 / 40
21 Produkční funkce v LR výnosy z rozsahu Kolikrát se zvýší výstup, když zvýšíme všechny vstupy tkrát (t > 1)? Tři možnosti produkční funkce f (x 1, x 2 ) má konstantní výnosy z rozsahu, pokud f (tx 1, tx 2 ) = tf (x 1, x 2 ), rostoucí výnosy z rozsahu, pokud f (tx 1, tx 2 ) > tf (x 1, x 2 ), klesající výnosy z rozsahu, pokud f (tx 1, tx 2 ) < tf (x 1, x 2 ). Příklady: konstantní replikace původní výroby,... rostoucí továrna na špendlíky, aerolinky, výroba letadel,... klesající nějaký výrobní faktor se nemění ve stejné proporci. Výnosy z rozsahu mohou být různé při různých výstupech. Např. při nízké výrobě rostoucí a při vysoké výrobě klesající. () 21 / 40
22 Příklady výnosy z rozsahu konkrétních produkčních funkcí 1) Jaké výnosy z rozsahu má produkční funkce f (x 1, x 2 ) = x 1/2 1 x 3/4 2? Nejdřív vynásobíme množství obou vstupů t > 1: f (tx 1, tx 2 ) = (tx 1 ) 1/2 (tx 2 ) 3/4 = t 5/4 x 1/2 1 x 3/4 2 = t 5/4 f (x 1, x 2 ) Rostoucí, protože f (tx 1, tx 2 ) > tf (x 1, x 2 ). 2) Jaké výnosy z rozsahu má produkční funkce f (x 1, x 2 ) = min{x 1, x 2 }? Když vynásobíme množství obou vstupů t > 1, dostaneme f (tx 1, tx 2 ) = min{tx 1, tx 2 } = t min{x 1, x 2 } = t f (x 1, x 2 ). Konstantní, protože f (tx 1, tx 2 ) = tf (x 1, x 2 ). () 22 / 40
23 PŘÍKLAD: Datová centra Internetové společnosti jako Google, Yahoo, Microsoft nebo Amazon mají po světě tisíce datových center. Datové centrum se sestává z polic, na kterých jsou počítače. Výkon se zvyšuje přidáním polic s počítači konstantní výnosy z rozsahu. () 23 / 40
24 PŘÍKLAD: Copy Exactly! Intel provozuje desítky provozů, které vyrábí a testují počítačové čipy. Výroba čipu je delikátní proces pro Intel je složité kontrolovat kvalitu v rozmanitém prostředí. Proto Intel přijal filosofii Copy Exactly! Každý provoz je stejný konstantní výnosy z rozsahu. () 24 / 40
25 Maximalizace zisku Firma si volí takový produkční plán, při kterém maximalizuje zisk. Předpokládáme dokonale konkurenční trhy VF a produkce: Firma nemůže ovlivnit ceny, za které nakupuje výrobní faktory, a za které prodává své výrobky. Zisk π je rozdíl mezi příjmy a náklady firmy. Pokud firma prodává n produktů (y 1,..., y n ) za ceny (p 1,..., p n ) a nakupuje m vstupů (x 1,..., x m ) za ceny (w 1,..., w m ), její zisk je π = n p i y i i=1 m w i x i. i=1 () 25 / 40
26 Ekonomický zisk Do nákladů patří všechny vstupy oceněné náklady příležitosti. Příklad: Když vlastník firmy pracuje ve své firmě a nevyplácí si mzdu, nebude mít účetní náklady, ale má náklady příležitosti. Explicitní náklady účetní náklady, Implicitní náklady nevstupují do účetnictví (náklady příležitosti). Dva typy zisku: Účetní zisk = příjmy explicitní náklady Ekonomický zisk = příjmy explicitní náklady implicitní náklady Vždy budeme používat ekonomický zisk. () 26 / 40
27 Maximalizace zisku v SR V SR alespoň jeden faktor fixní náklady na tento faktor firma platí, i když vyrábí nulový výstup = v SR může být firma ve ztrátě. Máme produkční funkci f (x 1, x 2 ) množství vstupu 2 x 2 je fixní, p je cena výstupu, w 1 a w 2 jsou ceny vstupů. Firma hledá takové množství vstupu 1, aby maximalizovala zisk: max x 1 π = pf (x 1, x 2 ) w 1 x 1 w 2 x 2. Z podmínky prvního řádu vyplývá, že pmp 1 (x 1, x 2 ) = w 1. Firma maximalizuje zisk, když se hodnota mezního produktu všech variabilních vstupů rovná jejim cenám. () 27 / 40
28 Maximalizace zisku v SR (pokračování) Izoziskové křivky kombinace x a y přinášející konstantní zisk π: π = py w 1 x 1 w 2 x 2 y = π p + w 2 x 2 p + w 1 p x 1. () 28 / 40
29 Komparativní statika Když zvýšíme cenu vstupu w 1, optimální x 1 se sníží (obr. A). Když zvýšíme cenu výstupu p, optimální x 1 se zvýší (obr. B). () 29 / 40
30 Příklad maximalizace zisku v SR Produkční funkce je f (x 1, x 2 ) = x 1/2 1 x 1/2 2, faktor 2 je fixní x 2 = 16 a ceny jsou (p, w 1, w 2 ) = (40, 10, 20). Jaké je optimální množství faktoru 1 x 1 a zisk firmy π? Dosadíme x 2 do produkční funkce firmy a získáme krátkodobou produkční funkci f (x 1, 16) = 4x 1/2 1. Zisková funkce firmy je π = pf (x 1, 16) w 1 x 1 w 2 x 2. Derivací této funkce podle x 1 získáme podmínku prvního řádu p MP 1 (x 1, 16) = w 1 x 1 = 64. Zisk firmy je π = pf (x 1, 16) w 1 x 1 w 2 x 2 = 320. () 30 / 40
31 Maximalizace zisku v LR V LR jsou všechny faktory variabilní firma nemůže být ve ztrátě. Firma hledá takové množství vstupu 1 a 2, aby maximalizovala zisk: max π = pf (x 1, x 2 ) w 1 x 1 w 2 x 2. x 1,x 2 Z podmínky prvního řádu vyplývá, že pmp 1 (x 1, x 2 ) = w 1 pmp 2 (x 1, x 2 ) = w 2. Firma maximalizuje zisk, když se hodnota mezního produktu všech vstupů rovná jejim cenám. () 31 / 40
32 Poptávka po faktoru Poptávka po faktoru 1 jaké množství faktoru x 1 nakoupím při daných cenách p, w 1 a w 2. Inverzní poptávka po faktoru 1 je w 1 = pmp 1 (x 1, x 2 ). Pokud je MP 1 (x 1, x 2 ) klesající, bude i křivka inverzní poptávky klesající. () 32 / 40
33 Projevená ziskovost Firma maximalizující zisk ukazuje, že jí zvolená kombinace vstupů a výstupů je přijatelný výrobní plán, který je ziskovější, než jiné přijatelné výrobní plány. Dva různé výběry při různých cenových úrovních: při cenách v čase t (p t, w t 1, w t 2) firma zvolí (y t, x t 1, x t 2), při cenách v čase s (p s, w s 1, w s 2) firma zvolí (y s, x s 1, x s 2). Slabý axiom maximalizace zisku (WAPM): Jestliže firma maximalizuje zisk a mezi časem t a s se nezmění její produkční funkce, pak musí platit následující nerovnice: p t y t w t 1x t 1 w t 2x t 2 p t y s w t 1x s 1 w t 2x s 2 (1) p s y s w s 1x s 1 w s 2x s 2 p s y t w s 1x t 1 w s 2x t 2 (2) () 33 / 40
34 Projevená ziskovost (pokračování) Nerovnice (1) a (2) můžeme upravit následujícím způsobem: Když nerovnici (2) vynásobíme 1 (a přehodíme strany), dostaneme p t y t w t 1x t 1 w t 2x t 2 p t y s w t 1x s 1 w t 2x s 2 p s y t + w s 1x t 1 + w s 2x t 2 p s y s + w s 1x s 1 + w s 2x s 2. Pokud platí tyto nerovnice, musí i pro součty obou stran platit, že (p t p s )y t (w t 1 w s 1)x t 1 (w t 2 w s 2)x t 2 (p t p s )y s (w t 1 w s 1)x s 1 (w t 2 w s 2)x s 2. Pokud u této nerovnice převedeme pravou stranu na levou stranu a dosadíme p za (p t p s ), y za (y t y s ), atd., dostaneme p y w 1 x 1 w 2 x 2 0. () 34 / 40
35 Projevená ziskovost (pokračování) Co vyplývá z výsledku p y w 1 x 1 w 2 x 2 0? Pokud se změní cena p a nezmění se w 1 a w 2, pak platí, že p y 0. Nikdy neplatí, že p > 0 a y < 0 nebo p < 0 a y > 0. = Nabídka dokonale konkurenční firmy není nikdy klesající. Pokud se změní cena vstupu w 1 a nezmění se p a w 2, pak platí, že w 1 x 1 0. Nikdy neplatí, že w 1 > 0 a x 1 > 0 nebo w 1 < 0 a x 1 < 0. = Poptávka po faktoru konkurenční firmy není nikdy rostoucí. () 35 / 40
36 Odhad technologie pomocí WAPM Je WAPM dostačující pro odvození technologie z chování firem? Ano, pokud firma maximalizuje zisk a nezměnila se její technologie, můžeme z jejích rozhodnutí odhadnout její technologii. Předpokládejte, že máme jeden vstup x 1 a jeden výstup y. V období t je vybraný produkční plán (x t 1, y t ) a izozisková funkce je π t = p t y w t 1x 1 y = π t /p t + (w t 1/p t )x 1. s je vybraný produkční plán (x s 1, y s ) a izozisková funkce je π s = p s y w s 1x 1 y = π s /p s + (w s 1/p s )x 1. Z WAMP vyplývá, že produkční plány ležící nad izoziskovými křivkami nejsou dostupné. Jinak by si je firma vybrala a zvýšila by tím svůj zisk. () 36 / 40
37 Odhad technologie pomocí WAPM (pokračování) Bílá plocha = produkční plány, které leží nad izoziskovou křivkou. Tzn. nejsou dostupné, takže nemůžou být součástí technologie. () 37 / 40
38 Odhad technologie pomocí WAPM (pokračování) Čím víc pozorujeme produkčních plánů při různých cenách, tím přesnější je odhad technologie (a produkční funkce). () 38 / 40
39 Shrnutí Technologická omezení firmy můžeme prezentovat pomocí produkční množiny nebo pomocí izokvant. Předpokládáme, že izokvanty jsou konvexní a monotónní. Předpokládáme, že mezní produkt klesá s rostoucím produktem. Technická míra substituce měří sklon izokvanty. V krátkém období jsou některé vstupy fixní, v dlouhém období jsou všechny variabilní. Výnosy z rozsahu říkají, jak se změní objem produkce, pokud změníme množství vstupů ve stejné proporci. () 39 / 40
40 Shrnutí (pokračování) Zisk je rozdíl mezi příjmy a náklady. Do nákladů počítáme i implicitní náklady. U firmy maximalizující zisk se hodnota mezního produktu každého variabilního faktoru musí rovnat jeho ceně. Z logiky maximalizace zisku vyplývá, že nabídka dokonale konkurenční firmy nesmí klesat a její poptávky po výrobních faktorech nesmí růst. Pokud dokonale konkurenční firma vykazuje konstantní výnosy z rozsahu, její dlouhodobé zisky musí být nulové. () 40 / 40
Minimalizace nákladů. Varian: Mikroekonomie: moderní přístup, kapitoly 19 a 20 Varian: Intermediate Microeconomics, 8e, Chapters 20 and 21 () 1 / 34
 Minimalizace nákladů a nákladové křivky Varian: Mikroekonomie: moderní přístup, kapitoly 19 a 20 Varian: Intermediate Microeconomics, 8e, Chapters 20 and 21 () 1 / 34 Na této přednášce se dozvíte co je
Minimalizace nákladů a nákladové křivky Varian: Mikroekonomie: moderní přístup, kapitoly 19 a 20 Varian: Intermediate Microeconomics, 8e, Chapters 20 and 21 () 1 / 34 Na této přednášce se dozvíte co je
Zisk Jan Čadil VŠE FNH
 Zisk Jan Čadil VŠE FNH Footer Text 12/10/2014 1 Ekonomický zisk Rozdíl mezi tržbami a náklady, včetně implicitních Firma má výstup q = f m 1,, m i. Obecně může mít více druhů výstupu (1 až n). Cenu produkce
Zisk Jan Čadil VŠE FNH Footer Text 12/10/2014 1 Ekonomický zisk Rozdíl mezi tržbami a náklady, včetně implicitních Firma má výstup q = f m 1,, m i. Obecně může mít více druhů výstupu (1 až n). Cenu produkce
Máte 1000 Kč a jdete si koupit svoji oblíbenou knihu?
 Volba a projevené preference Varian, Mikroekonomie: moderní přístup, kapitola 5 a oddíly 7.1 7.7 Varian, Intermediate Microeconomics, Chapter 5 and Sections 7.1 7.7 () 1 / 1 EXPERIMENT: Neúspěšný nákup
Volba a projevené preference Varian, Mikroekonomie: moderní přístup, kapitola 5 a oddíly 7.1 7.7 Varian, Intermediate Microeconomics, Chapter 5 and Sections 7.1 7.7 () 1 / 1 EXPERIMENT: Neúspěšný nákup
Kvízové otázky Obecná ekonomie I. Teorie firmy
 1. Firmy působí: a) na trhu výrobních faktorů b) na trhu statků a služeb c) na žádném z těchto trhů d) na obou těchto trzích Kvízové otázky Obecná ekonomie I. Teorie firmy 2. Firma na trhu statků a služeb
1. Firmy působí: a) na trhu výrobních faktorů b) na trhu statků a služeb c) na žádném z těchto trhů d) na obou těchto trzích Kvízové otázky Obecná ekonomie I. Teorie firmy 2. Firma na trhu statků a služeb
Rozpočtové omezení, preference a užitek
 Rozpočtové omezení, preference a užitek Varian, Mikroekonomie: moderní přístup, kapitoly 2, 3 a 4 Varian, Intermediate Microeconomics, 8e, Chapters 2, 3 a 4 1 / 43 Teorie spotřebitele Spotřebitelé si volí
Rozpočtové omezení, preference a užitek Varian, Mikroekonomie: moderní přístup, kapitoly 2, 3 a 4 Varian, Intermediate Microeconomics, 8e, Chapters 2, 3 a 4 1 / 43 Teorie spotřebitele Spotřebitelé si volí
Přijímací řízení ak. r. 2010/11 Kompletní znění testových otázek mikroekonomie. Správná odpověď je označena tučně
 řijímací řízení ak. r. 2010/11 Kompletní znění testových otázek mikroekonomie Správná odpověď je označena tučně 1. řebytek spotřebitele je rozdíl mezi a... a) cenou, mezními náklady b) cenou, celkovými
řijímací řízení ak. r. 2010/11 Kompletní znění testových otázek mikroekonomie Správná odpověď je označena tučně 1. řebytek spotřebitele je rozdíl mezi a... a) cenou, mezními náklady b) cenou, celkovými
základní východiska analýzy firmy krátkodobá produkční funkce výroba v dlouhém období, optimum firmy optimum firmy při různých úrovních nákladů a při
 3. PRODUKČNÍ ANAÝZA FIRMY OBSAH základní východiska analýzy firmy krátkodobá produkční funkce výroba v dlouhém období, optimum firmy optimum firmy při různých úrovních nákladů a při změnách cen VF výnosy
3. PRODUKČNÍ ANAÝZA FIRMY OBSAH základní východiska analýzy firmy krátkodobá produkční funkce výroba v dlouhém období, optimum firmy optimum firmy při různých úrovních nákladů a při změnách cen VF výnosy
Poptávka a Slutského rovnice Varian, Mikroekonomie: moderní přístup, kapitoly 6 a 8 Varian: Intermediate Microeconomics, 8e, Chapters 6 and 8
 Poptávka a Slutského rovnice Varian, Mikroekonomie: moderní přístup, kapitoly 6 a 8 Varian: Intermediate Microeconomics, 8e, Chapters 6 and 8 () 1 / 50 Na této přednášce se dozvíte na čem závisí poptávková
Poptávka a Slutského rovnice Varian, Mikroekonomie: moderní přístup, kapitoly 6 a 8 Varian: Intermediate Microeconomics, 8e, Chapters 6 and 8 () 1 / 50 Na této přednášce se dozvíte na čem závisí poptávková
Dokonalá konkurence. Mikroekonomie. Opakování. Řešení. Příklad. Příklad. Řešení Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU
 Opakování Mikroekonomie Dokonalá konkurence Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU U firmy v rámci dokonalé konkurence jsou výrobní náklady dány vztahem: TC = 20000 + 2 a) Jestliže tržní cena
Opakování Mikroekonomie Dokonalá konkurence Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU U firmy v rámci dokonalé konkurence jsou výrobní náklady dány vztahem: TC = 20000 + 2 a) Jestliže tržní cena
Mezi firmami v oligopolu dochází ke strategickým interakcím. Při zkoumání strategických interakcí používáme teorii her.
 Teorie her a oligopol Varian: Mikroekonomie: moderní přístup, oddíly 26.1-9, 27.1-3 a 27.7-8 Varian: Intermediate Microeconomics, Sections 27.1-9, 28.1-3, 28.7-8 () 1 / 36 Obsah přednášky V této přednášce
Teorie her a oligopol Varian: Mikroekonomie: moderní přístup, oddíly 26.1-9, 27.1-3 a 27.7-8 Varian: Intermediate Microeconomics, Sections 27.1-9, 28.1-3, 28.7-8 () 1 / 36 Obsah přednášky V této přednášce
Firma. Příklad zadání. Příklad řešení. Téma cvičení. náklady firmy. Příklady k opakování. Mikroekonomie. Příjmy, zisk Produkční analýza
 Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Téma cvičení Firma Příjmy, zisk Produkční analýza zadání y k opakování náklady firmy Q FC VC TC AC AVC AFC MC 0 X X X X X X X 1 5 5 X X X
Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Téma cvičení Firma Příjmy, zisk Produkční analýza zadání y k opakování náklady firmy Q FC VC TC AC AVC AFC MC 0 X X X X X X X 1 5 5 X X X
3. PRODUKČNÍ ANALÝZA FIRMY
 3. PRODUKČNÍ ANAÝZA FIRMY OBSAH základní východiska analýzy firmy krátkodobá produkční funkce výroba v dlouhém období, optimum firmy optimum firmy při různých úrovních nákladů a při změnách cen VF výnosy
3. PRODUKČNÍ ANAÝZA FIRMY OBSAH základní východiska analýzy firmy krátkodobá produkční funkce výroba v dlouhém období, optimum firmy optimum firmy při různých úrovních nákladů a při změnách cen VF výnosy
5. Trh analýza. Poptávka, nabídka, elasticity, užitková a produkční funkce.
 5. Trh analýza. Poptávka, nabídka, elasticity, užitková a produkční funkce. Teorie spotřebitele x teorie firmy 5.1.1 Teorie spotřebitele Ekonomie zkoumá preference mezi statky. Nezkoumá je ale přímo, nýbrž
5. Trh analýza. Poptávka, nabídka, elasticity, užitková a produkční funkce. Teorie spotřebitele x teorie firmy 5.1.1 Teorie spotřebitele Ekonomie zkoumá preference mezi statky. Nezkoumá je ale přímo, nýbrž
Firma. Spotřebitel. Téma cvičení. Mikroekonomie. Příjmy, zisk Produkční analýza. Opakování. Příklad. Příklad. Příklad
 Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Téma cvičení Firma Příjmy, zisk Produkční analýza Opakování Spotřebitel Máte danou funkci celkového užitku TU ve tvaru: 300X - 10X 2 (X značí
Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Téma cvičení Firma Příjmy, zisk Produkční analýza Opakování Spotřebitel Máte danou funkci celkového užitku TU ve tvaru: 300X - 10X 2 (X značí
Dokonale konkurenční odvětví
 Dokonale konkurenční odvětví Východiska určení výstupu pro maximalizaci zisku ekonomický zisk - je rozdíl mezi příjmy a ekonomickými náklady (alternativními náklady) účetní zisk - je rozdíl mezi příjmy
Dokonale konkurenční odvětví Východiska určení výstupu pro maximalizaci zisku ekonomický zisk - je rozdíl mezi příjmy a ekonomickými náklady (alternativními náklady) účetní zisk - je rozdíl mezi příjmy
Obvyklý tvar produkční funkce v krátkém období
 Produkční analýza firmy základní východiska analýzy firmy krátkodobá produkční funkce výroba v dlouhém období, optimum firmy optimum firmy při různých úrovních nákladů a při změnách cen VF výnosy z rozsahu
Produkční analýza firmy základní východiska analýzy firmy krátkodobá produkční funkce výroba v dlouhém období, optimum firmy optimum firmy při různých úrovních nákladů a při změnách cen VF výnosy z rozsahu
Mikroekonomie. Minulá přednáška - podstatné. Náklady firmy v krátkém a dlouhém období. Důležité vzorce. Náklady v krátkém období - graficky
 Minulá přednáška - podstatné Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Typologie nákladů firmy Náklady v krátkém období Náklady v dlouhém období Důležité vzorce TC = FC + VC AC =
Minulá přednáška - podstatné Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Typologie nákladů firmy Náklady v krátkém období Náklady v dlouhém období Důležité vzorce TC = FC + VC AC =
Nabídka firmy a nabídka odvětví Varian: Mikroekonomie: moderní přístup, kapitoly 21 a 22 Varian: Intermediate Microeconomics, 8e, Chapters 22 and 23
 Nabídka firmy a nabídka odvětví Varian: Mikroekonomie: moderní přístup, kapitoly 21 a 22 Varian: Intermediate Microeconomics, 8e, Chapters 22 and 23 () 1 / 39 Na této přednášce se dozvíte jaká jsou omezení
Nabídka firmy a nabídka odvětví Varian: Mikroekonomie: moderní přístup, kapitoly 21 a 22 Varian: Intermediate Microeconomics, 8e, Chapters 22 and 23 () 1 / 39 Na této přednášce se dozvíte jaká jsou omezení
7. Výrobní náklady. Motivace. Co se dnes naučíte. Naďa a Klára vaří ratatouille. Výrobní náklady 1
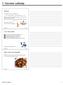 7. Výrobní náklady Motivace Cílem každé firmy je co nejvyšší zisk. zisk = celkové příjmy celkové náklady = TR TC Abychom porozuměli chování firmy, musíme rozumět tomu, co určuje její příjmy a náklady.
7. Výrobní náklady Motivace Cílem každé firmy je co nejvyšší zisk. zisk = celkové příjmy celkové náklady = TR TC Abychom porozuměli chování firmy, musíme rozumět tomu, co určuje její příjmy a náklady.
Teorie nákladů. Rozlišení zisku. Mikroekonomie. Účetní zisk. Ekonomický zisk. Normální zisk. Zisk firmy. Důležité. Účetní, ekonomický a normální zisk
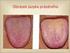 Zisk firmy Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Zisk (π) je rozdíl mezi celkovými příjmy a celkovými náklady. Π = TR - TC Je také vynásobený objem produkce rozdílem průměrného
Zisk firmy Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Zisk (π) je rozdíl mezi celkovými příjmy a celkovými náklady. Π = TR - TC Je také vynásobený objem produkce rozdílem průměrného
Mikroekonomie. Opakování - příklad. Řešení. Příklad - opakování. Příklad. Řešení Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU
 Opakování - příklad Mikroekonomie Máte danou funkci celkového užitku TU ve tvaru: 300X - 10X 2 (X značí spotřebované množství statku). Určete interval spotřeby (množství statku X) v kterém TU bude mít
Opakování - příklad Mikroekonomie Máte danou funkci celkového užitku TU ve tvaru: 300X - 10X 2 (X značí spotřebované množství statku). Určete interval spotřeby (množství statku X) v kterém TU bude mít
Formování cen na trzích výrobních faktorů
 Formování cen na trzích výrobních faktorů Na trzích výrobních faktorů jsou určujícími elementy poptávka a nabídka výrobního faktoru. Na trzích výrobků a služeb jsou domácnosti poptávající a firmy nabízející
Formování cen na trzích výrobních faktorů Na trzích výrobních faktorů jsou určujícími elementy poptávka a nabídka výrobního faktoru. Na trzích výrobků a služeb jsou domácnosti poptávající a firmy nabízející
Rozlišení zisku. Mikroekonomie. Účetní zisk = Ekonomický zisk. Normální zisk. Zisk firmy. Co je důležité pro členění zisku
 Zisk firmy Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Zisk (π) je rozdíl mezi celkovými příjmy a celkovými náklady. Π = TR - TC Je také vynásobený objem produkce rozdílem průměrného
Zisk firmy Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Zisk (π) je rozdíl mezi celkovými příjmy a celkovými náklady. Π = TR - TC Je také vynásobený objem produkce rozdílem průměrného
DK cena odvozená z trhu
 Dokonalá konkurence DK cena odvozená z trhu π (Kč) TR STC ZISK ZTRÁTA Q 1 Q 2 Q (ks) MR, MC (Kč/ks) MC MR Q 1 Q 2 Q (ks) ZiskfirmyvDK Nulový zisk v DK normální zisk Ztráta firmy v DK Křivka nabídky firmy
Dokonalá konkurence DK cena odvozená z trhu π (Kč) TR STC ZISK ZTRÁTA Q 1 Q 2 Q (ks) MR, MC (Kč/ks) MC MR Q 1 Q 2 Q (ks) ZiskfirmyvDK Nulový zisk v DK normální zisk Ztráta firmy v DK Křivka nabídky firmy
Motivace. Cílem každé firmy je co nejvyšší zisk. zisk = celkové příjmy celkové náklady = TR TC
 Výrobní náklady Motivace Cílem každé firmy je co nejvyšší zisk. zisk = celkové příjmy celkové náklady = TR TC Abychom porozuměli chování firmy, musíme rozumět tomu, co určuje její příjmy a náklady. Příjmy
Výrobní náklady Motivace Cílem každé firmy je co nejvyšší zisk. zisk = celkové příjmy celkové náklady = TR TC Abychom porozuměli chování firmy, musíme rozumět tomu, co určuje její příjmy a náklady. Příjmy
Firmy na dokonale konkurenčních trzích
 Firmy na dokonale konkurenčních trzích Motivace Každá firma musí učinit následující rozhodnutí: kolik vyrábět jakou cenu si účtovat s jakými výrobními faktory (kolik práce a kolik kapitálu) Tato rozhodnutí
Firmy na dokonale konkurenčních trzích Motivace Každá firma musí učinit následující rozhodnutí: kolik vyrábět jakou cenu si účtovat s jakými výrobními faktory (kolik práce a kolik kapitálu) Tato rozhodnutí
Firmy na dokonale konkurenčních trzích
 Firmy na dokonale konkurenčních trzích Motivace Každá firma musí učinit následující rozhodnutí: kolik vyrábět jakou cenu si účtovat s jakými výrobními faktory (kolik práce a kolik kapitálu) Tato rozhodnutí
Firmy na dokonale konkurenčních trzích Motivace Každá firma musí učinit následující rozhodnutí: kolik vyrábět jakou cenu si účtovat s jakými výrobními faktory (kolik práce a kolik kapitálu) Tato rozhodnutí
Mikroekonomie I. 5. přednáška Náklady firmy. Minulá přednáška - podstatné. Rovnováha spotřebitele - graf. Náklady firmy osnova přednášky
 Minulá přednáška - podstatné Mikroekonomie I. 5. přednáška Náklady firmy Celkový užitek Mezní užitek Je užitek měřitelný Indiferenční křivky spotřebitele Linie rozpočtu spotřebitele Optimum spotřebitele
Minulá přednáška - podstatné Mikroekonomie I. 5. přednáška Náklady firmy Celkový užitek Mezní užitek Je užitek měřitelný Indiferenční křivky spotřebitele Linie rozpočtu spotřebitele Optimum spotřebitele
ROVNOVÁHA. 5. Jak by se změnila účinnost fiskální politiky, pokud by spotřeba kromě důchodu závisela i na úrokové sazbě?
 ROVNOVÁHA Zadání 1. Použijte neoklasickou teorii rozdělování k předpovědi efektu následujících událostí na reálnou mzdu a reálnou cenu kapitálu: a) Vlna imigrace zvýší množství pracovníků v zemi. b) Zemětřesení
ROVNOVÁHA Zadání 1. Použijte neoklasickou teorii rozdělování k předpovědi efektu následujících událostí na reálnou mzdu a reálnou cenu kapitálu: a) Vlna imigrace zvýší množství pracovníků v zemi. b) Zemětřesení
5 FIRMA A SPOTŘEBITEL
 5 FIRMA A SPOTŘEBITEL 5.1 Firma 2 Firmy Zákon nabídky: Firmy jsou ochotny vyrábět a prodávat větší množství, když je cena jejich produkce vysoká = rostoucí křivka S P S Q 3 Cíl firem Ekonomický cíl maximalizace
5 FIRMA A SPOTŘEBITEL 5.1 Firma 2 Firmy Zákon nabídky: Firmy jsou ochotny vyrábět a prodávat větší množství, když je cena jejich produkce vysoká = rostoucí křivka S P S Q 3 Cíl firem Ekonomický cíl maximalizace
6. Teorie výroby Průvodce studiem: 6.2 Produkční analýza v krátkém období celkový (fyzický) produkt (TP)
 6. Teorie výroby Firma vystupuje na trhu finální produkce v pozici nabízejícího a současně na trhu výrobních faktorů v pozici poptávajícího. Firma používá různé vstupy (výrobní faktory), které ve výrobě
6. Teorie výroby Firma vystupuje na trhu finální produkce v pozici nabízejícího a současně na trhu výrobních faktorů v pozici poptávajícího. Firma používá různé vstupy (výrobní faktory), které ve výrobě
Struktura předpoklady modelu všeobecné rovnováhy pojem efektivnost hranice výrobních možností všeobecná rovnováha dosahování všeobecné rovnováhy a jej
 12. Všeobecná rovnováha Struktura předpoklady modelu všeobecné rovnováhy pojem efektivnost hranice výrobních možností všeobecná rovnováha dosahování všeobecné rovnováhy a její změna Literatura Soukupová
12. Všeobecná rovnováha Struktura předpoklady modelu všeobecné rovnováhy pojem efektivnost hranice výrobních možností všeobecná rovnováha dosahování všeobecné rovnováhy a její změna Literatura Soukupová
4. Křivka nabídky monopolní firmy je totožná s částí křivky mezních nákladů.
 Firma v nedokonalé konkurenci 1. Zdroji nedokonalé konkurence jsou: - jednak nákladové podmínky podnikání, - jednak. 2. Zapište vzorec Lernerova indexu. K čemu slouží? 3. Zakreslete celkový příjem monopolní
Firma v nedokonalé konkurenci 1. Zdroji nedokonalé konkurence jsou: - jednak nákladové podmínky podnikání, - jednak. 2. Zapište vzorec Lernerova indexu. K čemu slouží? 3. Zakreslete celkový příjem monopolní
OP3BK_FEK. Ekonomika. Jaro / 13:55 15:35 / učebna č.20
 OP3BK_FEK Ekonomika Jaro 2013 16.03.2013 / 13:55 15:35 / učebna č.20 Přehled témat (osnova): 1. Úvod do ekonomie Základní pojmy Vývoj ekonomie Aktuální problémy 2. Mikroekonomie Tržní struktury Dokonalá
OP3BK_FEK Ekonomika Jaro 2013 16.03.2013 / 13:55 15:35 / učebna č.20 Přehled témat (osnova): 1. Úvod do ekonomie Základní pojmy Vývoj ekonomie Aktuální problémy 2. Mikroekonomie Tržní struktury Dokonalá
Národní hospodářství poptávka a nabídka
 Národní hospodářství poptávka a nabídka Chování spotřebitele a poptávka Užitek a spotřebitelův přebytek Jedním ze základních problémů, které spotřebitel řeší, je, kolik určitého statku má kupovat a jak
Národní hospodářství poptávka a nabídka Chování spotřebitele a poptávka Užitek a spotřebitelův přebytek Jedním ze základních problémů, které spotřebitel řeší, je, kolik určitého statku má kupovat a jak
15 Poptávka na nedokonale konkurenčním trhu práce
 15 Poptávka na nedokonale konkurenčním trhu práce Existuje-li na trhu výstupu omezený počet firem nabízejících svou produkci, hovoříme o nedokonalé konkurenci, jejíž jednotlivé formy (monopol, oligopol
15 Poptávka na nedokonale konkurenčním trhu práce Existuje-li na trhu výstupu omezený počet firem nabízejících svou produkci, hovoříme o nedokonalé konkurenci, jejíž jednotlivé formy (monopol, oligopol
Bod uzavření firmy. Bod zvratu. Mikroekonomie. Důležité FC, VC, TC (graf) Náklady firmy - důležité. Průběh funkcí nákladů - grafy
 Důležité FC, VC, TC (graf) Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Náklady firmy - důležité Průběh funkcí nákladů - grafy TC = FC + VC AC = AFC + AVC AFC = FC/Q AVC = VC/Q MC =
Důležité FC, VC, TC (graf) Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Náklady firmy - důležité Průběh funkcí nákladů - grafy TC = FC + VC AC = AFC + AVC AFC = FC/Q AVC = VC/Q MC =
8. Firmy na dokonale konkurenčních trzích
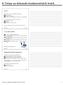 8. Firmy na dokonale konkurenčních trzích Motivace Každá firma musí učinit následující rozhodnutí: kolik vyrábět jakou cenu si účtovat s jakými výrobními faktory (kolik práce a kolik kapitálu) Tato rozhodnutí
8. Firmy na dokonale konkurenčních trzích Motivace Každá firma musí učinit následující rozhodnutí: kolik vyrábět jakou cenu si účtovat s jakými výrobními faktory (kolik práce a kolik kapitálu) Tato rozhodnutí
6 Nabídka na trhu výrobků a služeb
 6 Nabídka na trhu výrobků a služeb 1. Náklady firmy 2. Příjmy a zisk firmy 3. Rovnováha firmy na dokonale konkurenčním trhu 4. Nabídka firmy V ekonomii se rozlišují tři časové horizonty, ve vztahu k možnostem
6 Nabídka na trhu výrobků a služeb 1. Náklady firmy 2. Příjmy a zisk firmy 3. Rovnováha firmy na dokonale konkurenčním trhu 4. Nabídka firmy V ekonomii se rozlišují tři časové horizonty, ve vztahu k možnostem
Přebytek spotřebitele
 Přebytek spotřebitele a tržní poptávka Varian: Mikroekonomie: moderní přístup, kapitoly 14 a 15 Varian: Intermediate Microeconomics, 8e, Chapters 14 and 15 () 1 / 36 Na této přednášce se dozvíte jak měříme
Přebytek spotřebitele a tržní poptávka Varian: Mikroekonomie: moderní přístup, kapitoly 14 a 15 Varian: Intermediate Microeconomics, 8e, Chapters 14 and 15 () 1 / 36 Na této přednášce se dozvíte jak měříme
POPTÁVKA NA DOKONALE KONKURENČNÍM TRHU PRÁCE
 POPTÁVKA NA DOKONALE KONKURENČNÍM TRHU PRÁCE Firma maximalizuje zisk když platí Dokonalý trh práce-firma přicházející na tento trh je jednou z velkého počtu cenu práce nemůže ovlivnit Křivku nabídky práce
POPTÁVKA NA DOKONALE KONKURENČNÍM TRHU PRÁCE Firma maximalizuje zisk když platí Dokonalý trh práce-firma přicházející na tento trh je jednou z velkého počtu cenu práce nemůže ovlivnit Křivku nabídky práce
Teorie firmy (analýza nákladů a výnosů, rovnováha firmy)
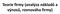 Teorie firmy (analýza nákladů a výnosů, rovnováha firmy) Povaha a podstata firmy Co je to firma? zisk Produkční funkce Definice produkční funkce Celkový produkt, průměrný produkt, mezní produkt Vztah mezního
Teorie firmy (analýza nákladů a výnosů, rovnováha firmy) Povaha a podstata firmy Co je to firma? zisk Produkční funkce Definice produkční funkce Celkový produkt, průměrný produkt, mezní produkt Vztah mezního
Preference Jan Čadil FNH VŠE 2014
 Preference Jan Čadil FNH VŠE 2014 Footer Text 3/24/2014 1 Racionalita Chování spotřebitele je založeno na předpokladu racionality. Tento předpoklad znamená, že spotřebitel volí neoptimálnější, resp. nejvíce
Preference Jan Čadil FNH VŠE 2014 Footer Text 3/24/2014 1 Racionalita Chování spotřebitele je založeno na předpokladu racionality. Tento předpoklad znamená, že spotřebitel volí neoptimálnější, resp. nejvíce
FAKULTA INFORMATIKY A MANAGEMENTU UNIVERZITA HRADEC KRÁLOVÉ VOLBA TECHNOLOGIE. Semestrální práce MIE2
 FAKULTA INFORMATIKY A MANAGEMENTU UNIVERZITA HRADEC KRÁLOVÉ VOLBA TECHNOLOGIE Semestrální práce MIE2 Vypracoval: Bc. Martin Petruželka Studijní obor: K-IM2 Emailová adresa: Martin.Petruzelka@uhk.cz Datum
FAKULTA INFORMATIKY A MANAGEMENTU UNIVERZITA HRADEC KRÁLOVÉ VOLBA TECHNOLOGIE Semestrální práce MIE2 Vypracoval: Bc. Martin Petruželka Studijní obor: K-IM2 Emailová adresa: Martin.Petruzelka@uhk.cz Datum
křivka MFC L roste dvakrát rychleji než AFC L
 10. Nedokonale konkurenční trh práce, nabídka práce Struktura charakteristika NedoKo.. trhu práce optimální množství práce v SR optimální množství práce v LR mzdová diskriminace monopsonu individuální
10. Nedokonale konkurenční trh práce, nabídka práce Struktura charakteristika NedoKo.. trhu práce optimální množství práce v SR optimální množství práce v LR mzdová diskriminace monopsonu individuální
13 Specifika formování poptávky firem po práci a kapitálu
 13 Specifika formování poptávky firem po práci a kapitálu Na rozdíl od trhu finálních statků, kde stranu poptávky tvořili jednotlivci (domácnosti) a stranu nabídky firmy, na trhu vstupů vytvářejí jednotlivci
13 Specifika formování poptávky firem po práci a kapitálu Na rozdíl od trhu finálních statků, kde stranu poptávky tvořili jednotlivci (domácnosti) a stranu nabídky firmy, na trhu vstupů vytvářejí jednotlivci
MAKROEKONOMIE. Blok č. 5: ROVNOVÁHA V UZAVŘENÉ EKONOMICE
 MAKROEKONOMIE Blok č. 5: ROVNOVÁHA V UZAVŘENÉ EKONOMICE CÍL A STRUKTURA TÉMATU.odpovědět na následující typy otázek: Kolik se toho v ekonomice vyprodukuje? Kdo obdrží důchody z produkce? Kdo nakoupí celkový
MAKROEKONOMIE Blok č. 5: ROVNOVÁHA V UZAVŘENÉ EKONOMICE CÍL A STRUKTURA TÉMATU.odpovědět na následující typy otázek: Kolik se toho v ekonomice vyprodukuje? Kdo obdrží důchody z produkce? Kdo nakoupí celkový
VOLBA TECHNOLOGIE.
 VOLBA TECHNOLOGIE ZÁKLADNÍ VÝCHODISKA ANALÝZY FIRMY Firma je charakterizována jako subjekt specializující se na výrobu, tj, přeměnu zdrojů(vstupů) na statky(výstup) Firma se specializuje na 3 hlavní činnosti-
VOLBA TECHNOLOGIE ZÁKLADNÍ VÝCHODISKA ANALÝZY FIRMY Firma je charakterizována jako subjekt specializující se na výrobu, tj, přeměnu zdrojů(vstupů) na statky(výstup) Firma se specializuje na 3 hlavní činnosti-
PR5 Poptávka na trhu výrobků a služeb
 PR5 Poptávka na trhu výrobků a služeb 5.1. Rovnováha spotřebitele 5.2. Indiferenční analýza od kardinalismu k ordinalismu 5.3. Poptávka, poptávané množství a jejich změny 5.4. Pružnost tržní poptávky Poptávka
PR5 Poptávka na trhu výrobků a služeb 5.1. Rovnováha spotřebitele 5.2. Indiferenční analýza od kardinalismu k ordinalismu 5.3. Poptávka, poptávané množství a jejich změny 5.4. Pružnost tržní poptávky Poptávka
Příjmové veličiny na trhu VF
 Trh práce Vysvětlivky: SR = short run = krátké období, množství kapitálových statků je fixní R = long run = dlouhé období, množství kapitálových statků je variabilni Příjmové veličiny na trhu VF Příjem
Trh práce Vysvětlivky: SR = short run = krátké období, množství kapitálových statků je fixní R = long run = dlouhé období, množství kapitálových statků je variabilni Příjmové veličiny na trhu VF Příjem
POPTÁVKA.
 POPTÁVKA INDIVIDUÁLNÍ POPTÁVKA Individuální poptávka-poptávka jednoho spotřebitele, závisí na: -ceně statku -cenách ostatních statků -důchodu spotřebitele Preference a očekávání předpokládáme za neměnné
POPTÁVKA INDIVIDUÁLNÍ POPTÁVKA Individuální poptávka-poptávka jednoho spotřebitele, závisí na: -ceně statku -cenách ostatních statků -důchodu spotřebitele Preference a očekávání předpokládáme za neměnné
Mikroekonomie. Opakování příklad 1. Řšení. Příklad 2. Příklad 5. Proč Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU 16 D
 Opakování příklad 1 Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Hodnota Edp = 0,1 znamená, že procentní změna množství při 10% změně ceny bude: a/ 0,2 b/ 2,5 c/ 5,0 d/ 1,0 e/ ze zadaných
Opakování příklad 1 Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Hodnota Edp = 0,1 znamená, že procentní změna množství při 10% změně ceny bude: a/ 0,2 b/ 2,5 c/ 5,0 d/ 1,0 e/ ze zadaných
Mikroekonomie Q FC VC Příklad řešení. Kontrolní otázky Příklad opakování zjistěte zbývající údaje
 Příklad opakování zjistěte zbývající údaje Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Q FC VC 0 20 1 10 2 18 3 24 4 36 Co lze zjistit? FC - pro Q = 1, 2, 3, 4 TC AC AVC AFC Příklad
Příklad opakování zjistěte zbývající údaje Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Q FC VC 0 20 1 10 2 18 3 24 4 36 Co lze zjistit? FC - pro Q = 1, 2, 3, 4 TC AC AVC AFC Příklad
STC = w.l + r.k fix = VC + FC
 Náklady a příjmy firmy definice nákladů náklady v krátkém období: - celkové, průměrné, mezní - fixní a variabilní náklady náklady v dlouhém období vztah mezi náklady v SR a LR: - obalová křivka příjmy
Náklady a příjmy firmy definice nákladů náklady v krátkém období: - celkové, průměrné, mezní - fixní a variabilní náklady náklady v dlouhém období vztah mezi náklady v SR a LR: - obalová křivka příjmy
Obsah. Poptávka spotřebitele - 1 - Petr Voborník
 Obsah Obsah... Poptávka spotřebitele.... ndividuální poptávka (po statku ).... Vliv změny důchodu spotřebitele na poptávku..... Důchodová spotřební křivka..... Druhy statků... 3 CC, kde je určitým druhem
Obsah Obsah... Poptávka spotřebitele.... ndividuální poptávka (po statku ).... Vliv změny důchodu spotřebitele na poptávku..... Důchodová spotřební křivka..... Druhy statků... 3 CC, kde je určitým druhem
0 z 25 b. Ekonomia: 0 z 25 b.
 Ekonomia: 1. Roste-li mzdová sazba,: nabízené množství práce se nemění nabízené množství práce může růst i klesat nabízené množství práce roste nabízené množství práce klesá Zvýšení peněžní zásoby vede
Ekonomia: 1. Roste-li mzdová sazba,: nabízené množství práce se nemění nabízené množství práce může růst i klesat nabízené množství práce roste nabízené množství práce klesá Zvýšení peněžní zásoby vede
Mikroekonomie I: Všeobecná rovnováha. Praha, VŠFS,
 PhDr. Praha, VŠFS, 13.12.2010 Podstata všeobecné rovnováhy Všeobecná rovnováha = rovnováha na všech trzích (trh statků a výrobních faktorů) Nelze zvýšit užitek nějakého spotřebitele, aniž bychom snížili
PhDr. Praha, VŠFS, 13.12.2010 Podstata všeobecné rovnováhy Všeobecná rovnováha = rovnováha na všech trzích (trh statků a výrobních faktorů) Nelze zvýšit užitek nějakého spotřebitele, aniž bychom snížili
Vymezení nákladů různá pojetí
 Obsah vymezení nákladů náklady v krátkém období vztah mezních, průměrných a celkových nákladů náklady v dlouhém období vztah mezi náklady v SR a LR vztah mezi produkční funkcí a funkcemi nákladů příjmy
Obsah vymezení nákladů náklady v krátkém období vztah mezních, průměrných a celkových nákladů náklady v dlouhém období vztah mezi náklady v SR a LR vztah mezi produkční funkcí a funkcemi nákladů příjmy
Mikroekonomie 1 -TOMÁŠ VOLEK (Prezentace 6) 1
 Obsah Podnik Výnosy Zisk Podnik Firma (podnik) je obecné označení pro ekonomicko - právní subjekt. Základními znaky rozlišující podnik od jiných institucí společnosti jsou: - -.. Základní cíl podniku je
Obsah Podnik Výnosy Zisk Podnik Firma (podnik) je obecné označení pro ekonomicko - právní subjekt. Základními znaky rozlišující podnik od jiných institucí společnosti jsou: - -.. Základní cíl podniku je
Přijímací zkoušky na navazující magisterské studium leden 2006 Zkouška z ekonomie Zadání
 Varianta C3 Strana 1 Přijímací zkoušky na navazující magisterské studium leden 2006 Zkouška z ekonomie Zadání Přečtěte si pozorně zadání každé otázky, vyberte variantu a označte křížkem na přiloženém listu
Varianta C3 Strana 1 Přijímací zkoušky na navazující magisterské studium leden 2006 Zkouška z ekonomie Zadání Přečtěte si pozorně zadání každé otázky, vyberte variantu a označte křížkem na přiloženém listu
M I K R O E K O N O M I E. orientační program cvičení. 3. Produkce, náklady, příjmy a zisk firmy. 31. 10. 2005
 Vysoká škola finanční a správní, o. p. s. zimní semestr 2005/06 bakalářské prezenční studium, středisko Most obor Řízení podniku a podnikové finance (RP) M I K R O E K O N O M I E orientační program cvičení
Vysoká škola finanční a správní, o. p. s. zimní semestr 2005/06 bakalářské prezenční studium, středisko Most obor Řízení podniku a podnikové finance (RP) M I K R O E K O N O M I E orientační program cvičení
11. Trhy výrobních faktorů Průvodce studiem: 11.1 Základní charakteristika trhu výrobních faktorů Poptávka po VF Nabídka výrobního faktoru
 11. Trhy výrobních faktorů V předchozích kapitolách jsme zkoumali způsob rozhodování firmy o výstupu a ceně v rámci různých tržních struktur (dokonalá a nedokonalá konkurence). Ačkoli se fungování firem
11. Trhy výrobních faktorů V předchozích kapitolách jsme zkoumali způsob rozhodování firmy o výstupu a ceně v rámci různých tržních struktur (dokonalá a nedokonalá konkurence). Ačkoli se fungování firem
29. mezní a průměrná produktivita práce MC a AC při 15 hodinách práce? AC = w = 4,5 Kč při 15 hodinách práce MC = w + L pro L = 15
 29. mezní a průměrná produktivita práce MC a AC při 15 hodinách práce? AC = w = 4,5 Kč při 15 hodinách práce MC = w + L pro L = 15 1 30. Optimum při nájmu výrobního faktoru Nabídka vstupu Z je dána rovnicí
29. mezní a průměrná produktivita práce MC a AC při 15 hodinách práce? AC = w = 4,5 Kč při 15 hodinách práce MC = w + L pro L = 15 1 30. Optimum při nájmu výrobního faktoru Nabídka vstupu Z je dána rovnicí
Metodický list pro druhé soustředění kombinovaného Bc. studia předmětu B_MiE_B, Mikroekonomie B Název tematického celku: Mikroekonomie B druhý blok
 Cíl tematického celku: pochopit problematiku rozhodování firmy, odvodit nabídkovou křivku Tento tématický celek je rozdělen do následujících dílčích témat: 1. dílčí téma: Podstata firmy 2. dílčí téma:
Cíl tematického celku: pochopit problematiku rozhodování firmy, odvodit nabídkovou křivku Tento tématický celek je rozdělen do následujících dílčích témat: 1. dílčí téma: Podstata firmy 2. dílčí téma:
Všeobecná rovnováha 1 Statistický pohled
 Makroekonomická analýza přednáška 4 1 Všeobecná rovnováha 1 Statistický pohled Předpoklady Úspory (resp.spotřeba) a investice (resp.kapitál), kterými jsme se zabývali v minulých lekcích, jsou spolu s technologickým
Makroekonomická analýza přednáška 4 1 Všeobecná rovnováha 1 Statistický pohled Předpoklady Úspory (resp.spotřeba) a investice (resp.kapitál), kterými jsme se zabývali v minulých lekcích, jsou spolu s technologickým
Literatura. Soukupová et al.: Mikroekonomie. Kapitoly 13-14, str Musil: Mikroekonomie středně pokročilý kurz. Kapitoly 9-10, str
 Struktura specifika trhu výrobních faktorů příjmové a nákladové veličiny podmínky maximalizace zisku dokonale konkurenční trh práce poptávka po práci firma prodávající výstup na DoKo. trhu poptávka po
Struktura specifika trhu výrobních faktorů příjmové a nákladové veličiny podmínky maximalizace zisku dokonale konkurenční trh práce poptávka po práci firma prodávající výstup na DoKo. trhu poptávka po
2. EKONOMICKÁ ROVNOVÁHA. slide 1
 2. EKONOMICKÁ ROVNOVÁHA slide 1 Předmětem přednášky je.odpovědět na následující otázky: Kolik se toho v ekonomice vyprodukuje? Kdo obdrží důchody z produkce? Kdo nakoupí celkový výstup? Co vyrovná poptávku
2. EKONOMICKÁ ROVNOVÁHA slide 1 Předmětem přednášky je.odpovědět na následující otázky: Kolik se toho v ekonomice vyprodukuje? Kdo obdrží důchody z produkce? Kdo nakoupí celkový výstup? Co vyrovná poptávku
2.. E K E ONOMI M C I KÁ K R OV O NOV O Á V H Á A H slide 0
 2. EKONOMICKÁ ROVNOVÁHA slide 0 Předmětem přednášky je.odpovědět na následující otázky: Kolik se toho v ekonomice vyprodukuje? Kdo obdrží důchody z produkce? Kdo nakoupí celkový výstup? Co vyrovná poptávku
2. EKONOMICKÁ ROVNOVÁHA slide 0 Předmětem přednášky je.odpovědět na následující otázky: Kolik se toho v ekonomice vyprodukuje? Kdo obdrží důchody z produkce? Kdo nakoupí celkový výstup? Co vyrovná poptávku
MODELY OLIGOPOLU COURNOTŮV MODEL, STACKELBERGŮV MODEL
 MODELY OLIGOPOLU COURNOTŮV MODEL, STACKELBERGŮV MODEL DOKONALÁ KONKURENCE Trh dokonalé konkurence je charakterizován velkým počtem prodávajících, kteří vyrábějí homogenní produkt a nemohou ovlivnit tržní
MODELY OLIGOPOLU COURNOTŮV MODEL, STACKELBERGŮV MODEL DOKONALÁ KONKURENCE Trh dokonalé konkurence je charakterizován velkým počtem prodávajících, kteří vyrábějí homogenní produkt a nemohou ovlivnit tržní
Funkce poptávky (lineární) Funkce nabídky. Křížová elasticita poptávky. Rovnovážné množství. Rovnovážná cena. Přebytek spotřebitele.
 Vzorce optávka a nabídka a b Funkce poptávky (lineární) m + n Funkce nabídky D * Cenová elasticita poptávky bodová + D + D * Důchodová elasticita poptávky * Cenová elasticita poptávky intervalová A B CD
Vzorce optávka a nabídka a b Funkce poptávky (lineární) m + n Funkce nabídky D * Cenová elasticita poptávky bodová + D + D * Důchodová elasticita poptávky * Cenová elasticita poptávky intervalová A B CD
a) Do produkční funkce firmy dosadíme počet jednotek práce, pro něž máme určit dosazený objem produkce
 Řešené příklady 1. Firma Karkulka, s.r.o šije červené čepečky. Produkční funkce firmy má tvar Q = 41. + 20. 2 (1/3). 3. Kde jsou hodiny práce za den. a) Určete, kolik firma ušije denně čepečků, pokud najme
Řešené příklady 1. Firma Karkulka, s.r.o šije červené čepečky. Produkční funkce firmy má tvar Q = 41. + 20. 2 (1/3). 3. Kde jsou hodiny práce za den. a) Určete, kolik firma ušije denně čepečků, pokud najme
DOKONALÁ KONKURENCE.
 DOKONALÁ KONKURENCE www.ekofun.cz ZÁKLADNÍ POJMY PLATNÉ PRO DOKONALOU I NEDOKONALOU KONKURENCI Cíl firmy je maximalizace zisku -největší(kladné) rozpětí mezi TR a TC Maximalizujeme zisk s ohlédnutím na
DOKONALÁ KONKURENCE www.ekofun.cz ZÁKLADNÍ POJMY PLATNÉ PRO DOKONALOU I NEDOKONALOU KONKURENCI Cíl firmy je maximalizace zisku -největší(kladné) rozpětí mezi TR a TC Maximalizujeme zisk s ohlédnutím na
Mikroekonomie. 1. Opakování příklad 1. Řešení. Opakování - Příklad 2. Příklad 2 - řešení P = 30 (6Q/5)
 1. Opakování příklad 1. Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Poptávka po obuvi je popsána rovnicí: Q D = 300 0,3P, (Q D je poptávané množství za měsíc. Nabídka v průběhu měsíce
1. Opakování příklad 1. Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Poptávka po obuvi je popsána rovnicí: Q D = 300 0,3P, (Q D je poptávané množství za měsíc. Nabídka v průběhu měsíce
Teorie her a ekonomické rozhodování. 9. Modely nedokonalých trhů
 Teorie her a ekonomické rozhodování 9. Modely nedokonalých trhů 9.1 Dokonalý trh Dokonalý trh Dokonalá informovanost kupujících Dokonalá informovanost prodávajících Nulové náklady na změnu dodavatele Homogenní
Teorie her a ekonomické rozhodování 9. Modely nedokonalých trhů 9.1 Dokonalý trh Dokonalý trh Dokonalá informovanost kupujících Dokonalá informovanost prodávajících Nulové náklady na změnu dodavatele Homogenní
Mikroekonomie I: Trh výrobních faktorů
 PhDr. Praha, VŠFS, 29.11.2010 Výrobní faktory Poptávka po výrobních faktorech Výrobní faktory = vzácné vstupy, které používáme k produkci statků-výstupu Tradiční výrobní faktory Prvotní výrobní faktory:
PhDr. Praha, VŠFS, 29.11.2010 Výrobní faktory Poptávka po výrobních faktorech Výrobní faktory = vzácné vstupy, které používáme k produkci statků-výstupu Tradiční výrobní faktory Prvotní výrobní faktory:
NABÍDKA.
 NABÍDKA www.ekofun.cz Agregátní nabídka -souhrn všech zamýšlených prodejů, se kterými přicházejí výrobci na trh Individuální nabídka -nabídka jednoho výrobce Dílčí (tržní) nabídka (S) -nabídka jediného
NABÍDKA www.ekofun.cz Agregátní nabídka -souhrn všech zamýšlených prodejů, se kterými přicházejí výrobci na trh Individuální nabídka -nabídka jednoho výrobce Dílčí (tržní) nabídka (S) -nabídka jediného
Dokonalá konkurence. Téma cvičení. Mikroekonomie Q FC VC Příklad řešení. Bod uzavření firmy
 opakování zjistěte zbývající údaje Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Q FC VC 0 20 1 10 2 18 3 24 4 36 Co lze zjistit? FC - pro Q = 1, 2, 3, 4 TC AC AVC AFC řešení opakování
opakování zjistěte zbývající údaje Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Q FC VC 0 20 1 10 2 18 3 24 4 36 Co lze zjistit? FC - pro Q = 1, 2, 3, 4 TC AC AVC AFC řešení opakování
Příjmy firmy můžeme rozdělit na celkové, průměrné a mezní.
 7 Příjmy firmy Příjmy firmy představují sumu peněžních prostředků, které firmě plynou z realizace její produkce, proto někteří autoři používají analogický pojem tržby. Jestliže vycházíme z cíle formy v
7 Příjmy firmy Příjmy firmy představují sumu peněžních prostředků, které firmě plynou z realizace její produkce, proto někteří autoři používají analogický pojem tržby. Jestliže vycházíme z cíle formy v
Mikroekonomie Nabídka, poptávka
 Téma cvičení č. 2: Mikroekonomie Nabídka, poptávka Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Podstatné z minulého cvičení Matematický pojmový aparát v Mikroekonomii Důležité minulé cvičení kontrolní
Téma cvičení č. 2: Mikroekonomie Nabídka, poptávka Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Podstatné z minulého cvičení Matematický pojmový aparát v Mikroekonomii Důležité minulé cvičení kontrolní
Struktura. formování poptávky po kapitálu odvození poptávky po investicích formování nabídky úspor Hayekův trojúhelník a jeho souvislosti
 11. Trh kapitálu Struktura formování poptávky po kapitálu odvození poptávky po investicích formování nabídky úspor Hayekův trojúhelník a jeho souvislosti Literatura Holman, R.: Mikroekonomie-středně pokročilý
11. Trh kapitálu Struktura formování poptávky po kapitálu odvození poptávky po investicích formování nabídky úspor Hayekův trojúhelník a jeho souvislosti Literatura Holman, R.: Mikroekonomie-středně pokročilý
Trh práce a politika zaměstnanosti Ing. Zuzana Hrdličková Konzultační hodiny: Po 14:30 15:30 Kancelář 602 (6. patro)
 Trh práce a politika zaměstnanosti Zuzana Hrdličková Trh práce a politika zaměstnanosti Ing. Zuzana Hrdličková Email: z.hrdlickova@mail.muni.cz Konzultační hodiny: Po 14:30 15:30 Kancelář 602 (6. patro)
Trh práce a politika zaměstnanosti Zuzana Hrdličková Trh práce a politika zaměstnanosti Ing. Zuzana Hrdličková Email: z.hrdlickova@mail.muni.cz Konzultační hodiny: Po 14:30 15:30 Kancelář 602 (6. patro)
FORMOVÁNÍ CEN NA TRZÍCH VÝROBNÍCH FAKTORŮ.
 ORMOVÁNÍ CEN NA TRZÍCH VÝROBNÍCH AKTORŮ www.ekoun.cz www.ekoun.cz ORMOVÁNÍ CEN NA TRZÍCH VÝROBNÍCH AKTORŮ Výrobní faktory: práce + kapitál (pro nás) Na trzích výrobních faktorů: - poptávku vytvářejí firmy
ORMOVÁNÍ CEN NA TRZÍCH VÝROBNÍCH AKTORŮ www.ekoun.cz www.ekoun.cz ORMOVÁNÍ CEN NA TRZÍCH VÝROBNÍCH AKTORŮ Výrobní faktory: práce + kapitál (pro nás) Na trzích výrobních faktorů: - poptávku vytvářejí firmy
Trhy výrobních faktorů
 Trhy výrobních faktorů Výrobní faktory Výrobními faktory (VF) je obecně vše, co slouží k produkci statků. Tedy jsou to vstupy, které používáme k produkci výstupu. Standardní hrubé dělení: práce, kapitál
Trhy výrobních faktorů Výrobní faktory Výrobními faktory (VF) je obecně vše, co slouží k produkci statků. Tedy jsou to vstupy, které používáme k produkci výstupu. Standardní hrubé dělení: práce, kapitál
Úvod do ekonomie Týden 10. Tomáš Cahlík
 Úvod do ekonomie Týden 10 Tomáš Cahlík Obsah Firmy Úvod rozhodování podle očekávaných nákladů a očekávaných výnosů Výroba Náklady Struktura trhu Dokonalá konkurence Monopol Nedokonalá konkurence Zkouškové
Úvod do ekonomie Týden 10 Tomáš Cahlík Obsah Firmy Úvod rozhodování podle očekávaných nákladů a očekávaných výnosů Výroba Náklady Struktura trhu Dokonalá konkurence Monopol Nedokonalá konkurence Zkouškové
Teorie spotřebitelské volby
 Teorie spotřebitelské volby Motivace MP #1: Lidé volí mezi alternativami. pokud koupí víc jednoho statku, zbude jim méně na nákup jiného statku pokud víc pracují, vydělají vyšší důchod a mohou víc spotřebovávat,
Teorie spotřebitelské volby Motivace MP #1: Lidé volí mezi alternativami. pokud koupí víc jednoho statku, zbude jim méně na nákup jiného statku pokud víc pracují, vydělají vyšší důchod a mohou víc spotřebovávat,
Produkční analýza. a) Co je to produkční funkce? Vyjadřuje max. objem produkce, jež je možno vyrobit danou kombinací VF při dané úrovni technologie.
 MIKROEKONOMIE 1 cvičení 9-13 [1] Produkční analýza a) Co je to produkční funkce? Vyjadřuje max. objem produkce, jež je možno vyrobit danou kombinací VF při dané úrovni technologie. b) Vysvětlete zákon
MIKROEKONOMIE 1 cvičení 9-13 [1] Produkční analýza a) Co je to produkční funkce? Vyjadřuje max. objem produkce, jež je možno vyrobit danou kombinací VF při dané úrovni technologie. b) Vysvětlete zákon
Studijní opora. Téma: Rozhodování firmy v podmínkách dokonalé konkurence.
 Studijní opora Název předmětu: Ekonomie I Zpracoval: Ing. Lenka Brizgalová, Ph.D. Téma: Rozhodování firmy v podmínkách dokonalé konkurence. Vzdělávací cíl: Téma Rozhodování firmy v podmínkách dokonalé
Studijní opora Název předmětu: Ekonomie I Zpracoval: Ing. Lenka Brizgalová, Ph.D. Téma: Rozhodování firmy v podmínkách dokonalé konkurence. Vzdělávací cíl: Téma Rozhodování firmy v podmínkách dokonalé
Základy ekonomie. Petr Musil: petrmusil1977@gmail.com
 Základy ekonomie Téma č. 2: Trh, nabídka, poptávka Petr Musil: petrmusil1977@gmail.com Obsah 1. Dělba práce 2. Směna, peníze 3. Trh 4. Cena 5. Nabídka 6. Poptávka 7. Tržní rovnováha 8. Konkurence Dělba
Základy ekonomie Téma č. 2: Trh, nabídka, poptávka Petr Musil: petrmusil1977@gmail.com Obsah 1. Dělba práce 2. Směna, peníze 3. Trh 4. Cena 5. Nabídka 6. Poptávka 7. Tržní rovnováha 8. Konkurence Dělba
Užitek a užitkové funkce Jan Čadil FNH VŠE
 Užitek a užitkové funkce Jan Čadil FNH VŠE Footer Text 3/24/2014 1 Užitek a preference Užitek je subjektivní pocit uspokojení potřeb (v našem případě pomocí spotřeby určitého statku/služby), v zásadě vyjadřuje
Užitek a užitkové funkce Jan Čadil FNH VŠE Footer Text 3/24/2014 1 Užitek a preference Užitek je subjektivní pocit uspokojení potřeb (v našem případě pomocí spotřeby určitého statku/služby), v zásadě vyjadřuje
Mikroekonomie I. Trh výrobních faktorů ekonomický koloběh. Křivka nabídky (S) Přednáška 3. Podstatné z minulé přednášky. Zákon rostoucí nabídky
 Trh výrobních faktorů ekonomický koloběh Mikroekonomie I 3. přednáška Poptávka substituční a důchodový efekt, konkurence, elasticita poptávky Přednáška 3. Křivka nabídky (S) Poptávka substituční a důchodový
Trh výrobních faktorů ekonomický koloběh Mikroekonomie I 3. přednáška Poptávka substituční a důchodový efekt, konkurence, elasticita poptávky Přednáška 3. Křivka nabídky (S) Poptávka substituční a důchodový
1. EKONOMIE jako věda o lidském jednání. Invisible hand ve společnosti směnných vztahů. Metodologie ekonomie, optimalizační chování a informace.
 5EN411 EKONOMIE II. PODMÍNKY UKONČENÍ KURZU: Získání 60 a více bodů ze 100. Na cvičení je možné získat max. 20 bodů: 2 malé testy po 10 bodech. Malé testy zahrnují příklady týkající se problémů řešených
5EN411 EKONOMIE II. PODMÍNKY UKONČENÍ KURZU: Získání 60 a více bodů ze 100. Na cvičení je možné získat max. 20 bodů: 2 malé testy po 10 bodech. Malé testy zahrnují příklady týkající se problémů řešených
Tržní síly nabídky a poptávky
 Tržní síly nabídky a poptávky Motivace Dělba práce zvyšuje bohatství. Zároveň vytváří vzájemnou závislost a potřebu koordinovat hospodářství. Ve svobodném světě však hospodářství nikdo neřídí a nekoordinuje
Tržní síly nabídky a poptávky Motivace Dělba práce zvyšuje bohatství. Zároveň vytváří vzájemnou závislost a potřebu koordinovat hospodářství. Ve svobodném světě však hospodářství nikdo neřídí a nekoordinuje
Otázky k přijímacímu řízení magisterského civilního studia
 Univerzita obrany Fakulta ekonomiky a managementu ----------------------------------------------------------------------------------------------------- Otázky k přijímacímu řízení magisterského civilního
Univerzita obrany Fakulta ekonomiky a managementu ----------------------------------------------------------------------------------------------------- Otázky k přijímacímu řízení magisterského civilního
8. Dokonalá konkurence
 8. Dokonalá konkurence Kompletní text ke kapitole viz. KRAFT, J., BEDNÁŘOVÁ, P, KOCOUREK, A. Ekonomie I. TUL Liberec, 2010. ISBN 978-80-7372-652-2; str.64-75 Dokonale konkurenční tržní prostředí lze charakterizovat
8. Dokonalá konkurence Kompletní text ke kapitole viz. KRAFT, J., BEDNÁŘOVÁ, P, KOCOUREK, A. Ekonomie I. TUL Liberec, 2010. ISBN 978-80-7372-652-2; str.64-75 Dokonale konkurenční tržní prostředí lze charakterizovat
Nejistota a rovnováha Varian: Mikroekonomie: moderní přístup, kapitoly 12 a 16 Varian: Intermediate Microeconomics, 8e, Chapters 12 and 16 () 1 / 49
 Nejistota a rovnováha Varian: Mikroekonomie: moderní přístup, kapitoly 12 a 16 Varian: Intermediate Microeconomics, 8e, Chapters 12 and 16 () 1 / 49 Na této přednášce se dozvíte jak vypadá rozhodování
Nejistota a rovnováha Varian: Mikroekonomie: moderní přístup, kapitoly 12 a 16 Varian: Intermediate Microeconomics, 8e, Chapters 12 and 16 () 1 / 49 Na této přednášce se dozvíte jak vypadá rozhodování
Vedoucí autorského kolektivu: Ing. Jana Soukupová, CSc. Tato publikace vychází s laskavým přispěním společnosti RWE Transgas, a. s.
 Autoři kapitol: Doc. Ing. Bronislava Hořejší, CSc. (kapitoly 1, 5, 6, 7, 8, 9, 10, 11, 13, 14, 15, 16) Doc. PhDr. Libuše Macáková, CSc. (kapitoly 4, 17.6, 18, 19) Prof. Ing. Jindřich Soukup, CSc. (kapitoly
Autoři kapitol: Doc. Ing. Bronislava Hořejší, CSc. (kapitoly 1, 5, 6, 7, 8, 9, 10, 11, 13, 14, 15, 16) Doc. PhDr. Libuše Macáková, CSc. (kapitoly 4, 17.6, 18, 19) Prof. Ing. Jindřich Soukup, CSc. (kapitoly
Mikroekonomie. Nabídka, poptávka. Kombinované studium 1. cv. Nabídka - rozlišujeme mezi: Nabídka (supply) S 10.10.2014
 Kombinované studium 1. cv. Mikroekonomie Nabídka, poptávka Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Nabídka (supply) S Nabídka představuje objem zboží, které jsou výrobci ochotni na trh dodat
Kombinované studium 1. cv. Mikroekonomie Nabídka, poptávka Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Nabídka (supply) S Nabídka představuje objem zboží, které jsou výrobci ochotni na trh dodat
Nejistota a rovnováha Varian: Mikroekonomie: moderní přístup, kapitoly 12 a 16 Varian: Intermediate Microeconomics, 8e, Chapters 12 and 16 1 / 42
 Nejistota a rovnováha Varian: Mikroekonomie: moderní přístup, kapitoly 12 a 16 Varian: Intermediate Microeconomics, 8e, Chapters 12 and 16 1 / 42 Na této přednášce se dozvíte jak vypadá rozhodování za
Nejistota a rovnováha Varian: Mikroekonomie: moderní přístup, kapitoly 12 a 16 Varian: Intermediate Microeconomics, 8e, Chapters 12 and 16 1 / 42 Na této přednášce se dozvíte jak vypadá rozhodování za
Řešení domácího úkolu
 Úkol 1 Řešení domácího úkolu Podrobný popis řešení - analogie na seminář IV. a) Napište produkční funkce Na 1 hektolitr Smoothie potřebujeme 72 jednotek práce Na 1 hektolitr Kofoly potřebujeme 36 jednotek
Úkol 1 Řešení domácího úkolu Podrobný popis řešení - analogie na seminář IV. a) Napište produkční funkce Na 1 hektolitr Smoothie potřebujeme 72 jednotek práce Na 1 hektolitr Kofoly potřebujeme 36 jednotek
Q 1. Výrobce 1. Spotřebitel 1 Q 2. Spotřebitel 2. Výrobce 2
 Mikroekonomie magisterský kurz - VŠFS Jiří Mihola, jiri.mihola@quick.cz, 2010 www.median-os.cz, www.ak-ol.cz Téma cvičení Příklady teorie všeobecné rovnováhy Model 2*2*2*2 Q 1 Q 2 Výrobce 1 Q 1 Spotřebitel
Mikroekonomie magisterský kurz - VŠFS Jiří Mihola, jiri.mihola@quick.cz, 2010 www.median-os.cz, www.ak-ol.cz Téma cvičení Příklady teorie všeobecné rovnováhy Model 2*2*2*2 Q 1 Q 2 Výrobce 1 Q 1 Spotřebitel
