|
|
|
- Stanislava Matějková
- před 8 lety
- Počet zobrazení:
Transkript
1 INFORMATIKA Dokazov n a objevov n v t v geometrii pomoc metod po ta ov algebry PAVEL PECH Pedagogick fakulta JU, esk Bud jovice 1. vod V posledn t etin dvac t ho stolet byly vyvinuty inn metody v automatick m dokazov n v t element rn geometrie. Pomoc t to teorie byly dok z ny a dokonce objeveny stovky netrivi ln ch v t. V semin i, kter jsem vedl v posledn ch letech napedagogick fakult Jiho esk univerzit, jsme pomoc teorie automatick ho dokazov n v t na po ta i e ili adu probl m element rn geometrie. Studenti, kte tento voliteln semin nav t vovali, byli v t inou ve tvrt m ro n ku studia u itelstv matematiky pro z kladn koly a pro koly st edn, t.j m li znalosti z kladn ho kurzu geometrie. Pomoc po ta e i klasick m zp sobem jsme vy et ovali adu loh { Heronovu formuli pro v po et obsahu troj- heln ka a jej zobecn n { Brahmaguptovu formuli pro v po et obsahu t tivov ho ty heln ka pomoc d lek jeho stran. D le Staudtovu formuli, Wallace{Simsonovu v tu a jej zobecn n, Napoleonovu v tu a dal podobn probl my. Zat mco klasick (syntetick ) metoda d v lep vhled do dan geometrick situace a t m umo uje i lep porozum n probl mu a v ce ukazuje kr su geometrie, pomoc po ta ov algebry na druh stran m eme e it slo it lohy, kter jsou klasick m zp sobem obt n e iteln. Pomoc po- ta ov algebry lze prov d t dokazov n matematick ch v t (automatic Matematika - fyzika - informatika /
2 theorem proving), odvozov n (automatic derivation) a objevov n (automatic discovery) nov ch v t. Lze t prov d t konstrukce, kter nen snadn sestrojit pomoc prav tka a kru tka, atd. V tomto l nku pod me stru n p ehled t to teorie. Pokud je mi zn mo, v e tin literatura k t to problematice neexistuje a tak z jemc m o hlub studium doporu uji vynikaj c publikaci [4], viz t [7], [10]. Na n kolika p kladech element rn geometrie v rovin je uk z no pou it metod po ta ov algebry, kter je v t inou dopln no i klasickou zp sobem e en. 2. Automatick dokazov n v t Nejprve trochuteorie.automatick dokazov n v t se zab v geometrick mi tvrzen mi, kter maj tvar H ) c, kde H je mno ina p edpoklad a c je z v r. Prvn m krokem je algebraizace geometrick ho probl mu vezvolen soustav sou adnic. Tato f ze je charakterizov na sestaven m mno iny p edpoklad H, kter maj tvar polynomick ch rovnic h 1 (x 1 x 2 ::: x n )=0 h 2 (x 1 x 2 ::: x n )=0 ::: h r (x 1 x 2 ::: x n )=0 az v ru c, kter je vyj d en rovnic c(x 1 x 2 ::: x n )=0 kde koecienty polynom jsou racion ln sla. Tedy algebraick tvar na- eho tvrzen je 8xf(h 1 (x) =0^ h 2 (x) =0^ ^h r (x) =0)) c(x) =0:g (1) C lem dal ho kroku je ov en pravdivosti neboli verikace tvrzen (1). M me rozhodnout, zda z v r tvrzen plyne z dan ch p edpoklad, nebo, co je tot, zda nulov mno ina z v ru c obsahuje nulovou mno inu p edpoklad H, tj. zda plat Zero(H) Zero c): K tomu sta uk zat, e polynom c pat do ide lu (h 1 ::: h r ): Zde kr tce p ipome me denici ide lu. Ide lem I kter je generov n polynomy (h 1 ::: h r ) zna me I =(h 1 ::: h r ) rozum me mno inu v ech polynom tvaru c 1 h 1 + c 2 h c r h r kde c 1 c 2 ::: c r jsou libovoln polynomy. Rozhodnut, zdali polynom c pat do dan ho ide lu I bylo je t doned vna velmi obt n m probl mem (tzv. ideal membership problem). 296 Matematika - fyzika - informatika /2006
3 V sedmdes t ch letech 20. stolet tento probl m vy e il Bruno Buchberger z univerzity v Linci pou it m algoritmu, kter se na po est sv ho objevitele naz v Buchberger v algoritmus. Ve v t in zn m ch matematick ch program (nap. Mathematica, Maple) je implementov n p kaz NF(c,I), zalo en na Buchbergerov algoritmu, pomoc kter ho um me danou ot zku rozhodnout. Jednodu e e eno, p kaz NF(c,I) nebo t norm ln forma polynomu c vzhledem k ide lu I d v zbytek p i d len polynomu c polynomy h 1 ::: h r kter mi je ide l I generov n. Pokud NF(c,I)=0, potom je zbytek roven nule a polynom c n le ide lu I, tj. lze ps t c = c 1 h 1 +c 2 h 2 ++c r h r kde c 1 c 2 ::: c r jsou n jak polynomy. Cel proces je zobecn n m Euklidova algoritmu p i d len polynomu polynomem o jedn prom nn, viz [4], kde je cel probl m podrobn vylo en. Nejjednodu zp sob, jak uk zat podstatu automatick ho dokazov n v t, je demonstrace na p kladu. M jme n sleduj c p klad. Doka te, e se v ky troj heln ka prot naj v jedin m bod. Nejprve zvol me vhodnou soustavu sou adnic, tj. takovou, aby vztahy, kter mi budeme analyticky popisovat geometrickou situaci byly co nejjednodu, obr. 1. ; Obr. 1 V ky troj heln ka ABC proch zej jedn m bodem { po ta ov d kaz Ozna me A =[0 0] B =[a 0] C =[b c] vrcholy troj heln ka ABC: Nyn vyj d me rovnice v ek v a v b v c : v a :(b ; a)x + cy =0 v b : bx + cy ; ab =0 v c : x ; b =0: Matematika - fyzika - informatika /
4 P edpokl dejme, e se v ky v b a v c prot naj v bod O =[s t], tj. e plat O 2 v b, bs + ct ; ab =0 O 2 v c, s ; b =0: Chceme uk zat, e v ka v a obsahuje bod O, tj. O 2 v a, (b ; a)s + ct =0: Tedy m me dok zat n sleduj c tvrzen 8s tf(bs + ct ; ab =0)^ (s ; b =0)) (b ; a)s + ct =0g: (2) Vtomto velmi jednoduch m p pad jsme schopni uk zat, e tvrzen (2) je pravdiv, dokonce ru n { bez u it po ta e. Uv domme si toti, e plat (b ; a)s + ct =1 (bs + ct ; ab) ; a (s ; b): (3) Vyj d ili jsme polynom z v ru (b ; a)s + ct jako line rn kombinaci polynom p edpoklad bs + ct ; ab and s ; b: Z platnosti rovnic bs + ct ; ab = =0 s ; b = 0 plyne z (3) platnost rovnice (b ; a)s + ct =0: Uk zali jsme, e polynom (b;a)s+ct n le ide lu I =(bs+ct;ab p;b): V programu CoCoA ), kter budeme pou vat, nap eme Use R::=Q[abcst] I:=Ideal(bs+ct-ab,s-b) NF((b-a)s+ct,I) Dostaneme odpov 0, tj. NF((b-a)s+ct,I)=0 a tvrzen (2) je pravdiv. Po ta ov d kaz je hotov. Uka me je t klasick d kaz tvrzen, e v ky troj heln ka se prot naj v jednom bod. M eme pou t n sleduj c postup: Vrcholy A B C troj heln ka vedeme rovnob ky s prot j mi stranami BC AC AB obr. 2. Dostaneme nov troj heln k A 0 B 0 C 0 v n m v ky v a v b v c troj heln ka ABC tvo osy stran. Nyn sta uk zat, e se osy stran troj heln ka A 0 B 0 C 0 prot naj v jednom bod. D kaz tohoto tvrzen p enech v me ten i. ) Software CoCoA je zdarma k dispozici na adrese Matematika - fyzika - informatika /2006
5 ; Obr. 2 V ky v a v b v c troj heln ka ABC proch zej jedn m bodem { klasick d kaz K d kazu tvrzen jsme nap. mohli pou t i Cevovu v tu apod. Klasick d kaz, kter jsme pr v uk zali, m l krom ady klad jeden podstatn nedostatek { pot ebovali jsme m t kl ov n pad, kter vede k e en probl mu. N kdy se v ak m e st t, e dn kl ov n pad nedostaneme. 3. Automatick odvozov n v t V dal sti se zam me na automatick odvozov n v t, kter v t inou odli ujeme od automatick ho objevov n v t, o kter m budeme hovo it v dal kapitole. Pod automatick m odvozov n m v t rozum me hled n geometrick ch tvrzen p edepsan ch vlastnost, kter plynou z dan ch p edpoklad. 3.1 Staudtova formule Obvykle za n me se studenty odvozen m Heronovy formule pro obsah troj heln ka. Proto e se v ak jedn o velmi zn m p pad, viz. nap. [7], uk eme danou metodu na n sleduj c m m n zn m m p kladu. Nech ABCD je rovinn ty heln k se stranami d lek a b c d a hlop kami e f. Vyj d ete obsah p ty heln ka ABCD pomoc a b c d e f. Uka me nejprve e en t to lohy metodou automatick ho odvozov n. Pot uk eme e en klasick, abychom mohli ob metody porovnat. Matematika - fyzika - informatika /
6 Zvolme syst m sou adnic tak e A =[0 0] B =[a 0] C =[x y] D = = [u v] a ozna me a = jabj b = jbcj c = jcdj d = jdaj e = jacj f = jbdj obr. 3. ; Obr. 3 Obsah ty heln ka ABCD vyj d en pomoc vzd lenost a b c d e f Pro d lky stran a hlop ek dostaneme: h 1 :(x ; a) 2 + y 2 = b 2 h 2 : (u ; x) 2 +(v ; y) 2 = c 2 h 3 : u 2 + v 2 = d 2 h 4 : x 2 + y 2 = e 2 h 5 : (u ; a) 2 + v 2 = f 2 : Obsah p ty heln ka ABCD m eme vyj d it s pou- it m sou adnic vrchol nap. tak, e ty heln k rozd l me kolmicemi na stranu AB kter proch zej vrcholy C D na dva pravo hl troj heln ky AD 0 D CC 0 B alichob n k D 0 C 0 CD: Potom snadno zjist me, e pro obsah p plat h 6 : p =1=2(ay + xv ; uy): Zrovnic h 1 h 2 ::: h 6 budeme eliminovat prom nn x y u v: Jinak e- eno, v ide lu I =(h 1 h 2 ::: h 6 ) hled me polynomy, kter obsahuj pouze prom nn a b c d e f p: Mezi t mito polynomy budeme hledat na formuli. V CoCoA nap eme Use R::= Q[xyuvabcdefp] I:=Ideal((x-a)^2+y^2-b^2,(u-x)^2+(v-y)^2-c^2,u^2+v^2-d^2,x^2+ y^2-e^2, (u-a)^2+v^2-f^2,p-1/2(ay+xv-uy)) Elim(x..v,I) Jako odpov dostaneme dva polynomy. Jeden z nich d v po prav hledan vztah 16p 2 =4e 2 f 2 ; (a 2 ; b 2 + c 2 ; d 2 ) 2 : (4) Tuto formuli, kter vyjad uje obsah ty heln ka pomoc v ech esti vz jemn ch vzd lenost mezi jeho ty mi vrcholy, publikoval Ch. R. Staudt v roce 1842, viz [9]. 300 Matematika - fyzika - informatika /2006
7 Druh polynom d v vztah pro vz jemnou z vislost mezi v emi esti vzd lenostmi a b c d e f vrchol ty heln ka. Jak dob e v me, ty heln k je zad n p ti prvky, nap. ty mi d lkami stran a jednou hlop kou (nikoliv jednozna n ). est vzd lenost tedy mus b t vz jemn z visl ch, co vyjad uje pr v nalezen Eulerova ty bodov relace [6]: e 4 f 2 + e 2 (a 2 b 2 ; a 2 c 2 ; b 2 d 2 + c 2 d 2 ; a 2 f 2 ; b 2 f 2 ; c 2 f 2 ; d 2 f 2 + f 4 )+ a 4 c 2 ; a 2 b 2 c 2 + a 2 c 4 ; a 2 b 2 d 2 + b 4 d 2 ; a 2 c 2 d 2 ; b 2 c 2 d 2 + b 2 d 4 ; a 2 c 2 f 2 + b 2 c 2 f 2 + a 2 d 2 f 2 ; b 2 d 2 f 2 =0: Eulerova ty bodov relace plyne z Cayley{Mengerova determinantu [2] pro objem V ty st nu, zn me-li d lky jeho v ech esti hran a b c d e f 288 V 2 = b 2 f 2 a 2 1 b 2 0 c 2 e 2 1 f 2 c 2 0 d 2 1 a 2 e 2 d 2 0 (5) polo me-li V = 0. Vztah (5) se li od Eulerovy ty bodov relace pouze okonstantn n sobek 2: Pozn mky: 1) M li bychom si uv domit, e Staudtova formule (4) plat p i dan m ozna en pro v echny tvary ty heln ka ABCD: Tedy nap. i v p pad, e ty heln k nen konvexn nebo dokonce kdy s m sebe prot n. Obsah p ty heln ka dan formul h 6 zahrnuje i tyto p pady a naz v se orientovan obsah. 2) Polo me-li v (4) nap. d =0potomse ty heln k zm n na troj heln k a dostaneme Heron v vzorec. Staudtova formule (4) je tedy zobecn n m Heronova vzorce. Nyn uk eme klasick zp sob nalezen Staudtovy formule (4). Zpravo hl ch troj heln k AED a DEC dostaneme jdej 2 = d 2 ;jaej 2 jdej 2 = c 2 ;jecj 2 a odtud Matematika - fyzika - informatika /
8 ; Obr. 4 Klasick d kaz Staudtovy formule d 2 ;jaej 2 = c 2 ;jecj 2 : (6) Analogicky z pravo hl ch troj heln k AF B a CFB dostaneme Se ten rovnost (6) a (7) d v a 2 ;jaf j 2 = b 2 ;jfcj 2 : (7) a 2 ; b 2 + c 2 ; d 2 = jaf j 2 ;jfcj 2 + jecj 2 ;jaej 2 : (8) Pravou stranu (8)m eme napsat ve tvaru (jaf j+jfcj)(jaf j;jfcj)+(jecj+jaej)(jecj;jaej) =2ejEFj tedy (a 2 ; b 2 + c 2 ; d 2 ) 2 =4e 2 jefj 2 : (9) D le plat jefj = f cos '. Dosazen do (9) d v (a 2 ; b 2 + c 2 ; d 2 ) 2 =4e 2 f 2 cos 2 ': (10) Nyn pou ijeme formuli pro obsah ty heln ka zn me-li d lky hlop ek e f a hel ' jimi sev en, viz nap. [1] p = 1 2 ef sin ': (11) Kone n dosazen m (10) do (11) s pou it m vztahu sin 2 ' = 1 ; cos 2 ' z sk me Staudtovu formuli (4). Na tomto p kladu m eme vid t, e automatick odvozen m e b t v ur it m smyslu snaz ne p i pou it klasick metody. 302 Matematika - fyzika - informatika /2006
9 3.2 Brahmaguptova formule Staudtovu formuli (4), kterou jsme odvodili v p edchoz sti pou ijeme kodvozen vzorce pro obsah t tivov ho ty heln ka. Je d n t tivov ty heln k ABCD (tj. jeho vrcholy le na kru nici) o stran ch d lek a b c d: Ur ete obsah p ty heln ka ABCD: Uva ujme nejprve p pad konvexn ho t tivov ho ty heln ka, viz obr. 5 vlevo. ; Obr. 5 Obsah t tivov ho ty heln ka vyj d en pomoc stran a b c d Podle Ptolemaiovy v ty plat vztah ef = ac + bd: P id me-li tuto podm nku k formuli (4), dostaneme eliminac prom nn ch e f hledanou formuli (eliminaci lze prov st v tomto p pad i ru n pouh m dosazen m). V CoCoA zad me Use R::=Q[abcdefp] I:=Ideal(16p^2-4e^2f^2+(a^2-b^2+c^2-d^2)^2,ac+bd-ef) Elim(e..f,I) Vyjde jedin polynom, kter vede na rovnici 16p 2 = ;(a 4 +b 4 +c 4 +d 4 )+2(a 2 b 2 +a 2 c 2 +a 2 d 2 +b 2 c 2 +b 2 d 2 +c 2 d 2 )+8abcd (12) nebo 16p 2 =(;a + b + c + d)(a ; b + c + d)(a + b ; c + d)(a + b + c ; d) a nebo, co je tot p = p (s ; a)(s ; b)(s ; c)(s ; d) (13) Matematika - fyzika - informatika /
10 kde s = 1 (a + b + c + d). To je zn m Brahmaguptova formule, (Brahmagupta, il v letech asi 665 v Indii). 2 Na obr. 5 vpravo vid me je t jin tvar t tivov ho ty heln ka ABCD p i t ch d lk ch stran a b c d: Vtomto p pad podle Ptolemaiovy v ty plat ef = bd ; ac: P id me-li tuto podm nku ke vztahu (4), dostaneme eliminac prom nn ch e f hledanou formuli pro p pad nekonvexn ho t tivov ho ty heln ka. Zad me Use R::=Q[abcdefp] I:=Ideal(16p^2-4e^2f^2+(a^2-b^2+c^2-d^2)^2, (ac-bd-ef)(ac-bd+ef)) Elim(e..f,I) a dostaneme polynom, kter vede na rovnici 16p 2 = ;(a 4 +b 4 +c 4 +d 4 )+2(a 2 b 2 +a 2 c 2 +a 2 d 2 +b 2 c 2 +b 2 d 2 +c 2 d 2 );8abcd (14) nebo 16p 2 =(a + b + c + d)(a + b ; c ; d)(a ; b + c ; d)(;a + b + c ; d): Ke stejn mu v sledku vede zb vaj c mo nost ef = ac ; bd: Pozn mka: Pro volbu a =2 b=1 c=1 d= 1 dostaneme pouze jedin tvar ty - heln ka, ve vzorci (14) vyjde toti napravo z porn slo. M eme tedy konstatovat, e pro dan d lky a b c d existuj nejv e dva ty heln ky sr zn mi obsahy p kter vypo teme podle vzorc (12) a (14). Klasick d kaz vynech v me. Je mo no jej naj t nap. v [2]. 3.3 Kiepertova hyperbola Automatick dokazov n a odvozov n si uk eme je t v n sleduj c m p kladu. Nad stranami troj heln ka ABC sestrojme podobn rovnoramenn troj- heln ky ABC 0, BCA 0, CAB 0 obr. Potom se p mky AA 0 BB 0 CC 0 prot naj v jednom bod. Zvolme soustavu sou adnic tak, e A =[0 0] B =[a 0] C =[b c] A 0 = =[k 1 k 2 ] B 0 =[l 1 l 2 ] C 0 =[m 1 m 2 ] obr Matematika - fyzika - informatika /2006
11 ; Obr. 6 P mky AA 0 BB 0 CC 0 se prot naj v bod S Nad stranami troj heln ka ABC sestrojme podobn rovnoramenn troj- heln ky ABC 0 BCA 0 CAB 0 (v echny vn troj heln ka ABC nebo dovnit ). Rovnoramenn troj heln k BCA 0 pop eme n sleduj c m zp sobem. Vrchol A 0 je koncov m bodem vektoru, jeho po tek je ve st edu strany BC od lcevjbcj kde v je n jak slo, a m t sm r jako vektor B ;C oto en o90 0 v kladn m smyslu, tj. plat (k 1 ;(a+b)=2 k 2 ;c=2) = v(c a ; b): Analogicky postupujeme u vrchol B 0 a C 0 : P mky AA 0 BB 0 CC 0 maj po ad rovnice k 1 y ; k 2 x =0 (l 1 ; a)y ; (x ; a)l 2 =0 (b ; m 1 )(y ; m 2 ) ; (x ; m 1 )(c ; m 2 )=0: P edpokl dejme, e S = [s 1 s 2 ] je spole n bod p mek AA 0 a BB 0. Chceme dok zat, e bod S le tak na p mce CC 0. Nap eme Use R::=Q[k[1..2]l[1..2]m[1..2]s[1..2]abcv] I:=Ideal(2k[1]-a-b-2vc,2k[2]-c-2va+2vb,2l[1]-b+2vc,2l[2]-c -2vb,2m[1]-a,m[2]+va,k[1]s[2]-k[2]s[1],(l[1]-a)s[2] -(s[1]-a)l[2]) NF((b-m[1])(s[2]-m[2])-(s[1]-m[1])(c-m[2]),I) Odpov je 0 co znamen, e se p mky AA 0 BB 0 CC 0 prot naj v jednom bod. N sleduje kr tk a elegantn klasick d kaz posledn ho tvrzen, kter publikoval O. Bottema [3], a kter si zaslou pozornost. D kaz je zalo en Matematika - fyzika - informatika /
12 na tzv. are ln metod [10], viz obr. 6. Plat a podobn Vid me, e plat jac 00 j=jc 00 Bj = obsah 4ACC 0 =obsah 4BCC 0 = = jacjjac 0 j sin(a + ')=jbcjjbc 0 j sin(b + ') = = jacj sin(a + ')=jbcj sin(b + ') jba 00 j=ja 00 Cj = jabj sin(b + ')=jacj sin(c + ') jcb 00 j=jb 00 Aj = jbcj sin(c + ')=jabj sin(a + '): jac 00 j jc 00 Bj jba00 j ja 00 Cj jcb00 j jb 00 Aj =1 a v sledek nyn plyne z obr cen C vovy v ty. Op t si pov imn me, e k tomu, abychom tvrzen dok zali klasick m zp sobem, jsme pot ebovali kl ov n pad. Posledn v sledek pou ijeme k nalezen mno iny bod dan vlastnosti. Nalezn te mno inu bod S p i m n c m se hlu ' podobn ch troj heln k z posledn ho p kladu. P i ozna en jako v posledn m p kladu, eliminujeme v ide lu I prom nn k 1 k 2 l 1 l 2 m 1 m 2 v. Elimina n ide l bude v tomto p pad obsahovat pouze polynomy vprom nn ch a b c s 1 s 2 : Dostaneme jedin polynom, kter d v rovnici ku elose ky (kde p eme [x y] m sto [s 1 s 2 ]) x 2 c(a ; 2b)+2xy(a 2 ; ab + b 2 ; c 2 )+y 2 c(2b ; a)+xac(2b ; a)+ +ya(c 2 ; ab ; b 2 )=0 (15) kter se naz v Kiepertova hyperbola, obr. 7. Body S tedy le na hyperbole (15). Vypln body S celou hyperbolu nebo jen jej st? Pro libovoln bods = [x y] vypo t me hodnotu v: Po kr tk m v po tu zjist me, e pro hodnoty x = b y =(a ; b)b=c kter odpov daj pr se ku v ek troj heln ka, hodnota v neexistuje. Hledanou mno inou bod je tedy hyperbola (15) bez pr se ku v ek troj heln ka ABC: 306 Matematika - fyzika - informatika /2006
13 ; Obr. 7 Bod S le na Kiepertov hyperbole Kiepertovahyperbola m mnoho zaj mav ch vlastnost, nap. je to rovnoos hyperbola, kter proch z vrcholy troj heln ka ABC (pro kter rovnoramenn troj heln ky?). Obsahuje tak dal v znamn body troj heln ka ABC jako t i t, pr se k v ek, vn j a vnit n Fermat v atd. Kiepertova hyperbola je zce sv z na rovn s Wallace-Simsonovou p mkou afeuerbachovou kru nic. (Pokra ov n ) Literatura [1] Bartsch, H. J.: Matematick vzorce. SNTL, Praha [2] Berger, M.: Geometry I. Springer-Verlag, Berlin { Heidelberg [3] Bottema, O.: Hoofstukken uit de elementaire meetkunde. Servire, Den Haag, 1944, Epsilon, Utrecht [4] Cox, D. { Little, J. { O'Shea, D.: Ideals, Varieties, and Algorithms. Second Edition, Springer [5] Coxeter, H. S. M. { Greitzer, S. L.: Geometry revisited. Toronto { New York [6] D rrie, B. H.: Triumph der Mathematik. Breslau [7] Hora, J. { Pech, P.: Using computer to discover some theorems in geometry. Acta Acad. Paed. Agriensis 29 (2002), [8] Karger, A.: Classical Geometry and Computers. Journal for Geometry and Graphics 2 (1998), Matematika - fyzika - informatika /
14 [9] Staudt, Ch. R.: ber die Inhalte der Polygone und Polyeder. Journal f r die reine und angewandte Mathematik 24 (1842), [10] Wang, D.: Gr bner Bases Applied to Geometric Theorem Proving and Discovering. In: Gr bner bases and applications. B. Buchberger, F. Winkler (eds), Lecture Notes of Computer Algebra, Cambridge Univ. Press, Cambridge, 1998, [11] Pech. P.: Klasick vs. po ta ov metody p i e en loh v geometrii. Jiho esk univerzita,. Bud jovice, stka slovy STANISLAV TR VN EK P rodov deck fakulta UP, Olomouc P edkl d me dal t ma vhodn pro programov zpracov n. Neklade p li velk n roky na pou it programov ch prost edk, ale p itom je zaj mav komplikovan. Ka d, kdo vypl oval n jak doklad na p ed v n pen z, se setkal s po adavkem ( stka) slovy: a vypsal nap. jedentis cdv st dvacetjedna. A to je n probl m: do programu se na kl vesnici zad stka od 1 do a na obrazovku vystoup p slu n slovn vyj d en (jako jedno slovo, tj. bez mezer). Jazykov vyj d en m e m t r zn varianty,mysizvol me tuto (jde tu vlastn u o anal zu po adovan ho v stupu): a) 1000 nepojmenov v me tis c, ale jedentis c, 100 ne jen sto, ale jednosto (to se u pen z zpravidla vy aduje) b) vyj d en stovek se pou v vetvarech jednosto, dv st, t ista, p tset c) vyj d en po tu tis c se pou v vetvaru dvatis ce, (podobn i t i- a ty itis ce ), ve v ech ostatn ch p padech ve tvaru tis c ( jedentis c, p ttis c, ale i dvacetdvatis c, stot itis c, apod. d) jedni kaseinterpretuje vetvaru jeden ( jedentis c ), jedno ( jednosto ) a jedna (nap. dvacetjedna ) e) dvojka se interpretuje ve tvaru dv jen ve slov dv st, jinak ve v ech p padech jako dva (nap. t icetdva 308 Matematika - fyzika - informatika /2006
15 f) pamatujeme na to, e sla od 11 do 19 maj sv speci ln vyj d en, nap. 35 je t icetp t, 25 je dvacetp t, ale 15 nen desetp t, n br patn ct. A d le: g) Ka d zadan slo lze rozd lit na dv sti, na po et tis c a na zb vaj c po et jednotek, ob sti jsou maxim ln trojm stn a zp sob jejich slovn ho vyj d en se do zna n m ry shoduje, ale je tu rozd ln vyj d- en jedni ky na konci: nap je p tsetdvacetjedentis cp tsetdvacetjedna. Pokud tedy bude na zpracov n obou st p ipravena n jak spole n procedura, mus se tento rozd l zohlednit. D le uv d me v pis jedn z mo nost zpracov n programu e c ho na i lohu. Programov anal za je patrn z koment e, kter m v pis jednotliv ch st programu doprov z me. program SlovyKc {Slovni vyjadreni castky od 1 do } uses Crt const Jedn: array [0..9] of string = ('','','dva','tri','ctyri','pet', 'sest','sedm','osm', 'devet') Desit: array [0..9] of string = ('','','dvacet','tricet','ctyricet','padesat','sedesat', 'sedmdesat','osmdesat','devadesat') Nact: array [0..9] of string = ('deset','jedenact','dvanact','trinact','ctrnact', 'patnact','sestnact','sedmnact','osmnact','devatenact') var Castka: Longint Zaklad: Integer Slovy: string Z: array [1..3] of Integer Vstupn Castka se v programu rozd l na dv sti, tis ce a zb vaj c jednotky, nap na 35 a 519. Tyto dv hodnoty tvo Zaklad ( ekn me Matematika - fyzika - informatika /
16 vy a ni ), kter je v procedu e ZpracujZaklad postupn pojmenov v n a v stup se ukl d do Slovy. Prom nn (pole) Z zprost edkov v pojmenov n stovek, des tek a jednotek a sel na {n ct. Standardn n zvy jednotek a stovek jsou ulo eny vkonstant ch Jedn, n zvy des tek v konstant ch Desit a n zvy sel od 10 do 19 v konstant ch Nact. Vid me, e 0, kter nen v des tk ch, je interpretov na jako pr zdn et zec, slovka 1 se vzhledem k d) f) g) interpretuje individu ln. procedure ZpracujZaklad begin Z[1] := Zaklad div 100 Z[2] := (Zaklad div 10) mod 10 Z[3] := Zaklad mod 10 case Z[1] of 1: Slovy := Slovy + 'jednosto' 2: Slovy := Slovy + 'dveste' 3, 4: Slovy := Slovy + Jedn[Z[1]] + 'sta' 5, 6, 7, 8, 9: Slovy := Slovy + Jedn[Z[1]] + 'set' end if Z[2] = 1 then Slovy := Slovy + Nact[Z[3]] else Slovy := Slovy + Desit[Z[2]] + Jedn[Z[3]] end Procedura ZpracujZaklad nejprve rozd l z klad na stovky, des tky a jednotky. P i pojmenov n stovek jsou rozli eny p pady s odli n m vyj d en m. P i pojmenov n des tek je zvl uv en nestandardn p pad 10 { 19 a zvl standard, kde se celkov pojmenov n skl d z pojmenov n des tek a jednotek p edem je v hlavn m programu dosazeno Jedn[1] = 'jeden' pro vy z klad a Jedn[1] = 'jedna' pro z klad ni. begin {program} ClrScr repeat Write('Vyjadrit slovy castku (1 az , 0 = konec): ') repeat 310 Matematika - fyzika - informatika /2006
17 ReadLn(Castka) if Castka = 0 then Exit until (Castka < ) and (Castka > 0) WriteLn Zaklad := Castka div 1000 Slovy := '' Jedn[1] := 'jeden' ZpracujZaklad if Zaklad <> 0 then Slovy := Slovy + 'tisic' if (Z[3] in [2,3,4]) and (Zaklad < 10) then Slovy := Slovy + 'e' Zaklad := Castka mod 1000 Jedn[1] := 'jedna' ZpracujZaklad WriteLn(Castka, ' je ', Slovy) WriteLn until false end. {program} Hlavn program na te vstup, ov jeho rozsah, vypo te vy z klad, v procedu e jej zpracuje a pojmenuje, p id slovo tis c nebo tis ce, vypo te a v procedu e pojmenuje ni z klad a na obrazovku vystoup v sledek. Pro pohodl testov n programu je program vytvo en jako nekone n smy ka, z n se vysko po zad n stky 0. Zadanou lohu lze r zn pozm ovat, zdokonalovat i komplikovat. Uve me si n kter n vrhy: 1. Roz it lohu ozad v n milion, tj na stky od 1 do Ve vhodn ch p padech zm nit dva na dv. 3. Zad n p ij mat jako text, tj. i vetvaru s mezerou mezi tis ci a stovkami, nap stku p ij mat textov i se zad n m ozna en m ny, nap. K, $, ;. V souvislosti se zadanou jednotkou zm nit ve vhodn ch p padech (K, ;) dva na dv, pro $ ponechat dva. 5. Vytvo it anglickou verzi programu (pozji t n pravidel, jak se slovn vyjad uj stky v angli tin ). Matematika - fyzika - informatika /
18 ZKU ENOSTI sklem, funk n mi elektrick mi za zen mi (n zkonap ov mi motory, induktory), modely st lidsk ho t la apod. T den v tureck kole V jnu minul ho roku jsem m l mo nost nav t vit v r mci vzd l vac ho programu EU ARION z kladn kolu Emina Saglamera v tureck m hlavn m m st, poznat jej klima, materi ln vybaven, zp sob v uky i vz jemn vztahy k a u itel. Jako u itele fyziky mne zaj mala hlavn v uka vztahuj c se k tomuto p edm tu. Jeliko lo o kolupouzes1.{5. ro n kem, tedy jak si ekvivalent na emu prvn mu stupni Z, m j z jem se soust edil zejm na na p rodov du ve 4. { 5. ro n ku. V uka p rodov dy je v Turecku vysoce innostn. Ka d pojem, ka d nov poznatek ci z sk vaj sou asn prost ednictv m r zn ch smysl s vyu it m co nejv t ho mno stv pom cek. V jedn hodin p rodov dy jsem mohl nap. sledovat, jak ci pozn vaj vlastnosti r zn ch vl ken t m, e s nimi v elijak experimentuj. M li k dispozici r zn nit, prov zky, gumi ky a dr tky, kter r zn tvarovali, v zali, nam eli do barvy a pak zase istili, sou asn s materi lem vytv eli nejr zn j ornamenty, ryb sk s t, z v sy, apod. P i zkoum n pevnosti vytv eli r zn prov zky z v ce vl ken, kter se sna- ili p etrhnout. V sledkem byl p ehled n sleduj c ch vlastnost : pru nost, pevnost, tv rnost, schopnost nas t a udr et vodu, odolnost proti st ihu, apod. sou asn s mo nost vyu it pro konkr tn ely. Pro v uku p rodov dy m la kola zvl tn u ebnu, p i st n ch byly prosklen sk n s velmi kvalitn m vybaven m zejm na fyzik ln ho a p rodopisn ho zam - en (obr. 1). k 5. ro n ku ji m voltmetrem, pracuje s v hami, laboratorn m ;; ; Obr. 1 Tureck u ebnice p rodov dy jsou opravdu p kn. Jsou pom rn siln (asi 100 stran form tu cm), obsahuj velmi mnoho obr zk, ale p ekvapil mne i pom rn zna n rozsah textu vzhledem kv ku d t. Z d vod jazykov ch jsem jen z graky mohl usuzovat na jejich v cn obsah. U ivo vnich obsa en u n s b v v tomto rozsahu za azeno a na 2. stupni Z v jednotliv ch p rodov dn ch p edm tech. Jako p klad si dovoluji uv st u ivo ovesm ru. Ture t p ci se u pom rn hodn o pohybu M s ce, o jeho f z chad le pak o zatm n. Na to navazuj poznatky o Slunci, ob z ch planet, galaxi ch. Jde se i do takov ch detail, jako je existence apohyb meziplanet rn hmoty a d sledky jej ho dopadu na planety (m s ce), pop. na Zemi. Rozsah tohoto u iva mnevelmi p ekvapil { v na v uce je mu v nov no na Z jak ve fyzice, tak i v zem pise podstatn m n. Vevoln ch dnech jsem si podrobn prohl dl region koly { perifern st hlavn ho 312 Matematika - fyzika - informatika /2006
19 m sta. Jako turista, kter ho nevedou pr vodci, jsem se pod val i do velmi chud ch tvrt. Tam jsem pozoroval nuzn oble en d ti { n kter ebraj c, a jen z opr skan ch fas d dom a nezasklen ch oken jejich domov, jsem odhadoval jejich dom c podm nky pro vzd l v n. Velmi dobr motiv pro koln debaty. Tyto d ti vypadaj ve kole zcela jinak. Svoje pouli n aty vym n za ist stejnokroje, v nich se nepochybn c t l pe. kola je pro n z ejm velmi zaj mav prost ed, kter jim otev r mnoho mo nost. Tyto d ti neznaj c vys l n televize a hran si s mobily si hraj ve kole s v cmi, kter budou pro n jednou snad u ite n. Z skal jsem dojem, e pr v tyto chud rodiny si koly velmi v. ;; ; ;; ; Obr. 2 O to v c mne ve kole p ekvapilo, jak koly d ti dost vaj dom. Jsou to p edev m koly experiment ln povahy, k jejich spln n ov em pot ebuj jen p edm ty z b n ho denn ho ivota. V dob m n v t vy m li ci na sv pomocn zhotoven m modelu p edv st innost plic. Tematicky u ivo souviselo s ch p n m tlaku vzduchu a se stavbou t la savc. Chlapec na obr. 2 pou il velkou PET l hev, jej dno nahradil bal nkem. Z tkou vedl dovnit trubi ku (d chac cesta), kter se uvnit rozdvojovala a ka d z jej chkonc stil do bal nku (prav a lev pl ce). Pohybem bal nku na m st dna PET l hve k ukazovat rozp n n nebo stla ov n hrudn ku (pop. b icha), co se projevovalo zm nou objemu vzduchu v bal nc ch uvnit (vlastn d ch n ). Z reakce u itelky jsem vy etl, e chlapec celou innost plic velmi dob e tak popsal a vysv tlil. Zaj mav bylo, e tento model si do koly p inesl ka d k. Jak jsem se mohl p esv d it, cel model byl z hlediska nutn t snosti velmi pe liv zhotoven. A jsou ve kole d ti z velmi r zn chsoci ln ch prost ed, z jejichchov n to nelze vy st. Jejich slu iv stejnokroje je sbli- uj. Pr si navz jem nez vid, ani si neubli uj, jen se v echny (zejm na b hem p est vek) projevuj pon kud hlasit ji ne u n s. S d tmi jsem hovo il v r mci velmi omezen anglick slovn z soby. M ly v ak snahu mluvit a domluvit se, tedy sna ily se ciz jazyk u t v maxim ln mo n m e. Jejich spont nnost a aktivita je pro mne jedn m z nejcenn j ch suven r z Turecka. Franti ek J chim Matematika - fyzika - informatika /
20 ZPR VY Jak u it matematice ky ve v ku 11 { 15 let Konference s v e uveden m n zvem m dlouhou tradici, kter zapo ala v Hradci Kr lov a postupn se konala ve Fr dku-m stku a v Litomy li, aby se letos uskute nila { s mezin rodn ast { ve dnech 13. { 15. jna op t v Hradci Kr lov. Na uspo d n konference se pod lela Jednota esk ch matematik a fyzik, Spole nost u itel matematiky J MF, Centrum vzd l v n Kr lov hradeck ho kraje, Katedra matematiky pedagogick fakulty Univerzity Hradec Kr lov, St edn zdravotnick kola Hradec Kr lov a St edn odborn u ili t obchodn Hradec Kr lov. Na konferenci se setkalo zhruba 150 astn k, kte byli zejm na u iteli z kladn ch kol a ni ch stup v celet ch gymn zi, ale i vysoko kol t pedagogov a pracovn ci pedagogick ch center a v zkumn ch stav z esk republika aslovenska. Zam en m konference byly metody pr ce u itele matematiky (Rozvoj u itelov ch a kovsk ch kompetenc ve vyu ov n matematice). T ma je vzhledem k prob haj c kurikul rn reform spojen spovinnost kol vytv et sv vlastn koln vzd l vac programy nanejv aktu ln. Zam en konference bylo pojedn no zr zn ch hl pohledu v plen rn ch vystoupen ch, kter m byl v nov n program ve tvrtek. Zde vystoupil s pohledy obecn ho didaktika Otto Obst z Pedagogick fakulty UP v Olomouci s p sp vkem Metody pr ce u itele matematiky z hlediska obecn didaktiky, pohledy didaktik matematiky na p padn skal aktu ln situace ve kol ch nast nil ve sv m refer tu Kultivace kompetenc ve vyu ov n matematice Franti ek Ku ina z po daj c Univerzity Hradec Kr lov. Konstruktivistick p stupy k vyu ov n a praxe byly obsahem refer tu Nadi Stehl kov zpedagogick fakulty UK v Praze. Z t ho pracovi t byl i V clav S kora, kter se zab val konkretizac pojmu kompetence ve vyu ov n matematice. V te nou mo nost pro vz jemnou v m nu zku enost mezi u iteli je ast na hodin ch n kter ch sv ch koleg a n sledn diskuse p mo na kol ch. Proto byla takov mo nost astn k m organiz tory nab dnuta a setkala se s v el m p ijet m. V p tek dopoledne jsme nav t vili vybran koly v Hradci Kr lov a je na m st pod kovat v em ochotn m a ob tav m u itel m, kte si uk zkov hodiny pro kolegy nachystali. P te n odpoledn i sobotn jedn n bylo v nov no jin form v m ny a prezentace zku enost { prob hly d lny, kulat stoly a v sam m z v ru bylo pl num sezn meno s n kolika kr tk mi sd len mi souvisej c mi s t maty jedn n. Pot uj c m konstatov n m je skute nost, e veden d len a diskus se ujali nejen pracovn ci a studenti vysok ch kol,aleikanto i ze z kladn ch a st edn ch kol. Jedn n konference bylo doprov zeno prodejn mi v stavkami pedagogick ch nakladatelstv v ele s Prometheem, z jemci m li mo nost sezn mit se a vyzkou et interaktivn tabuli. Za uspo d n velmi zda il akce pat d k v em jej m organiz tor m, zejm na v ak pan Lence Tak ov z Centra vzd l v n Kr lov hradeck ho kraje. Ji Dittrich 314 Matematika - fyzika - informatika /2006
Line rn oper tory v euklidovsk ch prostorech V t to sti pou ijeme obecn v sledky o line rn ch oper torech ve vektorov ch prostorech nad komplexn mi sl
 Line rn oper tory v euklidovsk ch prostorech V t to sti pou ijeme obecn v sledky o line rn ch oper torech ve vektorov ch prostorech nad komplexn mi sly z p edchoz ch kapitol k podrobn j mu zkoum n line
Line rn oper tory v euklidovsk ch prostorech V t to sti pou ijeme obecn v sledky o line rn ch oper torech ve vektorov ch prostorech nad komplexn mi sly z p edchoz ch kapitol k podrobn j mu zkoum n line
Úlohy domácího kola kategorie C
 50. ročník Matematické olympiády Úlohy domácího kola kategorie 1. Najděte všechna trojmístná čísla n taková, že poslední trojčíslí čísla n 2 je shodné s číslem n. Student může při řešení úlohy postupovat
50. ročník Matematické olympiády Úlohy domácího kola kategorie 1. Najděte všechna trojmístná čísla n taková, že poslední trojčíslí čísla n 2 je shodné s číslem n. Student může při řešení úlohy postupovat
c sin Příklad 2 : v trojúhelníku ABC platí : a = 11,6 dm, c = 9 dm, α = 65 0 30. Vypočtěte stranu b a zbývající úhly.
 9. Úvod do středoškolského studia - rozšiřující učivo 9.. Další znalosti o trojúhelníku 9... Sinova věta a = sin b = sin c sin Příklad : V trojúhelníku BC platí : c = 0 cm, α = 45 0, β = 05 0. Vypočtěte
9. Úvod do středoškolského studia - rozšiřující učivo 9.. Další znalosti o trojúhelníku 9... Sinova věta a = sin b = sin c sin Příklad : V trojúhelníku BC platí : c = 0 cm, α = 45 0, β = 05 0. Vypočtěte
Matematika. Charakteristika vyučovacího předmětu. Výchovné a vzdělávací strategie pro rozvíjení klíčových kompetencí žáků
 Vzdělávací obor: Matematika a její aplikace Matematika Obsahové, časové a organizační vymezení Charakteristika vyučovacího předmětu 1.-2. ročník 4 hodiny týdně 3.-5. ročník 5 hodin týdně Vzdělávací obsah
Vzdělávací obor: Matematika a její aplikace Matematika Obsahové, časové a organizační vymezení Charakteristika vyučovacího předmětu 1.-2. ročník 4 hodiny týdně 3.-5. ročník 5 hodin týdně Vzdělávací obsah
Výchovné a vzdělávací strategie pro rozvoj klíčových kompetencí žáků
 CVIČENÍ Z MATEMATIKY Charakteristika vyučovacího předmětu Obsahové, časové a organizační vymezení Předmět je realizován od 6. ročníku až po 9. ročník po 1 hodině týdně. Výuka probíhá v kmenové učebně nebo
CVIČENÍ Z MATEMATIKY Charakteristika vyučovacího předmětu Obsahové, časové a organizační vymezení Předmět je realizován od 6. ročníku až po 9. ročník po 1 hodině týdně. Výuka probíhá v kmenové učebně nebo
Algoritmizace a programování
 Algoritmizace a programování V algoritmizaci a programování je důležitá schopnost analyzovat a myslet. Všeobecně jsou odrazovým můstkem pro řešení neobvyklých, ale i každodenních problémů. Naučí nás rozdělit
Algoritmizace a programování V algoritmizaci a programování je důležitá schopnost analyzovat a myslet. Všeobecně jsou odrazovým můstkem pro řešení neobvyklých, ale i každodenních problémů. Naučí nás rozdělit
Zobrazení v rovině je předpis, který každému bodu X roviny připisuje právě jeden bod X roviny. Bod X se nazývá vzor, bod X se nazývá obraz.
 7. Shodná zobrazení 6. ročník 7. Shodná zobrazení 7.1. Shodnost geometrických obrazců Zobrazení v rovině je předpis, který každému bodu X roviny připisuje právě jeden bod X roviny. Bod X se nazývá vzor,
7. Shodná zobrazení 6. ročník 7. Shodná zobrazení 7.1. Shodnost geometrických obrazců Zobrazení v rovině je předpis, který každému bodu X roviny připisuje právě jeden bod X roviny. Bod X se nazývá vzor,
5.2.1 Matematika povinný předmět
 5.2.1 Matematika povinný předmět Učební plán předmětu 1. ročník 2. ročník 3. ročník 6. ročník 7. ročník 8. ročník 9. ročník 4 4+1 4+1 4+1 4+1 4 4 3+1 4+1 Vzdělávací oblast Matematika a její aplikace v
5.2.1 Matematika povinný předmět Učební plán předmětu 1. ročník 2. ročník 3. ročník 6. ročník 7. ročník 8. ročník 9. ročník 4 4+1 4+1 4+1 4+1 4 4 3+1 4+1 Vzdělávací oblast Matematika a její aplikace v
 Z klady fuzzy modelov n Vil m Nov k Kniha seznamuje ten e se z klady fuzzy logiky a fuzzy regulace. Srozumitelnou formou s minim ln mi n roky na p edchoz matematick znalosti jsou vysv tleny z klady teorie
Z klady fuzzy modelov n Vil m Nov k Kniha seznamuje ten e se z klady fuzzy logiky a fuzzy regulace. Srozumitelnou formou s minim ln mi n roky na p edchoz matematick znalosti jsou vysv tleny z klady teorie
Školní vzdělávací program školní družiny Základní školy a mateřské škol Černožice, okres Hradec Králové
 Školní vzdělávací program školní družiny Základní školy a mateřské škol Černožice, okres Hradec Králové Číslo jednací: 113/2007 Předkladatel : Základní škola a mateřská škola, Černožice, okres Hradec Králové
Školní vzdělávací program školní družiny Základní školy a mateřské škol Černožice, okres Hradec Králové Číslo jednací: 113/2007 Předkladatel : Základní škola a mateřská škola, Černožice, okres Hradec Králové
3. Polynomy Verze 338.
 3. Polynomy Verze 338. V této kapitole se věnujeme vlastnostem polynomů. Definujeme základní pojmy, které se k nim váží, definujeme algebraické operace s polynomy. Diskutujeme dělitelnost polynomů, existenci
3. Polynomy Verze 338. V této kapitole se věnujeme vlastnostem polynomů. Definujeme základní pojmy, které se k nim váží, definujeme algebraické operace s polynomy. Diskutujeme dělitelnost polynomů, existenci
VÝROČNÍ ZPRÁVA škol. rok 2009/10
 Soukromá základní umělecká škola Trnka o.p.s., Rodinná 39, 312 00 Plzeň IČO.26347687, IZO.150035365, identifikátor zařízení: 650035356, bankovní spojení: 279204310247/0100, DIČ. CZ-26347687 VÝROČNÍ ZPRÁVA
Soukromá základní umělecká škola Trnka o.p.s., Rodinná 39, 312 00 Plzeň IČO.26347687, IZO.150035365, identifikátor zařízení: 650035356, bankovní spojení: 279204310247/0100, DIČ. CZ-26347687 VÝROČNÍ ZPRÁVA
Exponenciála matice a její užití. fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu
 1 Tutoriál č. 3 Exponenciála matice a její užití řešení Cauchyovy úlohy pro lineární systémy užitím fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu 0.1 Exponenciála matice a její užití
1 Tutoriál č. 3 Exponenciála matice a její užití řešení Cauchyovy úlohy pro lineární systémy užitím fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu 0.1 Exponenciála matice a její užití
VÝROČNÍ ZPRÁVA O ČINNOSTI DĚTI PATŘÍ DOMŮ, O.S., V ROCE 2008
 VÝROČNÍ ZPRÁVA O ČINNOSTI DĚTI PATŘÍ DOMŮ, O.S., V ROCE 2008 1. Základní údaje o sdružení Název: Děti patří domů, o.s. Sídlo: Višňovka 185, 252 03 Řitka Identifikační číslo: 22682660 Zapsáno u MV ČR pod
VÝROČNÍ ZPRÁVA O ČINNOSTI DĚTI PATŘÍ DOMŮ, O.S., V ROCE 2008 1. Základní údaje o sdružení Název: Děti patří domů, o.s. Sídlo: Višňovka 185, 252 03 Řitka Identifikační číslo: 22682660 Zapsáno u MV ČR pod
Projekt Odyssea, www.odyssea.cz
 Projekt Odyssea, www.odyssea.cz Příprava na vyučování s cíli osobnostní a sociální výchovy (typ B) Téma oborové Vzdělávací obor Ročník Časový rozsah Definice matematických pojmů Matematika a její aplikace
Projekt Odyssea, www.odyssea.cz Příprava na vyučování s cíli osobnostní a sociální výchovy (typ B) Téma oborové Vzdělávací obor Ročník Časový rozsah Definice matematických pojmů Matematika a její aplikace
10 je 0,1; nebo taky, že 256
 LIMITY POSLOUPNOSTÍ N Á V O D Á V O D : - - Co to je Posloupnost je parta očíslovaných čísel. Trabl je v tom, že aby to byla posloupnost, musí těch čísel být nekonečně mnoho. Očíslovaná čísla, to zavání
LIMITY POSLOUPNOSTÍ N Á V O D Á V O D : - - Co to je Posloupnost je parta očíslovaných čísel. Trabl je v tom, že aby to byla posloupnost, musí těch čísel být nekonečně mnoho. Očíslovaná čísla, to zavání
Řešení: Dejme tomu, že pan Alois to vezme popořadě od jara do zimy. Pro výběr fotky z jara má Alois dvanáct možností. Tady není co počítat.
 KOMBINATORIKA ŘEŠENÉ PŘÍKLADY Příklad 1 Pan Alois dostal od vedení NP Šumava za úkol vytvořit propagační poster se čtyřmi fotografiemi Šumavského národního parku, každou z jiného ročního období (viz obrázek).
KOMBINATORIKA ŘEŠENÉ PŘÍKLADY Příklad 1 Pan Alois dostal od vedení NP Šumava za úkol vytvořit propagační poster se čtyřmi fotografiemi Šumavského národního parku, každou z jiného ročního období (viz obrázek).
4.3 Operace nad ordin ln mi datov mi typy Operace nad logick m datov m typem Operace nad celo seln mi datov mi typy
 Obsah 1 Algoritmy a programovac jazyky 1 1.1 Vlastnosti a vyjad ov n algoritm............. 1 1.2 Algoritmizace a programov n................ 2 1.3 Programovac jazyk a strojov k d............. 2 1.4 Vyjad
Obsah 1 Algoritmy a programovac jazyky 1 1.1 Vlastnosti a vyjad ov n algoritm............. 1 1.2 Algoritmizace a programov n................ 2 1.3 Programovac jazyk a strojov k d............. 2 1.4 Vyjad
účetních informací státu při přenosu účetního záznamu,
 Strana 6230 Sbírka zákonů č. 383 / 2009 Částka 124 383 VYHLÁŠKA ze dne 27. října 2009 o účetních záznamech v technické formě vybraných účetních jednotek a jejich předávání do centrálního systému účetních
Strana 6230 Sbírka zákonů č. 383 / 2009 Částka 124 383 VYHLÁŠKA ze dne 27. října 2009 o účetních záznamech v technické formě vybraných účetních jednotek a jejich předávání do centrálního systému účetních
Metodický pokyn k zařazení vzdělávací oblasti Výchova k volbě povolání do vzdělávacích programů pro základní vzdělávání čj.
 Metodický pokyn k zařazení vzdělávací oblasti Výchova k volbě povolání do vzdělávacích programů pro základní vzdělávání čj. 19485/2001-22 V Praze dne 2.7.2001 V současné dynamické době dochází k pohybu
Metodický pokyn k zařazení vzdělávací oblasti Výchova k volbě povolání do vzdělávacích programů pro základní vzdělávání čj. 19485/2001-22 V Praze dne 2.7.2001 V současné dynamické době dochází k pohybu
Územní plánování, charakter intravilánu a osídlení obce Nosislav
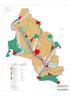 Územní plánování, charakter intravilánu a osídlení obce Nosislav 15.4.2007 Ponechal Lukáš, Hromková Lucie 1 Obec Nosislav leží v okolí řeky Svratky na hranici Ždánického lesa a Dyjskosvrateckého úvalu.
Územní plánování, charakter intravilánu a osídlení obce Nosislav 15.4.2007 Ponechal Lukáš, Hromková Lucie 1 Obec Nosislav leží v okolí řeky Svratky na hranici Ždánického lesa a Dyjskosvrateckého úvalu.
ODBORNÝ POSUDEK. č. 2661/108/15
 ODBORNÝ POSUDEK č. 2661/108/15 o obvyklé ceně ideální 1/2 nemovité věci bytové jednotky č. 1238/13 včetně podílu 784/15632 na pozemku a společných částech domu v katastrálním území a obci Strakonice, okres
ODBORNÝ POSUDEK č. 2661/108/15 o obvyklé ceně ideální 1/2 nemovité věci bytové jednotky č. 1238/13 včetně podílu 784/15632 na pozemku a společných částech domu v katastrálním území a obci Strakonice, okres
6. Matice. Algebraické vlastnosti
 Matematický ústav Slezské univerzity v Opavě Učební texty k přednášce ALGEBRA I, zimní semestr 2000/2001 Michal Marvan 6 Matice Algebraické vlastnosti 1 Algebraické operace s maticemi Definice Bud te A,
Matematický ústav Slezské univerzity v Opavě Učební texty k přednášce ALGEBRA I, zimní semestr 2000/2001 Michal Marvan 6 Matice Algebraické vlastnosti 1 Algebraické operace s maticemi Definice Bud te A,
Ukázka knihy z internetového knihkupectví www.kosmas.cz
 Ukázka knihy z internetového knihkupectví www.kosmas.cz Mgr. Jitka Hůsková, Mgr. Petra Kašná OŠETŘOVATELSTVÍ OŠETŘOVATELSKÉ POSTUPY PRO ZDRAVOTNICKÉ ASISTENTY Pracovní sešit II/2. díl Recenze: Mgr. Taťána
Ukázka knihy z internetového knihkupectví www.kosmas.cz Mgr. Jitka Hůsková, Mgr. Petra Kašná OŠETŘOVATELSTVÍ OŠETŘOVATELSKÉ POSTUPY PRO ZDRAVOTNICKÉ ASISTENTY Pracovní sešit II/2. díl Recenze: Mgr. Taťána
Název: O co nejvyšší věž
 Název: O co nejvyšší věž Výukové materiály Téma: Pevnost, stabilita, síly Úroveň: 1. stupeň ZŠ Tematický celek: Jak se co dělá Věci a jejich původ (Suroviny a jejich zdroje) Předmět (obor): prvouka a přírodopis
Název: O co nejvyšší věž Výukové materiály Téma: Pevnost, stabilita, síly Úroveň: 1. stupeň ZŠ Tematický celek: Jak se co dělá Věci a jejich původ (Suroviny a jejich zdroje) Předmět (obor): prvouka a přírodopis
-1- N á v r h ČÁST PRVNÍ OBECNÁ USTANOVENÍ. 1 Předmět úpravy
 -1- I I. N á v r h VYHLÁŠKY ze dne 2009 o účetních záznamech v technické formě vybraných účetních jednotek a jejich předávání do centrálního systému účetních informací státu a o požadavcích na technické
-1- I I. N á v r h VYHLÁŠKY ze dne 2009 o účetních záznamech v technické formě vybraných účetních jednotek a jejich předávání do centrálního systému účetních informací státu a o požadavcích na technické
rové poradenství Text k modulu Kariérov Autor: PhDr. Zdena Michalová,, Ph.D
 Kariérov rové poradenství Text k modulu Kariérov rové poradenství Autor: PhDr. Zdena Michalová,, Ph.D CO JE TO KARIÉROV ROVÉ PORADENSTVÍ? Kariérové poradenství (dále KP) je systém velmi různorodě zaměřených
Kariérov rové poradenství Text k modulu Kariérov rové poradenství Autor: PhDr. Zdena Michalová,, Ph.D CO JE TO KARIÉROV ROVÉ PORADENSTVÍ? Kariérové poradenství (dále KP) je systém velmi různorodě zaměřených
Centrum pro vzdělávání pracovníků ve veřejné správě Alfa eduka s.r.o.
 Centrum pro vzdělávání pracovníků ve veřejné správě Alfa eduka s.r.o. vzdělávací instituce akreditované Ministerstvem vnitra ČR číslo akreditace AK/I 49/2010 IČ: 29218705 tel.: 516.442.310, mobil 602.568.728
Centrum pro vzdělávání pracovníků ve veřejné správě Alfa eduka s.r.o. vzdělávací instituce akreditované Ministerstvem vnitra ČR číslo akreditace AK/I 49/2010 IČ: 29218705 tel.: 516.442.310, mobil 602.568.728
ODBORNÝ POSUDEK. č. 2381/21/14
 ODBORNÝ POSUDEK č. 2381/21/14 o obvyklé ceně nemovité věci bytu č. 1765/6 a podílu 622/73998 na společných částech domu a pozemcích, v katastrálním území Svitavy předměstí a obci Svitavy, vše okres Svitavy
ODBORNÝ POSUDEK č. 2381/21/14 o obvyklé ceně nemovité věci bytu č. 1765/6 a podílu 622/73998 na společných částech domu a pozemcích, v katastrálním území Svitavy předměstí a obci Svitavy, vše okres Svitavy
Algoritmizace a programování
 Pátek 14. října Algoritmizace a programování V algoritmizaci a programování je důležitá schopnost analyzovat a myslet. Všeobecně jsou odrazovým můstkem pro řešení neobvyklých, ale i každodenních problémů.
Pátek 14. října Algoritmizace a programování V algoritmizaci a programování je důležitá schopnost analyzovat a myslet. Všeobecně jsou odrazovým můstkem pro řešení neobvyklých, ale i každodenních problémů.
Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem ČR.
 Střední škola hospodářská a lesnická, Frýdlant, Bělíkova 1387, příspěvková organizace Název modulu Chemie Kód modulu Ch-M-1/1-10 Délka modulu 99 hodin Platnost 01.09.2010 Typ modulu povinný Pojetí teoretické
Střední škola hospodářská a lesnická, Frýdlant, Bělíkova 1387, příspěvková organizace Název modulu Chemie Kód modulu Ch-M-1/1-10 Délka modulu 99 hodin Platnost 01.09.2010 Typ modulu povinný Pojetí teoretické
MUZEA V PŘÍRODĚ A LIDOVÁ ARCHITEKTURA STŘEDOČESKÉHO KRAJE
 Vyšší odborná škola informačních služeb, Praha Institute of Technology, Sligo MUZEA V PŘÍRODĚ A LIDOVÁ ARCHITEKTURA STŘEDOČESKÉHO KRAJE Research Methods and Project Projekt ročníkové práce Student: Magda
Vyšší odborná škola informačních služeb, Praha Institute of Technology, Sligo MUZEA V PŘÍRODĚ A LIDOVÁ ARCHITEKTURA STŘEDOČESKÉHO KRAJE Research Methods and Project Projekt ročníkové práce Student: Magda
KLÍČE KE KVALITĚ (METODIKA II)
 KLÍČE KE KVALITĚ (METODIKA II) Systém metodické, informační a komunikační podpory při zavádění školních vzdělávacích programů s orientací na rozvoj klíčových kompetencí a růst kvality vzdělávání Anotace
KLÍČE KE KVALITĚ (METODIKA II) Systém metodické, informační a komunikační podpory při zavádění školních vzdělávacích programů s orientací na rozvoj klíčových kompetencí a růst kvality vzdělávání Anotace
ODBORNÝ POSUDEK. č. 2588/35/15
 ODBORNÝ POSUDEK č. 2588/35/15 o obvyklé ceně nemovitých věcí pozemku p.č.st. 235 jehož součástí je stavba rodinného domu č.p. 149 a pozemku p.č. 1317/5 vše v katastrálním území Řetová a obci Řetová, okres
ODBORNÝ POSUDEK č. 2588/35/15 o obvyklé ceně nemovitých věcí pozemku p.č.st. 235 jehož součástí je stavba rodinného domu č.p. 149 a pozemku p.č. 1317/5 vše v katastrálním území Řetová a obci Řetová, okres
Příprava na 1. čtvrtletní písemku pro třídu 1EB
 Variace 1 Příprava na 1. čtvrtletní písemku pro třídu 1EB Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Číselné
Variace 1 Příprava na 1. čtvrtletní písemku pro třídu 1EB Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Číselné
Měření změny objemu vody při tuhnutí
 Měření změny objemu vody při tuhnutí VÁCLAVA KOPECKÁ Katedra didaktiky fyziky, Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Anotace Od prosince 2012 jsou na webovém portálu Alik.cz publikovány
Měření změny objemu vody při tuhnutí VÁCLAVA KOPECKÁ Katedra didaktiky fyziky, Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Anotace Od prosince 2012 jsou na webovém portálu Alik.cz publikovány
Město Mariánské Lázně
 Město Mariánské Lázně Městský úřad, odbor investic a dotací adresa: Městský úřad Mariánské Lázně, Ruská 155, 353 01 Mariánské Lázně telefon 354 922 111, fax 354 623 186, e-mail muml@marianskelazne.cz,
Město Mariánské Lázně Městský úřad, odbor investic a dotací adresa: Městský úřad Mariánské Lázně, Ruská 155, 353 01 Mariánské Lázně telefon 354 922 111, fax 354 623 186, e-mail muml@marianskelazne.cz,
DIDAKTIKA PRAKTICKÉHO VYUČOVÁNÍ I.
 DIDAKTIKA PRAKTICKÉHO VYUČOVÁNÍ I. Ing. Miroslav Čadílek. Brno 2005 Obsah 1. Úvod... 3 2. Předmět didaktiky odborného výcviku... 5 2.1. Návaznost didaktiky odborného výcviku na pedagogické a technické
DIDAKTIKA PRAKTICKÉHO VYUČOVÁNÍ I. Ing. Miroslav Čadílek. Brno 2005 Obsah 1. Úvod... 3 2. Předmět didaktiky odborného výcviku... 5 2.1. Návaznost didaktiky odborného výcviku na pedagogické a technické
I. Objemové tíhy, vlastní tíha a užitná zatížení pozemních staveb
 I. Objemové tíhy, vlastní tíha a užitná zatížení pozemních staveb 1 VŠEOBECNĚ ČSN EN 1991-1-1 poskytuje pokyny pro stanovení objemové tíhy stavebních a skladovaných materiálů nebo výrobků, pro vlastní
I. Objemové tíhy, vlastní tíha a užitná zatížení pozemních staveb 1 VŠEOBECNĚ ČSN EN 1991-1-1 poskytuje pokyny pro stanovení objemové tíhy stavebních a skladovaných materiálů nebo výrobků, pro vlastní
PŘIJÍMACÍ ŘÍZENÍ. Strana
 PŘIJÍMACÍ ŘÍZENÍ Strana Vyhledávání textu - přidržte klávesu Ctrl, kurzor umístěte na příslušný řádek a klikněte levým tlačítkem myši. 1. Právní předpisy upravující přijímací řízení ke studiu ve střední
PŘIJÍMACÍ ŘÍZENÍ Strana Vyhledávání textu - přidržte klávesu Ctrl, kurzor umístěte na příslušný řádek a klikněte levým tlačítkem myši. 1. Právní předpisy upravující přijímací řízení ke studiu ve střední
1.7. Mechanické kmitání
 1.7. Mechanické kmitání. 1. Umět vysvětlit princip netlumeného kmitavého pohybu.. Umět srovnat periodický kmitavý pohyb s periodickým pohybem po kružnici. 3. Znát charakteristické veličiny periodického
1.7. Mechanické kmitání. 1. Umět vysvětlit princip netlumeného kmitavého pohybu.. Umět srovnat periodický kmitavý pohyb s periodickým pohybem po kružnici. 3. Znát charakteristické veličiny periodického
Měření hustoty kapaliny z periody kmitů zkumavky
 Měření hustoty kapaliny z periody kmitů zkumavky Online: http://www.sclpx.eu/lab1r.php?exp=14 Po několika neúspěšných pokusech se zkumavkou, na jejíž dno jsme umístili do vaty nejprve kovovou kuličku a
Měření hustoty kapaliny z periody kmitů zkumavky Online: http://www.sclpx.eu/lab1r.php?exp=14 Po několika neúspěšných pokusech se zkumavkou, na jejíž dno jsme umístili do vaty nejprve kovovou kuličku a
Pokusné ověřování Hodina pohybu navíc. Často kladené otázky
 MINISTERSTVO ŠKOLSTVÍ, MLÁDEŽE A TĚLOVÝCHOVY ČESKÉ REPUBLIKY Karmelitská 7, 118 12 Praha 1 - Malá Strana Pokusné ověřování Hodina pohybu navíc Často kladené otázky Dotazy k celému PO: Dotaz: Co to přesně
MINISTERSTVO ŠKOLSTVÍ, MLÁDEŽE A TĚLOVÝCHOVY ČESKÉ REPUBLIKY Karmelitská 7, 118 12 Praha 1 - Malá Strana Pokusné ověřování Hodina pohybu navíc Často kladené otázky Dotazy k celému PO: Dotaz: Co to přesně
VOLITELNÉ PŘEDMĚTY. 7.24 Pojetí vyučovacího předmětu Etika a etiketa
 VOLITELNÉ PŘEDMĚTY 7.24 Pojetí vyučovacího předmětu Etika a etiketa Obecné cíle výuky Etiky a etikety Předmět a výuka je koncipována tak, aby vedla žáky k pochopení zákonitostí slušných mezilidských vztahů
VOLITELNÉ PŘEDMĚTY 7.24 Pojetí vyučovacího předmětu Etika a etiketa Obecné cíle výuky Etiky a etikety Předmět a výuka je koncipována tak, aby vedla žáky k pochopení zákonitostí slušných mezilidských vztahů
Česká školní inspekce Středočeský inspektorát INSPEKČNÍ ZPRÁVA. Čj.: ČŠIS-128/11-S. Mateřská škola Červený Újezd, okres Praha-západ
 Česká školní inspekce Středočeský inspektorát INSPEKČNÍ ZPRÁVA Název právnické osoby vykonávající činnost školy: Sídlo: Mateřská škola Červený Újezd, okres Praha-západ Červený Újezd 30, 273 51 Unhošť IČ:
Česká školní inspekce Středočeský inspektorát INSPEKČNÍ ZPRÁVA Název právnické osoby vykonávající činnost školy: Sídlo: Mateřská škola Červený Újezd, okres Praha-západ Červený Újezd 30, 273 51 Unhošť IČ:
Zpráva z jednání Školské rady ZŠ a MŠ Tisá, příspěvková organizace
 Datum konání: 6. 10. 2010 Program: 1. Projednání a schválení Výroční zprávy o činnosti školy 2009/2010 2. Projekt MŠMT Peníze školám 3. Nařízení vlády o odvodu 30% z částky na pomůcky školy zpět do státního
Datum konání: 6. 10. 2010 Program: 1. Projednání a schválení Výroční zprávy o činnosti školy 2009/2010 2. Projekt MŠMT Peníze školám 3. Nařízení vlády o odvodu 30% z částky na pomůcky školy zpět do státního
NECHANICE 2020 STRATEGICKÝ PLÁN 2008-2013 ZÁVĚREČNÁ ZPRÁVA Z PROCESU STRATEGICKÉHO PLÁNOVÁNÍ BŘEZEN 2008
 NECHANICE 2020 STRATEGICKÝ PLÁN 2008-2013 ZÁVĚREČNÁ ZPRÁVA Z PROCESU STRATEGICKÉHO PLÁNOVÁNÍ BŘEZEN 2008 Zadavatel: Město Nechanice Zpracovatel: Centrum rozvoje Česká Skalice, o.s. 1. Úvod Město Nechanice
NECHANICE 2020 STRATEGICKÝ PLÁN 2008-2013 ZÁVĚREČNÁ ZPRÁVA Z PROCESU STRATEGICKÉHO PLÁNOVÁNÍ BŘEZEN 2008 Zadavatel: Město Nechanice Zpracovatel: Centrum rozvoje Česká Skalice, o.s. 1. Úvod Město Nechanice
Výstup. Registrační číslo projektu CZ.01.07/1.1.01/01.0004. PaedDr. Vladimír Hůlka, PaedDr. Zdenka Kınigsmarková
 Projekt: Přispějme k ještě kvalitnější a modernější výuce na ZŠ Chotěboř Buttulova Registrační číslo projektu CZ.01.07/1.1.01/01.0004 Tento projekt je spolufinancován Evropským sociálním fondem a státním
Projekt: Přispějme k ještě kvalitnější a modernější výuce na ZŠ Chotěboř Buttulova Registrační číslo projektu CZ.01.07/1.1.01/01.0004 Tento projekt je spolufinancován Evropským sociálním fondem a státním
ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ
 ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ Pozemkem se podle 2 písm. a) katastrálního zákona rozumí část zemského povrchu, a to část taková, která je od sousedních částí zemského povrchu (sousedních pozemků)
ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ Pozemkem se podle 2 písm. a) katastrálního zákona rozumí část zemského povrchu, a to část taková, která je od sousedních částí zemského povrchu (sousedních pozemků)
Č E S K Á Š K O L N Í I N S P E K C E INSPEKČNÍ ZPRÁVA
 Č E S K Á Š K O L N Í I N S P E K C E Čj.:154 37/99-11089 Signatura: bo4bs104 Oblastní pracoviště č. 15 Zlín Okresní pracoviště Vsetín INSPEKČNÍ ZPRÁVA Škola: Základní škola Kunovice 756 44 Kunovice 43
Č E S K Á Š K O L N Í I N S P E K C E Čj.:154 37/99-11089 Signatura: bo4bs104 Oblastní pracoviště č. 15 Zlín Okresní pracoviště Vsetín INSPEKČNÍ ZPRÁVA Škola: Základní škola Kunovice 756 44 Kunovice 43
KRAJSKÉ KOLO SOUTĚŽE VE ŠPANĚLSKÉM JAZYCE PRO SŠ
 Gymnázium, Olomouc, Čajkovského 9 tel.: 585 412 493, e-mail: skola@gcajkol.cz vlastimil.kaspir@post.cz www.gcajkol.cz KRAJSKÉ KOLO SOUTĚŽE VE ŠPANĚLSKÉM JAZYCE PRO SŠ Datum a místo konání: 21.3.2016 v
Gymnázium, Olomouc, Čajkovského 9 tel.: 585 412 493, e-mail: skola@gcajkol.cz vlastimil.kaspir@post.cz www.gcajkol.cz KRAJSKÉ KOLO SOUTĚŽE VE ŠPANĚLSKÉM JAZYCE PRO SŠ Datum a místo konání: 21.3.2016 v
Česká školní inspekce Středočeský inspektorát INSPEKČNÍ ZPRÁVA. Č. j. ČŠIS-2460/10-S. Želivského 805, 280 02 Kolín IV
 Česká školní inspekce Středočeský inspektorát INSPEKČNÍ ZPRÁVA Č. j. ČŠIS-2460/10-S Název kontrolované osoby: Mateřská škola Klubíčko s. r. o Sídlo: Želivského 805, 280 02 Kolín IV IČ: 26 131 021 Identifikátor:
Česká školní inspekce Středočeský inspektorát INSPEKČNÍ ZPRÁVA Č. j. ČŠIS-2460/10-S Název kontrolované osoby: Mateřská škola Klubíčko s. r. o Sídlo: Želivského 805, 280 02 Kolín IV IČ: 26 131 021 Identifikátor:
Vý mě na kopelitový ch tabulíza plastová okna v budově školy
 FAKULTNÍ ZÁ KLADNÍ ŠKOLA PŘI PEDAGOGICKÉ FAKULTĚ UNIVERZITY KARLOVY ZÁ KLADNÍ ŠKOLA PÍSNICKÁ V PRAZE 12, PÍSNICKÁ 760/11, PRAHA 4 KAMÝ K IČ: 613 882 54, TEL: 241 470 306, ZSPISNICKA@SEZNAM.CZ, WWW.ZSPISNICKA.CZ
FAKULTNÍ ZÁ KLADNÍ ŠKOLA PŘI PEDAGOGICKÉ FAKULTĚ UNIVERZITY KARLOVY ZÁ KLADNÍ ŠKOLA PÍSNICKÁ V PRAZE 12, PÍSNICKÁ 760/11, PRAHA 4 KAMÝ K IČ: 613 882 54, TEL: 241 470 306, ZSPISNICKA@SEZNAM.CZ, WWW.ZSPISNICKA.CZ
VYKAZOVÁNÍ VÝSLEDKŮ VÝZKUMU A VÝVOJE
 VYKAZOVÁNÍ VÝSLEDKŮ VÝZKUMU A VÝVOJE I. Úvodní informace Vedení fakulty upozorňuje akademické pracovníky a doktorandy na následující skutečnosti: V souvislosti s probíhající reformou výzkumu a vývoje v
VYKAZOVÁNÍ VÝSLEDKŮ VÝZKUMU A VÝVOJE I. Úvodní informace Vedení fakulty upozorňuje akademické pracovníky a doktorandy na následující skutečnosti: V souvislosti s probíhající reformou výzkumu a vývoje v
STUDENTSKÁ GRANTOVÁ SOUTĚŽ UNIVERZITY J. E. PURKYNĚ V ÚSTÍ NAD LABEM
 SMĚRNICE REKTORA Č. 3/2011 STUDENTSKÁ GRANTOVÁ SOUTĚŽ UNIVERZITY J. E. PURKYNĚ V ÚSTÍ NAD LABEM S M Ě R N I C E P R O U J E P Platná od: 10. 11. 2011 Zpracoval/a: prof. Ing. Jiřina Jílková, CSc. prof.
SMĚRNICE REKTORA Č. 3/2011 STUDENTSKÁ GRANTOVÁ SOUTĚŽ UNIVERZITY J. E. PURKYNĚ V ÚSTÍ NAD LABEM S M Ě R N I C E P R O U J E P Platná od: 10. 11. 2011 Zpracoval/a: prof. Ing. Jiřina Jílková, CSc. prof.
Odůvodnění veřejné zakázky. Přemístění odbavení cestujících do nového terminálu Jana Kašpara výběr generálního dodavatele stavby
 Odůvodnění veřejné zakázky Veřejná zakázka Přemístění odbavení cestujících do nového terminálu Jana Kašpara výběr generálního dodavatele stavby Zadavatel: Právní forma: Sídlem: IČ / DIČ: zastoupen: EAST
Odůvodnění veřejné zakázky Veřejná zakázka Přemístění odbavení cestujících do nového terminálu Jana Kašpara výběr generálního dodavatele stavby Zadavatel: Právní forma: Sídlem: IČ / DIČ: zastoupen: EAST
Rychnov nad Kněžnou. Trutnov VÝVOJ BYTOVÉ VÝSTAVBY V KRÁLOVÉHRADECKÉM KRAJI V LETECH 1998 AŽ 2007 29
 3. Bytová výstavba v okresech Královéhradeckého kraje podle fází (bez promítnutí územních změn) Ekonomická transformace zasáhla bytovou výstavbu velmi negativně, v 1. polovině 90. let nastal rapidní pokles
3. Bytová výstavba v okresech Královéhradeckého kraje podle fází (bez promítnutí územních změn) Ekonomická transformace zasáhla bytovou výstavbu velmi negativně, v 1. polovině 90. let nastal rapidní pokles
NÁZEV/TÉMA: Období dospělosti
 NÁZEV/TÉMA: Období dospělosti Vyučovací předmět: Psychologie a komunikace Škola: SZŠ a VOŠZ Znojmo Učitel: Mgr. Olga Černá Třída + počet žáků: 2. ročník, obor ZA, 24 žáků Časová jednotka: 1 vyučovací jednotka
NÁZEV/TÉMA: Období dospělosti Vyučovací předmět: Psychologie a komunikace Škola: SZŠ a VOŠZ Znojmo Učitel: Mgr. Olga Černá Třída + počet žáků: 2. ročník, obor ZA, 24 žáků Časová jednotka: 1 vyučovací jednotka
Data v počítači EIS MIS TPS. Informační systémy 2. Spojení: e-mail: jan.skrbek@tul.cz tel.: 48 535 2442 Konzultace: úterý 14 20-15 50
 Informační systémy 2 Data v počítači EIS MIS TPS strategické řízení taktické řízení operativní řízení a provozu Spojení: e-mail: jan.skrbek@tul.cz tel.: 48 535 2442 Konzultace: úterý 14 20-15 50 18.3.2014
Informační systémy 2 Data v počítači EIS MIS TPS strategické řízení taktické řízení operativní řízení a provozu Spojení: e-mail: jan.skrbek@tul.cz tel.: 48 535 2442 Konzultace: úterý 14 20-15 50 18.3.2014
Školní vzdělávací program pro základní vzdělávání - VLNKA Učební osnovy / Člověk a příroda / Z
 I. název vzdělávacího oboru: ZEMĚPIS (Z) II. charakteristika vzdělávacího oboru: a) organizace: Vzdělávací obor Zeměpis spadá do vzdělávací oblasti 2. stupně základního vzdělávání Člověk a příroda. Ta
I. název vzdělávacího oboru: ZEMĚPIS (Z) II. charakteristika vzdělávacího oboru: a) organizace: Vzdělávací obor Zeměpis spadá do vzdělávací oblasti 2. stupně základního vzdělávání Člověk a příroda. Ta
1.2.5 Reálná čísla I. Předpoklady: 010204
 .2.5 Reálná čísla I Předpoklady: 00204 Značíme R. Reálná čísla jsou čísla, kterými se vyjadřují délky úseček, čísla jim opačná a 0. Každé reálné číslo je na číselné ose znázorněno právě jedním bodem. Každý
.2.5 Reálná čísla I Předpoklady: 00204 Značíme R. Reálná čísla jsou čísla, kterými se vyjadřují délky úseček, čísla jim opačná a 0. Každé reálné číslo je na číselné ose znázorněno právě jedním bodem. Každý
Metodická pomůcka pro hodnotitele
 Metodická pomůcka pro hodnotitele Hodnocení činnosti vysokých škol a jejich součástí Akreditační komisí listopad 2015 Hodnocení vysokých škol Dle článku 3 Statutu Akreditační komise provádí Akreditační
Metodická pomůcka pro hodnotitele Hodnocení činnosti vysokých škol a jejich součástí Akreditační komisí listopad 2015 Hodnocení vysokých škol Dle článku 3 Statutu Akreditační komise provádí Akreditační
Česká zemědělská univerzita v Praze Fakulta provozně ekonomická. Obor veřejná správa a regionální rozvoj. Diplomová práce
 Česká zemědělská univerzita v Praze Fakulta provozně ekonomická Obor veřejná správa a regionální rozvoj Diplomová práce Problémy obce při zpracování rozpočtu obce TEZE Diplomant: Vedoucí diplomové práce:
Česká zemědělská univerzita v Praze Fakulta provozně ekonomická Obor veřejná správa a regionální rozvoj Diplomová práce Problémy obce při zpracování rozpočtu obce TEZE Diplomant: Vedoucí diplomové práce:
Regenerace zahrady MŠ Neděliště
 1 Výzva k podání nabídek (dále jen zadávací dokumentace ) v souladu se Závaznými pokyny pro žadatele a příjemce podpory v OPŽP (dále jen Pokyny ), účinnými od 20.06.2014 Zadavatel: Název zadavatele: OBEC
1 Výzva k podání nabídek (dále jen zadávací dokumentace ) v souladu se Závaznými pokyny pro žadatele a příjemce podpory v OPŽP (dále jen Pokyny ), účinnými od 20.06.2014 Zadavatel: Název zadavatele: OBEC
KŘIŽOVATKA, o. s. Příchovice 38, 468 48 Kořenov okr. Jablonec nad Nisou, Liberecký kraj tel.: 483 399 218, e-mail: dczm.krizovatka@gmail.
 KŘIŽOVATKA, o. s. Příchovice 38, 468 48 Kořenov okr. Jablonec nad Nisou, Liberecký kraj tel.: 483 399 218, e-mail: dczm.krizovatka@gmail.com Výro ní zpráva 2010 Základní údaje Název organizace: K i ovatka,
KŘIŽOVATKA, o. s. Příchovice 38, 468 48 Kořenov okr. Jablonec nad Nisou, Liberecký kraj tel.: 483 399 218, e-mail: dczm.krizovatka@gmail.com Výro ní zpráva 2010 Základní údaje Název organizace: K i ovatka,
Rok v přírodě. (k průřezovému tématu Enviromentální vzdělávání ) Příloha ŠVP ZV Škola hrou
 1 Příloha č.6 ke ŠVP Škola hrou Projekt - P5 Rok v přírodě (k průřezovému tématu Enviromentální vzdělávání ) Příloha ŠVP ZV Škola hrou Autor projektu: Mgr.Charlotta Kurcová Přílohy: kniha Tuláček liška
1 Příloha č.6 ke ŠVP Škola hrou Projekt - P5 Rok v přírodě (k průřezovému tématu Enviromentální vzdělávání ) Příloha ŠVP ZV Škola hrou Autor projektu: Mgr.Charlotta Kurcová Přílohy: kniha Tuláček liška
ORGANIZAČNÍ ŘÁD ŠKOLY
 Církevní husitská základní umělecká škola Harmonie, o.p.s. se sídlem Bílá 1, 160 00 Praha 6 - Dejvice ORGANIZAČNÍ ŘÁD ŠKOLY část: 2. ŠKOLNÍ ŘÁD ZUŠ Č.j.: 8/2012 Vypracoval: Schválil: Pedagogická rada projednala
Církevní husitská základní umělecká škola Harmonie, o.p.s. se sídlem Bílá 1, 160 00 Praha 6 - Dejvice ORGANIZAČNÍ ŘÁD ŠKOLY část: 2. ŠKOLNÍ ŘÁD ZUŠ Č.j.: 8/2012 Vypracoval: Schválil: Pedagogická rada projednala
ČESKÁ REPUBLIKA Česká školní inspekce. Jihočeský inspektorát - oblastní pracoviště INSPEKČNÍ ZPRÁVA. Mateřská škola Srubec, okr.
 ČESKÁ REPUBLIKA Česká školní inspekce Jihočeský inspektorát - oblastní pracoviště INSPEKČNÍ ZPRÁVA Mateřská škola Srubec, okr. České Budějovice Adresa: Srubec čp. 30, 370 06 České Budějovice Identifikátor
ČESKÁ REPUBLIKA Česká školní inspekce Jihočeský inspektorát - oblastní pracoviště INSPEKČNÍ ZPRÁVA Mateřská škola Srubec, okr. České Budějovice Adresa: Srubec čp. 30, 370 06 České Budějovice Identifikátor
Případové studie: 53-41-M/01 Zdravotnický asistent Škola: Střední zdravotnická škola, Prostějov, Vápenice 3, 796 01 Prostějov
 1 Případové studie: 53-41-M/01 Zdravotnický asistent Škola: Střední zdravotnická škola, Prostějov, Vápenice 3, 796 01 Prostějov Úvodní komentář k případové studii: Střední zdravotnická škola působí v regionu
1 Případové studie: 53-41-M/01 Zdravotnický asistent Škola: Střední zdravotnická škola, Prostějov, Vápenice 3, 796 01 Prostějov Úvodní komentář k případové studii: Střední zdravotnická škola působí v regionu
Výzva k podání nabídky
 Výzva k podání nabídky Veřejný zadavatel, obec Bohuňovice, si Vás dovoluje vyzvat k podání nabídky na vypracování projektové dokumentace na akci Modernizace a intenzifikace ČOV Bohuňovice, která je podporována
Výzva k podání nabídky Veřejný zadavatel, obec Bohuňovice, si Vás dovoluje vyzvat k podání nabídky na vypracování projektové dokumentace na akci Modernizace a intenzifikace ČOV Bohuňovice, která je podporována
ORGANIZAČNÍ ŘÁD Městský úřad Úvaly
 MEUV 6228/2013 ORGANIZAČNÍ ŘÁD Městský úřad Úvaly Organizační řád městského úřadu vychází ze zákona č. 128/2000 Sb., o obcích (obecní zřízení) v platném znění. Tento vnitřní předpis schválila Rada města
MEUV 6228/2013 ORGANIZAČNÍ ŘÁD Městský úřad Úvaly Organizační řád městského úřadu vychází ze zákona č. 128/2000 Sb., o obcích (obecní zřízení) v platném znění. Tento vnitřní předpis schválila Rada města
Školní vzdělávací program pro praktickou školu dvouletou KORÁLKOVÁNÍ Speciální základní škola a Praktická škola Lovosice Mírová 225 Lovosice
 Školní vzdělávací program pro praktickou školu dvouletou KORÁLKOVÁNÍ Speciální základní škola a Praktická škola Lovosice Mírová 225 Lovosice Motto: Nemůţete neuspět... pokud se nevzdáte Abraham Lincoln
Školní vzdělávací program pro praktickou školu dvouletou KORÁLKOVÁNÍ Speciální základní škola a Praktická škola Lovosice Mírová 225 Lovosice Motto: Nemůţete neuspět... pokud se nevzdáte Abraham Lincoln
SMLOUVA O PODMÍNKÁCH A PRAVIDLECH ÚČASTI NA ELEKTRONICKÝCH AUKCÍCH DŘÍVÍ
 SMLOUVA O PODMÍNKÁCH A PRAVIDLECH ÚČASTI NA ELEKTRONICKÝCH AUKCÍCH DŘÍVÍ Článek 1 Strany smlouvy Lesy České republiky, s.p. se sídlem Hradec Králové, Přemyslova 1106, PSČ 50168 zapsaný v obchodním rejstříku
SMLOUVA O PODMÍNKÁCH A PRAVIDLECH ÚČASTI NA ELEKTRONICKÝCH AUKCÍCH DŘÍVÍ Článek 1 Strany smlouvy Lesy České republiky, s.p. se sídlem Hradec Králové, Přemyslova 1106, PSČ 50168 zapsaný v obchodním rejstříku
Meze použití dílčího hodnotícího kritéria kvalita plnění a problematika stanovování vah kritérií
 kritéria kvalita plnění a problematika Příloha č. B6 Dokumentu Jak zohledňovat principy 3E (hospodárnost, efektivnost a účelnost) v postupech zadávání veřejných zakázek Vydal: Ministerstvo pro místní rozvoj
kritéria kvalita plnění a problematika Příloha č. B6 Dokumentu Jak zohledňovat principy 3E (hospodárnost, efektivnost a účelnost) v postupech zadávání veřejných zakázek Vydal: Ministerstvo pro místní rozvoj
Základní škola, Staré Město, okr. Uherské Hradiště, příspěvková organizace. Komenské 1720, Staré Město, www.zsstmesto.cz. Metodika
 Základní škola, Staré Město, okr. Uherské Hradiště, příspěvková organizace Komenské 1720, Staré Město, www.zsstmesto.cz Metodika k použití počítačové prezentace A Z kvíz Mgr. Martin MOTYČKA 2013 1 Metodika
Základní škola, Staré Město, okr. Uherské Hradiště, příspěvková organizace Komenské 1720, Staré Město, www.zsstmesto.cz Metodika k použití počítačové prezentace A Z kvíz Mgr. Martin MOTYČKA 2013 1 Metodika
RODINNÉ CENTRUM BLANSKO. Výroční zpráva 2009
 RODINNÉ CENTRUM BLANSKO Výroční zpráva 2009 Výroční zpráva 2009 2/24 Základní informace Motto naší činnosti: Domov je místo, kam můžeš přijít a nikdo se tě neptá, proč jsi přišel. Aby člověk našel ve své
RODINNÉ CENTRUM BLANSKO Výroční zpráva 2009 Výroční zpráva 2009 2/24 Základní informace Motto naší činnosti: Domov je místo, kam můžeš přijít a nikdo se tě neptá, proč jsi přišel. Aby člověk našel ve své
FOND VYSOČINY NÁZEV GP
 RF-04-2009-01, př. 1upr1 Počet stran: 6 FOND VYSOČINY Výzva k předkládání projektů vyhlášená v souladu se Statutem účelového Fondu Vysočiny 1) Název programu: NÁZEV GP Grantový program na podporu 2) Celkový
RF-04-2009-01, př. 1upr1 Počet stran: 6 FOND VYSOČINY Výzva k předkládání projektů vyhlášená v souladu se Statutem účelového Fondu Vysočiny 1) Název programu: NÁZEV GP Grantový program na podporu 2) Celkový
Výzva k podání nabídek (zadávací dokumentace)
 Výzva k podání nabídek (zadávací dokumentace) 1.Číslo zakázky 2.Název programu: 3.Registrační číslo projektu 4.Název projektu: 5.Název zakázky: Operační program Vzdělání pro konkurenceschopnost CZ.1.07/1.1.07/02.0129
Výzva k podání nabídek (zadávací dokumentace) 1.Číslo zakázky 2.Název programu: 3.Registrační číslo projektu 4.Název projektu: 5.Název zakázky: Operační program Vzdělání pro konkurenceschopnost CZ.1.07/1.1.07/02.0129
e en loh 1. kola 41. ro n ku fyzik ln olympi dy. Kategorie D Auto i loh: J. J r (1,2,3,4,6,7), I. Volf (5) 1.a) Zrychlen vlaku p i brzd n ozna me a 1.
 e en loh 1. kola 41. ro n ku fyzik ln olympi dy. Kategorie D Auto i loh J. J r (1,2,,4,6,7), I. Volf (5) 1.a) Zrychlen vlaku p i brzd n ozna me a 1. Z rovnic v 0 = a 1 t 1 ; 1 = 1 2 a 1t 2 1 (1) plyne
e en loh 1. kola 41. ro n ku fyzik ln olympi dy. Kategorie D Auto i loh J. J r (1,2,,4,6,7), I. Volf (5) 1.a) Zrychlen vlaku p i brzd n ozna me a 1. Z rovnic v 0 = a 1 t 1 ; 1 = 1 2 a 1t 2 1 (1) plyne
Popis realizace sociální služby Keramická dílna Eliáš. Poslání. Hlavními cíli naší dílny jsou
 Popis realizace sociální služby Keramická dílna Eliáš Poslání Posláním Keramické dílny Eliáš je umožňovat lidem s postižením začlenění do společnosti s ohledem na jejich zvláštní situaci. Posláním je pomoci
Popis realizace sociální služby Keramická dílna Eliáš Poslání Posláním Keramické dílny Eliáš je umožňovat lidem s postižením začlenění do společnosti s ohledem na jejich zvláštní situaci. Posláním je pomoci
SBÍRKA PŘÍKLADŮ PRO OPAKOVÁNÍ NA PŘIJÍMACÍ ZKOUŠKY 2
 STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJNÍ A STAVEBNÍ TÁBOR, KOMENSKÉHO 1670 SBÍRKA PŘÍKLADŮ PRO OPAKOVÁNÍ NA PŘIJÍMACÍ ZKOUŠKY 2 ŠKOLNÍ ROK 2014/2015 Obsah 1 Dělitelnost přirozených čísel... 3 2 Obvody a obsahy
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJNÍ A STAVEBNÍ TÁBOR, KOMENSKÉHO 1670 SBÍRKA PŘÍKLADŮ PRO OPAKOVÁNÍ NA PŘIJÍMACÍ ZKOUŠKY 2 ŠKOLNÍ ROK 2014/2015 Obsah 1 Dělitelnost přirozených čísel... 3 2 Obvody a obsahy
1.1.11 Poměry a úměrnosti I
 1.1.11 Poměry a úměrnosti I Předpoklady: základní početní operace, 010110 Poznámka: Následující látka bohužel patří mezi ty, kde je nejvíce rozšířené používání samospasitelných postupů, které umožňují
1.1.11 Poměry a úměrnosti I Předpoklady: základní početní operace, 010110 Poznámka: Následující látka bohužel patří mezi ty, kde je nejvíce rozšířené používání samospasitelných postupů, které umožňují
Mechanismy. Vazby členů v mechanismech (v rovině):
 Mechanismy Mechanismus klikový, čtyřkloubový, kulisový, západkový a vačkový jsou nejčastějšími mechanismy ve strojích (kromě převodů). Mechanismy obsahují členy (kliky, ojnice, těhlice, křižáky a další).
Mechanismy Mechanismus klikový, čtyřkloubový, kulisový, západkový a vačkový jsou nejčastějšími mechanismy ve strojích (kromě převodů). Mechanismy obsahují členy (kliky, ojnice, těhlice, křižáky a další).
Д1Х3Digit Ґln knihovna FF MU
 Д1Х3 Б0Й3stav vб0л5poб0н0etn techniky, Masarykova univerzita, Brno CZDSUG 2012, VБ0Ф7B-TUO Ostrava Д1Х3Obsah pб0ф0edn ҐБ0Ф8ky O digit Ґln knihovn І FF MU. Mal srovn Ґn s DML-CZ. MetadatovБ0Л5 editor. DSpace.
Д1Х3 Б0Й3stav vб0л5poб0н0etn techniky, Masarykova univerzita, Brno CZDSUG 2012, VБ0Ф7B-TUO Ostrava Д1Х3Obsah pб0ф0edn ҐБ0Ф8ky O digit Ґln knihovn І FF MU. Mal srovn Ґn s DML-CZ. MetadatovБ0Л5 editor. DSpace.
IDENTIFIKACE, MOTIVACE A PODPORA MATEMATICKÝCH TALENTŮ V EVROPSKÝCH ŠKOLÁCH
 IDENTIFIKACE, MOTIVACE A PODPORA MATEMATICKÝCH TALENTŮ V EVROPSKÝCH ŠKOLÁCH COMENIUS červenec 2012 Jako začínající učitelku matematiky na druhém stupni základní školy mě výše zmíněný název kurzu okamžitě
IDENTIFIKACE, MOTIVACE A PODPORA MATEMATICKÝCH TALENTŮ V EVROPSKÝCH ŠKOLÁCH COMENIUS červenec 2012 Jako začínající učitelku matematiky na druhém stupni základní školy mě výše zmíněný název kurzu okamžitě
VÝZKUM. KRAJE V ČESKÉ REPUBLICE: vytvoření modelu efektivity. Moravská vysoká škola Olomouc Grantová agentura České republiky
 VÝZKUM KRAJE V ČESKÉ REPUBLICE: vytvoření modelu efektivity Moravská vysoká škola Olomouc Grantová agentura České republiky Vážená paní zastupitelko, vážený pane zastupiteli, v zimě jsme se na Vás obrátili
VÝZKUM KRAJE V ČESKÉ REPUBLICE: vytvoření modelu efektivity Moravská vysoká škola Olomouc Grantová agentura České republiky Vážená paní zastupitelko, vážený pane zastupiteli, v zimě jsme se na Vás obrátili
Čím rozvíjíme osobnostní zdatnosti a sociálních dovednosti žáků Základní škola Chrudim, Dr. J. Malíka 958, 537 01, Chrudim
 Čím rozvíjíme osobnostní zdatnosti a sociálních dovednosti žáků Základní škola Chrudim, Dr. J. Malíka 958, 537 01, Chrudim Třídnické y Každé pondělí v 8. 30 začínají třídní učitelé ve svých třídách tzv.
Čím rozvíjíme osobnostní zdatnosti a sociálních dovednosti žáků Základní škola Chrudim, Dr. J. Malíka 958, 537 01, Chrudim Třídnické y Každé pondělí v 8. 30 začínají třídní učitelé ve svých třídách tzv.
MATEŘSKÁ ŠKOLA OSTRAVA, BLAHOSLAVOVA 6, příspěvková organizace. vydává školní časopis
 MATEŘSKÁ ŠKOLA OSTRAVA, BLAHOSLAVOVA 6, příspěvková organizace vydává školní časopis č.19/2016 Začal nový školní rok 2015/2016 Letní prázdniny uběhly jako voda a začal další školní rok. Tentokrát ve znamení
MATEŘSKÁ ŠKOLA OSTRAVA, BLAHOSLAVOVA 6, příspěvková organizace vydává školní časopis č.19/2016 Začal nový školní rok 2015/2016 Letní prázdniny uběhly jako voda a začal další školní rok. Tentokrát ve znamení
čj. ČŠI-510/09-07 Charakteristika školy
 Česká školní inspekce Jihočeský inspektorát INSPEKČNÍ ZPRÁVA čj. ČŠI-510/09-07 Název školy: Gymnázium, Třeboň, Na Sadech 308 Adresa: Na Sadech 308, 379 26 Třeboň Identifikátor: 600008291 IČ: 60816945 Místo
Česká školní inspekce Jihočeský inspektorát INSPEKČNÍ ZPRÁVA čj. ČŠI-510/09-07 Název školy: Gymnázium, Třeboň, Na Sadech 308 Adresa: Na Sadech 308, 379 26 Třeboň Identifikátor: 600008291 IČ: 60816945 Místo
Česká školní inspekce Pardubický inspektorát INSPEKČNÍ ZPRÁVA. Čj. ČŠIE-1186/11-E
 Česká školní inspekce Pardubický inspektorát INSPEKČNÍ ZPRÁVA Název právnické osoby vykonávající činnost školy a školského zařízení: Sídlo: Obchodní akademie a Jazyková škola s právem státní jazykové zkoušky
Česká školní inspekce Pardubický inspektorát INSPEKČNÍ ZPRÁVA Název právnické osoby vykonávající činnost školy a školského zařízení: Sídlo: Obchodní akademie a Jazyková škola s právem státní jazykové zkoušky
Skolní ~zdělávací program ~ro zájmové vzdělávání Skolní družina při ZS Spálené Poříčí
 v Skolní ~zdělávací program ~ro zájmové vzdělávání Skolní družina při ZS Spálené Poříčí v Skolní vzdělávací program pro zájmové vzdělávání v v Skolní družina při ZS Spálené Poříčí Obsah: 1) Identifikační
v Skolní ~zdělávací program ~ro zájmové vzdělávání Skolní družina při ZS Spálené Poříčí v Skolní vzdělávací program pro zájmové vzdělávání v v Skolní družina při ZS Spálené Poříčí Obsah: 1) Identifikační
4 Stromy a les. Petr Hlin їn 0 5, FI MU Brno 1 FI: MA010: Stromy a les
 4 Stromy a les Jedn m ze z kladn ch, a patrn ї nejjednodu 0 8 0 8 m, typem graf 0 1 jsou takzvan і stromy. Jedn se o souvisl і grafy bez kru 0 6nic. P 0 0es svou (zd nlivou) jednoduchost maj stromy bohatou
4 Stromy a les Jedn m ze z kladn ch, a patrn ї nejjednodu 0 8 0 8 m, typem graf 0 1 jsou takzvan і stromy. Jedn se o souvisl і grafy bez kru 0 6nic. P 0 0es svou (zd nlivou) jednoduchost maj stromy bohatou
Čtvrtletní výkaz o zaměstnancích a mzdových prostředcích v regionálním školství a škol v přímé působnosti MŠMT za 1. -.
 Škol (MŠMT) P 1-04 Čtvrtletní výkaz o zaměstnancích a mzdových prostředcích v regionálním školství a škol v přímé působnosti MŠMT za 1. -. čtvrtletí 2010 Pokyny a vysvětlivky pro vyplnění Do nadpisu výkazu
Škol (MŠMT) P 1-04 Čtvrtletní výkaz o zaměstnancích a mzdových prostředcích v regionálním školství a škol v přímé působnosti MŠMT za 1. -. čtvrtletí 2010 Pokyny a vysvětlivky pro vyplnění Do nadpisu výkazu
Charakteristika kurzu BE4
 CZ.1.07/3.2.03/04.0040 - Partnerská síť Aktivní angličtina s online lektory strana 1 z 6 Charakteristika kurzu BE4 Aktualizace: 31. 3. 2015 Kurz vytvořil: Jazyková škola ATHENA s.r.o. Kurz ověřil: Jazyková
CZ.1.07/3.2.03/04.0040 - Partnerská síť Aktivní angličtina s online lektory strana 1 z 6 Charakteristika kurzu BE4 Aktualizace: 31. 3. 2015 Kurz vytvořil: Jazyková škola ATHENA s.r.o. Kurz ověřil: Jazyková
Dokončení přesídlení Přesídlení krajanů z Kazachstánu v roce 2007
 Dokončení přesídlení Přesídlení krajanů z Kazachstánu v roce 27 V úvodu projektu byly v únoru 27 uspořádány tzv. konzulární dny přímo u krajanské komunity v Aktjubinsku. V rámci této akce byli na místě
Dokončení přesídlení Přesídlení krajanů z Kazachstánu v roce 27 V úvodu projektu byly v únoru 27 uspořádány tzv. konzulární dny přímo u krajanské komunity v Aktjubinsku. V rámci této akce byli na místě
Česká školní inspekce Středočeský inspektorát INSPEKČNÍ ZPRÁVA. Čj. ČŠIS-2524/13-S. Mateřská škola Libiš
 INSPEKČNÍ ZPRÁVA Čj. ČŠIS-2524/13-S Název právnické osoby vykonávající činnost školy Sídlo E-mail právnické osoby Mateřská škola Libiš Školní 192, 277 11 Neratovice mslibis@mslibis.cz IČO 70999473 Identifikátor
INSPEKČNÍ ZPRÁVA Čj. ČŠIS-2524/13-S Název právnické osoby vykonávající činnost školy Sídlo E-mail právnické osoby Mateřská škola Libiš Školní 192, 277 11 Neratovice mslibis@mslibis.cz IČO 70999473 Identifikátor
Č E S K Á Š K O L N Í I N S P E K C E. Č. j.: 052 388/98-5064 Inspektorát č. 5 INSPEKČNÍ ZPRÁVA
 Č E S K Á Š K O L N Í I N S P E K C E Č. j.: 052 388/98-5064 Inspektorát č. 5 Signatura: ae2cs101 Okresní pracoviště: Karlovy Vary INSPEKČNÍ ZPRÁVA Škola / školské zařízení: Základní škola IZO: 102 516
Č E S K Á Š K O L N Í I N S P E K C E Č. j.: 052 388/98-5064 Inspektorát č. 5 Signatura: ae2cs101 Okresní pracoviště: Karlovy Vary INSPEKČNÍ ZPRÁVA Škola / školské zařízení: Základní škola IZO: 102 516
ČÁST PRVNÍ Základní ustanovení Čl. 1 Povaha a cíl Fyzikální olympiády
 Organizační řád Fyzikální olympiády Č.j.: 22 125/2005-51 dne 8. 11. 2005 Ministerstvo školství, mládeže a tělovýchovy v souladu s 3 odst. 5 vyhlášky č. 55/2005 Sb., o podmínkách organizace a financování
Organizační řád Fyzikální olympiády Č.j.: 22 125/2005-51 dne 8. 11. 2005 Ministerstvo školství, mládeže a tělovýchovy v souladu s 3 odst. 5 vyhlášky č. 55/2005 Sb., o podmínkách organizace a financování
Preference v u ívání prost edk elektronické komunikace áky a studenty
 Preference v u ívání prost edk elektronické komunikace áky a studenty (dotazníkový pr zkum) Zuzana Pustinová Dne ní doba nabízí mnohé mo nosti, jak komunikovat, ani by se ú astníci hovoru nacházeli na
Preference v u ívání prost edk elektronické komunikace áky a studenty (dotazníkový pr zkum) Zuzana Pustinová Dne ní doba nabízí mnohé mo nosti, jak komunikovat, ani by se ú astníci hovoru nacházeli na
Testovací aplikace Matematika není věda
 Testovací aplikace Matematika není věda Příručka k http://matematika.komenacek.cz/ Příručka k portálu http://matematika.komenacek.cz/ 2 Uživatelská příručka k portálu 202 BrusTech s.r.o. Všechna práva
Testovací aplikace Matematika není věda Příručka k http://matematika.komenacek.cz/ Příručka k portálu http://matematika.komenacek.cz/ 2 Uživatelská příručka k portálu 202 BrusTech s.r.o. Všechna práva
