Konstrukce pravého úhlu pomocí kružítka 3 úlohy
|
|
|
- Silvie Lišková
- před 8 lety
- Počet zobrazení:
Transkript
1 Konstrukce pravého úhlu pomocí kružítka 3 úlohy Mgr. Jitka Koubová N{zev školy Z{kladní škola a Mateřsk{ škola Číslo projektu CZ N{zev šablony klíčové aktivity Inovace a zkvalitnění výuky prostřednictvím ICT Vzděl{vací oblast Matematika a její aplikace Vzděl{vací období 2. ředmět Matematika Téma hodiny Konstrukce pravého úhlu pomocí kružítka 3 úlohy Označení VY_32_INOVACE_14_Konstrukce pravého úhlu pomocí kružítka
2 Konstrukce pravého úhlu pomocí kružítka - rozdělením přímého úhlu 1. libovolně - osa úsečky 2. proch{zející bodem mimo přímku 3. proch{zející bodem na přímce
3 1. Osa úsečky Rozdělíme přímý úhel na dva pravé úhly pomocí osy úsečky sestroj úsečku Krok 1
4 1. Osa úsečky Rozdělíme přímý úhel na dva pravé úhly pomocí osy úsečky hrot kružítka zabodni do krajního bodu úsečky do kružítka vezmi více jak polovinu délky úsečky, toto je m{lo Krok 1
5 1. Osa úsečky Rozdělíme přímý úhel na dva pravé úhly pomocí osy úsečky hrot kružítka zabodni do krajního bodu úsečky do kružítka vezmi více jak polovinu délky úsečky, toto je st{le m{lo Krok 1
6 1. Osa úsečky Rozdělíme přímý úhel na dva pravé úhly pomocí osy úsečky hrot kružítka zabodni do krajního bodu úsečky můžeš začít toto je více jak polovina velikost úsečky Krok 1
7 1. Osa úsečky Rozdělíme přímý úhel na dva pravé úhly pomocí osy úsečky protni úsečku č{stí kružnice Krok 1
8 1. Osa úsečky Rozdělíme přímý úhel na dva pravé úhly pomocí osy úsečky protni úsečku č{stí kružnice Krok 1
9 1. Osa úsečky Rozdělíme přímý úhel na dva pravé úhly pomocí osy úsečky Krok 1
10 1. Osa úsečky Rozdělíme přímý úhel na dva pravé úhly pomocí osy úsečky Krok 1
11 1. Osa úsečky Rozdělíme přímý úhel na dva pravé úhly pomocí osy úsečky Krok 1
12 1. Osa úsečky Rozdělíme přímý úhel na dva pravé úhly pomocí osy úsečky V kružítku ponechej stejnou velikost opět protni úsečku č{stí kružnice Krok 1 Krok 2 hrot kružítka zabodni do druhého krajního bodu úsečky
13 1. Osa úsečky Rozdělíme přímý úhel na dva pravé úhly pomocí osy úsečky Krok 1 Krok 2
14 1. Osa úsečky Rozdělíme přímý úhel na dva pravé úhly pomocí osy úsečky Krok 1 Krok 2
15 1. Osa úsečky Rozdělíme přímý úhel na dva pravé úhly pomocí osy úsečky Krok 1 Krok 2
16 1. Osa úsečky použij pravítko ke spojení sestrojeného průsečíku s tímto průsečíkem Krok 1 Krok 2 Krok 3
17 1. Osa úsečky Rozdělili jsme přímý úhel na dva pravé úhly pomocí osy úsečky tady vznikne pravý úhel osa úsečky º 90º 1 2 tady také vznikne pravý úhel polovina úsečky Krok 1 Krok 2 Krok 3 Konec
18 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku Sestroj přímku Sestroj bod ležící mimo přímku Krok 1
19 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku Zde zabodni hrot kružítka rozevři kružítko tak, aby č{st kružnice protnula danou přímku ve dvou bodech takto je to m{lo Krok 1
20 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku rozevři kružítko tak, aby č{st kružnice protnula danou přímku ve dvou bodech takto je to dobré Krok 1
21 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku sestroj č{st kružnic a protni přímku ve dvou bodech Krok 1
22 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku Krok 1
23 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku Krok 1
24 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku Krok 1
25 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku Krok 1 Krok 2
26 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku ponechej v kružítku stejnou velikost Krok 1 Krok 2
27 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku zde zabodni hrot kružítka Krok 1 Krok 2
28 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku sestrojíme č{st kružnice Krok 1 Krok 2
29 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku sestrojíme č{st kružnice Krok 1 Krok 2
30 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku Krok 1 Krok 2
31 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku Krok 1 Krok 2
32 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku ponechej v kružítku stejnou velikost sestroj č{st kružnice zde zabodni hrot kružítka Krok 1 Krok 2 Krok 3
33 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku Krok 1 Krok 2 Krok 3
34 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku Krok 1 Krok 2 Krok 3
35 2. Kolmice proch{zející bodem ležícím mimo přímku Rozděl přímý úhel na dvě poloviny daným bodem ležícím mimo přímku Krok 1 Krok 2 Krok 3
36 2. Kolmice proch{zející bodem ležícím mimo přímku použij pravítko na spojení tohoto bodu s tímto bodem Krok 1 Krok 2 Krok 3 Zpět
37 2. Kolmice proch{zející bodem ležícím mimo přímku Rozdělili jsme přímý úhel na dvě poloviny daným bodem ležícím mimo přímku zde je pravý úhel Osa úsečky 90º 90º zde je také pravý úhel Krok 1 Krok 2 Krok 3 Konec
38 2. Kolmice proch{zející bodem ležícím na přímce Sestroj osu přímého úhlu bodem ležícím na přímce. Krok1
39 2. Kolmice proch{zející bodem ležícím na přímce zde zabodni hrot kružítka sestroj oblouk na obě strany z bodu Krok1
40 2. Kolmice proch{zející bodem ležícím na přímce zde zabodni hrot kružítka sestroj oblouk na obě strany z bodu Krok1
41 2. Kolmice proch{zející bodem ležícím na přímce Krok1
42 2. Kolmice proch{zející bodem ležícím na přímce ponech zde hrot kružítka sestrojíme oblouk i na druhou stranu od bodu Krok1
43 2. Kolmice proch{zející bodem ležícím na přímce Krok1
44 2. Kolmice proch{zející bodem ležícím na přímce Krok1
45 2. Kolmice proch{zející bodem ležícím na přímce zde zabodni vezmi do kružítka více jak polovinu Krok1 Krok2
46 2. Kolmice proch{zející bodem ležícím na přímce Krok1 Krok2
47 2. Kolmice proch{zející bodem ležícím na přímce ponech ve kružítku stejnou velikost zde zabodni sestroj č{st kružnice nad úsečkou Step1 Step2 Home
48 2. Kolmice proch{zející bodem ležícím na přímce Krok1 Krok2
49 2. Kolmice proch{zející bodem ležícím na přímce Krok1 Krok2
50 2. Kolmice proch{zející bodem ležícím na přímce Krok1 Krok2
51 2. Kolmice proch{zející bodem ležícím na přímce Krok1 Krok2
52 2. Kolmice proch{zející bodem ležícím na přímce ponech v kružítku stejnou velikost sestrojíme č{st kružnice nad úsečkou zde zabodni Krok1 Krok2 Krok3
53 2. Kolmice proch{zející bodem ležícím na přímce Krok1 Krok2 Krok3
54 2. Kolmice proch{zející bodem ležícím na přímce Krok1 Krok2 Krok3
55 2. Kolmice proch{zející bodem ležícím na přímce Krok1 Krok2 Krok3
56 2. Kolmice proch{zející bodem ležícím na přímce oužij pravítko ke spojení tohoto průsečíku s tímto bodem Krok1 Krok2 Krok3
57 2. Kolmice proch{zející bodem ležícím na přímce Zde je prvý úhel Kolmice bodem 90º 90º Krok1 Krok2 Krok3 Konec
58 Odkazy a materi{ly k tomuto tématu html - online ukázka konstrukce kolmice procházející daným bodem - online flashová ukázka + obrazový postu krok za krokem - názorné video v Aj - pracovní list na konstrukci kolmice k přímce daným bodem k vytištění ml - ještě jedna názorná ukázka krok za krokem - pracovní list na konstrukci kolmice procházející bodem k dané přímce k vytištění
Škola: Střední škola obchodní, České Budějovice, Husova 9
Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
ANOTACE VZDĚLÁVACÍCH MATERIÁLŮ IV/ 2 SADA č. 2, PL č. 36
ANOTACE VZDĚLÁVACÍCH MATERIÁLŮ IV/ 2 SADA č. 2, PL č. 36 Název školy Základní škola a Mateřská škola, Dětřichov nad Bystřicí okres Bruntál, příspěvková organizace Číslo projektu: CZ.1.07/1.4.00/21.21110
Svobodná chebská škola, základní škola a gymnázium s.r.o. Trojúhelník III. konstrukce trojúhelníku. Astaloš Dušan. frontální, fixační
METODICKÝ LIST DA35 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný obsah: Trojúhelník III. konstrukce trojúhelníku Astaloš Dušan Matematika šestý
Digitální učební materiál
Digitální učební materiál Projekt: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Příjemce: Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova
s dosud sestrojenými přímkami a kružnicemi. Abychom obrázky nezaplnili
Dělení úsečky ŠÁRKA GRGLITSOVÁ TOMÁŠ HOLAN Matematicko-fyzikální fakulta UK, Praha V tomto článku se budeme zabývat sadou geometrických úloh, které jsou tematicky podobné. Liší se jen hodnotou jednoho
3.3.5 Množiny bodů dané vlastnosti II (osa úsečky)
3.3.5 Množiny bodů dané vlastnosti II (osa úsečky) Předpoklady: 030304 Př. 1: Je dána úsečka, = 5,5cm. Narýsuj osu úsečky. Jakou vlastnost mají body ležící na této přímce? Pro všechny body na ose úsečky,
Kapitola 5. Seznámíme se ze základními vlastnostmi elipsy, hyperboly a paraboly, které
Kapitola 5 Kuželosečky Seznámíme se ze základními vlastnostmi elipsy, hyperboly a paraboly, které společně s kružnicí jsou známy pod společným názvem kuželosečky. Říká se jim tak proto, že každou z nich
MATEMATIKA. Problémy a úlohy, v nichž podrobujeme geometrický objekt nějaké transformaci
MATEMATIKA Úloha o čtverci a přímkách ŠÁRKA GERGELITSOVÁ TOMÁŠ HOLAN Matematicko-fyzikální fakulta UK, Praha Problémy a úlohy, v nichž podrobujeme geometrický objekt nějaké transformaci (například podobnosti)
Kružnice opsaná a kružnice vepsaná
1.7.13 Kružnice opsaná a kružnice vepsaná Předpoklady: 010712 Př. 1: Na obrázcích jsou znázorněny shodné trojúhelníky a různé kružnice k. Dvě z kružnic jsou speciální (jedinečné). Překresli obrázky těchto
Užití stejnolehlosti v konstrukčních úlohách
Užití stejnolehlosti v konstrukčních úlohách Příklad 1: Je dána kružnice k(o,r) a bod M ležící uvnitř kružnice k. Bodem M veďte tětivu AB, jejíž délka je bodem M rozdělena v poměru 2 : 1. Sestrojte obraz
Opakování ZŠ - Matematika - část geometrie - konstrukce
Opakování ZŠ - Matematika - část geometrie - konstrukce Základní útvary v rovině Bod je nejzákladnější geometrický pojem. Body zapisujeme písmeny velké abecedy: A, B, N, H, Přímka Přímky zapisujeme písmeny
ICT podporuje moderní způsoby výuky CZ.1.07/1.5.00/ Matematika analytická geometrie. Mgr. Pavel Liška
Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity IV/2 Inovace
KRUHOVÁ ŠROUBOVICE A JEJÍ VLASTNOSTI
KRUHOVÁ ŠROUBOVICE A JEJÍ VLASTNOSTI Šroubový pohyb vzniká složením otáčení kolem osy o a posunutí ve směru osy o, přičemž oba pohyby jsou spojité a rovnoměrné. Jestliže při pohybu po ose "dolů" je otáčení
P L A N I M E T R I E
M T E M T I K P L N I M E T R I E rovinná geometrie Základní planimetrické pojmy od - značí se velkými tiskacími písmeny, např.,,. P, Q. Přímka - značí se malými písmeny, např. a, b, p, q nebo pomocí bodů
Kružnice, úhly příslušné k oblouku kružnice
KRUŽNICE, KRUH Kružnice, úhly příslušné k oblouku kružnice Je dán bod S a kladné číslo r. Kružnice k(s;r) je množina všech bodů (roviny), které mají od bodu S vzdálenost r. Můžeme také říci. Kružnicí k
METODICKÉ LISTY Z MATEMATIKY pro gymnázia a základní vzdělávání
METODICKÉ LISTY Z MATEMATIKY pro gymnázia a základní vzdělávání Jaroslav Švrček a kolektiv Rámcový vzdělávací program pro základní vzdělávání Vzdělávací oblast: Matematika a její aplikace Tematický okruh:
prostorová definice (viz obrázek vlevo nahoře): elipsa je průsečnou křivkou rovinného
Elipsa Výklad efinice a ohniskové vlastnosti prostorová definice (viz obrázek vlevo nahoře): elipsa je průsečnou křivkou rovinného řezu na rotační kuželové ploše, jestliže řezná rovina není kolmá k ose
Shodná zobrazení v rovině osová a středová souměrnost Mgr. Martin Mach
Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
PLANIMETRIE. Mgr. Zora Hauptová TROJÚHELNÍK VY_32_INOVACE_MA_1_04
PLANIMETRIE Mgr. Zora Hauptová TROJÚHELNÍK VY_32_INOVACE_MA_1_04 OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/34.0116 Modernizace výuky na učilišti Název školy Název šablony Předmět Tematický celek
půdorysu; pro každý bod X v prostoru je tedy sestrojen pouze jeho nárys X 2 a pro jeho
Řešené úlohy Rotační paraboloid v kolmém promítání na nárysnu Příklad: V kolmém promítání na nárysnu sestrojte tečnou rovinu τ v bodě A rotačního paraboloidu, který má ohnisko F a svislou osu o, F o, rotace;
Perspektiva. Doplňkový text k úvodnímu cvičení z perspektivy. Obsahuje: zobrazení kružnice v základní rovině metodou osmi tečen
Perspektiva Doplňkový text k úvodnímu cvičení z perspektivy Obsahuje: úvodní pojmy určení skutečné velikosti úsečky zadané v různých polohách zobrazení kružnice v základní rovině metodou osmi tečen 1 Příklad
tečen a osu o π, V o; plochu omezte hranou vratu a půdorysnou a proved te rozvinutí
Řešené úlohy Rozvinutelná šroubová plocha v Mongeově promítání Příklad: V Mongeově promítání zobrazte půl závitu rozvinutelné šroubové plochy, jejíž hranou vratu je pravotočivá šroubovice, která prochází
Seznam pomůcek na hodinu technického kreslení
Seznam pomůcek na hodinu technického kreslení Sešit bez linek, formát A4 Psací potřeby propiska nebo pero, mikrotužky 2B, H Pravítko s ryskou Rovné pravítko Úhloměr Kružítko Šablona písma 3,5 mm Šablona
Digitální učební materiál
Digitální učební materiál Číslo projektu CZ07/500/34080 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/ Inovace a zkvalitnění výuky prostřednictvím ICT
ICT podporuje moderní způsoby výuky CZ.1.07/1.5.00/ Matematika - stereometrie. Mgr. Hedvika Novotná
Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity III/2
Výukový materiál zpracován v rámci oblasti podpory 1.5 EU peníze středním školám
Výukový materiál zpracován v rámci oblasti podpory 1.5 EU peníze středním školám Název školy Obchodní akademie a Hotelová škola Havlíčkův Brod Název OP OP Vzdělávání pro konkurenceschopnost Registrační
SEZNAM ANOTACÍ. CZ.1.07/1.5.00/ III/2 Inovace a zkvalitnění výuky prostřednictvím ICT VY_32_INOVACE_MA4 Analytická geometrie
SEZNAM ANOTACÍ Číslo projektu Číslo a název šablony klíčové aktivity Označení sady DUM Tematická oblast CZ.1.07/1.5.00/34.0527 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT VY_32_INOVACE_MA4 Analytická
Úhly a jejich vlastnosti
Úhly a jejich vlastnosti Pojem úhlu patří k nejzákladnějším pojmům geometrie. Zajímavé je, že úhel můžeme definovat několika různými způsoby, z nichž má každý své opodstatnění. Definice: Úhel je část roviny
Mgr. Monika Urbancová. a vepsané trojúhelníku
Název projektu Život jako leporelo Registrační číslo CZ.1.07/1.4.00/21.3763 Autor Mgr. Monika Urbancová Datum 28. 8. 2014 Ročník 6. ročník Vzdělávací oblast MATEMATIKA A JEJÍ APLIKACE Vzdělávací obor MATEMATIKA
Konkretizovaný výstup Konkretizované učivo Očekávané výstupy RVP. Zápis čísla v desítkové soustavě - porovnávání čísel - čtení a psaní čísel
Ročník: I. - vytváří si názoru představu o čísle 5, 10, 20 - naučí se vidět počty prvků do 5 bez počítání po jedné - rozpozná a čte čísla 0 5 - pozná a čte čísla 0 10 - určí a čte čísla 0 20 Číselná řada
ANOTACE nově vytvořených/inovovaných materiálů
ANOTACE nově vytvořených/inovovaných materiálů Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast CZ.1.07/1.5.00/34.1017 III/2 - Inovace a zkvalitnění výuky prostřednictvím ICT Analytická
SHODNÁ ZOBRAZENÍ V ROVINĚ
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol SHODNÁ
Omezíme se jen na lomené čáry, jejichž nesousední strany nemají společný bod. Jestliže A 0 = A n (pro n 2), nazývá se lomená čára uzavřená.
MNOHOÚHELNÍKY Vlastnosti mnohoúhelníků Lomená čára C 0 C C C 3 C 4 protíná samu sebe. Lomená čára A 0 A A... A n- A n (n ) se skládá z úseček A 0 A, A A,..., A n- A n, z nichž každé dvě sousední mají společný
1.1 Napište středovou rovnici kružnice, která má střed v počátku soustavy souřadnic a prochází bodem
Analytická geometrie - kružnice Napište středovou rovnici kružnice, která má střed v počátku soustavy souřadnic a prochází bodem A = ; 5 [ ] Napište středový i obecný tvar rovnice kružnice, která má střed
Další polohové úlohy
5.1.16 alší polohové úlohy Předpoklady: 5115 Průniky přímky s tělesem Př. 1: Je dána standardní krychle. Sestroj průnik přímky s krychlí pokud platí: leží na polopřímce, =, leží na polopřímce, =. Příklad
Přípravný kurz - Matematika
Přípravný kurz - Matematika Téma: Konstrukční úlohy Klíčová slova: rozbor, náčrt, popis, diskuse počtu řešení, kružnice opsaná a vepsaná Autor: trojúhelníku Mlynářová 12 19 9:02 Kontrukční úlohy Výsledkem
Střední příčky trojúhelníku
1.7.12 Střední příčky trojúhelníku Předpoklady: 010711 Př. 1: Narýsuj libovolný trojúhelník A (zvol ho tak, aby se co nejvíce lišil od trojúhelníku, který narýsoval soused). Najdi středy všech stran S
Základní geometrické tvary
Základní geometrické tvary č. 37 Matematika 1. Narýsuj bod A. 2. Narýsuj přímku b. 3. Narýsuj přímku, která je dána body AB. AB 4. Narýsuj polopřímku CD. CD 5. Narýsuj úsečku AB. 6. Doplň. Rýsujeme v rovině.
Výukový materiál zpracován v rámci oblasti podpory 1.5 EU peníze středním školám
Výukový materiál zpracován v rámci oblasti podpory 1.5 EU peníze středním školám Název školy Obchodní akademie a Hotelová škola Havlíčkův Brod Název OP OP Vzdělávání pro konkurenceschopnost Registrační
Využití Rhinoceros ve výuce předmětu Počítačová geometrie a grafika. Bítov Blok 1: Kinematika
Využití Rhinoceros ve výuce předmětu Počítačová geometrie a grafika Bítov 13.-17.8.2012 Blok 1: Kinematika Pro lepší orientaci v obrázku je vhodné umísťovat. Nabízí se dvě rychlé varianty. Buď pomocí příkazu
KRUŽNICE, KRUH, KULOVÁ PLOCHA, KOULE
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol KRUŽNICE,
DIGITÁLNÍ ARCHIV VZDĚLÁVACÍCH MATERIÁLŮ
DIGITÁLNÍ ARCHIV VZDĚLÁVACÍCH MATERIÁLŮ Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast CZ.1.07/1.5.00/34.0963 IV/2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti
Digitální učební materiál
Digitální učební materiál Projekt CZ.1.07/1.5.00/34.0415 Inovujeme, inovujeme Šablona III/2 Inovace a zkvalitnění výuky prostřednictvím ICT (DUM) Tematická oblast Základní aranžérské nářadí a pomůcky,
Definice: Kružnice je množina bodů v rovině, které mají od daného bodu (střed S) stejnou vzdálenost
Kuželosečky Kružnice Definice: Kružnice je množina bodů v rovině, které mají od daného bodu (střed S) stejnou vzdálenost (poloměr r).?! Co získáme, když v definici výraz stejnou nahradíme stejnou nebo
CZ.1.07/1.5.00/34.0527
Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
BA008 Konstruktivní geometrie. Kolmá axonometrie. pro kombinované studium. učebna Z240 letní semestr
BA008 Konstruktivní geometrie pro kombinované studium Kolmá axonometrie Jan Šafařík Jana Slaběňáková přednášková skupina P-BK1VS1 učebna Z240 letní semestr 2016-2017 31. března 2017 Základní literatura
PODOBNÁ ZOBRAZENÍ V ROVINĚ (včetně stejnolehlosti)
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol PODOBNÁ
Sada 1 Geodezie I. 05. Vytyčení kolmice a rovnoběžky
S třední škola stavební Jihlava Sada 1 Geodezie I 05. Vytyčení kolmice a rovnoběžky Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2
Shodná zobrazení. bodu B ležet na na zobrazené množině b. Proto otočíme kružnici b kolem
Shodná zobrazení Otočení Příklad 1. Jsou dány tři různé soustředné kružnice a, b a c. Sestrojte rovnostranný trojúhelník ABC tak, aby A ležel na a, B ležel na b a C ležel na c. Řešení. Zvolíme vrchol A
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Registrační číslo projektu Šablona Autor Název materiálu CZ.1.07/1.5.00/34.0951 III/2 INOVACE A ZKVALITNĚNÍ VÝUKY PROSTŘEDNICTVÍM ICT Mgr. Pavlína
Matematika - 4. ročník Vzdělávací obsah
Matematika - 4. ročník Čas.plán Téma Učivo Ročníkové výstupy žák podle svých schopností: Poznámka Září Opakování učiva 3. ročníku Počítaní do 20 Sčítání a odčítání do 20 Násobení a dělení číslem 2 Počítání
SEZNAM ANOTACÍ. CZ.1.07/1.5.00/34.0527 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT VY_32_INOVACE_MA3 Planimetrie
SEZNAM ANOTACÍ Číslo projektu Číslo a název šablony klíčové aktivity Označení sady DUM Tematická oblast CZ.1.07/1.5.00/34.0527 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT VY_32_INOVACE_MA3 Planimetrie
Vlasta Moravcová. Matematicko-fyzikální fakulta & Nad Ohradou 23 Univerzita Karlova v Praze Praha 3. Letní škola geometrie 2018,
KONSTRUKČNÍ ÚLOHY Katedra didaktiky matematiky Gymnázium Na Pražačce Matematicko-fyzikální fakulta & Nad Ohradou 23 Univerzita Karlova v Praze Praha 3 Letní škola geometrie 2018, 4. července 2018, Česká
ICT podporuje moderní způsoby výuky CZ.1.07/1.5.00/ Matematika planimetrie. Mgr. Tomáš Novotný
Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity IV/2 Inovace
Důkazy vybraných geometrických konstrukcí
Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 Ročníková práce Důkazy vybraných geometrických konstrukcí Vypracovala: Ester Sgallová Třída: 8.M Školní rok: 015/016 Seminář : Deskriptivní geometrie
Výuka geometrie na 2. stupni ZŠ
Výuka geometrie na 2. stupni ZŠ Úspěšnost žáků v geometrii, vytváření vědomostí, zdokonalování dovedností žáků i rozvíjení jejich schopností úzce souvisí s vytvářením postojů žáků k vyučování geometrii,
Rozvinutelné plochy. tvoří jednoparametrickou soustavu rovin a tedy obaluje rozvinutelnou plochu Φ. Necht jsou
Rozvinutelné plochy Rozvinutelná plocha je každá přímková plocha, pro kterou existuje izometrické zobrazení do rov iny, tj. lze ji rozvinout do roviny. Dá se ukázat, že každá rozvinutelná plocha patří
RNDr. Zdeněk Horák IX.
Jméno RNDr. Zdeněk Horák Datum 8. 10. 2014 Ročník IX. Vzdělávací oblast MATEMATIKA A JEJÍ APLIKACE Vzdělávací obor MATEMATIKA Tematický okruh KRUH, KRUŽNICE Téma klíčová slova Opakování učiva z tematického
5) Průnik rotačních ploch. A) Osy totožné (a kolmé k půdorysně) Bod R průniku ploch. 1) Pomocná plocha κ
5) Průnik rotačních ploch Bod R průniku ploch κ, κ : 1) Pomocná plocha κ ) Průniky : l κ κ, l κ κ 3) R l l Volba pomocné plochy pro průnik rotačních ploch závisí na poloze os ploch. Omezíme se pouze na
od zadaného bodu, vzdálenost. Bod je střed, je poloměr kružnice. Délka spojnice dvou bodů kružnice, která prochází středem
Kružnice Kružnice je množina všech bodů roviny, které mají od zadaného bodu, vzdálenost. Bod je střed, je poloměr kružnice. Délka spojnice dvou bodů kružnice, která prochází středem je průměr kružnice.
Digitální učební materiál
Digitální učební materiál Projekt Šablona CZ.1.07/1.5.00/34.0415 Inovujeme, inovujeme III/2 Inovace a zkvalitnění výuky prostřednictvím ICT (DUM) DUM č. VY_32_INOVACE_CH29_2_16 ŠVP Podnikání RVP 64-41-L/51
Projekt: Zlepšení výuky na ZŠ Schulzovy sady registrační číslo: CZ.1.07./1.4.00/ Mgr. Jakub Novák. Datum: Ročník: 9.
Projekt: Zlepšení výuky na ZŠ Schulzovy sady registrační číslo: CZ.1.07./1.4.00/1.581 VY_4_INOVACE_1NOV40 Autor: Mgr. Jakub Novák Datum: 10. 3. 013 Ročník: 9. Vzdělávací oblast: Matematika a její aplikace
Název: Tvorba obrázků pomocí grafického znázornění komplexních čísel
Název: Tvorba obrázků pomocí grafického znázornění komplexních čísel Autor: Mgr. Lukáš Saulich Název školy: Gymnázium Jana Nerudy, škola hl. města Prahy Předmět, mezipředmětové vztahy: matematika a její
Digitální učební materiál
Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/34.0802 Název projektu Zkvalitnění výuk prostřednictvím ICT Číslo a název šablon klíčové aktivit III/2 Inovace a zkvalitnění výuk prostřednictvím
KONSTRUKTIVNÍ GEOMETRIE
KONSTRUKTIVNÍ GEOMETRIE Přednáška Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipliny společného základu (reg. č. CZ.1.07/2.2.00/28.0021)
Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková. Výukový materiál
1 Výukový materiál Identifikační údaje škol Všší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 07 7 Varnsdorf, IČO: 1838387 www.vosassvdf.cz, tel. +2012372632 Číslo
16. Trojúhelník vlastnosti, prvky, konstrukční úlohy Vypracovala: Ing. Ludmila Všetulová, prosinec 2013
16. Trojúhelník vlastnosti, prvky, konstrukční úlohy Vypracovala: Ing. Ludmila Všetulová, prosinec 2013 Název školy Obchodní akademie a Střední odborné učiliště Veselí nad Moravou Název a číslo OP OP Vzdělávání
ANOTACE nově vytvořených/inovovaných materiálů
ANOTACE nově vytvořených/inovovaných materiálů Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast CZ.1.07/1.5.00/34.1017 III/2 - Inovace a zkvalitnění výuky prostřednictvím ICT Stereometrie
Sada 1 CAD Prostorové souřadnice v CAD systémech
S třední škola stavební Jihlava Sada 1 CAD1 05. Prostorové souřadnice v CAD systémech Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona:
Kinematika rektifikace oblouku (Sobotkova a Kochaňského), prostá cykloida, prostá epicykloida, úpatnice paraboly.
Kinematika rektifikace oblouku (Sobotkova a Kochaňského), prostá cykloida, prostá epicykloida, úpatnice paraboly. Výpočty trajektorií bodů při složených pohybech. Příklad 1: Je dána kružnice k s poloměrem
Univerzita Karlova v Praze Pedagogická fakulta
Univerzita Karlova v Praze Pedagogická fakulta SEMINÁRNÍ PRÁCE Z METOD ŘEŠENÍ 1 PLANIMETRIE 000/001 Cifrik, M-ZT První příklad ze zadávacích listů 1 Zadání: Sestrojte trojúhelník ABC, pokud je dáno: ρ
ROTAČNÍ PLOCHY. 1) Základní pojmy
ROTAČNÍ PLOCHY 1) Základní pojmy Rotační plocha vznikne rotací tvořicí křivky k kolem osy o. Pro zobrazení a konstrukce bude výhodnější nechat rotovat jednotlivé body tvořicí křivky. Trajektorii rotujícího
Digitální učební materiál
Digitální učební materiál Projekt: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Příjemce: Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova
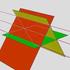
[obr. 1] Rozbor S 3 S 2 S 1. o 1. o 2 [obr. 2]
![[obr. 1] Rozbor S 3 S 2 S 1. o 1. o 2 [obr. 2]](/thumbs/51/27343209.jpg "[obr. 1] Rozbor S 3 S 2 S 1. o 1. o 2 [obr. 2]")
Příklad Do dané kruhové výseče s ostrým středovým úhlem vepište kružnici (obr. ). M k l V N [obr. ] Rozbor Oblouk l a hledaná kružnice k se dotýkají v bodě T, mají proto v tomto bodě společnou tečnu t.
Digitální učební materiál
Digitální učební materiál Projekt: Digitální učební materiály ve škole, registrační číslo projektu CZ107/1500/340527 Příjemce: Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371
A STEJNOLEHLOST,, EUKLIDOVYE VĚTY 2.
PODOBNOST A STEJNOLEHLOST,, EUKLIDOVYE VĚTY 2. ČÁST MAT. OT 2. OT. Č.. 15: SHODNÁS HODNÁ ZOBRAZENÍ V ROVINĚ, PODOBNOST A STEJNOLEHLOST,, EUKLIDOVYE VĚTY PODOBNOST KDE LÁTKU NAJDETE Kapitola Základy planimetrie
Voronoiův diagram. RNDr. Petra Surynková, Ph.D. Univerzita Karlova v Praze Matematicko-fyzikální fakulta
12 RNDr., Ph.D. Katedra didaktiky matematiky Univerzita Karlova v Praze Matematicko-fyzikální fakulta petra.surynkova@mff.cuni.cz http://surynkova.info Definice V( P) nad množinou bodů P { p v rovině 1,
Zadání domácích úkolů a zápočtových písemek
Konstruktivní geometrie (KG-L) Zadání domácích úkolů a zápočtových písemek Sestrojte elipsu, je-li dáno a = 5cm a b = 3cm. V libovolném bodě sestrojte její tečnu. Tento úkol je na krásu, tj. udělejte oskulační
O podobnosti v geometrii
O podobnosti v geometrii Kapitola IV. Stejnolehlost v polohových úlohách In: Jaroslav Šedivý (author): O podobnosti v geometrii. (Czech). Praha: Mladá fronta, 1963. pp. 48 60. Persistent URL: http://dml.cz/dmlcz/403487
3.MONGEOVO PROMÍTÁNÍ. Rovnoběžný průmět 3D těles na rovinu není vzájemně jednoznačné zobrazení, k obrazu neumíme jednoznačně určit objekt v prostoru
3.MONGEOVO PROMÍTÁNÍ A B E 3 E 2 Rovnoběžný průmět 3D těles na rovinu není vzájemně jednoznačné zobrazení, k obrazu neumíme jednoznačně určit objekt v prostoru 3.1.Kartézský souřadnicový systém O počátek
Vzdělávací materiál. vytvořený v projektu OP VK. Název školy: Gymnázium, Zábřeh, náměstí Osvobození 20. Číslo projektu: CZ.1.07/1.5.00/34.
Vzdělávací materiál vytvořený v projektu OP VK Název školy: Gymnázium, Zábřeh, náměstí Osvobození 20 Číslo projektu: Název projektu: Číslo a název klíčové aktivity: CZ.1.07/1.5.00/34.0211 Zlepšení podmínek
Matematika prima. Vazby a přesahy v RVP Mezipředmětové vztahy Průřezová témata. Očekávané výstupy z RVP Školní výstupy Učivo (U) Žák:
Matematika prima Očekávané výstupy z RVP Školní výstupy Učivo (U) využívá při paměťovém počítání komutativnost a asociativnost sčítání a násobení provádí písemné početní operace v oboru přirozených zaokrouhluje,
Gymnázium Christiana Dopplera, Zborovská 45, Praha 5. ROČNÍKOVÁ PRÁCE Technické osvětlení
Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 ROČNÍKOVÁ PRÁCE Technické osvětlení Vypracoval: Martin Hanuš Třída: 8.M Školní rok: 2015/2016 Seminář: Deskriptivní geometrie Prohlašuji, že jsem ročníkovou
Aplikace lineární perspektivy
Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 ROČNÍKOVÁ PRÁCE Aplikace lineární perspektivy Vypracoval: Jakub Sýkora Třída: 8.M Školní rok: 2015/2016 Seminář : Deskriptivní geometrie Prohlašuji,
Výukový matriál byl zpracován v rámci projektu OPVK 1.5 EU peníze školám. registrační číslo projektu:cz.1.07/1.5.00/
Výukový matriál byl zpracován v rámci projektu OPVK 1.5 EU peníze školám registrační číslo projektu:cz.1.07/1.5.00/34.1026 Autor: Mgr. Vladimír Mikel zpracováno: 28.11.2012 ročník (obor) tematická oblast
Digitální učební materiál
Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/4.080 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/ Inovace a zkvalitnění výuky prostřednictvím
Kuželoseč ky. 1.1 Elipsa
Kuželoseč ky 1.1 Elipsa Definice: Elipsa je množina všech bodů v 2, které mají od dvou pevných (různých) bodů v 2, zvaných ohniska (značíme F 1, F 2 ), stálý součet vzdáleností rovný 2a, který je větší
Fotogrammetrie. zpracovala Petra Brůžková. Fakulta Architektury ČVUT v Praze 2012
Fotogrammetrie zpracovala Petra Brůžková Fakulta Architektury ČVUT v Praze 2012 Fotogrammetrie je geometrický postup, který nám umožňuje určení tvaru, velikosti a polohy reálných objektů na základě fotografického
Čtyřúhelník. O b s a h : Čtyřúhelník. 1. Jak definovat čtyřúhelník základní vlastnosti. 2. Názvy čtyřúhelníků Deltoid Tětivový čtyřúhelník
Čtyřúhelník : 1. Jak definovat čtyřúhelník základní vlastnosti 2. Názvy čtyřúhelníků 2.1. Deltoid 2.2. Tětivový čtyřúhelník 2.3. Tečnový čtyřúhelník 2.4. Rovnoběžník 2.4.1. Základní vlastnosti 2.4.2. Výšky
JAK NA HYPERBOLU S GEOGEBROU
Trendy ve vzdělávání 015 JAK NA HYPERBOLU S GEOGEBROU KRIEG Jaroslav, CZ Resumé Článek ukazuje, jak pomocí GeoGebry snadno řešit úlohy, které vedou na konstrukci hyperboly, případně jak lehce zkonstruovat
Rozpis výstupů zima 2008 Geometrie
Rozpis výstupů zima 2008 Geometrie 20. 10. porovnávání úseček grafický součet úseček grafický rozdíl úseček... porovnávání úhlů grafický součet úhlů grafický rozdíl úhlů... osa úhlu úhly vedlejší a vrcholové...
Urci parametricke vyjadreni primky zadane body A[2;1] B[3;3] Urci, zda bod P [-3;5] lezi na primce AB, kde A[1;1] B[5;-3]
![Urci parametricke vyjadreni primky zadane body A[2;1] B[3;3] Urci, zda bod P [-3;5] lezi na primce AB, kde A[1;1] B[5;-3]](/thumbs/55/35554374.jpg "Urci parametricke vyjadreni primky zadane body A[2;1] B[3;3] Urci, zda bod P [-3;5] lezi na primce AB, kde A[1;1] B[5;-3]")
1 Parametricke vyjadreni primky Priklad 16 Priklad 17 Priklad 18 jestlize Urci parametricke vyjadreni primky zadane body A[2;1] B[3;3] Urci, zda bod P [-3;5] lezi na primce AB, kde A[1;1] B[5;-3] Urci,
Cabri pro začátečníky
Cabri pro začátečníky učební text RNDr. Ludmila Ciglerová 1. C T 1 T 3 O 1 1 A T 2 B H T G E F S D C A B R 1 Rýsování základních geometrických útvarů a) hlavní vodorovná lišta -Soubor, Upravit,Nastavit,
Do výtvarné výchovy se nakupují čtvrtky za cenu 5 Kč za kus. Kolik čtvrtek se nakoupí za 95 korun?
MATEMATIKA Součet bodů: Obor: 79-41-K/81 Opravil: Kontroloval: Vítáme vás u přijímacích zkoušek z matematiky a přejeme hodně úspěchů při řešení zadaných úloh. Úlohy můžete řešit v libovolném pořadí. 1.
Čtyři body na kružnici
Čtyři body na kružnici 10. listopadu 2015 Vojtěch Zlámal Čtyři body na kružnici 10. listopadu 2015 1 / 19 Problematika čtyř bodů na kružnici důkazové úlohy matematické soutěže nedostatečná metodika v učebnicích
VYTVÁŘENÍ GEOMETRICKÝCH PŘEDSTAV (u žáků se specifickými poruchami učení) Růžena Blažková
VYTVÁŘENÍ GEOMETRICKÝCH PŘEDSTAV (u žáků se specifickými poruchami učení) Růžena Blažková Geometrie je specifickou oblastí matematiky, která může být pro žáky, kteří mají poruchy v oblasti numerace a operací
Sada 1 CAD Kótování kótovací styl
S třední škola stavební Jihlava Sada 1 CAD1 06. Kótování kótovací styl Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2 - inovace
ZBORCENÉ PŘÍMKOVÉ PLOCHY ŘEŠENÉ PŘÍKLADY
ZBORCENÉ PŘÍMKOVÉ PLOCHY ŘEŠENÉ PŘÍKLADY Zpracovala: Kristýna Rožánková FA ČVUT 2011 ZBORCENÉ PŘÍMKOVÉ PLOCHY Zborcené přímkové plochy jsou určeny třemi křivkami k, l, m, které neleží na jedné rozvinutelné
Svobodná chebská škola, základní škola a gymnázium s.r.o. Vrcholové úhly. Souhlasné úhly
METODICKÝ LIST DA48 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný obsah: Úhly III. - Vztahy mezi úhly Astaloš Dušan Matematika šestý frontální,
Poznámka 1: Každý příklad začneme pro přehlednost do nového souboru tímto krokem:
Mongeovo promítání základní úlohy polohové (bod, přímka, rovina, bod v rovině, hlavní přímky roviny, rovina daná různoběžkami, průsečnice rovin, průsečík přímky s rovinou) Budeme pracovat v rovině nejlépe