2. Akustika, základní pojmy a veličiny v akustice
|
|
|
- Nikola Pešková
- před 9 lety
- Počet zobrazení:
Transkript
1 . Akustika, základní pojmy a veličiny v akustie. Předmět akustiky Akustika je definována jako věda zabývajíí se fyzikálními ději, které jsou spojeny se vznikem zvukového vlnění, jeho dalším šířením a vnímáním zvuku sluhovým orgánem. Vlnění hmotného prostředí, o jehož existeni se můžeme přesvědčit sluhem, se v běžné řeči i ve fyzie nazývá zvuk. Akustika se zabývá fyzikálními ději spojenými se vznikem zvukového vlnění, jeho šířením a vnímáním zvuku sluhem.. Rozdělení akustiky Obor akustika lze rozdělit na několik částí:. Fyzikální akustika zabývá se způsobem vzniku a šíření zvuku. Dále se zabývá odrazivostí a pohltivostí zvuku v různýh materiáleh.. Hudební akustika studuje zvuky včetně jejih kombinaí s ohledem na potřeby hudby. 3. Fyziologiká akustika zabývá se vznikem zvuku v hlasovém orgánu člověka a jeho vnímáním v sluhovém orgánu. 4. Stavební akustika zkoumá kvalitní podmínky poslehu hudby a řeči v obytnýh místnosteh a sáleh. 5. Elektroakustika zabývá se záznamem, reprodukí a šířením zvuku s využitím elektrikého proudu..3 Hluk jako environmentální faktor Hlukem bývá označován každý nepříjemný a nežádouí zvuk. Tato definie je ale subjektivní, protože pro někoho tentýž zvuk může být obtěžujíí a pro jiného přijatelný nebo dokone i příjemný. Hluk je definován jako zvuk, který člověka poškozuje (na zdraví, majetku nebo na životním prostředí), ruší nebo obtěžuje. Základním parametrem určujíím účinek zvuku je jeho intenzita. Člověk se neítí dobře v prostředí s velmi nízkou hladinou akustikého tlaku L pa frekvenčně váženého filtrem typu A. Hodnoty hladin okolo 0 db považuje spousta lidí za hluboké tiho. Hladina 30 db je považována za příjemné tiho. Při hladináh nad 65 db se již začínají projevovat účinky hluku především změnami vegetativníh reakí. Od 85 db výše již dohází k trvalým poruhám sluhu a ve větší míře se projevují účinky na vegetativní systém a elou nervovou soustavu. Od 30 db se obvykle účinky hluku mění na bolesti sluhového orgánu. Při hladináh a 60 db již dohází k protržení bubínku sluhového orgánu. Nadměrný hluk má rovněž negativní vliv na kvalitu a produktivitu práe a významně ohrožuje bezpečnost práe. Z těhto důvodů patří hluk k důležitým environmentálním faktorům..4 Metody eliminae hluku Existuje pět základníh metod boje proti hluku:
2 . Metoda reduke hluku ve zdroji spočívá v úplném odstranění zdroje hluku nebo se snížení jeho hlučnosti. Např. tlumením vibraí strojníh zařízení lze dosáhnout částečného snížení vyzařovaného hluku strojníh zařízení.. Metoda dispozie spočívá ve vhodném umístění hlučnýh strojů a zařízení (resp. elýh hlučnýh prostorů) od hráněnýh a méně hlučnýh prostorů. Této metody se využívá např. při územním plánování, projektování průmyslovýh zón, dopravníh komunikaí apod. tak, aby hlučné stroje a provozy neměly negativní vliv na akustikou pohodu v hráněnýh prostoreh (např. školy, školky, sídliště, nemonie, rekreační zóny apod.). 3. Metoda izolae spočívá ve zvukovém odizolování hlučného stroje, zařízení nebo elého hlučného prostoru od hráněného prostoru prostřednitvím zvukoizolačníh příček, stropů, krytů, zákrytů apod. 4. Metoda využívajíí zvukové pohltivosti materiálů spočívá ve shopnosti některýh materiálů a konstrukí pohlovat akustikou energii a transformovat ji na tepelnou energii. Aplikuje se především při snižování hlučnosti uvnitř místností. 5. Metoda využívajíí osobní ohranné pomůky tj. sluhátka, přilby nebo zvukově tlumií zátky vkládané do uha. Tato metoda se aplikuje, pokud z určitýh důvodů nelze použít žádnou z předhozíh metod nebo jestliže u těhto metod nedojde k dostatečnému snížení hlukové expozie člověka. Nejlepšíh výsledků v boji proti hluku lze dosáhnout využitím vhodnýh kombinaí výše uvedenýh metod..5 Zvuk Mehanikým vlněním pružného prostředí ve frekvenčním rozsahu 6 až kmitů za sekundu se nazývá zvuk, který se v daném pružném prostředí (tj. v kapalináh, plyneh nebo pevnýh látkáh) šíří konečnou ryhlostí. Jinak akustika se obeně zabývá mehanikými kmity ve větším frekvenčním rozsahu. Potom existují tři frekvenční pásma:. infrazvuk - mehaniké vlnění pružného prostředí s frekvení f < 6 Hz.. slyšitelný zvuk - mehaniké vlnění pružného prostředí ve frekvenčním pásmu od 6 Hz do 0 khz. 3. ultrazvuk - mehaniké vlnění pružného prostředí s frekvení f > Hz. Podstatou zvuku je mehaniké kmitání pružného prostředí ve frekvenčním rozsahu 6 až kmitů za sekundu. zdroj λ vlnoplohy Obr..: Šíření zvuku od zdroje
3 .6 Akustiké vlnění Zvuk se může šířit v kapalináh, plyneh nebo i pevnýh látkáh formou akustikého vlnění, jehož šíření je spojeno s přenosem energie. Částie daného prostředí se přitom nepohybují jednosměrně se šíříím se vlněním, ale kmitají pouze kolem svýh rovnovážnýh stavů. U plynů a kapalin se vyskytuje pouze podélné akustiké vlnění, protože tyto látky jsou pružné pouze ve smyslu objemové stlačitelnosti. V pevnýh elastikýh látkáh se může vyskytovat vlnění podélné i příčné. Tyto látky vykazují pevnost nejen v tahu a tlaku, ale i ve smyku. Kombinaí těhto namáhání vzniká i ohybové kmitání. Akustiké vlnění se šíří od zdroje zvuku ryhlostí šíření zvuku skrz dané prostředí ve vlnoploháh (viz obr..). Vlnoploha je harakteristiká tím, že ve všeh jejih bodeh je v daném čase stejný akustiký stav. Vzdálenost mezi vlnoplohami je vlnová délka λ. Kolmie na vlnoplohu je tzv. akustiký paprsek. Mezi pevnými látkami a plyny (resp. kapalinami) může doházet k přenosu kmitů. Každý hmotný element může být tzv. osilátorem, který je považován za akustiký osilátor. K nejjednodušším osilátorům patří pružina, struna, ladička apod..6. Lineární osilátor Nejjednodušším typem osilátoru je lineární osilátor (viz obr..). Jedná se o periodiký pohyb hmotného bodu, který probíhá po příme a je popsán difereniální rovnií: d y m + k y = 0, (.) d τ kde m je hmotnost kmitajíího hmotného bodu, y je výhylka, τ je čas a k je tuhost pružiny. Řešením rovnie (.) je rovnie volnýh netlumenýh kmitů hmotného bodu: y = y 0 sin( ω τ + ϕ ), (.) kde y 0 je amplituda výhylky kmitání, ω je vlastní kruhová frekvene a ϕ je fázový úhel. Vlastní kruhová frekvene je dána rovnií: k ω =. (.3) m k m y 0 y 0 Obr..: Lineární osilátor Časový průběh harmonikého netlumeného kmitání je znázorněn na obr..3. Z tohoto obrázku je zřejmé, že hmotný bod kmitá s amplitudou kmitání y 0 s periodou kmitání T.
4 Perioda kmitání je přitom taková doba, za kterou se hmotný bod dostane z rovnovážné polohy přes obě krajní polohy do původního stavu. Obr..3: Časový průběh harmonikého netlumeného kmitání.6. Kmitočet Kmitočet (resp. frekvene kmitání) f určuje počet kmitů za sekundu, které vykoná kmitajíí hmotný bod. Mezi frekvení kmitání a dobou kmitu T (resp. úhlovým kmitočtem ω) platí vztah: f ω = = T π. (.4) Kmitočet je roven převráené hodnotě periody kmitání..6.3 Celková energie kmitajíího bodu Při netlumeném harmonikém kmitání hmotného bodu platí zákon zahování energie, kdy elková energie E, která je dána součtem kinetiké energie E k a poteniální energie E p, je v průběhu kmitání neustále konstantní: E = E p + Ek = konst. (.5) Kinetiká energie kmitajíího hmotného bodu závisí na ryhlosti kmitání v hmotného bodu, která se stanoví derivaí výhylky kmitání dle rovnie (.): dy v = = y 0 ω os( ω τ + ϕ ) = v0 os( ω τ + ϕ ). (.6) dτ kde v 0 je amplituda ryhlosti kmitání. Kinetikou energii E k a poteniální energii E p (s využitím rovni (.) a (.3)) hmotného bodu lze vyjádřit z jejih základníh defini pomoí následujííh vztahů: E k = m v = m y0 ω os ( ω τ + ϕ ). (.7) E p = k y = m y0 ω sin ( ω τ + ϕ ). (.8) Po dosazení rovni (.7) a (.8) do rovnie (.5) a následnýh úpraváh se získá elková energie kmitajíího bodu:
5 Z výše uvedené rovnie je zřejmé, že elková energie při netlumeném harmonikém kmitání hmotného bodu zůstává stále konstantní. E = m y0 ω. (.9).6.4 Podélné vlnění v bodové řadě Prostorové vlnění je takový druh vlnění, které se šíří v trojrozměrném prostoru. Nejjednodušším typem vlnění je vlnění ve směru jedné souřadné osy. V tomto případě se jedná o podélné vlnění v bodové řadě. Na obr..4 je shématiky znázorněna bodová řada, ve které má nastat šíření podélného vlnění. Jednotlivé hmotné body daného prostředí se vzájemně ovlivňují mezimolekulárními silami, které jsou na obr..4 znázorněny ve formě pružinek. V této počáteční fázi před šířením rozruhu jsou tyto pružinky stejně stlačeny. Obr..4: Bodová řada před šířením akustikého vlnění Dojde-li k vyhýlení např. prvního bodu dané bodové řady, dojde k šíření akustiké vlny (viz obr..5.). Od prvního bodu se dále přenáší rozruh k dalším bodům konečnou ryhlostí šíření zvuku v daném prostředí. Na obr..5 je zřejmá poloha jednotlivýh bodů v konkrétním čase τ. Dále je zřejmé, že při šíření akustiké vlny dohází ke změnám vzdáleností mezi jednotlivými body. Může doházet ke zmenšení vzdálenosti dvou sousedníh bodů (tzn. pružiny jsou stlačeny) nebo naopak ke zvětšení vzdálenosti mezi dvěma sousedními body (tzn. pružiny jsou zředěny). Podobným způsobem lze zakreslit i kmitání molekul při příčném vlnění, při kterém je rovina pohybu molekul kolmá ke směru šíření akustikého signálu. τ = 0 T/ τ τ = T/4 τ = T/ x τ = 3T/4 Obr..5: Vývoj akustikého vlnění v bodové řadě V tehniké akustie se výhylka hmotného bodu, kterým je přenášen akustiký signál, je značena písmenem u. Její časová závislost je dána rovnií: u = u 0 sin( ω τ + ϕ ), (.0)
6 kde u 0 je amplituda akustiké výhylky. Budeme-li se zajímat o velikost akustiké výhylky ve vzdálenosti x od počátku při šíření rozruhu konstantní ryhlostí v homogenním prostředí, pak tento děj v daném místě x je opožděn o čas τ potřebný k uražení této dráhy: x τ =. (.) Potom akustiká výhylka kmitajíího bodu je dána vztahem: x u = u0 sin ω τ. (.) Záporné znaménko v rovnii. platí pro šíření vlny v kladném smyslu osy x. Podobně kladné znaménko ve výše uvedené rovnii platí pro šíření zvuku v záporném smyslu osy x..6.5 Vlnová délka Vlnová délka λ je určena vzdáleností mezi dvěma nejbližšími body bodové řady se stejným akustikým stavem v daném okamžiku. Resp. je to vzdálenost, kterou urazí akustiká vlna v průběhu jednoho kmitu T. Potom pro vlnovou délku platí vztah: λ = = T. (.3) f.6.6 Akustiká ryhlost Akustiká ryhlost v je taková ryhlost, se kterou kmitají jednotlivé částie prostředí, kterým se šíří zvuková vlna. První derivaí akustiké výhylky podle rovnie (.) je definována akustiká ryhlost: x x v = ω u0 os ω τ = v0 os ω τ, (.4) kde v 0 je amplituda akustiké ryhlosti. Pozor! Je třeba si uvědomit, že akustiká ryhlost v a ryhlost šíření zvuku jsou dvě zela odlišné veličiny. p s p b p Obr..6: Časový průběh elkového statikého tlaku p ve vzduhu τ
7 .6.7 Akustiký tlak Při šíření zvuku v bodové řadě (viz obr..5) jsou zřejmá místa se zředěním nebo zhuštěním části. Tomu odpovídají místa podtlaku a přetlaku. S tím souvisí změny elkového statikého tlaku vzduhu p s, který je dán součtem středního barometrikého tlaku p b a akustikého tlaku p (viz obr..6). Akustiký tlak p, který lidské uho vnímá již od hodnoty 0-5 Pa, je přitom zanedbatelný ve srovnání s barometrikým tlakem (p b 0 5 Pa). Průběh akustikého tlaku je analogiký s průběhem akustiké výhylky nebo akustiké ryhlosti. Pro harmoniký signál lze akustiký tlak vyjádřit rovnií: x p = p0 os ω τ, (.5) kde p 0 je amplituda akustikého tlaku. Z rovnie (.5) je zřejmé, že akustiký tlak závisí na kruhové frekveni ω, resp. kmitočtu f. Reálné zvuky v našem životním prostředí ale nejsou akustiké signály o jednom kmitočtu, ale skládají se z řady dílčíh signálů. Z tohoto důvodu je třeba u akustikýh veličin (jako je např. akustiký tlak, akustiká ryhlost nebo akustiký výkon) praovat s jejih frekvenčními spektry, která mohou být čárová (tzv. diskrétní) nebo spojitá..7 Ryhlost šíření zvuku V kapalináh a plyneh se může šířit pouze podélné vlnění, v pevnýh látkáh se může šířit též příčné vlnění. Všeobeně se zvuk nejryhleji šíří v pevnýh látkáh, nejpomaleji v plyneh. Pro srovnání jsou v tab.. uvedeny ryhlosti šíření podélného vlnění v některýh látkáh..7. Ryhlost šíření zvuku v kapalináh Ryhlost šíření podélného vlnění v kapalináh je dána vztahem: K =, (.6) ρ kde K je modul objemové pružnosti, ρ je hustota prostředí..7. Ryhlost šíření zvuku v plyneh Stanovení ryhlosti šíření zvuku v plyneh je složitější ve srovnání s šířením zvuku v kapalináh z důvodu dané stavové změny, která v plynu probíhá. Pro vlnění o kmitočteh f > 0 Hz jsou změny okamžitého akustikého tlaku velmi ryhlé a stavovou změnu lze považovat za adiabatikou. Potom pro ryhlost šíření zvuku v plyneh platí vztah: pb = κ, (.7) ρ kde κ je Poissonova konstanta. Speiálně pro vzduh v závislosti na teplotě t lze ryhlost šíření zvuku stanovit podle rovnie: t = 33,6 +, (.8) 73, kde t je teplota vzduhu ve C.
8 Látka L [m s - ] Vzduh 0 C 33 Vzduh 0 C 344 Dusík 0 C 334 Helium 0 C 97 Vodík 0 C 86 Voda 3 C 440 Petrolej 5 C 35 Aeton 0 C 90 Rtuť 0 C 45 Glyerin 0 C 93 Olovo 40 Bukové dřevo 3900 Hliník 4800 Oel 5750 Beton 300 Cihly 800 Sklo 570 Plexisklo 580 Tvrdá pryž 400 Měkká pryž 70 Tab..: Ryhlost šíření podélného vlnění v některýh látkáh.7.3 Ryhlost šíření zvuku v pevnýh látkáh Ryhlost šíření podélného vlnění v tenké tyči je dána vztahem: E L =, (.9) ρ kde E je Youngův modul pružnosti v tahu. Ryhlost šíření podélného vlnění v dese je určena rovnií: E L =, (.0) ρ µ ( ) kde µ je Poissonův poměr příčné kontrake, který se stanoví ze vztahu: E G µ =, (.) G kde G je modul pružnosti ve smyku. Ryhlost šíření příčného vlnění v pevnýh látkáh je dána vztahem: G T =. (.) ρ
9 V těleseh, u kterýh převládá jeden nebo dva rozměry oproti ostatním (např. v tyčíh nebo deskáh), vzniká kombinae podélného a příčného vlnění, tzv. ohybové vlnění. Toto vlnění je příčinou vyzařování zvuku. Pro ryhlost šíření ohybovýh vln v tyči platí vztah: B = π f 4E J, m (.3) kde J [kg m ] je moment setrvačnosti průřezu tyče, m [kg m - ] je hmotnost jednotkové délky tyče. Pro tyče obdélníkového průřezu lze rovnii (.3) upravit do tvaru: B =, 8 L h f, (.4) kde h je menší rozměr obdélníkového průřezu..8 Akustiký výkon Předpokládejme ve směru osy x šíření rovinné vlny, která dopadá na měřií plohu S (viz obr..7). Zvukové paprsky přitom s měřií plohou svírají úhel υ. Akustiký výkon je definován rovnií: de P =, (.5) dτ kde E je akustiká energie. Akustiký výkon je určen množstvím přenesené akustiké energie za jednotku času. Je-li akustiký výkon vztažen na jednotku plohy, zavádí se tzv. měrný akustiký výkon N [W/m ]: dp N =. (.6) ds osυ Pokud je ve všeh bodeh uvažované rovinné vlny stejný akustiký stav, lze rovnii (.6) zjednodušit do tvaru: P N =. (.7) S osυ υ S Obr..7: Šíření rovinné vlny na měřií plohu S Výkon je dán všeobeně součinem akustiké ryhlosti v a působíí síly F, která je úměrná součinu akustikého tlaku p a plohy S. Potom lze psát: P = F v = p S v. (.8) Pokud měřií ploha S je kolmá vzhledem ke zvukovým paprskům (osυ = ), pak lze na základě rovni (.7) a (.8) vyjádřit měrný akustiký výkon jako:
10 N = p v. (.9).9 Intenzita zvuku Intenzita zvuku závisí na měrném akustikém výkonu N a je dána rovnií: T I = Ndτ, (.30) T kde T je doba integrae, která je u harmonikýh signálů rovna době jedné periody. Řešení rovnie (.30) pro rovinnou vlnu je vztah pro intenzitu zvuku: p0 I = ρ ω u0 = = p ef v ef, (.3) ρ kde p ef a v ef jsou efektivní hodnoty tlaku a akustiké ryhlosti, pro které platí rovnie: 0 p 0 p ef =, (.3) v v 0 ef =. (.33) V tehniké akustie lze běžnými přístroji spolehlivě měřit akustiký tlak, ale ne akustikou ryhlost. U rovinné vlny se využívá té fyzikální skutečnosti, že poměr mezi akustikým tlakem a akustikou ryhlostí je konstantní a je roven poměru: p Z = = ρ = konst., (.34) v kde Z [N s/m 3 ]je tzv. měrný vlnový odpor prostředí, v němž se šíří akustiká vlna. Dosazením rovnie (.34) do rovnie (.3) se získá vztah pro intenzitu zvuku u rovinné vlny: pef I =. (.35) ρ Při šíření kulové vlny není akustiky tlak ve fázi s akustikou ryhlostí. Potom pro intenzitu zvuku kulové vlny platí rovnie: I = p ef vef os ϕ, (.36) kde ϕ je fázový úhel mezi akustikým tlakem a akustikou ryhlostí..0 Interferene akustikýh vln Šíří-li se bodovou řadou dvě nebo víe vlnění, výsledné vlnění se skládá metodou superpozie. Při šíření vlnění ve víe směreh je nutno tato vlnění skládat vektorově..0. Interferene vlnění o stejnýh frekveníh Předpokládejme dvě akustiká vlnění šíříí se v bodové řadě v kladném smyslu osy x o stejnýh kruhovýh frekveníh ω s příslušnými amplitudami akustiké výhylky (tzn. u 0 a u 0 ) a fázovými úhly (tzn. ϕ a ϕ ). Potom pro akustiké výhylky obou vlnění platí rovnie: x u = u0 sin ω τ + ϕ, (.37) x u = u0 sin ω τ + ϕ. (.38) Součtem předhozíh dvou rovni se získá amplituda výsledného vlnění:
11 x u = u0 sin ω τ + ϕ, (.39) kde u 0 je amplituda výsledného vlnění a ϕ je fázový úhel výsledného vlnění, pro které platí rovnie: u 0 = u0 + u0 u0 u0 os( ϕ ϕ ), (.40) u0 sin ϕ + u0 sin ϕ tg ϕ =. u0 os ϕ + u0 os ϕ (.4) Z rovnie (.39) je zřejmé, že výsledné vlnění je opět harmoniké vlnění šíříí se v kladném smyslu osy x se stejnou kruhovou frekvení ω jako obě dílčí akustiká vlnění. Má ale obeně jinou amplitudu u 0 a jiný fázový posun ϕ. Dále je zřejmé, že velikost amplitudy tohoto vlnění závisí na rozdílu fázovýh úhlů obou vlnění v rovnii (.40). Maximální amplituda výsledného vlnění nastane v případě, když: ϕ ϕ = n π, (.4) kde n je libovolné elé číslo (n = 0,,, 3.). Podobně minimální amplituda výsledného vlnění je dosažena za podmínky: ϕ ϕ = ( n + ) π. (.43) Zvláštním případem tohoto vlnění může být takové vlnění, kdy dohází k vzájemnému rušení obou vlnění při jejih skládání. Takový děj nastane tehdy, jestliže amplitudy obou vlnění jsou stejné a fázový posun mezi těmito vlněními je roven π (viz rovnie (.40))..0. Úplné stojaté vlnění Úplné stojaté vlnění je takový druh vlnění, při kterém se šíří proti sobě dvě vlnění se stejnými kruhovými frekvenemi a se stejnými amplitudami. Při úplném stojatém vlnění se šíří proti sobě dvě vlnění o stejnýh kruhovýh frekveníh a amplitudáh. Úplné stojaté vlnění je potom popsáno rovniemi: x u = u0 sin ω τ, (.44) x u = u0 sin ω τ +. (.45)
12 u kmitna u 0 u 0 x λ uzel Obr..8: Úplné stojaté vlnění Sečtením rovni (.44) a (.45) se získá rovnie pro akustikou výhylku úplného stojatého vlnění: x u = u + u = u 0 os ω sin( ω τ ) = U sin( ω τ ), (.46) kde U je amplituda úplného stojatého vlnění (v daném místě x) určená rovnií: x U = u 0 os ω. (.47) Z rovnie (.46) je patrné, že vlnění je opět harmoniké s kruhovou frekvení ω a jednotlivé částie kmitají se stejnou fází, ale obeně s jinou amplitudou U, protože U = f(x). Potom amplituda U bude maximální v takovýh místeh x, ve kterýh bude platit: ω x ω x os = ±, resp. = n π, (.48) kde n je libovolné elé číslo (n = 0,,, 3.). Maximální amplitudy se nazývají kmitny (viz obr..8). Tato místa jsou od sebe vzdáleny ve vzdálenosteh: λ x = n = n. (.49) f Podobně místa minimálníh (v tomto případě nulovýh) amplitud výsledného vlnění, které se nazývají tzv. uzly, jsou dosaženy za podmínky: ω x ω x π os = 0, resp. = ( n + ). (.50) Pro vzdálenost mezi uzly platí: λ x = ( n + ). (.5) 4 Úplné stojaté vlnění se v praxi vyskytuje při odrazu akustikého vlnění od překážky, jejíž odrazová ploha je akustiky tvrdá. V tomto případě se od této plohy odrazí veškerá dopadajíí akustiká energie. Běžně ale dohází k určitému pohlení akustiké energie danou překážkou. V těhto případeh vzniká při odrazu od dané překážky částečné stojaté vlnění.
13 .0.3 Částečné stojaté vlnění Úplné stojaté vlnění je takový druh vlnění, při kterém se šíří proti sobě dvě vlnění se stejnými kruhovými frekvenemi a s různými amplitudami. Při částečném stojatém vlnění se šíří proti sobě dvě vlnění o stejnýh kruhovýh frekveníh a různýh amplitudáh. částečné stojaté vlnění u úplné stojaté vlnění u 0 u 0 u 0 - u 0 u 0 + u 0 x postupné vlnění Obr..9: Částečné stojaté vlnění Částečné stojaté vlnění je potom popsáno rovniemi: x u = u0 sin ω τ, (.5) x u = u0 sin ω τ +. (.53) Sečtením rovni (.5) a (.53) se získá rovnie pro akustikou výhylku úplného stojatého vlnění: u = u + u x x = u0 os ω sin( ω τ ) + ( u0 u0 ) sin ω τ. (.54) Z rovnie (.54) je zřejmé, že částečné stojaté vlnění se skládá ze dvou složek. První složka harakterizuje úplné stojaté vlnění s amplitudou u 0 os(ω x/), druhý člen harakterizuje postupné vlnění s amplitudou (u 0 - u 0 ).. Výsledná intenzita zvuku při interfereni dvou vlnění Předpokládejme dva zdroje zvuku (viz obr..0), ze kterýh se šíří akustiké vlnění směrem k posluhači, v jehož místě je třeba stanovit výslednou intenzitu akustikého vlnění. V místě posluhače se v důsledku zdrojů zvuku vyskytují dva časově proměnlivé akustiké tlaky p (τ) a p (τ), jejihž součtem je určen výsledný akustiký tlak: p = p0 sin( ω τ + ϕ ) + p0 sin( ω τ + ϕ ). (.55)
14 Potom lze intenzitu zvuku vyjádřit vztahem: T p I = dτ = T ρ = 0 p0 + p ρ 0 p0 + ρ p 0 T T 0 sin. (.56) ( ω τ + ϕ ) dτ sin( ω τ + ϕ ) dτ p ( τ ) p ( τ ) Obr..0: Šíření vlnění ze dvou zdrojů zvuku Rovnie (.56) má dvě různá řešení v závislosti na velikosti kruhovýh frekvení jednotlivýh zdrojů zvuku. V případě rozdílnýh velikostí kruhovýh frekvení obou zvukovýh zdrojů (tzn. ω ω ), integrál v rovnii (.56) je roven nule a intenzita výsledného vlnění je dána vztahem: p0 + p0 I = = I + I. (.57) ρ Výsledná intenzita zvuku v případě rozdílnýh kruhovýh frekvení zdrojů zvuku je tedy rovna součtu součtu intenzit od jednotlivýh zdrojů zvuku. Pokud jsou kruhové frekvene obou zvukovýh zdrojů stejné (tzn. ω = ω ), integrál v rovnii (.56) je nenulový a intenzita výsledného vlnění je dána vztahem: p ef pef I = I + I + os( ϕ ϕ ). (.58) ρ. Hustota akustiké energie Hustota akustiké energie w [J/m 3 ] je energie obsažená v objemové jednote o elementárníh rozměreh dx, dy a dz. Je definována rovnií: de w =. (.59) dv Hustota akustiké energie je definována akustikou energií obsaženou v objemové jednote prostředí. Po dosazení rovnie (.9) do rovnie (.59) lze hustotu akustiké energie vyjádřit rovnií:
15 w = ρ ω u0. (.60) Porovná-li se výše uvedená rovnie s rovnií (.3) pro výpočet intenzity zvuku, lze potom psát: I = w. (.6).3 Testové otázky ke kapitole. Definujte, o je to zvuk. Jaké jsou druhy zvuku a jejih příslušná frekvenční pásma?. Definujte pojem hluk. Vyjmenujte (včetně příkladů) metody eliminae hluku. 3. Nakreslete prinip šíření zvuku ze zdroje. Definujte pojmy vlnová délka, vlnoploha, kmitočet. Napište základní vztah pro vlnovou délku včetně významu a jednotek jednotlivýh veličin. 4. Definujte pojmy akustiký tlak a akustiká ryhlost. Napište rovnie pro jejih výpočet včetně významu a jednotek jednotlivýh veličin. Vysvětlete pojmy ryhlost šíření zvuku a akustiká ryhlost jsou to tytéž veličiny? Pokud ne, rozlište tyto veličiny. 5. Ryhlost šíření zvuku v pevnýh látkáh, kapalináh a v plyneh. Jaké vlnění se vyskytuje v těhto médiíh. V kterýh látkáh se obeně šíří zvuk nejryhleji, resp. nejpomaleji. Uveďte základní vztahy včetně významu jednotlivýh veličin pro ryhlost šíření zvuku pro výše uvedená média. 6. Definujte pojmy akustiký výkon, měrný akustiký výkon a intenzita zvuku. Uveďte jejih definiční rovnie včetně významu jednotlivýh veličin. 7. Definujte pojmy úplné stojaté vlnění a částečné stojaté vlnění. Stanovte akustikou výhylku pro obě tyto vlnění. Zakreslete průběhy těhto vlnění. Co jsou to kmitny a uzly? Ze kterýh dvou složek se skládá částečné stojaté vlnění? 8. Definujte pojem hustota akustiké energie. Napište její základní vztah včetně významu a jednotek příslušnýh veličin. Jaký je vztah mezi intenzitou zvuku a hustotou akustiké energie? Uveďte ho.
Mechanické kmitání. Def: Hertz je frekvence periodického jevu, jehož 1 perioda trvá 1 sekundu. Y m
 Mehaniké kmitání Periodiký pohyb - harakterizován pravidelným opakováním pohybového stavu tělesa ( kyvadlo, těleso na pružině, píst motoru, struna na kytaře, nohy běžíího člověka ) - nejkratší doba, za
Mehaniké kmitání Periodiký pohyb - harakterizován pravidelným opakováním pohybového stavu tělesa ( kyvadlo, těleso na pružině, píst motoru, struna na kytaře, nohy běžíího člověka ) - nejkratší doba, za
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/ Vlnění
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Vlnění Vhodíme-li na klidnou vodní hladinu kámen, hladina se jeho dopadem rozkmitá a z místa rozruchu se začnou
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Vlnění Vhodíme-li na klidnou vodní hladinu kámen, hladina se jeho dopadem rozkmitá a z místa rozruchu se začnou
Mechanické kmitání a vlnění
 Mechanické kmitání a vlnění Pohyb tělesa, který se v určitém časovém intervalu pravidelně opakuje periodický pohyb S kmitavým pohybem se setkáváme např.: Zařízení, které volně kmitá, nazýváme mechanický
Mechanické kmitání a vlnění Pohyb tělesa, který se v určitém časovém intervalu pravidelně opakuje periodický pohyb S kmitavým pohybem se setkáváme např.: Zařízení, které volně kmitá, nazýváme mechanický
Vlnění. vlnění kmitavý pohyb částic se šíří prostředím. přenos energie bez přenosu látky. druhy vlnění: 1. a. mechanické vlnění (v hmotném prostředí)
 Vlnění vlnění kmitavý pohyb částic se šíří prostředím přenos energie bez přenosu látky Vázané oscilátory druhy vlnění: Druhy vlnění podélné a příčné 1. a. mechanické vlnění (v hmotném prostředí) b. elektromagnetické
Vlnění vlnění kmitavý pohyb částic se šíří prostředím přenos energie bez přenosu látky Vázané oscilátory druhy vlnění: Druhy vlnění podélné a příčné 1. a. mechanické vlnění (v hmotném prostředí) b. elektromagnetické
Izolaní materiály. Šastník Stanislav. 2. týden
 Izolaní materiály 2. týden Šastník Stanislav Vysoké uení technické v Brn, Fakulta stavební, Ústav technologie stavebních hmot a dílc, Veveí 95, 602 00 Brno, Tel: +420 5 4114 7507, Fax +420 5 4114 7502,
Izolaní materiály 2. týden Šastník Stanislav Vysoké uení technické v Brn, Fakulta stavební, Ústav technologie stavebních hmot a dílc, Veveí 95, 602 00 Brno, Tel: +420 5 4114 7507, Fax +420 5 4114 7502,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ PRŮVODCE GB01-P05 MECHANICKÉ VLNĚNÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ Prof. Ing. Bohumil Koktavý,CSc. FYZIKA PRŮVODCE GB01-P05 MECHANICKÉ VLNĚNÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA 2 OBSAH 1 Úvod...5
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ Prof. Ing. Bohumil Koktavý,CSc. FYZIKA PRŮVODCE GB01-P05 MECHANICKÉ VLNĚNÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA 2 OBSAH 1 Úvod...5
Jednotlivé body pouze kmitají kolem rovnovážných poloh. Tato poloha zůstává stálá.
 MECHANICKÉ VLNĚNÍ Dosud jsme při studiu uvažovali pouze harmonický pohyb izolované částice (hmotného bodu nebo tělesa), která konala kmitavý pohyb kolem rovnovážné polohy Jestliže takový objekt bude součástí
MECHANICKÉ VLNĚNÍ Dosud jsme při studiu uvažovali pouze harmonický pohyb izolované částice (hmotného bodu nebo tělesa), která konala kmitavý pohyb kolem rovnovážné polohy Jestliže takový objekt bude součástí
Interference vlnění
 8 Interference vlnění Umět vysvětlit princip interference Umět vysvětlit pojmy interferenčního maxima a minima 3 Umět vysvětlit vznik stojatého vlnění 4 Znát podobnosti a rozdíly mezi postupnýma stojatým
8 Interference vlnění Umět vysvětlit princip interference Umět vysvětlit pojmy interferenčního maxima a minima 3 Umět vysvětlit vznik stojatého vlnění 4 Znát podobnosti a rozdíly mezi postupnýma stojatým
1.8. Mechanické vlnění
 1.8. Mechanické vlnění 1. Umět vysvětlit princip vlnivého pohybu.. Umět srovnat a zároveň vysvětlit rozdíl mezi periodickým kmitavým pohybem jednoho bodu s periodickým vlnivým pohybem bodové řady. 3. Znát
1.8. Mechanické vlnění 1. Umět vysvětlit princip vlnivého pohybu.. Umět srovnat a zároveň vysvětlit rozdíl mezi periodickým kmitavým pohybem jednoho bodu s periodickým vlnivým pohybem bodové řady. 3. Znát
Zvuk. 1. základní kmitání. 2. šíření zvuku
 Zvuk 1. základní kmitání - vzduchem se šíří tlakové vzruchy (vzruchová vlna), zvuk je systémem zhuštěnin a zředěnin - podstatou zvuku je kmitání zdroje zvuku a tím způsobené podélné vlnění elastického
Zvuk 1. základní kmitání - vzduchem se šíří tlakové vzruchy (vzruchová vlna), zvuk je systémem zhuštěnin a zředěnin - podstatou zvuku je kmitání zdroje zvuku a tím způsobené podélné vlnění elastického
10. Energie a její transformace
 10. Energie a její transformace Energie je nejdůležitější vlastností hmoty a záření. Je obsažena v každém kousku hmoty i ve světelném paprsku. Je ve vesmíru a všude kolem nás. S energií se setkáváme na
10. Energie a její transformace Energie je nejdůležitější vlastností hmoty a záření. Je obsažena v každém kousku hmoty i ve světelném paprsku. Je ve vesmíru a všude kolem nás. S energií se setkáváme na
2. Vlnění. π T. t T. x λ. Machův vlnostroj
 2. Vlnění 2.1 Vlnění zvláštní případ pohybu prostředí Vlnění je pohyb v soustavě velkého počtu částic navzájem vázaných, kdy částice kmitají kolem svých rovnovážných poloh. Druhy vlnění: vlnění příčné
2. Vlnění 2.1 Vlnění zvláštní případ pohybu prostředí Vlnění je pohyb v soustavě velkého počtu částic navzájem vázaných, kdy částice kmitají kolem svých rovnovážných poloh. Druhy vlnění: vlnění příčné
ω=2π/t, ω=2πf (rad/s) y=y m sin ωt okamžitá výchylka vliv má počáteční fáze ϕ 0
 Kmity základní popis kmitání je periodický pohyb, při kterém těleso pravidelně prochází rovnovážnou polohou mechanický oscilátor zařízení vykonávající kmity Základní veličiny Perioda T [s], frekvence f=1/t
Kmity základní popis kmitání je periodický pohyb, při kterém těleso pravidelně prochází rovnovážnou polohou mechanický oscilátor zařízení vykonávající kmity Základní veličiny Perioda T [s], frekvence f=1/t
Elektromagnetický oscilátor
 Elektromagnetický oscilátor Již jsme poznali kmitání mechanického oscilátoru (závaží na pružině) - potenciální energie pružnosti se přeměňuje na kinetickou energii a naopak. T =2 m k Nejjednodušší elektromagnetický
Elektromagnetický oscilátor Již jsme poznali kmitání mechanického oscilátoru (závaží na pružině) - potenciální energie pružnosti se přeměňuje na kinetickou energii a naopak. T =2 m k Nejjednodušší elektromagnetický
Přednáší Kontakt: Ing. Michal WEISZ,Ph. Ph.D. Experimentáln. michal.weisz. weisz@vsb.cz. E-mail:
 AKUSTICKÁ MĚŘENÍ Přednáší a cvičí: Kontakt: Ing. Michal WEISZ,Ph Ph.D. CPiT pracoviště 9332 Experimentáln lní hluková a klimatizační laboratoř. Druhé poschodí na nové menze kl.: 597 324 303 E-mail: michal.weisz
AKUSTICKÁ MĚŘENÍ Přednáší a cvičí: Kontakt: Ing. Michal WEISZ,Ph Ph.D. CPiT pracoviště 9332 Experimentáln lní hluková a klimatizační laboratoř. Druhé poschodí na nové menze kl.: 597 324 303 E-mail: michal.weisz
DUM č. 14 v sadě. 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia
 projekt GML Brno Docens DUM č. 14 v sadě 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia Autor: Vojtěch Beneš Datum: 04.05.2014 Ročník: 1. ročník Anotace DUMu: Mechanické vlnění, zvuk Materiály
projekt GML Brno Docens DUM č. 14 v sadě 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia Autor: Vojtěch Beneš Datum: 04.05.2014 Ročník: 1. ročník Anotace DUMu: Mechanické vlnění, zvuk Materiály
Fyzikální podstata zvuku
 Fyzikální podstata zvuku 1. základní kmitání vzduchem se šíří tlakové vzruchy (vzruchová vlna), zvuk je systémem zhuštěnin a zředěnin podstatou zvuku je kmitání zdroje zvuku a tím způsobené podélné vlnění
Fyzikální podstata zvuku 1. základní kmitání vzduchem se šíří tlakové vzruchy (vzruchová vlna), zvuk je systémem zhuštěnin a zředěnin podstatou zvuku je kmitání zdroje zvuku a tím způsobené podélné vlnění
4. Akustika. 4.1 Úvod. 4.2 Rychlost zvuku
 4. Akustika 4.1 Úvod Fyzikálními ději, které probíhají při vzniku, šíření či vnímání zvuku, se zabývá akustika. Lidské ucho je schopné vnímat zvuky o frekvenčním rozsahu 16 Hz až 16 khz. Mechanické vlnění
4. Akustika 4.1 Úvod Fyzikálními ději, které probíhají při vzniku, šíření či vnímání zvuku, se zabývá akustika. Lidské ucho je schopné vnímat zvuky o frekvenčním rozsahu 16 Hz až 16 khz. Mechanické vlnění
Kmitání mechanického oscilátoru Mechanické vlnění Zvukové vlnění
 Mechanické kmitání a vlnění Kmitání mechanického oscilátoru Mechanické vlnění Zvukové vlnění Kmitání mechanického oscilátoru Kmitavý pohyb Mechanický oscilátor = zařízení, které kmitá bez vnějšího působení
Mechanické kmitání a vlnění Kmitání mechanického oscilátoru Mechanické vlnění Zvukové vlnění Kmitání mechanického oscilátoru Kmitavý pohyb Mechanický oscilátor = zařízení, které kmitá bez vnějšího působení
Druh učebního materiálu Anotace (metodický pokyn, časová náročnost, další pomůcky )
 Číslo šablony III/2 Číslo materiálu VY_32_INOVACE_F.6.18 Autor Stanislav Mokrý Vytvořeno 8.12.2013 Předmět, ročník Fyzika, 2. ročník Tematický celek Fyzika 2. - Mechanické kmitání a vlnění Téma Zvuk a
Číslo šablony III/2 Číslo materiálu VY_32_INOVACE_F.6.18 Autor Stanislav Mokrý Vytvořeno 8.12.2013 Předmět, ročník Fyzika, 2. ročník Tematický celek Fyzika 2. - Mechanické kmitání a vlnění Téma Zvuk a
I N V E S T I C E D O R O Z V O J E V Z D Ě L Á V Á N Í. x m. Ne čas!
 MECHANICKÉ VLNĚNÍ I N V E S T I C E D O R O Z V O J E V Z D Ě L Á V Á N Í uveďte rozdíly mezi mechanickým a elektromagnetickým vlněním zdroj mechanického vlnění musí. a to musí být přenášeno vhodným prostředím,
MECHANICKÉ VLNĚNÍ I N V E S T I C E D O R O Z V O J E V Z D Ě L Á V Á N Í uveďte rozdíly mezi mechanickým a elektromagnetickým vlněním zdroj mechanického vlnění musí. a to musí být přenášeno vhodným prostředím,
Jestliže rozkmitáme nějakou částici pevného, kapalného anebo plynného prostředí, tak síly pružnosti přenesou tento kmitavý pohyb na částici sousední
 Jestliže rozkmitáme nějakou částici pevného, kapalného anebo plynného prostředí, tak síly pružnosti přenesou tento kmitavý pohyb na částici sousední a ta jej zase předá svému sousedovi. Částice si tedy
Jestliže rozkmitáme nějakou částici pevného, kapalného anebo plynného prostředí, tak síly pružnosti přenesou tento kmitavý pohyb na částici sousední a ta jej zase předá svému sousedovi. Částice si tedy
Fyzika - Sexta, 2. ročník
 - Sexta, 2. ročník Fyzika Výchovné a vzdělávací strategie Kompetence komunikativní Kompetence k řešení problémů Kompetence sociální a personální Kompetence občanská Kompetence k podnikavosti Kompetence
- Sexta, 2. ročník Fyzika Výchovné a vzdělávací strategie Kompetence komunikativní Kompetence k řešení problémů Kompetence sociální a personální Kompetence občanská Kompetence k podnikavosti Kompetence
VY_32_INOVACE_FY.18 ZVUKOVÉ JEVY
 VY_32_INOVACE_FY.18 ZVUKOVÉ JEVY Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 Zvuk je mechanické vlnění v látkovém prostředí,
VY_32_INOVACE_FY.18 ZVUKOVÉ JEVY Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 Zvuk je mechanické vlnění v látkovém prostředí,
Akustické vlnění
 1.8.3. Akustické vlnění 1. Umět vysvětlit princip vzniku akustického vlnění.. Znát základní rozdělení akustického vlnění podle frekvencí. 3. Znát charakteristické veličiny akustického vlnění a jejich jednotky:
1.8.3. Akustické vlnění 1. Umět vysvětlit princip vzniku akustického vlnění.. Znát základní rozdělení akustického vlnění podle frekvencí. 3. Znát charakteristické veličiny akustického vlnění a jejich jednotky:
ZVUKOVÉ JEVY. Mgr. Jan Ptáčník - GJVJ - Fyzika - Tercie
 ZVUKOVÉ JEVY Mgr. Jan Ptáčník - GJVJ - Fyzika - Tercie Odraz zvuku Vznik ozvěny Dozvuk Několikanásobný odraz Ohyb zvuku Zvuk se dostává za překážky Překážka srovnatelná s vlnovou délkou Pružnost Působení
ZVUKOVÉ JEVY Mgr. Jan Ptáčník - GJVJ - Fyzika - Tercie Odraz zvuku Vznik ozvěny Dozvuk Několikanásobný odraz Ohyb zvuku Zvuk se dostává za překážky Překážka srovnatelná s vlnovou délkou Pružnost Působení
B. MECHANICKÉ KMITÁNÍ A VLNĚNÍ
 B. MECHANICKÉ KMITÁNÍ A VLNĚNÍ I. MECHANICKÉ KMITÁNÍ 8.1 Kmitavý pohyb a) mechanické kmitání (kmitavý pohyb) pohyb, při kterém kmitající těleso zůstává stále v okolí určitého bodu tzv. rovnovážné polohy
B. MECHANICKÉ KMITÁNÍ A VLNĚNÍ I. MECHANICKÉ KMITÁNÍ 8.1 Kmitavý pohyb a) mechanické kmitání (kmitavý pohyb) pohyb, při kterém kmitající těleso zůstává stále v okolí určitého bodu tzv. rovnovážné polohy
Rovinná harmonická elektromagnetická vlna
 Rovinná harmonická elektromagnetická vlna ---- 1. příklad -------------------------------- 2 GHz prochází prostředím s parametry: r 5, r 1, 0.005 S / m. Amplituda intenzity magnetického pole je H m 0.25
Rovinná harmonická elektromagnetická vlna ---- 1. příklad -------------------------------- 2 GHz prochází prostředím s parametry: r 5, r 1, 0.005 S / m. Amplituda intenzity magnetického pole je H m 0.25
Vysoká škola technická a ekonomická v Českých Budějovicích. Institute of Technology And Business In České Budějovice
 HLUK A VIBRACE Vysoká škola technická a ekonomická v Českých Budějovicích Institute of Technology And Business In České Budějovice Tento učební materiál vznikl v rámci projektu "Integrace a podpora studentů
HLUK A VIBRACE Vysoká škola technická a ekonomická v Českých Budějovicích Institute of Technology And Business In České Budějovice Tento učební materiál vznikl v rámci projektu "Integrace a podpora studentů
Akustická měření - měření rychlosti zvuku
 Akustická měření - měření rychlosti zvuku Úkol : 1. Pomocí přizpůsobené Kundtovy trubice určete platnost vztahu λ = v / f. 2. Určete rychlost zvuku ve vzduchu pomocí Kundtovy a Quinckeho trubice. Pomůcky
Akustická měření - měření rychlosti zvuku Úkol : 1. Pomocí přizpůsobené Kundtovy trubice určete platnost vztahu λ = v / f. 2. Určete rychlost zvuku ve vzduchu pomocí Kundtovy a Quinckeho trubice. Pomůcky
Obsah. Kmitavý pohyb. 2 Kinematika kmitavého pohybu 2. 4 Dynamika kmitavého pohybu 7. 5 Přeměny energie v mechanickém oscilátoru 9
 Obsah 1 Kmitavý pohyb 1 Kinematika kmitavého pohybu 3 Skládání kmitů 6 4 Dynamika kmitavého pohybu 7 5 Přeměny energie v mechanickém oscilátoru 9 6 Nucené kmity. Rezonance 10 1 Kmitavý pohyb Typy pohybů
Obsah 1 Kmitavý pohyb 1 Kinematika kmitavého pohybu 3 Skládání kmitů 6 4 Dynamika kmitavého pohybu 7 5 Přeměny energie v mechanickém oscilátoru 9 6 Nucené kmity. Rezonance 10 1 Kmitavý pohyb Typy pohybů
Hlavní body. Úvod do vlnění. Harmonické vlny. Energie a intenzita vlnění. Popis, periodicita v čase a prostoru Huygensův princip, odraz a lom vlnění
 Vlnění Úvod do vlnění Hlavní bod Harmoniké vln Popis, periodiia v čase a prosoru Hugensův prinip, odraz a lom vlnění Energie a inenzia vlnění Inerferene vln, Dopplerův jev Vln přenos kmiů prosorem Prosředím
Vlnění Úvod do vlnění Hlavní bod Harmoniké vln Popis, periodiia v čase a prosoru Hugensův prinip, odraz a lom vlnění Energie a inenzia vlnění Inerferene vln, Dopplerův jev Vln přenos kmiů prosorem Prosředím
6. Viskoelasticita materiálů
 6. Viskoelasticita materiálů Viskoelasticita materiálů souvisí se schopností materiálů tlumit mechanické vibrace. Uvažujme harmonické dynamické namáhání (tzn. střídavě v tahu a tlaku) materiálu v oblasti
6. Viskoelasticita materiálů Viskoelasticita materiálů souvisí se schopností materiálů tlumit mechanické vibrace. Uvažujme harmonické dynamické namáhání (tzn. střídavě v tahu a tlaku) materiálu v oblasti
3.1. Newtonovy zákony jsou základní zákony klasické (Newtonovy) mechaniky
 3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
VNITŘNÍ ENERGIE, TEPLO A PRÁCE
 VNITŘNÍ ENERGIE, TEPLO A PRÁCE 1. Vnitřní energie (U) Vnitřní energie je energie uložená v těleseh. Je těžké určit absolutní hodnotu. Pro většinu dějů to není nezbytné, protože ji nejsme shopni uvolnit
VNITŘNÍ ENERGIE, TEPLO A PRÁCE 1. Vnitřní energie (U) Vnitřní energie je energie uložená v těleseh. Je těžké určit absolutní hodnotu. Pro většinu dějů to není nezbytné, protože ji nejsme shopni uvolnit
7 Lineární elasticita
 7 Lineární elasticita Elasticita je schopnost materiálu pružně se deformovat. Deformace ideálně elastických látek je okamžitá (časově nezávislá) a dokonale vratná. Působí-li na infinitezimální objemový
7 Lineární elasticita Elasticita je schopnost materiálu pružně se deformovat. Deformace ideálně elastických látek je okamžitá (časově nezávislá) a dokonale vratná. Působí-li na infinitezimální objemový
Digitální učební materiál. III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Příjemce podpory Gymnázium, Jevíčko, A. K.
 Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/34.0802 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/2 Inovace a zkvalitnění výuky prostřednictvím
Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/34.0802 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/2 Inovace a zkvalitnění výuky prostřednictvím
4. V jednom krychlovém metru (1 m 3 ) plynu je 2, molekul. Ve dvou krychlových milimetrech (2 mm 3 ) plynu je molekul
 Fyzika 20 Otázky za 2 body. Celsiova teplota t a termodynamická teplota T spolu souvisejí známým vztahem. Vyberte dvojici, která tento vztah vyjadřuje (zaokrouhleno na celá čísla) a) T = 253 K ; t = 20
Fyzika 20 Otázky za 2 body. Celsiova teplota t a termodynamická teplota T spolu souvisejí známým vztahem. Vyberte dvojici, která tento vztah vyjadřuje (zaokrouhleno na celá čísla) a) T = 253 K ; t = 20
(test version, not revised) 9. prosince 2009
 Mechanické kmitání (test version, not revised) Petr Pošta pposta@karlin.mff.cuni.cz 9. prosince 2009 Obsah Kmitavý pohyb Kinematika kmitavého pohybu Skládání kmitů Dynamika kmitavého pohybu Přeměny energie
Mechanické kmitání (test version, not revised) Petr Pošta pposta@karlin.mff.cuni.cz 9. prosince 2009 Obsah Kmitavý pohyb Kinematika kmitavého pohybu Skládání kmitů Dynamika kmitavého pohybu Přeměny energie
Jaký význam má kritický kmitočet vedení? - nejnižší kmitočet vlny, při kterém se vlna začíná šířit vedením.
 Jaký význam má kritický kmitočet vedení? - nejnižší kmitočet vlny, při kterém se vlna začíná šířit vedením. Na čem závisí účinnost vedení? účinnost vedení závisí na činiteli útlumu β a na činiteli odrazu
Jaký význam má kritický kmitočet vedení? - nejnižší kmitočet vlny, při kterém se vlna začíná šířit vedením. Na čem závisí účinnost vedení? účinnost vedení závisí na činiteli útlumu β a na činiteli odrazu
Fyzika II, FMMI. 1. Elektrostatické pole
 Fyzika II, FMMI 1. Elektrostatické pole 1.1 Jaká je velikost celkového náboje (kladného i záporného), který je obsažen v 5 kg železa? Předpokládejme, že by se tento náboj rovnoměrně rozmístil do dvou malých
Fyzika II, FMMI 1. Elektrostatické pole 1.1 Jaká je velikost celkového náboje (kladného i záporného), který je obsažen v 5 kg železa? Předpokládejme, že by se tento náboj rovnoměrně rozmístil do dvou malých
Charakteristiky optického záření
 Fyzika III - Optika Charakteristiky optického záření / 1 Charakteristiky optického záření 1. Spektrální charakteristika vychází se z rovinné harmonické vlny jako elementu elektromagnetického pole : primární
Fyzika III - Optika Charakteristiky optického záření / 1 Charakteristiky optického záření 1. Spektrální charakteristika vychází se z rovinné harmonické vlny jako elementu elektromagnetického pole : primární
Mechanické kmitání (oscilace)
 Mechanické kmitání (oscilace) pohyb, při kterém se těleso střídavě vychyluje v různých směrech od rovnovážné polohy př. kyvadlo Příklady kmitavých pohybů kyvadlo v pendlovkách struna hudebního nástroje
Mechanické kmitání (oscilace) pohyb, při kterém se těleso střídavě vychyluje v různých směrech od rovnovážné polohy př. kyvadlo Příklady kmitavých pohybů kyvadlo v pendlovkách struna hudebního nástroje
Vlastnosti a zkoušení materiálů. Přednáška č.4 Úvod do pružnosti a pevnosti
 Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Příklady kmitavých pohybů. Mechanické kmitání (oscilace)
 Mechanické kmitání (oscilace) pohyb, při kterém se těleso střídavě vychyluje v různých směrech od rovnovážné polohy př. kyvadlo Příklady kmitavých pohybů kyvadlo v pendlovkách struna hudebního nástroje
Mechanické kmitání (oscilace) pohyb, při kterém se těleso střídavě vychyluje v různých směrech od rovnovážné polohy př. kyvadlo Příklady kmitavých pohybů kyvadlo v pendlovkách struna hudebního nástroje
1. Úvod do pružnosti a pevnosti
 1. Úvod do pružnosti a pevnosti Mechanika je nejstarší vědní obor a její nedílnou součástí je nauka o pružnosti a pevnosti. Pružností nazýváme schopnost pevných těles získat po odstranění vnějších účinků
1. Úvod do pružnosti a pevnosti Mechanika je nejstarší vědní obor a její nedílnou součástí je nauka o pružnosti a pevnosti. Pružností nazýváme schopnost pevných těles získat po odstranění vnějších účinků
Akustika. Rychlost zvukové vlny v v prostředí s hustotou ρ a modulem objemové pružnosti K
 zvuk každé mechanické vlnění v látkovém prostředí, které je schopno vyvolat v lidském uchu sluchový vjem akustika zabývá se fyzikálními ději spojenými se vznikem zvukového vlnění, jeho šířením a vnímáním
zvuk každé mechanické vlnění v látkovém prostředí, které je schopno vyvolat v lidském uchu sluchový vjem akustika zabývá se fyzikálními ději spojenými se vznikem zvukového vlnění, jeho šířením a vnímáním
PŘÍLOHA. Příloha 6. NAŘÍZENÍ V PŘENESENÉ PRAVOMOCI (EU) č. /..,
 EVROPSKÁ KOMISE V Bruselu dne 3.5.2013 C(2013) 2458 final PŘÍLOHA Příloha 6 k NAŘÍZENÍ V PŘENESENÉ PRAVOMOCI (EU) č. /.., kterým se doplňuje směrnie Evropského parlamentu a Rady 2010/30/EU, pokud jde o
EVROPSKÁ KOMISE V Bruselu dne 3.5.2013 C(2013) 2458 final PŘÍLOHA Příloha 6 k NAŘÍZENÍ V PŘENESENÉ PRAVOMOCI (EU) č. /.., kterým se doplňuje směrnie Evropského parlamentu a Rady 2010/30/EU, pokud jde o
UČIVO. Termodynamická teplota. První termodynamický zákon Přenos vnitřní energie
 PŘEDMĚT: FYZIKA ROČNÍK: SEXTA VÝSTUP UČIVO MEZIPŘEDM. VZTAHY, PRŮŘEZOVÁ TÉMATA, PROJEKTY, KURZY POZNÁMKY Zná 3 základní poznatky kinetické teorie látek a vysvětlí jejich praktický význam Vysvětlí pojmy
PŘEDMĚT: FYZIKA ROČNÍK: SEXTA VÝSTUP UČIVO MEZIPŘEDM. VZTAHY, PRŮŘEZOVÁ TÉMATA, PROJEKTY, KURZY POZNÁMKY Zná 3 základní poznatky kinetické teorie látek a vysvětlí jejich praktický význam Vysvětlí pojmy
Výukové texty pro předmět Měřící technika (KKS/MT) na téma Podklady k principu měření akustických projevů (hluk, akustický tlak, šíření v prostředí
 Výukové texty pro předmět Měřící technika (KKS/MT) na téma Podklady k principu měření akustických projevů (hluk, akustický tlak, šíření v prostředí Autor: Doc. Ing. Josef Formánek, Ph.D. Podklady k principu
Výukové texty pro předmět Měřící technika (KKS/MT) na téma Podklady k principu měření akustických projevů (hluk, akustický tlak, šíření v prostředí Autor: Doc. Ing. Josef Formánek, Ph.D. Podklady k principu
SNIŽOVÁNÍ HLUKU A VIBRACÍ
 SNIŽOVÁNÍ HLUKU A VIBRACÍ Doc. Ing. Richard Nový, CSc. a Ing. Miroslav Kučera Praha 009 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti OBSAH 1. Úvod 4 1.1 Hluk jako faktor životního
SNIŽOVÁNÍ HLUKU A VIBRACÍ Doc. Ing. Richard Nový, CSc. a Ing. Miroslav Kučera Praha 009 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti OBSAH 1. Úvod 4 1.1 Hluk jako faktor životního
Skládání různoběžných kmitů. Skládání kolmých kmitů. 1) harmonické kmity stejné frekvence :
 Skládání různoběžných kmitů Uvědomme si principiální bod tohoto problému : na jediný hmotný bod působí dvě nezávislé pružné síl ve dvou různých směrech. Jednotlivé mechanické pohb, které se budou skládat,
Skládání různoběžných kmitů Uvědomme si principiální bod tohoto problému : na jediný hmotný bod působí dvě nezávislé pružné síl ve dvou různých směrech. Jednotlivé mechanické pohb, které se budou skládat,
Elektrický signál - základní elektrické veličiny
 EVROPSKÝ SOCIÁLNÍ FOND Elektrický signál - základní elektrické veličiny PRAHA & EU INVESTUJEME DO VAŠÍ BUDOUCNOSTI Podpora kvality výuky informačních a telekomunikačních technologií ITTEL CZ.2.17/3.1.00/36206
EVROPSKÝ SOCIÁLNÍ FOND Elektrický signál - základní elektrické veličiny PRAHA & EU INVESTUJEME DO VAŠÍ BUDOUCNOSTI Podpora kvality výuky informačních a telekomunikačních technologií ITTEL CZ.2.17/3.1.00/36206
MECHANICKÉ KMITÁNÍ A VLNĚNÍ VLASTNÍ KMITÁNÍ MECHANICKÉHO OSCILÁTORU
 Předmět: Ročník: Vytvořil: Datum: FYZIKA PRVNÍ MGR. JÜTTNEROVÁ 9. 6. 2013 Název zpracovaného celku: MECHANICKÉ KMITÁNÍ A VLNĚNÍ VLASTNÍ KMITÁNÍ MECHANICKÉHO OSCILÁTORU Kmitavý pohyb Je periodický pohyb
Předmět: Ročník: Vytvořil: Datum: FYZIKA PRVNÍ MGR. JÜTTNEROVÁ 9. 6. 2013 Název zpracovaného celku: MECHANICKÉ KMITÁNÍ A VLNĚNÍ VLASTNÍ KMITÁNÍ MECHANICKÉHO OSCILÁTORU Kmitavý pohyb Je periodický pohyb
, p = c + jω nejsou zde uvedeny všechny vlastnosti viz lit.
 Statiké a dynamiké harakteristiky Úvod : Základy Laplaeovy transformae dále LT: viz lit. hlavní užití: - převádí difereniální rovnie na algebraiké (nehomogenní s konstantními koefiienty - usnadňuje řešení
Statiké a dynamiké harakteristiky Úvod : Základy Laplaeovy transformae dále LT: viz lit. hlavní užití: - převádí difereniální rovnie na algebraiké (nehomogenní s konstantními koefiienty - usnadňuje řešení
VLNOVÁ OPTIKA. Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník
 VLNOVÁ OPTIKA Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník Vlnová optika Světlo lze chápat také jako elektromagnetické vlnění. Průkopníkem této teorie byl Christian Huyghens. Některé jevy se dají
VLNOVÁ OPTIKA Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník Vlnová optika Světlo lze chápat také jako elektromagnetické vlnění. Průkopníkem této teorie byl Christian Huyghens. Některé jevy se dají
BIOMECHANIKA KINEMATIKA
 BIOMECHANIKA KINEMATIKA MECHANIKA Mechanika je nejstarším oborem fyziky (z řeckého méchané stroj). Byla původně vědou, která se zabývala konstrukcí strojů a jejich činností. Mechanika studuje zákonitosti
BIOMECHANIKA KINEMATIKA MECHANIKA Mechanika je nejstarším oborem fyziky (z řeckého méchané stroj). Byla původně vědou, která se zabývala konstrukcí strojů a jejich činností. Mechanika studuje zákonitosti
1 Rozdělení mechaniky a její náplň
 1 Rozdělení mechaniky a její náplň Mechanika je nauka o rovnováze a pohybu hmotných útvarů pohybujících se rychlostí podstatně menší, než je rychlost světla (v c). Vlastnosti skutečných hmotných útvarů
1 Rozdělení mechaniky a její náplň Mechanika je nauka o rovnováze a pohybu hmotných útvarů pohybujících se rychlostí podstatně menší, než je rychlost světla (v c). Vlastnosti skutečných hmotných útvarů
Fyzikální vzdělávání. 1. ročník. Učební obor: Kuchař číšník Kadeřník. Implementace ICT do výuky č. CZ.1.07/1.1.02/02.0012 GG OP VK
 Fyzikální vzdělávání 1. ročník Učební obor: Kuchař číšník Kadeřník 1 Vlnění a optika 1. ročník Učební obor: Kuchař číšník Kadeřník 2 mechanické kmitání a vlnění - základní druhy mechanického vlnění a jejich
Fyzikální vzdělávání 1. ročník Učební obor: Kuchař číšník Kadeřník 1 Vlnění a optika 1. ročník Učební obor: Kuchař číšník Kadeřník 2 mechanické kmitání a vlnění - základní druhy mechanického vlnění a jejich
Kapitola 2. o a paprsek sil lze ztotožnit s osou x (obr.2.1). sil a velikost rovnou algebraickému součtu sil podle vztahu R = F i, (2.
 Kapitola 2 Přímková a rovinná soustava sil 2.1 Přímková soustava sil Soustava sil ležící ve společném paprsku se nazývá přímková soustava sil [2]. Působiště všech sil m i lze posunout do společného bodu
Kapitola 2 Přímková a rovinná soustava sil 2.1 Přímková soustava sil Soustava sil ležící ve společném paprsku se nazývá přímková soustava sil [2]. Působiště všech sil m i lze posunout do společného bodu
TZB - VZDUCHOTECHNIKA
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ JIŘÍ HIRŠ, GÜNTER GEBAUER TZB - VZDUCHOTECHNIKA MODUL BT02-11 HLUK A CHVĚNÍ VE VZDUCHOTECHNICE STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ JIŘÍ HIRŠ, GÜNTER GEBAUER TZB - VZDUCHOTECHNIKA MODUL BT02-11 HLUK A CHVĚNÍ VE VZDUCHOTECHNICE STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU
kde a, b jsou konstanty závislé na střední frekvenci (viz tab. 5.1).
 5. Hluková kritéria Při hodnocení účinků hluku na člověka je třeba přihlížet na objektivní fyziologické reakce, produktivitu práce a subjektivní slovní reakce na podněty. Při měření účinků hluku na lidi
5. Hluková kritéria Při hodnocení účinků hluku na člověka je třeba přihlížet na objektivní fyziologické reakce, produktivitu práce a subjektivní slovní reakce na podněty. Při měření účinků hluku na lidi
Zvuk a hluk MGR. ALEŠ PEŘINA, PH. D.
 Zvuk a hluk MGR. ALEŠ PEŘINA, PH. D. Fyziologie slyšení Fyzikální podstata hluku Zvuk mechanické kmitání pružného prostředí Hz (Hertz): počet kmitů za sekundu Frekvenční rozsah slyšení u člověka: 16 Hz
Zvuk a hluk MGR. ALEŠ PEŘINA, PH. D. Fyziologie slyšení Fyzikální podstata hluku Zvuk mechanické kmitání pružného prostředí Hz (Hertz): počet kmitů za sekundu Frekvenční rozsah slyšení u člověka: 16 Hz
Fyzikální učebna vybavená audiovizuální technikou, interaktivní tabule, fyzikální pomůcky
 Předmět: Náplň: Třída: Počet hodin: Pomůcky: Fyzika (FYZ) Molekulová fyzika, termika 2. ročník, sexta 2 hodiny týdně Fyzikální učebna vybavená audiovizuální technikou, interaktivní tabule, fyzikální pomůcky
Předmět: Náplň: Třída: Počet hodin: Pomůcky: Fyzika (FYZ) Molekulová fyzika, termika 2. ročník, sexta 2 hodiny týdně Fyzikální učebna vybavená audiovizuální technikou, interaktivní tabule, fyzikální pomůcky
ÚLOHA 1 Ladi = 100 Hz = 340 m/s Úkoly: lnovou d él é ku k periodu T frekvenci f =? vlnovou délku =?
 ÚLOHA 1 Ladička má rekvenci 100 Hz. Kmitá ve vzduchu, kde je rychlost zvuku přibližně c 340 m/s. Úkoly: a) Jak lze u zvuku charakterizovat vlnovou délku λ? b) Jak lze u zvuku charakterizovat periodu T?
ÚLOHA 1 Ladička má rekvenci 100 Hz. Kmitá ve vzduchu, kde je rychlost zvuku přibližně c 340 m/s. Úkoly: a) Jak lze u zvuku charakterizovat vlnovou délku λ? b) Jak lze u zvuku charakterizovat periodu T?
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6
 OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
Vlnění, optika mechanické kmitání a vlnění zvukové vlnění elmag. vlny, světlo a jeho šíření zrcadla a čočky, oko druhy elmag. záření, rentgenové z.
 Vlnění, optika mechanické kmitání a vlnění zvukové vlnění elmag. vlny, světlo a jeho šíření zrcadla a čočky, oko druhy elmag. záření, rentgenové z. Mechanické vlnění představte si závaží na pružině, které
Vlnění, optika mechanické kmitání a vlnění zvukové vlnění elmag. vlny, světlo a jeho šíření zrcadla a čočky, oko druhy elmag. záření, rentgenové z. Mechanické vlnění představte si závaží na pružině, které
Mgr. Aleš Peřina, Ph. D.
 Mgr. Aleš Peřina, Ph. D. Fyziologie slyšení Fyzikální podstata hluku Zvuk mechanické kmitání pružného prostředí Hz (Hertz): počet kmitů za sekundu Frekvenční rozsah slyšení u člověka: 16 Hz - 16 khz Infrazvuk:
Mgr. Aleš Peřina, Ph. D. Fyziologie slyšení Fyzikální podstata hluku Zvuk mechanické kmitání pružného prostředí Hz (Hertz): počet kmitů za sekundu Frekvenční rozsah slyšení u člověka: 16 Hz - 16 khz Infrazvuk:
Zvukové jevy. Abychom slyšeli jakýkoli zvuk, musí být splněny tři základní podmínky: 1. musí existovat zdroj zvuku
 Zvukové jevy Abychom slyšeli jakýkoli zvuk, musí být splněny tři základní podmínky: 1. musí existovat zdroj zvuku 2. musí existovat látkové prostředí, kterým se zvuk šíří - ve vakuu se zvuk nešíří! 3.
Zvukové jevy Abychom slyšeli jakýkoli zvuk, musí být splněny tři základní podmínky: 1. musí existovat zdroj zvuku 2. musí existovat látkové prostředí, kterým se zvuk šíří - ve vakuu se zvuk nešíří! 3.
Taje lidského sluchu
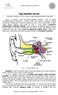 Taje lidského sluchu Markéta Kubánková, ČVUT v Praze, Fakulta biomedicínského inženýrství Sluch je jedním z pěti základních lidských smyslů. Zvuk je signál zprostředkovávající informace o okolním světě,
Taje lidského sluchu Markéta Kubánková, ČVUT v Praze, Fakulta biomedicínského inženýrství Sluch je jedním z pěti základních lidských smyslů. Zvuk je signál zprostředkovávající informace o okolním světě,
Určení počátku šikmého pole řetězovky
 2. Šikmé pole Určení počátku šikmého pole řetězovky d h A ϕ y A y x A x a Obr. 2.1. Souřadnie počátku šikmého pole Jestliže heme určit řetězovku, která je zavěšená v bodeh A a a je daná parametrem, je
2. Šikmé pole Určení počátku šikmého pole řetězovky d h A ϕ y A y x A x a Obr. 2.1. Souřadnie počátku šikmého pole Jestliže heme určit řetězovku, která je zavěšená v bodeh A a a je daná parametrem, je
Jaký obraz vytvoří rovinné zrcadlo? Zdánlivý, vzpřímený, stejně velký. Jaký obraz vytvoří vypuklé zrcadlo? Zdánlivý, vzpřímený, zmenšený
 Jan Olbrecht Jaký obraz vytvoří rovinné zrcadlo? Zdánlivý, vzpřímený, stejně velký Jaký obraz vytvoří vypuklé zrcadlo? Zdánlivý, vzpřímený, zmenšený Jaký typ lomu nastane při průchodu světla z opticky
Jan Olbrecht Jaký obraz vytvoří rovinné zrcadlo? Zdánlivý, vzpřímený, stejně velký Jaký obraz vytvoří vypuklé zrcadlo? Zdánlivý, vzpřímený, zmenšený Jaký typ lomu nastane při průchodu světla z opticky
I. část - úvod. Iva Petríková
 Kmitání mechanických soustav I. část - úvod Iva Petríková Katedra mechaniky, pružnosti a pevnosti Osah Úvod, základní pojmy Počet stupňů volnosti Příklady kmitavého pohyu Periodický pohy Harmonický pohy,
Kmitání mechanických soustav I. část - úvod Iva Petríková Katedra mechaniky, pružnosti a pevnosti Osah Úvod, základní pojmy Počet stupňů volnosti Příklady kmitavého pohyu Periodický pohy Harmonický pohy,
Kmity a mechanické vlnění. neperiodický periodický
 rozdělení časově proměnných pohybů (dějů): Mechanické kmitání neperiodický periodický ne(an)harmonický harmonický vlastní kmity nucené kmity - je pohyb HB (tělesa), při němž HB nepřekročí konečnou vzdálenost
rozdělení časově proměnných pohybů (dějů): Mechanické kmitání neperiodický periodický ne(an)harmonický harmonický vlastní kmity nucené kmity - je pohyb HB (tělesa), při němž HB nepřekročí konečnou vzdálenost
Mechanika kontinua. Mechanika elastických těles Mechanika kapalin
 Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
MĚŘENÍ RYCHLOSTI SVĚTLA
 MĚŘENÍ RYCHLOSTI SVĚTL Měřií potřeby 1) Základní jednotka se zdrojem a detektorem světla 2) Měřií dráha s délkovou stupnií 3) Měřič frekvene (čítač) 4) Dvojité zradlo, dvě spojné čočky 5) Osiloskop, spojovaí
MĚŘENÍ RYCHLOSTI SVĚTL Měřií potřeby 1) Základní jednotka se zdrojem a detektorem světla 2) Měřií dráha s délkovou stupnií 3) Měřič frekvene (čítač) 4) Dvojité zradlo, dvě spojné čočky 5) Osiloskop, spojovaí
ELEKTROMAGNETICKÉ KMITÁNÍ A VLNĚNÍ POJMY K ZOPAKOVÁNÍ. Testové úlohy varianta A
 Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Jitka Novosadová MGV_F_SS_3S3_D18_Z_OPAK_E_Elektromagneticke_kmitani_a_ vlneni_t Člověk a příroda Fyzika Elektromagnetické
Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Jitka Novosadová MGV_F_SS_3S3_D18_Z_OPAK_E_Elektromagneticke_kmitani_a_ vlneni_t Člověk a příroda Fyzika Elektromagnetické
Optika pro mikroskopii materiálů I
 Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
( ) Úloha č. 9. Měření rychlosti zvuku a Poissonovy konstanty
 Fyzikální praktikum IV. Měření ryhlosti zvuku a Poissonovy konstanty - verze Úloha č. 9 Měření ryhlosti zvuku a Poissonovy konstanty 1) Pomůky: Kundtova trubie, mikrofon se sondou, milivoltmetr, měřítko,
Fyzikální praktikum IV. Měření ryhlosti zvuku a Poissonovy konstanty - verze Úloha č. 9 Měření ryhlosti zvuku a Poissonovy konstanty 1) Pomůky: Kundtova trubie, mikrofon se sondou, milivoltmetr, měřítko,
Nauka o materiálu. Přednáška č.4 Úvod do pružnosti a pevnosti
 Nauka o materiálu Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze kluzu R e, odpovídající
Nauka o materiálu Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze kluzu R e, odpovídající
PRŮŘEZOVÉ CHARAKTERISTIKY
 . cvičení PRŮŘEZOVÉ CHRKTERISTIKY Poznámka Pojem průřezu zavádíme u prutových konstrukčních prvků. Průřez je rovinný obrazec, který vznikne myšleným řezem vedeným kolmo k podélné ose nedeformovaného prutu,
. cvičení PRŮŘEZOVÉ CHRKTERISTIKY Poznámka Pojem průřezu zavádíme u prutových konstrukčních prvků. Průřez je rovinný obrazec, který vznikne myšleným řezem vedeným kolmo k podélné ose nedeformovaného prutu,
Testovací příklady MEC2
 Testovací příklady MEC2 1. Určete, jak velká práce se vykoná při stlačení pružiny nárazníku železničního vagónu o w = 5 mm, když na její stlačení o w =15 mm 1 je zapotřebí síla F = 3 kn. 2. Jaké musí být
Testovací příklady MEC2 1. Určete, jak velká práce se vykoná při stlačení pružiny nárazníku železničního vagónu o w = 5 mm, když na její stlačení o w =15 mm 1 je zapotřebí síla F = 3 kn. 2. Jaké musí být
MĚŘENÍ RYCHLOSTI ŠÍŘENÍ ZVUKU V PLYNECH
 Úloha č. 6 MĚŘENÍ RYCHLOSTI ŠÍŘENÍ ZVUKU V PLYNECH ÚKOL MĚŘENÍ: 1. V zapojení dvou RC generátorů nalezněte na obrazovce osciloskopu Lissajousovy obrazce pro frekvence 1:1, 2:1, 3:1, 2:3 a 1:4 a zakreslete
Úloha č. 6 MĚŘENÍ RYCHLOSTI ŠÍŘENÍ ZVUKU V PLYNECH ÚKOL MĚŘENÍ: 1. V zapojení dvou RC generátorů nalezněte na obrazovce osciloskopu Lissajousovy obrazce pro frekvence 1:1, 2:1, 3:1, 2:3 a 1:4 a zakreslete
Jan Kaňka
 Jan Kaňka 21. 3. 2017 CO NÁS ČEKÁ Představení společnosti Akustika v interiérech Šíření zvuku Prostorová akustika Stavební akustika Psychoakustika Projekty v praxi Akustická řešení kancelářských prostor
Jan Kaňka 21. 3. 2017 CO NÁS ČEKÁ Představení společnosti Akustika v interiérech Šíření zvuku Prostorová akustika Stavební akustika Psychoakustika Projekty v praxi Akustická řešení kancelářských prostor
DUM označení: VY_32_INOVACE_... Jméno autora výukového materiálu: Ing. Jitka Machková Škola: Základní škola a mateřská škola Josefa Kubálka Všenory
 DUM označení: VY_32_INOVACE_... Jméno autora výukového materiálu: Ing. Jitka Machková Škola: Základní škola a mateřská škola Josefa Kubálka Všenory Karla Majera 370, 252 31 Všenory. Datum (období) vytvoření:
DUM označení: VY_32_INOVACE_... Jméno autora výukového materiálu: Ing. Jitka Machková Škola: Základní škola a mateřská škola Josefa Kubálka Všenory Karla Majera 370, 252 31 Všenory. Datum (období) vytvoření:
Světlo je elektromagnetické vlnění, které má ve vakuu vlnové délky od 390 nm do 770 nm.
 1. Podstata světla Světlo je elektromagnetické vlnění, které má ve vakuu vlnové délky od 390 nm do 770 nm. Vznik elektromagnetických vln (záření): 1. při pohybu elektricky nabitých částic s nenulovým zrychlením
1. Podstata světla Světlo je elektromagnetické vlnění, které má ve vakuu vlnové délky od 390 nm do 770 nm. Vznik elektromagnetických vln (záření): 1. při pohybu elektricky nabitých částic s nenulovým zrychlením
Měření a analýza mechanických vlastností materiálů a konstrukcí. 1. Určete moduly pružnosti E z ohybu tyče pro 4 různé materiály
 FP 1 Měření a analýza mechanických vlastností materiálů a konstrukcí Úkoly : 1. Určete moduly pružnosti E z ohybu tyče pro 4 různé materiály 2. Určete moduly pružnosti vzorků nepřímo pomocí měření rychlosti
FP 1 Měření a analýza mechanických vlastností materiálů a konstrukcí Úkoly : 1. Určete moduly pružnosti E z ohybu tyče pro 4 různé materiály 2. Určete moduly pružnosti vzorků nepřímo pomocí měření rychlosti
mechanická práce W Studentovo minimum GNB Mechanická práce a energie skalární veličina a) síla rovnoběžná s vektorem posunutí F s
 1 Mechanická práce mechanická práce W jednotka: [W] = J (joule) skalární veličina a) síla rovnoběžná s vektorem posunutí F s s dráha, kterou těleso urazilo 1 J = N m = kg m s -2 m = kg m 2 s -2 vyjádření
1 Mechanická práce mechanická práce W jednotka: [W] = J (joule) skalární veličina a) síla rovnoběžná s vektorem posunutí F s s dráha, kterou těleso urazilo 1 J = N m = kg m s -2 m = kg m 2 s -2 vyjádření
Skalární a vektorový popis silového pole
 Skalární a vektorový popis silového pole Elektrické pole Elektrický náboj Q [Q] = C Vlastnost materiálových objektů Interakce (vzájemné silové působení) Interakci (vzájemné silové působení) mezi dvěma
Skalární a vektorový popis silového pole Elektrické pole Elektrický náboj Q [Q] = C Vlastnost materiálových objektů Interakce (vzájemné silové působení) Interakci (vzájemné silové působení) mezi dvěma
, kde J [mol.m -2.s -1 ] je difuzní tok, D [m 2.s -1 ] je celkový
![, kde J [mol.m -2.s -1 ] je difuzní tok, D [m 2.s -1 ] je celkový , kde J [mol.m -2.s -1 ] je difuzní tok, D [m 2.s -1 ] je celkový](/thumbs/62/46575607.jpg) FM / DIFUZE I. I. a II. FICKŮV ZÁKON Jméno: St. sk.: Datum: Autor vičení: Ing. Eva Novotná, Ph.D., 4enov@seznam.z Potřebné moudro : Cílem vičení je vytvořit reálný pohled na důležitost, mnohotvárnost a
FM / DIFUZE I. I. a II. FICKŮV ZÁKON Jméno: St. sk.: Datum: Autor vičení: Ing. Eva Novotná, Ph.D., 4enov@seznam.z Potřebné moudro : Cílem vičení je vytvořit reálný pohled na důležitost, mnohotvárnost a
Ing. Jan Mareš, G r e i f a k u s t i k a s.r.o. Měření hluku tepelných čerpadel vzduch - voda
 Ing. Jan Mareš, G r e i f a k u s t i k a s.r.o. Měření hluku tepelných čerpadel vzduch - voda 1. Legislativa 2. Co je hladina akustického tlaku a výkonu 3. Hodnoty uváděné výrobci a jak s nimi pracovat
Ing. Jan Mareš, G r e i f a k u s t i k a s.r.o. Měření hluku tepelných čerpadel vzduch - voda 1. Legislativa 2. Co je hladina akustického tlaku a výkonu 3. Hodnoty uváděné výrobci a jak s nimi pracovat
Úvod Vibrace Hluk Zvuk
 Úvod Vibrace a hluk jsou součástí životního a pracovního prostředí všech živých organismů. Z tohoto důvodu je nutné se systematicky a cílevědomě starat o ochranu a tvorbu životního prostředí. Vibrace Vibrací
Úvod Vibrace a hluk jsou součástí životního a pracovního prostředí všech živých organismů. Z tohoto důvodu je nutné se systematicky a cílevědomě starat o ochranu a tvorbu životního prostředí. Vibrace Vibrací
3.2 Rovnice postupné vlny v bodové řadě a v prostoru
 3 Vlny 3.1 Úvod Vlnění můžeme pozorovat například na vodní hladině, hodíme-li do vody kámen. Mechanické vlnění je děj, při kterém se kmitání šíří látkovým prostředím. To znamená, že například zvuk, který
3 Vlny 3.1 Úvod Vlnění můžeme pozorovat například na vodní hladině, hodíme-li do vody kámen. Mechanické vlnění je děj, při kterém se kmitání šíří látkovým prostředím. To znamená, že například zvuk, který
Obsah. 1 Vznik a druhy vlnění. 2 Interference 3. 5 Akustika 9. 6 Dopplerův jev 12. přenosu energie
 Obsah 1 Vznik a druhy vlnění 1 2 Interference 3 3 Odraz vlnění. Stojaté vlnění 5 4 Vlnění v izotropním prostředí 7 5 Akustika 9 6 Dopplerův jev 12 1 Vznik a druhy vlnění Mechanické vlnění vzniká v látkách
Obsah 1 Vznik a druhy vlnění 1 2 Interference 3 3 Odraz vlnění. Stojaté vlnění 5 4 Vlnění v izotropním prostředí 7 5 Akustika 9 6 Dopplerův jev 12 1 Vznik a druhy vlnění Mechanické vlnění vzniká v látkách
Fyzikální vzdělávání. 1. ročník. Učební obor: Kuchař číšník Kadeřník. Implementace ICT do výuky č. CZ.1.07/1.1.02/ GG OP VK
 Fyzikální vzdělávání 1. ročník Učební obor: Kuchař číšník Kadeřník 1 1 Mechanika 1.1 Pohyby přímočaré, pohyb rovnoměrný po kružnici 1.2 Newtonovy pohybové zákony, síly v přírodě, gravitace 1.3 Mechanická
Fyzikální vzdělávání 1. ročník Učební obor: Kuchař číšník Kadeřník 1 1 Mechanika 1.1 Pohyby přímočaré, pohyb rovnoměrný po kružnici 1.2 Newtonovy pohybové zákony, síly v přírodě, gravitace 1.3 Mechanická
Základní úlohy a zkušební otázky předmětu Akustika oboru Aplikovaná fyzika
 Základní úlohy a zkušební otázky předmětu Akustika oboru Aplikovaná fyzika Úlohy pro 1. zápočtovou práci 1. Nakreslete časové rozvinutí elongace, rychlosti a zrychlení harmonického kmitavého pohybu během
Základní úlohy a zkušební otázky předmětu Akustika oboru Aplikovaná fyzika Úlohy pro 1. zápočtovou práci 1. Nakreslete časové rozvinutí elongace, rychlosti a zrychlení harmonického kmitavého pohybu během
Signál v čase a jeho spektrum
 Signál v čase a jeho spektrum Signály v časovém průběhu (tak jak je vidíme na osciloskopu) můžeme dělit na periodické a neperiodické. V obou případech je lze popsat spektrálně určit jaké kmitočty v sobě
Signál v čase a jeho spektrum Signály v časovém průběhu (tak jak je vidíme na osciloskopu) můžeme dělit na periodické a neperiodické. V obou případech je lze popsat spektrálně určit jaké kmitočty v sobě
Výukové texty. pro předmět. Měřící technika (KKS/MT) na téma
 Výukové texty pro předmět Měřící technika (KKS/MT) na téma Tvorba grafické vizualizace principu měření akustických projevů (hluk, akustický tlak, šíření v prostředí Autor: Doc. Ing. Josef Formánek, Ph.D.
Výukové texty pro předmět Měřící technika (KKS/MT) na téma Tvorba grafické vizualizace principu měření akustických projevů (hluk, akustický tlak, šíření v prostředí Autor: Doc. Ing. Josef Formánek, Ph.D.
Měření hlasitosti zvuku. Tematický celek: Zvuk. Úkol:
 Název: Měření hlasitosti zvuku. Tematický celek: Zvuk. Úkol: 1. Zopakuj si, co je to zvuk a ultrazvuk, jaké jsou jednotky hlasitosti zvuku. 2. Jak funguje zvukový senzor. 3. Navrhni robota pro měření hlasitosti
Název: Měření hlasitosti zvuku. Tematický celek: Zvuk. Úkol: 1. Zopakuj si, co je to zvuk a ultrazvuk, jaké jsou jednotky hlasitosti zvuku. 2. Jak funguje zvukový senzor. 3. Navrhni robota pro měření hlasitosti
5.6. Člověk a jeho svět
 5.6. Člověk a jeho svět 5.6.1. Fyzika ŠVP ZŠ Luštěnice, okres Mladá Boleslav verze 2012/2013 Charakteristika vyučujícího předmětu FYZIKA I. Obsahové vymezení Vyučovací předmět Fyzika vychází z obsahu vzdělávacího
5.6. Člověk a jeho svět 5.6.1. Fyzika ŠVP ZŠ Luštěnice, okres Mladá Boleslav verze 2012/2013 Charakteristika vyučujícího předmětu FYZIKA I. Obsahové vymezení Vyučovací předmět Fyzika vychází z obsahu vzdělávacího
