Úloha č. 9: Nelineární jevy v ultrarychlé optice
|
|
|
- Bohumír Prokop
- před 6 lety
- Počet zobrazení:
Transkript
1 Úloha č. 9: Nelineární jevy v ultrarychlé optice Pokročilé praktikum z optiky 1. října Úvod Ultrarychlá optika pracuje s optickými pulsy délky řádově jednotky až stovky femtosekund; díky tomu lze i s malými energiemi v optickém pulsu (typicky např. µj) dosáhnout velmi vysokých špičkových intenzit a pozorovat řadu nelineárních jevů, které jsou indukovány elektrickým polem záření. Brzy poté, co byly vyvinuty laserové zdroje s dostatečně krátkými impulsy, našly nelineární jevy v ultrarychlé optice četné uplatnění, např: při generaci vyšších harmonických, v diagnostice délky impulsu, generaci tzv. bílého kontinua, nebo při zesilování širokospektrálních optických pulsů. Právě těmito aplikacemi se budeme zabývat v této úloze. 1.1 Původ nelineárních jevů Uvažujme záření procházející bezeztrátovým dielektrikem. Dopadající elektromagnetické pole rozkmitává nabité částice a kmitající náboj vytváří nové elektromagnetické pole. Tento efekt je kvantitativně popsán pomocí vektorového pole polarizace P. Závislost polarizace na vnějším elektrickém poli je možno (za předpokladu hladkosti funkcí) rozvinout do Taylorova polynomu P = ε 0 ( χ (1) E + χ (2) EE + χ (3) EEE +... ), (1) kde χ (j) je susceptibilita j-tého řádu a z matematického hlediska se jedná o tenzor (j + 1)-tého řádu. Takto rozepsaná polarizace se projeví ve vlnové rovnici (2) na pravé straně; což má naznačit, že polarizace hraje v této rovnici roli budícího členu. Jedná se o vektorovou rovnici, kterou lze zjednodušit na skalární za předpokladu že dopadající (případně generované) vlny mají nějakou pevně danou polarizaci, která je vlastní polarizací daného materiálu (obvykle se jedná o lineární polarizaci). 2 E ε 0 µ 0 2 t 2 E = µ 0P, (2) V následujících odstavcích analyzujeme základní efekty spojené s nelinearitou druhého a třetího řádu. Obrázek 1: Ilustrace generace druhé harmonické. 1.2 Generace druhé harmonické Generace druhé harmonické je konverze čerpacího záření na záření s poloviční vlnovou délkou a dvojnásobnou frekvencí; jde o jeden z nejjednodušších a nejčastěji využívaných nelineárních procesů, který souvisí se susceptibilitou druhého řádu χ (2). Nejobvyklejší kolineární uspořádání zpravidla odpovídá obrázku 3. Pro optický puls s obdélníkovým profilem v prostoru i v čase lze dosáhnout účinnosti přes 90%, pro gaussovský svazek je však obvyklejší účinnost okolo 50 %. 1
2 Vysvětleme nyní princip vzniku druhé harmonické. Nechť lineárně polarizované harmonické záření popsané (pro jednoduchost skalární) hodnotou elektrického pole dopadá na materiál vykazující nelinearitu druhého řádu χ (2) (pro jednoduchost uvažujeme prostorovou souřadnici rovnou nule). Potom E = 1 2 ( E0 e iωt + E 0 e iωt) (3) Toto pole vybudí skrze susceptibilitu druhého řádu nové optické vlny polarizaci popsanou rovnicí (4), která obsahuje dvě nové frekvence: P = ε 0 χ (2) E 2 = ε 0 χ (2) 1 E 0 2 e i2ωt + E0 2 e i2ωt + 2E 2 0 (4) 4 }{{}}{{} SHG OR 1. Druhá harmonická zkráceně SHG (z anglického second harmonic generation), je vlna s dvojnásobnou frekvencí oproti dopadající vlně 2. Optická rektifikace zkráceně OR, je stejnosměrné napětí (vlna s nulovou frekvencí) generované jako konstantní dipólový moment v materiálu. Tento jev lze využít pro generaci tera-hertzového záření; v této úloze jej však nebudeme uvažovat. a Materiál s normální disperzí A B b A Fázově přizpůsobeno B n blue > n red V protifázi n blue = n red Ve fázi Obrázek 2: Vliv disperze na splnění podmínky fázového synchronizmu. Vlevo není kvůli disperzi podmínka synchronizmu splněna, druhá harmonická generovaná v různých místech materiálu se navzájem vyruší. Vpravo je podmínka synchronismu splněna a tak druhá harmonická v celém objemu konstruktivně nasčítá. Výše uvedené úvahy popsané rovnicí (4) platí pouze lokálně, v každém bodě dielektrika zvlášť. Celková účinnost konverze do druhé harmonické závisí na soufázovosti dílčích příspěvků druhé harmonické v celém objemu materiálu. Na obrázku 2 je naznačeno, jak tatáž dopadající vlna (říkejme jí základní harmonická) generuje druhou harmonickou ve dvou různých místech A a B. Přitom se může stát (viz 2a), že vlivem disperze v materiálu je fáze druhé harmonické, vygenerované v bodě A odlišná od fáze druhé harmonické vygenerované v bodě B. Za toto fázové rozladění je zodpovědný rozdílný index lomu základní a druhé harmonické, tj. disperze materiálu. Pokud by existoval materiál, který má stejný index lomu pro základní i druhou harmonickou, všechny dílčí příspěvky druhé harmonické z celého objemu materiálu by se konstruktivně sečetly. Tato podmínka pro účinnou generaci SHG je velmi důležitá a proto má vlastní název - podmínka fázového synchronismu; lze ji zapsat jako n ω = n 2ω, nebo ještě obecněji pomocí vlnových vektorů (rovnice (5)). Spolu se zákonem zachování energie (6) tvoří vektorová rovnice (5) čtyři základní podmínky pro generaci druhé harmonické. 2 k 1 = k 2 (5) 2ω 1 = ω 2, (6) n (ω ) e 2 y k pm θ n o (ω 2 ) pm x n (ω ) o 1 Obrázek 3: Diagram závislosti indexu lomu v závislosti na úhlu vlnového vektoru záření (v polárních souřadnicích. Diagram odpovídá tzv. negativnímu dvojlomnému prostředí, kdy při dané vlnové délce je n 0 n e. Úhel θ pm, při kterém platí n o (ω 1 ) = n e (ω 2 ) je hledaný úhel splňující podmínku fázového synchronismu. 2
3 kde ω 1 a k 1 je frekvence a vlnový vektor příslušející základní harmonické, ω 2 a k 2 přísluší druhé harmonické. Podmínky synchronismu je možné splnit ve vhodně orientovaném dvojlomném materiálu, pokud se podaří chromatická disperze vykompenzovat právě rozdílným indexem lomu extra-ordinární vlny. V této úloze budeme využívat krystalu BBO (β-barium borát), jsou indexy lomu uvedeny v následující tabulce: 800 nm 400 nm n o n e n o n e Průběh extra-ordinárního indexu lomu pro záření šířící se pod úhlem θ vůči optické ose v jednoosém krystalu je dán implicitně vztahem (7) 1 n e (θ) 2 = cos2 θ n 2 + sin2 θ o n 2 e (7) Odtud lze také vypočítat optimální orientaci krystalu vůči dopadajícímu záření tak, aby docházelo k účinné konverzi do druhé harmonické. 1.3 Parametrické zesílení Stejně, jako generace druhé harmonické, je parametrické zesílení nelineární jev druhého řádu, spojený se susceptibilitou χ (2). Při tomto procesu však vzájemně interagují tři různé vlnové délky. Během procesu předává intenzivní čerpací vlna s vyšší frekvencí ω 3 energii signálové vlně s nižší frekvencí ω 1 ; rozdílová energie je transformována do třetí vlny s rozdílovou frekvencí ω 2 = ω 3 ω 1. Parametrické zesilovače hrají významnou roli v laserové technice při generaci velmi intenzivních femtosekundových pulsů; parametrické generátory a zesilovače jsou rovněž žádané zdroje záření s přeladitelnou vlnovou délkou. A který člen nelineární polarizace je zodpovědný za parametrické zesílení? Odpověď na tuto otázku necháme studentům na rozmyšlenou; napovíme, že postup je velmi podobný jako ve vztazích (3) a (4), avšak jako vstupní pole bereme superpozici tří harmonických vln s frekvencemi splňující ω 3 = ω 1 + ω 2. Podobně, jako při generaci druhé harmonické, účinné parametrické zesílení je podmíněno splněním podmínek zákona zachování energie a fázového synchronismu. Pro třívlnové směšování mají tyto podmínky tvar k 3 = k 1 + k 2 (8) ω 3 = ω 1 + ω 2 (9) Jednotlivé interagující vlny 1-3 se nazývají po řadě signální, jalová a čerpací. Není přitom nezbytně nutné, aby se všechny tři interagující vlny šířily stejným směrem; podmínky fázového synchronismu lze dobře splnit i pro nekolineární uspořádání, přičemž rovnice (8) musí být splněna vektorově, jak je vidět na diagramu 4a. Tuto podmínku je možné splnit opět s využitím vhodně orientovaného dvojlomného krystalu. V této úloze použijeme krystal BBO v konfiguraci o + o e, což je zkrácený zápis faktu, že součet frekvencí ordinárně polarizovaného signálu a ordinárního jalového svazku dá frekvenci extraordinárně polarizovaného čerpání. Míra potřebného pootočení krystalu θ závisí na vlnové délce signálu a na úhlu α mezi čerpáním a signálem. Tato závislost (kterou lze získat vyřešením rovnic fázového synchronismu (8)) je na obrázku 4b, kde je vidět, že nekolineární uspořádání s úhlem α = 3.6 podporuje zesílení ve velmi široké spektrální oblasti. 1.4 Generace superkontinua Generace superkontinua je silně nelineární jev, při kterém dochází ke spojitému rozšíření spektrální čáry záření na kontinuum s šířkou pásma až několik stovek nanometrů; je možné jej komprimovataž na jednotky femtosekund a je často používaný jako sondovací (probe) svazek v pump-probe spektroskopii. Vygenerovat jej je možné zafokusováním femtosekundového svazku do téměř libovolného balkového dielektrika, či do fotonických/vlnovodných struktur. 3
4 a) b) krystalografická osa θ α k 2 k 1 k 3 θ deg α=7 α=5 α=3.6 α=2 α= λ, nm Obrázek 4: a) Grafické znázornění splnění podmínek fázového synchronismu pomocí dvojlomného krystalu natočeného pod úhlem θ. b) Řešení podmínek fázového synchronismu parametrického zesílení v krystalu BBO v závislosti na vlnové délce signálu a nekolineárním úhlu α. Pro α = 3, 6 je optimální úhel θ téměř konstantní v oblasti 500 až 700 nm. V této konfiguraci lze dosáhnout zesílení v široké spektrální oblasti. Z hlediska nelineární optiky je tento jev postaven především na nelinearitě třetího řádu (spojené se susceptibilitou χ (3) ), avšak mohou se projevovat i další efekty. Nelineární ( polarizace spojená se susceptibilitou třetího řádu má v případě jedné dopadající vlny (E = 1 2 E0 e iωt + E 0 e iωt) ) tvar (10). P = ε 0 χ (2) E 3 = ε 0 χ (2) 1 E0 3 e i3ωt + E0 3 e i3ωt + 3 E 0 2 ( E 0 e +iωt + E 0 e iωt) (10) 8 }{{}}{{} THG Kerrův jev Výsledkem interakce jsou dva nové jevy: 1. Generace třetí harmonické, jejíž účinnost je podmíněna splněním podmínky fázové synchronizace. Tento jev však v nehraje nyní klíčovou roli, nebudeme se jím dále proto zabývat. 2. Kerrův jev Jde o generaci stejné vlnové délky, jako budící vlna. Tento příspěvek má podobný tvar jako lineární polarizace (P Lin = ε 0 χ (1) E). Projeví se tedy jako nelineární změna indexu lomu materiálu, která je přímo úměrná E 2, tj. intenzitě. Ponechme na rozmyšlenou jednoduchou otázku, jak je to se splněním podmínky fázového synchronismu tohoto jevu? Kerrův jev přispívá k rozšíření spektra pulsu více způsoby; graficky jsou znázorněny na obrázku 5: 1. Autofokusace je důsledkem prostorového rozložení elektrického pole v gaussovském svazku. Uprostřed svazku je vyšší intenzita díky χ (3) nelinearitě i vyšší index lomu. To má za následek vznik gradientní čočky, která je nelineárně indukovaná samotným svazkem, čímž dochází k autofokusaci svazku. Nárůst intenzity na ose svazku dále zesiluje nelineární jevy, včetně samotné autofokusace, což může vést až ke kolapsu profilu svazku do velmi malé plochy a k poškození materiálu. Proti autofokusaci působí difrakce a nedestruktivní ionizace, která při velkých intenzitách přispívá ke snížení indexu lomu na ose svazku. Pokud nastane rovnováha mezi autofokusací na jedné straně a difrakcí a ionizací na straně druhé, může dojít k samovedení, kdy se puls šíří materiálem s velmi malým příčným průměrem na vzdálenost několik mm (viz obrázek 5a). 2. Automodulace fáze je důsledkem časově proměnné amplitudy elektrického pole v ultrakrátkém pulsu. Proces je znázorněn na obrázku 5b; nejintenzivnější část pulsu vidí vyšší index lomu než oblasti s nízkou intenzitou, dochází tedy k fázovému zpoždění optických vln ze středu pulsu směrem zadnímu kraji, čímž dojde k rozšíření spektra. 3. Self-steepening úzce souvisí z automodulací fáze; spolu se změnou fázové rychlosti totiž dochází i ke změně grupové rychlosti intenzivní části pulsu. To má za následek deformaci obálky impulsu pík pulsu se zpozdí a výrazně vzroste sklon sestupné hrany. V praxi to znamená, že se poruší symetrie v rozšiřování spektra preferovány jsou kratší vlnové délky. 4
5 a) Autofokusace a samovedení b) Původní puls Vliv automodulace fáze Vliv selfsteepeningu Pulsy letí tam Obrázek 5: a) Autofokusace umožňuje samovedení svazku v úzkém filamentu a zvýšení vlivu nelinearit b) Rozšíření spektra vlivem automodulace fáze a narušení symetrie kvůli self-steepeningu. Tmavší barva reprezentuje oblast s vyšším indexem lomu. 2 Experimentální uspořádání Zdrojem záření pro tuto úlohu je výkonný femtosekundový laserový systém Pulsar, jehož obvyklé výstupní parametry jsou shrnuty v tabulce 1. Energie v pulsu 5.5 mj Délka pulsu 55 fs Střední vln. délka 805 nm Šířka spektra 40 nm Opakovací frekvence 10 Hz Průměr svazku 8 mm Tabulka 1: Tabulka parametrů femtosekundového Ti:safírového systému. Popíšeme nyní samotný experiment, jehož schéma je uvedeno na obrázku 6. Pomocí klínu je malá část energie poslána skrz irisovou aperturu a čočku do krystalu safíru, kde je vygenerováno superkontinuum; následnou čočkou je pak divergentní široko-spektrální svazek zkolimován a nasměrován do krystalu BBO opa, kde je parametricky zesílen. Zbývající, energetičtější část pulsu projde skrze teleskop se zvětšením 1/2 (svazek se tedy zmenší) a je nasměrován do krystalu BBO shg, kde se část pulsu konvertuje do druhé harmonické (400 nm). Zatímco zbylá část energie pulsu na základní harmonické je oddělena pomocí dichroického zrcadla, druhá harmonická je nasměrována na druhý krystal BBO opa, kde slouží jako čerpání pro parametrické zesílení. 4 mj, 10 Hz, 55 fs, 800 nm Iris Klín L300 L-150 HR 800 nm L50 Safír 3 mm M 0.4 mj 400 nm SHG BBO, 2 mm Čerpání L40 Dichroické zrcadlo OPA BBO, 2 mm Signál Zpožďovací linka Obrázek 6: Schéma experimentu Celý systém má poměrně velké množství stupňů volnosti. Uvedeme výčet prvků, které lze během 5
6 experimentu nastavovat. Apertura za děličem svazku reguluje intenzitu záření při generaci superkontinua (jednak velikostí svazku a jednak difrakčně) Pozice safíru na ose z ovlivňuje stabilitu generovaného superkontinua. Pootočení safíru okolo osy z krystalický safír je dvojlomný; je třeba jej nastavit tak, aby nedocházelo k depolarizaci. Poloha čočky f=40 mm kolimující superkontinuum. Nastavíme tak, aby superkontinuum bylo mírně konvergentní. Zpoždění slouží k přesnému nastavení délek obou ramen. Orientace BBO shg určuje účinnost generace druhé harmonické (splnění fázového synchronismu). Nekolineární úhel α mezi čerpáním a signálem určuje maximální šířku pásma, ve které lze zesilovat. Optimum je pro α = 3, 6 uvnitř krystalu. Teleskop v čerpacím svazku na ten se raději nesahá, je to nebezpečné. Pootočení krystalu BBO opa okolo svislé osy zajišťuje splnění podmínek synchronismu OPA. Otočení krystalu BBO opa o 180 okolo horizontální osy změna z walk-off kompenzujícího uspořádání do walk-off nekompenzujícího a naopak. Ovlivňuje účinnost OPA a mění podmínku synchronismu pro parazitní jevy (SHG jalového svazku a signálu). 3 Zadání úlohy Před zahájením práce v laboratoři je třeba se seznámit s bezpečnostními pokyny: Laserový systém, se kterým budete pracovat, je systémem IV třídy. Při práci je povinnost studenta nosit ochranné brýle. Přitom je třeba mít na paměti, že rozsah vlnových délek, se kterými budete pracovat, pokrývá spojitě téměř celý rozsah viditelného spektra; dokonalé brýle pro tento experiment tedy neexistují. Proto je třeba dbát zvýšené opatrnosti i při práci s brýlemi. 3.1 Naladění systému 1. Naveďte svazek ze systému Pulsar do experimentální sestavy. Polarizace lineární, vertikální. 2. Vygenerujte jednovláknové superkontinuum; jeho depolarizaci potlačte vhodnou orientací safíru. 3. Vygenerujte čerpací svazek na druhé harmonické Ti:safíru. 4. Překryjte čerpací a signálový svazek v krystalu BBO opa 5. Optimalizujte všechny potřebné parametry pro účinné parametrické zesílení při jednom průchodu krystalem BBO opa v co nejširší šířce pásma. 3.2 Pozorování parametrického zesílení 1. Změřte energie vstupu, druhé harmonické, superkontinua a zesíleného signálu. 2. Změřte úhly α a θ. 3. Změřte spektrum superkontinua a zesíleného signálu. 4. Pozorujte parametrickou superfluorescenci. Jak se mění při otáčení krystalu v obou směrech? Jak se mění v přítomnosti/nepřítomnosti seedu? 5. Pokuste se prokázat přítomnost jalového svazku. Jaký je rozsah vlnových délek a úhel šíření idleru? 6
7 3.3 Časová charakteristika ultrakrátkých pulsů, měření disperze vyšších řádů 1. Změřte sérii spekter zesíleného signálu posouvaje postupně zpoždění mikrometrickým šroubem. Alespoň 10 spekter. 2. Vložte do svazku superkontinua tlustý optický materiál a opakujte měření z předchozího bodu. 3. Na základě naměřených dat z předchozích dvou bodů co nejpřesněji určete délku pulsu superkontinua pro oba dva případy. 4. Z naměřených dat vypočítejte disperzi prvního až třetího řádu (GD, GDD a TOD) superkontinua před a po průchodu tlustým materiálem. 5. Experimentálně získané disperzní charakteristiky materiálu porovnejte s teoretickou předpovědí disperze (ze znalosti Sellmeierových rovnic). 7
1 Zadání. 2 Úvod. Název a číslo úlohy 9 - Nelineární jevy v ultrarychlé optice. Měření provedli Jan Fait, Marek Vlk Vypracoval
 Název a číslo úlohy 9 - Nelineární jevy v ultrarychlé optice Datum měření 30.11.2015 Měření provedli Jan Fait, Marek Vlk Vypracoval Marek Vlk Datum 19.12.2015 Hodnocení 1 Zadání 1. Naladění systému; Naved
Název a číslo úlohy 9 - Nelineární jevy v ultrarychlé optice Datum měření 30.11.2015 Měření provedli Jan Fait, Marek Vlk Vypracoval Marek Vlk Datum 19.12.2015 Hodnocení 1 Zadání 1. Naladění systému; Naved
= , = (1) (2)
 Název a číslo úlohy Nelineární jevy v ultrarychlé optice úloha č. 9 Datum měření 30. 11. 2015 Měření provedli Jan Fait, Marek Vlk Vypracoval Jan Fait Datum 4. 12. 2015 Hodnocení Během úlohy jsme se seznámili
Název a číslo úlohy Nelineární jevy v ultrarychlé optice úloha č. 9 Datum měření 30. 11. 2015 Měření provedli Jan Fait, Marek Vlk Vypracoval Jan Fait Datum 4. 12. 2015 Hodnocení Během úlohy jsme se seznámili
Světlo jako elektromagnetické záření
 Světlo jako elektromagnetické záření Základní pojmy: Homogenní prostředí prostředí, jehož dané vlastnosti jsou ve všech místech v prostředí stejné. Izotropní prostředí prostředí, jehož dané vlastnosti
Světlo jako elektromagnetické záření Základní pojmy: Homogenní prostředí prostředí, jehož dané vlastnosti jsou ve všech místech v prostředí stejné. Izotropní prostředí prostředí, jehož dané vlastnosti
Metody nelineární optiky v Ramanově spektroskopii
 Metody nelineární optiky v Ramanově spektroskopii Využití optických nelinearit umožňuje přejít od tradičního studia rozptylu světla na fluktuacích, teplotních elementárních excitacích, ke studiu rozptylu
Metody nelineární optiky v Ramanově spektroskopii Využití optických nelinearit umožňuje přejít od tradičního studia rozptylu světla na fluktuacích, teplotních elementárních excitacích, ke studiu rozptylu
Rovinná monochromatická vlna v homogenním, neabsorbujícím, jednoosém anizotropním prostředí
 Rovinná monochromatická vlna v homogenním, neabsorbujícím, jednoosém anizotropním prostředí r r Další předpoklad: nemagnetické prostředí B = µ 0 H izotropně. Veškerá anizotropie pochází od interakce elektrických
Rovinná monochromatická vlna v homogenním, neabsorbujícím, jednoosém anizotropním prostředí r r Další předpoklad: nemagnetické prostředí B = µ 0 H izotropně. Veškerá anizotropie pochází od interakce elektrických
1. Pevnolátkový Nd:YAG laser v režimu volné generace a v režimu Q-spínání. 2. Zesilování laserového záření a generace druhé harmonické
 Úloha č. 1 pro laserová praktika KFE, FJFI, ČVUT v Praze, verze 2010/1 1. Pevnolátkový Nd:YAG laser v režimu volné generace a v režimu Q-spínání. 2. Zesilování laserového záření a generace druhé harmonické
Úloha č. 1 pro laserová praktika KFE, FJFI, ČVUT v Praze, verze 2010/1 1. Pevnolátkový Nd:YAG laser v režimu volné generace a v režimu Q-spínání. 2. Zesilování laserového záření a generace druhé harmonické
Elektromagnetické pole je generováno elektrickými náboji a jejich pohybem. Je-li zdroj charakterizován nábojovou hustotou ( r r
 Záření Hertzova dipólu, kulové vlny, Rovnice elektromagnetického pole jsou vektorové diferenciální rovnice a podle symetrie bývá vhodné je řešit v křivočarých souřadnicích. Základní diferenciální operátory
Záření Hertzova dipólu, kulové vlny, Rovnice elektromagnetického pole jsou vektorové diferenciální rovnice a podle symetrie bývá vhodné je řešit v křivočarých souřadnicích. Základní diferenciální operátory
PRAKTIKUM III. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009.
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III Úloha č. XXVI Název: Vláknová optika Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009 Odevzdal dne: Možný počet bodů
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III Úloha č. XXVI Název: Vláknová optika Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009 Odevzdal dne: Možný počet bodů
Jan Fait, Filip Grepl Jan Fait Datum Hodnocení
 Název a číslo úlohy Dvouvlnové směšování ve fotorefraktivním materiálu a fázová konjugace úloha č. 6 Datum měření 16. 10. 2015 Měření provedli Vypracoval Jan Fait, Filip Grepl Jan Fait Datum 22. 10. 2015
Název a číslo úlohy Dvouvlnové směšování ve fotorefraktivním materiálu a fázová konjugace úloha č. 6 Datum měření 16. 10. 2015 Měření provedli Vypracoval Jan Fait, Filip Grepl Jan Fait Datum 22. 10. 2015
Laserová technika prosince Katedra fyzikální elektroniky.
 Laserová technika 1 Aktivní prostředí Šíření optických impulsů v aktivním prostředí Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz. prosince 016 Program přednášek
Laserová technika 1 Aktivní prostředí Šíření optických impulsů v aktivním prostředí Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz. prosince 016 Program přednášek
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 18.4.2012 Jméno: Jakub Kákona Pracovní skupina: 2 Hodina: Po 7:30 Spolupracovníci: Viktor Polák Hodnocení: Měření s polarizovaným světlem Abstrakt V
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 18.4.2012 Jméno: Jakub Kákona Pracovní skupina: 2 Hodina: Po 7:30 Spolupracovníci: Viktor Polák Hodnocení: Měření s polarizovaným světlem Abstrakt V
Bakalářská práce. Generace součtové frekvence v daleké UV oblasti
 Univerzita Karlova v Praze Matematicko fyzikální fakulta Bakalářská práce Miroslav Martínek Generace součtové frekvence v daleké UV oblasti Katedra chemické fyziky a optiky Vedoucí bakalářské práce: RNDr.
Univerzita Karlova v Praze Matematicko fyzikální fakulta Bakalářská práce Miroslav Martínek Generace součtové frekvence v daleké UV oblasti Katedra chemické fyziky a optiky Vedoucí bakalářské práce: RNDr.
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 18.4.2012 Jméno: Jakub Kákona Pracovní skupina: 2 Hodina: Po 7:30 Spolupracovníci: Viktor Polák Hodnocení: Měření s polarizovaným světlem Abstrakt V
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 18.4.2012 Jméno: Jakub Kákona Pracovní skupina: 2 Hodina: Po 7:30 Spolupracovníci: Viktor Polák Hodnocení: Měření s polarizovaným světlem Abstrakt V
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 1.4.2011 Jméno: Jakub Kákona Pracovní skupina: 4 Ročník a kroužek: Pa 9:30 Spolupracovníci: Jana Navrátilová Hodnocení: Měření s polarizovaným světlem
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 1.4.2011 Jméno: Jakub Kákona Pracovní skupina: 4 Ročník a kroužek: Pa 9:30 Spolupracovníci: Jana Navrátilová Hodnocení: Měření s polarizovaným světlem
Neživá příroda I. Optické vlastnosti minerálů
 Neživá příroda I Optické vlastnosti minerálů 1 Charakter světla Světelný paprsek definuje: vlnová délka (λ): vzdálenost mezi následnými vrcholy vln, amplituda: výchylka na obě strany od rovnovážné polohy,
Neživá příroda I Optické vlastnosti minerálů 1 Charakter světla Světelný paprsek definuje: vlnová délka (λ): vzdálenost mezi následnými vrcholy vln, amplituda: výchylka na obě strany od rovnovážné polohy,
Jaký význam má kritický kmitočet vedení? - nejnižší kmitočet vlny, při kterém se vlna začíná šířit vedením.
 Jaký význam má kritický kmitočet vedení? - nejnižší kmitočet vlny, při kterém se vlna začíná šířit vedením. Na čem závisí účinnost vedení? účinnost vedení závisí na činiteli útlumu β a na činiteli odrazu
Jaký význam má kritický kmitočet vedení? - nejnižší kmitočet vlny, při kterém se vlna začíná šířit vedením. Na čem závisí účinnost vedení? účinnost vedení závisí na činiteli útlumu β a na činiteli odrazu
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE. Mikrovlny
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 25.3.2011 Jméno: Jakub Kákona Pracovní skupina: 4 Ročník a kroužek: Pa 9:30 Spolupracovníci: Jana Navrátilová Hodnocení: Mikrovlny Abstrakt V úloze je
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 25.3.2011 Jméno: Jakub Kákona Pracovní skupina: 4 Ročník a kroužek: Pa 9:30 Spolupracovníci: Jana Navrátilová Hodnocení: Mikrovlny Abstrakt V úloze je
Fyzika laserů. 4. dubna Katedra fyzikální elektroniky.
 Fyzika laserů Přitahováni frekvencí. Spektrum laserového záření. Modelocking Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 4. dubna 2013 Program přednášek 1.
Fyzika laserů Přitahováni frekvencí. Spektrum laserového záření. Modelocking Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 4. dubna 2013 Program přednášek 1.
Úloha č.6 Dvouvlnové směšování ve fotorefraktivním materiálu a fázová
 Úloha č.6 Dvouvlnové směšování ve fotorefraktivním materiálu a fázová konjugace 1 Teoretický úvod Dvouvlnové směšování neboli dvouvlnová interference ve fotorefraktivním (FRV) materiálu je proces, který
Úloha č.6 Dvouvlnové směšování ve fotorefraktivním materiálu a fázová konjugace 1 Teoretický úvod Dvouvlnové směšování neboli dvouvlnová interference ve fotorefraktivním (FRV) materiálu je proces, který
Jihočeská univerzita v Českých Budějovicích
 Jihočeská univerzita v Českých Budějovicích Pedagogická fakulta Katedra fyziky Měření nelineárních optických jevů generovaných femtosekundovými laserovými pulsy Generace superkontinua Bakalářská práce
Jihočeská univerzita v Českých Budějovicích Pedagogická fakulta Katedra fyziky Měření nelineárních optických jevů generovaných femtosekundovými laserovými pulsy Generace superkontinua Bakalářská práce
Optika pro mikroskopii materiálů I
 Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
Postupné, rovinné, monochromatické vlny v lineárním izotropním nemagnetickém prostředí
 Postupné, rovinné, monochromatické vlny v lineárním izotropním nemagnetickém prostředí Rovinné vlny 1 Při diskusi o řadě jevů je výhodné vycházet z rovinných vln. Vlny musí splňovat Maxwellovy rovnice
Postupné, rovinné, monochromatické vlny v lineárním izotropním nemagnetickém prostředí Rovinné vlny 1 Při diskusi o řadě jevů je výhodné vycházet z rovinných vln. Vlny musí splňovat Maxwellovy rovnice
Laboratorní úloha č. 7 Difrakce na mikro-objektech
 Laboratorní úloha č. 7 Difrakce na mikro-objektech Úkoly měření: 1. Odhad rozměrů mikro-objektů z informací uváděných výrobcem. 2. Záznam difrakčních obrazců (difraktogramů) vzniklých interakcí laserového
Laboratorní úloha č. 7 Difrakce na mikro-objektech Úkoly měření: 1. Odhad rozměrů mikro-objektů z informací uváděných výrobcem. 2. Záznam difrakčních obrazců (difraktogramů) vzniklých interakcí laserového
Karel Lemr. web: Karel Lemr Fotonové páry 1 / 26
 Kvantové zpracování informace s fotonovými páry Karel Lemr Společná laboratoř optiky UP Olomouc a FzÚ AVČR web: http://jointlab.upol.cz/lemr email: lemr@jointlab.upol.cz Karel Lemr Fotonové páry 1 / 26
Kvantové zpracování informace s fotonovými páry Karel Lemr Společná laboratoř optiky UP Olomouc a FzÚ AVČR web: http://jointlab.upol.cz/lemr email: lemr@jointlab.upol.cz Karel Lemr Fotonové páry 1 / 26
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK FYZIKÁLNÍ PRAKTIKUM III Úloha číslo: 16 Název: Měření indexu lomu Fraunhoferovou metodou Vypracoval: Ondřej Hlaváč stud. skup.: F dne:
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK FYZIKÁLNÍ PRAKTIKUM III Úloha číslo: 16 Název: Měření indexu lomu Fraunhoferovou metodou Vypracoval: Ondřej Hlaváč stud. skup.: F dne:
Použití nelineární optiky pro změnu vlnové délky laserových pulsů
 Univerzita Karlova v Praze Matematicko fyzikální fakulta Bakalářská práce Helena Reichlová Použití nelineární optiky pro změnu vlnové délky laserových pulsů Katedra chemické optiky a fyziky Vedoucí bakalářské
Univerzita Karlova v Praze Matematicko fyzikální fakulta Bakalářská práce Helena Reichlová Použití nelineární optiky pro změnu vlnové délky laserových pulsů Katedra chemické optiky a fyziky Vedoucí bakalářské
Akustooptický modulátor s postupnou a stojatou akustickou vlnou
 Úloha č. 8 pro laserová praktika KFE, FJFI, ČVUT v Praze, verze 2010/1 Akustooptický modulátor s postupnou a stojatou akustickou vlnou Akustooptické modulátory (AOM), někdy též nazývané Braggovské cely,
Úloha č. 8 pro laserová praktika KFE, FJFI, ČVUT v Praze, verze 2010/1 Akustooptický modulátor s postupnou a stojatou akustickou vlnou Akustooptické modulátory (AOM), někdy též nazývané Braggovské cely,
Řešení: Nejdříve musíme určit sílu, kterou působí kladka proti směru pohybu padajícího vědra a napíná tak lano. Moment síly otáčení kladky je:
 Přijímací zkouška na navazující magisterské studium - 16 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Jak dlouho bude padat
Přijímací zkouška na navazující magisterské studium - 16 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Jak dlouho bude padat
Laserová technika prosince Katedra fyzikální elektroniky.
 Laserová technika 1 Aktivní prostředí Šíření rezonančního záření dvouhladinovým prostředím Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program
Laserová technika 1 Aktivní prostředí Šíření rezonančního záření dvouhladinovým prostředím Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program
Fyzikální praktikum FJFI ČVUT v Praze
 Fyzikální praktikum FJFI ČVUT v Praze Úloha 4: Balrmerova série Datum měření: 13. 5. 016 Doba vypracovávání: 7 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V přípravě
Fyzikální praktikum FJFI ČVUT v Praze Úloha 4: Balrmerova série Datum měření: 13. 5. 016 Doba vypracovávání: 7 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V přípravě
Jméno a příjmení. Ročník. Měřeno dne Příprava Opravy Učitel Hodnocení. Vlnové vlastnosti světla difrakce, laser
 FYZIKÁLNÍ PRAKTIKUM Ústav fyziky FEKT VUT BRNO Jméno a příjmení Petr Švaňa Ročník 1 Předmět IFY Kroužek 38 ID 155793 Spolupracoval Měřeno dne Odevzdáno dne Lukáš Teuer 8.4.2013 22.4.2013 Příprava Opravy
FYZIKÁLNÍ PRAKTIKUM Ústav fyziky FEKT VUT BRNO Jméno a příjmení Petr Švaňa Ročník 1 Předmět IFY Kroužek 38 ID 155793 Spolupracoval Měřeno dne Odevzdáno dne Lukáš Teuer 8.4.2013 22.4.2013 Příprava Opravy
MODERNÍ METODY CHEMICKÉ FYZIKY I lasery a jejich použití v chemické fyzice Přednáška 5
 MODERNÍ METODY CHEMICKÉ FYZIKY I lasery a jejich použití v chemické fyzice Přednáška 5 Ondřej Votava J. Heyrovský Institute of Physical Chemistry AS ČR Opakování z minula Light Amplifier by Stimulated
MODERNÍ METODY CHEMICKÉ FYZIKY I lasery a jejich použití v chemické fyzice Přednáška 5 Ondřej Votava J. Heyrovský Institute of Physical Chemistry AS ČR Opakování z minula Light Amplifier by Stimulated
Úloha č. 7 - Disperze v optických vláknech
 Úloha č. 7 - Disperze v optických vláknech 1 Teoretický úvod Optické vláknové vlnovody jsou důležitou komponentou optických komunikačních sítí. Jejich nejvýznamnějšími parametry jsou měrný útlum a přenosová
Úloha č. 7 - Disperze v optických vláknech 1 Teoretický úvod Optické vláknové vlnovody jsou důležitou komponentou optických komunikačních sítí. Jejich nejvýznamnějšími parametry jsou měrný útlum a přenosová
Úloha 3: Mřížkový spektrometr
 Petra Suková, 2.ročník, F-14 1 Úloha 3: Mřížkový spektrometr 1 Zadání 1. Seřiďte spektrometr pro kolmý dopad světla(rovina optické mřížky je kolmá k ose kolimátoru) pomocí bočního osvětlení nitkového kříže.
Petra Suková, 2.ročník, F-14 1 Úloha 3: Mřížkový spektrometr 1 Zadání 1. Seřiďte spektrometr pro kolmý dopad světla(rovina optické mřížky je kolmá k ose kolimátoru) pomocí bočního osvětlení nitkového kříže.
Fyzika laserů. 7. března Katedra fyzikální elektroniky.
 Fyzika laserů Poloklasický popis šíření elmg. záření v rezonančním prostředí. Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 7. března 2013 Program přednášek
Fyzika laserů Poloklasický popis šíření elmg. záření v rezonančním prostředí. Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 7. března 2013 Program přednášek
1. Ze zadané hustoty krystalu fluoridu lithného určete vzdálenost d hlavních atomových rovin.
 1 Pracovní úkoly 1. Ze zadané hustoty krystalu fluoridu lithného určete vzdálenost d hlavních atomových rovin. 2. Proměřte úhlovou závislost intenzity difraktovaného rentgenového záření při pevné orientaci
1 Pracovní úkoly 1. Ze zadané hustoty krystalu fluoridu lithného určete vzdálenost d hlavních atomových rovin. 2. Proměřte úhlovou závislost intenzity difraktovaného rentgenového záření při pevné orientaci
Akustooptický modulátor s postupnou a stojatou akustickou vlnou
 Úloha č. 8 pro laserová praktika (ZPLT) KFE, FJFI, ČVUT, Praha v. 2017/2018 Akustooptický modulátor s postupnou a stojatou akustickou vlnou Akustooptické modulátory (AOM), někdy též nazývané Braggovské
Úloha č. 8 pro laserová praktika (ZPLT) KFE, FJFI, ČVUT, Praha v. 2017/2018 Akustooptický modulátor s postupnou a stojatou akustickou vlnou Akustooptické modulátory (AOM), někdy též nazývané Braggovské
Fyzikální korespondenční seminář MFF UK
 Úloha V.E... nezbedné fotony 1 bodů; (chybí statistiky) Spolu se zadáním úlohy vám přišly polarizační brýle. Máte tedy polarizační filtry. Když je dáte za sebe tak, aby směry jejich polarizace byly na
Úloha V.E... nezbedné fotony 1 bodů; (chybí statistiky) Spolu se zadáním úlohy vám přišly polarizační brýle. Máte tedy polarizační filtry. Když je dáte za sebe tak, aby směry jejich polarizace byly na
Praktikum školních pokusů 2
 Praktikum školních pokusů 2 Optika 3A Interference a difrakce světla Jana Jurmanová Přírodovědecká fakulta Masarykovy univerzity, Brno I Interference na dvojštěrbině Odvod te vztah pro polohu interferenčních
Praktikum školních pokusů 2 Optika 3A Interference a difrakce světla Jana Jurmanová Přírodovědecká fakulta Masarykovy univerzity, Brno I Interference na dvojštěrbině Odvod te vztah pro polohu interferenčních
4. Statika základní pojmy a základy rovnováhy sil
 4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
TEZE K DISERTAČNÍ PRÁCI ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE. Ing. Ondřej Novák
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAE Ing. Ondřej Novák Optické parametrické zesilování čerpovaných impulsů v nelineárních krystalech čerpaných jódovým fotodisociačním laserem TEE K DISERTAČNÍ PRÁCI České
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAE Ing. Ondřej Novák Optické parametrické zesilování čerpovaných impulsů v nelineárních krystalech čerpaných jódovým fotodisociačním laserem TEE K DISERTAČNÍ PRÁCI České
Základní otázky pro teoretickou část zkoušky.
 Základní otázky pro teoretickou část zkoušky. Platí shodně pro prezenční i kombinovanou formu studia. 1. Síla současně působící na elektrický náboj v elektrickém a magnetickém poli (Lorentzova síla) 2.
Základní otázky pro teoretickou část zkoušky. Platí shodně pro prezenční i kombinovanou formu studia. 1. Síla současně působící na elektrický náboj v elektrickém a magnetickém poli (Lorentzova síla) 2.
Fyzika II, FMMI. 1. Elektrostatické pole
 Fyzika II, FMMI 1. Elektrostatické pole 1.1 Jaká je velikost celkového náboje (kladného i záporného), který je obsažen v 5 kg železa? Předpokládejme, že by se tento náboj rovnoměrně rozmístil do dvou malých
Fyzika II, FMMI 1. Elektrostatické pole 1.1 Jaká je velikost celkového náboje (kladného i záporného), který je obsažen v 5 kg železa? Předpokládejme, že by se tento náboj rovnoměrně rozmístil do dvou malých
2 Nd:YAG laser buzený laserovou diodou
 2 Nd:YAG laser buzený laserovou diodou 15. května 2011 Základní praktikum laserové techniky Zpracoval: Vojtěch Horný Datum měření: 12. května 2011 Pracovní skupina: 1 Ročník: 3. Naměřili: Vojtěch Horný,
2 Nd:YAG laser buzený laserovou diodou 15. května 2011 Základní praktikum laserové techniky Zpracoval: Vojtěch Horný Datum měření: 12. května 2011 Pracovní skupina: 1 Ročník: 3. Naměřili: Vojtěch Horný,
V mnoha běžných případech v optickém oboru je zanedbáváno silové působení magnetické složky elektromagnetického pole na náboje v látce str. 3 6.
 Nekvantový popis interakce světla s pasivní látkou Zcela nekvantová fyzika nemůže interakci elektromagnetického záření s látkou popsat, např. atom jako soustava kladných a záporných nábojů by vůbec nebyl
Nekvantový popis interakce světla s pasivní látkou Zcela nekvantová fyzika nemůže interakci elektromagnetického záření s látkou popsat, např. atom jako soustava kladných a záporných nábojů by vůbec nebyl
z ), který je jejím Fourierovým obrazem. Naopak obrazová funkce g ( y, objeví v obrazové rovině bude Fourierovým obrazem funkce E(µ,ν).
 Prostorová filtrace Uvažujme uspořádání na obr. PF-1. Koherentně osvětlený předmět leží v předmětové rovině yz yz. Optickým systémem je v rovině yz (obrazová rovina) vytvořen obraz tohoto předmětu. V ohniskové
Prostorová filtrace Uvažujme uspořádání na obr. PF-1. Koherentně osvětlený předmět leží v předmětové rovině yz yz. Optickým systémem je v rovině yz (obrazová rovina) vytvořen obraz tohoto předmětu. V ohniskové
ρ = 0 (nepřítomnost volných nábojů)
 Učební text k přednášce UFY Světlo v izotropním látkovém prostředí Maxwellovy rovnice v izotropním látkovém prostředí: B rot + D rot H ( r, t) div D ρ rt, ( ) div B a materiálové vztahy D ε pro dielektrika
Učební text k přednášce UFY Světlo v izotropním látkovém prostředí Maxwellovy rovnice v izotropním látkovém prostředí: B rot + D rot H ( r, t) div D ρ rt, ( ) div B a materiálové vztahy D ε pro dielektrika
Generace 2. harmonické
 Generace. harmonické ω = + ω ω M M ˆ * A = i σ A A e i M ˆ A = i σ A e i = + ρ + + + + ig, + δ, z x k x y v, g, t t walkoff ( anizotropie) difrakce ( fokusace) i kz kz ( disp. pulsy grup. rych.) disperze
Generace. harmonické ω = + ω ω M M ˆ * A = i σ A A e i M ˆ A = i σ A e i = + ρ + + + + ig, + δ, z x k x y v, g, t t walkoff ( anizotropie) difrakce ( fokusace) i kz kz ( disp. pulsy grup. rych.) disperze
Laboratorní úloha č. 2 Vzájemná induktivní vazba dvou kruhových vzduchových cívek - Faradayův indukční zákon. Max Šauer
 Laboratorní úloha č. Vzájemná induktivní vazba dvou kruhových vzduchových cívek - Faradayův indukční zákon Max Šauer 14. prosince 003 Obsah 1 Popis úlohy Úkol měření 3 Postup měření 4 Teoretický rozbor
Laboratorní úloha č. Vzájemná induktivní vazba dvou kruhových vzduchových cívek - Faradayův indukční zákon Max Šauer 14. prosince 003 Obsah 1 Popis úlohy Úkol měření 3 Postup měření 4 Teoretický rozbor
Obecný Hookeův zákon a rovinná napjatost
 Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Praktikum III - Optika
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum III - Optika Úloha č. 13 Název: Vlastnosti rentgenového záření Pracoval: Matyáš Řehák stud.sk.: 13 dne: 3. 4. 2008 Odevzdal
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum III - Optika Úloha č. 13 Název: Vlastnosti rentgenového záření Pracoval: Matyáš Řehák stud.sk.: 13 dne: 3. 4. 2008 Odevzdal
MĚŘENÍ VLNOVÝCH DÉLEK SVĚTLA MŘÍŽKOVÝM SPEKTROMETREM
 MĚŘENÍ VLNOVÝCH DÉLEK SVĚTLA MŘÍŽKOVÝM SPEKTROMETREM Difrakce (ohyb) světla je jedním z několika projevů vlnových vlastností světla. Z těchto důvodů světlo při setkání s překážkou nepostupuje dále vždy
MĚŘENÍ VLNOVÝCH DÉLEK SVĚTLA MŘÍŽKOVÝM SPEKTROMETREM Difrakce (ohyb) světla je jedním z několika projevů vlnových vlastností světla. Z těchto důvodů světlo při setkání s překážkou nepostupuje dále vždy
Vibrace atomů v mřížce, tepelná kapacita pevných látek
 Vibrace atomů v mřížce, tepelná kapacita pevných látek Atomy vázané v mřížce nejsou v klidu. Míru jejich pohybu vyjadřuje podobně jako u plynů a kapalin teplota. - Elastické vlny v kontinuu neatomární
Vibrace atomů v mřížce, tepelná kapacita pevných látek Atomy vázané v mřížce nejsou v klidu. Míru jejich pohybu vyjadřuje podobně jako u plynů a kapalin teplota. - Elastické vlny v kontinuu neatomární
7 FYZIKÁLNÍ OPTIKA. Interference Ohyb Polarizace. Co je to ohyb? 27.2 Ohyb
 1 7 FYZIKÁLNÍ OPTIKA Interference Ohyb Polarizace Co je to ohyb? 27.2 Ohyb Ohyb vln je jev charakterizovaný odchylkou od přímočarého šíření vlnění v témže prostředí. Ve skutečnosti se nejedná o nový jev
1 7 FYZIKÁLNÍ OPTIKA Interference Ohyb Polarizace Co je to ohyb? 27.2 Ohyb Ohyb vln je jev charakterizovaný odchylkou od přímočarého šíření vlnění v témže prostředí. Ve skutečnosti se nejedná o nový jev
Úloha 15: Studium polovodičového GaAs/GaAlAs laseru
 Petra Suková, 2.ročník, F-14 1 Úloha 15: Studium polovodičového GaAs/GaAlAs laseru 1 Zadání 1. Změřte současně světelnou i voltampérovou charakteristiku polovodičového laseru. Naměřenézávislostizpracujtegraficky.Stanovteprahovýproud
Petra Suková, 2.ročník, F-14 1 Úloha 15: Studium polovodičového GaAs/GaAlAs laseru 1 Zadání 1. Změřte současně světelnou i voltampérovou charakteristiku polovodičového laseru. Naměřenézávislostizpracujtegraficky.Stanovteprahovýproud
ELEKTROMAGNETICKÉ KMITÁNÍ A VLNĚNÍ POJMY K ZOPAKOVÁNÍ. Testové úlohy varianta A
 Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Jitka Novosadová MGV_F_SS_3S3_D18_Z_OPAK_E_Elektromagneticke_kmitani_a_ vlneni_t Člověk a příroda Fyzika Elektromagnetické
Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Jitka Novosadová MGV_F_SS_3S3_D18_Z_OPAK_E_Elektromagneticke_kmitani_a_ vlneni_t Člověk a příroda Fyzika Elektromagnetické
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Příklady použití tenkých vrstev Jaromír Křepelka
 Příklady použití tenkých vrstev Jaromír Křepelka Příklad 01 Spočtěte odrazivost prostého rozhraní dvou izotropních homogenních materiálů s indexy lomu n 0 = 1 a n 1 = 1,52 v závislosti na úhlu dopadu pro
Příklady použití tenkých vrstev Jaromír Křepelka Příklad 01 Spočtěte odrazivost prostého rozhraní dvou izotropních homogenních materiálů s indexy lomu n 0 = 1 a n 1 = 1,52 v závislosti na úhlu dopadu pro
Měření absorbce záření gama
 Měření absorbce záření gama Úkol : 1. Změřte záření gama přirozeného pozadí. 2. Změřte záření gama vyzářené gamazářičem. 3. Změřte záření gama vyzářené gamazářičem přes absorbátor. 4. Naměřené závislosti
Měření absorbce záření gama Úkol : 1. Změřte záření gama přirozeného pozadí. 2. Změřte záření gama vyzářené gamazářičem. 3. Změřte záření gama vyzářené gamazářičem přes absorbátor. 4. Naměřené závislosti
Charakteristiky optického záření
 Fyzika III - Optika Charakteristiky optického záření / 1 Charakteristiky optického záření 1. Spektrální charakteristika vychází se z rovinné harmonické vlny jako elementu elektromagnetického pole : primární
Fyzika III - Optika Charakteristiky optického záření / 1 Charakteristiky optického záření 1. Spektrální charakteristika vychází se z rovinné harmonické vlny jako elementu elektromagnetického pole : primární
Elektromagnetické vlnění
 Elektromagnetické vlnění kolem vodičů elmag. oscilátoru se vytváří proměnné elektrické i magnetické pole http://www.walter-fendt.de/ph11e/emwave.htm Radiotechnika elmag vlnění vyzářené dipólem můžeme zachytit
Elektromagnetické vlnění kolem vodičů elmag. oscilátoru se vytváří proměnné elektrické i magnetické pole http://www.walter-fendt.de/ph11e/emwave.htm Radiotechnika elmag vlnění vyzářené dipólem můžeme zachytit
4. Z modové struktury emisního spektra laseru určete délku aktivní oblasti rezonátoru. Diskutujte,
 1 Pracovní úkol 1. Změřte současně světelnou i voltampérovou charakteristiku polovodičového laseru. Naměřené závislosti zpracujte graficky. Stanovte prahový proud i 0. 2. Pomocí Hg výbojky okalibrujte
1 Pracovní úkol 1. Změřte současně světelnou i voltampérovou charakteristiku polovodičového laseru. Naměřené závislosti zpracujte graficky. Stanovte prahový proud i 0. 2. Pomocí Hg výbojky okalibrujte
Polarizace čtvrtvlnovou destičkou
 Úkol : 1. Proměřte intenzitu lineárně polarizovaného světla jako funkci pozice analyzátoru. 2. Proměřte napětí na fotorezistoru ozářenou intenzitou světla za analyzátorem jako funkci úhlu mezi optickou
Úkol : 1. Proměřte intenzitu lineárně polarizovaného světla jako funkci pozice analyzátoru. 2. Proměřte napětí na fotorezistoru ozářenou intenzitou světla za analyzátorem jako funkci úhlu mezi optickou
Základní pojmy a vztahy: Vlnová délka (λ): vzdálenost dvou nejbližších bodů vlnění kmitajících ve stejné fázi
 LRR/BUBCV CVIČENÍ Z BUNĚČNÉ BIOLOGIE 1. SVĚTELNÁ MIKROSKOPIE A PREPARÁTY V MIKROSKOPII TEORETICKÝ ÚVOD: Mikroskopie je základní metoda, která nám umožňuje pozorovat velmi malé biologické objekty. Díky
LRR/BUBCV CVIČENÍ Z BUNĚČNÉ BIOLOGIE 1. SVĚTELNÁ MIKROSKOPIE A PREPARÁTY V MIKROSKOPII TEORETICKÝ ÚVOD: Mikroskopie je základní metoda, která nám umožňuje pozorovat velmi malé biologické objekty. Díky
Optické spektroskopie 1 LS 2014/15
 Optické spektroskopie 1 LS 2014/15 Martin Kubala 585634179 mkubala@prfnw.upol.cz 1.Úvod Velikosti objektů v přírodě Dítě ~ 1 m (10 0 m) Prst ~ 2 cm (10-2 m) Vlas ~ 0.1 mm (10-4 m) Buňka ~ 20 m (10-5 m)
Optické spektroskopie 1 LS 2014/15 Martin Kubala 585634179 mkubala@prfnw.upol.cz 1.Úvod Velikosti objektů v přírodě Dítě ~ 1 m (10 0 m) Prst ~ 2 cm (10-2 m) Vlas ~ 0.1 mm (10-4 m) Buňka ~ 20 m (10-5 m)
Vznik a šíření elektromagnetických vln
 Vznik a šíření elektromagnetických vln Hlavní body Rozšířený Coulombův zákon lektromagnetická vlna ve vakuu Zdroje elektromagnetických vln Přehled elektromagnetických vln Foton vlna nebo částice Fermatův
Vznik a šíření elektromagnetických vln Hlavní body Rozšířený Coulombův zákon lektromagnetická vlna ve vakuu Zdroje elektromagnetických vln Přehled elektromagnetických vln Foton vlna nebo částice Fermatův
FYZIKA II. Marek Procházka 1. Přednáška
 FYZIKA II Marek Procházka 1. Přednáška Historie Dělení optiky Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení
FYZIKA II Marek Procházka 1. Přednáška Historie Dělení optiky Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení
Modulace vlnoplochy. SLM vytváří prostorově modulovaný koherentní optický signál
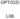 OPT/OZI L06 Modulace vlnoplochy prostorové modulátory světla (SLM) SLM vytváří prostorově modulovaný koherentní optický signál řízení elektronicky adresovaný SLM opticky adresovaný SLM technologie fotografická
OPT/OZI L06 Modulace vlnoplochy prostorové modulátory světla (SLM) SLM vytváří prostorově modulovaný koherentní optický signál řízení elektronicky adresovaný SLM opticky adresovaný SLM technologie fotografická
Úvod do laserové techniky
 Úvod do laserové techniky Světlo jako elektromagnetické záření I. část Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické v Praze jan.sulc@fjfi.cvut.cz 5. října 2016 Kontakty Ing. Jan
Úvod do laserové techniky Světlo jako elektromagnetické záření I. část Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické v Praze jan.sulc@fjfi.cvut.cz 5. října 2016 Kontakty Ing. Jan
Podle studijních textů k úloze [1] se divergence laserového svaku definuje jako
![Podle studijních textů k úloze [1] se divergence laserového svaku definuje jako Podle studijních textů k úloze [1] se divergence laserového svaku definuje jako](/thumbs/55/36333813.jpg) Úkoly 1. Změřte divergenci laserového svazku. 2. Z optické stavebnice sestavte Michelsonův interferometr. K rozšíření svazku sestavte Galileův teleskop. Ze známých ohniskových délek použitých čoček spočtěte,
Úkoly 1. Změřte divergenci laserového svazku. 2. Z optické stavebnice sestavte Michelsonův interferometr. K rozšíření svazku sestavte Galileův teleskop. Ze známých ohniskových délek použitých čoček spočtěte,
Měření a analýza mechanických vlastností materiálů a konstrukcí. 1. Určete moduly pružnosti E z ohybu tyče pro 4 různé materiály
 FP 1 Měření a analýza mechanických vlastností materiálů a konstrukcí Úkoly : 1. Určete moduly pružnosti E z ohybu tyče pro 4 různé materiály 2. Určete moduly pružnosti vzorků nepřímo pomocí měření rychlosti
FP 1 Měření a analýza mechanických vlastností materiálů a konstrukcí Úkoly : 1. Určete moduly pružnosti E z ohybu tyče pro 4 různé materiály 2. Určete moduly pružnosti vzorků nepřímo pomocí měření rychlosti
Fabry Perotův interferometr
 Fabry Perotův interferometr Princip Dvě zrcadla jsou sestavena tak aby tvořila tzv. Fabry Perotův interferometr, s jehož pomocí je vyšetřován svazek paprsků vycházejících z laseru. Při experimentu se pohybuje
Fabry Perotův interferometr Princip Dvě zrcadla jsou sestavena tak aby tvořila tzv. Fabry Perotův interferometr, s jehož pomocí je vyšetřován svazek paprsků vycházejících z laseru. Při experimentu se pohybuje
3.2.5 Odraz, lom a ohyb vlnění
 3..5 Odraz, lom a ohyb vlnění Předpoklady: 304 Odraz a lom vlnění na rozhranní dvou prostředí s různou rychlostí šíření http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=16.0 Rovinná vlna dopadá šikmo
3..5 Odraz, lom a ohyb vlnění Předpoklady: 304 Odraz a lom vlnění na rozhranní dvou prostředí s různou rychlostí šíření http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=16.0 Rovinná vlna dopadá šikmo
Fyzikální praktikum FJFI ČVUT v Praze
 Fyzikální praktikum FJFI ČVUT v Praze Úloha 9: Měření s polarizovaným světlem Datum měření: 29. 4. 2016 Doba vypracovávání: 8 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání
Fyzikální praktikum FJFI ČVUT v Praze Úloha 9: Měření s polarizovaným světlem Datum měření: 29. 4. 2016 Doba vypracovávání: 8 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání
Zvuk. 1. základní kmitání. 2. šíření zvuku
 Zvuk 1. základní kmitání - vzduchem se šíří tlakové vzruchy (vzruchová vlna), zvuk je systémem zhuštěnin a zředěnin - podstatou zvuku je kmitání zdroje zvuku a tím způsobené podélné vlnění elastického
Zvuk 1. základní kmitání - vzduchem se šíří tlakové vzruchy (vzruchová vlna), zvuk je systémem zhuštěnin a zředěnin - podstatou zvuku je kmitání zdroje zvuku a tím způsobené podélné vlnění elastického
1 Zadání. 2 Úvod. Název a číslo úlohy 6 - Dvouvlnové směšování ve fotorefraktivním materiálu a fázová konjugace. Měření provedli Marek Vlk Vypracoval
 Název a číslo úlohy 6 - Dvouvlnové směšování ve fotorefraktivním materiálu a fázová konjugace Datum měření 7.12.2015 Měření provedli Marek Vlk Vypracoval Marek Vlk Datum 2.1.2016 Hodnocení 1 Zadání 1.
Název a číslo úlohy 6 - Dvouvlnové směšování ve fotorefraktivním materiálu a fázová konjugace Datum měření 7.12.2015 Měření provedli Marek Vlk Vypracoval Marek Vlk Datum 2.1.2016 Hodnocení 1 Zadání 1.
VLNOVÁ OPTIKA. Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník
 VLNOVÁ OPTIKA Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník Vlnová optika Světlo lze chápat také jako elektromagnetické vlnění. Průkopníkem této teorie byl Christian Huyghens. Některé jevy se dají
VLNOVÁ OPTIKA Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník Vlnová optika Světlo lze chápat také jako elektromagnetické vlnění. Průkopníkem této teorie byl Christian Huyghens. Některé jevy se dají
4.2.3 ŠÍŘE FREKVENČNÍHO PÁSMA CHOROVÉHO ELEMENTU A DISTRIBUČNÍ FUNKCE VLNOVÝCH NORMÁL
 4.2.3 ŠÍŘE FREKVENČNÍHO PÁSMA CHOROVÉHO ELEMENTU A DISTRIBUČNÍ FUNKCE VLNOVÝCH NORMÁL V předchozích dvou podkapitolách jsme ukázali, že chorové emise se mohou v řadě případů šířit nevedeným způsobem. Připomeňme
4.2.3 ŠÍŘE FREKVENČNÍHO PÁSMA CHOROVÉHO ELEMENTU A DISTRIBUČNÍ FUNKCE VLNOVÝCH NORMÁL V předchozích dvou podkapitolách jsme ukázali, že chorové emise se mohou v řadě případů šířit nevedeným způsobem. Připomeňme
42 Polarizované světlo Malusův zákon a Brewsterův úhel
 42 Polarizované světlo Malusův zákon a rewsterův úhel ÚKOL 1. Ověřte platnost Malusova 1 zákona. 2. Změřte rewsterův 2 úhel a nalezněte relativní index lomu dvou prostředí. (Výslovnost: rewster ['bru:stər,
42 Polarizované světlo Malusův zákon a rewsterův úhel ÚKOL 1. Ověřte platnost Malusova 1 zákona. 2. Změřte rewsterův 2 úhel a nalezněte relativní index lomu dvou prostředí. (Výslovnost: rewster ['bru:stər,
Fyzika II. Marek Procházka Vlnová optika II
 Fyzika II Marek Procházka Vlnová optika II Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení složek vlnění s různou
Fyzika II Marek Procházka Vlnová optika II Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení složek vlnění s různou
Otázka 22(42) Přístroje pro měření signálů, metody pro měření v časové a frekvenční doméně. Přístroje
 Otázka 22(42) Přístroje pro měření signálů, metody pro měření v časové a frekvenční doméně Rozmanitost signálů v komunikační technice způsobuje, že rozdělení měřicích metod není jednoduché a jednoznačné.
Otázka 22(42) Přístroje pro měření signálů, metody pro měření v časové a frekvenční doméně Rozmanitost signálů v komunikační technice způsobuje, že rozdělení měřicích metod není jednoduché a jednoznačné.
Úvod do laserové techniky
 Úvod do laserové techniky Světlo jako elektromagnetické záření I. část Michal Němec Katedra fyzikální elektroniky České vysoké učení technické v Praze michal.nemec@fjfi.cvut.cz Kontakty Ing. Michal Němec,
Úvod do laserové techniky Světlo jako elektromagnetické záření I. část Michal Němec Katedra fyzikální elektroniky České vysoké učení technické v Praze michal.nemec@fjfi.cvut.cz Kontakty Ing. Michal Němec,
Balmerova série, určení mřížkové a Rydbergovy konstanty
 Balmerova série, určení mřížkové a Rydbergovy konstanty V tomto laboratorním cvičení zkoumáme spektrální čáry 1. řádu vodíku a rtuti pomocí difrakční mřížky (mřížkového spektroskopu). Známé spektrální
Balmerova série, určení mřížkové a Rydbergovy konstanty V tomto laboratorním cvičení zkoumáme spektrální čáry 1. řádu vodíku a rtuti pomocí difrakční mřížky (mřížkového spektroskopu). Známé spektrální
(Následující odstavce jsou zde uvedeny jen pro zájemce.) , sin2π, (2)
 Studium difrakčních jevů TEORIE doplněk: Odvození výrazů pro difrakční maxima (popř. minima) na štěrbině, dvojštěrbině a mřížce jsou zpravidla uvedena na středoškolské úrovni, což je založeno na vhodném
Studium difrakčních jevů TEORIE doplněk: Odvození výrazů pro difrakční maxima (popř. minima) na štěrbině, dvojštěrbině a mřížce jsou zpravidla uvedena na středoškolské úrovni, což je založeno na vhodném
Přehled posledních experimentů skupiny kvantové a nelineární optiky v Olomouci
 Přehled posledních experimentů skupiny kvantové a nelineární optiky v Olomouci Jan Soubusta, Antonín Černoch, Karel Lemr, Karol Bartkiewicz, Radek Machulka, Společná laboratoř optiky Univerzity Palackého
Přehled posledních experimentů skupiny kvantové a nelineární optiky v Olomouci Jan Soubusta, Antonín Černoch, Karel Lemr, Karol Bartkiewicz, Radek Machulka, Společná laboratoř optiky Univerzity Palackého
rychlostí šíření světla v tomto prostředí ku vakuu, n = c/v. Pro vzduch je index lomu přibližně 1, voda má 1.33, sklo od 1.5 do 1.9.
 1 Transport světla Pro popis šíření světla se může použít více metod v závislosti na okolnostech. Pokud je vlnová délka zanedbatelně malá nebo překážky, které klademe světlu do cesty, jsou mnohem větší
1 Transport světla Pro popis šíření světla se může použít více metod v závislosti na okolnostech. Pokud je vlnová délka zanedbatelně malá nebo překážky, které klademe světlu do cesty, jsou mnohem větší
Název a číslo materiálu VY_32_INOVACE_ICT_FYZIKA_OPTIKA
 Název a číslo materiálu VY_32_INOVACE_ICT_FYZIKA_OPTIKA OPTIKA ZÁKLADNÍ POJMY Optika a její dělení Světlo jako elektromagnetické vlnění Šíření světla Odraz a lom světla Disperze (rozklad) světla OPTIKA
Název a číslo materiálu VY_32_INOVACE_ICT_FYZIKA_OPTIKA OPTIKA ZÁKLADNÍ POJMY Optika a její dělení Světlo jako elektromagnetické vlnění Šíření světla Odraz a lom světla Disperze (rozklad) světla OPTIKA
Testové otázky za 2 body
 Přijímací zkoušky z fyziky pro obor MŽP K vypracování písemné zkoušky máte k dispozici 90 minut. Kromě psacích potřeb je povoleno používání kalkulaček. Pro úspěšné zvládnutí zkoušky je třeba získat nejméně
Přijímací zkoušky z fyziky pro obor MŽP K vypracování písemné zkoušky máte k dispozici 90 minut. Kromě psacích potřeb je povoleno používání kalkulaček. Pro úspěšné zvládnutí zkoušky je třeba získat nejméně
5.1 Modelování drátových antén v časové oblasti metodou momentů
 5.1 Modelování drátových antén v časové oblasti metodou momentů Základní teorie V kapitolách 4.1, 4.4 resp. 4.5 byly drátový dipól, mikropáskový dipól a flíčková anténa modelovány metodou momentů ve frekvenční
5.1 Modelování drátových antén v časové oblasti metodou momentů Základní teorie V kapitolách 4.1, 4.4 resp. 4.5 byly drátový dipól, mikropáskový dipól a flíčková anténa modelovány metodou momentů ve frekvenční
Elektromagnetický oscilátor
 Elektromagnetický oscilátor Již jsme poznali kmitání mechanického oscilátoru (závaží na pružině) - potenciální energie pružnosti se přeměňuje na kinetickou energii a naopak. T =2 m k Nejjednodušší elektromagnetický
Elektromagnetický oscilátor Již jsme poznali kmitání mechanického oscilátoru (závaží na pružině) - potenciální energie pružnosti se přeměňuje na kinetickou energii a naopak. T =2 m k Nejjednodušší elektromagnetický
Geometrická optika. předmětu. Obrazový prostor prostor za optickou soustavou (většinou vpravo), v němž může ležet obraz - - - 1 -
 Geometrická optika Optika je část fyziky, která zkoumá podstatu světla a zákonitosti světelných jevů, které vznikají při šíření světla a při vzájemném působení světla a látky. Světlo je elektromagnetické
Geometrická optika Optika je část fyziky, která zkoumá podstatu světla a zákonitosti světelných jevů, které vznikají při šíření světla a při vzájemném působení světla a látky. Světlo je elektromagnetické
4. V jednom krychlovém metru (1 m 3 ) plynu je 2, molekul. Ve dvou krychlových milimetrech (2 mm 3 ) plynu je molekul
 Fyzika 20 Otázky za 2 body. Celsiova teplota t a termodynamická teplota T spolu souvisejí známým vztahem. Vyberte dvojici, která tento vztah vyjadřuje (zaokrouhleno na celá čísla) a) T = 253 K ; t = 20
Fyzika 20 Otázky za 2 body. Celsiova teplota t a termodynamická teplota T spolu souvisejí známým vztahem. Vyberte dvojici, která tento vztah vyjadřuje (zaokrouhleno na celá čísla) a) T = 253 K ; t = 20
Laserové technologie v praxi I. Přednáška č.1. Fyzikální princip činnosti laserů. Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 2011
 Laserové technologie v praxi I. Přednáška č. Fyzikální princip činnosti laserů Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 0 LASER kvantový generátor světla Fyzikální princip činnosti laserů LASER zkratka
Laserové technologie v praxi I. Přednáška č. Fyzikální princip činnosti laserů Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 0 LASER kvantový generátor světla Fyzikální princip činnosti laserů LASER zkratka
Signál v čase a jeho spektrum
 Signál v čase a jeho spektrum Signály v časovém průběhu (tak jak je vidíme na osciloskopu) můžeme dělit na periodické a neperiodické. V obou případech je lze popsat spektrálně určit jaké kmitočty v sobě
Signál v čase a jeho spektrum Signály v časovém průběhu (tak jak je vidíme na osciloskopu) můžeme dělit na periodické a neperiodické. V obou případech je lze popsat spektrálně určit jaké kmitočty v sobě
Zdroje optického záření
 Metody optické spektroskopie v biofyzice Zdroje optického záření / 1 Zdroje optického záření tepelné výbojky polovodičové lasery synchrotronové záření Obvykle se charakterizují zářivostí (zářivý výkon
Metody optické spektroskopie v biofyzice Zdroje optického záření / 1 Zdroje optického záření tepelné výbojky polovodičové lasery synchrotronové záření Obvykle se charakterizují zářivostí (zářivý výkon
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE. Úloha 8: Mikrovlny. Abstrakt
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření:. 3. Úloha 8: Mikrovlny Jméno: Jiří Slabý Pracovní skupina: 4 Ročník a kroužek:. ročník,. kroužek, pondělí 3:3 Spolupracovala: Eliška Greplová Hodnocení:
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření:. 3. Úloha 8: Mikrovlny Jméno: Jiří Slabý Pracovní skupina: 4 Ročník a kroužek:. ročník,. kroužek, pondělí 3:3 Spolupracovala: Eliška Greplová Hodnocení:
Spektrální charakterizace mřížkového spektrografu
 Spektrální charakterizace mřížkového spektrografu Vedoucí: prof. RNDr. Petr Němec, Ph.D. (nemec@karlov.mff.cuni.cz), KCHFO MFF UK Analýza spektrálního složení světla je nedílnou součástí života každého
Spektrální charakterizace mřížkového spektrografu Vedoucí: prof. RNDr. Petr Němec, Ph.D. (nemec@karlov.mff.cuni.cz), KCHFO MFF UK Analýza spektrálního složení světla je nedílnou součástí života každého
Krystalografie a strukturní analýza
 Krystalografie a strukturní analýza O čem to dneska bude (a nebo také nebude): trocha historie aneb jak to všechno začalo... jak a čím pozorovat strukturu látek difrakce - tak trochu jiný mikroskop rozptyl
Krystalografie a strukturní analýza O čem to dneska bude (a nebo také nebude): trocha historie aneb jak to všechno začalo... jak a čím pozorovat strukturu látek difrakce - tak trochu jiný mikroskop rozptyl
DIFRAKCE ELEKTRONŮ V KRYSTALECH, ZOBRAZENÍ ATOMŮ
 DIFRAKCE ELEKTRONŮ V KRYSTALECH, ZOBRAZENÍ ATOMŮ T. Jeřábková Gymnázium, Brno, Vídeňská 47 ter.jer@seznam.cz V. Košař Gymnázium, Brno, Vídeňská 47 vlastik9a@atlas.cz G. Malenová Gymnázium Třebíč malena.vy@quick.cz
DIFRAKCE ELEKTRONŮ V KRYSTALECH, ZOBRAZENÍ ATOMŮ T. Jeřábková Gymnázium, Brno, Vídeňská 47 ter.jer@seznam.cz V. Košař Gymnázium, Brno, Vídeňská 47 vlastik9a@atlas.cz G. Malenová Gymnázium Třebíč malena.vy@quick.cz
Dualismus vln a částic
 Dualismus vln a částic Filip Horák 1, Jan Pecina 2, Jiří Bárdoš 3 1 Mendelovo gymnázium, Opava, Horaksro@seznam.cz 2 Gymnázium Jeseník, pecinajan.jes@mail.com 3 Gymnázium Teplice, jiri.bardos@post.gymtce.cz
Dualismus vln a částic Filip Horák 1, Jan Pecina 2, Jiří Bárdoš 3 1 Mendelovo gymnázium, Opava, Horaksro@seznam.cz 2 Gymnázium Jeseník, pecinajan.jes@mail.com 3 Gymnázium Teplice, jiri.bardos@post.gymtce.cz
Úloha 21: Studium rentgenových spekter
 Petra Suková, 3.ročník 1 Úloha 21: Studium rentgenových spekter 1 Zadání 1. S využitím krystalu LiF jako analyzátoru proveďte měření následujících rentgenových spekter: a) Rentgenka s Cu anodou. proměřte
Petra Suková, 3.ročník 1 Úloha 21: Studium rentgenových spekter 1 Zadání 1. S využitím krystalu LiF jako analyzátoru proveďte měření následujících rentgenových spekter: a) Rentgenka s Cu anodou. proměřte
