Temporální logiky. ČVUT FEL Katedra telekomunikační techniky, K prosince 2017
|
|
|
- Marian Kadlec
- před 6 lety
- Počet zobrazení:
Transkript
1 Temorální logiky Radek Mařík ČVUT FEL Katedra telekomunikační techniky, K rosince 2017 Radek Mařík Temorální logiky 6. rosince / 31
2 Obsah 1 Systém UPPAAL Postu modelování a ověřování 2 Základy temorálních logik Cesty výočtu a čas CTL* logika CTL logika 3 UPPAAL Secifikace ožadavků v UPPAAL 4 Hra NIM Secifikace ožadavků hry NIM Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
3 Systém UPPAAL Postu modelování a ověřování Tvorba automatu [UPP09] Automat očáteční ozice (dvojitá kružnice) Add Location ro řidání ozice Selection Tool ro ojmenování ozice Add Edge ro řidání hrany, rohnutí hran omocí myši v okoĺı konců dolní tabulka Position a Descrition ro analýzu chyb Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
4 Systém UPPAAL Postu modelování a ověřování Komozice systému [UPP09] Systém Systém... sít aralelních časovaných automatů (rocesů). Proces... instance arametrizovaného vzoru. Proces Pozice... jméno, invarianty Hrany... odmínky stráží (x >= 7), synchronizace (go[id]?), řiřazení (x = 0), Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
5 Systém UPPAAL Postu modelování a ověřování Pois vzoru (temlate) [UPP09] Parametrizovaný časový automat jméno, arametry, Lokální deklarace roměnné, synchronizační kanály, konstanty Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
6 Systém UPPAAL Postu modelování a ověřování Pois systému [UPP09] Globální deklarace globální celočíselné roměnné, globální hodiny, synchronizační kanály, konstanty Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
7 Systém UPPAAL Postu modelování a ověřování Definice systému [UPP09] Přiřazení rocesů deklarace instancí rocesu, vzory s úlně/částečně secifikovanými arametry, Definice systému seznam rocesů systému, Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
8 Základy temorálních logik Cesty výočtu a čas Přechody mezi konfiguracemi v Krikeho struktuře [Voj10] P1 P2 a c cs(p1) s 2 unlock(l) lock(l) lock(l) unlock(l) unlocked(l) s 1 b d cs(p2) s 3 mutex l; Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
9 Základy temorálních logik Cesty výočtu a čas Cesta v Krikeho struktuře [Voj10] Cesta Cesta π... v Krikeho struktuře M je nekonečná sekvence stavů π = s 0 s 1 s 3... taková, že i N..R(s i, s i+1 ). Π(M, s)... množina všech cest v M, které začínají v s S Sufix π i cesty π = s 0 s 1 s 3... s i s i+1 s i+2 je cesta π i = s i s i+1 s i+2 začínající v s i. s i = π[i] Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
10 Základy temorálních logik Cesty výočtu a čas Pojem času [Voj10] Abstrakce času Logický čas... racuje s (částečným) usořádáním stavů/událostí v chování systému. Fyzický čas... měření doby uběhlou mezi dvěma stavy/události. Čas ve verifikaci modelů Lineární čas... dovoluje se vyjadřovat ouze o dané lineární trase ve stavovém rostoru. Na všech trasách, x musí být následováno y. Na všech trasách, x musí být následováno y nebo z. Větvící se čas... dovoluje kvantifikovat (existenčně i univerzálně) možné budoucnosti očínaje daným stavem. Na stavový rostor se ohĺıží jako na rozvinutý nekonečný strom. Existuje trasa, kde následující stav je x. Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
11 Základy temorálních logik CTL* logika Výočetní strom [Voj10] Poisuje vlastnosti výočetního stromu unlocked(l) cs(p1) s 2 cs(p1) cs(p2) unlocked(l) s 1 unlocked(l) unlocked(l) cs(p2) s 3 cs(p1) cs(p2) cs(p1) cs(p2) Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
12 Základy temorálních logik CTL* logika CTL* formule [Voj10] Skládá se z atomické výroky logické sojky kvantifikátory cest temorální oerátory Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
13 Základy temorálních logik CTL* logika CTL* kvantifikátory a oerátory [Wik10, Voj10] Kvantifikátory cest oisují strukturu větvení vyočetního stromu E... existuje cesta výočtu z daného stavu. A... ro všechny cesty výočtů z daného stavu. Temorální oerátory určují vlastnosti cesty ve výočetním stromu X ϕ (next time, )... vlastnost ϕ latí ve druhém (následujícím) stavu cesty.. F ϕ (in future, )... vlastnost ϕ latí v nějakém stavu cesty. Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
14 CTL* oerátory Základy temorálních logik [Wik10, Voj10] CTL* logika Temorální oerátory Gϕ (globally, )... vlastnost ϕ latí ve všech stavech cesty. ψuϕ (until)... vlastnost ϕ latí v nějakém stavu cesty a vlastnost ψ latí řinejmenším ve všech ředcházejících stavech této cesty. ψrϕ (release)... vlastnost ϕ musí latit do (a včetně) stavu, kdy začne latit vlastnost ψ, okud takový stav existuje. Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
15 Základy temorálních logik CTL* logika CTL* syntax [Voj10] Necht AP je nerázdná množina atomických výroků. Syntax stavových formuĺı, které jsou ravdivé v daném stavu Jestliže AP, otom je stavová formule. Jestliže ϕ a ψ jsou stavové formule, otom ϕ, ϕ ψ, ϕ ψ jsou stavové formule. Jestliže ϕ je běhová formule, otom Eϕ a Aϕ jsou stavové formule. Syntax běhových formuĺı, které jsou ravdivé odél secifické cesty Jestliže ϕ je stavová formule, ak ϕ je také běhová formule. Jestliže ϕ a ψ jsou běhové formule, ak ϕ, ϕ ψ, ϕ ψ, X ϕ, F ϕ, Gϕ, ϕuψ a ϕrψ jsou běhové formule. CTL* je množina stavových formuĺı generovaných výše uvedenými ravidly. Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
16 Základy temorálních logik CTL* logika CTL* sémantika [Voj10] Necht je dána Krikeho struktura M = (S, T, I, s 0, L) nad množinou atomických výroků AP. Pro stavovou formuli ϕ nad AP, zaisujeme M, s = ϕ fakt, že ϕ latí v s S. Pro běhovou formuli ϕ nad AP, zaisujeme M, π = ϕ fakt, že ϕ latí odél cesty π v M. Necht s S, π je cesta v M, ϕ 1, ϕ 2 jsou stavové formule nad AP, AP, a ψ 1, ψ 2 jsou běhové formule nad AP. Pak relaci = definujeme induktivně následovně: M, s = iff L(s). M, s = ϕ 1 iff M, s = ϕ 1. M, s = ϕ 1 ϕ 2 iff M, s = ϕ 1 nebo M, s = ϕ 2. M, s = ϕ 1 ϕ 2 iff M, s = ϕ 1 a zároveň M, s = ϕ 2. M, s = Eψ 1 iff π Π(M, s).m, s = ψ 1. M, s = Aψ 1 iff π Π(M, s).m, s = ψ 1. Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
17 Základy temorálních logik CTL* logika CTL* sémantika [Voj10] Pokračování definice relace =: M, π = ϕ 1 iff M, s 0 = ϕ 1, s 0 = π[0]. M, π = ψ 1 iff M, π = ψ 1. M, π = ψ 1 ψ 2 iff M, π = ψ 1 nebo M, π = ψ 2. M, π = ψ 1 ψ 2 iff M, π = ψ 1 a zároveň M, π = ψ 2. M, π = X ψ 1 iff M, π 1 = ψ 1. M, π = F ψ 1 iff i 0.M, π i = ψ 1. M, π = Gψ 1 iff i 0.M, π i = ψ 1. M, π = ψ 1 Uψ 2 iff i 0.M, π i = ψ 2 a zároveň 0 j < i.m, π j = ψ 1. M, π = ψ 1 Rψ 2 iff i 0.( 0 j < i.m, π j = ψ 1 M, π i = ψ 2. Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
18 Základy temorálních logik CTL* logika CTL* základní oerátory [Voj10] Všechny CTL* oerátory lze odvodit z,, X, U a E: Nech AP, true (a false true) ϕ ψ ( ϕ ψ), F ϕ trueuϕ, Gϕ F ϕ, ϕrψ ( ϕu ψ), Aϕ E ϕ. Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
19 Základy temorálních logik CTL logika CTL syntaxe [Voj10] CTL je sublogikou CTL* běhové formule jsou omezeny na X ϕ, F ϕ, Gϕ, ϕuψ a ϕrψ, kde ϕ a ψ jsou stavové formule. Proto ouze 10 modálních CTL oerátorů: AX a EX AX EX AF a EF AF EF AG a EG AG EG Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
20 Základy temorálních logik CTL logika CTL modální oerátory [Voj10] Modální CTL oerátory: AU a EU A[ U q] E[ U q] q q q q AR a ER A[ R q] q E[ R q] q q q q Existují 3 základní CTL modální oerátory - EX, EG a EU: AX ϕ EX ϕ EF ϕ E[trueUϕ] AGϕ EF ϕ AF ϕ EG ϕ A[ϕUψ] E[ ψu( ϕ ψ)] EG ψ A[ϕRψ] E[ ϕu ψ] E[ϕRψ] A[ ϕu ψ] Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
21 UPPAAL Secifikace ožadavků v UPPAAL BNF gramatika secifikačního jazyka [UPP10] BNF gramatika A[]Exression E <> Exression E[]Exression A <> Exression Exression > Exression Poznámky Žadný výraz nesmí mít ostranní efekty. Výraz rocess.location testuje, zda určitý roces je v dané ozici. Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
22 UPPAAL Secifikace ožadavků v UPPAAL Příklady secifikačního jazyka [UPP10] BNF gramatika A[]1 < 2 Invariatně 1 < 2 E <> 1.csand2.cs Pravdivé, okud systém může dosáhnout stavu, ve kterém rocesy 1 a 2 jsou v jejich ozici cs A <> 1.csimlynot2.cs Invariantně rocess 1 v ozici cs imlikuje, že roces 2 není v ozici cs. A[]notdeadlock Invariantně, rocess neobsahuje deadlock. Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
23 Jednoduchá varianta NIM Hra NIM Secifikace ožadavků hry NIM NIM je hra založená na logice a strategii. Hrají 2 hráči. Hráč ři svém tahu odstraní jednu až MAX (2) věci (záalky, rotony) z řady. Vyhrává ten hráč, který odstraní oslední věc. Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
24 Klasická varianta NIM Hra NIM Secifikace ožadavků hry NIM NIM je hra založená na logice a strategii. Hrají 2 hráči. Hráči odebírají objekty z různých hromádek/řad. Hráč musí odstranit ři svém tahu alesoň jeden objekt. Hráč ři svém tahu odstraní libovolný očet objektů, které náleží všechny k jedné hromádce. Základní varianty hry: Normální... Vyhrává ten hráč, který odstraní oslední věc. Prohra... Prohrává ten hráč, který odstraní oslední věc. Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
25 Literatura I Hra NIM Secifikace ožadavků hry NIM UPPAAL 4.0: Small tutorial, November Tool environment for validation and verification of real-time systems (UPPAAL amhlet). htt:// Setember Tomas Vojnar. Formal analysis and verification. Lecture handouts, htt:// August Linear temoral logic. htt://en.wikiedia.org/wiki/linear temoral logic, November Radek Mařík (radek.marik@fel.cvut.cz) Temorální logiky 6. rosince / 31
Temporální logiky. Czech Technical University Faculty of Electrical Engineering Department of Telecommunication Engineering Prague CZ
 Temporální logiky Radek Mařík Czech Technical University Faculty of Electrical Engineering Department of Telecommunication Engineering Prague CZ December 5, 2017 Radek Mařík (radek.marik@fel.cvut.cz) Temporální
Temporální logiky Radek Mařík Czech Technical University Faculty of Electrical Engineering Department of Telecommunication Engineering Prague CZ December 5, 2017 Radek Mařík (radek.marik@fel.cvut.cz) Temporální
ČVUT FEL Katedra telekomunikační techniky, K prosince Radek Mařík Ověřování modelů II 6. prosince / 39
 Ověřování modelů II Radek Mařík ČVUT FEL Katedra telekomunikační techniky, K13132 6. prosince 2017 Radek Mařík (radek.marik@fel.cvut.cz) Ověřování modelů II 6. prosince 2017 1 / 39 Obsah 1 Temporální logiky
Ověřování modelů II Radek Mařík ČVUT FEL Katedra telekomunikační techniky, K13132 6. prosince 2017 Radek Mařík (radek.marik@fel.cvut.cz) Ověřování modelů II 6. prosince 2017 1 / 39 Obsah 1 Temporální logiky
ČVUT FEL, K December 12, Radek Mařík Ověřování modelů II December 12, / 30
 Ověřování modelů II Radek Mařík ČVUT FEL, K13133 December 12, 2010 Radek Mařík (marikr@felk.cvut.cz) Ověřování modelů II December 12, 2010 1 / 30 Obsah 1 Temporální logiky LTL logika 2 UPPAAL detaily Jazyk
Ověřování modelů II Radek Mařík ČVUT FEL, K13133 December 12, 2010 Radek Mařík (marikr@felk.cvut.cz) Ověřování modelů II December 12, 2010 1 / 30 Obsah 1 Temporální logiky LTL logika 2 UPPAAL detaily Jazyk
Verifikace Modelů a UPPAAL
 Verifikace Modelů a UPPAAL Radek Mařík ČVUT FEL, K13132 October 2, 2014 Radek Mařík (marikr@fel.cvut.cz) Verifikace Modelů a UPPAAL October 2, 2014 1 / 51 Obsah 1 Úvod Motivace Úvod do verifikace modelů
Verifikace Modelů a UPPAAL Radek Mařík ČVUT FEL, K13132 October 2, 2014 Radek Mařík (marikr@fel.cvut.cz) Verifikace Modelů a UPPAAL October 2, 2014 1 / 51 Obsah 1 Úvod Motivace Úvod do verifikace modelů
10. Techniky formální verifikace a validace
 Fakulta informačních technologií MI-NFA, zimní semestr 2011/2012 Jan Schmidt EVROPSKÝ SOCIÁLNÍ FOND PRAHA & EU: INVESTUJENE DO VAŠÍ BUDOUCNOSTI 10. Techniky formální verifikace a validace 1 Simulace není
Fakulta informačních technologií MI-NFA, zimní semestr 2011/2012 Jan Schmidt EVROPSKÝ SOCIÁLNÍ FOND PRAHA & EU: INVESTUJENE DO VAŠÍ BUDOUCNOSTI 10. Techniky formální verifikace a validace 1 Simulace není
Verifikace Modelů a UPPAAL
 Verifikace Modelů a UPPAAL Radek Mařík ČVUT FEL, K13133 September 6, 2011 Radek Mařík (marikr@felk.cvut.cz) Verifikace Modelů a UPPAAL September 6, 2011 1 / 51 Obsah 1 Úvod Motivace Úvod do verifikace
Verifikace Modelů a UPPAAL Radek Mařík ČVUT FEL, K13133 September 6, 2011 Radek Mařík (marikr@felk.cvut.cz) Verifikace Modelů a UPPAAL September 6, 2011 1 / 51 Obsah 1 Úvod Motivace Úvod do verifikace
Unbounded Model Checking
 Unbounded Model Checking Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze 25. října 2011 Evropský sociální fond Praha & EU: Investujeme do
Unbounded Model Checking Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze 25. října 2011 Evropský sociální fond Praha & EU: Investujeme do
IV113 Validace a verifikace. Převod LTL formule na Büchi automat. Jiří Barnat
 IV113 Validace a verifikace Převod LTL formule na Büchi automat Jiří Barnat Připomenutí IV113 úvod do validace a verifikace: LTL BA str. 2/26 Problém Kripkeho struktura M LTL formule ϕ M = ϕ? Řešení pomocí
IV113 Validace a verifikace Převod LTL formule na Büchi automat Jiří Barnat Připomenutí IV113 úvod do validace a verifikace: LTL BA str. 2/26 Problém Kripkeho struktura M LTL formule ϕ M = ϕ? Řešení pomocí
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti MI-SOC: 11 METODY VERIFIKACE SYSTÉMŮ NA ČIPU Hana Kubátov vá doc. Ing. Hana Kubátová, CSc. Katedra číslicového návrhu Fakulta 1 informačních
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti MI-SOC: 11 METODY VERIFIKACE SYSTÉMŮ NA ČIPU Hana Kubátov vá doc. Ing. Hana Kubátová, CSc. Katedra číslicového návrhu Fakulta 1 informačních
Temporální Logiky. Stefan Ratschan. Fakulta informačních technologíı. Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti 1 / 19
 Temporální Logiky Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze 10. října 2011 Evropský sociální fond Praha & EU: Investujeme do vaší
Temporální Logiky Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze 10. října 2011 Evropský sociální fond Praha & EU: Investujeme do vaší
Sémantika výrokové logiky. Alena Gollová Výroková logika 1/23
 Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
Model Checking pro Timed Automata. Jiří Vyskočil 2011
 Model Checking pro Timed Automata Jiří Vyskočil 2011 Časově kritické systémy korektnost fungování vestavěným a distribuovaných systémů závisí na: správném výsledku výpočtu správném načasování prováděných
Model Checking pro Timed Automata Jiří Vyskočil 2011 Časově kritické systémy korektnost fungování vestavěným a distribuovaných systémů závisí na: správném výsledku výpočtu správném načasování prováděných
Verifikace Modelů a UPPAAL
 Verifikace Modelů a UPPAAL Radek Mařík Czech Technical University Faculty of Electrical Engineering Department of Telecommunication Engineering Prague CZ November 7, 2017 Radek Mařík (radek.marik@fel.cvut.cz)
Verifikace Modelů a UPPAAL Radek Mařík Czech Technical University Faculty of Electrical Engineering Department of Telecommunication Engineering Prague CZ November 7, 2017 Radek Mařík (radek.marik@fel.cvut.cz)
Ověřování modelu pomocí automatů. Tomáš Masopust
 Ověřování modelu pomocí automatů Tomáš Masopust Brno, 2003 Obsah Úvod 3 1 Temporální logiky 5 1.1 Modely................................ 5 1.2 Computation Tree Logic....................... 7 1.3 Linear-time
Ověřování modelu pomocí automatů Tomáš Masopust Brno, 2003 Obsah Úvod 3 1 Temporální logiky 5 1.1 Modely................................ 5 1.2 Computation Tree Logic....................... 7 1.3 Linear-time
Výroková logika syntaxe a sémantika
 syntaxe a sémantika Jiří Velebil: AD0B01LGR 2015 Handout 01: & sémantika VL 1/16 1 Proč formální jazyk? 1 Přirozené jazyky jsou složité a často nejednoznačné. 2 Komunikace s formálními nástroji musí být
syntaxe a sémantika Jiří Velebil: AD0B01LGR 2015 Handout 01: & sémantika VL 1/16 1 Proč formální jazyk? 1 Přirozené jazyky jsou složité a často nejednoznačné. 2 Komunikace s formálními nástroji musí být
Úvod do informatiky. Miroslav Kolařík
 Úvod do informatiky přednáška první Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Co a k čemu je logika? 2 Výroky a logické spojky
Úvod do informatiky přednáška první Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Co a k čemu je logika? 2 Výroky a logické spojky
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2015/2016 1 / 18 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2015/2016 1 / 18 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
4.2 Syntaxe predikátové logiky
 36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
Výroková a predikátová logika - V
 Výroková a predikátová logika - V Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - V ZS 2015/2016 1 / 21 Dokazovací systémy VL Hilbertovský kalkul Hilbertovský
Výroková a predikátová logika - V Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - V ZS 2015/2016 1 / 21 Dokazovací systémy VL Hilbertovský kalkul Hilbertovský
Výroková a predikátová logika - VI
 Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
7 Jemný úvod do Logiky
 7 Jemný úvod do Logiky Základem přesného matematického vyjadřování je správné používání (matematické) logiky a logických úsudků. Logika jako filozofická discipĺına se intenzivně vyvíjí už od dob antiky,
7 Jemný úvod do Logiky Základem přesného matematického vyjadřování je správné používání (matematické) logiky a logických úsudků. Logika jako filozofická discipĺına se intenzivně vyvíjí už od dob antiky,
Úvod do predikátové logiky. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
 Úvod do predikátové logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 1 Relace Neuspořádaná vs. uspořádaná dvojice {m, n} je neuspořádaná dvojice. m, n je uspořádaná dvojice. (FLÚ AV ČR) Logika:
Úvod do predikátové logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 1 Relace Neuspořádaná vs. uspořádaná dvojice {m, n} je neuspořádaná dvojice. m, n je uspořádaná dvojice. (FLÚ AV ČR) Logika:
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2013/2014 1 / 20 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2013/2014 1 / 20 Základní syntax Jazyk Výroková logika je logikou
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Výroková logika. Sémantika výrokové logiky
 Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
Rezoluce ve výrokové logice
 Rezoluce ve výrokové logice Jiří Velebil: AD0B01LGR 2015 Rezoluce ve VL 1/13 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. 2 X nesplnitelná iff X = ff. 3 Hledání kritických důsledků X syntakticky.
Rezoluce ve výrokové logice Jiří Velebil: AD0B01LGR 2015 Rezoluce ve VL 1/13 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. 2 X nesplnitelná iff X = ff. 3 Hledání kritických důsledků X syntakticky.
Cyklické kódy. Alena Gollová, TIK Cyklické kódy 1/23
 Cyklické kódy 5. řednáška z algebraického kódování Alena Gollová, TIK Cyklické kódy 1/23 Obsah 1 Cyklické kódy Generující olynom - kódování Kontrolní olynom - objevování chyb Alena Gollová, TIK Cyklické
Cyklické kódy 5. řednáška z algebraického kódování Alena Gollová, TIK Cyklické kódy 1/23 Obsah 1 Cyklické kódy Generující olynom - kódování Kontrolní olynom - objevování chyb Alena Gollová, TIK Cyklické
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Sémantická věta o dedukci Věta Pro
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Sémantická věta o dedukci Věta Pro
TERMIKA VIII. Joule uv a Thompson uv pokus pro reálné plyny
 TERMIKA VIII Maxwellova rovnovážná rozdělovací funkce rychlostí Joule uv a Thomson uv okus ro reálné lyny 1 Maxwellova rovnovážná rozdělovací funkce rychlostí Maxwellova rychlostní rozdělovací funkce se
TERMIKA VIII Maxwellova rovnovážná rozdělovací funkce rychlostí Joule uv a Thomson uv okus ro reálné lyny 1 Maxwellova rovnovážná rozdělovací funkce rychlostí Maxwellova rychlostní rozdělovací funkce se
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti MI-SOC: 2 METODY VERIFIKACE SYSTÉMŮ NA ČIPU II doc. Ing. Hana Kubátová, CSc. Katedra číslicového návrhu Fakulta informačních technologii
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti MI-SOC: 2 METODY VERIFIKACE SYSTÉMŮ NA ČIPU II doc. Ing. Hana Kubátová, CSc. Katedra číslicového návrhu Fakulta informačních technologii
Výroková a predikátová logika - III
 Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2014/2015 1 / 21 Výroková logika Horn-SAT Horn-SAT Jednotková
Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2014/2015 1 / 21 Výroková logika Horn-SAT Horn-SAT Jednotková
Výroková a predikátová logika - III
 Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2017/2018 1 / 16 2-SAT 2-SAT Výrok je v k-cnf, je-li v CNF a
Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2017/2018 1 / 16 2-SAT 2-SAT Výrok je v k-cnf, je-li v CNF a
EKONOMETRIE 4. přednáška Modely chování spotřebitele
 EKONOMETRIE 4. řednáška Modely chování sotřebitele Rozočtové omezení Sotřebitel ři svém rozhodování resektuje tzv. rozočtové omezení x + x y, kde x i množství i-té sotřební komodity, i cena i-té sotřební
EKONOMETRIE 4. řednáška Modely chování sotřebitele Rozočtové omezení Sotřebitel ři svém rozhodování resektuje tzv. rozočtové omezení x + x y, kde x i množství i-té sotřební komodity, i cena i-té sotřební
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Stefan Ratschan. Fakulta informačních technologíı. Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
 Logika pro každodenní přežití Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
Logika pro každodenní přežití Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
Další (neklasické) logiky. Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20
 Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Databázové systémy. * relační kalkuly. Tomáš Skopal. - relační model
 Databázové systémy Tomáš Skopal - relační model * relační kalkuly Osnova přednášky relační kalkuly doménový n-ticový Relační kalkuly využití aparátu predikátové logiky 1. řádu pro dotazování rozšíření
Databázové systémy Tomáš Skopal - relační model * relační kalkuly Osnova přednášky relační kalkuly doménový n-ticový Relační kalkuly využití aparátu predikátové logiky 1. řádu pro dotazování rozšíření
Pro každé formule α, β, γ, δ platí: Pro každé formule α, β, γ platí: Poznámka: Platí právě tehdy, když je tautologie.
 Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
Analytická metoda aneb Využití vektorů v geometrii
 KM/GVS Geometrické vidění světa (Design) nalytická metoda aneb Využití vektorů v geometrii Použité značky a symboly R, C, Z obor reálných, komleních, celých čísel geometrický vektor R n aritmetický vektor
KM/GVS Geometrické vidění světa (Design) nalytická metoda aneb Využití vektorů v geometrii Použité značky a symboly R, C, Z obor reálných, komleních, celých čísel geometrický vektor R n aritmetický vektor
prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. BI-ZMA ZS 2009/2010
 Základní pojmy prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy
Základní pojmy prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy
Výroková logika - opakování
 - opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
- opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
Učební texty k státní bakalářské zkoušce Matematika Posloupnosti a řady funkcí. študenti MFF 15. augusta 2008
 Učební texty k státní bakalářské zkoušce Matematika Poslounosti a řady funkcí študenti MFF 15. augusta 2008 1 3 Poslounosti a řady funkcí Požadavky Sojitost za ředokladu stejnoměrné konvergence Mocninné
Učební texty k státní bakalářské zkoušce Matematika Poslounosti a řady funkcí študenti MFF 15. augusta 2008 1 3 Poslounosti a řady funkcí Požadavky Sojitost za ředokladu stejnoměrné konvergence Mocninné
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2018/2019 1 / 15 Platnost (pravdivost) Platnost ve struktuře
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2018/2019 1 / 15 Platnost (pravdivost) Platnost ve struktuře
Vlastnosti regulárních jazyků
 Vlastnosti regulárních jazyků Podobně jako u dalších tříd jazyků budeme nyní zkoumat následující vlastnosti regulárních jazyků: vlastnosti strukturální, vlastnosti uzávěrové a rozhodnutelné problémy pro
Vlastnosti regulárních jazyků Podobně jako u dalších tříd jazyků budeme nyní zkoumat následující vlastnosti regulárních jazyků: vlastnosti strukturální, vlastnosti uzávěrové a rozhodnutelné problémy pro
Obsah Předmluva Rekapitulace základních pojmů logiky a výrokové logiky Uvedení do predikátové logiky...17
 Obsah Předmluva...3 0. Rekapitulace základních pojmů logiky a výrokové logiky...11 0.1 Logika jako věda o vyplývání... 11 1. Uvedení do predikátové logiky...17 1.1 Základní terminologie... 17 1.2 Základní
Obsah Předmluva...3 0. Rekapitulace základních pojmů logiky a výrokové logiky...11 0.1 Logika jako věda o vyplývání... 11 1. Uvedení do predikátové logiky...17 1.1 Základní terminologie... 17 1.2 Základní
Predikátová logika: Axiomatizace, sémantické stromy, identita. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 13
 Predikátová logika: Axiomatizace, sémantické stromy, identita (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 13 Axiomatizace predikátové logiky Axiomatizace predikátové logiky Definice Hilbertovský
Predikátová logika: Axiomatizace, sémantické stromy, identita (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 13 Axiomatizace predikátové logiky Axiomatizace predikátové logiky Definice Hilbertovský
Základy logiky a teorie množin
 Pracovní text k přednášce Logika a teorie množin (I/2007) 1 1 Struktura přednášky Matematická logika 2 Výroková logika Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz Predikátová logika 1. řádu
Pracovní text k přednášce Logika a teorie množin (I/2007) 1 1 Struktura přednášky Matematická logika 2 Výroková logika Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz Predikátová logika 1. řádu
Markovovy řetězce se spojitým časem CTMC (Continuous time Markov Chain)
 Markovovy řetězce se soitým časem CTMC (Continuous time Markov Chain) 3 5 1 4 Markovovy rocesy X Diskrétní stavový rostor Soitý obor arametru t { } S e1, e,, en t R t 0 0 t 1 t t 3 t Proces e Markovův
Markovovy řetězce se soitým časem CTMC (Continuous time Markov Chain) 3 5 1 4 Markovovy rocesy X Diskrétní stavový rostor Soitý obor arametru t { } S e1, e,, en t R t 0 0 t 1 t t 3 t Proces e Markovův
Okruh č.3: Sémantický výklad predikátové logiky
 Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
platné nejsou Sokrates je smrtelný. (r) 1/??
 Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Úvěr a úvěrové výpočty 1
 Modely analýzy a syntézy lánů MAF/KIV) Přednáška 8 Úvěr a úvěrové výočty 1 1 Rovnice úvěru V minulých řednáškách byla ro stav dluhu oužívána rovnice 1), kde ředokládáme, že N > : d = a b + = k > N. d./
Modely analýzy a syntézy lánů MAF/KIV) Přednáška 8 Úvěr a úvěrové výočty 1 1 Rovnice úvěru V minulých řednáškách byla ro stav dluhu oužívána rovnice 1), kde ředokládáme, že N > : d = a b + = k > N. d./
Model tenisového utkání
 Model tenisového utkání Jan Šustek Semestrální rojekt do ředmětu Náhodné rocesy 2005 V této ráci se budu zabývat modelem tenisového utkání. Vstuními hodnotami budou úsěšnosti odání jednotlivých hráčů,
Model tenisového utkání Jan Šustek Semestrální rojekt do ředmětu Náhodné rocesy 2005 V této ráci se budu zabývat modelem tenisového utkání. Vstuními hodnotami budou úsěšnosti odání jednotlivých hráčů,
Logika Libor Barto. Výroková logika
 Logika Libor Barto Výroková logika Definice.(Jazyk výrokové logiky) Ve výrokové logice používáme tyto symboly: (1) Výrokové proměnné: velká písmena, případně opatřená indexy. (2) Výrokovéspojky:,,&,,,....
Logika Libor Barto Výroková logika Definice.(Jazyk výrokové logiky) Ve výrokové logice používáme tyto symboly: (1) Výrokové proměnné: velká písmena, případně opatřená indexy. (2) Výrokovéspojky:,,&,,,....
Predikátová logika. Teoretická informatika Tomáš Foltýnek
 Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Rekurentní rovnice, strukturální indukce
 , strukturální indukce Jiří Velebil: Y01DMA 23. února 2010: Strukturální indukce 1/19 Backusova-Naurova forma Například syntaxe formuĺı výrokové logiky kde a At. Poznámky 1 Relaxace BNF. ϕ ::= a tt (ϕ
, strukturální indukce Jiří Velebil: Y01DMA 23. února 2010: Strukturální indukce 1/19 Backusova-Naurova forma Například syntaxe formuĺı výrokové logiky kde a At. Poznámky 1 Relaxace BNF. ϕ ::= a tt (ϕ
Logika XI. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı BI-MLO, ZS 2011/12
 Logika XI. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Logika XI. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Predikátová logika dokončení
 Predikátová logika dokončení Jiří Velebil: X01DML 1. října 2010: Predikátová logika dokončení 1/18 Syntaktická analýza Jako ve výrokové logice (syntaktické stromy). Každý list úspěšného stromu je obsazen
Predikátová logika dokončení Jiří Velebil: X01DML 1. října 2010: Predikátová logika dokončení 1/18 Syntaktická analýza Jako ve výrokové logice (syntaktické stromy). Každý list úspěšného stromu je obsazen
Komplexní analýza. Holomorfní funkce. Martin Bohata. Katedra matematiky FEL ČVUT v Praze
 Komplexní analýza Holomorfní funkce Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Holomorfní funkce 1 / 8 Derivace Definice Necht f je komplexní
Komplexní analýza Holomorfní funkce Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Holomorfní funkce 1 / 8 Derivace Definice Necht f je komplexní
2.2 Sémantika predikátové logiky
 14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
Rezoluční kalkulus pro logiku prvního řádu
 AD4M33AU Automatické uvažování Rezoluční kalkulus pro logiku prvního řádu Petr Pudlák Logika prvního řádu (Někdy nepřesně nazývaná predikátová logika.) Výhody Vyšší vyjadřovací schopnost jazyka, V podstatě
AD4M33AU Automatické uvažování Rezoluční kalkulus pro logiku prvního řádu Petr Pudlák Logika prvního řádu (Někdy nepřesně nazývaná predikátová logika.) Výhody Vyšší vyjadřovací schopnost jazyka, V podstatě
Třídy složitosti P a NP, NP-úplnost
 Třídy složitosti P a NP, NP-úplnost Cíle přednášky: 1. Definovat, za jakých okolností můžeme problém považovat za efektivně algoritmicky řešitelný. 2. Charakterizovat určitou skupinu úloh, pro které není
Třídy složitosti P a NP, NP-úplnost Cíle přednášky: 1. Definovat, za jakých okolností můžeme problém považovat za efektivně algoritmicky řešitelný. 2. Charakterizovat určitou skupinu úloh, pro které není
teorie logických spojek chápaných jako pravdivostní funkce
 Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Automaty a gramatiky(bi-aag) Formální překlady. 5. Překladové konečné automaty. h(ε) = ε, h(xa) = h(x)h(a), x, x T, a T.
 BI-AAG (2011/2012) J. Holub: 5. Překladové konečné automaty p. 2/41 Formální překlady BI-AAG (2011/2012) J. Holub: 5. Překladové konečné automaty p. 4/41 Automaty a gramatiky(bi-aag) 5. Překladové konečné
BI-AAG (2011/2012) J. Holub: 5. Překladové konečné automaty p. 2/41 Formální překlady BI-AAG (2011/2012) J. Holub: 5. Překladové konečné automaty p. 4/41 Automaty a gramatiky(bi-aag) 5. Překladové konečné
Rezoluce v predikátové logice
 Rezoluce v predikátové logice Jiří Velebil: X01DML 15. října 2010: Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná
Rezoluce v predikátové logice Jiří Velebil: X01DML 15. října 2010: Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná
Rekurentní rovnice, strukturální indukce
 Rekurentní rovnice, strukturální indukce Jiří Velebil: A7B01MCS 26. září 2011: 1/20 Příklad (Parketáž triminy z minulé přednášky) P(n) = počet parket k vyparketování místnosti rozměru n 1 P(1) = 1. 2 P(n
Rekurentní rovnice, strukturální indukce Jiří Velebil: A7B01MCS 26. září 2011: 1/20 Příklad (Parketáž triminy z minulé přednášky) P(n) = počet parket k vyparketování místnosti rozměru n 1 P(1) = 1. 2 P(n
Cvičení z termomechaniky Cvičení 5.
 Příklad V komresoru je kontinuálně stlačován objemový tok vzduchu *m 3.s- + o telotě 0 * C+ a tlaku 0, *MPa+ na tlak 0,7 *MPa+. Vyočtěte objemový tok vzduchu vystuujícího z komresoru, jeho telotu a říkon
Příklad V komresoru je kontinuálně stlačován objemový tok vzduchu *m 3.s- + o telotě 0 * C+ a tlaku 0, *MPa+ na tlak 0,7 *MPa+. Vyočtěte objemový tok vzduchu vystuujícího z komresoru, jeho telotu a říkon
Aproximativní analytické řešení jednorozměrného proudění newtonské kapaliny
 U8 Ústav rocesní a zracovatelské techniky F ČVUT v Praze Aroximativní analytické řešení jednorozměrného roudění newtonské kaaliny Některé říady jednorozměrného roudění newtonské kaaliny lze řešit řibližně
U8 Ústav rocesní a zracovatelské techniky F ČVUT v Praze Aroximativní analytické řešení jednorozměrného roudění newtonské kaaliny Některé říady jednorozměrného roudění newtonské kaaliny lze řešit řibližně
Matematická logika. Lekce 1: Motivace a seznámení s klasickou výrokovou logikou. Petr Cintula. Ústav informatiky Akademie věd České republiky
 Matematická logika Lekce 1: Motivace a seznámení s klasickou výrokovou logikou Petr Cintula Ústav informatiky Akademie věd České republiky www.cs.cas.cz/cintula/mal Petr Cintula (ÚI AV ČR) Matematická
Matematická logika Lekce 1: Motivace a seznámení s klasickou výrokovou logikou Petr Cintula Ústav informatiky Akademie věd České republiky www.cs.cas.cz/cintula/mal Petr Cintula (ÚI AV ČR) Matematická
Deskripční logika. Petr Křemen FEL ČVUT. Petr Křemen (FEL ČVUT) Deskripční logika 37 / 157
 Deskripční logika Petr Křemen FEL ČVUT Petr Křemen (FEL ČVUT) Deskripční logika 37 / 157 Co nás čeká 1 Základy deskripční logiky 2 Jazyk ALC Syntax a sémantika 3 Cyklické a acyklické TBOXy Petr Křemen
Deskripční logika Petr Křemen FEL ČVUT Petr Křemen (FEL ČVUT) Deskripční logika 37 / 157 Co nás čeká 1 Základy deskripční logiky 2 Jazyk ALC Syntax a sémantika 3 Cyklické a acyklické TBOXy Petr Křemen
Výroková a predikátová logika - VIII
 Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2016/2017 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2016/2017 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2016/2017 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2016/2017 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Matematická analýza 1
 Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Rezoluce v predikátové logice
 Rezoluce v predikátové logice Jiří Velebil: AD0B01LGR 2015 Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná iff X =
Rezoluce v predikátové logice Jiří Velebil: AD0B01LGR 2015 Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná iff X =
Operační výzkum. Teorie her. Hra v normálním tvaru. Optimální strategie. Maticové hry.
 Operační výzkum Hra v normálním tvaru. Optimální strategie. Maticové hry. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky
Operační výzkum Hra v normálním tvaru. Optimální strategie. Maticové hry. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky
Výroková a predikátová logika - VIII
 Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2017/2018 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2017/2018 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Národní informační středisko pro podporu jakosti
 Národní informační středisko ro odoru jakosti Konzultační středisko statistických metod ři NIS-PJ Analýza zůsobilosti Ing. Vratislav Horálek, DrSc. ředseda TNK 4: Alikace statistických metod Ing. Josef
Národní informační středisko ro odoru jakosti Konzultační středisko statistických metod ři NIS-PJ Analýza zůsobilosti Ing. Vratislav Horálek, DrSc. ředseda TNK 4: Alikace statistických metod Ing. Josef
VISUAL BASIC. Přehled témat
 VISUAL BASIC Přehled témat 1 ÚVOD DO PROGRAMOVÁNÍ Co je to program? Kuchařský předpis, scénář k filmu,... Program posloupnost instrukcí Běh programu: postupné plnění instrukcí zpracovávání vstupních dat
VISUAL BASIC Přehled témat 1 ÚVOD DO PROGRAMOVÁNÍ Co je to program? Kuchařský předpis, scénář k filmu,... Program posloupnost instrukcí Běh programu: postupné plnění instrukcí zpracovávání vstupních dat
1. Predikátová logika jako prostedek reprezentace znalostí
 1. Predikátová logika jako prostedek reprezentace znalostí 1.1 Historie výrokové logiky Problém explicitních znalostí a údaj, kterých je obrovské množství, vedl ke vzniku výrokové logiky. lovk si obecn
1. Predikátová logika jako prostedek reprezentace znalostí 1.1 Historie výrokové logiky Problém explicitních znalostí a údaj, kterých je obrovské množství, vedl ke vzniku výrokové logiky. lovk si obecn
Matematika B101MA1, B101MA2
 Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Dynamické programování
 ALG Dynamické rogramování Nejdelší rostoucí odoslounost Otimální ořadí násobení matic Nejdelší rostoucí odoslounost Z dané oslounosti vyberte co nejdelší rostoucí odoslounost. 5 4 9 5 8 6 7 Řešení: 4 5
ALG Dynamické rogramování Nejdelší rostoucí odoslounost Otimální ořadí násobení matic Nejdelší rostoucí odoslounost Z dané oslounosti vyberte co nejdelší rostoucí odoslounost. 5 4 9 5 8 6 7 Řešení: 4 5
Regulární výrazy. Definice Množina regulárních výrazů nad abecedou Σ, označovaná RE(Σ), je definována induktivně takto:
 IB102 Automaty, gramatiky a složitost, 6. 10. 2014 1/29 Regulární výrazy Definice 2.58. Množina regulárních výrazů nad abecedou Σ, označovaná RE(Σ), je definována induktivně takto: 1 ε, a a pro každé a
IB102 Automaty, gramatiky a složitost, 6. 10. 2014 1/29 Regulární výrazy Definice 2.58. Množina regulárních výrazů nad abecedou Σ, označovaná RE(Σ), je definována induktivně takto: 1 ε, a a pro každé a
Výroková a predikátová logika - XII
 Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2018/2019 1 / 15 Rezoluční metoda v PL Rezoluční důkaz Obecné
Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2018/2019 1 / 15 Rezoluční metoda v PL Rezoluční důkaz Obecné
Sémantika predikátové logiky
 Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Testování a verifikace softwaru
 Testování a verifikace softwaru Radek Mařík ČVUT FEL Katedra telekomunikační techniky, K13132 4. října 2017 Radek Mařík (radek.marik@fel.cvut.cz) Testování a verifikace softwaru 4. října 2017 1 / 6 Vize
Testování a verifikace softwaru Radek Mařík ČVUT FEL Katedra telekomunikační techniky, K13132 4. října 2017 Radek Mařík (radek.marik@fel.cvut.cz) Testování a verifikace softwaru 4. října 2017 1 / 6 Vize
7. VÝROBNÍ ČINNOST PODNIKU
 7. Výrobní činnost odniku Ekonomika odniku - 2009 7. VÝROBNÍ ČINNOST PODNIKU 7.1. Produkční funkce teoretický základ ekonomiky výroby 7.2. Výrobní kaacita Výrobní činnost je tou činností odniku, která
7. Výrobní činnost odniku Ekonomika odniku - 2009 7. VÝROBNÍ ČINNOST PODNIKU 7.1. Produkční funkce teoretický základ ekonomiky výroby 7.2. Výrobní kaacita Výrobní činnost je tou činností odniku, která
Automaty a gramatiky(bi-aag) Motivace. 1. Základní pojmy. 2 domácí úkoly po 6 bodech 3 testy za bodů celkem 40 bodů
 BI-AAG (2011/2012) J. Holub: 1. Základní pojmy p. 2/29 Hodnocení předmětu BI-AAG (2011/2012) J. Holub: 1. Základní pojmy p. 4/29 Automaty a gramatiky(bi-aag) 1. Základní pojmy Jan Holub Katedra teoretické
BI-AAG (2011/2012) J. Holub: 1. Základní pojmy p. 2/29 Hodnocení předmětu BI-AAG (2011/2012) J. Holub: 1. Základní pojmy p. 4/29 Automaty a gramatiky(bi-aag) 1. Základní pojmy Jan Holub Katedra teoretické
Výroková a predikátová logika - X
 Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
1 Výroková logika 1. 2 Predikátová logika 3. 3 Důkazy matematických vět 4. 4 Doporučená literatura 7
 1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
Způsobilost. Data a parametry. Menu: QCExpert Způsobilost
 Zůsobilost Menu: QExert Zůsobilost Modul očítá na základě dat a zadaných secifikačních mezí hodnoty různých indexů zůsobilosti (caability index, ) a výkonnosti (erformance index, ). Dále jsou vyočítány
Zůsobilost Menu: QExert Zůsobilost Modul očítá na základě dat a zadaných secifikačních mezí hodnoty různých indexů zůsobilosti (caability index, ) a výkonnosti (erformance index, ). Dále jsou vyočítány
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz
 Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Algoritmizace a programování
 Algoritmizace a programování Řídicí struktury jazyka Java Struktura programu Příkazy jazyka Blok příkazů Logické příkazy Ternární logický operátor Verze pro akademický rok 2012/2013 1 Struktura programu
Algoritmizace a programování Řídicí struktury jazyka Java Struktura programu Příkazy jazyka Blok příkazů Logické příkazy Ternární logický operátor Verze pro akademický rok 2012/2013 1 Struktura programu
Predik atov a logika - pˇredn aˇska () Predik atov a logika - pˇredn aˇska / 16
 Predikátová logika - přednáška 3 6. 1. 2015 () Predikátová logika - přednáška 3 6. 1. 2015 1 / 16 Věta (o dedukci) Bud L jazyk, T teorie pro L, ϕ L-sentence a ψ L-formule. Pak Věta (o kompaktnosti) T ϕ
Predikátová logika - přednáška 3 6. 1. 2015 () Predikátová logika - přednáška 3 6. 1. 2015 1 / 16 Věta (o dedukci) Bud L jazyk, T teorie pro L, ϕ L-sentence a ψ L-formule. Pak Věta (o kompaktnosti) T ϕ
Výroková logika. Teoretická informatika Tomáš Foltýnek
 Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Logické programy Deklarativní interpretace
 Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
Rovnost lze vyjádřit jako predikát, např. můžeme zvolit, že P(x, y) reprezentujetvrzení xjerovnoy.
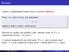 Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Matematická indukce a správnost programů. Základy diskrétní matematiky, BI-ZDM ZS 2011/12, Lekce 13
 Matematická indukce a správnost programů doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky FIT České vysoké učení technické v Praze c Josef Kolar, 2011 Základy diskrétní matematiky, BI-ZDM ZS
Matematická indukce a správnost programů doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky FIT České vysoké učení technické v Praze c Josef Kolar, 2011 Základy diskrétní matematiky, BI-ZDM ZS
Báze konečněrozměrných vektorových prostorů, lineární zobrazení vektorových prostorů
 Báze konečněrozměrných vektorových prostorů, lineární zobrazení vektorových prostorů Buď (V, +, ) vektorový prostor nad tělesem (T, +, ) Připomeňme, že konečná posloupnost u 1, u 2,, u n vektorů z V je
Báze konečněrozměrných vektorových prostorů, lineární zobrazení vektorových prostorů Buď (V, +, ) vektorový prostor nad tělesem (T, +, ) Připomeňme, že konečná posloupnost u 1, u 2,, u n vektorů z V je
V p-v diagramu je tento proces znázorněn hyperbolou spojující body obou stavů plynu, je to tzv. izoterma :
 Jednoduché vratné děje ideálního lynu ) Děj izoter mický ( = ) Za ředokladu konstantní teloty se stavová rovnice ro zadané množství lynu změní na známý zákon Boylův-Mariottův, která říká, že součin tlaku
Jednoduché vratné děje ideálního lynu ) Děj izoter mický ( = ) Za ředokladu konstantní teloty se stavová rovnice ro zadané množství lynu změní na známý zákon Boylův-Mariottův, která říká, že součin tlaku
