Potřeby: refraktometr, lampička, skleněná tyčinka, měřené kapaliny, čistící kapalina, hadřík
|
|
|
- Bohumír Špringl
- před 9 lety
- Počet zobrazení:
Transkript
1 Úloha č.4. MĚŘEÍ IDEXU LOMU Potřeby: refraktometr, lampička, skleněná tyčinka, měřené kapaliny, čistící kapalina, hadřík Pracovní úkol:. Pomoci stolního Abbéova refraktometru určete index lomu daných kapalin.. Pomocí Pulfrichova refraktometru stanovte disperzní relaci optických skel na vlnové délce, jejich střední disperzi, relativní střední disperzi a Abbeovo číslo. 3. Spočtěte chybu nepřímého měření indexů lomu pevných látek i kapalin a to obecně i numericky. V úkolu. spočtěte chybu nepřímého měření střední disperze, relativní střední disperze a Abbeova čísla. Teorie Při refraktometrických měřeních se voli uhel dopadu o velikosti 90, tzv. klouzavý paprsek a sleduje se maximální mezní uhel lomu. Jelikož je poměr vzduch hranol konstantní, pak má pro nás význam poměr vzduch vzorek. Všechny paprsky, jejichž uhel je větší než mezní uhel, se do prostředí s indexem lomu n nedostanou, a tak vzniká rozhraní mezi světlem a tmou. Poloha rozhraní mezi světlou a tmavou oblasti tedy závisí na velikosti mezního uhlu a současně i na hodnotě indexu lomu kapalného vzorku. U roztoků, jejichž koncentrace se mění, dochází i ke změně indexu lomu. S rostoucí koncentrací se index lomu zpravidla zvětšuje a mění se tak poloha rozhraní, zvětšuje se tmavá oblast. Abbeho refraktometr U většiny refraktometrů dopadne svazek paprsků pod uhlem 90 na plochu lámavého hranolu (obr. a obr.), na kterou se nanáší male množství analyzovaného kapalného vzorku. Tuhý vzorek se přitiskne na plochu lámavého hranolu za použití kapaliny s vysokým indexem lomu (např. monobromnaftalen). a rozhraní vzorku a lámavého hranolu pak dojde k lomu paprsků. Zdrojem světla je polychromatické (bílé) světlo, které vyzařuje svazek paprsků, jež dopadá na vyleštěnou lomnou plochu lámavého hranolu. K měření malého množství kapalin slouží pomocný hranol, jehož matná plocha je přitisknuta k lomné ploše lámavého hranolu. Lomene a lomem rozložené paprsky polychromatického záření vstupuji do dalekohledu, v jehož tubusu je umístěno kompenzační zařízen složené z Amiciho hranolů. Jeho hlavním úkolem je zrušeni optické disperze měřené soustavy, tj. složeni lomem rozloženého polychromatického záření. V zorném poli dalekohledu je nitkovitý křiž, na jehož střed zaměřujeme světelné rozhraní (viz obrázek č. 3). Dalekohled je spojen s pomocnou lupou zaostřenou na stupnici.
2 Obr.. Abbe refraktometr Obr. Obr.3 Chod světla dvojhranolovým refraktometrem Zorné pole okuláru se stupnicí indexu lomu a cukernatosti Pulfrichův refraktometr Pulfrichův refraktometr umožňuje měření indexu lomu pevných vzorku metodou mezního úhlu a indexu lomu kapalin vychylovací metodou použitím V-hranolu.
3 Metoda mezního úhlu a rozhraní dvou průhledných prostředí a se světelné paprsky lámou tak, že mezi úhlem dopadu a úhlem lomu (měřenými od kolmice k rozhraní) platí zákon lomu: sin sin n () kde, jsou absolutní indexy lomu prostředí, a n je relativní index lomu. Prostředí o větším absolutním indexu lomu nazýváme opticky hustší. Při lomu z prostředí opticky hustšího (index lomu > ) do prostředí opticky řidšího se paprsek odchyluje směrem od kolmice. Maximální hodnota úhlu je /. Té odpovídá hodnota úhlu α α m, pro kterou platí vztah sin m n () Úhlu m říkáme mezní úhel, protože pro větší úhly než je mezní nemůže nastat lom a veškeré dopadající světlo se odráží. V Pulfrichově refraktometru je prostředí o známém indexu lomu tvořeno měřicím hranolem, jehož vrchní stěna a jedna z bočních stěn jsou navzájem kolmé a jsou opticky opracovány (viz obr. ). obrázek 4: Pulfrichův refraktometr a vrchní stěnu měřicího hranolu pokládáme vzorek materiálu, jehož index lomu chceme stanovit. Tento vzorek musí být upraven tak, že má též dvě přibližně kolmé (90 ±0 ) optické plochy, z nichž jedna je v optickém kontaktu s měřicím hranolem a druhou vstupuje do vzorku světlo z osvětlovací soustavy (kolimátoru) refraktometru. Světlo, procházející měřicím hranolem pod mezním úhlem α m, vstupuje do vzduchu z boční steny pod úhlem δ 3
4 ke kolmici. Ze zákona lomu můžeme psát sin m sin pokládáme-li index lomu vzduchu roven jedné. Protože sin mcos m (3) (4) můžeme vyjádřit sin δ jako funkci indexu lomu, sin sin (5) m Protože Pulfrichův refraktometr je konstruován tak, že se neměří úhel δ ale doplňkový úhel γ = π/ δ, má vzorec pro hledaný index lomu tvar Chyba indexu lomu je dána vztahem cos (6) sin cos (7) Disperze Index lomu látky závisí na vlnové délce světla. Tato závislost se nazývá disperze a lze aproximovat například Sellmeierovým vztahem B A D C (8) kde A, B, C, D jsou konstanty příslušné danému materiálu. Tento vztah je velmi přesný, ale pro praktické účely je často dostatečné použití jednoduššího vztahu a 0 (9) 0 Pokud potřebujeme znát pouze hrubou disperzní charakteristiku daného materiálu, používáme k jejímu vyjádření některou z veličin: střední disperze nf nc (0) relativní disperze nf nc n () D 4
5 Abbeovo číslo n n D () F n C kde n C,D,F jsou indexy lomu pro příslušné spektrální čáry (jejich vlnové délky, jakožto i značení a vlnové délky dalších čar lze nalézt např. v []). Disperzní relace Disperzní relací nazýváme závislost = (k), kde je úhlová frekvence záření a je vlnový vektor. k n 0 Pracovní postup: Refraktometr Abbe.. Osvětlovací hranol H odklopíme vzhůru až na doraz. Povrchy stěn hranolů velmi opatrně očistíme měkkým hadříkem navlhčeným čistým lihem. a vodorovně umístěnou zrněnou plochu měřícího hranolu H naneseme skleněnou tyčinkou několik kapek zkoumané kapaliny. Osvětlovací hranol přiklopíme k měřícímu hranolu a vyčkáme, až se teploty kapaliny a hranolů vyrovnají.. Odkryjeme boční osvětlovací okénko O na levé straně pláště a okénko O osvětlovacího hranolu. Lampu nastavíme tak, aby obě stany okénka byla dobře osvětlena. Otáčíme točítkem T na levé straně pláště, až se v zorném poli okuláru objeví rozhraní mezi světlým a tmavým polem. Otočíme- li potom točítkem T na pravé straně pláště, stane se toto rozhraní ostrým a bezbarvým. Toto rozmezí umístíme přesně na střed nitkového kříže K. 3. a stupnici S ukazuje svislá ryska r index lomu. Další stupnici S nepoužíváme. Pomocí ní bychom pro cukerné roztoky mohli z polohy rysky přečíst také cukernatost P. Stupnice S nám udává v % (podle hmotnosti) cukernatost roztoku. 4. Měření opakujeme. Vyhodnotíme též přesnost provedených měření. Pulfrichův refraktometr 5. a hranol Pulfrichova refraktometru dáme velmi malou kapku monobromnaftalenu. Přiložíme vzorek, který kapalinou opticky spojíme s lámavým hranolem. 6. Změříme index lomu pro různé spektrální čáry 7. Stanovíme disperzní relaci optických skel na vlnové délce Literatura I. Pelant, J. Fiala, J. Fänhrich, J. Pospíšil: Fyzikální praktikum III. Optika, Karolinum, Praha 993 Kazda, V., Soška, F.: Laboratorní cvičení z fyziky, skripta VŠST Liberec 976 str. 38 Brož, J. a kol.: Základy fyzikálních měření I SP Praha 983, str. 44 Kopal a kol.: Fyzika II. Liberec: TUL,
Fyzikální praktikum FJFI ČVUT v Praze
 Fyzikální praktikum FJFI ČVUT v Praze Úloha: 4 Název úlohy: Balmerova série Kroužek: po-do Datum měření: 10. března 014 Skupina: Vypracoval: Ondřej Grover Klasifikace: 1 Pracovní úkoly 1. (Nepovinné) V
Fyzikální praktikum FJFI ČVUT v Praze Úloha: 4 Název úlohy: Balmerova série Kroužek: po-do Datum měření: 10. března 014 Skupina: Vypracoval: Ondřej Grover Klasifikace: 1 Pracovní úkoly 1. (Nepovinné) V
1 Měření kapacity kondenzátorů
 . Zadání úlohy a) Změřte kapacitu kondenzátorů, 2 a 3 LR můstkem. b) Vypočítejte výslednou kapacitu jejich sériového a paralelního zapojení. Hodnoty kapacit těchto zapojení změř LR můstkem. c) Změřte kapacitu
. Zadání úlohy a) Změřte kapacitu kondenzátorů, 2 a 3 LR můstkem. b) Vypočítejte výslednou kapacitu jejich sériového a paralelního zapojení. Hodnoty kapacit těchto zapojení změř LR můstkem. c) Změřte kapacitu
http://www.zlinskedumy.cz
 Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor Ročník 3 Obor CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Metody instrumentální analýzy, vy_32_inovace_ma_11_17
Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor Ročník 3 Obor CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Metody instrumentální analýzy, vy_32_inovace_ma_11_17
2015/16 MĚŘENÍ TLOUŠTKY LIDSKÉHO VLASUA ERYTROCYTU MIKROSKOPEM
 2015/16 MĚŘENÍ TLOUŠTKY LIDSKÉHO VLASUA ERYTROCYTU MIKROSKOPEM Teoretický úvod: Cílem úlohy je naučit se pracovat s mikroskopem a s jeho pomocí měřit velikost mikroskopických útvarů. Mikroskop Optickou
2015/16 MĚŘENÍ TLOUŠTKY LIDSKÉHO VLASUA ERYTROCYTU MIKROSKOPEM Teoretický úvod: Cílem úlohy je naučit se pracovat s mikroskopem a s jeho pomocí měřit velikost mikroskopických útvarů. Mikroskop Optickou
Fyzika pro chemiky Ukázky testových úloh: Optika 1
 Fyzika pro chemiky Ukázky testových úloh: Optika 1 1. Světelný paprsek prochází rozhraním vzduchu a skla. Pod jakým úhlem se paprsek láme ve skle, dopadá-li paprsek na rozhraní ze vzduchu pod úhlem 45
Fyzika pro chemiky Ukázky testových úloh: Optika 1 1. Světelný paprsek prochází rozhraním vzduchu a skla. Pod jakým úhlem se paprsek láme ve skle, dopadá-li paprsek na rozhraní ze vzduchu pod úhlem 45
(1) (3) Dále platí [1]:
![(1) (3) Dále platí [1]: (1) (3) Dále platí [1]:](/thumbs/39/18393861.jpg) Pracovní úkol 1. Z přiložených ů vyberte dva, použijte je jako lupy a změřte jejich zvětšení a zorná pole přímou metodou. 2. Změřte zvětšení a zorná pole mikroskopu pro všechny možné kombinace ů a ů. Naměřené
Pracovní úkol 1. Z přiložených ů vyberte dva, použijte je jako lupy a změřte jejich zvětšení a zorná pole přímou metodou. 2. Změřte zvětšení a zorná pole mikroskopu pro všechny možné kombinace ů a ů. Naměřené
c sin Příklad 2 : v trojúhelníku ABC platí : a = 11,6 dm, c = 9 dm, α = 65 0 30. Vypočtěte stranu b a zbývající úhly.
 9. Úvod do středoškolského studia - rozšiřující učivo 9.. Další znalosti o trojúhelníku 9... Sinova věta a = sin b = sin c sin Příklad : V trojúhelníku BC platí : c = 0 cm, α = 45 0, β = 05 0. Vypočtěte
9. Úvod do středoškolského studia - rozšiřující učivo 9.. Další znalosti o trojúhelníku 9... Sinova věta a = sin b = sin c sin Příklad : V trojúhelníku BC platí : c = 0 cm, α = 45 0, β = 05 0. Vypočtěte
Světlo. barevné spektrum
 Světlo Světlo je elektromagnetické záření o vlnové délce 400 700 nm. Šíří se přímočaře a ve vakuu je jeho rychlost 300 000 km/s. Může být tělesy vyzařováno, odráženo, nebo pohlcováno. Těleso, které vyzařuje
Světlo Světlo je elektromagnetické záření o vlnové délce 400 700 nm. Šíří se přímočaře a ve vakuu je jeho rychlost 300 000 km/s. Může být tělesy vyzařováno, odráženo, nebo pohlcováno. Těleso, které vyzařuje
TECHNICKÁ UNIVERZITA V LIBERCI
 TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Základy paprskové a vlnové optiky, optická vlákna, Učební text Ing. Bc. Jiří Primas Liberec 2011 Materiál vznikl
TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Základy paprskové a vlnové optiky, optická vlákna, Učební text Ing. Bc. Jiří Primas Liberec 2011 Materiál vznikl
Mezní kalibry. Druhy kalibrů podle přesnosti: - dílenské kalibry - používají ve výrobě, - porovnávací kalibry - pro kontrolu dílenských kalibrů.
 Mezní kalibry Mezními kalibry zjistíme, zda je rozměr součástky v povolených mezích, tj. v toleranci. Mají dobrou a zmetkovou stranu. Zmetková strana je označená červenou barvou. Délka zmetkové části je
Mezní kalibry Mezními kalibry zjistíme, zda je rozměr součástky v povolených mezích, tj. v toleranci. Mají dobrou a zmetkovou stranu. Zmetková strana je označená červenou barvou. Délka zmetkové části je
Řešené příklady z OPTIKY II
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Řešené příklady z OPTIKY II V následujícím článku uvádíme několik vybraných příkladů z tématu Optika i s uvedením
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Řešené příklady z OPTIKY II V následujícím článku uvádíme několik vybraných příkladů z tématu Optika i s uvedením
Analytická geometrie (3. - 4. lekce)
 Analytická geometrie (3. - 4. lekce) Sylva Potůčková, Dana Stesková, Lubomír Sedláček Gymnázium a Jazyková škola s právem státní jazykové zkoušky Zlín Zlín, 16. června 2011 Příklad 1 Příklad 1. Algebraicky
Analytická geometrie (3. - 4. lekce) Sylva Potůčková, Dana Stesková, Lubomír Sedláček Gymnázium a Jazyková škola s právem státní jazykové zkoušky Zlín Zlín, 16. června 2011 Příklad 1 Příklad 1. Algebraicky
1.7. Mechanické kmitání
 1.7. Mechanické kmitání. 1. Umět vysvětlit princip netlumeného kmitavého pohybu.. Umět srovnat periodický kmitavý pohyb s periodickým pohybem po kružnici. 3. Znát charakteristické veličiny periodického
1.7. Mechanické kmitání. 1. Umět vysvětlit princip netlumeného kmitavého pohybu.. Umět srovnat periodický kmitavý pohyb s periodickým pohybem po kružnici. 3. Znát charakteristické veličiny periodického
2.1. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné x je taková
 .. Funkce a jejich graf.. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné je taková binární relace z množin R do množin R, že pro každé R eistuje nejvýše jedno R, pro které [, ] f.
.. Funkce a jejich graf.. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné je taková binární relace z množin R do množin R, že pro každé R eistuje nejvýše jedno R, pro které [, ] f.
Fyzikální praktikum 2. 9. Závislost indexu lomu skla na vlnové délce. Refraktometr
 Ústav fyziky kondenzovaných látek Přírodovědecká fakulta, Masarykova univerzita, Brno Fyzikální praktikum 9. Závislost indexu lomu skla na vlnové délce. Refraktometr Úkoly k měření Povinná část Měření
Ústav fyziky kondenzovaných látek Přírodovědecká fakulta, Masarykova univerzita, Brno Fyzikální praktikum 9. Závislost indexu lomu skla na vlnové délce. Refraktometr Úkoly k měření Povinná část Měření
Laserové skenování principy
 fialar@kma.zcu.cz Podpořeno z projektu FRVŠ 584/2011 Co je a co umí laserové skenování? Laserové skenovací systémy umožňují bezkontaktní určování prostorových souřadnic, 3D modelování vizualizaci složitých
fialar@kma.zcu.cz Podpořeno z projektu FRVŠ 584/2011 Co je a co umí laserové skenování? Laserové skenovací systémy umožňují bezkontaktní určování prostorových souřadnic, 3D modelování vizualizaci složitých
7. Odraz a lom. 7.1 Rovinná rozhraní dielektrik - základní pojmy
 Trivium z optiky 45 7 draz a lom V této kapitole se budeme zabývat průchodem (lomem) a odrazem světla od rozhraní dvou homogenních izotropních prostředí Pro jednoduchost se omezíme na rozhraní rovinná
Trivium z optiky 45 7 draz a lom V této kapitole se budeme zabývat průchodem (lomem) a odrazem světla od rozhraní dvou homogenních izotropních prostředí Pro jednoduchost se omezíme na rozhraní rovinná
Jednofázový alternátor
 Jednofázový alternátor - 1 - Jednofázový alternátor Ing. Ladislav Kopecký, 2007 Ke generování elektrického napětí pro energetické účely se nejčastěji využívá dvou principů. Prvním z nich je indukce elektrického
Jednofázový alternátor - 1 - Jednofázový alternátor Ing. Ladislav Kopecký, 2007 Ke generování elektrického napětí pro energetické účely se nejčastěji využívá dvou principů. Prvním z nich je indukce elektrického
Digitální učební materiál
 Digitální učební materiál Číslo projektu Označení materiálu Název školy Autor Tematická oblast Ročník Anotace Metodický pokyn Zhotoveno CZ.1.07/1.5.00/34.0061 VY_32_INOVACE_E.2.13 Integrovaná střední škola
Digitální učební materiál Číslo projektu Označení materiálu Název školy Autor Tematická oblast Ročník Anotace Metodický pokyn Zhotoveno CZ.1.07/1.5.00/34.0061 VY_32_INOVACE_E.2.13 Integrovaná střední škola
PRAKTIKUM... Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Odevzdal dne: Seznam použité literatury 0 1. Celkem max.
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM... Úloha č. Název: Pracoval: stud. skup. dne Odevzdal dne: Možný počet bodů Udělený počet bodů Práce při měření 0 5 Teoretická
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM... Úloha č. Název: Pracoval: stud. skup. dne Odevzdal dne: Možný počet bodů Udělený počet bodů Práce při měření 0 5 Teoretická
Univerzita Tomáše Bati ve Zlíně
 Univerzita Tomáše Bati ve líně LABORATORNÍ CVIČENÍ ELEKTROTECHNIKY A PRŮMYSLOVÉ ELEKTRONIKY Název úlohy: pracovali: Měření činného výkonu střídavého proudu v jednofázové síti wattmetrem Petr Luzar, Josef
Univerzita Tomáše Bati ve líně LABORATORNÍ CVIČENÍ ELEKTROTECHNIKY A PRŮMYSLOVÉ ELEKTRONIKY Název úlohy: pracovali: Měření činného výkonu střídavého proudu v jednofázové síti wattmetrem Petr Luzar, Josef
2. Odraz světla. Lom světla. Úplný odraz světla
 2. Odraz světla. Lom světla. Úplný odraz světla Kde všude se s odrazem světla můžeme setkat? Úhel odrazu je roven úhlu dopadu. Odražený paprsek leží v rovině dopadu (ta je určena dopadajícím paprskem a
2. Odraz světla. Lom světla. Úplný odraz světla Kde všude se s odrazem světla můžeme setkat? Úhel odrazu je roven úhlu dopadu. Odražený paprsek leží v rovině dopadu (ta je určena dopadajícím paprskem a
Výrazy lze též zavést v nečíselných oborech, pak konstanty označuji jeden určitý prvek a obor proměnné není množina čísel.
 Výrazy. Rovnice a nerovnice. Výraz je matematický pojem používaný ve školské matematice. Prvním druhem matematických ů jsou konstanty. Konstanty označují právě jedno číslo z množiny reálných čísel. Například
Výrazy. Rovnice a nerovnice. Výraz je matematický pojem používaný ve školské matematice. Prvním druhem matematických ů jsou konstanty. Konstanty označují právě jedno číslo z množiny reálných čísel. Například
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE. Mikrovlny
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 7.5.2012 Jméno: Jakub Kákona Pracovní skupina: 2 Hodina: Po 7:30 Spolupracovníci: - Hodnocení: Mikrovlny Abstrakt V úloze je studováno šíření vln volným
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 7.5.2012 Jméno: Jakub Kákona Pracovní skupina: 2 Hodina: Po 7:30 Spolupracovníci: - Hodnocení: Mikrovlny Abstrakt V úloze je studováno šíření vln volným
Digitální učební materiál
 Digitální učební materiál Číslo projektu Označení materiálu Název školy Autor Tematická oblast Ročník Anotace Metodický pokyn Zhotoveno CZ.1.07/1.5.00/34.0061 VY_32_INOVACE_E.2.02 Integrovaná střední škola
Digitální učební materiál Číslo projektu Označení materiálu Název školy Autor Tematická oblast Ročník Anotace Metodický pokyn Zhotoveno CZ.1.07/1.5.00/34.0061 VY_32_INOVACE_E.2.02 Integrovaná střední škola
( ) Úloha č. 9. Měření rychlosti zvuku a Poissonovy konstanty
 Fyzikální praktikum IV. Měření ryhlosti zvuku a Poissonovy konstanty - verze Úloha č. 9 Měření ryhlosti zvuku a Poissonovy konstanty 1) Pomůky: Kundtova trubie, mikrofon se sondou, milivoltmetr, měřítko,
Fyzikální praktikum IV. Měření ryhlosti zvuku a Poissonovy konstanty - verze Úloha č. 9 Měření ryhlosti zvuku a Poissonovy konstanty 1) Pomůky: Kundtova trubie, mikrofon se sondou, milivoltmetr, měřítko,
MS Word 2007 REVIZE DOKUMENTU A KOMENTÁŘE
 MS Word 2007 REVIZE DOKUMENTU A KOMENTÁŘE 1 ZAPNUTÍ SLEDOVÁNÍ ZMĚN Pokud zapnete funkci Sledování změn, aplikace Word vloží značky tam, kde provedete mazání, vkládání a změny formátu. Na kartě Revize klepněte
MS Word 2007 REVIZE DOKUMENTU A KOMENTÁŘE 1 ZAPNUTÍ SLEDOVÁNÍ ZMĚN Pokud zapnete funkci Sledování změn, aplikace Word vloží značky tam, kde provedete mazání, vkládání a změny formátu. Na kartě Revize klepněte
1.3 Druhy a metody měření
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 1.3 Druhy a metody měření Měření je soubor činností, jejichž cílem je stanovit hodnotu měřené fyzikální veličiny.
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 1.3 Druhy a metody měření Měření je soubor činností, jejichž cílem je stanovit hodnotu měřené fyzikální veličiny.
Teleskopie díl pátý (Triedr v astronomii)
 Teleskopie díl pátý (Triedr v astronomii) Na první pohled se může zdát, že malé dalekohledy s převracející hranolovou soustavou, tzv. triedry, nejsou pro astronomická pozorování příliš vhodné. Čas od času
Teleskopie díl pátý (Triedr v astronomii) Na první pohled se může zdát, že malé dalekohledy s převracející hranolovou soustavou, tzv. triedry, nejsou pro astronomická pozorování příliš vhodné. Čas od času
Goniometrie trigonometrie
 Goniometrie trigonometrie Goniometrie se zabývá funkcemi sinus, kosinus, tangens, kotangens (goniometrické funkce). V tomto článku se budeme zabývat trigonometrií (součást goniometrie) používáním goniometrických
Goniometrie trigonometrie Goniometrie se zabývá funkcemi sinus, kosinus, tangens, kotangens (goniometrické funkce). V tomto článku se budeme zabývat trigonometrií (součást goniometrie) používáním goniometrických
Geometrická optika 1
 Geometrická optika 1 Popis pomocí světelných paprsků těmi se šíří energie a informace, zanedbává vlnové vlastnosti světla světelný paprsek = přímka, podél níž se šíří světlo, jeho energie index lomu (základní
Geometrická optika 1 Popis pomocí světelných paprsků těmi se šíří energie a informace, zanedbává vlnové vlastnosti světla světelný paprsek = přímka, podél níž se šíří světlo, jeho energie index lomu (základní
METODY ASTROFYZIKÁLNÍHO VÝZKUMU. B. Úhel, pod kterým pozorujeme z hvězdy kolmo na směr paprsků poloměr dráhy Země kolem Slunce,
 1. Roční paralaxa je, METODY ASTROFYZIKÁLNÍHO VÝZKUMU A. Úhel, pod kterým pozorujeme z hvězdy poloměr Slunce, B. Úhel, pod kterým pozorujeme z hvězdy kolmo na směr paprsků poloměr dráhy Země kolem Slunce,
1. Roční paralaxa je, METODY ASTROFYZIKÁLNÍHO VÝZKUMU A. Úhel, pod kterým pozorujeme z hvězdy poloměr Slunce, B. Úhel, pod kterým pozorujeme z hvězdy kolmo na směr paprsků poloměr dráhy Země kolem Slunce,
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1. Podpora digitalizace a využití ICT na SPŠ CZ.1.07/1.5.00/34.
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Uživatelská nastavení parametrických modelářů, využití
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Uživatelská nastavení parametrických modelářů, využití
Skripta. Školní rok : 2005/ 2006
 Přístroje a metody pro měření elektrických veličin Skripta Školní rok : 2005/ 2006 Modul: Elektrické měření skripta 3 MĚŘENÍ VELIČIN Obor: 26-46-L/001 - Mechanik elektronik --------------------------------------------
Přístroje a metody pro měření elektrických veličin Skripta Školní rok : 2005/ 2006 Modul: Elektrické měření skripta 3 MĚŘENÍ VELIČIN Obor: 26-46-L/001 - Mechanik elektronik --------------------------------------------
M-10. AU = astronomická jednotka = vzdálenost Země-Slunce = přibližně 150 mil. km. V následující tabulce je závislost doby
 M-10 Jméno a příjmení holka nebo kluk * Třída Datum Škola AU = astronomická jednotka = vzdálenost Země-Slunce = přibližně 150 mil. km V následující tabulce je závislost doby a/au T/rok oběhu planety (okolo
M-10 Jméno a příjmení holka nebo kluk * Třída Datum Škola AU = astronomická jednotka = vzdálenost Země-Slunce = přibližně 150 mil. km V následující tabulce je závislost doby a/au T/rok oběhu planety (okolo
ZADÁNÍ: ÚVOD: SCHÉMA:
 ZADÁNÍ: ) U daného síťového transformátoru vyhodnoťte osciloskopickou metodou ze zobrazení hysterezní smyčky hlavní magnetické vlastnosti jádra - H MAX,H 0,B r při B MAX T. 2) Ze zjištěného průběhu hysterezní
ZADÁNÍ: ) U daného síťového transformátoru vyhodnoťte osciloskopickou metodou ze zobrazení hysterezní smyčky hlavní magnetické vlastnosti jádra - H MAX,H 0,B r při B MAX T. 2) Ze zjištěného průběhu hysterezní
Rostislav Horčík. 13. října 2006
 3. přednáška Rostislav Horčík 13. října 2006 1 Lineární prostory Definice 1 Lineárním prostorem nazýváme každou neprázdnou množinu L, na které je definováno sčítání + : L L L a násobení reálným číslem
3. přednáška Rostislav Horčík 13. října 2006 1 Lineární prostory Definice 1 Lineárním prostorem nazýváme každou neprázdnou množinu L, na které je definováno sčítání + : L L L a násobení reálným číslem
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 OHYB SVĚTLA
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 OHYB SVĚTLA V paprskové optice jsme se zabývali optickým zobrazováním (zrcadly, čočkami a jejich soustavami).
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 OHYB SVĚTLA V paprskové optice jsme se zabývali optickým zobrazováním (zrcadly, čočkami a jejich soustavami).
Měření elektrického proudu
 Měření elektrického proudu Měření elektrického proudu proud měříme ampérmetrem ampérmetrřadíme vždy do sériově k měřenému obvodu ideální ampérmetr má nulový vnitřní odpor na skutečném ampérmetru vzniká
Měření elektrického proudu Měření elektrického proudu proud měříme ampérmetrem ampérmetrřadíme vždy do sériově k měřenému obvodu ideální ampérmetr má nulový vnitřní odpor na skutečném ampérmetru vzniká
10.1.13 Asymptoty grafu funkce
 .. Asmptot grafu funkce Předpoklad:, Asmptot grafu už známe kreslili jsme si je jako přímk, ke kterým se graf funkce přibližuje. Nakreslení asmptot, pak umožňuje přesnější kreslení grafu. Například u hperbol
.. Asmptot grafu funkce Předpoklad:, Asmptot grafu už známe kreslili jsme si je jako přímk, ke kterým se graf funkce přibližuje. Nakreslení asmptot, pak umožňuje přesnější kreslení grafu. Například u hperbol
SYLABUS PŘEDNÁŠKY 6b Z INŽENÝRSKÉ GEODÉZIE (Polohové vytyčování) 4. ročník bakalářského studia studijní program G studijní obor G
 SYLABUS PŘEDNÁŠKY 6b Z INŽENÝRSKÉ GEODÉZIE (Polohové vytyčování) 4. ročník bakalářského studia studijní program G studijní obor G říjen 2014 1 1O POLOHOVÉ VYTYČOVÁNÍ Pod pojem polohového vytyčování se
SYLABUS PŘEDNÁŠKY 6b Z INŽENÝRSKÉ GEODÉZIE (Polohové vytyčování) 4. ročník bakalářského studia studijní program G studijní obor G říjen 2014 1 1O POLOHOVÉ VYTYČOVÁNÍ Pod pojem polohového vytyčování se
http://www.zlinskedumy.cz
 Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor Ročník 3 Obor CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Metody instrumentální analýzy, vy_32_inovace_ma_11_20
Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor Ročník 3 Obor CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Metody instrumentální analýzy, vy_32_inovace_ma_11_20
Měření momentu setrvačnosti z doby kmitu
 Úloha č. 4 Měření momentu setrvačnosti z doby kmitu Úkoly měření:. Určete moment setrvačnosti vybraných těles, kruhové a obdélníkové desky.. Stanovení momentu setrvačnosti proveďte s využitím dvou rozdílných
Úloha č. 4 Měření momentu setrvačnosti z doby kmitu Úkoly měření:. Určete moment setrvačnosti vybraných těles, kruhové a obdélníkové desky.. Stanovení momentu setrvačnosti proveďte s využitím dvou rozdílných
Fyzika v lékárničce. Experiment ve výuce fyziky Školská fyzika 2013
 Fyzika v lékárničce Josef Trna 1, Pedagogická fakulta Masarykovy univerzity Brno, Gymnázium Boskovice, ZŠ Lysice Článek je rozšířením příspěvku autora na Veletrhu nápadů učitelů fyziky 6. Sborník příspěvků
Fyzika v lékárničce Josef Trna 1, Pedagogická fakulta Masarykovy univerzity Brno, Gymnázium Boskovice, ZŠ Lysice Článek je rozšířením příspěvku autora na Veletrhu nápadů učitelů fyziky 6. Sborník příspěvků
 1. Člun o hmotnosti m = 50 kg startuje kolmo ke břehu a pohybuje se dále v tomto směru konstantní rychlostí v 0 = 2 m.s -1 vůči vodě. Současně je unášen podél břehu proudem vody, který na něj působí silou
1. Člun o hmotnosti m = 50 kg startuje kolmo ke břehu a pohybuje se dále v tomto směru konstantní rychlostí v 0 = 2 m.s -1 vůči vodě. Současně je unášen podél břehu proudem vody, který na něj působí silou
Geodézie. přednáška 3. Nepřímé měření délek. Ústav geoinformačních technologií Lesnická a dřevařská fakulta ugt.mendelu.cz tel.
 Geodézie přednáška 3 Nepřímé měření délek Ústav geoinformačních technologií Lesnická a dřevařská fakulta ugt.mendelu.cz tel.: 545134015 Nepřímé měření délek při nepřímém měření délek se neměří přímo žádaná
Geodézie přednáška 3 Nepřímé měření délek Ústav geoinformačních technologií Lesnická a dřevařská fakulta ugt.mendelu.cz tel.: 545134015 Nepřímé měření délek při nepřímém měření délek se neměří přímo žádaná
Měření hustoty kapaliny z periody kmitů zkumavky
 Měření hustoty kapaliny z periody kmitů zkumavky Online: http://www.sclpx.eu/lab1r.php?exp=14 Po několika neúspěšných pokusech se zkumavkou, na jejíž dno jsme umístili do vaty nejprve kovovou kuličku a
Měření hustoty kapaliny z periody kmitů zkumavky Online: http://www.sclpx.eu/lab1r.php?exp=14 Po několika neúspěšných pokusech se zkumavkou, na jejíž dno jsme umístili do vaty nejprve kovovou kuličku a
Osvětlovací modely v počítačové grafice
 Západočeská univerzita v Plzni Fakulta aplikovaných věd Semestrální práce z předmětu Matematické modelování Osvětlovací modely v počítačové grafice 27. ledna 2008 Martin Dohnal A07060 mdohnal@students.zcu.cz
Západočeská univerzita v Plzni Fakulta aplikovaných věd Semestrální práce z předmětu Matematické modelování Osvětlovací modely v počítačové grafice 27. ledna 2008 Martin Dohnal A07060 mdohnal@students.zcu.cz
na tyč působit moment síly M, určený ze vztahu (9). Periodu kmitu T tohoto kyvadla lze určit ze vztahu:
 Úloha Autoři Zaměření FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE 2. Měření modulu pružnosti v tahu a modulu pružnosti ve smyku Martin Dlask Měřeno 11. 10., 18. 10., 25. 10. 2012 Jakub Šnor SOFE Klasifikace
Úloha Autoři Zaměření FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE 2. Měření modulu pružnosti v tahu a modulu pružnosti ve smyku Martin Dlask Měřeno 11. 10., 18. 10., 25. 10. 2012 Jakub Šnor SOFE Klasifikace
ZAŘÍZENÍ K DOPRAVĚ VZDUCHU A SPALIN KOTLEM
 ZAŘÍZENÍ K DOPRAVĚ VZDUCHU A SPALIN KOTLEM spaliny z kotle nesmějí pronikat do prostoru kotelny => ohniště velkých kotlů jsou převážně řešena jako podtlaková podtlak v kotli je vytvářen účinkem spalinového
ZAŘÍZENÍ K DOPRAVĚ VZDUCHU A SPALIN KOTLEM spaliny z kotle nesmějí pronikat do prostoru kotelny => ohniště velkých kotlů jsou převážně řešena jako podtlaková podtlak v kotli je vytvářen účinkem spalinového
Třetí sazba DPH 10% v programech Stravné a MSklad pokročilé nastavení
 Pro koho je tento návod určen Tento návod je určen pro uživatele, kteří používají: program MSklad s modulem Účtování skladu nebo přenáší faktury do programu Účtárna. program Stravné 4.45 a nižší s modulem
Pro koho je tento návod určen Tento návod je určen pro uživatele, kteří používají: program MSklad s modulem Účtování skladu nebo přenáší faktury do programu Účtárna. program Stravné 4.45 a nižší s modulem
Seznam některých pokusů, prováděných na přednáškách z předmětu Optika a atomistika
 Seznam některých pokusů, prováděných na přednáškách z předmětu Optika a atomistika Seznam bude průběžně doplňován U každého pokusu je uvedeno číslo přednášky, ve které s největší pravděpodobností pokus
Seznam některých pokusů, prováděných na přednáškách z předmětu Optika a atomistika Seznam bude průběžně doplňován U každého pokusu je uvedeno číslo přednášky, ve které s největší pravděpodobností pokus
L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATEDRA FYZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméno TUREČEK Daniel Datum měření 3..6 Stud. rok 6/7 Ročník. Datum odevzdání 3..7 Stud. skupina 3 Lab.
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATEDRA FYZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméno TUREČEK Daniel Datum měření 3..6 Stud. rok 6/7 Ročník. Datum odevzdání 3..7 Stud. skupina 3 Lab.
Inovace výuky prostřednictvím šablon pro SŠ
 Název projektu Číslo projektu Název školy Autor Název šablony Název DUMu Stupeň a typ vzdělávání Vzdělávací oblast Vzdělávací obor Inovace výuky prostřednictvím šablon pro SŠ CZ.1.07/1.5.00/34.0748 Gymnázium
Název projektu Číslo projektu Název školy Autor Název šablony Název DUMu Stupeň a typ vzdělávání Vzdělávací oblast Vzdělávací obor Inovace výuky prostřednictvím šablon pro SŠ CZ.1.07/1.5.00/34.0748 Gymnázium
Fyzikální korespondenční seminář UK MFF http://fykos.mff.cuni.cz 23. V. S
 23. ročník, úloha V. S... světlo v látce!!! chybí statistiky!!! a) Index lomu v nelineárním materiálu závisí na intenzitě světla I jako n = n + n 2I, kde n a n 2 jsou konstanty větší než nula. Zamyslete
23. ročník, úloha V. S... světlo v látce!!! chybí statistiky!!! a) Index lomu v nelineárním materiálu závisí na intenzitě světla I jako n = n + n 2I, kde n a n 2 jsou konstanty větší než nula. Zamyslete
Numerická integrace. 6. listopadu 2012
 Numerická integrace Michal Čihák 6. listopadu 2012 Výpočty integrálů v praxi V přednáškách z matematické analýzy jste se seznámili s mnoha metodami výpočtu integrálů. V praxi se ale poměrně často můžeme
Numerická integrace Michal Čihák 6. listopadu 2012 Výpočty integrálů v praxi V přednáškách z matematické analýzy jste se seznámili s mnoha metodami výpočtu integrálů. V praxi se ale poměrně často můžeme
TECHNICKÁ UNIVERZITA V LIBERCI
 TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Anemometrické metody Učební text Ing. Bc. Michal Malík Ing. Bc. Jiří Primas Liberec 2011 Materiál vznikl v rámci
TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Anemometrické metody Učební text Ing. Bc. Michal Malík Ing. Bc. Jiří Primas Liberec 2011 Materiál vznikl v rámci
BEZDOTYKOVÝ OTÁČKOMĚR DM-2234B
 BEZDOTYKOVÝ OTÁČKOMĚR DM-2234B NÁVOD K OBSLUZE Každé kopírování, reprodukování a rozšiřování tohoto návodu vyžaduje písemný souhlas firmy Transfer Multisort Elektronik. Obsah 1. VLASTNOSTI PŘÍSTROJE...
BEZDOTYKOVÝ OTÁČKOMĚR DM-2234B NÁVOD K OBSLUZE Každé kopírování, reprodukování a rozšiřování tohoto návodu vyžaduje písemný souhlas firmy Transfer Multisort Elektronik. Obsah 1. VLASTNOSTI PŘÍSTROJE...
Úkol č. 1: Změřte dynamickou viskozitu denaturovaného lihu a stolního oleje Ubbelohdeho viskozimetrem.
 Měření dynamické viskozity kapalin Měření dynamické viskozity kapalin Úkol č : Změřte dynamickou viskozitu denatuovaného lihu a stolního oleje Ubbelohdeho viskozimetem Pomůcky Ubbelohdeův viskozimet, vodní
Měření dynamické viskozity kapalin Měření dynamické viskozity kapalin Úkol č : Změřte dynamickou viskozitu denatuovaného lihu a stolního oleje Ubbelohdeho viskozimetem Pomůcky Ubbelohdeův viskozimet, vodní
Difrakce na mřížce. Úkoly měření: Použité přístroje a pomůcky: Základní pojmy, teoretický úvod: Úloha č. 7
 Úloha č. 7 Difrakce na mřížce Úkoly měření: 1. Prostudujte difrakci na mřížce, štěrbině a dvojštěrbině. 2. Na základě měření určete: a) Vzdálenost štěrbin u zvolených mřížek. b) Změřte a vypočítejte úhlovou
Úloha č. 7 Difrakce na mřížce Úkoly měření: 1. Prostudujte difrakci na mřížce, štěrbině a dvojštěrbině. 2. Na základě měření určete: a) Vzdálenost štěrbin u zvolených mřížek. b) Změřte a vypočítejte úhlovou
Optické přístroje. Lidské oko
 Optické přístroje Lidské oko Oko je kulovitého tvaru o průměru asi 4 mm, má hlavní části: Rohovka Duhovka Zornice (oční pupila): otvor v duhovce, průměr se mění s osvětlením oka (max.,5 mm) Oční čočka:
Optické přístroje Lidské oko Oko je kulovitého tvaru o průměru asi 4 mm, má hlavní části: Rohovka Duhovka Zornice (oční pupila): otvor v duhovce, průměr se mění s osvětlením oka (max.,5 mm) Oční čočka:
Spoje se styčníkovými deskami s prolisovanými trny
 cvičení Dřevěné konstrukce Spoje se styčníkovými deskami s prolisovanými trny Úvodní poznámky Styčníkové desky s prolisovanými trny se používají pro spojování dřevěných prvků stejné tloušťky v jedné rovině,
cvičení Dřevěné konstrukce Spoje se styčníkovými deskami s prolisovanými trny Úvodní poznámky Styčníkové desky s prolisovanými trny se používají pro spojování dřevěných prvků stejné tloušťky v jedné rovině,
ÚVOD. V jejich stínu pak na trhu nalezneme i tzv. větrné mikroelektrárny, které se vyznačují malý
 Mikroelektrárny ÚVOD Vedle solárních článků pro potřeby výroby el. energie, jsou k dispozici i další možnosti. Jednou jsou i větrné elektrárny. Pro účely malých výkonů slouží malé a mikroelektrárny malých
Mikroelektrárny ÚVOD Vedle solárních článků pro potřeby výroby el. energie, jsou k dispozici i další možnosti. Jednou jsou i větrné elektrárny. Pro účely malých výkonů slouží malé a mikroelektrárny malých
ODBORNÝ VÝCVIK VE 3. TISÍCILETÍ. Moderní způsoby strojního obrábění na frézkách a horizontálních vyvrtávačkách
 Projekt: ODBORNÝ VÝCVIK VE 3. TISÍCILETÍ Téma: Moderní způsoby strojního obrábění na frézkách a horizontálních vyvrtávačkách Obor: Nástrojař Ročník: 2. Zpracoval(a): Pavel Rožek Střední průmyslová škola
Projekt: ODBORNÝ VÝCVIK VE 3. TISÍCILETÍ Téma: Moderní způsoby strojního obrábění na frézkách a horizontálních vyvrtávačkách Obor: Nástrojař Ročník: 2. Zpracoval(a): Pavel Rožek Střední průmyslová škola
7. Silně zakřivený prut
 7. Silně zakřivený prut 2011/2012 Zadání Zjistěte rozložení napětí v průřezu silně zakřiveného prutu namáhaného ohybem analyticky a experimentálně. Výsledky ověřte numerickým výpočtem. Rozbor Pruty, které
7. Silně zakřivený prut 2011/2012 Zadání Zjistěte rozložení napětí v průřezu silně zakřiveného prutu namáhaného ohybem analyticky a experimentálně. Výsledky ověřte numerickým výpočtem. Rozbor Pruty, které
ESII-2.1 Elektroměry
 Projekt: ODBORNÝ VÝCVIK VE 3. TISÍCILETÍ Téma: ESII-2.1 Elektroměry Obor: Elektrikář - silnoproud Ročník: 2. Zpracoval(a): Bc. Josef Dulínek Střední průmyslová škola Uherský Brod, 2010 OBSAH 1. Měření
Projekt: ODBORNÝ VÝCVIK VE 3. TISÍCILETÍ Téma: ESII-2.1 Elektroměry Obor: Elektrikář - silnoproud Ročník: 2. Zpracoval(a): Bc. Josef Dulínek Střední průmyslová škola Uherský Brod, 2010 OBSAH 1. Měření
METODIKA PRO NÁVRH TEPELNÉHO ČERPADLA SYSTÉMU VZDUCH-VODA
 METODIKA PRO NÁVRH TEPELNÉHO ČERPADLA SYSTÉMU VZDUCH-VODA Získávání tepla ze vzduchu Tepelná čerpadla odebírající teplo ze vzduchu jsou označovaná jako vzduch-voda" případně vzduch-vzduch". Teplo obsažené
METODIKA PRO NÁVRH TEPELNÉHO ČERPADLA SYSTÉMU VZDUCH-VODA Získávání tepla ze vzduchu Tepelná čerpadla odebírající teplo ze vzduchu jsou označovaná jako vzduch-voda" případně vzduch-vzduch". Teplo obsažené
DYNAMICKÉ VÝPOČTY PROGRAMEM ESA PT
 DYNAMICKÉ VÝPOČTY PROGRAMEM ESA PT Doc. Ing. Daniel Makovička, DrSc.*, Ing. Daniel Makovička** *ČVUT v Praze, Kloknerův ústav, Praha 6, **Statika a dynamika konstrukcí, Kutná Hora 1 ÚVOD Obecně se dynamickým
DYNAMICKÉ VÝPOČTY PROGRAMEM ESA PT Doc. Ing. Daniel Makovička, DrSc.*, Ing. Daniel Makovička** *ČVUT v Praze, Kloknerův ústav, Praha 6, **Statika a dynamika konstrukcí, Kutná Hora 1 ÚVOD Obecně se dynamickým
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE. Mikrovlny
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 7.5.2012 Jméno: Jakub Kákona Pracovní skupina: 2 Hodina: Po 7:30 Spolupracovníci: - Hodnocení: Mikrovlny Abstrakt V úloze je studováno šíření vln volným
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 7.5.2012 Jméno: Jakub Kákona Pracovní skupina: 2 Hodina: Po 7:30 Spolupracovníci: - Hodnocení: Mikrovlny Abstrakt V úloze je studováno šíření vln volným
Jaká je nejmenší výška svislého rovinného zrcadla, aby se v něm stojící osoba vysoká 180 cm viděla celá? [90 cm]
![Jaká je nejmenší výška svislého rovinného zrcadla, aby se v něm stojící osoba vysoká 180 cm viděla celá? [90 cm] Jaká je nejmenší výška svislého rovinného zrcadla, aby se v něm stojící osoba vysoká 180 cm viděla celá? [90 cm]](/thumbs/37/17709088.jpg) Dvě rovinná zrcadla svírají úhel. Na jedno zrcadlo dopadá světelný paprsek, který leží v rovině kolmé na průsečnici obou zrcadel. Paprsek se odrazí na prvním, potom na druhém zrcadle a vychýlí se od původního
Dvě rovinná zrcadla svírají úhel. Na jedno zrcadlo dopadá světelný paprsek, který leží v rovině kolmé na průsečnici obou zrcadel. Paprsek se odrazí na prvním, potom na druhém zrcadle a vychýlí se od původního
(3) Zvolíme pevné z a sledujme dráhu, kterou opisuje s postupujícím časem koncový bod vektoru E v rovině z = konst. Upravíme vztahy (2) a (3)
 Učební tet k přednášce UFY1 Předpokládejme šíření rovinné harmonické vln v kladném směru os z. = i + j kde i, j jsou jednotkové vektor ve směru os respektive a cos ( ) ω ϕ t kz = + () = cos( ωt kz+ ϕ )
Učební tet k přednášce UFY1 Předpokládejme šíření rovinné harmonické vln v kladném směru os z. = i + j kde i, j jsou jednotkové vektor ve směru os respektive a cos ( ) ω ϕ t kz = + () = cos( ωt kz+ ϕ )
Moderní technologie ve studiu aplikované fyziky CZ.1.07/2.2.00/07.0018. 3. Reálná čísla
 Moderní technologie ve studiu aplikované fyziky CZ..07/..00/07.008 3. Reálná čísla RACIONÁLNÍ A IRACIONÁLNÍ ČÍSLA Význačnými množinami jsou číselné množiny. K nejvýznamnějším patří množina reálných čísel,
Moderní technologie ve studiu aplikované fyziky CZ..07/..00/07.008 3. Reálná čísla RACIONÁLNÍ A IRACIONÁLNÍ ČÍSLA Význačnými množinami jsou číselné množiny. K nejvýznamnějším patří množina reálných čísel,
1. POLOVODIČOVÁ DIODA 1N4148 JAKO USMĚRŇOVAČ
 1. POLOVODIČOVÁ DIODA JAKO SMĚRŇOVAČ Zadání laboratorní úlohy a) Zaznamenejte datum a čas měření, atmosférické podmínky, při nichž dané měření probíhá (teplota, tlak, vlhkost). b) Proednictvím digitálního
1. POLOVODIČOVÁ DIODA JAKO SMĚRŇOVAČ Zadání laboratorní úlohy a) Zaznamenejte datum a čas měření, atmosférické podmínky, při nichž dané měření probíhá (teplota, tlak, vlhkost). b) Proednictvím digitálního
Základní prvky a všeobecná lyžařská průprava
 Základní prvky a všeobecná lyžařská průprava Základní prvky a všeobecná lyžařská průprava na běžeckých lyžích Základními prvky nazýváme prvky elementární přípravy a pohybových dovedností, jejichž zvládnutí
Základní prvky a všeobecná lyžařská průprava Základní prvky a všeobecná lyžařská průprava na běžeckých lyžích Základními prvky nazýváme prvky elementární přípravy a pohybových dovedností, jejichž zvládnutí
ODBORNÝ VÝCVIK VE 3. TISÍCILETÍ MEII - 3.1 MĚŘENÍ ZÁKLADNÍCH EL. VELIČIN
 Projekt: ODBORNÝ VÝCVIK VE 3. TISÍCILETÍ Téma: MEII - 3.1 MĚŘENÍ ZÁKLADNÍCH EL. VELIČIN Obor: Mechanik Elektronik Ročník: 2. Zpracoval(a): Jiří Kolář Střední průmyslová škola Uherský Brod, 2010 Projekt
Projekt: ODBORNÝ VÝCVIK VE 3. TISÍCILETÍ Téma: MEII - 3.1 MĚŘENÍ ZÁKLADNÍCH EL. VELIČIN Obor: Mechanik Elektronik Ročník: 2. Zpracoval(a): Jiří Kolář Střední průmyslová škola Uherský Brod, 2010 Projekt
Pracovní list SVĚTELNÉ JEVY Jméno:
 Zadání projektu Optické jevy Časový plán: Zadání projektu, přidělení funkcí, časový a pracovní plán 9. 5. Vlastní práce 4 vyučovací hodiny do 22. 5. Prezentace 24.5. Test a odevzdání portfólií ke kontrole
Zadání projektu Optické jevy Časový plán: Zadání projektu, přidělení funkcí, časový a pracovní plán 9. 5. Vlastní práce 4 vyučovací hodiny do 22. 5. Prezentace 24.5. Test a odevzdání portfólií ke kontrole
5.2.2 Rovinné zrcadlo
 5.2.2 Rovinné zrcadlo ředpoklady: 5101, 5102, 5201 Terminologie pro přijímačky z fyziky Optická soustava = soustava optických prostředí a jejich rozhraní, která mění směr chodu světelných paprsků. Optické
5.2.2 Rovinné zrcadlo ředpoklady: 5101, 5102, 5201 Terminologie pro přijímačky z fyziky Optická soustava = soustava optických prostředí a jejich rozhraní, která mění směr chodu světelných paprsků. Optické
Indukční děliče napětí
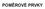 POMĚROVÉ PRVKY Indukční děliče napětí 2 Jednoduchý indukční dělič napětí k v D D i1 U Ui D 1α jβ U D k / m Jádro toroidního tvaru z materiálu s vysokou permeabilitou. Všechny sekce navinuty současně kabelem
POMĚROVÉ PRVKY Indukční děliče napětí 2 Jednoduchý indukční dělič napětí k v D D i1 U Ui D 1α jβ U D k / m Jádro toroidního tvaru z materiálu s vysokou permeabilitou. Všechny sekce navinuty současně kabelem
VY_52_INOVACE_2NOV70. Autor: Mgr. Jakub Novák. Datum: 19. 3. 2013 Ročník: 8. a 9.
 VY_52_INOVACE_2NOV70 Autor: Mgr. Jakub Novák Datum: 19. 3. 2013 Ročník: 8. a 9. Vzdělávací oblast: Člověk a příroda Vzdělávací obor: Fyzika Tematický okruh: Elektromagnetické a světelné děje Téma: Zapojení
VY_52_INOVACE_2NOV70 Autor: Mgr. Jakub Novák Datum: 19. 3. 2013 Ročník: 8. a 9. Vzdělávací oblast: Člověk a příroda Vzdělávací obor: Fyzika Tematický okruh: Elektromagnetické a světelné děje Téma: Zapojení
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE. Úloha č.4: Balmerova série
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 6.3.2011 Jméno: Jakub Kákona Pracovní skupina: 2 Hodina: Po 7:30 Spolupracovníci: Viktor Polák Hodnocení: Úloha č.4: Balmerova série Abstrakt V tomto
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 6.3.2011 Jméno: Jakub Kákona Pracovní skupina: 2 Hodina: Po 7:30 Spolupracovníci: Viktor Polák Hodnocení: Úloha č.4: Balmerova série Abstrakt V tomto
PROVOZNÍ CHARAKTERISTIKY OTOPNÝCH TĚLES
 ČVUT v Praze, Fakulta strojní Ústav techniky prostředí PROVOZNÍ CHARAKTERISTIKY OTOPNÝCH TĚLES Datum odevzdání: Měřicí skupina: Měřili: Semestr/rok: Datum měření: Zpráva o výsledcích experimentálních prací
ČVUT v Praze, Fakulta strojní Ústav techniky prostředí PROVOZNÍ CHARAKTERISTIKY OTOPNÝCH TĚLES Datum odevzdání: Měřicí skupina: Měřili: Semestr/rok: Datum měření: Zpráva o výsledcích experimentálních prací
UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE
 MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin
Metodika pro učitele Optika SŠ
 Metodika pro učitele Optika SŠ Základní charakteristika výukového programu: Popis: V šesti kapitolách se žáci seznámí se základními principy geometrické optiky, s optickými klamy a světelným spektrem.
Metodika pro učitele Optika SŠ Základní charakteristika výukového programu: Popis: V šesti kapitolách se žáci seznámí se základními principy geometrické optiky, s optickými klamy a světelným spektrem.
Fyzikální praktikum 3 - úloha 7
 Fyzikální praktikum 3 - úloha 7 Operační zesilovač, jeho vlastnosti a využití Teorie: Operační zesilovač je elektronická součástka využívaná v měřící, regulační a výpočetní technice. Ideální model má nekonečně
Fyzikální praktikum 3 - úloha 7 Operační zesilovač, jeho vlastnosti a využití Teorie: Operační zesilovač je elektronická součástka využívaná v měřící, regulační a výpočetní technice. Ideální model má nekonečně
(k 1)x k + 1. pro k 1 a x = 0 pro k = 1.
 . Funkce dvou a více proměnných. Úvod. Určete definiční obor funkce a proveďte klasifikaci bodů z R vzhledem k a rozhodněte zda je množina uzavřená či otevřená. Určete a načrtněte vrstevnice grafu funkce
. Funkce dvou a více proměnných. Úvod. Určete definiční obor funkce a proveďte klasifikaci bodů z R vzhledem k a rozhodněte zda je množina uzavřená či otevřená. Určete a načrtněte vrstevnice grafu funkce
4-149-563-02(1) Objektiv pro digitální jednookou zrcadlovku. Návod k obsluze. DT 50 mm F1.8 SAM SAL50F18. 2009 Sony Corporation
 4-149-563-02(1) Objektiv pro digitální jednookou zrcadlovku Návod k obsluze DT 50 mm F1.8 SAM SAL50F18 2009 Sony Corporation V tomto návodu najdete informace o používání tohoto objektivu. Poznámky k používání
4-149-563-02(1) Objektiv pro digitální jednookou zrcadlovku Návod k obsluze DT 50 mm F1.8 SAM SAL50F18 2009 Sony Corporation V tomto návodu najdete informace o používání tohoto objektivu. Poznámky k používání
Elektrické. MP - Ampérmetr A U I R. Naměřená hodnota proudu 5 A znamená, že měřená veličina je 5 x větší než jednotka - A
 Elektrické měření definice.: Poznávací proces jehož prvořadým cílem je zjištění: výskytu a velikosti (tzv. kvantifikace) měřené veličiny při využívání známých fyzikálních jevů a zákonů. MP - mpérmetr R
Elektrické měření definice.: Poznávací proces jehož prvořadým cílem je zjištění: výskytu a velikosti (tzv. kvantifikace) měřené veličiny při využívání známých fyzikálních jevů a zákonů. MP - mpérmetr R
SMĚRNICE EVROPSKÉHO PARLAMENTU A RADY 2009/76/ES
 L 201/18 Úřední věstník Evropské unie 1.8.2009 SMĚRNICE EVROPSKÉHO PARLAMENTU A RADY 2009/76/ES ze dne 13. července 2009 o hladině akustického tlaku kolových zemědělských a lesnických traktorů působícího
L 201/18 Úřední věstník Evropské unie 1.8.2009 SMĚRNICE EVROPSKÉHO PARLAMENTU A RADY 2009/76/ES ze dne 13. července 2009 o hladině akustického tlaku kolových zemědělských a lesnických traktorů působícího
1 Pracovní úkoly. 2 Vypracování. Úloha #9 Akustika.
 FYZIKÁLNÍ PRAKTIKUM I FJFI ƒvut v Praze Úloha #9 Akustika. Datum m ení: 18.10.2013 Skupina: 7 Jméno: David Roesel Krouºek: ZS 5 Spolupracovala: Tereza Schönfeldová Klasikace: 1 Pracovní úkoly 1. Domácí
FYZIKÁLNÍ PRAKTIKUM I FJFI ƒvut v Praze Úloha #9 Akustika. Datum m ení: 18.10.2013 Skupina: 7 Jméno: David Roesel Krouºek: ZS 5 Spolupracovala: Tereza Schönfeldová Klasikace: 1 Pracovní úkoly 1. Domácí
Metodický list - Coach
 Metodický list - Coach Optika POROVNÁNÍ SVITU ZÁŘIVKY A ŽÁROVKY Fyzikální princip Zářivka je nízkotlaká výbojka, která se používá jako zdroj světla. Tvoří ji zářivkové těleso, jehož základem je nejčastěji
Metodický list - Coach Optika POROVNÁNÍ SVITU ZÁŘIVKY A ŽÁROVKY Fyzikální princip Zářivka je nízkotlaká výbojka, která se používá jako zdroj světla. Tvoří ji zářivkové těleso, jehož základem je nejčastěji
Veletrh. Obr. 1. 1. Měřeni účinnosti ohřevu. Oldřich Lepil, Přírodovědecká fakulta UP Olomouc
 Oldřich Lepil, Přírodovědecká fakulta UP Olomouc Současný přístup ke školním demonstracím charakterizují na jedné straně nejrůznější moderní elektronické měřicí systémy převážně ve vazbě na počítač a na
Oldřich Lepil, Přírodovědecká fakulta UP Olomouc Současný přístup ke školním demonstracím charakterizují na jedné straně nejrůznější moderní elektronické měřicí systémy převážně ve vazbě na počítač a na
Gymnázium, Praha 10, Voděradská 2 Projekt OBZORY
 Gymnázium, Praha 10, Voděradská 2 Projekt OBZORY INDIVIDUÁLNÍ VÝUKA Matematika METODIKA Soustavy rovnic Mgr. Marie Souchová květen 2011 Tato část učiva následuje po kapitole Rovnice. Je rozdělena do částí
Gymnázium, Praha 10, Voděradská 2 Projekt OBZORY INDIVIDUÁLNÍ VÝUKA Matematika METODIKA Soustavy rovnic Mgr. Marie Souchová květen 2011 Tato část učiva následuje po kapitole Rovnice. Je rozdělena do částí
Posouzení únosnosti svaru se provádí podle zásad pružnosti a pevnosti v nebezpečném průřezu.
 Svarové spoje Posouzení únosnosti svaru se provádí podle zásad pružnosti a pevnosti v nebezpečném průřezu. Vybrané druhy svarů a jejich posouzení dle EN ČSN 1993-1-8. Koutový svar -T-spoj - přeplátovaný
Svarové spoje Posouzení únosnosti svaru se provádí podle zásad pružnosti a pevnosti v nebezpečném průřezu. Vybrané druhy svarů a jejich posouzení dle EN ČSN 1993-1-8. Koutový svar -T-spoj - přeplátovaný
Strojní pásová pila ProLine 520.450 H
 FIPAS-pily na kov s.r.o. Czech Strojní pásová pila ProLine 520.450 H 1. Zobrazení stroje Vyobrazení stroje slouží k informačním účelům a ukazuje konstrukčně podobný typ v ručním provedení. 2. Krátký popis
FIPAS-pily na kov s.r.o. Czech Strojní pásová pila ProLine 520.450 H 1. Zobrazení stroje Vyobrazení stroje slouží k informačním účelům a ukazuje konstrukčně podobný typ v ručním provedení. 2. Krátký popis
PÍSEMNÁ ZPRÁVA ZADAVATELE
 PÍSEMNÁ ZPRÁVA ZADAVATELE Identifikační údaje zadávacího řízení Název zakázky Dodávka pomůcek pro výuku fyziky a biologie část A, C, D, H Druh zakázky Dodávky zjednodušené podlimitní řízení Název projektu
PÍSEMNÁ ZPRÁVA ZADAVATELE Identifikační údaje zadávacího řízení Název zakázky Dodávka pomůcek pro výuku fyziky a biologie část A, C, D, H Druh zakázky Dodávky zjednodušené podlimitní řízení Název projektu
VÝVOJ POVLAKŮ PRO STAVEBNÍ APLIKACE. ABSTRACT anglicky
 VÝVOJ POVLAKŮ PRO STAVEBNÍ APLIKACE Ing. PAVEL WONDRAK AGC Flat Glass Czech, a.s., člen AGC Group; Teplice,Czech email: pavel.wondrak@eu.agc.com ABSTRACT anglicky The following papers explains the function
VÝVOJ POVLAKŮ PRO STAVEBNÍ APLIKACE Ing. PAVEL WONDRAK AGC Flat Glass Czech, a.s., člen AGC Group; Teplice,Czech email: pavel.wondrak@eu.agc.com ABSTRACT anglicky The following papers explains the function
Měření změny objemu vody při tuhnutí
 Měření změny objemu vody při tuhnutí VÁCLAVA KOPECKÁ Katedra didaktiky fyziky, Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Anotace Od prosince 2012 jsou na webovém portálu Alik.cz publikovány
Měření změny objemu vody při tuhnutí VÁCLAVA KOPECKÁ Katedra didaktiky fyziky, Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Anotace Od prosince 2012 jsou na webovém portálu Alik.cz publikovány
5 - Stanovení teoretické a experimentální hodnoty koeficientu prostupu tepla
 5 - Stanovení teoretické a experimentální hodnoty koeficientu prostupu tepla I Základní vztahy a definice Sdílením tepla rozumíme převod energie z místa s vyšší teplotou na místo s nižší teplotou vlivem
5 - Stanovení teoretické a experimentální hodnoty koeficientu prostupu tepla I Základní vztahy a definice Sdílením tepla rozumíme převod energie z místa s vyšší teplotou na místo s nižší teplotou vlivem
I. Objemové tíhy, vlastní tíha a užitná zatížení pozemních staveb
 I. Objemové tíhy, vlastní tíha a užitná zatížení pozemních staveb 1 VŠEOBECNĚ ČSN EN 1991-1-1 poskytuje pokyny pro stanovení objemové tíhy stavebních a skladovaných materiálů nebo výrobků, pro vlastní
I. Objemové tíhy, vlastní tíha a užitná zatížení pozemních staveb 1 VŠEOBECNĚ ČSN EN 1991-1-1 poskytuje pokyny pro stanovení objemové tíhy stavebních a skladovaných materiálů nebo výrobků, pro vlastní
HBG 60 ODSAVAČ PAR. Návod k instalaci a obsluze
 HBG 60 ODSAVAČ PAR Návod k instalaci a obsluze 1 POPIS Odsavač par lze instalovat ve filtrační nebo odtahové verzi. Filtrační verze (obr. 1) odsavač odsává vzduch z kuchyně nasycený párami a zápachy, čistí
HBG 60 ODSAVAČ PAR Návod k instalaci a obsluze 1 POPIS Odsavač par lze instalovat ve filtrační nebo odtahové verzi. Filtrační verze (obr. 1) odsavač odsává vzduch z kuchyně nasycený párami a zápachy, čistí
