1. ÚVOD 3. DRUHY DEFEKT
|
|
|
- Libuše Kučerová
- před 10 lety
- Počet zobrazení:
Transkript
1 Homogenizace dat dlouhodobých měření rychlostních polí přístroje MDI / SoHO Miroslav Klvaňa, Astronomický ústav Akademie věd České republiky, observatoř Ondřejov, Česká republika, Michal Švanda, Astronomický ústav Akademie věd České republiky, observatoř Ondřejov, Astronomický ústav University Karlovy v Praze, Česká republika, Václav Bumba, Astronomický ústav Akademie věd České republiky, observatoř Ondřejov, Česká republika, Abstrakt: Při zpracování rychlostních polí přístroje MDI družicové observatoře SoHO jsme v dlouhodobé sekvenci dopplergramů zjistili a odstranili řadu defektů, spojených jak s přístrojovými efekty, tak i se zpracováním a archivováním naměřených dopplergramů. V této práci popisujeme zjištěné defekty a způsoby jejich odstranění za účelem homogenizace 783 dopplergramů, měřených s šestihodinovou kadencí v časovém intervalu od do ÚVOD Snaha o ověření dynamické teorie slapových sil ve sluneční fotosféře (Krivtsov a kol., 2002) nás vedla ke zpracování značného množství dopplergramů, získaných přístrojem MDI družicové observatoře SoHO (Scherrer a kol., 1995). Na základě této teorie existuje předpoklad, že dopplerovské rychlostní pole Slunce by mohlo vykazovat charakteristické změny s periodou přibližně 120 dnů (Klvaňa a kol., 2005). Ověření efektu je možné na dlouhodobé homogenní řadě dopplergramů. Při použití primárních dat z archivu MDI/SoHO jsme však zjistili nesrovnalosti, které se promítaly do získaných výsledků takovou měrou, že tyto výsledky nebyly k ověření teorie použitelné. Bylo nutno přistoupit k prověření vlastností dat, která nám byla k tomuto účelu poskytnuta. 2. POUŽITÁ DATA Michelsonův interferometr (přístroj MDI) poskytuje filtrogramy slunečního disku v pěti vlnových délkách, pokrývajících rovnoměrně spektrální čáru Ni I s vlnovou délkou 676,88 nm. Z těchto filtrogramů se pak na základě modelu spektrální čáry počítá konfigurace rychlostního pole dopplergramu. Dopplergram celého slunečního disku je uložen dvoubajtově v matici 1024x1024 bodů. Dopplergramy jsou snímány v závislosti na pracovním programu s různou kadencí. Pro naše účely používáme standardní pracovní režim, měření dopplergramů po 6 hodinách. 3. DRUHY DEFEKTŮ V DOPPLERGRAMECH Pro naše účely jsme z dat SoHO vybrali interval 783 dnů měření přístroje MDI od do V tomto časovém intervalu se přístroj nacházel v režimu pravidelné registrace jednoho dopplergramu každých šest hodin. Dále diskutované problémy se týkají právě dat pravidelných šestihodinových měření Chyby v pořadí dopplergramů podle času První a možná nejzáludnější chybou byla záměna pořadí dopplergramů v datové řadě. Při bližším rozboru jsme zjistili, že údaje o čase pozorování v hlavičce dopplergramu jsou správně, ale vlastní pořadí snímků, označovaných a seřazených podle dne a pořadového čísla pozorování v tomto dni, může být chybné. Odstranění chyby: Pro sestavení časové sekvence po sobě jdoucích snímků nepoužívat jejich pořadí tak, jak byla data stažena z archívu SoHO, ale řadit snímky podle časů, uvedených v jejich hlavičkách Nedodržení časové pravidelnosti dopplergramů I když bychom očekávali, že v šestihodinovém režimu měření budou data registrována pravidelně po šesti hodinách, není tomu tak. Jsou běžné segmenty dat, kdy časy registrace jsou zcela chaotické a navázat je na pravidelný šestihodinový režim je prakticky nemožné. Tento efekt je často kombinován s vynechanými dopplergramy a zřejmě souvisí s poruchami měření. Odstranění chyby: Pokud pro naši práci potřebujeme pravidelnou časovou řadu spektroheliogramů, je jediným východiskem interpolace mezi sousedními snímky, vztažená k vynechaným časům v datové řadě.
2 3.3. Vynechané dopplergramy Vynechaných dopplergramů v jejich časové řadě je bohužel značné množství. Pokud při výpočtu započteme také zlomky dne, měli bychom mít v časové řadě použitého intervalu celkem 3133 dopplergramů. Reálný počet dopplergramů je však jen 2236, tzn. téměř jedna třetina dopplergramů chybí. Někdy vypadne celá řada po sobě následujících dopplergramů a proto tento efekt vede ke značným potížím v homogenizaci časové řady. Odstranění chyby: V určitých případech můžeme použít interpolaci podle bodu 3.2. Při interpolaci časové řady, v níž chybí několik dopplergramů za sebou může však taková interpolace vnést do interpolované řady rušivý efekt. V našem případě jsme tuto interpolaci prováděli, protože krátkodobé efekty by se v naší aplikaci neměly rušivě projevit Opakování stejných dopplergramů Při seřazení dopplergramů podle časů uvedených v jejich hlavičkách jsme zjistili, že některé dopplergramy v původní datové řadě se opakují (měly stejný čas pořízení). Odstranění chyby: Stejné dopplergramy není možno využít a proto je třeba je odstranit. V našem případě to bylo 48 dopplergramů. 3.5 Chybějící část dopplergramu Dopplergramy mohou být narušeny tak, že chybí horní část disku. Velikost chybějící oblasti je proměnná a tvoří ji jeden segment s chybějícími řádky (obr.1) Chybějící okraj disku Pokud je kolem dopplergramu vykresleno tenké světlé mezikruží je všechno v pořádku. Dopplergramy bez tohoto mezikruží však zobrazují pouze část slunečního disku (obr.2). Průměr dopplergramu, uvedený v jeho hlavičce neodpovídá vykreslenému průměru. Měřítko zobrazení v testovaných případech však zůstalo zachováno. Obr. 2.: Celý obraz slunečního disku s mezikružím a defektní obraz oříznutého disku, který poznáme podle toho, že mezikruží zde vždy chybí. Odstranění chyby: Tuto chybu v šestihodinových datech nelze odstranit a pokud by mohla celkový výsledek ovlivnit, je nutno všechny dopplergramy oříznout a zpracovávat jen jejich společnou část bez okrajů. My jsme se při zpracování omezili na společnou část dopplergramů Otočení obrazu disku V datové řadě jsme se setkali pouze s jedním dopplergramem, otočeným o devadesát stupňů (obr.3). Toto otočení nebylo v hlavičce dopplergramu zaznamenáno a proto tuto chybu není možno pomocí hlavičky identifikovat. Při práci s jinými daty SoHO jsme narazili na otočení magnetogramu o 180. Informaci o tomto otočení bylo možno z hlavičky zjistit. Obr. 1.: Defekty v obraze dopplergramu. Vlevo chybějící část obrazu, vpravo tři defektní řádky (na začátku a na konci dva řádky, uprostřed jen ten průběžný). Odstranění chyby: Eliminace chyby je problém. Především záleží na podmínkách konkrétní aplikace (viz bod 3.3). Pro naše účely jsme z těchto důvodů odstranili celkem 69 dopplergramů Defektní řádky Některé z dopplergramů mohou být narušeny chybnými řádky. Někdy chybí jen části řádku. Na nezmenšeném obraze při prohlížení dopplergramů je defekt většinou zřetelně viditelný (obr.1). Odstranění chyby: Pokud by tento defekt rušil, postačí většinou nahradit chybějící data interpolací okolních bodů. Pro naše účely jsme tyto defekty neodstraňovali. Obr. 3.: Správná poloha slunečního disku (vlevo) a chybná poloha s diskem, otočeným o 90 (vpravo). Odstranění chyby: Obraz je možno otočit zpět, ovšem pouze za předpokladu, že střed otáčení obrazu a střed disku jsou totožné. My jsme tento dopplergram odstranili.
3 4. TEST HOMOGENITY DAT Z hlediska našeho výzkumu se zajímáme o fluktuace dopplerovských rychlostních polí na slunečním disku během dlouhodobých pozorování. Tyto fluktuace zobrazujeme v mapách dopplerovských rychlostních polí, v nichž vertikálně vykreslujeme závislost intenzity těchto rychlostí na heliografické délce pro zadanou heliografickou šířku, horizontálně řadíme za sebou tyto informace, odečtené z jednotlivých dopplergramů celé časové řady. Mapu, sestrojenou z dopplergramů naší časové řady, vidíme na obr.4. V použité řadě byly odstraněny výše popsané defekty. Škála šedí znázorňuje dopplerovské rychlosti od -622 (černá) do 859 m/s. po sobě následujícími dopplergramy. Jak jsme zjistili později, způsobují tyto korekční posuvy nejen celkový posuv rychlostního pole, ale i jeho deformaci. Korekční posuvy hluboce narušují homogenitu časových řad dopplergramů. Z tohoto důvodu na obr.4 vidíme pouze korekční posuvy, ale žádnou další informaci o dopplerovských rychlostních polích a jejich fluktuacích. Při homogenizaci dlouhodobých časových řad je proto nezbytné tento defekt odstranit. 5. HOMOGENIZACE DOPPLERGRAMŮ 5.1. Identifikování korekčních posuvů Velké korekční posuvy se projeví náhlou změnou odstínu sousedních dopplergramů. Jak je vidět z obr.5, i pro značné korekční posuvy je jejich vizuální zjištění v dopplergramech je velmi obtížné. Obr.4.: Časový vývoj dopplerovských rychlostí na slunečním rovníku, vykreslený z původních dat. Škála šedí v rozsahu od -622 (černá) do 859 m/s poskytuje informaci prakticky pouze o korekčních posuvech. Žádné fluktuace zde nevidíme. Místo očekávané homogenní struktury jsme však obdrželi mapu, vertikálně rozdělenou na segmenty. Tak jsme zjistili, že v datech je přítomen další defekt, který na rozdíl od dříve popsaných defektů není snadno vizuálně identifikovatelný. Jedná se o nejkomplikovanější defekt, který se uplatňuje hlavně při zpracování dlouhých časových řad dopplergramů. Během provozu MDI dochází k pomalému posuvu výstupu Michelsonova interferometru k okraji jeho pracovního rozsahu. Důvody posuvu nejsou zcela jasné. Tento posuv, mající charakter dlouhodobého trendu, je čas od času korigován nastavením výstupu interferometru zpět do původního pracovního rozsahu. Obr. 5.: Vzhled dopplergramů před a za korekčním posuvem. Rozdíl v jasech obou disků, odpovídající změně rychlost m/sec, je téměř nepozorovatelný. Korekční posuvy mají charakter náhlé skokové změny dopplerovského rychlostního pole mezi dvěma Obr. 6.: Střední hodnota dopplerovského rychlostního pole centrální časti slunečního disku v závislosti na pořadovém čísle dopplergramu. Písmena A-E označují skokové změny jejich rychlostního pole, způsobené korekčními posuvy při nastavování interferometru. K nalezení dvou sousedních dopplergramů časové řady mezi nimiž ke korekčnímu posuvu došlo jsme použili křivku, vykreslenou na obr.6. Střední hodnotu dopplerovského rychlostního pole jsme získali integrací tohoto pole v oblasti 1200x1200 obl. sec, nacházející se v centrální části slunečního disku. Taková integrace dopplerovského rychlostního pole do značné míry potlačuje vlivy pětiminutových oscilací, supergranulace a diferenciální rotace. Výsledek integrace mohou ovlivnit osově a středově symetrická rychlostní pole jako např. modrý posuv a gravitační posuv, které však, jak předpokládáme, jsou dlouhodobě stabilní. Fyzikálně by tedy taková střední dopplerovská rychlost měla být konstantou, nezávislou na čase. Korekční posuvy a další přístrojové vlivy se pak projeví změnami této konstanty. Korekční posuvy, provedené během registrace časové řady dopplergramů, jsou na křivce korekčních posuvů na obr.6 velmi zřetelné. Proto z křivky snadno odečteme jak velikost korekčního posuvu rychlostního pole celého dopplergramu, tak i pořadová čísla
4 dopplergramů, mezi nimiž byla korekce provedena. Tyto údaje jsou spolu s označením korekčních posuvů podle obr.6. uvedeny v tabulce 1. TAB.1: Informace o provedených korekčních posuvech Označ. posuvu A B C D E Pořadová čísla dopplergramů Korekční posuv rychlosti [m/s] Odstranění korekčních posuvů Křivka korekčních posuvů na obr.6 nám dovoluje určit konkrétní dopplergramy, u nichž ke korekci došlo a velikost korekčních posuvů. Pokud tyto informace použijeme, můžeme skokové změny na křivce korekčních posuvů odstranit. Získáme tak monotónní homogenizační křivku pro zpracovávanou časovou řadu dopplergramů, vykreslenou na obr.7. čase registrace postupně tmavnout. Metoda může být vhodná pro zjištění vlivu trendů na změny rychlostního pole v různých místech disku Metoda B: Předpokládáme, že střední hodnota dopplerovské rychlosti každého z dopplergramů by měla být konstantou, nezávislou na čase (odstavec 5.1). Skokové změny dopplerovských rychlostí dopplergramů se projeví ve změně této konstanty. Vzhledem k tomu, že nám nejde o absolutní měření, ale o dlouhodobé změny v rychlostním poli, můžeme tuto konstantu položit rovnu nule. Jestliže rychlostní pole jednotlivých dopplergramů posuneme tak,aby střední hodnota jejich dopplerovské rychlosti byla rovna nule, odstraníme jak skokové změny, tak i trend v celé časové řadě a získáme tak na pohled zcela homogenní dopplergramy Výsledky aplikace obou metod: Mapa rozložení dopplerovských rychlostí na slunečním rovníku, zpracovaná pro celou časovou sérii dopplergramů metodou A je na obr.8a, výsledek aplikace metody B vidíme na obr.8b. Po odstranění skoků se v obr.8b začínají objevovat nové struktury rychlostního pole. Tato mapa zachovává trend, přítomný v časové řadě. V mapě na obr.8b je trend odstraněn. Přítomnost trendu v obr.8a zhoršuje vizualizaci rychlostních struktur. Kontrast obrazu klesá tím, že tutéž škálu šedí používáme pro větší rozsah zobrazovaných hodnot. Obr. 7.: Homogenizační křivka, získaná pro danou časovou řadu dopplergramů odstraněním skokových změn křivky na obr.5 posuvem jejích segmentů o konstanty korekčních posuvů Homogenizační křivka vykazuje dlouhodobý trend změny střední hodnoty dopplerovského rychlostního pole dopplergramů v oblasti středu disku, způsobený přístrojovými efekty. V místech skokových korekcí se charakter křivky nemění. Na základě tohoto faktu jsme předpokládali, že při korekčních posuvech se jedná pouze o posuv celého rychlostního pole dopplergramu o korekční konstantu a z toho jsme při dalším postupu vycházeli. Pro homogenizaci časové řady dopplergramů jsme použili tyto dvě následující metody: Metoda A: Rychlostní pole jednotlivých dopplergramů posuneme tak, aby střední hodnota dopplerovského rychlostního pole středu disku byla rovna hodnotě, odečtené pro daný dopplergram z homogenizační křivky na obr.7. Tímto způsobem odstraníme skoky v rychlostních polích, ale trend křivky na obr.7 zůstane zachován. Výsledné dopplergramy, homogenizované touto metodou, budou v závislosti na Obr. 8A.: Časový vývoj doppler. rychlostí na slunečním rovníku po zpracování dat mapy na obr.4. metodou A. Rychlostní pole je v rozsahu od (černá) do 77 m/s. Obr. 8B.: Časový vývoj doppler. rychlostí na slunečním rovníku po zpracování dat mapy na obr.4. metodou A. Rychlostní pole je v rozsahu od -137 (černá) do 146 m/s. Podle předpokladu v oblasti středu disku dostáváme v obou mapách hodnoty blízké nule. Celá struktura pásu je však vertikálně výrazně rozdělena na segmenty,
5 jejichž hranice korespondují s místy korekčních posuvů. Segmenty vznikají tím, že dopplerovské rychlosti pro tutéž heliografickou délku na sebe v místech korekčních posuvů většinou nenavazují. Z toho vyplývá, že během korekčního posuvu nedochází jen k posuvu rychlostního pole disku o korekční konstantu, ale současně se mění amplitudy dopplerovských rychlostí na celém disku. Důležitý závěr: Homogenizaci časové řady dopplergramů nelze provést pouze posuvem jejich rychlostního pole o korekční konstantu (tak, jak jsme původně předpokládali), ale je třeba vzít do úvahy i změnu převodní křivky dopplerovských rychlostí na hranicích jednotlivých segmentů jako funkci polohy korigovaného bodu na slunečním disku Převodní křivky pro rovník Po odstranění korekčních posuvů podle bodu 5.2. jsou v místech původních korekčních posuvů jak na obr.8a, tak i na obr.8b přítomna vertikální rozhraní, dělící obraz na segmenty. Hranice těchto segmentů je třeba odstranit, protože jinak budou tato rozhraní znemožňovat další zpracování. Vzhledem k dostatečné rychlosti korekčního posuvu se z hlediska dlouhodobých efektů fyzikální podmínky na disku před a po korekci prakticky nezmění. Můžeme proto předpokládat, že po odfiltrování krátkodobých změn budou rychlostní pole obou dopplergramů, pořízených před a po korekci, popisovat prakticky totéž rychlostní pole. Naší úlohou je nalézt takovou převodní křivku, která upraví rychlostní pole dopplergramu za hranicí segmentu tak, aby bylo totožné s polem předcházejícího dopplergramu. Hranice segmentů pak v obr.8a,b zmizí. Fyzikální podstatu změn rychlostních polí během korekčního posuvu neznáme a proto jsme použili experimentální přístup. Pro stanovení převodní křivky jsme vyzkoušeli dvě následující možnosti: Diferenční převodní křivka: Křivku pro danou hranici segmentu získáme tak, že pro dvojici dopplergramů, přiléhající k hranici segmentu sestrojíme diferenční křivku jako rozdíl obou dopplerovských rychlostních polí na rovníku v bodech, které mají stejnou heliografickou délku, v rozmezí heliografických délek od -54 do +54. Vliv krátkodobých lokálních rychlostí na výslednou křivku odstraníme předcházející filtrací obou dopplergramů gaussovským filtračním oknem 80x80 obl.sec. Při aplikaci diferenční křivky se k rychlostnímu poli korigovaného bodu přičítá hodnota, odečtená pro danou heliografickou délku korigovaného bodu z diferenční převodní křivky Multiplikační převodní křivka: Křivku pro danou hranici segmentu získáme podobným způsobem, jako diferenční převodní křivku. Postup se odlišuje tím, že místo rozdílu dopplerovských rychlostí použijeme jejich podíl. Dělení nulou se vyhneme konstantním posuvem rychlostního pole všech dopplergramů ve zpracovávané časové řadě do kladných hodnot. Při aplikaci multiplikační křivky se rychlostní pole korigovaných bodů (v posunuté rychlostní škále!!!) násobí hodnotou, odečtenou z křivky pro danou heliografickou délku korigovaného bodu. Konečné rychlostní pole korigovaného dopplergramu dostaneme zpětným odečtením hodnoty posuvu. Korekce dopplerovské rychlosti je v tomto případě úměrná velikosti korigované dopplerovské rychlosti, tzn. zdůrazňuje struktury v rychlostním poli Aplikace převodních křivek: Převodní křivky slouží k odstranění hranic mezi jednotlivými segmenty v mapách časového vývoje dopplerovských rychlostí na slunečním rovníku. Jejich počet je dán počtem hranic mezi segmenty, které chceme odstranit. Vidíme, že křivky na obr.9 se navzájem značně liší, protože částečně zachycují i lokální stav rychlostního pole. Obr. 9.: Převodní křivky pro hranice jednotlivých segmentů, zobrazené v posunutých rovinách. Hranice segmentů v mapách na obr.8a,b jsou podle obr.6 pojmenovány zleva doprava písmeny A-E. Kalibrační křivky je možno použít dvěma způsoby: V prvním případě odstraníme pouze defekty na hranicích segmentů (viz odstavec 5.4.) se zachováním starého trendu, případně se vznikem dalšího nového trendu, ve druhém případě (viz odstavec 5.5) odstraníme současně i trend v celé časové řadě dopplergramů Odstranění hranic segmentů pro celý rovník Hranice segmentů, patrné na obou obr.8 odstraníme aplikací diferenční nebo multiplikační převodní křivky postupně na všechny hranice segmentů. Převodní křivku vypočtenou pro první hranici segmentů, aplikujeme na rovníky všech dopplergramů segmentu, následujícího za touto hranicí. Dále vypočteme za použití již upravených dat převodní křivku pro následující hranici segmentů a celý postup opakujeme, dokud nezkorigujeme všechny dopplergramy. Pokud použijeme data obr.8a, bude v těchto strukturách zahrnut i trend. Vzhledem k tomu, že pro nás trend není důležitý, použili jsme k dalšímu zpracování data z obr.8b.
6 Odstranění trendů provedeme na základě úvahy o nulovém rychlostním poli na středu disku, popisované v odstavci jako metoda B. Rychlostní pole každého z vertikálních rovníkových řezů, upravené podle odstavce 4.4., posuneme odečtením jeho rychlosti na středu disku. Tímto způsobem odstraníme trend, projevující se posuvem rychlostního pole na středu disku. Výsledek postupu vidíme na obr.12. Obr.10.: Odstranění hranic segmentů aplikací diferenční převodní křivky na data Obr.8. Horizontální pruhy vznikly jako průvodní jev této metody. Porovnáním struktur, získaných zpracováním dat z obr.8b diferenční metodou (obr.10) a multiplikační (obr.11) metodou vidíme, že obě struktury se v tomto případě od sebe vizuálně prakticky neliší. Obr.13.: Zdůraznění konečných rychlostních struktur dat z obr.10 gaussovskou filtrací oknem fwhm = 80 obl.sec.. Konečné struktury, zdůrazněné filtrací obr.12, jsou vykresleny na obr.13. Rozdíl mezi původními daty na obr.4 a výsledkem na obr. 13 je zcela zásadní. Podařilo se nám zobrazit struktury dopplerovského rychlostního pole, které byly v původních datech skryty. Obr.11.: Odstranění hranic segmentů aplikací multiplikační převodní křivky na data Obr.8. Horizontální pruhy vznikly jako průvodní jev této metody. Průvodním jevem této korekce jsou v obou případech rušivé horizontální struktury, viditelné na obr.10 a obr.11, reprodukující profily jednotlivých převodních křivek, Tyto horizontální struktury odstraňujeme tak, že v každém řádku mapy nalezneme střední hodnotu dopplerovské rychlosti a tu odečteme od hodnoty rychlosti v každém bodě tohoto řádku Odstranění trendů Doposud jsme předpokládali, že tvar převodních křivek se podél jednoho segmentu nemění. Ve skutečnosti však převodní křivka na konci segmentu se liší od křivky na jejím začátku (viz obr.9), tzn. že podél segmentu dochází k její modifikaci. 6. ZÁVĚR Dopplergramy, získané s šestihodinovou kadencí přístrojem MDI/SoHO v časovém intervalu od do obsahovaly celkem devět defektů různého charakteru. Po odstranění uvedených defektů námi popisovanou metodou se podařilo homogenizovat časovou sérii dopplergramů do té míry, že jsme ji mohli použít ke studiu vývoje dopplerovského rychlostního pole na slunečním rovníku. Poděkování Tato práce byla realizována díky účinné podpoře grantového projektu GAČR 205/04/2129 a výzkumného záměru AVOZ SoHO data byla použita s laskavým svolením konsorcia SoHO/MDI. SoHO je projektem mezinárodní spolupráce ESA a NASA. LITERATURA: Klvaňa M., Švanda M., Krivtsov A.M., Bumba V., 2005: Hvar Observatory Bulletin 29 (2005) 1, Krivtsov A. M., Klvaňa M., Bumba V., 2002: Zborník referátov z 16. celoštátného slnečného seminára, Scherrer, P. H.; Bogart, R. S.; Bush, R. I.; Hoeksema, J. T.; Kosovichev, A. G.; Schou, J.; Rosenberg, W.; Springer, L.; Tarbell, T. D.; Title, A.; Wolfson, C. J.; Zayer, I.; MDI Engineering Team: 1995, Solar Physics, v. 162, p Obr.12.:Odstranění horizontálních pruhů z dat na obr.10 metodou posuvu rychlostního pole na středu disku.
Pohyby slunečního plazmatu, vyvolané slapovými silami
 Pohyby slunečního plazmatu, vyvolané slapovými silami Miroslav Klvaňa, Astronomický ústav Akademie věd České republiky, observatoř Ondřejov, Česká republika, mklvana @asu.cas.cz Michal Švanda, Astronomický
Pohyby slunečního plazmatu, vyvolané slapovými silami Miroslav Klvaňa, Astronomický ústav Akademie věd České republiky, observatoř Ondřejov, Česká republika, mklvana @asu.cas.cz Michal Švanda, Astronomický
Proudìní fotosférického plazmatu po sluneèním povrchu
 Proudìní fotosférického plazmatu po sluneèním povrchu M. Klvaòa, Astronomický ústav Akademie vìd Èeské republiky, observatoø Ondøejov, Èeská republika, mklvana@asu.cas.cz M. Švanda, Matematicko-fyzikální
Proudìní fotosférického plazmatu po sluneèním povrchu M. Klvaòa, Astronomický ústav Akademie vìd Èeské republiky, observatoø Ondøejov, Èeská republika, mklvana@asu.cas.cz M. Švanda, Matematicko-fyzikální
Pohyby slunečního plazmatu, vyvolané slapovými silami
 Pohyby slunečního plazmatu, vyvolané slapovými silami Miroslav Klvaňa, Astronomický ústav Akademie věd České republiky, observatoř Ondřejov, Česká republika, mklvana@asu.cas.cz Michal Švanda, Astronomický
Pohyby slunečního plazmatu, vyvolané slapovými silami Miroslav Klvaňa, Astronomický ústav Akademie věd České republiky, observatoř Ondřejov, Česká republika, mklvana@asu.cas.cz Michal Švanda, Astronomický
Magnetická a rychlostní pole v aktivní oblasti (NOAA 7757, 1994) a v jejím okolí
 Magnetická a rychlostní pole v aktivní oblasti (NOAA 7757, 1994) a v jejím okolí V. Bumba, Astronomický ústav Akademie věd České republiky, observatoř Ondřejov, Česká republika, bumba @asu.cas.cz M. Klvaňa,
Magnetická a rychlostní pole v aktivní oblasti (NOAA 7757, 1994) a v jejím okolí V. Bumba, Astronomický ústav Akademie věd České republiky, observatoř Ondřejov, Česká republika, bumba @asu.cas.cz M. Klvaňa,
Cyklické změny v dynamice sluneční konvektivní zóny
 Cyklické změny v dynamice sluneční konvektivní zóny P. Ambrož, Astronomický ústav AVČR, Ondřejov, pambroz @asu.cas.cz Abstrakt Na základě analýzy rozsáhlého materiálu evoluce fotosférických pozaďových
Cyklické změny v dynamice sluneční konvektivní zóny P. Ambrož, Astronomický ústav AVČR, Ondřejov, pambroz @asu.cas.cz Abstrakt Na základě analýzy rozsáhlého materiálu evoluce fotosférických pozaďových
Solární detektor oblačnosti
 Solární detektor oblačnosti Miroslav Klvaňa, Astronomický ústav Akademie věd České republiky, v.v.i. observatoř Ondřejov, Česká republika, mklvana @asu.cas.cz Michal Švanda, Astronomický ústav Akademie
Solární detektor oblačnosti Miroslav Klvaňa, Astronomický ústav Akademie věd České republiky, v.v.i. observatoř Ondřejov, Česká republika, mklvana @asu.cas.cz Michal Švanda, Astronomický ústav Akademie
Fotoelektrická měření magnetických a rychlostních polí. Miroslav Klvaňa, Astronomický ústav Akademie věd, observatoř Ondřejov
 Fotoelektrická měření magnetických a rychlostních polí Miroslav Klvaňa, Astronomický ústav Akademie věd, observatoř Ondřejov Zdroj našich informací Podle místa vzniku poskytují spektrální čáry informace
Fotoelektrická měření magnetických a rychlostních polí Miroslav Klvaňa, Astronomický ústav Akademie věd, observatoř Ondřejov Zdroj našich informací Podle místa vzniku poskytují spektrální čáry informace
Detekce pohybů supergranulárních struktur
 Detekce pohybů supergranulárních struktur M. Švanda, Astronomický ústav Univerzity Karlovy v Praze, Česká republika, svanda@asu.cas.cz M. Klvaňa, Astronomický ústav Akademie věd České republiky, observatoř
Detekce pohybů supergranulárních struktur M. Švanda, Astronomický ústav Univerzity Karlovy v Praze, Česká republika, svanda@asu.cas.cz M. Klvaňa, Astronomický ústav Akademie věd České republiky, observatoř
Studium časového vývoje erupcí v čarách vodíku a vápníku
 Studium časového vývoje erupcí v čarách vodíku a vápníku Eva Marková1) (eva.radec @seznam.cz) a Petr Heinzel2) (petr.heinzel @asu.cas.cz) 1) Sluneční sekce ČAS, 2) Astronomický ústav AV ČR, v.v.i. Ondřejov
Studium časového vývoje erupcí v čarách vodíku a vápníku Eva Marková1) (eva.radec @seznam.cz) a Petr Heinzel2) (petr.heinzel @asu.cas.cz) 1) Sluneční sekce ČAS, 2) Astronomický ústav AV ČR, v.v.i. Ondřejov
Pozorování Slunce s vysokým rozlišením. Michal Sobotka Astronomický ústav AV ČR, Ondřejov
 Pozorování Slunce s vysokým rozlišením Michal Sobotka Astronomický ústav AV ČR, Ondřejov Úvod Na Slunci se důležité děje odehrávají na malých prostorových škálách (desítky až stovky km). Granule mají typickou
Pozorování Slunce s vysokým rozlišením Michal Sobotka Astronomický ústav AV ČR, Ondřejov Úvod Na Slunci se důležité děje odehrávají na malých prostorových škálách (desítky až stovky km). Granule mají typickou
Derotátor, skener a depolarizátor obrazu Slunce
 Derotátor, skener a depolarizátor obrazu Slunce M. Klvaňa, Astronomický ústav Akademie věd České republiky, observatoř Ondřejov, Česká republika, mklvana @asu.cas.cz M. Sobotka, Astronomický ústav Akademie
Derotátor, skener a depolarizátor obrazu Slunce M. Klvaňa, Astronomický ústav Akademie věd České republiky, observatoř Ondřejov, Česká republika, mklvana @asu.cas.cz M. Sobotka, Astronomický ústav Akademie
Nyní využijeme slovník Laplaceovy transformace pro derivaci a přímé hodnoty a dostaneme běžnou algebraickou rovnici. ! 2 "
 ŘEŠENÉ PŘÍKLADY Z MB ČÁST Příklad Nalezněte pomocí Laplaceovy transformace řešení dané Cauchyho úlohy lineární diferenciální rovnice prvního řádu s konstantními koeficienty v intervalu 0,, které vyhovuje
ŘEŠENÉ PŘÍKLADY Z MB ČÁST Příklad Nalezněte pomocí Laplaceovy transformace řešení dané Cauchyho úlohy lineární diferenciální rovnice prvního řádu s konstantními koeficienty v intervalu 0,, které vyhovuje
Video-spektroheliograf pro měření fotosférických rychlostních polí
 Video-spektroheliograf pro měření fotosférických rychlostních polí Miroslav Klvaňa, Astronomický ústav Akademie věd České republiky, observatoř Ondřejov, Česká republika, mklvana @asu.cas.cz Václav Bumba,
Video-spektroheliograf pro měření fotosférických rychlostních polí Miroslav Klvaňa, Astronomický ústav Akademie věd České republiky, observatoř Ondřejov, Česká republika, mklvana @asu.cas.cz Václav Bumba,
Role magnetického pole při strukturování bílé koróny (interpretace pozorování zatmění z Angoly 2001)
 Role magnetického pole při strukturování bílé koróny (interpretace pozorování zatmění z Angoly 2001) Marcel Bělík, Hvězdárna v Úpici, belik @obsupice.cz Pavel Ambrož, AÚ AV ČR Ondřejov, pambroz @asu.cas.cz
Role magnetického pole při strukturování bílé koróny (interpretace pozorování zatmění z Angoly 2001) Marcel Bělík, Hvězdárna v Úpici, belik @obsupice.cz Pavel Ambrož, AÚ AV ČR Ondřejov, pambroz @asu.cas.cz
Analýza a zpracování digitálního obrazu
 Analýza a zpracování digitálního obrazu Úlohy strojového vidění lze přibližně rozdělit do sekvence čtyř funkčních bloků: Předzpracování veškerých obrazových dat pomocí filtrací (tj. transformací obrazové
Analýza a zpracování digitálního obrazu Úlohy strojového vidění lze přibližně rozdělit do sekvence čtyř funkčních bloků: Předzpracování veškerých obrazových dat pomocí filtrací (tj. transformací obrazové
Statistické zpracování naměřených experimentálních dat za rok 2012
 Statistické zpracování naměřených experimentálních dat za rok 2012 Popis dat: Experimentální data byla získána ze tří měřících sloupů označených pro jednoduchost názvy ZELENA, BILA a RUDA. Tyto měřící
Statistické zpracování naměřených experimentálních dat za rok 2012 Popis dat: Experimentální data byla získána ze tří měřících sloupů označených pro jednoduchost názvy ZELENA, BILA a RUDA. Tyto měřící
Graf I - Závislost magnetické indukce na proudu protékajícím magnetem. naměřené hodnoty kvadratické proložení. B [m T ] I[A]
![Graf I - Závislost magnetické indukce na proudu protékajícím magnetem. naměřené hodnoty kvadratické proložení. B [m T ] I[A] Graf I - Závislost magnetické indukce na proudu protékajícím magnetem. naměřené hodnoty kvadratické proložení. B [m T ] I[A]](/thumbs/27/10456203.jpg) Pracovní úkol 1. Proměřte závislost magnetické indukce na proudu magnetu. 2. Pomocí kamery změřte ve směru kolmém k magnetickému poli rozštěpení červené spektrální čáry kadmia pro 8-10 hodnot magnetické
Pracovní úkol 1. Proměřte závislost magnetické indukce na proudu magnetu. 2. Pomocí kamery změřte ve směru kolmém k magnetickému poli rozštěpení červené spektrální čáry kadmia pro 8-10 hodnot magnetické
2. Numerické výpočty. 1. Numerická derivace funkce
 2. Numerické výpočty Excel je poměrně pohodlný nástroj na provádění různých numerických výpočtů. V příkladu si ukážeme možnosti výpočtu a zobrazení diferenciálních charakteristik analytické funkce, přičemž
2. Numerické výpočty Excel je poměrně pohodlný nástroj na provádění různých numerických výpočtů. V příkladu si ukážeme možnosti výpočtu a zobrazení diferenciálních charakteristik analytické funkce, přičemž
Experimentální realizace Buquoyovy úlohy
 Experimentální realizace Buquoyovy úlohy ČENĚK KODEJŠKA, JAN ŘÍHA Přírodovědecká fakulta Univerzity Palackého, Olomouc Abstrakt Tato práce se zabývá experimentální realizací Buquoyovy úlohy. Jedná se o
Experimentální realizace Buquoyovy úlohy ČENĚK KODEJŠKA, JAN ŘÍHA Přírodovědecká fakulta Univerzity Palackého, Olomouc Abstrakt Tato práce se zabývá experimentální realizací Buquoyovy úlohy. Jedná se o
NESTABILITY VYBRANÝCH SYSTÉMŮ. Úvod. Vzpěr prutu. Petr Frantík 1
 NESTABILITY VYBRANÝCH SYSTÉMŮ Petr Frantík 1 Úvod Úloha pokritického vzpěru přímého prutu je řešena dynamickou metodou. Prut se statickým zatížením je modelován jako nelineární disipativní dynamický systém.
NESTABILITY VYBRANÝCH SYSTÉMŮ Petr Frantík 1 Úvod Úloha pokritického vzpěru přímého prutu je řešena dynamickou metodou. Prut se statickým zatížením je modelován jako nelineární disipativní dynamický systém.
Přehled matematického aparátu
 Přehled matematického aparátu Ekonomie je směsí historie, filozofie, etiky, psychologie, sociologie a dalších oborů je tak příslovečným tavicím kotlem ostatních společenských věd. Ekonomie však často staví
Přehled matematického aparátu Ekonomie je směsí historie, filozofie, etiky, psychologie, sociologie a dalších oborů je tak příslovečným tavicím kotlem ostatních společenských věd. Ekonomie však často staví
Návrh řídícího systému pro teleskop EST a kalibrace jeho souřadnicového systému
 Návrh řídícího systému pro teleskop EST a kalibrace jeho souřadnicového systému Miroslav Klvaňa, Astronomický ústav Akademie věd České republiky, v.v.i. observatoř Ondřejov, Česká republika, mklvana @asu.cas.cz
Návrh řídícího systému pro teleskop EST a kalibrace jeho souřadnicového systému Miroslav Klvaňa, Astronomický ústav Akademie věd České republiky, v.v.i. observatoř Ondřejov, Česká republika, mklvana @asu.cas.cz
2 Zpracování naměřených dat. 2.1 Gaussův zákon chyb. 2.2 Náhodná veličina a její rozdělení
 2 Zpracování naměřených dat Důležitou součástí každé experimentální práce je statistické zpracování naměřených dat. V této krátké kapitole se budeme věnovat určení intervalů spolehlivosti získaných výsledků
2 Zpracování naměřených dat Důležitou součástí každé experimentální práce je statistické zpracování naměřených dat. V této krátké kapitole se budeme věnovat určení intervalů spolehlivosti získaných výsledků
Rovinné přetvoření. Posunutí (translace) TEORIE K M2A+ULA
 Rovinné přetvoření Rovinné přetvoření, neboli, jak se také často nazývá, geometrická transformace je vlastně lineární zobrazení v prostoru s nějakou soustavou souřadnic. Jde v něm o přepočet souřadnic
Rovinné přetvoření Rovinné přetvoření, neboli, jak se také často nazývá, geometrická transformace je vlastně lineární zobrazení v prostoru s nějakou soustavou souřadnic. Jde v něm o přepočet souřadnic
Planety a sluneční aktivita
 Planety a sluneční aktivita V. Bumba, Astronomický ústav AVČR, Ondřejov, bumba @asu.cas.cz Abstrakt Pozorování ukazují, že pravidelnosti v rozložení slunečních magnetických polí korelují s oposicemi a
Planety a sluneční aktivita V. Bumba, Astronomický ústav AVČR, Ondřejov, bumba @asu.cas.cz Abstrakt Pozorování ukazují, že pravidelnosti v rozložení slunečních magnetických polí korelují s oposicemi a
Zajímavé vlastnosti sluneční atmosféry: magnetická a rychlostní pole
 Zajímavé vlastnosti sluneční atmosféry: magnetická a rychlostní pole Spektroskopie (nejen) ve sluneční fyzice LS 2011/2012 Michal Švanda Astronomický ústav MFF UK Astronomický ústav AV ČR Vliv na tvar
Zajímavé vlastnosti sluneční atmosféry: magnetická a rychlostní pole Spektroskopie (nejen) ve sluneční fyzice LS 2011/2012 Michal Švanda Astronomický ústav MFF UK Astronomický ústav AV ČR Vliv na tvar
Fyzikální sekce přírodovědecké fakulty Masarykovy univerzity v Brně FYZIKÁLNÍ PRAKTIKUM. Speciální praktikum z abc
 Fyzikální sekce přírodovědecké fakulty Masarykovy univerzity v Brně FYZIKÁLNÍ PRAKTIKUM Speciální praktikum z abc Zpracoval: Jan Novák Naměřeno: 1. ledna 2001 Obor: F Ročník: IV Semestr: IX Testováno:
Fyzikální sekce přírodovědecké fakulty Masarykovy univerzity v Brně FYZIKÁLNÍ PRAKTIKUM Speciální praktikum z abc Zpracoval: Jan Novák Naměřeno: 1. ledna 2001 Obor: F Ročník: IV Semestr: IX Testováno:
Soustavy lineárních rovnic
 Soustavy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních diferenciálních rovnic y = a (x)y + a (x)y + + a n (x)y n + f (x) y = a (x)y + a (x)y + + a n (x)y n + f (x). y n = a
Soustavy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních diferenciálních rovnic y = a (x)y + a (x)y + + a n (x)y n + f (x) y = a (x)y + a (x)y + + a n (x)y n + f (x). y n = a
Praktikum II Elektřina a magnetismus
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF K Praktikum II Elektřina a magnetismus Úloha č. V Název: Měření osciloskopem Pracoval: Matyáš Řehák stud.sk.: 13 dne: 1.1.28 Odevzdal dne:...
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF K Praktikum II Elektřina a magnetismus Úloha č. V Název: Měření osciloskopem Pracoval: Matyáš Řehák stud.sk.: 13 dne: 1.1.28 Odevzdal dne:...
Diferenciální rovnice 1
 Diferenciální rovnice 1 Základní pojmy Diferenciální rovnice n-tého řádu v implicitním tvaru je obecně rovnice ve tvaru,,,, = Řád diferenciální rovnice odpovídá nejvyššímu stupni derivace v rovnici použitému.
Diferenciální rovnice 1 Základní pojmy Diferenciální rovnice n-tého řádu v implicitním tvaru je obecně rovnice ve tvaru,,,, = Řád diferenciální rovnice odpovídá nejvyššímu stupni derivace v rovnici použitému.
Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného)
 Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného) 1 Obecný popis metody Particle Image Velocimetry, nebo-li zkráceně PIV, je měřící
Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného) 1 Obecný popis metody Particle Image Velocimetry, nebo-li zkráceně PIV, je měřící
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK FYZIKÁLNÍ PRAKTIKUM III Úloha číslo: 16 Název: Měření indexu lomu Fraunhoferovou metodou Vypracoval: Ondřej Hlaváč stud. skup.: F dne:
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK FYZIKÁLNÍ PRAKTIKUM III Úloha číslo: 16 Název: Měření indexu lomu Fraunhoferovou metodou Vypracoval: Ondřej Hlaváč stud. skup.: F dne:
= cos sin = sin + cos = 1, = 6 = 9. 6 sin 9. = 1 cos 9. = 1 sin 9. + 6 cos 9 = 1 0,939692621 6 ( 0,342020143) = 1 ( 0,342020143) + 6 0,939692621
 ŘEŠENÉ PŘÍKLADY Z MA+ULA ČÁST Příklad Bod má vůči souřadné soustavě souřadnice uvedené níže. Vypočtěte jeho souřadnice vzhledem k soustavě, která je vůči otočená dle zadání uvedeného níže. Výsledky zaokrouhlete
ŘEŠENÉ PŘÍKLADY Z MA+ULA ČÁST Příklad Bod má vůči souřadné soustavě souřadnice uvedené níže. Vypočtěte jeho souřadnice vzhledem k soustavě, která je vůči otočená dle zadání uvedeného níže. Výsledky zaokrouhlete
Algoritmizace prostorových úloh
 INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Úlohy nad rastrovými daty Daniela
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Úlohy nad rastrovými daty Daniela
MĚŘENÍ Laboratorní cvičení z měření. Měření oteplovací charakteristiky, část 3-3-4
 MĚŘENÍ Laboratorní cvičení z měření Měření oteplovací charakteristiky, část Číslo projektu: Název projektu: Šablona: III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Sada: 20 Číslo materiálu: VY_32_INOVACE_
MĚŘENÍ Laboratorní cvičení z měření Měření oteplovací charakteristiky, část Číslo projektu: Název projektu: Šablona: III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Sada: 20 Číslo materiálu: VY_32_INOVACE_
Sluneční dynamika. Michal Švanda Astronomický ústav AV ČR Astronomický ústav UK
 Sluneční dynamika Michal Švanda Astronomický ústav AV ČR Astronomický ústav UK Slunce: dynamický systém Neměnnost Slunce Iluze Slunce je proměnná hvězda Sluneční proměny Díky vývoji Dynamika hmoty Magnetická
Sluneční dynamika Michal Švanda Astronomický ústav AV ČR Astronomický ústav UK Slunce: dynamický systém Neměnnost Slunce Iluze Slunce je proměnná hvězda Sluneční proměny Díky vývoji Dynamika hmoty Magnetická
TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD. 9, m s.
 TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD Soustavu souřadnic spojenou se Zemí můžeme považovat prakticky za inerciální. Jen při několika jevech vznikají odchylky, které lze vysvětlit vlastním pohybem Země vzhledem
TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD Soustavu souřadnic spojenou se Zemí můžeme považovat prakticky za inerciální. Jen při několika jevech vznikají odchylky, které lze vysvětlit vlastním pohybem Země vzhledem
676 + 4 + 100 + 196 + 0 + 484 + 196 + 324 + 64 + 324 = = 2368
 Příklad 1 Je třeba prověřit, zda lze na 5% hladině významnosti pokládat za prokázanou hypotézu, že střední doba výroby výlisku je 30 sekund. Přitom 10 náhodně vybraných výlisků bylo vyráběno celkem 540
Příklad 1 Je třeba prověřit, zda lze na 5% hladině významnosti pokládat za prokázanou hypotézu, že střední doba výroby výlisku je 30 sekund. Přitom 10 náhodně vybraných výlisků bylo vyráběno celkem 540
Pohyb tělesa po nakloněné rovině
 Pohyb tělesa po nakloněné rovině Zadání 1 Pro vybrané těleso a materiál nakloněné roviny zjistěte závislost polohy tělesa na čase při jeho pohybu Výsledky vyneste do grafu a rozhodněte z něj, o jakou křivku
Pohyb tělesa po nakloněné rovině Zadání 1 Pro vybrané těleso a materiál nakloněné roviny zjistěte závislost polohy tělesa na čase při jeho pohybu Výsledky vyneste do grafu a rozhodněte z něj, o jakou křivku
Spektrální charakteristiky
 Spektrální charakteristiky Cíl cvičení: Měření spektrálních charakteristik filtrů a zdrojů osvětlení 1 Teoretický úvod Interakcí elektromagnetického vlnění s libovolnou látkou vzniká optický jev, který
Spektrální charakteristiky Cíl cvičení: Měření spektrálních charakteristik filtrů a zdrojů osvětlení 1 Teoretický úvod Interakcí elektromagnetického vlnění s libovolnou látkou vzniká optický jev, který
Měření modulů pružnosti G a E z periody kmitů pružiny
 Měření modulů pružnosti G a E z periody kmitů pružiny Online: http://www.sclpx.eu/lab2r.php?exp=2 V tomto experimentu vycházíme z pojetí klasického pokusu s pružinovým oscilátorem. Z periody kmitů se obvykle
Měření modulů pružnosti G a E z periody kmitů pružiny Online: http://www.sclpx.eu/lab2r.php?exp=2 V tomto experimentu vycházíme z pojetí klasického pokusu s pružinovým oscilátorem. Z periody kmitů se obvykle
Experimentáln. lní toků ve VK EMO. XXX. Dny radiační ochrany Liptovský Ján 10.11.-14.11.2008 Petr Okruhlica, Miroslav Mrtvý, Zdenek Kopecký. www.vf.
 Experimentáln lní měření průtok toků ve VK EMO XXX. Dny radiační ochrany Liptovský Ján 10.11.-14.11.2008 Petr Okruhlica, Miroslav Mrtvý, Zdenek Kopecký Systém měření průtoku EMO Měření ve ventilačním komíně
Experimentáln lní měření průtok toků ve VK EMO XXX. Dny radiační ochrany Liptovský Ján 10.11.-14.11.2008 Petr Okruhlica, Miroslav Mrtvý, Zdenek Kopecký Systém měření průtoku EMO Měření ve ventilačním komíně
Interpolace obrazu pro experimentální měřiče plošného teplotního rozložení
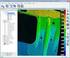 Interpolace obrazu pro experimentální měřiče plošného teplotního rozložení Bc. Zdeněk Martinásek Vysoké učení technické v Brně, Fakulta elektrotechniky a komunikačních technologií, Ústav telekomunikací,
Interpolace obrazu pro experimentální měřiče plošného teplotního rozložení Bc. Zdeněk Martinásek Vysoké učení technické v Brně, Fakulta elektrotechniky a komunikačních technologií, Ústav telekomunikací,
VYHODNOCENÍ LABORATORNÍCH ZKOUŠEK
 VYHODNOCENÍ LABORATORNÍCH ZKOUŠEK Deformace elastomerových ložisek při zatížení Z hodnot naměřených deformací elastomerových ložisek v jednotlivých měřících místech (jednotlivé snímače deformace) byly
VYHODNOCENÍ LABORATORNÍCH ZKOUŠEK Deformace elastomerových ložisek při zatížení Z hodnot naměřených deformací elastomerových ložisek v jednotlivých měřících místech (jednotlivé snímače deformace) byly
Obsah. Funkce grafu Zdrojová data pro graf Typ grafu Formátování prvků grafu Doporučení pro tvorbu grafů Zdroje
 Grafy v MS Excel Obsah Funkce grafu Zdrojová data pro graf Typ grafu Formátování prvků grafu Doporučení pro tvorbu grafů Zdroje Funkce grafu Je nejčastěji vizualizací při zpracování dat z různých statistik
Grafy v MS Excel Obsah Funkce grafu Zdrojová data pro graf Typ grafu Formátování prvků grafu Doporučení pro tvorbu grafů Zdroje Funkce grafu Je nejčastěji vizualizací při zpracování dat z různých statistik
Úvod. Zatmění Slunce 2006
 Dynamika polárních paprsků během zatmění Slunce 2006 Marková, E. 1, Bělík, M. 1, Druckmüller, M. 2, Druckmüllerová, H. 2 1 Hvězdárna v Úpici 2 VUT Brno Abstrakt: Velmi jemné detaily koronálních struktur
Dynamika polárních paprsků během zatmění Slunce 2006 Marková, E. 1, Bělík, M. 1, Druckmüller, M. 2, Druckmüllerová, H. 2 1 Hvězdárna v Úpici 2 VUT Brno Abstrakt: Velmi jemné detaily koronálních struktur
Nalezněte obecné řešení diferenciální rovnice (pomocí separace proměnných) a řešení Cauchyho úlohy: =, 0 = 1 = 1. ln = +,
 Příklad Nalezněte obecné řešení diferenciální rovnice (pomocí separace proměnných) a řešení Cauchyho úlohy: a) =, 0= b) =, = c) =2, = d) =2, 0= e) =, 0= f) 2 =0, = g) + =0, h) =, = 2 = i) =, 0= j) sin+cos=0,
Příklad Nalezněte obecné řešení diferenciální rovnice (pomocí separace proměnných) a řešení Cauchyho úlohy: a) =, 0= b) =, = c) =2, = d) =2, 0= e) =, 0= f) 2 =0, = g) + =0, h) =, = 2 = i) =, 0= j) sin+cos=0,
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Příklady použití tenkých vrstev Jaromír Křepelka
 Příklady použití tenkých vrstev Jaromír Křepelka Příklad 01 Spočtěte odrazivost prostého rozhraní dvou izotropních homogenních materiálů s indexy lomu n 0 = 1 a n 1 = 1,52 v závislosti na úhlu dopadu pro
Příklady použití tenkých vrstev Jaromír Křepelka Příklad 01 Spočtěte odrazivost prostého rozhraní dvou izotropních homogenních materiálů s indexy lomu n 0 = 1 a n 1 = 1,52 v závislosti na úhlu dopadu pro
Jednofaktorová analýza rozptylu
 I I.I Jednofaktorová analýza rozptylu Úvod Jednofaktorová analýza rozptylu (ANOVA) se využívá při porovnání několika středních hodnot. Často se využívá ve vědeckých a lékařských experimentech, při kterých
I I.I Jednofaktorová analýza rozptylu Úvod Jednofaktorová analýza rozptylu (ANOVA) se využívá při porovnání několika středních hodnot. Často se využívá ve vědeckých a lékařských experimentech, při kterých
Popis funkcí tlačítek jednotlivých modulů programu OGAMA
 Nevázaná příloha bakalářské práce VYUŽITÍ OPEN-SOURCE NÁSTROJŮ PRO PŘÍPRAVU, PRŮBĚH A VYHODNOCENÍ EYE-TRACKING EXPERIMENTŮ Popis funkcí tlačítek jednotlivých modulů programu OGAMA Michal KUČERA, 2014 Replay
Nevázaná příloha bakalářské práce VYUŽITÍ OPEN-SOURCE NÁSTROJŮ PRO PŘÍPRAVU, PRŮBĚH A VYHODNOCENÍ EYE-TRACKING EXPERIMENTŮ Popis funkcí tlačítek jednotlivých modulů programu OGAMA Michal KUČERA, 2014 Replay
Role magnetického pole při strukturování bílé koróny (interpretace pozorování zatmění z Angoly 2001)
 Role magnetického pole při strukturování bílé koróny (interpretace pozorování zatmění z Angoly 2001) Marcel Bělík, Hvězdárna v Úpici, belik@obsupice.cz Pavel Ambrož, AÚ AV ČR Ondřejov, pambroz@asu.cas.cz
Role magnetického pole při strukturování bílé koróny (interpretace pozorování zatmění z Angoly 2001) Marcel Bělík, Hvězdárna v Úpici, belik@obsupice.cz Pavel Ambrož, AÚ AV ČR Ondřejov, pambroz@asu.cas.cz
Topografické plochy KG - L MENDELU. KG - L (MENDELU) Topografické plochy 1 / 56
 Topografické plochy KG - L MENDELU KG - L (MENDELU) Topografické plochy 1 / 56 Obsah 1 Úvod 2 Křivky a body na topografické ploše 3 Řez topografické plochy rovinou 4 Příčný a podélný profil KG - L (MENDELU)
Topografické plochy KG - L MENDELU KG - L (MENDELU) Topografické plochy 1 / 56 Obsah 1 Úvod 2 Křivky a body na topografické ploše 3 Řez topografické plochy rovinou 4 Příčný a podélný profil KG - L (MENDELU)
Fázorové diagramy pro ideální rezistor, skutečná cívka, ideální cívka, skutečný kondenzátor, ideální kondenzátor.
 FREKVENČNĚ ZÁVISLÉ OBVODY Základní pojmy: IMPEDANCE Z (Ω)- charakterizuje vlastnosti prvku pro střídavý proud. Impedance je základní vlastností, kterou potřebujeme znát pro analýzu střídavých elektrických
FREKVENČNĚ ZÁVISLÉ OBVODY Základní pojmy: IMPEDANCE Z (Ω)- charakterizuje vlastnosti prvku pro střídavý proud. Impedance je základní vlastností, kterou potřebujeme znát pro analýzu střídavých elektrických
Základní jednotky v astronomii
 v01.00 Základní jednotky v astronomii Ing. Neliba Vlastimil AK Kladno 2005 Délka - l Slouží pro určení vzdáleností ve vesmíru Základní jednotkou je metr metr je definován jako délka, jež urazí světlo ve
v01.00 Základní jednotky v astronomii Ing. Neliba Vlastimil AK Kladno 2005 Délka - l Slouží pro určení vzdáleností ve vesmíru Základní jednotkou je metr metr je definován jako délka, jež urazí světlo ve
PRAKTIKUM I. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Pracoval: Pavel Ševeček stud. skup.: F/F1X/11 dne:
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I. Úloha č. VIII Název: Kalibrace odporového teploměru a termočlánku fázové přechody Pracoval: Pavel Ševeček stud. skup.:
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I. Úloha č. VIII Název: Kalibrace odporového teploměru a termočlánku fázové přechody Pracoval: Pavel Ševeček stud. skup.:
Střední průmyslová škola elektrotechnická a informačních technologií Brno
 Střední průmyslová škola elektrotechnická a informačních technologií Brno Číslo a název projektu: CZ.1.07/1.5.00/34.0521 Investice do vzdělání nesou nejvyšší úrok Autor: Ing. Bohumír Jánoš Tématická sada:
Střední průmyslová škola elektrotechnická a informačních technologií Brno Číslo a název projektu: CZ.1.07/1.5.00/34.0521 Investice do vzdělání nesou nejvyšší úrok Autor: Ing. Bohumír Jánoš Tématická sada:
EXPERIMENTÁLNÍ MECHANIKA 1. Jan Krystek
 EXPERIMENTÁLNÍ MECHANIKA 1 2. přednáška Jan Krystek 27. září 2017 ZÁKLADY TEORIE EXPERIMENTU EXPERIMENT soustava cílevědomě řízených činností s určitou posloupností CÍL EXPERIMENTU získání objektivních
EXPERIMENTÁLNÍ MECHANIKA 1 2. přednáška Jan Krystek 27. září 2017 ZÁKLADY TEORIE EXPERIMENTU EXPERIMENT soustava cílevědomě řízených činností s určitou posloupností CÍL EXPERIMENTU získání objektivních
Jasové transformace. Karel Horák. Rozvrh přednášky:
 1 / 23 Jasové transformace Karel Horák Rozvrh přednášky: 1. Úvod. 2. Histogram obrazu. 3. Globální jasová transformace. 4. Lokální jasová transformace. 5. Bodová jasová transformace. 2 / 23 Jasové transformace
1 / 23 Jasové transformace Karel Horák Rozvrh přednášky: 1. Úvod. 2. Histogram obrazu. 3. Globální jasová transformace. 4. Lokální jasová transformace. 5. Bodová jasová transformace. 2 / 23 Jasové transformace
Návrh frekvenčního filtru
 Návrh frekvenčního filtru Vypracoval: Martin Dlouhý, Petr Salajka 25. 9 2010 1 1 Zadání 1. Navrhněte co nejjednodušší přenosovou funkci frekvenčního pásmového filtru Dolní propusti typu Bessel, která bude
Návrh frekvenčního filtru Vypracoval: Martin Dlouhý, Petr Salajka 25. 9 2010 1 1 Zadání 1. Navrhněte co nejjednodušší přenosovou funkci frekvenčního pásmového filtru Dolní propusti typu Bessel, která bude
Nelineární obvody. V nelineárních obvodech však platí Kirchhoffovy zákony.
 Nelineární obvody Dosud jsme se zabývali analýzou lineárních elektrických obvodů, pasivní lineární prvky měly zpravidla konstantní parametr, v těchto obvodech platil princip superpozice a pro analýzu harmonického
Nelineární obvody Dosud jsme se zabývali analýzou lineárních elektrických obvodů, pasivní lineární prvky měly zpravidla konstantní parametr, v těchto obvodech platil princip superpozice a pro analýzu harmonického
1 Linearní prostory nad komplexními čísly
 1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
Kombinatorická minimalizace
 Kombinatorická minimalizace Cílem je nalézt globální minimum ve velké diskrétní množině, kde může být mnoho lokálních minim. Úloha obchodního cestujícího Cílem je najít nejkratší cestu, která spojuje všechny
Kombinatorická minimalizace Cílem je nalézt globální minimum ve velké diskrétní množině, kde může být mnoho lokálních minim. Úloha obchodního cestujícího Cílem je najít nejkratší cestu, která spojuje všechny
Laboratorní úloha č. 7 Difrakce na mikro-objektech
 Laboratorní úloha č. 7 Difrakce na mikro-objektech Úkoly měření: 1. Odhad rozměrů mikro-objektů z informací uváděných výrobcem. 2. Záznam difrakčních obrazců (difraktogramů) vzniklých interakcí laserového
Laboratorní úloha č. 7 Difrakce na mikro-objektech Úkoly měření: 1. Odhad rozměrů mikro-objektů z informací uváděných výrobcem. 2. Záznam difrakčních obrazců (difraktogramů) vzniklých interakcí laserového
SEMESTRÁLNÍ PRÁCE X. Aproximace křivek Numerické vyhlazování
 KATEDRA ANALYTICKÉ CHEMIE FAKULTY CHEMICKO TECHNOLOGICKÉ UNIVERSITA PARDUBICE - Licenční studium chemometrie LS96/1 SEMESTRÁLNÍ PRÁCE X. Aproximace křivek Numerické vyhlazování Praha, leden 1999 0 Úloha
KATEDRA ANALYTICKÉ CHEMIE FAKULTY CHEMICKO TECHNOLOGICKÉ UNIVERSITA PARDUBICE - Licenční studium chemometrie LS96/1 SEMESTRÁLNÍ PRÁCE X. Aproximace křivek Numerické vyhlazování Praha, leden 1999 0 Úloha
Úloha 3: Mřížkový spektrometr
 Petra Suková, 2.ročník, F-14 1 Úloha 3: Mřížkový spektrometr 1 Zadání 1. Seřiďte spektrometr pro kolmý dopad světla(rovina optické mřížky je kolmá k ose kolimátoru) pomocí bočního osvětlení nitkového kříže.
Petra Suková, 2.ročník, F-14 1 Úloha 3: Mřížkový spektrometr 1 Zadání 1. Seřiďte spektrometr pro kolmý dopad světla(rovina optické mřížky je kolmá k ose kolimátoru) pomocí bočního osvětlení nitkového kříže.
vzorek1 0.0033390 0.0047277 0.0062653 0.0077811 0.0090141... vzorek 30 0.0056775 0.0058778 0.0066916 0.0076192 0.0087291
 Vzorová úloha 4.16 Postup vícerozměrné kalibrace Postup vícerozměrné kalibrace ukážeme na úloze C4.10 Vícerozměrný kalibrační model kvality bezolovnatého benzinu. Dle následujících kroků na základě naměřených
Vzorová úloha 4.16 Postup vícerozměrné kalibrace Postup vícerozměrné kalibrace ukážeme na úloze C4.10 Vícerozměrný kalibrační model kvality bezolovnatého benzinu. Dle následujících kroků na základě naměřených
Diferenciální rovnice 3
 Diferenciální rovnice 3 Lineární diferenciální rovnice n-tého řádu Lineární diferenciální rovnice (dále jen LDR) n-tého řádu je rovnice tvaru + + + + = kde = je hledaná funkce, pravá strana a koeficienty
Diferenciální rovnice 3 Lineární diferenciální rovnice n-tého řádu Lineární diferenciální rovnice (dále jen LDR) n-tého řádu je rovnice tvaru + + + + = kde = je hledaná funkce, pravá strana a koeficienty
Matematické modelování dopravního proudu
 Matematické modelování dopravního proudu Ondřej Lanč, Alena Girglová, Kateřina Papežová, Lucie Obšilová Gymnázium Otokara Březiny a SOŠ Telč lancondrej@centrum.cz Abstrakt: Cílem projektu bylo seznámení
Matematické modelování dopravního proudu Ondřej Lanč, Alena Girglová, Kateřina Papežová, Lucie Obšilová Gymnázium Otokara Březiny a SOŠ Telč lancondrej@centrum.cz Abstrakt: Cílem projektu bylo seznámení
Systém vykonávající tlumené kmity lze popsat obyčejnou lineární diferenciální rovnice 2. řadu s nulovou pravou stranou:
 Pracovní úkol: 1. Sestavte obvod podle obr. 1 a změřte pro obvod v periodickém stavu závislost doby kmitu T na velikosti zařazené kapacity. (C = 0,5-10 µf, R = 0 Ω). Výsledky měření zpracujte graficky
Pracovní úkol: 1. Sestavte obvod podle obr. 1 a změřte pro obvod v periodickém stavu závislost doby kmitu T na velikosti zařazené kapacity. (C = 0,5-10 µf, R = 0 Ω). Výsledky měření zpracujte graficky
2. Kinematika bodu a tělesa
 2. Kinematika bodu a tělesa Kinematika bodu popisuje těleso nebo také bod, který se pohybuje po nějaké trajektorii, křivce nebo jinak definované dráze v závislosti na poloze bodu na dráze, rychlosti a
2. Kinematika bodu a tělesa Kinematika bodu popisuje těleso nebo také bod, který se pohybuje po nějaké trajektorii, křivce nebo jinak definované dráze v závislosti na poloze bodu na dráze, rychlosti a
Topologie rychlostního pole v různých vývojových fázích aktivní oblasti
 Topologie rychlostního pole v různých vývojových fázích aktivní oblasti V. Bumba, Astronomický ústav Akademie věd České republiky, observatoř Ondřejov, Česká republika, bumba @asu.cas.cz M. Klvaňa, Astronomický
Topologie rychlostního pole v různých vývojových fázích aktivní oblasti V. Bumba, Astronomický ústav Akademie věd České republiky, observatoř Ondřejov, Česká republika, bumba @asu.cas.cz M. Klvaňa, Astronomický
12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ
 56 12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ Těžiště I. impulsová věta - věta o pohybu těžiště II. impulsová věta Zákony zachování v izolované soustavě hmotných bodů Náhrada pohybu skutečných objektů pohybem
56 12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ Těžiště I. impulsová věta - věta o pohybu těžiště II. impulsová věta Zákony zachování v izolované soustavě hmotných bodů Náhrada pohybu skutečných objektů pohybem
APLIKACE SIMULAČNÍHO PROGRAMU ANSYS PRO VÝUKU MIKROELEKTROTECHNICKÝCH TECHNOLOGIÍ
 APLIKACE SIMULAČNÍHO PROGRAMU ANSYS PRO VÝUKU MIKROELEKTROTECHNICKÝCH TECHNOLOGIÍ 1. ÚVOD Ing. Psota Boleslav, Doc. Ing. Ivan Szendiuch, CSc. Ústav mikroelektroniky, FEKT VUT v Brně, Technická 10, 602
APLIKACE SIMULAČNÍHO PROGRAMU ANSYS PRO VÝUKU MIKROELEKTROTECHNICKÝCH TECHNOLOGIÍ 1. ÚVOD Ing. Psota Boleslav, Doc. Ing. Ivan Szendiuch, CSc. Ústav mikroelektroniky, FEKT VUT v Brně, Technická 10, 602
. je zlomkem. Ten je smysluplný pro jakýkoli jmenovatel různý od nuly. Musí tedy platit = 0
 Příklad 1 Určete definiční obor funkce: a) = b) = c) = d) = e) = 9 f) = Řešení 1a Máme určit definiční obor funkce =. Výraz je zlomkem. Ten je smysluplný pro jakýkoli jmenovatel různý od nuly. Musí tedy
Příklad 1 Určete definiční obor funkce: a) = b) = c) = d) = e) = 9 f) = Řešení 1a Máme určit definiční obor funkce =. Výraz je zlomkem. Ten je smysluplný pro jakýkoli jmenovatel různý od nuly. Musí tedy
Analýza reziduí gyroskopu
 Analýza reziduí gyroskopu Petr Šimeček Cílem studie bylo analyzovat přesnost tří neznámých gyroskopů, jež pro účely této studie budeme nazývat Gyroskop 1, Gyroskop 2 a Gyroskop 3. U prvních dvou gyroskopů
Analýza reziduí gyroskopu Petr Šimeček Cílem studie bylo analyzovat přesnost tří neznámých gyroskopů, jež pro účely této studie budeme nazývat Gyroskop 1, Gyroskop 2 a Gyroskop 3. U prvních dvou gyroskopů
GEODETICKÉ VÝPOČTY I.
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. TABELACE FUNKCE LINEÁRNÍ INTERPOLACE TABELACE FUNKCE Tabelace funkce se v minulosti často využívala z důvodu usnadnění
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. TABELACE FUNKCE LINEÁRNÍ INTERPOLACE TABELACE FUNKCE Tabelace funkce se v minulosti často využívala z důvodu usnadnění
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV MECHANIKY TĚLES, MECHATRONIKY A BIOMECHANIKY Komentovaný metodický list č. 1/4 Vytvořil: Ing. Oldřich Ševeček & Ing. Tomáš Profant, Ph.D.
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV MECHANIKY TĚLES, MECHATRONIKY A BIOMECHANIKY Komentovaný metodický list č. 1/4 Vytvořil: Ing. Oldřich Ševeček & Ing. Tomáš Profant, Ph.D.
6 Potenciály s δ funkcemi II
 6 Potenciály s δ funkcemi II 6.1 Periodická δ funkce (Diracův hřeben) Částice o hmotnosti M se pohybuje v jednorozměrné mřížce popsané periodickým potenciálem V(x) = c δ(x na), (6.1.1) n= kde a je vzdálenost
6 Potenciály s δ funkcemi II 6.1 Periodická δ funkce (Diracův hřeben) Částice o hmotnosti M se pohybuje v jednorozměrné mřížce popsané periodickým potenciálem V(x) = c δ(x na), (6.1.1) n= kde a je vzdálenost
Rozšíření rozsahu miliampérmetru a voltmetru, cejchování kompenzátorem
 FJFI ČVUT v Praze Fyzikální praktikum I Úloha 9 Verze 161010 Rozšíření rozsahu miliampérmetru a voltmetru, cejchování kompenzátorem Abstrakt: V úloze si osvojíte práci s jednoduchými elektrickými obvody.
FJFI ČVUT v Praze Fyzikální praktikum I Úloha 9 Verze 161010 Rozšíření rozsahu miliampérmetru a voltmetru, cejchování kompenzátorem Abstrakt: V úloze si osvojíte práci s jednoduchými elektrickými obvody.
Popisná statistika. Komentované řešení pomocí MS Excel
 Popisná statistika Komentované řešení pomocí MS Excel Vstupní data Máme k dispozici data o počtech bodů z 1. a 2. zápočtového testu z Matematiky I v zimním semestru 2015/2016 a to za všech 762 studentů,
Popisná statistika Komentované řešení pomocí MS Excel Vstupní data Máme k dispozici data o počtech bodů z 1. a 2. zápočtového testu z Matematiky I v zimním semestru 2015/2016 a to za všech 762 studentů,
4. Statika základní pojmy a základy rovnováhy sil
 4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
Měřicí přístroje a měřicí metody
 Měřicí přístroje a měřicí metody Základní elektrické veličiny určují kvalitativně i kvantitativně stav elektrických obvodů a objektů. Neelektrické fyzikální veličiny lze převést na elektrické veličiny
Měřicí přístroje a měřicí metody Základní elektrické veličiny určují kvalitativně i kvantitativně stav elektrických obvodů a objektů. Neelektrické fyzikální veličiny lze převést na elektrické veličiny
Nejdřív spočítáme jeden příklad na variaci konstant pro lineární diferenciální rovnici 2. řádu s kostantními koeficienty. y + y = 4 sin t.
 1 Variace konstanty Nejdřív spočítáme jeden příklad na variaci konstant pro lineární diferenciální rovnici 2. řádu s kostantními koeficienty. Příklad 1 Najděte obecné řešení rovnice: y + y = 4 sin t. Co
1 Variace konstanty Nejdřív spočítáme jeden příklad na variaci konstant pro lineární diferenciální rovnici 2. řádu s kostantními koeficienty. Příklad 1 Najděte obecné řešení rovnice: y + y = 4 sin t. Co
Stanovení kritických otáček vačkového hřídele Frotoru
 Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra mechaniky Stanovení ických otáček vačkového hřídele Frotoru Řešitel: oc. r. Ing. Jan upal Plzeň, březen 7 Úvod: Cílem předložené zprávy je
Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra mechaniky Stanovení ických otáček vačkového hřídele Frotoru Řešitel: oc. r. Ing. Jan upal Plzeň, březen 7 Úvod: Cílem předložené zprávy je
Automatická detekce anomálií při geofyzikálním průzkumu. Lenka Kosková Třísková NTI TUL Doktorandský seminář, 8. 6. 2011
 Automatická detekce anomálií při geofyzikálním průzkumu Lenka Kosková Třísková NTI TUL Doktorandský seminář, 8. 6. 2011 Cíle doktorandské práce Seminář 10. 11. 2010 Najít, implementovat, ověřit a do praxe
Automatická detekce anomálií při geofyzikálním průzkumu Lenka Kosková Třísková NTI TUL Doktorandský seminář, 8. 6. 2011 Cíle doktorandské práce Seminář 10. 11. 2010 Najít, implementovat, ověřit a do praxe
1 Co jste o sluneèních hodinách nevìdìli?
 1 Co jste o sluneèních hodinách nevìdìli? 1.1 Měsíční hodiny Drahomíra Pecinová Sluneční hodiny různých typů můžeme doplnit měsíčními hodinami a rozšířit tak jejich použití i na noci, kdy svítí Měsíc.
1 Co jste o sluneèních hodinách nevìdìli? 1.1 Měsíční hodiny Drahomíra Pecinová Sluneční hodiny různých typů můžeme doplnit měsíčními hodinami a rozšířit tak jejich použití i na noci, kdy svítí Měsíc.
SYLABUS PŘEDNÁŠKY 10 Z GEODÉZIE 1
 SYLABUS PŘEDNÁŠKY 10 Z GEODÉZIE 1 (Souřadnicové výpočty 4, Orientace osnovy vodorovných směrů) 1. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec
SYLABUS PŘEDNÁŠKY 10 Z GEODÉZIE 1 (Souřadnicové výpočty 4, Orientace osnovy vodorovných směrů) 1. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec
TERMINOLOGIE ... NAMĚŘENÁ DATA. Radek Mareček PŘEDZPRACOVÁNÍ DAT. funkční skeny
 PŘEDZPRACOVÁNÍ DAT Radek Mareček TERMINOLOGIE Session soubor skenů nasnímaných během jednoho běhu stimulačního paradigmatu (řádově desítky až stovky skenů) Sken jeden nasnímaný objem... Voxel elementární
PŘEDZPRACOVÁNÍ DAT Radek Mareček TERMINOLOGIE Session soubor skenů nasnímaných během jednoho běhu stimulačního paradigmatu (řádově desítky až stovky skenů) Sken jeden nasnímaný objem... Voxel elementární
Nastavení parametrů PID a PSD regulátorů
 Fakulta elektrotechniky a informatiky Univerzita Pardubice Nastavení parametrů PID a PSD regulátorů Semestrální práce z předmětu Teorie řídicích systémů Jméno: Jiří Paar Datum: 9. 1. 2010 Zadání Je dána
Fakulta elektrotechniky a informatiky Univerzita Pardubice Nastavení parametrů PID a PSD regulátorů Semestrální práce z předmětu Teorie řídicích systémů Jméno: Jiří Paar Datum: 9. 1. 2010 Zadání Je dána
1. Změřte průběh intenzity magnetického pole na ose souosých kruhových magnetizačních cívek
 1 Pracovní úkoly 1. Změřte průběh intenzity magnetického pole na ose souosých kruhových magnetizačních cívek (a) v zapojení s nesouhlasným směrem proudu při vzdálenostech 1, 16, 0 cm (b) v zapojení se
1 Pracovní úkoly 1. Změřte průběh intenzity magnetického pole na ose souosých kruhových magnetizačních cívek (a) v zapojení s nesouhlasným směrem proudu při vzdálenostech 1, 16, 0 cm (b) v zapojení se
Aplikovaná numerická matematika
 Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Výukový materiál v rámci projektu OPVK 1.5 Peníze středním školám
 Výukový materiál v rámci projektu OPVK 1.5 Peníze středním školám Číslo projektu: CZ.1.07/1.5.00/34.0883 Název projektu: Rozvoj vzdělanosti Číslo šablony: III/2 Datum vytvoření: 17. 12. 2012 Autor: MgA.
Výukový materiál v rámci projektu OPVK 1.5 Peníze středním školám Číslo projektu: CZ.1.07/1.5.00/34.0883 Název projektu: Rozvoj vzdělanosti Číslo šablony: III/2 Datum vytvoření: 17. 12. 2012 Autor: MgA.
CT - artefakty. Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová fyzika
 CT - artefakty Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová fyzika Artefakty v CT Systematické neshody v CT číslech v rekonstruovaném obraze oproti skutečné hodnotě koeficientu zeslabení
CT - artefakty Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová fyzika Artefakty v CT Systematické neshody v CT číslech v rekonstruovaném obraze oproti skutečné hodnotě koeficientu zeslabení
Diferenciální rovnice
 Diferenciální rovnice Průvodce studiem Touto kapitolou se náplň základního kurzu bakalářské matematiky uzavírá. Je tomu tak mimo jiné proto, že jsou zde souhrnně využívány poznatky získané studiem předchozích
Diferenciální rovnice Průvodce studiem Touto kapitolou se náplň základního kurzu bakalářské matematiky uzavírá. Je tomu tak mimo jiné proto, že jsou zde souhrnně využívány poznatky získané studiem předchozích
6 Algebra blokových schémat
 6 Algebra blokových schémat Operátorovým přenosem jsme doposud popisovali chování jednotlivých dynamických členů. Nic nám však nebrání, abychom přenosem popsali dynamické vlastnosti složitějších obvodů,
6 Algebra blokových schémat Operátorovým přenosem jsme doposud popisovali chování jednotlivých dynamických členů. Nic nám však nebrání, abychom přenosem popsali dynamické vlastnosti složitějších obvodů,
Měření parametrů světelných zdrojů a osvětlení
 FP 4 Měření parametrů světelných zdrojů a osvětlení Úkoly : 1. Určete a porovnejte normované prostorové vyzařovací charakteristiky určených světelných zdrojů (žárovky, LD dioda) pomocí fotogoniometru 2.
FP 4 Měření parametrů světelných zdrojů a osvětlení Úkoly : 1. Určete a porovnejte normované prostorové vyzařovací charakteristiky určených světelných zdrojů (žárovky, LD dioda) pomocí fotogoniometru 2.
M - Příprava na 1. zápočtový test - třída 3SA
 M - Příprava na 1. zápočtový test - třída 3SA Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento
M - Příprava na 1. zápočtový test - třída 3SA Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento
KFC/SEM, KFC/SEMA Rovnice, nerovnice
 KFC/SEM, KFC/SEMA Rovnice, nerovnice Požadované dovednosti: Řešení lineárních rovnic a nerovnic Řešení kvadratických rovnic Řešení rovnic s odmocninou Řešení rovnic s parametrem Řešení rovnic s absolutní
KFC/SEM, KFC/SEMA Rovnice, nerovnice Požadované dovednosti: Řešení lineárních rovnic a nerovnic Řešení kvadratických rovnic Řešení rovnic s odmocninou Řešení rovnic s parametrem Řešení rovnic s absolutní
Dělení. INP 2008 FIT VUT v Brně
 ělení INP 28 FIT VUT v Brně ělení čísel s pevnou řádovou čárkou Nejdříve se budeme zabývat dělením čísel s pevnou řádovou čárkou bez znaménka. Pro jednotlivé činitele operace dělení zavedeme symboly d
ělení INP 28 FIT VUT v Brně ělení čísel s pevnou řádovou čárkou Nejdříve se budeme zabývat dělením čísel s pevnou řádovou čárkou bez znaménka. Pro jednotlivé činitele operace dělení zavedeme symboly d
Přijímací zkouška na navazující magisterské studium Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy
 Přijímací zkouška na navazující magisterské studium 013 Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy Studijní program Učitelství pro základní školy - obor Učitelství fyziky
Přijímací zkouška na navazující magisterské studium 013 Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy Studijní program Učitelství pro základní školy - obor Učitelství fyziky
