Brloh VI Zadání Malého finále
|
|
|
- Jindřiška Kolářová
- před 8 lety
- Počet zobrazení:
Transkript
1 Brloh VI Zadání Malého finále Odpovědi odešlete prostřednictvím našich webových stránek 1 Abecední Zadání: Pišme za sebe znaky anglické abecedy stále dokola (tj. začneme písmenem A a poté, co napíšeme písmeno Z, budeme opět pokračovat písmenem A). Skončíme v ten moment, kdy bude rozdíl mezi počtem souhlásek a samohlásek roven Jaké poslední písmeno jsme napsali? Forma odpovědi: Písmeno Zadání: 2 Anglická matematika 3 Cesty v krychli Zadání: Určete, kolik existuje různých cest z bodu A do bodu G tak, že můžete chodit pouze po hranách krychle a máte projít právě 5 hran a po žádné hraně nesmíte jít opakovaně. Maximální počet odpovědí: Zde je maximální počet odpovědí upraven na 3 1
2 4 Čtyřnásobná Zadání: Nedopálený pták, který je tlučen, neboť uvádí štítky. Forma odpovědi: Jedno slovo 5 Genderová Zadání: Muž je jednoděložný a pojmenován po řeckém bohu duhy, žena je predátor na vrcholu mořského potravního řetězce. Jaký je jejich společný nástroj? Forma odpovědi: Vyplývá ze zadání 6 Krychlová Zadání: Kejtý na stole slepila stavbu z kostek. Na obrázku vidíte, jak stavba vypadá při pohledu shora. Čísla uprostřed čtverců udávají, kolik kostek je položených na sobě. Jack přišel a rozhodl se, že stavbu oblepí. Vystřihl si z papíru několik čtverců a ty nalepil na každou viditelnou stěnu (zespodu stavbu neoblepoval). Určete, kolik čtverců takto musel použít? 7 Matematický turnaj Zadání: Turnaje v řešení matematických úloh se zúčastnili nejlepší studenti z každé třídy 9. ročníku: Karel, Láďa, Marie, Norbert a Olga. Marie vyřešila více příkladů než Olga, ale méně než Láďa. Součet příkladů, který vyřešili Láďa a Norbert, byl menší než počet příkladů, které vyřešil Karel a Olga dohromady. Karel vyřešil méně příkladů než Marie. Určete, kdo byl na posledním místě, jestliže vyhrává student s největším počtem vyřešených příkladů. Forma odpovědi: Jméno Maximální počet odpovědí: Zde je maximální počet odpovědí upraven na 3 2
3 8 Nerovnoramenné váhy Zadání: Kupující chtěl koupit dvě a čtvrt kilo borůvek. Prodavačka zvážila zboží na pravé misce a na levou pokládala závaží. Kupující ale prodavačce nevěřil a požádal o převážení, přičemž položil borůvky na levou misku a závaží na pravou. Ukázalo se, že borůvek je 1,44 kg. Kolik vážily borůvky doopravdy? Forma odpovědi: Kilogramy zaokrouhlené na dvě desetinná místa. 9 Operační Zadání: Když se Bill jednoho sychravého podzimního rána v roce 2000 vzbudil, hlavou mu stále probíhal velmi podivný sen (nemluvě o tom, že mu v ní hučelo jako po výbuchu T.N.T.). Ležel na operačním stole a nad ním stál jeden podivný doktor, tři sestřičky a místnost osvětlovaly dva velké světelné reflektory. Ve svém životě zažil dvě operace. Jednu ještě v roce 95, kdy mu vzali slepé střevo, a druhou v roce 98, kdy nešťastně propadl oknem 7 metrů nad zemí a museli mu zašívat tržné rány po celém těle. Vlastně to bylo jen 8 ran, ale to není podstatné. Ani jedna z těchto operací však nevypadala jako ta ve snu. Ze svého snu si ještě pamatuje doktora s rouškou, zpod které vykukoval černý plnovous, a na jehož plášti byly zeleným nemocničním písmem vyšité iniciály X.P., které znamenaly Xavier Petófi. Dosti výstižné jméno k těm vousům, pomyslel si. Krom zvláštního doktora měl sen také zvláštní konec. Sedativa zabírala, oči se mu zavíraly a hodinky právě ukazovaly 10 hodin, když v tom doktor řekl: "Hasta la vista!" Forma odpovědi: Zadejte, co chybí 10 Presumpční Zadání: dříve v čase, později v čase, světlá stránka 11 Řezání hranolu Zadání: Kolik shodných pravidelných trojbokých hranolů, které mají hrany a výšky stejně dlouhé, lze vyrobit z pravidelného šestibokého hranolu výšky 1m a hrany délky 1m pomocí 24 řezů? Uvažujeme pouze rovinné řezy. 3
4 Zadání: Jaké je heslo? Forma odpovědi: Vyplývá ze zadání 12 Sedmnáct písmen 13 Skladná Zadání: V krabici jsou poskládány stejně velké bonboniéry tak, jak vidíte na obrázku. Krabice je až po okraj zaplněná a není v ní už žádné volné místo. Kolik nejméně bonboniér je v krabici? Zadání: Hledáme literární postavu. 14 Tabulka 5x5 Forma odpovědi: Celé jméno literární postavy Zadání: auto, zlá, dojí; krab, kyt, had Forma odpovědi: Vyplývá ze zadání 15 Tenzorová 4
5 16 Trocha víry Zadání: Maximální počet odpovědí: Zde je maximální počet odpovědí upraven na 3 17 Trojúhelníky Zadání: Je dána krychle. Určete, kolik je všech trojúhelníků, které mají vrcholy ve vrcholech krychle, ale neleží celé v žádné stěně této krychle. 18 Úspory na železnici Zadání: Na obrázku vidíme města, která jsou propojena železnicí. Určete, kolika různými způsoby můžeme zrušit některé tři tratě tak, aby se stále dalo mezi každými dvěma městy dostat po železnici. 5
6 19 Váhy Zadání: Určete hmotnosti jednotlivých závaží, jestliže jejich celková hmotnost je 136 kg. Forma odpovědi: Zadejte váhy závaží oddělené čárkou v tomto pořadí: pětiúhelník, smajlík, hvězda, mrak, válec, krychle Zadání: Co má místo zadku? 20 Vojenská 6
Autor: Jana Krchová Obor: Matematika. Hranoly
 Převeď na jednotky v závorce: Hranoly a) 0,5 cm 2 (mm 2 ) = 8,4 dm 2 (cm 2 ) = b) 2,3 m 2 (dm 2 ) = 0,078 m 2 (cm 2 ) = c) 0,09 ha (a) = 0,006 km 2 (a) = d) 4 a (m 2 ) = 540 cm 2 (m 2 ) = e) 23 cm 3 (mm
Převeď na jednotky v závorce: Hranoly a) 0,5 cm 2 (mm 2 ) = 8,4 dm 2 (cm 2 ) = b) 2,3 m 2 (dm 2 ) = 0,078 m 2 (cm 2 ) = c) 0,09 ha (a) = 0,006 km 2 (a) = d) 4 a (m 2 ) = 540 cm 2 (m 2 ) = e) 23 cm 3 (mm
Test žáka. Zdroj testu: Celoplošná zkouška 2. Školní rok 2012/2013 MATEMATIKA. Jméno: Třída: Škola: Termín provedení testu:
 Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Na obrázku jsou čtyři červené
Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Na obrázku jsou čtyři červené
Zadání: Lucka si vzala 20 kuliček a na každou z nich napsala nezáporné celé číslo. Z těchto kuliček
 1 Čtyřstěn z kuliček Zadání třetího kola Odpovědi odešlete prostřednictvím našich webových stránek http://brloh.math.muni.cz Zadání: Lucka si vzala 20 kuliček a na každou z nich napsala nezáporné celé
1 Čtyřstěn z kuliček Zadání třetího kola Odpovědi odešlete prostřednictvím našich webových stránek http://brloh.math.muni.cz Zadání: Lucka si vzala 20 kuliček a na každou z nich napsala nezáporné celé
1 Mobilní Forma odpovědi: Jedno slovo který je třetí mocninou jeho věku?
 Zadání prvního kola Odpovědi odešlete prostřednictvím našich webových stránek http://brloh.math.muni.cz 1 Mobilní Zadání: Co patří na místo otazníku? Forma odpovědi: Jedno slovo 2 Věková Zadání: V jakém
Zadání prvního kola Odpovědi odešlete prostřednictvím našich webových stránek http://brloh.math.muni.cz 1 Mobilní Zadání: Co patří na místo otazníku? Forma odpovědi: Jedno slovo 2 Věková Zadání: V jakém
Očekávaný výstup Žák zvládne náčrtek a rys jednoduchých hranolů, dosadí do vzorce, účelně použije kalkulátor Speciální vzdělávací žádné
 Název projektu Život jako leporelo Registrační číslo CZ.1.07/1.4.00/1.3763 utor Mgr. Martina Smolinková Datum 11. 1. 014 Ročník 9. Vzdělávací oblast Matematika a její aplikace Vzdělávací obor Matematika
Název projektu Život jako leporelo Registrační číslo CZ.1.07/1.4.00/1.3763 utor Mgr. Martina Smolinková Datum 11. 1. 014 Ročník 9. Vzdělávací oblast Matematika a její aplikace Vzdělávací obor Matematika
Geometrie. 1 Metrické vlastnosti. Odchylku boční hrany a podstavy. Odchylku boční stěny a podstavy
 1 Metrické vlastnosti 9000153601 (level 1): Úhel vyznačený na obrázku znázorňuje: eometrie Odchylku boční hrany a podstavy Odchylku boční stěny a podstavy Odchylku dvou protilehlých hran Odchylku podstavné
1 Metrické vlastnosti 9000153601 (level 1): Úhel vyznačený na obrázku znázorňuje: eometrie Odchylku boční hrany a podstavy Odchylku boční stěny a podstavy Odchylku dvou protilehlých hran Odchylku podstavné
Matematický KLOKAN 2006 kategorie Kadet (A) 15. (B) 16. (C) 17. (D) 13. (E) 14. (A) 5 (B) 3 (C) 4 (D) 2 (E) 6
 Matematický KLOKAN 2006 kategorie Kadet Úlohy za 3 body 1. Soutěž Klokan se koná každoročně od roku 1991. Kolikátý ročník soutěže probíhá v roce 2006? (A) 15. (B) 16. (C) 17. (D) 13. (E) 14. 2. Bod O je
Matematický KLOKAN 2006 kategorie Kadet Úlohy za 3 body 1. Soutěž Klokan se koná každoročně od roku 1991. Kolikátý ročník soutěže probíhá v roce 2006? (A) 15. (B) 16. (C) 17. (D) 13. (E) 14. 2. Bod O je
Otázky z kapitoly Stereometrie
 Otázky z kapitoly Stereometrie 10. února 015 Obsah 1 Krokované příklady (0 otázek) 1 Metrické vlastnosti (30 otázek) 1.1 Obtížnost 1 (16 otázek)....................................... 1. Obtížnost (14
Otázky z kapitoly Stereometrie 10. února 015 Obsah 1 Krokované příklady (0 otázek) 1 Metrické vlastnosti (30 otázek) 1.1 Obtížnost 1 (16 otázek)....................................... 1. Obtížnost (14
SMART Notebook verze Aug
 SMART Notebook verze 10.6.219.2 Aug 5 2010 Pořadové číslo projektu CZ.1.07/1.4.00/21.3007 Šablona č.: III/2 Datum vytvoření: 3.9.2012 Pro ročník: 6. až 9. Vzdělávací obor předmět: Matematika Klíčová slova:
SMART Notebook verze 10.6.219.2 Aug 5 2010 Pořadové číslo projektu CZ.1.07/1.4.00/21.3007 Šablona č.: III/2 Datum vytvoření: 3.9.2012 Pro ročník: 6. až 9. Vzdělávací obor předmět: Matematika Klíčová slova:
STEREOMETRIE, TĚLESA INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky
 STEREOMETRIE, TĚLESA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro nižší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu
STEREOMETRIE, TĚLESA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro nižší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu
Mateřská škola a Základní škola při dětské léčebně, Křetín 12
 VY_32_INOVACE_DUM.M.14 Mateřská škola a Základní škola při dětské léčebně, Křetín 12 Autor: Mgr. Miroslav Páteček Vytvořeno: duben 2012 Klíčová slova: Matematika a její aplikace Početní operace s přirozenými
VY_32_INOVACE_DUM.M.14 Mateřská škola a Základní škola při dětské léčebně, Křetín 12 Autor: Mgr. Miroslav Páteček Vytvořeno: duben 2012 Klíčová slova: Matematika a její aplikace Početní operace s přirozenými
Matematický KLOKAN kategorie Junior
 Matematický KLOKN 2008 kategorie Junior Úlohy za 3 body 1. Vkrabicích byly uloženy některé z karet označených,, I, O, U, jak ukazuje obrázek. Petr odebíral z každé krabice karty tak, aby na konci zbyla
Matematický KLOKN 2008 kategorie Junior Úlohy za 3 body 1. Vkrabicích byly uloženy některé z karet označených,, I, O, U, jak ukazuje obrázek. Petr odebíral z každé krabice karty tak, aby na konci zbyla
Zadání: Lucka si vzala 20 kuliček a na každou z nich napsala nezáporné celé číslo. Z těchto kuliček
 1 Čtyřstěn z kuliček Řešení třetího kola Odpovědi odešlete prostřednictvím našich webových stránek http://brloh.math.muni.cz Zadání: Lucka si vzala 20 kuliček a na každou z nich napsala nezáporné celé
1 Čtyřstěn z kuliček Řešení třetího kola Odpovědi odešlete prostřednictvím našich webových stránek http://brloh.math.muni.cz Zadání: Lucka si vzala 20 kuliček a na každou z nich napsala nezáporné celé
Matematický KLOKAN 2005 (A) 2 005 002 005 (B) 20 052 005 (C) 2 007 005 (D) 202 555 (E) 202 505 (A) 8 (B) 6 (C) 4 (D) 2 (E) 1
 Matematický KLOKAN 2005 kategorie Benjamín Úlohy za 3 body 1. Vypočítej 2 005. 100 + 2 005. (A) 2 005 002 005 (B) 20 052 005 (C) 2 007 005 (D) 202 555 (E) 202 505 2. Anička a Bětka mají dohromady 10 bonbonů.
Matematický KLOKAN 2005 kategorie Benjamín Úlohy za 3 body 1. Vypočítej 2 005. 100 + 2 005. (A) 2 005 002 005 (B) 20 052 005 (C) 2 007 005 (D) 202 555 (E) 202 505 2. Anička a Bětka mají dohromady 10 bonbonů.
Tělesa Geometrické těleso je prostorový omezený geometrický útvar. Jeho hranicí neboli povrchem je uzavřená plocha. Geometrická tělesa dělíme na
 Tělesa Geometrické těleso je prostorový omezený geometrický útvar. Jeho hranicí neboli povrchem je uzavřená plocha. Geometrická tělesa dělíme na mnohostěny a rotační tělesa. - Mnohostěny mají stěny, hrany
Tělesa Geometrické těleso je prostorový omezený geometrický útvar. Jeho hranicí neboli povrchem je uzavřená plocha. Geometrická tělesa dělíme na mnohostěny a rotační tělesa. - Mnohostěny mají stěny, hrany
Kategorie: U 1 pro žáky 1. ročníků učebních oborů
 Kategorie: U 1 pro žáky 1. ročníků učebních oborů 1) Kolika způsoby lze zaplatit částku 50 Kč, smíme-li použít pouze mince v hodnotě 1 Kč, 5 Kč a 10 Kč? ) Umocněte: 1 7 p3 q 3 r + 7pq r 3 = 3) Přeložíme-li
Kategorie: U 1 pro žáky 1. ročníků učebních oborů 1) Kolika způsoby lze zaplatit částku 50 Kč, smíme-li použít pouze mince v hodnotě 1 Kč, 5 Kč a 10 Kč? ) Umocněte: 1 7 p3 q 3 r + 7pq r 3 = 3) Přeložíme-li
Test žáka. Zdroj testu: Celoplošná zkouška 2. Školní rok 2012/2013 MATEMATIKA. Jméno: Třída: Škola: Termín provedení testu:
 Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 15. 10. 2013 Obtížnost 1 Úloha 1 Přednáška trvala 80 minut a skončila
Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 15. 10. 2013 Obtížnost 1 Úloha 1 Přednáška trvala 80 minut a skončila
PŘIJÍMACÍ ZKOUŠKY II.termín
 MATEMATIKA Obor: 79-41-K/81 Součet bodů: Opravil: Kontroloval: Vítejte na Gymnáziu v Omské u přijímacích zkoušek z matematiky. Dnes budete řešit úlohy čtverečkové a kostičkové. Úlohy můžete řešit v libovolném
MATEMATIKA Obor: 79-41-K/81 Součet bodů: Opravil: Kontroloval: Vítejte na Gymnáziu v Omské u přijímacích zkoušek z matematiky. Dnes budete řešit úlohy čtverečkové a kostičkové. Úlohy můžete řešit v libovolném
Zobrazení hranolu. Příklad 5: Sestrojte řez pravidelného šestibokého hranolu s podstavou v půdorysně rovinou ρ. Sestrojte síť seříznuté části.
 Zobrazení hranolu Příklad 1: Zobrazte pravidelný pětiboký hranol s podstavou v půdorysně π. Podstava je dána středem S a vrcholem A. Výška hranolu je v. Určete zbývající průmět bodu M pláště hranolu. 1
Zobrazení hranolu Příklad 1: Zobrazte pravidelný pětiboký hranol s podstavou v půdorysně π. Podstava je dána středem S a vrcholem A. Výška hranolu je v. Určete zbývající průmět bodu M pláště hranolu. 1
Test žáka. Zdroj testu: Celoplošná zkouška 2. Školní rok 2012/2013 MATEMATIKA. Jméno: Třída: Škola: Termín provedení testu:
 Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Železná trubka o délce 3 metry
Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Železná trubka o délce 3 metry
Vzdělávací obsah vyučovacího předmětu
 Vzdělávací obsah vyučovacího předmětu Matematika 6. ročník Zpracovala: Mgr. Michaela Krůtová Číslo a početní operace zaokrouhluje, provádí odhady s danou přesností, účelně využívá kalkulátor porovnává
Vzdělávací obsah vyučovacího předmětu Matematika 6. ročník Zpracovala: Mgr. Michaela Krůtová Číslo a početní operace zaokrouhluje, provádí odhady s danou přesností, účelně využívá kalkulátor porovnává
ZÁKLADNÍ ŠKOLA PŘI DĚTSKÉ LÉČEBNĚ Ostrov u Macochy, Školní 363 INOVACE VÝUKY CZ.1.07/1.4.00/21.0647
 ZÁKLADNÍ ŠKOLA PŘI DĚTSKÉ LÉČEBNĚ Ostrov u Macochy, Školní 363 INOVACE VÝUKY CZ.1.07/1.4.00/21.0647 Název vzdělávacího materiálu: VY_32_INOVACE_HRAVĚ16 Soutěž desetinná čísla, souměrnost, finanční matematika,
ZÁKLADNÍ ŠKOLA PŘI DĚTSKÉ LÉČEBNĚ Ostrov u Macochy, Školní 363 INOVACE VÝUKY CZ.1.07/1.4.00/21.0647 Název vzdělávacího materiálu: VY_32_INOVACE_HRAVĚ16 Soutěž desetinná čísla, souměrnost, finanční matematika,
Test žáka. Zdroj testu: Celoplošná zkouška 2. Školní rok 2012/2013 MATEMATIKA. Jméno: Třída: Škola: Termín provedení testu:
 Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Tatínek zaplatil za rozříznutí
Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Tatínek zaplatil za rozříznutí
Matematický KLOKAN kategorie Kadet
 Matematický KLOKAN 2009 www.matematickyklokan.net kategorie Kadet Úlohy za body. Hodnota kterého z výrazů je sudé číslo? (A) 2009 (B) 2 + 0 + 0 + 9 (C) 200 9 (D) 200 9 (E) 200 + 9 2. Hvězda na obrázku
Matematický KLOKAN 2009 www.matematickyklokan.net kategorie Kadet Úlohy za body. Hodnota kterého z výrazů je sudé číslo? (A) 2009 (B) 2 + 0 + 0 + 9 (C) 200 9 (D) 200 9 (E) 200 + 9 2. Hvězda na obrázku
Matematický KLOKAN 2006 kategorie Student
 atematický KLOKN 2006 kategorie Student (pro 3. a 4. roč. SŠ a septimu a oktávu osmiletých gymnázií) Vážení přátelé, v následujících 75 minutách vás čeká stejný úkol jako mnoho vašich vrstevníků v řadě
atematický KLOKN 2006 kategorie Student (pro 3. a 4. roč. SŠ a septimu a oktávu osmiletých gymnázií) Vážení přátelé, v následujících 75 minutách vás čeká stejný úkol jako mnoho vašich vrstevníků v řadě
Test žáka. Zdroj testu: Celoplošná zkouška 2. Školní rok 2012/2013 MATEMATIKA. Jméno: Třída: Škola: Termín provedení testu:
 Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Trojúhelník má jeden úhel tupý,
Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Trojúhelník má jeden úhel tupý,
PORG, přijímací zkoušky 2014 Matematika B, str. 1 Reg. číslo:
 PORG, přijímací zkoušky 2014 Matematika B, str. 1 Reg. číslo: 1. Toník se dopravuje ze školy domů autobusem číslo 176, který jezdí vždy v celou hodinu a pak dále po každých 15 minutách. Dnes dorazil Toník
PORG, přijímací zkoušky 2014 Matematika B, str. 1 Reg. číslo: 1. Toník se dopravuje ze školy domů autobusem číslo 176, který jezdí vždy v celou hodinu a pak dále po každých 15 minutách. Dnes dorazil Toník
Hranoly I. Předpoklady:
 11 Hranoly I Předpoklady: 01101 Pedagogická poznámka: Při výuce v sekundě se jako největší problém ukázalo počítání s výrazy Ačkoliv žáci písmenka používali bez větších problémů v jednoduchých vzorcích
11 Hranoly I Předpoklady: 01101 Pedagogická poznámka: Při výuce v sekundě se jako největší problém ukázalo počítání s výrazy Ačkoliv žáci písmenka používali bez větších problémů v jednoduchých vzorcích
Matematika. Vlastnosti početních operací s přirozenými čísly
 1 Matematika Matematika Učivo ŠVP výstupy Vlastnosti početních operací s přirozenými čísly Sčítání a odčítání dvojciferných čísel do 100 zpaměti i Sčítání a odčítání dvou trojciferných čísel do 1 000 a
1 Matematika Matematika Učivo ŠVP výstupy Vlastnosti početních operací s přirozenými čísly Sčítání a odčítání dvojciferných čísel do 100 zpaměti i Sčítání a odčítání dvou trojciferných čísel do 1 000 a
STEREOMETRIE 9*. 10*. 11*. 12*. 13*
 STEREOMETRIE Bod, přímka, rovina, polorovina, poloprostor, základní symboly označující přímku, bod, polorovinu, patří, nepatří, leží, neleží, vzájemná poloha dvou přímek v prostoru, vzájemná poloha dvou
STEREOMETRIE Bod, přímka, rovina, polorovina, poloprostor, základní symboly označující přímku, bod, polorovinu, patří, nepatří, leží, neleží, vzájemná poloha dvou přímek v prostoru, vzájemná poloha dvou
MATEMATIKA. 5. třída. Čemu se rovná uvedený součet v metrech? (A) 1,65015 m (B) 16,515 m (C) 16,0515 m (D) 16,5 m
 MATEMATIKA 5. třída 1. Jaké číslo je o 12 stovek, 4 desítky a 9 jednotek menší než 2000? (A) 751 (B) 861 (C) 1249 (D) 1831 2. Které z následujících tvrzení o pravoúhlém trojúhelníku je správné? (A) Dvě
MATEMATIKA 5. třída 1. Jaké číslo je o 12 stovek, 4 desítky a 9 jednotek menší než 2000? (A) 751 (B) 861 (C) 1249 (D) 1831 2. Které z následujících tvrzení o pravoúhlém trojúhelníku je správné? (A) Dvě
Svobodná chebská škola, základní škola a gymnázium s.r.o. Astaloš Dušan. frontální, fixační. samostatná práce, skupinová práce
 METODICKÝ LIST DA34 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný obsah: Trojúhelník I. obecný trojúhelník Astaloš Dušan Matematika šestý frontální,
METODICKÝ LIST DA34 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný obsah: Trojúhelník I. obecný trojúhelník Astaloš Dušan Matematika šestý frontální,
Obecné informace: Typy úloh a hodnocení:
 Obecné informace: Počet úloh: 30 Časový limit: 60 minut Max. možný počet bodů: 30 Min. možný počet bodů: 8 Povolené pomůcky: modrá propisovací tužka obyčejná tužka pravítko kružítko mazací guma Poznámky:
Obecné informace: Počet úloh: 30 Časový limit: 60 minut Max. možný počet bodů: 30 Min. možný počet bodů: 8 Povolené pomůcky: modrá propisovací tužka obyčejná tužka pravítko kružítko mazací guma Poznámky:
Název projektu: Poznáváme sebe a svět, chceme poznat více
 Název projektu: Poznáváme sebe a svět, chceme poznat více Registrační číslo projektu: CZ.1.07/1.4.00/21.2970 Identifikátor materiálu Název klíčové aktivity Vzdělávací oblast Vzdělávací předmět / obor Tematický
Název projektu: Poznáváme sebe a svět, chceme poznat více Registrační číslo projektu: CZ.1.07/1.4.00/21.2970 Identifikátor materiálu Název klíčové aktivity Vzdělávací oblast Vzdělávací předmět / obor Tematický
4. Vypočítejte objem dané krychle, jestliže víte, že objem krychle s hranou poloviční délky má objem 512 m 3.
 Didaktika matematiky DM 3 - příklady stereometrie Kvádr, krychle 1. Vypočítejte objem krychle, jejíž povrch je 96 cm 2. 2. Vypočítejte povrch krychle, jejíž objem je 512 cm 3. 3. Jedna stěna krychle má
Didaktika matematiky DM 3 - příklady stereometrie Kvádr, krychle 1. Vypočítejte objem krychle, jejíž povrch je 96 cm 2. 2. Vypočítejte povrch krychle, jejíž objem je 512 cm 3. 3. Jedna stěna krychle má
Finále SOUBOR OTÁZEK. ročník
 Finále SOUBOR OTÁZEK 6. ročník Co je Pangea a jaká je její filozofie? V dávných dobách prvohor a druhohor, tedy přibližně před 300 miliony let, nebyly jednotllivé kontinenty na naší planetě ještě rozdělené,
Finále SOUBOR OTÁZEK 6. ročník Co je Pangea a jaká je její filozofie? V dávných dobách prvohor a druhohor, tedy přibližně před 300 miliony let, nebyly jednotllivé kontinenty na naší planetě ještě rozdělené,
Přípravný kurz. k přijímacím zkouškám z matematiky pro uchazeče o studium na gymnáziu (čtyřletý obor) pro
 Příjímací zkoušky 01 Přípravný kurz k přijímacím zkouškám z matematiky pro uchazeče o studium na gymnáziu (čtyřletý obor) 1. Číselné obory 1.1. Doplňte číslo do rámečku tak, aby platila rovnost: 1.1.1.
Příjímací zkoušky 01 Přípravný kurz k přijímacím zkouškám z matematiky pro uchazeče o studium na gymnáziu (čtyřletý obor) 1. Číselné obory 1.1. Doplňte číslo do rámečku tak, aby platila rovnost: 1.1.1.
1.1.24 Skaláry a vektory
 1.1.4 Skaláry a vektory Předpoklady: 113 Př. 1: Vyřeš následující příklady: a) Na stole je položeno závaží o hmotnosti kg. Na závaží působí gravitační síla Země o velikosti 0 N a tlaková síla od stolu
1.1.4 Skaláry a vektory Předpoklady: 113 Př. 1: Vyřeš následující příklady: a) Na stole je položeno závaží o hmotnosti kg. Na závaží působí gravitační síla Země o velikosti 0 N a tlaková síla od stolu
Monika Cihelková, Jolana Nováková, učitelství pro 1. stupeň ZŠ, 4. ročník
 Hodina matematiky 21. 12. 2011 Monika Cihelková, Jolana Nováková, učitelství pro 1. stupeň ZŠ, 4. ročník 1. Úvod uvítání, představení vyučujících studentek (1min.) 2. Rozcvička (3min) 3. Hra Riskuj (15min)
Hodina matematiky 21. 12. 2011 Monika Cihelková, Jolana Nováková, učitelství pro 1. stupeň ZŠ, 4. ročník 1. Úvod uvítání, představení vyučujících studentek (1min.) 2. Rozcvička (3min) 3. Hra Riskuj (15min)
Jméno a příjmení. 2.1 Pokyny k otevřeným úlohám. 2.2 Pokyny k uzavřeným úlohám TESTOVÝ SEŠIT NEOTVÍREJTE, POČKEJTE NA POKYN!
 MATEMATIKA 9 M9PBD19C0T02 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 16 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby 1 Základní informace k zadání zkoušky Časový
MATEMATIKA 9 M9PBD19C0T02 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 16 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby 1 Základní informace k zadání zkoušky Časový
Pojmy: stěny, podstavy, vrcholy, podstavné hrany, boční hrany (celkem hran ),
 Tělesa 1/6 Tělesa 1.Mnohostěny n-boký hranol Pojmy: stěny, podstavy, vrcholy, podstavné hrany, boční hrany (celkem hran ), hranol kosý hranol kolmý (boční stěny jsou kolmé k rovině podstavy) pravidelný
Tělesa 1/6 Tělesa 1.Mnohostěny n-boký hranol Pojmy: stěny, podstavy, vrcholy, podstavné hrany, boční hrany (celkem hran ), hranol kosý hranol kolmý (boční stěny jsou kolmé k rovině podstavy) pravidelný
Desetinná čísla pracovní listy pro ročník stupňované podle náročnosti Irena Budínová Pedagogická fakulta MU
 Desetinná čísla pracovní listy pro 6. 7. ročník stupňované podle náročnosti Irena Budínová Pedagogická fakulta MU irena.budinova@seznam.cz Moderní výuka by se měla co nejvíce orientovat na individualitu
Desetinná čísla pracovní listy pro 6. 7. ročník stupňované podle náročnosti Irena Budínová Pedagogická fakulta MU irena.budinova@seznam.cz Moderní výuka by se měla co nejvíce orientovat na individualitu
Matematika - 6. ročník Vzdělávací obsah
 Matematika - 6. ročník Září Opakování učiva Obor přirozených čísel do 1000, početní operace v daném oboru Čte, píše, porovnává čísla v oboru do 1000, orientuje se na číselné ose Rozlišuje sudá a lichá
Matematika - 6. ročník Září Opakování učiva Obor přirozených čísel do 1000, početní operace v daném oboru Čte, píše, porovnává čísla v oboru do 1000, orientuje se na číselné ose Rozlišuje sudá a lichá
Jakýkoliv jiný způsob záznamu odpovědí (např. dva křížky u jedné úlohy) bude považován za nesprávnou odpověď.
 MATEMATIKA 5 M5PID16C0T01 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 16 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: psací a rýsovací potřeby Časový limit pro řešení didaktického testu je 60
MATEMATIKA 5 M5PID16C0T01 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 16 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: psací a rýsovací potřeby Časový limit pro řešení didaktického testu je 60
ILUSTRAÈNÍ TEST LIBERECKÝ KRAJ
 ILUSTRAÈNÍ TEST LIBERECKÝ KRAJ 5 NEOTVÍREJ, DOKUD NEDOSTANEŠ POKYN! Test obsahuje 30 úloh na 60 minut. Každá úloha má právì jedno správné øešení. Za správné øešení získáš 2 body. Za chybnou odpovìï ztratíš
ILUSTRAÈNÍ TEST LIBERECKÝ KRAJ 5 NEOTVÍREJ, DOKUD NEDOSTANEŠ POKYN! Test obsahuje 30 úloh na 60 minut. Každá úloha má právì jedno správné øešení. Za správné øešení získáš 2 body. Za chybnou odpovìï ztratíš
Matematický KLOKAN 2005 kategorie Junior
 Matematický KLOKAN 2005 kategorie Junior Vážení přátelé, v následujících 75 minutách vás čeká stejný úkol jako mnoho vašich vrstevníků v řadě dalších evropských zemí. V níže uvedeném testu je zadáno čtyřiadvacet
Matematický KLOKAN 2005 kategorie Junior Vážení přátelé, v následujících 75 minutách vás čeká stejný úkol jako mnoho vašich vrstevníků v řadě dalších evropských zemí. V níže uvedeném testu je zadáno čtyřiadvacet
3.2 OBJEMY A POVRCHY TĚLES
 . OBJEMY A POVRCHY TĚLES Krychle, kvádr, hranol Dochované matematické texty ze starého Egypta obsahují několik úloh na výpočet objemu čtverhranných obilnic tvaru krychle; lze předpokládat, že stejným způsobem
. OBJEMY A POVRCHY TĚLES Krychle, kvádr, hranol Dochované matematické texty ze starého Egypta obsahují několik úloh na výpočet objemu čtverhranných obilnic tvaru krychle; lze předpokládat, že stejným způsobem
Matematický KLOKAN kategorie Benjamín
 Matematický KLOKAN 2011 www.matematickyklokan.net kategorie Benjamín Úlohy za 3 body 1. Motocyklista ujel vzdálenost 28 km za 30 minut. Jakou průměrnou rychlostí jel? (A) 28 km/h (B) 36 km/h (C) 56 km/h
Matematický KLOKAN 2011 www.matematickyklokan.net kategorie Benjamín Úlohy za 3 body 1. Motocyklista ujel vzdálenost 28 km za 30 minut. Jakou průměrnou rychlostí jel? (A) 28 km/h (B) 36 km/h (C) 56 km/h
Tělesa můžeme v rovině zobrazit pomocí volného rovnoběžného promítání.
 9. Hranol 6. ročník 9. Hranol 9.1. Volné rovnoběžné promítání Tělesa můžeme v rovině zobrazit pomocí volného rovnoběžného promítání. Zásady : 1) Plochy, které jsou rovnoběžné s naší rýsovací plochou zobrazujeme
9. Hranol 6. ročník 9. Hranol 9.1. Volné rovnoběžné promítání Tělesa můžeme v rovině zobrazit pomocí volného rovnoběžného promítání. Zásady : 1) Plochy, které jsou rovnoběžné s naší rýsovací plochou zobrazujeme
Vektory I. Předpoklady: Pedagogická poznámka: První příklad je řešení domácího úkolu z minulé hodiny.
 1.1.5 Vektory I Předpoklady: 01014 Pedagogická poznámka: První příklad je řešení domácího úkolu z minulé hodiny. Pedagogická poznámka: V první části hodiny je třeba postupovat poměrně rychle, aby ještě
1.1.5 Vektory I Předpoklady: 01014 Pedagogická poznámka: První příklad je řešení domácího úkolu z minulé hodiny. Pedagogická poznámka: V první části hodiny je třeba postupovat poměrně rychle, aby ještě
SOUBOR OTÁZEK. ročník
 SOUBOR OTÁZEK 5. ročník Co je Pangea a jaká je její filozofie? V dávných dobách prvohor a druhohor, tedy přibližně před 300 miliony let, nebyly jednotllivé kontinenty na naší planetě ještě rozdělené, ale
SOUBOR OTÁZEK 5. ročník Co je Pangea a jaká je její filozofie? V dávných dobách prvohor a druhohor, tedy přibližně před 300 miliony let, nebyly jednotllivé kontinenty na naší planetě ještě rozdělené, ale
Mateřská škola a Základní škola při dětské léčebně, Křetín 12
 Mateřská škola a Základní škola při dětské léčebně, Křetín 12 VY_32_INOVACE_DUM.M.17 Autor: Mgr. Miroslav Páteček Vytvořeno: duben 2012 Matematika a její aplikace Klíčová slova: Třída: Anotace: Zlomky,
Mateřská škola a Základní škola při dětské léčebně, Křetín 12 VY_32_INOVACE_DUM.M.17 Autor: Mgr. Miroslav Páteček Vytvořeno: duben 2012 Matematika a její aplikace Klíčová slova: Třída: Anotace: Zlomky,
SOUTĚŽNÍ ÚLOHY 37. ročník regionální matematické soutěže žáků středních odborných škol, středních odborných učilišť a integrovaných středních škol
 Krajský úřad Pardubického kraje - odbor školství Jednota českých matematiků a fyziků, pobočka Pardubice Střední škola automobilní Ústí nad Orlicí 26.3.2019 SOUTĚŽNÍ ÚLOHY 37. ročník regionální matematické
Krajský úřad Pardubického kraje - odbor školství Jednota českých matematiků a fyziků, pobočka Pardubice Střední škola automobilní Ústí nad Orlicí 26.3.2019 SOUTĚŽNÍ ÚLOHY 37. ročník regionální matematické
Test žáka. Zdroj testu: Celoplošná zkouška 2. Školní rok 2012/2013 MATEMATIKA. Jméno: Třída: Škola: Termín provedení testu:
 Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Na obrázku jsou zakresleny dva
Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Na obrázku jsou zakresleny dva
Vzorové příklady k přijímacím zkouškám. 1) Doplňte číselné řady o další dvě čísla. a) 3, 6, 12, 24, 48, 96,... b) 875, 764, 653, 542, 431,...
 Vzorové příklady k přijímacím zkouškám ) Doplňte číselné řady o další dvě čísla. a), 6,, 4, 48, 96,... b) 87, 764, 6, 4, 4,... c), 6, 8,,, 0, 6,... d),,, 7,,, 7, 9,,... e) ; ; ; ; ; 8 ) Doplňte číslo místo.
Vzorové příklady k přijímacím zkouškám ) Doplňte číselné řady o další dvě čísla. a), 6,, 4, 48, 96,... b) 87, 764, 6, 4, 4,... c), 6, 8,,, 0, 6,... d),,, 7,,, 7, 9,,... e) ; ; ; ; ; 8 ) Doplňte číslo místo.
CVIČNÝ TEST 37. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15
 CVIČNÝ TEST 37 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Na staré hliněné desce je namalován čtverec
CVIČNÝ TEST 37 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Na staré hliněné desce je namalován čtverec
GEOMETRIE. Projekt byl podpořen z Evropského sociálního fondu. Praha & EU: Investujeme do vaší budoucnosti
 GEOMETRIE pracovní sešit pro 6. ročník Projekt byl podpořen z Evropského sociálního fondu. Praha & EU: Investujeme do vaší budoucnosti Tato publikace byla vytvořena v souladu s RVP ZV v rámci projektu
GEOMETRIE pracovní sešit pro 6. ročník Projekt byl podpořen z Evropského sociálního fondu. Praha & EU: Investujeme do vaší budoucnosti Tato publikace byla vytvořena v souladu s RVP ZV v rámci projektu
SOUBOR OTÁZEK. ročník
 SOUBOR OTÁZEK 6. ročník Co je Pangea a jaká je její filozofie? V dávných dobách prvohor a druhohor, tedy přibližně před 300 miliony let, nebyly jednotllivé kontinenty na naší planetě ještě rozdělené, ale
SOUBOR OTÁZEK 6. ročník Co je Pangea a jaká je její filozofie? V dávných dobách prvohor a druhohor, tedy přibližně před 300 miliony let, nebyly jednotllivé kontinenty na naší planetě ještě rozdělené, ale
MATEMATIKA PŘIJÍMACÍ ZKOUŠKA K 8LETÉMU STUDIU NA SŠ ROK 2013
 ILUSTRAČNÍ MATEMATIKA PŘIJÍMACÍ ZKOUŠKA K 8LETÉMU STUDIU NA SŠ ROK 203 POČET TESTOVÝCH POLOŽEK: 6 MAXIMÁLNÍ POČET BODŮ: 50 (00%) ČASOVÝ LIMIT PRO ŘEŠENÍ TESTU: 60 minut POVOLENÉ POMŮCKY ŘEŠITELE: psací
ILUSTRAČNÍ MATEMATIKA PŘIJÍMACÍ ZKOUŠKA K 8LETÉMU STUDIU NA SŠ ROK 203 POČET TESTOVÝCH POLOŽEK: 6 MAXIMÁLNÍ POČET BODŮ: 50 (00%) ČASOVÝ LIMIT PRO ŘEŠENÍ TESTU: 60 minut POVOLENÉ POMŮCKY ŘEŠITELE: psací
1. Vypočítejte: 775522 : 11. 2. Základní čtvercová síť má délky strany čtverců 1 cm. Určete obsah vyznačeného obrazce, odpověď zdůvodněte.
 Z A D Á N Í Gymnázium Ohradní Praha 4 / 5. třída / 03-04 / 1. kolo 1. Vypočítejte: 775522 : 11 2. Základní čtvercová síť má délky strany čtverců 1 cm. Určete obsah vyznačeného obrazce, odpověď zdůvodněte.
Z A D Á N Í Gymnázium Ohradní Praha 4 / 5. třída / 03-04 / 1. kolo 1. Vypočítejte: 775522 : 11 2. Základní čtvercová síť má délky strany čtverců 1 cm. Určete obsah vyznačeného obrazce, odpověď zdůvodněte.
Čtvercové puzzle úloha za 2 body
 Čtvercové puzzle úloha za 2 body Poskládejte uvedené dílky do čtverce 5 5 polí tak, aby v každém řádku a každém sloupci byla obarvena právě tři pole: jedno červené, jedno žluté a jedno modré. Úloha č.
Čtvercové puzzle úloha za 2 body Poskládejte uvedené dílky do čtverce 5 5 polí tak, aby v každém řádku a každém sloupci byla obarvena právě tři pole: jedno červené, jedno žluté a jedno modré. Úloha č.
Poměry a úměrnosti. Poměr dvou čísel je matematický zápis a : b, ve kterém a,b jsou nezáporná, nejčastěji přirozená čísla, symbol : čteme ku
 Poměry a úměrnosti Poměr dvou čísel je matematický zápis a : b, ve kterém a,b jsou nezáporná, nejčastěji přirozená čísla, symbol : čteme ku S poměrem lze pracovat jako se zlomkem a : b = a b porovnávat,
Poměry a úměrnosti Poměr dvou čísel je matematický zápis a : b, ve kterém a,b jsou nezáporná, nejčastěji přirozená čísla, symbol : čteme ku S poměrem lze pracovat jako se zlomkem a : b = a b porovnávat,
Algebrogramy. PaedDr. Libuše Sekaninová Martin Blahák (grafická úprava)
 Algebrogramy PaedDr. Libuše Sekaninová Martin Blahák (grafická úprava) Materiál byl zpracován v rámci projektu "Systémová podpora trvalého profesního rozvoje (CPD) pedagogických pracovníků propojením pedagogické
Algebrogramy PaedDr. Libuše Sekaninová Martin Blahák (grafická úprava) Materiál byl zpracován v rámci projektu "Systémová podpora trvalého profesního rozvoje (CPD) pedagogických pracovníků propojením pedagogické
MATEMATICKÉ DOVEDNOSTI
 Hodnocení výsledků vzdělávání žáků 9. tříd 005 MA0Z9 MATEMATICKÉ DOVEDNOSTI A Testový sešit obsahuje 7 úloh. Na řešení úloh máte 40 minut. Při řešení konstrukční úlohy užívejte rýsovací potřeby. V průběhu
Hodnocení výsledků vzdělávání žáků 9. tříd 005 MA0Z9 MATEMATICKÉ DOVEDNOSTI A Testový sešit obsahuje 7 úloh. Na řešení úloh máte 40 minut. Při řešení konstrukční úlohy užívejte rýsovací potřeby. V průběhu
Přehled vzdělávacích materiálů
 Přehled vzdělávacích materiálů Název školy Název a číslo OP Název šablony klíčové aktivity Název sady vzdělávacích materiálů Jméno tvůrce vzdělávací sady Číslo sady Anotace Základní škola Ţeliv Novými
Přehled vzdělávacích materiálů Název školy Název a číslo OP Název šablony klíčové aktivity Název sady vzdělávacích materiálů Jméno tvůrce vzdělávací sady Číslo sady Anotace Základní škola Ţeliv Novými
1. KOMBINATORIKA - PŘÍKLADY
 1. KOMBINATORIKA - PŘÍKLADY Úlohy k samostatnému řešení 1.1. Zjednodušte a vypočtěte: 1.2. Kolik třítónových akordů je možné zahrát z 8 tónů? 1.3. Kolik různých optických signálů je možno dát vytahováním
1. KOMBINATORIKA - PŘÍKLADY Úlohy k samostatnému řešení 1.1. Zjednodušte a vypočtěte: 1.2. Kolik třítónových akordů je možné zahrát z 8 tónů? 1.3. Kolik různých optických signálů je možno dát vytahováním
Základní škola Nýrsko, Školní ulice, příspěvková organizace. (www.sumavanet.cz/zsskolni/projekt2 zakladni.asp) MIŠ MAŠ
 Základní škola Nýrsko, Školní ulice, příspěvková organizace (www.sumavanet.cz/zsskolni/projekt2 zakladni.asp) Název projektu: MIŠ MAŠ Moderní Interaktivní Škola Možností a Šancí (pro každého žáka) Číslo
Základní škola Nýrsko, Školní ulice, příspěvková organizace (www.sumavanet.cz/zsskolni/projekt2 zakladni.asp) Název projektu: MIŠ MAŠ Moderní Interaktivní Škola Možností a Šancí (pro každého žáka) Číslo
12. VYTVÁŘENÍ GEOMETRICKÝCH PŘEDSTAV
 12. VYTVÁŘENÍ GEOMETRICKÝCH PŘEDSTAV Geometrie je specifickou oblastí matematiky, která může být pro děti, které mají poruchy v oblasti numerace a operací s přirozenými čísly, záchranou. Učitel sleduje
12. VYTVÁŘENÍ GEOMETRICKÝCH PŘEDSTAV Geometrie je specifickou oblastí matematiky, která může být pro děti, které mají poruchy v oblasti numerace a operací s přirozenými čísly, záchranou. Učitel sleduje
MATEMATIKA. základní úroveň obtížnosti DIDAKTICKÝ TEST MAGZD10C0T01. Testový sešit neotvírejte, počkejte na pokyn! Didaktický test obsahuje 20 úloh.
 MATEMATIKA základní úroveň obtížnosti MAGZD0C0T0 DIDAKTICKÝ TEST Didaktický test obsahuje 20 úloh. Časový limit pro řešení didaktického testu je uveden na záznamovém archu. Povolené pomůcky: psací a rýsovací
MATEMATIKA základní úroveň obtížnosti MAGZD0C0T0 DIDAKTICKÝ TEST Didaktický test obsahuje 20 úloh. Časový limit pro řešení didaktického testu je uveden na záznamovém archu. Povolené pomůcky: psací a rýsovací
MATEMATIKA. 3 hmotnosti nákupu a 2 kg. Kolik kilogramů. Nákup vážil 5. vážil celý nákup? (A) 4,25 kg (B) 4,5 kg (C) 5 kg (D) 5,25 kg 6.
 MATEMATIKA 9. třída. Nechť M je součet druhých mocnin prvních tří přirozených čísel a N součet těchto tří přirozených čísel. Které z následujících tvrzení je pravdivé? (A) M + N = 7 (B) M = 4N (C) M N
MATEMATIKA 9. třída. Nechť M je součet druhých mocnin prvních tří přirozených čísel a N součet těchto tří přirozených čísel. Které z následujících tvrzení je pravdivé? (A) M + N = 7 (B) M = 4N (C) M N
7/ Podstavou kolmého trojbokého hranolu ABCA BĆ je rovnoramenný trojúhelník ABC. Určete odchylku přímek: a) BA ; BC b) A B ; BC c) AB ; BC
 Stereometrie 1/ Je dána krychle ABCDEFGH. Uveďte všechny přímky, které procházejí bodem E a dalším vrcholem krychle a jsou s přímkou BC a) rovnoběžné b) různoběžné c) mimoběžné / Je dána krychle ABCDEFGH.
Stereometrie 1/ Je dána krychle ABCDEFGH. Uveďte všechny přímky, které procházejí bodem E a dalším vrcholem krychle a jsou s přímkou BC a) rovnoběžné b) různoběžné c) mimoběžné / Je dána krychle ABCDEFGH.
2.1 Pokyny k otevřeným úlohám. 2.2 Pokyny k uzavřeným úlohám TESTOVÝ SEŠIT NEOTVÍREJTE, POČKEJTE NA POKYN!
 MATEMATIKA DIDAKTICKÝ TEST Maimální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % Základní informace k zadání zkoušky Didaktický test obsahuje 26 úloh. Časový limit pro řešení didaktického testu je
MATEMATIKA DIDAKTICKÝ TEST Maimální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % Základní informace k zadání zkoušky Didaktický test obsahuje 26 úloh. Časový limit pro řešení didaktického testu je
Základní geometrické tvary
 Základní geometrické tvary č. 37 Matematika 1. Narýsuj bod A. 2. Narýsuj přímku b. 3. Narýsuj přímku, která je dána body AB. AB 4. Narýsuj polopřímku CD. CD 5. Narýsuj úsečku AB. 6. Doplň. Rýsujeme v rovině.
Základní geometrické tvary č. 37 Matematika 1. Narýsuj bod A. 2. Narýsuj přímku b. 3. Narýsuj přímku, která je dána body AB. AB 4. Narýsuj polopřímku CD. CD 5. Narýsuj úsečku AB. 6. Doplň. Rýsujeme v rovině.
MATEMATIKA 9. TŘÍDA. 0,5 b. Umocnění výrazu (x 2) 2 : 3 hmotnosti nákupu a 2 kg. Kolik kilogramů. Nákup vážil 5
 MATEMATIKA 9. TŘÍDA 1. Nechť M je součet druhých mocnin prvních tří přirozených čísel a N součet těchto tří přirozených čísel. Které z následujících tvrzení je pravdivé? (A) M + N = 17 (B) M = 4N (C) M
MATEMATIKA 9. TŘÍDA 1. Nechť M je součet druhých mocnin prvních tří přirozených čísel a N součet těchto tří přirozených čísel. Které z následujících tvrzení je pravdivé? (A) M + N = 17 (B) M = 4N (C) M
1.1 Základní pojmy prostorové geometrie. Předmětem studia prostorové geometrie je prostor, jehož prvky jsou body. Další
 Kapitola 1 Planimetrie a stereometrie Doplňky ke středoškolské látce 1.1 Základní pojmy prostorové geometrie 1.1.1 Axiomy Předmětem studia prostorové geometrie je prostor, jehož prvky jsou body. Další
Kapitola 1 Planimetrie a stereometrie Doplňky ke středoškolské látce 1.1 Základní pojmy prostorové geometrie 1.1.1 Axiomy Předmětem studia prostorové geometrie je prostor, jehož prvky jsou body. Další
ICT podporuje moderní způsoby výuky CZ.1.07/1.5.00/ Matematika - stereometrie. Mgr. Hedvika Novotná
 Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity III/2
Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity III/2
Vzdělávací obsah vyučovacího předmětu
 Vzdělávací obsah vyučovacího předmětu Matematika 7. ročník Zpracovala: Mgr. Michaela Krůtová Číslo a početní operace provádí početní operace v oboru celých a racionálních čísel zaokrouhluje, provádí odhady
Vzdělávací obsah vyučovacího předmětu Matematika 7. ročník Zpracovala: Mgr. Michaela Krůtová Číslo a početní operace provádí početní operace v oboru celých a racionálních čísel zaokrouhluje, provádí odhady
Základní pojmy: Objemy a povrchy těles Vzájemná poloha bodů, přímek a rovin Opakování: Obsahy a obvody rovinných útvarů
 1/13 Základní pojmy: Objemy a povrchy těles Vzájemná poloha bodů, přímek a rovin Opakování: Obsahy a obvody rovinných útvarů STEREOMETRIE Stereometrie - geometrie v prostoru - zabývá se vzájemnou polohou
1/13 Základní pojmy: Objemy a povrchy těles Vzájemná poloha bodů, přímek a rovin Opakování: Obsahy a obvody rovinných útvarů STEREOMETRIE Stereometrie - geometrie v prostoru - zabývá se vzájemnou polohou
Řezy těles rovinou III
 5.1.11 Řezy těles rovinou III Předpoklady: 050110 Ne vždy nám vystačí spojování bodů a dělaní rovnoběžek. Jako třeba bod b) posledního příkladu z minulé hodiny: Rovnoběžné jsou pouze podstavy nemůžeme
5.1.11 Řezy těles rovinou III Předpoklady: 050110 Ne vždy nám vystačí spojování bodů a dělaní rovnoběžek. Jako třeba bod b) posledního příkladu z minulé hodiny: Rovnoběžné jsou pouze podstavy nemůžeme
MATEMATIKA. 1 Základní informace k zadání zkoušky. 2 Pravidla správného zápisu řešení. 3.2 Pokyny k uzavřeným úlohám 7-15 DIDAKTICKÝ TEST
 MATEMATIKA PŘIJÍMACÍ ZKOUŠKY DIDAKTICKÝ TEST B TS-M5MBCINT Maximální bodové hodnocení: 50 bodů 1 Základní informace k zadání zkoušky Didaktický test obsahuje 15 úloh. Časový limit pro řešení didaktického
MATEMATIKA PŘIJÍMACÍ ZKOUŠKY DIDAKTICKÝ TEST B TS-M5MBCINT Maximální bodové hodnocení: 50 bodů 1 Základní informace k zadání zkoušky Didaktický test obsahuje 15 úloh. Časový limit pro řešení didaktického
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost.
 Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Jméno a příjmení. 2.1 Pokyny k otevřeným úlohám. 2.2 Pokyny k uzavřeným úlohám TESTOVÝ SEŠIT NEOTVÍREJTE, POČKEJTE NA POKYN!
 MATEMATIKA 7 M7PAD19C0T01 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 16 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby 1 Základní informace k zadání zkoušky Časový
MATEMATIKA 7 M7PAD19C0T01 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 16 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby 1 Základní informace k zadání zkoušky Časový
Název projektu: Poznáváme sebe a svět, chceme poznat více
 Název projektu: Poznáváme sebe a svět, chceme poznat více Registrační číslo projektu: CZ.1.07/1.4.00/21.2970 Identifikátor materiálu Název klíčové aktivity Vzdělávací oblast Vzdělávací předmět / obor Tematický
Název projektu: Poznáváme sebe a svět, chceme poznat více Registrační číslo projektu: CZ.1.07/1.4.00/21.2970 Identifikátor materiálu Název klíčové aktivity Vzdělávací oblast Vzdělávací předmět / obor Tematický
1. Opakování učiva 6. ročníku
 . Opakování učiva 6. ročníku.. Čísla, zlomek ) Z číslic, 6 a sestavte všechna trojciferná čísla tak, aby v každém z nich byly všechny tři číslice různé. ) Z číslic, 0, 3, sestavte všechna čtyřciferná čísla
. Opakování učiva 6. ročníku.. Čísla, zlomek ) Z číslic, 6 a sestavte všechna trojciferná čísla tak, aby v každém z nich byly všechny tři číslice různé. ) Z číslic, 0, 3, sestavte všechna čtyřciferná čísla
- 1 - 1. - osobnostní rozvoj cvičení pozornosti,vnímaní a soustředění při řešení příkladů,, řešení problémů
 - 1 - Vzdělávací oblast: Matematika a její aplikace Vyučovací předmět: Matematika 6.ročník Výstup Učivo Průřezová témata - čte, zapisuje a porovnává přirozená čísla s přirozenými čísly - zpaměti a písemně
- 1 - Vzdělávací oblast: Matematika a její aplikace Vyučovací předmět: Matematika 6.ročník Výstup Učivo Průřezová témata - čte, zapisuje a porovnává přirozená čísla s přirozenými čísly - zpaměti a písemně
MATEMATIKA 5. TŘÍDA. C) Tabulky, grafy, diagramy 1 - Tabulky, doplnění řady čísel podle závislosti 2 - Grafy, jízní řády 3 - Magické čtverce
 MATEMATIKA 5. TŘÍDA 1 - Přirozená čísla a číslo nula a číselná osa, porovnávání b zaokrouhlování c zápis čísla v desítkové soustavě d součet, rozdíl e násobek, činitel, součin f dělení, dělení se zbytkem
MATEMATIKA 5. TŘÍDA 1 - Přirozená čísla a číslo nula a číselná osa, porovnávání b zaokrouhlování c zápis čísla v desítkové soustavě d součet, rozdíl e násobek, činitel, součin f dělení, dělení se zbytkem
Žák plní standard v průběhu primy a sekundy, učivo absolutní hodnota v kvartě.
 STANDARDY MATEMATIKA 2. stupeň ČÍSLO A PROMĚNNÁ 1. M-9-1-01 Žák provádí početní operace v oboru celých a racionálních čísel; užívá ve výpočtech druhou mocninu a odmocninu 1. žák provádí základní početní
STANDARDY MATEMATIKA 2. stupeň ČÍSLO A PROMĚNNÁ 1. M-9-1-01 Žák provádí početní operace v oboru celých a racionálních čísel; užívá ve výpočtech druhou mocninu a odmocninu 1. žák provádí základní početní
Stereometrie pro učební obory
 Variace 1 Stereometrie pro učební obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz 1. Vzájemná poloha prostorových
Variace 1 Stereometrie pro učební obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz 1. Vzájemná poloha prostorových
Jméno a příjmení. 2.1 Pokyny k otevřeným úlohám. 2.2 Pokyny k uzavřeným úlohám TESTOVÝ SEŠIT NEOTVÍREJTE, POČKEJTE NA POKYN!
 MATEMATIKA 7 M7PBD19C0T02 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 16 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby 1 Základní informace k zadání zkoušky Časový
MATEMATIKA 7 M7PBD19C0T02 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 16 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby 1 Základní informace k zadání zkoušky Časový
Příklady pro přijímací zkoušku z matematiky školní rok 2012/2013
 Příklady pro přijímací zkoušku z matematiky školní rok 2012/2013 Test přijímací zkoušky bude obsahovat úlohy uzavřené, kdy žák vybírá správnou odpověď ze čtyř nabízených variant (správná je vždy právě
Příklady pro přijímací zkoušku z matematiky školní rok 2012/2013 Test přijímací zkoušky bude obsahovat úlohy uzavřené, kdy žák vybírá správnou odpověď ze čtyř nabízených variant (správná je vždy právě
Určete třetinu podílu čtvrtého čísla zleva a šestého čísla zprava podle číselné osy: Vypočtěte, kolik korun je 5 setin procenta ze 2 miliard korun.
 1. Operace s reálnými čísly Obsah jedné stěny krychle je 289 cm 2. Vypočítejte objem této krychle. [S= 4 913 cm 3 ] Určete třetinu podílu čtvrtého čísla zleva a šestého čísla zprava podle číselné osy:
1. Operace s reálnými čísly Obsah jedné stěny krychle je 289 cm 2. Vypočítejte objem této krychle. [S= 4 913 cm 3 ] Určete třetinu podílu čtvrtého čísla zleva a šestého čísla zprava podle číselné osy:
A[ 20, 70, 50] a výška v = 70, volte z V > z S ; R[ 40, 20, 80], Q[60, 70, 10]. α(90, 60, 70).
![A[ 20, 70, 50] a výška v = 70, volte z V > z S ; R[ 40, 20, 80], Q[60, 70, 10]. α(90, 60, 70). A[ 20, 70, 50] a výška v = 70, volte z V > z S ; R[ 40, 20, 80], Q[60, 70, 10]. α(90, 60, 70).](/thumbs/101/151863289.jpg) Úkoly k zápočtu z BA008 Všechny úkoly jsou povinné. Úkoly číslo 4, 7, 12, 14 budou uznány automaticky, pokud poslední den semestru, tj. 3. 5. 2019, budou všechny ostatní úkoly odevzdané a uznané. 1. Je
Úkoly k zápočtu z BA008 Všechny úkoly jsou povinné. Úkoly číslo 4, 7, 12, 14 budou uznány automaticky, pokud poslední den semestru, tj. 3. 5. 2019, budou všechny ostatní úkoly odevzdané a uznané. 1. Je
CVIČNÝ TEST 24. OBSAH I. Cvičný test 2. Mgr. Kateřina Nováková. II. Autorské řešení 6 III. Klíč 13 IV. Záznamový list 15
 CVIČNÝ TEST 24 Mgr. Kateřina Nováková OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 13 IV. Záznamový list 15 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Písemnou práci z chemie psalo všech 28 žáků ze
CVIČNÝ TEST 24 Mgr. Kateřina Nováková OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 13 IV. Záznamový list 15 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Písemnou práci z chemie psalo všech 28 žáků ze
MATEMATIKA 9 Přijímací zkoušky na nečisto
 787 Střední průmyslová škola stavební, Hradec Králové, Pospíšilova tř. MATEMATIKA 9 Přijímací zkoušky na nečisto 12.1.2017 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 17 Maximální bodové hodnocení: 50
787 Střední průmyslová škola stavební, Hradec Králové, Pospíšilova tř. MATEMATIKA 9 Přijímací zkoušky na nečisto 12.1.2017 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 17 Maximální bodové hodnocení: 50
Školní kolo soutěže Baltík 2009, kategorie C
 Úloha 1 Sídliště Počet bodů: 40 b Pracujte v 3D režimu s Baltíkem. a) Bílý a šedivý Baltík si postaví šachovnici o rozměru 6x6 políček následujícím způsobem. Předměty SGP21.sgpm a SGP22.sgpm upravte na
Úloha 1 Sídliště Počet bodů: 40 b Pracujte v 3D režimu s Baltíkem. a) Bílý a šedivý Baltík si postaví šachovnici o rozměru 6x6 políček následujícím způsobem. Předměty SGP21.sgpm a SGP22.sgpm upravte na
Logika je logika Úlohy na dvoudenní turnaj v Brně 2012
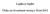 Logika je logika Úlohy na dvoudenní turnaj v Brně 2012 MOSTY Spojte všechny ostrovy (tj. kroužky s čísly) pomocí mostů tak, aby bylo možno dojít z každého ostrova na kterýkoliv jiný. Mosty je přitom dovoleno
Logika je logika Úlohy na dvoudenní turnaj v Brně 2012 MOSTY Spojte všechny ostrovy (tj. kroužky s čísly) pomocí mostů tak, aby bylo možno dojít z každého ostrova na kterýkoliv jiný. Mosty je přitom dovoleno
Test žáka. Zdroj testu: Celoplošná zkouška 2. Školní rok 2012/2013 MATEMATIKA. Jméno: Třída: Škola: Termín provedení testu:
 Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Kolik os souměrnosti má kruh?
Test žáka Zdroj testu: Celoplošná zkouška 2 Školní rok 2012/2013 MATEMATIKA Jméno: Třída: Škola: Termín provedení testu: Datum vytvoření: 14. 10. 2013 Obtížnost 1 Úloha 1 Kolik os souměrnosti má kruh?
Měsíc: učivo:. PROSINEC Numerace do 7, rozklad čísla 1 7. Sčítání a odčítání v oboru do 7, slovní úlohy.
 Předmět: MATEMATIKA Ročník: PRVNÍ Měsíc: učivo:. ZÁŘÍ Úvod k učivu o přirozeném čísle. Numerace do 5, čtení čísel 0-5. Vytváření souborů o daném počtu předmětů. Znaménka méně, více, rovná se, porovnávání
Předmět: MATEMATIKA Ročník: PRVNÍ Měsíc: učivo:. ZÁŘÍ Úvod k učivu o přirozeném čísle. Numerace do 5, čtení čísel 0-5. Vytváření souborů o daném počtu předmětů. Znaménka méně, více, rovná se, porovnávání
1. otázka. 2. otázka = Ve které z následujících možností je výsledek uvedeného výpočtu? 3. otázka
 1. otázka Paní Irena měla černé, bílé a černobílé kočky. elkově jich měla dvanáct. Z toho bylo šest černých a čtyři bílé. Jakou část z celkového počtu představují černobílé kočky? 2. otázka 24 + 12 3 5
1. otázka Paní Irena měla černé, bílé a černobílé kočky. elkově jich měla dvanáct. Z toho bylo šest černých a čtyři bílé. Jakou část z celkového počtu představují černobílé kočky? 2. otázka 24 + 12 3 5
I. kolo kategorie Z7
 68. ročník Matematické olympiády I. kolo kategorie Z7 Z7 I 1 Na každé ze tří kartiček je napsána jedna číslice různá od nuly (na různých kartičkách nejsou nutně různé číslice). Víme, že jakékoli trojmístné
68. ročník Matematické olympiády I. kolo kategorie Z7 Z7 I 1 Na každé ze tří kartiček je napsána jedna číslice různá od nuly (na různých kartičkách nejsou nutně různé číslice). Víme, že jakékoli trojmístné
