DOPLŇKOVÝ UČEBNÍ TEXT MATEMATIKA
|
|
|
- Iveta Krausová
- před 9 lety
- Počet zobrazení:
Transkript
1 DOPLŇKOVÝ UČEBNÍ TEXT MATEMATIKA 2. díl I. Rovnice a nerovnice II. Planimetrie Ondřej Kališ
2 Rovnice a nerovnice I. Rovnice a nerovnice I.1. Lineární rovnice a nerovnice I.1.A. Lineární rovnice Rovnice vyjadřuje rovnost dvou výrazů. Jejich úpravy, jimž se budeme v této kapitole věnovat, provádíme tak, že upravujeme zároveň obě strany, díky čemuž nepřestane rovnost platit; ačkoliv úpravy nikdy nesmí mít vliv na platnost rovnosti, může se stát, že mají vliv na množinu řešení, a proto musíme být hlavně u některých typů úprav opatrní. Lineární rovnice jsou takové rovnice, které obsahují polynom 1. stupně (lze je napsat ve tvaru ax = b); lineární se jim říká proto, že grafem polynomické funkce 1. stupně je přímka. Řešíme je tak, že je postupně upravujeme až na tvar: x = výsledek K tomu používáme ekvivalentní a důsledkové úpravy, přičemž: Ekvivalentní úpravy jsou takové, jež nemají vliv na množinu řešení (výsledek); patří mezi ně: 1) výměna stran rovnice 2) přičtení libovolného čísla k oběma stranám rovnice 3) vynásobení obou stran rovnice stejným číslem (kromě 0) (pozor: nemůžeme dělit rovnici výrazem s neznámou - pokud to nutně potřebujeme udělat, musíme nejprve prověřit (dosazením), zda řešením není V = 0, kde V je výraz, jímž dělíme) Důsledkové úpravy mají vliv na množinu řešení, a proto po jejich použití musíme vždy provést zkoušku (některé řešení nemusí být řešením původní rovnice). Příkladem důsledkové úpravy je umocnění obou stran rovnice na stejné číslo; po něm většinou vyjdou 2 řešení, z nichž řešením původní rovnice je jen jedno. Při odmocňování je naopak potřeba pamatovat na to, že x 2 = x, ale to zatím - při řešení lineárních rovnic - potřebovat nebudete. Úpravy pro přehlednost často zapisujeme napravo od rovnice za svislou čáru. I.1.B. Lineární nerovnice Nerovnice se vyznačuje tím, že hledáme, kdy je jeden výraz větší, nebo menší než druhý. Množinou řešení v R tedy většinou bývá interval, někdy prázdná množina, výjimečně také jedno číslo. Při řešení lineárních nerovnic používáme tentýž postup jako u rovnic. Rozdíl je v tom, že při násobení nerovnice záporným číslem musíme obrátit znak nerovnosti! Pokud nerovnici násobíme neznámou, musíme řešení rozdělit na dvě části (pro,,x 0 a,,x < 0 ); proto je lepší se tomu vyhýbat. I.2. Soustavy lineárních rovnic a nerovnic I.2.A. Soustavy rovnic Soustava rovnic je množina více rovnic, jež musí platit současně. K získání jednoznačného řešení je nutné, aby počet rovnic byl roven počtu neznámých; pokud je jich méně, musíme některou z neznámých vyjádřit na základě jiné (budeme ji považovat za proměnnou, protože nemáme dost informací, abychom určili její hodnotu); je-li rovnic více, vyjadřují některé totéž jako jiné, a proto jsou zbytečné, nebo soustava nemá řešení
3 Rovnice a nerovnice Soustavy lineárních rovnic řešíme jednou z těchto metod: Metoda sčítací je pro řešení běžných soustav asi vhodnější. Nejprve jednu nebo obě rovnice soustavy vynásobíme takovými čísly, aby po sečtení rovnic jedna z neznámých vypadla; pak obě rovnice sečteme. Metoda dosazovací se hodí hlavně k řešení soustav složitějších rovnic (např. kvadratických). Při užití této metody z jedné nerovnice vyjádříme jednu z neznámých a získaný výraz dosadíme do rovnice druhé. V obou případech nám vyjde řešení pouze pro jednu z neznámých, druhou získáme zpětným dosazením vyševší hodnoty neznámé do jedné z rovnic původní soustavy. I.2.B. Soustavy nerovnic Soustavy nerovnic řešíme velmi odlišně. Používá se k tomu grafické řešení, ale hlavně při řešení soustav nerovnic s jednou neznámou můžeme řešení jednotlivých nerovnic zapsat jako intervaly a určit jejich průnik (viz 1. díl). Při grafickém řešení budeme nejprve nahlížet na nerovnici jako na rovnici, z ní vyjádříme jednu z neznámých, abychom získali rovnici ve tvaru,,y = ax + b (jejímu grafickému znázornění se budeme podrobněji věnovat ve 3. dílu), tu zaneseme do grafu a jelikož se jedná o nerovnici, dosadíme libovolný bod (většinou [0;0]), zjistíme, zda pro něj nerovnost je/není splněná a na základě toho vyšrafujeme polorovinu na té straně od naší přímky, kde zvolený bod leží/neleží. Když takto zaneseme všechny nerovnice soustavy, snadno uvidíme, kde se všechny vyšrafované poloroviny překrývají, spočítáme průsečíky přímek, které potřebujeme (asi nikoho ani nenapadne, že by ten obrázek rýsoval), abychom zjistili krajní body intervalů řešení, a zapíšeme výsledek. I.3. Kvadratické rovnice a nerovnice I.3.A. Kvadratické rovnice Kvadratická rovnice je taková rovnice, jež obsahuje polynom 2. stupně; lze ji napsat ve tvaru: ax 2 + bx + c = 0 a ε R-{0} b, c ε R Každá kvadratická rovnice má v množině C právě dvě řešení, nemá-li dvojnásobný kořen (ten se považuje za dvě řešení, ale jedná se o jediné číslo). Pokud se jedná o rovnici, jejíž žádný koeficient není nulový, najdeme řešení nejlépe pomocí následujícího vzorce (použité označení koeficientů je stejné jako ve výše uvedené definici): x 1,2 = b± b2 4ac 2a Výraz pod odmocninou D=b 2 4ac se nazývá diskriminant a udává, jaká řešení bude rovnice mít: při D > 0 vyjdou dvě reálná řešení, při D = 0 vyjde jeden reálný dvojnásobný kořen, při D < 0 bude řešení komplexní, ale nikoliv reálné (v R tato rovnice nemá řešení); obě řešení navíc budou čísla komplexně sdružená (o tom se dočtete v 5. díle). Speciální případy kvadratických rovnic Ryze kvadratická rovnice (b = 0): Tuto prostě převedeme do tvaru x 2 = c a, pak musíme ještě pamatovat na to, že x 2 = x
4 Rovnice a nerovnice Například: x 2-9 = 0 x 2 = 9 x = 3 x 1,2 = +- 3 Kvadratická rovnice bez absolutního členu (c = 0): Takovou rovnici vyřešíme vytknutím neznámé a využitím pravidla, že aby se součin rovnal,,0, musí se rovnat,,0 aspoň jeden z činitelů. Takže třeba: x 2-2x = 0 x(x - 2) = 0 K = {0; 2} Některé kvadratické rovnice také můžeme snadno rozložit na součin, a to podle Vietových vzorců (viz níže); to mi však přijde většinou pracnější než použít vzorec uvedený v úvodu této kapitoly. Rozložení se často může hodit v případě, že rovnice má dvojnásobný kořen - v tom případě se používá vzorec: x 2 + 2rx + r 2 = (x + r) 2 Dvojnásobným kořenem pak je číslo,,-r. Vietovy vzorce Pro rovnici v normovaném tvaru x 2 + px + q = 0 platí: x 1 + x 2 = - p x 1 x 2 = q Díky těmto dvěma vzorcům můžeme kvadratickou rovnici roložit na součinový tvar, ale také zpětně určit rovnici při znalosti kořenů. Jen je třeba si uvědomit, že stejné kořeny má každá rovnice a(x 2 + px + q) = 0, kde a ε R-{0}. I.3.B. Kvadratické nerovnice Grafem kvadratické funkce je parabola protínající osu,,x v bodech, které jsou řešeními kvadratické rovnice. Pokud a > 0, je tato parabola otočená špičkou dolů, je-li a < 0, má parabola špičku nahoru. Na tom je založeno řešení kvadratických nerovnic - je jím buď interval mezi kořeny, nebo sjednocení intervalů vně kořenů, a to podle toho, zda je graf příslušné kvadratické funce zrovna nad, nebo pod osou,,x. Je tedy záhodno umět si jej představit. Například u takových jednoduchých kvadratických nerovnic: x 2-4x > 0 x(x + 4) > 0 K = (- ;0) U (4; ) x 2-4x < 0 K = (0;4) Pokud D < 0, funkce osu,,x neprotíná vůbec, a proto buď K = R, nebo K =. Pokud D = 0, funkce se osy,,x dotýká v jednom bodě, takže: x 2 + 2x + 1 = 0 K = {-1} x 2 + 2x + 1 > 0 K = R-{-1} x 2 + 2x K = R x 2 + 2x + 1 < 0 K = - 3 -
5 Rovnice a nerovnice x 2 + 2x K = {-1} I.4. Rovnice a nerovnice v součinovém a podílovém tvaru Pro řešení rovnic ve tvaru součinu (nebo podílu) polynomů používáme pravidlo zmíněné už u kvadratických rovnic - aby byl součin roven,,0, musí být alespoň jeden činitel roven,,0. Toto pravidlo tedy můžeme použít, pokud je na levé straně součin a na pravé,,0. Pak případně určíme podmínky a hned uvidíme řešení. U polynomů ve jmenovateli musíme nejprve určit podmínku, že se nesmějí rovnat 0. Při řešení nerovnic v součinovém (resp. podílovém) tvaru nejprve určíme nulové body (čísla, v nichž jsou jednotliví činitelé nuloví (tedy řešení příslušné rovnice)) - v nich funkce mění znaménko. Pak rozdělíme R na intervaly, jejichž hranicemi budou nulové body a dáme je do tabulky, kde v řádcích budou hodnoty jednotlivých polynomů v těchto intervalech; pro jeden z intervalů zjistíme, zda je celá funkce kladná, nebo záporná (záporná je, pokud je záporný lichý počet činitelů) a doplníme střídavě znaménka funkce v ostatních intervalech. Musíme dávat pozor na to, že ve dvojnásobném (přesněji v sudonásobném) kořeni se znaménko nemění! Například: x 1 2 x 3 2 x x 10 0 x {-10; 2} nulové body: -10; -1; 2; 3-1 je dvojnásobný kořen (- ;-10) (-10;-1) <-1;2) (2;3) <3; ) x (x + 1) x x celá fce K = (- ;-10) U (2;3> Při jisté praxi už nemusíte dělat tabulku a po určení nulových bodů a znaménka v jednom z intervalů dokážete výsledek napsat rovnou z hlavy nebo s načrtnutím číselné osy. I.5. Rovnice a nerovnice s absolutní hodnotou Pokud je neznámá v absolutní hodnotě, musíme řešení rozdělit na dva případy - pro výraz v abs. hodnotě nezáporný a záporný. Díky tomu můžeme absolutní hodnotu odstranit a řešíme dvě samostatné rovnice, případně nerovnice. Výsledkem bude sjednocení řešení obou rovnic (nerovnic) v příslušných intervalech. Je-li v rovnici absolutních hodnot více, bude i více dílčích řešení. K určení intervalů, v nichž budeme pracovat, je možné využít metodu nulových bodů (podobně jako v kapitole I.4.)
6 Rovnice a nerovnice x < 4/3: - 2x - 3x + 4 = 0-5x + 4 = 0-5x = -4 x = 4/5 Příklad: - 2x + 3x - 4 = 0 nulový bod: 4/3 K = {4/5; 4} x 4/3: - 2x + 3x - 4 = 0 x - 4 = 0 x = 4 I.6. Řešení rovnic a nerovnic substitucí Substituce znamená nahrazení části výrazu jednou neznámou. Můžeme ji buď označit novým písmenkem, nebo pouze uvažovat, že se jedná o jeden celek. Tím si někdy jen zjednodušíme zápis, ale mnohdy je tento krok nutný k úspěšnému vyřešení příkladu. Když zjistíme hodnotu zástupné proměnné, musíme se vždy vrátit k proměnné původní. Příklad: x x 2 x x 30=0 x 0 s=x x s 2 s 30=0 s 1,2 = 1± = 1± 121 = 1± s 1 = 5; s 2 =6 x 1 x 1 = 5 p= x 1 p 2 p= 5 p 2 p 5=0 p 1,2 = 1± = 1± Nemá řešení v R. x 2 x 2 =6 q= x 2 q 2 q=6 q 2 q 6=0 q 1,2 = 1± = 1± 25 = 1± q 1 = 3; q 2 =2 x 1 = 3 2. x 2 =2 2. x 1 =9 x 2 =4 Protože jsme umocňovali, musíme provést zkoušku (dosazením hodnot do původní rovnice): Pro x 1 zkouška nevyjde. Pro x 2 zkouška vyjde. K = {4} - 5 -
7 Rovnice a nerovnice Příklad, kde nebudeme zavádět nové označení: 4x 4-4x = 0 4(x 2 ) 2-4x = 0 x 2 1,2 = 4± = 4± = 1 2 x 2 1,2 = 1 2 x 1,2 =± 1 2 Protože není pěkné uvádět odmocninu ve jmenovateli (také kvůli dalšímu počítání), zlomek usměrníme (rozšíříme odmocninou ve jmenovateli): x 1,2 =± 1 2 =± =± 2 2 A to je výsledek. I.7. Rovnice a nerovnice s parametrem Parametr je proměnná. Nepovažujeme ji tedy za neznámou, nýbrž za číslo, a proto je součástí výsledku. Výsledkem je zpravidla vzorec, do nějž můžeme dosadit jakékoliv číslo z množiny, pro niž je definován, a proto je zvykem na závěr řešení uvést přehlednou tabulku, co se stane, pokud dosadíme čísla z různých intervalů. Počítání rovnic s parametrem ukazuje následující příklad: 4ax x - a + 8 = 0 a ε R 1) a = x + 8 = x = -8 x= 2 15 x= ) a 0 Zkoumáme znaménko diskriminantu: D = (4 15) 2-4 4a (-a+8) = a 2-128a = 16a 2-128a D > 0 16a 2-128a > 0 :16 a 2-8a + 15 > 0 a 1,2 = 8± = 8± 4 = 8± =4±1 a 1 =3; a 2 =5 a) a ε (- ;3) U (5; ) x 1,2 = 4 15± 16a2 128a 240 = 4 15±4 a2 8a 15 = 15± a2 8a 15 8a 8a 2a b) a = 3 x=
8 Rovnice a nerovnice c) a = 5 d) a ε (3;5) a x= (pouze pokud úlohu řešíme v C) x 1,2 = 15±i a2 8a 15 2a Tabulka řešení: 0 x= x= x= (- ;0) U (0;3) U (5; ) I.8. Rovnice vyšších stupňů x x 1,2 = 15± a2 8a 15 2a (3;5) x 1,2 = 15±i a2 8a 15 2a Rovnice snadno upravitelné na součinový tvar Nejsnáze z rovnic vyšších stupňů se řeší ty, jež lze snadno upravit na součinový tvar. Příklad nejjednoduššího případu: x 3 + 6x 2 + 8x = 0 x(x 2 + 6x + 8) = 0 x 1 = 0 x 2 + 6x + 8 = 0 x 2,3 = 6± = 6± 4 = 6±2 = 3± x 2 = 4; x 3 = 2 K = {-4; -2; 0} Obecné rovnice vyšších stupňů Při obecném řešení vycházíme z předpokladu, že je-li x 0 ε Q-{0} kořen rovnice vyjádřený zlomkem v základním tvaru x 0 = p/q, pak p je dělitelem absolutního členu a q dělitelem členu při nejvyšší mocnině. Nejprve samozřejmě dosazujeme celá čísla, jimiž je dělitelný absolutní člen, následně, pokud jsme nenalezli řešení, musíme přikročit k dosazování zlomků. Každá rovnice má právě tolik kořenů, jaký je její stupeň (ale může mít vícenásobné kořeny)
9 Rovnice a nerovnice Příklad: x 3 + 6x 2 + x - 14 = 0 x 1 ε {+-1; +-2; +-7; +-14} Postupným dosazením zjistíme, že x 1 = -2. (x 3 + 6x 2 + x - 14) : (x + 2) = x 2 + 4x - 7 x 2 + 4x - 7 = 0 x 2,3 = 4± = 4± = 4± 44 = 4±2 11 = 2± K = {-2-11; -2; } Reciproké rovnice Reciproké rovnice se dělí podle dvou kritérií na 4 druhy: a) I. druhu (kladně reciproké): a k = a n-k (např. 2x 3-3x 2-3x + 2 = 0) b) II. druhu (záporně reciproké): a k = -a n-k (např. 12x 4-25x x - 12 = 0) α) sudého stupně β) lichého stupně Vlasnosti reciprokých rovnic: 1) x 0 2) je-li x 1 kořenem, pak i x 1-1 je kořenem 3) prostřední člen rovnic sudého stupně (rovnice lichého stupně prostřední člen nemají) je u rovnic I. druhu libovolný, u rovnic II. druhu rovný 0 Řešení reciprokých rovnic: II. druh: 1) x 1 = 1 -> vydělím polynom (x - 1) I. druh, lichý stupeň: 1) x 1 = -1 -> vydělím polynom (x + 1) I. druh, sudý stupeň: 1) celou rovnici vydělím x n 2) vytknu stejné koeficienty 3) substituuju (x + x -1 ) n je nejvyšší mocnina k je jakákoliv mocnina vyskytující se v rovnici (k ε N 0 ; k n) - 8 -
10 Planimetrie II. Planimetrie Planimetrie je oblast matematiky, zabývající se útvary v rovině. V této kapitole se úmyslně nebudu věnovat problematice jejich sestrojování, neboť tuto spíše řemeslnou dovednost každý snad celkem snadno získá ve škole, případně jiným způsobem, avšak pro člověka, který již opustil střední školu, není příliš užitečná a jen by mu celou problematiku znepřehledňovala. II.1. Přímka, polopřímka, úsečka Přímka je jednorozměrný prostor. To znamená, že v jednom směru je nekončně dlouhá a ve všech ostatních směrech je její velikost,,0. K jednoznačnému určení přímky jsou potřeba právě dva body, nebo jeden bod a směr (zpravidla udávaný vektorem, ale tomu se budeme věnovat až v analytické geometrii). Dvourozměrnou obdobou přímky je rovina - ta je ve dvou na sebe kolmých směrech nekonečná a ve všech ostatních nulová. Dále existuje nám dobře známý trojrozměrný prostor (i těch existuje ve čtyřrozměrném a vyšším prostoru nekonečně mnoho), ale také prostory čtyřrozměrné, pětirozměrné a pravděpodobně i mnohem více rozměrné. Rovněž existuje bod, což je prostor bezrozměrný. To znamená, že má nulovou délku ve všech směrech. Jelikož se teď budeme pohybovat v rovině, budou nás z prostorů zajímat jen přímky a body. Bodem můžeme přímku rozdělit na dvě polopřímky. I ty jsou samozřejmě nekonečně dlouhé, ale z příslušného bodu jdou každá jen na jednu stranu. Dvěma body můžeme na přímce vymezit úsečku. Ta už má konkrétní délku. Ovšem i úsečka obsahuje nekonečně mnoho bodů, protože délka bodu je 0. II.2. Úhly Každé dvě přímky ležící v jedné rovině spolu svírají nějaký úhel. Pokud jsou přímky rovnoběžné, je velikost jejich úhlu 0 - říká se mu přímý. Protože přímka nemá směr, svírají vždy zároveň úhel o 180 větší. Úhel o 360 (případně násobky této hodnoty) větší znamená vždy tentýž úhel. Přímky kolmé svírají úhel pravý, tedy o velikosti 90. Úhel z intervalu (0 ; 90 ) se nazývá ostrý, z (90 ; 180 ) tupý. Úhly o velikostech (0 ; 180 ) jsou konvexní, (180 ; 360 ) nekonvexní. Kromě stupňů, kde pravý úhel má velikost 90, k udávání velikostí úhlů používáme ještě tyto jednotky: číslo (radián), kdy pravý úhel je π/2 a grad, kdy pravý úhel je 100 g. II.3. Trojúhelníky Trojúhelník (Δ) je množina tří bodů, které neleží v přímce, a tyto body spojujících úseček, přičemž ty body se nazývají vrcholy a úsečky strany
11 Planimetrie Strany a vrcholy samozřejmě můžeme označovat zcela libovolně, ale pro snazší orientaci zde použijeme takovýto obecný trojúhelník: Aby trojúhelník existoval, musí být splněna trojúhelníková nerovnost: a + b > c Samozřejmě, že v tomto případě, i vždy, pokud se jedná o obecný trojúhelník, je možná cyklická záměna, což znamená, že musí zároveň platit: a + c > b b + c > a Součet vnitřních úhlů trojúhelníka je úhel přímý, tedy: α + β + γ = 180 Výška trojúhelníka je úsečka z vrcholu kolmá na protější stranu, končící na této protější straně, nebo na jejím prodloužení. Obvykle se označuje v. Těžnice je spojnice středu strany a protějšího vrcholu (zpravidla se označuje t); průsečíkem těžnic je těžiště trojúhelníka. Těžiště se nachází vždy ve ⅓ délky těžnice, blíže ke straně. Střední příčka je spojnice středů dvou stran trojúhelníka; je vždy rovnoběžná se stranou, kterou neprotíná, a má oproti ní poloviční délku; Δ vytvořený středními příčkami je podobný původnímu Δ - má poloviční obvod a čtvrtinový obsah. Kružnice Δ opsaná prochází všemi vrcholy Δ. Kružnice Δ vepsaná se dotýká všech stran Δ, ležíc uvnitř něj. Středem kružnice opsané je průsečík os úhlů. Středem kružnice vepsané je průsečík os stran. Pomůcka: Kdyby to bylo opačně, poloměr by ležel na ose určující střed, takže by to bylo až moc jednoduché. Poloměr kružnice opsané se značívá r a její střed S. Poloměr kružnice vepsané bývá označován ρ a její střed O. Pomůcka: Kružnice vepsaná je v trojúhelníku sklíčená, proto kulatá písmena ρ a O. Také existují vždy tři kružnice Δ připsané, jež se dotýkají pokaždé jedné ze stran Δ a prodloužení zbylých dvou stran; středem kružnice Δ připsané je průsečík jedné osy vnitřního úhlu Δ a dvou os úhlů vnějších
12 Planimetrie Vzorce pro určení poloměrů kružnice opsané a vepsané: r= abc 4S ;r= a 2sinα ρ= 2S o (S je zde obsah Δ a o jeho obvod) Vzorce pro obvod a obsah trojúhelníka: o = a + b + c S = 0,5 a v a Heronův vzorec: S= s s a s b s c, kdes= o 2 II.3.A. Speciální případy trojúhelníků Rovnoramenné trojúhelníky Rovnoramenný trojúhelník se vyznačuje tím, že dvě z jeho stran jsou stejně dlouhé. Pokud jako c označíme stranu, jejíž délka je jiná než zbylých dvou (tedy základnu), tak platí: v c = t c, přičemž v c dělí ΔABC na dva pravoúhlé Δ, souměrné podle v c. Rovnostranné trojúhelníky Rovnostranný trojúhelník má všechny strany stejně dlouhé. Platí pro něj totéž jako pro Δ rovnoramenný, ovšem s tím, že je možná cyklická záměna, neboť za základnu lze považovat kteroukoliv ze stran. Navíc všechny vnitřní úhly rovnostranného Δ mají velikost 60. Pravoúhlé trojúhelníky Pravoúhlý trojúhelník má jeden úhlů pravý. Takovýto Δ je velmi užitečný, protože v něm platí Pythagorova věta, goniometrické funkce a eukleidovy věty. Těm se budeme věnovat v následující podkapitole. Stranám pravému úhlu přilehlým se říká odvěsny a straně protilehlé přepona
13 Planimetrie II.3.B. Vzorce pro pravoúhlý trojúhelník Nyní budeme uvažovat pravoúhlý trojúhelník s pravým úhlem při vrcholu C, tedy takovýto: Pythagorova věta Pythagorova věta říká, že součet druhých mocnin délek odvěsen je roven druhé mocnině délky přepony: a 2 + b 2 = c 2 Goniometrické funkce Goniometrické funce úhlů jsou definované jako poměry stran pravoúhlého trojúhelníka: sinα= a c cosα= b c tgα= a b Více si o nich povíme ve 4. díle doplňkových učebních textů. Eukleidovy věty Zde je patou výšky (P c ) přepona rozdělená na dvě části: - c a - část přepony blíže straně a - c b - část přepony blíže straně b Eukleidova věta o výšce: v 2 = c a c b Eukleidova věta o odvěsně: a 2 = c c a II.3.C. Sinová a cosinová věta Sinová a cosinová věta platí v každém trojúhelníku (nemusí být pravoúhlý). Věta sinová: Věta cosinová: a sinα = b sinβ = c sinγ a 2 = b 2 + c 2-2 b c cosα
14 Planimetrie II.4. Další mnohoúhelníky II.4.A. Obecné mnohoúhelníky Mnohoúhelník je rovinný útvar s přirozeným počtem vrcholů větším než 2, z nichž žádné 3 neleží v jedné přímce. Pravidelný mnohoúhelník je takový, který má všechny strany stejně dlouhé. Nejdůležitějšími mnohoúhelníky jsou trojúhelníky (viz výše) a čtyřúhelníky (viz níže), při znalostech práce s nimiž dokážeme pracovat s většinou rovinných útvarů. II.4.B. Čtyřúhelníky Zde se budeme stručně zabývat pouze speciálními případy čtyřúhelníků, jimiž jsou: - čtverec, jenž má všechny strany stejně dlouhé a všechny vnitřní úhly pravé - obdélník, jehož protilehlé strany jsou vždy stejně dlouhé a vnitřní úhly pravé - kosočtverec, jenž má stejně dlouhé strany (protilehlé strany jsou rovnoběžné), ale nepravé úhly - kosodélník, který má protilehlé strany stejně dlouhé (a rovnoběžné) a úhly nepravé - lichoběžník, jehož dvě strany jsou rovnoběžné a zbylé dvě různoběžné (může být obecný, rovnoramenný nebo pravoúhlý (s pravým úhlem na jedné straně)) Obsah čtverce: S = a 2 Obsah obdélníka: S = a b Obsah kosočtverce: S = a v S = e f (e a f jsou úhlopříčky kosočtverce) Obsah kosodélníka: S = a v a Obsah lichoběžníka: S = s v s= a c 2 (s je střední příčka lichoběžníka (spojnice středů jeho ramen), výška (v) je vzdálenost jeho základen) II.5. Kružnice a kruh Kružnice je množina všech bodů, jež mají od daného bodu - středu - stejnou vzdálenost, která je poloměrem kružnice. Jedná se o speciální případ elipsy, druh kuželosečky, o čemž si povíme více až v 6. díle. Kruh je množina všech bodů, jejichž vzdálenost od středu je menší nebo rovna poloměru. Tečna kružnice je taková přímka, jež má s kružnicí právě jeden společný bod. Je kolmá na poloměr a její vzdálenost od středu je rovna poloměru. Sečna kružnice protíná kružnici ve dvou bodech. Úsečka mezi průsečíky sečny s kružnicí se nazývá tětiva
15 Planimetrie Obvod a obsah kruhu se počítá s pomocí Ludolfova čísla - označovaného π - které vyjadřuje poměr obvodu kruhu k jeho průměru. Jeho přibližná hodnota je 3, , ale nejedná se o racionální číslo, a proto ho nevyčíslujeme, pokud opravdu nepotřebujeme získat výslednou hodnotu - ta bude vždy zaokrouhlená. Obvod kruhu: o = 2πr Obsah kruhu: S = πr 2 II.6. Zobrazení v rovině Zobrazení je předpis přiřazující každému bodu jeho obraz. Výchozí bod se nazývá vzor, výsledný bod pak obraz. II.6.A. Shodná zobrazení Shodné zobrazení je takové zobrazení, které zachovává délky úseček a velikosti úhlů. II.6.A.α. Osová souměrnost Osová souměrnost s osou o je shodné zobrazení, které přiřazuje každému bodu X bod X' tak, že přímka XX' je kolmá k o a Xo = X'o. Osová souměrnost s osou o se označuje O(o). Osová souměrnost je na rozdíl od níže uvedených shodných zobrazení shodnost nepřímá, protože obraz je vzhledem ke vzoru stranově převrácený. II.6.A.β. Středová souměrnost Středová souměrnost se středem S je shodné zobrazení, které přiřazuje každému bodu X bod X' tak, že pokud X S, S ε XX', a každopádně XS = X'S. Středová souměrnost se středem S se označuje S(S). II.6.A.γ. Posunutí (translace) Translace se směrem AB je shodné zobrazení, které přiřazuje každému bodu X bod X' tak, že orientované úsečky XX' a AB mají stejný směr i délku. Translace, jejímž směrem je orientovaná úsečka AB, se značí T(AB). II.6.A.δ. Otočení (rotace) Rotace daná orientovaným úhlem φ a středem S je shodné zobrazení, které přiřazuje každému bodu X bod X' tak, že XS = X'S a XSX' má směr a velikost φ (pokud X = S, pak X' = S). Rotace se středem S a úhlem φ se značí R(S,φ). II.6.B. Podobné zobrazení - stejnolehlost Podobné zobrazení zachovává úhly, ale úsečky zvětšuje podle daného kladného koeficientu. Příkladem podobného zobrazení je stejnolehlost (homotetie). Homotetie se středem S a koeficientem κ různým od 0 je podobné zobrazení s koeficientem κ, které přiřazuje bodu S bod S' = S a bodu X S bod X' tak, že platí SX' = κ. SX, přičemž pro κ > 0 leží bod X' na polopřímce SX a pro κ < 0 leží bod X' na polopřímce opačné pol. SX. Homotetie se středem S a koeficientem κ se značí H(S,κ)
16 Planimetrie Stejnolehlosti využíváme například chceme-li spojit daný bod (B) s průsečíkem dvou přímek (p, q) nacházejícím se kdesi daleko: Nejprve přetneme přímky p a q libovolnou další přímkou (r), čímž získáme průsečíky X a Y. Tyto body spojíme s bodem B (vzniknou přímky s, t) a sestrojíme přímku r' rovnoběžnou s r, čímž získáme body X' a Y', jsoucí opět průsečíky s p a q. Potom sestrojíme přímky s' a t' rovnoběžné s s a t procházející body X' a Y'. Průsečík s' a t' označíme B' a nyní spojíme body B a B', čímž získáme hledanou přímku b. Jak je vidět z tohoto příkladu, nejužitečnější je stejnolehlost trojúhelníků, na níž lze také stejnolehlost nejlépe ukázat, například na následujícím obrázku, kde jsou 3 stejnolehlé trojúhelníky a přímky spojující jejich vrcholy:
Kapitola I - Množiny bodů daných vlastností I.a Co je množinou všech bodů v rovině, které mají od daných dvou různých bodů stejnou vzdálenost? I.
 Kapitola I - Množiny bodů daných vlastností I.a Co je množinou všech bodů v rovině, které mají od daných dvou různých bodů stejnou vzdálenost? I.b Co je množinou středů všech kružnic v rovině, které prochází
Kapitola I - Množiny bodů daných vlastností I.a Co je množinou všech bodů v rovině, které mají od daných dvou různých bodů stejnou vzdálenost? I.b Co je množinou středů všech kružnic v rovině, které prochází
Kvadratické rovnice pro učební obory
 Variace 1 Kvadratické rovnice pro učební obory Autor: Mgr. Jaromír JUŘEK Kopírování a jkaékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
Variace 1 Kvadratické rovnice pro učební obory Autor: Mgr. Jaromír JUŘEK Kopírování a jkaékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
4. Výčtem prvků f: {[2,0],[3,1],[4,2],[5,3]}
![4. Výčtem prvků f: {[2,0],[3,1],[4,2],[5,3]} 4. Výčtem prvků f: {[2,0],[3,1],[4,2],[5,3]}](/thumbs/41/22269260.jpg) 1/27 FUNKCE Základní pojmy: Funkce, definiční obor, obor hodnot funkce Kartézská soustava souřadnic, graf funkce Opakování: Číselné množiny, úpravy výrazů, zobrazení čísel na reálné ose Funkce: Zápis:
1/27 FUNKCE Základní pojmy: Funkce, definiční obor, obor hodnot funkce Kartézská soustava souřadnic, graf funkce Opakování: Číselné množiny, úpravy výrazů, zobrazení čísel na reálné ose Funkce: Zápis:
15 s. Analytická geometrie lineárních útvarů
 5 s Analytická geometrie lineárních útvarů ) Na přímce: a) Souřadnice bodu na přímce: Bod P nazýváme počátek - jeho souřadnice je P [0] Nalevo od počátku leží čísla záporná, napravo čísla kladná. Každý
5 s Analytická geometrie lineárních útvarů ) Na přímce: a) Souřadnice bodu na přímce: Bod P nazýváme počátek - jeho souřadnice je P [0] Nalevo od počátku leží čísla záporná, napravo čísla kladná. Každý
ALGEBRA LINEÁRNÍ, KVADRATICKÉ ROVNICE
 ALGEBRA LINEÁRNÍ, KVADRATICKÉ ROVNICE A NEROVNICE, SOUSTAVY ROVNIC A NEROVNIC Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21.
ALGEBRA LINEÁRNÍ, KVADRATICKÉ ROVNICE A NEROVNICE, SOUSTAVY ROVNIC A NEROVNIC Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21.
Kvadratické rovnice pro studijní obory
 Variace 1 Kvadratické rovnice pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
Variace 1 Kvadratické rovnice pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
M - Rovnice - lineární a s absolutní hodnotou
 Rovnice a jejich ekvivalentní úpravy Co je rovnice Rovnice je matematický zápis rovnosti dvou výrazů. př.: x + 5 = 7x - M - Rovnice - lineární a s absolutní hodnotou Písmeno zapsané v rovnici nazýváme
Rovnice a jejich ekvivalentní úpravy Co je rovnice Rovnice je matematický zápis rovnosti dvou výrazů. př.: x + 5 = 7x - M - Rovnice - lineární a s absolutní hodnotou Písmeno zapsané v rovnici nazýváme
Různostranné obecné Rovnoramenné Rovnostranné. třetí, základna, je různá
 Trojúhelník Trojúhelník - AB určují tři body A, B,, které neleží na jedné přímce. Trojúhelník je rovněž možno považovat za průnik tří polorovin nebo tří konvexních úhlů. γ, γ, γ Body A, B,, se nazývají
Trojúhelník Trojúhelník - AB určují tři body A, B,, které neleží na jedné přímce. Trojúhelník je rovněž možno považovat za průnik tří polorovin nebo tří konvexních úhlů. γ, γ, γ Body A, B,, se nazývají
3.2.4 Podobnost trojúhelníků II
 3..4 odobnost trojúhelníků II ředpoklady: 33 ř. 1: Na obrázku jsou nakresleny podobné trojúhelníky. Zapiš jejich podobnost (aby bylo zřejmé, který vrchol prvního trojúhelníku odpovídá vrcholu druhého trojúhelníku).
3..4 odobnost trojúhelníků II ředpoklady: 33 ř. 1: Na obrázku jsou nakresleny podobné trojúhelníky. Zapiš jejich podobnost (aby bylo zřejmé, který vrchol prvního trojúhelníku odpovídá vrcholu druhého trojúhelníku).
2.4.11 Nerovnice s absolutní hodnotou
 .. Nerovnice s absolutní hodnotou Předpoklady: 06, 09, 0 Pedagogická poznámka: Hlavním záměrem hodiny je, aby si studenti uvědomili, že se neučí nic nového. Pouze používají věci, které dávno znají, na
.. Nerovnice s absolutní hodnotou Předpoklady: 06, 09, 0 Pedagogická poznámka: Hlavním záměrem hodiny je, aby si studenti uvědomili, že se neučí nic nového. Pouze používají věci, které dávno znají, na
ax + b = 0, kde a, b R, přímky y = ax + b s osou x (jeden, nekonečně mnoho, žádný viz obr. 1.1 a, b, c). Obr. 1.1 a Obr. 1.1 b Obr. 1.
 1 Rovnice, nerovnice a soustavy 11 Lineární rovnice Rovnice f(x) = g(x) o jedné neznámé x R, kde f, g jsou reálné funkce, se nazývá lineární rovnice, jestliže ekvivalentními úpravami dostaneme tvar ax
1 Rovnice, nerovnice a soustavy 11 Lineární rovnice Rovnice f(x) = g(x) o jedné neznámé x R, kde f, g jsou reálné funkce, se nazývá lineární rovnice, jestliže ekvivalentními úpravami dostaneme tvar ax
1. Kruh, kružnice. Mezi poloměrem a průměrem kružnice platí vztah : d = 2. r. Zapíšeme k ( S ; r ) Čteme kružnice k je určena středem S a poloměrem r.
 Kruh, kružnice, válec 1. Kruh, kružnice 1.1. Základní pojmy Kružnice je množina bodů mající od daného bodu stejnou vzdálenost. Daný bod označujeme jako střed kružnice. Stejnou vzdálenost nazýváme poloměr
Kruh, kružnice, válec 1. Kruh, kružnice 1.1. Základní pojmy Kružnice je množina bodů mající od daného bodu stejnou vzdálenost. Daný bod označujeme jako střed kružnice. Stejnou vzdálenost nazýváme poloměr
( ) ( ) ( ) 2 ( ) 2.7.16 Rovnice s neznámou pod odmocninou II. Předpoklady: 2715
 .7.6 Rovnice s neznámou pod odmocninou II Předpoklady: 75 Př. : Vyřeš rovnici y + + y = 4 y + + y = 4 / ( y + + y ) = ( 4) y + + 4 y + y + 4 y = 6 5y + 4 y + y = 8 5y + 4 y + y = 8 - v tomto stavu nemůžeme
.7.6 Rovnice s neznámou pod odmocninou II Předpoklady: 75 Př. : Vyřeš rovnici y + + y = 4 y + + y = 4 / ( y + + y ) = ( 4) y + + 4 y + y + 4 y = 6 5y + 4 y + y = 8 5y + 4 y + y = 8 - v tomto stavu nemůžeme
Vztah mezi dvěma čísly, které se rovnají, se nazývá rovnost, jako například : ( 2) 3 = 8 4 = 2 ; 16 = 4 ; 1 = 1 a podobně. 2
 Lineární rovnice o jedné neznámé O rovnicích obecně Vztah mezi dvěma čísly, které se rovnají, se nazývá rovnost, jako například : ( ) 8 ; 6 ; a podobně. ; Na rozdíl od rovností obsahuje rovnice kromě čísel
Lineární rovnice o jedné neznámé O rovnicích obecně Vztah mezi dvěma čísly, které se rovnají, se nazývá rovnost, jako například : ( ) 8 ; 6 ; a podobně. ; Na rozdíl od rovností obsahuje rovnice kromě čísel
2.8.9 Parametrické rovnice a nerovnice s absolutní hodnotou
 .8.9 Parametrické rovnice a nerovnice s absolutní hodnotou Předpoklady: 0,, 806 Pedagogická poznámka: Opět si napíšeme na začátku hodiny na tabuli jednotlivé kroky postupu při řešení rovnic (nerovnic)
.8.9 Parametrické rovnice a nerovnice s absolutní hodnotou Předpoklady: 0,, 806 Pedagogická poznámka: Opět si napíšeme na začátku hodiny na tabuli jednotlivé kroky postupu při řešení rovnic (nerovnic)
Maturitní okruhy z matematiky školní rok 2007/2008
 Maturitní okruhy z matematiky školní rok 2007/2008 1. ALGEBRAICKÉ VÝRAZY 2 2 2 3 3 3 a ± b ; a b ; a ± b ; a ± b 1.1. rozklad výrazů na součin: vytýkání, užití vzorců: ( ) ( ) 1.2. určování definičního
Maturitní okruhy z matematiky školní rok 2007/2008 1. ALGEBRAICKÉ VÝRAZY 2 2 2 3 3 3 a ± b ; a b ; a ± b ; a ± b 1.1. rozklad výrazů na součin: vytýkání, užití vzorců: ( ) ( ) 1.2. určování definičního
KONSTRUKČNÍ ÚLOHY ŘEŠENÉ UŽITÍM MNOŽIN BODŮ
 Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol KONSTRUKČNÍ
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol KONSTRUKČNÍ
STEREOMETRIE. Vzdálenost bodu od přímky. Mgr. Jakub Němec. VY_32_INOVACE_M3r0113
 STEREOMETRIE Vzdálenost bodu od přímky Mgr. Jakub Němec VY_32_INOVACE_M3r0113 VZDÁLENOST BODU OD PŘÍMKY V PROSTORU Při hledání vzdálenosti bodu od geometrického útvaru v prostoru je nutné si vždy úlohu
STEREOMETRIE Vzdálenost bodu od přímky Mgr. Jakub Němec VY_32_INOVACE_M3r0113 VZDÁLENOST BODU OD PŘÍMKY V PROSTORU Při hledání vzdálenosti bodu od geometrického útvaru v prostoru je nutné si vždy úlohu
2.7.2 Mocninné funkce se záporným celým mocnitelem
 .7. Mocninné funkce se záporným celým mocnitelem Předpoklady: 70 Mocninné funkce se záporným celým mocnitelem: znamená? 3 y = = = = 3 y y y 3 = ; = ; = ;.... Co to Pedagogická poznámka: Nechávám studenty,
.7. Mocninné funkce se záporným celým mocnitelem Předpoklady: 70 Mocninné funkce se záporným celým mocnitelem: znamená? 3 y = = = = 3 y y y 3 = ; = ; = ;.... Co to Pedagogická poznámka: Nechávám studenty,
( ) 2.5.7 Neúplné kvadratické rovnice. Předpoklady: 020501
 ..7 Neúplné kvadratické rovnice Předpoklady: Pedagogická poznámka: Tato hodina patří mezi vzácné výjimky, kdy naprostá většina studentů skončí více než pět minut před zvoněním. Nechávám je dělat něco jiného
..7 Neúplné kvadratické rovnice Předpoklady: Pedagogická poznámka: Tato hodina patří mezi vzácné výjimky, kdy naprostá většina studentů skončí více než pět minut před zvoněním. Nechávám je dělat něco jiného
1.1.1 Kvadratické rovnice (dosazení do vzorce) I
 .. Kvadratické rovnice (dosazení do vzorce) I Předpoklady: základní početní operace Rovnicí se nazývá vztah rovnosti mezi dvěma výrazy obsahujícími jednu nebo více neznámých. V této kapitole se budeme
.. Kvadratické rovnice (dosazení do vzorce) I Předpoklady: základní početní operace Rovnicí se nazývá vztah rovnosti mezi dvěma výrazy obsahujícími jednu nebo více neznámých. V této kapitole se budeme
M - Příprava na 2. zápočtový test pro třídu 2D
 M - Příprava na 2. zápočtový test pro třídu 2D Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento
M - Příprava na 2. zápočtový test pro třídu 2D Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento
KVADRATICKÉ ROVNICE A NEROVNICE (včetně řešení v C)
 Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol KVADRATICKÉ
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol KVADRATICKÉ
Soustavy lineárních rovnic
 1 Soustavy lineárních rovnic Příklad: Uvažujme jednoduchý příklad soustavy dvou lineárních rovnic o dvou neznámých x, y: x + 2y = 5 4x + y = 6 Ze střední školy známe několik metod, jak takové soustavy
1 Soustavy lineárních rovnic Příklad: Uvažujme jednoduchý příklad soustavy dvou lineárních rovnic o dvou neznámých x, y: x + 2y = 5 4x + y = 6 Ze střední školy známe několik metod, jak takové soustavy
4. R O V N I C E A N E R O V N I C E
 4. R O V N I C E A N E R O V N I C E 4.1 F U N K C E A J E J Í G R A F Funkce (definice, značení) Způsoby zadání funkce (tabulka, funkční předpis, slovní popis, graf) Definiční obor funkce (definice, značení)
4. R O V N I C E A N E R O V N I C E 4.1 F U N K C E A J E J Í G R A F Funkce (definice, značení) Způsoby zadání funkce (tabulka, funkční předpis, slovní popis, graf) Definiční obor funkce (definice, značení)
Matematika 9. ročník
 Matematika 9. ročník Náhradník NáhradníkJ evátá třída (Testovací klíč: PFFNINW) Počet správně zodpovězených otázek Počet nesprávně zodpovězených otázek 0 26 Počítání s čísly / Geometrie / Slovní úlohy
Matematika 9. ročník Náhradník NáhradníkJ evátá třída (Testovací klíč: PFFNINW) Počet správně zodpovězených otázek Počet nesprávně zodpovězených otázek 0 26 Počítání s čísly / Geometrie / Slovní úlohy
65. ročník matematické olympiády Řešení úloh klauzurní části školního kola kategorie B
 65. ročník matematické olympiády Řešení úloh klauzurní části školního kola kategorie B 1. Nejprve zjistíme, jak lze zapsat číslo 14 jako součet čtyř z daných čísel. Protože 4 + 3 3 < 14 < 4 4, musí takový
65. ročník matematické olympiády Řešení úloh klauzurní části školního kola kategorie B 1. Nejprve zjistíme, jak lze zapsat číslo 14 jako součet čtyř z daných čísel. Protože 4 + 3 3 < 14 < 4 4, musí takový
KVADRATICKÉ ROVNICE A NEROVNICE (početní a grafická řešení)
 KVADRATICKÉ ROVNICE A NEROVNICE (početní a grafická řešení) KVADRATICKÉ ROVNICE (početně) Teorie: Kvadratická rovnice o jedné neznámé se nazývá každá taková rovnice, kterou lze ekvivalentními úpravami
KVADRATICKÉ ROVNICE A NEROVNICE (početní a grafická řešení) KVADRATICKÉ ROVNICE (početně) Teorie: Kvadratická rovnice o jedné neznámé se nazývá každá taková rovnice, kterou lze ekvivalentními úpravami
UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE
 MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin
= musíme dát pozor na: jmenovatel 2a, zda je a = 0 výraz pod odmocninou, zda je > 0, < 0, = 0 (pak je jediný kořen)
 .8.7 Kvadratické rovnice s parametrem Předpoklady: 507, 803 Pedagogická poznámka: Na první pohled asi každého zarazí, že takřka celá hodina je psána jako příklady a studenti by ji měli vypracovat samostatně.
.8.7 Kvadratické rovnice s parametrem Předpoklady: 507, 803 Pedagogická poznámka: Na první pohled asi každého zarazí, že takřka celá hodina je psána jako příklady a studenti by ji měli vypracovat samostatně.
10. Polynomy a racionálně lomenné funkce
 10 Polynomy a racionálně lomenné funkce A Polynomy Definice 101 Reálný polynom stupně n (neboli mnohočlen) je funkce tvaru p(x) = a n x n + a n 1 x n 1 + + a 0, kde a 1,, a n R, a n 0, která každému komplexnímu
10 Polynomy a racionálně lomenné funkce A Polynomy Definice 101 Reálný polynom stupně n (neboli mnohočlen) je funkce tvaru p(x) = a n x n + a n 1 x n 1 + + a 0, kde a 1,, a n R, a n 0, která každému komplexnímu
Matematika - Tercie Matematika tercie Výchovné a vzdělávací strategie Učivo ŠVP výstupy
 - Tercie Matematika Výchovné a vzdělávací strategie Kompetence k řešení problémů Kompetence komunikativní Kompetence sociální a personální Kompetence občanská Kompetence k učení Kompetence pracovní Učivo
- Tercie Matematika Výchovné a vzdělávací strategie Kompetence k řešení problémů Kompetence komunikativní Kompetence sociální a personální Kompetence občanská Kompetence k učení Kompetence pracovní Učivo
{ } 9.1.9 Kombinace II. Předpoklady: 9108. =. Vypiš všechny dvoučlenné kombinace sestavené z těchto pěti prvků. Urči počet kombinací pomocí vzorce.
 9.1.9 Kombinace II Předpoklady: 9108 Př. 1: Je dána pěti prvková množina: M { a; b; c; d; e} =. Vypiš všechny dvoučlenné kombinace sestavené z těchto pěti prvků. Urči počet kombinací pomocí vzorce. Vypisujeme
9.1.9 Kombinace II Předpoklady: 9108 Př. 1: Je dána pěti prvková množina: M { a; b; c; d; e} =. Vypiš všechny dvoučlenné kombinace sestavené z těchto pěti prvků. Urči počet kombinací pomocí vzorce. Vypisujeme
EXPONENCIÁLNÍ A LOGARITMICKÁ FUNKCE
 Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol EXPONENCIÁLNÍ
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol EXPONENCIÁLNÍ
4.6.6 Složený sériový RLC obvod střídavého proudu
 4.6.6 Složený sériový LC obvod střídavého proudu Předpoklady: 41, 4605 Minulá hodina: odpor i induktance omezují proud ve střídavém obvodu, nemůžeme je však sčítat normálně, ale musíme použít Pythagorovu
4.6.6 Složený sériový LC obvod střídavého proudu Předpoklady: 41, 4605 Minulá hodina: odpor i induktance omezují proud ve střídavém obvodu, nemůžeme je však sčítat normálně, ale musíme použít Pythagorovu
Obsah. x y = 1 + x 2... 3 y = 3x + 1... 49. y = 2(x2 x + 1) (x 1) 2 101. x 3. y = x2 + 1 x 2 1... 191. y =... 149
 Průběh funkce Robert Mařík 26. září 28 Obsah y = 1 2............................. y = 1............................. 49 y = 2(2 1).......................... ( 1) 2 11 y =............................. 149
Průběh funkce Robert Mařík 26. září 28 Obsah y = 1 2............................. y = 1............................. 49 y = 2(2 1).......................... ( 1) 2 11 y =............................. 149
M - Příprava na 3. čtvrtletku třídy 1P, 1VK
 M - Příprava na 3. čtvrtletku třídy P, VK Souhrnný studijní materiál určený k přípravě na 3. čtvrtletní písemnou práci. Obsahuje učivo ledna až března. VARIACE Tento dokument byl kompletně vytvořen, sestaven
M - Příprava na 3. čtvrtletku třídy P, VK Souhrnný studijní materiál určený k přípravě na 3. čtvrtletní písemnou práci. Obsahuje učivo ledna až března. VARIACE Tento dokument byl kompletně vytvořen, sestaven
M - Matematika - třída 2ODK celý ročník
 M - Matematika - třída ODK celý ročník Obsahuje učivo celého školního roku 006/007. VARIACE Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu
M - Matematika - třída ODK celý ročník Obsahuje učivo celého školního roku 006/007. VARIACE Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu
Svobodná chebská škola, základní škola a gymnázium s.r.o. pochopení pojmů a výpočtů objemů a obvodů
 METODICKÝ LIST DA46 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný obsah: Obvod a obsah I. - obrazce Astaloš Dušan Matematika šestý frontální, fixační,
METODICKÝ LIST DA46 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný obsah: Obvod a obsah I. - obrazce Astaloš Dušan Matematika šestý frontální, fixační,
Důkazové metody. Teoretická informatika Tomáš Foltýnek
 Důkazové metody Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Matematický důkaz Jsou dány axiomy a věta (tvrzení, teorém), o níž chceme ukázat, zda platí. Matematický důkaz je nezpochybnitelné
Důkazové metody Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Matematický důkaz Jsou dány axiomy a věta (tvrzení, teorém), o níž chceme ukázat, zda platí. Matematický důkaz je nezpochybnitelné
KOMPLEXNÍ ČÍSLA INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky
 KOMPLEXNÍ ČÍSLA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu INVESTICE
KOMPLEXNÍ ČÍSLA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu INVESTICE
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita IV. Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma IV.. Kvadratické funkce, rovnice a nerovnice
Zvyšování kvality výuky technických oborů Klíčová aktivita IV. Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma IV.. Kvadratické funkce, rovnice a nerovnice
( ) 2.4.4 Kreslení grafů funkcí metodou dělení definičního oboru I. Předpoklady: 2401, 2208
 .. Kreslení grafů funkcí metodou dělení definičního oboru I Předpoklady: 01, 08 Opakování: Pokud jsme při řešení nerovnic potřebovali vynásobit nerovnici výrazem, nemohli jsme postupovat pro všechna čísla
.. Kreslení grafů funkcí metodou dělení definičního oboru I Předpoklady: 01, 08 Opakování: Pokud jsme při řešení nerovnic potřebovali vynásobit nerovnici výrazem, nemohli jsme postupovat pro všechna čísla
Základy matematiky kombinované studium 714 0365/06
 Základy matematiky kombinované studium 714 0365/06 1. Některé základní pojmy: číselné množiny, intervaly, operace s intervaly (sjednocení, průnik), kvantifikátory, absolutní hodnota čísla, vzorce: 2. Algebraické
Základy matematiky kombinované studium 714 0365/06 1. Některé základní pojmy: číselné množiny, intervaly, operace s intervaly (sjednocení, průnik), kvantifikátory, absolutní hodnota čísla, vzorce: 2. Algebraické
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita IV. Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma IV.. Kvadratické funkce, rovnice a nerovnice
Zvyšování kvality výuky technických oborů Klíčová aktivita IV. Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma IV.. Kvadratické funkce, rovnice a nerovnice
M - Příprava na 11. zápočtový test
 M - Příprava na 11. zápočtový test Určeno pro studenty dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu naleznete
M - Příprava na 11. zápočtový test Určeno pro studenty dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu naleznete
IRACIONÁLNÍ ROVNICE. x /() 2 (umocnění obou stran rovnice na druhou) 2x 4 9 /(-4) (ekvivalentní úpravy) Motivace: Teorie: Řešené úlohy:
 IRACIONÁNÍ ROVNICE Motivace: V řadě matematických úloh je nutno ovládat práci s odmocninami a rovnicemi, které obsahují neznámou pod odmocninou, mj. při vyjádření neznámé z technických vzorců. Znalosti
IRACIONÁNÍ ROVNICE Motivace: V řadě matematických úloh je nutno ovládat práci s odmocninami a rovnicemi, které obsahují neznámou pod odmocninou, mj. při vyjádření neznámé z technických vzorců. Znalosti
Předpokládané znalosti ze středoškolské matematiky. Pokuste se rozhodnout o pravdivosti následujících výroků a formulujte jejich negace.
 Předpokládané znalosti ze středoškolské matematiky 1. Matematická logika Výroky, složené výroky: konjunkce (, a zároveň ), disjukce (, nebo), negace výroků ( před nebo čárka nad označením výroku), implikace
Předpokládané znalosti ze středoškolské matematiky 1. Matematická logika Výroky, složené výroky: konjunkce (, a zároveň ), disjukce (, nebo), negace výroků ( před nebo čárka nad označením výroku), implikace
UNIVERZITA KARLOVA V PRAZE
 UNIVERZITA KARLOVA V PRAZE Pedagogická fakulta Katedra matematiky a didaktiky matematiky Vztahy mezi prvky trojúhelníku Relations among elements of a triangle Autor: Lucie Machovcová Vedoucí práce: RNDr.
UNIVERZITA KARLOVA V PRAZE Pedagogická fakulta Katedra matematiky a didaktiky matematiky Vztahy mezi prvky trojúhelníku Relations among elements of a triangle Autor: Lucie Machovcová Vedoucí práce: RNDr.
Funkce více proměnných
 Funkce více proměnných Funkce více proměnných Euklidův prostor Body, souřadnice, vzdálenost bodů Množina bodů, které mají od bodu A stejnou vzdálenost Uzavřený interval, otevřený interval Okolí bodu
Funkce více proměnných Funkce více proměnných Euklidův prostor Body, souřadnice, vzdálenost bodů Množina bodů, které mají od bodu A stejnou vzdálenost Uzavřený interval, otevřený interval Okolí bodu
Jak pracovat s absolutními hodnotami
 Jak pracovat s absolutními hodnotami Petr Matyáš 1 Co to je absolutní hodnota Absolutní hodnota čísla a, dále ji budeme označovat výrazem a, je jeho vzdálenost od nuly na ose x, tedy je to vždy číslo kladné.
Jak pracovat s absolutními hodnotami Petr Matyáš 1 Co to je absolutní hodnota Absolutní hodnota čísla a, dále ji budeme označovat výrazem a, je jeho vzdálenost od nuly na ose x, tedy je to vždy číslo kladné.
Digitální učební materiál
 Digitální učební materiál Projekt Šablona CZ.1.07/1.5.00/34.0415 Inovujeme, inovujeme III/2 Inovace a zkvalitnění výuky prostřednictvím ICT (DUM) DUM č. VY_32_INOVACE_CH29_1_16 ŠVP Podnikání RVP 64-41-L/51
Digitální učební materiál Projekt Šablona CZ.1.07/1.5.00/34.0415 Inovujeme, inovujeme III/2 Inovace a zkvalitnění výuky prostřednictvím ICT (DUM) DUM č. VY_32_INOVACE_CH29_1_16 ŠVP Podnikání RVP 64-41-L/51
1.3.1 Kruhový pohyb. Předpoklady: 1105
 .. Kruhový pohyb Předpoklady: 05 Předměty kolem nás se pohybují různými způsoby. Nejde pouze o přímočaré nebo křivočaré posuvné pohyby. Velmi často se předměty otáčí (a některé se přitom pohybují zároveň
.. Kruhový pohyb Předpoklady: 05 Předměty kolem nás se pohybují různými způsoby. Nejde pouze o přímočaré nebo křivočaré posuvné pohyby. Velmi často se předměty otáčí (a některé se přitom pohybují zároveň
Orientovaná úseka. Vektory. Souadnice vektor
 Vektory, operace s vektory Ž3 Orientovaná úseka Mjme dvojici bod A, B (na pímce, v rovin nebo prostoru), které spojíme a vznikne tak úseka. Pokud budeme rozlišovat, zda je spojíme od A k B nebo od B k
Vektory, operace s vektory Ž3 Orientovaná úseka Mjme dvojici bod A, B (na pímce, v rovin nebo prostoru), které spojíme a vznikne tak úseka. Pokud budeme rozlišovat, zda je spojíme od A k B nebo od B k
4 Algebraické rovnice a nerovnice
 Algebraické rovnice a nerovnice Matematika je stenografie abstraktního myšlení. Je-li používána správně, nenechává prostor žádné neurčitosti ani nepřesné interpretaci. (Louis de Broglie). Základní pojmy
Algebraické rovnice a nerovnice Matematika je stenografie abstraktního myšlení. Je-li používána správně, nenechává prostor žádné neurčitosti ani nepřesné interpretaci. (Louis de Broglie). Základní pojmy
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita IV. Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma IV.. Kvadratické funkce, rovnice a nerovnice
Zvyšování kvality výuky technických oborů Klíčová aktivita IV. Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma IV.. Kvadratické funkce, rovnice a nerovnice
2.8.10 Rovnice s neznámou pod odmocninou a parametrem
 .8.10 Rovnie s neznámou pod odmoninou a parametrem Předpoklady: 806, 808 Budeme postupovat stejně jako v předhozíh hodináh. Nejdříve si zopakujeme obený postup při řešení rovni s neznámou pod odmoninou
.8.10 Rovnie s neznámou pod odmoninou a parametrem Předpoklady: 806, 808 Budeme postupovat stejně jako v předhozíh hodináh. Nejdříve si zopakujeme obený postup při řešení rovni s neznámou pod odmoninou
Mária Sadloňová. Fajn MATIKA. 150 řešených příkladů (vzorek)
 Mária adloňová Fajn MATIKA (nejen) na přijímačky 50 řešených příkladů (vorek) 0 Mgr. Mária adloňová FajnMATIKA (nejen) na přijímačky 50 řešených příkladů (reklamní vorek) Mgr. Mária adloňová, 0 Vydavatel
Mária adloňová Fajn MATIKA (nejen) na přijímačky 50 řešených příkladů (vorek) 0 Mgr. Mária adloňová FajnMATIKA (nejen) na přijímačky 50 řešených příkladů (reklamní vorek) Mgr. Mária adloňová, 0 Vydavatel
Přehled učiva matematiky 7. ročník ZŠ
 Přehled učiva matematiky 7. ročník ZŠ I. ARITMETIKA 1. Zlomky a racionální čísla Jestliže rozdělíme něco (= celek) na několik stejných dílů, nazývá se každá část celku zlomkem. Zlomek tři čtvrtiny = tři
Přehled učiva matematiky 7. ročník ZŠ I. ARITMETIKA 1. Zlomky a racionální čísla Jestliže rozdělíme něco (= celek) na několik stejných dílů, nazývá se každá část celku zlomkem. Zlomek tři čtvrtiny = tři
Řešení: ( x = (1 + 2t, 2 5t, 2 + 3t, t); X = [1, 2, 2, 0] + t(2, 5, 3, 1), přímka v E 4 ; (1, 2, 2, 0), 0, 9 )
![Řešení: ( x = (1 + 2t, 2 5t, 2 + 3t, t); X = [1, 2, 2, 0] + t(2, 5, 3, 1), přímka v E 4 ; (1, 2, 2, 0), 0, 9 ) Řešení: ( x = (1 + 2t, 2 5t, 2 + 3t, t); X = [1, 2, 2, 0] + t(2, 5, 3, 1), přímka v E 4 ; (1, 2, 2, 0), 0, 9 )](/thumbs/39/20455694.jpg) . Vyjádřete koeficienty vektoru (, 8, 9) vzhledem k následující bázi vektorového prostoru V : (,, 5), (,, ), (5,, ). [,, ].. Určete všechny hodnoty parametru u, pro které vektor a patří do vektorového
. Vyjádřete koeficienty vektoru (, 8, 9) vzhledem k následující bázi vektorového prostoru V : (,, 5), (,, ), (5,, ). [,, ].. Určete všechny hodnoty parametru u, pro které vektor a patří do vektorového
Lokální a globální extrémy funkcí jedné reálné proměnné
 Lokální etrémy Globální etrémy Použití Lokální a globální etrémy funkcí jedné reálné proměnné Nezbytnou teorii naleznete Breviáři vyšší matematiky (odstavec 1.). Postup při hledání lokálních etrémů: Lokální
Lokální etrémy Globální etrémy Použití Lokální a globální etrémy funkcí jedné reálné proměnné Nezbytnou teorii naleznete Breviáři vyšší matematiky (odstavec 1.). Postup při hledání lokálních etrémů: Lokální
PLANIMETRIE, KONSTRUKČNÍ ÚLOHY V ROVINĚ
 PLANIMETRIE, KONSTRUKČNÍ ÚLOHY V ROVINĚ Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky
PLANIMETRIE, KONSTRUKČNÍ ÚLOHY V ROVINĚ Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky
(a) = (a) = 0. x (a) > 0 a 2 ( pak funkce má v bodě a ostré lokální maximum, resp. ostré lokální minimum. Pokud je. x 2 (a) 2 y (a) f.
 I. Funkce dvou a více reálných proměnných 5. Lokální extrémy. Budeme uvažovat funkci f = f(x 1, x 2,..., x n ), která je definovaná v otevřené množině G R n. Řekneme, že funkce f = f(x 1, x 2,..., x n
I. Funkce dvou a více reálných proměnných 5. Lokální extrémy. Budeme uvažovat funkci f = f(x 1, x 2,..., x n ), která je definovaná v otevřené množině G R n. Řekneme, že funkce f = f(x 1, x 2,..., x n
Učební dokument FUNKCE. Vyšetřování průběhu funkce. Mgr. Petra MIHULOVÁ. 4.roč.
 Učební dokument FUNKCE Vyšetřování průběhu funkce Mgr. Petra MIHULOVÁ.roč. Evropský sociální fond Praha a EU Investujeme do vaší budoucnosti Vyš etř ová ní přů be hů fůnkce á šeštřojení její ho gřáfů Určování
Učební dokument FUNKCE Vyšetřování průběhu funkce Mgr. Petra MIHULOVÁ.roč. Evropský sociální fond Praha a EU Investujeme do vaší budoucnosti Vyš etř ová ní přů be hů fůnkce á šeštřojení její ho gřáfů Určování
Věty o pravoúhlém trojúhelníku. Vztahy pro výpočet obvodu a obsahu. Eukleidova věta o výšce. Druhá mocnina výšky k přeponě je rovna součinu
 Věty o pravoúhlém trojúhelníku Eukleidova věta o výšce. Druhá mocnina výšky k přeponě je rovna součinu b v a obou úseků přepony: v 2 = c a c b c b c a Eukleidova věta o odvěsně A c B Druhá mocnina délky
Věty o pravoúhlém trojúhelníku Eukleidova věta o výšce. Druhá mocnina výšky k přeponě je rovna součinu b v a obou úseků přepony: v 2 = c a c b c b c a Eukleidova věta o odvěsně A c B Druhá mocnina délky
METODICKÉ LISTY Z MATEMATIKY pro gymnázia a základní vzdělávání
 METODICKÉ LISTY Z MATEMATIKY pro gymnázia a základní vzdělávání Jaroslav Švrček a kolektiv Rámcový vzdělávací program pro gymnázia Vzdělávací oblast: Matematika a její aplikace Tematický okruh: Číslo a
METODICKÉ LISTY Z MATEMATIKY pro gymnázia a základní vzdělávání Jaroslav Švrček a kolektiv Rámcový vzdělávací program pro gymnázia Vzdělávací oblast: Matematika a její aplikace Tematický okruh: Číslo a
INŽENÝRSKÁ MATEMATIKA LOKÁLNÍ EXTRÉMY
 INŽENÝRSKÁ MATEMATIKA LOKÁLNÍ EXTRÉMY FUNKCÍ DVOU PROMĚNNÝCH Robert Mařík 2. října 2009 Obsah z = x 4 +y 4 4xy + 30..................... 3 z = x 2 y 2 x 2 y 2........................ 18 z = y ln(x 2 +y)..........................
INŽENÝRSKÁ MATEMATIKA LOKÁLNÍ EXTRÉMY FUNKCÍ DVOU PROMĚNNÝCH Robert Mařík 2. října 2009 Obsah z = x 4 +y 4 4xy + 30..................... 3 z = x 2 y 2 x 2 y 2........................ 18 z = y ln(x 2 +y)..........................
Vzdělávací oblast: Matematika a její aplikace. Obor vzdělávací oblasti: Seminář z matematiky. Ročník: 7. Poznámky
 Vzdělávací oblast: Matematika a její aplikace Obor vzdělávací oblasti: Seminář z matematiky Ročník: 7. Výstupy - kompetence Učivo Průřezová témata,přesahy, a další poznámky - převádí jednotky délky, času,
Vzdělávací oblast: Matematika a její aplikace Obor vzdělávací oblasti: Seminář z matematiky Ročník: 7. Výstupy - kompetence Učivo Průřezová témata,přesahy, a další poznámky - převádí jednotky délky, času,
Kapitola 7: Integrál. 1/14
 Kapitola 7: Integrál. 1/14 Neurčitý integrál. Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f (x) x I nazýváme primitivní funkcí k
Kapitola 7: Integrál. 1/14 Neurčitý integrál. Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f (x) x I nazýváme primitivní funkcí k
2.1. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné x je taková
 .. Funkce a jejich graf.. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné je taková binární relace z množin R do množin R, že pro každé R eistuje nejvýše jedno R, pro které [, ] f.
.. Funkce a jejich graf.. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné je taková binární relace z množin R do množin R, že pro každé R eistuje nejvýše jedno R, pro které [, ] f.
Výrazy lze též zavést v nečíselných oborech, pak konstanty označuji jeden určitý prvek a obor proměnné není množina čísel.
 Výrazy. Rovnice a nerovnice. Výraz je matematický pojem používaný ve školské matematice. Prvním druhem matematických ů jsou konstanty. Konstanty označují právě jedno číslo z množiny reálných čísel. Například
Výrazy. Rovnice a nerovnice. Výraz je matematický pojem používaný ve školské matematice. Prvním druhem matematických ů jsou konstanty. Konstanty označují právě jedno číslo z množiny reálných čísel. Například
2.7.1 Mocninné funkce s přirozeným mocnitelem
 .7. Mocninné funkce s přirozeným mocnitelem Předpoklad: 0 Pedagogická poznámka: K následujícím třem hodinám je možné přistoupit dvěma způsob. Já osobně doporučuji postupovat podle učebnice. V takovém případě
.7. Mocninné funkce s přirozeným mocnitelem Předpoklad: 0 Pedagogická poznámka: K následujícím třem hodinám je možné přistoupit dvěma způsob. Já osobně doporučuji postupovat podle učebnice. V takovém případě
Gymnázium, Praha 10, Voděradská 2 Projekt OBZORY
 Gymnázium, Praha 10, Voděradská 2 Projekt OBZORY INDIVIDUÁLNÍ VÝUKA Matematika METODIKA Soustavy rovnic Mgr. Marie Souchová květen 2011 Tato část učiva následuje po kapitole Rovnice. Je rozdělena do částí
Gymnázium, Praha 10, Voděradská 2 Projekt OBZORY INDIVIDUÁLNÍ VÝUKA Matematika METODIKA Soustavy rovnic Mgr. Marie Souchová květen 2011 Tato část učiva následuje po kapitole Rovnice. Je rozdělena do částí
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita IV. Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma IV.. Kvadratické funkce, rovnice a nerovnice
Zvyšování kvality výuky technických oborů Klíčová aktivita IV. Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma IV.. Kvadratické funkce, rovnice a nerovnice
2.1 Pokyny k otevřeným úlohám. 2.2 Pokyny k uzavřeným úlohám TESTOVÝ SEŠIT NEOTVÍREJTE, POČKEJTE NA POKYN!
 MATEMATIKA+ DIDAKTICKÝ TEST Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % Základní informace k zadání zkoušky Didaktický test obsahuje 23 úloh. Časový limit pro řešení didaktického testu
MATEMATIKA+ DIDAKTICKÝ TEST Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % Základní informace k zadání zkoušky Didaktický test obsahuje 23 úloh. Časový limit pro řešení didaktického testu
Diferenciální počet funkcí jedné proměnné
 Diferenciální počet funkcí jedné proměnné 1 Diferenciální počet funkcí jedné proměnné - Úvod Diferenciální počet funkcí jedné proměnné - úvod V přírodě se neustále dějí změny. Naší snahou je nalézt příčiny
Diferenciální počet funkcí jedné proměnné 1 Diferenciální počet funkcí jedné proměnné - Úvod Diferenciální počet funkcí jedné proměnné - úvod V přírodě se neustále dějí změny. Naší snahou je nalézt příčiny
Geometrické vektory. Martina Šimůnková. Katedra aplikované matematiky. 9. března 2008
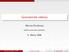 Geometrické vektory Martina Šimůnková Katedra aplikované matematiky 9. března 2008 Martina Šimůnková (KAP) Geometrické vektory 9. března 2008 1/ 27 Definice geometrického vektoru 1 Definice geometrického
Geometrické vektory Martina Šimůnková Katedra aplikované matematiky 9. března 2008 Martina Šimůnková (KAP) Geometrické vektory 9. března 2008 1/ 27 Definice geometrického vektoru 1 Definice geometrického
Číselné soustavy Ing. M. Kotlíková, Ing. A. Netrvalová Strana 1 (celkem 7) Číselné soustavy
 Číselné soustavy Ing. M. Kotlíková, Ing. A. Netrvalová Strana (celkem 7) Polyadické - zobrazené mnohočlenem desítková soustava 3 2 532 = 5 + 3 + 2 + Číselné soustavy Číslice tvořící zápis čísla jsou vlastně
Číselné soustavy Ing. M. Kotlíková, Ing. A. Netrvalová Strana (celkem 7) Polyadické - zobrazené mnohočlenem desítková soustava 3 2 532 = 5 + 3 + 2 + Číselné soustavy Číslice tvořící zápis čísla jsou vlastně
AUTORKA Barbora Sýkorová
 ČÍSLO SADY III/2 AUTORKA Barbora Sýkorová NÁZEV SADY: Číslo a proměnná číselné označení DUM NÁZEV DATUM OVĚŘENÍ DUM TŘÍDA ANOTACE PLNĚNÉ VÝSTUPY KLÍČOVÁ SLOVA FORMÁT (pdf,, ) 1 Pracovní list číselné výrazy
ČÍSLO SADY III/2 AUTORKA Barbora Sýkorová NÁZEV SADY: Číslo a proměnná číselné označení DUM NÁZEV DATUM OVĚŘENÍ DUM TŘÍDA ANOTACE PLNĚNÉ VÝSTUPY KLÍČOVÁ SLOVA FORMÁT (pdf,, ) 1 Pracovní list číselné výrazy
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.7/1../34.2 Šablona: III/2 Přírodovědné předměty
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.7/1../34.2 Šablona: III/2 Přírodovědné předměty
Pomůcka pro demonstraci momentu setrvačnosti
 Pomůcka pro demonstraci momentu setrvačnosti Cílem pomůcky je pochopit význam geometrických charakteristik pro pohybové chování těles na něž působí vnější síly. Princip pomůcky je velmi jednoduchý, jde
Pomůcka pro demonstraci momentu setrvačnosti Cílem pomůcky je pochopit význam geometrických charakteristik pro pohybové chování těles na něž působí vnější síly. Princip pomůcky je velmi jednoduchý, jde
Dualita v úlohách LP Ekonomická interpretace duální úlohy. Jiří Neubauer. Katedra ekonometrie FEM UO Brno
 Přednáška č. 6 Katedra ekonometrie FEM UO Brno Uvažujme obecnou úlohu lineárního programování, tj. úlohu nalezení takového řešení vlastních omezujících podmínek a 11 x 1 + a 1 x +... + a 1n x n = b 1 a
Přednáška č. 6 Katedra ekonometrie FEM UO Brno Uvažujme obecnou úlohu lineárního programování, tj. úlohu nalezení takového řešení vlastních omezujících podmínek a 11 x 1 + a 1 x +... + a 1n x n = b 1 a
Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y].
![Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y]. Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y].](/thumbs/91/104981778.jpg) Konzultace č. 6: Rovnice kružnice, poloha přímky a kružnice Literatura: Matematika pro gymnázia: Analytická geometrie, kap. 5.1 a 5. Sbírka úloh z matematiky pro SOŠ a studijní obory SOU. část, kap. 6.1
Konzultace č. 6: Rovnice kružnice, poloha přímky a kružnice Literatura: Matematika pro gymnázia: Analytická geometrie, kap. 5.1 a 5. Sbírka úloh z matematiky pro SOŠ a studijní obory SOU. část, kap. 6.1
Matematika ve 4. ročníku
 Matematika ve 4. ročníku září Čte a zapisuje přirozená čísla. učebnice strana 3 9 Počítá po stovkách a desítkách. chvilky strana 1 8 Čte, píše a zobrazuje čísla na číselné ose, teploměru, modelu. kalkulačka
Matematika ve 4. ročníku září Čte a zapisuje přirozená čísla. učebnice strana 3 9 Počítá po stovkách a desítkách. chvilky strana 1 8 Čte, píše a zobrazuje čísla na číselné ose, teploměru, modelu. kalkulačka
Mongeova projekce - řezy hranatých těles
 Mongeova projekce - řezy hranatých těles KG - L MENDELU KG - L (MENDELU) Mongeova projekce - řezy hranatých těles 1 / 73 Obsah 1 Zobrazení těles v základní poloze 2 Řez hranolu rovinou Osová afinita Sestrojení
Mongeova projekce - řezy hranatých těles KG - L MENDELU KG - L (MENDELU) Mongeova projekce - řezy hranatých těles 1 / 73 Obsah 1 Zobrazení těles v základní poloze 2 Řez hranolu rovinou Osová afinita Sestrojení
Edita Kolářová ÚSTAV MATEMATIKY
 Matematický seminář Edita Kolářová ÚSTAV MATEMATIKY Matematický seminář Obsah Přehled použité symboliky 4 Základní pojmy matematické logiky a teorie množin 5. Elementy matematické logiky.........................
Matematický seminář Edita Kolářová ÚSTAV MATEMATIKY Matematický seminář Obsah Přehled použité symboliky 4 Základní pojmy matematické logiky a teorie množin 5. Elementy matematické logiky.........................
Rovnice kuželoseček Petr Rys a Tomáš Zdráhal
 Rovnice kuželoseček Petr Rys a Tomáš Zdráhal ABSTRACT: The fact conic sections can be gained as an envelope of one-parametric system of lines in the plane is well known. The aim of this paper is to show
Rovnice kuželoseček Petr Rys a Tomáš Zdráhal ABSTRACT: The fact conic sections can be gained as an envelope of one-parametric system of lines in the plane is well known. The aim of this paper is to show
MONOTÓNNOST FUNKCE. Nechť je funkce f spojitá v intervalu I a nechť v každém vnitřním bodě tohoto intervalu existuje derivace f ( x)
 11.+12. přednáška S výjimkou velmi jednoduchých unkcí (lineární, parabolické) potřebujeme k vytvoření názorné představy o unkci a k načrtnutí jejího grau znát další inormace o unkci (intervaly monotónnosti,
11.+12. přednáška S výjimkou velmi jednoduchých unkcí (lineární, parabolické) potřebujeme k vytvoření názorné představy o unkci a k načrtnutí jejího grau znát další inormace o unkci (intervaly monotónnosti,
Svobodná chebská škola, základní škola a gymnázium s.r.o. Zlomky sčítání a odčítání. Dušan Astaloš. samostatná práce, případně skupinová práce
 METODICKÝ LIST DA2 Název tématu: Autor: Předmět: Zlomky sčítání a odčítání Dušan Astaloš Matematika Ročník:. Učebnice: Kapitola, oddíl: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný
METODICKÝ LIST DA2 Název tématu: Autor: Předmět: Zlomky sčítání a odčítání Dušan Astaloš Matematika Ročník:. Učebnice: Kapitola, oddíl: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný
INTEGRÁLNÍ POČET NEURČITÝ INTEGRÁL,
 INTEGRÁLNÍ POČET NEURČITÝ INTEGRÁL, URČITÝ INTEGRÁL Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve
INTEGRÁLNÍ POČET NEURČITÝ INTEGRÁL, URČITÝ INTEGRÁL Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve
9.2.5 Sčítání pravděpodobností I
 9.2.5 Sčítání pravděpodobností I Předpoklady: 9203 Pedagogická poznámka: Následující problém sice zadávám jako příklad, ale minimálně na začátku s žáky počítám na tabuli. I kvůli tomu, aby jejich úprava
9.2.5 Sčítání pravděpodobností I Předpoklady: 9203 Pedagogická poznámka: Následující problém sice zadávám jako příklad, ale minimálně na začátku s žáky počítám na tabuli. I kvůli tomu, aby jejich úprava
2.8.8 Kvadratické nerovnice s parametrem
 .8.8 Kvadratické nerovnice s arametrem Předoklady: 806 Pedagogická oznámka: Z hlediska orientace v tom, co studenti očítají, atří tato hodina určitě mezi nejtěžší během celého středoškolského studia. Proto
.8.8 Kvadratické nerovnice s arametrem Předoklady: 806 Pedagogická oznámka: Z hlediska orientace v tom, co studenti očítají, atří tato hodina určitě mezi nejtěžší během celého středoškolského studia. Proto
Vyučovací předmět Matematika Týdenní hodinová dotace 4 hodiny Ročník
 Vyučovací předmět Matematika Týdenní hodinová dotace 4 hodiny Ročník 1. Roční hodinová dotace 144 hodiny Výstupy Učivo Průřezová témata, mezipředmětové vztahy Žák provádí správně operace s množinami, množiny
Vyučovací předmět Matematika Týdenní hodinová dotace 4 hodiny Ročník 1. Roční hodinová dotace 144 hodiny Výstupy Učivo Průřezová témata, mezipředmětové vztahy Žák provádí správně operace s množinami, množiny
Výstupy - kompetence Téma - Učivo Průřezová témata,přesahy - čte, zapisuje a porovnává přirozená čísla. - přirozená čísla
 Vzdělávací oblast: Matematika a její aplikace Obor vzdělávací oblasti: Matematika Ročník: 6 Výstupy - kompetence Téma - Učivo Průřezová témata,přesahy - čte, zapisuje a porovnává přirozená čísla Opakování
Vzdělávací oblast: Matematika a její aplikace Obor vzdělávací oblasti: Matematika Ročník: 6 Výstupy - kompetence Téma - Učivo Průřezová témata,přesahy - čte, zapisuje a porovnává přirozená čísla Opakování
Zákonitosti, vztahy a práce s daty
 20mate matematika Jednotlivé kapitoly mají rozsah čtyř stran a každá kapitola je obohacena o rozšiřující učivo. sčítání a odčítání Zákonitosti, vztahy a práce s daty 1 Vyřeš úlohy. a) Součet všech čísel
20mate matematika Jednotlivé kapitoly mají rozsah čtyř stran a každá kapitola je obohacena o rozšiřující učivo. sčítání a odčítání Zákonitosti, vztahy a práce s daty 1 Vyřeš úlohy. a) Součet všech čísel
Řešení 3. série. typ čtverce o kolik se zvýší počet 1 x 1 2k + 1 2 x 2 2k 1 3 x 3 2k 3. . k x k 3 (k + 1) x (k + 1) 1
 Řešení 3 série Řešení S-I-3-1 Než se pustíme o řešení úlohy s n x n čtvercovými poli, zkusme ohalit princip na šachovnici s konkrétním počtem polí Na šachovnici 1 x 1 je pouze 1 čtverec Na šachovnici 2
Řešení 3 série Řešení S-I-3-1 Než se pustíme o řešení úlohy s n x n čtvercovými poli, zkusme ohalit princip na šachovnici s konkrétním počtem polí Na šachovnici 1 x 1 je pouze 1 čtverec Na šachovnici 2
Př. 3: Dláždíme čtverec 12 x 12. a) dlaždice 2 x 3 12 je dělitelné 2 i 3 čtverec 12 x 12 můžeme vydláždit dlaždicemi 2 x 3.
 1..20 Dláždění III Předpoklady: 01019 Př. 1: Najdi n ( 84,96), ( 84,96) D. 84 = 4 21 = 2 2 7 96 = 2 = 4 8 = 2 2 2 2 2 D 84,96 = 2 2 = 12 (společné části rozkladů) ( ) n ( 84,96) = 2 2 2 2 2 7 = 672 (nejmenší
1..20 Dláždění III Předpoklady: 01019 Př. 1: Najdi n ( 84,96), ( 84,96) D. 84 = 4 21 = 2 2 7 96 = 2 = 4 8 = 2 2 2 2 2 D 84,96 = 2 2 = 12 (společné části rozkladů) ( ) n ( 84,96) = 2 2 2 2 2 7 = 672 (nejmenší
derivace až do řádu n včetně. Potom existuje právě jeden polynom nejvýše n-tého stupně, který je aproximací funkce f v bodě x
 11+12 přednáška Některé aplikace derivací 1Věta o aproximaci unkce Nechť je libovolná unkce,která má v nějakém okolí bodu x derivace až do řádu n včetně Potom existuje právě jeden polynom nejvýše n-tého
11+12 přednáška Některé aplikace derivací 1Věta o aproximaci unkce Nechť je libovolná unkce,která má v nějakém okolí bodu x derivace až do řádu n včetně Potom existuje právě jeden polynom nejvýše n-tého
Profilová část maturitní zkoušky 2015/2016
 Střední průmyslová škola, Přerov, Havlíčkova 2 751 52 Přerov Profilová část maturitní zkoušky 2015/2016 TEMATICKÉ OKRUHY A HODNOTÍCÍ KRITÉRIA Studijní obor: 78-42-M/01 Technické lyceum Předmět: MATEMATIKA
Střední průmyslová škola, Přerov, Havlíčkova 2 751 52 Přerov Profilová část maturitní zkoušky 2015/2016 TEMATICKÉ OKRUHY A HODNOTÍCÍ KRITÉRIA Studijní obor: 78-42-M/01 Technické lyceum Předmět: MATEMATIKA
(k 1)x k + 1. pro k 1 a x = 0 pro k = 1.
 . Funkce dvou a více proměnných. Úvod. Určete definiční obor funkce a proveďte klasifikaci bodů z R vzhledem k a rozhodněte zda je množina uzavřená či otevřená. Určete a načrtněte vrstevnice grafu funkce
. Funkce dvou a více proměnných. Úvod. Určete definiční obor funkce a proveďte klasifikaci bodů z R vzhledem k a rozhodněte zda je množina uzavřená či otevřená. Určete a načrtněte vrstevnice grafu funkce
