POZNÁMKA: V USA se používá ještě Fahrenheitova teplotní stupnice. Převodní vztahy jsou vzhledem k volbě základních bodů složitější: 9 5
|
|
|
- Dalibor Tábor
- před 6 lety
- Počet zobrazení:
Transkript
1 TEPLO, TEPLOTA Tepelný stav látek je charakterizován veličinou termodynamická teplota T Jednotkou je kelvin T K Mezi Celsiovou a Kelvinovou teplotní stupnicí existuje převodní vztah T 73,5C t POZNÁMKA: V USA se používá ještě Fahrenheitova teplotní stupnice Převodní vztahy jsou vzhledem k volbě základních bodů složitější: 9 5 t F t C 3, t C t F Tepelný stav látek souvisí s tepelným (termickým) pohybem částic (molekul, atomů, iontů) V pevné látce částice kmitají kolem rovnovážných poloh, V kapalině částice kmitají kolem rovnovážných poloh, zároveň se mohou posouvat, V plynu se částice pohybují chaoticky Brownovým pohybem Jestliže se teplota látky zvýší, pak se zrychlí termický pohyb částic Při zahřívání se zvětší kinetická energie částic Teplota látky se zvýší dodáním tepelné energie (tepla) Q Jednotkou tepla je joule Q J Teplo, které je nutné dodat pevné látce nebo kapalině, aby se o určitý teplotní rozdíl T, vyjádříme vztahem zahřála T T dq mc dt Q mcdt Q mct T Q mct kde m je hmotnost látky, T, T je počáteční a konečná teplota, c je měrná tepelná kapacita Při ochlazení musíme stejné množství tepla odebrat Teplo vždy přechází z tělesa teplejšího na těleso studenější
2 Teplo přechází tak dlouho, až se teploty vyrovnají (5ºC) Kromě měrné tepelné kapacity c zavádíme ještě tepelnou kapacitu K Jednotkou K JK K mc, Q k T T Platí, že Q c m T Měrná tepelná kapacita je množství tepla, které je třeba dodat kg látky, aby se zahřála o jeden stupeň teplotního rozdílu Jednotkou je Jkg - K - Poznámka: měření ukázala, že závisí na teplotě a tlaku Při praktických výpočet, když nedochází k velkým teplotním a tlakovým změnám, můžeme c považovat za konstantní Rozlišujeme měrnou tepelnou kapacitu při zahřívání za stálého tlaku kapacitu při zahřívání za stálého objemu c V c p a měrnou tepelnou Pokud vyjadřujeme množství látky v molech, definujeme molární tepelnou kapacitu Molární tepelná kapacita je množství tepla, které je třeba dodat molu látky, aby se zahřála o jeden stupeň teplotního rozdílu Jednotkou je Jmol - K - Platí, že C M c - Kde M je molární hmotnost látky, M kgmol Pro pevné a kapalné látky se měrná a molární kapacita liší jen nepatrně a můžeme je v praxi zanedbat Pro plynné látky zavádíme molární tepelnou kapacitu při stálém tlaku C p a molární tepelnou kapacitu při stálém objemu C V Poměr je roven Poissonově konstantě kapa, jejich rozdíl podle Mayerovy rovnice plynové konstantě R 8,34JK - mol - C C p V C C p V R
3 Obě molární tepelné kapacity závisí na počtu stupňů volnosti i je to počet nezávislých parametrů, které určují danou veličinu nebo systém Rychlost, a tím energii, můžeme určit nejvýše třemi složkami rychlosti translačního pohybu v, v, v a třemi složkami rychlosti rotačního pohybu,, x y Jednoatomové molekuly i 3 Dvouatomové molekuly i 5 Tří a víceatomové molekuly i 6 z x y z Pak i i C V R C p R Toto pravidlo je v dobrém kvalitativním souhlasu s experimentálními výsledky za běžných a vyšších teplot Při nízkých teplotách molární tepelná kapacita všech pevných látek rychle klesá a v okolí absolutní nuly konverguje k nule Problém je řešen pomocí kvantové fyziky Fázové přeměny Fázová přeměna je děj, při kterém dochází ke změně skupenství látky Rozlišujeme tato skupenství: pevné kapalné plynné TÁNÍ, TUHNUTÍ Tání představuje fázovou přeměnu z pevné fáze na kapalnou Dochází k ní při zahřívání Krystalické látky tají při teplotě tání T t Ke změně skupenství je třeba dodat skupenské teplo tání Q l m, kde l t je měrné skupenské teplo tání, jednotkou je Jkg - Je to množství tepla, které je nutné dodat kg pevné látky, aby se přeměnila na kapalinu téže teploty Teplota zůstává během přeměny konstantní t Tuhnutí představuje změnu kapalného tělesa na pevné těleso Je to proces opačný k tání, který nastává při ochlazování
4 Krystalické látky mají pro chemicky čisté látky teplotu tuhnutí rovnu teplotě tání za téhož vnějšího tlaku Při tuhnutí je nutné látce odebrat teplo Q l m, aby se z ní stala pevná látka Má stejnou hodnotu jako skupenské teplo tání pevného tělesa z téže látky a stejné hmotnosti Amorfní látky postupně při zahřívání měknou Konkrétní teplota tání neexistuje Amorfní látky tuhnou postupně t Většina látek při tání objem zvětšuje a při tuhnutí zmenšuje VYPAŘOVÁNÍ, VAR, KONDENZACE Vypařování je přeměna kapalné látky na látku plynnou Probíhá vždy a za jakékoliv teploty a jen z povrchu kapaliny (čím větší povrch, tím rychlejší vypařování) Různé kapaliny se vypařují za stejných podmínek různou rychlostí Skupenské teplo vypařování Q l je teplo, které musí kapalina přijmout, aby se změnila na páru téže teploty lv je měrné skupenské teplo vypařování v m Var je speciální případ vypařování Kapalina se přeměňuje nejen na svém volném povrchu (jako u vypařování), ale také uvnitř svého objemu Přijímá-li kapalina teplo, var nastává při určité teplotě, tzv teplotě varu Teplota varu závisí na vnějším tlaku (např s nadmořskou výškou klesá) DIAGRAM SKUPENSKÝCH PŘEMĚN
5 Pevná látka se nejprve zahřeje na teplotu tání, pak dojde k přeměně na kapalinu a při dalším dodávání tepla Q se zahřívá kapalina až k bodu varu Pak se začne přeměňovat na páru SUBLIMACE, DESUBLIMACE Sublimace je změna pevné látky na látku plynnou (např jód, naftalen, kafr, suchý led (CO ) Během sublimace je nutné pevné látce dodat skupenské teplo sublimace Q l m l s je měrné skupenské teplo sublimace, jednotkou je Jkg - Desublimace je změna plynné látky na látku pevnou (např jinovatka) s Kalorimetrická rovnice Při vzájemném kontaktu si tělesa vyměňují tepelnou energii Q (teplo) Teplejší těleso o teplotě T, hmotnosti m a měrné tepelné kapacitě c předá teplo tělesu chladnějšímu o teplotě T, hmotnosti m a měrné tepelné kapacitě c
6 Tato výměna trvá do té doby, než se teplota obou těles ustálí na stejné teplotě T, platí T T T Teplejší těleso odevzdá teplo Q m c T T, chladnější těleso přijme teplo Q m c T T Při vzájemné styku dvou těles platí zákon zachování tepelné energie Stejné množství tepla, které teplejší těleso odevzdá, chladnější těleso přijme: m c Q Q T m c T T T POZNÁMKA: Tato rovnice platí za předpokladu, kdy nedochází k žádným tepelným ztrátám V ostatních případech je třeba rovnici pro jednotlivé případy sestavit 3 Teplotní roztažnost látek Při zahřívání látek libovolného skupenství dojde ke zvýšení kinetické energie částic látky a zvýšení jejich termického pohybu U pevných látek a kapalin se zvýší frekvence kmitů částice kolem rovnovážné polohy a zvětší se jejich rozkmit Tím dojde ke zvětšení střední vzdálenosti částic, pevná látka a většina kapalin zvětší své rozměry DÉLKOVÁ ROZTAŽNOST PEVNÝCH LÁTEK U některých těles převládá svou velikostí jeden z rozměrů (tyče, dráty), zbývající rozměry pak můžeme zanedbat Uvažujme, že počáteční délka tyče při počáteční teplotě t je l Potom při zahřátí tyče na teplotu t se tyč prodlouží na délku l Zavedeme absolutní změnu délky tyče l l Tato absolutní změna délky je l úměrná změně teploty t, původní délce l a materiálové konstantě součiniteli teplotní délkové roztažnosti - Pak platí, že l l t
7 Pak definujeme součinitele teplotní délkové roztažnosti l l t Z toho plyne jednotka součinitele teplotní délkové roztažnosti Jednotkou je K - Po úpravě dostaneme vztah pro novou délku l l t Kromě absolutního prodloužení Je to bezrozměrné číslo l zavádíme ještě relativní prodloužení l l PLOŠNÁ ROZTAŽNOST PEVNÝCH LÁTEK Některá tělesa jsou určená dvěma rozměry (desky) Třetí rozměr zanedbáváme Pak při zahřátí o teplotní rozdíl t dojde ke zvětšení obou hlavních rozměrů Jestliže uvažujeme desku o rozměrech a, b při teplotě t, pak po zahřátí na teplotu t získají oba rozměry novou velikost a a t, b b t Plocha při teplotě t pak bude S a b a tb t a b t S t t Vzhledem k malé hodnotě součinitele teplotní délkové roztažnosti můžeme člen t zanedbat Pak S S t OBJEMOVÁ ROZTAŽNOST PEVNÝCH LÁTEK A KAPALIN U pevných těles, jejichž všechny tři rozměry jsou nezanedbatelné, je a a t, b b t, c c t Objem při teplotě t pak bude V abc a t V 3 t t t bc Členy 3 t, t můžeme pro jejich malou hodnotu zanedbat Pak V V 3 t V t, kde 3 je součinitel teplotní objemové roztažnosti Jednotkou je K - Je v poměrně širokém rozsahu teplot stálý, tj nezávislý na teplotě U kapalin, které nemají stálý tvar, lze vyjádřit změnu objemu vztahem V V t Součinitel teplotní objemové roztažnosti kapalin není konstantní Kapaliny se roztahují nerovnoměrně
8 Při změně teploty se zvětšuje objem a nemění se hmotnost, proto dochází ke změně hustoty těles Platí m V V m t t Změny hustoty s teplotou jsou celkem malé, v praxi je lze zanedbávat, avšak při přesném měření, zejména u kapalin, je nutné k nim přihlížet 4 Tepelná vodivost Vedení se uplatňuje především u pevných látek Částice v teplejších oblastech kmitají s vyšší frekvencí a větším rozkmitem Svou kinetickou energii předávají částicím chladnějším Střední poloha částic se nemění Důležitým pojmem je teplotní spád pokles teploty v tělese, pak se tepelná energie Q přenáší z míst o vyšší teplotě T do míst o nižší teplotě T Množství přeneseného tepla pak je T T T Q S, Q S d d kde d je délka tělesa (šířka stěny) ve směru šíření, S je plocha kolmá ke směru šíření, je čas, během kterého dochází k šíření tepla, je součinitel tepelné vodivosti látky s jednotkou Wm - K - Množství tepla, které projde stěnou kolmou ke směru šíření tepla za s, představuje tepelný tok (tepelný výkon) Jestliže je stěna jednotková, pak zavádíme veličinu hustota tepelného toku q Jednotky jsou Platí Js W, q Jm s
9 Q q Q S Rozlišujeme vedení dvojího typu: Ustálené (stacionární) teploty T,T jsou trvale udržovány na stejných hodnotách (např vnější a vnitřní stěna domu), Neustálené (nestacionární) teploty T,T se po určité době vyrovnají Přestup tepla Tepelná energie přestupuje z kapaliny nebo plynu (tekutiny) do pevné látky, tam je vedena a pak opět může přestoupit z pevné látky do plynu nebo kapaliny Q T t Ts S, Kde je součinitel přestupu v prvním rozhraní, jednotka je Wm - K - T t je teplota tekutiny T t je teplota tekutiny Ts je teplota stěny T s je teplota stěny Při řešení uvažujeme, že hustota tepelného toku q je konstantní q = konst Přestup do stěny Vedení stěnou 3 Přestup do tekutiny q =α (T t Ts ) T T q s d q = α (T s T t ) q T t T s d q T s Ts q T s T t Sečtením rovnic dostaneme: T t T t d q
10 Tt Tt q d Pak množství prošlé tepelné energie je: Q = q S Q = Tt Tt S d Výraz ve jmenovateli představuje tepelný odpor R Proudění tepla je výrazné u kapalných a plynných látek, kdy dochází zároveň k proudění tekutiny Se zvětšením teploty klesne její hustota a teplejší tekutina tak vlivem vztlakové síly stoupá vzhůru Sálání je přenos tepelné energie prostřednictvím elektromagnetických vln, které se mohou šířit i vakuem Takto se přenáší tepelná energie ze Slunce PŘÍKLADY Na udržení stále teploty v místnosti se za hodinu spotřebuje 4, 6 J tepla Kolik vody proteče radiátorem ústředního topení za hodinu, jestliže má voda při vstupu do radiátoru teplotu 8 ºC a při výstupu 7 ºC? Měrná tepelná kapacita vody je 4 J kg - K - [ dm 3 za hodinu] Do nádrže obsahující 35 kg oleje teploty 33 K byl při kalení ponořen ocelový předmět teploty 73 K Vypočítejte, jaká je hmotnost tohoto předmětu, jestliže se po vnoření teplota oleje ustálila na 33 K Měrná tepelná kapacita oleje je 68 J kg - K - a oceli 46 J kg - K - [m = 4,8 kg] 3 Kolik tepla je třeba na ohřátí,5 litru vody v hliníkovém hrnci hmotnosti,4 kg z 83 K na 373 K? Měrná tepelná kapacita vody je 4 J kg - K - a hliníku je,9 3 J kg - K - [Q = 5,994 5 J] 4 Máme připravit do vany 8 litrů vody o teplotě 36 ºC Studená voda v koupelně má teplotu ºC a teplá 5 ºC Kolik které vody potřebujeme? [8 l studené a 5 l teplé vody] 5 Kolik tepla musíme dodat vodě v bazénu o rozměrech 4m,,5m,,5m, aby se ohřála ze 7 C na 5 C Bazén je plný (54 J) Kolik zaplatíme za ohřátí vody v bazénu, jestliže kwh stojí,35 Kč? (89 Kč)
11 6 Jaký je výkon vařiče, který ohřeje l vody o 4 C během 5 minut? Měrná tepelná kapacita vody je 4 56 W) 7 Určete účinnost parního stroje, který dodáním J tepla vykoná práci 4 J (4 %) 8 O kolik stupňů celsia se ohřejí l vody, jestliže jí dodáme 84 J tepla? Měrná tepelná kapacita vody je 4 ( C) 9 Určete účinnost parního stroje, který dodáním J tepla vykoná práci 4 J(4 %) Jak velké teplo musíme dodat 8 g ledu o teplotě C, aby změnil skupenství a po té se ohřál na C? Měrné skupenské teplo tání ledu je 33 kj/kg, měrná tepelná kapacita vody je 4 J/kg C(976 J) Kolik tepla odevzdá 5 l vody teploty 8 C, jestliže do ní vložíme 5 g ledu teploty C a ten se přemění na vodu teploty C? Měrné skupenské teplo tání ledu je 33 kj/kg, měrná tepelná kapacita vody je 4 J/kg C (6 5 J) O kolik klesne teplota vody? Kolik tepla je nutné odebrat 5 g vody teploty C, aby se přeměnila na led teploty - C? TEPLOTNÍ ROZTAŽNOST 3 Součinitel délkové teplotní roztažnosti skla je α = 8-6 K - Tyč má při teplotě t = C délku l = m Jakou má délku při teplotě t = 4 C? [l =,3 m] 4 Skleněná deska vsazená do stěny při teplotě t = C se někdy ohřeje na teplotu t = 6 C Rozměr desky je 5 m x 3 m O kolik se zvětší plocha? Součinitel délkové teplotní roztažnosti skla je α = 8-6 K - [ΔS = 9,6-3 m ] 5 Zjistěte, jaký je moment setrvačnosti tyče vzhledem k ose jdoucí jedním jejím koncem, změní-li se teplota tyče o Δt? [J = J (+ α Δ t)] 6 Zjistěte, jaký je moment setrvačnosti koule vzhledem k ose jdoucí jedním jejím koncem, změní-li se teplota tyče o Δt? [J = J (+ α Δ t)] VEDENÍ TEPLA Jeden konec ocelové tyče délky cm a průřezu 3 cm udržujeme na konstantní teplotě 3 C, druhý konec je uložen do tajícího ledu Určete, kolik ledu rozpustí tyč za minut, je-li možno zanedbat tepelné ztráty do okolí Součinitel tepelné vodivosti oceli je 47 Wm - K -, skupenské teplo tání ledu je 33 kj/kg
12 7 Měděná tyč délky 5 cm je připojena k ocelové tyči stejného průřezu a délky 8 cm Volný konec měděné tyče udržujeme na konstantní teplotě 5 C, volný konec ocelové tyče na teplotě C Určete hustotu tepelného toku v tyčích, je-li možno zanedbat ztráty do okolí Součinitel tepelné vodivosti mědi je 389 W m - K -, součinitel tepelné vodivosti oceli je 47 W m - K -, skupenské teplo tání ledu je 33 kj/kg 8 Určete množství tepla protékajícího cihlovou stěnou plochy 5x3 m o tloušťce 3 cm při povrchových teplotách C a - C Součinitel tepelné vodivosti cihly je,7 Wm - K - Určete množství uhlí potřebného ke kompenzaci těchto ztrát (výhřevnost hnědého uhlí je přibližně 4 MJkg -, černého uhlí 5 MJkg - 4 J 9 Jakou tloušťku zdi by nahradila 5 cm vrstva polystyrénu (Součinitel tepelné vodivosti polystyrenu je,4 Wm - K -, měrná tepelná vodivost cihly je,7 Wm - K - ) 87,5 cm Měděná tyč délky 5 cm je připojena k železné tyči stejného průřezu a délky 8 cm Volný konec měděné tyče udržujeme na teplotě 5 C, volný konec tyče železné na teplotě C Vypočítejte hustotu tepelného toku v tyčích a teplotu v dotykové ploše obou tyčí Součinitel tepelné vodivosti mědi 389 Wm - K -, součinitel tepelné vodivosti železa 59 Wm - K - Předpokládáme, že tepelným ztrátám do okolí se nám podařilo zabránit a teplo je přenášeno tyčemi ve směru jejich délky ustáleným vedením 3 75 Wm ;,7 C Hustota tepelného toku při ustáleném vedení Δ t = 5 C, t = C, l =,5 cm, = 398 Wm - K - měď l =,8 cm, = 59 Wm - K - železo q =?, t s
13 Kolik tepla za hodinu musí dodávat ústřední topení do místnosti, která má vnější stěnu plochy 5 m Tloušťka cihlového zdiva je,3 m, jeho součinitel tepelné vodivosti je,8 Wm - K - V místnosti požadujeme teplotu C, venkovní teplota je C Součinitelé přestupu tepla jsou 8 Wm - K - a 3 Wm - K - (při vnějším větru je součinitel přestupu větší) 6,98 J q = konst q =α (T T p ) q = α (T p T ) Q = q S Vypočítejte teplo prošlé m za sekundu stěnou kotle o tloušťce stěny mm a součiniteli tepelné vodivosti 6 Wm - K -, je-li uvnitř stěna pokryta vrstvou kotelního kamene o tloušťce mm a součiniteli tepelné vodivosti, Wm - K - Povrchové teploty jsou 5 C a C 5 kwm
6. Jaký je výkon vařiče, který ohřeje 1 l vody o 40 C během 5 minut? Měrná tepelná kapacita vody je W)
 TEPLO 1. Na udržení stále teploty v místnosti se za hodinu spotřebuje 4,2 10 6 J tepla. olik vody proteče radiátorem ústředního topení za hodinu, jestliže má voda při vstupu do radiátoru teplotu 80 ºC
TEPLO 1. Na udržení stále teploty v místnosti se za hodinu spotřebuje 4,2 10 6 J tepla. olik vody proteče radiátorem ústředního topení za hodinu, jestliže má voda při vstupu do radiátoru teplotu 80 ºC
TEPELNÉ JEVY. Mgr. Jan Ptáčník - GJVJ - Fyzika - Tercie
 TEPELNÉ JEVY Mgr. Jan Ptáčník - GJVJ - Fyzika - Tercie Vnitřní energie tělesa Každé těleso se skládá z látek. Látky se skládají z částic. neustálý neuspořádaný pohyb kinetická energie vzájemné působení
TEPELNÉ JEVY Mgr. Jan Ptáčník - GJVJ - Fyzika - Tercie Vnitřní energie tělesa Každé těleso se skládá z látek. Látky se skládají z částic. neustálý neuspořádaný pohyb kinetická energie vzájemné působení
měření teploty Molekulová fyzika a termika Teplotní délková roztažnost V praxi úlohy
 měření teploty Molekulová fyzika a termika rozdíl mezi stupnicí celsiovskou a termodynamickou př. str. 173 (nové vydání s. 172) teplo(to)měry roztažnost látek rtuťový, lihový, bimetalový vodivost polovodičů
měření teploty Molekulová fyzika a termika rozdíl mezi stupnicí celsiovskou a termodynamickou př. str. 173 (nové vydání s. 172) teplo(to)měry roztažnost látek rtuťový, lihový, bimetalový vodivost polovodičů
VNITŘNÍ ENERGIE. Mgr. Jan Ptáčník - GJVJ - Fyzika - 2. ročník - Termika
 VNITŘNÍ ENERGIE Mgr. Jan Ptáčník - GJVJ - Fyzika - 2. ročník - Termika Zákon zachování energie Ze zákona zachování mechanické energie platí: Ek + Ep = konst. Ale: Vnitřní energie tělesa Každé těleso má
VNITŘNÍ ENERGIE Mgr. Jan Ptáčník - GJVJ - Fyzika - 2. ročník - Termika Zákon zachování energie Ze zákona zachování mechanické energie platí: Ek + Ep = konst. Ale: Vnitřní energie tělesa Každé těleso má
Molekulová fyzika a termika:
 Molekulová fyzika a termika: 1. Měření teploty: 2. Délková roztažnost a Objemová roztažnost látek 3. Bimetal 4. Anomálie vody 5. Částicová stavba látek, vlastnosti látek 6. Atomová hmotnostní konstanta
Molekulová fyzika a termika: 1. Měření teploty: 2. Délková roztažnost a Objemová roztažnost látek 3. Bimetal 4. Anomálie vody 5. Částicová stavba látek, vlastnosti látek 6. Atomová hmotnostní konstanta
MOLEKULOVÁ FYZIKA A TERMODYNAMIKA
 MOLEKULOVÁ FYZIKA A TERMODYNAMIKA 2 metody zkoumání látek na základě vnějších projevů: I. KINETICKÁ TEORIE LÁTEK -studium vlastností látek na základě vnitřní struktury, pohybu a vzájemného působení jednotlivých
MOLEKULOVÁ FYZIKA A TERMODYNAMIKA 2 metody zkoumání látek na základě vnějších projevů: I. KINETICKÁ TEORIE LÁTEK -studium vlastností látek na základě vnitřní struktury, pohybu a vzájemného působení jednotlivých
Termodynamika. T [K ]=t [ 0 C] 273,15 T [ K ]= t [ 0 C] termodynamická teplota: Stavy hmoty. jednotka: 1 K (kelvin) = 1/273,16 část termodynamické
![Termodynamika. T [K ]=t [ 0 C] 273,15 T [ K ]= t [ 0 C] termodynamická teplota: Stavy hmoty. jednotka: 1 K (kelvin) = 1/273,16 část termodynamické Termodynamika. T [K ]=t [ 0 C] 273,15 T [ K ]= t [ 0 C] termodynamická teplota: Stavy hmoty. jednotka: 1 K (kelvin) = 1/273,16 část termodynamické](/thumbs/24/2778201.jpg) Termodynamika termodynamická teplota: Stavy hmoty jednotka: 1 K (kelvin) = 1/273,16 část termodynamické teploty trojného bodu vody (273,16 K = 0,01 o C). 0 o C = 273,15 K T [K ]=t [ 0 C] 273,15 T [ K ]=
Termodynamika termodynamická teplota: Stavy hmoty jednotka: 1 K (kelvin) = 1/273,16 část termodynamické teploty trojného bodu vody (273,16 K = 0,01 o C). 0 o C = 273,15 K T [K ]=t [ 0 C] 273,15 T [ K ]=
Název DUM: Změny skupenství v příkladech
 Základní škola národního umělce Petra Bezruče, Frýdek-Místek, tř. T. G. Masaryka 454 Zpracováno v rámci OP VK - EU peníze školám Jednička ve vzdělávání CZ.1.07/1.4.00/21.2759 Název DUM: Změny skupenství
Základní škola národního umělce Petra Bezruče, Frýdek-Místek, tř. T. G. Masaryka 454 Zpracováno v rámci OP VK - EU peníze školám Jednička ve vzdělávání CZ.1.07/1.4.00/21.2759 Název DUM: Změny skupenství
Základní poznatky. Teplota Vnitřní energie soustavy Teplo
 Molekulová fyzika a termika Základní poznatky Základní poznatky Teplota Vnitřní energie soustavy Teplo Termika = část fyziky zabývající se studiem vlastností látek a jejich změn souvisejících s teplotou
Molekulová fyzika a termika Základní poznatky Základní poznatky Teplota Vnitřní energie soustavy Teplo Termika = část fyziky zabývající se studiem vlastností látek a jejich změn souvisejících s teplotou
Vnitřní energie pevné látky < Vnitřní energie kapaliny < Vnitřní energie plynu (nejmenší energie)
 Změny skupenství Při změně tělesa z pevné látky na kapalinu nebo z kapaliny na plyn se jeho vnitřní energie zvyšuje musíme dodávat teplo (zahřívat). Při změně tělesa z plynu na kapalinu, nebo z kapaliny
Změny skupenství Při změně tělesa z pevné látky na kapalinu nebo z kapaliny na plyn se jeho vnitřní energie zvyšuje musíme dodávat teplo (zahřívat). Při změně tělesa z plynu na kapalinu, nebo z kapaliny
SKUPENSKÉ PŘEMĚNY POJMY K ZOPAKOVÁNÍ. Testové úlohy varianta A
 Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Jitka Novosadová MGV_F_SS_3S3_D11_Z_OPAK_T_Skupenske_premeny_T Člověk a příroda Fyzika Skupenské přeměny Opakování
Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Jitka Novosadová MGV_F_SS_3S3_D11_Z_OPAK_T_Skupenske_premeny_T Člověk a příroda Fyzika Skupenské přeměny Opakování
Digitální učební materiál
 Evidenční číslo materiálu: 516 Digitální učební materiál Autor: Mgr. Pavel Kleibl Datum: 22. 1. 2013 Ročník: 8. Vzdělávací oblast: Člověk a příroda Vzdělávací obor: Fyzika Tematický okruh: Energie Téma:
Evidenční číslo materiálu: 516 Digitální učební materiál Autor: Mgr. Pavel Kleibl Datum: 22. 1. 2013 Ročník: 8. Vzdělávací oblast: Člověk a příroda Vzdělávací obor: Fyzika Tematický okruh: Energie Téma:
F - Změny skupenství látek
 F - Změny skupenství látek Určeno jako učební text pro studenty dálkového studia a jako shrnující text pro studenty denního studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn
F - Změny skupenství látek Určeno jako učební text pro studenty dálkového studia a jako shrnující text pro studenty denního studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn
CELKOVÉ OPAKOVÁNÍ UČIVA + ZÁPIS DO ŠKOLNÍHO SEŠITU část 03 VNITŘNÍ ENERGIE, TEPLO.
 CELKOVÉ OPAKOVÁNÍ UČIVA + ZÁPIS DO ŠKOLNÍHO SEŠITU část 03 VNITŘNÍ ENERGIE, TEPLO. 01) Složení látek opakování učiva 6. ročníku: Všechny látky jsou složeny z částic nepatrných rozměrů (tj. atomy, molekuly,
CELKOVÉ OPAKOVÁNÍ UČIVA + ZÁPIS DO ŠKOLNÍHO SEŠITU část 03 VNITŘNÍ ENERGIE, TEPLO. 01) Složení látek opakování učiva 6. ročníku: Všechny látky jsou složeny z částic nepatrných rozměrů (tj. atomy, molekuly,
Mol. fyz. a termodynamika
 Molekulová fyzika pracuje na základě kinetické teorie látek a statistiky Termodynamika zkoumání tepelných jevů a strojů nezajímají nás jednotlivé částice Molekulová fyzika základem jsou: Látka kteréhokoli
Molekulová fyzika pracuje na základě kinetické teorie látek a statistiky Termodynamika zkoumání tepelných jevů a strojů nezajímají nás jednotlivé částice Molekulová fyzika základem jsou: Látka kteréhokoli
Teplota jedna ze základních jednotek soustavy SI, vyjadřována je v Kelvinech (značka K) další používané stupnice: Celsiova, Fahrenheitova
 1 Rozložení, distribuce tepla Teplota je charakteristika tepelného stavu hmoty je to stavová veličina, charakterizující termodynamickou rovnováhu systému. Teplo vyjadřuje kinetickou energii částic. Teplota
1 Rozložení, distribuce tepla Teplota je charakteristika tepelného stavu hmoty je to stavová veličina, charakterizující termodynamickou rovnováhu systému. Teplo vyjadřuje kinetickou energii částic. Teplota
Vnitřní energie, práce a teplo
 Vnitřní energie, práce a teplo Zákon zachování mechanické energie V izolované soustavě těles je v každém okamžiku úhrnná mechanická energie stálá. Mění se navzájem jen potenciální energie E p a kinetická
Vnitřní energie, práce a teplo Zákon zachování mechanické energie V izolované soustavě těles je v každém okamžiku úhrnná mechanická energie stálá. Mění se navzájem jen potenciální energie E p a kinetická
23_ 2 24_ 2 25_ 2 26_ 4 27_ 5 28_ 5 29_ 5 30_ 7 31_
 Obsah 23_ Změny skupenství... 2 24_ Tání... 2 25_ Skupenské teplo tání... 2 26_ Anomálie vody... 4 27_ Vypařování... 5 28_ Var... 5 29_ Kapalnění... 5 30_ Jak určíš skupenství látky?... 7 31_ Tepelné motory:...
Obsah 23_ Změny skupenství... 2 24_ Tání... 2 25_ Skupenské teplo tání... 2 26_ Anomálie vody... 4 27_ Vypařování... 5 28_ Var... 5 29_ Kapalnění... 5 30_ Jak určíš skupenství látky?... 7 31_ Tepelné motory:...
V izolované soustavě nedochází k výměně tepla s okolím. Dokonalá izolovaná soustava neexistuje, nejvíce se jí blíží kalorimetr nebo termoska.
 Teplo a vnitřní energie pracovní list Vnitřní energie Všechny tělesa se skládají z částic, které vykonávají neustálý a neuspořádaný pohyb a které na sebe navzájem silově působí. Částice uvnitř všech těles
Teplo a vnitřní energie pracovní list Vnitřní energie Všechny tělesa se skládají z částic, které vykonávají neustálý a neuspořádaný pohyb a které na sebe navzájem silově působí. Částice uvnitř všech těles
F8 - Změny skupenství Číslo variace: 1
 F8 - Změny skupenství Číslo variace: 1 1. K vypařování kapaliny dochází: při každé teplotě v celém jejím objemu pouze při teplotě 100 C v celém objemu kapaliny pouze při normální teplotě a normálním tlaku
F8 - Změny skupenství Číslo variace: 1 1. K vypařování kapaliny dochází: při každé teplotě v celém jejím objemu pouze při teplotě 100 C v celém objemu kapaliny pouze při normální teplotě a normálním tlaku
SKUPENSTVÍ LÁTEK Prima - Fyzika
 SKUPENSTVÍ LÁTEK Prima - Fyzika Skupenství látek Pevné skupenství Skupenství látek Skupenství látek Pevné skupenství Kapalné skupenství Skupenství látek Pevné skupenství Kapalné skupenství Plynné skupenství
SKUPENSTVÍ LÁTEK Prima - Fyzika Skupenství látek Pevné skupenství Skupenství látek Skupenství látek Pevné skupenství Kapalné skupenství Skupenství látek Pevné skupenství Kapalné skupenství Plynné skupenství
Základem molekulové fyziky je kinetická teorie látek. Vychází ze tří pouček:
 Molekulová fyzika zkoumá vlastnosti látek na základě jejich vnitřní struktury, pohybu a vzájemného působení částic, ze kterých se látky skládají. Termodynamika se zabývá zákony přeměny různých forem energie
Molekulová fyzika zkoumá vlastnosti látek na základě jejich vnitřní struktury, pohybu a vzájemného působení částic, ze kterých se látky skládají. Termodynamika se zabývá zákony přeměny různých forem energie
Termodynamika 2. UJOP Hostivař 2014
 Termodynamika 2 UJOP Hostivař 2014 Skupenské teplo tání/tuhnutí je (celkové) teplo, které přijme pevná látka při přechodu na kapalinu během tání nebo naopak Značka Veličina Lt J Nedochází při něm ke změně
Termodynamika 2 UJOP Hostivař 2014 Skupenské teplo tání/tuhnutí je (celkové) teplo, které přijme pevná látka při přechodu na kapalinu během tání nebo naopak Značka Veličina Lt J Nedochází při něm ke změně
V izolované soustavě nedochází k výměně tepla s okolím. Dokonalá izolovaná soustava neexistuje, nejvíce se jí blíží kalorimetr nebo termoska.
 Teplo a vnitřní energie pracovní list Vnitřní energie Všechny tělesa se skládají z částic, které vykonávají neustálý a neuspořádaný pohyb a které na sebe navzájem silově působí. Částice uvnitř všech těles
Teplo a vnitřní energie pracovní list Vnitřní energie Všechny tělesa se skládají z částic, které vykonávají neustálý a neuspořádaný pohyb a které na sebe navzájem silově působí. Částice uvnitř všech těles
Kalorimetrická rovnice, skupenské přeměny
 Základní škola Nový Bor, náměstí Míru 128, okres Česká Lípa, příspěvková organizace e mail: info@zsnamesti.cz; www.zsnamesti.cz; telefon: 487 722 010; fax: 487 722 378 Registrační číslo: CZ.1.07/1.4.00/21.3267
Základní škola Nový Bor, náměstí Míru 128, okres Česká Lípa, příspěvková organizace e mail: info@zsnamesti.cz; www.zsnamesti.cz; telefon: 487 722 010; fax: 487 722 378 Registrační číslo: CZ.1.07/1.4.00/21.3267
Vnitřní energie, práce a teplo
 Vnitřní energie, práce a teplo Míček upustíme z výšky na podlahu o Míček padá zvětšuje se, zmenšuje se. Celková mechanická energie se - o Míček se od země odrazí a stoupá vzhůru zvětšuje se, zmenšuje se.
Vnitřní energie, práce a teplo Míček upustíme z výšky na podlahu o Míček padá zvětšuje se, zmenšuje se. Celková mechanická energie se - o Míček se od země odrazí a stoupá vzhůru zvětšuje se, zmenšuje se.
ZMĚNY SKUPENSTVÍ LÁTEK
 ZMĚNY SKUPENSTVÍ LÁTEK TÁNÍ A TUHNUTÍ - OSNOVA Kapilární jevy příklad Skupenské přeměny látek Tání a tuhnutí Teorie s video experimentem Příklad KAPILÁRNÍ JEVY - OPAKOVÁNÍ KAPILÁRNÍ JEVY - PŘÍKLAD Jak
ZMĚNY SKUPENSTVÍ LÁTEK TÁNÍ A TUHNUTÍ - OSNOVA Kapilární jevy příklad Skupenské přeměny látek Tání a tuhnutí Teorie s video experimentem Příklad KAPILÁRNÍ JEVY - OPAKOVÁNÍ KAPILÁRNÍ JEVY - PŘÍKLAD Jak
Vnitřní energie. Teplo. Tepelná výměna.
 Vnitřní energie. Teplo. Tepelná výměna. A) Výklad: Vnitřní energie vnitřní energie označuje součet celkové kinetické energie částic (tj. rotační + vibrační + translační energie) a celkové polohové energie
Vnitřní energie. Teplo. Tepelná výměna. A) Výklad: Vnitřní energie vnitřní energie označuje součet celkové kinetické energie částic (tj. rotační + vibrační + translační energie) a celkové polohové energie
Vnitřní energie, práce, teplo.
 Vnitřní energie, práce, teplo. Vnitřní energie tělesa Částice uvnitř látek mají kinetickou a potenciální energii. Je to energie uvnitř tělesa, proto ji nazýváme vnitřní energie. Značíme ji písmenkem U
Vnitřní energie, práce, teplo. Vnitřní energie tělesa Částice uvnitř látek mají kinetickou a potenciální energii. Je to energie uvnitř tělesa, proto ji nazýváme vnitřní energie. Značíme ji písmenkem U
Měření teplotní roztažnosti
 KATEDRA EXPERIMENTÁLNÍ FYZIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO V OLOMOUCI FYZIKÁLNÍ PRAKTIKUM Z MOLEKULOVÉ FYZIKY A TERMODYNAMIKY Měření teplotní roztažnosti Úvod Zvyšování termodynamické teploty
KATEDRA EXPERIMENTÁLNÍ FYZIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO V OLOMOUCI FYZIKÁLNÍ PRAKTIKUM Z MOLEKULOVÉ FYZIKY A TERMODYNAMIKY Měření teplotní roztažnosti Úvod Zvyšování termodynamické teploty
Molekulová fyzika a termika
 Molekulová fyzika a termika Fyzika 1. ročník Vzdělávání pro konkurenceschopnost Inovace výuky oboru Informační technologie MěSOŠ Klobouky u Brna Mgr. Petr Kučera 1 Obsah témat v kapitole Molekulová fyzika
Molekulová fyzika a termika Fyzika 1. ročník Vzdělávání pro konkurenceschopnost Inovace výuky oboru Informační technologie MěSOŠ Klobouky u Brna Mgr. Petr Kučera 1 Obsah témat v kapitole Molekulová fyzika
1) Skupenství fáze, forma, stav. 2) 3 druhy skupenství (1 látky): pevné (led) kapalné (voda) plynné (vodní pára)
 SKUPENSTVÍ 1) Skupenství fáze, forma, stav 2) 3 druhy skupenství (1 látky): pevné (led) kapalné (voda) plynné (vodní pára) 3) Pevné látky nemění tvar, objem částice blízko sebe, pohybují se kolem urč.
SKUPENSTVÍ 1) Skupenství fáze, forma, stav 2) 3 druhy skupenství (1 látky): pevné (led) kapalné (voda) plynné (vodní pára) 3) Pevné látky nemění tvar, objem částice blízko sebe, pohybují se kolem urč.
R9.1 Molární hmotnost a molární objem
 Fyzika pro střední školy I 73 R9 M O L E K U L O V Á F Y Z I K A A T E R M I K A R9.1 Molární hmotnost a molární objem V čl. 9.5 jsme zavedli látkové množství jako fyzikální veličinu, která charakterizuje
Fyzika pro střední školy I 73 R9 M O L E K U L O V Á F Y Z I K A A T E R M I K A R9.1 Molární hmotnost a molární objem V čl. 9.5 jsme zavedli látkové množství jako fyzikální veličinu, která charakterizuje
Základy molekulové fyziky a termodynamiky
 Základy molekulové fyziky a termodynamiky Molekulová fyzika je částí fyziky, která zkoumá vlastnosti látek na základě jejich vnitřní struktury, pohybu a vzájemného silového působení částic, z nichž jsou
Základy molekulové fyziky a termodynamiky Molekulová fyzika je částí fyziky, která zkoumá vlastnosti látek na základě jejich vnitřní struktury, pohybu a vzájemného silového působení částic, z nichž jsou
Termomechanika cvičení
 KATEDRA ENERGETICKÝCH STROJŮ A ZAŘÍZENÍ Termomechanika cvičení 1. cvičení Ing. Michal Volf / 18.02.2019 Informace o cvičení Ing. Michal Volf Email: volfm@kke.zcu.cz Konzultace: po vzájemné dohodě prezentace
KATEDRA ENERGETICKÝCH STROJŮ A ZAŘÍZENÍ Termomechanika cvičení 1. cvičení Ing. Michal Volf / 18.02.2019 Informace o cvičení Ing. Michal Volf Email: volfm@kke.zcu.cz Konzultace: po vzájemné dohodě prezentace
Příklady k zápočtu molekulová fyzika a termodynamika
 Příklady k zápočtu molekulová fyzika a termodynamika 1. Do vody o teplotě t 1 70 C a hmotnosti m 1 1 kg vhodíme kostku ledu o teplotě t 2 10 C a hmotnosti m 2 2 kg. Do soustavy vzápětí přilijeme další
Příklady k zápočtu molekulová fyzika a termodynamika 1. Do vody o teplotě t 1 70 C a hmotnosti m 1 1 kg vhodíme kostku ledu o teplotě t 2 10 C a hmotnosti m 2 2 kg. Do soustavy vzápětí přilijeme další
Fyzika - Sexta, 2. ročník
 - Sexta, 2. ročník Fyzika Výchovné a vzdělávací strategie Kompetence komunikativní Kompetence k řešení problémů Kompetence sociální a personální Kompetence občanská Kompetence k podnikavosti Kompetence
- Sexta, 2. ročník Fyzika Výchovné a vzdělávací strategie Kompetence komunikativní Kompetence k řešení problémů Kompetence sociální a personální Kompetence občanská Kompetence k podnikavosti Kompetence
VLASTNOSTI VLÁKEN. 3. Tepelné vlastnosti vláken
 VLASNOSI VLÁKEN 3. epelné vlastnosti vláken 3.. Úvod epelné vlastnosti vláken jsou velice důležité, neboť jsou rozhodující pro volbu vhodných parametrů zpracování i použití vláken. Závisí na chemickém
VLASNOSI VLÁKEN 3. epelné vlastnosti vláken 3.. Úvod epelné vlastnosti vláken jsou velice důležité, neboť jsou rozhodující pro volbu vhodných parametrů zpracování i použití vláken. Závisí na chemickém
[381 m/s] 12. Ocelovou součást o hmotnosti m z = 4 kg, měrném teple c z = 420 J/kgK, zahřátou na teplotu t z = 900 C ponoříme do olejové lázně o
![[381 m/s] 12. Ocelovou součást o hmotnosti m z = 4 kg, měrném teple c z = 420 J/kgK, zahřátou na teplotu t z = 900 C ponoříme do olejové lázně o [381 m/s] 12. Ocelovou součást o hmotnosti m z = 4 kg, měrném teple c z = 420 J/kgK, zahřátou na teplotu t z = 900 C ponoříme do olejové lázně o](/thumbs/27/11706382.jpg) 3 - Termomechanika 1. Hustota vzduchu při tlaku p l = 0,2 MPa a teplotě t 1 = 27 C je ρ l = 2,354 kg/m 3. Jaká je jeho hustota ρ 0 při tlaku p 0 = 0,1MPa a teplotě t 0 = 0 C [1,29 kg/m 3 ] 2. Určete objem
3 - Termomechanika 1. Hustota vzduchu při tlaku p l = 0,2 MPa a teplotě t 1 = 27 C je ρ l = 2,354 kg/m 3. Jaká je jeho hustota ρ 0 při tlaku p 0 = 0,1MPa a teplotě t 0 = 0 C [1,29 kg/m 3 ] 2. Určete objem
Tepelná vodivost. střední rychlost. T 1 > T 2 z. teplo přenesené za čas dt: T 1 T 2. tepelný tok střední volná dráha. součinitel tepelné vodivosti
 Tepelná vodivost teplo přenesené za čas dt: T 1 > T z T 1 S tepelný tok střední volná dráha T součinitel tepelné vodivosti střední rychlost Tepelná vodivost součinitel tepelné vodivosti při T = 300 K součinitel
Tepelná vodivost teplo přenesené za čas dt: T 1 > T z T 1 S tepelný tok střední volná dráha T součinitel tepelné vodivosti střední rychlost Tepelná vodivost součinitel tepelné vodivosti při T = 300 K součinitel
Měření prostupu tepla
 KATEDRA EXPERIMENTÁLNÍ FYZIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO V OLOMOUCI FYZIKÁLNÍ PRAKTIKUM Z MOLEKULOVÉ FYZIKY A TERMODYNAMIKY Měření prostupu tepla Úvod Prostup tepla je kombinovaný případ
KATEDRA EXPERIMENTÁLNÍ FYZIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO V OLOMOUCI FYZIKÁLNÍ PRAKTIKUM Z MOLEKULOVÉ FYZIKY A TERMODYNAMIKY Měření prostupu tepla Úvod Prostup tepla je kombinovaný případ
Vnitřní energie, teplo a práce
 Přednáška 3 Vnitřní energie, teplo a práce 3.1 Vnitřní energie Pro popis stavu termodynamických soustav je výhodné zavést stavovou funkci, tzv. vnitřní energii soustavy U, která vyjadřuje charakter pohybu
Přednáška 3 Vnitřní energie, teplo a práce 3.1 Vnitřní energie Pro popis stavu termodynamických soustav je výhodné zavést stavovou funkci, tzv. vnitřní energii soustavy U, která vyjadřuje charakter pohybu
Termodynamika 1. UJOP Hostivař 2014
 Termodynamika 1 UJOP Hostivař 2014 Termodynamika Zabývá se tepelnými ději obecně. Existují 3 termodynamické zákony: 1. Celkové množství energie (všech druhů) izolované soustavy zůstává zachováno. 2. Teplo
Termodynamika 1 UJOP Hostivař 2014 Termodynamika Zabývá se tepelnými ději obecně. Existují 3 termodynamické zákony: 1. Celkové množství energie (všech druhů) izolované soustavy zůstává zachováno. 2. Teplo
ÚVODNÍ POJMY, VNITŘNÍ ENERGIE, PRÁCE A TEPLO POJMY K ZOPAKOVÁNÍ. Testové úlohy varianta A
 Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Jitka Novosadová MGV_F_SS_3S3_D08_Z_OPAK_T_Uvodni_pojmy_vnitrni_energie _prace_teplo_t Člověk a příroda Fyzika
Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Jitka Novosadová MGV_F_SS_3S3_D08_Z_OPAK_T_Uvodni_pojmy_vnitrni_energie _prace_teplo_t Člověk a příroda Fyzika
Termika. Nauka o teple se zabývá měřením teploty, tepla a tepelnými ději.
 Termika Nauka o teple se zabývá měřením teploty, tepla a tepelnými ději. 1. Vnitřní energie Brownův pohyb a difúze látek prokazují, že částice látek jsou v neustálém neuspořádaném pohybu. Proto mají kinetickou
Termika Nauka o teple se zabývá měřením teploty, tepla a tepelnými ději. 1. Vnitřní energie Brownův pohyb a difúze látek prokazují, že částice látek jsou v neustálém neuspořádaném pohybu. Proto mají kinetickou
Teplotní roztažnost. Teorie. Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
 Teplotní roztažnost Teorie Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Teplotní roztažnost souvisí se změnou rozměru zahřívaného těles Při zahřívání se tělesa zvětšují, při ochlazování
Teplotní roztažnost Teorie Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Teplotní roztažnost souvisí se změnou rozměru zahřívaného těles Při zahřívání se tělesa zvětšují, při ochlazování
Fyzikální vzdělávání. 1. ročník. Učební obor: Kuchař číšník Kadeřník. Implementace ICT do výuky č. CZ.1.07/1.1.02/02.0012 GG OP VK
 Fyzikální vzdělávání 1. ročník Učební obor: Kuchař číšník Kadeřník 1 2 Termika 2.1Teplota, teplotní roztažnost látek 2.2 Teplo a práce, přeměny vnitřní energie tělesa 2.3 Tepelné motory 2.4 Struktura pevných
Fyzikální vzdělávání 1. ročník Učební obor: Kuchař číšník Kadeřník 1 2 Termika 2.1Teplota, teplotní roztažnost látek 2.2 Teplo a práce, přeměny vnitřní energie tělesa 2.3 Tepelné motory 2.4 Struktura pevných
SBÍRKA ŘEŠENÝCH FYZIKÁLNÍCH ÚLOH
 SBÍRKA ŘEŠENÝCH FYZIKÁLNÍCH ÚLOH MECHANIKA MOLEKULOVÁ FYZIKA A TERMIKA ELEKTŘINA A MAGNETISMUS KMITÁNÍ A VLNĚNÍ OPTIKA FYZIKA MIKROSVĚTA TERMODYNAMICKÁ TEPLOTNÍ STUPNICE, TEPLOTA 1) Převeďte hodnoty v
SBÍRKA ŘEŠENÝCH FYZIKÁLNÍCH ÚLOH MECHANIKA MOLEKULOVÁ FYZIKA A TERMIKA ELEKTŘINA A MAGNETISMUS KMITÁNÍ A VLNĚNÍ OPTIKA FYZIKA MIKROSVĚTA TERMODYNAMICKÁ TEPLOTNÍ STUPNICE, TEPLOTA 1) Převeďte hodnoty v
T0 Teplo a jeho měření
 Teplo a jeho měření 1 Teplo 2 Kalorimetrie Kalorimetr 3 Tepelná kapacita 3.1 Měrná tepelná kapacita Měrná tepelná kapacita při stálém objemu a stálém tlaku Poměr měrných tepelných kapacit 3.2 Molární tepelná
Teplo a jeho měření 1 Teplo 2 Kalorimetrie Kalorimetr 3 Tepelná kapacita 3.1 Měrná tepelná kapacita Měrná tepelná kapacita při stálém objemu a stálém tlaku Poměr měrných tepelných kapacit 3.2 Molární tepelná
Měření teplotní roztažnosti
 KATEDRA EXPERIMENTÁLNÍ FYZIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO V OLOMOUCI FYZIKÁLNÍ PRAKTIKUM Z MOLEKULOVÉ FYZIKY A TERMODYNAMIKY Měření teplotní roztažnosti Úvod Zvyšování termodynamické teploty
KATEDRA EXPERIMENTÁLNÍ FYZIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO V OLOMOUCI FYZIKÁLNÍ PRAKTIKUM Z MOLEKULOVÉ FYZIKY A TERMODYNAMIKY Měření teplotní roztažnosti Úvod Zvyšování termodynamické teploty
3.2 Látka a její skupenství
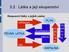 3.2 Látka a její skupenství Skupenství látky a jejich změny sublimace PEVNÁ LÁTKA tání desublimace tuhnutí PLYN vy pa řo vá ní KAPALINA zka pal ňo vá ní Látka a změna vnitřní energie Změna vnitřní energie
3.2 Látka a její skupenství Skupenství látky a jejich změny sublimace PEVNÁ LÁTKA tání desublimace tuhnutí PLYN vy pa řo vá ní KAPALINA zka pal ňo vá ní Látka a změna vnitřní energie Změna vnitřní energie
Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny
 Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny Hustota toku Zatím jsme studovali pouze soustavy, které byly v rovnovážném stavu není-li soustava v silovém poli, je hustota částic stejná
Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny Hustota toku Zatím jsme studovali pouze soustavy, které byly v rovnovážném stavu není-li soustava v silovém poli, je hustota částic stejná
5.7 Vlhkost vzduchu 5.7.5 Absolutní vlhkost 5.7.6 Poměrná vlhkost 5.7.7 Rosný bod 5.7.8 Složení vzduchu 5.7.9 Měření vlhkosti vzduchu
 Fázové přechody 5.6.5 Fáze Fázové rozhraní 5.6.6 Gibbsovo pravidlo fází 5.6.7 Fázový přechod Fázový přechod prvního druhu Fázový přechod druhého druhu 5.6.7.1 Clausiova-Clapeyronova rovnice 5.6.8 Skupenství
Fázové přechody 5.6.5 Fáze Fázové rozhraní 5.6.6 Gibbsovo pravidlo fází 5.6.7 Fázový přechod Fázový přechod prvního druhu Fázový přechod druhého druhu 5.6.7.1 Clausiova-Clapeyronova rovnice 5.6.8 Skupenství
KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE. 123MAIN tepelně-fyzikální parametry
 KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE 123MAIN tepelně-fyzikální parametry Vedení tepla v látkách: vedením (kondukcí) předání kinetické energie neuspořádaných tepelných pohybů. Přenos z míst vyšší
KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE 123MAIN tepelně-fyzikální parametry Vedení tepla v látkách: vedením (kondukcí) předání kinetické energie neuspořádaných tepelných pohybů. Přenos z míst vyšší
TERMIKA II. Stacionární vedení s dokonalou i nedokonalou izolací; Obecná rovnice vedení tepla; Přestup a prostup tepla;
 TERMIKA II Šíření tepla vedením, prouděním a zářením; Stacionární vedení s dokonalou i nedokonalou izolací; Nestacionární vedení tepla; Obecná rovnice vedení tepla; Přestup a prostup tepla; 1 Šíření tepla
TERMIKA II Šíření tepla vedením, prouděním a zářením; Stacionární vedení s dokonalou i nedokonalou izolací; Nestacionární vedení tepla; Obecná rovnice vedení tepla; Přestup a prostup tepla; 1 Šíření tepla
3 pokusy z termiky. Vojtěch Jelen Fyzikální seminář LS 2014
 3 pokusy z termiky Vojtěch Jelen Fyzikální seminář LS 2014 Obsah 1. Pokus online 2. Měření teploty cihly 3. Vypařování střely 1. Kalorimetrie Zabývá se měřením tepla a studuje vlastnosti látek a jejich
3 pokusy z termiky Vojtěch Jelen Fyzikální seminář LS 2014 Obsah 1. Pokus online 2. Měření teploty cihly 3. Vypařování střely 1. Kalorimetrie Zabývá se měřením tepla a studuje vlastnosti látek a jejich
ZÁKLADY STAVEBNÍ FYZIKY
 ZÁKLADY STAVEBNÍ FYZIKY Doc.Ing.Václav Kupilík, CSc. První termodynamická věta představuje zákon o zachování energie. Podle tohoto zákona nemůže energie samovolně vznikat nebo zanikat, ale může se pouze
ZÁKLADY STAVEBNÍ FYZIKY Doc.Ing.Václav Kupilík, CSc. První termodynamická věta představuje zákon o zachování energie. Podle tohoto zákona nemůže energie samovolně vznikat nebo zanikat, ale může se pouze
Fyzikální učebna vybavená audiovizuální technikou, interaktivní tabule, fyzikální pomůcky
 Předmět: Náplň: Třída: Počet hodin: Pomůcky: Fyzika (FYZ) Molekulová fyzika, termika 2. ročník, sexta 2 hodiny týdně Fyzikální učebna vybavená audiovizuální technikou, interaktivní tabule, fyzikální pomůcky
Předmět: Náplň: Třída: Počet hodin: Pomůcky: Fyzika (FYZ) Molekulová fyzika, termika 2. ročník, sexta 2 hodiny týdně Fyzikální učebna vybavená audiovizuální technikou, interaktivní tabule, fyzikální pomůcky
Termodynamika materiálů. Vztahy a přeměny různých druhů energie při termodynamických dějích podmínky nutné pro uskutečnění fázových přeměn
 Termodynamika materiálů Vztahy a přeměny různých druhů energie při termodynamických dějích podmínky nutné pro uskutečnění fázových přeměn Důležité konstanty Standartní podmínky Avogadrovo číslo N A = 6,023.10
Termodynamika materiálů Vztahy a přeměny různých druhů energie při termodynamických dějích podmínky nutné pro uskutečnění fázových přeměn Důležité konstanty Standartní podmínky Avogadrovo číslo N A = 6,023.10
LOGO. Změny skupenství
 Změny skupenství Látka existuje ve třech skupenstvích Pevném Kapalném Plynném Látka může přecházet z jednoho skupenství do druhého. Existují tedy tyto změny skupenství: Změny skupenství plyn sublimace
Změny skupenství Látka existuje ve třech skupenstvích Pevném Kapalném Plynném Látka může přecházet z jednoho skupenství do druhého. Existují tedy tyto změny skupenství: Změny skupenství plyn sublimace
KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE. 123TVVM tepelně-fyzikální parametry
 KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE 123TVVM tepelně-fyzikální parametry Vedení tepla v látkách: vedením (kondukcí) předání kinetické energie neuspořádaných tepelných pohybů. Přenos z míst vyšší
KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE 123TVVM tepelně-fyzikální parametry Vedení tepla v látkách: vedením (kondukcí) předání kinetické energie neuspořádaných tepelných pohybů. Přenos z míst vyšší
4. V jednom krychlovém metru (1 m 3 ) plynu je 2, molekul. Ve dvou krychlových milimetrech (2 mm 3 ) plynu je molekul
 Fyzika 20 Otázky za 2 body. Celsiova teplota t a termodynamická teplota T spolu souvisejí známým vztahem. Vyberte dvojici, která tento vztah vyjadřuje (zaokrouhleno na celá čísla) a) T = 253 K ; t = 20
Fyzika 20 Otázky za 2 body. Celsiova teplota t a termodynamická teplota T spolu souvisejí známým vztahem. Vyberte dvojici, která tento vztah vyjadřuje (zaokrouhleno na celá čísla) a) T = 253 K ; t = 20
UČIVO. Termodynamická teplota. První termodynamický zákon Přenos vnitřní energie
 PŘEDMĚT: FYZIKA ROČNÍK: SEXTA VÝSTUP UČIVO MEZIPŘEDM. VZTAHY, PRŮŘEZOVÁ TÉMATA, PROJEKTY, KURZY POZNÁMKY Zná 3 základní poznatky kinetické teorie látek a vysvětlí jejich praktický význam Vysvětlí pojmy
PŘEDMĚT: FYZIKA ROČNÍK: SEXTA VÝSTUP UČIVO MEZIPŘEDM. VZTAHY, PRŮŘEZOVÁ TÉMATA, PROJEKTY, KURZY POZNÁMKY Zná 3 základní poznatky kinetické teorie látek a vysvětlí jejich praktický význam Vysvětlí pojmy
Termika termika - teplota, teplo a práce termodynamické zákony tepelná vodivost - tepelná kapacita skupenské teplo
 Termika termika - teplota, teplo a práce termodynamické zákony tepelná vodivost - tepelná kapacita skupenské teplo teplo, teplota, práce, tepelná vodivost Teplo část vnitřní energie tělesa = součet kinetické
Termika termika - teplota, teplo a práce termodynamické zákony tepelná vodivost - tepelná kapacita skupenské teplo teplo, teplota, práce, tepelná vodivost Teplo část vnitřní energie tělesa = součet kinetické
VÝUKOVÝ MATERIÁL Ing. Yvona Bečičková Tematická oblast. Termika Číslo a název materiálu VY_32_INOVACE_0301_0220 Anotace
 VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
N_SFB. Stavebně fyzikální aspekty budov. Přednáška č. 3. Vysoká škola technická a ekonomická V Českých Budějovicích
 Vysoká škola technická a ekonomická V Českých Budějovicích N_ Stavebně fyzikální aspekty budov Přednáška č. 3 Přednášky: Ing. Michal Kraus, Ph.D. Cvičení: Ing. Michal Kraus, Ph.D. Garant: prof. Ing. Ingrid
Vysoká škola technická a ekonomická V Českých Budějovicích N_ Stavebně fyzikální aspekty budov Přednáška č. 3 Přednášky: Ing. Michal Kraus, Ph.D. Cvičení: Ing. Michal Kraus, Ph.D. Garant: prof. Ing. Ingrid
9. Struktura a vlastnosti plynů
 9. Struktura a vlastnosti plynů Osnova: 1. Základní pojmy 2. Střední kvadratická rychlost 3. Střední kinetická energie molekuly plynu 4. Stavová rovnice ideálního plynu 5. Jednoduché děje v plynech a)
9. Struktura a vlastnosti plynů Osnova: 1. Základní pojmy 2. Střední kvadratická rychlost 3. Střední kinetická energie molekuly plynu 4. Stavová rovnice ideálního plynu 5. Jednoduché děje v plynech a)
Jméno: _ podpis: ročník: č. studenta. Otázky typu A (0.25 bodů za otázku, správně je pouze jedna odpověď)
 Jméno: _ podpis: ročník: č. studenta Otázky typu A (0.25 bodů za otázku, správně je pouze jedna odpověď) 1. JEDNOTKA PASCAL JE DEFINOVÁNÁ JAKO a. N.m.s b. kg.m-1.s-2 c. kg.m-2 d. kg.m.s 2. KALORIMETRICKÁ
Jméno: _ podpis: ročník: č. studenta Otázky typu A (0.25 bodů za otázku, správně je pouze jedna odpověď) 1. JEDNOTKA PASCAL JE DEFINOVÁNÁ JAKO a. N.m.s b. kg.m-1.s-2 c. kg.m-2 d. kg.m.s 2. KALORIMETRICKÁ
Názvosloví Kvalita Výroba Kondenzace Teplosměnná plocha
 Názvosloví Kvalita Výroba Kondenzace Teplosměnná plocha Názvosloví páry Pro správné pochopení funkce parních systémů musíme znát základní pojmy spojené s párou. Entalpie Celková energie, příslušná danému
Názvosloví Kvalita Výroba Kondenzace Teplosměnná plocha Názvosloví páry Pro správné pochopení funkce parních systémů musíme znát základní pojmy spojené s párou. Entalpie Celková energie, příslušná danému
Přehled otázek z fyziky pro 2.ročník
 Přehled otázek z fyziky pro 2.ročník 1. Z jakých základních poznatků vychází teorie látek + důkazy. a) Látka kteréhokoli skupenství se skládá z částic molekul, atomů, iontů. b) Částice se v látce pohybují,
Přehled otázek z fyziky pro 2.ročník 1. Z jakých základních poznatků vychází teorie látek + důkazy. a) Látka kteréhokoli skupenství se skládá z částic molekul, atomů, iontů. b) Částice se v látce pohybují,
Termodynamika. Děj, který není kvazistatický, se nazývá nestatický.
 Termodynamika Zabývá se ději, při nichž se mění tepelná energie v jiné druhy energie (zejména mechanické). Studuje vlastnosti látek bez přihlédnutí k jejich mikrostruktuře. Je vystavěna na axiomech (0.,
Termodynamika Zabývá se ději, při nichž se mění tepelná energie v jiné druhy energie (zejména mechanické). Studuje vlastnosti látek bez přihlédnutí k jejich mikrostruktuře. Je vystavěna na axiomech (0.,
DUM č. 12 v sadě. 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia
 projekt GML Brno Docens DUM č. 12 v sadě 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia Autor: Vojtěch Beneš Datum: 03.05.2014 Ročník: 1. ročník Anotace DUMu: Kapaliny, změny skupenství Materiály
projekt GML Brno Docens DUM č. 12 v sadě 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia Autor: Vojtěch Beneš Datum: 03.05.2014 Ročník: 1. ročník Anotace DUMu: Kapaliny, změny skupenství Materiály
Laboratorní práce č. 2: Určení měrné tepelné kapacity látky
 Přírodní vědy moderně a interaktivně FYZIKA 4. ročník šestiletého a 2. ročník čtyřletého studia Laboratorní práce č. 2: Určení měrné tepelné kapacity látky Přírodní vědy moderně a interaktivně FYZIKA
Přírodní vědy moderně a interaktivně FYZIKA 4. ročník šestiletého a 2. ročník čtyřletého studia Laboratorní práce č. 2: Určení měrné tepelné kapacity látky Přírodní vědy moderně a interaktivně FYZIKA
TESTY Závěrečný test 2. ročník Skupina A
 1. Teplota tělesa se zvýšila o o C. Analogicky tomu lze říci, že se a) snížila o K. b) zvýšila o 93,15 K c) snížila o 53,15 K d) zvýšila o K. Částice v látce se pohybují a) neustáleným a uspořádaným pohybem
1. Teplota tělesa se zvýšila o o C. Analogicky tomu lze říci, že se a) snížila o K. b) zvýšila o 93,15 K c) snížila o 53,15 K d) zvýšila o K. Částice v látce se pohybují a) neustáleným a uspořádaným pohybem
12. Termomechanika par, Clausiova-Clapeyronova rovnice, parní tabulky, základni termodynamické děje v oblasti par
 1/18 12. Termomechanika par, Clausiova-Clapeyronova rovnice, parní tabulky, základni termodynamické děje v oblasti par Příklad: 12.1, 12.2, 12.3, 12.4, 12.5, 12.6, 12.7, 12.8, 12.9, 12.10, 12.11, 12.12,
1/18 12. Termomechanika par, Clausiova-Clapeyronova rovnice, parní tabulky, základni termodynamické děje v oblasti par Příklad: 12.1, 12.2, 12.3, 12.4, 12.5, 12.6, 12.7, 12.8, 12.9, 12.10, 12.11, 12.12,
II. VNITŘNÍ ENERGIE, PRÁCE A TEPLO
 II. VNITŘNÍ ENERGIE, PRÁCE A TEPLO 2.1 Vnitřní energie tělesa a) celková energie (termodynamické) soustavy E tvořena kinetickou energií E k jejího makroskopického pohybu jako celku potenciální energií
II. VNITŘNÍ ENERGIE, PRÁCE A TEPLO 2.1 Vnitřní energie tělesa a) celková energie (termodynamické) soustavy E tvořena kinetickou energií E k jejího makroskopického pohybu jako celku potenciální energií
Cvičení z termomechaniky Cvičení 2. Stanovte objem nádoby, ve které je uzavřený dusík o hmotnosti 20 [kg], teplotě 15 [ C] a tlaku 10 [MPa].
![Cvičení z termomechaniky Cvičení 2. Stanovte objem nádoby, ve které je uzavřený dusík o hmotnosti 20 [kg], teplotě 15 [ C] a tlaku 10 [MPa]. Cvičení z termomechaniky Cvičení 2. Stanovte objem nádoby, ve které je uzavřený dusík o hmotnosti 20 [kg], teplotě 15 [ C] a tlaku 10 [MPa].](/thumbs/25/6795424.jpg) Příklad 1 Stanovte objem nádoby, ve které je uzavřený dusík o hmotnosti 20 [kg], teplotě 15 [ C] a tlaku 10 [MPa]. m 20[kg], t 15 [ C] 288.15 [K], p 10 [MPa] 10.10 6 [Pa], R 8314 [J. kmol 1. K 1 ] 8,314
Příklad 1 Stanovte objem nádoby, ve které je uzavřený dusík o hmotnosti 20 [kg], teplotě 15 [ C] a tlaku 10 [MPa]. m 20[kg], t 15 [ C] 288.15 [K], p 10 [MPa] 10.10 6 [Pa], R 8314 [J. kmol 1. K 1 ] 8,314
Termomechanika 8. přednáška Doc. Dr. RNDr. Miroslav Holeček
 Termomechanika 8. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
Termomechanika 8. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
Kalorimetrická měření I
 KATEDRA EXPERIMENTÁLNÍ FYZIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO V OLOMOUCI FYZIKÁLNÍ PRAKTIKUM Z MOLEKULOVÉ FYZIKY A TERMODYNAMIKY Kalorimetrická měření I Úvod Teplo Teplo Q je určeno energií,
KATEDRA EXPERIMENTÁLNÍ FYZIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO V OLOMOUCI FYZIKÁLNÍ PRAKTIKUM Z MOLEKULOVÉ FYZIKY A TERMODYNAMIKY Kalorimetrická měření I Úvod Teplo Teplo Q je určeno energií,
VÝUKOVÝ MATERIÁL. 0301 Ing. Yvona Bečičková Termika VY_32_INOVACE_0301_0212 Teplotní roztažnost látek. Fyzika 2. ročník, učební obory Bez příloh
 VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
Měření měrného skupenského tepla tání ledu
 KATEDRA EXPERIMENTÁLNÍ FYZIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO V OLOMOUCI FYZIKÁLNÍ PRAKTIKUM Z MOLEKULOVÉ FYZIKY A TERMODYNAMIKY Měření měrného skupenského tepla tání ledu Úvod Tání, měrné
KATEDRA EXPERIMENTÁLNÍ FYZIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO V OLOMOUCI FYZIKÁLNÍ PRAKTIKUM Z MOLEKULOVÉ FYZIKY A TERMODYNAMIKY Měření měrného skupenského tepla tání ledu Úvod Tání, měrné
(test version, not revised) 24. listopadu 2010
 Změny skupenství (test version, not revised) Petr Pošta pposta@karlin.mff.cuni.cz 24. listopadu 2010 Obsah Tání Tuhnutí Sublimace a desublimace Vypařování a var. Kondenzace Sytá pára Fázový diagram Vodní
Změny skupenství (test version, not revised) Petr Pošta pposta@karlin.mff.cuni.cz 24. listopadu 2010 Obsah Tání Tuhnutí Sublimace a desublimace Vypařování a var. Kondenzace Sytá pára Fázový diagram Vodní
Fyzika, maturitní okruhy (profilová část), školní rok 2014/2015 Gymnázium INTEGRA BRNO
 1. Jednotky a veličiny soustava SI odvozené jednotky násobky a díly jednotek skalární a vektorové fyzikální veličiny rozměrová analýza 2. Kinematika hmotného bodu základní pojmy kinematiky hmotného bodu
1. Jednotky a veličiny soustava SI odvozené jednotky násobky a díly jednotek skalární a vektorové fyzikální veličiny rozměrová analýza 2. Kinematika hmotného bodu základní pojmy kinematiky hmotného bodu
Fyzikální chemie. Magda Škvorová KFCH CN463 magda.skvorova@ujep.cz, tel. 3302. 14. února 2013
 Fyzikální chemie Magda Škvorová KFCH CN463 magda.skvorova@ujep.cz, tel. 3302 14. února 2013 Co je fyzikální chemie? Co je fyzikální chemie? makroskopický přístup: (klasická) termodynamika nerovnovážná
Fyzikální chemie Magda Škvorová KFCH CN463 magda.skvorova@ujep.cz, tel. 3302 14. února 2013 Co je fyzikální chemie? Co je fyzikální chemie? makroskopický přístup: (klasická) termodynamika nerovnovážná
KAPALINY. Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda
 KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda Vlastnosti molekul kapalin V neustálém pohybu Ve stejných vzdálenostech, nejsou ale vázány Působí na sebe silami: odpudivé x přitažlivé Vlastnosti kapalin
KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda Vlastnosti molekul kapalin V neustálém pohybu Ve stejných vzdálenostech, nejsou ale vázány Působí na sebe silami: odpudivé x přitažlivé Vlastnosti kapalin
STRUKTURA PEVNÝCH LÁTEK A KAPALIN
 STRUKTURA PEVNÝCH LÁTEK A KAPALIN 19. ZMĚNY SKUPENSTVÍ, FÁZOVÝ DIAGRAM Autor: Ing. Eva Jančová DESS SOŠ a SOU spol. s r. o. SKUPENSTVÍ - Skupenství neboli stav je konkrétní forma látky, charakterizovaná
STRUKTURA PEVNÝCH LÁTEK A KAPALIN 19. ZMĚNY SKUPENSTVÍ, FÁZOVÝ DIAGRAM Autor: Ing. Eva Jančová DESS SOŠ a SOU spol. s r. o. SKUPENSTVÍ - Skupenství neboli stav je konkrétní forma látky, charakterizovaná
TÉMA: Molekulová fyzika a tepelné děje v plynech VNITŘNÍ ENERGIE TĚLESA
 U.. vnitřní energie tělesa ( termodynamické soustavy) je celková kinetická energie neuspořádaně se pohybujících částic tělesa ( molekul, atomů, iontů) a celková potenciální energie vzájemné polohy těchto
U.. vnitřní energie tělesa ( termodynamické soustavy) je celková kinetická energie neuspořádaně se pohybujících částic tělesa ( molekul, atomů, iontů) a celková potenciální energie vzájemné polohy těchto
FAKULTA STAVEBNÍ VUT V BRNĚ PŘIJÍMACÍ ŘÍZENÍ PRO AKADEMICKÝ ROK 2006 2007
 TEST Z FYZIKY PRO PŘIJÍMACÍ ZKOUŠKY ČÍSLO FAST-F-2006-01 1. Převeďte 37 mm 3 na m 3. a) 37 10-9 m 3 b) 37 10-6 m 3 c) 37 10 9 m 3 d) 37 10 3 m 3 e) 37 10-3 m 3 2. Voda v řece proudí rychlostí 4 m/s. Kolmo
TEST Z FYZIKY PRO PŘIJÍMACÍ ZKOUŠKY ČÍSLO FAST-F-2006-01 1. Převeďte 37 mm 3 na m 3. a) 37 10-9 m 3 b) 37 10-6 m 3 c) 37 10 9 m 3 d) 37 10 3 m 3 e) 37 10-3 m 3 2. Voda v řece proudí rychlostí 4 m/s. Kolmo
Laboratorní práce č. 2: Určení měrného skupenského tepla tání ledu
 Přírodní vědy moderně a interaktivně FYZIKA 1. ročník šestiletého studia Laboratorní práce č. 2: Určení měrného skupenského tepla tání ledu ymnázium Přírodní vědy moderně a interaktivně FYZIKA 1. ročník
Přírodní vědy moderně a interaktivně FYZIKA 1. ročník šestiletého studia Laboratorní práce č. 2: Určení měrného skupenského tepla tání ledu ymnázium Přírodní vědy moderně a interaktivně FYZIKA 1. ročník
PROCESY V TECHNICE BUDOV 11
 UNIVERZITA TOMÁŠE BATI VE ZLÍNĚ FAKULTA APLIKOVANÉ INFORMATIKY PROCESY V TECHNICE BUDOV 11 Dagmar Janáčová, Hana Charvátová, Zlín 2013 Tento studijní materiál vznikl za finanční podpory Evropského sociálního
UNIVERZITA TOMÁŠE BATI VE ZLÍNĚ FAKULTA APLIKOVANÉ INFORMATIKY PROCESY V TECHNICE BUDOV 11 Dagmar Janáčová, Hana Charvátová, Zlín 2013 Tento studijní materiál vznikl za finanční podpory Evropského sociálního
7. MECHANIKA TEKUTIN - statika
 7. - statika 7.1. Základní vlastnosti tekutin Obecným pojem tekutiny jsou myšleny. a. Mají společné vlastnosti tekutost, částice jsou od sebe snadno oddělitelné, nemají vlastní stálý tvar apod. Reálné
7. - statika 7.1. Základní vlastnosti tekutin Obecným pojem tekutiny jsou myšleny. a. Mají společné vlastnosti tekutost, částice jsou od sebe snadno oddělitelné, nemají vlastní stálý tvar apod. Reálné
Pomůcky, které poskytuje sbírka fyziky, a audiovizuální technika v učebně fyziky, interaktivní tabule a i-učebnice
 Předmět: Náplň: Třída: Počet hodin: Pomůcky: Fyzika (FYZ) Práce a energie, tepelné jevy, elektrický proud, zvukové jevy Tercie 1+1 hodina týdně Pomůcky, které poskytuje sbírka fyziky, a audiovizuální technika
Předmět: Náplň: Třída: Počet hodin: Pomůcky: Fyzika (FYZ) Práce a energie, tepelné jevy, elektrický proud, zvukové jevy Tercie 1+1 hodina týdně Pomůcky, které poskytuje sbírka fyziky, a audiovizuální technika
Základní škola národního umělce Petra Bezruče, Frýdek-Místek, tř. T. G. Masaryka 454. Název DUM: Teplo v příkladech I
 Základní škola národního umělce Petra Bezruče, Frýdek-Místek, tř. T. G. Masaryka 454 Zpracováno v rámci OP VK - EU peníze školám Jednička ve vzdělávání CZ.1.07/1.4.00/21.2759 Název DUM: Teplo v příkladech
Základní škola národního umělce Petra Bezruče, Frýdek-Místek, tř. T. G. Masaryka 454 Zpracováno v rámci OP VK - EU peníze školám Jednička ve vzdělávání CZ.1.07/1.4.00/21.2759 Název DUM: Teplo v příkladech
VÝUKOVÝ MATERIÁL. 0301 Ing. Yvona Bečičková Tematická oblast
 VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
Přehled základních fyzikálních veličin užívaných ve výpočtech v termomechanice. Autor Ing. Jan BRANDA Jazyk Čeština
 Identifikátor materiálu: ICT 2 41 Registrační číslo projektu CZ.1.07/1.5.00/34.0796 Název projektu Vzděláváme pro život Název příjemce podpory SOU plynárenské Pardubice název materiálu (DUM) Mechanika
Identifikátor materiálu: ICT 2 41 Registrační číslo projektu CZ.1.07/1.5.00/34.0796 Název projektu Vzděláváme pro život Název příjemce podpory SOU plynárenské Pardubice název materiálu (DUM) Mechanika
Ing. Stanislav Jakoubek
 Ing. Stanislav Jakoubek Číslo DUMu III/--3-09 III/--3-0 III/--3- III/--3- III/--3-3 Název DUMu Měrná tepelná kapacita Kalorimetr, kalorimetrická rovnice Přenos vnitřní energie vedením Přenos vnitřní energie
Ing. Stanislav Jakoubek Číslo DUMu III/--3-09 III/--3-0 III/--3- III/--3- III/--3-3 Název DUMu Měrná tepelná kapacita Kalorimetr, kalorimetrická rovnice Přenos vnitřní energie vedením Přenos vnitřní energie
I. 1) Mezinárodní soustava jednotek. 2) Vlastnosti kapalin a plynů. 3)Atmosférický, hydrostatický a celkový tlak.
 FYZIKA Pro potápěče je důležité znát přírodní zákony, které určují princip potápění. Bez této znalosti je těžké porozumět pravidlům, které je třeba dodržovat pro zachování bezpečnosti tohoto sportu. Rozdíl
FYZIKA Pro potápěče je důležité znát přírodní zákony, které určují princip potápění. Bez této znalosti je těžké porozumět pravidlům, které je třeba dodržovat pro zachování bezpečnosti tohoto sportu. Rozdíl
VÝUKOVÝ MATERIÁL. 0301 Ing. Yvona Bečičková Tematická oblast. Termika Číslo a název materiálu VY_32_INOVACE_0301_0215 Anotace
 VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
17. Základy přenosu tepla - přenosu tepla vedením, přenos tepla prouděním, nestacionární přenos tepla, prostup tepla, vyměníky tepla
 1/14 17. Základy přenosu tepla - přenosu tepla vedením, přenos tepla prouděním, nestacionární přenos tepla, prostup tepla, vyměníky tepla Příklad: 17.1, 17.2, 17.3, 17.4, 17.5, 17.6, 17.7, 17.8, 17.9,
1/14 17. Základy přenosu tepla - přenosu tepla vedením, přenos tepla prouděním, nestacionární přenos tepla, prostup tepla, vyměníky tepla Příklad: 17.1, 17.2, 17.3, 17.4, 17.5, 17.6, 17.7, 17.8, 17.9,
ABSOLVENTSKÁ PRÁCE ZÁKLADNÍ ŠKOLA, ŠKOLNÍ 24, BYSTRÉ 9. ROČNÍK. Změny skupenství. Filip Skalský, David Řehůřek
 ABSOLVENTSKÁ PRÁCE ZÁKLADNÍ ŠKOLA, ŠKOLNÍ 24, 569 92 BYSTRÉ 9. ROČNÍK Změny skupenství Filip Skalský, David Řehůřek ŠKOLNÍ ROK 2011/2012 Prohlašujeme, že jsme absolventskou práci vypracovali samostatně
ABSOLVENTSKÁ PRÁCE ZÁKLADNÍ ŠKOLA, ŠKOLNÍ 24, 569 92 BYSTRÉ 9. ROČNÍK Změny skupenství Filip Skalský, David Řehůřek ŠKOLNÍ ROK 2011/2012 Prohlašujeme, že jsme absolventskou práci vypracovali samostatně
