V okolí každého hmotného tělesa existuje gravitační pole, které se projevuje silovým působením na jiná hmotná tělesa.
|
|
|
- Ladislav Dušek
- před 9 lety
- Počet zobrazení:
Transkript
1 GRAVITAČNÍ POLE
2 V okolí kažého hmotného tělesa existuje avitační pole, kteé se pojevuje silovým působením na jiná hmotná tělesa. Gavitační pole zpostřekuje silové působení těles, aniž přitom musí ojít k jejich bezpostřenímu styku. Silové působení mezi tělesy je vžy vzájemné (le 3. Newtonova pohybového zákona) tzv. avitační inteakce Vzájemné přitažlivé síly, kteé jsou míou avitační inteakce tzv. avitační síly
3 NEWTONŮV VŠEOBECNÝ GRAVITAČNÍ ZÁKON - zobecnění výsleků J. Keplea o kinematice pohybu planet po va hmotné objekty po va libovolné HB o hmotnostech m, m F m m κ κ 6,67. - k -.m 3.s - je avitační konstanta, jejíž honota byla zjištěna expeimentálně Síla F leží na spojnici hmotných boů Kažé va hmotné boy se přitahují silou, kteá je přímo úměná součinu jejich hmotností a nepřímo úměná uhé mocnině jejich vzálenosti.
4 Vektoové vyjáření Newtonova zákona: - uvažujme hmotný bo o hmotnosti m v avitačním poli hmotného bou o hmotnosti m F m m κ κ m m 3 - vekto avitační síly má opačnou oientaci než polohový vekto (přitažlivá síla) Matematický vztah platí jen po va hmotné boy a tělesa nahaitelná hmotnými boy, jejichž velikost je poti jejich vzálenosti zanebatelná. Je také přesným vyjářením avitační síly vojice homoenních koulí, ke je vzálenost jejich střeů.
5 GRAVITAČNÍ KONSTANTA -honotu κ popvé změřil anlický fyzik H. Cavenish (798) κ 6,67. - k -.m 3.s - TORZNÍ VÁHY HENRY CAVENDISH
6 INTENZITA GRAVITAČNÍHO POLE -vektoová veličina učena poílem avitační síly, kteá v aném místě pole působí na hmotný bo o hmotnosti m, a této hmotnosti: K -intenzita popisuje pole v kažém boě jenoznačně -závisí pouze na poloze uvažovaného bou a na hmotnosti tělesa, kteé pole vytváří - jenotka: N.k - m.s - F m Pozn.: Jelikož kažé těleso je zojem postoově neomezeného avitačního pole, polínají se v kažém místě postou avitační pole jenotlivých těles. V aném boě postou se vektoy intenzity avitačních polí skláají.
7 RADIÁLNÍ (CENTRÁLNÍ) GRAVITAČNÍ POLE -centální avitační pole je postoově neomezené vektoový siločaový moel aiálního avitačního pole: pole vytvořené HB nebo homoenní koulí o hmotnosti M: - vektoové vyjáření: - smě vektou intenzity K K M κ F κ M m κ M 3 a) o aného hmotného bou, kteý je zojem tohoto pole b) o střeu stejnooé koule, kteá je zojem av. pole K M κ
8 HOMOGENNÍ GRAVITAČNÍ POLE - pole chaakteizované vektoem intenzity, kteý má v kažém boě tohoto pole stejnou velikost, stejný smě, stejnou oientaci - ealizace: v ostatečné vzálenosti o avitačního centa : v omezeném postou, v němž jsou změny velikosti a směu vektou intenzity zanebatelné a) b)
9 . NPZ: GRAVITAČNÍ ZRYCHLENÍ avitační síla při svém působení na tělesa uílí těmto tělesům zychlení tzv. avitační zychlení F Newtonův av. zákon: ma F F M m κ ma ma a a mm κ M κ F m a jenotka: m.s - avitační zychlení vučitém boě je ovno intenzitě avitačního pole v témže boě (co o velikosti, směu a oientace) K a vekto intenzity avitačního pole popisuje pole avitační zychlení chaakteizuje pohyb konkétního tělesa, kteé se v aném místě pole nachází
10 PŘÍKLAD: Mějme homoenní tyč élky L a hmotnosti m. Na poloužení tyče ve vzálenosti a o jenoho jejího konce se nachází hmotný bo o hmotnosti m. Učete sílu, kteou na sebe tyto objekty působí.
11 PRÁCE GRAVITAČNÍ SÍLY hmotný bo o hmotnosti m posuneme o element áhy poél půvoiče M F m elementání páce avitační síly: elementání páce vnější síly: (poti avitační síle) Mm Mm W F κ κ Mm Mm W F + κ + κ celková páce vnější síly při přemístění HB o hmotnosti m ze vzálenosti o HB o hmotnosti M o vzálenosti Mm Mm W + κ κ Mm Mm κ κ Mm κ Mm + κ
12 GRAVITAČNÍ POTENCIÁLNÍ ENERGIE - skalání veličina, kteá kvantitativně popisuje chování těles v avitačním poli jiných těles W E - páce avitační síly p avitační potenciální eneie EP W EP W + C C je aitivní (inteační) konstanta Potenciální eneie je učena pací, kteou vykoná avitační síla při přenesení hmotného bou z aného místa na vztažné místo a nezávisí na cestě, po níž se přenášení ěje. Inteační konstantu ve výazu po potenciální eneii učíme pomocí tzv. okajových pomínek (vztažný bo volíme v nekonečnu): po vymizí F E p E p Mm κ
13 GRAVITAČNÍ POTENCIÁLNÍ ENERGIE avitační potenciální eneie hmotného bou o hmotnosti m v avitačním poli hmotného bou o hmotnosti M - páce avitační síly: W E P Mm κ ( EP EP ) ( EP EP ) EP M F m W - páce vnější síly: Mm Mm κ κ ( EP EP ) + EP W W Mm Mm κ κ M F m F
14 POTENCIÁL GRAVITAČNÍHO POLE - skalání veličina chaakteizující avitační pole v učitém boě závisející pouze na vlastnostech tohoto pole (nikoli na vlastnostech tělesa v aném boě umístěného) - potenciál avitačního pole v aném boě postou je poíl avitační potenciální eneie, kteou má v tomto boě pomocné těleso (HB) o hmotnosti m a této hmotnosti E P ϕ jenotka: J.k m - N.m.k - m.s - po avitační pole HB o hmotnosti M a zvolíme-li vztažný bo v nekonečnu: M ϕ κ
15 MODEL ZEMĚ GRAVITAČNÍ POLE ZEMĚ - ve vztahu k jiným vesmíným objektům (planety, užice ) - Zemi považujme za homoenní kouli o poloměu R 6378 km a hmotnosti M 5,98. 4 k VE SKUTEČNOSTI: Země má tva blízký otačnímu elipsoiu hlavní poloosa (ovníkový polomě) 6378 km velejší poloosa (polání polomě) 6357 km Země není homoenní hustota oste směem o střeu Země hmotnost Země 5, k stření hustota Země 55 k.m -3
16 GRAVITAČNÍ ZRYCHLENÍ - avitační zychlení klesá s namořskou výškou (zvětšuje se vzálenost o střeu Země) - v namořské výšce h je vzálenost o střeu Země R + h M M M a κ κ κ + R ( R + h) R ( R h) a a + h R poku je h pp R a a + h R a h R a M κ R Pozn.: Ve výšce h 3,8 km je avitační zychlení jen o pomile menší než při hlaině moře ( ) a
17 POTENCIÁLNÍ ENERGIE TĚLES V GRAVITAČNÍM POLI ZEMĚ -mějme těleso o hmotnosti m ve vzálenosti o střeu Země - hmotnost Země ozn. M, polomě R A) na povchu Země: E P M m κ R E P M m κ B) ve výšce h na povchem Země: E M m κ P R + h páce vnější síly potřebná k vyzvenutí tělesa z povchu Země o výšky h (přemisťujeme poti avitační síle): W E p E M m κ R + h M m + κ R p κ M m R R + h
18 po h << R je páce: M m M m h M mh W κ κ + κ R h R R R + R M R použijeme-li vztah po avitační zychlení a κ páce vnějších sil: W ma h platí po malé namořské výšky
19 PŘÍKLAD: Jakou ychlostí musíme vypustit těleso z povchu Země, aby vystoupilo o výšky ovné poloměu Země?
20 TÍHOVÉ POLE ZEMĚ -ve vztahu k tělesům na povchu esp. v blízkosti povchu Země -komě avitační síly působí na tělesa o hmotnosti m síla setvačná F F S F o FS man mω F S mrω cos β Rcos β -tíhové pole Země je složené z avitačního pole Země a pole setvačných (ostřeivých) sil F G - výslenice sil působících na těleso na Zemi: F + F F G S F... tíhová síla, m je tíhové zychlení G F G smě tíhové síly efinuje svislý smě
21 TÍHOVÉ ZRYCHLENÍ tíhové zychlení závisí na namořské výšce i zeměpisné šířce: tíhové zychlení klesá s namořskou výškou tíhová síla klesá s namořskou výškou stejně jako tíhové zychlení F G m maximální je na zemských pólech (9,83 m.s - při hlaině moře) minimální je na ovníku (9,78 m.s - při hlaině moře) závislost je ána tvaem zemského elipsoiu a otací Země tíhové zychlení je vektoovým součtem avitačního zychlení a zychlení setvačného a + a s
22 POHYBY TĚLES V RADIÁLNÍM GRAVITAČNÍM POLI ZEMĚ - pohyby aketových střel, umělých užic Země, kosmických loí - poél tajektoie těchto těles se mění velikost i smě intenzity avitačního pole i avitačního zychlení - zanebáváme vliv avitačního pole Slunce, Měsíce a planet PRVNÍ KOSMICKÁ RYCHLOST (KRUHOVÁ RYCHLOST) ychlost, kteou musí mít těleso aby mohlo tvale obíhat kolem Země po kuhové áze o poloměu R + h opo vzuchu zanebáváme ostřeivá síla potřebná k užení ovnoměného pohybu po kužnici je ána avitační silou: mv M m κ pvní kosmická ychlost: v I M κ M κ R R R + h a R R + h -po přípa h<< R v I a R - 7,9 km.s
23 DRUHÁ KOSMICKÁ RYCHLOST (PARABOLICKÁ, ÚNIKOVÁ) - ychlost, kteou je třeba uělit tělesu ve výšce h, aby opustilo sféu zemské přitažlivosti -přepoklááme, že se těleso má vzálit o nekonečna (ke je potenciální eneie tělesa nulová) - ze zákona zachování mechanické eneie - otu platí: v a mv R R + h EP E II h P M m κ, po je v II, km.s - TŘETÍ KOSMICKÁ RYCHLOST (HYPERBOLICKÁ RYCHLOST) tajektoií užice je hypebola těleso opouští avitační pole Země a stává se umělou užicí Slunce, poku není její ychlost ostatečná k opuštění avitačního pole Slunce za přepoklau, že užici vypouštíme ve směu ychlosti, kteou obíhá Země kolem Slunce - v III 6,7 km.s
24
25 PŘÍKLAD:
26 POHYBY TĚLES V HOMOGENNÍM TÍHOVÉM POLI ZEMĚ - paamety tajektoie vženého tělesa malé ve sovnání s ozměy Země - tíhové zychlení je poél celé tajektoie tělesa konstantní - pohybová ovnice volného HB: ( ) F ma mv t -vyjáření pomocí souřanic: z z z y y y x x x F t z m t v m m a F t y m t v m a m F t x m t v m a m
27 VOLBA SOUSTAVY SOUŘADNIC: počátek vpočáteční poloze HB vekto počáteční ychlosti leží v ovině XY úhel, kteý svíá vekto ychlosti s klaným směem osy X je tzv. elevační úhel (úhel vhu) Pole počátečních pomínek pohybu ostáváme tyto přípay: volný pá vh svislý olů vh svislý vzhůu vh vooovný vh šikmý vzhůu souřanice síly ve zvolené soustavě souřanic: Fx F y m F z
28 Dosazení souřanic síly o pohybových ovnic: v x t, y t, souřanice ychlosti: y z 3 z t x k v t + k, v, k inteujeme inteační konstanty souřanice počáteční ychlosti v x v cosα, v y v sinα, v z souřanice polohy HB: x v x t + c, y t + v y t + c, z v z t + c3 inteační konstanty souřanice počáteční polohy HB x y, z, osaďme inteační konstanty inteujeme x v t, y t + v y t z v x, z t
29 A) VOLNÝ PÁD - ovnoměně zychlený pohyb s nulovou počáteční ychlostí - pohyb ve směu osy y x y v okamžitá ychlost: souřanice velikost v y t v souřanice HB y t, x t inteujeme B) VRH SVISLÝ DOLŮ - ovnoměně zychlený pohyb s nenulovou počáteční ychlostí -pohyb ve směu osy y x y v y v okamžitá ychlost: souřanice velikost v y v t v v + t inteujeme souřanice HB y v t t, x
30 C) VRH SVISLÝ VZHŮRU - ovnoměně zpomalený pohyb s nenulovou počáteční ychlostí - pohyb ve směu osy y x y v y v okamžitá ychlost v vy v t souřanice HB y v t t, x inteujeme oba výstupu po výška výstupu h v okamžiku opau v v y v v t h y celková oba vhu v t c
31 -pohyb v ovině xy -tajektoií je paabola -počáteční ychlost má smě osy x, úhel D) VRH VODOROVNÝ α -těleso se nachází na počátku na ose y ve výšce h x y h ( ), okamžitá ychlost v x v, v y t souřanice HB x y v t h t inteujeme x y h v vyloučením času z ovnic po souřanice HB oba vhu (po y ) h t s álka vhu (maximální x-ová souřanice) s v h velikost celkové ychlosti + v v h
32 E) VRH ŠIKMÝ VZHŮRU - pohyb v ovině xy, tajektoií je paabola -při uplatnění opou postřeí je tajektoií balistická křivka π -počáteční ychlost v svíá s osou x elevační úhel p α p -na počátku je hmotný bo v počátku soustavy souřanic x y okamžitá ychlost v v x y v v x v cosα sinα cos souřanice HB y vt sinα t y x t t α x α v cos oba výstupu (souřanice vcholu paaboly) po v y t α t h v α sin inteujeme vyloučení času obecná ovnice tajektoie
33 výška výstupu y h v sin α álka vhu po y celková oba vhu t s x s v v sinα sin α velikost okamžité ychlosti v vx + vy v y
34 závislost tvau tajektoie na elevačním úhlu vhu závislost tvau tajektoie na opou postřeí bez opou postřeí paabola balistická křivka
1.7. Mechanické kmitání
 1.7. Mechanické kmitání. 1. Umět vysvětlit princip netlumeného kmitavého pohybu.. Umět srovnat periodický kmitavý pohyb s periodickým pohybem po kružnici. 3. Znát charakteristické veličiny periodického
1.7. Mechanické kmitání. 1. Umět vysvětlit princip netlumeného kmitavého pohybu.. Umět srovnat periodický kmitavý pohyb s periodickým pohybem po kružnici. 3. Znát charakteristické veličiny periodického
MECHANICKÁ PRÁCE A ENERGIE
 MECHANICKÁ RÁCE A ENERGIE MECHANICKÁ RÁCE Konání práce je podmíněno silovým působením a pohybem Na čem závisí velikost vykonané práce Snadno určíme práci pro případ F s ráci nekonáme, pokud se těleso nepřemísťuje
MECHANICKÁ RÁCE A ENERGIE MECHANICKÁ RÁCE Konání práce je podmíněno silovým působením a pohybem Na čem závisí velikost vykonané práce Snadno určíme práci pro případ F s ráci nekonáme, pokud se těleso nepřemísťuje
Gravitační pole texty Jan Hrnčíř, Martin Klejch, 2005. Gravitační pole. Využití multimédií při výuce fyziky. Texty k multimediální prezentaci
 Gravitační pole Využití multimédií při výuce fyziky Texty k multimediální prezentaci Jan Hrnčíř jan.hrncir@gfxs.cz Martin Klejch martin.klejch@gfxs.cz Gymnázium F. X. Šaldy Liberec Obsah Obsah... 1 1.
Gravitační pole Využití multimédií při výuce fyziky Texty k multimediální prezentaci Jan Hrnčíř jan.hrncir@gfxs.cz Martin Klejch martin.klejch@gfxs.cz Gymnázium F. X. Šaldy Liberec Obsah Obsah... 1 1.
souřadné systémy geometrické určení polohy pevně spojené se vztažným tělesem
 souřadné systémy geometrické určení polohy pevně spojené se vztažným tělesem kartézský souřadný systém Z Y X kartézský souřadný systém Z Y X kartézský souřadný systém Z x y Y X kartézský souřadný systém
souřadné systémy geometrické určení polohy pevně spojené se vztažným tělesem kartézský souřadný systém Z Y X kartézský souřadný systém Z Y X kartézský souřadný systém Z x y Y X kartézský souřadný systém
Otázka 17. 17.1 Základy vyzařování elektromagnetických vln
 Otázka 17 Základy vyzařování elektomagnetických vln, přehled základních duhů antén a jejich základní paamety (vstupní impedance, směový diagam, zisk) liniové, plošné, eflektoové stuktuy, anténní řady.
Otázka 17 Základy vyzařování elektomagnetických vln, přehled základních duhů antén a jejich základní paamety (vstupní impedance, směový diagam, zisk) liniové, plošné, eflektoové stuktuy, anténní řady.
Mechanismy. Vazby členů v mechanismech (v rovině):
 Mechanismy Mechanismus klikový, čtyřkloubový, kulisový, západkový a vačkový jsou nejčastějšími mechanismy ve strojích (kromě převodů). Mechanismy obsahují členy (kliky, ojnice, těhlice, křižáky a další).
Mechanismy Mechanismus klikový, čtyřkloubový, kulisový, západkový a vačkový jsou nejčastějšími mechanismy ve strojích (kromě převodů). Mechanismy obsahují členy (kliky, ojnice, těhlice, křižáky a další).
Měření momentu setrvačnosti z doby kmitu
 Úloha č. 4 Měření momentu setrvačnosti z doby kmitu Úkoly měření:. Určete moment setrvačnosti vybraných těles, kruhové a obdélníkové desky.. Stanovení momentu setrvačnosti proveďte s využitím dvou rozdílných
Úloha č. 4 Měření momentu setrvačnosti z doby kmitu Úkoly měření:. Určete moment setrvačnosti vybraných těles, kruhové a obdélníkové desky.. Stanovení momentu setrvačnosti proveďte s využitím dvou rozdílných
Zobrazení v rovině je předpis, který každému bodu X roviny připisuje právě jeden bod X roviny. Bod X se nazývá vzor, bod X se nazývá obraz.
 7. Shodná zobrazení 6. ročník 7. Shodná zobrazení 7.1. Shodnost geometrických obrazců Zobrazení v rovině je předpis, který každému bodu X roviny připisuje právě jeden bod X roviny. Bod X se nazývá vzor,
7. Shodná zobrazení 6. ročník 7. Shodná zobrazení 7.1. Shodnost geometrických obrazců Zobrazení v rovině je předpis, který každému bodu X roviny připisuje právě jeden bod X roviny. Bod X se nazývá vzor,
Řešení úloh 1. kola 50. ročníku fyzikální olympiády. Kategorie D
 Řešení úloh 1. kola 50. ročníku fyzikální olympiády. Kategorie D Autořiúloh:J.Jírů(2,3,4,5,6),M.Jarešová,I.Volf(1),V.Vícha(7) 1.a) Dráha s 1,nakterésecyklistarozjíždí,jedánavztahem s 1 1 2 v1t11 2 24 3,6
Řešení úloh 1. kola 50. ročníku fyzikální olympiády. Kategorie D Autořiúloh:J.Jírů(2,3,4,5,6),M.Jarešová,I.Volf(1),V.Vícha(7) 1.a) Dráha s 1,nakterésecyklistarozjíždí,jedánavztahem s 1 1 2 v1t11 2 24 3,6
7.8 Kosmická loď o délce 100 m letí kolem Země a jeví se pozorovateli na Zemi zkrácena na 50 m. Jak velkou rychlostí loď letí?
 7. Speciální teorie relativity 7.1 Kosmonaut v kosmické lodi, přibližující se stálou rychlostí 0,5c k Zemi, vyšle směrem k Zemi světelný signál. Jak velká je rychlost signálu a) vzhledem k Zemi, b) vzhledem
7. Speciální teorie relativity 7.1 Kosmonaut v kosmické lodi, přibližující se stálou rychlostí 0,5c k Zemi, vyšle směrem k Zemi světelný signál. Jak velká je rychlost signálu a) vzhledem k Zemi, b) vzhledem
Kótování na strojnických výkresech 1.část
 Kótování na strojnických výkresech 1.část Pro čtení výkresů, tj. určení rozměrů nebo polohy předmětu, jsou rozhodující kóty. Z tohoto důvodu je kótování jedna z nejzodpovědnějších prací na technických
Kótování na strojnických výkresech 1.část Pro čtení výkresů, tj. určení rozměrů nebo polohy předmětu, jsou rozhodující kóty. Z tohoto důvodu je kótování jedna z nejzodpovědnějších prací na technických
Výsledky zpracujte do tabulek a grafů; v pracovní oblasti si zvolte bod a v tomto bodě vypočítejte diferenciální odpor.
 ZADÁNÍ: Změřte VA charakteristiky polovodičových prvků: 1) D1: germaniová dioda 2) a) D2: křemíková dioda b) D2+R S : křemíková dioda s linearizačním rezistorem 3) D3: výkonnová křemíková dioda 4) a) D4:
ZADÁNÍ: Změřte VA charakteristiky polovodičových prvků: 1) D1: germaniová dioda 2) a) D2: křemíková dioda b) D2+R S : křemíková dioda s linearizačním rezistorem 3) D3: výkonnová křemíková dioda 4) a) D4:
1 NÁPRAVA De-Dion Představuje přechod mezi tuhou nápravou a nápravou výkyvnou. Používá se (výhradně) jako náprava hnací.
 1 NÁPRAVA De-Dion Představuje přechod mezi tuhou nápravou a nápravou výkyvnou. Používá se (výhradně) jako náprava hnací. Skříň rozvodovky spojena s rámem zmenšení neodpružené hmoty. Přenos točivého momentu
1 NÁPRAVA De-Dion Představuje přechod mezi tuhou nápravou a nápravou výkyvnou. Používá se (výhradně) jako náprava hnací. Skříň rozvodovky spojena s rámem zmenšení neodpružené hmoty. Přenos točivého momentu
MODUL 3. ELEKTROMAGNETICKÉ POLE
 MODUL 3. ELEKTROMAGNETICKÉ POLE 3.1. ELEKTROSTATIKA 3.1.1. ELEKTRICKÝ NÁBOJ SHRNUTÍ Stavební jednotkou látky je atom. Skládá se z protonů, elektronů a neutronů. Elektrony a protony jsou nositeli elementárního
MODUL 3. ELEKTROMAGNETICKÉ POLE 3.1. ELEKTROSTATIKA 3.1.1. ELEKTRICKÝ NÁBOJ SHRNUTÍ Stavební jednotkou látky je atom. Skládá se z protonů, elektronů a neutronů. Elektrony a protony jsou nositeli elementárního
CVIČENÍ č. 8 BERNOULLIHO ROVNICE
 CVIČENÍ č. 8 BERNOULLIHO ROVNICE Výtok z nádoby, Průtok potrubím beze ztrát Příklad č. 1: Z injekční stříkačky je skrze jehlu vytlačovaná voda. Průměr stříkačky je D, průměr jehly d. Určete výtokovou rychlost,
CVIČENÍ č. 8 BERNOULLIHO ROVNICE Výtok z nádoby, Průtok potrubím beze ztrát Příklad č. 1: Z injekční stříkačky je skrze jehlu vytlačovaná voda. Průměr stříkačky je D, průměr jehly d. Určete výtokovou rychlost,
 1. Člun o hmotnosti m = 50 kg startuje kolmo ke břehu a pohybuje se dále v tomto směru konstantní rychlostí v 0 = 2 m.s -1 vůči vodě. Současně je unášen podél břehu proudem vody, který na něj působí silou
1. Člun o hmotnosti m = 50 kg startuje kolmo ke břehu a pohybuje se dále v tomto směru konstantní rychlostí v 0 = 2 m.s -1 vůči vodě. Současně je unášen podél břehu proudem vody, který na něj působí silou
Kritická síla imperfektovaných systémů
 Kritická síla imperfektovaných systémů Petr Frantík 1, Jiří Macur 2 Úvod V minulém století nově vzniklé obory, opírající se o studium silně nelineárních systémů, jako jsou teorie katastrof, teorie bifurkací
Kritická síla imperfektovaných systémů Petr Frantík 1, Jiří Macur 2 Úvod V minulém století nově vzniklé obory, opírající se o studium silně nelineárních systémů, jako jsou teorie katastrof, teorie bifurkací
L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATEDRA FYZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméno TUREČEK Daniel Datum měření 3..6 Stud. rok 6/7 Ročník. Datum odevzdání 3..7 Stud. skupina 3 Lab.
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATEDRA FYZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméno TUREČEK Daniel Datum měření 3..6 Stud. rok 6/7 Ročník. Datum odevzdání 3..7 Stud. skupina 3 Lab.
Název materiálu: Počasí a podnebí - opakování
 Základní škola Nový Bor, náměstí Míru 128, okres Česká Lípa, příspěvková organizace e-mail: info@zsnamesti.cz; www.zsnamesti.cz; telefon: 487 722 010; fax: 487 722 378 Registrační číslo: CZ.1.07/1.4.00/21.3267
Základní škola Nový Bor, náměstí Míru 128, okres Česká Lípa, příspěvková organizace e-mail: info@zsnamesti.cz; www.zsnamesti.cz; telefon: 487 722 010; fax: 487 722 378 Registrační číslo: CZ.1.07/1.4.00/21.3267
3. Dynamika. Obecné odvození: a ~ F a ~ m. Zrychlení je přímo úměrné F a nepřímo úměrné m. 3. 2. 1 Výpočet síly a stanovení jednotky newton. F = m.
 3. Dynamika Zabývá se říčinou ohybu (jak vzniká a jak se udržuje). Vše se odehrávalo na základě řesných okusů, vše shrnul Isac Newton v díle Matematické základy fyziky. Z díla vylývají 3 ohybové zákony.
3. Dynamika Zabývá se říčinou ohybu (jak vzniká a jak se udržuje). Vše se odehrávalo na základě řesných okusů, vše shrnul Isac Newton v díle Matematické základy fyziky. Z díla vylývají 3 ohybové zákony.
7. Odraz a lom. 7.1 Rovinná rozhraní dielektrik - základní pojmy
 Trivium z optiky 45 7 draz a lom V této kapitole se budeme zabývat průchodem (lomem) a odrazem světla od rozhraní dvou homogenních izotropních prostředí Pro jednoduchost se omezíme na rozhraní rovinná
Trivium z optiky 45 7 draz a lom V této kapitole se budeme zabývat průchodem (lomem) a odrazem světla od rozhraní dvou homogenních izotropních prostředí Pro jednoduchost se omezíme na rozhraní rovinná
ÚLOHY Z ELEKTŘINY A MAGNETIZMU SADA 2
 ÚLOHY Z ELEKTŘINY A MAGNETIZMU SADA Peter Dourmashkin MIT 6, překla: Vítězslav Kříha (7) Obsah SADA ÚLOHA 1: HLOUPÉ KONÍČKY ÚLOHA : BEN FRANKLIN ÚLOHA 3: ODPUZOVÁNÍ TYČÍ ÚLOHA 4: DIPÓL 3 ÚLOHA 5: KULOVÁ
ÚLOHY Z ELEKTŘINY A MAGNETIZMU SADA Peter Dourmashkin MIT 6, překla: Vítězslav Kříha (7) Obsah SADA ÚLOHA 1: HLOUPÉ KONÍČKY ÚLOHA : BEN FRANKLIN ÚLOHA 3: ODPUZOVÁNÍ TYČÍ ÚLOHA 4: DIPÓL 3 ÚLOHA 5: KULOVÁ
c sin Příklad 2 : v trojúhelníku ABC platí : a = 11,6 dm, c = 9 dm, α = 65 0 30. Vypočtěte stranu b a zbývající úhly.
 9. Úvod do středoškolského studia - rozšiřující učivo 9.. Další znalosti o trojúhelníku 9... Sinova věta a = sin b = sin c sin Příklad : V trojúhelníku BC platí : c = 0 cm, α = 45 0, β = 05 0. Vypočtěte
9. Úvod do středoškolského studia - rozšiřující učivo 9.. Další znalosti o trojúhelníku 9... Sinova věta a = sin b = sin c sin Příklad : V trojúhelníku BC platí : c = 0 cm, α = 45 0, β = 05 0. Vypočtěte
Posouzení únosnosti svaru se provádí podle zásad pružnosti a pevnosti v nebezpečném průřezu.
 Svarové spoje Posouzení únosnosti svaru se provádí podle zásad pružnosti a pevnosti v nebezpečném průřezu. Vybrané druhy svarů a jejich posouzení dle EN ČSN 1993-1-8. Koutový svar -T-spoj - přeplátovaný
Svarové spoje Posouzení únosnosti svaru se provádí podle zásad pružnosti a pevnosti v nebezpečném průřezu. Vybrané druhy svarů a jejich posouzení dle EN ČSN 1993-1-8. Koutový svar -T-spoj - přeplátovaný
E l e k t r o t e c h n i k a a i n f o r m a t i k a
 Varianta A Strana: 1/4 Osobní íslo uchaze e: Celkem bo : Test k p ijímacímu ízení ke stuiu na Fakult elektrotechnické Zápao eské univerzity v Plzni E l e k t r o t e c h n i k a a i n f o r m a t i k a
Varianta A Strana: 1/4 Osobní íslo uchaze e: Celkem bo : Test k p ijímacímu ízení ke stuiu na Fakult elektrotechnické Zápao eské univerzity v Plzni E l e k t r o t e c h n i k a a i n f o r m a t i k a
na tyč působit moment síly M, určený ze vztahu (9). Periodu kmitu T tohoto kyvadla lze určit ze vztahu:
 Úloha Autoři Zaměření FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE 2. Měření modulu pružnosti v tahu a modulu pružnosti ve smyku Martin Dlask Měřeno 11. 10., 18. 10., 25. 10. 2012 Jakub Šnor SOFE Klasifikace
Úloha Autoři Zaměření FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE 2. Měření modulu pružnosti v tahu a modulu pružnosti ve smyku Martin Dlask Měřeno 11. 10., 18. 10., 25. 10. 2012 Jakub Šnor SOFE Klasifikace
TECHNICKÁ UNIVERZITA V LIBERCI
 TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Základy paprskové a vlnové optiky, optická vlákna, Učební text Ing. Bc. Jiří Primas Liberec 2011 Materiál vznikl
TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Základy paprskové a vlnové optiky, optická vlákna, Učební text Ing. Bc. Jiří Primas Liberec 2011 Materiál vznikl
Lineární algebra. Vektorové prostory
 Lineární algebra Vektorové prostory Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo projektu:
Lineární algebra Vektorové prostory Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo projektu:
6. přednáška z předmětu GIS1 Souřadnicové systémy a transformace mezi nimi
 6. přednáška z předmětu GIS1 Souřadnicové systémy a transformace mezi nimi Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Pro přednášku byly použity texty a obrázky od Ing. Magdaleny Čepičkové
6. přednáška z předmětu GIS1 Souřadnicové systémy a transformace mezi nimi Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Pro přednášku byly použity texty a obrázky od Ing. Magdaleny Čepičkové
4.5.1 Magnety, magnetické pole
 4.5.1 Magnety, magnetické pole Předpoklady: 4101 Pomůcky: magnety, kancelářské sponky, papír, dřevěná dýha, hliníková kulička, měděná kulička (drát), železné piliny, papír, jehla (špendlík), korek (kus
4.5.1 Magnety, magnetické pole Předpoklady: 4101 Pomůcky: magnety, kancelářské sponky, papír, dřevěná dýha, hliníková kulička, měděná kulička (drát), železné piliny, papír, jehla (špendlík), korek (kus
Úkol č. 1: Změřte dynamickou viskozitu denaturovaného lihu a stolního oleje Ubbelohdeho viskozimetrem.
 Měření dynamické viskozity kapalin Měření dynamické viskozity kapalin Úkol č : Změřte dynamickou viskozitu denatuovaného lihu a stolního oleje Ubbelohdeho viskozimetem Pomůcky Ubbelohdeův viskozimet, vodní
Měření dynamické viskozity kapalin Měření dynamické viskozity kapalin Úkol č : Změřte dynamickou viskozitu denatuovaného lihu a stolního oleje Ubbelohdeho viskozimetem Pomůcky Ubbelohdeův viskozimet, vodní
ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ
 ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ Pozemkem se podle 2 písm. a) katastrálního zákona rozumí část zemského povrchu, a to část taková, která je od sousedních částí zemského povrchu (sousedních pozemků)
ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ Pozemkem se podle 2 písm. a) katastrálního zákona rozumí část zemského povrchu, a to část taková, která je od sousedních částí zemského povrchu (sousedních pozemků)
(3) Zvolíme pevné z a sledujme dráhu, kterou opisuje s postupujícím časem koncový bod vektoru E v rovině z = konst. Upravíme vztahy (2) a (3)
 Učební tet k přednášce UFY1 Předpokládejme šíření rovinné harmonické vln v kladném směru os z. = i + j kde i, j jsou jednotkové vektor ve směru os respektive a cos ( ) ω ϕ t kz = + () = cos( ωt kz+ ϕ )
Učební tet k přednášce UFY1 Předpokládejme šíření rovinné harmonické vln v kladném směru os z. = i + j kde i, j jsou jednotkové vektor ve směru os respektive a cos ( ) ω ϕ t kz = + () = cos( ωt kz+ ϕ )
Jan Březina. Technical University of Liberec. 17. března 2015
 TGH03 - stromy, ukládání grafů Jan Březina Technical University of Liberec 17. března 2015 Kružnice - C n V = {1, 2,..., n} E = {{1, 2}, {2, 3},..., {i, i + 1},..., {n 1, n}, {n, 1}} Cesta - P n V = {1,
TGH03 - stromy, ukládání grafů Jan Březina Technical University of Liberec 17. března 2015 Kružnice - C n V = {1, 2,..., n} E = {{1, 2}, {2, 3},..., {i, i + 1},..., {n 1, n}, {n, 1}} Cesta - P n V = {1,
3.1.5 Energie II. Předpoklady: 010504. Pomůcky: mosazná kulička, pingpongový míček, krabička od sirek, pružina, kolej,
 3.1.5 Energie II Předpoklady: 010504 Pomůcky: mosazná kulička, pingpongový míček, krabička od sirek, pružina, kolej, Př. 1: Při pokusu s odrazem míčku se během odrazu zdá, že se energie míčku "někam ztratila".
3.1.5 Energie II Předpoklady: 010504 Pomůcky: mosazná kulička, pingpongový míček, krabička od sirek, pružina, kolej, Př. 1: Při pokusu s odrazem míčku se během odrazu zdá, že se energie míčku "někam ztratila".
1.4.5 Rotující vztažné soustavy II
 145 Rotující ztažné soustay II Předpoklady: 1404 Vátíme se zpátky na pouť Př 1: Nakesli síly, kteé působí na tatínka z pohledu chlapce na kolotoči Vysětlují tyto síly jeho pohyb? F p F o F g Na tatínka
145 Rotující ztažné soustay II Předpoklady: 1404 Vátíme se zpátky na pouť Př 1: Nakesli síly, kteé působí na tatínka z pohledu chlapce na kolotoči Vysětlují tyto síly jeho pohyb? F p F o F g Na tatínka
Předmětem dražby jsou nemovité věci ve vlastnictví povinného, a to:
 Č.j. 198EX 13/06-121 Pův. sp. zn.: 59EX 13/06 Sp.zn.opr.: 1306 U s n e s e n í Mgr. Jaroslava Schafferová, soudní exekutor Exekutorského úřadu Brno venkov jmenovaný na základě rozhodnutí ministra spravedlnosti
Č.j. 198EX 13/06-121 Pův. sp. zn.: 59EX 13/06 Sp.zn.opr.: 1306 U s n e s e n í Mgr. Jaroslava Schafferová, soudní exekutor Exekutorského úřadu Brno venkov jmenovaný na základě rozhodnutí ministra spravedlnosti
1.2.5 Reálná čísla I. Předpoklady: 010204
 .2.5 Reálná čísla I Předpoklady: 00204 Značíme R. Reálná čísla jsou čísla, kterými se vyjadřují délky úseček, čísla jim opačná a 0. Každé reálné číslo je na číselné ose znázorněno právě jedním bodem. Každý
.2.5 Reálná čísla I Předpoklady: 00204 Značíme R. Reálná čísla jsou čísla, kterými se vyjadřují délky úseček, čísla jim opačná a 0. Každé reálné číslo je na číselné ose znázorněno právě jedním bodem. Každý
(k 1)x k + 1. pro k 1 a x = 0 pro k = 1.
 . Funkce dvou a více proměnných. Úvod. Určete definiční obor funkce a proveďte klasifikaci bodů z R vzhledem k a rozhodněte zda je množina uzavřená či otevřená. Určete a načrtněte vrstevnice grafu funkce
. Funkce dvou a více proměnných. Úvod. Určete definiční obor funkce a proveďte klasifikaci bodů z R vzhledem k a rozhodněte zda je množina uzavřená či otevřená. Určete a načrtněte vrstevnice grafu funkce
UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE
 MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin
Elektrické. MP - Ampérmetr A U I R. Naměřená hodnota proudu 5 A znamená, že měřená veličina je 5 x větší než jednotka - A
 Elektrické měření definice.: Poznávací proces jehož prvořadým cílem je zjištění: výskytu a velikosti (tzv. kvantifikace) měřené veličiny při využívání známých fyzikálních jevů a zákonů. MP - mpérmetr R
Elektrické měření definice.: Poznávací proces jehož prvořadým cílem je zjištění: výskytu a velikosti (tzv. kvantifikace) měřené veličiny při využívání známých fyzikálních jevů a zákonů. MP - mpérmetr R
Numerická integrace. 6. listopadu 2012
 Numerická integrace Michal Čihák 6. listopadu 2012 Výpočty integrálů v praxi V přednáškách z matematické analýzy jste se seznámili s mnoha metodami výpočtu integrálů. V praxi se ale poměrně často můžeme
Numerická integrace Michal Čihák 6. listopadu 2012 Výpočty integrálů v praxi V přednáškách z matematické analýzy jste se seznámili s mnoha metodami výpočtu integrálů. V praxi se ale poměrně často můžeme
14. Základy elektrostatiky
 4. Základy elektostatiky lektostatické pole existuje kolem všech elekticky nabitých tles. Tato tlesa na sebe vzájemn jeho postednictvím psobí. lektický náboj dva významy: a) vyjaduje stav elekticky nabitých
4. Základy elektostatiky lektostatické pole existuje kolem všech elekticky nabitých tles. Tato tlesa na sebe vzájemn jeho postednictvím psobí. lektický náboj dva významy: a) vyjaduje stav elekticky nabitých
Fakulta strojního inženýrství VUT v Brně Ústav konstruování. KONSTRUOVÁNÍ STROJŮ mechanismy. Přednáška 8
 Fakulta strojního inženýrství VUT v Brně Ústav konstruování KONSTRUOVÁNÍ STROJŮ mechanismy Přednáška 8 Převody s korigovanými ozubenými koly Obsah Převody s korigovanými ozubenými koly Výroba ozubení odvalováním
Fakulta strojního inženýrství VUT v Brně Ústav konstruování KONSTRUOVÁNÍ STROJŮ mechanismy Přednáška 8 Převody s korigovanými ozubenými koly Obsah Převody s korigovanými ozubenými koly Výroba ozubení odvalováním
Newtonův gravitační zákon Gravitační a tíhové zrychlení při povrchu Země Pohyby těles Gravitační pole Slunce
 Gavitační pole Newtonův gavitační zákon Gavitační a tíhové zychlení při povchu Země Pohyby těles Gavitační pole Slunce Úvod V okolí Země existuje gavitační pole. Země působí na každé těleso ve svém okolí
Gavitační pole Newtonův gavitační zákon Gavitační a tíhové zychlení při povchu Země Pohyby těles Gavitační pole Slunce Úvod V okolí Země existuje gavitační pole. Země působí na každé těleso ve svém okolí
MECHANICKÉ KMITÁNÍ A VLNĚNÍ
 Modularizace a modernizace studijního programu počáteční přípravy učitele fyziky Studijní modul MECHANICKÉ KMITÁNÍ A VLNĚNÍ Oldřich Lepil Olomouc 01 Zpracováno v rámci řešení projektu Evropského sociálního
Modularizace a modernizace studijního programu počáteční přípravy učitele fyziky Studijní modul MECHANICKÉ KMITÁNÍ A VLNĚNÍ Oldřich Lepil Olomouc 01 Zpracováno v rámci řešení projektu Evropského sociálního
MECHANIKA TUHÉ TĚLESO
 Projekt Efektivní Učení Reformou oblastí gymnaziálního vzělávání je spolufinancován Evropským sociálním fonem a státním rozpočtem České republiky. Implementace ŠVP MECHANIKA TUHÉ TĚLESO Učivo - Tuhé těleso
Projekt Efektivní Učení Reformou oblastí gymnaziálního vzělávání je spolufinancován Evropským sociálním fonem a státním rozpočtem České republiky. Implementace ŠVP MECHANIKA TUHÉ TĚLESO Učivo - Tuhé těleso
Geometrická optika 1
 Geometrická optika 1 Popis pomocí světelných paprsků těmi se šíří energie a informace, zanedbává vlnové vlastnosti světla světelný paprsek = přímka, podél níž se šíří světlo, jeho energie index lomu (základní
Geometrická optika 1 Popis pomocí světelných paprsků těmi se šíří energie a informace, zanedbává vlnové vlastnosti světla světelný paprsek = přímka, podél níž se šíří světlo, jeho energie index lomu (základní
Goniometrie trigonometrie
 Goniometrie trigonometrie Goniometrie se zabývá funkcemi sinus, kosinus, tangens, kotangens (goniometrické funkce). V tomto článku se budeme zabývat trigonometrií (součást goniometrie) používáním goniometrických
Goniometrie trigonometrie Goniometrie se zabývá funkcemi sinus, kosinus, tangens, kotangens (goniometrické funkce). V tomto článku se budeme zabývat trigonometrií (součást goniometrie) používáním goniometrických
SYLABUS PŘEDNÁŠKY 6b Z INŽENÝRSKÉ GEODÉZIE (Polohové vytyčování) 4. ročník bakalářského studia studijní program G studijní obor G
 SYLABUS PŘEDNÁŠKY 6b Z INŽENÝRSKÉ GEODÉZIE (Polohové vytyčování) 4. ročník bakalářského studia studijní program G studijní obor G říjen 2014 1 1O POLOHOVÉ VYTYČOVÁNÍ Pod pojem polohového vytyčování se
SYLABUS PŘEDNÁŠKY 6b Z INŽENÝRSKÉ GEODÉZIE (Polohové vytyčování) 4. ročník bakalářského studia studijní program G studijní obor G říjen 2014 1 1O POLOHOVÉ VYTYČOVÁNÍ Pod pojem polohového vytyčování se
Krajské kolo Fyzikální olympiády 53. ročník kategorie E
 Školská fyzika 01/4 Na pomoc FO Krajské kolo Fyzikální olympiády 53. ročník kategorie E Ivo olf, Pavel Kabrhel 1, Ústřední komise Fyzikální olympiády, niverzita Hradec Králové Krajské kolo Fyzikální olympiády
Školská fyzika 01/4 Na pomoc FO Krajské kolo Fyzikální olympiády 53. ročník kategorie E Ivo olf, Pavel Kabrhel 1, Ústřední komise Fyzikální olympiády, niverzita Hradec Králové Krajské kolo Fyzikální olympiády
MATEMATIKA I VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ JIŘÍ NOVOTNÝ ZÁKLADY LINEÁRNÍ ALGEBRY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ JIŘÍ NOVOTNÝ MATEMATIKA I ZÁKLADY LINEÁRNÍ ALGEBRY STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Typeset by L A TEX 2ε, Podpořeno projektem
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ JIŘÍ NOVOTNÝ MATEMATIKA I ZÁKLADY LINEÁRNÍ ALGEBRY STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Typeset by L A TEX 2ε, Podpořeno projektem
Normalizace fyzikálních veličin pro číslicové zpracování
 Noralzace fyzkálních velčn pro číslcové zpracování Vypracoval: Petr Kaaník Aktualzace: 15. října 2003 Kažý realzovaný říící systé usel projít vě hlavní stá. Nejprve je to vlastní návrh. Na záklaě ostupných
Noralzace fyzkálních velčn pro číslcové zpracování Vypracoval: Petr Kaaník Aktualzace: 15. října 2003 Kažý realzovaný říící systé usel projít vě hlavní stá. Nejprve je to vlastní návrh. Na záklaě ostupných
Příloha č. 3 VÝKONOVÉ UKAZATELE
 Příloha č. 3 VÝKONOVÉ UKAZATELE OBSAH 0. ÚVODNÍ USTANOVENÍ... 3 0.1. Vymezení obsahu přílohy... 3 0.2. Způsob vedení evidencí... 3 0.3. Hodnocené období... 4 1. VÝKONOVÉ UKAZATELE ODPADNÍ VODA... 5 1.1.
Příloha č. 3 VÝKONOVÉ UKAZATELE OBSAH 0. ÚVODNÍ USTANOVENÍ... 3 0.1. Vymezení obsahu přílohy... 3 0.2. Způsob vedení evidencí... 3 0.3. Hodnocené období... 4 1. VÝKONOVÉ UKAZATELE ODPADNÍ VODA... 5 1.1.
Analýza oběžného kola
 Vysoká škola báňská Technická univerzita 2011/2012 Analýza oběžného kola Radomír Bělík, Pavel Maršálek, Gȕnther Theisz Obsah 1. Zadání... 3 2. Experimentální měření... 4 2.1. Popis měřené struktury...
Vysoká škola báňská Technická univerzita 2011/2012 Analýza oběžného kola Radomír Bělík, Pavel Maršálek, Gȕnther Theisz Obsah 1. Zadání... 3 2. Experimentální měření... 4 2.1. Popis měřené struktury...
R O Z S U D E K J M É N E M R E P U B L I K Y
 6 Ads 10/2009-37 ČESKÁ REPUBLIKA R O Z S U D E K J M É N E M R E P U B L I K Y Nejvyšší správní soud rozhodl v senátu složeném z předsedkyně JUDr. Milady Tomkové a soudců JUDr. Jiřího Pally a JUDr. Bohuslava
6 Ads 10/2009-37 ČESKÁ REPUBLIKA R O Z S U D E K J M É N E M R E P U B L I K Y Nejvyšší správní soud rozhodl v senátu složeném z předsedkyně JUDr. Milady Tomkové a soudců JUDr. Jiřího Pally a JUDr. Bohuslava
Geometrie řízeného kola
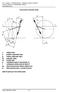 Geometie řízeného kola y ν δ z P O β z 2 3 1 4 ν δ β 4 p ϕ ϕ odklon kola příklon ejdového čepu záklon ejdového čepu polomě ejdu závlek kola vzdálenost bodu P od počátku O vzdálenost středu kola od bodu
Geometie řízeného kola y ν δ z P O β z 2 3 1 4 ν δ β 4 p ϕ ϕ odklon kola příklon ejdového čepu záklon ejdového čepu polomě ejdu závlek kola vzdálenost bodu P od počátku O vzdálenost středu kola od bodu
Vyvažování tuhého rotoru v jedné rovině přístrojem Adash 4900 - Vibrio
 Aplikační list Vyvažování tuhého rotoru v jedné rovině přístrojem Adash 4900 - Vibrio Ref: 15032007 KM Obsah Vyvažování v jedné rovině bez měření fáze signálu...3 Nevýhody vyvažování jednoduchými přístroji...3
Aplikační list Vyvažování tuhého rotoru v jedné rovině přístrojem Adash 4900 - Vibrio Ref: 15032007 KM Obsah Vyvažování v jedné rovině bez měření fáze signálu...3 Nevýhody vyvažování jednoduchými přístroji...3
a) Jaká je hodnota polytropického exponentu? ( 1,5257 )
 Ponorka se potopí do 50 m. Na dně ponorky je výstupní tunel o průměru 70 cm a délce, m. Tunel je napojen na uzavřenou komoru o objemu 4 m. Po otevření vnějšího poklopu vnikne z části voda tunelem do komory.
Ponorka se potopí do 50 m. Na dně ponorky je výstupní tunel o průměru 70 cm a délce, m. Tunel je napojen na uzavřenou komoru o objemu 4 m. Po otevření vnějšího poklopu vnikne z části voda tunelem do komory.
Analytická geometrie (3. - 4. lekce)
 Analytická geometrie (3. - 4. lekce) Sylva Potůčková, Dana Stesková, Lubomír Sedláček Gymnázium a Jazyková škola s právem státní jazykové zkoušky Zlín Zlín, 16. června 2011 Příklad 1 Příklad 1. Algebraicky
Analytická geometrie (3. - 4. lekce) Sylva Potůčková, Dana Stesková, Lubomír Sedláček Gymnázium a Jazyková škola s právem státní jazykové zkoušky Zlín Zlín, 16. června 2011 Příklad 1 Příklad 1. Algebraicky
( ) Úloha č. 9. Měření rychlosti zvuku a Poissonovy konstanty
 Fyzikální praktikum IV. Měření ryhlosti zvuku a Poissonovy konstanty - verze Úloha č. 9 Měření ryhlosti zvuku a Poissonovy konstanty 1) Pomůky: Kundtova trubie, mikrofon se sondou, milivoltmetr, měřítko,
Fyzikální praktikum IV. Měření ryhlosti zvuku a Poissonovy konstanty - verze Úloha č. 9 Měření ryhlosti zvuku a Poissonovy konstanty 1) Pomůky: Kundtova trubie, mikrofon se sondou, milivoltmetr, měřítko,
Moderní technologie ve studiu aplikované fyziky CZ.1.07/2.2.00/07.0018. 3. Reálná čísla
 Moderní technologie ve studiu aplikované fyziky CZ..07/..00/07.008 3. Reálná čísla RACIONÁLNÍ A IRACIONÁLNÍ ČÍSLA Význačnými množinami jsou číselné množiny. K nejvýznamnějším patří množina reálných čísel,
Moderní technologie ve studiu aplikované fyziky CZ..07/..00/07.008 3. Reálná čísla RACIONÁLNÍ A IRACIONÁLNÍ ČÍSLA Význačnými množinami jsou číselné množiny. K nejvýznamnějším patří množina reálných čísel,
Měření hustoty kapaliny z periody kmitů zkumavky
 Měření hustoty kapaliny z periody kmitů zkumavky Online: http://www.sclpx.eu/lab1r.php?exp=14 Po několika neúspěšných pokusech se zkumavkou, na jejíž dno jsme umístili do vaty nejprve kovovou kuličku a
Měření hustoty kapaliny z periody kmitů zkumavky Online: http://www.sclpx.eu/lab1r.php?exp=14 Po několika neúspěšných pokusech se zkumavkou, na jejíž dno jsme umístili do vaty nejprve kovovou kuličku a
http://cs.wikipedia.org/wiki/elektromotor
 http://cs.wikipedia.org/wiki/elektromotor Krokové motory princip funkce, metody řízení Občas se v praxi vyskytne potřeba pohonu, který umí přesně nastavit svoji polohu a tuto polohu i přes působící síly
http://cs.wikipedia.org/wiki/elektromotor Krokové motory princip funkce, metody řízení Občas se v praxi vyskytne potřeba pohonu, který umí přesně nastavit svoji polohu a tuto polohu i přes působící síly
MAGNETICKÉ POLE CÍVEK V HELMHOLTZOVĚ USPOŘÁDÁNÍ
 Úloha č. 6 a MAGNETICKÉ POLE CÍVEK V HELMHOLTZOVĚ USPOŘÁDÁNÍ ÚKOL MĚŘENÍ:. Změřte magnetickou indukci podél osy ovinných cívek po případy, kdy vdálenost mei nimi je ovna poloměu cívky R a dále R a R/..
Úloha č. 6 a MAGNETICKÉ POLE CÍVEK V HELMHOLTZOVĚ USPOŘÁDÁNÍ ÚKOL MĚŘENÍ:. Změřte magnetickou indukci podél osy ovinných cívek po případy, kdy vdálenost mei nimi je ovna poloměu cívky R a dále R a R/..
Krajská hospodářská komora Střední Čechy. Pravidla soutěže. Poznáváme firmy ve středních Čechách. 1. Pořadatel soutěže. 2. Termín konání soutěže
 Pravidla soutěže (dále jen pravidla soutěže ) Krajská hospodářská komora Střední Čechy Poznáváme firmy ve středních Čechách 1. Pořadatel soutěže se sídlem: Tyršova 106, 261 01 Příbram Zámeček s adresou
Pravidla soutěže (dále jen pravidla soutěže ) Krajská hospodářská komora Střední Čechy Poznáváme firmy ve středních Čechách 1. Pořadatel soutěže se sídlem: Tyršova 106, 261 01 Příbram Zámeček s adresou
VNITŘNÍ ENERGIE, PRÁCE A TEPLO
 VNITŘNÍ ENERGIE, PRÁCE A TEPLO Zákon zachování mechanické energie E celk. = = konst. Míček, který se odráží od země putuje do stále menší výšky, kam se část energie ztrácí? VNITŘNÍ ENERGIE TĚLESA Vnitřní
VNITŘNÍ ENERGIE, PRÁCE A TEPLO Zákon zachování mechanické energie E celk. = = konst. Míček, který se odráží od země putuje do stále menší výšky, kam se část energie ztrácí? VNITŘNÍ ENERGIE TĚLESA Vnitřní
Vítězslav Bártl. prosinec 2013
 VY_32_INOVACE_VB09_ČaP Jméno autora výukového materiálu Datum (období), ve kterém byl VM vytvořen Ročník, pro který je VM určen Vzdělávací oblast, vzdělávací obor, tematický okruh, téma Anotace Vítězslav
VY_32_INOVACE_VB09_ČaP Jméno autora výukového materiálu Datum (období), ve kterém byl VM vytvořen Ročník, pro který je VM určen Vzdělávací oblast, vzdělávací obor, tematický okruh, téma Anotace Vítězslav
Dodatečné informace č. 3 k zadávacím podmínkám
 Dodatečné informace č. 3 k zadávacím podmínkám Zakázka: Zadavatel: Evropské domy v krajích stavební úpravy objektu Nový Hluchák budova bez č.p. v areálu Pospíšilova 365, Hradec Králové Královéhradecký
Dodatečné informace č. 3 k zadávacím podmínkám Zakázka: Zadavatel: Evropské domy v krajích stavební úpravy objektu Nový Hluchák budova bez č.p. v areálu Pospíšilova 365, Hradec Králové Královéhradecký
U S N E S E N Í. I. Elektronické dražební jednání se koná dne 10.12.2015 v 09:00:00 hodin, prostřednictvím elektronického systému dražeb na adrese:
 Stránka 1 z 5 U S N E S E N Í JUDr. Vít Novozámský, soudní exekutor Exekutorského úřadu Brno-město se sídlem Bratislavská 73, 602 00 Brno-Město, Česká republika pověřený provedením exekuce, které vydal
Stránka 1 z 5 U S N E S E N Í JUDr. Vít Novozámský, soudní exekutor Exekutorského úřadu Brno-město se sídlem Bratislavská 73, 602 00 Brno-Město, Česká republika pověřený provedením exekuce, které vydal
Fyzika pro chemiky Ukázky testových úloh: Optika 1
 Fyzika pro chemiky Ukázky testových úloh: Optika 1 1. Světelný paprsek prochází rozhraním vzduchu a skla. Pod jakým úhlem se paprsek láme ve skle, dopadá-li paprsek na rozhraní ze vzduchu pod úhlem 45
Fyzika pro chemiky Ukázky testových úloh: Optika 1 1. Světelný paprsek prochází rozhraním vzduchu a skla. Pod jakým úhlem se paprsek láme ve skle, dopadá-li paprsek na rozhraní ze vzduchu pod úhlem 45
GEOMETRICKÁ TĚLESA. Mnohostěny
 GEOMETRICKÁ TĚLESA Geometrické těleso je prostorový geometrický útvar, který je omezený (ohraničený), tato hranice mu náleží. Jeho povrch tvoří rovinné útvary a také různé složitější plochy. Geometrická
GEOMETRICKÁ TĚLESA Geometrické těleso je prostorový geometrický útvar, který je omezený (ohraničený), tato hranice mu náleží. Jeho povrch tvoří rovinné útvary a také různé složitější plochy. Geometrická
Typové příklady ke zkoušce z Fyziky 1
 Mechanika hmotného bodu Typové příklady ke zkoušce z Fyziky 1 1. Těleso padá volným pádem. V bodě A své trajektorie má rychlost v 4 m s -1, v bodě B má rychlost 16 m s -1. Určete: a) vzdálenost bodů A,
Mechanika hmotného bodu Typové příklady ke zkoušce z Fyziky 1 1. Těleso padá volným pádem. V bodě A své trajektorie má rychlost v 4 m s -1, v bodě B má rychlost 16 m s -1. Určete: a) vzdálenost bodů A,
Všeobecné obchodní podmínky
 Všeobecné obchodní podmínky 1. Definice pojmů Pro účely těchto Všeobecných obchodních podmínek se následujícími pojmy rozumí: 1.1. 1.2. 1.3. 1.4. 1.5. 1.6. 1.7. 1.8. 1.9. 2. 2.1 2.2 2.3 2.4 2.5 3. 3.1
Všeobecné obchodní podmínky 1. Definice pojmů Pro účely těchto Všeobecných obchodních podmínek se následujícími pojmy rozumí: 1.1. 1.2. 1.3. 1.4. 1.5. 1.6. 1.7. 1.8. 1.9. 2. 2.1 2.2 2.3 2.4 2.5 3. 3.1
Jméno autora: Mgr. Zdeněk Chalupský Datum vytvoření: 14. 11. 2012 Číslo DUM: VY_32_INOVACE_12_FY_B
 Jméno autora: Mgr. Zdeněk Chalupský Datum vytvoření: 14. 11. 2012 Číslo DUM: VY_32_INOVACE_12_FY_B Ročník: I. Fyzika Vzdělávací oblast: Přírodovědné vzdělávání Vzdělávací obor: Fyzika Tematický okruh:
Jméno autora: Mgr. Zdeněk Chalupský Datum vytvoření: 14. 11. 2012 Číslo DUM: VY_32_INOVACE_12_FY_B Ročník: I. Fyzika Vzdělávací oblast: Přírodovědné vzdělávání Vzdělávací obor: Fyzika Tematický okruh:
Osvětlovací modely v počítačové grafice
 Západočeská univerzita v Plzni Fakulta aplikovaných věd Semestrální práce z předmětu Matematické modelování Osvětlovací modely v počítačové grafice 27. ledna 2008 Martin Dohnal A07060 mdohnal@students.zcu.cz
Západočeská univerzita v Plzni Fakulta aplikovaných věd Semestrální práce z předmětu Matematické modelování Osvětlovací modely v počítačové grafice 27. ledna 2008 Martin Dohnal A07060 mdohnal@students.zcu.cz
MECHANIKA TUHÉHO TĚLESA POJEM TUHÉ TĚLESO POHYBY TUHÉHO TĚLESA
 Předmět: Ročník: Vytvořil: Datum: YZIKA PRVNÍ MGR. JÜTTNEROVÁ 29. 0. 202 Název zpracovaného celku: MECHANIKA TUHÉHO TĚLESA POJEM TUHÉ TĚLESO Budeme uvažovat takové pohyby tělesa, při nichž nelze zanedbat
Předmět: Ročník: Vytvořil: Datum: YZIKA PRVNÍ MGR. JÜTTNEROVÁ 29. 0. 202 Název zpracovaného celku: MECHANIKA TUHÉHO TĚLESA POJEM TUHÉ TĚLESO Budeme uvažovat takové pohyby tělesa, při nichž nelze zanedbat
e en loh 1. kola 48. ro n ku fyzik ln olympi dy. Kategorie B Auto i loh: M. Jare ov (1, 2, 5, 6, 7), J. J r (4) a KVANT (3). Kone n prava P. ediv 1. l
 e en loh. kola 48. o n ku fyzik ln olympi y. Kategoie B Auto i loh: M. Jae ov (,, 5, 6, 7), J. J (4) a KVANT (). Kone n pava P. eiv. lohu bueme e it ve vzta n soustav, jej po tek je ve st eu M s ce a osy
e en loh. kola 48. o n ku fyzik ln olympi y. Kategoie B Auto i loh: M. Jae ov (,, 5, 6, 7), J. J (4) a KVANT (). Kone n pava P. eiv. lohu bueme e it ve vzta n soustav, jej po tek je ve st eu M s ce a osy
4. cvičení: Pole kruhové, rovinné, Tělesa editace těles (sjednocení, rozdíl, ), tvorba složených objektů
 4. cvičení: Pole kruhové, rovinné, Tělesa editace těles (sjednocení, rozdíl, ), tvorba složených objektů Příklad 1: Pracujte v pohledu Shora. Sestrojte kružnici se středem [0,0,0], poloměrem 10 a kružnici
4. cvičení: Pole kruhové, rovinné, Tělesa editace těles (sjednocení, rozdíl, ), tvorba složených objektů Příklad 1: Pracujte v pohledu Shora. Sestrojte kružnici se středem [0,0,0], poloměrem 10 a kružnici
Komutace a) komutace diod b) komutace tyristor Druhy polovodi ových m Usm ova dav
 V- Usměrňovače 1/1 Komutace - je děj, při němž polovodičová součástka (dioda, tyristor) přechází z propustného do závěrného stavu a dochází k tzv. zotavení závěrných vlastností součástky, a) komutace diod
V- Usměrňovače 1/1 Komutace - je děj, při němž polovodičová součástka (dioda, tyristor) přechází z propustného do závěrného stavu a dochází k tzv. zotavení závěrných vlastností součástky, a) komutace diod
Příklad 1.3: Mocnina matice
 Řešení stavových modelů, módy, stabilita. Toto cvičení bude věnováno hledání analytického řešení lineárního stavového modelu. V matematickém jazyce je takový model ničím jiným, než sadou lineárních diferenciálních
Řešení stavových modelů, módy, stabilita. Toto cvičení bude věnováno hledání analytického řešení lineárního stavového modelu. V matematickém jazyce je takový model ničím jiným, než sadou lineárních diferenciálních
Člověk a příroda - Přírodopis - 9. ročník. POZNÁMKY (průřezová témata, mezipředmětové vztahy) PŘEDMĚTOVÉ KOMPETENCE OČEKÁVANÉ VÝSTUPY UČIVO
 - způsobu myšlení, které vyžaduje ověřování vyslovovaných domněnek o přírodních faktech více nezávislými způsoby - charakterizuje postavení Země ve Sluneční soustavě a význam vytvoření základních podmínek
- způsobu myšlení, které vyžaduje ověřování vyslovovaných domněnek o přírodních faktech více nezávislými způsoby - charakterizuje postavení Země ve Sluneční soustavě a význam vytvoření základních podmínek
SBÍRKA PŘÍKLADŮ PRO OPAKOVÁNÍ NA PŘIJÍMACÍ ZKOUŠKY 2
 STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJNÍ A STAVEBNÍ TÁBOR, KOMENSKÉHO 1670 SBÍRKA PŘÍKLADŮ PRO OPAKOVÁNÍ NA PŘIJÍMACÍ ZKOUŠKY 2 ŠKOLNÍ ROK 2014/2015 Obsah 1 Dělitelnost přirozených čísel... 3 2 Obvody a obsahy
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJNÍ A STAVEBNÍ TÁBOR, KOMENSKÉHO 1670 SBÍRKA PŘÍKLADŮ PRO OPAKOVÁNÍ NA PŘIJÍMACÍ ZKOUŠKY 2 ŠKOLNÍ ROK 2014/2015 Obsah 1 Dělitelnost přirozených čísel... 3 2 Obvody a obsahy
ZAHRADNÍ DŘEVĚNÉ DOMKY
 ZAHRADNÍ DŘEVĚNÉ DOMKY Jak správně vybrat dřevěný domek? "Klasický dřevěný zahradní domek zajistí souznění Vaší zahrady s přírodou." www.lanitplast.cz 1.3.2016 1 Jak správně vybrat dřevěný domek Zahradní
ZAHRADNÍ DŘEVĚNÉ DOMKY Jak správně vybrat dřevěný domek? "Klasický dřevěný zahradní domek zajistí souznění Vaší zahrady s přírodou." www.lanitplast.cz 1.3.2016 1 Jak správně vybrat dřevěný domek Zahradní
3.1.4 Trojúhelník. Předpoklady: 3103. Každé tři různé body neležící v přímce určují trojúhelník. C. Co to je, víme. Jak ho definovat?
 3..4 Trojúhelní Předpolady: 303 Každé tři různé body neležící v přímce určují trojúhelní. o to je, víme. Ja ho definovat? Př. : Definuj trojúhelní jao průni polorovin. Trojúhelní je průni polorovin, a.
3..4 Trojúhelní Předpolady: 303 Každé tři různé body neležící v přímce určují trojúhelní. o to je, víme. Ja ho definovat? Př. : Definuj trojúhelní jao průni polorovin. Trojúhelní je průni polorovin, a.
Usnesení. r o z h o d l t a k t o :
 EXEKUTORSKÝ ÚŘAD CHEB MGR. DAVID KONCZ SOUDNÍ EXEKUTOR 26. dubna 10, Cheb 35002 tel., fax: +420 355 318 111, +420 355 318 110 e-mail: podatelna@eucheb.cz www.eucheb.cz IDDS: 9u8g8ka č.j. : 074 EX 08818/08-124
EXEKUTORSKÝ ÚŘAD CHEB MGR. DAVID KONCZ SOUDNÍ EXEKUTOR 26. dubna 10, Cheb 35002 tel., fax: +420 355 318 111, +420 355 318 110 e-mail: podatelna@eucheb.cz www.eucheb.cz IDDS: 9u8g8ka č.j. : 074 EX 08818/08-124
Instrukce Měření umělého osvětlení
 Instrukce Měření umělého osvětlení Označení: Poskytovatel programu PT: Název: Koordinátor: Zástupce koordinátora: Místo konání: PT1 UO-15 Zdravotní ústav se sídlem v Ostravě, Centrum hygienických laboratoří
Instrukce Měření umělého osvětlení Označení: Poskytovatel programu PT: Název: Koordinátor: Zástupce koordinátora: Místo konání: PT1 UO-15 Zdravotní ústav se sídlem v Ostravě, Centrum hygienických laboratoří
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Fotoefekt Fotoelektrický jev je jev, který v roce 1887 poprvé popsal Heinrich Hertz. Po nějakou dobu se efekt nazýval Hertzův efekt, ale
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Fotoefekt Fotoelektrický jev je jev, který v roce 1887 poprvé popsal Heinrich Hertz. Po nějakou dobu se efekt nazýval Hertzův efekt, ale
Znalecký posudek číslo 3804 144/08
 Znalecký posudek číslo 3804 144/08 O ceně nemovitosti: Bytová jednotka 1719/4 O S T R A V A katastrální území: Poruba - sever statutární město: Ostrava O B V Y K L Á T R Ž N Í C E N A Objednatel znaleckého
Znalecký posudek číslo 3804 144/08 O ceně nemovitosti: Bytová jednotka 1719/4 O S T R A V A katastrální území: Poruba - sever statutární město: Ostrava O B V Y K L Á T R Ž N Í C E N A Objednatel znaleckého
9. Lineárně elastická lomová mechanika K-koncepce. Únava a lomová mechanika Pavel Hutař, Luboš Náhlík
 9. Lineárně elastická lomová mechanika K-koncepce Únava a lomová mechanika Faktor intenzity napětí Předpokládáme ostrou trhlinu namáhanou třemi základními módy zatížení Zredukujeme-li obecnou trojrozměrnou
9. Lineárně elastická lomová mechanika K-koncepce Únava a lomová mechanika Faktor intenzity napětí Předpokládáme ostrou trhlinu namáhanou třemi základními módy zatížení Zredukujeme-li obecnou trojrozměrnou
Městský úřad ve Vratimově Odbor výstavby a životního prostředí Frýdecká 853, Vratimov
 Městský úřad ve Vratimově Odbor výstavby a životního prostředí Frýdecká 853, Vratimov muvrx001lpvj MUVRX001LPVJ Č.j. : MUVR 2967/2008 Sp.Zn. : SPIS 446/2008/VAŽP42 7 Vyřizuje : Svěnčíková Šárka Tel. :
Městský úřad ve Vratimově Odbor výstavby a životního prostředí Frýdecká 853, Vratimov muvrx001lpvj MUVRX001LPVJ Č.j. : MUVR 2967/2008 Sp.Zn. : SPIS 446/2008/VAŽP42 7 Vyřizuje : Svěnčíková Šárka Tel. :
Vyhláška č. 294/2015 Sb., kterou se provádějí pravidla provozu na pozemních komunikacích
 Změny 1 vyhláška č. 294/2015 Sb. Vyhláška č. 294/2015 Sb., kterou se provádějí pravidla provozu na pozemních komunikacích a která s účinností od 1. ledna 2016 nahradí vyhlášku č. 30/2001 Sb. Umístění svislých
Změny 1 vyhláška č. 294/2015 Sb. Vyhláška č. 294/2015 Sb., kterou se provádějí pravidla provozu na pozemních komunikacích a která s účinností od 1. ledna 2016 nahradí vyhlášku č. 30/2001 Sb. Umístění svislých
22 Cdo 2694/2015 ze dne 25.08.2015. Výběr NS 4840/2015
 22 Cdo 2694/2015 ze dne 25.08.2015 Výběr NS 4840/2015 22 Cdo 209/2012 ze dne 04.07.2013 C 12684 Bezúplatné nabytí členského podílu v bytovém družstvu jedním z manželů od jeho rodičů nepředstavuje investici
22 Cdo 2694/2015 ze dne 25.08.2015 Výběr NS 4840/2015 22 Cdo 209/2012 ze dne 04.07.2013 C 12684 Bezúplatné nabytí členského podílu v bytovém družstvu jedním z manželů od jeho rodičů nepředstavuje investici
KIS A JEJICH BEZPEČNOST I PŘENOS INFORMACÍ DOC. ING. BOHUMIL BRECHTA, CSC.
 KIS A JEJICH BEZPEČNOST I PŘENOS INFORMACÍ DOC. ING. BOHUMIL BRECHTA, CSC. Operační program Vzdělávání pro konkurenceschopnost Projekt: Vzdělávání pro bezpečnostní systém státu (reg. č.: CZ.1.01/2.2.00/15.0070)
KIS A JEJICH BEZPEČNOST I PŘENOS INFORMACÍ DOC. ING. BOHUMIL BRECHTA, CSC. Operační program Vzdělávání pro konkurenceschopnost Projekt: Vzdělávání pro bezpečnostní systém státu (reg. č.: CZ.1.01/2.2.00/15.0070)
TECHNICKÁ ZPRÁVA REKONSTRUKCE STÁVAJÍCÍHO ÚSEKU MÍSTNÍ KOMUNIKACE: PRŮSEČNÁ KŘIŽOVATKA V OBCI ŠLAPANICE
 TECHNICKÁ ZPRÁVA REKONSTRUKCE STÁVAJÍCÍHO ÚSEKU MÍSTNÍ KOMUNIKACE: PRŮSEČNÁ KŘIŽOVATKA V OBCI ŠLAPANICE Název stavby: Místo stavby: Kraj: Styková křižovatka v obci Šlapanice křížení ulic Bezručova a Sušilova
TECHNICKÁ ZPRÁVA REKONSTRUKCE STÁVAJÍCÍHO ÚSEKU MÍSTNÍ KOMUNIKACE: PRŮSEČNÁ KŘIŽOVATKA V OBCI ŠLAPANICE Název stavby: Místo stavby: Kraj: Styková křižovatka v obci Šlapanice křížení ulic Bezručova a Sušilova
Žáci mají k dispozici pracovní list. Formou kolektivní diskuze a výkladu si osvojí grafickou minimalizaci zápisu logické funkce
 Číslo projektu Číslo materiálu Název školy Autor Název Téma hodiny Předmět Ročník /y/ CZ.1.07/1.5.00/34.0394 VY_32_INOVACE_9_ČT_1.09_ grafická minimalizace Střední odborná škola a Střední odborné učiliště,
Číslo projektu Číslo materiálu Název školy Autor Název Téma hodiny Předmět Ročník /y/ CZ.1.07/1.5.00/34.0394 VY_32_INOVACE_9_ČT_1.09_ grafická minimalizace Střední odborná škola a Střední odborné učiliště,
2.6.4 Lineární lomené funkce s absolutní hodnotou
 .6. Lineární lomené funkce s absolutní hodnotou Předpoklady: 60, 603 Pedagogická poznámka: Hlavním cílem hodiny je nácvik volby odpovídajícího postupu. Proto je dobré nechat studentům chvíli, aby si metody
.6. Lineární lomené funkce s absolutní hodnotou Předpoklady: 60, 603 Pedagogická poznámka: Hlavním cílem hodiny je nácvik volby odpovídajícího postupu. Proto je dobré nechat studentům chvíli, aby si metody
269/2015 Sb. VYHLÁŠKA
 269/2015 Sb. - rozúčtování nákladů na vytápění a příprava teplé vody pro dům - poslední stav textu 269/2015 Sb. VYHLÁŠKA ze dne 30. září 2015 o rozúčtování nákladů na vytápění a společnou přípravu teplé
269/2015 Sb. - rozúčtování nákladů na vytápění a příprava teplé vody pro dům - poslední stav textu 269/2015 Sb. VYHLÁŠKA ze dne 30. září 2015 o rozúčtování nákladů na vytápění a společnou přípravu teplé
pracovní list studenta
 Výstup RVP: Klíčová slova: pracovní list studenta Rovnice a jejich soustavy Petra Směšná žák měří dané veličiny, analyzuje a zpracovává naměřená data, rozumí pojmu řešení soustavy dvou lineárních rovnic,
Výstup RVP: Klíčová slova: pracovní list studenta Rovnice a jejich soustavy Petra Směšná žák měří dané veličiny, analyzuje a zpracovává naměřená data, rozumí pojmu řešení soustavy dvou lineárních rovnic,
Vyřizuje: Tel.: Fax: E-mail: Datum: 6.8.2012. Oznámení o návrhu stanovení místní úpravy provozu na místní komunikaci a silnici
 M Ě S T S K Ý Ú Ř A D B L A N S K O ODBOR STAVEBNÍ ÚŘAD, oddělení silničního hospodářství nám. Svobody 32/3, 678 24 Blansko Pracoviště: nám. Republiky 1316/1, 67801 Blansko Město Blansko, nám. Svobody
M Ě S T S K Ý Ú Ř A D B L A N S K O ODBOR STAVEBNÍ ÚŘAD, oddělení silničního hospodářství nám. Svobody 32/3, 678 24 Blansko Pracoviště: nám. Republiky 1316/1, 67801 Blansko Město Blansko, nám. Svobody
