IA008 Computational logic Version: 6. května Formule je v konjunktivní normální formě (CNF), pokud má tvar α 1... α n,
|
|
|
- Kamil Svoboda
- před 5 lety
- Počet zobrazení:
Transkript
1 1 Převody do normálních forem Příklad 1.1: Vyjádřete následující formule v DNF pomocí pravdivostní tabulky a pomocí převodu logických spojek. a) (A B) C b) (A B) C c) (A B) (C D) Formule je v disjunktivní normální formě (DNF), pokud má tvar α 1... α n, kde α i = A i1... A iji a každé A ij je výroková proměnná nebo její negace. Příklad 1.2: Vyjádřete následující formule v CNF, a to pomocí pravdivostní tabulky a pomocí převodu logických spojek. a) (A B) ( A C) b) (A B) (A C) Formule je v konjunktivní normální formě (CNF), pokud má tvar α 1... α n, kde α i = A i1... A iji a A ij je výroková proměnná nebo její negace. Příklad 1.3: Víme, že můžeme provádět následující chemické reakce: MgO + H 2 Mg + H 2 O C + O 2 CO 2 CO 2 + H 2 O H 2 CO 3 K dispozici máme dále sloučeniny C, H 2, O 2 a MgO. Rezolucí dokažte, že H 2 CO 3 logicky vyplývá ze zadaných reakcí. Příklad 1.4: Převed te na prenexovou normální formu formule: a) y( xp(x,y) Q(y,z)) y( xr(x,y) Q(x,y)) b) xr(x,y) yp(x,y) c) ( x yq(x,y) x yp(x,y)) x yp(x,y) d) ( x yp(x,y) x yr(x,y)) x( yq(x,y)) Formule je v prenexové normání formě (PNF), pokud jsou všechny kvatifikátory na začátku formule, tj. formule má tvar Q 1 x 1 Q 2 x 2...Q n x n ϕ, kde Q 1,...,Q n {, } a ϕ je formule bez kvantifikátorů (tzv. otevřená formule). 2 Skolemizace a unifikace Začneme připomenutím následujících definic. Formle bez volných proměnných se nazývá sentence. 1
2 Necht ϕ(x 1,...,x n ) je formule s volnými proměnnými x 1,...,x n, kde n 0. Jejím univerzálním uzávěrem rozumíme formuli x 1... x n ϕ(x 1,...,x n ). Formule ϕ(x 1,...,x n ) je pravdivá v interpretaci I právě tehdy, když je v této interpretaci pravdivý její univerzální uzávěr, tj. pokud ϕ(x 1,...,x n ) je pravdivá v interpretaci I pro všechny valuace. Podobně, formule ϕ(x 1,...,x n ) je splnitelná, je-li splnitelný její univerzální uzávěr, tj. pokud existuje interpretace I taková, že ϕ(x 1,...,x n ) je pravdivá pro všechny valuace. Formule ϕ,ψ jsou equisatisfiable (ekvivalentní vzhledem ke splnitelnosti), pokud jsou obě splnitelné nebo obě nesplnitelné. Necht T je množina formulí. Formule ϕ je logickým důsledkem T (nebo ϕ logicky vyplývá z T, píšeme T = ϕ, ), pokud je ϕ pravdivá v každé interpretaci I, ve které jsou pravdivé všechny formule z T. Nyní si ukážeme, jak lze převést úlohu Dokažte, že ϕ je logickým důsledkem T do klauzulární formy (tj. konjunktivní normální formy), kde již může být dořešena rezoluční metodou. a) Nejprve nahradíme všechny formule s volnými proměnnými v T jejich univerzálními uzávěry. Vzniklou množinu sentencí označíme T. Má-li formule ϕ volné proměnné x 1,...,x n, nahradíme ji jejím univerzálním uzávěrem x 1... x n ϕ(x 1,...,x n ). Z výše uvedených definic plyne, že T = ϕ právě tehdy, když T = x 1... x n ϕ(x 1,...,x n ). b) T = x 1... x n ϕ(x 1,...,x n ) právě tehdy, když je množina sentencí T { x 1... x n ϕ(x 1,...,x n )} = T { x 1... x n ϕ(x 1,...,x n )} nesplnitelná. c) Všechny formule z množiny T { x 1... x n ϕ(x 1,...,x n )} převedeme do prenexního normální formy (PNF) a skolemizujeme (skolemizace vytvoří formuli, která je equisatisfiable původní formuli). Získanou množinu sentencí v PNF a bez existenčních kvantifikátorů označíme T. d) Nyní z každé formule z T odstraníme část s kvantifikátory (korektnost tohoto kroku opět vyplývá z výše uvedených definic) a zbylou část formule převedeme do konjunktivní normální formy. Konjunkci všech takto získaných formulí nazveme ψ. Platí T = ϕ právě tehdy, když ψ je nesplnitelná. Formuli ψ přepíšeme na množinu klauzulí a každou klauzuli nahradíme množinou jejích literálů. K důkazu nesplnitelnosti takto vytvořené množiny klauzulí můžeme použít rezoluční metodu. Pořadí některých částí výše uvedeného postupu lze zaměnit, např. převod do konjunktivní normální formy lze provést zaráz s převodem do PNF. Příklad 2.1: Proved te skolemizaci následujících formulí v PNF: a) y 1 x 1 y 2 x 2 [( P(x 1,y 1 ) Q(y 1,a)) (R(x 2,y 2 ) Q(x 1,y 2 ))] b) x 1 y 1 y 2 x 2 [( R(x 1,y 2 ) P(b,y 1 )) ( P(x 1,y 2 ) R(x 2,b))] c) x 1 y 1 x 2 (S(y 1 ) R(x 1,x 2 )) 2
3 Příklad 2.2: Najděte nejobecnější unifikátory (angl. most general unifiers, mgu) následujících množin literálů: a) S = {P(x,f(y),z),P(g(a),f(w),u),P(v,f(b),c)} b) T = {Q(h(x,y),w),Q(h(g(v),a),f(v)),Q(h(g(v),a),f(b))} Příklad 2.3: Najděte všechny rezolventy následujících dvojic klauzulí: a) C 1 = {P(x,y),P(y,z)},C 2 = { P(u,f(u))} b) C 1 = {P(x,x), R(x,f(x))},C 2 = {R(x,y),Q(y,z)} c) C 1 = {P(x,y), P(x,x),Q(x,f(x),z)},C 2 = { Q(f(x),x,z),P(x,z)} 3 Rezoluce Příklad 3.1: Dokažte, že platí následující vyplývání: a) { xp(x,x), x y z((p(x,y) P(y,z)) P(z,x))} = x y(p(x,y) P(y,x)) b) { x y z((p(x,y) P(y,z)) P(x,z)), x y(p(x,y) P(y,x))} = x y z((p(x,y) P(z,y)) P(x,z)) Příklad 3.2: Převed te následující tvrzení v přirozeném jazyce na formule predikátové logiky a dokažte jejich platnost. a) Předpokládejte, že platí následující tři tvrzení: Existuje drak (označme D/1). Draci spí (S/1) nebo loví (L/1). Když jsou draci hladoví (H/1), tak nespí. Důsledek: Když jsou draci hladoví, tak loví. b) Předpokládejte, že platí následující dvě tvrzení: Všichni holiči (B/1) holí (S/2) každého, kdo se neholí sám. Žádný holič neholí někoho, kdo se holí sám. Důsledek: Holiči neexistují. Příklad 3.3: Vyvrat te následující množinu klauzulí S = {{P(x), Q(x,f(y)), R(a)}, {R(x), Q(x,y)}, { P(x), Q(y,z)}, {P(x), R(x)}, {R(f(b))}, {Q(x,y), P(y)}} pomocí obecné rezoluce, lineární rezoluce, LI rezoluce, LD rezoluce a SLD rezoluce 1. 1 Viz materiály k předmětu IB101 přednáška). Úvod do logiky a logického programování (sedmá 3
4 4 SLD-stromy a rezoluce v Prologu Příklad 4.1: Nalezněte rezoluční vyvracení množiny klauzulí zadaných jako program a dotaz v Prologu. 1. r :- p, q. 5. t. 2. s :- p, q. 6. q. 3. v :- t, u. 7. u. 4. w :- v, s. 8. p.?- w. Příklad 4.2: Vytvořte SLD-strom pro následující program (Program 1.) a dotaz v Prologu a zjistěte, jak se projeví změna pořadí klauzulí (Program 2.) v definici programu na výsledné podobě SLD-stromu. Program 1: Program 2: 1. p :- q,r. 4. r :- q. 1. p :- r. 4. r. 2. p :- r. 5. r. 2. p :- q,r. 5. r :- q. 3. q :- p. 3. q :- p.?- p,q. Příklad 4.3: Sestrojte SLD-stromy pro následující programy a dotazy v jazyce Prolog: Program 1: Program 2: 1. p :- a,r. 5. r :- t,a. 1. p :- s,t. 5. r :- w. 2. a :- b. 6. r :- s. 2. p :- q. 6. r. 3. a. 7. s. 3. q. 7. s. 4. b :- a. 4. q :- r. 8. t :- w.?- p.?- p. Příklad 4.4: Napište SLD-strom pro následující program a dotaz. 1. p(f,g). 3. p(z,x) :- p(x,y), p(y,z). 2. p(x,x).?- p(y,f). Příklad 4.5: Vytvořte SLD-strom všech možných řešení k následujícímu programu a dotazu: 1. p(x,y) :- q(x,z), r(z,y). 7. s(x) :- t(x,a). 2. p(x,x) :- s(x). 8. s(x) :- t(x,b). 3. q(x,b). 9. s(x) :- t(x,x). 4. q(b,a). 10. t(a,b). 5. q(x,a) :- r(a,x). 11. t(b,a). 6. r(b,a).?- p(x,x). 4
5 Příklad 4.6: Zkonstruujte SLD vyvrácení cíle?- reverse([a,b,c],x). za předpokladu, že máme nadefinován predikát reverse/2 následovně: reverse(l1,l2) :- rev(l1,[],l2). rev([h T],A,L) :- rev(t,[h A],L). rev([],l,l). 5 Tabla ve výrokové logice Příklad 5.1: Sestrojte ukončené tablo s kořenem F(((C d) (D d)) (C D)), kde C,D,d jsou výrokové symboly. Příklad 5.2: Pomocí tabel dokažte, že následující formule jsou tautologické: a) (p q) (q p) b) ((p q) (p r)) (p (q r)) Příklad 5.3: Dokažte, že platí následující logické vyplývání: {q r,r (p q),p (q r)} = (p q). 6 Tabla v predikátové logice Příklad 6.1: Pomocí tabel dokažte, že následující formule jsou tautologie. a) Φ 1 xϕ(x) xϕ(x) b) Φ 2 x(p(x) Q(x)) ( xp(x) xq(x)) c) Φ 3 x(ϕ(x) ψ(x)) ( xϕ(x) xψ(x)) d) Φ 4 y x(p(x,y) P(x,x)) x y z(p(z,y) P(z,x)) Příklad 6.2: Dokažte, že formule xp(x) logicky vyplývá z předpokladů: x((q(x) R(x)) S(x)) x((r(x) P(x)) (Q(x) S(x))) Příklad 6.3: Pomocí tabel dokažte platnost následujících tvrzení. a) Předpokládejte, že platí následující tři tvrzení: Existuje drak (označme D/1). Draci spí (S/1) nebo loví (L/1). Když jsou draci hladoví (H/1), tak nespí. Důsledek: Když jsou draci hladoví, tak loví. 5
6 b) Předpokládejte, že platí následující dvě tvrzení: Všichni holiči (B/1) holí (S/2) každého, kdo se neholí sám. Žádný holič neholí někoho, kdo se holí sám. Důsledek: Holiči neexistují. 7 Tabla v modální logice Při konstrukci ukončeného kontradiktorického tabla v modální logice postupujeme podobně jako v případě logiky prvního řádu. Máme-li dokázat, že formule ϕ je tautologií (tj. platí ve všech světech všech Kripkeho rámců nad použitým jazykem modální logiky), stačí zkonstruovat kontradiktorické tablo s kořenem Fw ϕ. Každý uzel vytvářeného binárního stromu pak obsahuje výraz Fv ϕ nebo Tv ϕ. Narozdíl od logiky prvního řádu je tedy nutné brát v úvahu také svět, ve kterém danou položku redukujeme. Cesta v tablu je sporná (kontradiktorická), pokud se na ní vyskytuje položka Tv ϕ a zároveň Fv ϕ pro nějaký svět v a formuli ϕ. Kvůli technickému zjednodušení přijímáme konvenci, že jazyk modální logiky neobsahuje funkční symboly. Při expanzi položek Tv ( x)ϕ(x) a Fv ( x)ϕ(x) proto místo ground termů používáme pouze konstanty. Musíme však volit takové konstanty, o kterých víme, že se vyskytují ve světě v. Taková konstanta je bud součástí jazyka modální logiky, nebo se na expandované cestě již vyskytuje v nějaké položce týkající se světa v nebo nějakého jeho předchůdce (tj. světa w, pro který se na cestě vyskytuje wsv). Další možností je naopak volit konstantu, která se nevyskytuje nikde v celém tablu. Při expanzi položek Tv ( x)ϕ(x) a Fv ( x)ϕ(x) dosadíme namísto x libovolnou konstantu, která se dosud nevyskytuje v žádné položce tabla. Položky s operátory a redukujeme následovně. Při redukci položky Tv ϕ nebo Fv ϕ na cestu nejdříve přidáme výraz vsw, kde w je nějaký nový svět, který ještě v tablu nebyl použit. Poté přidáme nový uzel Tw ϕ resp. Fw ϕ. Položky typu Tv ϕ a Fv ϕ expandujeme na Tw ϕ a Fw ϕ, kde w je libovolný svět, pro který je na expandované cestě položka vsw. Pokud žádný takový svět neexistuje, můžeme položky považovat za redukované. Kořeny atomických tabel pro položky Tv ( x)ϕ(x), Fv ( x)ϕ(x), Tv ϕ a Fv ϕ bychom neměli při redukci vynechávat. Příklad 7.1: Pomocí tabel dokažte, že následující formule jsou tautologie. a) Φ 1 ( xϕ(x)) ( x ϕ(x)) b) Φ 2 ( (ϕ ψ)) (( ϕ ψ)) c) Φ 3 ( (ϕ xψ(x)) x(ϕ ψ(x))), x není volné ve formuli ϕ d) Φ 4 x(ϕ(x) ψ) ( xϕ(x) ψ), x není volné ve formuli ψ Příklad 7.2: Mějme modální tablo s kořenem Fw x ϕ(x) xϕ(x) definované v obrázku 1. Rozhodněte o korektnosti uvedeného důkazu a své tvrzení zdůvodněte. 6
7 Fw x ϕ(x) xϕ(x) Tw x ϕ(x) Fw xϕ(x) wsv Fv xϕ(x) Fv ϕ(c) Tw x ϕ(x) Tw ϕ(c) Tw ϕ(c) Tv ϕ(c) Obrázek 1: Příklad 7.3: Dokažte platnost úsudků: a) {ϕ} = ϕ b) { xϕ(x)} = xϕ(x) c) { xϕ(x)} = x ϕ(x) d) {ϕ ϕ} = ϕ ϕ 8 Induktivní logické programování Příklad 8.1: Jsou dány výrokové symboly a,b,c,d,e a tabulka + = pozitivní příklady = negativní příklad a b c d e třída
8 Najděte všechny specializace výrokové formule b. Vyznačte, které z nich pokrývají negativní příklad. Příklad 8.2: Napište část specializačního grafu s kořenem neteř(x,y), která bude obsahovat klauzuli: neteř(x,y) :- žena(x), sourozenec(y,z), rodič(z,x). 8
Výroková a predikátová logika - X
 Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
2.5 Rezoluční metoda v predikátové logice
 2.5. Rezoluční metoda v predikátové logice [101104-1520] 19 2.5 Rezoluční metoda v predikátové logice Rezoluční metoda v predikátové logice je obdobná stejnojmenné metodě ve výrokové logice. Ovšem vzhledem
2.5. Rezoluční metoda v predikátové logice [101104-1520] 19 2.5 Rezoluční metoda v predikátové logice Rezoluční metoda v predikátové logice je obdobná stejnojmenné metodě ve výrokové logice. Ovšem vzhledem
Rezoluční kalkulus pro logiku prvního řádu
 AD4M33AU Automatické uvažování Rezoluční kalkulus pro logiku prvního řádu Petr Pudlák Logika prvního řádu (Někdy nepřesně nazývaná predikátová logika.) Výhody Vyšší vyjadřovací schopnost jazyka, V podstatě
AD4M33AU Automatické uvažování Rezoluční kalkulus pro logiku prvního řádu Petr Pudlák Logika prvního řádu (Někdy nepřesně nazývaná predikátová logika.) Výhody Vyšší vyjadřovací schopnost jazyka, V podstatě
1 Pravdivost formulí v interpretaci a daném ohodnocení
 1 Pravdivost formulí v interpretaci a daném ohodnocení Než uvedeme konkrétní příklady, zopakujme si definici interpretace, ohodnocení a pravdivosti. Necht L je nějaký jazyk. Interpretaci U, jazyka L tvoří
1 Pravdivost formulí v interpretaci a daném ohodnocení Než uvedeme konkrétní příklady, zopakujme si definici interpretace, ohodnocení a pravdivosti. Necht L je nějaký jazyk. Interpretaci U, jazyka L tvoří
Predikátová logika. prvního řádu
 Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Logika. 5. Rezoluční princip. RNDr. Luděk Cienciala, Ph. D.
 Logika 5. Rezoluční princip RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216,
Logika 5. Rezoluční princip RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216,
Skolemizace. x(x + f(x) = 0). Interpretace f unární funkce, která pro daný
 Skolemizace převod formulí na formule bez existenčních kvantifikátorů v jazyce, který je rozšířen o tzv. Skolemovy funkce; zachovává splnitelnost idea převodu: formuli x 1... x n yp (x 1,..., x n, y) transformujeme
Skolemizace převod formulí na formule bez existenčních kvantifikátorů v jazyce, který je rozšířen o tzv. Skolemovy funkce; zachovává splnitelnost idea převodu: formuli x 1... x n yp (x 1,..., x n, y) transformujeme
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
Výroková a predikátová logika - VIII
 Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2016/2017 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2016/2017 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2016/2017 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2016/2017 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - V
 Výroková a predikátová logika - V Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - V ZS 2015/2016 1 / 21 Dokazovací systémy VL Hilbertovský kalkul Hilbertovský
Výroková a predikátová logika - V Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - V ZS 2015/2016 1 / 21 Dokazovací systémy VL Hilbertovský kalkul Hilbertovský
Výroková a predikátová logika - VIII
 Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2017/2018 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2017/2018 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Predikátová logika [Predicate logic]
![Predikátová logika [Predicate logic] Predikátová logika [Predicate logic]](/thumbs/74/70612837.jpg) Predikátová logika [Predicate logic] Přesněji predikátová logika prvého řádu. Formalizuje výroky o vlastnostech předmětů (entit) a vztazích mezi předměty, které patří do dané předmětné oblasti univerza.
Predikátová logika [Predicate logic] Přesněji predikátová logika prvého řádu. Formalizuje výroky o vlastnostech předmětů (entit) a vztazích mezi předměty, které patří do dané předmětné oblasti univerza.
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Výroková logika - opakování
 - opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
- opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
vhodná pro strojové dokazování (Prolog) metoda založená na vyvracení: dokazuje se nesplnitelnost formulí
 Rezoluce: další formální systém vhodná pro strojové dokazování (Prolog) metoda založená na vyvracení: dokazuje se nesplnitelnost formulí pracujeme s formulemi v nkf (též klauzulárním tvaru), ale používáme
Rezoluce: další formální systém vhodná pro strojové dokazování (Prolog) metoda založená na vyvracení: dokazuje se nesplnitelnost formulí pracujeme s formulemi v nkf (též klauzulárním tvaru), ale používáme
2.2 Sémantika predikátové logiky
 14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
Logika a logické programování
 Logika a logické programování témata ke zkoušce Poslední aktualizace: 16. prosince 2009 Zkouška je písemná, skládá se obvykle ze sedmi otázek (může být více nebo méně, podle náročnosti otázek), z toho
Logika a logické programování témata ke zkoušce Poslední aktualizace: 16. prosince 2009 Zkouška je písemná, skládá se obvykle ze sedmi otázek (může být více nebo méně, podle náročnosti otázek), z toho
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2015/2016 1 / 18 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2015/2016 1 / 18 Základní syntax Jazyk Výroková logika je logikou
Úvod do TI - logika Výroková logika - pokračování (3.přednáška) Marie Duží
 Úvod do TI - logika Výroková logika - pokračování (3.přednáška) Marie Duží marie.duzi@vsb.cz Normální formy formulí výrokové logiky Každé formuli výrokové logiky přísluší právě jedna pravdivostní funkce,
Úvod do TI - logika Výroková logika - pokračování (3.přednáška) Marie Duží marie.duzi@vsb.cz Normální formy formulí výrokové logiky Každé formuli výrokové logiky přísluší právě jedna pravdivostní funkce,
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2013/2014 1 / 20 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2013/2014 1 / 20 Základní syntax Jazyk Výroková logika je logikou
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Splnitelnost množin Definice Množina
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Splnitelnost množin Definice Množina
Výroková a predikátová logika - X
 Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2015/2016 1 / 22 Herbrandova věta Úvod Redukce nesplnitelnosti na
Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2015/2016 1 / 22 Herbrandova věta Úvod Redukce nesplnitelnosti na
Logika. 8. Automatické dokazování v predikátové logice (obecná rezoluční metoda)
 Logika 8. Automatické dokazování v predikátové logice (obecná rezoluční metoda) RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním
Logika 8. Automatické dokazování v predikátové logice (obecná rezoluční metoda) RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním
Marie Duží
 Marie Duží marie.duzi@vsb.cz Normální formy formulí výrokové logiky Každé formuli výrokové logiky přísluší právě jedna pravdivostní funkce, zobrazení {p, q, r } {0, 1} (pravdivostní tabulka). Naopak však
Marie Duží marie.duzi@vsb.cz Normální formy formulí výrokové logiky Každé formuli výrokové logiky přísluší právě jedna pravdivostní funkce, zobrazení {p, q, r } {0, 1} (pravdivostní tabulka). Naopak však
Unární je také spojka negace. pro je operace binární - příkladem může být funkce se signaturou. Binární je velká většina logických spojek
 Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Sémantika predikátové logiky
 Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Další (neklasické) logiky. Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20
 Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
(zkráceně jen formule), jestliže vznikla podle následujících pravidel:
 1 Kapitola 1 Výroková logika 1.1 Výroky 1.1.1 Výroky. Máme danou neprázdnou množinu A tzv. elementárních výroků (též jim říkáme logické nebo výrokové proměnné). Konečnou posloupnost prvků z množiny A,
1 Kapitola 1 Výroková logika 1.1 Výroky 1.1.1 Výroky. Máme danou neprázdnou množinu A tzv. elementárních výroků (též jim říkáme logické nebo výrokové proměnné). Konečnou posloupnost prvků z množiny A,
3.10 Rezoluční metoda ve výrokové logice
 3.10. Rezoluční metoda ve výrokové logice [070405-1102 ] 27 3.10 Rezoluční metoda ve výrokové logice Rezoluční metoda rozhoduje, zda daná množina klausulí je splnitelná nebo je nesplnitelná. Tím je také
3.10. Rezoluční metoda ve výrokové logice [070405-1102 ] 27 3.10 Rezoluční metoda ve výrokové logice Rezoluční metoda rozhoduje, zda daná množina klausulí je splnitelná nebo je nesplnitelná. Tím je také
Predikátová logika dokončení
 Predikátová logika dokončení Jiří Velebil: X01DML 1. října 2010: Predikátová logika dokončení 1/18 Syntaktická analýza Jako ve výrokové logice (syntaktické stromy). Každý list úspěšného stromu je obsazen
Predikátová logika dokončení Jiří Velebil: X01DML 1. října 2010: Predikátová logika dokončení 1/18 Syntaktická analýza Jako ve výrokové logice (syntaktické stromy). Každý list úspěšného stromu je obsazen
Predikátová logika. Teoretická informatika Tomáš Foltýnek
 Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Výroková a predikátová logika - VI
 Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
Pro každé formule α, β, γ, δ platí: Pro každé formule α, β, γ platí: Poznámka: Platí právě tehdy, když je tautologie.
 Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
Základy logiky a teorie množin
 Pracovní text k přednášce Logika a teorie množin (I/2007) 1 1 Struktura přednášky Matematická logika 2 Výroková logika Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz Predikátová logika 1. řádu
Pracovní text k přednášce Logika a teorie množin (I/2007) 1 1 Struktura přednášky Matematická logika 2 Výroková logika Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz Predikátová logika 1. řádu
Výroková a predikátová logika - XII
 Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2018/2019 1 / 15 Rezoluční metoda v PL Rezoluční důkaz Obecné
Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2018/2019 1 / 15 Rezoluční metoda v PL Rezoluční důkaz Obecné
Logika XI. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı BI-MLO, ZS 2011/12
 Logika XI. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Logika XI. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
1 Predikátová logika. 1.1 Syntax. jaký mohou mít formule význam (sémantiku). 1. Logických symbolů: 2. Speciálních (mimologických) symbolů:
 1 Predikátová logika 1.1 Syntax Podobně jako ve výrokové logice začneme nejprve se syntaxí predikátové logiky, která nám říká, co jsou správně utvořené formule predikátové logiky. V další části tohoto
1 Predikátová logika 1.1 Syntax Podobně jako ve výrokové logice začneme nejprve se syntaxí predikátové logiky, která nám říká, co jsou správně utvořené formule predikátové logiky. V další části tohoto
Rezoluce v predikátové logice
 Rezoluce v predikátové logice Jiří Velebil: X01DML 15. října 2010: Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná
Rezoluce v predikátové logice Jiří Velebil: X01DML 15. října 2010: Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Sémantická věta o dedukci Věta Pro
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Sémantická věta o dedukci Věta Pro
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Predik atov a logika - pˇredn aˇska () Predik atov a logika - pˇredn aˇska / 16
 Predikátová logika - přednáška 3 6. 1. 2015 () Predikátová logika - přednáška 3 6. 1. 2015 1 / 16 Věta (o dedukci) Bud L jazyk, T teorie pro L, ϕ L-sentence a ψ L-formule. Pak Věta (o kompaktnosti) T ϕ
Predikátová logika - přednáška 3 6. 1. 2015 () Predikátová logika - přednáška 3 6. 1. 2015 1 / 16 Věta (o dedukci) Bud L jazyk, T teorie pro L, ϕ L-sentence a ψ L-formule. Pak Věta (o kompaktnosti) T ϕ
Logické programy Deklarativní interpretace
 Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
Logika Libor Barto. Výroková logika
 Logika Libor Barto Výroková logika Definice.(Jazyk výrokové logiky) Ve výrokové logice používáme tyto symboly: (1) Výrokové proměnné: velká písmena, případně opatřená indexy. (2) Výrokovéspojky:,,&,,,....
Logika Libor Barto Výroková logika Definice.(Jazyk výrokové logiky) Ve výrokové logice používáme tyto symboly: (1) Výrokové proměnné: velká písmena, případně opatřená indexy. (2) Výrokovéspojky:,,&,,,....
Rezoluce v predikátové logice
 Rezoluce v predikátové logice Jiří Velebil: AD0B01LGR 2015 Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná iff X =
Rezoluce v predikátové logice Jiří Velebil: AD0B01LGR 2015 Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná iff X =
4.2 Syntaxe predikátové logiky
 36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
Cvičení ke kursu Klasická logika II
 Cvičení ke kursu Klasická logika II (12. května 2017) 1. Nechť P a Q jsou unární a R binární predikát. Dokažte, že následující formule jsou logicky platné, ale obrátíme-li (vnější) implikaci, ve všech
Cvičení ke kursu Klasická logika II (12. května 2017) 1. Nechť P a Q jsou unární a R binární predikát. Dokažte, že následující formule jsou logicky platné, ale obrátíme-li (vnější) implikaci, ve všech
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška třetí Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška třetí Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Formální systém výrokové logiky
 Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
Výroková a predikátová logika - III
 Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2014/2015 1 / 21 Výroková logika Horn-SAT Horn-SAT Jednotková
Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2014/2015 1 / 21 Výroková logika Horn-SAT Horn-SAT Jednotková
Logika. 2. Výroková logika. RNDr. Luděk Cienciala, Ph. D.
 Logika 2. Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216, Logika:
Logika 2. Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216, Logika:
popel, glum & nepil 16/28
 Lineární rezoluce další způsob zjemnění rezoluce; místo stromu směřujeme k lineární struktuře důkazu Lineární rezoluční odvození (důkaz) z Ë je posloupnost dvojic ¼ ¼ Ò Ò taková, že Ò ½ a 1. ¼ a všechna
Lineární rezoluce další způsob zjemnění rezoluce; místo stromu směřujeme k lineární struktuře důkazu Lineární rezoluční odvození (důkaz) z Ë je posloupnost dvojic ¼ ¼ Ò Ò taková, že Ò ½ a 1. ¼ a všechna
Úvod do teoretické informatiky(2017/2018) cvičení 6 1
 Úvod do teoretické informatiky(2017/2018) cvičení 6 1 Cvičení 6 Příklad 1: Pro každou z následujících sekvencí symbolů rozhodněte, zda se jedná o a) term, b) formuli predikátové logiky(používejte běžné
Úvod do teoretické informatiky(2017/2018) cvičení 6 1 Cvičení 6 Příklad 1: Pro každou z následujících sekvencí symbolů rozhodněte, zda se jedná o a) term, b) formuli predikátové logiky(používejte běžné
Základy logiky Logika a logické systémy. Umělá inteligence a rozpoznávání, LS
 Základy logiky 22. 4. 2015 Umělá inteligence a rozpoznávání, LS 2015 6-1 Logika je naukou, která se zabývá studiem lidského uvažování. Mezi základní úlohy logiky patří nalézání metod správného usuzování,
Základy logiky 22. 4. 2015 Umělá inteligence a rozpoznávání, LS 2015 6-1 Logika je naukou, která se zabývá studiem lidského uvažování. Mezi základní úlohy logiky patří nalézání metod správného usuzování,
Úvod do predikátové logiky. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
 Úvod do predikátové logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 1 Relace Neuspořádaná vs. uspořádaná dvojice {m, n} je neuspořádaná dvojice. m, n je uspořádaná dvojice. (FLÚ AV ČR) Logika:
Úvod do predikátové logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 1 Relace Neuspořádaná vs. uspořádaná dvojice {m, n} je neuspořádaná dvojice. m, n je uspořádaná dvojice. (FLÚ AV ČR) Logika:
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2018/2019 1 / 13 Dokončené tablo Chceme, aby dokončená bezesporná
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2018/2019 1 / 13 Dokončené tablo Chceme, aby dokončená bezesporná
Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka
 Celkové hodnocení BI-MLO (nevyplňujte!) Semestr Zkouška Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka BI-MLO Písemná zkouška 9. února 2016 Matematická logika FIT ČVUT v Praze Varianta B
Celkové hodnocení BI-MLO (nevyplňujte!) Semestr Zkouška Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka BI-MLO Písemná zkouška 9. února 2016 Matematická logika FIT ČVUT v Praze Varianta B
Místo pojmu výroková formule budeme používat zkráceně jen formule. Při jejich zápisu
 VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
Základní pojmy matematické logiky
 KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
Výroková a predikátová logika - IV
 Výroková a predikátová logika - IV Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IV ZS 2018/2019 1 / 17 Tablo metoda Tablo Tablo - příklady F (((p q)
Výroková a predikátová logika - IV Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IV ZS 2018/2019 1 / 17 Tablo metoda Tablo Tablo - příklady F (((p q)
Výroková a predikátová logika - III
 Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2017/2018 1 / 16 2-SAT 2-SAT Výrok je v k-cnf, je-li v CNF a
Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2017/2018 1 / 16 2-SAT 2-SAT Výrok je v k-cnf, je-li v CNF a
Výroková logika. Teoretická informatika Tomáš Foltýnek
 Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
teorie logických spojek chápaných jako pravdivostní funkce
 Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2018/2019 1 / 15 Platnost (pravdivost) Platnost ve struktuře
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2018/2019 1 / 15 Platnost (pravdivost) Platnost ve struktuře
Každé formuli výrokového počtu přiřadíme hodnotu 0, půjde-li o formuli nepravdivou, a hodnotu 1, půjde-li. α neplatí. β je nutná podmínka pro α
 1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
Přednáška 3: rozhodování o platnosti úsudku
 Přednáška 3: rozhodování o platnosti úsudku Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky Úsudky Úsudek je platný, jestliže nutně, za všech okolností, tj. při všech interpretacích, ve kterých
Přednáška 3: rozhodování o platnosti úsudku Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky Úsudky Úsudek je platný, jestliže nutně, za všech okolností, tj. při všech interpretacích, ve kterých
Úvod do informatiky. Miroslav Kolařík
 Úvod do informatiky přednáška první Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Co a k čemu je logika? 2 Výroky a logické spojky
Úvod do informatiky přednáška první Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Co a k čemu je logika? 2 Výroky a logické spojky
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška desátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. Obsah 1 Úvod do modální logiky 2 Logické programování a Prolog 3
Matematická logika přednáška desátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. Obsah 1 Úvod do modální logiky 2 Logické programování a Prolog 3
Predikátová logika. Z minula: 1. jazyk logiky 1. řádu. 2. term a formule. 3. interpretace jazyka (relační struktura) 4. Tarského definice pravdy
 1 Predikátová logika Z minula: 1. jazyk logiky 1. řádu 2. term a formule 3. interpretace jazyka (relační struktura) 4. Tarského definice pravdy 5. vázané a volné výskyty proměnných ve formuli 6. otevřené
1 Predikátová logika Z minula: 1. jazyk logiky 1. řádu 2. term a formule 3. interpretace jazyka (relační struktura) 4. Tarského definice pravdy 5. vázané a volné výskyty proměnných ve formuli 6. otevřené
Tableaux metody. Jiří Vyskočil 2011
 Tableaux metody Jiří Vyskočil 2011 Tableau [tabló] metoda Tableau metoda je další oblíbená metoda užívaná pro automatické dokazování vět v predikátové logice, ale i v dalších (modálních, temporálních,
Tableaux metody Jiří Vyskočil 2011 Tableau [tabló] metoda Tableau metoda je další oblíbená metoda užívaná pro automatické dokazování vět v predikátové logice, ale i v dalších (modálních, temporálních,
Přednáška 2: Formalizace v jazyce logiky.
 Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
Rezoluční kalkulus pro výrokovou logiku
 AD4M33AU Automatické uvažování Rezoluční kalkulus pro výrokovou logiku Petr Pudlák Výroková logika Výhody Jednoduchý jazyk. Rozhodnutelnost dokazatelnosti i nedokazatelnosti. Rychlejší algoritmy. Nevýhody
AD4M33AU Automatické uvažování Rezoluční kalkulus pro výrokovou logiku Petr Pudlák Výroková logika Výhody Jednoduchý jazyk. Rozhodnutelnost dokazatelnosti i nedokazatelnosti. Rychlejší algoritmy. Nevýhody
Výroková logika: splnitelnost, vyplývání, tautologie, úsudky. Splnitelnost. 1. Ověřte splnitelnost množiny formulí
 Splnitelnost 1. Ověřte splnitelnost množiny formulí 1 T = {(p q) r, q r, r s, p s} Splnitelnost 1. Ověřte splnitelnost množiny formulí 1 T = {(p q) r, q r, r s, p s} 2 F = {(p q r) ((s t) ( s t)), q r,
Splnitelnost 1. Ověřte splnitelnost množiny formulí 1 T = {(p q) r, q r, r s, p s} Splnitelnost 1. Ověřte splnitelnost množiny formulí 1 T = {(p q) r, q r, r s, p s} 2 F = {(p q r) ((s t) ( s t)), q r,
V této výukové jednotce se student seznámí se základními pojmy z teorie predikátového počtu.
 1 Predikátová logika Základní informace V této výukové jednotce se student seznámí se základními pojmy z teorie predikátového počtu. Výstupy z výukové jednotky Student se seznámí se základními termíny
1 Predikátová logika Základní informace V této výukové jednotce se student seznámí se základními pojmy z teorie predikátového počtu. Výstupy z výukové jednotky Student se seznámí se základními termíny
Výroková a predikátová logika - XIII
 Výroková a predikátová logika - XIII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XIII ZS 2013/2014 1 / 13 Úvod Algoritmická (ne)rozhodnutelnost Které
Výroková a predikátová logika - XIII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XIII ZS 2013/2014 1 / 13 Úvod Algoritmická (ne)rozhodnutelnost Které
2.1 Formule predikátové logiky. větám. Použijte k tomu predikátových symbolu uvedených v textu.
 6 Kapitola 2 Příklady z predikátové logiky 2.1 Formule predikátové logiky 2.1.1 Příklad. Napište formule predikátové logiky odpovídající následujícím větám. Použijte k tomu predikátových symbolu uvedených
6 Kapitola 2 Příklady z predikátové logiky 2.1 Formule predikátové logiky 2.1.1 Příklad. Napište formule predikátové logiky odpovídající následujícím větám. Použijte k tomu predikátových symbolu uvedených
Kapitola Výroky
 1 Kapitola 1 Výroková logika 1.1 Výroky 1.1.1 Příklad Rozhodněte, zda následující posloupnosti symbolú jsou výrokové formule. Jde-li o formuli, pak sestrojte její strom, určete její hloubku a uved te všechny
1 Kapitola 1 Výroková logika 1.1 Výroky 1.1.1 Příklad Rozhodněte, zda následující posloupnosti symbolú jsou výrokové formule. Jde-li o formuli, pak sestrojte její strom, určete její hloubku a uved te všechny
Okruh č.3: Sémantický výklad predikátové logiky
 Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz
 Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Řešení: Ano. Řešení: Ne.
 1 ÚLOHY Z PREDIKÁTOVÉ LOGIKY Instance, varianty. UF.1.1. Substituovatelnost. 1. Buď ϕ formule ( z)(x=z)&y < x a dále x, y, z různé proměnné, F unární funkční symbol, c konstantní symbol. Uveďte, zda je
1 ÚLOHY Z PREDIKÁTOVÉ LOGIKY Instance, varianty. UF.1.1. Substituovatelnost. 1. Buď ϕ formule ( z)(x=z)&y < x a dále x, y, z různé proměnné, F unární funkční symbol, c konstantní symbol. Uveďte, zda je
6. Logika a logické systémy. Základy logiky. Lucie Koloušková, Václav Matoušek / KIV. Umělá inteligence a rozpoznávání, LS
 Základy logiky Umělá inteligence a rozpoznávání, LS 2012 6-1 Logika je naukou, která se zabývá studiem lidského uvažování. Mezi základní úlohy logiky patří nalézání metod správného usuzování, tedy postupů,
Základy logiky Umělá inteligence a rozpoznávání, LS 2012 6-1 Logika je naukou, která se zabývá studiem lidského uvažování. Mezi základní úlohy logiky patří nalézání metod správného usuzování, tedy postupů,
platné nejsou Sokrates je smrtelný. (r) 1/??
 Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Matematická indukce, sumy a produkty, matematická logika
 Matematická indukce, sumy a produkty, matematická logika 8.9. -.0.009 Matematická indukce Jde o následující vlastnost přirozených čísel: Předpokládejme:. Nějaké tvrzení platí pro.. Platí-li tvrzení pro
Matematická indukce, sumy a produkty, matematická logika 8.9. -.0.009 Matematická indukce Jde o následující vlastnost přirozených čísel: Předpokládejme:. Nějaké tvrzení platí pro.. Platí-li tvrzení pro
Hilbertovský axiomatický systém
 Hilbertovský axiomatický systém Predikátová logika H 1 Šárka Vavrečková Ústav informatiky, FPF SU Opava Poslední aktualizace: 24. října 2008 Specifikace H 1 Jazyk L H1 přejímáme jazyk predikátové logiky
Hilbertovský axiomatický systém Predikátová logika H 1 Šárka Vavrečková Ústav informatiky, FPF SU Opava Poslední aktualizace: 24. října 2008 Specifikace H 1 Jazyk L H1 přejímáme jazyk predikátové logiky
Disjunktivní a konjunktivní lní tvar formule. 2.přednáška
 Disjunktivní a konjunktivní normáln lní tvar formule 2.přednáška Disjunktivní normáln lní forma Definice Řekneme, že formule ( A ) je v disjunktivním normálním tvaru (formě), zkráceně v DNF, jestliže je
Disjunktivní a konjunktivní normáln lní tvar formule 2.přednáška Disjunktivní normáln lní forma Definice Řekneme, že formule ( A ) je v disjunktivním normálním tvaru (formě), zkráceně v DNF, jestliže je
Rovnost lze vyjádřit jako predikát, např. můžeme zvolit, že P(x, y) reprezentujetvrzení xjerovnoy.
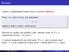 Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Negativní informace. Petr Štěpánek. S použitím materiálu M.Gelfonda a V. Lifschitze. Logické programování 15 1
 Negativní informace Petr Štěpánek S použitím materiálu M.Gelfonda a V. Lifschitze 2009 Logické programování 15 1 Negace jako neúspěch Motivace: Tvrzení p (atomická formule) neplatí, jestliže nelze odvodit
Negativní informace Petr Štěpánek S použitím materiálu M.Gelfonda a V. Lifschitze 2009 Logické programování 15 1 Negace jako neúspěch Motivace: Tvrzení p (atomická formule) neplatí, jestliže nelze odvodit
Úvod do logiky (PL): negace a ekvivalence vět mimo logický
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): negace a ekvivalence vět mimo logický čtverec
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): negace a ekvivalence vět mimo logický čtverec
Cvičení 4. negace konjunkce disjunkce implikace ekvivalence. a) Najděte UDNF, UKNF a stanovte log. důsledky. 1) [p (p q)] [( p q) (q p)]
![Cvičení 4. negace konjunkce disjunkce implikace ekvivalence. a) Najděte UDNF, UKNF a stanovte log. důsledky. 1) [p (p q)] [( p q) (q p)] Cvičení 4. negace konjunkce disjunkce implikace ekvivalence. a) Najděte UDNF, UKNF a stanovte log. důsledky. 1) [p (p q)] [( p q) (q p)]](/thumbs/92/108888591.jpg) Cvičení 4 negace konjunkce disjunkce implikace ekvivalence a) Najděte UDNF, UKNF a stanovte log. důsledky 1) [p (p q)] [( p q) (q p)] p q p q p q q p p A B C D E UEK UED A B C D E F 0 0 1 1 0 0 0 1 p q
Cvičení 4 negace konjunkce disjunkce implikace ekvivalence a) Najděte UDNF, UKNF a stanovte log. důsledky 1) [p (p q)] [( p q) (q p)] p q p q p q q p p A B C D E UEK UED A B C D E F 0 0 1 1 0 0 0 1 p q
Sémantika výrokové logiky. Alena Gollová Výroková logika 1/23
 Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
7 Jemný úvod do Logiky
 7 Jemný úvod do Logiky Základem přesného matematického vyjadřování je správné používání (matematické) logiky a logických úsudků. Logika jako filozofická discipĺına se intenzivně vyvíjí už od dob antiky,
7 Jemný úvod do Logiky Základem přesného matematického vyjadřování je správné používání (matematické) logiky a logických úsudků. Logika jako filozofická discipĺına se intenzivně vyvíjí už od dob antiky,
Výroková logika. Sémantika výrokové logiky
 Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
1 REZOLUČNÍ FORMÁLNÍ DŮKAZY
 Vážená kolegyně / vážený kolego, součástí Vašeho rozšiřujícího studia informatiky je absolvování předmětu Logika pro učitele 2, jehož cílem je v návaznosti na předmět Logika pro učitele 1 seznámení se
Vážená kolegyně / vážený kolego, součástí Vašeho rozšiřujícího studia informatiky je absolvování předmětu Logika pro učitele 2, jehož cílem je v návaznosti na předmět Logika pro učitele 1 seznámení se
Modely Herbrandovské interpretace
 Modely Herbrandovské interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 8 1 Uvedli jsme termové interpretace a termové modely pro logické programy a také nejmenší
Modely Herbrandovské interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 8 1 Uvedli jsme termové interpretace a termové modely pro logické programy a také nejmenší
Predikátová logika: Axiomatizace, sémantické stromy, identita. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 13
 Predikátová logika: Axiomatizace, sémantické stromy, identita (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 13 Axiomatizace predikátové logiky Axiomatizace predikátové logiky Definice Hilbertovský
Predikátová logika: Axiomatizace, sémantické stromy, identita (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 13 Axiomatizace predikátové logiky Axiomatizace predikátové logiky Definice Hilbertovský
Logika. 6. Axiomatický systém výrokové logiky
 Logika 6. Axiomatický systém výrokové logiky RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216,
Logika 6. Axiomatický systém výrokové logiky RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216,
Výroková a predikátová logika - XI
 Výroková a predikátová logika - XI Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XI ZS 2014/2015 1 / 21 Další dokazovací systémy PL Hilbertovský kalkul
Výroková a predikátová logika - XI Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XI ZS 2014/2015 1 / 21 Další dokazovací systémy PL Hilbertovský kalkul
