Úvod do predikátové logiky. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
|
|
|
- Šimon Rohla
- před 5 lety
- Počet zobrazení:
Transkript
1 Úvod do predikátové logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
2 Relace Neuspořádaná vs. uspořádaná dvojice {m, n} je neuspořádaná dvojice. m, n je uspořádaná dvojice. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
3 Kartézský součin Relace M N = { m, n ; m M, n N}. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
4 Relace Binární relace Definice Binární relace na množině M je podmnožina kartézského součinu M M. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
5 Relace Klasifikace relací R je reflexivní, když pro každé m platí mrm. R je symetrická, když pro každé m, n platí, že pokud mrn, pak nrm. R je tranzitivní, když pro každé m, n, o platí, že pokud mrn a nro, pak mro. R je relace ekvivalence, když je reflexivní, symetrická a tranzitivní. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
6 Relace Klasifikace relací R je antisymetrická, když pro každé m, n platí, že pokud mrn, pak neplatí nrm. R je ostré uspořádání, když R je tranzitivní a antisymetrická. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
7 Relace Klasifikace relací R je slabě antisymetrická, když pro každé m, n platí, že pokud mrn a nrm, pak n = m. R je neostré uspořádání, když R je reflexivní, tranzitivní a slabě antisymetrická. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
8 Klasifikace relací Relace R je funkce, když pro každé m, n, o platí, že pokud mrn a mro, pak n = o. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
9 Syntax klasické predikátové logiky Základní symboly predikátové logiky Základní symboly predikátové logiky: Mimologické symboly predikáty: A m, B m, C m,... jména: a, b, c,... Logické symboly výrokové operátory:,,,, kvantifikátory:, Proměnné: x, y, z,... Pomocné symboly: (, ) (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
10 Syntax klasické predikátové logiky Základní symboly predikátové logiky Základní symboly predikátové logiky: Mimologické symboly predikáty: A m, B m, C m,... jména: a, b, c,... Logické symboly výrokové operátory:,,,, kvantifikátory:, Proměnné: x, y, z,... Pomocné symboly: (, ) (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
11 Syntax klasické predikátové logiky Základní symboly predikátové logiky Základní symboly predikátové logiky: Mimologické symboly predikáty: A m, B m, C m,... jména: a, b, c,... Logické symboly výrokové operátory:,,,, kvantifikátory:, Proměnné: x, y, z,... Pomocné symboly: (, ) (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
12 Syntax klasické predikátové logiky Základní symboly predikátové logiky Základní symboly predikátové logiky: Mimologické symboly predikáty: A m, B m, C m,... jména: a, b, c,... Logické symboly výrokové operátory:,,,, kvantifikátory:, Proměnné: x, y, z,... Pomocné symboly: (, ) (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
13 Syntax klasické predikátové logiky Základní symboly predikátové logiky Základní symboly predikátové logiky: Mimologické symboly predikáty: A m, B m, C m,... jména: a, b, c,... Logické symboly výrokové operátory:,,,, kvantifikátory:, Proměnné: x, y, z,... Pomocné symboly: (, ) (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
14 Termy Syntax klasické predikátové logiky Proměnné a jména jsou termy. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
15 Syntax klasické predikátové logiky Gramatika: Elementární formule Pokud A je n-místný predikát a t 1,..., t n jsou termy, pak At 1,..., t n je elementární formule. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
16 Syntax klasické predikátové logiky Gramatika: Induktivní definice formule KPL Definice Každá elementární formule je formule. Jestliže ϕ je formule, pak ϕ je také formule. Pokud ϕ, ψ jsou formule, pak (ϕ ψ), (ϕ ψ), (ϕ ψ) a (ϕ ψ) jsou také formule. Jestliže ϕ je formule a x proměnná, pak xϕ a xϕ jsou formule. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
17 Syntax klasické predikátové logiky Gramatika: Induktivní definice formule KPL Definice Každá elementární formule je formule. Jestliže ϕ je formule, pak ϕ je také formule. Pokud ϕ, ψ jsou formule, pak (ϕ ψ), (ϕ ψ), (ϕ ψ) a (ϕ ψ) jsou také formule. Jestliže ϕ je formule a x proměnná, pak xϕ a xϕ jsou formule. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
18 Syntax klasické predikátové logiky Gramatika: Induktivní definice formule KPL Definice Každá elementární formule je formule. Jestliže ϕ je formule, pak ϕ je také formule. Pokud ϕ, ψ jsou formule, pak (ϕ ψ), (ϕ ψ), (ϕ ψ) a (ϕ ψ) jsou také formule. Jestliže ϕ je formule a x proměnná, pak xϕ a xϕ jsou formule. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
19 Syntax klasické predikátové logiky Gramatika: Induktivní definice formule KPL Definice Každá elementární formule je formule. Jestliže ϕ je formule, pak ϕ je také formule. Pokud ϕ, ψ jsou formule, pak (ϕ ψ), (ϕ ψ), (ϕ ψ) a (ϕ ψ) jsou také formule. Jestliže ϕ je formule a x proměnná, pak xϕ a xϕ jsou formule. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
20 Syntax klasické predikátové logiky Základní syntaktické pojmy konstrukce formule rozsah kvantifikátoru volné a vázané výskyty proměnných otevřené formule a uzavřené formule (sentence) (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
21 Formalizace Formalizace: Sylogistické formule SaP... x(sx Px) SeP... x(sx Px) SiP... x(sx Px) SoP... x(sx Px) (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
22 Formalizace, Obecný kvantifikátor se přirozeně váže k implikaci: x(......) Existenční kvantifikátor se přirozeně váže ke konjunkci: x(......) (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
23 Formalizace Cvičení: formalizujte následující věty Psi, kteří štěkají, nekoušou. Všichni lidé, kteří se něčeho bojí, jsou zbabělci. Někteří savci, kteří žijí ve vodě, nesnáší žraloky. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
24 Formalizace Cvičení: formalizujte následující věty Pokud někdo lže, tak i krade. Je k dispozici pokoj s výhledem. Není všechno zlato, co se třpytí. Pomeranče a citróny jsou citrusové plody. Jen hadům a ještěrkám se dobře daří v poušti. Petr má krásnou ženu, ona ho však nenávidí. Kdo jinému jámu kopá, sám do ní padá. Lidé se dělí na pracovité a líné. Tom se nepohodl se svým bratrem a syn ho pak našel mrtvého. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
25 Formalizace Cvičení: formalizujte následující věty Pokud někdo lže, tak i krade. Je k dispozici pokoj s výhledem. Není všechno zlato, co se třpytí. Pomeranče a citróny jsou citrusové plody. Jen hadům a ještěrkám se dobře daří v poušti. Petr má krásnou ženu, ona ho však nenávidí. Kdo jinému jámu kopá, sám do ní padá. Lidé se dělí na pracovité a líné. Tom se nepohodl se svým bratrem a syn ho pak našel mrtvého. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
26 Formalizace Cvičení: formalizujte následující věty Pokud někdo lže, tak i krade. Je k dispozici pokoj s výhledem. Není všechno zlato, co se třpytí. Pomeranče a citróny jsou citrusové plody. Jen hadům a ještěrkám se dobře daří v poušti. Petr má krásnou ženu, ona ho však nenávidí. Kdo jinému jámu kopá, sám do ní padá. Lidé se dělí na pracovité a líné. Tom se nepohodl se svým bratrem a syn ho pak našel mrtvého. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
27 Formalizace Cvičení: formalizujte následující věty Pokud někdo lže, tak i krade. Je k dispozici pokoj s výhledem. Není všechno zlato, co se třpytí. Pomeranče a citróny jsou citrusové plody. Jen hadům a ještěrkám se dobře daří v poušti. Petr má krásnou ženu, ona ho však nenávidí. Kdo jinému jámu kopá, sám do ní padá. Lidé se dělí na pracovité a líné. Tom se nepohodl se svým bratrem a syn ho pak našel mrtvého. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
28 Formalizace Cvičení: formalizujte následující věty Pokud někdo lže, tak i krade. Je k dispozici pokoj s výhledem. Není všechno zlato, co se třpytí. Pomeranče a citróny jsou citrusové plody. Jen hadům a ještěrkám se dobře daří v poušti. Petr má krásnou ženu, ona ho však nenávidí. Kdo jinému jámu kopá, sám do ní padá. Lidé se dělí na pracovité a líné. Tom se nepohodl se svým bratrem a syn ho pak našel mrtvého. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
29 Formalizace Cvičení: formalizujte následující věty Pokud někdo lže, tak i krade. Je k dispozici pokoj s výhledem. Není všechno zlato, co se třpytí. Pomeranče a citróny jsou citrusové plody. Jen hadům a ještěrkám se dobře daří v poušti. Petr má krásnou ženu, ona ho však nenávidí. Kdo jinému jámu kopá, sám do ní padá. Lidé se dělí na pracovité a líné. Tom se nepohodl se svým bratrem a syn ho pak našel mrtvého. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
30 Formalizace Cvičení: formalizujte následující věty Pokud někdo lže, tak i krade. Je k dispozici pokoj s výhledem. Není všechno zlato, co se třpytí. Pomeranče a citróny jsou citrusové plody. Jen hadům a ještěrkám se dobře daří v poušti. Petr má krásnou ženu, ona ho však nenávidí. Kdo jinému jámu kopá, sám do ní padá. Lidé se dělí na pracovité a líné. Tom se nepohodl se svým bratrem a syn ho pak našel mrtvého. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
31 Formalizace Cvičení: formalizujte následující věty Pokud někdo lže, tak i krade. Je k dispozici pokoj s výhledem. Není všechno zlato, co se třpytí. Pomeranče a citróny jsou citrusové plody. Jen hadům a ještěrkám se dobře daří v poušti. Petr má krásnou ženu, ona ho však nenávidí. Kdo jinému jámu kopá, sám do ní padá. Lidé se dělí na pracovité a líné. Tom se nepohodl se svým bratrem a syn ho pak našel mrtvého. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
32 Formalizace Cvičení: formalizujte následující věty Pokud někdo lže, tak i krade. Je k dispozici pokoj s výhledem. Není všechno zlato, co se třpytí. Pomeranče a citróny jsou citrusové plody. Jen hadům a ještěrkám se dobře daří v poušti. Petr má krásnou ženu, ona ho však nenávidí. Kdo jinému jámu kopá, sám do ní padá. Lidé se dělí na pracovité a líné. Tom se nepohodl se svým bratrem a syn ho pak našel mrtvého. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
33 Formalizace Cvičení: formalizujte následující věty Člověk, který ovládá všechny ctnosti, je ctnostný člověk, ale jsou ctnostní lidé, kteří všechny ctnosti neovládají. Každý syn má otce, ale ne každý otec má syna. Každý, kdo má všechny rád, zná někoho, kdo nemá nikoho rád. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
34 Sémantika predikátové logiky Pojem interpretace Interpretace I sestává z univerza objektů U I, což je nějaká neprázdná množina a navíc každému jménu přiřadí nějaký objekt univerza, každému jednomístnému predikátu přiřadí nějakou podmnožinu univerza, každému n-místnému predikátu přiřadí n-ární relaci na univerzu. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
35 Sémantika predikátové logiky Pojem interpretace Interpretace I sestává z univerza objektů U I, což je nějaká neprázdná množina a navíc každému jménu přiřadí nějaký objekt univerza, každému jednomístnému predikátu přiřadí nějakou podmnožinu univerza, každému n-místnému predikátu přiřadí n-ární relaci na univerzu. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
36 Sémantika predikátové logiky Pojem interpretace Interpretace I sestává z univerza objektů U I, což je nějaká neprázdná množina a navíc každému jménu přiřadí nějaký objekt univerza, každému jednomístnému predikátu přiřadí nějakou podmnožinu univerza, každému n-místnému predikátu přiřadí n-ární relaci na univerzu. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
37 Sémantika predikátové logiky Pojem interpretace Interpretace I sestává z univerza objektů U I, což je nějaká neprázdná množina a navíc každému jménu přiřadí nějaký objekt univerza, každému jednomístnému predikátu přiřadí nějakou podmnožinu univerza, každému n-místnému predikátu přiřadí n-ární relaci na univerzu. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
38 Valuace Sémantika predikátové logiky Valuace V v interpretaci I je funkce, která přiřazuje každé proměnné nějaký objekt z univerza interpretace I. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
39 Sémantika predikátové logiky Značení IV (t) = I(t), pokud t je jméno. IV (t) = V (t), pokud t je proměnná. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
40 Tarského definice pravdy Tarského definice pravdy elementární věty Předpokládejme, že A je jednomístný predikát a t je term. Pak IV = At ptk IV (t) I(A). Předpokládejme, že A je n-místný predikát. Pak IV = At 1,..., t n ptk IV (t 1 ),..., IV (t n ) I(A). (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
41 Tarského definice pravdy Tarského definice pravdy výrokové operátory IV = ϕ ptk není pravda, že IV = ϕ. IV = ϕ ψ ptk IV = ϕ a IV = ψ. IV = ϕ ψ ptk IV = ϕ nebo IV = ψ. IV = ϕ ψ ptk není pravda, že IV = ϕ nebo platí, že IV = ψ. IV = ϕ ψ ptk IV = ϕ právě tehdy, když IV = ψ (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
42 Tarského definice pravdy Kvantifikátory: Substituční strategie IV = xϕ ptk pro každé jméno a platí IV = ϕ x a. IV = xϕ ptk pro nějaké jméno a platí IV = ϕ x a. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
43 Tarského definice pravdy Varianta valuace Předpokládejme, že V je valuace v interpretaci I, o je nějaký objekt z univerza interpretace I, x je proměnná. V x o je tzv. x-varianta valuace V, kterou definujeme následujícím způsobem: V x o(y) = V (y), pro každou proměnnou y, která se liší od x. V x o(x) = o. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
44 Tarského definice pravdy Tarského definice pravdy kvantifikátory IV = xϕ ptk pro každé o U I platí IV x o = ϕ. IV = xϕ ptk pro nějaké o U I platí IV x o = ϕ. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
45 Tarského definice pravdy Platnost formule v interpretaci Definice I = ϕ ptk pro každé V v I platí IV = ϕ. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
46 Tarského definice pravdy Věta o platnosti sentencí v interpretaci Předpokládejme, že I je interpretace a ϕ je sentence. Pak platí: Bud I = ϕ, nebo I = ϕ. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
47 Tarského definice pravdy Model a kontra-model formule, model množiny formulí Definice Interpretace I je modelem formule ϕ p.t.k. I = ϕ. Interpretace I je kontra-modelem formule ϕ p.t.k. I není modelem formule ϕ. Interpretace I je modelem množiny formulí p.t.k. I je modelem každé formule z této množiny. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
48 Tarského definice pravdy Pojem vyplývání Definice Závěr vyplývá z předpokladů, když každý model předpokladů je modelem závěru. (Ekvivalentně: Neexistuje model předpokladů, který by současně byl kontra-modelem závěru.) Značíme: T = ϕ. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
49 Tarského definice pravdy Příklady Platí x yrxy = y xrxy Neplatí y xrxy = x yrxy Platný úsudek: Existuje příčina všech jevů. Z toho plyne, že každý jev má nějakou příčinu. Neplatný úsudek: Každý jev má nějakou příčinu. Z toho plyne, že existuje příčina všech jevů. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
50 Tarského definice pravdy Příklady Platí x yrxy = y xrxy Neplatí y xrxy = x yrxy Platný úsudek: Existuje příčina všech jevů. Z toho plyne, že každý jev má nějakou příčinu. Neplatný úsudek: Každý jev má nějakou příčinu. Z toho plyne, že existuje příčina všech jevů. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
51 Tarského definice pravdy Příklady Platí x yrxy = y xrxy Neplatí y xrxy = x yrxy Platný úsudek: Existuje příčina všech jevů. Z toho plyne, že každý jev má nějakou příčinu. Neplatný úsudek: Každý jev má nějakou příčinu. Z toho plyne, že existuje příčina všech jevů. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
52 Tarského definice pravdy Příklady Platí x yrxy = y xrxy Neplatí y xrxy = x yrxy Platný úsudek: Existuje příčina všech jevů. Z toho plyne, že každý jev má nějakou příčinu. Neplatný úsudek: Každý jev má nějakou příčinu. Z toho plyne, že existuje příčina všech jevů. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
53 Logická ekvivalence Tarského definice pravdy ϕ, ψ jsou logicky ekvivalentní formule, když ϕ = ψ a ψ = ϕ. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
54 Tarského definice pravdy Vztahy mezi kvantifikátory xϕ je log. ek. s x ϕ. xϕ je log. ek. s x ϕ. xϕ je log. ek. s x ϕ. xϕ je log. ek. s x ϕ. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
55 Tarského definice pravdy Další sémantické pojmy Sentence je logicky pravdivá, když je v každé interpretaci pravdivá. Sentence je logicky nepravdivá, když není v žádné interpretaci pravdivá. Sentence je splnitelná, když má model. Množina sentencí je splnitelná, když má model. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
56 Tarského definice pravdy Další sémantické pojmy Sentence je logicky pravdivá, když je v každé interpretaci pravdivá. Sentence je logicky nepravdivá, když není v žádné interpretaci pravdivá. Sentence je splnitelná, když má model. Množina sentencí je splnitelná, když má model. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
57 Tarského definice pravdy Další sémantické pojmy Sentence je logicky pravdivá, když je v každé interpretaci pravdivá. Sentence je logicky nepravdivá, když není v žádné interpretaci pravdivá. Sentence je splnitelná, když má model. Množina sentencí je splnitelná, když má model. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
58 Tarského definice pravdy Další sémantické pojmy Sentence je logicky pravdivá, když je v každé interpretaci pravdivá. Sentence je logicky nepravdivá, když není v žádné interpretaci pravdivá. Sentence je splnitelná, když má model. Množina sentencí je splnitelná, když má model. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
59 Tarského definice pravdy Další sémantické pojmy Sentence je logicky pravdivá, když je v každé interpretaci pravdivá. Sentence je logicky nepravdivá, když není v žádné interpretaci pravdivá. Sentence je splnitelná, když má model. Množina sentencí je splnitelná, když má model. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
Sylogistika. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 16
 (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 16 Výstavba logické teorie Sylogistika 1) Syntax základní symboly (logické, mimologické) gramatická pravidla (pojem formule) 2) Sémantika pojem interpretace
(FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 16 Výstavba logické teorie Sylogistika 1) Syntax základní symboly (logické, mimologické) gramatická pravidla (pojem formule) 2) Sémantika pojem interpretace
Predikátová logika dokončení
 Predikátová logika dokončení Jiří Velebil: X01DML 1. října 2010: Predikátová logika dokončení 1/18 Syntaktická analýza Jako ve výrokové logice (syntaktické stromy). Každý list úspěšného stromu je obsazen
Predikátová logika dokončení Jiří Velebil: X01DML 1. října 2010: Predikátová logika dokončení 1/18 Syntaktická analýza Jako ve výrokové logice (syntaktické stromy). Každý list úspěšného stromu je obsazen
Další (neklasické) logiky. Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20
 Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
Okruh č.3: Sémantický výklad predikátové logiky
 Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
1 Pravdivost formulí v interpretaci a daném ohodnocení
 1 Pravdivost formulí v interpretaci a daném ohodnocení Než uvedeme konkrétní příklady, zopakujme si definici interpretace, ohodnocení a pravdivosti. Necht L je nějaký jazyk. Interpretaci U, jazyka L tvoří
1 Pravdivost formulí v interpretaci a daném ohodnocení Než uvedeme konkrétní příklady, zopakujme si definici interpretace, ohodnocení a pravdivosti. Necht L je nějaký jazyk. Interpretaci U, jazyka L tvoří
Výroková a predikátová logika - VI
 Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Pro každé formule α, β, γ, δ platí: Pro každé formule α, β, γ platí: Poznámka: Platí právě tehdy, když je tautologie.
 Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
Unární je také spojka negace. pro je operace binární - příkladem může být funkce se signaturou. Binární je velká většina logických spojek
 Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Obsah Předmluva Rekapitulace základních pojmů logiky a výrokové logiky Uvedení do predikátové logiky...17
 Obsah Předmluva...3 0. Rekapitulace základních pojmů logiky a výrokové logiky...11 0.1 Logika jako věda o vyplývání... 11 1. Uvedení do predikátové logiky...17 1.1 Základní terminologie... 17 1.2 Základní
Obsah Předmluva...3 0. Rekapitulace základních pojmů logiky a výrokové logiky...11 0.1 Logika jako věda o vyplývání... 11 1. Uvedení do predikátové logiky...17 1.1 Základní terminologie... 17 1.2 Základní
Sémantika predikátové logiky
 Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
4.2 Syntaxe predikátové logiky
 36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
Úvod do logiky (PL): sémantika predikátové logiky
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): sémantika predikátové logiky doc. PhDr. Jiří
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): sémantika predikátové logiky doc. PhDr. Jiří
Matematická analýza 1
 Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Predikátová logika: Axiomatizace, sémantické stromy, identita. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 13
 Predikátová logika: Axiomatizace, sémantické stromy, identita (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 13 Axiomatizace predikátové logiky Axiomatizace predikátové logiky Definice Hilbertovský
Predikátová logika: Axiomatizace, sémantické stromy, identita (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 13 Axiomatizace predikátové logiky Axiomatizace predikátové logiky Definice Hilbertovský
Každé formuli výrokového počtu přiřadíme hodnotu 0, půjde-li o formuli nepravdivou, a hodnotu 1, půjde-li. α neplatí. β je nutná podmínka pro α
 1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
2.2 Sémantika predikátové logiky
 14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz
 Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Predikátová logika. Teoretická informatika Tomáš Foltýnek
 Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Výroková logika. Sémantika výrokové logiky
 Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
Přednáška 2: Formalizace v jazyce logiky.
 Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce
 Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
Predikátová logika. prvního řádu
 Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2018/2019 1 / 15 Platnost (pravdivost) Platnost ve struktuře
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2018/2019 1 / 15 Platnost (pravdivost) Platnost ve struktuře
prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. BI-ZMA ZS 2009/2010
 Základní pojmy prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy
Základní pojmy prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy
přednáška 2 Marie Duží
 Logika v praxi přednáška 2 Marie Duží marie.duzi@vsb.cz 1 1 Výroková logika Analyzuje způsoby skládání jednoduchých výroků do výroků složených pomocí logických spojek. Co je to výrok? Výrok je tvrzení,
Logika v praxi přednáška 2 Marie Duží marie.duzi@vsb.cz 1 1 Výroková logika Analyzuje způsoby skládání jednoduchých výroků do výroků složených pomocí logických spojek. Co je to výrok? Výrok je tvrzení,
Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka
 Celkové hodnocení BI-MLO (nevyplňujte!) Semestr Zkouška Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka BI-MLO Písemná zkouška 9. února 2016 Matematická logika FIT ČVUT v Praze Varianta B
Celkové hodnocení BI-MLO (nevyplňujte!) Semestr Zkouška Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka BI-MLO Písemná zkouška 9. února 2016 Matematická logika FIT ČVUT v Praze Varianta B
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
Výroková logika syntaxe a sémantika
 syntaxe a sémantika Jiří Velebil: AD0B01LGR 2015 Handout 01: & sémantika VL 1/16 1 Proč formální jazyk? 1 Přirozené jazyky jsou složité a často nejednoznačné. 2 Komunikace s formálními nástroji musí být
syntaxe a sémantika Jiří Velebil: AD0B01LGR 2015 Handout 01: & sémantika VL 1/16 1 Proč formální jazyk? 1 Přirozené jazyky jsou složité a často nejednoznačné. 2 Komunikace s formálními nástroji musí být
I) Příklady (převeďte následující věty do formulí PL1 a ověřte jejich ekvivalenci pomocí de Morganových zákonů):
 I) Příklady (převeďte následující věty do formulí PL1 a ověřte jejich ekvivalenci pomocí de Morganových zákonů): 1. Všechna prvočísla větší než 2 jsou lichá. Je-li prvočíslo větší než 2, pak je liché.
I) Příklady (převeďte následující věty do formulí PL1 a ověřte jejich ekvivalenci pomocí de Morganových zákonů): 1. Všechna prvočísla větší než 2 jsou lichá. Je-li prvočíslo větší než 2, pak je liché.
platné nejsou Sokrates je smrtelný. (r) 1/??
 Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
0. ÚVOD - matematické symboly, značení,
 0. ÚVOD - matematické symboly, značení, číselné množiny Výroky Výrok je každé sdělení, u kterého lze jednoznačně rozhodnout, zda je či není pravdivé. Každému výroku lze proto přiřadit jedinou pravdivostní
0. ÚVOD - matematické symboly, značení, číselné množiny Výroky Výrok je každé sdělení, u kterého lze jednoznačně rozhodnout, zda je či není pravdivé. Každému výroku lze proto přiřadit jedinou pravdivostní
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2015/2016 1 / 18 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2015/2016 1 / 18 Základní syntax Jazyk Výroková logika je logikou
Rezoluční kalkulus pro logiku prvního řádu
 AD4M33AU Automatické uvažování Rezoluční kalkulus pro logiku prvního řádu Petr Pudlák Logika prvního řádu (Někdy nepřesně nazývaná predikátová logika.) Výhody Vyšší vyjadřovací schopnost jazyka, V podstatě
AD4M33AU Automatické uvažování Rezoluční kalkulus pro logiku prvního řádu Petr Pudlák Logika prvního řádu (Někdy nepřesně nazývaná predikátová logika.) Výhody Vyšší vyjadřovací schopnost jazyka, V podstatě
Predik atov a logika - pˇredn aˇska () Predik atov a logika - pˇredn aˇska / 16
 Predikátová logika - přednáška 3 6. 1. 2015 () Predikátová logika - přednáška 3 6. 1. 2015 1 / 16 Věta (o dedukci) Bud L jazyk, T teorie pro L, ϕ L-sentence a ψ L-formule. Pak Věta (o kompaktnosti) T ϕ
Predikátová logika - přednáška 3 6. 1. 2015 () Predikátová logika - přednáška 3 6. 1. 2015 1 / 16 Věta (o dedukci) Bud L jazyk, T teorie pro L, ϕ L-sentence a ψ L-formule. Pak Věta (o kompaktnosti) T ϕ
Predikátová logika [Predicate logic]
![Predikátová logika [Predicate logic] Predikátová logika [Predicate logic]](/thumbs/74/70612837.jpg) Predikátová logika [Predicate logic] Přesněji predikátová logika prvého řádu. Formalizuje výroky o vlastnostech předmětů (entit) a vztazích mezi předměty, které patří do dané předmětné oblasti univerza.
Predikátová logika [Predicate logic] Přesněji predikátová logika prvého řádu. Formalizuje výroky o vlastnostech předmětů (entit) a vztazích mezi předměty, které patří do dané předmětné oblasti univerza.
Výroková a predikátová logika - X
 Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
teorie logických spojek chápaných jako pravdivostní funkce
 Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Logika Libor Barto. Výroková logika
 Logika Libor Barto Výroková logika Definice.(Jazyk výrokové logiky) Ve výrokové logice používáme tyto symboly: (1) Výrokové proměnné: velká písmena, případně opatřená indexy. (2) Výrokovéspojky:,,&,,,....
Logika Libor Barto Výroková logika Definice.(Jazyk výrokové logiky) Ve výrokové logice používáme tyto symboly: (1) Výrokové proměnné: velká písmena, případně opatřená indexy. (2) Výrokovéspojky:,,&,,,....
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Výroková logika. Teoretická informatika Tomáš Foltýnek
 Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2013/2014 1 / 20 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2013/2014 1 / 20 Základní syntax Jazyk Výroková logika je logikou
Úvod do logiky (PL): analýza vět přirozeného jazyka
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): analýza vět přirozeného jazyka doc. PhDr.
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): analýza vět přirozeného jazyka doc. PhDr.
Výroková a predikátová logika - XII
 Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2018/2019 1 / 15 Rezoluční metoda v PL Rezoluční důkaz Obecné
Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2018/2019 1 / 15 Rezoluční metoda v PL Rezoluční důkaz Obecné
Matematická logika. Lekce 1: Motivace a seznámení s klasickou výrokovou logikou. Petr Cintula. Ústav informatiky Akademie věd České republiky
 Matematická logika Lekce 1: Motivace a seznámení s klasickou výrokovou logikou Petr Cintula Ústav informatiky Akademie věd České republiky www.cs.cas.cz/cintula/mal Petr Cintula (ÚI AV ČR) Matematická
Matematická logika Lekce 1: Motivace a seznámení s klasickou výrokovou logikou Petr Cintula Ústav informatiky Akademie věd České republiky www.cs.cas.cz/cintula/mal Petr Cintula (ÚI AV ČR) Matematická
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2018/2019 1 / 13 Dokončené tablo Chceme, aby dokončená bezesporná
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2018/2019 1 / 13 Dokončené tablo Chceme, aby dokončená bezesporná
Okruh č.9: sémantické metody dokazování v PL1 model formule Tradiční Aristotelova logika kategorický sylogismus subjekt predikátové výroky
 Okruh č.9: sémantické metody dokazování v PL1 Pomocí metody Vennových diagramů a relačních struktur vytváříme grafický model situace, která je úsudkem vyjádřena. Ověřujeme, zda náš graficky znázorněný
Okruh č.9: sémantické metody dokazování v PL1 Pomocí metody Vennových diagramů a relačních struktur vytváříme grafický model situace, která je úsudkem vyjádřena. Ověřujeme, zda náš graficky znázorněný
1 Výroková logika 1. 2 Predikátová logika 3. 3 Důkazy matematických vět 4. 4 Doporučená literatura 7
 1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
Místo pojmu výroková formule budeme používat zkráceně jen formule. Při jejich zápisu
 VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
Základní pojmy matematické logiky
 KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
UDL 2004/2005 Cvičení č.6 řešení Strana 1/5
 UDL 2004/2005 Cvičení č.6 řešení Strana 1/5 Opakování pojmů relace a funkce Relace R nad množinami A, B je podmnožina kartézského součinu: R A B Kartézský součin množin A = {a 1, a 2,, a 4 }, B = {b 1,
UDL 2004/2005 Cvičení č.6 řešení Strana 1/5 Opakování pojmů relace a funkce Relace R nad množinami A, B je podmnožina kartézského součinu: R A B Kartézský součin množin A = {a 1, a 2,, a 4 }, B = {b 1,
7 Jemný úvod do Logiky
 7 Jemný úvod do Logiky Základem přesného matematického vyjadřování je správné používání (matematické) logiky a logických úsudků. Logika jako filozofická discipĺına se intenzivně vyvíjí už od dob antiky,
7 Jemný úvod do Logiky Základem přesného matematického vyjadřování je správné používání (matematické) logiky a logických úsudků. Logika jako filozofická discipĺına se intenzivně vyvíjí už od dob antiky,
Výroková a predikátová logika - VIII
 Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2016/2017 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2016/2017 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2016/2017 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2016/2017 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Logický důsledek. Petr Kuchyňka (7765@mail.muni.cz)
 Logický důsledek Petr Kuchyňka (7765@mail.muni.cz) Úvod P 1 Logický důsledek je hlavním předmětem zájmu logiky. Je to relace mezi premisami a závěry logicky platných úsudků: v logicky platném úsudku závěr
Logický důsledek Petr Kuchyňka (7765@mail.muni.cz) Úvod P 1 Logický důsledek je hlavním předmětem zájmu logiky. Je to relace mezi premisami a závěry logicky platných úsudků: v logicky platném úsudku závěr
Základy logiky a teorie množin
 Pracovní text k přednášce Logika a teorie množin (I/2007) 1 1 Struktura přednášky Matematická logika 2 Výroková logika Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz Predikátová logika 1. řádu
Pracovní text k přednášce Logika a teorie množin (I/2007) 1 1 Struktura přednášky Matematická logika 2 Výroková logika Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz Predikátová logika 1. řádu
B i n á r n í r e l a c e. Patrik Kavecký, Radomír Hamřík
 B i n á r n í r e l a c e Patrik Kavecký, Radomír Hamřík Obsah 1 Kartézský součin dvou množin... 3 2 Binární relace... 6 3 Inverzní relace... 8 4 Klasifikace binární relací... 9 5 Ekvivalence... 12 2 1
B i n á r n í r e l a c e Patrik Kavecký, Radomír Hamřík Obsah 1 Kartézský součin dvou množin... 3 2 Binární relace... 6 3 Inverzní relace... 8 4 Klasifikace binární relací... 9 5 Ekvivalence... 12 2 1
Výroková a predikátová logika - VIII
 Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2017/2018 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2017/2018 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Úvod do logiky. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 23
 Úvod do logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 23 Co je logika? Čeho se týkají logické zákony? Tři možnosti: (1) světa (2) myšlení (3) jazyka (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216
Úvod do logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 23 Co je logika? Čeho se týkají logické zákony? Tři možnosti: (1) světa (2) myšlení (3) jazyka (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216
LOGIKA VÝROKOVÁ LOGIKA
 LOGIKA Popisuje pravidla odvozování jedněch tvrzení z druhých. Je to myšlenková cesta ke správným závěrům. Vznikla jako součást filosofie. Zakladatelem byl Aristoteles. VÝROKOVÁ LOGIKA Obsahuje syntaktická,
LOGIKA Popisuje pravidla odvozování jedněch tvrzení z druhých. Je to myšlenková cesta ke správným závěrům. Vznikla jako součást filosofie. Zakladatelem byl Aristoteles. VÝROKOVÁ LOGIKA Obsahuje syntaktická,
Cvičení ke kursu Klasická logika II
 Cvičení ke kursu Klasická logika II (12. května 2017) 1. Nechť P a Q jsou unární a R binární predikát. Dokažte, že následující formule jsou logicky platné, ale obrátíme-li (vnější) implikaci, ve všech
Cvičení ke kursu Klasická logika II (12. května 2017) 1. Nechť P a Q jsou unární a R binární predikát. Dokažte, že následující formule jsou logicky platné, ale obrátíme-li (vnější) implikaci, ve všech
Úvod do informatiky. Miroslav Kolařík
 Úvod do informatiky přednáška první Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Co a k čemu je logika? 2 Výroky a logické spojky
Úvod do informatiky přednáška první Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Co a k čemu je logika? 2 Výroky a logické spojky
Sémantika výrokové logiky. Alena Gollová Výroková logika 1/23
 Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
Výroková a predikátová logika - III
 Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2017/2018 1 / 16 2-SAT 2-SAT Výrok je v k-cnf, je-li v CNF a
Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2017/2018 1 / 16 2-SAT 2-SAT Výrok je v k-cnf, je-li v CNF a
Výroková logika - opakování
 - opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
- opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška pátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška pátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
ZÁKLADY LOGIKY A METODOLOGIE
 ZÁKLADY LOGIKY A METODOLOGIE Metodický list č. 1 Téma: Předmět logiky a metodologie, základy logiky a formalizace. Toto téma lze rozdělit do tří základních tématických oblastí: 1) Předmět logiky a metodologie
ZÁKLADY LOGIKY A METODOLOGIE Metodický list č. 1 Téma: Předmět logiky a metodologie, základy logiky a formalizace. Toto téma lze rozdělit do tří základních tématických oblastí: 1) Předmět logiky a metodologie
1 Predikátová logika. 1.1 Syntax. jaký mohou mít formule význam (sémantiku). 1. Logických symbolů: 2. Speciálních (mimologických) symbolů:
 1 Predikátová logika 1.1 Syntax Podobně jako ve výrokové logice začneme nejprve se syntaxí predikátové logiky, která nám říká, co jsou správně utvořené formule predikátové logiky. V další části tohoto
1 Predikátová logika 1.1 Syntax Podobně jako ve výrokové logice začneme nejprve se syntaxí predikátové logiky, která nám říká, co jsou správně utvořené formule predikátové logiky. V další části tohoto
Predikátová logika Individua a termy Predikáty
 Predikátová logika Predikátová logika je rozšířením logiky výrokové o kvantifikační výrazy jako každý, všichni, někteří či žádný. Nejmenší jazykovou jednotkou, kterou byla výroková logika schopna identifikovat,
Predikátová logika Predikátová logika je rozšířením logiky výrokové o kvantifikační výrazy jako každý, všichni, někteří či žádný. Nejmenší jazykovou jednotkou, kterou byla výroková logika schopna identifikovat,
Formální systém výrokové logiky
 Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
RELACE, OPERACE. Relace
 RELACE, OPERACE Relace Užití: 1. K popisu (evidenci) nějaké množiny objektů či jevů, které lze charakterizovat pomocí jejich vlastnostmi. Entita je popsána pomocí atributů. Ty se vybírají z domén. Různé
RELACE, OPERACE Relace Užití: 1. K popisu (evidenci) nějaké množiny objektů či jevů, které lze charakterizovat pomocí jejich vlastnostmi. Entita je popsána pomocí atributů. Ty se vybírají z domén. Různé
Pojem binární relace patří mezi nejzákladnější matematické pojmy. Binární relace
 RELACE Pojem binární relace patří mezi nejzákladnější matematické pojmy. Binární relace slouží k vyjádření vztahů mezi prvky nějakých množin. Vztahy mohou být různé povahy. Patří sem vztah býti potomkem,
RELACE Pojem binární relace patří mezi nejzákladnější matematické pojmy. Binární relace slouží k vyjádření vztahů mezi prvky nějakých množin. Vztahy mohou být různé povahy. Patří sem vztah býti potomkem,
Logické programy Deklarativní interpretace
 Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
1. Základy logiky a teorie množin
 1. Základy logiky a teorie množin A. Logika Matematická logika vznikla v 19. století. Jejím zakladatelem byl anglický matematik G. Boole (1815 1864). Boole prosadil algebraické pojetí logiky a zavedl logické
1. Základy logiky a teorie množin A. Logika Matematická logika vznikla v 19. století. Jejím zakladatelem byl anglický matematik G. Boole (1815 1864). Boole prosadil algebraické pojetí logiky a zavedl logické
Logika a logické programování
 Logika a logické programování témata ke zkoušce Poslední aktualizace: 16. prosince 2009 Zkouška je písemná, skládá se obvykle ze sedmi otázek (může být více nebo méně, podle náročnosti otázek), z toho
Logika a logické programování témata ke zkoušce Poslední aktualizace: 16. prosince 2009 Zkouška je písemná, skládá se obvykle ze sedmi otázek (může být více nebo méně, podle náročnosti otázek), z toho
Modely Herbrandovské interpretace
 Modely Herbrandovské interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 8 1 Uvedli jsme termové interpretace a termové modely pro logické programy a také nejmenší
Modely Herbrandovské interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 8 1 Uvedli jsme termové interpretace a termové modely pro logické programy a také nejmenší
Výroková a predikátová logika - IV
 Výroková a predikátová logika - IV Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IV ZS 2018/2019 1 / 17 Tablo metoda Tablo Tablo - příklady F (((p q)
Výroková a predikátová logika - IV Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IV ZS 2018/2019 1 / 17 Tablo metoda Tablo Tablo - příklady F (((p q)
IA008 Computational logic Version: 6. května Formule je v konjunktivní normální formě (CNF), pokud má tvar α 1... α n,
 1 Převody do normálních forem Příklad 1.1: Vyjádřete následující formule v DNF pomocí pravdivostní tabulky a pomocí převodu logických spojek. a) (A B) C b) (A B) C c) (A B) (C D) Formule je v disjunktivní
1 Převody do normálních forem Příklad 1.1: Vyjádřete následující formule v DNF pomocí pravdivostní tabulky a pomocí převodu logických spojek. a) (A B) C b) (A B) C c) (A B) (C D) Formule je v disjunktivní
Klasická predikátová logika
 Klasická predikátová logika Matematická logika, LS 2012/13, závěrečná přednáška Libor Běhounek www.cs.cas.cz/behounek/teaching/malog12 PřF OU, 6. 5. 2013 Symboly klasické predikátové logiky Poznámky Motivace
Klasická predikátová logika Matematická logika, LS 2012/13, závěrečná přednáška Libor Běhounek www.cs.cas.cz/behounek/teaching/malog12 PřF OU, 6. 5. 2013 Symboly klasické predikátové logiky Poznámky Motivace
Logika. 2. Výroková logika. RNDr. Luděk Cienciala, Ph. D.
 Logika 2. Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216, Logika:
Logika 2. Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216, Logika:
Úvod do logiky (PL): ekvivalence a negace výroků logického
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): ekvivalence a negace výroků logického čtverce
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): ekvivalence a negace výroků logického čtverce
Výroková a predikátová logika - III
 Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2014/2015 1 / 21 Výroková logika Horn-SAT Horn-SAT Jednotková
Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2014/2015 1 / 21 Výroková logika Horn-SAT Horn-SAT Jednotková
1. Predikátová logika jako prostedek reprezentace znalostí
 1. Predikátová logika jako prostedek reprezentace znalostí 1.1 Historie výrokové logiky Problém explicitních znalostí a údaj, kterých je obrovské množství, vedl ke vzniku výrokové logiky. lovk si obecn
1. Predikátová logika jako prostedek reprezentace znalostí 1.1 Historie výrokové logiky Problém explicitních znalostí a údaj, kterých je obrovské množství, vedl ke vzniku výrokové logiky. lovk si obecn
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška třetí Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška třetí Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematika B101MA1, B101MA2
 Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Přednáška 3: rozhodování o platnosti úsudku
 Přednáška 3: rozhodování o platnosti úsudku Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky Úsudky Úsudek je platný, jestliže nutně, za všech okolností, tj. při všech interpretacích, ve kterých
Přednáška 3: rozhodování o platnosti úsudku Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky Úsudky Úsudek je platný, jestliže nutně, za všech okolností, tj. při všech interpretacích, ve kterých
Rovnost lze vyjádřit jako predikát, např. můžeme zvolit, že P(x, y) reprezentujetvrzení xjerovnoy.
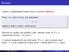 Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Matematika pro informatiky KMA/MATA
 Matematika pro informatiky KMA/MATA Informace k předmětu Mgr. Přemysl Rosa rosapr00@pf.jcu.cz, J349 Konzultační hodiny v ZS: úterý 10-11, čtvrtek 15-16 nebo individuálně po předchozí domluvě aktivní účast
Matematika pro informatiky KMA/MATA Informace k předmětu Mgr. Přemysl Rosa rosapr00@pf.jcu.cz, J349 Konzultační hodiny v ZS: úterý 10-11, čtvrtek 15-16 nebo individuálně po předchozí domluvě aktivní účast
Úvod do logiky (PL): analýza vět mimo logický čtverec
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): analýza vět mimo logický čtverec doc. PhDr.
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): analýza vět mimo logický čtverec doc. PhDr.
Stefan Ratschan. Fakulta informačních technologíı. Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
 Logika pro každodenní přežití Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
Logika pro každodenní přežití Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
Úvod do TI - logika Výroková logika (2.přednáška) Marie Duží
 Úvod do TI - logika Výroková logika (2.přednáška) Marie Duží marie.duzi@vsb.cz Výroková logika Analyzuje způsoby skládání jednoduchých výroků do výroků složených pomocí logických spojek. Co je to výrok?
Úvod do TI - logika Výroková logika (2.přednáška) Marie Duží marie.duzi@vsb.cz Výroková logika Analyzuje způsoby skládání jednoduchých výroků do výroků složených pomocí logických spojek. Co je to výrok?
Aritmetika s didaktikou I.
 Katedra matematiky PF UJEP Aritmetika s didaktikou I. KM1 / 0001 Přednáška 02 Opakování základních pojmů - 2. část O čem budeme hovořit: Binární relace a jejich vlastnosti Speciální typy binárních relací
Katedra matematiky PF UJEP Aritmetika s didaktikou I. KM1 / 0001 Přednáška 02 Opakování základních pojmů - 2. část O čem budeme hovořit: Binární relace a jejich vlastnosti Speciální typy binárních relací
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Sémantická věta o dedukci Věta Pro
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Sémantická věta o dedukci Věta Pro
Princip rozšíření a operace s fuzzy čísly
 Center for Machine Perception presents Princip rozšíření a operace s fuzzy čísly Mirko Navara Center for Machine Perception Faculty of Electrical Engineering Czech Technical University Praha, Czech Republic
Center for Machine Perception presents Princip rozšíření a operace s fuzzy čísly Mirko Navara Center for Machine Perception Faculty of Electrical Engineering Czech Technical University Praha, Czech Republic
Řešení: Ano. Řešení: Ne.
 1 ÚLOHY Z PREDIKÁTOVÉ LOGIKY Instance, varianty. UF.1.1. Substituovatelnost. 1. Buď ϕ formule ( z)(x=z)&y < x a dále x, y, z různé proměnné, F unární funkční symbol, c konstantní symbol. Uveďte, zda je
1 ÚLOHY Z PREDIKÁTOVÉ LOGIKY Instance, varianty. UF.1.1. Substituovatelnost. 1. Buď ϕ formule ( z)(x=z)&y < x a dále x, y, z různé proměnné, F unární funkční symbol, c konstantní symbol. Uveďte, zda je
Hilbertovský axiomatický systém
 Hilbertovský axiomatický systém Predikátová logika H 1 Šárka Vavrečková Ústav informatiky, FPF SU Opava Poslední aktualizace: 24. října 2008 Specifikace H 1 Jazyk L H1 přejímáme jazyk predikátové logiky
Hilbertovský axiomatický systém Predikátová logika H 1 Šárka Vavrečková Ústav informatiky, FPF SU Opava Poslední aktualizace: 24. října 2008 Specifikace H 1 Jazyk L H1 přejímáme jazyk predikátové logiky
Úvod do teoretické informatiky(2017/2018) cvičení 6 1
 Úvod do teoretické informatiky(2017/2018) cvičení 6 1 Cvičení 6 Příklad 1: Pro každou z následujících sekvencí symbolů rozhodněte, zda se jedná o a) term, b) formuli predikátové logiky(používejte běžné
Úvod do teoretické informatiky(2017/2018) cvičení 6 1 Cvičení 6 Příklad 1: Pro každou z následujících sekvencí symbolů rozhodněte, zda se jedná o a) term, b) formuli predikátové logiky(používejte běžné
